
Относительная ошибка
В практике геодезических измерений о точности измерений судят не только по абсолютной величине средней квадратической или предельной
погрешности, но и по величине относительной погрешности.
Относительной ошибкой называется отношение абсолютной ошибки к значению самой измеренной величины.
Относительную ошибку выражают в виде простой дроби, числитель которой — единица, а знаменатель — число, округленное до двух — трех значащих цифр с нулями.
отн = тl /l =1/(l / тl ), где l — значение измеряемой величины.
Относительная предельная ошибка:
отн. пр. = пр / l, где пр = 2(3)m
Например, относительная средняя квадратическая погрешность измерения линии длиной l = 110 м при тl = 2 см равна тl /l = 1/5500, а
|
относительная предельная погрешность при пр = 3m = 6 см, |
пр /l= |
|
1/1800. |
12

Пример. Длина линии местности измерена шесть раз. Требуется определить вероятнейшее значение длины линии и оценить точность выполненных измерений. Результаты измерений и вычислений записывают по форме, приведенной в таблице
|
№ п/п |
l, м |
, см |
2 ,см2 |
Вычисления |
|
1 |
121,75 |
-1 |
1 |
|
|
2 |
121,81 |
+5 |
25 |
|
|
3 |
121,77 |
+ 1 |
1 |
|
|
4 |
121,70 |
-6 |
36 |
|
|
5 |
121,73 |
-3 |
9 |
6121,79 +3 9
|
Среднее 121,76 Σ =-1 |
Σ = |
|
|
значени |
81 |
=12см |
|
е |
пр |
|
13

Вычислительная обработка результатов геодезических измерений
Для производства топографической съемки создается геодезическое съемочное обоснование в виде закрепленных на местности пунктов, координаты которых определены из геодезических линейно-угловых построений (сети триангуляции, теодолитные, тахеометрические, мензульные ходы, геодезические засечки). Высоты точек съемочных сетей определяются тригонометрическим или геометрическим нивелированием.
Съемочное обоснование развивается от пунктов опорной геодезической сети более высокого класса путем сгущения геодезической основы до плотности, обеспечивающей выполнение топографической съемки.
Самый распространенный вид съемочного планового обоснования – теодолитные ходы, опирающиеся на один или два исходных пункта.
Теодолитные ходы привязываются к пунктам опорной геодезической сети. Это выполняется для того, чтобы вершины теодолитных ходов были определены в существующей системе координат. Привязка выполняется различными способами. В результате ее выполнения на стороны и вершины теодолитного хода должны быть переданы дирекционный угол и координаты x, y.
Теодолитный ход не привязанный к пунктам опорной геодезической сети, носит название свободного, привязанный лишь в начальной точке – висячим.
14

Вычисление координат пунктов разомкнутого теодолитного хода
Исходными данными в теодолитном ходе являются координаты XA, YA пункта A и дирекционный угол αBA линии BA, который называется начальным
исходным дирекционным углом; этот угол может задаваться неявно через координаты пункта B, путем решения обратной геодезической задачи.
Измеряемые величины — это горизонтальные углы β1, β2,…, βn-1, βn и расстояния S1, S2,…, Sn-1, Sn.
Дирекционные углы сторон хода вычисляют последовательно по формулам передачи дирекционного угла через угол поворота.
Координаты пунктов хода получают из решения прямой геодезичеcкой задачи сначала от пункта A к пункту 2, затем от пункта 2 к пункту 3 и так далее до конца хода.
15

Прямая геодезическая задача
Дано:
координаты точки А (ХА ;YА ),
дирекционный угол направления АВ (αАВ),
горизонтальная проекция направления АВ (dАВ ).
Найти: координаты точки В (хВ уВ).
Решение:
Δх=± dАВ·cos rАВ= dАВ·cos αАВ;
Δу=± dАВ·sinrАВ= dАВ·sin αАВ.
Контроль вычисления приращений координат: d АВ 
Координаты искомой точки В определяются по формулам:
хВ=хА+Δх; уВ=уА+Δу.

ОБРАТНАЯ ГЕОДЕЗИЧЕСКАЯ ЗАДАЧА
Дано:
Координаты точек А (ХА ;YА ), В (ХВ; YВ).
Найти:
дирекционный угол направления АВ (αАВ),
горизонтальную проекцию направления АВ (dАВ ).
|
Решение: |
|
|
ΔХ = ХВ — ХА; |
ΔY = YВ — YА. |
По найденным значениям приращений координат ΔХ и ΔY в прямоугольном
|
треугольнике, вычисляют табличный угол |
||
|
(румб): |
tgr |
|
|
отсюда |
r arctg |
|
Зная дирекционный. угол направления и приращения координат, определяют горизонтальную проекцию направления:
|
d АВ |
d АВ |
d АВ 2 . 2 |
||||
|
; |
; |
|||||
|
sin АВ |
||||||
|
cos АВ |
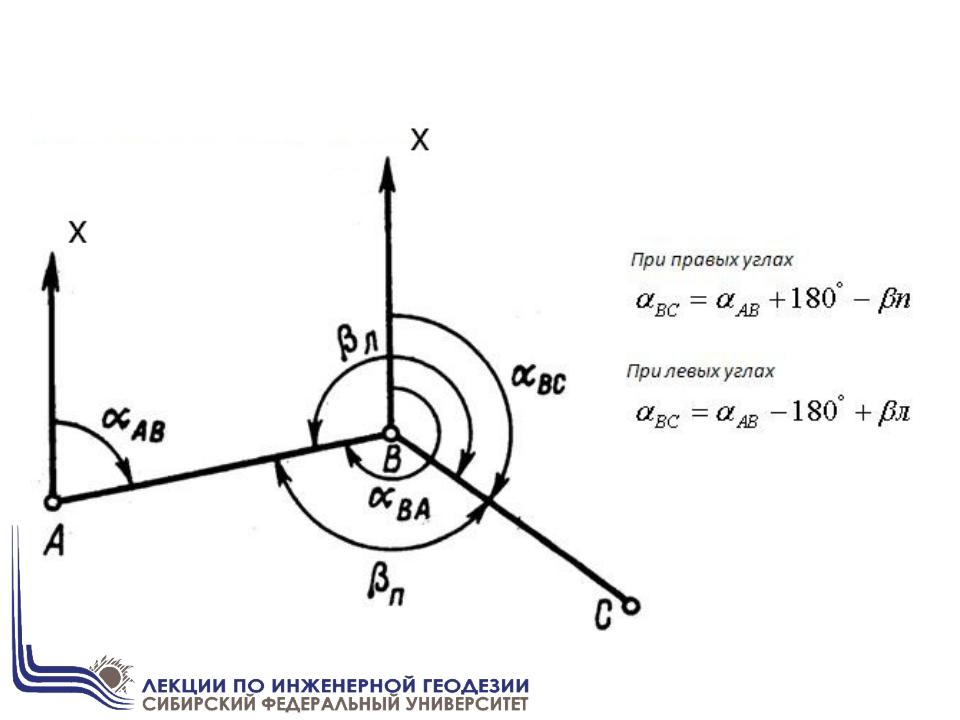
ПЕРЕДАЧА ДИРЕКЦИОННОГО УГЛА НА СТОРОНУ ТЕОДОЛИТНОГО ХОДА
В общем виде:
n n 1 180 прn n 1 180 л

180 л
В разомкнутом теодолитном ходе должны выполняться три условия: условие дирекционных углов и два координатных условия.
Вычислим последовательно дирекционные углы всех сторон хода,
используя формулу передачи дирекционного угла на последующую сторону хода: n n 1 180 пр или n n 1 .
Математическая запись условия дирекционных углов в разомкнутом теодолитном ходе для левых углов поворота:
(1)
Для правых углов поворота оно запишется так:
(2)
где αн , αк – дирекционные углы начальной и конечной выходных сторон,
между которыми прокладывается ход, n – число углов хода, включая
примычные.
Сумма углов, подсчитанная по формулам (1) и (2), называется теоретической суммой углов хода. Сумма измеренных углов вследствие
ошибок измерений, как правило, отличается от теоретической суммы на некоторую величину, называемую угловой невязкой и обозначаемую fβ:
(3)
19

|
f доп 2 m |
. |
|||
|
Допустимое значение угловой невязки: |
n |
(4) |
||
|
где n – число углов хода. |
|
Для теодолитных ходов mβ = 30″, поэтому: |
(5) |
|||
|
f доп 1 n. |
Присутствие ошибок в результатах измерений является причиной возникновения задачи уравнивания. Целью уравнивания является устранение невязок и повышение точности всех измеренных величин.
Обозначим поправку в измеренный угол Vβ и запишем условие:
откуда следует, что сумма угловых поправок равна угловой невязке с противоположным
|
знаком: |
V f . |
(7) |
|
При условии, что поправки в измеренные углы одинаковы, |
решение уравнения (7) |
|
|
получается в виде: |
V f / n. |
|
|
Исправленные значения углов вычисляются по формуле: |
||
|
i i(изм) V . |
(8) |
По исправленным углам поворота вычисляют дирекционные углы всех сторон хода; совпадение вычисленного и заданного значений конечного исходного дирекционного угла является контролем правильности обработки угловых измерений.
20

Координатные условия. Решая последовательно прямую геодезическую задачу, вычислим приращения координат по каждой стороне хода ΔXi и ΔYi :
|
Xвыч d cos d cos r |
(9) |
|||
|
Yвыч d sin d sin r |
(10) |
|||
|
где r – румб соответствующего дирекционного угла. |
X n X n 1 X |
|||
|
Координаты пунктов хода получим по формулам : |
(11) |
|||
|
Для конечной точки хода: Xкон Xнач Xi |
Yn Yn 1 Y |
(12) |
||
|
(13) |
||||
|
или |
Xi Xкон Xнач . |
(14) |
||
Аналогичная формула для суммы приращений ΔY имеет вид:
i кон нач . (15)
Получились еще два условия (14) и (15), которые называются координатными. Суммы приращений координат, подсчитанные по этим формулам, называются теоретическими суммами приращений. Вследствие ошибок измерения сторон суммы вычисленных приращений координат в общем случае не будут равны теоретическим суммам.
21
Соседние файлы в папке геодезия. все лекции
- #
- #
- #
- #
- #
- #
- #
8.1. Измерение длин линий мерными лентами и рулетками
Мерные приборы. Расстояния в геодезии измеряют мерными приборами и дальномерами. Мерными приборами называют ленты, рулетки, проволоки, которыми расстояние измеряют путём укладки мерного прибора в створе измеряемой линии. Дальномеры применяют оптические и светодальномеры.
Мерные ленты типа ЛЗ изготавливают из стальной полосы шириной до 2,5 см и длиной 20, 24 или 50 м. Наиболее распространены 20-метровые ленты. На концах лента имеет вырезы для фиксирования концов втыкаемыми в землю шпильками. На ленте отмечены метровые и дециметровые деления. Для хранения ленту наматывают на специальное кольцо. К ленте прилагается комплект из шести (или одиннадцати) шпилек.
Рулетки – узкие (до 10 мм) стальные ленты длиной 20, 30, 50, 75 или 100 м с миллиметровыми делениями. Для высокоточных измерений служат рулетки, изготовленные из инвара – сплава (64% железа, 35,5% никеля и 0,5% различных примесей), имеющего малый коэффициент линейного расширения. Для измерений пониженной точности применяют тесьмяные и фиберглассовые рулетки.
Компарирование. До применения мерных приборов их компарируют. Компарированием называется сравнение длины мерного прибора с другим прибором, длина которого точно известна.
Для компарирования ленты ЛЗ на ровной поверхности (например, досчатой, каменной) с помощью выверенной образцовой ленты отмеряют отрезок номинальной длины (20 м) и укладывают на том же месте проверяемую рабочую ленту. Совместив нулевой штрих ленты с началом отрезка, закрепляют конец ленты в этом положении. Затем ленту растягивают и линеечкой измеряют величину несовпадения конечного штриха ленты с концом отрезка, то есть отличие Dl длины ленты от номинала. В последующем эту величину используют для вычисления поправок за компарирование. Ими исправляют результаты измерений лентой. Если Dl не превышает 1-2 мм, поправкой за компарирование пренебрегают.
Для компарирования ленты в полевых условиях на ровной местности закрепляют концы базиса. Базис измеряют более точным прибором (светодальномером, рулеткой или лентой, проверенной на стационарном компараторе), а затем компарируемой лентой. Из сравнения результатов измерений получают поправку Dl. Измерения выполняют несколько раз и за окончательный результат принимают среднее.
Рулетки, предназначаемые для высокоточных измерений, компарируют на стационарных компараторах, где по результатам проверки длины ленты при разных температурах выводят уравнение её длины:
l = l0 + Dl + a l0 (t— t0). (8.1)
Здесь l — длина ленты при температуре t; l0 — номинальная длина; Dl — поправка к номинальной длине при температуре компарирования t0 ; a — температурный коэффициент линейного расширения. Для новых рулеток уравнение длины указывают в паспорте прибора.
Вешение линии. Перед измерением длины линии на её концах устанавливают вехи. Если длина линии превышает 100 м или на каких-то её участках не видны установленные вехи, то в их створе ставят дополнительные вехи (створом двух точек называют проходящую через них вертикальную плоскость). Вешение обычно ведут «на себя». Наблюдатель становится на провешиваемой линии у вехи A (рис. 8.1, а), а рабочий по его указаниям ставит веху 1 так, чтобы она закрыла собой веху B. Таким же образом последовательно устанавливают вехи 2, 3 и т. д. Установка вех в обратном порядке, то есть «от себя», является менее точной, так как ранее выставленные вехи закрывают видимость на последующие.
|
|
Рис. 8.1. Вешение линии: а – “на себя”; б – через препятствие; в – то же (вид в плане). |
Если точки A и B недоступны или между ними расположена возвышенность (рис. 8.1, б, в), то вехи ставят примерно на линии AB на возможно большем расстоянии друг от друга, но так, чтобы в точке C увидеть вехи B и D, а в точке D — вехи A и C. При этом рабочий в точке C по указаниям рабочего в точке D ставит свою веху в створ линии AD. Затем рабочий в точке D по указаниям рабочего в точке C переносит свою веху в точку D1, то есть в створ точек C и B. Затем из точки С веху переносят в точку С1 и так далее до тех пор, когда обе вехи окажутся в створе AB.
Измерение длин линий лентой. Ориентируясь по выставленным вехам, два мерщика откладывают ленту в створе линии, фиксируя концы ленты втыкаемыми в землю шпильками. По мере продвижения измерений задний мерщик вынимает из земли использованные шпильки и использует их для подсчета числа отложенных лент. Измеренное расстояние равно D=20n+r, где n — число отложенных целых лент и r – остаток (отсчет по последней ленте, меньший 20 м).
Длину измеряют дважды — в прямом и обратном направлениях. Расхождение не должно превышать 1/2000 (при неблагоприятных условиях — 1/1000). За окончательное значение принимают среднее.
Введение поправок. Измеренные расстояния исправляют поправками за компарирование, за температуру и за наклон.
Поправка за компарирование определяется по формуле
Dk = n Dl ,
где Dl — отличие длины ленты от 20 м и n — число уложенных лент. При длине ленты больше номинальной – поправка положительная, при длине меньше номинальной – отрицательная. Поправку за компарирование вводят в измеренные расстояния, если Dl > 2 мм.
Поправка за температуру определяется по формуле
Dt = aD(t—t0)
где a — термический коэффициент расширения (для стали a = 0,0000125); t и t0 — температура ленты во время измерений и при компарировании. Поправку Dt учитывают, если ½t—t0½>10°.
Поправка за наклон вводится для определения горизонтального проложения d измеренного наклонного расстояния D
d = D cosn , (8.2)
где n — угол наклона. Вместо вычисления по формуле (8.2) можно в измеренное расстояние D ввести поправку за наклон: d=D+Dn, где
Dn = d — D = D (cosn — 1) = -2D sin2 . (8.3)
По формуле (8.3) составляют таблицы, облегчающие вычисления.
Поправка за наклон имеет знак минус. При измерениях лентой ЛЗ поправку учитывают, когда углы наклона превышают 1°.
Если линия состоит из участков с разным уклоном, то находят горизонтальные проложения участков и результаты суммируют.
Углы наклона, необходимые для приведения длин линий к горизонту, измеряют эклиметром или теодолитом.
Эклиметр имеет внутри коробки 5 (рис. 8.2, а) круг с градусными делениями на его ободе. Круг вращается на оси и под действием укреплённого на нём груза 3 занимает положение, при котором нулевой диаметр круга горизонтален. К коробке прикреплена визирная трубка с двумя диоптрами — глазным 1 и предметным 4.
|
|
|
Рис. 8.2. Эклиметр: а – устройство; б – измерение угла наклона
Для измерения угла наклона n в точке B (рис. 8.2, б) ставят веху с меткой M на высоте глаза. Наблюдатель (в точке A), глядя в трубку 2 эклиметра, наводит её на точку M и нажатием кнопки 6 освобождает круг. Когда нулевой диаметр круга примет горизонтальное положение, против нити предметного диоптра 4 берут отсчёт угла наклона. Точность измерения угла эклиметром 15 — 30¢.
Поверку эклиметра выполняют измерением угла наклона одной и той же линии в прямом и обратном направлениях. Оба результата должны быть одинаковы. В противном случае надо переместить груз 3 в такое положение, при котором отсчёт будет равен среднему из прямого и обратного измерений.
Точность измерений лентой в разных условиях различна и зависит от многих причин — неточное укладывание ленты в створ, ее непрямолинейность, изменения температуры ленты, отклонения угла наклона ленты от измеренного эклиметром, неодинаковое натяжение ленты, ошибки фиксирования концов ленты, зависящие от характера грунта и др.
Приближённо точность измерений лентой ЛЗ считают равной 1:2000. При благоприятных условиях она в 1,5 – 2 раза выше, а при неблагоприятных – около 1:1000.
Измерение расстояний рулетками. Измерения рулеткой, выполняемые для составления плана местности, аналогичны измерениям лентой ЛЗ. Для измерений с более высокой точностью, необходимой, например, в разбивочных работах, выполняемых при строительстве сооружений, измеряемую линию расчищают, выравнивают и разбивают на отрезки по длине рулетки, забивая в створе линии до уровня земли колья и отмечая створ втыкаемыми в них иглами или ножами. При неровной поверхности на неё укладывают доски или даже делают мостки. Для измерения пролёта между соседними иглами (ножами) рулетку укладывают вдоль пролёта и натягивают с той же силой (50 или 100 H), что и при компарировании, используя для этого динамометр. Отсчёты по рулетке берут одновременно по команде против двух игл (лезвий ножей). Длину пролёта di определяют по формуле
di = П — З,
где П и З — передний (больший) и задний отсчёты по шкале рулетки. Полученный результат исправляют поправками за компарирование и температуру, используя уравнение длины рулетки (8.1).
Если линия имеет наклон, необходимо учесть поправку
,
где h — превышение между концами пролёта, измеряемое нивелиром.
Длина линии определится как сумма длин пролётов. Относительные ошибки расстояний при такой методике измерений 1:5000 — 1:10000.

Относительная ошибка
В практике геодезических измерений о точности измерений судят не только по абсолютной величине средней квадратической или предельной
погрешности, но и по величине относительной погрешности.
Относительной ошибкой называется отношение абсолютной ошибки к значению самой измеренной величины.
Относительную ошибку выражают в виде простой дроби, числитель которой — единица, а знаменатель — число, округленное до двух — трех значащих цифр с нулями.
отн = тl /l =1/(l / тl ), где l — значение измеряемой величины.
Относительная предельная ошибка:
отн. пр. = пр / l, где пр = 2(3)m
Например, относительная средняя квадратическая погрешность измерения линии длиной l = 110 м при тl = 2 см равна тl /l = 1/5500, а
|
относительная предельная погрешность при пр = 3m = 6 см, |
пр /l= |
|
1/1800. |
12

Пример. Длина линии местности измерена шесть раз. Требуется определить вероятнейшее значение длины линии и оценить точность выполненных измерений. Результаты измерений и вычислений записывают по форме, приведенной в таблице
|
№ п/п |
l, м |
, см |
2 ,см2 |
Вычисления |
|
1 |
121,75 |
-1 |
1 |
|
|
2 |
121,81 |
+5 |
25 |
|
|
3 |
121,77 |
+ 1 |
1 |
|
|
4 |
121,70 |
-6 |
36 |
|
|
5 |
121,73 |
-3 |
9 |
6121,79 +3 9
|
Среднее 121,76 Σ =-1 |
Σ = |
|
|
значени |
81 |
=12см |
|
е |
пр |
|
13

Вычислительная обработка результатов геодезических измерений
Для производства топографической съемки создается геодезическое съемочное обоснование в виде закрепленных на местности пунктов, координаты которых определены из геодезических линейно-угловых построений (сети триангуляции, теодолитные, тахеометрические, мензульные ходы, геодезические засечки). Высоты точек съемочных сетей определяются тригонометрическим или геометрическим нивелированием.
Съемочное обоснование развивается от пунктов опорной геодезической сети более высокого класса путем сгущения геодезической основы до плотности, обеспечивающей выполнение топографической съемки.
Самый распространенный вид съемочного планового обоснования – теодолитные ходы, опирающиеся на один или два исходных пункта.
Теодолитные ходы привязываются к пунктам опорной геодезической сети. Это выполняется для того, чтобы вершины теодолитных ходов были определены в существующей системе координат. Привязка выполняется различными способами. В результате ее выполнения на стороны и вершины теодолитного хода должны быть переданы дирекционный угол и координаты x, y.
Теодолитный ход не привязанный к пунктам опорной геодезической сети, носит название свободного, привязанный лишь в начальной точке – висячим.
14

Вычисление координат пунктов разомкнутого теодолитного хода
Исходными данными в теодолитном ходе являются координаты XA, YA пункта A и дирекционный угол αBA линии BA, который называется начальным
исходным дирекционным углом; этот угол может задаваться неявно через координаты пункта B, путем решения обратной геодезической задачи.
Измеряемые величины — это горизонтальные углы β1, β2,…, βn-1, βn и расстояния S1, S2,…, Sn-1, Sn.
Дирекционные углы сторон хода вычисляют последовательно по формулам передачи дирекционного угла через угол поворота.
Координаты пунктов хода получают из решения прямой геодезичеcкой задачи сначала от пункта A к пункту 2, затем от пункта 2 к пункту 3 и так далее до конца хода.
15

Прямая геодезическая задача
Дано:
координаты точки А (ХА ;YА ),
дирекционный угол направления АВ (αАВ),
горизонтальная проекция направления АВ (dАВ ).
Найти: координаты точки В (хВ уВ).
Решение:
Δх=± dАВ·cos rАВ= dАВ·cos αАВ;
Δу=± dАВ·sinrАВ= dАВ·sin αАВ.
Контроль вычисления приращений координат: d АВ 
Координаты искомой точки В определяются по формулам:
хВ=хА+Δх; уВ=уА+Δу.

ОБРАТНАЯ ГЕОДЕЗИЧЕСКАЯ ЗАДАЧА
Дано:
Координаты точек А (ХА ;YА ), В (ХВ; YВ).
Найти:
дирекционный угол направления АВ (αАВ),
горизонтальную проекцию направления АВ (dАВ ).
|
Решение: |
|
|
ΔХ = ХВ — ХА; |
ΔY = YВ — YА. |
По найденным значениям приращений координат ΔХ и ΔY в прямоугольном
|
треугольнике, вычисляют табличный угол |
||
|
(румб): |
tgr |
|
|
отсюда |
r arctg |
|
Зная дирекционный. угол направления и приращения координат, определяют горизонтальную проекцию направления:
|
d АВ |
d АВ |
d АВ 2 . 2 |
||||
|
; |
; |
|||||
|
sin АВ |
||||||
|
cos АВ |

ПЕРЕДАЧА ДИРЕКЦИОННОГО УГЛА НА СТОРОНУ ТЕОДОЛИТНОГО ХОДА
В общем виде:
n n 1 180 прn n 1 180 л

180 л
В разомкнутом теодолитном ходе должны выполняться три условия: условие дирекционных углов и два координатных условия.
Вычислим последовательно дирекционные углы всех сторон хода,
используя формулу передачи дирекционного угла на последующую сторону хода: n n 1 180 пр или n n 1 .
Математическая запись условия дирекционных углов в разомкнутом теодолитном ходе для левых углов поворота:
(1)
Для правых углов поворота оно запишется так:
(2)
где αн , αк – дирекционные углы начальной и конечной выходных сторон,
между которыми прокладывается ход, n – число углов хода, включая
примычные.
Сумма углов, подсчитанная по формулам (1) и (2), называется теоретической суммой углов хода. Сумма измеренных углов вследствие
ошибок измерений, как правило, отличается от теоретической суммы на некоторую величину, называемую угловой невязкой и обозначаемую fβ:
(3)
19

|
f доп 2 m |
. |
|||
|
Допустимое значение угловой невязки: |
n |
(4) |
||
|
где n – число углов хода. |
|
Для теодолитных ходов mβ = 30″, поэтому: |
(5) |
|||
|
f доп 1 n. |
Присутствие ошибок в результатах измерений является причиной возникновения задачи уравнивания. Целью уравнивания является устранение невязок и повышение точности всех измеренных величин.
Обозначим поправку в измеренный угол Vβ и запишем условие:
откуда следует, что сумма угловых поправок равна угловой невязке с противоположным
|
знаком: |
V f . |
(7) |
|
При условии, что поправки в измеренные углы одинаковы, |
решение уравнения (7) |
|
|
получается в виде: |
V f / n. |
|
|
Исправленные значения углов вычисляются по формуле: |
||
|
i i(изм) V . |
(8) |
По исправленным углам поворота вычисляют дирекционные углы всех сторон хода; совпадение вычисленного и заданного значений конечного исходного дирекционного угла является контролем правильности обработки угловых измерений.
20

Координатные условия. Решая последовательно прямую геодезическую задачу, вычислим приращения координат по каждой стороне хода ΔXi и ΔYi :
|
Xвыч d cos d cos r |
(9) |
|||
|
Yвыч d sin d sin r |
(10) |
|||
|
где r – румб соответствующего дирекционного угла. |
X n X n 1 X |
|||
|
Координаты пунктов хода получим по формулам : |
(11) |
|||
|
Для конечной точки хода: Xкон Xнач Xi |
Yn Yn 1 Y |
(12) |
||
|
(13) |
||||
|
или |
Xi Xкон Xнач . |
(14) |
||
Аналогичная формула для суммы приращений ΔY имеет вид:
i кон нач . (15)
Получились еще два условия (14) и (15), которые называются координатными. Суммы приращений координат, подсчитанные по этим формулам, называются теоретическими суммами приращений. Вследствие ошибок измерения сторон суммы вычисленных приращений координат в общем случае не будут равны теоретическим суммам.
21
Соседние файлы в папке геодезия. все лекции
- #
- #
- #
- #
- #
- #
- #
Добро пожаловать!
Войдите или зарегистрируйтесь сейчас!
Войти
-
- Регистрация:
- 13 мар 2010
- Сообщения:
- 14
- Симпатии:
- 0
какую информацию можно извлечь из относительной ошибки? например линейная погрешность или что то в этом роде. пожалуйста привидите пример.
#1
-
Форумчанин
- Регистрация:
- 16 авг 2008
- Сообщения:
- 5.141
- Симпатии:
- 630
- Адрес:
-
Химки
1/2000 = 1 м на 2 км
То есть, линейная погрешность в 1 м на 2 км хода дает 1/2000.#2
-
- Регистрация:
- 13 мар 2010
- Сообщения:
- 14
- Симпатии:
- 0
это я знаю, а еще что нибудь из нее нельзя извлечь?
#3
-
Форумчанин
- Регистрация:
- 16 авг 2008
- Сообщения:
- 5.141
- Симпатии:
- 630
- Адрес:
-
Химки
Попробуйте, может, получится;)
#4
-
Форумчанин
а вы что хотите извлечь то, вы расскажите причину столь странного интереса…
#5
-
- Регистрация:
- 13 мар 2010
- Сообщения:
- 14
- Симпатии:
- 0
нам преподаватель говорит, что относительная ошибка дает много информации, но не рассказывает, мол мы сами все знаем. а я кроме линейной погрешности ничего незнаю
#6
-
Форумчанин
- Регистрация:
- 5 мар 2010
- Сообщения:
- 175
- Симпатии:
- 4
- Адрес:
-
Москва
ну, скажем, на первый взгляд: в теодолитном ходе если угловая невязка в допуске а относительная ошибка слишком большая, то это логично говорит о том что у вас есть ошибка в длинах линий, если же вы проверили все длины линий и поняли что они все верны, а относительная ошибка хода по-прежнему вас не устраивает, то у вас ошибка как минимум в двух углах поворота, причем эти ошибки взаимно исключают друг друга.. (а преподаватели, к слову, пользуются относительной ошибкой часто для того что бы определить подгонялись ли углы в ходе или нет.. )
Случай с ошибкой в исходных данных тоже может быть выявлен таким образом..
#7
-
Форумчанин
Самую полезную для студента информацию несет не относительная ошибка, а абсолютные ошибки приращений координат. В случае, если в небольшом ходе Вы где-то пролетели с измерением длин линий лентой (на метр, двадцать метров, остаток до другого края ленты), ним легко узнать дир. угол линии, в которой сидит промах. Как — не скажу, сами догадайтесь.
И тогда в поисках ошибки не придется перемерять весь полигон.
#8
-
Форумчанин
Для теодолитного хода относительная ошибка вычисляется по формуле =√ΣΔX²+ ΣΔY²/P<1/2000, где ΣΔX, ΣΔY — суммы приращений координат, Р — периметр полигона, т.е. относительная ошибка позволяет определить еще и ошибку в вычислениях превышений.
Относительная ошибка как правило характеризует точность линейных измерений. Например, относительная ошибка нитяного дальномера составляет 1/300, ошибка измерения рулеткой 1/2000, значит линия в 50 м в первом случае будет определена с точностью ±17 см, а во втором ±2,5см#9
-
Форумчанин
- Регистрация:
- 5 мар 2010
- Сообщения:
- 175
- Симпатии:
- 4
- Адрес:
-
Москва
не понял.. а это то откуда?
#10
-
Форумчанин
- Регистрация:
- 30 ноя 2007
- Сообщения:
- 2.702
- Симпатии:
- 2.444
- Адрес:
-
Сибирь
А если промахнулись в двух линиях?
#11
-
Форумчанин
Извините приращений координат
#12
-
- Регистрация:
- 13 мар 2010
- Сообщения:
- 14
- Симпатии:
- 0
спасибо за участие в этом вопросе.
#13
-
Форумчанин
Тогда уже не узнать
Если трасса, и углы близки к 180 градусам, то тоже.
Но в теодолито-рулеточную эпоху этим методом пользовались частенько. Помогало.
#14
Поделиться этой страницей

Объясните решению задачи, пожалуйста! Даю 50 баллов
Результат измерения линии на местности в прямом направлении D пр = 160,00 м, а в обратном D обр = 160,10 м. Требуется определить
относительную погрешность f относ. измерения.
Р е ш е н и е. f отност. = дельта D/D, где D — абсолютная погрешность, определяемая как разность двух измерений, равная ±0,10 м, откуда
f относ. = 0,10/160,05=1/1600
Погрешности измерений, представление результатов эксперимента
- Шкала измерительного прибора
- Цена деления
- Виды измерений
- Погрешность измерений, абсолютная и относительная погрешность
- Абсолютная погрешность серии измерений
- Представление результатов эксперимента
- Задачи
п.1. Шкала измерительного прибора
Шкала – это показывающая часть измерительного прибора, состоящая из упорядоченного ряда отметок со связанной с ними нумерацией. Шкала может располагаться по окружности, дуге или прямой линии.
Примеры шкал различных приборов:
п.2. Цена деления
Цена деления измерительного прибора равна числу единиц измеряемой величины между двумя ближайшими делениями шкалы. Как правило, цена деления указана на маркировке прибора.
Алгоритм определения цены деления
Шаг 1. Найти два ближайшие пронумерованные крупные деления шкалы. Пусть первое значение равно a, второе равно b, b > a.
Шаг 2. Посчитать количество мелких делений шкалы между ними. Пусть это количество равно n.
Шаг 3. Разделить разницу значений крупных делений шкалы на количество отрезков, которые образуются мелкими делениями: $$ triangle=frac{b-a}{n+1} $$ Найденное значение (triangle) и есть цена деления данного прибора.
Пример определения цены деления:
 |
Определим цену деления основной шкалы секундомера. Два ближайших пронумерованных деления на основной шкале:a = 5 c b = 10 cМежду ними находится 4 средних деления, а между каждыми средними делениями еще 4 мелких. Итого: 4+4·5=24 деления. Цена деления: begin{gather*} triangle=frac{b-a}{n+1}\ triangle=frac{10-5}{24+1}=frac15=0,2 c end{gather*} |
п.3. Виды измерений
Вид измерений
Определение
Пример
Прямое измерение
Физическую величину измеряют с помощью прибора
Измерение длины бруска линейкой
Косвенное измерение
Физическую величину рассчитывают по формуле, куда подставляют значения величин, полученных с помощью прямых измерений
Определение площади столешницы при измеренной длине и ширине
п.4. Погрешность измерений, абсолютная и относительная погрешность
Погрешность измерений – это отклонение измеренного значения величины от её истинного значения.
Составляющие погрешности измерений
Причины
Инструментальная погрешность
Определяется погрешностью инструментов и приборов, используемых для измерений (принципом действия, точностью шкалы и т.п.)
Погрешность метода
Определяется несовершенством методов и допущениями в методике.
Погрешность теории (модели)
Определяется теоретическими упрощениями, степенью соответствия теоретической модели и реальности.
Погрешность оператора
Определяется субъективным фактором, ошибками экспериментатора.
Инструментальная погрешность измерений принимается равной половине цены деления прибора: $$ d=frac{triangle}{2} $$
Если величина (a_0) — это истинное значение, а (triangle a) — погрешность измерения, результат измерений физической величины записывают в виде (a=a_0pmtriangle a).
Абсолютная погрешность измерения – это модуль разности между измеренным и истинным значением измеряемой величины: $$ triangle a=|a-a_0| $$
Отношение абсолютной погрешности измерения к истинному значению, выраженное в процентах, называют относительной погрешностью измерения: $$ delta=frac{triangle a}{a_0}cdot 100text{%} $$
Относительная погрешность является мерой точности измерения: чем меньше относительная погрешность, тем измерение точнее. По абсолютной погрешности о точности измерения судить нельзя.
На практике абсолютную и относительную погрешности округляют до двух значащих цифр с избытком, т.е. всегда в сторону увеличения.
Значащие цифры – это все верные цифры числа, кроме нулей слева. Результаты измерений записывают только значащими цифрами.
Примеры значащих цифр:
0,403 – три значащих цифры, величина определена с точностью до тысячных.
40,3 – три значащих цифры, величина определена с точностью до десятых.
40,300 – пять значащих цифр, величина определена с точностью до тысячных.
В простейших измерениях инструментальная погрешность прибора является основной.
В таких случаях физическую величину измеряют один раз, полученное значение берут в качестве истинного, а абсолютную погрешность считают равной инструментальной погрешности прибора.
Примеры измерений с абсолютной погрешностью равной инструментальной:
- определение длины с помощью линейки или мерной ленты;
- определение объема с помощью мензурки.
Пример получения результатов прямых измерений с помощью линейки:
 |
Измерим длину бруска линейкой, у которой пронумерованы сантиметры и есть только одно деление между пронумерованными делениями. Цена деления такой линейки: begin{gather*} triangle=frac{b-a}{n+1}= frac{1 text{см}}{1+1}=0,5 text{см} end{gather*} Инструментальная погрешность: begin{gather*} d=frac{triangle}{2}=frac{0,5}{2}=0,25 text{см} end{gather*} Истинное значение: (L_0=4 text{см}) Результат измерений: $$ L=L_0pm d=(4,00pm 0,25) text{см} $$ Относительная погрешность: $$ delta=frac{0,25}{4,00}cdot 100text{%}=6,25text{%}approx 6,3text{%} $$ |
 |
Теперь возьмем линейку с n=9 мелкими делениями между пронумерованными делениями. Цена деления такой линейки: begin{gather*} triangle=frac{b-a}{n+1}= frac{1 text{см}}{9+1}=0,1 text{см} end{gather*} Инструментальная погрешность: begin{gather*} d=frac{triangle}{2}=frac{0,1}{2}=0,05 text{см} end{gather*} Истинное значение: (L_0=4,15 text{см}) Результат измерений: $$ L=L_0pm d=(4,15pm 0,05) text{см} $$ Относительная погрешность: $$ delta=frac{0,05}{4,15}cdot 100text{%}approx 1,2text{%} $$ |
Второе измерение точнее, т.к. его относительная погрешность меньше.
п.5. Абсолютная погрешность серии измерений
Измерение длины с помощью линейки (или объема с помощью мензурки) являются теми редкими случаями, когда для определения истинного значения достаточно одного измерения, а абсолютная погрешность сразу берется равной инструментальной погрешности, т.е. половине цены деления линейки (или мензурки).
Гораздо чаще погрешность метода или погрешность оператора оказываются заметно больше инструментальной погрешности. В таких случаях значение измеренной физической величины каждый раз немного меняется, и для оценки истинного значения и абсолютной погрешности нужна серия измерений и вычисление средних значений.
Алгоритм определения истинного значения и абсолютной погрешности в серии измерений
Шаг 1. Проводим серию из (N) измерений, в каждом из которых получаем значение величины (x_1,x_2,…,x_N)
Шаг 2. Истинное значение величины принимаем равным среднему арифметическому всех измерений: $$ x_0=x_{cp}=frac{x_1+x_2+…+x_N}{N} $$ Шаг 3. Находим абсолютные отклонения от истинного значения для каждого измерения: $$ triangle_1=|x_0-x_1|, triangle_2=|x_0-x_2|, …, triangle_N=|x_0-x_N| $$ Шаг 4. Находим среднее арифметическое всех абсолютных отклонений: $$ triangle_{cp}=frac{triangle_1+triangle_2+…+triangle_N}{N} $$ Шаг 5. Сравниваем полученную величину (triangle_{cp}) c инструментальной погрешностью прибора d (половина цены деления). Большую из этих двух величин принимаем за абсолютную погрешность: $$ triangle x=maxleft{triangle_{cp}; dright} $$ Шаг 6. Записываем результат серии измерений: (x=x_0pmtriangle x).
Пример расчета истинного значения и погрешности для серии прямых измерений:
Пусть при измерении массы шарика с помощью рычажных весов мы получили в трех опытах следующие значения: 99,8 г; 101,2 г; 100,3 г.
Инструментальная погрешность весов d = 0,05 г.
Найдем истинное значение массы и абсолютную погрешность.
Составим расчетную таблицу:
| № опыта | 1 | 2 | 3 | Сумма |
| Масса, г | 99,8 | 101,2 | 100,3 | 301,3 |
| Абсолютное отклонение, г | 0,6 | 0,8 | 0,1 | 1,5 |
Сначала находим среднее значение всех измерений: begin{gather*} m_0=frac{99,8+101,2+100,3}{3}=frac{301,3}{3}approx 100,4 text{г} end{gather*} Это среднее значение принимаем за истинное значение массы.
Затем считаем абсолютное отклонение каждого опыта как модуль разности (m_0) и измерения. begin{gather*} triangle_1=|100,4-99,8|=0,6\ triangle_2=|100,4-101,2|=0,8\ triangle_3=|100,4-100,3|=0,1 end{gather*} Находим среднее абсолютное отклонение: begin{gather*} triangle_{cp}=frac{0,6+0,8+0,1}{3}=frac{1,5}{3}=0,5 text{(г)} end{gather*} Мы видим, что полученное значение (triangle_{cp}) больше инструментальной погрешности d.
Поэтому абсолютная погрешность измерения массы: begin{gather*} triangle m=maxleft{triangle_{cp}; dright}=maxleft{0,5; 0,05right} text{(г)} end{gather*} Записываем результат: begin{gather*} m=m_0pmtriangle m\ m=(100,4pm 0,5) text{(г)} end{gather*} Относительная погрешность (с двумя значащими цифрами): begin{gather*} delta_m=frac{0,5}{100,4}cdot 100text{%}approx 0,050text{%} end{gather*}
п.6. Представление результатов эксперимента
Результат измерения представляется в виде $$ a=a_0pmtriangle a $$ где (a_0) – истинное значение, (triangle a) – абсолютная погрешность измерения.
Как найти результат прямого измерения, мы рассмотрели выше.
Результат косвенного измерения зависит от действий, которые производятся при подстановке в формулу величин, полученных с помощью прямых измерений.
Погрешность суммы и разности
Если (a=a_0+triangle a) и (b=b_0+triangle b) – результаты двух прямых измерений, то
- абсолютная погрешность их суммы равна сумме абсолютных погрешностей
$$ triangle (a+b)=triangle a+triangle b $$
- абсолютная погрешность их разности также равна сумме абсолютных погрешностей
$$ triangle (a-b)=triangle a+triangle b $$
Погрешность произведения и частного
Если (a=a_0+triangle a) и (b=b_0+triangle b) – результаты двух прямых измерений, с относительными погрешностями (delta_a=frac{triangle a}{a_0}cdot 100text{%}) и (delta_b=frac{triangle b}{b_0}cdot 100text{%}) соответственно, то:
- относительная погрешность их произведения равна сумме относительных погрешностей
$$ delta_{acdot b}=delta_a+delta_b $$
- относительная погрешность их частного также равна сумме относительных погрешностей
$$ delta_{a/b}=delta_a+delta_b $$
Погрешность степени
Если (a=a_0+triangle a) результат прямого измерения, с относительной погрешностью (delta_a=frac{triangle a}{a_0}cdot 100text{%}), то:
- относительная погрешность квадрата (a^2) равна удвоенной относительной погрешности
$$ delta_{a^2}=2delta_a $$
- относительная погрешность куба (a^3) равна утроенной относительной погрешности
$$ delta_{a^3}=3delta_a $$
- относительная погрешность произвольной натуральной степени (a^n) равна
$$ delta_{a^n}=ndelta_a $$
Вывод этих формул достаточно сложен, но если интересно, его можно найти в Главе 7 справочника по алгебре для 8 класса.
п.7. Задачи
Задача 1. Определите цену деления и объем налитой жидкости для каждой из мензурок. В каком случае измерение наиболее точно; наименее точно?
Составим таблицу для расчета цены деления:
| № мензурки | a, мл | b, мл | n | (triangle=frac{b-a}{n+1}), мл |
| 1 | 20 | 40 | 4 | (frac{40-20}{4+1}=4) |
| 2 | 100 | 200 | 4 | (frac{200-100}{4+1}=20) |
| 3 | 15 | 30 | 4 | (frac{30-15}{4+1}=3) |
| 4 | 200 | 400 | 4 | (frac{400-200}{4+1}=40) |
Инструментальная точность мензурки равна половине цены деления.
Принимаем инструментальную точность за абсолютную погрешность и измеренное значение объема за истинное.
Составим таблицу для расчета относительной погрешности (оставляем две значащих цифры и округляем с избытком):
| № мензурки | Объем (V_0), мл | Абсолютная погрешность (triangle V=frac{triangle}{2}), мл |
Относительная погрешность (delta_V=frac{triangle V}{V_0}cdot 100text{%}) |
| 1 | 68 | 2 | 3,0% |
| 2 | 280 | 10 | 3,6% |
| 3 | 27 | 1,5 | 5,6% |
| 4 | 480 | 20 | 4,2% |
Наиболее точное измерение в 1-й мензурке, наименее точное – в 3-й мензурке.
Ответ:
Цена деления 4; 20; 3; 40 мл
Объем 68; 280; 27; 480 мл
Самое точное – 1-я мензурка; самое неточное – 3-я мензурка
Задача 2. В двух научных работах указаны два значения измерений одной и той же величины: $$ x_1=(4,0pm 0,1) text{м}, x_2=(4,0pm 0,03) text{м} $$ Какое из этих измерений точней и почему?
Мерой точности является относительная погрешность измерений. Получаем: begin{gather*} delta_1=frac{0,1}{4,0}cdot 100text{%}=2,5text{%}\ delta_2=frac{0,03}{4,0}cdot 100text{%}=0,75text{%} end{gather*} Относительная погрешность второго измерения меньше. Значит, второе измерение точней.
Ответ: (delta_2lt delta_1), второе измерение точней.
Задача 3. Две машины движутся навстречу друг другу со скоростями 54 км/ч и 72 км/ч.
Цена деления спидометра первой машины 10 км/ч, второй машины – 1 км/ч.
Найдите скорость их сближения, абсолютную и относительную погрешность этой величины.
Абсолютная погрешность скорости каждой машины равна инструментальной, т.е. половине деления спидометра: $$ triangle v_1=frac{10}{2}=5 (text{км/ч}), triangle v_2=frac{1}{2}=0,5 (text{км/ч}) $$ Показания каждого из спидометров: $$ v_1=(54pm 5) text{км/ч}, v_2=(72pm 0,5) text{км/ч} $$ Скорость сближения равна сумме скоростей: $$ v_0=v_{10}+v_{20}, v_0=54+72=125 text{км/ч} $$ Для суммы абсолютная погрешность равна сумме абсолютных погрешностей слагаемых. $$ triangle v=triangle v_1+triangle v_2, triangle v=5+0,5=5,5 text{км/ч} $$ Скорость сближения с учетом погрешности равна: $$ v=(126,0pm 5,5) text{км/ч} $$ Относительная погрешность: $$ delta_v=frac{5,5}{126,0}cdot 100text{%}approx 4,4text{%} $$ Ответ: (v=(126,0pm 5,5) text{км/ч}, delta_vapprox 4,4text{%})
Задача 4. Измеренная длина столешницы равна 90,2 см, ширина 60,1 см. Измерения проводились с помощью линейки с ценой деления 0,1 см. Найдите площадь столешницы, абсолютную и относительную погрешность этой величины.
Инструментальная погрешность линейки (d=frac{0,1}{2}=0,05 text{см})
Результаты прямых измерений длины и ширины: $$ a=(90,20pm 0,05) text{см}, b=(60,10pm 0,05) text{см} $$ Относительные погрешности (не забываем про правила округления): begin{gather*} delta_1=frac{0,05}{90,20}cdot 100text{%}approx 0,0554text{%}approx uparrow 0,056text{%}\ delta_2=frac{0,05}{60,10}cdot 100text{%}approx 0,0832text{%}approx uparrow 0,084text{%} end{gather*} Площадь столешницы: $$ S=ab, S=90,2cdot 60,1 = 5421,01 text{см}^2 $$ Для произведения относительная погрешность равна сумме относительных погрешностей слагаемых: $$ delta_S=delta_a+delta_b=0,056text{%}+0,084text{%}=0,140text{%}=0,14text{%} $$ Абсолютная погрешность: begin{gather*} triangle S=Scdot delta_S=5421,01cdot 0,0014=7,59approx 7,6 text{см}^2\ S=(5421,0pm 7,6) text{см}^2 end{gather*} Ответ: (S=(5421,0pm 7,6) text{см}^2, delta_Sapprox 0,14text{%})


![inj_geo_1-245.jpg [image]](https://injzashita.com/images/inj_geo_all/inj_geo_1-245.jpg)
![inj_geo_1-247.jpg [image]](https://injzashita.com/images/inj_geo_all/inj_geo_1-247.jpg)
![inj_geo_1-248.jpg [image]](https://injzashita.com/images/inj_geo_all/inj_geo_1-248.jpg)

