Величина приборной погрешности
может быть найдена одним из следующих
способов:
-
Приборная погрешность может быть
указана или на самом приборе, или в
его паспорте (в описании лабораторной
работы).
-
Приборная погрешность электроизмерительных
приборов определяется по классу
точности прибора. Класс точности
указывается в нижней части шкалы
прибора, как правило, в виде числа,
обведенного в кружочек.

прибора равен
приборной погрешности, выраженной в
процентах от максимального значения,
измеряемого на данной шкале. Обозначим
класс точности прибора буквой N.
Тогда:
% . (3)
Таким образом, зная класс точности
прибора Nможно рассчитать
приборную погрешностьxпо формуле:
. (4)
Пример.Пусть необходимо
измерить силу тока амперметром класса
точности 0,05 и с диапазоном измерения
(0 — 10) А. Абсолютную погрешность определим
по формуле (4):
А.
Так как относительная погрешность
зависит от значения измеряемой величины,
то она оказывается тем меньше, чем ближе
значение измеряемой величины к предельному
значению шкалы. Так, в рассматриваемом
примере, если измеренное значение тока
оказалось бы равным 10А, то %, а если 1А, тоI= 0,5 %.
Следовательно, при работе с
многопредельными приборами, в целях
получения наименьшей погрешности
измерения, следует выбирать такой
предел измерения, при котором стрелка
прибора имела бы максимальное отклонение.
3. В остальных случаях, когда
отсутствует паспорт прибора и не указан
класс точности, приборную погрешность
следует считать равной половине
наименьшего деления шкалы прибора
(половине цены деления шкалы).
Пример.При измерении длины
обычной линейкой, у которой наименьшее
деление шкалы равно 1 мм, следует
считать приборную погрешность равной
0,5 мм.
2. Как определить случайную погрешность X?
Если после проведения нескольких
измерений одной и той же физической
величины обнаруживается, что она
принимает различные значения после
каждого измерения, то это свидетельствует
о наличии случайной погрешности
.
Допустим, что проделано nизмерений физической величиныx,
и полученыnеё различных
значений.
Оценку истинного значения
измеряемой величины x
принято находить как среднее арифметическое
значение результатов измерений:
.
(5)
Для того, чтобы вычислить
абсолютную погрешность xследует найти разности между каждым
из результатов отдельных измерений
и среднеарифметическим значением:

Величины
являютсяслучайными отклоненияминаблюдаемой величины от среднеарифметического
значения и могут оказаться как
положительными (еслиxx),
так и отрицательными (еслиxx).
За величину погрешности
принимается средняя абсолютная ошибка
измерения, равная среднему арифметическому
значению модулей случайных отклонений:

или
. (8)
Соседние файлы в папке Matobrabotka
- #
16.04.201531.74 Кб18МНК1.xls
- #
16.04.201522.02 Кб8МНК2.xls
- #
16.04.201518.43 Кб8МНК3.xls
- #
- #
- #
- #
ЛАБОРАТОРНАЯ РАБОТА 2
Прямые измерения
массы тела с помощью рычажных весов и определение полной погрешности измерений
Цель работы:
измерить массы трёх предложенных тел прямым способом и рассчитать полную погрешность
результатов прямых измерений.
Оборудование: три тела разной плотности, рычажные весы, разновес (набор гирь)
ТАОРЕТИЧЕСКИЕ СВЕДЕНИЯ
При определении
полной погрешности измеренного значения массы необходимо учитывать погрешность
весов , погрешность гирь
, и погрешность подбора гирь
.
Погрешность весов зависит от нагрузки линейно и
определяется по графику зависимости . Смотрите об этом §
75 учебника «физика-10» Пинский А.А. Вам необходимо построить такой график
самостоятельно в отчёте по следующим данным: при нагрузке погрешность весов
,
а при нагрузке погрешность весов
(см.§ 75). Зная, что зависимость
линейная, построение графика не составит
никакого труда.
Погрешность гирь ,
входящих в набор гирь (разновес) приводится в таблице 1. Смотрите также
§ 75 учебника «физика-10» Пинский А.А.
Таблица 1 Погрешность гирь
|
НОМИНАЛЬНОЕ |
ГРАНИЦЫ |
|
10 |
1 мг |
|
200 |
2 мг |
|
500 |
3 мг |
|
1г |
4 мг |
|
2г |
6 мг |
|
5 г |
8 мг |
|
10 г |
12 мг |
|
20 г |
20 мг |
|
50 г |
30 мг |
|
100 г |
40 мг |
Погрешность гирь
равна сумме погрешностей всех использованных гирь (формула 1)
(1)
Погрешность подбора гирь аналогична погрешности отсчёта и половине
значения наименьшей гири, находящейся на весах, или той, которая выводит весы
из равновесия (формула 2)
(2)
Таким образом, при прямом измерении массы тела
на весах граница абсолютной погрешности измерений (формула 3)
(3)
Ниже смотрите пример определения полной
погрешности массы тела, измеренной прямым способом на рычажных весах.
Пример определения полной погрешности
массы тела
Пусть весы
находятся в равновесии, если на чашке лежат гири со значениями массы: ,
,
. Тогда за результат измерения массы тела
принимается значение
(4)
Погрешность
весов при нагрузке равна
. Как было сказано выше, это определяется
по графику зависимости , который уже
необходимо построить.
Таким образом:
(5)
Погрешность
всех гирь определим, пользуясь таблицей 1,
(см. формулу 1):
(6)
Погрешность
подбора гирь определяем по значению наименьшей
гири на весах (см. формулу 2)
(7)
Полная
погрешность массы тела определяется как сумма всех
погрешностей (см. формулу 3)
(8)
Полная погрешность
округляется до одной значащей цифры (общее правило для любых измерений), поэтому
в нашем примере для погрешности получаем окончательно:
(9)
Результат измерения
массы записывается в интервальной форме:
Не забывайте, что
разряд последней цифры измеренного значения и разряд погрешности должны совпадать
(правило Брадиса-Крылова), поэтому в данном примере измеренное значение массы (см. формулу 4) округляется до разряда
десятых, т.к. погрешность находится в этом разряде (см. формулу 9)
Относительная
погрешность измерения массы определяется по
известной формуле:
ПРАКТИЧЕСКАЯ
ЧАСТЬ РАБОТЫ
ВНИМАНИЕ! Прежде
чем приступать к работе, вам необходимо изучить правила работы с весами. Обратитесь
к учебникам 7-го класса (Пёрышкин А.В. или Громов С.В.) и 10-го (Пинский А.А.).
Без знаний этих правил вас не допустят к работе.
Порядок
выполнения работы
- Определите массу
первого тела. Запишите значение массы в виде суммы масс всех гирь
находящихся на весах. Смотрите пример выше.
(результат в граммах)
- Постройте график
зависимости погрешности весов от нагрузки (смотрите теоретическую часть
работы) и по графику определите погрешность весов
(результат в миллиграммах)
- Пользуясь таблицей
1, определите погрешность всех гирь
(результат в миллиграммах)
- По значению наименьшей гири на весах (не в
наборе) определите погрешность подбора гирь
= (результат в миллиграммах)
- Полная
погрешность определяется как сумма всех погрешностей
= (результат выразите в граммах и
округлите до одной значащей цифры)
- Округлите
результат измерения массы (см. пункт 1 практической части) так, чтобы
последняя цифра в округлённом результате принадлежала тому же разряду, в
котором находится значащая цифра полной абсолютной погрешности (пункт 2).
- Результат
запишите в интервальной форме в соответствии с правилом Брадиса-Крылова
- Определите относительную погрешность
измерения массы
ПОВТОРИТЬ ИЗМЕРЕНИЯ
В СООТВЕТСТВИИ С ПУНКТАМИ 1-8 ДЛЯ ДВУХ ДРУГИХ ТЕЛ
ВСЕ ЗАПИСИ И
РАСЧЁТЫ ВЫПОЛНЯТЬ В ЛАБОРАТОРНАОЙ ТЕТРАДИ
ОТЧЁТ К РАБОТЕ ПОДГОТОВИТЬ
ПО ПЕРДЛАГАЕМОЙ ФОРМЕ (СМ.НИЖЕ)
ОТЧЁТ К РАБОТЕ № 2 ВЫПОЛНИЛ________________________
Цель работы:_____________________________________________________________________________
_________________________________________________________________________________________
Оборудование:_____________________________________________________________________________
Расчёт погрешности измерения массы первого
тела
(Выполняется в
соответствии с пунктами 1-8)
_________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________
Расчёт погрешности измерения массы второго
тела
(Выполняется в
соответствии с пунктами 1-8)
_________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________
Расчёт погрешности измерения массы третьего
тела
(Выполняется в
соответствии с пунктами 1-8)
_________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________
Вывод
_____________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________
КОНТРОЛЬНЫЕ ВОПРОСЫ (ОТВЕТИТЬ ПИСЬМЕННО И СДАТЬ С ОТЧЁТОМ)
1 Как определяется погрешность весов?
Ответ на вопрос 1__________________________________________________________________________
_____________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________
2 Как определяется погрешность гирь?
Ответ на вопрос
2__________________________________________________________________________
_____________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________
3 Как определяется погрешность подбора
гирь?
Ответ на вопрос
3__________________________________________________________________________
_____________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________
4 Как определяется полная абсолютная
погрешность измерения массы?
Ответ на вопрос
4__________________________________________________________________________
_____________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________
5 Как определяется относительная
погрешность и что она показывает?
Ответ на вопрос
5__________________________________________________________________________
_____________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________
6 Какие цифры числа являются значащими? В
чём состоит правило Брадиса-Крылова?
Ответ на вопрос
6__________________________________________________________________________
_____________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________
Физические величины характеризуются понятием «точность погрешности». Есть высказывание, что путем проведения измерений можно прийти к познанию. Так удастся узнать, какова высота дома или длина улицы, как и многие другие.
Введение
Разберемся в значении понятия «измерить величину». Процесс измерения заключается в том, чтобы сравнить её с однородными величинами, которые принимают в качестве единицы.
Для определения объёма используются литры, для вычисления массы применяются граммы. Чтобы было удобнее производить расчеты, ввели систему СИ международной классификации единиц.
За измерение длины вязли метры, массы – килограммы, объёма – кубические литры, времени – секунды, скорости – метры за секунду.
При вычислении физических величин не всегда нужно пользоваться традиционным способом, достаточно применить вычисление при помощи формулы. К примеру, для вычисления таких показателей, как средняя скорость, необходимо поделить пройденное расстояние на время, проведенное в пути. Так производятся вычисления средней скорости.
Применяя единицы измерения, которые в десять, сто, тысячу раз превышают показатели принятых измерительных единиц, их называют кратными.
Наименование каждой приставки соответствует своему числу множителя:
- Дека.
- Гекто.
- Кило.
- Мега.
- Гига.
- Тера.
В физической науке для записи таких множителей используется степень числа 10. К примеру, миллион обозначается как 106.
В простой линейке длина имеет единицу измерения – сантиметр. Она в 100 раз меньше метра. 15-сантиметровая линейка имеет длину 0,15 м.
Линейка является простейшим видом измерительных приборов для того, чтобы измерять показатели длины. Более сложные приборы представлены термометром – чтобы измерять температуру, гигрометром – чтобы определять влажность, амперметром – замерять уровень силы, с которой распространяется электрический ток.
Насколько точны будут показатели проведенных измерений?
Возьмем линейку и простой карандаш. Наша задача заключается в измерении длины этой канцелярской принадлежности.
Для начала потребуется определить, какова цена деления, указанная на шкале измерительного прибора. На двух делениях, которые являются ближайшими штрихами шкалы, написаны цифры, к примеру, «1» и «2».
Необходимо подсчитать, сколько делений заключено в промежутке этих цифр. При правильном подсчете получится «10». Вычтем от того числа, которое является большим, число, которое будет меньшим, и поделим на число, которое составляют деления между цифрами:
(2-1)/10 = 0,1 (см)
Так определяем, что ценой, определяющей деление канцелярской принадлежности, является число 0,1 см или 1 мм. Наглядно показано, как определяется показатель цены для деления с применением любого измерительного прибора.
Измеряя карандаш с длиной, которая немного меньше, чем 10 см, воспользуемся полученными знаниями. При отсутствии на линейке мелкого деления, следовал бы вывод, что предмет имеет длину 10 см. Это приблизительное значение названо измерительной погрешностью. Она указывает на тот уровень неточности, которая может допускаться при проведении измерений.
Определяя параметры длины карандаша с более высоким уровнем точности, большей ценой деления достигается большая измерительная точность, которая обеспечивает меньшую погрешность.
При этом абсолютно точного выполнения измерений не может быть. А показатели не должны превышать размеры цены деления.
Установлено, что размеры измерительной погрешности составляют ½ цены, которая указана на делениях прибора, который применяется для определения размеров.
После выполнения замеров карандаша в 9,7 см определим показатели его погрешности. Это промежуток 9,65 — 9,85 см.
Формулой, измеряющей такую погрешность, является вычисление:
А = а ± D (а)
А — в виде величины для измерительных процессов;
а — значение результата замеров;
D — обозначение абсолютной погрешности.
Если слаживать или вычитать величины с учетом погрешности, это число будет составлять сумму цифр, которые и обозначают погрешность, и имеются у каждой отдельно взятой величины.
При вычитании или складывании величин с погрешностью результат будет равен сумме показателей погрешности, которую составляет каждая отдельная величина.
Знакомство с понятием
Если рассматривать классификацию погрешностей в зависимости от способа её выражения, можно выделить такие разновидности:
- Абсолютную.
- Относительную.
- Приведенную.
Абсолютная погрешность измерений обозначается буквой «Дельта» прописной. Это понятие определяется в виде разности между измеренными и действительными значениями той физической величины, которая измеряется.
Выражением абсолютной погрешность измерений являются единицы той величины, которую необходимо измерить.
При измерении массы она будет выражаться, к примеру, в килограммах. Это не эталон точности измерений.
Как рассчитать погрешность прямых измерений?
Есть способы изображения погрешности измерения и их вычисления. Для этого важно уметь определять физическую величину с необходимой точностью, знать, что такое абсолютная погрешность измерений, что её никто никогда не сможет найти. Можно вычислить только её граничное значение.
Даже если условно употребляется этот термин, он указывает именно на граничные данные. Абсолютная и относительная погрешность измерений обозначаются одинаковыми буквами, разница в их написании.
При измерении длины абсолютная погрешность будет измеряться в тех единицах, в которых исчисляться длина. А относительная погрешность вычисляется без размеров, так как она является отношением абсолютной погрешности к результату измерения. Такую величину часто выражают в процентах или в долях.
Абсолютная и относительная погрешность измерений имеют несколько разных способов вычисления в зависимости от того, какой метод измерения физических величин.
Понятие прямого измерения
Абсолютная и относительная погрешность прямых измерений зависят от класса точности прибора и умения определять погрешность взвешивания.
Прежде чем говорить о том, как вычисляется погрешность, необходимо уточнить определения. Прямым называется измерение, при котором происходит непосредственное считывание результата с приборной шкалы.
Когда мы пользуемся термометром, линейкой, вольтметром или амперметром, то всегда проводим именно прямые измерения, так как применяем непосредственно прибор со шкалой.
Есть два фактора, которые влияют на результативность показаний:
- Погрешностью приборов.
- Погрешностью системы отсчета.
Граница абсолютной погрешности при прямых измерениях будет равна сумме погрешности, которую показывает прибор, и погрешности, которая происходит в процессе отсчета.
D = D (пр.) + D (отс.)
Пример с медицинским термометром
Показатели погрешности указаны на самом приборе. На медицинском термометре прописана погрешность 0,1 градусов Цельсия. Погрешность отсчета составляет половину цены деления.
D отс. = С/2
Если цена деления 0,1 градуса, то для медицинского термометра можно произвести вычисления:
D = 0,1o С + 0,1o С / 2 = 0,15o С
На тыльной стороне шкалы другого термометра есть ТУ и указано, что для правильности измерений необходимо погружать термометр всей тыльной частью. Точность измерения не указана. Остается только погрешность отсчета.
Если цена деления шкалы этого термометра равна 2o С, то можно измерять температуру с точностью до 1o С. Таковы пределы допускаемой абсолютной погрешности измерений и вычисление абсолютной погрешности измерений.
Особую систему вычисления точности используют в электроизмерительных приборах.
Точность электроизмерительных приборов
Чтобы задать точность таких устройств, используется величина, называемая классом точности. Для её обозначения применяют букву «Гамма». Чтобы точно произвести определение абсолютной и относительной погрешности измерений, нужно знать класс точности прибора, который указан на шкале.
Возьмем, к примеру, амперметр. На его шкале указан класс точности, который показывает число 0,5. Он пригоден для измерений на постоянном и переменном токе, относится к устройствам электромагнитной системы.
Это достаточно точный прибор. Если сравнить его со школьным вольтметром, видно, что у него класс точности – 4. Эту величину обязательно знать для дальнейших вычислений.
Применение знаний
Таким образом, D c = c (max) Х γ /100
Этой формулой и будем пользоваться для конкретных примеров. Воспользуемся вольтметром и найдем погрешность измерения напряжения, которое дает батарейка.
Подключим батарейку непосредственно к вольтметру, предварительно проверив, стоит ли стрелка на нуле. При подключении прибора стрелка отклонилась на 4,2 деления. Это состояние можно охарактеризовать так:
- Видно, что максимальное значение U для данного предмета равно 6.
- Класс точности –(γ) = 4.
- U(о) = 4,2 В.
- С=0,2 В
Пользуясь этими данными формулы, абсолютная и относительная погрешность измерений вычисляется так:
D U = DU (пр.)+ С/2
D U (пр.) = U (max) Х γ /100
D U (пр.) = 6 В Х 4/100 = 0, 24 В
Это погрешность прибора.
Расчет абсолютной погрешности измерений в этом случае будет выполнен так:
D U = 0,24 В + 0,1 В = 0,34 В
По рассмотренной формуле без труда можно узнать, как рассчитать абсолютную погрешность измерений.
Существует правило округления погрешностей. Оно позволяет найти средний показатель между границей абсолютной погрешности и относительной.
Учимся определять погрешность взвешивания
Это один из примеров прямых измерений. На особом месте стоит взвешивание. Ведь у рычажных весов нет шкалы. Научимся определять погрешность такого процесса. На точность измерения массы влияет точность гирь и совершенство самих весов.
Мы пользуемся рычажными весами с набором гирь, которые необходимо класть именно на правую чашу весов. Для взвешивания возьмем линейку.
Перед началом опыта нужно уравновесить весы. Линейку кладем на левую чашу.
Масса будет равна сумме установленных гирь. Определим погрешность измерения этой величины.
D m = D m (весов) + D m (гирь)
Погрешность измерения массы складывается из двух слагаемых, связанных с весами и гирями. Чтобы узнать каждую из этих величин, на заводах по выпуску весов и гирь продукция снабжается специальными документами, которые позволяют вычислить точность.
Применение таблиц
Воспользуемся стандартной таблицей. Погрешность весов зависит от того, какую массу положили на весы. Чем она больше, тем, соответственно, больше и погрешность.
Даже если положить очень легкое тело, погрешность будет. Этот связано с процессом трения, происходящим в осях.
Вторая таблица относится к набору гирь. На ней указано, что каждая из них имеет свою погрешность массы. 10-граммовая имеет погрешность в 1 мг, как и 20-граммовая. Просчитаем сумму погрешностей каждой из этих гирек, взятой из таблицы.
Удобно писать массу и погрешность массы в двух строчках, которые расположены одна под другой. Чем меньше гири, тем точнее измерение.
Итоги
В ходе рассмотренного материала установлено, что определить абсолютную погрешность невозможно. Можно лишь установить её граничные показатели. Для этого используются формулы, описанные выше в вычислениях. Данный материал предложен для изучения в школе для учеников 8-9 классов. На основе полученных знаний можно решать задачи на определение абсолютной и относительной погрешности.
Погрешность измерения
Содержание:
- Абсолютная погрешность — измерительный прибор
- 2. ПОГРЕШНОСТИ ИЗМЕРЕНИЙ
- Погрешность — измерительный прибор
- 4. ВЕСА РЕЗУЛЬТАТОВ НЕРАВНОТОЧНЫХ ИЗМЕРЕНИЙ
- Максимальная абсолютная погрешность
- а a изм аист ед.изм. 4
- Относительная
погрешность (5) – безразмерная величина, она измеряется в долях или процентах и
показывает какую часть от истинного значения измеряемой величины составляет
погрешность. - Например:
приборная погрешность
- Относительная
- 30 Поверка и калибровка си. Определения. Правовые основы.
- Расчёт ошибок косвенных измерений
Абсолютная погрешность — измерительный прибор
Абсолютная погрешность измерительного прибора представляет собой расхождение ( разность) между измеренным Ли и действительным ( истинным) Лд значениями измеряемой величины ДЛ — / 4н — Ац. Истинное значение измеряемой величины находят с учетом поправки. Поправка — это величина, обратная по знаку абсолютной погрешности: ДР — ДЛ Ал-А. Абсолютная погрешность электроизмерительных приборов со стрелочным показателем практически неизменна в пределах всей шкалы, поэтому с уменьшением значения измеряемой величины она возрастает. Для повышения точности измерения измеряемой величины на показывающих приборах со стрелочным указателем следует выбирать такие пределы измерения, чтобы отсчитывать показания примерно в пределах 2 / 3 всей шкалы.
Абсолютная погрешность измерительного прибора равна разности между показанием прибора и действительным ( точным) значением измеряемой величины.
Абсолютная погрешность измерительного прибора определяется разностью между показанием прибора и истинным значением измеряемой величины. Погрешность показаний прибора имеет своими источниками погрешности отдельных его элементов: чувствительного элемента, передаточного механизма и шкалы. Погрешность чувствительного элемента заключается в том, что действительная зависимость его перемещений от измеряемой величины не совпадает с расчетной, заложенной в схему прибора. Погрешность шкалы складывается из ошибки положения ее штрихов и эксцентриситета шкалы.
Абсолютной погрешностью измерительного прибора называется разность между его показанием и истинным значением измеряемой величины. Так как истинное значение измеряемой величины установить нельзя, в измерительной технике используется так называемое действительное значение, полученное с помощью образцового прибора.
Абсолютной погрешностью измерительного прибора называется разность между его показанием и истинным значением измеряемой величины. Поскольку последнее установить нельзя, то в измерительной технике используют так называемое действительное значение, полученное посредством образцового прибора.
Абсолютной погрешностью измерительного прибора называется разность между его показанием и истинным значением измеряемой величины Так как величину истинного значения измеряемой величины установить нельзя, в измерительной технике используется так называемое действительное значение, полученное с помощью образцового прибора.
Приведенная погрешность измерительного прибора — отношение абсолютной погрешности измерительного прибора к нормирующему значению, выраженное в процентах.
Корректность поставленных экспериментов доказана отсутствием превышения абсолютных ошибок измерения как при определении перемещений, так и напряжений над абсолютной погрешностью используемых измерительных приборов.
В некоторых случаях ( для образцовых и рабочих средств измерений повышенной точности) для исключения систематической погрешности показаний вводят поправку, равную абсолютной погрешности измерительного прибора.
Абсолютная погрешность измерительного прибора определяется разностью между показанием прибора и действительным значением измеряемой величины.
В данном разделе будут рассмотрены виды погрешностей, свойственные мерам, отдельным элементам и устройствам, а также средствам измерений в целом. Под абсолютной погрешностью меры понимают разность ( отклонение от номинального значения) между номинальным значением меры и истинным значением воспроизводимой ею величины. Так как истинное значение величины остается неизвестным, то на практике вместо него используют действительное значение величины. Следует различать абсолютную погрешность измерительного преобразователя по входу и по выходу. Абсолютную погрешность измерительного преобразователя по входу находят как разность между значением величины на входе преобразователя, определяемой в принципе по истинному значению величины на его выходе с помощью градуировочной характеристики, приписанной преобразователю, и истинным значением величины на входе преобразователя. Абсолютную погрешность измерительного преобразователя по выходу находят как разность между истинным значением величины на выходе преобразователя, отображающей измеряемую величину, и значением величины на выходе, определяемой в принципе по истинному значению величины на выходе с помощью градуировочной характеристики, приписанной преобразователю. Относительная погрешность измерительного прибора определяется как отношение абсолютной погрешности измерительного прибора к истинному значению измеряемой им величины.
При многократном измерении одной и той же величины каждый раз получают несколько отличающиеся результаты, как по абсолютной величине, так и по знакам, каким бы опытом не обладал исполнитель и какими бы высокоточными приборами он не пользовался.
Погрешности различают: грубые, систематические и случайные.
Появление грубых погрешностей (промахов) связано с серьезными ошибками при производстве измерительных работ. Эти ошибки легко выявляются и устраняются в результате контроля измерений.Систематические погрешностивходят в каждый результат измерений по строго определенному закону. Они обусловлены влиянием конструкции измерительных приборов, погрешностями градуировки их шкал, износом и т. д. (инструментальные погрешности)иливозникают из-за недоучета условий измерений и закономерностей их изменений, приближенности некоторых формул и др. (методические погрешности). Систематические погрешности делятся на постоянные (неизменные по знаку и вели чине) и переменные (изменяющие свою величину от одного измерения к другому по определенному закону).
Такие погрешности заранее определимы и могут быть сведены к необходимому минимуму путем введения соответствующих поправок.Например, заранее может быть учтено влияние кривизны Земли на точность определения вертикальных расстояний, влияние температуры воздуха и атмосферного давления при определении длин линий светодальномерами или электронными тахеометрами, заранее можно учесть влияние рефракции атмосферы и т. д.
Если не допускать грубых погрешностей и устранять систематические, то качество измерений будет определяться только случайными погрешностями. Эти погрешности неустранимы, однако их поведение подчиняется законам больших чисел. Их можно анализировать, контролировать и сводить к необходимому минимуму.
Для уменьшения влияния случайных погрешностей на результаты измерений прибегают к многократным измерениям, к улучшению условий работы, выбирают более совершенные приборы, методы измерений и осуществляют тщательное их производство.
Сопоставляя ряды случайных погрешностей равноточных измерений можно обнаружить, что они обладают следующими свойствами:
а) для данного вида и условий измерений случайные погрешности не могут превышать по абсолютной величине некоторого предела;
б) малые по абсолютной величине погрешности появляются чаще больших;
в) положительные погрешности появляются так же часто, как и равные им по абсолютной величине отрицательные;
г) среднее арифметическое из случайных погрешностей одной и той же величины стремится к нулю при неограниченном увеличении числа измерений.
Распределение ошибок, соответствующее указанным свойствам, называется нормальным (рис. 12.1).

Разность между результатом измерения некоторой величины (l) и ее истинным значением (X) называют абсолютной (истинной) погрешностью.
Δ = l — X
Истинное (абсолютно точное) значение измеряемой величины получить невозможно, даже используя приборы самой высокой точности и самую совершенную методику измерений. Лишь в отдельных случаях может быть известно теоретическое значение величины. Накопление погрешностей приводит к образованию расхождений между результатами измерений и действительными их значениями.Разность суммы практически измеренных (или вычисленных) величин и теоретического ее значения называется невязкой. Например, теоретическая сумма углов в плоском треугольнике равна 180º, а сумма измеренных углов оказалась равной 180º02′; тогда погрешность суммы измеренных углов составит +0º02′. Эта погрешность будет угловой невязкой треугольника.
Абсолютная погрешность не является, полным показателем точности выполненных работ. Например, если некоторая линия, фактическая длина которой составляет 1000 м, измерена землемерной лентой с ошибкой 0,5 м, а отрезок длиною 200 м – с ошибкой 0,2 м, то, несмотря на то, что абсолютная погрешность первого измерения больше второго, все же первое измерение было выполнено с точностью в два раза более высокой. Поэтому вводят понятие относительной погрешности:
Отношение абсолютной погрешности измеряемой величины Δ к измеренной величине l называют относительной погрешностью.
Относительные погрешности всегда выражаются дробью с числителем, равным единице (аликвотная дробь). Так, в приведенном выше примере относительная погрешность первого измерения составляет
,
а второго
Погрешность — измерительный прибор
Погрешность измерительных приборов часто выражают в процентах от диапазона шкалы. Такая погрешность называется приведенной относительной погрешностью.
Погрешности измерительных приборов подразделяются на основные и дополнительные.
Погрешность измерительного прибора определяется структурными и конструктивными особенностями самого прибора, свойствами примененных в нем материалов и элементов, особенностями технологии изготовления, градуировки.
Погрешность измерительного прибора определяется поверкой. Показания образцового прибора в этом случае считают действительным значением измеряемой величины. В процессе поверки на результаты многократных измерений воздействуют самые различные факторы как систематического, так и случайного характера, результатом чего являются систематические и случайные-ошибки измерения. Вычисление и суммирование этих ошибок производится по правилам теории вероятностей, причем систематические погрешности суммируются алгебраически, а для суммирования средних квадратичных значений погрешности необходимо учитывать вид закона распределения случайных погрешностей, взаимных корреляционных связей и степень достоверности определения результатов измерений.
Погрешность измерительного прибора представляет собой отклонение его показания от значения воздействующей на вход измеряемой величины. Поэтому источники погрешности измерительного прибора совпадают с таковыми для измерительного преобразователя.
Погрешность измерительного прибора, полученная при измерениях в нормальных условиях, называется основной погрешностью.
Погрешность измерительного прибора зависит от hoi решностей его отдельных viob. Суммирование погрешностей осуществляется по определенным правилам Систематические погрешности s, суммируют ал1ебраически с учетом собс.
Погрешность измерительного прибора в динамическом режиме возникает вследствие того, что время установления переходных процессов в приборе больше интервала изменения измеряемой величины. Опираясь на понятия теории случайных процессов, можно сказать, что эта погрешность заметно проявляется тогда, когда постоянная времени прибора превосходит интервал корреляции случайного процесса, реализация которого подана на вход прибора.
Погрешность измерительного прибора представляет собой разность между показаниями прибора и истинным значением измеряемой величины, а погрешность меры — разность между номинальным значением меры и истинным значением воспроизводимой ею величины.
|
Схема установки для измерения параметров транзистора. |
Погрешность измерительных приборов при этом весьма большая. Поэтому измеряют величину 1-а, равную отношению тока базы к току эмиттера. Ток эмиттера транзистора измеряют косвенно. Генератор тока подключают к нагрузочному сопротивлению в цепи коллектора, равному 50 ом, и вольтметром V измеряют падение напряжения на нем. Измеренный таким образом ток будет протекать через эмиттер, когда источник тока подключим к входной цепи транзистора. В этом положении ток базы определяют по падению напряжения на сопротивлении 1 ком, включенном в цепь базы.
Погрешности измерительных приборов бывают систематические и случайные. Систематические погрешности во многих случаях могут быть устранены поправкой или компенсированы.
Погрешность измерительного прибора представляет собой разность между показаниями прибора и истинным значением измеряемой величины, а погрешность меры — разность между номинальным значением меры и истинным значением воспроизводимой ею величины.
Погрешностей измерительных приборов, складывающихся из погрешности прибора, измеряющего данный параметр и из погрешностей приборов, по которым устанавливается режим работы ламп.
Погрешностью измерительного прибора называют отклонение его показаний от действительного значения измеряемой величины, определенного с известной более высокой точностью.
4. ВЕСА РЕЗУЛЬТАТОВ НЕРАВНОТОЧНЫХ ИЗМЕРЕНИЙ
При неравноточных измерениях, когда результаты каждого измерения нельзя считать одинаково надежными, уже нельзя обойтись определением простого арифметического среднего. В таких случаях учитывают достоинство (или надежность) каждого результата измерений.Достоинство результатов измерений выражают некоторым числом, называемым весом этого измерения. Очевидно, что арифметическое среднее будет иметь больший вес по сравнению с единичным измерением, а измерения, выполненные при использовании более совершенного и точного прибора, будут иметь большую степень доверия, чем те же измерения, выполненные прибором менее точным.
Поскольку условия измерений определяют различную величину средней квадратической погрешности, то последнюю и принято принимать в качестве основы оценки весовых значений, проводимых измерений. При этом веса результатов измерений принимают обратно пропорциональными квадратам соответствующих им средних квадратических погрешностей.
Так, если обозначить через р и Р веса измерений, имеющие средние квадратические погрешности соответственно m и µ, то можно записать соотношение пропорциональности:
Например, если µ средняя квадратическая погрешность арифметического среднего, а m – соответственно, одного измерения, то, как следует из
можно записать:
т. е. вес арифметического среднего в n раз больше веса единичного измерения.
Аналогичным образом можно установить, что вес углового измерения, выполненного 15-секундным теодолитом, в четыре раза выше веса углового измерения, выполненного 30-секундным прибором.
При практических вычислениях обычно вес одной какой-либо величины принимают за единицу и при этом условии вычисляют веса остальных измерений. Так, в последнем примере если принять вес результата углового измерения 30-секундным теодолитом за р = 1, то весовое значение результата измерения 15-секундным теодолитом составит Р = 4.
Максимальная абсолютная погрешность
|
Процесс зфавновсшивагия в цифровых приборах развертывающего уравновеши. |
В цифровых циклических приборах выходной код N приближается к искомому отсчету Nх с одной стороны, сверху или снизу, поэтому при АХп ч 0 максимальная абсолютная погрешность от квантования равна ступени & хк.
Здесь: Арн — максимальная абсолютная погрешность величины рн, равная половине единицы разряда последней значащей цифры в табличном значении рн; Ар и АГ — максимальные абсолютные погрешности измерения р и Т соответственно.
Абсолютная погрешность температурного предела смеси при использовании в расчете надежных экспериментальных данных по давлению пара чистых компонентов, растворимости и коэффициентам активности, как правило, не превышает максимальной абсолютной погрешности температурного предела компонентов смеси.
Абсолютная погрешность при изображении в ячейке чисел с запятой, фиксированной после определенного разряда, не превосходит по величине единицы младшего разряда, то есть, как говорят, максимальная абсолютная погрешность при этом постоянна. https://spb-evacuator.ru.
Для учета в модели однократной экстракции NRTL влияния воды, были дополнительно подобраны эмпирические коэффициенты бинарного взаимодействия воды с компонентами системы, применение которых при численных исследованиях существенно уменьшило погрешности моделирования в области содержания воды в экстрагенте выше 8 % об. По выходу рафината и содержанию в нем аренов максимальные абсолютные погрешности в этой области составляют 0 6 и 0 9 %, соответственно. Погрешности расчета по выходу экстракта и содержания в нем аренов снизились до 0 6 и 1 1 %, что составляет 4 8 и 1 4 % относительной по.
Следует отметить, что для измерения среднего фазового сдвига рассмотренным методом характерно уменьшение погрешности дискретности по сравнению с имеющей место при измерении одиночного интервала времени. Хотя максимальная абсолютная погрешность дискретности определения длительности одного интервала АГ составляет ГСЧ, результирующая погрешность за время измерения Ткзм уменьшается, так как результаты измерения всех k интервалов АГ суммируются, а возникновение частотной погрешности дискретности положительного или отрицательного знака равновероятно.
Рассмотрим погрешность от квантования. Следовательно, максимальная абсолютная погрешность от квантования будет равна единице.
Второй способ сводится к увеличению числа импульсов, заполняющих временные ворота, достигаемому умножением частоты исследуемого сигнала. При этом максимальная абсолютная погрешность меняется ( если неизменна длительность ворот), но уменьшается относительная погрешность. Осуществление данного способа сопряжено с применением дополнительного блока — умножителя частоты, что усложняет и удорожает аппаратуру.
Максимальную погрешность Дгд Т0 удобно учитывать через эквивалентное случайное изменение числа счетных импульсов Nx на 1 импульс. При этом максимальная абсолютная погрешность дискретизации может быть определена разностью значений частоты / получаемых по формулам (7.4) или (7.5) при Л 1 и Nx, и равна А.
Максимальные абсолютные погрешности показаний манометров Мп и Мв, исправленных на систематические погрешности приборов, принимаются равными 0 2н — 0 5 цены наименьшего деления шкалы, если эта величина не превышает вариации показаний прибора. В противном случае максимальная абсолютная погрешность равна вариации показа ний прибора, которая определяется при тарировании.
Максимальные абсолютные погрешности показаний манометров М и Мв, исправленных на систематические погрешности приборов, принимаются равными 0 2 — 0 5 цены наименьшего деления шкалы, если эта величина не превышает вариации показаний прибора. В ином случае максимальная абсолютная погрешность будет равна вариации показаний прибора, которая определяется при тарировании.
|
Вид кривой У 10 — 4Х2 и ее аппроксимация линейными отрезками. |
Точность результата зависит от того, в каком состоянии находится счетчик-интегратор в момент остановки цикла вычисления. Для этого значения получаем максимальную абсолютную погрешность — 5 импульсов младшего разряда.
Например, при отсчете или установке визира на логарифмической линейке длиной 250 мм ошибка не превышает 0 1 мм. Таким образом, обычно бывает известна максимальная абсолютная погрешность, получаемая при измерении величины х; обозначим эту погрешность через их.
а a изм аист ед.изм. 4
Это
размерная, положительная величина, характеризующая отклонение измеренного от
истинного значений.
Относительная погрешность – это
отношение абсолютной погрешности к истинному значению измеряемой величины.

Относительная
погрешность (5) – безразмерная величина, она измеряется в долях или процентах и
показывает какую часть от истинного значения измеряемой величины составляет
погрешность.
На
практике вместо неизвестного истинного значения используют среднее значение
измеряемой величины.
Формула (5) позволяет по
известной одной из характеристик определить другую. Часто вначале удобнее найти
относительную, а через неё абсолютную.
Если
измерение выполнено и погрешности определены, то окончательный результат
записывается в виде

что эквивалентно заданию
интервала, в котором лежит истинное значение искомой величины. И чем уже данный
интервал, тем точнее измерения и наоборот.
4.
Вычисление погрешностей.
За
абсолютную погрешность однократно измеряемой величины применяют приборную
погрешность.
Для
простых измерительных и цифровых приборов приборная погрешностьравная
половине цены деления прибора.
. (7)
Например:
приборная погрешность
миллиметровой линейки (с=1 мм/дел) равна, Δапр
= 0,5 мм.
штангенциркуля (с=0,05 мм/дел) – Δапр
= 0,025 мм.
эл.
секундомера (с=0,001 с/дел) – Δапр
= 0,0005 с.
Для
стрелочных электроизмерительных приборов приборная погрешность определятся
через класс точности прибора (характеристика прибора указанная на его
шкале).
,
(8)
представляющая
собой отношение приборной погрешности к максимальному значению измеряемой
прибором величины. Из (8) для приборной погрешности стрелочных
электроизмерительных приборов получаем:
ΔАприб. = 0,01 · К · Аmax
.
(9)
Часто
в расчетах приходится использовать физические и математические постоянные,
которые как правило выражаются сложными десятичными дробями
(π=
3.141593… , е = 2.718282… , с = 2.99792… · 108 м/с
qe =
1,60219… · 10-19 Kл , mе =
1.67265… · 10-31к2 и т.д.).
При
использовании постоянных мы вынуждены их округлять т.е. брать приближённые
значения, это также даёт вклад в погрешность. К погрешностям табличных величин
относятся так же как и к приборным.
За
погрешность табличной величины принимают половину единицы последнего разряда
табличной величины, выбранной с заданной точностью.
Например; при определении
плотности тела цилиндрической формы необходимо использовать число π.
Предварительно оговаривается точность расчётов (например вычисления проводят с
точностью до
четырёх значащих цифр).
Тогда используемое число π и погрешность Δπ соответственно будут равны:
π =
3.142, Δπ = 0.0005
и окончательная запись числа
π с погрешностью имеет вид:
б)
Погрешности многократно измеряемых величин.
Погрешности
многократных измерений в рамках линейной теории оцениваются по следующей схеме
30 Поверка и калибровка си. Определения. Правовые основы.
В
соответствии с законом РК «Об обеспечении
единства измерений» введены следующие
понятия:
— поверка
средства измерений —
совокупность операций, выполняемых
органами Государственной метрологической
службы (другими уполномоченными на то
органами, организациями) с целью
определения и подтверждения соответствия
средства измерений установленным
требованиям;
— калибровка
средств измерений —
совокупность операций, выполняемых с
целью определения и подтверждения
действительных значений метрологических
характеристик и/или пригодности к
применению средства измерений, не
подлежащего государственному
метрологическому контролю и надзору.
В
обоих случаях, как при поверке, так и
при калибровке, определяются метрологические
характеристики средств измерений,
причем часто по одной и той же методике,
называемой методикой
поверки,
но на этом их сходство заканчивается. Различия
между этими понятиями имеют
более принципиальный характер.
Во-первых,
в сферах распространения ГМКиН могут
применяться только поверенные СИ, а
калиброванные — не могут.
Во-вторых,
поверке могут подвергаться только СИ
утвержденного типа, то есть внесенные
в Государственный реестр СИ, а калибровке
— любые, в том числе нестандартизованные
и изготовленные в одном экземпляре.
В-третьих,
при поверке проверяется соответствие
СИ своему типу, внесенному в Государственный
реестр, тогда как при калибровке
определяются действительные
метрологические характеристики, которые
прибор имеет на момент калибровки.
Если
при поверке СИ обнаружено его несоответствие
хотя бы одному пункту утвержденного
типа, средство измерений должно быть
забраковано. При калибровке этому СИ
будут приписаны новые значения
метрологических характеристик.
Положительные
результаты поверки удостоверяются
поверительным клеймом или свидетельством
о поверке. Если средство измерений по
результатам поверки признано непригодным
к применению, оттиск поверительного
клейма и свидетельство о поверке
аннулируются и выписывается извещение
о непригодности или делаются соответствующие
записи в технической документации.
Результаты
калибровки удостоверяются калибровочным
знаком (клеймом), наносимым на средство
измерений, или сертификатом о калибровке,
а также, записью в эксплуатационных
документах. В соответствии с законом
РК «Об обеспечении единства измерений»
калибровка средств измерений является
процедурой добровольной и осуществляемой
по желанию владельца прибора с целью,
например, получения достоверных
результатов измерений, влияющих, в
конечном счете, на результаты труда.
ГМКиН на такие средства измерений не
распространяется.
Расчёт ошибок косвенных измерений
Пусть искомая
величина А
при выбранном
методе косвенных измерений рассчитывается
по формуле:
A
= f(x1
,x2
,x3
,…,xn
) (12)
где x1,x2,…,xn
— величины, найденные в результате прямых
измерений, с учётом ошибок о которых
шла речь выше. Из-за этих ошибок величина
«А»
так же будет определяться с ошибками.
Пусть X1,X2,…,XN
— значения f(x1
,x2
,x3
,…,xn), вычисленные
для разных серий измерений (x1,x2,…,xn).
Таблица 1
Таблица коэффициентов
Стьюдента
|
Число измерений |
Доверительная |
|||||
|
0.7 |
0.8 |
0.9 |
0.95 |
0.99 |
0.999 |
|
|
2 |
2.0 |
3.1 |
6.3 |
12.7 |
63.7 |
636.6 |
|
3 |
1.3 |
1.9 |
2.9 |
4.3 |
9.9 |
31.6 |
|
4 |
1.3 |
1.6 |
2.4 |
3.2 |
5.8 |
12.9 |
|
5 |
1.2 |
1.5 |
2.1 |
2.8 |
4.6 |
8.6 |
|
10 |
1.1 |
1.4 |
1.8 |
2.3 |
3.3 |
4.8 |
|
15 |
1.1 |
1.3 |
1.8 |
2.1 |
3.0 |
4.1 |
|
20 |
1.1 |
1.3 |
1.7 |
2.1 |
2.9 |
3.9 |
Абсолютной ошибкой
косвенных измерений, по аналогии с
абсолютной ошибкой прямых измерений,
называют разность между истинным
значением «А» и её значениями,
полученными в результате измерений:

Размерность
абсолютной ошибки совпадает с размерностью
определяемой величины. Относительной
ошибкой косвенных измерений называют
отвлечённое число:

Иногда относительную
ошибку выражают в процентах:

Для определения
величины «А» в формулах (12)…(15) по
теории
вероятностей
следует брать величину Х, которую можно
определить двумя способами:
1) А
= Х
= (Х1
+ Х2
+…+Хn)/n
(16)
2) A
= X
= f(x1
+ x2
+…+xn)
(17)
где x1,
x2
,…, xn
определяют по формуле (3). Если ошибки
измерений малы, то оба способа дают
практически тождественные результаты.
Рассмотрим способы
нахождения ошибки величины А,
определённой из косвенных измерений,
по найденным значениям оши
бок прямых измерений.
Выше отмечалось, что возможны различные
соотношения между приборной систематической
и случайными ошибками.
1-й случай. Преобладают
приборные ошибки. В этом случае можно
дать только оценку максимальной ошибки.
Формулы для нахождения предельной
ошибки косвенных измерений по внешнему
виду совпадают с формулами дифференциального
исчисления. В связи с этим для предельной
абсолютной ошибки используется формула:

а для расчёта
предельной относительной ошибки пригодна
фор
— 19 —
мула:

Формулы для расчёта
предельных ошибок некоторых часто
встречающихся функций, когда приборные
ошибки превышают случайные, приведены
в Таблице 2. Эти выражения легко
рассчитываются по формулам (18) и (19).
2-й случай. Преобладают
случайные ошибки. Для определения
среднеквадратичной ошибки теория
вероятностей даёт следующую формулу:

Относительная
ошибка вычисляется по формуле:

При выполнении
промежуточных расчётов необходимо
помнить, что число точных цифр в результате
расчётов не может увеличиваться. Поэтому
промежуточные результаты округляют,
сохраняя
1…2 избыточных
знака. При этом последующие цифры,
меньшие
5,отбрасываются;если
первая из отбрасываемых цифр больше 5,
то последняя из
оставшихся цифр увеличивается на
единицу. Ес
ли первая
отбрасываемая цифра 5, то предыдущая
цифра остаётся
без изменений,
если она чётная, и увеличивается на
единицу, если
она нечётная.
Выражения для среднеквадратичной ошибки
некоторых часто встречающихся функций
приведены в Таблице 3. Для определения
ошибок косвенных измерений используют
большую из инструментальной или случайной
ошибок прямого измерения.
Как определить погрешность прибора
Выполнение многих учебных и научно-исследовательских работ связано с проведением самых различных измерений физических величин. После получения результатов приборных измерений обычно следует их обработка. Для точного соответствия результатов вычислений картине эксперимента требуется учитывать допустимую погрешность измерений. Определение погрешности измерительных приборов осуществляется по особым методикам.

Инструкция
Используйте для определения абсолютной инструментальной погрешности, определяемой конструкцией прибора, специальные таблицы погрешности средств измерения. К примеру, для чертежной линейки длиной до 500 мм и ценой деления 1 мм абсолютная инструментальная погрешность равна плюс-минус 1 мм; а для микрометра с пределом измерения 25 мм и ценой 0,01 мм эта величина составит плюс-минус 0,005 мм.
Определите абсолютную погрешность отсчета. Она получается от не очень точного снятия показаний, отсчитываемых с помощью измерительных приборов и приспособлений. В большинстве случаев эта величина равна половине цены деления приборной шкалы. При измерении времени абсолютную погрешность отсчета примите равной цене деления секундомера (часов).
Вычислите максимальную абсолютную погрешность прямого наблюдения. Она определяется как результат сложения абсолютной инструментальной погрешности и абсолютной погрешности отсчета (если прочими видами погрешностей можно пренебречь):
А’ = Аи + Ао, где
А’ – максимальная абсолютная погрешность прямых наблюдений;
Аи – абсолютная инструментальная погрешность;
Ао – абсолютная погрешность отсчета.
При определении абсолютной погрешности измерения прибора округлите ее до одной значащей цифры. Численное значение результата измерительной процедуры округляют таким образом, чтобы последняя его цифра оказалась в том же разряде, что и цифра погрешности.
Если возникает необходимость в проведении повторных приборных измерений, осуществляемых в одинаковых контролируемых условиях, тогда погрешность, называемую здесь случайной, определите как среднее арифметическое погрешностей результатов всех измерений.
Чтобы определить абсолютную инструментальную погрешность электроизмерительного прибора, узнайте класс его точности. Его обычно указывают на шкале прибора или в техническом паспорте (описании).
Источники:
- определить стандартное отклонение
Войти на сайт
или
Забыли пароль?
Еще не зарегистрированы?
This site is protected by reCAPTCHA and the Google Privacy Policy and Terms of Service apply.
Погрешности измерений, представление результатов эксперимента
- Шкала измерительного прибора
- Цена деления
- Виды измерений
- Погрешность измерений, абсолютная и относительная погрешность
- Абсолютная погрешность серии измерений
- Представление результатов эксперимента
- Задачи
п.1. Шкала измерительного прибора
Шкала – это показывающая часть измерительного прибора, состоящая из упорядоченного ряда отметок со связанной с ними нумерацией. Шкала может располагаться по окружности, дуге или прямой линии.
Примеры шкал различных приборов:
п.2. Цена деления
Цена деления измерительного прибора равна числу единиц измеряемой величины между двумя ближайшими делениями шкалы. Как правило, цена деления указана на маркировке прибора.
Алгоритм определения цены деления
Шаг 1. Найти два ближайшие пронумерованные крупные деления шкалы. Пусть первое значение равно a, второе равно b, b > a.
Шаг 2. Посчитать количество мелких делений шкалы между ними. Пусть это количество равно n.
Шаг 3. Разделить разницу значений крупных делений шкалы на количество отрезков, которые образуются мелкими делениями: $$ triangle=frac{b-a}{n+1} $$ Найденное значение (triangle) и есть цена деления данного прибора.
Пример определения цены деления:
 |
Определим цену деления основной шкалы секундомера. Два ближайших пронумерованных деления на основной шкале:a = 5 c b = 10 cМежду ними находится 4 средних деления, а между каждыми средними делениями еще 4 мелких. Итого: 4+4·5=24 деления. Цена деления: begin{gather*} triangle=frac{b-a}{n+1}\ triangle=frac{10-5}{24+1}=frac15=0,2 c end{gather*} |
п.3. Виды измерений
Вид измерений
Определение
Пример
Прямое измерение
Физическую величину измеряют с помощью прибора
Измерение длины бруска линейкой
Косвенное измерение
Физическую величину рассчитывают по формуле, куда подставляют значения величин, полученных с помощью прямых измерений
Определение площади столешницы при измеренной длине и ширине
п.4. Погрешность измерений, абсолютная и относительная погрешность
Погрешность измерений – это отклонение измеренного значения величины от её истинного значения.
Составляющие погрешности измерений
Причины
Инструментальная погрешность
Определяется погрешностью инструментов и приборов, используемых для измерений (принципом действия, точностью шкалы и т.п.)
Погрешность метода
Определяется несовершенством методов и допущениями в методике.
Погрешность теории (модели)
Определяется теоретическими упрощениями, степенью соответствия теоретической модели и реальности.
Погрешность оператора
Определяется субъективным фактором, ошибками экспериментатора.
Инструментальная погрешность измерений принимается равной половине цены деления прибора: $$ d=frac{triangle}{2} $$
Если величина (a_0) — это истинное значение, а (triangle a) — погрешность измерения, результат измерений физической величины записывают в виде (a=a_0pmtriangle a).
Абсолютная погрешность измерения – это модуль разности между измеренным и истинным значением измеряемой величины: $$ triangle a=|a-a_0| $$
Отношение абсолютной погрешности измерения к истинному значению, выраженное в процентах, называют относительной погрешностью измерения: $$ delta=frac{triangle a}{a_0}cdot 100text{%} $$
Относительная погрешность является мерой точности измерения: чем меньше относительная погрешность, тем измерение точнее. По абсолютной погрешности о точности измерения судить нельзя.
На практике абсолютную и относительную погрешности округляют до двух значащих цифр с избытком, т.е. всегда в сторону увеличения.
Значащие цифры – это все верные цифры числа, кроме нулей слева. Результаты измерений записывают только значащими цифрами.
Примеры значащих цифр:
0,403 – три значащих цифры, величина определена с точностью до тысячных.
40,3 – три значащих цифры, величина определена с точностью до десятых.
40,300 – пять значащих цифр, величина определена с точностью до тысячных.
В простейших измерениях инструментальная погрешность прибора является основной.
В таких случаях физическую величину измеряют один раз, полученное значение берут в качестве истинного, а абсолютную погрешность считают равной инструментальной погрешности прибора.
Примеры измерений с абсолютной погрешностью равной инструментальной:
- определение длины с помощью линейки или мерной ленты;
- определение объема с помощью мензурки.
Пример получения результатов прямых измерений с помощью линейки:
 |
Измерим длину бруска линейкой, у которой пронумерованы сантиметры и есть только одно деление между пронумерованными делениями. Цена деления такой линейки: begin{gather*} triangle=frac{b-a}{n+1}= frac{1 text{см}}{1+1}=0,5 text{см} end{gather*} Инструментальная погрешность: begin{gather*} d=frac{triangle}{2}=frac{0,5}{2}=0,25 text{см} end{gather*} Истинное значение: (L_0=4 text{см}) Результат измерений: $$ L=L_0pm d=(4,00pm 0,25) text{см} $$ Относительная погрешность: $$ delta=frac{0,25}{4,00}cdot 100text{%}=6,25text{%}approx 6,3text{%} $$ |
 |
Теперь возьмем линейку с n=9 мелкими делениями между пронумерованными делениями. Цена деления такой линейки: begin{gather*} triangle=frac{b-a}{n+1}= frac{1 text{см}}{9+1}=0,1 text{см} end{gather*} Инструментальная погрешность: begin{gather*} d=frac{triangle}{2}=frac{0,1}{2}=0,05 text{см} end{gather*} Истинное значение: (L_0=4,15 text{см}) Результат измерений: $$ L=L_0pm d=(4,15pm 0,05) text{см} $$ Относительная погрешность: $$ delta=frac{0,05}{4,15}cdot 100text{%}approx 1,2text{%} $$ |
Второе измерение точнее, т.к. его относительная погрешность меньше.
п.5. Абсолютная погрешность серии измерений
Измерение длины с помощью линейки (или объема с помощью мензурки) являются теми редкими случаями, когда для определения истинного значения достаточно одного измерения, а абсолютная погрешность сразу берется равной инструментальной погрешности, т.е. половине цены деления линейки (или мензурки).
Гораздо чаще погрешность метода или погрешность оператора оказываются заметно больше инструментальной погрешности. В таких случаях значение измеренной физической величины каждый раз немного меняется, и для оценки истинного значения и абсолютной погрешности нужна серия измерений и вычисление средних значений.
Алгоритм определения истинного значения и абсолютной погрешности в серии измерений
Шаг 1. Проводим серию из (N) измерений, в каждом из которых получаем значение величины (x_1,x_2,…,x_N)
Шаг 2. Истинное значение величины принимаем равным среднему арифметическому всех измерений: $$ x_0=x_{cp}=frac{x_1+x_2+…+x_N}{N} $$ Шаг 3. Находим абсолютные отклонения от истинного значения для каждого измерения: $$ triangle_1=|x_0-x_1|, triangle_2=|x_0-x_2|, …, triangle_N=|x_0-x_N| $$ Шаг 4. Находим среднее арифметическое всех абсолютных отклонений: $$ triangle_{cp}=frac{triangle_1+triangle_2+…+triangle_N}{N} $$ Шаг 5. Сравниваем полученную величину (triangle_{cp}) c инструментальной погрешностью прибора d (половина цены деления). Большую из этих двух величин принимаем за абсолютную погрешность: $$ triangle x=maxleft{triangle_{cp}; dright} $$ Шаг 6. Записываем результат серии измерений: (x=x_0pmtriangle x).
Пример расчета истинного значения и погрешности для серии прямых измерений:
Пусть при измерении массы шарика с помощью рычажных весов мы получили в трех опытах следующие значения: 99,8 г; 101,2 г; 100,3 г.
Инструментальная погрешность весов d = 0,05 г.
Найдем истинное значение массы и абсолютную погрешность.
Составим расчетную таблицу:
| № опыта | 1 | 2 | 3 | Сумма |
| Масса, г | 99,8 | 101,2 | 100,3 | 301,3 |
| Абсолютное отклонение, г | 0,6 | 0,8 | 0,1 | 1,5 |
Сначала находим среднее значение всех измерений: begin{gather*} m_0=frac{99,8+101,2+100,3}{3}=frac{301,3}{3}approx 100,4 text{г} end{gather*} Это среднее значение принимаем за истинное значение массы.
Затем считаем абсолютное отклонение каждого опыта как модуль разности (m_0) и измерения. begin{gather*} triangle_1=|100,4-99,8|=0,6\ triangle_2=|100,4-101,2|=0,8\ triangle_3=|100,4-100,3|=0,1 end{gather*} Находим среднее абсолютное отклонение: begin{gather*} triangle_{cp}=frac{0,6+0,8+0,1}{3}=frac{1,5}{3}=0,5 text{(г)} end{gather*} Мы видим, что полученное значение (triangle_{cp}) больше инструментальной погрешности d.
Поэтому абсолютная погрешность измерения массы: begin{gather*} triangle m=maxleft{triangle_{cp}; dright}=maxleft{0,5; 0,05right} text{(г)} end{gather*} Записываем результат: begin{gather*} m=m_0pmtriangle m\ m=(100,4pm 0,5) text{(г)} end{gather*} Относительная погрешность (с двумя значащими цифрами): begin{gather*} delta_m=frac{0,5}{100,4}cdot 100text{%}approx 0,050text{%} end{gather*}
п.6. Представление результатов эксперимента
Результат измерения представляется в виде $$ a=a_0pmtriangle a $$ где (a_0) – истинное значение, (triangle a) – абсолютная погрешность измерения.
Как найти результат прямого измерения, мы рассмотрели выше.
Результат косвенного измерения зависит от действий, которые производятся при подстановке в формулу величин, полученных с помощью прямых измерений.
Погрешность суммы и разности
Если (a=a_0+triangle a) и (b=b_0+triangle b) – результаты двух прямых измерений, то
- абсолютная погрешность их суммы равна сумме абсолютных погрешностей
$$ triangle (a+b)=triangle a+triangle b $$
- абсолютная погрешность их разности также равна сумме абсолютных погрешностей
$$ triangle (a-b)=triangle a+triangle b $$
Погрешность произведения и частного
Если (a=a_0+triangle a) и (b=b_0+triangle b) – результаты двух прямых измерений, с относительными погрешностями (delta_a=frac{triangle a}{a_0}cdot 100text{%}) и (delta_b=frac{triangle b}{b_0}cdot 100text{%}) соответственно, то:
- относительная погрешность их произведения равна сумме относительных погрешностей
$$ delta_{acdot b}=delta_a+delta_b $$
- относительная погрешность их частного также равна сумме относительных погрешностей
$$ delta_{a/b}=delta_a+delta_b $$
Погрешность степени
Если (a=a_0+triangle a) результат прямого измерения, с относительной погрешностью (delta_a=frac{triangle a}{a_0}cdot 100text{%}), то:
- относительная погрешность квадрата (a^2) равна удвоенной относительной погрешности
$$ delta_{a^2}=2delta_a $$
- относительная погрешность куба (a^3) равна утроенной относительной погрешности
$$ delta_{a^3}=3delta_a $$
- относительная погрешность произвольной натуральной степени (a^n) равна
$$ delta_{a^n}=ndelta_a $$
Вывод этих формул достаточно сложен, но если интересно, его можно найти в Главе 7 справочника по алгебре для 8 класса.
п.7. Задачи
Задача 1. Определите цену деления и объем налитой жидкости для каждой из мензурок. В каком случае измерение наиболее точно; наименее точно?
Составим таблицу для расчета цены деления:
| № мензурки | a, мл | b, мл | n | (triangle=frac{b-a}{n+1}), мл |
| 1 | 20 | 40 | 4 | (frac{40-20}{4+1}=4) |
| 2 | 100 | 200 | 4 | (frac{200-100}{4+1}=20) |
| 3 | 15 | 30 | 4 | (frac{30-15}{4+1}=3) |
| 4 | 200 | 400 | 4 | (frac{400-200}{4+1}=40) |
Инструментальная точность мензурки равна половине цены деления.
Принимаем инструментальную точность за абсолютную погрешность и измеренное значение объема за истинное.
Составим таблицу для расчета относительной погрешности (оставляем две значащих цифры и округляем с избытком):
| № мензурки | Объем (V_0), мл | Абсолютная погрешность (triangle V=frac{triangle}{2}), мл |
Относительная погрешность (delta_V=frac{triangle V}{V_0}cdot 100text{%}) |
| 1 | 68 | 2 | 3,0% |
| 2 | 280 | 10 | 3,6% |
| 3 | 27 | 1,5 | 5,6% |
| 4 | 480 | 20 | 4,2% |
Наиболее точное измерение в 1-й мензурке, наименее точное – в 3-й мензурке.
Ответ:
Цена деления 4; 20; 3; 40 мл
Объем 68; 280; 27; 480 мл
Самое точное – 1-я мензурка; самое неточное – 3-я мензурка
Задача 2. В двух научных работах указаны два значения измерений одной и той же величины: $$ x_1=(4,0pm 0,1) text{м}, x_2=(4,0pm 0,03) text{м} $$ Какое из этих измерений точней и почему?
Мерой точности является относительная погрешность измерений. Получаем: begin{gather*} delta_1=frac{0,1}{4,0}cdot 100text{%}=2,5text{%}\ delta_2=frac{0,03}{4,0}cdot 100text{%}=0,75text{%} end{gather*} Относительная погрешность второго измерения меньше. Значит, второе измерение точней.
Ответ: (delta_2lt delta_1), второе измерение точней.
Задача 3. Две машины движутся навстречу друг другу со скоростями 54 км/ч и 72 км/ч.
Цена деления спидометра первой машины 10 км/ч, второй машины – 1 км/ч.
Найдите скорость их сближения, абсолютную и относительную погрешность этой величины.
Абсолютная погрешность скорости каждой машины равна инструментальной, т.е. половине деления спидометра: $$ triangle v_1=frac{10}{2}=5 (text{км/ч}), triangle v_2=frac{1}{2}=0,5 (text{км/ч}) $$ Показания каждого из спидометров: $$ v_1=(54pm 5) text{км/ч}, v_2=(72pm 0,5) text{км/ч} $$ Скорость сближения равна сумме скоростей: $$ v_0=v_{10}+v_{20}, v_0=54+72=125 text{км/ч} $$ Для суммы абсолютная погрешность равна сумме абсолютных погрешностей слагаемых. $$ triangle v=triangle v_1+triangle v_2, triangle v=5+0,5=5,5 text{км/ч} $$ Скорость сближения с учетом погрешности равна: $$ v=(126,0pm 5,5) text{км/ч} $$ Относительная погрешность: $$ delta_v=frac{5,5}{126,0}cdot 100text{%}approx 4,4text{%} $$ Ответ: (v=(126,0pm 5,5) text{км/ч}, delta_vapprox 4,4text{%})
Задача 4. Измеренная длина столешницы равна 90,2 см, ширина 60,1 см. Измерения проводились с помощью линейки с ценой деления 0,1 см. Найдите площадь столешницы, абсолютную и относительную погрешность этой величины.
Инструментальная погрешность линейки (d=frac{0,1}{2}=0,05 text{см})
Результаты прямых измерений длины и ширины: $$ a=(90,20pm 0,05) text{см}, b=(60,10pm 0,05) text{см} $$ Относительные погрешности (не забываем про правила округления): begin{gather*} delta_1=frac{0,05}{90,20}cdot 100text{%}approx 0,0554text{%}approx uparrow 0,056text{%}\ delta_2=frac{0,05}{60,10}cdot 100text{%}approx 0,0832text{%}approx uparrow 0,084text{%} end{gather*} Площадь столешницы: $$ S=ab, S=90,2cdot 60,1 = 5421,01 text{см}^2 $$ Для произведения относительная погрешность равна сумме относительных погрешностей слагаемых: $$ delta_S=delta_a+delta_b=0,056text{%}+0,084text{%}=0,140text{%}=0,14text{%} $$ Абсолютная погрешность: begin{gather*} triangle S=Scdot delta_S=5421,01cdot 0,0014=7,59approx 7,6 text{см}^2\ S=(5421,0pm 7,6) text{см}^2 end{gather*} Ответ: (S=(5421,0pm 7,6) text{см}^2, delta_Sapprox 0,14text{%})
Страница 1 из 6
-
lamen
Грустный lamen со своим жалким догматизмом.
Команда форума
АдминистраторВ этой теме буду писать что-то вроде краткой шпаргалки по погрешностям. Опять же, данный текст ни в коей мере не официальный и ссылаться на него недопустимо. Буду признателен за исправление любых ошибок и неточностей, которые могут быть в этом тексте.
Что такое погрешность?
Запись результата эксперимента вида
(
) означает, что если мы проведем очень много идентичных экспериментов, то в 70% полученные результаты будут лежать в интервале
, а в 30% — не будут.
Или, что тоже самое, если мы повторим эксперимент, то новый результат ляжет в доверительный интервал
с вероятностью, равной доверительной вероятности
.
Как округлять погрешность и результат?
Погрешность округляется до первой значащей цифры, если она не единица. Если единица — то до двух. При этом значащей цифрой называется любая цифра результата кроме нулей впереди.
Пример:
округляем до
или
или
но ни в коем случае не
или
, поскольку тут 2 значащие цифры — 2 и 0 после двойки.
округляем до
или
округляем до
или
или
Результат округляем таким образом, чтобы последняя значащая цифра результата соответствовала последней значащей цифре погрешности.
Примеры правильной записи:
мм
мм Держим тут в погрешности 2 значащие цифры потому что первая значащая цифра в погрешности — единица.
мм
Примеры неправильной записи:
мм. Здесь лишний знак в результате. Правильно будет
мм.
мм. Здесь лишний знак и в погрешности, и в результате. Правильно будет
мм.
В работе использую значение, данное мне просто в виде цифры. Например, масса грузиков. Какая у нее погрешность?
Если погрешность явно не указана, можно взять единицу в последнем разряде. То есть если написано m=1.35 г, то в качестве погрешность нужно взять 0.01 г.
Как считать погрешность сложной функции?
Есть функция от нескольких величин
У каждой из этих величин есть своя погрешность. Чтобы найти погрешность функции надо сделать следующее:
символ
означает частную производную f по x. Подробнее про частные производные здесь.
Как вообще правильно посчитать погрешность?
Положим, вы меряли одну и ту же величину x несколько (n) раз. Получили набор значений.
. Вам необходимо посчитать погрешность разброса, посчитать приборную погрешность и сложить их вместе.
По пунктам.
1. Считаем погрешность разброса
Если все значения совпали — никакого разброса у вас нет. Иначе — есть погрешность разброса
, которую надо вычислить. Для начала вычисляется среднеквадратичная погрешность среднего:
здесь
означает среднее по всем
.
Погрешность разбросаполучается умножением среднеквадратичной погрешности среднего на коэффициент Стьюдента
, который зависит от выбранной вами доверительной вероятности
и числа измерений n:
.
Коэффициенты Стьюдента
берем из нижеприведенной таблицы. Доверительная вероятность
выбитается произвольно, число измерений n мы также знаем.
2. Считаем приборную погрешность среднего
Если погрешности разных точек разные, то по формуле
При этом естественно, у всех
доверительная вероятность должна быть одинаковой.
3. Складываем среднее с разбросом
Погрешности всегда складываются как корень из квадратов:
При этом нужно убедиться, что доверительные вероятности с которыми были вычислены
и
совпадают.
Как по графику определить приборную погрешность среднего? Ну т.е., используя метод парных точек или метод наименьших квадратов, мы найдем погрешность разброса среднего сопротивления. Как найти приборную погрешность среднего сопротивления?
И в МНК и в методе парных точек можно дать строгий ответ на этот вопрос. Для МНК форума в Светозарове есть («Основы…», раздел про метод наименьших квадратов), а для парных точек первое, что приходит в голову (в лоб, что называется) это посчитать приборную погрешность каждого углового коэффициента. Ну и далее по всем пунктам…
Если же не хочешь мучиться, то в лабниках дан простой способ для оценки приборной погрешности углового коэффициента, именно из МНК следующий (например перед работой 1 в лабнике «Электроизмерительные приборы. …» последняя страница Метод.рекомендаций).
, где
— величина максимального отклонения по оси Y точки с погрешностью от проведенной прямой, а в знаменателе стоит ширина области нашего графика по оси Y. Аналогично по оси X.
На магазине сопротивлений написан класс точности: 0,05/4*10^-6? Как из этого найти погрешность прибора?Это означает, что предельная относительная погрешность прибора (в процентах) имеет вид:
, где
— наибольшее значение сопротивления магазина, а
— номинальное значение включённого сопротивления.
Легко видеть, что второе слагаемое важно тогда, когда мы работаем на очень малых сопротивлениях.Подробнее всегда можно посмотреть в паспорте прибора. Паспорт можно найти в интернете, забив марку прибора в гугл.
Литература про погрешности
Рецептурная информация про то как считать погрешности дана во введениях к практикумам, в частности, во вводной части к практикуму «Измерительные приборы».
Гораздо больше информации по этому поводу можно найти в рекомендованной для первокурсников книге:
В.В. Светозаров «Элементарная обработка результатов измерений»В качестве дополнительной (для первокурсников дополнительной) литературы можно порекомендовать:
В.В.Светозаров «Основы статистической обработки результатов измерений»И уж тем кто хочет окончательно во всем разобраться непременно стоит заглянуть сюда:
Дж. Тейлор. «Введение в теорию ошибок»Спасибо Lexxus’у за нахождение и размещение у себя на сайте этих замечательных книжек.
-
Lexxus
Немного великий
Администратор
VIPА разве не
? -
lamen
Грустный lamen со своим жалким догматизмом.
Команда форума
АдминистраторНеа. Последняя значащая цифра результата должна отвечать последней значащей цифре погрешности.
Если мы держим миллиметры в погрешности, то почему их надо убирать в результате? -
0,98 можно округлить так:
?
-
Lexxus
Немного великий
Администратор
VIP[quote name=’Silver MC’s’ post=’379424′ date=’Oct 5 2010, 16:00′]
0,98 можно округлить так:?
[/quote]
0.98 можно округлять до 1.0, если погрешность получилась 0.195 и более.
В противном случае, округлять до 1.0 нельзя. -
Lexxus
Немного великий
Администратор
VIPlamen, а вот кстати. Если результат измерения получился, скажем, 4, а погрешность — скажем, 20 (ну, мало ли).
В точности следуя описанной выше логике, я должен округлить результат до порядка первой значащей цифры погрешности (в нашем случае — до десятков), т.е. записать?
-
lamen
Грустный lamen со своим жалким догматизмом.
Команда форума
Администратор[quote name=’Silver MC’s’ post=’379424′ date=’Oct 5 2010, 16:00′]
0,98 можно округлить так:?
[/quote]0,98 это результат или погрешность?
[quote name=’Lexxus’ post=’379428′ date=’Oct 5 2010, 16:53′]
lamen, а вот кстати. Если результат измерения получился, скажем, 4, а погрешность — скажем, 20 (ну, мало ли).
В точности следуя описанной выше логике, я должен округлить результат до порядка первой значащей цифры погрешности (в нашем случае — до десятков), т.е. записать?
[/quote]
Да, именно так, если я правильно понимаю. Связано, как я понимаю, с тем, что погрешность округления самой погрешности в этом случае превысит результат.
То есть я понимаю, что четверка несет в себе некую информацию, которая убивается округлением. Но по сравнению с самой погрешностью, и с ее ошибкой округления, это уже все мало.
-
А в чем разница 2х примеров? Во втором случае оба числа просто на порядок меньше. Нельзя их записать как-то типа
. Это, разве, не полностью аналогичный случай к правильному варианту записи?
-
lamen
Грустный lamen со своим жалким догматизмом.
Команда форума
АдминистраторВ первом случае первая цифра в погрешности — единица. Из-за этого мы держим в погрешности 2 знака, чтобы минимизировать ошибку округления погрешности. Во втором — четверка. И мы оставляем только один знак.
-
Т.е.
— правильно?
Думаю, тогда стоит в инструкции более ясно написать, почему предыдущее не правильно.
-
lamen
Грустный lamen со своим жалким догматизмом.
Команда форума
АдминистраторДа. А +- 4.2 — неправильно.Предлагай. У меня-то глаз замылен, мне все кажется понятным
.
-
результат
-
lamen
Грустный lamen со своим жалким догматизмом.
Команда форума
Администратор[quote name=’Silver MC’s’ post=’379443′ date=’Oct 5 2010, 17:41′]
результат
[/quote]
Тогда тебе Lexxus ответил.[quote name=’Chameleon’ post=’379445′ date=’Oct 5 2010, 17:42′]
как так «завернуто»
[/quote]Слишком сложно для восприятия, имхо. Смешано в кучу правильное и неправильное. Я чуть выше, в примерах правильной записи, добавил строчку, поясняющую различие. И, кстати, про единицу сказано выше.
-
т.е.если погрешность 0.1 при при результате 0.98 то при округлении я получу 0.9
-
lamen
Грустный lamen со своим жалким догматизмом.
Команда форума
Администратор -
[quote name=’Silver MC’s’ date=’Oct 5 2010, 18:19′]
[snapback]379453[/snapback]т.е.если погрешность 0.1 при при результате 0.98 то при округлении я получу 0.9[/quote]
Нет. Если погрешность 0,1, то дадо писать так: $0.98pm0.10
Если в погрешности 1я значащая цифра 1, то второй знак обязателен.
PS Если преподаватели немного посвирепствуют, то никакие мануалы и не нужны. Кстати в Светозарове то же самое написано, что и тут. -
Мне кажется, стоит еще написать:
1. как округлять пятерку в последнем разряде (у преподавателей разных кафедр похоже требования разные)
1.56
1.54
1.55
1.52. на пальцах объяснить что значит частная производная с простеньким примерчиком
Если надо — текст попозже напишу
-
lamen
Грустный lamen со своим жалким догматизмом.
Команда форума
АдминистраторNick_, а надо ли тут так вдаваться в математику? тем более в элементарную, вроде правил округления?
-
Lexxus
Немного великий
Администратор
VIPПроблема в том, что функции многих переменных и частные производные в курсе матанализа, кажется, где-то ближе к концу первого семестра.
Страница 1 из 6
Поделиться этой страницей













![[IMG]](http://corum.mephist.ru/tex/images/b7cd22a4bb1c3d8abaa342cd2ada4701.gif) (
(![[IMG]](http://corum.mephist.ru/tex/images/48291f83278dbe78bb6d25c83d42b779.gif) ) означает, что если мы проведем очень много идентичных экспериментов, то в 70% полученные результаты будут лежать в интервале
) означает, что если мы проведем очень много идентичных экспериментов, то в 70% полученные результаты будут лежать в интервале ![[IMG]](http://corum.mephist.ru/tex/images/e52740eb8c1ca9095d2a4e17d036ebec.gif) , а в 30% — не будут.
, а в 30% — не будут.![[IMG]](http://corum.mephist.ru/tex/images/dad2cde42eb00bcf43e15d68d3efabab.gif) .
.![[IMG]](http://corum.mephist.ru/tex/images/fe09543b974240017f246c36f0e20bad.gif) округляем до
округляем до ![[IMG]](http://corum.mephist.ru/tex/images/a5cada5c2d1ccb4b76fbda0fb521adb3.gif) или
или ![[IMG]](http://corum.mephist.ru/tex/images/b4bebab07d35bbb43ec16714f5ed87c8.gif) или
или ![[IMG]](http://corum.mephist.ru/tex/images/2e68c7fa8bf3791b61039377fa19d559.gif) но
но ![[IMG]](http://corum.mephist.ru/tex/images/f9c474b6e9e0acb125b588c2978f94e4.gif) или
или ![[IMG]](http://corum.mephist.ru/tex/images/42a0f383586370bf8d25ece709fbb3e8.gif) , поскольку тут 2 значащие цифры — 2 и 0 после двойки.
, поскольку тут 2 значащие цифры — 2 и 0 после двойки. ![[IMG]](http://corum.mephist.ru/tex/images/d5d51f35586a0011459580a47c329c1c.gif) округляем до
округляем до ![[IMG]](http://corum.mephist.ru/tex/images/bf7e5189fad7ab2880e4fc7c5411fea9.gif) или
или ![[IMG]](http://corum.mephist.ru/tex/images/9182580f66fbbe10919734c8448a2b0e.gif)
![[IMG]](http://corum.mephist.ru/tex/images/74ccc55c5f11b678eee65f6d66b9a60d.gif) округляем до
округляем до ![[IMG]](http://corum.mephist.ru/tex/images/60673e2250d177e624ad95b43064ca5e.gif) или
или ![[IMG]](http://corum.mephist.ru/tex/images/af619a318dbcab2d7ff6c6654f907177.gif) или
или ![[IMG]](http://corum.mephist.ru/tex/images/b928ec2d5d3d00612d6b75b0024e52e6.gif)
![[IMG]](http://corum.mephist.ru/tex/images/5e73d4508bfbc87a12895031f6919e08.gif) мм
мм ![[IMG]](http://corum.mephist.ru/tex/images/e51638f79ed91c6edb4a330fbfeb683c.gif) мм Держим тут в погрешности 2 значащие цифры потому что первая значащая цифра в погрешности — единица.
мм Держим тут в погрешности 2 значащие цифры потому что первая значащая цифра в погрешности — единица. ![[IMG]](http://corum.mephist.ru/tex/images/03ffd1a1b9f618fd926a47a5ca0fc293.gif) мм
мм ![[IMG]](http://corum.mephist.ru/tex/images/96072c008b0f5d6a865359f39cd1e082.gif) мм. Здесь лишний знак в результате. Правильно будет
мм. Здесь лишний знак в результате. Правильно будет ![[IMG]](http://corum.mephist.ru/tex/images/13bbbaf0c29b751a6c22008eb7f9f7b1.gif) мм.
мм. ![[IMG]](http://corum.mephist.ru/tex/images/2291014f831b0fd0257924da54867d23.gif) мм. Здесь лишний знак и в погрешности, и в результате. Правильно будет
мм. Здесь лишний знак и в погрешности, и в результате. Правильно будет ![[IMG]](http://corum.mephist.ru/tex/images/27b6e5ddc95fcf2627e37957689fa579.gif) У каждой из этих величин есть своя погрешность. Чтобы найти погрешность функции надо сделать следующее:
У каждой из этих величин есть своя погрешность. Чтобы найти погрешность функции надо сделать следующее:![[IMG]](http://corum.mephist.ru/tex/images/cf5c3f00f8d2fe027241a59955d5ceae.gif)
![[IMG]](http://corum.mephist.ru/tex/images/8fbdcb7dc81fe147175bc997b0fb2119.gif) означает частную производную f по x. Подробнее про частные производные здесь.
означает частную производную f по x. Подробнее про частные производные здесь.![[IMG]](http://corum.mephist.ru/tex/images/a0311888c35b344c57ef62341814562b.gif) . Вам необходимо посчитать погрешность разброса, посчитать приборную погрешность и сложить их вместе.
. Вам необходимо посчитать погрешность разброса, посчитать приборную погрешность и сложить их вместе.![[IMG]](http://corum.mephist.ru/tex/images/693eacf86ab361cc13fe5e292519b7c3.gif) , которую надо вычислить. Для начала вычисляется среднеквадратичная погрешность среднего:
, которую надо вычислить. Для начала вычисляется среднеквадратичная погрешность среднего:![[IMG]](http://corum.mephist.ru/tex/images/c7f83b4f19066a525f2969ce1c8ce372.gif)
![[IMG]](http://corum.mephist.ru/tex/images/4c795de483c9c9897980b7ba74c847fc.gif) означает среднее по всем
означает среднее по всем ![[IMG]](http://corum.mephist.ru/tex/images/fac074461d1491da3757d3b266ebf89c.gif) .
. ![[IMG]](http://corum.mephist.ru/tex/images/c5a8793748b3bf6f4c68fac5db40c651.gif) , который зависит от выбранной вами доверительной вероятности
, который зависит от выбранной вами доверительной вероятности ![[IMG]](http://corum.mephist.ru/tex/images/ceb95147a8605f55cd8513ecd26cc1fd.gif) .
. 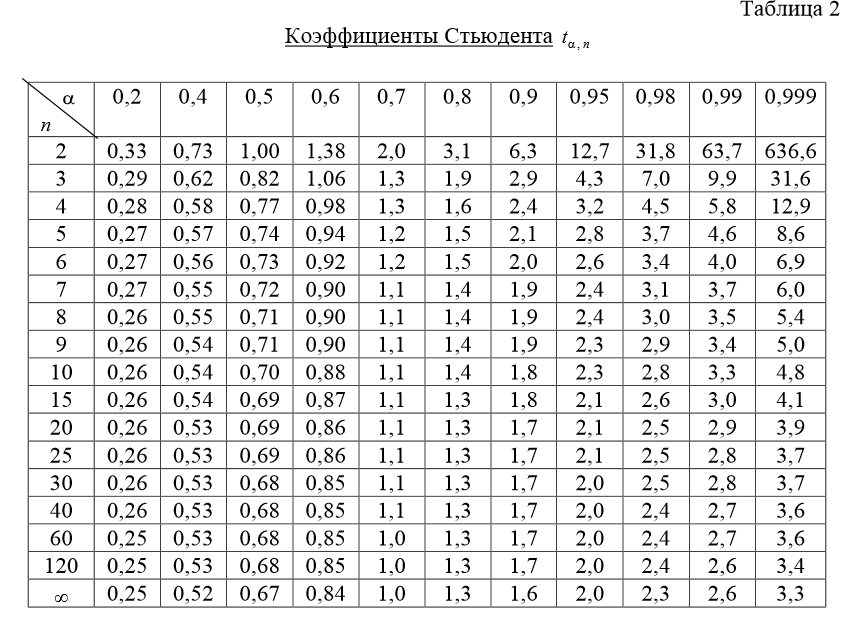
![[IMG]](http://corum.mephist.ru/tex/images/bb6c84165e61208b5b7b94e889085f7f.gif)
![[IMG]](http://corum.mephist.ru/tex/images/80a15ae9b42d82e8676bae47fcab70b3.gif) доверительная вероятность должна быть одинаковой.
доверительная вероятность должна быть одинаковой. ![[IMG]](http://corum.mephist.ru/tex/images/b853078084cb450336d8305ee3ff0051.gif)
![[IMG]](http://corum.mephist.ru/tex/images/c391ad2e2574b7c9ffb7f64916b97dc2.gif) и
и ![[IMG]](http://corum.mephist.ru/tex/images/e3f04bbaaa490a4d496e19c05c63f31e.gif) совпадают.
совпадают. 
![[IMG]](http://corum.mephist.ru/tex/images/59b6fc687986871e08a4def089688bbf.gif) , где
, где ![[IMG]](http://corum.mephist.ru/tex/images/a5f06e8811bf82a53ff629bd97e8417e.gif) — величина максимального отклонения по оси Y точки с погрешностью от проведенной прямой, а в знаменателе стоит ширина области нашего графика по оси Y. Аналогично по оси X.
— величина максимального отклонения по оси Y точки с погрешностью от проведенной прямой, а в знаменателе стоит ширина области нашего графика по оси Y. Аналогично по оси X.![[IMG]](http://corum.mephist.ru/tex/images/fd7f8eb5a1972f4158afd23480837110.gif) , где
, где ![[IMG]](http://corum.mephist.ru/tex/images/8f29cb2c179bfc115aa33e7730d3954d.gif) — наибольшее значение сопротивления магазина, а
— наибольшее значение сопротивления магазина, а ![[IMG]](http://corum.mephist.ru/tex/images/7d47b66519d27f5821540aa071c3d561.gif) — номинальное значение включённого сопротивления.
— номинальное значение включённого сопротивления. ![[IMG]](http://corum.mephist.ru/tex/images/e1b00eb5241498c481dfb7468c96e465.gif)
![[IMG]](http://corum.mephist.ru/tex/images/805bb957d0aecb7e839faacecb86f1de.gif) ?
?
![[IMG]](http://corum.mephist.ru/tex/images/d482ffddae86743b780638e2194d1cb2.gif) ?
?

![[IMG]](http://corum.mephist.ru/tex/images/795e28a5ddba8232883f37576bbf11cf.gif) . Это, разве, не полностью аналогичный случай к правильному варианту записи?
. Это, разве, не полностью аналогичный случай к правильному варианту записи?
![[IMG]](http://corum.mephist.ru/tex/images/e7493bf11a89e41c4c62b4e8aee498a5.gif) — правильно?
— правильно?