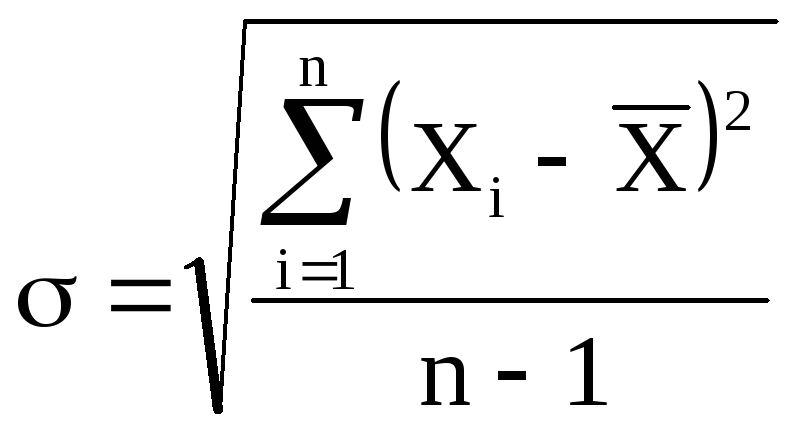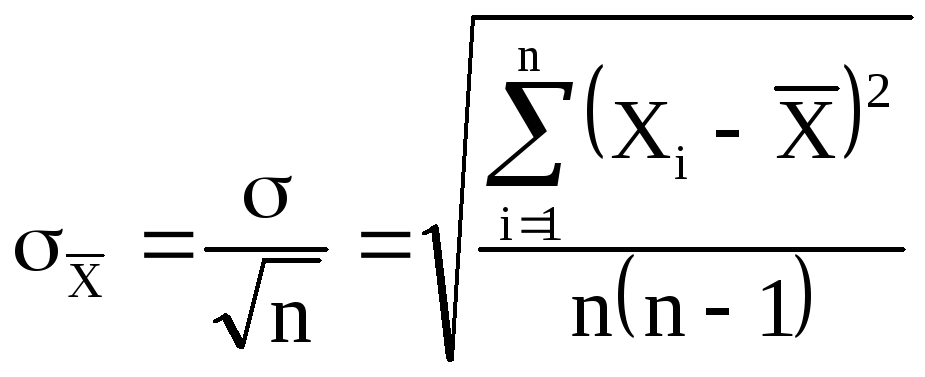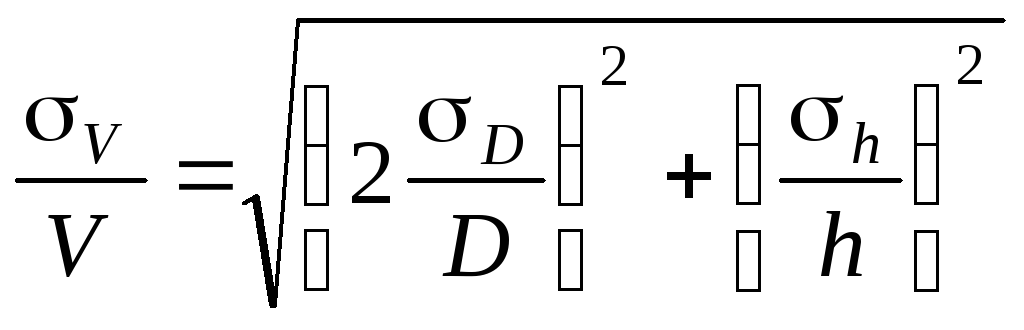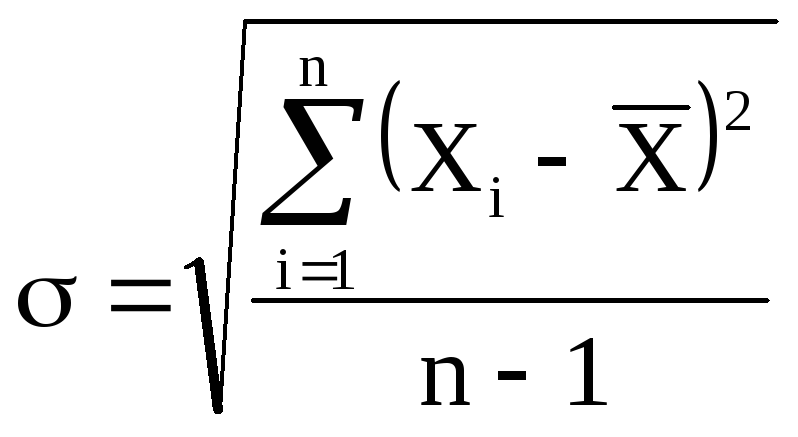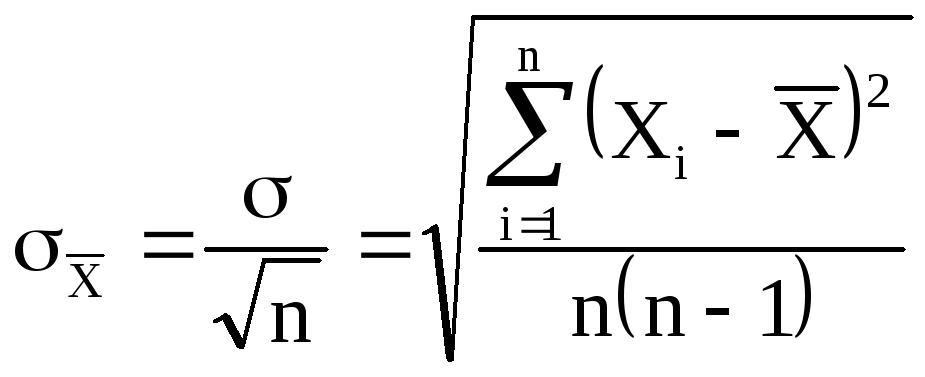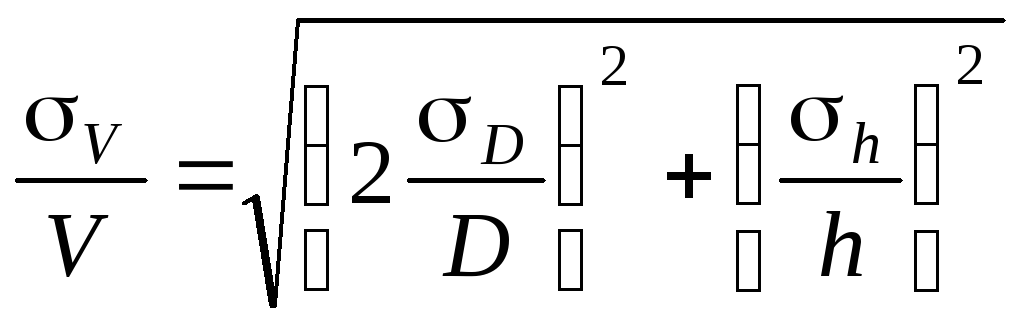17 авг. 2022 г.
читать 3 мин
В статистике регрессионный анализ — это метод, который мы используем для понимания взаимосвязи между переменной-предиктором x и переменной отклика y.
Когда мы проводим регрессионный анализ, мы получаем модель, которая сообщает нам прогнозируемое значение для переменной ответа на основе значения переменной-предиктора.
Один из способов оценить, насколько «хорошо» наша модель соответствует заданному набору данных, — это вычислить среднеквадратичную ошибку , которая представляет собой показатель, который говорит нам, насколько в среднем наши прогнозируемые значения отличаются от наших наблюдаемых значений.
Формула для нахождения среднеквадратичной ошибки, чаще называемая RMSE , выглядит следующим образом:
СКО = √[ Σ(P i – O i ) 2 / n ]
куда:
- Σ — причудливый символ, означающий «сумма».
- P i — прогнозируемое значение для i -го наблюдения в наборе данных.
- O i — наблюдаемое значение для i -го наблюдения в наборе данных.
- n — размер выборки
Технические примечания:
- Среднеквадратичную ошибку можно рассчитать для любого типа модели, которая дает прогнозные значения, которые затем можно сравнить с наблюдаемыми значениями набора данных.
- Среднеквадратичную ошибку также иногда называют среднеквадратичным отклонением, которое часто обозначается аббревиатурой RMSD.
Далее рассмотрим пример расчета среднеквадратичной ошибки в Excel.
Как рассчитать среднеквадратичную ошибку в Excel
В Excel нет встроенной функции для расчета RMSE, но мы можем довольно легко вычислить его с помощью одной формулы. Мы покажем, как рассчитать RMSE для двух разных сценариев.
Сценарий 1
В одном сценарии у вас может быть один столбец, содержащий предсказанные значения вашей модели, и другой столбец, содержащий наблюдаемые значения. На изображении ниже показан пример такого сценария:
Если это так, то вы можете рассчитать RMSE, введя следующую формулу в любую ячейку, а затем нажав CTRL+SHIFT+ENTER:
=КОРЕНЬ(СУММСК(A2:A21-B2:B21) / СЧЕТЧ(A2:A21))
Это говорит нам о том, что среднеквадратическая ошибка равна 2,6646 .
Формула может показаться немного сложной, но она имеет смысл, если ее разобрать:
= КОРЕНЬ( СУММСК(A2:A21-B2:B21) / СЧЕТЧ(A2:A21) )
- Во-первых, мы вычисляем сумму квадратов разностей между прогнозируемыми и наблюдаемыми значениями, используя функцию СУММСК() .
- Затем мы делим на размер выборки набора данных, используя COUNTA() , который подсчитывает количество непустых ячеек в диапазоне.
- Наконец, мы извлекаем квадратный корень из всего вычисления, используя функцию SQRT() .
Сценарий 2
В другом сценарии вы, возможно, уже вычислили разницу между прогнозируемыми и наблюдаемыми значениями. В этом случае у вас будет только один столбец, отображающий различия.
На изображении ниже показан пример этого сценария. Прогнозируемые значения отображаются в столбце A, наблюдаемые значения — в столбце B, а разница между прогнозируемыми и наблюдаемыми значениями — в столбце D:
Если это так, то вы можете рассчитать RMSE, введя следующую формулу в любую ячейку, а затем нажав CTRL+SHIFT+ENTER:
=КОРЕНЬ(СУММСК(D2:D21) / СЧЕТЧ(D2:D21))
Это говорит нам о том, что среднеквадратическая ошибка равна 2,6646 , что соответствует результату, полученному в первом сценарии. Это подтверждает, что эти два подхода к расчету RMSE эквивалентны.
Формула, которую мы использовали в этом сценарии, лишь немного отличается от той, что мы использовали в предыдущем сценарии:
= КОРЕНЬ (СУММСК(D2 :D21) / СЧЕТЧ(D2:D21) )
- Поскольку мы уже рассчитали разницу между предсказанными и наблюдаемыми значениями в столбце D, мы можем вычислить сумму квадратов разностей с помощью функции СУММСК().только со значениями в столбце D.
- Затем мы делим на размер выборки набора данных, используя COUNTA() , который подсчитывает количество непустых ячеек в диапазоне.
- Наконец, мы извлекаем квадратный корень из всего вычисления, используя функцию SQRT() .
Как интерпретировать среднеквадратичную ошибку
Как упоминалось ранее, RMSE — это полезный способ увидеть, насколько хорошо регрессионная модель (или любая модель, которая выдает прогнозируемые значения) способна «соответствовать» набору данных.
Чем больше RMSE, тем больше разница между прогнозируемыми и наблюдаемыми значениями, а это означает, что модель регрессии хуже соответствует данным. И наоборот, чем меньше RMSE, тем лучше модель соответствует данным.
Может быть особенно полезно сравнить RMSE двух разных моделей друг с другом, чтобы увидеть, какая модель лучше соответствует данным.
Для получения дополнительных руководств по Excel обязательно ознакомьтесь с нашей страницей руководств по Excel , на которой перечислены все учебные пособия Excel по статистике.
From Wikipedia, the free encyclopedia
In statistics, the mean squared error (MSE)[1] or mean squared deviation (MSD) of an estimator (of a procedure for estimating an unobserved quantity) measures the average of the squares of the errors—that is, the average squared difference between the estimated values and the actual value. MSE is a risk function, corresponding to the expected value of the squared error loss.[2] The fact that MSE is almost always strictly positive (and not zero) is because of randomness or because the estimator does not account for information that could produce a more accurate estimate.[3] In machine learning, specifically empirical risk minimization, MSE may refer to the empirical risk (the average loss on an observed data set), as an estimate of the true MSE (the true risk: the average loss on the actual population distribution).
The MSE is a measure of the quality of an estimator. As it is derived from the square of Euclidean distance, it is always a positive value that decreases as the error approaches zero.
The MSE is the second moment (about the origin) of the error, and thus incorporates both the variance of the estimator (how widely spread the estimates are from one data sample to another) and its bias (how far off the average estimated value is from the true value).[citation needed] For an unbiased estimator, the MSE is the variance of the estimator. Like the variance, MSE has the same units of measurement as the square of the quantity being estimated. In an analogy to standard deviation, taking the square root of MSE yields the root-mean-square error or root-mean-square deviation (RMSE or RMSD), which has the same units as the quantity being estimated; for an unbiased estimator, the RMSE is the square root of the variance, known as the standard error.
Definition and basic properties[edit]
The MSE either assesses the quality of a predictor (i.e., a function mapping arbitrary inputs to a sample of values of some random variable), or of an estimator (i.e., a mathematical function mapping a sample of data to an estimate of a parameter of the population from which the data is sampled). The definition of an MSE differs according to whether one is describing a predictor or an estimator.
Predictor[edit]
If a vector of 



In other words, the MSE is the mean 

In matrix notation,
where 



The MSE can also be computed on q data points that were not used in estimating the model, either because they were held back for this purpose, or because these data have been newly obtained. Within this process, known as statistical learning, the MSE is often called the test MSE,[4] and is computed as
Estimator[edit]
The MSE of an estimator 

This definition depends on the unknown parameter, but the MSE is a priori a property of an estimator. The MSE could be a function of unknown parameters, in which case any estimator of the MSE based on estimates of these parameters would be a function of the data (and thus a random variable). If the estimator 
The MSE can be written as the sum of the variance of the estimator and the squared bias of the estimator, providing a useful way to calculate the MSE and implying that in the case of unbiased estimators, the MSE and variance are equivalent.[5]
Proof of variance and bias relationship[edit]
An even shorter proof can be achieved using the well-known formula that for a random variable 



But in real modeling case, MSE could be described as the addition of model variance, model bias, and irreducible uncertainty (see Bias–variance tradeoff). According to the relationship, the MSE of the estimators could be simply used for the efficiency comparison, which includes the information of estimator variance and bias. This is called MSE criterion.
In regression[edit]
In regression analysis, plotting is a more natural way to view the overall trend of the whole data. The mean of the distance from each point to the predicted regression model can be calculated, and shown as the mean squared error. The squaring is critical to reduce the complexity with negative signs. To minimize MSE, the model could be more accurate, which would mean the model is closer to actual data. One example of a linear regression using this method is the least squares method—which evaluates appropriateness of linear regression model to model bivariate dataset,[6] but whose limitation is related to known distribution of the data.
The term mean squared error is sometimes used to refer to the unbiased estimate of error variance: the residual sum of squares divided by the number of degrees of freedom. This definition for a known, computed quantity differs from the above definition for the computed MSE of a predictor, in that a different denominator is used. The denominator is the sample size reduced by the number of model parameters estimated from the same data, (n−p) for p regressors or (n−p−1) if an intercept is used (see errors and residuals in statistics for more details).[7] Although the MSE (as defined in this article) is not an unbiased estimator of the error variance, it is consistent, given the consistency of the predictor.
In regression analysis, «mean squared error», often referred to as mean squared prediction error or «out-of-sample mean squared error», can also refer to the mean value of the squared deviations of the predictions from the true values, over an out-of-sample test space, generated by a model estimated over a particular sample space. This also is a known, computed quantity, and it varies by sample and by out-of-sample test space.
Examples[edit]
Mean[edit]
Suppose we have a random sample of size 




which has an expected value equal to the true mean 
where 
For a Gaussian distribution, this is the best unbiased estimator (i.e., one with the lowest MSE among all unbiased estimators), but not, say, for a uniform distribution.
Variance[edit]
The usual estimator for the variance is the corrected sample variance:
This is unbiased (its expected value is 
where 

However, one can use other estimators for 

then we calculate:
This is minimized when
For a Gaussian distribution, where 



Further, while the corrected sample variance is the best unbiased estimator (minimum mean squared error among unbiased estimators) of variance for Gaussian distributions, if the distribution is not Gaussian, then even among unbiased estimators, the best unbiased estimator of the variance may not be 
Gaussian distribution[edit]
The following table gives several estimators of the true parameters of the population, μ and σ2, for the Gaussian case.[9]
| True value | Estimator | Mean squared error |
|---|---|---|
 |
 = the unbiased estimator of the population mean, = the unbiased estimator of the population mean,  |

|
 |
 = the unbiased estimator of the population variance, = the unbiased estimator of the population variance,  |

|
 |
 = the biased estimator of the population variance, = the biased estimator of the population variance,  |

|
 |
 = the biased estimator of the population variance, = the biased estimator of the population variance,  |

|
Interpretation[edit]
An MSE of zero, meaning that the estimator 

Values of MSE may be used for comparative purposes. Two or more statistical models may be compared using their MSEs—as a measure of how well they explain a given set of observations: An unbiased estimator (estimated from a statistical model) with the smallest variance among all unbiased estimators is the best unbiased estimator or MVUE (Minimum-Variance Unbiased Estimator).
Both analysis of variance and linear regression techniques estimate the MSE as part of the analysis and use the estimated MSE to determine the statistical significance of the factors or predictors under study. The goal of experimental design is to construct experiments in such a way that when the observations are analyzed, the MSE is close to zero relative to the magnitude of at least one of the estimated treatment effects.
In one-way analysis of variance, MSE can be calculated by the division of the sum of squared errors and the degree of freedom. Also, the f-value is the ratio of the mean squared treatment and the MSE.
MSE is also used in several stepwise regression techniques as part of the determination as to how many predictors from a candidate set to include in a model for a given set of observations.
Applications[edit]
- Minimizing MSE is a key criterion in selecting estimators: see minimum mean-square error. Among unbiased estimators, minimizing the MSE is equivalent to minimizing the variance, and the estimator that does this is the minimum variance unbiased estimator. However, a biased estimator may have lower MSE; see estimator bias.
- In statistical modelling the MSE can represent the difference between the actual observations and the observation values predicted by the model. In this context, it is used to determine the extent to which the model fits the data as well as whether removing some explanatory variables is possible without significantly harming the model’s predictive ability.
- In forecasting and prediction, the Brier score is a measure of forecast skill based on MSE.
Loss function[edit]
Squared error loss is one of the most widely used loss functions in statistics[citation needed], though its widespread use stems more from mathematical convenience than considerations of actual loss in applications. Carl Friedrich Gauss, who introduced the use of mean squared error, was aware of its arbitrariness and was in agreement with objections to it on these grounds.[3] The mathematical benefits of mean squared error are particularly evident in its use at analyzing the performance of linear regression, as it allows one to partition the variation in a dataset into variation explained by the model and variation explained by randomness.
Criticism[edit]
The use of mean squared error without question has been criticized by the decision theorist James Berger. Mean squared error is the negative of the expected value of one specific utility function, the quadratic utility function, which may not be the appropriate utility function to use under a given set of circumstances. There are, however, some scenarios where mean squared error can serve as a good approximation to a loss function occurring naturally in an application.[10]
Like variance, mean squared error has the disadvantage of heavily weighting outliers.[11] This is a result of the squaring of each term, which effectively weights large errors more heavily than small ones. This property, undesirable in many applications, has led researchers to use alternatives such as the mean absolute error, or those based on the median.
See also[edit]
- Bias–variance tradeoff
- Hodges’ estimator
- James–Stein estimator
- Mean percentage error
- Mean square quantization error
- Mean square weighted deviation
- Mean squared displacement
- Mean squared prediction error
- Minimum mean square error
- Minimum mean squared error estimator
- Overfitting
- Peak signal-to-noise ratio
Notes[edit]
- ^ This can be proved by Jensen’s inequality as follows. The fourth central moment is an upper bound for the square of variance, so that the least value for their ratio is one, therefore, the least value for the excess kurtosis is −2, achieved, for instance, by a Bernoulli with p=1/2.
References[edit]
- ^ a b «Mean Squared Error (MSE)». www.probabilitycourse.com. Retrieved 2020-09-12.
- ^ Bickel, Peter J.; Doksum, Kjell A. (2015). Mathematical Statistics: Basic Ideas and Selected Topics. Vol. I (Second ed.). p. 20.
If we use quadratic loss, our risk function is called the mean squared error (MSE) …
- ^ a b Lehmann, E. L.; Casella, George (1998). Theory of Point Estimation (2nd ed.). New York: Springer. ISBN 978-0-387-98502-2. MR 1639875.
- ^ Gareth, James; Witten, Daniela; Hastie, Trevor; Tibshirani, Rob (2021). An Introduction to Statistical Learning: with Applications in R. Springer. ISBN 978-1071614174.
- ^ Wackerly, Dennis; Mendenhall, William; Scheaffer, Richard L. (2008). Mathematical Statistics with Applications (7 ed.). Belmont, CA, USA: Thomson Higher Education. ISBN 978-0-495-38508-0.
- ^ A modern introduction to probability and statistics : understanding why and how. Dekking, Michel, 1946-. London: Springer. 2005. ISBN 978-1-85233-896-1. OCLC 262680588.
{{cite book}}: CS1 maint: others (link) - ^ Steel, R.G.D, and Torrie, J. H., Principles and Procedures of Statistics with Special Reference to the Biological Sciences., McGraw Hill, 1960, page 288.
- ^ Mood, A.; Graybill, F.; Boes, D. (1974). Introduction to the Theory of Statistics (3rd ed.). McGraw-Hill. p. 229.
- ^ DeGroot, Morris H. (1980). Probability and Statistics (2nd ed.). Addison-Wesley.
- ^ Berger, James O. (1985). «2.4.2 Certain Standard Loss Functions». Statistical Decision Theory and Bayesian Analysis (2nd ed.). New York: Springer-Verlag. p. 60. ISBN 978-0-387-96098-2. MR 0804611.
- ^ Bermejo, Sergio; Cabestany, Joan (2001). «Oriented principal component analysis for large margin classifiers». Neural Networks. 14 (10): 1447–1461. doi:10.1016/S0893-6080(01)00106-X. PMID 11771723.
Средняя квадратичная ошибка.
При ответственных
измерениях, когда необходимо знать
надежность полученных результатов,
используется средняя квадратичная
ошибка (или
стандартное отклонение), которая
определяется формулой
(5)
Величина
характеризует отклонение отдельного
единичного измерения от истинного
значения.
Если мы вычислили
по n
измерениям среднее значение
по формуле (2), то это значение будет
более точным, то есть будет меньше
отличаться от истинного, чем каждое
отдельное измерение. Средняя квадратичная
ошибка среднего значения
равна
(6)
где — среднеквадратичная
ошибка каждого отдельного измерения,
n
– число
измерений.
Таким образом,
увеличивая число опытов, можно уменьшить
случайную ошибку в величине среднего
значения.
В настоящее время
результаты научных и технических
измерений принято представлять в виде
(7)
Как показывает
теория, при такой записи мы знаем
надежность полученного результата, а
именно, что истинная величина Х с
вероятностью 68% отличается от
не более, чем на
.
При использовании
же средней арифметической (абсолютной)
ошибки (формула 2) о надежности результата
ничего сказать нельзя. Некоторое
представление о точности проведенных
измерений в этом случае дает относительная
ошибка (формула 4).
При выполнении
лабораторных работ студенты могут
использовать как среднюю абсолютную
ошибку, так и среднюю квадратичную.
Какую из них применять указывается
непосредственно в каждой конкретной
работе (или указывается преподавателем).
Обычно если число
измерений не превышает 3 – 5, то
можно использовать среднюю абсолютную
ошибку. Если число измерений порядка
10 и более, то следует использовать более
корректную оценку с
помощью средней квадратичной ошибки
среднего (формулы 5 и 6).
Учет систематических ошибок.
Увеличением числа
измерений можно уменьшить только
случайные ошибки опыта, но не
систематические.
Максимальное
значение систематической ошибки обычно
указывается на приборе или в его паспорте.
Для измерений с помощью обычной
металлической линейки систематическая
ошибка составляет не менее 0,5 мм; для
измерений штангенциркулем –
0,1 – 0,05 мм;
микрометром – 0,01 мм.
Часто в качестве
систематической ошибки берется половина
цены деления прибора.
На шкалах
электроизмерительных приборов указывается
класс точности. Зная класс точности К,
можно вычислить систематическую ошибку
прибора ∆Х по формуле
где К – класс
точности прибора, Хпр – предельное
значение величины, которое может быть
измерено по шкале прибора.
Так, амперметр
класса 0,5 со шкалой до 5А измеряет ток с
ошибкой не более
Среднее значение
полной погрешности складывается из
случайной и систематической
погрешностей.
Ответ с учетом
систематических и случайных ошибок
записывается в виде
Погрешности косвенных измерений
В физических
экспериментах чаще бывает так, что
искомая физическая величина сама на
опыте измерена быть не может, а является
функцией других величин, измеряемых
непосредственно. Например, чтобы
определить объём цилиндра, надо измерить
диаметр D и высоту h, а затем вычислить
объем по формуле
Величины D и h будут измерены с
некоторой ошибкой. Следовательно,
вычисленная величина
V
получится также с некоторой ошибкой.
Надо уметь выражать погрешность
вычисленной величины через погрешности
измеренных величин.
Как и при прямых
измерениях можно вычислять среднюю
абсолютную (среднюю арифметическую)
ошибку или среднюю квадратичную ошибку.
Общие правила
вычисления ошибок для обоих случаев
выводятся с помощью дифференциального
исчисления.
Пусть искомая
величина φ является функцией нескольких
переменных Х,
У, Z…
φ(Х,
У, Z…).
Путем прямых
измерений мы можем найти величины
,
а также оценить их средние абсолютные
ошибки
…
или средние квадратичные ошибки Х,
У,
Z…
Тогда средняя
арифметическая погрешность
вычисляется по формуле
где
— частные
производные от φ по
Х, У, Z. Они
вычисляются для средних значений
…
Средняя квадратичная
погрешность вычисляется по формуле
Пример.
Выведем формулы погрешности для
вычисления объёма цилиндра.
а) Средняя
арифметическая погрешность.
Величины
D и h
измеряются соответственно с ошибкой
D
и h.
Погрешность
величины объёма будет равна
б) Средняя
квадратичная погрешность.
Величины
D и h
измеряются соответственно с ошибкой
D, h.
Погрешность
величины объёма будет равна
Если формула
представляет выражение удобное для
логарифмирования (то есть произведение,
дробь, степень), то удобнее вначале
вычислять относительную погрешность.
Для этого (в случае средней арифметической
погрешности) надо проделать следующее.
1. Прологарифмировать
выражение.
2. Продифференцировать
его.
3. Объединить
все члены с одинаковым дифференциалом
и вынести его за скобки.
4. Взять выражение
перед различными дифференциалами по
модулю.
5. Заменить
значки дифференциалов d
на значки абсолютной погрешности .
В итоге получится
формула для относительной погрешности
Затем,
зная ,
можно вычислить абсолютную погрешность
=
Пример.
Аналогично можно
записать относительную среднюю
квадратичную погрешность
Правила
представления результатов измерения
следующие:
-
погрешность должна
округляться до одной значащей цифры:
правильно = 0,04,
неправильно —
= 0,0382;
-
последняя значащая
цифра результата должна быть того же
порядка величины, что и погрешность:
правильно
= 9,830,03,
неправильно —
= 9,8260,03;
-
если результат
имеет очень большую или очень малую
величину, необходимо использовать
показательную форму записи — одну и ту
же для результата и его погрешности,
причем запятая десятичной дроби должна
следовать за первой значащей цифрой
результата:
правильно —
= (5,270,03)10-5,
неправильно —
= 0,00005270,0000003,
= 5,2710-50,0000003,
=
= 0,0000527310-7,
= (5273)10-7,
= (0,5270,003)
10-4.
-
Если результат
имеет размерность, ее необходимо
указать:
правильно – g=(9,820,02)
м/c2,
неправильно – g=(9,820,02).
Соседние файлы в папке Отчеты_Погрешность
- #
- #
- #
- #
- #
17 авг. 2022 г.
читать 3 мин
В статистике регрессионный анализ — это метод, который мы используем для понимания взаимосвязи между переменной-предиктором x и переменной отклика y.
Когда мы проводим регрессионный анализ, мы получаем модель, которая сообщает нам прогнозируемое значение для переменной ответа на основе значения переменной-предиктора.
Один из способов оценить, насколько «хорошо» наша модель соответствует заданному набору данных, — это вычислить среднеквадратичную ошибку , которая представляет собой показатель, который говорит нам, насколько в среднем наши прогнозируемые значения отличаются от наших наблюдаемых значений.
Формула для нахождения среднеквадратичной ошибки, чаще называемая RMSE , выглядит следующим образом:
СКО = √[ Σ(P i – O i ) 2 / n ]
куда:
- Σ — причудливый символ, означающий «сумма».
- P i — прогнозируемое значение для i -го наблюдения в наборе данных.
- O i — наблюдаемое значение для i -го наблюдения в наборе данных.
- n — размер выборки
Технические примечания:
- Среднеквадратичную ошибку можно рассчитать для любого типа модели, которая дает прогнозные значения, которые затем можно сравнить с наблюдаемыми значениями набора данных.
- Среднеквадратичную ошибку также иногда называют среднеквадратичным отклонением, которое часто обозначается аббревиатурой RMSD.
Далее рассмотрим пример расчета среднеквадратичной ошибки в Excel.
Как рассчитать среднеквадратичную ошибку в Excel
В Excel нет встроенной функции для расчета RMSE, но мы можем довольно легко вычислить его с помощью одной формулы. Мы покажем, как рассчитать RMSE для двух разных сценариев.
Сценарий 1
В одном сценарии у вас может быть один столбец, содержащий предсказанные значения вашей модели, и другой столбец, содержащий наблюдаемые значения. На изображении ниже показан пример такого сценария:
Если это так, то вы можете рассчитать RMSE, введя следующую формулу в любую ячейку, а затем нажав CTRL+SHIFT+ENTER:
=КОРЕНЬ(СУММСК(A2:A21-B2:B21) / СЧЕТЧ(A2:A21))
Это говорит нам о том, что среднеквадратическая ошибка равна 2,6646 .
Формула может показаться немного сложной, но она имеет смысл, если ее разобрать:
= КОРЕНЬ( СУММСК(A2:A21-B2:B21) / СЧЕТЧ(A2:A21) )
- Во-первых, мы вычисляем сумму квадратов разностей между прогнозируемыми и наблюдаемыми значениями, используя функцию СУММСК() .
- Затем мы делим на размер выборки набора данных, используя COUNTA() , который подсчитывает количество непустых ячеек в диапазоне.
- Наконец, мы извлекаем квадратный корень из всего вычисления, используя функцию SQRT() .
Сценарий 2
В другом сценарии вы, возможно, уже вычислили разницу между прогнозируемыми и наблюдаемыми значениями. В этом случае у вас будет только один столбец, отображающий различия.
На изображении ниже показан пример этого сценария. Прогнозируемые значения отображаются в столбце A, наблюдаемые значения — в столбце B, а разница между прогнозируемыми и наблюдаемыми значениями — в столбце D:
Если это так, то вы можете рассчитать RMSE, введя следующую формулу в любую ячейку, а затем нажав CTRL+SHIFT+ENTER:
=КОРЕНЬ(СУММСК(D2:D21) / СЧЕТЧ(D2:D21))
Это говорит нам о том, что среднеквадратическая ошибка равна 2,6646 , что соответствует результату, полученному в первом сценарии. Это подтверждает, что эти два подхода к расчету RMSE эквивалентны.
Формула, которую мы использовали в этом сценарии, лишь немного отличается от той, что мы использовали в предыдущем сценарии:
= КОРЕНЬ (СУММСК(D2 :D21) / СЧЕТЧ(D2:D21) )
- Поскольку мы уже рассчитали разницу между предсказанными и наблюдаемыми значениями в столбце D, мы можем вычислить сумму квадратов разностей с помощью функции СУММСК().только со значениями в столбце D.
- Затем мы делим на размер выборки набора данных, используя COUNTA() , который подсчитывает количество непустых ячеек в диапазоне.
- Наконец, мы извлекаем квадратный корень из всего вычисления, используя функцию SQRT() .
Как интерпретировать среднеквадратичную ошибку
Как упоминалось ранее, RMSE — это полезный способ увидеть, насколько хорошо регрессионная модель (или любая модель, которая выдает прогнозируемые значения) способна «соответствовать» набору данных.
Чем больше RMSE, тем больше разница между прогнозируемыми и наблюдаемыми значениями, а это означает, что модель регрессии хуже соответствует данным. И наоборот, чем меньше RMSE, тем лучше модель соответствует данным.
Может быть особенно полезно сравнить RMSE двух разных моделей друг с другом, чтобы увидеть, какая модель лучше соответствует данным.
Для получения дополнительных руководств по Excel обязательно ознакомьтесь с нашей страницей руководств по Excel , на которой перечислены все учебные пособия Excel по статистике.
In statistics, the mean squared error (MSE)[1] or mean squared deviation (MSD) of an estimator (of a procedure for estimating an unobserved quantity) measures the average of the squares of the errors—that is, the average squared difference between the estimated values and the actual value. MSE is a risk function, corresponding to the expected value of the squared error loss.[2] The fact that MSE is almost always strictly positive (and not zero) is because of randomness or because the estimator does not account for information that could produce a more accurate estimate.[3] In machine learning, specifically empirical risk minimization, MSE may refer to the empirical risk (the average loss on an observed data set), as an estimate of the true MSE (the true risk: the average loss on the actual population distribution).
The MSE is a measure of the quality of an estimator. As it is derived from the square of Euclidean distance, it is always a positive value that decreases as the error approaches zero.
The MSE is the second moment (about the origin) of the error, and thus incorporates both the variance of the estimator (how widely spread the estimates are from one data sample to another) and its bias (how far off the average estimated value is from the true value).[citation needed] For an unbiased estimator, the MSE is the variance of the estimator. Like the variance, MSE has the same units of measurement as the square of the quantity being estimated. In an analogy to standard deviation, taking the square root of MSE yields the root-mean-square error or root-mean-square deviation (RMSE or RMSD), which has the same units as the quantity being estimated; for an unbiased estimator, the RMSE is the square root of the variance, known as the standard error.
Definition and basic properties[edit]
The MSE either assesses the quality of a predictor (i.e., a function mapping arbitrary inputs to a sample of values of some random variable), or of an estimator (i.e., a mathematical function mapping a sample of data to an estimate of a parameter of the population from which the data is sampled). The definition of an MSE differs according to whether one is describing a predictor or an estimator.
Predictor[edit]
If a vector of 



In other words, the MSE is the mean 

In matrix notation,
where 



The MSE can also be computed on q data points that were not used in estimating the model, either because they were held back for this purpose, or because these data have been newly obtained. Within this process, known as statistical learning, the MSE is often called the test MSE,[4] and is computed as
Estimator[edit]
The MSE of an estimator 

This definition depends on the unknown parameter, but the MSE is a priori a property of an estimator. The MSE could be a function of unknown parameters, in which case any estimator of the MSE based on estimates of these parameters would be a function of the data (and thus a random variable). If the estimator 
The MSE can be written as the sum of the variance of the estimator and the squared bias of the estimator, providing a useful way to calculate the MSE and implying that in the case of unbiased estimators, the MSE and variance are equivalent.[5]
Proof of variance and bias relationship[edit]
An even shorter proof can be achieved using the well-known formula that for a random variable 



But in real modeling case, MSE could be described as the addition of model variance, model bias, and irreducible uncertainty (see Bias–variance tradeoff). According to the relationship, the MSE of the estimators could be simply used for the efficiency comparison, which includes the information of estimator variance and bias. This is called MSE criterion.
In regression[edit]
In regression analysis, plotting is a more natural way to view the overall trend of the whole data. The mean of the distance from each point to the predicted regression model can be calculated, and shown as the mean squared error. The squaring is critical to reduce the complexity with negative signs. To minimize MSE, the model could be more accurate, which would mean the model is closer to actual data. One example of a linear regression using this method is the least squares method—which evaluates appropriateness of linear regression model to model bivariate dataset,[6] but whose limitation is related to known distribution of the data.
The term mean squared error is sometimes used to refer to the unbiased estimate of error variance: the residual sum of squares divided by the number of degrees of freedom. This definition for a known, computed quantity differs from the above definition for the computed MSE of a predictor, in that a different denominator is used. The denominator is the sample size reduced by the number of model parameters estimated from the same data, (n−p) for p regressors or (n−p−1) if an intercept is used (see errors and residuals in statistics for more details).[7] Although the MSE (as defined in this article) is not an unbiased estimator of the error variance, it is consistent, given the consistency of the predictor.
In regression analysis, «mean squared error», often referred to as mean squared prediction error or «out-of-sample mean squared error», can also refer to the mean value of the squared deviations of the predictions from the true values, over an out-of-sample test space, generated by a model estimated over a particular sample space. This also is a known, computed quantity, and it varies by sample and by out-of-sample test space.
Examples[edit]
Mean[edit]
Suppose we have a random sample of size 




which has an expected value equal to the true mean 
where 
For a Gaussian distribution, this is the best unbiased estimator (i.e., one with the lowest MSE among all unbiased estimators), but not, say, for a uniform distribution.
Variance[edit]
The usual estimator for the variance is the corrected sample variance:
This is unbiased (its expected value is 
where 

However, one can use other estimators for 

then we calculate:
This is minimized when
For a Gaussian distribution, where 



Further, while the corrected sample variance is the best unbiased estimator (minimum mean squared error among unbiased estimators) of variance for Gaussian distributions, if the distribution is not Gaussian, then even among unbiased estimators, the best unbiased estimator of the variance may not be 
Gaussian distribution[edit]
The following table gives several estimators of the true parameters of the population, μ and σ2, for the Gaussian case.[9]
| True value | Estimator | Mean squared error |
|---|---|---|
 |
 = the unbiased estimator of the population mean, = the unbiased estimator of the population mean,  |

|
 |
 = the unbiased estimator of the population variance, = the unbiased estimator of the population variance,  |

|
 |
 = the biased estimator of the population variance, = the biased estimator of the population variance,  |

|
 |
 = the biased estimator of the population variance, = the biased estimator of the population variance,  |

|
Interpretation[edit]
An MSE of zero, meaning that the estimator 

Values of MSE may be used for comparative purposes. Two or more statistical models may be compared using their MSEs—as a measure of how well they explain a given set of observations: An unbiased estimator (estimated from a statistical model) with the smallest variance among all unbiased estimators is the best unbiased estimator or MVUE (Minimum-Variance Unbiased Estimator).
Both analysis of variance and linear regression techniques estimate the MSE as part of the analysis and use the estimated MSE to determine the statistical significance of the factors or predictors under study. The goal of experimental design is to construct experiments in such a way that when the observations are analyzed, the MSE is close to zero relative to the magnitude of at least one of the estimated treatment effects.
In one-way analysis of variance, MSE can be calculated by the division of the sum of squared errors and the degree of freedom. Also, the f-value is the ratio of the mean squared treatment and the MSE.
MSE is also used in several stepwise regression techniques as part of the determination as to how many predictors from a candidate set to include in a model for a given set of observations.
Applications[edit]
- Minimizing MSE is a key criterion in selecting estimators: see minimum mean-square error. Among unbiased estimators, minimizing the MSE is equivalent to minimizing the variance, and the estimator that does this is the minimum variance unbiased estimator. However, a biased estimator may have lower MSE; see estimator bias.
- In statistical modelling the MSE can represent the difference between the actual observations and the observation values predicted by the model. In this context, it is used to determine the extent to which the model fits the data as well as whether removing some explanatory variables is possible without significantly harming the model’s predictive ability.
- In forecasting and prediction, the Brier score is a measure of forecast skill based on MSE.
Loss function[edit]
Squared error loss is one of the most widely used loss functions in statistics[citation needed], though its widespread use stems more from mathematical convenience than considerations of actual loss in applications. Carl Friedrich Gauss, who introduced the use of mean squared error, was aware of its arbitrariness and was in agreement with objections to it on these grounds.[3] The mathematical benefits of mean squared error are particularly evident in its use at analyzing the performance of linear regression, as it allows one to partition the variation in a dataset into variation explained by the model and variation explained by randomness.
Criticism[edit]
The use of mean squared error without question has been criticized by the decision theorist James Berger. Mean squared error is the negative of the expected value of one specific utility function, the quadratic utility function, which may not be the appropriate utility function to use under a given set of circumstances. There are, however, some scenarios where mean squared error can serve as a good approximation to a loss function occurring naturally in an application.[10]
Like variance, mean squared error has the disadvantage of heavily weighting outliers.[11] This is a result of the squaring of each term, which effectively weights large errors more heavily than small ones. This property, undesirable in many applications, has led researchers to use alternatives such as the mean absolute error, or those based on the median.
See also[edit]
- Bias–variance tradeoff
- Hodges’ estimator
- James–Stein estimator
- Mean percentage error
- Mean square quantization error
- Mean square weighted deviation
- Mean squared displacement
- Mean squared prediction error
- Minimum mean square error
- Minimum mean squared error estimator
- Overfitting
- Peak signal-to-noise ratio
Notes[edit]
- ^ This can be proved by Jensen’s inequality as follows. The fourth central moment is an upper bound for the square of variance, so that the least value for their ratio is one, therefore, the least value for the excess kurtosis is −2, achieved, for instance, by a Bernoulli with p=1/2.
References[edit]
- ^ a b «Mean Squared Error (MSE)». www.probabilitycourse.com. Retrieved 2020-09-12.
- ^ Bickel, Peter J.; Doksum, Kjell A. (2015). Mathematical Statistics: Basic Ideas and Selected Topics. Vol. I (Second ed.). p. 20.
If we use quadratic loss, our risk function is called the mean squared error (MSE) …
- ^ a b Lehmann, E. L.; Casella, George (1998). Theory of Point Estimation (2nd ed.). New York: Springer. ISBN 978-0-387-98502-2. MR 1639875.
- ^ Gareth, James; Witten, Daniela; Hastie, Trevor; Tibshirani, Rob (2021). An Introduction to Statistical Learning: with Applications in R. Springer. ISBN 978-1071614174.
- ^ Wackerly, Dennis; Mendenhall, William; Scheaffer, Richard L. (2008). Mathematical Statistics with Applications (7 ed.). Belmont, CA, USA: Thomson Higher Education. ISBN 978-0-495-38508-0.
- ^ A modern introduction to probability and statistics : understanding why and how. Dekking, Michel, 1946-. London: Springer. 2005. ISBN 978-1-85233-896-1. OCLC 262680588.
{{cite book}}: CS1 maint: others (link) - ^ Steel, R.G.D, and Torrie, J. H., Principles and Procedures of Statistics with Special Reference to the Biological Sciences., McGraw Hill, 1960, page 288.
- ^ Mood, A.; Graybill, F.; Boes, D. (1974). Introduction to the Theory of Statistics (3rd ed.). McGraw-Hill. p. 229.
- ^ DeGroot, Morris H. (1980). Probability and Statistics (2nd ed.). Addison-Wesley.
- ^ Berger, James O. (1985). «2.4.2 Certain Standard Loss Functions». Statistical Decision Theory and Bayesian Analysis (2nd ed.). New York: Springer-Verlag. p. 60. ISBN 978-0-387-96098-2. MR 0804611.
- ^ Bermejo, Sergio; Cabestany, Joan (2001). «Oriented principal component analysis for large margin classifiers». Neural Networks. 14 (10): 1447–1461. doi:10.1016/S0893-6080(01)00106-X. PMID 11771723.
In statistics, the mean squared error (MSE)[1] or mean squared deviation (MSD) of an estimator (of a procedure for estimating an unobserved quantity) measures the average of the squares of the errors—that is, the average squared difference between the estimated values and the actual value. MSE is a risk function, corresponding to the expected value of the squared error loss.[2] The fact that MSE is almost always strictly positive (and not zero) is because of randomness or because the estimator does not account for information that could produce a more accurate estimate.[3] In machine learning, specifically empirical risk minimization, MSE may refer to the empirical risk (the average loss on an observed data set), as an estimate of the true MSE (the true risk: the average loss on the actual population distribution).
The MSE is a measure of the quality of an estimator. As it is derived from the square of Euclidean distance, it is always a positive value that decreases as the error approaches zero.
The MSE is the second moment (about the origin) of the error, and thus incorporates both the variance of the estimator (how widely spread the estimates are from one data sample to another) and its bias (how far off the average estimated value is from the true value).[citation needed] For an unbiased estimator, the MSE is the variance of the estimator. Like the variance, MSE has the same units of measurement as the square of the quantity being estimated. In an analogy to standard deviation, taking the square root of MSE yields the root-mean-square error or root-mean-square deviation (RMSE or RMSD), which has the same units as the quantity being estimated; for an unbiased estimator, the RMSE is the square root of the variance, known as the standard error.
Definition and basic properties[edit]
The MSE either assesses the quality of a predictor (i.e., a function mapping arbitrary inputs to a sample of values of some random variable), or of an estimator (i.e., a mathematical function mapping a sample of data to an estimate of a parameter of the population from which the data is sampled). The definition of an MSE differs according to whether one is describing a predictor or an estimator.
Predictor[edit]
If a vector of 



In other words, the MSE is the mean 

In matrix notation,
where 



The MSE can also be computed on q data points that were not used in estimating the model, either because they were held back for this purpose, or because these data have been newly obtained. Within this process, known as statistical learning, the MSE is often called the test MSE,[4] and is computed as
Estimator[edit]
The MSE of an estimator 

This definition depends on the unknown parameter, but the MSE is a priori a property of an estimator. The MSE could be a function of unknown parameters, in which case any estimator of the MSE based on estimates of these parameters would be a function of the data (and thus a random variable). If the estimator 
The MSE can be written as the sum of the variance of the estimator and the squared bias of the estimator, providing a useful way to calculate the MSE and implying that in the case of unbiased estimators, the MSE and variance are equivalent.[5]
Proof of variance and bias relationship[edit]
An even shorter proof can be achieved using the well-known formula that for a random variable 



But in real modeling case, MSE could be described as the addition of model variance, model bias, and irreducible uncertainty (see Bias–variance tradeoff). According to the relationship, the MSE of the estimators could be simply used for the efficiency comparison, which includes the information of estimator variance and bias. This is called MSE criterion.
In regression[edit]
In regression analysis, plotting is a more natural way to view the overall trend of the whole data. The mean of the distance from each point to the predicted regression model can be calculated, and shown as the mean squared error. The squaring is critical to reduce the complexity with negative signs. To minimize MSE, the model could be more accurate, which would mean the model is closer to actual data. One example of a linear regression using this method is the least squares method—which evaluates appropriateness of linear regression model to model bivariate dataset,[6] but whose limitation is related to known distribution of the data.
The term mean squared error is sometimes used to refer to the unbiased estimate of error variance: the residual sum of squares divided by the number of degrees of freedom. This definition for a known, computed quantity differs from the above definition for the computed MSE of a predictor, in that a different denominator is used. The denominator is the sample size reduced by the number of model parameters estimated from the same data, (n−p) for p regressors or (n−p−1) if an intercept is used (see errors and residuals in statistics for more details).[7] Although the MSE (as defined in this article) is not an unbiased estimator of the error variance, it is consistent, given the consistency of the predictor.
In regression analysis, «mean squared error», often referred to as mean squared prediction error or «out-of-sample mean squared error», can also refer to the mean value of the squared deviations of the predictions from the true values, over an out-of-sample test space, generated by a model estimated over a particular sample space. This also is a known, computed quantity, and it varies by sample and by out-of-sample test space.
Examples[edit]
Mean[edit]
Suppose we have a random sample of size 




which has an expected value equal to the true mean 
where 
For a Gaussian distribution, this is the best unbiased estimator (i.e., one with the lowest MSE among all unbiased estimators), but not, say, for a uniform distribution.
Variance[edit]
The usual estimator for the variance is the corrected sample variance:
This is unbiased (its expected value is 
where 

However, one can use other estimators for 

then we calculate:
This is minimized when
For a Gaussian distribution, where 



Further, while the corrected sample variance is the best unbiased estimator (minimum mean squared error among unbiased estimators) of variance for Gaussian distributions, if the distribution is not Gaussian, then even among unbiased estimators, the best unbiased estimator of the variance may not be 
Gaussian distribution[edit]
The following table gives several estimators of the true parameters of the population, μ and σ2, for the Gaussian case.[9]
| True value | Estimator | Mean squared error |
|---|---|---|
 |
 = the unbiased estimator of the population mean, = the unbiased estimator of the population mean,  |

|
 |
 = the unbiased estimator of the population variance, = the unbiased estimator of the population variance,  |

|
 |
 = the biased estimator of the population variance, = the biased estimator of the population variance,  |

|
 |
 = the biased estimator of the population variance, = the biased estimator of the population variance,  |

|
Interpretation[edit]
An MSE of zero, meaning that the estimator 

Values of MSE may be used for comparative purposes. Two or more statistical models may be compared using their MSEs—as a measure of how well they explain a given set of observations: An unbiased estimator (estimated from a statistical model) with the smallest variance among all unbiased estimators is the best unbiased estimator or MVUE (Minimum-Variance Unbiased Estimator).
Both analysis of variance and linear regression techniques estimate the MSE as part of the analysis and use the estimated MSE to determine the statistical significance of the factors or predictors under study. The goal of experimental design is to construct experiments in such a way that when the observations are analyzed, the MSE is close to zero relative to the magnitude of at least one of the estimated treatment effects.
In one-way analysis of variance, MSE can be calculated by the division of the sum of squared errors and the degree of freedom. Also, the f-value is the ratio of the mean squared treatment and the MSE.
MSE is also used in several stepwise regression techniques as part of the determination as to how many predictors from a candidate set to include in a model for a given set of observations.
Applications[edit]
- Minimizing MSE is a key criterion in selecting estimators: see minimum mean-square error. Among unbiased estimators, minimizing the MSE is equivalent to minimizing the variance, and the estimator that does this is the minimum variance unbiased estimator. However, a biased estimator may have lower MSE; see estimator bias.
- In statistical modelling the MSE can represent the difference between the actual observations and the observation values predicted by the model. In this context, it is used to determine the extent to which the model fits the data as well as whether removing some explanatory variables is possible without significantly harming the model’s predictive ability.
- In forecasting and prediction, the Brier score is a measure of forecast skill based on MSE.
Loss function[edit]
Squared error loss is one of the most widely used loss functions in statistics[citation needed], though its widespread use stems more from mathematical convenience than considerations of actual loss in applications. Carl Friedrich Gauss, who introduced the use of mean squared error, was aware of its arbitrariness and was in agreement with objections to it on these grounds.[3] The mathematical benefits of mean squared error are particularly evident in its use at analyzing the performance of linear regression, as it allows one to partition the variation in a dataset into variation explained by the model and variation explained by randomness.
Criticism[edit]
The use of mean squared error without question has been criticized by the decision theorist James Berger. Mean squared error is the negative of the expected value of one specific utility function, the quadratic utility function, which may not be the appropriate utility function to use under a given set of circumstances. There are, however, some scenarios where mean squared error can serve as a good approximation to a loss function occurring naturally in an application.[10]
Like variance, mean squared error has the disadvantage of heavily weighting outliers.[11] This is a result of the squaring of each term, which effectively weights large errors more heavily than small ones. This property, undesirable in many applications, has led researchers to use alternatives such as the mean absolute error, or those based on the median.
See also[edit]
- Bias–variance tradeoff
- Hodges’ estimator
- James–Stein estimator
- Mean percentage error
- Mean square quantization error
- Mean square weighted deviation
- Mean squared displacement
- Mean squared prediction error
- Minimum mean square error
- Minimum mean squared error estimator
- Overfitting
- Peak signal-to-noise ratio
Notes[edit]
- ^ This can be proved by Jensen’s inequality as follows. The fourth central moment is an upper bound for the square of variance, so that the least value for their ratio is one, therefore, the least value for the excess kurtosis is −2, achieved, for instance, by a Bernoulli with p=1/2.
References[edit]
- ^ a b «Mean Squared Error (MSE)». www.probabilitycourse.com. Retrieved 2020-09-12.
- ^ Bickel, Peter J.; Doksum, Kjell A. (2015). Mathematical Statistics: Basic Ideas and Selected Topics. Vol. I (Second ed.). p. 20.
If we use quadratic loss, our risk function is called the mean squared error (MSE) …
- ^ a b Lehmann, E. L.; Casella, George (1998). Theory of Point Estimation (2nd ed.). New York: Springer. ISBN 978-0-387-98502-2. MR 1639875.
- ^ Gareth, James; Witten, Daniela; Hastie, Trevor; Tibshirani, Rob (2021). An Introduction to Statistical Learning: with Applications in R. Springer. ISBN 978-1071614174.
- ^ Wackerly, Dennis; Mendenhall, William; Scheaffer, Richard L. (2008). Mathematical Statistics with Applications (7 ed.). Belmont, CA, USA: Thomson Higher Education. ISBN 978-0-495-38508-0.
- ^ A modern introduction to probability and statistics : understanding why and how. Dekking, Michel, 1946-. London: Springer. 2005. ISBN 978-1-85233-896-1. OCLC 262680588.
{{cite book}}: CS1 maint: others (link) - ^ Steel, R.G.D, and Torrie, J. H., Principles and Procedures of Statistics with Special Reference to the Biological Sciences., McGraw Hill, 1960, page 288.
- ^ Mood, A.; Graybill, F.; Boes, D. (1974). Introduction to the Theory of Statistics (3rd ed.). McGraw-Hill. p. 229.
- ^ DeGroot, Morris H. (1980). Probability and Statistics (2nd ed.). Addison-Wesley.
- ^ Berger, James O. (1985). «2.4.2 Certain Standard Loss Functions». Statistical Decision Theory and Bayesian Analysis (2nd ed.). New York: Springer-Verlag. p. 60. ISBN 978-0-387-96098-2. MR 0804611.
- ^ Bermejo, Sergio; Cabestany, Joan (2001). «Oriented principal component analysis for large margin classifiers». Neural Networks. 14 (10): 1447–1461. doi:10.1016/S0893-6080(01)00106-X. PMID 11771723.
Средняя квадратичная ошибка.
При ответственных
измерениях, когда необходимо знать
надежность полученных результатов,
используется средняя квадратичная
ошибка (или
стандартное отклонение), которая
определяется формулой
(5)
Величина
характеризует отклонение отдельного
единичного измерения от истинного
значения.
Если мы вычислили
по n
измерениям среднее значение
по формуле (2), то это значение будет
более точным, то есть будет меньше
отличаться от истинного, чем каждое
отдельное измерение. Средняя квадратичная
ошибка среднего значения
равна
(6)
где — среднеквадратичная
ошибка каждого отдельного измерения,
n
– число измерений.
Таким образом,
увеличивая число опытов, можно уменьшить
случайную ошибку в величине среднего
значения.
В настоящее время
результаты научных и технических
измерений принято представлять в виде
(7)
Как показывает
теория, при такой записи мы знаем
надежность полученного результата, а
именно, что истинная величина Х с
вероятностью 68% отличается от
не более, чем на
.
При использовании
же средней арифметической (абсолютной)
ошибки (формула 2) о надежности результата
ничего сказать нельзя. Некоторое
представление о точности проведенных
измерений в этом случае дает относительная
ошибка (формула 4).
При выполнении
лабораторных работ студенты могут
использовать как среднюю абсолютную
ошибку, так и среднюю квадратичную.
Какую из них применять указывается
непосредственно в каждой конкретной
работе (или указывается преподавателем).
Обычно если число
измерений не превышает 3 – 5, то
можно использовать среднюю абсолютную
ошибку. Если число измерений порядка
10 и более, то следует использовать более
корректную оценку с помощью средней
квадратичной ошибки среднего (формулы
5 и 6).
Учет систематических ошибок.
Увеличением числа
измерений можно уменьшить только
случайные ошибки опыта, но не
систематические.
Максимальное
значение систематической ошибки обычно
указывается на приборе или в его паспорте.
Для измерений с помощью обычной
металлической линейки систематическая
ошибка составляет не менее 0,5 мм; для
измерений штангенциркулем –
0,1 – 0,05 мм;
микрометром – 0,01 мм.
Часто в качестве
систематической ошибки берется половина
цены деления прибора.
На шкалах
электроизмерительных приборов указывается
класс точности. Зная класс точности К,
можно вычислить систематическую ошибку
прибора ∆Х по формуле
где К – класс
точности прибора, Хпр – предельное
значение величины, которое может быть
измерено по шкале прибора.
Так, амперметр
класса 0,5 со шкалой до 5А измеряет ток с
ошибкой не более
Погрешность
цифрового прибора равна единице
наименьшего индицируемого разряда.
Среднее значение
полной погрешности складывается из
случайной и систематической
погрешностей.
Ответ с учетом
систематических и случайных ошибок
записывается в виде
Погрешности косвенных измерений
В физических
экспериментах чаще бывает так, что
искомая физическая величина сама на
опыте измерена быть не может, а является
функцией других величин, измеряемых
непосредственно. Например, чтобы
определить объём цилиндра, надо измерить
диаметр D и высоту h, а затем вычислить
объем по формуле
Величины D и h будут измерены с
некоторой ошибкой. Следовательно,
вычисленная величина V
получится также с некоторой ошибкой.
Надо уметь выражать погрешность
вычисленной величины через погрешности
измеренных величин.
Как и при прямых
измерениях можно вычислять среднюю
абсолютную (среднюю арифметическую)
ошибку или среднюю квадратичную ошибку.
Общие правила
вычисления ошибок для обоих случаев
выводятся с помощью дифференциального
исчисления.
Пусть искомая
величина φ является функцией нескольких
переменных Х,
У, Z…
φ(Х,
У, Z…).
Путем прямых
измерений мы можем найти величины
,
а также оценить их средние абсолютные
ошибки
…
или средние квадратичные ошибки Х,
У,
Z…
Тогда средняя
арифметическая погрешность
вычисляется по формуле
где
— частные
производные от φ по
Х, У, Z. Они
вычисляются для средних значений
…
Средняя квадратичная
погрешность вычисляется по формуле
Пример.
Выведем формулы погрешности для
вычисления объёма цилиндра.
а) Средняя
арифметическая погрешность.
Величины
D и h
измеряются соответственно с ошибкой
D
и h.
Погрешность
величины объёма будет равна
б) Средняя
квадратичная погрешность.
Величины
D и h
измеряются соответственно с ошибкой
D,
h.
Погрешность
величины объёма будет равна
Если формула
представляет выражение удобное для
логарифмирования (то есть произведение,
дробь, степень), то удобнее вначале
вычислять относительную погрешность.
Для этого (в случае средней арифметической
погрешности) надо проделать следующее.
1. Прологарифмировать
выражение.
2. Продифференцировать
его.
3. Объединить
все члены с одинаковым дифференциалом
и вынести его за скобки.
4. Взять выражение
перед различными дифференциалами по
модулю.
5. Заменить
значки дифференциалов d
на значки абсолютной погрешности .
В итоге получится
формула для относительной погрешности
Затем,
зная ,
можно вычислить абсолютную погрешность
=
Пример.
Аналогично можно
записать относительную среднюю
квадратичную погрешность
Правила
представления результатов измерения
следующие:
-
погрешность должна
округляться до одной значащей цифры:
правильно = 0,04,
неправильно —
= 0,0382;
-
последняя значащая
цифра результата должна быть того же
порядка величины, что и погрешность:
правильно
= 9,830,03,
неправильно —
= 9,8260,03;
-
если результат
имеет очень большую или очень малую
величину, необходимо использовать
показательную форму записи — одну и ту
же для результата и его погрешности,
причем запятая десятичной дроби должна
следовать за первой значащей цифрой
результата:
правильно —
= (5,270,03)10-5,
неправильно —
= 0,00005270,0000003,
= 5,2710-50,0000003,
=
= 0,0000527310-7,
= (5273)10-7,
= (0,5270,003)
10-4.
-
Если результат
имеет размерность, ее необходимо
указать:
правильно – g=(9,820,02)
м/c2,
неправильно – g=(9,820,02).
Соседние файлы в папке Методички физика
- #
02.04.2015275.46 Кб37оформление заготовки и отчета.ppt
- #
Среднеквадратичная ошибка (Mean Squared Error) – Среднее арифметическое (Mean) квадратов разностей между предсказанными и реальными значениями Модели (Model) Машинного обучения (ML):
Рассчитывается с помощью формулы, которая будет пояснена в примере ниже:
$$MSE = frac{1}{n} × sum_{i=1}^n (y_i — widetilde{y}_i)^2$$
$$MSEspace{}{–}space{Среднеквадратическая}space{ошибка,}$$
$$nspace{}{–}space{количество}space{наблюдений,}$$
$$y_ispace{}{–}space{фактическая}space{координата}space{наблюдения,}$$
$$widetilde{y}_ispace{}{–}space{предсказанная}space{координата}space{наблюдения,}$$
MSE практически никогда не равен нулю, и происходит это из-за элемента случайности в данных или неучитывания Оценочной функцией (Estimator) всех факторов, которые могли бы улучшить предсказательную способность.
Пример. Исследуем линейную регрессию, изображенную на графике выше, и установим величину среднеквадратической Ошибки (Error). Фактические координаты точек-Наблюдений (Observation) выглядят следующим образом:
Мы имеем дело с Линейной регрессией (Linear Regression), потому уравнение, предсказывающее положение записей, можно представить с помощью формулы:
$$y = M * x + b$$
$$yspace{–}space{значение}space{координаты}space{оси}space{y,}$$
$$Mspace{–}space{уклон}space{прямой}$$
$$xspace{–}space{значение}space{координаты}space{оси}space{x,}$$
$$bspace{–}space{смещение}space{прямой}space{относительно}space{начала}space{координат}$$
Параметры M и b уравнения нам, к счастью, известны в данном обучающем примере, и потому уравнение выглядит следующим образом:
$$y = 0,5252 * x + 17,306$$
Зная координаты реальных записей и уравнение линейной регрессии, мы можем восстановить полные координаты предсказанных наблюдений, обозначенных серыми точками на графике выше. Простой подстановкой значения координаты x в уравнение мы рассчитаем значение координаты ỹ:
Рассчитаем квадрат разницы между Y и Ỹ:
Сумма таких квадратов равна 4 445. Осталось только разделить это число на количество наблюдений (9):
$$MSE = frac{1}{9} × 4445 = 493$$
Само по себе число в такой ситуации становится показательным, когда Дата-сайентист (Data Scientist) предпринимает попытки улучшить предсказательную способность модели и сравнивает MSE каждой итерации, выбирая такое уравнение, что сгенерирует наименьшую погрешность в предсказаниях.
MSE и Scikit-learn
Среднеквадратическую ошибку можно вычислить с помощью SkLearn. Для начала импортируем функцию:
import sklearn
from sklearn.metrics import mean_squared_errorИнициализируем крошечные списки, содержащие реальные и предсказанные координаты y:
y_true = [5, 41, 70, 77, 134, 68, 138, 101, 131]
y_pred = [23, 35, 55, 90, 93, 103, 118, 121, 129]Инициируем функцию mean_squared_error(), которая рассчитает MSE тем же способом, что и формула выше:
mean_squared_error(y_true, y_pred)
Интересно, что конечный результат на 3 отличается от расчетов с помощью Apple Numbers:
496.0Ноутбук, не требующий дополнительной настройки на момент написания статьи, можно скачать здесь.
Автор оригинальной статьи: @mmoshikoo
Фото: @tobyelliott
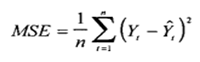
- Для чего нужна среднеквадратическая ошибка прогноза;
- Как она рассчитывается.
+ сможете скачать пример расчета в Excel.
MSE (mean squared error) – среднеквадратическая ошибка прогноза.
MSE – среднеквадратическая ошибка прогноза применяется в ситуациях, когда нам надо подчеркнуть большие ошибки и выбрать модель, которая дает меньше больших ошибок прогноза.
Грубые ошибки становятся заметнее за счет того, что ошибку прогноза мы возводим в квадрат. И модель, которая дает нам меньшее значение среднеквадратической ошибки, можно сказать, что что у этой модели меньше грубых ошибок.
Как рассчитать среднеквадратическую ошибку?
- Рассчитываем ошибку для каждого значения модели;
- Возводим ошибку в квадрат;
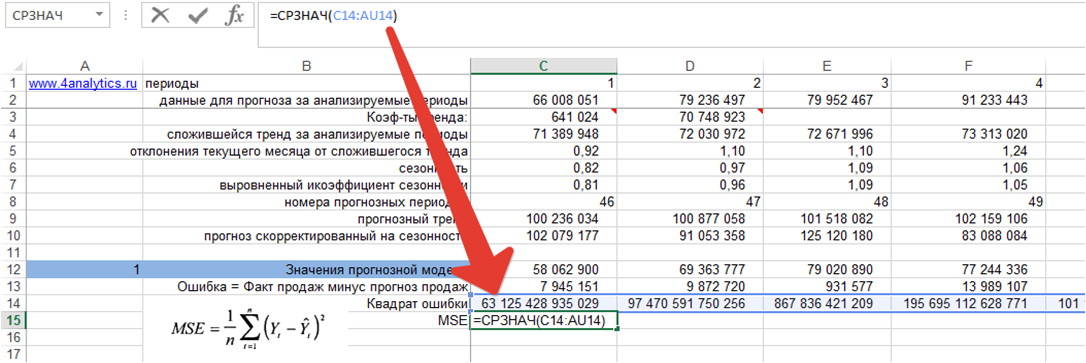
- Рассчитываем среднее по квадрату ошибки, т.е. среднеквадратическую ошибку MSE:
Скачайте файл с примером расчета ошибки MSE
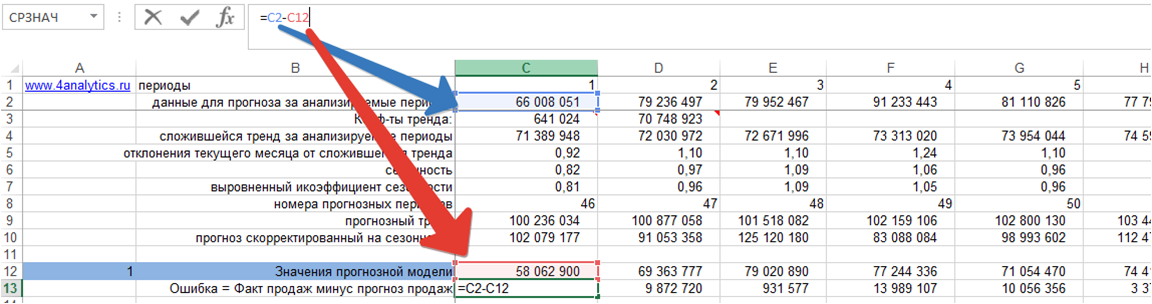
1. Ошибка = фактические продаж минус значения прогнозной модели для каждого момента времени:
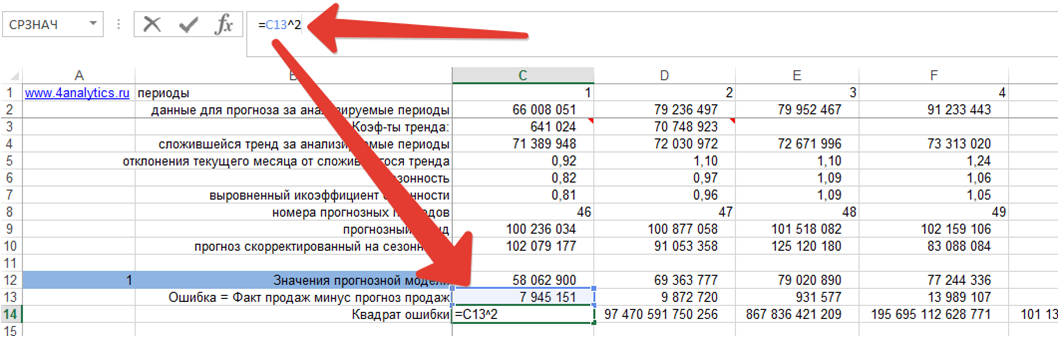
2. Возводим ошибку в квадрат для каждого момента времени:
3. Рассчитываем среднеквадратическую ошибку MSE, для этого определяем среднее значение квадратов ошибок:
Скачайте файл с примером расчета ошибки MSE
Из данной статьи вы узнали, для чего использовать среднеквадратическую ошибку прогноза и как ее рассчитать. Если у вас остались вопросы, пожалуйста, задавайте в комментариях, буду рад помочь!
Присоединяйтесь к нам!
Скачивайте бесплатные приложения для прогнозирования и бизнес-анализа:
- Novo Forecast Lite — автоматический расчет прогноза в Excel.
- 4analytics — ABC-XYZ-анализ и анализ выбросов в Excel.
- Qlik Sense Desktop и QlikView Personal Edition — BI-системы для анализа и визуализации данных.
Тестируйте возможности платных решений:
- Novo Forecast PRO — прогнозирование в Excel для больших массивов данных.
Получите 10 рекомендаций по повышению точности прогнозов до 90% и выше.
Зарегистрируйтесь и скачайте решения
Статья полезная? Поделитесь с друзьями
Загрузить PDF
Загрузить PDF
Стандартной ошибкой называется величина, которая характеризует стандартное (среднеквадратическое) отклонение выборочного среднего. Другими словами, эту величину можно использовать для оценки точности выборочного среднего. Множество областей применения стандартной ошибки по умолчанию предполагают нормальное распределение. Если вам нужно рассчитать стандартную ошибку, перейдите к шагу 1.
-
1
Запомните определение среднеквадратического отклонения. Среднеквадратическое отклонение выборки – это мера рассеянности значения. Среднеквадратическое отклонение выборки обычно обозначается буквой s. Математическая формула среднеквадратического отклонения приведена выше.
-
2
Узнайте, что такое истинное среднее значение. Истинное среднее является средним группы чисел, включающим все числа всей группы – другими словами, это среднее всей группы чисел, а не выборки.
-
3
Научитесь рассчитывать среднеарифметическое значение. Среднеаримфетическое означает попросту среднее: сумму значений собранных данных, разделенную на количество значений этих данных.
-
4
Узнайте, что такое выборочное среднее. Когда среднеарифметическое значение основано на серии наблюдений, полученных в результате выборок из статистической совокупности, оно называется “выборочным средним”. Это среднее выборки чисел, которое описывает среднее значение лишь части чисел из всей группы. Его обозначают как:
-
5
Усвойте понятие нормального распределения. Нормальные распределения, которые используются чаще других распределений, являются симметричными, с единичным максимумом в центре – на среднем значении данных. Форма кривой подобна очертаниям колокола, при этом график равномерно опускается по обе стороны от среднего. Пятьдесят процентов распределения лежит слева от среднего, а другие пятьдесят процентов – справа от него. Рассеянность значений нормального распределения описывается стандартным отклонением.
-
6
Запомните основную формулу. Формула для вычисления стандартной ошибки приведена выше.
Реклама
-
1
Рассчитайте выборочное среднее. Чтобы найти стандартную ошибку, сначала нужно определить среднеквадратическое отклонение (поскольку среднеквадратическое отклонение s входит в формулу для вычисления стандартной ошибки). Начните с нахождения средних значений. Выборочное среднее выражается как среднее арифметическое измерений x1, x2, . . . , xn. Его рассчитывают по формуле, приведенной выше.
- Допустим, например, что вам нужно рассчитать стандартную ошибку выборочного среднего результатов измерения массы пяти монет, указанных в таблице:
Вы сможете рассчитать выборочное среднее, подставив значения массы в формулу:
- Допустим, например, что вам нужно рассчитать стандартную ошибку выборочного среднего результатов измерения массы пяти монет, указанных в таблице:
-
2
Вычтите выборочное среднее из каждого измерения и возведите полученное значение в квадрат. Как только вы получите выборочное среднее, вы можете расширить вашу таблицу, вычтя его из каждого измерения и возведя результат в квадрат.
- Для нашего примера расширенная таблица будет иметь следующий вид:
-
3
Найдите суммарное отклонение ваших измерений от выборочного среднего. Общее отклонение – это сумма возведенных в квадрат разностей от выборочного среднего. Чтобы определить его, сложите ваши новые значения.
- В нашем примере нужно будет выполнить следующий расчет:
Это уравнение дает сумму квадратов отклонений измерений от выборочного среднего.
- В нашем примере нужно будет выполнить следующий расчет:
-
4
Рассчитайте среднеквадратическое отклонение ваших измерений от выборочного среднего. Как только вы будете знать суммарное отклонение, вы сможете найти среднее отклонение, разделив ответ на n -1. Обратите внимание, что n равно числу измерений.
- В нашем примере было сделано 5 измерений, следовательно n – 1 будет равно 4. Расчет нужно вести следующим образом:
-
5
Найдите среднеквадратичное отклонение. Сейчас у вас есть все необходимые значения для того, чтобы воспользоваться формулой для нахождения среднеквадратичного отклонения s.
- В нашем примере вы будете рассчитывать среднеквадратичное отклонение следующим образом:
Следовательно, среднеквадратичное отклонение равно 0,0071624.
Реклама
- В нашем примере вы будете рассчитывать среднеквадратичное отклонение следующим образом:
-
1
Чтобы вычислить стандартную ошибку, воспользуйтесь базовой формулой со среднеквадратическим отклонением.
- В нашем примере вы сможете рассчитать стандартную ошибку следующим образом:
Таким образом в нашем примере стандартная ошибка (среднеквадратическое отклонение выборочного среднего) составляет 0,0032031 грамма.
- В нашем примере вы сможете рассчитать стандартную ошибку следующим образом:
Советы
- Стандартную ошибку и среднеквадратическое отклонение часто путают. Обратите внимание, что стандартная ошибка описывает среднеквадратическое отклонение выборочного распределения статистических данных, а не распределения отдельных значений
- В научных журналах понятия стандартной ошибки и среднеквадратического отклонения несколько размыты. Для объединения двух величин используется знак ±.
Реклама
Об этой статье
Эту страницу просматривали 47 997 раз.
Была ли эта статья полезной?
В статистике , то средний квадрат ошибка ( СКО ) [1] [2] , или среднее отклонение в квадрате ( МСД ) из оценки (методик для оценки в ненаблюдаемом количестве) измеряет среднее из квадратов ошибок , то есть, то среднеквадратичная разница между расчетными значениями и фактическими значениями. MSE — это функция риска , соответствующая ожидаемому значению квадрата потери ошибок. [ согласно кому? ] [ требуется разъяснение ]Тот факт, что MSE почти всегда строго положительна (а не равна нулю), объясняется случайностью или тем, что оценщик не учитывает информацию, которая могла бы дать более точную оценку. [3]
MSE — это показатель качества оценщика. Поскольку оно вычисляется из квадрата евклидова расстояния , оно всегда является положительным значением, а ошибка уменьшается по мере приближения к нулю. [ требуется разъяснение ]
MSE — это второй момент (о происхождении) ошибки, [ требуется пояснение ] и, таким образом, включает в себя как дисперсию оценки (насколько широко разброс оценок от одной выборки данных к другой), так и ее смещение (насколько далеко от среднее оценочное значение от истинного значения). [ необходимая цитата ] Для несмещенного оценщика MSE — это дисперсия оценщика. Как и дисперсия, MSE имеет те же единицы измерения, что и квадрат оцениваемой величины. По аналогии со стандартным отклонением извлечение квадратного корня из MSE дает среднеквадратичную ошибку илисреднеквадратичное отклонение (RMSE или RMSD), которое имеет те же единицы, что и оцениваемая величина; для несмещенной оценки RMSE — это квадратный корень из дисперсии , известный как стандартная ошибка .
Определение и основные свойства
СКО либо оценивает качество предсказателя (т.е. функция отображения произвольных входов к выборке значений некоторой случайной величины ), либо из оценки (т.е. математическая функция отображения выборки данных для оценки в параметре из население , из которого отбирают данные). Определение MSE различается в зависимости от того, описывается ли предсказатель или оценщик.
Предиктор
Если вектор прогнозы генерируются из выборки точки данных по всем переменным, и — вектор наблюдаемых значений прогнозируемой переменной, при этом являясь предсказанными значениями (например, по методу наименьших квадратов ), то MSE в пределах выборки предсказателя вычисляется как
Другими словами, MSE — это среднее из квадратов ошибок . Это легко вычисляемая величина для конкретного образца (и, следовательно, зависит от образца).
В матричных обозначениях
куда является а также это матрица.
СКО также можно вычислить по q точкам данных, которые не использовались при оценке модели, либо потому, что они не использовались для этой цели, либо потому, что эти данные были получены заново. В этом процессе (известном как перекрестная проверка ) MSE часто называют среднеквадратической ошибкой прогноза [ необходима ссылка ] и вычисляется как
Оценщик
MSE оценщика по неизвестному параметру определяется как [2]
Это определение зависит от неизвестного параметра, но MSE априори является свойством оценщика. MSE может быть функцией неизвестных параметров, и в этом случае любая оценка MSE, основанная на оценках этих параметров, будет функцией данных (и, следовательно, случайной величиной). Если оценщик выводится как статистика выборки и используется для оценки некоторого параметра совокупности, тогда ожидание относится к распределению выборки статистики выборки.
MSE может быть записано как сумма дисперсии оценки и квадрата смещения оценки, обеспечивая полезный способ вычисления MSE и подразумевая, что в случае несмещенных оценок MSE и дисперсия эквивалентны. [4]
Доказательство отношения отклонения и предвзятости
В качестве альтернативы у нас есть
Еще более короткое доказательство, использующее известную формулу, что для случайной величины (и в частности для ),
, является:
Но в реальном случае моделирования MSE можно описать как добавление дисперсии модели, систематической ошибки модели и неснижаемой неопределенности [ необходима ссылка ] [ требуется пояснение ] . В соответствии с этим соотношением, MSE оценщиков можно просто использовать для сравнения эффективности , которое включает в себя информацию о дисперсии и смещении оценщика. Это называется критерием MSE.
В регрессе
В регрессионном анализе построение графиков является более естественным способом просмотра общей тенденции всех данных. Среднее значение расстояния от каждой точки до прогнозируемой регрессионной модели может быть вычислено и показано как среднеквадратичная ошибка. Возведение в квадрат критически важно для уменьшения сложности с отрицательными знаками. Чтобы свести к минимуму MSE, модель могла бы быть более точной, что означало бы, что модель ближе к фактическим данным. Одним из примеров линейной регрессии с использованием этого метода является метод наименьших квадратов -Какой оценивает уместность модели линейной регрессии к модели двухмерного набора данных , [5] , но чьи ограничение связано с известным распределением данных.
Термин среднеквадратичная ошибка иногда используется для обозначения несмещенной оценки дисперсии ошибки: остаточная сумма квадратов, деленная на количество степеней свободы . Это определение известной вычисленной величины отличается от приведенного выше определения вычисленной MSE предиктора тем, что используется другой знаменатель. Знаменатель — это размер выборки, уменьшенный на количество параметров модели, оцененных на основе тех же данных, ( n — p ) для p регрессоров или ( n — p -1), если используется перехват (см. Ошибки и остатки в статистике для более подробной информации. ). [6]Хотя MSE (как определено в этой статье) не является объективной оценкой дисперсии ошибок, она согласована , учитывая согласованность предсказателя.
В регрессионном анализе «среднеквадратичная ошибка», часто называемая среднеквадратической ошибкой прогноза или « среднеквадратической ошибкой вне выборки», также может относиться к среднему значению квадратов отклонений прогнозов от истинных значений в зависимости от тестовое пространство вне выборки , сгенерированное моделью, оцененной по определенному пространству выборки . Это также известная вычисляемая величина, и она варьируется в зависимости от образца и тестового пространства вне выборки.
Примеры
Среднее
Предположим, у нас есть случайная выборка размера от населения, . Предположим, что образцы были выбраны с заменой . Это единицы выбираются по одному, и ранее выбранные единицы по-прежнему могут быть выбраны для всех рисует. Обычная оценка дляэто среднее значение по выборке [1]
ожидаемое значение которого равно истинному среднему значению (так что это беспристрастно) и среднеквадратичная ошибка
куда — дисперсия населения .
Для гауссовского распределения это лучшая несмещенная оценка (т. Е. С самой низкой MSE среди всех несмещенных оценок), но не, скажем, для равномерного распределения .
Дисперсия
Обычной оценкой дисперсии является скорректированная выборочная дисперсия :
Это беспристрастно (его ожидаемое значение ), поэтому также называется несмещенной дисперсией выборки, а ее MSE равна [7]
куда — четвертый центральный момент распределения или популяции, иэто избыточный эксцесс .
Однако можно использовать другие оценки для которые пропорциональны , и соответствующий выбор всегда может дать более низкую среднеквадратичную ошибку. Если мы определим
затем рассчитываем:
Это сводится к минимуму, когда
Для гауссова распределения , где, это означает, что MSE минимизируется при делении суммы на . Минимальный избыточный эксцесс составляет, [a] что достигается распределением Бернулли с p = 1/2 (подбрасывание монеты), а MSE минимизируется дляСледовательно, независимо от эксцесса, мы получаем «лучшую» оценку (в смысле наличия более низкой MSE), немного уменьшая несмещенную оценку; это простой пример оценщика усадки : один «сжимает» оценщик до нуля (уменьшает несмещенный оценщик).
Кроме того, хотя скорректированная дисперсия выборки является лучшей несмещенной оценкой (минимальная среднеквадратическая ошибка среди несмещенных оценок) дисперсии для гауссовских распределений, если распределение не является гауссовым, то даже среди несмещенных оценок лучшая несмещенная оценка дисперсии может не быть
Гауссово распределение
В следующей таблице приведены несколько оценок истинных параметров совокупности μ и σ 2 для гауссовского случая. [8]
| Истинное значение | Оценщик | Среднеквадратичная ошибка |
|---|---|---|
| = несмещенная оценка среднего значения генеральной совокупности , | ||
| = несмещенная оценка дисперсии генеральной совокупности , | ||
| = смещенная оценка дисперсии генеральной совокупности , | ||
| = смещенная оценка дисперсии генеральной совокупности , |
Интерпретация
MSE равна нулю, что означает, что оценщик предсказывает наблюдения параметра с идеальной точностью является идеальным (но обычно невозможным).
Значения MSE могут использоваться для сравнительных целей. Две или более статистических моделей можно сравнить с использованием их MSE — в качестве меры того, насколько хорошо они объясняют данный набор наблюдений: несмещенная оценка (оцененная на основе статистической модели) с наименьшей дисперсией среди всех несмещенных оценок является лучшей несмещенной оценкой или MVUE (Несмещенная оценка минимальной дисперсии).
Как анализ дисперсии, так и методы линейной регрессии оценивают MSE как часть анализа и используют оцененную MSE для определения статистической значимости изучаемых факторов или предикторов. Цель экспериментального плана состоит в том, чтобы построить эксперименты таким образом, чтобы при анализе наблюдений MSE была близка к нулю относительно величины по крайней мере одного из оцененных эффектов лечения.
При одностороннем дисперсионном анализе MSE можно вычислить путем деления суммы квадратов ошибок и степени свободы. Кроме того, значение f представляет собой отношение среднего квадрата обработки и MSE.
MSE также используется в нескольких методах пошаговой регрессии как часть определения того, сколько предикторов из набора кандидатов включить в модель для данного набора наблюдений.
Приложения
- Минимизация MSE является ключевым критерием при выборе оценщиков: см. Минимальную среднеквадратичную ошибку . Среди несмещенных оценщиков минимизация MSE эквивалентна минимизации дисперсии, а оценщик, который делает это, является несмещенной оценкой с минимальной дисперсией . Однако смещенная оценка может иметь более низкую MSE; см. смещение оценки .
- В статистическом моделировании MSE может представлять разницу между фактическими наблюдениями и значениями наблюдений, предсказанными моделью. В этом контексте он используется для определения степени, в которой модель соответствует данным, а также возможности удаления некоторых независимых переменных без значительного ущерба для предсказательной способности модели.
- В прогнозировании и прогнозировании , то оценка Шиповник является мерой успешности прогнозов на основе MSE.
Функция потери
Квадратичная потеря ошибок — одна из наиболее широко используемых функций потерь в статистике [ необходима цитата ] , хотя ее широкое использование проистекает больше из математического удобства, чем из соображений фактических потерь в приложениях. Карл Фридрих Гаусс , который ввел использование среднеквадратичной ошибки, осознавал ее произвол и был согласен с возражениями против нее на этих основаниях. [3] Математические преимущества среднеквадратичной ошибки особенно очевидны при ее использовании при анализе эффективности линейной регрессии , поскольку она позволяет разделить вариацию в наборе данных на вариации, объясняемые моделью, и вариации, объясняемые случайностью.
Критика
Использование среднеквадратичной ошибки без вопросов подвергалось критике со стороны теоретика принятия решений Джеймса Бергера . Среднеквадратичная ошибка — это отрицательное значение ожидаемого значения одной конкретной функции полезности , квадратичной функции полезности, которая может не быть подходящей функцией полезности для использования в данном наборе обстоятельств. Однако есть некоторые сценарии, в которых среднеквадратичная ошибка может служить хорошим приближением к функции потерь, естественным образом возникающей в приложении. [9]
Подобно дисперсии , среднеквадратичная ошибка имеет тот недостаток, что сильно взвешиваются выбросы . [10] Это результат возведения в квадрат каждого члена, который фактически дает больший вес большим ошибкам, чем малым. Это свойство, нежелательное для многих приложений, заставило исследователей использовать альтернативы, такие как средняя абсолютная ошибка или те, которые основаны на медиане .
См. Также
- Компромисс смещения и дисперсии
- Оценщик Ходжеса
- Оценка Джеймса – Стейна
- Средняя процентная ошибка
- Среднеквадратичная ошибка квантования
- Среднеквадратичное взвешенное отклонение
- Среднеквадратичное смещение
- Среднеквадратичная ошибка прогноза
- Минимальная среднеквадратичная ошибка
- Оценщик минимальной среднеквадратичной ошибки
- Переоснащение
- Пиковое отношение сигнал / шум
Примечания
- ^ Это можно доказать с помощью неравенства Йенсена следующим образом. Четвертый центральный момент является верхней границей квадрата дисперсии, так что наименьшее значение для их отношения равно единице, следовательно, наименьшее значение для избыточного эксцесса равно −2, что достигается, например, Бернулли с p = 1. / 2.
Ссылки
- ^ a b «Список вероятностных и статистических символов» . Математическое хранилище . 2020-04-26 . Проверено 12 сентября 2020 .
- ^ a b «Среднеквадратичная ошибка (MSE)» . www.probabilitycourse.com . Проверено 12 сентября 2020 .
- ^ a b Lehmann, EL; Казелла, Джордж (1998). Теория точечного оценивания (2-е изд.). Нью-Йорк: Спрингер. ISBN 978-0-387-98502-2. Руководство по ремонту 1639875 .
- ^ Вакерли, Деннис; Менденхолл, Уильям; Шеффер, Ричард Л. (2008). Математическая статистика с приложениями (7-е изд.). Белмонт, Калифорния, США: Высшее образование Томсона. ISBN 978-0-495-38508-0.
- ^ Современное введение в вероятность и статистику: понимание, почему и как . Деккинг, Мишель, 1946-. Лондон: Спрингер. 2005. ISBN 978-1-85233-896-1. OCLC 262680588 .CS1 maint: другие ( ссылка )
- ^ Steel, RGD, и Torrie, JH, Принципы и процедуры статистики со специальной ссылкой на биологические науки. , Макгроу Хилл , 1960, стр. 288.
- ^ Настроение, А .; Graybill, F .; Боэс, Д. (1974). Введение в теорию статистики (3-е изд.). Макгроу-Хилл. п. 229 .
- ^ ДеГрут, Моррис Х. (1980). Вероятность и статистика (2-е изд.). Эддисон-Уэсли.
- ^ Бергер, Джеймс О. (1985). «2.4.2 Некоторые стандартные функции потерь». Статистическая теория принятия решений и байесовский анализ (2-е изд.). Нью-Йорк: Springer-Verlag. п. 60 . ISBN 978-0-387-96098-2. Руководство по ремонту 0804611 .
- ^ Бермеджо, Серхио; Кабестани, Джоан (2001). «Ориентированный анализ главных компонентов для классификаторов с большой маржой». Нейронные сети . 14 (10): 1447–1461. DOI : 10.1016 / S0893-6080 (01) 00106-X . PMID 11771723 .
В статистика, то среднеквадратичная ошибка (MSE)[1][2] или среднеквадратическое отклонение (MSD) из оценщик (процедуры оценки ненаблюдаемой величины) измеряет средний квадратов ошибки — то есть средний квадрат разницы между оценочными и фактическими значениями. MSE — это функция риска, соответствующий ожидаемое значение квадрата ошибки потери. Тот факт, что MSE почти всегда строго положительный (а не нулевой), объясняется тем, что случайность или потому что оценщик не учитывает информацию это может дать более точную оценку.[3]
MSE — это мера качества оценки — она всегда неотрицательна, а значения, близкие к нулю, лучше.
МСЭ — второй момент (о происхождении) ошибки и, таким образом, включает в себя как отклонение оценщика (насколько разбросаны оценки от одного образец данных другому) и его предвзятость (насколько далеко среднее оценочное значение от истинного значения). Для объективный оценщик, MSE — это дисперсия оценки. Как и дисперсия, MSE имеет те же единицы измерения, что и квадрат оцениваемой величины. По аналогии с стандартное отклонение, извлечение квадратного корня из MSE дает среднеквадратичную ошибку или среднеквадратичное отклонение (RMSE или RMSD), который имеет те же единицы, что и оцениваемое количество; для несмещенной оценки RMSE — это квадратный корень из отклонение, известный как стандартная ошибка.
Определение и основные свойства
MSE либо оценивает качество предсказатель (т.е. функция, отображающая произвольные входные данные в выборку значений некоторых случайная переменная ) или оценщик (т.е. математическая функция отображение образец данных для оценки параметр из численность населения из которого берутся данные). Определение MSE различается в зависимости от того, описывается ли предсказатель или оценщик.
Предсказатель
Если вектор 


Другими словами, MSE — это иметь в виду 

В матрица обозначение
куда 



MSE также можно вычислить на q точки данных, которые не использовались при оценке модели, либо потому, что они были задержаны для этой цели, либо потому, что эти данные были получены заново. В этом процессе (известном как перекрестная проверка ), MSE часто называют среднеквадратичная ошибка прогноза, и вычисляется как
Оценщик
MSE оценщика 

Это определение зависит от неизвестного параметра, но MSE априори свойство оценщика. MSE может быть функцией неизвестных параметров, и в этом случае любой оценщик MSE на основе оценок этих параметров будет функцией данных (и, следовательно, случайной величиной). Если оценщик 
MSE можно записать как сумму отклонение оценщика и квадрата предвзятость оценщика, обеспечивая полезный способ вычисления MSE и подразумевая, что в случае несмещенных оценок MSE и дисперсия эквивалентны.[4]
Доказательство отношения дисперсии и предвзятости
- В качестве альтернативы у нас есть
Но в реальном случае моделирования MSE можно описать как добавление дисперсии модели, систематической ошибки модели и неснижаемой неопределенности. Согласно соотношению, MSE оценщиков может быть просто использована для эффективность сравнение, которое включает информацию о дисперсии и смещении оценки. Это называется критерием MSE.
В регрессе
В регрессивный анализ, построение графиков — более естественный способ просмотра общей тенденции всех данных. Среднее значение расстояния от каждой точки до прогнозируемой регрессионной модели может быть вычислено и показано как среднеквадратичная ошибка. Возведение в квадрат критически важно для уменьшения сложности с отрицательными знаками. Чтобы свести к минимуму MSE, модель может быть более точной, что означает, что модель ближе к фактическим данным. Одним из примеров линейной регрессии с использованием этого метода является метод наименьших квадратов —Который оценивает соответствие модели линейной регрессии модели двумерный набор данных[5], но чье ограничение связано с известным распределением данных.
Период, термин среднеквадратичная ошибка иногда используется для обозначения объективной оценки дисперсии ошибки: остаточная сумма квадратов делится на количество степени свободы. Это определение известной вычисленной величины отличается от приведенного выше определения вычисленной MSE предиктора тем, что используется другой знаменатель. Знаменатель — это размер выборки, уменьшенный на количество параметров модели, оцененных на основе тех же данных, (н-р) за п регрессоры или (п-п-1) если используется перехват (см. ошибки и остатки в статистике Больше подробностей).[6] Хотя MSE (как определено в этой статье) не является объективной оценкой дисперсии ошибки, она последовательный, учитывая непротиворечивость предсказателя.
В регрессионном анализе «среднеквадратичная ошибка», часто называемая среднеквадратичная ошибка прогноза или «среднеквадратичная ошибка вне выборки», также может относиться к среднему значению квадратичные отклонения прогнозов на основе истинных значений в тестовом пространстве вне выборки, сгенерированных моделью, оцененной в конкретном пространстве выборки. Это также известная вычисляемая величина, которая зависит от образца и тестового пространства вне образца.
Примеры
Иметь в виду
Предположим, у нас есть случайная выборка размера 




ожидаемое значение которого равно истинному среднему значению 
куда 
Для Гауссово распределение, это лучший объективный оценщик (то есть с самой низкой MSE среди всех несмещенных оценок), но не, скажем, для равномерное распределение.
Дисперсия
Обычной оценкой дисперсии является исправлено выборочная дисперсия:
Это объективно (его ожидаемое значение 
куда 

Однако можно использовать другие оценки для 

затем рассчитываем:
Это сводится к минимуму, когда
Для Гауссово распределение, куда 



Далее, хотя исправленная дисперсия выборки является лучший объективный оценщик (минимальная среднеквадратичная ошибка среди несмещенных оценок) дисперсии для гауссовских распределений, если распределение не является гауссовым, то даже среди несмещенных оценок лучшая несмещенная оценка дисперсии может не быть
Гауссово распределение
В следующей таблице приведены несколько оценок истинных параметров популяции, μ и σ.2, для гауссова случая.[8]
| Истинное значение | Оценщик | Среднеквадратичная ошибка |
|---|---|---|
 |
 = несмещенная оценка Средняя численность населения, = несмещенная оценка Средняя численность населения,  |
 |
 |
 = несмещенная оценка дисперсия населения, = несмещенная оценка дисперсия населения,  |
 |
 |
 = смещенная оценка дисперсия населения, = смещенная оценка дисперсия населения,  |
 |
 |
 = смещенная оценка дисперсия населения, = смещенная оценка дисперсия населения,  |
 |
Интерпретация
MSE равна нулю, что означает, что оценщик 

Значения MSE могут использоваться для сравнительных целей. Два и более статистические модели можно сравнить, используя их MSE — как меру того, насколько хорошо они объясняют данный набор наблюдений: несмещенная оценка (рассчитанная на основе статистической модели) с наименьшей дисперсией среди всех несмещенных оценок — это оценка лучший объективный оценщик или MVUE (несмещенная оценка минимальной дисперсии).
Обе линейная регрессия методы, такие как дисперсионный анализ оценить MSE как часть анализа и использовать оценочную MSE для определения Статистическая значимость изучаемых факторов или предикторов. Цель экспериментальная конструкция состоит в том, чтобы построить эксперименты таким образом, чтобы при анализе наблюдений MSE была близка к нулю относительно величины по крайней мере одного из оцененных эффектов лечения.
В односторонний дисперсионный анализ, MSE можно вычислить путем деления суммы квадратов ошибок и степени свободы. Кроме того, значение f — это отношение среднего квадрата обработки и MSE.
MSE также используется в нескольких пошаговая регрессия методы как часть определения того, сколько предикторов из набора кандидатов включить в модель для данного набора наблюдений.
Приложения
- Минимизация MSE является ключевым критерием при выборе оценщиков: см. минимальная среднеквадратичная ошибка. Среди несмещенных оценщиков минимизация MSE эквивалентна минимизации дисперсии, а оценщик, который делает это, является несмещенная оценка минимальной дисперсии. Однако смещенная оценка может иметь более низкую MSE; видеть систематическая ошибка оценки.
- В статистическое моделирование MSE может представлять разницу между фактическими наблюдениями и значениями наблюдений, предсказанными моделью. В этом контексте он используется для определения степени, в которой модель соответствует данным, а также возможности удаления некоторых объясняющих переменных без значительного ущерба для прогнозирующей способности модели.
- В прогнозирование и прогноз, то Оценка Бриера это мера умение прогнозировать на основе MSE.
Функция потерь
Квадратичная потеря ошибок — одна из наиболее широко используемых функции потерь в статистике[нужна цитата ], хотя его широкое использование проистекает больше из математического удобства, чем из соображений реальных потерь в приложениях. Карл Фридрих Гаусс, который ввел использование среднеквадратичной ошибки, сознавал ее произвол и был согласен с возражениями против нее на этих основаниях.[3] Математические преимущества среднеквадратичной ошибки особенно очевидны при ее использовании при анализе производительности линейная регрессия, поскольку он позволяет разделить вариацию в наборе данных на вариации, объясняемые моделью, и вариации, объясняемые случайностью.
Критика
Использование среднеквадратичной ошибки без вопросов подвергалось критике со стороны теоретик решений Джеймс Бергер. Среднеквадратичная ошибка — это отрицательное значение ожидаемого значения одного конкретного вспомогательная функция, квадратичная функция полезности, которая может не подходить для использования в данном наборе обстоятельств. Однако есть некоторые сценарии, в которых среднеквадратичная ошибка может служить хорошим приближением к функции потерь, естественным образом возникающей в приложении.[9]
подобно отклонение, среднеквадратичная ошибка имеет тот недостаток, что выбросы.[10] Это результат возведения в квадрат каждого члена, который фактически дает больший вес большим ошибкам, чем малым. Это свойство, нежелательное для многих приложений, заставило исследователей использовать альтернативы, такие как средняя абсолютная ошибка, или основанные на медиана.
Смотрите также
- Компромисс смещения и дисперсии
- Оценщик Ходжеса
- Оценка Джеймса – Стейна
- Средняя процентная ошибка
- Среднеквадратичная ошибка квантования
- Среднеквадратичное взвешенное отклонение
- Среднеквадратичное смещение
- Среднеквадратичная ошибка прогноза
- Минимальная среднеквадратичная ошибка
- Оценщик минимальной среднеквадратичной ошибки
- Пиковое отношение сигнал / шум
Примечания
- ^ Это может быть доказано Неравенство Дженсена следующим образом. Четвертый центральный момент является верхней границей квадрата дисперсии, так что наименьшее значение для их отношения равно единице, следовательно, наименьшее значение для избыточный эксцесс равно −2, что достигается, например, Бернулли с п=1/2.
Рекомендации
- ^ а б «Список вероятностных и статистических символов». Математическое хранилище. 2020-04-26. Получено 2020-09-12.
- ^ а б «Среднеквадратичная ошибка (MSE)». www.probabilitycourse.com. Получено 2020-09-12.
- ^ а б Lehmann, E. L .; Казелла, Джордж (1998). Теория точечного оценивания (2-е изд.). Нью-Йорк: Спрингер. ISBN 978-0-387-98502-2. Г-Н 1639875.
- ^ Вакерли, Деннис; Менденхолл, Уильям; Шеаффер, Ричард Л. (2008). Математическая статистика с приложениями (7-е изд.). Белмонт, Калифорния, США: Высшее образование Томсона. ISBN 978-0-495-38508-0.
- ^ Современное введение в вероятность и статистику: понимание, почему и как. Деккинг, Мишель, 1946-. Лондон: Спрингер. 2005 г. ISBN 978-1-85233-896-1. OCLC 262680588.CS1 maint: другие (ссылка на сайт)
- ^ Стил, Р.Г.Д., и Торри, Дж. Х., Принципы и процедуры статистики с особым акцентом на биологические науки., Макгроу Хилл, 1960, стр.288.
- ^ Настроение, А .; Graybill, F .; Боэс, Д. (1974). Введение в теорию статистики (3-е изд.). Макгроу-Хилл. п.229.
- ^ ДеГрут, Моррис Х. (1980). вероятность и статистика (2-е изд.). Эддисон-Уэсли.
- ^ Бергер, Джеймс О. (1985). «2.4.2 Некоторые стандартные функции потерь». Статистическая теория принятия решений и байесовский анализ (2-е изд.). Нью-Йорк: Springer-Verlag. п.60. ISBN 978-0-387-96098-2. Г-Н 0804611.
- ^ Бермехо, Серхио; Кабестани, Джоан (2001). «Ориентированный анализ главных компонентов для классификаторов с большой маржой». Нейронные сети. 14 (10): 1447–1461. Дои:10.1016 / S0893-6080 (01) 00106-X. PMID 11771723.
Среднеквадратичная ошибка (Mean Squared Error) – Среднее арифметическое (Mean) квадратов разностей между предсказанными и реальными значениями Модели (Model) Машинного обучения (ML):
Рассчитывается с помощью формулы, которая будет пояснена в примере ниже:
$$MSE = frac{1}{n} × sum_{i=1}^n (y_i — widetilde{y}_i)^2$$
$$MSEspace{}{–}space{Среднеквадратическая}space{ошибка,}$$
$$nspace{}{–}space{количество}space{наблюдений,}$$
$$y_ispace{}{–}space{фактическая}space{координата}space{наблюдения,}$$
$$widetilde{y}_ispace{}{–}space{предсказанная}space{координата}space{наблюдения,}$$
MSE практически никогда не равен нулю, и происходит это из-за элемента случайности в данных или неучитывания Оценочной функцией (Estimator) всех факторов, которые могли бы улучшить предсказательную способность.
Пример. Исследуем линейную регрессию, изображенную на графике выше, и установим величину среднеквадратической Ошибки (Error). Фактические координаты точек-Наблюдений (Observation) выглядят следующим образом:
Мы имеем дело с Линейной регрессией (Linear Regression), потому уравнение, предсказывающее положение записей, можно представить с помощью формулы:
$$y = M * x + b$$
$$yspace{–}space{значение}space{координаты}space{оси}space{y,}$$
$$Mspace{–}space{уклон}space{прямой}$$
$$xspace{–}space{значение}space{координаты}space{оси}space{x,}$$
$$bspace{–}space{смещение}space{прямой}space{относительно}space{начала}space{координат}$$
Параметры M и b уравнения нам, к счастью, известны в данном обучающем примере, и потому уравнение выглядит следующим образом:
$$y = 0,5252 * x + 17,306$$
Зная координаты реальных записей и уравнение линейной регрессии, мы можем восстановить полные координаты предсказанных наблюдений, обозначенных серыми точками на графике выше. Простой подстановкой значения координаты x в уравнение мы рассчитаем значение координаты ỹ:
Рассчитаем квадрат разницы между Y и Ỹ:
Сумма таких квадратов равна 4 445. Осталось только разделить это число на количество наблюдений (9):
$$MSE = frac{1}{9} × 4445 = 493$$
Само по себе число в такой ситуации становится показательным, когда Дата-сайентист (Data Scientist) предпринимает попытки улучшить предсказательную способность модели и сравнивает MSE каждой итерации, выбирая такое уравнение, что сгенерирует наименьшую погрешность в предсказаниях.
MSE и Scikit-learn
Среднеквадратическую ошибку можно вычислить с помощью SkLearn. Для начала импортируем функцию:
import sklearn
from sklearn.metrics import mean_squared_errorИнициализируем крошечные списки, содержащие реальные и предсказанные координаты y:
y_true = [5, 41, 70, 77, 134, 68, 138, 101, 131]
y_pred = [23, 35, 55, 90, 93, 103, 118, 121, 129]Инициируем функцию mean_squared_error(), которая рассчитает MSE тем же способом, что и формула выше:
mean_squared_error(y_true, y_pred)
Интересно, что конечный результат на 3 отличается от расчетов с помощью Apple Numbers:
496.0Ноутбук, не требующий дополнительной настройки на момент написания статьи, можно скачать здесь.
Автор оригинальной статьи: @mmoshikoo
Фото: @tobyelliott


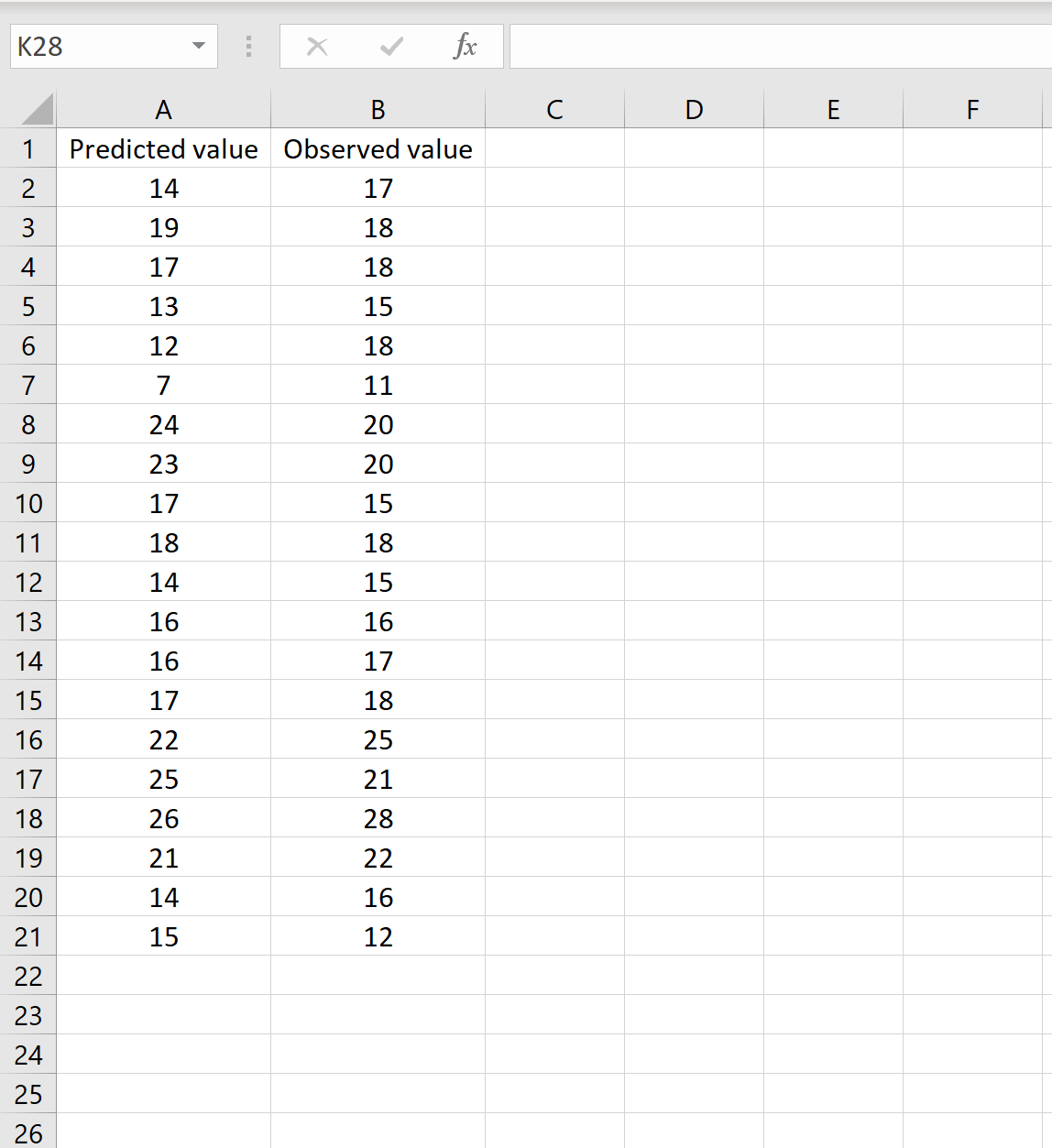
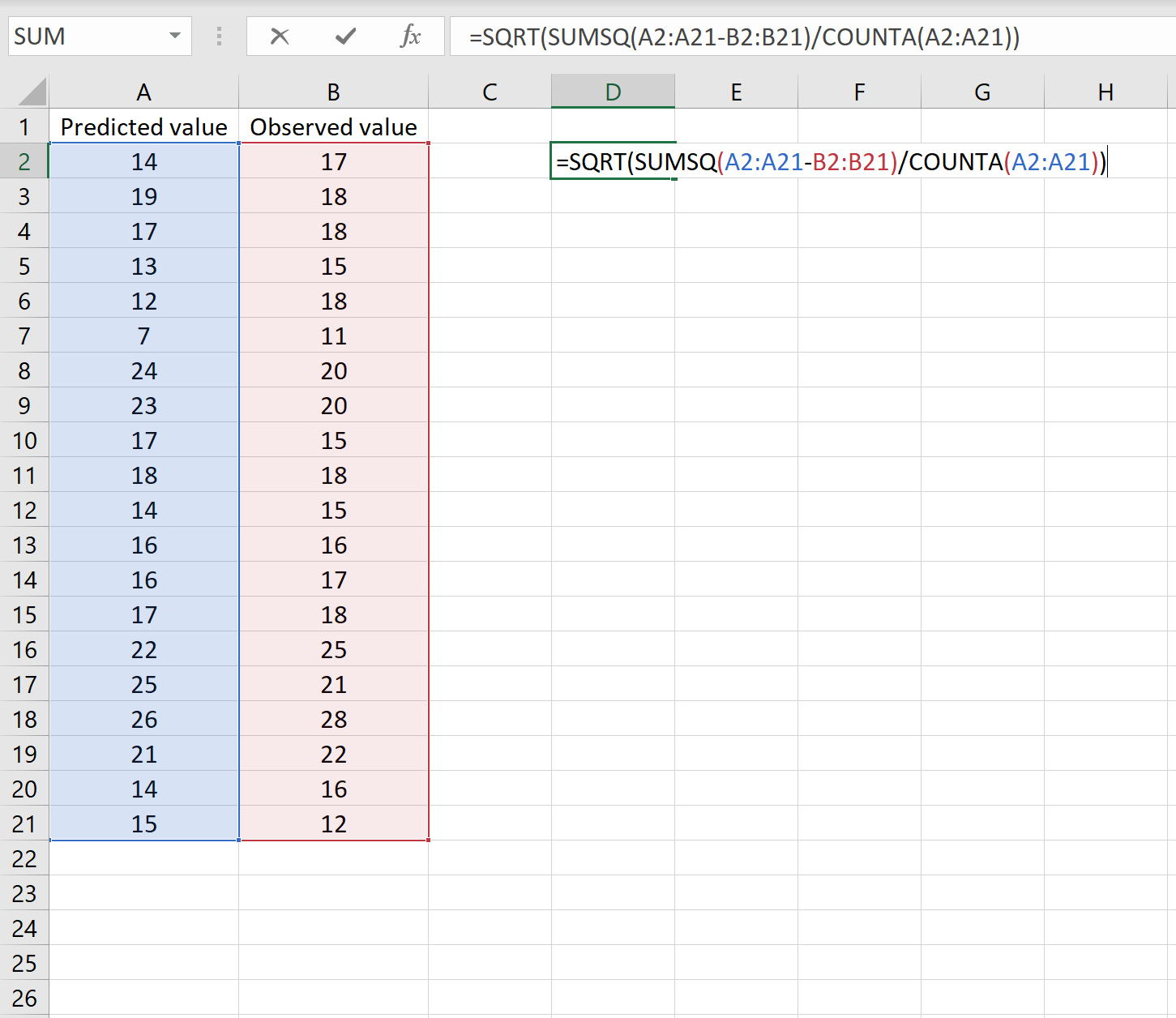
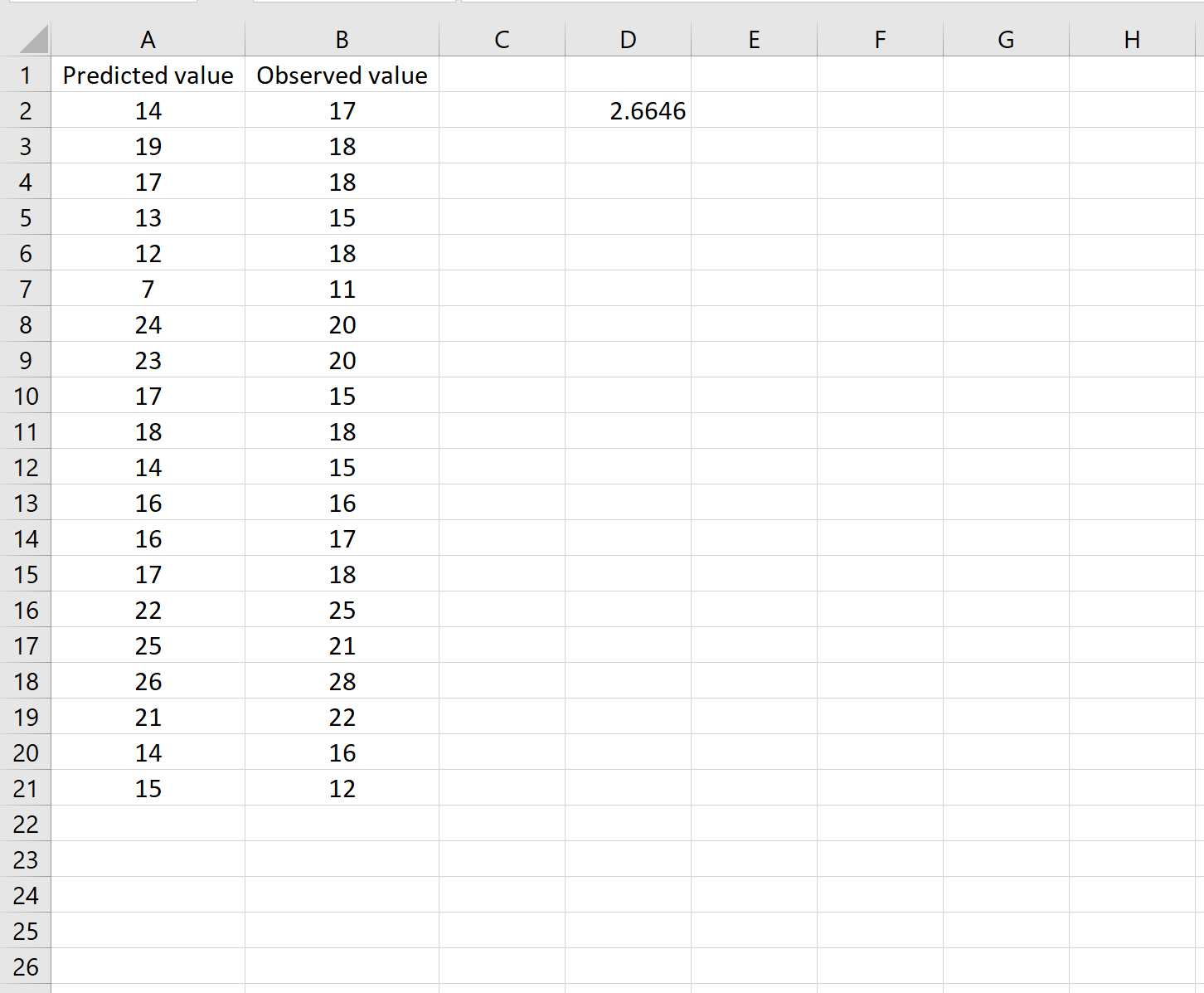
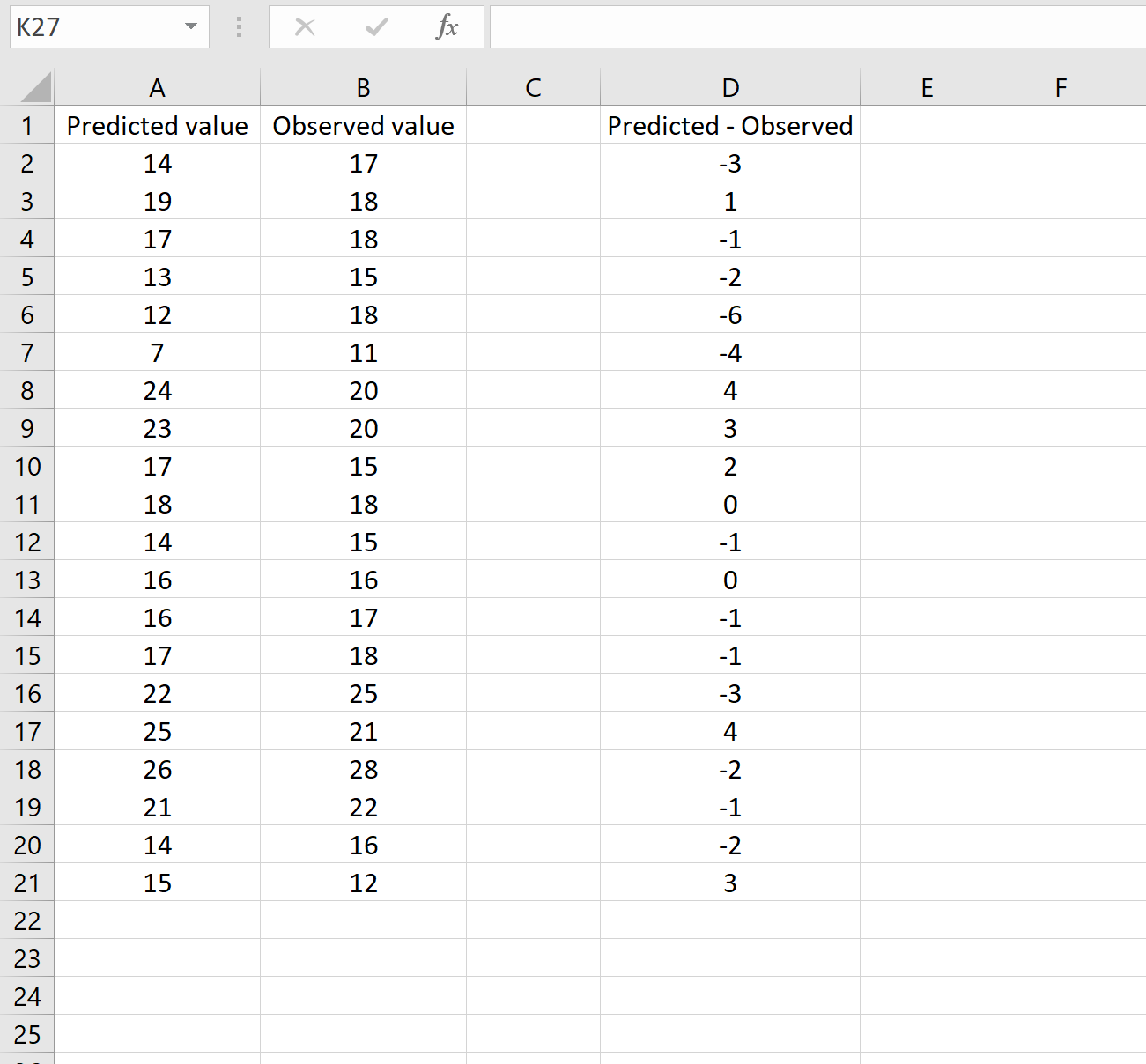
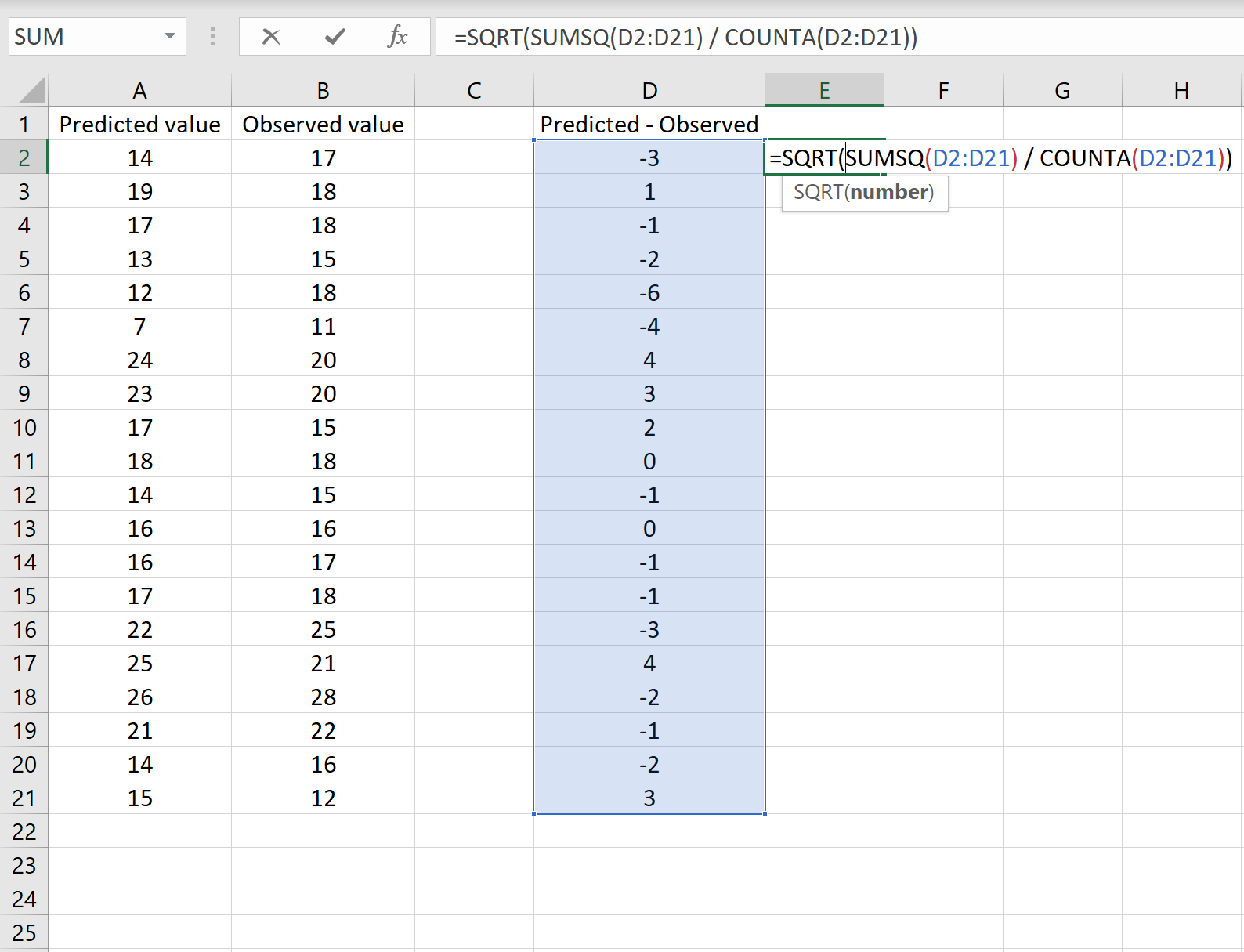
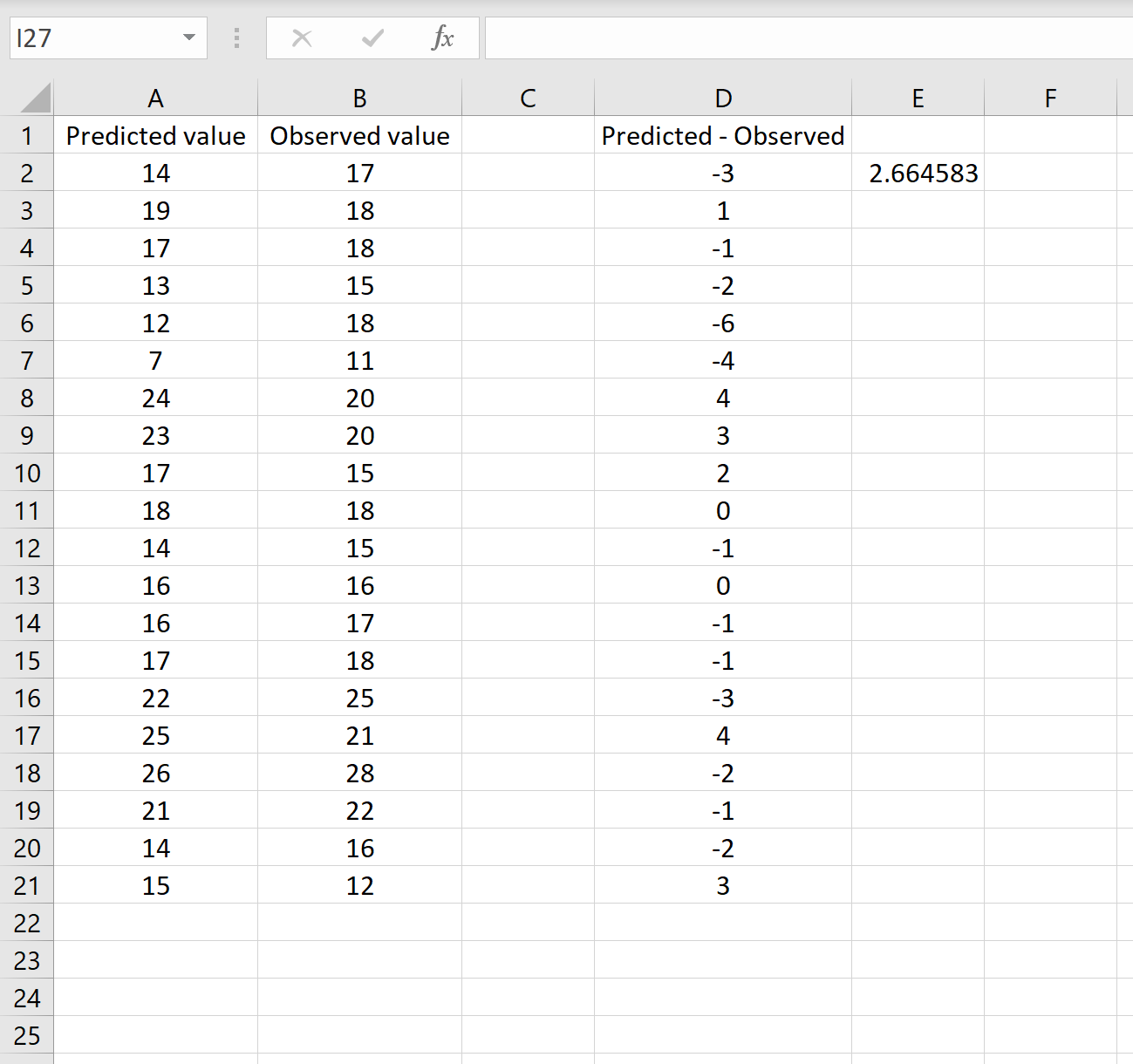



![{displaystyle operatorname {MSE} ({hat {theta }})=operatorname {E} _{theta }left[({hat {theta }}-theta )^{2}right].}](https://wikimedia.org/api/rest_v1/media/math/render/svg/9a0e1b3bac58f9ba2d2f4ff8b85b2e35a8f4bf78)

![{displaystyle {begin{aligned}operatorname {MSE} ({hat {theta }})&=operatorname {E} _{theta }left[({hat {theta }}-theta )^{2}right]\&=operatorname {E} _{theta }left[left({hat {theta }}-operatorname {E} _{theta }[{hat {theta }}]+operatorname {E} _{theta }[{hat {theta }}]-theta right)^{2}right]\&=operatorname {E} _{theta }left[left({hat {theta }}-operatorname {E} _{theta }[{hat {theta }}]right)^{2}+2left({hat {theta }}-operatorname {E} _{theta }[{hat {theta }}]right)left(operatorname {E} _{theta }[{hat {theta }}]-theta right)+left(operatorname {E} _{theta }[{hat {theta }}]-theta right)^{2}right]\&=operatorname {E} _{theta }left[left({hat {theta }}-operatorname {E} _{theta }[{hat {theta }}]right)^{2}right]+operatorname {E} _{theta }left[2left({hat {theta }}-operatorname {E} _{theta }[{hat {theta }}]right)left(operatorname {E} _{theta }[{hat {theta }}]-theta right)right]+operatorname {E} _{theta }left[left(operatorname {E} _{theta }[{hat {theta }}]-theta right)^{2}right]\&=operatorname {E} _{theta }left[left({hat {theta }}-operatorname {E} _{theta }[{hat {theta }}]right)^{2}right]+2left(operatorname {E} _{theta }[{hat {theta }}]-theta right)operatorname {E} _{theta }left[{hat {theta }}-operatorname {E} _{theta }[{hat {theta }}]right]+left(operatorname {E} _{theta }[{hat {theta }}]-theta right)^{2}&&operatorname {E} _{theta }[{hat {theta }}]-theta ={text{const.}}\&=operatorname {E} _{theta }left[left({hat {theta }}-operatorname {E} _{theta }[{hat {theta }}]right)^{2}right]+2left(operatorname {E} _{theta }[{hat {theta }}]-theta right)left(operatorname {E} _{theta }[{hat {theta }}]-operatorname {E} _{theta }[{hat {theta }}]right)+left(operatorname {E} _{theta }[{hat {theta }}]-theta right)^{2}&&operatorname {E} _{theta }[{hat {theta }}]={text{const.}}\&=operatorname {E} _{theta }left[left({hat {theta }}-operatorname {E} _{theta }[{hat {theta }}]right)^{2}right]+left(operatorname {E} _{theta }[{hat {theta }}]-theta right)^{2}\&=operatorname {Var} _{theta }({hat {theta }})+operatorname {Bias} _{theta }({hat {theta }},theta )^{2}end{aligned}}}](https://wikimedia.org/api/rest_v1/media/math/render/svg/2ac524a751828f971013e1297a33ca1cc4c38cd6)
![{displaystyle {begin{aligned}operatorname {MSE} ({hat {theta }})&=mathbb {E} [({hat {theta }}-theta )^{2}]\&=operatorname {Var} ({hat {theta }}-theta )+(mathbb {E} [{hat {theta }}-theta ])^{2}\&=operatorname {Var} ({hat {theta }})+operatorname {Bias} ^{2}({hat {theta }})end{aligned}}}](https://wikimedia.org/api/rest_v1/media/math/render/svg/864646cf4426e2b62a3caf9460382eec1a77fe4e)

![{displaystyle operatorname {MSE} left({overline {X}}right)=operatorname {E} left[left({overline {X}}-mu right)^{2}right]=left({frac {sigma }{sqrt {n}}}right)^{2}={frac {sigma ^{2}}{n}}}](https://wikimedia.org/api/rest_v1/media/math/render/svg/b4647a2cc4c8f9a4c90b628faad2dcf80c4aae84)



![{displaystyle {begin{aligned}operatorname {MSE} (S_{a}^{2})&=operatorname {E} left[left({frac {n-1}{a}}S_{n-1}^{2}-sigma ^{2}right)^{2}right]\&=operatorname {E} left[{frac {(n-1)^{2}}{a^{2}}}S_{n-1}^{4}-2left({frac {n-1}{a}}S_{n-1}^{2}right)sigma ^{2}+sigma ^{4}right]\&={frac {(n-1)^{2}}{a^{2}}}operatorname {E} left[S_{n-1}^{4}right]-2left({frac {n-1}{a}}right)operatorname {E} left[S_{n-1}^{2}right]sigma ^{2}+sigma ^{4}\&={frac {(n-1)^{2}}{a^{2}}}operatorname {E} left[S_{n-1}^{4}right]-2left({frac {n-1}{a}}right)sigma ^{4}+sigma ^{4}&&operatorname {E} left[S_{n-1}^{2}right]=sigma ^{2}\&={frac {(n-1)^{2}}{a^{2}}}left({frac {gamma _{2}}{n}}+{frac {n+1}{n-1}}right)sigma ^{4}-2left({frac {n-1}{a}}right)sigma ^{4}+sigma ^{4}&&operatorname {E} left[S_{n-1}^{4}right]=operatorname {MSE} (S_{n-1}^{2})+sigma ^{4}\&={frac {n-1}{na^{2}}}left((n-1)gamma _{2}+n^{2}+nright)sigma ^{4}-2left({frac {n-1}{a}}right)sigma ^{4}+sigma ^{4}end{aligned}}}](https://wikimedia.org/api/rest_v1/media/math/render/svg/cf22322412b8454c706d78671e5d94208675a6e0)