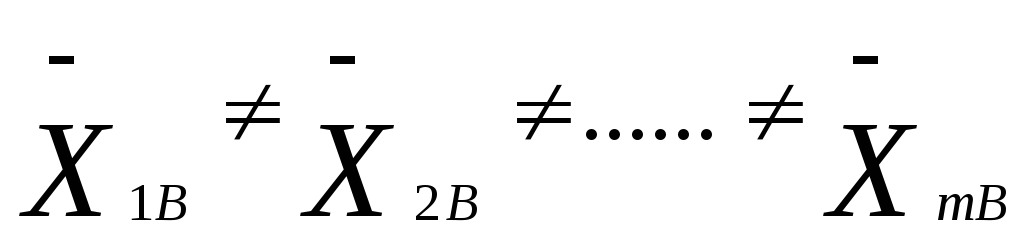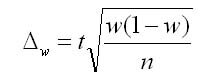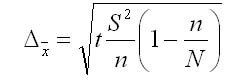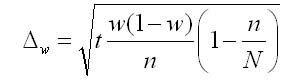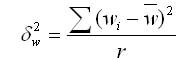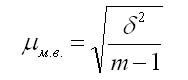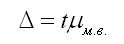. Данная задача
решается в такой последовательности:
1.1)
из генеральной совокупности численностью
в N
единиц механическим способом
осуществляется выборка численностью
единиц, при этом численность выборки
должна меньше тридцать единиц
1.2)
по выборочной совокупности определяется
выборочная средняя, как оценка для
средней генеральной ; при ее расчете
может быть использована формула
средней арифметической простой

вариационным рядом распределения )
средней арифметической взвешенной
1.3)
по выборочной совокупности определяется
значение выборочного среднего
квадратического отклонения по формулам
:


определяется как средняя взвешенная
) ;
1.4)
определяется средняя ошибка выборочной
средней
1.5) устанавливается
доверительный уровень вероятности
( Р );
1.6)
для принятого доверительного уровня
вероятности по таблицам распределения
t-
Стьюдента находят значение коэффициента
t
;
1.7)
определяются границы предельной
ошибки
;
1.8)
с принятым доверительным уровнем
вероятности генеральная средняя
находится в интервале
0
=
±
;
Сравниваем
полученные на основе малых выборок
границы с границами полученными на
основе больших выборок
2.Определение
необходимой численности выборки
Условие
: величина предельной ошибки задана
и составила с установленным доверительным
уровнем вероятности величину
( ошибку берем несколько большую чем
полученную в задаче 1 ) ;
Требуется
определить
какова должна быть минимальная
численность выборки для обеспечения
заданной ошибки
Решение
:
2.1)
поскольку для формирования выборки
планируется использовать механический
отбор, необходимую численность выборки
определим по формуле :

при
этом величину дисперсии возьмем
из первой задачи, а величину коэффициента
t
из таблиц распределения t-
Стьюдента . По полученному результату
сделаем выводы .
3. Определение вероятности появления заданной ошибки
Условие
: величина предельной ошибки задана
и составила с установленным доверительным
уровнем вероятности величину
,
задана также численность выборки (
при этом ошибку задаем меньшую, чем
полученную в задаче 1, а выборку в
пределах 30 единиц, то есть малую )
Требуется
определить
какова гарантия ( какова вероятность
), что при заданной численности выборки
ошибка не выйдет за установленные
границы.
Решение
3.1
) с уровнем вероятности связан
коэффициент t
распределения Стьюдента . Исходя из
равенства
=
, находим

3.2
) по таблицам распределения t
– Стьюдента находим искомый уровень
вероятности (Р)
Занятие
7 Проведение типического отбора.
Определение ошибок при типическом
отборе
Модуль 2. Модульная
единица 8
Условие
: Имеется
генеральная совокупность численностью
в N
единиц
Требуется
: Провести
типический отбор численностью в n
единиц . Определить ошибки выборки.
Решение
1.1)
установим наличие в генеральной
совокупности качественно отличных
частей. Разобьем генеральную совокупность
на m
качественно
отличных частей ( групп ) ;
1.2)
определим численность каждой группы
(части) в генеральной совокупности ();
1.3
) определим представительство каждой
группы генеральной совокупности в
выборке :

1.4
) из каждой группы генеральной
совокупности в соответствии с ее
представительством механическим
способом произведем выборку.; по каждой
единице попавшей в выборку запишем
значение признака —, при этом индексI
– означает номер группы, а индекс j
– номер наблюдения в группе.
1.5)
определим среднее значение признака
по выборке
=
1.6
) рассчитаем среднюю ошибку выборочной
средней по формуле
1.7
) для нахождения средней внутригрупповой
дисперсии воспользуемся формулой :
Чтобы
воспользоваться этой формулой надо
предварительно найти средние значения
признака по группам выборочной
совокупности
и квадраты каждого из значений
попавших в выборку.
1.8
) зная среднюю ошибку рассчитаем
предельную ошибку выборочной средней

, для чего предварительно в соответствии
с принятым уровнем доверия ( Р ) по
таблицам ( t
– нормального распределения или t
–Стьюдента ) находим значение
нормированного отклонения t
Занятие
8 Критерий
как критерий согласия и независимости
Модуль2. Модульные
единицы 9,10, 11
Задача1
Критерий
как
критерий согласия
Условие
: имеется
распределение выборочной совокупности
по группам
Требуется
: установить
соответствует ли распределение по
группам в генеральной совокупности,
из которой произведена выборка,
некоторой пропорции
Решение
1.1)
выдвинем две гипотезы: Н0
( нулевая гипотеза ) – распределение
генеральной совокупности по группам
соответствует ожидаемой пропорции
и НА
(альтернативная гипотеза )
распределение генеральной совокупности
ожидаемой пропорции не соответствует;
1.2 ) установим
уровень значимости (α )и соответственно
1- α = β -достоверность вывода;
1.3
) в качестве критерия для проверки
выдвинутых гипотез используем
параметрический критерий
,
поскольку наблюдения по группам
независимы друг от друга;
1.4
) рассчитаем фактическое значение
критерия по формуле :
факт
=

где— фактические численности по группам
( интервалам) выборки— ожидаемые численности, причем в
качестве ожидаемых берутся численности
соответствующие нулевой гипотезе
(Н0 );
1.5 ) этапы расчета
критерия оформим в таблице
|
Этапы расчета критерия |
Формула расчета |
Группы |
||||
|
1 |
2 |
3 |
4 |
5 |
||
|
Фактические |
ni |
|||||
|
Ожидаемые |
ñi |
|||||
|
Разности |
ni |
|||||
|
Квадрат |
(ni |
|||||
|
Отношение |
(ni |
1.6
) сумма по последней строке таблицы
даст фактическое значение критерия(
)
1
.7 ) сравним фактическое значение
критерия с табличным , которое найдем
с принятым уровнем значимости и
числом степеней свободы равнымm-1,
где m
— число интервалов (групп) . Сравнение
позволит сделать вывод о справедливости
нулевой или альтернативной гипотезы
( еслипринимается нулевая гипотеза, если
—
альтернативная )
Задача
2 Критерий
как критерий независимости
Условие
: имеется
распределение выборочной совокупности
по двум признакам;
Требуется
: установить
взаимосвязаны или нет распределения
по этим признакам в генеральной
совокупности
Решение
.
Выборочные данные в этом случае
представлены в виде такой , например,
таблицы с двумя входами
|
Группы |
Группы |
Итого |
|||
|
а |
В |
с |
d |
||
|
А |
|
… |
… |
… |
|
|
В |
… |
… |
… |
… |
|
|
С |
… |
… |
… |
|
|
|
Итого |
|
|
|
|
|
2.1)
выдвинем гипотезы : нулевую — распределение
по первому признаку не зависит от
распределения по второму и альтернативную
о наличии взаимосвязи между
распределениями
2.2) определимся
с уровнем значимости ;
2.3)
в качестве критерия для проверки
выдвинутых гипотез воспользуемся
критерием
,
используя его как критерий независимости;
2.4 ) фактическое
значение критерия рассчитаем по
формуле

ожидаемые частоты при этом должны
соответствовать нулевой гипотезе о
независимости распределений и
определяются по формуле

то есть для нахождения ожидаемой
частоты с координатами : строкаs
и столбец
p
надо
обратиться к фактическим частотам ,
найти произведение итога по строке s
на итог
по столбцу
р и полученное
произведение разделить на общую
численность совокупности.
. При
определении ожидаемых частот естественно
следует производить округление до
целых значений.
2.4
) Результаты расчетов ожидаемых частот
оформляются в таблице аналогичной
выше приведенной Правильность расчета
ожидаемых частот проверяется сравнением
итогов по строкам и столбцам для
фактических и ожидаемых частот. Эти
итоги должны совпадать ( за счет
округления могут иметь место несовпадения
в несколько единиц ). Численность
каждой ожидаемой частоты должна
превышать 5 единиц, в противном случае
прежде чем рассчитывать фактическое
значение критерия следует произвести
объединение интервалов.
2.5
) в заключение найденное фактическое
значение критерия (факт)
следует сравнить с табличным (табл
), при этом
табличное значение зависит от
установленного уровня значимости и
от числа степеней свободы, которое в
данном аспекте использования критерия
рассчитывается по формулеdf
(
= (k-1)(l=1),
где к
и l
— соответственно
число строк
и столбцов. В зависимости от соотношения
факт
и
табл
принимается
соответственно или нулевая или
альтернативная гипотезы.
Занятие
9Критерий
как критерий однородности
Модуль 2. Модульные
единицы 9, 12
Условие
: имеются две выборочных совокупности,
каждая из которых распределена по
одному и тому же признаку .
Требуется:
установить одинаковым или нет является
распределение двух генеральных
совокупностей , из которых сделаны
выборки.
Решение
1.1
) в качестве нулевой гипотезы выдвинем
предположение , что две генеральные
совокупности однородны по составу. В
качестве альтернативной выдвинем
предположение, что совокупности не
однородны;
1.2 ) установим
уровень значимости;
1.3)
в качестве критерия для проверки
выдвинутых гипотез воспользуемся
критерием
,
используя его в качестве критерия
однородности ;
1.4 ) рассчитаем
фактическое значение критерия по
формуле
:

где
— численность каждойj
– ой из к
групп в
первой совокупности ;
— общая численность первой выборочной
совокупности ;— численность каждойj-
ой из к
групп второй совокупности ;
— общая численность второй выборочной
совокупности ;
–ой группы в первой выборке ;

ой группы во второй выборочной
совокупности ;
+
— общая численность группыj
в обеих выборочных совокупностях. Ход
расчетов фактического значения
критерия следует оформить в таблице
Таблица
К
расчету фактического значения критерия
|
Группы (интервалы) |
Первая |
Вторая |
Доля |
Квадрат разности долей |
Сумма частот по интер- валам (В) |
Отно шение А/В |
|
|
первая выборка |
вторая выборка |
||||||
|
|
|
|
|
( |
|
||
|
А |
|||||||
|
В |
|||||||
|
С |
|||||||
|
Итого |
|
|
1.6
) находим табличное значение критерия
с принятым уровнем значимости (
) и числом степеней свободы, которое
в данном случае равноdf
(=
k
-1, где k
— число групп, на которое подразделена
каждая из совокупностей;
1.7
) сопоставляя фактическое значение
рассматриваемого критерия с табличным
формулируется соответствующий вывод;
Занятие 10 Проверка
гипотезы относительно генеральной
средней
Модуль2. Модульная
единица 13
Условие
: имеется
генеральная
совокупность численностью N
единиц.
Требуется
: установить
равна ли средняя в этой совокупности
величине а
Решение
1.1)
из генеральной
совокупности механическим способом
произведем большую выборку численностью
n
единиц. По каждой единице, попавшей в
выборке зарегистрируем значение
признака
;
1.2
) рассчитаем среднюю по выборке
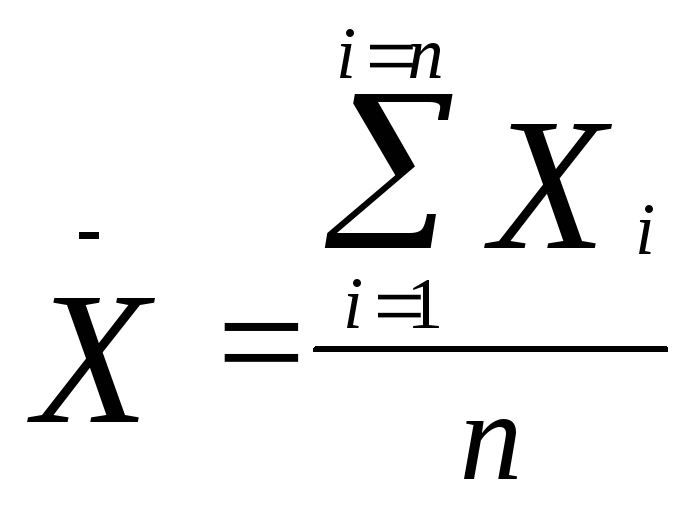
1.3
) сформулируем нулевую и рабочую
гипотезы . В качестве нулевой гипотезы
выдвигается предположение
В качестве альтернативной гипотезы
выдвинем две( ненаправленная альтернативная
гипотеза ) иили
( направленная альтернативная )
гипотеза.;
1.4
) в качестве критериев для проверки
выдвинутых гипотез использоваться
два : критерий t
–нормального распределения или
критерий t-Стьюдента
;
1.5 ) установим
уровень значимости;.
1.6
) рассчитаем фактическое значения
критерия . по данным выборки по
алгоритму

— рассчитанное по выборке значение
средней ;
-предполагаемое
в генеральной совокупности среднее
значение признака ;
=
— средняя ошибка выборочной средней
,
1.7
) найдем табличное значение критерия
— при ненаправленной альтернативной
гипотезе t
–нормального распределения зависит
только от уровня значимости. В случае
направленной гипотезы, табличное
значение следует брать с удвоенным
его уровнем (),
хотя окончательный вывод формулируется
с принятым заранее уровнем. Если
используется критерийt-Стьюдента
, то его табличное значение , кроме
уровня значимости, зависит от числа
степеней свободы : d
f
()
=
1.8
) сформулируем окончательный вывод
относительно выдвинутых гипотез по
схеме : еслипринимается
,
если— альтернативная с учетом ее содержания
( направленная или ненаправленная )
Занятие
11 Проверка гипотезы относительно
средних по данным двух выборок
Модуль2 . Модульная
единица 14
Задача
1 Проверка гипотезы относительно двух
средних по данным двух независимых
выборок
Условие
: имеются
две малых выборки .
Требуется
: на основании имеющихся выборок
установить имеют ли место различия
между средними по генеральным
совокупностям, из которых произведены
выборки
Решение
-
)
вначале следует установить характер
двух выборок; если выборки независимые,
то последующие шаги состоят в следующем
1.2)
выдвигаем две гипотезы : Н 0
:
,
и НА :
(ненаправленную
) или направленную НА
:
или наоборот
1.2) определяемся
с уровнем значимости
1.3
) поскольку выборки малые в качестве
критерия для проверки обозначенных
выше гипотез используется критерий t
— Стьюдента
1.4
) определяемся с ситуацией к которой
принадлежат исходные данные , для чего
проверяем вспомогательную гипотезу
: Н0 :и соответственно НА
:.
Проверка этой вспомогательной
гипотезы производится на основе
критерияF
– критерия; фактическое значение
критерия рассчитывается так:

еслиили

если,
гдеи
— дисперсии по выборкам; фактическое
значение критерия сопоставляется
с табличным, которое зависит от
принятого уровня значимости и от числа
степеней свободы для дисперсий по
первой выборкеd
f
()1
= n1
– 1 и по
второй выборке d
f
()2
=п2
— 1
. Принятие решение о равенстве или
неравенстве дисперсий по генеральным
совокупностям происходит по традиционной
схеме.
1.6)
в зависимости от ситуации , к которой
принадлежат исходные данные ,
фактическое значение критерия t-
Стьюдента рассчитывается по следующим
алгоритмам :
При
первой ситуации
(равны численности выборок , равны и
дисперсии)

— среднее значение признака по первой
выборке ;— среднее значение признака по второй
выборке ,при этом разность между
средними берется по абсолютной величине.

усредненная дисперсия
При
второй ситуации
( дисперсии равны, но численности
выборок не равны ) фактическое значение
критерия находится по формуле

усредненной дисперсии будет выглядеть
так :
При
третьей ситуации ( при
равенстве численности выборок, дисперсии
не равны)
фактическое значение критерия
определяется по формуле

При
четвертой ситуации
( нет равенства в дисперсиях и в
численности выборок ) фактическое
значение критерия определяется
аналогично как и при третьей;
1.7)
находим табличное значение критерия
t-Стьюдента
: для первых трех ситуаций , кроме
уровня значимости оно зависит от числа
степеней свободы , которое для первых
двух ситуаций определяется по формуле:
d
f
()
= (. Для третьей ситуации при определении
числа степеней свободы следует внести
поправку и формула приобретает вид :
d
f
()
= [ (]
[0,5 +
Для
четвертой ситуации
табличное значение критерия является
расчетной величиной и определяется
по формуле :

гдеи
— табличные значения критерияt
– Стьюдента для первой и второй
выборок, соответственно с числом
степеней свободы
и
;
1.8
) Сравнивая фактическое и табличное
значения критерия формулируем
соответствующий вывод о выдвинутых
гипотезах , при этом при направленной
гипотезе для всех ситуаций табличное
значение критерия берется с удвоенным
уровнем значимости.
Задача
2 Проверка гипотезы относительно
средних при зависимых выборках
Условие
: имеются
две малых выборки .
Требуется
: на основании имеющихся выборок
установить имеют ли место различия
между средними по генеральным
совокупностям, из которых произведены
выборки
Решение
2.1)
вначале следует установить характер
двух выборок; если выборки зависимые,
то последующие шаги состоят в следующем
2.2
) выдвигаем гипотезы : в качестве
нулевой выдвигается предположение,
что средняя разность попарно
взаимосвязанных наблюдений в
генеральной совокупности равна 0 (
нулю ) , то есть
,
в качестве альтернативной ненаправленной, альтернативной направленной
или
.
2.3
) определяемся с уровнем значимости ;
2.4
) в качестве критерия для проверки
выдвинутых гипотез воспользуемся
критерием t
– Стьюдента;
2.5
) фактическое значение критерия
устанавливаем по формуле

гдесредняя разность для
попарно взаимосвязанных наблюдений
по 2- выборкам. Для ее нахождения вначале
необходимо найти разность по каждой
изпар наблюдений , то есть
,
а затем их среднее значение

разностей .
2.6
) фактическое значение критерия
сопоставляется с табличным, при этом
число степеней свободы для нахождения
табличного значения определяется по
формуле d
f
()
=
; формулируем, вытекающие из сравнения
выводы.
Занятие 12
Проверка
гипотезы относительно доли признака.
Проверка гипотезы о принадлежности
резко выделяющегося значения признака
изучаемой совокупности
Модуль 2 Модульная
единица 15
Задача
1 Проверка гипотезы относительно доли
признака
Условия
: имеется
генеральная совокупность, в которой
единицы характеризуются неким
качественным признаком, имеющим
альтернативный характер.
Требуется
: на основе
большой выборки установить равна
ли в генеральной совокупности доля
единиц с определенным качеством величине
Q
Решение:
1.1)
из генеральной совокупности произведем
механическим способом выборку
численностью n
единиц; подсчитаем число единиц в
выборке с определенным качеством (m
) ; найдем выборочную долю этих единиц
1.1)
выдвинем две гипотезы Н9
: Р=Q
и альтернативная РQ;
1.2 ) определимся
с уровнем значимости ;
1.3
) поскольку выборки большие , для
проверки выдвинутых гипотез воспользуемся
критерием t
– нормального распределения;
1.4
) рассчитаем фактическое значение
критерия по формуле

гдеp
– доля единиц определенного качества
по выборке, g
— доля единиц противоположного
качества по выборке ; n
– численность выборки;
1.5
) сравним фактическое значение критерия
с табличным, которое зависит только от
уровня значимости и сделаем
соответствующий вывод.
Задача 2 Проверка
гипотезы относительно доли признака
в двух генеральных совокупностях
Условие
: имеются
две генеральных совокупности, в которых
единицы характеризуются неким
качественным признаком, имеющим
альтернативный характер.
Требуется:
установить
равны или нет в двух генеральных
совокупностях доли единиц одинакового
качества
Решение :
2.1
) из каждой генеральной совокупности
произведем выборки численностью
и
единиц;
2.2
) по каждой выборке установим число
единиц определенного качества 
и
);
2.3
) по каждой выборке найдем долю единиц
определенного качества :


2.4
) выдвинем гипотезы : нулевую о
равенстве долей в двух генеральных
совокупностях ,
то
есть:
.и
альтернативную — ненаправленную:
или направленную —
:
(
:
);
2.5 ) определимся
с уровнем значимости;
2.6
) в качестве критерия для проверки
выдвинутых гипотез используется
критерий t
— нормального распределения;
2.7
) расчет фактического значения
критерия может производится по двум
алгоритмам : если каждая из выборочных
доли () лежит в интервале
,
то формула для расчета фактического
значения критерия будет следующей
—
доля единиц с определенным качеством
по первой выборке ;—
доля таких единиц по второй выборке
;,
— доля единиц с противоположным качест-
вом
соответственно по первой и второй
выборкам ;
и
численности выборок.
Если
же хотя бы одна из выборочных долей
лежит вне указанного выше интервала,
то для расчета фактического значения
критерия требуется предварительное
( фи ) преобразование выборочных
долей, при этом значениянаходятся по специальным таблицам.
Фактическое значение критерияt
–нормального распределения находят
по формуле :

где
и
— преобразованные значения выборочных
долей.
2.8
) по таблицам находим критическое
значение критерия; сравнивая его
фактическое значение с табличным
формулируем вывод относительно
выдвинутых гипотез
Задача
3 Проверка гипотезы о принадлежности
резко выделяющегося значения признака
изучаемой совокупности
Условие
: имеется
выборочная совокупность.
Требуется
: установить
принадлежат ли максимальное и минимальное
значение признака исследуемой
совокупности .
Решение
3.1
) выдвинем гипотезы : в качестве
нулевой гипотезы выдвигается
предположение , что резко выделяющиеся
значение признака принадлежат
исследуемой совокупности , в качестве
альтернативной – не принадлежат;
3.2 ) определимся
с уровнем значимости ;
3.3)
для проверки выдвинутых гипотез
воспользуемся критерием Диксона;
3.4)
рассчитаем фактическое значение
критерия , при этом для оценки
максимального значения признака
фактическое значение данного критерия
определяем по формуле : М =
—
максимальное значение признака
относительно которого выдвигается
гипотеза ;— значение признака предшествующее в
ранжированном ряду максимальному;—
минимальное в ранжированном ряду
значение признака;
для
оценки минимального значения
признака , фактическое значение
критерия Диксона определяем по формуле
М =
где— минимальное значение признака
относительно которого выдвигается
гипотеза ;—
следующее за минимальным в ранжированном
ряду значение признака ;—
максимальное значение признака.
3.5
) фактическое значение критерия
сравниваем с табличным, формулируем
соответствующие выводы
Занятие
13 Однофакторный дисперсионный анализ
Модуль 3. Модульные
единицы 16,17
Условие
: имеются
выборочные данные по результатам
однофакторного многовариантного
эксперимента, число наблюдений по
вариантам опыта ( выборкам ) одинаково
Требуется
: установить
наличие или отсутствие различий
между вариантами в генеральных
совокупностях.
Решение
1.1
) выдвигаем две гипотезы, в качестве
нулевой — все m
генеральных
средних равны между собой , то есть
:
; в качестве альтернативной выдвигается
предположение, что хотя бы две генеральных
средних не равны между собой ;:
;
1.2 ) определяемся
с уровнем значимости ;
1.3
) в качестве критерия при воспользуемся
критерием F-Фишера.
1.4
) фактическое значение критерия
определим по формуле

.
Если в ходе расчетов дисперсий
оказалось , чтокритерийF-Фишера
не рассчитывается , а сразу признается
справедливой нулевая гипотеза о
равенстве генеральных средних.. Для
получения необходимых дисперсий
вначале следует разложить общий
объем вариации на составные части в
соответствии с известным законом:
. Поскольку речь идет о выборочных
дисперсияхдля их получения необходимо
соответствующие объемы вариации
разделить на их степени свободы – для
межгрупповой вариации :df
()
=m-1
, где m
– число средних ;для внутригрупповой
вариации df
()=
(N-1)-(m-1),
где N
– общее число наблюдений по всем
выборкам, то есть

1.5
) найдем табличное значение критерия,
которое зависит от уровня значимости
и от степеней свободы df
()
=m-1
и df
()=
(N-1)-(m-1),
Сравнение фактического значения
критерия с табличным позволяет
сформулировать соответствующие
выводы.
1.6
) если по F
– критерию была принята альтернативная
гипотеза , то следует провести
конкретизацию дисперсионного анализа
с использованием критерия Q-
Тьюки
Использование
критерия Q
— Тьюки в целях конкретизации включает
следующие шаги :
1.6.1
) рассчитываем средние значения признака
по группам (выборкам )
,
…..
;
1.6.2
) полученные средние ранжируем , например
ранжированный ряд может выглядеть
так :
,
…..
;
1.6.3
) находим разности первого порядка,
под которыми понимаются
разности
между средними соседними в ранжированном
ряду, например,
—
;
и так далее;
1.6.4
) находим разности второго порядка,
то есть разности между средними стоящими
в ранжированном ряду через одну позицию,
то есть
—
,
и так далее.
1.6.5 ) находим
разности следующих порядков , если для
этого имеются необходимые средние;
1.6.6
) относительно каждой из разностей
выдвигаются две гипотезы : нулевая
( Н0 ) –в
генеральной совокупности разность
равна 0 ( нулю ) иными словами в генеральной
совокупности соответствующие средние
равны между собой и альтернативная
(НА )
— в генеральной совокупности разность
нулю не равна, то есть соответствующие
генеральные средние не равны между
собой ;
1.6.7)
для каждой разности находим ее среднюю
ошибку по формуле :

где
— внутригрупповая дисперсия,
—
число наблюдений в каждой группе (
выборке ).
1.6.8
) каждую из разностей первого порядка
разделим на среднюю ошибку , получим
фактические значения критерия Q-Тьюки
для разностей первого порядка , то есть


1.6.9
) полученные фактические значения
критерия Q-Тьюки
сравниваем с табличным, которое для
всех разностей первого порядка
одинаково. Табличное значение критерия
Q-Тьюки
зависит от уровня значимости, числа
степеней свободы внутригрупповой
вариации и от величины k
, которая для разностей первого порядка
равна 2 . Сравнение позволяет принять
относительно пары средних или нулевую
гипотезу ( средние равны между собой
) или альтернативную гипотезу ( средние
составляющие пару не равны между собой
);
1.6.10
) каждую из разностей второго порядка
разделим на среднюю ошибку и получим
фактические значения критерия Q-Тьюки
для разностей второго порядка. Все
фактические значения критерия Q-Тьюки
сравниваются с одним и тем же табличным
, которое зависит от принятого уровня
значимости, числа степеней свободы
внутригрупповой вариации и величины
k
, которая для разностей второго порядка
равна 3. Сравнение даст основание для
принятия нулевой ( равенство средних
) или альтернативной ( неравенство
средних ) гипотезы.
Аналогичная
процедура осуществляется относительно
разностей третьего, четвертого и так
далее порядков.
Занятие 14
Двухфакторный дисперсионный анализ
Модуль3. Модульные
единицы 16, 17
Условие
: имеются
данные по результатам двухфакторного
эксперимента; число наблюдений по
вариантам одинаково.
Требуется
:
установить наличие или отсутствиеразличий по
вариантам и наличия или отсутствия
эффекта взаимодействия факторов.
Решение
-
)
Выдвинем
три пары гипотез :
первая:
:

:
(
то есть средние по вариантам первого
фактора равны соответственно хотя
бы две из них не равны между собой );
вторая
:
:

:
(
то есть средние по вариантам второго
фактора равны соответственно хотя
бы две из них не равны между собой );
третья:
:
эффект
взаимодействия отсутствует и
:эффект
взаимодействия
имеет место ;
-
) определимся с
уровнем значимости ; -
)
гипотезы проверим на основе критерия
F-
Фишера -
)
расчет трех фактических значений
критерия F-
Фишера произведем
на
основе стандартной программы Excel/
1.5)
полученные фактические значения
критерия сравним с табличными, которые
находятся при следующих степенях
свободы :
для
первой пары гипотез
df
(A)=
k-1
— для большей дисперсии, при этом
k
— число средних ( вариантов ) по первому
фактору) и d
f
(вг) = ( N-1)-
(km
-1)- для меньшей дисперсии, при этом N
– общее число наблюдений, m-
вариантов по второму фактору;
для
второй пары гипотез
df
(B)=
m-1
( для большей дисперсии, при этом
m
— число средних ( вариантов ) по второму
фактору) и d
f
(вг) = ( N-1)-
(km
-1)- для меньшей дисперсии, при этом N
– общее число наблюдений, m-
вариантов по второму фактору;
для
третьей пары гипотез df
(АB)=
( km-1
) –(k-1)-(m-1
) — для большей дисперсии, и d
f
(вг) = ( N-1)-
(km
-1)- для меньшей дисперсии,
Сравнение
фактических и табличных значений
критерия позволит сделать соответствующие
выводы;
1.6
) при принятии альтернативной гипотезы
по первому или второму фактору следует
провести конкретизацию результатов
дисперсионного анализа с использованием
критерия Q-Тьюки,
по методике , изложенной в занятии №13
Занятие
15 Расчет и анализ уравнения парной
корреляционной связи
Модуль 3. Модульные
единицы 18, 19
Условия
: имеются
данные об изменении по единицам
совокупности двух признаков.
Требуется
: построить
, решить и проанализировать уравнение
корреляционной связи
Решение
1.1
) вначале следует уяснить
причинно-следственные связи, выяснить
соподчиненность признаков, то есть
какой из них являются причиной
(факторным признаком ) , а какой
следствием ( признакам результативным).
1.2
) далее следует выбрать вид уравнения;
для выбора вида уравнения необходимо
построить график, где на оси абсцисс
откладываются значения факторного
признака, а на оси ординат значения
признака результативного. Поскольку
по определению одному и тому же значению
факторного признака соответствует
множество неопределенных значений
признака результативного, в результате
указанных выше действий мы получим
некоторую совокупность точек , то
есть корреляционное поле. Общий вид
корреляционного поля позволит
высказать предположение о виде
уравнения.
1.3
) после выбора уравнения следующим
шагом является расчет коэффициентов
уравнения. Расчет коэффициентов
уравнения производится на основе
метода наименьших квадратов. , который
реализуется построением и решением
системы так нормальных уравнений.
Если в качестве уравнения корреляционной
связи между y
и x
выбрано
уравнение прямой
,
где система нормальных уравнений,
как будет такой :
;
1.4
) для построения системы уравнений
следует произвести предварительные
расчеты:—
суммы значений результативного
признака;
—
суммы значений факторного признака
;—
суммы произведений факторного и
результативного признаков ;—
суммы квадратов значений факторного
признака;n-
число наблюдений ;
1.5
) решая систему уравнений относительно
a
и b
получим
необходимые значения коэффициентов.
Правильность расчета коэффициентов
проверяем равенством
1.6 ) раскроем
содержание коэффициентов уравнения:
а
является
условным началом содержательной
интерпретации не подлежит; коэффициент
в
— коэффициент регрессии . Он показывает
на сколько в
среднем изменится
результативный признак при изменении
факторного на единицу.
1.7)
рассчитаем коэффициент корреляции
по формуле

где
среднее произведение результативного
и факторного признаков;—
средние значения результативного и
факторного признака;—
средние квадратические отклонения
по результативному и факторному
признакам;
1.8
) возведем в квадрат коэффициент
корреляции, получим коэффициент
детерминации
, раскроем содержание коэффициента
детерминации, то есть установим долю
воспроизведенной вариации в общем
объеме вариации результативного
признака
Занятие
16 Расчет и анализ уравнения множественной
корреляции
Модуль 3. Модульные
единицы 18.19
Условие
: по единицам
выборочной совокупности имеются данные
о значениях результативного и 3-х
факторных признаков.
Требуется
: построить
и
проанализировать
уравнение
множественной корреляции;
Решение
:
1.1
) предполагая линейный характер
зависимости результативного и факторных
признаков , коэффициенты уравнения, а
также коэффициенты множественной
корреляции и детерминации определим
используя стандартную программу
«Регрессия» EXCEL
1.2
) проанализируем полученные коэффициенты
уравнения и показатели тесноты связи;
1.3
) найдем по каждому из трех факторов
стандартизированные коэффициенты
регрессии по формулам :

, где
—
бета – коэффициент поi-
му фактору ;— коэффициент чистой регрессии по
этому фактору ;— средние квадратические отклонения
соответственно поi-ому
факторному признаку и признаку
результативному ;
Эi
=
, где Эi-
коэффициент эластичности по i
–ому фактору,
—
коэффициент регрессии по поi
–ому фактору,

–ому фактору и результативному
признаку.
Величины
, необходимые для расчета бета-коэффициентов
и коэффициентов эластичности получим
используя стандартную программу
«Описательная статистика» EXCEL
;
1.4
) раскроем содержание коэффициентов
, учитывая, что
—
бета – коэффициент показывает насколько
своих средних квадратических отклонений
в среднем изменится результативный
признак при изменении соответствующего
фактора на свое среднее квадратическое
отклонение., а коэффициент эластичности
показывает на сколько долей ( процентов
) в среднем изменится результативный
признак при изменении соответствующего
фактора на долю ( процент ). По величине
стандартизированных коэффициентов
регрессии расставим факторы по
степени их влияния на результат .
1.5 ) рассчитаем
коэффициенты отдельного определения
по формуле :
.
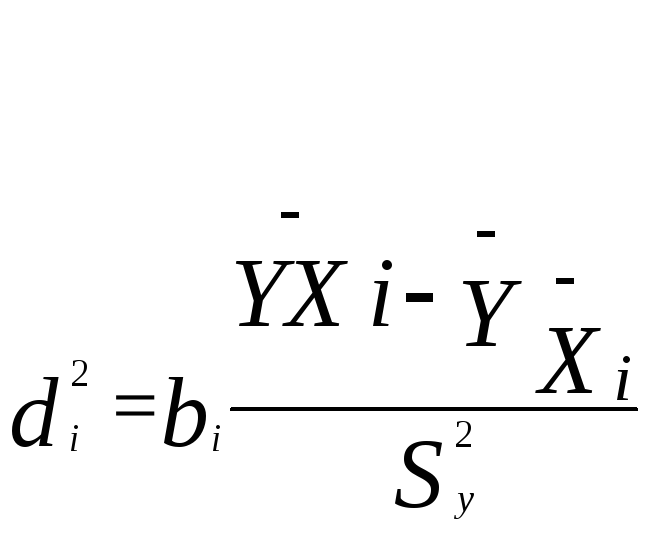
дроби ( разность между средним
произведением и произведением средних
— это ковариация признаков ,— коэффициент чистой регрессии по
соответствующему фактору ;— дисперсия результативного признака..
Значение ковариации находится
использованием стандартной программы
«Ковариация «EXCEL,значение
дисперсии уже известно ( из п 1.4 )
1.6
) проанализируем коэффициенты отдельного
определения, установив вклад каждого
фактора в воспроизведенную вариацию
результативного признака.
Занятие 17 Оценка
выборочных показателей связи
Модуль3. Модульные
единицы 18, 19
Условие
: имеется
уравнение связи полученное по выборочным
данным ( см занятие 15 ).
Требуется
: оценить
полученные по выборке показатели
связи.
Решение
1.1
) во- первых следует проверить гипотезу
о существенности уравнения в целом.
Эта гипотеза проверяется на основе
критерия F
– Фишера, фактическое значение которого
определяется как отношение

соответствующие объемы вариации (и
)
следует разделить на их число степеней
свободы,
гдеm-
число параметров уравнения;
, гдеn-
число наблюдений на основе которых
построено уравнение связи. Полученное
фактическое значение критерия
сравнивается с табличным (),
которое зависит от уровня значимости
и числа степеней свободы воспроизведенной
и остаточной вариации. Еслипринимается гипотеза о несущественности
уравнения и дальнейшая оценка
показателей связи не требуется, если
жепринимается гипотеза о существенности
уравнения и требуется дальнейшая
оценка показателей связи. Расчет
фактического значения критерияF
произведем используя стандартную
программу «Регрессия» EXCEL.
В выходной таблице этой программы даны
также степени свободы, необходимые
для определения табличного значения
критерия
1.2
) проверим гипотезу относительно
выборочного коэффициента регрессии
. для чего вначале выдвинем гипотезы
нулевую в генеральной совокупности
коэффициент регрессии В=0 и
альтернативную — в генеральной
совокупности этот коэффициенты нулю
не равен (В≠0
).
1.3) определимся
с уровнем значимости;
1.4
) поскольку при построении уравнения
была использована малая выборка, то
проверку гипотезы относительно
коэффициента регрессии проведем с
использованием критерия t-Стьюдента
.
Фактическое
значение данного критерия найдем по
формуле

где—
выборочный коэффициент регрессии.
— средняя ошибка коэффициента регрессии,
которая рассчитываем по формуле
где—
остаточная вариация результативного
признака;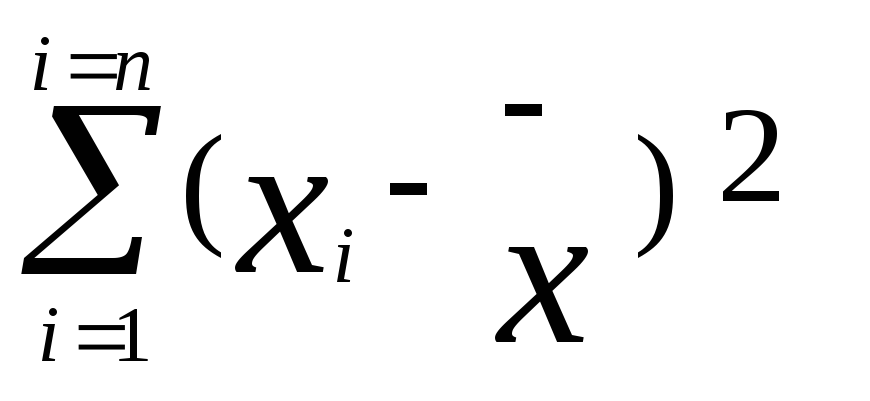
объем вариации факторного признака.
Остаточную
вариацию результативного признака
находим на основе выходной таблицы
программы «Регрессия « EXCEL
Объем вариации факторного признака
на основе программы « Описательная
статистика«
1.5
) фактическое значение критерия
сравниваются с табличным , которое
кроме уровня значимости зависит от
числа степеней свободы, которое равно
,
гдеn
–число наблюдений, m-
число параметров уравнения. По результатам
сравнения формулируем соответствующий
вывод. Если была принята альтернативная
гипотеза, то находим границы коэффициента
регрессии в генеральной совокупности
: В = b ±,
где—
предельная ошибка коэффициента
регрессии, определяемая по формуле
1.6)
проверим гипотезу относительно
коэффициента корреляции . Для чего
вначале выдвинем гипотезы : нулевую
R=0
и альтернативную
— в генеральной совокупности эти
коэффициент корреляции
R≠
0.
Определимся
с уровнем значимости.
В
качестве критерия надо воспользоваться
критерием t
– Стьюдента, поскольку выборка малая.
Фактическое
значение критерия рассчитаем по
формуле

где

при этом r-
выборочный коэффициент корреляции
Фактическое
значение критерия сравниваются с
табличным , которое кроме уровня
значимости зависит от числа степеней
свободы, которое равно
,
гдеn
–число наблюдений, m-
число параметров уравнения. По результатам
сравнения формулируем соответствующий
вывод.
Если
была принята альтернативная гипотеза
о существенности коэффициента
корреляции следует найти его границы
в генеральной совокупности R=
r
±,
где
—
предельная ошибка коэффициента
корреляции равная
ГЛОССАРИЙ УМК
дисциплины «МАТЕМАТИЧЕСКАЯ СТАТИСТИКА»
|
Термин |
Содержание |
|
Вариация |
Изменчивость, |
|
— |
Общая |
|
-вариации |
Разность |
|
Гипотеза |
Предположение |
|
-статистическая |
Предположение |
|
Гистограмма |
Графическое |
|
Граница |
Черта, |
|
— |
Интервал |
|
Дисперсия |
Один |
|
Корреляция |
Особый |
|
Коэффициент |
Отношение |
|
— |
Отношение |
|
— |
Показатель |
|
— |
Показатель |
|
— |
Один |
|
— |
Один |
|
Критерий |
Инструмент |
|
Медиана |
Значение |
|
Мода |
Значение |
|
НСР |
Наибольшая |
|
Область |
Территория |
|
— |
Совокупность |
|
— |
Совокупность |
|
Огива |
Графическое |
|
Отклонение |
Отличие |
|
— |
Один |
|
-стандартное |
Один |
|
Оценка |
Статистическая |
|
Ошибка |
Заблуждение, |
|
— |
Разница |
|
— |
Возможные |
|
Полигон |
Графическое |
|
Признак |
Одно |
|
Ряд |
Расположение |
|
— |
Расположение |
|
— |
Упорядочение |
|
Совокупность |
Собрание |
|
— |
Совокупность |
|
— |
Специально |
|
Средняя |
Некий |
|
Степень |
Число |
|
Частота |
Число, |
|
Уровень |
Некое |
|
-значимости |
Вероятность |
|
-доверия |
Вероятность |
ТЕСТОВЫЕ
ЗАДАНИЯ ИТОГОВОГО КОНТРОЛЯ
УМК
«МАТЕМАТИЧЕСКАЯ
СТАТИСТИКА»
ТЕСТ 1
«Статистическая
совокупность – это собрание единиц
…..
-
.. каждая из которых
индивидуальна по набору признаков; -
…каждая
из которых имеет одно и более общих
свойств (признаков) со всеми другими
единицами; -
…каждая
из которых , хотя бы по одному признаку
, имеет одинаковые значения;
ТЕСТ 2
«Признак -это…..
-
качественная
особенность единицы совокупности; -
…качественная
или количественная особенность
единицы совокупности; -
..количественная
особенность единицы совокупности;
ТЕСТ 3
«Дискретный
признак – это…
1….. качественный
признак;
2….. количественный
признак , который может принимать
любые
значения;
3.
…. количественный признак, который
может принимать лишь отдель-
ные , чаще
целочисленные значения.
ТЕСТ 4
Ранжированный
ряд распределения единиц- это
-
… расположение
единиц в порядке получения информации
о них; -
…. расположение
единиц в зависимости от числа признаков
их характеризующих; -
… расположение
единиц в таком порядке, какой считает
целесообразным исследователь; -
… расположение
единиц совокупности в порядке
возрастания или убывания значения
количественного признака.
ТЕСТ
5
Огива распределения
:
-
Всегда параллельна
оси абсцисс -
Всегда параллельна
оси ординат -
Может
иметь любой угол наклона по отношению
к оси абсцисс
ТЕСТ
6
Если в совокупности
несколько единиц имеют одинаковые
значения
количественного
признака, то…
-
….ранжированный
ряд не построит -
… все единицы,
имеющие одинаковое значение признака
должны иметь одинаковый номер в
ранжированном ряду; -
…единицы
имеющие одинаковое значения признака
должны иметь разные номера в
ранжированном ряду.
ТЕСТ
7
Можно
ли построить вариационный ряд
распределения по качественному
признаку ?
-
Нельзя, можно
построить только ранжированный ряд -
Можно
только в том случае, если качественный
признак имеет -
три и более
градаций ( уровней ) -
Можно в любом
случае
ТЕСТ
8
Что отражается
в правой колонке вариационного ряда
распределения
дискретного
признака ?
1.Частоты
для отдельных значений признака
2.
Значения признака, расположенные в
том порядке как трешил исследователь
3.Значения
признака , расположенные в порядке их
возрастания
4.Значения
признака расположенные в порядке их
убывания.
ТЕСТ
9
Каково
содержание частоты в вариационном
ряду распределения дискретного
признака ?
1.
Это число единиц, имеющих минимальное
значение признака
2.
Это число единиц , имеющих максимальное
значение признака
3. Это число единиц
с одинаковым значением признака
ТЕСТ
10
Чем
отличается частота в интервальном
ряду распределения от частоты в
дискретном ряду распределения ?
-
Ничем
-
Частота
в интервальном ряду относится ко всем
значениям , входящим в интервала в
дискретном к – одному единственному
значению
ТЕСТ
11
Что такое шаг
интервала ?
-
Количество
выделенных интервалов. -
Разность
между верхней и нижней границами
каждого из интервалов -
Разность
между максимальным и минимальным
значениями признака в совокупности -
Полусумма
верхней и нижней границей каждого
из интервалов
ТЕСТ
12
Как рассчитать
шаг интервала ?
1.Надо
численность совокупности разделить
на число интервалов
2.Надо
максимальное значение признака
разделить на число интервалов
3.
Надо разность между максимальным и
минимальным значением
признака разделить
на число интервалов
ТЕСТ
13
Как определить
границы первого интервала ?
-
Нижняя граница
— минимальное значение признака;
верхняя минимальное значение признака
плюс шаг интервала
2.
Нижняя граница -шаг интервала ;
верхняя удвоенный шаг ин-
тервала
3. Нижняя
граница –максимальное значение
признака, верхняя
максимальное
значение минус шаг интервала
ТЕСТ 14
Чему равна верхняя
граница последнего интервала ?
-
Максимальному
значению признака, если шаг интервала
определен без округления -
Больше
максимального значения признака ,
если шаг интервала определен с
округлением
3. Меньше
максимального значения признака
ТЕСТ 15
В
какой интервал ( первый или второй )
следует отнести единицу совокупности,
имеющую значение признака равное
верхней границе первого интервала ?
-
В первый
-
Во второй
-
Ни в какой
-
В первый и во
второй -
В один из интервалов
ТЕСТ 16
Что включает в
себя количественная характеристика
рядов распределения ?
-
Показатели
центральной тенденции -
Показатели
ассиметрии распределения -
Показатели
вариации -
Шаг интервала
в интервальном вариационном ряду -
Показатели
эксцесса распределения
ТЕСТ 17
Какие
показатели из перечисленных показателей
следует отнести к показателям центральной
тенденции ?
-
Коэффициент
вариации -
Стандартное
отклонение -
Средняя
арифметическая -
Мода
ТЕСТ 18
Для
расчета каких из перечисленных
показателей центральной тенденции в
интервальном ряду распределения
используются все без исключения частоты
?
-
Средняя
арифметическая -
Мода
-
Медиана
ТЕСТ 19
Если
в вариационном ряду дискретного
признака , где максимальные частоты
сосредоточены в конце ряда рассчитать
среднюю арифметическую простую и
среднюю арифметическую взвешенную,
какая из них будет больше ?
-
Средняя простая
-
Средняя взвешенная
-
Они будут равны
между собой
ТЕСТ 20
Чему
равен объем вариации , если в совокупности
численностью в 10 единиц среднее
квадратическое отклонение равно 1
-
100
-
1
-
10
-
0,1
ТЕСТ 21
Что произойдет
с дисперсией признака, если все
индивидуальные значения признака
одновременно уменьшить на 10 и увеличить
в 2 раза ?
-
Не изменится
-
Уменьшится на 10
-
Увеличиться в 2
раза -
Увеличится в 5
раз -
Увеличится в 4
раза
ТЕСТ 22
Какой из показателей
вариации можно использовать для
сравнения вариации разных по содержанию
признаков ?
-
Размах вариации
-
Коэффициент
вариации -
Объем вариации
ТЕСТ 23
Какие
из перечисленных показателей
характеризуют среднюю колеблемость
признака ?
-
Размах вариации
-
Объем вариации
-
Дисперсия
-
Среднее
квадратическое отклонение -
Коэффициент
вариации
ТЕСТ 24
Чему равна
дисперсия качественного альтернативного
признака, если средняя равна 0,2.
-
0,8
-
0,4
-
0,16
-
0,04
ТЕСТ 25
Как
преобразовать любое распределение,
чтобы средняя арифметическая по новому
распределению оказалась равной 0 ?
-
Каждое
значение признака разделить на
среднюю арифметическую -
Каждое
значение признака умножить на среднюю
арифметическую -
Каждое
значение признака увеличить на
среднюю арифметическую -
Каждое
значение признака уменьшить на среднюю
арифметическую
ТЕСТ 26
Как преобразовать
исходное распределение, чтобы среднее
квадратическое отклонение по новому
распределению оказалось равным 1 ?
-
Каждое
значение признака уменьшить на среднее
значение -
Каждое
значение признака разделить на среднее
квадратическое отклонение -
Каждое
значение признака увеличить на
среднюю арифметическую -
Каждое
значение признака умножить на
стандартное отклонение
ТЕСТ 27
Что
следует использовать в качестве
значения признака при расчете средней
арифметической в интервальном ряду
распределения ?
-
Середину каждого
интервала -
Нижнюю границу
каждого интервала -
Верхнюю границу
каждого интервала
ТЕСТ 28
Если
модальным является первый интервал,
чему равна частота предшествующего
модальному интервала ?
-
Нулю
-
Единице
-
Двум
ТЕСТ 29
Чему равна
накопленная частота для максимального
значения признака ?
-
.Частоте для
этого значения признака -
Общей численности
совокупности -
Половине общей
численности совокупности
ТЕСТ 30
Если
сложить треть моды и две трети средней
арифметической, то получим приближенное
значение :
-
Медианы
-
Средней
арифметической -
Моды
ТЕСТ 31
Объем вариации
в расчете на единицу совокупности это
-
Коэффициент
вариации -
Среднее
квадратическое отклонение -
Дисперсия
-
Размах вариации
ТЕСТ 32
В
какой формуле для расчета дисперсии
используются квадраты значений признака
-
В основной,
раскрывающей содержание вариации -
В рабочее
-
Ни в какой
ТЕСТ 33
Какой
из объемов вариации ( межгрупповой или
внутригрупповой ) больше, если
корреляционное отношение равно 0,
-
.Межгрупповая
-
.Внутригрупповая
-
Они равны между
собой
ТЕСТ 34
Чему равна
межгрупповая вариация, если корреляционное
отношение равно 1 ?
-
Равна внутригрупповой
-
Равна
-
Равна общей
вариации
ТЕСТ 35
Какая из совокупностей
составляет часть другой
-
Выборочная –часть
генеральной -
Генеральная –
часть выборочной -
Выборочная
и генеральная совокупности равны по
численности
ТЕСТ 36
Что такое оценка
?
-
Одна
из количественных характеристик
генеральной совокупности -
Количественная
характеристика выборочной совокупности,
которая используется для соответствующей
количественной характеристики
совокупности генеральной
3.Суждение
о форме распределения выборочной
совокупности
ТЕСТ
37
Что представляет
собой конкретная ошибка выборки ?
-
Ошибка
при определении значения признака
по конкретной единице совокупности -
Разница
статистической характеристики
конкретной выборки и
соответствующего
параметра генеральной совокупности
ТЕСТ 38
Что представляет
собой средняя ошибка выборки ?
-
Среднюю
арифметическую из всех возможных
конкретных ошибок
выборки
-
Среднюю
гармоническую из всех возможных
конкретных ошибок -
Среднюю
квадратическую из всех возможных
ошибок выборки -
Среднюю
геометрическую из всех возможных
конкретных ошибок выборки
ТЕСТ 39
Как
изменится средняя ошибка выборочной
средней , если численность выборки
увеличить в 4 раза ?
-
Не изменится
-
Увеличится в 4
раза -
.Уменьшится в 4
раза -
Увеличится в 2
раза -
Уменьшится в 2
раза
ТЕСТ 40
Как изменится
средняя ошибка выборочной средней,
если выборочная дисперсия увеличится
в 9 раз , а численность выборки в 4 раза
-
Не изменится
-
Увеличится в 9
раз -
Увеличится в 3
раза -
Увеличится в 1.5
раза -
Уменьшится в 4
раза
ТЕСТ 41
При какой выборочной
доле имеет место ее наибольшая ошибка
-
0,1
-
0,2
-
0,3
-
0,4
-
0,5
ТЕСТ 42
По какому закону
распределяются конкретные ошибки
оценок при больших выборках ?
-
По закону Пуассона
-
По нормальному
закону -
По
закону распределения t
– Стьюдента
ТЕСТ 43
По
какому закону распределяются конкретные
ошибки оценок при малых выборках ?
-
По нормальному
закону -
По
закону распределения t-
Стьюдента -
По закону
распределения Госсета -
По закону
распределения Фишера
ТЕСТ 44
Доверительный
уровень вероятности это ….
-
..вероятность
не допустить разницы между оценкой
и параметром -
генеральной
совокупности -
.вероятность
появления ошибки, равной заданной (
определенной) -
.вероятность
появления ошибки меньше или равной
заданной (оп-
ределенной )
-
вероятность
появления ошибки больше заданной (
определенной )
ТЕСТ 45
Как задается
величина предельно допустимой ошибки
?
-
В виде конкретного
значения -
В виде интервала,
за пределы которого ошибка не выйдет -
В
виде всех возможных значений за
пределами заданного интервала
ТЕСТ 46
Может ли
генеральная средняя выйти за границы,
установленные при ее интервальной
оценке с доверительным уровнем
вероятности Р ?
-
Не может
-
Может при
непредвиденных обстоятельствах. -
Может
только в том случае, если исследователь
ошибся в расчетах -
Может с вероятностью
1-Р
ТЕСТ 47
Каково
должно быть соотношение выборочной
и генеральной совокупностей, чтобы
при замене повторного отбора на
бесповторный предельная ошибка
уменьшилась бы в 2 раза ?
-
0,25
-
0,50
-
0,75
-
0,90
ТЕСТ 48
Какая
из предельных ошибок будет меньше :
установленная на основе случайного
повторного или на основе механического
отбора ?
-
Они будут равны
между собой -
На основе
повторного отбора -
На основе
механического отбора
ТЕСТ 49
Какой
из способов отбора предполагает
предварительное разбиение генеральной
совокупности на качественно отличные
части ?
-
Типический
-
Серийный
-
Механический
ТЕСТ 50
При
каком из способов отбора, используемая
при расчете ошибок дисперсия будет
наименьшей ?
-
При случайном
повторном -
При случайном
бесповторном -
При механическом
-
При типическом
-
При серийном
ТЕСТ
51
Что такое
статистическая гипотеза ?
-
Предположение
о необходимом соотношении генеральной
и выборочной совокупностей -
Предположение
об алгоритмах расчета параметров
выборочной совокупности -
Предположение
о статистической характеристике или
о законе распределения генеральной
совокупности -
Предположение
о возможных ошибках выборки
ТЕСТ
53
Сколько
гипотез должно быть выдвинуто на
первом этапе их проверки ?
-
Две
-
Одна
ТЕСТ
54
Что такое уровень
значимости ?
-
Весомость
вывода о гипотезе в ходе его
дальнейшего практического использования -
Вероятность
допустить ошибку первого рода при
формулировании
вывода
относительно выдвинутой гипотезы
-
Величина
указывающая на целесообразность
повторной проверки
выдвинутой
гипотезы
ТЕСТ
55
Что представляет
собой ошибка первого рода ?
-
Отказ от верной
нулевой гипотезы -
Принятие ложной
нулевой гипотезы . -
Ошибка при расчете
фактического значения критерия -
Ошибка
в формулировке вывода относительно
выдвинутой нулевой гипотезы
ТЕСТ 56
Что
представляет собой ошибка второго
рода ?
-
Отказ от верной
нулевой гипотезы -
Принятие ложной
нулевой гипотезы . -
Ошибка при расчете
фактического значения критерия -
Ошибка
в формулировке вывода относительно
выдвинутой нулевой
гипотезы
ТЕСТ
57
Если
уровень значимости уменьшить , то
вероятность допущения какого рода
ошибки снижается ?
-
Первого рода
-
Второго рода
-
Ошибок первого
и второго рода
ТЕСТ
58
Если
уровень значимости увеличить, то
вероятность допущения какого рода
ошибки уменьшается ?
-
Первого рода
-
Второго рода
-
Ошибок первого
и второго рода
ТЕСТ
59
Что такое
статистический критерий ?
-
Математический
инструмент для проверки выдвинутых
гипотез -
Некоторое
соотношение между генеральной и
выборочной совокуп- ностью
позволяющее на основе выборки без
больших погрешностей сделать заключение
о генеральной совокупности -
Случайная
величина .имеющая закон распределения
ТЕСТ
60
Что представляет
собой фактическое значение критерия
?
-
Значение
критерия , рассчитанное по генеральной
совокупности -
Значение
критерия, рассчитанное по выборочной
совокупности -
Значение
критерия , полученное в ранее
проведенных исследованиях -
Среднее
из нескольких полученных по
выборкам значений крите-
рия
ТЕСТ
61
Что представляет
собой табличное ( критическое )
значение критерия ?
-
Это
значение критерия, при сравнении с
которым формулируется вывод
относительно выдвинутых гипотез -
Это
максимально возможное в силу игры
случая значение случай
ной величины,
получившей название критерия
-
Это
такое значение критерия, которое
позволяет установить правильно или
нет произведены расчеты по выборке
ТЕСТ
62
Что такое область
согласия ?
-
Все
возможные значения критерия, при
которых принимается альтернативная
гипотеза -
Все
возможные значения критерия , при
которых приходим к выводу о
необходимости повторной проверки
выдвинутой гипотезы -
Все
возможные значения критерия, при
которых соглашаемся с выдвинутой
нулевой гипотезой -
Все
возможные значения критерия, при
которых соглашаемся о возможном
согласии как с нулевой , так и с
альтернативной гипотезой.
ТЕСТ
63
Что представляет
собой критическая область ?
-
Все
возможные значения критерия, при
которых принимается нулевая гипотеза -
Все
возможные значения критерия , при
которых не может быть принята ни
нулевая, ни альтернативная гипотеза -
Все
возможные значения критерия, при
которых есть основание принять
альтернативную гипотезу
ТЕСТ
64
При
каких фактических значениях критерия
нулевая гипотеза обычно отвергается
?
-
Только при
равных табличному -
Только при
значениях больше табличного -
При
значениях меньше или равных табличному
ТЕСТ 65
Какие
из названных критериев используются
при проверке гипотез относительно
распределения численностей
-
Критерий
t
— Стьюдент -
Критерий
F-
Фишера -
Критерий
Госсета -
Критерий
Тьюки -
—
Пирсона
ТЕСТ
66
Если
требуется проверить гипотезу о
соответствии фактического распределения
нормальному, то в каком аспекте
используется в этом случае критерий
—Пирсона
?
-
Как критерий
согласия -
Как критерий
независимости -
Как критерий
однородности
ТЕСТ 67
Если
требуется установить по данным
выборочного распределения взаимосвязаны
ли специализация предприятий и степень
их убыточности, то в каком аспекте
используется критерий
—Пирсона
?
-
Как критерий
согласия -
Как критерий
независимости -
Как критерий
однородности
ТЕСТ 68
Если
требуется установить на основе двух
выборок одинаков ли состав
полей
по степени их засоренности , то критерий
—Пирсона
используется
как критерий …..
-
однородности
-
… независимости
-
… однородности
ТЕСТ 69
В
формуле для расчета фактического
значения критерия
—Пирсона
:
=
,что
представляют собой
?
-
Фактические
численности по группам ( интервалам
) выборки -
Ожидаемые
численности по группам ( интервалам
) -
Долю каждого
интервала в общей численности выборки
ТЕСТ 70
В
формуле для расчета фактического
значения критерия
—Пирсона
=
,что
представляют собой
-
Фактические
численности по группам ( интервалам
) выборки -
Ожидаемые
численности по группам ( интервалам -
Долю каждого
интервала в общей численности выборки
ТЕСТ 71
В
чем смысл ожидаемых частот (
) при использовании критерия
—Пирсона
в качестве критерия согласия
-
Так
распределялась бы выборочная
совокупность в соответствии с
нулевой гипотезой -
Так
распределялась бы выборка при
соответствии фактического
распределения
ожидаемому
-
Это
некоторое стандартное распределение,
которое должно присутствовать в
любом случае
ТЕСТ 72
В
чем смысл ожидаемых частот при
использовании критерия
—Пирсона
как критерия независимости ?
-
Такие
частоты должны иметь место при
независимости распределений по двум
признакам -
Такие
частоты должны иметь место при
справедливости нулевой гипотезы -
Это
некий постоянный стандарт с каким
должны сравниваться все распределения
по 2- м признакам.
ТЕСТ 73
Как
проверить правильность расчета
ожидаемых частот при использовании
критерия
—Пирсона
в качестве критерия независимости
-
Повторным
расчетом -
Сравнением
сумм фактических и ожидаемых частот
по столбцам строкам таблиц
распределения по 2- м признакам -
Сравнением общей
численности фактических и ожидаемых
частот.
ТЕСТ 74
Если в каком
–либо интервале ( группе ) его частота
оказалось менее
5 единиц , каковы
будут последующие действия ?
-
.Исключить данную
группу из последующих расчетов -
Объединить
данный интервал с соседним и независимо
от численности объединенного интервала
продолжить расчеты -
Осуществлять
объединение до тех пор , пока в
объединенном интервале будет не менее
5 единиц -
Проигнорировав
этот факт , продолжать расчеты
ТЕСТ 75
От
чего зависит табличное значение
критерия
—Пирсона
?
-
От численности
выборки ( выборок ) -
.От числа выделенных
групп ( интервалов ) -
От числа степеней
свободы -
От уровня значимости
ТЕСТ 76
При
каком из аспектов использования
критерия
—Пирсона
в алгоритме расчета фактического
значении критерия отсутствуют ожидаемые
частоты ?
-
Как критерий
согласия -
Как критерий
однородности -
Как критерий
независимости
ТЕСТ 77
Какую из гипотез
следует отнести к направленной ?
-
-
-
=
а
ТЕСТ 78
Какой критерий
используется при проверке гипотезы
относительно
генеральной
средней при численности выборки в 40
единиц ?
-
t
–Cтьюдента -
t-
нормального распределения -
F
–Фишера -
t-
Госсета
ТЕСТ 79
Дополните
выражение: « Если в качестве альтернативной
присутствует направленная гипотеза,
то табличное значение критерия следует
брать….
-
…..с установленным
заранее уровнем значимости -
….
с удвоенным по сравнению с заранее
установленным уровнем зна чимости -
……с
уменьшенным вдвое против принятого
заранее уровнем значимости
ТЕСТ 80
Какой критерий
используется при проверке гипотез
относительно средних
по данным 2- выборок
-
t
–Cтьюдента -
t-
нормального распределении -
F
–Фишера -
t-
Госсета -
Критерий знаков
ТЕСТ 81
Дополните выражение
: « Две выборки относятся к независимым
если,,,
-
наблюдения
в каждой из них не зависят друг от
друга» -
наблюдения
по двум выборкам попарно между собой
взаимосвя-
заны»
-
….по
двум выборкам отсутствует попарная
взаимосвязь наблюдений»
ТЕСТ 82
Дополните
выражение: « Две выборки относятся к
зависимым , если…
-
наблюдения
в каждой из них не зависят друг от
друга» -
….наблюдения
по двум выборкам попарно между собой
взаимосвя-
заны»
-
.по
двум выборкам отсутствует попарная
взаимосвязь наблюдений»
ТЕСТ 83
В
случае независимых выборок нулевая
гипотеза выдвигается относительно :
-
Каждой из
генеральных средних -
Разности между
генеральными средними -
Средней разности
по двум генеральным совокупностям -
Равенства
генеральных средних
ТЕСТ 84
В
случае зависимых выборок нулевая
гипотеза выдвигается относительно :
-
Каждой из
генеральных средних -
.Разности между
генеральными средними -
Средней разности
по двум генеральным совокупностям -
Равенства
генеральных средних -
Равенстве
средней разности 0 ( нулю ) в двух
генеральных совокуп-
ностях
ТЕСТ 85
Для
чего при проверке гипотезы относительно
двух средних должна быть проведена
проверка вспомогательной гипотезы ?
-
Чтобы установить
равны ли численности выборок -
Чтобы
установить равны ли дисперсии в
генеральных совокупностях . -
Чтобы
установить равны ли численности по
выборкам и равны ли дисперсии в
генеральных совокупностях
ТЕСТ 86
В
каких из перечисленных ниже ситуаций
требуется предварительный расчет
усредненной дисперсии двух выборок ?
-
Численности
выборок равны, равны дисперсии по
генеральным совокупностям -
Численности
выборок не равны, но дисперсии по
генеральным совокуп-
ностям равны
между собой
-
Численности
выборок равны, но дисперсии по
генеральным совокупностям не равны
между собой -
Численности
выборок не равны, не равны и дисперсии.
ТЕСТ 87
При
какой ниже ситуаций для определения
числа степеней свободы используется
поправка ?
-
Численности
выборок равны, равны дисперсии по
генеральным совокупностям -
Численности
выборок не равны, но дисперсии по
генеральным совокупностям равны между
собой -
Численности
выборок равны, но дисперсии по
генеральным совокуп-
ностям
не равны
-
Численности
выборок не равны, не равны и дисперсии.
ТЕСТ 88
При какой из
перечисленных ситуаций критическое
значение критерия
является расчетной
величиной ?
-
Численности
выборок равны, равны дисперсии по
генеральным совокупностям -
Численности
выборок не равны, но дисперсии по
генеральным совокупностям равны между
собой -
Численности
выборок равны, но дисперсии по
генеральным совокупностям не равны
между собой -
Численности
выборок не равны, не равны и дисперсии.
ТЕСТ 89
Если численности
каждой из двух независимых выборок
увеличивается, а дисперсии остаются
неизменными, вероятность принятия
какой гипотезы возрастает ?
-
Нулевой
-
Альтернативной
-
Ни той , ни другой
ТЕСТ 90
Если
числа пар взаимосвязанных наблюдений
уменьшается, а дисперсия разностей
остается неизменной , вероятность
принятия какой гипотезы возрастает ?
-
Ни той , ни другой
-
Альтернативной
-
Нулевой
ТЕСТ 91
Что такое НСР ?
-
Наименьшая
случайная разность -
Наибольшая
случайная разность -
Наименьшая
существенная разность -
Наибольшая
существенная разность
ТЕСТ 92
Если
разность между выборочными средними
больше НСР, какую из гипотез следует
принять ?
-
.Нулевую
-
Альтернативную
-
Ни ту , ни другую
ТЕСТ 93
Какой
критерий используется при проверке
гипотезы о равенстве долей альтернативного
признака в двух генеральных совокупностях
?
-
t
–Cтьюдента -
t-
нормального распределении -
F
–Фишера -
t-
Госсета
ТЕСТ 94
В
каком случае при проверке гипотезы
относительно долей признака в двух
генеральных совокупностях требуется
предварительное фи- преобразование
?
-
Только если
выборочные доли равны между собой -
Только если каждая
из долей меньше 0,1 -
Только если каждая
из долей больше чем 0,9 -
Если хотя бы одна
из долей меньше 0,1 или больше 0,9
ТЕСТ 95
Если выборочные
средние равны между собой, какая из
гипотез должна быть принята без
дополнительных расчетов ?
-
Нулевая
-
Альтернативная
-
Ни та, ни другая
ТЕСТ 96
Относительно
каких статистических характеристик
выдвигаются гипотезы при дисперсионном
анализе ?
-
Относительно
двух дисперсий -
Относительно
одной средней -
Относительно
нескольких средних -
Относительно
одной дисперсии
ТЕСТ 97
В чем состоит
содержание альтернативной гипотезы
при дисперсионном анализе ?
-
Сравниваемые
дисперсии не равны между собой -
Все сравниваемые
средние не равны между собой -
Хотя бы две
генеральные средние не равны между
собой -
Межгрупповая
дисперсии больше дисперсии
внутригрупповой
ТЕСТ 98
Если
внутригрупповая вариация больше
вариации межгрупповой , следует ли
продолжать дисперсионный анализ или
сразу согласиться с Н0
либо с НА
?
-
Следует
продолжить, определив необходимые
дисперсии ? -
Следует
согласиться с
Н0 -
Следует
согласиться с НА
ТЕСТ 99
Если
внутригрупповая дисперсия оказалась
равной межгрупповой, каковы должны
последовать действия, проводящего
дисперсионный анализ ?
-
Согласиться
с нулевой гипотезой о равенстве
генеральных средних -
Согласиться
с альтернативной гипотезой о наличии
хотя бы пары средних неравных между
собой -
Рассчитать
фактическое значение критерия F
ТЕСТ 100
Какая
дисперсия всегда должна быть в
числителе при расчете критерия F-Фишера
?
-
Любая
-
Только
внутригрупповая -
В любом случае
межгрупповая -
Межгрупповая,
если она больше внутригрупповой
ТЕСТ 101
От
чего зависит табличное значение
критерия F-Фишера
?
-
От принятого
уровня значимости -
От числа степеней
свободы общей вариации -
От числа степеней
свободы межгрупповой вариации -
От числа степеней
свободы внутригрупповой вариации -
От
величины фактического значения
критерия F-Фишера
ТЕСТ 102
В чем смысл
конкретизации результатов дисперсионного
анализа ?
-
Уточнить верно
ли проведены расчеты дисперсий -
Установить
какие из генеральных средних
оказались равными между собой -
Уточнить
какие из генеральных средних не равны
между собой
ТЕСТ 103
Верно
ли высказывание : « При конкретизации
результатов дисперсионного анализа
все средние генеральные оказались
равными между собой»
-
Верно
-
Может быть верным
и неверным -
Не
верно, это может иметь место вследствие
допущенных ошибок в расчетах
ТЕСТ 104
Можно
ли при конкретизации дисперсионного
анализа прийти к выводу, что все
генеральные средние не равны между
собой ?
-
Вполне возможно
-
Возможно в
исключительных случаях -
Невозможно в
принципе. -
Возможно только
при допущении ошибок в расчетах
ТЕСТ 105
Если
по критерию F-Фишера
была принята нулевая гипотеза
требуется ли конкретизация
дисперсионного анализа ?
-
Требуется
-
Не требуется
-
По усмотрению
проводящего дисперсионный анализ
ТЕСТ 106
В каком случае
для конкретизации результатов
дисперсионного анализа используется
критерий Тьюки.
-
Если число
наблюдений по группам ( выборкам )
одинаково -
Если число
наблюдений по группам ( выборкам )
разное -
Если имеются
выборки как с равными ,так и с
неравными чис-
ленностями
ТЕСТ 107
Что
представляет собой НСР при конкретизации
результатов дисперсионного анализа
на основе критерия Тьюки ?
-
Произведение
средней ошибки на фактическое значение
критерия
Тьюки
-
Произведение
средней ошибки на табличное значение
критерия
Тьюки
-
Отношение
каждой разницы между выборочными
средними к
средней
ошибке
-
Разность между
выборочными средними
ТЕСТ 108
Если выборочная
совокупность разбита на группы по 2-
признакам на сколько источников как
минимум должна быть разбита общая
вариация признака ?
-
На 2
-
На 3
-
На 4
-
На 5
-
На 6
ТЕСТ 109
Если
наблюдения по выборкам ( группам )
являются зависимыми , на сколько
источников должна быть разбита общая
вариация ( группировочный признак
один ) ?
-
на 2
-
на 3
-
на 4
-
на 5
ТЕСТ 110
Каков источник
( причина ) межгрупповой вариации
-
Игра случая
-
Совместное
действие игры случая и фактора -
Действие фактора
( факторов) -
Выяснится после
проведения дисперсионного анализа
ТЕСТ 111
Каков источник
( причина ) внутригрупповой вариации
?
-
Игра случая
-
Совместное
действие игры случая и фактора -
Действие фактора
( факторов) -
Выяснится после
проведения дисперсионного анализа
ТЕСТ 112
Если
каждому значению аргумента соответствует
несколько четко определенных значений
функции, то какой это вид связи ?
-
Функциональная
-
Корреляционная
-
Стохастическая
ТЕСТ 113
Какой
этап построения корреляционного
уравнения связи является первым ?
-
Определение вида
уравнения -
Расчет параметров
уравнения связи -
Интерпретация
коэффициентов уравнения связи -
Установление
причинно-следственных отношений
между признаками
ТЕСТ 115
На
основании чего устанавливается
наличие причинно- следственных
отношений между признаками ?
-
На основе
показателей тесноты связи -
На основе
коэффициентов регрессии -
На основе
теоретического анализа предмета
исследования
ТЕСТ 116
Какие способы
определения вида уравнения используются
?
-
Построение
графиков -
Перебор различных
видов уравнений -
Теоретический
анализ характера взаимосвязей
ТЕСТ 117
Какие
из перечисленных требований к
признакам и совокупности при построении
уравнения корреляции аналогичны тем,
которые должны выполняться при расчете
средних ?
-
Факторные
признаки должны быть между собой
независимы -
Численность
совокупности должна быть достаточно
большой -
Совокупность
должна быть качественно однородной
ТЕСТ 118
Чем
определяется область существования
корреляционного уравнения связи ?
-
Численностью
совокупности -
Границами
изменения в исходной совокупности
значений результативного признака -
Границами
изменения в исходной совокупности
значений результативного и факторного
признаков -
Границами
изменения в исходной совокупности
значений факторных признаков
ТЕСТ 119
Каково
содержание параметра а
в корреляционном уравнении связи :
У = а + в Х ?
-
Значение У при
Х = 0 -
Значение
У при Х = 0, если Х =0 находится в
области существования корреляционного
уравнения связи -
Содержательного
смысла не имеет, если Х =0 находится
вне области существования
корреляционного уравнения связи
ТЕСТ 120
Каково содержание
коэффициента регрессии ?
-
Такое же как
уравнении функциональной связи -
Среднее
изменение результативного признака
при изменении фактора на 1 -
Содержательного
смысла не имеет
ТЕСТ 121
В чем отличие
коэффициента полной регрессии от
коэффициента чистой
регрессии ?
-
Отличий нет
-
Коэффициент
чистой регрессии имеет место в
уравнениях множественной связи, а
полной –в уравнениях парной связи -
Коэффициент
чистой регрессии имеет место в
уравнениях парной связи, а полной —
в уравнениях множественной связи -
Все зависит от
величины ( полноты) коэффициента
регрессии
ТЕСТ 122
Какой из
коэффициентов регрессии ( полной или
чистой ) учитывает влияние других
факторов, включенных в уравнение связи
?
-
Чистой регрессии
-
Полной регрессии
-
Ни тот , ни другой
-
Все зависит от
величины коэффициента регрессии
ТЕСТ 123
Как проверить
правильность расчета коэффициентов
парного уравнения связи ?
-
Повторно сделать
расчеты. -
Посмотреть
насколько расчетные по уравнению
значения результативного признака
отличаются от фактических -
Проверить
по фактическим данным равенство
ТЕСТ 124
На основе каких
коэффициентов регрессии можно сравнить
факторы по степени их влияния на
результат ?
-
Коэффициентов
чистой регрессии -
Коэффициентов
эластичности -
Коэффициентов
полной регрессии -
Бета-коэффициентов
ТЕСТ 125
Каково содержание
воспроизведенной вариации результативного
признака ?
-
Изменчивость
результативного признака связанная
с изменением случайных причин -
Это
изменчивость результативного
связанная с изменением как фактора,
так и случайных причин -
Это
сопряженное изменение результативного
и факторного признака -
Это
изменчивость результативного признака
, связанная с изменением факторного
признака
ТЕСТ 126
Каково содержание
остаточной вариации результативного
признака ?
-
Это
изменчивость результативного
признака связанная с изменением
случайных причин -
Это изменчивость
результативного связанная с изменением
как фактора, так и случайных причин -
Это
сопряженное изменение результативного
и факторного признака -
Это
изменчивость результативного признака
, связанная с изменением факторного
признака.
ТЕСТ 127
Отношение
каких объемов вариации представляет
собой коэффициент детерминации ?
-
Общей к остаточной
-
Остаточной к
воспроизведенной -
3..Воспроизведенной
к остаточной -
4.Воспроизведенной
к общей
ТЕСТ 128
Если
связь есть, но она не функциональная,
что больше коэффициент корреляции
или коэффициент детерминации ?
-
Они равны между
собой -
Коэффициент
корреляции -
Коэффициент
детерминации
ТЕСТ 129
Если
коэффициент корреляции равен нулю
, где проходит линия регрессии ?
-
на совпадает со
средним значением результативного
признак
2.Она
перпендикулярна О оси ОХ
ТЕСТ 130
Если
теснота связи увеличивается как ведет
себя угол наклона линии регрессии по
отношению к оси ОХ ?
-
Не меняется
-
Возрастает
-
Уменьшается
ТЕСТ 131
Можно
ли разложить коэффициент множественной
детерминации по факторам ?
-
Нельзя
-
Можно на
коэффициенты отдельного определения
ВОПРОСЫ
ДЛЯ ИТОГОВОГО КОНТРОЛЯ
-
Что такое
статистическая совокупность ? -
Что есть
определяющее свойство? -
Какие признаки
относятся количественным ? -
.В чем отличие
признаков дискретных и непрерывных
? -
В чем отличие
первичных и вторичных признаков ? -
. Что такое
ранжированный ряд распределения ? -
Как
называется графическая форма
ранжированного ряда и как она выглядит
? -
Каково содержание
колонок в дискретном вариационном
ряду -
Как определить
число интервалов ? -
Как определить
шаг интервала ? -
Как определить
границы интервалов ? -
Что
произойдет с дисперсией признака,
если все значения признака одновременно
уменьшить на 10 и увеличить в 2 раза ? -
Какие
математические свойства средней
арифметической и среднего квадратического
отклонения совпадают ? -
В
партии продукции на некачественную
приходится 10 %. Определить коэффициент
вариации -
Какой
показатель вариации может быть
использован для сравнения вариации
нескольких признаков ? Почему ? -
Определить
объем вариации , если среднее
квадратическое отклонение равно 5, а
совокупность состоит из 4-х единиц. -
Какие
показатели характеризуют среднюю
колеблемость признака в совокупности
? -
Определить
дисперсию альтернативного признака,
если известно, что средняя в 3 раза
превышает среднее квадратическое
отклонение -
Имеется
распределение с параметрами : средняя
арифметическая равна 10, среднее
квадратическое отклонение равно 4.
Используя математические свойства
средней арифметической и среднего
квадратического отклонения получить
распределение с параметрами : средняя
арифметическая равна 0, среднее
квадратическое 1 -
Во
сколько раз межгрупповая вариация
меньше внутригрупповой, если
корреляционное отношение равно 0,25 -
Групповые средние
по совокупности равны соответственно
25, 100, 250.Группы равной численности.
Найти общую среднюю -
Найти межгрупповую
вариацию по следующим данным
|
№ группы |
Средняя |
Число единиц в |
|
1 |
5 |
5 |
|
2 |
7 |
5 |
|
3 |
…. |
…. |
В целом по
совокупности 10
15
-
Определите
межгрупповую вариацию, если по 3-м
группам имеются
следующие значения
признака:
1 группа : 2, 3, 4
2 группа 10, 12, 11
3 группа 25, 26,
24
-
Каково содержание
выборочного метода ? -
Что такое
генеральная совокупность? -
Что такое
выборочная совокупность ? -
Каково содержание
оценки ? -
Каковы
научные условия применения выборочного
метода -
.Какова
природа конкретной, средней и предельной
ошибок ? -
Каков источник
систематической ошибки ? -
.Какие
различия в знаках ( + , — ) имеют
систематические и случайные ошибки? -
Каковы основные
пути уменьшения средней и предельной
ошибки ? -
При какой выборочной
доле имеет место ее наибольшая ошибка
? -
При какой доле
признака имеет место ее наименьшая
ошибка 7 -
При
каких выборках ( больших или малых )
при прочих равных условиях имеет место
большая предельная ошибка ? -
Как
определить границы генеральной
средней с заданной вероятностью? -
Как определить
границы генеральной доли ? -
При
использовании каких выборок ( больших
или малых ) границы генеральной средней
будут шире ? -
Какова
вероятность того, что генеральная
средняя окажется вне установленных
границ ? -
Каков смысл
необходимой численности выборки ? -
В каком случае
следует определять вероятность
появления ошибки ? -
Чем
отличается случайный повторный отбор
от отбора бесповторного ? -
При
каком отборе повторном или бесповторном
будет больше средняя ошибка? -
Какова
последовательность проведения
механического отбора ? -
Какую
долю от генеральной совокупности
должна составлять выборка, чтобы при
бесповторном отборе средняя ошибка
уменьшилась в 2 раза ? -
Почему при
типическом отборе имеет место
наименьшая ошибка ? -
Какая
формула для определения предельной
ошибки используется при механическом
отборе ? -
В чем состоит
особенность серийного отбора ? -
Что
такое представительство групп в выборке
при проведении типического отбора
? -
Что есть
статистическая гипотеза ? -
.Каково должно
быть содержание нулевой гипотезы ? -
Что такое
статистический критерий ? -
Каково содержание
области согласия ? -
Каково содержание
критической области ? -
Что представляют
собой уровень значимости ? -
В чем состоит
содержание ошибок первого рода ? -
В чем состоит
содержание ошибок второго рода ? -
Какая
нулевая гипотеза выдвигается при
проверке гипотезы о соответствии
фактического распределения ожидаемому
? -
Какова
формула расчета фактического значения
критерия
при использовании его в аспекте
согласия ? -
Отчего
зависит табличное значение критерияпри использовании его в качестве
критерия согласия ? -
В
каком случае критерий
используется
как критерий независимости ? -
Какая
гипотеза выступает в качестве нулевой
при использовании критерия
в аспекте независимости ? Почему ?
-
Какой
алгоритм расчета фактического
значения критерия
используется при использовании его
в качестве критерия независимости ? -
Каков
алгоритм расчета ожидаемых частот
при использовании критерия
в качестве критерия независимости
? -
Как
установить число степеней свободы
при использовании критерия
как критерия независимости ?
-
В
каком случае критерий
используется как критерий однородности
? -
При
каком аспекте использования критерияпри расчете его фактического значения
не используются ожидаемые ( теоретические
численности )? -
От
каких величин зависит главным образом
фактическое значение критерия
при использовании его в аспекте
однородности ? -
Чем
отличаются направленная и ненаправленная
альтернативные гипотезы ? -
Какие
критерии используются при проверке
гипотезы относительно генеральной
средней ? -
Совпадают
или нет критические области при
направленной и ненаправленной
альтернативной гипотезах? -
Как
установить табличное значение
критерия при направленной и ненаправленной
гипотезах ? -
В чем разница
между выборками зависимыми и независимыми
? -
Как формулируется
нулевая гипотеза о средних при
независимых выборках ? -
Какие
четыре ситуации возможны при проверке
гипотезы относительно двух средних
при независимых выборках? -
При
каких ситуациях необходим расчет
усредненной дисперсии ? -
В
чем особенность расчета числа степеней
свободы при неравных дисперсиях ? -
Что такое НСР ?
-
Как формулируется
нулевая гипотеза при зависимых
выборках ? -
Каков
алгоритм расчета фактического
значения критерия t-
Стьюдента при зависимых выборках ? -
Как
формулируется нулевая гипотеза
относительно доли признака в генеральной
совокупности ? -
Как
формулируется нулевая гипотеза
относительно доли признака в двух
генеральных совокупностях? -
Какой
критерий используется при проверке
гипотезы относительно доли признака
? -
Как
меняется алгоритм расчета фактического
значения критерия в зависимости от
величины выборочной доли ? -
Какие
критерии используются при проверке
гипотезы о принадлежности единицы
исследуемой совокупности ? -
Каковы
алгоритмы расчета фактического
значения критерия Диксона, если резко
выделяется максимальное значение
признака ? Минимальное значение
признака ? -
Каково назначение
дисперсионного анализа ? -
Каково
содержание нулевой гипотезы при
дисперсионном анализе ? -
Каково
содержание альтернативной гипотезы
при дисперсионном анализе ? -
Какой
параметрический критерий используется
при дисперсионном анализе? -
Какие
дисперсии используются для расчета
фактического значения критерия F
–Фишера ? -
В
каком случае без расчета фактического
значения критерия F
–Фишера можно принять нулевую
гипотезу? -
От
чего зависит табличное значение
критерия F
–Фишера ? -
В
чем состоит конкретизация результатов
дисперсионного анализа? -
В
каком случае для конкретизации
используется критерий Q-Тьюки -
Что представляют
собой разницы первого, второго порядков
? -
Как
найти фактическое значение критерия
Q-Тьюки
? -
От
чего зависит табличное значение
критерия Q-Тьюки
? -
Какова
будет нулевая гипотеза , если уровни
фактора ( группировочного признака)
представляют собой выборку ?
100.Как
раскладывается общий объем вариации
при группировке данных по двум признакам
?
101.В
каком случае выделяется вариация по
повторностям ()
?
102.В
чем состоит отличие корреляционной
связи от функциональной? 103.Каковы
этапы построения корреляционного
уравнения связи ?
104.Какие
существуют требования к признакам и
совокупности при построении уравнения
связи ?
105.Как выбрать
вид уравнения связи ?
106.Каким методом
определяются коэффициенты уравнения
?
107.Каково содержание
коэффициентов уравнения ?
108.В
чем отличие коэффициентов полной и
чистой регрессии ?
109.Какие
существуют стандартизированные
коэффициенты регрессии ?
110.Каков
алгоритм расчета стандартизированных
коэффициентов регрессии ?
111.Какие показатели
используются для характеристики тесноты
связи 112.Какова формула расчета
коэффициента детерминации ?
113.Как
рассчитать коэффициент корреляции
при парной линейной связи ?
114.Каков интервал
возможных значений показателей тесноты
связи ?
115.Какой
критерий используется для проверки
гипотезы относительно уравнения в
целом ?
116.В
чем состоит оценка выборочных
коэффициентов регрессии и корреляции
?
117.
Как найти границы коэффициента регрессии
в генеральной совокупности ?
118
.Как найти границы коэффициента
корреляции в генеральной совокупности
?
Калькулятор для расчета достаточного объема выборки
Калькулятор ошибки выборки для доли признака
Калькулятор ошибки выборки для среднего значения
Калькулятор значимости различий долей
Калькулятор значимости различий средних
1. Формула (даже две)
Бытует заблуждение, что чем больше объем генеральной совокупности, тем больше должен быть объем выборки маркетингового исследования. Это отчасти так, когда объем выборки сопоставим с размером генеральной совокупности. Например, при опросах организаций (B2B).
Если речь идет об исследовании жителей городов, то не важно, Москва это или Рязань – оптимальный объем выборки будет одинаков в обоих городах. Этот принцип следует из закона больших чисел и применим, только если выборка простая случайная.
На рис.1. пример выборки 15000 человек (!) при опросе в муниципальном районе. Возможно, от численности населения взяли 10%?
Размер выборки никогда не рассчитывается как процент от генеральной совокупности!
Рис.1. Размер выборки 15000 человек, как реальный пример некомпетентности (или хуже).
В таких случаях для расчета объема выборки используется следующая формула:

где
n – объем выборки,
Z – коэффициент, зависящий от выбранного исследователем доверительного уровня,
p – доля респондентов с наличием исследуемого признака,
q = 1 – p – доля респондентов, у которых исследуемый признак отсутствует,
∆ – предельная ошибка выборки.
Доверительный уровень – это вероятность того, что реальная доля лежит в границах полученного доверительного интервала: выборочная доля (p) ± ошибка выборки (Δ). Доверительный уровень устанавливает сам исследователь в соответствии со своими требованиями к надежности полученных результатов. Чаще всего применяются доверительные уровни, равные 0,95 или 0,99. В маркетинговых исследованиях, как правило, выбирается доверительный уровень, равный 0,95. При этом уровне коэффициент Z равен 1,96.
Значения p и q чаще всего неизвестны до проведения исследования и принимаются за 0,5. При этом значении размер ошибки выборки максимален.
Допустимая предельная ошибка выборки выбирается исследователем в зависимости от целей исследования. Считается, что для принятия бизнес-решений ошибка выборки должна быть не больше 4%. Этому значению соответствует объем выборки 500-600 респондентов. Для важных стратегических решений целесообразно минимизировать ошибку выборки.
Рассмотрим кривую зависимости ошибки выборки от ее объема (Рис.2).

Рис.2. Зависимость ошибки выборки от ее объема при 95% доверительном уровне
Как видно из диаграммы, с ростом объема выборки значение ошибки уменьшается все медленнее. Так, при объеме выборки 1500 человек предельная ошибка выборки составит ±2,5%, а при объеме 2000 человек – ±2,2%. То есть, при определенном объеме выборки дальнейшее его увеличение не дает значительного выигрыша в ее точности.
Подходы к решению проблемы:
Случай 1. Генеральная совокупность значительно больше выборки:

Случай 2. Генеральная совокупность сопоставима с объемом выборки: (см. раздел исследований B2B)

где
n – объем выборки,
N – объем генеральной совокупности,
Z – коэффициент, зависящий от выбранного исследователем доверительного уровня,
p – доля респондентов с наличием исследуемого признака,
q = 1 – p – доля респондентов, у которых исследуемый признак отсутствует, (значения p и q обычно принимаются за 0,5, поскольку точно неизвестны до проведения исследования)
∆ – предельная ошибка выборки.
Например,
рассчитаем ошибку выборки объемом 1000 человек при 95% доверительном уровне, если генеральная совокупность значительно больше объема выборки:
Ошибка выборки = 1,96 * КОРЕНЬ(0,5*0,5/1000) = 0,031 = ±3,1%
При расчете объема выборки следует также учитывать стоимость проведения исследования. Например, при цене за 1 анкету 200 рублей стоимость опроса 1000 человек составит 200 000 рублей, а опрос 1500 человек будет стоить 300 000 рублей. Увеличение затрат в полтора раза сократит ошибку выборки всего на 0,6%, что обычно неоправданно экономически.
2. Причины «раздувать» выборку
Анализ полученных данных обычно включает в себя и анализ подвыборок, объемы которых меньше основной выборки. Поэтому ошибка для выводов по подвыборкам больше, чем ошибка по выборке в целом. Если планируется анализ подгрупп / сегментов, объем выборки должен быть увеличен (в разумных пределах).
Рис.3 демонстрирует данную ситуацию. Если для исследования авиапассажиров используется выборка численностью 500 человек, то для выводов по выборке в целом ошибка составляет 4,4%, что вполне приемлемо для принятия бизнес-решений. Но при делении выборки на подгруппы в зависимости от цели поездки, выводы по каждой подгруппе уже недостаточно точны. Если мы захотим узнать какие-либо количественные характеристики группы пассажиров, совершающих бизнес-поездку и покупавших билет самостоятельно, ошибка полученных показателей будет достаточно велика. Даже увеличение выборки до 2000 человек не обеспечит приемлемой точности выводов по этой подвыборке.

Рис.3. Проектирование объема выборки с учетом необходимости анализа подвыборок
Другой пример – анализ подгрупп потребителей услуг торгово-развлекательного центра (Рис.4).

Рис.4. Потенциальный спрос на услуги торгово-развлекательного центра
При объеме выборки в 1000 человек выводы по каждой отдельной услуге (например, социально-демографический профиль, частота пользования, средний чек и др.) будут недостаточно точными для использования в бизнес планировании. Особенно это касается наименее популярных услуг (Таблица 1).
Таблица 1. Ошибка по подвыборкам потенциальных потребителей услуг торгово-развлекательного центра при выборке 1000 чел.

Чтобы ошибка в самой малочисленной подвыборке «Ночной клуб» составила меньше 5%, объем выборки исследования должен составлять около 4000 человек. Но это будет означать 4-кратное удорожание проекта. В таких случаях возможно компромиссное решение:
- увеличение выборки до 1800 человек, что даст достаточную точность для 6 самых популярных видов услуг (от кинотеатра до парка аттракционов);
- добор 200-300 пользователей менее популярных услуг с опросом по укороченной анкете (см. Таблицу 2).
Таблица 2. Разница в ошибке выборки по подвыборкам при разных объемах выборки.

При обсуждении с исследовательским агентством точности результатов планируемого исследования рекомендуется принимать во внимание бюджет, требования к точности результатов в целом по выборке и в разрезе подгрупп. Если бюджет не позволяет получить информацию с приемлемой ошибкой, лучше пока отложить проект (или поторговаться).
КАЛЬКУЛЯТОРЫ ДЛЯ РАСЧЕТА СТАТИСТИЧЕСКИХ ПОКАЗАТЕЛЕЙ И ОПРЕДЕЛЕНИЯ ЗНАЧИМОСТИ РАЗЛИЧИЙ:
КАЛЬКУЛЯТОР ДЛЯ РАСЧЕТА
ДОСТАТОЧНОГО ОБЪЁМА ВЫБОРКИ
Доверительный уровень:
Ошибка выборки (?):
%
Объём генеральной совокупности (N):
(можно пропустить, если больше 100 000)
РЕЗУЛЬТАТ
Один из важных вопросов, на которые нужно ответить при планировании исследования, — это оптимальный объем выборки. Слишком маленькая выборка не сможет обеспечить приемлемую точность результатов опроса, а слишком большая приведет к лишним расходам.
Онлайн-калькулятор объема выборки поможет рассчитать оптимальный размер выборки, исходя из максимально приемлемого для исследователя размера ошибки выборки.
Все дальнейшие формулы и расчеты относятся только к простой случайной выборке!
Формулы для других типов выборки отличаются.
Объем выборки рассчитывается по следующим формулам
1) если объем выборки значительно меньше генеральной совокупности:

2) если объем выборки сопоставим с объемом генеральной совокупности:

В приведенных формулах:
Z – коэффициент, зависящий от выбранного исследователем доверительного уровня. Доверительный уровень (или доверительная вероятность) – это вероятность того, что реальное значение измеряемого показателя (по всей генеральной совокупности) находится в пределах доверительного интервала, полученного в исследовании. Доверительный уровень выбирает сам исследователь, исходя из требований к надежности результатов исследования. В маркетинговых исследованиях обычно применяется 95%-й доверительный уровень. Ему соответствует значение Z = 1,96.
N – объем генеральной совокупности. Генеральная совокупность – это все люди, которые изучаются в исследовании (например, все покупатели соков и нектаров, постоянно проживающие в Москве и Московской области). Если генеральная совокупность значительно больше объема выборки (в сотни и более раз), ее размером можно пренебречь (формула 1).
p – доля респондентов с наличием исследуемого признака. Например, если 20% опрошенных заинтересованы в новом продукте, то p = 0,2.
q = 1 — p – доля респондентов, у которых исследуемый признак отсутствует. Значения p и q обычно принимаются за 0,5, поскольку точно неизвестны до проведения исследования. При этом значении размер ошибки выборки максимален. В данном калькуляторе значения p и q по умолчанию равны 0,5.
Δ– предельная ошибка выборки (для доли признака), приемлемая для исследователя. Считается, что для принятия бизнес-решений ошибка выборки не должна превышать 4%.
n – объем выборки. Объем выборки – это количество людей, которые опрашиваются в исследовании.
ПРИМЕР РАСЧЕТА ОБЪЕМА ВЫБОРКИ:
Допустим, мы хотим рассчитать объем выборки, предельная ошибка которой составит 4%. Мы принимаем доверительный уровень, равный 95%. Генеральная совокупность значительно больше выборки. Тогда объем выборки составит:
n = 1,96 * 1,96 * 0,5 * 0,5 / (0,04 * 0,04) = 600,25 ≈ 600 человек
Таким образом, если мы хотим получить результаты с предельной ошибкой 4%, нам нужно опросить 600 человек.
КАЛЬКУЛЯТОР ОШИБКИ ВЫБОРКИ ДЛЯ ДОЛИ ПРИЗНАКА
Доверительный уровень:
Объём выборки (n):
Объём генеральной совокупности (N):
(можно пропустить, если больше 100 000)
Доля признака (p):
%
РЕЗУЛЬТАТ
Зная объем выборки исследования, можно рассчитать значение ошибки выборки (или, другими словами, погрешность выборки).
Если бы в ходе исследования мы могли опросить абсолютно всех интересующих нас людей, мы могли бы быть на 100% уверены в полученном результате. Но ввиду экономической нецелесообразности сплошного опроса применяют выборочный подход, когда опрашивается только часть генеральной совокупности. Выборочный метод не гарантирует 100%-й точности измерения, но, тем не менее, вероятность ошибки может быть сведена к приемлемому минимуму.
Все дальнейшие формулы и расчеты относятся только к простой случайной выборке! Формулы для других типов выборки отличаются.
Ошибка выборки для доли признака рассчитывается по следующим формулам.
1) если объем выборки значительно меньше генеральной совокупности:
(в данной формуле не используется показатель объема генеральной совокупности N)
2) если объем выборки сопоставим с объемом генеральной совокупности:

В приведенных формулах:
Z – коэффициент, зависящий от выбранного исследователем доверительного уровня. Доверительный уровень (или доверительная вероятность) – это вероятность того, что реальное значение измеряемого показателя (по всей генеральной совокупности) находится в пределах доверительного интервала, полученного в исследовании. Доверительный уровень выбирает сам исследователь, исходя из требований к надежности результатов исследования. В маркетинговых исследованиях обычно применяется 95%-й доверительный уровень. Ему соответствует значение Z = 1,96.
N – объем генеральной совокупности. Генеральная совокупность – это все люди, которые изучаются в исследовании (например, все покупатели шоколада, постоянно проживающие в Москве). Если генеральная совокупность значительно больше объема выборки (в сотни и более раз), ее размером можно пренебречь (формула 1).
n – объем выборки. Объем выборки – это количество людей, которые опрашиваются в исследовании. Существует заблуждение, что чем больше объем генеральной совокупности, тем больше должен быть и объем выборки маркетингового исследования. Это отчасти так, когда объем выборки сопоставим с объемом генеральной совокупности. Например, при опросах организаций (B2B). Если же речь идет об исследовании жителей городов, то не важно, Москва это или Рязань – оптимальный объем выборки будет одинаков в обоих городах. Этот принцип следует из закона больших чисел и применим, только если выборка простая случайная. ВАЖНО: если предполагается сравнивать какие-то группы внутри города, например, жителей разных районов, то выборку следует рассчитывать для каждой такой группы.
p – доля респондентов с наличием исследуемого признака. Например, если 20% опрошенных заинтересованы в новом продукте, то p = 0,2.
q = 1 — p – доля респондентов, у которых исследуемый признак отсутствует. Значения p и q обычно принимаются за 0,5, поскольку точно неизвестны до проведения исследования. При этом значении размер ошибки выборки максимален.
Δ– предельная ошибка выборки.
Таким образом, зная объем выборки исследования, мы можем заранее оценить показатель ее ошибки.
А получив значение p, мы можем рассчитать доверительный интервал для доли признака: (p — ∆; p + ∆)
ПРИМЕР РАСЧЕТА ОШИБКИ ВЫБОРКИ ДЛЯ ДОЛИ ПРИЗНАКА:
Например, в ходе исследования были опрошены 1000 человек (n=1000). 20% из них заинтересовались новым продуктом (p=0,2). Рассчитаем показатель ошибки выборки по формуле 1 (выберем доверительный уровень, равный 95%):
∆ = 1,96 * КОРЕНЬ (0,2*0,8/1000) = 0,0248 = ±2,48%
Рассчитаем доверительный интервал:
(p — ∆; p + ∆) = (20% — 2,48%; 20% + 2,48%) = (17,52%; 22,48%)
Таким образом, с вероятностью 95% мы можем быть уверены, что реальная доля заинтересованных в новом продукте (среди всей генеральной совокупности) находится в пределах полученного диапазона (17,52%; 22,48%).
Если бы мы выбрали доверительный уровень, равный 99%, то для тех же значений p и n ошибка выборки была бы больше, а доверительный интервал – шире. Это логично, поскольку, если мы хотим быть более уверены в том, что наш доверительный интервал «накроет» реальное значение признака, то интервал должен быть более широким.
КАЛЬКУЛЯТОР ОШИБКИ ВЫБОРКИ ДЛЯ СРЕДНЕГО ЗНАЧЕНИЯ
Доверительный уровень:
Объём выборки (n):
Объём генеральной совокупности (N):
(можно пропустить, если больше 100 000)
Среднее значение (x̄):
Стандартное отклонение (s):
РЕЗУЛЬТАТ
Зная объем выборки исследования, можно рассчитать значение ошибки выборки (или, другими словами, погрешность выборки).
Если бы в ходе исследования мы могли опросить абсолютно всех интересующих нас людей, мы могли бы быть на 100% уверены в полученном результате. Но ввиду экономической нецелесообразности сплошного опроса применяют выборочный подход, когда опрашивается только часть генеральной совокупности. Выборочный метод не гарантирует 100%-й точности измерения, но, тем не менее, вероятность ошибки может быть сведена к приемлемому минимуму.
Все дальнейшие формулы и расчеты относятся только к простой случайной выборке! Формулы для других типов выборки отличаются.
Ошибка выборки для среднего значения рассчитывается по следующим формулам.
1) если объем выборки значительно меньше генеральной совокупности:

(в данной формуле не используется показатель объема генеральной совокупности N)
2) если объем выборки сопоставим с объемом генеральной совокупности:

В приведенных формулах:
Z – коэффициент, зависящий от выбранного исследователем доверительного уровня. Доверительный уровень (или доверительная вероятность) – это вероятность того, что реальное значение измеряемого показателя (по всей генеральной совокупности) находится в пределах доверительного интервала, полученного в исследовании. Доверительный уровень выбирает сам исследователь, исходя из требований к надежности результатов исследования. В маркетинговых исследованиях обычно применяется 95%-й доверительный уровень. Ему соответствует значение Z = 1,96
N – объем генеральной совокупности. Генеральная совокупность – это все люди, которые изучаются в исследовании (например, все покупатели мороженого, постоянно проживающие в Москве). Если генеральная совокупность значительно больше объема выборки (в сотни и более раз), ее размером можно пренебречь (формула 1).
n – объем выборки. Объем выборки – это количество людей, которые опрашиваются в исследовании. Существует заблуждение, что чем больше объем генеральной совокупности, тем больше должен быть и объем выборки маркетингового исследования. Это отчасти так, когда объем выборки сопоставим с объемом генеральной совокупности. Например, при опросах организаций (B2B). Если же речь идет об исследовании жителей городов, то не важно, Москва это или Рязань – оптимальный объем выборки будет одинаков в обоих городах. Этот принцип следует из закона больших чисел и применим, только если выборка простая случайная. ВАЖНО: если предполагается сравнивать какие-то группы внутри города, например, жителей разных районов, то выборку следует рассчитывать для каждой такой группы.
s — выборочное стандартное отклонение измеряемого показателя. В идеале на месте этого аргумента должно быть стандартное отклонение показателя в генеральной совокупности (σ), но так как обычно оно неизвестно, используется выборочное стандартное отклонение, рассчитываемое по следующей формуле:
где, x ̅ – среднее арифметическое показателя, xi– значение i-го показателя, n – объем выборки
Δ– предельная ошибка выборки.
Зная среднее значение показателя x ̅ и ошибку ∆, мы можем рассчитать доверительный интервал для среднего значения:(x ̅ — ∆; x ̅ + ∆)
ПРИМЕР РАСЧЕТА ОШИБКИ ВЫБОРКИ ДЛЯ СРЕДНЕГО ЗНАЧЕНИЯ:
Например, в ходе исследования были опрошены 1000 человек (n=1000). Каждого из них попросили указать их примерную среднюю сумму покупки (средний чек) в известной сети магазинов. Среднее арифметическое всех ответов составило 500 руб. (x ̅=500), а стандартное отклонение составило 120 руб. (s=120). Рассчитаем показатель ошибки выборки по формуле 1 (выберем доверительный уровень, равный 95%):
∆ = 1,96 * 120 / КОРЕНЬ (1000) = 7,44
Рассчитаем доверительный интервал:
(x ̅ — ∆; x ̅ + ∆) = (500 – 7,44; 500 + 7,44) = (492,56; 507,44)
Таким образом, с вероятностью 95% мы можем быть уверены, что значение среднего чека по всей генеральной совокупности находится в границах полученного диапазона: от 492,56 руб. до 507,44 руб.
КАЛЬКУЛЯТОР ЗНАЧИМОСТИ РАЗЛИЧИЙ ДОЛЕЙ
Доверительный уровень:
| Измерение 1 | Измерение 2 | |
| Доля признака (p): | % | % |
| Объём выборки (n): |
РЕЗУЛЬТАТ
Если в прошлогоднем исследовании вашу марку вспомнили 10% респондентов, а в исследовании текущего года – 15%, не спешите открывать шампанское, пока не воспользуетесь нашим онлайн-калькулятором для оценки статистической значимости различий.
Сравнивая два разных значения, полученные на двух независимых выборках, исследователь должен убедиться, что различия статистически значимы, прежде чем делать выводы.
Как известно, выборочные исследования не обеспечивают 100%-й точности измерения (для этого пришлось бы опрашивать всю целевую аудиторию поголовно, что слишком дорого). Тем не менее, благодаря методам математической статистики, мы можем оценить точность результатов любого количественного исследования и учесть ее в выводах.
В приведенном здесь калькуляторе используется двухвыборочный z-тест для долей. Для его применения должны соблюдаться следующие условия:
- Обе выборки – простые случайные
- Выборки независимы (между значениями двух выборок нет закономерной связи)
- Генеральные совокупности значительно больше выборок
- Произведения n*p и n*(1-p), где n=размер выборки а p=доля признака, – не меньше 5.
В калькуляторе используются следующие вводные данные:
Доверительный уровень (или доверительная вероятность) – это вероятность того, что реальное значение измеряемого показателя (по всей генеральной совокупности) находится в пределах доверительного интервала, полученного в исследовании. Доверительный уровень выбирает сам исследователь, исходя из требований к надежности результатов исследования. В маркетинговых исследованиях обычно применяется 95%-й доверительный уровень.
Доля признака (p) – доля респондентов с наличием исследуемого признака. Например, если 20% опрошенных заинтересованы в новом продукте, то p = 0,2.
Объем выборки (n) – это количество людей, которые опрашиваются в исследовании.
Результат расчетов – вывод о статистической значимости или незначимости различий двух измерений.
КАЛЬКУЛЯТОР ЗНАЧИМОСТИ РАЗЛИЧИЙ СРЕДНИХ
Доверительный уровень:
| Измерение 1 | Измерение 2 | |
| Среднее значение (x̄): | ||
| Стандартное отклонение (s): | ||
| Объём выборки (n): |
РЕЗУЛЬТАТ
Допустим, выборочный опрос посетителей двух разных ТРЦ показал, что средний чек в одном из них равен 1000 рублей, а в другом – 1200 рублей. Следует ли отсюда вывод, что суммы среднего чека в двух этих ТРЦ действительно отличаются?
Сравнивая два разных значения, полученные на двух независимых выборках, исследователь должен убедиться, что различия статистически значимы, прежде чем делать выводы.
Как известно, выборочные исследования не обеспечивают 100%-й точности измерения (для этого пришлось бы опрашивать всю целевую аудиторию поголовно, что слишком дорого). Тем не менее, благодаря методам математической статистики, мы можем оценить точность результатов любого количественного исследования и учесть ее в выводах.
В приведенном здесь калькуляторе используется двухвыборочный z-тест для средних значений. Для его применения должны соблюдаться следующие условия:
- Обе выборки – простые случайные
- Выборки независимы (между значениями двух выборок нет закономерной связи)
- Генеральные совокупности значительно больше выборок
- Распределения значений в выборках близки к нормальному распределению.
В калькуляторе используются следующие вводные данные:
Доверительный уровень (или доверительная вероятность) – это вероятность того, что реальное значение измеряемого показателя (по всей генеральной совокупности) находится в пределах доверительного интервала, полученного в исследовании. Доверительный уровень выбирает сам исследователь, исходя из требований к надежности результатов исследования. В маркетинговых исследованиях обычно применяется 95%-й доверительный уровень.
Среднее значение ( ̅x) – среднее арифметическое показателя.
Стандартное отклонение (s) – выборочное стандартное отклонение измеряемого показателя. В идеале на месте этого аргумента должно быть стандартное отклонение показателя в генеральной совокупности (σ), но так как обычно оно неизвестно, используется выборочное стандартное отклонение, рассчитываемое по следующей формуле:
где, x ̅ – среднее арифметическое показателя, xi– значение i-го показателя, n – объем выборки
Объем выборки (n) – это количество людей, которые опрашиваются в исследовании.
Результат расчетов – вывод о статистической значимости или незначимости различий двух измерений.
Вы можете подписаться на уведомления о новых материалах СканМаркет
11.2. Оценка результатов выборочного наблюдения
11.2.1. Средняя и предельная ошибки выборки. Построение доверительных границ для средней и доли
Средняя ошибка выборки показывает, насколько отклоняется в среднем параметр выборочной совокупности от соответствующего параметра генеральной. Если рассчитать среднюю из ошибок всех возможных выборок определенного вида заданного объема (n), извлеченных из одной и той же генеральной совокупности, то получим их обобщающую характеристику — среднюю ошибку выборки (
В теории выборочного наблюдения выведены формулы для определения 
Например, если применяется повторная собственно случайная выборка, то 


При бесповторном собственно случайном отборе в формулы вносится поправка (1 — n/N):


Вероятность получения именно такой величины ошибки всегда равна 0,683. На практике же предпочитают получать данные с большей вероятностью, но это приводит к возрастанию величины ошибки выборки.
Предельная ошибка выборки (

Если ошибку выборки увеличить в два раза (t = 2), то получим гораздо большую вероятность того, что она не превысит определенного предела (в нашем случае — двойной средней ошибки) — 0,954. Если взять t = 3, то доверительная вероятность составит 0,997 — практически достоверность.
Уровень предельной ошибки выборки зависит от следующих факторов:
- степени вариации единиц генеральной совокупности;
- объема выборки;
- выбранных схем отбора (бесповторный отбор дает меньшую величину ошибки);
- уровня доверительной вероятности.
Если объем выборки больше 30, то значение t определяется по таблице нормального распределения, если меньше — по таблице распределения Стьюдента.
Приведем некоторые значения коэффициента доверия из таблицы нормального распределения.
Таблица
11.2.
| Значение доверительной вероятности P | 0,683 | 0,954 | 0,997 |
|---|---|---|---|
| Значение коэффициента доверия t | 1,0 | 2,0 | 3,0 |
Доверительный интервал для среднего значения признака и для доли в генеральной совокупности устанавливается следующим образом:
Итак, определение границ генеральной средней и доли состоит из следующих этапов:
Ошибки выборки при различных видах отбора
- Собственно случайная и механическая выборка. Средняя ошибка собственно случайной и механической выборки находятся по формулам, представленным в табл. 11.3.
Таблица
11.3.
Формулы для расчета средней ошибки собственно случайной и механической выборки (
 |
|
где |
Пример 11.2. Для изучения уровня фондоотдачи было проведено выборочное обследование 90 предприятий из 225 методом случайной повторной выборки, в результате которого получены данные, представленные в таблице.
Таблица
11.4.
| Уровень фондоотдачи, руб. | До 1,4 | 1,4-1,6 | 1,6-1,8 | 1,8-2,0 | 2,0-2,2 | 2,2 и выше | Итого |
|---|---|---|---|---|---|---|---|
| Количество предприятий | 13 | 15 | 17 | 15 | 16 | 14 | 90 |
В рассматриваемом примере имеем 40%-ную выборку (90 : 225 = 0,4, или 40%). Определим ее предельную ошибку и границы для среднего значения признака в генеральной совокупности по шагам алгоритма:
- По результатам выборочного обследования рассчитаем среднее значение и дисперсию в выборочной совокупности:
Таблица
11.5.
| Результаты наблюдения | Расчетные значения | |||
|---|---|---|---|---|
| уровень фондоотдачи, руб., xi | количество предприятий, fi | середина интервала, xixb4 | xixb4fi | xixb42fi |
| До 1,4 | 13 | 1,3 | 16,9 | 21,97 |
| 1,4-1,6 | 15 | 1,5 | 22,5 | 33,75 |
| 1,6-1,8 | 17 | 1,7 | 28,9 | 49,13 |
| 1,8-2,0 | 15 | 1,9 | 28,5 | 54,15 |
| 2,0-2,2 | 16 | 2,1 | 33,6 | 70,56 |
| 2,2 и выше | 14 | 2,3 | 32,2 | 74,06 |
| Итого | 90 | — | 162,6 | 303,62 |
Выборочная средняя
Выборочная дисперсия изучаемого признака
- Определяем среднюю ошибку повторной случайной выборки
- Зададим вероятность, на уровне которой будем говорить о величине предельной ошибки выборки. Чаще всего она принимается равной 0,999; 0,997; 0,954.
Для наших данных определим предельную ошибку выборки, например, с вероятностью 0,954. По таблице значений вероятности функции нормального распределения (см. выдержку из нее, приведенную в Приложении 1) находим величину коэффициента доверия t, соответствующего вероятности 0,954. При вероятности 0,954 коэффициент t равен 2.
- Предельная ошибка выборки с вероятностью 0,954 равна
- Найдем доверительные границы для среднего значения уровня фондоотдачи в генеральной совокупности
Таким образом, в 954 случаях из 1000 среднее значение фондоотдачи будет не выше 1,88 руб. и не ниже 1,74 руб.
Выше была использована повторная схема случайного отбора. Посмотрим, изменятся ли результаты обследования, если предположить, что отбор осуществлялся по схеме бесповторного отбора. В этом случае расчет средней ошибки проводится по формуле
Тогда при вероятности равной 0,954 величина предельной ошибки выборки составит:
Доверительные границы для среднего значения признака при бесповторном случайном отборе будут иметь следующие значения:
Сравнив результаты двух схем отбора, можно сделать вывод о том, что применение бесповторной случайной выборки дает более точные результаты по сравнению с применением повторного отбора при одной и той же доверительной вероятности. При этом, чем больше объем выборки, тем существеннее сужаются границы значений средней при переходе от одной схемы отбора к другой.
По данным примера определим, в каких границах находится доля предприятий с уровнем фондоотдачи, не превышающим значения 2,0 руб., в генеральной совокупности:
- рассчитаем выборочную долю.
Количество предприятий в выборке с уровнем фондоотдачи, не превышающим значения 2,0 руб., составляет 60 единиц. Тогда
m = 60, n = 90, w = m/n = 60 : 90 = 0,667;
- рассчитаем дисперсию доли в выборочной совокупности

- средняя ошибка выборки при использовании повторной схемы отбора составит
Если предположить, что была использована бесповторная схема отбора, то средняя ошибка выборки с учетом поправки на конечность совокупности составит
- зададим доверительную вероятность и определим предельную ошибку выборки.
При значении вероятности Р = 0,997 по таблице нормального распределения получаем значение для коэффициента доверия t = 3 (см. выдержку из нее, приведенную в Приложении 1):
- установим границы для генеральной доли с вероятностью 0,997:
Таким образом, с вероятностью 0,997 можно утверждать, что в генеральной совокупности доля предприятий с уровнем фондоотдачи, не превышающим значения 2,0 руб., не меньше, чем 54,7%, и не больше 78,7%.
- Типическая выборка. При типической выборке генеральная совокупность объектов разбита на k групп, тогда
N1 + N2 + … + Ni + … + Nk = N.
Объем извлекаемых из каждой типической группы единиц зависит от принятого способа отбора; их общее количество образует необходимый объем выборки
n1 + n2 + … + ni + … + nk = n.
Существуют следующие два способа организации отбора внутри типической группы: пропорциональной объему типических групп и пропорциональной степени колеблемости значений признака у единиц наблюдения в группах. Рассмотрим первый из них, как наиболее часто используемый.
Отбор, пропорциональный объему типических групп, предполагает, что в каждой из них будет отобрано следующее число единиц совокупности:
n = ni · Ni/N
где ni — количество извлекаемых единиц для выборки из i-й типической группы;
n — общий объем выборки;
Ni — количество единиц генеральной совокупности, составивших i-ю типическую группу;
N — общее количество единиц генеральной совокупности.
Отбор единиц внутри групп происходит в виде случайной или механической выборки.
Формулы для оценивания средней ошибки выборки для среднего и доли представлены в табл. 11.6.
Таблица
11.6.
Формулы для расчета средней ошибки выборки (

Здесь 
Пример 11.3. В одном из московских вузов проведено выборочное обследование студентов с целью определения показателя средней посещаемости вузовской библиотеки одним студентом за семестр. Для этого была использована 5%-ная бесповторная типическая выборка, типические группы которой соответствуют номеру курса. При отборе, пропорциональном объему типических групп, получены следующие данные:
Таблица
11.7.
| Номер курса | Всего студентов, чел., Ni | Обследовано в результате выборочного наблюдения, чел., ni | Среднее число посещений библиотеки одним студентом за семестр, xi | Внутригрупповая выборочная дисперсия,  |
|---|---|---|---|---|
| 1 | 650 | 33 | 11 | 6 |
| 2 | 610 | 31 | 8 | 15 |
| 3 | 580 | 29 | 5 | 18 |
| 4 | 360 | 18 | 6 | 24 |
| 5 | 350 | 17 | 10 | 12 |
| Итого | 2 550 | 128 | 8 | — |
Число студентов, которое необходимо обследовать на каждом курсе, рассчитаем следующим образом:
- общий объем выборочной совокупности:
n = 2550/130*5 =128 (чел.);
- количество единиц, отобранных из каждой типической группы:
аналогично для других групп:
n2 = 31 (чел.);
n3 = 29 (чел.);
n4 = 18 (чел.);
n5 = 17 (чел.).
Проведем необходимые расчеты.
- Выборочная средняя, исходя из значений средних типических групп, составит:
- Средняя из внутригрупповых дисперсий
- Средняя ошибка выборки:
С вероятностью 0,954 находим предельную ошибку выборки:
- Доверительные границы для среднего значения признака в генеральной совокупности:
Таким образом, с вероятностью 0,954 можно утверждать, что один студент за семестр посещает вузовскую библиотеку в среднем от семи до девяти раз.
- Малая выборка. В связи с небольшим объемом выборочной совокупности те формулы для определения ошибок выборки, которые использовались нами ранее при «больших» выборках, становятся неподходящими и требуют корректировки.
Среднюю ошибку малой выборки определяют по формуле
Предельная ошибка малой выборки:
Распределение значений выборочных средних всегда имеет нормальный закон распределения (или приближается к нему) при п > 100, независимо от характера распределения генеральной совокупности. Однако в случае малых выборок действует иной закон распределения — распределение Стьюдента. В этом случае коэффициент доверия находится по таблице t-распределения Стьюдента в зависимости от величины доверительной вероятности Р и объема выборки п. В Приложении 1 приводится фрагмент таблицы t-распределения Стьюдента, представленной в виде зависимости доверительной вероятности от объема выборки и коэффициента доверия t.
Пример 11.4. Предположим, что выборочное обследование восьми студентов академии показало, что на подготовку к контрольной работе по статистике они затратили следующее количество часов: 8,5; 8,0; 7,8; 9,0; 7,2; 6,2; 8,4; 6,6.
Оценим выборочные средние затраты времени и построим доверительный интервал для среднего значения признака в генеральной совокупности, приняв доверительную вероятность равной 0,95.
- Среднее значение признака в выборке равно
- Значение среднего квадратического отклонения составляет
- Средняя ошибка выборки:
- Значение коэффициента доверия t = 2,365 для п = 8 и Р = 0,95 .
- Предельная ошибка выборки:
- Доверительный интервал для среднего значения признака в генеральной совокупности:
То есть с вероятностью 0,95 можно утверждать, что затраты времени студента на подготовку к контрольной работе находятся в пределах от 6,9 до 8,5 ч.
11.2.2. Определение численности выборочной совокупности
Перед непосредственным проведением выборочного наблюдения всегда решается вопрос, сколько единиц исследуемой совокупности необходимо отобрать для обследования. Формулы для определения численности выборки выводят из формул предельных ошибок выборки в соответствии со следующими исходными положениями (табл. 11.7):
- вид предполагаемой выборки;
- способ отбора (повторный или бесповторный);
- выбор оцениваемого параметра (среднего значения признака или доли).
Кроме того, следует заранее определиться со значением доверительной вероятности, устраивающей потребителя информации, и с размером допустимой предельной ошибки выборки.
Таблица
11.8.
Формулы для определения численности выборочной совокупности

Примечание: при использовании приведенных в таблице формул рекомендуется получаемую численность выборки округлять в большую сторону для обеспечения некоторого запаса в точности.
Пример 11.5. Рассчитаем, сколько из 507 промышленных предприятий следует проверить налоговой инспекции, чтобы с вероятностью 0,997 определить долю предприятий с нарушениями в уплате налогов. По данным прошлого аналогичного обследования величина среднего квадратического отклонения составила 0,15; размер ошибки выборки предполагается получить не выше, чем 0,05.
При использовании повторного случайного отбора следует проверить
При бесповторном случайном отборе потребуется проверить
Как видим, использование бесповторного отбора позволяет проводить обследование гораздо меньшего числа объектов.
Пример 11.6. Планируется провести обследование заработной платы на предприятиях отрасли методом случайного бесповторного отбора. Какова должна быть численность выборочной совокупности, если на момент обследования в отрасли число занятых составляло 100 000 чел.? Предельная ошибка выборки не должна превышать 100 руб. с вероятностью 0,954. По результатам предыдущих обследований заработной платы в отрасли известно, что среднее квадратическое отклонение составляет 500 руб.
Следовательно, для решения поставленной задачи необходимо включить в выборку не менее 100 человек.
Калькулятор для расчета достаточного объема выборки
Калькулятор ошибки выборки для доли признака
Калькулятор ошибки выборки для среднего значения
Калькулятор значимости различий долей
Калькулятор значимости различий средних
1. Формула (даже две)
Бытует заблуждение, что чем больше объем генеральной совокупности, тем больше должен быть объем выборки маркетингового исследования. Это отчасти так, когда объем выборки сопоставим с размером генеральной совокупности. Например, при опросах организаций (B2B).
Если речь идет об исследовании жителей городов, то не важно, Москва это или Рязань – оптимальный объем выборки будет одинаков в обоих городах. Этот принцип следует из закона больших чисел и применим, только если выборка простая случайная.
На рис.1. пример выборки 15000 человек (!) при опросе в муниципальном районе. Возможно, от численности населения взяли 10%?
Размер выборки никогда не рассчитывается как процент от генеральной совокупности!
Рис.1. Размер выборки 15000 человек, как реальный пример некомпетентности (или хуже).
В таких случаях для расчета объема выборки используется следующая формула:

где
n – объем выборки,
Z – коэффициент, зависящий от выбранного исследователем доверительного уровня,
p – доля респондентов с наличием исследуемого признака,
q = 1 – p – доля респондентов, у которых исследуемый признак отсутствует,
∆ – предельная ошибка выборки.
Доверительный уровень – это вероятность того, что реальная доля лежит в границах полученного доверительного интервала: выборочная доля (p) ± ошибка выборки (Δ). Доверительный уровень устанавливает сам исследователь в соответствии со своими требованиями к надежности полученных результатов. Чаще всего применяются доверительные уровни, равные 0,95 или 0,99. В маркетинговых исследованиях, как правило, выбирается доверительный уровень, равный 0,95. При этом уровне коэффициент Z равен 1,96.
Значения p и q чаще всего неизвестны до проведения исследования и принимаются за 0,5. При этом значении размер ошибки выборки максимален.
Допустимая предельная ошибка выборки выбирается исследователем в зависимости от целей исследования. Считается, что для принятия бизнес-решений ошибка выборки должна быть не больше 4%. Этому значению соответствует объем выборки 500-600 респондентов. Для важных стратегических решений целесообразно минимизировать ошибку выборки.
Рассмотрим кривую зависимости ошибки выборки от ее объема (Рис.2).

Рис.2. Зависимость ошибки выборки от ее объема при 95% доверительном уровне
Как видно из диаграммы, с ростом объема выборки значение ошибки уменьшается все медленнее. Так, при объеме выборки 1500 человек предельная ошибка выборки составит ±2,5%, а при объеме 2000 человек – ±2,2%. То есть, при определенном объеме выборки дальнейшее его увеличение не дает значительного выигрыша в ее точности.
ШПАРГАЛКА (скопируйте ссылку или текст)
Подходы к решению проблемы:
Случай 1. Генеральная совокупность значительно больше выборки:

Случай 2. Генеральная совокупность сопоставима с объемом выборки: (см. раздел исследований B2B)

где
n – объем выборки,
N – объем генеральной совокупности,
Z – коэффициент, зависящий от выбранного исследователем доверительного уровня,
p – доля респондентов с наличием исследуемого признака,
q = 1 – p – доля респондентов, у которых исследуемый признак отсутствует, (значения p и q обычно принимаются за 0,5, поскольку точно неизвестны до проведения исследования)
∆ – предельная ошибка выборки.
Например,
рассчитаем ошибку выборки объемом 1000 человек при 95% доверительном уровне, если генеральная совокупность значительно больше объема выборки:
Ошибка выборки = 1,96 * КОРЕНЬ(0,5*0,5/1000) = 0,031 = ±3,1%
При расчете объема выборки следует также учитывать стоимость проведения исследования. Например, при цене за 1 анкету 200 рублей стоимость опроса 1000 человек составит 200 000 рублей, а опрос 1500 человек будет стоить 300 000 рублей. Увеличение затрат в полтора раза сократит ошибку выборки всего на 0,6%, что обычно неоправданно экономически.
2. Причины «раздувать» выборку
Анализ полученных данных обычно включает в себя и анализ подвыборок, объемы которых меньше основной выборки. Поэтому ошибка для выводов по подвыборкам больше, чем ошибка по выборке в целом. Если планируется анализ подгрупп / сегментов, объем выборки должен быть увеличен (в разумных пределах).
Рис.3 демонстрирует данную ситуацию. Если для исследования авиапассажиров используется выборка численностью 500 человек, то для выводов по выборке в целом ошибка составляет 4,4%, что вполне приемлемо для принятия бизнес-решений. Но при делении выборки на подгруппы в зависимости от цели поездки, выводы по каждой подгруппе уже недостаточно точны. Если мы захотим узнать какие-либо количественные характеристики группы пассажиров, совершающих бизнес-поездку и покупавших билет самостоятельно, ошибка полученных показателей будет достаточно велика. Даже увеличение выборки до 2000 человек не обеспечит приемлемой точности выводов по этой подвыборке.

Рис.3. Проектирование объема выборки с учетом необходимости анализа подвыборок
Другой пример – анализ подгрупп потребителей услуг торгово-развлекательного центра (Рис.4).

Рис.4. Потенциальный спрос на услуги торгово-развлекательного центра
При объеме выборки в 1000 человек выводы по каждой отдельной услуге (например, социально-демографический профиль, частота пользования, средний чек и др.) будут недостаточно точными для использования в бизнес планировании. Особенно это касается наименее популярных услуг (Таблица 1).
Таблица 1. Ошибка по подвыборкам потенциальных потребителей услуг торгово-развлекательного центра при выборке 1000 чел.

Чтобы ошибка в самой малочисленной подвыборке «Ночной клуб» составила меньше 5%, объем выборки исследования должен составлять около 4000 человек. Но это будет означать 4-кратное удорожание проекта. В таких случаях возможно компромиссное решение:
- увеличение выборки до 1800 человек, что даст достаточную точность для 6 самых популярных видов услуг (от кинотеатра до парка аттракционов);
- добор 200-300 пользователей менее популярных услуг с опросом по укороченной анкете (см. Таблицу 2).
Таблица 2. Разница в ошибке выборки по подвыборкам при разных объемах выборки.

При обсуждении с исследовательским агентством точности результатов планируемого исследования рекомендуется принимать во внимание бюджет, требования к точности результатов в целом по выборке и в разрезе подгрупп. Если бюджет не позволяет получить информацию с приемлемой ошибкой, лучше пока отложить проект (или поторговаться).
КАЛЬКУЛЯТОРЫ ДЛЯ РАСЧЕТА СТАТИСТИЧЕСКИХ ПОКАЗАТЕЛЕЙ И ОПРЕДЕЛЕНИЯ ЗНАЧИМОСТИ РАЗЛИЧИЙ:
КАЛЬКУЛЯТОР ДЛЯ РАСЧЕТА
ДОСТАТОЧНОГО ОБЪЁМА ВЫБОРКИ
Доверительный уровень:
Ошибка выборки (?):
%
Объём генеральной совокупности (N):
(можно пропустить, если больше 100 000)
РЕЗУЛЬТАТ
Один из важных вопросов, на которые нужно ответить при планировании исследования, — это оптимальный объем выборки. Слишком маленькая выборка не сможет обеспечить приемлемую точность результатов опроса, а слишком большая приведет к лишним расходам.
Онлайн-калькулятор объема выборки поможет рассчитать оптимальный размер выборки, исходя из максимально приемлемого для исследователя размера ошибки выборки.
Все дальнейшие формулы и расчеты относятся только к простой случайной выборке!
Формулы для других типов выборки отличаются.
Объем выборки рассчитывается по следующим формулам
1) если объем выборки значительно меньше генеральной совокупности:

2) если объем выборки сопоставим с объемом генеральной совокупности:

В приведенных формулах:
Z – коэффициент, зависящий от выбранного исследователем доверительного уровня. Доверительный уровень (или доверительная вероятность) – это вероятность того, что реальное значение измеряемого показателя (по всей генеральной совокупности) находится в пределах доверительного интервала, полученного в исследовании. Доверительный уровень выбирает сам исследователь, исходя из требований к надежности результатов исследования. В маркетинговых исследованиях обычно применяется 95%-й доверительный уровень. Ему соответствует значение Z = 1,96.
N – объем генеральной совокупности. Генеральная совокупность – это все люди, которые изучаются в исследовании (например, все покупатели соков и нектаров, постоянно проживающие в Москве и Московской области). Если генеральная совокупность значительно больше объема выборки (в сотни и более раз), ее размером можно пренебречь (формула 1).
p – доля респондентов с наличием исследуемого признака. Например, если 20% опрошенных заинтересованы в новом продукте, то p = 0,2.
q = 1 — p – доля респондентов, у которых исследуемый признак отсутствует. Значения p и q обычно принимаются за 0,5, поскольку точно неизвестны до проведения исследования. При этом значении размер ошибки выборки максимален. В данном калькуляторе значения p и q по умолчанию равны 0,5.
Δ– предельная ошибка выборки (для доли признака), приемлемая для исследователя. Считается, что для принятия бизнес-решений ошибка выборки не должна превышать 4%.
n – объем выборки. Объем выборки – это количество людей, которые опрашиваются в исследовании.
ПРИМЕР РАСЧЕТА ОБЪЕМА ВЫБОРКИ:
Допустим, мы хотим рассчитать объем выборки, предельная ошибка которой составит 4%. Мы принимаем доверительный уровень, равный 95%. Генеральная совокупность значительно больше выборки. Тогда объем выборки составит:
n = 1,96 * 1,96 * 0,5 * 0,5 / (0,04 * 0,04) = 600,25 ≈ 600 человек
Таким образом, если мы хотим получить результаты с предельной ошибкой 4%, нам нужно опросить 600 человек.
КАЛЬКУЛЯТОР ОШИБКИ ВЫБОРКИ ДЛЯ ДОЛИ ПРИЗНАКА
Доверительный уровень:
Объём выборки (n):
Объём генеральной совокупности (N):
(можно пропустить, если больше 100 000)
Доля признака (p):
%
РЕЗУЛЬТАТ
Зная объем выборки исследования, можно рассчитать значение ошибки выборки (или, другими словами, погрешность выборки).
Если бы в ходе исследования мы могли опросить абсолютно всех интересующих нас людей, мы могли бы быть на 100% уверены в полученном результате. Но ввиду экономической нецелесообразности сплошного опроса применяют выборочный подход, когда опрашивается только часть генеральной совокупности. Выборочный метод не гарантирует 100%-й точности измерения, но, тем не менее, вероятность ошибки может быть сведена к приемлемому минимуму.
Все дальнейшие формулы и расчеты относятся только к простой случайной выборке! Формулы для других типов выборки отличаются.
Ошибка выборки для доли признака рассчитывается по следующим формулам.
1) если объем выборки значительно меньше генеральной совокупности:
(в данной формуле не используется показатель объема генеральной совокупности N)
2) если объем выборки сопоставим с объемом генеральной совокупности:

В приведенных формулах:
Z – коэффициент, зависящий от выбранного исследователем доверительного уровня. Доверительный уровень (или доверительная вероятность) – это вероятность того, что реальное значение измеряемого показателя (по всей генеральной совокупности) находится в пределах доверительного интервала, полученного в исследовании. Доверительный уровень выбирает сам исследователь, исходя из требований к надежности результатов исследования. В маркетинговых исследованиях обычно применяется 95%-й доверительный уровень. Ему соответствует значение Z = 1,96.
N – объем генеральной совокупности. Генеральная совокупность – это все люди, которые изучаются в исследовании (например, все покупатели шоколада, постоянно проживающие в Москве). Если генеральная совокупность значительно больше объема выборки (в сотни и более раз), ее размером можно пренебречь (формула 1).
n – объем выборки. Объем выборки – это количество людей, которые опрашиваются в исследовании. Существует заблуждение, что чем больше объем генеральной совокупности, тем больше должен быть и объем выборки маркетингового исследования. Это отчасти так, когда объем выборки сопоставим с объемом генеральной совокупности. Например, при опросах организаций (B2B). Если же речь идет об исследовании жителей городов, то не важно, Москва это или Рязань – оптимальный объем выборки будет одинаков в обоих городах. Этот принцип следует из закона больших чисел и применим, только если выборка простая случайная. ВАЖНО: если предполагается сравнивать какие-то группы внутри города, например, жителей разных районов, то выборку следует рассчитывать для каждой такой группы.
p – доля респондентов с наличием исследуемого признака. Например, если 20% опрошенных заинтересованы в новом продукте, то p = 0,2.
q = 1 — p – доля респондентов, у которых исследуемый признак отсутствует. Значения p и q обычно принимаются за 0,5, поскольку точно неизвестны до проведения исследования. При этом значении размер ошибки выборки максимален.
Δ– предельная ошибка выборки.
Таким образом, зная объем выборки исследования, мы можем заранее оценить показатель ее ошибки.
А получив значение p, мы можем рассчитать доверительный интервал для доли признака: (p — ∆; p + ∆)
ПРИМЕР РАСЧЕТА ОШИБКИ ВЫБОРКИ ДЛЯ ДОЛИ ПРИЗНАКА:
Например, в ходе исследования были опрошены 1000 человек (n=1000). 20% из них заинтересовались новым продуктом (p=0,2). Рассчитаем показатель ошибки выборки по формуле 1 (выберем доверительный уровень, равный 95%):
∆ = 1,96 * КОРЕНЬ (0,2*0,8/1000) = 0,0248 = ±2,48%
Рассчитаем доверительный интервал:
(p — ∆; p + ∆) = (20% — 2,48%; 20% + 2,48%) = (17,52%; 22,48%)
Таким образом, с вероятностью 95% мы можем быть уверены, что реальная доля заинтересованных в новом продукте (среди всей генеральной совокупности) находится в пределах полученного диапазона (17,52%; 22,48%).
Если бы мы выбрали доверительный уровень, равный 99%, то для тех же значений p и n ошибка выборки была бы больше, а доверительный интервал – шире. Это логично, поскольку, если мы хотим быть более уверены в том, что наш доверительный интервал «накроет» реальное значение признака, то интервал должен быть более широким.
КАЛЬКУЛЯТОР ОШИБКИ ВЫБОРКИ ДЛЯ СРЕДНЕГО ЗНАЧЕНИЯ
Доверительный уровень:
Объём выборки (n):
Объём генеральной совокупности (N):
(можно пропустить, если больше 100 000)
Среднее значение (x̄):
Стандартное отклонение (s):
РЕЗУЛЬТАТ
Зная объем выборки исследования, можно рассчитать значение ошибки выборки (или, другими словами, погрешность выборки).
Если бы в ходе исследования мы могли опросить абсолютно всех интересующих нас людей, мы могли бы быть на 100% уверены в полученном результате. Но ввиду экономической нецелесообразности сплошного опроса применяют выборочный подход, когда опрашивается только часть генеральной совокупности. Выборочный метод не гарантирует 100%-й точности измерения, но, тем не менее, вероятность ошибки может быть сведена к приемлемому минимуму.
Все дальнейшие формулы и расчеты относятся только к простой случайной выборке! Формулы для других типов выборки отличаются.
Ошибка выборки для среднего значения рассчитывается по следующим формулам.
1) если объем выборки значительно меньше генеральной совокупности:

(в данной формуле не используется показатель объема генеральной совокупности N)
2) если объем выборки сопоставим с объемом генеральной совокупности:

В приведенных формулах:
Z – коэффициент, зависящий от выбранного исследователем доверительного уровня. Доверительный уровень (или доверительная вероятность) – это вероятность того, что реальное значение измеряемого показателя (по всей генеральной совокупности) находится в пределах доверительного интервала, полученного в исследовании. Доверительный уровень выбирает сам исследователь, исходя из требований к надежности результатов исследования. В маркетинговых исследованиях обычно применяется 95%-й доверительный уровень. Ему соответствует значение Z = 1,96
N – объем генеральной совокупности. Генеральная совокупность – это все люди, которые изучаются в исследовании (например, все покупатели мороженого, постоянно проживающие в Москве). Если генеральная совокупность значительно больше объема выборки (в сотни и более раз), ее размером можно пренебречь (формула 1).
n – объем выборки. Объем выборки – это количество людей, которые опрашиваются в исследовании. Существует заблуждение, что чем больше объем генеральной совокупности, тем больше должен быть и объем выборки маркетингового исследования. Это отчасти так, когда объем выборки сопоставим с объемом генеральной совокупности. Например, при опросах организаций (B2B). Если же речь идет об исследовании жителей городов, то не важно, Москва это или Рязань – оптимальный объем выборки будет одинаков в обоих городах. Этот принцип следует из закона больших чисел и применим, только если выборка простая случайная. ВАЖНО: если предполагается сравнивать какие-то группы внутри города, например, жителей разных районов, то выборку следует рассчитывать для каждой такой группы.
s — выборочное стандартное отклонение измеряемого показателя. В идеале на месте этого аргумента должно быть стандартное отклонение показателя в генеральной совокупности (σ), но так как обычно оно неизвестно, используется выборочное стандартное отклонение, рассчитываемое по следующей формуле:
где, x ̅ – среднее арифметическое показателя, xi– значение i-го показателя, n – объем выборки
Δ– предельная ошибка выборки.
Зная среднее значение показателя x ̅ и ошибку ∆, мы можем рассчитать доверительный интервал для среднего значения:(x ̅ — ∆; x ̅ + ∆)
ПРИМЕР РАСЧЕТА ОШИБКИ ВЫБОРКИ ДЛЯ СРЕДНЕГО ЗНАЧЕНИЯ:
Например, в ходе исследования были опрошены 1000 человек (n=1000). Каждого из них попросили указать их примерную среднюю сумму покупки (средний чек) в известной сети магазинов. Среднее арифметическое всех ответов составило 500 руб. (x ̅=500), а стандартное отклонение составило 120 руб. (s=120). Рассчитаем показатель ошибки выборки по формуле 1 (выберем доверительный уровень, равный 95%):
∆ = 1,96 * 120 / КОРЕНЬ (1000) = 7,44
Рассчитаем доверительный интервал:
(x ̅ — ∆; x ̅ + ∆) = (500 – 7,44; 500 + 7,44) = (492,56; 507,44)
Таким образом, с вероятностью 95% мы можем быть уверены, что значение среднего чека по всей генеральной совокупности находится в границах полученного диапазона: от 492,56 руб. до 507,44 руб.
КАЛЬКУЛЯТОР ЗНАЧИМОСТИ РАЗЛИЧИЙ ДОЛЕЙ
Доверительный уровень:
| Измерение 1 | Измерение 2 | |
| Доля признака (p): | % | % |
| Объём выборки (n): |
РЕЗУЛЬТАТ
Если в прошлогоднем исследовании вашу марку вспомнили 10% респондентов, а в исследовании текущего года – 15%, не спешите открывать шампанское, пока не воспользуетесь нашим онлайн-калькулятором для оценки статистической значимости различий.
Сравнивая два разных значения, полученные на двух независимых выборках, исследователь должен убедиться, что различия статистически значимы, прежде чем делать выводы.
Как известно, выборочные исследования не обеспечивают 100%-й точности измерения (для этого пришлось бы опрашивать всю целевую аудиторию поголовно, что слишком дорого). Тем не менее, благодаря методам математической статистики, мы можем оценить точность результатов любого количественного исследования и учесть ее в выводах.
В приведенном здесь калькуляторе используется двухвыборочный z-тест для долей. Для его применения должны соблюдаться следующие условия:
- Обе выборки – простые случайные
- Выборки независимы (между значениями двух выборок нет закономерной связи)
- Генеральные совокупности значительно больше выборок
- Произведения n*p и n*(1-p), где n=размер выборки а p=доля признака, – не меньше 5.
В калькуляторе используются следующие вводные данные:
Доверительный уровень (или доверительная вероятность) – это вероятность того, что реальное значение измеряемого показателя (по всей генеральной совокупности) находится в пределах доверительного интервала, полученного в исследовании. Доверительный уровень выбирает сам исследователь, исходя из требований к надежности результатов исследования. В маркетинговых исследованиях обычно применяется 95%-й доверительный уровень.
Доля признака (p) – доля респондентов с наличием исследуемого признака. Например, если 20% опрошенных заинтересованы в новом продукте, то p = 0,2.
Объем выборки (n) – это количество людей, которые опрашиваются в исследовании.
Результат расчетов – вывод о статистической значимости или незначимости различий двух измерений.
КАЛЬКУЛЯТОР ЗНАЧИМОСТИ РАЗЛИЧИЙ СРЕДНИХ
Доверительный уровень:
| Измерение 1 | Измерение 2 | |
| Среднее значение (x̄): | ||
| Стандартное отклонение (s): | ||
| Объём выборки (n): |
РЕЗУЛЬТАТ
Допустим, выборочный опрос посетителей двух разных ТРЦ показал, что средний чек в одном из них равен 1000 рублей, а в другом – 1200 рублей. Следует ли отсюда вывод, что суммы среднего чека в двух этих ТРЦ действительно отличаются?
Сравнивая два разных значения, полученные на двух независимых выборках, исследователь должен убедиться, что различия статистически значимы, прежде чем делать выводы.
Как известно, выборочные исследования не обеспечивают 100%-й точности измерения (для этого пришлось бы опрашивать всю целевую аудиторию поголовно, что слишком дорого). Тем не менее, благодаря методам математической статистики, мы можем оценить точность результатов любого количественного исследования и учесть ее в выводах.
В приведенном здесь калькуляторе используется двухвыборочный z-тест для средних значений. Для его применения должны соблюдаться следующие условия:
- Обе выборки – простые случайные
- Выборки независимы (между значениями двух выборок нет закономерной связи)
- Генеральные совокупности значительно больше выборок
- Распределения значений в выборках близки к нормальному распределению.
В калькуляторе используются следующие вводные данные:
Доверительный уровень (или доверительная вероятность) – это вероятность того, что реальное значение измеряемого показателя (по всей генеральной совокупности) находится в пределах доверительного интервала, полученного в исследовании. Доверительный уровень выбирает сам исследователь, исходя из требований к надежности результатов исследования. В маркетинговых исследованиях обычно применяется 95%-й доверительный уровень.
Среднее значение ( ̅x) – среднее арифметическое показателя.
Стандартное отклонение (s) – выборочное стандартное отклонение измеряемого показателя. В идеале на месте этого аргумента должно быть стандартное отклонение показателя в генеральной совокупности (σ), но так как обычно оно неизвестно, используется выборочное стандартное отклонение, рассчитываемое по следующей формуле:
где, x ̅ – среднее арифметическое показателя, xi– значение i-го показателя, n – объем выборки
Объем выборки (n) – это количество людей, которые опрашиваются в исследовании.
Результат расчетов – вывод о статистической значимости или незначимости различий двух измерений.
Вы можете подписаться на уведомления о новых материалах СканМаркет
Предельная ошибка выборки
Предельная ошибка — максимально возможное расхождение средних или максимум ошибок при заданной вероятности ее появления.
1. Предельную ошибку выборки для средней при повторном отборе в контрольных по статистике в ВУЗах рассчитывают по формуле:
где t — нормированное отклонение — «коэффициент доверия», который зависит от вероятности, гарантирующей предельную ошибку выборки;
мю х — средняя ошибка выборки.
2. Предельная ошибка выборки для доли при повторном отборе определяется по формуле:
3. Предельная ошибка выборки для средней при бесповторном отборе:
4. Предельная ошибка выборки для доли при бесповторном отборе:
Предельная относительная ошибка выборки
Предельную относительную ошибку выборки определяют как процентное соотношение предельной ошибки выборки к соответствующей характеристике выборочной совокупности. Она определяется таким образом:
Малая выборка
Теория малых выборок была разработана английским статистиком Стьюдентом в начале 20 века. В 1908 г. он выявил специальное распределение, которое позволяет и при малых выборках соотносить t и доверительную вероятность F(t). При n больше 100 дают такие же результаты, что и таблицы интеграла вероятностей Лапласа, при 30 < n < 100 различия получаются незначительные. Поэтому на практике к малым выборкам относятся выборки объемом менее 30 единиц.
Средняя и предельная ошибки для малой выборки
В малой выборке средняя ошибка рассчитывается по формуле:
Предельная ошибка малой выборки рассчитывается по формуле:
где t — отношение Стьюдента
Источник: Балинова B.C. Статистика в вопросах и ответах: Учеб. пособие. — М.: ТК. Велби, Изд-во Проспект, 2004. — 344 с.
Материалы сайта
Обращаем Ваше внимание на то, что все материалы опубликованы для образовательных целей.
11.2. Оценка результатов выборочного наблюдения
11.2.1. Средняя и предельная ошибки выборки. Построение доверительных границ для средней и доли
Средняя ошибка выборки показывает, насколько отклоняется в среднем параметр выборочной совокупности от соответствующего параметра генеральной. Если рассчитать среднюю из ошибок всех возможных выборок определенного вида заданного объема (n), извлеченных из одной и той же генеральной совокупности, то получим их обобщающую характеристику — среднюю ошибку выборки (
В теории выборочного наблюдения выведены формулы для определения 
Например, если применяется повторная собственно случайная выборка, то 


При бесповторном собственно случайном отборе в формулы вносится поправка (1 — n/N):


Вероятность получения именно такой величины ошибки всегда равна 0,683. На практике же предпочитают получать данные с большей вероятностью, но это приводит к возрастанию величины ошибки выборки.
Предельная ошибка выборки (

Если ошибку выборки увеличить в два раза (t = 2), то получим гораздо большую вероятность того, что она не превысит определенного предела (в нашем случае — двойной средней ошибки) — 0,954. Если взять t = 3, то доверительная вероятность составит 0,997 — практически достоверность.
Уровень предельной ошибки выборки зависит от следующих факторов:
- степени вариации единиц генеральной совокупности;
- объема выборки;
- выбранных схем отбора (бесповторный отбор дает меньшую величину ошибки);
- уровня доверительной вероятности.
Если объем выборки больше 30, то значение t определяется по таблице нормального распределения, если меньше — по таблице распределения Стьюдента.
Приведем некоторые значения коэффициента доверия из таблицы нормального распределения.
| Значение доверительной вероятности P | 0,683 | 0,954 | 0,997 |
|---|---|---|---|
| Значение коэффициента доверия t | 1,0 | 2,0 | 3,0 |
Доверительный интервал для среднего значения признака и для доли в генеральной совокупности устанавливается следующим образом:
Итак, определение границ генеральной средней и доли состоит из следующих этапов:
Ошибки выборки при различных видах отбора
- Собственно случайная и механическая выборка. Средняя ошибка собственно случайной и механической выборки находятся по формулам, представленным в табл. 11.3.
 |
|
где |
Пример 11.2. Для изучения уровня фондоотдачи было проведено выборочное обследование 90 предприятий из 225 методом случайной повторной выборки, в результате которого получены данные, представленные в таблице.
| Уровень фондоотдачи, руб. | До 1,4 | 1,4-1,6 | 1,6-1,8 | 1,8-2,0 | 2,0-2,2 | 2,2 и выше | Итого |
|---|---|---|---|---|---|---|---|
| Количество предприятий | 13 | 15 | 17 | 15 | 16 | 14 | 90 |
В рассматриваемом примере имеем 40%-ную выборку (90 : 225 = 0,4, или 40%). Определим ее предельную ошибку и границы для среднего значения признака в генеральной совокупности по шагам алгоритма:
- По результатам выборочного обследования рассчитаем среднее значение и дисперсию в выборочной совокупности:
| Результаты наблюдения | Расчетные значения | |||
|---|---|---|---|---|
| уровень фондоотдачи, руб., xi | количество предприятий, fi | середина интервала, xixb4 | xixb4fi | xixb42fi |
| До 1,4 | 13 | 1,3 | 16,9 | 21,97 |
| 1,4-1,6 | 15 | 1,5 | 22,5 | 33,75 |
| 1,6-1,8 | 17 | 1,7 | 28,9 | 49,13 |
| 1,8-2,0 | 15 | 1,9 | 28,5 | 54,15 |
| 2,0-2,2 | 16 | 2,1 | 33,6 | 70,56 |
| 2,2 и выше | 14 | 2,3 | 32,2 | 74,06 |
| Итого | 90 | — | 162,6 | 303,62 |
Выборочная средняя
Выборочная дисперсия изучаемого признака
- Определяем среднюю ошибку повторной случайной выборки
- Зададим вероятность, на уровне которой будем говорить о величине предельной ошибки выборки. Чаще всего она принимается равной 0,999; 0,997; 0,954.
Для наших данных определим предельную ошибку выборки, например, с вероятностью 0,954. По таблице значений вероятности функции нормального распределения (см. выдержку из нее, приведенную в Приложении 1) находим величину коэффициента доверия t, соответствующего вероятности 0,954. При вероятности 0,954 коэффициент t равен 2.
- Предельная ошибка выборки с вероятностью 0,954 равна
- Найдем доверительные границы для среднего значения уровня фондоотдачи в генеральной совокупности
Таким образом, в 954 случаях из 1000 среднее значение фондоотдачи будет не выше 1,88 руб. и не ниже 1,74 руб.
Выше была использована повторная схема случайного отбора. Посмотрим, изменятся ли результаты обследования, если предположить, что отбор осуществлялся по схеме бесповторного отбора. В этом случае расчет средней ошибки проводится по формуле
Тогда при вероятности равной 0,954 величина предельной ошибки выборки составит:
Доверительные границы для среднего значения признака при бесповторном случайном отборе будут иметь следующие значения:
Сравнив результаты двух схем отбора, можно сделать вывод о том, что применение бесповторной случайной выборки дает более точные результаты по сравнению с применением повторного отбора при одной и той же доверительной вероятности. При этом, чем больше объем выборки, тем существеннее сужаются границы значений средней при переходе от одной схемы отбора к другой.
По данным примера определим, в каких границах находится доля предприятий с уровнем фондоотдачи, не превышающим значения 2,0 руб., в генеральной совокупности:
- рассчитаем выборочную долю.
Количество предприятий в выборке с уровнем фондоотдачи, не превышающим значения 2,0 руб., составляет 60 единиц. Тогда
m = 60, n = 90, w = m/n = 60 : 90 = 0,667;
- рассчитаем дисперсию доли в выборочной совокупности

- средняя ошибка выборки при использовании повторной схемы отбора составит
Если предположить, что была использована бесповторная схема отбора, то средняя ошибка выборки с учетом поправки на конечность совокупности составит
- зададим доверительную вероятность и определим предельную ошибку выборки.
При значении вероятности Р = 0,997 по таблице нормального распределения получаем значение для коэффициента доверия t = 3 (см. выдержку из нее, приведенную в Приложении 1):
- установим границы для генеральной доли с вероятностью 0,997:
Таким образом, с вероятностью 0,997 можно утверждать, что в генеральной совокупности доля предприятий с уровнем фондоотдачи, не превышающим значения 2,0 руб., не меньше, чем 54,7%, и не больше 78,7%.
- Типическая выборка. При типической выборке генеральная совокупность объектов разбита на k групп, тогда
N1 + N2 + … + Ni + … + Nk = N.
Объем извлекаемых из каждой типической группы единиц зависит от принятого способа отбора; их общее количество образует необходимый объем выборки
n1 + n2 + … + ni + … + nk = n.
Существуют следующие два способа организации отбора внутри типической группы: пропорциональной объему типических групп и пропорциональной степени колеблемости значений признака у единиц наблюдения в группах. Рассмотрим первый из них, как наиболее часто используемый.
Отбор, пропорциональный объему типических групп, предполагает, что в каждой из них будет отобрано следующее число единиц совокупности:
n = ni · Ni/N
где ni — количество извлекаемых единиц для выборки из i-й типической группы;
n — общий объем выборки;
Ni — количество единиц генеральной совокупности, составивших i-ю типическую группу;
N — общее количество единиц генеральной совокупности.
Отбор единиц внутри групп происходит в виде случайной или механической выборки.
Формулы для оценивания средней ошибки выборки для среднего и доли представлены в табл. 11.6.

|
Здесь 
Пример 11.3. В одном из московских вузов проведено выборочное обследование студентов с целью определения показателя средней посещаемости вузовской библиотеки одним студентом за семестр. Для этого была использована 5%-ная бесповторная типическая выборка, типические группы которой соответствуют номеру курса. При отборе, пропорциональном объему типических групп, получены следующие данные:
| Номер курса | Всего студентов, чел., Ni | Обследовано в результате выборочного наблюдения, чел., ni | Среднее число посещений библиотеки одним студентом за семестр, xi | Внутригрупповая выборочная дисперсия, 
|
|---|---|---|---|---|
| 1 | 650 | 33 | 11 | 6 |
| 2 | 610 | 31 | 8 | 15 |
| 3 | 580 | 29 | 5 | 18 |
| 4 | 360 | 18 | 6 | 24 |
| 5 | 350 | 17 | 10 | 12 |
| Итого | 2 550 | 128 | 8 | — |
Число студентов, которое необходимо обследовать на каждом курсе, рассчитаем следующим образом:
- общий объем выборочной совокупности:
n = 2550/130*5 =128 (чел.);
- количество единиц, отобранных из каждой типической группы:
аналогично для других групп:
n2 = 31 (чел.);
n3 = 29 (чел.);
n4 = 18 (чел.);
n5 = 17 (чел.).
Проведем необходимые расчеты.
- Выборочная средняя, исходя из значений средних типических групп, составит:
- Средняя из внутригрупповых дисперсий
- Средняя ошибка выборки:
С вероятностью 0,954 находим предельную ошибку выборки:
- Доверительные границы для среднего значения признака в генеральной совокупности:
Таким образом, с вероятностью 0,954 можно утверждать, что один студент за семестр посещает вузовскую библиотеку в среднем от семи до девяти раз.
- Малая выборка. В связи с небольшим объемом выборочной совокупности те формулы для определения ошибок выборки, которые использовались нами ранее при «больших» выборках, становятся неподходящими и требуют корректировки.
Среднюю ошибку малой выборки определяют по формуле
Предельная ошибка малой выборки:
Распределение значений выборочных средних всегда имеет нормальный закон распределения (или приближается к нему) при п > 100, независимо от характера распределения генеральной совокупности. Однако в случае малых выборок действует иной закон распределения — распределение Стьюдента. В этом случае коэффициент доверия находится по таблице t-распределения Стьюдента в зависимости от величины доверительной вероятности Р и объема выборки п. В Приложении 1 приводится фрагмент таблицы t-распределения Стьюдента, представленной в виде зависимости доверительной вероятности от объема выборки и коэффициента доверия t.
Пример 11.4. Предположим, что выборочное обследование восьми студентов академии показало, что на подготовку к контрольной работе по статистике они затратили следующее количество часов: 8,5; 8,0; 7,8; 9,0; 7,2; 6,2; 8,4; 6,6.
Оценим выборочные средние затраты времени и построим доверительный интервал для среднего значения признака в генеральной совокупности, приняв доверительную вероятность равной 0,95.
- Среднее значение признака в выборке равно
- Значение среднего квадратического отклонения составляет
- Средняя ошибка выборки:
- Значение коэффициента доверия t = 2,365 для п = 8 и Р = 0,95 .
- Предельная ошибка выборки:
- Доверительный интервал для среднего значения признака в генеральной совокупности:
То есть с вероятностью 0,95 можно утверждать, что затраты времени студента на подготовку к контрольной работе находятся в пределах от 6,9 до 8,5 ч.
11.2.2. Определение численности выборочной совокупности
Перед непосредственным проведением выборочного наблюдения всегда решается вопрос, сколько единиц исследуемой совокупности необходимо отобрать для обследования. Формулы для определения численности выборки выводят из формул предельных ошибок выборки в соответствии со следующими исходными положениями (табл. 11.7):
- вид предполагаемой выборки;
- способ отбора (повторный или бесповторный);
- выбор оцениваемого параметра (среднего значения признака или доли).
Кроме того, следует заранее определиться со значением доверительной вероятности, устраивающей потребителя информации, и с размером допустимой предельной ошибки выборки.
 |
Примечание: при использовании приведенных в таблице формул рекомендуется получаемую численность выборки округлять в большую сторону для обеспечения некоторого запаса в точности.
Пример 11.5. Рассчитаем, сколько из 507 промышленных предприятий следует проверить налоговой инспекции, чтобы с вероятностью 0,997 определить долю предприятий с нарушениями в уплате налогов. По данным прошлого аналогичного обследования величина среднего квадратического отклонения составила 0,15; размер ошибки выборки предполагается получить не выше, чем 0,05.
При использовании повторного случайного отбора следует проверить
При бесповторном случайном отборе потребуется проверить
Как видим, использование бесповторного отбора позволяет проводить обследование гораздо меньшего числа объектов.
Пример 11.6. Планируется провести обследование заработной платы на предприятиях отрасли методом случайного бесповторного отбора. Какова должна быть численность выборочной совокупности, если на момент обследования в отрасли число занятых составляло 100 000 чел.? Предельная ошибка выборки не должна превышать 100 руб. с вероятностью 0,954. По результатам предыдущих обследований заработной платы в отрасли известно, что среднее квадратическое отклонение составляет 500 руб.
Следовательно, для решения поставленной задачи необходимо включить в выборку не менее 100 человек.







 —
— )2
)2