Что мы узнали? — Абсолютные и относительные погрешности используются для оценки точности измерений. Абсолютной погрешностью называют разницу между точным и приближенным числом. Относительная погрешность – это отношение абсолютной погрешности числа к самому числу. На практике используют относительную погрешность, так как она является более точной.
Как определить относительную и абсолютную погрешность?
Физические величины и погрешности их измерений — Задачей физического эксперимента является определение числового значения измеряемых физических величин с заданной точностью. Сразу оговоримся, что при выборе измерительного оборудования часто нужно также знать диапазон измерения и какое именно значение интересует: например, среднеквадратическое значение (СКЗ) измеряемой величины в определённом интервале времени, или требуется измерять среднеквадратическое отклонение (СКО) (для измерения переменной составляющей величины), или требуется измерять мгновенное (пиковое) значение.
- При измерении переменных физических величин (например, напряжение переменного тока) требуется знать динамические характеристики измеряемой физической величины: диапазон частот или максимальную скорость изменения физической величины,
- Эти данные, необходимые при выборе измерительного оборудования, зависят от физического смысла задачи измерения в конкретном физическом эксперименте,
Итак, повторимся: задачей физического эксперимента является определение числового значения измеряемых физических величин с заданной точностью. Эта задача решается с помощью прямых или косвенных измерений, При прямом измерении осуществляется количественное сравнение физической величины с соответствующим эталоном при помощи измерительных приборов.
- Отсчет по шкале прибора указывает непосредственно измеряемое значение.
- Например, термометр дает значения измеряемой температуры, а вольтметр – значение напряжения.
- При косвенных измерениях интересующая нас физическая величина находится при помощи математических операций над непосредственно измеренными физическими величинами (непосредственно измеряя напряжение U на резисторе и ток I через него, вычисляем значение сопротивления R = U / I ).
Точность прямых измерений некоторой величины X оценивается величиной погрешности или ошибки, измерений относительно действительного значения физической величины X Д, Действительное значение величины X Д (согласно РМГ 29-99 ) – это значение физической величины, полученное экспериментальным путем и настолько близкое к истинному значению, что в поставленной измерительной задаче может быть использовано вместо него.
Различают абсолютную (∆ X) и относительную (δ) погрешности измерений. Абсолютная погрешность измерения – это п огрешность средства измерений, выраженная в единицах измеряемой физической величины, характеризующая абсолютное отклонение измеряемой величины от действительного значения физической величины: ∆X = X – X Д,
Относительная погрешность измерения – это п огрешность измерения, выраженная отношением абсолютной погрешности измерения к действительному значению измеряемой величины. Обычно относительную погрешность выражают в процентах: δ = (∆X / Xд) * 100%, При оценке точности косвенных измерений некоторой величины X 1, функционально связанной с физическими величинами X 2, X 3,, X 1 = F (X 2, X 3, ), учитывают погрешности прямых измерений каждой из величин X 2, X 3, и характер функциональной зависимости F (),
Что такое абсолютная относительная и приведенная погрешность?
Абсолютные,относительные и приведенные погрешности измерений Абсолютная погрешность – это разница между измеренной датчиком величиной Хизм и действительным значением Хд этой величины. Действительное значение Хд измеряемой величины это найденное экспериментально значение измеряемой величины максимально близкое к ее истинному значению. Говоря простым языком действительное значение Хд это значение, измеренное эталонным прибором, или сгенерированное калибратором или задатчиком высокого класса точности.
Абсолютная погрешность выражается в тех же единицах измерения, что и измеряемая величина (например, в м3/ч, мА, МПа и т.п.). Так как измеренная величина может оказаться как больше, так и меньше ее действительного значения, то погрешность измерения может быть как со знаком плюс (показания прибора завышены), так и со знаком минус (прибор занижает).
См. Абсолютная погрешность микрокомпьютерного расходомера скоростемера МКРС Относительная погрешность – это отношение абсолютной погрешности измерения Δ к действительному значению Хд измеряемой величины. Относительная погрешность выражается в процентах, либо является безразмерной величиной, а также может принимать как положительные, так и отрицательные значения. См. О тносительная погрешность ультразвукового уровнемера ЭХО-АС-01 Приведенная погрешность – это отношение абсолютной погрешности измерения Δ к нормирующему значению Хn, постоянному во всем диапазоне измерения или его части. Нормирующее значение Хn зависит от типа шкалы датчика КИП:
Если шкала датчика односторонняя и нижний предел измерения равен нулю (например, шкала датчика от 0 до 150 м3/ч), то Хn принимается равным верхнему пределу измерения (в нашем случае Хn = 150 м3/ч). Если шкала датчика односторонняя, но нижний предел измерения не равен нулю (например, шкала датчика от 30 до 150 м3/ч), то Хn принимается равным разности верхнего и нижнего пределов измерения (в нашем случае Хn = 150-30 = 120 м3/ч). Если шкала датчика двухсторонняя (например, от -50 до +150 ˚С), то Хn равно ширине диапазона измерения датчика (в нашем случае Хn = 50+150 = 200 ˚С).
Приведенная погрешность выражается в процентах, либо является безразмерной величиной, а также может принимать как положительные, так и отрицательные значения. Довольно часто в описании на тот или иной датчик указывается не только диапазон измерения, например, от 0 до 50 мг/м3, но и диапазон показаний, например, от 0 до 100 мг/м3.
Что такое абсолютная ошибка?
Смотреть что такое «Ошибка Абсолютная» в других словарях: —
ОШИБКА, АБСОЛЮТНАЯ — абсолютная величина расхождения (разности) между величиной признака (показателя), установленной на основе статистического наблюдения, и действительной его величиной. Понятие А.о. используется, главным образом, при выборочном наблюдении Большой экономический словарь ОШИБКА, АБСОЛЮТНАЯ — Абсолютное значение (то есть безотносительно к знаку) различия между наблюдаемым значением и истинным значением измерения. Например, переоценка чьего то роста на два дюйма приводит к такой абсолютной ошибке, как переоценка на два дюйма Толковый словарь по психологии абсолютная ошибка — абсолютная погрешность — Тематики электросвязь, основные понятия Синонимы абсолютная погрешность EN absolute error Справочник технического переводчика абсолютная ошибка — absoliučioji paklaida statusas T sritis Kūno kultūra ir sportas apibrėžtis Matas, rodantis skirtumą tarp išmatuotos reikšmės ir matuojamojo dydžio tikrosios reikšmės. Absoliučioji paklaida nustatoma pagal vieno arba kelių bandymų rezultatų Sporto terminų žodynas АБСОЛЮТНАЯ ОШИБКА — См. ошибка, абсолютная Толковый словарь по психологии абсолютная погрешность — absoliučioji paklaida statusas T sritis Kūno kultūra ir sportas apibrėžtis Matas, rodantis skirtumą tarp išmatuotos reikšmės ir matuojamojo dydžio tikrosios reikšmės. Absoliučioji paklaida nustatoma pagal vieno arba kelių bandymų rezultatų Sporto terminų žodynas Абсолютная пустота — Doskonała próżnia Жанр: Сборник рассказов Автор: Станислав Лем Язык оригинала: польский Год написания: 1971 год Википедия Абсолютная ошибка (точность) прогноза метеорологической величины — Абсолютная ошибка (точность) прогноза метеорологической величины: разность между прогностическим значением метеорологической величины и фактически наблюдавшимся ее значением. Источник: РД 52.27.724 2009. Руководящий документ. Наставление по Официальная терминология абсолютная ошибка измерений — — Тематики релейная защита EN absolute error of measurement Справочник технического переводчика Ошибка измерения — Погрешность измерения оценка отклонения величины измеренного значения величины от её истинного значения. Погрешность измерения является характеристикой (мерой) точности измерения. Поскольку выяснить с абсолютной точностью истинное значение любой Википедия
Чему равна относительная погрешность измерения?
Точность числа определяется его относительной погрешностью. Относительная погрешность – это отношение абсолютной погрешности к самому числу. Относительную погрешность принято выражать в процентах, то есть, умножать полученное отношение на 100 %.
Как определяется абсолютная погрешность?
Абсолютная погрешность меры — разность между номинальным значением меры и истинным (действительным) значением воспроизводимой ею величины. Абсолютная погрешность измерительного прибора представляется разностью между показанием прибора и истинным (действительным) значением измеряемой величины.
Что определяет относительную погрешность?
При изготовлении стандартных образцов понятия абсолютной и относительной погрешности используют для определения и представления неточности результатов измерений. Погрешности измерения – отклонение результатов измерения от «истинного» значения измеряемой величины, возникающее из-за несовершенства результатов измерений.
- Выразить погрешность измерения можно и в абсолютных и в относительных величинах.
- Абсолютная погрешность измерения – погрешность измерения, выраженная в единицах измеряемой величины.
- Если требуется смесь кислорода в азоте с концентрацией кислорода – 100 ppm, абсолютная по-грешность измерения также будет выражаться в ppm.
В случае с поверочными смесями чаще всего в абсолютная погрешность выражается %, ppm, или в мг/м3. Относительная погрешность — отношение абсолютной погрешности концентрации к действительному значению концентрации, выраженное в процентах. Действительное значение – значение, определенное прибором высокого класса точности, т.е.
Как определяется ошибка измерения?
Измерение физических величин основано на том, что физика исследует объективные закономерности, которые происходят в природе. Найти значение физической величины — умножить конкретное число на единицу измерения данной величины, которая стандартизирована ( эталоны ).
расположение наблюдателя относительно измерительного прибора: если на линейку смотреть сбоку, погрешность измерений произойдёт по причине неточного определения полученного значения;деформация измерительного прибора: металлические и пластиковые линейки могут изогнуться, сантиметровая лента растягивается со временем;несоответствие шкалы прибора эталонным значениям: при множественном копировании эталонов может произойти ошибка, которая будет множиться;физический износ шкалы измерений, что приводит к невозможности распознавания значений.
Рассмотрим на примере измерения длины бруска линейкой с сантиметровой шкалой. Рис. (1). Линейка и брусок Внимательно рассмотрим шкалу. Расстояние между двумя соседними метками составляет (1) см. Если этой линейкой измерять брусок, который изображён на рисунке, то правый конец бруска будет находиться между (9) и (10) метками.
- У нас есть два варианта определения длины этого бруска. (1).
- Если мы заявим, что длина бруска — (9) сантиметров, то недостаток длины от истинной составит более половины сантиметра ((0,5) см (= 5) мм). (2).
- Если мы заявим, что длина бруска — (10) сантиметров, то избыток длины от истинной составит менее половины сантиметра ((0,5) см (= 5) мм).
Погрешность измерений — это отклонение полученного значения измерения от истинного. Погрешность измерительного прибора равна цене деления прибора. Для первой линейки цена деления составляет (1) сантиметр. Значит, погрешность этой линейки (1) см. Если нам необходимо произвести более точные измерения, то следует поменять линейку на другую, например, с миллиметровыми делениями. Рис. (2). Деревянная линейка Если же необходимы ещё более точные измерения, то нужно найти прибор с меньшей ценой деления, например, штангенциркуль. Существуют штангенциркули с ценой деления (0,1) мм и (0,05) мм, Рис. (3). Штангенциркуль На процесс измерения влияют следующие факторы: масштаб шкалы прибора, который определяет значения делений и расстояние между ними; уровень экспериментальных умений. Считается, что погрешность прибора превосходит по величине погрешность метода вычисления, поэтому за абсолютную погрешность принимают погрешность прибора.
Как зависит приведенная относительная погрешность от показания прибора?
Приведенная погрешность пропорциональна абсолютной погрешности, поэтому, если абсолютная погрешность измерительного прибора постоянна во всем диапазон измерения, то приведенная будет также постоянной.
Что показывает средняя абсолютная ошибка?
MAPE – средняя абсолютная ошибка в процентах используется: —
- Для оценки точности прогноза;
- Показывает на сколько велики ошибки в сравнении со значениями ряда;
- Хороша для сравнения 1-й модели для разных рядов;
- Используется для сравнения разных моделей для одного ряда;
- Оценки экономического эффекта, за счет повышения точности прогноза.
В данной статье мы рассмотрим, как рассчитать MAPE в Excel и как ее использовать. Формула расчета MAPE: Где:
- Y t – фактический объем продаж за анализируемый период;
- Ŷ t — значение прогнозной модели за аналазируемый период;
- n — количество периодов.
Для того, чтобы рассчитать среднюю абсолютную ошибку мы:
- Рассчитываем значение модели прогноза — Ŷ t;
- Рассчитываем ошибку прогноза;
- Берем ошибку по модулю;
- Определяем абсолютную ошибку;
- Рассчитываем среднюю абсолютную ошибку в процентах — MAPE.
Что называется относительной погрешностью приближенного значения?
Чтобы узнать, на сколько приближенное значение отличается от точного, надо из большего числа вычесть меньшее. Иначе говоря, надо найти модуль разности точного и приближенного значений. Этот модуль разности называют абсолютной погрешностью. Абсолютной погрешностью, или, короче, погрешностью приближенного числа, называется разность между этим числом и его точным значе нием (из большего числа вычитается меньшее).
Пример 1. На предприятии 1284 рабочих и служащих. При округлении этого числа до 1300 абсолютная погрешность составляет 1300 – 1284 = 16. При округлении до 1280 абсолютная погрешность составляет 1284 – 1280 = 4. Относительной погрешностью приближенного числа называется отношение абсолютной погрешности приближенного числа к самому этому числу.
Пример 2. В школе 197 учащихся. Округляем это число до 200. Абсолютная погрешность составляет 200 – 197 = 3. Относительная погрешность равна (frac ) или, округленно, (frac ) = 1,5 %. В большинстве случаев невозможно узнать точное значение приближенного числа, а значит, и точную величину погрешности.
Как найти ошибку прогноза?
18 Янв Ошибка прогнозирования: как рассчитать и применять. — Posted at 11:37h in Статьи Основной задачей при управлении запасами является определение объема пополнения, то есть, сколько необходимо заказать поставщику. При расчете этого объема используется несколько параметров — сколько будет продано в будущем, за какое время происходит пополнение, какие остатки у нас на складе и какое количество уже заказано у поставщика.
- То, насколько правильно мы определим эти параметры, будет влиять на то, будет ли достаточно товара на складе или его будет слишком много.
- Но наибольшее влияние на эффективность управления запасами влияет то, насколько точен будет прогноз.
- Многие считают, что это вообще основной вопрос в управлении запасами.
Действительно, точность прогнозирования очень важный параметр. Поэтому важно понимать, как его оценивать. Это важно и для выявления причин дефицитов или неликвидов, и при выборе программных продуктов для прогнозирования продаж и управления запасами. В данной статье я представила несколько формул для расчета точности прогноза и ошибки прогнозирования.
- Кроме этого, вы сможете скачать файлы с примерами расчетов этого показателя.
- Статистические методы Для оценки прогноза продаж используются статистические оценки Оценка ошибки прогнозирования временного ряда.
- Самый простой показатель – отклонение факта от прогноза в количественном выражении.
- В практике рассчитывают ошибку прогнозирования по каждой отдельной позиции, а также рассчитывают среднюю ошибку прогнозирования.
Следующие распространенные показатели ошибки относятся именно к показателям средних ошибок прогнозирования. К ним относятся: MAPE – средняя абсолютная ошибка в процентах где Z(t) – фактическое значение временного ряда, а – прогнозное. Данная оценка применяется для временных рядов, фактические значения которых значительно больше 1. Например, оценки ошибки прогнозирования энергопотребления почти во всех статьях приводятся как значения MAPE. Если же фактические значения временного ряда близки к 0, то в знаменателе окажется очень маленькое число, что сделает значение MAPE близким к бесконечности – это не совсем корректно.
Как найти абсолютную погрешность напряжения?
На рисунке показана часть шкалы вольтметра. Абсолютная погрешность измерения напряжения равна цене деления вольтметра. В ответ запишите показания прибора с учетом погрешности измерений, не разделяя их пробелом или запятой. Шкала вольтметра проградуирована в вольтах.
Как определяется абсолютная погрешность при прямых измерениях?
Абсолютную погрешность прямых измерений определяют суммой абсолютной инструментальной погрешности и абсолютной погрешности отсчёта Δx = Δ и x + Δ о x при условии, что случайная погрешность и погрешность вычисления или отсутствуют, или незначительны и ими можно пренебречь.
Как найти абсолютную погрешность приближения?
Абсолютной погрешностью или погрешностью приближенного числа называется разность между этим числом и его точным значением (из большего числа вычитается меньшее). Рассчитаем абсолютную погрешность 7,4 — 7 = 0,4. Ответ: абсолютная погрешность приближения 7.4 числом 7 равна 0,4.
Как найти относительную погрешность математика?
Чтобы узнать, на сколько приближенное значение отличается от точного, надо из большего числа вычесть меньшее. Иначе говоря, надо найти модуль разности точного и приближенного значений. Этот модуль разности называют абсолютной погрешностью. Абсолютной погрешностью, или, короче, погрешностью приближенного числа, называется разность между этим числом и его точным значе нием (из большего числа вычитается меньшее).
Пример 1. На предприятии 1284 рабочих и служащих. При округлении этого числа до 1300 абсолютная погрешность составляет 1300 – 1284 = 16. При округлении до 1280 абсолютная погрешность составляет 1284 – 1280 = 4. Относительной погрешностью приближенного числа называется отношение абсолютной погрешности приближенного числа к самому этому числу.
Пример 2. В школе 197 учащихся. Округляем это число до 200. Абсолютная погрешность составляет 200 – 197 = 3. Относительная погрешность равна (frac ) или, округленно, (frac ) = 1,5 %. В большинстве случаев невозможно узнать точное значение приближенного числа, а значит, и точную величину погрешности.
Как найти абсолютную погрешность в физике?
Измерение физических величин основано на том, что физика исследует объективные закономерности, которые происходят в природе. Найти значение физической величины — умножить конкретное число на единицу измерения данной величины, которая стандартизирована ( эталоны ).
расположение наблюдателя относительно измерительного прибора: если на линейку смотреть сбоку, погрешность измерений произойдёт по причине неточного определения полученного значения;деформация измерительного прибора: металлические и пластиковые линейки могут изогнуться, сантиметровая лента растягивается со временем;несоответствие шкалы прибора эталонным значениям: при множественном копировании эталонов может произойти ошибка, которая будет множиться;физический износ шкалы измерений, что приводит к невозможности распознавания значений.
Рассмотрим на примере измерения длины бруска линейкой с сантиметровой шкалой. Рис. (1). Линейка и брусок Внимательно рассмотрим шкалу. Расстояние между двумя соседними метками составляет (1) см. Если этой линейкой измерять брусок, который изображён на рисунке, то правый конец бруска будет находиться между (9) и (10) метками.
- У нас есть два варианта определения длины этого бруска. (1).
- Если мы заявим, что длина бруска — (9) сантиметров, то недостаток длины от истинной составит более половины сантиметра ((0,5) см (= 5) мм). (2).
- Если мы заявим, что длина бруска — (10) сантиметров, то избыток длины от истинной составит менее половины сантиметра ((0,5) см (= 5) мм).
Погрешность измерений — это отклонение полученного значения измерения от истинного. Погрешность измерительного прибора равна цене деления прибора. Для первой линейки цена деления составляет (1) сантиметр. Значит, погрешность этой линейки (1) см. Если нам необходимо произвести более точные измерения, то следует поменять линейку на другую, например, с миллиметровыми делениями. Рис. (2). Деревянная линейка Если же необходимы ещё более точные измерения, то нужно найти прибор с меньшей ценой деления, например, штангенциркуль. Существуют штангенциркули с ценой деления (0,1) мм и (0,05) мм, Рис. (3). Штангенциркуль На процесс измерения влияют следующие факторы: масштаб шкалы прибора, который определяет значения делений и расстояние между ними; уровень экспериментальных умений. Считается, что погрешность прибора превосходит по величине погрешность метода вычисления, поэтому за абсолютную погрешность принимают погрешность прибора.
Как определить абсолютную погрешность измерительного прибора?
Абсолютная погрешность косвенных измерений определяется по формуле ΔA=A пр ε (ε выражается десятичной дробью).
Как найти относительную погрешность приближенного значения?
Погрешность и точность приближения. Найдем значение функции у = х 2 при х=1,5 и при х=2,1. Можно найти значение функции двумя способами: по формуле и с помощью графика. С помощью графика приближенные значения функции равны: при х = 1,5 у ≈ 2,3; при х = 2,1 у ≈ 4,4.
Разница между абсолютной ошибкой и относительной ошибкой
Автор:
Charles Brown
Дата создания:
9 Февраль 2021
Дата обновления:
2 Июнь 2023
Содержание
- Ключевое различие — абсолютная ошибка против относительной ошибки
- Что такое абсолютная ошибка?
- Что такое относительная ошибка?
- В чем разница между абсолютной ошибкой и относительной ошибкой?
-
Ключевое различие — абсолютная ошибка против относительной ошибки
Абсолютная ошибка и относительная ошибка — это два способа указания ошибок в экспериментальных измерениях, хотя существует разница между абсолютной ошибкой и относительной ошибкой на основе их расчета. Большинство измерений в научных экспериментах содержат ошибки из-за инструментальных ошибок и ошибок человека. В некоторых случаях для конкретного измерительного прибора существует заранее определенное постоянное значение абсолютной погрешности. (Наименьшее показание. Например: — линейка = +/- 1 мм.) Это разница между истинным значением и экспериментальным значением. Однако относительная ошибка варьируется в зависимости от экспериментального значения и абсолютной ошибки. Он определяется отношением абсолютной ошибки к экспериментальному значению. Таким образом ключевое отличие между абсолютной ошибкой и относительной ошибкой, абсолютная ошибкаэтовеличина разницы между точным значением и приближением в то время как Относительная погрешность рассчитывается путем деления абсолютной погрешности на величину точного значения.
Что такое абсолютная ошибка?
Абсолютная ошибка — это показатель неопределенности измерения. Другими словами, он измеряет, в какой степени истинное значение может отличаться от экспериментального. Абсолютная погрешность выражается в тех же единицах, что и измерения.
Пример: Допустим, мы хотим измерить длину карандаша с помощью линейки с миллиметровыми отметками. Мы можем измерить его длину с точностью до миллиметра. Если вы получите значение 125 мм, оно будет выражено как 125 +/- 1 мм. Абсолютная погрешность составляет +/- 1 мм.
Что такое относительная ошибка?
Относительная ошибка зависит от двух переменных; абсолютная погрешность и экспериментальное значение измерения. Следовательно, эти два параметра должны быть известны для расчета относительной ошибки. Относительная ошибка вычисляется как отношение абсолютной ошибки к экспериментальному значению. Выражается в процентах или дробях; так что в нем нет единиц.
Относительная ошибка интегрирования Монте-Карло для вычисления числа пи
В чем разница между абсолютной ошибкой и относительной ошибкой?
Определение абсолютной ошибки и относительной ошибки
Абсолютная ошибка:
Абсолютная ошибка — это значение Δx (+ или — значение), где x — переменная; это физическая погрешность измерения. Он также известен как фактическая ошибка измерения.
Другими словами, это разница между истинным значением и экспериментальным значением.
Абсолютная ошибка = фактическое значение — измеренное значение
Относительная ошибка:
Относительная ошибка — это отношение абсолютной ошибки (Δx) к измеренному значению (x). Он выражается либо в процентах (процентная погрешность), либо в виде дроби (дробная погрешность).
Единицы и расчет абсолютной погрешности и относительной погрешности
Единицы
Абсолютная ошибка:
Он имеет те же единицы измерения, что и измеренное значение. Например, если вы измеряете длину книги в сантиметрах (см), абсолютная ошибка также будет иметь те же единицы.
Относительная ошибка:
Относительная погрешность может быть выражена в виде дроби или процента. Однако у обоих нет единицы в стоимости.
Расчет ошибок
Пример 1:Фактическая длина земли составляет 500 футов. Измерительный прибор показывает, что длина составляет 508 футов.
Абсолютная ошибка:
Абсолютная ошибка = [Фактическое значение — измеренное значение] = [508-500] футов = 8 футов
Относительная ошибка:
В процентах:
В виде дроби:
Пример 2:
Студент хотел измерить высоту стены в комнате. Он измерил значение с помощью метровой линейки (с точностью до миллиметра), оно составило 3,215 м.
Абсолютная ошибка:
Абсолютная погрешность = +/- 1 мм = +/- 0,001 м (Наименьшее значение, которое можно прочитать с помощью линейки)
Относительная ошибка:
Относительная погрешность = Абсолютная погрешность ÷ Экспериментальное значение = 0,001 м ÷ 3,215 м * 100 = 0,0003%
Абсолютная и относительная погрешность

4.2
Средняя оценка: 4.2
Всего получено оценок: 2201.
4.2
Средняя оценка: 4.2
Всего получено оценок: 2201.
Абсолютную и относительную погрешность используют для оценки неточности в производимых расчетах с высокой сложностью. Также они используются в различных измерениях и для округления результатов вычислений. Рассмотрим, как определить абсолютную и относительную погрешность.
Опыт работы учителем математики — более 33 лет.
Абсолютная погрешность
Абсолютной погрешностью числа называют разницу между этим числом и его точным значением.
Рассмотрим пример: в школе учится 374 ученика. Если округлить это число до 400, то абсолютная погрешность измерения равна 400-374=26.
Для подсчета абсолютной погрешности необходимо из большего числа вычитать меньшее.
Существует формула абсолютной погрешности. Обозначим точное число буквой А, а буквой а – приближение к точному числу. Приближенное число – это число, которое незначительно отличается от точного и обычно заменяет его в вычислениях. Тогда формула будет выглядеть следующим образом:
Δа=А-а. Как найти абсолютную погрешность по формуле, мы рассмотрели выше.
На практике абсолютной погрешности недостаточно для точной оценки измерения. Редко когда можно точно знать значение измеряемой величины, чтобы рассчитать абсолютную погрешность. Измеряя книгу в 20 см длиной и допустив погрешность в 1 см, можно считать измерение с большой ошибкой. Но если погрешность в 1 см была допущена при измерении стены в 20 метров, это измерение можно считать максимально точным. Поэтому в практике более важное значение имеет определение относительной погрешности измерения.
Записывают абсолютную погрешность числа, используя знак ±. Например, длина рулона обоев составляет 30 м ± 3 см. Границу абсолютной погрешности называют предельной абсолютной погрешностью.
Относительная погрешность
Относительной погрешностью называют отношение абсолютной погрешности числа к самому этому числу. Чтобы рассчитать относительную погрешность в примере с учениками, разделим 26 на 374.
Получим число 0,0695, переведем в проценты и получим 7 %. Относительную погрешность обозначают процентами, потому что это безразмерная величина. Относительная погрешность – это точная оценка ошибки измерений. Если взять абсолютную погрешность в 1 см при измерении длины отрезков 10 см и 10 м, то относительные погрешности будут соответственно равны 10 % и 0,1 %. Для отрезка длиной в 10 см погрешность в 1 см очень велика, это ошибка в 10 %. А для десятиметрового отрезка 1 см не имеет значения, всего 0,1 %.
Различают систематические и случайные погрешности. Систематической называют ту погрешность, которая остается неизменной при повторных измерениях. Случайная погрешность возникает в результате воздействия на процесс измерения внешних факторов и может изменять свое значение.
Правила подсчета погрешностей
Для номинальной оценки погрешностей существует несколько правил:
- при сложении и вычитании чисел необходимо складывать их абсолютные погрешности;
- при делении и умножении чисел требуется сложить относительные погрешности;
- при возведении в степень относительную погрешность умножают на показатель степени.
Приближенные и точные числа записываются при помощи десятичных дробей. Берется только среднее значение, поскольку точное может быть бесконечно длинным. Чтобы понять, как записывать эти числа, необходимо узнать о верных и сомнительных цифрах.
Верными называются такие цифры, разряд которых превосходит абсолютную погрешность числа. Если же разряд цифры меньше абсолютной погрешности, она называется сомнительной. Например, для дроби 3,6714 с погрешностью 0,002 верными будут цифры 3,6,7, а сомнительными – 1 и 4. В записи приближенного числа оставляют только верные цифры. Дробь в этом случае будет выглядеть таким образом – 3,67.
Что мы узнали?
Абсолютные и относительные погрешности используются для оценки точности измерений. Абсолютной погрешностью называют разницу между точным и приближенным числом. Относительная погрешность – это отношение абсолютной погрешности числа к самому числу. На практике используют относительную погрешность, так как она является более точной.
Тест по теме
Доска почёта

Чтобы попасть сюда — пройдите тест.
-
Светлана Лобанова-Асямолова
10/10
-
Валерий Соломин
10/10
-
Анастасия Юшкова
10/10
-
Ксюша Пономарева
7/10
-
Паша Кривов
10/10
-
Евгений Холопик
9/10
-
Guzel Murtazina
10/10
-
Максим Аполонов
10/10
-
Olga Bimbirene
9/10
-
Света Колодий
10/10
Оценка статьи
4.2
Средняя оценка: 4.2
Всего получено оценок: 2201.
А какая ваша оценка?
Абсолютная и относительная погрешности (ошибки).
Пусть некоторая
величина x
измерена n
раз. В результате получен ряд значений
этой величины: x1,
x2,
x3,
…, xn
Величиной, наиболее
близкой к действительному значению,
является среднее арифметическое этих
результатов:
Отсюда следует,
что каждое физическое измерение должно
быть повторено несколько раз.
Разность между
средним значением
измеряемой
величины и значением отдельного измерения
называется абсолютной
погрешностью отдельного измерения:
(13)
Абсолютная
погрешность может быть как положительной,
так и отрицательной и измеряется в тех
же единицах, что и измеряемая величина.
Средняя абсолютная
ошибка результата — это среднее
арифметическое значений абсолютных
погрешностей отдельных измерений,
взятых по абсолютной величине (модулю):
(14)
Отношения
называются относительными погрешностями
(ошибками) отдельных измерений.
Отношение средней
абсолютной погрешности результата
к среднему арифметическому значению
измеряемой величины называют относительной
ошибкой результата и выражают в процентах:
Относительная
ошибка характеризует точность измерения.
Законы распределения случайных величин.
Результат измерения
физической величины зависит от многих
факторов, влияние которых заранее учесть
невозможно. Поэтому значения, полученные
в результате прямых измерений какого
— либо параметра, являются случайными,
обычно не совпадающие между собой.
Следовательно, случайные
величины —
это такие величины, которые в зависимости
от обстоятельств могут принимать те
или иные значения. Если случайная
величина принимает только определенные
числовые значения, то она называется
дискретной.
Например,
количество заболеваний в данном регионе
за год, оценка, полученная студентом на
экзамене, энергия электрона в атоме и
т.д.
Непрерывная
случайная величина принимает любые
значения в данном интервале.
Например: температура
тела человека, мгновенные скорости
теплового движения молекул, содержание
кислорода в воздухе и т.д.
Под событием
понимается всякий результат или исход
испытания. В теории вероятностей
рассматриваются события, которые при
выполнение некоторых условий могут
произойти, а могут не произойти. Такие
события называются
случайными.
Например, событие, состоящее в появлении
цифры 1 при выполнении условия — бросания
игральной кости, может произойти, а
может не произойти.
Если событие
неизбежно происходит в результате
каждого испытания, то оно называется
достоверным.
Событие называется невозможным,
если оно вообще не происходит ни при
каких условиях.
Два события,
одновременное появление которых
невозможно, называются несовместными.
Пусть случайное
событие А в серии из n
независимых испытаний произошло m
раз, тогда отношение:
называется
относительной частотой события А. Для
каждой относительной частоты выполняется
неравенство:
При небольшом
числе опытов относительная частота
событий в значительной мере имеет
случайный характер и может заметно
изменяться от одной группы опытов к
другой. Однако при увеличении числа
опытов частота событий все более теряет
свой случайный характер и приближается
к некоторому постоянному положительному
числу, которое является количественной
мерой возможности реализации случайного
события А. Предел, к которому стремится
относительная частота событий при
неограниченном увеличении числа
испытаний, называется статистической
вероятностью события:
Например, при
многократном бросании монеты частота
выпадения герба будет лишь незначительно
отличаться от ½. Для достоверного события
вероятность Р(А) равна единице. Если
Р=0, то событие невозможно.
Математическим
ожиданием
дискретной случайной величины называется
сумма произведений всех ее возможных
значений хi
на вероятность этих значений рi:
Статистическим
аналогом математического ожидания
является среднее арифметическое значений
:
,
где mi
— число дискретных случайных величин,
имеющих значение хi.
Для непрерывной
случайной величины математическим
ожиданием служит интеграл:
,
где р(х) — плотность
вероятности.
Отдельные значения
случайной величины группируются около
математического ожидания. Отклонение
случайной величины от ее математического
ожидания (среднего значения) характеризуется
дисперсией,
которая для дискретной случайной
величины определяется формулой:
(15)
(16)
Дисперсия имеет
размерность случайной величины. Для
того, чтобы оценивать рассеяние
(отклонение) случайной величины в
единицах той же размерности, введено
понятие среднего
квадратичного отклонения
σ(Х), которое
равно корню квадратному из дисперсии:
(17)
Вместо среднего
квадратичного отклонения иногда
используется термин «стандартное
отклонение».
Всякое отношение,
устанавливающее связь между всеми
возможными значениями случайной величины
и соответствующими им вероятностями,
называется законом
распределения случайной величины.
Формы задания закона распределения
могут быть разными:
а) ряд распределения
(для дискретных величин);
б) функция
распределения;
в) кривая распределения
(для непрерывных величин).
Существует
относительно много законов распределения
случайных величин.
Нормальный
закон распределения случайных
величин (закон
Гаусса).
Случайная величина
распределена по
нормальному закону, если ее плотность
вероятности f(x)
определяется формулой:
(18),
где <x>
— математическое ожидание (среднее
значение) случайной величины <x>
= M
(X);
—
среднее квадратичное отклонение;
—
основание натурального логарифма
(неперово число);
f
(x)
– плотность вероятности (функция
распределения вероятностей).
Многие случайные
величины (в том числе все случайные
погрешности) подчиняются нормальному
закону распределения (закону Гаусса).
Для этого распределения наиболее
вероятным значением
измеряемой
величины
является
её среднее
арифметическое
значение.
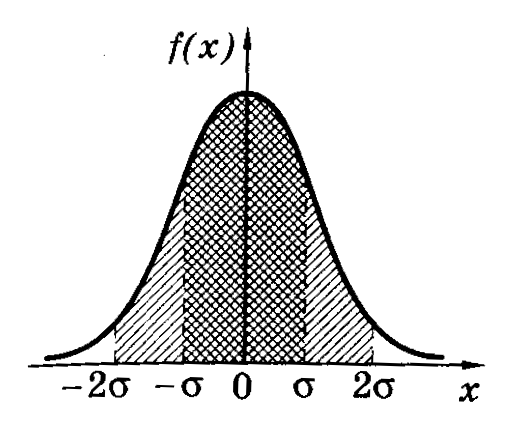
График нормального
закона распределения изображен на
рисунке (колоколообразная кривая).
Кривая симметрична
относительно прямой х=<x>=α,
следовательно, отклонения случайной
величины вправо и влево от <x>=α
равновероятны. При х=<x>±
кривая асимптотически приближается к
оси абсцисс. Если х=<x>,
то функция распределения вероятностей
f(x)
максимальна и принимает вид:
(19)
Таким образом,
максимальное значение функции fmax(x)
зависит от величины среднего квадратичного
отклонения. На рисунке изображены 3
кривые распределения. Для кривых 1 и 2
<x>
= α = 0 соответствующие значения среднего
квадратичного отклонения различны, при
этом 2>1.
(При увеличении
кривая распределения становится более
пологой, а при уменьшении
– вытягивается вверх). Для кривой 3 <x>
= α ≠ 0 и 3
= 2.
Закон
распределения
молекул в газах по скоростям называется
распределением
Максвелла.
Функция плотности вероятности попадания
скоростей молекул в определенный
интервал
теоретически была определена в 1860 году
английским физиком Максвеллом
. На рисунке
распределение Максвелла представлено
графически. Распределение движется
вправо или влево в зависимости от
температуры газа (на рисунке Т1
< Т2).
Закон распределения Максвелла определяется
формулой:
(20),
где mо
– масса молекулы, k
– постоянная Больцмана, Т – абсолютная
температура газа,
—
скорость молекулы.
Распределение
концентрации молекул газа в атмосфере
Земли (т.е.
в силовом поле) в зависимости от высоты
было дано австрийским физиком Больцманом
и называется
распределением
Больцмана:
(21)
Где n(h)
– концентрация молекул газа на высоте
h,
n0
– концентрация у поверхности Земли, g
– ускорение свободного падения, m
– масса молекулы.
Распределение
Больцмана.
Совокупность всех
значений случайной величины называется
простым
статистическим рядом.
Так как простой статистический ряд
оказывается большим, то его преобразуют
в вариационный
статистический
ряд или интервальный
статистический ряд. По интервальному
статистическому ряду для оценки вида
функции распределения вероятностей по
экспериментальным данным строят
гистограмму
– столбчатую
диаграмму. (Гистограмма – от греческих
слов “histos”–
столб и “gramma”–
запись).
n
-
h
Гистограмма
распределения Больцмана.
Для построения
гистограммы интервал, содержащий
полученные значения случайной величины
делят на несколько интервалов xi
одинаковой ширины. Для каждого интервала
подсчитывают число mi
значений случайной величины, попавших
в этот интервал. После этого вычисляют
плотность частоты случайной величины
для каждого интервала xi
и среднее значение случайной величины
<xi
> в каждом интервале.
Затем по оси абсцисс
откладывают интервалы xi,
являющиеся основаниями прямоугольников,
высота которых равна
(или
высотой
– плотностью относительной частоты
).
Расчетами показано,
что вероятность попадания нормально
распределенной случайной величины в
интервале значений от <x>–
до <x>+
в среднем равна 68%. В границах вдвое
более широких (<x>–2;
<x>+2)
размещается в среднем 95% всех значений
измерений, а в интервале (<x>–3;<x>+3)
– уже 99,7%. Таким образом, вероятность
того, что отклонение значений нормально
распределенной случайной величины
превысит 3
(
– среднее квадратичное отклонение)
чрезвычайно мала (~0,003). Такое событие
можно считать практически невозможным.
Поэтому границы <x>–3
и <x>+3
принимаются за границы практически
возможных значений нормально распределенной
случайной величины («правило трех
сигм»).
Если число измерений
(объем выборки) невелико (n<30),
дисперсия вычисляется по формуле:
(22)
Уточненное среднее
квадратичное отклонение отдельного
измерения вычисляется по формуле:
(23)
Напомним, что для
эмпирического распределения по выборке
аналогом математического ожидания
является среднее арифметическое значение
<x>
измеряемой величины.
Чтобы дать
представление о точности и надежности
оценки измеряемой величины, используют
понятия доверительного интервала и
доверительной вероятности.
Доверительным
интервалом
называется интервал (<x>–x,
<x>+x),
в который по определению попадает с
заданной вероятностью действительное
(истинное) значение измеряемой величины.
Доверительный интервал характеризует
точность полученного результата: чем
уже доверительный интервал, тем меньше
погрешность.
Доверительной
вероятностью
(надежностью)
результата серии измерений называется
вероятность того, что истинное значение
измеряемой величины попадает в данный
доверительный интервал (<x>±x).
Чем больше величина доверительного
интервала, т.е. чем больше x,
тем с большей надежностью величина <x>
попадает в этот интервал. Надежность
выбирается самим исследователем
самостоятельно, например, =0,95;
0,98. В медицинских и биологических
исследованиях, как правило, доверительную
вероятность (надежность) принимают
равной 0,95.
Если величина х
подчиняется нормальному закону
распределения Гаусса, а <x>
и <>
оцениваются по выборке (числу измерений)
и если объем выборки невелик (n<30),
то интервал (<x>
– t,n<>,
<x>
+ t,n<>)
будет доверительным интервалом для
известного параметра х с доверительной
вероятностью .
Коэффициент t,n
называется коэффициентом
Стьюдента
(этот коэффициент был предложен в 1908 г.
английским математиком и химиком В.С.
Госсетом, публиковавшим свои работы
под псевдонимом «Стьюдент» – студент).
Значении коэффициента
Стьюдента t,n
зависит от доверительной вероятности
и числа измерений n
(объема выборки). Некоторые значения
коэффициента Стьюдента приведены в
таблице 1.
Таблица 1
|
n |
|
||||||
|
0,6 |
0,7 |
0,8 |
0,9 |
0,95 |
0,98 |
0,99 |
|
|
2 |
1,38 |
2,0 |
3,1 |
6,3 |
12,7 |
31,8 |
63,7 |
|
3 |
1,06 |
1,3 |
1,9 |
2,9 |
4,3 |
7,0 |
9,9 |
|
4 |
0,98 |
1,3 |
1,6 |
2,4 |
3,2 |
4,5 |
5,8 |
|
5 |
0,94 |
1,2 |
1,5 |
2,1 |
2,8 |
3,7 |
4,6 |
|
6 |
0,92 |
1,2 |
1,5 |
2,0 |
2,6 |
3,4 |
4,0 |
|
7 |
0,90 |
1,1 |
1,4 |
1,9 |
2,4 |
3,1 |
3,7 |
|
8 |
0,90 |
1,1 |
1,4 |
1,9 |
2,4 |
3,0 |
3,5 |
|
9 |
0,90 |
1,1 |
1,4 |
1,9 |
2,3 |
2,9 |
3,4 |
|
10 |
0,88 |
1,1 |
1,4 |
1,9 |
2,3 |
2,8 |
3,3 |
В таблице 1 в верхней
строке заданы значения доверительной
вероятности
от 0,6 до 0,99, в левом столбце – значение
n.
Коэффициент Стьюдента следует искать
на пересечении соответствующих строки
и столбца.
Окончательный
результат измерений записывается в
виде:
(25)
Где
– полуширина доверительного интервала.
Результат серии
измерений оценивается относительной
погрешностью:
(26)
Соседние файлы в предмете [НЕСОРТИРОВАННОЕ]
- #
- #
- #
- #
- #
- #
- #
- #
- #
- #
- #
-
-
May 8 2015, 14:46
Абсолютные ,относительные и приведенные погрешности измерений
Абсолютная погрешность – это разница между измеренной датчиком величиной Хизм и действительным значением Хд этой величины.
Действительное значение Хд измеряемой величины это найденное экспериментально значение измеряемой величины максимально близкое к ее истинному значению. Говоря простым языком действительное значение Хд это значение, измеренное эталонным прибором, или сгенерированное калибратором или задатчиком высокого класса точности. Абсолютная погрешность выражается в тех же единицах измерения, что и измеряемая величина (например, в м3/ч, мА, МПа и т.п.). Так как измеренная величина может оказаться как больше, так и меньше ее действительного значения, то погрешность измерения может быть как со знаком плюс (показания прибора завышены), так и со знаком минус (прибор занижает).
См.Абсолютная погрешность микрокомпьютерного расходомера скоростемера МКРС
Относительная погрешность – это отношение абсолютной погрешности измерения Δ к действительному значению Хд измеряемой величины.
Относительная погрешность выражается в процентах, либо является безразмерной величиной, а также может принимать как положительные, так и отрицательные значения.
См.Относительная погрешность ультразвукового уровнемера ЭХО-АС-01
Приведенная погрешность – это отношение абсолютной погрешности измерения Δ к нормирующему значению Хn, постоянному во всем диапазоне измерения или его части.
Нормирующее значение Хn зависит от типа шкалы датчика КИП:
- Если шкала датчика односторонняя и нижний предел измерения равен нулю (например, шкала датчика от 0 до 150 м3/ч), то Хn принимается равным верхнему пределу измерения (в нашем случае Хn = 150 м3/ч).
- Если шкала датчика односторонняя, но нижний предел измерения не равен нулю (например, шкала датчика от 30 до 150 м3/ч), то Хn принимается равным разности верхнего и нижнего пределов измерения (в нашем случае Хn = 150-30 = 120 м3/ч).
- Если шкала датчика двухсторонняя (например, от -50 до +150 ˚С), то Хn равно ширине диапазона измерения датчика (в нашем случае Хn = 50+150 = 200 ˚С).
Приведенная погрешность выражается в процентах, либо является безразмерной величиной, а также может принимать как положительные, так и отрицательные значения.
Довольно часто в описании на тот или иной датчик указывается не только диапазон измерения, например, от 0 до 50 мг/м3, но и диапазон показаний, например, от 0 до 100 мг/м3. Приведенная погрешность в этом случае нормируется к концу диапазона измерения, то есть к 50 мг/м3, а в диапазоне показаний от 50 до 100 мг/м3 погрешность измерения датчика не определена вовсе – фактически датчик может показать все что угодно и иметь любую погрешность измерения. Диапазон измерения датчика может быть разбит на несколько измерительных поддиапазонов, для каждого из которых может быть определена своя погрешность как по величине, так и по форме представления. При этом при поверке таких датчиков для каждого поддиапазона могут применяться свои образцовые средства измерения, перечень которых указан в методике поверки на данный прибор.