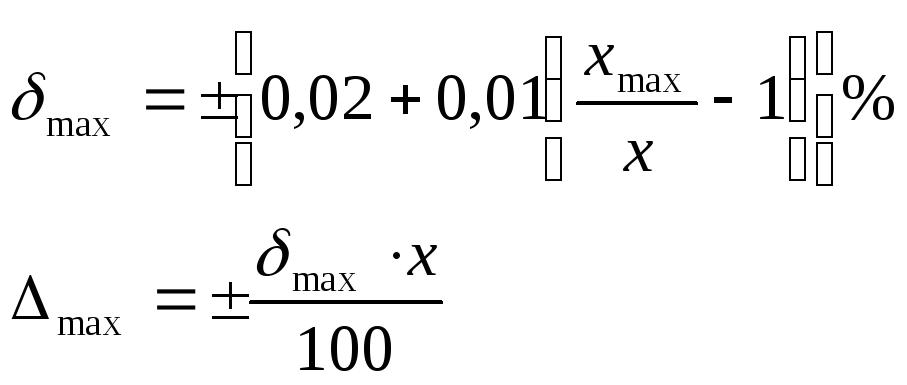Какие ошибки называются инструментальными

Инструментальные погрешности

Инструментальными называют погрешности, причина которых заключается в свойствах применяемых средств измерений. Эти свойства могут вызывать погрешности различного характера.

В общем случае инструментальные погрешности можно разделить на: инструментальные погрешности, являющиеся следствием несовершенства или неправильности технологии изготовления средств измерений; инструментальные погрешности, присущие данной конструкции; инструментальные погрешности, являющиеся следствием износа, старения или неисправности средств измерений.

Инструментальные погрешности, присущие данной конструкции

Одним из характерных источников погрешностей рассматриваемого вида, присущих почти всем средствам измерений, которые имеют подвижные части, является некоторая свобода перемещения этих частей, помимо движения, соответствующего принципу действия устройства. В зависимости от конструкции узла, в котором возникает такая свобода перемещения, а также от традиций той или иной отрасли приборостроения говорят о наличие «люфта», «зазора», «мертвого», «свободного» или «холостого хода» и т. д.

Еще одной причиной инструментальных погрешностей является трение в сочленениях подвижных деталей приборов.

Так, в средствах измерений, в которых при измерении приходится вращать или перемещать отдельные детали (например, в микрометрах), большое трение затрудняет правильную установку вращаемой детали и может привести к возникновению чрезмерно большого или чрезмерно малого давления на измеряемый объект.

Инструментальные погрешности, являющиеся следствием несовершенства или неправильности технологии изготовления средств измерений

Всем средствам измерений, имеющим шкалу, в большей или меньшей степени присущи погрешности, возникшие в результате неточности нанесения отметок шкалы, так называемые погрешности градуировки. В тех случаях, когда деления шкалы строго равномерны, как, например, в устройствах для измерения длины, отметки на шкалы наносятся механически при помощи соответствующих приспособлений. Несовершенство конструкции, износ или неисправности этих приспособлений могут привести к тому, что некоторые или все отметки окажутся смещенными в ту или иную сторону. При этом в процессе измерения результаты всегда будут содержать одну и ту же погрешность.

Более или менее точные измерительные приборы, шкалы которых неравномерны, градуируют нередко вручную. Процесс градуировки осуществляется следующим образом. Градуируемый измерительный прибор с основанием, подготовленным для нанесения шкалы, и образцовый измерительный прибор, погрешности которого значительно меньше предельно допускаемых для градуируемо, подключают к регулируемому источнику измеряемой величины. Устанавливая различные значения измеряемой величины показаниям образцового измерительного прибора, одновременно наносят отметки на шкалу градуируемого измерительного прибора. Уже на этом этапе возможно появление погрешностей, например, вследствие того, что исполнитель при нанесении отметки дет смотреть не строго перпендикулярно к плоскости шкалы, результате нанесенная им отметка окажется смещенной влево :и вправо от правильного положения (погрешность от параллакса). При градуировке на шкалу наносят только основные отметки, т. е. отметки, против которых ставят числовые значения (называть их «оцифрованными» не рекомендуется).

Промежуточные отметки в соответствии с характером шкалы наносят на глаз или при помощи приспособлений различной степени сложности. На этом этапе возможно появление погрешностей градуировки вследствие глазомерных ошибок или несовершенства приспособления, недостаточно точно воспроизводящего малых делениях характер неравномерности шкалы. Эти погрешности опасны тем, что при поверке средств измерений, как правило, ограничиваются сличением их показаний с показаниями образцового измерительного устройства также только на числовых метках.

Таким образом, систематические погрешности на промежуточных отметках могут остаться незамеченными.

Числовые, а иногда и промежуточные отметки при описанном особе градуировки наносят предварительно «вчерне», например виде карандашных точек, после чего вычерчивают шкалу тушью или иным способом. На этом этапе может возникнуть дополни-льная градуировочная погрешность, например, от того, что при нанесении штриха определенной ширины (а не толщины, как иногда говорят) его середина может оказаться смещенной по отношению к точке, поставленной при градуировке.

Таким образом, возможность появления инструментальных погрешностей в результате градуировки весьма значительна. Принимаются меры к тому, чтобы погрешности градуировки были меньше погрешностей, допускаемых для данного средства измерения, однако в какой-то степени они все же остаются. Их отрицательное влияние становится особенно заметно в процессе эксплуатации средств измерений, когда возрастают другие погрешности, например, вследствие износа деталей, старения материала, нарушения регулировки. Тогда суммарная погрешность может выйти за допускаемые пределы раньше срока естественного износа.

В последнее время стремятся изготовлять печатные шкалы (типографским, фотографическим и другими способами) не только для средств измерений массового выпуска, но и для более точных. В этом случае при конструировании предусматривают способы регулирования средств измерений, позволяющие «подогнать» их показания к шкале. Разумеется, и при этом способе неизбежны градуировочные погрешности.

Инструментальные погрешности, являющиеся следствием износа, старения или неисправности средств измерений.

Износ и старение материалов могут быть причиной появления погрешностей, имеющих некоторые характерные особенности. Так, совершенно очевидно, что средства измерений изнашиваются непрерывно и постепенно в процессе эксплуатации со скоростью, зависящей от интенсивности эксплуатации. Следовательно, и погрешности, появляющиеся в результате износа, как правило, возрастают постепенно. Однако рост этот происходит настолько медленно, что в определенный отрезок времени мы можем принимать погрешности, явившиеся следствием износа, постоянными и даже пользоваться соответствующими поправками. Только тогда, когда эти погрешности достигнут установленного предела, дальнейшее применение данного средства измерений считается недопустимым.

Типичным примером в этом отношении являются гири. Их износ всегда идет в одном направлении — постепенно уменьшается их масса. Характер износа гирь заставляет изготовлять их с положительным запасом массы. Масса новой гири всегда больше номинальной в пределах, допускаемых для данного класса гирь.

Другим примером являются концевые меры длины — плитки. В процессе эксплуатации и при ремонтах их размер постепенно уменьшается. Плитками пользуются до тех пор, пока их размер не достигнет установленного для них предела, после чего их или переводят в другой класс, или переаттестовывают, или, наконец, изымают из применения в качестве мер.

Несколько иначе обстоит дело со старением. Под старением понимают изменение каких-либо свойств материалов с течением времени, а иногда и в зависимости от условий применения или хранения.

Процесс старения может протекать различно. Старение может привести к потере каких-либо свойств, имеющих значение для средства измерений, или к постепенной их стабилизации. Одним из характерных примеров старения второго вида является старение манганина. Манганин—это сплав меди, марганца, никеля и некоторых других компонентов, добавляемых иногда в небольших количествах. Обладая сравнительно большим удельным электрическим сопротивлением, манганин в то же время имеет незначительный температурный коэффициент сопротивления. Термоэлектродвижущая сила (т. э. д. с), которая возникает в спае манганина с медью при его нагревании, относительно невелика. Благодаря этим качествам манганин широко применяется в электроприборостроении. Однако манганин имеет одно отрицательное свойство — с течением времени его сопротивление хотя и медленно, но изменяется. По истечении двух-трех лет процесс этот практически прекращается и сопротивление изделия из манганина стабилизируется.

Были разработаны приемы искусственного ускорения процесса старения манганина, стабилизации его свойств. Так как полной стабилизации все же достичь не удается, то для более точных приборов, в которых эта остаточная нестабильность влияет на показания, в первые годы эксплуатации проводят более частые поверки.

В особо ответственных случаях готовое изделие выдерживают годами без применения — до полной стабилизации его свойств, например, катушки сопротивления высшей точности. Во время выдержки ведутся периодические наблюдения за изменением их сопротивления.

Как видим, в данном случае процесс старения обратен процессу износа — с течением времени качество и надежность измерительного устройства улучшаются.

Манганин — не единственный пример старения материала в области измерительной техники. Так, в некоторых концевых мерах длины, изготовляемых из стали, также была обнаружена тенденция к изменению с течением времени их размеров, причем в сторону увеличения. Это явление назвали «ростом» плиток. Меры борьбы с этим явлением те же, что и в отношении манганина — искусственная стабилизация и более частая поверка до наступления надежной естественной стабилизации.

Неисправностей, которые являются или точнее могут являться причиной появления систематических погрешностей, множество. Перечислить их нет никакой возможности. Можно указать на деформации или коррозию деталей измерительного механизма, не прекращающих, но изменяющих характер взаимодействия отдельных его частей. Часто неисправность измерительного устройства является следствием его перегрузки. Перегрузка — механическая, электрическая, тепловая или какая-либо иная — может вызвать устойчивое «остаточное» изменение в материале или в механизме средства измерений и явиться причиной появления или изменения систематической погрешности.

Неисправности, ведущие к появлению небольших систематических погрешностей, гораздо опаснее тех, которые вызывают большие погрешности. Большие систематические погрешности сравнительно быстро обнаруживаются «на глаз», например, по значительному несоответствию результатов измерения ожидаемым. Небольшие систематические погрешности, в два — четыре раза превышающие допускаемые, могут в течение более или менее длительного времени оставаться незамеченными. Такие незамеченные погрешности могут принести огромный вред, особенно при большом числе измерений.

Особую опасность представляет появление или изменение систематических погрешностей в образцовых средствах измерений, применяемых для поверки других средств измерений. Мало того, что каждое средство измерений, поверенное или отградуированное по такому образцовому средству измерений, с самого начала будет нести в себе скрытую погрешность, оно будет передавать эту погрешность всем объектам, которые с его помощью будут измеряться или поверяться. Если вред, приносимый скрытой систематической погрешностью рабочего средства измерений, можно было бы выразить математически, то для выражения вреда, приносимого скрытой систематической погрешностью образцового средства измерений, это выражение следовало бы возвести в квадрат или даже в четвертую степень для случая поверки образцового средства измерений следующего, более низкого, разряда.

Из этого сопоставления роли систематических погрешностей рабочих и образцовых средств измерений наглядно видна важность особой тщательности проведения поверки образцовых средств измерений.

Данный обзор инструментальных погрешностей не является исчерпывающим. Его цель — подсказать читателю необходимость и пути анализа возможных систематических погрешностей, которые могут внести в результаты измерения применяемые измерительные устройства.

Похожие материалы

        ошибки наблюдений и измерений, обусловленные несовершенством инструментов (т. е. неизбежными отличиями реального инструмента от инструмента «идеального», представляемого его геометрической схемой), а также неточностью установки инструмента в рабочем положении. Учёт И. о. имеет значение при измерениях, требующих высокой точности. Пренебрежение их учётом влечёт за собой систематические ошибки, которые в значительной мере могут обесценить результаты измерений.

         Особенно большое значение учёт И. о. имеет в астрономии, геодезии и др. науках, требующих точнейших измерений. В связи с этим разработка методов исследования И. о. и исключения их влияния на результаты наблюдений и измерений является одной из главных задач теории измерительных инструментов.

         И. о. могут быть подразделены на 3 категории: 1) ошибки, зависящие от несовершенства изготовления отдельных частей инструмента. Эти ошибки не могут быть ни устранены, ни изменены наблюдателем, но они тщательно исследуются, а вызываемые ими погрешности исключаются или введением соответствующих поправок, или рационально построенной методикой измерений, устраняющей их влияние на окончательные результаты. К этой категории И. о. относятся: ошибки штрихов разделённых кругов, по которым делаются отсчёты направлений на наблюдаемые предметы; ошибки штрихов шкал измерительных приборов; ошибки эксцентриситета, происходящие от несовпадения центра вращения разделённого круга или алидады с центром делений круга; периодические и ходовые ошибки винтов микрометров, связанные с несовершенством их нарезки или монтировки; ошибки от прогиба частей инструмента; ошибки, связанные с оптикой инструмента: дисторсия, астигматизм, кома и др.

         2) Ошибки, зависящие от погрешностей сборки и юстировки инструмента, а также от недостаточной точности его установки в положении, требуемом теорией данного способа наблюдений. К этим ошибкам относятся: коллимационная ошибка, заключающаяся в отклонении от 90° угла между визирной линией и осью вращения трубы; ошибки, связанные с наклонением горизонтальной оси инструмента к горизонту и неточностью его установки в нужном азимуте; неточная центрировка линз объектива; некоторые ошибки регистрирующей аппаратуры и др. И. о. этой категории, обнаруживаемые поверками инструмента, могут быть сведены к минимуму перемещением отдельных частей инструмента, предусматриваемым их конструкцией. Остающиеся неустранёнными малые доли этих ошибок определяются с помощью вспомогательных приспособлений (уровень, надир-горизонт, коллиматоры и т. п.) или выводятся из наблюдений (например, ошибка азимута) и влияние их учитывается при обработке наблюдений.

         3) Ошибки, связанные с изменением свойств инструмента с течением времени, в частности обусловленные изменением температуры; к этой же категории ошибок относится суммарный эффект всех прочих погрешностей, не учитываемых теорией инструмента. Эти И. о. наиболее сложны. Проявляясь систематически и не обнаруживаясь явно в процессе наблюдений и измерений, они особенно вредны. Выявляются они только при измерениях одних и тех же величин разными инструментами. Так, при сравнении координат звёзд, полученных из наблюдений на разных обсерваториях, или поправок радиосигналов точного времени, определённых различными службами времени, всегда обнаруживаются систематические разности, которые обычно в полтора-два раза, а иногда и в пять-шесть раз превосходят присущие данным методам и инструментам случайные ошибки. Одной из важных задач является нахождение, тщательное исследование и, по возможности, устранение причин, вызывающих И. о. этой категории.

Лит.: Блажко С. Н., Курс практической астрономии, 3 изд., М.—Л., 1951; Зверев М. С., Исследование результатов астрономических наблюдений Службы времени ГАИШ за 1941—44 гг., «Труды Государственного астрономического института им. П. К. Штернберга», 1950, т. 18. в. 2; Щеглов В. П., Опыт исследования некоторых систематических ошибок…, «Астрономический журнал», 1950, т. 27, в. 6; Васильев В. М., О разностях температуры отдельных частей трех пассажных инструментов Службы времени, там же, 1952, т. 29, в. 6; Павлов Н. Н., О термических эффектах в перекладывающихся пассажных инструментах, там же, 1953, т. 30, в. 1.

Источники
погрешностей (инструментальные и
методические погрешности, влияние
помех, субъективные ошибки). Номинальная
и реальная функция преобразования,
абсолютная и относительная погрешность
средства измерений, основная и
дополнительная погрешности. Пределы
допускаемых погрешностей, классы
точности средств измерений. Выявление
и уменьшение систематических погрешностей.
Оценка случайных погрешностей.
Доверительный интервал и доверительная
вероятность. Оценка погрешностей
косвенных измерений. Обработка результатов
измерений. [1:
с.23…35,40,41,53,54,56…61; 2:
с.22…53; 3:
с.48…91; 4:
с.21,22,35…52,63…71, 72…77,85…93].

II.1. Основные сведения и методические указания.

Одним из
основополагающих понятий Метрологии
является понятие погрешности измерений.

Погрешностью
измерения
называют отклонение измеренного

значения физической
величины от её истинного значения.

Погрешность
измерений, в общем случае, может быть
вызвана следующими причинами:

1. Несовершенством
   принципа действия и недостаточным
   качеством элементов используемого
   средства измерения.

2. Несовершенством
   метода измерений и влиянием используемого
   средства измерения на саму измеряемую
   величину, зависящим от способа
   использования данного средства
   измерения.

3. Субъективными
   ошибками экспериментатора.

Так как истинное
значение измеряемой величины никогда
неизвестно (в противном случае отпадает
необходимость в проведении измерений),
то численное значение погрешности
измерений может быть найдено только
приближенно. Наиболее близким к истинному
значению измеряемой величины является
значение, которое может быть получено
при использовании эталонных средств
измерений (средств измерений наивысшей
точности). Это значение условились
называть действительным
значением измеряемой величины.
Действительное значение также является
неточным, однако, из-за малой погрешности
эталонных средств измерений, погрешностью
определения действительного значения
пренебрегают.

Классификация
погрешностей

1. По форме представления
   различают понятия абсолютной погрешности
   измерений и относительной погрешности
   измерений.

Абсолютной
погрешностью
измерений называют разность между

измеренным и
действительным значениями измеряемой

величины:

,

где ∆ — абсолютная
погрешность,

–измеренное
значение,

–действительное
значение измеряемой величины.

Абсолютная
погрешность имеет размерность измеряемой
величины. Знак абсолютной погрешности
будет положительным, если измеренное
значение больше действительного, и
отрицательным в противном случае.

Относительной
погрешностью
называют отношение абсолютной

погрешности к
действительному значению измеряемой
величины:

где δ – относительная
погрешность.

Чаще всего
относительную погрешность определяют
приближенно в процентах от измеренного
значения:

Относительная
погрешность показывает, какую часть (в
%) от измеренного значения составляет
абсолютная погрешность. Относительная
погрешность позволяет нагляднее, чем
абсолютная погрешность, судить о точности
измеренного значения.

1. По источникам
   происхождения погрешности подразделяют
   на следующие виды:

— инструментальные
погрешности;

— методические
погрешности;

— субъективные
погрешности, допущенные экспериментатором
.

Инструментальными
называются погрешности, которые
принадлежат данному типу средств
измерения, могут быть определены при
их испытаниях и занесены в паспорт
средства измерения в виде пределов
допускаемых погрешностей.

Инструментальная
погрешность возникает из-за несовершенства
принципа действия и недостаточно
высокого качества элементов, применяемых
в конструкции средства измерений. По
этой причине реальная передаточная
характеристика каждого экземпляра
средства измерений в большей или меньшей
степени отличается от номинальной
(расчетной) передаточной характеристики.
Отличие реальной характеристики средства
измерений от номинальной (рис.1) определяет
величину инструментальной погрешности
средства измерений.

Рис.1. Иллюстрация
к определению понятия инструментальной

погрешности.

Здесь: 1 – номинальная
характеристика средства измерений;

2 – реальная
характеристика средства измерений.

Как видно из рис.1,
при изменении измеряемой величины,
инструментальная погрешность может
иметь различные значения (как положительные,
так и отрицательные).

При создании
средств измерений какой-либо физической
величины, к сожалению, не удается
полностью избавиться от реакции этого
средства измерений на изменение других
(не измеряемых) величин. Наряду с
чувствительностью средства измерения
к измеряемой величине, оно всегда
реагирует (хотя и существенно в меньшей
степени) на изменение условий эксплуатации.
По этой причине инструментальную
погрешность подразделяют на основную
погрешность и дополнительную
погрешности.

Основной
погрешностью
называют погрешность, имеющую место

в случае применения
средства измерений в нормальных условиях

эксплуатации.

Номенклатура
влияющих на средство измерений величин
и диапазоны их изменений определяются
разработчиками в качестве нормальных
условий для каждого типа средств
измерений. Нормальные условия эксплуатации
всегда указываются в техническом
паспорте средства измерений. Если
эксперимент выполняется в условиях,
отличных от нормальных для данного
средства измерений, его реальная
характеристика искажается сильнее, чем
в нормальных условиях. Погрешности,
которые при этом возникают, называют
дополнительными.

Дополнительной
погрешностью
называют погрешность средств

измерений, которая
возникает в условиях, отличающихся от

нормальных, но
входящих в допустимую рабочую область
условий

эксплуатации.

Рабочие условия
эксплуатации, так же как и нормальные,
в обязательном порядке приводятся в
техническом паспорте средств измерений.

Инструментальная
погрешность средств измерений
определенного типа не должна превышать
некоторого заданного значения – так
называемой предельно допустимой основной
погрешности средств измерений данного
типа. Фактическая основная погрешность
каждого конкретного экземпляра этого
типа является при этом случайной
величиной и может принимать различные
значения, иногда даже равные нулю, но в
любом случае инструментальная погрешность
не должна превышать заданного предельного
значения. Если это условие не выполняется,
средство измерений должно быть изъято
из обращения.

Методическими
называются погрешности, которые возникают
из-за неудачного выбора экспериментатором
средства измерения для решения
поставленной задачи. Они не могут быть
приписаны средству измерения и приведены
в его паспорте.

Методические
погрешности измерения зависят как от
характеристик применяемого средства
измерений, так и во многом от параметров
самого объекта измерения. Неудачно
выбранные средства измерений могут
исказить состояние объекта измерений.
При этом методическая составляющая
погрешности может оказаться существенно
больше инструментальной.

Субъективными
погрешностями
называют погрешности,

допускаемые
самим экспериментатором при проведении

измерений.

Этот тип погрешностей
связан обычно с невнимательностью
экспериментатора: применение прибора
без устранения смещения нуля, неправильное
определение цены деления шкалы, неточный
отсчет доли деления, ошибки в подключении
и т.п.

1. По характеру
   проявления погрешности измерений
   подразделяют на:

— систематические
погрешности;

— случайные
погрешности;

— промахи (грубые
ошибки).

Систематической
называют погрешность, которая при
повторных измерениях одной и той же
величины остается постоянной, или
изменяется закономерно.

Систематические
погрешности обусловлены как несовершенством
метода измерений и влиянием средства
измерений на измеряемый объект, так и
отклонением реальной передаточной
характеристики применяемого средства
измерений от номинальной характеристики.

Постоянные
систематические погрешности средств
измерений могут быть выявлены и численно
определены в результате сличения их
показаний с показаниями эталонных
средств измерений. Такие систематические
погрешности могут быть уменьшены
регулировкой приборов или введением
соответствующих поправок. Следует
заметить, что полностью исключить
систематические погрешности средств
измерений не удается, так как их реальные
передаточные характеристики изменяются
при изменении условий эксплуатации.
Кроме этого всегда имеют место так
называемые прогрессирующие погрешности
(возрастающие или убывающие), вызванные
старением элементов входящих в состав
средств измерений. Прогрессирующие
погрешности могут быть скорректированы
регулировкой или введением поправок
лишь на некоторое время.

Таким образом,
даже после регулировки или введения
поправок, всегда имеет место так
называемая неисключенная систематическая
погрешность результата измерений.

Случайной
называют погрешность, которая при
повторных измерениях одной и той же
величины принимает различные значения.

Случайные погрешности
обусловлены хаотичным характером
изменений физических величин (помех),
влияющих на передаточную характеристику
средства измерений, суммированием помех
с измеряемой величиной, а также наличием
собственных шумов средства измерений.
При создании средств измерений
предусматриваются специальные меры
защиты от помех: экранирование входных
цепей, использование фильтров, применение
стабилизированных источников питающего
напряжения и т.д. Это позволяет уменьшить
величину случайных погрешностей при
проведении измерений. Как правило, при
повторных измерениях одной и той же
величины результаты измерений либо
совпадают, либо отличаются на одну, две
единицы младшего разряда. В такой
ситуации случайной погрешностью
пренебрегают и оценивают только величину
неисключенной систематической
погрешности.

Наиболее сильно
случайные погрешности проявляются при
измерении малых значений физических
величин. Для повышения точности в таких
случаях производятся многократные
измерения с последующей статистической
обработкой результатов методами теории
вероятности и математической статистики.

Промахами
называют грубые погрешности, существенно
превышающие ожидаемые погрешности при
данных условиях проведения измерений.

Промахи большей
частью возникают из-за субъективных
ошибок экспериментатора или из-за сбоев
в работе средства измерений при резких
изменениях условий эксплуатации (броски
или провалы сетевого напряжения, грозовые
разряды и т.п.) Обычно промахи легко
выявляются при повторных измерениях и
исключаются из рассмотрения.

Оценка погрешностей
косвенных измерений.

При косвенных
измерениях результат измерений
определяется по функциоральной
зависимости от результатов прямых
измерений. Поэтому погрешность косвенных
измерений определяется как полный
дифференциал этой функции от величин,
измеряемых с помощью прямых измерений.

;

Где:
—
предельные абсолютные погрешности
результатов прямых

измерений;

—
предельная абсолютная погрешность
результата косвенного

измерения;

—
соответствующие предельные относительные
погрешности.

—
функциональная связь между искомой
измеряемой величиной и

величинами,
подвергающимися прямым измерениям.

Статистическая
обработка результатов измерений

Из-за влияния на
средство измерений помех различного
происхождения (изменение температуры
окружающей среды, электромагнитных
полей, вибраций, изменения частоты и
амплитуды сетевого напряжения, изменения
атмосферного давления, влажности и
т.д.), а также из-за наличия собственных
шумов элементов, входящих в состав
измерительных приборов, результаты
повторных измерений одной и той же
физической величины (особенно ее малых
значений) будут в большей или меньшей
степени отличаться друг от друга. В этом
случае результат измерений является
случайной величиной, которая характеризуется
наиболее вероятным значением и разбросом
(рассеянием) результатов повторных
измерений вблизи наиболее вероятного
значения. Если при повторных измерениях
одной и той же величины результаты
измерений не отличаются друг от друга,
то это означает, что разрешающая
способность отсчетного устройства не
позволяет обнаружить это явление. В
этом случае случайная составляющая
погрешности измерений является
несущественной и ею можно пренебречь.
При этом неисключенную систематическую
погрешность результата измерений
оценивают по величине пределов допускаемых
погрешностей применяемых средств
измерений. Если же при повторных
измерениях одной и той же величины
наблюдается разброс показаний, то это
означает, что наряду с большей или
меньшей неисключенной систематической
погрешностью, имеет место и случайная
погрешность, принимающая при повторных
измерениях различные значения.

Для определения
наиболее вероятного значения измеряемой
величины при наличии случайных
погрешностей и для оценки погрешности,
с которой определено это наиболее
вероятное значение, применяется
статистическая обработка результатов
измерений. Статистическая обработка
результатов серии измерений при
проведении экспериментов позволяет
решить следующие задачи.

1. Более точно
   определить результат измерения путем
   усреднения отдельных наблюдений.

2. Оценить область
   неопределенности уточненного результата
   измерений.

Основной смысл
усреднения результатов измерений
заключается в том, что найденная
усредненная оценка имеет меньшую
случайную погрешность, чем отдельные
результаты, по которым эта усредненная
оценка определяется. Следовательно
усреднение не устраняет полностью
случайного характера усредненного
результата, а лишь уменьшает ширину
полосы его неопределенности.

Таким образом, при
статистической обработке, прежде всего,
определяют наиболее вероятное значение
измеряемой величины путем вычисления
среднего арифметического всех отсчетов:

где: x_i
– результат i
– го измерения;

n
– число проведенных измерений в данной
серии измерений.

После этого
оценивают отклонение результатов
отдельных измерений x_i
от этой оценки среднего значения
;.

Затем находят
оценку среднеквадратического отклонения
наблюдений, характеризующую степень
рассеяния результатов отдельных
наблюдений вблизи,
по формуле:

.

Точность оценки
наиболее вероятного значения измеряемой
величины
зависит от числа наблюдений.
Нетрудно убедиться в том, что результаты
нескольких оценокпо одному и тому же числуотдельных измерений будут отличаться.
Таким образом, сама оценкатакже является случайной величиной. В
связи с этим вычисляется оценка
среднеквадратического отклонения
результата измерения,
которую обозначают.
Эта оценка характеризует степень
разброса значенийпо отношению к истинному значению
результата, т.е. характеризует точность
результата, полученного усреднением
результата многократных измерений.
Следовательно, поможет быть оценена систематическая
составляющая результата серии измерений.
Для различныхона определяется по формуле:

Следовательно,
точность результата многократных
измерений увеличивается с ростом числа
последних.

Однако в большинстве
практических случаев нам важно определить
не просто степень рассеивания значения
погрешности при проведении серии
измерений (т.е. величину
),
а оценить вероятность возникновения
погрешности измерения, не превышающую
допустимую, т.е. не выходящую за пределы
некоторого заданного интервала разброса
получаемых погрешностей.

Доверительным
интервалом
называют
интервал, который с заданной вероятностью,
называемой
доверительной вероятностью
накрывает истинное значение измеряемой
величины.

При определении
доверительных интервалов необходимо,
прежде всего, учитывать, что закон
распределения погрешностей, получаемых
при проведении многократных измерений,
при числе измерений в серии меньше 30,
описывается не нормальным законом
распределения, а так называемым законом
распределения Стьюдента. И, в этих
случаях, величину доверительного
интервала обычно оценивают по формуле:

,

где
— так называемый коэффициент Стьюдента.

В табл.4.1 приведены
значения коэффициентов Стьюдента
в зависимости от заданной доверительной
вероятности и числа проведенных
наблюдений.
При выполнении измерений обычно задаются
доверительной вероятностью 0,95 или 0,99.

Таблица 4.1

Значения
коэффициентов Стьюдента
.

n
0,5	0,6	0,7	0,8	0,9	0,95	0,98	0,99
2	1,00	1,38	1,96	3,08	6,31	12,71	31,82	63,66
3	0,82	1,06	1,34	1,89	2,92	4,30	6,97	9,93
4	0,77	0,98	1,25	1,64	2,35	3,18	4,54	5,84
5	0,74	0,94	1,19	1,53	2,13	2,78	3,75	4,60
6	0,73	0,92	1,16	1,48	2,02	2,62	3,37	4,03
7	0,72	0,91	1,13	1,44	1,94	2,45	3,14	3,71
8	0,71	0,90	1,12	1,42	1,90	2,37	3,00	3,50
9	0,71	0,89	1,11	1,40	1,86	2,31	2,90	3,36
10	0,70	0,88	1,10	1,38	1,83	2,26	2,82	3,25
16	0,69	0,87	1,07	1,34	1,75	2,13	2,60	2,95
25	0,69	0,86	1,06	1,32	1,71	2,06	2,49	2,80

При изучении
материалов данного раздела следует
хорошо уяснить, что погрешности
результатов измерений и погрешности
средств измерений – не идентичные
понятия. Погрешность средства измерения
это его свойство, характеристика, для
описания которого используют ряд правил,
закрепленных в стандартах и нормативных
документах. Это та доля погрешности
измерения, которая определяется только
самим средством измерения. Погрешность
же измерений (результата измерений) –
это число, которое характеризует границы
неопределенности значения измеряемой
величины. В нее, кроме погрешности
средства измерений, могут входить
составляющие погрешности, порожденные
применяемым методом измерения
(методические погрешности), действием
влияющих (неизмеряемых) величин,
погрешность отсчета и др.

Нормирование
погрешностей средств измерения.

Точность СИ
определяется предельно-допустимыми
погрешностями, которые могут быть
получены при его использовании.

Нормированием
погрешностей средств измерений называют

процедуру
назначения допустимых границ основной
и

дополнительных
погрешностей, а также выбор формы
указания

этих границ
в нормативно-технической документации.

Пределы допускаемой
основной и дополнительных погрешностей
определяются разработчиками для каждого
типа средств измерений на стадии
подготовки производства. В зависимости
от назначения средства измерений и
характера изменения погрешности в
пределах диапазона измерений нормируется
для средств измерений различного типа
либо предельно-допустимое значение
основной абсолютной погрешности, либо
предельно-допустимое значение основной
приведенной погрешности, либо
предельно-допустимое значение основной
относительной погрешности.

Для каждого типа
средств измерений характер изменения
погрешности в пределах диапазона
измерений зависит от принципа действия
этого средства измерений и может быть
самым разнообразным. Однако, как показала
практика, среди этого многообразия
часто удается выделить три типовых
случая, предопределяющих выбор формы
представления пределов допускаемой
погрешности. Типовые варианты отклонения
реальных передаточных характеристик
средств измерений от номинальной
характеристики и соответствующие им
графики изменения предельных значений
абсолютной и относительной погрешностей
в зависимости от измеряемой величины
приведены на рис 2.

Если реальная
передаточная характеристика средства
измерений смещена по отношению к
номинальной (1-й график на рис.2а),
абсолютная погрешность, возникающая
при этом, (1-й график на рис.2б), не зависит
от измеряемой величины.

Составляющую
погрешности средства измерений, не
зависящую от измеряемой величины,
называют аддитивной
погрешностью.

Если угол наклона
реальной передаточной характеристики
средства измерений отличается от
номинального (2-й график на рис. 2а), то
абсолютная погрешность будет линейно
зависеть от измеряемой величины (2-й
график на рис. 2б).

Составляющую
погрешности средства измерений, линейно
зависящую от измеряемой величины,
называют мультипликативной
погрешностью.

Если реальная
передаточная характеристика средства
измерений смещена по отношению к
номинальной и угол ее наклона отличается
от номинального (3-й график на рис. 2а),
то в этом случае имеет место как
аддитивная, так и мультипликативная
погрешность.

Аддитивная
погрешность возникает из-за неточной
установки нулевого значения перед
началом измерений, ухода нуля в процессе
измерений, из-за наличия трений в опорах
измерительного механизма, из-за наличия
термо-эдс в контактных соединениях и
т.д.

Мультипликативная
погрешность возникает при изменении
коэффициентов усиления или ослабления
входных сигналов (например, при изменении
температуры окружающей среды, или
вследствие старения элементов), из-за
изменения значений, воспроизводимых
мерами, встроенными в измерительные
приборы, из-за изменений жесткости
пружин, создающих противодействующий
момент в электромеханических приборах
и т.д.

Ширина полосы
неопределенности значений абсолютной
(рис.2б) и относительной (рис.2в) погрешностей
характеризует разброс и изменение в
процессе эксплуатации индивидуальных
характеристик множества находящихся
в обращении средств измерений определенного
типа.

А) Нормирование
пределов допускаемой основной погрешности
для

средств
измерений с преобладающей аддитивной
погрешностью.

Для средств
измерений с преобладающей аддитивной
погрешностью (1-й график на рис.2) удобно
нормировать одним числом предельно-допустимое
значение абсолютной погрешности (∆_max=
±а). В этом случае фактическая абсолютная
погрешность ∆ каждого экземпляра
средства измерений данного типа на
различных участках шкалы может иметь
различные значения, но не должна превышать
предельно-допустимой величины (∆ ≤
±а). В многопредельных измерительных
приборах с преобладающей аддитивной
погрешностью для каждого предела
измерений пришлось бы указывать свое
значение предельно допустимой абсолютной
погрешности. К сожалению, как видно из
1-го графика на рис.2в, нормировать одним
числом предел допускаемой относительной
погрешности в различных точках шкалы
не представляется возможным. По этой
причине для средств измерений с
преобладающей аддитивной погрешностью
часто нормируют одним числом значение
так называемой основной приведенной
относительной
погрешности

,

где X_N
– нормирующее значение.

Таким способом,
например, нормируются погрешности
большинства электромеханических и
электронных приборов со стрелочными
индикаторами. В качестве нормирующего
значения X_N
обычно используется предел измерений
(X_N
= X_max),
удвоенное значение предела измерений
(если нулевая отметка находится в
середине шкалы), или длина шкалы (для
приборов с неравномерной шкалой). Если
X_N
= X_max,
то значение приведенной погрешности γ
равно пределу допускаемой относительной
погрешности средства измерений в точке,
соответствующей пределу измерений. По
заданному значению предела допускаемой
основной приведенной погрешности легко
определить предел допускаемой основной
абсолютной погрешности для каждого
предела измерений многопредельного
прибора:.

После этого для
любой отметки шкалы X
может быть произведена оценка
предельно-допустимой основной
относительной погрешности:

.

Б) Нормирование
пределов допускаемой основной погрешности
для

средств измерений
с преобладающей мультипликативной

погрешностью.

Как видно из рис.2
(2-й график), для средств измерений с
преобладающей мультипликативной
погрешностью, одним числом удобно
нормировать предел допускаемой основной
относительной погрешности (рис.2в) δ_max=
± b∙100%.
В этом случае, фактическая относительная
погрешность каждого экземпляра средства
измерений данного типа на различных
участках шкалы может иметь различные
значения, но не должна превышать предельно
допустимой величины (δ ≤ ± b∙100%).
По заданному значению предельно
допустимой относительной погрешности
δ_max
для любой точки шкалы может быть
произведена оценка предельно-допустимой
абсолютной погрешности:

.

К числу средств
измерений с преобладающей мультипликативной
погрешностью относится большинство
многозначных мер, счетчики электрической
энергии, счетчики воды, расходомеры и
др. Следует отметить, что для реальных
средств измерений с преобладающей
мультипликативной погрешностью не
удается полностью устранить аддитивную
погрешность. По этой причине в технической
документации всегда указывается
наименьшее значение измеряемой величины,
для которого предел допускаемой основной
относительной погрешности ещё не
превышает заданного значения δ_max.
Ниже этого наименьшего значения
измеряемой величины погрешность
измерений не нормируется и является
неопределенной.

В) Нормирование
пределов допускаемой основной погрешности
для

средств измерений
с соизмеримой аддитивной и мультипликативной

погрешностью.

Если аддитивная
и мультипликативная составляющая
погрешности средства измерений соизмеримы
(3-й график на рис.2), то задание
предельно-допустимой погрешности одним
числом не представляется возможным. В
этом случае либо нормируется предел
допускаемой абсолютной основной
погрешности (указываются предельно-допустимые
значения a
и b),
либо (чаще всего) нормируется предел
допускаемой относительной основной
погрешности. В последнем случае численные
значения предельно-допустимых
относительных погрешностей в различных
точках шкалы оцениваются по формуле:

,

где X_max
– предел измерений;

X
— измеренное значение;

d
=

— значение приведенной к пределу измерений

аддитивной
составляющей основной погрешности;

с =
— значение результирующей относительной

основной
погрешности в точке, соответствующей
пределу

измерений.

Рассмотренным
выше способом (указанием численных
значений c
и d)
нормируются, в частности, предельно-допустимые
значения относительной основной
погрешности цифровых измерительных
приборов. В этом случае относительные
погрешности каждого экземпляра средств
измерений определенного типа не должны
превышать установленных для этого типа
средств измерений значений
предельно-допустимой погрешности:

.

При этом абсолютная
основная погрешность определяется по
формуле

.

Г)
Нормирование дополнительных погрешностей.

Наиболее часто
пределы допускаемых дополнительных
погрешностей указывают в технической
документации либо одним значением для
всей рабочей области величины, влияющей
на точность средства измерений (иногда
несколькими значениями для поддиапазонов
рабочей области влияющей величины),
либо отношением предела допускаемой
дополнительной погрешности к интервалу
значений влияющей величины. Пределы
допускаемых дополнительных погрешностей
указываются на каждой , влияющей на
точность средства измерений величине.
При этом, как правило, значения
дополнительных погрешностей устанавливают
в виде дольного или кратного значения
предела допускаемой основной погрешности.
Например, в документации может быть
указано, что при температуре окружающей
среды за пределами нормальной области
температур, предел допускаемой
дополнительной погрешности, возникающей
по этой причине, не должен превышать
0,2% на 10^о С.

Классы
точности средств измерений.

Исторически по
точности средства измерений подразделяют
на классы. Иногда их называют классами
точности, иногда классами допуска,
иногда просто классами.

Класс точности
средства измерений
– это его характеристика, отражающая
точностные возможности средств измерений
данного типа.

Допускается
буквенное или числовое обозначение
классов точности. Средствам измерений,
предназначенным для измерения двух и
более физических величин, допускается
присваивать различные классы точности
для каждой измеряемой величины. Средствам
измерений с двумя или более переключаемыми
диапазонами измерений также допускается
присваивать два или более класса
точности.

Если нормируется
предел допускаемой абсолютной основной
погрешности, или в различных поддиапазонах
измерений установлены разные значения
пределов допускаемой относительной
основной погрешности, то , как правило,
применяется буквенное обозначение
классов. Так, например платиновые
термометры сопротивления изготовляют
с классом допуска А
или классом
допуска В.
При этом для
класса А
установлен
предел допускаемой абсолютной основной
погрешности
,
а для классаВ
—
,
где– температура измеряемой среды.

Если для средств
измерений того или иного типа нормируется
одно значение предельно-допустимой
приведенной основной погрешности, или
одно значение предельно-допустимой
относительной основной погрешности,
или указываются значения c
и d,
то для обозначения классов точности
используются десятичные числа. В
соответствии с ГОСТом 8.401-80 для обозначения
классов точности допускается применение
следующих чисел:

1∙10ⁿ;
1,5∙10ⁿ;
2∙10ⁿ;
2,5∙10ⁿ;
4∙10ⁿ;
5∙10ⁿ;
6∙10ⁿ,
где n
= 0, -1, -2, и т.д.

Для средств
измерений с преобладающей аддитивной
погрешностью численное значение класса
точности выбирается из указанного ряда
равным предельно-допустимому значению
приведенной основной погрешности,
выраженной в процентах. Для средств
измерений с преобладающей мультипликативной
погрешностью численное значение класса
точности соответствует пределу
допускаемой относительной основной
погрешности также выраженной в процентах.
Для средств измерений с соизмеримыми
аддитивными и мультипликативными
погрешностями числа с
и d
также
выбираются из указанного выше ряда. При
этом класс точности средства измерений
обозначается двумя числами, разделенными
косой чертой, например, 0,05/0,02. В этом
случае с
= 0,05%; d
= 0,02%. Примеры
обозначений классов точности в
документации и на средствах измерений,
а также расчетные формулы для оценки
пределов допускаемой основной погрешности
приведены в Таблице 1.

Правила округления
и записи результата измерений.

Нормирование
пределов допускаемых погрешностей
средств измерений производится указанием
значения погрешностей с одной или двумя
значащими цифрами. По этой причине при
расчете значений погрешностей измерений
также должны быть оставлены только
первые одна или две значащие цифры. Для
округления используются следующие
правила:

1. Погрешность
   результата измерения указывается двумя
   значащими цифрами, если первая из них
   не более 2, и одной цифрой, если первая
   из них 3 и более.

2. Показание прибора
   округляется до того же десятичного
   разряда, которым заканчивается
   округленное значение абсолютной
   погрешности.

3. Округление
   производится в окончательном ответе,
   промежуточные вычисления выполняют с
   одной – двумя избыточными цифрами.

Пример 1:

— показание прибора
— 5,361 В;

— вычисленное
значение абсолютной погрешности — ±
0,264 В;

— округленное
значение абсолютной погрешности — ±
0,26 В;

— результат измерения
— (5,36 ± 0,26) В.

Таблица
1

Примеры обозначения
классов точности средств измерений и
расчетные

формулы для оценки
пределов допускаемой основной погрешности.

Форма представления нормируемой основной погрешности	Примеры обозначения класса точности	Расчетные формулы для оценки пределов допускаемой основной погрешности	Примечания
В документации	На средствах измерений
Нормируется предел допускаемой абсолютной основной погрешности	Варианты: — класс B; — класс допуска В; — класс точностиВ.	В	или или	Значения a иb приводятся в документации на средство измерений.
Нормируется предел допускаемой приведенной основной погрешности	Варианты: — класс точности 1,5 2,5 — не обозначается.	1,5	гдепредел измерений.	Для приборов с равномерной шкалой и нулевой отметкой в начале шкалы
Варианты: — класс точности 2,5; — не обозначается		— предел допускаемой абсолютной погрешности в мм. — длина всей шкалы.	Для приборов с неравномерной шкалой. Длина шкалы указывается в документации.
Нормируется предел допускаемой относительной основной погрешности	Класс точности 0,5.	0,5		Для средств измерений с преобладающей мультипликативной погрешностью.
Варианты: — класс точности 0,02/0,01; -не обозначается.	0,02/0,01		Для средств измерений с соизмеримыми аддитивной и мультипликативной погрешностью

Пример 2:

— показание прибора
– 35,67 мА;

— вычисленное
значение абсолютной погрешности — ±
0,541 мА;

— округленное
значение абсолютной погрешности — ± 0,5
мА;

— результат измерений
– (35,7 ± 0,5) мА.

Пример 3:

— вычисленное
значение относительной погрешности –
± 1,268 %;

— округленное
значение относительной погрешности –
± 1,3 %.

Пример 4:

— вычисленное
значение относительной погрешности —
± 0,367 %;

— округленное
значение относительной погрешности —
± 0,4 %.

II.2.
Вопросы для самопроверки

1. Чем вызываются
   погрешности измерений?

2. Перечислите
   разновидности погрешностей, возникающих
   в процессе измерений?

3. Какая разница
   между абсолютной, относительной и
   приведенной погрешностями измерения
   и в чем смысл их введения?

4. Чем отличается
   основная погрешность измерения от
   дополнительной?

5. Чем отличается
   методическая погрешность измерения
   от инструментальной?

6. Чем отличается
   систематическая погрешность измерения
   от случайной?

7. Что понимается
   под аддитивной и мультипликативной
   оставляющими погрешности?

8. В каких случаях
   целесообразно использовать статистическую
   обработку результатов измерений?

9. Какие статистические
   характеристики обработки наиболее
   часто используются на практике?

10. Как оценивается
    неисключенная систематическая
    погрешность при статистической обработке
    результатов измерений?

11. Что характеризует
величина среднеквадратического
отклонения ?

12. В чем заключается
суть понятий «доверительной вероятности»
и «доверительного интервала», используемых
при статистической обработке результатов
измерений?

13. В чем заключается
разность понятий «погрешность измерения»
и

«погрешность
средства измерения»?

Погрешность средств измерения и результатов измерения. 

Погрешности средств измерений – отклонения метрологических свойств или параметров средств измерений от номинальных, влияющие на погрешности результатов измерений (создающие так называемые инструментальные ошибки измерений).
Погрешность результата измерения – отклонение результата измерения от действительного (истинного) значения измеряемой величины.

Инструментальные и методические погрешности. 

Методическая погрешность обусловлена несовершенством метода измерений или упрощениями, допущенными при измерениях. Так, она возникает из-за использования приближенных формул при расчете результата или неправильной методики измерений. Выбор ошибочной методики возможен из-за несоответствия (неадекватности) измеряемой физической величины и ее модели.

Причиной методической погрешности может быть не учитываемое взаимное влияние объекта измерений и измерительных приборов или недостаточная точность такого учета. Например, методическая погрешность возникает при измерениях падения напряжения на участке цепи с помощью вольтметра, так как из-за шунтирующего действия вольтметра измеряемое напряжение уменьшается. Механизм взаимного влияния может быть изучен, а погрешности рассчитаны и учтены.

Инструментальная погрешность обусловлена несовершенством применяемых средств измерений. Причинами ее возникновения являются неточности, допущенные при изготовлении и регулировке приборов, изменение параметров элементов конструкции и схемы вследствие старения. В высокочувствительных приборах могут сильно проявляться их внутренние шумы.

Статическая и динамическая погрешности.

• Статическая погрешность измерений – погрешность результата измерений, свойственная условиям статического измерения, то есть при измерении постоянных величин после завершения переходных процессов в элементах приборов и преобразователей.
  Статическая погрешность средства измерений возникает при измерении с его помощью постоянной величины. Если в паспорте на средства измерений указывают предельные погрешности измерений, определенные в статических условиях, то они не могут характеризовать точность его работы в динамических условиях.
• Динамическая погрешность измерений – погрешность результата измерений, свойственная условиям динамического измерения. Динамическая погрешность появляется при измерении переменных величин и обусловлена инерционными свойствами средств измерений. Динамической погрешностью средства измерений является разность между погрешностью средсва измерений в динамических условиях и его статической погрешностью, соответствующей значению величины в данный момент времени. При разработке или проектировании средства измерений следует учитывать, что увеличение погрешности измерений и запаздывание появления выходного сигнала связаны с изменением условий.

Статические и динамические погрешности относятся к погрешностям результата измерений. В большей части приборов статическая и динамическая погрешности оказываются связаны между собой, поскольку соотношение между этими видами погрешностей зависит от характеристик прибора и характерного времени изменения величины. 

Систематическая и случайная погрешности. 

Систематическая погрешность измерения – составляющая погрешности измерения, остающаяся постоянной или закономерно изменяющаяся при повторных измерениях одной и той же физической величины. Систематические погрешности являются в общем случае функцией измеряемой величины, влияющих величин (температуры, влажности, напряжения питания и пр.) и времени. В функции измеряемой величины систематические погрешности входят при поверке и аттестации образцовых приборов.

Причинами возникновения систематических составляющих погрешности измерения являются:

• отклонение параметров реального средства измерений от расчетных значений, предусмотренных схемой;
• неуравновешенность некоторых деталей средства измерений относительно их оси вращения, приводящая к дополнительному повороту за счет зазоров, имеющихся в механизме;
• упругая деформация деталей средства измерений, имеющих малую жесткость, приводящая к дополнительным перемещениям;
• погрешность градуировки или небольшой сдвиг шкалы;
• неточность подгонки шунта или добавочного сопротивления, неточность образцовой измерительной катушки сопротивления;
• неравномерный износ направляющих устройств для базирования измеряемых деталей;
• износ рабочих поверхностей, деталей средства измерений, с помощью которых осуществляется контакт звеньев механизма;
• усталостные измерения упругих свойств деталей, а также их естественное старение;
• неисправности средства измерений.

Случайной погрешностью называют составляющие погрешности измерений, изменяющиеся случайным образом при повторных измерениях одной и той же величины. Случайные погрешности определяются совместным действием ряда причин: внутренними шумами элементов электронных схем, наводками на входные цепи средств измерений, пульсацией постоянного питающего напряжения, дискретностью счета.

Погрешности адекватности и градуировки. 

Погрешность градуировки средства измерений – погрешность действительного значения величины, приписанного той или иной отметке шкалы средства измерений в результате градуировки.

Погрешностью адекватности модели называют погрешность при выборе функциональной зависимости. Характерным примером может служить построение линейной зависимости по данным, которые лучше описываются степенным рядом с малыми нелинейными членами.

Погрешность адекватности относится к измерениям для проверки модели. Если зависимость параметра состояния от уровней входного фактора задана при моделировании объекта достаточно точно, то погрешность адекватности оказывается минимальной. Эта погрешность может зависеть от динамического диапазона измерений, например, если однофакторная зависимость задана при моделировании параболой, то в небольшом диапазоне она будет мало отличаться от экспоненциальной зависимости. Если диапазон измерений увеличить, то погрешность адекватности сильно возрастет.

Абсолютная, относительная и приведенная погрешности. 

Абсолютная погрешность – алгебраическая разность между номинальным и действительным значениями измеряемой величины. Абсолютная погрешность измеряется в тех же единицах измерения, что и сама величина, в расчетах её принято обозначать греческой буквой – ∆. На рисунке ниже ∆X и ∆Y – абсолютные погрешности.

Относительная погрешность – отношение абсолютной погрешности к тому значению, которое принимается за истинное. Относительная погрешность является безразмерной величиной, либо измеряется в процентах, в расчетах обозначается буквой – δ.

Приведённая погрешность – погрешность, выраженная отношением абсолютной погрешности средства измерений к условно принятому значению величины, постоянному во всем диапазоне измерений или в части диапазона. Вычисляется по формуле

где Xn – нормирующее значение, которое зависит от типа шкалы измерительного прибора и определяется по его градуировке:

– если шкала прибора односторонняя и нижний предел измерений равен нулю (например диапазон измерений 0…100), то Xn определяется равным верхнему пределу измерений (Xn=100);
– если шкала прибора односторонняя, нижний предел измерений больше нуля, то Xn определяется как разность между максимальным и минимальным значениями диапазона (для прибора с диапазоном измерений 30…100, Xn=Xmax-Xmin=100-30=70);
– если шкала прибора двухсторонняя, то нормирующее значение равно ширине диапазона измерений прибора (диапазон измерений -50…+50, Xn=100).

Приведённая погрешность является безразмерной величиной, либо измеряется в процентах.

Аддитивные и мультипликативные погрешности.

• Аддитивной погрешностью называется погрешность, постоянную в каждой точке шкалы.
• Мультипликативной погрешностью называется погрешность, линейно возрастающую или убывающую с ростом измеряемой величины.

Различать аддитивные и мультипликативные погрешности легче всего по полосе погрешностей (см.рис.).

Если абсолютная погрешность не зависит от значения измеряемой величины, то полоса определяется аддитивной погрешностью (а). Иногда аддитивную погрешность называют погрешностью нуля.

Если постоянной величиной является относительная погрешность, то полоса погрешностей меняется в пределах диапазона измерений и погрешность называется мультипликативной (б). Ярким примером аддитивной погрешности является погрешность квантования (оцифровки).

Класс точности измерений зависит от вида погрешностей. Рассмотрим класс точности измерений для аддитивной и мультипликативной погрешностей:

– для аддитивной погрешности:
аддитивная погрешность 
где Х – верхний предел шкалы, ∆0 – абсолютная аддитивная погрешность.
– для мультипликативной погрешности:
мультипликативная погрешность 
порог чувствительности прибора – это условие определяет порог чувствительности прибора (измерений).