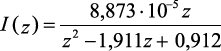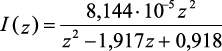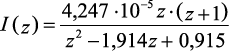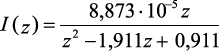В чем заключается сущность моделирова
ния ?
*Это замещение
одного объекта (оригинала) другим
(моделью) и фиксация или
изучение ,,свойств
оригинала путем исследования свойств
модели.
Моделирование-это
процесс физического познания реальной
системы.
Моделирование-это процесс описания
реальной системы с использованием
средств вычислительной техники.
Моделирование- это познание физических
процессов.
В теории моделирования что понимается
под объектом-оригина
лом ?
Компьютерная
технология
Эта воображаемая
система.
*Объектом-оригиналом
может быть естественная и исскуственная,
реальная или ,воображаемая
система.
Это реальные процессы.
Что
понимается под математичес
кой
моделью ?
Математическая
модель-это описание реального объекта
с помощью дифференциальных ,,уравнений.
Математическая модель это модель
разработанная математиком.
*Представление
изучаемого явления, процесса или
объекта с помощью математических
,,соотношений и формул.
Математическая модель-это описание
объекта с помощью систем уравнений.
Чем начинается процесс моделирования
?
Процесс моделирования начинается с
разработки программы.
*Процесс
моделирования начинается с формализации
объекта.
Моделирование
начинается с выбора средств моделирования.
Правильных ответов нет.
В чем заключается целесообраз
ность моделирова
ния ?
*Когда у
модели отсутствуют те признаки
оригинала, которые препятствуют его
исследованию.
Моделирование
целесообразно использовать тогда,
когда исследователь имеет достаточного
,,опыта для проведения
эксперимента.
Для получения
большого числа значений искомых
параметром.
Все ответы
правильны.
Что за собой представляет теория
моделирова
ния ?
Это теория разработки моделей.
* Это
взаимосвязанная совокупность
положений, определений методов и
средств создания и , , , ,
изучения моделей.
Совокупность
методов создания моделей.
Теория замещения одних объектов
(оригиналов) другими объектами
(моделями) и исследования
свойств объектов на их моделях.
Что понимается под предметом теории
моделирова
ния?
Модели
реальных объектов или систем.
*Совокупность
положений определений, методов или
средств моделирования и сами модели.
Программные
средства для разработки моделей
Методы
теории моделирования.
Какие
модели в знаете ?
Физическая,
масштабная, географическая,
математическая, химическая
*Математическая,имитационная,оптимизационная,масштабная,аналоговая
Физическая
,аналоговая, математическая, абстрактная,
вычислительная.
Физические, математические, социальные.
Какие
методы используются для исследования
математической модели.
Аналитические,
численные, дифференциальные, графические.
Аналитические,
имитационные, визуальные, графические.
*Аналитические,
численные, имитационные, качественные
Интегральные и асимптотические.
С проблемой
моделирования мы сталкиваемся в двух
случаях?
*В процессах
познания и управления.
В процессах
прогнозирования и анализа.
В процессах
наблюдения и алгоритмизации.
В производственных процессах и
явлениях.
Что понимается под управлением в
теории моделирова
ния ?
Процесс
достижения целевого состояния.
*Процесс
целенаправленного воздействия на
объект.
Процесс
создания управляющего устройства.
Управление-эта корректировка и
настройка параметров объекта.
Какие типы
объектов Вы знаете ?
*Статический,динамический,стохостический,детерминированный,линейный,нелинейный.
Статический,динамический,детерминированный,стохостический,нелинейный,идентификационный
Динамический,статический,имитационный,стохостический,линейный,нелинейный
Правильных ответов нет.
Что такая
концептуальная модель ?
Эта системная
модель.
Эта
содержательная, абстрактная модель
определяющая состав и структуру
объекта.
Модель
отражающая статику системы
Эта первоначальная модель.
Концетуальная
модель включает в себя следующие
процедуры:
Стратификация, детализация, выделение
процессов локализация, структуризация.
*Стратификация,
детализация ,выделение процессов,
централизация, локализация
Стратификация,
детализация, децентрализация,
локализация, оптимизация.
Локализация и стратифика.
Объект и
внешняя среда имеют следующие параметры.
*Качественные,
функциональные, количественные.
Качественные,
показательные, детерминированные.
Случайные,
идеализированные, стохастические
Идеализированные.
Поиск
математических зависимостей между
входными и выходными переменными
,,по собранными
опытным данным может выполняется с
помощью следующих ,,методов:
Статический,
корреляционный, не линейный анализ.
*Регрессионный,
корреляционный, дисперсионный анализ.
Экспериментальный,
математический, алгоритмический
анализ.
Дисперсионный
анализ.
Основные цели создания математичес
кой модели.
Формализация
структуры и процесса работы объекта.
Представить
процесс, допускающий аналитическое
исследование объекта.
*Оба ответа
правильные.
Нет
правильных ответов
Что понимается под аналитическим
методом исследования математичес
кой модели
?
Исследования
объекта с помощью математического
анализа
*Преобразование
математической модели к виду явных
аналитических зависимостей между ,,
характеристиками и параметрами
объекта и внешних воздействий.
Формульное
описание структуры объекта.
Этот-
метод статического моделирова
ния.
Сущность численных методов исследования
математичес
кой модели.
*Математическая модель, т.е.система
уравнений или дифференциальные
уравнения
,,решаются
численными (итерационными) методами.
Результатом
исследования систем численными
методами являются множества значений
искомых ,,величин для
конечного набора значений параметров
системы и входных переменных.
Метод
для анализа больших систем.
Реальный объект имитируется на
машине.
Какие виды математичес
ких модели
Вы знаете ?
Обобщенные
,агрегативные , кусочно-линейные,
стохастические сети, системы массового
,,обслуживания,
непрерывно-детерминированные, случайные
*Стохастические,
автоматные,дискретно-детерминистические,системы,массового
,,обслуживания.
Стохастические,
временные, табличные, автоматные;
системы массового обслуживания.
Массовые, табличные, электрические.
Что Вы понимаете под средствами
моделирова
ния ?
Технические
средства алгоритмические языки, языки
моделирования автоматизированные
,,системы моделирования,
эксперимент.
Технические
средства, компьютерные средства,
информационные средства, системы
,,моделирования, языки
моделирования.
*Технические
средства, алгоритмические языки, языки
моделирования, автоматизированные,,системы
моделирования
Технические, гибридные, алгоритмические
языки.
В чем
заключается проверка адекватности
модели ?
соответствия
модели к объекту.
Проверки
основных параметров объекта.
*В анализе
соразмерности модели с системой, а
также равнозначности системе.
Проверке
моделей элементов.
Какие виды
проверок модели Вы знаете ?
*Проверка моделей элементов, проверка
моделей внешних воздействий, проверка
формализованной и ,,математической
модели, проверка программной модели,
проверка
,,способов
измерения и вычисления выходных
характеристик.
Проверка
концептуальной модели, проверка
физической модели проверка измерительной
модели.
Проверка
модели элементов системы, проверка
программной модели, проверка
инструментальных ,,ошибок
программирования ,проверка гипотезы.
Проверка только концептуаль
ной модели
Как достигается цель моделирова
ния ?
Цель
моделирования достигается путем
алгоритмизации модели
Цель
моделирования достигается упрощением
системы.
*Цель
моделирования достигается исследованием
разработанной модели.
Цель моделирования достигается путем
корректировки модели.
Какие виды
методов используются для исследования
сложных систем ?
Аналитический,
численный, количественный,
экспериментальный
*Аналитический
,численный, имитационный качественный.
Аналитический,
временный имитационный, численный.
Математический, электрическийпневматический.
В чем
заключается стратегическое планирование
?
*В проведении
экспериментов в выборе определенных
сочетаний параметров и ,,последовательности
проведения экспериментов.
В стратегическом
исследовании системы.
В минимизации
суммарных отклонений результатов
моделирования.
Уменьшение
длительности машинного эксперимента.
Что такое тактическое планирование
эксперимен
тов ?
Увеличение
времени моделирования
Специальные
приемы обработки результатов для
уменьшения дисперсии.
*Совокупность
методов уменьшения длительности
малинного эксперимента.
Метод для уменьшения дисперсии.
Какими
методами уменьшаются ошибки моделирования
?
*Увеличение
периода моделирования, сбор статистики
по истечении некоторого времени.
Увеличением
числа замером, увеличением числа
параметром.
Сбор статистики
в конце периода моделирования.
Корреляционным, регрессион
ным.
В каких целях используются результаты
моделирова
ния ?
Для проверки
результатов работы системы управления.
Для уменьшения
использования машинных ресурсов.
*Для
принятия решения о работоспособности
системы, для выбора лучшего проектного
варианта ,,или для
оптимизации системы.
Для математической формализации
системы.
Что означает
планирование экспериментов с моделью
?
*Такой план
проведения машинных экспериментов,
когда имеется возможности получения
,,необходимой информации
об исследуемой системе при ограничениях
на ресурсы
Последовательность
экспериментов на машине с целью
получения точной информации об объекте.
Такой план
проведения машинных экспериментов,
когда затраты машинной памяти будут
,,минимальными.
Эта количествен
ная
Что означает
априорная информация об объекте?
Эта информация
о количестве входных параметров
объекта.
Эта информация
о внешней среде .
*Эта информация
о структуре идентифицируемого объекта.
Это информация,
которая необходима иметь после
эксперимента с моделью
Что означает
апостериорная информация?
Эта информация
о состоянии объекта.
*Эта информация
полученная после наблюдения входа и
выхода объекта.
Эта информация
о взаимодействии элементов системы.
Статическая.
Какой
характер имеет априорная информация?
Количественный.
*Качественный.
Динамический.
Линейная
Какими
признаками характеризуется структура
объекта?
Динамичность,
стохастичность, нелинейность,
дискретность.
Статичность,
детерминированность, линейность,
дискретность.
*Ответы 1
и 2 верны.
Шаговый, адаптивный, аналитический
Что означает
идентификация объекта?
Определение
оператора объекта.
*Определение
оператора модели.
Нахождение
идентичных входных и выходных параметров
объекта.
Процедура для определения близости
модели к объекту
Как
оценивается близость объекта и модели
?
Полиномом.
Тригонометрической
функцией.
*Функцией
невязки.
Функцией потерь
В чем заключается решение задачи
идентифика
ции?
Решение
системы нелинейных уравнений.
Решение
задачи минимизации функционала.
*Ответы 1
и 2 верны.
Разработке моделирующего алгоритма
Что понимается под структурной
идентифика
цией?
*Процесс
определения структуры оператора
моделей.
Процесс
определения структуры оператора
объекта.
Процесс
определения структуры элементов
объекта.
Все
ответы правильны
По каким признакам можно классифицировать
методы идентифика
ции?
*Активность,
адаптивность, дискретность
Активность,
стохастичность, динамичность.
Стохастичность,
линейность, пассивность.
Линейность, нелинейность, динамичность
Что
понимается под структурой модели?
Совокупность
элементов, составляющая систему.
Взаимодействие
элементов системы.
* Вид оператора с точностью до его
коэффициентов.
Степень
полинома аппроксимирующая модель
Для чего
ранжируется входные и выходные
параметры объекта ?
Для определения
структуре модели.
*Какие именно
входы и выходы объекта будут включены
в его модель.
Для измерения
внешних воздействий.
Для определения неизвестных параметров
системы
Что такое
ранг входа или выхода объекта?
*Целое число,
определяющее существ верности
(важности) параметра, влияющий наибольшим
,,образом на реализацию
цели в объекте.
Упорядочивающий
номер входных или выходных параметров.
Код входного
параметра.
Метод реакции, метод цепей
Какие
методы ранжирования Вы знаете?
Метод
экспертных оценок, метод упорядочивания.
Метод
имитации, метод зацикливания.
*Метод
непосредственного ранжирования, метод
парных сравнений.
Метод
реакции, метод цепей
Для чего
используется критерий согласованности
экспертов?
Для оценки
корреляции мнений экспертов.
Для оценки
максимальной дисперсии рангов.
*Для оценки
степени согласованности экспертов.
Для
оценки структуры модели
Как
определяется рациональное число
входов и выходов объекта?
*Экспертным
способом.
Алгоритмическим
способом.
Игровым
способом.
Арбитражным способом
Какими
свойствами обладает простейший по
ток?
Стационарность,
линейность, ординарность.
Стационарность,
ординарность, динамичность.
*Стационарность,
ординарность, отсутствие последействия.
Нелинейность, активность, дискретность
Какой
процесс называется Марковским?
*Случайный
процесс вероятностные характеристики
который зависит только от его состояния
в ,,данный момент.
Случайный
процесс вероятностные характеристики
который зависит от прошлого состояния.
Случайный
процесс вероятностные характеристики
который зависит только от времени.
Случайный процесс с динамическим
характером в будущем
Для чего
используется уравнение Колмогорова
?
Для определения
стационарных режимов работы система.
Для изучения
переходных режимов системе.
*Для вычисления
финальных вероятностей состояний
система.
Для
изучения стационарности системы
При каких
условиях существует финальные
вероятности состояний ?
Если существует
в системе особые состояния.
*Если число состояний конечно и из
каждого состояния можно перейти в
любое
,,другое
за конечное число шагов.
Если система
имеет динамический характер.
Если число состояний бесконечно
Какие
модели описываются дифференциальными
уравнениями ?
*Непрерывно-детерминированные.
Непрерывно-стохастические.
Непрерывно-линейные.
Линейно-стохастические
Для чего используется
процессы
обработки результатов моделирова
ния?
Для получения
интегральных характеристик
Для сжатия
данных
Для вычисления
коеффицента регрессии
* Ответы 1 и
2 верны
Для чего используется
результаты моделирова
ния?
Для модернизации
системы
Для обеспечения
устойчивости системы
*Для обеспечения
оптимального режима
Не знаю
Что
понимается под эмпирической моделью?
*Аналитический
зависимость между характеристиками
и факторами объекта
Зависимость
между параметрами объекта
Модель
учитывающий воздействие внешних
факторов
Модель
объекта без учёта помех
Что такое
регрессионный анализ?
Анализ
объекта для определения структуры
объекта
Метод для
анализа устойчивости объекта
*Метод для
определения вида соотношения между
зависимыми переменными
Все ответы
правильны
Какие види
методов используются для исследования
сложных систем?
Аналитический
Численный
Имитационный
*Все ответы
правильны
Что
понимается под анализом чувствительность
и системы?
Анализ
взаимодействия системы
Анализ
устойчивости характеристик системы
*Проверка
устойчивости характеристик системы
к возможным отклонение значений
параметров
Не знаю
Определение
задачи идентификации
Идентификация
это проверка подобия модели к объекту
Идентификация
это настройка модели
Идентификация
это планирование эксперимента с
моделью
*Построение
модели объекта по результатам наблюдений
входа и выхода объекта
Какие трудности возникают в задачах
идентифика
ции?
Трудности
связанные с определением структуры
объекта
Трудности
связанные с настройкой параметров
объекта
*Трудности
с определением класса оператора
объекта
Не знаю
Как
кодируется структура объекта?
С двумя
кодами
С пятью
кодами
*С четырьмя
кодами
С тремя
кодами
Чем
характеризуется экспоненциальное
распределение?
Плотностью
распределения
Сложностью
распределения
*Интенсивностью
распределения
отключением
Какой поток
событий называется рекуррентным?
*Если поток
стационарен, ординарен
Если поток
простейший
Если поток
детерминистический
Нет правильных
ответов
Модель
размножения и гибели эта модель:
*Эта Марковская
модель с дискретным числом состояний
и непрерывным временем
Биологическая
модель с непрерывным временем
Химическая
модель с дискретным временем
Информационная
модель
Что такое
математическая схема?
Схема для
изображения объекта исследований
Схема для
представления характеристики объекта
*Математический
аппарат для описания объекта
Все ответы
правильны
Основные
характеристики вычислительных систем:
Коэффициент
загрузки, число заявок в системе, длина
очереди
*Время
реакции, коэффициент загрузки, число
заявок, длина очереди
Поток
обслуженных заявок получившие отказ
Время
обслуживания, время ожидания
Типы систем
массого обслуживания:
одноканальная
многоканального
*Все ответы
правильны
С приоритетом
Пропускная
способность системы определяется:
Количеством
заявок в системе
Не знаю
*Среднее
число заявок
Ответы 1 и 3
верны
Что такое
переходной процесс в объекте?
*Период
окончания нестационарного процесса
в объекте
Время
необходимое для установления
периодического процесса
Процесс
затухания шума
Ответы 1 и 3
верны
Процедура
имитационного моделирования это:
Копирование
реального процесса в машину
* создание
логика- аналитической (математической)модели
системы и внешних воздействий
Имитация
модели в фиксированный момент времени
Не знаю
Система
массового обслуживания может имеет
фаз обслуживания:
Один
Два
Три
*Конечное
множество
Основная
идея имитационного моделирования
основывается на метод:
*Статических
испытаний
Динамических
испытаний
Стохастических
испытаний
Все ответы
правильны
Какие
методы имитационного моделирования
Вы знаете?
По принципу
особых состояний
По принципу
Δt
По принципу
обратной связи
*Ответы 1 и
2 верны
По ходу имитационного моделирования
выходные характерис
тики
Измеряются,
записываются, фиксируются
*Измеряются,
фиксируются, обрабатываются
Только
вычисляются
Нет правильных
ответов
В результате
имитационного моделирования получается:
*Одна из
возможных реализации многомерного
процесса в интервале времени
Многих
реализаций одномерных процессов
Ответы 1 и 2
Не
знаю
Измеряемые характерис
тики вичислитиль
ных систем:
Каждого
потока
Устройства
Заявки
Ответы 1 и 2
верны
Для чего
проводится повторный эксперимент?
Для исследования
стационарных процессов
Для изучения
устойчивых процессов
*Для получения
характеристик нестационарных процессов
Не знаю
Что такое
агрегат?
Агрегат эта
преобразователь одной энергии в другую
Агрегат
устройства для вычисления характеристик
объекта
*Устройства
с общим входом и выходом
Все ответы
правильны
Какими
свойствами обладает функция невязки
модели?
Вогнутости
вниз
Унимодальность
Выпукла вниз
Не знаю
Как
называется процедура определения
конкретного значения случайного число
с заданным законом распределения?
Случайным
испытанием
Фиксированным
испытанием
Бросанием
жребия
*Ответы 1 и
2 верны
В чём
заключается идея моделирования
случайных процессов?
Определяется
случайное число
*Определяется
последовательность случайных величин
Вычисляется
число из интервала от 0 до 1
Все ответы
верны
Какие
методы генерации случайных величин
Вы знаете?
*мультипликативный
Ассоциативный
Комульятивный
Не знаю
Укажите
средства формализованного описания
процессов функционирования объектов
Агрегативные
системы
Стохастические
сети
Системы
массового обслуживания
*Все ответы
верны
Что
понимается под автоматом?
Непрерывные
устройство преобразующее
Дискретное
устройства
Устройства
с памятью
*Все ответы
верны
Функция
переходов автомата задаётся в виде:
Таблицами
Матрицами
Графами
*Все ответы
верны
Функция
выходов автомата задаётся в виде:
Таблицы,
диаграммы
*Таблицы,
матрицы, графа
Матрицы,
формулы, графически
Только
матрицы
Имитационное моделирование
предназначен для моделирова
ния:
Дискретных
процессов
Непрерывных
процессов
*Ответы 1 и
2 верны
Правильных
ответов нет
По какими
причинами отличаются модель от объекта?
Не учетом
случайных факторов
По принятым
аппроксимациям
По интерполяции
*Все ответы
верны
По проверкам
адекватности модели к объекту
выявляются:
*Недопустимое
рассогласование модели и объекта
Адаптивные
свойства модели
Не знаю
Динамические
свойства объекта
В процессе
моделирования для стохастических
характеристик объекта можно построить:
Эмпирическую
характер объекта
*Эмпирическую
плотность распределения
Не знаю
Стационарную
характеристику объекта
Найдите
правильное значения критерия
согласованности экспертов.
W=2
W=5
*W=0.2
W= -2
Найдите
правильный ранжированный ряд параметров
объекта.
3,7,6,2,5,4
7,6,5,4,3,2,1
5,4,3,2,1,6
*1,2,3,4,5,6
Что такое
адаптивное модель?
*Модель
объектов, которые уточняются по
лиренакопления данных об объектов
Модель
объектов без учета флуктуации и помех
Модель с
памятью
Модель без
памяти
Что понимается кибернетически
подходом при моделирова
нии?
Аналитический
метод
Статический
метод
Динамический
метод
*Метод
основанный на пассивный эксперимент
Как
определяется степень достоверности
полученных из эксперимента оценок
характеристик объекта.
Методом
уменьшения погрешностей
С помощью
уточнения параметров объекта
*С помощью
статического анализа уравнения
регрессии и его коэффициентов
Все ответы
верны
Какие
методы моделирования являются
статическими?
Математической
статичестики
*Все ответы
верны
Теория
случайных функции
Теория
экстремальных экспериментов
Что понимается под потерей метода
и идентифика
ции?
Время
Средства
Энергия
*Все ответы
верны
Функция
невязки означает:
Близость
модели к объекту
Близость
модели к системе
Близость
модели к процессу
*Все ответы
верны
Оценка
взаимосвязанности параметров
оценивается с помощью:
Коэффициента
дисперсии
Коэффициента
нагрузки
*Коэффициента
корреляции
Коэффициента
загрузки
В каких
случаях можно найти аналитическуюзависимость
между характеристиками объекта и
входными параметрами?
*Если факторы
количественные
Если факторы
эмпирические
Если факторы
качественные
Не знаю
В чем
заключается сущность уравнения
Колмогорова?
Эта система
нелинейных уравнений
Эта система
рекуррентных уравнений
Эта система
неоднородных уравнений
*Эта система
однородных уравнений
Что
понимается под дисперизацией в системах
массового обслуживания?
Управления
потоком обслуженных требований
*Управлением
входящего потока заявок
Управления
регистрации заявок
Управление
приоритетом заявок
Как уменьшить дисперсию в окончательной модели машинного обучения
Перевод
Ссылка на автора
Конечная модель машинного обучения обучается на всех доступных данных, а затем используется для прогнозирования новых данных.
Проблема с большинством окончательных моделей заключается в том, что они страдают от различий в своих прогнозах.
Это означает, что каждый раз, когда вы подгоняете модель, вы получаете немного другой набор параметров, который, в свою очередь, будет давать немного разные прогнозы. Иногда более, а иногда менее умело, чем вы ожидали.
Это может быть неприятно, особенно если вы хотите развернуть модель в операционной среде.
В этом посте вы узнаете, как думать о дисперсии модели в окончательной модели, и о методах, которые можно использовать для уменьшения дисперсии в прогнозах из окончательной модели.
Прочитав этот пост, вы узнаете:
- Проблема с отклонениями в прогнозах, сделанных окончательной моделью.
- Как измерить дисперсию модели и как обычно учитывается дисперсия при оценке параметров.
- Методы, которые вы можете использовать для уменьшения различий в прогнозах, сделанных окончательной моделью.
Давайте начнем.
Финальная модель
После того, как вы обнаружили, какая модель и гиперпараметры приводят к лучшим навыкам в вашем наборе данных, вы готовы подготовить окончательную модель.
Окончательная модель обучается на всех доступных данных, например, учебные и тестовые наборы.
Это модель, которую вы будете использовать для прогнозирования новых данных, если вы не знаете результатов.
Окончательная модель является результатом вашего прикладного проекта машинного обучения.
Чтобы узнать больше о подготовке окончательной модели, смотрите пост:
- Как обучить окончательной модели машинного обучения
Смещение и дисперсия
Компромисс отклонения является концептуальной идеей в прикладном машинном обучении, чтобы помочь понять источники ошибок в моделях.
- предвзятостьотносится к допущениям в алгоритме обучения, которые сужают область изучения. Это полезно, поскольку может ускорить обучение и привести к стабильным результатам за счет предположения, отличающегося от реальности.
- отклонениеотносится к чувствительности алгоритма обучения к особенностям обучающих данных, например, шум и конкретные наблюдения. Это хорошо, так как модель будет специализироваться на данных за счет изучения случайного шума и изменяться каждый раз, когда она обучается на разных данных.
Компромисс между отклонениями является концептуальным инструментом для размышлений об этих источниках ошибок и о том, как они всегда находятся в равновесии.
Больше смещения в алгоритме означает, что меньше дисперсии, и обратное также верно.
Вы можете узнать больше о компромиссе смещения дисперсии в этом посте:
- Нежное введение в компромисс с отклонениями в машинном обучении
Вы можете контролировать этот баланс.
Многие алгоритмы машинного обучения имеют гиперпараметры, которые прямо или косвенно позволяют вам контролировать компромисс смещения.
Например,КвКБлижайшие соседи — один из примеров. МаленькийКрезультаты в прогнозах с высокой дисперсией и низким смещением. БольшойКрезультаты в прогнозах с небольшой дисперсией и большим смещением.
Проблема дисперсии в конечных моделях
У большинства финальных моделей есть проблема: они страдают от дисперсии.
Каждый раз, когда модель обучается по алгоритму с высокой дисперсией, вы получите немного другой результат.
Немного другая модель, в свою очередь, сделает несколько иные прогнозы, к лучшему или к худшему.
Это проблема с обучением окончательной модели, так как мы должны использовать модель для прогнозирования реальных данных, когда мы не знаем ответа, и мы хотим, чтобы эти прогнозы были как можно более хорошими.
Мы хотим максимально возможную версию модели, которую мы можем получить.
Мы хотим, чтобы дисперсия разыгралась в нашу пользу.
Если мы не можем этого достичь, по крайней мере, мы хотим, чтобы дисперсия не упала против нас при прогнозировании.
Измерение дисперсии в окончательной модели
В окончательной модели есть два распространенных источника дисперсии:
- Шум в тренировочных данных.
- Использование случайности в алгоритме машинного обучения.
Первый тип мы представили выше.
Второй тип воздействует на те алгоритмы, которые используют случайность во время обучения.
Три распространенных примера включают в себя:
- Выбор случайных точек разделения в случайном лесу.
- Случайная инициализация веса в нейронных сетях.
- Перетасовка тренировочных данных при стохастическом градиентном спуске.
Вы можете измерить оба типа дисперсии в вашей конкретной модели, используя ваши данные обучения.
- Дисперсия алгоритма измерения: Дисперсия, вызванная стохастической природой алгоритма, может быть измерена путем повторения оценки алгоритма в том же наборе обучающих данных и вычисления дисперсии или стандартного отклонения навыка модели.
- Измерение дисперсии обучающих данных: Дисперсия, введенная обучающими данными, может быть измерена путем повторения оценки алгоритма на разных выборках обучающих данных, но с фиксированным начальным числом для генератора псевдослучайных чисел, после чего вычисляется дисперсия или стандартное отклонение навыка модели.
Часто комбинированную дисперсию оценивают, выполняя повторную перекрестную проверку в k-кратном размере для обучающего набора данных, затем вычисляя дисперсию или стандартное отклонение навыка модели.
Уменьшить дисперсию оценки
Если мы хотим уменьшить количество отклонений в прогнозе, мы должны добавить смещение.
Рассмотрим случай простой статистической оценки параметра совокупности, такой как оценка среднего значения по небольшой случайной выборке данных.
Одна оценка среднего будет иметь высокую дисперсию и низкое смещение.
Это интуитивно понятно, потому что если бы мы повторили этот процесс 30 раз и вычислили стандартное отклонение расчетных средних значений, мы бы увидели большой разброс.
Решения для уменьшения дисперсии также интуитивно понятны.
Повторите оценку для множества различных небольших выборок данных из домена и рассчитайте среднее значение оценок, опираясь на Центральная предельная теорема,
Среднее из оценочных средних будет иметь меньшую дисперсию. Мы увеличили смещение, предполагая, что среднее из оценок будет более точной оценкой, чем единичная оценка.
Другой подход заключается в том, чтобы резко увеличить размер выборки данных, по которой мы оцениваем среднее значение популяции, опираясь на закон больших чисел,
Уменьшить дисперсию конечной модели
Принципы, используемые для уменьшения дисперсии для статистики населения, также могут быть использованы для уменьшения дисперсии конечной модели.
Мы должны добавить предвзятость.
В зависимости от конкретной формы конечной модели (например, дерево, вес и т. Д.) Вы можете проявить творческий подход с этой идеей.
Ниже приведены три подхода, которые вы можете попробовать.
Если возможно, я рекомендую разработать тестовую систему, чтобы экспериментировать и находить подход, который лучше всего работает или наиболее подходит для вашего конкретного набора данных и алгоритма машинного обучения.
1. Предсказания ансамбля от финальных моделей
Вместо подгонки одной финальной модели вы можете установить несколько финальных моделей.
Вместе группа финальных моделей может быть использована в качестве ансамбля.
Для заданного входного сигнала каждая модель в ансамбле делает прогноз, а окончательный выходной прогноз принимается как среднее из прогнозов моделей.
Анализ чувствительности может использоваться для измерения влияния размера ансамбля на дисперсию прогноза.
2. Параметры ансамбля из окончательных моделей
Как указано выше, можно создать несколько конечных моделей вместо одной конечной модели.
Вместо вычисления среднего значения прогнозов из окончательных моделей можно построить единую окончательную модель как ансамбль параметры группы финальных моделей.
Это имеет смысл только в тех случаях, когда каждая модель имеет одинаковое количество параметров, таких как веса нейронной сети или коэффициенты регрессии.
Например, рассмотрим модель линейной регрессии с тремя коэффициентами [b0, b1, b2]. Мы могли бы подобрать группу моделей линейной регрессии и рассчитать конечное значение b0 как среднее значение параметров b0 в каждой модели и повторить этот процесс для b1 и b2.
Опять же, анализ чувствительности может быть использован для измерения влияния размера ансамбля на дисперсию прогноза.
3. Увеличьте размер набора обучающих данных
Опираясь на закон больших чисел, возможно, самый простой подход к уменьшению дисперсии модели заключается в подборе модели для большего количества обучающих данных.
В тех случаях, когда больше данных недоступно, возможно, вместо них можно использовать методы дополнения данных.
Рекомендуется провести анализ чувствительности размера набора обучающих данных к прогнозируемой дисперсии, чтобы найти точку убывающей отдачи.
Хрупкое мышление
Существуют подходы к подготовке окончательной модели, которые направлены на то, чтобы дисперсия в конечной модели работала для вас, а не против вас.
Общность этих подходов заключается в том, что они ищут единственную наилучшую окончательную модель.
Два примера включают в себя:
- Почему бы не исправить случайное семя?Вы можете исправить случайное семя при установке окончательной модели. Это будет ограничивать дисперсию, обусловленную стохастической природой алгоритма.
- Почему бы не использовать раннюю остановку?Вы можете проверить мастерство модели по набору удерживающих во время тренировки и прекратить тренировку, когда навык модели на удерживающем наборе начинает ухудшаться.
Я бы сказал, что эти подходы и подобные им хрупки.
Возможно, вы можете играть в азартные игры и стремиться к тому, чтобы дисперсия разыгралась в вашу пользу. Это может быть хорошим подходом к соревнованиям по машинному обучению, в которых нет реальных недостатков проигрыша.
Я не буду.
Я думаю, что безопаснее стремиться к лучшей средней производительности и ограничивать недостатки.
Я думаю, что хитрость в выборе компромисса между смещением и окончательной моделью заключается в том, чтобы думать в образцах, а не в единичных моделях. Оптимизировать для средней производительности модели.
Дальнейшее чтение
Этот раздел предоставляет больше ресурсов по теме, если вы хотите углубиться.
- Как обучить окончательной модели машинного обучения
- Нежное введение в компромисс с отклонениями в машинном обучении
- Bias-Variance Tradeoff в Википедии
- Ансамбли контрольных точек: методы ансамбля из одного учебного процесса, 2017
Резюме
В этом посте вы узнали, как думать о дисперсии модели в окончательной модели, и о методах, которые можно использовать для уменьшения дисперсии в прогнозах из окончательной модели.
В частности, вы узнали:
- Проблема с отклонениями в прогнозах, сделанных окончательной моделью.
- Как измерить дисперсию модели и как обычно учитывается дисперсия при оценке параметров.
- Методы, которые вы можете использовать для уменьшения различий в прогнозах, сделанных окончательной моделью.
У вас есть вопросы?
Задайте свои вопросы в комментариях ниже, и я сделаю все возможное, чтобы ответить.
Можно выделить три источника ошибок моделирования:
1) погрешность моделирования , связанная с неточностью самой ММ;
2) погрешность численного решения уравнений модели, связанных с применением численных методов;
3) любая реализация численных методов на ЭВМ связана с ошибками округления .
Общая ошибка моделирования будет удовлетворять следующему неравенству:
Если мы находимся в рамках одной ММ, то влиять на первый источник ошибок нет возможности, поэтому такую ошибку часто считают неустранимой. На остальные два источника ошибок можно влиять выбором метода решения и разрядностью представления числе в ЭВМ. Обычно выбор считают приемлемым, если на порядок меньше
, а
порядок меньше
.
Пусть точное значение выходной переменной , предсказанной по модели
, равно
. Ошибка моделирования определяется нормой
, в качестве которой наиболее часто используют следующие величины:
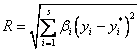
где bi – весовые коэффициенты, учитывающие относительную важность i-и точки (увеличение b, приводит при стремлении уменьшить R к уменьшению, прежде всего отклонения в i-й точке, так как это отклонение искусственно увеличено за счет относительно большого значения весового коэффициента);
Относительная ошибка определяется соотношением (обычно точное значение не известно)
3.2. Экспериментальное исследование погрешностей моделирования
Проведем исследование погрешностей цифрового фильтра, описываемого разностным уравнением (1.105) [89]. Одним из основных параметров численной модели является период дискретизации, который влияет как на погрешность моделирования, так и на чувствительность к устойчивости численной модели. Для устойчивости численного моделирования необходимо, чтобы значения модулей полюсов передаточной функции W(z) были меньше единицы. Так, например, при уменьшении периода дискретизации погрешность моделирования уменьшается, но, в тоже время, увеличивается чувствительность к неустойчивости решения и объем обрабатываемой информации [76]. Кроме того, погрешность моделирования и чувствительность к устойчивости z-форм зависят от моделируемого объекта, а именно для колебательного звена от параметра затухания, поэтому исследуем влияние параметра затухания и периода дискретизации на погрешность численного моделирования.
В качестве примера на рис. 3.1 и 3.2 представлены графики переходного процесса тока в цепи с последовательным соединением R, L, C элементов при численном моделировании с помощью операторно-дискретного метода [87]. Уравнения моделируемых переходных процессов для апериодического и колебательного режимов имеют следующий вид:
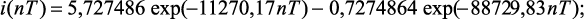
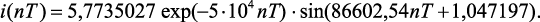
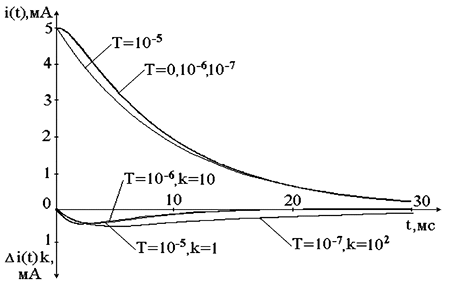
Рис. 3.1. Графики свободной составляющей и погрешностей в z-ветви
при апериодическом характере переходного процесса
Обычно в теории автоматического управления для оценки погрешности временной выходной функции используется методика интегральных квадратичных оценок [52], требующая вычислений в каждом такте временной функции. Из результатов ранее проведенных исследований следует, что вид функции ошибок совпадает с видом моделируемой функции [87], поскольку эти функции имеют общие корни характеристического уравнения.
Из представленных графиков абсолютных погрешностей (в масштабе k) тока в цепи следует, что вид графиков погрешностей совпадает с видом моделируемых функций. По этой причине нет необходимости проводить интегральные квадратичные оценки погрешности по большому количеству точек и при исследовании можно ограничиться одной максимальной погрешностью, то есть погрешностью в одной точке, что значительно сокращает объем вычислений. На основании проведенных исследований установлено, что результаты, полученные по упрощенной методике, полностью совпадают с результатами, полученными с помощью методики интегральных квадратичных оценок.
В источнике [76] приведены результаты исследования влияния параметра затухания на погрешность моделирования переходной функции с помощью следующих методов: прямой разности; обратной разности, метода трапеций и операторно-дискретного метода. Эти исследования были выполнены при ограниченном числе значений (параметров) ξ и с. Для получения более полной информации о точности моделирования необходимы зависимости погрешностей численных методов от с при различных значениях ξ в их предполагаемых диапазонах. Для вычисления погрешности при заданных параметрах ξ и с необходимо определить переходную функцию с помощью численного метода и сравнить ее с точным решением, полученным аналитически. Далее этого необходимо вычислять значения максимальной абсолютной погрешности для каждого значения с всего диапазона при одном значении параметра ξ. Затем необходимо выполнить эту операцию для другого значения ξ и по полученным значениям построить семейство графиков δ = f(с) при различных значениях ξ.
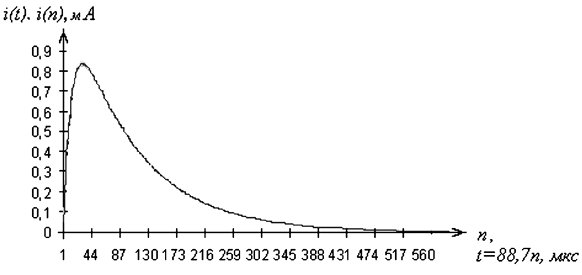
Рис. 3.2. Графики свободной составляющей и погрешностей в z-ветви
при колебательном характере переходного процесса
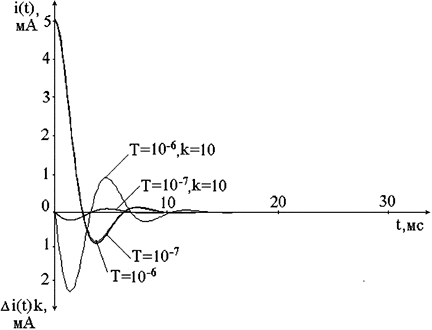
Рис. 3.3. Графики свободных составляющих тока в z-ветви
Графики свободных составляющих тока, полученные классическим методом, методами прямой, обратной разности, методом трапеций визуально совпадают (рис. 3.3). На рис. 3.4 представлены графики абсолютных погрешностей моделирования с помощью указанных методов.
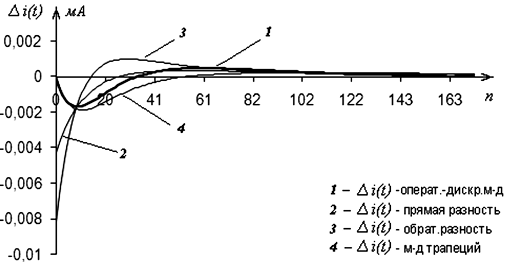
Рис. 3.4. Графики абсолютных погрешностей свободных составляющих тока в z-ветви, полученные численными методами расчета
Аналитическое выражение тока в z-ветви, его z-изображения и значения максимальной погрешности Δimax при различных методах моделирования занесены в табл. 3.1.
Таблица 3
Аналитическое выражение тока в z-ветви, его z-изображения и значения максимальной погрешности Δimax при различных методах моделирования
|
№ п/п |
Методы расчета |
Аналитическое выражение тока i(t) и его z-изображения I(z) |
∆imax |
|
1 |
Классический метод |
i(t) = 1,291·10–3·(e–11270·t – e–88730·t) |
– |
|
2 |
Прямая разность |
|
4,247·10–5 |
|
3 |
Обратная разность |
|
8,144·10–5 |
|
4 |
Метод трапеций |
|
1,863·10–5 |
|
5 |
Операторно-дискретный метод |
|
1,639·10–5 |
Из проведенного выше описания следует, что моделирование отдельных этапов и обобщение их результатов является довольно трудоемкой операцией. Поэтому для решения этой задачи была разработана компьютерная программа, позволяющая выполнять все выше перечисленные операции и представить результаты в компактной форме. Данная компьютерная программа позволяет получать численно значения импульсной или переходной характеристик с помощью трех видов аппроксимации, таких как прямая разность, обратная разность, метод трапеций и операторно-дискретного метода, сравнивать численное решение с точным и вычислять максимальные абсолютные погрешности при различных параметрах численной модели.
Работа программы начинается с ввода исходных данных, а именно диапазонов изменения и шагов моделирования для с и ξ, значения периода собственных колебаний Т0 и временного диапазона моделирования (0; Tmax). Для вычисления погрешностей численного моделирования предварительно определяется точное решение этой задачи. Дискретная переходная характеристика определяется с помощью рекуррентной формулы по коэффициентам числителя и знаменателя передаточной функции и при численном задании входного воздействия.
Выражения дискретных передаточных функций получены с помощью указанных методов z-моделирования и представлены в табл. 3.1, по которым определяются коэффициенты числителя и знаменателя а0, а1, а2, b0, b1, b2. Для каждого значения с при минимальном значении ξmin определяется дискретная переходная характеристика и погрешность численного решения. Из значений абсолютной погрешности всего временного диапазона выбирается и запоминается максимальное значение. По сохраненным значениям строится зависимость погрешности от относительного периода дискретизации. Затем эта операция осуществляется для каждого значения ξ < ξmax. Результаты численного моделирования представляются в виде таблиц в программе Excel, по которым осуществляется построение графических зависимостей.
Анализ функциональных зависимостей погрешностей моделирования от относительного периода дискретизации и параметров передаточной функции позволяет выявлять причины возникновения погрешностей и выбирать параметры численных моделей, а также решать вопрос о применимости метода для решения конкретной задачи.
На рис. 3.5 представлены графические зависимости максимальных абсолютных погрешностей моделирования от относительного периода дискретизации. Анализ зависимостей погрешностей в большом диапазоне значений позволит получить вывод об устойчивости численных решений.
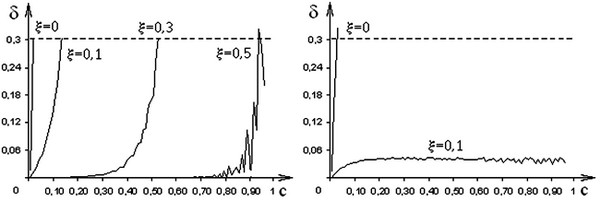
а б
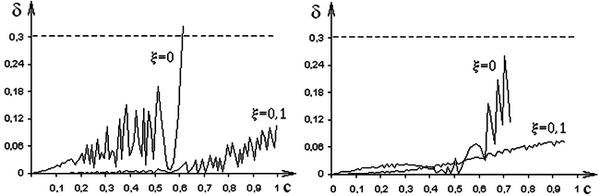
в г
Рис. 3.5. Зависимости δ = f(c) (0 < c < 1)
для различных значений ξ, полученные методами:
а – прямой разности; б – обратной разности;
в – трапеций; г – операторно-дискретным
Из анализа графиков следует, что при некоторых значениях с зависимости имеют расходящийся колебательный характер, что является признаком неустойчивости. Поэтому по этим графикам можно определять области устойчивости для параметра с. Из анализа графиков (рис. 3.5, а, б)
следует, что при моделировании колебательного звена без затухания (ξ = 0) наблюдается резкое увеличение погрешности при ограниченном диапазоне с, особенно при использовании методов прямой и обратной разностей. Графики погрешностей (рис. 3.5, в, г) имеют признаки неустойчивости, но имеют больший диапазон устойчивости в сравнении с предыдущими методами. Необходимо отметить, что при ξ → 1 уменьшаются погрешности для всех методов моделирования в широком диапазоне с. Из анализа графических зависимостей следует, что при моделировании колебательных звеньев с малым значением коэффициента затухания (ξ → 1) целесообразно использовать операторно-дискретный метод, который по сравнению с другими методами не требует жестких условий к выбору относительного периода дискретизации.
На рис. 3.6 показаны зависимости, позволяющие количественно оценить погрешности моделирования при использовании различных методов. При этом значения относительного периода дискретизации были заданы в диапазоне практического использования c = 0…0,1.
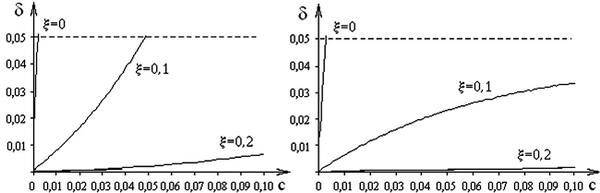
а б
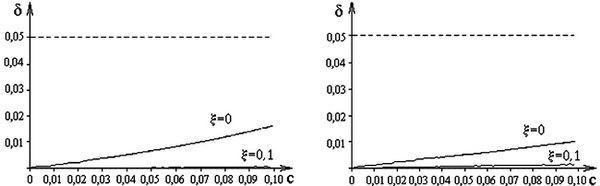
в г
Рис. 3.6. Зависимости δ = f(c) (0 < c < 1)
при различных ξ, полученные методами:
а – прямой разности; б – обратной разности;
в – трапеций; г – операторно-дискретным методом
Из сравнения погрешностей различных методов следует, что минимальные погрешности моделирования обеспечивают только два метода: метод трапеций и операторно-дискретный метод. Наибольшие погрешности имеет метод прямой разности. Так, например, методами прямой и обратной разностей моделировать колебательное звено без затухания (ξ = 0) можно только в очень ограниченном диапазоне с (рис. 3.6, а, б).
Из анализа погрешностей методов прямой и обратной разностей (рис. 3.6 а, б) следует, что погрешность моделирования метода
обратной разности меньше погрешности метода прямой разности при соответствующих значениях ξ. Анализ графиков (рис. 3.6, в, г), полученных с помощью метода трапеций и операторно-дискретного метода показывает, что эти методы позволяют, в сравнении с предыдущими методами, расширить диапазон выбора с при ξ = 0. Наименьшую погрешность имеет операторно-дискретный метод (рис. 3.6, г), который позволяет моделировать колебательный режим даже при ξ = 0, несколько большие погрешности имеет метод Тустена (рис. 3.6, в), однако формула перехода от непрерывной функции к импульсной функции для метода Тустена несколько сложнее. Из вышеприведенного анализа следует, что при моделировании колебательных звеньев целесообразно использовать операторно-дискретный метод, который не предъявляет жестких условий к выбору значений с. Наибольшие значения погрешностей по сравнению с другими методами имеет метод прямой разности и поэтому этот метод не целесообразно использовать при моделировании. При обработке результатов экспериментальных исследований были использованы методы математической статистики [34]. На рис. 3.6 приведены графики математических ожиданий исследуемых функциональных зависимостей, максимальные значения среднеквадратических отклонений не превышали 5 % от максимального значения функций во всех исследованиях.
Обычно выделяют три группы погрешностей: неустранимая погрешность; погрешность метода; вычислительная погрешность. Неустранимая погрешность порождается: а) неточностью входных данных в математическом описании задачи; б) несоответствия математической модели реальной задаче. Погрешность метода возникает из-за того, что используются приближенные методы. А погрешность вычислений возникает при вводе-выводе и при выполнении математических операций, а также при округлениях. Попробуем привести несколько практических приемов для уменьшения влияния вычислительной погрешности на результаты вычислений.
1. Сложение чисел необходимо проводить по мере их возрастания так как в машинной арифметике из-за погрешности округления существенен порядок выполнения операций.
2. В некоторых случаях имеет смысл выполнить предварительные преобразования вычисляемого выражения.
Например, вместо (a+b)^2 для случая, когда одно число намного меньше другого, лучше использовать выражение: a^2+2ab+b^2. Перемножение большого и маленького числа: 2ab позволит слегка поправить ситуацию.
3. Необходимо исключать вычитание двух почти равных чисел, тем более когда такая разность находится в знаменателе выражения.
4. Если числа равны a и b почти равны, то вычитание этих чисел следует производить раньше, чем деление или умножение.
К примеру, следует отдать предпочтение выражению (a-b)/c, а не выражению a/c-b/c. Во-первых здесь меньше операций (смотри пункт 3 и 6), а во-вторых, после деления числа станут меньше и еще меньше будут отличаться друг от друга, что может привести к обращению разности в ноль.
5. При перемножении нескольких чисел надо сразу перемножать самое большое число и самое маленькое, так как умножение друг на друга нескольких маленьких чисел может привести к появлению машинного нуля.
6. Всегда следует стремиться к уменьшению числа арифметических операций. Это объясняется тем, что чем больше операций, тем больше суммирующие погрешности.