Какую роль играет стандартная ошибка - Не ошибается лишь тот, кто ничего не делает!

From Wikipedia, the free encyclopedia

For a value that is sampled with an unbiased normally distributed error, the above depicts the proportion of samples that would fall between 0, 1, 2, and 3 standard deviations above and below the actual value.

The standard error (SE)^[1] of a statistic (usually an estimate of a parameter) is the standard deviation of its sampling distribution^[2] or an estimate of that standard deviation. If the statistic is the sample mean, it is called the standard error of the mean (SEM).^[1]

The sampling distribution of a mean is generated by repeated sampling from the same population and recording of the sample means obtained. This forms a distribution of different means, and this distribution has its own mean and variance. Mathematically, the variance of the sampling mean distribution obtained is equal to the variance of the population divided by the sample size. This is because as the sample size increases, sample means cluster more closely around the population mean.

Therefore, the relationship between the standard error of the mean and the standard deviation is such that, for a given sample size, the standard error of the mean equals the standard deviation divided by the square root of the sample size.^[1] In other words, the standard error of the mean is a measure of the dispersion of sample means around the population mean.

In regression analysis, the term «standard error» refers either to the square root of the reduced chi-squared statistic or the standard error for a particular regression coefficient (as used in, say, confidence intervals).

Standard error of the sample mean[edit]

Exact value[edit]

Suppose a statistically independent sample of observations ${displaystyle x_{1},x_{2},ldots ,x_{n}}$ is taken from a statistical population with a standard deviation of sigma . The mean value calculated from the sample, , will have an associated standard error on the mean, ${displaystyle {sigma }_{bar {x}}}$ , given by:^[1]

${displaystyle {sigma }_{bar {x}} ={frac {sigma }{sqrt {n}}}}$ .

Practically this tells us that when trying to estimate the value of a population mean, due to the factor , reducing the error on the estimate by a factor of two requires acquiring four times as many observations in the sample; reducing it by a factor of ten requires a hundred times as many observations.

Estimate[edit]

The standard deviation sigma of the population being sampled is seldom known. Therefore, the standard error of the mean is usually estimated by replacing sigma with the sample standard deviation $sigma _{x}$ instead:

${displaystyle {sigma }_{bar {x}} approx {frac {sigma _{x}}{sqrt {n}}}}$

As this is only an estimator for the true «standard error», it is common to see other notations here such as:

${displaystyle {widehat {sigma }}_{bar {x}}approx {frac {sigma _{x}}{sqrt {n}}}}$

or alternately ${displaystyle {s}_{bar {x}} approx {frac {s}{sqrt {n}}}}$ .

A common source of confusion occurs when failing to distinguish clearly between:

Accuracy of the estimator[edit]

When the sample size is small, using the standard deviation of the sample instead of the true standard deviation of the population will tend to systematically underestimate the population standard deviation, and therefore also the standard error. With n = 2, the underestimate is about 25%, but for n = 6, the underestimate is only 5%. Gurland and Tripathi (1971) provide a correction and equation for this effect.^[3] Sokal and Rohlf (1981) give an equation of the correction factor for small samples of n < 20.^[4] See unbiased estimation of standard deviation for further discussion.

Derivation[edit]

The standard error on the mean may be derived from the variance of a sum of independent random variables,^[5] given the definition of variance and some simple properties thereof. If ${displaystyle x_{1},x_{2},ldots ,x_{n}}$ is a sample of independent observations from a population with mean and standard deviation sigma , then we can define the total

${displaystyle T=(x_{1}+x_{2}+cdots +x_{n})}$

which due to the Bienaymé formula, will have variance

${displaystyle operatorname {Var} (T)approx {big (}operatorname {Var} (x_{1})+operatorname {Var} (x_{2})+cdots +operatorname {Var} (x_{n}){big )}=nsigma ^{2}.}$

where we’ve approximated the standard deviations, i.e., the uncertainties, of the measurements themselves with the best value for the standard deviation of the population. The mean of these measurements is simply given by

The variance of the mean is then

${displaystyle operatorname {Var} ({bar {x}})=operatorname {Var} left({frac {T}{n}}right)={frac {1}{n^{2}}}operatorname {Var} (T)={frac {1}{n^{2}}}nsigma ^{2}={frac {sigma ^{2}}{n}}.}$

The standard error is, by definition, the standard deviation of which is simply the square root of the variance:

${displaystyle sigma _{bar {x}}={sqrt {frac {sigma ^{2}}{n}}}={frac {sigma }{sqrt {n}}}}$

For correlated random variables the sample variance needs to be computed according to the Markov chain central limit theorem.

Independent and identically distributed random variables with random sample size[edit]

There are cases when a sample is taken without knowing, in advance, how many observations will be acceptable according to some criterion. In such cases, the sample size is a random variable whose variation adds to the variation of such that,

${displaystyle operatorname {Var} (T)=operatorname {E} (N)operatorname {Var} (X)+operatorname {Var} (N){big (}operatorname {E} (X){big )}^{2}}$

^[6]

If has a Poisson distribution, then with estimator . Hence the estimator of becomes ${displaystyle nS_{X}^{2}+n{bar {X}}^{2}}$ , leading the following formula for standard error:

${displaystyle operatorname {Standard~Error} ({bar {X}})={sqrt {frac {S_{X}^{2}+{bar {X}}^{2}}{n}}}}$

(since the standard deviation is the square root of the variance)

Student approximation when σ value is unknown[edit]

In many practical applications, the true value of σ is unknown. As a result, we need to use a distribution that takes into account that spread of possible σ’s.
When the true underlying distribution is known to be Gaussian, although with unknown σ, then the resulting estimated distribution follows the Student t-distribution. The standard error is the standard deviation of the Student t-distribution. T-distributions are slightly different from Gaussian, and vary depending on the size of the sample. Small samples are somewhat more likely to underestimate the population standard deviation and have a mean that differs from the true population mean, and the Student t-distribution accounts for the probability of these events with somewhat heavier tails compared to a Gaussian. To estimate the standard error of a Student t-distribution it is sufficient to use the sample standard deviation «s» instead of σ, and we could use this value to calculate confidence intervals.

Note: The Student’s probability distribution is approximated well by the Gaussian distribution when the sample size is over 100. For such samples one can use the latter distribution, which is much simpler.

Assumptions and usage[edit]

An example of how is used is to make confidence intervals of the unknown population mean. If the sampling distribution is normally distributed, the sample mean, the standard error, and the quantiles of the normal distribution can be used to calculate confidence intervals for the true population mean. The following expressions can be used to calculate the upper and lower 95% confidence limits, where is equal to the sample mean, is equal to the standard error for the sample mean, and 1.96 is the approximate value of the 97.5 percentile point of the normal distribution:

Upper 95% limit

{displaystyle ={bar {x}}+(operatorname {SE} times 1.96),}

and

Lower 95% limit

In particular, the standard error of a sample statistic (such as sample mean) is the actual or estimated standard deviation of the sample mean in the process by which it was generated. In other words, it is the actual or estimated standard deviation of the sampling distribution of the sample statistic. The notation for standard error can be any one of SE, SEM (for standard error of measurement or mean), or S_E.

Standard errors provide simple measures of uncertainty in a value and are often used because:

in many cases, if the standard error of several individual quantities is known then the standard error of some function of the quantities can be easily calculated;
when the probability distribution of the value is known, it can be used to calculate an exact confidence interval;
when the probability distribution is unknown, Chebyshev’s or the Vysochanskiï–Petunin inequalities can be used to calculate a conservative confidence interval; and
as the sample size tends to infinity the central limit theorem guarantees that the sampling distribution of the mean is asymptotically normal.

Standard error of mean versus standard deviation[edit]

In scientific and technical literature, experimental data are often summarized either using the mean and standard deviation of the sample data or the mean with the standard error. This often leads to confusion about their interchangeability. However, the mean and standard deviation are descriptive statistics, whereas the standard error of the mean is descriptive of the random sampling process. The standard deviation of the sample data is a description of the variation in measurements, while the standard error of the mean is a probabilistic statement about how the sample size will provide a better bound on estimates of the population mean, in light of the central limit theorem.^[7]

Put simply, the standard error of the sample mean is an estimate of how far the sample mean is likely to be from the population mean, whereas the standard deviation of the sample is the degree to which individuals within the sample differ from the sample mean.^[8] If the population standard deviation is finite, the standard error of the mean of the sample will tend to zero with increasing sample size, because the estimate of the population mean will improve, while the standard deviation of the sample will tend to approximate the population standard deviation as the sample size increases.

Extensions[edit]

Finite population correction (FPC)[edit]

The formula given above for the standard error assumes that the population is infinite. Nonetheless, it is often used for finite populations when people are interested in measuring the process that created the existing finite population (this is called an analytic study). Though the above formula is not exactly correct when the population is finite, the difference between the finite- and infinite-population versions will be small when sampling fraction is small (e.g. a small proportion of a finite population is studied). In this case people often do not correct for the finite population, essentially treating it as an «approximately infinite» population.

If one is interested in measuring an existing finite population that will not change over time, then it is necessary to adjust for the population size (called an enumerative study). When the sampling fraction (often termed f) is large (approximately at 5% or more) in an enumerative study, the estimate of the standard error must be corrected by multiplying by a »finite population correction» (a.k.a.: FPC):^[9]
^[10]

${displaystyle operatorname {FPC} ={sqrt {frac {N-n}{N-1}}}}$

which, for large N:

${displaystyle operatorname {FPC} approx {sqrt {1-{frac {n}{N}}}}={sqrt {1-f}}}$

to account for the added precision gained by sampling close to a larger percentage of the population. The effect of the FPC is that the error becomes zero when the sample size n is equal to the population size N.

This happens in survey methodology when sampling without replacement. If sampling with replacement, then FPC does not come into play.

Correction for correlation in the sample[edit]

Expected error in the mean of A for a sample of n data points with sample bias coefficient ρ. The unbiased standard error plots as the ρ = 0 diagonal line with log-log slope −½.

If values of the measured quantity A are not statistically independent but have been obtained from known locations in parameter space x, an unbiased estimate of the true standard error of the mean (actually a correction on the standard deviation part) may be obtained by multiplying the calculated standard error of the sample by the factor f:

$f={sqrt {frac {1+rho }{1-rho }}},$

where the sample bias coefficient ρ is the widely used Prais–Winsten estimate of the autocorrelation-coefficient (a quantity between −1 and +1) for all sample point pairs. This approximate formula is for moderate to large sample sizes; the reference gives the exact formulas for any sample size, and can be applied to heavily autocorrelated time series like Wall Street stock quotes. Moreover, this formula works for positive and negative ρ alike.^[11] See also unbiased estimation of standard deviation for more discussion.

References[edit]

^ ^a ^b ^c ^d Altman, Douglas G; Bland, J Martin (2005-10-15). «Standard deviations and standard errors». BMJ: British Medical Journal. 331 (7521): 903. doi:10.1136/bmj.331.7521.903. ISSN 0959-8138. PMC 1255808. PMID 16223828.
^ Everitt, B. S. (2003). The Cambridge Dictionary of Statistics. CUP. ISBN 978-0-521-81099-9.
^ Gurland, J; Tripathi RC (1971). «A simple approximation for unbiased estimation of the standard deviation». American Statistician. 25 (4): 30–32. doi:10.2307/2682923. JSTOR 2682923.
^ Sokal; Rohlf (1981). Biometry: Principles and Practice of Statistics in Biological Research (2nd ed.). p. 53. ISBN 978-0-7167-1254-1.
^ Hutchinson, T. P. (1993). Essentials of Statistical Methods, in 41 pages. Adelaide: Rumsby. ISBN 978-0-646-12621-0.
^ Cornell, J R, and Benjamin, C A, Probability, Statistics, and Decisions for Civil Engineers, McGraw-Hill, NY, 1970, ISBN 0486796094, pp. 178–9.
^ Barde, M. (2012). «What to use to express the variability of data: Standard deviation or standard error of mean?». Perspect. Clin. Res. 3 (3): 113–116. doi:10.4103/2229-3485.100662. PMC 3487226. PMID 23125963.
^ Wassertheil-Smoller, Sylvia (1995). Biostatistics and Epidemiology : A Primer for Health Professionals (Second ed.). New York: Springer. pp. 40–43. ISBN 0-387-94388-9.
^ Isserlis, L. (1918). «On the value of a mean as calculated from a sample». Journal of the Royal Statistical Society. 81 (1): 75–81. doi:10.2307/2340569. JSTOR 2340569. (Equation 1)
^ Bondy, Warren; Zlot, William (1976). «The Standard Error of the Mean and the Difference Between Means for Finite Populations». The American Statistician. 30 (2): 96–97. doi:10.1080/00031305.1976.10479149. JSTOR 2683803. (Equation 2)
^ Bence, James R. (1995). «Analysis of Short Time Series: Correcting for Autocorrelation». Ecology. 76 (2): 628–639. doi:10.2307/1941218. JSTOR 1941218.

Источник

Среднее арифметическое, как известно, используется для получения обобщающей характеристики некоторого набора данных. Если данные более-менее однородны и в них нет аномальных наблюдений (выбросов), то среднее хорошо обобщает данные, сведя к минимуму влияние случайных факторов (они взаимопогашаются при сложении).

Когда анализируемые данные представляют собой выборку (которая состоит из случайных значений), то среднее арифметическое часто (но не всегда) выступает в роли приближенной оценки математического ожидания. Почему приближенной? Потому что среднее арифметическое – это величина, которая зависит от набора случайных чисел, и, следовательно, сама является случайной величиной. При повторных экспериментах (даже в одних и тех же условиях) средние будут отличаться друг от друга.

Для того, чтобы на основе статистического анализа данных делать корректные выводы, необходимо оценить возможный разброс полученного результата. Для этого рассчитываются различные показатели вариации. Но то исходные данные. И как мы только что установили, среднее арифметическое также обладает разбросом, который необходимо оценить и учитывать в дальнейшем (в выводах, в выборе метода анализа и т.д.).

Интуитивно понятно, что разброс средней должен быть как-то связан с разбросом исходных данных. Основной характеристикой разброса средней выступает та же дисперсия.

Дисперсия выборочных данных – это средний квадрат отклонения от средней, и рассчитать ее по исходным данным не составляет труда, например, в Excel предусмотрены специальные функции. Однако, как же рассчитать дисперсию средней, если в распоряжении есть только одна выборка и одно среднее арифметическое?

Расчет дисперсии и стандартной ошибки средней арифметической

Чтобы получить дисперсию средней арифметической нет необходимости проводить множество экспериментов, достаточно иметь только одну выборку. Это легко доказать. Для начала вспомним, что средняя арифметическая (простая) рассчитывается по формуле:

где x_i – значения переменной,
n – количество значений.

Теперь учтем два свойства дисперсии, согласно которым, 1) — постоянный множитель можно вынести за знак дисперсии, возведя его в квадрат и 2) — дисперсия суммы независимых случайных величин равняется сумме соответствующих дисперсий. Предполагается, что каждое случайное значение x_i обладает одинаковым разбросом, поэтому несложно вывести формулу дисперсии средней арифметической:

Используя более привычные обозначения, формулу записывают как:

где σ² – это дисперсия, случайной величины, причем генеральная.

На практике же, генеральная дисперсия известна далеко не всегда, точнее совсем редко, поэтому в качестве оной используют выборочную дисперсию:

Стандартное отклонение средней арифметической называется стандартной ошибкой средней и рассчитывается, как квадратный корень из дисперсии.

Формула стандартной ошибки средней при использовании генеральной дисперсии

Формула стандартной ошибки средней при использовании выборочной дисперсии

Последняя формула на практике используется чаще всего, т.к. генеральная дисперсия обычно не известна. Чтобы не вводить новые обозначения, стандартную ошибку средней обычно записывают в виде соотношения стандартного отклонения выборки и корня объема выборки.

Назначение и свойство стандартной ошибки средней арифметической

Стандартная ошибка средней много, где используется. И очень полезно понимать ее свойства. Посмотрим еще раз на формулу стандартной ошибки средней:

Числитель – это стандартное отклонение выборки и здесь все понятно. Чем больше разброс данных, тем больше стандартная ошибка средней – прямо пропорциональная зависимость.

Посмотрим на знаменатель. Здесь находится квадратный корень из объема выборки. Соответственно, чем больше объем выборки, тем меньше стандартная ошибка средней. Для наглядности изобразим на одной диаграмме график нормально распределенной переменной со средней равной 10, сигмой – 3, и второй график – распределение средней арифметической этой же переменной, полученной по 16-ти наблюдениям (которое также будет нормальным).

Судя по формуле, разброс стандартной ошибки средней должен быть в 4 раза (корень из 16) меньше, чем разброс исходных данных, что и видно на рисунке выше. Чем больше наблюдений, тем меньше разброс средней.

Казалось бы, что для получения наиболее точной средней достаточно использовать максимально большую выборку и тогда стандартная ошибка средней будет стремиться к нулю, а сама средняя, соответственно, к математическому ожиданию. Однако квадратный корень объема выборки в знаменателе говорит о том, что связь между точностью выборочной средней и размером выборки не является линейной. Например, увеличение выборки с 20-ти до 50-ти наблюдений, то есть на 30 значений или в 2,5 раза, уменьшает стандартную ошибку средней только на 36%, а со 100-а до 130-ти наблюдений (на те же 30 значений), снижает разброс данных лишь на 12%.

Лучше всего изобразить эту мысль в виде графика зависимости стандартной ошибки средней от размера выборки. Пусть стандартное отклонение равно 10 (на форму графика это не влияет).

Видно, что примерно после 50-ти значений, уменьшение стандартной ошибки средней резко замедляется, после 100-а – наклон постепенно становится почти нулевым.

Таким образом, при достижении некоторого размера выборки ее дальнейшее увеличение уже почти не сказывается на точности средней. Этот факт имеет далеко идущие последствия. Например, при проведении выборочного обследования населения (опроса) чрезмерное увеличение выборки ведет к неоправданным затратам, т.к. точность почти не меняется. Именно поэтому количество опрошенных редко превышает 1,5 тысячи человек. Точность при таком размере выборки часто является достаточной, а дальнейшее увеличение выборки – нецелесообразным.

Подведем итог. Расчет дисперсии и стандартной ошибки средней имеет довольно простую формулу и обладает полезным свойством, связанным с тем, что относительно хорошая точность средней достигается уже при 100 наблюдениях (в этом случае стандартная ошибка средней становится в 10 раз меньше, чем стандартное отклонение выборки). Больше, конечно, лучше, но бесконечно увеличивать объем выборки не имеет практического смысла. Хотя, все зависит от поставленных задач и цены ошибки. В некоторых опросах участие принимают десятки тысяч людей.

Дисперсия и стандартная ошибка средней имеют большое практическое значение. Они используются в проверке гипотез и расчете доверительных интервалов.

Поделиться в социальных сетях:

Источник

Когда мы подгоняем регрессионную модель к набору данных, нас часто интересует, насколько хорошо регрессионная модель «подходит» к набору данных. Две метрики, обычно используемые для измерения согласия, включают R -квадрат (R2) и стандартную ошибку регрессии , часто обозначаемую как S.

В этом руководстве объясняется, как интерпретировать стандартную ошибку регрессии (S), а также почему она может предоставить более полезную информацию, чем R 2 .

Стандартная ошибка по сравнению с R-квадратом в регрессии

Предположим, у нас есть простой набор данных, который показывает, сколько часов 12 студентов занимались в день в течение месяца, предшествующего важному экзамену, а также их баллы за экзамен:

Если мы подгоним простую модель линейной регрессии к этому набору данных в Excel, мы получим следующий результат:

R-квадрат — это доля дисперсии переменной отклика, которая может быть объяснена предикторной переменной. При этом 65,76% дисперсии экзаменационных баллов можно объяснить количеством часов, потраченных на учебу.

Стандартная ошибка регрессии — это среднее расстояние, на которое наблюдаемые значения отклоняются от линии регрессии. В этом случае наблюдаемые значения отклоняются от линии регрессии в среднем на 4,89 единицы.

Если мы нанесем фактические точки данных вместе с линией регрессии, мы сможем увидеть это более четко:

Обратите внимание, что некоторые наблюдения попадают очень близко к линии регрессии, в то время как другие не так близки. Но в среднем наблюдаемые значения отклоняются от линии регрессии на 4,19 единицы .

Стандартная ошибка регрессии особенно полезна, поскольку ее можно использовать для оценки точности прогнозов. Примерно 95% наблюдений должны находиться в пределах +/- двух стандартных ошибок регрессии, что является быстрым приближением к 95% интервалу прогнозирования.

Если мы заинтересованы в прогнозировании с использованием модели регрессии, стандартная ошибка регрессии может быть более полезной метрикой, чем R-квадрат, потому что она дает нам представление о том, насколько точными будут наши прогнозы в единицах измерения.

Чтобы проиллюстрировать, почему стандартная ошибка регрессии может быть более полезной метрикой для оценки «соответствия» модели, рассмотрим другой пример набора данных, который показывает, сколько часов 12 студентов занимались в день в течение месяца, предшествующего важному экзамену, а также их экзаменационная оценка:

Обратите внимание, что это точно такой же набор данных, как и раньше, за исключением того, что все значения s сокращены вдвое.Таким образом, студенты из этого набора данных учились ровно в два раза дольше, чем студенты из предыдущего набора данных, и получили ровно половину экзаменационного балла.

Обратите внимание, что R-квадрат 65,76% точно такой же, как и в предыдущем примере.

Однако стандартная ошибка регрессии составляет 2,095 , что ровно вдвое меньше стандартной ошибки регрессии в предыдущем примере.

Если мы нанесем фактические точки данных вместе с линией регрессии, мы сможем увидеть это более четко:

Обратите внимание на то, что наблюдения располагаются гораздо плотнее вокруг линии регрессии. В среднем наблюдаемые значения отклоняются от линии регрессии на 2,095 единицы .

Таким образом, несмотря на то, что обе модели регрессии имеют R-квадрат 65,76% , мы знаем, что вторая модель будет давать более точные прогнозы, поскольку она имеет более низкую стандартную ошибку регрессии.

Преимущества использования стандартной ошибки

Стандартную ошибку регрессии (S) часто бывает полезнее знать, чем R-квадрат модели, потому что она дает нам фактические единицы измерения. Если мы заинтересованы в использовании регрессионной модели для получения прогнозов, S может очень легко сказать нам, достаточно ли точна модель для прогнозирования.

Например, предположим, что мы хотим создать 95-процентный интервал прогнозирования, в котором мы можем прогнозировать результаты экзаменов с точностью до 6 баллов от фактической оценки.

Наша первая модель имеет R-квадрат 65,76%, но это ничего не говорит нам о том, насколько точным будет наш интервал прогнозирования. К счастью, мы также знаем, что у первой модели показатель S равен 4,19. Это означает, что 95-процентный интервал прогнозирования будет иметь ширину примерно 2*4,19 = +/- 8,38 единиц, что слишком велико для нашего интервала прогнозирования.

Наша вторая модель также имеет R-квадрат 65,76%, но опять же это ничего не говорит нам о том, насколько точным будет наш интервал прогнозирования. Однако мы знаем, что вторая модель имеет S 2,095. Это означает, что 95-процентный интервал прогнозирования будет иметь ширину примерно 2*2,095= +/- 4,19 единиц, что меньше 6 и, следовательно, будет достаточно точным для использования для создания интервалов прогнозирования.

Дальнейшее чтение

Введение в простую линейную регрессию
Что такое хорошее значение R-квадрата?

Источник

Стандартное определение ошибки

Стандартная ошибка или SE измеряет точность с помощью выборочного распределения, которое означает, что популяция использует стандартное отклонение. Другими словами, его можно понимать как меру дисперсии выборочного среднего, относящегося к средним значениям генеральной совокупности. Его не следует путать со стандартным отклонением. Это выше, потому что стандартные ошибки используют выборочные данные или статистику, в то время как стандартные отклонения используют параметры или данные населения.

Оглавление

Стандартное определение ошибки
- Стандартная формула ошибки
- Шаги, чтобы найти стандартную ошибку
- Примеры стандартной ошибки
- Интерпретация стандартной ошибки
- Разница между стандартной ошибкой и стандартным отклонением
- Заключение
- Рекомендуемые статьи

Стандартная формула ошибки

Можно представить это следующим образом:

Шаги, чтобы найти стандартную ошибку

На первом этапе необходимо вычислить среднее значение, суммируя все образцы, а затем разделив их на общее количество образцов.
На втором этапе отклонение для каждого измерения должно быть рассчитано от среднего значения, т. е. путем вычитания отдельного измерения.
На третьем шаге нужно возвести в квадрат каждое отклонение от среднего. Таким образом, отрицательные квадраты станут положительными.
На четвертом шаге необходимо просуммировать квадраты отклонений. Для этого нужно сложить все числа, полученные на шаге 3.
На пятом шаге сумма, полученная на четвертом шаге, должна делиться на одну цифру меньше объема выборки.
На шестом шаге нужно извлечь квадратный корень из числа, полученного на пятом шаге. Результат должен быть SD или стандартным отклонением.
Необходимо рассчитать SE, разделив стандартное отклонение на квадратный корень из N (размер выборки).
На последнем шаге вычтите SE из среднего значения. Соответственно, нужно записать этот номер. Затем добавьте SE к среднему и запишите результат.

Примеры стандартной ошибки

Ниже приведены примеры стандартных ошибок.

.free_excel_div{фон:#d9d9d9;размер шрифта:16px;радиус границы:7px;позиция:относительная;margin:30px;padding:25px 25px 25px 45px}.free_excel_div:before{content:»»;фон:url(центр центр без повтора #207245;ширина:70px;высота:70px;позиция:абсолютная;верх:50%;margin-top:-35px;слева:-35px;граница:5px сплошная #fff;граница-радиус:50%} Вы можете скачать этот шаблон стандартной ошибки Excel здесь – Стандартный шаблон ошибки Excel

Пример №1

Смертность от рака в выборке из 100 человек составляет 20 процентов, а во второй выборке из 100 человек — 30 процентов. Оцените значимость контраста в уровне смертности.

Решение

Используйте приведенные ниже данные.

=КОРЕНЬ(20*80/(100)+(30*70/(100)))
=6,08

Z= 20-30/6,08
Z= -1,64

Пример #2

Они выбрали случайную выборку из 5 баскетболистов мужского пола. Их рост 175, 170, 177, 183 и 169 (в см). Во-первых, найдите SE среднего значения этой высоты (в см).

Решение

= (175+170+177+183+169)/5
Среднее значение выборки = 174,8

Расчет выборочного стандартного отклонения

=КОРЕНЬ(128,80)
Стандартное отклонение выборки =5,67450438

= 5,67450438/КОРЕНЬ(5)
= 2,538

Пример №3

Среднее значение прибыли для выборки из 41 предприятия составляет 19, а стандартное отклонение клиентов составляет 6,6. Сначала найдите SE среднего.

Решение

Используйте приведенные ниже данные.

Расчет стандартной ошибки

= 6,6/кв.кв.(41)
= 1,03

Интерпретация стандартной ошибки

Стандартная ошибка функционирует очень похоже на описательная статистика поскольку это позволяет исследователю разработать доверительные интервалы. Доверительные интервалы. Доверительный интервал относится к степени неопределенности, связанной с конкретной статистикой, и часто используется вместе с погрешностью. Доверительный интервал = среднее значение выборки ± критический фактор × стандартное отклонение выборки. читайте больше об уже полученной статистике выборки. Кроме того, это помогает оценить интервалы, в которые должны попадать параметры. SE среднего и SE оценки — две обычно используемые статистики SE.

SE среднего позволяет исследователю разработать доверительный интервал, в который попадет среднее значение генеральной совокупности. Можно использовать 1-P в качестве формулы, которая означает вероятность того, что среднее значение совокупности Среднее значение совокупности Среднее значение совокупности является средним или средним значением всех значений в данной совокупности и рассчитывается как сумма всех значений в совокупности, обозначаемая суммой X, разделенной по количеству значений в популяции, которое обозначается N. Подробнее попадет в доверительный интервал.

SE оценки в основном используется различными исследователями. Его можно использовать вместе с мерой корреляции. Это позволяет исследователям построить доверительный интервал под фактической корреляцией населения, которая должна падать. Можно использовать SE оценки для определения точности оценки корреляции населения.

SE помогает указать точность оценки параметров совокупности выборочной статистики.

Разница между стандартной ошибкой и стандартным отклонением

Стандартная ошибка и стандартное отклонение — это две разные темы, которые не следует путать друг с другом. Краткая форма стандартной ошибки — SE, а аббревиатура стандартного отклонения — SD. Это связано с тем, что SE выборки действительно означает оценку расстояния между средним значением выборки и средним значением генеральной совокупности и помогает оценить точность выборки. оценивать. В то же время SD измеряет количество дисперсии. В статистике дисперсия (или разброс) является средством описания степени распределения данных вокруг центрального значения или точки. Это помогает понять распределение данных или изменчивость. Как правило, это степень, в которой отдельные лица, принадлежащие к одной и той же выборке, отличаются от среднего значения выборки.

Заключение

Стандартная ошибка измеряет точность среднего значения и оценки. Он предлагает полезный способ количественной оценки ошибки выборки. SE полезен, поскольку он представляет собой общее количество ошибок выборки, связанных с процессами выборки. Стандартная ошибка оценки и стандартная ошибка среднего — две обычно используемые статистики SE.

Стандартная ошибка оценки позволяет делать прогнозы, но не указывает на точность прогноза. Он измеряет точность регрессии. Регрессия. Регрессионный анализ — это статистический подход к оценке взаимосвязи между 1 зависимой переменной и 1 или более независимыми переменными. Он широко используется в инвестиционном и финансовом секторах для дальнейшего улучшения продуктов и услуг. читать далее, в то время как стандартная ошибка среднего помогает исследователю определить доверительный интервал, в который, скорее всего, попадет среднее значение генеральной совокупности. Можно понимать SEM как статистику или параметр среднего.

интерпретация

Стандартная ошибка дает представление о качестве оцениваемого параметра. Чем больше имеется индивидуальных значений, тем меньше стандартная ошибка и тем точнее можно оценить неизвестный параметр. Стандартная ошибка делает измеренный разброс (стандартное отклонение) двух наборов данных с разными размерами выборки сопоставимым путем нормализации стандартного отклонения к размеру выборки.

Если неизвестный параметр оценивается с помощью нескольких образцов, результаты будут отличаться от образца к образцу. Конечно, это изменение происходит не из-за изменения неизвестного параметра (потому что он фиксирован), а из-за случайных влияний, например Б. Неточности измерения. Стандартная ошибка — это стандартное отклонение оцененных параметров во многих выборках. Как правило, уменьшение стандартной ошибки вдвое требует увеличения размера выборки в четыре раза.

В отличие от этого, стандартное отклонение отображает фактический разброс в популяции , который также присутствует с высочайшей точностью измерения и бесконечным количеством индивидуальных измерений (например, для распределения веса, распределения по размерам, ежемесячного дохода). Он показывает, близки ли отдельные значения друг к другу или данные широко разбросаны.

пример

Предположим, вы изучаете популяцию старшеклассников с точки зрения их интеллекта. Таким образом, неизвестный параметр — это средний уровень интеллекта детей, посещающих среднюю школу. Если случайная выборка размера (например, с детьми) отбирается из этой совокупности , то среднее значение может быть вычислено по всем результатам измерений . Если после этой выборки будет нарисована другая случайная выборка с тем же количеством дочерних элементов и будет определено среднее значение, два средних значения не будут точно совпадать. Если нарисовать большое количество других случайных выборок из диапазона , то можно определить разброс всех эмпирически определенных средних значений вокруг среднего значения генеральной совокупности. Этот разброс — стандартная ошибка. Поскольку среднее значение выборки является наилучшей оценкой среднего значения генеральной совокупности, стандартная ошибка представляет собой разброс эмпирических средних значений вокруг среднего значения генеральной совокупности. Он показывает не распределение интеллекта детей, а точность рассчитанного среднего значения.

обозначение

Для обозначения стандартной ошибки используются различные термины, чтобы отличить ее от стандартного отклонения генеральной совокупности и прояснить, что это разброс оцениваемого параметра выборок:

оценивать

Поскольку стандартное отклонение генеральной совокупности включено в стандартную ошибку, стандартное отклонение генеральной совокупности должно быть оценено с использованием максимально точного оценщика, чтобы оценить стандартную ошибку.

Доверительные интервалы и тесты

Стандартная ошибка также играет важную роль в доверительных интервалах и тестах . Если оценка соответствует ожиданиям и, по крайней мере, приблизительно нормально распределена ( ), то
${ Displaystyle { mathcal {N}} ( vartheta, sigma ^ {2} ({ hat { vartheta}}))}$

${ displaystyle { frac {{ hat { vartheta}} - vartheta} { sigma ({ hat { vartheta}})}} приблизительно { mathcal {N}} (0; 1)}$

Исходя из этого, — для неизвестного параметра можно указать доверительные интервалы :

${ Displaystyle P ({ шляпа { vartheta}} - z_ {1- alpha / 2} sigma ({ hat { vartheta}}) leq vartheta leq { hat { vartheta}} + z_ {1- alpha / 2} sigma ({ hat { vartheta}})) = 1- alpha}$

или сформулировать тесты, например Б. принимает ли параметр определенное значение :

против.

а результаты статистики теста:

${ displaystyle V = { frac {{ hat { vartheta}} - vartheta _ {0}} { sigma ({ hat { vartheta}})}} приблизительно { mathcal {N}} ( 0; 1)}$

$z_ {1- alpha / 2}$ это — квантиль стандартного нормального распределения , а также критическое значение для сформулированного теста. Как правило, его нужно оценивать по выборке, чтобы

${ displaystyle V = { frac {{ hat { vartheta}} - vartheta _ {0}} {{ hat { sigma}} ({ hat { vartheta}})}} приблизительно t_ { n-1}}$

где — количество наблюдений. Для t-распределение можно аппроксимировать стандартным нормальным распределением.

Стандартная ошибка среднего арифметического

Стандартная ошибка среднего арифметического такая же

$sigma ( overline {X}) = frac { sigma} { sqrt {n}}$ ,

где обозначает стандартное отклонение единичного измерения.

Вывод

Среднее значение размера выборки определяется как

$overline x = frac1n sum_ {i = 1} ^ nx_i.$

Глядя на оценщик

$overline {X} = frac {1} {n} sum_ {i = 1} ^ n X_i$

с независимыми, одинаково распределенными случайными величинами с конечной дисперсией стандартная ошибка определяется как квадратный корень из дисперсии . Используя правила расчета дисперсий и уравнение Биенайме, можно рассчитать :
$sigma ^ {2}$

$sigma ( overline {X}) ^ 2 = operatorname {Var} left ( overline X right) = operatorname {Var} left ( frac 1n sum_ {i = 1} ^ n X_i right ) = frac 1 {n ^ 2} operatorname {Var} left ( sum_ {i = 1} ^ n X_i right) = frac 1 {n ^ 2} sum_ {i = 1} ^ n имя оператора {Var} left (X_i right) = frac 1 {n ^ 2} n sigma ^ 2 = frac { sigma ^ 2} n$

откуда следует формула для стандартной ошибки. Если это так , то аналогично следует
$operatorname {Var} (X_i) = sigma_i ^ 2$

$sigma ( overline {X}) ^ 2 = frac {1} {n ^ 2} sum_ {i = 1} ^ n sigma_i ^ 2$

Расчет

Предполагая выборочное распределение, стандартная ошибка может быть рассчитана с использованием дисперсии выборочного распределения:

в биномиальном распределении с параметрами

$sigma _ { bar x, mathrm {binom}} = frac { sqrt {N cdot p cdot (1-p)}} { sqrt n}$

$sigma _ { bar x, mathrm {exp}} = frac {1} { lambda sqrt n}$

$sigma _ { bar x, mathrm {poisson}} = sqrt { frac { lambda} {n}}$

Обозначьте это

Если стандартная ошибка среднего должна быть оценена, тогда дисперсия оценивается с помощью скорректированной дисперсии выборки .
$sigma ^ {2}$

пример

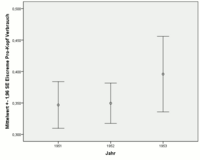
Для данных по мороженому рассчитывались среднее арифметическое, стандартная ошибка и стандартное отклонение за 1951, 1952 и 1953 годы для потребления мороженого на душу населения (измеряемого в пинтах ).

год	В среднем	Стандартная ошибка среднего	Стандартное отклонение	Количество наблюдений
1951 г.	0,34680	0,01891	0,05980	10
1952 г.	0,34954	0,01636	0,05899	13-е
1953 г.	0,39586	0,03064	0,08106	7-е

Для 1951 и 1952 годов расчетные средние значения и стандартные отклонения, а также числа наблюдений примерно одинаковы. Следовательно, оцененные стандартные ошибки также дают примерно такое же значение. В 1953 г., с одной стороны, количество наблюдений меньше, а стандартное отклонение больше. Таким образом, стандартная ошибка почти вдвое превышает стандартные ошибки 1951 и 1952 годов.

Графическое представление может быть выполнено с помощью гистограммы ошибок . Справа показаны 95% интервалы оценки для 1951, 1952 и 1953 годов. Если функция выборки, по крайней мере, приблизительно нормально распределена, то 95% интервалы оценки задаются с помощью, а также средними значениями выборки и дисперсиями выборки.
${ displaystyle { bar {x_ {j}}} pm 1 {,} 96 cdot s_ {j} / { sqrt {n_ {j}}}}$ $bar {x} _j$ s_j ^ 2

Здесь также ясно видно, что среднее значение для 1953 г. может быть оценено более неточно, чем средние значения для 1951 и 1952 гг. (Более длинная полоса для 1953 г.).

Стандартная ошибка коэффициентов регрессии в модели простой регрессии

Классическая модель регрессии для простой линейной регрессии предполагает , что
${ displaystyle Y_ {i} = beta _ {0} + beta _ {1} x_ {i} + varepsilon _ {i}}$

с наблюдениями, сделанными при беге. Для оценщиков

${ displaystyle { hat { beta}} _ {1} = { frac { sum _ {i} (x_ {i} - { overline {x}}) (Y_ {i} - { overline { Y}})} { sum _ {i} (x_ {i} - { overline {x}}) ^ {2}}}}$

а также

${ displaystyle { hat { beta}} _ {0} = { overline {Y}} - { hat { beta}} _ {1} { overline {x}}}$

затем результаты

${ displaystyle { hat { beta}} _ {1} sim { mathcal {N}} ( beta _ {1}, sigma _ {{ hat { beta}} _ {1}} ^ {2} cdot a_ {1}) ,}$

и . ${ displaystyle { hat { beta}} _ {0} sim { mathcal {N}} ( beta _ {0}, sigma _ {{ hat { beta}} _ {0}} ^ {2} cdot a_ {0})}$

В стандартные ошибки коэффициентов регрессии определяются

${ displaystyle sigma _ {{ hat { beta}} _ {1}} = operatorname {SD} ({ hat { beta}} _ {1}) = sigma { sqrt { underbrace { frac {1} { sum nolimits _ {i = 1} ^ {n} (x_ {i} - { overline {x}}) ^ {2}}} _ {=: a_ {1}}} } = sigma cdot { sqrt {a_ {1}}}}$

а также

${ displaystyle sigma _ {{ hat { beta}} _ {0}} = operatorname {SD} ({ hat { beta}} _ {0}) = sigma { sqrt { underbrace { frac { sum nolimits _ {i = 1} ^ {n} x_ {i} ^ {2}} {n sum nolimits _ {i = 1} ^ {n} (x_ {i} - { над чертой {x}}) ^ {2}}} _ {=: a_ {0}}}} = sigma cdot { sqrt {a_ {0}}}}$

Пример : Для данных по мороженому была проведена простая линейная регрессия для потребления мороженого на душу населения (измеренного в поллитрах) со средней недельной температурой (в градусах Фаренгейта) в качестве независимой переменной. Оценка регрессионной модели привела к:

{ displaystyle { text {Потребление на душу населения}} = 0 {,} 20686 + 0 {,} 00311 cdot { text {Температура}}}

модель	Нестандартизированные коэффициенты	Стандартизированные коэффициенты	Т	Sig.
	Коэффициенты регрессии	Стандартная ошибка
постоянный	0,20686	0,02470		8,375	0,000
температура	0,00311	0,00048	0,776	6,502	0,000

Хотя расчетный коэффициент регрессии для средней недельной температуры очень мал, расчетная стандартная ошибка дала еще меньшее значение. Точность оценки коэффициента регрессии в 6,5 раз меньше, чем самого коэффициента.

Отношение к логарифмической вероятности

Термин также известен как стандартная ошибка оценки максимального правдоподобия , где в функции логарифмического правдоподобия и представляет собой наблюдаемую информацию Фишера (информация Фишера вместо оценки ML ). ${ displaystyle sigma ({ hat { theta}} _ {ML}) = { frac {1} { sqrt {- { frac { partial ^ {2}} { partial theta ^ {2 }}} ell ({ hat { theta}} _ {ML})}}}}$ ${ displaystyle - { frac { partial ^ {2}} { partial theta ^ {2}}} ell ({ hat { theta}} _ {ML})}$ ${ displaystyle { hat { theta}} _ {ML}}$

Смотри тоже

Стандартная ошибка регрессии

Индивидуальные доказательства

↑ ^a^b Котешвара Рао Кадияла (1970): Проверка независимости регрессионных нарушений. В: Econometrica , 38, 97-117.
↑ ^а^б финики мороженого. In: Data and Story Library , по состоянию на 16 февраля 2010 г.
↑ Приложение: логарифм правдоподобия и доверительные интервалы. Проверено 14 июля 2021 года .

Источник

Standard error of the sample mean[edit]

Exact value[edit]

Estimate[edit]

Accuracy of the estimator[edit]

Derivation[edit]

Independent and identically distributed random variables with random sample size[edit]

Student approximation when σ value is unknown[edit]

Assumptions and usage[edit]

Standard error of mean versus standard deviation[edit]

Extensions[edit]

Finite population correction (FPC)[edit]

Correction for correlation in the sample[edit]

See also[edit]

References[edit]

Расчет дисперсии и стандартной ошибки средней арифметической

Назначение и свойство стандартной ошибки средней арифметической

Стандартная ошибка по сравнению с R-квадратом в регрессии

Преимущества использования стандартной ошибки

Стандартное определение ошибки

Стандартная формула ошибки

Шаги, чтобы найти стандартную ошибку

Примеры стандартной ошибки

Интерпретация стандартной ошибки

Разница между стандартной ошибкой и стандартным отклонением

Заключение

Рекомендуемые статьи

интерпретация

пример

обозначение

оценивать

Доверительные интервалы и тесты

Стандартная ошибка среднего арифметического

Вывод

Расчет <img decoding="async" src="https://wikimedia.org/api/rest_v1/media/math/render/svg/59f59b7c3e6fdb1d0365a494b81fb9a696138c36" alt=" сигма " />

пример

Стандартная ошибка коэффициентов регрессии в модели простой регрессии

Отношение к логарифмической вероятности

Смотри тоже

Индивидуальные доказательства

Расчет