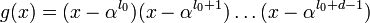Коррекция ошибок рида соломона

Кодирование Рида-Соломона для чайников

Есть способ передавать данные, теряя часть по пути, но так, чтобы потерянное можно было вернуть по прибытии. Это третья, завершающая часть моего простого изложения алгоритма избыточного кодирования по Риду-Соломону. Реализовать это в коде не прочитав первую, или хотя бы вторую часть на эту тему будет проблематично, но чтобы понять для себя что можно сделать с использованием кодировки Рида-Соломона, можно ограничиться прочтением этой статьи.

Что может этот код?

Итак, что из себя представляет избыточный код Рида-Соломона с практической точки зрения? Допустим, есть у нас сообщение – «DON’T PANIC». Если добавить к нему несколько избыточных байт, допустим 6 штук: «rrrrrrDON’T PANIC» (каждый r – это рассчитанный по алгоритму байт), а затем передать через какую-нибудь среду с помехами, или сохранить там, где данные могут понемногу портиться, то по окончании передачи или хранения у нас может остаться такое, например: «rrrrrrDON’AAAAAAA» (6 байт оказались с ошибкой). Если мы знаем номера байтов, где вместо букв, которые были при создании кода, вдруг оказались какие-нибудь «A», то мы можем полностью восстановить сообщение в исходное «rrrrrrDON’T PANIC». После этого можно для красоты убрать избыточные символы. Теперь текст можно печатать на обложку.

Вообще, избыточных символов к сообщению мы можем добавить сколько угодно. Количество избыточных символов равно количеству исправляемых ошибок (это верно лишь в том случае, когда нам известны номера позиций ошибок). Как правило, ошибки, положение которых известно, называют erasures. Благозвучного перевода найти не могу («стирание» мне не кажется благозвучным), так что в дальнейшем я буду применять термин «опечатки» и ставить его в кавычки (прекрасно понимаю, что этот термин обычно несёт похожий, но другой смысл). Исправление «опечаток» полезно, например, при восстановлении блоков QR кода, которые по какой-либо причине не удалось прочитать.

Также код Рида-Соломона позволяет исправлять ошибки, положение которых неизвестно, но тогда на каждую одну исправляемую ошибку должно приходиться 2 избыточных символа. «rrrrrrDON’T PANIC», принятые как «rrrrrrDO___ PANIC» легко будут исправлены без дополнительной информации. Неправильно принятый байт, положение которого неизвестно, в дальнейшем я буду называть «ошибкой» и тоже брать в кавычки.

Можно комбинировать исправление «ошибок» и «опечаток». Если, например, есть 3 избыточных символа, то можно исправить одну «ошибку» и одну «опечатку». Ещё раз обращу внимание на то, что чтобы исправить «опечатку», нужно каким-то образом (не связанным с алгоритмом Рида-Соломона) узнать номер байта «опечатки». Что важно, и «ошибки» и «опечатки» могут быть исправлены алгоритмом и в избыточных байтах тоже.

Стоит отметить, что если количество переданных и принятых байт отличается, то здесь код Рида-Соломона практически бессилен. То есть, если на расшифровку попадёт такое: «rrrrrrDO’AIC», то ничего сделать не получится, если, конечно, неизвестно какие позиции у пропавших букв.

Как закодировать сообщение?

Здесь уже не обойтись без понимания арифметики с полиномами в полях Галуа. Ранее мы научились представлять сообщения в виде полиномов и проводить операции сложения, умножения и деления над ними. Уже этого почти достаточно, чтобы создать код Рида-Соломона из сообщения. Единственно, для того, чтобы это сделать понадобится ещё полином-генератор. Это результат такого произведения:

Где – это примитивный член поля (как правило, выбирают 2), а – это количество избыточных символов. То есть, прежде чем создавать код Рида-Соломона из сообщения, нужно определиться с количеством избыточных символов, которое мы считаем достаточным, затем перемножить биномы вида в количестве штук по правилам перемножения полиномов. Для любого сообщения можно использовать один и тот же полином-генератор, и любое сообщение в таком случае будет закодировано с одним и тем же количеством избыточных символов.

Пример: Мы решили использовать 4 избыточных символа, тогда нужно составить такое выражение:

Так как мы работаем с полем Галуа с характеристикой 2, то вместо минуса можно смело писать плюс, не боясь никаких последствий. Жаль, что это не работает с количеством денег после похода в магазин. Итак, возводим в степень, и перемножаем (по правилам поля Галуа GF[256], порождающий полином 285):

Необязательное дополнение

Легко заметить (правда легко – надо лишь взглянуть на произведение биномов), что корнями получившегося полинома будут как раз степени примитивного члена: 2, 4, 8, 16. Что самое интересное, если взять какой-нибудь другой полином, умножить его на (4 – в данном случае это количество избыточных символов), получится тот же самый полином, только с нулями в коэффициентах перед первыми 4 младшими степенями, а затем разделить его на полином-генератор, и прибавить остаток от деления к нашему полиному с 4 нулями, то его корнями также будут эти 4 числа (2, 4, 8, 16).

Выражение выше есть полином-генератор, который необходим для того, чтобы закодировать сообщение любой длины, добавив к нему 4 избыточных символа, которые позволят скорректировать 2 «ошибки» или 4 «опечатки».

Прежде чем приводить пример кодирования, нужно договориться об обозначениях. Полиномы, записанные «по-математически» с иксами и степенями выглядят довольно-таки громоздко. На самом деле, при написании программы достаточно знать коэффициенты полинома, а степени можно узнать из положения этих коэффициентов. Таким образом полученный в примере выше полином-генератор можно записать так: {116, 231, 216, 30, 1}. Также, для ещё большей компактности, можно опустить скобки и запятые и записать всё в шестнадцатеричном представлении: 74 E7 D8 1E 01. Выходит в 2 раза короче. Надо отметить, что если в «математической» записи мы не пишем члены, коэффициенты которых равны нулю, то при принятой здесь шестнадцатеричной записи они обязательны, и, например, нужно записывать так: или 00 00 00 00 0A. Там, где «математическая» запись позволит более понятно объяснить суть, я буду прибегать к ней.

Итак, чтобы представить сообщение «DON’T PANIC» в полиномиальной форме, с учётом соглашения выше достаточно просто записать его байты:

44 4F 4E 27 54 20 50 41 4E 49 43.

Чтобы создать код Рида-Соломона с 4 избыточными символами, сдвигаем полином вправо на 4 позиции (что эквивалентно умножению его на ):

00 00 00 00 44 4F 4E 27 54 20 50 41 4E 49 43

Теперь делим полученный полином на полином-генератор (74 E7 D8 1E 01), берём остаток от деления (DB 22 58 5C) и записываем вместо нулей к полиному, который мы делили. (это эквивалентно операции сложения):

DB 22 58 5C 44 4F 4E 27 54 20 50 41 4E 49 43

Вот эта строка как раз и будет кодом Рида-Соломона для сообщения «DON’T PANIC» с 4 избыточными символами.

Некоторые пояснения

Как раскодировать сообщение?

Здесь всё посложнее будет. Ненамного, но всё же. Вопрос про раскодировать, собственно «не вопрос!» – убираем избыточные символы и остаётся исходное сообщение. Вопрос в том, как узнать, были ли ошибки при передаче, и если были, то как их исправить.

В первую очередь нужно отметить, что при проверке на наличие ошибок нужно знать количество избыточных символов. А во-вторую – надо научиться считать значение полинома при определённом . Про количество избыточных символов нам должен заранее сообщить тот, кто кодировал сообщение, а вот чтобы вычислить значение полинома нужно написать ещё одну функцию для работы с полиномами. Это элементарщина – просто вместо подставляется нужное значение. Но пример, всё же, никогда не помешает.

Пример: Нужно вычислить полиномпри . Подставляем, возводим в степень: , перемножаем, , складываем и получаем число . Сложение, умножение и возведение в степень здесь по правилам поля Галуа GF[256] (порождающий полином 285)

Код приводить не буду, оставлю ссылку на гитхаб. Там всё что я описывал в этой и предыдущих статьях реализовано на C#, в виде демо-приложения (собирается под win в VS2019, бинарник тоже выложен). Можно посмотреть как работает арифметика в поле Галуа, а также посмотреть, как работает кодирование Рида-Соломона.

Итак, прежде чем исправлять «ошибки» или «опечатки» нужно узнать есть ли они. Элементарно. Нужно вычислить полином принятого сообщения с избыточными символами при равном степеням примитивного члена. Это те же числа, которые мы использовали при составлении полинома-генератора: , – количество избыточных символов, – примитивный член. Если ошибок нет, то все вычисленные значения будут равны нулю. Закодированное ранее сообщение «DON’T PANIC» с 4 избыточными символами, в виде полинома в шестнадцатеричном представлении:

DB 22 58 5C 44 4F 4E 27 54 20 50 41 4E 49 43,

если вычислить этот полином при равном 2, 4, 8, 16, то получатся значения: 0, 0, 0, 0, ведь здесь сообщение точно в таком же виде, в котором оно и было закодировано. Если изменить хотя бы один байт, например, последний символ сделаем более правильным: 42 вместо 43:

DB 22 58 5C 44 4F 4E 27 54 20 50 41 4E 49 42,

то результат такого же вычисления станет равным 13, 18, B5, 5D. Эти значения называются синдромами. Их тоже можно принять за полином. Тогда это будет полином синдромов.

Итак, чтобы узнать есть ли ошибки в принятом сообщении, нужно посчитать полином синдромов. Если он состоит из одних нулей (также можно говорить, что он равен нулю), то ошибок нет.

Важное, но совсем занудное дополнение

Что же делать, если синдром не равен нулю? Конечно же исправлять ошибки! Для начала рассмотрим случай с «опечатками», когда мы точно знаем номера позиций некорректно принятых байт. Ошибёмся намеренно в нашем закодированном сообщении 4 раза, столько же, сколько у нас избыточных символов:

DB 22 58 5C 44 4F 4E 27 54 20 41 41 41 41 41

41 – это буква A, поэтому их 5 подряд получилось. Позиции ошибок считаются слева направо, начиная с 0. Для удобства используем шестнадцатеричную систему при нумерации:

00 01 02 03 04 05 06 07 08 09 0A 0B 0C 0D 0E
DB 22 58 5C 44 4F 4E 27 54 20 50 41 4E 49 43
DB 22 58 5C 44 4F 4E 27 54 20 41 41 41 41 41

Позиции ошибок: 0A 0C 0D 0E.

Итак, если мы находимся на стороне приёмника, то у нас есть следующая информация:

• Сообщение с 4 избыточными символами;

• само сообщение: DB 22 58 5C 44 4F 4E 27 54 20 41 41 41 41 41;

• В сообщении есть ошибки в позициях 0A 0C 0D 0E.

Этого достаточно, чтобы восстановить сообщение в исходное состояние. Но обо всём по порядку.

Для продолжения необходимо разучить ещё одну операцию с полиномами в полях Галуа — взятие формальной производной от полинома. Формальная производная полинома в поле Галуа похожа на обычную производную. Формальной она называется потому, что в полях вроде GF[256] нет дробных чисел, и соответственно нельзя определить производную, как отношение бесконечно малых величин. Вычисляется похоже на обычную производную, но с особенностями. Если при обычном дифференцировании , то для формальной производной в поле Галуа с основанием 2, формула для дифференцирования члена такая: . Это значит, что достаточно просто переписать полином, начиная с первой степени (нулевая выкидывается) и у оставшегося убрать (обнулить, извиняюсь) члены с нечётными степенями. Пример:

Необходимо найти производную

(Это рандомный полином, не связан с примером). Производная суммы равна сумме производных, соответственно применяем формулу для производной члена и получаем:

Или, если записывать в шестнадцатеричном виде, то это же самое выглядит так:

(01 2D A5 C6 8C DF )’ = 2D 00 C6 00 DF .

Думаю, что из примера в шестнадцатеричном виде проще всего составить алгоритм нахождения формальной производной.

Теперь можно уже исправить «опечатки»? Как бы не так! Нужно ещё два полинома. Полином-локатор и полином ошибок.

Полином-локатор – это полином, корнями которого являются числа обратные примитивному члену в степени позиции ошибки. Сложно? Можно проще. Полином-локатор это произведение вида

где – это примитивный член, и так далее – это позиции ошибок.

Пример: у нас есть позиции ошибок 10, 12, 13, 14; примитивный член тогда полином локатор будет таким:

Перемножаем и получаем полином-локатор для позиций ошибок 10, 12, 13, 14:

Или в шестнадцатеричной записи: 01 2D A5 C6 8C.

Про полином-локатор нужно понять следующее: из него можно получить позиции ошибок, и наоборот – из позиций ошибок можно получить полином-локатор. По сути, это две разные записи одного и того же – позиций ошибок.

Полином ошибок – его по-разному называют в разных статьях, он не так уж и сложен. Представляет из себя произведение полинома синдромов и полином-локатора, с отброшенными старшими степенями. Продолжая пример, найдём полином ошибок для искажённого сообщения:

DB 22 58 5C 44 4F 4E 27 54 20 41 41 41 41 41

Полином синдромов: 72 BD 22 5B

Произведение полинома синдромов и полинома-локатора не буду расписывать в «математическом» виде, напишу так:

(72 BD 22 5B)(01 2D A5 C6 8C) = 72 4B 10 22 D9 C0 57 15

У результата оставляем количество младших членов, равное количеству избыточных символов, в нашем случае их 4, старшие степени просто выбрасываем, они не нужны. Остаётся

72 4B 10 22

Это и есть полином ошибок.

Осталось посчитать амплитуды ошибок. Звучит угрожающе, но на деле это просто значения, которые нужно прибавить к искажённым символам сообщения чтобы получились неискажённые символы. Для этого воспользуемся алгоритмом Форни. Здесь придётся привести фрагмент кода, словами расписать так, чтобы было понятно, очень сложно.

Функция принимает на входе

• полином синдромов (Syndromes),

• полином, в котором члены – позиции ошибок (ErrPos),

• количество избыточных символов (NumOfErCorrSymbs).

Класс GF_Byte — это просто байт, для которого переопределены арифметические операции так, чтобы они выполнялись по правилам поля Галуа GF[256], класс GF_Poly – Это полином в поле Галуа. По сути, массив GF_Byte. Для него также переопределны арифметические операции так, чтобы они выполнялись по правилам арифметики с полиномами в полях Галуа.

public static GF_Poly FindMagnitudesFromErrPos(
   GF_Poly Syndromes,
   GF_Poly ErrPos,
   uint NumOfErCorrSymbs)
{
 	//Вычисление локатора из позиций ошибок
	GF_Poly Locator = CalcLocatorPoly(ErrPos);
	//Произведение для вычисления полинома ошибок
	GF_Poly Product = Syndromes * Locator;
	//Полином ошибок. DiscardHiDeg оставляет указаное количество младших степеней
	GF_Poly ErrPoly = Product.DiscardHiDeg(NumOfErCorrSymbs);
	//Производная локатора
	GF_Poly LocatorDer = Locator.FormalDerivative();
	//Здесь будут амплитуды ошибок. Количество членов - это самая большая позиция ошибки
	GF_Poly Magnitudes = new GF_Poly(ErrPos.GetMaxCoef());

	//Перебор каждой заданной позиции ошибки
	for (uint i = 0; i < ErrPos.Len; i++) {
		//число обратное примитивному члену в степени позиции ошибки
		GF_Byte Xi = 1 / GF_Byte.Pow_a(ErrPos[i]);
		//значение полинома ошибок при x = Xi
		GF_Byte W = ErrPoly.Eval(Xi);
		//значение производной локатора при x = Xi
		GF_Byte L = LocatorDer.Eval(Xi);
		//Это как раз и будет найденное значение ошибки,
		//которое надо вычесть из ошибочного символа, чтобы он стал не ошибочным
		GF_Byte Magnitude = W / L;
		//запоминаем найденную амплитуду в текущей позиции ошибки
		Magnitudes[ErrPos[i]] = Magnitude;
	}            
	return Magnitudes;
}

Если скормить функции следующие параметры:

• полином синдромов 72 BD 22 5B

• полином, в котором члены — позиции ошибок 0A 0C 0D 0E

• количество символов коррекции ошибок 4,

то на выходе она даст полином амплитуд ошибок:

00 00 00 00 00 00 00 00 00 00 11 00 0F 08 02.

Теперь можно прибавить полученное к искажённому сообщению

DB 22 58 5C 44 4F 4E 27 54 20 41 41 41 41 41

(по правилам сложения полиномов, конечно же), и на выходе получится исходное сообщение:

DB 22 58 5C 44 4F 4E 27 54 20 50 41 4E 49 43.

Первые 4 байта — это избыточные символы. Если бы в них оказались «опечатки», то разницы никакой для алгоритма нет, разве что они нам не нужны после исправления. Можно их просто отбросить:

44 4F 4E 27 54 20 50 41 4E 49 43 Это исходное сообщение «DON’T PANIC».

Здесь должно быть понятно, как исправлять ошибки, положение которых известно. Само по себе уже это может нести практическую пользу. В QR кодах на обшарпанных стенах могут стереться некоторые квадратики, и программа, которая их расшифровывает сможет определить в каких именно местах находятся байты, которые не удалось прочитать, которые «стёрлись» – erasures, или как мы договорились писать по-русски «опечатки». Но нам этого, конечно же недостаточно. Мы хотим уметь выявлять испорченные байты без дополнительной информации, чтобы передавать их по радио, или по лазерному лучу, или записывать на диски (кого я обманываю? CD давно мертвы), может быть, захотим реализовать передачу через ультразвук под водой, чтобы управлять моделью подводной лодки, а какие-нибудь неблагодарные дельфины будут портить случайные данные своими песнями. Для всего этого нам понадобится уметь выявлять, в каких именно байтах при передаче попортились биты.

Как найти позиции ошибок?

Вспомним про полином-локатор. Его можно составить из заранее известных позиций ошибок, а ещё его можно вычислить из полинома-синдромов и количества избыточных символов. Есть не один алгоритм, который позволяет это сделать. Здесь будет алгоритм алгоритм Берлекэмпа-Мэсси. Если хочется много математики, то гугл с википедией на неё не скупятся. Я, если честно, не вник до конца в циклические полиномы и прочее-прочее-прочее. Стыдно, немножко, конечно, но я взял реализацию этого алгоритма с сайта Wikiversity переписал его на C#, и постарался сделать его более доходчивым и читаемым:

public static GF_Poly CalcLocatorPoly(GF_Poly Syndromes, uint NumOfErCorrSymbs) {
	//Алгоритм Берлекэмпа-Мэсси
	GF_Poly Locator;
	GF_Poly Locator_old;
	
	//Присваиваем локатору инициализирующее значение (1*X^0)
	Locator = new GF_Poly(new byte[] { 1 });
	Locator_old = new GF_Poly(Locator);

	uint Synd_Shift = 0;

	for (uint i = 0; i < NumOfErCorrSymbs; i++) {
		uint K = i + Synd_Shift;
		GF_Byte Delta = Syndromes[K];

		for (uint j = 1; j < Locator.Len; j++) {
			Delta += Locator[j] * Syndromes[K - j];
		}
		//Умножение полинома на икс (эквивалентно сдвигу вправо на 1 байт)
		Locator_old = Locator_old.MultiplyByXPower(1);
		if (Delta.val != 0) {
			if (Locator_old.Len > Locator.Len) {
				GF_Poly Locator_new = Locator_old.Scale(Delta);
				Locator_old = Locator.Scale(Delta.Inverse());
				Locator = Locator_new;
			}
			//Scale – умножение на константу. Можно было бы
			//вместо использования Scale 
			//умножить на полином нулевой степени. Разницы нет, но так короче:
			Locator += Locator_old.Scale(Delta);
		}
	}
	return Locator;
}

Пояснения по коду

Класс GF_Poly по сути – обёртка над массивом GF_Byte. Есть ещё одна особенность. Свойство Lenght любого массива — возвращает количество его элементов независимо от значений элементов. Здесь Len — возвращает количество членов полинома. Массив может быть любой длины, но если начиная с какого-то номера все элементы равны нулю, то старшая степень полинома — это последний ненулевой элемент.

Приведённый алгоритм считает локатор. Если количество «ошибок» больше, чем количество избыточных символов, поделённое на 2, то алгоритм не сработает правильно.

Если в сообщении, которое мы используем для примера –

DB 22 58 5C 44 4F 4E 27 54 20 50 41 4E 49 43,

ошибиться в нулевом и последнем символе (2 «ошибки», мы притворяемся, что не знаем в каких позициях ошиблись), получится такой полином:

02 22 58 5C 44 4F 4E 27 54 20 50 41 4E 49 01,

Полином синдромов для него 4B A7 E8 BD. Если выполнить функцию, приведённую выше с параметрами 4B A7 E8 BD, и 4 (количество избыточных символов), то она вернёт нам такой полином: 01 12 13. Это не похоже на позиции ошибок, которые мы ожидаем, но полином-локатор содержит в себе информацию о позициях ошибок, ведь это «полином, корнями которого являются числа обратные примитивному члену в степени позиции ошибки». Из этого, если немного поскрипеть мозгами или ручкой по бумаге следует, что позиция ошибки – это логарифм числа по основанию примитивного члена, обратного корню полинома.

E – позиция ошибки, a – примитивный член (2, как правило), R – корень полинома.

Что-ж, будем искать корни в поле. Поиск корней полинома в поле Галуа занятие лёгкое и непыльное. В GF[256] может быть 256 чисел всего, так что иксу негде разгуляться. Просто считаем полином 256 раз, подставляя вместо x число, и если полином посчитался как нуль, то записываем к массиву с корнями текущее значение x. Дальше считаем по формуле и получаем позиции ошибок 00 и 0E, именно там где они и были допущены. Теперь эти значения вместе с синдромами и цифрой 4 можно скармливать алгоритму Форни, чтобы он исправил «ошибки» также, как он исправлял «опечатки».

Ещё пара пояснений

Если у нас есть 4 избыточных символа, при этом мы знаем что есть 2 «опечатки» в известных позициях, то алгоритм Берлекэмпа-Мэсси сможет найти ещё одну «ошибку». Но для этого его нужно будет совсем немного модифицировать. Всего то надо там где мы писали

	//Присваиваем локатору инициализирующее значение (1*X^0)
	Locator = new GF_Poly(new byte[] { 1 });

нужно локатор инициализировать не единичным полиномом, а полиномом-локатором, рассчитанным из известных позиций ошибок. И ещё изменить пару строчек. Весь код, напомню, есть на гитхабе.

Надеюсь материал в этой статье поможет тем, кто захочет в каком-нибудь своём проекте реализовать избыточное кодирование без сторонних библиотек. Просьба: Если что-то не понятно, не стесняйтесь комментировать. Постараюсь ответить на вопросы, или внести правки в статью.

Reed–Solomon codes are a group of error-correcting codes that were introduced by Irving S. Reed and Gustave Solomon in 1960.^[1]
They have many applications, the most prominent of which include consumer technologies such as MiniDiscs, CDs, DVDs, Blu-ray discs, QR codes, data transmission technologies such as DSL and WiMAX, broadcast systems such as satellite communications, DVB and ATSC, and storage systems such as RAID 6.

Reed–Solomon codes operate on a block of data treated as a set of finite-field elements called symbols. Reed–Solomon codes are able to detect and correct multiple symbol errors. By adding t = n − k check symbols to the data, a Reed–Solomon code can detect (but not correct) any combination of up to t erroneous symbols, or locate and correct up to ⌊t/2⌋ erroneous symbols at unknown locations. As an erasure code, it can correct up to t erasures at locations that are known and provided to the algorithm, or it can detect and correct combinations of errors and erasures. Reed–Solomon codes are also suitable as multiple-burst bit-error correcting codes, since a sequence of b + 1 consecutive bit errors can affect at most two symbols of size b. The choice of t is up to the designer of the code and may be selected within wide limits.

There are two basic types of Reed–Solomon codes – original view and BCH view – with BCH view being the most common, as BCH view decoders are faster and require less working storage than original view decoders.

History[edit]

Reed–Solomon codes were developed in 1960 by Irving S. Reed and Gustave Solomon, who were then staff members of MIT Lincoln Laboratory. Their seminal article was titled «Polynomial Codes over Certain Finite Fields». (Reed & Solomon 1960). The original encoding scheme described in the Reed & Solomon article used a variable polynomial based on the message to be encoded where only a fixed set of values (evaluation points) to be encoded are known to encoder and decoder. The original theoretical decoder generated potential polynomials based on subsets of k (unencoded message length) out of n (encoded message length) values of a received message, choosing the most popular polynomial as the correct one, which was impractical for all but the simplest of cases. This was initially resolved by changing the original scheme to a BCH code like scheme based on a fixed polynomial known to both encoder and decoder, but later, practical decoders based on the original scheme were developed, although slower than the BCH schemes. The result of this is that there are two main types of Reed Solomon codes, ones that use the original encoding scheme, and ones that use the BCH encoding scheme.

Also in 1960, a practical fixed polynomial decoder for BCH codes developed by Daniel Gorenstein and Neal Zierler was described in an MIT Lincoln Laboratory report by Zierler in January 1960 and later in a paper in June 1961.^[2] The Gorenstein–Zierler decoder and the related work on BCH codes are described in a book Error Correcting Codes by W. Wesley Peterson (1961).^[3] By 1963 (or possibly earlier), J. J. Stone (and others) recognized that Reed Solomon codes could use the BCH scheme of using a fixed generator polynomial, making such codes a special class of BCH codes,^[4] but Reed Solomon codes based on the original encoding scheme, are not a class of BCH codes, and depending on the set of evaluation points, they are not even cyclic codes.

In 1969, an improved BCH scheme decoder was developed by Elwyn Berlekamp and James Massey, and has since been known as the Berlekamp–Massey decoding algorithm.

In 1975, another improved BCH scheme decoder was developed by Yasuo Sugiyama, based on the extended Euclidean algorithm.^[5]

In 1977, Reed–Solomon codes were implemented in the Voyager program in the form of concatenated error correction codes. The first commercial application in mass-produced consumer products appeared in 1982 with the compact disc, where two interleaved Reed–Solomon codes are used. Today, Reed–Solomon codes are widely implemented in digital storage devices and digital communication standards, though they are being slowly replaced by Bose–Chaudhuri–Hocquenghem (BCH) codes. For example, Reed–Solomon codes are used in the Digital Video Broadcasting (DVB) standard DVB-S, in conjunction with a convolutional inner code, but BCH codes are used with LDPC in its successor, DVB-S2.

In 1986, an original scheme decoder known as the Berlekamp–Welch algorithm was developed.

In 1996, variations of original scheme decoders called list decoders or soft decoders were developed by Madhu Sudan and others, and work continues on these types of decoders – see Guruswami–Sudan list decoding algorithm.

In 2002, another original scheme decoder was developed by Shuhong Gao, based on the extended Euclidean algorithm.^[6]

Applications[edit]

Data storage[edit]

Reed–Solomon coding is very widely used in mass storage systems to correct
the burst errors associated with media defects.

Reed–Solomon coding is a key component of the compact disc. It was the first use of strong error correction coding in a mass-produced consumer product, and DAT and DVD use similar schemes. In the CD, two layers of Reed–Solomon coding separated by a 28-way convolutional interleaver yields a scheme called Cross-Interleaved Reed–Solomon Coding (CIRC). The first element of a CIRC decoder is a relatively weak inner (32,28) Reed–Solomon code, shortened from a (255,251) code with 8-bit symbols. This code can correct up to 2 byte errors per 32-byte block. More importantly, it flags as erasures any uncorrectable blocks, i.e., blocks with more than 2 byte errors. The decoded 28-byte blocks, with erasure indications, are then spread by the deinterleaver to different blocks of the (28,24) outer code. Thanks to the deinterleaving, an erased 28-byte block from the inner code becomes a single erased byte in each of 28 outer code blocks. The outer code easily corrects this, since it can handle up to 4 such erasures per block.

The result is a CIRC that can completely correct error bursts up to 4000 bits, or about 2.5 mm on the disc surface. This code is so strong that most CD playback errors are almost certainly caused by tracking errors that cause the laser to jump track, not by uncorrectable error bursts.^[7]

DVDs use a similar scheme, but with much larger blocks, a (208,192) inner code, and a (182,172) outer code.

Reed–Solomon error correction is also used in parchive files which are commonly posted accompanying multimedia files on USENET. The distributed online storage service Wuala (discontinued in 2015) also used Reed–Solomon when breaking up files.

Bar code[edit]

Almost all two-dimensional bar codes such as PDF-417, MaxiCode, Datamatrix, QR Code, and Aztec Code use Reed–Solomon error correction to allow correct reading even if a portion of the bar code is damaged. When the bar code scanner cannot recognize a bar code symbol, it will treat it as an erasure.

Reed–Solomon coding is less common in one-dimensional bar codes, but is used by the PostBar symbology.

Data transmission[edit]

Specialized forms of Reed–Solomon codes, specifically Cauchy-RS and Vandermonde-RS, can be used to overcome the unreliable nature of data transmission over erasure channels. The encoding process assumes a code of RS(N, K) which results in N codewords of length N symbols each storing K symbols of data, being generated, that are then sent over an erasure channel.

Any combination of K codewords received at the other end is enough to reconstruct all of the N codewords. The code rate is generally set to 1/2 unless the channel’s erasure likelihood can be adequately modelled and is seen to be less. In conclusion, N is usually 2K, meaning that at least half of all the codewords sent must be received in order to reconstruct all of the codewords sent.

Reed–Solomon codes are also used in xDSL systems and CCSDS’s Space Communications Protocol Specifications as a form of forward error correction.

Space transmission[edit]

One significant application of Reed–Solomon coding was to encode the digital pictures sent back by the Voyager program.

Voyager introduced Reed–Solomon coding concatenated with convolutional codes, a practice that has since become very widespread in deep space and satellite (e.g., direct digital broadcasting) communications.

Viterbi decoders tend to produce errors in short bursts. Correcting these burst errors is a job best done by short or simplified Reed–Solomon codes.

Modern versions of concatenated Reed–Solomon/Viterbi-decoded convolutional coding were and are used on the Mars Pathfinder, Galileo, Mars Exploration Rover and Cassini missions, where they perform within about 1–1.5 dB of the ultimate limit, the Shannon capacity.

These concatenated codes are now being replaced by more powerful turbo codes:

Constructions (encoding)[edit]

The Reed–Solomon code is actually a family of codes, where every code is characterised by three parameters: an alphabet size q, a block length n, and a message length k, with k < n ≤ q. The set of alphabet symbols is interpreted as the finite field of order q, and thus, q must be a prime power. In the most useful parameterizations of the Reed–Solomon code, the block length is usually some constant multiple of the message length, that is, the rate R = k/n is some constant, and furthermore, the block length is equal to or one less than the alphabet size, that is, n = q or n = q − 1.^{[citation needed]}

Reed & Solomon’s original view: The codeword as a sequence of values[edit]

There are different encoding procedures for the Reed–Solomon code, and thus, there are different ways to describe the set of all codewords.
In the original view of Reed & Solomon (1960), every codeword of the Reed–Solomon code is a sequence of function values of a polynomial of degree less than k. In order to obtain a codeword of the Reed–Solomon code, the message symbols (each within the q-sized alphabet) are treated as the coefficients of a polynomial p of degree less than k, over the finite field F with q elements.
In turn, the polynomial p is evaluated at n ≤ q distinct points of the field F, and the sequence of values is the corresponding codeword. Common choices for a set of evaluation points include {0, 1, 2, …, n − 1}, {0, 1, α, α², …, αⁿ⁻²}, or for n < q, {1, α, α², …, αⁿ⁻¹}, … , where α is a primitive element of F.

Formally, the set of codewords of the Reed–Solomon code is defined as follows:

Since any two distinct polynomials of degree less than agree in at most points, this means that any two codewords of the Reed–Solomon code disagree in at least positions. Furthermore, there are two polynomials that do agree in points but are not equal, and thus, the distance of the Reed–Solomon code is exactly . Then the relative distance is , where is the rate. This trade-off between the relative distance and the rate is asymptotically optimal since, by the Singleton bound, every code satisfies .
Being a code that achieves this optimal trade-off, the Reed–Solomon code belongs to the class of maximum distance separable codes.

While the number of different polynomials of degree less than k and the number of different messages are both equal to , and thus every message can be uniquely mapped to such a polynomial, there are different ways of doing this encoding. The original construction of Reed & Solomon (1960) interprets the message x as the coefficients of the polynomial p, whereas subsequent constructions interpret the message as the values of the polynomial at the first k points and obtain the polynomial p by interpolating these values with a polynomial of degree less than k. The latter encoding procedure, while being slightly less efficient, has the advantage that it gives rise to a systematic code, that is, the original message is always contained as a subsequence of the codeword.

Simple encoding procedure: The message as a sequence of coefficients[edit]

In the original construction of Reed & Solomon (1960), the message is mapped to the polynomial with

The codeword of is obtained by evaluating at different points of the field . Thus the classical encoding function for the Reed–Solomon code is defined as follows:

This function is a linear mapping, that is, it satisfies for the following -matrix with elements from :

This matrix is the transpose of a Vandermonde matrix over . In other words, the Reed–Solomon code is a linear code, and in the classical encoding procedure, its generator matrix is .

Systematic encoding procedure: The message as an initial sequence of values[edit]

There is an alternative encoding procedure that also produces the Reed–Solomon code, but that does so in a systematic way. Here, the mapping from the message to the polynomial works differently: the polynomial is now defined as the unique polynomial of degree less than such that

To compute this polynomial from , one can use Lagrange interpolation.
Once it has been found, it is evaluated at the other points of the field.
The alternative encoding function for the Reed–Solomon code is then again just the sequence of values:

Since the first entries of each codeword coincide with , this encoding procedure is indeed systematic.
Since Lagrange interpolation is a linear transformation, is a linear mapping. In fact, we have , where

Discrete Fourier transform and its inverse[edit]

A discrete Fourier transform is essentially the same as the encoding procedure; it uses the generator polynomial p(x) to map a set of evaluation points into the message values as shown above:

The inverse Fourier transform could be used to convert an error free set of n < q message values back into the encoding polynomial of k coefficients, with the constraint that in order for this to work, the set of evaluation points used to encode the message must be a set of increasing powers of α:

However, Lagrange interpolation performs the same conversion without the constraint on the set of evaluation points or the requirement of an error free set of message values and is used for systematic encoding, and in one of the steps of the Gao decoder.

The BCH view: The codeword as a sequence of coefficients[edit]

In this view, the message is interpreted as the coefficients of a polynomial . The sender computes a related polynomial of degree where and sends the polynomial . The polynomial is constructed by multiplying the message polynomial , which has degree , with a generator polynomial of degree that is known to both the sender and the receiver. The generator polynomial is defined as the polynomial whose roots are sequential powers of the Galois field primitive

For a «narrow sense code», .

Systematic encoding procedure[edit]

The encoding procedure for the BCH view of Reed–Solomon codes can be modified to yield a systematic encoding procedure, in which each codeword contains the message as a prefix, and simply appends error correcting symbols as a suffix. Here, instead of sending , the encoder constructs the transmitted polynomial such that the coefficients of the largest monomials are equal to the corresponding coefficients of , and the lower-order coefficients of are chosen exactly in such a way that becomes divisible by . Then the coefficients of are a subsequence of the coefficients of . To get a code that is overall systematic, we construct the message polynomial by interpreting the message as the sequence of its coefficients.

Formally, the construction is done by multiplying by to make room for the check symbols, dividing that product by to find the remainder, and then compensating for that remainder by subtracting it. The check symbols are created by computing the remainder :

The remainder has degree at most , whereas the coefficients of in the polynomial are zero. Therefore, the following definition of the codeword has the property that the first coefficients are identical to the coefficients of :

As a result, the codewords are indeed elements of , that is, they are divisible by the generator polynomial :^[10]

Properties[edit]

The Reed–Solomon code is a [n, k, n − k + 1] code; in other words, it is a linear block code of length n (over F) with dimension k and minimum Hamming distance The Reed–Solomon code is optimal in the sense that the minimum distance has the maximum value possible for a linear code of size (n, k); this is known as the Singleton bound. Such a code is also called a maximum distance separable (MDS) code.

The error-correcting ability of a Reed–Solomon code is determined by its minimum distance, or equivalently, by , the measure of redundancy in the block. If the locations of the error symbols are not known in advance, then a Reed–Solomon code can correct up to erroneous symbols, i.e., it can correct half as many errors as there are redundant symbols added to the block. Sometimes error locations are known in advance (e.g., «side information» in demodulator signal-to-noise ratios)—these are called erasures. A Reed–Solomon code (like any MDS code) is able to correct twice as many erasures as errors, and any combination of errors and erasures can be corrected as long as the relation 2E + S ≤ n − k is satisfied, where is the number of errors and is the number of erasures in the block.

The theoretical error bound can be described via the following formula for the AWGN channel for FSK:^[11]

and for other modulation schemes:

where , , , is the symbol error rate in uncoded AWGN case and is the modulation order.

For practical uses of Reed–Solomon codes, it is common to use a finite field with elements. In this case, each symbol can be represented as an -bit value.
The sender sends the data points as encoded blocks, and the number of symbols in the encoded block is . Thus a Reed–Solomon code operating on 8-bit symbols has symbols per block. (This is a very popular value because of the prevalence of byte-oriented computer systems.) The number , with , of data symbols in the block is a design parameter. A commonly used code encodes eight-bit data symbols plus 32 eight-bit parity symbols in an -symbol block; this is denoted as a code, and is capable of correcting up to 16 symbol errors per block.

The Reed–Solomon code properties discussed above make them especially well-suited to applications where errors occur in bursts. This is because it does not matter to the code how many bits in a symbol are in error — if multiple bits in a symbol are corrupted it only counts as a single error. Conversely, if a data stream is not characterized by error bursts or drop-outs but by random single bit errors, a Reed–Solomon code is usually a poor choice compared to a binary code.

The Reed–Solomon code, like the convolutional code, is a transparent code. This means that if the channel symbols have been inverted somewhere along the line, the decoders will still operate. The result will be the inversion of the original data. However, the Reed–Solomon code loses its transparency when the code is shortened. The «missing» bits in a shortened code need to be filled by either zeros or ones, depending on whether the data is complemented or not. (To put it another way, if the symbols are inverted, then the zero-fill needs to be inverted to a one-fill.) For this reason it is mandatory that the sense of the data (i.e., true or complemented) be resolved before Reed–Solomon decoding.

Whether the Reed–Solomon code is cyclic or not depends on subtle details of the construction. In the original view of Reed and Solomon, where the codewords are the values of a polynomial, one can choose the sequence of evaluation points in such a way as to make the code cyclic. In particular, if is a primitive root of the field , then by definition all non-zero elements of take the form for , where . Each polynomial over gives rise to a codeword . Since the function is also a polynomial of the same degree, this function gives rise to a codeword ; since holds, this codeword is the cyclic left-shift of the original codeword derived from . So choosing a sequence of primitive root powers as the evaluation points makes the original view Reed–Solomon code cyclic. Reed–Solomon codes in the BCH view are always cyclic because BCH codes are cyclic.

[edit]

Designers are not required to use the «natural» sizes of Reed–Solomon code blocks. A technique known as «shortening» can produce a smaller code of any desired size from a larger code. For example, the widely used (255,223) code can be converted to a (160,128) code by padding the unused portion of the source block with 95 binary zeroes and not transmitting them. At the decoder, the same portion of the block is loaded locally with binary zeroes. The Delsarte–Goethals–Seidel^[12] theorem illustrates an example of an application of shortened Reed–Solomon codes. In parallel to shortening, a technique known as puncturing allows omitting some of the encoded parity symbols.

BCH view decoders[edit]

The decoders described in this section use the BCH view of a codeword as a sequence of coefficients. They use a fixed generator polynomial known to both encoder and decoder.

Peterson–Gorenstein–Zierler decoder[edit]

Daniel Gorenstein and Neal Zierler developed a decoder that was described in a MIT Lincoln Laboratory report by Zierler in January 1960 and later in a paper in June 1961.^[13] The Gorenstein–Zierler decoder and the related work on BCH codes are described in a book Error Correcting Codes by W. Wesley Peterson (1961).^[14]

Formulation[edit]

The transmitted message, , is viewed as the coefficients of a polynomial s(x):

As a result of the Reed-Solomon encoding procedure, s(x) is divisible by the generator polynomial g(x):

where α is a primitive element.

Since s(x) is a multiple of the generator g(x), it follows that it «inherits» all its roots.

Therefore,

The transmitted polynomial is corrupted in transit by an error polynomial e(x) to produce the received polynomial r(x).

Coefficient e_i will be zero if there is no error at that power of x and nonzero if there is an error. If there are ν errors at distinct powers i_k of x, then

The goal of the decoder is to find the number of errors (ν), the positions of the errors (i_k), and the error values at those positions (e_ik). From those, e(x) can be calculated and subtracted from r(x) to get the originally sent message s(x).

Syndrome decoding[edit]

The decoder starts by evaluating the polynomial as received at points . We call the results of that evaluation the «syndromes», S_j. They are defined as:

Note that because has roots at , as shown in the previous section.

The advantage of looking at the syndromes is that the message polynomial drops out. In other words, the syndromes only relate to the error, and are unaffected by the actual contents of the message being transmitted. If the syndromes are all zero, the algorithm stops here and reports that the message was not corrupted in transit.

Error locators and error values[edit]

For convenience, define the error locators X_k and error values Y_k as:

Then the syndromes can be written in terms of these error locators and error values as

This definition of the syndrome values is equivalent to the previous since .

The syndromes give a system of n − k ≥ 2ν equations in 2ν unknowns, but that system of equations is nonlinear in the X_k and does not have an obvious solution. However, if the X_k were known (see below), then the syndrome equations provide a linear system of equations that can easily be solved for the Y_k error values.

Consequently, the problem is finding the X_k, because then the leftmost matrix would be known, and both sides of the equation could be multiplied by its inverse, yielding Y_k

In the variant of this algorithm where the locations of the errors are already known (when it is being used as an erasure code), this is the end. The error locations (X_k) are already known by some other method (for example, in an FM transmission, the sections where the bitstream was unclear or overcome with interference are probabilistically determinable from frequency analysis). In this scenario, up to errors can be corrected.

The rest of the algorithm serves to locate the errors, and will require syndrome values up to , instead of just the used thus far. This is why 2x as many error correcting symbols need to be added as can be corrected without knowing their locations.

Error locator polynomial[edit]

There is a linear recurrence relation that gives rise to a system of linear equations. Solving those equations identifies those error locations X_k.

Define the error locator polynomial Λ(x) as

The zeros of Λ(x) are the reciprocals . This follows from the above product notation construction since if then one of the multiplied terms will be zero , making the whole polynomial evaluate to zero.

Let be any integer such that . Multiply both sides by and it will still be zero.

Sum for k = 1 to ν and it will still be zero.

Collect each term into its own sum.

Extract the constant values of that are unaffected by the summation.

These summations are now equivalent to the syndrome values, which we know and can substitute in! This therefore reduces to

Subtracting from both sides yields

Recall that j was chosen to be any integer between 1 and v inclusive, and this equivalence is true for any and all such values. Therefore, we have v linear equations, not just one. This system of linear equations can therefore be solved for the coefficients Λ_i of the error location polynomial:

The above assumes the decoder knows the number of errors ν, but that number has not been determined yet. The PGZ decoder does not determine ν directly but rather searches for it by trying successive values. The decoder first assumes the largest value for a trial ν and sets up the linear system for that value. If the equations can be solved (i.e., the matrix determinant is nonzero), then that trial value is the number of errors. If the linear system cannot be solved, then the trial ν is reduced by one and the next smaller system is examined. (Gill n.d., p. 35)

Find the roots of the error locator polynomial[edit]

Use the coefficients Λ_i found in the last step to build the error location polynomial. The roots of the error location polynomial can be found by exhaustive search. The error locators X_k are the reciprocals of those roots. The order of coefficients of the error location polynomial can be reversed, in which case the roots of that reversed polynomial are the error locators (not their reciprocals ). Chien search is an efficient implementation of this step.

Calculate the error values[edit]

Once the error locators X_k are known, the error values can be determined. This can be done by direct solution for Y_k in the error equations matrix given above, or using the Forney algorithm.

Calculate the error locations[edit]

Calculate i_k by taking the log base of X_k. This is generally done using a precomputed lookup table.

Fix the errors[edit]

Finally, e(x) is generated from i_k and e_ik and then is subtracted from r(x) to get the originally sent message s(x), with errors corrected.

Example[edit]

Consider the Reed–Solomon code defined in GF(929) with α = 3 and t = 4 (this is used in PDF417 barcodes) for a RS(7,3) code. The generator polynomial is

If the message polynomial is p(x) = 3 x² + 2 x + 1, then a systematic codeword is encoded as follows.

Errors in transmission might cause this to be received instead.

The syndromes are calculated by evaluating r at powers of α.

Using Gaussian elimination:

Λ(x) = 329 x² + 821 x + 001, with roots x₁ = 757 = 3⁻³ and x₂ = 562 = 3⁻⁴

The coefficients can be reversed to produce roots with positive exponents, but typically this isn’t used:

R(x) = 001 x² + 821 x + 329, with roots 27 = 3³ and 81 = 3⁴

with the log of the roots corresponding to the error locations (right to left, location 0 is the last term in the codeword).

To calculate the error values, apply the Forney algorithm.

Ω(x) = S(x) Λ(x) mod x⁴ = 546 x + 732

Λ'(x) = 658 x + 821

e₁ = −Ω(x₁)/Λ'(x₁) = 074

e₂ = −Ω(x₂)/Λ'(x₂) = 122

Subtracting from the received polynomial r(x) reproduces the original codeword s.

Berlekamp–Massey decoder[edit]

The Berlekamp–Massey algorithm is an alternate iterative procedure for finding the error locator polynomial. During each iteration, it calculates a discrepancy based on a current instance of Λ(x) with an assumed number of errors e:

and then adjusts Λ(x) and e so that a recalculated Δ would be zero. The article Berlekamp–Massey algorithm has a detailed description of the procedure. In the following example, C(x) is used to represent Λ(x).

Example[edit]

Using the same data as the Peterson Gorenstein Zierler example above:

The final value of C is the error locator polynomial, Λ(x).

Euclidean decoder[edit]

Another iterative method for calculating both the error locator polynomial and the error value polynomial is based on Sugiyama’s adaptation of the extended Euclidean algorithm .

Define S(x), Λ(x), and Ω(x) for t syndromes and e errors:

The key equation is:

For t = 6 and e = 3:

The middle terms are zero due to the relationship between Λ and syndromes.

The extended Euclidean algorithm can find a series of polynomials of the form

A_i(x) S(x) + B_i(x) x^t = R_i(x)

where the degree of R decreases as i increases. Once the degree of R_i(x) < t/2, then

A_i(x) = Λ(x)

B_i(x) = −Q(x)

R_i(x) = Ω(x).

B(x) and Q(x) don’t need to be saved, so the algorithm becomes:

R−1 := xt
R0  := S(x)
A−1 := 0
A0  := 1
i := 0
while degree of Ri ≥ t/2
  i := i + 1
  Q := Ri-2 / Ri-1
  Ri := Ri-2 - Q Ri-1
  Ai := Ai-2 - Q Ai-1

to set low order term of Λ(x) to 1, divide Λ(x) and Ω(x) by A_i(0):

Λ(x) = A_i / A_i(0)

Ω(x) = R_i / A_i(0)

A_i(0) is the constant (low order) term of A_i.

Example[edit]

Using the same data as the Peterson–Gorenstein–Zierler example above:

Λ(x) = A₂ / 544 = 329 x² + 821 x + 001

Ω(x) = R₂ / 544 = 546 x + 732

Decoder using discrete Fourier transform[edit]

A discrete Fourier transform can be used for decoding.^[15] To avoid conflict with syndrome names, let c(x) = s(x) the encoded codeword. r(x) and e(x) are the same as above. Define C(x), E(x), and R(x) as the discrete Fourier transforms of c(x), e(x), and r(x). Since r(x) = c(x) + e(x), and since a discrete Fourier transform is a linear operator, R(x) = C(x) + E(x).

Transform r(x) to R(x) using discrete Fourier transform. Since the calculation for a discrete Fourier transform is the same as the calculation for syndromes, t coefficients of R(x) and E(x) are the same as the syndromes:

Use through as syndromes (they’re the same) and generate the error locator polynomial using the methods from any of the above decoders.

Let v = number of errors. Generate E(x) using the known coefficients to , the error locator polynomial, and these formulas

Then calculate C(x) = R(x) − E(x) and take the inverse transform (polynomial interpolation) of C(x) to produce c(x).

Decoding beyond the error-correction bound[edit]

The Singleton bound states that the minimum distance d of a linear block code of size (n,k) is upper-bounded by n − k + 1. The distance d was usually understood to limit the error-correction capability to ⌊(d−1) / 2⌋. The Reed–Solomon code achieves this bound with equality, and can thus correct up to ⌊(n−k) / 2⌋ errors. However, this error-correction bound is not exact.

In 1999, Madhu Sudan and Venkatesan Guruswami at MIT published «Improved Decoding of Reed–Solomon and Algebraic-Geometry Codes» introducing an algorithm that allowed for the correction of errors beyond half the minimum distance of the code.^[16] It applies to Reed–Solomon codes and more generally to algebraic geometric codes. This algorithm produces a list of codewords (it is a list-decoding algorithm) and is based on interpolation and factorization of polynomials over and its extensions.

Soft-decoding[edit]

The algebraic decoding methods described above are hard-decision methods, which means that for every symbol a hard decision is made about its value. For example, a decoder could associate with each symbol an additional value corresponding to the channel demodulator’s confidence in the correctness of the symbol. The advent of LDPC and turbo codes, which employ iterated soft-decision belief propagation decoding methods to achieve error-correction performance close to the theoretical limit, has spurred interest in applying soft-decision decoding to conventional algebraic codes. In 2003, Ralf Koetter and Alexander Vardy presented a polynomial-time soft-decision algebraic list-decoding algorithm for Reed–Solomon codes, which was based upon the work by Sudan and Guruswami.^[17]
In 2016, Steven J. Franke and Joseph H. Taylor published a novel soft-decision decoder.^[18]

MATLAB example[edit]

Encoder[edit]

Here we present a simple MATLAB implementation for an encoder.

function encoded = rsEncoder(msg, m, prim_poly, n, k)
    % RSENCODER Encode message with the Reed-Solomon algorithm
    % m is the number of bits per symbol
    % prim_poly: Primitive polynomial p(x). Ie for DM is 301
    % k is the size of the message
    % n is the total size (k+redundant)
    % Example: msg = uint8('Test')
    % enc_msg = rsEncoder(msg, 8, 301, 12, numel(msg));

    % Get the alpha
    alpha = gf(2, m, prim_poly);

    % Get the Reed-Solomon generating polynomial g(x)
    g_x = genpoly(k, n, alpha);

    % Multiply the information by X^(n-k), or just pad with zeros at the end to
    % get space to add the redundant information
    msg_padded = gf([msg zeros(1, n - k)], m, prim_poly);

    % Get the remainder of the division of the extended message by the
    % Reed-Solomon generating polynomial g(x)
    [~, remainder] = deconv(msg_padded, g_x);

    % Now return the message with the redundant information
    encoded = msg_padded - remainder;

end

% Find the Reed-Solomon generating polynomial g(x), by the way this is the
% same as the rsgenpoly function on matlab
function g = genpoly(k, n, alpha)
    g = 1;
    % A multiplication on the galois field is just a convolution
    for k = mod(1 : n - k, n)
        g = conv(g, [1 alpha .^ (k)]);
    end
end

Decoder[edit]

Now the decoding part:

function [decoded, error_pos, error_mag, g, S] = rsDecoder(encoded, m, prim_poly, n, k)
    % RSDECODER Decode a Reed-Solomon encoded message
    %   Example:
    % [dec, ~, ~, ~, ~] = rsDecoder(enc_msg, 8, 301, 12, numel(msg))
    max_errors = floor((n - k) / 2);
    orig_vals = encoded.x;
    % Initialize the error vector
    errors = zeros(1, n);
    g = [];
    S = [];

    % Get the alpha
    alpha = gf(2, m, prim_poly);

    % Find the syndromes (Check if dividing the message by the generator
    % polynomial the result is zero)
    Synd = polyval(encoded, alpha .^ (1:n - k));
    Syndromes = trim(Synd);

    % If all syndromes are zeros (perfectly divisible) there are no errors
    if isempty(Syndromes.x)
        decoded = orig_vals(1:k);
        error_pos = [];
        error_mag = [];
        g = [];
        S = Synd;
        return;
    end

    % Prepare for the euclidean algorithm (Used to find the error locating
    % polynomials)
    r0 = [1, zeros(1, 2 * max_errors)]; r0 = gf(r0, m, prim_poly); r0 = trim(r0);
    size_r0 = length(r0);
    r1 = Syndromes;
    f0 = gf([zeros(1, size_r0 - 1) 1], m, prim_poly);
    f1 = gf(zeros(1, size_r0), m, prim_poly);
    g0 = f1; g1 = f0;

    % Do the euclidean algorithm on the polynomials r0(x) and Syndromes(x) in
    % order to find the error locating polynomial
    while true
        % Do a long division
        [quotient, remainder] = deconv(r0, r1);
        % Add some zeros
        quotient = pad(quotient, length(g1));

        % Find quotient*g1 and pad
        c = conv(quotient, g1);
        c = trim(c);
        c = pad(c, length(g0));

        % Update g as g0-quotient*g1
        g = g0 - c;

        % Check if the degree of remainder(x) is less than max_errors
        if all(remainder(1:end - max_errors) == 0)
            break;
        end

        % Update r0, r1, g0, g1 and remove leading zeros
        r0 = trim(r1); r1 = trim(remainder);
        g0 = g1; g1 = g;
    end

    % Remove leading zeros
    g = trim(g);

    % Find the zeros of the error polynomial on this galois field
    evalPoly = polyval(g, alpha .^ (n - 1 : - 1 : 0));
    error_pos = gf(find(evalPoly == 0), m);

    % If no error position is found we return the received work, because
    % basically is nothing that we could do and we return the received message
    if isempty(error_pos)
        decoded = orig_vals(1:k);
        error_mag = [];
        return;
    end

    % Prepare a linear system to solve the error polynomial and find the error
    % magnitudes
    size_error = length(error_pos);
    Syndrome_Vals = Syndromes.x;
    b(:, 1) = Syndrome_Vals(1:size_error);
    for idx = 1 : size_error
        e = alpha .^ (idx * (n - error_pos.x));
        err = e.x;
        er(idx, :) = err;
    end

    % Solve the linear system
    error_mag = (gf(er, m, prim_poly)  gf(b, m, prim_poly))';
    % Put the error magnitude on the error vector
    errors(error_pos.x) = error_mag.x;
    % Bring this vector to the galois field
    errors_gf = gf(errors, m, prim_poly);

    % Now to fix the errors just add with the encoded code
    decoded_gf = encoded(1:k) + errors_gf(1:k);
    decoded = decoded_gf.x;

end

% Remove leading zeros from Galois array
function gt = trim(g)
    gx = g.x;
    gt = gf(gx(find(gx, 1) : end), g.m, g.prim_poly);
end

% Add leading zeros
function xpad = pad(x, k)
    len = length(x);
    if len < k
        xpad = [zeros(1, k - len) x];
    end
end

Reed Solomon original view decoders[edit]

The decoders described in this section use the Reed Solomon original view of a codeword as a sequence of polynomial values where the polynomial is based on the message to be encoded. The same set of fixed values are used by the encoder and decoder, and the decoder recovers the encoding polynomial (and optionally an error locating polynomial) from the received message.

Theoretical decoder[edit]

Reed & Solomon (1960) described a theoretical decoder that corrected errors by finding the most popular message polynomial. The decoder only knows the set of values to and which encoding method was used to generate the codeword’s sequence of values. The original message, the polynomial, and any errors are unknown. A decoding procedure could use a method like Lagrange interpolation on various subsets of n codeword values taken k at a time to repeatedly produce potential polynomials, until a sufficient number of matching polynomials are produced to reasonably eliminate any errors in the received codeword. Once a polynomial is determined, then any errors in the codeword can be corrected, by recalculating the corresponding codeword values. Unfortunately, in all but the simplest of cases, there are too many subsets, so the algorithm is impractical. The number of subsets is the binomial coefficient, , and the number of subsets is infeasible for even modest codes. For a code that can correct 3 errors, the naïve theoretical decoder would examine 359 billion subsets.

Berlekamp Welch decoder[edit]

In 1986, a decoder known as the Berlekamp–Welch algorithm was developed as a decoder that is able to recover the original message polynomial as well as an error «locator» polynomial that produces zeroes for the input values that correspond to errors, with time complexity , where is the number of values in a message. The recovered polynomial is then used to recover (recalculate as needed) the original message.

Example[edit]

Using RS(7,3), GF(929), and the set of evaluation points a_i = i − 1

a = {0, 1, 2, 3, 4, 5, 6}

If the message polynomial is

p(x) = 003 x² + 002 x + 001

The codeword is

c = {001, 006, 017, 034, 057, 086, 121}

Errors in transmission might cause this to be received instead.

b = c + e = {001, 006, 123, 456, 057, 086, 121}

The key equations are:

Assume maximum number of errors: e = 2. The key equations become:

Using Gaussian elimination:

Q(x) = 003 x⁴ + 916 x³ + 009 x² + 007 x + 006

E(x) = 001 x² + 924 x + 006

Q(x) / E(x) = P(x) = 003 x² + 002 x + 001

Recalculate P(x) where E(x) = 0 : {2, 3} to correct b resulting in the corrected codeword:

c = {001, 006, 017, 034, 057, 086, 121}

Gao decoder[edit]

In 2002, an improved decoder was developed by Shuhong Gao, based on the extended Euclid algorithm.^[6]

Example[edit]

Using the same data as the Berlekamp Welch example above:

Q(x) = R₂ = 266 x⁴ + 086 x³ + 798 x² + 311 x + 532

E(x) = A₂ = 708 x² + 176 x + 532

divide Q(x) and E(x) by most significant coefficient of E(x) = 708. (Optional)

Q(x) = 003 x⁴ + 916 x³ + 009 x² + 007 x + 006

E(x) = 001 x² + 924 x + 006

Q(x) / E(x) = P(x) = 003 x² + 002 x + 001

Recalculate P(x) where E(x) = 0 : {2, 3} to correct b resulting in the corrected codeword:

c = {001, 006, 017, 034, 057, 086, 121}

See also[edit]

• BCH code
• Cyclic code
• Chien search
• Berlekamp–Massey algorithm
• Forward error correction
• Berlekamp–Welch algorithm
• Folded Reed–Solomon code

Notes[edit]

References[edit]

Further reading[edit]

• Gill, John (n.d.), EE387 Notes #7, Handout #28 (PDF), Stanford University, archived from the original (PDF) on June 30, 2014, retrieved April 21, 2010
• Hong, Jonathan; Vetterli, Martin (August 1995), «Simple Algorithms for BCH Decoding» (PDF), IEEE Transactions on Communications, 43 (8): 2324–2333, doi:10.1109/26.403765
• Lin, Shu; Costello, Jr., Daniel J. (1983), Error Control Coding: Fundamentals and Applications, New Jersey, NJ: Prentice-Hall, ISBN 978-0-13-283796-5
• Massey, J. L. (1969), «Shift-register synthesis and BCH decoding» (PDF), IEEE Transactions on Information Theory, IT-15 (1): 122–127, doi:10.1109/tit.1969.1054260
• Peterson, Wesley W. (1960), «Encoding and Error Correction Procedures for the Bose-Chaudhuri Codes», IRE Transactions on Information Theory, IT-6 (4): 459–470, doi:10.1109/TIT.1960.1057586
• Reed, Irving S.; Solomon, Gustave (1960), «Polynomial Codes over Certain Finite Fields», Journal of the Society for Industrial and Applied Mathematics, 8 (2): 300–304, doi:10.1137/0108018
• Welch, L. R. (1997), The Original View of Reed–Solomon Codes (PDF), Lecture Notes
• Berlekamp, Elwyn R. (1967), Nonbinary BCH decoding, International Symposium on Information Theory, San Remo, Italy
• Berlekamp, Elwyn R. (1984) [1968], Algebraic Coding Theory (Revised ed.), Laguna Hills, CA: Aegean Park Press, ISBN 978-0-89412-063-3
• Cipra, Barry Arthur (1993), «The Ubiquitous Reed–Solomon Codes», SIAM News, 26 (1)
• Forney, Jr., G. (October 1965), «On Decoding BCH Codes», IEEE Transactions on Information Theory, 11 (4): 549–557, doi:10.1109/TIT.1965.1053825
• Koetter, Ralf (2005), Reed–Solomon Codes, MIT Lecture Notes 6.451 (Video), archived from the original on 2013-03-13
• MacWilliams, F. J.; Sloane, N. J. A. (1977), The Theory of Error-Correcting Codes, New York, NY: North-Holland Publishing Company
• Reed, Irving S.; Chen, Xuemin (1999), Error-Control Coding for Data Networks, Boston, MA: Kluwer Academic Publishers

External links[edit]

Information and tutorials[edit]

• Introduction to Reed–Solomon codes: principles, architecture and implementation (CMU)
• A Tutorial on Reed–Solomon Coding for Fault-Tolerance in RAID-like Systems
• Algebraic soft-decoding of Reed–Solomon codes
• Wikiversity:Reed–Solomon codes for coders
• BBC R&D White Paper WHP031
• Geisel, William A. (August 1990), Tutorial on Reed–Solomon Error Correction Coding, Technical Memorandum, NASA, TM-102162
• Concatenated codes by Dr. Dave Forney (scholarpedia.org).
• Reid, Jeff A. (April 1995), CRC and Reed Solomon ECC (PDF)

Implementations[edit]

• FEC library in C by Phil Karn (aka KA9Q) includes Reed–Solomon codec, both arbitrary and optimized (223,255) version
• Schifra Open Source C++ Reed–Solomon Codec
• Henry Minsky’s RSCode library, Reed–Solomon encoder/decoder
• Open Source C++ Reed–Solomon Soft Decoding library
• Matlab implementation of errors and-erasures Reed–Solomon decoding
• Octave implementation in communications package
• Pure-Python implementation of a Reed–Solomon codec

4.2. Введение в коды Рида-Соломона: принципы, архитектура и реализация

Коды Рида-Соломона были предложены в 1960 году Ирвином Ридом (Irving S. Reed) и Густавом Соломоном (Gustave Solomon), являвшимися сотрудниками Линкольнской лаборатории МТИ. Ключом к использованию этой технологии стало изобретение эффективного алгоритма декодирования Элвином Беликамфом (Elwyn Berlekamp; http://en.wikipedia.org/wiki/Berlekamp-Massey_algorithm), профессором Калифорнийского университета (Беркли). Коды Рида-Соломона (см. также http://www.4i2i.com/reed_solomon_codes.htm) базируются на блочном принципе коррекции ошибок и используются в огромном числе приложений в сфере цифровых телекоммуникаций и при построении запоминающих устройств. Коды Рида-Соломона применяются для исправления ошибок во многих системах:

• устройствах памяти (включая магнитные ленты, CD, DVD, штриховые коды, и т.д.);
• беспроводных или мобильных коммуникациях (включая сотовые телефоны, микроволновые каналы и т.д.);
• спутниковых коммуникациях;
• цифровом телевидении / DVB (digital video broadcast);
• скоростных модемах, таких как ADSL, xDSL и т.д.

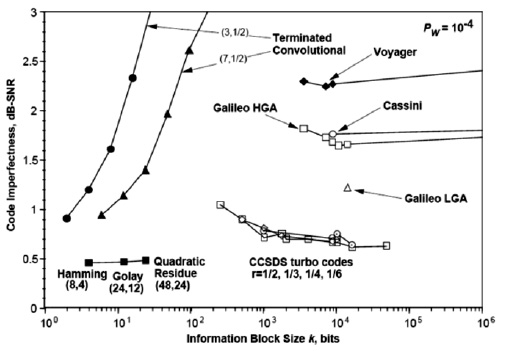
На
рис.
4.3 показаны практические приложения (дальние космические проекты) коррекции ошибок с использованием различных алгоритмов (Хэмминга, кодов свертки, Рида-Соломона и пр.). Данные и сам рисунок взяты из http://en.wikipedia.org/wiki/Reed-Solomon_error_correction.

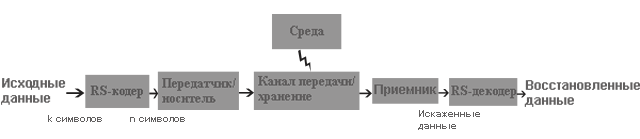
Типовая система представлена ниже (см. http://www.4i2i.com/reed_solomon_codes.htm)

Кодировщик Рида-Соломона берет блок цифровых данных и добавляет дополнительные «избыточные» биты. Ошибки происходят при передаче по каналам связи или по разным причинам при запоминании (например, из-за шума или наводок, царапин на CD и т.д.). Декодер Рида-Соломона обрабатывает каждый блок, пытается исправить ошибки и восстановить исходные данные. Число и типы ошибок, которые могут быть исправлены, зависят от характеристик кода Рида-Соломона.

Свойства кодов Рида-Соломона

Коды Рида-Соломона являются субнабором кодов BCH и представляют собой линейные блочные коды. Код Рида-Соломона специфицируются как RS(n,k) s -битных символов.

Это означает, что кодировщик воспринимает k информационных символов по s битов каждый и добавляет символы четности для формирования n символьного кодового слова. Имеется nk символов четности по s битов каждый. Декодер Рида-Соломона может корректировать до t символов, которые содержат ошибки в кодовом слове, где 2t = n–k.

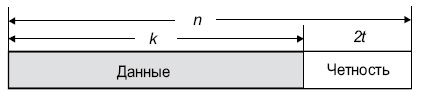
Диаграмма, представленная ниже, показывает типовое кодовое слово Рида-Соломона:

Пример. Популярным кодом Рида-Соломона является RS(255, 223) с 8-битными символами. Каждое кодовое слово содержит 255 байт, из которых 223 являются информационными и 32 байтами четности. Для этого кода

n = 255, k = 223, s = 8

2t = 32, t = 16

Декодер может исправить любые 16 символов с ошибками в кодовом слове: то есть ошибки могут быть исправлены, если число искаженных байт не превышает 16.

При размере символа s, максимальная длина кодового слова ( n ) для кода Рида-Соломона равна n = 2^s – 1.

Например, максимальная длина кода с 8-битными символами ( s = 8 ) равна 255 байтам.

Коды Рида-Соломона могут быть в принципе укорочены путем обнуления некоторого числа информационных символов на входе кодировщика (передавать их в этом случае не нужно). При передаче данных декодеру эти нули снова вводятся в массив.

Пример. Код (255, 223), описанный выше, может быть укорочен до (200, 168). Кодировщик будет работать с блоком данных 168 байт, добавит 55 нулевых байт, сформирует кодовое слово (255, 223) и передаст только 168 информационных байт и 32 байта четности.

Объем вычислительной мощности, необходимой для кодирования и декодирования кодов Рида-Соломона, зависит от числа символов четности. Большое значение t означает, что большее число ошибок может быть исправлено, но это потребует большей вычислительной мощности по сравнению с вариантом при меньшем t.

Ошибки в символах

Одна ошибка в символе происходит, когда 1 бит символа оказывается неверным или когда все биты неверны.

Пример. Код RS(255,223) может исправить до 16 ошибок в символах. В худшем случае, могут иметь место 16 битовых ошибок в разных символах (байтах). В лучшем случае, корректируются 16 полностью неверных байт, при этом исправляется 16 x 8 = 128 битовых ошибок.

Коды Рида-Соломона особенно хорошо подходят для корректировки кластеров ошибок (когда неверными оказываются большие группы бит кодового слова, следующие подряд).

Декодирование

Алгебраические процедуры декодирования Рида-Соломона могут исправлять ошибки и потери. Потерей считается случай, когда положение неверного символа известно. Декодер может исправить до t ошибок или до 2t потерь. Данные о потере (стирании) могут быть получены от демодулятора цифровой коммуникационной системы, т.е. демодулятор помечает полученные символы, которые вероятно содержат ошибки.

Когда кодовое слово декодируется, возможны три варианта.

1. Если 2s + r < 2t ( s ошибок, r потерь), тогда исходное переданное кодовое слово всегда будет восстановлено. В противном случае
2. Декодер детектирует ситуацию, когда он не может восстановить исходное кодовое слово. или
3. Декодер некорректно декодирует и неверно восстановит кодовое слово без какого-либо указания на этот факт.

Вероятность каждого из этих вариантов зависит от типа используемого кода Рида-Соломона, а также от числа и распределения ошибок.

Коды Рида — Соломона (англ. Reed–Solomon codes) — недвоичные циклические коды, позволяющие исправлять ошибки в блоках данных. Элементами кодового вектора являются не биты, а группы битов (блоки). Очень распространены коды Рида — Соломона, работающие с байтами (октетами).

Код Рида — Соломона является частным случаем БЧХ-кода.

В настоящее время широко используется в системах восстановления данных с компакт-дисков, при создании архивов с информацией для восстановления в случае повреждений, в помехоустойчивом кодировании.

[править] История

Код Рида — Соломона был изобретён в 1960 году сотрудниками лаборатории Линкольна Массачуссетского технологического института Ирвином Ридом (англ.) и Густавом Соломоном (англ.). Идея использования этого кода была представлена в статье «Polynomial Codes over Certain Finite Fields». Первое применение код Рида — Соломона получил в 1982 году в серийном выпуске компакт-дисков. Эффективные алгоритмы декодирования были предложены в 1969 году Элвином Берлекэмпом (англ.) и Джэймсом Месси (алгоритм Берлекэмпа — Мэсси) и в 1977 году Давидом Мандельбаумом (англ.) (метод, использующий Алгоритм Евклида ^[1]).

[править] Формальное описание

Коды Рида — Соломона являются важным частным случаем БЧХ-кода, корни порождающего полинома которого лежат в том же поле, над которым строится код (). Пусть — элемент поля порядка . Если — примитивный элемент, то его порядок равен , то есть . Тогда нормированный полином минимальной степени над полем , корнями которого являются подряд идущих степеней элемента , является порождающим полиномом кода Рида — Соломона над полем :

где — некоторое целое число (в том числе 0 и 1), с помощью которого иногда удается упростить кодер. Обычно полагается . Степень многочлена равна .

Длина полученного кода , минимальное расстояние (минимальное расстояние d линейного кода является минимальным из всех расстояний Хемминга всех пар кодовых слов, см. Линейный код). Код содержит проверочных символов, где обозначает степень полинома; число информационных символов . Таким образом и код Рида — Соломона является разделимым кодом с максимальным расстоянием (является оптимальным в смысле границы Синглтона).

Кодовый полином может быть получен из информационного полинома , , путем перемножения и :

[править] Свойства

Код Рида — Соломона над , исправляющий ошибок, требует проверочных символов и с его помощью исправляются произвольные пакеты ошибок длиной и меньше. Согласно теореме о границе Рейгера, коды Рида — Соломона являются оптимальными с точки зрения соотношения длины пакета и возможности исправления ошибок — используя дополнительных проверочных символов исправляется ошибок (и менее).

Теорема (граница Рейгера). Каждый линейный блоковый код, исправляющий все пакеты длиной и менее, должен содержать, по меньшей мере, проверочных символов.

Код, двойственный коду Рида — Соломона, есть также код Рида-Соломона. Двойственным кодом для циклического кода называется код, порожденный его проверочным многочленом.

Матрица порождает код Рида — Соломона тогда и только тогда когда любой минор матрицы отличен от нуля.

При выкалывании или укорочении кода Рида-Соломона снова получается код Рида — Соломона. Выкалывание — операция, состоящая в удалении одного проверочного символа. Длина кода уменьшается на единицу, размерность сохраняется. Расстояние кода должно уменьшиться на единицу, ибо в противном случае удаленный символ был бы бесполезен.Укорочение — фиксируем произвольный столбец кода и выбираем только те векторы, которые в данном столбце содержат 0. Это множество векторов образует подпространство.

[править] Исправление многократных ошибок

Код Рида — Соломона является одним из наиболее мощных кодов, исправляющих многократные пакеты ошибок. Применяется в каналах, где пакеты ошибок могут образовываться столь часто, что их уже нельзя исправлять с помощью кодов, исправляющих одиночные ошибки.

-код Рида — Соломона над полем с кодовым расстоянием можно рассматривать как -код над полем , который может исправлять любую комбинацию ошибок, сосредоточенную в или меньшем числе блоков из m символов. Наибольшее число блоков длины , которые может затронуть пакет длины , где , не превосходит , поэтому код, который может исправить блоков ошибок, всегда может исправить и любую комбинацию из пакетов общей длины , если .

[править] Практическая реализация

Кодирование с помощью кода Рида — Соломона может быть реализовано двумя способами: систематическим и несистематическим (см. [1], описание кодировщика).

При несистематическом кодировании информационное слово умножается на некий неприводимый полином в поле Галуа. Полученное закодированное слово полностью отличается от исходного и для извлечения информационного слова нужно выполнить операцию декодирования и уже потом можно проверить данные на содержание ошибок. Такое кодирование требует большие затраты ресурсов только на извлечение информационных данных, при этом они могут быть без ошибок.

При систематическом кодировании к информационному блоку из символов приписываются проверочных символов, при вычислении каждого проверочного символа используются все символов исходного блока. В этом случае нет затрат ресурсов при извлечении исходного блока, если информационное слово не содержит ошибок, но кодировщик/декодировщик должен выполнить операций сложения и умножения для генерации проверочных символов. Кроме того, так как все операции проводятся в поле Галуа, то сами операции кодирования/декодирования требуют много ресурсов и времени. Быстрый алгоритм декодирования, основанный на быстром преобразовании Фурье, выполняется за время порядка .

[править] Кодирование

При операции кодирования информационный полином умножается на порождающий многочлен. Умножение исходного слова длины на неприводимый полином при систематическом кодировании можно выполнить следующим образом:

Кодировщик строится из сдвиговых регистров, сумматоров и умножителей. Сдвиговый регистр состоит из ячеек памяти, в каждой из которых находится один элемент поля Галуа.

Существует и другая процедура кодирования (более практичная и простая). Положим — примитивный элемент поля , и пусть — вектор информационных символов , а значит — информационный многочлен. Тогда вектор есть вектор кода Рида — Соломона , соответствующий информационному вектору . Этот способ кодирования показывает , что для кода РС вообще не нужно знать порождающего многочлена и порождающей матрицы коды, достаточно знать разложение поля по примитивному элементу и размерность кода (длина кода в этом случае определяется как ). Все дело в том , что за разностью полностью скрывается порождающий многочлен и кодовое расстояние.

[править] Декодирование

Декодировщик, работающий по авторегрессивному спектральному методу декодирования, последовательно выполняет следующие действия:

• Вычисляет синдром ошибки
• Строит полином ошибки
• Находит корни данного полинома
• Определяет характер ошибки
• Исправляет ошибки

[править] Вычисление синдрома ошибки

Вычисление синдрома ошибки выполняется синдромным декодером, который делит кодовое слово на порождающий многочлен. Если при делении возникает остаток, то в слове есть ошибка. Остаток от деления является синдромом ошибки.

[править] Построение полинома ошибки

Вычисленный синдром ошибки не указывает на положение ошибок. Степень полинома синдрома равна , что много меньше степени кодового слова . Для получения соответствия между ошибкой и ее положением в сообщении строится полином ошибок. Полином ошибок реализуется с помощью алгоритма Берлекэмпа — Месси, либо с помощью алгоритма Евклида. Алгоритм Евклида имеет простую реализацию, но требует больших затрат ресурсов. Поэтому чаще применяется более сложный, но менее затратоемкий алгоритм Берлекэмпа — Месси. Коэффициенты найденного полинома непосредственно соответствуют коэффициентам ошибочных символов в кодовом слове.

[править] Нахождение корней

На этом этапе ищутся корни полинома ошибки, определяющие положение искаженных символов в кодовом слове. Реализуется с помощью процедуры Ченя, равносильной полному перебору. В полином ошибок последовательно подставляются все возможные значения, когда полином обращается в ноль — корни найдены.

[править] Определение характера ошибки и ее исправление

По синдрому ошибки и найденным корням полинома с помощью алгоритма Форни определяется характер ошибки и строится маска искаженных символов. Однако для кодов РС существует более простой способ отыскания характера ошибок. Как показано в ^[2] для кодов РС с произвольным множеством последовательных нулей

где формальная производная по многочлена локаторов ошибок ,а

Далее после того как маска найдена , она накладывается на кодовое слово с помощью операции XOR и искаженные символы восстанавливаются. После этого отбрасываются проверочные символы и получается восстановленное информационное слово.

[править] Алгоритм Судана

В данное время стали применяться принципиально новые методы декодирования , например алгоритм предложенный в 1997году Мадху Суданом ^[3].

[править] Удлинение кодов РС

Удлинение кодов РС — это процедура, при которой увеличивается длина и расстояние кода (при этом код ещё находится на границе Синглтона и алфавит кода не изменяется),а количество информационных символов кода не изменяется^[4]. Такая процедура увеличивает корректирующую способность кода. Рассмотрим удлинение кода РС на один символ. Пусть — вектор кода РС, порождающий многочлен которого есть . Пусть теперь . Покажем ,что добавление к вектору символа увеличит его вес до ,если . Многочлен, соответствующий вектору кода, можно расписать как , но тогда с учётом выражения для получим . , так как 1 не принадлежит списку корней порождающего многочлена. Но и , так как в этом случае ,что увеличило бы расстояние кода вопреки условию, это значит что и вес кода увеличился, за счёт добавления нового символа . Новые параметры кода , удлиненный вектор . Проверочная матрица не удлиненного кода имеет вид

Тогда проверочная матрица, удлиненного на один символ РС кода будет

[править] Применение

Сразу после появления (60-е годы 20-го века) коды Рида — Соломона стали применяться в качестве внешних кодов в каскадных конструкциях, использующихся в спутниковой связи. В подобных конструкциях -ые символы РС(их может быть несколько) кодируются внутренними сверточными кодами. На приемном конце эти символы декодируются мягким алгоритмом Витерби (эффективный в каналах с АБГШ) . Такой декодер будет исправлять одиночные ошибки в q-ичных символах , когда же возникнут пакетные ошибки и некоторые пакеты q-ичных символов будут декодированы неправильно, тогда внешний декодер Рида — Соломона исправит пакеты этих ошибок. Таким образом будет достигнута требуемая надежность передачи информации (^[5]).

В настоящий момент коды Рида — Соломона имеют очень широкую область применения благодаря их способности находить и исправлять многократные пакеты ошибок.

[править] Запись и хранение информации

Код Рида — Соломона используется при записи и чтении в контроллерах оперативной памяти, при архивировании данных, записи информации на жесткие диски (ECC), записи на CD/DVD диски. Даже если поврежден значительный объем информации, испорчено несколько секторов дискового носителя, то коды Рида — Соломона позволяют восстановить большую часть потерянной информации. Также используется при записи на такие носители, как магнитные ленты и штрихкоды.

[править] Запись на CD-ROM

Возможные ошибки при чтении с диска появляются уже на этапе производства диска, так как сделать идеальный диск при современных технологиях невозможно. Также ошибки могут быть вызваны царапинами на поверхности диска, пылью и т. д. Поэтому при изготовлении читаемого компакт-диска используется система коррекции CIRC (Cross Interleaved Reed Solomon Code). Эта коррекция реализована во всех устройствах, позволяющих считывать данные с CD дисков, в виде чипа с прошивкой firmware. Нахождение и коррекция ошибок основана на избыточности и перемежении (redundancy & interleaving). Избыточность примерно 25 % от исходной информации.

При записи на аудиокомпакт-диски используется стандарт Red Book. Коррекция ошибок происходит на двух уровнях C1 и C2. При кодировании на первом этапе происходит добавление проверочных символов к исходным данным, на втором этапе информация снова кодируется. Кроме кодирования осуществляется также перемешивание (перемежение) байтов, чтобы при коррекции блоки ошибок распались на отдельные биты, которые легче исправляются. На первом уровне обнаруживаются и исправляются ошибочные блоки длиной один и два байта (один и два ошибочных символа соответственно). Ошибочные блоки длиной три байта обнаруживаются и передаются на следующий уровень. На втором уровне обнаруживаются и исправляются ошибочные блоки, возникшие в C2, длиной 1 и 2 байта. Обнаружение трех ошибочных символов является фатальной ошибкой и не может быть исправлено.

[править] Беспроводная и мобильная связь

Этот алгоритм кодирования используется при передаче данных по сетям WiMAX, в оптических линиях связи, в спутниковой и радиорелейной связи. Метод прямой коррекции ошибок в проходящем трафике (Forward Error Correction, FEC) основывается на кодах Рида — Соломона.

[править] Примеры кодирования

[править] 16-ричный (15,11) код Рида — Соломона

Пусть . Тогда

.

Степень равна 4, и . Каждому элементу поля можно сопоставить 4 бита. Информационный многочлен является последовательностью 11 символов из , что эквивалентно 44 битам, а все кодовое слово является набором из 60 бит.

[править] 8-ричный (7,3) код Рида — Соломона

Пусть . Тогда

.

Пусть информационный многочлен имеет вид

.

Кодовое слово несистематического кода запишется в виде

что представляет собой последовательность семи восьмеричных символов.

[править] Альтернативный метод кодирования 9-ричного (8,4) кода Рида — Соломона

Построим поле Галуа по модулю многочлена .Пусть его корень, тогда , таблица поля имеет вид:

Пусть информационный многочлен , далее производя соответствующие вычисления над построенным полем получим

В итоге построен вектор кода РС с параметрами .На этом кодирование законченно. Заметим ,что при этом способе нам не потребовался проверочный многочлен кода^[4].

[править] Примеры декодирования

Пусть поле генерируется примитивным элементом, неприводимый многочлен которого . Тогда . Пусть . Тогда порождающий многочлен кода РС равен . Пусть теперь принят многочлен . Тогда . Тогда ключевая система уравнений получается в виде

Теперь рассмотрим Евклидов алгоритм решения этой системы уравнений.

• Начальные условия:

Алгоритм останавливается, так как отсюда следует, что

Далее полный перебор по алгоритму Чени выдает нам позиции ошибок ,это .Потом по формуле получаем что

Таким образом декодированный вектор . Декодирование завершено, исправлены две ошибки^[6].

[править] Примечания

[править] Литература

• Питерсон У., Уэлдон Э. Коды, исправляющие ошибки. — М.: Мир, 1976. — С. 596.
• Блейхут Р. Теория и практика кодов, контролирующих ошибки = Theory and Practice of Error Control Codes. — М.: Мир, 1986. — 576 с.
• Берлекэмп Э. Алгебраическая теория кодирования = Algebraic Coding Theory. — М.: Мир, 1971. — С. 478.
• Егоров С.И. Коррекция ошибок в информационных каналах периферийных устройств ЭВМ. — Курск: КурскГТУ, 2008. — С. 252.
• Сагалович Ю. Л. Введение в алгебраические коды: Учебное пособие. — М.: МФТИ, 2007. — 262 с. — ISBN 5-7417-0191-4
• Морелос-Сарагоса Р. Искусство помехоустойчивого кодирования. Методы, алгоритмы, применение / пер. с англ. В. Б. Афанасьева. — М.: Техносфера, 2006. — 320 с. — (Мир связи). — 2000 экз. — ISBN 5-94836-035-0
• М. Вернер Основы кодирования. — Техносфера, 2004. — 288 с. — ISBN 5-94836-019-9

[править] Ссылки

• Могущество кодов Рида — Соломона или информация, воскресшая из пепла (статья Криса Касперски)
• Помехоустойчивое кодирование в пакетных сетях (статья В. Варгаузина)
• Error Correcting Code (ECC)
• CD-R диски, технология изнутри
• Формат CD
• Коды Рида-Соломона

[править] См. также

• Конечное поле
• Обнаружение и исправление ошибок
• Циклический код
• Код Боуза — Чоудхури — Хоквингема
• Турбо-код

Коды Рида — Соломона — недвоичные циклические коды, позволяющие исправлять ошибки в блоках данных. Элементами кодового вектора являются не биты, а группы битов (блоки). Очень распространены коды Рида — Соломона, работающие с байтами (октетами).

Код Рида — Соломона является частным случаем БЧХ-кода.

В настоящее время широко используется в системах восстановления данных с компакт-дисков, при создании архивов с информацией для восстановления в случае повреждений, в помехоустойчивом кодировании.

История

Код Рида — Соломона был изобретён в 1960 году сотрудниками лаборатории Линкольна Массачуссетского технологического института Ирвином Ридом (англ.) и Густавом Соломоном (англ.). Идея использования этого кода была представлена в статье «Polynomial Codes over Certain Finite Fields». Первое применение код Рида — Соломона получил в 1982 году в серийном выпуске компакт-дисков. Эффективный алгоритм декодирования был предложен в 1969 году Элвином Берлекэмпом (англ.) и Джэймсом Месси (англ.)

Формальное описание

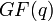
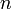
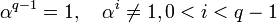
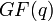
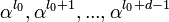
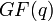
Коды Рида — Соломона являются важным частным случаем БЧХ-кода, корни порождающего полинома которого лежат в том же поле, над каким и строится код (m = 1). Пусть α — элемент поля порядка . Если α — примитивный элемент, то его порядок равен q − 1, то есть . Тогда нормированный полином g(x) минимальной степени над полем , корнями которого являются d − 1 подряд идущих степеней элемента α, является порождающим полиномом кода Рида — Соломона над полем :

где l₀ — некоторое целое число (в том числе 0 и 1), с помощью которого иногда удается упростить кодер. Обычно полагается l₀ = 1. Степень многочлена 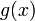равна d − 1.

Длина полученного кода n, минимальное расстояние d (минимальное расстояние d линейного кода является минимальным из всех расстояний Хемминга всех пар кодовых слов, см. Линейный код). Код содержит r = d − 1 = deg(g(x)) проверочных символов, где deg() обозначает степень полинома; число информационных символов k = n − r = n − d + 1. Таким образом 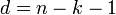и код Рида — Соломона является разделимым кодом с максимальным расстоянием (является оптимальным в смысле границы Синглтона).

Кодовый полином c(x) может быть получен из информационного полинома m(x), 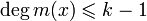, путем перемножения m(x) и g(x):

c(x) = m(x)g(x)

Свойства

Код Рида — Соломона над 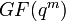, исправляющий t ошибок, требует 2t проверочных символов и с его помощью исправляются произвольные пакеты длиной t и меньше. Согласно теореме о границе Рейгера, коды Рида — Соломона являются оптимальными с точки зрения соотношения длины пакета и возможности исправления ошибок — используя 2t дополнительных проверочных символов исправляются t ошибок (и менее).

Теорема (граница Рейгера). Каждый линейный блоковый код, исправляющий все пакеты длиной t и менее, должен содержать по меньшей мере 2t проверочных символов.

Исправление многократных ошибок

Код Рида — Соломона является одним из наиболее мощных кодов, исправляющих многократные пакеты ошибок. Применяется в каналах, где пакеты ошибок могут образовываться столь часто, что их уже нельзя исправлять с помощью кодов, исправляющих одиночные ошибки.

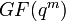
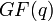
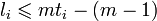
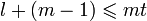
(q^m − 1,q^m − 1 − 2t)-код Рида — Соломона над полем с кодовым расстоянием d = 2t + 1 можно рассматривать как ((q^m − 1)m,(q^m − 1 − 2t)m)-код над полем , который может исправлять любую комбинацию ошибок, сосредоточенную в t или меньшем числе блоков из m символов. Наибольшее число блоков длины m, которые может затронуть пакет длины l_i, где , не превосходит t_i, поэтому код, который может исправить t блоков ошибок, всегда может исправить и любую комбинацию из p пакетов общей длины l, если .

Практическая реализация

Кодирование с помощью кода Рида — Соломона может быть реализовано двумя способами: систематическим и несистематическим (см. [1], описание кодировщика).

При несистематическом кодировании информационное слово умножается на некий неприводимый полином в поле Галуа. Полученное закодированное слово полностью отличается от исходного и для извлечения информационного слова нужно выполнить операцию декодирования и уже потом можно проверить данные на содержание ошибок. Такое кодирование требует большие затраты ресурсов только на извлечение информационных данных, при этом они могут быть без ошибок.

При систематическом кодировании к информационному блоку из k символов приписываются 2t проверочных символов, при вычислении каждого проверочного символа используются все k символов исходного блока. В этом случае нет затрат ресурсов при извлечении исходного блока, если информационное слово не содержит ошибок, но кодировщик/декодировщик должен выполнить k(n − k) операций сложения и умножения для генерации проверочных символов. Кроме того, так как все операции проводятся в поле Галуа, то сами операции кодирования/декодирования требуют много ресурсов и времени. Быстрый алгоритм декодирования, основанный на быстром преобразовании Фурье, выполняется за время порядка lnn².

Кодирование

При операции кодирования информационный полином умножается на порождающий многочлен. Умножение исходного слова S длины k на неприводимый полином при систематическом кодировании можно выполнить следующим образом:

Кодировщик строится из сдвиговых регистров, сумматоров и умножителей. Сдвиговый регистр состоит из ячеек памяти, в каждой из которых находится один элемент поля Галуа.

Декодирование

Декодировщик, работающий по авторегрессивному спектральному методу декодирования, последовательно выполняет следующие действия:

• Вычисляет синдром ошибки
• Строит полином ошибки
• Находит корни данного полинома
• Определяет характер ошибки
• Исправляет ошибки

Вычисление синдрома ошибки

Вычисление синдрома ошибки выполняется синдромным декодером, который делит кодовое слово на порождающий многочлен. Если при делении возникает остаток, то в слове есть ошибка. Остаток от деления является синдромом ошибки.

Построение полинома ошибки

Вычисленный синдром ошибки не указывает на положение ошибок. Степень полинома синдрома равна 2t, что много меньше степени кодового слова n. Для получения соответсвия между ошибкой и ее положением в сообщении строится полином ошибок. Полином ошибок реализуется с помощью алгоритма Берлекэмпа — Месси, либо с помощью алгоритма Евклида. Алгоритм Евклида имеет простую реализацию, но требует больших затрат ресурсов. Поэтому чаще применяется более сложный, но менее затратоемкий алгоритм Берлекэмпа — Месси. Коэффициенты найденного полинома непосредственно соответствуют коэффициентам ошибочных символов в кодовом слове.

Нахождение корней

На этом этапе ищутся корни полинома ошибки, определяющие положение искаженных символов в кодовом слове. Реализуется с помощью процедуры Ченя, равносильной полному перебору. В полином ошибок последовательно подставляются все возможные значения, когда полином обращается в ноль — корни найдены.

Определение характера ошибки и ее исправление

По синдрому ошибки и найденным корням полинома с помощью алгоритма Форни определяется характер ошибки и строится маска искаженных символов. Эта маска накладывается на кодовое слово с помощью операции XOR и искаженные символы восстанавливаются. После этого отбрасываются проверочные символы и получается восстановленное информационное слово.

Применение

В настоящий момент коды Рида — Соломона имеют очень широкую область применения благодаря их способности находить и исправлять многократные пакеты ошибок.

Запись и хранение информации

Код Рида — Соломона используется при записи и чтении в контроллерах оперативной памяти, при архивировании данных, записи информации на жесткие диски (

Запись на CD-ROM

Возможные ошибки при чтении с диска появляются уже на этапе производства диска, так как сделать идеальный диск при современных технологиях невозможно. Так же ошибки могут быть вызваны царапинами на поверхности диска, пылью и т. д. Поэтому при изготовлении читаемого компакт-диска используется система коррекции CIRC (Cross Interleaved Reed Solomon Code). Эта коррекция реализована во всех устройствах, позволяющих считывать данные с CD дисков, в виде чипа с прошивкой firmware. Нахождение и коррекция ошибок основана на избыточности и перемежении (redundancy & interleaving). Избыточность примерно 25 % от исходной информации.

При записи на цифровые аудиокомпакт-диски (Compact Disc Digital Audio — CD-DA) используется стандарт Red Book. Коррекция ошибок происходит на двух уровнях C1 и C2. При кодировании на первом этапе происходит добавление проверочных символов к исходным данным, на втором этапе информация снова кодируется. Кроме кодирования осуществляется также перемешивание (перемежение) байтов, чтобы при коррекции блоки ошибок распались на отдельные биты, которые легче исправляются. На первом уровне обнаруживаются и исправляются ошибочные блоки длиной один и два байта (один и два ошибочных символа соответсвенно). Ошибочные блоки длиной три байта обнаруживаются и передаются на следующий уровень. На втором уровне обнаруживаются и исправляются ошибочные блоки, возникшие в C2, длиной 1 и 2 байта. Обнаружение трех ошибочных символа является фатальной ошибкой, не могут быть исправлены.

Беспроводная и мобильная связь

Этот алгоритм кодирования используется при передаче данных по сетям оптических линиях связи, в спутниковой и радиорелейной связи. Метод прямой коррекции ошибок в проходящем трафике (Forward Error Correction, FEC) основывается на кодах Рида — Соломона.

Примеры кодов

16-ричный (15,11) код Рида — Соломона

Пусть t = 2,l₀ = 1. Тогда

g(x) = (x − α)(x − α²)(x − α³)(x − α⁴) = x⁴ + α¹³x³ + α⁶x² + α³x + α¹⁰

.

Степень g(x) равна 4, n − k = 4 и k = 11. Каждому элементу поля GF(16) можно сопоставить 4 бита. Информационный многочлен является последовательностью 11 символов из GF(16), что эквивалентно 44 битам, а все кодовое слово является набором из 60 бит.

8-ричный (7,3) код Рида — Соломона

Пусть t = 2,l₀ = 4. Тогда

g(x) = (x − α⁴)(x − α⁵)(x − α⁶)(x − α⁰) = x⁴ + α⁶x³ + α⁶x² + α³x + α

.

Пусть информационный многочлен имеет вид

m(x) = α⁴x² + x + α³

.

Кодовое слово несистематического кода запишется в виде

c(x) = m(x)g(x) = (α⁴x² + x + α³)(x⁴ + α⁶x³ + α⁶x² + α³x + α) = α⁴x⁶ + αx⁵ + α⁶x⁴ + 0x³ + 0x² + α⁵x + α⁴

что представляет собой последовательность семи восьмеричных символов.

Примечания

Литература

• Питерсон У., Уэлдон Э. Коды, исправляющие ошибки. — М.: Мир, 1976. — С. 596.
• Блейхут Р. Теория и практика кодов, контролирующих ошибки = Theory and practice of error control codes. — М.: Мир, 1986. — С. 576.
• Берлекэмп Э. Алгебраическая теория кодирования = Algebraic Coding Theory. — М.: Мир, 1971. — С. 478.

Ссылки

• Могущество кодов Рида — Соломона или информация, воскресшая из пепла (статья Криса Касперски)
• Помехоустойчивое кодирование в пакетных сетях (статья В. Варгаузина)
• Error Correcting Code (ECC)
• CD-R диски, технология изнутри
• Формат CD

См. также

• Конечное поле
• Обнаружение и исправление ошибок
• Циклический код
• Код Боуза — Чоудхури — Хоквингема
• Турбо-код