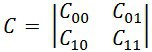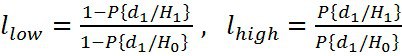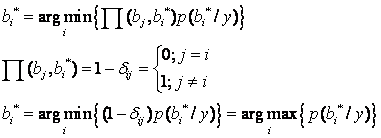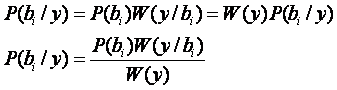ГЛАВА 2. Обнаружение и различение сигналов
В литературе задача оценки сообщения, принадлежащего дискретному конечному ансамблю, называется обычно «задачей различения m сигналов». Дискретная модель хорошо подходит для описания сообщений в цифровых системах передачи информации, таких, как цифровая телеметрическая система или система передачи дискретных сообщений. Объем ансамбля определяется выбранным методом приема (посимвольным, пословным и т.д.). Число m при пословном приеме равно числу кодовых комбинаций (команд); при посимвольном приеме – основанию кода. В частности, при посимвольном приеме двоичного кода m=2.
Практически работа любой радиосистемы начинается с обнаружения сигнала, при этом по наблюдаемой реализации смеси требуется определить, имеется ли в смеси сигнал или он отсутствует. Если случай отсутствия сигнала можно отождествить с одним значением сообщения х0, а наличия – с другим х1, то задача обнаружения сведется к задаче различения двух значений сообщения и принципиально ничем не будет отличаться от задачи посимвольного приема двоичной информации. Может встретиться ситуация, например, в системе передачи дискретных сообщений, когда на заданном интервале времени может или передаваться сигнал, соответствующий одному из возможных значений сообщения, или ничего не передаваться. Система обработки в этом случае должна вынести решение о том, имеется ли в наблюдаемой смеси сигнал, и если да, то какой именно. В литературе эта задача называется задачей различения m сигналов с обнаружением. Ясно, что и эта задача приводится к общей задачи различения m + 1 сигналов, если в ансамбль сообщений ввести дополнительный («нулевой») сигнал, соответствующий отсутствию сигнала в смеси.
Таким образом, одной из наиболее важных проблем радиообнаружения является отыскание оптимальных способов выделения сигналов при наличии помех. Оптимальными методами обнаружения называются такие, которые обеспечивают наилучшее выделение сигналов из смеси сигнала с помехой.
В результате процесса обнаружения должно быть выдано решение о наличии или отсутствии сигнала в смеси, действующей на входе обнаружителя.
2.1. Обнаружение сигналов как статистическая задача
Пусть на вход обнаружителя поступает сумма сигнала u(t) и шума n(t), представляющая собой непрерывный случайный процесс, x(t) = au(t) + n(t); u(t) – полностью известный сигнал, т.е. такой сигнал, единственным неизвестным параметром которого является сообщение а. В простейшем случае при обнаружении сообщения а может принимать два значения: а = а0 = 0 или а = а1 = 1.
Рекомендуемые материалы
Когда а0 = 0, сигнал на входе обнаружителя отсутствует, когда а1 = 1, сигнал на входе обнаружителя присутствует. Априорные вероятности присутствия и отсутствия сигнала на входе обнаружителя равны Р(а1) и Р(а0) соответственно.
Обнаружитель анализирует колебание x(t) в течение заранее выбранного (конечного) интервала времени Т и должен на основании анализа воспроизвести сообщение а. Функцию x(t), ограниченную во времени Т, будем называть реализацией колебания.
В настоящее время для решения подобных задач широко применяются методы математической статистики. Основной задачей ее является установление законов распределения случайных величин на основе результатов наблюдения над этими величинами.
В случае обнаружения сигналов реализация колебания x(t) является непрерывной функцией времени (при непрерывном или дискретном сигнале u(t) в смеси) с ограниченным спектром.
Представим x(t) выборочными значениями(x1, …,xn), взятыми в соответствии с теоремой Котельникова с интервалом Δt = 1/F, где F – ширина спектра колебания x(t). При этом, объем выборки определится соотношением:
n = T/ΔT = TF (2.1)
На основании анализа выборки x1, …,xn обнаружитель должен оценить параметр а. Очевидно точность оценки зависит от объема выборки при неограниченном времени наблюдения Т. Однако на практике Т ограниченно, а с увеличением объема выборки при Т = const погрешность оценки не устремляется к нулю. Выборка, у которой n → ∞ при Т = const, называется непрерывной.
Поскольку в задачах обнаружения оценка дискретная (а=0 или1), при конечном объеме выборки можно лишь с некоторыми вероятностями высказать статистические гипотезы. Следовательно, решение задачи обнаружения сводится к проверке двух альтернативных (противоположных) статистических гипотез. Гипотеза H1— сигнал во входной смеси есть и гипотеза H0— сигнала нет.
Решение статистической задачи обнаружения сигнала в шуме имеет следующую последовательность:
¨ Выбор и обоснование критериев оптимальности.
¨ Нахождение математического правила решения задачи оптимального обнаружения.
¨ Реализация правила решения с помощью радиотехнических средств (нахождение структурной схемы обнаружителя).
¨ Исследование характеристик оптимального обнаружителя.
¨ Сравнение оптимального и реального обнаружителей.
2.2. Критерии оптимальности обнаружения. Отношение правдоподобия
Критерием оптимальности называется правило, по которому из всех
возможных обнаружителей можно выбрать наилучший.
Пусть сообщение принимает два значения: а0 = 0 и а1 = 1 с априорными вероятностями Р(а0) и Р(а1) соответственно.
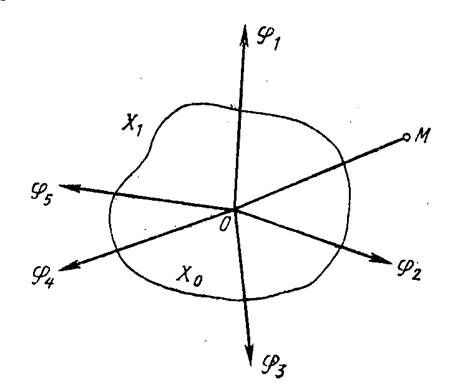
В результате наблюдения выборки x1, …,xn должно быть получено одно из двух взаимоисключающих решений: А1 – сигнал есть, А0 — сигнала нет. Каждая возможная выборка представляется в многомерном пространстве одной точкой. Оптимальный обнаружитель должен разделить пространство выборок на два подпространства Х1 и Х0 (соприкасающихся, но непересекающихся) (рис. 2.1.). Если точка М, соответствующая
k-й выборке (x1, …,xn), попадет в подпространство Х1, — принимается решение А1, в противном случае принимается решение А0.
При решении задачи возможны ошибки двух видов – ложные тревоги (с вероятностью Рл) и пропуски сигналов (с вероятностью Рп). Ложные тревоги имеют место в случае, когда в отсутствии сигнала выборка попадает в пространство Х1. Пропуски сигналов имеют место, если при наличии сигнала на входе обнаружителя выборка попадает в Х0.
Из рис. 2.1. следует, что если подпространство Х1 выбрать равным нулю, то Рл = 0, Рп = 1. Если же выбрать равным нулю подпространство Х0, то Рл = 1, Рп = 0. Таким образом, путем изменения границ подпространств Х1 и Х0 можно получить любое соотношение между вероятностями Рл и Рп. Уменьшая Рл, мы тем самым увеличиваем Рп, и наоборот.
Рис. 2.1. Пространство выборок
Оптимальный обнаружитель должен наилучшим образом по определенному критерию разделить пространство выборок Х на два подпространства: Х1 и Х0. Наиболее распространенными критериями оптимальности обнаружения являются следующие:
1. Критерий минимума среднего риска

где rл и rп – «весовые» коэффициенты, выбираемые, исходя из значимости каждой ошибки.
Величина 
2. Критерий минимальной «взвешенной» вероятности ошибки

где a и b – весовые коэффициенты.
3. Критерий минимума вероятности полной ошибки (или критерий
идеального наблюдателя, или критерий Зигерта-Котельникова)

4. Критерий Неймана – Пирсона


Величиной Рл задаются, исходя из физической постановки задачи. При этом Рп минимизируют.
Если априорные вероятности Р(а0) и Р(а1) неизвестны, что имеет место во многих случаях, то критерием 
Рассмотрим подробнее критерий минимальной «взвешенной»
вероятности ошибки.
Обозначим отношение 

где 

Если при наличии сигнала выборка (х1,…,хn) попадет в область Х1, то имеет место правильное обнаружение. Вероятность правильного обнаружения


откуда

Из (2.6), (2.8) и (2.9)

Следовательно, оптимальный обнаружитель должен обеспечивать максимум интеграла в (2.11)

Это возможно при положительной подынтегральной разности

т.е. 

Таким образом, оптимальный обнаружитель должен вычислять величину

определяемую отношением функций правдоподобия 



при 

при 

Все критерии дают оптимальное решение задачи обнаружения, основанное на вычислении отношения правдоподобия и сравнения его с порогом. Отличаются критерии лишь выбором порога.
Для критерия минимума среднего риска

Для критерия минимума взвешенной вероятности ошибки

Для критерия Неймана – Пирсона 
2.3. Бинарное обнаружение полностью известного сигнала
Положим, что сигнал u(t) известен точно. Сообщение а принимает два значения: а=а0=0 и а=а1=1, с априорными вероятностями Р(а0) и Р(а1) соответственно.
Колебание на входе обнаружителя x(t)=au(t)+n(t), n(t) – нормальный белый шум.
На основании теоремы Котельникова представим колебание x(t) выборкой (х1, …хn) и найдем функцию правдоподобия для выборки в отсутствие сигнала

Функция правдоподобия для выборки в присутствии сигнала

В выражениях (2.18) и (2.19) дисперсии равны в силу физической симметрии и определяются соотношением

где N0 – спектральная мощность шума; F=1/Dt.
Подставим значения s2 в выражения (2.18) и (2.19) и перейдем от суммы к интегралу, устремив 


Отношение правдоподобия

где 

Отношение правдоподобия для полностью известного сигнала имеет следующий вид:

Для вынесения решения необходимо сравнить 

Если 

Если 

Реализовать правило решения (2.24) радиотехническими методами, т.е. построить обнаружитель, который вычислял бы 
Поскольку 

Если z(T) > z0 – сигнал есть,
Если z(T) < z0 — сигнала нет.
Схема оптимального обнаружителя представлена на рис. 2.2 и состоит из перемножителя, интегратора и порогового устройства (ПУ).
Рис. 2.2. Схема оптимального обнаружителя
При вычислении корреляционного интеграла z(T) осуществляются переход от многомерного распределения n выборочных значений напряжения на входе обнаружителя к одномерному распределению напряжения z(T) на его выходе в момент времени Т в результате накопления (суммирования) n выборочных значений в течение длительности выборки Т.
Если входная выборка представляет собой шум n, то zn(T) определяет напряжение шума на выходе коррелятора. Если выборка – смесь сигнала с шумом, то znc(T) можно рассматривать на выходе как аддитивную смесь, поскольку операции суммирования и интегрирования линейные.
Переход от суммы выборочных значений при n→∞ и Т=const к интегралу осуществляется на основании теоремы Котельникова. Напряжение шума на выходе коррелятора

Напряжение смеси

Эти напряжения есть максимальные значения отклика коррелятора на шум и смесь соответственно. Превышение порога z0 величиной znc(T) есть правильное обнаружение и вероятность превышения и называется вероятностью правильного обнаружения Р0, а превышение порога z0 величиной zn(T) с вероятностью Рл называется ложной тревогой.
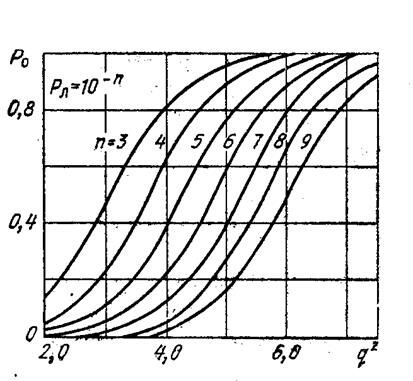
Основными показателями обнаружителя являются рабочие характеристики. Каждая характеристика определяет зависимость Р0, Рл и q2(q2-отношение сигнал/шум). На рис. 2.3 даны качественные характеристики.
Рис. 2.3. Качественные характеристики обнаружителя.
Из анализа этих характеристик следует:
¨ вероятность правильного обнаружения Р0=0 при вероятности ложной тревоги Рл=0.
¨ чем больше отношение сигнал/шум при заданной вероятности ложной тревоги Рл, тем больше вероятность правильного обнаружения Р0.
¨ Если изменять порог z0 от 0 до ∞, то Р0 и Рл будут изменяться от 1 до 0.
По характеристикам можно определить пороговое отношение
сигнал/шум, которое удовлетворяет заданным вероятностям Р0 и Рл. Найденному значению 

Для расчета и построения характеристик обнаружения необходимо знать закон распределения отклика коррелятора z(T).
В отсутствии сигнала отклик определяется шумами на входе обнаружителя и может дать ложную тревогу. Величина отклика сравнивается с порогом z0 и вероятностью того, что zn(T) превысит порог z0, называется вероятностью ложной тревоги.
Закон распределения zn(T) будет нормальным с нулевым средним значением. Дисперсия, которая определяет мощность шума на выходе коррелятора:

Сренеквадратичное напряжение шума на выходе коррелятора 

С увеличением порога ограничения z0 вероятность Рл уменьшается. Аналитически вероятность ложной тревоги определяется выражением

В присутствии на входе обнаружителя отклик коррелятора на смесь сигнала с шумом

Первый интеграл выражения (2.31) равен Е и определяет амплитуду напряжения на входе коррелятора, которое численно равно энергии входного сигнала и, следовательно, является максимально возможной величиной. Второй интеграл определяет флюктуацию с нулевым средним значением отклика (напряжение шумов) коррелятора.
Случайная величина znс(T) распределена по нормальному закону

Распределения Wn(z) и Wnc(z) отличаются средними значениями, дисперсии откликов одинаковы.
Вероятность правильного обнаружения вычисляется по формуле

После преобразований вероятность правильного обнаружения

Порог ограничения вычисляется в соответствии с выбранным критерием оптимальности.
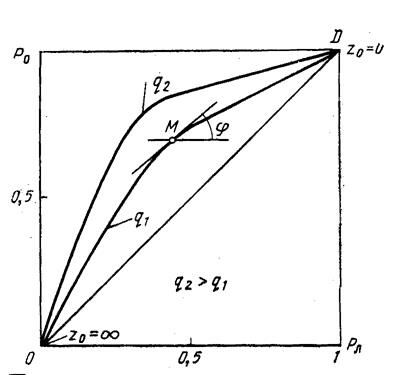
Зависимость Р0 от q2 при Рл=const называется характеристикой обнаружения. Для различных значений Рл можно построить семейство характеристик обнаружения. Характеристики обнаружения для полностью известного сигнала изображены на рис. 2.4
Рис. 2.4. Характеристики обнаружения для полностью известного сигнала
2.4. Обнаружение сигнала со случайной начальной фазой
Рассмотрим задачу обнаружения сигнала, у которой фаза высокочастотного колебания изменяется по случайному закону. Плотность распределения фазы 
Выражение для корреляционного интеграла через огибающую и фазу запишется в виде:

где

Отношение правдоподобия для полностью известного сигнала равно:

которое является случайной функцией β.
Отношение правдоподобия для сигнала со случайной фазой:

Показатель экспоненты является постоянной величиной, 
Если Z(T) > Z0 – сигнал есть, если Z(T) < Z0 – сигнала нет.
Структурная схема обнаружителя, включающая два квадратурных канала, представлена на рис. 2.5 В каждом канале вычисляется корреляционный интеграл z1 (T) и z2(T) соответственно. В квадратичном детекторе (Кв.Д.) осуществляется операция возведения в квадрат; после вычисления величины 
Рис. 2.5. Структурная схема обнаружителя
В качестве опорных напряжений на умножителях используются сдвинутые по фазе на π/2 колебания высокой или промежуточной частоты 

Вероятность правильного обнаружения равна:

где 
2.5. Бинарное обнаружение сигнала со случайными амплитудой и начальной фазой
Для сигнала 

Схема оптимального обнаружителя сигнала со случайными амплитудой и начальной фазой не отличается от схемы оптимального обнаружителя сигнала со случайной фазой. По-прежнему оптимальной является квадратурная схема обработки. Изменяется только оптимальный порог, который вычисляется по формуле

По этой зависимости можно построить характеристики обнаружения

Особенность характеристик обнаружителя со случайными амплитудой и начальной фазой состоит в том, что с ростом q2 вероятность обнаружения увеличивается сначала быстро, после достижения значений q2=0,5…0,6 это увеличение замедляется, а затем становится очень медленным.
Таким образом, характеристики обнаружения для сигнала со случайной начальной фазой сдвигаются в сторону увеличения отношения сигнал/шум, т.е. для обнаружения сигнала требуется большое напряжение его на входе, чем для полностью известного сигнала. Для сигнала со случайной амплитудой и начальной фазой отклик является случайной функцией амплитуды и фазы, поэтому необходимо усреднить отношение правдоподобия и по амплитуде, и по фазе. Характеристики обнаружения сдвигаются еще правее, за исключением участка, где отношение сигнал/шум меньше единицы. Флюктуации амплитуды при q2 < 1 несколько увеличивают вероятность обнаружения.
2.6. Обнаружение сигнала в виде пачки радиоимпульсов
В радиолокации часто применяют сигналы, представляющие собой последовательность из N импульсов, которую для краткости называют пачкой импульсов.
Каждый импульс ui(t) такой пачки полностью характеризуется амплитудой ai, частотой fi, начальной фазой φi, длительностью τi, моментом возникновения ti.
Если зависимость между всеми параметрами импульсов пачки в месте приема полностью известна, то такие импульсы и такая пачка называются когерентными. В противном случае пачка называется некогерентной.
2.6.1. Когерентная пачка импульсов с полностью известными параметрами
Пачка с полностью известными параметрами является частным случаем, полностью известного сигнала и для нее справедливы все расчетные формулы для известного случая. Энергия сигнала u(t): 

Следовательно, все приведенные выше формулы для вероятностей ошибок будут справедливы и для пачки импульсов, если в них понимать под Е энергию всех импульсов пачки, равную сумме энергий всех N импульсов пачки. Если суммарная энергия пачки импульсов такая же, как и у одиночного импульсного сигнала, ошибки обнаружения не изменяются.
Структурная схема обнаружителя для пачки подобна изображенной на рис. 2.2. Однако в этом случае на перемножитель нужно подавать «копию» сигнала в виде пачки радиоимпульсов. Максимальное значение отклика коррелятора будет в момент окончания пачки.
2.6.2. Некогерентная пачка радиоимпульсов с независимыми флюктуациями амплитуды
Сигнал в этом случае запишется так: 

При независимых флюктуациях амплитуды импульсов отношение правдоподобия для всего сигнала можно представить в виде произведения отношений правдоподобия для импульсов, тогда:

После выполнения операции умножения в показателе экспоненты будет сумма откликов на каждый импульс пачки. Поскольку 

Так же, как и для одиночного импульса, отклик Z(T) будет пропорционален энергии входного сигнала, т.е. энергии пачки импульсов. Результат сравнивают с порогом Z0, выбранным на основании критерия оптимальности. Схема обнаружителя аналогична данной на рис. 2.5. Разница будет состоять в том, что копии сигналов, подаваемых на перемножители, в данном случае представляют собой пачки радиоимпульсов.
2.7. Различение детерминированных сигналов на фоне белого гауссовского шума
Корреляционная функция белого шума со спектральной плотностью N0 равна 

где сj определяется по формуле 

Для ортогональных сигналов :
2.8. Принцип работы цифровых обнаружителей и различителей сигналов
Оптимальные алгоритмы обнаружения и различения сигналов, как известно, заключаются в накоплении сигнала за длительность входной реализации, сравнении с порогом и измерении параметров сигнала. Реализация алгоритмов в аналоговой форме имеет существенные недостатки:
¨ Аналоговым накопителям свойственно насыщение, в результате которого уменьшается отношение сигнал/шум при накоплении сигналов.
¨ Результаты накопления изменяются в процессе эксплуатации за счет нестабильности элементов динамической памяти.
¨ Нет возможности полной автоматизации процесса обработки сигналов.
¨ Оценка параметров сигналов в процессе обзора сопровождается ошибками, существенно превышающими потенциальные.
Цифровые алгоритмы квазиоптимальны за счет потерь в отношении сигнал/шум при квантовании смеси по амплитуде и дискретизации по времени. Кроме того, реализация алгоритмов в цифровой форме осуществляется на стандартных элементах вычислительной техники, что упрощает конструкции, снижает вес и габариты, увеличивает надежность.
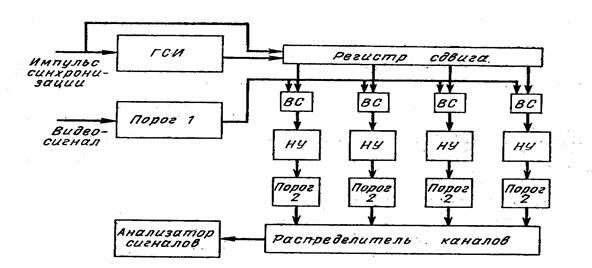
Рис. 2.6. Цифровая схема обнаружения
На рис. 2.6 дана простейшая схема цифровой схемы обнаружения сигналов. Схема включает квантователь по уровню смеси сигнала с шумом (пороговое устройство 1), дискретизатор по времени, выполненный в виде генератора стандартных импульсов (ГСИ), многоканальную схему измерения дальности, включающую регистр сдвига, вентили совпадений (ВС) и накопители сигналов (НУ), распределитель каналов (коммутатор) и анализатор сигналов.
2.9. Дискретизация и квантование непрерывных сигналов
Длительность и период дискретизации выбирают так, чтобы последовательность дискретных значений непрерывного сигнала в течение времени наблюдения позволила восстановить исходный сигнал с заданной точностью.
Вероятность обнаружения смеси Z(t):

Из этого выражения следует, что с увеличением μ увеличивается вероятность обнаружения сигнала и тем больше, чем меньше исходная вероятность Р01.
Следовательно, увеличение периода квантования приводит к увеличению вероятности обнаружения сигнала, но при этом уменьшается разрешающая способность и точность измерения дальности. Поэтому период квантования Т0 выбирается из условий получения заданной точности измерения при ограниченной сложности измерительного устройства.
Информация в лекции «4 Режущие многогранные пластины» поможет Вам.
Квантование амплитуд сигналов на два уровня означает определение наличия или отсутствия сигнала в дискретном по времени выборочном значении сигнала. На выходе бинарного квантователя появляются 1 и 0 в присутствии сигнала с вероятностью правильного обнаружения

и пропуска сигнала Рп = 1 – Р0, а в отсутствие сигнала с вероятностью ложной тревоги

и правильного необнаружения Рн = 1 – Рл. Функции Wnc(Z) и Wn(Z) – распределение смеси сигнала с шумом и шума на выходе детектора огибающей.
После логарифмирования отношения правдоподобия 
Критерий МП получается из критерия
минимального среднего риска, если
принять, что П12 = 1/P(S1),
П21 = 1/P(S2).
При этом оптимальный приемник принимает
решение таким образом, что минимизируется
значение
l п = P(y2/S1)
+ P(y1/S2).
(2.3)
Критерий МП иногда называется критерием
минимума потерь информации, так как
оптимальное правило решения в этом
случае устанавливает границу
подпространства (рис.1.2) так, чтобы
уменьшить вероятность искажения того
сигнала, вероятность передачи которого
меньше (следовательно, этот сигнал
содержит больше информации).
Критерий МП применяется в системах
связи также в тех случаях, когда априорные
вероятности Р(S1)и
P(S2)неизвестны.
3. Критерий идеального наблюдателя.
Если весовые коэффициенты П12
= П21=1, то критерий
минимального среднего риска минимизирует
среднюю вероятность ошибки
pош
= P(S1)P(y2/S1)
+ P(S2)P(y1/S2)
(2.4)
и называется критерием идеального
наблюдателя.
Критерий идеального наблюдателя широко
применяется в системах связи, когда
искажения любого сигнала одинаково
нежелательны и совпадает с критерием
МП, если вероятности Р(S1)
= P(S2) = 0,5.
4. Критерий Неймана-Пирсона.
В некоторых системах передачи информации
(системах радиолокации, некоторых
системах сигнализации) имеется
необходимость фиксирования (задания)
одной из условных вероятностей Р(у1/S2)илиР(у2/S1).При этом оптимальный приемник принимает
решение таким образом, чтобы минимизировать
ту условную вероятность, которая не
задана. Критерий оптимальности, который
используется таким приемником называетсякритерием Неймана-Пирсона.
Например, задана вероятность пропуска
сигнала S1, то естьР(у2/S1)
= ..Тогда
критерий Неймана-Пирсона требует
минимизации условной вероятностиР(у1/S2),обеспечивая заданное значение.
ВероятностьР(у1/S2)обычно обозначается ,тогда (1-)
= Р(у2/S2)называется качеством решения.Правило решения Неймана-Пирсона
обеспечивает(min )
илимах(1- )при =
const.
Приемник при использовании критерия
Неймана-Пирсона строится таким образом,
чтобы получить достаточно малую
вероятность пропуска cигнала(цели )
Р(у2/S1)=..С тем, что при этом может (несмотря на
минимизацию=Р(у1/S2))
оказаться много ложных тревог, приходится
мириться. В этом и заключается сущность
данного критерия.
3. Отношение правдоподобия
Различение сигналов в приемном устройстве
обычно осуществляют путем установления
некоторого «порога» на выходе
приемника, фактически играющего роль
«границы подпространств» сигналов
S1 иS2
.
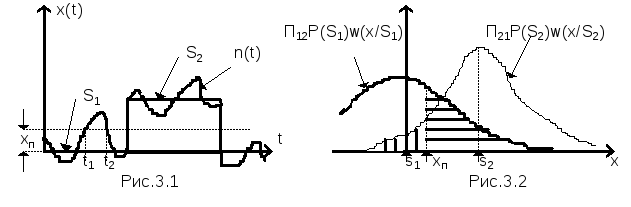
На рис. 3.1. приведен некоторый дискретный
сигнал х(t)(импульсы постоянного
тока), на который накладывается
флюктуационная помеха и проведена
пунктирная линия, соответствующая
выбранному порогухп.
Если величина x(t) < xп
, приемник выдает сигналS1,
если жеx(t)>xп ,приемник выдает сигнал S2.
Как видно из рисунка, на отрезке времениt1, t2под
действием сильной помехи величина х
> xп, т. е. в этом случае
приемник может выдать сигналS2
, хотя передавалсяS1.
Различные критерии приема дискретных
сигналов фактически отличаются способом
установления величины порога. Данная
задача проще всего решается с помощью
«отношения правдоподобия«. Для
рассмотрения этого вопроса обратимся
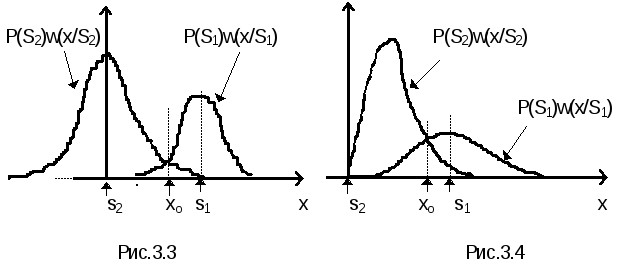
к рис. 3. 2.
Если бы на входе приемника отсутствовали
помехи, мы имели бы дело с «чистыми»
сигналами S1 иS2
и задача разделения сигналов
была бы очень проста. При наличии же
помех сигналы искажаются и для их
описания приходится использовать
вероятностное пространство. Сами сигналы
вместе с помехами описываются уже
функциями плотности вероятности w(x/S1)и w(x/S2), которые изображены
на рис. 3.2. (эти функции умножены также
на весовые коэффициентыП12Р(S1)иП21Р(S2)).На этом же рисунке показан порог хп.
Заштрихованная часть рисунка левее хп
имеет площадь, равную
П21Р(S2)w(x/S2)dx
= П21Р(S2)P(x/S2),
(3.1)
а заштрихованная часть правее хпимеет площадь, равную
П12Р(S1)w(x/S1)dx
= П12Р(S1)P(x/S1),
(3.2)
Сумма этих величин, в
соответствии с формулой (2.1), есть средний
рискRср. Из рис. 3.2. видно,
чтоRсрбудет минимальным,
когда минимальна суммарная площадь под
кривыми. Это будет в том случае, если
величинахп соответствует
точке пересечения кривых на рис. 3.2.
Следовательно, условием полученияmin{Rср} является такой
порогхп,при котором
наступает равенство ординат приведенных
кривых, т. е.
П12Р(S1)w(x/S1)dx
= П21Р(S2)w(x/S2),
(3.3)
откуда получаем следующее соотношение:
. (3.4)
Стоящее слева выражение называется
отношением правдоподобия
(х) =
,(3.5)
а w(x/S i),которая
представляет собой плотность вероятности
того, что принятый сигнал х образовался
при передаче сигнала Si
, обычно называетсяфункцией
правдоподобия (функцией правдоподобия
является также любая монотонная функция
от w(x/Si),напримерlog[
w(x/Si)]).
Чем больше значение w(x/S i),тем более вероятно, чтохсодержит
сигналSi(это очевидно из
рис. 3.2). Справа стоящее выражение
называетсяпороговым отношением
правдоподобия
0 =
.
(3.6)
Приемник, использующий отношение
правдоподобия, работает следующим
образом.
1. Анализируя поступающий на его вход
сигнал, вычисляет отношение правдоподобия
(х).
2. По известным значениям априорных
вероятностей Р(S1)иP(S2),а также заданным
весовым коэффициентомП21и П12, вычисляется пороговое
отношение правдоподобия 0.
3. Величина (х)сравнивается с0,
если (х)
> 0,
приемник выдает сигнал S1,
в противном случае
сигнал S2 .
(3.7)
Выражение (3.7) является правилом решения
Ф(х)решающего устройства, показанного
на рис.1.3.
Правило решения (3.7) является общим для
двоичных систем связи, использующих
любой критерий оптимального приема ;
отличие только в значении порога 0
.
Если приемник работает по критерию
минимального среднего риска, величина
0определяется формулой (3.6).
Для критерия идеального наблюдателя,
в этой формуле коэффициенты
П12 = П21= 1 и тогда0
= P(S2)/ P(S1), (3.8)
Для критерия максимального правдоподобия
П12
= 1/ P(S1)
, П21
= 1/ Р(S2),
тогда
0
=1. (3.9)
Если приемник использует критерий
Неймана-Пирсона, то отношение правдоподобия
(х) становится
случайной величиной, так как в равенстве
(3.1) Р(у1/S2)
=(задается
потребителем). Пороговое отношение
правдоподобия определяется как верхний
предел интеграла
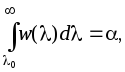
где w()— плотность распределения отношения
правдоподобия (х).
Правило принятия решения приемником
с использованием отношения правдоподобия
рассмотрим на следующих примерах.
Условия задачи.
Пусть на вход приемника поступает
аддитивная смесь сигнала (дискретная
амплитудная модуляция) и помехи:
, где i=1,2;
n(t)флюктуационная помеха типа гауссовского
шума с дисперсией.
На протяжении длительности одной
элементарной посылки в решающей схеме
приемника в синхронные моменты времени
t1иt2произведено два отсчета(замера) сигналаx(t), причем t
= t2-t1больше
интервала корреляции помехиn(t).
Измеренные значенияx(t1)=x1= 0,2 B; x(t2)=x2= 0,3B. Амплитуда
сигнала A=0,4 B.
Определить отношение правдоподобия
и принять решение по критерию идеального
наблюдателя, какой из двух сигналов (S1или S2)поступил на вход
приемника для двух случаев:
а);
б);
.
Решение задачи(когерентный
прием).
1. Найдем отношение правдоподобия .
Плотность вероятности сигнала
x(t)=S1(t)+n(t)имеет вид
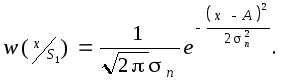
Так как на протяжении элементарного
сигнала производятся два отсчета, то
для нахождения отношения правдоподобия
требуется найти двухмерную плотность
вероятностей w2(x1x2/s1).
Учитывая, что отсчеты некоррелированы
(t больше
интервала корреляции), а помеха
распределена по гауссовскому закону,
эти отсчеты можно считать независимыми.
В этом случае двухмерная плотность
вероятностей равна произведению
одномерных плотностей
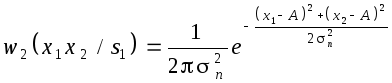
Аналогично
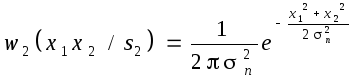
Отношение правдоподобия
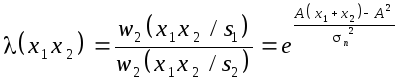
Подставляя численные значения A,n,
x1, x2,получим:
(0,2;0,3)= 2,7.
2.Применяем правило решения (3.7 ).
а) Пороговое отношение правдоподобия
приP(s1)=P(s2)=0,5
.
В нашем случае (x1x2)=2,7
> 0=1
и приемник выдает сигнал S1.
б)Пороговое отношение правдоподобия
приP(s1)=0,2 и P(s2)=0,8
.
В этом случае (x1x2)=2,7
< 0=4
и приемник выдает сигналS2.
Полученные результаты вполне объяснимы:
в случае a)измеренное значениеx(t1)=0,2B соответствует
половине амплитудыА=0,4В, а измеренное
значениеx(t2)=0,3Bближе
к сигналуS1, поэтому при
равной вероятности сигналов приемник
выдает решение в пользу сигналаS1;
в случаеб) измеренные значения
сигнала ближе кS1, но зато
сигналS2(t)встречается
в 4 раза чаще, чем сигналS1(t),
и точное решение задачи с учетом всех
обстоятельств во втором случае получается
в пользу сигнала S2.
Решение задачи(некогерентный прием).
Решим эту же задачу в предположении,
что в приемнике используется обычный
амплитудный детектор .
Найдем отношение правдоподобия для
этого случая. Плотность вероятности
x(t) при передаче сигнала S1(t)определяется обобщенным законом Релея
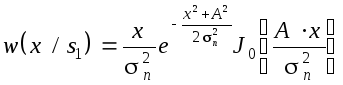
а плотность вероятности x(t) при
передаче сигналаS2(t)определяется простым законом Релея
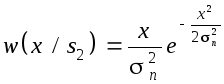
Как и в предыдущем примере, отношение
правдоподобия будет определяться
отношением двухмерных плотностей
вероятности. После простых преобразований
получаем
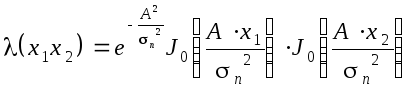
Подставляя сюда численные значения
А, n,
x1, x2,получим
.
Как и в предыдущем примере, а)0=1
и б) 0=4.
В обоих случаях (x1x2)<0и в обоих случаях приемник выдает
решение в пользу сигнала S2(t).
Сравнивая случаи принятия решения
решающей схемой приемника при когерентном
и некогерентном приеме, невольно
возникает вопрос: почему получаются
разные результаты в случае а).
Дело в том, что при когерентном приеме
сигналы x(t)распределены по
гауссовскому закону и оптимальный порогxo, определяемый точкой
пересечения функций P(S1)w(x/s1)иP(S2)w(x/s2)
(рис. 3.3),в этом случае (когдаP(S1)
=P(S2)и0=1)
соответствует половине амплитуды
сигнала S1(t); измеренные
же значения сигналаx(t)близки к
пороговому значению и ближе к сигналу
S1(t). Однако при некогерентном
приеме сигналы x(t)распределены по
законам Релея и оптимальный порогxoзначительно выше, чем половина амплитуды
сигнала S1(t) (рис. 3.4).
Поэтому те же измеренные значенияx(t1)иx(t2)оказываются
дальше от порога в области сигналаS2(t)
и решающая схема приемника при
заданных в условиях задачи вероятностях
сигналовS1(t)иS2(t)выдает решение в пользу сигналаS2(t).
Учитывая, что при когерентном приеме
уровень помех на входе решающей схемы
существенно ниже, чем при некогерентном,
более вероятно, что ошибочное решение
принял некогерентный приемник.
Соседние файлы в папке CHIN
- #
- #
- #
- #
ГЛАВА 2. Обнаружение и различение сигналов
В литературе задача оценки сообщения, принадлежащего дискретному конечному ансамблю, называется обычно «задачей различения m сигналов». Дискретная модель хорошо подходит для описания сообщений в цифровых системах передачи информации, таких, как цифровая телеметрическая система или система передачи дискретных сообщений. Объем ансамбля определяется выбранным методом приема (посимвольным, пословным и т.д.). Число m при пословном приеме равно числу кодовых комбинаций (команд); при посимвольном приеме – основанию кода. В частности, при посимвольном приеме двоичного кода m=2.
Практически работа любой радиосистемы начинается с обнаружения сигнала, при этом по наблюдаемой реализации смеси требуется определить, имеется ли в смеси сигнал или он отсутствует. Если случай отсутствия сигнала можно отождествить с одним значением сообщения х0, а наличия – с другим х1, то задача обнаружения сведется к задаче различения двух значений сообщения и принципиально ничем не будет отличаться от задачи посимвольного приема двоичной информации. Может встретиться ситуация, например, в системе передачи дискретных сообщений, когда на заданном интервале времени может или передаваться сигнал, соответствующий одному из возможных значений сообщения, или ничего не передаваться. Система обработки в этом случае должна вынести решение о том, имеется ли в наблюдаемой смеси сигнал, и если да, то какой именно. В литературе эта задача называется задачей различения m сигналов с обнаружением. Ясно, что и эта задача приводится к общей задачи различения m + 1 сигналов, если в ансамбль сообщений ввести дополнительный («нулевой») сигнал, соответствующий отсутствию сигнала в смеси.
Таким образом, одной из наиболее важных проблем радиообнаружения является отыскание оптимальных способов выделения сигналов при наличии помех. Оптимальными методами обнаружения называются такие, которые обеспечивают наилучшее выделение сигналов из смеси сигнала с помехой.
В результате процесса обнаружения должно быть выдано решение о наличии или отсутствии сигнала в смеси, действующей на входе обнаружителя.
2.1. Обнаружение сигналов как статистическая задача
Пусть на вход обнаружителя поступает сумма сигнала u(t) и шума n(t), представляющая собой непрерывный случайный процесс, x(t) = au(t) + n(t); u(t) – полностью известный сигнал, т.е. такой сигнал, единственным неизвестным параметром которого является сообщение а. В простейшем случае при обнаружении сообщения а может принимать два значения: а = а0 = 0 или а = а1 = 1.
Рекомендуемые материалы
Когда а0 = 0, сигнал на входе обнаружителя отсутствует, когда а1 = 1, сигнал на входе обнаружителя присутствует. Априорные вероятности присутствия и отсутствия сигнала на входе обнаружителя равны Р(а1) и Р(а0) соответственно.
Обнаружитель анализирует колебание x(t) в течение заранее выбранного (конечного) интервала времени Т и должен на основании анализа воспроизвести сообщение а. Функцию x(t), ограниченную во времени Т, будем называть реализацией колебания.
В настоящее время для решения подобных задач широко применяются методы математической статистики. Основной задачей ее является установление законов распределения случайных величин на основе результатов наблюдения над этими величинами.
В случае обнаружения сигналов реализация колебания x(t) является непрерывной функцией времени (при непрерывном или дискретном сигнале u(t) в смеси) с ограниченным спектром.
Представим x(t) выборочными значениями(x1, …,xn), взятыми в соответствии с теоремой Котельникова с интервалом Δt = 1/F, где F – ширина спектра колебания x(t). При этом, объем выборки определится соотношением:
n = T/ΔT = TF (2.1)
На основании анализа выборки x1, …,xn обнаружитель должен оценить параметр а. Очевидно точность оценки зависит от объема выборки при неограниченном времени наблюдения Т. Однако на практике Т ограниченно, а с увеличением объема выборки при Т = const погрешность оценки не устремляется к нулю. Выборка, у которой n → ∞ при Т = const, называется непрерывной.
Поскольку в задачах обнаружения оценка дискретная (а=0 или1), при конечном объеме выборки можно лишь с некоторыми вероятностями высказать статистические гипотезы. Следовательно, решение задачи обнаружения сводится к проверке двух альтернативных (противоположных) статистических гипотез. Гипотеза H1— сигнал во входной смеси есть и гипотеза H0— сигнала нет.
Решение статистической задачи обнаружения сигнала в шуме имеет следующую последовательность:
¨ Выбор и обоснование критериев оптимальности.
¨ Нахождение математического правила решения задачи оптимального обнаружения.
¨ Реализация правила решения с помощью радиотехнических средств (нахождение структурной схемы обнаружителя).
¨ Исследование характеристик оптимального обнаружителя.
¨ Сравнение оптимального и реального обнаружителей.
2.2. Критерии оптимальности обнаружения. Отношение правдоподобия
Критерием оптимальности называется правило, по которому из всех
возможных обнаружителей можно выбрать наилучший.
Пусть сообщение принимает два значения: а0 = 0 и а1 = 1 с априорными вероятностями Р(а0) и Р(а1) соответственно.
В результате наблюдения выборки x1, …,xn должно быть получено одно из двух взаимоисключающих решений: А1 – сигнал есть, А0 — сигнала нет. Каждая возможная выборка представляется в многомерном пространстве одной точкой. Оптимальный обнаружитель должен разделить пространство выборок на два подпространства Х1 и Х0 (соприкасающихся, но непересекающихся) (рис. 2.1.). Если точка М, соответствующая
k-й выборке (x1, …,xn), попадет в подпространство Х1, — принимается решение А1, в противном случае принимается решение А0.
При решении задачи возможны ошибки двух видов – ложные тревоги (с вероятностью Рл) и пропуски сигналов (с вероятностью Рп). Ложные тревоги имеют место в случае, когда в отсутствии сигнала выборка попадает в пространство Х1. Пропуски сигналов имеют место, если при наличии сигнала на входе обнаружителя выборка попадает в Х0.
Из рис. 2.1. следует, что если подпространство Х1 выбрать равным нулю, то Рл = 0, Рп = 1. Если же выбрать равным нулю подпространство Х0, то Рл = 1, Рп = 0. Таким образом, путем изменения границ подпространств Х1 и Х0 можно получить любое соотношение между вероятностями Рл и Рп. Уменьшая Рл, мы тем самым увеличиваем Рп, и наоборот.
Рис. 2.1. Пространство выборок
Оптимальный обнаружитель должен наилучшим образом по определенному критерию разделить пространство выборок Х на два подпространства: Х1 и Х0. Наиболее распространенными критериями оптимальности обнаружения являются следующие:
1. Критерий минимума среднего риска

где rл и rп – «весовые» коэффициенты, выбираемые, исходя из значимости каждой ошибки.
Величина 
2. Критерий минимальной «взвешенной» вероятности ошибки

где a и b – весовые коэффициенты.
3. Критерий минимума вероятности полной ошибки (или критерий
идеального наблюдателя, или критерий Зигерта-Котельникова)

4. Критерий Неймана – Пирсона


Величиной Рл задаются, исходя из физической постановки задачи. При этом Рп минимизируют.
Если априорные вероятности Р(а0) и Р(а1) неизвестны, что имеет место во многих случаях, то критерием 
Рассмотрим подробнее критерий минимальной «взвешенной»
вероятности ошибки.
Обозначим отношение 

где 

Если при наличии сигнала выборка (х1,…,хn) попадет в область Х1, то имеет место правильное обнаружение. Вероятность правильного обнаружения


откуда

Из (2.6), (2.8) и (2.9)

Следовательно, оптимальный обнаружитель должен обеспечивать максимум интеграла в (2.11)

Это возможно при положительной подынтегральной разности

т.е. 

Таким образом, оптимальный обнаружитель должен вычислять величину

определяемую отношением функций правдоподобия 



при 

при 

Все критерии дают оптимальное решение задачи обнаружения, основанное на вычислении отношения правдоподобия и сравнения его с порогом. Отличаются критерии лишь выбором порога.
Для критерия минимума среднего риска

Для критерия минимума взвешенной вероятности ошибки

Для критерия Неймана – Пирсона 
2.3. Бинарное обнаружение полностью известного сигнала
Положим, что сигнал u(t) известен точно. Сообщение а принимает два значения: а=а0=0 и а=а1=1, с априорными вероятностями Р(а0) и Р(а1) соответственно.
Колебание на входе обнаружителя x(t)=au(t)+n(t), n(t) – нормальный белый шум.
На основании теоремы Котельникова представим колебание x(t) выборкой (х1, …хn) и найдем функцию правдоподобия для выборки в отсутствие сигнала

Функция правдоподобия для выборки в присутствии сигнала

В выражениях (2.18) и (2.19) дисперсии равны в силу физической симметрии и определяются соотношением

где N0 – спектральная мощность шума; F=1/Dt.
Подставим значения s2 в выражения (2.18) и (2.19) и перейдем от суммы к интегралу, устремив 


Отношение правдоподобия

где 

Отношение правдоподобия для полностью известного сигнала имеет следующий вид:

Для вынесения решения необходимо сравнить 

Если 

Если 

Реализовать правило решения (2.24) радиотехническими методами, т.е. построить обнаружитель, который вычислял бы 
Поскольку 

Если z(T) > z0 – сигнал есть,
Если z(T) < z0 — сигнала нет.
Схема оптимального обнаружителя представлена на рис. 2.2 и состоит из перемножителя, интегратора и порогового устройства (ПУ).
Рис. 2.2. Схема оптимального обнаружителя
При вычислении корреляционного интеграла z(T) осуществляются переход от многомерного распределения n выборочных значений напряжения на входе обнаружителя к одномерному распределению напряжения z(T) на его выходе в момент времени Т в результате накопления (суммирования) n выборочных значений в течение длительности выборки Т.
Если входная выборка представляет собой шум n, то zn(T) определяет напряжение шума на выходе коррелятора. Если выборка – смесь сигнала с шумом, то znc(T) можно рассматривать на выходе как аддитивную смесь, поскольку операции суммирования и интегрирования линейные.
Переход от суммы выборочных значений при n→∞ и Т=const к интегралу осуществляется на основании теоремы Котельникова. Напряжение шума на выходе коррелятора

Напряжение смеси

Эти напряжения есть максимальные значения отклика коррелятора на шум и смесь соответственно. Превышение порога z0 величиной znc(T) есть правильное обнаружение и вероятность превышения и называется вероятностью правильного обнаружения Р0, а превышение порога z0 величиной zn(T) с вероятностью Рл называется ложной тревогой.
Основными показателями обнаружителя являются рабочие характеристики. Каждая характеристика определяет зависимость Р0, Рл и q2(q2-отношение сигнал/шум). На рис. 2.3 даны качественные характеристики.
Рис. 2.3. Качественные характеристики обнаружителя.
Из анализа этих характеристик следует:
¨ вероятность правильного обнаружения Р0=0 при вероятности ложной тревоги Рл=0.
¨ чем больше отношение сигнал/шум при заданной вероятности ложной тревоги Рл, тем больше вероятность правильного обнаружения Р0.
¨ Если изменять порог z0 от 0 до ∞, то Р0 и Рл будут изменяться от 1 до 0.
По характеристикам можно определить пороговое отношение
сигнал/шум, которое удовлетворяет заданным вероятностям Р0 и Рл. Найденному значению 

Для расчета и построения характеристик обнаружения необходимо знать закон распределения отклика коррелятора z(T).
В отсутствии сигнала отклик определяется шумами на входе обнаружителя и может дать ложную тревогу. Величина отклика сравнивается с порогом z0 и вероятностью того, что zn(T) превысит порог z0, называется вероятностью ложной тревоги.
Закон распределения zn(T) будет нормальным с нулевым средним значением. Дисперсия, которая определяет мощность шума на выходе коррелятора:

Сренеквадратичное напряжение шума на выходе коррелятора 

С увеличением порога ограничения z0 вероятность Рл уменьшается. Аналитически вероятность ложной тревоги определяется выражением

В присутствии на входе обнаружителя отклик коррелятора на смесь сигнала с шумом

Первый интеграл выражения (2.31) равен Е и определяет амплитуду напряжения на входе коррелятора, которое численно равно энергии входного сигнала и, следовательно, является максимально возможной величиной. Второй интеграл определяет флюктуацию с нулевым средним значением отклика (напряжение шумов) коррелятора.
Случайная величина znс(T) распределена по нормальному закону

Распределения Wn(z) и Wnc(z) отличаются средними значениями, дисперсии откликов одинаковы.
Вероятность правильного обнаружения вычисляется по формуле

После преобразований вероятность правильного обнаружения

Порог ограничения вычисляется в соответствии с выбранным критерием оптимальности.
Зависимость Р0 от q2 при Рл=const называется характеристикой обнаружения. Для различных значений Рл можно построить семейство характеристик обнаружения. Характеристики обнаружения для полностью известного сигнала изображены на рис. 2.4
Рис. 2.4. Характеристики обнаружения для полностью известного сигнала
2.4. Обнаружение сигнала со случайной начальной фазой
Рассмотрим задачу обнаружения сигнала, у которой фаза высокочастотного колебания изменяется по случайному закону. Плотность распределения фазы 
Выражение для корреляционного интеграла через огибающую и фазу запишется в виде:

где

Отношение правдоподобия для полностью известного сигнала равно:

которое является случайной функцией β.
Отношение правдоподобия для сигнала со случайной фазой:

Показатель экспоненты является постоянной величиной, 
Если Z(T) > Z0 – сигнал есть, если Z(T) < Z0 – сигнала нет.
Структурная схема обнаружителя, включающая два квадратурных канала, представлена на рис. 2.5 В каждом канале вычисляется корреляционный интеграл z1 (T) и z2(T) соответственно. В квадратичном детекторе (Кв.Д.) осуществляется операция возведения в квадрат; после вычисления величины 
Рис. 2.5. Структурная схема обнаружителя
В качестве опорных напряжений на умножителях используются сдвинутые по фазе на π/2 колебания высокой или промежуточной частоты 

Вероятность правильного обнаружения равна:

где 
2.5. Бинарное обнаружение сигнала со случайными амплитудой и начальной фазой
Для сигнала 

Схема оптимального обнаружителя сигнала со случайными амплитудой и начальной фазой не отличается от схемы оптимального обнаружителя сигнала со случайной фазой. По-прежнему оптимальной является квадратурная схема обработки. Изменяется только оптимальный порог, который вычисляется по формуле

По этой зависимости можно построить характеристики обнаружения

Особенность характеристик обнаружителя со случайными амплитудой и начальной фазой состоит в том, что с ростом q2 вероятность обнаружения увеличивается сначала быстро, после достижения значений q2=0,5…0,6 это увеличение замедляется, а затем становится очень медленным.
Таким образом, характеристики обнаружения для сигнала со случайной начальной фазой сдвигаются в сторону увеличения отношения сигнал/шум, т.е. для обнаружения сигнала требуется большое напряжение его на входе, чем для полностью известного сигнала. Для сигнала со случайной амплитудой и начальной фазой отклик является случайной функцией амплитуды и фазы, поэтому необходимо усреднить отношение правдоподобия и по амплитуде, и по фазе. Характеристики обнаружения сдвигаются еще правее, за исключением участка, где отношение сигнал/шум меньше единицы. Флюктуации амплитуды при q2 < 1 несколько увеличивают вероятность обнаружения.
2.6. Обнаружение сигнала в виде пачки радиоимпульсов
В радиолокации часто применяют сигналы, представляющие собой последовательность из N импульсов, которую для краткости называют пачкой импульсов.
Каждый импульс ui(t) такой пачки полностью характеризуется амплитудой ai, частотой fi, начальной фазой φi, длительностью τi, моментом возникновения ti.
Если зависимость между всеми параметрами импульсов пачки в месте приема полностью известна, то такие импульсы и такая пачка называются когерентными. В противном случае пачка называется некогерентной.
2.6.1. Когерентная пачка импульсов с полностью известными параметрами
Пачка с полностью известными параметрами является частным случаем, полностью известного сигнала и для нее справедливы все расчетные формулы для известного случая. Энергия сигнала u(t): 

Следовательно, все приведенные выше формулы для вероятностей ошибок будут справедливы и для пачки импульсов, если в них понимать под Е энергию всех импульсов пачки, равную сумме энергий всех N импульсов пачки. Если суммарная энергия пачки импульсов такая же, как и у одиночного импульсного сигнала, ошибки обнаружения не изменяются.
Структурная схема обнаружителя для пачки подобна изображенной на рис. 2.2. Однако в этом случае на перемножитель нужно подавать «копию» сигнала в виде пачки радиоимпульсов. Максимальное значение отклика коррелятора будет в момент окончания пачки.
2.6.2. Некогерентная пачка радиоимпульсов с независимыми флюктуациями амплитуды
Сигнал в этом случае запишется так: 

При независимых флюктуациях амплитуды импульсов отношение правдоподобия для всего сигнала можно представить в виде произведения отношений правдоподобия для импульсов, тогда:

После выполнения операции умножения в показателе экспоненты будет сумма откликов на каждый импульс пачки. Поскольку 

Так же, как и для одиночного импульса, отклик Z(T) будет пропорционален энергии входного сигнала, т.е. энергии пачки импульсов. Результат сравнивают с порогом Z0, выбранным на основании критерия оптимальности. Схема обнаружителя аналогична данной на рис. 2.5. Разница будет состоять в том, что копии сигналов, подаваемых на перемножители, в данном случае представляют собой пачки радиоимпульсов.
2.7. Различение детерминированных сигналов на фоне белого гауссовского шума
Корреляционная функция белого шума со спектральной плотностью N0 равна 

где сj определяется по формуле 

Для ортогональных сигналов :
2.8. Принцип работы цифровых обнаружителей и различителей сигналов
Оптимальные алгоритмы обнаружения и различения сигналов, как известно, заключаются в накоплении сигнала за длительность входной реализации, сравнении с порогом и измерении параметров сигнала. Реализация алгоритмов в аналоговой форме имеет существенные недостатки:
¨ Аналоговым накопителям свойственно насыщение, в результате которого уменьшается отношение сигнал/шум при накоплении сигналов.
¨ Результаты накопления изменяются в процессе эксплуатации за счет нестабильности элементов динамической памяти.
¨ Нет возможности полной автоматизации процесса обработки сигналов.
¨ Оценка параметров сигналов в процессе обзора сопровождается ошибками, существенно превышающими потенциальные.
Цифровые алгоритмы квазиоптимальны за счет потерь в отношении сигнал/шум при квантовании смеси по амплитуде и дискретизации по времени. Кроме того, реализация алгоритмов в цифровой форме осуществляется на стандартных элементах вычислительной техники, что упрощает конструкции, снижает вес и габариты, увеличивает надежность.
Рис. 2.6. Цифровая схема обнаружения
На рис. 2.6 дана простейшая схема цифровой схемы обнаружения сигналов. Схема включает квантователь по уровню смеси сигнала с шумом (пороговое устройство 1), дискретизатор по времени, выполненный в виде генератора стандартных импульсов (ГСИ), многоканальную схему измерения дальности, включающую регистр сдвига, вентили совпадений (ВС) и накопители сигналов (НУ), распределитель каналов (коммутатор) и анализатор сигналов.
2.9. Дискретизация и квантование непрерывных сигналов
Длительность и период дискретизации выбирают так, чтобы последовательность дискретных значений непрерывного сигнала в течение времени наблюдения позволила восстановить исходный сигнал с заданной точностью.
Вероятность обнаружения смеси Z(t):

Из этого выражения следует, что с увеличением μ увеличивается вероятность обнаружения сигнала и тем больше, чем меньше исходная вероятность Р01.
Следовательно, увеличение периода квантования приводит к увеличению вероятности обнаружения сигнала, но при этом уменьшается разрешающая способность и точность измерения дальности. Поэтому период квантования Т0 выбирается из условий получения заданной точности измерения при ограниченной сложности измерительного устройства.
Информация в лекции «4 Режущие многогранные пластины» поможет Вам.
Квантование амплитуд сигналов на два уровня означает определение наличия или отсутствия сигнала в дискретном по времени выборочном значении сигнала. На выходе бинарного квантователя появляются 1 и 0 в присутствии сигнала с вероятностью правильного обнаружения

и пропуска сигнала Рп = 1 – Р0, а в отсутствие сигнала с вероятностью ложной тревоги

и правильного необнаружения Рн = 1 – Рл. Функции Wnc(Z) и Wn(Z) – распределение смеси сигнала с шумом и шума на выходе детектора огибающей.
После логарифмирования отношения правдоподобия 
Аннотация
В статье рассмотрены основы статистической обработки сигналов и методы их оптимальной обработки* на фоне шума.
Оптимальная обработка
*Под оптимальной обработкой в радиолокации понимают такую операцию над входной реализацией**, приводящей к повышению вероятности правильно обнаружения полезного сигнала, как правило, известной формы, при условии наличия во входной реализации шума в виде случайного процесса с известным или неизвестным законом распределения.
**Процесс наблюдаемый на входе приёмника. Строго говоря, назвать его «Входной сигнал» нельзя, так как в теории связи «Шум» и «Сигнал» — антонимы.
Введение
Основной задачей радиотехники является приём, передача и обработка информации с использованием в качестве переносчика – радиосигнала. Главное требование, предъявляемое к радиотехническим системам – получение своевременной и достоверной информации от источника к потребителю. Однако этому мешает физика принципов работы приёмопередающих устройств и среды распространения сигнала, суть которой заключается во флюктуации физических параметров системы и случайным значением принимаемого сигнала, имеющего шумовую составляющую, также относящуюся к стохастическим процессам.
На текущий момент, самый эффективный способ различения полезных сигналов на фоне шумов и помех является оптимальная обработка, реализуемая, как правило, сравнением принимаемой входной реализации с априорно известной формой полезного сигнала. При этом шумы, которые по своей природе процесс слабокоррелированный, вносят меньший вклад в величину, показывающую степень этого сравнения и называющуюся коэффициентом корреляции. Таким образом, любая задача обнаружения сводится к проверке минимум двух гипотез. В общем случае задача обнаружения состоит из двух гипотез: H_0 – сигнал отсутствует на входе приёмного устройства, H_1 – сигнал присутствует на входе приёмного устройства. Различные алгоритмы обнаружения обеспечивают различную вероятность правильного обнаружения P{d_1/H_1} при различных прочих статистических параметрах. Для сравнения эффективности алгоритмов обнаружения существуют критерии, а так как обрабатываются вероятностные величины, то характер этих критериев статистический. Иными словами критерий можно определить как мерило сравнения.
Статистические критерии обнаружения
Большая часть алгоритмов обнаружения радиолокационных целей включают в себя следующие этапы:
- Прием входной реализации
- Формирование порога на основе априорной или апостериорной информации.
- Оптимальная фильтрация входной реализации
- Принятие решения о наличии сигнала/цели
При этом очередность приёма входной реализации и формирования порога зависит непосредственно от типа алгоритма. Алгоритмы, формирующие порог на основе апостериорной информации о принятой входной реализации называют адаптивными [1]. Критерий выбирается эмпирически исходя из типа задачи. Например: при выборе места работы обычно рассматривают два критерия:
- Максимума отношения заработанных денег к затраченной силе.
- Максимума удовольствия, получаемого от работы.
К сожалению, современные реалии ставят в приоритет такого специалиста, навыки которого позволяли бы как можно быстрее выпустить продукцию и максимизировать прибыль компании. И зачастую второй критерий либо отбрасывается, либо при анализе ситуации ему присваивается низкий приоритет. Показатель, в данном случае, определяющий приоритет критериев, называется его мощностью.
В математической статистике мощность критерия определяется, как вероятность не совершить ошибку второго рода при принятии решения. В нашем случае ошибка второго рода — это не устроится на оптимальную для себя работу, в общем же случае это ложное принятие за истину события соответствующего гипотезе H_0.
Разумеется, универсальных критериев не существует. Так, например, критерий, имеющий наибольшую мощность, в решении одной задачи, в решении другой может оказаться наихудшим по этому показателю.
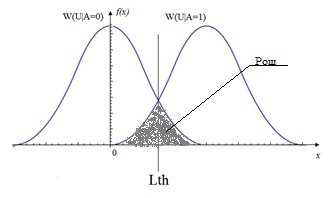
Критерий минимального среднего риска (критерий Байеса)
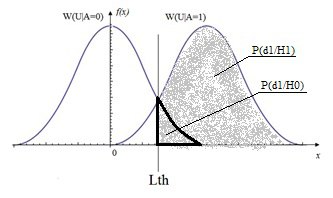
Рис.1 График распределения условной плотности вероятности наличия W(U|A=1) и отсутствия W(U|A=0) с вероятностями ошибок
Пусть A = 1 соответствует наличию сигнала s(t), а A = 0 – его отсутствию. Множество решений d вырождается в два: d_0 →A=1 and d_1→A=0.
При решении задачи бинарного обнаружения задача эквивалентна проверке гипотезы H_1 о том, что А = 1, при альтернативной гипотезе H_0 о том, что А = 0, а функция потерь переходит в квадратную матрицу:
Таким образом, условный риск при A = 0 равен r_0= C_00 P{d_0/H_0 }+ C_01 P{d_1/H_0 }=C_00 (1-P{d_1/H_0 })+ C_01 P{d_1/H_0 }, а при A = 1 равен r_1= C_10 P{d_0/H_1 }+ C_11 P{d_1/H_1}=C_10 (1-P{d_1/H_1} )+C_11 P{d_1/H_1}, где P{d_1/H_1} – вероятность правильного обнаружения, а P{d_1/H_0 } – вероятность ложной тревоги.
Средний риск определяется как r ̅=qr_0+pr_1, где q – априорная вероятность отсутствия сигнала, а p – априорная вероятность присутствия сигнала и определяет средние потери при ложной тревоге и пропуске цели [2]. Например: при использовании такого критерия для выставления порога срабатывания пожарной сигнализации, стоимость риска при ложной тревоге – вызов пожарной службы, а при пропуске – стоимость вещей в сгоревшей квартире или офисе.
На рис.1 проиллюстрированы графики распределения плотности вероятности при наличии и отсутствии сигнала, также выделены зоны, площадь которых численно равна вероятностям ошибок при принятии решения. Ввиду стохастической природы явлений рассматриваемых в данном примере, распределения имеют ненулевую дисперсию. Согласно критерию минимального среднего риска лучшим алгоритмом обнаружения сигнала будет тот, у которого величина r ̅ будет минимальна [2].
Критерий максимума апостериорной вероятности (максимального правдоподобия)
Этот критерий получается из критерия минимального среднего риска при условии, что потери при совершении ошибки обратно пропорциональны вероятности их совершения C_01=1/P{d_0}, C_10=1/P{d_1}. При этом порог оптимального обнаружителя выставляется таким образом, чтобы минимизировать сумму вероятностей ошибок P_ош=P{d_0/H_1 }+P{d_1/H_0 } (см рис.2).
Рис.2 График распределения условной плотности вероятности наличия W(U|A=1) и отсутствия W(U|A=0) с вероятностью ошибки
Двухпороговый критерий Вальда
В случаях, когда большую роль играет время наблюдения за процессом, например при наличии нескольких каналов и одного обнаружителя или круговом обзоре РЛС, применяют критерий последовательной проверки гипотез Вальда также известный под названием двухпороговый.
Рис.3 График распределения условной плотности вероятности наличия W(U|A=1) и отсутствия W(U|A=0) с вероятностью правильного обнаружения и вероятностью ложной тревоги
По этому критерию область определения вероятности делится на три подобласти, разделяемыми двумя порогами, определяемыми вероятностями правильного обнаружения и ложной тревоги (см.рис 3):
Критерий Вальда является оптимальным в смысле минимизации среднего времени наблюдения по большому количеству экспериментов [4]. Так как наиболее предпочтительным для радиолокации является сокращение длительности процедуры обнаружения, современные реалии ведут к всё более активному использованию этого критерия [5].
Критерий Неймана-Пирсона
Большим минусом критериев Байесовского класса является необходимость априорного знания элементов матрицы потерь. Например: при пропуске вражеского бомбардировщика на союзную территорию стоимость рисков не поддается исчислению.
В критерии Неймана-Пирсона фиксируется время обнаружения. Оптимальным будет алгоритм с максимальной вероятностью правильного обнаружения P{d_1/H_1 }, при условии, что вероятность ложной тревоги P{d_1/H_0 } не превышает заданной величины [6].
В виду того, что критерий Неймана-Пирсона не требует знания априорных вероятностей ситуаций A = 1 и A = 0, в радиолокации его используют одним из основных [5].
Заключение
При разработке обнаружителей очень важно осознанно выбирать критерий оптимальности, ведь, как уже упоминалось ранее, каждый критерий имеет максимальную мощность в какой-либо определенной ситуации и применение иных может привести к нежелательным последствиям.
Список использованных источников:
[1] Bulyakulov R.R. The adaptive threshold device // Processing of the 2014 IEEE North West Russia Section Young Researches in Electrical and Electronic Engineering Conference. P.165.
doi: 10.1109/EIConRusNW.2016.7448237
[2] Бакулев, П.А. Радиолокационные системы. Учебник для ВУЗов / П.А. Бакулев; М.: Радиотехника, 2004. – 46 с.
[3] Юревич, Е.И. Теория автоматического управления / Е.И. Юревич; М.: Энергия, 1969
[4] Богатырев, А.А. Стандартизация статистических методов управления качеством / А. А. Богатырев, Ю. Д. Филиппов; М.: Изд-во стандартов, 1989. – 42 с.
[5] Храменков, А.С. Сопоставительный анализ радиолокационных обнаружителей, основанных на критерии неймана-пирсона и последовательном критерии отношения вероятностей /А.С. Храменков, С.Н. Ярмолик // доклады БГУИР №6(76) Минск, 2013.
[6] Васильев, К.К. Методы обработки сигналов: Учебное пособие / К.К. Васильев; Ульяновск, 2001.
Минимум — вероятность — ошибка
Cтраница 1
Минимум вероятности ошибки Р0 оптимальной системы можно оценить следующим образом: оптимальная стратегия Торпа для упрощенной игры дает выигрыш в 49 5 % игр. В большинстве разыгранных партий вначале делаются 3 правильных решения.
[1]
Во многих алгоритмах поиск минимума вероятности ошибки заменяется поиском решающего правила заданного вида, минимизирующего число ошибок на обучающей последовательности. Однако часто оказывается, что, построив более сложное решающее правило, можно добиться уменьшения числа ошибок на обучающей выборке, тогда как вероятность ошибки классификации векторов генеральной совокупности не падает, а наоборот, возрастает. Поэтому, в соответствии с теоретическими положениями части первой, в предлагаемом комплексе алгоритмов решающее правило выбирается по более сложному критерию, учитывающему соотношение числа ошибок на обучающей выборке, сложности правила и длины выборки.
[2]
Таким образом, система, оптимальная в смысле критерия минимума вероятности ошибки, оказывается частным случаем байесо-вой системы при простой функции потерь.
[3]
Во всех таких случаях оптимальной моделью распознавания образов двух классов считают такую модель, которая реализует минимум вероятности ошибки одного вида при данном значении вероятности ошибки другого вида. Условие минимума вероятности ошибки одного вида при заданной вероятности ошибки другого вида обычно называется критерием Неймана-Пирсона.
[4]
Из формулы (1.4.3) следует, что для заданных исходных величин N, V, т, г существует величина попт, которая обеспечивает минимум вероятности ошибки. При заданной вероятности ошибки Ра можно из формулы (1.4.4) найти необходимую величину мопт, а затем из формулы (1.4.3) длительность импульса т0, при которой получается необходимое значение погт.
[5]
Начало развитию теории оптимизации нелинейных систем положила работа В. А. Котельникова [73], в которой впервые была решена задача обнаружения сигнала, зависящего от конечного числа неизвестных параметров, на фоне белого шума по критерию минимума вероятности ошибки, а также задача оценки параметров сигнала, принимаемого на фоне белого шума.
[6]
Во всех таких случаях оптимальной моделью распознавания образов двух классов считают такую модель, которая реализует минимум вероятности ошибки одного вида при данном значении вероятности ошибки другого вида. Условие минимума вероятности ошибки одного вида при заданной вероятности ошибки другого вида обычно называется критерием Неймана-Пирсона.
[7]
Почему такое правило обеспечивает минимум вероятности ошибки при выборе гипотез.
[8]
Условием ( 20) критическое множество определяется неоднозначно. Выбирают ту из возможностей, которая обеспечивает минимум вероятности ошибки второго рода, или, что то же самое, максимум мощности критерия.
[9]
В [1,4] получены зависимости д ( z), характеризующие эффективность систем на оптимальных режимах работы. Оптимальными режимами работы называются такие режимы, которые обеспечивают минимум вероятности ошибки при условии, что величина z принимает заданное значение. На рис. 1 представлены зависимости q ( z), характеризующие эффективность сравниваемых систем на оптимальных режимах. На рис. 1 показаны кривые 3, 4 ( и 0 5, х — 0), свидетельствующие о больших возможностях повышения эффективности в системах со сравнением.
[10]
В § 8.3 дан эвристический вывод выражения для пропускной способности канала с фильтром и аддитивным стационарным гауссовым шумом. В § 8.4 и 8.5 это исследование продолжено со строгим анализом пропускной способности и верхних границ для минимума достижимой вероятности ошибки. Однако проведенный анализ не был полным; в нем не учитывалась интерференция между последовательными кодовыми словами. Последняя задача остается открытой для исследования.
[11]
Пропуск сигнала и ложная тревога являются ошибками при обнаружении. В соответствии с критерием так называемого идеального наблюдателя системой оптимальной фильтрации при обнаружении считается такая система обработки, с помощью которой обеспечивается минимум вероятности ошибок. При таком критерии в приемном устройстве должно осуществляться определение вероятностей наличия и отсутствия сигнала на входе приемника и сравнение между собой этих вероятностей. В соответствии с тем, какая из вероятностей больше, и принимается решение о наличии или отсутствии сигнала. Вероятность совершить ошибку при этом, естественно, оказывается наименьшей. Под входным напряжением приемника обычно понимается напряжение на нагрузке антенны. Здесь же под входным понимается напряжение на входе оптимального фильтра.
[12]
В задачах обнаружения сигналов имеет значение не величина ошибки, а сам факт ее наличия или отсутствия. Сигнал W считается обнаруженным, если величина его на выходе системы не меньше некоторого порогового значения С и наоборот. Тогда минимум вероятности ошибки системы ( обнаружение сигнала, когда его нет, и наоборот — фиксация его отсутствия при наличии сигнала) служит критерием оптимальности обнаружения сигнала.
[13]
Здесь логарифм отношения правдоподобия играет во многом ту же самую роль, как в гл. При декодировании по максимуму правдоподобия сообщение 1 декодируется, когда rlt 2 ( у) 0, а сообщение 2 — в противном случае. При декодировании по минимуму вероятности ошибки с априорными вероятностями qt и qz сообщение 1 декодируется, когда rlt 2 ( У) ln ( 9a / 9i) — Заметим, что при п N величины уп опускаются из рассмотрения, так как эти величины не зависят от посланного сообщения и не влияют на значение логарифма отношения правдоподобия. Даже если W бесконечно в (8.2.12), r1: 2 ( у) вполне определено, хотя предел условных плотностей вероятностей в (8.2.14) не существует.
[14]
Для простоты в теореме рассматриваются лишь дискретные каналы без памяти. Она, очевидно, остается справедливой всегда, когда С может быть выражена как максимум средней взаимной информации и вместе с тем интерпретирована с помощью теоремы кодирования. Весьма примечательно, что этот минимум вероятности ошибки может быть однозначно определен с помощью столь малого числа параметров.
[15]
Страницы:
1
2
УДК 519. 248
метод нелинейной параметрической идентификации
с использованием критерия минимума вероятности
ошибки оценивания
© 2008 г. П.А. Кучеренко
Ростовский государственный университет путей сообщения, 344038, г. Ростов-на-Дону, пл. Ростовского Стрелкового Полка Народного Ополчения, 2. pavelpost83@mail.ru
Rostov State University of Means of Сommunication, 344038, Rostov-on-Don, Rostovskogo Strelkovogo Polka Narodnogo Opolchehija sq, 2. pavelpost83@mail. ru
Показана актуальность исследования альтернативных (по отношению к традиционным) методов стохастической нелинейной параметрической идентификации. Предложен синтез процедуры идентификации параметра дискретного наблюдателя с использованием критерия минимума вероятности ошибки оценивания. Рассмотрен численный пример, иллюстрирующий эффективность предлагаемого подхода.
Ключевые слова: нелинейная параметрическая идентификация, стохастический дискретный объект, оптимальный дискретный фильтр Калмана, цифровая обработка сигналов.
The relevance of the alternative (related to the traditional) methods of stochastic nonlinear parametric identification is performed in the paper. The identification procedure of the parameter of the discrete observer based on the minimum criterion of the estimation error probability is produced. The numerical example which demonstrates an efficiency of the offered method is considered.
Keywords: nonlinear parametric identification, stochastic discrete object, optimal discrete Kalman filter, digital signal processing.
Существующие в настоящее время методы решения задачи стохастической параметрической идентификации требуют, как правило, для своей удовлетворительной реализации принятия целого ряда крайне упрощающих ограничений — линейности модели измерителя относительно параметров, необходимости нормального вида распределения аддитивных помех наблюдаемых сигналов и др. Это в большинстве реальных ситуаций оказывает значительное отрицательное влияние на качественные характеристики процедуры идентификации и как следствие снижает потенциально возможную точность получаемых оценок параметров [1-4].
Проведение исследований, направленных на синтез методов и алгоритмов, позволяющих в значительной (или полной) мере устранить недостатки традиционных методов, представляется весьма актуальным как с практической, таки с теоретическойточекзрения.
Для решения данной задачи ниже рассмотрим подход, позволяющий, во-первых, избавиться от существующих ограничений разработанных методов, а во-вторых, повысить потенциальную точность процедуры идентификации за счет использования обобщенных вероятностных критериев, зависящих в общем случае нелинейно от апостериорной плотности распределения вектора состояния.
Для упрощения изложения синтеза процедуры идентификации и его наглядности остановимся подробнее на скалярных уравнениях, определяющих в общем случае нелинейную модель исследуемого объекта и структуру его наблюдателя (обобщение на векторный случай, как это будет очевидно из последующих построений, особенностей не имеет).
Постановка задачи параметрической идентификации
Пусть дискретный объект задан в общем случае нелинейным разностным уравнением х/( = /'(х/( |) + п ,
где п — шум объекта с известной плотностью вероятности д(п); х^ — переменная состояния в к-й момент времени; / — известная нелинейная функция.
Наблюдение переменных состояния в дискретном времени осуществляется измерителем, описываемым в общем случае также нелинейным уравнением (уравнением наблюдения) следующего вида: гк = /(с. хк) + н>, где с — неизвестный искомый параметр наблюдателя; м> — шум наблюдения с известной плотностью вероятности g(w); % — известная нелинейная функция наблюдения; 2 к — дискретный отсчет сигнала наблюдения.
Для сокращения дальнейшей записи набор дискретных отсчетов сигнала наблюдения 21 (/=1..к) обок
значим через 2^ .
В рассматриваемом общем нелинейном стохастическом случае задача идентификации неизвестного параметра с может быть сформулирована как задача нахождения такого его значения, при котором величина некоторого нелинейного вероятностного функционала, зависящего от апостериорной плотности распределения переменных состояния, принимала бы наибольшее (наименьшее) значение. (Иными словами, как задача определения параметра, удовлетворяющего некоторому вероятностному критерию оптимальности J).
Исходя из физического смысла поставленной задачи идентификации, в качестве критерия J используем далее критерий минимума апостериорной плотности вероятности (АПВ) текущей ошибки оценивания а переменных состояния объекта на выбранном интервале ее предельно допустимого изменения — от о~П1П1 до о~|гах ,
т.е. J = min J p(<Jk | zx )dak, где ak =xk — xk , xk —
c а ^ min
текущие ошибки оценивания и переменной состояния объекта; р(рк | zf) — апостериорная плотность вероятности ошибки оценивания.
Учитывая линейную зависимость значений ошибки су ]: и переменной состояния хк: сгк =хк-хк, выразим АПВ ошибки оценивания р(<т/; | zf) через АПВ переменной состояния p(xk | zx) (выражение для которой будет получено ниже): p(<ykzx) =
= p(ak+xk I zf).
В этом случае критерий идентификации можно представить следующим образом:
^шах ,
J = min J p(<Jk I zx )dak =
с Л-
max ,
= min J p(ak+xkzl)dak.
C <T ^ mm
В результате проделанных построений поставленная задача сводится к отысканию плотности
р(сгк + хк | 2 ) и последующему определению значения искомого параметра из условия минимума критериальной функции (1).
Синтез метода нелинейной параметрической идентификации
Для определения АПВ р(сгк + хк ) предварительно используем выражение для АПВ р(хк | zx ) с последующей соответствующей заменой переменных.
Известно [5], что АПВ информационного параметра х для к-го момента времени р(хк | zx) определяется выражением
р(ч 14) =
I Р(хк-1 I z *)’ Р(хк I xk-)dxk- ■ p(zk I хк) (2)
h ¿-Ь
+00 +00
где к = ^ ^ р(Хк~1′ 2*~1>)’ Р<уЧ ‘ хк-№хк-1 х
хР(2к ч)<Лхк-
Условная плотность вероятности р(хк хк_х) в правой части этой формулы может быть получена из исходного уравнения объекта при известном виде плотности распределения вероятности значений шума п (в предположении их взаимной статистической независимости): р{хк хк_х) = ц{хк — /(хк_.
Аналогичным образом из уравнения наблюдения можно определить и входящую в (2) функцию правдоподобия: р(гк хк) = — х(с, хк)) .
Так как АПВ р(хк_хгх ‘) в правой части равенства (2) является известной функцией (определенной на предыдущем шаге), рекуррентный алгоритм определения АПВ переменной состояния для к-го момента времени при наличии дискретных отсчетов сигнала
наблюдения zх принимает вид
Р(xk I zl ) =
I p(xk-i1 z kxk~f (xk-i))dxk-i
h (c)
,g(zk ~X(c>xk))
h (c)
(3)
где
к (с) = | | р(хк_хгх~ )-д(хк — ¡{хк_х))йхк_х х
—оо —оо
-Х(с-хк))Лхк-
Производя соответствующую замену переменных в (3) и обозначив критериальную функцию через Г1(с), критерий (1) представим в следующем компактном виде:
J = mmQ(c), (4)
где
Q(с) = j р(сгк +xkzx )dak =
(5)
i р(хк-\z l)-q(iCTk+xk)-f(xk-))dxk-
h (c)
g(zk -Х(с,(гк +xk)) ‘ *
h (c)
da
k-
Здесь важно отметить, что в общем случае решения поставленной задачи оценка переменной состояния
хк, входящая в (5), представляет собой некоторый функционал (оператор) Ь от апостериорной плотности распределения переменной состояния, т.е.
хк =Ь^{хк ) , и следовательно, в силу выражения (3) является нелинейной функцией от искомого пара-
метра с : Хк=и (с).
Тогда выражение критериальной функции в (4) окончательно можно представить в следующем обобщенном виде: £2(с) =
i р(хк-11z 1)-чКРк+иf(xk-)hxk-
-со_
*
h (c)
*
h (с)
der i-
(6)
c
Идентификация параметра, удовлетворяющего критерию (4), предполагает минимизацию критериальной функции (6). Для этой цели в зависимости от конкретного вида получаемой функции (Л(с) можно использовать известные и широко применяемые методы оптимизации: градиентный, Ньютона, сопряженных направлений, различные прямые методы и прочие, выбор которых определяется особенностями исследуемого объекта и его наблюдателя.
Для иллюстрации эффективности использования предложенного подхода рассмотрим пример.
Стохастический дискретный объект задан разностным уравнением — + п. Х| = 3 . где и -белый гауссовский шум с нулевым средним и дисперсией Б„ = 0,01.
Наблюдение переменных состояния в дискретном времени осуществляется измерителем, описываемым уравнением = с ■ хк + м>, где с — неизвестный искомый параметр наблюдателя (для рассматриваемого далее модельного примера выберем исходное значение искомого параметра с— 2): — белый гауссовский шум с нулевым средним и дисперсией £>„, = 0,35.
Априорную плотность вероятности для первой итерации алгоритма (к=2) выберем нормальной с дисперсией £>о =1,5 и математическим ожиданием 2,5. При этом интересно отметить, что отклонения среднего значения априорной плотности от начального значения переменной состояния не оказывают в дальнейшем существенного влияния на качество процедуры идентификации (алгоритм идентификации к ним устойчив).
Для определения текущего значения оценки переменной состояния объекта был использован оптимальный фильтр Калмана [5], который в рассматри-
ваемом случае имеет вид
+ K
k
Rk =
zk-c-xk-1
Xk=U{c)= =xk- +
Ri
x =2.5 : K,.= с
D ,
2 А
iНе можете найти то, что вам нужно? Попробуйте сервис подбора литературы.
Rk-1 +Dn Dw
■ R = 1,5
Определение оценки искомого параметра с на очередном шаге алгоритма осуществлялось, исходя из условия, определяемого выбранным критерием J, и предварительного задания границ допустимого интервала изменения текущей ошибки наблюдения (<тП1П1 =-1,5, °»пих = )- а также замены бесконечных пределов интегрирования по переменной состояния х на конечные значения, удовлетворяющие точностным требованиям к алгоритму оценки (хпл п = 0, х11ИХ = 5 ).
На рисунке представлена полученная в результате моделирования зависимость критериальной функции П(с) от искомого параметра наблюдателя на А-м шаге алгоритма (к=200).
Интегралы, входящие в (5), определялись численно с использованием квадратурных формул с шагом Дсг = Ат = 0,02 .
Как показали результаты моделирования, вид приведенной на рисунке зависимости является характерным для критериальных функций, получаемых на различных итерациях алгоритма (5). Здесь важно отметить, что, являясь многоэкстремальными, критериальные функции на различных шагах алгоритма (рисунок) принимают свои наименьшие значения в районе истинного значения искомого параметра с = 2 .
О(с) 2,2
3,0
2,8
2,6
2,4
2,2
2,0
0,5
1,0
1,5
2,0
2,5
3,0 С
Зависимость критериальной функции от искомого параметра (к=200)
Для минимизации критериальной функции на очередном шаге алгоритма, т.е. для однозначного определения численного значения текущей оценки искомого параметра, целесообразно, задав некоторый интервал возможных значений параметра с (в примере был выбран интервал 0 < с < 8). воспользоваться одним из методов прямой минимизации. В данном случае использовался модифицированный симплексный метод Бокса прямой минимизации Нелдера-Мида, обладающий достаточной вычислительной эффективностью и удобной программной реализацией [6].
Результаты компьютерного моделирования процедуры нелинейной параметрической идентификации показали, что при выборе количества дискретных значений сигнала наблюдения т>300 отклонение оценки параметра наблюдателя с от его истинного значения с=2 не превышает 8 % от его величины.
Таким образом, результаты проведенных исследований подтверждают принципиальную возможность эффективной реализации метода нелинейной параметрической идентификации с использованием критерия минимума АПВ текущей ошибки оценивания.
Полученное выше выражение (6) определяет общий вид алгоритма нелинейной параметрической идентификации, обладающего рядом принципиально новых свойств. К их числу следует отнести: более высокий по сравнению с традиционными методами уровень потенциальной точности процесса идентификации за счет использования обобщенных вероятностных критериев, зависящих в общем случае нелинейно от апостериорной плотности распределения вектора состояния и позволяющих охватить самый широкий класс условий оптимальности по точности; инвариантность к виду плотности распределения вероятности шума как объекта, так и наблюдателя; возможность применения метода для нелинейных объек-
1
1
тов и наблюдателей, в том числе при нелинейной зависимости функции наблюдения от параметра.
Таким образом, предложенный метод нелинейной параметрической идентификации на основе обобщенных вероятностных критериев может быть весьма эффективно использован в самых различных областях связи, управления, метрологии и т.д.
Литература
1. Гроп Д. Методы идентификации систем. М., 1979.
2. Петров Б.Н. и др. Теория моделей в процессах управления. М., 1978.
3. Справочник по теории автоматического управления
/ Под ред. А. Красовского. М., 1987.
4. Хуторцев В.В., Соколов С.В., Шевчук П.С. Современные принципы управления и фильтрации в стохастических системах. М., 2001.
5. Тихонов В.И., Харисов В.Н. Статистический анализ и синтез радиотехнических устройств и систем. М., 1991.
6. Bunday B.D. Basic Optimization Methods. L., 1984.
Поступила в редакцию_14 ноября 2007 г.
1)
В системе связи
все ошибки одинаково нежелательны.
2)
Чем реже
передается какое-либо сообщение, тем это сообщение является более неожиданным
для получателя. В этой ситуации считается, что пропустить редкое сообщение
очень не желательно.
В соответствии с этим, 2 алгоритма.
Оказывается, что в первом случае, когда все ошибки одинаково нежелательны,
алгоритм обеспечит минимальную полную вероятность ошибки (минимальная
среднестатистическая вероятность ошибки). Второй алгоритм минимизирует
среднеарифметическую вероятность ошибки.
Для таких двух матриц риска
существует 2 названия критериев оптимальности:
1)
Критерий
минимальной средней вероятности ошибки (дальше узнаем, что для этого же
критерия существуют и другие названия, которые важны для профессионалов;
наиболее распространенное название — критерий максимальной апостериорной
вероятности (MAP-алгоритм)).
2)
Штраф за ошибку
тем больше, чем реже сообщение передается. Этот критерий обеспечивает
минимальную среднеарифметическую вероятность ошибки. Профессиональное название:
критерий (правило) максимального правдоподобия (критерий максимума отношения
правдоподобия). (Log-MAP)
Алгоритм оптимального приема по
критерию минимума средней вероятности ошибки (Log—MAP, MAP-алгоритмы)
Итак, при простой матрице рисков
получаем следующее правило:
Вычисление апостериорной вероятности:
—
априорная вероятность передачи символа
—
условная плотность вероятности (какова вероятность у, если известно, что
произошло событие ).