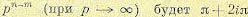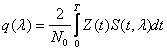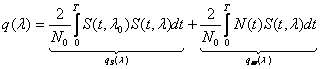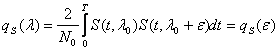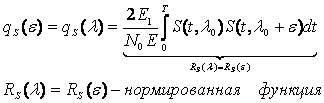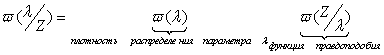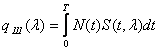Критерий минимума среднеквадратичной ошибки - Не ошибается лишь тот, кто ничего не делает!

Критерий — минимум — среднеквадратичная ошибка

Cтраница 1

Критерий минимума среднеквадратичной ошибки используется для решения более сложных задач по сравнению с задачей определения оптимальных параметров при известной структуре системы.
[1]

Идея приближения по критерию минимума среднеквадратичной ошибки, как уже указывалось, не единственна.
[2]

Тх корректирующего устройства по критерию минимума среднеквадратичной ошибки, если полезный сигнал и помеха независимы и приложены к одной точке системы.
[3]

Первое из этих условий удовлетворялось и при синтезе по критерию минимума среднеквадратичной ошибки.
[4]

Адекватность полученной модели и необходимость ее коррекции оценивают чаще всего по критерию минимума среднеквадратичной ошибки. Этот метод наиболее целесообразен.
[5]

Причем объем вычислений может быть значительно уменьшен за счет незначительного ухудшения качества, фильтрации по критерию минимума среднеквадратичной ошибки.
[6]

В большинстве практически встречающихся случаев представляется возможным, хотя бы в первом приближении, рассматривать процессы изменения технологических величин или других производственных показателей как стационарные случайные функции с нормальным распределением. Поэтому обычно критерий минимума среднеквадратичной ошибки является наиболее приемлемым в качестве критерия наилучшего предсказания в большинстве рассматриваемых задач управления.
[7]

Кроме того, по критерию минимума среднеквадратичной ошибки определяются оптимальная структура и передаточная функция замкнутой системы, обеспечивающие минимальную величину погрешности.
[8]

Анализ и синтез нелинейных систем с неизвестной структурой предлагается проводить с помощью многопеременных прямоугольных функций. Практически реализуемый алгоритм с применением этих функций получен на основе критерия минимума среднеквадратичной ошибки. Алгоритм применим при входных стационарных сигналах с произвольной плотностью распределения вероятностей.
[9]

Задача заключается в оценке значений, к-рые реализация рассматриваемого процесса ( или нек-рых его параметров, таких, как ср. Здесь в большинстве случаев определяется инвариантный во времени линейный реализуемый фильтр, оптимизирующий оценку по критерию минимума среднеквадратичной ошибки. Возможны и часто желательны др. критерии, но указанный критерий отличается математич. Для решения задач такого рода часто применяется теория Винера — Колмогорова. В этой теории предполагается, что сигнал S ( t) характеризуется только статистич. Мешающий шум N ( t) представляет также чисто случайный процесс, комбинируется с сигналом аддитивно и может быть с ним связан статистически. Далее предполагается, что накопление и обработка данных совершаются только над прошлым процессов на входе, к-рые считаются стационарными в широком смысле и имеющими положительно определенные ковариант-ные ф-ции. Кроме того, в большинстве случаев реализуются оптимальные линейные фильтры, к-рые не только реализуемы, но также и инвариантны во времени. При этих условиях импульсная переходная ф-ция линейного фильтра определяется из интегр.
[10]

Задача заключается в оценке значений, к-рые реализация рассматриваемого процесса ( или нек-рых его параметров, таких, как ср. Здесь в большинство случаев определяется инвариантный во времени линейный реализуемый фильтр, оптимизирующий оценку по критерию минимума среднеквадратичной ошибки. Возможны и часто желательны др. критерии, но указанный критерий отличается математич. Для решения задач такого рода часто применяется теория Винера — Колмогорова. В этой теории предполагается, что сигнал S ( t) характеризуется только статпстич. Мешающий шум N ( t) представляет также чисто случайный процесс, комбинируется с сигналом аддитивно и может быть с ним связан статистически. Далее предполагается, что накопление и обработка данных совершаются только над прошлым процессов па входе, к-рые считаются стационарными в широком смысле и имеющими положительно определенные ковариант-ные ф-ции. Кроме того, в большинстве случаев реализуются оптимальные линейные фильтры, к-рые не только реализуемы, но также и инвариантны во времени. При этих условиях импульсная переходная ф-ция линейного фильтра определяется из интегр.
[11]

После определения среднеквадратичной ошибки необходимо обеспечить минимальное значение ее. Наиболее просто задача решается путем минимизации среднеквадратичной ошибки по тому или иному параметру системы при заданных воздействиях. В качестве параметров, которые желательно сделать оптимальными на основе критерия минимума среднеквадратичной ошибки, могут рассматриваться различные постоянные, имеющие большое значение для определения динамических свойств системы.
[12]

Страницы:

Источник

Анализ систем на основе критерия минимума среднеквадратичной ошибки [c.189]

Если ковариационные функции процессов Х( ) и У(/) известны точно, то можно воспользоваться винеровским критерием минимума среднеквадратичной ошибки Этот критерий утверждает, что функция /г(и) должна быть выбрана так, чтобы минимизировать среднеквадратичную ошибку шумовой компоненты, т е [c.190]

Синтез следящих систем. Одно из первых инженерных применений анализа на основе критерия минимума среднеквадратичной ошибки было сделано при синтезировании следящих систем для зенитных орудий и в радиолокационных следящих системах [5] Например, от радиолокационной следящей системы требуется, чтобы она следила за самолетом несмотря на возмущения отра- [c.189]

Другое применение критерий минимума среднеквадратичной ошибки находит в задаче об идентификации системы В этом случае в распоряжении имеются входной сигнал и соответствующий ему выходной сигнал от некоторой системы, требуется вывести линейное приближение к этой системе для дальнейшего его использования при управлении или моделировании Предположим, например, что система представляет собой черный ящик (рис 5 7). Если вход является реализацией случайного процесса Х 1), то выход можно рассматривать как реализацию случайного процесса У(0< где [c.190]

Оптимальное в любом смысле корреляционное окно, например (7 2 3), будет зависеть от неизвестного спектра Гхх(/). Этот недостаток свойствен не только спектральному анализу Вообще говоря, справедливо правило, согласно которому наилучший план действий должен опираться на некоторые представления об истинном положении вещей Следовательно, очень валено проводить четкое различие между планированием спектрального анализа до сбора данных и самим анализом данных, после того как они собраны Мы хотели бы использовать критерии минимума среднеквадратичной ошибки или какой-нибудь аналогичный критерий до проведения спектрального анализа, чтобы решить, например, какой длины нужно взять запись Но после того как данные собраны, могло бы оказаться, что наши представления относительно Гхх (/) были абсолютно неправильны [c.26]

Если плотность вероятности ге ([х у) симметрична относительно среднего значения гпг [х у и унимодальна (т. е. монотонно невозрастающая функция [х — /П] [х у ), то байесовская оценка (5.18) совпадает с оценкой по критерию максимума апостериорной плотности вероятности. В этом случае функция С (х) не должна быть обязательно выпуклой, а лишь монотонно неубывающей функцией х (см. приложение С). Так как нормальная плотность вероятности унимодальна, то всегда, когда плотность вероятности ге ([х I у) нормальна, оценка по максимуму апостериорной плотности вероятности совпадает с широким классом байесовских оценок, который включает оценки по минимуму среднеквадратичной ошибки (или минимуму дисперсии). [c.158]

Источник

From Wikipedia, the free encyclopedia

In statistics, the mean squared error (MSE)^[1] or mean squared deviation (MSD) of an estimator (of a procedure for estimating an unobserved quantity) measures the average of the squares of the errors—that is, the average squared difference between the estimated values and the actual value. MSE is a risk function, corresponding to the expected value of the squared error loss.^[2] The fact that MSE is almost always strictly positive (and not zero) is because of randomness or because the estimator does not account for information that could produce a more accurate estimate.^[3] In machine learning, specifically empirical risk minimization, MSE may refer to the empirical risk (the average loss on an observed data set), as an estimate of the true MSE (the true risk: the average loss on the actual population distribution).

The MSE is a measure of the quality of an estimator. As it is derived from the square of Euclidean distance, it is always a positive value that decreases as the error approaches zero.

The MSE is the second moment (about the origin) of the error, and thus incorporates both the variance of the estimator (how widely spread the estimates are from one data sample to another) and its bias (how far off the average estimated value is from the true value).^{[citation needed]} For an unbiased estimator, the MSE is the variance of the estimator. Like the variance, MSE has the same units of measurement as the square of the quantity being estimated. In an analogy to standard deviation, taking the square root of MSE yields the root-mean-square error or root-mean-square deviation (RMSE or RMSD), which has the same units as the quantity being estimated; for an unbiased estimator, the RMSE is the square root of the variance, known as the standard error.

Definition and basic properties[edit]

The MSE either assesses the quality of a predictor (i.e., a function mapping arbitrary inputs to a sample of values of some random variable), or of an estimator (i.e., a mathematical function mapping a sample of data to an estimate of a parameter of the population from which the data is sampled). The definition of an MSE differs according to whether one is describing a predictor or an estimator.

Predictor[edit]

If a vector of predictions is generated from a sample of data points on all variables, and is the vector of observed values of the variable being predicted, with hat{Y} being the predicted values (e.g. as from a least-squares fit), then the within-sample MSE of the predictor is computed as

${displaystyle operatorname {MSE} ={frac {1}{n}}sum _{i=1}^{n}left(Y_{i}-{hat {Y_{i}}}right)^{2}.}$

In other words, the MSE is the mean ${textstyle left({frac {1}{n}}sum _{i=1}^{n}right)}$ of the squares of the errors ${textstyle left(Y_{i}-{hat {Y_{i}}}right)^{2}}$ . This is an easily computable quantity for a particular sample (and hence is sample-dependent).

In matrix notation,

${displaystyle operatorname {MSE} ={frac {1}{n}}sum _{i=1}^{n}(e_{i})^{2}={frac {1}{n}}mathbf {e} ^{mathsf {T}}mathbf {e} }$

where $e_{i}$ is ${displaystyle (Y_{i}-{hat {Y_{i}}})}$ and is the column vector.

The MSE can also be computed on q data points that were not used in estimating the model, either because they were held back for this purpose, or because these data have been newly obtained. Within this process, known as statistical learning, the MSE is often called the test MSE,^[4] and is computed as

${displaystyle operatorname {MSE} ={frac {1}{q}}sum _{i=n+1}^{n+q}left(Y_{i}-{hat {Y_{i}}}right)^{2}.}$

Estimator[edit]

The MSE of an estimator with respect to an unknown parameter theta is defined as^[1]

${displaystyle operatorname {MSE} ({hat {theta }})=operatorname {E} _{theta }left[({hat {theta }}-theta )^{2}right].}$

This definition depends on the unknown parameter, but the MSE is a priori a property of an estimator. The MSE could be a function of unknown parameters, in which case any estimator of the MSE based on estimates of these parameters would be a function of the data (and thus a random variable). If the estimator is derived as a sample statistic and is used to estimate some population parameter, then the expectation is with respect to the sampling distribution of the sample statistic.

The MSE can be written as the sum of the variance of the estimator and the squared bias of the estimator, providing a useful way to calculate the MSE and implying that in the case of unbiased estimators, the MSE and variance are equivalent.^[5]

${displaystyle operatorname {MSE} ({hat {theta }})=operatorname {Var} _{theta }({hat {theta }})+operatorname {Bias} ({hat {theta }},theta )^{2}.}$

Proof of variance and bias relationship[edit]

${displaystyle {begin{aligned}operatorname {MSE} ({hat {theta }})&=operatorname {E} _{theta }left[({hat {theta }}-theta )^{2}right]\&=operatorname {E} _{theta }left[left({hat {theta }}-operatorname {E} _{theta }[{hat {theta }}]+operatorname {E} _{theta }[{hat {theta }}]-theta right)^{2}right]\&=operatorname {E} _{theta }left[left({hat {theta }}-operatorname {E} _{theta }[{hat {theta }}]right)^{2}+2left({hat {theta }}-operatorname {E} _{theta }[{hat {theta }}]right)left(operatorname {E} _{theta }[{hat {theta }}]-theta right)+left(operatorname {E} _{theta }[{hat {theta }}]-theta right)^{2}right]\&=operatorname {E} _{theta }left[left({hat {theta }}-operatorname {E} _{theta }[{hat {theta }}]right)^{2}right]+operatorname {E} _{theta }left[2left({hat {theta }}-operatorname {E} _{theta }[{hat {theta }}]right)left(operatorname {E} _{theta }[{hat {theta }}]-theta right)right]+operatorname {E} _{theta }left[left(operatorname {E} _{theta }[{hat {theta }}]-theta right)^{2}right]\&=operatorname {E} _{theta }left[left({hat {theta }}-operatorname {E} _{theta }[{hat {theta }}]right)^{2}right]+2left(operatorname {E} _{theta }[{hat {theta }}]-theta right)operatorname {E} _{theta }left[{hat {theta }}-operatorname {E} _{theta }[{hat {theta }}]right]+left(operatorname {E} _{theta }[{hat {theta }}]-theta right)^{2}&&operatorname {E} _{theta }[{hat {theta }}]-theta ={text{const.}}\&=operatorname {E} _{theta }left[left({hat {theta }}-operatorname {E} _{theta }[{hat {theta }}]right)^{2}right]+2left(operatorname {E} _{theta }[{hat {theta }}]-theta right)left(operatorname {E} _{theta }[{hat {theta }}]-operatorname {E} _{theta }[{hat {theta }}]right)+left(operatorname {E} _{theta }[{hat {theta }}]-theta right)^{2}&&operatorname {E} _{theta }[{hat {theta }}]={text{const.}}\&=operatorname {E} _{theta }left[left({hat {theta }}-operatorname {E} _{theta }[{hat {theta }}]right)^{2}right]+left(operatorname {E} _{theta }[{hat {theta }}]-theta right)^{2}\&=operatorname {Var} _{theta }({hat {theta }})+operatorname {Bias} _{theta }({hat {theta }},theta )^{2}end{aligned}}}$

An even shorter proof can be achieved using the well-known formula that for a random variable , ${textstyle mathbb {E} (X^{2})=operatorname {Var} (X)+(mathbb {E} (X))^{2}}$ . By substituting with, , we have

${displaystyle {begin{aligned}operatorname {MSE} ({hat {theta }})&=mathbb {E} [({hat {theta }}-theta )^{2}]\&=operatorname {Var} ({hat {theta }}-theta )+(mathbb {E} [{hat {theta }}-theta ])^{2}\&=operatorname {Var} ({hat {theta }})+operatorname {Bias} ^{2}({hat {theta }})end{aligned}}}$

But in real modeling case, MSE could be described as the addition of model variance, model bias, and irreducible uncertainty (see Bias–variance tradeoff). According to the relationship, the MSE of the estimators could be simply used for the efficiency comparison, which includes the information of estimator variance and bias. This is called MSE criterion.

In regression[edit]

In regression analysis, plotting is a more natural way to view the overall trend of the whole data. The mean of the distance from each point to the predicted regression model can be calculated, and shown as the mean squared error. The squaring is critical to reduce the complexity with negative signs. To minimize MSE, the model could be more accurate, which would mean the model is closer to actual data. One example of a linear regression using this method is the least squares method—which evaluates appropriateness of linear regression model to model bivariate dataset,^[6] but whose limitation is related to known distribution of the data.

The term mean squared error is sometimes used to refer to the unbiased estimate of error variance: the residual sum of squares divided by the number of degrees of freedom. This definition for a known, computed quantity differs from the above definition for the computed MSE of a predictor, in that a different denominator is used. The denominator is the sample size reduced by the number of model parameters estimated from the same data, (n−p) for p regressors or (n−p−1) if an intercept is used (see errors and residuals in statistics for more details).^[7] Although the MSE (as defined in this article) is not an unbiased estimator of the error variance, it is consistent, given the consistency of the predictor.

In regression analysis, «mean squared error», often referred to as mean squared prediction error or «out-of-sample mean squared error», can also refer to the mean value of the squared deviations of the predictions from the true values, over an out-of-sample test space, generated by a model estimated over a particular sample space. This also is a known, computed quantity, and it varies by sample and by out-of-sample test space.

Examples[edit]

Mean[edit]

Suppose we have a random sample of size from a population, $X_{1},dots ,X_{n}$ . Suppose the sample units were chosen with replacement. That is, the units are selected one at a time, and previously selected units are still eligible for selection for all draws. The usual estimator for the is the sample average

$overline{X}=frac{1}{n}sum_{i=1}^n X_i$

which has an expected value equal to the true mean (so it is unbiased) and a mean squared error of

${displaystyle operatorname {MSE} left({overline {X}}right)=operatorname {E} left[left({overline {X}}-mu right)^{2}right]=left({frac {sigma }{sqrt {n}}}right)^{2}={frac {sigma ^{2}}{n}}}$

where $sigma ^{2}$ is the population variance.

For a Gaussian distribution, this is the best unbiased estimator (i.e., one with the lowest MSE among all unbiased estimators), but not, say, for a uniform distribution.

Variance[edit]

The usual estimator for the variance is the corrected sample variance:

${displaystyle S_{n-1}^{2}={frac {1}{n-1}}sum _{i=1}^{n}left(X_{i}-{overline {X}}right)^{2}={frac {1}{n-1}}left(sum _{i=1}^{n}X_{i}^{2}-n{overline {X}}^{2}right).}$

This is unbiased (its expected value is $sigma ^{2}$ ), hence also called the unbiased sample variance, and its MSE is^[8]

${displaystyle operatorname {MSE} (S_{n-1}^{2})={frac {1}{n}}left(mu _{4}-{frac {n-3}{n-1}}sigma ^{4}right)={frac {1}{n}}left(gamma _{2}+{frac {2n}{n-1}}right)sigma ^{4},}$

where $mu _{4}$ is the fourth central moment of the distribution or population, and is the excess kurtosis.

However, one can use other estimators for $sigma ^{2}$ which are proportional to $S^2_{n-1}$ , and an appropriate choice can always give a lower mean squared error. If we define

${displaystyle S_{a}^{2}={frac {n-1}{a}}S_{n-1}^{2}={frac {1}{a}}sum _{i=1}^{n}left(X_{i}-{overline {X}},right)^{2}}$

then we calculate:

${displaystyle {begin{aligned}operatorname {MSE} (S_{a}^{2})&=operatorname {E} left[left({frac {n-1}{a}}S_{n-1}^{2}-sigma ^{2}right)^{2}right]\&=operatorname {E} left[{frac {(n-1)^{2}}{a^{2}}}S_{n-1}^{4}-2left({frac {n-1}{a}}S_{n-1}^{2}right)sigma ^{2}+sigma ^{4}right]\&={frac {(n-1)^{2}}{a^{2}}}operatorname {E} left[S_{n-1}^{4}right]-2left({frac {n-1}{a}}right)operatorname {E} left[S_{n-1}^{2}right]sigma ^{2}+sigma ^{4}\&={frac {(n-1)^{2}}{a^{2}}}operatorname {E} left[S_{n-1}^{4}right]-2left({frac {n-1}{a}}right)sigma ^{4}+sigma ^{4}&&operatorname {E} left[S_{n-1}^{2}right]=sigma ^{2}\&={frac {(n-1)^{2}}{a^{2}}}left({frac {gamma _{2}}{n}}+{frac {n+1}{n-1}}right)sigma ^{4}-2left({frac {n-1}{a}}right)sigma ^{4}+sigma ^{4}&&operatorname {E} left[S_{n-1}^{4}right]=operatorname {MSE} (S_{n-1}^{2})+sigma ^{4}\&={frac {n-1}{na^{2}}}left((n-1)gamma _{2}+n^{2}+nright)sigma ^{4}-2left({frac {n-1}{a}}right)sigma ^{4}+sigma ^{4}end{aligned}}}$

This is minimized when

$a=frac{(n-1)gamma_2+n^2+n}{n} = n+1+frac{n-1}{n}gamma_2.$

For a Gaussian distribution, where , this means that the MSE is minimized when dividing the sum by a=n+1 . The minimum excess kurtosis is ,^[a] which is achieved by a Bernoulli distribution with p = 1/2 (a coin flip), and the MSE is minimized for ${displaystyle a=n-1+{tfrac {2}{n}}.}$ Hence regardless of the kurtosis, we get a «better» estimate (in the sense of having a lower MSE) by scaling down the unbiased estimator a little bit; this is a simple example of a shrinkage estimator: one «shrinks» the estimator towards zero (scales down the unbiased estimator).

Further, while the corrected sample variance is the best unbiased estimator (minimum mean squared error among unbiased estimators) of variance for Gaussian distributions, if the distribution is not Gaussian, then even among unbiased estimators, the best unbiased estimator of the variance may not be $S^2_{n-1}.$

Gaussian distribution[edit]

The following table gives several estimators of the true parameters of the population, μ and σ², for the Gaussian case.^[9]

True value	Estimator	Mean squared error
	= the unbiased estimator of the population mean, $overline{X}=frac{1}{n}sum_{i=1}^n(X_i)$	$operatorname{MSE}(overline{X})=operatorname{E}((overline{X}-mu)^2)=left(frac{sigma}{sqrt{n}}right)^2$
${displaystyle theta =sigma ^{2}}$	= the unbiased estimator of the population variance, $S^2_{n-1} = frac{1}{n-1}sum_{i=1}^nleft(X_i-overline{X},right)^2$	$operatorname{MSE}(S^2_{n-1})=operatorname{E}((S^2_{n-1}-sigma^2)^2)=frac{2}{n - 1}sigma^4$
${displaystyle theta =sigma ^{2}}$	= the biased estimator of the population variance, $S^2_{n} = frac{1}{n}sum_{i=1}^nleft(X_i-overline{X},right)^2$	$operatorname{MSE}(S^2_{n})=operatorname{E}((S^2_{n}-sigma^2)^2)=frac{2n - 1}{n^2}sigma^4$
${displaystyle theta =sigma ^{2}}$	= the biased estimator of the population variance, $S^2_{n+1} = frac{1}{n+1}sum_{i=1}^nleft(X_i-overline{X},right)^2$	$operatorname{MSE}(S^2_{n+1})=operatorname{E}((S^2_{n+1}-sigma^2)^2)=frac{2}{n + 1}sigma^4$

Interpretation[edit]

An MSE of zero, meaning that the estimator predicts observations of the parameter theta with perfect accuracy, is ideal (but typically not possible).

Values of MSE may be used for comparative purposes. Two or more statistical models may be compared using their MSEs—as a measure of how well they explain a given set of observations: An unbiased estimator (estimated from a statistical model) with the smallest variance among all unbiased estimators is the best unbiased estimator or MVUE (Minimum-Variance Unbiased Estimator).

Both analysis of variance and linear regression techniques estimate the MSE as part of the analysis and use the estimated MSE to determine the statistical significance of the factors or predictors under study. The goal of experimental design is to construct experiments in such a way that when the observations are analyzed, the MSE is close to zero relative to the magnitude of at least one of the estimated treatment effects.

In one-way analysis of variance, MSE can be calculated by the division of the sum of squared errors and the degree of freedom. Also, the f-value is the ratio of the mean squared treatment and the MSE.

MSE is also used in several stepwise regression techniques as part of the determination as to how many predictors from a candidate set to include in a model for a given set of observations.

Applications[edit]

Minimizing MSE is a key criterion in selecting estimators: see minimum mean-square error. Among unbiased estimators, minimizing the MSE is equivalent to minimizing the variance, and the estimator that does this is the minimum variance unbiased estimator. However, a biased estimator may have lower MSE; see estimator bias.
In statistical modelling the MSE can represent the difference between the actual observations and the observation values predicted by the model. In this context, it is used to determine the extent to which the model fits the data as well as whether removing some explanatory variables is possible without significantly harming the model’s predictive ability.
In forecasting and prediction, the Brier score is a measure of forecast skill based on MSE.

Loss function[edit]

Squared error loss is one of the most widely used loss functions in statistics^{[citation needed]}, though its widespread use stems more from mathematical convenience than considerations of actual loss in applications. Carl Friedrich Gauss, who introduced the use of mean squared error, was aware of its arbitrariness and was in agreement with objections to it on these grounds.^[3] The mathematical benefits of mean squared error are particularly evident in its use at analyzing the performance of linear regression, as it allows one to partition the variation in a dataset into variation explained by the model and variation explained by randomness.

Criticism[edit]

The use of mean squared error without question has been criticized by the decision theorist James Berger. Mean squared error is the negative of the expected value of one specific utility function, the quadratic utility function, which may not be the appropriate utility function to use under a given set of circumstances. There are, however, some scenarios where mean squared error can serve as a good approximation to a loss function occurring naturally in an application.^[10]

Like variance, mean squared error has the disadvantage of heavily weighting outliers.^[11] This is a result of the squaring of each term, which effectively weights large errors more heavily than small ones. This property, undesirable in many applications, has led researchers to use alternatives such as the mean absolute error, or those based on the median.

Notes[edit]

^ This can be proved by Jensen’s inequality as follows. The fourth central moment is an upper bound for the square of variance, so that the least value for their ratio is one, therefore, the least value for the excess kurtosis is −2, achieved, for instance, by a Bernoulli with p=1/2.

References[edit]

^ ^a ^b «Mean Squared Error (MSE)». www.probabilitycourse.com. Retrieved 2020-09-12.
^ Bickel, Peter J.; Doksum, Kjell A. (2015). Mathematical Statistics: Basic Ideas and Selected Topics. Vol. I (Second ed.). p. 20. If we use quadratic loss, our risk function is called the mean squared error (MSE) …
^ ^a ^b Lehmann, E. L.; Casella, George (1998). Theory of Point Estimation (2nd ed.). New York: Springer. ISBN 978-0-387-98502-2. MR 1639875.
^ Gareth, James; Witten, Daniela; Hastie, Trevor; Tibshirani, Rob (2021). An Introduction to Statistical Learning: with Applications in R. Springer. ISBN 978-1071614174.
^ Wackerly, Dennis; Mendenhall, William; Scheaffer, Richard L. (2008). Mathematical Statistics with Applications (7 ed.). Belmont, CA, USA: Thomson Higher Education. ISBN 978-0-495-38508-0.
^ A modern introduction to probability and statistics : understanding why and how. Dekking, Michel, 1946-. London: Springer. 2005. ISBN 978-1-85233-896-1. OCLC 262680588.{{cite book}}: CS1 maint: others (link)
^ Steel, R.G.D, and Torrie, J. H., Principles and Procedures of Statistics with Special Reference to the Biological Sciences., McGraw Hill, 1960, page 288.
^ Mood, A.; Graybill, F.; Boes, D. (1974). Introduction to the Theory of Statistics (3rd ed.). McGraw-Hill. p. 229.
^ DeGroot, Morris H. (1980). Probability and Statistics (2nd ed.). Addison-Wesley.
^ Berger, James O. (1985). «2.4.2 Certain Standard Loss Functions». Statistical Decision Theory and Bayesian Analysis (2nd ed.). New York: Springer-Verlag. p. 60. ISBN 978-0-387-96098-2. MR 0804611.
^ Bermejo, Sergio; Cabestany, Joan (2001). «Oriented principal component analysis for large margin classifiers». Neural Networks. 14 (10): 1447–1461. doi:10.1016/S0893-6080(01)00106-X. PMID 11771723.

Источник

достаточно простом выражении для дисперсии это может быть определено непосредственным дифференцированием и приравниванием нулю частных производных.

В более сложных случаях приходится искать минимум дисперсии путем числового задания интересующих параметров и построения соответствующих графиков.

Другая постановка задачи при расчете по критерию минимума среднеквадратичной ошибки заключается в том, что ставится вопрос о нахождении оптимальной структуры и значений параметров автоматической системы, при которых обеспечивается получение теоретического минимума среднеквадратичной ошибки при заданных вероятностных характеристиках полезного сигнала и помехи. Эта задача будет решена, если найти, например, передаточную функцию

замкнутой системы 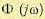, при которой обеспечивается получение теоретического минимума среднеквадратичной ошибки.

Задача относится к категории вариационных задач. Приведем здесь некоторые результаты ее решения [120] для случая, когда полезный сигнал g (t) и помеха f (I) представляют собой центрированные стационарные случайные процессы, приложенные на входе системы. Перед системой ставится задача преобразовывать входной сигнал g (t) так, чтобы на ее выходе воспроизводилась величина h (t), связанная с g (t) некоторой формулой преобразования

тде Н (р) — преобразующий оператор.

Так, например, при 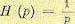получится задача интегрирования входного сигнала, при Н(р)=р — задача дифференцирования, при H(р) = 1 — задача простого воспроизведения со

сглаживанием помехи (обычная следящая система при наличии помех), при 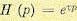— статистическое упреждение (предсказание) и т. п.

На основании изложенного ошибку системы можно представить в виде

(11.130)

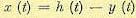
Выходная величина системы регулирования

(11.131)

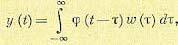
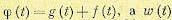
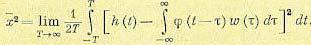
где — весовая функция замкнутой системы. Подставляя (11.130) и (11.131) в формулу (11.129), получаем

(11.132)

Задача заключается в том, чтобы найти частотную передаточную функцию замкнутой системы, связанную с весовой функцией преобразованием Фурье

(11.133)

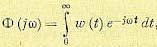
таким образом, чтобы минимизировать значение .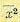

Раскроем в выражении (11.132) скобки и изменим порядок интегрирования:

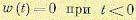
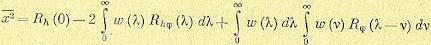
Так как в реальных системах , то нижние пределы интегрирования в (11.138) надо положить равными нулю. В результате получим

(11.139)

Из последнего выражения видно, что оптимальная весовая функция, соответствующая минимуму среднего квадрата ошибки, определяется только видом корреляционных функций полезного сигнала и помехи.

Можно показать [120], что необходимое и достаточное условие минимизации выражения (11.139), которое должно быть наложено на весовую функцию, заключается в том, чтобы она была решением интегрального уравнения Винера — Хопфа

(11.140)

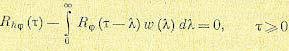
Оптимальная передаточная функция (11.133), соответствующая оптимальной весовой функции, являющейся решением уравнения (11.140), может быть представлена в виде

(11.141)

где

(11.142)

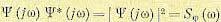
Вчастном случае, когда преобразующий оператор Н(р) = 1, т. е в так называемом случае оптимального сглаживания, имеем

Вэтом случае решение (11.141) может быть представлено в более простом виде:

(11.143)

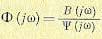
Числитель этого выражения определяется следующим образом. Рассмотрим следующее выражение:

(11.144)

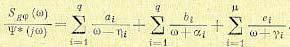
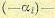
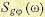
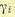
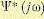
Здесь , расположенные в верхней полуплоскости, полюсы , расположенные в нижней полуплоскости, причем полюсы предполагаются простыми, а — нули . Тогда

(11.145)

При реализации в системе оптимальной передаточной функции получится теоретический минимум среднего квадрата ошибки. Этот минимум определяется выражением или, в другом виде,

(11.146)

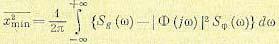
или, в другом виде,

(11.147).

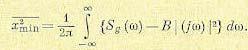
Рассмотрим иллюстративный пример. Предположим, что полезному сигналу и помехе на входе системы регулирования соответствуют спектральные плотности:

причем корреляция между ними отсутствует и 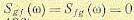. Найдем спектральную плотность, соответствующую (11.136):

Отсюда знаменатель искомой передаточной функции (11.143)

Отбросив первый член в скобках, соответствующий полюсу в нижней полуплоскости, находим числитель искомой передаточной функции (11.143):

Нахождение оптимальной передаточной функции еще не означает, что реальная автоматическая система может быть выполнена оптимальной, так как реализация ее может быть сопряжена с большими трудностями. Оптимальную передаточную функцию, за исключением простейших случаев, следует считать идеальной функцией, к которой по возможности надо стремиться при выполнении реальной автоматической системы. Теория оптимальных систем излагается в работах [26, 108, 120, 121].

ГЛАВА 12. МЕТОДЫ СИНТЕЗА СИСТЕМ АВТОМАТИЧЕСКОГО РЕГУЛИРОВАНИЯ

§ 12.1. Общие соображения

Под синтезом системы автоматического регулирования понимается направленный расчет, имеющий конечной целью отыскание рациональной структуры системы и установление оптимальных величин параметров ее отдельных звеньев. По отношению к основе синтеза в настоящее время имеются разные точки зрения.

Синтез можно трактовать как пример вариационной задачи и рассматривать такое построение системы автоматического регулирования, при котором для данных условий работы (управляющие и возмущающие воздействия, помехи, ограничения по времени работы и т. п.) обеспечивается теоретический минимум ошибки.

Синтез также можно трактовать как инженерную задачу, сводящуюся к такому построению системы автоматического регулирования, при котором обеспечивается выполнение технических требований к ней. Подразумевается, что из.многих возможных решений Инженер, проектирующий систему, будет выбирать те, которые являются оптимальными с точки зрения существующих конкретных условий и требований к габаритам, весу, простоте, надежности и т. п.

Иногда в понятие инженерного синтеза вкладывается еще более узкий смысл и рассматривается синтез, имеющий целью определение вида и параметров корректирующих средств, которые необходимо добавить к некоторой неизменяемой части системы регулирования (объект с регулятором), чтобы обеспечить требуемые динамические качества.

При инженерном синтезе системы автоматического регулирования необходимо обеспечить, во-первых, требуемую точность и, во-вторых, приемлемый характер переходных процессов.

Решение первой задачи в большинстве случаев сводится к определению требуемого общего коэффициента усиления системы и, в случае необходимости,— вида корректирующих средств, повышающих точность системы (регулирование по управляющему и возмущающему воздействиям, изодром-ные механизмы и т. п.). Эта задача может решаться при помощи определения ошибок в типовых режимах на основе тех критериев точности, которые были изложены в главе 8. Решение этой задачи, как правило, не сопряжено с трудностями принципиального или вычислительного характера, так как критерии точности достаточно просты для их практического использования. В сложных случаях можно прибегать к помощи моделирования. Решение оказывается сравнительно простым вследствие необходимости установления значений относительно небольшого числа параметров. В простейшем случае необходимо найти только общий коэффициент усиления системы.

Решение второй задачи — обеспечение приемлемых переходных процессов — оказывается почти всегда более трудным вследствие большого числа варьируемых параметров и многозначности решения задачи демпфирования системы. Поэтому существующие инженерные методы часто ограничиваются решением только второй задачи, так как их авторы считают, что обеспечение требуемой точности может быть достаточно просто сделано на основании использования существующих критериев точности и совершенствования их практически не требуется.

В настоящее время для целей синтеза систем автоматического регулирования широко используются электронные и электромеханические вычислительные машины, позволяющие производить полное или частичное моделирование проектируемой системы. При таком моделировании становится возможным наиболее полно исследовать влияние различных факторов нелинейности, зависимость параметров от времени и т. п.

Однако моделирование на вычислительных машинах не может заменить расчетных методов проектирования, которые во многих случаях позволяют исследовать вопрос в общем виде и среди многих решений найти оптимальное. Поэтому, несмотря на развитие и распространение машинных методов синтеза, теория должна располагать собственными методами, которые дополняли бы моделирование и являлись бы теоретической базой при отыскании оптимального решения.

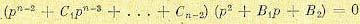
§ 12.2. Корневой метод

Наиболее простой корневой метод разработан Т. Н. Соколовым [117]. Сущность его сводится к следующему. [В соответствии с изложенным в § 12.1 рассматривается только задача

.получения приемлемых динамических качеств при заданном значении общего коэффициента усиления, т. е. последнего члена характеристического уравнения.]

Пусть имеется характеристическое уравнение системы

(12.1)

С точки зрения скорейшего затухания переходного процесса важно, чтобы вещественные части всех корней характеристического уравнения были наибольшими. Сумма вещественных частей всех корней численно равна первому коэффициенту характеристического уравнения (12.1). Поэтому при заданной величине этого коэффициента наивыгоднейшие результаты получаются при равенстве вещественных частей всех корней/ Однако расчеты и исследования построенных систем показывают, что стремление удовлетворить поставленному требованию приводит к совершенно нереальным конструктивным характеристикам отдельных звеньев. Эти расчеты и исследования показывают, что из общего числа корней характеристического уравнения всегда можно выделить два или три корня с меньшей по абсолютному значению вещественной частью, которые и определяют ход основного процесса. Остальные же корни характеризуют быстро затухающие составляющие, оказывающие влияние только на начальной стадии переходного процесса.

Примем, что основной характер переходного процесса определяется двумя корнями. Тогда уравнение (12.1) удобно представить в виде

(12.2)

Второй сомножитель (12.2) и будет определять основной характер процесса.

Для уменьшения погрешностей проектируемой системы важно, чтобы коэффициент В2 в основном множителе имел возможно большую величину. Однако чрезмерное увеличение В2 приводит к колебательному характеру переходного процесса.

Оптимальное соотношение между коэффициентами B1 и В2 определяется из условия получения затухания за один период 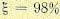, которому соответствует выражение (см. §8.6)

(12.3)

где 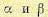— вещественная и мнимая части комплексного корня, характеризующего основной процесс. Учитывая соотношения:

(12.4)

Множитель 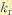определяющий соотношение между коэффициентами основного множителя характеристического уравнения, является критерием переходного режима, зависящим от выбранной степени затухания. Формула (12.4) показывает желаемое соотношение между коэффициентами характеристического уравнения, к которому надо стремиться при проектировании системы. Это должно осуществляться введением различных корректирующих средств.

Из (12.3) можно также получить требуемое соотношение между мнимой и вещественной частями корня (колебательность):

(12.5)

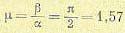
В ряде случаев для описания основного переходного процесса оказывается более целесообразным воспользоваться уравнением третьей степени

(12.6)

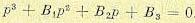
Это уравнение можно представить в виде

(12.7)

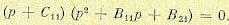
Между коэффициентами уравнений (12.6) и (12.7) имеют место соотношения:

Положим, что во втором множителе (12.7) по-прежнему

(12.8)

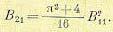
Поэтому корни характеристического уравнения (12.6) и (12.7) равны: (12.9)

(12.10)

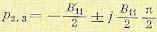
Так как вещественная часть корней должна быть возможно большей, то целесообразно задать

(12.11)

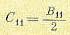
и, следовательно,

Подставив полученные значения в формулы разложения, находим зависимость между коэффициентами основного уравнения. Если В1 задано, то

Эти соотношения должны реализоваться при проектировании системы регулирования. Корни основного уравнения

Выбор уравнения для описания основной составляющей переходного процесса зависит от структурной схемы проектируемой системы.

Рассмотрим теперь связь между основной и дополнительной составляющими переходного процесса для заданного затухания ξ (8.40). Для этой цели полезно представить характеристическое уравнение (12.1) в таком виде:

(12.19)

где — произвольно выбранный среднегеометрический корень, А1, . . . , . ., Аn-1 — безразмерные коэффициенты.

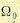
Записанное в такой форме уравнение третьей степени принимает вид

Разлагая его на множители, находим

Соотношения для коэффициентов:

(12.21)

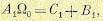
Введем коэффициент а и положим

откуда

Таким образом, безразмерные коэффициенты А1 и A2 являются функциями критерия переходного процесса &ш зависящего от. желаемой степени затухания и коэффициента разложения а, определяющего соотношение постоянных времени затухания отдельных составляющих.

Следовательно, обе составляющие переходного процесса затухают с одинаковой скоростью. Аналогичным образом можно получить выражения для коэффициентов

характеристического уравнения четвертой, пятой и более высоких степеней [117].

Синтез системы регулирования начинается с того, что для выбранной структурной схемы и введенных корректирующих средств находится характеристическое уравнение. Затем варьируются параметры основного канала регулирования и корректирующих средств таким образом, чтобы получить требуемые значения коэффициентов характеристического уравнения

(12.1) или (12.20).

Этот метод оказывается достаточно эффективным в случае сравнительно невысокой степени характеристического уравнения (n=2-4). В более сложных случаях обеспечить требуемые значения коэффициентов характеристического уравнения оказывается затруднительно, так как некоторые параметры системы и корректирующих средств могут влиять сразу на несколько коэффициентов характеристического уравнения.

Недостатком этого метода является также то, что необходимо задаваться видом корректирующих средств. Поэтому получаемое решение будет во многом зависеть от опытности проектанта.

§ 12.3. Метод корневых годографов

Качество системы регулирования с точки зрения быстродействия и запаса устойчивости может характеризоваться расположением корней числителя и знаменателя передаточной функции замкнутой системы, т. е. расположением нулей и полюсов передаточной функции (§ 8.6).

Зная эти корни, можно изобразить их расположение на комплексной плоскости корней. При расчете регулируемой системы целесообразно проследить, как меняется общая картина расположения корней при изменении отдельных параметров, например общего коэффициента усиления, постоянных времени корректирующих цепей и т. п., с целью установления оптимальных значений этих параметров.

При плавном изменении значения какого-либо параметра корни будут перемещаться на плоскости корней, прочерчивая некоторую кривую, которую будем называть корневым

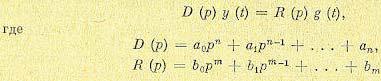
годографом или траекторией корней. Построив траектории всех корней, можно выбрать такое значение варьируемого параметра, которое соответствует наилучшему расположению корней.

Первый способ построения траекторий корней заключается в следующем. Пусть имеется дифференциальное уравнение замкнутой системы, записанное для регулируемой величины при наличии задающего воздействия (5.3):

Это уравнение записано здесь для случая равенства нулю возмущающих воздействий. Оно может быть записано также для любого возмущающего-воздействия. Это не изменит его формы и не отразится на дальнейших рассуждениях.

Передаточная функция замкнутой системы

(12.29)

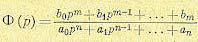
Полюсы передаточной функции, т. е. корни знаменателя, обозначим через , а

ее нули (корни числителя) —через .

Коэффициенты числителя и знаменателя (12.29) определенным образом выражены через параметры регулируемого объекта, регулятора и корректирующих устройств. Если нужно

выбрать величину какого-либо параметра 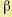(постоянная времени, коэффициент усиления и т. п.), входящего как угодно в коэффициенты (12.29), то необходимо принять некоторые постоянные

значения для всех остальных параметров, а для искомого параметра 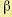задавать различные

числовые значения внутри реально возможных пределов изменения этого параметра в данной системе регулирования. Для каждого из этих вариантов необходимо затем вычислить корни числителя и знаменателя (12.29). Результаты вычислений можно свести в таблицу, на основании которой легко строятся все траектории корней.

Если нужно выбрать два или несколько параметров регулируемой системы, то такого рода вычисления нужно проделать несколько раз, меняя каждый раз один из параметров при заданных значениях всех остальных.

Вычисление корней при этом можно производить любым численным методом, возможно более простым, так как ввиду приближенности корневой оценки здесь не требуется большой точности вычислений. В настоящее время имеются электрические устройства, позволяющие строить на экране траектории корней непосредственно по заданным коэффициентам уравнения.

Из простых численных методов определения корней можно рекомендовать, например, метод последовательных делений [98].

Другой способ построения траекторий корней, разработанный Ивэнсом и Э. Г. Удерманом [128], в отличие от первого, пригодного для выбора любого параметра системы, специально приспособлен для выбора общего коэффициента усиления передаточной функции разомкнутой системы (5.10), которую запишем следующим образом:

(12.30)

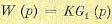
Здесь К = Кr — общий коэффициент усиления разомкнутой системы, имеющий размерность сек-r, где r — степень астатизма; G1 (р) — операторная часть передаточной функции разомкнутой системы.

Характеристическое уравнение системы может быть записано в виде

(12.31)

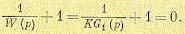
Обозначим полюсы и нули передаточной функции разомкнутой системы соответственно через 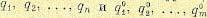. Тогда

Каждый сомножитель в выражении (12.32) можно изобразить в виде вектора на комплексной плоскости (рис. 12.1), где р — текущая точка. Обозначим длину (модуль) каждого

вектора в знаменателе (12.32) через , а в числителе — через Соответственно угол между вектором и положительным направлением оси вещественных

(аргумент) для знаменателя обозначим , а для числителя — . По правилу перемножения комплексных чисел согласно формуле (12.32) найдем, что G (р) будет представлять собой вектор с длиной г ж аргументом ф, причем

(12.33)

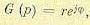
где

Траектории корней (рис. 12.1) строятся таким образом, чтобы они удовлетворяли условию (12.38). После этого по формуле (12.34) для каждой

конкретной комбинации корней можно вычислить А и величину r, а затем по формуле (12.37) — общий коэффициент усиления К.

Для упрощения построения траекторий корней используются следующие свойства. 1.При К = 0 корни характеристического уравнения замкнутой системы совпадают с

полюсами передаточной функции разомкнутой системы W (р) или G (р), так как согласно (12.31) при К = 0 имеем .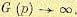

2. При корни стремятся к нулям передаточной функции разомкнутой системы, так

как при из (12.31) получаем . Но количество нулей равно m, в то время как количество корней n >m. Поэтому остальные n — m корней уходят в бесконечность, так как

еще при . Для последних n-m корней можно определить направления асимптот на основании (12.31) и (12.32). При больших имеем соответственно

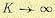
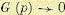
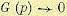
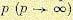
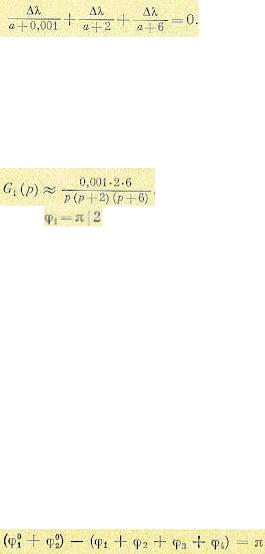
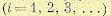
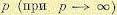
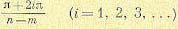
откуда аргумент комплексного числа и, значит, аргумент числа , т. е. наклон искомых асимптот, будет

(12.41)

3.На вещественной оси траектории корней представляют собой отрезки прямой, соединяющие нули и полюсы функции G (р), расположенные на этой оси. Началом траекторий на вещественной оси служит нуль, расположенный правее всех остальных.

4.Если траектория отклоняется от вещественной оси, то положение точки р = а, в которой траектория отходит от этой оси, можно оценить из того условия, что при малом отклонении 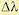, от вещественной оси приращение угла (12.35), обусловленное влиянием полюсов и нулей функции G (р), расположенных на оси влево от искомой точки, должно уничтожаться приращением этого же угла, обусловленным влиянием полюсов и нулей О (р), расположенных вправо от этой точки.

Так, например, пусть имеется функция

(12.42)

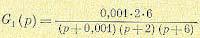
При К = 0 траектории исходят из точек (—0,001), (—2) и (—6), лежащих на вещественной

оси. Отрезки траекторий лежат между точками (—0,001) ж (—2) и между (—6) и . Применяя правило 4, можем записать

Решение этого квадратного уравнения дает .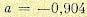

5. Положение точки, в которой траектория пересекает мнимую ось при переходе в правую полуплоскость комплексной переменной р, часто можно оценить, пренебрегая влиянием малого по абсолютной величине полюса функции G (р).

Рассмотрим в качестве примера опять функцию (12.42). При значительных по модулю величинах комплексной переменной р эту функцию можно с хорошей точностью аппроксимировать функцией

Тогда (рис. 12.2) и, следовательно, условие (12.38) сводится к равенству

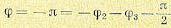
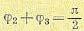
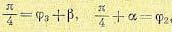
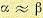
и Рассматривая график на рис. 12.2, можно заметить, что

откуда следует, что . Это равенство и представляет собой условие для определения точки пересечения В.

6. Направление касательной к траектории при выходе ее из какого-либо полюса или при подходе к какому-либо нулю нетрудно определить путем вычисления угла между этой касательной в данном полюсе или нуле и вещественной осью. При таком вычислении используется зависимость (12.38) для аргументов всех нулей и полюсов, расположенных по условию в левой полуплоскости комплексной переменной р.

На рис. 12.3 изображены траектории корней передаточной функции G (р), имеющей два нуля и два полюса на вещественной оси и одну пару комплексных сопряженных полюсов. При

достаточно малом удалении точки р от полюса q4 углы 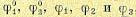, соответствующие

остальным нулям и полюсам, останутся неизменными. Таким образом, в силу (12.38) угол 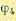найдется из уравнения I

Источник

Применим закон распределения равновероятности:

(4)

Подставляя (1) и (2) и (4) и вводя обозначения с фазой

Последовательная схема может быть
также реализована на основе СФ.

Нормальные
и аномальные ошибки.

Необходимо рассматривать

,
тогда

если ,
либо соответствует , то

Эта же задача стоит при
радиоизмерениях. И она может решаться при построении оптимального устройства, с
различными критериями.

Статистические
критерии оценки непрерывных параметров

сигнала.

Cуществуют
следующие критерии:

ü
Критерий максимума функции правдоподобия.

ü
максимальная апостериорная плотность распределения вероятности
параметра .

ü
Критерий минимума средне квадратичной ошибки.

ü
Критерий Баеса.

Распишем каждый критерий более
подробно.

Критерий максимального
правдоподобия.

оценка
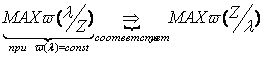
максимального правдоподобия.

Критерий максимальной
апостериорной вероятности.

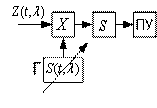
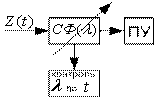
Рассмотрим статистическую схему:

Оценивается значение
максимального параметра.

Критерий минимальной средне
квадратичной ошибки.

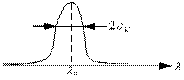
Ошибки, связанные с фиксацией , не выходящие за пределы
корреляционного пика называются нормальные ошибки (инстр. ошибки,
ошибки шума).

Шумовая составляющая:

Дисперсия:

Шумовая составляющая имеет вид , но её особенность, что
количество сигнальных выбросов тем больше, чем больше шумовой уровень.

При регистрации шумовой выброс
может быть принят за сигнальный выброс. Ошибка может составить , а нормальные ошибки не выходят за
корреляционные пределы. Вероятность появления аномальных ошибок характеризует
неправильность измерения вообще.

При проектировании задают
соотношение сигнал/шум, чтобы избежать аномальных ошибок.

А среднеквадратичная ошибка
параметра .

Расчёт среднеквадратической ошибки.

Рассмотрим формулу исходя из
геометрического происхождения сигнала.

Источник

Критерий — минимум — среднеквадратичная ошибка

Definition and basic properties[edit]

Predictor[edit]

Estimator[edit]

Proof of variance and bias relationship[edit]

In regression[edit]

Examples[edit]

Mean[edit]

Variance[edit]

Gaussian distribution[edit]

Interpretation[edit]

Applications[edit]

Loss function[edit]

Criticism[edit]

See also[edit]

Notes[edit]

References[edit]