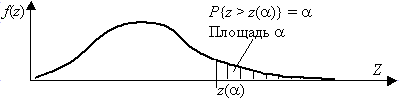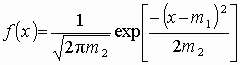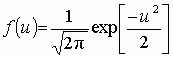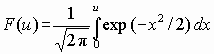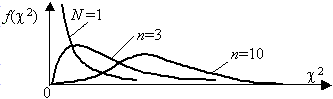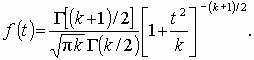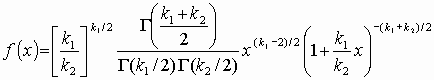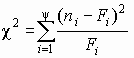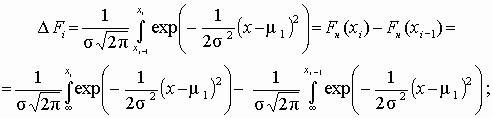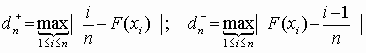Ошибки I и II рода при проверке гипотез, мощность
Общий обзор
Принятие неправильного решения
Мощность и связанные факторы
Проверка множественных гипотез
Общий обзор
Большинство проверяемых гипотез сравнивают между собой группы объектов, которые испытывают влияние различных факторов.
Например, можно сравнить эффективность двух видов лечения, чтобы сократить 5-летнюю смертность от рака молочной железы. Для данного исхода (например, смерть) сравнение, представляющее интерес (например, различные показатели смертности через 5 лет), называют эффектом или, если уместно, эффектом лечения.
Нулевую гипотезу выражают как отсутствие эффекта (например 5-летняя смертность от рака молочной железы одинаковая в двух группах, получающих разное лечение); двусторонняя альтернативная гипотеза будет означать, что различие эффектов не равно нулю.
Критериальная проверка гипотезы дает возможность определить, достаточно ли аргументов, чтобы отвергнуть нулевую гипотезу. Можно принять только одно из двух решений:
- отвергнуть нулевую гипотезу и принять альтернативную гипотезу
- остаться в рамках нулевой гипотезы
Важно: В литературе достаточно часто встречается понятие «принять нулевую гипотезу». Хотелось бы внести ясность, что со статистической точки зрения принять нулевую гипотезу невозможно, т.к. нулевая гипотеза представляет собой достаточно строгое утверждение (например, средние значения в сравниваемых группах равны ).
Поэтому фразу о принятии нулевой гипотезы следует понимать как то, что мы просто остаемся в рамках гипотезы.
Принятие неправильного решения
Возможно неправильное решение, когда отвергают/не отвергают нулевую гипотезу, потому что есть только выборочная информация.
| Верная гипотеза | |||
|---|---|---|---|
| H0 | H1 | ||
| Результат
применения критерия |
H0 | H0 верно принята | H0 неверно принята
(Ошибка второго рода) |
| H1 | H0 неверно отвергнута
(Ошибка первого рода) |
H0 верно отвергнута |
Ошибка 1-го рода: нулевую гипотезу отвергают, когда она истинна, и делают вывод, что имеется эффект, когда в действительности его нет. Максимальный шанс (вероятность) допустить ошибку 1-го рода обозначается α (альфа). Это уровень значимости критерия; нулевую гипотезу отвергают, если наше значение p ниже уровня значимости, т. е., если p < α.
Следует принять решение относительно значения а прежде, чем будут собраны данные; обычно назначают условное значение 0,05, хотя можно выбрать более ограничивающее значение, например 0,01.
Шанс допустить ошибку 1-го рода никогда не превысит выбранного уровня значимости, скажем α = 0,05, так как нулевую гипотезу отвергают только тогда, когда p< 0,05. Если обнаружено, что p > 0,05, то нулевую гипотезу не отвергнут и, следовательно, не допустят ошибки 1-го рода.
Ошибка 2-го рода: не отвергают нулевую гипотезу, когда она ложна, и делают вывод, что нет эффекта, тогда как в действительности он существует. Шанс возникновения ошибки 2-го рода обозначается β (бета); а величина (1-β) называется мощностью критерия.
Следовательно, мощность — это вероятность отклонения нулевой гипотезы, когда она ложна, т.е. это шанс (обычно выраженный в процентах) обнаружить реальный эффект лечения в выборке данного объема как статистически значимый.
В идеале хотелось бы, чтобы мощность критерия составляла 100%; однако это невозможно, так как всегда остается шанс, хотя и незначительный, допустить ошибку 2-го рода.
К счастью, известно, какие факторы влияют на мощность и, таким образом, можно контролировать мощность критерия, рассматривая их.
Мощность и связанные факторы
Планируя исследование, необходимо знать мощность предложенного критерия. Очевидно, можно начинать исследование, если есть «хороший» шанс обнаружить уместный эффект, если таковой существует (под «хорошим» мы подразумеваем, что мощность должна быть по крайней мере 70-80%).
Этически безответственно начинать исследование, у которого, скажем, только 40% вероятности обнаружить реальный эффект лечения; это бесполезная трата времени и денежных средств.
Ряд факторов имеют прямое отношение к мощности критерия.
Объем выборки: мощность критерия увеличивается по мере увеличения объема выборки. Это означает, что у большей выборки больше возможностей, чем у незначительной, обнаружить важный эффект, если он существует.
Когда объем выборки небольшой, у критерия может быть недостаточно мощности, чтобы обнаружить отдельный эффект. Эти методы также можно использовать для оценки мощности критерия для точно установленного объема выборки.
Вариабельность наблюдений: мощность увеличивается по мере того, как вариабельность наблюдений уменьшается.
Интересующий исследователя эффект: мощность критерия больше для более высоких эффектов. Критерий проверки гипотез имеет больше шансов обнаружить значительный реальный эффект, чем незначительный.
Уровень значимости: мощность будет больше, если уровень значимости выше (это эквивалентно увеличению допущения ошибки 1-го рода, α, а допущение ошибки 2-го рода, β, уменьшается).
Таким образом, вероятнее всего, исследователь обнаружит реальный эффект, если на стадии планирования решит, что будет рассматривать значение р как значимое, если оно скорее будет меньше 0,05, чем меньше 0,01.
Обратите внимание, что проверка ДИ для интересующего эффекта указывает на то, была ли мощность адекватной. Большой доверительный интервал следует из небольшой выборки и/или набора данных с существенной вариабельностью и указывает на недостаточную мощность.
Проверка множественных гипотез
Часто нужно выполнить критериальную проверку значимости множественных гипотез на наборе данных с многими переменными или существует более двух видов лечения.
Ошибка 1-го рода драматически увеличивается по мере увеличения числа сравнений, что приводит к ложным выводам относительно гипотез. Следовательно, следует проверить только небольшое число гипотез, выбранных для достижения первоначальной цели исследования и точно установленных априорно.
Можно использовать какую-нибудь форму апостериорного уточнения значения р, принимая во внимание число выполненных проверок гипотез.
Например, при подходе Бонферрони (его часто считают довольно консервативным) умножают каждое значение р на число выполненных проверок; тогда любые решения относительно значимости будут основываться на этом уточненном значении р.
Связанные определения:
p-уровень
Альтернативная гипотеза, альтернатива
Альфа-уровень
Бета-уровень
Гипотеза
Двусторонний критерий
Критерий для проверки гипотезы
Критическая область проверки гипотезы
Мощность
Мощность исследования
Мощность статистического критерия
Нулевая гипотеза
Односторонний критерий
Ошибка I рода
Ошибка II рода
Статистика критерия
Эквивалентные статистические критерии
В начало
Содержание портала
Ошибки первого и второго рода
Выдвинутая гипотеза
может быть правильной или неправильной,
поэтому возникает необходимость её
проверки. Поскольку проверку производят
статистическими методами, её называют
статистической. В итоге статистической
проверки гипотезы в двух случаях может
быть принято неправильное решение, т.
е. могут быть допущены ошибки двух родов.
Ошибка первого
рода состоит в том, что будет отвергнута
правильная гипотеза.
Ошибка второго
рода состоит в том, что будет принята
неправильная гипотеза.
Подчеркнём, что
последствия этих ошибок могут оказаться
весьма различными. Например, если
отвергнуто правильное решение «продолжать
строительство жилого дома», то эта
ошибка первого рода повлечёт материальный
ущерб: если же принято неправильное
решение «продолжать строительство»,
несмотря на опасность обвала стройки,
то эта ошибка второго рода может повлечь
гибель людей. Можно привести примеры,
когда ошибка первого рода влечёт более
тяжёлые последствия, чем ошибка второго
рода.
Замечание 1.
Правильное решение может быть принято
также в двух случаях:
-
гипотеза принимается,
причём и в действительности она
правильная; -
гипотеза отвергается,
причём и в действительности она неверна.
Замечание 2.
Вероятность совершить ошибку первого
рода принято обозначать через
;
её называют уровнем значимости. Наиболее
часто уровень значимости принимают
равным 0,05 или 0,01. Если, например, принят
уровень значимости, равный 0,05, то это
означает, что в пяти случаях из ста
имеется риск допустить ошибку первого
рода (отвергнуть правильную гипотезу).
Статистический
критерий проверки нулевой гипотезы.
Наблюдаемое значение критерия
Для проверки
нулевой гипотезы используют специально
подобранную случайную величину, точное
или приближённое распределение которой
известно. Обозначим эту величину в целях
общности через
.
Статистическим
критерием
(или просто критерием) называют случайную
величину
,
которая служит для проверки нулевой
гипотезы.
Например, если
проверяют гипотезу о равенстве дисперсий
двух нормальных генеральных совокупностей,
то в качестве критерия
принимают отношение исправленных
выборочных дисперсий:
Эта величина
случайная, потому что в различных опытах
дисперсии принимают различные, наперёд
неизвестные значения, и распределена
по закону Фишера – Снедекора.
Для проверки
гипотезы по данным выборок вычисляют
частные значения входящих в критерий
величин и таким образом получают частное
(наблюдаемое) значение критерия.
Наблюдаемым
значением
называют значение критерия, вычисленное
по выборкам. Например, если по двум
выборкам найдены исправленные выборочные
дисперсиии
,
то наблюдаемое значение критерия
Критическая
область. Область принятия гипотезы.
Критические точки
После выбора
определённого критерия множество всех
его возможных значений разбивают на
два непересекающихся подмножества:
одно из них содержит значения критерия,
при которых нулевая гипотеза отвергается,
а другая – при которых она принимается.
Критической
областью называют совокупность значений
критерия, при которых нулевую гипотезу
отвергают.
Областью принятия
гипотезы (областью допустимых значений)
называют совокупность значений критерия,
при которых гипотезу принимают.
Основной принцип
проверки статистических гипотез можно
сформулировать так: если наблюдаемое
значение критерия принадлежит критической
области – гипотезу отвергают, если
наблюдаемое значение критерия принадлежит
области принятия гипотезы – гипотезу
принимают.
Поскольку критерий
— одномерная случайная величина, все её
возможные значения принадлежат некоторому
интервалу. Поэтому критическая область
и область принятия гипотезы также
являются интервалами и, следовательно,
существуют точки, которые их разделяют.
Критическими
точками (границами)
называют точки, отделяющие критическую
область от области принятия гипотезы.
Различают
одностороннюю (правостороннюю или
левостороннюю) и двустороннюю критические
области.
Правосторонней
называют критическую область, определяемую
неравенством
>
,
где— положительное число.
Левосторонней
называют критическую область, определяемую
неравенством
<
,
где— отрицательное число.
Односторонней
называют правостороннюю или левостороннюю
критическую область.
Двусторонней
называют критическую область, определяемую
неравенствами
где
.
В частности, если
критические точки симметричны относительно
нуля, двусторонняя критическая область
определяется неравенствами ( в
предположении, что
>0):
,
или равносильным неравенством
.
Отыскание
правосторонней критической области
Как найти критическую
область? Обоснованный ответ на этот
вопрос требует привлечения довольно
сложной теории. Ограничимся её элементами.
Для определённости начнём с нахождения
правосторонней критической области,
которая определяется неравенством
>
,
где>0.
Видим, что для отыскания правосторонней
критической области достаточно найти
критическую точку. Следовательно,
возникает новый вопрос: как её найти?
Для её нахождения
задаются достаточной малой вероятностью
– уровнем значимости
.
Затем ищут критическую точку,
исходя из требования, чтобы при условии
справедливости нулевой гипотезы
вероятность того, критерийпримет значение, большее
,
была равна принятому уровню значимости:
Р(>
)=
.
Для каждого критерия
имеются соответствующие таблицы, по
которым и находят критическую точку,
удовлетворяющую этому требованию.
Замечание 1.
Когда
критическая точка уже найдена, вычисляют
по данным выборок наблюдаемое значение
критерия и, если окажется, что
>
,
то нулевую гипотезу отвергают; если же<
,
то нет оснований, чтобы отвергнуть
нулевую гипотезу.
Пояснение. Почему
правосторонняя критическая область
была определена, исходя из требования,
чтобы при справедливости нулевой
гипотезы выполнялось соотношение
Р(>
)=
?
(*)
Поскольку вероятность
события
>
мала (
— малая вероятность), такое событие при
справедливости нулевой гипотезы, в силу
принципа практической невозможности
маловероятных событий, в единичном
испытании не должно наступить. Если всё
же оно произошло, т.е. наблюдаемое
значение критерия оказалось больше,
то это можно объяснить тем, что нулевая
гипотеза ложна и, следовательно, должна
быть отвергнута. Таким образом, требование
(*) определяет такие значения критерия,
при которых нулевая гипотеза отвергается,
а они и составляют правостороннюю
критическую область.
Замечание 2.
Наблюдаемое значение критерия может
оказаться большим
не потому, что нулевая гипотеза ложна,
а по другим причинам (малый объём выборки,
недостатки методики эксперимента и
др.). В этом случае, отвергнув правильную
нулевую гипотезу, совершают ошибку
первого рода. Вероятность этой ошибки
равна уровню значимости.
Итак, пользуясь требованием (*), мы с
вероятностьюрискуем совершить ошибку первого рода.
Замечание 3. Пусть
нулевая гипотеза принята; ошибочно
думать, что тем самым она доказана.
Действительно, известно, что один пример,
подтверждающий справедливость некоторого
общего утверждения, ещё не доказывает
его. Поэтому более правильно говорить,
«данные наблюдений согласуются с нулевой
гипотезой и, следовательно, не дают
оснований её отвергнуть».
На практике для
большей уверенности принятия гипотезы
её проверяют другими способами или
повторяют эксперимент, увеличив объём
выборки.
Отвергают гипотезу
более категорично, чем принимают.
Действительно, известно, что достаточно
привести один пример, противоречащий
некоторому общему утверждению, чтобы
это утверждение отвергнуть. Если
оказалось, что наблюдаемое значение
критерия принадлежит критической
области, то этот факт и служит примером,
противоречащим нулевой гипотезе, что
позволяет её отклонить.
Отыскание
левосторонней и двусторонней критических
областей***
Отыскание
левосторонней и двусторонней критических
областей сводится (так же, как и для
правосторонней) к нахождению соответствующих
критических точек. Левосторонняя
критическая область определяется
неравенством
<
(
<0).
Критическую точку находят, исходя из
требования, чтобы при справедливости
нулевой гипотезы вероятность того, что
критерий примет значение, меньшее,
была равна принятому уровню значимости:
Р(<
)=
.
Двусторонняя
критическая область определяется
неравенствами
Критические
точки находят, исходя из требования,
чтобы при справедливости нулевой
гипотезы сумма вероятностей того, что
критерий примет значение, меньшееили большее
,
была равна принятому уровню значимости:
.
(*)
Ясно, что критические
точки могут быть выбраны бесчисленным
множеством способов. Если же распределение
критерия симметрично относительно нуля
и имеются основания (например, для
увеличения мощности) выбрать симметричные
относительно нуля точки (-
)и
(
>0),
то
Учитывая (*), получим
.
Это соотношение
и служит для отыскания критических
точек двусторонней критической области.
Критические точки находят по соответствующим
таблицам.
Дополнительные
сведения о выборе критической области.
Мощность критерия
Мы строили
критическую область, исходя из требования,
чтобы вероятность попадания в неё
критерия была равна
при условии, что нулевая гипотеза
справедлива. Оказывается целесообразным
ввести в рассмотрение вероятность
попадания критерия в критическую область
при условии, что нулевая гипотеза неверна
и, следовательно, справедлива конкурирующая.
Мощностью критерия
называют вероятность попадания критерия
в критическую область при условии, что
справедлива конкурирующая гипотеза.
Другими словами, мощность критерия есть
вероятность того, что нулевая гипотеза
будет отвергнута, если верна конкурирующая
гипотеза.
Пусть для проверки
гипотезы принят определённый уровень
значимости и выборка имеет фиксированный
объём. Остаётся произвол в выборе
критической области. Покажем, что её
целесообразно построить так, чтобы
мощность критерия была максимальной.
Предварительно убедимся, что если
вероятность ошибки второго рода (принять
неправильную гипотезу) равна
,
то мощность равна 1-.
Действительно, если— вероятность ошибки второго рода, т.е.
события «принята нулевая гипотеза,
причём справедливо конкурирующая», то
мощность критерия равна 1 —.
Пусть мощность 1
—
возрастает; следовательно, уменьшается
вероятностьсовершить ошибку второго рода. Таким
образом, чем мощность больше, тем
вероятность ошибки второго рода меньше.
Итак, если уровень
значимости уже выбран, то критическую
область следует строить так, чтобы
мощность критерия была максимальной.
Выполнение этого требования должно
обеспечить минимальную ошибку второго
рода, что, конечно, желательно.
Замечание 1.
Поскольку вероятность события «ошибка
второго рода допущена» равна
,
то вероятность противоположного события
«ошибка второго рода не допущена» равна
1 —,
т.е. мощности критерия. Отсюда следует,
что мощность критерия есть вероятность
того, что не будет допущена ошибка
второго рода.
Замечание 2. Ясно,
что чем меньше вероятности ошибок
первого и второго рода, тем критическая
область «лучше». Однако при заданном
объёме выборки уменьшить одновременно
и
невозможно; если уменьшить
,
тобудет возрастать. Например, если принять
=0,
то будут приниматься все гипотезы, в
том числе и неправильные, т.е. возрастает
вероятностьошибки второго рода.
Как же выбрать
наиболее целесообразно? Ответ на этот
вопрос зависит от «тяжести последствий»
ошибок для каждой конкретной задачи.
Например, если ошибка первого рода
повлечёт большие потери, а второго рода
– малые, то следует принять возможно
меньшее.
Если
уже выбрано, то, пользуясь теоремой Ю.
Неймана и Э.Пирсона, можно построить
критическую область, для которойбудет минимальным и, следовательно,
мощность критерия максимальной.
Замечание 3.
Единственный способ одновременного
уменьшения вероятностей ошибок первого
и второго рода состоит в увеличении
объёма выборок.
Соседние файлы в папке Лекции 2 семестр
- #
- #
- #
- #
Ошибки первого рода (англ. type I errors, α errors, false positives) и ошибки второго рода (англ. type II errors, β errors, false negatives) в математической статистике — это ключевые понятия задач проверки статистических гипотез. Тем не менее, данные понятия часто используются и в других областях, когда речь идёт о принятии «бинарного» решения (да/нет) на основе некоего критерия (теста, проверки, измерения), который с некоторой вероятностью может давать ложный результат.
Содержание
- 1 Определения
- 2 О смысле ошибок первого и второго рода
- 3 Вероятности ошибок (уровень значимости и мощность)
- 4 Примеры использования
- 4.1 Компьютеры
- 4.1.1 Компьютерная безопасность
- 4.1.2 Фильтрация спама
- 4.1.3 Вредоносное программное обеспечение
- 4.1.4 Поиск в компьютерных базах данных
- 4.1.5 Оптическое распознавание текстов (OCR)
- 4.1.6 Досмотр пассажиров и багажа
- 4.1.7 Биометрия
- 4.2 Массовая медицинская диагностика (скрининг)
- 4.3 Медицинское тестирование
- 4.4 Исследования сверхъестественных явлений
- 4.1 Компьютеры
- 5 См. также
- 6 Примечания
Определения
Пусть дана выборка 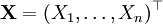
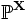
где H0 — нулевая гипотеза, а H1 — альтернативная гипотеза. Предположим, что задан статистический критерий
,
сопоставляющий каждой реализации выборки 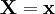
- Распределение
выборки
соответствует гипотезе H0, и она точно определена статистическим критерием, то есть
.
- Распределение
выборки
соответствует гипотезе H0, но она неверно отвергнута статистическим критерием, то есть
.
- Распределение
выборки
соответствует гипотезе H1, и она точно определена статистическим критерием, то есть
.
- Распределение
выборки
соответствует гипотезе H1, но она неверно отвергнута статистическим критерием, то есть
.
Во втором и четвертом случае говорят, что произошла статистическая ошибка, и её называют ошибкой первого и второго рода соответственно.
| Верная гипотеза | |||
|---|---|---|---|
| H0 | H1 | ||
| Результат применения критерия |
H0 | H0 верно принята | H0 неверно принята (Ошибка второго рода) |
| H1 | H0 неверно отвергнута (Ошибка первого рода) |
H0 верно отвергнута |
О смысле ошибок первого и второго рода
Как видно из вышеприведённого определения, ошибки первого и второго рода являются взаимно-симметричными, то есть если поменять местами гипотезы H0 и H1, то ошибки первого рода превратятся в ошибки второго рода и наоборот. Тем не менее, в большинстве практических ситуаций путаницы не происходит, поскольку принято считать, что нулевая гипотеза H0 соответствует состоянию «по умолчанию» (естественному, наиболее ожидаемому положению вещей) — например, что обследумый человек здоров, или что проходящий через рамку металлодетектора пассажир не имеет запрещённых металлических предметов. Соответственно, альтернативная гипотеза H1 обозначает противоположную ситуацию, которая обычно трактуется как менее вероятная, неординарная, требующая какой-либо реакции.
С учётом этого ошибку первого рода часто называют ложной тревогой — например, анализ крови показал наличие заболевания, хотя на самом деле человек здоров, или металлодетектор выдал сигнал тревоги, сработав на металлическую пряжку ремня.
Соответственно, ошибку второго рода иногда называют пропуском события — человек болен, но анализ крови этого не показал, или у пассажира имеется холодное оружие, но рамка металлодетектора его не обнаружила (например, из-за того, что чувствительность рамки отрегулирована на обнаружение только очень массивных металлических предметов).
Ниже, в разделе Примеры использования, подробно рассматривается применение понятий ошибок первого и второго рода в различных областях.
Вероятности ошибок (уровень значимости и мощность)
Для проверки статистических гипотез используют так называемые критерии согласия. Для них вероятности ошибок первого и второго рода играют значительную роль.
Вероятность ошибки первого рода при проверке статистических гипотез назывют уровнем значимости и обычно обозначают греческой буквой α (отсюда название α-errors).
Вероятность ошибки второго рода не имеет какого-то особого общепринятого названия, на письме обозначается греческой буквой β (отсюда β-errors). Однако с этой величиной тесно связана другая, имеющая большое статистическое значение — мощность критерия. Она вычисляется по формуле (1 − β). Таким образом, чем выше мощность, тем меньше вероятность совершить ошибку второго рода.
В статистических тестах обычно приходится идти на компромисс между приемлемым уровнем ошибок первого и второго рода. Зачастую для принятия решения используется пороговое значение, которое может варьироваться с целью сделать тест более строгим или, наоборот, более мягким. Этим пороговым значением является уровень значимости, которым задаются при проверке статистических гипотез. Например, в случае металлодетектора повышение чувствительности прибора приведёт к увеличению риска ошибки первого рода (ложная тревога), а понижение чувствительности — к увеличению риска ошибки второго рода (пропуск запрещённого предмета).
Примеры использования
Компьютеры
Понятия ошибок первого и второго рода широко используются в области компьютеров и программного обеспечения.
Компьютерная безопасность
Наличие уязвимостей в вычислительных системах приводит тому, что приходится, с одной стороны, решать задачу сохранения целостности компьютерных данных, а с другой стороны — обеспечивать нормальный доступ легальных пользователей к этим данным (см. компьютерная безопасность). Moulton (1983, с.125) отмечает, что в данном контексте возможны следующие нежелательные ситуации:
- когда авторизованные пользователи классифицируются как нарушители (ошибки первого рода)
- когда нарушители классифицируются как авторизованные пользователи (ошибки второго рода)
Фильтрация спама
Ошибка первого рода происходит, когда механизм блокировки/фильтрации спама ошибочно классифицирует легитимное email-сообщение как спам и препятствует его нормальной доставке. В то время как большинство «анти-спам» алгоритмов способны блокировать/фильтровать большой процент нежелательных email-сообщений, гораздо более важной задачей является минимизировать число «ложных тревог» (ошибочных блокировок нужных сообщений).
Ошибка второго рода происходит, когда анти-спам система ошибочно пропускает нежелательное сообщение, классифицируя его как «не спам». Низкий уровень таких ошибок является индикатором эффективности анти-спам алгоритма.
Вредоносное программное обеспечение
Понятие ошибки первого рода также ипользуется, когда антивирусное программное обеспечение ошибочно классифицирует безвредный файл как вирус. Неверное обнаружение может быть вызвано особенностями эвристики, либо неправильной сигнатурой вируса в базе данных. Подобные проблемы могут происходить также и с анти-троянскими и анти-
Поиск в компьютерных базах данных
При поиске в базе данных, к ошибкам первого рода можно отнести документы, которые выдаются поиском, несмотря на их иррелевантность (несоответствие) поисковому запросу. Ошибочные срабатывания характерны для полнотекстового поиска, когда поисковый алгоритм анализирует полные тексты всех хранимых в базе данных документов и пытается найти соответствия одному или нескольким терминам, заданным пользователем в запросе.
Большинство ложных срабатываний обусловлены сложностью естественных языков, многозначностью слов: например, «home» может обозначать как «место проживания человека», так и «корневую страницу веб-сайта». Число подобных ошибок может быть снижено за счёт использования специального словаря. Однако, это решение относительно дорогое, поскольку подобный словарь и разметка документов (индексирование) должны создаваться экспертом.
Оптическое распознавание текстов (OCR)
Разнообразные детектирующие алгоритмы нередко выдают ошибки первого рода. Программное обеспечение оптического распознавания текстов может распознать букву «a» в ситуации, когда на самом деле изображены несколько точек, которые используемый алгоритм расценил как «a».
Досмотр пассажиров и багажа
Ошибки первого рода регулярно встречаются каждый день в комьютерных системах предварительного досмотра пассажиров в аэропортах. Установленные в них детекторы предназначены для предотвращения проноса оружия на борт самолёта; тем не менее, уровень чувствительности в них зачастую настраивается настолько высоко, что много раз за день они срабатывают на незначительные предметы, такие как ключи, пряжки ремней, монеты, мобильные телефоны, гвозди в подошвах обуви и т. п. (см. обнаружение взрывчатых веществ, металлодетекторы).
Таким образом, соотношение числа ложных тревог (идентифицикация благопристойного пассажира как террориста) к числу правильных срабатываний (обнаружение действительно запрещённых предметов) очень велико.
Биометрия
Ошибки первого и второго рода являются большой проблемой в системах биометрического сканирования, использующих распознавание радужной оболочки или сетчатки глаза, черт лица и т. д. Такие сканирующие системы могут ошибочно отождествить кого-то с другим, «известным» системе человеком, информация о котором хранится в базе данных (к примеру, это может быть лицо, имеющее право входа в систему, или подозреваемый преступник и т. п.). Противоположной ошибкой будет неспособность системы распознать легитимного зарегистрированного пользователя, или опознать подозреваемого в преступлении.[1]
Массовая медицинская диагностика (скрининг)
В медицинской практике есть существенное различие между скринингом и тестированием:
- Скрининг включает в себя относительно дешёвые тесты, которые проводятся для большой группы людей при отсутствии каких-либо клинических признаков болезни (например, мазок Папаниколау).
- Тестирование подразумевает гораздо более дорогие, зачастую инвазивные, процедуры, которые проводятся только для тех, у кого проявляются клинические признаки заболевания, и которые в основном применяются для подтверждения предполагаемого диагноза.
К примеру, в большинстве штатов в США обязательно прохождение новорожденными процедуры скрининга на оксифенилкетонурию и гипотиреоз, помимо других врождённых аномалий. Несмотря на высокий уровень ошибок первого рода, эти процедуры скрининга считаются целесообразными, поскольку они существенно увеличивают вероятность обнаружения этих расстройств на самой ранней стадии.[2]
Простые анализы крови, используемые для скрининга потенциальных доноров на ВИЧ и гепатит, имеют существенный уровень ошибок первого рода; однако в арсенале врачей есть гораздо более точные (и, соответственно, дорогие) тесты для проверки, действительно ли человек инфицирован каким-либо из этих вирусов.
Возможно, наиболее широкие дискуссии вызывают ошибки первого рода в процедурах скрининга на рак груди (маммография). В США уровень ошибок первого рода в маммограммах достигает 15 %, это самый высокий показатель в мире.[3] Самый низкий уровень наблюдается в Нидерландах, 1 %.[4]
Медицинское тестирование
Ошибки второго рода являются существенной проблемой в медицинском тестировании. Они дают пациенту и врачу ложное убеждение, что заболевание отсутствует, в то время как в действительности оно есть. Это зачастую приводит к неуместному или неадекватному лечению. Типичным примером является доверие результатам кардиотестирования при выявлении коронарного атеросклероза, хотя известно, что кардиотестирование выявляет только те затруднения кровотока в коронарной артерии, которые вызваны стенозом.
Ошибки второго рода вызывают серьёзные и трудные для понимания проблемы, особенно когда искомое условие является широкораспространённым. Если тест с 10%-ным уровнем ошибок второго рода используется для обследования группы, где вероятность «истинно-положительных» случаев составляет 70 %, то многие отрицательные результаты теста окажутся ложными. (См. Теорему Байеса).
Ошибки первого рода также могут вызывать серьёзные и трудные для понимания проблемы. Это происходит, когда искомое условие является редким. Если уровень ошибок первого рода у теста составляет один случай на десять тысяч, но в тестируемой группе образцов (или людей) вероятность «истинно-положительных» случаев составляет в среднем один случай на миллион, то большинство положительных результатов этого теста будут ложными.[5]
Исследования сверхъестественных явлений
Термин ошибка первого рода был взят на вооружение исследователями в области паранормальных явлений и привидений для описания фотографии или записи или какого-либо другого свидетельства, которое ошибочно трактуется как имеющее паранормальное происхождение — в данном контексте ошибка первого рода — это какое-либо несостоятельное «медиа-свидетельство» (изображение, видеозапись, аудиозапись и т. д.), которое имеет обычное объяснение.[6]
См. также
- Ложное срабатывание (ошибка первого рода)
- Статистическая значимость
Примечания
- ↑ Данный пример как раз характеризует случай, когда классификация ошибок будет зависеть от назначения системы: если биометрическое сканирование используется для допуска сотрудников (нулевая гипотеза: «проходящий сканирование человек действительно является сотрудником»), то ошибочное отождествление будет ошибкой второго рода, а «неузнавание» — ошибкой первого рода; если же сканирование используется для опознания преступников (нулевая гипотеза: «проходящий сканирование человек не является преступником»), то ошибочное отождествление будет ошибкой первого рода, а «неузнавание» — ошибкой второго рода.
- ↑ Относительно скрининга новорожденных, последние исследования показали, что количество ошибок первого рода в 12 раз больше, чем количество верных обнаружений (Gambrill, 2006. [1])
- ↑ Одним из последствий такого высокого уровня ошибок первого рода в США является то, что за произвольный 10-летний период половина обследуемых американских женщин получают как минимум одну ложноположительную маммограмму. Такие ошибочные маммограммы обходятся дорого, приводя к ежегодным расходам в 100 миллионов долларов на последующее (ненужное) лечение. Кроме того, они вызывают излишнюю тревогу у женщин. В результате высокого уровня подобных ошибок первого рода в США, примерно у 90-95 % женщин, получивших хотя бы раз в жизни положительную маммограмму, на самом деле заболевание отсутствует.
- ↑ Наиболее низкие уровни этих ошибок наблюдаются в северной Европе, где маммографические плёнки считываются дважды, и для дополнительного тестирования устанавливается повышенное пороговое значение (высокий порог снижает статистическую эффективность теста).
- ↑ Вероятность того, что выдаваемый тестом результат окажется ошибкой первого рода, может быть вычислена при помощи Теоремы Байеса.
- ↑ На некоторых сайтах приведены примеры ошибок первого рода, например: Атлантическое Сообщество Паранормальных явлений (The Atlantic Paranormal Society, TAPS) и Морстаунская организация по Исследованию Привидений (Moorestown Ghost Research).
Wikimedia Foundation.
2010.
Сущность задачи проверки статистических гипотез
Статистическая гипотеза
—
представляет собой некоторое предположение о законе
распределения случайной величины или о параметрах этого закона,
формулируемое на основе выборки.
Примерами статистических гипотез являются предположения: генеральная
совокупность распределена по экспоненциальному закону; математические
ожидания двух экспоненциально распределенных выборок равны друг другу. В
первой из них высказано предположение о виде закона распределения, а во
второй – о параметрах двух распределений. Гипотезы, в основе которых
нет никаких допущений о конкретном виде закона распределения, называют непараметрическими, в противном случае – параметрическими.
Гипотезу, утверждающую, что различие между
сравниваемыми характеристиками отсутствует, а наблюдаемые отклонения
объясняются лишь случайными колебаниями в выборках, на основании которых
производится сравнение, называют нулевой (основной) гипотезой и обозначают Н0. Наряду с основной гипотезой рассматривают и альтернативную (конкурирующую, противоречащую) ей гипотезу Н1. И если нулевая гипотеза будет отвергнута, то будет иметь место альтернативная гипотеза.
Различают простые и сложные гипотезы. Гипотезу называют простой, если она однозначно характеризует параметр распределения случайной величины.
Например, если l
является параметром экспоненциального распределения, то гипотеза Н0 о равенстве l
=10 – простая гипотеза. Сложной называют гипотезу, которая состоит из конечного или бесконечного множества простых гипотез. Сложная гипотеза Н0 о неравенстве l
> 10 состоит из бесконечного множества простых гипотез Н0 о равенстве l
=bi , где bi – любое число, большее 10. Гипотеза Н0
о том, что математическое ожидание нормального распределения равно двум
при неизвестной дисперсии, тоже является сложной. Сложной гипотезой
будет предположение о распределении случайной величины Х по нормальному закону, если не фиксируются конкретные значения математического ожидания и дисперсии.
Проверка гипотезы основывается на вычислении
некоторой случайной величины – критерия, точное или приближенное
распределение которого известно. Обозначим эту величину через z, ее значение является функцией от элементов выборки z=z(x1, x2, …, xn).
Процедура проверки гипотезы предписывает каждому значению критерия одно
из двух решений – принять или отвергнуть гипотезу. Тем самым все
выборочное пространство и соответственно множество значений критерия
делятся на два непересекающихся подмножества S0 и S1. Если значение критерия z попадает в область S0, то гипотеза принимается, а если в область S1, – гипотеза отклоняется. Множество S0называется областью принятия гипотезы или областью допустимых значений, а множество S1 – областью отклонения гипотезы или критической областью.
Выбор одной области однозначно определяет и другую область.
Принятие или отклонение гипотезы Н0 по
случайной выборке соответствует истине с некоторой вероятностью и, соответственно,
возможны два рода ошибок.
Ошибка первого рода
—
возникает с вероятностью a тогда, когда отвергается верная гипотеза Н0 и принимается конкурирующая гипотеза Н1.
Ошибка второго рода
—
возникает с вероятностью b в том случае, когда принимается неверная гипотеза Н0, в то время как справедлива конкурирующая гипотеза Н1.
Доверительная вероятность – это вероятность не совершить ошибку первого рода и принять верную гипотезу Н0.
Вероятность отвергнуть ложную гипотезу Н0 называется мощностью критерия.
Следовательно, при проверке гипотезы возможны четыре варианта исходов, табл. 3.1.
Таблица 3.1.
| Гипотеза Н0 | Решение | Вероятность | Примечание |
| Верна | Принимается | 1–a | Доверительная вероятность |
| Отвергается | a | Вероятность ошибки первого рода | |
| Неверна | Принимается | b | Вероятность ошибки второго рода |
| Отвергается | 1–b | Мощность критерия |
Например, рассмотрим случай, когда некоторая несмещенная оценка параметра q
вычислена по выборке объема n, и эта оценка имеет плотность распределения f(q
), рис. 3.1.
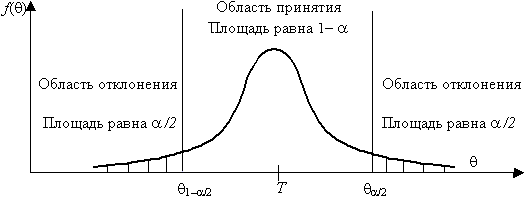
Рис. 3.1. Области и отклонения гипотезы
Предположим, что истинное значение оцениваемого параметра равно Т. Если рассматривать гипотезу Н0 о равенстве q
=Т, то насколько велико должно быть различие между q
и Т, чтобы эту гипотезу отвергнуть. Ответить на данный вопрос
можно в статистическом смысле, рассматривая вероятность достижения
некоторой заданной разности между q
и Т на основе выборочного распределения параметра q
.
Целесообразно полагать одинаковыми значения вероятности выхода параметра q
за нижний и верхний пределы интервала. Такое допущение во многих
случаях позволяет минимизировать доверительный интервал, т.е. повысить
мощность критерия проверки. Суммарная вероятность того, что параметр q
выйдет за пределы интервала с границами q
1–a
/2 и q
a
/2, составляет величину a
. Эту величину следует выбрать настолько
малой, чтобы выход за пределы интервала был маловероятен. Если оценка
параметра попала в заданный интервал, то в таком случае нет оснований
подвергать сомнению проверяемую гипотезу, следовательно, гипотезу
равенства q
=Т можно принять. Но если после получения
выборки окажется, что оценка выходит за установленные пределы, то в этом
случае есть серьезные основания отвергнуть гипотезу Н0. Отсюда следует, что вероятность допустить ошибку первого рода равна a
(равна уровню значимости критерия).
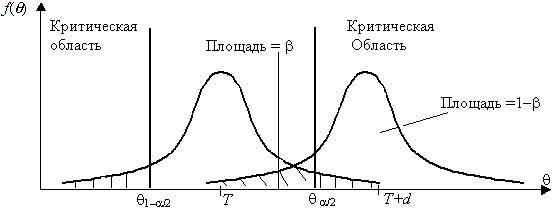
Если предположить, например, что истинное значение параметра в действительности равно Т+d, то согласно гипотезе Н0 о равенстве q
=Т – вероятность того, что оценка параметра q
попадет в область принятия гипотезы, составит b
, рис. 3.2.
При заданном объеме выборки вероятность совершения ошибки первого рода можно уменьшить, снижая уровень значимости a
. Однако при этом увеличивается вероятность ошибки второго рода b
(снижается мощность критерия). Аналогичные рассуждения можно провести для случая, когда истинное значение параметра равно Т – d.
Единственный способ уменьшить обе вероятности состоит
в увеличении объема выборки (плотность распределения оценки параметра
при этом становится более «узкой»). При выборе критической области
руководствуются правилом Неймана – Пирсона: следует так выбирать
критическую область, чтобы вероятность a
была мала, если гипотеза верна, и велика в противном случае. Однако выбор конкретного значения a
относительно произволен. Употребительные значения лежат в пределах от
0,001 до 0,2. В целях упрощения ручных расчетов составлены таблицы
интервалов с границами q
1–a
/2 и q
a
/2 для типовых значений a
и различных способов построения критерия.
При выборе уровня значимости необходимо учитывать
мощность критерия при альтернативной гипотезе. Иногда большая мощность
критерия оказывается существеннее малого уровня значимости, и его
значение выбирают относительно большим, например 0,2. Такой выбор
оправдан, если последствия ошибок второго рода более существенны, чем
ошибок первого рода. Например, если отвергнуто правильное решение
«продолжить работу пользователей с текущими паролями», то ошибка первого
рода приведет к некоторой задержке в нормальном функционировании
системы, связанной со сменой паролей. Если же принято решения не менять
пароли, несмотря на опасность несанкционированного доступа посторонних
лиц к информации, то эта ошибка повлечет более серьезные последствия.
В зависимости от сущности проверяемой гипотезы и
используемых мер расхождения оценки характеристики от ее теоретического
значения применяют различные критерии. К числу наиболее часто
применяемых критериев для проверки гипотез о законах распределения
относят критерии хи-квадрат Пирсона, Колмогорова, Мизеса, Вилкоксона, о
значениях параметров – критерии Фишера, Стьюдента.
3.2. Типовые распределения
При проверке гипотез широкое применение находит ряд
теоретических законов распределения. Наиболее важным из них является
нормальное распределение. С ним связаны распределения хи-квадрат,
Стьюдента, Фишера, а также интеграл вероятностей. Для указанных законов
функции распределения аналитически не представимы. Значения функций
определяются по таблицам или с использованием стандартных процедур
пакетов прикладных программ. Указанные таблицы обычно построены в целях
удобства проверки статистических гипотез в ущерб теории распределений –
они содержат не значения функций распределения, а критические значения
аргумента z(a
).
Для односторонней критической области z(a
) = z1–a
, т.е. критическое значение аргумента z(a
) соответствует квантили z1–a
уровня 1– a
, так как 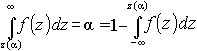
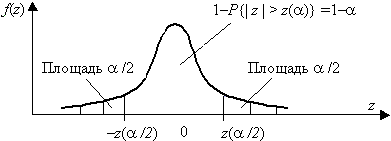
Для двусторонней критической области, с уровнем значимости a , размер левой области a 2, правой a 1 (a 1+a 2=a ), рис. 3.4. Значения z(a 2) и z(a 1) связаны с квантилями распределения соотношениями z(a 1)=z1–a 1, z(a 2)=za 2, так как 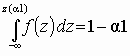
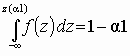
Рис. 3.4. Двусторонняя критическая область
Нормальное распределение
Этот вид распределения является наиболее важным в
связи с центральной предельной теоремой теории вероятностей:
распределение суммы независимых случайных величин стремится к
нормальному с увеличением их количества при произвольном законе
распределения отдельных слагаемых, если слагаемые обладают конечной
дисперсией. Так как реальные физические явления часто представляют собой
результат суммарного воздействия многих факторов, то в таких случаях
нормальное распределение является хорошим приближением наблюдаемых
значений. Функция плотности нормального распределения
(3.1)
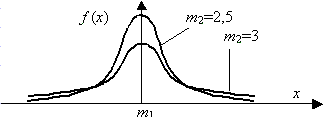
– унимодальная, симметричная, аргумент х может принимать любые действительные значения, рис. 3.5.
Рис. 3.5. Плотность нормального распределения
Функция плотности нормального распределения стандартизованной величины u имеет вид:
Вычисление значений функции распределения Ф(u) для стандартизованного неотрицательного аргумента u (u ³
0) можно произвести с помощью полинома наилучшего приближения [9, стр. 694]
Ф(u)= 1– 0,5(1 + 0,196854u + 0,115194u2 +
+ 0,000344u3 + 0,019527u4)– 4.(3.2)
Такая аппроксимация обеспечивает абсолютную ошибку не более 0,00025. Для вычисления Ф(u) в области отрицательных значений стандартизованного аргумента u (u<0) следует воспользоваться свойством симметрии нормального распределения Ф(u) = 1 –Ф(–u).
Иногда в справочниках вместо значений функции Ф(u) приводят значения интеграла вероятностей
, u > 0.(3.3)
Интеграл вероятностей связан с функцией нормального распределения соотношением Ф(u) = 0,5 + F(u).
Распределение хи-квадрат
Распределению хи-квадрат (c
2-распределению) с k степенями свободы соответствует распределение суммы 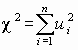
k. Функция плотности распределения хи-квадрат с k степенями свободы
, xі0,(3.4)
где х = c
2, Г(k/2) – гамма-функция.
Число степеней свободы k определяет количество независимых слагаемых в выражении для c
2. Функция плотности при k, равном одному или двум, – монотонная, а при k >2 – унимодальная, несимметричная, рис. 3.6.
Рис. 3.6. Плотность распределения хи-квадрат
Математическое ожидание и дисперсия величины c
2 равны соответственно k и 2k.
Распределение хи-квадрат является частным случаем более общего
гамма-распределения, а величина, равная корню квадратному из хи-квадрат с
двумя степенями свободы, подчиняется распределению Рэлея.
С увеличением числа степеней свободы (k >30) распределение хи-квадрат приближается к нормальному распределению с математическим ожиданием k и дисперсией 2k. В таких случаях критическое значение c 2(k; a ) » u1– a (k, 2k), где u1– a (k, 2k) – квантиль нормального распределения. Погрешность аппроксимации не превышает нескольких процентов.
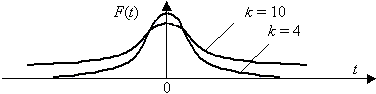
Распределение Стьюдента
Распределение Стьюдента (t-распределение, предложено в 1908 г. английским статистиком В. Госсетом, публиковавшим научные труды под псевдонимом Student) характеризует распределение случайной величины 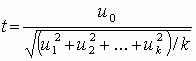
(3.5)
Величина k
характеризует количество степеней свободы. Плотность распределения –
унимодальная и симметричная функция, похожая на нормальное
распределение, рис. 3.7.
Область изменения аргумента t от –Ґ
до Ґ
. Математическое ожидание и дисперсия равны 0 и k/(k–2) соответственно, при k>2.
По сравнению с нормальным распределение Стьюдента более пологое, оно
имеет меньшую дисперсию. Это отличие заметно при небольших значениях k,
что следует учитывать при проверке статистических гипотез (критические
значения аргумента распределения Стьюдента превышают аналогичные
показатели нормального распределения). Таблицы распределения содержат
значения для односторонней или двусторонней критической области.
Распределение Стьюдента применяется для описания ошибок выборки при k Ј 30. При k >100 данное распределение практически соответствует нормальному, для 30 < k < 100 различия между распределением Стьюдента и нормальным распределением составляют несколько процентов. Поэтому относительно оценки ошибок малыми считаются выборки объемом не более 30 единиц, большими – объемом более 100 единиц. При аппроксимации распределения Стьюдента нормальным распределением для односторонней критической области вероятность Р{t> t(k; a )} = u1– a (0, k/(k–2)), где u1– a (0, k/(k–2)) – квантиль нормального распределения. Аналогичное соотношение можно составить и для двусторонней критической области.
Распределение Фишера
Распределению Р.А. Фишера (F-распределению Фишера – Снедекора) подчиняется случайная величина х =[(y1/k1)/(y2/k2)],равная отношению двух случайных величин у1и у2, имеющих хи-квадрат распределение с k1 и k2 степенями свободы. Область изменения аргумента х от 0 до ¥
. Плотность распределения
.(3.6)
В этом выражении k1обозначает число степеней свободы величины y1 с большей дисперсией, k2– число степеней свободы величины y2 с меньшей дисперсией. Плотность распределения – унимодальная, несимметричная, рис. 3.8.
Рис. 3.8. Плотность распределения Фищера
Математическое ожидание случайной величины х равно k2/(k2–2) при k2>2, дисперсия т2 = [2 k22 (k1+k2–2)]/[k1(k2–2)2(k2–4)] при k2 > 4. При k1 > 30 и k2 > 30 величина х распределена приближенно нормально с центром (k1 – k2)/(2 k1 k2) и дисперсией (k1 + k2)/(2 k1 k2).
3.3. Проверка гипотез о законе распределения
Обычно сущность проверки гипотезы о законе распределения ЭД заключается в следующем. Имеется выборка ЭД фиксированного объема, выбран или известен вид закона распределения генеральной совокупности. Необходимо оценить по этой выборке параметры закона, определить степень согласованности ЭД и выбранного закона распределения, в котором параметры заменены их оценками. Пока не будем касаться способов нахождения оценок параметров распределения, а рассмотрим только вопрос проверки согласованности распределений с использованием наиболее употребительных критериев.
Критерий хи-квадрат К. Пирсона
Использование этого критерия основано на применении такой меры (статистики) расхождения между теоретическим F(x) и эмпирическим распределением Fп(x), которая приближенно подчиняется закону распределения c
2. Гипотеза Н0
о согласованности распределений проверяется путем анализа распределения
этой статистики. Применение критерия требует построения статистического
ряда.
Итак, пусть выборка представлена статистическим рядом с количеством разрядов y
. Наблюдаемая частота попаданий в i-й разряд ni. В соответствии с теоретическим законом распределения ожидаемая частота попаданий в i-й разряд составляет Fi. Разность между наблюдаемой и ожидаемой частотой составит величину (n i – Fi). Для нахождения общей степени расхождения между F(x) и Fп(x) необходимо подсчитать взвешенную сумму квадратов разностей по всем разрядам статистического ряда
.(3.7)
Величина c
2 при неограниченном увеличении n
имеет распределение хи-квадрат (асимптотически распределена как
хи-квадрат). Это распределение зависит от числа степеней свободы k, т.е. количества независимых значений слагаемых в выражении (3.7). Число степеней свободы равно числу y
минус число линейных связей, наложенных на выборку. Одна связь
существует в силу того, что любая частота может быть вычислена по
совокупности частот в оставшихся y
– 1 разрядах. Кроме того, если параметры распределения неизвестны
заранее, то имеется еще одно ограничение, обусловленное подгонкой
распределения к выборке. Если по выборке определяются f
параметров распределения, то число степеней свободы составит k=y
– f
–1.
Область принятия гипотезы Н0 определяется условием c
2£
c
2(k;a
), где c
2(k;a
) – критическая точка распределения хи-квадрат с уровнем значимости a
. Вероятность ошибки первого рода равна a
, вероятность ошибки второго рода четко определить нельзя, потому что
существует бесконечно большое множество различных способов несовпадения
распределений. Мощность критерия зависит от количества разрядов и объема
выборки. Критерий рекомендуется применять при n>200, допускается применение при n>40, именно при таких условиях критерий состоятелен (как правило, отвергает неверную нулевую гипотезу).
Пример 3.1. Проверить с помощью критерия
хи-квадрат гипотезу о нормальности распределения случайной величины,
представленной статистическим рядом в табл. 2.4 при уровне значимости a
= 0,05.
Решение. В примере 2.3 были вычислены значения оценок моментов: m
1=27,51, m
2 = 0,91, s
= 0,96. На основе табл. 2.4 построим табл. 3.2, иллюстрирующую расчеты.
Таблица 3.2
| Номер интервала, i | 1 | 2 | 3 | 4 | 5 | 6 |
| n i | 5 | 9 | 10 | 9 | 5 | 6 |
| xi | 26,37 | 26,95 | 27,53 | 28,12 | 28,70 | ¥ |
| F(xi) | 0,117 | 0,280 | 0,508 | 0,737 | 0,892 | 1 |
|
D Fi |
0,117 | 0,166 | 0,228 | 0,228 | 0,155 | 0,108 |
| Fi | 5,148 | 7,304 | 10,032 | 10,032 | 6,820 | 4,752 |
| (ni —Fi)2/Fi | 0,004 | 0,394 | 0,0001 | 0,1062 | 0,486 | 0,328 |
В этой таблице:
ni – частота попаданий элементов выборки в i-й интервал;
xi – верхняя граница i-го интервала;
F(xi) – значение функции нормального распределения;
D
Fi – теоретическое значение вероятности попадания случайной величины в i-й интервал
Fi = D
Fi*n – теоретическая частота попадания случайной величины в i-й интервал;
(n i – Fi)2/Fi – взвешенный квадрат отклонения.
Для нормального закона возможные значения случайной величины лежат в диапазоне от – ¥
до ¥
, поэтому при расчетах оценок вероятностей крайний левый и крайний правый интервалы расширяются до – ¥
и ¥
соответственно. Вычислить значения функции нормального распределения
можно, воспользовавшись стандартными функциями табличного процессора или
полиномом наилучшего приближения.
Сумма взвешенных квадратов отклонения c 2=1,32. Число степеней свободы k=6–1–2=3 (уклонения связаны линейным соотношением 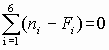
Критерий А.Н. Колмогорова
Для применения критерия А.Н. Колмогорова ЭД требуется
представить в виде вариационного ряда (ЭД недопустимо объединять в
разряды). В качестве меры расхождения между теоретической F(x) и эмпирической Fn(x) функциями распределения непрерывной случайной величины Х используется модуль максимальной разностиdn = max|F(x) — Fn(x)|.
(3.8)
А.Н. Колмогоров доказал, что какова бы ни была функция распределения F(x) величины Х при неограниченном увеличении количества наблюдений n функция распределения случайной величины dn 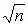
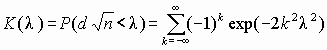
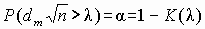
Во-первых, в точном соответствии с условиями его применения необходимо пользоваться следующим соотношением
где
Во-вторых, условия применения критерия
предусматривают, что теоретическая функция распределения известна
полностью (известны вид функции и ее параметры). Но на практике
параметры обычно неизвестны и оцениваются по ЭД. Это приводит к
завышению значения вероятности соблюдения нулевой гипотезы, т.е.
повышается риск принять в качестве правдоподобной гипотезу, которая
плохо согласуется с ЭД (повышается вероятность совершить ошибку второго
рода). В качестве меры противодействия такому выводу следует увеличить
уровень значимости a
, приняв его равным 0,1 – 0,2, что приведет к уменьшению зоны допустимых отклонений.
Пример 3.2. Проверить с помощью критерия А.Н.
Колмогорова гипотезу о том, что ЭД, представленные в табл. 2.3,
подчиняются нормальному распределению при уровне значимости a
=0,1.
Решение. Исходные данные и результаты
вычислений сведены в табл. 3.3. Необходимые вычисления можно провести с
использованием табличного процессора: значение эмпирической функции
распределения Fn(xi)=i/44; значения теоретической функции F(xi) – это значение функции нормального распределения в точке xi.
| i | 1 | 2 | 3 | 4 | 5 | 6 | 7 | 8 | 9 | 10 | 11 |
| xi | 25,79 | 25,98 | 25,98 | 26,12 | 26,13 | 26,49 | 26,52 | 26,60 | 26,66 | 26,69 | 26,74 |
| Fn(xi) | 0,023 | 0,046 | 0,068 | 0,091 | 0,114 | 0,136 | 0,159 | 0,182 | 0,204 | 0,227 | 0,250 |
| F(xi) | 0,036 | 0,055 | 0,055 | 0,073 | 0,075 | 0,144 | 0,151 | 0,170 | 0,188 | 0,196 | 0,211 |
| dn+ | 0,014 | 0,009 | 0,013 | 0,018 | 0,038 | 0,008 | 0,008 | 0,012 | 0,016 | 0,032 | 0,039 |
| dn— | 0,036 | 0,032 | 0,010 | 0,005 | 0,016 | 0,031 | 0,014 | 0,011 | 0,006 | 0,009 | 0,016 |
| i | 12 | 13 | 14 | 15 | 16 | 17 | 18 | 19 | 20 | 21 | 22 |
| xi | 26,85 | 26,90 | 26,91 | 26,96 | 27,02 | 27,11 | 27,19 | 27,21 | 27,28 | 27,30 | 27,38 |
| Fn(xi) | 0,273 | 0,296 | 0,318 | 0,341 | 0,364 | 0,386 | 0,409 | 0,432 | 0,455 | 0,477 | 0,500 |
| F(xi) | 0,246 | 0,263 | 0,267 | 0,284 | 0,305 | 0,337 | 0,371 | 0,378 | 0,406 | 0,412 | 0,447 |
| dn+ | 0,027 | 0,032 | 0,051 | 0,057 | 0,059 | 0,050 | 0,038 | 0,054 | 0,049 | 0,065 | 0,053 |
| dn— | 0,004 | 0,010 | 0,028 | 0,034 | 0,036 | 0,027 | 0,015 | 0,031 | 0,026 | 0,042 | 0,031 |
| i | 23 | 24 | 25 | 26 | 27 | 28 | 29 | 30 | 31 | 32 | 33 |
| xi | 27,40 | 27,49 | 27,64 | 27,66 | 27,71 | 27,78 | 27,89 | 27,89 | 28,01 | 28,10 | 28,11 |
| Fn(xi) | 0,523 | 0,546 | 0,568 | 0,591 | 0,614 | 0,636 | 0,659 | 0,682 | 0,705 | 0,727 | 0,750 |
| F(xi) | 0,456 | 0,492 | 0,555 | 0,561 | 0,583 | 0,610 | 0,656 | 0,656 | 0,701 | 0,731 | 0,735 |
| dn+ | 0,067 | 0,053 | 0,013 | 0,030 | 0,031 | 0,026 | 0,003 | 0,026 | 0,003 | 0,004 | 0,015 |
| dn— | 0,044 | 0,031 | 0,010 | 0,007 | 0,008 | 0,003 | 0,019 | 0,003 | 0,020 | 0,027 | 0,008 |
| i | 34 | 35 | 36 | 37 | 38 | 39 | 40 | 41 | 42 | 43 | 44 |
| xi | 28,37 | 28,38 | 28,50 | 28,63 | 28,67 | 28,90 | 28,99 | 28,99 | 29,03 | 29,12 | 29,28 |
| Fn(xi) | 0,773 | 0,795 | 0,818 | 0,841 | 0,864 | 0,886 | 0,909 | 0,932 | 0,955 | 0,977 | 1,000 |
| F(xi) | 0,817 | 0,819 | 0,851 | 0,879 | 0,888 | 0,928 | 0,939 | 0,940 | 0,944 | 0,954 | 0,968 |
| dn+ | 0,044 | 0,024 | 0,032 | 0,038 | 0,024 | 0,042 | 0,030 | 0,008 | 0,010 | 0,024 | 0,032 |
| dn— | 0,067 | 0,046 | 0,055 | 0,061 | 0,047 | 0,064 | 0,053 | 0,031 | 0,013 | 0,001 | 0,009 |
В данном примере максимальные значения dn+ и dn–одинаковы и равны 0,067. Из табл. П.1 при a =0,1 найдем l =1,22. Для n=44 критическое значение 0,184. Поскольку величина max dn=0,067 меньше критического значения, гипотеза о принадлежности выборки нормальному закону не отвергается.
Критерий Мизеса
В качестве меры различия теоретической функции распределения F(x) и эмпирической Fn(x) по критерию Мизеса (критерию w
2) выступает средний квадрат отклонений по всем значениям аргумента x
(3.9)
Статистика критерия
(3.10)
При неограниченном увеличении n существует предельное распределение статистики nw
n2. Задав значение вероятности a
можно определить критические значения nw
n2(a
). Проверка гипотезы о законе распределения осуществляется обычным образом: если фактическое значение nw
n2окажется больше критического или равно ему, то согласно критерию Мизеса с уровнем значимости a
гипотеза Но о том, что закон распределения генеральной совокупности соответствует F(x), должна быть отвергнута.
Пример 3.3. Проверить с помощью критерия
Мизеса гипотезу о том, что ЭД, представленные вариационным рядом, табл.
2.3, подчиняются нормальному распределению при уровне значимости a
= 0,1.
Решение. Исходные данные и результаты вычислений представлены в табл. 3.4.
| i | 1 | 2 | 3 | 4 | 5 | 6 | 7 | 8 | 9 | 10 | 11 |
| xi | 25,79 | 25,98 | 25,98 | 26,12 | 26,13 | 26,49 | 26,52 | 26,60 | 26,66 | 26,69 | 26,74 |
| Fn(xi) | 0,011 | 0,034 | 0,057 | 0,080 | 0,102 | 0,125 | 0,148 | 0,171 | 0,193 | 0,216 | 0,237 |
| F(xi) | 0,036 | 0,055 | 0,055 | 0,073 | 0,075 | 0,144 | 0,151 | 0,170 | 0,188 | 0,196 | 0,211 |
|
D i |
0,618 | 0,429 | 0,003 | 0,047 | 0,726 | 0,378 | 0,009 | 0,000 | 0,025 | 0,409 | 0,742 |
| i | 12 | 13 | 14 | 15 | 16 | 17 | 18 | 19 | 20 | 21 | 22 |
| xi | 26,85 | 26,90 | 26,91 | 26,96 | 27,02 | 27,11 | 27,19 | 27,21 | 27,28 | 27,30 | 27,38 |
| Fn(xi) | 0,261 | 0,284 | 0,307 | 0,330 | 0,352 | 0,375 | 0,398 | 0,421 | 0,443 | 0,466 | 0,489 |
| F(xi) | 0,246 | 0,263 | 0,267 | 0,284 | 0,305 | 0,337 | 0,371 | 0,378 | 0,406 | 0,412 | 0,447 |
|
D i |
0,231 | 0,439 | 1,572 | 2,071 | 2,243 | 1,467 | 0,717 | 1,790 | 1,391 | 2,866 | 1,755 |
| i | 23 | 24 | 25 | 26 | 27 | 28 | 29 | 30 | 31 | 32 | 33 |
| xi | 27,40 | 27,49 | 27,64 | 27,66 | 27,71 | 27,78 | 27,89 | 27,89 | 28,01 | 28,10 | 28,11 |
| Fn(xi) | 0,511 | 0,534 | 0,557 | 0,580 | 0,602 | 0,625 | 0,648 | 0,671 | 0,693 | 0,716 | 0,739 |
| F(xi) | 0,456 | 0,492 | 0,555 | 0,561 | 0,583 | 0,610 | 0,656 | 0,656 | 0,701 | 0,731 | 0,735 |
|
D i |
3,103 | 1,765 | 0,003 | 0,332 | 0,374 | 0,216 | 0,063 | 0,213 | 0,067 | 0,238 | 0,013 |
| I | 34 | 35 | 36 | 37 | 38 | 39 | 40 | 41 | 42 | 43 | 44 |
| xi | 28,37 | 28,38 | 28,50 | 28,63 | 28,67 | 28,90 | 28,99 | 28,99 | 29,03 | 29,12 | 29,28 |
| Fn(xi) | 0,761 | 0,784 | 0,807 | 0,830 | 0,852 | 0,875 | 0,898 | 0,921 | 0,943 | 0,966 | 0,989 |
| F(xi) | 0,817 | 0,819 | 0,851 | 0,879 | 0,888 | 0,928 | 0,939 | 0,940 | 0,944 | 0,954 | 0,968 |
|
D i |
3,090 | 1,230 | 1,908 | 2,461 | 1,271 | 2,791 | 1,737 | 0,381 | 0,001 | 0,149 | 0,432 |
В этой таблице:
Fn(xi)=(i–0,5)/44 – значение эмпирической функции распределения;
F(xi) – значение теоретической функции распределения, соответствует значению функции нормального распределения в точке xi;
D
i =1000[Fn(xi) – F(xi)]2 .Здесь масштабный множитель 1000 введен для удобства отображения данных в таблице, при расчетах он не используется.
Критическое значение статистики критерия Мизеса при заданном уровне значимости равно 0,347, табл. П.2. Фактическое значение статистики , что меньше критического значения. Следовательно, гипотеза Н0 не противоречит имеющимся данным.
Достоинством критерия Мизеса является быстрая
сходимость к предельному закону, для этого достаточно не менее 40
наблюдений в области часто используемых на практике больших значений nw
n (а не несколько сот, как для критерия хи-квадрат).
Сопоставляя возможности различных критериев,
необходимо отметить следующие особенности. Критерий Пирсона устойчив к
отдельным случайным ошибкам в ЭД. Однако его применение требует
группирования данных по интервалам, выбор которых относительно
произволен и подвержен противоречивым рекомендациям. Критерий
Колмогорова слабо чувствителен к виду закона распределения и подвержен
влиянию помех в исходной выборке, но прост в применении. Критерий Мизеса
имеет ряд общих свойств с критерием Колмогорова: оба основаны
непосредственно на результатах наблюдения и не требуют построения
статистического ряда, что повышает объективность выводов; оба не
учитывают уменьшение числа степеней свободы при определении параметров
распределения по выборке, а это ведет к риску принятия ошибочной
гипотезы. Их предпочтительно применять в тех случаях, когда параметры
закона распределения известны априори, например, при проверке датчиков
случайных чисел.
При проверке гипотез о законе распределения следует
помнить, что слишком хорошее совпадение с выбранным законом
распределения может быть обусловлено некачественным экспериментом
(“подчистка” ЭД) или предвзятой предварительной обработкой результатов
(некоторые результаты отбрасываются или округляются).
Выбор критерия проверки гипотезы относительно
произволен. Разные критерии могут давать различные выводы о
справедливости гипотезы, окончательное заключение в таком случае
принимается на основе неформальных соображений. Точно также нет
однозначных рекомендаций по выбору уровня значимости.
Рассмотренный подход к проверке гипотез, основанный
на применении специальных таблиц критических точек распределения,
сложился в эпоху «ручной» обработки ЭД, когда наличие таких таблиц
существенно снижало трудоемкость вычислений. В настоящее время
математические пакеты включают процедуры вычисления стандартных функций
распределений, что позволяет отказаться от использования таблиц, но
может потребовать изменения правил проверки. Например, соблюдению
гипотезы Н0 соответствует такое значение функции распределения критерия, которое не превышает значение доверительной вероятности 1– a
(оценка статистики критерия соответствует доверительному интервалу). В
частности, для примера 3.1 значение статистики критерия хи-квадрат равно
1,318. А значение функции
распределения хи-квадрат для этого значения аргумента при трех степенях
свободы составляет 0,275, что меньше доверительной вероятности 0,95.
Следовательно, нет оснований отвергать нулевую гипотезу.
Тема 3.5.
СТАТИСТИЧЕСКИЕ ГИПОТЕЗЫ
План лекции:
-
Понятие гипотезы.
-
Схема статистической
проверки гипотезы.
Список литературы:
-
Вентцель, Е.С.
Теория вероятностей [Текст] / Е.С.
Вентцель. – М.: Высшая школа, 2006. – 575 с. -
Гмурман, В.Е. Теория
вероятностей и математическая статистика
[Текст] / В.Е. Гмурман. — М.: Высшая школа,
2007. — 480 с. -
Кремер, Н.Ш. Теория
вероятностей и математическая статистика
[Текст] / Н.Ш.
Кремер — М: ЮНИТИ, 2002. – 543 с.
п.1. Понятие
гипотезы.
Одна
из
часто
встречающихся на практике задач,
связанных с применением статистических
методов, состоит в решении вопроса о
том, должно ли на основании данной
выборки быть принято или, напротив,
отвергнуто некоторое предположение
(гипотеза) относительно генеральной
совокупности (случайной величины).
Например,
новое
лекарство испытано на определенном
числе людей. Можно ли сделать по
данным результатам лечения обоснованный
вывод о том, что новое лекарство более
эффективно, чем применявшиеся ранее
методы лечения? Аналогичный вопрос
логично задать, говоря о новом правиле
поступления в вуз, о новом методе
обучения, о пользе быстрой ходьбы, о
преимуществах новой модели автомобиля
или технологического процесса и т.
д.
Процедура
сопоставления высказанного предположения
(гипотезы) с выборочными данными
называется проверкой
гипотез.
Задачи
статистической проверки гипотез ставятся
в следующем виде: относительно некоторой
генеральной совокупности высказывается
та или иная гипотеза Н.
Из
этой генеральной совокупности извлекается
выборка. Требуется указать правило, при
помощи которого можно было бы по выборке
решить вопрос о том, следует ли
отклонить
гипотезу Н
или
принять
ее.
Следует
отметить, что статистическими методами
гипотезу можно
только опровергнуть или не опровергнуть,
но
не доказать. Например,
для
проверки утверждения (гипотеза Н)
автора,
что «в рукописи нет ошибок», рецензент
прочел (изучил)
несколько страниц рукописи.
Если
он обнаружил хотя бы одну ошибку, то
гипотеза Н
отвергается,
в противном случае — не отвергается,
говорят, что «результат проверки с
гипотезой согласуется».
Выдвинутая
гипотеза может быть правильной или
неправильной, поэтому возникает
необходимость ее проверки.
Под
статистической
гипотезой (или
просто гипотезой)
понимают
всякое высказывание (предположение) о
генеральной совокупности, проверяемое
по
выборке.
Статистические
гипотезы делятся на гипотезы о параметрах
распределения известного вида (это
так называемые параметрические
гипотезы)
и гипотезы о виде неизвестного
распределения (непараметрические
гипотезы).
Например,
статистическими являются гипотезы:
-
генеральная
совокупность распределена по закону
Пуассона; -
дисперсии
двух нормальных совокупностей равны
между собой.
В
первой гипотезе сделано предположение
о виде неизвестного распределения, во
второй – о параметрах двух известных
распределений.
Гипотеза
«на Марсе есть жизнь» не является
статистической, т.к. в ней не идёт речь
ни о виде, ни о параметрах распределения.
Наряду
с выдвинутой гипотезой рассматривают
и противоречащую ей гипотезу. Если
выдвинутая гипотеза будет отвергнута,
то имеет место противоречащая гипотеза.
Таким
образом, одну из гипотез выделяют в
качестве основной
(или
нулевой)
и
обозначают Но,
а другую, являющуюся логическим отрицанием
Н0,
т. е. противоположную Но
—
в качестве конкурирующей
(или
альтернативной)
гипотезы
и обозначают Н1.
Гипотезу,
однозначно фиксирующую распределение
наблюдений, называют простой
(в
ней идет речь об одном значении параметра),
в противном случае — сложной.
Например,
гипотеза Но,
состоящая
в том что математическое ожидание
случайной
величины
X
равно ао,
т.е. М(Х)=ао
является
простой. В качестве альтернативной
гипотезы можно рассматривать гипотезу
Н1:
М(Х)≠
ао
(сложная
гипотеза).
Имея
две гипотезы Но
и
Н1,
надо
на основе выборки Х1,…
,Хп
принять
либо основную гипотезу Н0,
либо
конкурирующую Н1.
Правило,
по которому принимается решение принять
или отклонить гипотезу Но
(соответственно,
отклонить или принять Н1),
называется
статистическим
критерием К (или
просто критерием)
проверки
гипотезы Но.
Проверку
гипотез осуществляют на основании
результатов выборки Х1,
Х2,…,
Хп,
из
которых формируют функцию выборки Кп
=К(Х1,
Х2,…,
Хn),
называемой статистикой
критерия.
Основной
принцип проверки гипотез состоит
в следующем. Множество возможных
значений статистики критерия Кп
разбивается
на два непересекающихся подмножества:
критическую
область S,
т.
е. область отклонения гипотезы Но
и
область
принятия
этой
гипотезы. Если фактически наблюдаемое
значение статистики критерия (т. е.
значение критерия, вычисленное по
выборке: Кнабл
=К(х1,х2,…,
хп))
попадает
в критическую область S,
то
основная гипотеза Но
отклоняется
и принимается альтернативная гипотеза
Н1;
если
же Кнабл
попадает
в
,
то
принимается Но,
а
Н1
отклоняется.
При
проверке гипотезы может быть принято
неправильное решение, т.
е. могут быть допущены ошибки двух родов:
Ошибка
первого рода состоит
в том, что отвергается нулевая гипотеза
Но,
когда
на самом деле она верна.
Ошибка
второго рода состоит
в том, что отвергается альтернативная
гипотеза Н1,
когда
она на самом деле верна.
Рассматриваемые
случаи наглядно иллюстрирует следующая
таблица.
|
Гипотеза |
Отвергается |
Принимается |
|
верна |
ошибка |
правильное |
|
неверна |
правильное |
ошибка |
Вероятность
ошибки 1-го рода (обозначается через α)
называется
уровнем
значимости критерия.
Очевидно,
α
= P(Н1Но).
Чем
меньше α,
тем
меньше вероятность отклонить верную
гипотезу. Допустимую ошибку 1-го рода
обычно задают заранее.
В
одних случаях считается возможным
пренебречь событиями, вероятность
которых меньше 0,05 (α=
0,05
означает, что в среднем в 5 случаях из
100 испытаний верная гипотеза будет
отвергнута), в других случаях, когда
речь идет, например, о разрушении
сооружений, гибели судна и т. п., нельзя
пренебречь обстоятельствами, которые
могут появиться с вероятностью,
равной
0,001.
Обычно
для α
используются
стандартные значения: α
= 0,05;
0,01; 0,005; 0,001.
Вероятность
ошибки 2-го рода обозначается через β,
т.е.
β
= Р(Н0Н1).
Величину
1- β,
т.
е. вероятность недопущения ошибки 2-го
рода (отвергнуть неверную гипотезу
принять верную Н1),
называется
мощностью
критерия.
Чем
больше мощность критерия, тем вероятность
ошибки 2-го рода меньше, что, конечно,
желательно (как и уменьшение α).
Последствия
ошибок 1-го, 2-го рода могут быть совершенно
различными: в одних случаях надо
минимизировать α,
в
другом — β.
Так,
применительно к производству, к торговле
можно сказать, что α
—
риск поставщика (т.е. забраковка по
выборке всей партии изделий, удовлетворяющих
стандарту), β — риск потребителя (т.е.
прием по выборке всей партии изделий,
не удовлетворяющей стандарту);
применительно к судебной системе, ошибка
1-го рода приводит к оправданию виновного,
ошибка 2-го рода — осуждению невиновного.
Или, например, если отвергнуто правильное
решение «продолжить строительство
жилого дома», то эта ошибка первого рода
повлечёт материальный ущерб; если же
принято неправильное решение «продолжать
строительство», несмотря на опасность
обвала стройки, то эта ошибка второго
рода может повлечь гибель людей.
Отметим,
что одновременное
уменьшение ошибок 1-го
и 2-го рода возможно лишь при увеличении
объема выборок. Поэтому
обычно при заданном уровне значимости
α
отыскивается
критерий с наибольшей мощностью.
п.2. Схема
статистической проверки гипотезы.
Методика
проверки гипотез сводится к следующему:
-
Располагая
выборкой Х1,
Х2,…,Хп,
формируют
нулевую гипотезу Но
и
альтернативную Н1. -
В
каждом конкретном случае подбирают
статистику критерия Кп=К(Х1,Х2,…,
Хп). -
По
статистике критерия Кп
и
уровню значимости а
определяют
критическую область S
(и).
Для
ее отыскания достаточно найти критическую
точку kкр,
т.е. границу (или квантиль), отделяющую
область S
от.
Границы
областей определяются, соответственно,
из соотношений: Р(Kп
>
kкр)
= а,
для
правосторонней критической области S;
Р(Kп
<kкр)
= а,
для
левосторонней критической области
S;
Р(Kп
<
)
= Р(Kп
>
)
=,
для двусторонней критической области
S.
Для
каждого критерия имеются соответствующие
таблицы, по которым и находят
критическую точку, удовлетворяющую
приведенным выше соотношениям.
-
Для
полученной реализации выборки
подсчитывают значение критерия, т.е.
Кнабл
=К(х1,х2,…,
хп)=
k. -
Если
(например,
для правосторонней области S),
то нулевую гипотезу Н0
отвергают, если же
(),
то нет оснований, чтобы отвергнуть
гипотезу Но.
Во
многих случаях закон распределения
изучаемой случайно величины неизвестен,
но есть основания предположить, что он
имеет вполне определенный вид: нормальный,
биномиальный или какой-либо другой.
Пусть
необходимо проверить гипотезу Но
о
том, что случайная
величина
X
подчиняется
определенному закону распределения,
заданному функцией распределения Fо(х),
т.
е. Но:
Fх(х)=Fо(х).
Под
альтернативной гипотезой Н1
будем
понимать в данном случае то, что просто
не выполнена основная (т.е. Н1:
Fх(х)≠
Fо(х)).
Для
проверки гипотезы о распределении
случайной величины X
проведем
выборку, которую оформим в виде
статистического ряда:
|
xi |
x1 |
x2 |
… |
Xm |
|
ni |
n1 |
n2 |
… |
nm |
где
—
объем выборки.
Требуется
сделать заключение: согласуются ли
результаты наблюдений с высказанным
предположением. Для этого используем
специально подобранную величину —
критерий согласия.
Критерием
согласия называют
статистический критерий проверки
гипотезы о предполагаемом законе
неизвестного распределения. (Он
используется для проверки согласия
предполагаемого вида распределения
с опытными данными на основании выборки.)
Существуют
различные критерии согласия: Пирсона,
Колмогорова, Фишера, Смирнова и др.
Критерий согласия Пирсона — наиболее
часто употребляемый критерий для
проверки простой гипотезы о законе
распределения.
Рассмотрим
применение критерия согласия Пирсона
для проверки гипотезы о нормальном
распределении исследуемой случайной
величины X.
По
результатам выборки подсчитывают:
— эмпирическую абсолютную частоту для
каждого варианта;
—
оценку математического ожидания;
— несмещённую оценку среднего
квардатического отклонения; числа
в предположении нормальности случайной
величины X
с параметрами
,
;
числа
— теоретические частоты, где n
– объем выборки.
В
качестве критерия проверки нулевой
гипотезы примем случайную величину
.
Доказано, что при
закон распределения этой случайной
величины, независимо от закона
распределения изучаемой величины X,
стремиться к известному закону
с f
степенями
свободы. Число f
находят из равенства
,
где i
– число частичных интервалов, r
– число параметров предполагаемого
распределения. В случае нормального
закона r=2.
Построим
правостороннюю критическую область,
исходя из требования, что вероятность
попадания критерия в эту область, в
предположении справедливости нулевой
гипотезы, была равна принятому уровню
значимости α:
.
Точка
по данным f
и α находится по таблице критических
точек распределения
.
На основании выборки вычисляем
.
Если
,
то нулевую гипотезу отвергают, в противном
случае её можно принять.
5
Проверка корректности А/Б тестов
Время на прочтение
8 мин
Количество просмотров 7.7K
Хабр, привет! Сегодня поговорим о том, что такое корректность статистических критериев в контексте А/Б тестирования. Узнаем, как проверить, является критерий корректным или нет. Разберём пример, в котором тест Стьюдента не работает.
Меня зовут Коля, я работаю аналитиком данных в X5 Tech. Мы с Сашей продолжаем писать серию статей по А/Б тестированию, это наша третья статья. Первые две можно посмотреть тут:
-
Стратификация. Как разбиение выборки повышает чувствительность A/Б теста
-
Бутстреп и А/Б тестирование
Корректный статистический критерий
В А/Б тестировании при проверке гипотез с помощью статистических критериев можно совершить одну из двух ошибок:
-
ошибку первого рода – отклонить нулевую гипотезу, когда на самом деле она верна. То есть сказать, что эффект есть, хотя на самом деле его нет;
-
ошибку второго рода – не отклонить нулевую гипотезу, когда на самом деле она неверна. То есть сказать, что эффекта нет, хотя на самом деле он есть.
Совсем не ошибаться нельзя. Чтобы получить на 100% достоверные результаты, нужно бесконечно много данных. На практике получить столько данных затруднительно. Если совсем не ошибаться нельзя, то хотелось бы ошибаться не слишком часто и контролировать вероятности ошибок.
В статистике ошибка первого рода считается более важной. Поэтому обычно фиксируют допустимую вероятность ошибки первого рода, а затем пытаются минимизировать вероятность ошибки второго рода.
Предположим, мы решили, что допустимые вероятности ошибок первого и второго рода равны 0.1 и 0.2 соответственно. Будем называть статистический критерий корректным, если его вероятности ошибок первого и второго рода равны допустимым вероятностям ошибок первого и второго рода соответственно.
Как сделать критерий, в котором вероятности ошибок будут равны допустимым вероятностям ошибок?
Вероятность ошибки первого рода по определению равна уровню значимости критерия. Если уровень значимости положить равным допустимой вероятности ошибки первого рода, то вероятность ошибки первого рода должна стать равной допустимой вероятности ошибки первого рода.
Вероятность ошибки второго рода можно подогнать под желаемое значение, меняя размер групп или снижая дисперсию в данных. Чем больше размер групп и чем ниже дисперсия, тем меньше вероятность ошибки второго рода. Для некоторых гипотез есть готовые формулы оценки размера групп, при которых достигаются заданные вероятности ошибок.
Например, формула оценки необходимого размера групп для гипотезы о равенстве средних:
где и
– допустимые вероятности ошибок первого и второго рода,
– ожидаемый эффект (на сколько изменится среднее),
и
– стандартные отклонения случайных величин в контрольной и экспериментальной группах.
Проверка корректности
Допустим, мы работаем в онлайн-магазине с доставкой. Хотим исследовать, как новый алгоритм ранжирования товаров на сайте влияет на среднюю выручку с покупателя за неделю. Продолжительность эксперимента – одна неделя. Ожидаемый эффект равен +100 рублей. Допустимая вероятность ошибки первого рода равна 0.1, второго рода – 0.2.
Оценим необходимый размер групп по формуле:
import numpy as np
from scipy import stats
alpha = 0.1 # допустимая вероятность ошибки I рода
beta = 0.2 # допустимая вероятность ошибки II рода
mu_control = 2500 # средняя выручка с пользователя в контрольной группе
effect = 100 # ожидаемый размер эффекта
mu_pilot = mu_control + effect # средняя выручка с пользователя в экспериментальной группе
std = 800 # стандартное отклонение
# исторические данные выручки для 10000 клиентов
values = np.random.normal(mu_control, std, 10000)
def estimate_sample_size(effect, std, alpha, beta):
"""Оценка необходимого размер групп."""
t_alpha = stats.norm.ppf(1 - alpha / 2, loc=0, scale=1)
t_beta = stats.norm.ppf(1 - beta, loc=0, scale=1)
var = 2 * std ** 2
sample_size = int((t_alpha + t_beta) ** 2 * var / (effect ** 2))
return sample_size
estimated_std = np.std(values)
sample_size = estimate_sample_size(effect, estimated_std, alpha, beta)
print(f'оценка необходимого размера групп = {sample_size}')оценка необходимого размера групп = 784Чтобы проверить корректность, нужно знать природу случайных величин, с которыми мы работаем. В этом нам помогут исторические данные. Представьте, что мы перенеслись в прошлое на несколько недель назад и запустили эксперимент с таким же дизайном, как мы планировали запустить его сейчас. Дизайн – это совокупность параметров эксперимента, таких как: целевая метрика, допустимые вероятности ошибок первого и второго рода, размеры групп и продолжительность эксперимента, техники снижения дисперсии и т.д.
Так как это было в прошлом, мы знаем, какие покупки совершили пользователи, можем вычислить метрики и оценить значимость отличий. Кроме того, мы знаем, что эффекта на самом деле не было, так как в то время эксперимент на самом деле не запускался. Если значимые отличия были найдены, то мы совершили ошибку первого рода. Иначе получили правильный результат.
Далее нужно повторить эту процедуру с мысленным запуском эксперимента в прошлом на разных группах и временных интервалах много раз, например, 1000.
После этого можно посчитать долю экспериментов, в которых была совершена ошибка. Это будет точечная оценка вероятности ошибки первого рода.
Оценку вероятности ошибки второго рода можно получить аналогичным способом. Единственное отличие состоит в том, что каждый раз нужно искусственно добавлять ожидаемый эффект в данные экспериментальной группы. В этих экспериментах эффект на самом деле есть, так как мы сами его добавили. Если значимых отличий не будет найдено – это ошибка второго рода. Проведя 1000 экспериментов и посчитав долю ошибок второго рода, получим точечную оценку вероятности ошибки второго рода.
Посмотрим, как оценить вероятности ошибок в коде. С помощью численных синтетических А/А и А/Б экспериментов оценим вероятности ошибок и построим доверительные интервалы:
def run_synthetic_experiments(values, sample_size, effect=0, n_iter=10000):
"""Проводим синтетические эксперименты, возвращаем список p-value."""
pvalues = []
for _ in range(n_iter):
a, b = np.random.choice(values, size=(2, sample_size,), replace=False)
b += effect
pvalue = stats.ttest_ind(a, b).pvalue
pvalues.append(pvalue)
return np.array(pvalues)
def print_estimated_errors(pvalues_aa, pvalues_ab, alpha):
"""Оценивает вероятности ошибок."""
estimated_first_type_error = np.mean(pvalues_aa < alpha)
estimated_second_type_error = np.mean(pvalues_ab >= alpha)
ci_first = estimate_ci_bernoulli(estimated_first_type_error, len(pvalues_aa))
ci_second = estimate_ci_bernoulli(estimated_second_type_error, len(pvalues_ab))
print(f'оценка вероятности ошибки I рода = {estimated_first_type_error:0.4f}')
print(f' доверительный интервал = [{ci_first[0]:0.4f}, {ci_first[1]:0.4f}]')
print(f'оценка вероятности ошибки II рода = {estimated_second_type_error:0.4f}')
print(f' доверительный интервал = [{ci_second[0]:0.4f}, {ci_second[1]:0.4f}]')
def estimate_ci_bernoulli(p, n, alpha=0.05):
"""Доверительный интервал для Бернуллиевской случайной величины."""
t = stats.norm.ppf(1 - alpha / 2, loc=0, scale=1)
std_n = np.sqrt(p * (1 - p) / n)
return p - t * std_n, p + t * std_n
pvalues_aa = run_synthetic_experiments(values, sample_size, effect=0)
pvalues_ab = run_synthetic_experiments(values, sample_size, effect=effect)
print_estimated_errors(pvalues_aa, pvalues_ab, alpha)оценка вероятности ошибки I рода = 0.0991
доверительный интервал = [0.0932, 0.1050]
оценка вероятности ошибки II рода = 0.1978
доверительный интервал = [0.1900, 0.2056]Оценки вероятностей ошибок примерно равны 0.1 и 0.2, как и должно быть. Всё верно, тест Стьюдента на этих данных работает корректно.
Распределение p-value
Выше рассмотрели случай, когда тест контролирует вероятность ошибки первого рода при фиксированном уровне значимости. Если решим изменить уровень значимости с 0.1 на 0.01, будет ли тест контролировать вероятность ошибки первого рода? Было бы хорошо, если тест контролировал вероятность ошибки первого рода при любом заданном уровне значимости. Формально это можно записать так:
Для любого выполняется
.
Заметим, что в левой части равенства записано выражение для функции распределения p-value. Из равенства следует, что функция распределения p-value в точке X равна X для любого X от 0 до 1. Эта функция распределения является функцией распределения равномерного распределения от 0 до 1. Мы только что показали, что статистический критерий контролирует вероятность ошибки первого рода на заданном уровне для любого уровня значимости тогда и только тогда, когда при верности нулевой гипотезы p-value распределено равномерно от 0 до 1.
При верности нулевой гипотезы p-value должно быть распределено равномерно. А как должно быть распределено p-value при верности альтернативной гипотезы? Из условия для вероятности ошибки второго рода следует, что
.
Получается, график функции распределения p-value при верности альтернативной гипотезы должен проходить через точку , где
и
– допустимые вероятности ошибок конкретного эксперимента.
Проверим, как распределено p-value в численном эксперименте. Построим эмпирические функции распределения p-value:
import matplotlib.pyplot as plt
def plot_pvalue_distribution(pvalues_aa, pvalues_ab, alpha, beta):
"""Рисует графики распределения p-value."""
estimated_first_type_error = np.mean(pvalues_aa < alpha)
estimated_second_type_error = np.mean(pvalues_ab >= alpha)
y_one = estimated_first_type_error
y_two = 1 - estimated_second_type_error
X = np.linspace(0, 1, 1000)
Y_aa = [np.mean(pvalues_aa < x) for x in X]
Y_ab = [np.mean(pvalues_ab < x) for x in X]
plt.plot(X, Y_aa, label='A/A')
plt.plot(X, Y_ab, label='A/B')
plt.plot([alpha, alpha], [0, 1], '--k', alpha=0.8)
plt.plot([0, alpha], [y_one, y_one], '--k', alpha=0.8)
plt.plot([0, alpha], [y_two, y_two], '--k', alpha=0.8)
plt.plot([0, 1], [0, 1], '--k', alpha=0.8)
plt.title('Оценка распределения p-value', size=16)
plt.xlabel('p-value', size=12)
plt.legend(fontsize=12)
plt.grid()
plt.show()
plot_pvalue_distribution(pvalues_aa, pvalues_ab, alpha, beta)P-value для синтетических А/А тестах действительно оказалось распределено равномерно от 0 до 1, а для синтетических А/Б тестов проходит через точку .
Кроме оценок распределений на графике дополнительно построены четыре пунктирные линии:
-
диагональная из точки [0, 0] в точку [1, 1] – это функция распределения равномерного распределения на отрезке от 0 до 1, по ней можно визуально оценивать равномерность распределения p-value;
-
вертикальная линия с
– пороговое значение p-value, по которому определяем отвергать нулевую гипотезу или нет. Проекция на ось ординат точки пересечения вертикальной линии с функцией распределения p-value для А/А тестов – это вероятность ошибки первого рода. Проекция точки пересечения вертикальной линии с функцией распределения p-value для А/Б тестов – это мощность теста (мощность = 1 —
).
-
две горизонтальные линии – проекции на ось ординат точки пересечения вертикальной линии с функцией распределения p-value для А/А и А/Б тестов.
График с оценками распределения p-value для синтетических А/А и А/Б тестов позволяет проверить корректность теста для любого значения уровня значимости.
Некорректный критерий
Выше рассмотрели пример, когда тест Стьюдента оказался корректным критерием для случайных данных из нормального распределения. Может быть, все критерии всегда работаю корректно, и нет смысла каждый раз проверять вероятности ошибок?
Покажем, что это не так. Немного изменим рассмотренный ранее пример, чтобы продемонстрировать некорректную работу критерия. Допустим, мы решили увеличить продолжительность эксперимента до 2-х недель. Для каждого пользователя будем вычислять стоимость покупок за первую неделю и стоимость покупок за второю неделю. Полученные стоимости будем передавать в тест Стьюдента для проверки значимости отличий. Положим, что поведение пользователей повторяется от недели к неделе, и стоимости покупок одного пользователя совпадают.
def run_synthetic_experiments_two(values, sample_size, effect=0, n_iter=10000):
"""Проводим синтетические эксперименты на двух неделях."""
pvalues = []
for _ in range(n_iter):
a, b = np.random.choice(values, size=(2, sample_size,), replace=False)
b += effect
# дублируем данные
a = np.hstack((a, a,))
b = np.hstack((b, b,))
pvalue = stats.ttest_ind(a, b).pvalue
pvalues.append(pvalue)
return np.array(pvalues)
pvalues_aa = run_synthetic_experiments_two(values, sample_size)
pvalues_ab = run_synthetic_experiments_two(values, sample_size, effect=effect)
print_estimated_errors(pvalues_aa, pvalues_ab, alpha)
plot_pvalue_distribution(pvalues_aa, pvalues_ab, alpha, beta)оценка вероятности ошибки I рода = 0.2451
доверительный интервал = [0.2367, 0.2535]
оценка вероятности ошибки II рода = 0.0894
доверительный интервал = [0.0838, 0.0950]Получили оценку вероятности ошибки первого рода около 0.25, что сильно больше уровня значимости 0.1. На графике видно, что распределение p-value для синтетических А/А тестов не равномерно, оно отклоняется от диагонали. В этом примере тест Стьюдента работает некорректно, так как данные зависимые (стоимости покупок одного человека зависимы). Если бы мы сразу не догадались про зависимость данных, то оценка вероятностей ошибок помогла бы нам понять, что такой тест некорректен.
Итоги
Мы обсудили, что такое корректность статистического теста, посмотрели, как оценить вероятности ошибок на исторических данных и привели пример некорректной работы критерия.
Таким образом:
-
корректный критерий – это критерий, у которого вероятности ошибок первого и второго рода равны допустимым вероятностям ошибок первого и второго рода соответственно;
-
чтобы критерий контролировал вероятность ошибки первого рода для любого уровня значимости, необходимо и достаточно, чтобы p-value при верности нулевой гипотезы было распределено равномерно от 0 до 1.
Скачать материал

Скачать материал


- Сейчас обучается 385 человек из 62 регионов


- Сейчас обучается 262 человека из 64 регионов




Описание презентации по отдельным слайдам:
-
1 слайд
Основы теории проверки статистических гипотез.
Доцент Аймаханова А.Ш.
-
2 слайд
План лекции:
1. Статистические гипотезы в медико-
биологических исследованиях.
2. Параметрические критерии различий.
3. Непараметрические критерии.
4. Критерии согласия. -
3 слайд
Процедура сопоставления высказанного предположения (гипотезы) с выборочными данными называется проверкой гипотез.
Задачи статистической проверки гипотез:
Относительно некоторой генеральной совокупности высказывается та или иная гипотеза Н0.
Из этой генеральной совокупности извлекается выборка.
Требуется указать правило, при помощи которого можно было бы по выборке решить вопрос о том, следует ли отклонить гипотезу Н0 или принять ее. -
4 слайд
Статистическая гипотеза- это предположение о виде распределения или о величинах неизвестных параметров генеральной совокупности, которая может быть проверена на основании выборочных показателей.
Примеры статистических гипотез:
Генеральная совокупность распределена по нормальному закону Гаусса.
Дисперсии двух нормальных совокупностей равны между собой. -
5 слайд
Статистические гипотезы
Параметрические Непараметрические
-
6 слайд
Нулевой гипотезой Н0 называется основная гипотеза, которая проверяется.
Альтернативной гипотезой Н1, называется гипотеза, конкурирующая с нулевой, то есть противоречащая ей.
Простой называют гипотезу, содержащую только одно предположение. a=a0
Сложной называют гипотезу, которая состоит из конечного или бесконечного числа простых гипотез.
Статистическим критерием проверки гипотезы Н0 называется правило, по которому принимается решение принять или отклонить гипотезу Н0. -
7 слайд
Основной принцип проверки гипотез
Проверку гипотез осуществляют на основании результатов выборки X1,X2,…,Xn , из которых формируют функцию выборки Tn=T(X1,X2,…,Xn ), называемой статистикой критерия.Tn=T(X1,X2,…,Xn )
критическая область S область принятия гипотезы
-
8 слайд
Возможные ошибки при проверке гипотез
Первого рода Второго рода
-
9 слайд
Уровнем значимости критерия () называется вероятность допустить ошибку 1-го рода.
Вероятность ошибки 2-го рода обозначается через β.
Мощностью критерия называется вероятность недопущения ошибки 2-го рода (1- β).
Р(отвергнуть Н0/Н0 верна) или Р(Н1/Н0)
βР(принять Н0/Н0 неверна) или βР(Н0 /Н1)
1-βР(принять Н1/Н1 верна)
Чем больше мощность критерия, тем вероятность ошибки 2-го рода меньше.
Разумное соотношение между и β находят, исходя из тяжести последствий каждой из ошибок. -
10 слайд
Методика проверки гипотез:
1. Формирование нулевой Н0 и альтернативной Н1 гипотез исходя из выборки X1,X2,…,Xn .
2. Подбор статистики критерия Tn=T(X1,X2,…,Xn )
3. По статистике критерия Tn и уровню значимости определяют критическую точку tкр, то есть границу, отделяющую область от S.
4. Для полученной реализации выборки Х=(X1,X2,…,Xn ) подсчитывают значение критерия, то есть Tнабл=T(X1,X2,…,Xn )t
5. Если tS (например, t> tкр для правосторонней области S), то нулевую гипотезу Н0 отвергают; если же t (t <tкр), то нет оснований, чтобы отвергнуть гипотезу Н0. -
11 слайд
t-критерий Стьюдента:
Общий вид: -
12 слайд
Случай независимых выборок.
df= n1+n2-2
n1=n2=n
df=n-1
n1≠n2 -
13 слайд
Случай зависимых выборок.
df=n-1
-
14 слайд
Вывод:
Критерий Стьюдента может быть использован для проверки гипотезы о различии средних только для двух групп.
Критерий Стьюдента применяется в случае малых выборок, что характерно для медико- биологических экспериментов.
Если схема эксперимента предполагает большее число групп, воспользуйтесь дисперсионным анализом.
Если критерий Стьюдента был использован для проверки различий между несколькими группами, то истинный уровень значимости можно получить, умножив уровень значимости, на число возможных сравнений. -
15 слайд
F- критерий Фишера:
1>2
df1=n1-1, df2=n2-1 -
16 слайд
Критерии различия называют непараметрическими, если он не базируется на предположении о типе распределения генеральной совокупности и не использует параметры этой совокупности.
Применение непараметрических методов целесообразно:
на этапе разведочного анализа;
при малом числе наблюдений (до 30);
когда нет уверенности в соответствии данных закону нормального распределения. -
17 слайд
Непараметрические критерии представлены основными группами:
критерии различия между группами
независимых выборок;
критерии различия между группами
зависимых выборок. -
18 слайд
Различия между независимыми группами
U критерий Манна-Уитни
двухвыборочный критерий
Колмогорова – Смирнова. -
19 слайд
Различия между зависимыми группами
z – критерий знаков
Т – критерий Уилкоксона парных
сравнений -
20 слайд
Критерии согласия:
Критерием согласия называют статистический критерий проверки гипотезы о предполагаемом законе неизвестного распределения.Пирсона (Хи-квадрат),
Колмогорова,
Фишера,
Смирнова. -
21 слайд
Критерий согласия χ2 (хи-квадрат) Пирсона.
Н0: «между эмперическим распределением и теоретической моделью нет никакого различия».Если эмпирические частоты (ni) сильно отличаются от теоретических (npi) ,то проверяемую гипотезу Но следует отвергнуть; в противном случае-принять.
-
22 слайд
Критерий согласия χ2 (хи-квадрат) Пирсона.
n-объем выборки
k-число интервалов разбиения выборки
ni-число значений выборки, попавших в і-й интервал
npi — теоретическая частота попадания значений случайной величины Х в і-й интервал. -
23 слайд
Критерий согласия χ2 (хи-квадрат) Пирсона.
илиО-фактически наблюдаемое число
Е- теоретически ожидаемое число -
24 слайд
Поправка Йейтса
Для распределения признаков, которые принимают всего 2 значения.
-
25 слайд
Правило применения критерия χ2.
*По формуле вычисляют — выборочное
значение статистики критерия.
*выбрав уровень значимости α критерия,
по таблице -распределения находим критическую точку*Если ≤ , то гипотеза Н0 не противоречит опытным данным;
если > , то гипотеза Н0 отвергается.
Неоходимым условием применения критерия Пирсона является наличие в каждом из интервалов не менее 5 наблюдений -
26 слайд
ЛИТЕРАТУРА:
Медик В.А.,Токмачев М.С.,Фишман Б.Б.Статистика в медицине и биологии. М.: Медицина, 2000.
Лукьянова Е.А. Медицинская статистика.- М.: Изд. РУДН, 2002.
Рокицкий П.Ф. Биологическая статистика.- Высшая школа, 1973.
И.В. Павлушков и др. Основы высшей математики и математической статистики.
(учебник для медицинских и фармацевтических вузов) М., «ГЭОТАР — МЕД»; 2003 -
Найдите материал к любому уроку, указав свой предмет (категорию), класс, учебник и тему:
6 276 033 материала в базе
- Выберите категорию:
- Выберите учебник и тему
- Выберите класс:
-
Тип материала:
-
Все материалы
-
Статьи
-
Научные работы
-
Видеоуроки
-
Презентации
-
Конспекты
-
Тесты
-
Рабочие программы
-
Другие методич. материалы
-
Найти материалы
Другие материалы
- 20.12.2020
- 223
- 2
- 06.12.2020
- 228
- 2
- 19.11.2020
- 383
- 8
- 12.11.2020
- 567
- 9
- 23.10.2020
- 207
- 1
- 15.10.2020
- 593
- 2
- 22.09.2020
- 225
- 4
- 14.09.2020
- 115
- 0
Вам будут интересны эти курсы:
-
Курс повышения квалификации «Педагогическая риторика в условиях реализации ФГОС»
-
Курс повышения квалификации «Основы управления проектами в условиях реализации ФГОС»
-
Курс профессиональной переподготовки «Организация логистической деятельности на транспорте»
-
Курс профессиональной переподготовки «Логистика: теория и методика преподавания в образовательной организации»
-
Курс повышения квалификации «Финансы: управление структурой капитала»
-
Курс профессиональной переподготовки «Разработка эффективной стратегии развития современного вуза»
-
Курс профессиональной переподготовки «Управление информационной средой на основе инноваций»
-
Курс профессиональной переподготовки «Риск-менеджмент организации: организация эффективной работы системы управления рисками»
-
Курс профессиональной переподготовки «Организация деятельности специалиста оценщика-эксперта по оценке имущества»
-
Курс профессиональной переподготовки «Методика организации, руководства и координации музейной деятельности»
-
Курс профессиональной переподготовки «Организация и управление службой рекламы и PR»
Презентация на тему «Основы теории проверки статистических гипотез»
-
Скачать презентацию (0.18 Мб)
-
52 загрузки -
5.0 оценка
Ваша оценка презентации
Оцените презентацию по шкале от 1 до 5 баллов
- 1
- 2
- 3
- 4
- 5
Комментарии
Добавить свой комментарий
Аннотация к презентации
Презентация powerpoint для студентов на тему «Основы теории проверки статистических гипотез». Содержит 27 слайдов. Скачать файл 0.18 Мб. Самая большая база качественных презентаций. Смотрите онлайн с анимацией или скачивайте на компьютер. Средняя оценка: 5.0 балла из 5.
-
Формат
pptx (powerpoint)
-
Количество слайдов
27
-
Слова
-
Конспект
Отсутствует
Содержание
-
Слайд 1
Основы теории проверки статистических гипотез.
Доцент Аймаханова А.Ш.
-
Слайд 2
План лекции:
1. Статистические гипотезы в медико-
биологических исследованиях.
2. Параметрические критерии различий.
3. Непараметрические критерии.
4. Критерии согласия. -
Слайд 3
Процедура сопоставления высказанного предположения (гипотезы) с выборочными данными называется проверкой гипотез.
Задачи статистической проверки гипотез:
Относительно некоторой генеральной совокупности высказывается та или иная гипотеза Н0.
Из этой генеральной совокупности извлекается выборка.
Требуется указать правило, при помощи которого можно было бы по выборке решить вопрос о том, следует ли отклонить гипотезу Н0 или принять ее. -
Слайд 4
Статистическая гипотеза- это предположение о виде распределения или о величинах неизвестных параметров генеральной совокупности, которая может быть проверена на основании выборочных показателей.
Примеры статистических гипотез:
Генеральная совокупность распределена по нормальному закону Гаусса.
Дисперсии двух нормальных совокупностей равны между собой. -
Слайд 5
Статистические гипотезы
Параметрические Непараметрические
-
Слайд 6
Нулевой гипотезой Н0 называется основная гипотеза, которая проверяется.
Альтернативной гипотезой Н1, называется гипотеза, конкурирующая с нулевой, то есть противоречащая ей.
Простойназывают гипотезу, содержащую только одно предположение. a=a0
Сложной называют гипотезу, которая состоит из конечного или бесконечного числа простых гипотез.
Статистическим критерием проверки гипотезы Н0 называется правило, по которому принимается решение принять или отклонить гипотезу Н0. -
Слайд 7
Основной принцип проверки гипотез
Проверку гипотез осуществляют на основании результатов выборки X1,X2,…,Xn , из которых формируют функцию выборки Tn=T(X1,X2,…,Xn ), называемой статистикой критерия.
Tn=T(X1,X2,…,Xn )
критическая область S область принятия гипотезы
-
Слайд 8
Возможные ошибки при проверке гипотез
Первого рода Второго рода
-
Слайд 9
Уровнем значимости критерия ()называется вероятность допустить ошибку 1-го рода.
Вероятность ошибки 2-го рода обозначается через β.
Мощностью критерия называется вероятность недопущения ошибки 2-го рода (1- β).
Р(отвергнуть Н0/Н0 верна) или Р(Н1/Н0)
βР(принять Н0/Н0 неверна) или βР(Н0 /Н1)
1-βР(принять Н1/Н1 верна)
Чем больше мощность критерия, тем вероятность ошибки 2-го рода меньше.
Разумное соотношение между и β находят, исходя из тяжести последствий каждой из ошибок. -
Слайд 10
Методика проверки гипотез:
1. Формирование нулевой Н0 и альтернативной Н1 гипотез исходя из выборки X1,X2,…,Xn .
2. Подбор статистики критерия Tn=T(X1,X2,…,Xn )
3. По статистике критерия Tn и уровню значимости определяют критическую точку tкр, то есть границу, отделяющую область от S.
4. Для полученной реализации выборки Х=(X1,X2,…,Xn ) подсчитывают значение критерия, то есть Tнабл=T(X1,X2,…,Xn )t
5. Если tS (например, t> tкр дляправосторонней области S), то нулевую гипотезу Н0 отвергают; если же t (t -
Слайд 11
t-критерий Стьюдента:
Общий вид:
-
Слайд 12
Случай независимых выборок.
df= n1+n2-2
n1=n2=n
df=n-1
n1≠n2
-
Слайд 13
Случай зависимых выборок.
df=n-1
-
Слайд 14
Вывод:
Критерий Стьюдента может быть использован для проверки гипотезы о различии средних только для двух групп.
Критерий Стьюдента применяется в случае малых выборок, что характерно для медико- биологических экспериментов.
Если схема эксперимента предполагает большее число групп, воспользуйтесь дисперсионным анализом.
Если критерий Стьюдента был использован для проверки различий между несколькими группами, то истинный уровень значимости можно получить, умножив уровень значимости, на число возможных сравнений. -
Слайд 15
F- критерий Фишера:
1>2
df1=n1-1, df2=n2-1 -
Слайд 16
Критерии различия называют непараметрическими, если он не базируется на предположении о типе распределения генеральной совокупности и не использует параметры этой совокупности.
Применение непараметрических методовцелесообразно:
на этапе разведочного анализа;
при малом числе наблюдений (до 30);
когда нет уверенности в соответствии данных закону нормального распределения. -
Слайд 17
Непараметрические критерии представленыосновными группами:
критерии различия между группами
независимых выборок;
критерии различия между группами
зависимых выборок. -
Слайд 18
Различия между независимыми группами
U критерий Манна-Уитни
двухвыборочный критерий
Колмогорова – Смирнова. -
Слайд 19
Различия между зависимыми группами
z – критерий знаков
Т – критерий Уилкоксона парных
сравнений -
Слайд 20
Критерии согласия:
Критерием согласияназывают статистический критерий проверки гипотезы о предполагаемом законе неизвестного распределения.
Пирсона (Хи-квадрат),
Колмогорова,
Фишера,
Смирнова. -
Слайд 21
Критерий согласия χ2 (хи-квадрат) Пирсона.
Н0: «между эмперическим распределением и теоретической моделью нет никакого различия».
Если эмпирические частоты (ni) сильно отличаются от теоретических (npi) ,то проверяемую гипотезу Но следует отвергнуть; в противном случае-принять.
-
Слайд 22
n-объем выборки
k-число интервалов разбиения выборки
ni-число значений выборки, попавших в і-й интервал
npi — теоретическая частота попадания значений случайной величины Х в і-й интервал. -
Слайд 23
или
О-фактически наблюдаемое число
Е- теоретически ожидаемое число -
Слайд 24
Поправка Йейтса
Для распределения признаков, которые принимают всего 2 значения.
-
Слайд 25
Правило применения критерия χ2.
*По формуле вычисляют — выборочное
значение статистики критерия.
*выбрав уровень значимости α критерия,
по таблице -распределения находим критическую точку*Если ≤ , то гипотеза Н0 не противоречит опытным данным;
если > , то гипотеза Н0 отвергается.
Неоходимым условием применения критерия Пирсонаявляется наличие в каждом из интервалов не менее 5 наблюдений -
Слайд 26
ЛИТЕРАТУРА:
Медик В.А.,Токмачев М.С.,Фишман Б.Б.Статистика в медицине и биологии. М.: Медицина, 2000.
Лукьянова Е.А. Медицинская статистика.- М.: Изд. РУДН, 2002.
Рокицкий П.Ф. Биологическая статистика.- Высшая школа, 1973.
И.В. Павлушков и др. Основы высшей математики и математической статистики.
(учебник для медицинских и фармацевтических вузов) М., «ГЭОТАР — МЕД»; 2003 -
Слайд 27
СПАСИБО ЗА ВНИМАНИЕ.
Посмотреть все слайды
Сообщить об ошибке
Похожие презентации












Спасибо, что оценили презентацию.
Мы будем благодарны если вы поможете сделать сайт лучше и оставите отзыв или предложение по улучшению.
Добавить отзыв о сайте

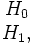
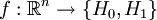 ,
,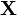 соответствует гипотезе
соответствует гипотезе 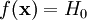 .
.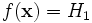 .
.