Новая IP-камера IPEYE-B1-SUR-2.8-12-03 это экономичное решение для круглосуточного аудио и видео мониторинга на улице при любых погодных условиях. Модель оснащена современным сенсором с прогрессивным сканированием, подсветкой, аудиовходом и технологией трехмерного шумоподавления
Использование мегапиксельного CMOS сенсора позволяет получить хорошее изображение в разрешении 1280*720 точек. За счет наличия технологии трехмерного шумоподавления выполняется понижение шумов за счет сравнения кадров, а так же снижаются пространственные шумы. Вся сцена обрабатывается так, что каждая часть изображения становится четкой и свободной от шумов. Вариофокальный объектив с переменным фокусным расстоянием от 2.8 до 12мм обеспечивает гибкость при выборе обозреваемых территорий, от широких помещений до длинных узких коридоров. Благодаря аудиовходу можно подключить внешний микрофон и осуществлять запись звука на объекте видеонаблюдения. Прочный металлический корпус обеспечивает камере хорошую защиту от внешних механических воздействий. Камера безотказно работает в широком диапазоне температур от -40 до +50°C.
B1-SUR-2.8-12-03 универсальная IP-камера. Вы можете осуществлять запись локально на регистратор, флэшку, компьютер или сервер, либо писать в облако, подключив камеру к сети интернет. За счет уникальной технологии, разработанной в компании АЙПИАЙ, вам не потребуется статический IP адрес, настройка DDNS и установка дополнительного программного обеспечения. Простое добавление камеры в облако производится в несколько действий, а использование мобильных приложений (Android, iOS) позволит контролировать ситуацию из любой точки мира, где есть интернет. Так же камера поддерживает ПО по стандарту Onvif (Trassir, Macroscop, Линия и т.д.). Российский разработчик. Сделано в Санкт-Петербурге. Гарантия 3 года.
- Тип камеры
- Буллет
- Разрешение
- 1Mpx (1280*720)
- Сенсор
- JX-H42, 1/4″
- Светочувствительность
- 0.1 лк (день) /0.01 лк (ночь)
- Скорость кадров
- до 25 к/сек для всех разрешений
- Объектив
- 2.8-12 мм
- Угол обзора по горизонтали
- от 17° до 67°
- Угол обзора по вертикали
- от 10° до 41°
- Подсветка
- Да, до 30 м
- Звук
- Аудиовход
- Темп. режим
- -40°C — 50°C
- Запись в облако
- Да
- Wifi
- Нет
- Грозозащита
- Нет
- Onvif
- 2.4
- POE
- Нет
- USB
- Нет
- Встр. обогрев
- Нет
- Класс защиты
- IP 66
- Материал корпуса
- Металл
- Питание
- 12B (DC)
- Вес нетто/Вес брутто
- 840 гр./ 960 гр.
- Габариты упаковки
- 235x134x130 мм
Документация
| Сертификат соответствия | Скачать |
| Руководство для добавления камер IPEYE в облачный сервис | Скачать |
| Руководство к Web-интерфейсу камер IPEYE | Скачать |
| Руководство к личному кабинету пользователя сервиса IPEYE | Скачать |
| Инструкция по установке и использованию программы UC | Скачать |
| Руководство к мобильным приложениям IPEYE | Скачать |
Программы для Windows
| Утилита для настройки и добавления камер в облако «IPEYE HELPER» | Скачать |
| Клиент видеонаблюдения для камер IPEYE UC версия 4.6 (64 бит / x64) | Скачать |
| Клиент видеонаблюдения для камер IPEYE UC версия 4.6 (32 бит / x86) | Скачать |
| ActiveX плагин для камер видеонаблюдения IPEYE | Скачать |
Мобильные приложения
Вопрос по видеонаблюдению
Здравствуйте. Установил 5 IP камер IPEYE и видеорегистратор Hunter. Все камеры подключены к облаку IPEYE и на трех проплачена запись по движению. Видеорегистратор тоже подключен к своему облаку. Также запись ведется на видеорегистратор. В течении суток из сети пропадает одно из устройств. Это может быть как камера так и видеорегистратор, а может пропасть всё кроме какой нибудь одной камеры. Всегда по разному. В камерах и видеорегистраторе IP адреса статические. Когда добавляю камеры в видеорегистратор, он сам как то меняет подсеть в камерах. Может камеры надо прописывать вручную? Последний раз подключил 4 камеры без видеорегистратора прямо к роутеру и снова в течении суток ушла в offline одна камера, а три оставшиеся работают уже неделю. Камеры ушедшие в offline, не видит даже HELPER, можно вернуть к жизни только перезагрузкой по питанию. Как можно сделать , чтобы камера зависла ? Пробовал дома выставить в камере IP адрес смартфона и после подключения камеры включал его. Так роутер присваивал ему уже другой адрес. Конфлик адресов не получился. Провайдер интернета даёт 25Мбит. Проверял скорость, на отдачу доходит до 50Мбит. Камеры прошиты новой прошивкой. Три такие работают в садоводствах на въезде. Каждая камера подключена к своему роутеру и работает от 4G модема. Даже когда скорость падала до 164кбит, камера не висла. Она то в сети , то в offline. Проплатил интернет и все работает без перезагрузки по питанию. В чем может быть причина ?
Спрашивает , 2019-03-24 12:50:59
Камера hi3516ev300
Прошивка
Версия:2.2.05.11-lite
Сборка:master+8cdf302, 2022-05-11
Mahestic master+b5bceef, 2022-05-09
Перестает писаться через rtsp поток в облако ipeye, в vlc долго очень прогружает картинку и потом она замирает на месте.
В это же время в другое облако(двор24) котрое получает также поток через rtsp идет запись без прерываний. Обычно перестает работать ночью. Детектор что камера перестала работать и что она офлайн в ipeye не срабатывает.
ipeye + vlc одновременно перестают работать корректно.
После перезагрузки камеры начинают работать корректно.
По тикету нет никакой информации, как можно воспроизвести проблему (отсутствуют шаги, логи, скриншоты и т.п.)
Шаги воспроизведения:
Прошил камеру через coupler
Обновил до версий указаных в тикете
Подключил поток в ipeye
Через сутки открываем камеру в ipeye — картинка не грузится, в архиве также не грузится
Открываем поток в vlc получаем статичную картинку.
Перезагружаем камеру и все снова работает как часы.
Куда прикрепить лог и конфиг? Здесь постоянно пишет ошибку
Лог можно поместить в zip архив и прикрепить к тикету
Судя по логам — у вас сетевые проблемы. Для подробного анализа нужны будут:
- Кусок лога Majestic в момент наблюдания проблемы (либо указать временной промежуток, когда возникает эта проблема)
- Кусок лога со стороны VLC в этот же период с ключом
-vvv - Дамп трафика между устройствами (можно сделать на клиенте, камере или промежуточном устройстве между ними)
Как сделать дамп трафика?
Перед камерой стоит роутер микротик, на нем настроен проброс порта 554 на камеру.
По поводу сети пробовал открывать поток напрямую по внешнему ip(также как работало до прошивки oipc).
При подключении vlc сначала долго думает(видимо идет буферизация) потом появляется статическая картинка. В логи на камере никаких ошибок не пишет.
Также пробовал подключаться по локальному ip через впн, проблема таже, только в логи сначала пишет что соединение запрещено(типа авторизацию не проходит), потом через несколько секунд проходит и картинка появляется статическиая.
Проблема решается перезагрузкой камеры(попробую перезагрузку только маджестика, забыл проверить)
Проблема набюдается на двух камерах в разных городах.
Причем завсиание идет ночью или вечером при включеном ночном режиме, но может это совпадение
но я так понимаю wireshark можно и на стороне клиента с vlc запустить?
лог из консоли vlc -vvv в момент проблем
vlclog.txt
ы
ответ техподдержки ipeye
Рекомендация — обновить прошивку если есть на что, или раз в 12 часов ребутать камеру для того что бы на ней счетчик таймштампа обнулялся.
Подробнее:
Камера когда отдает поток она фреймы маркирует временем — выстраивая таким образом линию времени, и эта камера 15 числа в 9 утра подключилась и стала слать видео подписывая фреймы таймштампами.
И вот в 9 вечера камера доходит в значении таймштампа до какого-то числа, которое является максимальным для данного типа и вместо того что бы переполнить его и начать отсчет заново и продолжать линию времени — оно так и остается на одном месте.
То есть все фреймы которые прилетели после 9 вечера 15 числа помечены одной и той же временной меткой поэтому и проблемы с архивом — файлы есть, но судя по данным в них они произошли все в единый момент времени.
Потом 16 в 8:30 камеру перезагрузили и она начала отсчитывать все заново
У нас есть функция — калькуляция таймштампа на основе фпс.
Но и она не поможет — потому что камера заявляет 25 фпс а по факту он там где-то 12-13
Есть еще проблема с теми же таймштампами. Даже если мы камеру перезапускаем каждые 11 часов, то в архиве файлы всреано не корректные и при скачивании и просмотре в vlc идет сильная рассинхронизация звука и картинки.
По словам техподдержки ipeye эта проблема связано с теми же таймштампами.
В другом облаке если камеру не перезапускать то часть архива просто пишется без звука и просматривается как на ускореной перемотке. При скачивании также ускореная перемотка без звука.
Проблема вызвана ошибкой, которая добавлена при недавнем рефакторинге в библиотеке SmolRTSP, после ее исправления в Majestic также она исчезнет
А какая старая версия majestic в которой еще нет этой ошибки? попробую пока на ней поработать
Просьба проверить последнюю версию, был возвращен старый алгоритм расчета временных меток
Проверил, проблема устранена
|
|
эта статья нужны дополнительные цитаты для проверка. Пожалуйста помоги улучшить эту статью к добавление цитат в надежные источники. Материал, не полученный от источника, может быть оспорен и удален. |
А критическая масса это наименьшее количество делящийся материал, необходимый для устойчивого ядерная цепная реакция. Критическая масса делящегося материала зависит от его ядерный свойства (в частности, его ядерное деление поперечное сечение ), плотность, форма, обогащение, чистота, температура и окружение. Концепция важна в конструкция ядерного оружия.
Объяснение критичности
Когда ядерная цепная реакция в массе делящегося материала является самоподдерживающейся, говорят, что масса находится в критический состояние, в котором нет увеличения или уменьшения мощности, температуры или нейтрон Население.
Числовая мера критической массы зависит от эффективный коэффициент размножения нейтронов k, среднее количество нейтронов, высвобождаемых за одно событие деления, которые вызывают другое событие деления, а не поглощаются или покидают материал. Когда k = 1, масса критична, и цепная реакция самоподдерживающаяся.
А субкритический Масса — это масса делящегося материала, не способного выдерживать цепную реакцию деления. Популяция нейтронов, вводимых в подкритическую сборку, будет экспоненциально уменьшаться. В таком случае, k < 1. Постоянная скорость спонтанных делений вызывает пропорционально постоянный уровень нейтронной активности. Константа пропорциональности увеличивается как k увеличивается.
А сверхкритический масса — это та, которая после начала деления будет происходить с возрастающей скоростью. Материал может прийти в равновесие (т.е. снова станет критическим) при повышенной температуре / мощности или самоуничтожится. В случае сверхкритичности k > 1.
Из-за спонтанное деление сверхкритическая масса подвергнется цепной реакции. Например, сферическая критическая масса чистого уран-235 (235U) с массой около 52 кг (115 фунтов) будет испытывать около 15 событий спонтанного деления в секунду.[нужна цитата ] Вероятность того, что одно такое событие вызовет цепную реакцию, зависит от того, насколько масса превышает критическую массу. Если есть уран-238 (238U) в настоящее время скорость спонтанного деления будет намного выше. Деление также может быть инициировано нейтронами, образованными космические лучи.
Изменение точки критичности
Масса, при которой возникает критичность, может быть изменена путем изменения определенных атрибутов, таких как топливо, форма, температура, плотность и установка вещества, отражающего нейтроны. Эти атрибуты имеют сложные взаимодействия и взаимозависимости. В этих примерах описаны только самые простые идеальные случаи:
Варьируя количество топлива
Топливная сборка может быть критической при почти нулевой мощности. Если бы идеальное количество топлива было добавлено к слегка подкритической массе для создания «точно критической массы», деление было бы самоподдерживающимся только для одного поколения нейтронов (тогда потребление топлива снова делает сборку подкритической).
Если бы идеальное количество топлива было добавлено к слегка подкритической массе, чтобы создать едва сверхкритическую массу, температура сборки увеличилась бы до начального максимума (например: 1K выше температуры окружающей среды), а затем через некоторое время понизится до температуры окружающей среды, поскольку топливо, израсходованное во время деления, снова возвращает сборку в докритичность.
Изменение формы
Масса может быть точно критической, не будучи идеальной однородной сферой. Более точное уточнение формы до идеальной сферы сделает массу сверхкритической. И наоборот, изменение формы на менее совершенную сферу снизит ее реактивность и сделает ее подкритической.
Изменение температуры
Масса может быть критической при определенной температуре. Сечения деления и поглощения возрастают с уменьшением относительной скорости нейтронов. При повышении температуры топлива нейтроны заданной энергии появляются быстрее, и поэтому деление / поглощение менее вероятно. Это связано с Доплеровское уширение из 238U-резонанс, но является общим для всех видов топлива / поглотителей / конфигураций. Если пренебречь очень важными резонансами, полное нейтронное сечение каждого материала показывает обратную зависимость от относительной скорости нейтронов. Горячее топливо всегда менее реактивно, чем холодное (избыточное / недостаточное замедление в LWR это отдельная тема). Тепловое расширение, связанное с повышением температуры, также вносит свой вклад в отрицательный коэффициент реактивности, поскольку атомы топлива отдаляются друг от друга. Масса, которая является критической при комнатной температуре, будет докритической в среде, где температура выше комнатной, только из-за теплового расширения.
Изменение плотности массы
Чем выше плотность, тем ниже критическая масса. Плотность материала при постоянной температуре можно изменять, изменяя давление или натяжение или изменяя кристаллическую структуру (см. аллотропы плутония ). Идеальная масса станет подкритической, если ей позволено расшириться, или, наоборот, та же масса станет сверхкритической при сжатии. Изменение температуры также может изменить плотность; однако влияние на критическую массу затем усложняется температурными эффектами (см. «Изменение температуры») и тем, расширяется или сжимается материал при повышении температуры. Предполагая, что материал расширяется с температурой (обогащенный уран-235 при комнатной температуре, например), в точно критическом состоянии, он станет докритическим при нагревании до более низкой плотности или станет сверхкритическим при охлаждении до более высокой плотности. Говорят, что такой материал имеет отрицательный температурный коэффициент реактивности, что указывает на то, что его реакционная способность снижается при повышении температуры. Использование такого материала в качестве топлива означает, что деление уменьшается при повышении температуры топлива.
Использование отражателя нейтронов
Окружение сферической критической массы отражатель нейтронов дополнительно снижает массу, необходимую для критичности. Обычным материалом для отражателя нейтронов является бериллий металл. Это уменьшает количество нейтронов, покидающих делящийся материал, что приводит к увеличению реактивности.
Использование тампера
В бомбе плотная оболочка из материала, окружающая делящееся ядро, будет по инерции содержать расширяющийся делящийся материал. Это увеличивает эффективность. Тампер также имеет тенденцию действовать как отражатель нейтронов. Поскольку в бомбе используются быстрые нейтроны (а не нейтроны, замедляемые отражением от легких элементов, как в реакторе), нейтроны, отраженные тампером, замедляются из-за их столкновений с ядрами тампера, а также потому, что отраженным нейтронам требуется время, чтобы вернуться. делящемуся ядру им требуется гораздо больше времени, чтобы поглощаться делящимся ядром. Но они вносят свой вклад в реакцию и могут снизить критическую массу в четыре раза.[1] Кроме того, если тампер представляет собой (например, обедненный) уран, он может делиться из-за нейтронов высокой энергии, генерируемых первичным взрывом. Это может значительно увеличить выход, особенно если еще больше нейтронов генерируется при синтезе изотопов водорода в так называемой усиленной конфигурации.
Критический размер
Критический размер — это минимальный размер активной зоны ядерного реактора или ядерного оружия, который может быть изготовлен для определенного геометрического расположения и состава материала. Критический размер должен как минимум включать достаточно расщепляющегося материала для достижения критической массы. Если размер активной зоны реактора меньше определенного минимума, через его поверхность выходит слишком много нейтронов деления, и цепная реакция не поддерживается.
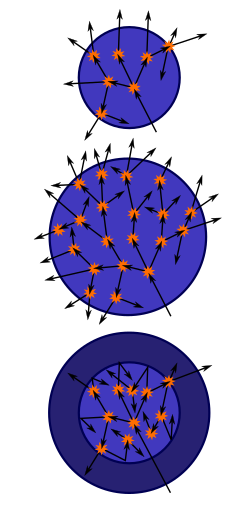
Критическая масса голого шара
Вершина: А сфера делящегося материала слишком мал, чтобы позволить цепная реакция стать самодостаточным, как нейтроны Сгенерированно с помощью деления может слишком легко сбежать.
Середина: Увеличивая массу сферы до критической, реакция может стать самоподдерживающейся.
Дно: Окружив исходную сферу отражатель нейтронов увеличивает эффективность реакций, а также позволяет реакции становиться самоподдерживающейся.
Форма с минимальной критической массой и наименьшими физическими размерами — сфера. Критические массы голой сферы при нормальной плотности актиниды перечислены в следующей таблице. Большая часть информации о массах голых сфер считается засекреченной, поскольку она важна для конструкции ядерного оружия, но некоторые документы были рассекречены.[2]
| Нуклид | Период полураспада (у) |
Критическая масса (кг) |
Диаметр (см) |
Ссылка |
|---|---|---|---|---|
| уран-233 | 159,200 | 15 | 11 | [3] |
| уран-235 | 703,800,000 | 52 | 17 | [3] |
| нептуний-236 | 154,000 | 7 | 8.7 | [4] |
| нептуний-237 | 2,144,000 | 60 | 18 | [5][6] |
| плутоний-238 | 87.7 | 9.04–10.07 | 9.5–9.9 | [7] |
| плутоний-239 | 24,110 | 10 | 9.9 | [3][7] |
| плутоний-240 | 6561 | 40 | 15 | [3] |
| плутоний-241 | 14.3 | 12 | 10.5 | [8] |
| плутоний-242 | 375,000 | 75–100 | 19–21 | [8] |
| америций-241 | 432.2 | 55–77 | 20–23 | [9] |
| америций-242m | 141 | 9–14 | 11–13 | [9] |
| америций-243 | 7370 | 180–280 | 30–35 | [9] |
| кюрий -243 | 29.1 | 7.34–10 | 10–11 | [10] |
| кюрий -244 | 18.1 | 13.5–30 | 12.4–16 | [10] |
| кюрий -245 | 8500 | 9.41–12.3 | 11–12 | [10] |
| кюрий -246 | 4760 | 39–70.1 | 18–21 | [10] |
| кюрий -247 | 15,600,000 | 6.94–7.06 | 9.9 | [10] |
| берклий -247 | 1380 | 75.7 | 11.8-12.2 | [11] |
| берклий -249 | 0.9 | 192 | 16.1-16.6 | [11] |
| калифорний -249 | 351 | 6 | 9 | [4] |
| калифорний -251 | 900 | 5.46 | 8.5 | [4] |
| калифорний -252 | 2.6 | 2.73 | 6.9 | [12] |
| эйнштейний -254 | 0.755 | 9.89 | 7.1 | [11] |
Критическая масса низкосортного урана сильно зависит от сорта: с 20% 235U более 400 кг; с 15% 235У, это значительно больше 600 кг.
Критическая масса обратно пропорциональна квадрату плотности. Если плотность на 1% больше, а масса на 2% меньше, то объем меньше на 3%, а диаметр на 1% меньше. Вероятность попадания нейтрона на см пройденного пути в ядро пропорциональна плотности. Отсюда следует, что увеличение плотности на 1% означает, что расстояние, пройденное до выхода из системы, будет на 1% меньше. Это то, что необходимо учитывать при попытке более точных оценок критических масс изотопов плутония, чем приблизительные значения, приведенные выше, поскольку металлический плутоний имеет большое количество различных кристаллических фаз, плотность которых может сильно варьироваться.
Обратите внимание, что не все нейтроны участвуют в цепной реакции. Некоторые убегают, а другие проходят радиационный захват.
Позволять q обозначают вероятность того, что данный нейтрон вызывает деление в ядре. Считайте только быстрые нейтроны, и разреши ν обозначают количество мгновенных нейтронов, генерируемых при делении ядра. Например, ν ≈ 2.5 для урана-235. Тогда критичность наступает, когда ν · q = 1. Зависимость этого от геометрии, массы и плотности проявляется через фактор q.
Учитывая полное взаимодействие поперечное сечение σ (обычно измеряется в сараи ), длина свободного пробега быстрого нейтрона 

Однако еще раз отметим, что это лишь приблизительная оценка.
По общей массе M, ядерная масса м, плотность ρ и фактор выдумки ж учитывающим геометрические и другие эффекты, критичность соответствует
что явно восстанавливает вышеупомянутый результат, что критическая масса обратно пропорциональна квадрату плотности.
В качестве альтернативы, можно выразить это более кратко, используя поверхностную плотность массы Σ:
где фактор ж был переписан как f ‘ чтобы учесть тот факт, что эти два значения могут различаться в зависимости от геометрических эффектов и того, как определяется Σ. Например, для голого твердого шара размером 239Критичность Pu составляет 320 кг / м3.2, независимо от плотности, и для 235U при 550 кг / м2. В любом случае критичность зависит от типичного нейтрона, «видящего» такое количество ядер вокруг себя, что поверхностная плотность ядер превышает определенный порог.
Это применяется в ядерном оружии имплозивного типа, где сферическая масса делящегося материала, которая существенно меньше критической массы, становится сверхкритической за счет очень быстрого увеличения ρ (и, следовательно, Σ) (см. Ниже). Действительно, сложные программы создания ядерного оружия могут создать функциональное устройство из меньшего количества материала, чем требуется для более примитивных программ оружия.
Помимо математики, есть простой физический аналог, который помогает объяснить этот результат. Представьте, что из выхлопной трубы выходят пары дизельного топлива. Сначала пары кажутся черными, затем постепенно вы можете без проблем видеть сквозь них. Это происходит не потому, что общее сечение рассеяния всех частиц сажи изменилось, а потому, что сажа рассеялась. Если рассматривать прозрачный куб длиной L на стороне, залитой сажей, затем оптическая глубина этой среды обратно пропорционально квадрату L, и поэтому пропорциональна поверхностной плотности частиц сажи: мы можем облегчить просмотр воображаемого куба, просто увеличив куб.
Некоторые неопределенности способствуют определению точного значения критических масс, включая (1) подробное знание сечений деления, (2) расчет геометрических эффектов. Эта последняя проблема послужила значительной мотивацией для разработки Метод Монте-Карло в вычислительной физике Николай Метрополис и Станислав Улам. Фактически, даже для однородной твердой сферы точный расчет отнюдь не является тривиальным. Наконец, обратите внимание, что расчет также может быть выполнен в предположении континуального приближения для переноса нейтронов. Это сводит его к проблеме распространения. Однако, поскольку типичные линейные размеры не намного больше, чем длина свободного пробега, такое приближение применимо лишь в незначительной степени.
Наконец, обратите внимание, что для некоторых идеализированных геометрий критическая масса формально может быть бесконечной, а для описания критичности используются другие параметры. Например, рассмотрим бесконечный лист расщепляющегося материала. Для любой конечной толщины это соответствует бесконечной массе. Однако критичность достигается только тогда, когда толщина этой плиты превышает критическое значение.
Важность конструкции ядерного оружия
Если два куска подкритического материала не собрать вместе достаточно быстро, ядерная преддонация (шипеть ) может произойти, в результате чего очень небольшой взрыв разнесет большую часть материала на части.
Пока не требуется детонация, ядерное оружие должны поддерживаться в субкритическом состоянии. В случае урановой бомбы это может быть достигнуто путем хранения топлива в нескольких отдельных частях, каждая ниже критический размер либо потому, что они слишком маленькие, либо неправильной формы. Чтобы произвести детонацию, куски урана быстро собираются вместе. В Маленький мальчик, это было достигнуто путем выстрела куска урана («бублика») в ствол пистолета на другой кусок («шип»). Эта конструкция называется орудие деления пушечного типа.
Теоретическая 100% чистота 239Оружие из полиуретана также может быть сконструировано как оружие пушечного типа, как предложенное Манхэттенским проектом. Тонкий человек дизайн. На самом деле это непрактично, потому что даже «оружейный класс» 239Pu загрязнен небольшим количеством 240Pu, который имеет сильную склонность к спонтанному делению. Из-за этого оружие типа пушки разумного размера будет подвергаться ядерной реакции (преддонация ) до того, как массы плутония будут в состоянии, чтобы произойти полноценный взрыв.
Вместо этого плутоний присутствует в виде подкритической сферы (или другой формы), которая может быть или не быть полой. Детонация производится при взрыве кумулятивный заряд окружая сферу, увеличивая плотность (и схлопывая полость, если она есть), чтобы произвести срочный критический конфигурация. Это известно как оружие имплозивного типа.
Оперативная критичность
Событие деления должно высвободить, в среднем, более одного свободного нейтрона желаемого уровня энергии для поддержания цепной реакции, и каждый должен найти другие ядра и вызвать их деление. Большая часть нейтронов, высвобождаемых в результате деления, происходит сразу же после этого события, но часть из них приходит позже, когда продукты деления распадаются, что может произойти в среднем от микросекунд до минут. Это удачно для атомной энергетики, поскольку без этой задержки «критическое состояние» было бы немедленно катастрофическим событием, как в случае ядерной бомбы, где более 80 поколений цепной реакции происходят менее чем за микросекунду, что слишком быстро для человек или даже машина, чтобы отреагировать. Физики выделяют два важных момента в постепенном увеличении потока нейтронов: критический, когда цепная реакция становится самоподдерживающейся благодаря вкладу обоих видов генерации нейтронов,[13] и срочный критический, где только немедленные «мгновенные» нейтроны будут поддерживать реакцию без необходимости в нейтронах распада. Атомные электростанции работают между этими двумя точками реактивность, в то время как выше критической точки находится область ядерного оружия и некоторых аварий на атомной электростанции, таких как Чернобыльская катастрофа.
Удобная единица измерения реактивности предложена Луи Слотин: что из доллар и центы.
Смотрите также
- Критичность аварии
- Безопасность ядерной критичности
- Геометрическая форма и деформация материала
Рекомендации
- ^ Сербер, Роберт, The Los Alamos Primer: Первые лекции о том, как построить атомную бомбу, (Калифорнийский университет Press, 1992) ISBN 0-520-07576-5 Оригинальный «LA-1» 1943 года, рассекреченный в 1965 году, плюс комментарии и историческое введение
- ^ Переоценка критических характеристик некоторых систем быстрых нейтронов в Лос-Аламосе
- ^ а б c d Конструкция и материалы ядерного оружия, Веб-сайт Инициативы по ядерной угрозе.[мертвая ссылка ][ненадежный источник? ]
- ^ а б c Заключительный отчет, оценка данных о безопасности ядерной критичности и предельных значений для актинидов на транспорте, Французская Республика, Институт радиозащиты и защиты от несчастных случаев, Департамент защиты и безопасности несчастных случаев.
- ^ Глава 5, Завтра проблемы? Разделенные нептуний 237 и америций, Проблемы контроля делящегося материала (1999), isis-online.org
- ^ П. Вайс (26 октября 2002 г.). «Нептуниум Ядерное? Малоизученный металл становится критическим». Новости науки. 162 (17): 259. Дои:10.2307/4014034. Архивировано из оригинал 15 декабря 2012 г.. Получено 7 ноября 2013.
- ^ а б Обновленные оценки критической массы плутония-238, Министерство энергетики США: Управление научно-технической информации
- ^ а б Амори Б. Ловинс, Ядерное оружие и плутоний для энергетических реакторов, Природа, Vol. 283, No. 5750, pp. 817–823, 28 февраля 1980 г.
- ^ а б c Диас, Хемант; Танкок, Найджел; Клейтон, Анджела (2003). «Расчет критической массы для 241Являюсь, 242 кв.м.Я и 243Являюсь» (PDF). Вызовы на пути к обеспечению глобальной ядерной безопасности. Материалы седьмой Международной конференции по безопасности ядерной критичности. II. Токай, Ибараки, Япония: Японский научно-исследовательский институт атомной энергии. С. 618–623.
- ^ а б c d е Окуно, Хироши; Кавасаки, Хиромицу (2002). «Расчет критических и докритических масс кюрия-243–247 на основе JENDL-3.2 для пересмотра ANSI / ANS-8.15». Журнал ядерной науки и технологий. 39 (10): 1072–1085. Дои:10.1080/18811248.2002.9715296.
- ^ а б c Institut de Radioprotection et de Sûreté Nucléaire: «Оценка ядерной безопасности по критичности. Данные и пределы для актинидов на транспорте», п. 16
- ^ Кэри Саблетт, Ядерное оружие. Часто задаваемые вопросы: Раздел 6.0. Ядерные материалы. 20 февраля 1999 г.
- ^ Родос, Ричард (1995). Темное Солнце: Создание водородной бомбы.В описании советского эквивалента стартапа CP1 в Чикагском университете в 1942 году подробно описывается долгое ожидание этих запоздалых нейтронов.
In nuclear engineering, a critical mass is the smallest amount of fissile material needed for a sustained nuclear chain reaction. The critical mass of a fissionable material depends upon its nuclear properties (specifically, its nuclear fission cross-section), density, shape, enrichment, purity, temperature, and surroundings. The concept is important in nuclear weapon design.
Explanation of criticality[edit]
When a nuclear chain reaction in a mass of fissile material is self-sustaining, the mass is said to be in a critical state in which there is no increase or decrease in power, temperature, or neutron population.
A numerical measure of a critical mass is dependent on the effective neutron multiplication factor k, the average number of neutrons released per fission event that go on to cause another fission event rather than being absorbed or leaving the material. When k = 1, the mass is critical, and the chain reaction is self-sustaining.
A subcritical mass is a mass of fissile material that does not have the ability to sustain a fission chain reaction. A population of neutrons introduced to a subcritical assembly will exponentially decrease. In this case, k < 1. A steady rate of spontaneous fissions causes a proportionally steady level of neutron activity. The constant of proportionality increases as k increases.
A supercritical mass is one which, once fission has started, will proceed at an increasing rate. The material may settle into equilibrium (i.e. become critical again) at an elevated temperature/power level or destroy itself. In the case of supercriticality, k > 1.
Due to spontaneous fission a supercritical mass will undergo a chain reaction. For example, a spherical critical mass of pure uranium-235 (235U) with a mass of about 52 kilograms (115 lb) would experience around 15 spontaneous fission events per second.[citation needed] The probability that one such event will cause a chain reaction depends on how much the mass exceeds the critical mass. If there is uranium-238 (238U) present, the rate of spontaneous fission will be much higher. Fission can also be initiated by neutrons produced by cosmic rays.
Changing the point of criticality[edit]
The mass where criticality occurs may be changed by modifying certain attributes such as fuel, shape, temperature, density and the installation of a neutron-reflective substance. These attributes have complex interactions and interdependencies. These examples only outline the simplest ideal cases:
Varying the amount of fuel[edit]
It is possible for a fuel assembly to be critical at near zero power. If the perfect quantity of fuel were added to a slightly subcritical mass to create an «exactly critical mass», fission would be self-sustaining for only one neutron generation (fuel consumption then makes the assembly subcritical again).
Similarly, if the perfect quantity of fuel were added to a slightly subcritical mass, to create a barely supercritical mass, the temperature of the assembly would increase to an initial maximum (for example: 1 K above the ambient temperature) and then decrease back to the ambient temperature after a period of time, because fuel consumed during fission brings the assembly back to subcriticality once again.
Changing the shape[edit]
A mass may be exactly critical without being a perfect homogeneous sphere. More closely refining the shape toward a perfect sphere will make the mass supercritical. Conversely changing the shape to a less perfect sphere will decrease its reactivity and make it subcritical.
Changing the temperature[edit]
A mass may be exactly critical at a particular temperature. Fission and absorption cross-sections increase as the relative neutron velocity decreases. As fuel temperature increases, neutrons of a given energy appear faster and thus fission/absorption is less likely. This is not unrelated to Doppler broadening of the 238U resonances but is common to all fuels/absorbers/configurations. Neglecting the very important resonances, the total neutron cross-section of every material exhibits an inverse relationship with relative neutron velocity. Hot fuel is always less reactive than cold fuel (over/under moderation in LWR is a different topic). Thermal expansion associated with temperature increase also contributes a negative coefficient of reactivity since fuel atoms are moving farther apart. A mass that is exactly critical at room temperature would be sub-critical in an environment anywhere above room temperature due to thermal expansion alone.
Varying the density of the mass[edit]
The higher the density, the lower the critical mass. The density of a material at a constant temperature can be changed by varying the pressure or tension or by changing crystal structure (see allotropes of plutonium). An ideal mass will become subcritical if allowed to expand or conversely the same mass will become supercritical if compressed. Changing the temperature may also change the density; however, the effect on critical mass is then complicated by temperature effects (see «Changing the temperature») and by whether the material expands or contracts with increased temperature. Assuming the material expands with temperature (enriched uranium-235 at room temperature for example), at an exactly critical state, it will become subcritical if warmed to lower density or become supercritical if cooled to higher density. Such a material is said to have a negative temperature coefficient of reactivity to indicate that its reactivity decreases when its temperature increases. Using such a material as fuel means fission decreases as the fuel temperature increases.
Use of a neutron reflector[edit]
Surrounding a spherical critical mass with a neutron reflector further reduces the mass needed for criticality. A common material for a neutron reflector is beryllium metal. This reduces the number of neutrons which escape the fissile material, resulting in increased reactivity.
Use of a tamper[edit]
In a bomb, a dense shell of material surrounding the fissile core will contain, via inertia, the expanding fissioning material, which increases the efficiency. This is known as a tamper. A tamper also tends to act as a neutron reflector. Because a bomb relies on fast neutrons (not ones moderated by reflection with light elements, as in a reactor), the neutrons reflected by a tamper are slowed by their collisions with the tamper nuclei, and because it takes time for the reflected neutrons to return to the fissile core, they take rather longer to be absorbed by a fissile nucleus. But they do contribute to the reaction, and can decrease the critical mass by a factor of four.[1] Also, if the tamper is (e.g. depleted) uranium, it can fission due to the high energy neutrons generated by the primary explosion. This can greatly increase yield, especially if even more neutrons are generated by fusing hydrogen isotopes, in a so-called boosted configuration.
Critical size[edit]
The critical size is the minimum size of a nuclear reactor core or nuclear weapon that can be made for a specific geometrical arrangement and material composition. The critical size must at least include enough fissionable material to reach critical mass. If the size of the reactor core is less than a certain minimum, too many fission neutrons escape through its surface and the chain reaction is not sustained.
Critical mass of a bare sphere[edit]
Top: A sphere of fissile material is too small to allow the chain reaction to become self-sustaining as neutrons generated by fissions can too easily escape.
Middle: By increasing the mass of the sphere to a critical mass, the reaction can become self-sustaining.
Bottom: Surrounding the original sphere with a neutron reflector increases the efficiency of the reactions and also allows the reaction to become self-sustaining.
The shape with minimal critical mass and the smallest physical dimensions is a sphere. Bare-sphere critical masses at normal density of some actinides are listed in the following table. Most information on bare sphere masses is considered classified, since it is critical to nuclear weapons design, but some documents have been declassified.[2]
| Nuclide | Half-life (y) |
Critical mass (kg) |
Diameter (cm) |
Ref |
|---|---|---|---|---|
| uranium-233 | 159,200 | 15 | 11 | [3] |
| uranium-235 | 703,800,000 | 52 | 17 | [3] |
| neptunium-236 | 154,000 | 7 | 8.7 | [4] |
| neptunium-237 | 2,144,000 | 60 | 18 | [5][6] |
| plutonium-238 | 87.7 | 9.04–10.07 | 9.5–9.9 | [7] |
| plutonium-239 | 24,110 | 10 | 9.9 | [3][7] |
| plutonium-240 | 6561 | 40 | 15 | [3] |
| plutonium-241 | 14.3 | 12 | 10.5 | [8] |
| plutonium-242 | 375,000 | 75–100 | 19–21 | [8] |
| americium-241 | 432.2 | 55–77 | 20–23 | [9] |
| americium-242m | 141 | 9–14 | 11–13 | [9] |
| americium-243 | 7370 | 180–280 | 30–35 | [9] |
| curium-243 | 29.1 | 7.34–10 | 10–11 | [10] |
| curium-244 | 18.1 | 13.5–30 | 12.4–16 | [10] |
| curium-245 | 8500 | 9.41–12.3 | 11–12 | [10] |
| curium-246 | 4760 | 39–70.1 | 18–21 | [10] |
| curium-247 | 15,600,000 | 6.94–7.06 | 9.9 | [10] |
| berkelium-247 | 1380 | 75.7 | 11.8-12.2 | [11] |
| berkelium-249 | 0.9 | 192 | 16.1-16.6 | [11] |
| californium-249 | 351 | 6 | 9 | [4] |
| californium-251 | 900 | 5.46 | 8.5 | [4] |
| californium-252 | 2.6 | 2.73 | 6.9 | [12] |
| einsteinium-254 | 0.755 | 9.89 | 7.1 | [11] |
The critical mass for lower-grade uranium depends strongly on the grade: with 20% 235U it is over 400 kg; with 15% 235U, it is well over 600 kg.
The critical mass is inversely proportional to the square of the density. If the density is 1% more and the mass 2% less, then the volume is 3% less and the diameter 1% less. The probability for a neutron per cm travelled to hit a nucleus is proportional to the density. It follows that 1% greater density means that the distance travelled before leaving the system is 1% less. This is something that must be taken into consideration when attempting more precise estimates of critical masses of plutonium isotopes than the approximate values given above, because plutonium metal has a large number of different crystal phases which can have widely varying densities.
Note that not all neutrons contribute to the chain reaction. Some escape and others undergo radiative capture.
Let q denote the probability that a given neutron induces fission in a nucleus. Consider only prompt neutrons, and let ν denote the number of prompt neutrons generated in a nuclear fission. For example, ν ≈ 2.5 for uranium-235. Then, criticality occurs when ν·q = 1. The dependence of this upon geometry, mass, and density appears through the factor q.
Given a total interaction cross section σ (typically measured in barns), the mean free path of a prompt neutron is 

Note again, however, that this is only a rough estimate.
In terms of the total mass M, the nuclear mass m, the density ρ, and a fudge factor f which takes into account geometrical and other effects, criticality corresponds to
which clearly recovers the aforementioned result that critical mass depends inversely on the square of the density.
Alternatively, one may restate this more succinctly in terms of the areal density of mass, Σ:
where the factor f has been rewritten as f’ to account for the fact that the two values may differ depending upon geometrical effects and how one defines Σ. For example, for a bare solid sphere of 239Pu criticality is at 320 kg/m2, regardless of density, and for 235U at 550 kg/m2.
In any case, criticality then depends upon a typical neutron «seeing» an amount of nuclei around it such that the areal density of nuclei exceeds a certain threshold.
This is applied in implosion-type nuclear weapons where a spherical mass of fissile material that is substantially less than a critical mass is made supercritical by very rapidly increasing ρ (and thus Σ as well) (see below). Indeed, sophisticated nuclear weapons programs can make a functional device from less material than more primitive weapons programs require.
Aside from the math, there is a simple physical analog that helps explain this result. Consider diesel fumes belched from an exhaust pipe. Initially the fumes appear black, then gradually you are able to see through them without any trouble. This is not because the total scattering cross section of all the soot particles has changed, but because the soot has dispersed. If we consider a transparent cube of length L on a side, filled with soot, then the optical depth of this medium is inversely proportional to the square of L, and therefore proportional to the areal density of soot particles: we can make it easier to see through the imaginary cube just by making the cube larger.
Several uncertainties contribute to the determination of a precise value for critical masses, including (1) detailed knowledge of fission cross sections, (2) calculation of geometric effects. This latter problem provided significant motivation for the development of the Monte Carlo method in computational physics by Nicholas Metropolis and Stanislaw Ulam. In fact, even for a homogeneous solid sphere, the exact calculation is by no means trivial. Finally, note that the calculation can also be performed by assuming a continuum approximation for the neutron transport. This reduces it to a diffusion problem. However, as the typical linear dimensions are not significantly larger than the mean free path, such an approximation is only marginally applicable.
Finally, note that for some idealized geometries, the critical mass might formally be infinite, and other parameters are used to describe criticality. For example, consider an infinite sheet of fissionable material. For any finite thickness, this corresponds to an infinite mass. However, criticality is only achieved once the thickness of this slab exceeds a critical value.
Criticality in nuclear weapon design[edit]
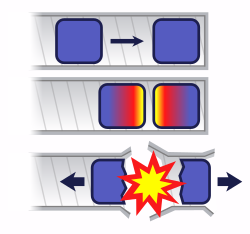
If two pieces of subcritical material are not brought together fast enough, nuclear predetonation (fizzle) can occur, whereby a very small explosion will blow the bulk of the material apart.
Until detonation is desired, a nuclear weapon must be kept subcritical. In the case of a uranium gun-type bomb, this can be achieved by keeping the fuel in a number of separate pieces, each below the critical size either because they are too small or unfavorably shaped. To produce detonation, the pieces of uranium are brought together rapidly. In Little Boy, this was achieved by firing a piece of uranium (a ‘doughnut’) down a gun barrel onto another piece (a ‘spike’). This design is referred to as a gun-type fission weapon.
A theoretical 100% pure 239Pu weapon could also be constructed as a gun-type weapon, like the Manhattan Project’s proposed Thin Man design. In reality, this is impractical because even «weapons grade» 239Pu is contaminated with a small amount of 240Pu, which has a strong propensity toward spontaneous fission. Because of this, a reasonably sized gun-type weapon would suffer nuclear reaction (predetonation) before the masses of plutonium would be in a position for a full-fledged explosion to occur.
Instead, the plutonium is present as a subcritical sphere (or other shape), which may or may not be hollow. Detonation is produced by exploding a shaped charge surrounding the sphere, increasing the density (and collapsing the cavity, if present) to produce a prompt critical configuration. This is known as an implosion type weapon.
Prompt criticality[edit]
The event of fission must release, on the average, more than one free neutron of the desired energy level in order to sustain a chain reaction, and each must find other nuclei and cause them to fission. Most of the neutrons released from a fission event come immediately from that event, but a fraction of them come later, when the fission products decay, which may be on the average from microseconds to minutes later. This is fortunate for atomic power generation, for without this delay «going critical» would be an immediately catastrophic event, as it is in a nuclear bomb where upwards of 80 generations of chain reaction occur in less than a microsecond, far too fast for a human, or even a machine, to react. Physicists recognize two points in the gradual increase of neutron flux which are significant: critical, where the chain reaction becomes self-sustaining thanks to the contributions of both kinds of neutron generation,[13] and prompt critical, where the immediate «prompt» neutrons alone will sustain the reaction without need for the decay neutrons. Nuclear power plants operate between these two points of reactivity, while above the prompt critical point is the domain of nuclear weapons and some nuclear power accidents, such as the Chernobyl disaster.
See also[edit]
- Criticality (status)
- Criticality accident
- Nuclear criticality safety
- Geometric and material buckling
References[edit]
- ^ Serber, Robert, The Los Alamos Primer: The First Lectures on How to Build an Atomic Bomb, (University of California Press, 1992) ISBN 0-520-07576-5 Original 1943 «LA-1», declassified in 1965, plus commentary and historical introduction
- ^ Reevaluated Critical Specifications of Some Los Alamos Fast-Neutron Systems
- ^ a b c d Nuclear Weapons Design & Materials, The Nuclear Threat Initiative website.[dead link][unreliable source?]
- ^ a b c Final Report, Evaluation of nuclear criticality safety data and limits for actinides in transport, Republic of France, Institut de Radioprotection et de Sûreté Nucléaire, Département de Prévention et d’étude des Accidents.
- ^ Chapter 5, Troubles tomorrow? Separated Neptunium 237 and Americium, Challenges of Fissile Material Control (1999), isis-online.org
- ^
P. Weiss (26 October 2002). «Neptunium Nukes? Little-studied metal goes critical». Science News. 162 (17): 259. doi:10.2307/4014034. Archived from the original on 15 December 2012. Retrieved 7 November 2013. - ^ a b Updated Critical Mass Estimates for Plutonium-238, U.S. Department of Energy: Office of Scientific & Technical Information
- ^ a b Amory B. Lovins, Nuclear weapons and power-reactor plutonium, Nature, Vol. 283, No. 5750, pp. 817–823, February 28, 1980
- ^ a b c Dias, Hemanth; Tancock, Nigel; Clayton, Angela (2003). «Critical Mass Calculations for 241Am, 242mAm and 243Am» (PDF). Challenges in the Pursuit of Global Nuclear Criticality Safety. Proceedings of the Seventh International Conference on Nuclear Criticality Safety. Vol. II. Tokai, Ibaraki, Japan: Japan Atomic Energy Research Institute. pp. 618–623.
- ^ a b c d e Okuno, Hiroshi; Kawasaki, Hiromitsu (2002). «Critical and Subcritical Mass Calculations of Curium-243 to -247 Based on JENDL-3.2 for Revision of ANSI/ANS-8.15». Journal of Nuclear Science and Technology. 39 (10): 1072–1085. doi:10.1080/18811248.2002.9715296.
- ^ a b c Institut de Radioprotection et de Sûreté Nucléaire: «Evaluation of nuclear criticality safety. data and limits for actinides in transport», p. 16
- ^ Carey Sublette, Nuclear Weapons Frequently Asked Questions: Section 6.0 Nuclear Materials February 20, 1999
- ^ Rhodes, Richard (1 August 1995). Dark Sun: The Making of the Hydrogen Bomb. Simon & Schuster. ISBN 978-0-68-480400-2. LCCN 95011070. OCLC 456652278. OL 7720934M. Wikidata Q105755363 – via Internet Archive.In the description of the Soviet equivalent of the CP1 startup at the University of Chicago in 1942, the long waits for those tardy neutrons is described in detail