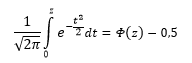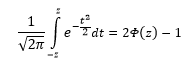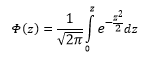Кривая ошибок кривая гаусса обладает следующими свойствами - Не ошибается лишь тот, кто ничего не делает!

Интегральная
предельная теорема Ляпунова устанавливает
условия, при которых возникает наиболее
важный и наиболее часто встречающийся
в природе нормальный закон распределения,
имеющий плотность

(1.62)

где, как было
установлено нами в задаче 1.169, а
= М_х,
σ = √D_x.

Теорему Ляпунова
упрощенно можно сформулировать так:
если некоторая случайная величина есть
сумма достаточно большого числа других
случайных независимых величин,
отклоняющихся от своих математических
ожиданий на весьма малые величины по
сравнению с отклонениями суммарной
величины, то закон распределения этой
суммарной случайной величины будет
близок к нормальному.

На основании этой
теоремы можно полагать, что ошибки
измерений подчиняются нормальному
закону, так как они складываются из
суммы большого числа элементарных
ошибок. По этой же причине координаты
попадания в цель при стрельбе подчиняются
этому закону распределения. Таких
примеров можно привести много.

Для вычисления
вероятностей попадания в интервал при
нормальном законе распределения
можно воспользоваться формулой

P{a<X<b} = F (b) —
F(a),

где интегральная
функция

(1.63)

Если ввести новую
переменную

Z = (x — M_x)/σ, (1.64)

обладающую
свойствами (см. 1.168) M_z
= 0, σ_z
= 0, то можно
написать для нее

Рисунок 18.

Тогда, очевидно,

P{a
< x
< b}
= P{t₁< z
< t₂}
= F(t₂)
— F(t₁),

где
t₂
=
(b—M_x)/a;
t₁
=
(a
— M_x)/σ.

Для функции F(t)
имеются
таблицы, однако более удобно пользоваться
другой, связанной с ней аналитически
функцией

(1.65)

обладающей свойством
Ф(- t)
= — Ф(t)
(нечетная
функция).

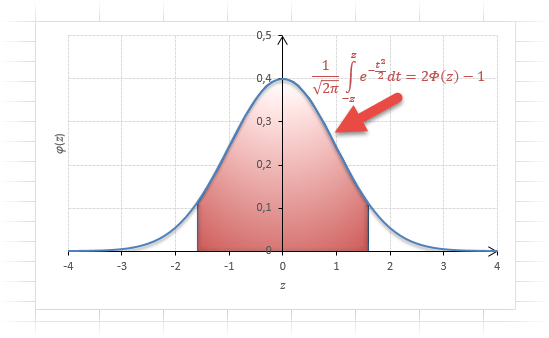
Функция Ф(t)
численно равна заштрихованной площади
в осях х и
φ(x)
(рис. 18, а) и в осях t
и φ(t)
(рис. 18, б).

Как видно из рис.
18, б,
имеет место
связь

(1.66)

(F(t)
есть
площадь под кривой φ(t),
ограниченная
справа абсциссой t).
Подставив
формулу (1.66) в выражение

Р{а <
X
< b}
= Р{t₁
< X
< t₂}
= F(t₁)
– F(t₂).

Получим

Р{а < Х < b)
= 1/2{Ф(t₂)
-Ф (t₁)}.
(1.67)

Если
пределы t₂
и
t₁
изменения
случайной переменной z
таковы,
что t₂
= |t₁|
= t,
то можно
написать

,
(1.68)

откуда
следует, что функция Ф(t)
представляет
собой вероятность попадания
в интервал, симметричный относительно
математического ожидания.

Для функций Ф(t)
составлены таблицы (см. прил. IV).
В случае
их отсутствия применяют формулу

(1.69)

Функцию
Ф(t)
называют интегралом вероятностей, или
функцией Лапласа.
Последнее ее название связано с так
называемой интегральной
теоремой Лапласа, который доказал, что
при большом числе испытаний
п число
появлений интересующего нас события k
заключено
в
пределах

Р{а < k
< b}
= {Ф(t₂)-Ф(t₁)}.
(1.70)

Ярким
примером случайной величины, подчиненной
нормальному закону
распределения, является случайная
ошибка измерений, определяемая
по формуле

В
теории ошибок измерений существует
важнейшее понятие — истинное
значение измеряемой величины X,
а величина

Δ_i=x_i
— X
, (1.71)

называется
истинной ошибкой измерения. Выражение
(1.71) можно переписать
в виде

Δ_i=x_i
— M_X
+
M_X
— X
= Q_i
+ c.

Величину
с
называют
систематической ошибкой измерения,
которая
может быть как постоянной, так и переменной
величиной (подробнее
см. [2]).

В классической
теории ошибок принимают постулат 1

М_Х= Х,

т. е. полагают, что
систематические ошибки в измерениях
отсутствуют,
(это свойство называют несмещенностью)
или их исключают правильной
постановкой методики измерений. Тогда,
очевидно, будем иметь
свойства Δ_i= Q_i и

Постулат
2 предполагает, что ошибки Δ_i
подчинены нормальному закону
распределения с плотностью

(1.72)

или, если перейти
к нормированной величине
,

(1.73)

Причем

,
(1.74)

Выражение (1.72)
часто записывается в виде

(1.75)

где

— так называемая мера точности.

Свойства
случайных ошибок, вытекающие из указанных
двух постулатов
и проявляющиеся при массовых испытаниях,
могут быть охарактеризованы
следующим образом.

Свойство
1. Случайные
ошибки по абсолютной величине с заданной
вероятностью
Р
не
превосходят определенного предела,
равного tσ,
где
t
— коэффициент
такой, что Р
= Ф(t).
Так, например,
из 100 ошибок с
вероятностью Р
=
0,67 не превосходят предел, равный σ,
67
ошибок, 95
ошибок с вероятностью 0,95 не превосходят
2σ
и т. д.

Свойство
2. Положительные
и отрицательные случайные ошибки, равные
по абсолютной величине, равновозможны,
т. е.

Р{Δ > 0} = Р{Δ < 0}
= 1/2.

Свойство
3. Среднее
арифметическое из значений случайной
ошибки
при неограниченном возрастании числа
наблюдений имеет свойство
компенсации,
т. е.

вер

.
(1.76)

Систематические
ошибки этим свойством обладают редко.

Свойство
4. Малые
по абсолютной величине случайные ошибки
встречаются
чаще, чем большие.

Плотность
нормального распределения ошибок Δ_i
(1.72) или (1.73) называют
кривой ошибок, или кривой Гаусса.

1.183. Вычислить ординаты кривой нормального
распределения для значений Δ
= 0, σ, 2σ, Зσ, если σ = 0,47″. По полученным
данным построить кривую распределения.
Вычисления проконтролировать по таблице
(прил. II).

Решение. Прежде
всего, имеем

Вычисления располагаем в табл. 1.

Таблица
1

Δ_i	t	-h²Δ² = -t²/2		y		y = y’ h
0 σ	0	0	1	0,851	0,564	0,850
1 σ	1	— 0,50	0,607	0,516	0,342	0,516
2 σ	2	-2,0	0,136	0,115	0,076	0,115
3 σ	3	— 4,5	0,010	0,008	0,0063	0,008

Примечания:

(Построение кривой
ошибок дано на рис. 19).

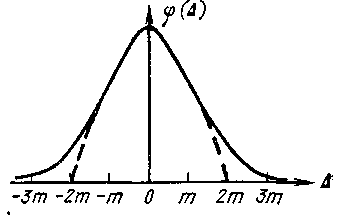
Рисунок 19.

При построении кривой ошибок масштабы
выбирают так, чтобы обеспечить
наглядность,

Кривая Гаусса обладает следующими
свойствами:

функция φ(Δ) четная, т. е. φ(Δ) = φ(- Δ), и
кривая симметрична относительно
оси ординат;
кривая Гаусса лежит выше оси абсцисс;
кривая Гаусса имеет максимум в точке
Δ = 0;
поскольку кривая имеет максимум и в то
же время асимптотически приближается
к оси Δ, то она имеет две точки перегиба
— одну справа, другую слева от оси φ(Δ),
причем абсцисса точек перегиба Δ = σ;
касательные к кривой в точках перегиба
пересекают ось абсцисс в точках Δ = ±2σ
(см. рис. 19).

1.184. Выполнено 64 измерения. Найти
вероятность того, что:

число положительных ошибок будет
заключено в пределах 24 ≤ k
≤ 40;.
в пределах 16 ≤ k ≤
40.

Решение. 1) Так
как число испытаний достаточно велико,
то для решения задачи применим формулу
(1.70). Находим

Поэтому, так как t₂
= | t | , то по
формуле (1.68)

Р {24 ≤ k ≤ 40} =
Ф (2) = 0,954.

2) Вычисляем t₂
= 2; t₁ = —
4.

На основании формулы (1.70) имеем

Р{16 ≤ k ≤ 40} = 1/2
{Ф(t₂)
— Ф(t₁)}
= 1/2 {Ф(2) — Ф(- 4)}.

По свойству (1.65) с помощью таблицы прил.
IV находим

Р {16 ≤ k ≤
40} = 1/2
{0,954 + 1,000} =0,977,

где

Учитывая теорему Ляпунова и вспомнив
выражение (1.56), показывающее, что число
k можно представить
в виде суммы достаточно большого числа
слагаемых, можно прийти к выводу, что
случайная величина k
приближенно подчинена нормальному
закону распределения. Поэтому понятным
становится и выражение (1.21) как частный
случай (1.62).

Выражение (1.69) можно записать также в
виде

Но величина Q = n/k
есть частота появления события, а
величина pq/n
= σ_Q есть
с. к. о. частоты (см. 1.171). Поэтому вероятность
отклонения частоты от вероятности по
абсолютной величине на заданное число
ε = tσ_Q
определим по формуле

(1.77)

1.185. Монету
бросают 100 раз. Найти вероятность того,
что отклонение частоты появления герба
от вероятности по абсолютной величине
не превзойдет величину ε = 0,1.

Решение. На
основании формулы (1.77) имеем

Так как ε = tσ_Q
= 0,1, σ_Q
= √(pq/n)
= √(1/400) = 1/20, то t
= 2,0.

1.186. Бюффон
бросил монету 4040 раз, причем герб выпал
2048 раз. Можно ли считать полученное
отклонение числа появлений герба от
2020 случайным или же оно обусловлено
систематической причиной?

Решение.
Расхождение эмпирической частоты
Бюффона от теоретической можно
считать случайным, если вероятность
того, что при 4040 бросаниях монеты
отклонение числа выпадений герба от
2020 равно или больше по абсолютной
величине, чем у Бюффона, достаточно
большая. Пусть т — число выпадений
герба при 4040 бросаниях монеты. Находим
вероятность

Р( | т — 2020 | < 28) = 0,622.

Поэтому вероятность противоположного
события, т. е. того, что | k
— 2020 | ≥ 28, равна 1 — 0,6217 = 0,3783. Так как
эта вероятность достаточно большая, то
результат Бюффона можно считать
обусловленным случайными причинами.

1.187. Проведено
700 независимых испытаний, в каждом из
которых вероятность наступлений
события А равна 0,7. Найти вероятность
того, что частота появлений события А
окажется заключенной между 460 и 600.

Ответ: 0,993.

1.188. Найти
вероятность того, что число мальчиков
среди 1000 новорожденных больше 480, но
меньше 540 (вероятность рождения мальчика
принять равной 0,515).

Ответ: 0,929.

1.189. Вероятность
выпуска радиолампы с дефектом равна
0,03. Найти максимально возможное
отклонение ξ частости от 0,03 среди 2000
радиоламп, чтобы вероятность получить
отклонение, по абсолютной величине
меньшее ξ, была равна 0,999.

Ответ: 0,013.

1.190. Произведено
1000 независимых испытаний с вероятностью
наступления интересующего нас события
А в отдельном испытании 0,01. Найти
границы, в которых с вероятностью 0,99
заключена частость наступлений события
А.

Ответ: 0,0019.

1.191. В каждой из
1000 колод по 36 карт. Из каждой колоды
вынимают на удачу две карты. Чему
равна вероятность, того, что число пар
хотя бы с одним тузом заключено между
100 и 200?

Ответ: 0,159.

1.192. Найти такое
число k, чтобы с
вероятностью, приблизительно равной
0,7, число выпадений герба при 4000 бросаний
монеты было заключено между 3000 и k.

Ответ: 925.

1.193. Найти
вероятность того, что в партии из 800
изделий отклонение числа изделий первого
сорта от наивероятнейшего числа не
превысит по абсолютной величине
50, если вероятность появления изделия
первого сорта равна 0,7. Ответ: 0,9999.

Таблица 2

Число ошибок, n	Заданное предельное значение \|Δ\|	t	Ф(t)	P(Δ > tσ) = 1 – Ф(t)	Число ошибок	Контроль
Превышающих заданное Δ k = n (1 – Ф(t))	Укладывающихся в предел от 0 до ± tσ
100	1,0	1	0,6827	0,3173	32	68	100
100	2,0	2	0,9545	0,455	5	95	100
100	2,5	2,5	0,9876	0,0124	1	99	100
1000	3,0	3,0	0,9973	0,0027	3	997	1000

Вычислить интеграл вероятностей для
t == 0,30; 0,40; 0,50, 0,60 по формуле
(1.69) и сравнить его с табличным.
Вычислить наиболее возможное число
ошибок Δ из общего их числа п = 100,
превышающих по абсолютной величине:

а) одинарное с. к. о. измерений, т. е.
σ;

б) удвоенное с. к. о., т. е. 2σ;

в) 2,5σ;

г) утроенное с. к. о., т. е. 3σ, при п =
1000.

Решение. По
условию задачи имеем при п = 100 а) | Δ
| > σ; б) | Δ | > 2σ; в) | Δ | > 2,5σ при п =
1000; г) | Δ | > 3σ. Необходимо определить:

а) Р{| Δ | > σ }; б) Р{| Δ | > 2σ }; в) Р{| Δ |
> 2,5σ }; г) Р{| Δ | > 3σ } Определив Ф(t)
по таблице (прил. IV),
сведем результаты вычислений в
табл. 2.

1.196. Вероятность
появления ошибки в пределах от — 10 до
10″ равна 0,95, т. е. Р{| Δ | < 10″} = 0,95.
Вычислить с. к. о. измерений, если М
| Δ | = 0.

Решение. Так как
Ф(t) = 0,95, то по
таблице функции Ф(t)
обратным интерполированием находим t
= 1,96. Но t = (Δ –
M | Δ |)/σ = 10″/σ = 1,96,
откуда σ = 5,1″.

1.197. Найти
вероятность того, что ошибка измерений
Д по абсолютной величине не превзойдет
предел 4″ < | Δ | < 6″, если σ = 10″.

Решение. На
основании теоремы сложения имеем

Р {4 < | Δ | < 6} = Р {-
6 < Δ < — 4} + Р {4 < Δ
< 6}.

Можно написать

Р {4 < | Δ | < 6} = 2Р
{4 < Δ < 6} = Ф (6/10) – Ф
(4/10) = 0,452 — 0,311 =0,141.

1.198. Угол
измеряется с систематической ошибкой
в сторону завышения, равной 1,2″. Найти
вероятность того, что отклонение
измеренного значения угла х от
истинного X (т. е. ошибка
измерения Δ_i
= x_i
— X) не превзойдет
по абсолютной величине 1,6″, если с. к.
о. измерения σ = 0,8″.

Решение. Так как
ошибки измерений подчиняются нормальному
закону, то искомая вероятность

Р {- 1,6″ < Δ < 1,6″}
= 1/2 {Ф (t₁)
— Ф (t₂)},

где t₂ =
(1,6″ — 1,2″)/0,8″ = 0,5″, t₁
= (-1,6″ — 1,2″)/0,8″ = — 3,5 (систематическая
ошибка рассматривается как М [ Δ ] ).
Поэтому

Р {- 1,6 < Δ < 1,6} = — {Ф
(0,5) – Ф (-3,5)} = 1/2 {0,383 + 1,000} = 0,691.

1.199. Найти ту же
вероятность, но при условии отсутствия
систематической ошибки.

Ответ: 0,95.

Вероятным (средним) отклонением г
называется величина, больше и меньше
которой (по абсолютной величине) ошибки
в ряде наблюдений равновозможны, т. е.
Р{|Δ| < r} = 1/2.

Установить связь r
и σ при нормальном законе
распределения.

Ответ: r
= 0,67 σ.

1.200. Найти
вероятность того, что ошибка Д не
превзойдет предел, равный: а) 2;
б) 2r.

Ре ш е н и е.

поэтому

б)

поэтому

1.201. Определить
вероятность того, что ошибка измерения
Δ не превзойдет по абсолютной величине
следующих пределов:

1) 1,25σ; 2) 1,50 σ; 3) 1,75 σ; 4) 2,00 σ; 5) 2,25 σ; 6) 2,50 σ;
7) 2,75 σ; 3,00 σ; 9) 3,25 σ; 10) 3,50 σ.

Вычислить, сколько ошибок не выйдет за
эти пределы, если всех ошибок 1000.

При некоторых условиях инструмент
обеспечивает измерения с точностью
σ = 10″. Найти вероятность того, что
при измерениях этим инструментом в
тех же условиях ошибка по абсолютной
величине не превзойдет 6,0″.
Известно вероятное отклонение на 1 км
нивелирного хода r
= 2,0 мм. Определить вероятность того,
что среднее отклонение на 1 км хода при
нивелировании в таких же условиях
окажется не более 4,0 мм.
В каких пределах (- х; + х) можно
с вероятностью 0,495 ожидать появление
ошибки Δ, т. е. P (|
Δ | ≤ х) = 0,495, если σ = 15?
С. к. о. σ = 15 мм. Установить вероятность
того, что ошибка измерения по
абсолютному значению превысит 30 мм.
Вероятность того, что ошибка по абсолютной
величине превзойдет 4,0″, равна 0,823.
Вычислить вероятное и среднее отклонения.
В каких пределах (- х; + x)
можно с вероятностью 0,75 ожидать появления
ошибки, если вероятное отклонение равно
12 мм?
Вероятность появления ошибки в пределах
(- 5,0; + 5,0″) равна 0,75, т. е. Р
(| Δ | ≤ 5,0″) = 0,75.
Вычислить среднее и вероятное отклонения.
Найти вероятность появления ошибки в
пределах. (- 6,0; + 6,0 мм), если вероятное
отклонение равно 2,0 мм.
В каких пределах (- х; + х) можно с
вероятностью 0,683 ожидать появления
ошибки, если σ = 5,0″.

Вероятность появления ошибки в пределах
(- 10; + 10 мм) равна 0,89. Определить среднее
и вероятное отклонения.
С. к. о. σ = 13″. Определить вероятность
того, что ошибка измерения по
абсолютной величине будет заключаться
в пределах от 10 до 20″.
Вероятное отклонение равно r
= 2,4 мм. Найти вероятность того, что
ошибка измерения по абсолютной величине
будет находиться в пределах от 1,0 до
5,0 мм.

Источник

Вероятность и статистика объединены благодаря двум фактам. Первый факт: явление статистической устойчивости. Второй факт: во многих статистических наблюдениях статистическая устойчивость может быть описана с помощью только одной функции, которая была введена великим немецким математиком Карлом Гауссом ((1777)–(1855)). Эта функция имеет вид:

ϕ(x)=12πe−x22.

График функции y=ϕ(x) имеет своё название — гауссова кривая. Эта кривая «колоколообразного» вида. График обладает следующими свойствами.

имеет один максимум;
симметричен относительно оси ординат;
площадь под гауссовой кривой равна единице;
график очень быстро асимптотически приближается к оси абсцисс.

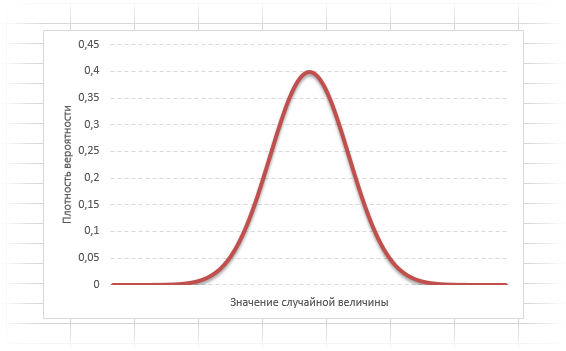
Рис. (1). Гауссова кривая.

Проведём оценку площади под гауссовой кривой на отрезке −3;3. Получим более (0,99), т. е. более 99% всей площади.

Гистограммы распределения большого объёма информации для удобства подвергаются выравниванию и заменяются на функции, имеющие простую аналитическую запись. Они называются выравнивающими функциями.

График выравнивающей функции является гауссовой кривой. Её называют ещё кривой нормального распределения.

Рис. (2). Кривая нормального распределения.

Рассмотрим простой прибор (называется доска Гальтона). От верхнего отверстия равномерно идут вниз разветвляющиеся ходы.Шарики, поступающие в прибор, случайным образом находят свою траекторию и попадают в определённую ячейку. Распределение шариков подтверждает закон Гаусса.

Рис. (3). Доска Гальтона.

Источники:

Рис. 1. Гауссова кривая, © ЯКласс.

Рис. 2. Кривая нормального распределения, © ЯКласс.

Рис. 3. Доска Гальтона, © ЯКласс.

Источник

В статье подробно показано, что такое нормальный закон распределения случайной величины и как им пользоваться при решении практически задач.

Нормальное распределение в статистике

История закона насчитывает 300 лет. Первым открывателем стал Абрахам де Муавр, который придумал аппроксимацию биномиального распределения еще 1733 году. Через много лет Карл Фридрих Гаусс (1809 г.) и Пьер-Симон Лаплас (1812 г.) вывели математические функции.

Лаплас также обнаружил замечательную закономерность и сформулировал центральную предельную теорему (ЦПТ), согласно которой сумма большого количества малых и независимых величин имеет нормальное распределение.

Нормальный закон не является фиксированным уравнением зависимости одной переменной от другой. Фиксируется только характер этой зависимости. Конкретная форма распределения задается специальными параметрами. Например, у = аx + b – это уравнение прямой. Однако где конкретно она проходит и под каким наклоном, определяется параметрами а и b. Также и с нормальным распределением. Ясно, что это функция, которая описывает тенденцию высокой концентрации значений около центра, но ее точная форма задается специальными параметрами.

Кривая нормального распределения Гаусса имеет следующий вид.

График нормального распределения напоминает колокол, поэтому можно встретить название колоколообразная кривая. У графика имеется «горб» в середине и резкое снижение плотности по краям. В этом заключается суть нормального распределения. Вероятность того, что случайная величина окажется около центра гораздо выше, чем то, что она сильно отклонится от середины.

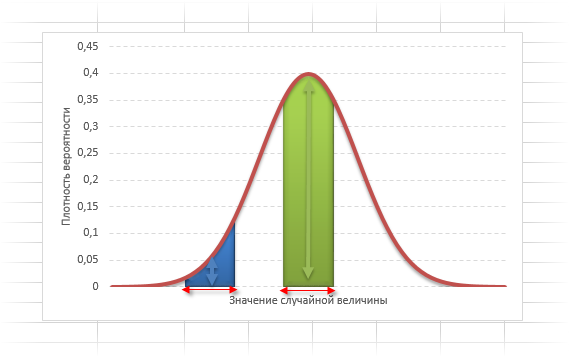
На рисунке выше изображены два участка под кривой Гаусса: синий и зеленый. Основания, т.е. интервалы, у обоих участков равны. Но заметно отличаются высоты. Синий участок удален от центра, и имеет существенно меньшую высоту, чем зеленый, который находится в самом центре распределения. Следовательно, отличаются и площади, то бишь вероятности попадания в обозначенные интервалы.

Формула нормального распределения (плотности) следующая.

Формула состоит из двух математических констант:

π – число пи 3,142;

е – основание натурального логарифма 2,718;

двух изменяемых параметров, которые задают форму конкретной кривой:

m – математическое ожидание (в различных источниках могут использоваться другие обозначения, например, µ или a);

σ² – дисперсия;

ну и сама переменная x, для которой высчитывается плотность вероятности.

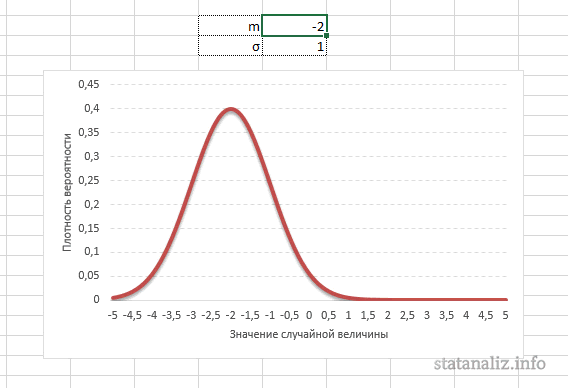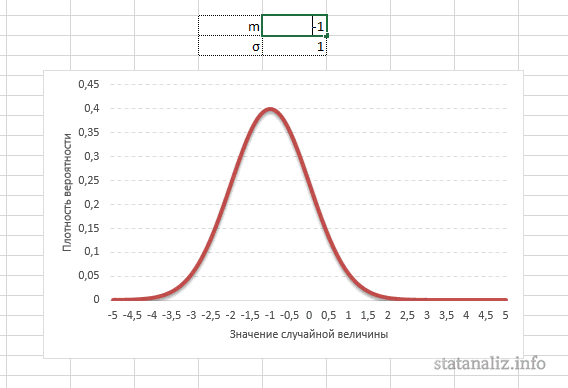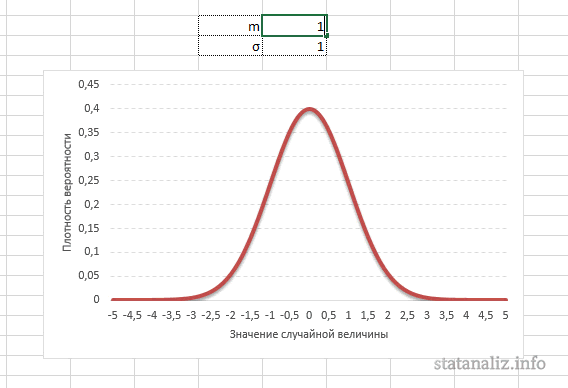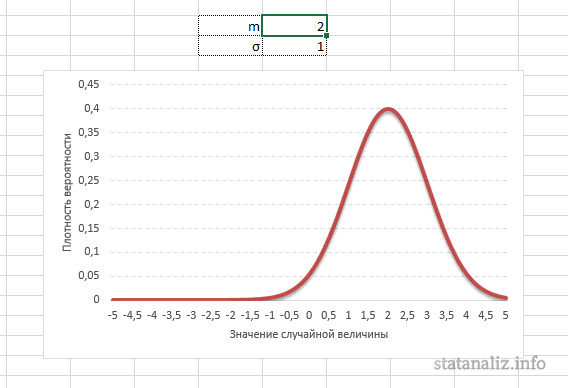
Конкретная форма нормального распределения зависит от 2-х параметров: математического ожидания (m) и дисперсии (σ²). Кратко обозначается N(m, σ²) или N(m, σ). Параметр m (матожидание) определяет центр распределения, которому соответствует максимальная высота графика. Дисперсия σ² характеризует размах вариации, то есть «размазанность» данных.

Параметр математического ожидания смещает центр распределения вправо или влево, не влияя на саму форму кривой плотности.

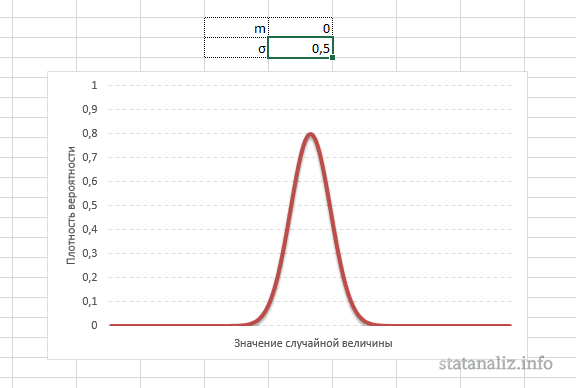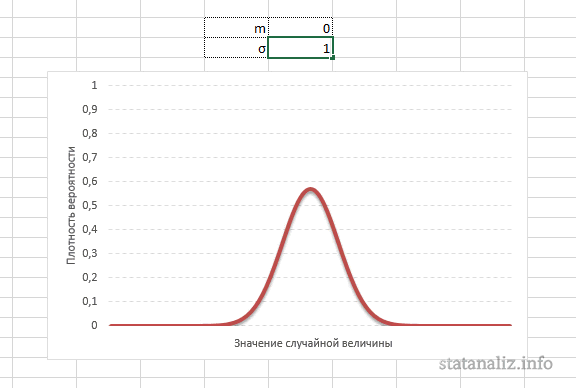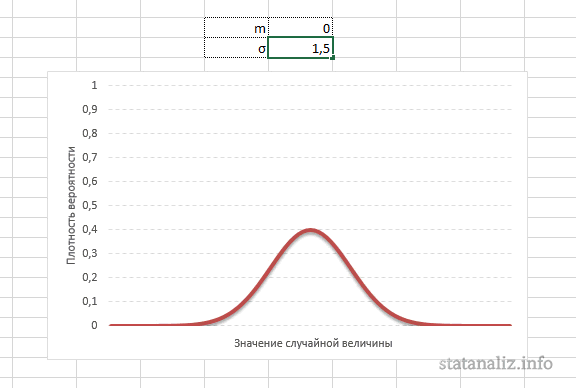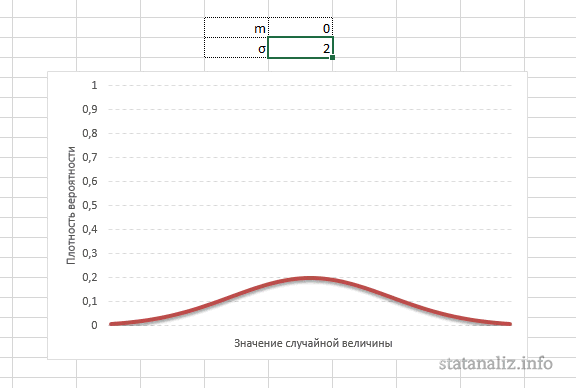
А вот дисперсия определяет остроконечность кривой. Когда данные имеют малый разброс, то вся их масса концентрируется у центра. Если же у данных большой разброс, то они «размазываются» по широкому диапазону.

Плотность распределения не имеет прямого практического применения. Для расчета вероятностей нужно проинтегрировать функцию плотности.

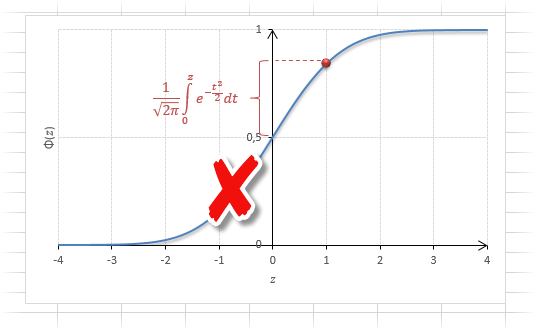
Вероятность того, что случайная величина окажется меньше некоторого значения x, определяется функцией нормального распределения:

Используя математические свойства любого непрерывного распределения, несложно рассчитать и любые другие вероятности, так как

P(a ≤ X < b) = Ф(b) – Ф(a)

Стандартное нормальное распределение

Нормальное распределение зависит от параметров средней и дисперсии, из-за чего плохо видны его свойства. Хорошо бы иметь некоторый эталон распределения, не зависящий от масштаба данных. И он существует. Называется стандартным нормальным распределением. На самом деле это обычное нормальное нормальное распределение, только с параметрами математического ожидания 0, а дисперсией – 1, кратко записывается N(0, 1).

Любое нормальное распределение легко превращается в стандартное путем нормирования:

где z – новая переменная, которая используется вместо x;
m – математическое ожидание;
σ – стандартное отклонение.

Для выборочных данных берутся оценки:

Среднее арифметическое и дисперсия новой переменной z теперь также равны 0 и 1 соответственно. В этом легко убедиться с помощью элементарных алгебраических преобразований.

В литературе встречается название z-оценка. Это оно самое – нормированные данные. Z-оценку можно напрямую сравнивать с теоретическими вероятностями, т.к. ее масштаб совпадает с эталоном.

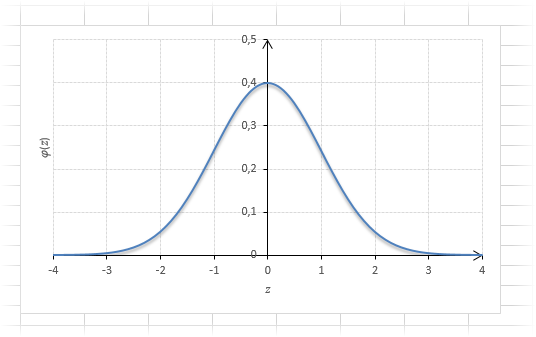
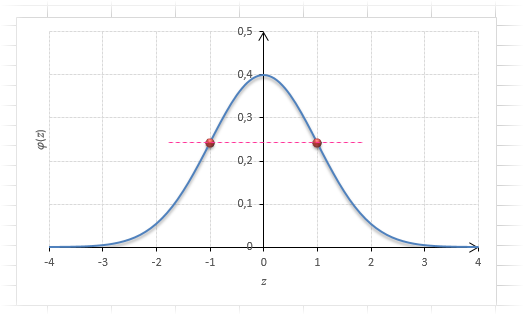
Посмотрим теперь, как выглядит плотность стандартного нормального распределения (для z-оценок). Напомню, что функция Гаусса имеет вид:

Подставим вместо (x-m)/σ букву z, а вместо σ – единицу, получим функцию плотности стандартного нормального распределения:

График плотности:

Центр, как и ожидалось, находится в точке 0. В этой же точке функция Гаусса достигает своего максимума, что соответствует принятию случайной величиной своего среднего значения (т.е. x-m=0). Плотность в этой точке равна 0,3989, что можно посчитать даже в уме, т.к. e⁰=1 и остается рассчитать только соотношение 1 на корень из 2 пи.

Таким образом, по графику хорошо видно, что значения, имеющие маленькие отклонения от средней, выпадают чаще других, а те, которые сильно отдалены от центра, встречаются значительно реже. Шкала оси абсцисс измеряется в стандартных отклонениях, что позволяет отвязаться от единиц измерения и получить универсальную структуру нормального распределения. Кривая Гаусса для нормированных данных отлично демонстрирует и другие свойства нормального распределения. Например, что оно является симметричным относительно оси ординат. В пределах ±1σ от средней арифметической сконцентрирована большая часть всех значений (прикидываем пока на глазок). В пределах ±2σ находятся большинство данных. В пределах ±3σ находятся почти все данные. Последнее свойство широко известно под названием правило трех сигм для нормального распределения.

Функция стандартного нормального распределения позволяет рассчитывать вероятности.

Понятное дело, вручную никто не считает. Все подсчитано и размещено в специальных таблицах, которые есть в конце любого учебника по статистике.

Таблица нормального распределения

Таблицы нормального распределения встречаются двух типов:

— таблица плотности;

— таблица функции (интеграла от плотности).

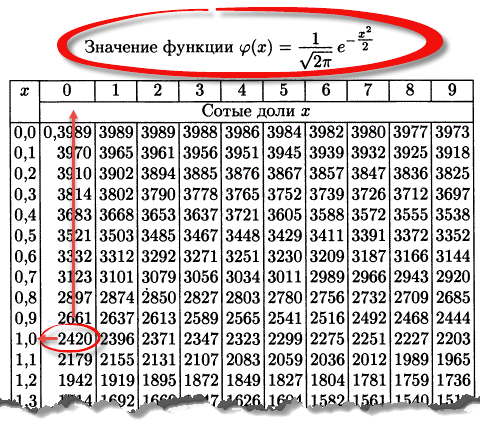
Таблица плотности используется редко. Тем не менее, посмотрим, как она выглядит. Допустим, нужно получить плотность для z = 1, т.е. плотность значения, отстоящего от матожидания на 1 сигму. Ниже показан кусок таблицы.

В зависимости от организации данных ищем нужное значение по названию столбца и строки. В нашем примере берем строку 1,0 и столбец 0, т.к. сотых долей нет. Искомое значение равно 0,2420 (0 перед 2420 опущен).

Функция Гаусса симметрична относительно оси ординат. Поэтому φ(z)= φ(-z), т.е. плотность для 1 тождественна плотности для -1, что отчетливо видно на рисунке.

Чтобы не тратить зря бумагу, таблицы печатают только для положительных значений.

На практике чаще используют значения функции стандартного нормального распределения, то есть вероятности для различных z.

В таких таблицах также содержатся только положительные значения. Поэтому для понимания и нахождения любых нужных вероятностей следует знать свойства стандартного нормального распределения.

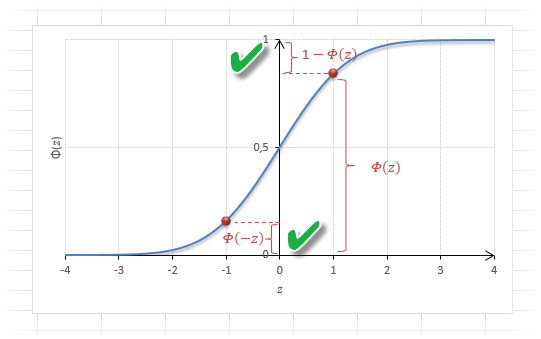
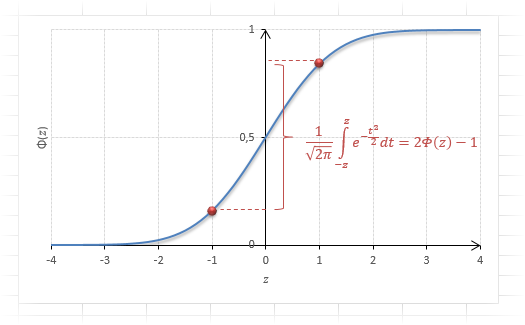
Функция Ф(z) симметрична относительно своего значения 0,5 (а не оси ординат, как плотность). Отсюда справедливо равенство:

Это факт показан на картинке:

Значения функции Ф(-z) и Ф(z) делят график на 3 части. Причем верхняя и нижняя части равны (обозначены галочками). Для того, чтобы дополнить вероятность Ф(z) до 1, достаточно добавить недостающую величину Ф(-z). Получится равенство, указанное чуть выше.

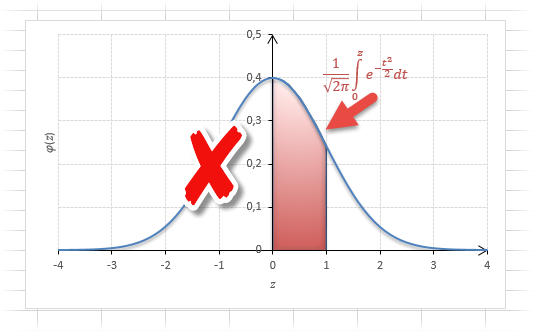
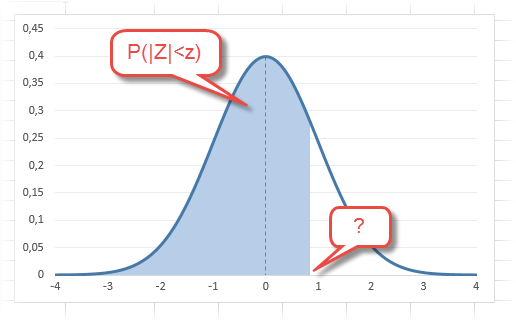
Если нужно отыскать вероятность попадания в интервал (0; z), то есть вероятность отклонения от нуля в положительную сторону до некоторого количества стандартных отклонений, достаточно от значения функции стандартного нормального распределения отнять 0,5:

Для наглядности можно взглянуть на рисунок.

На кривой Гаусса, эта же ситуация выглядит как площадь от центра вправо до z.

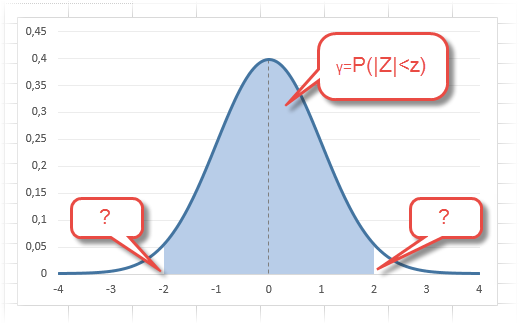
Довольно часто аналитика интересует вероятность отклонения в обе стороны от нуля. А так как функция симметрична относительно центра, предыдущую формулу нужно умножить на 2:

Рисунок ниже.

Под кривой Гаусса это центральная часть, ограниченная выбранным значением –z слева и z справа.

Указанные свойства следует принять во внимание, т.к. табличные значения редко соответствуют интересующему интервалу.

Для облегчения задачи в учебниках обычно публикуют таблицы для функции вида:

Если нужна вероятность отклонения в обе стороны от нуля, то, как мы только что убедились, табличное значение для данной функции просто умножается на 2.

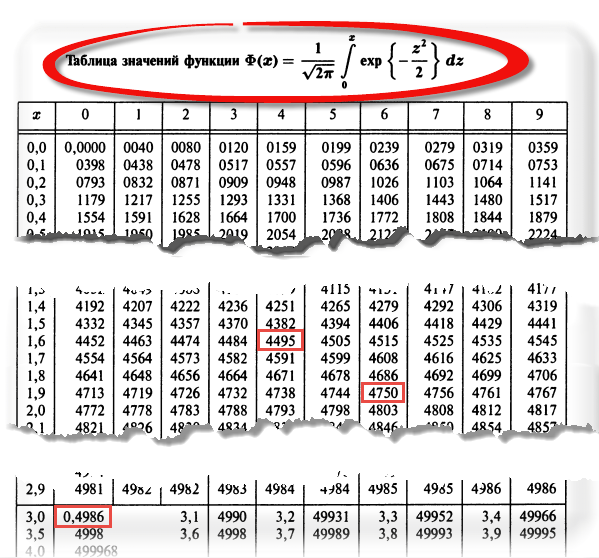
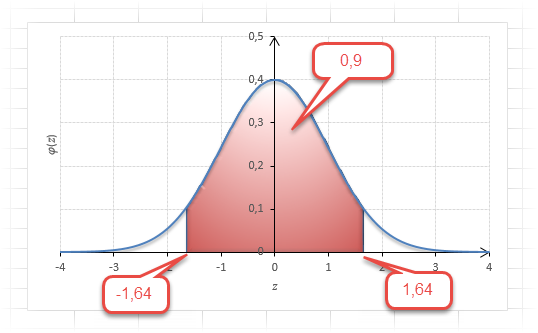
Теперь посмотрим на конкретные примеры. Ниже показана таблица стандартного нормального распределения. Найдем табличные значения для трех z: 1,64, 1,96 и 3.

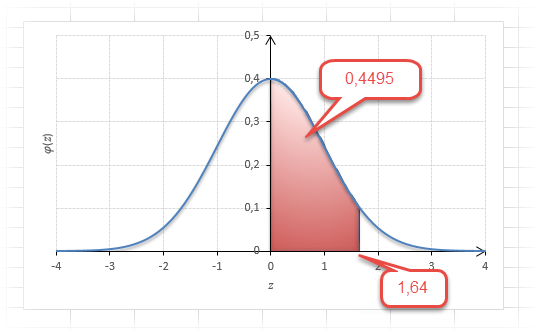
Как понять смысл этих чисел? Начнем с z=1,64, для которого табличное значение составляет 0,4495. Проще всего пояснить смысл на рисунке.

То есть вероятность того, что стандартизованная нормально распределенная случайная величина попадет в интервал от 0 до 1,64, равна 0,4495. При решении задач обычно нужно рассчитать вероятность отклонения в обе стороны, поэтому умножим величину 0,4495 на 2 и получим примерно 0,9. Занимаемая площадь под кривой Гаусса показана ниже.

Таким образом, 90% всех нормально распределенных значений попадает в интервал ±1,64σ от средней арифметической. Я не случайно выбрал значение z=1,64, т.к. окрестность вокруг средней арифметической, занимающая 90% всей площади, иногда используется для проверки статистических гипотез и расчета доверительных интервалов. Если проверяемое значение не попадает в обозначенную область, то его наступление маловероятно (всего 10%).

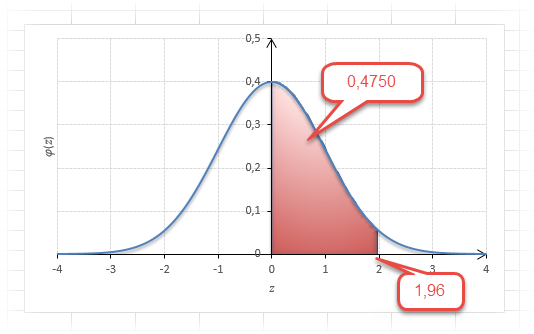
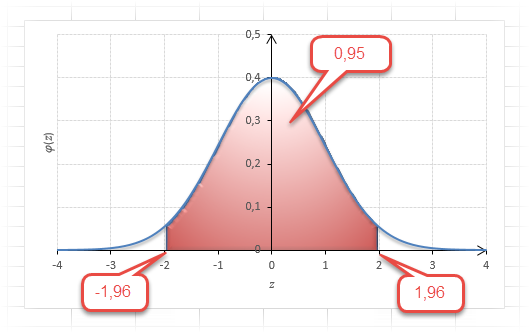
Для проверки гипотез, однако, чаще используется интервал, накрывающий 95% всех значений. Половина вероятности от 0,95 – это 0,4750 (см. второе выделенное в таблице значение).

Для этой вероятности z=1,96. Т.е. в пределах почти ±2σ от средней находится 95% значений. Только 5% выпадают за эти пределы.

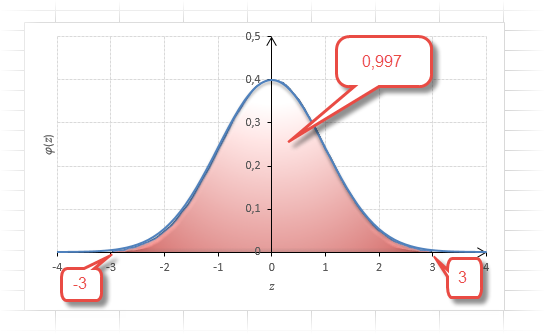
Еще одно интересное и часто используемое табличное значение соответствует z=3, оно равно по нашей таблице 0,4986. Умножим на 2 и получим 0,997. Значит, в рамках ±3σ от средней арифметической заключены почти все значения.

Так выглядит правило 3 сигм для нормального распределения на диаграмме.

С помощью статистических таблиц можно получить любую вероятность. Однако этот метод очень медленный, неудобный и сильно устарел. Сегодня все делается на компьютере. Далее переходим к практике расчетов в Excel.

В Excel есть несколько функций для подсчета вероятностей или обратных значений нормального распределения.

Функция НОРМ.СТ.РАСП

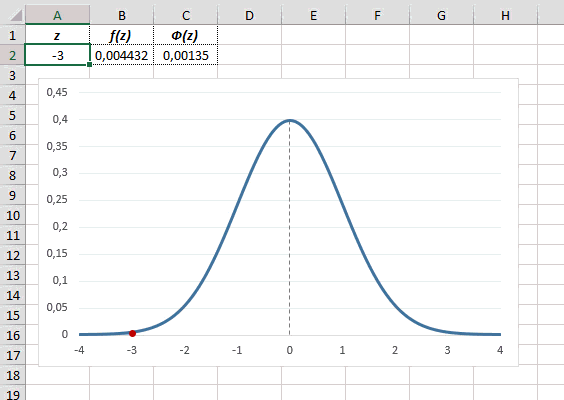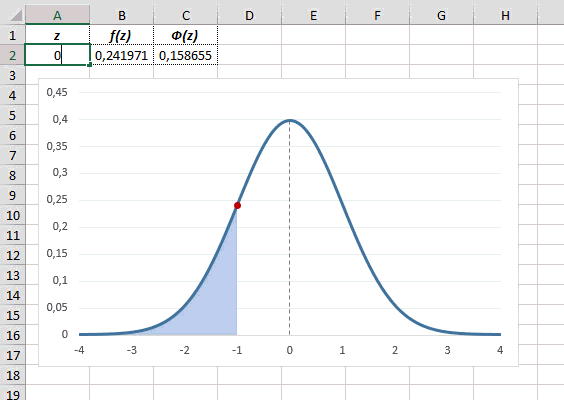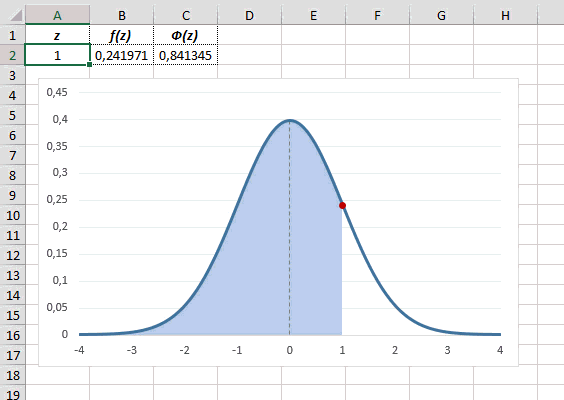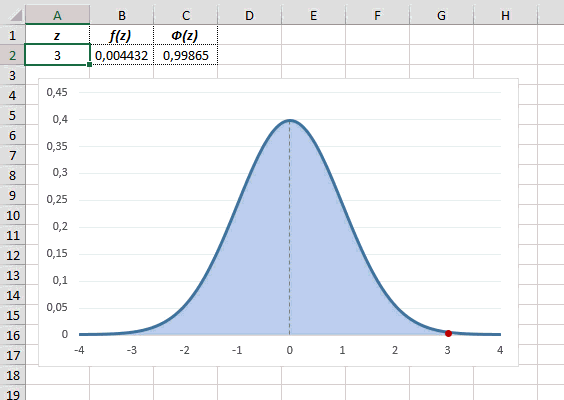
Функция НОРМ.СТ.РАСП предназначена для расчета плотности ϕ(z) или вероятности Φ(z) по нормированным данным (z).

=НОРМ.СТ.РАСП(z;интегральная)

z – значение стандартизованной переменной

интегральная – если 0, то рассчитывается плотность ϕ(z), если 1 – значение функции Ф(z), т.е. вероятность P(Z<z).

Рассчитаем плотность и значение функции для различных z: -3, -2, -1, 0, 1, 2, 3 (их укажем в ячейке А2).

Для расчета плотности потребуется формула =НОРМ.СТ.РАСП(A2;0). На диаграмме ниже – это красная точка.

Для расчета значения функции =НОРМ.СТ.РАСП(A2;1). На диаграмме – закрашенная площадь под нормальной кривой.

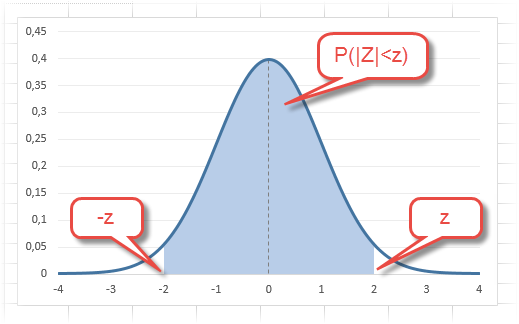
В реальности чаще приходится рассчитывать вероятность того, что случайная величина не выйдет за некоторые пределы от средней (в среднеквадратичных отклонениях, соответствующих переменной z), т.е. P(|Z|<z).

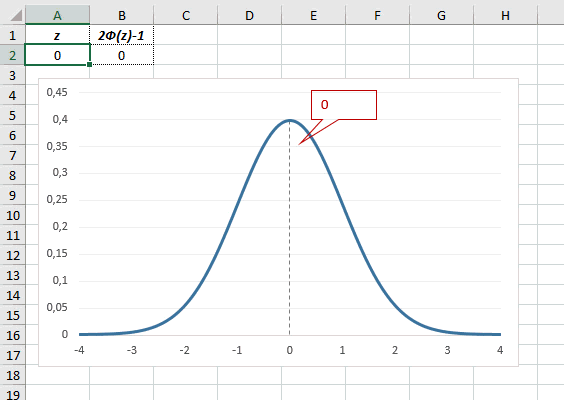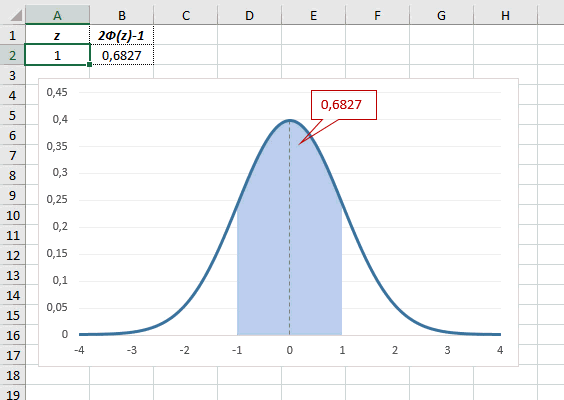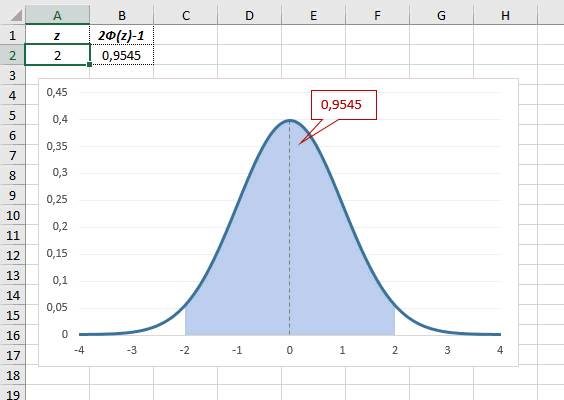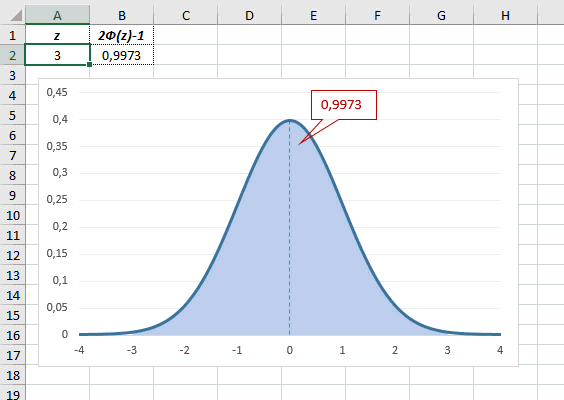
Определим, чему равна вероятность попадания случайной величины в пределы ±1z, ±2z и ±3z от нуля. Потребуется формула 2Ф(z)-1, в Excel =2*НОРМ.СТ.РАСП(A2;1)-1.

На диаграмме отлично видны основные основные свойства нормального распределения, включая правило трех сигм. Функция НОРМ.СТ.РАСП – это автоматическая таблица значений функции нормального распределения в Excel.

Может стоять и обратная задача: по имеющейся вероятности P(Z<z) найти стандартизованную величину z ,то есть квантиль стандартного нормального распределения.

Функция НОРМ.СТ.ОБР

НОРМ.СТ.ОБР рассчитывает обратное значение функции стандартного нормального распределения. Синтаксис состоит из одного параметра:

=НОРМ.СТ.ОБР(вероятность)

вероятность – это вероятность.

Данная формула используется так же часто, как и предыдущая, ведь по тем же таблицам искать приходится не только вероятности, но и квантили.

Например, при расчете доверительных интервалов задается доверительная вероятность, по которой нужно рассчитать величину z.

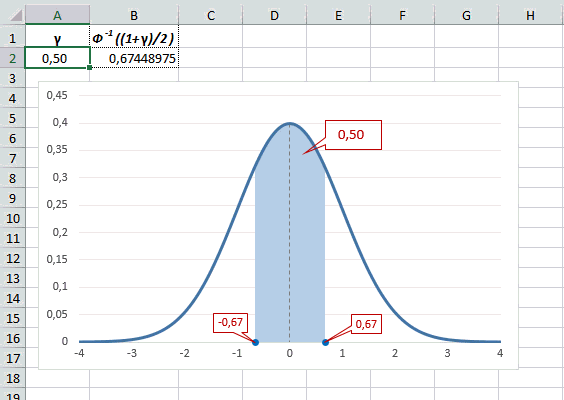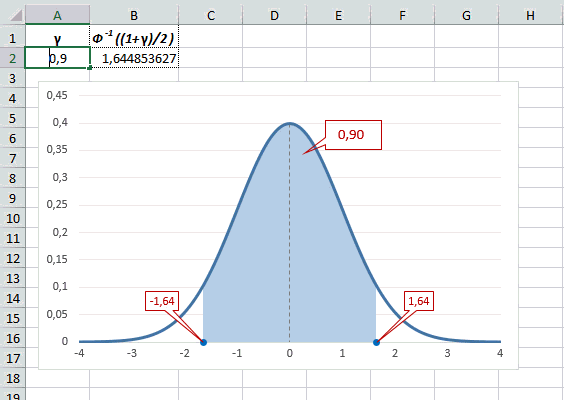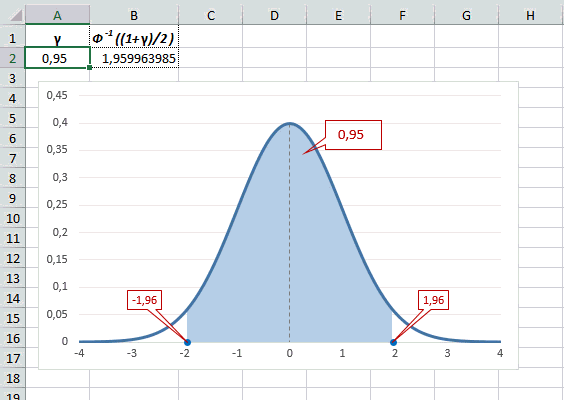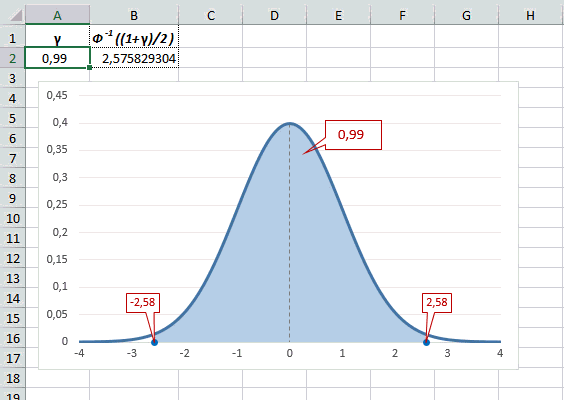
Учитывая то, что доверительный интервал состоит из верхней и нижней границы и то, что нормальное распределение симметрично относительно нуля, достаточно получить верхнюю границу (положительное отклонение). Нижняя граница берется с отрицательным знаком. Обозначим доверительную вероятность как γ (гамма), тогда верхняя граница доверительного интервала рассчитывается по следующей формуле.

Рассчитаем в Excel значения z (что соответствует отклонению от средней в сигмах) для нескольких вероятностей, включая те, которые наизусть знает любой статистик: 90%, 95% и 99%. В ячейке B2 укажем формулу: =НОРМ.СТ.ОБР((1+A2)/2). Меняя значение переменной (вероятности в ячейке А2) получим различные границы интервалов.

Доверительный интервал для 95% равен 1,96, то есть почти 2 среднеквадратичных отклонения. Отсюда легко даже в уме оценить возможный разброс нормальной случайной величины. В общем, доверительным вероятностям 90%, 95% и 99% соответствуют доверительные интервалы ±1,64, ±1,96 и ±2,58 σ.

В целом функции НОРМ.СТ.РАСП и НОРМ.СТ.ОБР позволяют произвести любой расчет, связанный с нормальным распределением. Но, чтобы облегчить и уменьшить количество действий, в Excel есть несколько других функций. Например, для расчета доверительных интервалов средней можно использовать ДОВЕРИТ.НОРМ. Для проверки статистической гипотезы о средней арифметической есть формула Z.ТЕСТ.

Рассмотрим еще пару полезных формул с примерами.

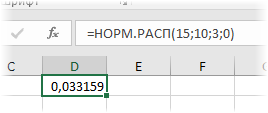
Функция НОРМ.РАСП

Функция НОРМ.РАСП отличается от НОРМ.СТ.РАСП лишь тем, что ее используют для обработки данных любого масштаба, а не только нормированных. Параметры нормального распределения указываются в синтаксисе.

=НОРМ.РАСП(x;среднее;стандартное_откл;интегральная)

x – значение (или ссылка на ячейку), для которого рассчитывается плотность или значение функции нормального распределения

среднее – математическое ожидание, используемое в качестве первого параметра модели нормального распределения

стандартное_откл – среднеквадратичное отклонение – второй параметр модели

интегральная – если 0, то рассчитывается плотность, если 1 – то значение функции, т.е. P(X<x).

Например, плотность для значения 15, которое извлекли из нормальной выборки с матожиданием 10, стандартным отклонением 3, рассчитывается так:

Если последний параметр поставить 1, то получим вероятность того, что нормальная случайная величина окажется меньше 15 при заданных параметрах распределения. Таким образом, вероятности можно рассчитывать напрямую по исходным данным.

Функция НОРМ.ОБР

Это квантиль нормального распределения, т.е. значение обратной функции. Синтаксис следующий.

=НОРМ.ОБР(вероятность;среднее;стандартное_откл)

вероятность – вероятность

среднее – матожидание

стандартное_откл – среднеквадратичное отклонение

Назначение то же, что и у НОРМ.СТ.ОБР, только функция работает с данными любого масштаба.

Пример показан в ролике в конце статьи.

Моделирование нормального распределения

Для некоторых задач требуется генерация нормальных случайных чисел. Готовой функции для этого нет. Однако В Excel есть две функции, которые возвращают случайные числа: СЛУЧМЕЖДУ и СЛЧИС. Первая выдает случайные равномерно распределенные целые числа в указанных пределах. Вторая функция генерирует равномерно распределенные случайные числа между 0 и 1. Чтобы сделать искусственную выборку с любым заданным распределением, нужна функция СЛЧИС.

Допустим, для проведения эксперимента необходимо получить выборку из нормально распределенной генеральной совокупности с матожиданием 10 и стандартным отклонением 3. Для одного случайного значения напишем формулу в Excel.

=НОРМ.ОБР(СЛЧИС();10;3)

Протянем ее на необходимое количество ячеек и нормальная выборка готова.

Для моделирования стандартизованных данных следует воспользоваться НОРМ.СТ.ОБР.

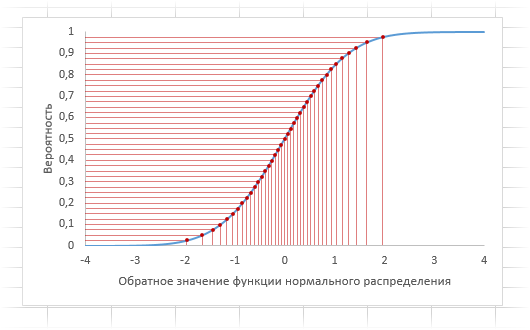
Процесс преобразования равномерных чисел в нормальные можно показать на следующей диаграмме. От равномерных вероятностей, которые генерируются формулой СЛЧИС, проведены горизонтальные линии до графика функции нормального распределения. Затем от точек пересечения вероятностей с графиком опущены проекции на горизонтальную ось.

На выходе получаются значения с характерной концентрацией около центра. Вот так обратный прогон через функцию нормального распределения превращает равномерные числа в нормальные. Excel позволяет за несколько секунд воспроизвести любое количество выборок любого размера.

Как обычно, прилагаю ролик, где все вышеописанное показывается в действии.

Скачать файл с примером.

Поделиться в социальных сетях:

Источник

Кривая Гаусса

Авторы
Руководители
Файлы работы
Наградные документы

Садовникова А.Д. 1

1МАОУ «Гимназия №6» г. Перми

Шитоева А.О. 1

1МАОУ «Гимназия №6» г. Перми

Текст работы размещён без изображений и формул.
Полная версия работы доступна во вкладке «Файлы работы» в формате PDF

Введение

В современном мире жизнь каждого учащегося во многом зависит от сдачи экзаменов, ведь именно этот способ проверки знаний ставят в приоритет большинство учебных заведений.

Актуальность. Многие ученики считают, что результаты, которые они получают в ходе этих тестов, недостоверно отражают уровень их интеллекта. Изучив эту проблему более глубоко, мы узнали, что составители общероссийских тестов пользуются кривой Гаусса, т.е. кривой нормального распределения, а это значит, что их результаты должны ей соответствовать. Поэтому, в своей научно-исследовательской работе мы решили определить соответствуют ли задания ОГЭ, ЕГЭ и ВПР гауссовой кривой.

Цель работы: изучить применение кривой Гаусса составителями контрольных тестов и выяснить, соответствуют ли общепринятые экзамены кривой нормального распределения

Задачи:

1)Анализ литературы и сбор информации по теме «Кривые линии. Кривая Гаусса»

2)Проведение общепринятых школами тестов для обучающихся экзаменуемых классов

3)Произведение статистического анализа результатов теста

4)Сравнение полученных графиков с кривой Гаусса

5)Обобщение и систематизация полученных результатов

Методы исследования:

1)Изучение литературы и интернет источников

2)Статистический анализ

4)Тестирование учащихся

5)Построение графиков

6)Сравнение

7)Синтез полученной информации

Объект исследования: кривая Гаусса

Предмет исследования: тесты для учащихся 5, 9 и 11 классов

Глава 1. Теоретические аспекты исследования кривых линий

1.1. Понятие кривой линии

Кривая линия — это множество точек пространства, координаты которых являются функциями одной переменной. Термин «кривая» в разных разделах математики определяется по-разному.

Кривую линию можно рассматривать как траекторию движения точки на плоскости или в пространстве, а также как совокупность точек, удовлетворяющих определенному уравнению. Кривая линия может являться результатом пересечения между собой кривых поверхностей или кривой поверхности и плоскости..

Каждая кривая включает в себя геометрические элементы, которые составляют её определитель, т.е. совокупность независимых условий, однозначно определяющих эту кривую.

Различны и способы задания кривых:

Аналитический — кривая задана математическим уравнением;

Графический — кривая задана визуально на носителе графической информации;

Табличный — кривая задана координатами последовательного ряда точек.

Уравнением кривой линии называется такое соотношение между переменными, которому удовлетворяют координаты точки, принадлежащей кривой.

В основу классификации кривых положена природа их уравнений.

1.2. Алгебраические и трансцендентные кривые линии

Кривые подразделяются на алгебраические и трансцендентные в зависимости от того, являются ли их уравнения алгебраическими или трансцендентными в прямоугольной системе координат.

Закономерные линии описываются уравнениями и делятся на алгебраические второго и высшего порядков и трансцендентные, описываемые тригонометрическими функциями. Кривая линия, представленная в декартовых координатах уравнением n— й степени, называется алгебраической кривой n-го порядка.

Порядок плоской алгебраической кривой линии определяется наибольшим числом точек её пересечения прямой линией. Любая прямая линия может пересекать алгебраическую кривую линию n-го порядка не более чем в n точках.

Трансцендентные кривые в отличие от алгебраических могут иметь бесконечное количество точек пересечения с прямой, точек перегиба, вершин и т.п.

Кривая линия как траектория движущейся точки должна быть непрерывной.

Движущаяся точка в любом положении должна иметь определенное направление движения. Это направление указывает прямая (касательная), проходящая через рассматриваемую точку

Кривизна произвольной кривой линии в различных точках различна, в отдельных точках она может быть равна нулю. Такие точки называются точками спрямления.

Кривизна в каждой из точек плоской кривой а определяется с помощью соприкасающейся в этой точке окружности.

1.3. Кривая Гаусса

Распределением называется закономерность встречаемости признака и разных его значений. Форма распределения является некоторой обобщенной характеристикой выборки.

Распределение частоты полученных результатов в виде графиков и гистограмм дает важную предварительную информацию о форме распределения признака, а именно о том, какие значения встречаются реже, какие чаще, насколько выражена изменчивость признака. Выделяют следующие типичные формы эмпирического распределения.

Равномерное распределение — когда все значения встречаются с одинаковой частотой.

Симметричное распределение — когда с одинаковой частотой встречаются крайние значения признака.

Асимметричное распределение — может быть левосторонним (когда преобладает частота малых значений) или правосторонним (когда преобладает частота больших значений).

Нормальное распределение — идеальный стандарт распределения, когда крайние значения встречаются редко и частота встречаемости постепенно повышается от крайних к серединным значениям признака.

Нормальный закон распределения играет важнейшую роль в применении математико-статистических методов в психологии. Он лежит в основе измерений, разработки тестовых шкал, методов проверки гипотез.

Нормальное распределение — вид распределения переменных, характеризуемый тем, что крайние значения признака в нем появляются достаточно редко, а значения, близкие к средней величине, — достаточно часто. Нормальным такое распределение называется потому, что оно очень часто встречалось в естественнонаучных исследованиях и казалось «нормой» всякого массового проявления признаков. Это распределение следует закону, открытому в разное время: Муавром в 1733 г. в Англии, Гауссом в 1809 г. в Германии и Лапласом в 1812 г. во Франции.

Процентное распределение случаев под нормальной кривой

График нормального распределения представляет симметричную унимодальную колоколообразную кривую (верхняя часть колокола), осью которой является вертикаль (ордината), проведенная через точку 0.

Закон нормального распределения имеет следующую формулировку: «Если индивидуальная изменчивость некоторого свойства есть следствие действия множества причин, то распределение частот для всего многообразия проявлений этого свойства в генеральной совокупности соответствует кривой нормального распределения» (Наследов А. Д., 2007, с. 51).

Чтобы установить, подчиняется ли эмпирическое распределение изучаемой величины нормальному закону, необходимо сопоставить сведения о свойствах этой величины и условиях ее изучения со свойствами функций нормального распределения. Это сопоставление вначале является качественным, а потом осуществляется специальными количественными методами (Сыромятников И. В., 2005).

Подтверждение нормального закона распределения будет означать, что полученная эмпирическая кривая не требует нормализации. Распределение можно рассматривать как репрезентативное по отношению к генеральной совокупности и на его основе определить репрезентативные оценочные нормы.

Если распределение отличается от нормального, то это означает, что либо выборка нерепрезентативна генеральной совокупности, либо измерения произведены не в шкале равных интервалов.

Наиболее важным общим свойством разных кривых нормального распределения является одинаковая доля площади под кривой между одними и теми же двумя значениями признака, выраженными в единицах стандартного отклонения.

М ± о соответствует 68 % (точно — 68,26 %) площади;

М ± 2о соответствует 95 % (точно — 95,44 %) площади;

М±3а соответствует 100 % (точно — 99,72 %) площади.

Полезно знать, что если распределение является нормальным, то:

90 % всех случаев располагается в диапазоне значений М ± 1,64 о;

95 % всех случаев располагается в диапазоне значений М± 1,96 а;

99 % всех случаев располагается в диапазоне значений М±2,58 о.

График функции y=ϕ(x) называют гауссовой кривой. Это «колоколообразная» кривая. Она имеет единственную точку максимума, симметрична относительно оси ординат, площадь под этой кривой равна единице. Она очень быстро асимптотически приближается к оси абсцисс.

Графики функций выравнивающих гистограммы похожи друг на друга. Все эти кривые распределения получаются из гауссовой кривой. Её часто называют кривой нормального распределения.

1.4. Правила построения кривой нормального распределения

Один из способов построения нормальной кривой по опытным данным наблюдений (либо экспериментов) заключается в следующем:

* находят и например, по методу произведений;

* находят ординаты (выравнивающие частоты) теоретической кривой по формуле где сумма наблюдаемых частот, разность между двумя соседними вариантами

* строят точки в прямоугольной системе координат и соединяют их плавной линией.

Близость выравнивающих частот к наблюдаемым подтверждает правильность допущения о том, что обследуемый признак распределен нормально.

В качестве иллюстрации, рассмотрим следующий пример.

Построим нормальную кривую по данным

варианта	15	20	25	30	35	40	45	50	55
частота	6	13	38	74	106	85	30	10	4

Рис. 5.

На рис. 4 построена нормальная (теоретическая) кривая по выравнивающим частотам (см. рис. 4) и полигон наблюдаемых частот (они изображены на рис. 5).

Сравнение графиков визуально показывает, что построенная теоретическая кривая удовлетворительно отражает данные наблюдений.

Для того, чтобы более уверенно считать, что данные наблюдений свидетельствуют о нормальном распределении признака, необходимо использовать специальные правила (их называют критериями согласия)

Глава 2. Практическое исследование соответствия кривой Гаусса контрольным тестам

Изучив теоретический материал по данной теме, мы приступили к практической части. Для анализа были взяты 150 учеников МАОУ «Гимназия №6»: 36 учеников 11-х классов, 55 учеников 9-х классов и 59 учеников 5-х классов. В нашей школе были проведены тесты ОГЭ, ЕГЭ и ВПР в соответствующих параллелях, на основе результатов этих тестов были составлены графики, сопоставляемые с гауссовой кривой. На оси ординат графиков расположено кол-во человек, получивших тот или иной балл, а на оси абсцисс – результат, переведенный из первичных баллов в стобалльную систему

2.1. Статистический анализ тестов ТЕГЭ (ЕГЭ)

Результаты первой группы (результаты ТЕГЭ среди 11-х классов)

На полученных нами графиках видно, что, если мы учитываем небольшую погрешность, то результаты ТЕГЭ по русскому языку и математике соответствуют кривой Гаусса. Значит, задания для проверки знаний одиннадцатиклассников составлены верно и показывают реальный уровень подготовки учеников по данному предмету.

2.2.Статистический анализ тестов ТОГЭ (ОГЭ)

Результаты второй группы (ТОГЭ среди 9-х классов)

Проверив группу девятых классов, можно сделать вывод, что тест ТОГЭ по математике составлен правильно, т.к. результаты по этому предмету выстраиваются в кривую Гаусса. А тест по русскому языку, напротив, отражает, что экзамен оказался слишком простым для учеников гимназии, вследствие чего выявлено слишком большое количество высоких показателей.

Также мы решили узнать, соответствуют ли результаты ОГЭ-2019 по Российской Федерации получившимся в ходе исследования выводам. Поскольку статистика учеников по России находится в общем доступе, мы ее проанализировали и составили графики:

Проведя статистический анализ, мы видим, что получен аналогичный итог: результаты по русскому языку много выше результатов по математике, а значит, тест ОГЭ-2019 по русскому языку оценивает учеников необъективно.

2.3.Статистический анализ тестов ВПР

Результаты третьей группы (ВПР и промежуточный тест для 5-х классов)

Проанализировав графики третьей группы, можно сказать, что результаты схожи с результатами в девятых классах: тест по математике составлен таким образом, что объективно оценивает знания учеников, его результаты соответствуют гауссовой кривой, а тест по русскому языку показал слишком большое количество высоких результатов (его можно считать составленным неверно)

Заключение

Выводы

Проделав научно-исследовательскую работу, можно сделать следующие выводы:

1)Кривая Гаусса довольно часто используется создателями тестов, ведь статистический анализ работ, соответствующих ей, показывает более достоверные результаты оценки знаний учащихся.

2)Тесты ТЕГЭ (а значит и ЕГЭ) составлены верно, т.к. они легко сопоставляются с кривой Гаусса. Это говорит о том, что при поступлении в ВУЗы учитывается объективный уровень изучения предмета.

3)Графики, составленные по ТОГЭ и ВПР, говорят о том, что тесты имеют упрощенный уровень по русскому языку, ведь детей, сдавших экзамен на оценку «отлично» значительно больше, нежели имеющих не проходной балл или оценку «удовлетворительно».

Можно сделать предположение, что экзамен по русскому языку учащиеся сдают на более высокий балл, потому что это их родной язык. Но в таком случае составителям заданий нужно учитывать этот критерий и подбирать задания сложнее, чем на данный момент, если они хотят добиться высокого уровня подготовки по данному предмету.

Список использованных источников и литературы

1) Гаусс, К.Ф. Труды по теории чисел / Пер. с англ. Под ред. И.М. Виноградова. — М.: ЁЁ Медиа, 2012 – 978 с.

2) Гауссова кривая, закон больших чисел [Электронный ресурс] // Кривая Гаусса. URL: https://www.yaklass.ru/p/algebra/11-klass/matematicheskaia—statistika-9176/gauscova—krivaia—zakon—bolshikh—chisel-10288/re-161d12ad-5034-4bae-8bcb-204dcd940823 / (дата обращения — 07.01.2020)

3) Инженерная графика [Электронный ресурс] // Кривые линии, общие сведения о кривых линиях и проецировании. URL: https://studme.org/84071/tehnika/krivye_linii / (дата обращения — 11.01.2020)

4) Казарян, М.Э. Алгебраические кривые по направлению к пространствам модулей / М.Э. Казарян, С.К. Ландо, В.В. Прасолов. – М:. — МЦНМО, 2019 – 274 с.

5) Мир математики: в 40т. Т.4: Жуан Гомес. Когда прямые искривляются. Неевклидовы геометрии. / Пер. с англ. – М.: — Де Агостини, 2014 – 160с.

6) Начертательная геометрия [Электронный ресурс] // Лекция №7-1. Кривые линии . URL:https://vuzlit.ru/843223/-_krivye_linii#369/ (дата обращения: 11.01.2020)

7) Построение нормальной кривой распределения по опытным данным [Электронный ресурс] // URL: http://po—teme.com.ua/vysshaya—matematika/prikladnaya—matematika/2038-postroenie—normalnoj—krivoj—raspredeleniya—po—opytnym—dannym. / (дата обращения — 07.01.2020)

Психодиагностика ребенка [Электронный ресурс] // Кривая нормального распределения Гаусса и гистограмма. URL: https://studref.com/415556/psihologiya/krivaya_normalnogo_raspredeleniya_gaussa_gistogramma / (дата обращения — 04.01.2020)

9) Харрис, Дж. Модули кривых. Вводный курс / Дж. Харрис, Я. Моррисон. – М:. – Мир, 2004 — 448 с.

Просмотров работы: 1115

Источник