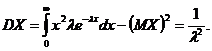Лабораторная работа № 29
Изучение распределения случайных ошибок измерений
Неконтролируемые причины, приводящие к появлению ошибок измерений, могут быть самыми разнообразными: это и неопределённость самой измеряемой величины1, и колебания других величин, не имеющих прямого отношения к измеряемой величине, но влияющих на показания приборов и вообще на результат измерений, и несовершенство процедуры измерений, приборов и органов чувств экспериментатора. Независимо от их природы мы можем объединить все такие искажающие влияния под общим названием помехи или шума, который накладывается на «полезный сигнал» – истинное значение измеряемой величины xист. Результат измерения xизм является суммой полезного сигнала xист и сигнала помехи
δx , т. е. ошибки
|
xизм |
= xист +δx |
(I) |
|
В отдельных опытах ошибка δx |
принимает значения δx j |
(j = 1, 2, …– номер |
измерения), которые никак не связаны между собой и совершенно непредсказуемы. Такие величины носят название случайных, и для их описания применяются методы математической статистики (теории вероятностей).
Результат измерения xизм, поскольку он содержит случайную величину – ошибку,
также является случайной величиной, принимающей в отдельных опытах значения:
Полезно обратить внимание на терминологию. Как в математике следует различать саму функцию и принимаемые ею численные значения, так и здесь мы говорим о величинах
δx , xизм и о значениях δx j , x j , которые они принимают в отдельных опытах. Это
1 Надо помнить, что, проводя измерения какой-либо физической величины, мы всегда имеем в виду какую-нибудь модель, упрощающую реальную действительность. Например, если мы будем говорить о «диаметре d Земли», приближенно считая её шаром, то при измерениях, естественно, обнаружатся колебания d, вызванные расхождением между моделью и действительностью. Под «истинным значением» d естественно понимать какое-то среднее значение. Мы можем улучшить модель, вводя вместо диаметра более адекватные понятия размеров, но любая модель рано или поздно наталкивается на подобные трудности.

различие не всегда проводится в словесных определениях: говорят, что δx – ошибка
(величина), а δx j – ошибки (значения этой величины).
В действительности мы не знаем истинного значения измеряемой величины2 и
соответственно не знаем значений ошибки. Нам известны только значения x j , которые
принимает величина xизм; о них мы и будем говорить в дальнейшем.
Результаты отдельных экспериментов, как уже говорилось, непредсказуемы, но это не значит, что они не подчинены никакой закономерности. Действительно, помехи обусловлены реальными физическими воздействиями, каждое из которых подчинено каким-то законам. Совместное действие большого числа отдельных независимых помех приводит к невозможности предсказать результат отдельного измерения, но их закономерный характер позволяет установить, насколько часто будет встречаться то или иное конкретное значение xизм при большом числе повторных измерений. Иначе говоря, законы, которым подчиняются результаты измерений, существуют и имеют статистический характер.
Мы можем поставить задачу – установить эти законы и воспользоваться ими для достижения основной цели – получить из опыта возможно лучшую оценку истинного значения измеряемой величины x и охарактеризовать качество этой оценки.
Итак, мы должны выяснить, как часто случайная величина xизм принимает определенные наперед заданные значения x1, x2 ,…. Заметим, прежде всего, что в таком виде вопрос не имеет смысла. Действительно, если физическая величина x может принимать непрерывный ряд значений, то xизм может быть любым числом. Тогда вероятность обнаружить среди конечного набора численных значений какое-то наперед заданное число практически равна нулю.
Если вы попросите всех ваших сокурсников назвать произвольные числа из интервала 0…10 – найдется ли среди них число 4.9487526750002? Число 5, вероятно, найдется, но природа не имеет человеческой склонности к целым числам!
2 При градуировке приборов, т.е. при наличии двух приборов – более и менее точного – показание эталонного или образцового прибора часто может быть с достаточной для практических целей точностью принято за истинное значение, т. е. мы можем предполагать, что соответствующая ошибка мала (но, конечно, не равна нулю).

Содержательным будет только вопрос, сколько значений xизм лежит в определенном интервале, например x1 < xизм < x2 . Предположим, что мы провели N измерений
|
величины |
x |
и получили набор значений |
xизм. Выделим |
на оси |
x |
такой интервал |
||||||
|
xmin < x < xmax , что все значения лежат внутри этого интервала. Разобьем его |
на |
m |
||||||||||
|
равных отрезков длиной ∆x = |
xmax − xmin |
и |
подсчитаем, |
сколько |
значений xизм |
из |
||||||
|
m |
||||||||||||
|
общего числа |
N результатов измерений попадает в каждый из этих промежутков. |
Пусть, |
||||||||||
|
например, |
в |
промежутке ∆xk от xk = xmin +k∆x до xk+1 = xk |
+∆x |
лежит |
∆nk |
|||||||
|
результатов3. Построим на каждом отрезке [xk , xk+1 ] (k = 0,1,2,…m −1) |
прямоугольник |
|||||||||||
|
с высотой |
∆nk |
. |
||||||||||
|
N∆x |
||||||||||||
|
Мы |
получим тогда график, подобный |
показанному |
на Рис.1 |
и |
называемый |
гистограммой.
|
∆nk / N |
p ( x ) |
|||||||||||
|
35 |
||||||||||||
|
3 |
5 |
|||||||||||
|
30 |
3 |
0 |
||||||||||
|
25 |
2 |
5 |
||||||||||
|
20 |
2 |
0 |
||||||||||
|
15 |
1 |
5 |
||||||||||
|
10 |
1 |
0 |
||||||||||
|
5 |
5 |
|||||||||||
|
0 |
0 |
|||||||||||
|
1 0 |
1 1 |
1 2 |
1 3 |
1 4 |
1 5 |
|||||||
|
10 |
11 |
12 |
13 |
14 |
15 |
|||||||
|
X |
||||||||||||
|
X |
||||||||||||
|
Рис.1. |
Рис.2. |
Площадь каждого из прямоугольников равна ∆Nnk – относительной частоте
попадания результатов в промежуток ∆xk .
3 для определенности можно договориться относить к этому отрезку также значения xизм, равные в точности x

Если число измерений N невелико, гистограмма может иметь довольно неправильный вид, зависящий от случайного выпадения тех или иных значений xизм, но если N растет, то в форме гистограммы все в большей и большей степени проявляются закономерности, определяемые физической природой процессов, происходящих при измерении. В пределе4,
|
при N → ∞, относительная частота |
∆nk |
принимает вполне определенное (уже не |
|
|
N |
|||
случайное) значение, которое называется вероятностью попадания xизм в интервал
∆xk :
|
P(xk ≤ xизм < xk +1 )= |
∆n |
|
|
lim |
N |
k |
|
N →∞ |
|
Если мы, кроме того, устремим m к бесконечности, |
так что ∆x → 0 , то верхушки |
||
|
прямоугольников на Рис.1 сольются в плавную кривую (см. Рис.2), ординаты которой |
|||
|
∆n |
k |
||
|
p(x)= lim lim |
(3) |
||
|
∆x→0 N →∞ N∆x |
представляют собой значения плотности вероятности получения результата xизм = x .
Если мы выделим на оси абсцисс произвольный промежуток a ≤ x ≤ b , то площадь,
заключенная под этой кривой между отрезками x = a и x = b , равна вероятности того,
что x попадает в указанный промежуток: P(a ≤ xизм ≤ b) отсюда название функции p(x) – плотность вероятности.
Кривая плотности распределения вероятностей, подобная показанной на Рис.2, наиболее полно отражает условия эксперимента и дает наиболее детальные предсказания о поведении случайной величины xизм. Никакие более конкретные предсказания, касающиеся результатов отдельных измерений, невозможны. С другой стороны, самое большее, что можно
4 Определение «предела» в теории вероятностей не совпадает с аналогичным определением в математическом анализе, и мы здесь не вполне правомерно используем обозначение «lim». В теории вероятностей само «стремление» к «пределу» носит вероятностный характер.

p(x)
p(x)
xист
получить из опыта – это построить настолько хорошую гистограмму (для таrих больших N и
|
m), что она будет практически совпадать с кривой |
p(x). |
|||
|
Гистограмма и кривая плотности вероятности p(x) для случайной величины |
xизм |
|||
|
описывают также |
распределение |
ошибок, |
т.е. значений случайной величины |
|
|
δx = xизм − xист |
. Действительно, |
достаточно |
перенести начало координат в |
точку |
x = xист, и тогда на оси абсцисс вместо xизм будут отложены значения δx . Таким образом,
эти кривые характеризуют точность эксперимента. Если они имеют вид острого пика,
вершина которого близка к (δx = 0) , а по обе стороны от вершины наблюдается резкий спад функции , то эксперимент имеет высокую точность (большие ошибки встречаются реже). Если существует заметное неравенство частот появления ошибок положительного и отрицательного знака, то гистограмма становится несимметричной и при этом вершина пика отклоняется от x = xист. Большая ширина пика означает наличие сильных помех случайного характера.
На практике редко удается провести такое большое число измерений, чтобы можно было построить хорошую гистограмму, поэтому вместо графического построения кривой распределения обычно определяют расчётом параметры функции . Для этого нужно,
конечно, сделать какие-то предположения о форме этой функциональной зависимости. Можно показать5, что если ошибки вызываются очень большим набором независимых помех, каждая из которых вносит очень малый положительный или отрицательный вклад, то возникает распределение ошибок по так называемому нормальному закону,
описываемое функцией Гаусса:
|
1 |
(x−x |
)2 |
1 δx2 |
||||||||||||||
|
1 |
− |
ист |
1 |
− |
|||||||||||||
|
p(x) = p(δx) = |
2 |
σ |
2 |
= |
e |
2 |
σ |
2 |
|||||||||
|
2π |
e |
2π |
, |
(4) |
|||||||||||||
где e = 2.718281828… – основание натуральных логарифмов.
5 Это доказывает так называемая «центральная предельная теорема» теории вероятностей

Формула (4) содержит только два параметра – xист и σ – и зная их, можно целиком построить кривую p(x).
Условия, при которых ошибки распределены по нормальному закону, часто выполняются на опыте. В качестве удобного приближения этот закон нередко используют при обработке наблюдений и тогда, когда реальное распределение отличается от нормального.
Функция Гаусса (Рис.3)
p(δx)
0.4
0.2
|
0 |
-3 |
-2 |
-1 |
0 |
1 |
2 |
3 |
δx |
Рис.3. Функция Гаусса.
имеет следующие основные свойства, которые легко понять исходя из упомянутых предпосылок её вывода:
1. Кривая p(x) симметрична относительно xист – положительные и отрицательные ошибки встречаются одинаково часто. Это и естественно, если все помехи имеют абсолютно случайный характер (а тогда нет систематического преобладания случайных ошибок положительного знака над отрицательными).
2.Кривая p(x) имеет вид колокола: пик ее лежит при x = xист (δx = 0); довольно тупая вершина указывает на то, что любые малые значения ошибок почти равновероятны, а затем наблюдается быстрый спад, указывающий на малую вероятность больших ошибок. Это
ипонятно, так как для получения большой ошибки все источники помех должны одновременно дать вклад одного знака, что случается очень редко.
3.Полная площадь под кривой p(x) равна 1 (это обеспечивается нормировочным
|
множителем |
1 |
перед экспонентой). Это необходимое условие, так как вероятность |
|
2πσ |

xизм
p(x)
совершения хоть какой-нибудь ошибки равна единице (достоверное событие), иначе говоря,
|
из N |
измерений |
все |
N обязательно содержат какую-нибудь ошибку из интервала |
|
−∞ <δx < ∞. |
|||
|
4. |
Функция |
p(x) |
нигде не обращается в нуль, так что с какой-то (хотя бы очень |
малой) вероятностью ошибка может иметь сколь угодно большую величину. Этот результат получается, если число источников помех принимается не просто очень большим, а
бесконечным. Осторожнее будет говорить, что p(x) практически равна нулю при очень больших δx .
Параметр σ характеризует ширину распределения: при δx =σ величина p(x) в

заключена большая часть площади под кривой p(x): 68%, иначе говоря, 68% всех результатов имеют ошибку, по абсолютной величине не превосходящую σ . В то же время
|
95% результатов измерений удовлетворяют условию |
δx |
< 2σ , |
а 99.7% – условию |
|||||
|
δx |
<3σ . |
|||||||
|
Ввиду важного значения параметров σ и σ 2 оба они имеют специальные названия: |
||||||||
|
σ 2 называется дисперсией случайной величины |
xизм или |
δx , а σ называется |
среднеквадратической ошибкой (в соответствии с физическим смыслом, о котором речь пойдет чуть ниже).
Если мы проведем очень большое число измерений, позволяющее построить
гистограмму, совпадающую с кривой плотности вероятности , то оценку истинного
значения измеряемой величины даст положение пика этой кривой. Более удобным и более
точным методом получения этой оценки будет вычисление среднего значения (черта
над обозначением величины здесь и дальше означает усреднение по большому числу N измерений):

|
1 |
N |
1 |
m |
||||||
|
= |
∑x j ≈ |
∑xk ∆nk = |
|||||||
|
xизм |
|||||||||
|
N j=1 |
N k =1 |
(5) |
|||||||
|
m |
∆nk |
m |
|||||||
|
= ∑xk |
∆xk ≈ ∑xk p(xk )∆xk |
||||||||
|
N∆xk |
|||||||||
|
k =1 |
k =1 |
||||||||
|
(напомним, что j – номер измерения, а k |
– номер одного из отрезков, на которые мы |
разбили интервал изменения величины xизм. Здесь последовательно выполнены следующее операции.
1. Величины x j разбиты на m групп, в каждой из которых xk ≤ x j < xk +∆xk ,
2.в каждой группе все x j приближенно заменены на xk ,
3.величины N∆∆nxkk приближенно заменены на p(xk ) .
|
Если N → ∞, m → ∞, то приближенные |
равенства станут точными, и, в силу |
|||||
|
симметрии функции p(x) относительно точки x = xист мы получим |
= xист. |
|||||
|
xизм |
||||||
|
Действительно, перепишем последнее равенство в (5) в виде |
||||||
|
m |
m |
|||||
|
= ∑(xk − xист) p(xk )∆xk + xист∑p(xk )∆xk = xист |
||||||
|
xизм |
(6) |
|||||
|
k =1 |
k =1 |
Здесь первая сумма равна нулю, поскольку каждому положительному слагаемому
δxk p(δxk ) соответствует равное ему по модулю отрицательное слагаемое
−δxk p(−δxk ) , ведь p(x)– четная функция! Вторая сумма равна единице, поскольку она представляет собой площадь под всей кривой p(x). Остается в итоге множитель перед второй суммой.
Если число измерений N конечно, то равенство xизм = xист уже не будет точным,
|
но и в этом случае |
xизм |
является наилучшей оценкой истинного значения |
x . Будем |
||||
|
обозначать эту найденную оценку через x0 : |
|||||||
|
x0 ≡ |
≈ xист |
||||||
|
xизм |
(7) |
||||||

|
Для определения |
ширины |
кривой |
p(x) несколько удобнее не графический, а |
|||||
|
расчетный метод. Вычислим средний квадрат ошибки: |
||||||||
|
1 |
N |
m |
∆nk |
|||||
|
δx2 |
= |
∑δx2j |
≈ ∑δxk2 |
∆xk ≈ ∑δxk2 p(xk )∆xk |
(7) |
|||
|
N |
||||||||
|
j=1 |
k =1 |
N∆xk |
(здесь выполнены те же преобразования, что и в (5) ). Последняя сумма для функции (4) вычисляется методами интегрального исчисления, и вычисление дает
Средний квадрат ошибки отдельного измерения равен дисперсии, а σ имеет смысл среднеквадратической ошибки. В действительности именно формулы (8) считаются
|
определением величины σ , независимо |
от вида распределения p(x). Так, для |
|||||||
|
распределения |
||||||||
|
1 |
при |
δx ≤ a |
||||||
|
p(x) = |
2a |
|||||||
|
при |
δx ≤ a |
|||||||
|
0 |
||||||||
|
из определения (8) следует: σ = a |
. |
|||||||
|
3 |
||||||||
|
Если мы провели небольшое число измерений n и нашли оценку истинного значения |
||||||||
|
1 |
n |
|||||||
|
x0 |
= |
∑x j |
(9) |
|||||
|
n j =1 |
||||||||
то нас будет, конечно, интересовать качество этой оценки. Подчеркнем, прежде всего, что x0
есть случайная величина (функция n случайных величин – результатов отдельных измерений), так что следует говорить в действительности, о распределении величины x0 , т.
е. о вероятности встретить различные значения x0 . Методами интегрального исчисления можно показать, что, если распределение величины xизм является гауссовым, то и распределение оценки x0 будет иметь такую же функциональную форму:

|
1 |
(x |
−x |
)2 |
||||||||||||||||||||||||||||||||
|
1 |
− |
0 |
ист |
||||||||||||||||||||||||||||||||
|
2 |
σ2 |
||||||||||||||||||||||||||||||||||
|
p(x0 ) = |
2π |
e |
0 |
(10) |
|||||||||||||||||||||||||||||||
|
Центр этого распределения, естественно, также лежит при |
x0 = xист , но величина |
||||||||||||||||||||||||||||||||||
|
дисперсии σ0 |
будет другой, мы без труда найдем дисперсию величины |
x0 элементарными |
|||||||||||||||||||||||||||||||||
|
методами, исходя из формулы, аналогичной (8): |
|||||||||||||||||||||||||||||||||||
|
σ02 = |
|||||||||||||||||||||||||||||||||||
|
(x0 − xист )2 |
(11) |
||||||||||||||||||||||||||||||||||
|
где среднее уже, конечно, |
не по n измерениям, |
как в (9), а по очень большому числу |
N |
||||||||||||||||||||||||||||||||
|
возможных серий таких измерений, по |
n измерений в каждой. |
Подставляя x0 из (9), |
|||||||||||||||||||||||||||||||||
|
получим после громоздких, но тривиальных выкладок |
|||||||||||||||||||||||||||||||||||
|
1 |
n |
2 |
1 |
n |
2 |
||||||||||||||||||||||||||||||
|
σ |
02 = |
∑x j − xист |
= |
∑(x j |
− xист) |
= |
|||||||||||||||||||||||||||||
|
n |
j=1 |
n |
j=1 |
||||||||||||||||||||||||||||||||
|
1 |
n |
2 |
n |
n |
|||||||||||||||||||||||||||||||
|
= |
∑(x j |
− xист)2 + |
∑ |
∑(xi − xист)(x j |
− xист) |
||||||||||||||||||||||||||||||
|
n |
2 |
n |
2 |
||||||||||||||||||||||||||||||||
|
j=1 |
|||||||||||||||||||||||||||||||||||
|
j=1 i= j+1 |
|||||||||||||||||||||||||||||||||||
|
n одинаковых слагаемых |
= |
=σ 2 . |
|||||||||||||||||||||||||||||||||
|
Под знаком первой суммы стоит |
δx2j |
δx2 |
Под |
знаком второй суммы стоит среднее произведение ошибок двух независимых измерений,
δxiδx j . Поскольку ошибки одинаково часто бывают положительными и отрицательными,
это среднее будет, очевидно, нулем.
Таким образом,
|
σ02 = |
1 |
nσ 2 = |
1 |
σ 2 |
(13) |
||
|
n2 |
n |
||||||
Дисперсия среднего из результатов n измерений в n раз меньше, чем дисперсия
результата отдельного измерения, следовательно, x0 – оценка для xист , в 
Содержание
- Виды кривых распределения вероятностей
- Получаем кривую плотности распределения вероятности случайного процесса
- Функция плотности распределения
Виды кривых распределения вероятностей



Закон Гаусса (нормального распределения). Для оценки случайной погрешности наиболее часто используется кривая Гаусса или кривая нормального распределения плотности вероятностей, которая является симметричной относительно максимума.
Такому закону (кривой) с некоторым приближением подчиняется рассеяние погрешностей измерения размеров, массы и других механических и физических величин, характеризующих свойства материала (например, условной вязкости ЛКМ).
Закон Гаусса хорошо описывает разброс экспериментальных данных, когда результат измерения зависит от многих равнозначных по величине факторов.
Симметричная кривая, изображающая плотность распределения вероятности по нормальному закону определяется уравнением: 
где P(x) — плотность распределения вероятности Р;

Q и s — параметры распределения Р; х — аргумент функции плотности распределения Р, т.е. случайная величина — — ¥ 2 . Площадь под кривой численно равна 1. Т.е. вероятность попадания величины х в диапазон от — ¥ до ¥ равна 1.
В ряде случаев характер рассеяние эмпирических значений случайной величины подчиняется другим законам распределения (Максвелла, Вейбулла, Пуансона и др.)
Источник
Получаем кривую плотности распределения вероятности случайного процесса
В ходе моей трудовой деятельности неоднократно возникала необходимость построить кривую плотности распределения вероятности по имеющемуся набору числовых данных большого объема различной природы, как случайных, так и не очень. Бывало и такое, что по некоторым причинам, использовать при этом сторонние библиотеки, решающие вопрос, было нежелательно. Приходилось обходится своими силами.
Помнится, когда впервые возникла задача такого рода, с ходу решить ее не получилось, при кажущейся, на первый взгляд, относительной простоте вопроса, на его решение пришлось потратить некоторое количество времени и обратиться при этом к тематической литературе. Немного покопавшись в поиске Хабра обнаружил, что нет статей, которые могли бы помочь решить такую задачу. В связи с этим я хотел бы простым и понятным языком рассказать коллегам по цеху, как можно построить плотность распределения вероятности какого либо процесса, представленного некоторой числовой последовательностью своими силами, не используя методы сторонних библиотек для научных расчетов, например, таких как Pandas или Seaborn. Думаю, что научиться это делать или просто освежить тему в памяти было бы полезно многим аналитикам данных, разработчикам, инженерам, научным работникам и другим специалистам.
Для решения задачи будем использовать Python и сторонний модуль Matplotlib, который поможет легко и наглядно визуализировать полученные результаты и удостовериться в их адекватности. Из Pandas возьмем только DataFrame для удобства.
Допустим, что в исходных данных имеется совокупность числовых значений, представляющая собой, например, некоторый процесс. Случайный он или нет на самом деле не имеет для нас никакого значения. Иными словами — имеем некоторый набор чисел, плотность распределения вероятности которых нам нужно построить для тех или иных целей.
В данном случае предлагаю не забивать голову формулами, а сосредоточиться на понимании сути вопроса и принципа его решения. Если уловить смысл, то несложные формулы вы совершенно легко сможете написать самостоятельно. А вот код на Python мы напишем, будет интереснее математических формул (заодно и вспомним принципы работы с Matplotlib).
Итак, опишем процесс простым и понятным языком. Для решения вопроса нам нужно пройти через следующие этапы:
определяем количество элементов в рассматриваемой выборке;
кривую плотности распределения будем строить на основе гистограммы, это означает, что нам нужно поделить диапазон изменения значений (учитываем минимальное и максимальное значение) в нашей выборке на какое-то количество интервалов, тем самым узнать ширину одного интервала. Чем больше интервалов, тем более детализована будет кривая распределения (но есть нюанс, неоправданно большое количество интервалов разбиения делать не нужно);
определяем, какое количество чисел из нашей выборки входит в каждый интервал;
количество вхождений в каждый интервал делим на произведение ширины интервала на количество чисел в нашей выборке, таким образом получаем значения кривой плотности распределения вероятности по оси ординат;
сопоставляем вычисленные значения для пункта выше для каждого интервала с серединой соответствующего интервала, таким образом получаем значения кривой плотности распределения вероятности по оси абсцисс.
Проверяем корректность описанного способа следующим образом:
генерируем четыре выборки случайных чисел для четырех видов распределений соответственно: Релея, гамма, Вейбулла и экспоненциального;
рассчитываем кривые плотности распределения вероятности для соответствующих распределений по известным формулам;
получаем своими силами плотность распределения вероятности для каждой выборки, используя описанный выше алгоритм;
на отдельных графиках совмещаем полученный в пункте выше результат для каждой выборки с соответствующей кривой плотности распределения, рассчитанной по известной формуле (например, можно взять из любого справочника по математической статистике или Википедии).
Напишем код на Python. Все должно быть понятно, поскольку есть комментарии (они существенно увеличили количество строк, но с ними все гораздо яснее).
В результате выполнения кода имеем следующие кривые (визуализированы с помощью Matplotlib).
На рисунке можно увидеть совпадения кривой плотности распределения вероятности, полученной нами самостоятельно (красный цвет) для распределений Релея, гамма, Вейбулла и экспоненциального с соответствующими кривыми этих распределений, вычисленных по общеизвестным формулам (синий цвет). В связи с этим можно сделать вывод об адекватности нашего алгоритма определения кривой плотности распределения случайных (или неслучайных) процессов и пользоваться им для оценки плотности распределения той или иной числовой выборки.
Источник
Функция плотности распределения



Пусть имеется непрерывная случайная величина X с функцией распределения F(х), которая для большинства практических ситуаций обладает свойством непрерывности и дифференцируемости. Вычислим вероятность попадания этой случайной величины на промежуток оси абсцисс от х до х+Δх:

Определим отношение этой вероятности к длине промежутка, на котором она сосредоточена.

Это будет средняя вероятность, приходящаяся на единицу длины этого промежутка, другими словами — средняя плотность вероятности. Будем теперь уменьшать длину промежутка Δх до нуля, переходя к пределу:

В пределе получаем производную от функции распределения, которая обычно обозначается
С другой стороны, функция распределения F(x) является первообразной для функции плотности f(x) так, что может быть записано следующее соотношение: 
Определенная таким образом функция f(х) характеризует как бы плотность, с которой распределяются значения случайной величины в данной точке. Эта функция называется плотностью распределения (или «плотностью вероятности») непрерывной случайной величины X.
основные свойства плотности распределения.
1. Плотность распределения есть неотрицательная функция:
Это свойство непосредственно вытекает из того, что функция распределенияF(х) есть неубывающая функция.
2. Интеграл в бесконечных пределах от плотности распределения равен единице:
Это соотношение следует из соотношений: 
Геометрически основные свойства плотности распределения означают, что вся кривая графика функции плотности распределения лежит не ниже оси абсцисс. Кроме того, полная площадь, ограниченная кривой графика функции плотности распределения и осью абсцисс, равна единице.
Случайные величины, которые принимают числовые значения, отделенные на числовой оси друг от друга конечными промежутками, называются дискретными случайными величинами.
Закон распределения дискретной случайной величины может быть заданграфически. Для чего в прямоугольной системе координатстроятточки M1(x1, p1), M2(x2, p2). Mn(xn, pn), гдеxi, (значения на оси абсцисс) — возможные значения случайной величины X, а pi. (значения на оси ординат) -вероятности,соответствующиезначениям xi.Построенные таким образом точки соединяют отрезками прямых. Полученная графическая фигура называется многоугольником распределения или полигоном.
Статистический ряд часто оформляется графически в виде так называемой гистограммы. Гистограмма строится следующим образом. По оси абсцисс откладываются интервалы группировки, и на каждом из интервалов как на основании строится прямоугольник, площадь которого равна соответствующей относительной частоте. Для построения гистограммы нужно частоту каждого интервала разделить на его длину и полученное число взять в качестве высоты прямоугольника. Из способа построения гистограммы следует, что полная площадь ее равна единице.
Очевидно, при увеличении объема выборки будет увеличиваться и общее число интервалов группировки, а длины интервалов будут уменьшаться, при этом гистограмма будет все более приближаться к некоторой кривой, ограничивающей площадь равную единице. Нетрудно убедиться, что эта кривая представляет собой график плотности распределения исходной случайной величины Х.
Полигон также является графическим представлением статистического ряда. Полигон образуется ломаной линией, отрезки прямых линий которой, соединяют точки координатной плоскости (х, у). Координата х – является центром некоторого интервала группировки, а координата у равна относительной частоте встречаемости значений выборки на данном интервале.
(дополнительно) Случайные величины, которые принимают числовые значения, отделенные на числовой оси друг от друга конечными промежутками, называются дискретными случайными величинами.
Закон распределения дискретной случайной величины может быть заданграфически. Для чего в прямоугольной системе координатстроятточки M1(x1, p1), M2(x2, p2). Mn(xn, pn), гдеxi, (значения на оси абсцисс) — возможные значения случайной величины X, а pi. (значения на оси ординат) -вероятности,соответствующиезначениям xi.Построенные таким образом точки соединяют отрезками прямых. Полученная графическая фигура называется многоугольником распределения или полигоном.
31 Экспоненциальное распределение вероятностей
Плотность показательного распределения имеет вид: 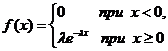
Здесь λ > 0 постоянный параметр.
Функция распределения экспоненциального закона выражается следующим образом:

Для случайной величины, распределенной по экспоненциальному закону математическое ожидание равно:
Дисперсия может быть найдена следующим образом:
32 Теорема умножения вероятностей
Условные вероятности
Допустим, что из общего числа N человек страдает дальтонизмом NА человек. Все N человек делятся на N1женщин и N2 мужчин, N1 + N2 = N. Случайное событие H1состоит в том, что наугад выбранный человек является женщиной, а событие H2 состоит в том, что наугад выбранный человек является мужчиной. Случайное событие А состоит в том, что наугад выбранный человек (мужчина или женщина) страдает дальтонизмом
Для вероятностей (классических) рассмотренных событий имеют место следующие соотношения:
Будем интересоваться дальтонизмом не всех людей, а отдельно дальтонизмом женщин и мужчин. Найдём вероятность того, что наугад выбранная женщина страдает дальтонизмом; очевидно, эта вероятность равна отношению числа женщин, страдающих дальтонизмом, пусть это будет 
Здесь выражение Р(АН1) обозначена как раз вероятность произведения (одновременного наступления) событий А и H1 (случайно выбранная женщина страдает дальтонизмом).
Заметим, что выражение для условной вероятности было получено в предположении применимости классического определения вероятностей (когда все элементарные события равновероятны). Тем не менее, в общем случае условная вероятность определяется аналогичным образом.
Пусть Н — некоторое случайное событие, имеющее ненулевую вероятность, и А — произвольное случайное событие. Условной вероятностью события А при условии Н (при справедливости гипотезы Н) называется величина, определённая соотношением: 
Иногда слова «при условии Н» заменяют словами «если известно, что Н произошло». Условные вероятности остаются неопределёнными, когда гипотеза Н имеет нулевую вероятность.
В противоположность условным вероятностям для большей ясности может использоваться термин безусловная вероятность.
Теоретически, переход от безусловных вероятностей к условным приводит к замене пространства элементарных исходов Ω. на пространство элементарных исходов Н, являющееся частью исходного пространства Ω. Но всякая часть исходного пространства элементарных исходов является его подмножеством, а значит, по определению, случайным событием, которое мы называем Н. Отсюда следует, что все общие теоремы о вероятностях справедливы также и для условных вероятностей. Например, условная вероятность события 
Формула 

С другой стороны, если 
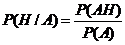
Полученную формулу называют теоремой умножения вероятностей для так называемых зависимых событийА и Н. События А и Н могут бытьнезависимыми, если появление одного из них никак не влияет на вероятность появления другого, то есть условная вероятность события А в предположении, что Н произошло, совершенно такая же, как и без этого предположения: Р(А/Н) = Р(А).
Для независимых событий формула умножения вероятностей имеет вид: 


Свойство независимости событий взаимно, и имеет место и для противоположных событий.
Таким образом, для независимых событий теорема умножения вероятностей формулируется следующим образом: вероятность произведения независимых событий равна произведению их вероятностей.
33 Поле случайных событий
Рассматривается некоторая система S подмножеств множества Ω. Элементы системы S называются случайными событиями. Предполагаются, что для системы S выполняются следующие условия:
1. S в качестве элемента содержит множество Ω. То есть ΩÎS.
2. Если А и В — подмножества множества Ω и входят в S в качестве элементов, то в качестве элементов S содержит также множества 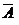

При этом под 
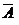
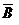
Поскольку в S в качестве элемента входит все множество Ω, то согласно второму требованию S содержит также 
Очевидно, что второе требование влечет за собой принадлежность к множеству S сумм, произведений и дополнений конечного числа событий, принадлежащих S. Таким образом, рассмотренные элементарные операции над случайными событиями не могут вывести за пределы множества случайных событий.
Система событий S, удовлетворяющая приведенным выше условиям, называется полем событий.
34Геометрическое определение вероятностей
Допустим, что на плоскости имеется некоторая область W и в ней содержится другая область w. В область W наудачу бросается точка и спрашивается, чему равна вероятность того, что точка попадет в область w. При этом выражению «точка бросается наудачу в область W» придается следующий смысл: брошенная точка может попасть в любую точку области W, вероятность попасть в какую-либо часть области W пропорциональна площади этой части (либо длине, если рассматриваются области на прямой линии) и не зависит от ее расположения и формы.
Таким образом, по определению, вероятность попадания в область w при бросании наудачу точки в область W определяется следующим образом:
35Аксиоматическое построение теории вероятностей
Изначально постулируется наличие множества (пространства) Ω элементарных событий. Что представляют собой элементы этого множества для логического развития теории вероятностей безразлично. Далее рассматривается некоторая система S подмножеств множества Ω. Элементы системы S называются случайными событиями. Предполагаются, что для системы S выполняются следующие условия:
1. S в качестве элемента содержит множество Ω. То есть ΩÎS.
2. Если А и В — подмножества множества Ω и входят в S в качестве элементов, то в качестве элементов S содержит также множества 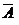

При этом под 
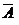
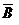
Поскольку в S в качестве элемента входит все множество Ω, то согласно второму требованию S содержит также 
Очевидно, что второе требование влечет за собой принадлежность к множеству S сумм, произведений и дополнений конечного числа событий, принадлежащих S. Таким образом, рассмотренные элементарные операции над случайными событиями не могут вывести за пределы множества случайных событий.
Система событий S, удовлетворяющая приведенным выше условиям, называется полем событий.
При аксиоматическом построении теории вероятностей от поля событий требуется выполнение и следующего условия:
3. Если подмножества А1, А2, . . , Аn, . . . множества Ω являются элементами множества S, то и их бесконечное объединение (сумма) А1+А2+ . . .+ Аn+. . . и бесконечное пересечение (произведение) А1А2. . . Аn. . . также являются элементами S.
Множество S, образованное описанным способом, носит название борелевского поля событий.
Изложенный таким образом способ определения случайного события вполне согласуется с представлениями, полученными выше при рассмотрении конкретных примеров.
Естественно вводятся и следующие определения. Если два случайных события А и В не имеют в своем составе одних и тех же элементов множества Ω, то естественно их называть несовместимыми.
Случайное событие Ω называется достоверным событием, а случайное событие Æ (пустое множество) — невозможным событием. События А и 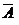
Аксиоматическое определение вероятностей включает следующие утверждения:
1. Каждому случайному событию А из борелевского поля событий S ставится в соответствие неотрицательное число Р(А), называемое его вероятностью. Иными словами, на множестве S всевозможных событий А вводится функция Р, называемая вероятностной мерой.
Из перечисленных аксиом может быть получен ряд важных утверждений.
1. Вероятность невозможного события равна нулю. Р(Æ) = 0.
2. Для любого события А вероятность события 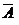

3. Вероятность любого события АÎS заключена между нулем и единицей так, что 0 ≤ Р(А) ≤ 1.
4. Если событие А влечет за собой событие В, (то есть 
Приведенное аксиоматическое построение вероятности в терминах теории множеств есть не что иное, как введение на множестве Ω нормированной, счетно-аддитивной, неотрицательной меры Р, определенной для всех элементов множества S.
Таким образом при аксиоматическом определении понятия вероятности должно быть указано исходное множество элементарных событий Ω, множество случайных событий Sи определенная на S функция Р. Совокупность этих трех составляющих <Ω, S,Р>называется вероятностным пространством.
36Случайные величины и их распределения
Случайной величиной называется величина, которая в результате случайного опыта может принять то или другое значение, заранее неизвестное.Случайные величины, которые принимают числовые значения, отделенные на числовой оси друг от друга конечными промежутками, называются дискретными случайными величинами.
Случайные величины могут относиться и к другому типу.Значения таких случайных величин заполняют некоторый участок числовой оси без промежутков, а сами такие случайные величины называютсянепрерывными
Источник
Кривая — распределение — ошибка
Cтраница 1
Кривая распределения ошибок характеризует точность эксперимента. Пологая кривая отражает наличие больших случайных ошибок.
[1]
Параметр а характеризует форму кривой распределения ошибок тонкости помола. Так как площадь кривой распределения всегда должна оставаться равной единице, то при увеличении а кривая распределения ошибок тонкости помола становится более плоской ( кривая /, рис. 49), растягиваясь вдоль оси абсцисс; при уменьшении а кривая распределения вытягивается вверх ( кривая 2) -, одновременно сжимаясь с боков, и становится более иглообразной.
[2]
Каждому значению а отвечает своя кривая распределения ошибок. Так, на рис. 4 6 видно, что для кривой, имеющей а 3 %, ошибки, превышающие 9 %, практически не встречаются, а для кривой, соответствующей а 6 %, такие ошибки появляются довольно часто.
[4]
Каждому значению а отвечает своя кривая распределения ошибок. Так, на рис. 4 6 видно, что для кривой, имеющей о 3 %, ошибки, превышающие 9 %, практически не встречаются, а для кривой, соответствующей а 6 %, такие ошибки появляются довольно часто.
[6]
Кривую нормального распределения часто называют гауссовской кривой распределения ошибок в честь немецкого математика Гаусса — одного из основателей статистической теории ошибок.
[8]
Такое определение величины 5 основано на анализе кривой распределения ошибок, показанной выше, и, следовательно, на более реалистическом подходе к установлению меры точности результатов измерений. Можно показать, что при случайном распределении ошибок ( или, правильнее сказать, отклонений) одно стандартное отклонение s указывает границы выше и ниже среднего арифметического значения, в которых заключено 68 26 % вероятности обнаружить результат любого измерения.
[9]
Хромачографический пик, как уже отмечалось, практически принимает форму кривой распределения ошибок но Гауссу. В таком виде пик записывается с помощью дифференциальных детекторов.
[10]
Параметр а характеризует форму кривой распределения ошибок тонкости помола. Так как площадь кривой распределения всегда должна оставаться равной единице, то при увеличении а кривая распределения ошибок тонкости помола становится более плоской ( кривая /, рис. 49), растягиваясь вдоль оси абсцисс; при уменьшении а кривая распределения вытягивается вверх ( кривая 2) -, одновременно сжимаясь с боков, и становится более иглообразной.
[11]
Одна из основных задач хроматографии состоит в том, чтобы получить хорошее разделение. О качестве разделения судят по числу пиков и по расстоянию, на каком они находятся друг от друга. Кривая распределения концентраций вещества на выходе из хроматографической колонки близка к кривой распределения ошибок Гаусса, поэтому абсолютного разделения двух компонентов достигнуть невозможно.
[12]
Чем дальше, тем сильнее в такой ситуации люди будут стремиться получить такую счетную единицу, изменение ценности которой было бы более тесно увязано с общей тенденцией, и даже, быть может, вынуждены будут использовать в качестве счетной единицы что-то такое, что нельзя использовать в качестве средства обмена. Кривая, представляющая дисперсию изменений цен в виде доли всех продаж, произведенных за определенный период по возросшим или снизившимся по сравнению с предыдущим периодом ценам, будучи построена по логарифмической шкале, должна, конечно, иметь одну и ту же форму, независимо от того, используем мы в качестве измерителя цен деньги или какой-нибудь товар. Мы, вероятно, получим кривую в виде нормальной ( гауссовой) кривой распределения ошибок. Случайные отклонения от нее в ту или другую сторону, насколько мы способны предсказать, будут взаимно погашаться, и количество их будет уменьшаться с ростом величины отклонения. Большинство ценовых изменений будет вызываться смещением спроса с соответствующим падением некоторых цен и повышением других; относительно мелкие смещения такого рода будут, вероятно, более частыми, чем крупные. Общий уровень цен, выраженный в деньгах со стабильной в данном смысле ценностью и представленный данной кривой, не должен в этом случае меняться, а объемы сделок, совершаемых по ценам, возросшим или упавшим на некоторый процент, должны уравновешивать друг друга. Это минимизирует ошибки — не обязательно отдельных индивидуумов, но всего общества в целом. И хотя никакое индексное число, обычно исчисляемое для этих целей, не поможет полностью подтвердить то, что мы предположили, достаточно точное приближение к измерению такого эффекта вполне достижимо.
[13]
На каждом интервале строят прямоугольник, высота которого равна частоте ( абсолютной или относительной) появления результата в данном интервале. Соединив середины верхних сторон прямоугольников плавной линией, получают экспериментальную кривую распределения результатов измерения. Для этого начало координат совмещают со средним значением частоты ( см. рис. 1.5), а на ось абсцисс, не меняя масштаба, наносят шкалу ошибок. Кривая распределения ошибок дает сведения о вероятности появления той или иной ошибки.
[14]
Страницы:
1
График фиг. 7 указывает на удовлетворительную сходимость результатов расчета по предлагаемому методу с кривой ошибок Гаусса. Это дает основание считать, что ошибки расчета носят случайный характер. Следовательно, основное расчетное уравнение (II) в первом приближении правильно учитывает связи между наиболее существенными для топочного процесса величинами. [c.94]
На рис. 3.2Й приведены теоретическая кривая плотности вероятности для линейной функции Ь (t) при = 0,85 и эмпирический полигон распределения ошибок измерений одной и той же детали разными штангенциркулями, разными контролерами, производимых в неодинаковых производственных условиях. На том же рисунке нанесена кривая гауссова распределения. Сопоставление интегральных кривых закона Гаусса и распределения с линейной функцией Ь (/) [c.101]
Многочисленными опытами доказано, что распределение случайных ошибок, возникающих в размерах при механической обработке деталей, сборке механизмов, а также при снятии показаний, приближается к закону нормального распределения (к закону Гаусса), который выражается кривой, представленной на рис. 234. [c.372]
Величина коэфициента больше — 1 и меньше +1 и зависит от закона распределения. В табл. 1 даны значения величин и As для того случая, когда закон распределения ошибок размеров всех производимых деталей есть закон Гаусса, а поле допуска годных деталей различным образом расположено относительно кривой и имеет различную величину. Взаимное расположение поля допуска н кривой распределения определяем с помощью координаты Хм — вершины кривой распределения относительно середины поля допуска, выражая её в долях половины поля допуска [c.99]
Распределение случайных ошибок во многих видах физических измерений является распределением Гаусса, или нормальным распределением. Можно показать, что даже если сами ошибки не подчиняются этому закону, средние значения групп измерений описываются распределением, которое для очень больших групп приближается к нормальному [4]. Если принять, что результаты экспериментов соответствуют гауссовой кривой, то тогда по среднему отклонению можно определить стандартное отклонение, ибо, как нетрудно показать, [c.15]
Кривую нормального распределения часто называют гауссовской кривой распределения ошибок в честь немецкого математика Гаусса — одного из основателей статистической теории ошибок. [c.392]
Распределение скоростей, соответствующее этому асимптотическому решению, изображено на рис. 9.11. Примечательно, что по форме оно совпадает с кривой Гаусса для нормального распределения ошибок. Согласно еде- [c.176]
Статистическая обработка дает для каждого параметра закон распределения ошибок единичных замеров, близкий к нормальному распределению Гаусса (рис. 25, а—г). В частности, кривая распределения для частоты ударов свидетельствует о том, что около 50% всех замеров имеют погрешность менее 2 уд мин, т. е. 0,5%, что указывает на незначительную вариацию этого параметра. [c.63]
К этому виду относится кривая нормального закона распределения ошибок (кривая Гаусса) [c.203]
Однако, как было замечено Рейхардтом [67] и Сквайром [82], не следует придавать слишком большого значения этому совпадению. Хорошо известно, что использованные уравнения пограничного слоя относятся к параболическому типу, как и уравнение теплопроводности [31, гл. IIJ, и что любое такое уравнение типа уравнения диффузии дает асимптотически колоколообразное распределение функции первоначально сосредоточенного источника. Так, например [98, гл. XXII], профиль скорости, выведенный из соотношений (14.11а) и (14.116), пренебрежимо мало отличается от кривой ошибок Гаусса, полученной из обычного уравнения теплопроводности, как, например, в гл. XII, п. 5. [c.392]
Пояснение к таблице. Ошибки размеров всех производимых деталей подчиняются закону распределения Гаусса. В графе 6 дана величина поля допуска в зависимости от величины среднего квадратического отклонения ошибок размеров всех производимых деталей, а также в зависимости от величины среднего ква-дратическогоотклонения только ошибок деталей, признаваемых годными. Графа 2 определяет взаимное расположение кривой распределения и поля допуска. При fjL == О кривая распределения расположена симметрично относительно поля допуска, точки М иО совпадают. При н-5 > О вершина кривой распределения смешена относительно середины поля допуска в сторону возрастания размера а при < О — смещена в сторону убывания этого размера. Обеими графами полностью определяется поле допуска относительно кривой распре- [c.99]
Кривые аберраций в форме параболических зависимостей, которые мы рисовали до сих пор (см. рис. 6.6), справедливы только в рамках теории аберраций третьего порядка. Наличие аберраций высших порядков меняет форму кривых, причем задача оптика-вычислителя заключается в том, чтобы ати изменения были направлены в нужную Сторону, чтобы они компенсировали остаточные аберрации третьего порядка и друг друга. Расчеты по формулам аберраций пятого, а тем боле еще более высоких порядков, столь сложны, что ими никто не пользуется. Строгий тригонометрический расчет хода лучей, в основе которого лежит закон преломления Снеллиуса ( 1.1), позволяет построить графики аберраций и следы пересечения каждого из лучей с выбранной фокальной поверхностью, так называемые точечные диаграммы, включающие влияние аберраций всех порядков. Кривые аберраций реального объектива в процессе его изготовления, отличающиеся от расчетных из-за неизбежных ошибок изготовления, оптик-практик строит по результатам измерений последних отрезков разных зон объектива. Более того, опытный оптик может так ретушировать отдельные зоны той или иной поверхности объектива (зональная ретушь), чтобы уменьшить остаточную сферическую аберрацию объектива и увеличить концентрацию энергии в изображении точечного объекта. Посмотрим, какая форма кривой аберрации является оптимальной для визуальных и фотографических наблюдений. Сферическая аберрация двухлинзового ахромата должна быть наилучшим образом исправлена для наиболее эффективных лучей (Я.=0,5550 мкм для вмуального объектива и Я=0,4400 мкм для фотографического объектива). В этих же. тучах должна лежать вершина хроматической кривой вторичного спектра. Длч получения от визуального объектива максимального разрешения необходимо, чтобы в нем была наилучшим образом исправлена волновая аберрация. Она будет минимальна, если ход характеризующей ее кривой будет иметь вид, представленный сплошной кривой на рис. 6.15, а. Продольная сферическая аберрация оказывается исправленной для внешней зоны у = 0/2 = Я, а п.тос-кость наилучшей фокусировки, смещенной относительно плоскости Гаусса на величину Д, если точка А (точка пересечения графика продольной сферической аберрации с новой плоскостью фокусировки) находится приблизительно на зоне у = 0,5Н (рис. 6.15, б). В объективе, предназначенном для фотографических работ, необходимо добиваться минимального кружка рассеяния, т. е. минимальной угловой аберрации % (рис. 6.15, в). Этому соответствует слегка недоисправленная продольная сферическая аберрация. [c.198]
Материал из MachineLearning.
Перейти к: навигация, поиск
Содержание
- 1 Задача классификации
- 2 TPR и FPR
- 3 ROC-кривая
- 4 Площадь под ROC-кривой AUC
- 5 Алгоритм построения ROC-кривой
- 6 Чувствительность и специфичность
- 7 История
- 8 См. также
- 9 Ссылки
Кривая ошибок или ROC-кривая – графичекая характеристика качества бинарного классификатора, зависимость доли верных положительных классификаций от доли ложных положительных классификаций при варьировании порога решающего правила. Преимуществом ROC-кривой является её инвариантность относительно отношения цены ошибки I и II рода.
Задача классификации
Рассмотрим задачу классификации в случае двух классов, называемых «положительным» и «отрицательным». Обозначим множество классов через . Большинство известных классификаторов могут быть представлены в виде
где
— произвольный объект,
— дискриминантная функция,
— вектор параметров, определяемый по обучающей выборке,
— порог.
Уравнение определяет разделяющую поверхность.
Примером является линейный классификатор, в котором дискриминантная функция имеет вид скалярного произведения вектора описания объекта на вектор параметров:
.
Пусть – цена ошибки (штраф за ошибку) на объекте класса
.
Для байесовского классификатора при достаточно общих предположениях доказано, что оптимальное значение порога зависит только от соотношения цены ошибок:
тогда как оптимальное значение вектора параметров , наоборот, зависит от выборки и не зависит от цены ошибок.
Таким образом, варьирование порога для многих классификаторов эквивалентно варьированию отношения цены ошибок на отрицательных и положительных объектах.
На практике цены ошибок зависят от особенностей конкретной задачи (например, от различных экономических соображений или экспертных оценок) и могут многократно пересматриваться.
Заметим, что частным случаем линейного байесовского классификатора является логистическая регрессия.
ROC-кривая наглядно представляет, каким будет качество классификации при различных и фиксированном
.
TPR и FPR
Пусть задана выборка объектов с соответствующими им верными ответами
.
Тогда для классификатора можно определить две характеристики качества:
- Доля ложных положительных классификаций (False Positive Rate, FPR):
- Доля верных положительных классификаций (True Positive Rate, TPR):
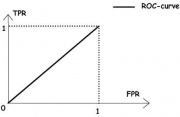
ROC-кривая
Рис.1. «Случайное гадание».
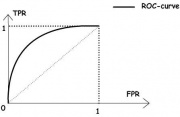
Рис.2. «Хороший» классификатор.
ROC-кривая показывает зависимость TPR от FPR при варьировании порога .
Она проходит из точки , соответствующей максимальному значению
, в точку
, соответствующую минимальному значению
.
При все объекты классифицируются как отрицательные, и ошибки возникают на всех положительных объектах,
,
.
При все объекты классифицируются как положительные, и ошибки возникают на всех отрицательных объектах,
,
.
ROC-кривая монотонно не убывает.
Чем выше лежит кривая, тем лучше качество классификации.
На рисунке 1 приведена ROC-кривая, соответствующая худшему случаю — алгоритму «случайного гадания».
На рисунке 2 изображён общий случай.
Лучший случай — это кривая, проходящая через точки
ROC-кривая может быть вычислена по любой выборке. Однако ROC-кривая, вычисленная по обучающей выборке, является оптимистично смещённой влево-вверх вследствие переобучения. Величину этого смещения предсказать довольно трудно, поэтому на практике ROC-кривую всегда оценивают по независомой тестовой выборке.
Площадь под ROC-кривой AUC
Площадь под ROC-кривой AUC (Area Under Curve) является агрегированной характеристикой качества классификации, не зависящей от соотношения цен ошибок.
Чем больше значение AUC, тем «лучше» модель классификации.
Данный показатель часто используется для сравнительного анализа нескольких моделей классификации.
Алгоритм построения ROC-кривой
Следующий алгоритм строит ROC-кривую за обращений к дискриминантной функции.
Входные данные:
Результат:
1. вычислить количество представителей классови
в выборке:
; 2. упорядочить выборку
по убыванию значений
; 3. установить начальную точку ROC-кривой:
;
; 4. для всех
если
, то сместиться на один шаг вправо:
;
; 5. иначе сместиться на один шаг вверх:
;
Чувствительность и специфичность
Наряду с FPR и TPR используют также показатели чувствительности и специфичности, которые также изменяются в интервале :
Модель с высокой чувствительностью часто дает истинный результат при наличии положительного исхода (обнаруживает положительные примеры). Наоборот, модель с высокой специфичностью чаще дает истинный результат при наличии отрицательного исхода (обнаруживает отрицательные примеры). Если рассуждать в терминах медицинской диагностики, где модель классификации пациентов на больных и здоровых называется диагностическим тестом, то получится следующее:
- чувствительный диагностический тест проявляется в гипердиагностике – максимальном предотвращении пропуска больных;
- специфичный диагностический тест диагностирует только доподлинно больных. Это важно в случае, когда, например, лечение больного связано с серьезными побочными эффектами и гипердиагностика пациентов нежелательна.
История
Термин операционная характеристика приёмника (Receiver Operating Characteristic, ROC) пришёл из теории обработки сигналов.
Эту характеристику впервые ввели во время II мировой войны, после поражения американского военного флота в Пёрл Харборе в 1941 году, когда была осознана проблема повышения точности распознавания самолётов противника по радиолокационному сигналу. Позже нашлись и другие применения: медицинская диагностика, приёмочный контроль качества, кредитный скоринг, предсказание лояльности клиентов, и т.д.
См. также
- Линейный классификатор
- Логистическая регрессия
Ссылки
- Логистическая регрессия и ROC-анализ
- RoC-curve (english wikipedia)