Среднеквадратичная ошибка (Mean Squared Error) – Среднее арифметическое (Mean) квадратов разностей между предсказанными и реальными значениями Модели (Model) Машинного обучения (ML):
Рассчитывается с помощью формулы, которая будет пояснена в примере ниже:
$$MSE = frac{1}{n} × sum_{i=1}^n (y_i — widetilde{y}_i)^2$$
$$MSEspace{}{–}space{Среднеквадратическая}space{ошибка,}$$
$$nspace{}{–}space{количество}space{наблюдений,}$$
$$y_ispace{}{–}space{фактическая}space{координата}space{наблюдения,}$$
$$widetilde{y}_ispace{}{–}space{предсказанная}space{координата}space{наблюдения,}$$
MSE практически никогда не равен нулю, и происходит это из-за элемента случайности в данных или неучитывания Оценочной функцией (Estimator) всех факторов, которые могли бы улучшить предсказательную способность.
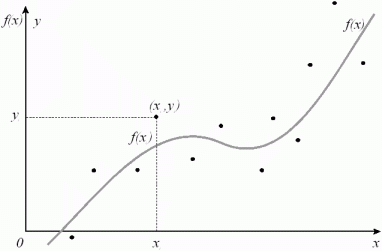
Пример. Исследуем линейную регрессию, изображенную на графике выше, и установим величину среднеквадратической Ошибки (Error). Фактические координаты точек-Наблюдений (Observation) выглядят следующим образом:
Мы имеем дело с Линейной регрессией (Linear Regression), потому уравнение, предсказывающее положение записей, можно представить с помощью формулы:
$$y = M * x + b$$
$$yspace{–}space{значение}space{координаты}space{оси}space{y,}$$
$$Mspace{–}space{уклон}space{прямой}$$
$$xspace{–}space{значение}space{координаты}space{оси}space{x,}$$
$$bspace{–}space{смещение}space{прямой}space{относительно}space{начала}space{координат}$$
Параметры M и b уравнения нам, к счастью, известны в данном обучающем примере, и потому уравнение выглядит следующим образом:
$$y = 0,5252 * x + 17,306$$
Зная координаты реальных записей и уравнение линейной регрессии, мы можем восстановить полные координаты предсказанных наблюдений, обозначенных серыми точками на графике выше. Простой подстановкой значения координаты x в уравнение мы рассчитаем значение координаты ỹ:
Рассчитаем квадрат разницы между Y и Ỹ:
Сумма таких квадратов равна 4 445. Осталось только разделить это число на количество наблюдений (9):
$$MSE = frac{1}{9} × 4445 = 493$$
Само по себе число в такой ситуации становится показательным, когда Дата-сайентист (Data Scientist) предпринимает попытки улучшить предсказательную способность модели и сравнивает MSE каждой итерации, выбирая такое уравнение, что сгенерирует наименьшую погрешность в предсказаниях.
MSE и Scikit-learn
Среднеквадратическую ошибку можно вычислить с помощью SkLearn. Для начала импортируем функцию:
import sklearn
from sklearn.metrics import mean_squared_errorИнициализируем крошечные списки, содержащие реальные и предсказанные координаты y:
y_true = [5, 41, 70, 77, 134, 68, 138, 101, 131]
y_pred = [23, 35, 55, 90, 93, 103, 118, 121, 129]Инициируем функцию mean_squared_error(), которая рассчитает MSE тем же способом, что и формула выше:
mean_squared_error(y_true, y_pred)
Интересно, что конечный результат на 3 отличается от расчетов с помощью Apple Numbers:
496.0Ноутбук, не требующий дополнительной настройки на момент написания статьи, можно скачать здесь.
Автор оригинальной статьи: @mmoshikoo
Фото: @tobyelliott
Среднеквадратичное приближение функций
Время на прочтение
3 мин
Количество просмотров 57K
На днях нужно было написать программу, вычисляющую среднеквадратичное приближение функции, заданной таблично, по степенному базису — методом наименьших квадратов. Сразу оговорюсь, что тригонометрический базис я не рассматривал и в этой статье его брать не буду. В конце статьи можно найти исходник программы на C#.
Теория
Пусть значения приближаемой функции f(x) заданы в N+1 узлах f(x0), …, f(xN). Аппроксимирующую функцию будем выбирать из некоторого параметрического семейства F(x, c), где c = (c0, …, cn)T — вектор параметров, N > n.
Принципиальным отличием задачи среднеквадратичного приближения от задачи интерполяции является то, что число узлов превышает число параметров. В данном случае практически всегда не найдется такого вектора параметров, для которого значения аппроксимирующей функции совпадали бы со значениями аппроксимируемой функции во всех узлах.
В этом случае задача аппроксимации ставится как задача поиска такого вектора параметров c = (c0, …, cn)T, при котором значения аппроксимирующей функции как можно меньше отклонялись бы от значений аппроксимируемой функции F(x, c) в совокупности всех узлов.
Графически задачу можно представить так
Запишем критерий среднеквадратичного приближения для метода наименьших квадратов:
J( c) = √ (Σi=0N[f(xi) — F(x, c) ]2) →min
Подкоренное выражение представляет собой квадратичную функцию относительно коэффициентов аппроксимирующего многочлена. Она непрерывна и дифференцируема по c0, …, cn. Очевидно, что ее минимум находится в точке, где все частные производные равны нулю. Приравнивая к нулю частные производные, получим систему линейных алгебраических уравнений относительно неизвестных (искомых) коэффициентов многочлена наилучшего приближения.
Метод наименьших квадратов может быть применен для различных параметрических функций, но часто в инженерной практике в качестве аппроксимирующей функции используются многочлены по какому-либо линейно независимому базису {φk(x), k=0,…,n}:
F(x, c) = Σk=0n[ckφk(x)].
В этом случае система линейных алгебраических уравнений для определения коэффициентов будет иметь вполне определенный вид:
a00c0 + a01c1 +… + a0ncn = b0
a10c0 + a11c1 +… + a1ncn = b1
…
an0c0 + an1c1 +… + anncn = bn
akj = Σi=0N [φk(xi)φj(xi) ], bj = Σi=0N[f(xi)φj(xi) ]
Чтобы эта система имела единственное решение необходимо и достаточно, чтобы определитель матрицы А (определитель Грама) был отличен от нуля. Для того, чтобы система имела единственное решение необходимо и достаточно чтобы система базисных функций φk(x), k=0,…,n была линейно независимой на множестве узлов аппроксимации.
В этой статье рассматривается среднеквадратичное приближение многочленами по степенному базису {φk(x) = xk, k=0,…,n}.
Пример
А теперь перейдем к примеру. Требуется вывести эмпирическую формулу для приведенной табличной зависимости f(х), используя метод наименьших квадратов.
| x | 0,75 | 1,50 | 2,25 | 3,00 | 3,75 |
| y | 2,50 | 1,20 | 1,12 | 2,25 | 4,28 |
Примем в качестве аппроксимирующей функцию
y = F(x) = c0 + c1x + c2x2, то есть, n=2, N=4
Система уравнений для определения коэффициентов:
a00c0 + a01c1 +… + a0ncn = b0
a10c0 + a11c1 +… + a1ncn = b1
…
an0c0 + an1c1 +… + anncn = bn
akj = Σi=0N[φk(xi)φj(xi) ], bj = Σi=0N[f(xi)φj(xi) ]
Коэффициенты вычисляются по формулам:
a00 = N + 1 = 5, a01 = Σi=0Nxi = 11,25, a02 = Σi=0Nxi2 = 30,94
a10 = Σi=0Nxi = 11,25, a11 = Σi=0Nxi2 = 30,94, a12 = Σi=0Nxi3 = 94,92
a20 = Σi=0Nxi2 = 30,94, a21 = Σi=0Nxi3 = 94,92, a22 = Σi=0Nxi4 = 303,76
b0 = Σi=0Nyi = 11,25, b1 = Σi=0Nxiyi = 29, b2 = Σi=0Nxi2yi = 90,21
Решаем систему уравнений и получаем такие значения коэффициентов:
c0 = 4,822, c1 = -3,882, c2 = 0,999
Таким образом
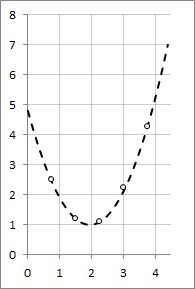
y = 4,8 — 3,9x + x2
График получившейся функции
Релизация на C#
А теперь перейдем к тому, как написать код, который бы строил такую матрицу. А тут, оказывается, все совсем просто:
private double[,] MakeSystem(double[,] xyTable, int basis)
{
double[,] matrix = new double[basis, basis + 1];
for (int i = 0; i < basis; i++)
{
for (int j = 0; j < basis; j++)
{
matrix[i, j] = 0;
}
}
for (int i = 0; i < basis; i++)
{
for (int j = 0; j < basis; j++)
{
double sumA = 0, sumB = 0;
for (int k = 0; k < xyTable.Length / 2; k++)
{
sumA += Math.Pow(xyTable[0, k], i) * Math.Pow(xyTable[0, k], j);
sumB += xyTable[1, k] * Math.Pow(xyTable[0, k], i);
}
matrix[i, j] = sumA;
matrix[i, basis] = sumB;
}
}
return matrix;
}На входе функция получает таблицу значений функций — матрицу, в первом столбце которой содержатся значения x, во втором, соответственно, y, а также значение степенного базиса.
Сначала выделяется память под матрицу, в которую будут записаны коэффициенты для решения системы линейных уравнений. Затем, собственно, составляем матрицу — в sumA записываются значения коэффициентов aij, в sumB — bi, все по формуле, указанной выше в теоретической части.
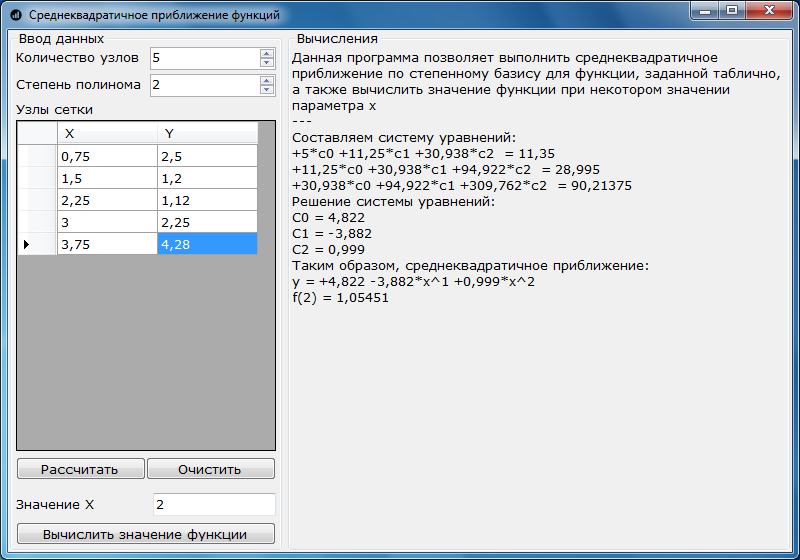
Для решения составленной системы линейных алгебраических уравнений в моей программе используется метод Гаусса. Архив с проектом можно скачать по ссылке.
Скриншот работы программы на примере, решенном выше:
Используемые источники:
Сулимова В.В. Методические указания по курсу «Вычислительный практикум» — Тула, ТулГУ, 2009 — 65 с.
Лабораторная
работа № 18.
Аппроксимация
функции, заданной таблично методом
наименьших квадратов
Общие сведения
Пусть
в результате наблюдений получена таблица
совместно наблюдаемых значений:
Таблица 1
-
x
y
Требуется
найти некоторую функцию, заданную
аналитически и удовлетворительно
описывающую зависимость y
от x. Приближенное
представление исходной функции с помощью
другой функции называется ее аппроксимацией.
Выбор вида аппроксимирующей функции
остается за исследователем и зависит
от ряда соображений. Как правило,
предпочтение отдается достаточно
простым функциям: линейной, квадратичной,
экспоненциальной, логарифмической,
обратно пропорциональной. Зачастую
выбору конкретной зависимости помогает
анализ графика табличной функции, а
также физические основания. Выберем
класс аппроксимирующих функций, зависящий
от нескольких параметров:
(1)
Подставив
в формулу (1) эмпирическое значение
переменной x=
xi
, получим
теоретическое значение величины y=yiт
, вычисленное
по формуле
(2)
Разности
называются отклонениями и представляют
ошибку аппроксимации одного значения
данной табличной функции. Для оценки
качества аппроксимации функции в целом
требуется оценить суммарную ошибку.
Есть разные способы
оценки суммарной ошибки аппроксимации,
Чаще всего оценивают суммарную
квадратичную ошибку, равную сумме
квадратов отклонений эмпирических
значений функции от теоретических:
(3)
Параметры a1,
a2,
… , am
должны быть определены из условия
минимума суммарной квадратичной ошибки.
Запишем необходимое условие экстремума
функции многих переменных S(a1,
a2,
… , am):
(4)
Формулы
(4) представляют собой систему m
уравнений с m
неизвестными для определения наилучших
значений параметров. Если функция (1)
линейна относительно параметров a1,
a2,
… , am,
то система
(4) представляет собой систему линейных
уравнений.
Метод определения
параметров из условия минимума суммарной
квадратичной ошибки называется методом
наименьших квадратов.
Задаваясь конкретным
видом зависимости (1), а именно
-
линейной функцией
y=a1+a2x.
(5)
-
квадратичной
функцией
y=a1+a2x+a3x2.
(6)
-
экспоненциальной
функцией:
.
(7)
-
логарифмической
функцией
,
(8
и т.д., можно получить
конкретный вид системы для определения
параметров; зная параметры, можно
вычислить теоретические значения и
построить как график экспериментальной
зависимости, так и теоретической.
Достоверность
аппроксимации
Квадратичная
ошибка (погрешность) аппроксимации
функции в соответствии с формулой (3)
равна
.
С
целью оценки относительной погрешности
при аппроксимации функции рассматривают
величину суммарной погрешности по
отношению к общему разбросу данных.
Общий разброс данных складывается из
отклонений теоретических значений от
среднего
и
эмпирических значений от теоретических
значений. Вводятся обозначения
(9)
(10)
(11)
Величина
(12)
называется
коэффициентом детерминированности и
характеризует меру точности аппроксимации
табличных данных функцией любого вида.
Если К2
= 1, то ошибка
аппроксимации равна 0 и теоретические
значения функции совпадают с эмпирическими
значениями.
Табличный
процессор MS
Excel
содержит встроенные функции для
определения параметров аппроксимации
методом наименьших квадратов, а также
автоматические средства построения
графика аппроксимирующей функции.
Графики аппроксимирующих функций в
Excel
называются линиями тренда.
Задание 1
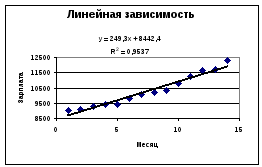
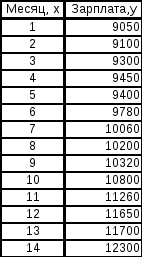
Построить
график зависимости зарплаты от текущего
месяца, если рассматривался период
относительно устойчивого роста зарплаты
в течение четырнадцати месяцев. Данные
представлены в таблице 2. Построить
графики аппроксимирующих функций (линии
тренда)с помощью встроенных средств MS
Excel
Таблица 2
Решение
-
Открыть
MS
Excel -
Набрать
таблицу данных и оформить ее по образцу -
Сохранить
файл в личной папке -
Построить
график данной функции, заданной таблично
с применением Мастера диаграмм. При
этом выбрать Тип диаграммы – Точечный,
Вид диаграммы – соответствующей
отдельным точкам графика -
Далее
построить график линейной аппроксимирующей
функции – линию тренда, заданную
линейным уравнением. Для этого выполним
следующие действия
а) выделим щелчком
мыши график функции;
б) вызовем
контекстное меню щелчком правой кнопки
в) выполним команду
Добавить линию тренда, которая вызовет
диалоговое окно этой команды;
г) в диалоговом
окне команды Линия тренда зададим Тип
аппроксимации — линейная на вкладке
Тип;
д) перейдем на
вкладку окна Параметра, где установим
опции:
показывать на
диаграмме уравнение;
поместить
на диаграмму величину достоверности
аппроксимации R^2;
е) подтвердить
выбор нажатием клавиши OK
Результат построения
представлен на рис.
-
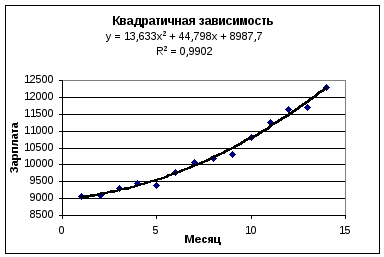
Построить
график квадратичной аппроксимации –
квадратичную линию тренда и найти
уравнение квадратичной аппроксимации.
Для решения этой задачи нужно повторить
все действия пунктов 4, 5, но при
построении линии тренда выбрать Тип
аппроксимации -Полиномиальная степени
2. Если вторая линия тренда строится
на той же диаграмме что и первая, то
нужно выполнить только п.5 -
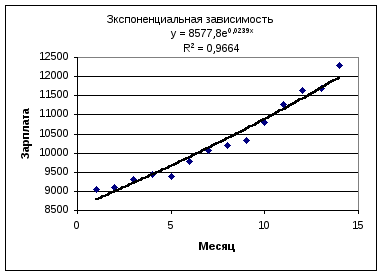
Построить
график экспоненциальной аппроксимации.
Решение очевидно
Результаты решения
задачи 1 показаны на рис.1-3.
Рис. 2.
Рис. 3.
Сравним различные
способы аппроксимации эмпирических
данных различными аналитическими
функциями. Наибольшее значение
коэффициента детерминированности
соответствует квадратичной аппроксимации.
Задание
2
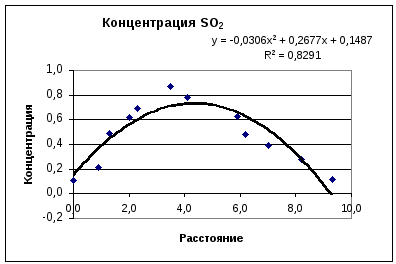
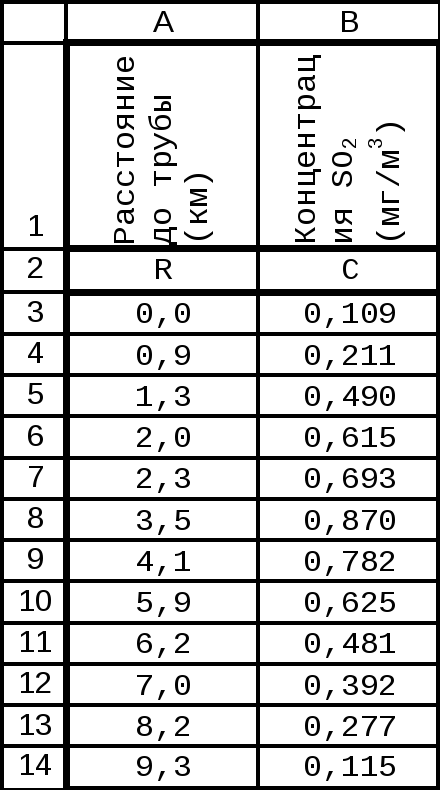
Построить
график зависимости загрязнения воздуха
сернистым газом от расстояния до
источника загрязнения (высокой трубы)
и определить, в каком диапазоне расстояний
концентрация превосходят предельно
допустимую. Предельно допустимая
концентрация равна С=0,:6 мг/и3.
Наблюдения проводились на различных
расстояниях от источника загрязнения
период наименьшей интенсивности.
Данные получены
в утренние часы при наименьших выбросах
промышленного объекта. В дневное и
вечернее время загрязненность выше
Решение:
-
Предварительно
выполним сортировку данных. Для этого
выделим ряды данных по R
и C вместе с заголовками
и выполним команду Данные|Сортировка.
В диалоговом окне укажем Сортировку
по возрастанию и по ряду R.
2.
Таблица 2
4.
Сравнение
квадратичной линии тренда и графика
исходной функции показывает, что выбор
уравнения аппроксимации не является
удачным. Попробуем использовать
полиномиальную аппроксимацию данной
функции степени 3. Результат , показанный
на рис.5, иллюстрирует улучшение качества
аппроксимации, т.к. в большей степени
учтена асимметричность исходной функции
и сложность ее формы.
Рис. 5.
0
Соседние файлы в папке prepod
- #
- #
- #
- #
- #
- #
Цель
работы. Изучить возможности синтеза
сигналов с помощью ряда Фурье по
ортогональной системе тригонометрических
функций. Синтезировать периодические
сигналы различной формы и исследовать
влияние числа ортогональных составляющих
на погрешность аппроксимации.
4.1. Разложение сигналов в обобщенный ряд фурье
4.1.1. Спектры простейших периодических функций
Если
функция
четная (симметричная относительно оси
ординат), т.е.
,
то в этом случае
;
(4.1)
.
(4.2)
Разложение
функции будет следующим
. (4.3)
Аналогично
для нечетной функции можно найти, что
. (4.4)
На
рис. 4.1 показана последовательность
прямоугольных импульсов которую можно
рассматривать как четную функцию.
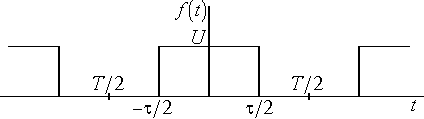
Рис.
4.1. Последовательность прямоугольных
импульсов
По
формуле (4.1) находим амплитуду
-й
гармоники:
. (4.5)
Постоянная
составляющая будет равна
;
. (4.6)
где
–
скважность импульсов. Разложение функции
запишется в виде:
. (4.7)
Графически
амплитудный и фазовый спектры прямоугольных
импульсов показаны на рис. 4.2.
Расстояния
между отдельными спектральными
составляющими обратно пропорциональны
периоду следования импульсов —
,
а положение нулей кратно
.
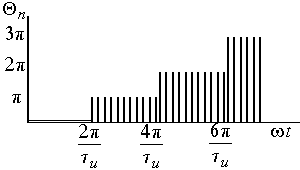
а) б)
Рис.
4.2. Амплитудный и фазовый спектры
прямоугольных импульсов
Можно
показать, что для импульсов, представленных
на рис. 4.3, разложения в ряд Фуре будут
иметь следующий вид:
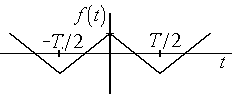
а) б)
Рис.
4.3. Пилообразное колебание и треугольные
импульсы
для
периодического пилообразного колебания
(рис 4.3,а);
; (4.8)
для
периодической последовательности
треугольных импульсов (рис.4.3,б):
. (4.9)
4.1.2. Мощность и действующее значение периодического сигнала
Пусть
несинусоидальный периодический ток
течет через активное сопротивление
.
Средняя за период мощность будет равна
. (4.10)
здесь
мгновенная мощность. Представим функцию
в виде ряда Фурье (4.6), тогда
.
Возводя
в квадрат и интегрируя каждое из слагаемых
можно убедиться, что только интегралы
вида:
, 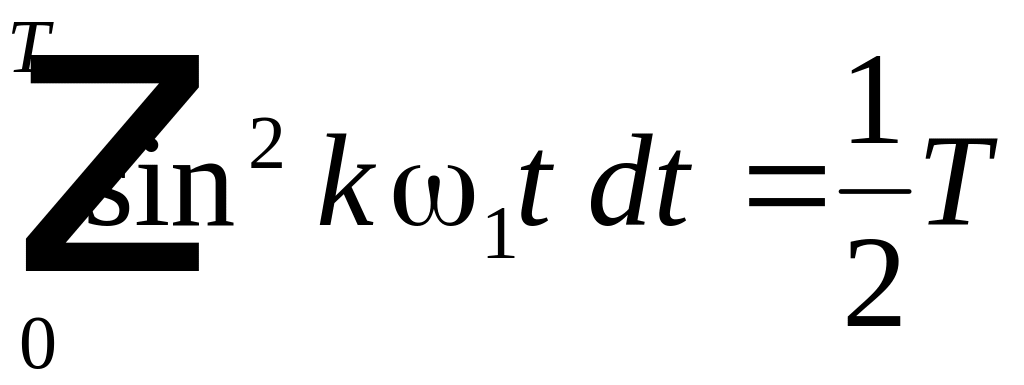
имеют
значения, не равные 0. Все остальные
интегралы равны нулю Поэтому после
интегрирования получим
,
где
. (4.11)
;
;
. (4.12)
Величины
,
,
,
,
… называют действующими значениями
тока. Аналогично вычисляются и
действующие значения напряжения. Если
сопротивление
Ом, то мощность равна
. (4.13)
Последнее
выражение справедливо для любой
периодической функции, т.е.
. (4.14)
В
таком виде последнее соотношение носит
название равенства Парсеваля.
4.1.3. Среднеквадратическая погрешность аппроксимации
Представим
приближенно функцию
разложением в усеченный ряд по
ортонормированным базисным функциям
(см. п. 2.1)
(4.15)
и
определим коэффициенты
так, чтобы минимизировать среднеквадратическую
погрешность:
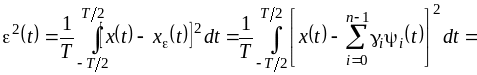
.
С
учетом (2.4) можно записать
. (4.16)
Погрешность
принимает минимальное значение, если
,
т.е. если коэффициенты разложения в
усеченном представлении (4.15) являются
коэффициентами обобщенного ряда Фурье.
Исходя из (4.16) можно записать
или
. (4.17)
Неравенство
(4.17) называют неравенством Бесселя.
С ростом
величина среднеквадратической погрешности
уменьшается. Если при
среднеквадратическая погрешность
стремится к нулю, то систему базисных
функций
называют полной. Эта система функций
является также замкнутой, т.к. для
любой функции
неравенство (4.17) переходит при
в равенство.
Точность
аппроксимации периодических сигналов
зависит от числа членов ряда при конечном
числе членов ряда. Относительную
среднеквадратическую погрешность
аппроксимации периодической функции
конечным числом членов ряда Фурье можно
определить по формуле :
. (4.18)
где
— средняя мощность сигнала;
— средняя мощность
-й
ортогональной составляющей сигнала.
Экспериментальное
значение погрешности аппроксимации
может быть найдено следующим образом.
Пусть имеется
экспериментально полученных точек
сигнала. Известен также теоретический
вид зависимости. Тогда погрешность
аппроксимации может быть вычислена
следующим образом
, (4.19)
где
— теоретическое значение отсчета сигнала
в момент времени
.
Соседние файлы в предмете [НЕСОРТИРОВАННОЕ]
- #
- #
- #
- #
- #
- #
- #
- #
- #
- #
- #
Остаточный член ряда Фурье. Погрешности приближения функций. Численное дифференцирование
Страницы работы
Содержание работы
12.Остаточный член ряда Фурье.
Для функции f(x) Î L2[a,b]
обобщенный ряд Фурье сходится к ней в среднеквадратичном смысле и методическая
погрешность аппроксимации может быть определена выражением (1.48)
Представим
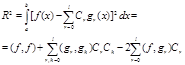 |
Имея ввиду, что функции gr(x), rÎ[0,l] ортогональны, а коэфиценты Фурье вычисляются по
соотношению (1.51) получим
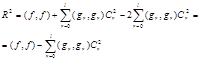 |
oткуда
(1.54)
а если gr(x), rÎ[0,l] ортонормированные, то
(1.55)
Если на приближаемую функцию
наложить дополнительные ограничения, то обобщенный ряд Фурье может сходиться к ней
и в равномерном смысле. Например, необходимым и достаточным условием
равномерной сходимости обобщенного ряда Фурье по полиномам Лежандра или
Чебышева к f(x) на [a,b]. Независимо от типа сходимости, иногда оказывается
необходимо оценить погрешность аппроксимации на [a,b] в
виде максимального отклонения ряда Фурье от приближаемой f(x), что
можно осущесвить дав оценку остаточного члена ряда Фурье
(1.56)
Однако в общнм случае
аппроксимации таких оценок не существует. В частности, же, например, для (l+1) раз
дифферинцируемых функций f(x), xÎ[a,b]
(1.57)
где a(x) –
значение частичной суммы ряда Фурье на [a,b].Если
более конкретизировать
задачу аппроксимации, положив
в качестве базисных функций ряда Фурье полиномы Чебышева, то
(1.58)
Оценка остаточного члена ряда
Фурье для непрерывной, преиодической, периода 2p функции f(x)
(1.59)
где K – некоторая
константа, определение которой, вообще говоря, проблематично, l
— максимальное значение скорости изменения f(x) на
интервале аппроксимации. Оценки (1.57) ¸(1.59) являются
неконструктивными, поскольку содержат в себе параметры, определение которых
практически невозможны или вызывают существенные трудности. Представляется
целесообразным в случае неоходимости оценку остаточного члена (1.56) давать по
некоторой модели аппроксимируемой функции, которая принадлежит к тому же
классу, что и f(x), но в то же время является наиболее неблагоприятной в
отношении точности аппроксимации. Учитывая наиболее вероятную с практической
точки зрения априорную информацию об аппроксимируемой функции, за такую модель
может быть принята функция вида
(1.60)
где fmin и
fmax – минимальное и максимальное значение f(x) на [a,b], WМ –
максимальное значение круговой частоты спектра аппроксимируемой функции, если
таковая информация может быть получена, или
WМ = VМ / AМ
где VМ – максимальная скорость изменения f(x) на [a,b]. При
аппроксимации модели (1.60) обобщенными рядами Фурье по полиномам Лежандра и
Чебышева первого рода были получены экспериментальные номограммы
которые позволили дать оценки остаточных членов в
следующем аналитическом виде
(1.61)
где K≈0,212(5,3125 + l) для полиномов
Лежандра и Kl =4
для полиномов Чебышевва. Следует отметить, что модельная оценка (1.61)
совпадает с оценкой (1.58), если модели положить AМ = 1,
a
имея в виду, что
13.Погрншности приближения функций.
Результирующая погрешноси
приближения функции f(x), xÎ[a,b] в виде некоторой F(x), xÎ[a,b]
вобщем случае складывается составляющих .
1. Методическая погрешность
используемого способа приближения, возникающая из-за отбрасывания остаточного
члена при опрнделении F(x). Данная погрешность уменьшается с увеличением числа
слагаемых в F(x), и в ряде случаев её удаётся оценить.
2. Погрешность приближенных
вычислений ЭВМ, которые, в свою очередь, можно подразделить на две группы:
Методическая погрешность,
возникающая в результате использования численных методовпри реализации
алгоритмов вычислений требуемых параметров. Данная погрешность имеет место,
например, при исппользовании квадратурных формул численного интегрирования для
определения коэфициентов Фурье. Эта погрешность может быть уменьшена за счет
использования более точного вычислительного алгоритма и оценена в виде
методической погрешности данного алгоритма.
Вычислительная погрешность,
порождаемая конечностью разрядной сетки памяти ЭВМ и зависящая (при выбранном
алгоритме) от возможностей используемой вычислительной техники.
3. Погрешность от неточного
задания исходных данных, которая носит случайный характер и может быть оценена
вероятностными характеристиками. На пример, при аппроксимации некоторой
функции f*(x)=f(x)+ sf(x), где
sf(x) –
погрешности, искажающие истинную f(x) и
характеризуемые математическим ожиданием М{sf(x)}=0
и дисперсией D{sf(x)}=s2, увеличение числа учитываемых членов ряда Фурье
приводит к тому, что математическое ожидание случайной погрешности определения
коэффициентов Фурье остаётся нулевым, а вот дисперсия возрастает.
Анализируя поведение
приведённых погрешностей в зависимости от числа слагаемых в приближающей F(x),
можно сделать вывод, что увеличение количества учитываемых членов в F(x)
приводит к тому, чтометодическая погрешность приближения уменьшается, в то
время как все остальные, связанные, как правило, свычислением коэфициентов
приближающей функции, возрастает. Таким образом, существует некое оптимальное
значение числа учитываемых членов функции F(x),
превышение которого приведёт к увеличению результирующей погрешности, поскольку
скорость нарастания вычислительной погрешности становится больше, чем скорость
уменьшения методической.
Похожие материалы
- Аппроксимация кубическим сплайном (моделирование сплайн-интерполяции)
- Вычисление корней многочлена p(x) = x6 + 5×5 – 7×4 + 3×3 – 6×2 + x +12 различными методами. Решение обыкновенных дифференциальных уравнений
- Использование методов вычислительной математики для решения задач с использованием доступных средств компьютерной поддержки
Информация о работе
Тип:
Ответы на экзаменационные билеты
Уважаемый посетитель!
Чтобы распечатать файл, скачайте его (в формате Word).
Ссылка на скачивание — внизу страницы.
From Wikipedia, the free encyclopedia
In statistics, the mean squared error (MSE)[1] or mean squared deviation (MSD) of an estimator (of a procedure for estimating an unobserved quantity) measures the average of the squares of the errors—that is, the average squared difference between the estimated values and the actual value. MSE is a risk function, corresponding to the expected value of the squared error loss.[2] The fact that MSE is almost always strictly positive (and not zero) is because of randomness or because the estimator does not account for information that could produce a more accurate estimate.[3] In machine learning, specifically empirical risk minimization, MSE may refer to the empirical risk (the average loss on an observed data set), as an estimate of the true MSE (the true risk: the average loss on the actual population distribution).
The MSE is a measure of the quality of an estimator. As it is derived from the square of Euclidean distance, it is always a positive value that decreases as the error approaches zero.
The MSE is the second moment (about the origin) of the error, and thus incorporates both the variance of the estimator (how widely spread the estimates are from one data sample to another) and its bias (how far off the average estimated value is from the true value).[citation needed] For an unbiased estimator, the MSE is the variance of the estimator. Like the variance, MSE has the same units of measurement as the square of the quantity being estimated. In an analogy to standard deviation, taking the square root of MSE yields the root-mean-square error or root-mean-square deviation (RMSE or RMSD), which has the same units as the quantity being estimated; for an unbiased estimator, the RMSE is the square root of the variance, known as the standard error.
Definition and basic properties[edit]
The MSE either assesses the quality of a predictor (i.e., a function mapping arbitrary inputs to a sample of values of some random variable), or of an estimator (i.e., a mathematical function mapping a sample of data to an estimate of a parameter of the population from which the data is sampled). The definition of an MSE differs according to whether one is describing a predictor or an estimator.
Predictor[edit]
If a vector of 



In other words, the MSE is the mean 

In matrix notation,
where 



The MSE can also be computed on q data points that were not used in estimating the model, either because they were held back for this purpose, or because these data have been newly obtained. Within this process, known as statistical learning, the MSE is often called the test MSE,[4] and is computed as
Estimator[edit]
The MSE of an estimator 

This definition depends on the unknown parameter, but the MSE is a priori a property of an estimator. The MSE could be a function of unknown parameters, in which case any estimator of the MSE based on estimates of these parameters would be a function of the data (and thus a random variable). If the estimator 
The MSE can be written as the sum of the variance of the estimator and the squared bias of the estimator, providing a useful way to calculate the MSE and implying that in the case of unbiased estimators, the MSE and variance are equivalent.[5]
Proof of variance and bias relationship[edit]
An even shorter proof can be achieved using the well-known formula that for a random variable 



But in real modeling case, MSE could be described as the addition of model variance, model bias, and irreducible uncertainty (see Bias–variance tradeoff). According to the relationship, the MSE of the estimators could be simply used for the efficiency comparison, which includes the information of estimator variance and bias. This is called MSE criterion.
In regression[edit]
In regression analysis, plotting is a more natural way to view the overall trend of the whole data. The mean of the distance from each point to the predicted regression model can be calculated, and shown as the mean squared error. The squaring is critical to reduce the complexity with negative signs. To minimize MSE, the model could be more accurate, which would mean the model is closer to actual data. One example of a linear regression using this method is the least squares method—which evaluates appropriateness of linear regression model to model bivariate dataset,[6] but whose limitation is related to known distribution of the data.
The term mean squared error is sometimes used to refer to the unbiased estimate of error variance: the residual sum of squares divided by the number of degrees of freedom. This definition for a known, computed quantity differs from the above definition for the computed MSE of a predictor, in that a different denominator is used. The denominator is the sample size reduced by the number of model parameters estimated from the same data, (n−p) for p regressors or (n−p−1) if an intercept is used (see errors and residuals in statistics for more details).[7] Although the MSE (as defined in this article) is not an unbiased estimator of the error variance, it is consistent, given the consistency of the predictor.
In regression analysis, «mean squared error», often referred to as mean squared prediction error or «out-of-sample mean squared error», can also refer to the mean value of the squared deviations of the predictions from the true values, over an out-of-sample test space, generated by a model estimated over a particular sample space. This also is a known, computed quantity, and it varies by sample and by out-of-sample test space.
Examples[edit]
Mean[edit]
Suppose we have a random sample of size 




which has an expected value equal to the true mean 
where 
For a Gaussian distribution, this is the best unbiased estimator (i.e., one with the lowest MSE among all unbiased estimators), but not, say, for a uniform distribution.
Variance[edit]
The usual estimator for the variance is the corrected sample variance:
This is unbiased (its expected value is 
where 

However, one can use other estimators for 

then we calculate:
This is minimized when
For a Gaussian distribution, where 



Further, while the corrected sample variance is the best unbiased estimator (minimum mean squared error among unbiased estimators) of variance for Gaussian distributions, if the distribution is not Gaussian, then even among unbiased estimators, the best unbiased estimator of the variance may not be 
Gaussian distribution[edit]
The following table gives several estimators of the true parameters of the population, μ and σ2, for the Gaussian case.[9]
| True value | Estimator | Mean squared error |
|---|---|---|
 |
 = the unbiased estimator of the population mean, = the unbiased estimator of the population mean,  |

|
 |
 = the unbiased estimator of the population variance, = the unbiased estimator of the population variance,  |

|
 |
 = the biased estimator of the population variance, = the biased estimator of the population variance,  |

|
 |
 = the biased estimator of the population variance, = the biased estimator of the population variance,  |

|
Interpretation[edit]
An MSE of zero, meaning that the estimator 

Values of MSE may be used for comparative purposes. Two or more statistical models may be compared using their MSEs—as a measure of how well they explain a given set of observations: An unbiased estimator (estimated from a statistical model) with the smallest variance among all unbiased estimators is the best unbiased estimator or MVUE (Minimum-Variance Unbiased Estimator).
Both analysis of variance and linear regression techniques estimate the MSE as part of the analysis and use the estimated MSE to determine the statistical significance of the factors or predictors under study. The goal of experimental design is to construct experiments in such a way that when the observations are analyzed, the MSE is close to zero relative to the magnitude of at least one of the estimated treatment effects.
In one-way analysis of variance, MSE can be calculated by the division of the sum of squared errors and the degree of freedom. Also, the f-value is the ratio of the mean squared treatment and the MSE.
MSE is also used in several stepwise regression techniques as part of the determination as to how many predictors from a candidate set to include in a model for a given set of observations.
Applications[edit]
- Minimizing MSE is a key criterion in selecting estimators: see minimum mean-square error. Among unbiased estimators, minimizing the MSE is equivalent to minimizing the variance, and the estimator that does this is the minimum variance unbiased estimator. However, a biased estimator may have lower MSE; see estimator bias.
- In statistical modelling the MSE can represent the difference between the actual observations and the observation values predicted by the model. In this context, it is used to determine the extent to which the model fits the data as well as whether removing some explanatory variables is possible without significantly harming the model’s predictive ability.
- In forecasting and prediction, the Brier score is a measure of forecast skill based on MSE.
Loss function[edit]
Squared error loss is one of the most widely used loss functions in statistics[citation needed], though its widespread use stems more from mathematical convenience than considerations of actual loss in applications. Carl Friedrich Gauss, who introduced the use of mean squared error, was aware of its arbitrariness and was in agreement with objections to it on these grounds.[3] The mathematical benefits of mean squared error are particularly evident in its use at analyzing the performance of linear regression, as it allows one to partition the variation in a dataset into variation explained by the model and variation explained by randomness.
Criticism[edit]
The use of mean squared error without question has been criticized by the decision theorist James Berger. Mean squared error is the negative of the expected value of one specific utility function, the quadratic utility function, which may not be the appropriate utility function to use under a given set of circumstances. There are, however, some scenarios where mean squared error can serve as a good approximation to a loss function occurring naturally in an application.[10]
Like variance, mean squared error has the disadvantage of heavily weighting outliers.[11] This is a result of the squaring of each term, which effectively weights large errors more heavily than small ones. This property, undesirable in many applications, has led researchers to use alternatives such as the mean absolute error, or those based on the median.
See also[edit]
- Bias–variance tradeoff
- Hodges’ estimator
- James–Stein estimator
- Mean percentage error
- Mean square quantization error
- Mean square weighted deviation
- Mean squared displacement
- Mean squared prediction error
- Minimum mean square error
- Minimum mean squared error estimator
- Overfitting
- Peak signal-to-noise ratio
Notes[edit]
- ^ This can be proved by Jensen’s inequality as follows. The fourth central moment is an upper bound for the square of variance, so that the least value for their ratio is one, therefore, the least value for the excess kurtosis is −2, achieved, for instance, by a Bernoulli with p=1/2.
References[edit]
- ^ a b «Mean Squared Error (MSE)». www.probabilitycourse.com. Retrieved 2020-09-12.
- ^ Bickel, Peter J.; Doksum, Kjell A. (2015). Mathematical Statistics: Basic Ideas and Selected Topics. Vol. I (Second ed.). p. 20.
If we use quadratic loss, our risk function is called the mean squared error (MSE) …
- ^ a b Lehmann, E. L.; Casella, George (1998). Theory of Point Estimation (2nd ed.). New York: Springer. ISBN 978-0-387-98502-2. MR 1639875.
- ^ Gareth, James; Witten, Daniela; Hastie, Trevor; Tibshirani, Rob (2021). An Introduction to Statistical Learning: with Applications in R. Springer. ISBN 978-1071614174.
- ^ Wackerly, Dennis; Mendenhall, William; Scheaffer, Richard L. (2008). Mathematical Statistics with Applications (7 ed.). Belmont, CA, USA: Thomson Higher Education. ISBN 978-0-495-38508-0.
- ^ A modern introduction to probability and statistics : understanding why and how. Dekking, Michel, 1946-. London: Springer. 2005. ISBN 978-1-85233-896-1. OCLC 262680588.
{{cite book}}: CS1 maint: others (link) - ^ Steel, R.G.D, and Torrie, J. H., Principles and Procedures of Statistics with Special Reference to the Biological Sciences., McGraw Hill, 1960, page 288.
- ^ Mood, A.; Graybill, F.; Boes, D. (1974). Introduction to the Theory of Statistics (3rd ed.). McGraw-Hill. p. 229.
- ^ DeGroot, Morris H. (1980). Probability and Statistics (2nd ed.). Addison-Wesley.
- ^ Berger, James O. (1985). «2.4.2 Certain Standard Loss Functions». Statistical Decision Theory and Bayesian Analysis (2nd ed.). New York: Springer-Verlag. p. 60. ISBN 978-0-387-96098-2. MR 0804611.
- ^ Bermejo, Sergio; Cabestany, Joan (2001). «Oriented principal component analysis for large margin classifiers». Neural Networks. 14 (10): 1447–1461. doi:10.1016/S0893-6080(01)00106-X. PMID 11771723.








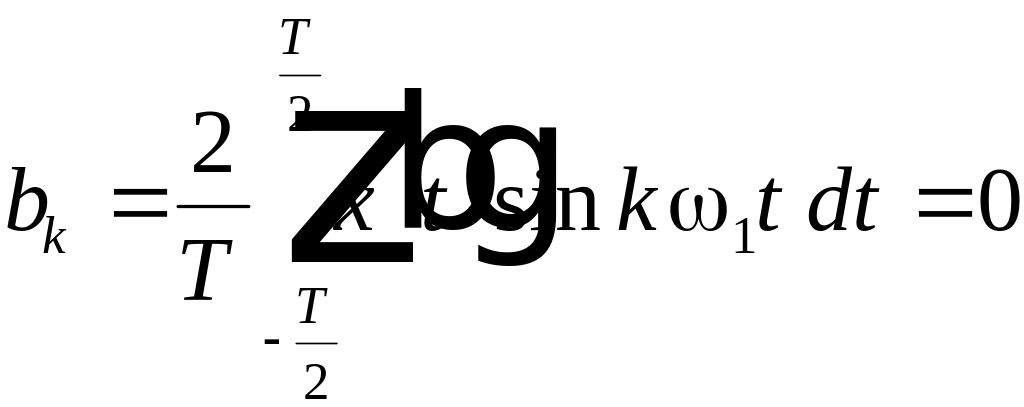
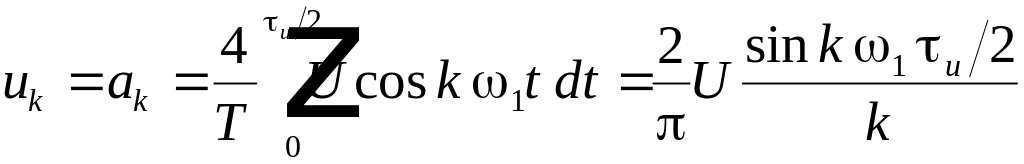
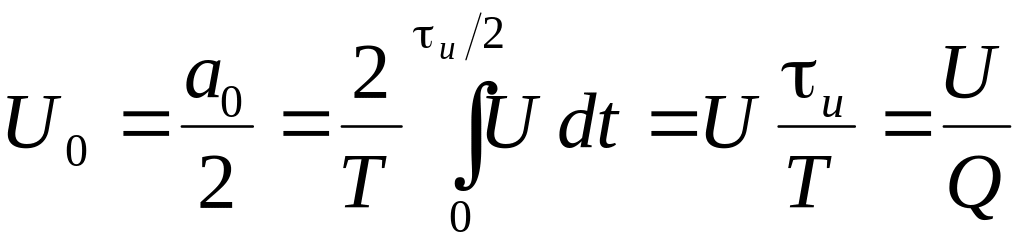
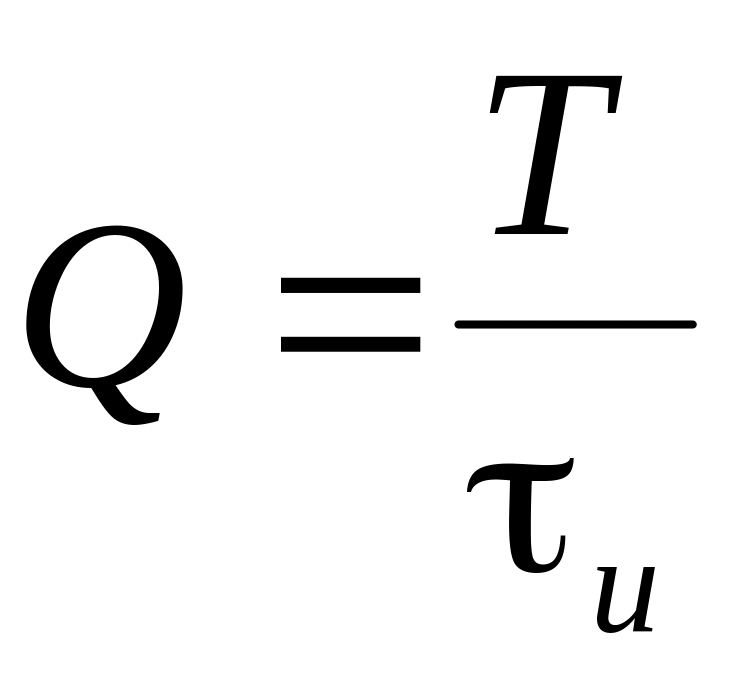
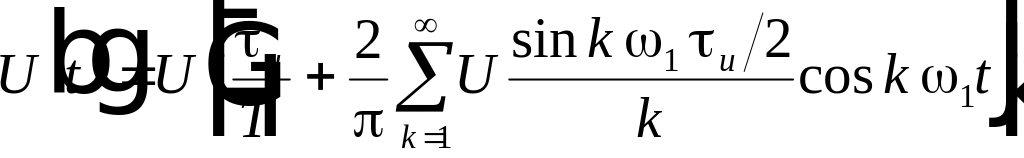
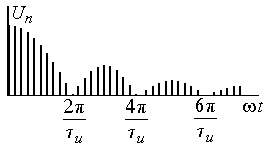
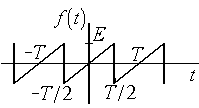
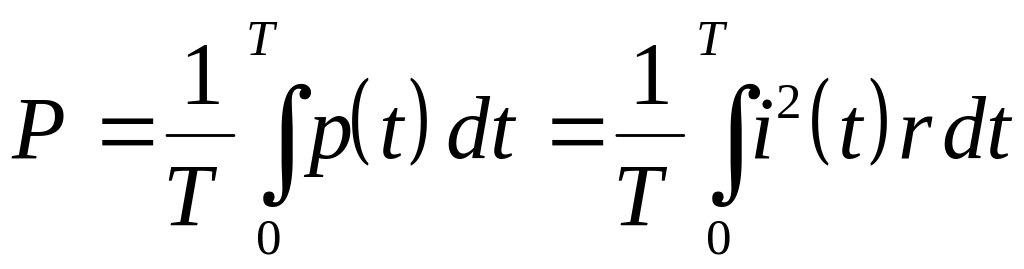
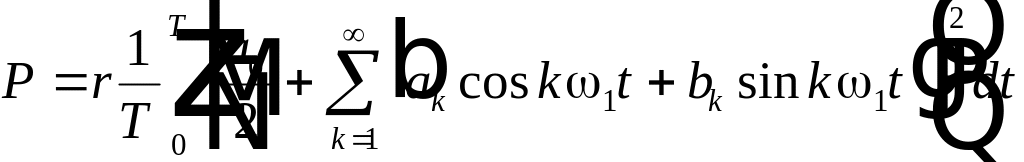
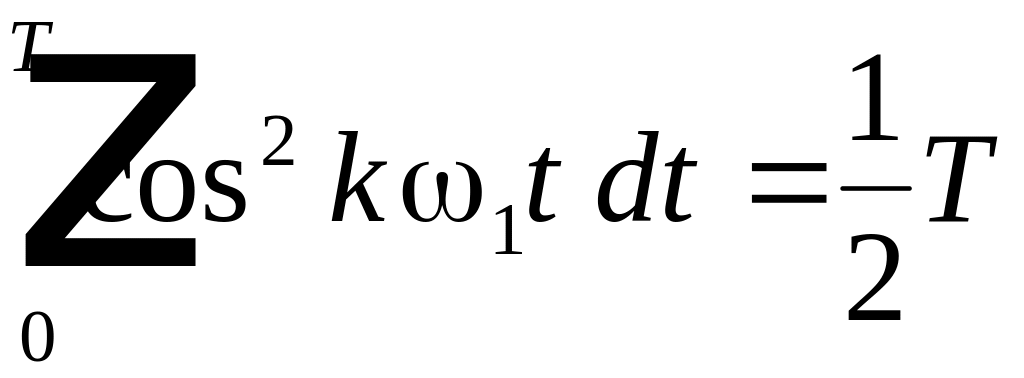
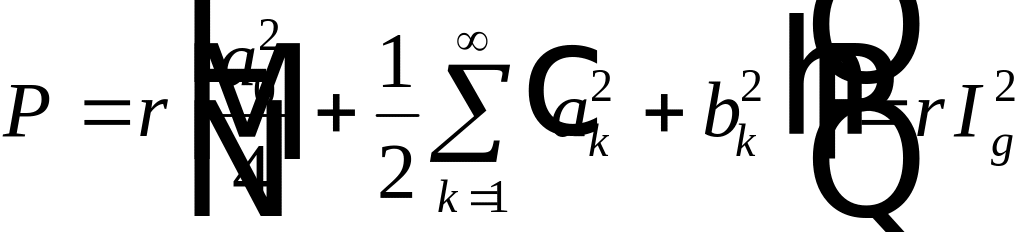
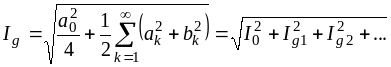

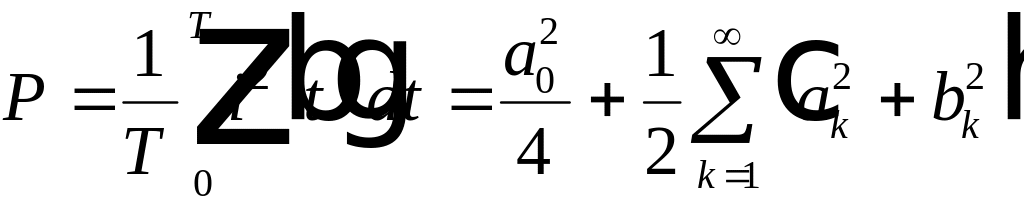
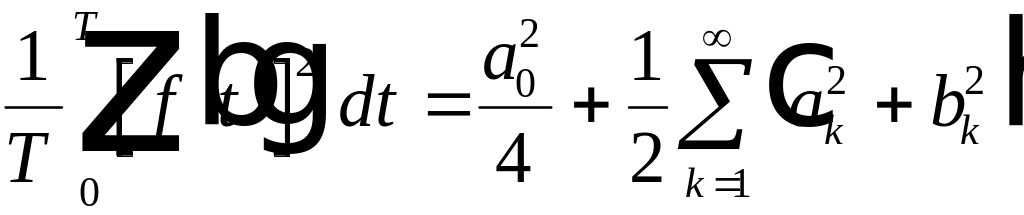
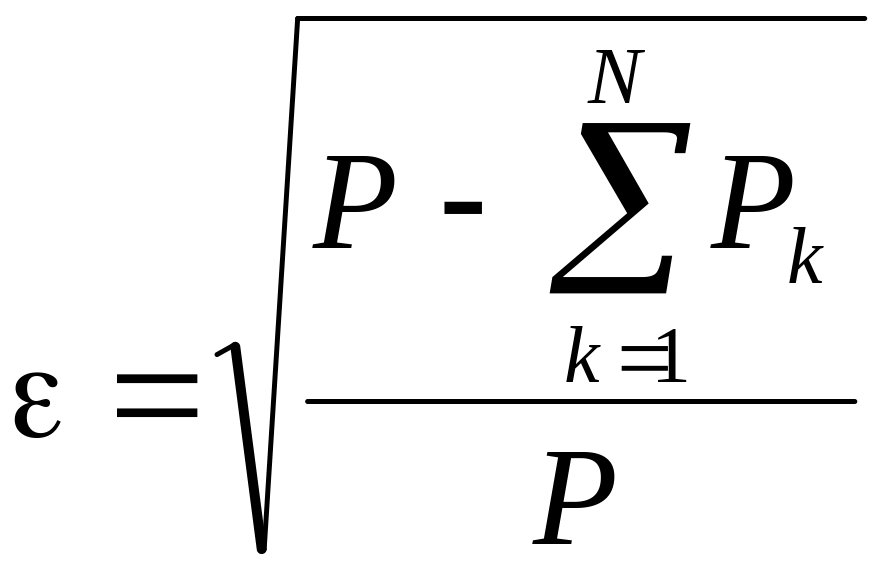
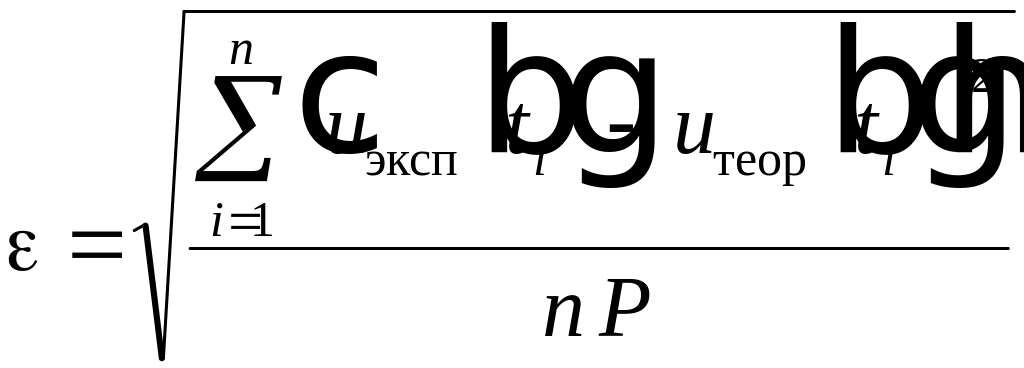



![{displaystyle operatorname {MSE} ({hat {theta }})=operatorname {E} _{theta }left[({hat {theta }}-theta )^{2}right].}](https://wikimedia.org/api/rest_v1/media/math/render/svg/9a0e1b3bac58f9ba2d2f4ff8b85b2e35a8f4bf78)

![{displaystyle {begin{aligned}operatorname {MSE} ({hat {theta }})&=operatorname {E} _{theta }left[({hat {theta }}-theta )^{2}right]\&=operatorname {E} _{theta }left[left({hat {theta }}-operatorname {E} _{theta }[{hat {theta }}]+operatorname {E} _{theta }[{hat {theta }}]-theta right)^{2}right]\&=operatorname {E} _{theta }left[left({hat {theta }}-operatorname {E} _{theta }[{hat {theta }}]right)^{2}+2left({hat {theta }}-operatorname {E} _{theta }[{hat {theta }}]right)left(operatorname {E} _{theta }[{hat {theta }}]-theta right)+left(operatorname {E} _{theta }[{hat {theta }}]-theta right)^{2}right]\&=operatorname {E} _{theta }left[left({hat {theta }}-operatorname {E} _{theta }[{hat {theta }}]right)^{2}right]+operatorname {E} _{theta }left[2left({hat {theta }}-operatorname {E} _{theta }[{hat {theta }}]right)left(operatorname {E} _{theta }[{hat {theta }}]-theta right)right]+operatorname {E} _{theta }left[left(operatorname {E} _{theta }[{hat {theta }}]-theta right)^{2}right]\&=operatorname {E} _{theta }left[left({hat {theta }}-operatorname {E} _{theta }[{hat {theta }}]right)^{2}right]+2left(operatorname {E} _{theta }[{hat {theta }}]-theta right)operatorname {E} _{theta }left[{hat {theta }}-operatorname {E} _{theta }[{hat {theta }}]right]+left(operatorname {E} _{theta }[{hat {theta }}]-theta right)^{2}&&operatorname {E} _{theta }[{hat {theta }}]-theta ={text{const.}}\&=operatorname {E} _{theta }left[left({hat {theta }}-operatorname {E} _{theta }[{hat {theta }}]right)^{2}right]+2left(operatorname {E} _{theta }[{hat {theta }}]-theta right)left(operatorname {E} _{theta }[{hat {theta }}]-operatorname {E} _{theta }[{hat {theta }}]right)+left(operatorname {E} _{theta }[{hat {theta }}]-theta right)^{2}&&operatorname {E} _{theta }[{hat {theta }}]={text{const.}}\&=operatorname {E} _{theta }left[left({hat {theta }}-operatorname {E} _{theta }[{hat {theta }}]right)^{2}right]+left(operatorname {E} _{theta }[{hat {theta }}]-theta right)^{2}\&=operatorname {Var} _{theta }({hat {theta }})+operatorname {Bias} _{theta }({hat {theta }},theta )^{2}end{aligned}}}](https://wikimedia.org/api/rest_v1/media/math/render/svg/2ac524a751828f971013e1297a33ca1cc4c38cd6)
![{displaystyle {begin{aligned}operatorname {MSE} ({hat {theta }})&=mathbb {E} [({hat {theta }}-theta )^{2}]\&=operatorname {Var} ({hat {theta }}-theta )+(mathbb {E} [{hat {theta }}-theta ])^{2}\&=operatorname {Var} ({hat {theta }})+operatorname {Bias} ^{2}({hat {theta }})end{aligned}}}](https://wikimedia.org/api/rest_v1/media/math/render/svg/864646cf4426e2b62a3caf9460382eec1a77fe4e)

![{displaystyle operatorname {MSE} left({overline {X}}right)=operatorname {E} left[left({overline {X}}-mu right)^{2}right]=left({frac {sigma }{sqrt {n}}}right)^{2}={frac {sigma ^{2}}{n}}}](https://wikimedia.org/api/rest_v1/media/math/render/svg/b4647a2cc4c8f9a4c90b628faad2dcf80c4aae84)



![{displaystyle {begin{aligned}operatorname {MSE} (S_{a}^{2})&=operatorname {E} left[left({frac {n-1}{a}}S_{n-1}^{2}-sigma ^{2}right)^{2}right]\&=operatorname {E} left[{frac {(n-1)^{2}}{a^{2}}}S_{n-1}^{4}-2left({frac {n-1}{a}}S_{n-1}^{2}right)sigma ^{2}+sigma ^{4}right]\&={frac {(n-1)^{2}}{a^{2}}}operatorname {E} left[S_{n-1}^{4}right]-2left({frac {n-1}{a}}right)operatorname {E} left[S_{n-1}^{2}right]sigma ^{2}+sigma ^{4}\&={frac {(n-1)^{2}}{a^{2}}}operatorname {E} left[S_{n-1}^{4}right]-2left({frac {n-1}{a}}right)sigma ^{4}+sigma ^{4}&&operatorname {E} left[S_{n-1}^{2}right]=sigma ^{2}\&={frac {(n-1)^{2}}{a^{2}}}left({frac {gamma _{2}}{n}}+{frac {n+1}{n-1}}right)sigma ^{4}-2left({frac {n-1}{a}}right)sigma ^{4}+sigma ^{4}&&operatorname {E} left[S_{n-1}^{4}right]=operatorname {MSE} (S_{n-1}^{2})+sigma ^{4}\&={frac {n-1}{na^{2}}}left((n-1)gamma _{2}+n^{2}+nright)sigma ^{4}-2left({frac {n-1}{a}}right)sigma ^{4}+sigma ^{4}end{aligned}}}](https://wikimedia.org/api/rest_v1/media/math/render/svg/cf22322412b8454c706d78671e5d94208675a6e0)
