Наверное, нет человека, который не использовал бы слово «логика». Умозаключения, кажущиеся нам правильными, мы называем «логичными». А если кто-то поступает странно, мы говорим, что в его действиях отсутствует логика. Но на самом деле, логика это не только разумный ход рассуждений. Это целая наука, изучающая, как из одних суждений следует истинность или ложность других. Сегодня мы поговорим о том, что она собой представляет, какие законы логики и формы логического мышления существуют, а также выясним, какие функции выполняет эта наука.
Что такое логика?
Логика – это наука о формах, приёмах и операциях мышления, позволяющих устанавливать или опровергать истинность определенных утверждений, исходя из заведомо известных фактов. Сложно сказать точно, когда она возникла. Отдельные элементы логики присутствуют в работах древнегреческих, древнекитайских и древнеиндийских мыслителей 6-5 веков до н. э., но первым её основные принципы сформулировал Аристотель в 4 веке до н. э.
Изначально она возникла как направление в философии, но со временем развилась в сложную систему знаний и стала самостоятельной научной дисциплиной – формальной логикой. От остальных наук, изучающих мышление, она отличается тем, что абстрагируется от содержания размышлений и высказываний, а изучает их структуру и внутренние закономерности.
Термин «логика» образован от греческого слова λόγος (логос – мысль, слово, причина). Сегодня у него есть два основных значения. Им может обозначаться как научная дисциплина, изучающая закономерности мыслительных процессов и логических построений, так и совокупность правил, которых необходимо придерживаться при построении непротиворечивых умозаключений.
Объект и предмет логики
Как и любая наука, логика имеет объект и предмет изучения. Объектом логики является мышление человека – отображение различных явлений и процессов в его мыслях, а также построение умозаключений на основе уже имеющихся знаний о внешнем мире. Здесь следует отметить, что мышление является объектом не только для логики, но и для большого количества других наук.
Предмет логики – это система закономерностей правильного мышления. По сути, логика изучает один аспект познавательного мышления – законы и принципы, ведущие к построению непротиворечивых умозаключений. А поскольку философия изучает все аспекты познания мира, логика является философской наукой.
Формы логического мышления
Форма мышления – это структура мысли, определяющая взаимосвязи между отдельными её элементами.
Существует три основных формы мышления:
- Понятие. Это мысль о конкретном объекте, явлении или свойстве. Это может быть кто-то одушевленный (другой человек), что-то материальное (автомобиль) или нематериальное (любовь).
- Суждение. Это цепочка взаимосвязанных понятий. К примеру, у нас есть понятие о том, что ответственность – это хорошо. И если мы думаем о том, что какой-то человек ответственный – это суждение, состоящее из двух понятий (человек + качество).
- Умозаключение. Это вывод, который делается на основе нескольких суждений и при этом содержит в себе новую информацию. К примеру, если мы знаем, что наш знакомый является ответственным человеком, мы можем сделать вывод, что ему можно доверять.
Какие бы мысли ни крутились сейчас в вашей головы, каждая из них относится к одной из этих трёх форм. Наш жизненный опыт включает знание миллионов разных понятий, которые мы мгновенно объединяем в суждения и делаем на их основе определённые умозаключения.
Законы логики
Существует 4 закона, знание которых позволяет лучше понять, что такое логика. Придерживаясь этих законов, можно гарантированно делать правильные и логичные умозаключения при условии наличия достаточного количества точно установленных фактов:
1. Закон тождества
Суть данного закона состоит в том, что суждение сохраняет своё предметное и смысловое значение в рамках одного контекста (например, в пределах одного логического рассуждения). Иными словами, недопустимо в процессе размышления подменять одно значение понятия или суждения другим, поскольку это приведёт к ложному выводу.
К примеру, утверждение «Выучить новый язык можно, общаясь с носителями на житейские темы» истинно в отношение английского или испанского языка, но слабо применимо к языкам программирования. Подобная подмена понятий является одним из грубых нарушений закона тождества. В данном примере она очевидна, но в некоторых случаях она используется как успешный демагогический приём.
2. Закон непротиворечия
Этот закон (называемый также «законом противоречия») гласит, что два высказывания, противоречащих друг другу, не могут быть истинными одновременно. Как минимум одно из них ложно. К примеру, если на столе лежит шар, полностью выкрашенный в один цвет, утверждения «Этот шар белый» и «Этот шар чёрный» не могут быть истинными одновременно. Но они оба вполне могут быть ложными, если шар, к примеру, красный.
Есть три основных типа логических противоречий:
- Контактные. Это два несовместимых логических высказывания, следующих друг за другом.
- Дистантные. Это взаимоисключающие высказывания, разделенные определенным интервалом.
- Мнимые. Это кажущиеся противоречия, которых на самом деле нет, если понимать контекст, в котором делается утверждение (например, «Это красная смородина. А жёлтая она, потому что ещё зелёная»).
Контактные противоречия обычно не пытаются скрыть. Их используют сознательно, чтобы смягчить негативное высказывание («Ты хорошо справился, но это не совсем то, о чём я просил») или, наоборот, усилить его («Отлично! Ты опять всё испортил!»). Дистантные противоречия могут применять демагоги, чтобы запутать собеседника, но чаще их используют по ошибке неопытные или плохо подготовившиеся ораторы.
3. Закон исключённого третьего
Если одно суждение отрицает другое, то одно из них является ложным, а второе – истинным. Здесь важно не путать, что подразумевается под отрицанием.
К примеру, утверждения «Этот шар белый» и «Этот шар чёрный» являются всего лишь взаимоисключающими. А отрицающими друг друга являются утверждения «Этот шар белый» и «Этот шар не белый» (одно из них обязательно является истинным, какого бы цвета ни был шар).
4. Закон достаточного основания
Этот закон ввёл Готфрид Лейбниц. Его суть состоит в том, что для того, чтобы считать утверждение истинным, необходимо располагать однозначными доказательствами, исключающими другие варианты. В повседневной жизни люди пренебрегают этим законом логики чаще, чем любым другим, делая однозначные выводы по косвенным фактам.
К примеру, если в середине лета вы несколько дней подряд не видели соседа, которого обычно встречаете ежедневно, можно предположить, что он уехал в отпуск. Скорее всего, так и есть, но всё же этот вывод противоречит закону достаточного основания, поскольку нельзя исключать, к примеру, болезнь или командировку.
Нарушение законов логики
Когда законы логики нарушаются, возникают логические ошибки. Существует три основных типа логических ошибок:
- паралогизмы – ошибки, возникающие в результате непреднамеренного нарушения законов логики;
- софизмы – логические ошибки, возникающие в результате намеренного нарушения законов логики;
- парадоксы – ошибки, возникающие не из-за нарушения законов логики, а из-за неясности некоторых принципов.
Софизмы – это основной инструмент в софистике. Они используются для того, чтобы запутать собеседника, подвести его к неправильным выводам или заставить выглядеть глупо перед окружающими. Парадоксы могут возникать, в частности, когда смешиваются количественные и качественные характеристики предметов и явлений либо присутствуют неявные условия. В таком случае рассуждение, выглядящее логически правильным, может приводить к выводам, противоречащим действительности или другому логически правильному рассуждению.
В качестве примера можно привести «Парадокс кучи». Его суть состоит в следующем: если из кучи гравия убрать 1 камешек, куча останется кучей, однако если продолжать этот процесс, то в какой-то момент куча перестанет существовать. Противоречие здесь в том, что убирание одного (любого!) камня не должно приводить к исчезновению кучи. И всё же она исчезает именно от того, что из неё убирают один камень. Причина этого парадокса в том, что не сформулирована взаимосвязь между количественными и качественными характеристиками кучи.
Другой пример логической ошибки – известная апория Зенона про Ахиллеса, который никогда не догонит черепаху. Условие парадокса специально формулируется так, чтобы исключить из рассмотрения точку пути, в которой атлет обгоняет черепаху. В результате доказательство того, что он не сможет этого сделать, не противоречит законам логики. Ошибка заложена в самой формулировке задачи, в которой неявно присутствует условие «На отрезке до точки X».
Виды логики
Объясняя, что такое логика, обычно говорят в первую очередь о формальной логике. При этом существует ещё два раздела, фактически являющихся самостоятельными дисциплинами: математическая (символическая) логика и диалектическая логика. Рассмотрим каждый из разделов подробнее.
1. Формальная логика
Формальная логика – это научная дисциплина, изучающая структуру и истинность утверждений. Её создателем считается Аристотель (4 век до н. э.), рассматривавший её как возможность оперировать формальными фактами, абстрагируясь от их природы и содержания. Это позволяет обеспечить логическую правильность суждений, поскольку анализу подвергается только структура утверждения, но не его содержание.
По сути, наше мышление подчиняется формальной логике. Основываясь на имеющихся фактах, мы делаем логические выводы и принимаем решения. Однако мы не можем полностью абстрагироваться от природы и содержания суждений, кроме того, эмоции могут оказывать очень сильное влияние на наши выводы и действия. Поэтому людям свойственны нелогичные поступки.
2. Математическая логика
Изначально это была часть формальной логики, но в 19 веке она выделилась в самостоятельный раздел (при этом в ней по-прежнему соблюдаются все принципы формальной логики). Она пополнилась новыми математическими методами и специализированными нотациями. Благодаря этому символическая логика превратилась в мощный инструмент, применяемый современными науками при решении задач и доказательстве теорий.
Данная модель делает процесс познания более точным, поскольку в ней слова естественных языков с размытым смыслом заменяются формальными определениями, исключающими двусмысленность и размытость суждений. Все суждения математической логики формулируются на точном языке, не допускающем неоднозначных трактовок. Для таких языков чётко определена семантика (значения терминов) и синтаксис (совокупность формул или правил построения объектов языка).
3. Диалектическая логика
Это философская дисциплина, изучающая мышление вообще. Её основателем считается немецкий философ Георг Гегель (1770-1831). Она основывается на формальной логике, и всё же в ней учитывается содержание явлений, объектов и процессов. В ней используются такие принципы как:
- принцип объективности;
- принцип всесторонности;
- принцип историзма (выявление закономерностей в истории рассматриваемого объекта);
- принцип конкретности (принятие в расчёт особенностей конкретного объекта и условий его существований).
Зачем нужна логика?
Главная цель логики заключается в том, чтобы обеспечить эффективный инструментарий для поиска решений и доказательств, применимый в любых сферах знаний. Благодаря логике мы можем оперировать фактами, достоверность которых установлена и доказана. Логика необходима при решении таких задач как:
- Познание. В любой науке все накопленные знания взаимосвязаны между собой логическими связями. Часть этих знаний получена эмпирически, а часть – благодаря теоретическому анализу с использованием логики.
- Разрешение спорных ситуаций. В любой сфере жизни могут возникать спорные ситуации, в которых сталкиваются противоположные точки зрения. И найти истину помогает логический анализ. К примеру, судебное разбирательство строится на применении формальной логики для поиска истины и определения степени правоты каждой из сторон.
- Продуктивное общение. Общаясь с кем-то, мы стараемся излагать свои мыли логично, чтобы быть понятыми однозначно. При этом мы рассчитываем, что наш собеседник руководствуется теми же правилами логического мышления, что и мы.
- Поиск ответов. В любой сфере знаний при поиске ответов, решений и доказательств используются правила формальной или математической логики.
Заключение
Логика – это наука о правильном мышлении и о способах рассуждения, не ведущих к ошибочным выводам. Это одна из важнейших научных дисциплин, ведь её принципами и законами пользуются все существующие науки. И даже если мы этого не замечаем, вся наша жизнь подчинена логике. Мы используем её в быту и общении, она заложена в законах, которые мы соблюдаем, без неё был бы невозможен научно-технический прогресс, достижениями которого мы пользуемся ежедневно.
Задача
логики состоит в том, чтобы научить
человека сознательно применять
законы и формы мышления и на основе
этого логичнее мыслить и, следовательно,
правильнее познавать окружающий
мир.
Знание
логики повышает культуру мышления,
вырабатывает навык мыслить более
«грамотно», развивает критическое
отношение к своим и чужим мыслям.
Поэтому мнение, будто изучение логики
не имеет практического значения,
несостоятельно.
Мыслить
логично — это значит мыслить точно и
последовательно, не допускать
противоречий в своих рассуждениях,
уметь вскрывать логические ошибки.
Эти качества мышления имеют большое
значение в любой области научной и
практической деятельности, в том числе
и в работе экономиста и менеджера, юриста
и психолога, требующей точности мышления,
обоснованности выводов.
Умение
логически мыслить, помогает избегать
ошибок в рассуждениях, а также найти
ошибку и исправить ее. Логически не
образованному человеку сделать это
довольно сложно, и поэтому, как правило,
он горазд упорствовать в своих ошибках.
Знакомство с множеством возможных
логических ошибок формирует чувство
опасности и ответственности в мышлении.
Поэтому человек приучается сначала
думать, продумывать мыслительный
материал, а затем говорить, имея в виду
возможность доказать сказанное. Для
него будет непозволительной роскошью
сначала говорить, а уже потом думать,
что же он сказал.
В
логике можно найти эффективные приемы
ведения спора, полемики и публичного
выступления. Она предлагает средства
убеждения, доказывания и межличностного
общения. Логика разрабатывает также
интеллектуальную основу ораторского
искусства.
Общественное
значение логики состоит в том, что она
исследует формы, разрабатывает методы
и приемы мышления, используемые всеми
другими науками. В качестве примеров
таких общенаучных методов познания
можно привести индукцию, дедукцию,
аналогию. В определенном смысле каждую
науку действительно можно считать
прикладной логикой потому, что каждая
из них пользуется логическими формами,
законами и методами мышления.
Значение
математической логики заключается
прежде всего в том, что она выступает
средством автоматизации мыслительного
процесса, создания искусственного
интеллекта.
Перечисленные
аспекты логики отражают ее полезность
в самых различных направлениях. Однако
при такой «всеобщей» полезности логики
ее значение для ряда наук и видов
практической деятельности особенно
существенно. В частности, это относится
к юриспруденции. Известно, что своими
успехами легендарный Шерлок Холмс
обязан способности логически мыслить
и мастерски пользоваться дедуктивным
методом. В сфере следственной, судебной,
адвокатской практики, где решаются
вопросы человеческих судеб, цена
логической ошибки особенно велика, и
она может оказаться роковой. Здесь
логическое знание является необходимым
компонентом профессиональной деятельности.
III. Предмет формальной логики
Предмет
логики составляют:
—
Законы, которым подчиняется мышление
в процессе познания объективного мира.
— Формы
мыслительного процесса — понятия,
суждения и умозаключения.
—
Методы получения нового выводного
знания — сходства, различия сопутствующих
изменений, остатков и другие.
—
Способы доказательства истинности
полученных знаний: прямое и косвенное
доказательство, опровержение и т.д.
Итак,
в современном понимании, логика
— это наука о законах и формах правильного
мышления.
Выше
уже упоминалось, что «логика» обозначает
формальную логику и логику диалектическую.
Формальная в свою очередь подразделяется
на традиционную и символическую, или
математическую.
Логика
изучает мышление. Она рассматривает
этот объект с точки зрения его функций
и структуры, т.е. роли и значения в
познании и практической деятельности,
и в то же время с точки зрения составляющих
его элементов, а также связей и отношений
между ними. Логика может быть кратко
определена как наука
о формах и законах правильного мышления,
ведущего к истине.
Основными
чертами мышления являются:
1.
Мышление возникает не само по себе,
зависит от реального мира — действительности
— и определяется ею.
2.
Мышление воспроизводит действительность
в виде мыслей о ней, которые определенным
образом связанны между собой и
взаимодействуют друг с другом.
3.
Мышление есть не прямое отражение, а
основанное на имеющихся знаниях. Это
отражение не отдельно взятого предмета
или явления, оно носит обобщенный
характер, охватывая сразу множество
предметов и явлений.
4.
Основой мышления является общественная
практика.
Мышление
обладает громадной активностью. Оно
служит средством ориентации человека
в окружающем мире, предпосылкой и
условием его существования. Возникая
на базе материально-производственной
деятельности людей, оно оказывает на
нее обратное воздействие, творит «вторую
природу». При этом мышление и само
стремительно развивается и разрастается.
Мышление
неразрывно связано с языком.
Какая бы мысль ни возникла в голове
человека, она может возникнуть и
существовать лишь в словах и предложениях.
При помощи языка люди выражают и
закрепляют результаты своей мыслительной
работы, обмениваясь мыслями, добиваются
взаимного понимания.
Язык
— это знаковая информационная система,
выполняющая функцию формирования,
хранения и передачи информации в процессе
познания действительности и общения
между людьми.
Основным
материалом при конструировании языка
выступают используемые в нем знаки.
Знак — это любой чувственно воспринимаемый
(зрительно, на слух или иным способом)
предмет, выступающий представителем
другого предмета. Среди различных знаков
выделяются два вида: знаки-образы и
знаки-символы.
Знаки-образы
имеют определенное сходство с обозначаемыми
предметами. Примеры таких знаков: копии
документов; дактилоскопические
отпечатки пальцев; фотоснимки; некоторые
дорожные знаки с изображением детей,
пешеходов и других объектов. Знаки-символы
не имеют сходства с обозначаемыми
предметами. Например: нотные знаки;
знаки азбуки Морзе; буквы в алфавитах
национальных языков.
Языки
делятся на естественные
и искусственные.
Естественным
является язык,
возникший исторически в процессе общения
членов определенной социальной группы.
Например, национальные языки. Искусственные
языки создаются
людьми для каких-либо специальных целей.
Например, язык математики, химии, азбука
Морзе и т.п.
Ранее
мы отмечали, что нас интересует формальная
логика. В её основе находятся простые
формы и законы.
Введем
понятие логической
формы.
Логическая
форма — это
структура мысли, способ связи ее
элементов. Поясним
это на примере такой логической формы
как суждение. Суждение
обозначает мысль, утверждающую или
отрицающую что-либо о чем-либо. Предмет
мысли называется субъектом
суждения и обозначается
буквой S.
То, что мы утверждаем о субъекте, его
признак, называется предикатом
и обозначается буквой Р.
Отношения между субъектом и предикатом
фиксируется словами-связками
«есть», «суть», «является» и т.п. Например:
«Все законы являются нормативными
актами». В так называемом стандартном
виде это суждение представляется
формулой: «Все S
суть Р». В ней
отчетливо выражено строение мысли,
способ связи ее элементов. Посредством
логических союзов можно строить более
сложные мысли, образуя более сложные
логические формы.
Основными
логическими формами являются понятие,
суждение, умозаключение, доказательство.
Мышление
проявляется в различных формах, но при
этом обнаруживает определенные
закономерности.
Логический
закон — внутренняя,
необходимая, существенная связь между
мыслями, рассматриваемая со стороны их
формы. Основные
формально-логические законы: закон
тождества, закон противоречия, закон
исключенного третьего и закон достаточного
основания.
Логика
правильное мышление, ведущее к истине.
Истинность
относится к содержанию
мыслей, а правильность
— к их форме.
Под
истиной подразумевается такое содержание
мысли, которое соответствует самой
действительности, что проверяется
практикой. Например, я читаю книгу и
говорю: «Сейчас я читаю книгу». Вы можете
сказать сейчас является ли это суждение
истинным или ложным.
Истинность
мышления —
свойство воспроизводить действительность
такой, какова она есть. Ложность
мышления —
свойство искажать содержание
действительности, извращать его.
Правильность
мышления —
способность мышления воспроизводить
в структуре мысли объективную структуру
действительности.
Неправильность мышления
— его способность искажать структурные
связи и отношения вещей. Таким
образом, категории правильности и
неправильности применимы к логическим
операциям с понятиями, суждениями, а
также к строению умозаключений и
доказательств.
Предметом
формальной логики как
науки являются
логические формы мышления.
Формальной она называются потому, что
основное внимание уделяет форме,
правильным способам рассуждений,
отвлекаясь от конкретного содержания
мыслей.
Наше
знание о мире существует в двух видах:
непосредственное
знание, которое мы
получаем из воздействия предметов на
наши органы чувств и выводное
знание, получаемое
в процессе рассуждения. Логика
устанавливает правила и законы, которым
должна соответствовать мысленная
деятельность.
Итак,
Логика — это теория рассуждений и их
элементов, которая отличает правильные
рассуждения от неправильных на основании
одной только их формы.
Литература:
1.
ГетмановаА.Д. Логика.
Учебник. Изд. «Омега-Л»,2009, стр.3-24
2.
Иванов Е.А. Логика. Учебник для студентов
юридических вузов и факультетов. М.:
Волтерс Клувер, 2007. — 416 – ISBN
5-466-00105-8 (в пер.). стр.1-38.
3.
Брушинкин В.Н. Логика. Электр. Книга. Гл.
1
Соседние файлы в предмете [НЕСОРТИРОВАННОЕ]
- #
- #
- #
- #
- #
- #
- #
- #
- #
- #
- #
Привет, Вы узнаете про логика, Разберем основные ее виды и особенности использования. Еще будет много подробных примеров и описаний. Для того чтобы лучше понимать что такое
логика, логика как наука, функции логики , настоятельно рекомендую прочитать все из категории Логика.
логика (др.-греч. λογική — это «наука о правильном мышлении», «способность к рассуждению» от др.-греч. λόγος — «логос», «рассуждение», «мысль», «разум», «смысл») — нормативная наука о законах логики и приемах интеллектуальной (мыслительной) познавательной деятельности
Поскольку новое знание получают посредством разума, логика также определяется как наука о формах и законах мышления. Так как мышление оформляется в языке в виде рассуждения, частными случаями которого являются доказательство и опровержение, логика иногда определяется как наука о способах рассуждения или наука о способах доказательств и опровержений. Поскольку мышление проявляется только в языке, то логика, исследуя законы мысли, обращается к языку как к единственному доступному ей материалу .
логика как наука изучает методы достижения истины в процессе познания опосредованным путем, не из чувственного опыта, а из знаний, полученных ранее, поэтому ее также можно определить как науку о способах получения выводного знания.
В любой науке логика служит одним из основных инструментов . Логика является подразделом не только философии, но и математики, а булева алгебра — одной из основ информатики .
Основными разделами логики являются теория рассуждений (имеющая 2 варианта: теорию дедуктивных рассуждений и теорию правдоподобных рассуждений), металогика и логическая методология .
В связи с тем, что результаты мыслительной деятельности выражаются в языковой форме, исследования в логике сопряжены с изучением языковых конструкций. Этим занимается логическая семиотика, которая включает в себя логическую синтактику, логическую семантику и логическую прагматику .
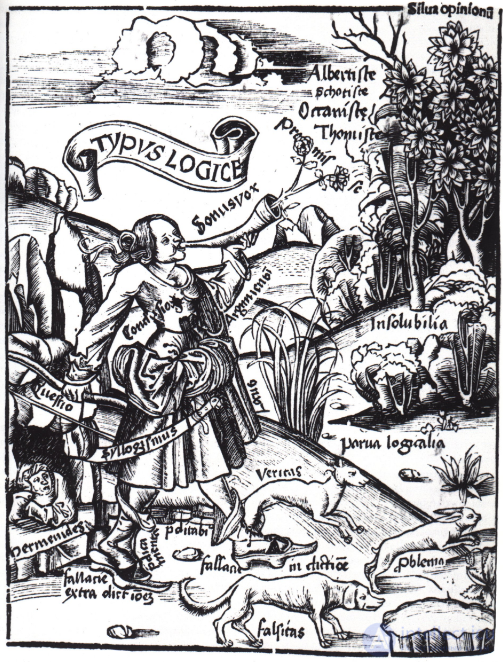
Грегор Рейш. «Логика представляет ее центральные темы», Margarita Philosophica, 1503/08 (?). Две собаки veritas (с лат. — «истина») и falsitas (с лат. — «ложь») преследуют зайца problema (с лат. — «проблема»), логика, вооруженная мечом силлогизма, спешит позади. Слева внизу в гроте изображен Парменид, с которым логическая аргументация проложила себе путь в философию.
Сущность логики
Классическая логическая теория далеко не совершенна: основное ее содержание формулируется на особом, созданном для своих целей языке, использует предметное мышление. В ней не предполагается использование контроля прагматических ошибок, погрешностей, нелинейностей используемых систем отсчета, пограничных ошибок описания, релятивизма масштабирования (относительность предметов и их пространственных характеристик, к примеру: человек велик относительно муравья, но в то же время мал относительно слона) и т. п. Вследствие чего принято считать нормальным факт наличия в ее языке парадоксов и априорных утверждений, кустовых эффектов словаря и т. п.
Подобно тому как умение говорить существовало еще до возникновения науки грамматики, так и искусство правильно мыслить существовало задолго до науки логики. Логические операции: определение, классификация, доказательство, опровержение и др. — нередко применяются каждым человеком в его мыслительной деятельности неосознанно и с погрешностями. Некоторые склонны считать собственное мышление естественным процессом, не требующим анализа и контроля больше, чем, скажем, дыхание или движение, но реальное мышление не сводится просто к логической последовательности. В процессе решения возникающих задач также существенны: интуиция, эмоции, образное видение мира и многое другое . Однако нестрогость мышления еще не значит, что оно не подчинено логике .
Основная цель (функция) логики всегда оставалась неизменной: исследование того, как из одних утверждений можно выводить другие. При этом предполагается, что вывод зависит только от способа связи входящих в него утверждений и их строения, а не от их конкретного содержания. Изучая, «что из чего следует», логика выявляет наиболее общие или, как говорят, формальные условия правильного мышления. Сфера конкретных интересов логики существенно менялась на протяжении ее истории.
Значение слова
Слово «логика» используется также в значениях «внутренняя закономерность, присущая тем или иным явлениям» или «правильный, разумный ход рассуждений» . В частности этим словом могут называться следующие вещи в:
- процессе мышления — когда говорится о логичном и нелогичном мышлении, где последовательность утверждений соответствует изученным в логике схемам, в отличие от полностью бессвязных и рассуждений по аналогии с произвольными понравившимися автору образами или стереотипами.
- электронике — вид схем, предназначенных для обработки информации и управления. В отличие от силовых схем трансформации и распределения энергии. И маломощных, но обрабатывающих атомарные сигналы — фильтрации, регистрации, генерации.
- произвольных явлениях — приписываемое или обнаруженное в них определенное функционирование, повторяющиеся процессы, которые могут быть описаны в логических категориях — состояние, подчинение, отражение, зависимость и т. п.
Неформальная, формальная, символическая и диалектическая логика
Неформальная логика (термин принят прежде всего в англоязычной литературе) — исследование аргументации в естественном языке. Одной из главных задач ее является исследование логических ошибок — см. Логическая семантика, философская логика, теория аргументации, логический анализ языка. Любой вывод, сделанный на естественном языке, обладает чисто формальным содержанием (смысл рассуждения может быть разделен на форму мысли и собственно содержание), если можно показать, что он является частным применением абстрактного универсального правила, которое отвлекается от всякого конкретного предмета, свойства или отношения. Именно этот вывод с чисто формальным содержанием называют логическим выводом и основным предметом логики. Анализ вывода, который раскрывает это чисто формальное содержание, называется формальной логикой.
Символическая логика изучает символические абстракции, которые фиксируют формальную структуру логического вывода.
Диалектическая логика — наука о мышлении в марксизме. Здесь понятие мышления употребляется в смысле Логоса как предмета античной философии, а диалектическая логика — уже в смысле отдельной науки, как физика или формальная логика. Диалектическое рассуждение учитывает законы формальной логики. Вместе с тем, осуществляя анализ динамики перехода понятий в свою противоположность, оно допускает, что противоположности совпадают, ориентируется на законы диалектики.
В рамках формальной логики имеется группа логик, именуемых неклассическими (иногда также используется термин «альтернативные логики»). Эта группа логик существенно отличается от классических логик путем различных вариаций законов и правил (например, логики, отменяющие закон исключенного третьего, меняющие таблицы истинности и т. д.). Благодаря этим вариациям возможно построение различных моделей логических следствий и логической истины .
Отношение к другим наукам
Исторически логика изучалась как часть философии и риторики. Сейчас символическая логика также изучается как часть математики, информатики.
1. В чем ценность логики?
– Логика беспристрастна. Язык ее сухой, а-эмоциональный. Сила ее в том, чтобы предупредить, предостеречь об опасности. И в этом отношении логика вне конкуренции.
2. Чему учит логика?
– Сложному умению ориентироваться в жизненных обстоятельствах и принимать правильное решение. Малейшая ошибка в логике доказательств может привести к катастрофе. Современному человеку, нацеленному быть образованным, умным, не хватает античного понимания логики – как согласования одной мысли с другой, умения слушать и слышать. Всему этому учили Сократ, Платон и особенно Аристотель – один из самых универсальных мыслителей, основатель научного языка.
3. Где можно научиться логике? Как считает Непейвода, логике можно научиться самостоятельно.
– Это трудно, а значит, возможно!
Металогика
Металогика
Метатеоретические проблемы логики
- Непротиворечивость формализованных теорий
- Полнота формализованных теорий
- Разрешимость формализованных теорий
- Независимость аксиом формализованных теорий
- Корректность формальной системы
- Определимость
- Сравнительный анализ логических теорий
Концепции логики
Концепции логики различаются между собой прежде всего по способам решения метатеоретических проблем логики, связанных с основаниями математики:
- Психологизм
- Логицизм
- Формализм (математика)
- Интуиционизм
- Конструктивная математика
- Консерватизм (логика)
Проблемы аксиоматизации теории множеств
- Логические парадоксы
- Семантические парадоксы
История логики
Хотя многие культуры выработали сложные системы рассуждения, логика как эксплицитный анализ методов рассуждения получила основательное развитие изначально только в трех традициях: в китайской, индийской и греческой . Об этом говорит сайт https://intellect.icu . Хотя точные даты не слишком достоверны (особенно в случае Индии). Современная логика, разработанная формально изощренно, происходит в конечном счете из греческой традиции (аристотелевской логики), которая, однако, была воспринята не напрямую, а при посредничестве и комментаторской деятельности арабо-мусульманских философов и средневековых европейских логиков. Можно выделить следующие исторические и региональные формы логики (приведены также их наименования, исторически существовавшие и принятые в литературе по истории формальной логики)
- Древнекитайская логика
- Индийская логика
- Европейская и ближневосточная логика: традиционная логика (в широком смысле)
- Античная и раннесредневековая логика: диалектика
- Средневековая логика
- Арабская и еврейская средневековая логика
- Восточнохристианская средневековая логика
- Западноевропейская средневековая логика: схоластическая логика, диалектика
- Логика европейского Возрождения; диалектика
- Логика Нового времени: традиционная логика (в узком смысле), формальная логика
- Современная логика (общемировая, со второй половины XIX века): математическая логика, символическая логика, логистика (последнее — как правило, в западной литературе).
Логика в своем развитии прошла три порога:
- порог формализации рассуждений (во всех трех традициях)
- введение условных (символических, буквенных и числовых) обозначений (только европейская традиционная логика)
- научная революция, с которой началась современная логика, — математизация (внесение в логику математических методов).
Логика в Древнем Китае
Логика в Китае появилась в период появления большого количества школ, конкуренции и дискуссий между ними. Современник Конфуция Мо-цзы («Учитель Мо», «Мудрец Мо»; V—IV вв. до н. э) был известен как основатель моизма (школы мо цзя), представители которой занимались поиском источников достоверного рассуждения и условий его правильности. В области аргументации они предпочитали разработку рассуждения по аналогии разработке дедукции. В процессе анализа семантики языка моисты разработали метод классификации имен по степени их общности и деления вещей по видам (метод «трех правил», «трех фа»).
Одно из ответвлений моизма, логики (мин цзя, школа имен, V—III вв. до н. э), приступило к исследованию собственно формальной логики (ее представители подошли к открытию категорического силлогизма ранее или одновременно с ее формулировкой Аристотелем).
Позднее, при династии Цинь, эта линия исследований исчезла в Китае, поскольку тогда философия легизма жестоко подавляла все остальные философские школы. Вновь логика в Китае появилась только с проникновением туда индийской логики буддистов и далее сильно отстала от развития европейской и ближневосточной логики.
Индийская логика
Истоки логики в Индии можно проследить в грамматических текстах V века до н. э.. Две из шести ортодоксально-индуистских (ведийских) школ индийской философии — ньяя и вайшешика — занимались методологией познания, из этого проблемного поля и выделилась логика.
Само название школы «ньяя» значит «логика». Главным ее достижением была разработка логики и методологии, ставших впоследствии общим достоянием (ср. аристотелевская логика в Европе). Основным текстом школы были Ньяя-сутры Акшапады Гаутамы (II век н. э.). Поскольку ньяики считали единственным путем освобождения от страданий достижение надежного знания, они разрабатывали тонкие методы отличения надежных источников знания от ложных мнений. Есть только четыре источника знания (четыре праманы): восприятие, умозаключение, сравнение и свидетельство. Строгая пятичленная схема умозаключения включала в себя: начальную посылку, основание, пример, приложение и вывод.
Буддийская философия (не входившая в число шести ортодоксальных школ) была главным оппонентом ньяиков в логике. Нагарджуна, основатель мадхьямики («срединного пути»), развил рассуждение, известное как «чатушкоти», или тетралемма. Этот четырехсторонний аргумент систематически проверял и отклонял утверждение высказывания, его отрицание, соединение утверждения и отрицания и, наконец, отклонение и его утверждения, и его отрицания.
У Дигнаги и его последователя Дхармакирти буддийская логика достигла вершины. Центральным пунктом их анализа было установление (определение) необходимой логической присущности (включенности в определение), «вьяпти», также известное как «неизменное следование» или «убеждение». Для этой цели они развили учение об «апоха» или различении, о правилах включения признаков в определение или исключения их из него.
Школа навья-ньяя («новая ньяя», «новая логика») была основана в XIII веке Ганешей Упадхьяей из Митилы, автора «Таттвачинтамами» («Сокровище мысли о реальности»). Впрочем, и он опирался на работы своих предшественников X века.[источник не указан 133 дня]
Европейская и ближневосточная логика
В истории европейской логики можно выделить этапы:
- аристотелевский (традиционный) продолжался сотни лет, в течение которых логика развивалась очень медленно;
- схоластический этап развития, пик которого приходится на XIV век;
- нововременной этап.
Логика античности
Основателем логики в древнегреческой философии считается древнегреческий философ Аристотель, так как полагается, что он вывел первую логическую теорию. Предшественниками Аристотеля в развитии логической науки в Древней Греции были Парменид, Зенон Элейский, Сократ и Платон. Аристотель же впервые систематизировал доступные знания о логике, обосновал формы и правила логического мышления. Его цикл сочинений «Органон» состоит из шести работ, посвященных логике: «Категории», «Об истолковании», «Топика», «Первая аналитика» и «Вторая аналитика», «Софистические опровержения».
После Аристотеля в Древней Греции логика также разрабатывалась представителями школы стоиков. Большой вклад в развитие этой науки внесли оратор Цицерон и древнеримский теоретик ораторского искусства Квинтилиан
Логика в Средневековье
По мере приближения к Средним векам логика получала более широкое распространение. Ее начали разрабатывать арабоязычные исследователи, например, Аль-Фараби (ок. 870—950 гг.). Средневековая логика называется схоластической, а ее расцвет в XIV веке связывают с именами ученых Уильяма Оккама, Альберта Саксонского и Уолтера Берли.
Логика в эпоху Возрождения и в Новое время
Этот исторический период в логике отмечается появлением множества крайне значимых для науки публикаций.
Френсис Бэкон в 1620 году опубликовывает свой «Новый органон», содержащий основы индуктивных методов, усовершенствованных позднее Джоном Стюартом Миллем и получивших название методов установления причинных связей между явлениями Бэкона-Милля. Суть индукции (обобщения) — в восхождении (в процессе познания) от частных случаев к общим правилам. Также необходимо искать причины своих ошибок.
В 1662 году в Париже издан учебник «Логика Пор-Рояля», авторами которого являются П. Николь и А. Арно, создавшие логическое учение на основе методологических принципов Рене Декарта.
Современная логика
В конце XIX — начале XX веков были заложены основы т. н. математической, или символической, логики. Ее суть заключается в том, что для обнаружения истинностного значения выражений естественного языка можно применять математические методы. Именно использование символической логики отличает современную логическую науку от традиционной.
Огромный вклад в развитие символической логики внесли такие ученые, как Дж. Буль, О. де Морган, Г. Фреге, Ч. Пирс и др. В XX веке математическая логика оформилась в качестве самостоятельной дисциплины в рамках логической науки.
Начало XX века ознаменовалось становлением идей неклассической логики, многие важные положения которой были предвосхищены и/или заложены Н. А. Васильевым и И. Е. Орловым.
В середине XX века развитие вычислительной техники привело к появлению логических элементов, логических блоков и устройств вычислительной техники, что было связано с дополнительной разработкой таких областей логики, как проблемы логического синтеза, логическое проектирование и проблемы логического моделирования логических устройств и средств вычислительной техники.
В 80-х годах XX века начались исследования в области искусственного интеллекта на базе языков и систем логического программирования. Началось и создание экспертных систем с использованием и развитием автоматического доказательства теорем, а также методов доказательного программирования для верификации алгоритмов и программ для ЭВМ.
В 80-е годы начались также изменения в образовании. Появление персональных компьютеров в средних школах привело к созданию учебников информатики с изучением элементов математической логики для объяснения логических принципов работы логических схем и устройств вычислительной техники, а также принципов логического программирования для компьютеров пятого поколения, и разработке учебников информатики с изучением языка исчисления предикатов для проектирования баз знаний.
Основные понятия науки логики
Понятия логики, необходимые для понимания предмета:
- Абстракция
- Адаптация
- Аналогия
- Антиномия
- Аргументация
- Ассоциация
- Гипотеза
- Дедукция
- Доказательство
- Доказуемость
- Законы логики
- Индукция
- Истинность
- Классификация
- Обобщение
- Определение
- Опровержение
- Парадокс
- Паралогия
- Понятие
- Признак
- Семантика
- Силлогизм
- Софизм
- Софистика
- Суждение
- Тавтология
- Теория
- Умозаключение
- Формальный язык
Традиционная логика
Дедуктивное и индуктивное рассуждение в традиционной логике
- Индукция
- Дедукция
- Трансдукция
Силлогистика
- Силлогизм
- Силлогистические теории
Законы логики
Закон логики — это общезначимый принцип какой-либо логической теории, формула которого принимает значение «истина» при любых допустимых в этой теории значениях нелогических символов. В логических исчислениях их теоремы, доказуемые с использованием дедуктивных средств исчисления, тоже признаются логическими законами. В традиционной логике было четыре основных логических закона[10]:
- Закон тождества постулирует, что в процессе рассуждения понятия и суждения должны употребляться в одном и том же смысле[11].
- Закон непротиворечия гласит, что два противоречащих суждения не могут быть одновременно истинными. По крайней мере одно из них ложно[12]
- Закон достаточного основания говорит о том, что каждое осмысленное выражение (понятие, суждение) может считаться достоверным только в том случае, если оно было доказано, то есть были приведены достаточные основания, в силу которых его можно считать истинным[13].
- Закон исключенного третьего утверждает, что любое высказывание или истинно, или ложно, третьего не дано[14].
В некоторых теориях современной логики применимы не все традиционные логические законы[10].
См. : Законы де Моргана, Закон Клавия и Законы деления
Классическая математическая логика
Основные статьи: Математическая логика и Классическая логика
Аппарат математической логики
Алгебра логики
Пропозициональная логика
Логика высказываний
- (Пропозициональная логика)
Логика предикатов
Логика предикатов
- Логика кванторов
- Логика первого порядка
- Логика второго порядка
Исчисления и логические методы
- Разрешимость
- Семантическое древо
- Таблицы Бета
- Аксиоматика
- Натуральный вывод
- Исчисление секвенций
Логическая семантика
Логическая семантика
- Алгебраические семантики
- Теоретико-множественные семантики
- Реляционные семантики возможных миров
- Проблема содержательности семантик логических систем
- Категорная семантика
- Теория семантических категорий
Теория моделей
Теория моделей
Теория доказательств
Теория доказательств
Теории логического вывода
- Теории логического вывода (теория логического вывода)
- Теории следования (теория следования)
- Теории импликаций (теория импликаций)
- Материальная импликация
Неклассические логики
Логики с неклассическим пониманием следования
- Релевантная логика
- Паранепротиворечивая логика
- Немонотонные логики
- Динамическая логика
Логики, отменяющие закон исключенного третьего
- Интуиционистская логика
- Конструктивная логика
- Логика квантовой механики
Логики, меняющие таблицы истинности
Многозначные логики
- Многозначная логика
- Двузначная логика
- Трехзначная логика
Логики, расширяющие состав высказывания
- Логика вопросов
- Логика оценок
- Логика норм
Модальная логика
- Модальность
- Алетические модальности (алетическая модальность, алетическая модальная логика, алетические модальные логики)
- Деонтические модальности (деонтическая модальность, деонтическая модальная логика, деонтические модальные логики)
- Эпистемологические модальности (эпистемологическая модальность, эпистемологическая модальная логика, эпистемологические модальные логики)
- Временные модальности (временная модальность, временные модальные логики, временная модальная логика)
- Строгая импликация
- Материальная импликация
Недедуктивные логические теории
- Индуктивная логика
- Вероятностная логика
- Логика решений
- Логика нечетких понятий (логика нечетких множеств, нечеткая логика)
- Аналогия (умозаключение по аналогии)
Другие неклассические логики
- Категориальная логика
- Комбинаторная логика — это логика, которая заменяет переменные функциями с целью прояснить такие интуитивные операции с переменными, как подстановка. Построенная на базе комбинаторной логики система арифметики содержит все частично рекурсивные функции и избегает геделевской неполноты.
- Кондициональная логика (условная логика). Ее предмет — истинность условных предложений (в частности, сослагательного наклонения). Логика контрафактических утверждений.
функции логики
1. Познавательная функция логики.
Как и всякая наука вообще, логика имеет дело с открытием и исследованием объективных законов, с той лишь существенной разницей, что это законы не внешнего мира, а мышления. В этом смысле, занимая важное место в общей системе познания мира, а мышления. В этом смысле, занимая место в общей системе познания мира, она выполняет прежде всего общенаучную — познавательную функцию, т.е. объяснительную и предсказательную. Она дает более или менее точное объяснение определенной группы явлений и процессов мышления, а на этой основе — предсказание, при каких условиях возможно достижение истинных знаний и каковы последствия неправильного хода рассуждения.
2. Мировоззренческая функция логики.
Логика, как отмечалось выше, особая наука. Если в естественных и общественных науках мышление служит лишь средством познания действительности, то в логике — непосредственной целью познания. Поэтому, раскрывая закономерности мышления как одной из важнейших сфер исследования наряду с природой и обществом, эта наука тем самым вносит свой, и притом весомый, вклад в то или иное решение фундаментальной философской проблемы — отношение мышления к бытию. Следовательно, она активно участвует в формировании мировоззрения людей — более или менее стройной совокупности их обобщенных взглядов на мир в целом и на отношении человека к этому миру. Вот в каком смысле говорится о ее мировоззренческой функции.
3. Методологическая функция логики.
Как и любая теория вообще, логическая теория, будучи результатом предшествующего познания своего объекта, становится средством, а следовательно, методом его дальнейшего познания. Но как весьма широкая теория, которая исследует процесс мышления, проявляющаяся во всех науках без исключения, логика обеспечивает и их определенным методом познания.
4. Идеологическая функция логики.
Зарождаясь и развиваясь в классовом обществе, логика никогда не была нейтральной в идеологической борьбе. Она служила важным средством обоснования одной идеологии, орудием борьбы с другой. В ней самой всегда развертывалось идейное противоборство важнейших философских направлений — материализма, и идеализма, диалектики и метафизики. Отсюда — ее идеологическая функция.
Свои важнейшие функции логика выполняла всегда, на всех этапах своего развития, хотя появлялись они в разное время по-разному. В современных условиях ее роль и значение особенно возрастают. Потребность в логике, особенно в символической, становится все более ощутимой- в обстановке нового этапа развертывания научно-технической революции, связанного с широкой информатизацией производства, управления, обслуживания.
Значение и применение логики
Достижения формальной логики применяются в юриспруденции, психологии, лингвистике, теории управления, педагогике и др. науках. Некоторые разделы логики являются теоретической основой математики, теории информации, кибернетики.
При изучении логики развиваются:
- точное мышление и ясная речь;
- умение убеждать и обосновывать свои идеи;
- умение спорить;
- привычка анализировать свои и чужие рассуждения, что помогает нам справиться с софистикой и ложью.
Но все же главное значение логики в том, что она приучает думать и усиливает мыслительные способности человека.
Вау!! 😲 Ты еще не читал? Это зря!
- Логические символы
- тесты по логике ,
- термины по логике , понятия логики ,
- Определение
- Классификация
- Абстракция
- Идеализация
- Аксиоматизация
- Формализация
- Аргументация
- Методология науки
- Логическое программирование
- Логика в информатике
- Доказательное программирование
- Автоматическое доказательство теорем
- Когнитивная психология
- Аналитическая философия
- Динамическая логика
- Трансцендентальная логика
- Философская логика
В общем, мой друг ты одолел чтение этой статьи об логика. Работы в переди у тебя будет много. Смело пишикоментарии, развивайся и счастье окажется в ваших руках.
Надеюсь, что теперь ты понял что такое логика, логика как наука, функции логики
и для чего все это нужно, а если не понял, или есть замечания,
то нестесняся пиши или спрашивай в комментариях, с удовольствием отвечу. Для того чтобы глубже понять настоятельно рекомендую изучить всю информацию из категории
Логика
Ло́гика [греч. λογική (τέχνη) – наука и искусство разговаривать и размышлять, от λόγος – слово, мысль, счёт], нормативная наука о законах, формах и приёмах интеллектуальной (мыслительной) познавательной деятельности. Логика представляет собой разветвлённую и многоплановую науку, в составе которой можно выделить теорию рассуждений (дедуктивных и правдоподобных), металогику и логическую методологию.
Так как работа интеллекта реализуется в языковой форме, исследования в логике тесно связаны с изучением языковых конструкций и ведутся в рамках т. н. логической семиотики, которая распадается на логическую синтактику, логическую семантику и логическую прагматику.
В логической синтактике язык и строящиеся на его основе логические теории изучаются с их формальной (структурной) стороны. Здесь определяются алфавиты языков логических теорий, задаются правила построения из знаков этих алфавитов различных сложных языковых конструкций – термов, формул, выводов, теорий и т. д. Осуществляется синтаксическое членение множества языковых выражений на функторы и аргументы, постоянные и переменные, определяются понятия логической формы выражения, логического подлежащего и логического сказуемого, осуществляется построение различных логических теорий и анализ способов оперирования в них.
В логической семантике язык изучается с его содержательной стороны. При этом все выражения языка, в зависимости от их значений, распределяются по классам – семантическим категориям. Среди последних выделяют предложения, дескриптивные и логические термины. Для логики как науки особое значение имеют логические термины, ибо процедурная сторона интеллектуальной работы с информацией определяется смыслом данных терминов. К их числу относятся такие слова и словосочетания, как «и», «или», «если… то», «неверно, что», «всякий», «любой», «некоторый» и многие другие (см. Логические операции). Центральным понятием логической семантики является понятие истины, с которым тесно связано понятие интерпретации. Под последней имеется в виду процедура приписывания языковым выражениям значений, ассоциированных с некоторым классом предметов, называемым универсумом рассуждения. Те интерпретации, при которых каждое предложение, входящее в множество предложений G, принимает значение «истина», называют моделями для G. Понятие модели исследуется в специальной семантической теории – теории моделей.
При анализе логических проблем нередко требуется учитывать также и интерпретатора (субъекта). Например, рассмотрение такой логической теории, как теория аргументации, спора, дискуссии, невозможно без учёта целей и намерений участников диспута. Во многих случаях применяемые здесь приёмы полемики зависят от желаний одной из спорящих сторон поставить своего противника в неудобное положение, сбить его с толку, навязать ему определённое видение обсуждаемой проблемы. Рассмотрение этих вопросов входит в круг проблем логической прагматики.
При логическом анализе понятий, суждений, императивов, вопросов в языковых выражениях осуществляется замена дескриптивных терминов или простых предложений на переменные соответствующих типов. В результате этого выявляется логическая форма выражений. Так, заменяя дескриптивные термины «человек» и «смертен» в предложении «Всякий человек смертен» переменными, получаем логическую форму «Всякий S является P», содержание которой задаётся интерпретацией всех предложений данной формы.
Главным разделом логики является теория рассуждений, а в последней особое место занимает теория дедуктивных рассуждений. В ней определяются понятия логического закона и логического следования. К числу логических законов относят такие логические формы мыслей, которые при любой интерпретации входящих в них переменных всегда превращаются в истинные предложения. Так, выражения вида «Если p, то p», «Неверно, что p и не-p», «p или не-p», «Если для каждого x верно, что x обладает свойством P, то существует такой x, что x обладает свойством P» являются в классической логике соответственно логическими законами тождества, противоречия, исключённого третьего и подчинения. Логическое следование определяется как такое отношение между посылками A1, A2, …, An и заключением B, когда любая интерпретация, делающая все посылки истинными утверждениями, делает и заключение истинным.
На основе понятий логического следования и логического закона формулируются логические правила вывода. Главная их особенность состоит в том, что они гарантируют обязательное (необходимое) получение истинного заключения, если применяются к истинным посылкам. Иначе говоря, справедливость этих правил зависит лишь от их логической формы и совершенно не зависит от конкретного содержания наших рассуждений.
Ныне этот раздел представлен различными логическими теориями, отличающимися друг от друга типами анализируемых в них рассуждений, логическими правилами и логическими законами. Так, в зависимости от глубины анализа высказываний выделяют логику высказываний (пропозициональную логику) и кванторные теории – логику предикатов. В первой анализируются такие типы рассуждений, которые не зависят от внутренней структуры простых предложений. В отличие от этого, в логике предикатов анализ рассуждений осуществляется с учётом внутренней структуры простых предложений. По способу представления логической теории различают семантическое (например, табличное построение высказываний классической логики) и синтаксическое её представление в виде некоторой формальной дедуктивной теории – исчисления.
Логические теории делятся на классические и неклассические. Если современная классическая логика развивалась главным образом для решения проблем математики, в силу чего она даже получила название математической логики, то причиной возникновения неклассических логик явилось стремление использовать аппарат логики для решения философских, в частности гносеологических, проблем (множество неклассических логик называются философскими). Так, попытки учесть такую особенность ряда высказываний, которая связана с неопределённостью их истинностной оценки, когда мы не можем сказать, истинны они или ложны, привели к построению большого числа разнообразных систем многозначной логики. Включение в рамки логического анализа высказываний с модальными операторами породило разнообразные системы модальной логики: алетические, в которых изучаются высказывания с операторами «необходимо», «возможно», «случайно»; временны́е – высказывания с временны́ми характеристиками; эпистемические – высказывания с операторами «доказано», «опровергнуто», «знает, что» и другими; аксиологические – высказывания с операторами «добро», «зло», «хорошо», «плохо», «прекрасно», «безобразно». Попытки избавиться от парадоксов материальной импликации привели к построению систем релевантной логики, обосновывающих следование по смыслу, и систем паранепротиворечивой логики, не принимающих принцип классической логики, согласно которому из противоречия следует всё что угодно. Включение в рамки логического анализа вопросительных и побудительных высказываний породило различные варианты логики вопросов и деонтической логики. Строятся различные варианты логики изменения и динамическая логика. Потребности логического анализа рассуждений в области квантовой механики вызвали к жизни квантовую логику, анализ рассуждений о массовых случайных событиях потребовал развития вероятностной логики.
В современной логике постоянно возникают всё новые и новые логические теории, в которых изучаются новые типы рассуждений и высказываний, требующие введения новых типов правил и законов.
Построение логики в форме исчислений привело к созданию ещё одного важного раздела современной логики – металогики. В последней исследуются свойства, которыми обладают логические теории: непротиворечивость, полнота, наличие разрешающих процедур, независимость исходных дедуктивных принципов, а также различные отношения между теориями и самими логическими исчислениями. В этом смысле металогика является саморефлексией логики относительно своих построений.
Кроме анализа дедуктивных рассуждений, важнейшая задача логики – исследование и других приёмов интеллектуальной познавательной деятельности. К их числу относятся выработка и формулировка понятий, установление их видов и различных способов оперирования с ними (деление, классификация), определение терминов, построение и проверка гипотез, а также исследование правдоподобных рассуждений (индукции и аналогии), теории измерения, объяснения и предсказания. Этот круг вопросов составляет предмет методологии дедуктивных, эмпирических и гуманитарных наук.
На протяжении тысячелетий логика была обязательной дисциплиной школьного и университетского образования, т. к. выполняла общекультурную задачу пропедевтики правильности рассуждений. Современная логика в полном объёме сохранила за собой эту дидактическую функцию. Однако развитие в последнее время мощного аппарата современной логики позволило ей стать и важной прикладной дисциплиной. Помимо использования логики в области оснований математики, важными прикладными областями её применения являются лингвистика и в особенности информатика. Логическая проблематика проникает в юриспруденцию, а также в этику, эстетику и другие сферы знания.
Логика в Античности
Теории дедукции, созданные в 4 в. до н. э. Аристотелем и представителями мегарской школы, стали основой последующего развития логики в Европе. Евклид из Мегары широко использовал как доказательство от противного, так и аргументы, по форме близкие к силлогистическим. Аристотель в «Топике» сформулировал основное правило исчисления высказываний – правило «отделения заключения» – modus ponens (разрешающее при истинности высказываний «если A, то B» и «A» «отделить» высказывание «B» как истинное заключение). Он ввёл понятие высказывания как истинной или ложной речи, открыл атрибутивную форму речи (в отличие от грамматической) – как утверждения или отрицания «чего-либо о чём-то», определил «простое высказывание» как атрибутивное отношение двух терминов, открыл изоморфизм атрибутивных и объёмных отношений и правила силлогизма. Созданная Аристотелем законченная теория дедукции – силлогистика – реализовала для определённых способов рассуждения выведение логических следствий при помощи механических приёмов, родственных алгоритмам. Представитель мегарской школы Евбулид из Милета, споривший с Аристотелем, сформулировал парадоксы «лжец», «лысый», «куча» и несколько софизмов. Диодор Крон и его ученик Филон из Мегары предложили параллельные уточнения отношения логического следования посредством понятия импликации. Диодор Крон толковал импликацию как модальную (необходимую) условную связь, а Филон – как материальную (не учитывающую связь высказываний по содержанию).
Логические идеи мегариков были восприняты стоиками. Хрисипп принял критерий Филона для условного суждения и принцип двузначности как онтологическую предпосылку логики. В сочинениях стоиков логика высказываний предшествует аристотелевской силлогистике, оформляясь в систему правил построения и правил вывода высказываний. Последние по примеру Аристотеля тоже стали называть силлогизмами. Была сформулирована идея дедукции: заключение B следует из посылок A1, A2, …, An, когда B не может быть ложным при истинности каждой из этих посылок. Аргументы, основанные на понимании высказываний только исходя из их отношения истинно/ложно, стоики называли формальными; они могут вести от ложных посылок к истинным следствиям. Если же во внимание принималась содержательная истинность посылок, формальные аргументы назывались истинными. Если посылки и заключения соотносились как причины и следствия, аргументы назывались доказывающими. В общем случае «доказывающие аргументы» стоиков предполагали понятие о естественных законах. Стоики считали их аналитическими и отрицали возможность их доказательства посредством аналогии и индукции. Т. о., развитое стоиками учение о доказательстве вело за пределы логики в область теории познания, и здесь им противостоял радикальный эмпиризм представителей школы Эпикура, защищавших опыт, аналогию, индукцию и положивших начало индуктивной логике (Филодем из Гадары).
Для поздней Античности характерно эклектическое сочетание логических идей Аристотеля и стоицизма. Вклад в логику ограничивался преимущественно переводческой и комментаторской деятельностью поздних представителей перипатетической школы (Боэт Сидонский, Александр Эгский, Адраст, Гермин, Александр Афродисийский, Гален и др.) и неоплатоников (Порфирий, Прокл, Симпликий, Марий Викторин, Апулей, Августин, Боэций, Кассиодор и др.). У Боэция, по-видимому, впервые появляются понятия «субъект», «предикат», «связка», ставшие на протяжении последующих столетий основой анализа высказываний. Из нововведений этого периода заслуживают внимания логический квадрат (quadrata formula) Апулея, реформированный позднее Боэцием; дихотомическое деление понятий и учение о видах и родах Порфирия; зачатки истории логики у Секста Эмпирика и Диогена Лаэртия; наконец, ставшая с тех пор общепринятой латинизированная логическая терминология, восходящая к сочинениям Цицерона и латинским переводам из аристотелевского «Органона», выполненным Боэцием. Логика у неоплатоников постепенно сближается с грамматикой. В энциклопедическом «Сатириконе» Марциана Капеллы логика объявляется необходимым элементом гуманитарного образования в качестве одного из семи свободных искусств.
Логика в Средние века
Значительное влияние на развитие европейской средневековой логики оказала арабская логика. Уже в 1-й половине 9 в. на арабский язык были переведены сочинения Аристотеля и греческих перипатетиков. Аль-Фараби в своих основополагающих комментариях к трудам Аристотеля развивал учение о доказательстве, изучал взаимосвязь логики и грамматики, его имя носит разработанная им интерпретация аристотелевской проблемы будущей случайности. Ибн Сина создал оригинальную теорию временнóй модальной силлогистики, разрабатывал логику высказываний, отсутствующую у Аристотеля. Традиция аль-Фараби была продолжена Ибн Рушдом, комментарии которого к аристотелевской логике и метафизике уже к началу 13 в. были переведены на латинский язык и получили большую известность в Европе.
В Европе в 12–13 вв., когда стали известными произведения Аристотеля, в рамках латинской схоластики возникла оригинальная логика (logica modernorum). Её основы намечены уже в «Диалектике» П. Абеляра, но окончательное оформление она получает в конце 13 – середине 15 вв. в работах У. Шервуда, Петра Испанского, Иоанна Дунса Скота, Вальтера Бурлея (Бёрли), У. Оккама, Ж. Буридана, Альберта Саксонского, Павла Венецианского. В сочинениях этих авторов строго разделяются логическая и фактическая истинность, и логика понимается как формальная дисциплина о принципах всякого знания (modi scientiarum omnium), предметом которой являются не эмпирические, а абстрактные объекты – универсалии. Складывается представление о двояком использовании языка: для выражения мысли о внеязыковых фактах, когда термины «употребляются», и для выражения мысли о самом языке, когда термины «упоминаются». Учение о логических операциях логики высказываний и логики предикатов с использованием кванторных слов «все» и «существует» стало естественным основанием для различения между «формой» и «содержанием» суждений. Учение о «следовании» основывалось на различии между импликацией материальной и формальной (тавтологичной): для первой можно указать контрпример, для второй – нет. Поэтому материальная импликация рассматривалась как выражение фактического следования, а формальная – логического, с которым естественно связывалось понятие о логических законах. Средневековые логики открыли многочисленные законы логики высказываний, составлявшей основу их теории дедукции и, как и у стоиков, считавшейся более общей, чем аристотелевская силлогистика. В этот же период впервые зародилась идея «автоматизации» процесса логического вывода (логическая машина Р. Луллия).
Средневековые дискуссии о поставленной Аристотелем проблеме логического статуса высказываний о будущих случайных событиях и в связи с этим о совместимости всеведения Бога со свободой воли человека привели к введению в логику третьего истинностного значения и связи логических модальностей со временем. Особый интерес здесь представляют работы Оккама, автора фундаментального труда «Summa totius logicae».
Логика в Новое время
Эпоха Возрождения стала эпохой кризиса для дедуктивной логики. Её воспринимали как основу схоластического мышления, оперирующего схемами умозаключений, в которых посылки устанавливаются авторитетом веры, а не познания. Руководствуясь общим принципом «вместо абстракций – опыт», дедуктивной логике стали противопоставлять логику «естественного мышления», под которой обычно подразумевались интуиция и воображение. Леонардо да Винчи и Ф. Бэкон переоткрывают античную идею индукции и индуктивного метода, выступая с резкой критикой силлогизма. И лишь немногие, подобно падуанцу Я. Дзабарелле («Логические труды» – «Opera logica», 1578), пробуют вернуть в методологию научной мысли традиционную логическую дедукцию, освободив её от схоластической интерпретации.
В 17 в. Г. Галилей использует гипотетико-дедуктивный метод для образования абстракций, восполняющих данные опытных наблюдений. Критическое отношение к схоластике и одновременная реабилитация дедукции (правда, при некотором снижении интереса к формальной стороне доказательств) характерны для логики картезианства, систематически изложенной в сочинении А. Арно и П. Николя «Логика, или Искусство мыслить» (1662) и вошедшей в историю под названием «Логика Пор-Рояля». Логика представлена здесь как рабочий инструмент всех других наук, поскольку она принуждает к строгим формулировкам мысли. Р. Декарт реабилитировал дедукцию (из аксиом) как «верный путь» к познанию, подчиняя её более точному методу всеобщей науки о «порядке и мере» – mathesis universalis, простейшими примерами которой он считал алгебру и геометрию. В том же ключе работали И. Юнг («Гамбургская логика» – «Logica Hamburgensis», 1638), Б. Паскаль («О геометрическом разуме» – «De l’esprit géométrique»), А. Гейлинкс («Логика…» – «Logica…», 1662), Дж. Саккери («Наглядная логика» – «Logica demonstrativa», 1697) и в особенности Г. В. Лейбниц, который идею mathesis universalis доводит до идеи calculus rationator – универсального искусственного языка, свободного от недостатков, присущих естественным языкам, и способного точно и однозначно выражать мысли. Лейбниц считал, что можно создать универсальный алгоритм, который позволит провести доказательство всех известных истин и составить тем самым «энциклопедию доказательств». Пытаясь реализовать этот замысел, Лейбниц предложил несколько вариантов арифметизации логики. В одном из них каждому термину сопоставлялось простое число, каждому сложному, составленному из простых, – произведение простых чисел. Эта идея сыграла впоследствии важную роль в математике и логике благодаря, в частности, работам К. Гёделя. Для проверки истин разума, по Лейбницу, достаточно законов аристотелевской логики; для проверки истин факта, т. е. эмпирических истин, нужен ещё закон достаточного основания.
Исходным пунктом индуктивной логики Нового времени послужили методологические идеи Ф. Бэкона, систематически же логика, исследующая «обобщающие выводы» как заключения, основанные на установлении причинной связи между явлениями, была разработана Дж. С. Миллем (1843), который опирался, в свою очередь, на идеи Дж. Гершеля. Индуктивная логика 19 в., центральным вопросом которой был вопрос о способах обоснования эмпирических заключений о закономерных (регулярных) связях явлений, в 20 в., с одной стороны, трансформировалась в вероятностную логику, а с другой – приобрела новую жизнь в современной математической статистике и в работах по искусственному интеллекту, т. е. вышла за пределы логики в собственном смысле слова.
Главной линией последующего развития логической мысли стало формирование математической логики, связанное прежде всего с работами Дж. Буля, У. С. Джевонса, Дж. Венна, О. де Моргана, П. С. Порецкого, Г. Фреге, Дж. Пеано, Б. Рассела, А. Уайтхеда, Д. Гильберта, К. Гёделя, А. Тарского и многих других.
Логика в России
Первым оригинальным российским сочинением по логике стали «Письма к немецкой принцессе» («Lettres à une princesse d’Allemagne…», vol. 1–3, 1767–1772; в русском переводе – «Письма о разных физических и филозофических материях…», ч. 1–3, 1768–1774) логика Л. Эйлера, с именем которого связаны широко используемые в логике графические схемы (круги Эйлера), основанные на трактовке понятий с точки зрения их объёмов. В связи с потребностями университетского преподавания в 1-й половине 19 в. появляется целый ряд сочинений по логике (А. С. Лубкин, П. Д. Лодий и др.). Во 2-й половине 19 в. публикуются самобытные сочинения российских авторов в области как традиционной (философской) логики (М. И. Владиславлев, М. И. Каринский, А. И. Введенский, Н. Я. Грот, Л. В. Рутковский), так и новой тогда математической логики. Введенский, автор учебника «Логика, как часть теории познания» (1909), различал «логику открытия» новых истин и «логику проверки» истин, уже установленных. Каринский (1880) предложил оригинальную классификацию выводов (отличную от классификаций Аристотеля, Дж. С. Милля и В. Вундта), основанную на сравнительном анализе отношений тождества между субъектами и предикатами суждений, участвующих в выводе (дополнена Рутковским, 1899). Систематическая разработка логики отношений была предпринята С. И. Поварниным. Первым представителем математического направления в логике 2-й половины 19 в. стал П. С. Порецкий (цикл работ с 1884 по 1904). Н. А. Васильев в 1910–1913 гг. разработал систему «воображаемой» логики, не содержащей онтологического закона противоречия и ставшей предвестником паранепротиворечивой логики. Различая три формы суждений – утвердительные, отрицательные и противоречивые (индифферентные), он сформулировал также закон исключённого четвёртого. В конце 19 в. появляются российские обзоры истории логики М. И. Владиславлева (1872), М. М. Троицкого (1886), П. Э. Лейкфельда (1890). Широкое распространение получил «Учебник логики» Г. И. Челпанова (9 изданий до 1917).
После 1917 г., в связи с прекращением преподавания логики в школах и вузах и осуждением «формальной логики» как разновидности антидиалектического мышления, логические исследования вплоть до 1950-х гг. осуществлялись главным образом в области математики.
Частичная аксиоматизация интуиционистской логики была дана А. Н. Колмогоровым («О принципе tertium non datur», 1925), в работах которого, а также В. И. Гливенко (1929) проанализированы взаимоотношения между классической пропозициональной и интуиционистской логикой. В 1924 г. М. И. Шейнфинкель заложил основы комбинаторной логики. В 1928 г. И. Е. Орлов предвосхитил такие направления неклассической логики, как релевантная и паранепротиворечивая логика, а также ввёл общепринятые сейчас модальные аксиомы S4 и правило, называемое ныне правилом Гёделя. В это же время И. И. Жегалкин предложил арифметизацию классической логики (полиномы Жегалкина). В 1938 г. в кандидатской диссертации В. И. Шестаков (одновременно с К. Шенноном) применил аппарат алгебры логики для синтеза и анализа релейно-контактных переключательных схем. Российские математики внесли существенный вклад в решение проблем неразрешимости. Первый в мире результат в этой области принадлежит А. А. Маркову, который в 1947 г. (ранее Э. Л. Поста) доказал неразрешимость проблемы тождества слов в полугруппах, а П. С. Новиков в 1955 г. доказал неразрешимость этой проблемы в конечно определённой группе. В 1970 г. Ю. В. Матиясевич доказал алгоритмическую нераспознаваемость наличия решений у диофантовых уравнений, решив тем самым десятую проблему Гильберта.
С. А. Яновская в 1936 г. начала читать первый в России курс математической логики на механико-математическом факультете МГУ, а в 1946 г. – там же на философском факультете; благодаря её усилиям переведены на русский язык классические труды по логике (Д. Гильберта и В. Аккермана, А. Тарского, Р. Карнапа, С. К. Клини и др.). В 1946 г. восстановлено преподавание логики в школах и вузах, стали переиздаваться дореволюционные учебники по формальной логике (Г. И. Челпанов) и издаваться новые (В. Ф. Асмус). В 1940-х гг. открыты кафедры логики на философских факультетах МГУ и ЛГУ и образован сектор логики в Институте философии АН СССР.
Вокруг созданной в 1959 г. на механико-математическом факультете МГУ кафедры математической логики во главе с А. А. Марковым образовались три научные школы, связанные с именами Маркова, А. Н. Колмогорова и П. С. Новикова (автора первого систематического курса по математической логике, опубликованного в 1959). В школе Маркова были получены результаты по конструктивной логике и семантике, теории нормальных алгоритмов, конструктивной математике, по поиску логического вывода и логике доказуемости, модальным логикам. В школе Колмогорова исследовались теория рекурсии и её применения, теория множеств, проблема разрешимости в классической логике, суперинтуиционистские логики и булева сложность. В 1952 г. Колмогоров предложил общее определение алгоритма (машина Колмогорова – В. А. Успенского) и наряду с Марковым заложил основы теории алгоритмов сложности. В школе Новикова исследовались проблемы сводимости Поста, неразрешимости теорем для некоторых проблем алгоритмической алгебры, получены результаты в теории булевой сложности и в области алгебры функций k-значной логики. Новиковым совместно с С. И. Адяном было получено решение проблемы Бернсайда о периодических группах. А. И. Мальцевым в 1959 г. основана сибирская научная школа алгебры и логики (после Мальцева её возглавил Ю. Л. Ершов), в 1962 г. – специализированный журнал «Алгебра и логика». Главные результаты школы получены в области теории моделей, теории рекурсии, разрешимости/неразрешимости алгебраических теорий в области суперинтуиционистских и модальных логик.
В 1938 г. Д. А. Бочвар создал трёхзначную логику, предназначенную для решения парадокса Рассела. В 1950-х гг. А. В. Кузнецов и С. В. Яблонский, а позднее А. И. Мальцев разработали аппарат для изучения функциональных свойств многозначных логик, используемый сейчас повсеместно.
Важным событием явилось издание первой в России «Философской энциклопедии» (т. 1–5, 1960–1970), в которой логика впервые в истории отечественной философской мысли была представлена в её современном виде с активным участием логиков-математиков. В 1960–1970-х гг. в области философской логики разрабатывались проблемы образования абстракций и их видов, теория понятий (Е. К. Войшвилло), теория определений, силлогистика, вопросы логической семантики, логика аргументации, логический аппарат для интеллектуальных систем (В. К. Финн). В школе В. А. Смирнова исследовались взаимоотношение теорий и классификация логики, теория логического следования, разрешимость логических исчислений, неклассической логики. На философском факультете ЛГУ в 1977 г. для философских факультетов университетов был издан первый учебник «Формальная логика», вторая часть которого посвящена символической логике. С 1993 г. сектором логики Института философии РАН издаётся ежегодник «Логические исследования».
Логика в Индии
Индийская логика представляет собой совокупность концепций относительно инструментов получения знания и контроля за рассуждениями, созданных в индийских религиозно-философских системах. Включает учение об инструментах достоверного познания (прамана-вада), логическую семантику, теории логического вывода (анумана), аргументации и полемики, теорию отношений, классификацию логических ошибок. Формальная логика как самостоятельная наука в Индии не сложилась. Включённость логических концепций в эпистемологию обусловила их самобытный характер, выражающийся: 1) в своеобразных проблемах и методологии; 2) в неоднозначности (нередко метафоричности) логической терминологии; 3) в понимании логической истины как относительной, низшей (самврити-сатья), обслуживающей потребности эмпирической, низшей реальности (самврити-сат). Трактовка логической истины как соответствующей установленным формальным правилам сближает индийскую логику с европейской.
Истоком логико-эпистемологических концепций в Индии, так же как и в Древней Греции, стало искусство ведения публичных споров. Об этом свидетельствуют как множество терминов для его обозначения, так и сохранение диалогической формы в качестве основной при написании теоретических сочинений по всем отраслям знания. В медицинском трактате «Чарака самхита» (78 н. э.) приводится список из 36 специальных методов интерпретации текстов, обсуждаемых в процессе диспута, и 34 специальных термина, регламентирующих ведение публичного спора. Во входящем в «Абхидхамма-питаку» сочинении Тиссы Могалипутты (около 255 до н. э.) «Каттхаватху» перечисляются ступени дискуссии, в том числе напоминающие элементы пятичленного силлогизма школы ньяя. В числе предлогических концепций, выдвинутых в древний период, – пятичленная и десятичленная формы аргументации, «семичастный паралогизм» последователей джайнизма, применявшиеся буддистами методы опровержения, использовавшиеся в «Милинда паньхе» вопросы, поднимающие оппонентов «на рога дилеммы».
Оформление собственно логико-эпистемологического комплекса – прамана-вады и ньяя-шастры (науки о методах познания) – происходит во 2–13 вв., когда все школы вовлекаются в обсуждение проблем познания и форм рассуждения и в результате дискуссий создают свои систематизированные учения, содержащие логические концепции. Тогда же теория полемики теряет свою самостоятельность и становится одним из разделов «науки о познании». Этот период открывают «Ньяя-сутры» Гаутамы Акшапады (2–4 вв.). Ключевыми фигурами в логике Средних веков были найяики Ватсьяяна (5 в.) и Уддйотакара, представитель синкретической ньяя-вайшешики Бхасарваджня, буддисты Нагарджуна, Асанга и Васубандху, Дигнага, Дхармакирти и Дхармоттара (около 750–810), мимансак Кумарила Бхатта, вайшешик Прашастапада, джайны Умасвати, Кундакунда, Сиддхасена Дивакара (около 480–550), Джинабхадра Гани (484–588), Сиддхасена Гани (6 в.), Самантабхадра (6 в.), Видьянанда (9 в.).
Центральной проблемой индийской логики этого периода стала проблема вывода (анумана). Представленная в «Ньяя-сутрах» (I.1. 32–39) и комментариях к ним концепция «пятичленного силлогизма» (панча-аваява-анумана) получила широкое распространение и до появления буддийской теории вывода стала общепризнанной. «Пятичленный силлогизм» содержит следующие члены: 1) тезис: «Звук не вечен»; 2) основание: «Потому что он сотворён»; 3) пример, который мог быть либо положительным, либо отрицательным: «Как горшок» или «Что не невечно, то непроизводно, как душа»; 4) применение, положительное (при положительном примере) или отрицательное (при отрицательном примере): «Так и здесь» или «Здесь не так»; 5) заключение: «Поэтому звук не вечен».
В рамках концепции вывода рассматривались вопросы семантики и разрабатывались теории разнообразных отношений между терминами-знаками и объектами, их свойствами и действиями или представлениями, выступающими в роли обозначаемого. Среди множества отношений – вритти (присутствие), вьяпти (проникновение), тадатмья (тождество), самйога (контакт), разъединение (вибхага), самавая (внутренняя присущность) и другие, опосредующие переход от вещей или представлений о вещах к знаниям. Отношение вьяпти, игравшее в выводе роль, аналогичную отношению логического следования в западной традиции, интерпретировалось неоднозначно различными школами и было предметом дискуссий. У найяиков и мимансаков вьяпти понималось как «проникновение» между терминами умозаключения, у буддистов, а вслед за ними и у вайшешиков – как логическое следование, обеспечиваемое выполнением правила трайрупья (трёхаспектности) для основания вывода, у джайнов – как «неразрывная связь среднего и большего терминов» (авинабхава), достигаемая при наличии однозначного соответствия названных терминов.
С 6 по 9 вв. логику развивали буддисты, совершившие своего рода переворот в теории вывода: они ввели в него общую посылку (повысив таким образом его надёжность и приблизив к дедуктивному умозаключению) и впервые отделили вывод в качестве формы умозаключения от диалектической формы аргументации. Собственно прамана-вада была создана буддистами сравнительно поздно (в конце 5 – 7 вв.), но индийская логика поднялась на принципиально новый уровень благодаря идеям Дигнаги и Дхармакирти, опиравшихся на достижения в теории диалектики Нагарджуны, Асанги и его брата Васубандху, которые не создали, однако, систематизированных теорий познания и логики. Вкладом Нагарджуны стало использование трёх форм аргументации – «тетралеммы» (Р. Робинсон), или «четырёхчастного отрицания», опровержения тезиса оппонента методом от противного и опровержения тезиса оппонента методом сведения к абсурду. Нагарджуна первым поколебал позиции пятичленного силлогизма найяиков, заявив, что необходимыми для доказательства («доказывающими») являются только три члена: тезис может быть усмотрен через основание и пример, следовательно, применение и повторяющее тезис заключение излишни. Это положило начало не утихавшим в течение нескольких сотен лет спорам о количестве членов силлогизма, результатом которых стало разделение Дигнагой вывода на два вида: «для себя» (свартха-анумана), аналог логической формы энтимемы («На горе огонь, так как там дым»), и «для других» (парартха-анумана) – аналог логической формы доказательства. Вывод «для себя» он определил как двучленный, а «для других» – как трёхчленный. Трёхчленный вывод представлял у буддистов бестезисную форму доказательства и формулировался в следующих высказываниях: 1) «[Всё] производное не вечно» – бо́льшая посылка; 2) «Как горшок и т. д.» – пример по сходству; 3) «Слово также производно» – меньшая посылка. Тезис данного доказательства, представляющий собой заключение приведённого силлогизма, формулировать не предполагалось, т. к. оно, по мнению буддистов, было очевидно: «Следовательно, слово не вечно». Значительный вклад в развитие буддийской эпистемологии и логики был внесён также Шантаракшитой и Камалашилой (оба 8 в.).
Буддисты считали, что знание, полученное с помощью вывода, не имеет отношения к реальности; всё, что сообщается нам мышлением о феноменальном мире, иллюзорно, «сконструировано» по особым законам разума. Главным свойством интеллектуальных конструкций является, согласно Дхармакирти, их способность быть выраженными в слове. Выводное знание понималось как новое состояние сознания познающего субъекта, следующее за восприятием логического признака объекта и обоснованием неразрывной связи между этим объектом и его логическим признаком. Ядром буддийского учения о выводе было правило «трёхаспектности» среднего термина (трайрупья) и классификация выводов в зависимости от разновидностей среднего термина: «основанные на причинно-следственной связи» (карья-анумана), «основанные на тождестве» (свабхава-анумана) и «отрицательные выводы» (анупалабдхи-анумана), для которых буддисты насчитывали 11 модусов. Правило трайрупья включало в вывод общие посылки, отсутствовавшие в пятичленном силлогизме найяиков. В соответствии с этим средний термин вывода должен был быть распределён в меньшей посылке, всегда присутствовать там, где есть больший и меньший термины, и отсутствовать там, где названные термины отсутствуют. В разрабатывавшейся буддистами теории значений (апоха-вада) обосновывалось чисто отрицательное значение всех имён и высказываний, т. е. решались проблемы логической семантики.
В 9 в. найяик Джаянта Бхатта объединил достижения буддистов и школы ньяя. Он принял дигнаговское разделение вывода на вывод «для себя» и «для других», усложнил правило трайрупья для среднего термина силлогизма, дополнив его двумя пунктами и превратив в правило «пятиаспектности». В логике вайшешиков правило трайрупья ввёл Прашастапада, сохранив при этом приверженность пятичленной модели вывода.
С появлением в 13 в. навья-ньяи (началом её считается трактат Гангеши Упадхьяи «Таттвачинтамани» – «Драгоценная мысль об истине») наступило время расцвета индийской логики. Основываясь на реалистической онтологии ньяи-вайшешики, представители навья-ньяи попытались показать, как категории «присутствуют» в объектах, что происходит во время получения знаний посредством четырёх инструментов-праман – восприятия, вывода, сравнения, слова – и их вербализации. Они ввели при этом ряд принципиально новых для индийской логики технических терминов и соответствующих концепций. Их логико-эпистемологическая доктрина описывает познающее мышление не столько со стороны его структуры, сколько со стороны природы тех процессов, результатом которых является знание связей между двумя когнитивными актами. При этом в когнитивном процессе различаются эпистемологический и логический аспекты. Теоретиками навья-ньяи были Вардхамана (середина 14 в.), Джаядева (Мишра) Пакшадхара (около 1425–1550), Рагхунатха Широмани (около 1475–1550), Васудева Сарвабхаума (около 1450–1525) и др. Они усовершенствовали логическую терминологию (ввели определения многих терминов) и двигались по направлению к формализации логики.
Со 2-й половины 17 в. перестали появляться новые логико-эпистемологические концепции. Ныне ньяя-вада, понимаемая как синкретическая теория познания и логики, остаётся обязательной составной частью классического религиозного образования. Продолжается деятельность комментаторов классических философских сочинений по ньяя-шастре в религиозных центрах Индии (в частности, в Нава-Наланде и Вайшали) и Тибета (в Лхасе); во многих учебных заведениях Индии существуют кафедры ньяи, где сочинения индийских логиков исследуются специалистами по санскритской литературе и индийской философии. На рубеже 20–21 вв. к логике навья-ньяи стали обращаться индийские логики и математики, считающие её наиболее подходящей для создания языков программирования.
Логика в Китае
Ориентированные на целостный логико-лингвистический анализ и эристическую проблематику (определение терминов, иерархизация категорий, выявление парадоксов, классификация правильных высказываний и т. п.), методологические построения древнекитайских философов, главным образом «школы имён» (мин цзя), школы моистов (мо цзя) и Сюнь-цзы, имеют в целом протологический характер, оставаясь диалектикой в её первоначальном смысле (ср. общий в этой сфере термин «бянь» – «красноречие/спор/диалектика»).
Истинность приводимых в наиболее логизированном трактате философской классики – «Мо-цзы» – образцовых высказываний зависит не только от того, какие иероглифы их составляют, но и от того, в каком значении они употребляются. В главном трактате «школы имён» – «Гунсунь Лун-цзы» – содержатся прямые нормативные высказывания о зависимости логической аргументации от языковой формы. Особенности этой протологической мысли определялись также иероглифическим характером китайской письменности. Аристотель стал основателем формальной логики в Европе, в частности, благодаря использованию букв для обозначения переменных. В Китае же не было таких не имеющих собственных лексических значений универсальных знаков, как буквы греческого алфавита; единственным видом китайских иероглифов, способных выполнять функцию переменных, являются циклические знаки (десятеричные «небесные стволы» и двенадцатеричные «земные ветви»), именно так и используемые в современной логической литературе под влиянием западной логики. Несмотря на некоторые общие свойства с буквами, циклические знаки принципиально отличаются тем, что не являются элементами для всех прочих иероглифов, как буквы – для слов. Кроме того, общий натуралистический характер традиционной китайской философии, отсутствие развитой идеалистической доктрины, подобной, например, платонизму, благодаря которому произошло осознание понятий как логически взаимосвязанных нематериальных сущностей, стали препятствием для развития формальной логики в Китае.
Впервые китайцев познакомили с логической теорией индийские буддисты. Совершивший в 7 в. паломничество в Индию Сюань Цзан для обозначения индийской логики создал термин «инь-мин» («освещение оснований», семантическая калька с санскритского «хету-видья»). В 17 в. появились переводы логических сочинений Аристотеля (М. Риччи), португальского учебника формальной логики (Ли Чжицзао, 1564/1565 – 1630), в начале 20 в. – логические работы Дж. С. Милля (Янь Фу, 1903) и У. С. Джевонса (Янь Фу, 1908; Ван Говэй, 1909); Ху Ши после учёбы в США выпустил новаторскую монографию «Развитие логического метода в древнем Китае» («The development of the logical method in ancient China», 1922). Употреблявшиеся при этом для передачи термина «логика» выражения «мин-ли-сюэ» (учение об именах и принципах), «мин-сюэ» (учение об именах), «ли-цзэ-сюэ» (учение о принципах и правилах) и «бянь-сюэ» (учение о различениях, диалектика, эристика) демонстрировали три обычные тенденции сведения логики к онтологии (учение о принципах – ли), лингвистике (учение об именах – мин) или эристике (учение о различениях в споре – бянь) и поддерживали представление о связи с исконной протологической традицией. Осознание специфики западной логики вызвало потребность в термине, подчёркивающем её принципиальную новизну для Китая. В период республики (1912–1949) им стал заимствованный из Японии «ронригаку»/«лунь-ли-сюэ» (учение о принципах суждений), а в КНР стандартизировалась фонетическая транскрипция «лоцзи(-сюэ)» (логика, учение о логике, наука логика), применённая ещё Янь Фу. Западные исследования китайской логики, начатые в 20 в. А. Форке (1867–1944; Германия), П. Массон-Урселем (1882–1956; Франция) и А. Масперо (1883–1945), продолжили Я. Хмелевский (1916–1998; Польша), А. Ч. Грэм (1919–1990; Великобритания), Ч. Хансен (род. 1942; США), К. Харбсмайер (род. 1946; Норвегия), в России – В. С. Спирин (1929–1992), А. М. Карапетьянц (род. 1943), А. И. Кобзев (род. 1953), А. А. Крушинский (род. 1953).
Ввиду отсутствия в китайском письменно-литературном языке вэньянь глагола-связки «быть» и производной от него субъектно-предикатной структуры предложения, являющейся лингвистически адекватной формой выражения логического закона тождества, в Китае не было выработано понятие тождества в логическом смысле. Грамматическая структура предложения в вэньяне характеризует лишь взаимосвязь описываемых в нём объектов, ничего не говоря о соотношении объёмов их понятий и более соответствуя логике отношений, чем логике предикатов или силлогистике Аристотеля, адекватной древнегреческому языку. Согласно Дж. Нидему, «отношение (лянь) было, возможно, более фундаментальной категорией китайской мысли, чем субстанция». Базовые категории (фань – «обратность», дуй – «супротивность», мао-дунь – «несовместность», буквально – [всепробивающее] копьё и [непробиваемый] щит) и даже сами отрицания (фэй, бу) здесь двусмысленны, что не позволяет однозначно судить, идёт ли речь о противоречии или противоположности, т. е. отношении A и не-A или A и Z, что делает нерелевантным закон исключённого третьего. Пытаясь определить «обоюдную допустимость/недопустимость» контрарно-контрадикторных альтернатив, Дэн Си, Чжуан-цзы, моисты и Хань Фэй последовательно перебрали все сочетания отрицания и конъюнкции. В итоге у них возобладала потенциально богатая идея антиконъюнкции (способной быть единственной исходной связкой для пропозиционального исчисления, что на Западе впервые около 1860 осознал Ч. Пирс, а в 1913 опубликовал американский логик Г. М. Шеффер). Антиконъюнкция же логически выражает несовместность, за которой, в свою очередь, стоит отношение противоположности. Отсюда проистекает неэксклюзивность китайских классификаций и традиция определений с помощью антонимов, синонимов и омонимов, а не через род и видовое отличие («логика противоположности», или «коррелятивной дуальности», согласно Чжан Дунсуню, 1884/1887 – 1972/1973). Другая фундаментальная для логики категория – «тун» [«одинаковость, равенство, подобие, совпадение, совместимость, (объ)единение»] – охватывает два принципиально разных понятия – тождества и подобия, что сущностно связано с недифференцированностью противоречия и противоположности, строго различавшихся в Европе после Аристотеля. Внутри синкретичных понятийных комплексов «подобие – тождество» и «противоположность – противоречие» главенство принадлежало первым, неформализуемым семантическим полюсам – «подобию» и «противоположности». «Тождество» и «противоречие» приобретают первостепенное значение, когда речь идёт об одном и том же объекте (субстанции, сущности), «подобие» и «противоположность» – когда о разных. Если для анализа единичного объекта наиболее важно то, чем он является и чем не является или с какими признаками отождествляем и какие ему противоречат, то для сопоставления разных объектов наиболее важно то, в чём они подобны друг другу и в чём противоположны. Концепция «сходства/подобия/одинаковости по роду» (тун лэй) играла роль теоретического базиса «коррелятивного (ассоциативного) мышления». Категория «тун», общая для протологики и нумерологии (сяншучжи-сюэ), подразумевает принципиальную множественность своих объектов, в онтологическом аспекте объединяемых в определённую целостность («единение»), в гносеологическом – охватываемых коррелятивной связью («родственностью»).
Не проводя чёткой границы между идеальным понятием/смыслом и материальным знаком/словом (то и другое есть «имя» – мин), китайские философы не выработали логической концепции общего как идеальной сущности, присущей целому классу материальных объектов. Поэтому китайские классификации не соблюдали соотношения общего и частного, признавая вместе с тем принцип «исходя из одного – знать многое»: «Посредством одного/единого познаётся десять тысяч/универсум» («Сюнь-цзы», гл. 5), при этом одним/единым в «Дао дэ цзине» (§ 21) называлось дао, «имя» которого «с древности до современности служит для постижения [всего] множества наименований». Одно/единое понимается, т. о., как конкретная целостность, а не абстрактная общность. Логически оно выступает репрезентативной абстракцией, представляющей выбранный объект собранием всех рассматриваемых признаков. Пиктографический этимон термина «общий» (гун), применявшегося в классификации имён/понятий, изображал две сведённые вместе руки, откуда самое общее значение – «сводить вместе, соединять», а не «отвлекать, абстрагировать», т. е. «разъединять». Это рождает идею соединяющего, т. е. центрального, начала: «Тридцать спиц соединяются (гун) в одной ступице» («Дао дэ цзин», § 11); здесь фиксируется связь через «спицы» между «обобщающим» центром – ступицей и «обобщаемой» периферией – ободом; предполагается подобное спице прямое материальное соединение означающего («имени») с означаемым («вещью/реалией»). Процедура обобщения становится объединением определённой совокупности материальных объектов (в том числе имён) вокруг центрального (главного) члена, что, согласно Сюнь-цзы, даёт в итоге «связующее имя» (юэ мин). Имя считалось одним из элементов обозначаемого им (концентрирующегося вокруг него) класса вещей, о чём с парадоксальной заострённостью свидетельствует изречение Хуэй Ши (380/350 – 300/260 до н. э.): «У петуха три ноги», в котором наряду с двумя физическими ногами имеется в виду и само слово «нога». В лексическом плане аналог репрезентативной абстракции – имя нарицательное (гун мин – «генерализирующее имя»). В «Мо-цзы» (глава 42) введён термин «сы мин» («частное имя») для обозначения собственных имён, которые назывались также просто именами.
Философские термины обозначали и определённый класс явлений в целом, и отдельный элемент этого класса. Например, «небо» (тянь) – это один член космологической триады «небо, человек, земля» и вся она целиком («природа») и т. п. В классе A, состоящем из элементов a … z, выделяется репрезентативный (главный, наиболее характерный) элемент x, обозначение которого переносится (уподобляется-отождествляется) на все остальные элементы (a = x, b = x … z = x), а затем – и на весь класс, т. е. осуществляется генерализация A = X. Классы объектов в китайском языке представляются именно как материальные множества, а не идеальные наборы абстрагированных признаков, требующих в качестве предпосылки лексические индивидуализации. Для репрезентации такого класса объектов степень общности репрезентирующего термина не имеет принципиального значения, т. е. общее может быть представлено посредством частного (индивидуального), а частное (индивидуальное) – посредством общего, поскольку репрезентация и генерализация не опираются на логически прояснённую родо-видовую иерархию.
При классификации и определении понятий китайские философы апеллировали не только к их логическому содержанию, но и к материальной форме: учитывались количество используемых знаков, их фонетика и графика. Подход к именам (словам) как к материальным объектам обусловливал также визуализацию и геометризацию представлений об их взаимных соотношениях. Та методологическая структурирующая роль, которую в Европе играла логика, в Китае принадлежала геометризированной комбинаторике, т. е. нумерологии. Генерализирующему обобщению присущи два аспекта – арифметический и геометрический, в которых обобщающий член соотносится с крайним (начальным, конечным – дуань) или центральным (срединным – чжун) элементом (т. е. в первом аспекте – с числом, во втором – с соответствующей позицией в традиционных матричных символах, представляющих собой симметричные геометрические или стереометрические фигуры). Идею «генерализации» передаёт синоним и омоним термина «гун», совмещающий «общее» (например, «общественное») с «главным» (например, «господин»). Если объём общего понятия в европейской логике составляют все единичные члены множества, определённого содержанием этого понятия, то объём репрезентативной абстракции – это единственный, центральный член множества, определяемого её содержанием. Выделение такого репрезентирующего члена может быть произведено по самым разным основаниям, предполагающим ценностный и нормативный подход. Сам понятийно-терминологический аппарат нацеливал внимание китайских философов на анализ соотносительной ценности и нормативных взаимоотношений отдельных вещей в мире и мира в целом как их совокупности. Характерная для Европы логика истинностных значений не соответствовала ценностно-нормативным установкам китайских мыслителей и не была ими создана.
Бирюков Борис Владимирович, Кузичева Зинаида Андреевна, Новоселов Михаил Михайлович, Карпенко Александр Степанович, Канаева Наталия Алексеевна, Кобзев Артем Игоревич
Дата публикации: 5 апреля 2023 г. в 15:24 (GMT+3)
1.1. Логика как наука
Логика относится к числу древнейших наук, первые учения которой о формах и способах рассуждений возникли еще в цивилизациях Древнего Востока (Китай, Индия). В западную культуру принципы и методы логики вошли главным образом благодаря усилиям античных греков. Развитая политическая жизнь в греческих государствах-полисах, борьба разных партий за влияние на массы свободных граждан, стремление решать возникавшие имущественные и иные конфликты через суд — все это требовало умения убеждать людей, защищать свою позицию на различных народных форумах, в государственных учреждениях, судебных заседаниях и т.п.
Искусство убеждения, ведения спора, мастерства обоснованно защищать свое мнение и возражать оппоненту в ходе спора и полемики культивировалось в рамках античной риторики, ориентированной на совершенствование ораторской речи, и эристики — специального учения о споре. Первые учителя риторики многое сделали для распространения и развития знаний о мастерстве убеждения, приемах спора и построения публичной речи, обращая особое внимание на эмоционально-психологические, нравственные и ораторские ее стороны и особенности. Однако впоследствии, когда школы риторики стали возглавлять софисты, они стремились научить своих учеников не поискам истины в ходе спора, а скорее выигрышу, победе в словесном состязании любой ценой. В этих целях широко использовались преднамеренные логические ошибки, которые в дальнейшем стали называть софизмами, а также разнообразные психологические уловки и приемы для отвлечения внимания оппонента, внушения, переключения спора с основной темы на второстепенные моменты и т.п.
Против этой тенденции в риторике решительно выступили великие античные философы Сократ, Платон и Аристотель, которые считали главным средством убеждения — обоснованность содержащихся в ораторской речи суждений, их правильную связь в процессе рассуждений, т.е. вывода одних суждений из других. Именно для анализа рассуждений и была создана Аристотелем (IV век до н.э.) первая система логики, названная силлогистикой. Она представляет собой простейшую, но вместе с тем наиболее часто используемую форму дедуктивных умозаключений, в которых заключение (вывод) получается из посылок по правилам логической дедукции. Заметим, что термин дедукция в переводе с латинского означает вывод.
Для пояснения сказанного обратимся к античному силлогизму:
Все люди смертны.
Кай — человек.
________________________________
Следовательно, Кай смертен.
Здесь, как и в других силлогизмах, умозаключение совершается от общего знания о некотором классе предметов и явлений к знанию частному и единичному. Сразу же подчеркнем, что в других случаях дедукция может осуществляться от частного к частному или от общего к общему.
Главное, что объединяет все дедуктивные умозаключения, состоит в том, что заключение в них следует из посылок по логическим правилам вывода и имеет достоверный, объективный характер. Другими словами, заключение не зависит от воли, желаний и предпочтений рассуждающего субъекта. Если вы принимаете посылки такого умозаключения, то обязаны принять и его заключение.
Часто также заявляют, что определяющим признаком дедуктивных умозаключений является логически необходимый характер заключения, его достоверная истинность. Иначе говоря, в таких умозаключениях истинностное значение посылок полностью переносится на заключение. Вот почему дедуктивные умозаключения обладают наибольшей силой убеждения и широко применяются не только для доказательства теорем в математике, но и всюду, где необходимы достоверные заключения.
Очень часто в учебниках логика определяется как наука о законах правильного мышления или же принципах и способах правильных умозаключений. Поскольку, однако, остается неясным, какое мышление считается правильным, то в первой части определения содержится скрытая тавтология, так как неявно предполагается, что такая правильность достигается при соблюдении правил логики. Во второй части предмет логики определяется точнее, ибо главная задача логики сводится к анализу умозаключений, т.е. к выявлению способов получения одних суждений из других. Нетрудно заметить, что когда говорят о правильных умозаключениях, то неявно или даже явно имеют в виду дедуктивную логику. Именно в ней только и существуют вполне определенные правила для логического вывода заключений из посылок, с которыми мы познакомимся более детально в дальнейшем. Часто дедуктивную логику отождествляют также с формальной логикой на том основании, что последняя изучает формы умозаключений в отвлечении от конкретного содержания суждений. Такой взгляд, однако, не учитывает других способов и форм рассуждений, которые широко применяются как в опытных науках, изучающих природу, так и в социально-экономических и гуманитарных науках, опирающихся на факты и результаты общественной жизни. Да и в повседневной практике мы часто делаем обобщения и строим предположения, исходя из наблюдения частных случаев.
Рассуждения подобного рода, в которых на основе исследования и проверки каких-либо частных случаев приходят к заключению о неизученных случаях или о всех явлениях класса в целом, называют индуктивными. Термин индукция означает наведение и хорошо выражает сущность таких рассуждений. В них обычно изучаются свойства и отношения некоторого числа членов определенного класса предметов и явлений. Выявленное в результате этого общее свойство или отношение затем переносится на неисследованные члены или на весь класс полностью. Очевидно, что такое заключение не может считаться достоверно истинным, ибо среди неисследованных членов класса и тем более всего класса в целом могут оказаться члены, которые не обладают предполагаемым общим свойством. Поэтому заключения индукции имеют не достоверный, а лишь вероятностный характер. Часто такие заключения называют также правдоподобными, гипотетическими или предположительными, так как они не гарантируют достижение истины, а лишь наводят на нее. Они имеют эвристический (поисковый), а не достоверный характер, помогая искать истину, а не доказывать ее. Наряду с индуктивными рассуждениями сюда относят также выводы по аналогии и статистические обобщения.
Отличительная особенность подобных недедуктивных рассуждений состоит в том, что в них заключение не следует логически, т.е. по правилам дедукции, из посылок. Посылки лишь с той или иной степенью подтверждают заключение, делают его более или менее вероятным или правдоподобным, но не гарантируют его достоверной истинности. На этом основании вероятностные рассуждения иногда явно недооцениваются, считаются второстепенными, вспомогательными и даже исключаются из логики.
Такое отношение к недедуктивной и, в частности к индуктивной логике объясняется в основном следующими причинами:
• Во-первых, — и это главное — проблематический, вероятностный характер индуктивных заключений и связанная с ним зависимость результатов от имеющихся данных, неотделимость от посылок, незавершенность заключений. Ведь с получением новых данных меняется и вероятность таких выводов.
• Во-вторых, наличие субъективных моментов в оценке вероятностного логического отношения между посылками и заключением рассуждения. Одному эти посылки, например факты и свидетельства, могут показаться убедительными, другому — нет. Один считает, что они достаточно сильно подтверждают заключение, другой придерживается противоположного мнения. Подобных разногласий не возникает при дедуктивном выводе.
• В-третьих, такое отношение к индукции объясняется также историческими обстоятельствами. Когда впервые возникла индуктивная логика, то ее создатели, в частности Ф. Бэкон, верили, что с помощью ее канонов, или правил, можно открывать новые истины в опытных науках чуть ли не чисто механическим путем. «Наш же путь открытия наук, — писал он, — немногое оставляет остроте и силе дарования, но почти уравнивает их. Подобно тому как для проведения прямой или описания совершенного круга много значат твердость, умелость и испытанность руки, если действовать только рукой, — мало или совсем ничего не значит, если пользоваться циркулем и линейкой. Так обстоит и с нашим методом». Говоря современным языком, творцы индуктивной логики рассматривали свои каноны как алгоритмы открытия. С развитием науки становилось все более очевидным, что с помощью таких правил (или алгоритмов) можно открывать лишь простейшие эмпирические связи между наблюдаемыми на опыте явлениями и характеризующими их величинами. Открытие же сложных связей и глубоких теоретических законов требовали использования всех средств и методов эмпирического и теоретического исследования, максимального применения психических и интеллектуальных способностей ученых, их опыта, интуиции и таланта. А это не могло не породить негативного отношения к механическому подходу к открытию, существовавшему раньше в индуктивной логике.
• В-четвертых, расширение форм дедуктивных умозаключений, появление логики отношений и, в особенности, применение математических методов для анализа дедукции, которое завершилось созданием символической (или математической) логики во многом способствовало выдвижению на первый план именно дедуктивной логики.
Все это делает понятным, почему нередко предпочитают определять логику как науку о способах, правилах и законах дедуктивных умозаключений или как теорию логического вывода. Но нельзя забывать, что индукция, аналогия и статистика являются важными способами эвристического поиска истины, а потому они служат рациональными методами рассуждений. Ведь поиск истины можно вести наудачу, путем проб и ошибок, но такой способ крайне неэффективен, хотя иногда и используется. Наука к нему прибегает весьма редко, поскольку она ориентируется на поиск организованный, целенаправленный и системный.
Надо также учитывать, что общие истины (эмпирические и теоретические законы, принципы, гипотезы и обобщения), которые используются как посылки дедуктивных умозаключений, невозможно установить дедуктивно. Но нам могут возразить, что они не открываются и индуктивно. Тем не менее поскольку индуктивные рассуждения ориентируются на поиск истины, то они оказываются более полезным эвристическим средством исследования. Разумеется, в ходе проверки предположений и гипотез используется и дедукция, в частности для вывода следствий из них. Поэтому нельзя противопоставлять дедукцию индукции, поскольку в реальном процессе научного познания они предполагают и дополняют друг друга.
Следовательно логику можно определить как науку о рациональных методах рассуждений, которые охватывают как анализ правил дедукции (вывода заключений из посылок), так и исследование степени подтверждения вероятностных или правдоподобных заключений (гипотез, обобщений, предположений и т.д.).
Традиционная логика, которая сформировалась на основе логического учения Аристотеля, дополнилась в дальнейшем методами индуктивной логики, сформулированными Ф. Бэконом и систематизированными Дж.С. Миллем. Именно эта логика в течение долгого времени преподавалась в школах и университетах под именем формальной логики.
Возникновение математической логики коренным образом изменило отношение между дедуктивной и недедуктивной логиками, которое существовало в традиционной логике. Это изменение было сделано в пользу дедукции. Благодаря символизации и применению математических методов сама дедуктивная логика приобрела строго формальный характер. По сути дела, такую логику вполне правомерно рассматривать как математическую модель дедуктивных умозаключений. Нередко поэтому ее считают современной ступенью развития формальной логики, но забывают при этом добавить, что речь идет о дедуктивной логике.
Нередко также говорят, что математическая логика сводит процесс рассуждения к построению различных систем исчислений и тем самым заменяет естественный процесс мышления вычислениями. Однако модель всегда связана с упрощениями, поэтому она не может заменить оригинал. Действительно, математическая логика ориентируется прежде всего на математические доказательства, следовательно, абстрагируется от характера посылок (или аргументов), их обоснованности и приемлемости. Она считает такие посылки заданными или ранее доказанными.
Между тем в реальном процессе рассуждения, в споре, дискуссии, полемике анализ и оценка посылок приобретает особо важное значение. В ходе аргументации приходится выдвигать определенные тезисы и утверждения, находить убедительные доводы в их защиту, исправлять и дополнять их, приводить контраргументы и т.д. Здесь приходится обращаться уже к неформальным и недедуктивным способам рассуждений, в частности к индуктивному обобщению фактов, выводам по аналогии, статистическому анализу и т.д.
Рассматривая логику как науку о рациональных способах рассуждений, мы не должны забывать о других формах мышления — понятиях и суждениях, с освещения которых начинается любой учебник логики. Но суждения и тем более понятия играют вспомогательную роль в логике. С их помощью становится более ясной структура умозаключений, связь суждений в различных видах рассуждений. Понятия же входят в структуру любого суждения в виде субъекта, т. е. предмета мысли, и предиката — как признака, характеризующего субъект, а именно утверждающего наличие или отсутствие у предмета мысли определенного свойства. В нашем изложении мы придерживаемся общепринятой традиции и начинаем обсуждение с анализа понятий и суждений, а затем более подробно освещаем дедуктивные и недедуктивные способы рассуждений. В главе, где анализируются суждения, рассматриваются элементы исчисления высказываний, с которых обычно открывается любой курс математической логики.
Элементы логики предикатов освещаются в следующей главе, где в качестве частного случая рассматривается теория категорического силлогизма. Современные формы недедуктивных рассуждений нельзя, очевидно, понять без четкого разграничения логической и статистической интерпретации вероятности, поскольку под вероятностью подразумевается чаще всего как раз ее статистическое истолкование, которое имеет вспомогательное значение в логике. В связи с этим в главе, посвященной вероятностным рассуждениям, мы специально останавливаемся на выяснении различия между двумя интерпретациями вероятности и более подробно разъясняем особенности логической вероятности.
Таким образом, весь характер изложения в книге ориентирует читателя на то, что дедукция и индукция, достоверность и вероятность, движение мысли от общего к частному и от частного к общему не исключают, а скорее дополняют друг друга в общем процессе рационального рассуждения, направленного как на поиск истины, так и ее доказательство.
Читайте также
§ 2. ФОРМАЛЬНАЯ ЛОГИКА КАК НАУКА
§ 2. ФОРМАЛЬНАЯ ЛОГИКА КАК НАУКА
Чтобы дать определение логической формы мысли и указать способы выявления логических форм различных мыслей, выделим среди выражений естественного языка термины, называемые логическими. К ним относятся союзы “и”, “или”, “если…, то…”,
Глава 1. ЛОГИКА КАК НАУКА
Глава 1. ЛОГИКА КАК НАУКА
Освоение проблем формальной логики требует глубокого понимания, в первую очередь, ее объекта и предмета как науки, уяснения методологической роли для конкретного вида деятельности. При этом решаются не только теоретические задачи. Познание
А. Логика
А. Логика
I. Задача логики
Форма науки сама составляет предмет особой науки, и эта наука – логика – всегда одна и та же, совершенно независимо от разнообразия объектов знания. Именно вследствие этого логика не может теоретически основываться на какой-либо одной науке,
3. Частная наука и универсальная наука.
3. Частная наука и универсальная наука.
— Если все знание внутренне взаимосвязано и постольку есть единое знание, сама собою напрашивается неопределенная мысль об одной-единственной универсальной науке. В таком случае, насколько вообще возможно деление, имело бы силу
Глава I ЛОГИКА КАК НАУКА
Глава I ЛОГИКА КАК НАУКА
§ 1. РОЛЬ МЫШЛЕНИЯ В ПОЗНАНИИ
Логика — наука о законах и формах, приемах и операциях мышления, с помощью которой человек познает окружающий мир. Данное определение предполагает прежде всего выяснение вопроса, сформулированного в названии
Логика
Логика
Существуют ли специфические тенденции в логике, связанные с наукой второй половины XX века? Анализ структуры теории относительности и квантовой механики приводит к представлению о мобильности исходных математических и логических норм науки, которая в
§ 2. ФОРМАЛЬНАЯ ЛОГИКА КАК НАУКА
§ 2. ФОРМАЛЬНАЯ ЛОГИКА КАК НАУКА
Чтобы дать определение логической формы мысли и указать способы выявления логических форм различных мыслей, выделим среди выражений естественного языка термины, называемые логическими. К ним относятся союзы “и”, “или”, “если…, то…”,
Вводный раздел. Логика как наука
Вводный раздел. Логика как наука
Прежде чем непосредственно приступить к проблематике логики, необходимо иметь хотя бы общее представление о самой этой науке — уяснить себе ее предмет, познакомиться с историей ее возникновения и развития вплоть до наших дней, осмыслить
§ 1. Логика как наука о типах порядка
§ 1. Логика как наука о типах порядка
В предыдущих главах мы видели, что обоснованность доказательства зависит не от истинности или ложности посылок, а от их формы, или структуры. В качестве фундаментальной задачи логики мы признали изучение этих объективных отношений
Глава 4. НАУКА САКРАЛЬНАЯ И НАУКА ПРОФАНИЧЕСКАЯ
Глава 4. НАУКА САКРАЛЬНАЯ И НАУКА ПРОФАНИЧЕСКАЯ
Выше мы показали, что в традиционных цивилизациях в основе всего лежит интеллектуальная интуиция. Иными словами, в таких цивилизациях самым существенным является чисто метафизическая доктрина, а все остальное проистекает
139. Логика
139. Логика
Деятельность может обеспечить только одну половину мудрости; другая половина зависит от воспринимающей бездеятельности. В конечном счете, спор между теми, кто основывает логику на «истине» и теми, кто основывает ее на «исследовании», происходит из различия в
Логика открытия и логика оправдания гипотезы
Логика открытия и логика оправдания гипотезы
В стандартной модели развития теории, которая разрабатывалась в рамках позитивистской традиции, логика открытия и логика обоснования резко разделялись и противопоставлялись друг другу. Отголоски этого противопоставления
Наука сакральная и наука для профанов
Наука сакральная и наука для профанов
Ранее мы уже говорили, что в традиционных обществах в основе всего находится интеллектуальная интуиция. Иначе говоря, метафизическая доктрина является самым важным элементом такого общества, а все остальные области человеческой
2. Наука не рождается из мифа, но наука всегда мифологична
2. Наука не рождается из мифа, но наука всегда мифологична
В связи с этим я категорически протестую против второго лженаучного предрассудка, заставляющего утверждать, что мифология предшествует науке, что наука появляется из мифа, что некоторым историческим эпохам, в
V. Логика
V. Логика
Пресловутый «скептицизм» Гассенди был не итогом, выводом его философии, а необходимой и исторически оправданной ее предпосылкой — не эпилогом, а прологом его неоэпикуреизма. Расчищая путь мысли от схоластических преград, он вместе с тем побуждал ее не