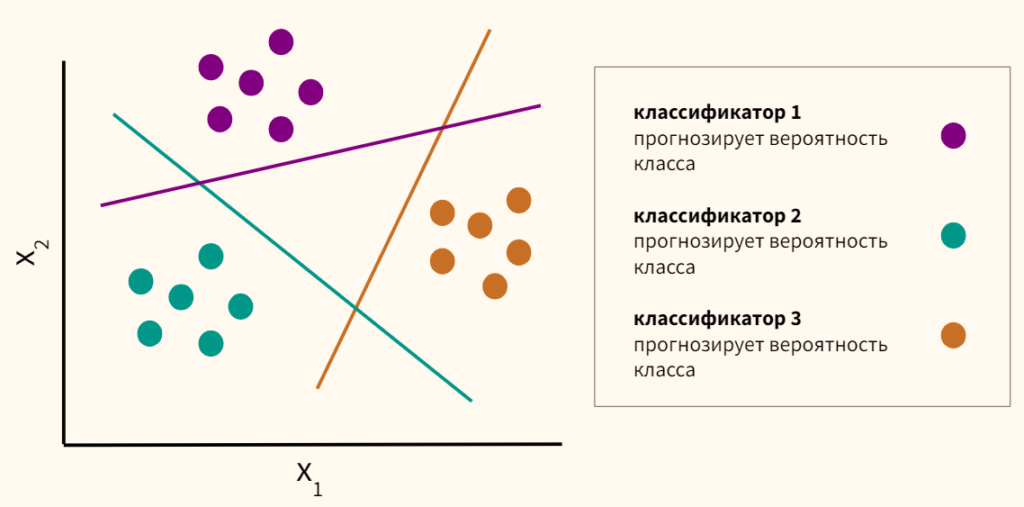
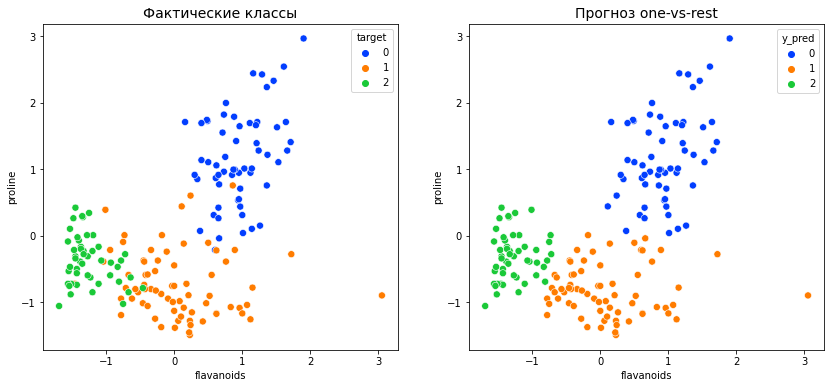
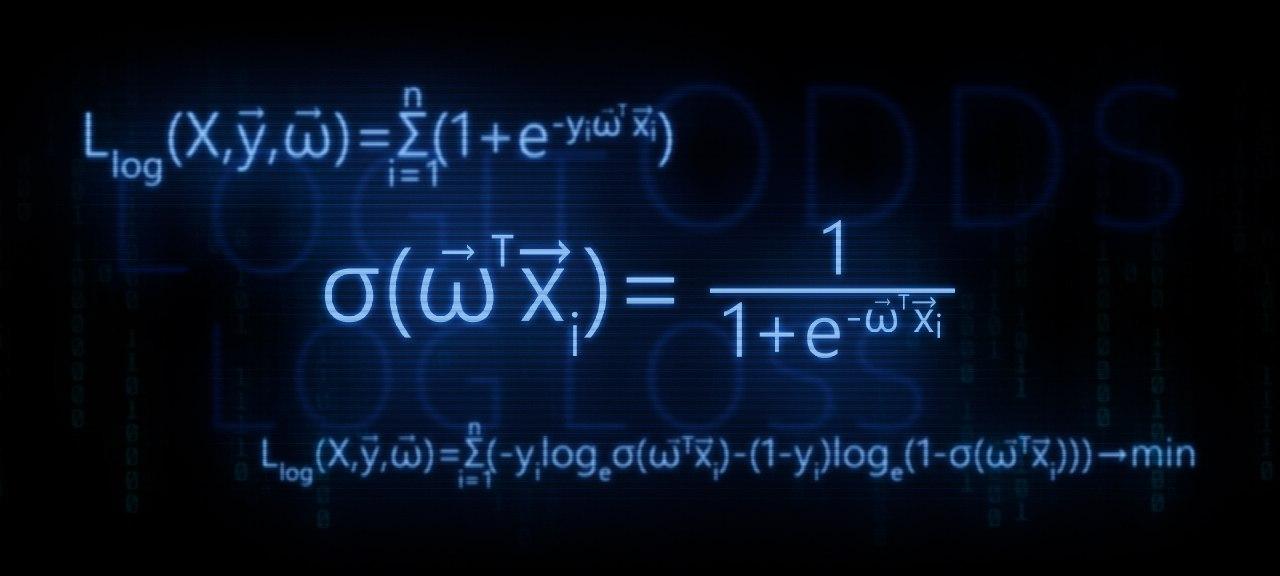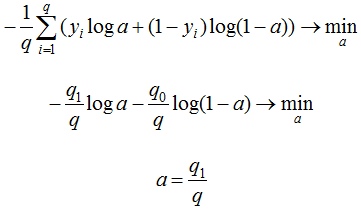Эту функцию называют также «логлосс» (logloss / log_loss), перекрёстной / кросс-энтропией (Cross Entropy) и часто используют в задачах классификации. Разберёмся, почему её используют и какой смысл она имеет. Для чтения поста нужна неплохая ML-математическая подготовка, но даже новичкам я бы рекомендовал почитать (хотя я не очень заботился, чтобы «всё объяснялось на пальцах»).
Начнём издалека…
Вспомним, как решается задача линейной регрессии. Итак, мы хотим получить линейную функцию (т.е. веса w), которая приближает целевое значение с точностью до ошибки:
Здесь мы предположили, что ошибка нормально распределена, x – признаковое описание объекта (возможно, в нём есть и фиктивный константный признак, чтобы в линейной функции был свободный член). Тогда мы знаем как распределены ответы нашей функции и можем записать функцию правдоподобия выборки (т.е. произведение плотностей, в которые подставлены значения из обучающей выборки) и воспользоваться методом максимального правдоподобия (в котором для определения значений параметров берётся максимум правдоподобия, а чаще – его логарифма):
В итоге оказывается, что максимизация правдоподобия эквивалентна минимизации среднеквадратичной ошибки (MSE), т.е. эта функция ошибки не зря широко используется в задачах регрессии. Кроме того, что она вполне логична, легко дифференцируема по параметрам и легко минимизируется, она ещё и теоретически обосновывается с помощью метода максимального правдоподобия в случае, если линейная модель соответствует данным с точностью до нормального шума.
Давайте ещё посмотрим, как реализуется метод стохастического градиента (SGD) для минимизации MSE: надо взять производную функции ошибки для конкретного объекта и записать формулу коррекции весов в виде «шага в сторону антиградиента»:
Получили, что веса линейной модели при её обучении методом SGD корректируются с помощью добавки вектора признаков. Коэффициент, с которым добавляют, зависит от «агрессивности алгоритма» (параметр альфа, который называют темпом обучения) и разности «ответ алгоритма – правильный ответ». Кстати, если разница нулевая (т.е. на данном объекте алгоритм выдаёт точный ответ), то коррекция весов не производится.
Log Loss
Теперь давайте, наконец, поговорим о «логлоссе». Рассматриваем задачу классификации с двумя классами: 0 и 1. Обучающую выборку можно рассматривать, как реализацию обобщённой схемы Бернулли: для каждого объекта генерируется случайная величина, которая с вероятностью p (своей для каждого объекта) принимает значение 1 и с вероятностью (1–p) – 0. Предположим, что мы как раз и строим нашу модель так, чтобы она генерировала правильные вероятности, но тогда можно записать функцию правдоподобия:
После логарифмирования правдоподобия получили, что его максимизация эквивалентна минимизации последнего записанного выражения. Именно его и называют «логистической функции ошибки». Для задачи бинарной классификации, в которой алгоритм должен выдать вероятность принадлежности классу 1, она логична ровно настолько, насколько логична MSE в задаче линейной регрессии с нормальным шумом (поскольку обе функции ошибки выводятся из метода максимального правдоподобия).
Часто гораздо более понятна такая запись logloss-ошибки на одном объекте:
Отметим неприятное свойство логосса: если для объекта 1го класса мы предсказываем нулевую вероятность принадлежности к этому классу или, наоборот, для объекта 0го – единичную вероятность принадлежности к классу 1, то ошибка равна бесконечности! Таким образом, грубая ошибка на одном объекте сразу делает алгоритм бесполезным. На практике часто логлосс ограничивают каким-то большим числом (чтобы не связываться с бесконечностями).
Если задаться вопросом, какой константный алгоритм оптимален для выборки из q_1 представителей класса 1 и q_0 представителей класса 0, q_1 + q_0 = q , то получим
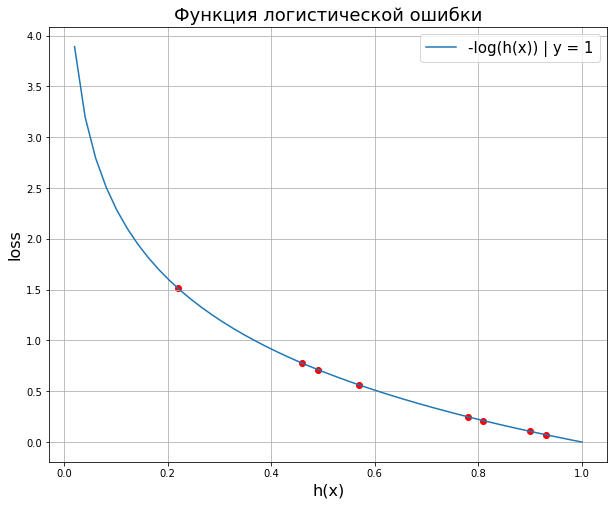
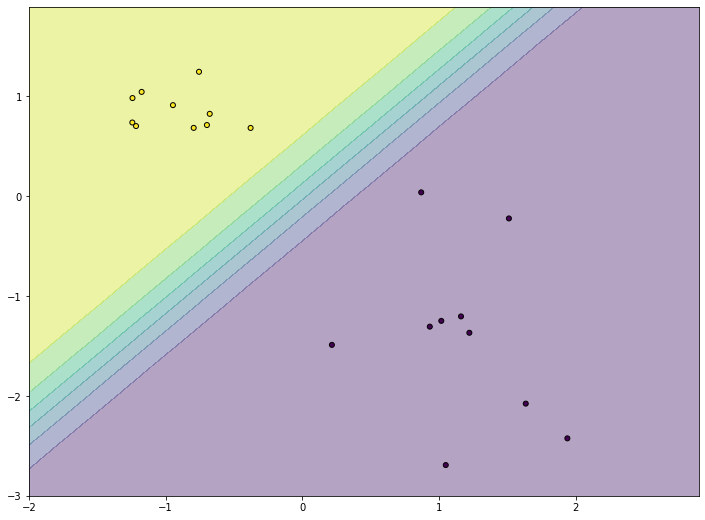
Последний ответ получается взятием производной и приравниванием её к нулю. Описанную задачу приходится решать, например, при построении решающих деревьев (какую метку приписывать листу, если в него попали представители разных классов). На рис. 2 изображён график log_loss-ошибки константного алгоритма для выборки из четырёх объектов класса 0 и 6 объектов класса 1.
Представим теперь, что мы знаем, что объект принадлежит к классу 1 вероятностью p, посмотрим, какой ответ оптимален на этом объекте с точки зрения log_loss: матожидание нашей ошибки
Для минимизации ошибки мы опять взяли производную и приравняли к нулю. Мы получили, что оптимально для каждого объекта выдавать его вероятность принадлежности к классу 1! Таким образом, для минимизации log_loss надо уметь вычислять (оценивать) вероятности принадлежности классам!
Если подставить полученное оптимальное решение в минимизируемый функционал, то получим энтропию:
Это объясняет, почему при построении решающих деревьев в задачах классификации (а также случайных лесов и деревьях в бустингах) применяют энтропийный критерий расщепления (ветвления). Дело в том, что оценка принадлежности к классу 1 часто производится с помощью среднего арифметического меток в листе. В любом случае, для конкретного дерева эта вероятность будет одинакова для всех объектов в листе, т.е. константой. Таким образом, энтропия в листе примерно равна логлосс-ошибке константного решения. Используя энтропийный критерий мы неявно оптимизируем логлосс!
В каких пределах может варьироваться logloss? Ясно, что минимальное значение 0, максимальное – +∞, но эффективным максимальным можно считать ошибку при использовании константного алгоритма (вряд же мы в итоге решения задачи придумаем алгоритм хуже константы?!), т.е.
Интересно, что если брать логарифм по основанию 2, то на сбалансированной выборке это отрезок [0, 1].
Связь с логистической регрессией
Слово «логистическая» в названии ошибки намекает на связь с логистической регрессией – это как раз метод для решения задачи бинарной классификации, который получает вероятность принадлежности к классу 1. Но пока мы исходили из общих предположений, что наш алгоритм генерирует эту вероятность (алгоритмом может быть, например, случайный лес или бустинг над деревьями). Покажем, что тесная связь с логистической регрессией всё-таки есть… посмотрим, как настраивается логистическая регрессия (т.е. сигмоида от линейной комбинации) на эту функцию ошибки методом SGD.
Как видим, корректировка весов точно такая же, как и при настройке линейной регрессии! На самом деле, это говорит о родстве разных регрессий: линейной и логистической, а точнее, о родстве распределений: нормального и Бернулли. Желающие могут внимательно почитать лекцию Эндрю Ына.
Во многих книгах логистической функцией ошибки (т.е. именно «logistic loss») называется другое выражение, которое мы сейчас получим, подставив выражение для сигмоиды в logloss и сделав переобозначение: считаем, что метки классов теперь –1 и +1, тогда
Полезно посмотреть на график функции, центральной в этом представлении:
Как видно, это сглаженный (всюду дифференцируемый) аналог функции max(0, x), которую в глубоком обучении принято называть ReLu (Rectified Linear Unit). Если при настройке весов минимизировать logloss, то таким образом мы настраиваем классическую логистическую регрессию, если же использовать ReLu, чуть-чуть подправить аргумент и добавить регуляризацию, то получаем классическую настройку SVM:
выражение под знаком суммы принято называть Hinge loss. Как видим, часто с виду совсем разные методы можно получать «немного подправив» оптимизируемые функции на похожие. Между прочим, при обучении RVM (Relevance vector machine) используется тоже очень похожий функционал:
Связь с расхождением Кульбака-Лейблера
Расхождение (дивергенцию) Кульбака-Лейблера (KL, Kullback–Leibler divergence) часто используют (особенно в машинном обучении, байесовском подходе и теории информации) для вычисления непохожести двух распределений. Оно определяется по следующей формуле:
где P и Q – распределения (первое обычно «истинное», а второе – то, про которое нам интересно, насколько оно похоже на истинное), p и q – плотности этих распределений. Часто KL-расхождение называют расстоянием, хотя оно не является симметричным и не удовлетворяет неравенству треугольника. Для дискретных распределений формулу записывают так:
P_i, Q_i – вероятности дискретных событий. Давайте рассмотрим конкретный объект x с меткой y. Если алгоритм выдаёт вероятность принадлежности первому классу – a, то предполагаемое распределение на событиях «класс 0», «класс 1» – (1–a, a), а истинное – (1–y, y), поэтому расхождение Кульбака-Лейблера между ними
что в точности совпадает с logloss.
Настройка на logloss
Один из методов «подгонки» ответов алгоритма под logloss – калибровка Платта (Platt calibration). Идея очень простая. Пусть алгоритм порождает некоторые оценки принадлежности к 1му классу – a. Метод изначально разрабатывался для калибровки ответов алгоритма опорных векторов (SVM), этот алгоритм в простейшей реализации разделяет объекты гиперплоскостью и просто выдаёт номер класса 0 или 1, в зависимости от того, с какой стороны гиперплоскости объект расположен. Но если мы построили гиперплоскость, то для любого объекта можем вычислить расстояние до неё (со знаком минус, если объект лежит в полуплоскости нулевого класса). Именно эти расстояния со знаком r мы будем превращать в вероятности по следующей формуле:
неизвестные параметры α, β обычно определяются методом максимального правдоподобия на отложенной выборке (calibration set).
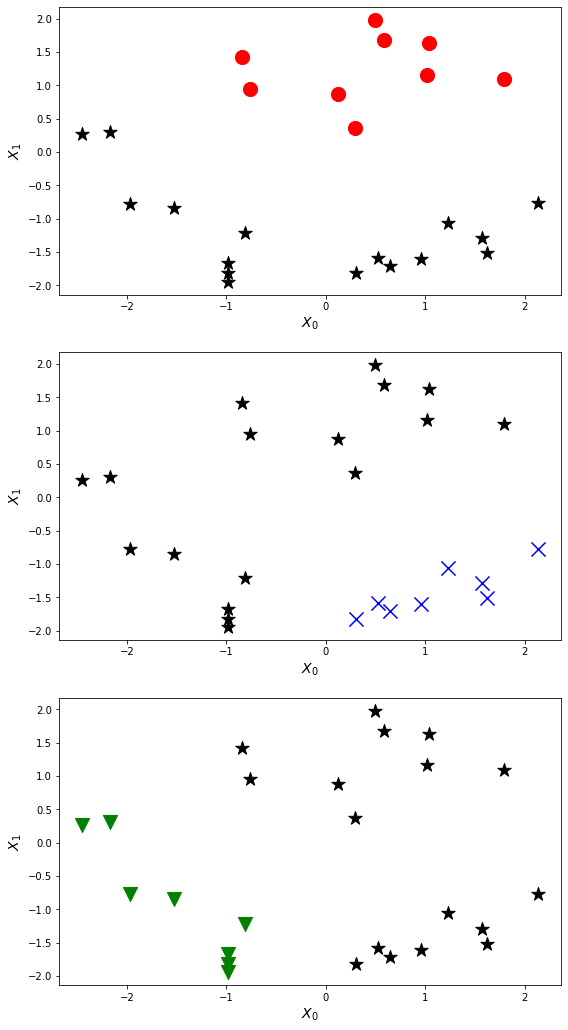
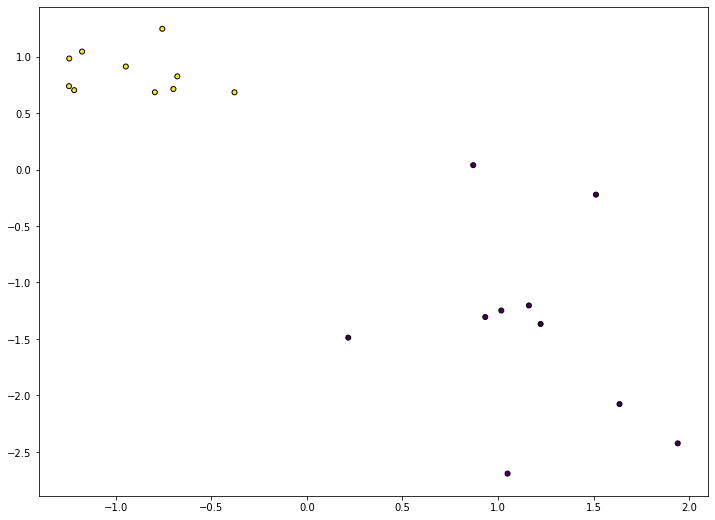
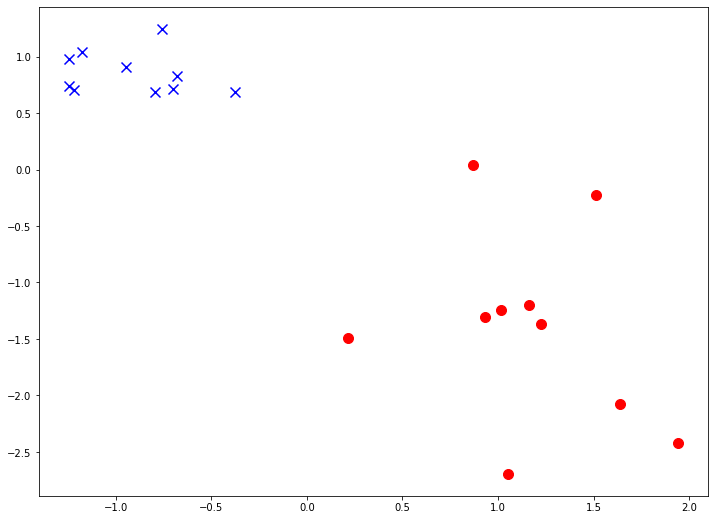
Проиллюстрируем применение метода на реальной задаче, которую автор решал недавно. На рис. показаны ответы (в виде вероятностей) двух алгоритмов: градиентного бустинга (lightgbm) и случайного леса (random forest).
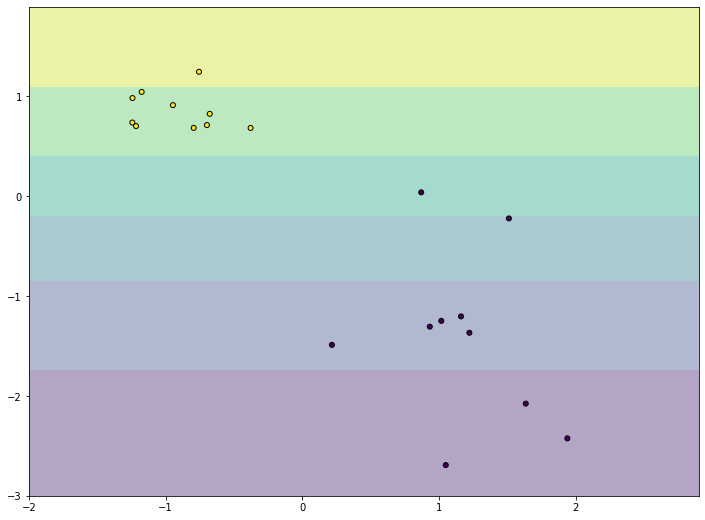
Видно, что качество леса намного ниже и он довольно осторожен: занижает вероятности у объектов класса 1 и завышает у объектов класса 0. Упорядочим все объекты по возрастанию вероятностей (RF), разобьем на k равных частей и для каждой части вычислим среднее всех ответов алгоритма и среднее всех правильных ответов. Результат показан на рис. 5 – точки изображены как раз в этих двух координатах.
Нетрудно видеть, что точки располагаются на линии, похожей на сигмоиду – можно оценить параметр сжатия-растяжения в ней, см. рис. 6. Оптимальная сигмоида показана розовым цветом на рис. 5. Если подвергать ответы такой сигмоидной деформации, то логлосс-ошибка случайного леса снижается с 0.37 до 0.33.
Обратите внимание, что здесь мы деформировали ответы случайного леса (это были оценки вероятности – и все они лежали на отрезке [0, 1]), но из рис. 5 видно, что для деформации нужна именно сигмоида. Практика показывает, что в 80% ситуаций для улучшения logloss-ошибки надо деформировать ответы именно с помощью сигмоиды (для меня это также часть объяснения, почему именно такие функции успешно используются в качестве функций активаций в нейронных сетях).
Ещё один вариант калибровки – монотонная регрессия (Isotonic regression).
Многоклассовый logloss
Для полноты картины отметим, что logloss обобщается и на случай нескольких классов естественным образом:
здесь q – число элементов в выборке, l – число классов, a_ij – ответ (вероятность) алгоритма на i-м объекте на вопрос принадлежности его к j-му классу, y_ij=1 если i-й объект принадлежит j-му классу, в противном случае y_ij=0.
На посошок…
В каждом подобном посте я стараюсь написать что-то из мира машинного обучения, что, с одной стороны, просто и понятно, а с другой – изложение этого не встречается больше нигде. Например, есть такой естественный вопрос: почему в задачах классификации при построении решающих деревьев используют энтропийный критерий расщепления? Во всех курсах его (критерий) преподносят либо как эвристику, которую «вполне естественно использовать», либо говорят, что «энтропия похожа на кросс-энтропию». Сейчас стоимость некоторых курсов по машинному обучению достигает нескольких сотен тысяч рублей, но «профессиональные инструкторы» не могут донести простую цепочку:
- в статистической теории обучения настройка алгоритма производится максимизацией правдоподобия,
- в задаче бинарной классификации это эквивалентно минимизации логлосса, а сам минимум как раз равен энтропии,
- поэтому использование энтропийного критерия фактически эквивалентно выбору расщепления, минимизирующего логлосс.
Если Вы всё-таки отдали несколько сотен тысяч рублей, то можете проверить «профессиональность инструктора» следующими вопросами:
- Энтропия в листе примерно равна logloss-ошибке константного решения. Почему не использовать саму ошибку, а не приближённое значение? Или, как часто происходит в задачах оптимизации, её верхнюю оценку?
- Минимизации какой ошибки соответствует критерий расщепления Джини?
- Можно показать, что если в задаче бинарной классификации использовать в качестве функции ошибки среднеквадратичное отклонение, то также, как и для логлосса, оптимальным ответом на объекте будет вероятность его принадлежности к классу 1. Почему тогда не использовать такую функцию ошибки?
Ответы типа «так принято», «такой функции не существует», «это только для регрессии», естественно, заведомо неправильные. Если Вам не ответят с такой же степенью подробности, как в этом посте, то Вы точно переплатили;)
П.С. Что ещё почитать…
В этом блоге я публиковал уже несколько постов по метрикам качества…
- AUC ROC (площадь под кривой ошибок)
- Задачки про AUC (ROC)
- Знакомьтесь, Джини
И буквально на днях вышла классная статья Дмитрия Петухова про коэффициент Джини, читать обязательно:
- Коэффициент Джини. Из экономики в машинное обучение
В этой статье, мы будем разбирать теоретические выкладки преобразования функции линейной регрессии в функцию обратного логит-преобразования (иначе говорят, функцию логистического отклика). Затем, воспользовавшись арсеналом метода максимального правдоподобия, в соответствии с моделью логистической регрессии, выведем функцию потерь Logistic Loss, или другими словами, мы определим функцию, с помощью которой в модели логистической регрессии подбираются параметры вектора весов
.
План статьи:
- Повторим о прямолинейной зависимости между двумя переменными
- Выявим необходимость преобразования функции линейной регрессии
в функцию логистического отклика
- Проведем преобразования и выведем функцию логистического отклика
- Попытаемся понять, чем плох метод наименьших квадратов при подборе параметров
функции Logistic Loss
- Используем метод максимального правдоподобия для определения функции подбора параметров
:
5.1. Случай 1: функция Logistic Loss для объектов с обозначением классов 0 и 1:
5.2. Случай 2: функция Logistic Loss для объектов с обозначением классов -1 и +1:
Статья изобилует простыми примерами, в которых все расчеты легко произвести устно или на бумаге, в некоторых случаях может потребоваться калькулятор. Так что подготовьтесь 
Данная статья в большей мере рассчитана на датасайнтистов с начальным уровнем познаний в основах машинного обучения.
В статье также будет приведен код для отрисовки графиков и расчетов. Весь код написан на языке python 2.7. Заранее поясню о «новизне» используемой версии — таково одно из условий прохождения известного курса от Яндекса на не менее известной интернет-площадке онлайн образования Coursera, и, как можно предположить, материал подготовлен по мотивам этого курса.
01. Прямолинейная зависимость
Вполне резонно задать вопрос — причем здесь прямолинейная зависимость и логистическая регрессия?
Все просто! Логистическая регрессия представляет собой одну из моделей, которые относятся к линейному классификатору. Простыми словами, задачей линейного классификатора является предсказание целевых значений
от переменных (регрессоров)
. При этом считается, что зависимость между признаками
и целевыми значениями
линейная. Отсюда собственно и название классификатора — линейный. Если очень грубо обобщить, то в основе модели логистической регрессии лежит предположение о наличии линейной зависимости между признаками
и целевыми значениями
. Вот она — связь.
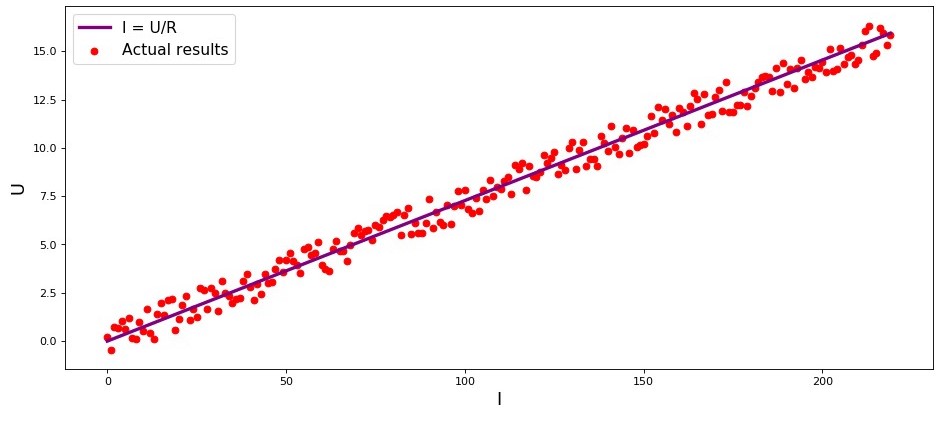
В студии первый пример, и он, правильно, о прямолинейной зависимости исследуемых величин. В процессе подготовки статьи наткнулся на пример, набивший уже многим оскомину — зависимость силы тока от напряжения («Прикладной регрессионный анализ», Н.Дрейпер, Г.Смит). Здесь мы его тоже рассмотрим.
В соответствии с законом Ома:
, где
— сила тока,
— напряжение,
— сопротивление.
Если бы мы не знали закон Ома, то могли бы найти зависимость эмпирически, изменяя
и измеряя
, поддерживая при этом
фиксированным. Тогда мы бы увидели, что график зависимости
от
дает более или менее прямую линию, проходящую через начало координат. Мы сказали «более или менее», так как, хотя зависимость фактически точная, наши измерения могут содержать малые ошибки, и поэтому точки на графике, возможно не попадут строго на линию, а будут разбросаны вокруг нее случайным образом.
График 1 «Зависимость
от
»
Код отрисовки графика
import matplotlib.pyplot as plt
%matplotlib inline
import numpy as np
import random
R = 13.75
x_line = np.arange(0,220,1)
y_line = []
for i in x_line:
y_line.append(i/R)
y_dot = []
for i in y_line:
y_dot.append(i+random.uniform(-0.9,0.9))
fig, axes = plt.subplots(figsize = (14,6), dpi = 80)
plt.plot(x_line,y_line,color = 'purple',lw = 3, label = 'I = U/R')
plt.scatter(x_line,y_dot,color = 'red', label = 'Actual results')
plt.xlabel('I', size = 16)
plt.ylabel('U', size = 16)
plt.legend(prop = {'size': 14})
plt.show()
02. Необходимость преобразований уравнения линейной регрессии
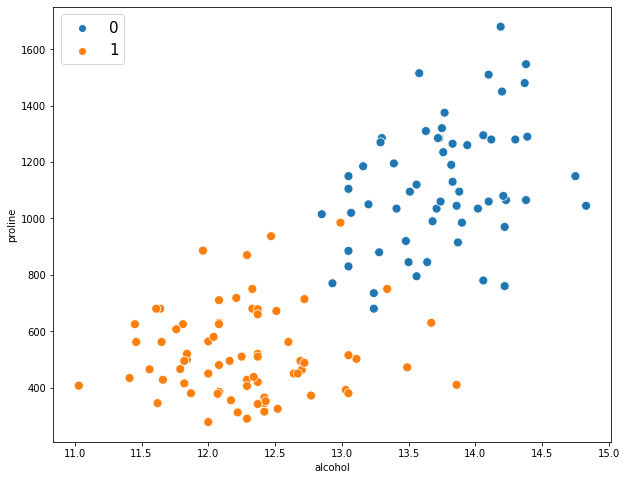
Рассмотрим очередной пример. Представим, что мы работаем в банке и перед нами задача определить вероятность возврата кредита заемщиком в зависимости от некоторых факторов. Для упрощения задачи, рассмотрим только два фактора: месячная зарплата заемщика и месячный размер платежа на погашение кредита.
Задача очень условная, но на этом примере мы сможем понять, почему для ее решения недостаточно применения функции линейной регрессии, а также узнаем какие преобразования с функцией требуется провести.
Возвращаемся к примеру. Понятно, что чем выше зарплата, тем больше заемщик сможет ежемесячно направлять на погашение кредита. При этом, для определенного диапазона зарплат эта зависимость будет вполне себе линейная. Например, возьмем диапазон зарплат от 60.000Р до 200.000Р и предположим, что в указанном диапазоне заработных плат, зависимость размера ежемесячного платежа от размера заработной платы — линейная. Допустим, для указанного диапазона размера заработных плат было выявлено, что соотношение зарплаты к платежу не может опускаться ниже 3 и еще у заемщика должно оставаться в запасе 5.000Р. И только в таком случае, мы будем считать, что заемщик вернет кредит банку. Тогда, уравнение линейной регрессии примет вид:
где
,
,
,
— зарплата
-го заемщика,
— платеж по кредиту
-го заемщика.
Подставляя в уравнение зарплату и платеж по кредиту с фиксированными параметрами
можно принять решение о выдаче или отказе кредита.
Забегая вперед, отметим, что, при заданных параметрах
функция линейной регрессии, применяемая в функции логистичиеского отклика будет выдавать большие значения, которые затруднят проведение расчетов по определению вероятностей погашения кредита. Поэтому, предлагается уменьшить наши коэффициенты, скажем так, в 25.000 раз. От этого преобразования в коэффициентах, решение о выдачи кредита не изменится. Запомним этот момент на будущее, а сейчас чтобы было еще понятнее, о чем речь, рассмотрим ситуация с тремя потенциальными заемщиками.
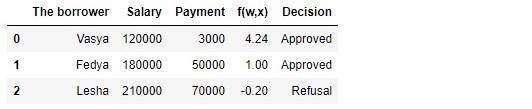
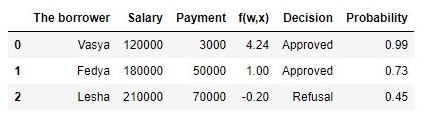
Таблица 1 «Потенциальные заемщики»
Код для формирования таблицы
import pandas as pd
r = 25000.0
w_0 = -5000.0/r
w_1 = 1.0/r
w_2 = -3.0/r
data = {'The borrower':np.array(['Vasya', 'Fedya', 'Lesha']),
'Salary':np.array([120000,180000,210000]),
'Payment':np.array([3000,50000,70000])}
df = pd.DataFrame(data)
df['f(w,x)'] = w_0 + df['Salary']*w_1 + df['Payment']*w_2
decision = []
for i in df['f(w,x)']:
if i > 0:
dec = 'Approved'
decision.append(dec)
else:
dec = 'Refusal'
decision.append(dec)
df['Decision'] = decision
df[['The borrower', 'Salary', 'Payment', 'f(w,x)', 'Decision']]
В соответствии с данными таблицы, Вася при зарплате в 120.000Р хочет получить такой кредит, чтобы ежемесячного гасить его по 3.000Р. Нами было определено, что для одобрения кредита, размер заработной платы Васи должен превышать в три раза размер платежа, и чтобы еще оставалось 5.000Р. Этому требованию Вася удовлетворяет:
. Остается даже 106.000Р. Несмотря на то, что при расчете
мы уменьшили коэффициенты
в 25.000 раз, результат получили тот же — кредит может быть одобрен. Федя тоже получит кредит, а вот Леше, несмотря на то, что он получает больше всех, придется поумерить свои аппетиты.
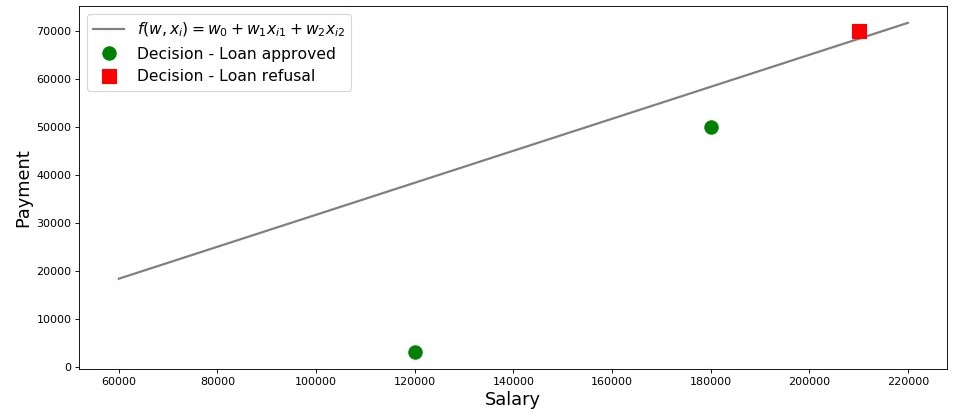
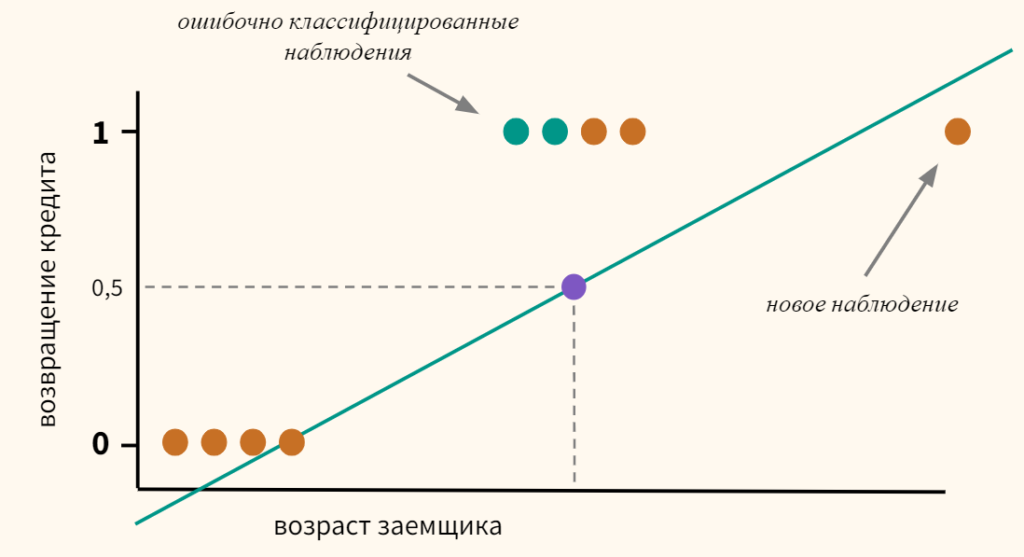
Нарисуем график по такому случаю.
График 2 «Классификация заемщиков»
Код для отрисовки графика
salary = np.arange(60000,240000,20000)
payment = (-w_0-w_1*salary)/w_2
fig, axes = plt.subplots(figsize = (14,6), dpi = 80)
plt.plot(salary, payment, color = 'grey', lw = 2, label = '$f(w,x_i)=w_0 + w_1x_{i1} + w_2x_{i2}$')
plt.plot(df[df['Decision'] == 'Approved']['Salary'], df[df['Decision'] == 'Approved']['Payment'],
'o', color ='green', markersize = 12, label = 'Decision - Loan approved')
plt.plot(df[df['Decision'] == 'Refusal']['Salary'], df[df['Decision'] == 'Refusal']['Payment'],
's', color = 'red', markersize = 12, label = 'Decision - Loan refusal')
plt.xlabel('Salary', size = 16)
plt.ylabel('Payment', size = 16)
plt.legend(prop = {'size': 14})
plt.show()
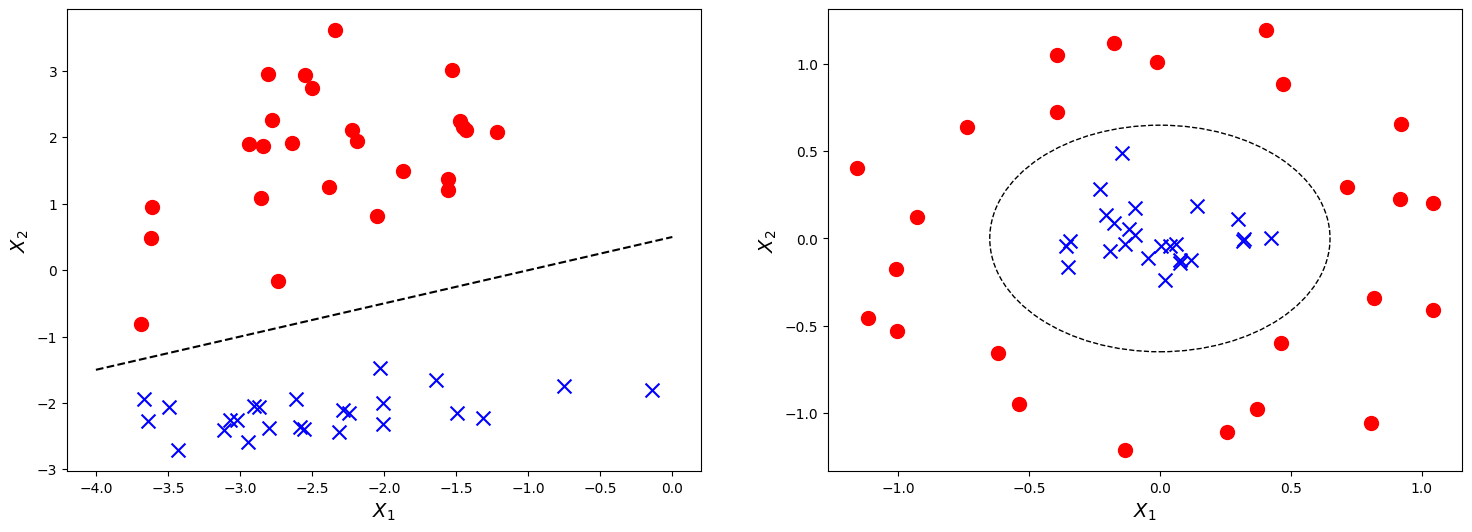
Итак, наша прямая, построенная в соответствии с функцией
, отделяет «плохих» заемщиков от «хороших». Те заемщики, у кого желания не совпадают с возможностями находятся выше прямой (Леша), те же, кто способен согласно параметрам нашей модели, вернуть кредит, находятся под прямой (Вася и Федя). Иначе можно сказать так — наша прямая разделяет заемщиков на два класса. Обозначим их следующим образом: к классу
отнесем тех заемщиков, которые скорее всего вернут кредит, к классу
или
отнесем тех заемщиков, которые скорее всего не смогут вернуть кредит.
Обобщим выводы из этого простенького примера. Возьмем точку
и, подставляя координаты точки в соответствующее уравнение прямой
, рассмотрим три варианта:
- Если точка находится под прямой, и мы относим ее к классу
, то значение функции
будет положительным от
до
. Значит мы можем считать, что вероятность погашения кредита, находится в пределах
. Чем больше значение функции, тем выше вероятность.
- Если точка находится над прямой и мы относим ее к классу
или
, то значение функции будет отрицательным от
до
. Тогда мы будем считать, что вероятность погашения задолженности находится в пределах
и, чем больше по модулю значение функции, тем выше наша уверенность.
- Точка находится на прямой, на границе между двумя классами. В таком случае значение функции
будет равно
и вероятность погашения кредита равна
.
Теперь, представим, что у нас не два фактора, а десятки, заемщиков не три, а тысячи. Тогда вместо прямой у нас будет m-мерная плоскость и коэффициенты
у нас будут взяты не с потолка, а выведены по всем правилам, да на основе накопленных данных о заемщиках, вернувших или не вернувших кредит. И действительно, заметьте, мы сейчас отбираем заемщиков при уже известных коэффициентах
. На самом же деле, задача модели логистической регрессии как раз и состоит в том, чтобы определить параметры
, при которых значение функции потерь Logistic Loss будет стремиться к минимальному. Но о том, как рассчитывается вектор
, мы еще узнаем в 5-м разделе статьи. А пока возвращаемся на землю обетованную — к нашему банкиру и трем его клиентам.
Благодаря функции
мы знаем кому можно дать кредит, а кому нужно отказать. Но с такой информацией к директору идти нельзя, ведь от нас хотели получить вероятность возврата кредита каждым заемщиком. Что делать? Ответ простой — нам нужно как-то преобразовать функцию
, значения которой лежат в диапазоне
на функцию, значения которой будут лежать в диапазоне
. И такая функция существует, ее называют функцией логистического отклика или обратного-логит преобразования. Знакомьтесь:
Посмотрим по шагам как получается функция логистического отклика. Отметим, что шагать мы будем в обратную сторону, т.е. мы предположим, что нам известно значение вероятности, которое лежит в пределах от
до
и далее мы будем «раскручивать» это значение на всю область чисел от
до
.
03. Выводим функцию логистического отклика
Шаг 1. Переведем значения вероятности в диапазон 
На время трансформации функции
в функцию логистического отклика
мы оставим в покое нашего кредитного аналитика, а вместо этого пройдемся по букмекерским конторам. Нет, конечно, ставки делать мы не будем, все что нас там интересует, так это смысл выражения, например, шанс 4 к 1. Шансы, знакомые всем делающим ставки игрокам, являются соотношением «успехов» к «неуспехам». С точки зрения вероятностей, шансы — это вероятность наступления события, деленная на вероятность того, что событие не произойдет. Запишем формулу шанса наступления события
:
, где
— вероятность наступления события,
— вероятность НЕ наступления события
Например, если вероятность того, что молодой, сильный и резвый конь по прозвищу «Ветерок» обойдет на скачках старую и дряблую старушку по кличке «Матильда» равняется
, то шансы на успех «Ветерка» составят
к
и наоборот, зная шансы, нам не составит труда вычислить вероятность
:
Таким образом, мы научились «переводить» вероятность в шансы, которые принимают значения от
до
. Сделаем еще один шаг и научимся «переводить» вероятность на всю числовую прямую от
до
.
Шаг 2. Переведем значения вероятности в диапазон 
Шаг этот очень простой — прологарифмируем шансы по основанию числа Эйлера
и получим:
Теперь мы знаем, что если
, то вычислить значение
будет очень просто и, более того, оно должно быть положительным:
. Так и есть.
Ради любопытства проверим, что если
, тогда мы ожидаем увидеть отрицательное значение
. Проверяем:
. Все верно.
Теперь мы знаем как перевести значение вероятности от
до
на всю числовую прямую от
до
. В следующем шаге сделаем все наоборот.
А пока, отметим, что в соответствии с правилами логарифмирования, зная значение функции
, можно вычислить шансы:
Этот способ определения шансов нам пригодится на следующем шаге.
Шаг 3. Выведем формулу для определения 
Итак, мы научились, зная
, находить значения функции
. Однако, на самом деле нам нужно все с точностью до наоборот — зная значение
находить
. Для этого обратимся к такому понятию как обратная функция шансов, в соответствии с которой:
В статье мы не будем выводить вышеобозначенную формулу, но проверим на цифрах из примера выше. Мы знаем, что при шансах равными 4 к 1 (
), вероятность наступления события равна 0.8 (
). Сделаем подстановку:
. Это совпадает с нашими вычислениями, проведенными ранее. Двигаемся далее.
На прошлом шаге мы вывели, что
, а значит можно сделать замену в обратной функции шансов. Получим:
Разделим и числитель и знаменатель на
, тогда:
На всякий пожарный, дабы убедиться, что мы нигде не ошиблись, сделаем еще одну небольшую проверку. На шаге 2, мы для
определили, что
. Тогда, подставив значение
в функцию логистического отклика, мы ожидаем получить
. Подставляем и получаем:
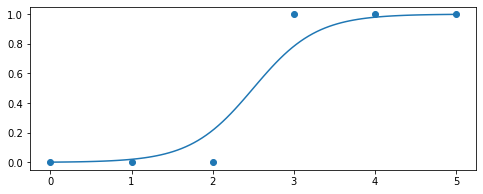
Поздравляю вас, уважаемый читатель, мы только что вывели и протестировали функцию логистического отклика. Давайте посмотрим на график функции.
График 3 «Функция логистического отклика»
Код для отрисовки графика
import math
def logit (f):
return 1/(1+math.exp(-f))
f = np.arange(-7,7,0.05)
p = []
for i in f:
p.append(logit(i))
fig, axes = plt.subplots(figsize = (14,6), dpi = 80)
plt.plot(f, p, color = 'grey', label = '$ 1 / (1+e^{-w^Tx_i})$')
plt.xlabel('$f(w,x_i) = w^Tx_i$', size = 16)
plt.ylabel('$p_{i+}$', size = 16)
plt.legend(prop = {'size': 14})
plt.show()
В литературе также можно встретить название данной функции как сигмоид-функция. По графику хорошо заметно, что основное изменение вероятности принадлежности объекта к классу происходит на относительно небольшом диапазоне
, где-то от
до
.
Предлагаю вернуться к нашему кредитному аналитику и помочь ему с вычислением вероятности погашения кредитов, иначе он рискует остаться без премии 
Таблица 2 «Потенциальные заемщики»
Код для формирования таблицы
proba = []
for i in df['f(w,x)']:
proba.append(round(logit(i),2))
df['Probability'] = proba
df[['The borrower', 'Salary', 'Payment', 'f(w,x)', 'Decision', 'Probability']]
Итак, вероятность возврата кредита мы определили. В целом, это похоже на правду.
Действительно, вероятность того что Вася при зарплате в 120.000Р сможет ежемесячно отдавать в банк 3.000Р близка к 100%. Кстати, мы должны понимать, что банк может выдать кредит и Леше в том случае, если политикой банка предусмотрено, например, кредитовать клиентов с вероятностью возврата кредита более, ну скажем, 0.3. Просто в таком случае банк сформирует больший резерв под возможные потери.
Также следует отметить, что соотношение зарплаты к платежу не менее 3 и с запасом в 5.000Р было взято с потолка. Поэтому нам нельзя было использовать в первоначальном виде вектор весов
. Нам требовалось сильно уменьшить коэффициенты и в таком случае мы разделили каждый коэффициент на 25.000, то есть по сути мы подогнали результат. Но это сделано было специально, чтобы упростить понимание материала на начальном этапе. В жизни, же нам потребуется не выдумывать и подгонять коэффициенты, а находить их. Как раз в следующих разделах статьи мы выведем уравнения, с помощью которых подбираются параметры
.
04. Метод наименьших квадратов при определении вектора весов  в функции логистического отклика
в функции логистического отклика
Нам уже известен такой метод подбора вектора весов
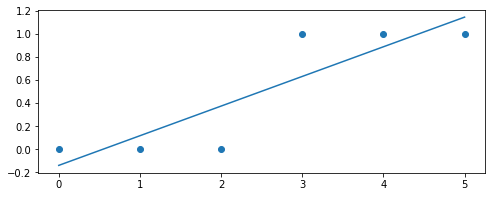
, как метод наименьших квадратов (МНК) и собственно, почему бы нам тогда не использовать его в задачах бинарной классификации? Действительно, ничто не мешает использовать МНК, только вот данный способ в задачах классификации дает результаты менее точные, нежели Logistic Loss. Этому есть теоретическое обоснование. Давайте для начала посмотрим на один простой пример.
Предположим, что наши модели (использующие MSE и Logistic Loss) уже начали подбор вектора весов
и мы остановили расчет на каком-то шаге. Неважно, в середине, в конце или в начале, главное, что у нас уже есть какие-то значения вектора весов и допустим, что на этом шаге, вектора весов
для обеих моделей не имеют различий. Тогда возьмем полученные веса и подставим их в функцию логистического отклика (
) для какого-нибудь объекта, который относится к классу
. Исследуем два случая, когда в соответствии с подобранным вектором весов наша модель сильно ошибается и наоборот — модель сильно уверена в том, что объект относится к классу
. Посмотрим какие штрафы будут «выписаны» при использовании МНК и Logistic Loss.
Код для расчета штрафов в зависимости от используемой функции потерь
# класс объекта
y = 1
# вероятность отнесения объекта к классу в соответствии с параметрами w
proba_1 = 0.01
MSE_1 = (y - proba_1)**2
print 'Штраф MSE при грубой ошибке =', MSE_1
# напишем функцию для вычисления f(w,x) при известной вероятности отнесения объекта к классу +1 (f(w,x)=ln(odds+))
def f_w_x(proba):
return math.log(proba/(1-proba))
LogLoss_1 = math.log(1+math.exp(-y*f_w_x(proba_1)))
print 'Штраф Log Loss при грубой ошибке =', LogLoss_1
proba_2 = 0.99
MSE_2 = (y - proba_2)**2
LogLoss_2 = math.log(1+math.exp(-y*f_w_x(proba_2)))
print '**************************************************************'
print 'Штраф MSE при сильной уверенности =', MSE_2
print 'Штраф Log Loss при сильной уверенности =', LogLoss_2
Случай с грубой ошибкой — модель относит объект к классу
с вероятностью в 0,01
Штраф при использовании МНК составит:
Штраф при использовании Logistic Loss составит:
Случай с сильной уверенностью — модель относит объект к классу
с вероятностью в 0,99
Штраф при использовании МНК составит:
Штраф при использовании Logistic Loss составит:
Этот пример хорошо иллюстрирует, что при грубой ошибке функция потерь Log Loss штрафует модель значительно сильнее, чем MSE. Давайте теперь разберемся, каковы теоретические предпосылки использования функции потерь Log Loss в задачах классификации.
05. Метод максимального правдоподобия и логистическая регрессия
Как и было обещано в начале, статья изобилует простыми примерами. В студии очередной пример и старые гости — заемщики банка: Вася, Федя и Леша.
На всякий пожарный, перед тем как развивать пример, напомню, что в жизни мы имеем дело с обучающей выборкой из тысяч или миллионов объектов с десятками или сотнями признаков. Однако здесь цифры взяты так, чтобы они легко укладывались в голове начинающего датасайнтеста.
Возвращаемся к примеру. Представим, что директор банка решил выдать кредит всем нуждающимся, несмотря на то, что алгоритм подсказывал не выдавать его Леше. И вот прошло достаточно времени и нам стало известно кто из трех героев погасил кредит, а кто нет. Что и следовало ожидать: Вася и Федя погасили кредит, а Леша — нет. Теперь давайте представим, что этот результат будет для нас новой обучающей выборкой и, при этом у нас как будто исчезли все данные о факторах, влияющих на вероятность погашения кредита (зарплата заемщика, размер ежемесячного платежа). Тогда интуитивно мы можем полагать, что каждый третий заемщик не возвращает банку кредит или другими словами вероятность возврата кредита следующим заемщиком
. Этому интуитивному предположению есть теоретическое подтверждение и основывается оно на методе максимального правдоподобия, часто в литературе его называют принципом максимального правдоподобия.
Для начала познакомимся с понятийным аппаратом.
Правдоподобие выборки — это вероятность получения именно такой выборки, получения именно таких наблюдений / результатов, т.е. произведение вероятностей получения каждого из результатов выборки (например, погашен или не погашен кредит Васей, Федей и Лешей одновременно).
Функция правдоподобия связывает правдоподобие выборки со значениями параметров распределения.
В нашем случае, обучающая выборка представляет собой обобщённую схему Бернулли, в которой случайная величина принимает всего два значения:
или
. Следовательно, правдоподобие выборки можно записать как функцию правдоподобия от параметра
следующим образом:
Вышеуказанную запись можно интерпретировать так. Совместная вероятность того, что Вася и Федя погасят кредит равна
, вероятность того что Леша НЕ погасит кредит равна
(так как имело место именно НЕ погашение кредита), следовательно совместная вероятность всех трех событий равна
.
Метод максимального правдоподобия — это метод оценки неизвестного параметра путём максимизации функции правдоподобия. В нашем случае требуется найти такое значение
, при котором
достигает максимума.
Откуда собственно идея – искать значение неизвестного параметра, при котором функция правдоподобия достигает максимума? Истоки идеи проистекают из представления о том, что выборка – это единственный, доступный нам, источник знания о генеральной совокупности. Все, что нам известно о генеральной совокупности, представлено в выборке. Поэтому, все, что мы можем сказать, так это то, что выборка – это наиболее точное отражение генеральной совокупности, доступное нам. Следовательно, нам требуется найти такой параметр, при котором имеющаяся выборка становится наиболее вероятной.
Очевидно, мы имеем дело с оптимизационной задачей, в которой требуется найти точку экстремума функции. Для нахождения точки экстремума необходимо рассмотреть условие первого порядка, то есть приравнять производную функции к нулю и решить уравнение относительно искомого параметра. Однако поиски производной произведения большого количества множителей могут оказаться делом затяжным, чтобы этого избежать существует специальный прием — переход к логарифму функции правдоподобия. Почему возможен такой переход? Обратим внимание на то, что мы ищем не сам экстремум функции
, а точку экстремума, то есть то значение неизвестного параметра
, при котором
достигает максимума. При переходе к логарифму точка экстремума не меняется (хотя сам экстремум будет отличаться), так как логарифм — монотонная функция.
Давайте, в соответствии с вышеизложенным, продолжим развивать наш пример с кредитами у Васи, Феди и Леши. Для начала перейдем к логарифму функции правдоподобия:
Теперь мы можем с легкостью продифференцировать выражение по
:
И наконец, рассмотрим условие первого порядка — приравняем производную функции к нулю:
Таким образом, наша интуитивная оценка вероятности погашения кредита
была теоретически обоснована.
Отлично, но что нам теперь делать с такой информацией? Если мы будем считать, что каждый третий заемщик не вернет банку деньги, то последний неизбежно разорится. Так-то оно так, да только при оценке вероятности погашения кредита равной
мы не учли факторы, влияющие на возврат кредита: заработная плата заемщика и размер ежемесячного платежа. Вспомним, что ранее мы рассчитали вероятность возврата кредита каждым клиентом с учетом этих самых факторов. Логично, что и вероятности у нас получились отличные от константы равной
.
Давайте определим правдоподобие выборок:
Код для расчетов правдоподобий выборок
from functools import reduce
def likelihood(y,p):
line_true_proba = []
for i in range(len(y)):
ltp_i = p[i]**y[i]*(1-p[i])**(1-y[i])
line_true_proba.append(ltp_i)
likelihood = []
return reduce(lambda a, b: a*b, line_true_proba)
y = [1.0,1.0,0.0]
p_log_response = df['Probability']
const = 2.0/3.0
p_const = [const, const, const]
print 'Правдоподобие выборки при константном значении p=2/3:', round(likelihood(y,p_const),3)
print '****************************************************************************************************'
print 'Правдоподобие выборки при расчетном значении p:', round(likelihood(y,p_log_response),3)
Правдоподобие выборки при константном значении :
Правдоподобие выборки при расчете вероятности погашения кредита с учетом факторов :
Правдоподобие выборки с вероятностью, посчитанной в зависимости от факторов оказалось выше правдоподобия при константном значении вероятности. О чем это говорит? Это говорит о том, что знания о факторах позволили подобрать более точно вероятность погашения кредита для каждого клиента. Поэтому, при выдаче очередного кредита, правильнее будет использовать, предложенную в конце 3-го раздела статьи, модель оценки вероятности погашения задолженности.
Но тогда, если нам требуется максимизировать функцию правдоподобия выборки, то почему бы не использовать какой-нибудь алгоритм, который будет выдавать вероятности для Васи, Феди и Леши, например, равными 0.99, 0.99 и 0.01 соответственно. Возможно такой алгоритм и хорошо себя проявит на обучающей выборке, так как приблизит значение правдоподобия выборки к
, но, во-первых, у такого алгоритма будут, скорее всего трудности с обобщающей способностью, во-вторых, этот алгоритм будет точно не линейным. И если, методы борьбы с переобучением (равно слабая обобщающая способность) явно не входят в план этой статьи, то по второму пункту давайте пройдемся подробнее. Для этого, достаточно ответить на простой вопрос. Может ли вероятность погашения кредита Васей и Федей быть одинаковой с учетом известных нам факторов? С точки зрения здравой логики конечно же нет, не может. Так на погашение кредита Вася будет отдавать 2.5% своей зарплаты в месяц, а Федя — почти 27,8%. Также на графике 2 «Классификация клиентов» мы видим, что Вася находится значительно дальше от линии, разделяющей классы, чем Федя. Ну и наконец, мы знаем, что функция
для Васи и Феди принимает различные значения: 4.24 для Васи и 1.0 для Феди. Вот если бы Федя, например, зарабатывал на порядок больше или кредит поменьше просил, то тогда вероятности погашения кредита у Васи и Феди были бы схожими. Другими словами, линейную зависимость не обманешь. И если бы мы действительно рассчитали коэффициенты
, а не взяли их с потолка, то могли бы смело заявить, что наши значения
лучше всего позволяют оценить вероятность погашения кредита каждым заемщиком, но так как мы условились считать, что определение коэффициентов
было проведено по всем правилам, то мы так и будем считать — наши коэффициенты позволяют дать лучшую оценку вероятности

Однако мы отвлеклись. В этом разделе нам надо разобраться как определяется вектор весов
, который необходим для оценки вероятности возврата кредита каждым заемщиком.
Кратко резюмируем, с каким арсеналом мы выступаем на поиски коэффициентов
:
1. Мы предполагаем, что зависимость между целевой переменной (прогнозным значением) и фактором, оказывающим влияние на результат — линейная. По этой причине применяется функция линейной регрессии вида
, линия которого делит объекты (клиентов) на классы
и
или
(клиенты, способные погасить кредит и не способные). В нашем случае уравнение имеет вид
.
2. Мы используем функцию обратного логит-преобразования вида
для определения вероятности принадлежности объекта к классу
.
3. Мы рассматриваем нашу обучающую выборку как реализацию обобщенной схемы Бернулли, то есть для каждого объекта генерируется случайная величина, которая с вероятностью
(своей для каждого объекта) принимает значение 1 и с вероятностью
– 0.
4. Мы знаем, что нам требуется максимизировать функцию правдоподобия выборки с учетом принятых факторов для того, чтобы имеющаяся выборка стала наиболее правдоподобной. Другими словами, нам нужно подобрать такие параметры, при которых выборка будет наиболее правдоподобной. В нашем случае подбираемый параметр — это вероятность погашения кредита
, которая в свою очередь зависит от неизвестных коэффициентов
. Значит нам требуется найти такой вектор весов
, при котором правдоподобие выборки будет максимальным.
5. Мы знаем, что для максимизации функции правдоподобия выборки можно использовать метод максимального правдоподобия. И мы знаем все хитрые приемы для работы с этим методом.
Вот такая многоходовочка получается 
А теперь вспомним, что в самом начале статьи мы хотели вывести два вида функции потерь Logistic Loss в зависимости от того как обозначаются классы объектов. Так повелось, что в задачах классификации с двумя классами, классы обозначают как
и
или
. В зависимости от обозначения, на выходе будет соответствующая функция потерь.
Случай 1. Классификация объектов на  и
и 
Раннее, при определении правдоподобия выборки, в котором вероятность погашения задолженности заемщиком рассчитывалась исходя из факторов и заданных коэффициентов
, мы применили формулу:
На самом деле
— это значение функции логистического отклика
при заданном векторе весов
Тогда нам ничто не мешает записать функцию правдоподобия выборки так:
Бывает так, что иногда, некоторым начинающим аналитикам сложно сходу понять, как эта функция работает. Давайте рассмотрим 4 коротких примера, которые все прояснят:
1. Если
(т.е. в соответствии с обучающей выборкой объект относится к классу +1), а наш алгоритм
определяет вероятность отнесения объекта к классу
равной 0.9, то вот этот кусочек правдоподобия выборки будет рассчитываться так:
2. Если
, а
, то расчет будет таким:
3. Если
, а
, то расчет будет таким:
4. Если
, а
, то расчет будет таким:
Очевидно, что функция правдоподобия будет максимизироваться в случаях 1 и 3 или в общем случае — при правильно отгаданных значениях вероятностей отнесения объекта к классу
.
В связи с тем, что при определении вероятности отнесения объекта к классу
нам не известны только коэффициенты
, то мы их и будем искать. Как и говорилось выше, это задача оптимизации, в которой для начала нам требуется найти производную от функции правдоподобия по вектору весов
. Однако предварительно имеет смысл упростить себе задачу: производную будем искать от логарифма функции правдоподобия.
Почему после логарифмирования, в функции логистической ошибки, мы поменяли знак с
на
. Все просто, так как в задачах оценки качества модели принято минимизировать значение функции, то мы умножили правую часть выражения на
и соответственно вместо максимизации, теперь минимизируем функцию.
Собственно, сейчас, на ваших глазах была много страдальчески выведена функция потерь — Logistic Loss для обучающей выборки с двумя классами:
и
.
Теперь, для нахождения коэффициентов, нам потребуется всего лишь найти производную функции логистической ошибки и далее, используя численные методы оптимизации, такие как градиентный спуск или стохастический градиентный спуск, подобрать наиболее оптимальные коэффициенты
. Но, учитывая, уже не малый объем статьи, предлагается провести дифференцирование самостоятельно или, быть может, это будет темой для следующей статьи с большим количеством арифметики без столь подробных примеров.
Случай 2. Классификация объектов на  и
и 
Подход здесь будет такой же, как и с классами
и
, но сама дорожка к выводу функции потерь Logistic Loss, будет более витиеватой. Приступаем. Будем для функции правдоподобия использовать оператор «если…, то…». То есть, если
-ый объект относится к классу
, то для расчета правдоподобия выборки используем вероятность
, если объект относится к классу
, то в правдоподобие подставляем
. Вот так выглядит функция правдоподобия:
На пальцах распишем как это работает. Рассмотрим 4 случая:
1. Если
и
, то в правдоподобие выборки «пойдет»
2. Если
и
, то в правдоподобие выборки «пойдет»
3. Если
и
, то в правдоподобие выборки «пойдет»
4. Если
и
, то в правдоподобие выборки «пойдет»
Очевидно, что в 1 и 3 случае, когда вероятности были правильно определены алгоритмом, функция правдоподобия будет максимизироваться, то есть именно это мы и хотели получить. Однако, такой подход достаточно громоздок и далее мы рассмотрим более компактную запись. Но для начала, логарифмируем функцию правдоподобия с заменой знака, так как теперь мы будем минимизировать ее.
Подставим вместо
выражение
:
Упростим правое слагаемое под логарифмом, используя простые арифметические приемы и получим:
А теперь настало время избавиться от оператора «если…, то…». Заметим, что когда объект
относится к классу
, то в выражении под логарифмом, в знаменателе,
возводится в степень
, если объект относится к классу
, то $e$ возводится в степень
. Следовательно запись степени можно упростить — объединить оба случая в один:
. Тогда функция логистической ошибки примет вид:
В соответствии с правилами логарифмирования, перевернем дробь и вынесем знак «
» (минус) за логарифм, получим:
Перед вами функция потерь logistic Loss, которая применяется в обучающей выборке с объектами относимых к классам:
и
.
Что ж, на этом моменте я откланиваюсь и мы завершаем статью.
Предыдущая работа автора — «Приводим уравнение линейной регрессии в матричный вид»
Вспомогательные материалы
1. Литература
1) Прикладной регрессионный анализ / Н. Дрейпер, Г. Смит – 2-е изд. – М.: Финансы и статистика, 1986 (перевод с английского)
2) Теория вероятностей и математическая статистика / В.Е. Гмурман — 9-е изд. — М.: Высшая школа, 2003
3) Теория вероятностей / Н.И. Чернова — Новосибирск: Новосибирский государственный университет, 2007
4) Бизнес-аналитика: от данных к знаниям / Паклин Н. Б., Орешков В. И. — 2-е изд. — Санкт-Петербург: Питер, 2013
5) Data Science Наука о данных с нуля / Джоэл Грас — Санкт-Петербург: БХВ Петербург, 2017
6) Практическая статистика для специалистов Data Science / П.Брюс, Э.Брюс — Санкт-Петербург: БХВ Петербург, 2018
2. Лекции, курсы (видео)
1) Суть метода максимального правдоподобия, Борис Демешев
2) Метод максимального правдоподобия в непрерывном случае, Борис Демешев
3) Логистическая регрессия. Открытый курс ODS, Yury Kashnitsky
4) Лекция 4, Евгений Соколов (с 47 минуты видео)
5) Логистическая регрессия, Вячеслав Воронцов
3. Интернет-источники
1) Линейные модели классификации и регрессии
2) Как легко понять логистическую регрессию
3) Логистическая функция ошибки
4) Независимые испытания и формула Бернули
5) Баллада о ММП
6) Метод максимального правдоподобия
7) Формулы и свойства логарифмов

Почему число ?
9) Линейный классификатор
9) Jupyter notebook на гитхабе
Эту функцию называют также «логлосс» (logloss / log_loss), перекрёстной / кросс-энтропией (Cross Entropy) и часто используют в задачах классификации. Разберёмся, почему её используют и какой смысл она имеет. Для чтения поста нужна неплохая ML-математическая подготовка, но даже новичкам я бы рекомендовал почитать (хотя я не очень заботился, чтобы «всё объяснялось на пальцах»).
Начнём издалека…
Вспомним, как решается задача линейной регрессии. Итак, мы хотим получить линейную функцию (т.е. веса w), которая приближает целевое значение с точностью до ошибки:
Здесь мы предположили, что ошибка нормально распределена, x – признаковое описание объекта (возможно, в нём есть и фиктивный константный признак, чтобы в линейной функции был свободный член). Тогда мы знаем как распределены ответы нашей функции и можем записать функцию правдоподобия выборки (т.е. произведение плотностей, в которые подставлены значения из обучающей выборки) и воспользоваться методом максимального правдоподобия (в котором для определения значений параметров берётся максимум правдоподобия, а чаще – его логарифма):
В итоге оказывается, что максимизация правдоподобия эквивалентна минимизации среднеквадратичной ошибки (MSE), т.е. эта функция ошибки не зря широко используется в задачах регрессии. Кроме того, что она вполне логична, легко дифференцируема по параметрам и легко минимизируется, она ещё и теоретически обосновывается с помощью метода максимального правдоподобия в случае, если линейная модель соответствует данным с точностью до нормального шума.
Давайте ещё посмотрим, как реализуется метод стохастического градиента (SGD) для минимизации MSE: надо взять производную функции ошибки для конкретного объекта и записать формулу коррекции весов в виде «шага в сторону антиградиента»:
Получили, что веса линейной модели при её обучении методом SGD корректируются с помощью добавки вектора признаков. Коэффициент, с которым добавляют, зависит от «агрессивности алгоритма» (параметр альфа, который называют темпом обучения) и разности «ответ алгоритма – правильный ответ». Кстати, если разница нулевая (т.е. на данном объекте алгоритм выдаёт точный ответ), то коррекция весов не производится.
Log Loss
Теперь давайте, наконец, поговорим о «логлоссе». Рассматриваем задачу классификации с двумя классами: 0 и 1. Обучающую выборку можно рассматривать, как реализацию обобщённой схемы Бернулли: для каждого объекта генерируется случайная величина, которая с вероятностью p (своей для каждого объекта) принимает значение 1 и с вероятностью (1–p) – 0. Предположим, что мы как раз и строим нашу модель так, чтобы она генерировала правильные вероятности, но тогда можно записать функцию правдоподобия:
После логарифмирования правдоподобия получили, что его максимизация эквивалентна минимизации последнего записанного выражения. Именно его и называют «логистической функции ошибки». Для задачи бинарной классификации, в которой алгоритм должен выдать вероятность принадлежности классу 1, она логична ровно настолько, насколько логична MSE в задаче линейной регрессии с нормальным шумом (поскольку обе функции ошибки выводятся из метода максимального правдоподобия).
Часто гораздо более понятна такая запись logloss-ошибки на одном объекте:
Отметим неприятное свойство логосса: если для объекта 1го класса мы предсказываем нулевую вероятность принадлежности к этому классу или, наоборот, для объекта 0го – единичную вероятность принадлежности к классу 1, то ошибка равна бесконечности! Таким образом, грубая ошибка на одном объекте сразу делает алгоритм бесполезным. На практике часто логлосс ограничивают каким-то большим числом (чтобы не связываться с бесконечностями).
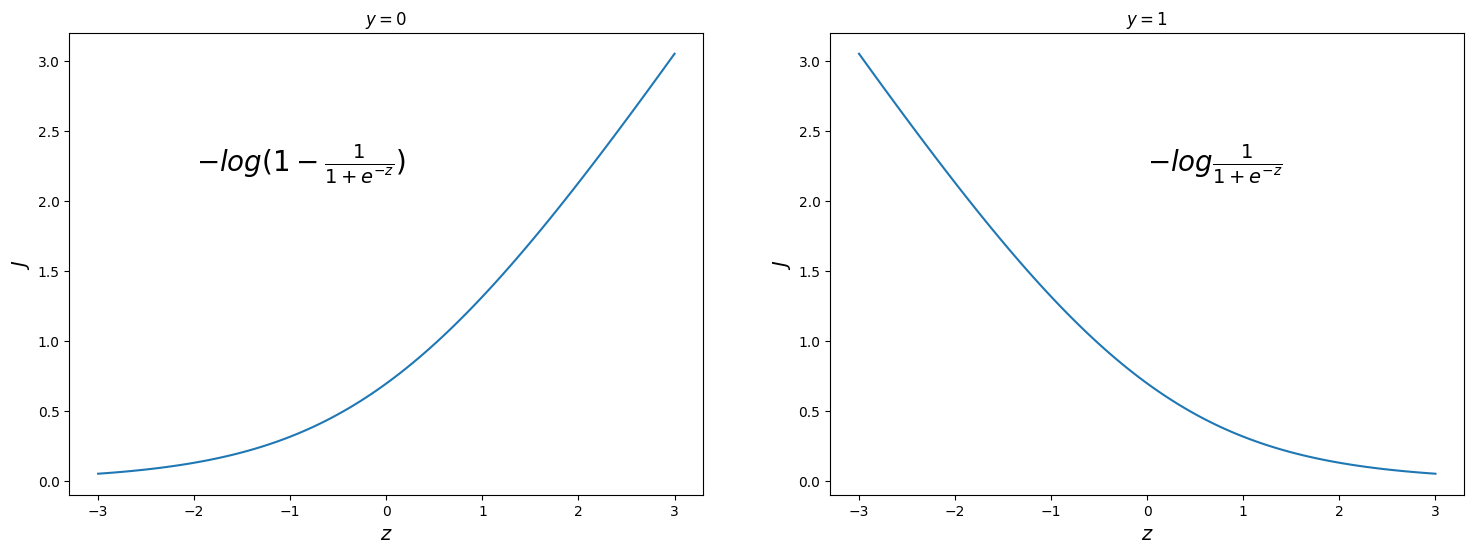
Если задаться вопросом, какой константный алгоритм оптимален для выборки из q_1 представителей класса 1 и q_0 представителей класса 0, q_1 + q_0 = q , то получим
Последний ответ получается взятием производной и приравниванием её к нулю. Описанную задачу приходится решать, например, при построении решающих деревьев (какую метку приписывать листу, если в него попали представители разных классов). На рис. 2 изображён график log_loss-ошибки константного алгоритма для выборки из четырёх объектов класса 0 и 6 объектов класса 1.
Представим теперь, что мы знаем, что объект принадлежит к классу 1 вероятностью p, посмотрим, какой ответ оптимален на этом объекте с точки зрения log_loss: матожидание нашей ошибки
Для минимизации ошибки мы опять взяли производную и приравняли к нулю. Мы получили, что оптимально для каждого объекта выдавать его вероятность принадлежности к классу 1! Таким образом, для минимизации log_loss надо уметь вычислять (оценивать) вероятности принадлежности классам!
Если подставить полученное оптимальное решение в минимизируемый функционал, то получим энтропию:
Это объясняет, почему при построении решающих деревьев в задачах классификации (а также случайных лесов и деревьях в бустингах) применяют энтропийный критерий расщепления (ветвления). Дело в том, что оценка принадлежности к классу 1 часто производится с помощью среднего арифметического меток в листе. В любом случае, для конкретного дерева эта вероятность будет одинакова для всех объектов в листе, т.е. константой. Таким образом, энтропия в листе примерно равна логлосс-ошибке константного решения. Используя энтропийный критерий мы неявно оптимизируем логлосс!
В каких пределах может варьироваться logloss? Ясно, что минимальное значение 0, максимальное – +∞, но эффективным максимальным можно считать ошибку при использовании константного алгоритма (вряд же мы в итоге решения задачи придумаем алгоритм хуже константы?!), т.е.
Интересно, что если брать логарифм по основанию 2, то на сбалансированной выборке это отрезок [0, 1].
Связь с логистической регрессией
Слово «логистическая» в названии ошибки намекает на связь с логистической регрессией – это как раз метод для решения задачи бинарной классификации, который получает вероятность принадлежности к классу 1. Но пока мы исходили из общих предположений, что наш алгоритм генерирует эту вероятность (алгоритмом может быть, например, случайный лес или бустинг над деревьями). Покажем, что тесная связь с логистической регрессией всё-таки есть… посмотрим, как настраивается логистическая регрессия (т.е. сигмоида от линейной комбинации) на эту функцию ошибки методом SGD.
Как видим, корректировка весов точно такая же, как и при настройке линейной регрессии! На самом деле, это говорит о родстве разных регрессий: линейной и логистической, а точнее, о родстве распределений: нормального и Бернулли. Желающие могут внимательно почитать лекцию Эндрю Ына.
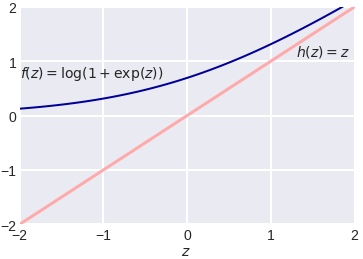
Во многих книгах логистической функцией ошибки (т.е. именно «logistic loss») называется другое выражение, которое мы сейчас получим, подставив выражение для сигмоиды в logloss и сделав переобозначение: считаем, что метки классов теперь –1 и +1, тогда
Полезно посмотреть на график функции, центральной в этом представлении:
Как видно, это сглаженный (всюду дифференцируемый) аналог функции max(0, x), которую в глубоком обучении принято называть ReLu (Rectified Linear Unit). Если при настройке весов минимизировать logloss, то таким образом мы настраиваем классическую логистическую регрессию, если же использовать ReLu, чуть-чуть подправить аргумент и добавить регуляризацию, то получаем классическую настройку SVM:
выражение под знаком суммы принято называть Hinge loss. Как видим, часто с виду совсем разные методы можно получать «немного подправив» оптимизируемые функции на похожие. Между прочим, при обучении RVM (Relevance vector machine) используется тоже очень похожий функционал:
Связь с расхождением Кульбака-Лейблера
Расхождение (дивергенцию) Кульбака-Лейблера (KL, Kullback–Leibler divergence) часто используют (особенно в машинном обучении, байесовском подходе и теории информации) для вычисления непохожести двух распределений. Оно определяется по следующей формуле:
где P и Q – распределения (первое обычно «истинное», а второе – то, про которое нам интересно, насколько оно похоже на истинное), p и q – плотности этих распределений. Часто KL-расхождение называют расстоянием, хотя оно не является симметричным и не удовлетворяет неравенству треугольника. Для дискретных распределений формулу записывают так:
P_i, Q_i – вероятности дискретных событий. Давайте рассмотрим конкретный объект x с меткой y. Если алгоритм выдаёт вероятность принадлежности первому классу – a, то предполагаемое распределение на событиях «класс 0», «класс 1» – (1–a, a), а истинное – (1–y, y), поэтому расхождение Кульбака-Лейблера между ними
что в точности совпадает с logloss.
Настройка на logloss
Один из методов «подгонки» ответов алгоритма под logloss – калибровка Платта (Platt calibration). Идея очень простая. Пусть алгоритм порождает некоторые оценки принадлежности к 1му классу – a. Метод изначально разрабатывался для калибровки ответов алгоритма опорных векторов (SVM), этот алгоритм в простейшей реализации разделяет объекты гиперплоскостью и просто выдаёт номер класса 0 или 1, в зависимости от того, с какой стороны гиперплоскости объект расположен. Но если мы построили гиперплоскость, то для любого объекта можем вычислить расстояние до неё (со знаком минус, если объект лежит в полуплоскости нулевого класса). Именно эти расстояния со знаком r мы будем превращать в вероятности по следующей формуле:
неизвестные параметры α, β обычно определяются методом максимального правдоподобия на отложенной выборке (calibration set).
Проиллюстрируем применение метода на реальной задаче, которую автор решал недавно. На рис. показаны ответы (в виде вероятностей) двух алгоритмов: градиентного бустинга (lightgbm) и случайного леса (random forest).
Видно, что качество леса намного ниже и он довольно осторожен: занижает вероятности у объектов класса 1 и завышает у объектов класса 0. Упорядочим все объекты по возрастанию вероятностей (RF), разобьем на k равных частей и для каждой части вычислим среднее всех ответов алгоритма и среднее всех правильных ответов. Результат показан на рис. 5 – точки изображены как раз в этих двух координатах.
Нетрудно видеть, что точки располагаются на линии, похожей на сигмоиду – можно оценить параметр сжатия-растяжения в ней, см. рис. 6. Оптимальная сигмоида показана розовым цветом на рис. 5. Если подвергать ответы такой сигмоидной деформации, то логлосс-ошибка случайного леса снижается с 0.37 до 0.33.
Обратите внимание, что здесь мы деформировали ответы случайного леса (это были оценки вероятности – и все они лежали на отрезке [0, 1]), но из рис. 5 видно, что для деформации нужна именно сигмоида. Практика показывает, что в 80% ситуаций для улучшения logloss-ошибки надо деформировать ответы именно с помощью сигмоиды (для меня это также часть объяснения, почему именно такие функции успешно используются в качестве функций активаций в нейронных сетях).
Ещё один вариант калибровки – монотонная регрессия (Isotonic regression).
Многоклассовый logloss
Для полноты картины отметим, что logloss обобщается и на случай нескольких классов естественным образом:
здесь q – число элементов в выборке, l – число классов, a_ij – ответ (вероятность) алгоритма на i-м объекте на вопрос принадлежности его к j-му классу, y_ij=1 если i-й объект принадлежит j-му классу, в противном случае y_ij=0.
На посошок…
В каждом подобном посте я стараюсь написать что-то из мира машинного обучения, что, с одной стороны, просто и понятно, а с другой – изложение этого не встречается больше нигде. Например, есть такой естественный вопрос: почему в задачах классификации при построении решающих деревьев используют энтропийный критерий расщепления? Во всех курсах его (критерий) преподносят либо как эвристику, которую «вполне естественно использовать», либо говорят, что «энтропия похожа на кросс-энтропию». Сейчас стоимость некоторых курсов по машинному обучению достигает нескольких сотен тысяч рублей, но «профессиональные инструкторы» не могут донести простую цепочку:
- в статистической теории обучения настройка алгоритма производится максимизацией правдоподобия,
- в задаче бинарной классификации это эквивалентно минимизации логлосса, а сам минимум как раз равен энтропии,
- поэтому использование энтропийного критерия фактически эквивалентно выбору расщепления, минимизирующего логлосс.
Если Вы всё-таки отдали несколько сотен тысяч рублей, то можете проверить «профессиональность инструктора» следующими вопросами:
- Энтропия в листе примерно равна logloss-ошибке константного решения. Почему не использовать саму ошибку, а не приближённое значение? Или, как часто происходит в задачах оптимизации, её верхнюю оценку?
- Минимизации какой ошибки соответствует критерий расщепления Джини?
- Можно показать, что если в задаче бинарной классификации использовать в качестве функции ошибки среднеквадратичное отклонение, то также, как и для логлосса, оптимальным ответом на объекте будет вероятность его принадлежности к классу 1. Почему тогда не использовать такую функцию ошибки?
Ответы типа «так принято», «такой функции не существует», «это только для регрессии», естественно, заведомо неправильные. Если Вам не ответят с такой же степенью подробности, как в этом посте, то Вы точно переплатили;)
П.С. Что ещё почитать…
В этом блоге я публиковал уже несколько постов по метрикам качества…
- AUC ROC (площадь под кривой ошибок)
- Задачки про AUC (ROC)
- Знакомьтесь, Джини
И буквально на днях вышла классная статья Дмитрия Петухова про коэффициент Джини, читать обязательно:
- Коэффициент Джини. Из экономики в машинное обучение
Кирилл Нестеркин представляет топ 10 самых частых ошибок, которые совершают абсолютно все логисты. Вы наверняка в каких-то пунктах узнаете себя. Этот материал основан на собственном опыте и опыте коллег, в частности Василия Дмитриенко, который поучаствовал косвенно в создании этого топа. Он предоставил информацию, которую я тоже взял за основу. Спасибо ему большое за то, что он поучаствовал в создании данного топа логистических ошибок.
Пойдем по списку в обратном порядке от 10-го к первому. Первые пункты — это те ошибки, которые приводят к максимальным финансовым потерям. Десятый пункт — это минимальные финансовые потери. Скажем так, это больше могут быть репутационные потери или какие-то неприятности в мелких ситуациях.
Этот топ ошибок логистов в основном основан на нашем практическом опыте по экспедированию грузов. Это не работы с собственным транспортом, а именно экспедирование грузов, то есть грубо говоря в сфере посреднических логистических услуг.
Ошибки — это не прерогатива начинающих! У опытных логистов их просто меньше!
- Работа с биржей автоперевозок АвтоТрансИнфо (АТИ)
- Работа с контактами нового клиента
- Контроль исполнения заявки со стороны логиста
- Проблемы с необъективными сроками и формой оплаты
- Проверка заявки перед отправкой
- Проблемы оплаты с НДС и без НДС
- Ошибки в стоимости доставки
- Ошибки в полноте данных для исполнения заявки
- Риски работы под честное слово
- Мошенничество в перевозках и безопасность
Работа с биржей автоперевозок АвтоТрансИнфо (АТИ)
Десятый пункт это неправильная работа с АТИ. любого логиста это происходит бывает выставляет груз забывает про этот груз он где-то висит уходит вниз списка его никто не обновляет соответственно нет нет нет звонков от перевозчиков логист влаги что звонит клиент спрашивает где груз? Особенно такое бывает зоопарке, когда несколько грузов логиста висит.
Он забывает про какой-то груз, не обновляет его, ему никто не звонит. Потом он не понимает, что такое происходит, почему этот груз не закрывается, водители не находятся.
Все банально просто. Работает такая человеческая психология естественно водителям перевозчикам интереснее забрать как можно быстрее груз по максимальной цене. Соответственно они будут смотреть первые строчки списка заявок что есть в нужном направлении и естественно водители в первую очередь звонят по первым строчкам. Грузы надо обновлять чаще, при этом надо корректно выставлять грузы. Любые некорректности или отсутствие значимых данных приводят к потерям времени и денег.
Работа с контактами нового клиента
Пункт номер девять это контакты нового клиента, что я имею под этим в виду? Зачастую бывает так, что клиент какой-то новый звонит на городской телефон на мобильный телефон. Звонит предоставляет какой-то груз. Логист записывает данные или сразу же выставляют в АСИ по этому грузу. Все хорошо, кладет трубку ищет по этому грузу транспорт, но вот проблема контактные данные то этого клиента он забыл записать. Да такое бывает. Иногда бывает так, что люди позвонят на городской номер, логист в спешке, если у него тем более несколько заявок висит, быстренько принял заявку, но не спросил, как вас зовут и как с вами связаться. Зачастую бывает так, что у городских телефонов нет определения номера и логисту уже некуда перезвонить. Или бывает такая ситуация, когда логиста много звонков ему на мобильный и он не записал , как зовут человека, как называется компании не сохранил у себя в контактах телефоне. Потом он просто открывает телефон видит вот такой вот список с разными номерами. Ему там и водители звонят и клиенты и какие-то личные там переговоры и так далее. И такой вот список приходится прозванивать, узнавать не вы ли давали груз. Может быть уже пока дозвонишься до этого человека груз уже заберут какие-то конкуренты, другие транспортные компании. Поэтому такая вот ошибка. Зачастую логисты держат перед собой такой вот блокнотик рабочий, где можно и нужно делать пометки. Принял груз обязательно записал контакты быстренько для себя. Как то это выделил рамочкой, скобками или маркером, что это важный какой-то груз. Но, во всяком случае, здесь уже на бумаге он будет даже если вам звонят на мобильный телефон — все равно записываете сюда номер телефона, кто вам звонил и и обязательно продублируйте номер телефона, потому что потом в длинном списке этих контактов будет тяжело найти этого клиента.
Контроль исполнения заявки со стороны логиста
Пункт номер восемь логист не контролирует исполнение заявки. Он заключил заявку, машина должна загрузиться. с клиентом оформил, с перевозчиком заключил заявку. Но помимо того, что он просто оформил заявки, необходимо все контролировать. Позвонить в день загрузки, позвонить в день следования, вот машина едет позвонить и узнать, как у тебя дела все ли нормально не сломался, где ты едешь. В день выгрузки — все ли нормально подписали тебе документы и так далее. Если не контролировать эту загрузку, то может получиться так, что, например, клиент звонит и спрашивает, а где машина? Почему она долго не едет, а логист понимает, что елки-палки, а я ж не позвонил по этой заявке. Я же не узнал, где он. Логист говорит, что да, сейчас узнаю и вам перезвоню. Это выглядит не очень компетентно, когда логист исполняет заявку, но при этом даже не знает, что происходит с этим водителем. Еще хуже, когда информацию получает первым клиент. Клиент вам звонит и говорит — вы в курсе, что у вас водитель сломался? Это выглядит очень некрасиво и более того, если не контролировать исполнение заявки, то на выгрузке могут произойти какие-то неприятности. Например, долго не выгружают машину, случилась проблема с краном и так далее, нет доверенности, вот тупо нет доверенности. Просто нужно сделать один звоночек, как у тебя дела? Водитель говорит, что на него нет доверенности. Соответственно мы звоним нашему клиенту и говорим, что машину не разгружают из-за отсутствия доверенности. Доверенность предоставляют и заявка исполняется. Это как пример, но ситуации бывают разные и из-за того, что логисты забывают контролировать само исполнение ситуация приходит к такому моменту, что решить оперативно уже сложно. А можно было бы, если контролировать на всем протяжении исполнения.
Проблемы с необъективными сроками и формой оплаты
Пункт номер семь — необъективные сроки и форма оплаты перевозчику. Например, когда клиент говорит, что он будет оплачивать по оригиналам ТТН бухгалтерских документов, а переводчик говорит, что я вам отправлю сканы. Я все отправлю, честное слово. Все вложу и отправлю, как есть. В общем хорошо, логист доверяется словам перевозчика, перевозчик присылает документы, оказывается в конверте нет таки ТТН В итоге вы знаете, что ТТН потерялась, мы не можем выставить документы на оплату клиенту, о перевозчику мы уже оплатили по скану, потому что так договорился логист и происходит такая вот нелепая ситуация. Вроде, как логист поверил в такую форму оплаты, с перевозчиком договорился по сканам, хотя клиент платит по оригиналам. Ну и получается, что нам приходится восстанавливать эти ТТН. Приходится тратить на это время. Перевозчику, как вы понимаете, уже наплевать, потому что он уже свои деньги получил. Он шевелится уже не особо-то хочет. Если клиент платит за 30 дней банковских по оригиналам ТТН, некоторые логисты берут и договаривается по сканам ТТН, да еще и наличкой, а клиент платит НДС, то здесь компания начинает терять, потому что эти деньги мы по сути замораживаем под этого перевозчика. Платим из своих средств, из своего фонда и эти деньги вернутся нам еще не скоро, поэтому вот такая ошибка.
Проверка заявки перед отправкой
Шестой пункт он уже более сильно влияет на финансовую ситуацию в компании. Отсутствие проверки заявки перед отправкой. Такая ошибка бывает и старых и у новых логистов, и опытных и у неопытных — без разницы. Что я имею ввиду, когда логист уже оформил заявку и необходимо отправить перевозчику и заказчику зачастую бывает так, что логист, который находится в запарке какой-то или находится где-то мысленно в другом месте , занят какими-то посторонними делами и так далее, его отвлекают. Тогда он может просто перепутать заявки и отправить заявку с заказчиком на электронку перевозчика, а заявку перевозчика может отправить на электронку заказчику. Происходит такая вот нелепая ситуация — все стороны сделки узнают, кто с кем работает по каким ставкам, по каким срокам оплаты по какой форме оплаты. Логисту приходится оправдываться, как перед переводчиком, так и перед заказчиком, выдумывать какие-то отмазки, поэтому смотрите внимательно перед тем, как отправить заявку по электронной почте и обязательно проверьте ту ли заявку вы прикрепили к вашему электронному письму и туда ли вы ее отправляете. Это очень важно.
Чем больше опыта у логиста, тем более сложные ошибки он совершает!
Проблемы оплаты с НДС и без НДС
Ошибка номер пять, который может привести к тому, что компания может потерять деньги. Я ее так назвал «с НДС и без НДС». Особенно часто это происходит с новичками в логистике, которые еще ненедопонимают, что такое безнал, что такое НДС, что такое без НДС. И зачастую бывают такие ситуации, когда, например, но клиент дал заявку, говорит вот заявка стоит 50 тысяч рублей надо отвезти с Москвы в Уфу от 50000 рублей с НДС. Логист начинает искать по этой заявке перевозчика, находит перевозчика за 45 тысяч рублей и думает о, как здорово сейчас я заработаю 5000 рублей. Это круто, когда приходит время оформления заявки он присылает заявку перевозчику, перевозчик говорит, что вы мне пишете 45 тысяч рублей с НДС — же мы же с вами без НДС договаривались. Новенький логист может не понимать, что с ндс и без ндс абсолютно разные вещи. У нас есть определенная инструкция по этой теме в формате word, как рассчитывается те или иные ситуации, когда клиент платит с НДС и без НДС наличкой, как рассчитываться с перевозчиком. Нужно сделать определенную инструкцию для ваших логистов, чтобы они понимали, что такое с НДС, что такое без НДС и как рассчитывать при этом выгоду со сделки, то есть вашу маржу. Очень важно донести то логистов умение правильно выбирать формы оплаты и понимать, в чем разница между с НДС и без НДС.
Постепенно мы с вами приближаемся к нашей тройки лидеров.
Ошибки в стоимости доставки
Четвертый пункт это некорректная стоимость доставки. Это, когда логист может, например, в транспорте быть, а ему клиент звонит — мне срочно нужно посчитать стоимость доставки. При этом иногда логисты забывают задать какие-то уточняющие вопросы, например, этот заказчик говорит мне нужно отвезти груз из Казани в московскую область , а куда там в московскую область не ясно. Надо было бы задать этому клиенту вопрос, куда именно, а может быть это вообще какой-то дальний район — область большая. Не очень приятно — может быть это вообще несколько точек московской области, может быть это в центре Москвы и тогда это уже вообще проблема. На садовое кольцо, вы сами знаете, заехать не каждый сможет, а он говорит мне рассчитайте стоимость на фуру в московскую область. А на разные районы московской области это совершенно разные ставки. Но клиент торопит и логист в спешке называют какую-то наобум цену. Через неделю этот клиент перезванивает говорит отвезти груз как вы мне называли там за 40 тысяч рублей. Тут логист начинает уже нормально разбираться с заказом, он начинает задавать какие-то конкретные наводящие вопросы и тут понимает, что фактически то он с ценой облажался. Если это клиент новый, то приходится как-то выкручиваться из ситуации, ставить прибыль в ноль, если вы хотите зацепиться за этого клиента. Либо ставить в небольшой минус, если это старый клиент, то приходится как-то оправдываться пытаться хоть что-то здесь выиграть. Хотя бы в ноль или с небольшой маржинальностью.
Такая вот ситуация происходит довольно часто. В итоге это приводит к тому, что фирма теряет деньги.
Ошибки в полноте данных для исполнения заявки
Позиция номер три это, когда логист не указывает полные данные в заявке. Здесь очень важно указывать конкретные четкие данные по дате загрузки, по времени загрузки, особенно маршрут загрузки с полным указанием адреса области, района, региона и так далее. Важно указывать габариты и обязательно какие-то особые требования к погрузке. Например, требуется двенадцать крепежных ремней, требуются коники. Требуется, например, верхняя расстановка со снятием задней балки. Забудет написать дату и время погрузки. Машина приезжает к шести вечера оказывается ее ждали к 14-00, а никто не знал в заявке это не прописано. Клиент кричит, выставляет опоздание, мы ничего не можем предъявить перевозчику, так как мы его об этом не уведомили в письменном виде по поводу населенных пунктов. Логисты зачастую забывают написать, что это определенно какая-то область, не просто там населенный пункт особенно это касается, когда прописывают в заявках акие-то маленькие населенные пункты. Забывают прописать, что это такая-то область нижегородская область и такой-то район. Бывает так, что даже в одном регионе в одной области бывает несколько поселков с одним именем и они находятся на больших расстояниях друг друга. Поэтому обязательно нужно прописывать — какая область, какой район у этого населенного пункта. Все это нужно обязательно указывать в заявке и более того нужно обязательно прописывать контактные данные на выгрузке и на загрузке, чтобы водитель максимально быстро нашел эту загрузку и лишний раз вас не теребил, не спрашивал, как доехать, куда повернуть. То есть обязательно указывать полные данные в заявке максимально полные какие только можно. И, чтобы к вам потом юридически не было никаких вопросов вот эта ситуация может привести действительно к финансовым потерям вплоть до штрафных санкций за срыв погрузки за опоздание это все очень серьезно.
Риски работы под честное слово
Пункт номер два это работа под честное слово, что я имею ввиду этот пункт он вытекает по сути из пункта 3. Очень важно, чтобы у вас было документально закреплены все ваши отношения, как с перевозчиком так и с заказчиком. У вас обязательно должны быть подтвержденные заявки, как минимум с перевозчиком и заказчиком, а еще лучше, чтобы были оформлены договоры либо, чтобы это было договор-заявка, где были прописаны определенные штрафные санкции, требования и обязанности. У нас произошла ситуация, когда, например, наш постоянный клиент подогнал нам скажем так другого клиента. Есть такой вот заказчик — ищет транспорт, помогите ему найти. Мы находим заявку.
При этом клиент грамотно вошел в доверие, что и без заявки там все нормально. Мы не заключили заявку с этим заказчиком и в итоге получилось так, что этот груз оказался ненадлежащего качества. Нам пришлось этот груз возвращать обратно в точку загрузки. При этом клиент не подписал никакие ТТН, не подписал заявки, договор не подписал и мы не можем подать в суд и обосновать сумму претензии. Работа под честное слово это худшее, что можно придумать. Под любыми предлогами обязательно требуйте подтвержденные заявки от заказчика и тем более от переводчика. Это все очень важно, потому что это действительно приводит к серьезным финансовым потерям. Если перевозчик вам сорвал загрузку, то заказчик естественно вам выставит штраф, перевозчику вы в свою очередь ничего не сможете предъявить, потому что заявки, так как таковой и нет. Это всё серьёзно, к этому нужно отнестись очень внимательно.
Ошибок не совершает только тот, кто ничего не делает! Вопрос только в том все ли вы делаете, чтобы их было меньше!
Мошенничество в перевозках и безопасность
И завершаем наш топ халатная проверка перевозчика, как я уже говорю безопасность безопасность еще раз безопасность. Никогда не экономьте на безопасности особенно в сфере грузоперевозок. Поймите, это очень серьезная вещь, когда логист относится халатно к проверке перевозчика. Ну висит у него несколько заявок до ему скинули данные он так в спешке что-то посмотрел, но у него нет какого-то четкого алгоритма, какого то чек-листа по проверке. Он действует интуитивно — что знает то смотрит. А в запарке логист может просто халатно к этому отнестись или что-то не досмотреть, что-то не увидеть, а когда у него есть конкретные пункты перед глазами, что нужно делать, конкретные четкие инструкции, он уже следует этим инструкциям и ни одного пункта не пропускает. К проверке перевозчиков относиться нужно очень внимательно, потому что настолько сейчас профессионально начали действовать мошенники, что я довольно часто сталкиваюсь с разнообразными мошенническими схемами. Мне пишут периодически, рассказывают о разных схемах мошенничества, в которых задействуют даже женщин. Мужчины более склонны доверять женщинам и, когда мы слышим женский голос, мы думаем вряд ли наверное будут там обманывать, красть груз и так далее. Ничего подобного! Последнее время задействует даже женщин в мошеннических схемах. Под разным соусом падают одни и те же мошеннические схемы, поэтому с этим будьте особо внимательны. Я именно сделал акцент на перевозчике не на заказчике, потому что именно при проверке перевозчика могут быть допущены ошибки, которые приведут к максимальным потерям. Груз украдут на 5 миллионов. Если вы недопроверили нового заказчика ну, что вы там потеряете — ставку за перевозку, ну пусть будет это 100 тысяч. Вы потеряете не так много, чем при проверке при халатной проверке перевозчика. Поэтому к этому моменту относиться нужно особо внимательно!
Источник
Все курсы > Оптимизация > Занятие 5
Как мы уже знаем, несмотря на название, логистическая регрессия решает задачу классификации. Сегодня мы подробно разберем принцип работы и составные части алгоритма логистической регрессии, а также построим модели с одной и несколькими независимыми переменными.
Бинарная логистическая регрессия
Задача бинарной классификации
Вернемся к задаче кредитного скоринга, про которую мы говорили, когда обсуждали принцип машинного обучения. Предположим, что мы собрали данные и выявили зависимость возвращения кредита (ось y) от возраста заемщика (ось x).
Как мы видим, в среднем более молодые заемщики реже возвращают кредит. Возникает вопрос, с помощью какой модели можно описать эту зависимость? Казалось бы, можно построить линейную регрессию таким образом, чтобы она выдавала некоторое значение и, если это значение окажется ниже 0,5 — отнести наблюдение к классу 0, если выше — к классу 1.
- Если $ f_w(x) < 0,5 rightarrow hat{y} = 0 $
- Если $ f_w(x) geq 0,5 rightarrow hat{y} = 1 $
Однако, даже если предположить, что мы удачно провели линию регрессии (а на графике выше мы действительно провели ее вполне удачно), и наша модель может делать качественный прогноз, появление новых данных сместит эту границу, и, как следствие, ничего не добавит, а только ухудшит точность модели.
Теперь часть наблюдений, принадлежащих к классу 1, будет ошибочно отнесено моделью к классу 0.
Кроме этого, линейная регрессия по оси y выдает значения, сильно выходящие за пределы интересующего нас интервала от нуля до единицы.
Откроем ноутбук к этому занятию⧉
|
1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 18 19 |
# помимо стандартных библиотек мы также импортируем библиотеку warnings # она позволит скрыть предупреждения об ошибках import numpy as np import pandas as pd import matplotlib.pyplot as plt import seaborn as sns import warnings # кроме того, импортируем датасеты библиотеки sklearn from sklearn import datasets # а также функции для расчета метрики accuracy и построения матрицы ошибок from sklearn.metrics import accuracy_score, confusion_matrix # построенные нами модели мы будем сравнивать с результатом # класса LogisticRegression библиотеки sklearn from sklearn.linear_model import LogisticRegression # среди прочего, мы построим модели полиномиальной логистической регрессии from sklearn.preprocessing import PolynomialFeatures |
Функция логистической регрессии
Сигмоида
Возможно решение упомянутых выше сложностей — пропустить значение линейной регрессии через сигмоиду (sigmoid function), которая при любом значении X не выйдет из необходимого нам диапазона $0 leq h(x) leq 1 $. Напомню формулу и график сигмоиды.
$$ g(z) = frac{1}{1+e^{-z}} $$
Примечание: обратие внимание, когда z представляет собой большое отрицательное число, знаменатель становится очень большим $ 1 + e^{-(-5)} approx 148, 413 $ и значение сигмоиды стремится к нулю; когда z является большим положительным числом, знаменатель, а вместе с ним и все выражение стремятся к единице $ 1 + e^{-(5)} approx 0,0067 $.
Тогда мы можем построить линейную модель, значение которой будет подаваться в сигмоиду.
$$ z = Xtheta rightarrow h_{theta}(x) = frac{1}{1+e^{-(Xtheta)}} $$
В этом смысле никакой ошибки в названии «логистическая регрессия». Этот алгоритм решает задачу классификации через модель линейной регрессии.
Если вы не помните, почему мы записали множественную линейную функцию как $theta x$, посмотрите предыдущую лекцию.
Приведем код на Питоне.
|
def h(x, thetas): z = np.dot(x, thetas) return 1.0 / (1 + np.exp(—z)) |
Теперь посмотрим, как интерпретировать коэффициенты.
Интерпретация коэффициентов
Для любого значения x через $ h_{theta}(x) $ мы будем получать вероятность от 0 до 1, что объект принадлежит к классу y = 1. Например, если класс 1 означает, что заемщик вернул кредит, то $ h_{theta}(x) = 0,8 $ говорит о том, что согласно нашей модели (с параметрами $theta$), для данного заемщика (x) вероятность возвращения кредита состаляет 80 процентов.
В общем случае мы можем записать вероятность вот так.
$$ h_{theta}(x) = P(y = 1 | x; theta) $$
Это выражение можно прочитать как вероятность принадлежности к классу 1 при условии x с параметрами $theta$ (probability of y = 1 given x, parameterized by $theta$).
Поскольку, как мы помним, сумма вероятностей событий, образующих полную группу, всегда равна единице, вероятность принадлежности к классу 0 будет равна
$$ P(y = 0 | x; theta) = 1-P(y = 1 | x; theta) $$
Решающая граница
Решающая граница (decision boundary) — это порог, который определяет к какому классу отнести то или иное наблюдение. Если выбрать порог на уровне 0,5, то все что выше или равно этому порогу мы отнесем к классу 1, все что ниже — к классу 0.
$$ y = 1, h_{theta}(x) geq 0,5 $$
$$ y = 0, h_{theta}(x) < 0,5 $$
Теперь обратите внимание на сигмоиду. Сигмоида $ g(z) $ принимает значения больше 0,5, если $ z geq 0 $, а так как $ z = Xtheta $, то можно сказать, что
- $h_{theta}(x) geq 0,5$ и $ y = 1$, когда $ Xtheta geq 0 $, и соответственно
- $h_{theta}(x) < 0,5 $ и $ y = 0$, когда $ Xtheta < 0 $.
Уравнение решающей границы
Предположим, что у нас есть два признака $x_1$ и $x_2$. Вместе они образуют так называемое пространство ввода (input space), то есть все имеющиеся у нас наблюдения. Мы можем представить его на координатной плоскости, дополнительно выделив цветом наблюдения, относящиеся к разным классам.
Кроме того, представим, что мы уже построили модель логистической регрессии, и она провела для нас соответствующую границу между двумя классами.
Возникает вопрос. Как, зная коэффициенты $theta_0$, $theta_1$ и $theta_2$ модели, найти уравнение линии решающей границы? Для начала договоримся, что уравнение решающией границы будет иметь вид $x_2 = mx_1 + c$, где m — наклон прямой, а c — сдвиг.
Теперь вспомним, что модель с двумя признаками (до подачи в сигмоиду) имеет вид
$$ z = theta_0 + theta_1 x_1 + theta_2 x_2 $$
Также не забудем, что граница проходит там, где $ h_{theta}(x) = 0,5 $, а значит z = 0. Значит,
$$ 0 = theta_0 + theta_1 x_1 + theta_2 x_2 $$
Чтобы найти с (то есть сдвиг линии решающей границы вдоль оси $x_2$) приравняем $x_1$ к нулю и решим для $x_2$ (именно эта точка и будет сдвигом c).
$$ 0 = theta_0 + 0 + theta_2 x_2 rightarrow x_2 = -frac{theta_0}{theta_2} rightarrow c = -frac{theta_0}{theta_2} $$
Теперь займемся наклоном m. Возьмем некоторую точку на линии решающей границы с координатами $(x_1^a, x_2^a)$, $(x_1^b, x_2^b)$. Тогда наклон m будет равен
$$ m = frac{x_2^b-x_2^a}{x_1^b-x_1^a} $$
Так как эти точки расположены на решающей границе, то справедливо, что
$$ 0 = theta_1x_1^b + theta_2x_2^b + theta_0-(theta_1x_1^a + theta_2x_2^a + theta_0) $$
$$ -theta_2(x_2^b-x_2^a) = theta_1(x_1^b-x_1^a) $$
А значит,
$$ frac{x_2^b-x_2^a}{x_1^b-x_1^a} = -frac{theta_1}{theta_2} rightarrow m = -frac{theta_1}{theta_2} $$
Вычислительная устойчивость сигмоиды
При очень больших отрицательных или положительных значениях z может возникнуть переполнение памяти (overflow).
|
# возьмем большое отрицательное значение z = —999 1 / (1 + np.exp(—z)) |
|
RuntimeWarning: overflow encountered in exp 0.0 |
Преодолеть это ограничение и добиться вычислительной устойчивости (numerical stability) алгоритма можно с помощью следующего тождества.
$$ g(z) = frac{1}{1+e^{-z}} = frac{1}{1+e^{-z}} times frac{e^z}{e^z} = frac{e^z}{e^z(1+e^{-z})} = frac {e^z}{e^z + 1} $$
Что интересно, первая часть тождества устойчива при очень больших положительных значениях z.
|
z = 999 1 / (1 + np.exp(—z)) |
При этом вторая стабильна при очень больших отрицательных значениях.
|
z = —999 np.exp(z) / (np.exp(z) + 1) |
Объединим обе части с помощью условия с if.
|
def stable_sigmoid(z): if z >= 0: return 1 / (1 + np.exp(—z)) else: return np.exp(z) / (np.exp(z) + 1) |
Примечание. Мы не использовали более лаконичный код, например, функцию np.where(), потому что эта функция прежде чем применить условие рассчитывает оба сценария (в данном случае обе части тождества), а это ровно то, чего мы хотим избежать, чтобы не возникло ошибки. Простое условие с if препятствует выполнению той части кода, которая нам не нужна.
Остается написать линейную функцию и подать ее результат в сигмоиду.
|
def h(x, thetas): z = np.dot(x, thetas) return np.array([stable_sigmoid(value) for value in z]) |
Протестируем код. Предположим, что в нашем датасете четыре наблюдения и три коэффициента. Схематично расчеты будут выглядеть следующим образом.
Пропишем это на Питоне.
|
# возьмем массив наблюдений 4 х 3 с числами от 1 до 12 x = np.arange(1, 13).reshape(4, 3) # и трехмерный вектор коэффициентов thetas = np.array([—3, 1, 1]) # подадим их в модель h(x, thetas) |
|
array([0.88079708, 0.26894142, 0.01798621, 0.00091105]) |
Модель работает корректно. Теперь обсудим, как ее обучать, то есть какую функцию потерь использовать для оптимизации параметров $theta$.
Logistic loss или функция кросс-энтропии
В модели логистической регрессии мы не можем использовать MSE. Дело в том, что если мы поместим результат сигмоиды (представляющей собою нелинейную функцию) в MSE, то на выходе получим невыпуклую функцию (non-convex), глобальный минимум которой довольно сложно найти.
Вместо MSE мы будем использовать функцию логистической ошибки, которую еще называют функцией бинарной кросс-энтропии (log loss, binary cross-entropy loss).
График и формула логистической ошибки
Вначале посмотрим на нее на графике.
Разберемся, как она работает. Наша модель $h_{theta}(x)$ может выдавать вероятность от 0 до 1, фактические значения $y$ только 0 и 1.
Сценарий 1. Предположим, что для конкретного заемщика в обучающем датасете истинное значение/ целевой класс записан как 1 (то есть заемщик вернул кредит). Тогда «срабатывает» синяя ветвь графика и ошибка измеряется по ней. Соответственно, чем ближе выдаваемая моделью вероятность к единице, тем меньше ошибка.
$$ -log(P(y = 1 | x; theta)) = -log(h_{theta}(x)), y = 1 $$
Сценарий 2. Заемщик не вернул кредит и его целевая переменная записана как 0. Тогда срабатывает оранжевая ветвь. Ошибка модели будет минимальна при значениях близких к нулю.
$$ -log(1-P(y = 1 | x; theta)) = -log(1-h_{theta}(x)), y = 0 $$
Добавлю, что минус логарифм в данном случае очень удачно отвечает нашему желанию иметь нулевую ошибку при правильном прогнозе и наказать алгоритм высокой ошибкой (асимптотически стремящейся к бесконечности) в случае неправильного прогноза.
В итоге нам нужно будет найти сумму вероятностей принадлежности к классу 1 для сценария 1 и сценария 2.
$$ J(theta) = begin{cases} -log(h_{theta}(x)) | y=1 -log(1-h_{theta}(x)) | y=0 end{cases} $$
Однако, для каждого наблюдения нам нужно учитывать только одну из вероятностей (либо $y=1$, либо $y=0$). Как нам переключаться между ними? На самом деле очень просто.
В качестве переключателя можно использовать целевую переменную. В частности, умножим левую часть функции на y, а правую на 1-y. Тогда если речь идет о классе 1 первая часть умножится на единицу, вторая на ноль и исчезнет. Если речь идет о классе 0, произойдет обратное, исчезнет левая часть, а правая останется. Получается
$$ J(theta) = -frac{1}{n} sum y cdot log(h_{theta}(x)) + (1-y) cdot log(1-h_{theta}(x)) $$
Рассмотрим ее работу на учебном примере.
Расчет логистической ошибки
Предположим, мы построили модель и для каждого наблюдения получили некоторый прогноз (вероятность).
|
# выведем результат работы модели (вероятности) y_pred и целевую переменную y output = pd.DataFrame({ ‘y’ :[1, 1, 1, 0, 0, 1, 1, 0], ‘y_pred’ :[0.93, 0.81, 0.78, 0.43, 0.54, 0.49, 0.22, 0.1] }) output |
Найдем вероятность принадлежности к классу 1.
|
# оставим вероятность, если y = 1, и вычтем вероятность из единицы, если y = 0 output[‘y=1 prob’] = np.where(output[‘y’] == 0, 1 — output[‘y_pred’], output[‘y_pred’]) output |
Возьмем отрицательный логарифм из каждой вероятности.
|
output[‘-log’] = —np.log(output[‘y=1 prob’]) output |
Выведем каждое из получившихся значений на графике.
|
1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 18 19 |
plt.figure(figsize = (10, 8)) # создадим точки по оси x в промежутке от 0 до 1 x_vals = np.linspace(0, 1) # выведем кривую функции логистической ошибки plt.plot(x_vals, —np.log(x_vals), label = ‘-log(h(x)) | y = 1’) # выведем каждое из значений отрицательного логарифма plt.scatter(output[‘y=1 prob’], output[‘-log’], color = ‘r’) # зададим заголовок, подписи к осям, легенду и сетку plt.xlabel(‘h(x)’, fontsize = 16) plt.ylabel(‘loss’, fontsize = 16) plt.title(‘Функция логистической ошибки’, fontsize = 18) plt.legend(loc = ‘upper right’, prop = {‘size’: 15}) plt.grid() plt.show() |
Как мы видим, так как мы всегда выражаем вероятность принадлежности к классу 1, графически нам будет достаточно одной ветви. Остается сложить результаты и разделить на количество наблюдений.
Окончательный вариант
Напишем функцию логистической ошибки, которую будем использовать в нашем алгоритме.
|
def objective(y, y_pred): # рассчитаем функцию потерь для y = 1, добавив 1e-9, чтобы избежать ошибки при log(0) y_one_loss = y * np.log(y_pred + 1e—9) # также рассчитаем функцию потерь для y = 0 y_zero_loss = (1 — y) * np.log(1 — y_pred + 1e—9) # сложим и разделим на количество наблюдений return —np.mean(y_zero_loss + y_one_loss) |
Проверим ее работу на учебных данных.
|
# проверим ее работу на учебных данных objective(output[‘y’], output[‘y_pred’]) |
Теперь займемся поиском производной.
Производная функции логистической ошибки
Предположим, что $G(theta)$ — одна из частных производных описанной выше функции логистической ошибки $J(theta)$,
$$ G = y cdot log(h) + (1-y) cdot log(1-h) $$
где h — это сигмоида $1/1+e^{-z}$, а $z(theta)$ — линейная функция $xtheta$. Тогда по chain rule нам нужно найти производные следующих функций
$$ frac{partial G}{partial theta} = frac{partial G}{partial h} cdot frac{partial h}{partial z} cdot frac{partial z}{partial theta} $$
Производная логарифмической функции
Начнем с производной логарифмической функции.
$$ frac{partial}{partial x} ln f(x) = frac{1}{f(x)} $$
Теперь, помня, что x и y — это константы, найдем первую производную.
$$ frac{partial G}{partial h} left[ y cdot log(h) + (1-y) cdot log(1-h) right] $$
$$ = y cdot frac{partial G}{partial h} [log(h)] + (1-y) cdot frac{partial G}{partial h} [log(1-h)] $$
$$ = frac{1}{h}y + frac{1}{1-h} cdot frac{partial G}{partial h} [1-h] cdot (1-y) $$
Упростим выражение (не забыв про производную разности).
$$ = frac{h}{y} + frac{frac{partial G}{partial h} (1-h) (1-y)}{1-h} = frac{h}{y}+frac{(0-1)(1-y)}{1-h} $$
$$ = frac{y}{h}-frac{1-y}{1-h} = frac{y-h}{h(1-h)} $$
Теперь займемся производной сигмоиды.
Производная сигмоиды
Вначале упростим выражение.
$$ frac{partial h}{partial z} left[ frac{1}{1+e^{-z}} right] = frac{partial h}{partial z} left[ (1+e^{-z})^{-1}) right] $$
Теперь перейдем к нахождению производной
$$ = -(1+e^{-z})^{-2}) cdot (-e^{-z}) = frac{e^{-z}}{(1+e^{-z})^2} $$
$$ = frac{1}{1+e^{-z}} cdot frac{e^{-z}}{1+e^{-z}} = frac{1}{1+e^{-z}} cdot frac{(1+e^{-z})-1}{1+e^{-z}} $$
$$ = frac{1}{1+e^{-z}} cdot left( frac{1+e^{-z}}{1+e^{-z}}-frac{1}{1+e^{-z}} right) $$
$$ = frac{1}{1+e^{-z}} cdot left( 1-frac{1}{1+e^{-z}} right) $$
В терминах предложенной выше нотации получается
$$ h(1-h) $$
Производная линейной функции
Наконец найдем производную линейной функции.
$$ frac{partial z}{partial theta} = x $$
Перемножим производные и найдем градиент по каждому из признаков j для n наблюдений.
$$ frac{partial J}{partial theta} = frac{y-h}{h(1-h)} cdot h(1-h) cdot x_j cdot frac{1}{n} = x_j cdot (y-h) cdot frac{1}{n} $$
Замечу, что хотя производная похожа на градиент функции линейной регрессии, на самом деле это разные функции, $h$ в данном случае это сигмоида.
Для нахождения градиента (всех частных производных одновременно) перепишем формулу в векторной нотации.
$$ nabla_{theta} J = X^T(h(Xtheta)-y) times frac{1}{n} $$
Схематично для четырех наблюдений и трех коэффициентов нахождение градиента будет выглядеть следующим образом.
Объявим соответствующую функцию.
|
def gradient(x, y, y_pred, n): return np.dot(x.T, (y_pred — y)) / n |
На всякий случай напомню, что прогнозные значения (y_pred) мы получаем с помощью объявленной ранее функции $h(x, thetas)$.
Подготовка данных
В качестве примера возьмем встроенный в sklearn датасет, в котором нам предлагается определить класс вина по его характеристикам.
|
# импортируем датасет о вине из модуля datasets data = datasets.load_wine() # превратим его в датафрейм df = pd.DataFrame(data.data, columns = data.feature_names) # добавим целевую переменную df[‘target’] = data.target # посмотрим на первые три строки df.head(3) |
Целевая переменная
Посмотрим на количество наблюдений и признаков (размерность матрицы), а также уникальные значения (классы) в целевой переменной.
|
df.shape, np.unique(df.target) |
|
((178, 14), array([0, 1, 2])) |
Как мы видим, у нас три класса, а должно быть два, потому что пока что мы создаем алгоритм бинарной классификации. Отфильтруем значения так, чтобы осталось только два класса.
|
# применим маску датафрейма и удалим класс 2 df = df[df.target != 2] # посмотрим на результат df.shape, df.target.unique() |
|
((130, 14), array([0, 1])) |
Отбор признаков
Наша целевая переменная выражена бинарной категорией или, как еще говорят, находится на дихотомической шкале (dichotomous variable). В этом случае применять коэффициент корреляции Пирсона не стоит и можно использовать точечно-бисериальную корреляцию (point-biserial correlation). Рассчитаем корреляцию признаков и целевой переменной нашего датасета.
|
1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 |
# импортируем модуль stats из библиотеки scipy from scipy import stats # создадим два списка, один для названий признаков, второй для корреляций columns, correlations = [], [] # пройдемся по всем столбцам датафрейма кроме целевой переменной for col in df.drop(‘target’, axis = 1).columns: # поместим название признака в список columns columns.append(col) # рассчитаем корреляцию этого признака с целевой переменной # и поместим результат в список корреляций correlations.append(stats.pointbiserialr(df[col], df[‘target’])[0]) # создадим датафрейм на основе заполненных списков # и применим градиентную цветовую схему pd.DataFrame({‘column’: columns, ‘correlation’: correlations}).style.background_gradient() |
Наиболее коррелирующим с целевой переменной признаком является пролин (proline). Визуально оценим насколько сильно отличается этот показатель для классов вина 0 и 1.
|
# зададим размер графика plt.figure(figsize = (10, 8)) # на точечной диаграмме выведем пролин по оси x, а класс вина по оси y sns.scatterplot(x = df.proline, y = df.target, s = 80); |
Теперь посмотрим на зависимость двух признаков (спирт и пролин) от целевой переменной.
|
# зададим размер графика plt.figure(figsize = (10, 8)) # на точечной диаграмме по осям x и y выведем признаки, # с помощью параметра hue разделим соответствующие классы целевой переменной sns.scatterplot(x = df.alcohol, y = df.proline, hue = df.target, s = 80) # добавим легенду, зададим ее расположение и размер plt.legend(loc = ‘upper left’, prop = {‘size’: 15}) # выведем результат plt.show() |
В целом можно сказать, что классы линейно разделимы (другими словами, мы можем провести прямую между ними). Поместим признаки в переменную X, а целевую переменную — в y.
|
X = df[[‘alcohol’, ‘proline’]] y = df[‘target’] |
Масштабирование признаков
Как и в случае с линейной регрессией, для алгоритма логистической регрессии важно, чтобы признаки были приведены к одному масштабу. Для этого используем стандартизацию.
|
# т.е. приведем данные к нулевому среднему и единичному СКО X = (X — X.mean()) / X.std() X.head() |
Проверим результат.
|
X.alcohol.mean(), X.alcohol.std(), X.proline.mean(), X.proline.std() |
|
(6.8321416900009635e-15, 1.0, -5.465713352000771e-17, 1.0) |
Теперь мы готовы к созданию и обучению модели.
Обучение модели
Вначале объявим уже знакомую нам функцию, которая добавит в датафрейм столбец под названием x0, заполненный единицами.
|
def add_ones(x): # важно! метод .insert() изменяет исходный датафрейм return x.insert(0,‘x0’, np.ones(x.shape[0])) |
Применим ее к нашему датафрейму с признаками.
|
# добавим столбец с единицами add_ones(X) # и посмотрим на результат X.head() |
Создадим вектор начальных весов (он будет состоять из нулей), а также переменную n, в которой будет храниться количество наблюдений.
|
thetas, n = np.zeros(X.shape[1]), X.shape[0] thetas, n |
|
(array([0., 0., 0.]), 130) |
Кроме того, создадим список, в который будем записывать размер ошибки функции потерь.
Теперь выполним основную работу по минимизации функции потерь и поиску оптимальных весов (выполнение кода ниже у меня заняло около 30 секунд).
|
# в цикле из 20000 итераций for i in range(20000): # рассчитаем прогнозное значение с текущими весами y_pred = h(X, thetas) # посчитаем уровень ошибки при текущем прогнозе loss_history.append(objective(y, y_pred)) # рассчитаем градиент grad = gradient(X, y, y_pred, n) # используем градиент для улучшения весов модели # коэффициент скорости обучения будет равен 0,001 thetas = thetas — 0.001 * grad |
Посмотрим на получившиеся веса и финальный уровень ошибки.
|
# чтобы посмотреть финальный уровень ошибки, # достаточно взять последний элемент списка loss_history thetas, loss_history[—1] |
|
(array([ 0.23234188, -1.73394252, -1.89350543]), 0.12282503517421262) |
Модель обучена. Теперь мы можем сделать прогноз и оценить результат.
Прогноз и оценка качества
Прогноз модели
Объявим функцию predict(), которая будет предсказывать к какому классу относится то или иное наблюдение. От функции $h(x, thetas)$ эта функция будет отличаться тем, что выдаст не только вероятность принадлежности к тому или иному классу, но и непосредственно сам предполагаемый класс (0 или 1).
|
def predict(x, thetas): # найдем значение линейной функции z = np.dot(x, thetas) # проведем его через устойчивую сигмоиду probs = np.array([stable_sigmoid(value) for value in z]) # если вероятность больше или равна 0,5 — отнесем наблюдение к классу 1, # в противном случае к классу 0 # дополнительно выведем значение вероятности return np.where(probs >= 0.5, 1, 0), probs |
Вызовем функцию predict() и запишем прогноз класса и вероятность принадлежности к этому классу в переменные y_pred и probs соответственно.
|
# запишем прогноз класса и вероятность этого прогноза в переменные y_pred и probs y_pred, probs = predict(X, thetas) # посмотрим на прогноз и вероятность для первого наблюдения y_pred[0], probs[0] |
|
(0, 0.022908352078195617) |
Здесь важно напомнить, что вероятность близкая к нулю говорит о пренадлжености к классу 0. В качестве упражнения выведите класс последнего наблюдения и соответствующую вероятность.
Метрика accuracy и матрица ошибок
Оценим результат с помощью метрики accuracy и матрицы ошибок.
|
# функцию accuracy_score() мы импортировали в начале ноутбука accuracy_score(y, y_pred) |
|
# функцию confusion_matrix() мы импортировали в начале ноутбука # столбцами будут прогнозные значения (Forecast), # строками — фактические (Actual) pd.DataFrame(confusion_matrix(y, y_pred), columns = [‘Forecast 0’, ‘Forecast 1’], index = [‘Actual 0’, ‘Actual 1’]) |
Как мы видим, алгоритм ошибся пять раз. Дважды он посчитал, что наблюдение относится к классу 1, хотя на самом деле это был класс 0, и трижды, наоборот, неверно отнес класс 1 к классу 0.
Решающая граница
Выше мы уже вывели уравнение решающей границы. Воспользуемся им, чтобы визуально оценить насколько удачно классификатор справился с поставленной задачей.
|
# рассчитаем сдвиг (c) и наклон (m) линии границы c, m = —thetas[0]/thetas[2], —thetas[1]/thetas[2] c, m |
|
(0.1227046263531282, -0.915731474695505) |
|
# найдем минимальное и максимальное значения для спирта (ось x) xmin, xmax = min(X[‘alcohol’]), max(X[‘alcohol’]) # найдем минимальное и максимальное значения для пролина (ось y) ymin, ymax = min(X[‘proline’]), max(X[‘proline’]) # запишем значения оси x в переменную xd xd = np.array([xmin, xmax]) xd |
|
array([-2.15362589, 2.12194856]) |
|
# подставим эти значения, а также значения сдвига и наклона в уравнение линии yd = m * xd + c # в результате мы получим координаты двух точек, через которые проходит линия границы (xd[0], yd[0]), (xd[1], yd[1]) |
|
((-2.1536258890738247, 2.0948476376971197), (2.1219485561396647, -1.8204304541886445)) |
|
1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 18 19 20 21 22 23 24 25 26 |
# зададим размер графика plt.figure(figsize = (11, 9)) # построим пунктирную линию по двум точкам, найденным выше plt.plot(xd, yd, ‘k’, lw = 1, ls = ‘—‘) # дополнительно отобразим наши данные sns.scatterplot(x = X[‘alcohol’], y = X[‘proline’], hue = y, s = 70) # которые снова снабдим легендой plt.legend(loc = ‘upper left’, prop = {‘size’: 15}) # минимальные и максимальные значения по обеим осям будут границами графика plt.xlim(xmin, xmax) plt.ylim(ymin, ymax) # по желанию, разделенные границей половинки можно закрасить # tab: означает, что цвета берутся из палитры Tableau # plt.fill_between(xd, yd, ymin, color=’tab:blue’, alpha = 0.2) # plt.fill_between(xd, yd, ymax, color=’tab:orange’, alpha = 0.2) # а также добавить обозначения переменных в качестве подписей к осям # plt.xlabel(‘x_1’) # plt.ylabel(‘x_2’) plt.show() |
На графике хорошо видны те пять значений, в которых ошибся наш классификатор.
Написание класса
Остается написать класс бинарной логистической регрессии.
|
1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 18 19 20 21 22 23 24 25 26 27 28 29 30 31 32 33 34 35 36 37 38 39 40 41 42 43 44 45 46 47 48 49 50 51 52 53 54 55 56 57 58 59 60 61 62 63 64 65 66 67 68 69 70 71 72 73 74 75 |
class LogReg(): # в методе .__init__() объявим переменные для весов и уровня ошибки def __init__(self): self.thetas = None self.loss_history = [] # метод .fit() необходим для обучения модели # этому методу мы передадим признаки и целевую переменную # кроме того, мы зададим значения по умолчанию # для количества итераций и скорости обучения def fit(self, x, y, iter = 20000, learning_rate = 0.001): # метод создаст «правильные» копии датафрейма x, y = x.copy(), y.copy() # добавит столбец из единиц self.add_ones(x) # инициализирует веса и запишет в переменную n количество наблюдений thetas, n = np.zeros(x.shape[1]), x.shape[0] # создадим список для записи уровня ошибки loss_history = [] # в цикле равном количеству итераций for i in range(iter): # метод сделает прогноз с текущими весами y_pred = self.h(x, thetas) # найдет и запишет уровень ошибки loss_history.append(self.objective(y, y_pred)) # рассчитает градиент grad = self.gradient(x, y, y_pred, n) # и обновит веса thetas -= learning_rate * grad # метод выдаст веса и список с историей ошибок self.thetas = thetas self.loss_history = loss_history # метод .predict() делает прогноз с помощью обученной модели def predict(self, x): # метод создаст «правильную» копию модели x = x.copy() # добавит столбец из единиц self.add_ones(x) # рассчитает значения линейной функции z = np.dot(x, self.thetas) # передаст эти значения в сигмоиду probs = np.array([self.stable_sigmoid(value) for value in z]) # выдаст принадлежность к определенному классу и соответствующую вероятность return np.where(probs >= 0.5, 1, 0), probs # ниже приводятся служебные методы, смысл которых был разобран ранее на занятии def add_ones(self, x): return x.insert(0,‘x0’, np.ones(x.shape[0])) def h(self, x, thetas): z = np.dot(x, thetas) return np.array([self.stable_sigmoid(value) for value in z]) def objective(self, y, y_pred): y_one_loss = y * np.log(y_pred + 1e—9) y_zero_loss = (1 — y) * np.log(1 — y_pred + 1e—9) return —np.mean(y_zero_loss + y_one_loss) def gradient(self, x, y, y_pred, n): return np.dot(x.T, (y_pred — y)) / n def stable_sigmoid(self, z): if z >= 0: return 1 / (1 + np.exp(—z)) else: return np.exp(z) / (np.exp(z) + 1) |
Проверим работу написанного нами класса. Вначале подготовим данные и обучим модель.
|
# проверим работу написанного нами класса # поместим признаки и целевую переменную в X и y X = df[[‘alcohol’, ‘proline’]] y = df[‘target’] # приведем признаки к одному масштабу X = (X — X.mean())/X.std() # создадим объект класса LogReg model = LogReg() # и обучим модель model.fit(X, y) # посмотрим на атрибуты весов и финального уровня ошибки model.thetas, model.loss_history[—1] |
|
(array([ 0.23234188, —1.73394252, —1.89350543]), 0.12282503517421262) |
Затем сделаем прогноз и оценим качество модели.
|
# сделаем прогноз y_pred, probs = model.predict(X) # и посмотрим на класс первого наблюдения и вероятность y_pred[0], probs[0] |
|
(0, 0.022908352078195617) |
|
# рассчитаем accuracy accuracy_score(y, y_pred) |
|
# создадим матрицу ошибок pd.DataFrame(confusion_matrix(y, y_pred), columns = [‘Forecast 0’, ‘Forecast 1’], index = [‘Actual 0’, ‘Actual 1’]) |
Модель показала точно такой же результат. Методы класса LogReg работают. Теперь давайте сравним работу нашего класса с классом LogisticRegression библиотеки sklearn.
Сравнение с sklearn
Обучение модели
Вначале обучим модель.
|
# подготовим данные X = df[[‘alcohol’, ‘proline’]] y = df[‘target’] X = (X — X.mean())/X.std() # создадим объект класса LogisticRegression и запишем его в переменную model model = LogisticRegression() # обучим нашу модель model.fit(X, y) # посмотрим на получившиеся веса модели model.intercept_, model.coef_ |
|
(array([0.30838852]), array([[-2.09622008, -2.45991159]])) |
Прогноз
Теперь необходимо сделать прогноз и найти соответствющие вероятности. В классе LogisticRegression библиотеки sklearn метод .predict() отвечает за предсказание принадлежности к определенному классу, а метод .predict_proba() отвечает за вероятность такого прогноза.
|
# выполним предсказание класса y_pred = model.predict(X) # и найдем вероятности probs = model.predict_proba(X) # посмотрим на класс и вероятность первого наблюдения y_pred[0], probs[0] |
|
(0, array([0.9904622, 0.0095378])) |
Модель предсказала для первого наблюдения класс 0. При этом, обратите внимание, что метод .predict_proba() для каждого наблюдения выдает две вероятности, первая — это вероятность принадлежности к классу 0, вторая — к классу 1.
Оценка качества
Рассчитаем метрику accuracy.
|
accuracy_score(y, y_pred) |
И построим матрицу ошибок.
|
pd.DataFrame(confusion_matrix(y, y_pred), columns = [‘Forecast 0’, ‘Forecast 1’], index = [‘Actual 0’, ‘Actual 1’]) |
Как мы видим, хотя веса модели и предсказанные вероятности немного, ее точность осталась неизменной.
Решающая граница
Построим решающую границу.
|
# найдем сдвиг и наклон для уравнения решающей границы c, m = —model.intercept_ / model.coef_[0][1], —model.coef_[0][0] / model.coef_[0][1] c, m |
|
(array([0.12536569]), -0.8521526076691505) |
|
# посмотрим на линию решающей границы plt.figure(figsize = (11, 9)) xmin, xmax = min(X[‘alcohol’]), max(X[‘alcohol’]) ymin, ymax = min(X[‘proline’]), max(X[‘proline’]) xd = np.array([xmin, xmax]) yd = m*xd + c plt.plot(xd, yd, ‘k’, lw=1, ls=‘—‘) sns.scatterplot(x = X[‘alcohol’], y = X[‘proline’], hue = y, s = 70) plt.legend(loc = ‘upper left’, prop = {‘size’: 15}) plt.xlim(xmin, xmax) plt.ylim(ymin, ymax) plt.show() |
Бинарная полиномиальная регрессия
Идея бинарной полиномиальной логистической регрессии (binary polynomial logistic regression) заключается в том, чтобы использовать полином внутри сигмоиды и соответственно создать нелинейную границу между двумя классами.
Полиномиальные признаки
Уравнение полинома на основе двух признаков будет выглядеть следующим образом.
$$ y = theta_{0}x_0 + theta_{1}x_1 + theta_{2}x_2 + theta_{3} x_1^2 + theta_{4} x_1x_2 + theta_{5} x_2^2 $$
Реализуем этот алгоритм на практике и посмотрим улучшатся ли результаты. Вначале, подготовим и масштабируем данные.
|
# подготовим и X = df[[‘alcohol’, ‘proline’]] y = df[‘target’] # масштабируем данные X = (X — X.mean())/X.std() |
Теперь преобразуем наши данные так, как если бы мы использовали полином второй степени.
Смысл создания полиномиальных признаков мы детально разобрали на занятии по множественной линейной регрессии.
|
# создадим объект класса PolynomialFeatures # укажем, что мы хотим создать полином второй степени polynomial_features = PolynomialFeatures(degree = 2) # преобразуем данные с помощью метода .fit_transform() X_poly = polynomial_features.fit_transform(X) |
Сравним исходные признаки с полиномиальными.
|
# посмотрим на первое наблюдение X.head(1) |
|
# должно получиться шесть признаков X_poly[:1] |
|
array([[1. , 1.44685785, 0.77985116, 2.09339765, 1.12833378, 0.60816783]]) |
Моделирование и оценка качества
Обучим модель, сделаем прогноз и оценим результат.
|
# создадим объект класса LogisticRegression poly_model = LogisticRegression() # обучим модель на полиномиальных признаках poly_model = poly_model.fit(X_poly, y) # сделаем прогноз y_pred = poly_model.predict(X_poly) # рассчитаем accuracy accuracy_score(y_pred, y) |
Построим матрицу ошибок.
|
pd.DataFrame(confusion_matrix(y, y_pred), columns = [‘Forecast 0’, ‘Forecast 1’], index = [‘Actual 0’, ‘Actual 1’]) |
Для того чтобы визуально оценить качество модели, построим два графика: фактических классов и прогнозных. Вначале создадим датасет, в котором будут исходные признаки (alcohol, proline) и прогнозные значения (y_pred).
|
# сделаем копию исходного датафрейма с нужными признаками predictions = df[[‘alcohol’, ‘proline’]].copy() # и добавим новый столбец с прогнозными значениями predictions[‘y_pred’] = y_pred # посмотрим на результат predictions.head(3) |
|
1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 18 19 20 |
# создадим два подграфика с помощью функции plt.subplots() # расположим подграфики на одной строке fig, (ax1, ax2) = plt.subplots(1, 2, # пропишем размер, figsize = (14, 6), # а также расстояние между подграфиками по горизонтали gridspec_kw = {‘wspace’ : 0.2}) # на левом подграфики выведем фактические классы sns.scatterplot(data = df, x = ‘alcohol’, y = ‘proline’, hue = ‘target’, palette = ‘bright’, s = 50, ax = ax1) ax1.set_title(‘Фактические классы’, fontsize = 14) # на правом — прогнозные sns.scatterplot(data = predictions, x = ‘alcohol’, y = ‘proline’, hue = ‘y_pred’, palette = ‘bright’, s = 50, ax = ax2) ax2.set_title(‘Прогноз’, fontsize = 14) # зададим общий заголовок fig.suptitle(‘Бинарная полиномиальная регрессия’, fontsize = 16) plt.show() |
Как вы видите, нам не удалось добиться улучшения по сравнению с обычной полиномиальной регрессией.
Напомню, что создание подграфиков мы подробно разобрали на занятии по исследовательскому анализу данных.
В качестве упражнения предлагаю вам выяснить, какая степень полинома позволит улучшить результат прогноза на этих данных и насколько, таким образом, улучшится качество предсказаний.
Перейдем ко второй части нашего занятия.
Мультиклассовая логистическая регрессия
Как поступить, если нужно предсказать не два класса, а больше? Сегодня мы рассмотрим два подхода: one-vs-rest и кросс-энтропию. Начнем с того, что подготовим данные.
Подготовка данных
Вернем исходный датасет с тремя классами.
|
# вновь импортируем датасет о вине data = datasets.load_wine() # превратим его в датафрейм df = pd.DataFrame(data.data, columns = data.feature_names) # приведем признаки к одному масштабу df = (df — df.mean())/df.std() # добавим целевую переменную df[‘target’] = data.target # убедимся, что у нас присутствуют все три класса df.target.value_counts() |
|
1 71 0 59 2 48 Name: target, dtype: int64 |
В целевой переменной большое двух классов, а значит точечно-бисериальный коэффициент корреляции мы использовать не можем. Воспользуемся корреляционным отношением (correlation ratio).
|
# код ниже был подробно разобран на предыдущем занятии def correlation_ratio(numerical, categorical): values = np.array(numerical) ss_total = np.sum((values.mean() — values) ** 2) cats = np.unique(categorical, return_inverse = True)[1] ss_betweengroups = 0 for c in np.unique(cats): group = values[np.argwhere(cats == c).flatten()] ss_betweengroups += len(group) * (group.mean() — values.mean()) ** 2 return np.sqrt(ss_betweengroups/ss_total) |
|
# создадим два списка, один для названий признаков, второй для значений корреляционного отношения columns, correlations = [], [] # пройдемся по всем столбцам датафрейма кроме целевой переменной for col in df.drop(‘target’, axis = 1).columns: # поместим название признака в список columns columns.append(col) # рассчитаем взаимосвязь этого признака с целевой переменной # и поместим результат в список значений корреляционного отношения correlations.append(correlation_ratio(df[col], df[‘target’])) # создадим датафрейм на основе заполненных списков # и применим градиентную цветовую схему pd.DataFrame({‘column’: columns, ‘correlation’: correlations}).style.background_gradient() |
Теперь наибольшую корреляцию с целевой переменной показывают флавоноиды (flavanoids) и пролин (proline). Их и оставим.
|
df = df[[‘flavanoids’, ‘proline’, ‘target’]].copy() df.head(3) |
Посмотрим насколько легко можно разделить эти классы.
|
# зададим размер графика plt.figure(figsize = (10, 8)) # построим точечную диаграмму с двумя признаками, разделяющей категориальной переменной будет класс вина sns.scatterplot(x = df.flavanoids, y = df.proline, hue = df.target, palette = ‘bright’, s = 100) # добавим легенду plt.legend(loc = ‘upper left’, prop = {‘size’: 15}) plt.show() |
Перейдем непосредственно к алгоритмам мультиклассовой логистической регрессии. Начнем с подхода one-vs-rest.
Подход one-vs-rest
Подход one-vs-rest или one-vs-all предполагает, что мы отделяем один класс, а остальные наоборот объединяем. Так мы поступаем с каждым классом и строим по одной модели логистической регрессии относительно каждого из класса. Например, если у нас три класса, то у нас будет три модели логистической регрессии. Далее мы смотрим на получившиеся вероятности и выбираем наибольшую.
$$ h_theta^{(i)}(x) = P(y = i | x; theta), i in {0, 1, 2} $$
При таком подходе сам по себе алгоритм логистической регрессии претерпевает лишь несущественные изменения, главное правильно подготовить данные для обучения модели.
Подготовка датасетов
|
# поместим признаки и данные в соответствующие переменные x1, x2 = df.columns[0], df.columns[1] target = df.target.unique() target |
|
1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 18 19 20 21 22 23 24 |
# сделаем копии датафреймов ovr_0, ovr_1, ovr_2 = df.copy(), df.copy(), df.copy() # в каждом из них сделаем целевым классом 0-й, 1-й или 2-й классы # например, в ovr_0 нулевым будет класс 0, а классы 1 и 2 первым ovr_0[‘target’] = np.where(df[‘target’] == target[0], 1, 0) ovr_1[‘target’] = np.where(df[‘target’] == target[1], 1, 0) ovr_2[‘target’] = np.where(df[‘target’] == target[2], 1, 0) # выведем разделение на классы на графике fig, (ax1, ax2, ax3) = plt.subplots(1, 3, figsize = (16, 4), gridspec_kw = {‘wspace’: 0.2, ‘hspace’: 0.08}) sns.scatterplot(data = ovr_0, x = x1, y = x2, hue = ‘target’, s = 50, ax = ax1) ax1.set_title(‘Прогнозирование класса 0’, fontsize = 14) sns.scatterplot(data = ovr_1, x = x1, y = x2, hue = ‘target’, s = 50, ax = ax2) ax2.set_title(‘Прогнозирование класса 1’, fontsize = 14) sns.scatterplot(data = ovr_2, x = x1, y = x2, hue = ‘target’, s = 50, ax = ax3) ax3.set_title(‘Прогнозирование класса 2’, fontsize = 14) plt.show() |
Обучение моделей
|
models = [] # поочередно обучим каждую из моделей for ova_n in [ovr_0, ovr_1, ovr_2]: X = ova_n[[‘flavanoids’, ‘proline’]] y = ova_n[‘target’] model = LogReg() model.fit(X, y) # каждую обученную модель поместим в список models.append(model) |
|
# убедимся, что все работает # например, выведем коэффициенты модели 1 models[0].thetas |
|
array([-0.99971466, 1.280398 , 2.04834457]) |
Прогноз и оценка качества
|
# вновь перенесем данные из исходного датафрейма X = df[[‘flavanoids’, ‘proline’]] y = df[‘target’] # в список probs будем записывать результат каждой модели # для каждого наблюдения probs = [] for model in models: _, prob = model.predict(X) probs.append(prob) |
|
# очевидно, для каждого наблюдения у нас будет три вероятности # принадлежности к целевому классу probs[0][0], probs[1][0], probs[2][0] |
|
(0.9161148288779738, 0.1540913395345091, 0.026621132600103174) |
|
# склеим и изменим размерность массива таким образом, чтобы # строки были наблюдениями, а столбцы вероятностями all_probs = np.concatenate(probs, axis = 0).reshape(len(probs), —1).T all_probs.shape |
|
# каждая из 178 строк — это вероятность одного наблюдения # принадлежать к классу 0, 1, 2 all_probs[0] |
|
array([0.91611483, 0.15409134, 0.02662113]) |
Обратите внимание, при использовании подхода one-vs-rest вероятности в сумме не дают единицу!
|
# например, первое наблюдение вероятнее всего принадлежит к классу 0 np.argmax(all_probs[0]) |
|
# найдем максимальную вероятность в каждой строке, # индекс вероятности [0, 1, 2] и будет прогнозом y_pred = np.argmax(all_probs, axis = 1) # рассчитаем accuracy accuracy_score(y, y_pred) |
|
# выведем матрицу ошибок pd.DataFrame(confusion_matrix(y, y_pred), columns = [‘Forecast 0’, ‘Forecast 1’, ‘Forecast 2’], index = [‘Actual 0’, ‘Actual 1’, ‘Actual 2’]) |
Сравним фактическое и прогнозное распределение классов на точечной диаграмме.
|
1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 18 19 |
predictions = df[[‘flavanoids’, ‘proline’]].copy() predictions[‘y_pred’] = y_pred fig, (ax1, ax2) = plt.subplots(1, 2, figsize = (14, 6), gridspec_kw = {‘wspace’: 0.2, ‘hspace’: 0.08}) sns.scatterplot(data = df, x = ‘flavanoids’, y = ‘proline’, hue = ‘target’, palette = ‘bright’, s = 50, ax = ax1) ax1.set_title(‘Фактические классы’, fontsize = 14) sns.scatterplot(data = predictions, x = ‘flavanoids’, y = ‘proline’, hue = ‘y_pred’, palette = ‘bright’, s = 50, ax = ax2) ax2.set_title(‘Прогноз one-vs-rest’, fontsize = 14) plt.show() |
Написание класса
Поместим достигнутый выше результат в класс.
|
1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 18 19 20 21 22 23 24 25 26 27 28 29 30 31 32 33 34 35 36 37 38 39 40 41 42 43 44 45 46 47 48 49 50 51 52 53 54 55 56 57 58 59 60 61 62 63 64 65 66 67 68 69 70 71 72 73 74 75 76 77 78 79 80 81 82 83 84 85 |
class OVR_LogReg(): def __init__(self): self.models_thetas = [] self.models_loss = [] def fit(self, x, y, iter = 20000, learning_rate = 0.001): dfs = self.preprocess(x, y) models_thetas, models_loss = [], [] for ovr_df in dfs: x = ovr_df.drop(‘target’, axis = 1).copy() y = ovr_df.target.copy() self.add_ones(x) loss_history = [] thetas, n = np.zeros(x.shape[1]), x.shape[0] for i in range(iter): y_pred = self.h(x, thetas) loss_history.append(self.objective(y, y_pred)) grad = self.gradient(x, y, y_pred, n) thetas -= learning_rate * grad models_thetas.append(thetas) models_loss.append(loss_history) self.models_thetas = models_thetas self.models_loss = models_loss def predict(self, x): x = x.copy() probs = [] self.add_ones(x) for t in self.models_thetas: z = np.dot(x, t) prob = np.array([self.stable_sigmoid(value) for value in z]) probs.append(prob) all_probs = np.concatenate(probs, axis = 0).reshape(len(probs), —1).T y_pred = np.argmax(all_probs, axis = 1) return y_pred, all_probs def preprocess(self, x, y): x, y = x.copy(), y.copy() x[‘target’] = y classes = x.target.unique() dfs = [] ovr_df = None for c in classes: ovr_df = x.drop(‘target’, axis = 1).copy() ovr_df[‘target’] = np.where(x[‘target’] == classes[c], 1, 0) dfs.append(ovr_df) return dfs def add_ones(self, x): return x.insert(0,‘x0’, np.ones(x.shape[0])) def h(self, x, thetas): z = np.dot(x, thetas) return np.array([self.stable_sigmoid(value) for value in z]) def objective(self, y, y_pred): y_one_loss = y * np.log(y_pred + 1e—9) y_zero_loss = (1 — y) * np.log(1 — y_pred + 1e—9) return —np.mean(y_zero_loss + y_one_loss) def gradient(self, x, y, y_pred, n): return np.dot(x.T, (y_pred — y)) / n def stable_sigmoid(self, z): if z >= 0: return 1 / (1 + np.exp(—z)) else: return np.exp(z) / (np.exp(z) + 1) |
Проверим класс в работе.
|
X = df[[‘flavanoids’, ‘proline’]] y = df[‘target’] model = OVR_LogReg() model.fit(X, y) y_pred, probs = model.predict(X) accuracy_score(y_pred, y) |
Сравнение с sklearn
Сравним с sklearn. Для того чтобы применить подход one-vs-rest в классе LogisticRegression, необходимо использовать значение параметра multi_class = ‘ovr’.
|
X = df[[‘flavanoids’, ‘proline’]] y = df[‘target’] ovr_model = LogisticRegression(multi_class = ‘ovr’) ovr_model = ovr_model.fit(X, y) y_pred = ovr_model.predict(X) accuracy_score(y_pred, y) |
Мультиклассовая полиномиальная регрессия
Как мы увидели в предыдущем разделе, линейная решающая граница допустила некоторое количество ошибок. Попробуем улучшить результат, применив мультиклассовую полиномиальную логистическую регрессию.
|
X = df[[‘flavanoids’, ‘proline’]] y = df[‘target’] polynomial_features = PolynomialFeatures(degree = 7) X_poly = polynomial_features.fit_transform(X) poly_ovr_model = LogisticRegression(multi_class = ‘ovr’) poly_ovr_model = poly_ovr_model.fit(X_poly, y) y_pred = poly_ovr_model.predict(X_poly) accuracy_score(y_pred, y) |
Как мы видим результат, по сравнению с моделью sklearn без полиномиальных признаков, стал чуть лучше. Однако это было достигнуто за счет полинома достаточно высокой степени (degree = 7), что неэффективно с точки зрения временной сложности алгоритма.
Посмотрим, какие нелинейные решающие границы удалось построить алгоритму.
|
predictions = df[[‘flavanoids’, ‘proline’]].copy() predictions[‘y_pred’] = y_pred fig, (ax1, ax2) = plt.subplots(1, 2, figsize = (14, 6), gridspec_kw = {‘wspace’: 0.2, ‘hspace’: 0.08}) sns.scatterplot(data = df, x = ‘flavanoids’, y = ‘proline’, hue = ‘target’, palette = ‘bright’, s = 50, ax = ax1) ax1.set_title(‘Фактические классы’, fontsize = 14) sns.scatterplot(data = predictions, x = ‘flavanoids’, y = ‘proline’, hue = ‘y_pred’, palette = ‘bright’, s = 50, ax = ax2) ax2.set_title(‘Полиномиальная регрессия’, fontsize = 14) plt.show() |
Softmax Regression
Еще один подход при создании мультиклассовой логистической регрессии заключается в том, чтобы не разбивать многоклассовые данные таким образом, чтобы использовать бинарный классификатор, а сразу применять функции, которые подходят для работы с множеством классов.
Такую регрессию часто называют Softmax Regression из-за того, что в ней используется уже знакомая нам по занятию об основах нейросетей функция softmax. Вначале подготовим данные.
Подготовка признаков
Возьмем признаки flavanoids и proline и добавим столбец из единиц.
|
def add_ones(x): # важно! метод .insert() изменяет исходный датафрейм return x.insert(0,‘x0’, np.ones(x.shape[0])) |
|
X = df[[‘flavanoids’, ‘proline’]] add_ones(X) X.head(3) |
Кодирование целевой переменной
Напишем собственную функцию для one-hot encoding.
|
def ohe(y): # количество примеров и количество классов examples, features = y.shape[0], len(np.unique(y)) # нулевая матрица: количество наблюдений x количество признаков zeros_matrix = np.zeros((examples, features)) # построчно проходимся по нулевой матрице и с помощью индекса заполняем соответствующее значение единицей for i, (row, digit) in enumerate(zip(zeros_matrix, y)): zeros_matrix[i][digit] = 1 return zeros_matrix |
|
y = df[‘target’] y_enc = ohe(df[‘target’]) y_enc[:3] |
|
array([[1., 0., 0.], [1., 0., 0.], [1., 0., 0.]]) |
Такой же результат можно получить с помощью класса LabelBinarizer.
|
lb = LabelBinarizer() lb.fit(y) lb.classes_ |
|
y_lb = lb.transform(y) y_lb[:5] |
|
array([[1, 0, 0], [1, 0, 0], [1, 0, 0], [1, 0, 0], [1, 0, 0]]) |
Инициализация весов
Создадим нулевую матрицу весов. Она будет иметь размерность: количество признаков (строки) х количество классов (столбцы). Приведем схематичный пример для четырех наблюдений, трех признаков (включая сдвиг $theta_0$) и трех классов.
Инициализируем веса.
|
thetas = np.zeros((3, 3)) thetas |
|
array([[0., 0., 0.], [0., 0., 0.], [0., 0., 0.]]) |
Функция softmax
Подробнее изучим функцию softmax. Приведем формулу.
$$ text{softmax}(z)_{i} = frac{e^{z_i}}{sum_{k=1}^N e^{z_k}} $$
Рассмотрим ее реализацию на Питоне.
Напомню, что $ z = (-Xtheta) $. Соответственно в нашем случае мы будем умножать матрицу 178 x 3 на 3 x 3.
В результате получим матрицу 178 x 3, где каждая строка — это прогнозные значения принадлежности одного наблюдения к каждому из трех классов.
|
z = np.dot(—X, thetas) z.shape |
Так как мы умножаем на ноль, при первой итерации эти значения будут равны нулю.
|
array([[0., 0., 0.], [0., 0., 0.], [0., 0., 0.], [0., 0., 0.], [0., 0., 0.]]) |
Для того чтобы обеспечить вычислительную устойчивость softmax мы можем вычесть из z максимальное значение в каждой из 178 строк (пока что, опять же на первой итерации, оно равно нулю).
$$ text{softmax}(z)_{i} = frac{e^{z_i-max(z)}}{sum_{k=1}^N e^{z_k-max(z)}} $$
|
# axis = -1 — это последняя ось # keepdims = True сохраняет размерность (в данном случае двумерный массив) np.max(z, axis = —1, keepdims = True)[:5] |
|
array([[0.], [0.], [0.], [0.], [0.]]) |
|
z = z — np.max(z, axis = —1, keepdims = True) z[:5] |
|
array([[0., 0., 0.], [0., 0., 0.], [0., 0., 0.], [0., 0., 0.], [0., 0., 0.]]) |
Смысл такого преобразования⧉ в том, что оно делает значения z нулевыми или отрицательными.
|
arr = np.array([—2, 3, 0, —7, 6]) arr — max(arr) |
|
array([ -8, -3, -6, -13, 0]) |
Далее, число возводимое в увеличивающуюся отрицательную степень стремится к нулю, а не к бесконечности и, таким образом, не вызывает переполнения памяти. Найдем числитель и знаменатель из формулы softmax.
|
numerator = np.exp(z) numerator[:5] |
|
array([[1., 1., 1.], [1., 1., 1.], [1., 1., 1.], [1., 1., 1.], [1., 1., 1.]]) |
|
denominator = np.sum(numerator, axis = —1, keepdims = True) denominator[:5] |
|
array([[3.], [3.], [3.], [3.], [3.]]) |
Разделим числитель и знаменатель и, таким образом, вычислим вероятность принадлежности каждого из наблюдений (строки результата) к одному из трех классов (столбцы).
|
softmax = numerator / denominator softmax[:5] |
|
array([[0.33333333, 0.33333333, 0.33333333], [0.33333333, 0.33333333, 0.33333333], [0.33333333, 0.33333333, 0.33333333], [0.33333333, 0.33333333, 0.33333333], [0.33333333, 0.33333333, 0.33333333]]) |
На первой итерации при одинаковых $theta$ мы получаем, что логично, одинаковые вероятности принадлежности к каждому из классов. Напишем функцию.
|
def stable_softmax(x, thetas): z = np.dot(—x, thetas) z = z — np.max(z, axis = —1, keepdims = True) numerator = np.exp(z) denominator = np.sum(numerator, axis = —1, keepdims = True) softmax = numerator / denominator return softmax |
|
probs = stable_softmax(X, thetas) probs[:3] |
|
array([[0.33333333, 0.33333333, 0.33333333], [0.33333333, 0.33333333, 0.33333333], [0.33333333, 0.33333333, 0.33333333]]) |
Примечание. Обратите внимание, что сигмоида — это частный случай функции softmax для двух классов $[z_1, 0]$. Вероятность класса $z_1$ будет равна
$$ softmax(z_1) = frac{e^{z_1}}{e^{z_1}+e^0} = frac{e^{z_1}}{e^{z_1}+1} $$
Если разделить и числитель, и знаменатель на $e^{z_1}$, то получим
$$ sigmoid(z_1) = frac{e^{z_1}}{1 + e^{-z_1}} $$
Вычислять вероятность принадлежности ко второму классу нет необходимости, достаточно вычесть результат сигмроиды из единицы.
Теперь нужно понять, насколько сильно при таких весах ошибается наш алгоритм.
Функция потерь
Вспомним функцию бинарной кросс-энтропии. То есть функции ошибки для двух классов.
$$ L(y, theta) = -frac{1}{n} sum y cdot log(h_{theta}(x)) + (1-y) cdot log(1-h_{theta}(x)) $$
Напомню, что y выступает в роли своего рода переключателя, сохраняющего одну из частей выражения, и обнуляющего другую. Теперь посмотрите на функцию категориальной (многоклассовой) кросс-энтропии (categorical cross-entropy).
$$ L(y_{ohe}, softmax) = -sum y_{ohe} log(softmax) $$
Разберемся, что здесь происходит. $y_{ohe}$ содержит закодированную целевую переменную, например, для наблюдения класса 0 [1, 0, 0], softmax содержит вектор вероятностей принадлежности набюдения к каждому из классов, например, [0,3 0,4 0,3] (мы видим, что алгоритм ошибается).
В данном случае закодированная целевая переменная также выступает в виде перерключателя. Здесь при умножении «срабатывает» только первая вероятность $1 times 0,3 + 0 times 0,4 + 0 times 0,4 $. Если подставить в формулу, то получаем (np.sum() добавлена для сохранения единообразия с формулой выше, в данном случае у нас одно наблюдение и сумма не нужна)
|
y_ohe = np.array([1, 0, 0]) softmax = np.array([0.3, 0.4, 0.4]) —np.sum(y_ohe * np.log(softmax)) |
Если бы модель в своих вероятностях ошибалась бы меньше, то и общая ошибка была бы меньше.
|
y_ohe = np.array([1, 0, 0]) softmax = np.array([0.4, 0.3, 0.4]) —np.sum(y_ohe * np.log(softmax)) |
Функция $-log$ позволяет снижать ошибку при увеличении вероятности верного (сохраненного переключателем) класса.
|
x_arr = np.linspace(0.001,1, 100) sns.lineplot(x=x_arr,y=—np.log(x_arr)) plt.title(‘Plot of -log(x)’) plt.xlabel(‘x’) plt.ylabel(‘-log(x)’); |
Напишем функцию.
|
# добавим константу в логарифм для вычислительной устойчивости def cross_entropy(probs, y_enc, epsilon = 1e—9): n = probs.shape[0] ce = —np.sum(y_enc * np.log(probs + epsilon)) / n return ce |
Рассчитаем ошибку для нулевых весов.
|
ce = cross_entropy(probs, y_enc) ce |
Для снижения ошибки нужно найти градиент.
Градиент
Приведем формулу градиента без дифференцирования.
$$ nabla_{theta}J = frac{1}{n} times X^T cdot (y_{ohe}-softmax) $$
По сути, мы умножаем транспонированную матрицу признаков (3 x 178) на разницу между закодированной целевой переменной и вероятностями функции softmax (178 x 3).
|
def gradient_softmax(X, probs, y_enc): # если не добавить функцию np.array(), будет выводиться датафрейм return np.array(1 / probs.shape[0] * np.dot(X.T, (y_enc — probs))) |
|
gradient_softmax(X, probs, y_enc) |
|
array([[-0.00187266, 0.06554307, -0.06367041], [ 0.31627721, 0.02059572, -0.33687293], [ 0.38820566, -0.28801792, -0.10018774]]) |
Обучение модели, прогноз и оценка качества
Выполним обучение модели.
|
loss_history = [] # в цикле for i in range(30000): # рассчитаем прогнозное значение с текущими весами probs = stable_softmax(X, thetas) # посчитаем уровень ошибки при текущем прогнозе loss_history.append(cross_entropy(probs, y_enc, epsilon = 1e—9)) # рассчитаем градиент grad = gradient_softmax(X, probs, y_enc) # используем градиент для улучшения весов модели thetas = thetas — 0.002 * grad |
Посмотрим на получившиеся коэффициенты (напомню, что первая строка матрицы это сдвиг (intercept, $theta_0$)) и достигнутый уровень ошибки.
|
array([[ 0.11290134, -0.90399727, 0.79109593], [-1.7550965 , -0.7857371 , 2.5408336 ], [-1.93839311, 1.77140542, 0.16698769]]) |
|
loss_history[0], loss_history[—1] |
|
(1.0986122856681098, 0.2569641080523888) |
Сделаем прогноз и оценим качество.
|
y_pred = np.argmax(stable_softmax(X, thetas), axis = 1) |
|
accuracy_score(y, y_pred) |
|
pd.DataFrame(confusion_matrix(y, y_pred), columns = [‘Forecast 0’, ‘Forecast 1’, ‘Forecast 2’], index = [‘Actual 0’, ‘Actual 1’, ‘Actual 2’]) |
Написание класса
Объединим созданные выше компоненты в класс.
|
1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 18 19 20 21 22 23 24 25 26 27 28 29 30 31 32 33 34 35 36 37 38 39 40 41 42 43 44 45 46 47 48 49 50 51 52 |
class SoftmaxLogReg(): def __init__(self): self.loss_ = None self.thetas_ = None def fit(self, x, y, iter = 30000, learning_rate = 0.002): loss_history = [] self.add_ones(x) y_enc = self.ohe(y) thetas = np.zeros((x.shape[1], y_enc.shape[1])) for i in range(iter): probs = self.stable_softmax(x, thetas) loss_history.append(self.cross_entropy(probs, y_enc, epsilon = 1e—9)) grad = self.gradient_softmax(x, probs, y_enc) thetas = thetas — 0.002 * grad self.thetas_ = thetas self.loss_ = loss_history def predict(self, x, y): return np.argmax(self.stable_softmax(x, thetas), axis = 1) def stable_softmax(self, x, thetas): z = np.dot(—x, thetas) z = z — np.max(z, axis = —1, keepdims = True) numerator = np.exp(z) denominator = np.sum(numerator, axis = —1, keepdims = True) softmax = numerator / denominator return softmax def cross_entropy(self, probs, y_enc, epsilon = 1e—9): n = probs.shape[0] ce = —np.sum(y_enc * np.log(probs + epsilon)) / n return ce def gradient_softmax(self, x, probs, y_enc): return np.array(1 / probs.shape[0] * np.dot(x.T, (y_enc — probs))) def add_ones(self, x): return x.insert(0,‘x0’, np.ones(x.shape[0])) def ohe(self, y): examples, features = y.shape[0], len(np.unique(y)) zeros_matrix = np.zeros((examples, features)) for i, (row, digit) in enumerate(zip(zeros_matrix, y)): zeros_matrix[i][digit] = 1 return zeros_matrix |
Обучим модель, сделаем прогноз и оценим качество.
|
X = df[[‘flavanoids’, ‘proline’]] y = df[‘target’] model = SoftmaxLogReg() model.fit(X, y) model.thetas_, model.loss_[—1] |
|
(array([[ 0.11290134, -0.90399727, 0.79109593], [-1.7550965 , -0.7857371 , 2.5408336 ], [-1.93839311, 1.77140542, 0.16698769]]), 0.2569641080523888) |
|
y_pred = model.predict(X, y) accuracy_score(y, y_pred) |
Сравнение с sklearn
Для того чтобы использовать softmax логистическую регрессию в sklearn, соответствующему классу нужно передать параметр multi_class = ‘multinomial’.
|
X = df[[‘flavanoids’, ‘proline’]] y = df[‘target’] # создадим объект класса LogisticRegression и запишем его в переменную model model = LogisticRegression(multi_class = ‘multinomial’) # обучим нашу модель model.fit(X, y) # посмотрим на получившиеся веса модели model.intercept_, model.coef_ |
|
(array([ 0.09046097, 1.12593099, -1.21639196]), array([[ 1.86357908, 1.89698292], [ 0.86696131, -1.43973164], [-2.73054039, -0.45725129]])) |
|
y_pred = model.predict(X) accuracy_score(y, y_pred) |
Подведем итог
Сегодня мы разобрали множество разновидностей и подходов к использованию линейной регрессии. Давайте систематизируем изученный материал с помощью следующей схемы.
Рассмотрим обучение нейронных сетей.
Содержание
- Логистическая функция ошибки
- Логистическая функция ошибки
- Начнём издалека…
- Log Loss
- Связь с логистической регрессией
- Настройка на logloss
- Многоклассовый logloss
Логистическая функция ошибки
Эту функцию называют также «логлосс» (logloss / log_loss), перекрёстной / кросс-энтропией (Cross Entropy) и часто используют в задачах классификации. Разберёмся, почему её используют и какой смысл она имеет. Для чтения поста нужна неплохая ML-математическая подготовка, но даже новичкам я бы рекомендовал почитать (хотя я не очень заботился, чтобы «всё объяснялось на пальцах»).
Вспомним, как решается задача линейной регрессии. Итак, мы хотим получить линейную функцию (т.е. веса w), которая приближает целевое значение с точностью до ошибки:
Здесь мы предположили, что ошибка нормально распределена, x – признаковое описание объекта (возможно, в нём есть и фиктивный константный признак, чтобы в линейной функции был свободный член). Тогда мы знаем как распределены ответы нашей функции и можем записать функцию правдоподобия выборки (т.е. произведение плотностей, в которые подставлены значения из обучающей выборки) и воспользоваться методом максимального правдоподобия (в котором для определения значений параметров берётся максимум правдоподобия, а чаще – его логарифма):
В итоге оказывается, что максимизация правдоподобия эквивалентна минимизации среднеквадратичной ошибки (MSE), т.е. эта функция ошибки не зря широко используется в задачах регрессии. Кроме того, что она вполне логична, легко дифференцируема по параметрам и легко минимизируется, она ещё и теоретически обосновывается с помощью метода максимального правдоподобия в случае, если линейная модель соответствует данным с точностью до нормального шума.
Давайте ещё посмотрим, как реализуется метод стохастического градиента (SGD) для минимизации MSE: надо взять производную функции ошибки для конкретного объекта и записать формулу коррекции весов в виде «шага в сторону антиградиента»:
Получили, что веса линейной модели при её обучении методом SGD корректируются с помощью добавки вектора признаков. Коэффициент, с которым добавляют, зависит от «агрессивности алгоритма» (параметр альфа, который называют темпом обучения) и разности «ответ алгоритма – правильный ответ». Кстати, если разница нулевая (т.е. на данном объекте алгоритм выдаёт точный ответ), то коррекция весов не производится.
Теперь давайте, наконец, поговорим о «логлоссе». Рассматриваем задачу классификации с двумя классами: 0 и 1. Обучающую выборку можно рассматривать, как реализацию обобщённой схемы Бернулли: для каждого объекта генерируется случайная величина, которая с вероятностью p (своей для каждого объекта) принимает значение 1 и с вероятностью (1–p) – 0. Предположим, что мы как раз и строим нашу модель так, чтобы она генерировала правильные вероятности, но тогда можно записать функцию правдоподобия:
После логарифмирования правдоподобия получили, что его максимизация эквивалентна минимизации последнего записанного выражения. Именно его и называют «логистической функции ошибки». Для задачи бинарной классификации, в которой алгоритм должен выдать вероятность принадлежности классу 1, она логична ровно настолько, насколько логична MSE в задаче линейной регрессии с нормальным шумом (поскольку обе функции ошибки выводятся из метода максимального правдоподобия).
Часто гораздо более понятна такая запись logloss-ошибки на одном объекте:
Отметим неприятное свойство логосса: если для объекта 1го класса мы предсказываем нулевую вероятность принадлежности к этому классу или, наоборот, для объекта 0го – единичную вероятность принадлежности к классу 1, то ошибка равна бесконечности! Таким образом, грубая ошибка на одном объекте сразу делает алгоритм бесполезным.На практике часто логлосс ограничивают каким-то большим числом (чтобы не связываться с бесконечностями).
Если задаться вопросом, какой константный алгоритм оптимален для выборки из q_1 представителей класса 1 и q_ представителей класса 0, q_1+ q_0 = q , то получим
Последний ответ получается взятием производной и приравниванием её к нулю. Описанную задачу приходится решать, например, при построении решающих деревьев (какую метку приписывать листу, если в него попали представители разных классов). На рис. 2 изображён график log_loss-ошибки константного алгоритма для выборки из четырёх объектов класса 0 и 6 объектов класса 1.
Представим теперь, что мы знаем, что объект принадлежит к классу 1 вероятностью p, посмотрим, какой ответ оптимален на этом объекте с точки зрения log_loss: матожидание нашей ошибки
Для минимизации ошибки мы опять взяли производную и приравняли к нулю. Мы получили, что оптимально для каждого объекта выдавать его вероятность принадлежности к классу 1! Таким образом, для минимизации log_loss надо уметь вычислять (оценивать) вероятности принадлежности классам!
Если подставить полученное оптимальное решение в минимизируемый функционал, то получим энтропию:
Это объясняет, почему при построении решающих деревьев в задачах классификации (а также случайных лесов и деревьях в бустингах) применяют энтропийный критерий расщепления (ветвления). Дело в том, что оценка принадлежности к классу 1 часто производится с помощью среднего арифметического меток в листе. В любом случае, для конкретного дерева эта вероятность будет одинакова для всех объектов в листе, т.е. константой. Таким образом, энтропия в листе примерно равна логлосс-ошибке константного решения. Используя энтропийный критерий мы неявно оптимизируем логлосс!
В каких пределах может варьироваться logloss? Ясно, что минимальное значение 0, максимальное – +?, но эффективным максимальным можно считать ошибку при использовании константного алгоритма (вряд же мы в итоге решения задачи придумаем алгоритм хуже константы?!), т.е.
Интересно, что если брать логарифм по основанию 2, то на сбалансированной выборке это отрезок [0, 1].
Связь с логистической регрессией
Слово «логистическая» в названии ошибки намекает на связь с логистической регрессией – это как раз метод для решения задачи бинарной классификации, который получает вероятность принадлежности к классу 1. Но пока мы исходили из общих предположений, что наш алгоритм генерирует эту вероятность (алгоритмом может быть, например, случайный лес или бустинг над деревьями). Покажем, что тесная связь с логистической регрессией всё-таки есть… посмотрим, как настраивается логистическая регрессия (т.е. сигмоида от линейной комбинации) на эту функцию ошибки методом SGD.
Как видим, корректировка весов точно такая же, как и при настройке линейной регрессии! На самом деле, это говорит о родстве разных регрессий: линейной и логистической, а точнее, о родстве распределений: нормального и Бернулли. Желающие могут внимательно почитать лекцию Эндрю Ына.
Во многих книгах логистической функцией ошибки (т.е. именно «logistic loss») называется другое выражение, которое мы сейчас получим, подставив выражение для сигмоиды в logloss и сделав переобозначение: считаем, что метки классов теперь –1 и +1, тогда
Полезно посмотреть на график функции, центральной в этом представлении:
Как видно, это сглаженный (всюду дифференцируемый) аналог функции max(0, x), которую в глубоком обучении принято называть ReLu (Rectified Linear Unit). Если при настройке весов минимизировать logloss, то таким образом мы настраиваем классическую логистическую регрессию, если же использовать ReLu, чуть-чуть подправить аргумент и добавить регуляризацию, то получаем классическую настройку SVM:
выражение под знаком суммы принято называть Hinge loss. Как видим, часто с виду совсем разные методы можно получать «немного подправив» оптимизируемые функции на похожие. Между прочим, при обучении RVM(Relevance vector machine) используется тоже очень похожий функционал:
Связь с расхождением Кульбака-Лейблера
Расхождение (дивергенцию) Кульбака-Лейблера (KL, Kullback–Leibler divergence) часто используют (особенно в машинном обучении, байесовском подходе и теории информации) для вычисления непохожести двух распределений. Оно определяется по следующей формуле:
где P и Q – распределения (первое обычно «истинное», а второе – то, про которое нам интересно, насколько оно похоже на истинное), p и q – плотности этих распределений. Часто KL-расхождение называют расстоянием, хотя оно не является симметричным и не удовлетворяет неравенству треугольника. Для дискретных распределений формулу записывают так:
что в точности совпадает с logloss.
Настройка на logloss
Один из методов «подгонки» ответов алгоритма под logloss – калибровка Платта (Platt calibration). Идея очень простая. Пусть алгоритм порождает некоторые оценки принадлежности к 1му классу – a. Метод изначально разрабатывался для калибровки ответов алгоритма опорных векторов(SVM), этот алгоритм в простейшей реализации разделяет объекты гиперплоскостью и просто выдаёт номер класса 0 или 1, в зависимости от того, с какой стороны гиперплоскости объект расположен. Но если мы построили гиперплоскость, то для любого объекта можем вычислить расстояние до неё (со знаком минус, если объект лежит в полуплоскости нулевого класса). Именно эти расстояния со знаком r мы будем превращать в вероятности по следующей формуле:
неизвестные параметры ?, ? обычно определяются методом максимального правдоподобия на отложенной выборке (calibration set).
Проиллюстрируем применение метода на реальной задаче, которую автор решал недавно. На рис. показаны ответы (в виде вероятностей) двух алгоритмов: градиентного бустинга (lightgbm) и случайного леса (random forest).
Видно, что качество леса намного ниже и он довольно осторожен: занижает вероятности у объектов класса 1 и завышает у объектов класса 0. Упорядочим все объекты по возрастанию вероятностей (RF), разобьем на kравных частей и для каждой части вычислим среднее всех ответов алгоритма и среднее всех правильных ответов. Результат показан на рис. 5 – точки изображены как раз в этих двух координатах.
Нетрудно видеть, что точки располагаются на линии, похожей на сигмоиду – можно оценить параметр сжатия-растяжения в ней, см. рис. 6. Оптимальная сигмоида показана розовым цветом на рис. 5. Если подвергать ответы такой сигмоидной деформации, то логлосс-ошибка случайного леса снижается с 0.37 до 0.33.
Обратите внимание, что здесь мы деформировали ответы случайного леса (это были оценки вероятности – и все они лежали на отрезке [0, 1]), но из рис. 5 видно, что для деформации нужна именно сигмоида. Практика показывает, что в 80% ситуаций для улучшения logloss-ошибки надо деформировать ответы именно с помощью сигмоиды (для меня это также часть объяснения, почему именно такие функции успешно используются в качестве функций активаций в нейронных сетях).
Ещё один вариант калибровки – монотонная регрессия (Isotonic regression).
Для полноты картины отметим, что logloss обобщается и на случай нескольких классов естественным образом:
здесь q – число элементов в выборке, l – число классов, a_ij – ответ (вероятность) алгоритма на i-м объекте на вопрос принадлежности его к j-му классу, y_ij=1 если i-й объект принадлежит j-му классу, в противном случае y_ij=0.
Источник
Логистическая функция ошибки
Эту функцию называют также «логлосс» (logloss / log_loss), перекрёстной / кросс-энтропией (Cross Entropy) и часто используют в задачах классификации. Разберёмся, почему её используют и какой смысл она имеет. Для чтения поста нужна неплохая ML-математическая подготовка, но даже новичкам я бы рекомендовал почитать (хотя я не очень заботился, чтобы «всё объяснялось на пальцах»).
Начнём издалека…
Вспомним, как решается задача линейной регрессии. Итак, мы хотим получить линейную функцию (т.е. веса w), которая приближает целевое значение с точностью до ошибки:
Здесь мы предположили, что ошибка нормально распределена, x – признаковое описание объекта (возможно, в нём есть и фиктивный константный признак, чтобы в линейной функции был свободный член). Тогда мы знаем как распределены ответы нашей функции и можем записать функцию правдоподобия выборки (т.е. произведение плотностей, в которые подставлены значения из обучающей выборки) и воспользоваться методом максимального правдоподобия (в котором для определения значений параметров берётся максимум правдоподобия, а чаще – его логарифма):
В итоге оказывается, что максимизация правдоподобия эквивалентна минимизации среднеквадратичной ошибки (MSE), т.е. эта функция ошибки не зря широко используется в задачах регрессии. Кроме того, что она вполне логична, легко дифференцируема по параметрам и легко минимизируется, она ещё и теоретически обосновывается с помощью метода максимального правдоподобия в случае, если линейная модель соответствует данным с точностью до нормального шума.
Давайте ещё посмотрим, как реализуется метод стохастического градиента (SGD) для минимизации MSE: надо взять производную функции ошибки для конкретного объекта и записать формулу коррекции весов в виде «шага в сторону антиградиента»:
Получили, что веса линейной модели при её обучении методом SGD корректируются с помощью добавки вектора признаков. Коэффициент, с которым добавляют, зависит от «агрессивности алгоритма» (параметр альфа, который называют темпом обучения) и разности «ответ алгоритма – правильный ответ». Кстати, если разница нулевая (т.е. на данном объекте алгоритм выдаёт точный ответ), то коррекция весов не производится.
Log Loss
Теперь давайте, наконец, поговорим о «логлоссе». Рассматриваем задачу классификации с двумя классами: 0 и 1. Обучающую выборку можно рассматривать, как реализацию обобщённой схемы Бернулли: для каждого объекта генерируется случайная величина, которая с вероятностью p (своей для каждого объекта) принимает значение 1 и с вероятностью (1– p) – 0. Предположим, что мы как раз и строим нашу модель так, чтобы она генерировала правильные вероятности, но тогда можно записать функцию правдоподобия:
После логарифмирования правдоподобия получили, что его максимизация эквивалентна минимизации последнего записанного выражения. Именно его и называют «логистической функции ошибки». Для задачи бинарной классификации, в которой алгоритм должен выдать вероятность принадлежности классу 1, она логична ровно настолько, насколько логична MSE в задаче линейной регрессии с нормальным шумом (поскольку обе функции ошибки выводятся из метода максимального правдоподобия).
Часто гораздо более понятна такая запись logloss-ошибки на одном объекте:
Отметим неприятное свойство логосса: если для объекта 1го класса мы предсказываем нулевую вероятность принадлежности к этому классу или, наоборот, для объекта 0го – единичную вероятность принадлежности к классу 1, то ошибка равна бесконечности! Таким образом, грубая ошибка на одном объекте сразу делает алгоритм бесполезным.На практике часто логлосс ограничивают каким-то большим числом (чтобы не связываться с бесконечностями).
Если задаться вопросом, какой константный алгоритм оптимален для выборки из q_1 представителей класса 1 и q_0 представителей класса 0, q_1+ q_0 = q , то получим
Последний ответ получается взятием производной и приравниванием её к нулю. Описанную задачу приходится решать, например, при построении решающих деревьев (какую метку приписывать листу, если в него попали представители разных классов). На рис. 2 изображён график log_loss-ошибки константного алгоритма для выборки из четырёх объектов класса 0 и 6 объектов класса 1.
Представим теперь, что мы знаем, что объект принадлежит к классу 1 вероятностью p, посмотрим, какой ответ оптимален на этом объекте с точки зрения log_loss: матожидание нашей ошибки
Для минимизации ошибки мы опять взяли производную и приравняли к нулю. Мы получили, что оптимально для каждого объекта выдавать его вероятность принадлежности к классу 1! Таким образом, для минимизации log_loss надо уметь вычислять (оценивать) вероятности принадлежности классам!
Если подставить полученное оптимальное решение в минимизируемый функционал, то получим энтропию:
Это объясняет, почему при построении решающих деревьев в задачах классификации (а также случайных лесов и деревьях в бустингах) применяют энтропийный критерий расщепления (ветвления). Дело в том, что оценка принадлежности к классу 1 часто производится с помощью среднего арифметического меток в листе. В любом случае, для конкретного дерева эта вероятность будет одинакова для всех объектов в листе, т.е. константой. Таким образом, энтропия в листе примерно равна логлосс-ошибке константного решения. Используя энтропийный критерий мы неявно оптимизируем логлосс!
В каких пределах может варьироваться logloss? Ясно, что минимальное значение 0, максимальное – +∞, но эффективным максимальным можно считать ошибку при использовании константного алгоритма (вряд же мы в итоге решения задачи придумаем алгоритм хуже константы?!), т.е.
Интересно, что если брать логарифм по основанию 2, то на сбалансированной выборке это отрезок [0, 1].
Связь с логистической регрессией
Слово «логистическая» в названии ошибки намекает на связь с логистической регрессией – это как раз метод для решения задачи бинарной классификации, который получает вероятность принадлежности к классу 1. Но пока мы исходили из общих предположений, что наш алгоритм генерирует эту вероятность (алгоритмом может быть, например, случайный лес или бустинг над деревьями). Покажем, что тесная связь с логистической регрессией всё-таки есть… посмотрим, как настраивается логистическая регрессия (т.е. сигмоида от линейной комбинации) на эту функцию ошибки методом SGD.
Как видим, корректировка весов точно такая же, как и при настройке линейной регрессии! На самом деле, это говорит о родстве разных регрессий: линейной и логистической, а точнее, о родстве распределений: нормального и Бернулли. Желающие могут внимательно почитать лекцию Эндрю Ына.
Во многих книгах логистической функцией ошибки (т.е. именно «logistic loss») называется другое выражение, которое мы сейчас получим, подставив выражение для сигмоиды в logloss и сделав переобозначение: считаем, что метки классов теперь –1 и +1, тогда
Полезно посмотреть на график функции, центральной в этом представлении:
Как видно, это сглаженный (всюду дифференцируемый) аналог функции max(0, x), которую в глубоком обучении принято называть ReLu (Rectified Linear Unit). Если при настройке весов минимизировать logloss, то таким образом мы настраиваем классическую логистическую регрессию, если же использовать ReLu, чуть-чуть подправить аргумент и добавить регуляризацию, то получаем классическую настройку SVM:
выражение под знаком суммы принято называть Hinge loss. Как видим, часто с виду совсем разные методы можно получать «немного подправив» оптимизируемые функции на похожие. Между прочим, при обучении RVM(Relevance vector machine) используется тоже очень похожий функционал:
Связь с расхождением Кульбака-Лейблера
Расхождение (дивергенцию) Кульбака-Лейблера (KL, Kullback–Leibler divergence) часто используют (особенно в машинном обучении, байесовском подходе и теории информации) для вычисления непохожести двух распределений. Оно определяется по следующей формуле:
где P и Q – распределения (первое обычно «истинное», а второе – то, про которое нам интересно, насколько оно похоже на истинное), p и q – плотности этих распределений. Часто KL-расхождение называют расстоянием, хотя оно не является симметричным и не удовлетворяет неравенству треугольника. Для дискретных распределений формулу записывают так:
что в точности совпадает с logloss.
Настройка на logloss
Один из методов «подгонки» ответов алгоритма под logloss – калибровка Платта (Platt calibration). Идея очень простая. Пусть алгоритм порождает некоторые оценки принадлежности к 1му классу – a. Метод изначально разрабатывался для калибровки ответов алгоритма опорных векторов(SVM), этот алгоритм в простейшей реализации разделяет объекты гиперплоскостью и просто выдаёт номер класса 0 или 1, в зависимости от того, с какой стороны гиперплоскости объект расположен. Но если мы построили гиперплоскость, то для любого объекта можем вычислить расстояние до неё (со знаком минус, если объект лежит в полуплоскости нулевого класса). Именно эти расстояния со знаком r мы будем превращать в вероятности по следующей формуле:
неизвестные параметры α, β обычно определяются методом максимального правдоподобия на отложенной выборке (calibration set).
Проиллюстрируем применение метода на реальной задаче, которую автор решал недавно. На рис. показаны ответы (в виде вероятностей) двух алгоритмов: градиентного бустинга (lightgbm) и случайного леса (random forest).
Видно, что качество леса намного ниже и он довольно осторожен: занижает вероятности у объектов класса 1 и завышает у объектов класса 0. Упорядочим все объекты по возрастанию вероятностей (RF), разобьем на kравных частей и для каждой части вычислим среднее всех ответов алгоритма и среднее всех правильных ответов. Результат показан на рис. 5 – точки изображены как раз в этих двух координатах.
Нетрудно видеть, что точки располагаются на линии, похожей на сигмоиду – можно оценить параметр сжатия-растяжения в ней, см. рис. 6. Оптимальная сигмоида показана розовым цветом на рис. 5. Если подвергать ответы такой сигмоидной деформации, то логлосс-ошибка случайного леса снижается с 0.37 до 0.33.
Обратите внимание, что здесь мы деформировали ответы случайного леса (это были оценки вероятности – и все они лежали на отрезке [0, 1]), но из рис. 5 видно, что для деформации нужна именно сигмоида. Практика показывает, что в 80% ситуаций для улучшения logloss-ошибки надо деформировать ответы именно с помощью сигмоиды (для меня это также часть объяснения, почему именно такие функции успешно используются в качестве функций активаций в нейронных сетях).
Ещё один вариант калибровки – монотонная регрессия (Isotonic regression).
Многоклассовый logloss
Для полноты картины отметим, что logloss обобщается и на случай нескольких классов естественным образом:
здесь q – число элементов в выборке, l – число классов, a_ij – ответ (вероятность) алгоритма на i-м объекте на вопрос принадлежности его к j-му классу, y_ij=1 если i-й объект принадлежит j-му классу, в противном случае y_ij=0.
Источник
Логистика важна практически во всех направлениях бизнеса. Если она не отлажена должным образом, то сроки и стоимость транспортировки будут неуклонно расти, что негативно скажется на прибыли и лояльности клиентов. В условиях жесткой конкуренции и финансового кризиса важно не допустить такого исхода, поэтому мы совместно со специалистами сервиса CRMBOX расскажем об основных проблемах с логистикой, о которых лучше побеспокоиться заранее.
1. Плохая информационная поддержка процесса транспортировки
И отправителю, и получателю очень важно отслеживать текущий статус отправления. Особенно если речь идет о крупных поставках товаров, от которых зависит маркетинговая стратегия.
Приведем пример: Nike выпускает новую коллекцию кроссовок, и между магазинами начинается настоящая война за каждого потенциального покупателя. Для последнего же будет крайне важно получить новый продукт как можно быстрее, что заставит его сравнивать способы и сроки доставки и искать самое выгодное предложение. Имея четко проработанную логистику, ты сможешь точно определить, сколько времени займет доставка, и предложить удобные способы отслеживания, что, в свою очередь, позволит увеличить шансы твоей компании в конкурентной борьбе.
В наше время самым оптимальным вариантом остается трекинг груза по промежуточным пунктам. Так ты сможешь понять, отправлен ли товар, прошел ли он границу и таможню, прибыл ли в пункт промежуточного хранения и так далее. Понимание точного местоположения позволит корректировать действия и бизнес-стратегию компании. В случае новой коллекции кроссовок ты сможешь вовремя запустить рекламу, открыть предзаказы с более точными сроками получения, подготовить промоматериалы, оптимизировать товарооборот и вовремя скорректировать товарную матрицу. Поэтому вопрос трекинга и информационного сопровождения очень важен, так как позволяет контролировать ситуацию и четко планировать этапы работы. Так клиент сможет понимать, где его посылка в конкретный момент времени.
2. Неэффективное выстраивание маршрутов
От того, насколько тщательно проработан маршрут, зависит не только срок доставки, но и величина транспортных издержек. При его составлении должны учитываться все факторы, особенно если пересекаются международные границы. В зависимости от размеров пошлины, стоимости растаможки, проезда по платным дорогам или стоимости топлива в конкретном регионе может быть намного выгоднее отправить груз через другую страну, чтобы сократить расходы. Добиться минимальных расходов без потери скорости доставки поможет система автоматизации, которая учитывает все важные факторы. Например, система управления логистикой CRMBOX позволяет не только автоматически рассчитывать тарифы и выставлять счета, но и оптимизировать прием заявок в режиме 24/7 и поэтапно отслеживать действия клиентов, поставщиков и сотрудников, минимизируя ошибки и тем самым ускоряя весь рабочий процесс.
3. Отсутствие промежуточных пунктов хранения
Эта проблема особенно актуальна для тех сфер бизнеса, чьи логистические маршруты пролегают через международные границы. Прохождение таможенных проверок и оформления может занять немало времени. Заказчику, в свою очередь, важно, чтобы за этот период с грузом ничего не случилось. Поэтому логистический маршрут должен учитывать специальные охраняемые территории, где транспорт и его содержимое будут находиться в целости и сохранности на период прохождения проверок или отдыха водителя. К сожалению, в России дефицит подобных парковок и стоянок. Расстояние между ними напрямую обуславливает особенности построения маршрута.
4. Неотлаженная оптимизация внутренних процессов
Одновременно в мире обрабатываются тысячи заявок, что нередко приводит к сбоям и ошибкам, из-за которых многие компании несут огромные финансовые и репутационные потери. И это только этап обработки заявок, а если прибавить к этому погрузку, оформление, транспортировку, декларирование, то получим целую цепочку, каждое звено которой может дать сбой.
Чтобы не допустить этого, все внутренние процессы должны быть четко оптимизированы. Лучшим решением в таком случае будет подключение CRM-системы, которая адаптирована под работу с доставкой и позволит контролировать и отслеживать всё в одном месте. Отличный пример — CRMBOX, который поддерживает интеграцию с «1С», платежными системами, сайтом. Это будет удобно не только для твоих сотрудников, которые смогут решать все возникающие вопросы в одном окне, но и для клиентов, которым будет доступен онлайн-калькулятор для расчета стоимости и просмотр статуса заказа.
5. Сложности при транспортировке на большие расстояния
Отличный пример — скоропортящиеся или хрупкие товары. Для них требуются не только соответствующая упаковка, но и определенные условия транспортировки. Некоторые товары могут просто не перенести её, если транспорт не оборудован системами терморегулирования. Особенно актуально это при смене климатических зон, когда температура из значительного минуса переходит в высокий плюс. Хрупкий товар также не доедет в целости, если подвеска машины имеет плохую амортизацию, а содержимое никак не зафиксировано. Прибавь сюда особенности рельефа, состояние дорог и общую проходимость транспорта.
Предусмотреть все эти нюансы помогут специалисты логистических компаний. Они изучат особенности и требования к транспортировке груза и подберут решения, при которых товары не испытают воздействия внешних факторов. Например, для скоропортящихся продуктов они предусмотрят влажность и требования к температуре, а для хрупких — способы дополнительной упаковки, распределения внутри контейнера и фиксации груза.
CRMBOX — система управления логистикой и доставкой, позволяющая упорядочить обработку заявок, автоматизировать оплату, управлять ключевыми процессами, отслеживать работу курьеров и поставщиков, контролировать тарификацию и многое другое. Все ключевые инструменты для решения основных задач будут собраны в одном месте, а адаптивная верстка позволит пользоваться полным функционалом сервиса с любого устройства. И это даже не половина возможностей, которые тебе откроются, если ты будешь работать с CRMBOX.
Узнать больше о CRMBOX
Все курсы > Оптимизация > Занятие 5
Как мы уже знаем, несмотря на название, логистическая регрессия решает задачу классификации. Сегодня мы подробно разберем принцип работы и составные части алгоритма логистической регрессии, а также построим модели с одной и несколькими независимыми переменными.
Бинарная логистическая регрессия
Задача бинарной классификации
Вернемся к задаче кредитного скоринга, про которую мы говорили, когда обсуждали принцип машинного обучения. Предположим, что мы собрали данные и выявили зависимость возвращения кредита (ось y) от возраста заемщика (ось x).
Как мы видим, в среднем более молодые заемщики реже возвращают кредит. Возникает вопрос, с помощью какой модели можно описать эту зависимость? Казалось бы, можно построить линейную регрессию таким образом, чтобы она выдавала некоторое значение и, если это значение окажется ниже 0,5 — отнести наблюдение к классу 0, если выше — к классу 1.
- Если $ f_w(x) < 0,5 rightarrow hat{y} = 0 $
- Если $ f_w(x) geq 0,5 rightarrow hat{y} = 1 $
Однако, даже если предположить, что мы удачно провели линию регрессии (а на графике выше мы действительно провели ее вполне удачно), и наша модель может делать качественный прогноз, появление новых данных сместит эту границу, и, как следствие, ничего не добавит, а только ухудшит точность модели.
Теперь часть наблюдений, принадлежащих к классу 1, будет ошибочно отнесено моделью к классу 0.
Кроме этого, линейная регрессия по оси y выдает значения, сильно выходящие за пределы интересующего нас интервала от нуля до единицы.
Откроем ноутбук к этому занятию⧉
|
1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 18 19 |
# помимо стандартных библиотек мы также импортируем библиотеку warnings # она позволит скрыть предупреждения об ошибках import numpy as np import pandas as pd import matplotlib.pyplot as plt import seaborn as sns import warnings # кроме того, импортируем датасеты библиотеки sklearn from sklearn import datasets # а также функции для расчета метрики accuracy и построения матрицы ошибок from sklearn.metrics import accuracy_score, confusion_matrix # построенные нами модели мы будем сравнивать с результатом # класса LogisticRegression библиотеки sklearn from sklearn.linear_model import LogisticRegression # среди прочего, мы построим модели полиномиальной логистической регрессии from sklearn.preprocessing import PolynomialFeatures |
Функция логистической регрессии
Сигмоида
Возможное решение упомянутых выше сложностей — пропустить значение линейной регрессии через сигмоиду (sigmoid function), которая при любом значении X не выйдет из необходимого нам диапазона $0 leq h(x) leq 1 $. Напомню формулу и график сигмоиды.
$$ g(z) = frac{1}{1+e^{-z}} $$

Примечание: обратие внимание, когда z представляет собой большое отрицательное число, знаменатель становится очень большим $ 1 + e^{-(-5)} approx 148, 413 $ и значение сигмоиды стремится к нулю; когда z является большим положительным числом, знаменатель, а вместе с ним и все выражение стремятся к единице $ 1 + e^{-(5)} approx 0,0067 $.
Тогда мы можем построить линейную модель, значение которой будет подаваться в сигмоиду.
$$ z = Xtheta rightarrow h_{theta}(x) = frac{1}{1+e^{-(Xtheta)}} $$
В этом смысле никакой ошибки в названии «логистическая регрессия» нет. Этот алгоритм решает задачу классификации через модель линейной регрессии.
Если вы не помните, почему мы записали множественную линейную функцию как $theta x$, посмотрите предыдущую лекцию.
Приведем код на Питоне.
|
def h(x, thetas): z = np.dot(x, thetas) return 1.0 / (1 + np.exp(—z)) |
Теперь посмотрим, как интерпретировать коэффициенты.
Интерпретация коэффициентов
Для любого значения x через $ h_{theta}(x) $ мы будем получать вероятность от 0 до 1, что объект принадлежит к классу y = 1. Например, если класс 1 означает, что заемщик вернул кредит, то $ h_{theta}(x) = 0,8 $ говорит о том, что согласно нашей модели (с параметрами $theta$), для данного заемщика (x) вероятность возвращения кредита состаляет 80 процентов.
В общем случае мы можем записать вероятность вот так.
$$ h_{theta}(x) = P(y = 1 | x; theta) $$
Это выражение можно прочитать как вероятность принадлежности к классу 1 при условии x с параметрами $theta$ (probability of y = 1 given x, parameterized by $theta$).
Поскольку, как мы помним, сумма вероятностей событий, образующих полную группу, всегда равна единице, вероятность принадлежности к классу 0 будет равна
$$ P(y = 0 | x; theta) = 1-P(y = 1 | x; theta) $$
Решающая граница
Решающая граница (decision boundary) — это порог, который определяет к какому классу отнести то или иное наблюдение. Если выбрать порог на уровне 0,5, то все что выше или равно этому порогу мы отнесем к классу 1, все что ниже — к классу 0.
$$ y = 1, h_{theta}(x) geq 0,5 $$
$$ y = 0, h_{theta}(x) < 0,5 $$
Теперь обратите внимание на сигмоиду. Сигмоида $ g(z) $ принимает значения больше 0,5, если $ z geq 0 $, а так как $ z = Xtheta $, то можно сказать, что
- $h_{theta}(x) geq 0,5$ и $ y = 1$, когда $ Xtheta geq 0 $, и соответственно
- $h_{theta}(x) < 0,5 $ и $ y = 0$, когда $ Xtheta < 0 $.
Уравнение решающей границы
Предположим, что у нас есть два признака $x_1$ и $x_2$. Вместе они образуют так называемое пространство ввода (input space), то есть все имеющиеся у нас наблюдения. Мы можем представить это пространство на координатной плоскости, дополнительно выделив цветом наблюдения, относящиеся к разным классам.
Кроме того, представим, что мы уже построили модель логистической регрессии, и она провела для нас соответствующую границу между двумя классами.

Возникает вопрос. Как, зная коэффициенты $theta_0$, $theta_1$ и $theta_2$ модели, найти уравнение линии решающей границы? Для начала договоримся, что уравнение решающией границы будет иметь вид $x_2 = mx_1 + c$, где m — наклон прямой, а c — сдвиг.
Теперь вспомним, что модель с двумя признаками (до подачи в сигмоиду) имеет вид
$$ z = theta_0 + theta_1 x_1 + theta_2 x_2 $$
Также не забудем, что граница проходит там, где $ h_{theta}(x) = 0,5 $, а значит z = 0. Значит,
$$ 0 = theta_0 + theta_1 x_1 + theta_2 x_2 $$
Чтобы найти с (то есть сдвиг линии решающей границы вдоль оси $x_2$) приравняем $x_1$ к нулю и решим для $x_2$ (именно эта точка и будет сдвигом c).
$$ 0 = theta_0 + 0 + theta_2 x_2 rightarrow x_2 = -frac{theta_0}{theta_2} rightarrow c = -frac{theta_0}{theta_2} $$
Теперь займемся наклоном m. Возьмем некоторую точку на линии решающей границы с координатами $(x_1^a, x_2^a)$, $(x_1^b, x_2^b)$. Тогда наклон m будет равен
$$ m = frac{x_2^b-x_2^a}{x_1^b-x_1^a} $$
Так как эти точки расположены на решающей границе, то справедливо, что
$$ 0 = theta_1x_1^b + theta_2x_2^b + theta_0-(theta_1x_1^a + theta_2x_2^a + theta_0) $$
$$ -theta_2(x_2^b-x_2^a) = theta_1(x_1^b-x_1^a) $$
А значит,
$$ frac{x_2^b-x_2^a}{x_1^b-x_1^a} = -frac{theta_1}{theta_2} rightarrow m = -frac{theta_1}{theta_2} $$
Вычислительная устойчивость сигмоиды
При очень больших отрицательных или положительных значениях z может возникнуть переполнение памяти (overflow).
|
# возьмем большое отрицательное значение z = —999 1 / (1 + np.exp(—z)) |
|
RuntimeWarning: overflow encountered in exp 0.0 |
Преодолеть это ограничение и добиться вычислительной устойчивости (numerical stability) алгоритма можно с помощью следующего тождества.
$$ g(z) = frac{1}{1+e^{-z}} = frac{1}{1+e^{-z}} times frac{e^z}{e^z} = frac{e^z}{e^z(1+e^{-z})} = frac {e^z}{e^z + 1} $$
Что интересно, первая часть тождества устойчива при очень больших положительных значениях z.
|
z = 999 1 / (1 + np.exp(—z)) |
При этом вторая стабильна при очень больших отрицательных значениях.
|
z = —999 np.exp(z) / (np.exp(z) + 1) |
Объединим обе части с помощью условия.
|
def stable_sigmoid(z): if z >= 0: return 1 / (1 + np.exp(—z)) else: return np.exp(z) / (np.exp(z) + 1) |
Примечание. Мы не использовали более лаконичный код, например, функцию np.where(), потому что эта функция прежде чем применить условие рассчитывает оба сценария (в данном случае обе части тождества), а это ровно то, чего мы хотим избежать, чтобы не возникло ошибки. Простое условие с if препятствует выполнению той части кода, которая нам не нужна.
Можно также использовать функцию expit() библиотеки scipy.
|
from scipy.special import expit expit(999), expit(—999) |
Остается написать линейную функцию и подать ее результат в сигмоиду.
|
def h(x, thetas): z = np.dot(x, thetas) return np.array([stable_sigmoid(value) for value in z]) |
Протестируем код. Предположим, что в нашем датасете четыре наблюдения и три коэффициента. Схематично расчеты будут выглядеть следующим образом.
Пропишем это на Питоне.
|
# возьмем массив наблюдений 4 х 3 с числами от 1 до 12 x = np.arange(1, 13).reshape(4, 3) # и трехмерный вектор коэффициентов thetas = np.array([—3, 1, 1]) # подадим их в модель h(x, thetas) |
|
array([0.88079708, 0.26894142, 0.01798621, 0.00091105]) |
Модель работает корректно. Теперь обсудим, как ее обучать, то есть какую функцию потерь использовать для оптимизации параметров $theta$.
Logistic loss или функция кросс-энтропии
В модели логистической регрессии мы не можем использовать MSE. Дело в том, что если мы поместим результат сигмоиды (представляющей собою нелинейную функцию) в MSE, то на выходе получим невыпуклую функцию (non-convex), глобальный минимум которой довольно сложно найти.

Вместо MSE мы будем использовать функцию логистической ошибки, которую еще называют функцией бинарной кросс-энтропии (log loss, binary cross-entropy loss).
График и формула функции логистической ошибки
Вначале посмотрим на нее на графике.

Разберемся, как она работает. Наша модель $h_{theta}(x)$ может выдавать вероятность от 0 до 1, фактические значения $y$ только 0 и 1.
Сценарий 1. Предположим, что для конкретного заемщика в обучающем датасете истинное значение/ целевой класс записан как 1 (то есть заемщик вернул кредит). Тогда «срабатывает» синяя ветвь графика и ошибка измеряется по ней. Соответственно, чем ближе выдаваемая моделью вероятность к единице, тем меньше ошибка.
$$ -log(P(y = 1 | x; theta)) = -log(h_{theta}(x)), y = 1 $$
Сценарий 2. Заемщик не вернул кредит и его целевая переменная записана как 0. Тогда срабатывает оранжевая ветвь. Ошибка модели будет минимальна при значениях, близких к нулю.
$$ -log(1-P(y = 1 | x; theta)) = -log(1-h_{theta}(x)), y = 0 $$
Добавлю, что минус логарифм в данном случае очень удачно отвечает нашему желанию иметь нулевую ошибку при правильном прогнозе и наказать алгоритм высокой ошибкой (асимптотически стремящейся к бесконечности) в случае неправильного прогноза.
В итоге нам нужно будет найти сумму вероятностей принадлежности к классу 1 для сценария 1 и сценария 2.
$$ J(theta) = begin{cases} -log(h_{theta}(x)) | y=1 \ -log(1-h_{theta}(x)) | y=0 end{cases} $$
Однако, для каждого наблюдения нам нужно учитывать только одну из вероятностей (либо $y=1$, либо $y=0$). Как нам переключаться между ними? На самом деле очень просто.
В качестве переключателя можно использовать целевую переменную. В частности, умножим левую часть функции на $y$, а правую на $1-y$. Тогда, если речь идет о классе 1, первая часть умножится на единицу, вторая на ноль и исчезнет. Если речь идет о классе 0, произойдет обратное, исчезнет левая часть, а правая останется. Получается
$$ J(theta) = -frac{1}{n} sum y cdot log(h_{theta}(x)) + (1-y) cdot log(1-h_{theta}(x)) $$
Рассмотрим ее работу на учебном примере.
Расчет логистической ошибки
Предположим, мы построили модель и для каждого наблюдения получили некоторый прогноз (вероятность).
|
# выведем результат работы модели (вероятности) y_pred и целевую переменную y output = pd.DataFrame({ ‘y’ :[1, 1, 1, 0, 0, 1, 1, 0], ‘y_pred’ :[0.93, 0.81, 0.78, 0.43, 0.54, 0.49, 0.22, 0.1] }) output |
Найдем вероятность принадлежности к классу 1.
|
# оставим вероятность, если y = 1, и вычтем вероятность из единицы, если y = 0 output[‘y=1 prob’] = np.where(output[‘y’] == 0, 1 — output[‘y_pred’], output[‘y_pred’]) output |
Возьмем отрицательный логарифм из каждой вероятности.
|
output[‘-log’] = —np.log(output[‘y=1 prob’]) output |
Выведем каждое из получившихся значений на графике.
|
1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 18 19 |
plt.figure(figsize = (10, 8)) # создадим точки по оси x в промежутке от 0 до 1 x_vals = np.linspace(0, 1) # выведем кривую функции логистической ошибки plt.plot(x_vals, —np.log(x_vals), label = ‘-log(h(x)) | y = 1’) # выведем каждое из значений отрицательного логарифма plt.scatter(output[‘y=1 prob’], output[‘-log’], color = ‘r’) # зададим заголовок, подписи к осям, легенду и сетку plt.xlabel(‘h(x)’, fontsize = 16) plt.ylabel(‘loss’, fontsize = 16) plt.title(‘Функция логистической ошибки’, fontsize = 18) plt.legend(loc = ‘upper right’, prop = {‘size’: 15}) plt.grid() plt.show() |
Как мы видим, так как мы всегда выражаем вероятность принадлежности к классу 1, графически нам будет достаточно одной ветви. Остается сложить результаты и разделить на количество наблюдений.
Окончательный вариант
Напишем функцию логистической ошибки, которую будем использовать в нашем алгоритме.
|
def objective(y, y_pred): # рассчитаем функцию потерь для y = 1, добавив 1e-9, чтобы избежать ошибки при log(0) y_one_loss = y * np.log(y_pred + 1e—9) # также рассчитаем функцию потерь для y = 0 y_zero_loss = (1 — y) * np.log(1 — y_pred + 1e—9) # сложим и разделим на количество наблюдений return —np.mean(y_zero_loss + y_one_loss) |
Проверим ее работу на учебных данных.
|
objective(output[‘y’], output[‘y_pred’]) |
Теперь займемся поиском производной.
Производная функции логистической ошибки
Предположим, что $G(theta)$ — одна из частных производных описанной выше функции логистической ошибки $J(theta)$,
$$ G = y cdot log(h) + (1-y) cdot log(1-h) $$
где h — это сигмоида $1/1+e^{-z}$, а $z(theta)$ — линейная функция $xtheta$. Тогда по chain rule нам нужно найти производные следующих функций
$$ frac{partial G}{partial theta} = frac{partial G}{partial h} cdot frac{partial h}{partial z} cdot frac{partial z}{partial theta} $$
Производная логарифмической функции
Начнем с производной логарифмической функции.
$$ frac{partial}{partial x} ln f(x) = frac{1}{f(x)} $$
Теперь, помня, что x и y — это константы, найдем первую производную.
$$ frac{partial G}{partial h} left[ y cdot log(h) + (1-y) cdot log(1-h) right] $$
$$ = y cdot frac{partial G}{partial h} [log(h)] + (1-y) cdot frac{partial G}{partial h} [log(1-h)] $$
$$ = frac{1}{h}y + frac{1}{1-h} cdot frac{partial G}{partial h} [1-h] cdot (1-y) $$
Упростим выражение (не забыв про производную разности).
$$ = frac{h}{y} + frac{frac{partial G}{partial h} (1-h) (1-y)}{1-h} = frac{h}{y}+frac{(0-1)(1-y)}{1-h} $$
$$ = frac{y}{h}-frac{1-y}{1-h} = frac{y-h}{h(1-h)} $$
Теперь займемся производной сигмоиды.
Производная сигмоиды
Вначале упростим выражение.
$$ frac{partial h}{partial z} left[ frac{1}{1+e^{-z}} right] = frac{partial h}{partial z} left[ (1+e^{-z})^{-1}) right] $$
Теперь перейдем к нахождению производной
$$ = -(1+e^{-z})^{-2}) cdot (-e^{-z}) = frac{e^{-z}}{(1+e^{-z})^2} $$
$$ = frac{1}{1+e^{-z}} cdot frac{e^{-z}}{1+e^{-z}} = frac{1}{1+e^{-z}} cdot frac{(1+e^{-z})-1}{1+e^{-z}} $$
$$ = frac{1}{1+e^{-z}} cdot left( frac{1+e^{-z}}{1+e^{-z}}-frac{1}{1+e^{-z}} right) $$
$$ = frac{1}{1+e^{-z}} cdot left( 1-frac{1}{1+e^{-z}} right) $$
В терминах предложенной выше нотации получается
$$ h(1-h) $$
Производная линейной функции
Наконец найдем производную линейной функции.
$$ frac{partial z}{partial theta} = x $$
Перемножим производные и найдем градиент по каждому из признаков j для n наблюдений.
$$ frac{partial J}{partial theta} = frac{y-h}{h(1-h)} cdot h(1-h) cdot x_j cdot frac{1}{n} = x_j cdot (y-h) cdot frac{1}{n} $$
Замечу, что хотя производная похожа на градиент функции линейной регрессии, на самом деле это разные функции, $h$ в данном случае сигмоида.
Для нахождения градиента (всех частных производных одновременно) перепишем формулу в векторной нотации.
$$ nabla_{theta} J = X^T(h(Xtheta)-y) times frac{1}{n} $$
Схематично для четырех наблюдений и трех коэффициентов нахождение градиента будет выглядеть следующим образом.
Объявим соответствующую функцию.
|
def gradient(x, y, y_pred, n): return np.dot(x.T, (y_pred — y)) / n |
На всякий случай напомню, что прогнозные значения (y_pred) мы получаем с помощью объявленной ранее функции $h(x, thetas)$.
Подготовка данных
В качестве примера возьмем встроенный в sklearn датасет, в котором нам предлагается определить класс вина по его характеристикам.
|
# импортируем датасет о вине из модуля datasets data = datasets.load_wine() # превратим его в датафрейм df = pd.DataFrame(data.data, columns = data.feature_names) # добавим целевую переменную df[‘target’] = data.target # посмотрим на первые три строки df.head(3) |
Целевая переменная
Посмотрим на количество наблюдений и признаков (размерность матрицы), а также уникальные значения (классы) в целевой переменной.
|
df.shape, np.unique(df.target) |
|
((178, 14), array([0, 1, 2])) |
Как мы видим, у нас три класса, а должно быть два, потому что пока что мы создаем алгоритм бинарной классификации. Отфильтруем значения так, чтобы осталось только два класса.
|
# применим маску датафрейма и удалим класс 2 df = df[df.target != 2] # посмотрим на результат df.shape, df.target.unique() |
|
((130, 14), array([0, 1])) |
Отбор признаков
Наша целевая переменная выражена бинарной категорией или, как еще говорят, находится на дихотомической шкале (dichotomous variable). В этом случае применять коэффициент корреляции Пирсона не стоит и можно использовать точечно-бисериальную корреляцию (point-biserial correlation). Рассчитаем корреляцию признаков и целевой переменной нашего датасета.
|
1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 |
# импортируем модуль stats из библиотеки scipy from scipy import stats # создадим два списка, один для названий признаков, второй для корреляций columns, correlations = [], [] # пройдемся по всем столбцам датафрейма кроме целевой переменной for col in df.drop(‘target’, axis = 1).columns: # поместим название признака в список columns columns.append(col) # рассчитаем корреляцию этого признака с целевой переменной # и поместим результат в список корреляций correlations.append(stats.pointbiserialr(df[col], df[‘target’])[0]) # создадим датафрейм на основе заполненных списков # и применим градиентную цветовую схему pd.DataFrame({‘column’: columns, ‘correlation’: correlations}).style.background_gradient() |
Наиболее коррелирующим с целевой переменной признаком является пролин (proline). Визуально оценим насколько сильно отличается этот показатель для классов вина 0 и 1.
|
# зададим размер графика plt.figure(figsize = (10, 8)) # на точечной диаграмме выведем пролин по оси x, а класс вина по оси y sns.scatterplot(x = df.proline, y = df.target, s = 80); |
Теперь посмотрим на зависимость двух признаков (спирт и пролин) от целевой переменной.
|
# зададим размер графика plt.figure(figsize = (10, 8)) # на точечной диаграмме по осям x и y выведем признаки, # с помощью параметра hue разделим соответствующие классы целевой переменной sns.scatterplot(x = df.alcohol, y = df.proline, hue = df.target, s = 80) # добавим легенду, зададим ее расположение и размер plt.legend(loc = ‘upper left’, prop = {‘size’: 15}) # выведем результат plt.show() |
В целом можно сказать, что классы линейно разделимы (другими словами, мы можем провести прямую между ними). Поместим признаки в переменную X, а целевую переменную — в y.
|
X = df[[‘alcohol’, ‘proline’]] y = df[‘target’] |
Масштабирование признаков
Как и в случае с линейной регрессией, для алгоритма логистической регрессии важно, чтобы признаки были приведены к одному масштабу. Для этого используем стандартизацию.
|
# т.е. приведем данные к нулевому среднему и единичному СКО X = (X — X.mean()) / X.std() X.head() |
Проверим результат.
|
X.alcohol.mean(), X.alcohol.std(), X.proline.mean(), X.proline.std() |
|
(6.8321416900009635e-15, 1.0, -5.465713352000771e-17, 1.0) |
Теперь мы готовы к созданию и обучению модели.
Обучение модели
Вначале объявим уже знакомую нам функцию, которая добавит в датафрейм столбец под названием x0, заполненный единицами.
|
def add_ones(x): # важно! метод .insert() изменяет исходный датафрейм return x.insert(0,‘x0’, np.ones(x.shape[0])) |
Применим ее к нашему датафрейму с признаками.
|
# добавим столбец с единицами add_ones(X) # и посмотрим на результат X.head() |
Создадим вектор начальных весов (он будет состоять из нулей), а также переменную n, в которой будет храниться количество наблюдений.
|
thetas, n = np.zeros(X.shape[1]), X.shape[0] thetas, n |
|
(array([0., 0., 0.]), 130) |
Кроме того, создадим список, в который будем записывать размер ошибки функции потерь.
Теперь выполним основную работу по минимизации функции потерь и поиску оптимальных весов (выполнение кода ниже у меня заняло около 30 секунд).
|
# в цикле из 20000 итераций for i in range(20000): # рассчитаем прогнозное значение с текущими весами y_pred = h(X, thetas) # посчитаем уровень ошибки при текущем прогнозе loss_history.append(objective(y, y_pred)) # рассчитаем градиент grad = gradient(X, y, y_pred, n) # используем градиент для улучшения весов модели # коэффициент скорости обучения будет равен 0,001 thetas = thetas — 0.001 * grad |
Посмотрим на получившиеся веса и финальный уровень ошибки.
|
# чтобы посмотреть финальный уровень ошибки, # достаточно взять последний элемент списка loss_history thetas, loss_history[—1] |
|
(array([ 0.23234188, -1.73394252, -1.89350543]), 0.12282503517421262) |
Модель обучена. Теперь мы можем сделать прогноз и оценить результат.
Прогноз и оценка качества
Прогноз модели
Объявим функцию predict(), которая будет предсказывать к какому классу относится то или иное наблюдение. От функции $h(x, thetas)$ эта функция будет отличаться тем, что выдаст не только вероятность принадлежности к тому или иному классу, но и непосредственно сам предполагаемый класс (0 или 1).
|
def predict(x, thetas): # найдем значение линейной функции z = np.dot(x, thetas) # проведем его через устойчивую сигмоиду probs = np.array([stable_sigmoid(value) for value in z]) # если вероятность больше или равна 0,5 — отнесем наблюдение к классу 1, # в противном случае к классу 0 # дополнительно выведем значение вероятности return np.where(probs >= 0.5, 1, 0), probs |
Вызовем функцию predict() и запишем прогноз класса и вероятность принадлежности к этому классу в переменные y_pred и probs соответственно.
|
# запишем прогноз класса и вероятность этого прогноза в переменные y_pred и probs y_pred, probs = predict(X, thetas) # посмотрим на прогноз и вероятность для первого наблюдения y_pred[0], probs[0] |
|
(0, 0.022908352078195617) |
Здесь важно напомнить, что вероятность, близкая к нулю, говорит о пренадлжености к классу 0. В качестве упражнения выведите класс последнего наблюдения и соответствующую вероятность.
Метрика accuracy и матрица ошибок
Оценим результат с помощью метрики accuracy и матрицы ошибок.
|
# функцию accuracy_score() мы импортировали в начале ноутбука accuracy_score(y, y_pred) |
|
# функцию confusion_matrix() мы импортировали в начале ноутбука # столбцами будут прогнозные значения (Forecast), # строками — фактические (Actual) pd.DataFrame(confusion_matrix(y, y_pred), columns = [‘Forecast 0’, ‘Forecast 1’], index = [‘Actual 0’, ‘Actual 1’]) |
Как мы видим, алгоритм ошибся пять раз. Дважды он посчитал, что наблюдение относится к классу 1, хотя на самом деле это был класс 0, и трижды, наоборот, неверно отнес класс 1 к классу 0.
Решающая граница
Выше мы уже вывели уравнение решающей границы. Воспользуемся им, чтобы визуально оценить насколько удачно классификатор справился с поставленной задачей.
|
# рассчитаем сдвиг (c) и наклон (m) линии границы c, m = —thetas[0]/thetas[2], —thetas[1]/thetas[2] c, m |
|
(0.1227046263531282, -0.915731474695505) |
|
# найдем минимальное и максимальное значения для спирта (ось x) xmin, xmax = min(X[‘alcohol’]), max(X[‘alcohol’]) # найдем минимальное и максимальное значения для пролина (ось y) ymin, ymax = min(X[‘proline’]), max(X[‘proline’]) # запишем значения оси x в переменную xd xd = np.array([xmin, xmax]) xd |
|
array([-2.15362589, 2.12194856]) |
|
# подставим эти значения, а также значения сдвига и наклона в уравнение линии yd = m * xd + c # в результате мы получим координаты двух точек, через которые проходит линия границы (xd[0], yd[0]), (xd[1], yd[1]) |
|
((-2.1536258890738247, 2.0948476376971197), (2.1219485561396647, -1.8204304541886445)) |
|
1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 18 19 20 21 22 23 24 25 26 |
# зададим размер графика plt.figure(figsize = (11, 9)) # построим пунктирную линию по двум точкам, найденным выше plt.plot(xd, yd, ‘k’, lw = 1, ls = ‘—‘) # дополнительно отобразим наши данные, sns.scatterplot(x = X[‘alcohol’], y = X[‘proline’], hue = y, s = 70) # которые снова снабдим легендой plt.legend(loc = ‘upper left’, prop = {‘size’: 15}) # минимальные и максимальные значения по обеим осям будут границами графика plt.xlim(xmin, xmax) plt.ylim(ymin, ymax) # по желанию, разделенные границей половинки можно закрасить # tab: означает, что цвета берутся из палитры Tableau # plt.fill_between(xd, yd, ymin, color=’tab:blue’, alpha = 0.2) # plt.fill_between(xd, yd, ymax, color=’tab:orange’, alpha = 0.2) # а также добавить обозначения переменных в качестве подписей к осям # plt.xlabel(‘x_1’) # plt.ylabel(‘x_2’) plt.show() |
На графике хорошо видны те пять значений, в которых ошибся наш классификатор.
Написание класса
Остается написать класс бинарной логистической регрессии.
|
1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 18 19 20 21 22 23 24 25 26 27 28 29 30 31 32 33 34 35 36 37 38 39 40 41 42 43 44 45 46 47 48 49 50 51 52 53 54 55 56 57 58 59 60 61 62 63 64 65 66 67 68 69 70 71 72 73 74 75 |
class LogReg(): # в методе .__init__() объявим переменные для весов и уровня ошибки def __init__(self): self.thetas = None self.loss_history = [] # метод .fit() необходим для обучения модели # этому методу мы передадим признаки и целевую переменную # кроме того, мы зададим значения по умолчанию # для количества итераций и скорости обучения def fit(self, x, y, iter = 20000, learning_rate = 0.001): # метод создаст «правильные» копии датафрейма x, y = x.copy(), y.copy() # добавит столбец из единиц self.add_ones(x) # инициализирует веса и запишет в переменную n количество наблюдений thetas, n = np.zeros(x.shape[1]), x.shape[0] # создадим список для записи уровня ошибки loss_history = [] # в цикле равном количеству итераций for i in range(iter): # метод сделает прогноз с текущими весами y_pred = self.h(x, thetas) # найдет и запишет уровень ошибки loss_history.append(self.objective(y, y_pred)) # рассчитает градиент grad = self.gradient(x, y, y_pred, n) # и обновит веса thetas -= learning_rate * grad # метод выдаст веса и список с историей ошибок self.thetas = thetas self.loss_history = loss_history # метод .predict() делает прогноз с помощью обученной модели def predict(self, x): # метод создаст «правильную» копию модели x = x.copy() # добавит столбец из единиц self.add_ones(x) # рассчитает значения линейной функции z = np.dot(x, self.thetas) # передаст эти значения в сигмоиду probs = np.array([self.stable_sigmoid(value) for value in z]) # выдаст принадлежность к определенному классу и соответствующую вероятность return np.where(probs >= 0.5, 1, 0), probs # ниже приводятся служебные методы, смысл которых был разобран ранее def add_ones(self, x): return x.insert(0,‘x0’, np.ones(x.shape[0])) def h(self, x, thetas): z = np.dot(x, thetas) return np.array([self.stable_sigmoid(value) for value in z]) def objective(self, y, y_pred): y_one_loss = y * np.log(y_pred + 1e—9) y_zero_loss = (1 — y) * np.log(1 — y_pred + 1e—9) return —np.mean(y_zero_loss + y_one_loss) def gradient(self, x, y, y_pred, n): return np.dot(x.T, (y_pred — y)) / n def stable_sigmoid(self, z): if z >= 0: return 1 / (1 + np.exp(—z)) else: return np.exp(z) / (np.exp(z) + 1) |
Проверим работу написанного нами класса. Вначале подготовим данные и обучим модель.
|
# проверим работу написанного нами класса # поместим признаки и целевую переменную в X и y X = df[[‘alcohol’, ‘proline’]] y = df[‘target’] # приведем признаки к одному масштабу X = (X — X.mean())/X.std() # создадим объект класса LogReg model = LogReg() # и обучим модель model.fit(X, y) # посмотрим на атрибуты весов и финального уровня ошибки model.thetas, model.loss_history[—1] |
|
(array([ 0.23234188, —1.73394252, —1.89350543]), 0.12282503517421262) |
Затем сделаем прогноз и оценим качество модели.
|
# сделаем прогноз y_pred, probs = model.predict(X) # и посмотрим на класс первого наблюдения и вероятность y_pred[0], probs[0] |
|
(0, 0.022908352078195617) |
|
# рассчитаем accuracy accuracy_score(y, y_pred) |
|
# создадим матрицу ошибок pd.DataFrame(confusion_matrix(y, y_pred), columns = [‘Forecast 0’, ‘Forecast 1’], index = [‘Actual 0’, ‘Actual 1’]) |
Модель показала точно такой же результат. Методы класса LogReg работают. Теперь давайте сравним работу нашего класса с классом LogisticRegression библиотеки sklearn.
Сравнение с sklearn
Обучение модели
Вначале обучим модель.
|
# подготовим данные X = df[[‘alcohol’, ‘proline’]] y = df[‘target’] X = (X — X.mean())/X.std() # создадим объект класса LogisticRegression и запишем его в переменную model model = LogisticRegression() # обучим модель model.fit(X, y) # посмотрим на получившиеся веса модели model.intercept_, model.coef_ |
|
(array([0.30838852]), array([[-2.09622008, -2.45991159]])) |
Прогноз
Теперь необходимо сделать прогноз и найти соответствующие вероятности. В классе LogisticRegression библиотеки sklearn метод .predict() отвечает за предсказание принадлежности к определенному классу, а метод .predict_proba() отвечает за вероятность такого прогноза.
|
# выполним предсказание класса y_pred = model.predict(X) # и найдем вероятности probs = model.predict_proba(X) # посмотрим на класс и вероятность первого наблюдения y_pred[0], probs[0] |
|
(0, array([0.9904622, 0.0095378])) |
Модель предсказала для первого наблюдения класс 0. При этом, обратите внимание, что метод .predict_proba() для каждого наблюдения выдает две вероятности, первая — это вероятность принадлежности к классу 0, вторая — к классу 1.
Оценка качества
Рассчитаем метрику accuracy.
|
accuracy_score(y, y_pred) |
И построим матрицу ошибок.
|
pd.DataFrame(confusion_matrix(y, y_pred), columns = [‘Forecast 0’, ‘Forecast 1’], index = [‘Actual 0’, ‘Actual 1’]) |
Как мы видим, хотя веса модели и предсказанные вероятности немного отличаются, ее точность осталась неизменной.
Решающая граница
Построим решающую границу.
|
# найдем сдвиг и наклон для уравнения решающей границы c, m = —model.intercept_ / model.coef_[0][1], —model.coef_[0][0] / model.coef_[0][1] c, m |
|
(array([0.12536569]), -0.8521526076691505) |
|
# посмотрим на линию решающей границы plt.figure(figsize = (11, 9)) xmin, xmax = min(X[‘alcohol’]), max(X[‘alcohol’]) ymin, ymax = min(X[‘proline’]), max(X[‘proline’]) xd = np.array([xmin, xmax]) yd = m*xd + c plt.plot(xd, yd, ‘k’, lw=1, ls=‘—‘) sns.scatterplot(x = X[‘alcohol’], y = X[‘proline’], hue = y, s = 70) plt.legend(loc = ‘upper left’, prop = {‘size’: 15}) plt.xlim(xmin, xmax) plt.ylim(ymin, ymax) plt.show() |
Бинарная полиномиальная регрессия
Идея бинарной полиномиальной логистической регрессии (binary polynomial logistic regression) заключается в том, чтобы использовать полином внутри сигмоиды и соответственно создать нелинейную границу между двумя классами.
Полиномиальные признаки
Уравнение полинома на основе двух признаков будет выглядеть следующим образом.
$$ y = theta_{0}x_0 + theta_{1}x_1 + theta_{2}x_2 + theta_{3} x_1^2 + theta_{4} x_1x_2 + theta_{5} x_2^2 $$
Реализуем этот алгоритм на практике и посмотрим, улучшатся ли результаты. Вначале, подготовим и масштабируем данные.
|
X = df[[‘alcohol’, ‘proline’]] y = df[‘target’] X = (X — X.mean())/X.std() |
Теперь преобразуем наши данные так, как если бы мы использовали полином второй степени.
Смысл создания полиномиальных признаков мы детально разобрали на занятии по множественной линейной регрессии.
|
# создадим объект класса PolynomialFeatures # укажем, что мы хотим создать полином второй степени polynomial_features = PolynomialFeatures(degree = 2) # преобразуем данные с помощью метода .fit_transform() X_poly = polynomial_features.fit_transform(X) |
Сравним исходные признаки с полиномиальными.
|
# посмотрим на первое наблюдение X.head(1) |
|
# должно получиться шесть признаков X_poly[:1] |
|
array([[1. , 1.44685785, 0.77985116, 2.09339765, 1.12833378, 0.60816783]]) |
Моделирование и оценка качества
Обучим модель, сделаем прогноз и оценим результат.
|
# создадим объект класса LogisticRegression poly_model = LogisticRegression() # обучим модель на полиномиальных признаках poly_model = poly_model.fit(X_poly, y) # сделаем прогноз y_pred = poly_model.predict(X_poly) # рассчитаем accuracy accuracy_score(y_pred, y) |
Построим матрицу ошибок.
|
pd.DataFrame(confusion_matrix(y, y_pred), columns = [‘Forecast 0’, ‘Forecast 1’], index = [‘Actual 0’, ‘Actual 1’]) |
Для того чтобы визуально оценить качество модели, построим два графика: фактических классов и прогнозных. Вначале создадим датасет, в котором будут исходные признаки (alcohol, proline) и прогнозные значения (y_pred).
|
# сделаем копию исходного датафрейма с нужными признаками predictions = df[[‘alcohol’, ‘proline’]].copy() # и добавим новый столбец с прогнозными значениями predictions[‘y_pred’] = y_pred # посмотрим на результат predictions.head(3) |
|
1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 18 19 20 |
# создадим два подграфика с помощью функции plt.subplots() # расположим подграфики на одной строке fig, (ax1, ax2) = plt.subplots(1, 2, # пропишем размер, figsize = (14, 6), # а также расстояние между подграфиками по горизонтали gridspec_kw = {‘wspace’ : 0.2}) # на левом подграфике выведем фактические классы sns.scatterplot(data = df, x = ‘alcohol’, y = ‘proline’, hue = ‘target’, palette = ‘bright’, s = 50, ax = ax1) ax1.set_title(‘Фактические классы’, fontsize = 14) # на правом — прогнозные sns.scatterplot(data = predictions, x = ‘alcohol’, y = ‘proline’, hue = ‘y_pred’, palette = ‘bright’, s = 50, ax = ax2) ax2.set_title(‘Прогноз’, fontsize = 14) # зададим общий заголовок fig.suptitle(‘Бинарная полиномиальная регрессия’, fontsize = 16) plt.show() |
Как вы видите, нам не удалось добиться улучшения по сравнению с обычной полиномиальной регрессией.
Напомню, что создание подграфиков мы подробно разобрали на занятии по исследовательскому анализу данных.
В качестве упражнения предлагаю вам выяснить, какая степень полинома позволит улучшить результат прогноза на этих данных и насколько, таким образом, улучшится качество предсказаний.
Перейдем ко второй части нашего занятия.
Мультиклассовая логистическая регрессия
Как поступить, если нужно предсказать не два класса, а больше? Сегодня мы рассмотрим два подхода: one-vs-rest и кросс-энтропию. Начнем с того, что подготовим данные.
Подготовка данных
Вернем исходный датасет с тремя классами.
|
# вновь импортируем датасет о вине data = datasets.load_wine() # превратим его в датафрейм df = pd.DataFrame(data.data, columns = data.feature_names) # приведем признаки к одному масштабу df = (df — df.mean())/df.std() # добавим целевую переменную df[‘target’] = data.target # убедимся, что у нас присутствуют все три класса df.target.value_counts() |
|
1 71 0 59 2 48 Name: target, dtype: int64 |
В целевой переменной большое двух классов, а значит точечно-бисериальный коэффициент корреляции мы использовать не можем. Воспользуемся корреляционным отношением (correlation ratio).
|
# код ниже был подробно разобран на предыдущем занятии def correlation_ratio(numerical, categorical): values = np.array(numerical) ss_total = np.sum((values.mean() — values) ** 2) cats = np.unique(categorical, return_inverse = True)[1] ss_betweengroups = 0 for c in np.unique(cats): group = values[np.argwhere(cats == c).flatten()] ss_betweengroups += len(group) * (group.mean() — values.mean()) ** 2 return np.sqrt(ss_betweengroups/ss_total) |
|
# создадим два списка, один для названий признаков, второй для значений корреляционного отношения columns, correlations = [], [] # пройдемся по всем столбцам датафрейма кроме целевой переменной for col in df.drop(‘target’, axis = 1).columns: # поместим название признака в список columns columns.append(col) # рассчитаем взаимосвязь этого признака с целевой переменной # и поместим результат в список значений корреляционного отношения correlations.append(correlation_ratio(df[col], df[‘target’])) # создадим датафрейм на основе заполненных списков # и применим градиентную цветовую схему pd.DataFrame({‘column’: columns, ‘correlation’: correlations}).style.background_gradient() |
Теперь наибольшую корреляцию с целевой переменной показывают флавоноиды (flavanoids) и пролин (proline). Их и оставим.
|
df = df[[‘flavanoids’, ‘proline’, ‘target’]].copy() df.head(3) |
Посмотрим, насколько легко можно разделить эти классы.
|
# зададим размер графика plt.figure(figsize = (10, 8)) # построим точечную диаграмму с двумя признаками, разделяющей категориальной переменной будет класс вина sns.scatterplot(x = df.flavanoids, y = df.proline, hue = df.target, palette = ‘bright’, s = 100) # добавим легенду plt.legend(loc = ‘upper left’, prop = {‘size’: 15}) plt.show() |
Перейдем непосредственно к алгоритмам мультиклассовой логистической регрессии. Начнем с подхода one-vs-rest.
Подход one-vs-rest
Подход one-vs-rest или one-vs-all предполагает, что мы отделяем один класс, а остальные наоборот объединяем. Так мы поступаем с каждым классом и строим по одной модели логистической регрессии относительно каждого из класса. Например, если у нас три класса, то у нас будет три модели логистической регрессии. Далее мы смотрим на получившиеся вероятности и выбираем наибольшую.
$$ h_theta^{(i)}(x) = P(y = i | x; theta), i in {0, 1, 2} $$
При таком подходе сам по себе алгоритм логистической регрессии претерпевает лишь несущественные изменения, главное правильно подготовить данные для обучения модели.
Подготовка датасетов
|
# поместим признаки и данные в соответствующие переменные x1, x2 = df.columns[0], df.columns[1] target = df.target.unique() target |
|
1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 18 19 20 21 22 23 24 |
# сделаем копии датафреймов ovr_0, ovr_1, ovr_2 = df.copy(), df.copy(), df.copy() # в каждом из них сделаем целевым классом 0-й, 1-й или 2-й классы # например, в ovr_0 первым классом будет класс 0, а классы 1 и 2 — нулевым ovr_0[‘target’] = np.where(df[‘target’] == target[0], 1, 0) ovr_1[‘target’] = np.where(df[‘target’] == target[1], 1, 0) ovr_2[‘target’] = np.where(df[‘target’] == target[2], 1, 0) # выведем разделение на классы на графике fig, (ax1, ax2, ax3) = plt.subplots(1, 3, figsize = (16, 4), gridspec_kw = {‘wspace’: 0.2, ‘hspace’: 0.08}) sns.scatterplot(data = ovr_0, x = x1, y = x2, hue = ‘target’, s = 50, ax = ax1) ax1.set_title(‘Прогнозирование класса 0’, fontsize = 14) sns.scatterplot(data = ovr_1, x = x1, y = x2, hue = ‘target’, s = 50, ax = ax2) ax2.set_title(‘Прогнозирование класса 1’, fontsize = 14) sns.scatterplot(data = ovr_2, x = x1, y = x2, hue = ‘target’, s = 50, ax = ax3) ax3.set_title(‘Прогнозирование класса 2’, fontsize = 14) plt.show() |
Обучение моделей
|
models = [] # поочередно обучим каждую из моделей for ova_n in [ovr_0, ovr_1, ovr_2]: X = ova_n[[‘flavanoids’, ‘proline’]] y = ova_n[‘target’] model = LogReg() model.fit(X, y) # каждую обученную модель поместим в список models.append(model) |
|
# убедимся, что все работает # например, выведем коэффициенты модели 1 models[0].thetas |
|
array([-0.99971466, 1.280398 , 2.04834457]) |
Прогноз и оценка качества
|
# вновь перенесем данные из исходного датафрейма X = df[[‘flavanoids’, ‘proline’]] y = df[‘target’] # в список probs будем записывать результат каждой модели # для каждого наблюдения probs = [] for model in models: _, prob = model.predict(X) probs.append(prob) |
|
# очевидно, для каждого наблюдения у нас будет три вероятности # принадлежности к целевому классу probs[0][0], probs[1][0], probs[2][0] |
|
(0.9161148288779738, 0.1540913395345091, 0.026621132600103174) |
|
# склеим и изменим размерность массива таким образом, чтобы # строки были наблюдениями, а столбцы вероятностями all_probs = np.concatenate(probs, axis = 0).reshape(len(probs), —1).T all_probs.shape |
|
# каждая из 178 строк — это вероятность одного наблюдения # принадлежать к классу 0, 1, 2 all_probs[0] |
|
array([0.91611483, 0.15409134, 0.02662113]) |
Обратите внимание, при использовании подхода one-vs-rest вероятности в сумме не дают единицу.
|
# например, первое наблюдение вероятнее всего принадлежит к классу 0 np.argmax(all_probs[0]) |
|
# найдем максимальную вероятность в каждой строке, # индекс вероятности [0, 1, 2] и будет прогнозом y_pred = np.argmax(all_probs, axis = 1) # рассчитаем accuracy accuracy_score(y, y_pred) |
|
# выведем матрицу ошибок pd.DataFrame(confusion_matrix(y, y_pred), columns = [‘Forecast 0’, ‘Forecast 1’, ‘Forecast 2’], index = [‘Actual 0’, ‘Actual 1’, ‘Actual 2’]) |
Сравним фактическое и прогнозное распределение классов на точечной диаграмме.
|
1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 18 |
predictions = df[[‘flavanoids’, ‘proline’]].copy() predictions[‘y_pred’] = y_pred fig, (ax1, ax2) = plt.subplots(1, 2, figsize = (14, 6), gridspec_kw = {‘wspace’: 0.2, ‘hspace’: 0.08}) sns.scatterplot(data = df, x = ‘flavanoids’, y = ‘proline’, hue = ‘target’, palette = ‘bright’, s = 50, ax = ax1) ax1.set_title(‘Фактические классы’, fontsize = 14) sns.scatterplot(data = predictions, x = ‘flavanoids’, y = ‘proline’, hue = ‘y_pred’, palette = ‘bright’, s = 50, ax = ax2) ax2.set_title(‘Прогноз one-vs-rest’, fontsize = 14) plt.show() |
Написание класса
Поместим достигнутый выше результат в класс.
|
1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 18 19 20 21 22 23 24 25 26 27 28 29 30 31 32 33 34 35 36 37 38 39 40 41 42 43 44 45 46 47 48 49 50 51 52 53 54 55 56 57 58 59 60 61 62 63 64 65 66 67 68 69 70 71 72 73 74 75 76 77 78 79 80 81 82 83 84 85 |
class OVR_LogReg(): def __init__(self): self.models_thetas = [] self.models_loss = [] def fit(self, x, y, iter = 20000, learning_rate = 0.001): dfs = self.preprocess(x, y) models_thetas, models_loss = [], [] for ovr_df in dfs: x = ovr_df.drop(‘target’, axis = 1).copy() y = ovr_df.target.copy() self.add_ones(x) loss_history = [] thetas, n = np.zeros(x.shape[1]), x.shape[0] for i in range(iter): y_pred = self.h(x, thetas) loss_history.append(self.objective(y, y_pred)) grad = self.gradient(x, y, y_pred, n) thetas -= learning_rate * grad models_thetas.append(thetas) models_loss.append(loss_history) self.models_thetas = models_thetas self.models_loss = models_loss def predict(self, x): x = x.copy() probs = [] self.add_ones(x) for t in self.models_thetas: z = np.dot(x, t) prob = np.array([self.stable_sigmoid(value) for value in z]) probs.append(prob) all_probs = np.concatenate(probs, axis = 0).reshape(len(probs), —1).T y_pred = np.argmax(all_probs, axis = 1) return y_pred, all_probs def preprocess(self, x, y): x, y = x.copy(), y.copy() x[‘target’] = y classes = x.target.unique() dfs = [] ovr_df = None for c in classes: ovr_df = x.drop(‘target’, axis = 1).copy() ovr_df[‘target’] = np.where(x[‘target’] == classes[c], 1, 0) dfs.append(ovr_df) return dfs def add_ones(self, x): return x.insert(0,‘x0’, np.ones(x.shape[0])) def h(self, x, thetas): z = np.dot(x, thetas) return np.array([self.stable_sigmoid(value) for value in z]) def objective(self, y, y_pred): y_one_loss = y * np.log(y_pred + 1e—9) y_zero_loss = (1 — y) * np.log(1 — y_pred + 1e—9) return —np.mean(y_zero_loss + y_one_loss) def gradient(self, x, y, y_pred, n): return np.dot(x.T, (y_pred — y)) / n def stable_sigmoid(self, z): if z >= 0: return 1 / (1 + np.exp(—z)) else: return np.exp(z) / (np.exp(z) + 1) |
Проверим класс в работе.
|
X = df[[‘flavanoids’, ‘proline’]] y = df[‘target’] model = OVR_LogReg() model.fit(X, y) y_pred, probs = model.predict(X) accuracy_score(y_pred, y) |
Сравнение с sklearn
Для того чтобы применить подход one-vs-rest в классе LogisticRegression, необходимо использовать значение параметра multi_class = ‘ovr’.
|
X = df[[‘flavanoids’, ‘proline’]] y = df[‘target’] ovr_model = LogisticRegression(multi_class = ‘ovr’) ovr_model = ovr_model.fit(X, y) y_pred = ovr_model.predict(X) accuracy_score(y_pred, y) |
Мультиклассовая полиномиальная регрессия
Как мы увидели в предыдущем разделе, линейная решающая граница допустила некоторое количество ошибок. Попробуем улучшить результат, применив мультиклассовую полиномиальную логистическую регрессию.
|
X = df[[‘flavanoids’, ‘proline’]] y = df[‘target’] polynomial_features = PolynomialFeatures(degree = 7) X_poly = polynomial_features.fit_transform(X) poly_ovr_model = LogisticRegression(multi_class = ‘ovr’) poly_ovr_model = poly_ovr_model.fit(X_poly, y) y_pred = poly_ovr_model.predict(X_poly) accuracy_score(y_pred, y) |
Результат, по сравнению с моделью sklearn без полиномиальных признаков, стал чуть лучше. Однако это было достигнуто за счет полинома достаточно высокой степени (degree = 7), что неэффективно с точки зрения временной сложности алгоритма.
Посмотрим, какие нелинейные решающие границы удалось построить алгоритму.
|
predictions = df[[‘flavanoids’, ‘proline’]].copy() predictions[‘y_pred’] = y_pred fig, (ax1, ax2) = plt.subplots(1, 2, figsize = (14, 6), gridspec_kw = {‘wspace’: 0.2, ‘hspace’: 0.08}) sns.scatterplot(data = df, x = ‘flavanoids’, y = ‘proline’, hue = ‘target’, palette = ‘bright’, s = 50, ax = ax1) ax1.set_title(‘Фактические классы’, fontsize = 14) sns.scatterplot(data = predictions, x = ‘flavanoids’, y = ‘proline’, hue = ‘y_pred’, palette = ‘bright’, s = 50, ax = ax2) ax2.set_title(‘Полиномиальная регрессия’, fontsize = 14) plt.show() |
Softmax Regression
Еще один подход при создании мультиклассовой логистической регрессии заключается в том, чтобы не разбивать многоклассовые данные на несколько датасетов и использовать бинарный классификатор, а сразу применять функции, которые подходят для работы с множеством классов.
Такую регрессию часто называют Softmax Regression из-за того, что в ней используется уже знакомая нам по занятию об основах нейросетей функция softmax. Вначале подготовим данные.
Подготовка признаков
Возьмем признаки flavanoids и proline и добавим столбец из единиц.
|
def add_ones(x): # важно! метод .insert() изменяет исходный датафрейм return x.insert(0,‘x0’, np.ones(x.shape[0])) |
|
X = df[[‘flavanoids’, ‘proline’]] add_ones(X) X.head(3) |
Кодирование целевой переменной
Напишем собственную функцию для one-hot encoding.
|
def ohe(y): # количество примеров и количество классов examples, features = y.shape[0], len(np.unique(y)) # нулевая матрица: количество наблюдений x количество признаков zeros_matrix = np.zeros((examples, features)) # построчно проходимся по нулевой матрице и с помощью индекса заполняем соответствующее значение единицей for i, (row, digit) in enumerate(zip(zeros_matrix, y)): zeros_matrix[i][digit] = 1 return zeros_matrix |
|
y = df[‘target’] y_enc = ohe(df[‘target’]) y_enc[:3] |
|
array([[1., 0., 0.], [1., 0., 0.], [1., 0., 0.]]) |
Такой же результат можно получить с помощью класса LabelBinarizer.
|
lb = LabelBinarizer() lb.fit(y) lb.classes_ |
|
y_lb = lb.transform(y) y_lb[:5] |
|
array([[1, 0, 0], [1, 0, 0], [1, 0, 0], [1, 0, 0], [1, 0, 0]]) |
Инициализация весов
Создадим нулевую матрицу весов. Она будет иметь размерность: количество признаков (строки) х количество классов (столбцы). Приведем схематичный пример для четырех наблюдений, трех признаков (включая сдвиг $theta_0$) и трех классов.
Инициализируем веса.
|
thetas = np.zeros((3, 3)) thetas |
|
array([[0., 0., 0.], [0., 0., 0.], [0., 0., 0.]]) |
Функция softmax
Подробнее изучим функцию softmax. Приведем формулу.
$$ text{softmax}(z)_{i} = frac{e^{z_i}}{sum_{k=1}^N e^{z_k}} $$
Рассмотрим ее реализацию на Питоне.
Напомню, что $ z = (-Xtheta) $. Соответственно в нашем случае мы будем умножать матрицу 178 x 3 на 3 x 3.
В результате получим матрицу 178 x 3, где каждая строка — это прогнозные значения принадлежности одного наблюдения к каждому из трех классов.
|
z = np.dot(—X, thetas) z.shape |
Так как мы умножаем на ноль, при первой итерации эти значения будут равны нулю.
|
array([[0., 0., 0.], [0., 0., 0.], [0., 0., 0.], [0., 0., 0.], [0., 0., 0.]]) |
Для того чтобы обеспечить вычислительную устойчивость softmax мы можем вычесть из z максимальное значение в каждой из 178 строк (пока что, опять же на первой итерации, оно равно нулю).
$$ text{softmax}(z)_{i} = frac{e^{z_i-max(z)}}{sum_{k=1}^N e^{z_k-max(z)}} $$
|
# axis = -1 — это последняя ось # keepdims = True сохраняет размерность (в данном случае двумерный массив) np.max(z, axis = —1, keepdims = True)[:5] |
|
array([[0.], [0.], [0.], [0.], [0.]]) |
|
z = z — np.max(z, axis = —1, keepdims = True) z[:5] |
|
array([[0., 0., 0.], [0., 0., 0.], [0., 0., 0.], [0., 0., 0.], [0., 0., 0.]]) |
Смысл такого преобразования⧉ в том, что оно делает значения z нулевыми или отрицательными.
|
arr = np.array([—2, 3, 0, —7, 6]) arr — max(arr) |
|
array([ -8, -3, -6, -13, 0]) |
Далее, число возводимое в увеличивающуюся отрицательную степень стремится к нулю, а не к бесконечности и, таким образом, не вызывает переполнения памяти. Найдем числитель и знаменатель из формулы softmax.
|
numerator = np.exp(z) numerator[:5] |
|
array([[1., 1., 1.], [1., 1., 1.], [1., 1., 1.], [1., 1., 1.], [1., 1., 1.]]) |
|
denominator = np.sum(numerator, axis = —1, keepdims = True) denominator[:5] |
|
array([[3.], [3.], [3.], [3.], [3.]]) |
Разделим числитель и знаменатель и, таким образом, вычислим вероятность принадлежности каждого из наблюдений (строки результата) к одному из трех классов (столбцы).
|
softmax = numerator / denominator softmax[:5] |
|
array([[0.33333333, 0.33333333, 0.33333333], [0.33333333, 0.33333333, 0.33333333], [0.33333333, 0.33333333, 0.33333333], [0.33333333, 0.33333333, 0.33333333], [0.33333333, 0.33333333, 0.33333333]]) |
На первой итерации при одинаковых $theta$ мы получаем, что логично, одинаковые вероятности принадлежности к каждому из классов. Напишем функцию.
|
def stable_softmax(x, thetas): z = np.dot(—x, thetas) z = z — np.max(z, axis = —1, keepdims = True) numerator = np.exp(z) denominator = np.sum(numerator, axis = —1, keepdims = True) softmax = numerator / denominator return softmax |
|
probs = stable_softmax(X, thetas) probs[:3] |
|
array([[0.33333333, 0.33333333, 0.33333333], [0.33333333, 0.33333333, 0.33333333], [0.33333333, 0.33333333, 0.33333333]]) |
Примечание. Обратите внимание, что сигмоида — это частный случай функции softmax для двух классов $[z_1, 0]$. Вероятность класса $z_1$ будет равна
$$ softmax(z_1) = frac{e^{z_1}}{e^{z_1}+e^0} = frac{e^{z_1}}{e^{z_1}+1} $$
Если разделить и числитель, и знаменатель на $e^{z_1}$, то получим
$$ sigmoid(z_1) = frac{e^{z_1}}{1 + e^{-z_1}} $$
Вычислять вероятность принадлежности ко второму классу нет необходимости, достаточно вычесть результат сигмоиды из единицы.
Теперь нужно понять, насколько сильно при таких весах ошибается наш алгоритм.
Функция потерь
Вспомним функцию бинарной кросс-энтропии. То есть функции ошибки для двух классов.
$$ L(y, theta) = -frac{1}{n} sum y cdot log(h_{theta}(x)) + (1-y) cdot log(1-h_{theta}(x)) $$
Напомню, что y выступает в роли своего рода переключателя, сохраняющего одну из частей выражения, и обнуляющего другую. Теперь посмотрите на функцию категориальной (многоклассовой) кросс-энтропии (categorical cross-entropy).
$$ L(y_{ohe}, softmax) = -sum y_{ohe} log(softmax) $$
Разберемся, что здесь происходит. $y_{ohe}$ содержит закодированную целевую переменную, например, для наблюдения класса 0 [1, 0, 0], softmax содержит вектор вероятностей принадлежности наблюдения к каждому из классов, например, [0,3 0,4 0,3] (мы видим, что алгоритм ошибается).
В данном случае закодированная целевая переменная также выступает в виде переключателя. Здесь при умножении «срабатывает» только первая вероятность $1 times 0,3 + 0 times 0,4 + 0 times 0,4 $. Если подставить в формулу, то получаем (np.sum() добавлена для сохранения единообразия с формулой выше, в данном случае у нас одно наблюдение и сумма не нужна).
|
y_ohe = np.array([1, 0, 0]) softmax = np.array([0.3, 0.4, 0.4]) —np.sum(y_ohe * np.log(softmax)) |
Если бы модель в своих вероятностях ошибалась меньше, то и общая ошибка была бы меньше.
|
y_ohe = np.array([1, 0, 0]) softmax = np.array([0.4, 0.3, 0.4]) —np.sum(y_ohe * np.log(softmax)) |
Функция $-log$ позволяет снижать ошибку при увеличении вероятности верного (сохраненного переключателем) класса.
|
x_arr = np.linspace(0.001,1, 100) sns.lineplot(x=x_arr,y=—np.log(x_arr)) plt.title(‘Plot of -log(x)’) plt.xlabel(‘x’) plt.ylabel(‘-log(x)’); |
Напишем функцию.
|
# добавим константу в логарифм для вычислительной устойчивости def cross_entropy(probs, y_enc, epsilon = 1e—9): n = probs.shape[0] ce = —np.sum(y_enc * np.log(probs + epsilon)) / n return ce |
Рассчитаем ошибку для нулевых весов.
|
ce = cross_entropy(probs, y_enc) ce |
Для снижения ошибки нужно найти градиент.
Градиент
Приведем формулу градиента без дифференцирования.
$$ nabla_{theta}J = frac{1}{n} times X^T cdot (y_{ohe}-softmax) $$
По сути, мы умножаем транспонированную матрицу признаков (3 x 178) на разницу между закодированной целевой переменной и вероятностями функции softmax (178 x 3).
|
def gradient_softmax(X, probs, y_enc): # если не добавить функцию np.array(), будет выводиться датафрейм return np.array(1 / probs.shape[0] * np.dot(X.T, (y_enc — probs))) |
|
gradient_softmax(X, probs, y_enc) |
|
array([[-0.00187266, 0.06554307, -0.06367041], [ 0.31627721, 0.02059572, -0.33687293], [ 0.38820566, -0.28801792, -0.10018774]]) |
Обучение модели, прогноз и оценка качества
Выполним обучение модели.
|
loss_history = [] # в цикле for i in range(30000): # рассчитаем прогнозное значение с текущими весами probs = stable_softmax(X, thetas) # посчитаем уровень ошибки при текущем прогнозе loss_history.append(cross_entropy(probs, y_enc, epsilon = 1e—9)) # рассчитаем градиент grad = gradient_softmax(X, probs, y_enc) # используем градиент для улучшения весов модели thetas = thetas — 0.002 * grad |
Посмотрим на получившиеся коэффициенты (напомню, что первая строка матрицы это сдвиг (intercept, $theta_0$)) и достигнутый уровень ошибки.
|
array([[ 0.11290134, -0.90399727, 0.79109593], [-1.7550965 , -0.7857371 , 2.5408336 ], [-1.93839311, 1.77140542, 0.16698769]]) |
|
loss_history[0], loss_history[—1] |
|
(1.0986122856681098, 0.2569641080523888) |
Сделаем прогноз и оценим качество.
|
y_pred = np.argmax(stable_softmax(X, thetas), axis = 1) |
|
accuracy_score(y, y_pred) |
|
pd.DataFrame(confusion_matrix(y, y_pred), columns = [‘Forecast 0’, ‘Forecast 1’, ‘Forecast 2’], index = [‘Actual 0’, ‘Actual 1’, ‘Actual 2’]) |
Написание класса
Объединим созданные выше компоненты в класс.
|
1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 18 19 20 21 22 23 24 25 26 27 28 29 30 31 32 33 34 35 36 37 38 39 40 41 42 43 44 45 46 47 48 49 50 51 52 |
class SoftmaxLogReg(): def __init__(self): self.loss_ = None self.thetas_ = None def fit(self, x, y, iter = 30000, learning_rate = 0.002): loss_history = [] self.add_ones(x) y_enc = self.ohe(y) thetas = np.zeros((x.shape[1], y_enc.shape[1])) for i in range(iter): probs = self.stable_softmax(x, thetas) loss_history.append(self.cross_entropy(probs, y_enc, epsilon = 1e—9)) grad = self.gradient_softmax(x, probs, y_enc) thetas = thetas — 0.002 * grad self.thetas_ = thetas self.loss_ = loss_history def predict(self, x, y): return np.argmax(self.stable_softmax(x, thetas), axis = 1) def stable_softmax(self, x, thetas): z = np.dot(—x, thetas) z = z — np.max(z, axis = —1, keepdims = True) numerator = np.exp(z) denominator = np.sum(numerator, axis = —1, keepdims = True) softmax = numerator / denominator return softmax def cross_entropy(self, probs, y_enc, epsilon = 1e—9): n = probs.shape[0] ce = —np.sum(y_enc * np.log(probs + epsilon)) / n return ce def gradient_softmax(self, x, probs, y_enc): return np.array(1 / probs.shape[0] * np.dot(x.T, (y_enc — probs))) def add_ones(self, x): return x.insert(0,‘x0’, np.ones(x.shape[0])) def ohe(self, y): examples, features = y.shape[0], len(np.unique(y)) zeros_matrix = np.zeros((examples, features)) for i, (row, digit) in enumerate(zip(zeros_matrix, y)): zeros_matrix[i][digit] = 1 return zeros_matrix |
Обучим модель, сделаем прогноз и оценим качество.
|
X = df[[‘flavanoids’, ‘proline’]] y = df[‘target’] model = SoftmaxLogReg() model.fit(X, y) model.thetas_, model.loss_[—1] |
|
(array([[ 0.11290134, -0.90399727, 0.79109593], [-1.7550965 , -0.7857371 , 2.5408336 ], [-1.93839311, 1.77140542, 0.16698769]]), 0.2569641080523888) |
|
y_pred = model.predict(X, y) accuracy_score(y, y_pred) |
Сравнение с sklearn
Для того чтобы использовать softmax логистическую регрессию в sklearn, соответствующему классу нужно передать параметр multi_class = ‘multinomial’.
|
X = df[[‘flavanoids’, ‘proline’]] y = df[‘target’] # создадим объект класса LogisticRegression и запишем его в переменную model model = LogisticRegression(multi_class = ‘multinomial’) # обучим нашу модель model.fit(X, y) # посмотрим на получившиеся веса модели model.intercept_, model.coef_ |
|
(array([ 0.09046097, 1.12593099, -1.21639196]), array([[ 1.86357908, 1.89698292], [ 0.86696131, -1.43973164], [-2.73054039, -0.45725129]])) |
|
y_pred = model.predict(X) accuracy_score(y, y_pred) |
Подведем итог
Сегодня мы разобрали множество разновидностей и подходов к использованию логистической регрессии. Давайте систематизируем изученный материал с помощью следующей схемы.
Рассмотрим обучение нейронных сетей.
Что такое классификация в машинном обучении?
Задача классификации на практике встречается гораздо чаще, чем регрессия. По счастливому совпадению, и решать ее в каком-то смысле гораздо проще. Формально, задача классификации состоит в предсказании какого-то дискретного значения, в противоположность регрессии — предсказанию непрерывного значения. Но в реальности задачи классификации очень непохожи на регрессионные. Задачи регрессии — часто экономические или статистические — состоят именно в прогнозировании некоторого уровня какой-то величины. Задача классификации (как, впрочем и следует из названия) сводится к отнесению конкретного объекта к одному из заранее известных классов. Вот эта “метка” — название класса — и выступает в роли целевой переменной. И, совершенно естественно, что классов может быть только конечное количество, поэтому целевая переменная — дискретная.
Классификация в машинном обучении — задача отнесения объекта по совокупности его характеристик к одному из заранее известных классов.
Важно, что классы должны быть заранее известны. Мы должны знать сколько их всего, и к какому классу относится каждый объект обучающей выборки. Если чего-то из этого мы не знаем, то это уже совершенно другая задача — кластеризация — которая относится к обучению без учителя. А для классификации в датасете должны быть приведены метки классов для каждого объекта. Иначе говорят, что датасет должен быть “размечен”. Если у нас этих данных нет, то данные надо разметить — указать для каждого объекта правильный класс.
Задачи классификации очень разнообразны. Почти любая прикладная задача машинного обучения может быть представлена в виде классификации. Например — распознавание объектов на изображении. Мы все пользуемся умными камерами в смартфонах, которые умеют автоматически определять, есть ли лицо на изображении в объективе. Вот там как раз работает алгоритм классификации, который разделяет все изображения на два класса — имеющих лицо и не имеющих. Другой пример — определение, является электронное письмо спамом или нет. Здесь так же идет разделение объектов на два класса. Или, например, выявление подозрительных банковских транзакций.
Все эти примеры имеют одну общую черту — в них идет речь о двух классах. Это примеры так называемой бинарной классификации. Такая постановка задачи действительно встречается довольно часто. И все эти задачи можно сформулировать как определение наличия или отсутствия какого-либо признака у объекта. Например, наличие лица на фото, подозрительности транзакции, и так далее. Но вообще не все задачи классификации обязаны быть бинарными. Иногда случается такое, что классов больше двух. Тогда мы говорим о задаче множественной классификации. Например, вместо распознавания конкретного объекта на изображении весьма распространена задача определения, какой именно объект изображен.
Это называется задача идентификации объекта. К задачам множественной классификации еще относятся, например, рубрикация текстов — определение тематики текста, классификация изображений, сегментация рынка, классификация товаров, и еще множество других. Более того, к задачам классификации относятся такие задачи, про которые вообще с первого взгляда непонятно, куда их относить и как их решать. Типичный пример — машинный перевод. При всей своей специфике, его тоже можно представить как задачу классификации — подбор следующего слова в тексте, соответствующего контексту и тексту на другом языке. Так как мы выбираем какое-то оптимальное значение из пусть большого, но не бесконечного количества значений — всех возможных слов языка. Так что перевод — это очень множественная, но все-таки классификация. То же можно сказать и о задаче генерации текста. Аналогично к классификации относится распознавание рукописных или сканированных текстов, преобразование речи в текст и многие другие задачи обработки естественных языков.
Кроме бинарной и множественной классификации еще выделяют одноклассовую и мультиклассовую. Одноклассовая — это когда один объект может принадлежать только одному классу. В мультиклассовой классификации каждый объект может принадлежать сразу нескольким классам. Например, текст может относиться сразу к нескольким темам. А на изображении может присутствовать сразу несколько объектов. Отдельно выделяют нечеткую классификацию — это когда объект может принадлежать некоторым классам с разной принадлежностью или вероятностью.
Некоторые прикладные задачи сводятся к элементарным задачам менее очевидным способом. Например, генерация текста, также как и машинный перевод — это всего лишь определение, какое слово должно идти следующим в переводе при известном контексте ии переводе. То есть для выбора каждого очередного слова в итоговом тексте решается задача выбора одного из сотен тысяч слов. Но тем не менее это всего лишь классификация — выбор их конечного набора вариантов. Другой пример — локация объектов на изображении. Здесь картинка разбивается на множество возможных “рамок” и для каждой из них решается задача классификации — содержит эта конкретная рамка нужное изображение или нет. Так что действительно, практически любая задача может быть переформулирована как задача классификации
Еще следует отметить, что иногда имеет смысл преобразовать задачу регрессии в классификацию. Например, рассмотрим задачу предсказания цены финансового актива. Из-за того, что на цену актива влияют множество факторов, эта задача очень сложная, ведь мы выбираем из бесконечно большого количества вариантов. Но ее можно решать по-другому. Зачастую нам не важен конкретный уровень будущего значения цены, важнее то, будет цена больше или меньше, чем текущая. В таком случае, можно заменить сложную и зачастую нерешаемую задачу предсказания уровня более простой задачей предсказания тренда. У тренда можно выделить конечное число состояний — восходящий, нисходящий или боковой. То есть мы выбираем из, например, трех вариантов — будет цена больше, меньше или примерно такая же, как текущая. Другими словами мы заменили задачу регрессии классификацией. И такой прием используется очень часто.
Выводы:
- Классификация — это задача машинного обучения, которая выражается в предсказании дискретного значения.
- Классификация — это задача обучения с учителем, поэтому в датасете должны быть “правильные ответы” — значения целевой переменной.
- Классификация — самая распространенная задача машинного обучения на практике.
- Классификация бывает бинарной и множественной, одноклассовой и мультиклассовой.
- Примеры задач классификации — распознавание объектов, генерация текстов, подбор тематики текстов, идентификация объектов на изображениях, распознавание речи, машинный перевод и так далее.
- Почти любую практическую задачу машинного обучения можно сформулировать как задачу классификации.
Как определяется задача классификации?
Итак, рассмотрим математическую формализацию задачи классификации. В такой задаче, так же как и в регрессии, на вход модели подается вектор признаков $ x^{(i)} = (x_1, x_2, … x_n)$. Как и ранее, введем искусственный признак $ x_0 = 1 $. Он нужен для удобства представления многих моделей классификации. Можете представлять его как еще один столбец в датасете, в котором во всех строчках стоят единицы.
Функция гипотезы в таком случае будет иметь точно такой же вид: $ y = h_theta (x) $. Существенное отличие в том, что целевая переменная $y$ будет принимать одно из конечного множества значений: $ y in lbrace y_1, y_2, …, y_k rbrace $, где $k$ — это количество классов. Набор данных для можно представить как множество пар, состоящих из вектора признаков и значения целевой переменной.
[{(x_1, y_1), (x_2, y_2), (x_3, y_3), …, (x_m, y_m)}]
Этот же набор данных иногда представляют как матрицу признаков (состоящую из векторов-строк для каждого объекта выборки) и вектора целевое переменной, также для каждого объекта выборки.
Сами метки классов в данных могут обозначаться как угодно, обычно текстом. В численных моделях гораздо удобнее представлять их в виде чисел. Но большинство реализаций моделей классификации прекрасно умеет работать и с нечисловыми метками классов. Поэтому условно, для удобства будем считать, что:
[y_i in {0, 1, 2, 3, …, k}]
В дальнейшем для лучшего интуитивного понимания задач и алгоритмов классификации мы будем изображать объекты из датасета в виде точек на двумерном графике. А цвет или форма точек будут показывать, какому классу они относятся. Это хорошее визуальное представление. Но следует помнить, что на практике входной вектор может иметь сколько угодно измерений. То есть в датасете может быть сколько угодно признаков у каждого объекта. Тысячу или миллион признаков невозможно изобразить на графике, но это вполне может встретиться на практике.
Как мы уже говорили, классов тоже может быть произвольное количество. Но мы в начале будем рассматривать именно бинарную классификацию. Более сложные модели множественной или мультиклассовой классификации все равно строятся на основе бинарной. И на этих алгоритмах мы тоже остановимся. В такой формулировке мы будем предполагать, что $ y in lbrace 0, 1 rbrace $, где 0 обычно принимается как «отрицательный класс» и 1 как «положительный класс», но вы можете назначить этим значениям любое представление. Как мы говорили, бинарная классификация — это часто про обнаружение какого-то признака у объекта, то есть положительный класс — это объекты, у которых этот признак присутствует, а отрицательный — это объекты, у которых этого признака нет. Хотя чисто математически, нет никакой разницы, как вы обозначите классы, это скорее общепринятое соглашение, которое облегчает понимание моделей и алгоритмов.
Выводы:
- На вход модели классификации подается вектор признаков объекта.
- На выходе модель классификации предсказывает одно из конечного набора значений — метку класса объекта.
- Мы часто будем изображать классификацию на графике, но имейте в виду, что на практике это обычно многомерная задача.
- Обычно сначала рассматривается бинарная классификация, остальные типы строятся на ее основе.
- Бинарная классификация — это про наличие или отсутствие какого-либо признака у объекта.
Логистическая регрессия
Одним из самых простых и распространенных алгоритмов классификации является логистическая регрессия. Пусть название «логистическая регрессия» не вводит в заблуждение. Метод назван таким образом по историческим причинам и на самом деле является подходом к проблемам классификации, а не регрессионным задачам. В следующих частях мы рассмотрим и принципиально другие модели классификации, но именно на примере логистической регрессии проще всего понять, как работает алгоритм классификации и какие общепринятые приемы и обозначения в ней используются. Логистическая регрессия это один из самых простых алгоритмов классификации, а что еще важнее — он очень похож и основан на уже известной нам модели линейной регрессии.
Перед рассмотрением сути метода логистической регрессии нужно задаться вопросом: почему мы не можем применить для классификации уже известные нам методы линейной регрессии? В самом деле, пусть модель предсказывает непрерывное значение, а мы будем его интерпретировать, как 0 или 1. Рассмотрим простой пример, в котором есть только один атрибут (отложен по горизонтальной оси), и на его основе мы хотим предсказать бинарное значение целевой переменной. Представим эти значения как 0 или 1 и отложим на вертикальной оси. Вот как может выглядеть датасет в таком виде:
Здесь явно наблюдается тенденция, что в имеющихся данных у положительных объектов значения атрибута выше, чем у отрицательных. Конечно, это такие идеализированные, искусственные данные, но на этом примере мы попытаемся понять главный принцип классификации. На этих данных вполне можно обучить модель парной линейной регрессии. Именно на этом датасете она может выглядеть примерно так:
Но так как нам надо предсказывать точно либо 0, либо 1, придется ввести специальное пороговое значение. Например, если модель выдает значение больше 0.5, мы предсказываем положительный класс, если меньше — то отрицательный. Это вполне нормальный способ перевести непрерывное значение в дискретное, многие реальные модели классификации этим приемом успешно пользуются. Но в этом подходе заключается проблема. Регрессионные модели по сути своей неограничены и их значение может возрастать или убывать сколько угодно. Как это может быть проблемой? Давайте предположим, что в наших данных появилась еще одна точка:
Эта новая точка никак не изменяет общую картину, она прекрасно вписывается в уже имеющееся распределение данных, ничему не противоречит. Эта точка только подтверждает общую тенденцию, что у положительных объектов более высокий уровень факторной переменной. Но давайте посмотрим, что эта новая точка сделает с нашей моделью. Если мы изобразим предыдущую линию регрессии с учетом этой новой точки то получим следующую картину:
Эта модель даст огромную ошибку в появившейся новой точке. Поэтому если мы обучим регрессионную модель заново, то алгоритм обучения регрессии вынужденно сместит линию модели вниз, вот так:
Получается, что линия регрессии очень чувствительна к расположению точек, которые никак не влияют на общую тенденцию и принцип классификации. Но из-за этих расположений старое значение порога, которое мы выбрали, ориентируясь на предыдущую модель, уже не будет разделять классы правильно. То есть нам каждый раз придется вручную подбирать значение этого самого порога.
Это очень неудобно и ненадежно. И происходит потому, что регрессионные функции как правило неограничены. Но в принципе идея использовать регрессию здравая. Надо только преобразовать нашу функцию таким образом, чтобы вместо области значений $ y in (-inf, inf) $ она имела, скажем, $ y in (0, 1) $.Это можно легко сделать, используя нелинейное преобразование. Например, так:
[h_b (x) = g(z) = frac{1}{1 + e^{-z}}]
В этой формуле $ z = X cdot vec{b}$, то есть обычная линейная комбинация значений факторов и параметров. По сути, это и есть результат работы модели линейной регрессии, но теперь эта линейная комбинация передается в нелинейное преобразование, которое ограничивает область значений и сверху и снизу. За счет этого, значение функции гипотезы будет ограничено и асимптотически приближаться к 1 при неограниченном увеличении $z$ и приближаться к 0 при неограниченном уменьшении $z$. При использовании такого преобразования график функции гипотезы будет выглядеть так:
Сама эта нелинейная функция называется логистической или сигмоидной функцией. Именно из-за ее применения вся модель называется логистической регрессией. В принципе, можно использовать и другие нелинейные функции, которые имеют ограниченную область значений, например, арктангенс. Но на практике логистическая функция используется гораздо чаще, потому что она проще и работать с ней дальше гораздо удобнее. Не забывайте, что для машинного обучения мало определить саму функцию гипотезы, надо еще составить алгоритм обучения, то есть подбора параметров. Об этом и поговорим дальше.
Кто знаком с математической статистикой знает, что логистическая функция очень похожа на функцию, которая задает нормальное распределение. Кроме того, в нейронных сетях логистическая функция часто используется в качестве функции активации. Аналогия между логистической регрессией и нейронными сетями, кстати, глубже. чем может показаться с первого взгляда. Но это предмет рассмотрения в следующих главах. А пока лишь заметим, что логистическая функция очень важна и часто используется в разных разделах математики.
В такой формулировке значение функции гипотезы $h_theta (x)$ всегда будет лежать в диапазоне от 0 до 1. Поэтому это значение может быть проинтерпретировано как вероятность того, что данный объект принадлежит к положительному классу. Например, $h_theta (x) = 0.7$ дает нам вероятность 70%, что класс данного объекта — положительный. Другими словами,
[h_b(x) = P(y=1 vert x, vec{b}) = 1 — P(y=0 vert x, vec{b})]
Вероятность того, что наше предсказание равно 0, то есть класс данного объекта — отрицательный, является просто дополнением вероятности того, что класс положительных (например, если вероятность положительного равна 70%, то вероятность отрицательного класса равна 30%).
Для практического использования логистической регрессии для классификации также необходимо выбрать значение порога. По умолчанию он берется равным 0,5. Принципиальное отличие от использования обычной линейной функции в том, что значение порога не будет так сильно зависеть от конкретного расположения точек. И поэтому не нужно каждый раз вручную подбирать его значение после каждого обучения модели. Логистическая регрессия устроена таким образом, что значение порога 0,5 всегда в среднем дает неплохие результаты классификации, и поэтому его можно использовать, не анализируя конкретное распределение точек выборки.
Выводы:
- Логистическая регрессия — это самый простой алгоритм бинарной классификации.
- Можно взять регрессионную модель и ввести пороговое значение.
- Обычная регрессия плохо работает в задачах классификации за счет своей чувствительности и неограниченности.
- Метод логистической регрессии основан на применении логистической или сигмоидной функции.
- Результат работы логистической функции часто интерпретируется как вероятность отнесения объекта к положительному классу.
- Для четкой классификации обычно выбирают некоторое пороговое значение, обычно — 0,5.
Граница принятия решений
Вернемся к пороговому значению функции гипотезы, ведь оно играет в понимании и интерпретации модели логистической регрессии. Чтобы получить дискретную классификацию, то есть конкретное значение целевой переменной 0 или 1, мы можем перевести непрерывное значение функции гипотезы, используя тот самый порог (по умолчанию, 0,5), следующим образом:
[h_b (x) ge 0.5 rightarrow y=1]
[h_b (x) lt 0.5 rightarrow y=0]
Логистическая функция $g$ ведет себя таким образом, что когда ее вход равен нулю, ее выход равен 0,5. Если входное значение больше нуля, то значение логистической функции будет больше, и наоборот. Напомним, что на вход ей подается линейная комбинация атрибутов и признаков, то есть значение линейной регрессии. Следует запомнить особые случаи значений логистической функции:
[z = 0 rightarrow h_b (x) = 0.5]
[z = -inf rightarrow h_b (x) = 0]
[z = inf rightarrow h_b (x) = 1]
Таким образом, область пространства признаков, где $z = 0$ формирует границу между областью, точки которой модель относит к положительному классу и областью, точки которой модель относит к отрицательному. Граница принятия решения — это линия, которая разделяет область, где y = 0 и где y = 1. Она создается нашей функцией гипотезы. Так как мы используем линейную функцию внутри логистической, граница принятия решений такой модели всегда будет прямой линией, плоскостью или, в общем случае, гиперплоскостью.
Граница принятия решения существует в любой модели классификации, не только в логистической регрессии. Это граница, которая отделяет область точек, классифицируемых как один определенный класс. Граница принятия решения есть и в моделях множественной классификации. Вообще, форма и сложность границы принятия решения — это одна из основных характеристик моделей машинного обучения для классификаций. Если возможно изобразить границу принятия решения графически, это всегда дает очень полное представление о работе модели. К сожалению, это можно сделать только в очень маломерных случаях, либо при использовании специальных методов, типа алгоритмов понижения размерности.
Форма границы принятия решения полностью определяется видом модели, который мы применяем. В данном случае мы имеем линейную функцию. Поэтому граница тоже может быть только линейной. Если бы мы взяли другую функцию, например, полином второй степени, то граница принятия решения была бы поверхностью второго порядка. Именно поэтому логистическая регрессия считается именно линейной моделью. Несмотря на то, что в ней используется нелинейное преобразование, граница принятия решения в этой модели всегда линейна.
А вот конкретное положение границы принятия решения зависит от значений параметров модели. И именно это мы и подбираем в ходе машинного обучения. Поэтому процесс обучения модели классификации можно представить как процесс нахождения оптимальной границы принятия решения. Отсюда, кстати, следует основное ограничение метода логистической регрессии. Она будет показывать хорошие результаты тогда, когда объекты нашей выборки могут быть разделены гиперплоскостью.
Такое свойство датасета называется линейной разделимостью. Имейте в виду, что это свойство именно данных, а не модели. На рисунке слева вы видите линейно разделимые данные, а справа — неразделимые. И логистическая регрессия хорошо работает именно на линейно разделимых данных. Поэтому важным этапом предварительного анализа данных является анализ, разделимы ли данные линейно. От этого зависит, какие модели на них будут хорошо работать.
И не забывайте, что данные у нас обычно многомерны. Это значит, что нельзя так просто нарисовать их на графике и понять визуально, разделимы они или нет. Ведь двумерный график — это лишь проекция многомерного многообразия на определенные оси. И то, что разделимо в высших размерностях может не показаться таким в проекции.
Если данные не являются линейно разделимыми, в них есть существенная нелинейная составляющая, то логистическая регрессия будет на них работать уже не так эффективно. Точно также, как линейная регрессия плохо работает, если зависимость между факторами и целевой переменной описывается нелинейной функцией. В таком случае к этим данным нужно пробовать применять другие, более сложные виды моделей. О них мы поговорим в следующих главах.
Выводы:
- Граница принятия решений — это область, отделяющая один класс от другого.
- Форма границы принятия решения определяется видом используемой модели.
- Данные бывают линейно разделимые или нет.
- Логистическая регрессия — это линейный метод, поэтому она хорошо работает с линейно разделимыми данными.
- Если данные линейно неразделимы можно попробовать ввести в модель полиномиальные признаки.
Функция ошибки и градиентный спуск для логистической регрессии
Для использования логистической регрессии как модели машинного обучения нужно определить алгоритм обучения, то есть подбор оптимальных параметров. Для этого мы будем использовать тот же алгоритм градиентного спуска, который изучали применительно к линейной регрессии. В его основе — манипулирование функцией ошибки модели, которая показывает, насколько модель соответствует данным. К сожалению, мы уже не можем использовать ту же самую функцию ошибки, которую мы используем для линейной регрессии, потому что логистическая функция породит немонотонную производную, имеющую множество локальных оптимумов. Другими словами, это не будет выпуклая функция.
Вместо этого функция ошибки для логистической регрессии выглядит немного сложнее. Начнем ее рассматривать с самого начала. Также, как и в прошлом случае, ошибка всей модели строится как среднее из ошибок, измеренных в каждой точке данных. Это можно записать с помощью условных обозначений так:
[J(vec{b}) = frac{1}{m} sum_{i-1}^{m} Cost(h_b(x), y)]
А вот сами индивидуальные ошибки будут строиться немного по-другому. Напомним, что сейчас мы рассматриваем индивидуальные точки данных. Для начала рассмотрим случай, когда истинное значение целевой переменной равно 1, то есть данный объект принадлежит положительному классу. Тогда мы хотим, чтобы значение логистической функции было как можно ближе к 1. Чем ближе значение сигмоиды к единице, тем меньше для нас будет ошибка. В предельном случае, когда значение будет равно единице (такое невозможно, так как сигмоида только стремится к единице, но никогда не достигает ее), ошибка должна быть нулевой. А если значение сигмоиды приближается к нулю, то это значит, что ошибка растет. Чем ближе к нулю, тем больше ошибка. Если значение логистической функции равно нулю (также в пределе), то ошибка бесконечна. для моделирования такого поведения опять-таки можно использовать разные функции, но традиционно в логистической регрессии применяются логарифмы. Если взять логарифм с противоположным знаком, то мы добьемся как раз нужного эффекта. Так что если $y=1$, то ошибка в конкретной точке будет записываться так:
[Cost(h_b(x), y vert y=1) = -log(h_b(x)) = -log(frac{1}{1 + e^{-z}})]
Для противоположного случая, когда $y=0$, то есть объект принадлежит отрицательному классу, ситуация прямо противоположная. Нужно считать, что ошибка нулевая, если значение сигмоиды равно нулю, а если оно равно единице — то ошибка бесконечна. Для этого можно просто взять логарифм от $1 — g(z)$. Обратите внимание, что это имеет смысл, так как мы точно знаем, что значение сигмоиды всегда лежит от 0 до 1 (не включая концы). Поэтому нам неважно, как ведет себя функция ошибки, если ее аргумент будет какой-то другой, вне этого диапазона. Итак, для второго случая индивидуальная ошибка будет вычисляться так:
[Cost(h_b(x), y vert y=0) = -log(1 — h_b(x)) = -log(1 — frac{1}{1 + e^{-z}})]
Чем больше конкретная функция гипотезы отклоняется от реального значения $y$, тем больше получающая функция ошибки. Если гипотеза равна истинным значениям $y$, то ошибка равна 0. Это поведение функции ошибки в индивидуальной точке можно понять, посмотрев на два графика, которые иллюстрируют поведение функции ошибки в зависимости от аргумента сигмоиды, то есть линейной комбинации:
Мы можем представить два рассмотренных условных случая функции ошибки в одно выражение, используя тот факт, что истинные значения $y$ могут принимать только значения 0 или 1:
[Cost(h_b(x), y) = — y cdot log(h_b(x)) — (1 — y)(1 — log(h_b(x)))]
Обратите внимание, что когда $y$ равно 1, то второе слагаемое будет равен нулю и не повлияет на результат. Если $y$ равно 0, то, наоборот, первое слагаемое будет равен нулю и не повлияет на результат. Это математическию трюк позволяет выразить функцию в виде единой формулы, а не набора условных выражений, как в кусочных функциях. Это очень полезно и удобно для последующих манипуляций с этой функцией.
Заметим, что при такой функции ошибки она в каждой точке будет ненулевая. Идеальный случай, когда ошибка равна нулю недостижим на практике, так как значение сигмоиды только бесконечно приближается к границам (значениям 0 и 1), но никогда не может достичь их. Именно такая функция ошибки имеет несколько критичных преимуществ перед какими-нибудь другими, которые мы могли бы изобрести. Во-первых, она будет выпукла, то есть иметь один глобальный оптимум, как в случае с линейной регрессией. Во-вторых, она везде дифференцируема, так как использует только гладкие функции, мы смогли даже избавиться от кусочности, представив ее в виде одного выражения. И в-третьих, при ее дифференцировании функции логарифма и экспоненты в какой-то момент прекрасно сократятся, что значительно упростит выражение для градиента.
Доказательство того, что функция ошибки унимодальна, также как и подробное ее дифференцирование выходит за рамки данного учебника, но представляет собой неплохое упражнение по продвинутому математическому анализу для интересующихся.
Мы можем полностью сформулировать общую функцию ошибки следующим образом:
[J(vec{b}) = -frac{1}{m} sum_{i-1}^{m} y_i cdot log(h_b(x_i)) + (1 — y_i)(1 — log(h_b(x_i)))]
Теперь для полноценного определения алгоритма градиентного спуска нужно взять частные производные этой функции по всем параметрам. Продифференцировав ее найдем частную производную функции ошибки:
[frac{partial}{partial b_i} J(vec{b}) = frac{1}{m} sum_{i=1}^{m} (h_b (x_i) -y_i) x_i]
Обратите внимание, что мы получили точно такое же выражение, что и в случае с линейной регрессией. Также, как и в том случае, формула для частной производной выражена через функцию гипотезы. И опять же это не случайно. Так мы получаем, что алгоритм градиентного спуска полностью аналогичен для логистической и для линейной регрессии.
Напомним, что общая форма градиентного спуска:
[b_i := b_i -alpha frac{partial}{partial b_i} J(b)]
Подставляя выражение для частной производной получаем следующее выражение:
[b_i := b_i — frac{alpha}{m} sum_{i=1}^{m} (h_b (x) -y)x_i]
Обратите внимание, что этот алгоритм полностью идентичен тому, который мы использовали в линейной регрессии. Именно поэтому мы выразили эту формулу в терминах функции гипотезы, не раскрывая дальше $h_b(x)$. Также, как и раньше метод градиентного спуска подразумевает, что нужно обновлять все значения $b$ одновременно.
Многоклассовая классификация: один против всех
До сих пор мы рассматривали алгоритм логистической регрессии, который может решать только проблему бинарной классификации. Более того, некоторые математические выкладки активно используют тот факт, что целевая переменная может принимать только значения 0 или 1. Как же его безболезненно обобщить на случай, когда классов больше? Теперь мы рассмотрим классификацию данных более чем в двух категориях. Вместо $y = lbrace 0, 1 rbrace$ мы расширим наше определение так, чтобы
[y = lbrace 0,1 … n rbrace]
Пример набора данных для задачи множественной классификации, содержащих два признака и три класса можно увидеть на рисунке:
Алгоритм классификации в данном случае очень прост. Мы берем последовательно каждый имеющийся класс в данных, делаем его “положительным”, а все остальные — “отрицательными”, и обучаем модель, которая стремится отделить данный класс от остальных. Схематично алгоритм классификации “один против всех” можно увидеть на рисунке:
В этом случае мы делим нашу задачу на $ n + 1 $ (потому что индекс начинается с 0) бинарных задач классификации. В каждом из них мы прогнозируем вероятность того, что $y$ является членом одного из наших классов. То есть мы обучаем сразу множество моделей, столько, сколько у нас есть классов. Так что на каждый класс в задаче будет своя собственная модель, которая для определенного объекта выдает вероятность принадлежности этого объекта к соответствующему классу. Для каждого конкретного объекта все модели выдают такой вектор вероятностей:
[h_b^{(0)} = P(y=0 vert x, vec{b});]
[h_b^{(1)} = P(y=1 vert x, vec{b});]
[…]
[h_b^{(n)} = P(y=n vert x, vec{b});]
Другими словами, построив несколько моделей бинарной классификации мы можем использовать их, чтобы получить оценки вероятности принадлежности любого объекта ко всем имеющимся классам. После этого для окончательной классификации выбирается тот класс, чья модель дала наивысший результат. Другими словами, мы с помощью нескольких моделей оцениваем, к какому классу вероятнее всего принадлежит данный объект и выбираем для окончательной классификации тот класс, чья вероятность выше остальных.
Данный метод называется “один против всех” (one vs all или one vs rest). Это название подчеркивает тот факт, что для каждого класса оценивается вероятность принадлежности объекта к нему, в сравнении с вероятностью принадлежности к любому из всех остальных классов. Надо отметить, что во всех современных программных инструментах для машинного обучения, он уже реализован и встроен в существующие методы классификации, так что разработчику не придется программировать его специально.
Кроме того, чуть позже мы познакомимся с моделями, которые сами по себе способны решать задачи множественной классификации, а значит, не требуют реализации схемы “один против всех”. Она нужна только для моделей, которые способны решать только бинарную классификацию, чтобы “приспособить” их для задач, где классов больше двух.
Обратите внимание, что формулировка данного алгоритма не предполагает использование порогового значения. Вероятности принадлежности объекта к классам могут быть любые. Нам важно выбрать среди них максимум. Даже есть все эти вероятности меньше 50%, все равно мы выберем тот класс, к которому данный объект больше всего подходит. Более того, в среднем, эти вероятности обратно пропорциональны количеству классов в задаче. То есть если в конкретной проблеме, например, 50 000 классов, то не стоит ожидать, что объект будет принадлежать одному из них с вероятностью 90%. Здесь скорее речь пойдет о выборе между 0,028% и 0,025%.
У этого алгоритма есть еще одна характерная черта. С его помощью можно решать задачи мультиклассификации. Напомним, это такие, в которых один конкретный объект может принадлежать нескольким классам одновременно. Такие задачи часто формулируются как придание объекту набора меток. Например, добавление релевантных тегов к посту в социальных сетях. Естественно, что у отдельно взятому посту можно придать достаточно много тегов. В данном случае теги служат классами, но задача мультиклассовая. Другой пример — распознавание объектов на изображении. На конкретной картинке может же быть не один объект, а несколько, произвольное количество. Так вот, при использовании алгоритма “один против всех” можно брать как итоговый не один класс с максимальной вероятностью, а сразу несколько. Стратегии отбора классов бывают разные: в одной задаче можно брать фиксированное количество лучше подходящих классов, в других — брать любое количество классов, вероятности которых больше определенного порога.
Конечно, есть у данного алгоритма и оборотная сторона. Его применение не очень целесообразно, если в задачу уж очень большое количество классов. Ведь тогда придется обучить и использовать точно такое же количество моделей. А это может быть как затратно по процессорному времени, то есть обучение будет проходить слишком медленно, так и затратно по памяти, ведь все эти модели, их параметры надо хранить для осуществления предсказания. Может, стоит рассмотреть другие виды моделей классификации, которые решают множественные задачи сами по себе.
Выводы:
- Существуют методы классификации, которые сами по себе могут решать задачи множественной классификации.
- Для тех, которые не умеют, существует алгоритм “один против всех”.
- В нем строится столько бинарных моделей, сколько классов существует в задаче.
- Данный алгоритм уже не зависит от выбора порогового значения.
- Этот алгоритм еще может решать проблемы мультиклассификации.
- Для задач с очень большим количеством классов этот алгоритм может быть неэффективен.
Практическое построение классификации
Как подготовить данные для классификации?
Для решения задач классификации в языке программирования Python с использованием sklearn остается справедливым все то, о чем мы говорили в конце предыдущей части о подготовке данных для регрессионных задач. Так же нам нужно сформировать два массива данных — двумерный массив признаков X и одномерный массив значений целевой переменной y.
Раньше, в векторе значений целевой переменной находились сами численные значения. В данных для классификации метки классов могут обозначаться разными способами — числом, названием, аббревиатурой. Дальше мы будем подразумевать, что значения в массиве y заданы просто числами — [0, 1], если классов два (бинарная классификация), [0, 1, 2] — если классов три и так далее. Если в вашем датасете это не так и классы обозначаются как-то по другому, то обратитесь к одной из следующих частей, где мы обсуждаем преобразование и подготовку данных.
Здесь хотелось бы упомянуть еще об одной полезной функции библиотеки sklearn — процедурной генерации датасетов. Данная библиотека включает в себя несколько функций, которые используются для создания случайных наборов данных для тестирования моделей машинного обучения. В частности, существует функция make_classification, которая позволяет быстро создать случайный набор данных для классификации, обладающий определенными свойствами. Вы можете настроить количество точек, количество классов и признаков, насколько они будут линейно разделимы. Более полно информацию об этой и других функциях смотрите в официальной документации sklearn, в разделе, посвященном пакету datasets. Приведем пример использования этой функции:
1
2
3
from sklearn.datasets import make_classification
X, Y = make_classification( n_features=2)
В результате мы получаем и массив признаков и вектор значений целевой переменной. Они уже готовы для использования в моделях классификации.
Если возможно, всегда нужно стремится визуализировать данные, которые вы собираетесь анализировать. В случае с данными для классификации это немного сложнее, чем для парной регрессии, ведь нам нужно на графике как-то выделить классы. Можно воспользоваться встроенной возможностью задания цвета точек через массив вот так:
1
2
plt.scatter(X[:, 0], X[:, 1], marker="o", c=Y, s=25, edgecolor="k")
plt.show()
Обратите внимание, что в данном случае мы явно указываем, какие признаки будут расположены по осям. В данном примере мы откладываем первый столбец (с индексом 0) по горизонтальной оси, а второй (с индексом 1) — по вертикальной. Вот так это выглядит на графике:
Есть другой способ — визуализировать каждый класс отдельно. В таком случае мы можем более гибко управлять отображением разных классов — задавать явно произвольные цвета, размеры, форму маркеров точек. Обратите внимание, как в данном примере используется условная индексация одного массива (признаков) другим массивом (целевой переменной):
1
2
3
plt.scatter(X[:, 0][Y==0], X[:, 1][Y==0], marker="o", c='r', s=100)
plt.scatter(X[:, 0][Y==1], X[:, 1][Y==1], marker="x", c='b', s=100)
plt.show()
Вот так это выглядит на графике:
Помимо визуализации с данными такой структуры можно работать абсолютно так же, как и с данными для регрессии.
Как реализовать логистическую регрессию?
Рассмотрим простейшую модель логистической регрессии. Как мы увидели в этой главе, она мало чем отличается от модели линейной регрессии, поэтому возьмем за основу класс, который реализовали в предыдущей части, посвященной задаче регрессии.
Мы будем рассматривать двумерную задачу классификации. То есть у нас будет два непрерывных признака — $x_1$ и $x_2$. Поэтому в модели будет 3 параметра — $b_0, b_1, b_2$. Еще мы предполагаем решение бинарной задачи, так как множественная классификация решается отдельным алгоритмом “один-против-всех”
Ключевым отличием метода predict будет то, что мы считаем линейную комбинацию, а затем считаем логистическую функцию от нее:
1
2
3
def predict(self, x):
x1, x2 = x
z = self.b0 + self.b1 * x1 + self.b2 * x2
Модифицируем функцию ошибки так, чтобы она соответствовала формуле логарифмической ошибки для логистической регрессии:
1
2
def error(self, X, Y):
return -sum(Y * np.log2(self.predict(X)) + (1 - Y) *(1 - np.log2(self.predict(X)))) / len(X[0])
Теперь перейдем к методу градиентного спуска. И вот здесь все останется поразительно похожим на линейную регрессию, за исключением большего количества параметров:
1
2
3
4
5
6
7
8
9
def BGD(self, X, Y):
alpha = 0.5
for _ in range(1000):
dJ0 = sum(self.predict(X) - Y) /len(X)
dJ1 = sum((self.predict(X) - Y) * X[0]) /len(X[0])
dJ2 = sum((self.predict(X) - Y) * X[1]) /len(X[0])
self.b0 -= alpha * dJ0
self.b1 -= alpha * dJ1
self.b2 -= alpha * dJ2
Полностью код, реализующий метод логистической регрессии, выглядит так:
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
class hypothesis(object):
"""Модель логистической регрессии"""
def __init__(self):
self.b0 = 0
self.b1 = 0
self.b2 = 1
def predict(self, x):
x1, x2 = x
z = self.b0 + self.b1 * x1 + self.b2 * x2
return 1 / (1 + np.exp(-z))
def error(self, X, Y):
return -sum(Y * np.log2(self.predict(X)) + (1 - Y) *(1 - np.log2(self.predict(X)))) / len(X[0])
def BGD(self, X, Y):
alpha = 0.5
for _ in range(1000):
dJ0 = sum(self.predict(X) - Y) /len(X)
dJ1 = sum((self.predict(X) - Y) * X[0]) /len(X[0])
dJ2 = sum((self.predict(X) - Y) * X[1]) /len(X[0])
self.b0 -= alpha * dJ0
self.b1 -= alpha * dJ1
self.b2 -= alpha * dJ2
Обратите внимание на задание начальных значений параметров. В данном примере мы создаем регрессию со следующими значениями параметров по умолчанию: $b_0 = 0; b_1 = 0; b_2 = 1$. Задание одного из параметров в 1 нужно будет потом, чтобы получился более понятный график модели без обучения. На практике можно задавать начальные значения всеми нулями.
Как оценить качество классификационной модели?
После создания модели логистической регрессии логичным шагом будет вывести ее на график вместе с точками данных. Проблема в том, что это не так просто, как в случае с линейной регрессией, так как мы имеем два измерения признаков плюс еще значение самой функции модели. Для того, чтобы наглядно увидеть, как сочетается значение модели с точками воспользуемся построением контурного графика.
Для начала создадим экземпляр модели с параметрами по умолчанию:
1
2
3
4
hyp = hypothesis()
print(hyp.predict((0, 0)))
J = hyp.error(X, Y)
print("initial error:", J)
Теперь надо подготовить равномерные данные для рисования функции гипотезы. Нам понадобится создать двумерную сетку. К счастью, в numpy есть необходимые элементы. Подробный разбор кода выходит за рамки данного пособия, так как использует продвинутые возможности библиотеки numpy. Если вам интересно, как работает этот код, обратитесь к документации к используемым методам:
1
2
3
4
xx, yy = np.meshgrid(
np.arange(X.min(axis=0)[0]-1, X.max(axis=0)[0]+1, 0.01),
np.arange(X.min(axis=0)[1]-1, X.max(axis=0)[1]+1, 0.01))
XX = np.array(list(zip(xx.ravel(), yy.ravel()))).reshape((-1, 2))
В данном коде мы создаем двумерную матрицу, содержащую все комбинации значений признаков в заданном диапазоне. Другими словами, мы создаем равномерную сетку в прямоугольнике от минимального до максимального значения каждого признака (отступая для красоты 1 в обоих направлениях). Попробуйте вывести получившиеся переменные, чтобы понять принцип построения данной сетки. А после мы используем матрицу XX как исходные данные для модели:
1
2
Z = hyp.predict(XX)
Z = Z.reshape(xx.shape)
Данный код выполнит предсказание модели в каждой точке нашей сетки. Эти данные мы сможем использовать для того, чтобы построить контурный график вот так:
1
2
3
plt.contourf(xx, yy, Z, alpha=0.4)
plt.scatter(X[:, 0][Y==0], X[:, 1][Y==0], marker="o", c='r', s=100)
plt.scatter(X[:, 0][Y==1], X[:, 1][Y==1], marker="x", c='b', s=100)
В итоге мы должны получить график, похожий на следующий рисунок:
На графике мы видим наши точки данных, они выглядят так же, как и в предыдущих частях. Кроме него график заполняет заливка цветом. Цвет показывает значение функции гипотезы в данной точке. Так как мы задавали начальные значения параметров модели специально, параметр $b_2 = 1$ дает нам такой ровный градиент, который увеличивается равномерно с ростом значения признака $x_1$. Конечно, такой градиент никак не учитывает положение точек. Это и логично, ведь наша модель еще не обучена. Давайте запустим градиентный спуск и увидим модель после обучения:
1
2
3
4
5
6
7
8
hyp.BGD(X, Y)
Z = hyp.predict((xx, yy))
Z = Z.reshape(xx.shape)
plt.contourf(xx, yy, Z, alpha=0.4)
plt.scatter(X.T[:, 0], X.T[:, 1], marker="o", c=Y, s=25, edgecolor="k")
plt.show()
Обратите внимание, что мы переиспользуем сетку, которую создавали на предыдущем шаге. Ведь сами значения не меняются, меняется только набор значений модели. После обучения вы должны увидеть примерно такой график:
На нем мы видим, что функция гипотезы подстроилась к точкам таким образом, чтобы для точек положительного класса (желтых) выдавать значения, близкие к единице (желтая область), а для точек отрицательного класса (черных) — значения, близкие к нулю (фиолетовая область). То есть модель стала гораздо лучше соответствовать данным. Посередине между двумя областями мы видим более узкую полоску градиента. Это область, для точек которой модель не уверена в своих предсказаниях и выдает значения, ближе к 0,5. Именно в этой полосе располагается граница принятия решения нашей модели.
Как построить простую классификацию в scikit-learn?
Так же, как и в случае с линейной регрессией, самостоятельная реализация данного метода нужна только для того, чтобы на практике прочувствовать алгоритм его работы. В реальной жизни лучше всего пользоваться существующими профессиональными реализациями. Именно поэтому мы используем sklearn. Работа с моделью классификации в этой библиотеке практически не отличается от работы с линейной регрессией. Для начала нужно импортировать нужный класс, создать его экземпляр и обучить его на имеющихся данных:
1
2
3
4
5
6
7
from sklearn import linear_model
X = X.T
reg = linear_model.LogisticRegression()
reg.fit(X, Y)
print(reg.score(X, Y))
Обратите внимание, на то, что названия методов полностью совпадают у всех моделей машинного обучения в этой библиотеке. За счет этого ей очень приятно и просто пользоваться — у всех моделей единый интерфейс.
Точно так же, как и в самостоятельной реализации мы можем использовать модель для построения предсказания по сетке и для построения контурного графика. Давайте сравним самостоятельную реализацию логистической регрессии с библиотечной:
1
2
3
4
5
6
7
Z = reg.predict(XX)
Z = Z.reshape(xx.shape)
plt.figure(figsize=(12, 9))
plt.contourf(xx, yy, Z, alpha=0.4)
plt.scatter(X[:, 0][Y==0], X[:, 1][Y==0], marker="o", c='r', s=100)
plt.scatter(X[:, 0][Y==1], X[:, 1][Y==1], marker="x", c='b', s=100)
В результате выполнения данного кода вы должны увидеть график наподобие следующего:
Обратите внимание, что граница принятия решения расположена примерно в том же месте, что и у нашей реализации. Однако полоса “неопределенности”, область, где проявляется цветовой градиент, значительно уже. На библиотечной модели ее вообще почти невозможно разглядеть. Это не значит, что наша модель обучилась хуже. Ведь наша модель все еще способна точно отделить точки обучающей выборки разных классов. Но библиотечная модель обучилась “сильнее” — она более уверенно классифицирует точки, которые ближе к границе принятия решения.