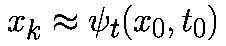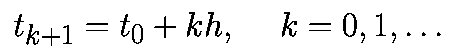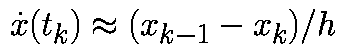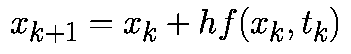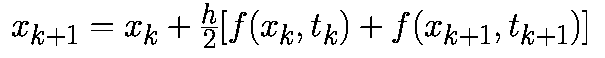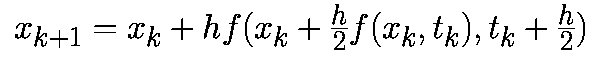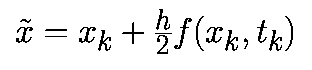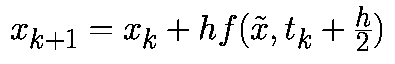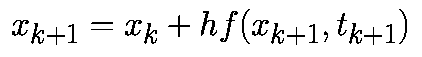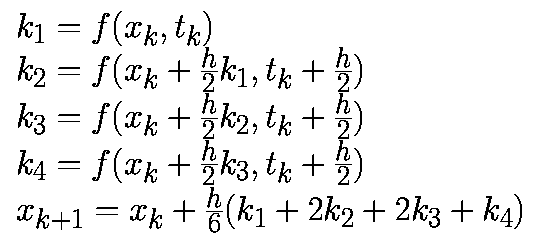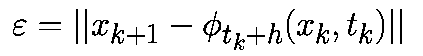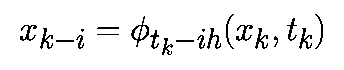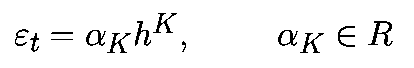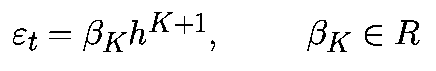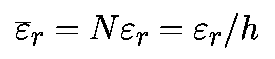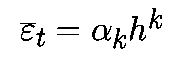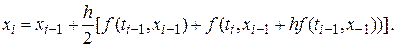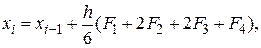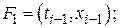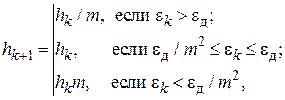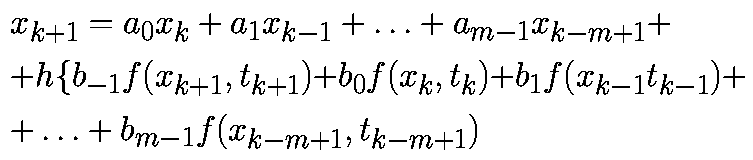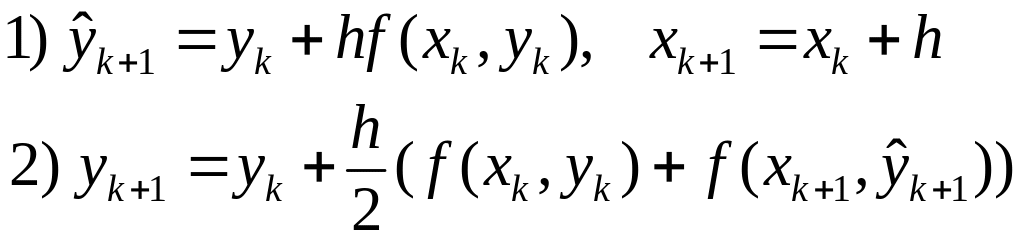Локальная и глобальная ошибки дискретизации при численном интегрировании дифференциальных уравнений
последовательностью точек x0,x1. в соответствующие моменты времени t0,t1. Значения точек должны удоволетворять приближенному равенству
Если специально не оговорено иное, то предполагается, что моменты времени выбираются через равные интервалы с величиной шага h>0, то есть
Аппроксимируем производную в момент времени tk соотношением
При такой аппроксимации уравнение (1) примет вид:
Формула (2) известна как прямой метод Эйлера.
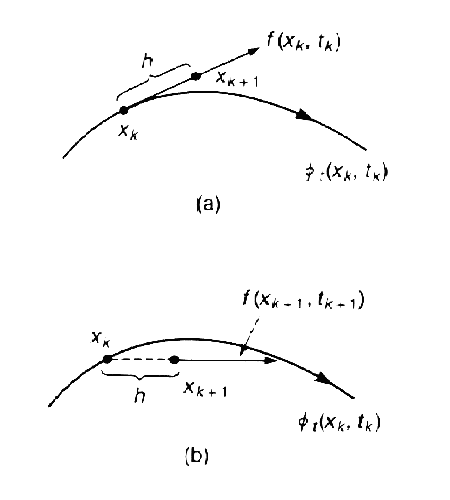
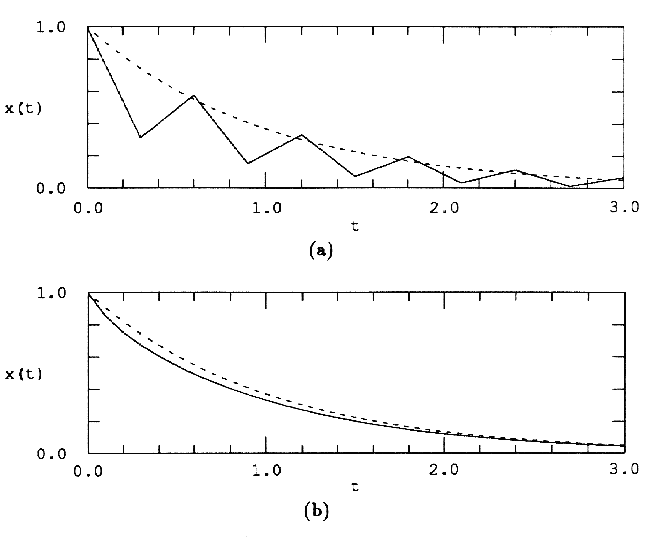
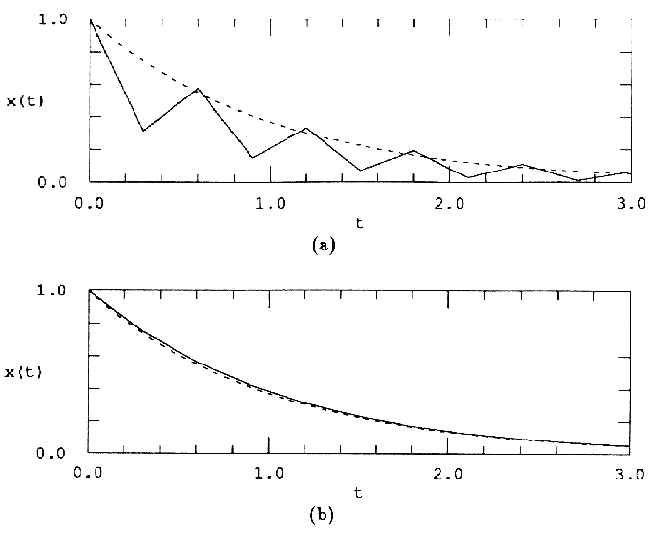
На рис.1(a) показана графическая интерпретация прямого метода Эйлера. На (k+1)-ом шаге векторное поле предполагается (локально) постоянным со значением f(xk,tk).
Рис.1 Иллюстрация алгоритмов (а) прямого метода Эйлера, (b) обратного метода Эйлера
Меньшее значение величины шага h в итоге дает точки аппроксимации чаще и, как демонстрирует рис.2, приводит к большей точности интегрирования, что приобретает математический смысл, поскольку (2) стремится к (1) при h->0.
Рис.2 Влияние величины шага. Уравнение dx/dt=-6x+5t -t интегрируется от x=1 прямым методом Эйлера при h=0.3 (а) и при h=0.1 (b). Точное решение показано штриховой линией.
Обратный метод Эйлера подобен прямому, но есть одно отличие в аппроксимации для производной
Такая аппроксимация дает формулу обратного метода Эйлера:
На рис.1(b) показана геометрическая интерпретация обратного метода Эйлера. На (k+1)-ом шаге векторное поле предполагается (локально) постоянным со значением f(xk+1,tk+1).
Обратный метод Эйлера — это пример неявного алгоритма интегрирования , где xk+1 является функцией от самой себя. И напротив, прямой метод Эйлера представляет собой явный алгоритм. В неявных алгоритмах для определения xk+1 требуются дополнительные вычисления, но они по сравнению с аналогичными прямыми алгоритмами более устойчивы и дают более высокую точность вычислений (см. рис.3). Возможно это обусловлено наличием члена xk+1 в правой части формулы, что может рассматриваться как вид обратной связи.
Рис.3 Та же система, что и на рис.2 проинтегрирована от x0=1.0 с h=0.3 (a) прямым методом Эйлера, (b) обратным методом Эйлера. Точное решение показано штриховой линией.
Трапецеидальный алгоритм имеет вид:
Имеется целое семейство уравнений Рунге-Кутта второго порядка. Мы рассмотрим модифицированный алгоритм Эйлера-Коши, заданный соотношением:
Из этой формулы следует, что модифицированный алгоритм Эйлера-Коши включает два этапа. На первом этапе с помощью прямого метода Эйлера происходит перемещение на пол шага вперед к моменту времени (tk+h/2):
На втором этапе это промежуточное значение используется для аппроксимации векторного поля с помощью итераций Эйлера прямого типа:
Как и в случае алгоритма второго порядка метод Рунге-Кутта четвертого порядка относится к явным алгоритмам. Он использует промежуточные моменты времени для для вычисления состояния в момент времени tk+1. Следующие формулы определяют алгоритм Рунге-Кутта четвертого порядка:
Для определенных выше алгоритмов на каждом шаге требуется только одна начальная точка xk. Такие алгоритмы называются одношаговыми. Одношаговые алгоритмы высокого порядка имеют высокую точность, но они не эффективны, если велики затраты на вычисление f. Например, алгоритм Рунге-Кутта четвертого порядка требует на шаге четыре значения f. Кроме того, на текущем шаге не выполняются оценки функций с целью их использования на последующих шагах.
В отличие от одношаговых алгоритмов, многошаговые алгоритмы повторно используют предыдущую информацию о траектории. В m-шаговом алгоритме для определения xk+1 используют m предыдущих точек xk, xk-1. xk-m+1 и значения f в этих точках. Общая формула m-шагового алгоритма имеет вид
Локальная ошибка определяется как ошибка на шаге алгоритма:
Для m-шаговых алгоритмов предполагается, что предыдущие m точек xk-i при i=0. m-1 являются точно заданными, т.е.
Ошибка усечения — это локальная ошибка, которая получилась бы в результате выполнения алгоритма на компьютере с бесконечной точностью.
Другими словами, подразумевается, что эта локальная ошибка возникает помимо ошибки округления. Также важно помнить, что для m-шаговых алгоритмов предыдущие m точек xk. xk-m+1 предполагаются точно заданными.
Ошибка усечения берет свое название от алгоритмов, основанных на рядах Тейлора (например, Рунге-Кутта). Эти алгоритмы были бы точными, если бы использовались полные (бесконечные) ряды. Ошибка возникает при усечении ряда до конечного числа членов.
Ошибка усечения зависит только от алгоритма. Она не зависит от используемого компьютера и, следовательно, может быть проанализирована. Для алгоритмов Рунге-Кутта K-го порядка, при подходящих условиях, локальная ошибка усечения представляет собой
где «альфа» зависит от K, f и xk, но не зависит от h. Для многошагового алгоритма K-го порядка локальная ошибка усечения имеет вид
Глобальнае ошибка округления — это простое накопление локальных ошибок округления. Если локальная ошибка составляет «эпсилон», то ошибка округления на единичном интервале будет
Подобно ошибке округления, локальная ошибка усечения также накапливается с каждым шагом. Для одношаговых алгоритмов K-го порядка локальная ошибка усечения составляет
Если пренебречь зависимостью ak от xk, то на единичном интервале времени ошибка усечения будет:
Порядок метода интегрирования.
Дата добавления: 2015-06-12 ; просмотров: 3180 ; Нарушение авторских прав
Главный вопрос при использовании любого численного метода состоит в оценке точности приближенных вычислений 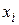
· ошибка дискретизации, возникающая в результате замены дифференциального уравнения (3.1) разностной аппроксимацией (3.2);
· ошибка округления, накопившаяся при выполнении арифметических операций.
При этом доминирующей является, как правило, ошибка дискретизации.
Будем считать, что все вычисления проводятся точно. Интуитивно ясно, что при 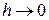
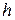
Введем величину 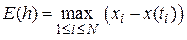
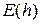
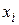
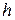
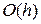
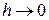
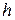
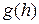
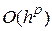
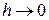
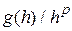
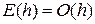
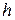
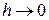
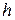
Очевидно, что повышение порядка метода позволяет повысить точность интегрирования при той же величине шага интегрирования 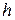
Рассмотрим, например, явный одношаговый метод Хьюна (или метод Рунге – Кутты второго порядка). Он определяется формулой
Сравнивая его с методом Эйлера легко заметить, что значение 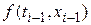
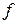
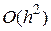
Наиболее знаменитым из методов Рунге – Кутты, а возможно и из всех методов численного интегрирования, является классический метод четвертого порядка, задаваемый формулой
где
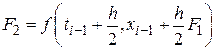
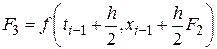
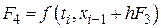
Суть метода в том, что вектор-функция правых частей системы ОДУ определяется не только в узлах сетки, но и в промежуточных точках интервала 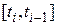
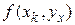
Как видно, повышение порядка метода связано с повышением затрат на вычисление значений функции 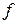
Для многошаговых методов порядок напрямую связан с объемом информации, используемой на каждом шаге. В частности, двух и трехшаговые методы Адамса – Бишфорта, задаваемые формулами (3.10) и (3.11) имеют второй и третий порядок, соответственно.
3.2.6. Процедуры численного моделирования
с автоматическим выбором шага
Данный раздел касается не выбора того или иного метода интегрирования, а реализации самой процедуры интегрирования на ЭВМ.
Выше уже отмечалось, что выбор шага интегрирования связан с динамическими свойствами моделируемого объекта. Для явных методов он должен быть меньше минимальной постоянной времени объекта, с тем, чтобы обеспечить устойчивость и позволить моделировать самые высокочастотные составляющие процесса. Неявные методы позволяют использовать больший шаг, но общий характер зависимости остается тем же самым. В то же время, на интервале моделирования характер моделируемых процессов может меняться. Например, в большинстве реальных систем высокочастотные составляющие переходного процесса затухают быстрее, чем низкочастотные, и процесс со временем приобретает более плавный характер. Это наводит на мысль организовать процедуру моделирования таким образом, чтобы шаг интегрирования менялся в процессе работы алгоритма. Там, где решение меняется плавно, можно вести интегрирование с относительно большим шагом. В областях же, где решение изменяется резко, необходимо считать с маленьким шагом. Проблема заключается в том, как определить величину шага, с которым следует начать следующий шаг интегрирования.
На выбор шага, как обычно влияют два фактора – точность и устойчивость. Шаг целесообразно поддерживать таким, чтобы погрешность интегрирования не превышала допустимого значения и величина шага при этом была максимально возможной.
Обычный подход состоит в оценке локальной ошибки дискретизации и, в зависимости от ее величины, уменьшении или увеличении текущего значения шага.
Два простых способа состоят либо в прохождении последнего шага интегрирования с половинным шагом и сравнении двух полученных результатов, либо в использовании двух методов интегрирования, имеющих разный порядок. Оба эти способа требуют дополнительных вычислений значений 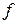
Первый способ реализует правило Рунге [29, 23], при котором ошибка дискретизации определяется по формуле
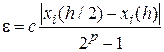
где 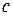
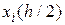
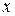
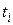
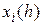
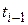
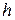
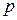
Для метода Эйлера формула Рунге дает
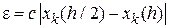
для метода Рунге – Кутты 4-го порядка
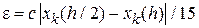
Величина погрешности аппроксимации на каждом шаге 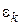
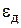
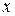
При автоматическом выборе шага наиболее популярным является алгоритм «трех зон» [29]:
где 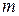
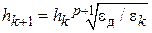
где 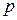
3.2.7. Особенности численного интегрирования
технических систем
Обширный набор методов численного интегрирования, которым обладают современные пакеты моделирования, позволяет эффективно решать самые различные задачи исследования технических систем, но при этом возникает проблема выбора наиболее подходящего метода
и правильного задания его параметров. Очень часто пользователь задает только интервал интегрирования и не обращает внимания на другие опции решателя. При решении простых задач с умеренной точностью такой подход вполне допустим, однако при решении сложных задач неудачный выбор метода либо неправильное задание его параметров может привести к неоправданно большим затратам машинного времени либо, вообще, к невозможности получить правильное решение.
Таким образом, для профессиональной работы с любым моделирующим программным обеспечением пользователь должен обладать некоторыми знаниями о реализованных в нем численных методах
и применимости их к требуемому кругу задач.
Практика показала, что наличие в технических системах объектов различной физической природы приводит к тому, что процессы в них характеризуются разнотемповостью, т.е. наличием быстрых и медленных составляющих движения. Кроме того, возможно одновременное присутствие как монотонных, так и медленно затухающих гармонических составляющих. Свойство системы содержать в своем переходном процессе существенно различные по своим спектральным характеристикам составляющие принято называть жесткостью[27].
Примером жесткой системы может служить робототехническая система, в которой быстрые составляющие связаны с включением тормозных устройств и демпферов, взятием или освобождением груза.
Жесткость часто является следствием избыточности модели, связанной с введением в нее малозначащих составляющих. Однако на этапе предварительных исследований такой избыточности трудно избежать. С другой стороны, часто жесткость имеет принципиальный характер и неучет быстрых движений может привести к неадекватности модели.
Жесткие системы требуют особого подхода к процедуре численного интегрирования, так как наличие быстрых и медленных составляющих в спектре движений предъявляет совершенно разные требования к методам интегрирования. Необходимо уметь оценивать характеристики жесткости и использовать эти оценки для выбора или настройки процедуры интегрирования.
Пусть исследуемая система 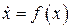
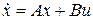
Матрица 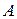
Составляющие движения (обычно называемые модами), связанные с собственными значениями 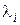
Исходя из распределения собственных значений матрицы Якоби на комплексной плоскости, можно назвать жесткой системой ОДУ такую систему, у которой матрица Якоби имеет различающиеся на несколько порядков максимальное и минимальное по модулю собственные значения.
Оценкой жесткости системы ОДУ обычно считается число обусловленности матрицы Якоби
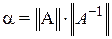
где 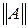
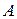
Для целей управления процессом моделирования под числом обусловленности чаще понимают отношение модулей максимального и минимального собственных значений матрицы
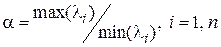
К жестким относят системы ОДУ, у которых 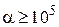
Для нелинейной системы матрицу Якоби можно определить после ее линеаризации в рабочей точке, как это описано в разд. 3.2.2.
Элементами матрицы Якоби являются частные производные от
нелинейной вектор функции 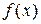
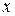
При умеренных значениях числа обусловленности 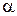
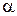
При моделировании такой системы в начальный момент времени инициируются все, или большинство мод, как быстрых так и медленных. Однако через некоторое время быстрые моды затухают и решение сходится к медленному движению.
Исследователя могут интересовать и быстрые и медленные составляющие движения. В этом случае, целесообразно использование явных методов в сочетании с эффективной процедурой изменения величины шага интегрирования в зависимости от состояния моделируемой системы. Это позволит достаточно точно смоделировать быстрые движения и избежать чрезмерных затрат машинного времени, так как явные методы требуют минимальных временных затрат на каждый шаг интегрирования.
Если исследователя мало интересуют быстро затухающие движения, но отбросить их на этапе формирования модели у него нет достаточных оснований, предпочтительными являются неявные методы, которые в сумме способны дать меньшее время интегрирования при удовлетворительном качестве. Такие методы подавляют все составляющие решения, соответствующие большим по модулю собственным значениям (если только шаг не выбран очень малым).
Изложенные рекомендации по выбору методов интегрирования жестких систем предполагают, что исследователь хорошо знаком с особенностями объекта. Например, если речь идет о проектировании или оптимизации системы управления некоторого хорошо изученного объекта, то выбор метода интегрирования может быть проведен путем сравнения нескольких вариантов. Если же объект недостаточно исследован, то эффективными могут оказаться процедуры, обладающие элементами адаптации к особенностям объекта.
Некоторые современные моделирующие программные комплексы содержат наборы методов, расчетные формулы которых настраиваются на решаемую задачу, используя для этого оценки некоторых параметров, обычно, собственных значений якобиана. Особенно перспективными считаются явные адаптивные методы, не требующие при своей реализации вычисления матрицы Якоби и решения алгебраических уравнений [27]. Такие методы есть, в частности, среди решателей ОДУ программного комплекса «МВТУ».
3.3. Моделирование гибридных (событийно-управляемых)
технических систем
Технические системы, по определению, относятся к сложным техническим системам. Одной из особенностей этих систем является то, что поведение многих из них определяется событиями, происходящими как внутри этих систем, так и в окружающей среде. Соответственно, они обладают как непрерывной, так и дискретной динамикой, находящимися в сложном взаимодействии. Подобные системы часто называют гибридными системами [20, 21]. В отечественной литературе также используются синонимы – непрерывно-дискретные, системы с переменной структурой, реактивные, событийно-управляемые.
Примерами гибридных технических систем могут служить системы управления, используемые в промышленности (автоматизированные технологические процессы), в быту (сложные бытовые приборы), в военной области (высокотехнологичные виды вооружений), в сфере космонавтики, транспорта и связи.
Гибридное поведение может быть связано со следующими факторами:
· совместное функционирование непрерывных и дискретных объектов. Подобное поведение является типовым для непрерывных объектов (механических, гидравлических и т.д.) управляемых цифровыми регуляторами, например, для ИСЗ. Управление может формироваться как в фиксированные моменты времени, так и асинхронно, в зависимости от изменения фазовых координат объекта;
· гибридное поведение, связанное с особенностями физических процессов в непрерывных объектах. Например, учет в моделях механических систем таких эффектов как сухое трение или люфт может быть реализован в виде некоторых логических условий, меняющих модель системы;
· гибридное поведение, обусловленное изменением состава системы.
Все перечисленные факторы являются типичными для технических систем.
Учет дискретной динамики приводит к тому, что фазовое пространство гибридных систем разбивается на области с различным поведением, при этом фазовая траектория в зависимости от происходящих событий оказывается то в одной области фазового пространства, то в другой. Достижение фазовой траекторией границы областей является событием, приводящим к смене поведения.
События могут быть как внутренними, так и внешними. Например, при моделировании робота-манипулятора внутренние события могут быть связаны с типовыми нелинейностями механической части, а внешние – являться следствием взаимодействия со средой.
Очевидной и удобной моделью систем, управляемых событиями, является конечно-автоматная модель. Например, можно использовать конечный автомат, чтобы описать автоматическую передачу автомобиля. Передача имеет ряд состояний: парковка, нейтраль, движение, реверс и т.д. Система переходит из одного состояния в другое, когда водитель перемещает рычаг из одной позиции в другую, например, из позиции парковка в нейтральное положение.
При всей ее простоте и наглядности конечно-автоматная модель достаточно строга и формальна. Однако классическое графическое представление конечных автоматов обладает рядом недостатков. Главным недостатком является отсутствие понятия времени, что предполагает статичность состояний. Другие недостатки – отсутствие иерархии состояний, обобщения переходов, средств выражения прерываний
и продолжения нормальной работы после их обработки [11].
Для полноценного компьютерного моделирования физики процессов необходимо обеспечить сопряжение непрерывной составляющей поведения системы и логики работы управляющих ей устройств (дискретная компонента). Математический аппарат описания в данном случае – это система уравнений, но не дифференциальных, а дифференциально-алгебраическо-логических, для которых отсутствует стройная теория и единый подход.
В настоящее время для моделирования систем, управляемых событиями, широко используется предложенный Д. Харелом [7] визуальный формализм – Statechart (карты состояний и переходов). Карты состояния были разработаны применительно к моделированию дискретных систем, однако они могут служить хорошей основой и для моделирования гибридных систем, т.е. с их помощью можно описать поведение системы как в дискретном, так и в непрерывном времени [8]. Основные
неграфические компоненты таких диаграмм – это событие и действие, основные графические компоненты – состояние и переход.
Событие – нечто, происходящее вне рассматриваемой системы, возможно требующее некоторых ответных действий. События могут быть вызваны поступлением некоторых данных или некоторых задающих сигналов со стороны человека или некоторой другой части системы. События считаются мгновенными.
Действия –это реакции моделируемой системы на события. Подобно событиям, действия принято считать мгновенными.
Состояние –условия, в которых моделируемая система пребывает некоторое время, в течение которого она ведет себя одинаковым образом. В диаграмме переходов состояния представлены прямоугольными полями со скругленными углами.
Переход – изменение состояния, обычно вызываемое некоторым событием. Как правило, состояние соответствует промежутку времени между двумя такими событиями. Переходы показываются в диаграммах переходов линиями со стрелками, указывающими направление перехода. Каждому переходу могут быть сопоставлены условия, при выполнении которых переход осуществляется.
С каждым переходом и каждым состоянием могут быть соотнесены некоторые действия. Действия могут дополнительно обозначаться как действия, выполняемые однократно при входе в состояние; действия, выполняемые многократно внутри некоторого состояния; действия, выполняемые однократно при выходе из состояния.
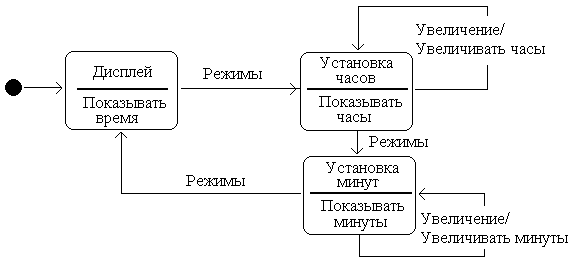
В [25] качестве примера простой дискретной системы (частного случая гибридной системы) рассмотрена диаграмма (карта) состояний и переходов цифровых часов, представленная на рис. 3.4.
Рис. 3.4. Диаграмма состояний и переходов цифровых часов
На часах имеется две кнопки: Кнопка Режима и Кнопка Увеличения. Нажатие любой из них генерирует событие, которое может вызывать переход из одного состояния в другое. Имеются три состояния: Дисплей, Установка Часов и Установка Минут. Состояние Дисплей – начальное состояние (что обозначается стрелкой, направленной от блока перехода по умолчанию в виде черного круга). Нажатие кнопки Режимы в состоянии Дисплей вызывает появление события Режимы и переход в состояние Установка часов. В состоянии Установка Часов, событие Режимы вызывает переход к состоянию Установка Минут, тогда как событие Увеличение увеличивает текущее время (число часов), которое отображается на экране, причем это происходит без изменения состояния. Каждому состоянию часов соответствует действие, записанное ниже горизонтальной линии. Оно начинает выполняться после того, как переход в это состояние произошел.
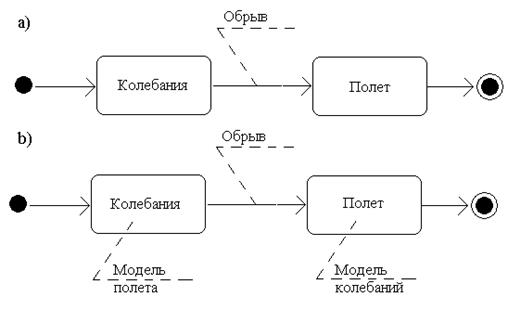
В [21] в качестве примера рассмотрена модель, которая описывает поведение маятника в виде шарика на нити, у которого в некоторый момент времени (событие «Обрыв») рвется нить. У этой модели два состояния – «Колебания» и «Полет». Оба описываются системами дифференциальных уравнений, каждая из которых является динамической системой. Карта поведений представляет собой совокупность состояний и переходов. В любой момент времени только одно состояние является текущим.
На рис. 3.5, а показана карта состояний обрывающегося маятника, на которой кроме двух обычных состояний помещены два особых состояния – начальное и конечное.
Рис. 3.5. Карта состояний и карта поведений обрывающегося маятника
В общем случае для состояния могут быть определены входные воздействия, выходные воздействия, а также локальная деятельность. Последовательность входных воздействий выполняется при каждом входе в состояние, последовательность выходных действий – при каждом выходе. Локальные действия выполняются все время, пока состояние является текущим.
Рис. 3.5, а отражает качественное поведение маятника. Для получения количественной картины необходимо связать с каждым состоянием локальное действие, в частности, интегрирование систем уравнений «Модель колебаний» и «Модель полета», как это сделано на рис. 3.5, b. Карта состояний, дополненная моделями состояний, названа в [20] картой поведения гибридной системы.
Одна из доступных реализаций концепции гибридного моделирования реализована в пакете StateFlow среды MATLAB, который кратко описан в главе 5. Также следует выделить отечественный пакет Model Vision Studium, ориентированный на моделирование сложных поведений [19].
Глава 4
Автоматизированное моделирование
технических объектов
Исторический экскурс. Необходимость автоматизации процессов моделирования технических объектов возникла практически одновременно с появлением вычислительных машин. Однако, исторически, разные этапы моделирования автоматизировались в разное время. Первым этапом следует считать создание библиотек численных методов исследования систем. Сами численные методы были разработаны задолго до появления ЭВМ и предназначались, прежде всего, для решения задач небесной механики. Так как первоначально расчеты велись вручную, алгоритмы методов были хорошо отлажены и оптимизированы. К концу 70-х годов прошлого столетия были созданы специализированные коллекции численных методов практически для всех областей численного анализа.
Дальнейшие шаги на пути автоматизации моделирования были связаны с разработкой систем автоматизированного проектирования (САПР) и систем автоматизации вычислительного эксперимента – пакетов прикладных программ. Автоматизации подлежали стандартные расчеты и оформление результатов экспериментов. Как правило, эти системы создавались под определенную предметную область, прежде всего, в наукоемких отраслях (космическая, авиация и т.д.). Для создания большинства пакетов прикладных программ для численных расчетов использовался язык Фортран, хорошо приспособленный именно для этих целей. Подобные пакеты создавались годами, их модификация и развитие требовали специальных знаний в предметной области, численных методах и программировании.
Наиболее трудно автоматизируемым этапом явился процесс построения модели. Ручная подготовка модели сложного технического объекта связана с большим объемом преобразований, в которых легко допустить ошибку. Использование систем автоматизации моделирования (САМ) позволило существенно повысить производительность труда, снизить число ошибок и, во многих случаях, исключить необходимость привлечение программистов к решению конкретных предметных задач. Опираясь на САМ, специалист в предметной (прикладной) области может самостоятельно создавать достаточно сложные модели.
При использовании системы автоматизированного моделирования исследователь формулирует математическую модель исследуемой системы на формальном входном языке моделирования. На ранних этапах развития САМ, когда отсутствовали возможности прямого изображения структуры модели на экране монитора, использовались методы кодирования структурной информации [1, 6]. Программа модели представляла собой последовательность вызовов процедур, каждая из которых являлась моделью структурного компонента. После связывания с модулями исполняющей системы пакета моделирования список компонентов преобразовывался в независимую исполняемую программу.
В современных системах автоматизированного моделирования, исходя из соображений удобства восприятия человеком, используются, как правило, графические средства задания исходной информации о модели. Переход к изображению структуры системы на экране монитора позволил исключить этап ручного кодирования схемы, однако потребовал разработки нового принципа организации самого процесса численных расчетов – принципа Data Flow, или принципа потока данных.
Можно отметить следующие факторы, способствующие внедрению систем автоматизированного моделирования:
· трудоемкость получения математической модели сложных технических объектов, связанная с опасностью совершить ошибку в многочисленных преобразованиях модельных выражений;
· необходимость многовариантного моделирования, при котором необходимо иметь для одного объекта несколько моделей, отличающихся по сложности;
· желание иметь дружественный интерфейс с программой и возможность оперативно вносить изменения в модель, что проще всего на основе использования графических языков задания исходной информации.
4.1. Особенности современных систем
автоматизированного моделирования
Современные профессиональные САМ имеют следующие отличительные черты [31]:
· поддержка иерархического проектирования как сверху – вниз, так и снизу – вверх, за счет реализации многоуровневого моделирования и метода локальной детализации модели;
· компонентное моделирование на основе использования библиотек, содержащих большое число графических и функциональных описаний компонентов, причем эти библиотеки открыты для добавления в них новых описаний, которые может сделать сам пользователь;
· графический пользовательский интерфейс, сочетающий графические средства формирования визуального образа исследуемого технического устройства с автоматической генерацией модели всей схемы по ее структурному описанию;
· наличие интерактивной рабочей среды проектирования (управляющей оболочки, монитора), т.е. специальной программы, из которой можно запускать все или большинство других программ пакета, не обращаясь к услугам штатной операционной системы;
· наличие в современных САПР и САМ постпроцессоров моделирования, что позволяет не только просматривать в удобной для пользователя форме результаты моделирования, но и обрабатывать эти результаты;
· наличие встроенных средств численного моделирования рабочего процесса в режиме реального времени или в режиме масштабирования модельного времени;
· реализация механизмов продвижения модельного времени, основанных как на принципе 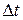
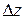
· интегрируемость с другими пакетами аналогичного назначения, которая обеспечивается соответствующими программами – конверторами, позволяющими импортировать и экспортировать данные из одной системы в другую;
· наличие средств, обеспечивающие формирование виртуальных аналогов измерительно-управляющей аппаратуры.
Если САМ предназначена для решения исследовательских задач, то к перечисленным качествам добавляются возможности активного вычислительного эксперимента [21]. В частности:
· визуализация результатов во время эксперимента;
· возможность интерактивного вмешательства в ход моделирования;
· возможность использования 2D и 3D анимации.
4.2. Иерархическое проектирование
и многоуровневое моделирование технических систем
С точки зрения инженера, основное назначение моделирования – поддержка процедур проектирования технических объектов и систем. Процедуры проектирования работают с моделями объектов реального мира и должны быть подстроены под их свойства.
Сложные системы имеют, как правило, иерархическую структуру. Естественные возможности человека позволяют оперативно обрабатывать не более 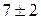
Такой подход, известный как иерархическое проектирование [21, 31], является типовым при разработке сложных технических объектов и заключается в разбиении исходной задачи на подзадачи.
В процессе проектирования сложной системы формируются определенные представления о системе, отражающие ее существенные свойства с той или иной степенью подробности. В этих представлениях можно выделить составные части – уровни проектирования. В один уровень, как правило, включаются представления, имеющие общую физическую основу и допускающие для своего описания использование одного и того же математического аппарата. Уровни проектирования можно выделять по степени подробности, с какой отражаются свойства проектируемого объекта. Тогда их называют горизонтальными (иерархическими) уровнями проектирования.
В результате такого подхода объект проектирования декомпозируется на фрагменты (подсхемы) и проектирование каждого из них ведется в определенном смысле самостоятельно. На каждом уровне иерархии этот принцип применяется вновь, что позволяет заменить решение одной сложной задачи многократным решением задач меньшей размерности.
При иерархическом проектировании разработчику достаточно держать в поле зрения лишь один фрагмент объекта. Остальные части лишь имитируют внешнюю среду, т.е. взаимодействие проектируемого фрагмента с другими частями объекта.
Использование принципа иерархического проектирования позволяет ограничить текущую сложность проекта на приемлемом уровне, за счет того, что в каждый момент времени разработчик имеет дело только с двумя смежными уровнями декомпозиции объекта – структурным описанием проектируемого в данный момент фрагмента и функциональным описанием внешней среды.
Инструментальной поддержкой иерархического проектирования является многоуровневое моделирование.При многоуровневом моделировании различные фрагменты представляются на различных уровнях иерархии, т.е. с разной степенью детальности. Например, проектируемая в настоящий момент времени часть объекта раскрыта до уровня элементарных динамических компонентов и имитируется структурной моделью, а остальные фрагменты представлены на соседнем более высоком уровне в виде функциональных моделей.
Завершив проектирование одного фрагмента, разработчик может свернуть его в функциональный блок и перейти к детальной модели следующего фрагмента, с которым он собирается работать. Эта процедура повторяется многократно, на разных уровнях иерархии проектируемого объекта. Достоинством такого подхода является то, что в поле зрения разработчика находится в каждый момент времени минимум
необходимой информации, не перегруженной лишними деталями. Описанный метод проектирования называется методом локальной детализации объекта.
Программной поддержкой многоуровневого моделирования, реализованной в большинстве языков графического программирования, является процедура инкапсуляции, которая позволяет «свернуть» любой смысловой фрагмент графического представления в единичный блок. Кроме того, что инкапсуляция служит основой получения иерархически структурированных моделей, она так же позволяет расширить библиотеку базовых блоков блоками пользователя, которые, впоследствии, можно многократно использовать (например, типовые динамические звенья).
Такой возможностью обладает, в частности, пакет LabVIEW, пакет Simulink и основанные на нем пакеты SimMechanics и SimPower. Пакеты IDEF-моделирования (ERWIN, BPWIN) принципиально основаны на многоуровневом изображении объектов.
4.4. Архитектура программ
автоматизированного моделирования
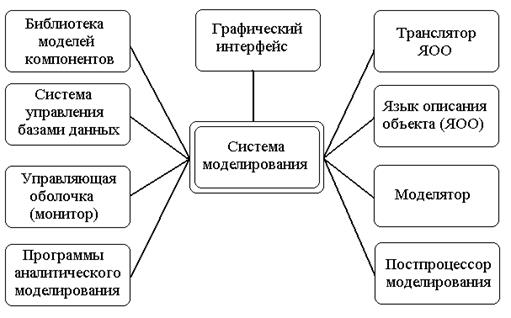
Существующие инструментальные средства автоматизированного моделирования могут относиться к разным предметным областям и существенно различаться по своим возможностям, но их модульные структуры мало отличаются друг от друга. На рис. 4.1 представлена типовая структура современного пакета визуального компонентного моделирования. Рассмотрим более детально назначение и особенности основных элементов этой структуры.
4.4.1. Графический интерфейс программ математического
моделирования динамических систем
Графический интерфейс является в настоящее время стандартным компонентом современной САМ. Он создает дружественный интерфейс между пользователем и программой, дает возможность оперировать с графическими образами вместо аналитических выражений. Это значительно облегчает работу в САМ и снижает вероятность ошибок при вводе информации о системе.
Рис. 4.1. Модульная структура
системы автоматизированного моделирования
Графический пользовательский интерфейс позволяет вводить информацию об исследуемой системе путем «рисования» на экране монитора проектируемой схемы в виде, понятном широкому кругу специалистов. Формой графического представления информации о моделируемой системе могут быть [16]:
· операторно-структурные схемы, принятые в ТАУ;
· функциональные и принципиальные схемы различных физических устройств;
· кинематические схемы механизмов;
· блок-схемы алгоритмов и другие графические модели.
Однако простым «рисованием» роль графического интерфейса не ограничивается. Задачами графического интерфейса, кроме того, могут быть [16]:
· контроль за соблюдением некоторых правил в процессе создания графического изображения на экране монитора (обычно накладываются ограничения на способы соединения компонентов и т.п.);
· преобразование информации о схеме в команды для моделирующей программы (моделятора);
· контроль за процессом моделирования, визуализация результатов моделирования.
П.5. Локальные и глобальные погрешности одношаговых методов решения ДУ
(метода Эйлера и методов Рунге-Кутта 2го, 4го порядка).
Теорема 6.1:
Если локальная погрешность метода 

как и при численном интегрировании, при переходе от локальной погрешности к глобальной, точность метода уменьшается на порядок. (6.8):
| Методы | Локальная | Глобальная |
| Эйлер | const*h 2 | const*h |
| Р.–К. 2го порядка по времени | const*h 3 | const*h 2 |
| Р.–К. 2го порядка по производной | const*h 3 | const*h 2 |
| Р.–К. 4го порядка | const*h 5 | const*h 4 |
Как и при численном интегрировании, порядок метода – степень h в глобальной погрешности.
П.6. Многошаговые методы решения ДУ и СДУ.
Все рассмотренные ранее методы – одношаговые, т.к. для нахождения 



В k-шаговом методе используются значения с k предыдущих шагов.
Многошаговые методы, как правило, дают лучший результат, чем одношаговые, в силу того, что более устойчивы к вычислительным погрешностям. Многошаговых методов много, самый распространенный среди них – метод Милна.
Формулы метода Милна:

Метод Милна – 4х шаговый (т.к. использует 4 предыдущих значения) и имеет 4-ый порядок точности. Перед применением метода Милна нам надо знать 4y, следовательно, необходимо сделать хотя бы 3 шага каким-нибудь одношаговым методом.
П.7. Оценка погрешности решения ДУ и СДУ методом двойного пересчета. Коррекция решения.
Используя такую же идею, как и в численном интегрировании, находим решение ДУ на [a,b] дважды с шагом h и с шагом h/2. Получим следующую картину:


Сравниваем попарно, если расхождение между 


Метод двойного пересчёта при решении ДУ и СДУ практически единственный имеет возможность для оценки погрешностей, так как иные формулы очень сложны и требуют оценок различных производных.
Как и при ЧИ, при решении ДУ и СДУ после 2го пересчёта в качестве точного решения выгодно брать не 


Метод двойного пересчёта применим не только лишь при ЧИ, при решении ДУ и СДУ, но и при решении других численных методов.
П.7. Краевые задачи для дифференциальных уравнений.
Выше рассматривалось решение ДУ и СДУ с начальными условиями, заданными в одной точке, так называемую задачу Коши, но для ДУ высших порядков часто бывает необходимо решить не з. Коши, а так называемую краевую задачу, т.е. начальные условия, которые заданы в разных точках.
Рассмотрим простейшую краевую задачу для ДУ 2го порядка:

А мы умеем решать:

В (6.11) нам известно 

Метод стрельб
После пристрелки и определения интервала [a,b],
где идёт смена знака, запускаем МПД или МХ.
На практике это выглядит так, как будто мы
решаем уравнение 
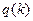
решение задачи Коши (6.11) в точке b при
П.9. Что делать, если ДУ не может быть разрешено относительно старшей производной?
Так как ДУ не может быть решено относительно старшей производной, то тогда на каждом шаге решаем нелинейное уравнение относительно y ( n) (все остальные неизвестные y,y’,y”,…, y ( n-1) -к этому моменту уже известны).
Решать уравнение относительно старшей производной любым методом(Хорд, МПД, Ньютона).
Замечание:
Таким образом, если ДУ не разрешается относительно старшей производной, то у нас возникает дополнительный цикл (самый внутренний) при написании программы.
Типы и классификация ошибок численного интегрирования
Современный численный метод одновременно с решением задачи Коши должен вычислять значение или оценку ошибки. Первый такой метод был предложен Мсрсоном в 1959 году (метод Рунгс-Кутта-Мсрсона). Теоретически таких методов описано достаточно много. Однако хороших практических реализаций в виде алгоритмов или прикладных программ мало. Рассмотрим причины возникновения ошибки при решении задачи Коши. Эта ошибка складывается из следующих компонент.
- 1. Неустранимая погрешность исходных данных. На нее повлиять нельзя, но учесть необходимо.
- 2. Локальная ошибка метода. Ее величина определяется порядком р используемого метода и зависит от шага: е,
()(h p *’). Эта ошибка связана с отбрасыванием остатка ряда при разложении точного решения в ряд по шагу при условии, что вес исходные данные заданы точно и вычисления проводятся без ошибок округления.
Если производить расчет на малом отрезке интегрирования, то ошибкой округления можно пренебречь, и преобладающей становится ошибка метода. Но когда количество шагов велико, ошибки округления накапливаются и становятся преобладающими. Экспериментально устаО а
количестве шагов взаимодействуют, в результате возникает общая ошибка, накопленная на веем отрезке интегрирования при применении данного метода. Эта общая ошибка ?г называется глобальной ошибкой. Известно, что при интегрировании на отрезке |0; Т|
Здесь множитель Т)(Т) зависит только от вида функции f(x) и нс зависит от шага интегрирования. Соотношение (7.9) называют правилом Рунге.
Общая ошибка ?у, порожденная всеми составляющими, сеть их сумма (рис. 7.1). Существует оптимальное значение шага /Г, обеспечивающее наименьшую суммарную ошибку. В случае, изображенном на рис. 7.1, отклонение от этого оптимального значения нс вызывает силь-
„ _ , „ , ного изменения ошибки. Возможно, однако, си-
Рнс.7.1. Суммарная ошибка
численного интегрирования туация, когда график суммарной ошибки столь крут, что даже малое изменение шага вызывает резкий рост суммарной ошибки. Такая ситуация характеризует вычислительную неустойчивость процесса интегрирования.
Полученную в результате интегрирования ошибку нужно уметь оценивать. Кроме того, полезно иметь возможность сознательно так выбирать шаг интегрирования, чтобы влиять на величину ошибки.
Наиболее популярный метод вычисления локальной ошибки основан на разложении решения в ряд по шагу. Если используется метод порядка р. то остаток ряда начинается с члена, содержащего
Очевидно, именно этот член и характеризует величину ошибки. Значит, следует оценить значение величины R. Будем считать, что при малом /| на протяжении шага R = const. Пусть на некотором шаге с номером г выбрана точка t е [tr‘,tnl]. Тогда x(t’) — точное, а х*/, — вычисленное при интегрировании с шагом /; значение искомой функции. Можно считать, что на шаге
Теперь разобьем шаг на два, длины —. и вычислим то же значение,
выполнив два шага интегрирования. Будем считать, что величина R при этом нс изменилась. Получим:
Вычитая уравнения, можно получить
И можно считать, что при интегрировании с постоянным шагом И верно соотношение
Таким образом, схема выбора величины /г на шаге для достижения заданной точности Очакова:
1. при известном х, с шагом /г вычислить тг+/;
источники:
http://life-prog.ru/2_14935_poryadok-metoda-integrirovaniya.html
http://megalektsii.ru/s20945t2.html
http://bstudy.net/718789/ekonomika/tipy_klassifikatsiya_oshibok_chislennogo_integrirovaniya
Ошибка метода Эйлера
Представленный
метод аппроксимации решения задачи
Коши называется разностным. Решение
представляет собой совокупность
отдельных точек, называемых узловыми.
При
использовании разностных методов
существует два источника ошибок: ошибка
дискретизации, возникающая в результаты
замены дифференциального уравнения
разностной аппроксимацией (2.5), и ошибка
округления, накопившаяся при выполнении
арифметических операций. Будем считать,
что значения
вычисляются точно, так что погрешности
обусловлены только ошибкой дискретизации.
Введем величину, равную наибольшему
отклонению аппроксимации от точного
решения на отрезке
|
|
(3.1) |
называемую
глобальной
ошибкой дискретизации
(иногда эту величину называют глобальной
ошибкой усечения).
Отметим, что
зависит от величины шага
,
поскольку предполагается, что приближения
вычисляют при заданном значении
.
Интуитивно ожидаем, что при уменьшении
ошибка дискретизации будет убывать и,
в частности, при стремлении
к нулю, так же будет стремиться к нулю.
Теорема
(ошибка дискретизации метода Эйлера).
Если функция
имеет ограниченную частную производную
по второй переменной и если решение
задачи Коши имеет ограниченную вторую
производную, то глобальная ошибка
дискретизации метода Эйлера
.
Порядок
метода численного интегрирования
показывает, от какой степени шага зависит
величина ошибки.
Локальная
(или шаговая)
ошибка метода – это ошибка, совершаемая
на одном шаге. Очевидно, что от шага к
шагу, т. е. при многократном применении
формулы метода, возможно наложение
ошибок. За
шагов, т. е. в точке
,
образуется глобальная
ошибка.
Порядок
глобальной ошибки (относительно шага
)
на единицу ниже, чем порядок локальной
ошибки, а порядком глобальной ошибки и
определяется порядок соответствующего
численного процесса решения задачи
Коши.
Глобальная
ошибка метода Эйлера есть
,
т. е. данный метод имеет первый порядок.
Иными словами, размер шага и ошибка для
метода Эйлера связаны линейно. Практическим
следствием этого факта является ожидание
того, что при уменьшении
приближенное решение будет все более
точным и при стремлении
к нулю будет стремиться к точному решению
с линейной скоростью
;
т.е. ожидаем, что при уменьшении шага
вдвое ошибка уменьшится примерно в два
раза. Такое поведение ошибки демонстрируется
на следующем примере.
Поскольку
в методе Эйлера ошибка достаточно велика
и от шага к шагу накапливается, а точность
пропорциональна количеству вычислений,
то метод Эйлера обычно применяют для
грубых расчетов, для оценки поведения
системы в принципе. Для точных
количественных расчетов применяют
более точные методы.
Метод Хьюна
Следующий
подход представляет новую идею построения
алгоритмов решения задачи Коши. Пусть
|
на с начальным условием |
Для
получения решения в точке
,
можем воспользоваться теоремой о
вычислнии определенного интеграла:
|
|
где
первообразная от
является
искомой функцией
.
Если разрешить уравнение последнее
уравнение относительно
,
получим
|
|
Теперь
можно применить численные методы
нахождения интеграла. Воспользуемся
методом трапеций с шагом
,
получим:
|
|
Правая
часть формулы включает в себя еще не
найденное значение
.
Для его нахождения воспользуемся методом
Эйлера. Получим конечную формулу,
именуемую методом
Хьюна (синонимы:
метод
Хойна,
метод
Эйлера-Коши):
|
|
Продолжая
процесс, получим последовательность
точек, аппроксимирующих кривую решения
.
Метод Хьюна относится к классу методов
прогноза-коррекции. На каждом шаге метод
Эйлера используется для предсказания,
а метод трапеций для уточнения конечного
значения. Общие формулы для шага метода
Хьюна:
|
|
Соседние файлы в предмете [НЕСОРТИРОВАННОЕ]
- #
- #
- #
- #
- #
- #
- #
- #
- #
- #
- #
При рассмотрении численных методов решения задачи Коши выделяют следующие погрешности
1) локальную (ошибку);
2) глобальную (ошибку);
3) вычислений на ЭВМ;
4) общую.
Локальная погрешность – это погрешность, допущенная на данном шаге , при условии, что предыдущие значения вычислены точно и отсутствуют ошибки округления. Другими словами, решается задача Коши:
где известно точное значение . Тогда локальная погрешность
равна:
,
где – решение разностной задачи в отсутствие ошибок округления, а
– значение точного решения дифференциальной задачи в точке
.
Глобальная погрешность – это разность между вычисленным решением разностной задачи в отсутствии ошибок округления и точным решением. То есть, решается задача Коши:
Глобальная погрешность R равна:
,
где – вычисленное в отсутствие ошибок округления решение разностной задачи в точке
;
– точное решение задачи Коши в этой же точке.
Для частного случая, когда функция не зависит от y, то есть
, глобальная погрешность равна сумме локальных погрешностей.
В общем случае для устойчивых дифференциальных задач Коши глобальная погрешность будет меньше суммы локальных погрешностей, но для неустойчивых дифференциальных задач Коши глобальная погрешность больше суммы локальных погрешностей.
Общая погрешность – это сумма глобальной погрешности и погрешности вычислений на ЭВМ. Другими словами, общая погрешность – это разность между вычисленным и точным решениями с учетом ошибок округления на ЭВМ.
При оценке точности численного метода решения задачи Коши важной характеристикой является порядок метода. Разностная задача имеет порядок k по h, если для глобальной погрешности справедливо: . Для локальной погрешности в этом случае справедливо равенство
. Условия для глобальной и локальной погрешности можно записать в эквивалентном виде:
,
,
где c, c1 – положительные константы, не зависящие от h.
Численные методы решения задачи Коши
Основные понятия и определения
Обыкновенным дифференциальным уравнением называется уравнение, связывающее независимую переменную [math]x[/math], неизвестную функцию [math]y(x)[/math] этой независимой переменной и ее производные [math]y'(x),y»(x),ldots,y^{(n)}(x)colon[/math]
[math]F bigl(x,y(x), y'(x),ldots,y^{(n)}(x)bigr)=0,qquad mathsf{(6.1)}[/math]
где [math]F(x,y, y’,ldots,y^{(n)})[/math] — функция указанных аргументов, заданная в некоторой области их изменения.
Порядком дифференциального уравнения называется порядок старшей производной, входящей в уравнение.
Если в соотношении (6.1) функция [math]F[/math] такова, что его можно представить в виде
[math]y^{(n)}= f bigl(x,y(x),ldots,y^{(n-1)}(x)bigr),qquad mathsf{(6.2)}[/math]
то уравнение называется обыкновенным дифференциальным уравнением л-го порядка, разрешенным относительно старшей производной.
Уравнение называется линейным, если функция [math]f[/math] линейна относительно искомой функции и ее производных, т.е. если уравнение может быть записано в виде
[math]a_n(x)y^{(n)}+ a_{n-1}y^{(n-1)}+ ldots+a_0(x)= f(x),[/math]
(6.3)
где [math]a_n(x),a_{n-1}(x),ldots,a_0(x),f(x)[/math] — известные в общем случае нелинейные функции от [math]x[/math].
Решением дифференциального уравнения n-го порядка называется функция [math]y(x)[/math], непрерывная на некотором интервале [math](a,b)[/math] вместе со своими производными до [math](n-1)[/math] порядка включительно, имеющая производную [math]y^{(n)}(x)[/math] и такая, что подстановка [math]y(x)[/math] в уравнение обращает его в тождество.
График решения дифференциального уравнения называется интегральной кривой.
Одной из важнейших задач в теории и приложениях дифференциальных уравнений является задана Коши (начальная задана), в которой требуется найти решение дифференциального уравнения, удовлетворяющее заданным начальным условиям. Для уравнения (6.2) она записывается следующим образом:
[math]begin{gathered}y^{(n)}= f bigl(x,y(x),ldots,y^{(n-1)}(x)bigr),\ y(x_0)=y_0,~ y'(x_0)=y’_0,~ ldots,~ y^{(n-1)}(x_0)= y_0^{(n-1)},end{gathered}[/math]
(6.4)
где [math]x_0in (a,b),~ y_0,y’_0,ldots,y_0^{(n-1)}[/math] — заданные числа.
Теорема 6.1 (о существовании и единственности решения задачи Коши (6.4)). Пусть выполнены следующие условия:
а) функция [math]f(x,y,ldots,y^{(n-1)})[/math] определена и непрерывна в некоторой замкнутой области [math]overline{D}[/math], а также имеет в [math]overline{D}[/math] ограниченные частные производные по переменным [math]y,y’,ldots,y^{(n-1)}[/math];
б) точка [math](x_0,y_0,y’_0,ldots,y_0^{(n-1)})[/math] лежит внутри области [math]overline{D}[/math].
Тогда решение задачи Коши (6.4) существует и единственно.
Общим решением дифференциального уравнения л-го порядка в области [math]Gsubset overline{D}[/math] ([math]overline{D}[/math] — область, в которой выполнены условия теоремы 6.1) называется функция [math]y=y(x,C_1,ldots,C_n)[/math], зависящая от [math]n[/math] произвольных постоянных, и такая, что при подстановке в уравнение она обращает его в тождество при любых значениях [math]C_1,ldots,C_n[/math]. Геометрически общее решение в области [math]G[/math] представляет собой семейство непересекающихся интегральных кривых, полностью покрывающих всю область.
Общим интегралом дифференциального уравнения называется соотношение вида [math]varphi(x,y,C_1,ldots,C_n)=0[/math], неявно определяющее общее решение.
При конкретных значениях [math]C_1,ldots,C_n[/math], включая [math]pminfty[/math], из общего решения выделяется частное решение, а общий интефал становится частным интегралом. В каждой точке [math](x,y)[/math] частного решения или частного интефала выполняются условия теоремы 6.1.
Наряду с проблемой решения дифференциальных уравнений л-го порядка на практике возникает проблема решения систем обыкновенных дифференциальных уравнений первого порядка, связывающих независимую переменную [math]x[/math], неизвестные функции [math]y_1(x),ldots, y_n(x)[/math] и их производные [math]y’_1(x),ldots, y’_n(x)[/math].
В случае, если уравнения разрешимы относительно производных, систему можно записать в нормальной форме Коши (где [math]f_i(x,y_1,ldots,y_n),~ i=overline{1,n}[/math] — известные функции):
[math]left{! begin{aligned}&frac{dy_1}{dx}= f_1(x,y_1,ldots,y_n),\ &frac{dy_2}{dx}= f_2(x,y_1,ldots,y_n),\ &quadvdots\ &frac{dy_n}{dx}= f_n(x,y_1,ldots,y_n). end{aligned}right.[/math]
(6.5)
Решением системы (6.5) называется совокупность [math]n[/math] функций [math]y_1(x),ldots, y_n(x)[/math], непрерывных на некотором интервале (д,6), такая, что подстановка этих функций в (6.5) обращает все уравнения в тождества.
Задача Коши для системы (6.5) состоит в нахождении решения системы, удовлетворяющего начальным условиям (где [math]y_{1,0},y_{2,0},ldots,y_{n,0}[/math] — известные числа):
[math]y_1(x_0)=y_{1,0},quad y_2(x_0)=y_{2,0},quad ldots,quad y_n(x_0)=y_{n,0}.[/math]
(6.6)
В векторной форме задача Коши (6.5),(6.6) имеет вид
[math]Y’= F(x,Y),quad Y(x_0)=Y_0,[/math]
(6.7)
где [math]Y=(y_1,ldots,y_n)^T,~ F(x,Y)= bigl(f_1(x,Y),ldots, f_n(x,Y)bigr)^T,~ Y_0= bigl(y_{1,0},ldots, y_{n,0}bigr)^T[/math].
Теорема 6.2 (о существовании и единственности решения задачи Коши (6.5),(6.6)). Пусть выполнены следующие условия:
а) функции [math]f_i(x,y_1,ldots,y_n),~ i=overline{1,n}[/math], определены и непрерывны в некоторой замкнутой области [math]overline{D}[/math], а также имеют в [math]overline{D}[/math] ограниченные частные производные по переменным [math]y_1,ldots,y_n[/math];
б) точка [math](x_0,y_{1,0},y_{2,0},ldots,y_{n,0})[/math] лежит внутри области [math]overline{D}[/math].
Тогда решение задачи Коши (6.5),(6.6) существует и единственно.
Замечания.
1. Во многих практических приложениях независимая переменная обозначается через [math]t[/math] и имеет смысл времени, поэтому задача Коши называется начальной задачей.
2. Понятия общего и частного решений, общего и частного интегралов для уравнения первого порядка и систем совпадают по форме, если заменить функцию [math]y(x)[/math] на вектор-функцию [math]Y(x),~ f(x,y)[/math] на [math]F(x,Y)[/math], а [math]y_0[/math] — на [math]Y_0[/math].
Численные методы, рассматриваемые в данном разделе, пригодны для решения задач Коши, записанных в форме (6.5),(6.6). Чтобы решить задачу Коши (6.4) этими методами, ее необходимо привести к системе [math]n[/math] уравнений первого порядка, т.е. к виду (6.5),(6.6).
Обозначая [math]y_1(x)=y(x),~ y_2(x)= y'(x),~ldots,~ y_n(x)= y^{(n-1)}(x)[/math], получаем
[math]left{! begin{aligned}&frac{dy_1}{dx}=y_2, &quad & y_1(x_0)=y_0,\ &frac{dy_2}{dx}=y_3, &quad & y_2(x_0)=y’_0,\[-4pt] &quadvdots &quad &quadvdots\[-2pt] &frac{dy_n}{dx}=f(x,y_1,ldots,y_n), &quad & y_n(x_0)=y^{(n-1)}_0. end{aligned}right.[/math]
(6.8)
Получим точное решение модельного примера, используемого далее для демонстрации применения различных численных методов.
Пример 6.1. Найти аналитическое решение задачи Коши [math]Ty’+y=1,~ y(0)=0[/math], где [math]T>0[/math] — известное число, называемое постоянной времени.
Решение
Решение задачи Коши найдем с помощью известной методики.
1. Определим общее решение однородного уравнения [math]Ty’+y=0[/math]. Поскольку корень [math]lambda=-1!!not{phantom{|}},T[/math] соответствующего характеристического уравнения [math]Tlambda+1=0[/math] действительный, то [math]y_0(x)=Ce^{lambda x}= Ce^{-x!not{phantom{|}},,T}[/math] — общее решение однородного уравнения.
2. Частное решение неоднородного уравнения ищется в форме [math]y_{text{ch}}=A[/math], где [math]A=text{const}[/math]. После подстановки в решаемое уравнение получаем [math]y_{text{ch}}=1[/math].
3. Общее решение неоднородного уравнения получается как сумма общего решения однородного уравнения и частного решения неоднородного уравнения:
[math]y(x)= y_0(x)+ y_{text{ch}}= Ce^{-x!not{phantom{|}},,T}+1.[/math]
Ему соответствует семейство интегральных кривых, характеризующееся параметром [math]C[/math], который может принимать произвольные значения.
4. Частное решение неоднородного уравнения находим из начального условия: [math]y(0)=C+1=0[/math]. Отсюда [math]C=-1[/math] и [math]y(x)=1-e^{-x!not{phantom{|}},,T}[/math].
Пример 6.2. Записать дифференциальное уравнение второго порядка [math]2y»+y’+4y=6sin{x},~ y(0)=1,~ y'(0)=2[/math], в виде системы дифференциальных уравнений в нормальной форме Коши.
Решение
Введем обозначения: [math]y_1(x)=y(x),~ y_2(x)=y’_1(x)[/math] и запишем уравнение в форме [math]y»=-frac{1}{2}y’-2y+3sin{x}[/math], разрешенной относительно старшей производной. Тогда получим
[math]left{!begin{aligned}&y’_1=y_2,&quad &y_1(0)=1,\ &y’_2=-frac{1}{2}y_2-2y_1+3sin{x},&quad &y_2(0)=2. end{aligned}right.[/math]
Численные и приближенно-аналитические методы решения задачи Коши в отличие от аналитических методов позволяют найти искомую функцию [math]y(x)[/math] лишь приближенно. Но при этом численные методы являются более универсальными, так как с их помощью можно приближенно решать многие из задач, точные решения которых аналитическими методами не могут быть найдены. Аналитическими методами в основном решаются только линейные задачи и некоторые типы нелинейных задач, в то время как для численных методов эти ограничения отсутствуют.
Чтобы упростить изложение и в силу того, что численные методы легко обобщаются на системы уравнений, в дальнейшем будем рассматривать решение задачи Коши для уравнения первого порядка
[math]y’=f(x,y),quad y(x_0)=y_0,quad xin(a,b).[/math]
(6.9)
Численное решение задачи ищется в узлах сетки [math]Omega_n= {x_0,x_1,ldots,x_n}[/math], где [math]h_{i+1}=x_{i+1}-x_{i},~ i=overline{0,n-1}[/math] — расстояние между соседними узлами, называемое шагом интегрирования (параметром сетки). Если [math]h_{i+1}=h=text{const}[/math], сетка называется равномерной (регулярной), а если [math]h_{i+1}=text{var}[/math] — неравномерной (нерегулярной). В случае равномерной сетки узлы находятся по формуле [math]x_{i}= x_0+ih,~ i=overline{0,n}[/math], а в случае неравномерной (где [math]delta_{i+1}= frac{h_{i+1}}{h_{i}}[/math] — параметр нерегулярности):
[math]x_1=x_0+h_1,quad x_2=x_1+h_2=x_1+delta_2h_1,quad ldots,quad x_{i+1}=x_{i}+ delta_{i+1}h_{i},quadldots, quad x_n=x_{n-1}+delta_{n}h_{n-1}.[/math]
Решение находится в виде последовательности значений [math]widehat{y}_0,widehat{y}_1, widehat{y}_2,ldots, widehat{y}_n[/math], являющихся приближением значений [math]y_0,y(x_1),y(x_2),ldots,y(x_n)[/math] точного решения [math]y(x)[/math] в узлах сетки [math]Omega_{n}[/math] (рис. 6.1).
Сеточное представление [math]y(x_i),~i=overline{0,n}[/math], известной функции [math]y(x)[/math] (точного решения задачи Коши) называется проекцией [math]y(x)[/math] на сетку [math]Omega_n[/math].
Дискретные и непрерывно-дискретные методы
Численные методы решения обыкновенных дифференциальных уравнений делятся на две группы:
– дискретные методы, позволяющие найти решение только в узлах сетки. Эти методы называются еще разностными методами или методами сеток;
– непрерывно-дискретные методы, основанные на использовании дискретных методов и сплайн-функций для восполнения численных результатов. Они позволяют найти непрерывные решения дифференциальных уравнений.
Дискретные методы (методы сеток) подразделяются на явные и неявные. Значение [math]widehat{y}_{i+1}[/math], на (i+1)-м шаге может определяться явно:
[math]widehat{y}_{i+1}= Phi(x_{i-k+1},ldots, x_{i-1}, x_{i}, widehat{y}_{i-k+1}, ldots, widehat{y}_{i-1},widehat{y}_{i}),[/math]
(6.10)
где [math]Phi(.)[/math] — некоторая функция, зависящая от конкретного метода (кроме последней рассчитанной точки [math](x_{i},widehat{y}_{i})[/math] могут использоваться еще [math](k-1)[/math] предыдущих точек), или неявно:
[math]widehat{y}_{i+1}= Phi(x_{i-k+1},ldots, x_{i-1}, x_{i},x_{i+1}, widehat{y}_{i-k+1}, ldots, widehat{y}_{i-1},widehat{y}_{i},widehat{y}_{i+1}),[/math]
(6.11)
где искомая величина [math]widehat{y}_{i+1}[/math] входит одновременно и в левую, и в правую часть.
Явные и неявные методы делятся также на одношаговые и многошаговые (k-шаговые). В одношаговых методах для расчета очередной точки [math](x_{i+1},widehat{y}_{i+1})[/math] требуется информация только о последней рассчитанной точке [math](x_{i},widehat{y}_{i})[/math]. В k-шаговых методах для нахождения точки [math]x_{i+1},widehat{y}_{i+1}[/math] требуется информация о [math]k[/math] предыдущих точках (рис. 6.2).
Формулы (6.10),(6.11) в общем случае представляют собой нелинейные уравнения относительно [math]widehat{y}_{i+1}[/math] и называются разностными схемами.
Численный алгоритм (метод) называется устойчивым, если численные результаты непрерывно зависят от входных данных и если погрешность остается ограниченной при заданных пределах изменения параметров численного алгоритма (шагов сетки, числа итераций и др.).
Сходимость приближенных методов является основной проблемой, от успешного преодоления которой зависит точность решения всей задачи. Численный алгоритм называется сходящимся, если при стремлении его параметров к определенным предельным значениям, например, при [math]hto0[/math] (или при [math]stoinfty[/math], где [math]s[/math] — число итераций), результаты стремятся к точному решению.
При известном точном решении некоторой модельной задачи сходимость может быть проверена следующим образом. Фиксируется некоторая точка [math]x>x_0[/math] и строится последовательность сеток [math]Omega_{n}[/math], таких, что [math]hto0,[/math] [math]x=x_{n}= x_{0}+nh[/math]. Здесь для простоты считаем, что все сетки, образующие указанную последовательность, являются равномерными. Тогда, если [math]|widehat{y}_{n}-y(x_{n})|to0[/math] при [math]hto0~ (ntoinfty)[/math], то метод является сходящимся в точке [math]x[/math]. Если метод сходится в каждой точке [math]xin[c,d]subset (a,b)[/math], то он сходящийся на [math][c,d][/math].
Локальная и глобальная ошибки
Локальной ошибкой численного метода на (i+1) -м шаге называется величина
[math]varepsilon_{i+1}(h)= widehat{y}_{i+1}-y(x_{i+1}),[/math]
где [math]y(x_{i+1})[/math] — значение точного решения при [math]x=x_{i+1}[/math], а [math]widehat{y}_{i+1}[/math] — приближенное решение, получаемое по формуле (6.10) или (6.11) при условии, что вместо приближенных значений [math]widehat{y}_{i}, widehat{y}_{i-1},ldots, widehat{y}_{i-k+1}[/math] используются значения, соответствующие точному решению, т.е. [math]y(x_{i}), y(x_{i-1}),ldots, y(x_{i-k-1})[/math].
Глобальной ошибкой называется величина [math]e_{n}(h)= widehat{y}_{n}-y(x_{n})[/math], где [math]widehat{y}_{n}[/math] — значение, получаемое по формулам (6.10) или (6.11) при [math]i=n-1[/math].
Глобальная ошибка определяется:
а) ошибками округления и ошибками арифметических действий, обусловленными числом разрядов компьютера и характером выполняемых операций для расчета значения искомой функции в очередной точке [math]x_{i+1}[/math];
б) методическими ошибками, определяемыми выбранным алгоритмом;
в) переходными ошибками, обусловленными тем, что при расчете значения р/+1 вместо точных значений [math]y(x_{i}), y(x_{i-1}),ldots, y(x_{i-k-1})[/math] берутся приближенные значения [math]widehat{y}_{i}, widehat{y}_{i-1},ldots, widehat{y}_{i-k+1}[/math], полученные на предыдущих шагах.
Локальные ошибки «переносятся» в точку [math]x_n[/math] и формируют глобальную ошибку.
Число [math]p[/math] называется порядком (точностью) численного метода, если его глобальная ошибка есть [math]O[/math] большое от [math]h^p[/math], то есть [math]e_n(h)= O(h^p)[/math].
На практике в качестве характеристики точности метода часто используется величина [math]varepsilon(h)= max_{i=0,1,ldots,n}bigl|widehat{y}_{i}-y(x_{i})bigr|[/math].
Рассмотрим введенные понятия более подробно на примере явных одношаговых методов, построенных для задачи (6.9). При этом формулу (6.10) представим в виде
[math]widehat{y}_{i+1}= widehat{y}_{i}+hcdot Psi(widehat{y}_{i},x_{i},h),[/math]
где [math]Psi(widehat{y}_{i},x_{i},h)[/math] — некоторая функция, определяемая конструкцией того или иного метода.
Обозначим [math]y(x,x_{i},widehat{y}_{i})[/math] — решение задачи Коши [math]u’=f(x,u),~ u(x_{i})= widehat{y}_{i}[/math]. Тогда локальная ошибка определяется выражением
[math]varepsilon_{i+1}(h)= widehat{y}_{i}+ hcdot Psi(widehat{y}_{i},x_{i},h)-y(x_{i+1}, x_{i}, widehat{y}_{i}).[/math]
Геометрическая интерпретация возникновения локальных и глобальной ошибок изображена на рис. 6.3.
Можно показать, что если локальная ошибка имеет порядок [math](p+1)[/math], то есть [math]varepsilon_{i+1}(h)= O(h^{p+1})[/math], то глобальная погрешность имеет на единицу меньший порядок, т.е. [math]e_{n}(h)= O(h^p)[/math].
Перейдем теперь к рассмотрению устойчивости численных методов. Она проверяется на «тестовом примере»
[math]y’=mucdot y,quad y(0)=1,[/math]
(6.12)
где [math]mu[/math] — в общем случае комплексная константа. Дифференциальное уравнение в (6.12) является простейшим линейным уравнением, и для него можно получить значимые критерии устойчивости в явной форме.
Устойчивость методов решения задачи Коши
Метод называется устойчивым (ограниченно устойчивым), если существует такое число [math]h_{text{kr}}>0[/math], что при использовании метода для решения задачи (6.12), где [math]operatorname{Re}mu<0[/math], с шагом [math]0<h<h_{text{kr}}[/math] при [math]itoinfty[/math] глобальная ошибка ограничена. Величина [math]h_{text{kr}}[/math] называется критическим шагом. Если [math]h>h_{text{kr}}[/math], глобальная ошибка может неограниченно возрастать.
В ограниченно устойчивых методах при задании величины шага [math]h[/math] необходимо учитывать значение критического шага [math]h_{text{kr}}[/math]. Для сложных дифференциальных уравнений и систем нахождение [math]h_{text{kr}}[/math] является самостоятельной задачей, а свойство ограниченной устойчивости предупреждает вычислителя о возможных проблемах. Поэтому на практике становится актуальной задача конструирования таких методов, которые были бы устойчивы при любом значении шага, а его величина выбиралась бы только исходя из желаемой точности расчетов (при этом класс решаемых задач может быть ограничен).
Метод называется A-устойчивым, если при его применении с любым фиксированным положительным шагом [math]h[/math] все численные решения задачи (6.12) с комплексной константой [math]mu~(operatorname{Re}mu<0)[/math] стремятся к нулю при [math]itoinfty[/math].
Область A-устойчивости — совокупность значений [math]h[/math] и [math]mu[/math], удовлетворяющих условию [math]operatorname{Re}(hmu)<0[/math]. Она изображена на рис. 6.4,а. Выполнение свойства A-устойчивости является желательным, поскольку если решение задачи (6.12) асимптотически устойчиво (в силу условия [math]operatorname{Re}mu<0[/math] корень характеристического уравнения находится в левой полуплоскости), то погрешность численного решения стремится к нулю при любой величине шага [math]h>0[/math].
При исследовании устойчивости численного метода необходимо использовать соответствующую ему разностную схему для решения задачи (6.12) и привести ее к линейному разностному уравнению с постоянными коэффициентами:
[math]a_ny(i+n)+ a_{n-1}y(i+n-1)+ldots+a_0y(i)=g(i),quad i=0,1,2,ldots[/math]
Известно, что критерием устойчивости решения линейного разностного уравнения является требование расположения корней [math]lambda_{i}[/math] соответствующего характеристического уравнения [math]a_n lambda^n+ a_{n-1}lambda^{n-1}+ ldots+a_0=0[/math] внутри круга единичного радиуса с центром в начале координат, т.е.
[math]|lambda_{i}|<1,quad i=overline{1,n}.[/math]
(6.13)
Замечания
1. Численные методы, которые можно представить в виде (где |[math]|alpha_0|+|beta_0|ne0,~ f_{i+1-j}= f(x_{i+1-j}, widehat{y}_{i+1-j})[/math] называются линейными k-шаговыми методами)
[math]sumlimits_{j=0}^{k} bigl(alpha_{j}cdot widehat{y}_{i+1-j}+ hcdot beta_{j}cdot f_{i+1-j}bigr)=0.[/math]
(6.14)
Обозначим [math]textstyle{rho(xi)= sumlimits_{j=0}^{k} alpha_{j}xi^{k-j},~ sigma(xi)= sumlimits_{j=0}^{k} beta_{j}xi^{k-j}}[/math]. Линейный многошаговый метод является устойчивым, если для фиксированного значения [math]hmu[/math] корни уравнения
[math]rho(xi)+hcdotmucdot sigma(xi)=0[/math]
(6.15)
лежат внутри круга единичного радиуса с центром в начале координат.
2. Для ограниченно устойчивых методов важной задачей является нахождение величины критического шага [math]h_{text{kr}}[/math]. Если константа [math]mu[/math] в уравнении (6.12) действительная, то можно найти интервал устойчивости.
3. Существуют определения, смягчающие свойство A-устойчивости. Приведем одно из них. Метод называется A(α)-устойчивым, [math]alphain(0,pi!!not{phantom{|}},2)[/math], если при его применении все численные решения уравнения (6.12) с фиксированным положительным шагом [math]h[/math] стремятся к нулю при [math]itoinfty[/math] для всех [math]mu[/math], удовлетворяющих условию [math]|arg(-mu)|<alpha,~ |mu|ne0[/math], где [math]arg(-mu)[/math] — аргумент комплексного числа [math](-mu)[/math]. Область A(α)-устойчивости показана на рис. 6.4,5. Это условие применимо и для линейных систем с постоянными коэффициентами [math]y’=Ay[/math], где [math]A[/math] — матрица коэффициентов, имеющая собственные значения [math]lambda_{i},~ i=overline{1,n}[/math]. Геометрическая интерпретация изображена на рис. 6.4,в.
4. Можно показать, что явные линейные многошаговые методы не могут быть A-устойчивыми.
Математический форум (помощь с решением задач, обсуждение вопросов по математике).
Если заметили ошибку, опечатку или есть предложения, напишите в комментариях.
Ошибки усечения при численном интегрировании бывают двух видов:
- локальные ошибки усечения — ошибка, вызванная одной итерацией, и
- глобальные ошибки усечения — совокупная ошибка, вызванная множеством итераций.
Определения
Предположим, у нас есть непрерывное дифференциальное уравнение
и мы хотим вычислить приближение истинного решения с дискретными временными шагами . Для простоты предположим, что временные шаги равномерно распределены:
Предположим, мы вычисляем последовательность одношаговым методом вида
Эта функция называется функцией приращения , и ее можно интерпретировать как оценку наклона .
Ошибка локального усечения
Локальная ошибка усечения является ошибкой , что наше приращение функции, вызывает в течение одной итерации, предполагая , что совершенное знание истинного решения на предыдущей итерации.
Более формально локальная ошибка усечения на шаге вычисляется из разницы между левой и правой частями уравнения для приращения :
Численный метод является непротиворечивым, если локальная ошибка усечения равна (это означает, что для каждого существует такая, что для всех ; см. Небольшие обозначения ). Если функция приращения непрерывна, то метод непротиворечив, если и только если ,.
Кроме того, мы говорим, что численный метод имеет порядок,
Глобальная ошибка усечения
Глобальная ошибка усечения является накоплением локальной погрешности усечения за все итерации, предполагая совершенное знание истинного решения на начальном этапе времени.
Более формально глобальная ошибка усечения во времени определяется следующим образом:
Численный метод сходится, если глобальная ошибка усечения стремится к нулю, когда размер шага стремится к нулю; другими словами, численное решение сходится к точному решению: .
Связь между локальными и глобальными ошибками усечения
Иногда можно вычислить верхнюю границу глобальной ошибки усечения, если мы уже знаем локальную ошибку усечения. Для этого требуется, чтобы наша функция приращения работала достаточно хорошо.
Глобальная ошибка усечения удовлетворяет рекуррентному соотношению:
Это сразу следует из определений. Теперь предположим, что функция приращения липшицева по второму аргументу, то есть существует такая константа , что для всех и и мы имеем:
Тогда глобальная ошибка удовлетворяет оценке
Из приведенной выше оценки глобальной ошибки следует, что если функция в дифференциальном уравнении непрерывна по первому аргументу и липшицева по второму аргументу (условие из теоремы Пикара – Линделёфа ), а функция приращения непрерывна во всех аргументы и непрерывность Липшица во втором аргументе, то глобальная ошибка стремится к нулю, когда размер шага приближается к нулю (другими словами, численный метод сходится к точному решению).
Расширение линейных многоступенчатых методов
Теперь рассмотрим линейный многоступенчатый метод , задаваемый формулой
Таким образом, следующее значение численного решения вычисляется согласно
Следующая итерация линейного многоступенчатого метода зависит от предыдущих итераций s . Таким образом, в определении локальной ошибки усечения теперь предполагается, что все предыдущие s итерации соответствуют точному решению:
Опять же, метод непротиворечив, если и имеет порядок p, если . Не изменилось и определение глобальной ошибки усечения.
Связь между локальными и глобальными ошибками усечения немного отличается от более простой настройки одношаговых методов. Для линейных многошаговых методов требуется дополнительная концепция, называемая нулевой стабильностью, чтобы объяснить связь между локальными и глобальными ошибками усечения. Линейные многоступенчатые методы, удовлетворяющие условию нулевой устойчивости, имеют такое же соотношение между локальными и глобальными ошибками, что и одношаговые методы. Другими словами, если линейный многоступенчатый метод устойчив к нулю и непротиворечив, то он сходится. И если линейный многоступенчатый метод устойчив к нулю и имеет локальную ошибку , то его глобальная ошибка удовлетворяет .
Смотрите также
- Порядок точности
- Численное интегрирование
- Численные обыкновенные дифференциальные уравнения
- Ошибка усечения
Ноты
Ссылки
- Изерлес, Ари (1996), Первый курс численного анализа дифференциальных уравнений , Cambridge University Press , ISBN 978-0-521-55655-2.
- Сули, Эндре; Майерс, Дэвид (2003), Введение в численный анализ , Cambridge University Press , ISBN 0521007941.
внешние ссылки
- Примечания к ошибкам усечения и методам Рунге-Кутта
- Ошибка усечения метода Эйлера
Ошибки усечения в численное интегрирование бывают двух видов:
- локальные ошибки усечения — ошибка, вызванная одной итерацией, и
- глобальные ошибки усечения — совокупная ошибка, вызванная множеством итераций.
Определения
Предположим, у нас есть непрерывное дифференциальное уравнение
и мы хотим вычислить приближение 


Предположим, мы вычисляем последовательность 
Функция 

Ошибка локального усечения
В локальная ошибка усечения 

Более формально локальная ошибка усечения, 


[1][2]
Численный метод последовательный если локальная ошибка усечения 






Кроме того, мы говорим, что численный метод имеет порядок 





Глобальная ошибка усечения
В глобальная ошибка усечения это накопление локальная ошибка усечения на всех итерациях, предполагая полное знание истинного решения на начальном временном шаге.[нужна цитата ]
Более формально, глобальная ошибка усечения, 

[5]
Численный метод сходящийся если глобальная ошибка усечения становится равной нулю, когда размер шага становится равным нулю; другими словами, численное решение сходится к точному решению: 
Связь между локальными и глобальными ошибками усечения
Иногда возможно вычислить верхнюю границу глобальной ошибки усечения, если мы уже знаем локальную ошибку усечения. Для этого требуется, чтобы наша функция приращения работала достаточно хорошо.
Глобальная ошибка усечения удовлетворяет рекуррентному соотношению:
Это сразу следует из определений. Теперь предположим, что функция приращения равна Липшицева непрерывная во втором аргументе, то есть существует постоянная 



Тогда глобальная ошибка удовлетворяет оценке
[7]
Из приведенной выше оценки глобальной ошибки следует, что если функция 


Расширение линейных многоступенчатых методов
Теперь рассмотрим линейный многоступенчатый метод, задаваемый формулой
Таким образом, следующее значение численного решения вычисляется согласно
Следующая итерация линейного многоступенчатого метода зависит от предыдущего s повторяется. Таким образом, в определении локальной ошибки усечения теперь предполагается, что предыдущие s все итерации соответствуют точному решению:
[9]
Опять же, метод непротиворечив, если 

Связь между локальными и глобальными ошибками усечения немного отличается от более простой настройки одношаговых методов. Для линейных многоступенчатых методов существует дополнительная концепция, называемая нулевая стабильность необходим для объяснения связи между локальными и глобальными ошибками усечения. Линейные многоступенчатые методы, удовлетворяющие условию нулевой устойчивости, имеют такое же соотношение между локальными и глобальными ошибками, что и одношаговые методы. Другими словами, если линейный многоступенчатый метод устойчив к нулю и непротиворечив, то он сходится. И если линейный многоступенчатый метод устойчив к нулю и имеет локальную ошибку 

Смотрите также
- Порядок точности
- Численное интегрирование
- Численные обыкновенные дифференциальные уравнения
- Ошибка усечения
Заметки
- ^ Gupta, G.K .; Sacks-Davis, R .; Тишер П. Э. (март 1985 г.). «Обзор последних достижений в решении ODE». Вычислительные опросы. 17 (1): 5–47. CiteSeerX 10.1.1.85.783. Дои:10.1145/4078.4079.
- ^ Сюли и Майерс 2003, п. 317, звонки
ошибка усечения.
- ^ Сюли и Майерс 2003, стр. 321 и 322
- ^ Изерлес 1996, п. 8; Сюли и Майерс 2003, п. 323
- ^ Сюли и Майерс 2003, п. 317
- ^ Изерлес 1996, п. 5
- ^ Сюли и Майерс 2003, п. 318
- ^ Сюли и Майерс 2003, п. 322
- ^ Сюли и Майерс 2003, п. 337, использует другое определение, разделив его по существу на час
- ^ Сюли и Майерс 2003, п. 340
использованная литература
- Изерлес, Арье (1996), Первый курс численного анализа дифференциальных уравнений, Издательство Кембриджского университета, ISBN 978-0-521-55655-2.
- Сули, Эндре; Майерс, Дэвид (2003), Введение в численный анализ, Издательство Кембриджского университета, ISBN 0521007941.
внешние ссылки
- Примечания к ошибкам усечения и методам Рунге-Кутта
- Ошибка усечения метода Эйлера