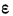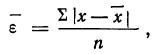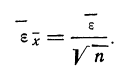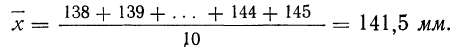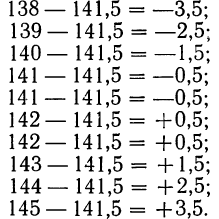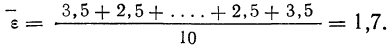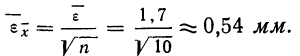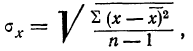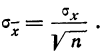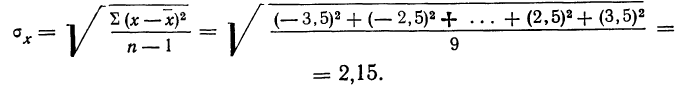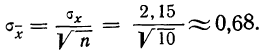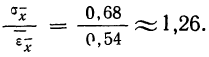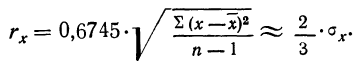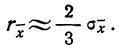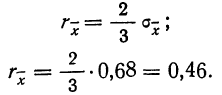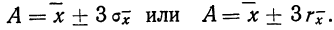Математическое ожидание — ошибка
Cтраница 1
Математическое ожидание ошибки называется систематической ошибкой, ее среднее квадратическое отклонение — среднеквадра-тической ошибкой. Анализ качества систем управления сводится к определению указанных ошибок по вероятностным характеристикам случайных внешних воздействий.
[2]
Математическое ожидание ошибки слежения равно ее среднеарифметическому значению.
[3]
Система имеет математическое ожидание ошибки тст 0 и центрированную составляющую С, подчиненную нормальному закону распределения.
[4]
Известно, что математическое ожидание ошибки уменьшается с увеличением частоты замеров и с уменьшением скорости линейного изменения коэффициентом.
[5]
В этом случае математическое ожидание ошибки равно нулю.
[6]
Учитывая, что при усечении математическое ожидание ошибки квантования отлично от нуля, более целесообразно использовать округление.
[7]
При совпадении ПФ с видом г математическое ожидание ошибки прогноза будет равно нулю.
[9]
Получаемые вероятностные оценки поступают на сумматор 2, который определяет величину математического ожидания ошибок Мп для каждой из сравниваемых кодовых комбинаций.
[10]
Формулы (5.5.12) и (5.5.14) характеризуют собой общие выражения соответственно корреляционной функции и математического ожидания ошибки положения для партии механизмов.
[11]
При приеме в целом принятая кодовая комбинация будет ошибочной, если при математическом ожидании ошибок на ее длине Мл Мп mln и зафиксированное значение кодовой комбинации содержит любые варианты ошибок.
[12]
Согласно соотношению ( 11) каждому из возможных состояний канала связи соответствует случайная величина математического ожидания ошибок Мс, которая через финальные вероятности состояний принятой модели может указать на наличие того или иного состояния с некоторой вероятностью правдоподобия рс.
[13]
Чтобы упростить сравнение указанных методов, будем полагать, что первичные параметры взаимонезависимы, а математическое ожидание ошибок ( допусков) равно нулю.
[14]
Функция потерь) в общем случае является функционалом от выходных сигналов объекта и модели или от математического ожидания ошибок оценок параметров.
[15]
Страницы:
1
2
Содержание:
Ошибки измерения: Опыт убеждает, что измерения объектов не могут быть произведены абсолютно точно и каждое конкретное измерение дает лишь, как правило, приближенное значение величины явления, истинное значение которой (A) нам неизвестно. Ошибки измерения (
Рассмотрим такие измерения, которые производятся одним наблюдателем, одним и тем же инструментом, в одинаковых условиях, т. е. равноточные измерения.
Различают два вида ошибок измерения:
- систематические ошибки, т. е. такие, которые при данных условиях проведения измерения имеют вполне определенное значение (например, ошибка измерительного прибора);
- случайные — такие, которые являются результатом взаимодействия большого числа незначительных в отдельности факторов и имеют в каждом отдельном случае различные значения.
Задача математической статистики — предусмотреть возможность возникновения систематических ошибок и добиться их ликвидации или сведения к минимуму.
Случайные ошибки измерения обладают рядом свойств: при большом числе измерений крупные ошибки встречаются реже мелких и число положительных ошибок примерно равно числу отрицательных, вследствие чего сумма всех ошибок близка к нулю.
Если ошибки получаются весьма малыми по сравнению с величиной явления, то ими просто пренебрегают или считаются с наибольшей возможной ошибкой, чтобы обезопасить себя от влияния случайной неточности.
В теории ошибок изучаются те ошибки, которые, являясь, с одной стороны, ошибками случайного характера, по своему абсолютному значению настолько велики, что ими пренебречь нельзя, а с другой стороны, для них существует закон, позволяющий установить зависимость между величиной ошибки и вероятностью ее появления. Закон случайных ошибок, полученный Гауссом, состоит в том, что случайные ошибки подчиняются закону нормального распределения.
Средняя ошибка сводного результата измерения
Принимая за действительное значение измеряемой величины при равноточном измерении среднюю арифметическую из всех результатов n измерений, можно охарактеризовать точность одного измерения с помощью средней арифметической из абсолютных величин значений ошибок:
где n — число измерений, х — численное значение отдельных измерений,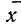 
— средняя арифметическая из результатов измерений.
За меру точности соответствия принятой средней арифметической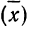 
истинному значению измеряемой величины (A) принимают среднюю ошибку сводного результата измерения, вычисляемую по формуле:
Пример 1. Произведено 10-кратное измерение размера детали (в мм), давшее следующие, расположенные в возрастающем порядке результаты: 138; 139; 140; 141; 141; 142; 142; 143; 144; 145.
Охарактеризуем сначала точность одного измерения, т. е. вычислим среднюю арифметическую из абсолютных значений ошибок. Для этой цели вычислим среднюю арифметическую из результатов измерений:
Найдем ошибки измерения:
Следовательно:
Теперь можно вычислить среднюю ошибку сводного результата измерения:
Значит, мерой точности соответствия 141,5 мм истинной величине размера детали является средняя ошибка, равная 0,54 мм.
Средняя квадратическая ошибка
Если в качестве меры точности одного измерения принять не среднюю арифметическую из абсолютных значений ошибок (средняя ошибка), а среднюю квадратическую из ошибок измерений, т. е.
то средняя квадратическая ошибка найденной средней арифметической из ошибок измерения вычисляется по формуле:
Между средней -квадратической ошибкой и средней ошибкой сводного результата измерения существует связь: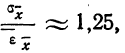 
если случайные ошибки подчиняются Гауссову закону нормального распределения.
Пример 2. Используя данные предыдущего примера, находим меру точности одного измерения, т. е. среднюю квадратическую ошибку:
Затем исчисляем среднюю квадратическую ошибку найденной средней арифметической, равной 141,5 мм:
Сопоставляя среднюю квадратическую ошибку сводного результата измерения со средней ошибкой, получаем:
Вероятная ошибка
За меру точности одного измерения иногда принимают вероятную ошибку:
Тогда в качестве вероятной ошибки сводного результата измерения используют соотношение:
Пример 3. Используя данные предыдущих примеров, находим вероятную ошибку сводного результата измерения:
Наиболее вероятные границы сводных результатов измерения
Математическое ожидание случайной ошибки равно нулю. В качестве значения измеряемой величины применяется средняя арифметическая всех измерений (если они равноточны). Использование отклонений результатов измерений (х) от средней из них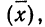 
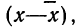
называемых в теории ошибок «кажущимися ошибками» 
позволяет произвести оценку точности соответствия средней арифметической неизвестному истинному значению измеряемой величины (A).
Для этой цели используют удвоенную или утроенную среднюю квадратическую ошибку сводного результата измерения или его вероятную ошибку и получают:
Найденные границы неизвестной истинной величины в случае, если ошибки подчинены нормальному закону распределения Гаусса (чаще всего так и бывает), соблюдаются с большой вероятностью (0,997 и 0,954).
Пример 4. По данным предыдущих примеров находим границы истинного значения размера детали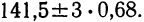 
Значит, истинное значение размера детали находится в границах от 141,5—2,04 до 141,5+2,04.
- Методы математической статистики
- Комбинаторика — правила, формулы и примеры
- Классическое определение вероятности
- Геометрические вероятности
- Законы распределения случайных величин
- Дисперсионный анализ
- Математическая обработка динамических рядов
- Корреляция — определение и вычисление
11
ЛЕКЦИЯ 4.
Случайные
погрешности измерений и способы их
описания.
При выполнении
повторных измерений одной и той же
величины легко убедиться, что результаты
отдельных измерений отличаются друг
от друга. Это объясняется действием
случайных погрешностей. Случайные
погрешности вызываются большим числом
причин, действующих независимо друг от
друга. Их нельзя исключить опытным
путем, но их влияние на результат
измерения можно оценить, проведя ряд
наблюдений одной и той же величины.
Результат измерения всегда содержит
как систематическую С,
так и случайную погрешности, т.е.
,
поэтому погрешность результата измерения
в общем случае нужно рассматривать как
случайную величину. Тогда систематическая
погрешность есть математическое ожидание
этой величины, а случайная погрешность
– центрированная случайная величина.
Со статистических позиций можно дать
следующие определения составляющих
погрешности.
Систематическая
погрешность
– отклонение математического ожидания
mx
результатов
наблюдений от истинного значения А
измеряемой величины:
.
Случайная
погрешность
— разность между результатом единичного
наблюдения и математическим ожиданием
результатов:
.
Математическое
ожидание погрешности
равно математическому ожиданию
систематической составляющей погрешности,
так как математическое ожидание случайной
погрешности всегда равно нулю:
.
Законы распределения случайных величин
Полным описанием
случайной величины, а, следовательно,
и погрешности является ее закон
распределения. Этим законом распределения
и определяется характер появления
различных результатов отдельных
измерений в ряду наблюдений.
В практике
электрических измерений встречаются
различные законы распределения. Это
равномерное (прямоугольное) распределение,
нормальное распределение Гаусса,
распределение 2
(хи-квадрат), распределение t-Стьюдента
и др. Одним из наиболее распространенных
законов распределения погрешностей
является нормальный закон (Гаусса),
который базируется на центральной
предельной теореме теории вероятностей,
согласно которой нормальное распределение
плотности вероятности имеет сумма
бесконечно большого числа бесконечно
малых случайных возмущений с любыми
распределениями. Применительно к
измерениям это означает, что нормальное
распределение случайных погрешностей
возникает тогда, когда на результат
измерения действует множество случайных
возмущений и ни одно из которых не
является преобладающим. Практически,
суммарное воздействие даже сравнительно
небольшого числа возмущений приводит
к закону распределения результатов и
погрешностей измерений, близкому к
нормальному. Закон нормального
распределения имеет фундаментальное
значение для теории обработки результатов
измерений. Он позволяет вести расчеты
даже тогда, когда действительный закон
неизвестен.
Математически
нормальное распределение случайных
погрешностей может быть представлено
формулой
,
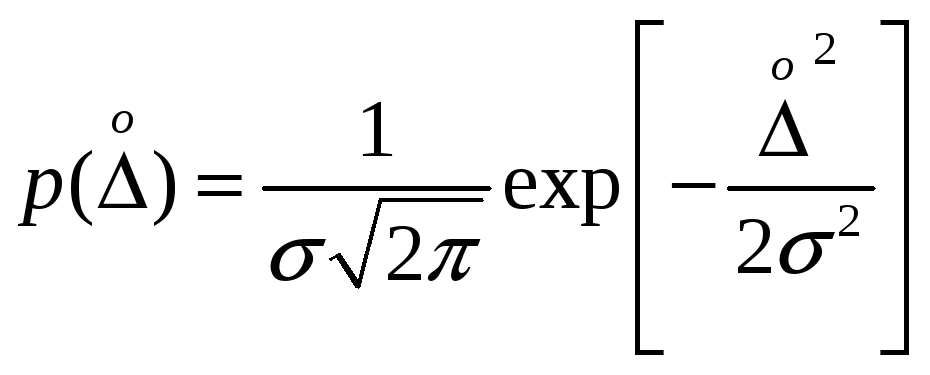
где p(
)
– плотность вероятности случайной
погрешности
;
s — среднее
квадратическое отклонение.
Характер
кривых, описываемых этим уравнением
для двух значений s
(
),
показан на рис.4.1.
Из этих кривых
видно, что чем меньше s,
тем чаще встречаются малые случайные
погрешности, т.е. тем точнее выполнены
измерения. Кривые симметричны относительно
оси ординат, так как положительные и
отрицательные погрешности встречаются
одинаково часто.
Основные
характеристики законов распределения.
Основными
характеристиками являются математическое
ожидание и дисперсия.
Математическое
ожидание ряда наблюдений есть
величина, относительно которой
рассеиваются результаты отдельных
измерений. Если систематическая
погрешность отсутствует, и разброс
результатов отдельных измерений
обусловлен только случайной погрешностью,
то математическим ожиданием такого
ряда наблюдений будет истинное значение
измеряемой величины. Если же результаты
отдельных измерений кроме случайной
погрешности содержат постоянную
систематическую погрешность, то
математическое ожидание ряда наблюдений
будет смещено от истинного значения
измеряемой величины на значение
систематической погрешности.
Дисперсия D
ряда наблюдений характеризует степень
рассеивания (разброса) результатов
отдельных наблюдений вокруг математического
ожидания. Чем меньше дисперсия, тем
меньше разброс отдельных результатов,
тем точнее выполнены измерения.
Следовательно, дисперсия может служить
характеристикой точности проведенных
измерений. Однако, дисперсия выражается
в единицах в квадрате измеряемой
величины. Поэтому в качестве характеристики
точности ряда наблюдений наиболее часто
применяют среднее квадратическое
отклонение результата наблюдения (СКО)
s,
равное корню квадратному из дисперсии
с положительным знаком и выражаемое в
единицах измеряемой величины. Среднее
квадратическое отклонение, отнесенное
к значению измеряемой величины, может
быть выражено в относительных единицах
или процентах.
Соседние файлы в предмете [НЕСОРТИРОВАННОЕ]
- #
- #
- #
- #
- #
- #
- #
- #
- #
- #
- #
#статьи
- 19 апр 2022
-
0
Ошибка выжившего, лёгкая рука и математическое ожидание: почему мы всегда в минусе
Хозяин казино всегда будет в выигрыше. Чтобы убедиться в этом, достаточно знать три простых концепции из статистики.
Кадр: фильм «Казино „Рояль“»
Переводчик-фрилансер. Увлечён своей профессией. Переводит полезные статьи на разные темы — от IT до путешествий, урбанистики и социологии. Занимается лингвистическими исследованиями.
Об авторе
Аналитик данных и основатель курсов Data36. Создаёт подробные и точные практические руководства и записывает видеокурсы в помощь изучающим Data Science.
Представьте: вы сидите в казино, крупье раскручивает рулетку, и шарик начинает скакать. Скачет, скачет, и кажется, вот оно — красное! А потом он делает ещё одно движение. Нет, чёрное! Вы снова всё проиграли и идёте домой без гроша в кармане.
Надеюсь, с вами такого не произойдёт, потому что вы не ходите в казино, не покупаете лотерейные билеты и вообще не играете на деньги. В этой статье я расскажу о трёх статистических концепциях, которые подтверждают мысль о том, что играть на деньги — плохая затея.
Эти концепции часто используются в проектах с обработкой и анализом данных, поэтому не удивляйтесь, что в статье я поднимаю тему азартных игр, — вы сможете применить эти знания в своей работе.
Истории успеха цепляют, их любит каждый. Многие слышали о счастливчиках, сделавших ставки на спорт и получивших большие суммы, вернувшихся из Вегаса с 10 тысячами долларов, выигравших в лотерею путешествие мечты. В общем, победивших по-крупному.
Эти истории всегда заканчиваются тем, что кто-то срывает куш. В этом вся фишка, это логично. Моя бабушка никогда не расскажет, как на прошлой неделе она в очередной раз купила несколько лотерейных билетов и опять ничего не выиграла. Но она обязательно вспомнит, как в 2003 году выиграла в этой лотерее 6 тысяч долларов.
А почему? Потому что проигрывать — скучно. Ведь это постоянно происходит с каждым из нас, а вот побеждать — весело, и даже спустя несколько лет об этом будет интересно рассказать.
Истории успеха увлекают, поэтому они остаются в нашей памяти, а скучные мы забываем. Вот почему эта концепция называется «ошибка выжившего». Но при чём здесь ошибка?
Систематическая ошибка выжившего — тип смещения выборки, возникающий, если при принятии решения человек опирается только на примеры «выживших» (тех, кто добился успеха), но не учитывает статистику по «погибшим» (тех, у кого не получилось прийти к такому же результату), поскольку данных по ним мало или они отсутствуют.
Хрестоматийным примером ошибки выжившего стало открытие математика Абрахама Вальда во время Второй мировой войны. Чтобы уменьшить потери авиации, командование поставило перед Вальдом задачу определить самые уязвимые места самолёта в воздушном бою.
До этого военные инженеры изучали повреждения машин, вернувшихся с поля боя, и укрепляли наиболее повреждённые части. Вальд выдвинул парадоксальную, на первый взгляд, гипотезу: если самолёт смог вернуться на базу, то попадания в него были не критичны.
Следовательно, укреплять нужно те места, где у «выживших» нет пробоин, — ведь повреждённые в них самолёты не возвращаются. Это помогло снизить потери американской авиации и сохранить жизни многих лётчиков.
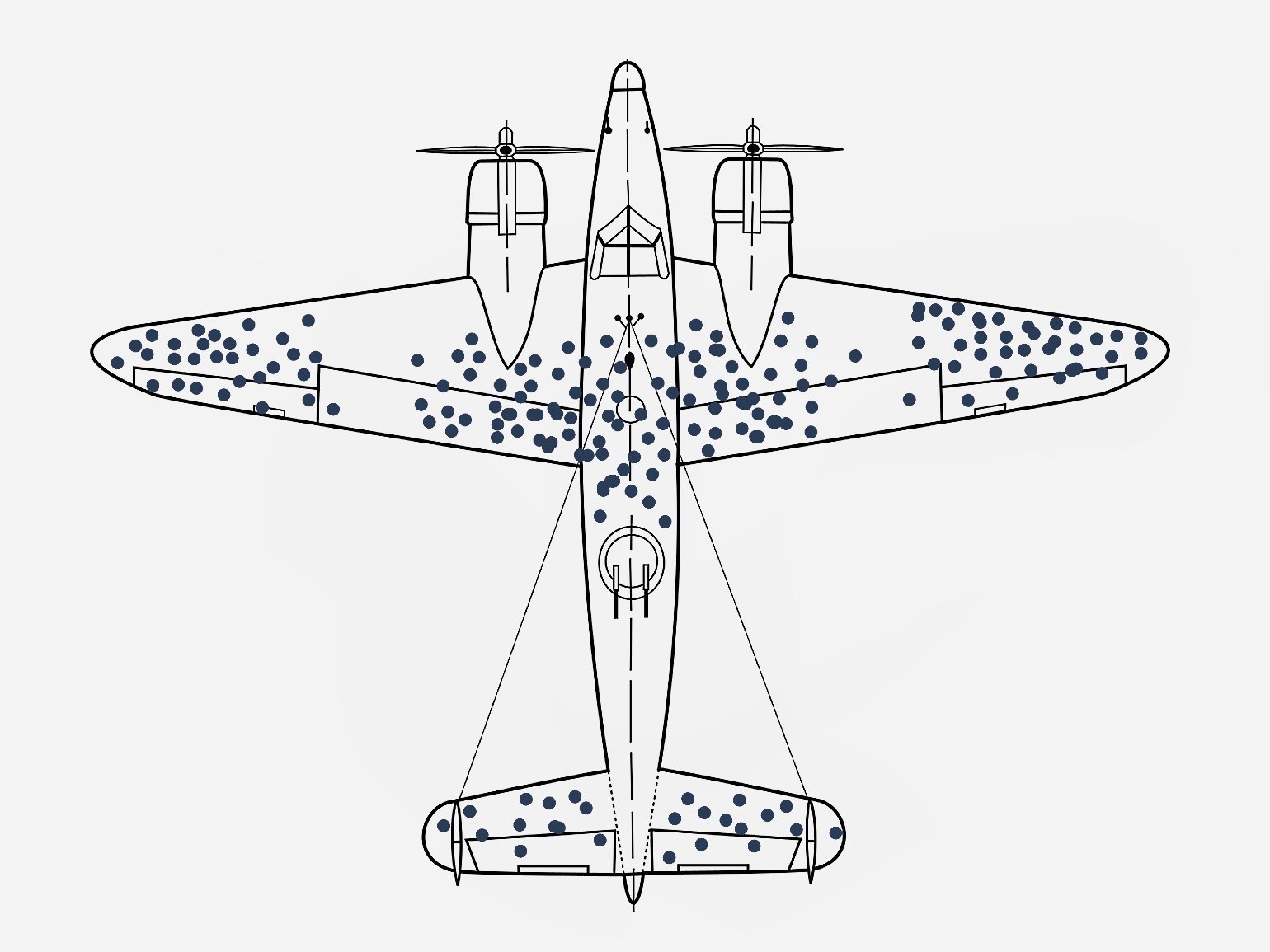
Изображение: Wikimedia Commons
Вот как это работает: мозг слышит историю успеха — это один элемент данных. Затем он слышит ещё одну историю, и ещё одну — и так далее. Истории о неудачах тоже попадаются — но этих историй мало, в отличие от неудач в реальной статистике.
В итоге мозг воспринимает непропорционально много историй успеха и относительно мало историй неудач. Неосознанно, на основе искажённых данных, формируется ложное представление, и мы начинаем думать, что у нас гораздо больше шансов выиграть, хотя реальные статистические данные показывают обратное.
Так устроен мой глупый мозг. Да и не только мой — ваш работает точно так же. Мы все люди и все интуитивно верим, что у нас есть больший шанс на победу, чем на самом деле. И почти все казино и букмекеры стремятся усилить этот эффект как только могут (привет «Азино три топора» и Вите АК).
Если бы не ошибка выжившего, мы бы оценивали свои шансы на победу более трезво и, возможно, никто бы никогда не играл на деньги. Поэтому, если вам рассказывают какую-то историю успеха, всегда помните, что она не даёт полной картины — на самом деле только хозяин казино всегда в выигрыше.
Кстати, я уже не раз повторил эту фразу, но так и не объяснил, что за ней стоит.
Я не буду вдаваться в подробности того, как рассчитать математическое ожидание. Если вам это интересно, прочитайте статью Expected Value (Formula, Explanation, Everyday Usage and a Game).
Но давайте вернёмся к нашей концепции. Математическое ожидание показывает, что в среднем можно получить, если сделать одну и ту же ставку несколько раз.
Звучит сложновато, поэтому приведу очень простой пример. Когда мы подбрасываем монетку, с вероятностью пятьдесят на пятьдесят выпадет либо орёл, либо решка.
Обычно всё довольно справедливо — например, вы сделали ставку, подбросили монетку, и выпала решка. В таком случае ваша сумма удваивается. Если выпал орёл, вы проигрываете свои деньги. Когда вы подбросите монетку, скажем, тысячу раз, количество ваших побед и поражений сравняется, а средний доход будет стремиться к нулю. Это означает, что математическое ожидание такой игры — 0 рублей.
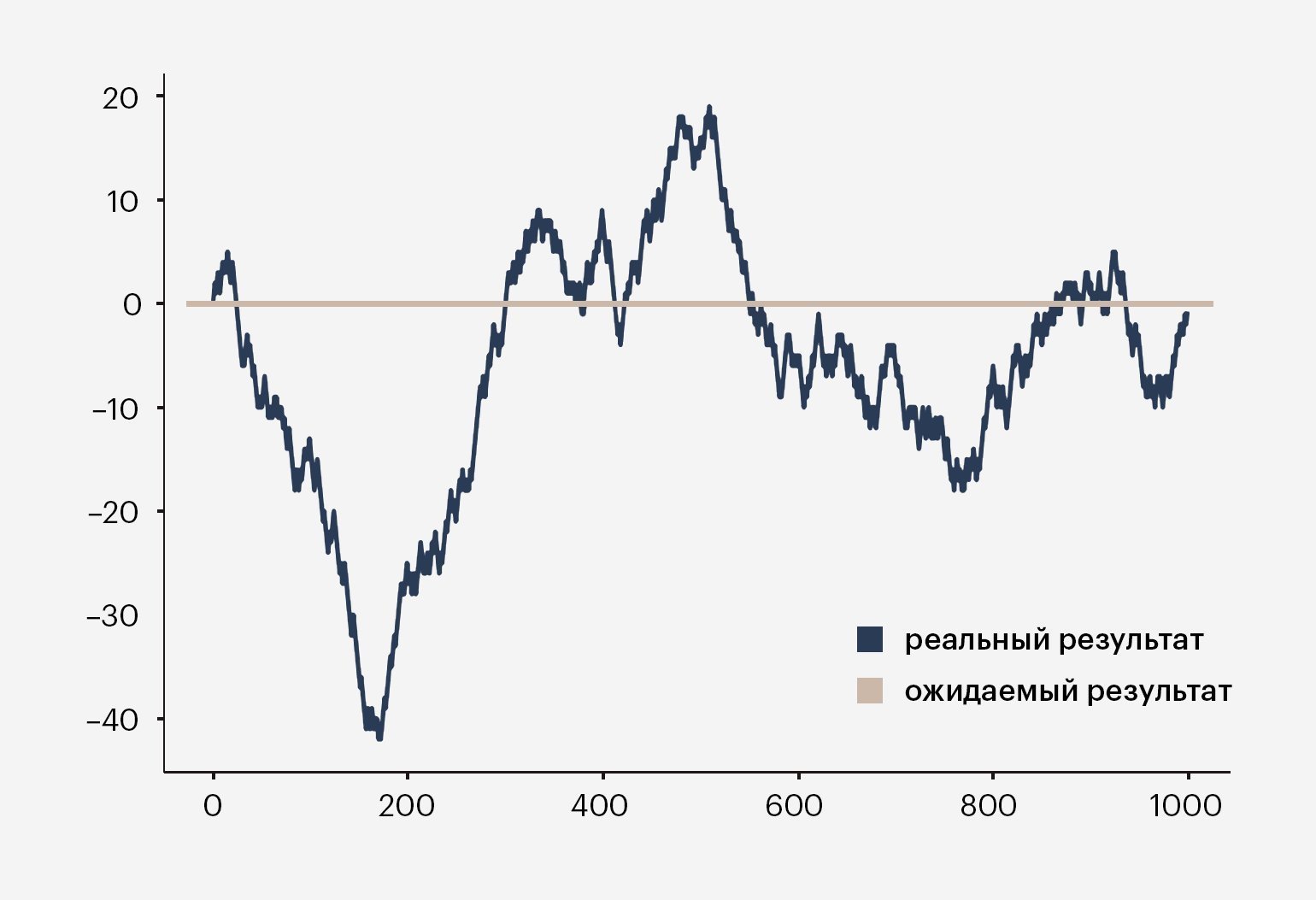
Источник: Tomi Mester. Инфографика: Skillbox Media
Рулетка устроена схожим образом: есть красные и чёрные секторы. Но когда вы играете в рулетку, у вас немного меньше шансов победить, чем в игре с монеткой. Если вы ставите тысячу рублей, математическое ожидание в таком случае не 0, а −27 рублей за раунд. Кажется, что это небольшая сумма, но за тысячу раундов вы проиграете уже 27 тысяч рублей. Статистика неумолима.
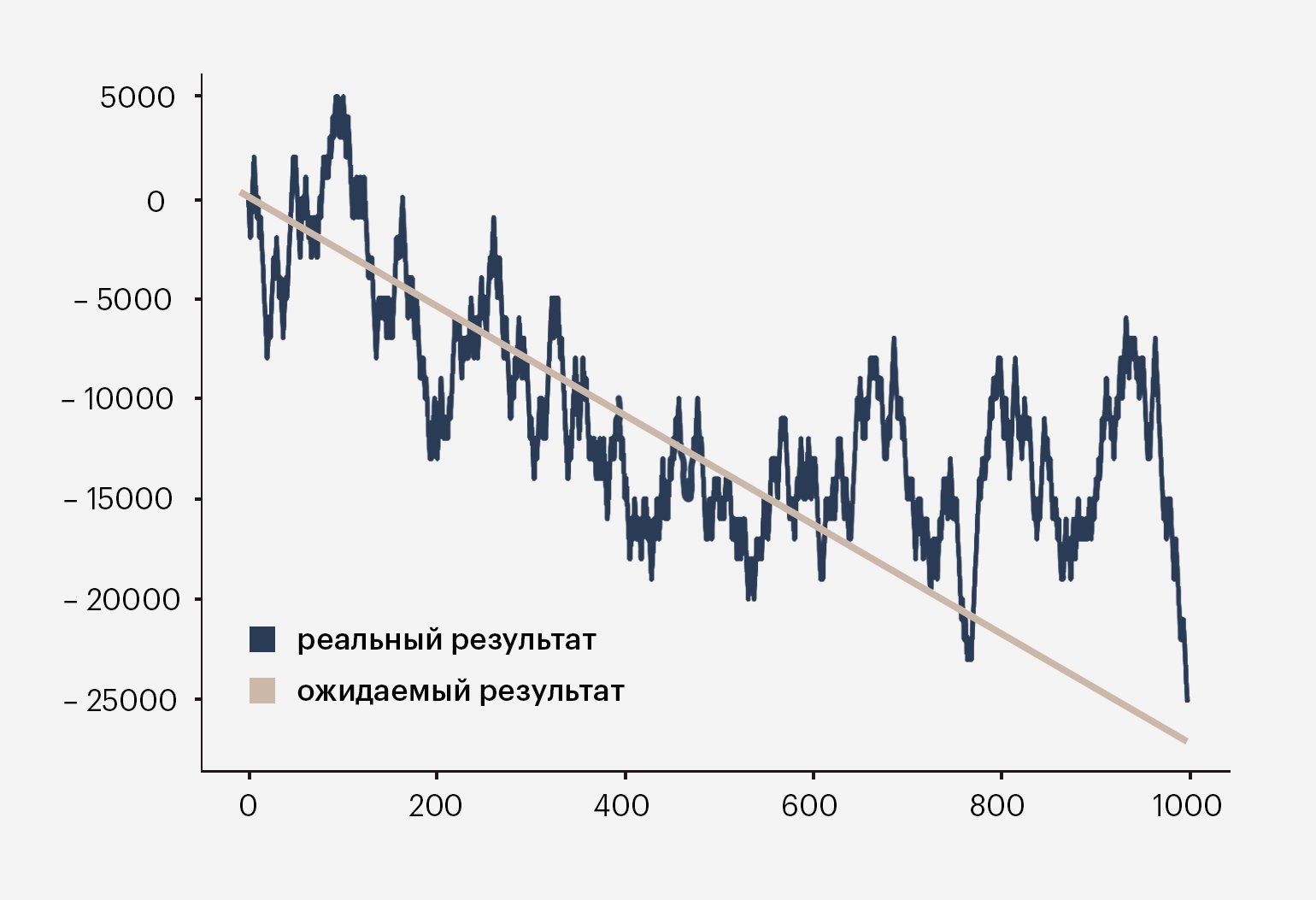
Источник: Tomi Mester. Инфографика: Skillbox Media
Да, конечно, математическое ожидание — это теоретическая величина, но она всегда даёт о себе знать на практике: чем больше игр вы проводите, тем больше проигрываете.
Суть в том, что рулетка — это игра с отрицательным математическим ожиданием. Шансы на выигрыш в ней просчитаны так, чтобы в конечном итоге вы оказались в минусе. Да никто особо и не скрывает, что все игры в казино устроены таким образом. Вот почему хозяин всегда будет в плюсе.
А с помощью этой концепции можно объяснить, почему мы не выходим из игры, когда побеждаем несколько раз подряд.
Прежде всего, не забывайте, что нашему мозгу очень сложно понять, как работают вероятности, то есть крайне маловероятные события. Например, шанс, что вам выпадет орёл 10 раз подряд, составляет менее 0,1%. Но если выборка достаточно большая — скажем, вы подбросили монетку 100 тысяч раз, — орёл неизбежно выпадет, причём не один раз.
То же самое может произойти, если, допустим, вы играете в рулетку уже тысячу раундов. Очень вероятно, что несколько раз вам повезёт, а когда везёт, может показаться, что у вас лёгкая рука. Вы начинаете поднимать планку и увеличивать ставки в надежде, что сможете выжать максимум из своего везения. Но правда в том, что удача — это просто счастливая случайность. По статистике, каждому время от времени везёт.
В мире азартных игр никакой лёгкой руки нет — выигрывают так же быстро, как проигрывают. От статистики не уйдёшь — чем больше играешь, тем больше шансов остаться ни с чем. Если же, несмотря ни на что и вопреки здравому смыслу, вы пойдёте в казино и даже выиграете, лучшее, что вы можете сделать, — это быстро унести оттуда ноги и наслаждаться своим везением.
Научитесь: Профессия BI-аналитик
Узнать больше
Математическое ожидание
Предмет
Естествознание
Разместил
🤓 grovevadtio1980
👍 Проверено Автор24
понятие теории вероятности, среднее значение, является характеристикой распределения значений случайной величины. Математическое ожидание случайной величины X, которая может принимать значение X1, Х2, Х3, …, Хп с вероятностями Р1, Р2, …, Рk, определяется как ΕΧ = Σ РКХК- Если же X — непрерывная случайная величина с функцией плотности f, то ЕХ = xf(x) dx.
Научные статьи на тему «Математическое ожидание»
Доверительные интервалы для оценки математического ожидания
Доверительный интеграл для оценки математического ожидания при известном ${mathbf sigma }$
Для начала…
Пусть варианты генеральной совокупности имеет нормальное распределение с математическим ожиданием $a$…
Таблица значений функции $Фleft(tright).$
Доверительный интеграл для оценки математического ожидания…
Найти доверительный интервал для оценки математического ожидания данного распределения.
Статья от экспертов
Математическое ожидание функции
В статье рассмотрены решения различных задач, связанных со случайными явлениями, современная теория вероятностей. Рассмотрена задача об определении числовых характеристик функции при заданном законе распределения аргументов.
Математическое ожидание
В противном случае говорят, что интеграл и, тем самым, математическое ожидание не существует….
Если математические ожидания $Mxi $, $Meta $ существуют, то $M(xi pm eta )$ существует….
Если математические ожидания $Mxi $, $Meta $ существуют, то $M(xi cdot eta )$ существует….
Геометрически математическое ожидание численно равно абсциссе центра тяжести интеграла (5)….
Проверить свойства $3, 4$ математического ожидания.
Решение.
Статья от экспертов
Об оценке математического ожидания периодически коррелированного случайного процесса
Строится и исследуется непараметрическая оценка математического ожидания m(t) периодически коррелированного случайного процесса X(t) по его реализации конечного объема. Формулируется рекомендации по выбору ключевого параметра оценки функции m(t).
Повышай знания с онлайн-тренажером от Автор24!
- Напиши термин
- Выбери определение из предложенных или загрузи свое
-
Тренажер от Автор24 поможет тебе выучить термины с помощью удобных и приятных
карточек