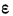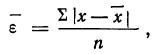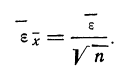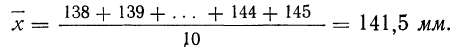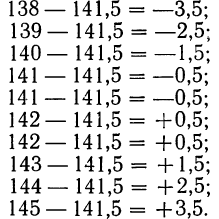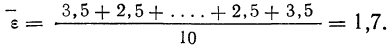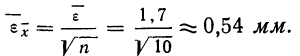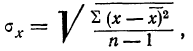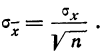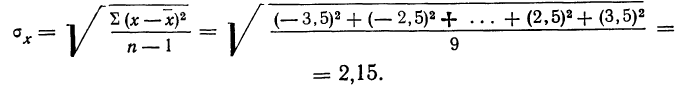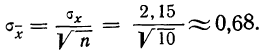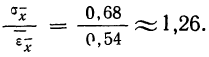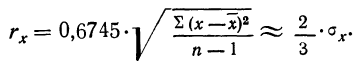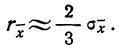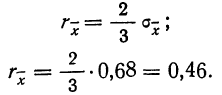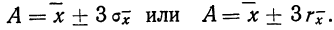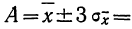Математическая теория ошибок - Не ошибается лишь тот, кто ничего не делает!

Тео́рия оши́бок, раздел математической статистики, посвящённый построению выводов о численных значениях приближённо измеренных величин и об ошибках (погрешностях) измерений. Повторные измерения одной и той же постоянной величины дают, как правило, различные результаты, т. к. каждое измерение содержит некоторую ошибку. Различают три основных вида ошибок: систематические, грубые и случайные. Систематические ошибки постоянно либо преувеличивают, либо преуменьшают результаты измерений и происходят от определённых причин (неправильной установки измерительных приборов, влияния окружающей среды и т. д.), систематически влияющих на результаты измерений и изменяющих их в одном направлении. Оценка систематических ошибок производится с помощью методов, выходящих за пределы математической статистики. Например, в астрономии при измерении величины угла между направлением на светило и плоскостью горизонта систематическая ошибка является суммой двух ошибок: систематической ошибки, которую даёт прибор при отсчёте данного угла (инструментальная ошибка) и систематической ошибки, обусловленной преломлением лучей света в атмосфере (рефракция). Инструментальная ошибка учитывается с помощью таблицы или графика поправок для данного прибора; ошибку, связанную с рефракцией (для углов, меньших 80°), можно достаточно точно вычислить теоретически. Грубые ошибки возникают в результате просчёта, неправильного чтения показаний измерительного прибора и т. п. Результаты измерений, содержащие грубые ошибки, как правило, сильно отличаются от других результатов измерений и поэтому часто бывают хорошо заметны. Случайные ошибки происходят от различных случайных причин, действующих при каждом из отдельных измерений непредсказуемым образом то в сторону уменьшения, то в сторону увеличения результата.

Теория ошибок занимается изучением лишь случайных и грубых ошибок. Основные задачи теории ошибок: определение законов распределения случайных ошибок, построение статистических оценок неизвестных величин по результатам измерений, вычисление погрешностей таких оценок и устранение грубых ошибок.

Пусть в результате nn независимых измерений некоторой неизвестной величины μmu получены значения X1,X2,…,XnX_1,X_2,dots,X_n. Разности

δ1=X1−μ, δ2=X2−μ, …, δn=Xn−μdelta_1=X_1-mu,, delta_2=X_2-mu, ,dots, , delta_n=X_n-muназываются истинными ошибками; в терминах вероятностной теории ошибок все δidelta_i рассматриваются как случайные величины, независимость измерений понимается как взаимная независимость случайных величин δ1,…,δndelta_1, dots, delta_n. При этом измерения называются равноточными (в широком смысле), если эти величины имеют одно и то же распределение. Т. о., истинные ошибки равноточных измерений суть независимые одинаково распределённые случайные величины. При этом математическое ожидание истинных ошибок b=Eδ1=…=Eδnb=text{E}delta_1=ldots =text{E}delta_n называется систематической ошибкой, а разности δ1−b,…,δn−bdelta_1-b,dots,delta_n-b – случайными ошибками. Отсутствие систематической ошибки означает, что b=0b=0, в этом случае δ1,…,δndelta_1,dots,delta_n суть случайные ошибки. Величину 1/(2σ)1/(sqrt{2}sigma), где σsigma – квадратичное отклонение ошибок δ1,…,δndelta_1,dots,delta_n, называют мерой точности (при наличии систематической ошибки мера точности есть 1/2(b2+σ2)1/sqrt{2(b^2+sigma^2)}. Равноточность измерений в узком смысле понимается как одинаковость меры точности всех результатов измерений. Наличие грубых ошибок означает нарушение равноточности (как в широком, так и в узком смысле) для некоторых отдельных измерений.

В качестве оценки неизвестной величины μ mu обычно берут арифметическое среднее из результатов измерений X1,…,XnX_1,dots,X_n:

X‾=1n∑i=1nXi,displaystyleoverline X=frac{1}{n}sum^n_{i=1}X_i,а разности Δ1=X1−X‾,…,Δn−X‾Delta_1=X_1- overline X, dots, Delta_n — overline X называются кажущимися ошибками. Выбор X‾overline X в качестве оценки для μmu основан на том, что при достаточно большом числе nn равноточных измерений, лишённых систематической ошибки, оценка X‾overline X с вероятностью, сколь угодно близкой к единице, сколь угодно мало отличается от неизвестной величины μmu (это связано с Законом больших чисел); оценка X‾overline X лишена систематической ошибки (оценки с таким свойством называются несмещёнными оценками); дисперсия этой оценки есть

DX‾=E(X‾−μ)2=σ2/n.text Doverline X=text E(overline X-mu)^2=sigma^2/n.Опыт показывает, что практически очень часто случайные ошибки имеют распределения, близкие к нормальным (это объясняется центральной предельной теоремой). В этом случае распределение величины X‾overline X мало отличается от нормального распределения с математическим ожиданием μmu и дисперсией σ2/nsigma^2/n. Если распределение величин δ1,…,δndelta_1,dots,delta_n в точности нормально, то дисперсия всякой другой несмещённой оценки для μmu, например медианы, не меньше DX‾text Doverline X. Если же распределение величин δ1,…,δndelta_1,dots,delta_n отлично от нормального, то последнее свойство может не иметь места.

Если дисперсия σ2sigma^2 отдельных измерений заранее неизвестна, то для её оценки пользуются величиной

s2=1n−1∑i=1nΔi2;displaystyle s^2=frac{1}{n-1}sum^n_{i=1}Delta^2_i;

s2s^2 – несмещённая оценка для σ2sigma^2, т. к. Es2=σ2text E s^2=sigma^2.

Если случайные ошибки δ1,…,δndelta_1,dots,delta_n имеют нормальное распределение, то отношение

t=(X‾−μ)nst=dfrac{(overline X -mu)sqrt{n}}{s}имеет распределение Стьюдента с n−1n-1 степенью свободы. Этим можно воспользоваться для оценки погрешности приближённого равенства μ≈X‾mu approx overline X (см. Метод наименьших квадратов). Величина

χ2=(n−1)s2σ2chi^2=dfrac{(n-1)s^2}{sigma^2}при тех же предположениях имеет распределение хи-квадрат с n−1n-1 степенью свободы. Это позволяет оценить погрешность приближённого равенства σ≈ssigma approx s. Относительная погрешность ∣s−σ∣/s|s-sigma|/s не превосходит числа qq с вероятностью

ω=F(z2,n−1)−F(z1,n−1),omega=F(z^2,n-1)-F(z_1,n-1),
где F(z,n−1)F(z, n-1) – функция распределения хи-квадрат, а

z1=n−11+q,z2=n−11−q.z_1=dfrac{sqrt{n-1}}{1+q},quad z_2 = dfrac{sqrt{n-1}}{1-q}.

Дата публикации: 1 августа 2022 г. в 13:27 (GMT+3)

Источник

Основные
понятия теории ошибок.
Оценка точности
наблюдений.

Для
последующей ясности, в этой статье, под
наблюдениями будем подразумевать
совокупность одиночных измерений
определенной величины: разница в блеске,
показание шкалы микрометра и прочее.
Это величина называется измеряемой или
наблюдаемой. По особенности проведения,
все наблюдения можно разделить на две
группы: равноточные и неравноточные. К
первой категории относятся такие
наблюдения, которые были выполнены
одним человеком, на одном приборе
(инструменте) в сравнительно короткий
промежуток времени (то есть одинаковое
воздействие внешних факторов). Во вторую
категорию, естественно, попадают те
наблюдения, которые не соответствуют
одному, нескольким или всем условиям
принадлежности к равноточным наблюдениям.
В этой статье не будут описаны точностные
расчеты для наблюдений второй категории,
они более сложны и громоздки, и применяются
чаще в обработке геодезических измерений
и при комплексных астронаблюдениях.
Планируется подробно остановится на
неравноточных измерениях в следующей
статье из этого цикла, которая будет
содержать основные принципы совместного
уравнивания результатов наблюдений по
способу наименьших квадратов.

Типы
погрешностей наблюдений и особенности
их учета

Любое
измерение в реальных условиях производится
с погрешностью, которую можно разделить
на две составляющие — систематическую
и случайную. Систематическая погрешность
возникает в основном из-за ограниченной
точности измерительных приборов,
отчетных механизмов, а так же в связи с
отсутствием учета второстепенных
факторов, влияющих на измерения, или,
если этот учет ведется не корректно.
Систематические погрешности ведут к
одностороннему искажению результатов
наблюдений (постоянное завышение или
занижение значения измеряемой величины).
Их главная особенность — в ходе поверок
инструментов и тестовых измерений
вполне реально выявить такие погрешности
(найти их численные значения и знаки),
и тем самым свести их влияние на результаты
наблюдений к минимуму. Случайные
погрешности появляются из-за
непредсказуемых, хаотичных причин,
искажающих результаты наблюдений. Их
особенность в том, что они приводят к
получению разных значений измерений
при их многократных повторах, проведенных
в одинаковых условиях. Выявить случайные
погрешности из отдельных замеров
практически невозможно, но зато при
достаточном количестве однородных
измерений вполне реально «свести на
нет» их совокупное влияние на результаты
наблюдений. Такое минимизирование
случайных искажений данных основано
на ряде процедур, которые в свою очередь
базируются на выводах и следствиях
теории ошибок. Теория ошибок — математическая
дисциплина, изучающая законы и особенности
«поведения» погрешностей (ошибок)
измерений. Например, нормальное
распределение, эффект взаимной компенсации
по знакам и так далее. Возникла эта
дисциплина, как одно из многочисленных
«ответвлений» от Теории Вероятностей.
Математическая обработка различна для
обоих видов погрешностей. Учет
систематической составляющей есть
процесс почти уникальный для каждого
типа приборов и инструментов, для
различных природных и прочих факторов,
в том числе для каждого отдельного
наблюдателя (так называемая личная
ошибка, которую обычно классифицируют
как подтип систематической составляющей).
Случайные ошибки подчиняются универсальным
законам, которые можно применять не
только при наблюдениях разных объектов
и измерениях разных величин, но и в
разных науках — будь то астрономия,
физика или геодезия. Основные принципы
обработки везде одни и те же. Впрочем
существует еще один класс погрешностей
— грубая ошибка, или ложное измерение.

Точностной
расчет для серии равноточных наблюдений

Рассмотрим
алгоритм первичной обработки серии
равноточных наблюдений. Пусть мы получили
массив замеров измеряемой величины
«Х», который имеет вид: X1, X2, …, Xn,
где n — количество замеров на сеансе.

Находим
среднее арифметическое значение «Х»
на сеансе:

Xs
= ( X1 + X2 + … + Xn ) / n

Рассчитываем
отклонения среднего значения от
измеренных:

d1
= X1 — Xs, d2 = X2 — Xs, …, dn = Xn — Xs

Определяем
среднюю квадратическую погрешность
одного измерения, это параметр, который
характеризует среднюю точность
проведения одного замера:

MX
= SQR ( ( d1 ^ 2 + d2 ^ 2 + … + dn ^ 2 ) / ( n — 1 ) )

Находим
среднюю квадратическую ошибку среднего
арифметического, которая определяет
надежность полученного результата:

MXs
= MX / SQR ( n )

Рассчитываем
относительную погрешность результата
наблюдений:

U
( в процентах ) = ( MXs * 100% ) / Xs

Таким
образом, получаем, что наиболее вероятное
значение измеряемой величины на сеансе
имеет значение:

Xsv
= Xs + MXs

Особенности
точностного расчета для прямых и
косвенных измерений

По
признаку анализирования получаемой
при наблюдении информации, измерения
делятся на прямые и косвенные. При прямых
измерениях значение исследуемой величины
измеряют непосредственно, например
момент или промежуток времени. При
косвенных измерениях, искомую величину
рассчитывают по определенной формуле,
в которую входят величины, измеряемые
непосредственно, а так же заданные
значения вспомогательных величин и
констант, то есть можем записать: Y = F (
X1, X2, …, Xn ), где Y — искомая величина, а X1,
X2, …, Xn — ее аргументы, измеряемые
непосредственно. Пример косвенного
измерения: исходя из снятых отчетов по
окулярному микрометру, впоследствии
переходим к координатам объекта. Важной
задачей при обработке косвенных
наблюдений является определение
погрешности искомой величины по известным
погрешностям величин ее составляющих.
Формула, которая связывает эти параметры,
имеет следующий вид:

MY
= SQR ( ( ( dY / dX1 ) ^ 2 ) * MX1 ^ 2 + ( dY / dX2 ) ^ 2 ) * MX2 ^ 2
+ …
… +
( dY / dXn ) ^ 2 ) * MXn ^ 2 ),

где
( Di / dXi ) — частная производная функции Y
= F ( X1, X2, …, Xn ) по аргументу Xi, вычисленная
в точке Xi.

Пример:
А теперь еще раз «пробежимся» по
описанной выше методики оценки точности
проведенных наблюдений, но уже на базе
конкретного случая. При наблюдениях
деталей на диске Юпитера, на протяжении
ночи были сделаны несколько
зарисовок/фотографий. 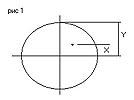На
всех рисунках/фотографиях отмечено
точечное образование, находящееся в
южном полушарии и медленно передвигающееся
параллельно экватору за счет суточного
вращения планеты. Задача: определить
широту наблюдаемого образования — по
всей видимости ядра нового мощного
антициклона, на которые богата бурная
юпитерианская атмосфера. С изображения
Юпитера снимем два линейных значения:
расстояние от экватора (его легко
прочертить учитывая значительное сжатие
планеты) до полюса — Y и расстояние от
экватора до зафиксированного образования.
(см. рис 1). Так как масштаб зарисовок/фотографий
может быть разным, вычислим для всех
изображений относительные значения
величины Х ( Y приравняем к единице).
Далее приводится таблица с примером
вычисления средних квадратических
погрешностей одного наблюдения и всего
результата.

Xs
= 2.88 / 8 = 0.360
MX = SQR ( 0.0114 / 8 — 1 ) = 0.040
MXs =
0.040 / SQR ( 8 ) = 0.014
U = ( 0.014 * 100% ) / 0.360 =
3.889%
Xsv = 0.360 + 0.014, или: 0.346 <= Xsv <= 0.374

Но,
результат получен в относительной
линейной мере. Переход к широте в градусах
осуществляется по формуле: B = ARCSIN ( X / Y
), а с учетом того, что Y — единичный
отрезок: Bs = ARCSIN ( X ) = ARCSIN ( 0.360 ) = 21.1002° =
21° 06.01′ Для вычисления средней квадратической
погрешности определения широты объекта
в градусной мере, воспользуемся выражением
описанным в параграфе о прямых и косвенных
наблюдениях, принимая во внимание, что
Y — константа ( Y = 1 ). Находим производную
функции B ( X ): ( dB / dX ) = 1 / SQR ( 1 — X ^ 2 ).
Вычисляем погрешность результата
наблюдений в градусной мере: MBsv = ( r * MXs
) / SQR ( 1 — Xs ^ 2 ), где r — коэффициент перехода
из радианной меры в градусную ( r = 57.2958
). MBsv = (r * 0.014 ) / SQR ( 1 — 0.360 ^ 2 ) = 0.8598° = 51.59′. U
=( 0.8598 * 100% ) / 21.002 = 4.094%

Итог:
Средняя вероятная широта образования,
зафиксированного на диске Юпитера,
составляет: Bsv = 21° 06.01′ + 51.59′, или: 20°14.42′
<= Bsv <= 21°57.60′.

Все
описанные в этой статье этапы обработки
легко программируются (для нахождения
частных производных можно воспользоваться
одним из численных методов, например
Рунге — Кутта), и поэтому впоследствии
не будут отнимать почти никакого времени
— необходимо только создать массив или
файл исходных данных — значений измеренных
величин. Стоит еще добавить, что точностной
расчет проведенных измерений помимо
своего основного назначения (оценка
надежности исследований) имеет еще и
другую немаловажную роль. Проводя изо
дня в день, из месяца в месяц определенный
вид работ, наблюдатель может следить,
как в динамике прогрессирует (или
регрессирует) достоверность и качество
информации, источником которой он
является, то есть проводить своеобразный
самоконтроль. И будет очень неплохо,
если последняя в этой статье фраза в
скобках так и останется «закрытой».

5.
В технических характеристиках приборов
приведены различные данные диапазонов
измерения
и отображения.
В диапазонах
измерения
наших приборов
представлены пределы измерений
с учетом внешних активных сопротивлений
измерительных проводников стандартной
…

Соседние файлы в папке Лабораторные работы

#
#
#
#
02.05.201416.9 Кб31Расчеты к лабе2.xls

Источник

Математическая теория — ошибка

Cтраница 1

Математическая теория ошибок, применимая исключительно к случайным погрешностям, показывает зависимость точности результата от многократности измерений одной и той же величины.
[1]

В математической теории ошибок доказывается, что ошибка среднего арифметического из п определений в УП раз меньше ошибки единичного определения.
[2]

В математической теории ошибок доказывается, что ошибка среднего арифметического из п определений в — Гп раз меньше ошибки единичного определения.
[3]

В математической теории ошибок рассматриваются только случайные ошибки. Будем предполагать, что систематические ошибки и грубые просчеты совершенно исключены.
[4]

В математической теории ошибок доказывается, что ошибка среднего арифметического из п определений в У п раз меньше ошибки единичного определения.
[5]

Применять математическую теорию ошибок можно только к случайным погрешностям, поэтому до начала обработки результатов измерения этими методами следует исключить все систематические погрешности ц промахи.
[6]

Ответ на это может дать только математическая теория ошибок, с некоторыми основами которой должен быть знаком каждый аналитик.
[7]

Во втором случае численные методы применяются в своей обычной форме численного интегрирования, производящегося при иллюстрации качественных выводов HSL весьма большие промежутки времени, О важнейших примерах такого применения мы будем говорить несколько ниже специально, а теперь отметим только, что подобное использование машинной техники приводит обычно к малообоснованным результатам, что обусловливается постепенным накоплением ошибок численного интегрирования и отсутствием надежных способов контроля, так как математическая теория ошибок численного интегрирования еще только начинает развиваться и пока еще далека от совершенства.
[8]

Случайные погрешности не могут быть устранены, но их влияние может быть учтено. Расчетам случайных погрешностей посвящен целый раздел математической теории ошибок — статистическая оценка результатов анализа.
[9]

Подобный расчет ошибки допустим только при ориентировочных определениях. Для более точных расчетов необходимо пользоваться математической теорией ошибок и вычислять не средние арифметические ошибки, а средние квадратичные ошибки определения.
[10]

Такое же согласование наблюдается и на линии насыщения. Принимая во внимание согласование полученных нами значений плотности аргона с наиболее достоверными данными других авторов как в газообразном, так и в жидком состояниях, а также исходя из общей оценки погрешности измерений на основании математической теории ошибок, погрешность приводимых в табл. 1 данных авторы оценивают как не превышающую 0 1 %; погрешность данных в газообразной области — как не превышающую 0 2 %, причем максимальная погрешность относится к околокритической области.
[11]

Каждая новая область применения математической статистики требует своего особого методического подхода. Опыт, полученный при статистических исследованиях в одной области, нельзя механически переносить на соседние, даже, казалось бы, близкие области. В частности, например, математическая теория ошибок, разработанная, исходя из задач метрологии и геодезии, не может быть без существенного видоизменения перенесена в область аналитической химии.
[12]

Как указывалось в главе I, каждое измерение сопровождается некоторой погрешностью. Следовательно, и результат, найденный на основании каких-то измерений, несмотря на частичную компенсацию погрешностей, будет также не свободен от ошибки. Вычисление возможной величины ошибки результата производят на основании математической теории ошибок, основными приемами которой должен владеть каждый аналитик.
[13]

Как указывалось в § I, каждое измерение сопровождается некоторой погрешностью. Следовательно, и результат, найденный на основании каких-то измерений, несмотря на частичную компенсацию погрешностей, будет также не свободен от ошибки. Вычисление возможной величины ошибки результата производят на основании математической теории ошибок, основными приемами которой должен владеть каждый аналитик.
[14]

Страницы:

Источник

The true value of a measured constant and the theory of errors.
Hist. Scientiarum, vol. 17, 2007, pp. 38 – 48

Введение

Понятие истинное значение было всегда связано с измерениями, и лишь математическая статистика почти изменила это положение. Впрочем, появилось оно, видимо, только в эпоху градусных измерений в конце XVII в. Наше второе понятие, теория ошибок, мы определяем как статистический метод (или сама статистика) в приложении к обработке наблюдений в экспериментальной науке. Её определение, принятое в математике (Никулин 1999), вводит в заблуждение, поскольку ограничивает её рассмотрением нормального распределения. Сам термин теория ошибок ввёл Ламберт в 1765 г.

Среднее арифметическое и истинное значение

Picard (1693/1729, с. 330, 335, 343) первым назвал среднее арифметическое истинным(véritable) значением (измеренного угла триангуляции). Следующим и более подробным автором был Ламберт. Вначале он (1760, § 286) заявил, что

Поскольку погрешности встречаются тем чаще, чем они меньше, в каждом данном случае повторных экспериментов более часто появляющиеся величины ближе расположены к среднему значению, или также к истинному значению.

В § 290 он добавил, что погрешность среднего арифметического намного меньше, чем у отдельного наблюдения и что поэтому среднее арифметическое ближе к истинному значению. Затем Ламберт (1765, § 3) убеждал, что ошибки наблюдения, говоря современным языком, обладают чётной плотностью распределения вероятностей:

Среднее большого числа экспериментов должно перемещаться тем ближе к истине, чем больше экспериментов повторено. Ибо, среди всех случаев, которые только можно представить себе, наиболее вероятен тот, при котором равные крупные отклонения в ту и другую сторону происходят одинаково часто.

Он, как и некоторые позднейшие авторы, см. ниже, молчаливо, но почти прямо предположил, что плотность одновершинна и не относится к плохим, типа распределения Коши, при котором одно наблюдение не хуже среднего. Но, конечно же, Ламберт ничего не обосновал. Только Симпсон в 1756 г. по существу доказал второе утверждение Ламберта, да и то лишь для двух распределений.

Стремление среднего к значению соответствующего теоретического параметра теперь называется свойством состоятельности, которое имеет место для линейных оценок вообще; впрочем, это замечание вряд ли имеет значение для нас.

Следующим автором был Лаплас. Он (1795/1912, с. 161) утверждал, что при неограниченном возрастании числа наблюдений их среднее стремится к определённому числу, так что

Если неограниченно увеличивать число наблюдений или экспериментов, их средний результат будет стремиться к постоянному члену. Поэтому, если взять по обе его стороны сколь угодно малый интервал, то вероятность, что средний результат окажется в нём, в конце концов будет отличаться от уверенности меньше любой назначенной величины. Этот член и есть сама истина, если только положительные и отрицательные ошибки равновероятны.

Лаплас (1810а/1898, с. 303) дословно повторил это высказывание, и примерно в то же время (1810b/1979, с. 110/272) сообщил то же самое чуть в иной форме: не сама истина, а сливается с истиной. А в своём Опыте (1814/1999, с. 843 правый столбец), первоначальным наброском которого были его Лекции 1795 г., мы находим: Чем многочисленнее наблюдения, и чем менее они расходятся, тем ближе их результаты к истине. Он добавил, что наилучшие средние результаты определяются при помощи теории вероятностей. Известно, что Лаплас усиленно пропагандировал метод наименьших квадратов (МНКв) и был одним из его создателей (создателем его практически почти не применимого варианта), так что здесь, обсуждая случай одного неизвестного, он, конечно же, имел в виду среднее арифметическое.

Гаусс (1809, § 177), в своём первом обосновании принципа наименьших квадратов, предположил, в частности, что среднее арифметическое является вероятнейшим значением искомой константы или близким к нему. Вслед за Лапласом Пуассон (1811, с. 136; 1824, с. 297; 1829, с. 12 и 19) применял термин истинное значение (vraie valeur) и по существу заявил, что это значение является средним из бесконечно большого количества измерений.

Определение

Формальное определение предложил Фурье (1826/1890, с. 533 – 534):

Предположим […], что собрано большое число наблюденных значений [некоторой константы] и что их сумма разделена на [их] число […], что дало для среднего значения величину А; мы уже заметили, что почти то же самое значение А будет определено при применении очень большого числа других наблюдений. Вообще, если исключить особые и отвлеченные случаи, которые мы совсем не будем рассматривать, выведенное подобным образом среднее значение из громадного числа наблюдений нисколько не изменяется. Оно имеет определенную величину Н, и можно сказать, что средний результат бесконечного числа наблюдений есть неизменное количество, в котором больше нет ничего случайного и которое имеет достоверное отношение к сути наблюденных событий. Именно эту неизменную величину Н мы имеем в виду как истинный объект исследования.

Мы не нашли ни единой ссылки на это высказывание; возможно, впрочем, что оно считалось очевидным. Многие авторы по сути повторяли его независимо и друг от друга, и, видимо, от Фурье: Гаусс, во всех своих сочинениях по обработке наблюдений; Пуанкаре (1896/1999, § 113, с. 145); Марков (1899/1951, с. 250); Whittaker & Robinson(1924/1958, с. 215 прим.); Колмогоров (1946, название § 7). И только Марков (1900/1924, с. 323) с присущей ему строгостью заметил, начиная свою главу о МНКв, что

Прежде всего необходимо допустить существование числа, приближённые величины которых доставляются наблюдениями.

Аналогичное замечание о неизвестной вероятности Марков привёл на с. 352; первое появилось во всяком случае в издании 1908 г., второе – в 1913 г.

Вероятность (см. выше) не существует в реальном мире, по крайней мере в обычном смысле, и это обобщение понятия истинного значения существенно для естествоиспытателей, хотя и не для чистого математика-Маркова. Гаусс (1816, §§ 3 и 4), который был и тем и другим, многократно рассматривал истинные значения меры точности наблюдений, см. также соответствующее высказывание Фишера и других авторов в нашем §4.

Заметим нежелание Маркова выходить за пределы математики: он так и не упомянул истинного значения; напомним, что он не привёл ни одного примера приложения своих цепей в естествознании.

Определение Фурье эвристически напоминает знаменитое определение вероятности по Мизесу. Вот что последний (1919/1964, с. 40 и 46) заявил, во многом повторив своего предшественника (и самого себя):

Истинное среднее значение наблюдения (т. е. такое, которое должно появиться как среднее, если ряд наблюдений продолжать до бесконечности) […].

Истинное среднее значение является лишь величиной, которая должна появиться по определению понятия вероятности как среднее арифметическое, когда серия извлечений продолжается до бесконечности.

В 1919 г. соответствующие страницы были 80 и 87. Именно в указанном сочинении Мизес впервые ввёл свою частотную теорию. Иначе говоря, он ввёл понятие вероятности (Wahrscheinlichkeitsbegriff) как её частотное определение. Теперь, извлечения: пусть урна содержит белые и чёрные шары и m белых шаров и n чёрных было извлечено с возвращением по одному. Тогда, как утверждал Мизес, отношение m/n приближается к неизвестному соотношению белых и чёрных шаров. Он таким образом пояснил, но прямо не определил связи истинного значения и частотной вероятности.

Обратимся теперь к автору (Eisenhart 1963/1969, с. 30 – 31), обсуждавшему метрологию, важную научную дисциплину, которую вряд ли затрагивают статистики при их (редком) упоминании теории ошибок:

Истинное значение некоторой величины […] – это предельное среднее в мыслимом образцовом процессе. […] Масса стандарта массы […] определяется […] как масса металлического содержания стандарта плюс масса среднего объёма воздуха, адсорбированного его поверхностью при стандартных условиях. Я надеюсь, что в теории и практике измерений традиционный термин истинное значение будет отброшено и заменено более подходящим, как, например, искомое (target) значение.

Итак, Эйзенхарт по существу повторил Фурье, но он явно указал (как это должно было быть ясно с самого начала), что остаточная систематическая ошибка включается в истинное значение. Далее, образцовый процесс в метрологии подразумевает постоянство внешних условий, но в практической астрономии и геодезии наблюдать следует при различных (но благоприятных) условиях, чтобы по возможности исключать систематические погрешности. Надежда Эйзенхарта не осуществилась, хотя определённый смысл в ней был: отказ от философских терминов.

Математическая статистика

Считается, что математическая статистика отказалась от истинных значений, заменив их параметрами плотности (или функций распределения). Действительно, Фишер (1922, с. 309 – 310) ввёл понятия состоятельности, эффективности и достаточности статистических оценок без всяких ссылок на теорию ошибок или истинные значения. Но на следующей же странице мы читаем:

Чисто словесная путаница помешала чётко формулировать статистические задачи, ибо обычно [Биометрическая школа] применяет то же название среднее, стандартное отклонение, коэффициент корреляции и т. д. и для истинного значения, которое мы хотели бы узнать, но можем лишь оценивать, и для частного значения, которого удаётся достичь нашими методами оценивания.

Итак, истинное значение было ещё живо в математической статистике. Вот ещё несколько примеров. Словарь (Александров 1962) упоминал истинную корреляцию, истинные средние и значение. Болшев (1964, с. 566) рассматривал истинное значение параметра. Он комментировал Бернштейна (1941/1964), который обсуждал истинную вероятность неравенства (§ 5, с. 390). И вот наш современник Hald (1998, с. 91): До сих пор мы рассматривали только оценку истинного положения параметра сдвига… И он неоднократно упоминал истинные значения в главах 5 и 6. Так же поступали другие авторы (Уилкс 1962, § 101) и, позже, снова Хальд (Hald 2007, c. 105).

Но существует и неверное мнение о ненужности обсуждаемого нами термина (Chatterjee2003, с. 264):

Методы теории ошибок редко применялись вне этих узких областей [астрономии и геодезии] и синдром истинного значения в конце концов был оставлен.

Будем великодушны и скажем, что автор написал узкие (narrow), имея в виду ограниченные, и что о метрологии он позабыл. Но есть ведь и геофизика (магнетизм, ускорение силы тяжести), есть физика (скорость света в пустоте, масса электрона). Далее (с. 273), Кетле будто бы сдерживался синдромом истинного значения, и, что следовало косвенно, уклонения были для него менее важны. Кетле повинен во многих грехах, но только никак не в этом (Шейнин 1986), см. также § 5.

Синдром означал мнение или поведение, типичное либо для данного человека, либо при обсуждении некоторой проблемы (есть и чисто медицинское определение), и какой-то синдром мы усматриваем у самого автора! Наконец, поскольку Chatterjee (с. 248 – 249) всё ещё верит в существование мифической теоремы Гаусса – Маркова [iv, § 6.12], мы сомневаемся, что он достаточно знаком с историей статистики (и особенно с историей обработки наблюдений).

Промежуточная стадия

Обычно Гальтон считается первым, кто отошёл от истинных значений (и теории ошибок вообще). Так (Eisenhart 1978, с. 382), в 1908 г. он указывал:

Основные цели гауссового закона ошибок в некотором смысле точно противоположны моим. Они были направлены на исключение или принятие в расчёт погрешностей, но эти ошибки или уклонения были именно тем, что я хотел сохранить и про что выяснить.

Закон ошибок здесь не при чём, а теория ошибок стремится уменьшить влияние погрешностей. Высказывание Гальтона интересно лишь тем, что он противопоставил Гаусса статистике. Но существовала и промежуточная стадия между математической статистикой и теорией ошибок, и формально начало ей положил Кондорсе (1805/1986, с. 604):

Теория средних значений […] является введением к социальной математике. […] В каждой физической и математической науке одинаково полезно иметь средние значения наблюдений или результатов экспериментов.

На той же странице он определённо отделил эту теорию от теории исчисления вероятностей, но не пояснил этой мысли и не определил новую теорию. Он (с. 555 – 559) также рассуждал о связи среднего арифметического (только для конечного числа измерений) и неизвестного истинного значения и заметил (с. 555), что следует различать два вида средних, см. ниже. Вообще же соображения Кондорсе следует воспринимать крайне осторожно. В приложении теории вероятностей к судебной статистике неопределённость и противоречивость [его рассуждений] не имеет равных (Todhunter 1865, с. 352). В самой теории вероятностей он следовал за Даламбером, см. его письмо французскому государственному деятелю Тюрго 1772 г. (Henry 1883/1970, с. 97 – 98), чьи потрясающие ошибки хорошо известны, а про его биографии Эйлера и Даниила Бернулли лучше умолчать.

Но теория средних величин действительно возникла, хотя быть может только в мыслях учёных. Она представлялась общее теории ошибок, потому что дополнительно исследовала средние из переменных величин или состояний, и только в этом смысле мы её признаём.

Вот одно из соответствующих утверждений Кетле (1846, с. 65):

Принимая средние, можно иметь в виду две вполне различные вещи. Можно стараться определить число, которое реально существует, но можно и вычислять число, которое даёт нам наиболее близкое возможное представление о многих однородных объектах, отличающихся друг от друга по величине.

То же сказал несколько позже Давидов (1857, с. 14), который добавил (с. 16), что различие существенно только в связи со свойствами уклонений от среднего. Изучение средних значений или состояний, а не истинных значений, но также и не законов распределения вероятностей, было необходимой стадией в развитии естественных наук [viii, § 4.1]. Сошлёмся теперь на Гильберта (1901/1969, Проблема № 6), одного из последних учёных, упомянувших теорию средних значений, которая больше заведомо не существует; как промежуточную, её поделили статистика (к которой её отнёс уже Кетле) и теория ошибок.

В астрономии отход от промежуточной стадии яснее всего, видимо, выразил Каптейн (1906, с. 397):

Так же, как физик […] не может надеяться проследить ни за какой отдельной молекулой в её движении, но всё же может вывести важные заключения, как только определит среднюю скорость всех молекул и частоту установленных отклонений от этого среднего, так же […] наша основная надежда будет состоять в определении средних и частот.

Выводы

Известно, что развитие математики было неизменно связано с её непрестанным удалением от природы (например, от натуральных чисел к действительным, а затем к мнимым числам), и что чем дальше, тем она становилась абстрактнее, и тем полезнее оказывалась для своих приложений. В частности, общий переход от истинных значений к оценкам параметров функций в математической статистике был шагом в верном направлении.

Но подчеркнём, что наука измерения реальных объектов и обработки собранных наблюдений вовсе не отказалась от истинных значений и что даже сама статистика их не забыла. Что Мизес (§ 3) также нашёл возможным определить истинное значение (правда, не формально) и косвенно связать его со своей теорией, явно подкрепило нашу точку зрения. Конечно, его теория относится к естествознанию, а не к математике, но ведь и теория ошибок лишь частично относится к последней. Утверждение Chatterjee (§ 4) и, возможно, аналогичное мнение других авторов следует отвергнуть.

Идеи и методы математической статистики должны быть в какой-то степени восприняты в теории ошибок, и в первую очередь мы имеем в виду оценку точности. О теории корреляции и дисперсионном анализе также нельзя забывать, но они в нашем контексте не появлялись.

Библиография

Александров П. С., редактор (1962), Англо-русский словарь математических терминов. М.

Бернштейн С. Н. (1941), О доверительных вероятностях Фишера. В книге автора (1964, с. 386 – 393).

— (1964), Собрание сочинений, т. 4. Без места.

Большев Л. Н. (1964), Комментарий к статье Бернштейн (1941). В книге Бернштейн (1964, с. 566 – 569).

Гаусс К. Ф. (1809, латин.), Теория движения небесных тел. В книге Гаусс (1957, с. 89 – 109).

— (1816, нем.), Определение точности наблюдений. Там же, с. 111 – 120.

— (1957), Избранные геодезические сочинения, т. 1. М.

Гильберт Д. (1901, нем), Проблемы Гильберта. М., 1969.

Давидов А. Ю. (1857), Теория средних величин. Речи и отчёт, произнесённые в торж. собр. Моск. унив. М., отдельная пагинация.

Колмогоров А. Н. (1946), К обоснованию метода наименьших квадратов. Успехи математич. наук, т. 1, с. 57 – 71.

Марков А. А. (1899), Закон больших чисел и способ наименьших квадратов. В книге автора (1951, с. 231 – 251).

— (1900), Исчисление вероятностей. М., 1924.

— (1951), Избранные труды. Без места.

Никулин М. С. (1999), Случайная ошибка. В книге Прохоров (1999, с. 587).

Прохоров Ю.В., редактор (1999), Вероятность и математическая статистика. Энциклопедия. М.

Пуанкаре А. (1896, франц.), Теория вероятностей. Ижевск, 1999.

Шейнин О. Б., Sheynin O. B. (1986), Quetelet as a statistican. Arch. Hist. Ex. Sci., vol. 36, pp. 281 – 325.

Уилкс С. С. (1962, англ.), Математическая статистика. М., 1967.

Chatterjee S. K. (2003), Statistical Thought: a Perspective and History. Oxford.

Condorcet M. J. A. Caritat de (1805), Elémens du calcul des probabilités et son application aux jeux de hasard, a la loterie, et aux jugemens des hommes. In author’s book Sur les élections et autres textes. No place, 1986, pp. 483 – 623.

Eisenhart C. (1963), Realistic evaluation of the precision and accuracy of instrument calibration systems. In Ku, Editor (1969), Precision Measurement and Calibrations. Washington, pp. 21 – 47.

— (1978), Gauss. In Kruskal W., Tanur Judith M., Editors. Intern. Enc. of Statistics, vols 1 – 2. New York, single paging, pp. 378 – 386.

Fisher R. A. (1922), On the mathematical foundations of theoretical statistics. Phil. Trans. Roy. Soc., vol. A222, pp. 309 – 368.

Fourier J. B. J. (1826), Sur les résultats moyens déduits d’un grand nombre d’observations. Oeuvr., t. 2. Paris, 1890, pp. 525 – 545.

Hald A. (1998), History of Probability and Statistics and Their Applications from 1750 to 1930. New York.

— (2007), History of Parametric Statistical Inference from Bernoulli to Fisher, 1713 – 1935. New York.

Henry M. Ch. (1883), Correspondance inédite de Condorcet et de Turgot. Genève, 1970.

Kapteyn J. C. (1906), Statistical methods in stellar astronomy. [Reports] Intern. Congr. Arts & Sci. St. Louis – Boston 1904. No place, vol. 4, pp. 396 – 425.

Lambert J. H. (1760, in Latin), Photometria. Augsburg. Соответствующий материал не был включен в немецкий перевод книги в серии Ostwald Klassiker. Цитата в тексте переведена с немецкого перевода отрывка в книге Schneider (1988, p. 228).

— (1765), Theorie der Zuverlässigkeit der Beobachtungen und Versuche. In author’s Beyträge zum Gebrauche der Mathematik und deren Anwendung, Tl. 1. Berlin, pp. 424 – 488.

Laplace P. S. (1795), Leçons de mathématiques. Oeuvr. Compl., t. 14. Paris, 1912, pp. 10 – 177.

— (1810a), Sur les approximations des formules qui sont fonctions de très grands nombres et sur leur application aux probabilités. Ibidem, t. 12. Paris, 1898, pp. 301 – 345.

— (1810b), Notice sur les probabilités. In Gillispie C. C. (1979), Mémoires inédites ou anonymes de Laplace. Revue d’histoire des sciences, t. 32, pp. 223 – 279.

— (1814, франц.), Опыт философии теории вероятностей. В книге Прохоров 1999, с. 834 – 863).

Mises R. von (1919), Fundamentalsätze der Wahrscheinlichkeitsrechnung. Math. Z., Bd. 4, pp. 1 – 97. Partly reprinted in author’s Selected Papers, vol. 2. Providence, Rhode Island, 1964, pp. 35 – 56.

Picard J. (1693), Observations astronomiques faites en divers endroits du royaume en 1672, 1673, 1674. Mém. Acad. Roy. Sci. 1666 – 1699, t. 7, 1729, pp. 329 – 347.

Poisson S.-D. (1811), Review of a memoir of Laplace. Nouv. bull. sciences. Soc. philomatique Paris, t. 2, No. 35, pp. 132 – 136.

— (1824), Sur la probabilité des résultats moyens des observations. Connaissance des tems pour 1827, pp. 273 – 302.

— (1829), Second part of same. Ibidem pour 1832, pp. 3 – 22 of second paging.

Quetelet A. (1846), Lettres sur la théorie des probabilités. Bruxelles.

Schneider I., Herausgeber (1988), Die Entwicklung der Wahrscheinlichkeitstheorie von den Anfängen bis 1933. Darmstadt.

Todhunter I. (1865), History of the Mathematical Theory of Probability. New York, 1949, 1965.

Whittaker E.T., Robinson G. (1924), The Calculus of Observations. London – Glasgow, 1958. Уиттекер Э., Робинсон Г. (1935), Математическая обработка результатов наблюдений. М.

Оригинал: https://7i.7iskusstv.com/y2022/nomer5/oshejnin/

Отдав голос за данное произведение, Вы оказываете влияние на его общий рейтинг, а также на рейтинг автора и журнала опубликовавшего этот текст.

Источник

Содержание:

Ошибки измерения: Опыт убеждает, что измерения объектов не могут быть произведены абсолютно точно и каждое конкретное измерение дает лишь, как правило, приближенное значение величины явления, истинное значение которой (A) нам неизвестно. Ошибки измерения (

Рассмотрим такие измерения, которые производятся одним наблюдателем, одним и тем же инструментом, в одинаковых условиях, т. е. равноточные измерения.

Различают два вида ошибок измерения:

систематические ошибки, т. е. такие, которые при данных условиях проведения измерения имеют вполне определенное значение (например, ошибка измерительного прибора);
случайные — такие, которые являются результатом взаимодействия большого числа незначительных в отдельности факторов и имеют в каждом отдельном случае различные значения.

Задача математической статистики — предусмотреть возможность возникновения систематических ошибок и добиться их ликвидации или сведения к минимуму.

Случайные ошибки измерения обладают рядом свойств: при большом числе измерений крупные ошибки встречаются реже мелких и число положительных ошибок примерно равно числу отрицательных, вследствие чего сумма всех ошибок близка к нулю.

Если ошибки получаются весьма малыми по сравнению с величиной явления, то ими просто пренебрегают или считаются с наибольшей возможной ошибкой, чтобы обезопасить себя от влияния случайной неточности.

В теории ошибок изучаются те ошибки, которые, являясь, с одной стороны, ошибками случайного характера, по своему абсолютному значению настолько велики, что ими пренебречь нельзя, а с другой стороны, для них существует закон, позволяющий установить зависимость между величиной ошибки и вероятностью ее появления. Закон случайных ошибок, полученный Гауссом, состоит в том, что случайные ошибки подчиняются закону нормального распределения.

Средняя ошибка сводного результата измерения

Принимая за действительное значение измеряемой величины при равноточном измерении среднюю арифметическую из всех результатов n измерений, можно охарактеризовать точность одного измерения с помощью средней арифметической из абсолютных величин значений ошибок:

где n — число измерений, х — численное значение отдельных измерений, — средняя арифметическая из результатов измерений.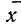

За меру точности соответствия принятой средней арифметической 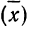истинному значению измеряемой величины (A) принимают среднюю ошибку сводного результата измерения, вычисляемую по формуле:

Пример 1. Произведено 10-кратное измерение размера детали (в мм), давшее следующие, расположенные в возрастающем порядке результаты: 138; 139; 140; 141; 141; 142; 142; 143; 144; 145.

Охарактеризуем сначала точность одного измерения, т. е. вычислим среднюю арифметическую из абсолютных значений ошибок. Для этой цели вычислим среднюю арифметическую из результатов измерений:

Найдем ошибки измерения:

Следовательно:

Теперь можно вычислить среднюю ошибку сводного результата измерения:

Значит, мерой точности соответствия 141,5 мм истинной величине размера детали является средняя ошибка, равная 0,54 мм.

Средняя квадратическая ошибка

Если в качестве меры точности одного измерения принять не среднюю арифметическую из абсолютных значений ошибок (средняя ошибка), а среднюю квадратическую из ошибок измерений, т. е.

то средняя квадратическая ошибка найденной средней арифметической из ошибок измерения вычисляется по формуле:

Между средней -квадратической ошибкой и средней ошибкой сводного результата измерения существует связь: 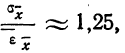если случайные ошибки подчиняются Гауссову закону нормального распределения.

Пример 2. Используя данные предыдущего примера, находим меру точности одного измерения, т. е. среднюю квадратическую ошибку:

Затем исчисляем среднюю квадратическую ошибку найденной средней арифметической, равной 141,5 мм:

Сопоставляя среднюю квадратическую ошибку сводного результата измерения со средней ошибкой, получаем:

Вероятная ошибка

За меру точности одного измерения иногда принимают вероятную ошибку:

Тогда в качестве вероятной ошибки сводного результата измерения используют соотношение:

Пример 3. Используя данные предыдущих примеров, находим вероятную ошибку сводного результата измерения:

Наиболее вероятные границы сводных результатов измерения

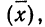
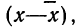
Математическое ожидание случайной ошибки равно нулю. В качестве значения измеряемой величины применяется средняя арифметическая всех измерений (если они равноточны). Использование отклонений результатов измерений (х) от средней из них называемых в теории ошибок «кажущимися ошибками» позволяет произвести оценку точности соответствия средней арифметической неизвестному истинному значению измеряемой величины (A).

Для этой цели используют удвоенную или утроенную среднюю квадратическую ошибку сводного результата измерения или его вероятную ошибку и получают:

Найденные границы неизвестной истинной величины в случае, если ошибки подчинены нормальному закону распределения Гаусса (чаще всего так и бывает), соблюдаются с большой вероятностью (0,997 и 0,954).

Пример 4. По данным предыдущих примеров находим границы истинного значения размера детали 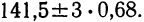Значит, истинное значение размера детали находится в границах от 141,5—2,04 до 141,5+2,04.

Методы математической статистики
Комбинаторика — правила, формулы и примеры
Классическое определение вероятности
Геометрические вероятности
Законы распределения случайных величин
Дисперсионный анализ
Математическая обработка динамических рядов
Корреляция — определение и вычисление

Источник