Муниципальное казенное общеобразовательное учреждение
«Средняя общеобразовательная школа №1» г. Поворино
Тема проекта:
«Анализ математических ошибок, приведших к катастрофам»
Проект по математике
ученицы 9б класса
Федосовой Валерии
Научный руководитель. учитель:
Карташова С. А.
Предмет математика
г. Поворино
2020-2021 учебный год
Содержание…………………………………………………………………….2
Введение……………………………………………………………………….3
Глава I Основная
часть………………………………………………………..4
§ 1. Анкетирование………………………..………..…………………………….4
§ 2. Десять
простых, но дорогостоящих математических ошибок в истории…………………………….….…………………………..……………5
§ 3. Математические ошибки,
которые привели к значительным катастрофам……………………………………………………………………11
Заключение…………………………………………………………………………16
Список использованных источников и литературы ………………………….17
Введение
В математических
вопросах
нельзя
пренебрегать даже
самыми мелкими
ошибками.
И. Ньютон
Мне хотелось бы сказать
вначале: «Дети! Учите математику! Потому что когда вы станете взрослыми, одна
маленькая ошибка может стоить жизни многим людям». Не верите? В своем проекте я
попытаюсь это доказать.
Гипотеза: математическая
ошибка может привести как к курьёзным ситуациям, так и к серьёзным проблемам
(авариям, катастрофам, разрушениям).
Тема моей работы: «Анализ Математических
ошибок, приведших к катастрофам».
Цель: собрать
информацию о последствиях математической ошибки; показать значимость
математической ошибки.
Задачи:
• исследовать типичные
ошибки одноклассников;
• провести анкетирование
среди одноклассников на тему «К чему может привести математическая ошибка?»;
• найти примеры ошибок,
которые приводили к курьёзным ситуациям;
•найти в Интернете ответ
на вопрос: были ли случаи, когда математические ошибки, повлекли за собой
серьёзные проблемы: катастрофы, аварии, разрушения.
Методы
исследования:
• изучение источников:
литературы, энциклопедий, сайтов в Интернете;
• наблюдения,
сопоставления;
• анализ и классификация
ошибок в работах учащихся 9 класса;
• отбор и классификация
материала.
Глава
I Основная часть.
Человечество
ошибается — и делает это отнюдь не редко. Когда дело касается крупных строений
или сложной техники, даже малейший огрех может привести к катастрофе.
Расплачивается же за это жизнью не сам конструктор, а доверившиеся его работе
люди. В истории бывали случаи, когда чудовищные катастрофы возникали
вследствие, казалось бы, небольших ошибок или чьей-то непредусмотрительности.
Иногда в этих катастрофах оказывались виноваты конкретные люди, отвечавшие за
безопасность и допустившие небрежность, иногда несчастье происходило в результате
череды маловероятных совпадений.
Минимальная
ошибка в расчетах может обернуться катастрофой, если речь идет о точных науках.
Здесь нет места словам «примерно» и «приблизительно». Одна
маленькая ошибка может стоить жизни многим людям.
Если вы считаете,
что это пустые слова, то я приведу реальные истории, которые подтверждают нашу
тревогу.
1. Анкетирование
Я провела
анкетирование среди одноклассников. В нем приняли участие 43 ученика
(Приложения №1 и №2). Обучающимся 9-х классов было предложено ответить на
следующие вопросы:
1.
Как часто
на уроках математики вы допускаете ошибки?
2.
Задумывались
ли вы о последствиях математической ошибки?
3.
Знакомы
ли вам примеры, когда математическая ошибка привела к катастрофе?
4.
Подумайте
и запишите, к чему может привести математическая ошибка?
5.
Хотели бы
вы познакомиться с курьёзными случаями математических ошибок?
На вопрос «Как
часто на уроках математики вы допускаете ошибки?» ответили «часто» и «почти
всегда» — 37 человек. На вопрос «Задумывались ли вы о последствиях математической
ошибки?» ответили «нет» — 39 человек. На вопрос «Знакомы ли вам примеры, когда
математическая ошибка привела к катастрофе?» ответили «нет» — 39 человек. На
вопрос «Хотели бы вы познакомиться с курьёзными случаями математических
ошибок?» ответили положительно – 41 человек. Анкетирование показало, что
школьники не задумываются о последствиях математической ошибки.
Наблюдения на
уроках математики и анализ ошибок в тетрадях одноклассников показал, что
ошибками могут стать неправильные расчёты, неправильное применение определений,
аксиом, теорем, незнание формул, правил. Ряд ошибок одноклассники допускают
из-за неразборчивого почерка, неаккуратно выполненного чертежа, по невнимательности.
Некоторые ошибки носят курьёзный характер.
Начну с простого.
2. Десять простых, но дорогостоящих
математических ошибок в истории.
Многие ненавидят
математику, хотя мир работает на математике. Огромные суммы денег и
оборудование стоимостью в миллионы долларов были потеряны просто потому, что
кто-то допустил небольшую математическую ошибку. Компьютеры также допускают
подобные ошибки, но в них можно винить людей, так как именно они занимались
программированием.
Чтобы было ясно,
некоторые бедствия были вызваны ошибками, связанными со сложной математикой,
которая, возможно, проще, чем, кажется. Тем не менее, здесь, в основном,
смехотворно простые ошибки, которые даже ученик начальной школы не мог бы
допустить.
2. 10. Атака ракет типа
«Скад» в войне в Персидском заливе
25 февраля 1991
года иракская ракета «Скад» нанесла удар по базе армии США в Даране, Саудовской
Аравии, убив 28 солдат и ранив ещё 100. Катастрофа была неожиданной, если
учесть, что база была защищена системой ПВО «Патриот». Расследования показали,
что система не пыталась перехватить «Скад».
Ошибка была
связана с программным обеспечением, питающим часы системы. Часы записывали
время в десятых секундах (одна десятая секунды), но сохраняли эти данные в виде
целого числа. Для этого они преобразовывали время в 24-битное число с плавающей
точкой. Однако округление времени при их преобразовании привело к постепенному
увеличению погрешности в работе системы. В результате система не смогла
перехватить ракеты после 20 часов непрерывного использования.
Во время атаки
рассматриваемая ракетная батарея «Патриот» проработала 100 часов. Разница во
времени была такова, что она искала не в той части неба входящую ракету и
поэтому не нашла цели.
Армия США была
проинформирована об этой проблеме с программным обеспечением и выпустила
обновление 16 февраля. Обновление достигло базы в Дхаране 26 февраля, на
следующий день после атаки.
2.9. Испанская программа
подводных лодок S-80
В 2003 году
Испания запустила программу подводных лодок S-80 на сумму 2,7 миллиарда
долларов для строительства четырёх дизель-электрических подводных лодок для ВМС
Испании. Испания почти завершила строительство одной из них в 2013 году, когда
обнаружила, что лодка на 70 тонн тяжелее, чем должна была быть. Испанский флот
боялся, что подводная лодка никогда не всплывёт, если уйдёт под воду.
Подводная лодка
оказалась тяжёлой после того, как кто-то поставил десятичную точку в
неправильном месте во время вычислений. Никто не обнаружил ошибку, пока первая
субмарина не была закончена, а остальные три уже строились. Позже Испания
подписала контракт на 14 миллионов долларов с Electric Boat из Гротона, штат
Коннектикут, чтобы те помогли им снизить вес 2200-тонной подводной лодки.
2.8. Рейс 143Air Canada
В июле 1983 года
самолёт Boeing 767 Air Canada, летевший из Оттавы в Эдмонтон с 69 пассажирами и
членами экипажа, вынужден был совершить аварийную посадку после того, как
закончился запас топлива на высоте 12500 м. Двигатели внезапно потеряли
мощность, и самолёт начал снижаться к земле. Он пролетел 100 километров до
посадки в Гимли, Манитоба.
Он приземлился на
ипподроме, который изначально был взлётно-посадочной полосой. К счастью, никто
не погиб. Однако два человека получили лёгкие травмы, а носовая часть была
разрушена. Эта посадка принесла Рейсу 143 прозвище «Планёр Гимли».
Авария была
связана с ошибкой преобразования. Air Canada использовала британскую систему
мер, но перешла на метрическую, которую уже использовал этот Boeing 767.
Наземные экипажи Air Canada использовали британскую систему при заправке
самолёта. Они измеряли топливо в фунтах вместо килограммов.
Один килограмм равен
2,2 фунта. Это означало, что у самолёта было всего около половины количества
топлива, необходимого для завершения полёта. Пилоты не заметили расхождений,
потому что датчик топлива не работал. Наземные экипажи использовали капельные
палочки для измерения топлива во время заполнения резервуаров.
Интересно, что
наземные экипажи ошиблись дважды. Первый раз в Монреале, а второй – в Оттаве.
Самолёт совершил перелёт из Монреаля в Оттаву без происшествий, но буквально
столкнулся с проблемами, когда летел из Оттавы в Эдмонтон.
2.7.Потопление «Вазы»
10 августа 1628
года Швеция запустила новый, хорошо вооружённый и большой военный корабль:
«Ваза». Судно едва проплыло 20 минут, когда затонуло менее чем в миле от
берега. Тридцать человек погибли в результате потопления. Корабль был позже
найден в 20-м веке и сейчас хранится в Музее Вазы.
Историки измерили
весь корабль и обнаружили, что его строители использовали две разные единицы
измерения. Одной был шведский фут, а другой – амстердамский фут. Шведский фут
составляет 30,48 см, в то время как амстердамский – 27,94 см.
Разница между
обеими единицами измерения привела к тому, что одна сторона оказалась тяжелее
другой. Вот почему корабль наклонился в сторону и быстро затонул после того,
как по нему ударили два порыва ветра. Историки добавляют, что влияние ветра
было усугублено тем фактом, что верх корабля был тяжелее его дна.
2.6. Крушение Mars Climate
Orbiter.
Mars Climate
Orbiter был совместным проектом компании Lockheed Martin и NASA / JPL
стоимостью 125 миллионов долларов. Проект получил неловкое завершение, когда
орбитальный аппарат, скорее всего, потерпел крушение на Марсе из-за простой
ошибки преобразования в 1999 году. Lockheed Martin использовал британскую
систему мер при программировании программного обеспечения, но НАСА использовало
метрическую систему.
Инженеры НАСА
обнаружили бы ошибку, если бы обратили внимание. Однако они этого не сделали.
Никто не понимал, что что-то не так во время девятимесячного путешествия Mars Climate
Orbiter на Марс. Ошибка стала очевидной только тогда, когда НАСА потеряло связь
с орбитальным аппаратом.
В ответ на
инцидент Джон Логсдон из Института космической политики Университета имени
Джорджа Вашингтона сказал, что всё это было «глупо». Джон Пайк из Федерации
американских учёных добавил: «Было неловко потерять космический корабль из-за
такой простой математической ошибки».
2.5.Взрыв ракеты Ariane 5
4 июня 1996 года
ракета Ariane 5 Европейского космического агентства взорвалась через 37 секунд
после взлёта. На борту космического корабля находились четыре спутника. Ракета
и спутники стоили 370 миллионов долларов. Авария была связана с целочисленной
ошибкой переполнения в программном обеспечении, используемом для запуска
ракеты.
Целочисленное переполнение
– это математическая ошибка, которая возникает, когда числа, сгенерированные
системой, превышают объём памяти этой системы. Ariane 5 работала на 16-битном
программном обеспечении, способном хранить числа до 32767. Ракете удалось
создать числа намного больше этого.
Европейское
космическое агентство использовало то же программное обеспечение, что и в
ракетах Ariane 4. У них были проблемы с Ariane 5, потому что она была быстрее,
чем Ariane 4. Чем быстрее, тем больше числа. Программное обеспечение не может
обрабатывать большие показания, из-за чего ракета становится негодной. Наземный
контроль приказал самоуничтожиться.
2.4. Выплата дивидендов и
выкуп акций Банка Америки
Федеральная
резервная система регулярно заставляет банки проходить стресс-тесты. Стресс-тест
– это анализ финансового состояния банка в условиях стимулированной негативной
экономической ситуации. Стресс-тесты необходимы, чтобы определить, достаточно
ли силён банк, чтобы преодолеть страшную рецессию или финансовый кризис.
В 2014 году Банк
Америки показал, что впервые после финансового кризиса 2008 года он прошёл
стресс-тест Федеральной резервной системы. Банк добавил, что собирается
выплатить дивиденды своим акционерам и выкупить акции на 4 миллиарда долларов.
Позже банк отозвал заявление и обнаружил, что допустил некоторые ошибки.
Банк Америки не
прошёл стресс-тест. Он только думал, что сделал это, потому что допустил ошибку
в определении стоимости некоторых облигаций, принадлежащих его дочерней
компании, Merrill Lynch. Акционеры были недовольны, и акции банка упали на 9
миллиардов долларов (пять процентов от общей стоимости) в тот же день, когда
была обнаружена ошибка.
2.3. Проблема моста в
Лауфенбурге
Некоторое время
назад Германия и Швейцария договорились построить мост через Рейн между своими
городами по обе стороны, оба под названием Лауфенбург. В соответствии с
соглашением, каждая страна должна была начать строительство со своей стороны
реки и встретиться посередине. Мост близился к завершению в 2003 году, когда
обе страны поняли, что одна половина моста была на 54 сантиметра выше, чем
другая.
Ошибка возникла
из-за того, что каждая страна по-своему определила термин «уровень моря».
Большинство стран используют разные методы определения уровня моря, учитывая,
что он не везде одинаков. Германия для его определения использует Северное
море, а Швейцария предпочитает Средиземное.
Разница между
соответствующими уровнями моря в этих странах составляла 27 сантиметров.
Германия и Швейцария знали об этом и учли это в своих расчётах. Тем не менее,
кто-то сделал так, что несоответствие удвоилось, в результате чего одна сторона
моста стала на 54 сантиметра выше, чем следовало.
2.2. Проблема негабаритного
поезда во Франции
В 2014 году
Societe Nationale des Chemins de Fer francai (SNCF), государственный
железнодорожный оператор Франции, обнаружил, что его новые скоростные поезда
были слишком широкими для 1300 станций по всей стране. Проблема заключалась в
том, что он заказал 1860 поездов у Alstom из Франции и Bombardier из Канады.
SNCF определил, что необходимо уменьшить ширину поездов, чтобы станции могли их
разместить. Ошибка обошлась в миллионы евро.
Этот инцидент
вызвал некоторое недовольство во Франции; Министр транспорта назвал это
«комично трагическим». Canard Enchaine, еженедельная сатирическая газета,
сделала карикатуру, в которой пассажирам на платформе было приказано «втянуть
животы», когда один из новых поездов подошёл к станции.
Ошибка произошла
потому, что французские вокзалы различаются по размеру. SNCF знал об этом и
просил Reseau ferre de France (RFF), который отвечал за пути, измерить
пространство возле путей. У SNCF и RFF возникли некоторые проблемы после того,
как выяснилось, что RFF пропустил 1300 старых станций в своих первоначальных
расчётах. Эти станции были уже, чем другие. Было слишком поздно, так как
некоторые поезда уже доставили, а другие находились в стадии строительства.
2.1.Ошибка муниципального
совета Амстердама на 188 миллионов евро
В декабре 2013
года финансовое управление городского совета Амстердама отправило 188 миллионов
евро более чем 10000 бедных семей, проживающих в городе. Позже город обнаружил,
что совершил ошибку в платежах. Изначально планировалось направить 1,8 миллиона
евро, а не 188 миллионов евро.
Платёжное
программное обеспечение было запрограммировано в центах, а не в евро. Люди
получили 15500 евро вместо 155 евро и в одном случае 34000 евро вместо 340
евро.
К счастью, город
смог вернуть все деньги, за исключением 2,4 миллиона евро, когда в новостях
ошибка была обнародована. Ожидалось, что городу будет сложно вернуть 1,2
миллиона евро. Это значительная сумма вместе с 300000 евро, которые город уже
потратил на ликвидацию последствий бедствия.
Человеческий
фактор – самая главная причина различных катастроф. И обидно бывает, когда
огромный труд многих людей губится из-за «незначительных» ошибок в расчетах, а
то и вовсе из-за глупости тех, кто эти расчеты делал.
3.Математические ошибки,
которые привели к значительным катастрофам
Приведу еще
несколько примеров.
3.1..Самолет с квадратными
иллюминаторами
Реактивное
авиастроение в 1950-х годах только начиналось. Первым лайнером стала «Комета» –
детище de Havilland. Это был ультрасовременный реактивный пассажирский самолёт
с уникальными для того времени техническими характеристиками и герметичной
кабиной. К сожалению, в 1954-м две «Кометы» развалились прямо в полёте. Погибло
56 человек. Причина проста: квадратные иллюминаторы.
Это была одна из
тех досадных мелочей, которые легко упустить при проектировании. Как оказалось,
круглые иллюминаторы позволяют давлению распределяться по всему фюзеляжу, и не
дают разорвать самолет на куски.
Возьмем плитку
шоколада. Как вы думаете, в каком месте она переломится, если на неё
надавить? Правильно, вдоль этих выемок.
Так вот,
квадратное окно состоит из четырех 90-градусных выемок, а стало быть, у него
есть четыре слабых места. Если бы на ваш дом надавили, то трещина непременно
прошла бы через угол какого-нибудь окна. Вы замечали, что иллюминаторы во всех
самолётах круглые? Это делается не для красоты – круглая форма не позволяет
разорвать самолёт на куски. Давление распределяется по всей кривой, вместо
того, чтобы идти трещинами по углам (как выяснилось) и разрывать самолёт в
клочья.
Выяснить это было
нелегко. Эксперты понятия не имели, почему конструкция самолёта разваливается,
пока не протестировали структуру путём многократной симуляции давления на
кабину. Конечно же, фюзеляж, в конце концов, лопнул, и разрыв начинался как раз
с этих пресловутых углов.
С тех пор
иллюминаторы у всех самолётов только круглые.
3.2 Прямые взлетно-посадочные
полосы на авианосцах
Не надо быть
пилотом, чтобы понять – посадить самолёт на авианосец чрезвычайно сложно. Эта
взлетно-посадочная полоса в миниатюре, напичканная другими самолётами, вдобавок
ещё и качается на волнах.
Но была и ещё
одна проблема.
Первые авианосцы
имели прямые полосы для взлета и посадки и были очень опасны как для самолетов,
заходящих на посадку, так и для тех, которые ожидают взлета.
Дело в том, что
истребители, которые не поймали тормозной трос, «сваливались» с
полосы, и часто врезались в другие самолеты. Чтобы хоть как-то обезопасить
авианосцы, было решено использовать перехватывающие сети, но и они не помогали.
Позже было решено
отвернуть посадочную полосу на 9 градусов влево, и количество аварий сократилось
в разы: пилоты, которые не успевали поймать тормозной трос, могли быстро дать
«полный газ» и зайти на второй круг без угрозы для остальных
самолетов.
3.3 Цельный мост в США
Мост
Такома-Нэрроуз в американском штате Вашингтон — один из крупнейших в США
висячих мостов. Его открыли 1 июля 1940 года и считали настоящим чудом: общая
длина моста составляла 1,8 км, и при этом он был цельным.
Но 7 ноября 1940
года из-за сильных порывов ветра (скорость ветра достигала 65 км/час) рухнул
центральный пролет моста. В это время на мосту была одна машина, водителю
которой удалось вовремя выбраться из салона и убежать.
Так что, железные
«кружева», которых так много на современных мостах, сделаны не для
красоты или экономии металла, а, чтобы пропускать воздух. В 1943 году мост
открыли заново и добавили в него открытые фермы, стойки жесткости,
деформационные швы и системы гашения вибраций.
3.4 Петли на дверях ночного
клуба
Клуб Cocoanut
Grove был самым модным местом Бостона в 30-х годах прошлого века. По
документам, заведение вмещало 460 человек, но во время праздников туда
набивалось куда больше народу.
В 1942 году
помощник официанта не мог найти розетку и решил подсветить себе дорогу спичкой.
Он оглянуться не успел, как за считанные секунды вспыхнули декорации, и пламя
перебросилось в зал. За несколько минут 492 человека погибли в огне.
Расследование, которое провели пожарные, показало, что такого количества жертв
можно было бы избежать, если бы двери клуба открывались наружу, а не вовнутрь
заведения.
3.5 Центральный винт, который
не может менять направление движения
Многие эксперты
сходятся во мнение, что причина крушения «Титаника» является
механической. Дело в том, что на теплоходе было установлено три винта: два
наружных, которые приводились в движение турбинами и большой центральный,
управляемый паровой турбиной. Но пар не может менять направление движения, и
поэтому мощный центральный винт вращался только в одну сторону. Вероятно
поэтому, когда помощник капитана Мэрдок отдал приказ «полный назад»,
внешние винты завертелись в обратную сторону, а центральный (самый мощный)
просто остановился. Это существенно уменьшило маневренность судна. У паровых
турбин по сравнению с их поршневыми аналогами есть существенное преимущество –
сочетание меньшего размера и большей эффективности. Но есть и недостаток – они
могут вращаться только в одну сторону. Если бы центральный винт, в случае
необходимости, мог дать задний ход, и не мешал управлять движением судна (или
если бы они вообще не давали задний ход), то вполне возможно, что Титаник
вообще не задел бы айсберг, и жизни 1514 человек и восьми собак оказались бы
вне опасности.
3.6 Несущественное изменение
дизайна
Владельцы Hyatt
Regency – нового отеля в Канзас Сити, мечтали, чтобы отель был необычный.
Архитектурная фирма, ответственная за дизайн здания, выступила с предложением сделать
несколько галерей, которые крепились бы к потолку. Недостаток проекта был в
том, что один длинный стержень был заменен на два коротких. Первоначальный
план заключался в том, чтобы расположить две галереи одна над другой, причём
обе должны были поддерживаться одним длинным стержнем, прикреплённым к потолку.
Вся конструкция висит на одном длинном стержне, что делает её настолько же
прочной, насколько и сложной для сборки – стержень должен проходить сквозь обе
галереи.
Но с большими
деталями сложно управляться – затащить в дом стол гораздо легче в разобранном
виде. Кроме того, у стержня должна быть резьба по всей длине – чтобы можно было
закрутить гайку до верхней галереи. Сталелитейная компания, ответственная за
изготовление стержня, внесла в конструкцию одно небольшое изменение – заменила
один длинный стержень двумя короткими.
Это небольшое
изменение убило 114 человек, покалечило 216 и обошлось компании в 140 миллионов
долларов по судебным искам.
Один стержень,
две гайки. Каждая гайка должна была нести вес только своей собственной
платформы. После изменения дизайна получилось, что верхняя гайка должна была
нести вес двух галерей. И вот, однажды ночью во время конкурса танцев несущая
гайка не выдержала, и обе галереи рухнули.
В ходе
последующих судебных разбирательств выяснилось, что ни сталелитейная компания,
ни инженерные фирмы, отвечающие за строительство, не потрудились даже сделать
расчёт, который показал бы этот изъян.
Заключение
Мною был собран и
оформлен материал о последствиях математической ошибки. Продемонстрирована
значимость математической ошибки.
Нашла своё
подтверждение гипотеза: математическая ошибка может привести не только к
курьёзным ситуациям, но и к серьёзным проблемам (авариям, катастрофам,
разрушениям). В ходе работы над темой я научилась разбирать математические
ошибки и поняла, что их поиск – очень полезное занятие.
Поиск ошибок
приучает внимательно и настороженно продвигаться вперед, тщательно следить за
точностью формулировок, правильностью записи чертежей, за законностью математических
операций. Если нашел ошибку, значит, ты ее осознал, а осознание ошибки
предупреждает от ее повторения в дальнейших математических рассуждениях.
Главный вывод
исследования: последствия даже маленьких математических ошибок могут быть
непредсказуемыми. Необходимо помнить об этом каждому и учиться находить и
своевременно исправлять свои ошибки. Взять себе за правило: не позволять себе
допускать даже самых незначительных математических ошибок.
Поэтому, хочется
сказать: «Ребята, уделяйте достаточно внимания изучению математики за школьной
партой!» Дело в том, что когда мы станем взрослыми, то даже одна очень
маленькая ошибка может стоить жизни многим людям.
Список использованных источников и литературы
1. Савин, А.П. Энциклопедический словарь юного математика / А.П.Савин.
— М.: Педагогика, 1989.-352 с.
2. Перельман, Я. И. Занимательная алгебра / Я.И.Перельман — Москва:
Государственное издательство физико-математической литературы, 1959.- 184 с.
3. Игнатьев, Е.И. В царстве смекалки / Е.И.Игнатьев — Москва:
Наука, 1984.- 192 с.
4.Гарднер, М. Математические чудеса и тайны / М.Гарднер —
Москва: Наука, 1982.- 128 с
5.РИА Новости (RIA.RU).
6.http://mixednews.ru/archives/15234
7.http://hijos.ru/2011/11/06/matematicheskie-kinolyapy
8.https://www.liveinternet.ru/community/for_men_only/post265675202/
9.https://pikabu.ru/story/10_prostyikh_no_dorogostoyashchikh_matematicheskikh_oshibok_v_istorii_6912640
Муниципальное казённое общеобразовательное учреждение
«Мармыжанская средняя общеобразовательная школа»
Советского района Курской области
Проектно-исследовательская работа
«К чему приводят
математические ошибки»
Выполнила:
Помогаева Виктория,
ученица 9 класса
Руководитель:
Гладилина Елена Петровна,
учитель математики
п. им. Ленина
2021 г.
Содержание
- Введение……………………………………………………………………3
- План работы над проектом………………………………………………..5
- Основная часть……………………………………………………………..6
- Математические ошибки на ТВ……………………………………….6
- Математические ошибки при использовании разных единиц измерения ………………………………………………………………7
- Математические ошибки при программировании…………………..10
- Математические ошибки в реальной жизни…………………………12
- Заключение………………………………………………………………..14
- Использованная литература………………………………………………15
-
Введение
«В математических вопросах нельзя
пренебрегать даже самыми мелкими
ошибками».
И. Ньютон.
Мы постоянно слышим от учителя на уроках математики: «Будьте внимательными, не делайте ошибок», и все делаем эти ошибки. Чаще всего просто в вычислениях. Думаем, что если бы мы пользовались на уроках математики и на экзаменах калькуляторами, то этих ошибок бы не было. Для нас, учеников, эти ошибки могут привести к неудовлетворительной оценке на уроке или, самое страшное, на экзамене. Во взрослой жизни все уже производят расчеты с помощью калькуляторов или ЭВМ. Неужели и там бывают математические ошибки? Почему они возникают и к каким последствиям могут привести?
Гипотеза: математическая ошибка может привести как к курьёзным ситуациям, так и к серьёзным проблемам (авариям, катастрофам, разрушениям)
Актуальность проекта:
Актуальность данной проблемы имеет как личный аспект, так и масштабный характер (ошибиться может каждый). Но к чему может привести математическая ошибка – это ключевой вопрос, в котором и хотелось разобраться. Ведь математика касается всех сфер нашей жизни, как частной, так и в масштабе государства.
Цель проекта: собрать и оформить информацию о последствиях математической ошибки; показать значимость математической ошибки.
Задачи проекта:
- найти примеры ошибок, которые приводили к курьёзным ситуациям;
- найти ответ на вопрос: были ли случаи, когда математические ошибки, повлекли за собой серьёзные проблемы: катастрофы, аварии, разрушения.
- найти ответ на вопрос: как может нам навредить математическая неграмотность.
- Поделиться информацией с одноклассниками
- План работы над проектом
- Наблюдения, сопоставления по теме проекта
- Нахождение информации о математических ошибках на телевидении
- Нахождение информации о математических ошибках, приведших к катастрофам, авариям. Попытаться их классифицировать.
- Поиск информации о математических ошибках в жизненных ситуациях
- Создание презентации к проекту
- Оформление проекта, защита проекта
- Показ одноклассникам презентации
- Основная часть
Изучая математику, мы уже можем заметить какие-то ошибки у взрослых. Например, многие путают понятия «число» и «цифра». Даже в средствах массовой информации говорят: «получилась солидная цифра», «цифра сто двадцать пять», «а теперь сопоставим полученные многозначные цифры», «сложив полученные цифры, получим…». Но ведь в математике цифр всего 10, а чисел — бесконечное множество и только с числами можно
проводить различные математические действия. Лишь, упоминая официальные показатели, например статистические данные, допускается говорить слово «цифра».
Часто мы слышим от взрослых, что когда температура воздуха изменилась с -100С до -200С, то «она стала больше». Но ведь -10 больше, чем -20. Поэтому грамотнее говорить, что температура понизилась.
Но все это всего лишь показывает математическую неграмотность человека и не может привести к какой-либо трагедии.
Введя запрос в Интернете «математические ошибки» я нашла много интересного. С этой информацией я и хочу поделиться.
- Математические ошибки на ТВ
- «Сериал «Звездный путь» Военный суд, 1967 г. Керк говорит, что компьютер может усилить звук в число раз, равное «единице в сороковой степени», а это равно единице». [1]
- Математическая ошибка Юрия Дудя о кратчайшем расстоянии между двумя объектами на Земле. Расстояние определяется не по параллели, а по диаметральному сечению.
- В комедийном фильме 1965 года «Операция „ы“ и другие приключения Шурика» Леонида Гайдая герой Михаила Пуговкина — прораб СМУ, рассказывая о достижениях в строительстве, говорит: «Если поставить этажи один на другой, то мы получим здание в два раза выше, чем всемирно известная Эйфелева башня или втрое выше, чем знаменитый Нотр-Дам де Пари».[1]
На самом деле, высота Эйфелевой башни 325 м (325*2=650), а Нотр-Дам де Пари — 35 м (35*3=105). - Кадр из американской программы новостей. Всего проголосовало 193% избирателей.
- 4 декабря 2011 года в России прошли выборы. Тогда на ТВ появилась такая интересная информация: «В Воронежской области насчитали 128,96% голосов. Однако, в Ростовской области и того больше — 146,47%. Свердловская область — 115,35%».
Такие ошибки часто называют «киноляпы» или «курьёзные ошибки». Замечают их не все, и они не приводят к какой-либо трагедии.
А теперь рассмотрим более серьезные ошибки в истории человечества.
Ошибки при использовании разных единиц измерения
Почти каждая страна в мире использует метрическую систему мер, Кроме Соединённых Штатов. Обычно это не особо большая проблема. Но на протяжении всей истории было несколько случаев, когда использование разных систем измерения величин приводило к катастрофическим результатам.
а) Потопление военного корабля «Ваза»
«10 августа 1628 года Швеция запустила новый, хорошо вооружённый и большой военный корабль «Ваза». Судно едва проплыло 20 минут, когда затонуло менее чем в миле от берега. Тридцать человек погибли в результате потопления. Корабль был позже найден в 20-м веке и сейчас хранится в Музее Вазы.
Историки измерили весь корабль и обнаружили, что его строители использовали две разные единицы измерения. Одной был шведский фут, а другой – амстердамский фут. Шведский фут составляет 30,48 см, в то время как амстердамский – 27,94 см.
Разница между обеими единицами измерения привела к тому, что одна сторона оказалась тяжелее другой. Вот почему корабль наклонился в сторону и быстро затонул после того, как по нему ударили два порыва ветра. Историки добавляют, что влияние ветра было усугублено тем фактом, что верх корабля был тяжелее его дна». [3]
б) В самолёте Air Canada закончилось топливо (1983 год)
«В июле 1983 года самолёт Boeing 767 Air Canada, летевший из Оттавы в Эдмонтон с 69 пассажирами и членами экипажа, вынужден был совершить аварийную посадку после того, как закончился запас топлива на высоте 12500 м. Двигатели внезапно потеряли мощность, и самолёт начал снижаться к земле.
Авария была связана с ошибкой преобразования. Air Canada использовала британскую систему мер, но перешла на метрическую, которую уже использовал этот Boeing 767. Наземные экипажи Air Canada использовали британскую систему при заправке самолёта. Они измеряли топливо в фунтах вместо килограммов.
Один килограмм равен 2,2 фунта. Это означало, что у самолёта было всего около половины количества топлива, необходимого для завершения полёта.
К счастью, 69 пассажиров на борту отделались незначительными травмами». [2]
в) Крушение орбитального аппарата Mars Climate Orbiter
«Mars Climate Orbiter был совместным проектом компании Lockheed Martin и NASA / JPL стоимостью 125 миллионов долларов. Проект получил неловкое завершение, когда орбитальный аппарат, скорее всего, потерпел крушение на Марсе из-за простой ошибки преобразования в 1999 году. Lockheed Martin использовал британскую систему мер при программировании программного обеспечения, но НАСА использовало метрическую систему.
Инженеры НАСА обнаружили бы ошибку, если бы обратили внимание. Однако они этого не сделали. Никто не понимал, что что-то не так во время девятимесячного путешествия Mars Climate Orbiter на Марс. Ошибка стала очевидной только тогда, когда НАСА потеряло связь с орбитальным аппаратом.
В ответ на инцидент Джон Логсдон из Института космической политики Университета имени Джорджа Вашингтона сказал, что всё это было «глупо». Джон Пайк из Федерации американских учёных добавил: «Было неловко потерять космический корабль из-за такой простой математической ошибки». [2]
г) Крушение американских горок в Токио (2003 год)
«В декабре 2003 года в токийском Диснейленде один из автомобилей аттракциона «Космическая гора» внезапно сошел с рельсов из-за сломанной оси. Почему сломалась ось? Согласно официальному отчёту, выпущенному в январе 2004 года, ось была не того размера, потому что существовала путаница в метрической и английской системах мер.
К счастью, никто из людей, не пострадал». [2]
д) Если вы думаете, что в нашей стране таких ошибок быть не может, то ошибаетесь. Вот, что рассказывает очевидец: «Привезли, значит, нам на завод какие-то нестандартные ж/д цистерны под концентрированную серную кислоту. …на них указана ёмкость — но, правда, в галлонах. Ну, мы ж не дураки: в инете полно калькуляторов по переводу единиц измерения! Пересчитываем в кубометры, задаём автомату указание, сколько наливать, ждём, когда отключится… А вот кислота начинает литься через край! Срочно вырубаем, но пролив уже есть, что, мягко говоря, неприятно. Последствия пролива устранили, стали разбираться, и выяснилось, что галлоны разные бывают! Судя по всему, мы посчитали объём цистерны в классических английских галлонах, а есть ещё и американские, которые меньше, и в которых эта самая ёмкость была указана на цистернах». [4]
(Американский галлон равен 3,785411784 литра. Британский галлон — 4,5461 литра)
3) Математические ошибки при программировании
Огромные суммы денег и оборудование стоимостью в миллионы долларов были потеряны просто потому, что кто-то допустил небольшую математическую ошибку. Компьютеры также допускают подобные ошибки, но в них можно винить людей, так как именно они занимались программированием.
а) «25 февраля 1991 года иракская ракета «Скад» нанесла удар по базе армии США в Даране, Саудовская Аравия, убив 28 солдат и ранив ещё 100. Катастрофа была неожиданной, если учесть, что база была защищена системой ПВО «Патриот». Расследования показали, что система не пыталась перехватить «Скад».
Ошибка была связана с программным обеспечением, питающим часы системы. Часы записывали время в десятых секундах (одна десятая секунды), но сохраняли эти данные в виде целого числа. Для этого они преобразовывали время в 24-битное число с плавающей точкой. Однако округление времени при их преобразовании привело к постепенному увеличению погрешности в работе системы. В результате система не смогла перехватить ракеты после 20 часов непрерывного использования.
Во время атаки рассматриваемая ракетная батарея «Патриот» проработала 100 часов. Разница во времени была такова, что она искала не в той части неба входящую ракету и поэтому не нашла цели. Армия США была проинформирована об этой проблеме с программным обеспечением и выпустила обновление 16 февраля. Обновление достигло базы в Дхаране 26 февраля, на следующий день после атаки». [4]
б) Испанская программа подводных лодок S-80
В 2003 году Испания запустила программу подводных лодок S-80 на сумму 2,7 миллиарда долларов для строительства чётырех дизель-электрических подводных лодок для ВМС Испании. Испания почти завершила строительство одной из них в 2013 году, когда обнаружила, что лодка на 70 тонн тяжелее, чем должна была быть. Испанский флот боялся, что подводная лодка никогда не всплывёт, если уйдёт под воду.
Подводная лодка оказалась тяжёлой после того, как кто-то поставил десятичную точку в неправильном месте во время вычислений. Никто не обнаружил ошибку, пока первая субмарина не была закончена, а остальные три уже строились. Позже Испания подписала контракт на 14 миллионов долларов с Electric Boat из Гротона, штат Коннектикут, чтобы те помогли им снизить вес 2200-тонной подводной лодки.
в) Взрыв ракеты Ariane 5
4 июня 1996 года ракета Ariane 5 Европейского космического агентства взорвалась через 37 секунд после взлёта. На борту космического корабля находились четыре спутника. Ракета и спутники стоили 370 миллионов долларов. Авария была связана с целочисленной ошибкой переполнения в программном обеспечении, используемом для запуска ракеты.
Целочисленное переполнение – это математическая ошибка, которая возникает, когда числа, сгенерированные системой, превышают объём памяти этой системы. Ariane 5 работала на 16-битном программном обеспечении, способном хранить числа до 32767. Ракете удалось создать числа намного больше этого.
Европейское космическое агентство использовало то же программное обеспечение, что и в ракетах Ariane 4. У них были проблемы с Ariane 5, потому что она была быстрее, чем Ariane 4. Чем быстрее, тем больше числа. Программное обеспечение не может обрабатывать большие показания, из-за чего ракета становится негодной. Наземный контроль приказал самоуничтожиться.
г) Разрушение ракеты — носителя «Протон-М» в 2010 году.
РИА новости сообщает: «К неудачному запуску трех спутников системы ГЛОНАСС могла привести математическая ошибка в программе, заложенной в бортовой комплекс ракеты — носителя. Сейчас ее эксперты занимаются выяснением всех обстоятельств аварии. По некоторым данным, ракета-носитель «Протон-М» после запуска отклонилась от заданной траектории на восемь градусов. Дмитрий Медведев поручил найти виновных в утрате спутников и проверить расходование средств на выполнение программы создания отечественной навигационной группировки». [5]
Все приведённые выше примеры заставляют задуматься над тем, что фактов, когда математическая ошибка ведет к серьёзным авариям, катастрофам, разрушениям значительно больше, чем можно было себе представить.
4)Математические ошибки в реальной жизни
Но, не все мы станем программистами, инженерами и т. д. Но математические ошибки в любой сфере деятельности могут причинить вред тебе самому и тем, кто тебя окружает. Есть люди, которые преднамеренно пользуются нашей математической неграмотностью. Я приведу лишь несколько примеров.
Вот некоторые уловки маркетологов в магазинах и супермаркетах:
1) «Снижение стоимости продукта всего на копейки, рубль может существенно увеличивать продажи. Все дело в том, что даже мизерное снижение стоимости товара дает нам чувство экономии. Для многих покупателей покупка продукта по 999 руб. воспринимается заметно выгодней, чем по цене в 1000 рублей. Этот эффект называют «эффектом левой цифры».
Благодаря подобной уловке маркетологи заставляют клиентов воспринимать только крайние левые числа. Например, психологически многие клиенты, купившие товар по цене 999 руб., воспринимают покупку по цене 900 рублей.
Примечательно, что эта ситуация для цен типа 549 и 550 рублей не производит такой же эффект, хотя разница в ценах составляет тот же 1 рубль. Но в этом примере в обоих сценариях психологически люди считают, что приобретают товар за 500 руб.
Именно поэтому разница между этими ценами не создает восприятия сбережения. Но почему так происходит? Все дело в том, что наш мозг обычно обращает внимание только на первую цифру. На уроках математики мы учимся округлять, делать прикидки, и если будем делать это автоматически, то не попадемся на эту уловку». [6]
2) Вес продукта
«Замечали такое, что ваш любимый товар внезапно становился дешевле? Например, молоко, сливочное масло, сок, майонез и т. д. Нередко маркетологи идут на хитрую уловку: снижают стоимость товара, уменьшая при этом вес. Поэтому, в следующий раз, когда вы захотите, не глядя бросить в корзину самый дешёвый товар, внимательно изучите его этикетку. Возможно, он несколько легче своих аналогов, а его цена дешевле лишь на 1 рубль». [6]
3)Микрокредиты
«Тема микрозаймов сейчас более чем актуальна в России. Это подтверждают цифры. Только по предварительным данным, за 2019 год 11 млн российских граждан взяли в долг больше 200 млрд руб. С каждым годом эти цифры увеличиваются примерно на четверть. Около 40 % клиентов МФО в России – это люди в возрасте 25–36 лет, другими словами, трудоспособное население.
Рассчитать, какой процент переплаты будет начислен, также очень просто. Если ставка равна 1 % в день, а заем берется на 15 дней, то переплата составит 15 %. За 20 дней переплата возрастет до 20 %, за 30 дней – до 30 % и т. д.» [7]
Прежде чем брать кредит, подумайте, сможете ли вы его погасить вовремя, и стоит ли столько процентов переплачивать.
- Заключение.
Вывод: Мною был собран и оформлен материал о последствиях математической ошибки. Продемонстрирована значимость математической ошибки. Нашла своё подтверждение гипотеза: математическая ошибка может привести не только к курьёзным ситуациям, но и к серьёзным проблемам. Последствия даже маленьких математических ошибок могут быть непредсказуемыми.
В нашем мире от математики зависит больше, чем когда-либо в истории, и поэтому цена ошибок, намного выше.
Человеческий фактор – самая главная причина различных катастроф. И обидно бывает, когда огромный труд многих людей губится из-за «незначительных» ошибок в расчетах, а то и вовсе из-за глупости тех, кто эти расчеты делал.
Поэтому, хочется сказать: «Ребята, уделяйте достаточно внимания изучению математики за школьной партой!» Дело в том, что когда мы станем взрослыми, то даже одна очень маленькая ошибка может стоить жизни многим людям.
Список литературы
Источники, представленные в Internet:
- http://hijos.ru/2011/11/06/matematicheskie-kinolyapy/
- https://m.fishki.net/3118774-10-dorogostojawih-matematicheskih-oshibok/gallery-7117630-photo.html
- https://ru.wikipedia.org/wiki/Ваза_(корабль)
- https://pikabu.ru/story/10_prostyikh_no_dorogostoyashchikh_matematicheskikh_oshibok_v_istorii_6912640
- РИА Новости (RIA.RU).
- https://basetop.ru/samyie-hitryie-marketingovyie-ulovki-dlya-povyisheniya-prodazh/
- https://iklife.ru/finansy/zajmy/chto-takoe-mikrozajm-prostymi-slovami.html
Разделы презентаций
- Разное
- Английский язык
- Астрономия
- Алгебра
- Биология
- География
- Геометрия
- Детские презентации
- Информатика
- История
- Литература
- Математика
- Медицина
- Менеджмент
- Музыка
- МХК
- Немецкий язык
- ОБЖ
- Обществознание
- Окружающий мир
- Педагогика
- Русский язык
- Технология
- Физика
- Философия
- Химия
- Шаблоны, картинки для презентаций
- Экология
- Экономика
- Юриспруденция
Содержание
-
1.
Математические неожиданности 8 класс -
2.
Цель:Найти математические задачи, приводящие к парадоксам.Исследовать решение -
3.
Задачи: дать определение понятием «софизм» и «парадокс» -
4.
Методы исследования:Сбор информации, обработка данных, наблюдение, сравнение, анализ, обобщение. -
5.
«Софизм» и «Парадокс» -
6.
СофизмЛожное умозаключение, которое, тем не менее, при поверхностном рассмотрении кажется правильным. -
7.
ПарадоксЭто нечто необычное и удивительное, то, что расходится с привычными ожиданиями, здравым смыслом и жизненным опытом. -
8.
Их отличие С софизмом их различает то, что парадокс — не преднамеренно полученный противоречивый результат. -
9.
Классификация математических неожиданностейАлгебраические Геометрические Арифметические Логические -
10.
Алгебраические софизмыАлгебраические софизмы – намеренно скрытые ошибки в уравнениях и числовых выражениях -
11.
Арифметические софизмыАрифметические софизмы – это числовые выражения, имеющие неточность или ошибку, не заметную с первого взгляда. -
12.
Геометрические софизмыГеометрические софизмы – это умозаключения, обосновывающие какую-нибудь заведомую нелепость, связанную с геометрическими фигурами ми. -
13.
Логичесике софизмыЧем больше учишься, тем больше знаешь.Чем -
14.
Многообразие парадоксов -
15.
Парадокс парикмахера В одной деревне жил единственный парикмахер-мужчина. -
16.
Основные типы геометрических парадоксов -
17.
Невозможный треугольник -
18.
Бесконечная лестница -
19.
Космическая вилка -
20.
Сумасшедший ящик -
21.
Имп-Арт — искусство парадоксальных картин -
22.
Имп-Арт — искусство парадоксальных картин -
23.
Имп-Арт — искусство парадоксальных картин -
24.
Выводы:Итак, в процессе работы:я узнала, что называется -
25.
Спасибо за внимание! -
26.
Скачать презентанцию
Цель:Найти математические задачи, приводящие к парадоксам.Исследовать решение этих задач.Найти, где скрыты ошибки, подготовить презентацию по этой теме для использования на уроках математики.
Слайды и текст этой презентации
Слайд 1Математические неожиданности
Автор: Жевнерова Альвина, 8 класс
Руководитель: Демченкова С. В.

Слайд 2Цель:
Найти математические задачи, приводящие к парадоксам.
Исследовать решение этих задач.
Найти, где
скрыты ошибки, подготовить презентацию по этой теме для использования на
уроках математики.

Слайд 3Задачи:
дать определение понятием «софизм» и «парадокс» , узнать ,в
чем их отличие;
классифицировать математические неожиданности;
научиться находить ошибки в готовых
решениях,
математических задач;
подготовить презентацию .

Слайд 4Методы исследования:
Сбор информации, обработка данных, наблюдение, сравнение, анализ, обобщение.

Слайд 6Софизм
Ложное умозаключение, которое, тем не менее, при поверхностном рассмотрении кажется
правильным.

Слайд 7Парадокс
Это нечто необычное и удивительное, то, что расходится с привычными
ожиданиями, здравым смыслом и жизненным опытом.

Слайд 8Их отличие
С софизмом их различает то, что парадокс —
не преднамеренно полученный противоречивый результат.

Слайд 9Классификация математических неожиданностей
Алгебраические
Геометрические
Арифметические
Логические

Слайд 10Алгебраические софизмы
Алгебраические софизмы – намеренно скрытые ошибки в уравнениях и
числовых выражениях
Слайд 11Арифметические софизмы
Арифметические софизмы – это числовые выражения, имеющие неточность или
ошибку, не заметную с первого взгляда.

Слайд 12Геометрические софизмы
Геометрические софизмы – это умозаключения, обосновывающие какую-нибудь заведомую нелепость,
связанную с геометрическими фигурами ми.

Слайд 13Логичесике софизмы
Чем больше учишься, тем больше знаешь.
Чем больше знаешь, тем
больше забываешь.
Чем больше забываешь, тем меньше знаешь.
Чем меньше знаешь, тем
меньше забываешь.
Но чем меньше забываешь, тем больше знаешь.
Так для чего учиться?

Слайд 15Парадокс парикмахера
В одной деревне жил единственный парикмахер-мужчина. Здесь был издан
указ: «Парикмахер имеет право брить тех и только тех жителей
деревни, которые не бреются сами». Спрашивается, может ли парикмахер брить сам себя?

Слайд 16Основные типы геометрических парадоксов

Слайд 21
Имп-Арт — искусство парадоксальных картин

Слайд 22
Имп-Арт — искусство парадоксальных картин

Слайд 23
Имп-Арт — искусство парадоксальных картин

Слайд 24Выводы:
Итак, в процессе работы:
я узнала, что называется «софизмом «и «парадоксом»,
и в чём их отличия;
проклассифицировала софизмы в соответствии с разделами
математики, к которым они принадлежат;
рассмотрела четыре основных вида геометрических парадоксов, которые вызвали у меня особый интерес, так как нашли своё отражение в имп-арт – искусстве парадоксальных картин.

IХ муниципальная
научно — практическая конференция
старшеклассников «Будущее науки»
Секция математических наук
Научно-исследовательская работа на тему
ОШИБКИ В РАСЧЕТАХ – ПРИЧИНЫ МНОГИХ КАТАСТРОФ
Работу выполнил: ученик 9Т класса
МАОУ ВСОШ №3 с УИОП
Фатеев Кирилл
Научный руководитель:
Семеняченко Татьяна Васильевна,
учитель математики
Домодедово 2016
Содержание:
-
ВВЕДЕНИЕ ………………………………………………….…3
-
АНКЕТИРОВАНИЕ ОДНОКЛАССНИКОВ…………………5
-
ПРИМЕРЫ МАТЕМАТИЧЕСКИХ ОШИБОК
3.1 Самолет с квадратными иллюминаторами………………..6
3.2 Прямые взлетно-посадочные полосы на авианосцах…….7
3.3 Цельный мост в США………………………………………7
3.4 Петли на дверях ночного клуба……………………………8
3.5 Центральный винт, который не может менять
направление движения………………………………………….8
3.6 Несущественное изменение дизайна………………………9
Заключение…………….…………………………………………..10
Список литературы……………………….……………………….11
Приложение №1…………………………….…………….……….12
Приложение №2……………………………….………….……….13
В математических вопросах нельзя пренебрегать даже самыми мелкими ошибками.
И. Ньютон
-
ВВЕДЕНИЕ
Объект исследования: одноклассники, источники о глобальных катастрофах.
Гипотеза: математическая ошибка может привести как к курьёзным ситуациям, так и к серьёзным проблемам (авариям, катастрофам, разрушениям)
Цель исследования: собрать информацию о последствиях математической ошибки; показать значимость математической ошибки.
Задачи:
исследовать типичные ошибки одноклассников;
провести анкетирование среди одноклассников на тему «К чему может привести математическая ошибка?»;
найти примеры ошибок, которые приводили к курьёзным ситуациям;
найти в Интернете ответ на вопрос: были ли случаи, когда математические ошибки, повлекли за собой серьёзные проблемы: катастрофы, аварии, разрушения.
Методы исследования:
изучение источников: литературы, энциклопедий, сайтов в Интернете;
наблюдения, сопоставления;
анализ и классификация ошибок в работах учащихся 9 класса;
отбор и классификация материала.
Человечество ошибается — и делает это отнюдь не редко. Когда дело касается крупных строений или сложной техники, даже малейший огрех может привести к катастрофе. Расплачивается же за это жизнью не сам конструктор, а доверившиеся его работе люди. В истории бывали случаи, когда чудовищные катастрофы возникали вследствие, казалось бы, небольших ошибок или чьей-то непредусмотрительности. Иногда в этих катастрофах оказывались виноваты конкретные люди, отвечавшие за безопасность и допустившие небрежность, иногда несчастье происходило в результате череды маловероятных совпадений.
Минимальная ошибка в расчетах может обернуться катастрофой, если речь идет о точных науках. Здесь нет места словам «примерно» и «приблизительно». Одна маленькая ошибка может стоить жизни многим людям.
Если вы считаете, что это пустые слова, то мы приведем реальные истории, которые подтверждают нашу тревогу.
-
АНКЕТИРОВАНИЕ ОДНОКЛАССНИКОВ
Мы провели анкетирование среди одноклассников. В нем приняли участие 40 учеников (Приложения №1 и №2). Обучающимся 9-х классов было предложено ответить на следующие вопросы:
1. Как часто на уроках математики вы допускаете ошибки?
2. Задумывались ли вы о последствиях математической ошибки?
3. Знакомы ли вам примеры, когда математическая ошибка привела к катастрофе?
4. Подумайте и запишите, к чему может привести математическая ошибка?
5. Хотели бы вы познакомиться с курьёзными случаями математических ошибок?
На вопрос «Как часто на уроках математики вы допускаете ошибки?» ответили «часто» и «почти всегда» — 35 человек. На вопрос «Задумывались ли вы о последствиях математической ошибки?» ответили «нет» — 31 человек. На вопрос «Знакомы ли вам примеры, когда математическая ошибка привела к катастрофе?» ответили «нет» — 29 человек. На вопрос «Хотели бы вы познакомиться с курьёзными случаями математических ошибок?» ответили положительно – 32 человек. Анкетирование показало, что школьники не задумываются о последствиях математической ошибки.
Наблюдения на уроках математики и анализ ошибок в тетрадях одноклассников показал, что ошибками могут стать неправильные расчёты, неправильное применение определений, аксиом, теорем, незнание формул, правил. Ряд ошибок одноклассники допускают из-за неразборчивого почерка, неаккуратно выполненного чертежа, по невнимательности. Некоторые ошибки носят курьёзный характер.
Человеческий фактор – самая главная причина различных катастроф. И обидно бывает, когда огромный труд многих людей губится из-за «незначительных» ошибок в расчетах, а то и вовсе из-за глупости тех, кто эти расчеты делал.
-
ПРИМЕРЫ МАТЕМАТИЧЕСКИХ ОШИБОК
3.1 Самолет с квадратными иллюминаторами
Реактивное авиастроение в 1950-х годах только начиналось. Первым лайнером стала «Комета» – детище de Havilland. Это был ультрасовременный реактивный пассажирский самолёт с уникальными для того времени техническими характеристиками и герметичной кабиной. К сожалению, в 1954-м две «Кометы» развалились прямо в полёте. Погибло 56 человек. Причина проста: квадратные иллюминаторы.
Это была одна из тех досадных мелочей, которые легко упустить при проектировании. Как оказалось, круглые иллюминаторы позволяют давлению распределяться по всему фюзеляжу, и не дают разорвать самолет на куски.
Вот плитка шоколада. Как вы думаете, в каком месте она переломится, если на неё надавить? Правильно, вдоль этих выемок.
Так вот, квадратное окно состоит из четырех 90-градусных выемок, а стало быть, у него есть четыре слабых места. Если бы на ваш дом надавили, то трещина непременно прошла бы через угол какого-нибудь окна. Вы замечали, что иллюминаторы во всех самолётах круглые? Это делается не для красоты – круглая форма не позволяет разорвать самолёт на куски. Давление распределяется по всей кривой, вместо того, чтобы идти трещинами по углам (как выяснилось) и разрывать самолёт в клочья.
Выяснить это было нелегко. Эксперты понятия не имели, почему конструкция самолёта разваливается, пока не протестировали структуру путём многократной симуляции давления на кабину. Конечно же, фюзеляж, в конце концов, лопнул, и разрыв начинался как раз с этих пресловутых углов.
С тех пор иллюминаторы у всех самолётов только круглые.
3.2 Прямые взлетно-посадочные полосы на авианосцах
Не надо быть пилотом, чтобы понять – посадить самолёт на авианосец чрезвычайно сложно. Эта взлетно-посадочная полоса в миниатюре, напичканная другими самолётами, вдобавок ещё и качается на волнах.
Но была и ещё одна проблема…
Первые авианосцы имели прямые полосы для взлета и посадки и были очень опасны как для самолетов, заходящих на посадку, так и для тех, которые ожидают взлета.
Дело в том, что истребители, которые не поймали тормозной трос, «сваливались» с полосы, и часто врезались в другие самолеты. Чтобы хоть как-то обезопасить авианосцы, было решено использовать перехватывающие сети, но и они не помогали.
Позже было решено отвернуть посадочную полосу на 9 градусов влево, и количество аварий сократилось в разы: пилоты, которые не успевали поймать тормозной трос, могли быстро дать «полный газ» и зайти на второй круг без угрозы для остальных самолетов.
3.3 Цельный мост в США
Мост Такома-Нэрроуз в американском штате Вашингтон — один из крупнейших в США висячих мостов. Его открыли 1 июля 1940 года и считали настоящим чудом: общая длина моста составляла 1,8 км, и при этом он был цельным.
Но 7 ноября 1940 года из-за сильных порывов ветра (скорость ветра достигала 65 км/час) рухнул центральный пролет моста. В это время на мосту была одна машина, водителю которой удалось вовремя выбраться из салона и убежать.
Так что, железные «кружева», которых так много на современных мостах, сделаны не для красоты или экономии металла, а, чтобы пропускать воздух. В 1943 году мост открыли заново и добавили в него открытые фермы, стойки жесткости, деформационные швы и системы гашения вибраций.
3.4 Петли на дверях ночного клуба
Клуб Cocoanut Grove был самым модным местом Бостона в 30-х годах прошлого века. По документам, заведение вмещало 460 человек, но во время праздников туда набивалось куда больше народу.
В 1942 году помощник официанта не мог найти розетку и решил подсветить себе дорогу спичкой. Он оглянуться не успел, как за считанные секунды вспыхнули декорации, и пламя перебросилось в зал. За несколько минут 492 человека погибли в огне. Расследование, которое провели пожарные, показало, что такого количества жертв можно было бы избежать, если бы двери клуба открывались наружу, а не вовнутрь заведения.
3.5 Центральный винт, который не может менять направление движения
Многие эксперты сходятся во мнение, что причина крушения «Титаника» является механической. Дело в том, что на теплоходе было установлено три винта: два наружных, которые приводились в движение турбинами и большой центральный, управляемый паровой турбиной. Но пар не может менять направление движения, и поэтому мощный центральный винт вращался только в одну сторону. Вероятно поэтому, когда помощник капитана Мэрдок отдал приказ «полный назад», внешние винты завертелись в обратную сторону, а центральный (самый мощный) просто остановился. Это существенно уменьшило маневренность судна. У паровых турбин по сравнению с их поршневыми аналогами есть существенное преимущество – сочетание меньшего размера и большей эффективности. Но есть и недостаток – они могут вращаться только в одну сторону. Если бы центральный винт, в случае необходимости, мог дать задний ход, и не мешал управлять движением судна (или если бы они вообще не давали задний ход), то вполне возможно, что Титаник вообще не задел бы айсберг, и жизни 1514 человек и восьми собак оказались бы вне опасности.
3.6 Несущественное изменение дизайна
Владельцы Hyatt Regency – нового отеля в Канзас Сити, мечтали, чтобы отель был необычный. Архитектурная фирма, ответственная за дизайн здания, выступила с предложением сделать несколько галерей, которые крепились бы к потолку. Недостаток проекта был в том, что один длинный стержень был заменен на два коротких. Первоначальный план заключался в том, чтобы расположить две галереи одна над другой, причём обе должны были поддерживаться одним длинным стержнем, прикреплённым к потолку. Вся конструкция висит на одном длинном стержне, что делает её настолько же прочной, насколько и сложной для сборки – стержень должен проходить сквозь обе галереи.
Но с большими деталями сложно управляться – затащить в дом стол гораздо легче в разобранном виде. Кроме того, у стержня должна быть резьба по всей длине – чтобы можно было закрутить гайку до верхней галереи. Сталелитейная компания, ответственная за изготовление стержня, внесла в конструкцию одно небольшое изменение – заменила один длинный стержень двумя короткими.
Это небольшое изменение убило 114 человек, покалечило 216 и обошлось компании в 140 миллионов долларов по судебным искам.
Один стержень, две гайки. Каждая гайка должна была нести вес только своей собственной платформы. После изменения дизайна получилось, что верхняя гайка должна была нести вес двух галерей. И вот, однажды ночью во время конкурса танцев несущая гайка не выдержала, и обе галереи рухнули.
В ходе последующих судебных разбирательств выяснилось, что ни сталелитейная компания, ни инженерные фирмы, отвечающие за строительство, не потрудились даже сделать расчёт, который показал бы этот изъян.
ЗАКЛЮЧЕНИЕ
Нами был собран и оформлен материал о последствиях математической ошибки. Продемонстрирована значимость математической ошибки.
Нашла своё подтверждение гипотеза: математическая ошибка может привести не только к курьёзным ситуациям, но и к серьёзным проблемам (авариям, катастрофам, разрушениям). В ходе работы над темой мы научилась разбирать математические ошибки и поняли, что их поиск – очень полезное занятие. Поиск ошибок приучает внимательно и настороженно продвигаться вперед, тщательно следить за точностью формулировок, правильностью записи чертежей, за законностью математических операций. Если нашел ошибку, значит, ты ее осознал, а осознание ошибки предупреждает от ее повторения в дальнейших математических рассуждениях.
Главный вывод исследования: последствия даже маленьких математических ошибок могут быть непредсказуемыми. Необходимо помнить об этом каждому и учиться находить и своевременно исправлять свои ошибки. Взять себе за правило: не позволять себе допускать даже самых незначительных математических ошибок.
Человеческий фактор – самая главная причина различных катастроф. И обидно бывает, когда огромный труд многих людей губится из-за «незначительных» ошибок в расчетах, а то и вовсе из-за глупости тех, кто эти расчеты делал.
Поэтому, хочется сказать: «Ребята, уделяйте достаточно внимания изучению математики за школьной партой!» Дело в том, что когда мы станем взрослыми, то даже одна очень маленькая ошибка может стоить жизни многим людям.
БИБЛИОГРАФИЯ
1. А.П.Савин Энциклопедический словарь юного математика – М.: Педагогика, 1989.-352 с.
2. Я.И.Перельман Занимательная алгебра – Москва: Государственное издательство физико-математической литературы, 1959.- 184 с.
3. Е.И.Игнатьев В царстве смекалки – Москва: Наука, 1984.- 192 с.
4. М.Гарднер Математические чудеса и тайны — Москва: Наука, 1982.- 128 с. Источники, представленные в Internet:
5. РИА Новости (RIA.RU).
6. http://mixednews.ru/archives/15234
7. http://hijos.ru/2011/11/06/matematicheskie-kinolyapy
ПРИЛОЖЕНИЕ №1
АНКЕТА
-
Как часто на уроках математики вы допускаете ошибки?
а) часто;
б) почти всегда;
в) иногда;
г) никогда.
2. Задумывались ли вы о последствиях математической ошибки?
а) да;
б) нет.
3. Знакомы ли вам примеры, когда математическая ошибка привела к катастрофе?
а) да;
б) нет.
4. Подумайте и запишите, к чему может привести математическая ошибка?
_________________________________________________________________________________________________________________________________________________________________________________
5. Хотели бы вы познакомиться с курьёзными случаями математических ошибок?
а) да;
б) нет;
в) не знаю.
ПРИЛОЖЕНИЕ №2
РЕЗУЛЬТАТЫ АНКЕТИРОВАНИЯ
Слайды и текст этой презентации
Слайд 1
Описание слайда:
Математическая
теория катастроф
Факультет лазерной и световой инженерии
Слайд 2
Описание слайда:
Теория катастроф
Теория катастроф — раздел
математики, включающий в себя теорию
бифуркаций дифференциальных уравнений
(динамических систем) и теорию
особенностей гладких отображений.
Слайд 3
Описание слайда:
Термины «катастрофа» и «теория катастроф» были
Термины «катастрофа» и «теория катастроф» были
введены Рене Томом (René Thom) и Кристофером
Зиманом (Christopher Zeeman) в конце 1960-х — начале
1970-х годов («катастрофа» в данном контексте
означает резкое качественное изменение объекта при
плавном количественном изменении параметров, от
которых он зависит). Одной из главных задач теории
катастроф является получение так называемой
нормальной формы исследуемого объекта
(дифференциального уравнения или отображения) в
окрестности «точки катастрофы» и построенная на этой
основе классификация объектов.
Слайд 4
Описание слайда:
Теория катастроф нашла многочисленные
Теория катастроф нашла многочисленные
применения в различных областях
прикладной математики,
физики,
экономике.
Слайд 5
Описание слайда:
История
История
Начало математической теории катастроф положили
классические работы великого российско-немецкого
математика Леонарда Эйлера по теории устойчивости –
многообразной дисциплине, изучающей закономерности
поведения систем под действием внешних воздействий. В
работах Эйлера наибольшее развитие
получила теория устойчивости
механических систем. Действительно,
именно механика как старейшая наука,
впервые столкнулась с проблемами
устойчивости. Эйлер впервые строго
поставил и решил задачу устойчивости
состояния равновесия механический
системы — стержня, сжатого сжимающей
силой (эластика Эйлера).
Слайд 6
Описание слайда:
Первые фундаментальные результаты в
Первые фундаментальные результаты в
области динамических
систем, относящиеся к
теории катастроф,
принадлежат А. Пуанкаре
(метод нормальных форм
в теории дифференциальных
уравнений) и А. А. Андронову
(бифуркации динамических систем).
Слайд 7
Описание слайда:
Основы теории особенностей гладких
Основы теории особенностей гладких
отображений были заложены прежде
всего в трудах американского тополога
Хасслера Уитни (Hassler Whitney) в 1940-х
1950-х годах, которым предшествовала
лемма Морса о нормальной форме
функции в окрестности невырожденной
критической точки.
Слайд 8
Описание слайда:
В конце 1960-х годов развитием этого направления
В конце 1960-х годов развитием этого направления
занялся известный французский математик и
филдсовский лауреат 1958 года Рене Том. Однако
популярность идеи Уитни и Тома приобрели благодаря
нескольким публикациям К. Зимана в 1970-х годах,
который активно пропагандировал теорию катастроф,
сравнивая её значение с изобретением математического
анализа и говоря о «революции в математике». Бурное
развитие теории катастроф в 1970-е — 1990-е годы
связано с деятельностью Дж. Боардмана, Е. Брискорна,
Дж. Брюса, Дж. Мазера, Б. Мальгранжа, Р. Тома,
Т. Волла, К. Зимана и особенно В. И. Арнольда и его
учеников (А. Н. Варченко, В. А. Васильев, А. Б. Гивенталь,
В. В. Горюнов, С. М. Гусейн-Заде, А. А. Давыдов,
В. М. Закалюкин, В. Д. Седых и др.).
Слайд 9
Описание слайда:
Семь элементарных катастроф по Тому
Теория катастроф анализирует критические
точки (репетиции) потенциальной функции, то
есть точки, где не только первая производная
функции равна нулю, но и равны нулю же
производные более высокого порядка.
Динамика развития таких точек может быть
изучена при помощи разложения потенциальной
функции в рядах Тейлора посредством малых
изменений входных параметров.
Слайд 10
Описание слайда:
Если точки роста складываются не просто в случайный
Если точки роста складываются не просто в случайный
узор, но формируют структурированную область
стабильности, эти точки существуют как организующие
центры для особых геометрических структур с низким
уровнем катастрофичности, с высоким уровнем
катастрофичности в окружающих их областях фазового
пространства. Если потенциальная функция зависит от
трёх или меньшего числа активных переменных, и пяти
или менее активных параметров, то в этом случае
существует всего семь обобщённых структур
описанных геометрий бифуркаций, которым можно
приписать стандартные формы разложений в ряды
Тейлора, в которые можно разложить репетиции при
помощи диффеоморфизма (гладкой трансформации,
обращение которой также гладко). Сегодня эти семь
фундаментальных типов катастроф известны под
именами, которые им дал Рене Том.
Слайд 11
Описание слайда:
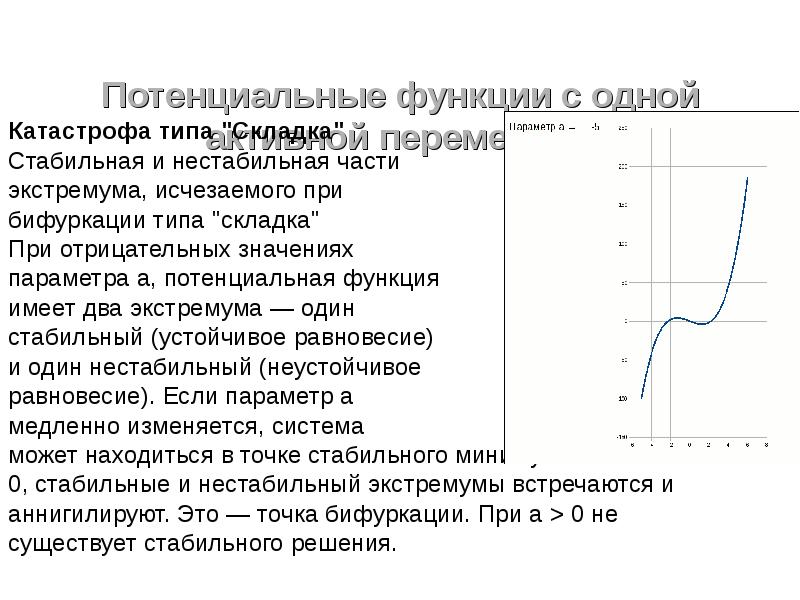
Потенциальные функции с одной активной переменной
Катастрофа типа «Складка»
Стабильная и нестабильная части
экстремума, исчезаемого при
бифуркации типа «складка»
При отрицательных значениях
параметра a, потенциальная функция
имеет два экстремума — один
стабильный (устойчивое равновесие)
и один нестабильный (неустойчивое
равновесие). Если параметр a
медленно изменяется, система
может находиться в точке стабильного минимума. Но если a =
0, стабильные и нестабильный экстремумы встречаются и
аннигилируют. Это — точка бифуркации. При a > 0 не
существует стабильного решения.
Слайд 12
Описание слайда:
Катастрофа типа «Сборка«
Катастрофа типа «Сборка«
Диаграмма катастрофы «сборка» с точкой возврата, на
которой показаны кривые (коричневые, красные) по
переменной x, удовлетворяющие выражению для
параметров (a, b), кривые показаны для непрерывно
изменяющегося параметра b при различных значениях
параметра a. Вне геометрического места точек
возврата (синяя область) для каждой точки (a, b) в
фазовом пространстве существует
только одно экстремальное значение
переменной x. Внутри точек
возврата существует два
различных значения x, которые
дают локальные минимумы
функции V(x) для каждой пары
(a, b). При этом указанные
значения разделены локальным максимумом.
Слайд 13
Описание слайда:
Катастрофа типа «Ласточкин хвост»
Катастрофа типа «Ласточкин хвост»
Управляющее пространство в данном
типе катастроф является трёхмерным.
Каскад бифуркаций в фазовом
пространстве состоит из трёх
поверхностей бифуркаций типа
«свёртки», которые
встречаются на двух
кривых бифуркаций с
точками возврата,
которые в конечном
итоге встречаются в
одной точке, представляющей собой
бифуркацию типа «ласточкин хвост»».
Слайд 14
Описание слайда:
Катастрофа типа «Бабочка«
Катастрофа типа «Бабочка«
В зависимости от значений параметров потенциальная
функция может иметь три, два или один локальный
минимум, причём все минимумы разделены областями
с бифуркациями типа «свёртка». В точке с
поэтичным наименованием «бабочка» встречаются три
различные пространства (трёхмерных плоскости) таких
бифуркаций типа «свёртка»,
две поверхности бифуркаций
с точками возврата и скривая
бифуркаций типа «ласточкин
хвост». Все эти бифуркации
пропадают в одной точке и
преобразуются в простую
структуру с точкой возврата
тогда, когда значение
параметра a
становится положительным.
Слайд 15
Описание слайда:
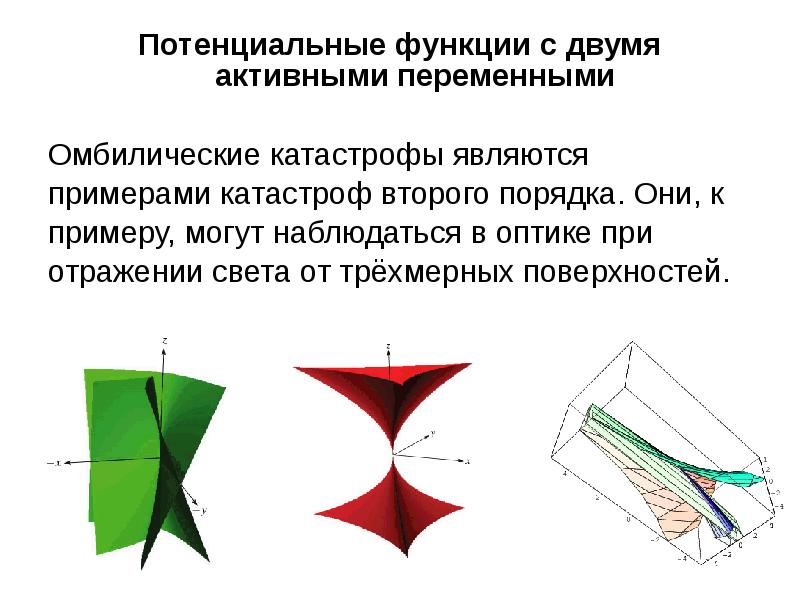
Потенциальные функции с двумя активными переменными
Потенциальные функции с двумя активными переменными
Омбилические катастрофы являются
примерами катастроф второго порядка. Они, к
примеру, могут наблюдаться в оптике при
отражении света от трёхмерных поверхностей.
Слайд 16
Описание слайда:
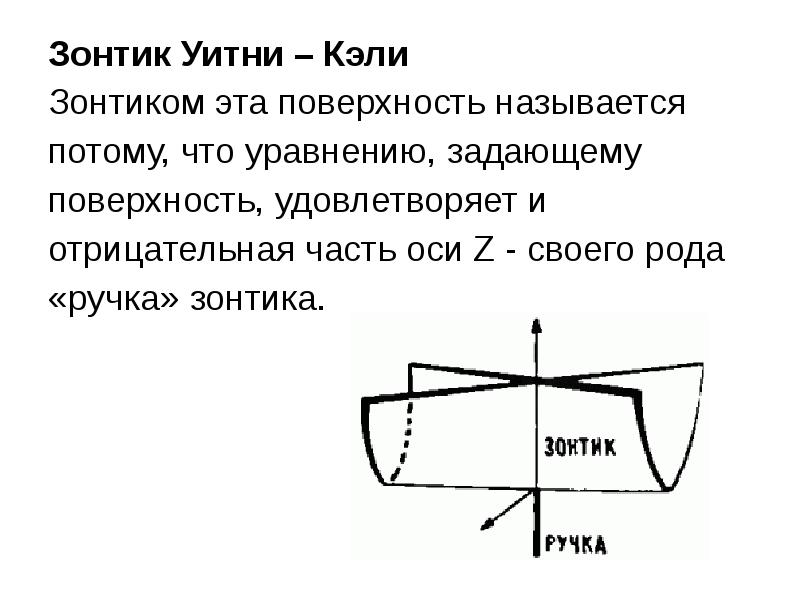
Зонтик Уитни – Кэли
Зонтик Уитни – Кэли
Зонтиком эта поверхность называется
потому, что уравнению, задающему
поверхность, удовлетворяет и
отрицательная часть оси Z — своего рода
«ручка» зонтика.
Слайд 17
Описание слайда:
Запись и классификация катастроф по Арнольду
В. И. Арнольд предложил классификацию катастроф, использующую глубокие связи с теорией групп Ли.
A0 — несингулярная точка: .
A1 — локальный экстремум: устойчивый минимум или неустойчивый максимум .
A2 — складка
A3 — сборка
A4 — ласточкин хвост
A5 — бабочка
Ak — бесконечная последовательность форм от одной
переменной
D4+ — кошелёк = гиперболическая омбилика
D4- — пирамида = эллиптическая омбилика
D5 — параболическая омбилика
Dk — бесконечная последовательность других омбилик
E6 — символическая омбилика
E7
E8
В теории сингулярности есть объекты, которые соответствуют
большинству других простых групп Ли.
Слайд 18
Описание слайда:
Применения теории катастроф
Создание и развитие этой части
математического анализа было связано с
широкими возможностями наглядного
моделирования некоторых сложных явлений,
особенно тех, которые встречаются при
описании самых разных естественных явлений
(радуга, каустика, устойчивость сложных
систем, колебания и разрушение в
строительной механике, поведение в этологии,
и даже бунты в тюрьмах)
Слайд 19
Описание слайда:
Спасибо за внимание
Список литературы:
В. И. Арнольд. В.И. АРНОЛЬД О ТЕОРИИ КАТАСТРОФ — Наука и жизнь, 1989, № 10
В. И. Арнольд. Теория катастроф — М., 1990
Стегний В. Н. Архитектоника генома, системные мутации и эволюция — Новосибирск: Изд-во НГУ, 1993. — 143 с.
Дубинин Н. П. Эволюция популяций и радиация. — М.: Атомиздат, 1966. — 744 с.
Вид и видообразование. // Соросовский Образовательный Журнал. — 1997. — № 4. — С. 2—10.