Математика метод проб и ошибок 5 класс

 «Метод проб и
ошибок»

Основные цели:

Предметные:

1) Сформировать представление о методе проб и ошибок,
умение использовать его в простейших случаях для решения уравнений.

2) Тренировать умение решать составные уравнения.

 
Ход урока:

1 Мотивация к учебной
деятельности.

Приветствие. Настрой на работу

2. Актуализация знаний

  
Все задания учащиеся выполняют
на индивидуальных карточках.

— Начнём работать по плану,
какой первый шаг? (Повторяем ранее изученное.)

  
На доске карточка с заданием № 1

– Подберите корень уравнения: . (5.)

–
Объясните способ решения, который вы использовали. (…)

–
А есть ли у этого уравнения другие корни? (…)

  
На доске карточка с заданием № 2

– Вспомните, как была построена математическая модель
задачи 3.

  
Учащиеся показывают результаты
выполнения задания, проводится, если необходимо коррекция ошибок, выбирается
одна из предложенных моделей: х(х + 3) = 70.

— Какой
из предложенных алгоритмов (алгоритмы висят на доске) вы использовали при
построении данной модели?

  
Учащиеся выбирают алгоритм и
обосновывают свой выбор.

— Что вы
сейчас повторили? (Алгоритм построение математической модели по тексту задач
третьего типа, решение уравнений способом подбора.)

— К
какому пункту плана вы можете приступать? (К рассмотрению пробного задания.)

– Решите задачу 3, используя построенную математическую
модель.

— На
какие вопросы вам надо ответить прежде, чем пробовать выполнить задание? (Что
нового в этом задании, какая наша цель, какая тема урока.)

—
Обсудите в группах эти вопросы и подготовьте на них ответы.

  
На работу группам отводится 1
минута. Затем одна группа представляет свой вариант ответов, а другие группы
дополняют, корректируют ответ.

Вариант ответа: надо решить
задачу, но сначала надо решить уравнение, в котором оба множителя не известны,
тема: «Решение задач третьего типа».

  
Если работа в группах будет
затруднена, организовать подводящий диалог.

— Что
нового в задании?

— Какая
цель стоит перед вами?

— В чём
особенность, получившего уравнения?

—
Сформулируйте тему урока.

— Что
теперь надо сделать? (Попробовать выполнить задание.)

—
Внимание задание: решите уравнение, которое является моделью задачи.

  
На работу отводится 1 минута.
Учащиеся показывают свои результаты.

Вариант первый: учитель
фиксирует, что нет ответов.

— Что
показало пробное задания? (Мы не смогли решить уравнение, в котором оба
множителя не известны.)

Вариант второй: учитель
фиксирует, что нет правильных ответов.

—
Сформулируйте своё затруднение. (Мы не смогли правильно решить уравнение, в
котором оба множителя неизвестны.)

Вариант третий: учитель
фиксирует, что есть правильные ответы.

— Вы
можете доказать, что вы правильно решили уравнение? (Да, подставить найденное
число в уравнение и проверить, получится ли верное равенство.)

— А
объяснить, почему именно так надо решать уравнение, как вы это делали, и вы
можете доказать, что других корней нет, ведь произведение равно 70 если
множители равны 7 и 10 или 2 и 35, или 5 и 14? (Нет.)

— Что вы
не можете сделать? (Мы не можем обосновать свои действия при решении уравнения,
не можем доказать, что других корней нет.)

— Что
теперь вы должны сделать? (Подумать, почему так получилось.)

3. Выявление места и причины затруднения

– Какое задание вы должны были выполнить? (Решить
уравнение .)

— Как вы
пробовали решать уравнение? (Пробовали использовать алгоритм, который построили
на прошлом уроке, пробовали подбирать.)

— В каком
месте у вас возникло затруднение? (В уравнении, для которого был построен
алгоритм, неизвестны два слагаемых, а в данном уравнении два множителя,
преобразование левой части не дало результата, подобрать корень не хватило
время, трудно, не знаем, как доказать, что других корней нет.)

– Почему вы не смогли решить, получившееся уравнение, или
не можете доказать, что решали правильно, и других корней нет? (У нас нет
способа решения уравнений, в котором неизвестны оба множителя.)

– Получившееся уравнение является моделью, какого типа
задач? (Третьего типа.)

– Значит, если вы не можете решить уравнение, вы сможете
решить задачу? (Нет, не сможем.)

— Какие
следующие шага вы должны предпринять? (Мы должны уточнить цель нашей работы,
составить план действий.)

4. Построение
проекта выхода из затруднения

– Уточните цель деятельности? (Найти способ решения
уравнений, составленного по формуле произведения, и в котором оба множителя
неизвестны.)

– Что вам даст умение решать уравнения такого вида?
(Решать задачи третьего типа.)

— Каким
способом вы можете решить это уравнение? (Способом подбора.)

—
Составьте план действий. (Подобрать корни, найти способ для доказательства, что
других корней нет.)

5. Реализация
построенного проекта

  
Дальше можно организовать работу
в группах. Группы работают по предложенному плану в течение 3 минут. Затем одна
из групп по желанию выставляет свою версию, и обосновывает её. Остальные группы
либо высказывают согласие с этой версией, либо поясняют, чем и почему их
вариант отличается от других. Во время ответа группы учитель фиксирует способ
поиска решения. Поиск способа доказательства, что других корней нет, может вызвать
затруднение.

  
Возможный вариант ответа детей:
угадываем корень, делаем проверку, если угадали, то записываем ответ, если не
угадали, т.е. при проверке не получили верное равенство, то угадываем дальше.

– А как можно ещё найти решение уравнения, но так, чтобы
не сидеть, и не гадать корень? (Можно брать любые числа и проверять: являются,
взятые числа корнями уравнения или нет, подставляя их вместо переменной.)

— И до
каких пор будете брать числа? (Пока не найдём корень уравнения.)

– Молодцы! Вы, верно, указали один из методов решения
таких уравнений. Попробуйте дать название такому методу.

  
Учащиеся предлагают свои
варианты. В итоге учитель вводит название метода «метод проб и ошибок».

– Приведите пример из жизни, где используется метод проб
и ошибок. (…)

– Вы нашли, что x = 7. Как доказать, что других
корней нет?

  
Доказательство проводится в
беседе с учащимися.

— Другие
корни, если они есть либо меньше 7, либо больше 7. Исследуйте, каким будет x(x + 3), если x < 7? (Первый
множитель меньше 7, второй меньше 10, значит произведение меньше 70.)

— Исследуйте,
каким будет x(x + 3), если x > 7? (Первый множитель
больше 7, второй больше 10, значит произведение больше 70.)

— Вы
доказали, что других корней нет? (Да доказали.)

— Я вам
предлагаю из блоков составить алгоритм решения уравнений.

  
У каждой группы блоки

	Придать переменной любое правдоподобное значение		Подставить его в уравнение
	Докажи, что других решений нет
		Взять другое правдоподобное значение переменной

  
Учащиеся в течение 1 минуты
выполняют задание. Одна из групп представляет свою версию, и обосновывают её.
Остальные группы работают на дополнение, уточнение.

  
Задача учителя на данном этапе –
организовать согласование всех полученных версий.

— Как можно проверить, что вы правильно открыли новые знания?

Учащиеся сопоставляют свой вариант
с эталоном 1 на стр. 97 учебника.

  
После этого он выставляет
собственный вариант и сравнивает его с итоговой версией класса

Вариант 1                                                                                         Вариант
2

		1. Придать переменной любое правдоподобное значение. 2. Подставить его в уравнение. 3. Найти значение левой и правой части уравнения и сравнить полученные числа. 4. Если значения не равны, то перейти к пункту 1, если значения равны, то перейти к пункту 5. 5. Доказать, что других решений нет.

Да                                           Нет

6. Первичное закрепление во внешней
речи

№ 168 (4)

  
Задание выполняет ученик у
доски.

1) Прочитать задачу. «Площадь прямоугольника равна 64 дм²,
а его длина в 4 раза больше ширины. Каков периметр прямоугольника?»

2)
Проверить соответствие между единицами измерения величин: единицы измерения
величин согласованы.

3) Определить взаимосвязи между описанными в ней величинами: в задаче
говориться о площади прямоугольника – 64 дм², а длина в 4 раза
больше ширины. Надо найти периметр прямоугольника.

4) Обозначить одну из неизвестных величин буквой: обозначим ширину – х
дм.

5)
Выразить остальные неизвестные величины через введенную букву, составим
таблицу:

6) Составить уравнение: x × 4x = 64

7)
Решить уравнение методом проб и ошибок:

Придать переменной любое правдоподобное значение: x = 3.

Подставить его в уравнение, проверить является число корнем:

если x = 3, то 3 × 4 × 3 = 64;

                                            36 = 64 (Н)

Число 3 не является корнем.

Взять другое правдоподобное значение переменной: x = 4

Подставить его в уравнение, проверить является число корнем:

если x = 4, то 4 × 4 × 4 = 64 (В)

Число 4 является корнем.

Доказать, что других корней нет:

если x < 4, то
x ×
4x < 64

если x > 4, то
x ×
4x > 64

Ответить на вопрос задачи: ширина участка – 4 дм

4 × 4 = 16 (дм) – длина участка.

(4 + 16) × 2 = 40 (дм) периметр прямоугольника.

Ответ: периметр равен 40 дм.

№ 168 (2)

  
Задание выполняется в парах.

  
Результаты выполнения № 168

7. Самостоятельная работа с
самопроверкой

  
Для самостоятельной работы
предлагается выполнить № 168 (1).

  
Результаты выполнения № 168 (1)
проверяются

8. Включение в систему знаний и
повторение.

— Какие ещё уравнения вы умеете решать? (Составные
уравнения.)

— Выполните № 179 (2).

  
Задание выполняет один ученик у
доски с комментарием.

60 × (у : 40 + 4) = 720;

Находим множитель. Чтобы найти неизвестный множитель
надо произведение разделить на известный множитель:

у : 40 + 4 = 720 : 60;

у : 40 + 4 = 12;

Находим первое слагаемое. Чтобы найти неизвестное
слагаемое надо из суммы вычесть известное слагаемое:

у : 40 = 12 – 4;

у : 40 = 8;

Находим делимое. Чтобы найти делимое надо частное умножить
на делитель:

у = 8 × 40;

у = 320

9. Рефлексия деятельности на уроке

– Какая основная цель стояла сегодня на уроке? (Вывести способ решения
уравнения с двумя неизвестными множителями.)

– Назовите этот метод (Метод проб и ошибок.)

– В чём заключается этот метод? (Вместо переменной в
уравнение подставляем любые числа и проверяем, является взятое число корнем
уравнения и делаем это до тех пор пока не найдём решение.)

– Что ещё необходимо при использовании этого метода?
(Доказывать, что найденное решение единственное.)

– Проанализируйте и оцените свою работу на уроке.

Домашнее задание: п. 1.2.2. (задача 3), эталон; № 177 (1); № 178 (а); № 179 (1 или 3 на
выбор); № 180* — по желанию.

Метод проб и ошибок

в решении текстовых задач.

При решении текстовых задач многие учащиеся испытывают затруднения. Главная задача учителя научить решать ученика различные типы текстовых задач. Процесс решения текстовых задач развивает у учащихся логическое мышление, учат находить выход из проблем реальной жизни, дает почувствовать уверенность в своих силах.

Текстовые задачи можно разбить на два основных класса:

• текстовые арифметические задачи;

• текстовые задачи на составление уравнений.

Причем это разделение довольно условно. Многие текстовые арифметические задачи можно решить с помощью уравнений, а задачи на составление уравнений (систем уравнений) часто решают по действиям, а если это не получается, то используют метод проб и ошибок или метод перебора.

Мне бы хотелось продемонстрировать решение ряда задач этими методами.

Задача №1

Одна сторона прямоугольного участка земли на 3 м больше другой его стороны. Площадь участка равна 70 м². Найти размеры этого участка.

Пусть x м ширина участка, (x+3) м – длина участка, а площадь x·(x+3) м²,

что по условию задачи равно 70 м². Чтобы найти размеры участка надо составить уравнение x·(x+3)=70 и решить его. Но в 5^ом классе такие учащиеся решать еще не могут. Поэтому попробуем подобрать решение «экспериментально», так называемым методом проб и ошибок.

1. пусть x=4, т.е. 4·(4+3)=28, 28≠70;

2. x=6, т.е. 6·(6+3)=54, 54≠70;

3. x=7, т.е. 7·(7+3)=70, 70=70 верно.

Т.е. мы увидели, что метод проб и ошибок позволяет найти ответ даже в случае, когда математический модель представляет собой новый, не изученный еще объект. Но, решая задачи этим способом, следует помнить, что подбор одного решения не гарантирует полноты решения. Поэтому необходимы обоснования того, что найдены все возможные решения.

В нашей задаче, если бы x было больше 7,то x+310 и x·(x+3)70, если наоборот xx+3 x·(x+3)

Задачи для учащихся.

Переведи условие задачи на математический язык и найди решение методом проб и ошибок.

1. Площадь прямоугольника равна 68 дм², а длина больше ширины на 13 дм. Каковы стороны этого прямоугольника?

2. Ширина прямоугольника на 9 см меньше длины, а площадь равна 90 см². Найти стороны прямоугольника.

3. Найти периметр прямоугольника, площадь которого составляет 18 м², а ширина в 2 раза меньше длины.

4. Площадь прямоугольника равна 64 дм², а его длина в 4 раза больше ширины. Чему равен периметр прямоугольника?

5. Длину прямоугольника уменьшили на 3 см, а ширину увеличили на 4 см и получили квадрат. Найти сторону квадрата, если площадь прямоугольника равна 30 см².

6. После того как ширину прямоугольника увеличили на 1 м, а длину уменьшили на 5 м, получили квадрат. Чему равна площадь квадрата, если площадь прямоугольника 91 м².

7. Длина прямоугольника на 5 м больше ширины, а площадь составляет 24 м². каковы стороны этого прямоугольника?

8. Длину прямоугольника уменьшили в 2 раза, а ширину увеличили на 1 дм и получили квадрат. Найти сторону квадрата, если площадь прямоугольника 60 дм².

9. Найти периметр прямоугольника, у которого ширина на 4 см меньше длины, а площадь составляет 32 см².

10)Одна из сторон прямоугольника на 20 см больше другой. Если

большую сторону уменьшить в 3 раза, а меньшую сторону увеличить

в 2 раза, то площадь нового прямоугольника будет равна 200 см².

Найти стороны данного прямоугольника.

Метод перебора при

нахождении НОД.

Рассмотрим еще один метод – метод перебора. Т.к. предыдущий метод решения задач – метод проб и ошибок не дает уверенности в том, что найдены все искомые значения. Поэтому для обоснования полноты решения требуются дополнительные, иногда очень непростые рассуждения. В этом недостаток метода проб и ошибок. Но он исключен в методе полного перебора.

Полный перебор требует, как правило, больших усилий и большого времени. Однако внимательный анализ условия часто позволяет найти систему перебора, охватывающую все возможные варианты, но более короткую, чем «лобовой» перебор.

Задача. На экскурсию едут 252 ученика школы. Для них заказаны

несколько автобусов. Однако выяснилось, что если заказать

автобусы, вмещающие на 6 человек больше, то автобусов

потребуется на один меньше. Сколько больших автобусов надо

заказать?

Составим таблицу.

Т.к. по условию в большой автобус вмещается на 6 детей больше, чем в маленький, то разность 252 : x — 252 : (x+1) = 6. Значит решением задачи является число X, удовлетворяющее равенству: 252 : x — 252 : (x+1) = 6.

Но можно получить более простую математическую модель этой задачи, обозначив дополнительно буквой Y число детей, которых можно разместить в большом автобусе.

Очевидно, что в этом случае математической моделью задачи являются два равенства:

1. xy = 252;

2. (x+1)·(y-6) = 252.

Искомые числа x и y должны удовлетворять как первому, так и

второму равенству. Найдем эти числа x и y.

Из равенства xy = 252 можно заметить, что числа x и y не могут быть

больше, чем 252. Однако и в этом случае «лобовой» перебор потребовал бы рассмотрения огромного числа вариантов. Но более внимательный анализ первого равенства показывает, что числа x и y – это парные делители 252: при делении 252 на x получается y, и наоборот. Следовательно, достаточно рассмотреть лишь парные делители числа 252, причем для случая, когда y6 (y-60).

Составим таблицу:

+1

— 6

Анализ второго равенства позволяет еще больше сократить число возможных вариантов. Оно означает, что число (x+1) и (y-6) так же являются парными делителями 252. Из таблицы видно, что такими свойствами обладает только пара x=6, y=42.

Ответ: для экскурсии надо заказать 6 больших автобусов.

Задачи для учащихся.

1. Сумма цифр двузначного числа равна 15. Если эти цифры поменять местами, то получится число, которое на 27 меньше исходного. Найти эти числа.

2. Сумма цифр двузначного числа равна 12. число, записанное теми же цифрами, но в обратном порядке, составляет ⁴ /₇ исходного числа. Найти эти числа.

3. Одно из двух натуральных чисел на 4 больше другого. Найди эти числа, если их произведение равно 96.

4. У причала находилось 6 лодок, часть из которых была двухместными, а часть трехместными. Всего в эти лодки может поместиться 14 человек. Сколько двухместных и трехместных лодок было у причала?

5. Прямоугольный газон обнесен изгородью, длинна которой 30 м. Площадь газона 56 м². Найди длины газона, если известно, что они выражаются натуральными числами.

6. В несколько посылок упаковали 36 книг и 54 журнала, распределив их между посылками поровну. В каждой посылке книг на 2 меньше, чем журналов. Сколько получилось посылок?

7. Произведение двух натуральных чисел равно 72. Найти эти числа, если одно из них больше другого на 6.

8. На турбазе имеются палатки и домики, общее число которых равно 25. в каждом домике живут 4 человека, а в палатке – 2 человека. Сколько на турбазе палаток и сколько домиков, если всего на этой турбазе отдыхают 70 человек?

9. Прямоугольный участок земли обнесен забором, длина которого 40 м. Площадь участка 96 м². Найти длины сторон этого участка, если известно, что они выражаются натуральными числами.

Еще один тип задач, которые решаются методом перебора.

Задумано двузначное число, которое на 52 больше произведения своих цифр. Какое число задумано?

Пусть xy – задуманное двузначное число, где x – цифра десятков, а y – цифра единиц. Тогда их произведение равно xy. Само двузначное число можно записать как 10x+y. По условию 10x+y на 52 больше произведения своих цифр xy. Т.е. должно выполняться равенство 10x+y= xy+52, которое является математической моделью данной задачи.

Решается это уравнение методом перебора. Полный перебор можно провести, рассматривая последовательно все значения x от 1 до 9 и подбирая в каждом случае соответствующее значение y от 0 до 9.

Однако этот перебор можно сократить, если заметить, что первая часть данного равенства больше 52. Значит, и первая его часть, т.е. задуманное число, больше 52. Поэтому неизвестное число x не меньше 5, и можно рассматривать только пять значений x – от 5 до 9.

При x=5 будем иметь равенство 50+y=5y+52, оно невозможно, т.к. 50+yy+52.

При x=6 60+y=6y+52 | -y

60=5y+52

5y=8 невозможно для натурального y.

При x=7 70+y=7y+52

70=6y+52

6y=18

y=3 Число 73

При x=8 80+y=8y+52

80=7y+52

7y=28

y=4 Число 87

При x=9 90+y=9y+52

38=8y невозможно

Таким образом, задумано либо 73, либо 84.

Условие задачи не дает возможности ответить на этот вопрос. Поэтому два ответа: 73 или 84.

Задачи для учащихся.

Метод перебора используется при доказательстве общих утверждений, где необходимо вводить буквенные обозначения.

Например: Доказать, что сумма любых трех последовательных натуральных чисел делится на 3.

1 сл. 1,2,3 1+2+3=6, 6:3=2

2 сл. 5,6,7 5+6+7=18, 18:3=6

3 сл. 21,22,23 21+22+23=66 66:3=22

и т.д.

Возьмем произведение натурального числа и обозначим его n. Тогда следующие за ним два числа соответственно равны n+1 и n+2.

Их сумма: n+(n+1)+(n+2)=3n+3=3(n+1) делится на 3, т.к. один из множителей делится на 3.

Человечество берет свое начало несколько тысяч лет назад. И на протяжении всего этого времени оно неустанно развивается. Причин на это было всегда много, но без изобретательности человека это просто не представлялось бы возможным. Метод проб и ошибок был и является в настоящее время одним из основных.

Описание способа

Четко зафиксированного в исторических документах применения данного метода мало. Но, несмотря на это, он заслуживает особого внимания.

Метод проб и ошибок – это способ, при котором решение задачи достигается подбором вариантов до тех пор, пока результат не станет правильным (например, в математике) или приемлемым (при изобретении новых методов в науке).

Человечество всегда пользовалось данным методом. Ориентировочно век назад психологи пытались найти общее между людьми, которые использовали данный способ познания. И им это удалось. Человек, который ищет ответ на поставленную задачу, вынужден подбирать варианты, ставить эксперименты и смотреть на результат. Это продолжается до тех пор, пока не приходит озарение по данному вопросу. Экспериментатор выходит на новую ступень мышления в данном вопросе.

Метод в мировой истории

Одним из самых известных людей, кто применял данный способ, был Эдисон. Все знают его историю изобретения лампочки. Он экспериментировал до тех пор, пока не получилось. Но Эдисон усовершенствовал данный метод. При поиске решения он разделял задачи между людьми, которые работали на него. Соответственно материала по теме получалось намного больше, чем при работе одного человека. И на основании полученных данных метод проб и ошибок имел большой успех в деятельности Эдисона. Благодаря этому человеку появились исследовательские институты, которые применяют, в том числе, и этот метод.

Степени трудности

У данного метода есть несколько уровней сложности. Они были так разделены для лучшего усвоения. Задача первого уровня считается легкой, и на поиск ее решения затрачивается немного сил. Но и вариантов ответов она имеет не так много. С повышением степени трудности растет и сложность поставленной задачи. Метод проб и ошибок 5 класса – самый труднорешаемый и затратный по времени.

Необходимо учитывать, что при возрастании уровня сложности растет и объем знаний, которыми обладает человек. Чтобы лучше понимать, о чем идет речь, рассмотрим технику. Первый и второй уровни позволяют изобретателям ее усовершенствовать. На последней ступени сложности создается совершенно новый продукт.

Например, известен случай, когда молодые люди темой дипломной работы взяли труднорешаемую задачу из аэронавигации. Студенты не обладали такими же знаниями, как многие ученые, которые работали в данной области, но благодаря широкому спектру знаний ребят у них получилось найти ответ. И причем область решения оказалась в самом далеком от науки кондитерском деле. Казалось бы, что это невозможно, но это факт. Молодым людям было даже выдано авторское свидетельство на их изобретение.

Преимущества метода

Первым достоинством можно по праву считать творческий подход. Задачи методом проб и ошибок решаемые позволяют задействовать оба полушария головного мозга для поиска ответа.

Стоит привести в пример, как строились лодки. Раскопки показывают, как на протяжении столетий деталь за деталью менялась форма. Исследователи постоянно пробовали что-то новое. Если лодка тонула, то эту форму вычеркивали, если оставалась держаться на воде, то принимали это к сведению. Таким образом, в итоге было найдено компромиссное решение.

Если поставленная задача не слишком сложная, то данный метод занимает немного времени. У некоторых возникающих проблем может быть десять вариантов, один или два из которых окажутся правильными. Но если рассматривать, например, робототехнику, то в данном случае без применения других методов исследования могут затянуться на десятки лет и принесут миллионы вариантов.

Разделение задач на несколько уровней позволяет оценить, насколько быстрым и возможным представляется поиск решения. Это сокращает время для принятия решения. И при сложных задачах можно использовать метод проб и ошибок параллельно с другими.

Недостатки метода

С развитием технологий и науки данный метод начал терять свою популярность.

В некоторых областях просто нерационально создавать тысячи образцов, чтобы менять по одному элементу. Поэтому зачастую теперь используют другие методы, основанные на конкретных знаниях. Для этого стали изучаться природа вещей, взаимодействие элементов друг с другом. Стали использоваться математические расчеты, научные обоснования, эксперименты и опыт прошлого.

Метод проб и ошибок все так же отлично используется в творчестве. Но строить автомобиль таким способом уже кажется глупым и неактуальным. Поэтому теперь, при нынешнем уровне развития цивилизации, нужно в точных науках по большей части использовать другие методы.

Часто при рассматриваемом способе задача может описывать много совершенно незначительных вещей и не учитывать априори важные вещи. Например, изобретатель пенициллина (антибиотик) утверждал, что при правильном подходе лекарство могли изобрести лет на двадцать раньше его. Это поспособствовало бы спасению огромного количества жизней.

При сложных задачах часто бывают ситуации, когда сам вопрос лежит в одной области знаний, а его решение — совершенно в другой.

Не всегда исследователь уверен, что ответ вообще будет найден.

Автор метода проб и ошибок

Кто конкретно изобрел это способ познания, мы никогда не узнаем. Точнее мы знаем, что это явно был изобретательный человек, которым, скорее всего, руководило желание улучшить свою жизнь.

В древности люди были достаточно ограничены во многих вещах. Все изобреталось именно этим методом. Тогда еще не было каких-то фундаментальных знаний в области физики, математики, химии и прочих важных наук. Поэтому приходилось действовать наугад. Именно так добыли огонь, чтобы защищаться от хищников, готовить пищу и обогревать жилище. Оружие, чтобы добывать пропитание, лодки — для передвижения по рекам. Все было изобретено при столкновении человека с трудностью. Но каждый раз решаемая проблема приводила к более качественному уровню жизни.

Известно, что многие ученые использовали этот метод в своих трудах.

Однако именно описание метода и активное использование мы наблюдаем у физиолога Торндайка в конце девятнадцатого века.

Исследования Торндайка

Пример метода проб и ошибок можно рассмотреть в научных трудах ученого-физиолога. Он ставил различные поведенческие эксперименты с животными, помещая их в специальные коробки.

Один из экспериментов выглядел приблизительно следующим образом. Кошка, помещенная в ящик, ищет выход. Сама коробка может иметь 1 вариант открытия: нужно было нажать на пружинку — и дверца распахивалась. Животное применяло много действий (так называемых проб), и большинство из них оказывались неудачными. Кошка так и оставалась в коробке. Но после некоторого набора вариантов животному удавалось нажать на пружинку и выбраться из ящика. Таким образом, кошка, попадая в коробку, с течением времени запоминала варианты развития событий. И выбиралась из ящика за более короткое время.

Торндайк доказал, что метод действителен, и хоть результат не линеен, но со временем, при повторении аналогичных действий, решение приходит практически моментально.

Решение задач методом проб и ошибок

Примеров этого способа великое множество, однако стоит привести один очень интересный.

В начале двадцатого века жил известный конструктор двигателей для авиации Микулин. В то время наблюдалось огромное количество авиакатастроф из-за магнето, то есть искра зажигания через некоторое время полета исчезала. Много было экспериментов и размышлений о причине, но ответ пришел в совершенно неожиданной ситуации.

Александр Александрович встретил на улице мужчину с подбитым глазом. В тот момент к нему и пришло озарение, что человек без одного глаза видит намного хуже. Он поделился этим наблюдением с авиатором Уточкиным. Когда установили в самолеты второе магнето, количество авиакатастроф значительно уменьшилось. А Уточкин некоторое время выплачивал после каждого показательного полета Микулину денежные вознаграждения.

Применение способа в математике

Достаточно часто метод проб и ошибок в математике применяется в школах как способ развития логического мышления и проверки скорости поиска вариантов. Это позволяет разнообразить процесс обучения и внести элементы игры.

Часто можно встретить в школьных учебниках задания с формулировкой «реши уравнение методом проб и ошибок». В данном случае необходимо подбирать варианты ответа. Когда найден правильный ответ, он просто доказывается уже практически, то есть проводятся необходимые расчеты. В итоге мы удостоверяемся, что это единственно верный ответ.

Пример практической задачи

Метод проб и ошибок в математике 5 класса (в последних изданиях) часто фигурирует. Приведем пример.

Необходимо назвать, какие стороны могут быть у прямоугольника. При условии, что площадь (S) = 32 см, а периметр (P) = 24 см.

Решение данной задачи: предположим, что длина одной стороны 4. Значит и длина еще одной стороны такая же.

Получаем следующее уравнение:

24 – 4 – 4 = 16

16 делим на 2 = 8

8 см – это ширина.

Проверяем по формуле площади. S = A*B = 8*4 = 32 сантиметра. Как мы видим, решение верное. Так же можно вычислить и периметр. По формуле получается следующий расчет Р = 2* (А + В) = 2* (4 + = 24.

В математике метод проб и ошибок не всегда отлично подходит для поиска решений. Зачастую можно использовать более подходящие способы, при этом затрачивается меньше времени. Но для развития мышления данный метод имеется в арсенале каждого педагога.

Теория решения изобретательских задач

В ТРИЗ метод проб и ошибок считается одним из самых неэффективных. Когда человек попадает в необычную для него затруднительную ситуацию, то действия наугад, скорее всего, будут безрезультатными. Можно потратить много времени и в результате не добиться успеха. Теория решения изобретательских задач основана на уже известных закономерностях, и обычно используются другие методы познания. Часто ТРИЗ используют в воспитании детей, делая этот процесс интересным и увлекательным для ребенка.

Выводы

Рассмотрев данный метод, можно с уверенностью сказать, что он достаточно интересный. Несмотря на недостатки, он часто используется в решении творческих задач.

Однако не всегда он позволяет добиться нужного результата. Никогда исследователь не знает, когда стоит прекратить поиски или, может, стоит сделать еще пару усилий и гениальное изобретение появится на свет. Также непонятно, сколько времени будет затрачено.

Если вы решили использовать данный метод для решения какой-либо проблемы, то должны понимать, что ответ порой может находиться в совершенно неожиданной области. Но это позволяет взглянуть на поиск с разных точек зрения. Возможно, придется набросать несколько десятков вариаций, а может, и тысячи. Но лишь упорство и вера в успех приведут к нужному результату.

Иногда этот метод используют как дополнительный. Например, на начальном этапе для сужения поиска. Либо когда исследование было проведено многими способами и зашло в тупик. В этом случае творческая составляющая метода позволит найти компромиссное решение проблемы.

Метод проб и ошибок часто применяют в педагогической деятельности. Он позволяет детям на собственном опыте находить решения в различных жизненных ситуациях. Это учит их запоминать правильные типы поведения, которые приняты в обществе.

Художники используют данный способ для поиска вдохновения.

Метод стоит опробовать в обыденной жизни при решении проблем. Возможно, какие-то вещи предстанут вам по-другому.

Введение

Проблемы обычного школьного урока привлекают к себе в последнее время особенно пристальное внимание. От школы и от учителя требуют не только дать знания, сформировать программные умения и навыки у всех учащихся, а главное, научить школьников творчески распоряжаться ими.

Но в большинстве случаев, учащиеся ориентируются на указания учителя, а самостоятельно организовывать свои действия не умеют. Умение решать задачи является одним из основных показателей уровня математического развития, глубины освоения учебного материала. Ребенок с первых дней занятий в школе встречается с задачей. С начала и до конца обучения в школе математическая задача неизменно помогает ученику вырабатывать правильные математические понятия, глубже выяснять различные стороны взаимосвязей в окружающей его жизни, дает возможность применять изучаемые теоретические положения. Текстовые задачи — традиционно трудный для значительной части школьников материал. Однако в школьном курсе математики ему придается большое значение, так как такие задачи способствуют развитию логического мышления, речи и других качеств продуктивной деятельности обучающихся.

Задачи в обучении математике занимают важное место: это и цель, и средство обучения. Умение решать задачи — показатель обученности и развития учащихся. Научиться решать математические задачи очень важно, т.к., зная подходы к решению математических задач, учащиеся тем самым обучаются взаимодействию с любой задачей, которых достаточно много в других школьных предметах и в жизни вообще. Тем самым формируется жизненная позиция ученика как активной, самостоятельной личности.

Функции, цели обучения самой математики: воспитание, развитие, обучение молодого поколения. Отдельная задача может нести в себе различную информацию из различных областей знаний, расширять кругозор, воздействовать на познавательные возможности, может нести эстетическую нагрузку.

Цель: описание методов и способов решения текстовой задачи в курсе изучения математики 5 – 6 классов.

Объект работы: текстовые задачи в курсе математики основной школы.

Предмет работы: решение текстовых разными способами и методами.

В соответствии с целью исследования необходимо решить следующие задачи:

• изучить научную литературу по данной проблеме;

• рассмотреть классификации, методы и способы решения текстовых задач;

• описать методы и способы решения задач в 5 — 6 классах.

При решении задач требуется, чтобы учащиеся не только знали правила, определения, формулировки, но и понимали их смысл, значение, умели применять их в конкретных ситуациях. В процессе обучения должны объединиться строго научное изложение учителя с высказываниями, рассуждениями, вопросами, усилиями в преодолении трудностей со стороны учащихся.

Методы и способы решения тестовых задач

Существуют различные методы решения текстовых задач:

• арифметический,

• алгебраический,

• геометрический,

• логический,

• практический,

• табличный,

• комбинированный,

• метод проб и ошибок.

В основе каждого метода лежат различные виды математических моделей.

Например, при алгебраическом методе решения задачи составляются уравнения или неравенства, при геометрическом — строятся диаграммы или графики. Решение задачи логическим методом начинается с составления алгоритма.

Следует иметь в виду, что практически каждая задача в рамках выбранного метода допускает решение с помощью различных моделей. Так, используя алгебраический метод, ответ на требование одной и той же задачи можно получить, составив и решив совершенно разные уравнения, используя логический метод — построив разные алгоритмы. Ясно, что в этих случаях мы так же имеем дело с различными методами решения конкретной задачи, которые называю способы решения.

Иногда для краткости изложения, вместо того чтобы говорить, что задача решена определенным способом в рамках, например, арифметического метода, будем говорить, что «задача решена арифметическим способом» или «задача решена арифметическим методом», а то и просто — «задача решена арифметически».

Арифметический метод. Решить задачу арифметическим методом — значит найти ответ на требование задачи посредством выполнения арифметических действий над числами. Одну и ту де задачу во многих случаях можно решить различными арифметическими способами. Задача считается решенной различными способами, если ее решения отличаются связями между данными и искомыми, положенными в основу решений, или последовательностью этих связей.

Алгебраический метод. Решить задачу алгебраическим методом — это значит найти ответ на требование задачи, составив и решив уравнение или системы уравнений (или неравенств). Одну и ту же задачу можно так же решить различными алгебраическими способами. Задача считается решенной различными способами, если для ее решения составлены различные уравнения или системы уравнений (неравенств), в основе составления которых лежат различные соотношения между данными и искомыми.

Геометрический метод. Решить задачу геометрическим методом — значит найти ответ на требование задачи, используя геометрические построения или свойства геометрических фигур.

Логический метод. Решить задачу логическим методом — это значит найти ответ на требование задачи, как правило, не выполняя вычислений, а только используя логические рассуждения.

Практический метод. Решить задачу практическим методом — значит найти ответ на требования задачи, выполнив практические действия с предметами или их копиями (моделями, макетами).

Табличный метод позволяет видеть задачу целиком это- решение путем занесения содержания задачи в соответствующим образом организованную таблицу.

Комбинированный метод позволяет получить ответ на требование задачи более простым путем.

Метод проб и ошибок (самый примитивный), в нем ответ на вопрос задачи угадывается. Но и здесь основные моменты решения — выбор пробных ответов на вопрос задачи и проверка их соответствия условию осуществляется с помощью мыслительных операций, необходимых при решении любым путем. Угадывание ответа требует интуиции, без которой невозможно никакое решение.

Методы решения могут быть разные, но способ решения, лежащий в их основе, может быть один.

Примеры решения текстовых задач в 5 — 6 классе

Решение задач по-разному – мощное средство постижения мира, осознание разнообразия свойств и отношений его элементов. Разные методы и способы решения — средство развития познавательного интереса, умения отстаивать свою точку зрения, способности слышать и понимать других людей.

Арифметический метод.

Пример. Поют в хоре и занимаются танцами 82 студента, занимаются танцами и художественной гимнастикой 32 студента, а поют в хоре и занимаются художественной гимнастикой 78 студентов. Сколько студентов поют в хоре, занимаются танцами и художественной гимнастикой отдельно, если известно, что каждый студент занимается только чем-то одним?

Решение.

1-й способ.

1) 82 32 + 78 = 192 (чел.) — удвоенное число студентов, поющих в хоре, занимающихся танцами и художественной гимнастикой;

2) 192 : 2 = 96 (чел.) — поют в хоре, занимаются танцами и художественной гимнастикой;

3) 96 – 32 = 64 (чел.) — поют в хоре;

4) 96 – 78 = 18 (чел.) — занимаются танцами;

5) 96 – 82 = 14 (чел.) — занимаются художественной гимнастикой.

2-й способ.

1) 82 – 32 = 50 (чел.) — настолько больше студентов поют в хоре, чем

занимаются художественной гимнастикой;

2) 50 + 78 = 128 (чел.) — удвоенное число студентов, поющих в хоре;

3) 128 : 2 = 64 (чел.) — поют в хоре;

4) 78 – 64 = 14 (чел.) — занимаются художественной гимнастикой;

5) 82 – 64 = 18 (чел.) — занимаются танцами.

Ответ: 64 студента поют в хоре, 14 студентов занимаются художественной гимнастикой, 18 студентов занимаются танцами.

Алгебраический метод.

Пример 1. Рабочий может сделать определенное число деталей за три дня. Если он в день будет делать на 10 деталей больше, то справится с заданием за два дня. Какова первоначальная производительность рабочего и сколько деталей он должен сделать?

Решение.

1-й способ. Пусть х д. в день — первоначальная производительность рабочего. Тогда (х + 10) д. в день — новая производительность, Зх д. – число деталей, которое он должен сделать. По условию получаем уравнение Зх = 2(х + 10), решив которое найдем х = 20. первоначальная производительность рабочего 20 деталей в день, он должен сделать 60 деталей.

2-й способ.

Пусть х д. – число деталей, которое должен сделать рабочий. Тогда д. в день — новая производительность, ( – 10) д. в день – первоначальная производительность рабочего по условию получаем уравнение х = 3( – 10), решив которое найдем х = 60. Рабочий должен сделать 60 деталей, его первоначальная производительность 20 деталей в день.

Ответ: 20 деталей в день; 60 деталей.

Приме 2. На солнышке грелось несколько кошек. У них вместе лап на 10 больше, чем ушей. Сколько кошек грелось на солнышке?

Решение.

1 способ.

Так как лап на 10 больше чем ушей.

Составим и решим уравнение:
4х – 2х = 10
2х = 10   │: 2
х = 5

Ответ: 5 кошек грелось на солнышке. 

2 способ

1. На сколько лап больше чем ушей у одной кошки?
   4 – 2 = 2 (шт.)

2. Сколько кошек грелось на солнышке?
   10 : 2 = 5 (шт.)

Ответ: 5 кошек грелось на солнышке. 

Пример 3. В хозяйстве имеются куры и овцы. Сколько тех и других, если известно, что у них вместе 19 голов и 46 ног?

Решение.

Так как у кур и овец ног всего 46.
Составим и решим уравнение:
2х + 4(19 – х) = 46

Составленное уравнение учащиеся решают самостоятельно, с последующей проверкой.

2х + 76 – 4х = 46
-2х = -30 │: (-2)
х = 15
15 шт. – куры
19 – 15 = 4 (шт.) – овцы

Ответ: 15 кур, 4 овц

Геометрический метод.

Пример. Из двух городов А и В, расстояние между которыми 250 км, навстречу друг другу выехали два туриста. Скорость движения первого равна 20 км/ч, второго – ЗО км/ч. Через сколько часов туристы встретятся?

Решение.

1-й способ. Математическую модель задачи представим в виде диаграммы. Причем длину одного отрезка по вертикали за 10 км. Длину одного отрезка по горизонтали — за 1 ч. Отложим на вертикальной прямой отрезок АВ, равный 250 км. Он будет изображать расстояние между городами. Для удобства проведем еще одну ось времени через точку В. затем на вертикальных прямых станем откладывать отрезки пути, пройденные каждым туристом за 1 ч, 2 ч, 3 ч и т. д. Из чертежа видим, что через 5 ч они встретятся.

2-й способ. В прямоугольной системе координат по горизонтали отложим время движения (в часах), по вертикали — расстояние (в километрах).

Примем длину одного отрезка по вертикали за 10 км, а длину одного отрезка по горизонтали – за 1 ч. Построим графики, характеризующие движение каждого туриста. Движение первого туриста определяется функцией y = 20х, второго – y= 250 – З0х. Абсцисса точки их пересечения (точки О) указывает, через сколько часов туристы встретятся. Из чертежа видно, что ее значение равно 5. Ордината указывает, на каком расстоянии от пункта А произойдет встреча. Ее значение равно 100.

3-й способ. Пусть время движения туристов до встречи изображается отрезком ОТ, а скорость сближения — отрезком OS. Тогда площадь S прямоугольника OSOT соответствует расстоянию между городами А и В. Учитывая, что туристы сближаются каждый час на 20 + 30 = 50 (км), расстояние между городами равно 250 км, имеем уравнение 250 = 50 · ОТ, решив которое находим ОТ = 5 (ч). Итак, туристы встретятся через 5 ч.

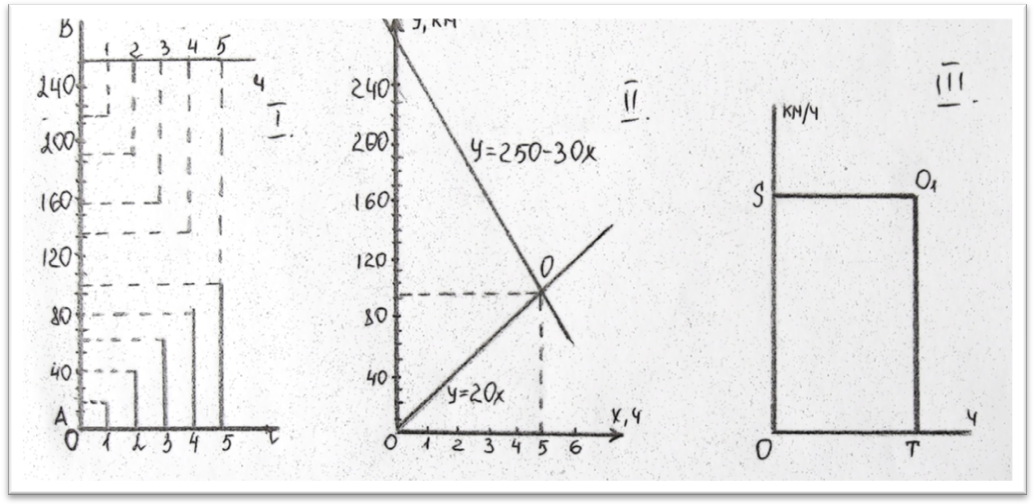
Логический метод.

Пример 1.: Кто из учеников Саша, Сергей, Дима и Андрей играет, а кто не играет в шахматы, если известно следующее:

а) если Саша и Сергей играет, то Дима не играет;

б) если Сергей не играет, то играют Дима и Андрей;

в) Дима играет.

 Решение.

Если Саша и Сережа играют, то Дима не играет.

Если играют Дима и Андрей, то Сережа не играет.

Так как Дима по условию играет в шахматы значит – это Дима и Андрей играют в шахматы.

Ответ: в шахматы играют ученики Дима и Андрей, а Саша и Сергей – не играют.

Практический метод.

Пример. Некто истратил 30 р. Своих денег, после чего удвоил оставшиеся деньги. Затем он истратил 60 р., после чего опять удвоил оставшиеся деньги. Когда он еще истратил 90 р., у него осталось 70р. Сколько денег было вначале?

Решение:

Чтобы определить, сколько денег было первоначально, возьмем оставшееся количество денег и выполним обратные операции в обратном порядке. Берем оставшиеся 70 р., добавляем к ним истраченные 90 р. (160 р.), затем делим эту сумму пополам и узнаем, сколько денег было до того, как второй раз удвоили оставшиеся деньги (80 р.). После этого добавляем 60 р. и находим, сколько денег было до того, как истратили 60 р. (140 р.). Делим эту сумму пополам и узнаем, сколько денег было до того, как первый раз удвоили оставшиеся деньги (70 р.), прибавляем истраченные в первый раз 30 р. и находим первоначальное количество денег (100 р.). Ответ: первоначально было 100 р.

Табличный метод

Пример. С одного участка собрали 1440 центнеров пшеницы, а с другого, площадь которого на 12 гектар меньше, собрали 1080 центнеров. Найти площадь первого участка, если известно, что на первом участке собирали пшеницы с каждого гектара на 2 ц больше, чем на втором.

Анализ задачи показывает, что в ней рассматривается сбор урожая пшеницы с двух участков, при этом этот сбор характеризуется тремя величинами: массой собранной пшеницы, площадью участка и урожаем с одного гектара. Исходя из этого, составим таблицу для схематической записи условий и требований задачи. Неизвестные величины, встречающиеся в задаче, запишем в таблице буквами, притом искомое обозначим буквой х:

В этой схематической записи выделены все условия, их объекты и характеристики. Указано и требование задачи: найти площадь первого участка. В то же время эта запись очень компактная, наглядная и полностью заменяет саму формулировку задачи.

Комбинированный метод

Пример. Четыре товарища купили телевизор. Первый внес половину суммы, вносимой остальными, второй — треть того, что внесли все его товарищи, третий — четверть того, что все его товарищи, четвертый — оставшиеся 650 р. Сколько было уплачено за телевизор?

Решение:

Пусть первый товарищ внес х р., второй – у р., третий – z р. тогда, решая задачу чисто алгебраическим методом, по условию задачи получим достаточно громоздкую систему трех уравнений с тремя неизвестными.

Решение начнем алгебраическим методом.

Пусть первый товарищ вне х р., тогда все остальные внесли 2х р. Отсюда находим стоимость телевизора: (р.). Значит, первый внес стоимости телевизора. Пусть второй внес у р., тогда все остальные внесли Зу р. Отсюда находим стоимость телевизора: (р.). Значит, второй внес стоимости телевизора.

Пусть третий внес z р., тогда все остальные внесли 4z р. Отсюда находим стоимость телевизора: (p.). Значит, третий внес стоимости телевизора.

Продолжим решение арифметическим методом.

Первый, второй и третий внесли стоимости телевизора. Значит, четвертый внес остальные стоимости. По условию это составляет 650 р. Следовательно, телевизор стоит р.

Ответ: 3 000 р.

Метод проб и ошибок

Методы решения могут быть разные, но способ решения, лежащий в их основе, может быть один.

Например, при алгебраическом методе решения задачи составляются уравнения или неравенства, при геометрическом — строятся диаграммы или графики. Решение задачи логическим методом начинается с составления алгоритма.

Пример. Площадь прямоугольника равна 180 см², его ширина на 8 см меньше длины. Найти длину и ширину этого прямоугольника.

Построим математическую модель задачи:

Подбираем решение «экспериментально», методом проб и ошибок.

Найдем значение x, такие, что значение выражения x · (x – равно 180. По смыслу задачи x 8.

Пусть x = 9, то 9 · (9 – ≠ 180.

И 9 слишком маленькое число.

Возьмем x =17, то 17· (17 – ≠ 180

x = 18, то 18 · (18 – =180

x = 19, то 19 · (19 – ≠ 180

Итак, если x = 18, то x – 8 = 10.

Ответ: длина 18 см, ширина 10 см.

Пример. Найти методом проб и ошибок натуральные корни уравнения x² – 8x + 15=0

Найдем значения x, такие, что x² – 8x + 15 равно 0.

Возьмем x = 2, то 2² – 8 · 2 + 15 ≠ 0

x = 3, то 3² – 8 · 3 + 15 = 0

Один натуральный корень найден, продолжим исследование:

X = 4, то 4² – 8 · 4 + 15 ≠ 0,

x = 5, то 5² – 8 · 5 + 15 = 0,

x = 6, то 6² – 8 · 6 + 15 ≠ 0

Оказалось, что уравнение имеет 2 натуральных корня. Больше быть не может.

Ответ: 3 и 5

Пример. Найти число x, если выполняется равенство x ·(17 – x)= 70.

Найдем такое число х, чтобы значение выражения х · (17 – х) было равно 70.

x = 6, то 6 · (17 – 6) = 66

х = 7, то 7 · (17 – 7) 70

х = 8, то 8 · (17 – 70

х = 9, то 9 · (17 – 9) 70

х = 10, то 10 · (17 – 10) = 70

Ответ: х = 7 и х = 10.

Следует иметь в виду, что практически каждая задача в рамках выбранного метода допускает решение с помощью различных моделей. Так, используя алгебраический метод, ответ на требование одной и той же задачи можно получить, составив и решив совершенно разные уравнения, используя логический метод — построив разные алгоритмы. Ясно, что в этих случаях мы так же имеем дело с различными методами решения конкретной задачи, которые называю способы решения.

Заключение

Для достижения цели данного исследования были выполнены следующие задачи:

1. Был произведен анализ некоторой методической и школьной литературы с точки зрения изучения общих методов решения задач в школе на уроках математики.

2. На основе изученного материла, были описаны методы и способы решения текстовых задач, в основной школе. С кратким описанием и приведением примеров.

3. В результате были описаны наиболее часто встречающиеся методы используемые в школьном курсе математики в 5 – 6 классах.

Таким образом, была достигнута цель данного исследования: описать методы и способы решения текстовой задачи в курсе изучения математики 5 – 6 классов.

Общеобразовательное значение курса математики, как и любого другого предмета, состоит, прежде всего, в тех общих понятиях, которые он даёт и которые расширяют кругозор и способы подхода человека к явлениям жизни. С этой точки зрения математика важна, во-первых, своей логикой, последовательностью и точностью выводов. Во-вторых, математика полезна тем, что она трудна. Её абстрактные строгие рассуждения требуют больших и длительных умственных усилий, требуют не столько памяти, сколько понимания и соображения. (А.Д. Александров).

Литература

1. Бизам, Д. Игра и логика. 85 логических задач //Д. Бизам, Я. Герцег.– М.: Мир, 1975.– 358 с. : ил.

2. Ванцян А.Г. «Математика» 5 класс// А.Г. Ванцян. – М.: Просвещение, 2009.- с.

3. Виленкин Н.Я. Математика: Учебник для 5 класса общеобразовательных учреждений// Н.Я.Виленкин, В.И. Жохов, А.С.Чесноков, С.И.Шварцбурд. – М.: Мнемозина: 1999-2004. – 384 с.

4. Виленкин Н.Я. Математика: Учебник для 6 класса общеобразовательных учреждений// Н.Я.Виленкин, В.И. Жохов, А.С.Чесноков, С.И.Шварцбурд. – М.: Мнемозина, 1999-2004. – 384 с.

5. Кочагин В.В. Математика // Тематические тренировочные задания/ В. В. Кочагин, М. Н. Кочагина. – М.: Просвещение, 2008.

6. Гаврилова Т.Д. Занимательная математика. 5 – 11 классы. (Как сделать уроки математики нескучными)// Т.Д. Гаврилова. – Волгоград: Учитель, 2005. — 96 с.

7. Дорофеев, Г.В. Математика: 5 кл. : учеб. для общеобразоват. учреждений. В 2 ч. Ч. 1 // Г.В. Дорофеев, Л.Г. Петерсон.– М.: Баласс, С-инфо, 1996.– 176 с. : ил.

8. Дорофеев, Г.В. Математика: 5 кл. : учеб. для общеобразоват. учреждений. В 2 ч. Ч. 2 / Г.В. Дорофеев, Л.Г. Петерсон.– М.: Баласс, С-инфо, 1997.– 240 с. : ил.

9. Дорофеев, Г.В. Математика: 5 кл. : учеб. для общеобразоват. учреждений. / Г.В. Дорофеев, И.Ф. Шарыгин, С.Б. Суворова.– 3-е изд.– М.: Просвещение, 2000.– 368 с.: ил.

1. Дорофеев, Г.В. Математика: 6 кл. : учеб. для общеобразоват. учреждений. В 3 ч. Ч. 2 / Г.В. Дорофеев, Л.Г. Петерсон.– М.: Баласс, С-инфо, 1999.– 129 с.: ил.

2. Дорофеев, Г.В. Математика: 6 кл. : учеб. для общеобразоват. учреждений. В 3 ч. Ч. 3 / Г.В. Дорофеев, Л.Г. Петерсон.– М.: Баласс, С-инфо, 2002.– 176 с. : ил.

3. Зак, А.З. 600 игровых задач для развития логического мышления школьников // А.З. Зак.– Ярославль: Академия развития, 1998.– 192 с. : ил.

4. Колягин, Ю.М. Задачи в обучении математике. В 2 ч. Ч. 2: Обучение математике через задачи и обучение решению задач // Ю.М. Колягин.– М.: Просвещение, 1977.– 139 с.

5. Кордемский, Б.А. Математическая смекалка // Б.А. Кордемский.– М.: Наука, 1991.– 377 с.

6. Лихтарников, Л.М. Логические задачи: книга для учащихся 3-7 кл. / Л.М. Лихтарников.– Новгород: НГПИ, 1995.– 288 с.

7. Мираков, Т.Н. Развивающие задачи на уроках математики в 5-8 классах: пособие для учителя // Т.Н. Мираков.– Львов: Квантор.– 1991.– 94 с. : ил.

8. Оганесян В.А. Методика преподавания математики в средней школе. Общая методика: учебное пособие для студ. физ.-мат. фак. пед. ин-тов // В.А. Оганесян, Ю.М. Колягин, Г.Л. Луканин и др.– М.: Просвещение, 1980.– 480 с.

9. Епишева О.Б. Учить школьников учиться математике: Формирование приемов учебной деятельности: кн. Для учителей //О.Б. Епишева В.И.. Крупин. – М.: Просвещение, 2000. – с. 102-136.

10. Мерзляк. А. Г. Математика: 5 кл.: учебник для общеобразовательных учреждений // А. Г. Мерзляк, В. Б. Полонский, М. С. Якир. − М.: Вентана-Граф, 2012.

11. Мерзляк А. Г. Дидактические материалы по математике для 5 класса // А. Г. Мерзляк, В. Б. Полонский, М. С. Якир. − М.: Вентана-Граф, 2012.

12. Никольский С.М. Арифметика: Учебник для 5 класса общеобразовательных учреждений// С.М.Никольский, М.К. Потапов, Н.Н.Решетников, А.В.Шевкин. – М.: Просвещение, 1999-2005. – 255 с.

13. Полякова, Т.С. История математического образования в России. Два века. – М.: Изд. Московского ун-та, 2002.

14. Темербекова, А.А. Методика преподавания математики: Учеб. пособие для студ. высш. учеб. заведений// А.А. Темербекова. – М.: Гуманит. изд. центр ВЛАДОС, 2003. – 490 с.

15. Шевкин А.В. Обучение решению текстовых задач в 5-6 классах.: Книга для учителя// А.В. Шевкин. – М.:Галс плюс, 1998. – 168 с.

16. Шевкин А.В. Материалы курса “Текстовые задачи в школьном курсе математики”: Лекции 1 – 4// А.В.Шевкин. М.: Педагогический университет “Первое сентября”, 2006. – 88 с.

17. Шевкин А.В. Роль текстовых задач в школьном курсе математике. Математика.// А.В. Шевкин– 2005. – № 17. – c. 23-30.

18. Ресурсы Интернет: http: //www.eidos.ru/journal/2002/0920.htm

19. Ресурсы Интернет: http://www.erudition.ru

20. Ресурсы Интернет: http:// docs.google.com

21. Ресурсы Интернет: http://ipk.admin.tstu.ru/sputnik

23