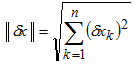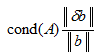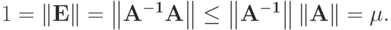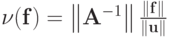Матрица ошибок – это метрика производительности классифицирующей модели Машинного обучения (ML).
Когда мы получаем данные, то после очистки и предварительной обработки, первым делом передаем их в модель и, конечно же, получаем результат в виде вероятностей. Но как мы можем измерить эффективность нашей модели? Именно здесь матрица ошибок и оказывается в центре внимания.
Матрица ошибок – это показатель успешности классификации, где классов два или более. Это таблица с 4 различными комбинациями сочетаний прогнозируемых и фактических значений.
Давайте рассмотрим значения ячеек (истинно позитивные, ошибочно позитивные, ошибочно негативные, истинно негативные) с помощью «беременной» аналогии.
Истинно позитивное предсказание (True Positive, сокр. TP)
Вы предсказали положительный результат, и женщина действительно беременна.
Истинно отрицательное предсказание (True Negative, TN)
Вы предсказали отрицательный результат, и мужчина действительно не беременен.
Ошибочно положительное предсказание (ошибка типа I, False Positive, FN)
Вы предсказали положительный результат (мужчина беременен), но на самом деле это не так.
Ошибочно отрицательное предсказание (ошибка типа II, False Negative, FN)
Вы предсказали, что женщина не беременна, но на самом деле она беременна.
Давайте разберемся в матрице ошибок с помощью арифметики.
Пример. Мы располагаем датасетом пациентов, у которых диагностируют рак. Зная верный диагноз (столбец целевой переменной «Y на самом деле»), хотим усовершенствовать диагностику с помощью модели Машинного обучения. Модель получила тренировочные данные, и на тестовой части, состоящей из 7 записей (в реальных задачах, конечно, больше) и изображенной ниже, мы оцениваем, насколько хорошо прошло обучение.
Модель сделала свои предсказания для каждого пациента и записала вероятности от 0 до 1 в столбец «Предсказанный Y». Мы округляем эти числа, приводя их к нулю или единице, с помощью порога, равного 0,6 (ниже этого значения – ноль, пациент здоров). Результаты округления попадают в столбец «Предсказанная вероятность»: например, для первой записи модель указала 0,5, что соответствует нулю. В последнем столбце мы анализируем, угадала ли модель.
Теперь, используя простейшие формулы, мы рассчитаем Отзыв (Recall), точность результата измерений (Precision), точность измерений (Accuracy), и наконец поймем разницу между этими метриками.
Отзыв
Из всех положительных значений, которые мы предсказали правильно, сколько на самом деле положительных? Подсчитаем, сколько единиц в столбце «Y на самом деле» (4), это и есть сумма TP + FN. Теперь определим с помощью «Предсказанной вероятности», сколько из них диагностировано верно (2), это и будет TP.
$$Отзыв = frac{TP}{TP + FN} = frac{2}{2 + 2} = frac{1}{2}$$
Точность результата измерений (Precision)
В этом уравнении из неизвестных только FP. Ошибочно диагностированных как больных здесь только одна запись.
$$Точностьspaceрезультатаspaceизмерений = frac{TP}{TP + FP} = frac{2}{2 + 1} = frac{2}{3}$$
Точность измерений (Accuracy)
Последнее значение, которое предстоит экстраполировать из таблицы – TN. Правильно диагностированных моделью здоровых людей здесь 2.
$$Точностьspaceизмерений = frac{TP + TN}{Всегоspaceзначений} = frac{2 + 2}{7} = frac{4}{7}$$
F-мера точности теста
Эти метрики полезны, когда помогают вычислить F-меру – конечный показатель эффективности модели.
$$F-мера = frac{2 * Отзыв * Точностьspaceизмерений}{Отзыв + Точностьspaceизмерений} = frac{2 * frac{1}{2} * frac{2}{3}}{frac{1}{2} + frac{2}{3}} = 0,56$$
Наша скромная модель угадывает лишь 56% процентов диагнозов, и такой результат, как правило, считают промежуточным и работают над улучшением точности модели.
SkLearn
С помощью замечательной библиотеки Scikit-learn мы можем мгновенно определить множество метрик, и матрица ошибок – не исключение.
from sklearn.metrics import confusion_matrix
y_true = [2, 0, 2, 2, 0, 1]
y_pred = [0, 0, 2, 2, 0, 2]
confusion_matrix(y_true, y_pred)Выводом будет ряд, состоящий из трех списков:
array([[2, 0, 0],
[0, 0, 1],
[1, 0, 2]])Значения диагонали сверху вниз слева направо [2, 0, 2] – это число верно предсказанных значений.
Фото: @opeleye
4 года назад · 4866 просмотров
Даже у самой отлаженной системы бывают сбои. Может, мир немного сошел с ума и реальность уже не так реальна? Давайте посмотрим на примеры, доказывающие, что мы все-таки живем в Матрице!
1. Мода — ничто, индивидуальность — все. Ой, или наоборот?

Источник:
2. Да ладно!

Источник:
3. Очки и клетчатая рубашка — популярное сочетание

Источник:
4. Клонировали?

Источник:
5. Или этих?

Источник:
6. «Пока ждал с отцом в больнице, заметил сбой в матрице»

Источник:
7. Вы тоже это видите?

Источник:
8. Что есть реальность вообще?

Источник:
9. Похоже на роботов

Источник:
10. Опять глюки

Источник:
11. Кто-то точно баловался с кнопками CTRL+C и CTRL+V

Источник:
12.

Источник:
13. Серьезный глюк

Источник:
14.

Источник:
15. Жаль, что низ не совпал

Источник:
16.

Источник:
17. Бабушки кое-что знают о стиле

Источник: Инстаграм (запрещён в РФ)
18.

Источник: Инстаграм (запрещён в РФ)
19.

Источник: Инстаграм (запрещён в РФ)
Источник:
Кто-то называет их двойниками, кто-то зовёт их доппельгангерами, замечая в этом нечто зловещее, ну а кто-то твёрдо уверен, что это просто глюк в Матрице, как учил нас Нео. Мы конечно не можем точно сказать существует ли Матрица на самом деле, но то, что она постоянно сбоит — однозначно. Эти фотографии в очередной раз доказывают, что прямо сейчас мы все лежим в колбах с жидкостью с подключенными к нашим телам трубками. Сегодня мы предлагаем вам снова сделать вид, что ничего не произошло и просто похихикать над этими забавными фото, списав всё на простое совпадение. Тссс.. сейчас выйдет женщина в красном..
Увидев это, Нео назвал бы это «дежавю»
Просто обедающие женщины с одинаковыми причёсками, свитерами и блузками
Сбой в метро. Четыре блондинки в черном пальто подряд
Две незнакомые женщины в жёлтых шарфах, бежевом пальто и с синими волосами.. Всё ещё не верите в Матрицу?
Словно одна и та же женщина на разных этапах жизни
[region:bone:inline_1]
Девушка просто хотела сфотографировать своего парня в музее, но внезапно обнаружила его двойника на фоне
У них одинаковый цвет волос, свитера одного цвета и все они немного склонили голову влево.. Кажется, здесь творится что-то странное
Этот парень отправился на отдых в Таиланд и случайно оказался рядом с парнем, который выглядел точно также, как он
Внезапные близнецы на концерте Coldplay
Трое одинаковых спящих мужчин, сидящих один за другим. Это не фильм. Это реальная жизнь
[region:bone:inline_2]
Слишком много полос на одном фото
Может сбой в Матрице, а может просто корпоративная офисная униформа
Где же ещё можно встретить своего доппельгангера как не на технологической конференции
Дети на велосипедах — классический жуткий признак фильмов ужасов. И это фото не исключение
Эти двое друзей появились на вечеринке в одной и той же одежде от футболки и до обуви
[region:bone:inline_3]
Очевидно розовая блузка и бежевые капри — униформа всех мам в Канаде
Тут Матрица решила замести следы, вручив девушкам разные пакеты
Трудно не начать верить в Матрицу, когда видишь такое
Эти мужчины не знают друг друга, но по всей видимости они одеваются в одном и том же магазине
Эти парни одеты в одинаковую одежду и кажется они знают друг друга. Матрица или просто близнецы?
[region:bone:inline_2]
Две копии спина к спине
Сбой в Матрице на овощном рынке
«Был на работе, как вдруг мы заметили фантастическое сходство»
Интересно, они читают одну и ту же статью? Знаешь, Матрица, это уже слишком
Казалось бы, в этом фото нет ничего необычного, но этот мужчина клянётся, что у него всего одна пара таких тапочек
[region:bone:inline_2]
Пришли на фестиваль пива и встретили пару, одетую точно также, как и они
Это фото можно объяснить тем, что возможно это очень маленький город, в котором есть всего один магазин с одеждой, и в котором все одеваются
Три парня на одной и той же работе в одинаковых чёрных поло с белыми полосами
Такие персонажи встречаются не так часто и какова была вероятность встретить двух одинаковых в одном и том же месте?
И ещё глюки в Матрице или 20 незнакомых людей, которые выглядят одинаково.
Содержание:
Сбои в матрице или глюки мозга: проверь себя
Сбои матрицы на экране: легендарные фразы больше не легендарные?
Сбои, глюки в «текстурах» матрицы или аномалии?
Восстание клонов или невероятные совпадения в вашем городе
Совпадения и сбои матрицы — вы были правы?
В матрицу можно верить или не верить, но жить в ней приходится. Пересматривая легендарное кино про Нео, Тринити, агентов Смит, мультфильм про мишек «Бернштейн», вольно-невольно задумываешься о сбоях матрицы, ищешь глюки в реальной жизни, волнуешься, объясняешь себе невероятные совпадения и случаи. Давайте вообразим, что действительно помещены в колбы с жидкостью, а наши тела подключены трубками… Добро пожаловать, в аттракцион невероятных совпадений, моментов, глюков, сбоев матрицы 2020! Что не так с этим миром? Апдейт, перезагрузка, пристегнитесь!
Можешь ли ты доверять миру, в котором живешь?
Сбои в матрице или глюки мозга: проверь себя
В 2003 году шведский философ Ник Бостром выдвинул гипотезу, что мы живем в симуляции. Гипотеза о матрице — очередная загадка Вселенной, а сбои, глюки, невероятные совпадения выносят нас за рамки действительности, перемещают в искусственную реальность.
Подмена реальности возможна!
Невероятные совпадения, дежавю, сбои, глюки матрицы хотя бы однажды случаются. Хотите, докажем? Ответьте на 10 странных, но простых вопросов, из которых в пяти случаях — вы будете сомневаться, в пяти других — уверенно отвечать, но правильно ли…
- Какого цвета штаны у Карлсона?
- С какой стороны Австралии находится Новая Зеландия?
- Был ли у старухи Шапокляк зонтик?
- В кадре из кинофильма «Кавказская пленница», какого цвета на Шурике смирительная рубашка?
- Представьте хоть одну загадочную статую на о. Пасха в шляпе? Получилось?
- Сколько океанов на планете?
- Носил ли повязку на глазу Кутузов?
- Вспомните, как выглядит статуя Родена «Мыслитель». Какой части головы касается его рука?
- Советские солдаты устанавливали флаг над немецким рейхстагом. Чтобы было изображено на флаге: серп, молот, звезда?
- Есть ли в глазницах черепа кость?
Готовьтесь снять трубку по первому звонку, кто знает — что там на другой стороне…
Необычные совпадения, эффект Манделы, сбои, глюки матрицы окружают нашу жизнь повсюду. Внезапно пламя на спичке больше не отбрасывает тень на стенах, а из памяти стираются достоверные факты истории.
До сих пор тайна: существует ли матрица, из которой можно было бы выбраться?
Сбои матрицы на экране: легендарные фразы больше не легендарные?
Привычное высказывание «Спасение утопающих — дело рук самих утопающих!» — наглая ложь, сбой и глюк матрицы. «Дело помощи утопающим — дело рук самих утопающих» — так верно. Кстати, Почтальон Печкин был не злой, а вредный, когда у него велосипеда не было! Еще одно недоразумение — отсутствие в истории факта, что Хрущев стучал ботинком по трибуне во время выступления на Ассамблеи ООН. А Ельцин, представьте себе, никогда не говорил фразу «Я устал, я ухожу!», вместо этого: «Я ухожу в отставку!».
Код матрицы, кажется, несовершенен, что подтверждают сбои и глюки
Сбои, глюки в «текстурах» матрицы или аномалии?
В Израиле, например, есть три дороги, в которых любая жидкость, вылитая на поверхность течет вверх, а не вниз. Еще один сбой или глюк матрицы — долина падающих птиц в горах индийского штата Ассам, где в августе с ночного неба падают птицы. В полуобморочном состоянии они даже не пытаются вырваться из рук.
В науке есть масса пробелов, которые не могут объяснить до сих пор великие гении
Конкретный сбой и глюк воображения происходит над морем возле замка Франка-Кастелло, где возникает сцена огромной битвы, слышатся крики и звон оружия. Историки допускают версию, что битва между греками и турками заблудилась во времени. Этот мираж, совпадение или глюк до сих пор необъясним.
Отличать реальность ото сна не всегда получается…
Грандиозный сбой в матрице происходил в 1994 году летом в Вашингтоне (штат Оаквилль), когда на жителей города пошел дождь из… желе. После этого, все разом заболели гриппом, совпадение? А необъяснимый случай или сбой в матрице записали в историю, как природную аномалию, глюк.
Глюки матрицы происходят постоянно: код неверен?
Восстание клонов или невероятные совпадения в вашем городе
Встречали одинаковых людей в метрополитене, на автобусной остановке, в толпе рядом? Незнакомых между собой одинаково одетых женщин, мужчин… Глюки матрицы происходят где угодно: на стоянке, в аэропорту, музеях, театрах, супермаркетах. Невероятные совпадения и сбои в повседневной жизни заставляют нас зависнуть во временном парадоксе, удивиться и выстроить десяток непредсказуемых теорий о существовании матрицы.
Эффект близнецов часто встречается в самых необычных местах
Совпадения и сбои матрицы — вы были правы?
Вернемся к мини-тесту вначале статьи, чтобы узнать, живете ли вы в матрице со сбоями и невероятными глюками? Выдохните, если вы помните, что у Карлсона штаны белые, а смирительная рубашка Шурика в кадре — абсолютно черная. Глюк, совпадение, сбой? Мыслитель Родена кулаком упирается не ко лбу, а ладонью к подбородку, а еще:
Новая Зеландия находится к Югу от Австралии, а не к Северу
У старухи Шапокляк никогда не было зонтика в руках, представляете?
У статуй на о. Пасха действительно есть шляпы, погуглите!
Кутузов не носил на глазу повязку…
…и, наверное, как и вы не знал, что в глазницах черепа есть все-таки кость!
На флаге над немецким рейхстагом изображено все: серп, молот и звезда
Кто-то назовет совпадения, глюки или сбой в матрице последствиями Black Friday, теорией существования двойников или заговоров, флешмобом, пранком или возможностями фотошопа… А вы попробуйте выйти на улицу летом в закат, перед дождем, когда разряжен воздух! Сбой в матрице покажет «реальность» в фиолетово-розовых красках, даже без очков. Удивительно, правда?
Netflix рекомендует к просмотру «Черное зеркало», «Измерение 404» со всеми ответами о матрице!
Влияние обусловленности матрицы на точность решения системы с ней
В этом разделе мы рассмотрим, как ошибки
в элементах вектора правой части и в
матрице системы линейных уравнений Ax
= b могут повлиять на решение этой системы.
Обратимся сначала к случаю внесения
возмущений в вектор правой части b. Итак,
мы решаем две системы
причем предполагается, что каждую из
систем мы решаем точно, а основной
возникающий вопрос — насколько будет
отличаться решение x системы (1) от решения
системы (2) с возмущением в правой части
δb. Это довольно важный вопрос, поскольку
элементы правой части могут быть получены
как результат некоторых измерений,
соответственно содержащий погрешность
δbk в каждой компоненте bk. Хотелось бы,
чтобы при измерении одной и той же
величины (каждый раз со своими, небольшими
погрешностями) соответствующие решения
систем с мало отличающимися правыми
частями также не очень сильно отличались
друг от друга. К сожалению, так бывает
не всегда. Причиной этому — характеристика
матрицы, называемая ее обусловленностью.
Об этом и пойдет дальше речь.
Сначала требуется ввести меру близости
векторов
и
x, т.е. вектора ошибки
. Мерой величины вектора является норма
(определяться она может по-разному).
Возьмем пока в качестве нормы обычную
евклидову норму вектора (квадратный
корень из суммы квадратов его компонент),
т.е.
соответственно
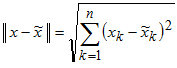
где n — число неизвестных и уравнений
в системе. Кроме векторной нормы для
оценки величины вектора нам понадобится
еще и матричная норма для оценки величины
матрицы. Возьмем матричную норму, которая
определяется следующим образом (она
называется спектральной):
т.е. спектральная матричная норма равна
квадратному корню из максимального
собственного числа матрицы ATA. В MATLAB
имеется функция norm для вычисления норм
матриц и векторов, которая, в частности,
умеет вычислять приведенные выше нормы.
Почему мы выбрали именно такие нормы
векторов и матриц, подробно объясняется
в разделе Получение неравенства для
ошибки, согласованная норма матрицы,
где приведено немного выкладок и
определений. Это связано с оценкой,
которой мы будем пользоваться для ошибки
в решении системы (вывод этого неравенства
также приведен в упомянутом разделе):
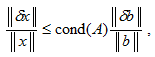
Здесь через обозначено число обусловленности
матрицы , которое определяется так:
Из приведенного неравенства следует,
что чем больше число обусловленности
матрицы системы, тем больше может быть
относительная ошибка в решении
при небольшой ошибке в правой части
Рассмотрим классический пример плохо
обусловленной матрицы — матрицу
Гильберта — и выясним, как ошибка в
правой части системы влияет на ошибку
в решении. Матрица Гильберта определяется
следующим образом
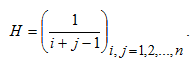
Для создания матрицы Гильберта в MATLAB
предусмотрена функция hilb, входной
аргумент которой задает размер матрицы.
Возьмем небольшую матрицу 6 на 6:
n = 6;
H = hilb(n)
H =
1.0000 0.5000 0.3333 0.2500 0.2000 0.1667
0.5000 0.3333 0.2500 0.2000 0.1667 0.1429
0.3333 0.2500 0.2000 0.1667 0.1429 0.1250
0.2500 0.2000 0.1667 0.1429 0.1250 0.1111
0.2000 0.1667 0.1429 0.1250 0.1111 0.1000
0.1667 0.1429 0.1250 0.1111 0.1000 0.0909
Далее вычислим такую правую часть
системы b, что все компоненты ее решения
x равны единице:
x =
ones(n, 1);
b =
H*x
b =
2.4500
1.5929
1.2179
0.9956
0.8456
0.7365
Видим, что ни в матрице, ни в векторе
правой части нет ничего «подозрительного»,
все числа не сильно отличаются друг от
друга. Теперь сформируем возмущенную
правую часть b + δb, добавив в вектор b
небольшие числа порядка 10-5 и решим
систему с возмущенной правой частью
для получения вектора .
delta_b
= 1e-5*(1:n)’;
x_tilda
= H(b + delta_b)
x_tilda =
0.9978
1.0735
0.4288
2.6632
-1.0160
1.8593
Видно, что полученное решение далеко
от точного, где должны быть все единицы.
Вычислим относительную ошибку в решении
и в правой части (функция norm по умолчанию
вычисляет евклидову норму вектора):
delta_x
= x — x_tilda;
LEFT
= norm(delta_x)/norm(x)
LEFT
=
1.1475
RIGHT
= norm(delta_b)/norm(b)
RIGHT =
2.7231e-005
Итак, ошибка в решении порядка единицы,
хотя изменения в правой части были
порядка 10-5. Это полностью укладывается
в приведенное выше неравенство для
ошибки. Действительно, вычислим число
обусловленности cond(H) при помощи функции
MATLAB, которая называется cond и по умолчанию
вычисляет
для спектральной нормы матрицы
c = cond(H)
c =
1.4951e+007
Итак
= LEFT ≈ 1.1475 меньше
= c* RIGHT ? 1.4951e+07 * 2.7231e-05 ≈ 407
и неравенство выполнено (даже с некоторым
запасом).
При увеличении размера матрицы Гильберта
ошибка в решении будет только расти
(это несложно проверить, задавая n = 7, 8,
…). Причем, при n = 12 выведется сообщение
о том, что матрица плохообусловлена и
решение может оказаться неверным
Warning:
Matrix is close to singular or badly scaled.
Results
may be inaccurate. RCOND = 2.409320e-017.
В качестве меры обусловленности здесь
выбрана величина RCOND равная единице,
деленной на оценку числа обусловленности
(число обусловленности оценивается по
достаточно быстрому алгоритму, который
работает намного быстрее, чем cond, о чем
более подробно написано в справке по
функции rcond). Если значение RCOND мало, то
матрица считается плохообусловленной.
Увеличение ошибки в решении при увеличении
размера матрицы Гильберта происходит
из-за того, что число обусловленности
матрицы Гильберта растет очень быстро
с ее размером. В этом несложно убедиться
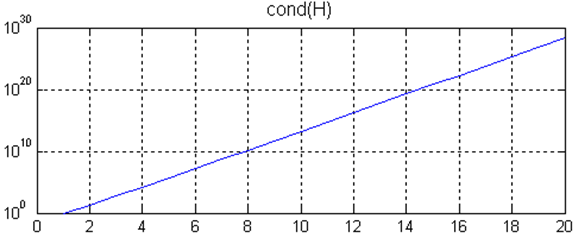
при помощи простого цикла и функции
semilogy (масштаб по оси ординат —
логарифмический):
N =
1:20; C = zeros(1, 20);
for
n = N
H = hilb(n);
C(n) = cond(H);
end
semilogy(N, C)
grid
on, title(‘cond(H)’), xlabel(‘n’)
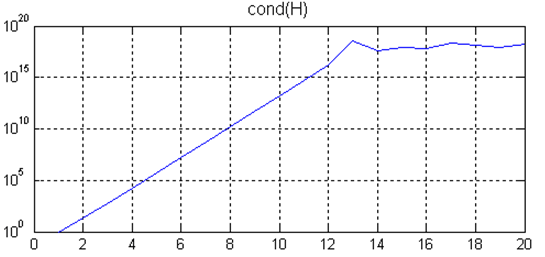
Кстати, поскольку функция cond находит
число обусловленности при помощи
численного метода (а именно сингулярного
разложения для нахождения сингулярных
чисел), то число обусловленности после
n = 12 вычисляется уже неверно, на самом
деле оно должно расти и дальше, в чем
можно убедиться при помощи символьных
вычислений в MATLAB и операций с заданным
числом значащих цифр
N =
1:20; C = zeros(1, N);
digits(60)
for n = N
H = vpa(sym(hilb(n))); % вычисление матрицы
Гильберта с точностью до 60-го знака
sigma = svd(H); % нахождение сингулярных
чисел матрицы Гильберта
% вычисление числа обусловленности
матрицы Гильберта
C(n) = max(double(sigma))/min(double(sigma));
end
semilogy(N, C)
grid
on, title(‘cond(H)’), xlabel(‘n’)
Рассмотрим теперь три важных момента,
касающихся данного примера.
Первый из них — решение системы Hx = b (с
вектором правой части, соответствующим
решению из единиц) при помощи оператора
обратной косой черты не даст точные
единицы, погрешность будет уже в десятом
знаке (хотя в MATLAB все вычисления по
умолчанию выполняются с двойной
точностью)
format
long
Hb
ans
=
0.99999999999916
1.00000000002391
0.99999999983793
1.00000000042209
0.99999999953366
1.00000000018389
Так происходит из-за того, что при
вычислении вектора b при умножении
матрицы H на вектор из всех единиц мы
уже заложили в него некоторую погрешность.
Кроме того, ошибки округления в процессе
решения системы также сыграли свою роль
и плохая обусловленность матрицы (даже
небольшого размера) привела к таким
ошибкам в решении. Действительно, для
матриц небольшого размера с небольшим
числом обусловленности такого эффекта
наблюдаться не будет. Возьмем матрицу
6 на 6 из случайных чисел, вычислим ее
число обусловленности
A = rand(n);
cond(A)
ans =
57.35245279907571
Затем сформируем правую часть,
соответствующую точному решению из
всех единиц
x = ones(n, 1);
b = A*x;
и решим систему, получив в результате
хорошую точность
>> Ab
ans =
1.00000000000000
1.00000000000000
1.00000000000000
1.00000000000000
1.00000000000000
1.00000000000000
Второй важный момент связан с определителем
матрицы. Вычислим определитель матрицы
Гильберта размера 6 на 6, с которой мы
решали систему
>> det(hilb(6))
ans =
5.3673e-018
Определитель оказывается достаточно
мал, откуда можно сделать неверный
вывод, что источник проблемы большой
ошибки в решении при небольшом возмущении
правой части системы — малость
определителя. В действительности это
не так, если определитель системы мал,
то это не означает плохой обусловленности
матрицы и, следовательно, большой ошибки
в решении. Действительно, возьмем матрицу
A = [1e-40 1e-42 1e-42
1e-42 1e-40 1e-42
1e-42 1e-42 1e-40];
Ее определитель очень мал, порядка
10-121
det(A)
ans =
9.9970e-121
(слово «очень», конечно условно, но он
меньше определителя матрицы Гильберта
размера 6 на 6, при решении системы с
которой у нас возникли проблемы). Однако,
малость определителя никак не повлияет
на ошибку в решении при возмущении
правой части системы, что несложно
показать, сформировав систему с известным
решением, внеся возмущения в правую
часть и решив систему:
x =
[1e40; 1e40; 1e40];
b =
A*x;
delta_b
= 1e-5*[1; 2; 3];
x_tilda
= A(b+delta_b);
delta_x
= x — x_tilda;
LEFT
= norm(delta_x)/norm(x)
RIGHT
= norm(delta_b)/norm(b)
LEFT =
2.1272e-005
RIGHT =
2.1179e-005
Итак, относительная ошибка в решении
практически равна относительной ошибке
в правой части, поскольку число
обусловленности приведенной выше
матрицы A немного больше 1, а именно:
c = cond(A)
c =
1.0303
И, наконец, рассмотрим третий вопрос,
касающийся достижения знака равенства
в неравенстве для ошибки в решении
Т.е., говоря другими словами, выясним:
может ли быть такая ситуация, когда мы
делаем небольшое относительное возмущение
правой части системы, скажем 10-5, число
обусловленности матрицы системы равно
1010, а в решении получается относительная
ошибка 105. Можно проделать массу примеров,
перебирая различные матрицы, не получить
достижения равенства и ошибочно
заключить, что это всего лишь завышенная
оценка сверху для ошибки в решении.
Однако, это не так, в чем нас убеждает
следующий пример
A = [2.1005632211074903e+009 2.4405728346208658e+009
2.6288320556007657e+009 3.9543845780862803e+009
5.6384551998346877e+008
6.5511289861702812e+008 7.0564654322518432e+008
1.0614591390422670e+009
1.9531852931707768e+009 2.2693394431935925e+009
2.4443901805698233e+009 3.6769404175323849e+009
2.2044117415857959e+009 2.5612308917984776e+009
2.7587973499916158e+009 4.1498830928366508e+009];
b =
[ -5.7373057243726833e-001
-1.5400413072907607e-001
-5.3347697688693385e-001
-6.0209490373259589e-001];
delta_b
= [-0.71685839091451e-5
0.54786619630709e-5
0.37746931527138e-5
0.20850322383081e-5];
в котором относительное возмущение
правой части равно 10-5
RIGHT
= norm(delta_b)/norm(b)
RIGHT =
1.0000e-005
Относительная ошибка в решении системы
оказывается 105
x =
Ab;
x_tilda
= A(b+delta_b);
delta_x
= x — x_tilda;
LEFT
= norm(delta_x)/norm(x)
LEFT =
1.0000e+005
И происходит так потому, что
1) в этом примере число обусловленности
матрицы A равно 1010;
c = cond(A)
c =
1.0000e+010
2) неравенство для ошибки в решении
переходит в равенство.
Если установить формат long, то мы увидим,
что LEFT, RIGHT и число обусловленности не
в точности 105, 10-5 и 1010, соответственно,
но это вызвано ошибками округлений. При
решении в точной арифметике, равенство
получилось бы точным, что можно показать
аналитически (см. раздел Получение
неравенства для ошибки, согласованная
норма матрицы, подробнее про norm и cond).
В предыдущих примерах мы предполагали,
что матрица не содержит ошибок, а ошибки
могут быть только в правой части системы
линейных уравнений. На практике может
оказаться, что элементы матрицы системы
заданы с ошибками, т.е. вместо системы
Ax = b
мы решаем систему
В этом случае мы так же можем оценить
погрешность в решении, и в оценку снова
входит число обусловленности матрицы
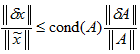
В самом общем случае ошибки могут быть
как в матрице, так и в векторе правой
части, и соответствующая оценка
погрешности в решении имеет более
сложный вид
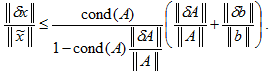
2.3. Обусловленность СЛАУ. Число обусловленности матрицы
Понятия согласованных норм матриц и векторов позволяют оценить погрешности,
возникающие при численном решении СЛАУ. Пусть и матрица, и правая часть системы заданы с некоторой погрешностью, тогда наряду с системой
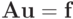 |
( 2.4) |
рассматривается система
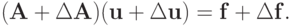 |
( 2.5) |
Теорема. Пусть правая часть и невырожденная матрица СЛАУ (2.4)
вида 



, где 

неравенству
Доказательство.
Из (2.5) следует, что 
Вводя обозначение 
Заметим, что
т.к.
Тогда для оценки относительной погрешности решения окончательно получим
 |
( 2.6) |
При 
 |
( 2.7) |
если в (2.5) положить 
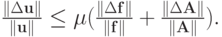 |
( 2.8) |
В результате получено важное соотношение, показывающее, на сколько возрастают относительные ошибки решения СЛАУ в случае наличия относительных ошибок при задании правых частей и элементов матриц.
Величина
 |
( 2.9) |
называется числом обусловленности матрицы 

При 

Пример. Решением системы
будет пара чисел u = v = 1.
Внесем возмущение в правые части системы:
При этом решение заметно изменится: u = 2,97; v = -0,99. Воспользовавшись выбранными согласованными нормами, получим
Значит,
, что согласуется с результатами решения возмущенной и невозмущенной задач. Для невозмущенной задачи 
Рассмотрим еще одно важное свойство. Число обусловленности матрицы, как
было показано ранее, можно определить, как 
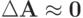
Можно ли найти более тонкую оценку отношения 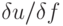
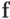
от 
Его можно определить как точную верхнюю грань отношения
по 
Далее,
с другой стороны
Параметр 
, причем 

Можно также показать, что для симметричной матрицы 
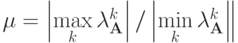
и соотношения
, которое предлагается доказать самостоятельно.
Методы решения систем линейных алгебраических уравнений (СЛАУ) с примерами
Содержание:
Методы решения систем линейных алгебраических уравнений (СЛАУ)
Метод Крамера
Определение: Системой линейных алгебраических уравнений (СЛАУ) называется выражение
Определение: Определитель, составленный из коэффициентов при неизвестных, называется главным определителем системы
Крамер предложил следующий метод решения СЛАУ: умножим главный определитель на 
Второй столбец умножим на 



Согласно записи СЛАУ первый столбец получившегося определителя представляет собой столбец свободных коэффициентов, т.е.
Определение: Определитель 
Поступая аналогично тому, как описано выше, найдем все вспомогательные определители СЛАУ:
31. Для того чтобы найти вспомогательный определитель i, надо в главном определителе СЛАУ заменить столбец i на столбец свободных коэффициентов.
Определение: Полученные выше соотношения называются формулами Крамера. Используя формулы Крамера, находят неизвестные величины 
Пример:
Решить СЛАУ методом Крамера
Решение:
Прежде всего, обращаем внимание на то, что в последнем уравнении переменные записаны в неправильном порядке, в этом случае говорят, что СЛАУ записана в ненормализованном виде. Нормализуем СЛАУ, для чего запишем неизвестные в последнем уравнении системы в правильном порядке, чтобы одноименные неизвестные были записаны друг под другом
Найдем главный определитель СЛАУ (раскрываем по первой строке)
Так как главный определитель системы отличен от нуля, то СЛАУ имеет единственное решение. Найдем три вспомогательных определителя
Воспользуемся формулами Крамера
Замечание: После нахождения решения СЛАУ надо обязательно провести проверку, для чего найденные числовые значения неизвестных подставляется в нормализованную систему линейных алгебраических уравнений.
Выполним проверку 
Матричный способ решения СЛАУ
Для решения СЛАУ матричным способом введем в рассмотрение матрицу, составленную из коэффициентов при неизвестных 

Тогда СЛАУ можно записать в матричном виде 





Пример:
Решить СЛАУ матричным способом
Решение:
Введем в рассмотрение следующие матрицы
Найдем матрицу 
Пример:
Решение:
Найдем алгебраические дополнения всех элементов 


Отсюда находим, что х = 1; y = l; z = l.
Метод Гаусса
Метод Гаусса или метод исключения неизвестных состоит в том, чтобы за счет элементарных преобразований привести СЛАУ к треугольному виду. Покажем использование расширенной матрицы, составленной из коэффициентов при неизвестных и расширенной за счет столбца свободных коэффициентов, для приведения СЛАУ к треугольному виду на примере системы, рассматриваемой в этой лекции. Расширенная матрица для СЛАУ имеет вид:
Замечание: В методе Гаусса желательно, чтобы первая строка расширенной матрицы начиналась с единицы.
Обменяем в расширенной матрице первую и вторую строки местами, получим 

Умножим элементы первой строки на (—1) и прибавим к соответствующим элементам третьей строки 

Из первого уравнения находим, что х = 1.
Вывод: Из вышеизложенного материала следует, что вне зависимости от
способа решения СЛАУ всегда должен получаться один и тот же ответ.
Замечание: После нахождения решения СЛАУ надо обязательно выполнить проверку, то есть подставить полученные значения неизвестных в заданную СЛАУ и убедиться в тождественности левой части всех равенств системы соответствующим правым частям. Отметим, что задание СЛАУ всегда верно, то есть, если проверка показывает нарушение оговоренной тождественности, то надо искать ошибку в проведенных вычислениях.
Ранг матрицы. Теорема Кронекера-Капелли
Определение: Рангом матрицы 
Если 
При вычислении ранга необходимо начинать вычислять миноры 2 порядка, затем миноры 3 порядка и так далее, пока не будут найдены миноры, обращающиеся в нуль. Если все миноры порядка p равны нулю, то и все миноры, порядок которых больше p, равны нулю.
Пример:
Найти ранг матрицы
Решение:
Очевидно, что среди миноров второго порядка есть миноры отличные от нуля, например, 


Теорема Кронекера-Капелли (критерий совместности СЛАУ). Для совместности системы линейных алгебраических уравнений (СЛАУ) необходимо и достаточно, чтобы ранг расширенной матрицы совпадал с рангом основной матрицы, составленной из коэффициентов при неизвестных величинах.
Следствия из теоремы Кронекера — Капелли
Следствие: Если ранг матрицы совместной системы равен числу неизвестных, то система имеет единственное решение (то есть она определенная).
Следствие: Если ранг матрицы совместной системы меньше числа неизвестных, то система имеет бесчисленное множество решений (т.е. она неопределенная).
В случае неопределенной системы решения ищут следующим образом: выбираются главные неизвестные, число которых равно рангу, а остальные неизвестные считаются свободными; далее главные неизвестные выражаются через свободные и получают множество решений, зависящих от свободных неизвестных. Это множество решений называется общим решением системы. Придавая свободным неизвестным различные произвольные значения, получим бесчисленное множество решений, каждое из которых называется частным решением системы.
| Рекомендую подробно изучить предметы: |
|
| Ещё лекции с примерами решения и объяснением: |
- Скалярное произведение и его свойства
- Векторное и смешанное произведения векторов
- Преобразования декартовой системы координат
- Бесконечно малые и бесконечно большие функции
- Критерий совместности Кронекера-Капелли
- Формулы Крамера
- Матричный метод
- Экстремум функции
При копировании любых материалов с сайта evkova.org обязательна активная ссылка на сайт www.evkova.org
Сайт создан коллективом преподавателей на некоммерческой основе для дополнительного образования молодежи
Сайт пишется, поддерживается и управляется коллективом преподавателей
Whatsapp и логотип whatsapp являются товарными знаками корпорации WhatsApp LLC.
Cайт носит информационный характер и ни при каких условиях не является публичной офертой, которая определяется положениями статьи 437 Гражданского кодекса РФ. Анна Евкова не оказывает никаких услуг.
Устойчивость решения СЛАУ относительно исходных данных
(или обусловленность задач и вычислений)
Рассмотрим систему линейных алгебраических уравнений

Будем считать, что det A ¹ 0, 
Матрица А и вектор правой части 
Естественно встает вопрос, как эти погрешности (возмущения) исходных данных влияют на точность решения. Чтобы на него ответить, надо познакомиться с особой характеристикой матриц, которую называют обусловленностью [3].
G Говорят, что задача, модель или вычисление плохо обусловлены, если они чувствительны к малым изменениям (возмущениям) входящих в нее величин, т.е. исходных данных. В противном случае – хорошо обусловлена.
Таким образом, обусловленность характеризует устойчивость решения системы относительно исходных данных
Введем еще одно определение: задача решения СЛАУ является корректной, если решение существует, единственно (detA¹0) и непрерывно зависит от исходных данных (матриц А и В), т.е. малым изменениям исходных данных соответствуют малые изменения решения задачи.
Прежде всего, оговорим различие между плохо обусловленной задачей и плохо обусловленными вычислениями.
Если задача плохо обусловлена, то никакие усилия, потраченные на организацию изощренных вычислений, не могут дать правильный ответ, исключая случайность. С плохо обусловленными задачами можно столкнуться при расчетах стержневых систем методами строительной механики, например,
- при расчете рам методом перемещений, если два узла соединены очень жесткой частью конструкции;
- или при расчете конструкции методом сил, если выбрать основную систему так, что перемещение в устраняемой связи, соответствующее приложенной в ней паре нагрузок, равно или меньше перемещений в других устраненных связях от этой же нагрузки.
Все плохо обусловленные вычисления являются результатом применения численно неустойчивых алгоритмов. Например, метод исключения Гаусса без выбора главного элемента может обладать таким недостатком.
У плохо обусловленной матрицы обратная матрица является неустойчивой, т.е. элементы обратной матрицы значительно изменяются при малом изменении элементов исходной матрицы.
n Пример 3.7.Рассмотримплохо обусловленнуюсистему, записанную в матричном виде:
Если изменить правые части на 0,1 и принять их равными


Если принять величину 1-го коэффициента в 1-ом уравнении равной 4,99 вместо 5, то получим решение 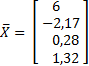
Существенно изменится при этом и обратная матрица.
Следует отметить, что чем больше порядок системы, тем сильнее сказывается влияние небольших возмущений коэффициентов системы на ее решение.
Обусловленность матрицы (системы) является качественной характеристикой, хотя мы будем стараться оценить ее количественно. Существует несколько способов оценки обусловленности.
Например, обусловленность матрицы (системы) можно оценить с помощью величины, называемой мерой обусловленности m(A):
где 

Число m(A), часто обозначаемое cond A (от английского слова conditioned — «обусловленный»), служит также коэффициентом роста относительных погрешностей при неточном задании элементов матрицы А.
Чем больше m(A) ,тем сильнее сказываются возмущения в исходных данных на решении системы линейных уравнений. Если число m(A) велико, то система считается плохо обусловленной. Говорить о том, «что такое хорошо, а что такое плохо» в отрыве от контекста решаемой задачи почти бессмысленно, так как здесь могут играть роль размерность задачи, точность, с которой должно быть найдено ее решение, точность представления чисел в ЭВМ и т.п. Однако можно дать оценку снизу меры обусловленности. Число обусловленности m(A) не может быть меньше 1. Матрица, а соответственно и система, будет хорошо обусловленной, если m(A) стремится к единице.
n Пример 3.8. Оценим обусловленность матриц А и В:
A =
Решение:
Обратные матрицы равны:
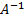
Вычислим меры обусловленности. Для этого найдем нормы матрицы А:
Мера обусловленности m(A) = 12´0,292=4,506 невелика и матрица А хорошо обусловлена.
Нормы матрицы В:
Мера обусловленности m(B) = 21´8421=176841 очень большая и матрица Вплохо обусловлена.
Примеры решения СЛАУ с использованием электронных таблиц MS Excel
Реализация метода Гаусса
Рассмотрим решение системы линейных алгебраических уравнений (пример 3.1) методом Гаусса, используя таблицы Excel.
Последовательность действий
Введем расширенную матрицу системы, как показано на рис.3.3, в ячейки А3:D5.

Прямой ход метода Гаусса.
1. Поделим элементы 1-ой строки на а11 .Для этого в ячейку А7 введем формулу
и скопируем ее вправо до конца строки.
2. Умножим элементы 1-ой строки на (–а21 ) и прибавим ко 2-й строке. Для этого введем формулу
и скопируем ее вправо до конца строки.
3. Умножим элементы 1-ой строки на (–а31 ) и прибавим к 3-й строке. Для этого введем формулу
и скопируем ее вправо до конца строки.
Таким образом исключили неизвестное х1 из 2-го и 3-го уравнений системы (смотри 1-й шаг рис.3.3).
Осталось исключить неизвестное х2 из 3-го уравнения системы. Для этого реализуем описанный выше алгоритм для 2-й и 3-й строк (смотри 2-й шаг рис.3.3).
На этом прямой ход метода Гаусс закончен, матрица системы приведена к треугольному виду.
Обратный ход метода Гаусса.
Найдем последовательно неизвестные, начиная с последней строки. Для этого в ячейки G12:G14 запишем формулы:
G3=D12-C12*G4 (для вычисления x2);
G2=D11-C11*G4-B11*G3 (для вычисления x1).
Число обусловленности матрицы и оценки погрешности решения систем линейных алгебраических уравнений
Число обусловленности матрицы и оценки погрешности решения систем линейных алгебраических уравнений — раздел Философия, Численные методы линейной алгебры Компьютерные Вычисления Являются Приближенными В Силу Того, Что Действительны.
Компьютерные вычисления являются приближенными в силу того, что действительные числа представляются конечным числом десятичных разрядов. Относительная погрешность представления действительных чисел в формате double составляет приблизительно 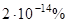
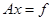
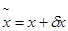
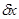
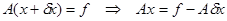
Таким образом, в условиях приближенности вычислений вместо исходной системы уравнений фактически решается некоторая возмущенная задача, точное решение которой и является приближенным решением, полученным в процессе вычислений. Рассмотрим, как возмущения правой части системы ЛАУ связаны с погрешностью ее решения при условии, что все промежуточные вычисления выполняются точно.
Итак, пусть правая часть системы возмущена – задана с абсолютной погрешностью 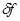
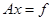
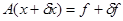
где 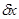
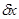

Несложные преобразования позволяют получить из уравнения (2.18) оценку нормы абсолютной величины погрешности:
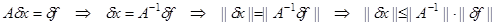
Заметим, что последнее неравенство (2.19) выражает устойчивость решения по правой части, и (согласно условию (1.15)) требование устойчивости эквивалентно требованию ограниченности нормы обратной матрицы системы ЛАУ. Из постановки задачи имеем
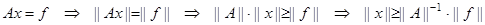
Из неравенств (2.19) и (2.20) следует оценка относительной погрешности возмущенной задачи:

Оценка (2.21) выражает зависимость относительной погрешности решения возмущенной задачи от относительной величины возмущения правой части в произвольной норме векторного пространства. В частности, согласно (2.21), погрешность возмущенной задачи пропорционально возрастает с ростом возмущений правой части, причем коэффициент пропорциональности определяется произведением норм матриц 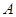
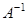
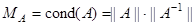
характеризующее зависимость относительной погрешности решения системы ЛАУ от величины относительного возмущения правой части, называется числом обусловленности матрицы. Если число обусловленности матрицы велико, то говорят, что данная матрица плохо обусловлена. Если число обусловленности близко к единице, то матрица считается хорошо обусловленной. Обычно для оценки числа обусловленности используется спектральная норма матриц, которая является подчиненной для евклидовой векторной нормы. Для симметричных матриц число обусловленности определяется отношением модулей наибольшего и наименьшего собственного значения матрицы.
Плохая обусловленность матрицы системы ЛАУ характеризует сильную чувствительность решения задачи к погрешности входных данных (малая ошибка входных данных приводит к существенному изменению решения). Аналогичным образом плохо обусловленные системы ЛАУ реагируют и на погрешности промежуточных вычислений. Так, например, в процессе приведения матрицы системы к треугольному виду выполняется ряд преобразований ее коэффициентов. В итоге, на этапе обратного хода метода Гаусса решается задача с возмущенными коэффициентами матрицы и полная оценка относительной погрешности должна исходить из следующей возмущенной задачи:
.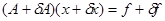
Если матрица возмущенной задачи (2.23) не вырожденная, то возмущения коэффициентов матрицы могут быть соотнесены с возмущениями правой части и вместо задачи (2.23) достаточно рассмотреть задачу
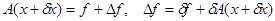
для которой имеет место оценка (2.21). На практике величина 
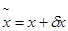
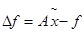
Вектор 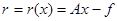
Оценки числа обусловленности матриц требуют вычисления обратной матрицы или, по крайней мере, оценки максимального и минимального собственных значений в случае симметричных матриц. В силу этого практическая оценка фактической точности приближенного решения системы ЛАУ согласно неравенству (2.21) представляет собой сложную задачу. Тем не менее, для ряда практически значимых случаев оценка (2.21) представляется полезной в плане контроля точности вычислений.
1. Доказать, что число обусловленности матрицы не меньше единицы
источники:
http://lektsia.com/6x31e9.html
http://allrefs.net/c1/48zvh/p7/
Предположим, что матрица и правая часть системы заданы неточно и вместо предъявленной к решению системы

в действительности должна была решаться некоторая система

Пусть известны оценки 

Сначала выделим главный член погрешности. Будем обозначать решения (1) и (2) через X и 




Вычитая из этого равенства (1), получим

откуда

b

Если 





Отсюда следует оценка погрешности

Строгая оценка погрешности получается следующим образом. Вследствие (3) выполняется неравенство

Предположим, что 


Довольно распространен случай, когда погрешность матрицы системы существенно меньше погрешности правой части. В качестве модели этой ситуации будем рассматривать случай точного задания матрицы системы. Тогда, полагая в 

Для качественной характеристики связи между погрешностями правой части и решения вводятся понятия обусловленности системы и обусловленности матрицы системы. Абсолютные погрешности правой части и решения системы зависят от масштабов, которыми измеряются коэффициенты системы. Поэтому удобнее характеризовать свойства системы через связь между относительными погрешностями правой части и решения.
Соответственно этому в качестве меры обусловленности системы принимается число

Отсюда получаем оценку относительной погрешности решения через меру обусловленности системы и относительную погрешность правой части:

Так как 

и

Иногда удобнее иметь более грубую характеристику свойств системы только через свойства матрицы А. Эту характеристику 

связывающую относительные погрешности правой части и решения только через свойства матрицы системы. Так как

то

Поскольку любая норма матрицы не меньше ее наибольшего по модулю собственного значения, то 


Таким образом,

В частности, при 


Следовательно, в случае нормы 

Рассмотрим вопрос о погрешности решения вследствие округления в ЭВМ правой части. Пусть, как обычно, t -двоичная разрядность чисел в ЭВМ. Каждый элемент 



Следовательно,

При практической работе вопрос: о строгой оценке погрешности полученного приближенного решения системы линейных уравнений с помощью полученных неравенств или каким-либо иным способом возникает редко. Однако информация о порядке погрешности решения часто полезна для получения качественных выводов о том, с какой точностью разумно решать задачу. Соотношения (4), (5) оценивают сверху погрешность решения, являющуюся следствием погрешности исходных данных. Из равенства (3) видно, что оценки (4), (5) довольно точны, поэтому обычно не имеет смысла стремиться получать решение задачи с погрешностью, существенно меньшей чем 
Системы уравнений и матрицы с большими значениями мер обусловленности принято называть плохо обусловленными, а с малыми — хорошо обусловленными. Если правая часть (4), оценивающая погрешность решения через погрешность исходных данных, или оценка вычислительной погрешности недопустимо велики, то полезно принять во внимание какую-то дополнительную информацию о решении рассматриваемой задачи. Подход к решению такой задачи должен быть таким же, как в случае некорректных задач.
Рассмотрим простейший случай, когда А — симметричная матрица. Пусть 




При реально заданной правой части 

Коэффициент 



При небольших 






Первый способ. Задавая некоторое 


записывается в виде

Так как

то наличие малого параметра а несущественно изменит слагаемые, соответствующие большим 


Это означает, что введение параметра 



Второй способ заключается в следующем. Будем решать систему уравнений каким-либо итерационным способом. Рассмотрим случай итераций по формуле

при некотором начальном приближении 

Подставим эти выражения в (7) и, приравнивая коэффициенты при 

Последовательно выражая каждое 

Если 


поэтому 










В других случаях решение задачи находят, минимизируя некоторый функционал, близкий к 


Успешность применения описанных приемов в случае несимметричных матриц А в существенной степени зависит от структуры жордановой формы и от ряда свойств матрицы. Здесь часто решение находят, минимизируя функционал

при малых 


Другая группа методов основана на представлении матрицы системы А в виде

где G и Р — ортогональные матрицы, а 



Большинство из описанных методов решения систем уравнений с плохо обусловленной матрицей относится к методам регуляризации.
Задача 1. Пусть 


1. Вычислить матрицу 



2. Выписать явно решение системы 
3. Выписать явно через правую часть 


4. Попытаться качественно описать эффект, достигаемый за счет применения такой регуляризации.
Объясним еще одну причину, по которой стараются избегать симметризации матриц, предложенной в § 6. Сначала посмотрим, что происходит, когда операция симметризации применяется формально в случае симметричной матрицы. Тогда 



Если 




Задача 2. Существуют ли несимметричные матрицы, для которых 
Рассмотрим еще один метод решения плохо обусловленных систем линейных алгебраических уравнений. Пусть

Относительно А будем считать, что в спектре матрицы 

Заметим, что в силу наших предположений относительно собственных значений матрицы 
Назовем решением X уравнения (8) вектор, который минимизирует функционал невязки, а именно,

здесь и далее в этом параграфе под нормой мы будем понимать евклидову норму вектора. Выписывая уравнение Эйлера для функционала 

Уравнение (10), в отличие от (8), всегда имеет решение. Действительно, непосредственной проверкой убеждаемся, что 



Описываемый ниже метод заключается в минимизации функционала 

Пусть 





Если приближение 



Наряду с приближениями 

Выпишем условия минимума функционала 


Заметим, что при поиске минимума 










откуда

При таком выборе 

и

Суммируя вышесказанное, получаем следующий алгоритм:
1) Вычисляем векторы 




2) Выбираем 

3) Если 


4) Следующее приближение 

Найдем трудоемкость метода. Для этого оценим число арифметических операций на шаге. Прежде всего заметим, что предварительные операции (этап 1) требуют в общем случае 
Этап 3 итерационного метода требует 

Таким образом, общая трудоемкость метода составляет 

Отметим также, что 

Исследуем сходимость итерационного метода. Имеет место
Лемма. Пусть 




Доказательство. Положим

Покажем, что функционал 






Пусть для определенности 

откуда и следует непрерывность рассматриваемого функционала.
Предположим, что утверждение леммы неверно. Тогда существует последовательность 





В силу непрерывности функционала 

Следовательно, при 

Отсюда следует, что 








Теорема. Последовательность приближений 



Постоянная q при этом зависит от выбора базиса 
Доказательство. Так как 


Из (14), (15) следует, что невязки 

Положим 

Поскольку 


и мы находимся в условиях предыдущей леммы. Тогда из условий леммы следует оценка

Из (14) и (15) имеем

откуда, учитывая (16), получаем оценку

Применяя к полученному неравенству оценку (18), имеем

откуда следует цепочка соотношений

Таким образом, последовательность 



Описанный выше метод решения систем уравнений с плохо обусловленными матрицами особенно эффективен в случае, когда априорная информация представлена в виде каких-либо сведений о структурных особенностях искомого решения; например, когда известны базисные функции 
Особенно эффективен данный метод в случае, когда q достаточно мало. Другими словами, для эффективного применения данного метода надо иметь разумную параметризацию исходной задачи. Довольно часто это можно сделать на основе априорной информации о решении. Например, если известно, что решение представляет собой некоторый колебательный процесс с небольшим числом гармоник, номера которых, вообще говоря, неизвестны.
Изложенный выше метод может быть обоснован также и в случае, когда спуск осуществляется не по одномерным подпространствам, соответствующим координатным осям в базисе