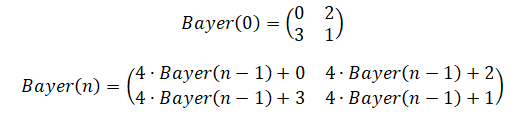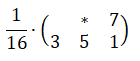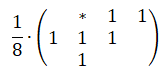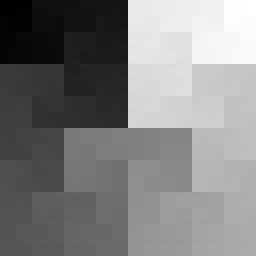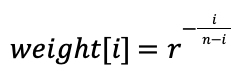Покажем
последовательность решения бизнес-задачи
сегментации абонентов с помощью подхода,
который основан на алгоритме Кохонена.
Решение состоит из двух шагов:
-
кластеризации
объектов алгоритмом Кохонена; -
построения и
интерпретации карты Кохонена.
В программе Deductor
сети и карты
Кохонена реализованы в обработчике
Карта Кохонена,
где содержатся сам алгоритм Кохонена
и специальный визуализатор Карта
Кохонена.
В Deductor
канонический
алгоритм Кохонена дополнен рядом
возможностей.
-
Алгоритм Кохонена
применяется к сети Кохонена, состоящей
из ячеек, упорядоченных на плоскости.
По умолчанию размер карты равен 16×12,
что соответствует 192 ячейкам. В выходном
наборе данных алгоритм Кохонена
формирует поля
Номер ячейки
и
Расстояние до центра ячейки. -
Ячейки карты с
помощью специальной дополнительной
процедуры объединяются в кластеры. Эта
процедура –
алгоритм k-means,
причем имеется
возможность автоматически определять
количество кластеров. В выходном наборе
данных алгоритм k-means
формирует
поля
Номер кластера
и
Расстояние до центра кластера. -
Каждый входной
признак может иметь весовой коэффициент
от 0 до 100%, который влияет на расчет
евклидова расстояния между векторами.
Импортируйте в
Deductor
набор данных
из файла mobile.txt.
Запустите
Мастер
обработки
и выберите узел
Карта Кохонена.
Установите все поля, кроме
Код, входными
(рис. 4.1).
Рис.
4.1.
Установка входных полей в алгоритме
Кохонена
На этой же вкладке
при нажатии кнопки
Настройка нормализации
откроется окно, где можно задать
значимость каждого входного поля.
Оставьте значимость всех полей без
изменений.
Поскольку любой
метод кластеризации, в том числе алгоритм
Кохонена, субъективен, смысл в выделении
отдельного тестового множества, как
правило, отсутствует. Оставьте в обучающем
множестве 100% записей (рис. 4.2).
На третьей вкладке
задаются размер и форма карты Кохонена
(рис. 4.3). Увеличьте размер карты до 24×18
(соотношение рекомендуется делать
кратным 4:3).
Рис.
4.2.
Разбиение набора данных на обучающее
и тестовое множества
Рис.
4.3.
Параметры будущей карты Кохонена
На следующем шаге
оставьте все без изменений (рис. 4.4).
Наконец, на последнем
шаге, предшествующем обучению,
настраиваются параметры обучения
алгоритма Кохонена (рис. 4.5).
Здесь задаются
следующие опции.
Способ
начальной инициализации карты
определяет, как будут установлены
начальные веса нейронов карты. Удачно
выбранный способ инициализации может
существенно ускорить обучение и привести
к получению более качественных
результатов. Доступны три варианта.
Рис.
4.4.
Параметры остановки алгоритма Кохонена
Рис.
4.5.
Параметры обучения сети Кохонена
-
Случайными
значениями
– начальные веса нейронов будут
инициированы случайными значениями. -
Из обучающего
множества –
в качестве начальных весов будут
использоваться случайные
примеры из обучающего множества. -
Из собственных
векторов –
начальные веса нейронов карты будут
проинициализированы значениями
подмножества гиперплоскости, через
которую проходят два главных собственных
вектора матрицы ковариации входных
значений обучающей выборки.
При выборе способа
начальной инициализации нужно
руководствоваться следующей информацией:
-
объемом обучающей
выборки; -
количеством эпох,
отведенных для обучения; -
размером карты.
Между указанными
параметрами и способом начальной
инициализации существует много
зависимостей. Выделим несколько главных.
-
Если объем обучающей
выборки значительно (в 100 раз и более)
превышает число ячеек карты и время
обучения не играет первоочередной
роли, то лучше выбрать инициализацию
случайными значениями. -
Если объем обучающей
выборки не очень велик, время обучения
ограниченно или если необходимо
уменьшить вероятность появления после
обучения пустых ячеек, в которые не
попало ни одного экземпляра обучающей
выборки, то следует использовать
инициализацию примерами из обучающего
множества. -
Инициализацию из
собственных векторов можно использовать
при любом стечении обстоятельств.
Именно этот способ лучше выбирать при
первом ознакомлении с данными.
Единственное замечание: вероятность
появления пустых ячеек после обучения
выше, чем при инициализации примерами
из обучающего множества.
Скорость
обучения
–
задается скорость обучения в начале и
в конце обучения сети Кохонена.
Рекомендуемые значения: 0,1-0,3 в начале
обучения и 0,05-0,005 в конце.
Радиус
обучения
–
задается радиус обучения в начале и в
конце обучения сети Кохонена, а также
тип функции соседства. Вначале радиус
обучения должен быть достаточно большим
–
примерно половина размера карты
(максимальное линейное расстояние от
любого нейрона до другого любого нейрона)
или меньше, а в конце –
достаточно малым, 1 или меньше. Начальный
радиус в Deductor
подбирается
автоматически в зависимости от размера
карты.
В этом же блоке
задается вид функции соседства: гауссова
или ступенчатая. Если функция соседства
ступенчатая, то «соседями» нейрона-победителя
будут считаться все нейроны, линейное
расстояние до которых не больше текущего
радиуса обучения. Если применяется
гауссова функция соседства, то «соседями»
нейрона-победителя будут считаться все
нейроны карты, но в разной степени. При
использовании гауссовой функции
соседства обучение проходит более
плавно и равномерно, так как одновременно
изменяются веса всех нейронов, что может
дать немного лучший результат, чем, если
бы использовалась ступенчатая функция.
Однако и времени на обучение требуется
больше, поскольку в каждой эпохе
корректируются все нейроны.
Кластеризация
–
в этой области указываются параметры
алгоритма k-means,
который
запускается после алгоритма Кохонена
для кластеризации ячеек карты.
Здесь нужно либо
позволить алгоритму автоматически
определить число кластеров, либо сразу
зафиксировать его. Следует знать, что
автоматически подбираемое число
кластеров не всегда приводит к желаемому
результату: оно может быть слишком
большим, поэтому рассчитывать на эту
опцию можно только на этапе исследования
данных.
Нажмите кнопку
Пуск
–
в следующем окне можно будет увидеть
динамику процесса обучения сети Кохонена
(рис. 4.6). По умолчанию алгоритм делает
500 итераций (эпох). Если предварительно
установить флажок
Рестарт,
то веса нейронов будут проинициализированы
согласно выбранному на предыдущем шаге
способу инициализации, иначе обучение
начнется с текущих весовых коэффициентов
(это справедливо только при повторной
настройке узла).
Рис. 4.6.
Обучение сети Кохонена
Для обученной сети
Кохонена предлагается специализированный
визуализатор –
Карта Кохонена.
Параметры ее отображения задаются на
одноименной вкладке мастера (рис. 4.7).
Область
Список допустимых отображений карты
содержит три группы –
Входные столбцы, Выходные столбцы
и
Специальные.
Последние не связаны с каким-либо полем
набора данных, а служат для анализа всей
карты.
-
Матрица
расстояний
применяется для визуализации структуры
кластеров, полученных в результате
обучения карты. Большое значение говорит
о том, что данный нейрон сильно отличается
от окружающих и относится к другому
классу. -
Матрица
ошибок квантования
отображает среднее расстояние от
расположения примеров до центра ячейки.
Расстояние считается как евклидово.
Матрица ошибок квантования показывает,
насколько хорошо обучена сеть Кохонена.
Чем меньше среднее расстояние до центра
ячейки, тем ближе к ней расположены
примеры и тем лучше модель.
Рис.
4.7.
Параметры карты Кохонена
Матрица
плотности попадания
отображает количество объектов, попавших
в ячейку.
Кластеры
–
ячейки карты Кохонена, объединенные в
кластеры алгоритмом k-means.
Проекция
Саммона –
матрица, являющаяся результатом
проецирования многомерных данных на
плоскость. При этом данные, расположенные
рядом в исходной многомерной выборке,
будут расположены рядом и на плоскости.
Дополнительно справа имеется еще ряд
настроек.
Способ
раскрашивания ячеек –
цветная палитра или градация серого.
Цветная палитра нагляднее, однако если
потребуется встраивать карту Кохонена
в отчет с последующей распечаткой на
бумажном носителе, то лучше выбрать
серую цветовую схему.
Сглаживание
цветов карты –
цвета на картах будут сглажены, то есть
будет обеспечен более плавный переход
цветов. Это поможет устранить случайные
выбросы.
Границы
ячеек –
установка данного флажка позволит
включить отображение границ ячеек на
карте.
Границы
кластеров –
установка данного флажка позволит
включить отображение границ кластеров
на всех картах. Этот режим удобен для
анализа структуры кластеров.
Размер
ячейки по умолчанию –
указывается размер ячейки на карте в
пикселях (по умолчанию 16).
Текущая ячейка
отображается на карте маленькой
окружностью черного цвета. Изменить
текущую ячейку просто: щелкнуть кнопкой
мыши на нужном участке карты. Внизу
каждой карты на градиентной шкале в
желтом прямоугольнике отображается
числовое значение признака, соответствующее
цвету ячейки.
На рис. 4.8 приведены
получившиеся карты Кохонена. По матрице
плотности попадания видно, что в одной
ячейке сосредоточилось 259 объектов. Эта
ячейка выделяется белым цветом. Можно
приступать к интерпретации результатов
кластеризации.
Рис.
4.8.
Карты Кохонена для сегментации абонентов
сети сотовой связи
Попробуем выделить
на карте изолированные области
самостоятельно (без использования
встроенного метода группировки ячеек
алгоритмом k-means).
Анализируя карту
Возраст
(рис. 4.8), видим, что четко выделяются три
возрастные группы: молодежь, люди
среднего возраста и люди старше 45 лет.
Остановимся
подробнее на молодежи. Она неоднородна
–
здесь можно выделить несколько кластеров.
Первый расположен в правом нижнем углу
(рис. 4.10). Абоненты этой условной зоны
активно и продолжительно разговаривают
по телефону вечером и ночью, отправляют
много SMS-сообщений,
соответственно, и тратят на разговоры
больше денег, чем другие представители
возрастной группы. Обратите внимание,
что в этот кластер попала львиная доля
тех, кто увлекается ночными разговорами.
Можно предположить, что это студенты и
молодежь, часто проводящие вечера вне
дома.
Рис.
4.10.
Кластер «Активная молодежь»
Вверху (рис. 4.11)
сосредоточилась небольшая по числу
ячеек группа молодежи, которая не
отличается активностью разговоров ни
днем, ни вечером, ни тем более ночью, и,
как следствие, ежемесячные расходы на
связь у представителей этого кластера
невелики.
Рис.
4.11.
Кластер молодежи с пониженным потреблением
услуг связи
Остальные люди в
этой возрастной группе ничем особенным
не выделяются: умеренные расходы на
связь и преимущественно вечерние
разговоры. Можно предположить, что сюда
попала наибольшая часть молодежи. Таким
образом, в молодежной возрастной группе
мы обнаружили три кластера.
Продолжим
интерпретацию карты Кохонена и теперь
остановимся на людях зрелого и пенсионного
возраста. Обратим внимание на ярко
выраженный сгусток в верхней области,
в котором практически по всем признакам,
кроме SMS,
наблюдаются
высокие значения, в том числе по звонкам
в другие города и страны (рис. 4.12). Это
так называемые VIP-клиенты:
бизнесмены, руководители, топ-менеджеры.
Они преимущественно зрелого возраста,
очень много разговаривают днем и вечером
(скорее всего, по работе) и практически
не пользуются SMS-услугами.
Месячные расходы на связь у этой категории
абонентов самые высокие.
Рис.
4.12.
Кластер «VIP-клиенты»
Чуть выше в небольшом
кластере наблюдается противоположная
картина: люди практически не пользуются
услугами сотовой сети (рис. 4.13). Вероятнее
всего, это пенсионеры, которым мобильная
связь нужна преимущественно для приема
входящих звонков, сами же они почти не
звонят. Их расходы на связь самые низкие,
возможно, из-за того, что единственным
их доходом является пенсия.
Рис.
4.13.
Пенсионеры, практически не делающие
исходящих звонков
Изучим статистические
характеристики этой группы людей.
Нажмите кнопку
Показать/скрыть
окно данных,
затем –
кнопку
Изменить
способ фильтрации
и установите
Фильтр
по выделенному.
Там же переключитесь в режим статистики
(кнопка
Способ
отображения).
Колонка
Среднее
даст следующие вычисленные значения
(табл. 4.2).
Таблица
4.2.
Статистические характеристики кластера
5
|
№ |
Признак |
Среднее |
|
1 |
Возраст |
65,7 |
|
2 |
Среднемесячный |
41,5 |
|
3 |
Средняя |
2,1 |
|
4 |
Звонков |
9,3 |
|
5 |
Звонков |
6,4 |
|
6 |
Звонков |
0,0 |
|
7 |
Звонки |
0 |
|
8 |
Звонки |
0 |
|
9 |
Доля |
6,3 |
|
10 |
Количество |
0 |
Остальных людей
в возрастной группе «Зрелый и пенсионный
возраст» объединяет то, что они в основном
звонят вечером и не используют SMS-сервис.
С большой долей вероятности можно
утверждать, что сюда входят работающие
пенсионеры, дачники, родители
совершеннолетних детей.
Осталась последняя,
средневозрастная группа. Это кластер
работающих людей. В нем можно отметить
группу тех, кто совершает мало звонков
вечером.
По площади, которую
занимают на карте Кохонена условно
выделенные кластеры, судить о мощности
каждого из них трудно: в разных ячейках
содержится различное число объектов.
Поэтому рекомендуется фиксировать
число объектов, попавших в каждый
кластер. Зная мощность кластера, можно
дополнительно оценить его прибыльность
–
сумму по признаку
Среднемесячный расход
(табл. 4.3).
Таблица
4.3.
Мощности кластеров
|
№ кластера |
Условное |
Мощность |
Прибыльность |
|
1 |
Активная |
||
|
2 |
Молодежь, |
||
|
3 |
Основная |
||
|
4 |
VIP-клиенты |
||
|
5 |
«Малоговорящие» |
569 |
23613,5 |
|
6 |
Активная |
||
|
7 |
Работающие |
Теперь включите
автоматическую группировку ячеек в
кластеры:
Настроить
отображения – Кластеры.
При установленном флажке
Автоматически
определить количество кластеров
(с уровнем значимости 1,00) получится
16
кластеров (рис. 4.14, а). Это очень много,
поэтому следует принудительно установить,
скажем, 6 кластеров (рис. 4.14, б).
а
б
Рис.
4.14.
Варианты автоматической группировки
ячеек алгоритмом k-means:
а – автоматическое число кластеров, б
– ручное задание числа кластеров, равное
6
Видно, что
автоматический алгоритм k-means
при 6 кластерах
выделил целиком кластер «Зрелый и
пенсионный возраст», раздробились
группы «Молодежь» и «Люди среднего
возраста». Не были явно выделены кластеры
2, 4 и 5 из табл. 4.3. Тем не менее, автоматическая
группировка ячеек в Deductor
имеет одно
важное преимущество: в наборе данных
появляется столбец
Кластер
с номером, который можно использовать
в дальнейшем, в частности «прогонять»
новые объекты и получать для них номер
кластера.
Соседние файлы в предмете [НЕСОРТИРОВАННОЕ]
- #
- #
- #
- #
- #
- #
- #
- #
- #
- #
- #
Подборка по базе: Курсовая Работа Максимов 19-КОП.odt, Практическая работа №1.docx, Самостоятельная работа к теме 2.1.2.docx, Практическая работа №1.docx, Практическая работа (11).docx, Практическая работа.doc, Контрольная работа по Базам данныхНазароваС.docx, Козлов В.А. Практическая работа №2..docx, Курсовая работа. Теоретические основы дошкольного образования (Д, Практическая работа 4.docx
Решение задачи
Откройте сценарий som. ded для изучения дальнейшего материала.
Покажем последовательность решения бизнес-задачи сегментации абонентов с помощью подхода, который основан на алгоритме Кохонена, которая состоит из двух шагов:
- кластеризация объектов алгоритмом Кохонена;
- построение и интерпретация карты Кохонена.
В Deductor Studio сети и карты Кохонена реализованы в обработчике Карта Кохонена, где содержатся сам алгоритм Кохонена и специальный визуализатор Карта Кохонена.
В Deductor канонический алгоритм Кохонена дополнен рядом возможностей, а именно:
- Алгоритм Кохонена применяется к сети Кохонена, состоящих из ячеек, упорядоченных на плоскости. По умолчанию размер карты равен 16 х 12, что соответствует 192 ячейкам. В выходном наборе данных алгоритм Кохонена формирует поля Номер ячейки и Расстояние до центра ячейки.
- Ячейки карты с помощью специальной дополнительной процедуры объединяются в кластеры. Эта процедура – алгоритм k-means, причем имеется возможность
автоматически определять количество кластеров. В выходном наборе данных алгоритм k- means формирует поля Номер кластера и Расстояние до центра кластера.
Каждый входной признак может иметь весовой коэффициент от 0 до 100%, последний влияет на расчет евклидового расстояния между векторами.
Для построения профилей клиентов воспользуется сетями и картами Кохонена. Импортируем в Deductor набор данных из файла mobile. txt . Запустим мастер обработки и выберем узел Карта Кохонена . Установим все поля, кроме Код, входными.

Рисунок 1 – Настройка назначений столбцов
На этой же вкладки при нажатии кнопки Настройка нормализации … откроется окно, где
можно задать значимость каждого входного поля. Оставим значимость одинаковой для всех полей без изменений.
Замечание

Поскольку любой метод кластеризации, в том числе и алгоритм Кохонена, субъективен, смысл в выделении отдельного, тестового множества, как правило, отсутствует. Оставим в обучающем 100
% записей (рисунок 2).
Рисунок 2 – Разбиение набора данных на обучающее и тестовое множества
На третьей вкладке задаются размер и форма карты Кохонена (рисунок 3). Пока что согласимся с настройками по умолчанию – шестиугольные ячейки, размер 16х12.

Рисунок 3 – Параметры будущей карты Кохонена
На следующем шаге также оставим все без изменений (рисунок 4).
Рисунок 4 – Параметры остановки алгоритма Кохонена
Наконец, на последнем шаге, предшествующем обучению, настраиваются параметры обучения алгоритма Кохонена (рисунок 5).
Здесь задаются следующие опции.

Рисунок 5 – Параметры обучения сети Кохонена
Способ начальной инициализации кар ты определяет, как будут установлены начальные веса нейронов карты. Удачно выбранный способ инициализации может существенно ускорить обучение и привести к получению более качественных результатов. Доступны три варианта:
Случайнымизначениями– начальные веса нейронов будут инициированы случайными значениями
- Изобучающегомножества– в качестве начальных весов будут использоваться случайные примеры из обучающего множества.
- Изсобственныхвекторов– начальные веса нейронов карты будут проинициализированы значениями подмножества гиперплоскости, через которую проходят два главных собственных вектора матрицы ковариации входных значений обучающей выборки.
При выборе способа начальной инициализации (рисунок 6)следует руководствоваться следующей информацией:
- объемом обучающей выборки;
- количеством эпох, отведенных для обучения;
- размером карты.
Между указанными параметрами и способом начальной инициализации существует много зависимостей. Выделим несколько главных.
- Если объем обучающей выборки значительно (в 100 и более) превышает число ячеек карты и время обучения не играет первоочередной роли, то лучше выбрать
инициализациюслучайнымизначениями, т.к. это даст меньшую вероятность попадания в локальный минимум ошибки кластеризации.
- Если объем обучающей выборки не очень велик, время обучения ограниченно или необходимо уменьшить вероятность появления после обучения пустых ячеек, в которые не попало ни одного экземпляра обучающей выборки, то следует использовать
инициализациюпримерамиизобучающегомножества.
- Инициализацию из собственных векторов можно использовать при любом стечении обстоятельств. Единственное замечание: вероятность появления пустых ячеек после обучения выше, чем при инициализации примерами из обучающего множества. Именно этот способ лучше выбирать при первом ознакомлении с данными.
Скорость обучения – задается скорость обучения в начале и в конце обучения сети Кохонена. Рекомендуемые значения: 0,1–0,3 в начале и 0,05–0,005 в конце обучения.
Радиус обучения – задается радиус обучения в начале и в конце обучения сети Кохонена. Радиус в начале должен быть достаточно большой – примерно половина или меньше размера карты (максимальное линейное расстояние от любого нейрона до другого любого нейрона). а в конце – достаточно малым, примерно 1 или меньше. Начальный радиус в Deductor подбирается автоматически в зависимости от размера карты.
В этом же блоке задается Функция соседства : Гауссова или Ступенчатая. Если функция соседства Ступенчатая, то «соседями» для нейрона-победителя будут считаться все нейроны, линейное расстояние до которых не больше текущего радиуса обучения. Если используется Гауссова функция соседства, то «соседями» для нейрона- победителя будут считаться все нейроны карты, но в разной степени полноты.
При использовании Гауссовой функции соседства обучение проходит более плавно и равномерно, так как одновременно изменяются веса всех нейронов, что может дать немного лучший результат, чем если бы использовалась ступенчатая функция. Однако время, необходимое на обучение, требуется немного большее, по причине того, что на каждой эпохе корректируются все нейроны.
Кластеризация – в этой области указываются параметры алгоритма k-means (G-means), который запускается после алгоритма Кохонена для группировки ячеек карты. Здесь нужно только определить, позволить алгоритму автоматически определить число кластеров (G-means), или сразу зафиксировать его (k-means). Следует знать, что автоматически подбираемое число кластеров не всегда приводит к желаемому результату – число кластеров может предлагаться слишком большим, поэтому рассчитывать на эту опцию можно только на этапе исследования данных.
В следующем окне, нажав кнопку Пуск, можно будет увидеть динамику процесса обучения сети Кохонена (рисунок 6). По умолчанию алгоритм делает 500 итераций (эпох). Если предварительно установить флаг Рестарт , то веса нейронов будут проинициализированы согласно выбранному на предыдущем шаге способу инициализации, иначе обучение начнется с текущих весовых коэффициентов (это справедливо только при повторной настройке узла).

Рисунок 6 – Обучение сети Кохонена
К обученной сети Кохонена предлагается специализированный визуализатор – Карта
Кохонена . Параметры ее отображения задаются на специальной вкладке мастера (рисунок 7).
Список допустимых отображений карты содержит три группы – входные поля, выходные поля и специальные. Последние не связаны с каким-либо полем набора данных, а служат для анализа всей карты.
- Матрицарасстоянийприменяется для визуализации структуры кластеров, полученных в результате обучения карты. Большое значение говорит о том, что данный нейрон сильно отличается от окружающих и относится к другому классу.
- Матрицаошибокквантования– отображает среднее расстояние от расположения
примеров до центра ячейки. Расстояние считается как евклидово расстояние. Матрица ошибок квантования показывает, насколько хорошо обучена сеть Кохонена. Чем меньше среднее расстояние до центра ячейки, тем ближе к ней расположены примеры, и тем лучше модель.
- Матрицаплотностипопадания– отображает количество объектов, попавших в ячейку.
- Кластеры– ячейки карты Кохонена, объединенные в кластеры алгоритмом k-means.
Проекция Саммона – матрица, являющаяся результатом проецирования многомерных данных на плоскость. При этом данные, расположенные рядом в исходной многомерной выборке, будут расположены рядом и на плоскости
Рисунок 7 – Настройки визуализатора «Карта Кохонена»
Дополнительно справа имеется еще ряд настроек:
- Способраскрашиванияячеек–цветная палитра и или градация серого. Цветная палитра нагляднее, однако, если вам потребуется встраивать карту Кохонена в печатный отчет с последующей распечаткой на бумажный носитель, то лучше выбрать серую цветовую схему.
- Сглаживаниецветовкарты– цвета на картах будут сглажены, т.е. будет обеспечен более плавный переход цветов. Это поможет устранить случайные выбросы.
- Границыячеек– установка данного флажка позволяет включить отображение границ ячеек на карте.
- Границыкластеров– установка данного флага позволит включить отображение границ кластеров на всех картах. Этот режим удобен для анализа структуры кластеров.
- Размерячейки– указывается размер ячейки на карте в пикселях (по умолчанию 16).
Данное окно установки параметров карты можно будет в любой момент вызвать кнопкой
Настроить отображения… на панели инструментов визуализатора.
Посмотрим на получившуюся при настройках по умолчанию карту (рисунок 8 и файл som. ded ).
Рисунок 9 – Фрагмент карты Кохонена, построенной при стандартных настройках
Текущая ячейка отображается на карте маленькой окружностью черного цвета. Изменить текущую ячейку просто: щелкнуть мышью в нужный участок карты. Внизу каждого отображения на градиентной шкале в желтом прямоугольнике отображается числовое значение признака, соответствующее ее цвету.
При работе с картой доступны операции, выполняемые с помощью кнопок на панели инструментов визуализатора или контекстного меню, вызываемого правой кнопкой мыши в любом окне карты.
Ряд кнопок ( Границы ячеек ,
Границы кластеров ,
Настроить
отображения… ) дублирует параметры, задаваемые в окне мастера настройки визуализатора (рисунок 7). Действия остальных кнопок описаны в таблице 2.
Таблица 2
| Команда | Описание | |
| Настроить кластеры… | Вызывается диалоговое окно Настройка кластеров , в котором можно изменять количество кластеров для уже
построенной карты. По сути, запускается алгоритм k- means для кластеризации ячеек карты с новым числом кластеров |
|
| Изменить режим работы | Устанавливает один из четырех режимов работы (простой, выделение, рисование контура, установка меток), который влияет на поведение при выделении ячейки. При открытии карты устанавливается простой режим | |
| Отображать выделенные ячейки | Показывать или скрывать выделенные ячейки на всех картах | |
| Отображать контур | Показывать или скрывать ломаную линию,
предназначенную для дополнительного выделения ячеек на картах |
|
| Отображать метки | Показывать или скрывать текстовые метки для ячеек | |
| Уменьшить/увеличить карты | Каждый щелчок по данной кнопке позволяет уменьшить/увеличить размер всех открытых окон
отображений карты одновременно. Аналогично изменению параметра Размер ячейки по умолчанию |
|
| Расположить встык | Расположить все открытые окна отображений карты рядом друг с другом | |
| Показать/скрыть окно данных | Показать/скрыть в нижней части окна визуализатора таблицу, в которой будут отображаться примеры обучающей выборки |
Замечание

Вернемся к сегментации заемщиков. По матрице плотности попадания видно (рис. 9), что в одной ячейке сосредоточилось 259 объектов. Эта ячейка выделяется желто-красным цветом. В
принципе, можно остановиться на этом варианте кластеризации и приступить к интерпретации карты. Забегая вперед, скажем, что карта с увеличенным масштабом оказалась лучше, так как позволила «разглядеть» кластер, который не удавалось обнаружить при размере карты 16х12. Поэтому здесь универсальных рецептов нет. Понять, лучше или хуже карта Кохонена, можно только сравнив ее с картами, построенными при других настройках, сравнив матрицы ошибок квантования и матрицы плотности попадания.
Поэтому построим еще одну карту Кохонена, увеличив ее размер в 1,5 раза до 24х18 и изменив способ инициализации («из обучающего множества») для снижения вероятности образования пустых ячеек. При размере карты 24х18 она имеет 432 ячейки, значит, на 1 ячейку приходится в среднем по 20 примеров. Полученная карта Кохонена изображена на рисунке 9 (см. также
som. ded ).

Рисунок 9 – Карты Кохонена масштаба 24х18 для сегментации абонентов сети сотовой связи
Попробуем выделить на карте изолированные области самостоятельно без использования встроенного метода группировки ячеек алгоритмом k-means.
Анализируя отображение карты Возраст (рисунок 10), видим, что четко выделяются три возрастные группы: молодежь, люди среднего возраста и люди старше 45 лет.

Рисунок 10 – Деление по возрастным группам
Остановимся подробнее на молодежи. Она не однородна, здесь можно выделить несколько кластеров. Первый расположился в правом нижнем углу (рисунок 11). Абоненты этой условной зоны на карте активно и продолжительно говорят вечером и ночью, отправляют много SMS- сообщений, соответственно, и тратят на разговоры больше денег, чем другая молодежь. Обратите внимание, что в этот кластер попала «львиная» доля людей, пользующихся ночными разговорами. Можно предположить, что это часть студентов и молодежи, часто проводящая вечера вне дома.

Рисунок 11 – Деление по возрастным группам
Вверху (рисунок 12) сосредоточилась небольшая по числу ячеек группа молодежи, которая не отличается активностью разговоров и SMS ни днем, ни вечером, ни, тем более, ночью, и, как следствие, их ежемесячные расходы на связь невелики
Рисунок 12 – Кластер молодежи с пониженным потреблением услуг связи
Остальные люди в возрастной группе молодежи ничем особенным не выделяются: умеренные расходы на связь и преимущественно вечерние разговоры. Можно предположить, что сюда попала наибольшая часть молодежи.
Таким образом, в молодой возрастной группе мы обнаружили три кластера. Продолжим интерпретацию карты Кохонена и возьмем людей зрелого и пенсионного возраста. Обратим внимание на ярко выраженный сгусток в нижней области, в котором практически по всем
признакам, кроме SMS, наблюдаются высокие значения, в том числе по звонкам в другие города и страны (рисунок 13). Это так называемые VIP-клиенты: бизнесмены, руководители, топ-
менеджеры. Они преимущественно зрелого возраста, очень много разговаривают днем и вечером (скорее всего по работе) и практически не пользуются SMS-услугами. Месячные расходы на связь этой категории абонентов самые высокие.

Рисунок 13 – Кластер «VIP-клиенты»
Чуть выше в небольшом кластере наблюдается противоположная картина – люди практически не пользуются услугами сотовой сети (рисунок 14). Вероятнее всего это пенсионеры, которые имеют мобильную связь преимущественно для приема входящих звонков, а сами практически не совершают звонков. Их расходы на связь самые низкие, возможно, из-за того, что единственным их доходом является пенсия.

Рисунок 14 – Пенсионеры, практически не делающие исходящих звонков
Изучим статистические характеристики этой группы людей. Для этого нажмем на кнопку
Показать окно данных и установим Фильтр по выделенному , а потом
переключимся в режим статистики. Колонка Среднее даст следующие вычисленные значения (таблица 3).
| N | Признак | Среднее значение |
| 1 | Возраст | 64,5 |
| 2 | Среднемесячный расход | 49,7 |
| 3 | Средняя продолжительность разговоров, мин. | 2,1 |
| 4 | Звонков днем за месяц | 13,4 |
| 5 | Звонков вечером за месяц | 7,4 |
| 6 | Звонков ночью за месяц | 0,3 |
| 7 | Звонки в другие города | 0,5 |
| 8 | Звонки в другие страны | 0,05 |
| 9 | Доля звонков на стационарные телефоны, % | 5,7 |
| 10 | Количество SMS в месяц | 1,6 |
Остальных людей в возрастной группе Зрелый и пенсионный возраст объединяет то, что они в основном звонят вечером и и не используют SMS-сервис. С большой долей вероятности можно утверждать, что сюда входят работающие пенсионеры, дачники, родители совершеннолетних детей.
Осталась последняя, средневозрастная группа. Это кластер работающих людей. В нем можно отметить группу тех, кто совершает мало звонков вечером.
По площади, которую занимают на карте Кохонена условно выделенные кластеры, судить о мощности каждого из них трудно: в разных ячейках содержится различное число объектов.
Поэтому рекомендуется фиксировать число объектов, попавших в каждый кластер. Зная мощность кластера, в нашей задаче можно дополнительно оценить его прибыльность – сумму по полю Среднемесячный расход (таблица 4).
Таблица 4
| N кластера | Условное название кластера | Мощность кластера | Прибыльность кластера |
| 1 | Активная молодежь | 370 (8%) | 281 413 (12%) |
| 2 | Молодежь, мало пользующаяся услугами | 157 (3,5%) | 49 863 (2,2%) |
| 3 | Основная молодежь | 890 (20%) | 458 763 (20%) |
| 4 | VIP-клиенты | 152 (3,4%) | 424 378 (18,7%) |
| 5 | «Малоговорящие» пенсионеры | 274 (6%) | 13 640 (0,6%) |
| 6 | Активная группа зрелого и пенсионного возраста | 1461 (33,1%) | 530 751 (33,8%) |
| 7 | Работающие люди среднего возраста | 1188 (26%) | 514 842 (22,7%) |
Теперь включим автоматическую группировку ячеек в кластеры: Настроить отображения ►
Кластеры . При установленном флаге Автоматически опр еделить количество
кластеров будет работать алгоритм G-means и получится 11 кластеров (рисунок 16а). Это очень много, поэтому принудительно установим, скажем, 6 кластеров (рисунок 16б).


Рисунок 16 – Варианты автоматической группировки ячеек алгоритмом k-means, а – автоматическое число кластеров, б – ручное задание числа кластеров, равное 6
Видно, что автоматический алгоритм k-means при 6 кластерах выделил целиком кластер Зрелый и пенсионный возраст, раздробились группы Молодежь и Люди среднего возраста. Не были явно выделены кластеры №2, 4 и 5 из таблицы 3. Тем не менее, автоматическая группировка ячеек в Deductor имеет одно важное преимущество: в наборе данных появляется столбец Кластер с его номером, поэтому его можно использовать в дальнейшем, в частности, «прогонять» новые объекты и получать для них № кластера.
Кластеризация «новых» объектов
Наша карта Кохонена способна «прогонять» через себя новые объекты и относить их к той или иной ячейке, к тому или иному кластеру. Механизм этой операции прост: для нового объекта рассчитывается расстояние до всех центров ячеек и объект считается принадлежащим к том
ячейке, расстояние до которой минимально. А зная номер ячейки, определяется номер кластера.
В сценарии som. ded приведен пример «прогона» нового объекта (из файла
mobile 1 abonent. txt ) с использованием обработчика Скрипт .
Прогнозирование с помощью карт Кохонена
Ранее упоминалось, что опционально обработчик Карта Кохонена может иметь выходные поля. Как они будут использоваться? Представим, что в нашей задаче столбец Возраст не входной, а выходной. Он не будет использоваться при кластеризации. Однако после построения карты Кохонена появляется возможность для новых абонентов определять их возраст, зная остальные
параметры: число звонков, среднемесячный расход и т.д. Иначе говоря, с помощью кластеризации будет решаться задача регрессии или классификации.
Механизм работы этого следующий. Если выходное поле – дискретное, то выходом ячейки (по этому выходному полю) будет являться самое распространенное значение выходного поля тех строчек данных, которые «попали» в данную ячейку. Если же выходное поле – это непрерывное
поле, то выходом ячейки (по этому выходному полю) будет являться среднее значений выходного поля тех строчек данных, которые «попали» в данную ячейку.
Ограничения использования карт Кохонена в Deductor
В Deductor Studio алгоритм Кохонена ориентирован на работу преимущественно с числовыми типами данных, а также с упорядоченными (ординальными) типами. Обработка данных в полях, значения которых нельзя упорядочить будет приводить к некорректным результатам.
Упорядочивание ординальных типов осуществляется на вкладке Настройка нормализации…
Практическая работа:
- Изучите сценарий som. ded , прилагающийся к занятию. Выделите множества ячеек подобным образом, как это демонстрировалось на рисунках 10-13.
- Опишите, какими услугами и с какой частотой пользуются люди из средневозрастной группы.
- Проанализируйте людей, попавших в ячейку 48.
- Постройте карту Кохонена для сегментации абонентов, сделав поле Возраст выходным. Насколько сильно изменилась карта? Проведите эксперимент в визуализаторе Что-если: введите свои данные в поля Количество звонков, Среднемесячный расход и т.д. и
спрогнозируйте свой возраст.
- Превратите карту Кохонена в обычную сеть Кохонена с шестью выходными нейронами.
- Найдите в справке и самостоятельно изучите отображение Проекция Саммона.
Вопросы для проверки:
- Как выделить множество ячеек на карте и посмотреть объекты, попавшие в них?
- Как поставить текстовую метку на ячейке?
- Как проще всего посмотреть статистику по объектам, попавшим в ячейку?
- Какой кластер в приведенной бизнес-задаче, скорее всего, не удалось бы обнаружить при масштабе карты 16 х 12?
- В каких случаях следует задавать значимость входных полей?
- Как карта Кохонена может использоваться в задаче восстановления пропусков в данных? Опишите шаги, необходимые для этого.
- Почему при кластеризации в обработчике Карта Кохонена могут быть выходные поля? Каково их предназначение?
- В каком случае для карты Кохонена лучше установить цветовую палитру в серых тонах? Почему?
Мне всегда нравилась визуальная эстетика дизеринга (dithering, псевдотонирование, псевдосмешение цветов), но я не знал о том, как он применяется. Поэтому я провёл кое-какие изыскания. Эта статья может содержать отголоски ностальгии, но в ней не будет никаких следов Лены.
Как я сюда попал?
Я, конечно, припозднился, но, наконец, поиграл в «Return of the Obra Dinn», самую свежую игру Лукаса Поупа, создателя знаменитой «Papers Please». «Obra Dinn» — это история-головоломка, которую я могу только порекомендовать. Но я программист, и моё любопытство этот проект разжёг тем, что это — 3D-игра (созданная с использованием движка Unity), которая рендерится с использованием всего лишь двух цветов и с применением дизеринга. Видимо, это называется «дизерпанк», и мне это нравится.
Дизеринг, как я изначально его понимал, это техника, основанная на применении лишь небольшого количества цветов из некоей палитры. Цвета так хитро комбинируются, что мозгу зрителя кажется, что он видит множество цветов. Например, глядя на предыдущий рисунок, вам, возможно, покажется, что на нём представлено несколько уровней светлоты. А на самом деле их всего два — полностью белый цвет и полностью чёрный.
Тот факт, что я никогда не видел 3D-игру с дизерингом, подобным этому, возможно, объясняется тем, что цветовые палитры — это, в основном, достояние прошлого. Вы, может быть, помните работу в Windows 95 в 16-цветном режиме и игры вроде «Monkey Island».
Уже давно у нас имеется 8 бит на цветовой канал пикселя, что позволяет каждому пикселю на экране выводить один из 16 миллионов цветов. А учитывая то, что на горизонте виднеются технологии HDR и WCG, компьютерная графика уходит ещё дальше от ситуаций, в которых может хотя бы понадобиться какая-нибудь форма дизеринга. Но в «Obra Dinn», несмотря ни на что, дизеринг, всё же, используется. Эта игра вновь зажгла во мне давно забытую любовь. Я, после работы в Squoosh, кое-что знал о дизеринге. Поэтому был особенно впечатлён тем, как в этой игре дизеринг остаётся стабильным при перемещении и вращении камеры в трёхмерном пространстве. Мне хотелось разобраться с тем, как всё это работает.
Как оказалось, Лукас Поуп написал пост на форуме, в котором рассказал о том, какие техники дизеринга используются в игре, и о том, как они применяются в трёхмерном пространстве. Он проделал большую работу, чтобы сделать дизеринг стабильным при перемещениях камеры. После прочтения того поста я провалился в кроличью нору, а в этом материале я постараюсь рассказать о том, что там нашёл.
Дизеринг
Что такое дизеринг?
Из Википедии можно узнать о том, что дизеринг — это намеренное внесение в сигнал некоей разновидности шума, используемое для рандомизации ошибки квантования. Эта техника применима не только к изображениям. Она, до наших дней, используется и в звукозаписи. Но это — ещё одна кроличья нора, в которую можно будет провалиться как-нибудь в другой раз. Начнём с квантования.
Квантование
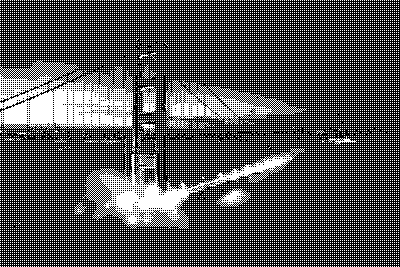
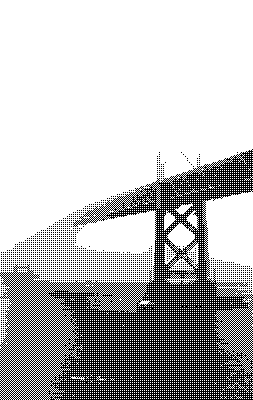
Квантование — это процесс отображения большого набора значений на меньший, обычно конечный, набор значений. В дальнейшем я, приводя примеры, буду использовать два следующих изображения.
Обе чёрно-белые фотографии представлены в 256 оттенках серого. Если нужно будет использовать меньше цветов — например — только чёрный и белый, чтобы сделать изображения монохромными, придётся поменять цвет каждого пикселя, сделать каждый из них или полностью чёрным, или полностью белым. При таком сценарии чёрный и белый цвета называются «цветовой палитрой», а процесс изменения характеристик пикселей, которые не используют цвета из нашей палитры, называется «квантованием». Так как не все цвета из исходных изображений имеются в нашей цветовой палитре, это неизбежно приведёт к появлению ошибки, называемой «ошибкой квантования». Примитивное решение этой задачи заключается в том, чтобы квантовать каждый пиксель, приведя его цвет к цвету из палитры, наиболее близкому к исходному цвету пикселя.
Обратите внимание: определение того, какие цвета «близки друг к другу» — это вопрос, открытый для интерпретации. Ответ на него зависит от того, как измеряют расстояние между двумя цветами. Я исхожу из предположения о том, что мы, в идеале, измеряем расстояние между цветами с использованием психовизуальной модели. Но в большинстве найденных мной публикаций просто используется евклидово расстояние в RGB-кубе, вычисляемое по формуле .
Учитывая то, что наша палитра состоит лишь из чёрного и белого цветов, мы можем использовать светлоту пикселя для того чтобы решить, в какой цвет его квантовать. Светлота 0 — это чёрный цвет, светлота 1 — белый, а всё, что между ними, должно идеально коррелировать с человеческим восприятием. Таким образом, светлота 0.5 даст приятный средне-серый цвет. Для квантования заданного цвета нам лишь нужно сравнить его светлоту с 0.5, и, если светлота больше 0.5 — взять белый цвет, а если меньше — взять чёрный. Такое квантование вышеприведённых изображений приводит к… неудовлетворительным результатам.
grayscaleImage.mapSelf(brightness =>
brightness > 0.5
? 1.0
: 0.0
);Обратите внимание: здесь приведены примеры рабочего кода, созданного на базе вспомогательного класса GrayImageF32N0F8, который я написал для демонстрационного материала к этой статье. Он похож на интерфейс ImageData, но использует Float32Array, имеет лишь один цветовой канал, представляющий значения между 0.0 и 1.0, и содержит множество вспомогательных функций. Исходный код можно найти здесь.
Гамма-коррекция
Я завершил написание этой статьи и решил, так сказать, одним глазком глянуть на то, как будут выглядеть градиенты от чёрного к белому с использованием различных алгоритмов дизеринга. Результаты показали, что я не учёл того самого, что всегда становится проблемой при работе с изображениями. Речь идёт о цветовых пространствах. Я написал предложение «идеально коррелирует с человеческим восприятием», а сам не следовал этой идее.
Мои демонстрационные материалы созданы с использованием веб-технологий, и, самое главное, с помощью <canvas> и ImageData, а они, в момент написания статьи, предусматривали использование цветового пространства sRGB. Это — старая спецификация (от 1996 года), в которой сопоставление значений и цветов смоделировано для отражения поведения CRT-мониторов. Хотя в наши дни почти никто не пользуется такими мониторами, sRGB всё ещё считается «безопасным» цветовым пространством, которое правильно выводится любым дисплеем. В результате — это цветовое пространство, по умолчанию, применяемое на веб-платформе. Но цветовое пространство sRGB нелинейно, то есть — (0.5,0.5,0.5) в sRGB — это не тот цвет, который человек видит, когда смешивают 50% (0,0,0) и (1, 1, 1). Это — тот цвет, который получают, подав половину мощности, необходимой для вывода полностью белого цвета, на электронно-лучевую трубку.
Обратите внимание: я, при выводе большинства изображений в этой статье, применил свойство image-rendering: pixelated;. Это позволяет увеличивать страницу и реально видеть пиксели изображений. Но на устройствах с дробным значением devicePixelRatio это может привести к появлению артефактов. Если вы не уверены в том, что именно выводится на вашем экране — откройте изображение отдельно, в новой вкладке браузера.
На этом изображении видно, что градиент после дизеринга светлеет слишком быстро. Если нужно, чтобы 0.5 был бы цветом, находящимся между чёрным и белым цветами (как это воспринимается людьми), нужно преобразовать изображение из цветового пространства sRGB в RGB. Сделать это можно, прибегнув к процессу, называемому «гамма-коррекцией». В Википедии можно найти следующие формулы, предназначенные для преобразования между цветовым пространством sRGB и линейным RGB.
Применив эти преобразования, мы получаем (более) точный дизеринг градиента.
Дизеринг со случайным шумом (random noise)
Вспомним, что говорится о дизеринге в Википедии. Дизеринг — это намеренное внесение в сигнал некоей разновидности шума, используемое для рандомизации ошибки квантования. С квантованием мы разобрались, а теперь поговорим о шуме. О намеренном внесении шума в сигнал.
Вместо того чтобы квантовать каждый пиксель напрямую, мы добавляем к пикселям шум, значения которого находятся между -0.5 и 0.5. Идея тут в том, что некоторые пиксели теперь будут квантоваться к «неправильным» цветам, но то, как часто это происходит, зависит от изначальной светлоты пикселя. Чёрные пиксели всегда остаются чёрными, белые всегда остаются белыми, а средне-серые будут, примерно в 50% случаев, оказываться чёрными. Со статистической точки зрения общая ошибка квантования снижается, а наш мозг охотно сделает всё остальное и поможет нам увидеть, так сказать, общую картину.
grayscaleImage.mapSelf(brightness =>
brightness + (Math.random() - 0.5) > 0.5
? 1.0
: 0.0
);Этот результат показался мне довольно-таки неожиданным! Не назову его «хорошим», видеоигры из 90-х показали нам, что такие картинки могут выглядеть куда лучше. Но перед нами — быстрый способ, не требующий особых усилий, позволяющий получить больше деталей на монохромном изображении. И если бы я понимал слово «дизеринг» буквально, то на этом я и окончил бы статью. Но это — далеко не всё.
Дизеринг с упорядоченным шумом (ordered dithering)
Вместо того чтобы говорить о том, какой именно шум добавить к изображению перед квантованием, можно изменить точку зрения и обсудить настройку порога квантования.
// Добавление шума
grayscaleImage.mapSelf(brightness =>
brightness + Math.random() - 0.5 > 0.5
? 1.0
: 0.0
);
// Настройка порога квантования
grayscaleImage.mapSelf(brightness =>
brightness > Math.random()
? 1.0
: 0.0
);В контексте монохромного дизеринга, где порог квантования равен 0.5, эти два подхода эквивалентны:
brightness+rand()-0.5 > 0.5
↔ brightness > 1.0-rand()
↔ brightness > rand()Положительный момент этого подхода в том, что мы можем говорить о «матрице пороговых значений». Матрицы пороговых значений можно визуализировать. Это облегчит обсуждение того, почему результирующее изображение выглядит так, как выглядит. Ещё их можно вычислять заранее и использовать многократно, что делает процесс дизеринга детерминистическим и поддающимся параллелизации на уровне каждого пикселя. В результате дизеринг можно выполнять на GPU в виде шейдера. Именно так сделано в «Return of the Obra Dinn»! Есть несколько различных подходов к генерированию матриц пороговых значений, но все они каким-то образом упорядочивают шум, который добавляют к изображению. Отсюда и название этого метода — «дизеринг с упорядоченным шумом», или «дизеринг с упорядоченным возбуждением».
Матрица пороговых значений для вышеприведённого примера дизеринга — это, в буквальном смысле, матрица, полная случайных пороговых значений, называемых ещё «белым шумом» (white noise). Это название пришло из сферы обработки сигналов, где каждая частота имеет одинаковую интенсивность, как, например, в белом свете.
Дизеринг Байера (Bayer dithering)
Дизеринг Байера использует в роли матрицы пороговых значений матрицу Байера. Эти сущности названы в честь Брюса Байера, создателя фильтра Байера, который до наших дней используется в цифровых фотоаппаратах. Каждый пиксель светочувствительной матрицы может регистрировать лишь яркость света. Но если перед отдельными пикселями по-умному разместить цветные фильтры, можно восстановить цветное изображение посредством алгоритма демозаизации. Шаблон для этих фильтров — это тот же шаблон, что используется в дизеринге Байера.
Матрицы Байера бывают разных размеров, которые я, в итоге, стал называть «уровнями». Матрица Байера уровня 0 — это матрица 2×2. Уровень 1 — это матрица 4×4. А матрица уровня — это матрица
. Матрицу уровня n можно рекурсивно вычислить из матрицы уровня
(хотя в Википедии, кроме того, упомянут алгоритм, основанный на работе с отдельными ячейками). Если ваше изображение оказалось больше, чем матрица Байера, можно обработать его, расположив несколько матриц пороговых значений рядом друг с другом.
Матрица Байера уровня n содержит числа от 0 до После того, как вы нормализуете матрицу Байера, то есть — разделите на
, её можно использовать как матрицу пороговых значений:
const bayer = generateBayerLevel(level);
grayscaleImage.mapSelf((brightness, { x, y }) =>
brightness > bayer.valueAt(x, y, { wrap: true })
? 1.0
: 0.0
);Хочу отметить тут одну деталь: дизеринг Байера использующий матрицы, такие, которые определены выше, даст итоговое изображение, которые будет светлее исходного. Например — в области, где каждый пиксель имеет светлоту 1/255=0.4%, матрица Байера размера 2×2 сделает белым каждый из четырёх пикселей, что даст итоговую среднюю светлоту в 25%. Эта ошибка становится меньше при применении матриц Байера более высоких уровней, но фундаментальное отклонение от оригинала при этом остаётся таким же.
На нашем «тёмном» тестовом изображении небо не полностью чёрное, оно, при применении матрицы Байера уровня 0, оказывается значительно светлее. Хотя ситуация улучшается на более высоких уровнях, альтернативным решением может стать инвертирование отклонения, что приводит к получению изображений, которые темнее оригинала. Это делается путём обращения механизма использования матрицы Байера:
const bayer = generateBayerLevel(level);
grayscaleImage.mapSelf((brightness, { x, y }) =>
//Обратите внимание на “1 -” в следующей строке
brightness > 1 - bayer.valueAt(x, y, { wrap: true })
? 1.0
: 0.0
);Я использовал исходное определение матрицы Байера для «светлого» изображения и инвертированную версию для «тёмного» изображения. Лично мне больше всего нравятся результаты, полученные на уровнях 1 и 3.
Дизеринг с синим шумом (blue noise)
И у подхода к дизерингу, когда применяется белый шум, и у того, где используется матрица Байера, конечно, есть недостатки. Для дизеринга Байера, например, характерно наложение на изображение повторяющихся структур, которые, особенно, если увеличить изображение, оказываются заметными. Белый шум — это набор случайных значений, что неизбежно ведёт к появлению на матрице пороговых значений «кластеров» из светлых пикселей и «пустот» из тёмных пикселей. Эти факты можно сделать более очевидными, если наклонить, или, если это для вас слишком сложно, алгоритмически размыть матрицу пороговых значений. «Кластеры» и «пустоты» могут плохо подействовать на результаты дизеринга. Если тёмные области изображения придутся на один из «кластеров» — в соответствующей области выходного изображения будут потеряны детали (и, наоборот, для светлых областей изображения, пришедшихся на «пустоты»).
Существует разновидность шума, называемая «синим шумом», нацеленная на решение этой проблемы. Этот шум называют «синим» из-за того, что сигналы более высоких частот в нём имеют более высокие интенсивности, чем сигналы более низких частот (как в случае с синим светом). Убирая или заглушая низкие частоты, можно сделать так, что «кластеры» и «пустоты» оказываются менее выраженными. Дизеринг с синим шумом выполняется так же быстро, как и дизеринг с белым шумом — в итоге это просто матрица пороговых значений, но генерирование синего шума немного сложнее и ресурсозатратнее.
Наиболее распространённый алгоритм генерирования синего шума, похоже, это «метод пустот и кластеров» («void-and-cluster method») Роберта Улични. Вот публикация, где это описано. По-моему, описание алгоритма не отличается интуитивной понятностью, а теперь, когда я его реализовал, я убедился в том, что он описан в чрезмерно абстрактном стиле. Но алгоритм это весьма толковый!
Алгоритм основан на идее, в соответствии с которой можно найти пиксель, являющийся частью «кластера» или «пустоты», обработав изображение с помощью эффекта размытия по Гауссу и найдя самый светлый (или, соответственно, самый тёмный) пиксель на размытом изображении. После инициализации чёрного изображения с помощью нескольких случайно расположенных белых пикселей, алгоритм приступает к непрерывной замене пикселей «кластеров» и «пустот», стремясь как можно равномернее распределить по изображению белые пиксели. После этого каждому пикселю назначается номер между 0 и (где
— общее количество пикселей) в соответствии с их важностью для формирования «кластеров» и «пустот». Подробности об этом смотрите здесь.
Моя реализация этого алгоритма работает хорошо, но не очень быстро, так как я не тратил много времени на её оптимизацию. На моём MacBook 2018 года генерирование текстуры синего шума размером 64×64 занимает около минуты. Для наших целей этого достаточно. Если нужно что-то побыстрее — стоит обратить внимание на оптимизацию, касающуюся эффекта размытия по Гауссу, но не в пространственной области, а в частотной области.
Отступление: конечно, я, когда это узнал, увидел интересную задачу, которую просто не мог не решить. Перспективность этой оптимизации объясняется свёрткой (это — внутренний механизм размытия по Гауссу), которой приходится проходиться по каждому полю ядра размытия по Гауссу для каждого пикселя изображения. Но если перевести и изображение, и ядро размытия по Гауссу в частотную область (используя один из многих алгоритмов быстрого преобразования Фурье), свёртка превращается в поэлементное умножение. Так как размер целевой текстуры синего шума — это степень двойки — я мог реализовать хорошо исследованный in-place-вариант алгоритма быстрого преобразования Фурье Кули — Тьюки. После нескольких первоначальных неудач я смог уменьшить время генерирования текстуры синего шума на 50%. Код у меня получился довольно-таки посредственный, поэтому тут найдётся место и для дальнейших оптимизаций.
Синий шум основан на размытии по Гауссу, которое вычисляется на тороидальной структуре (это — замысловатый способ сказать, что алгоритм на краях изображения «сворачивается»). В результате изображение можно бесшовно «замостить» текстурами синего шума. Поэтому можно воспользоваться текстурой размера 64×64 и покрыть её копиями всё изображение. Дизеринг с синим шумом даёт приятную, сбалансированную отрисовку деталей, не выдавая заметных повторяющихся паттернов. Итоговое изображение смотрится органично.
Дизеринг с рассеянием ошибки (error diffusion)
Все вышеописанные подходы к дизерингу основаны на том факте, что ошибки квантования статистически сглаживаются из-за того, что пороговые значения в соответствующей матрице распределены равномерно. Но есть и другой подход к квантованию, связанный с рассеянием ошибки. Вы, скорее всего, встречались с ним, если когда-нибудь интересовались дизерингом. Применяя этот подход, мы не просто выполняем квантование изображения, надеясь, что, в среднем, ошибка квантования останется незначительной. Вместо этого мы измеряем ошибку квантования и рассеиваем эту ошибку на соседние пиксели, влияя на то, как они будут квантоваться. Мы, по сути, в процессе работы меняем изображение, которое хотим подвергнуть дизерингу. Это делает процесс преобразования изображения, по сути, последовательным.
Предостережение: одним из больших плюсов алгоритмов рассеяния ошибки, о котором мы не говорим в этом материале, является тот факт, что эти алгоритмы способны работать с произвольными цветовыми палитрами. А дизеринг с упорядоченным шумом требует, чтобы цвета на цветовой палитре были бы расположены с равными интервалами. Подробнее об этом я расскажу как-нибудь в другой раз.
Почти все подходы к дизерингу с рассеиванием ошибки, которые я собираюсь рассмотреть, используют «матрицу рассеяния», которая определяет то, как ошибка квантования текущего пикселя распространяется по соседним пикселям. При работе с такими матрицами часто считается, что пиксели изображения просматриваются сверху вниз и слева направо — так же, как читают тексты жители Запада. Это важно, так как ошибка может быть рассеяна лишь на пиксели, которые ещё не подверглись квантованию. Если вы будете обходить изображения в порядке, не соответствующем тому, на который рассчитана матрица рассеяния, соответствующим образом отразите матрицу.
Дизеринг с «простым» двумерным рассеянием ошибки
Примитивный подход к дизерингу с рассеянием ошибки предусматривает распространение ошибки квантования на пиксель, который находится ниже текущего, и на пиксель, находящийся справа от него. Это можно описать следующей матрицей:
Алгоритм рассеяния ошибки посещает каждый пиксель изображения (в правильном порядке), квантует текущий пиксель и измеряет ошибку квантования. Обратите внимание на то, что значение ошибки квантования имеет знак, то есть — оно может быть отрицательным, если квантование делает пиксель светлее, чем исходный пиксель. Затем части ошибки добавляют к соседним пикселям в соответствии с матрицей. Потом этот процесс повторяется для следующего пикселя.
Пошаговая визуализация алгоритма рассеяния ошибки
Эта анимация предназначена для визуализации алгоритма, но она не способна показать то, как результаты дизеринга соотносятся с оригиналом изображения. Области размером 4×4 пикселя вряд ли достаточно для того, чтобы рассеять и усреднить ошибки квантования. Но тут можно видеть то, что если пиксель в ходе квантования делается светлее, то соседние пиксели, чтобы это скомпенсировать, делаются темнее (и наоборот).
Но простота матрицы рассеяния делает рассматриваемый подход к дизерингу подверженным появлению различимых паттернов, вроде паттернов в виде линий, которые можно видеть на вышеприведённых изображениях.
Дизеринг по алгоритму Флойда — Стейнберга (Floyd-Steinberg)
Алгоритм Флойда — Стейнберга — это, пожалуй, один из самых известных алгоритмов рассеяния ошибки, а, возможно, это — самый известный алгоритм, применяемый при дизеринге изображений. Он использует более сложную матрицу рассеяния ошибок, которая позволяет распределять ошибку на все непосещённые пиксели, являющиеся непосредственными соседями текущего пикселя. Числа в этой матрице тщательно подобраны для того чтобы как можно сильнее уменьшить возможность образования повторяющихся паттернов.
Применение алгоритма Флойда — Стейнберга — это большой шаг вперёд в нашем исследовании, так как это позволяет предотвращать возникновение множества паттернов. Но и при его применении большие пространства изображения с незначительным количеством деталей всё ещё могут выглядеть не очень хорошо.
Дизеринг по алгоритму Джарвиса — Джудиса — Нинке (Jarvis-Judice-Ninke)
В алгоритме Джарвиса — Джудиса — Нинке используется ещё большая матрица рассеяния ошибки. Ошибка распределяется на большее количество пикселей, а не только на те, которые находятся в непосредственной близости от текущего пикселя.
Использование такой матрицы рассеяния ошибки ведёт к дальнейшему снижению вероятности образования паттернов. И хотя на тестовых изображениях имеются паттерны в виде линий, теперь они не так сильно бросаются в глаза.
Дизеринг по алгоритму Аткинсона (Atkinson)
Алгоритм Аткинсона был разработан в компании Apple Биллом Аткинсоном и получил известность благодаря его использованию в ранних компьютерах Macintosh.
Стоит отметить, что матрица рассеяния ошибки Аткинсона состоит из шести единиц, но она нормализуется с использованием 1/8, то есть — она не переносит всю ошибку на соседние пиксели, увеличивая воспринимаемую контрастность изображения.
Дизеринг по алгоритму Римерсма (Riemersma)
Честно говоря, на алгоритм Римерсма я наткнулся случайно. Я, пока исследовал другие алгоритмы, нашёл одну обстоятельную статью, в которой было написано об этом алгоритме. Такое ощущение, что он не особенно широко известен, но он мне очень понравился. Понравились мне и те идеи, на которых он основан. Вместо того, чтобы, ряд за рядом, обходить изображение, он обходит изображение по кривой Гильберта. С технической точки зрения тут подошла бы любая кривая, заполняющая пространство. Но рекомендуется использовать именно кривую Гильберта. Этот алгоритм довольно просто реализовать с использованием генераторов. Благодаря этому алгоритм нацелен на то, чтобы взять лучшее из алгоритмов дизеринга с упорядоченным шумом и с рассеянием ошибки. Речь идёт об ограничении количества пикселей, на которые может подействовать один пиксель, а так же о приятном внешнем виде результата (и о скромных требованиях к памяти).
У кривой Гильберта есть свойство «локальности», которое выражается в том, что пиксели, находящиеся близко друг к другу на кривой, находятся близко друг к другу и на изображении. При таком подходе нам не нужно использовать матрицу рассеяния ошибки. Вместо этого достаточно применить последовательность рассеяния ошибки длиной n. Для квантования текущего пикселя к нему добавляются n последних ошибок квантования с весами, заданными в последовательности рассеяния ошибки. В вышеупомянутой статье для задания весов используется экспоненциальный спад. Ошибке квантования предыдущего пикселя назначается вес 1, самой старой ошибке квантования в списке назначается маленький, вычисляемый по особой формуле, вес . Для вычисления
-го веса используется следующая формула:
В статье рекомендуется использовать , а минимальный размер списка значений —
, но, выполняя тесты, я обнаружил, что лучше всего выглядит изображение с
и
Результат выглядит чрезвычайно органично, почти так же приятно, как после дизеринга с синим шумом. И, в то же время, дизеринг по алгоритму Римерсма легче реализовать, чем оба предыдущих варианта. Это, правда, всё равно, алгоритм, основанный на рассеянии ошибки, то есть — он обрабатывает данные последовательно и не подходит для выполнения на GPU.
Я выбираю синий шум, дизеринг Байера и алгоритм Римерсма
«Return of the Obra Dinn» — это 3D-игра, поэтому в ней необходимо использовать дизеринг с упорядоченным шумом для того чтобы выполнять соответствующий код в виде шейдера. В ней используется и дизеринг Байера, и дизеринг с синим шумом. Я поддерживаю создателей игры в этом выборе и тоже считаю, что, с эстетической точки зрения, они дают наиболее приятные результаты. Дизеринг Байера даёт немного больше структуры, а изображения после дизеринга с синим шумом выглядят очень естественно и органично. Я, кроме того, хочу особо выделить дизеринг по алгоритму Римерсма, и мне хочется узнать о том, как он показывает себя на изображениях с многоцветной палитрой.
Большая часть окружения в «Obra Dinn» рендерится с применением дизеринга с синим шумом. Люди и другие интересные объекты обрабатываются с помощью дизеринга Байера. Это создаёт интересный визуальный контраст и выделяет их, не нарушая общую эстетику игры. Напомню, что подробности о том, почему в игре всё сделано именно так, и о том, как обрабатываются перемещения камеры, можно почитать в посте Лукаса Поупа.
Если вы хотите испытать разные алгоритмы дизеринга на своём изображении — взгляните на мою демо-страницу, использованную для создания всех примеров к этой статье. Учитывайте, что мои реализации алгоритмов дизеринга не относятся к разряду самых быстрых. Поэтому, если вы решите «скормить» моей программе 20-мегапиксельную JPEG-фотографию — её обработка займёт некоторое время.
Обратите внимание на то, что у меня такое ощущение, что в Safari я наткнулся на деоптимизацию. Так, в Chrome на работу моего генератора синего шума требуется примерно 30 секунд, а в Safari — более 20 минут. А вот в Safari Tech Preview генератор работает гораздо быстрее.
Уверен, что то, о чём я рассказал — это до крайности нишевая тема, но мне понравилось побывать в этой кроличьей норе. Если вам есть что сказать о дизеринге, если вы этим занимались — с радостью вас послушаю.
Благодарности и дополнительные материалы
Благодарю Лукаса Поупа за его игры и за источник визуального вдохновения.
Благодарю Кристофа Питерса за его замечательную статью о генерировании синего шума.
О, а приходите к нам работать? 🤗 💰
Мы в wunderfund.io занимаемся высокочастотной алготорговлей с 2014 года. Высокочастотная торговля — это непрерывное соревнование лучших программистов и математиков всего мира. Присоединившись к нам, вы станете частью этой увлекательной схватки.
Мы предлагаем интересные и сложные задачи по анализу данных и low latency разработке для увлеченных исследователей и программистов. Гибкий график и никакой бюрократии, решения быстро принимаются и воплощаются в жизнь.
Сейчас мы ищем плюсовиков, питонистов, дата-инженеров и мл-рисерчеров.
Присоединяйтесь к нашей команде.
Sensors
Andrea Colagrossi, … Matteo Battilana, in Modern Spacecraft Guidance, Navigation, and Control, 2023
Quantization errors
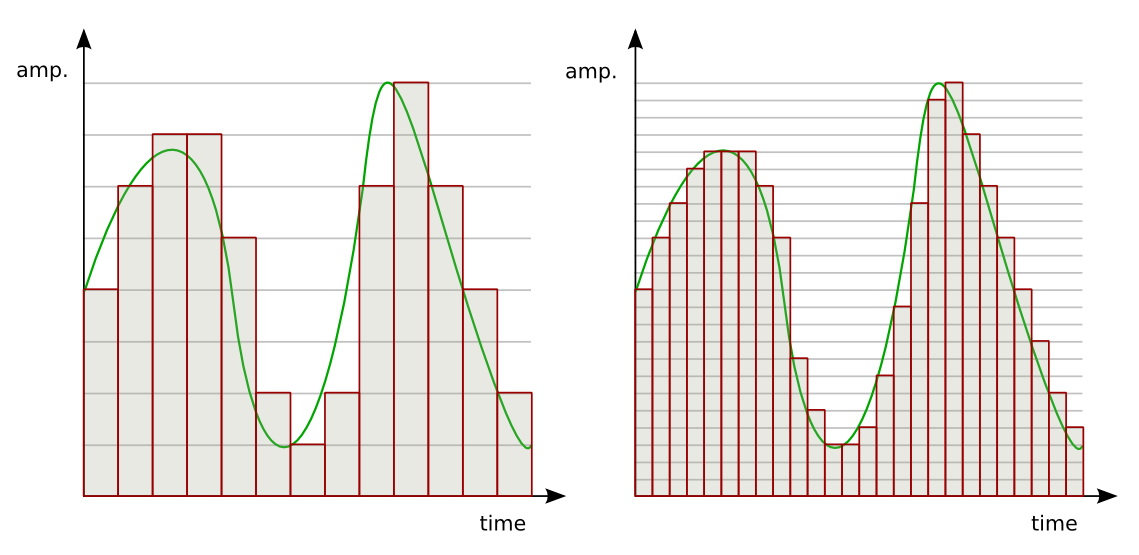
Quantization error is a systematic error resulting from the difference between the continuous input value and its quantized output, and it is like round-off and truncation errors. This error is intrinsically associated with the AD conversion that maps the input values from a continuous set to the output values in a countable set, often with a finite number of elements. The quantization error is linked to the resolution of the sensor. Namely, a high-resolution sensor has a small quantization error. Indeed, the maximum quantization error is smaller than the resolution interval of the output, which is associated to the least significant bit representing the smallest variation that can be represented digitally:
LSB=FSR2NBIT
where FSR is the full-scale range of the sensor, and NBIT is the number of bits (i.e., the resolution) used in the AD converter to represent the sensor’s output. Quantization errors are typically not corrected, and the discrete values of the output are directly elaborated by the GNC system, which is designed to operate on digital values.
Fig. 6.9 shows a convenient model block to simulate quantization errors.
Figure 6.9. Quantization error model.
Read full chapter
URL:
https://www.sciencedirect.com/science/article/pii/B9780323909167000068
Digital Filters
Marcio G. Siqueira, Paulo S.R. Diniz, in The Electrical Engineering Handbook, 2005
2.11 Quantization in Digital Filters
Quantization errors in digital filters can be classified as:
- •
-
Round-off errors derived from internal signals that are quantized before or after more down additions;
- •
-
Deviations in the filter response due to finite word length representation of multiplier coefficients; and
- •
-
Errors due to representation of the input signal with a set of discrete levels.
A general, digital filter structure with quantizers before delay elements can be represented as in Figure 2.23, with the quantizers implementing rounding for the granular quantization and saturation arithmetic for the overflow nonlinearity.
FIGURE 2.23. Digital Filter Including Quantizers at the Delay Inputs
The criterion to choose a digital filter structure for a given application entails evaluating known structures with respect to the effects of finite word length arithmetic and choosing the most suitable one.
2.11.1 Coefficient Quantization
Approximations are known to generate digital filter coefficients with high accuracy. After coefficient quantization, the frequency response of the realized digital filter will deviate from the ideal response and eventually fail to meet the prescribed specifications. Because the sensitivity of the filter response to coefficient quantization varies with the structure, the development of low-sensitivity digital filter realizations has raised significant interest (Antoniou, 1993; Diniz et al., 2002).
A common procedure is to design the digital filter with infinite coefficient word length satisfying tighter specifications than required, to quantize the coefficients, and to check if the prescribed specifications are still met.
2.11.2 Quantization Noise
In fixed-point arithmetic, a number with a modulus less than one can be represented as follows:
(2.84)x=b0b1b2b3…bb,
where b0 is the sign bit and where b1b2b3 … bb represent the modulus using a binary code. For digital filtering, the most widely used binary code is the two’s complement representation, where for positive numbers b0 = 0 and for negative numbers b0 = 1. The fractionary part of the number, called x2 here, is represented as:
(2.85)x2={xif b0=0.2−|x|if b0=1.
The discussion here concentrates in the fixed-point implementation.
A finite word length multiplier can be modeled in terms of an ideal multiplier followed by a single noise source e(n) as shown in Figure 2.24.
FIGURE 2.24. Model for the Noise Generated after a Multiplication
For product quantization performed by rounding and for signal levels throughout the filter much larger than the quantization step q = 2−b, it can be shown that the power spectral density of the noise source ei(n) is given by:
(2.86)Pei(z)=q212=2−2b12.
In this case, ei(n) represents a zero mean white noise process. We can consider that in practice, ei(n) and ek(n + l) are statistically independent for any value of n or l (for i ≠ k). As a result, the contributions of different noise sources can be taken into consideration separately by using the principle of superposition.
The power spectral density of the output noise, in a fixed-point digital-filter implementation, is given by:
(2.87)Py(z)=σe2Σi=1KGi(z)Gi(z−1),
where Pei(ejw)=σe2, for all i, and each Gi(z) is a transfer function from multiplier output (gi(n)) to the output of the filter as shown in Figure 2.25. The word length, including sign, is b + 1 bits, and K is the number of multipliers of the filter.
FIGURE 2.25. Digital Filter Including Scaling and Noise Transfer Functions.
2.11.3 Overflow Limit Cycles
Overflow nonlinearities influence the most significant bits of the signal and cause severe distortion. An overflow can give rise to self-sustained, high-amplitude oscillations known as overflow limit cycles. Digital filters, which are free of zero-input limit cycles, are also free of overflow oscillations if the overflow nonlinearities are implemented with saturation arithmetic, that is, by replacing the number in overflow by a number with the same sign and with maximum magnitude that fits the available wordlength.
When there is an input signal applied to a digital filter, overflow might occur. As a result, input signal scaling is required to reduce the probability of overflow to an acceptable level. Ideally, signal scaling should be applied to ensure that the probability of overflow is the same at each internal node of the digital filter. This way, the signal-to-noise ratio is maximized in fixed-point implementations.
In two’s complement arithmetic, the addition of more than two numbers will be correct independently of the order in which they are added even if overflow occurs in a partial summation as long as the overall sum is within the available range to represent the numbers. As a result, a simplified scaling technique can be used where only the multiplier inputs require scaling. To perform scaling, a multiplier is used at the input of the filter section as illustrated in Figure 2.25.
It is possible to show that the signal at the multiplier input is given by:
(2.88)xi(n)=12πj∮cXi(z)zn−1dz=12π∫02πFi(ejω)X(ejω)ejωndω,
where c is the convergence region common to Fi(z) and X(z).
The constant λ is usually calculated by using Lp norm of the transfer function from the filter input to the multiplier input Fi(z), depending on the known properties of the input signal. The Lp norm of Fi(z) is defined as:
(2.89)‖Fi(ejω)‖p=[12π∫02π|Fi(ejω)|pdω]1p,
for each p ≥ 1, such that ∫02π|Fi(ejω)|pdω≤∞. In general, the following inequality is valid:
(2.90)|xi(n)| ≤ ‖Fi‖p‖X‖q, (1p+1q=1),
for p, q = 1, 2 and ∞.
The scaling guarantees that the magnitudes of multiplier inputs are bounded by a number Mmax when |x(n)| ≤ Mmax. Then, to ensure that all multiplier inputs are bounded by Mmax we must choose λ as follows:
(2.91)λ=1Max{‖F1‖p,…,‖F1‖p,…, ‖FK‖p},
which means that:
(2.92)‖F′i(ejω)‖p≤1, for‖X(ejω)‖q ≤ Mmax.
The K is the number of multipliers in the filter.
The norm p is usually chosen to be infinity or 2. The L∞ norm is used for input signals that have some dominating frequency component, whereas the L2 norm is more suitable for a random input signal. Scaling coefficients can be implemented by simple shift operations provided they satisfy the overflow constraints.
In case of modular realizations, such as cascade or parallel realizations of digital filters, optimum scaling is accomplished by applying one scaling multiplier per section.
As an illustration, we present the equation to compute the scaling factor for the cascade realization with direct-form second-order sections:
(2.93)λi=1‖∏j=1i−1Hj(z)Fi(z)‖p,
where:
Fi(z)=1z2+m1iz+m2i.
The noise power spectral density is computed as:
(2.94)Py(z)=σe2[3+3λ12∏i=1mHi(z)Hi(z−1)+5Σj=2m1λj2∏i=jmHi(z)Hi(z−1)],
whereas the output noise variance is given by:
(2.95)σo2=σe2[3+3λ12||∏i=1mHi(ejω)||22+5Σj=2m1λj2||∏i=jmHi(ejω)||22].
As a design rule, the pairing of poles and zeros is performed as explained here: poles closer to the unit circle pair with closer zeros to themselves, such that ||Hi(z)||p is minimized for p = 2 or p = ∞.
For ordering, we define the following:
(2.96)Pi=| |Hi(z)| |∞| |Hi(z)| |2.
For L2 scaling, we order the section such that Pi is decreasing. For L∞ scaling, Pi should be increasing.
2.11.4 Granularity Limit Cycles
The quantization noise signals become highly correlated from sample to sample and from source to source when signal levels in a digital filter become constant or very low, at least for short periods of time. This correlation can cause autonomous oscillations called granularity limit cycles.
In recursive digital filters implemented with rounding, magnitude truncation,72 and other types of quantization, limitcycles oscillations might occur.
In many applications, the presence of limit cycles can be harmful. Therefore, it is desirable to eliminate limit cycles or to keep their amplitude bounds low.
If magnitude truncation is used to quantize particular signals in some filter structures, it can be shown that it is possible to eliminate zero-input limit cycles. As a consequence, these digital filters are free of overflow limit cycles when overflow nonlinearities, such as saturation arithmetic, are used.
In general, the referred methodology can be applied to the following class of structures:
- •
-
State-space structures: Cascade and parallel realization of second-order state-space structures includes design constraints to control nonlinear oscillations (Diniz and Antoniou, 1986).
- •
-
Wave digital filters: These filters emulate doubly terminated lossless filters and have inherent stability under linear conditions as well as in the nonlinear case where the signals are subjected to quantization (Fettweis, 1986).
- •
-
Lattice realization: Modular structures allowing easy limit cycles elimination (Gray and Markel, 1975).
Read full chapter
URL:
https://www.sciencedirect.com/science/article/pii/B9780121709600500621
Biomedical signals and systems
Sri Krishnan, in Biomedical Signal Analysis for Connected Healthcare, 2021
2.2.1 Noise power
The quantization error (e) or noise tends to have a random behavior, and they could be mathematically represented using statistical variables. Power of a random variable with a probability density function of p(e) could be obtained by computing the second-order statistics of variance, and it is denoted by
σ2=∫−q/2q/2e2p(e)de
A good assumption for p(e) is a uniform probability density function which will have a value of 1/q over the range of −q/2 to q/2.
=∫−q/2q/2e2·1qde=q212
Read full chapter
URL:
https://www.sciencedirect.com/science/article/pii/B9780128130865000049
Measurement of high voltages
E. Kuffel, … J. Kuffel, in High Voltage Engineering Fundamentals (Second Edition), 2000
Static errors
The quantization error is present because the analogue value of each sample is transformed into a digital word. This A-to-D conversion entails a quantization of the recorder’s measuring range into a number of bands or code bins, each represented by its central value which corresponds to a particular digital code or level. The number of bands is given by 2N, where N is the resolution of the A-to-D converter. The digital output to analogue input relationship of an ideal digitizer is shown diagrammatically in Fig. 3.49. For any input in the range (iΔVav – 0.5 * ΔVav to iΔVav + 0.5 * ΔVav), where iΔVav is the voltage corresponding to the width of each code bin, or one least significant bit (LSB), and iΔVav is the centre voltage corresponding to the i th code, an ideal digitizer will return a value of Ii. Therefore, the response of an ideal digitizer to a slowly increasing linear ramp would be a stairway such as that shown in Fig. 3.50. A quick study of these figures reveals the character of the quantization error associated with the ideal A-to-D conversion process. The maximum error possible is equivalent to a voltage corresponding to ±(½) of an LSB. For an ideal digital recorder, this quantization would be the only source of error in the recorded samples. For a real digital recorder, this error sets the absolute upper limit on the accuracy of the readings. In the case of an 8-bit machine, this upper limit would be 0.39 per cent of the recorder’s full-scale deflection. The corresponding maximum accuracy (lowest uncertainty) of a 10-bit recorder is 0.10 per cent of its full-scale deflection.
Figure 3.49. Analogue input to digital output relation of an ideal A/D converter
Figure 3.50. Response of an ideal A/D converter to a slowly rising ramp
The error caused by discrete time sampling is most easily demonstrated with reference to the recording of sinusoidal signals. As an example we can look at the discrete time sampling error introduced in the measurement of a single cycle of a pure sine wave of frequency f, which is sampled at a rate of four times its frequency. When the sinusoid and the sampling clock are in phase, as shown in Fig. 3.51, a sample will fall on the peak value of both positive and negative half-cycles. The next closest samples will lie at π/2 radians from the peaks. As the phase of the clock is advanced relative to the input sinusoid the sample points which used to lie at the peak values will move to lower amplitude values giving an error (Δ) in the measurement of the amplitude (A) of
Figure 3.51. Sample points with sinusoid and sampling clock in phase. (Error in peak amplitude = 0)
Δ = A(1 − cos ϕ)
where ϕ is the phase shift in the sample points. This error will increase until ϕ – π/4 (Fig. 3.52). For ϕ > π/4 the point behind the peak value will now be closer to the peak and the error will decrease for a ϕ in the range of π/4 to π/2. The maximum per unit value of the discrete time sampling error is given by eqn 3.93,
Figure 3.52. Sample points with sampling clock phase advanced to π/4 with respect to the sinusoid. Error in peak amplitude (Δ) is at a maximum
(3.93)Δmax=I−cos(πfts)
where ts is the recorder’s sampling interval and f the sinewave frequency.
The maximum errors obtained through quantization and sampling when recording a sinusoidal waveform are shown in Fig. 3.53. The plotted quantities were calculated for an 8-bit 200-MHz digitizer.
Figure 3.53. Sampling and quantization errors of an ideal recorder
In a real digital recorder, an additional two categories of errors are introduced. The first includes the instrument’s systematic errors. These are generally due to the digitizer’s analogue input circuitry, and are present to some degree in all recording instruments. They include such errors as gain drift, linearity errors, offset errors, etc. They can be compensated by regular calibration without any net loss in accuracy. The second category contains the digitizer’s dynamic errors. These become important when recording high-frequency or fast transient signals. The dynamic errors are often random in nature, and cannot be dealt with as simply as their systematic counterparts and are discussed below.
Read full chapter
URL:
https://www.sciencedirect.com/science/article/pii/B9780750636346500046
Remaining useful life prediction
Yaguo Lei, in Intelligent Fault Diagnosis and Remaining Useful Life Prediction of Rotating Machinery, 2017
6.3.4.3 RUL Prediction
The constructed indicator WMQE is further input into the RUL prediction module. In this module, a PF-based prediction algorithm is utilized to predict RUL of the rotating machinery whose degradation processes are described using a variant of Paris–Erdogan model. The Paris–Erdogan model is formulated as
(6.96)dxdt=c(Δδ)γ, Δδ=mx
where x represents the semicrack length, t is the number of stress cycles (i.e., the fatigue life), c, γ, and m are material constants which are determined by tests, and Δδ is amplitude of stress intensity factor roughly proportional to the square root of x.
It is seen from Eq. (6.96) that there are several model parameters in the Paris–Erdogan model, that is, c, γ, and m, which are difficult to measure during the operation process of the rotating machinery. For convenient application, the Paris–Erdogan model is transformed into the following format with α=cmγ and β = γ/2.
(6.97)dxdt=αxβ.
Then, the above function is rewritten into the following state space model.
(6.98)xk=xk−1+αk−1xk−1βΔtkαk=αk−1zk=xk+νk,
where αk−1 is a random variable following a normal distribution of Nμα,σα2, β is a constant parameter, Δtk=tk−tk−1, zk is the measured WMQE value at tk and νk is the measurement noise following the normal distribution of N0,σν2. With the transformation of the Paris–Erdogan model, the model parameters are more convenient to estimate according to the measurements. In addition, the state space model inherits the superiority of the Paris–Erdogan model in describing the general degradation processes. Therefore, it is supposed to be a good model for a general degradation process.
After the transformation, the unknown model parameters are changed to be Θ=μα,σα2,β,σν2′, where (·)′ denotes the vector transposition. Then, the measured WMQE values constructed from vibration signals are input into the model, and the model parameters are initialized using MLE. It is assumed that there are a series of measurements z0:M=z0,…,zM′ at ordered times t0,…,tM. According to Eq. (6.98), zk is formulated as follows:
(6.99)zk=xk−1+αkxk−1βΔtk+νk.
The degradation state xk−1 has the following relationship with the measurement zk−1.
(6.100)xk−1=zk−1−νk−1.
The degradation state xk−1 is hard to be acquired in real applications. If the measurement noise νk−1 is small enough compared with the measurement itself, it is negligible and xk−1 is approximated by zk−1. Let T=z0βΔt1,…,zM−1βΔtM′. z1:M=z1,…,zM′ is multivariate normally distributed, which is denoted as follows:
(6.101)z1:M∼Nz0:M−1+μαT,σα2TT′+σν2IM,
where IM is an identity matrix of order M.
Let Δz1:M=z1−z0,…,zM−zM−1′, and the log-likelihood function of the unknown parameters based on the measurements is expressed as
(6.102)ℓΘ|z0:M=−M2ln2π−12lnσα2TT′+σν2IM −12Δz1:M−μαT′σα2TT′+σν2IM−1Δz1:M−μαT =−M2ln2π−M2lnσα2−12lnTT′+σ˜ν2IM −12σα2Δz1:M−μαT′σα2TT′+σν2IM−1Δz1:M−μαT,
with σ~ν2=σν2/σα2. The first partial derivatives of ℓΘ|z0:M with respect to μα and σα2 are calculated and formulated with
(6.103)∂ℓΘ|z0:M∂μα=1σα2T′TT′+σ~ν2IM-1Δz1:M−μαT,
(6.104)∂ℓΘ|z0:M∂σα2=−M2σα2+12σα4Δz1:M−μαT′TT′+σ~ν2IM−1Δz1:M−μαT.
Let ∂ℓΘ|z0:M/∂μα=0 and ∂ℓΘ|z0:M/∂σα2=0. The MLE results of μα and σα2 are
(6.105)μα=T′TT′+σ~ν2IM−1Δz1:MT′TT′+σ~ν2IM−1T,
(6.106)σα2=Δz1:M−μαT′TT′+σ~ν2IM−1Δz1:M−μαTM.
With Eqs. (6.105) and (6.106) substituted into Eq. (6.102), the log-likelihood function is reduced into a two-variable function about β and σ~ν2, which is denoted by
(6.107)ℓΘ|z0:M=−M2ln2π−M2lnσα2−12lnTT′+σ~ν2IM−M2.
The MLE values of β and σ~ν2 are obtained by maximizing the log-likelihood function (6.107) through two-dimensional optimizing. Then the MLE values of β and σ~ν2 are substituted into Eqs. (6.105) and (6.106), and the MLE values of μα and σα2 are acquired. The value of σν2 is calculated with σ~ν2 multiplied by σα2. Finally, all of the unknown parameters Θ=μα,σα2,β,σν2′ are initialized.
After parameter initialization, the model parameters are further updated and the RUL is predicted using a PF-based prediction algorithm. Based on the initialized parameters, a series of initial particles y0nn=1:Ns are sampled from the initial PDF of the system state p(y0n|Θ0)∼N(y0,Q0) with
(6.108)y0=x0μα and Q0=000σα2.
Ns is the number of particles and the weight of each particle is set to be 1/Ns. Then new particles ykni=1:Ns are obtained following
(6.109)ykn=xknμαn=xk−1n+μαnxk−1nβΔtkμαn.
When the new measurement zk at tk is available, each particle weight is updated and normalized by
(6.110)wkn=wk−1npzk|ykn, w~kn=wkn∑n=1Nswkn,
where
(6.111)pzk|ykn=12πσνexp−12zk−xknσν2.
The particles are resampled according to the particle weights and their weights are reset to be 1/Ns. After that, the RUL is predicted based on the resampled particles. The RUL lk at tk is defined as
(6.112)lk=inflk:xlk+tk≥λ|x1:k,
where λ is a prespecified failure threshold. Each particle is transmitted following the transition function of Eq. (6.98) from current state until the state value exceeds the failure threshold, and the RUL lknn=1:Ns predicted using each particle is acquired. Then the PDF of the RUL is approximated by
(6.113)plk|z0:k=∑n=1Nsw~knδlk−lkn.
Read full chapter
URL:
https://www.sciencedirect.com/science/article/pii/B9780128115343000068
Orbit and Attitude Sensors
Enrico Canuto, … Carlos Perez Montenegro, in Spacecraft Dynamics and Control, 2018
Exercise 1
Prove that the quantization error defined by Eq. (8.6) is bounded by |n˜y(i)|≤ρy/2 and under the random assumption has zero mean and variance equal to ρy2/12. □
A typical model of the random error d˜ in Eq. (8.4), which includes quantization errors, is the linear continuous-time stochastic state equation
(8.7)x˜˙(t)=A˜x˜+G˜w˜d˜(t)=C˜x˜+D˜w˜E{w˜(t)}=0,E{w˜(t)w˜T(t+τ)}=S˜w2δ(τ)E{x˜(0)}=x˜0,E{(x˜(0)−x˜0)(x˜(0)−x˜0)T}=P˜0≥0E{(x˜(0)−x˜0)w˜T(0)}=0,
which is similar to the DT Eq. (4.159) of Section 4.8.1. Eq. (8.7) being continuous-time, the eigenvalues of the state matrix A˜ are assumed to lie on the imaginary axis and when equal to zero may be multiple. The statistics in Eq. (8.7) assumes that w˜ is a zero-mean second-order stationary white noise with constant spectral density S˜w2, and impulsive covariance, where δ(τ) denotes a Dirac delta (see Sections 13.2.1 and 13.7.3Section 13.2.1Section 13.7.3). The initial state may be modeled as a random vector with mean value x˜0 and covariance matrix P˜0, but is uncorrelated from any simultaneous white noise as expressed by the last identity in Eq. (8.7). This uncorrelation has been already referred to as the causality constraint. In principle, Eq. (8.7) may be unobservable from the output d˜ and uncontrollable by the noise w˜, because the output d˜ may include polynomial and trigonometric components (deterministic signals) just driven by the initial state x˜0. For instance, a trigonometric component tuned to the angular frequency ω˜ corresponds to a second-order subsystem with eigenvalues ±jω˜. A first-order polynomial corresponds to a second-order subsystem with a pair of zero eigenvalues and a single eigenvector. The mixed case of stochastic processes and deterministic signals can be simplified by assuming that trigonometric and polynomial components are the free response of the equations driven by w˜, and that Eq. (8.7) is observable and controllable.
The simplest model of the class in Eq. (8.7), which is common to inertial sensors (accelerometers in Section 8.4 and gyroscopes in Section 8.5), is the scalar first-order random drift [32]:
(8.8)x˜˙(t)=w˜x,x˜(0)=x˜0d˜(t)=x˜+w˜dE{x˜(0)}=x˜0,var{x˜}=σ02,E{(x˜−x˜0)w˜T(0)}=0w˜=[w˜xw˜d],E{w˜(t)}=0,E{w˜(t)w˜T(t+τ)}=[S˜wx200S˜wd2]δ(τ),
where, if [unit] denotes the unit of measurement of x˜, we find S˜wx2 in [(unit/s)2Hz−1] and S˜wd2 in [unit2Hz−1]. The initial state x˜0 accounts for a constant bias and is uncorrelated with any simultaneous noise; the scalar input noise w˜x and the output noise w˜d in Eq. (8.8) are uncorrelated with each other. The output process d˜ is nonstationary and the autocorrelation is given by
(8.9)R˜d(t,t+τ)=S˜wx2min(t,t+τ)+S˜wd2δ(τ).
Although x˜ is nonstationary, the spectral density S˜x2(f) can be defined through the AS equation x˜˙=−εx˜+w˜x, where ε > 0 must be sufficiently smaller than the cutoff frequency f0 to be defined in the next paragraph. We can write the following identities:
(8.10)S˜d2(f)=S˜x2(f)+S˜wd2=S˜wx2(2πf)2+S˜wd2,f>ε2π=fεσ˜x2=limf→∞∫0fS˜x2νdν<∞,
where if, for f < ε, S˜x2(f) is bounded, also the variance σ˜x2 is bounded. The Bode plot of S˜d(f) is approximately flat for f>f0=2π−1S˜wx/S˜wd>fε and has a −20 dB/decade slope for fε < f < f0. The first PSD in the first row of Eq. (8.10) is a first-order random walk, which is known, in the realm of inertial sensors, as the (long-term) bias instability of the sensor. The name is appropriate because it describes the long-term fluctuations—bounded because of ε—around the mean sensor bias x˜0. The square root of the second term S˜wd corresponds to the minimum-valued profile of the overall spectral density. Let us call it, as already anticipated, noise floor, although the name sometimes refers to the whole instrument noise (here referred to as the background noise). In the realm of inertial sensors, it is known as the velocity random walk in the case of linear accelerometers, the unit being [m/(s2Hz)], and the angular random walk (ARW) in the case of gyroscopes, the unit being[rad/(sHz)]. The name, which may cause same confusion, is justified by the fact that when either of the two measurements (linear acceleration and angular rate) is time integrated for generating either velocity or attitude measurements, the integrated noise floor becomes a random walk. By restricting to gyroscopes, the ARW unit [rad/(sHz)] is usually simplified to [rad/s], de facto to the non-SI unit [degree/hour]. Indeed, the simplified unit is at the same time the unit of S˜wd and the unit of the root mean square (RMS) σ¯w(t,Δt) of the random walk increment w¯d(t,Δt)=∫tt+Δtw˜d(τ)dτ, namely:
(8.11)σ¯w(t,Δt)=E{1Δt(∫tt+Δtw˜d(τ)dτ)2}=S˜wd.
Read full chapter
URL:
https://www.sciencedirect.com/science/article/pii/B9780081007006000088
Sampling Theory
Luis Chaparro, in Signals and Systems Using MATLAB (Second Edition), 2015
8.3.2 Quantization and Coding
Amplitude discretization of the sampled signal xs(t) is accomplished by a quantizer consisting of a number of fixed amplitude levels against which the sample amplitudes {x(nTs)} are compared. The output of the quantizer is one of the fixed amplitude levels that best represents {x(nTs)} according to some approximation scheme. The quantizer is a non-linear system.
Independent of how many levels or, equivalently, of how many bits are allocated to represent each level of the quantizer, in general there is a possible error in the representation of each sample. This is called the quantization error. To illustrate this, consider the 2-bit or four-level quantizer shown in Figure 8.12. The input of the quantizer are the samples {x(nTs)}, which are compared with the values in the bins [-2Δ,-Δ],[-Δ,0],[0,Δ], and [Δ,2Δ]. Depending on which of these bins the sample falls in it is replaced by the corresponding levels -2Δ,-Δ,0, or Δ, respectively. The value of the quantization step Δ for the four-level quantizer is
Figure 8.12. Four-level quantizer and coder.
(8.23)Δ=dynamic range of signal2b=2max|x(t)|22
where b = 2 is number of bits of the code assigned to each level. The bits assigned to each of the levels uniquely represents the different levels [-2Δ,-Δ,0,Δ]. As to how to approximate the given sample to one of these levels, it can be done by rounding or by truncating. The quantizer shown in Figure 8.12 approximates by truncation, i.e., if the sample kΔ≤x(nTs)<(k+1)Δ, for k = −2, −1,0,1, then it is approximated by the level kΔ.
To see how quantization and coding are done, and how to obtain the quantization error, let the sampled signal be
x(nTs)=x(t)|t=nTS
The given four-level quantizer is such that if the sample x(nTs) is such that
(8.24)kΔ≤x(nTs)<(k+1)Δ⇒xˆ(nTs)=kΔk=-2,-1,0,1
The sampled signal x(nTs) is the input of the quantizer and the quantized signal xˆ(nTs) is its output. So that whenever
-2Δ≤x(nTs)<-Δ⇒xˆ(nTs)=-2Δ-Δ≤x(nTs)<0⇒xˆ(nTs)=-Δ0≤x(nTs)<Δ⇒xˆ(nTs)=0Δ≤x(nTs)<2Δ⇒xˆ(nTs)=Δ
To transform the quantized values into unique binary 2-bit values, one could use a code such as
xˆ(nTs)⇒binary code-2Δ10-Δ110Δ00Δ01
which assigns a unique 2 bit binary number to each of the 4 quantization levels. Notice that the first bit of this code can be considered a sign bit, “1” for negative levels and “0” for positive levels.
If we define the quantization error as
ε(nTs)=x(nTs)-xˆ(nTs)
and use the characterization of the quantizer given by Equation (8.24) as
xˆ(nTs)≤x(nTs)≤xˆ(nTs)+Δ
by subtracting xˆ(nTs) from each of the terms gives that the quantization error is bounded as follows
(8.25)0≤ε(nTs)≤Δ
i.e., the quantization error for the four-level quantizer being considered is between 0 and Δ. This expression for the quantization error indicates that one way to decrease the quantization error is to make the quantization step Δsmaller. Increasing the number of bits of the A/D converter makes Δ smaller (see Equation (8.23) where the denominator is 2 raised to the number of bits) which in turn makes smaller the quantization error, and improves the quality of the A/D converter.
In practice, the quantization error is random and so it needs to be characterized probabilistically. This characterization becomes meaningful when the number of bits is large, and when the input signal is not a deterministic signal. Otherwise, the error is predictable and thus not random. Comparing the energy of the input signal to the energy of the error, by means of the so-called signal to noise ratio (SNR), it is possible to determine the number of bits that are needed in a quantizer to get a reasonable quantization error.
Example 8.5
Suppose we are trying to decide between an 8 and a 9 bit A/D converter for a certain application where the signals in this application are known to have frequencies that do not exceed 5 kHz. The dynamic range of the signals is 10 volts, so that the signal is bounded as −5 ≤ x(t) ≤ 5. Determine an appropriate sampling period and compare the percentage of error for the two A/Ds of interest.
Solution
The first consideration in choosing the A/D converter is the sampling period, so we need to get an A/D converter capable of sampling at fs = 1/Ts > 2 fmax samples/second. Choosing fs = 4 fmax = 20 k samples/second then Ts = 1/20 msec/sample or 50 microseconds/sample. Suppose then we look at the 8-bit A/D converter, the quantizer has 28 = 256 levels so that the quantization step is Δ=10/256 volts and if we use a truncation quantizer the quantization error would be
0≤ε(nTs)≤10/256
If we find that objectionable we can then consider the 9-bit A/D converter, with a quantizer of 29 = 512 levels and the quantization step Δ=10/512 or half that of the 8-bit A/D converter, and
0≤ε(nTs)≤10/512
So that by increasing one bit we cut the quantization error in half from the previous quantizer. Inputting a signal of constant amplitude 5 into the 9-bit A/D gives a quantization error of [(10/512)/5] × 100% = (100/256)% ≈ 0.4% in representing the input signal. For the 8-bit A/D it would correspond to 0.8% error. ▪
Read full chapter
URL:
https://www.sciencedirect.com/science/article/pii/B9780123948120000085
Compression
StéphaneMallat , in A Wavelet Tour of Signal Processing (Third Edition), 2009
Weighted Quantization and Regions of Interest
Visual distortions introduced by quantization errors of wavelet coefficients depend on the scale 2j. Errors at large scales are more visible than at fine scales [481]. This can be taken into account by quantizing the wavelet coefficients with intervals Δj=Δwj that depend on the scale 2j. For R¯≤1 bit/pixel, wj = 2−j is appropriate for the three finest scales. The distortion in (10.34) shows that choosing such weights is equivalent to minimizing a weighted mean-square error.
Such a weighted quantization is implemented like in (10.35) by quantizing weighted wavelet coefficients fB[m]/wj with a uniform quantizer. The weights are inverted during the decoding process. JPEG-2000 supports a general weighting scheme that codes weighted coefficients w[m]fB[m] where w[m] can be designed to emphasize some region of interest Ω ⊂ [0, 1]2 in the image. The weights are set to w[m] = w > 1 for the wavelet coefficients fB[m]=〈f,ψj,p,q1〉 where the support of ψj,p,q1 intersects Ω. As a result, the wavelet coefficients inside Ω are given a higher priority during the coding stage, and the region Ω is coded first within the compressed stream. This provides a mechanism to more precisely code regions of interest in images—for example, a face in a crowd.
Read full chapter
URL:
https://www.sciencedirect.com/science/article/pii/B9780123743701000148
Signal and Image Representation in Combined Spaces
Zoran. Cvetković, Martin. Vetterli, in Wavelet Analysis and Its Applications, 1998
6.1 Two lemmas on frames of complex exponentials
Estimates of bounds on the quantization error in Subsection 4.3 are derived from the next two lemmas [5].
Lemma 1
Letejλnωbe a frame in L2[− σ, σ]. If M is any constant and {μn} is a sequence satisfying |μn − λn| ≤ M, for all n, then there is a number C = C(M, σ, {λn}) such that
(6.1.1)∑n|fμn|2∑n|fλn|2≤C
for every cr-bandlimited signal f(x).
Lemma 2
Letejλnωbe a frame in L2[− σ, σ], with bounds 0 < A ≤ B < ∞ and δ a given positive number. If a sequence { μn } satisfies | λn − μn < δ for all n, then for every σ-bandlimited signal f(x)
(6.1.2)A1−C2||f||2≤∑n|fμn|2≤B(1+C)2||f||2,
where
(6.1.3)C=BAeγδ−12
Remark 1
If δ in the statement of Lemma 2 is chosen small enough, so that C is less then 1, then ejμnω is also a frame in L2[− σ, σ]. Moreover, there exists some δ 1/4 ({λn},σ), such that whenever δ < δ 1/4 ({λn }, σ), ejμnω is a frame with frame bounds A/A and 9B/4.
Read full chapter
URL:
https://www.sciencedirect.com/science/article/pii/S1874608X98800125
Live HDR Video Broadcast Production
I.G. Olaizola, … J. Gorostegui, in High Dynamic Range Video, 2017
1.4.1 Banding
Banding effects are directly related to quantization errors. As the dynamic range increases, the quantization effects become more noticeable and banding artifacts arise. To avoid this, smaller quantization steps must be taken, but this requires a higher bitdepth (from 8 to 10 or 12 in order to have backwards compatibility with existing infrastructures, and ideally 14 or 16 bits) and nonlinear transform functions based on the HVS that minimize the observable banding effects. Nowadays, this is partially solved by the electro-optical transfer function (EOTF) and opto-electronic transfer function (OETF) mapping curves that will be introduced in a further section.
Read full chapter
URL:
https://www.sciencedirect.com/science/article/pii/B978012809477800008X
Ошибки квантования
В реальных
устройствах цифровой обработки сигналов
необходимо учитывать
эффекты, обусловленные квантованием
входных сигналов
и конечной разрядностью всех регистров.
Источниками ошибок
в процессах обработки сигналов являются
округление (усечение)
результатов арифметических операций,
шум аналого-цифрового квантования
входных аналоговых сигналов, неточность
реализации характеристик цифровых
фильтров из-за округления их коэффициентов
(параметров). В дальнейшем с целью
упрощения анализа предполагается, что
вес источники ошибок независимы и не
коррелируют с входным сигналом (хотя
мы и рассмотрим явление предельных
циклов, обусловленных коррелированным
шумом округления).
Эффект квантования
приводят в конечном итоге к погрешностями выходных сигналах цифровых фильтров
(ЦФ), а в некоторыхслучаяхи к неустойчивым
режимам. Выходную ошибку ЦФ будем
рассчитыватькаксуперпозицию ошибок, обусловленных
каждым независимымисточником.
Квантование
чисел– нелинейная операция;m-разрядное
двоичное числоА
представляетсяb-разрядным
двоичнымчислом
B=F(A),
причем b
< m. В
результате квантования число А
представляется
с ошибкой
е
=B–А= F(А)
–А.
Шаг квантования
Q
=
2–b
определяется весом младшего
числовогоразряда.
При квантовании
используется усечение или округление.
Усечение
числаА
состоит в отбрасываниит
– b
младших разрядов числа, при этом
ошибка усечения
eус=
Fус(А) –А.
Оценим величину
ошибки в предположении m
» b.
Для положительных чисел при любом
способе кодирования –2–b
<еус
0. Для
отрицательных чисел при использовании
прямого и обратного кодов ошибка усечения
неотрицательна: 0еус
< 2–b,
а в дополнительном коде эта ошибка
неположительна: 0еус
> –2–b.
Таким образом, во всех случаях
абсолютное значение ошибки усечения
не превосходит шага квантования:maxeус
< 2–b
=Q.
Округление
m-разрядного
числаA
доb
разрядов (b «
m)b-й
разряд остается неизменным или
увеличивается на единицув
зависимости от соотношения (больше –
меньше) между отбрасываемой дробью
0,аb+1…ат
и величиной
,
гдеаi–i-й
разряд числаA;
i =
b+1,
…,m.
Округление можно практически выполнить
путемприбавления
единицы к (b+1)-му
разряду и усечения полученного числа
до b разрядов.
В таком случае ошибка округления еoк
=
fок(А)–
А
при всех способах кодирования лежит в
пределах
–2–(b+1)
<
еoк
< 2–(b+1)
(1.11)
и, следовательно,
max<2–b
= Q/2.
(1.12)
В задачах ЦОС
ошибки квантования чисел рассматриваются
как стационарный
шумоподобный процесс с равномерным
распределением
вероятности по диапазону распределения
ошибок квантования.
(nT)
x(nT)
e(nT)
Рис. 3. Линейная модель квантования
сигналов:
(nT) —дискретный
или m-разрядный
цифровой сигнал (m
> b);
x(nT) —квантованный
b-разрядный
цифровой сигнал;
e(nT)
= x(nT)
–f(nT)
— ошибка
квантования.
Квантование
дискретных сигналов состоит в
представлении отсчета
(выборки сигнала) числамиx(nT),
содержащими b
числовых разрядов. Квантование сигналов,
как и квантование
чисел – нелинейная операция. Однако
при анализе процессов в ЦФ целесообразно
использовать линейную модель квантования
сигналов – рис. 3.
Верхнее значение ошибки квантования
определяетсясоотношением
(1.11) или (1.12).
Вероятностные
оценки ошибок квантования основаны на
предположениях о том, что
последовательностье(пТ)являетсястационарным
случайным процессом с равномерным
распределением вероятности по
диапазону ошибок квантования ие(пТ)
не коррелирован
с f(nT).
Математическое
ожидание (среднее значение) e
и дисперсия
ошибки квантованияе
определяются
по формулам:
=E(е)
=,
=
=
=E(е2)
–,
где ре
— плотность вероятности ошибки. По
этим формуламвычисляются
математическое ожидание и дисперсия
для ошибок
округления и усечения:
=
=
В логарифмическоммасштабе
=
Лекция 2
Вычислите ошибку квантования
В этом примере показано, как вычислить и сравнить статистику ошибки квантования сигнала при использовании различных методов округления.
Во-первых, случайный сигнал создается, который порождает линейную оболочку столбцов квантизатора.
Затем сигнал квантуется, соответственно, с округлением методов ‘фиксируют’, ‘ставят в тупик’, ‘перекрывают’, ‘самый близкий’, и ‘конвергентный’, и статистические данные сигнала оцениваются.
Теоретическая функция плотности вероятности ошибки квантования будет вычислена с ERRPDF, теоретическое среднее значение ошибки квантования будет вычислено с ERRMEAN, и теоретическое отклонение ошибки квантования будет вычислено с ERRVAR.
Равномерно распределенный случайный сигнал
Сначала мы создаем равномерно распределенный случайный сигнал, который охватывает область-1 к 1 из квантизаторов фиксированной точки, на которые мы посмотрим.
q = quantizer([8 7]);
r = realmax(q);
u = r*(2*rand(50000,1) - 1); % Uniformly distributed (-1,1)
xi=linspace(-2*eps(q),2*eps(q),256);
Фиксация: вокруг по направлению к нулю.
Заметьте, что с округлением ‘фиксации’, функция плотности вероятности вдвое более широка, чем другие. Поэтому отклонение в четыре раза больше чем это других.
q = quantizer('fix',[8 7]); err = quantize(q,u) - u; f_t = errpdf(q,xi); mu_t = errmean(q); v_t = errvar(q); % Theoretical variance = eps(q)^2 / 3 % Theoretical mean = 0 fidemo.qerrordemoplot(q,f_t,xi,mu_t,v_t,err)
Estimated error variance (dB) = -46.8586 Theoretical error variance (dB) = -46.9154 Estimated mean = 7.788e-06 Theoretical mean = 0
Пол: вокруг к минус бесконечность.
Пол, округляющийся, часто называется усечением, когда используется с целыми числами и числами фиксированной точки, которые представлены в дополнении two. Это — наиболее распространенный режим округления процессоров DSP, потому что это требует, чтобы никакое оборудование не реализовало. Пол не производит квантованные значения, которые являются как близко к истинным значениям, когда ROUND будет, но это имеет то же отклонение, и маленькие сигналы, которые варьируются по знаку, будут обнаружены, тогда как в ROUND они будут потеряны.
q = quantizer('floor',[8 7]); err = quantize(q,u) - u; f_t = errpdf(q,xi); mu_t = errmean(q); v_t = errvar(q); % Theoretical variance = eps(q)^2 / 12 % Theoretical mean = -eps(q)/2 fidemo.qerrordemoplot(q,f_t,xi,mu_t,v_t,err)
Estimated error variance (dB) = -52.9148 Theoretical error variance (dB) = -52.936 Estimated mean = -0.0038956 Theoretical mean = -0.0039062
Потолок: вокруг к плюс бесконечность.
q = quantizer('ceil',[8 7]); err = quantize(q,u) - u; f_t = errpdf(q,xi); mu_t = errmean(q); v_t = errvar(q); % Theoretical variance = eps(q)^2 / 12 % Theoretical mean = eps(q)/2 fidemo.qerrordemoplot(q,f_t,xi,mu_t,v_t,err)
Estimated error variance (dB) = -52.9148 Theoretical error variance (dB) = -52.936 Estimated mean = 0.0039169 Theoretical mean = 0.0039062
Вокруг: вокруг к самому близкому. Вничью, вокруг к самой большой величине.
Вокруг более точно, чем пол, но все значения, меньшие, чем eps (q), округлены, чтобы обнулить и потеряны — также.
q = quantizer('nearest',[8 7]); err = quantize(q,u) - u; f_t = errpdf(q,xi); mu_t = errmean(q); v_t = errvar(q); % Theoretical variance = eps(q)^2 / 12 % Theoretical mean = 0 fidemo.qerrordemoplot(q,f_t,xi,mu_t,v_t,err)
Estimated error variance (dB) = -52.9579 Theoretical error variance (dB) = -52.936 Estimated mean = -2.212e-06 Theoretical mean = 0
Конвергентный: вокруг к самому близкому. Вничью, вокруг к даже.
Конвергентное округление устраняет смещение, введенное обычным «раундом», вызванным, всегда округляя связь в том же направлении.
q = quantizer('convergent',[8 7]); err = quantize(q,u) - u; f_t = errpdf(q,xi); mu_t = errmean(q); v_t = errvar(q); % Theoretical variance = eps(q)^2 / 12 % Theoretical mean = 0 fidemo.qerrordemoplot(q,f_t,xi,mu_t,v_t,err)
Estimated error variance (dB) = -52.9579 Theoretical error variance (dB) = -52.936 Estimated mean = -2.212e-06 Theoretical mean = 0
Сравнение самых близких по сравнению с конвергентным
Функция плотности вероятности появления ошибки для конвергентного округления затрудняет, чтобы различать от того из раунда-к-самому-близкому путем рассмотрения графика.
Ошибка p.d.f. из конвергентных
f(err) = 1/eps(q), for -eps(q)/2 <= err <= eps(q)/2, and 0 otherwise
в то время как ошибка p.d.f. из раунда
f(err) = 1/eps(q), for -eps(q)/2 < err <= eps(q)/2, and 0 otherwise
Обратите внимание на то, что ошибка p.d.f. из конвергентных симметрично, в то время как вокруг немного склоняется к положительному.
Единственной разницей является направление округления вничью.
x=(-3.5:3.5)'; [x convergent(x) nearest(x)]
ans =
-3.5000 -4.0000 -3.0000
-2.5000 -2.0000 -2.0000
-1.5000 -2.0000 -1.0000
-0.5000 0 0
0.5000 0 1.0000
1.5000 2.0000 2.0000
2.5000 2.0000 3.0000
3.5000 4.0000 4.0000
Постройте функцию помощника
Функция помощника, которая использовалась, чтобы сгенерировать графики в этом примере, описана ниже.
type(fullfile(matlabroot,'toolbox','fixedpoint','fidemos','+fidemo','qerrordemoplot.m')) %#ok<*NOPTS>
function qerrordemoplot(q,f_t,xi,mu_t,v_t,err)
%QERRORDEMOPLOT Plot function for QERRORDEMO.
% QERRORDEMOPLOT(Q,F_T,XI,MU_T,V_T,ERR) produces the plot and display
% used by the example function QERRORDEMO, where Q is the quantizer
% whose attributes are being analyzed; F_T is the theoretical
% quantization error probability density function for quantizer Q
% computed by ERRPDF; XI is the domain of values being evaluated by
% ERRPDF; MU_T is the theoretical quantization error mean of quantizer Q
% computed by ERRMEAN; V_T is the theoretical quantization error
% variance of quantizer Q computed by ERRVAR; and ERR is the error
% generated by quantizing a random signal by quantizer Q.
%
% See QERRORDEMO for examples of use.
% Copyright 1999-2014 The MathWorks, Inc.
v=10*log10(var(err));
disp(['Estimated error variance (dB) = ',num2str(v)]);
disp(['Theoretical error variance (dB) = ',num2str(10*log10(v_t))]);
disp(['Estimated mean = ',num2str(mean(err))]);
disp(['Theoretical mean = ',num2str(mu_t)]);
[n,c]=hist(err);
figure(gcf)
bar(c,n/(length(err)*(c(2)-c(1))),'hist');
line(xi,f_t,'linewidth',2,'color','r');
% Set the ylim uniformly on all plots
set(gca,'ylim',[0 max(errpdf(quantizer(q.format,'nearest'),xi)*1.1)])
legend('Estimated','Theoretical')
xlabel('err'); ylabel('errpdf')
Дорогие читатели, меня зовут Феликс Арутюнян. Я студент, профессиональный скрипач. В этой статье хочу поделиться с Вами отрывком из моей презентации, которую я представил в университете музыки и театра Граца по предмету прикладная акустика.
Рассмотрим теоретические аспекты преобразования аналогового (аудио) сигнала в цифровой.
Статья не будет всеохватывающей, но в тексте будут гиперссылки для дальнейшего изучения темы.
Чем отличается цифровой аудиосигнал от аналогового?
Аналоговый (или континуальный) сигнал описывается непрерывной функцией времени, т.е. имеет непрерывную линию с непрерывным множеством возможных значений (рис. 1).
рис. 1
Цифровой сигнал — это сигнал, который можно представить как последовательность определенных цифровых значений. В любой момент времени он может принимать только одно определенное конечное значение (рис. 2).
рис. 2
Аналоговый сигнал в динамическом диапазоне может принимать любые значения. Аналоговый сигнал преобразуется в цифровой с помощью двух процессов — дискретизация и квантование. Очередь процессов не важна.
Дискретизацией называется процесс регистрации (измерения) значения сигнала через определенные промежутки (обычно равные) времени (рис. 3).
рис. 3
Квантование — это процесс разбиения диапазона амплитуды сигнала на определенное количество уровней и округление значений, измеренных во время дискретизации, до ближайшего уровня (рис. 4).
рис. 4
Дискретизация разбивает сигнал по временной составляющей (по вертикали, рис. 5, слева).
Квантование приводит сигнал к заданным значениям, то есть округляет сигнал до ближайших к нему уровней (по горизонтали, рис. 5, справа).
рис. 5
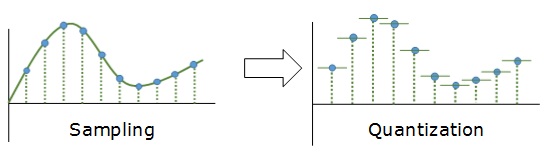
Эти два процесса создают как бы координатную систему, которая позволяет описывать аудиосигнал определенным значением в любой момент времени.
Цифровым называется сигнал, к которому применены дискретизация и квантование. Оцифровка происходит в аналого-цифровом преобразователе (АЦП). Чем больше число уровней квантования и чем выше частота дискретизации, тем точнее цифровой сигнал соответствует аналоговому (рис. 6).
рис. 6
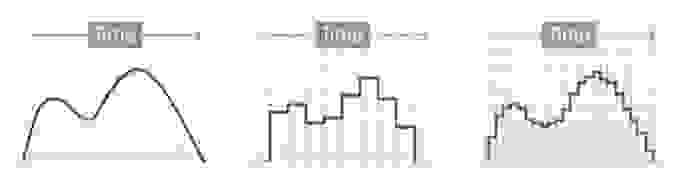
Уровни квантования нумеруются и каждому уровню присваивается двоичный код. (рис. 7)
рис. 7
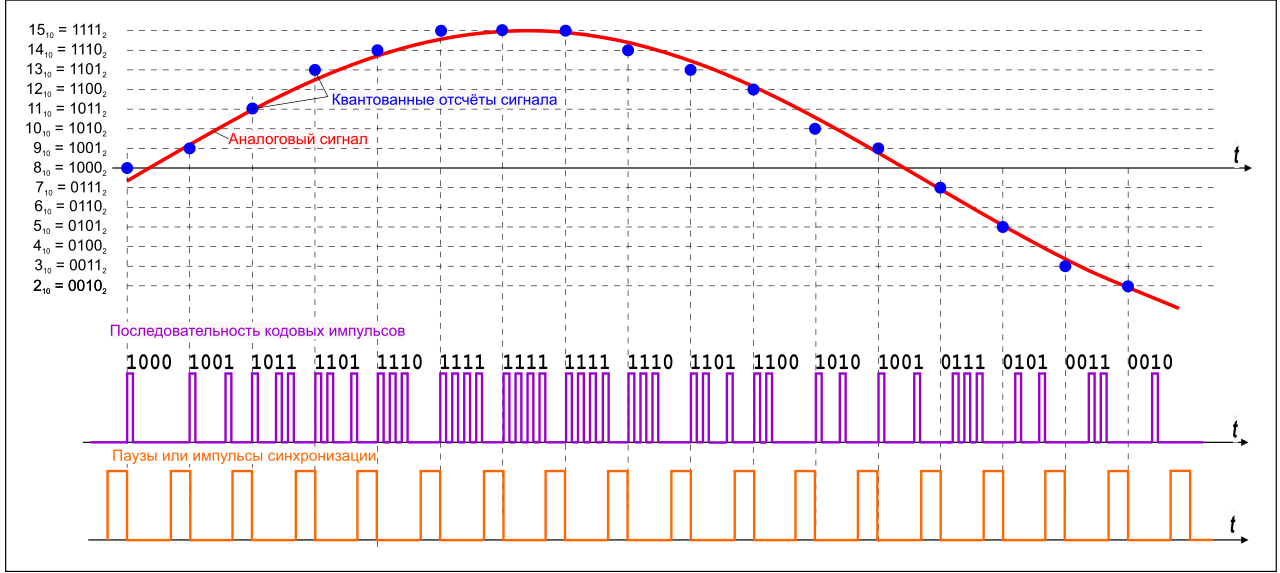
Количество битов, которые присваиваются каждому уровню квантования называют разрядностью или глубиной квантования (eng. bit depth). Чем выше разрядность, тем больше уровней можно представить двоичным кодом (рис. 8).
рис. 8.
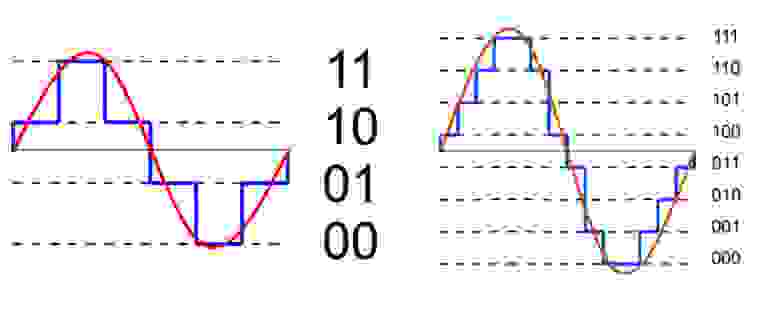
Данная формула позволяет вычислить количество уровней квантования:
Если N — количество уровней квантования,
n — разрядность, то
Обычно используют разрядности в 8, 12, 16 и 24 бит. Несложно вычислить, что при n=24 количество уровней N = 16,777,216.
При n = 1 аудиосигнал превратится в азбуку Морзе: либо есть «стук», либо нету. Существует также разрядность 32 бит с плавающей запятой. Обычный компактный Аудио-CD имеет разрядность 16 бит. Чем ниже разрядность, тем больше округляются значения и тем больше ошибка квантования.
Ошибкой квантований называют отклонение квантованного сигнала от аналогового, т.е. разница между входным значением и квантованным значением
(
)
Большие ошибки квантования приводят к сильным искажениям аудиосигнала (шум квантования).
Чем выше разрядность, тем незначительнее ошибки квантования и тем лучше отношение сигнал/шум (Signal-to-noise ratio, SNR), и наоборот: при низкой разрядности вырастает шум (рис. 9).
рис. 9
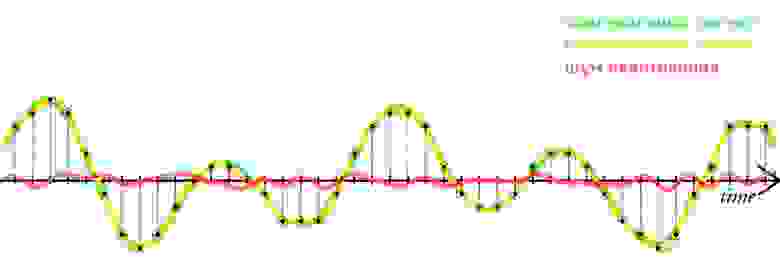
Разрядность также определяет динамический диапазон сигнала, то есть соотношение максимального и минимального значений. С каждым битом динамический диапазон вырастает примерно на 6dB (Децибел) (6dB это в 2 раза; то есть координатная сетка становиться плотнее, возрастает градация).
рис. 10. Интенсивность шумов при разрядности 6 бит и 8 бит
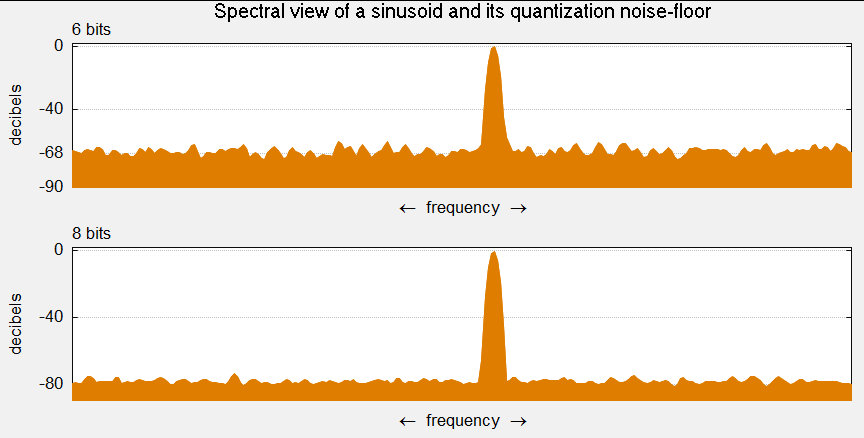
Ошибки квантования (округления) из-за недостаточного количество уровней не могут быть исправлены.
шум квантования
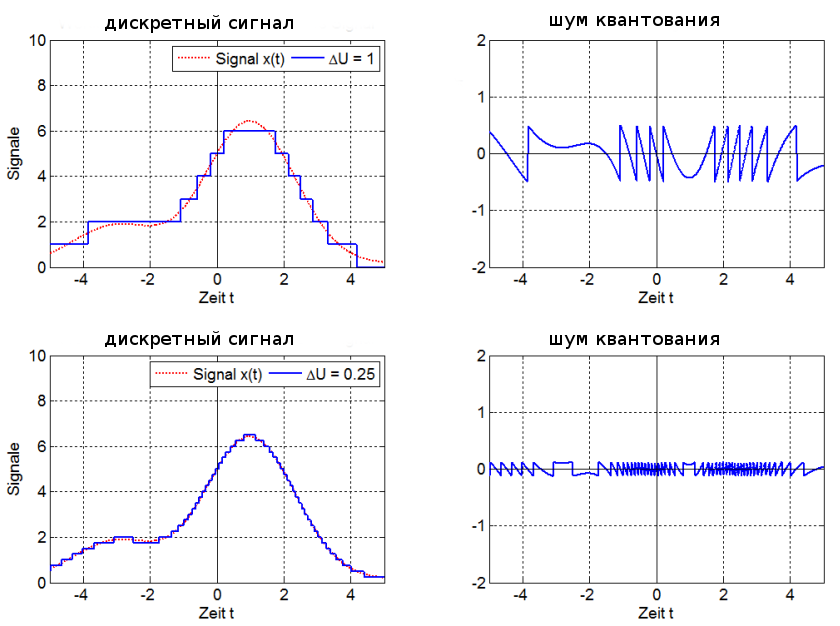
амплитуда сигнала при разрядности 1 бит (сверху) и 4 бит
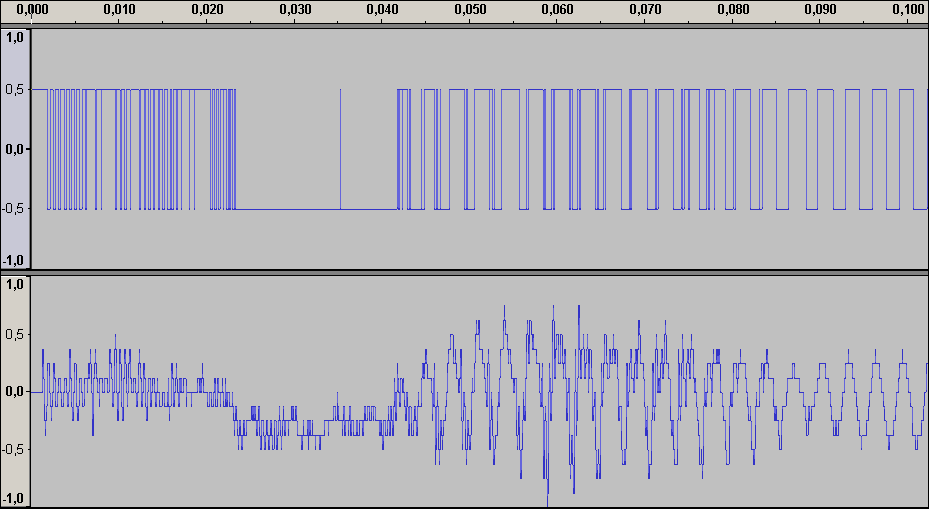
Аудиопример 1: 8bit/44.1kHz, ~50dB SNR
примечание: если аудиофайлы не воспроизводятся онлайн, пожалуйста, скачивайте их.
Аудиопример 1
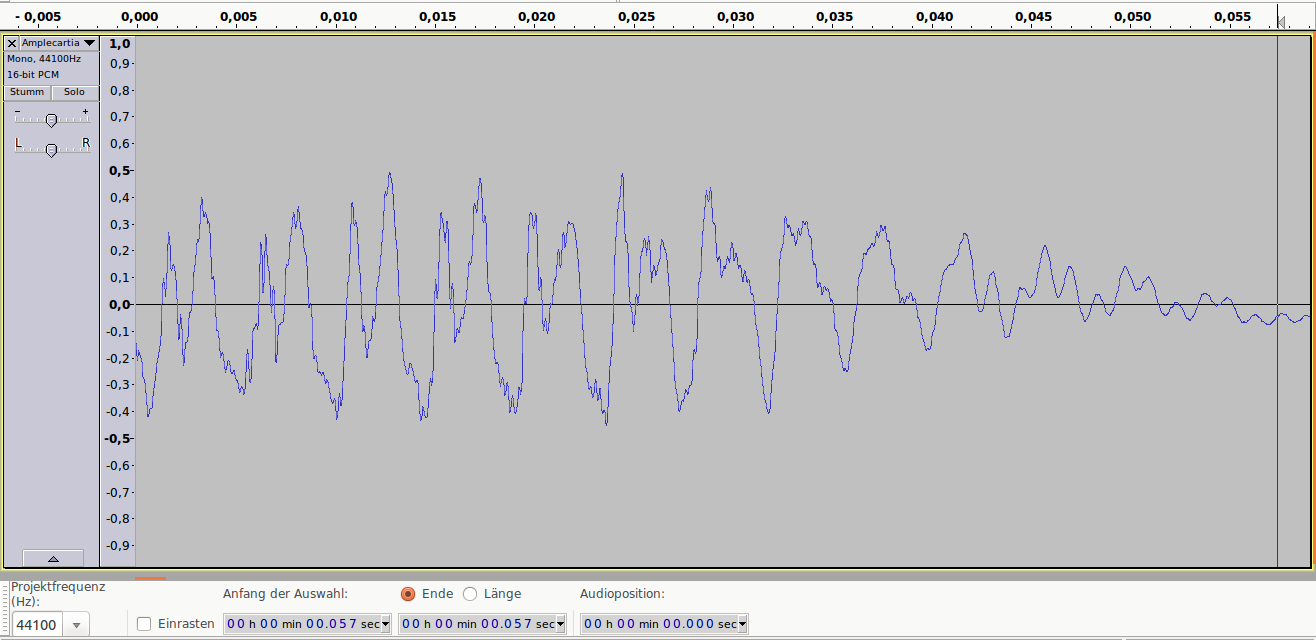
Аудиопример 2: 4bit/48kHz, ~25dB SNR
Аудиопример 2
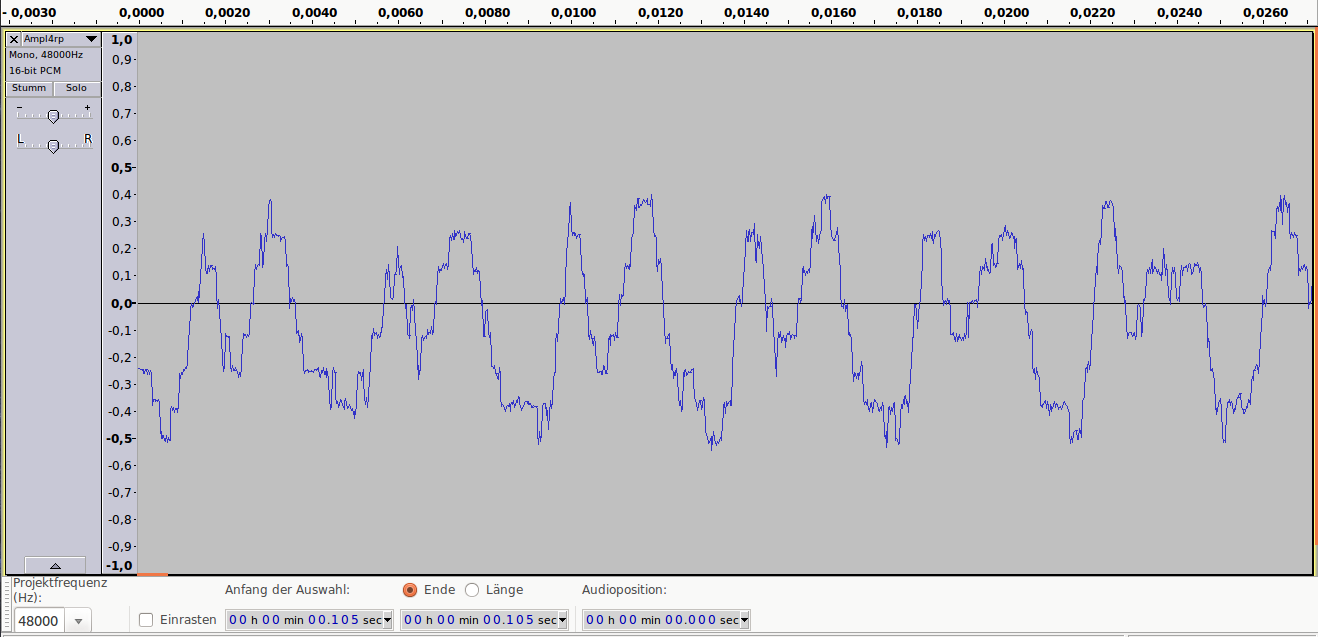
Аудиопример 3: 1bit/48kHz, ~8dB SNR
Аудиопример 3
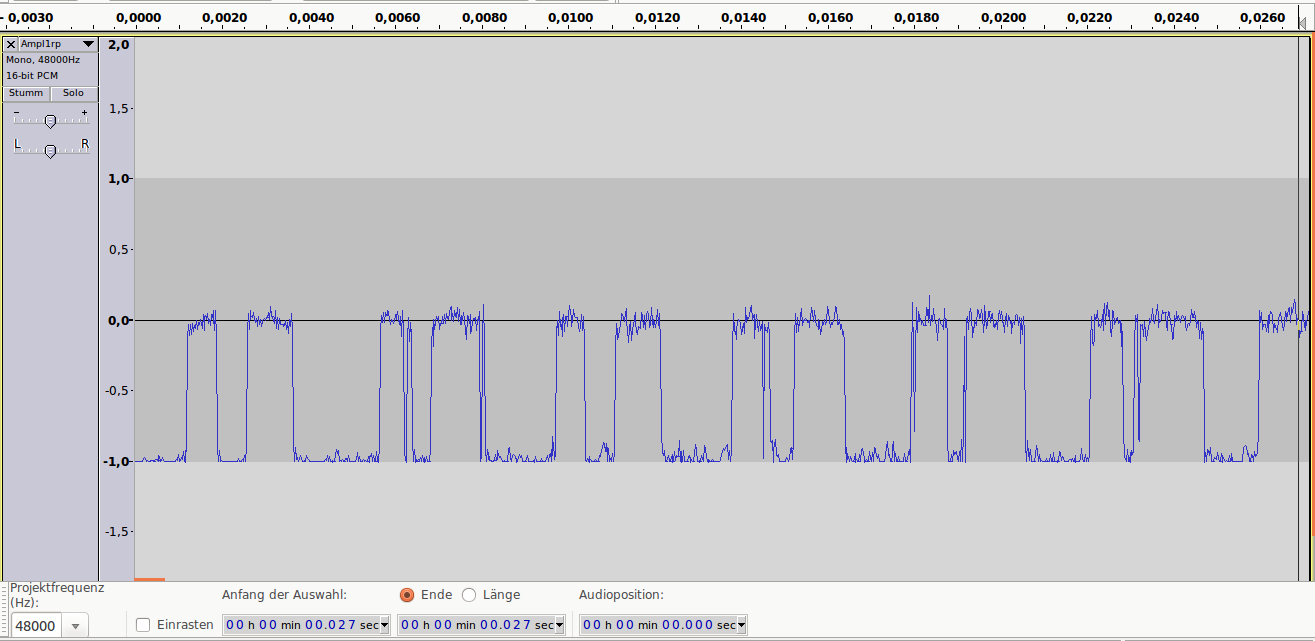
Теперь о дискретизации.
Как уже говорили ранее, это разбиение сигнала по вертикали и измерение величины значения через определенный промежуток времени. Этот промежуток называется периодом дискретизации или интервалом выборок. Частотой выборок, или частотой дискретизации (всеми известный sample rate) называется величина, обратная периоду дискретизации и измеряется в герцах. Если
T — период дискретизации,
F — частота дискретизации, то
Чтобы аналоговый сигнал можно было преобразовать обратно из цифрового сигнала (точно реконструировать непрерывную и плавную функцию из дискретных, «точечных» значении), нужно следовать теореме Котельникова (теорема Найквиста — Шеннона).
Теорема Котельникова гласит:
Если аналоговый сигнал имеет финитный (ограниченной по ширине) спектр, то он может быть восстановлен однозначно и без потерь по своим дискретным отсчетам, взятым с частотой, строго большей удвоенной верхней частоты.
Вам знакомо число 44.1kHz? Это один из стандартов частоты дискретизации, и это число выбрали именно потому, что человеческое ухо слышит только сигналы до 20kHz. Число 44.1 более чем в два раза больше чем 20, поэтому все частоты в цифровом сигнале, доступные человеческому уху, могут быть преобразованы в аналоговом виде без искажении.
Но ведь 20*2=40, почему 44.1? Все дело в совместимости с стандартами PAL и NTSC. Но сегодня не будем рассматривать этот момент. Что будет, если не следовать теореме Котельникова?
Когда в аудиосигнале встречается частота, которая выше чем 1/2 частоты дискретизации, тогда возникает алиасинг — эффект, приводящий к наложению, неразличимости различных непрерывных сигналов при их дискретизации.
Алиасинг
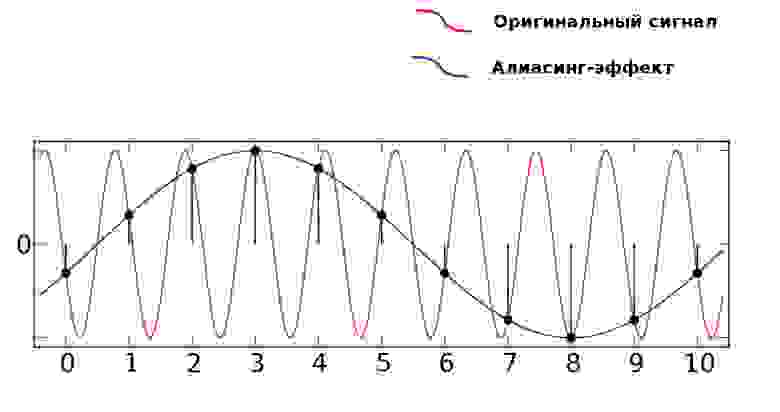
Как видно из предыдущей картинки, точки дискретизации расположены так далеко друг от друга, что при интерполировании (т.е. преобразовании дискретных точек обратно в аналоговый сигнал) по ошибке восстанавливается совершенно другая частота.
Аудиопример 4: Линейно возрастающая частота от ~100 до 8000Hz. Частота дискретизации — 16000Hz. Нет алиасинга.
Спектральный анализ
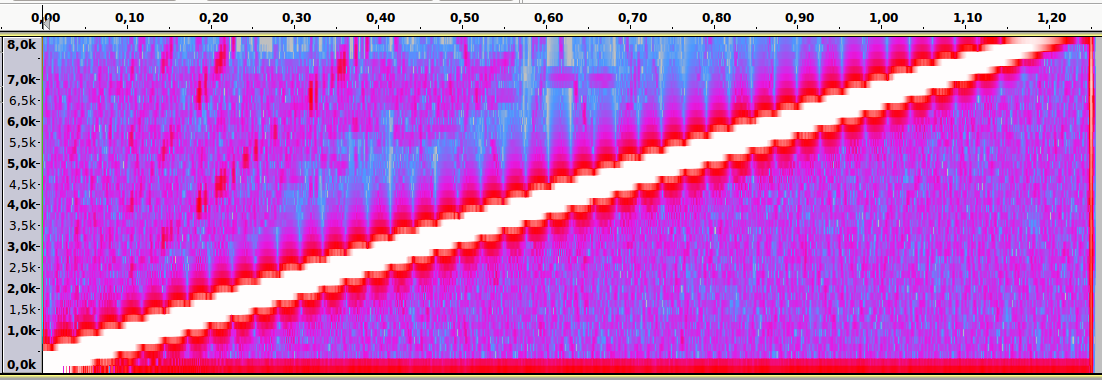
Аудиопример 5: Тот же файл. Частота дискретизации — 8000Hz. Присутствует алиасинг
Спектральный анализ
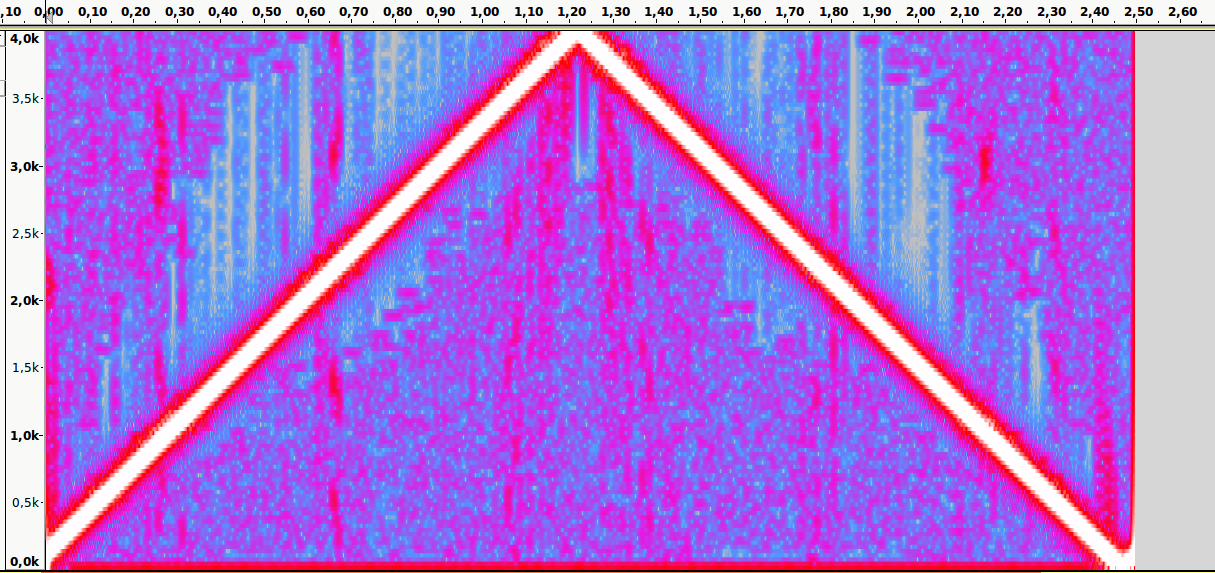
Пример:
Имеется аудиоматериал, где пиковая частота — 2500Hz. Значит, частоту дискретизации нужно выбрать как минимум 5000Hz.
Следующая характеристика цифрового аудио это битрейт. Битрейт (bitrate) — это объем данных, передаваемых в единицу времени. Битрейт обычно измеряют в битах в секунду (Bit/s или bps). Битрейт может быть переменным, постоянным или усреднённым.
Следующая формула позволяет вычислить битрейт (действительна только для несжатых потоков данных):
Битрейт = Частота дискретизации * Разрядность * Количество каналов
Например, битрейт Audio-CD можно рассчитать так:
44100 (частота дискретизации) * 16 (разрядность) * 2 (количество каналов, stereo)= 1411200 bps = 1411.2 kbit/s
При постоянном битрейте (constant bitrate, CBR) передача объема потока данных в единицу времени не изменяется на протяжении всей передачи. Главное преимущество — возможность довольно точно предсказать размер конечного файла. Из минусов — не оптимальное соотношение размер/качество, так как «плотность» аудиоматериала в течении музыкального произведения динамично изменяется.
При кодировании переменным битрейтом (VBR), кодек выбирает битрейт исходя из задаваемого желаемого качества. Как видно из названия, битрейт варьируется в течение кодируемого аудиофайла. Данный метод даёт наилучшее соотношение качество/размер выходного файла. Из минусов: точный размер конечного файла очень плохо предсказуем.
Усреднённый битрейт (ABR) является частным случаем VBR и занимает промежуточное место между постоянным и переменным битрейтом. Конкретный битрейт задаётся пользователем. Программа все же варьирует его в определенном диапазоне, но не выходит за заданную среднюю величину.
При заданном битрейте качество VBR обычно выше чем ABR. Качество ABR в свою очередь выше чем CBR: VBR > ABR > CBR.
ABR подходит для пользователей, которым нужны преимущества кодирования VBR, но с относительно предсказуемым размером файла. Для ABR обычно требуется кодирование в 2 прохода, так как на первом проходе кодек не знает какие части аудиоматериала должны кодироваться с максимальным битрейтом.
Существуют 3 метода хранения цифрового аудиоматериала:
- Несжатые («сырые») данные
- Данные, сжатые без потерь
- Данные, сжатые с потерями
Несжатый (RAW) формат данных
содержит просто последовательность бинарных значений.
Именно в таком формате хранится аудиоматериал в Аудио-CD. Несжатый аудиофайл можно открыть, например, в программе Audacity. Они имеют расширение .raw, .pcm, .sam, или же вообще не имеют расширения. RAW не содержит заголовка файла (метаданных).
Другой формат хранения несжатого аудиопотока это WAV. В отличие от RAW, WAV содержит заголовок файла.
Аудиоформаты с сжатием без потерь
Принцип сжатия схож с архиваторами (Winrar, Winzip и т.д.). Данные могут быть сжаты и снова распакованы любое количество раз без потери информации.
Как доказать, что при сжатии без потерь, информация действительно остаётся не тронутой? Это можно доказать методом деструктивной интерференции. Берем две аудиодорожки. В первой дорожке импортируем оригинальный, несжатый wav файл. Во второй дорожке импортируем тот же аудиофайл, сжатый без потерь. Инвертируем фазу одного из дорожек (зеркальное отображение). При проигрывании одновременно обеих дорожек выходной сигнал будет тишиной.
Это доказывает, что оба файла содержат абсолютно идентичные информации (рис. 11).
рис. 11
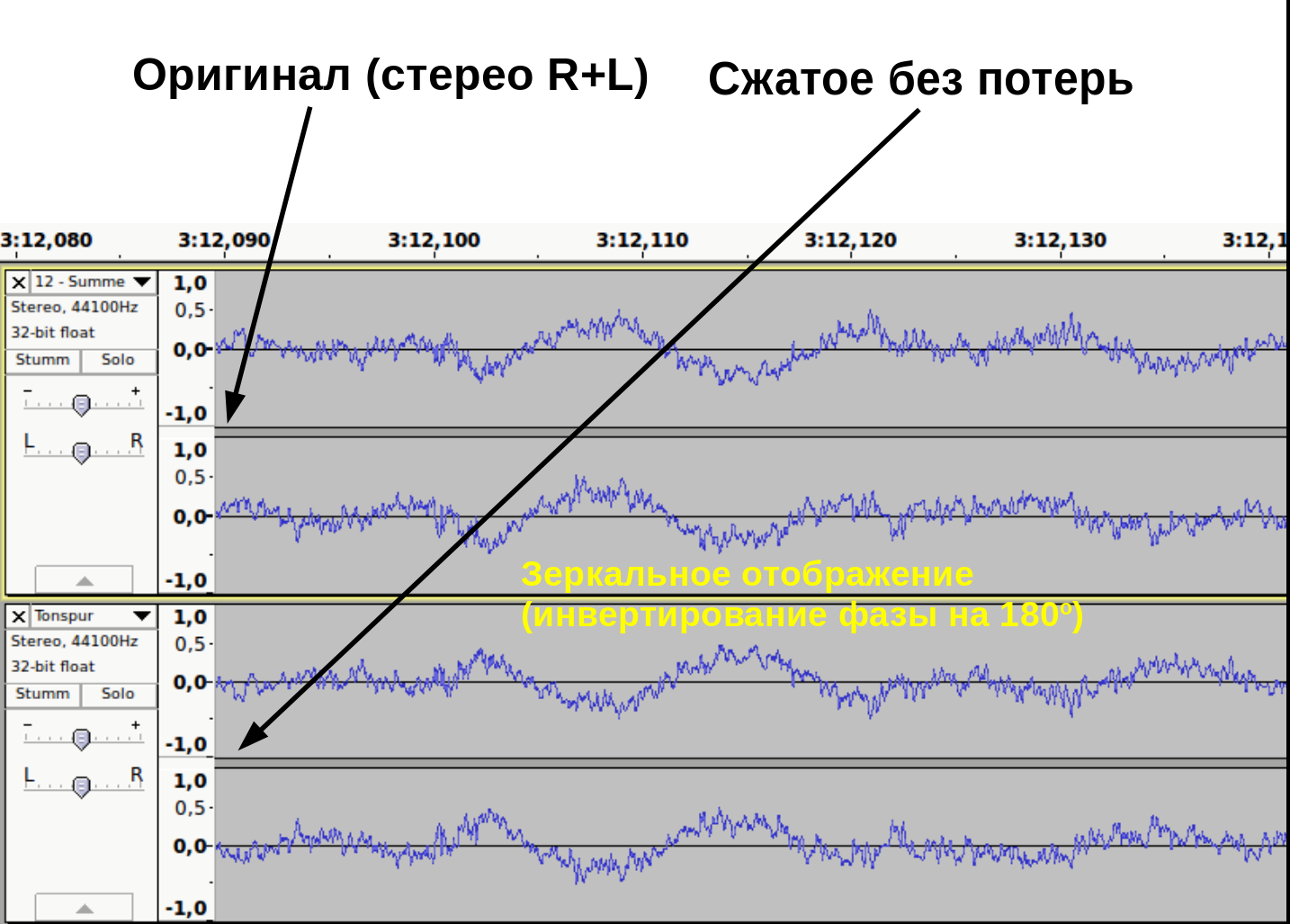
Кодеки сжатия без потерь: flac, WavPack, Monkey’s Audio…
При сжатии с потерями
акцент делается не на избежание потерь информации, а на спекуляцию с субъективными восприятиями (Психоакустика). Например, ухо взрослого человек обычно не воспринимает частоты выше 16kHz. Используя этот факт, кодек сжатия с потерями может просто жестко срезать все частоты выше 16kHz, так как «все равно никто не услышит разницу».
Другой пример — эффект маскировки. Слабые амплитуды, которые перекрываются сильными амплитудами, могут быть воспроизведены с меньшим качеством. При громких низких частотах тихие средние частоты не улавливаются ухом. Например, если присутствует звук в 1kHz с уровнем громкости в 80dB, то 2kHz-звук с громкостью 40dB больше не слышим.
Этим и пользуется кодек: 2kHz-звук можно убрать.
Спектральный анализ кодека mp3 с разными уровнями компрессии
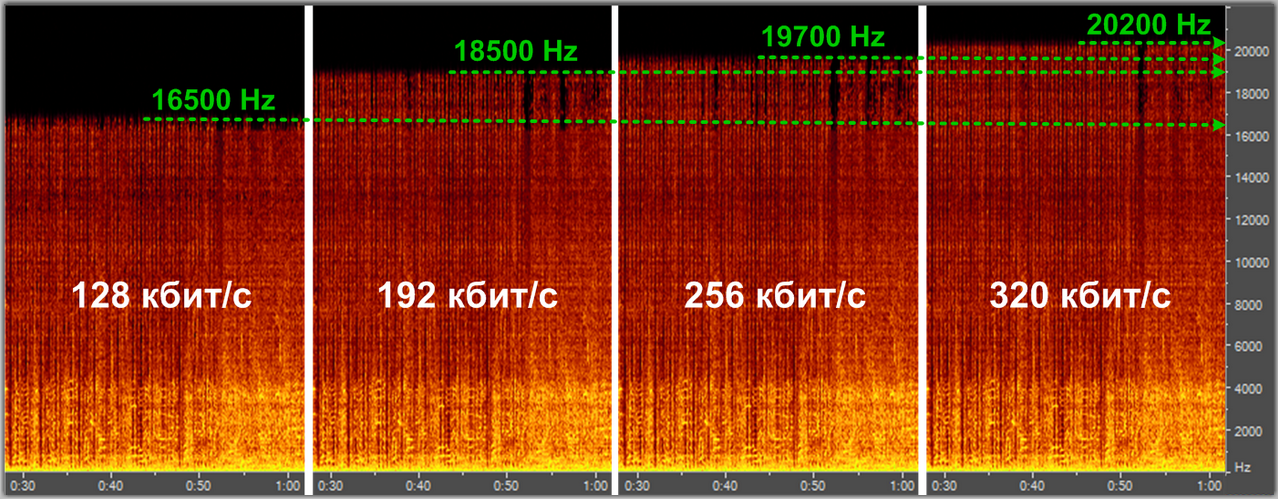
Кодеки сжатия с потерям: mp3, aac, ogg, wma, Musepack…
Спасибо за внимание.
UPD:
Если по каким-либо причинам аудиофайлы не загружаются, можете их скачать здесь: cloud.mail.ru/public/HbzU/YEsT34i4c

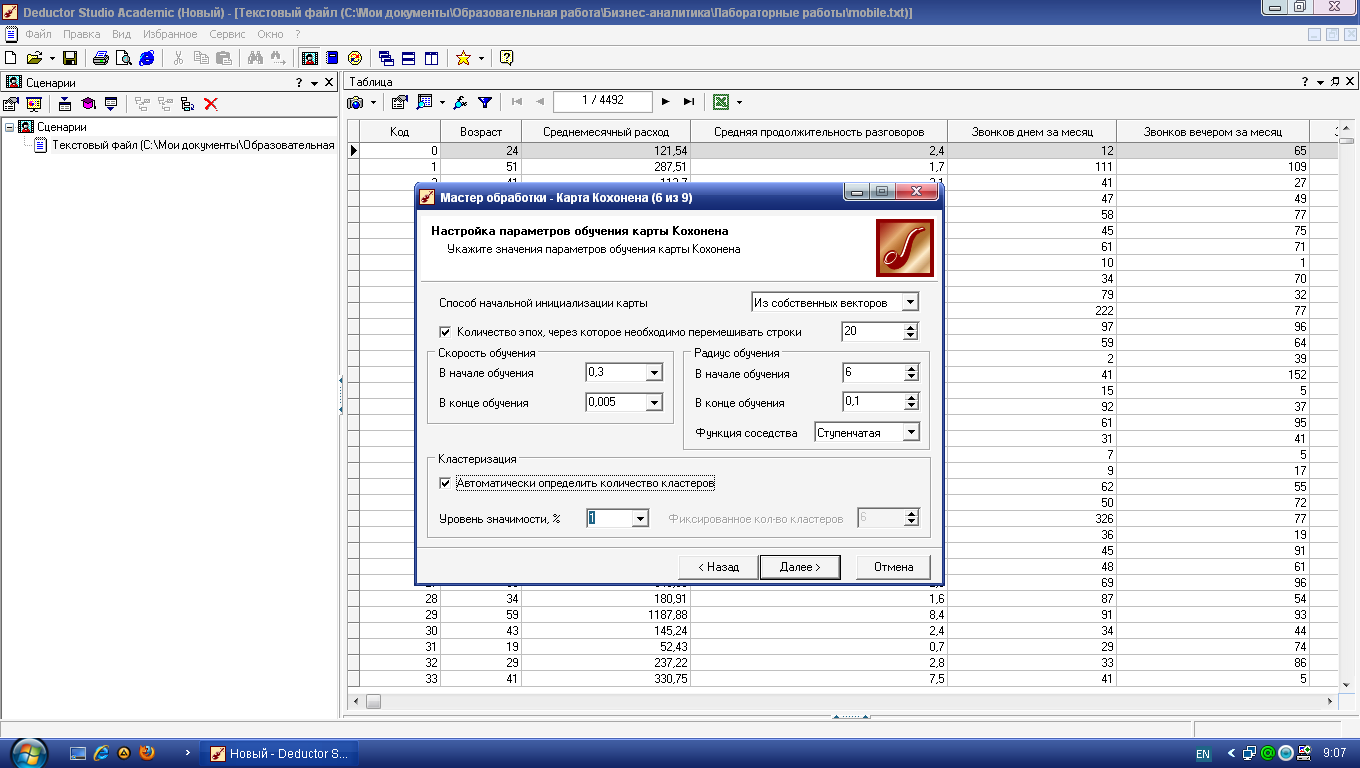
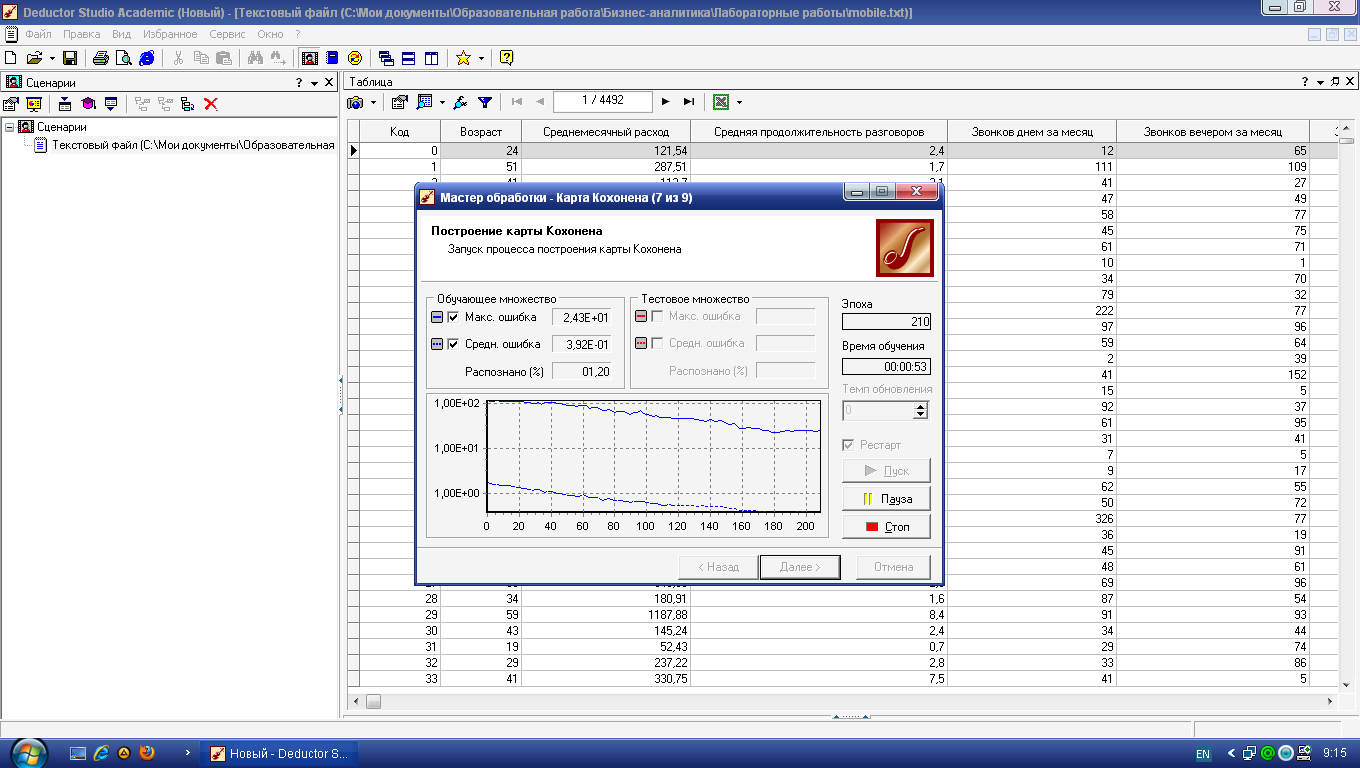
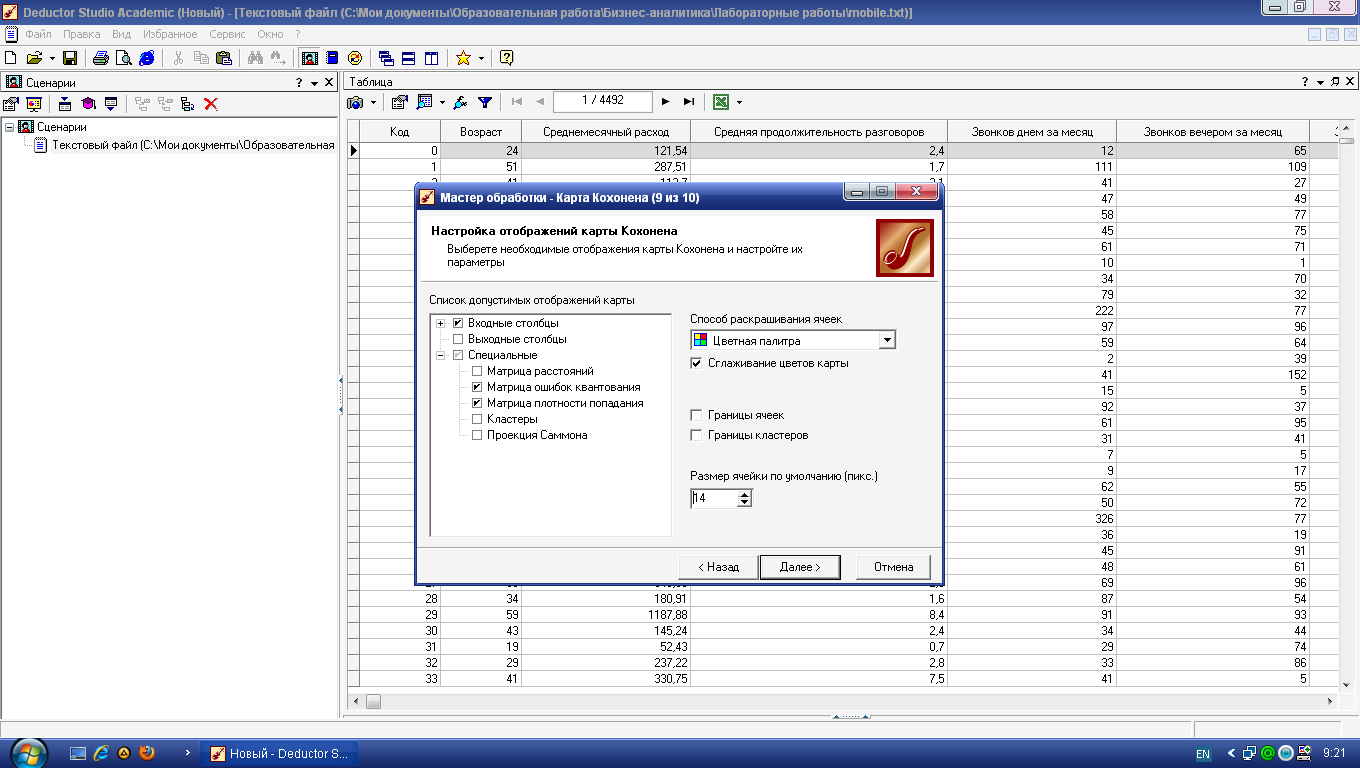
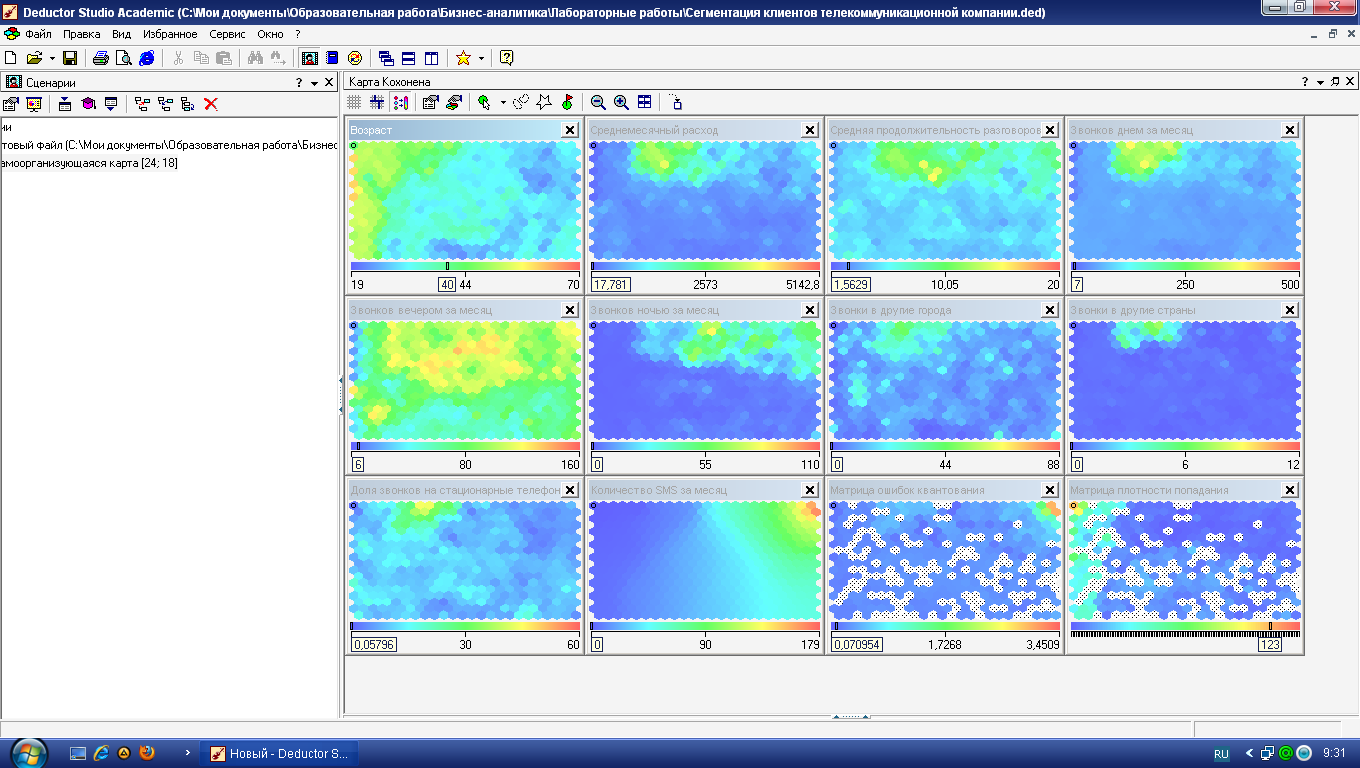
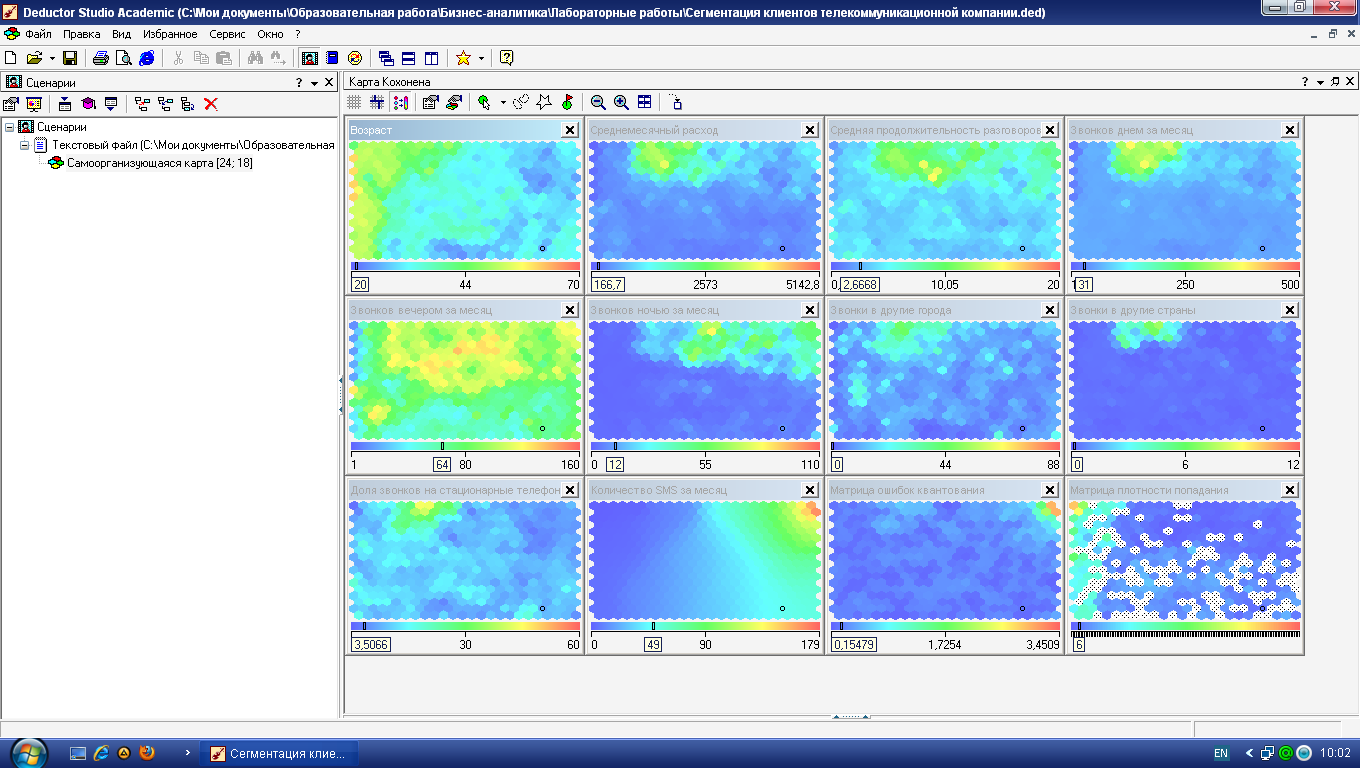
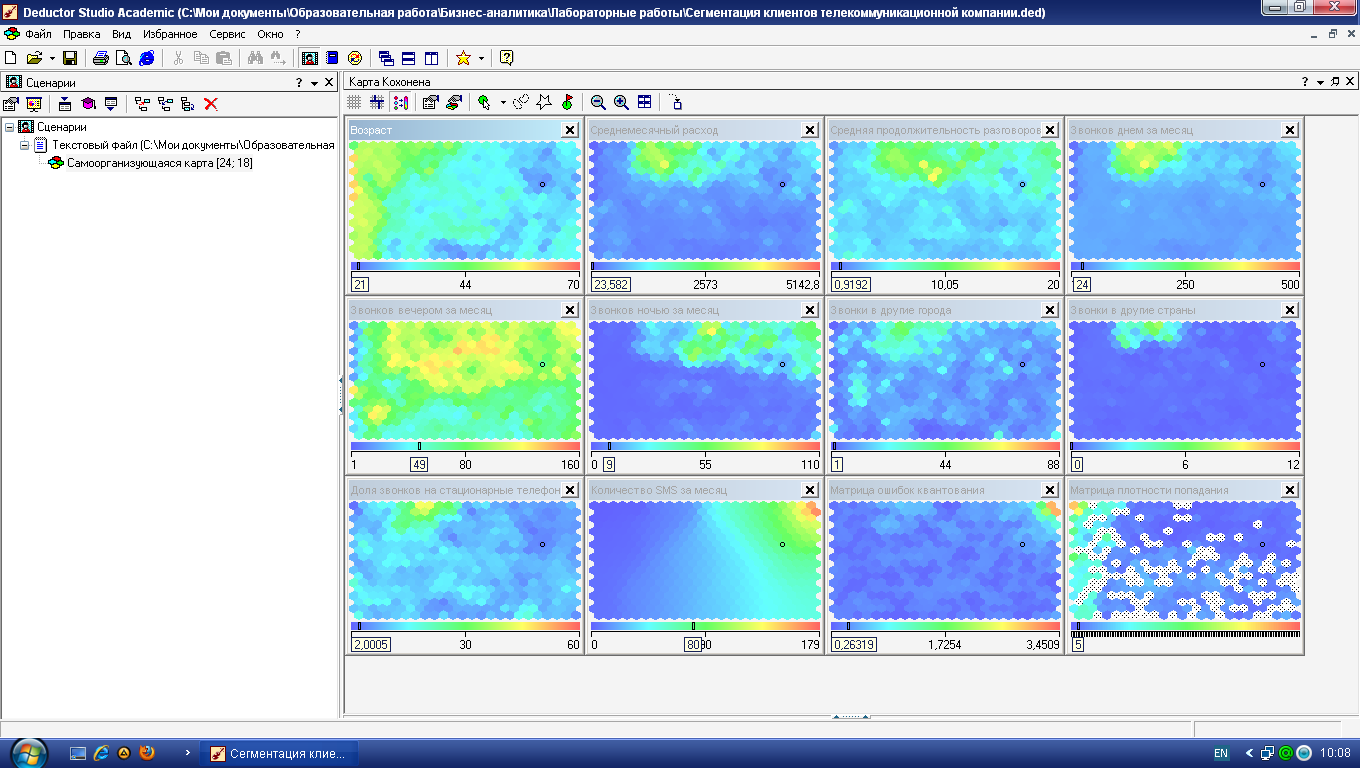

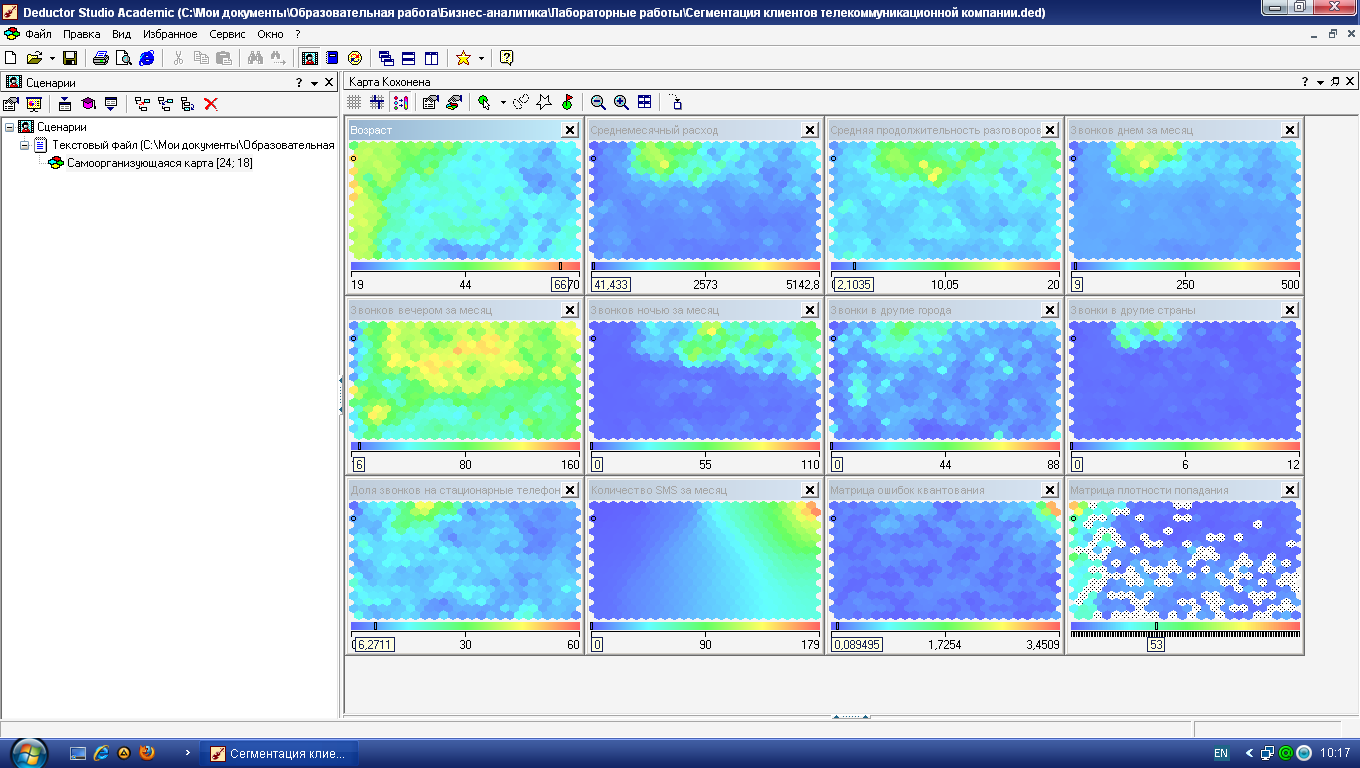
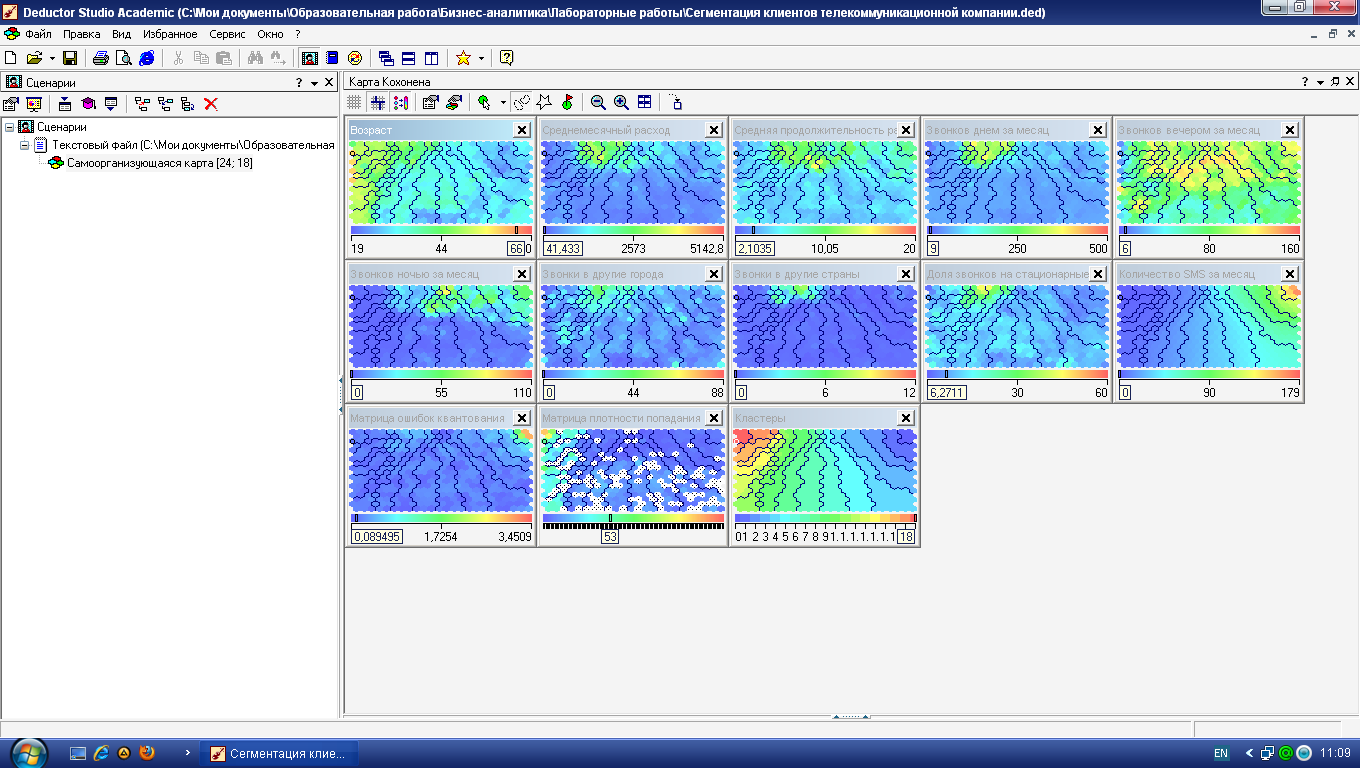
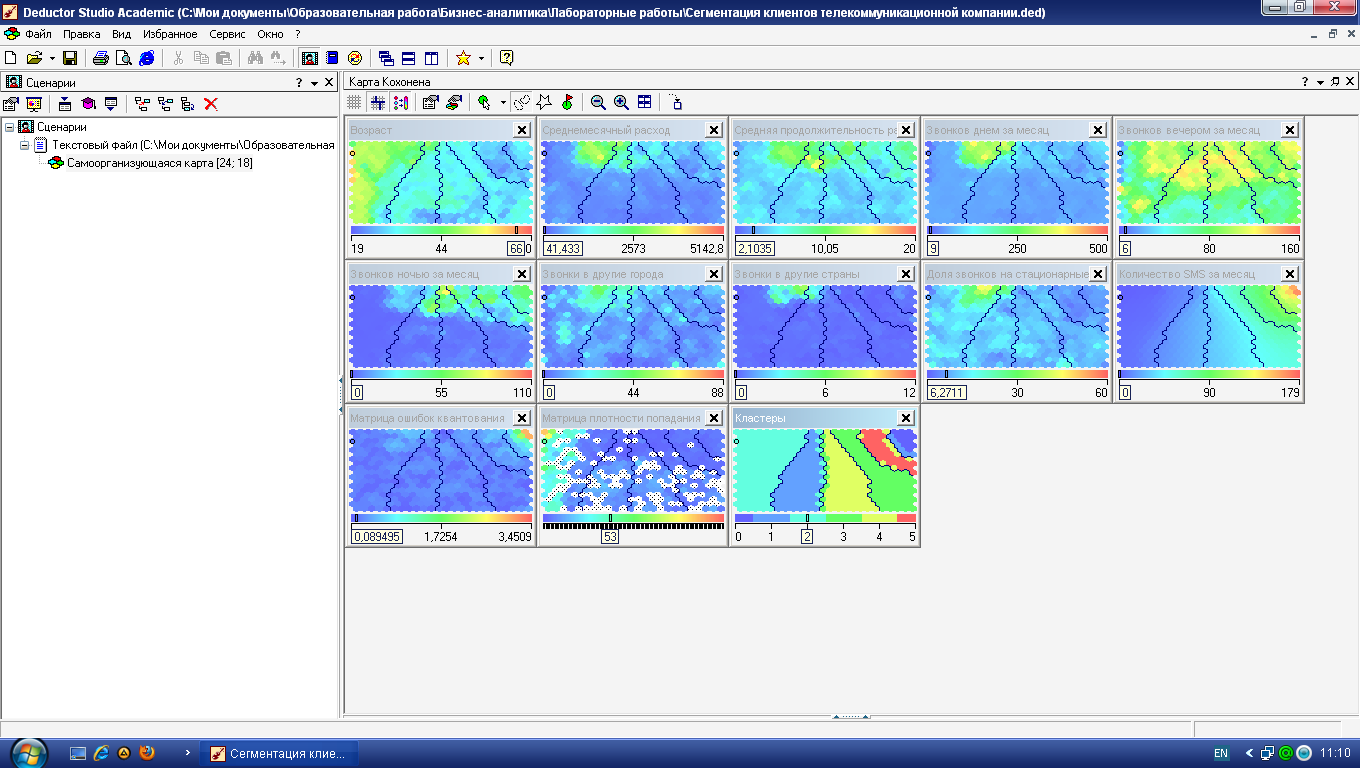







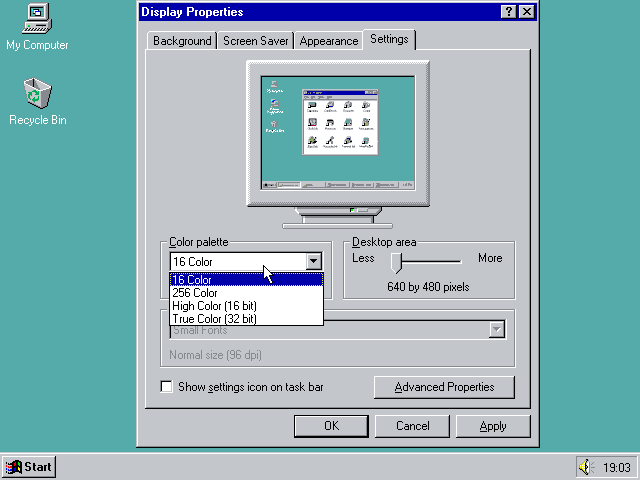
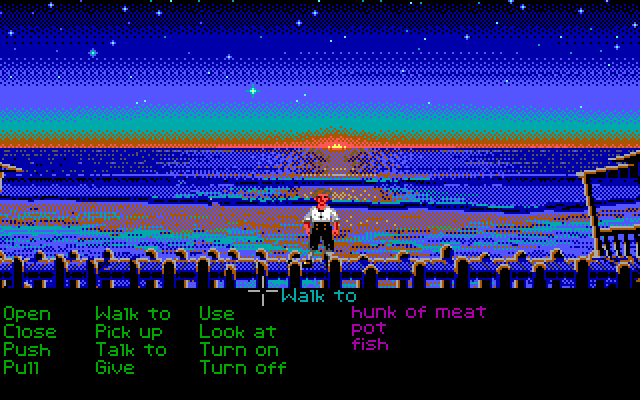




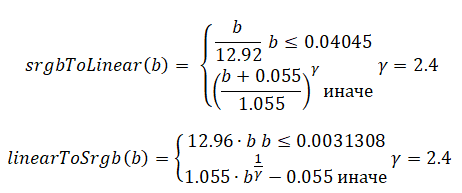

![К каждому пикселю перед квантованием добавлен случайный шум [-0.5; 0.5] К каждому пикселю перед квантованием добавлен случайный шум [-0.5; 0.5]](https://habrastorage.org/getpro/habr/upload_files/e3c/5c7/ebb/e3c5c7ebb28469d03e33342b53d75046.png)