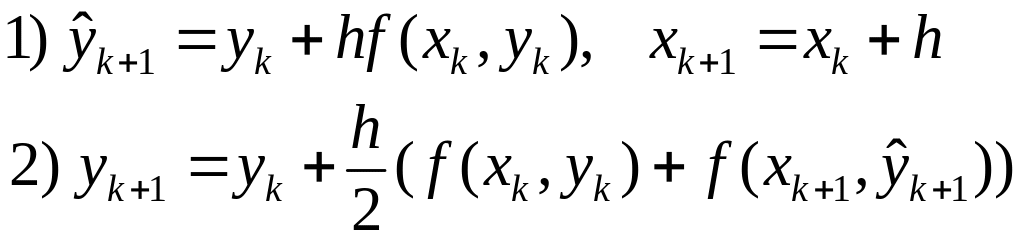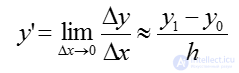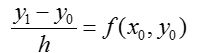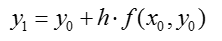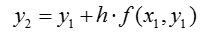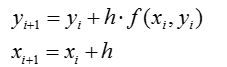Ошибка метода Эйлера
Представленный
метод аппроксимации решения задачи
Коши называется разностным. Решение
представляет собой совокупность
отдельных точек, называемых узловыми.
При
использовании разностных методов
существует два источника ошибок: ошибка
дискретизации, возникающая в результаты
замены дифференциального уравнения
разностной аппроксимацией (2.5), и ошибка
округления, накопившаяся при выполнении
арифметических операций. Будем считать,
что значения
вычисляются точно, так что погрешности
обусловлены только ошибкой дискретизации.
Введем величину, равную наибольшему
отклонению аппроксимации от точного
решения на отрезке
|
|
(3.1) |
называемую
глобальной
ошибкой дискретизации
(иногда эту величину называют глобальной
ошибкой усечения).
Отметим, что
зависит от величины шага
,
поскольку предполагается, что приближения
вычисляют при заданном значении
.
Интуитивно ожидаем, что при уменьшении
ошибка дискретизации будет убывать и,
в частности, при стремлении
к нулю, так же будет стремиться к нулю.
Теорема
(ошибка дискретизации метода Эйлера).
Если функция
имеет ограниченную частную производную
по второй переменной и если решение
задачи Коши имеет ограниченную вторую
производную, то глобальная ошибка
дискретизации метода Эйлера
.
Порядок
метода численного интегрирования
показывает, от какой степени шага зависит
величина ошибки.
Локальная
(или шаговая)
ошибка метода – это ошибка, совершаемая
на одном шаге. Очевидно, что от шага к
шагу, т. е. при многократном применении
формулы метода, возможно наложение
ошибок. За
шагов, т. е. в точке
,
образуется глобальная
ошибка.
Порядок
глобальной ошибки (относительно шага
)
на единицу ниже, чем порядок локальной
ошибки, а порядком глобальной ошибки и
определяется порядок соответствующего
численного процесса решения задачи
Коши.
Глобальная
ошибка метода Эйлера есть
,
т. е. данный метод имеет первый порядок.
Иными словами, размер шага и ошибка для
метода Эйлера связаны линейно. Практическим
следствием этого факта является ожидание
того, что при уменьшении
приближенное решение будет все более
точным и при стремлении
к нулю будет стремиться к точному решению
с линейной скоростью
;
т.е. ожидаем, что при уменьшении шага
вдвое ошибка уменьшится примерно в два
раза. Такое поведение ошибки демонстрируется
на следующем примере.
Поскольку
в методе Эйлера ошибка достаточно велика
и от шага к шагу накапливается, а точность
пропорциональна количеству вычислений,
то метод Эйлера обычно применяют для
грубых расчетов, для оценки поведения
системы в принципе. Для точных
количественных расчетов применяют
более точные методы.
Метод Хьюна
Следующий
подход представляет новую идею построения
алгоритмов решения задачи Коши. Пусть
|
на с начальным условием |
Для
получения решения в точке
,
можем воспользоваться теоремой о
вычислнии определенного интеграла:
|
|
где
первообразная от
является
искомой функцией
.
Если разрешить уравнение последнее
уравнение относительно
,
получим
|
|
Теперь
можно применить численные методы
нахождения интеграла. Воспользуемся
методом трапеций с шагом
,
получим:
|
|
Правая
часть формулы включает в себя еще не
найденное значение
.
Для его нахождения воспользуемся методом
Эйлера. Получим конечную формулу,
именуемую методом
Хьюна (синонимы:
метод
Хойна,
метод
Эйлера-Коши):
|
|
Продолжая
процесс, получим последовательность
точек, аппроксимирующих кривую решения
.
Метод Хьюна относится к классу методов
прогноза-коррекции. На каждом шаге метод
Эйлера используется для предсказания,
а метод трапеций для уточнения конечного
значения. Общие формулы для шага метода
Хьюна:
|
|
Соседние файлы в предмете [НЕСОРТИРОВАННОЕ]
- #
- #
- #
- #
- #
- #
- #
- #
- #
- #
- #
(Figure 1) Illustration of the Euler method. The unknown curve is in blue, and its polygonal approximation is in red.
In mathematics and computational science, the Euler method (also called the forward Euler method) is a first-order numerical procedure for solving ordinary differential equations (ODEs) with a given initial value. It is the most basic explicit method for numerical integration of ordinary differential equations and is the simplest Runge–Kutta method. The Euler method is named after Leonhard Euler, who first proposed it in his book Institutionum calculi integralis (published 1768–1870).[1]
The Euler method is a first-order method, which means that the local error (error per step) is proportional to the square of the step size, and the global error (error at a given time) is proportional to the step size.
The Euler method often serves as the basis to construct more complex methods, e.g., predictor–corrector method.
Geometrical description[edit]
Purpose and why it works[edit]
Consider the problem of calculating the shape of an unknown curve which starts at a given point and satisfies a given differential equation. Here, a differential equation can be thought of as a formula by which the slope of the tangent line to the curve can be computed at any point on the curve, once the position of that point has been calculated.
The idea is that while the curve is initially unknown, its starting point, which we denote by 

Take a small step along that tangent line up to a point 




First-order process[edit]
When given the values for 











The value of 





Higher-order process[edit]
While the Euler method integrates a first-order ODE, any ODE of order 

we implement the following formula until we reach the approximation of the solution to the ODE at the desired time:
These first-order systems can be handled by Euler’s method or, in fact, by any other scheme for first-order systems.[4]
Example[edit]
Given the initial value problem
we would like to use the Euler method to approximate 
Using step size equal to 1 (h = 1)[edit]
(Figure 2) Illustration of numerical integration for the equation 

The Euler method is
so first we must compute 


By doing the above step, we have found the slope of the line that is tangent to the solution curve at the point 



The next step is to multiply the above value by the step size 
Since the step size is the change in 


The above steps should be repeated to find 


Due to the repetitive nature of this algorithm, it can be helpful to organize computations in a chart form, as seen below, to avoid making errors.
-
0 1 0 1 1 1 2 1 2 1 2 1 2 4 2 4 2 4 1 4 8 3 8 3 8 1 8 16
The conclusion of this computation is that 



Using other step sizes[edit]
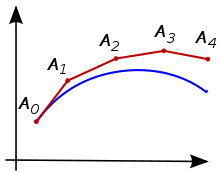
(Figure 3) The same illustration for
As suggested in the introduction, the Euler method is more accurate if the step size 
-
step size result of Euler’s method error 1 16.00 38.60 0.25 35.53 19.07 0.1 45.26 09.34 0.05 49.56 05.04 0.025 51.98 02.62 0.0125 53.26 01.34
The error recorded in the last column of the table is the difference between the exact solution at 
Other methods, such as the midpoint method also illustrated in the figures, behave more favourably: the global error of the midpoint method is roughly proportional to the square of the step size. For this reason, the Euler method is said to be a first-order method, while the midpoint method is second order.
We can extrapolate from the above table that the step size needed to get an answer that is correct to three decimal places is approximately 0.00001, meaning that we need 400,000 steps. This large number of steps entails a high computational cost. For this reason, higher-order methods are employed such as Runge–Kutta methods or linear multistep methods, especially if a high accuracy is desired.[6]
Derivation[edit]
The Euler method can be derived in a number of ways. Firstly, there is the geometrical description above.
Another possibility is to consider the Taylor expansion of the function 

The differential equation states that 
A closely related derivation is to substitute the forward finite difference formula for the derivative,
in the differential equation 
Finally, one can integrate the differential equation from 

Now approximate the integral by the left-hand rectangle method (with only one rectangle):
Combining both equations, one finds again the Euler method.[9] This line of thought can be continued to arrive at various linear multistep methods.
Local truncation error[edit]
The local truncation error of the Euler method is the error made in a single step. It is the difference between the numerical solution after one step, 

For the exact solution, we use the Taylor expansion mentioned in the section Derivation above:
The local truncation error (LTE) introduced by the Euler method is given by the difference between these equations:
This result is valid if 
This shows that for small 


A slightly different formulation for the local truncation error can be obtained by using the Lagrange form for the remainder term in Taylor’s theorem. If 
![xi in [t_{0},t_{0}+h]](https://wikimedia.org/api/rest_v1/media/math/render/svg/21216efa1ba4d1d6558385ff51b38a37f3ffc42f)
[11]
In the above expressions for the error, the second derivative of the unknown exact solution 

Global truncation error[edit]
The global truncation error is the error at a fixed time 




This intuitive reasoning can be made precise. If the solution 


where 




![{textstyle L={text{max}}{bigl (}{frac {d}{dy}}{bigl [}f(t,y){bigr ]}{bigr )}}](https://wikimedia.org/api/rest_v1/media/math/render/svg/ba728dd212212c1c8a66e2d520cccefb2eb4a3c5)

![{textstyle M={text{max}}{bigl (}{frac {d^{2}}{dt^{2}}}{bigl [}y(t){bigr ]}{bigr )}}](https://wikimedia.org/api/rest_v1/media/math/render/svg/c177ecf4975a19fed7289dabbce7aa2b74a1e555)


The precise form of this bound is of little practical importance, as in most cases the bound vastly overestimates the actual error committed by the Euler method.[16] What is important is that it shows that the global truncation error is (approximately) proportional to 
Numerical stability[edit]
(Figure 4) Solution of 


The Euler method can also be numerically unstable, especially for stiff equations, meaning that the numerical solution grows very large for equations where the exact solution does not. This can be illustrated using the linear equation
The exact solution is 



(Figure 5) The pink disk shows the stability region for the Euler method.
If the Euler method is applied to the linear equation 

illustrated on the right. This region is called the (linear) stability region.[18] In the example, 


This limitation — along with its slow convergence of error with 
Rounding errors[edit]
In step 



Modifications and extensions[edit]
A simple modification of the Euler method which eliminates the stability problems noted above is the backward Euler method:
This differs from the (standard, or forward) Euler method in that the function 

Other modifications of the Euler method that help with stability yield the exponential Euler method or the semi-implicit Euler method.
More complicated methods can achieve a higher order (and more accuracy). One possibility is to use more function evaluations. This is illustrated by the midpoint method which is already mentioned in this article:
.
This leads to the family of Runge–Kutta methods.
The other possibility is to use more past values, as illustrated by the two-step Adams–Bashforth method:
This leads to the family of linear multistep methods. There are other modifications which uses techniques from compressive sensing to minimize memory usage[21]
In popular culture[edit]
In the film Hidden Figures, Katherine Goble resorts to the Euler method in calculating the re-entry of astronaut John Glenn from Earth orbit.[22]
See also[edit]
- Crank–Nicolson method
- Gradient descent similarly uses finite steps, here to find minima of functions
- List of Runge-Kutta methods
- Linear multistep method
- Numerical integration (for calculating definite integrals)
- Numerical methods for ordinary differential equations
Notes[edit]
- ^ Butcher 2003, p. 45; Hairer, Nørsett & Wanner 1993, p. 35
- ^ Atkinson 1989, p. 342; Butcher 2003, p. 60
- ^ Butcher 2003, p. 45; Hairer, Nørsett & Wanner 1993, p. 36
- ^ Butcher 2003, p. 3; Hairer, Nørsett & Wanner 1993, p. 2
- ^ See also Atkinson 1989, p. 344
- ^ Hairer, Nørsett & Wanner 1993, p. 40
- ^ Atkinson 1989, p. 342; Hairer, Nørsett & Wanner 1993, p. 36
- ^ Atkinson 1989, p. 342
- ^ Atkinson 1989, p. 343
- ^ Butcher 2003, p. 60
- ^ Atkinson 1989, p. 342
- ^ Stoer & Bulirsch 2002, p. 474
- ^ Atkinson 1989, p. 344
- ^ Butcher 2003, p. 49
- ^ Atkinson 1989, p. 346; Lakoba 2012, equation (1.16)
- ^ Iserles 1996, p. 7
- ^ Butcher 2003, p. 63
- ^ Butcher 2003, p. 70; Iserles 1996, p. 57
- ^ Butcher 2003, pp. 74–75
- ^ Butcher 2003, pp. 75–78
- ^ Unni, M. P.; Chandra, M. G.; Kumar, A. A. (March 2017). «Memory reduction for numerical solution of differential equations using compressive sensing». 2017 IEEE 13th International Colloquium on Signal Processing Its Applications (CSPA): 79–84. doi:10.1109/CSPA.2017.8064928. ISBN 978-1-5090-1184-1. S2CID 13082456.
- ^ Khan, Amina (9 January 2017). «Meet the ‘Hidden Figures’ mathematician who helped send Americans into space». Los Angeles Times. Retrieved 12 February 2017.
References[edit]
- Atkinson, Kendall A. (1989). An Introduction to Numerical Analysis (2nd ed.). New York: John Wiley & Sons. ISBN 978-0-471-50023-0.
- Ascher, Uri M.; Petzold, Linda R. (1998). Computer Methods for Ordinary Differential Equations and Differential-Algebraic Equations. Philadelphia: Society for Industrial and Applied Mathematics. ISBN 978-0-89871-412-8.
- Butcher, John C. (2003). Numerical Methods for Ordinary Differential Equations. New York: John Wiley & Sons. ISBN 978-0-471-96758-3.
- Hairer, Ernst; Nørsett, Syvert Paul; Wanner, Gerhard (1993). Solving ordinary differential equations I: Nonstiff problems. Berlin, New York: Springer-Verlag. ISBN 978-3-540-56670-0.
- Iserles, Arieh (1996). A First Course in the Numerical Analysis of Differential Equations. Cambridge University Press. ISBN 978-0-521-55655-2.
- Stoer, Josef; Bulirsch, Roland (2002). Introduction to Numerical Analysis (3rd ed.). Berlin, New York: Springer-Verlag. ISBN 978-0-387-95452-3.
- Lakoba, Taras I. (2012), Simple Euler method and its modifications (PDF) (Lecture notes for MATH334), University of Vermont, retrieved 29 February 2012
- Unni, M P. (2017). «Memory reduction for numerical solution of differential equations using compressive sensing». 2017 IEEE 13th International Colloquium on Signal Processing & its Applications (CSPA). IEEE CSPA. pp. 79–84. doi:10.1109/CSPA.2017.8064928. ISBN 978-1-5090-1184-1. S2CID 13082456.
External links[edit]
Media related to Euler method at Wikimedia Commons
- Euler method implementations in different languages by Rosetta Code
- «Euler method», Encyclopedia of Mathematics, EMS Press, 2001 [1994]
Иллюстрация метода Эйлера. Неизвестная кривая отображается синим цветом, а ее полигональная аппроксимация — красным.
В математика и вычислительная наука, то Метод Эйлера (также называемый прямой метод Эйлера) является первым порядком числовой процедура решения обыкновенные дифференциальные уравнения (ODE) с заданным Первоначальный значение. Это самый простой явный метод за численное интегрирование обыкновенных дифференциальных уравнений и это самый простой Метод Рунге – Кутты. Метод Эйлера назван в честь Леонард Эйлер, который лечил это в своей книге Institutionum Calculi Integratedis (опубликовано 1768–1870 гг.).[1]
Метод Эйлера — это метод первого порядка, что означает, что локальная ошибка (ошибка на шаг) пропорциональна квадрату размера шага, а глобальная ошибка (ошибка в данный момент времени) пропорциональна размеру шага. Метод Эйлера часто служит основой для построения более сложных методов, например, метод предиктора – корректора.
Неформальное геометрическое описание
Рассмотрим задачу вычисления формы неизвестной кривой, которая начинается в данной точке и удовлетворяет данному дифференциальному уравнению. Здесь дифференциальное уравнение можно представить как формулу, по которой склон из касательная линия к кривой можно вычислить в любой точке кривой, после того как положение этой точки будет вычислено.
Идея состоит в том, что, хотя кривая изначально неизвестна, ее начальная точка, которую мы обозначим 

Сделайте небольшой шаг по касательной до точки 




Выберите значение 



Значение 





Хотя метод Эйлера интегрирует ОДУ первого порядка, любое ОДУ порядка N можно представить в виде системы ОДУ первого порядка: для обработки уравнения
,
введем вспомогательные переменные 
Это система первого порядка по переменной 
Пример
Учитывая проблему начального значения
мы хотели бы использовать метод Эйлера для аппроксимации 
Используя размер шага равный 1 (час = 1)
Иллюстрация численного интегрирования уравнения 

Метод Эйлера
поэтому сначала мы должны вычислить 


Выполнив вышеуказанный шаг, мы нашли наклон линии, касательной к кривой решения в точке 



Следующим шагом будет умножение указанного выше значения на размер шага. 
Поскольку размер шага — это изменение 


Вышеуказанные шаги следует повторить, чтобы найти 


Из-за повторяющегося характера этого алгоритма может быть полезно организовать вычисления в виде диаграммы, как показано ниже, чтобы избежать ошибок.
-
0 1 0 1 1 1 2 1 2 1 2 1 2 4 2 4 2 4 1 4 8 3 8 3 8 1 8 16
Вывод этого вычисления заключается в том, что 



Пример кода MATLAB
Чисто; clc; Закрыть('все');y0 = 1;t0 = 0;час = 1; % попытка: h = 0,01tn = 4; % равно: t0 + h * n, где n - количество шагов[т, у] = Эйлер(t0, y0, час, tn);участок(т, у, 'b');% точное решение (y = e ^ t):тт = (t0:0.001:tn);гг = exp(тт);держать('на');участок(тт, гг, 'р');держать('выключенный');легенда('Эйлер', 'Точный');функция [t, y] = Эйлер (t0, y0, h, tn) fprintf('% 10s% 10s% 10s% 15s n', 'я', 'yi', 'ти', 'ф (йи, ти)'); fprintf('% 10d% + 10.2f% + 10.2f% + 15.2f n', 0, y0, t0, ж(y0, t0)); т = (t0:час:tn)'; у = нули(размер(т)); у(1) = y0; за i = 1: 1: длина (t) - 1 у(я + 1) = у(я) + час * ж(у(я), т(я)); fprintf('% 10d% + 10.2f% + 10.2f% + 15.2f n', я, у(я + 1), т(я + 1), ж(у(я + 1), т(я + 1))); конецконец% в этом случае f (y, t) = f (y)функцияdydt =ж(у, т)dydt = у;конец% ВЫХОД:% i yi ti f (yi, ti)% 0 +1.00 +0.00 +1.00% 1 +2.00 +1.00 +2.00% 2 +4.00 +2.00 +4.00% 3 +8.00 +3.00 +8.00% 4 +16.00 +4.00 +16.00% ПРИМЕЧАНИЕ: Код также выводит сравнительный график
Пример кода R
Графический вывод кода языка программирования R для поставленного примера
Ниже приведен код примера в Язык программирования R.
# ============# РЕШЕНИЕ# y '= y, где y' = f (t, y)# тогда:ж <- функция(ти,у) у# НАЧАЛЬНЫЕ ЗНАЧЕНИЯ:t0 <- 0y0 <- 1час <- 1tn <- 4# Метод Эйлера: определение функцииЭйлер <- функция(t0, y0, час, tn, dy.dt) { # dy.dt: производная функция # t последовательность: тт <- seq(t0, tn, к=час) # таблица с количеством строк, равным tt элементов: таблица <- data.frame(ти=тт) таблица$йи <- y0 # Инициализирует yi с y0 таблица$Dy.dt [1] <- dy.dt(таблица$ти [1],y0) # производная за (я в 2:Nrow(таблица)) { таблица$yi [i] <- таблица$йи [я-1] + час*таблица$Dy.dt [i-1] # Для следующей итерации: таблица$Dy.dt [i] <- dy.dt(таблица$ти [я],таблица$yi [i]) } возвращаться(таблица)}# Метод Эйлера: применение функциир <- Эйлер(t0, y0, час, tn, ж)rownames(р) <- 0:(Nrow(р)-1) # совпадать с индексом n# Точное решение для этого случая: y = exp (t)# добавлен как дополнительный столбец к rр$у <- exp(р$ти)# ТАБЛИЦА с результатами:Распечатать(р)участок(р$ти, р$у, тип="л", Col="красный", lwd=2)линии(р$ти, р$йи, Col="синий", lwd=2)сетка(Col="чернить")легенда("верх", легенда = c("Точный", «Эйлер»), lwd=2, Col = c("красный", "синий"))# ВЫХОД:## ti yi Dy.dt y# 0 0 1 1 1.000000# 1 1 2 2 2.718282# 2 2 4 4 7.389056# 3 3 8 8 20.085537# 4 4 16 16 54.598150# ПРИМЕЧАНИЕ: Код также выводит график сравнения
Использование других размеров шага
Та же иллюстрация для час = 0.25.
Как было предложено во введении, метод Эйлера более точен, если размер шага 
-
размер шага результат метода Эйлера ошибка 1 16.00 38.60 0.25 35.53 19.07 0.1 45.26 9.34 0.05 49.56 5.04 0.025 51.98 2.62 0.0125 53.26 1.34
Ошибка, записанная в последнем столбце таблицы, представляет собой разницу между точным решением при 
Другие методы, такие как метод средней точки также показано на рисунках, ведут себя более благоприятно: глобальная ошибка метода средней точки примерно пропорциональна квадрат размера шага. По этой причине метод Эйлера называется методом первого порядка, а метод средней точки — методом второго порядка.
Мы можем экстраполировать из приведенной выше таблицы, что размер шага, необходимый для получения ответа, верного с точностью до трех десятичных знаков, составляет приблизительно 0,00001, что означает, что нам нужно 400 000 шагов. Такое большое количество шагов влечет за собой большие вычислительные затраты. По этой причине люди обычно используют альтернативные методы более высокого порядка, такие как Методы Рунге – Кутты или же линейные многоступенчатые методы, особенно если требуется высокая точность.[6]
Вывод
Метод Эйлера можно получить разными способами. Во-первых, это геометрическое описание выше.
Другая возможность — рассмотреть Расширение Тейлора функции 

Дифференциальное уравнение утверждает, что 
Близко родственный вывод — замена форвардного конечная разница формула для производной,
в дифференциальном уравнении 
Наконец, можно проинтегрировать дифференциальное уравнение из 

Теперь аппроксимируем интеграл левой метод прямоугольника (только с одним прямоугольником):
Комбинируя оба уравнения, мы снова получаем метод Эйлера.[9] Эту мысль можно продолжить, чтобы прийти к различным линейные многоступенчатые методы.
Ошибка локального усечения
В локальная ошибка усечения метода Эйлера — это ошибка, сделанная за один шаг. Это разница между численным решением после одного шага, 

Для точного решения воспользуемся разложением Тейлора, упомянутым в разделе Вывод над:
Локальная ошибка усечения (LTE), вносимая методом Эйлера, определяется разницей между этими уравнениями:
Этот результат действителен, если 
Это показывает, что для небольших 


Несколько иную формулировку локальной ошибки усечения можно получить, используя форму Лагранжа для остаточного члена в Теорема Тейлора. Если 
![xi in [t_ {0}, t_ {0} + h]](https://wikimedia.org/api/rest_v1/media/math/render/svg/21216efa1ba4d1d6558385ff51b38a37f3ffc42f)
[11]
В приведенных выше выражениях для ошибки вторая производная неизвестного точного решения 

[12]
Глобальная ошибка усечения
В глобальная ошибка усечения ошибка в фиксированное время 




Это интуитивное рассуждение можно уточнить. Если решение 

куда 



Точная форма этой границы не имеет большого практического значения, так как в большинстве случаев оценка значительно переоценивает фактическую ошибку, допущенную методом Эйлера.[16] Важно то, что он показывает, что глобальная ошибка усечения (приблизительно) пропорциональна 
Численная стабильность
Решение 


Метод Эйлера также можно численно неустойчивый, особенно для жесткие уравнения, что означает, что численное решение становится очень большим для уравнений, в которых нет точного решения. Это можно проиллюстрировать с помощью линейного уравнения
Точное решение 



Розовый диск показывает область устойчивости метода Эйлера.
Если применить метод Эйлера к линейному уравнению 

показано справа. Эта область называется (линейной) регион стабильности.[18] В этом примере 


Это ограничение, наряду с медленной сходимостью ошибки с час— означает, что метод Эйлера используется нечасто, за исключением простого примера численного интегрирования.
Ошибки округления
Обсуждение до сих пор игнорировало последствия ошибка округления. В ногу п метода Эйлера ошибка округления примерно равна величине εуп где ε — машина эпсилон. Предполагая, что все ошибки округления примерно одинакового размера, объединенная ошибка округления в N шаги примерно Nεу0 если все ошибки указывают в одном направлении. Поскольку количество шагов обратно пропорционально размеру шага час, полная ошибка округления пропорциональна ε / час. В действительности, однако, крайне маловероятно, что все ошибки округления указывают в одном направлении. Если вместо этого предполагается, что ошибки округления являются независимыми случайными величинами, то ожидаемая общая ошибка округления пропорциональна 
Таким образом, для чрезвычайно малых значений размера шага ошибка усечения будет небольшой, но эффект ошибки округления может быть большим. Большей части эффекта ошибки округления можно легко избежать, если компенсированное суммирование используется в формуле метода Эйлера.[20]
Модификации и расширения
Простая модификация метода Эйлера, которая устраняет проблемы устойчивости, отмеченные в предыдущем разделе, — это обратный метод Эйлера:
Он отличается от (стандартного или прямого) метода Эйлера тем, что функция 

Другие модификации метода Эйлера, способствующие устойчивости, дают экспоненциальный метод Эйлера или полунеявный метод Эйлера.
Более сложные методы позволяют достичь более высокого порядка (и большей точности). Одна из возможностей — использовать больше оценок функций. Это иллюстрируется метод средней точки о котором уже упоминалось в этой статье:
.
Это приводит к семье Методы Рунге – Кутты.
Другая возможность — использовать больше прошлых значений, как показано двухэтапным методом Адамса – Башфорта:
Это приводит к семье линейные многоступенчатые методы. Существуют и другие модификации, в которых используются методы сжатия данных для минимизации использования памяти.[21]
В популярной культуре
В фильме Скрытые фигуры, Кэтрин Гобл прибегает к методу Эйлера при расчете повторного входа космонавта Джон Гленн с околоземной орбиты.[22]
Смотрите также
- Метод Кранка – Николсона
- Градиентный спуск аналогично использует конечные шаги, чтобы найти минимум функций
- Список методов Рунге-Кутта
- Линейный многоступенчатый метод
- Численное интегрирование (для вычисления определенных интегралов)
- Численные методы решения обыкновенных дифференциальных уравнений
Примечания
- ^ Мясник 2003, п. 45; Хайрер, Норсетт и Ваннер, 1993 г., п. 35 год
- ^ Аткинсон 1989, п. 342; Мясник 2003, п. 60
- ^ Мясник 2003, п. 45; Хайрер, Норсетт и Ваннер, 1993 г., п. 36
- ^ Мясник 2003, п. 3; Хайрер, Норсетт и Ваннер, 1993 г., п. 2
- ^ Смотрите также Аткинсон 1989, п. 344
- ^ Хайрер, Норсетт и Ваннер, 1993 г., п. 40
- ^ Аткинсон 1989, п. 342; Хайрер, Норсетт и Ваннер, 1993 г., п. 36
- ^ Аткинсон 1989, п. 342
- ^ Аткинсон 1989, п. 343
- ^ Мясник 2003, п. 60
- ^ Аткинсон 1989, п. 342
- ^ Stoer & Bulirsch, 2002 г., п. 474
- ^ Аткинсон 1989, п. 344
- ^ Мясник 2003, п. 49
- ^ Аткинсон 1989, п. 346; Лакоба 2012, уравнение (1.16)
- ^ Изерлес 1996, п. 7
- ^ Мясник 2003, п. 63
- ^ Мясник 2003, п. 70; Изерлес 1996, п. 57
- ^ Мясник 2003, стр. 74–75
- ^ Мясник 2003, стр. 75–78
- ^ Unni, M. P .; Chandra, M. G .; Кумар, А. А. (март 2017 г.). «Сокращение памяти для численного решения дифференциальных уравнений с использованием сжатия». 13-й Международный коллоквиум IEEE по приложениям обработки сигналов (CSPA), 2017 г.: 79–84. Дои:10.1109 / CSPA.2017.8064928. ISBN 978-1-5090-1184-1. S2CID 13082456.
- ^ Хан, Амина. «Познакомьтесь с математиком« Скрытых фигур », который помог отправить американцев в космос». Лос-Анджелес Таймс. Получено 12 февраля 2017.
Рекомендации
- Аткинсон, Кендалл А. (1989). Введение в численный анализ (2-е изд.). Нью-Йорк: Джон Уайли и сыновья. ISBN 978-0-471-50023-0.
- Ascher, Uri M .; Петцольд, Линда Р. (1998). Компьютерные методы решения обыкновенных дифференциальных и дифференциально-алгебраических уравнений. Филадельфия: Общество промышленной и прикладной математики. ISBN 978-0-89871-412-8.
- Мясник, Джон С. (2003). Численные методы решения обыкновенных дифференциальных уравнений.. Нью-Йорк: Джон Уайли и сыновья. ISBN 978-0-471-96758-3.
- Хайрер, Эрнст; Норсетт, Сиверт Пол; Ваннер, Герхард (1993). Решение обыкновенных дифференциальных уравнений I: нежесткие задачи. Берлин, Нью-Йорк: Springer-Verlag. ISBN 978-3-540-56670-0.
- Изерлес, Арье (1996). Первый курс численного анализа дифференциальных уравнений. Издательство Кембриджского университета. ISBN 978-0-521-55655-2.
- Стоер, Йозеф; Булирш, Роланд (2002). Введение в численный анализ (3-е изд.). Берлин, Нью-Йорк: Springer-Verlag. ISBN 978-0-387-95452-3.
- Лакоба, Тарас И. (2012), Простой метод Эйлера и его модификации (PDF) (Конспект лекций для MATH334), Университет Вермонта, получено 29 февраля 2012
- Унни, М. П. (2017). «Сокращение памяти для численного решения дифференциальных уравнений с использованием сжатия». 13-й Международный коллоквиум по обработке сигналов и ее приложениям (CSPA), 2017 г.. IEEE CSPA. С. 79–84. Дои:10.1109 / CSPA.2017.8064928. ISBN 978-1-5090-1184-1. S2CID 13082456.
внешняя ссылка
СМИ, связанные с Метод Эйлера в Wikimedia Commons
- Реализации метода Эйлера на разных языках к Код Розетты
- «Метод Эйлера», Энциклопедия математики, EMS Press, 2001 [1994]
Привет, сегодня поговорим про метод эйлера, обещаю рассказать все что знаю. Для того чтобы лучше понимать что такое
метод эйлера, уточненный метод эйлера , настоятельно рекомендую прочитать все из категории Моделирование и Моделирование систем.
метод эйлера — простейший численный метод решения систем обыкновенных дифференциальных уравнений. Впервые описан Леонардом Эйлером в 1768 году в работе «Интегральное исчисление». Метод Эйлера является явным, одношаговым методом первого порядка точности. Он основан на аппроксимации интегральной кривой кусочно-линейной функцией, так называемой ломаной Эйлера.
Описание метода
Ломаная Эйлера (красная линия) — приближенное решение в пяти узлах задачи Коши и точное решение этой задачи (выделено синим цветом)
Пусть дана задача Коши для уравнения первого порядка:
где функция определена на некоторой области
. Решение ищется на интервале
. На этом интервале введем узлы:
Приближенное решение в узлах , которое обозначим через
, определяется по формуле:
Эти формулы непосредственно обобщаются на случай систем обыкновенных дифференциальных уравнений.
Оценка погрешности метода на шаге и в целом
Погрешность на шаге или локальная погрешность — это разность между численным решением после одного шага вычисления и точным решением в точке
. Численное решение задается формулой
Точное решение можно разложить в ряд Тейлора:
Локальную ошибку получаем, вычитая из второго равенства первое:
Это справедливо, если {displaystyle y} имеет непрерывную вторую производную . Другим достаточным условием справедливости этой оценки, из которого вытекает предыдущее и которое обычно может быть легко проверено, является непрерывная дифференцируемость
по обоим аргументам .
Погрешность в целом, глобальная или накопленная погрешность — это погрешность в последней точке произвольного конечного отрезка интегрирования уравнения. Для вычисления решения в этой точке требуется шагов, где
длина отрезка. Поэтому глобальная погрешность метода
.
Таким образом, метод Эйлера является методом первого порядка — имеет погрешность на шаге и погрешность в целом
.
Значение метода Эйлера
Метод Эйлера являлся исторически первым методом численного решения задачи Коши . Об этом говорит сайт https://intellect.icu . О. Коши использовал этот метод для доказательства существования решения задачи Коши. Ввиду невысокой точности и вычислительной неустойчивости для практического нахождения решений задачи Коши метод Эйлера применяется редко. Однако в виду своей простоты метод Эйлера находит свое применение в теоретических исследованиях дифференциальных уравнений, задач вариационного исчисления и ряда других математических проблем.
Характеристика метода Эйлера
- Метод Эйлера является одношаговым методом, то есть для расчета последующей точки необходимо знать только координаты предыдущей.
- Данный метод использует явную схему. В правой части формулы Эйлера стоят все известные величины.
- Метод Эйлера не является устойчивым методом, поэтому он применяется только для ОДУ, решением которых являются достаточно гладкие функции.
- Этот метод характеризуется первым порядком точности (точность низкая).
Модификации и обобщения
Модифицированный метод Эйлера с пересчетом
Повысить точность и устойчивость вычисления решения можно с помощью неявного метода Эйлера следующего вида.
Прогноз:
.
Коррекция:
.
Для повышения точности корректирующую итерацию можно повторить, подставляя .
Модифицированный метод Эйлера с пересчетом имеет второй порядок точности, однако для его реализации необходимо как минимум дважды вычислять . Метод Эйлера с пересчетом представляет собой разновидность методов Рунге-Кутты (предиктор-корректор).
Двухшаговый метод Адамса — Башфорта
Другой способ повысить точность метода заключается в использовании не одного, а нескольких вычисленных ранее значений функции:
Это линейный многошаговый метод.
Реализации на языках программирования
Реализация на языке Си для функции .
#include
double func(double x, double y)
{
return 6*x*x+5*x*y; // функция первой производной
}
int main(int argc, char** argv)
{
int i, n;
double x, y, h;
h = 0.01; // шаг
n = 10; // количество итераций
x = 1; // x0
y = 1; // y0
for (i = 0; i < n; i++)
{
y += h * func(x, y); // вычисление yi
x += h;
}
return EXIT_SUCCESS;
}
Реализация на языке Python 3.7:
# n - количество итераций, h - шаг, (x, y) - начальная точка
def Euler(n = 10, h = 0.01, x = 1, y = 1):
for i in range(n):
y += h * function(x, y)
x += h
return x, y # решение
def function(x, y):
return 6 * x**2 + 5 * x * y # функция первой производной
print(Euler())
Улучшенный метод Эйлера
Метод Эйлера для расчета дифференциальных уравнений имеет небольшую точность расчета. Как было показано ранее (см. Лекцию 10. Численные методы интегрирования дифференциальных уравнений. Метод Эйлера), точность расчета у него зависит от размера шага линейно, зависимость точности от шага — первой степени. То есть, чтобы увеличить точность в 10 раз, надо уменьшить шаг в 10 раз. На практике интересуются более совершенными методами. Вопрос стоит так: можно ли увеличить точность на порядок, но при этом сэкономить на количестве вычислений? Да, такие методы есть. Модифицированный метод Эйлера имеет точность второго порядка. В методе Эйлера производная берется в начале шага и по ней прогнозируется движение системы на конец шага, считая, что во время шага производная неизменна. То есть в течение всего шага производная считается той, какой она была в самом начале шага. Это основной источник неточности.
Улучшение метода состоит в том, что берется производная не в начале шага, а как промежуточное или среднее на разных участках одного шага. В разных вариантах метода вычисляют несколько производных в разных частях шага и усредняют их. Конечно, в этом случае число вычислений увеличивается, — но не в десятки раз, — а вот точность возрастает на порядок, в этом и состоит выигрыш.
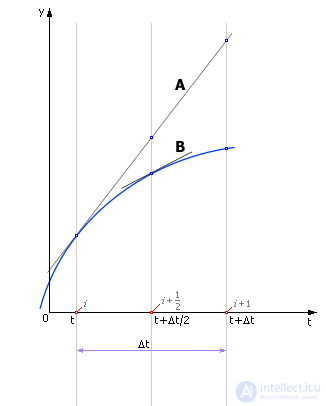
Пусть, как и прежде (см. Лекцию 10. Численные методы интегрирования дифференциальных уравнений. Метод Эйлера), требуется решить уравнение y‘ = f(x, y, t). Идея уточненного метода Эйлера состоит в том, что производную вычисляют не в i-ой точке, а между двумя соседними точками: i иi + 1. Данная процедура состоит из следующих шагов:
- в точке i вычисляют значение производной:
f(xi, yi, t); - делают пол-шага и вычисляют значение функции на середине отрезка:
yi + 1/2 = yi + f(xi, yi, t) · Δt/2; - в точке i + 1/2 вычисляют производную:
f(xi + 1/2, yi + 1/2, t + Δt/2); - делается полный шаг из точки i в точку i + 1 по значению уточненной производной:
yi + 1 =yi + f(xi + 1/2, yi + 1/2, t + Δt/2) · Δt; - значение t увеличивается: t := t + Δt. Вся процедура повторяется сначала.
Данный метод обладает точностью Ο2(h), то есть на порядок выше, чем метод Эйлера, при увеличении числа вычислений всего в 2 раза.
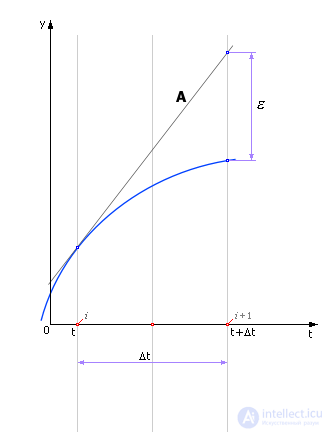
На рис. 14.1 показано, какой будет ошибка ε (расхождение между реальным и вычисленным теоретическим значением), если шаг делается по значению производной, вычисленной в точке i, как это делается в методе Эйлера. Эта ошибка может быть достаточно велика!
Рис. 14.1. Движение реальной и расчетной системы по методу Эйлера и расхождение между ними (ошибка)
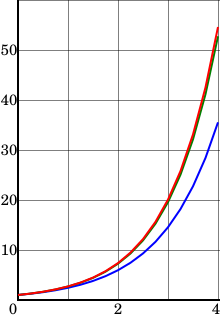
На рис. 14.2 показано, как по значению производной, вычисленной в точке i, делается полшага до точки t + Δt/2 (направление производной показано линией A). И в точке t + Δt/2 вычисляют новую производную. Касательная в точке t + Δt/2 будет другой — линия B. Ее наклон равен производной в точке t + Δt/2.
Рис. 14.2. Уточнение значения производной внутри шага расчета
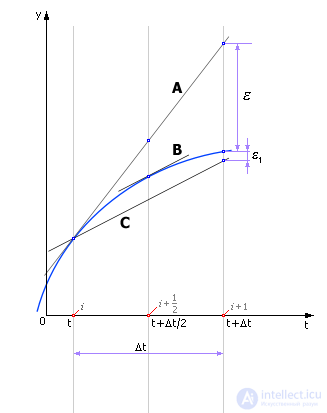
Далее переносят линию B обратно в точку t. Это соответствует тому, что из точки t снова делается, — но уже полный, — шаг Δt до точки t + Δt по направлению, соответствующему линии C(рис. 14.3). Линия C параллельна B. То есть значение производной в точке t берется искусственно равным производной в точке t + Δt/2. Ошибка расчета (см. ε1) во многих случаях при этом уменьшается.
Рис. 14.3. Движение реальной системы и системы, рассчитанной модифицированным методом Эйлера, и расхождение между ними (ошибка). На рисунке для сравнения показан результат, вычисленный по методу Эйлера
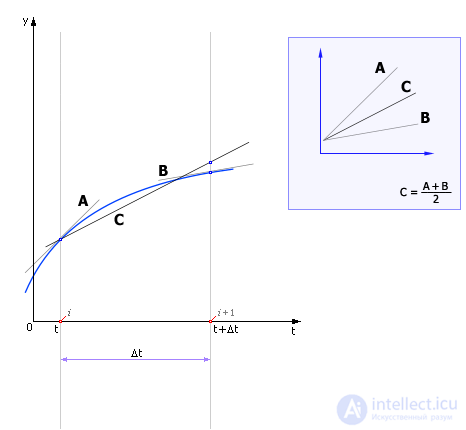
Существует другой вариант модифицированного метода Эйлера, когда производную для того, чтобы сделать шаг из точки i, берут не в i-ой точке и не в i + 1/2, а как среднее арифметическое двух производных: производной в точке i (направление производной показано на рис. 14.4 линией A) и производной в точке i + 1 (направление производной показано линией B). Направление «средней» производной показано линией C.
Рис. 14.4. Расчет движения системы по среднему значению производной на шаге
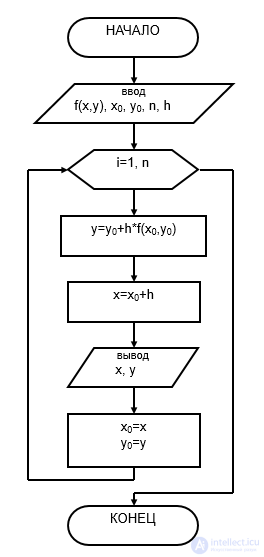
Блок схема и алгоритм метода Эйлера
Решение ОДУ 1-го порядка
Общий вид ОДУ 1-го порядка:
F(x, y, y’)=0
Уравнение разрешаем относительно старшей производной:
y’=f(x, y)
Начальная точка: x0, y0.
Количество точек на интегральной кривой решения n
Шаг h, с которым будет изменяться значение аргумента.
Метод Эйлера
y’=f(x, y)
Представляем производную функции y’ в виде конечной разности.
За величину приращения аргумента Dx принимается величина шага h:
Тогда:
Аналогично:
В общем виде: — формула Эйлера
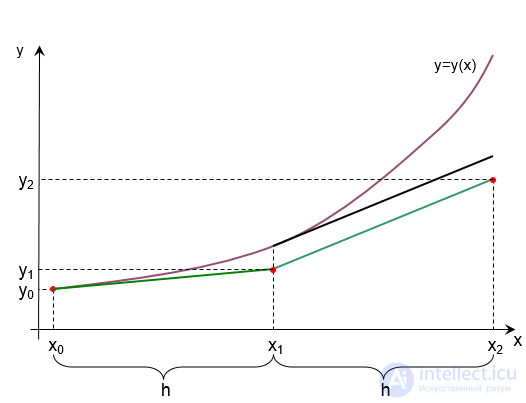
Графическая интерпретация метода Эйлера
Предположим, что мы имеем истинное решение ОДУ: y=y(x).
От начальной точки (x0, y0) проводим касательную к графику до пересечения с линией x=x1. Получаем новую точку (x1, y1).
Из графика видно, что с увеличением количества шагов погрешность возрастает.
Если величину шага h уменьшить, то результат получится более точным.
Блок-схема метода Эйлера
Вау!! 😲 Ты еще не читал? Это зря!
- Метод Рунге — Кутты метод рунге-кутты ,
- задача Коши общие понятия дифференциальных уравнений первого порядка , задача коши , дифференциальные уравнения первого порядка , ду первого порядка ,
- метод Адамса
- метод Хенричи
- аппроксимация функций , интерполяция , интерполяция функций , аппроксимация ,
Я что-то не договорил про метод эйлера, тогда сделай замечание в комментариях Надеюсь, что теперь ты понял что такое метод эйлера, уточненный метод эйлера
и для чего все это нужно, а если не понял, или есть замечания,
то нестесняся пиши или спрашивай в комментариях, с удовольствием отвечу. Для того чтобы глубже понять настоятельно рекомендую изучить всю информацию из категории
Моделирование и Моделирование систем