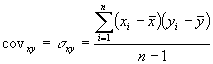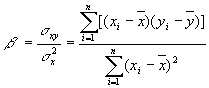Модель исправления ошибок

Векторная модель коррекции ошибок

Рассмотрим модель р-го порядка:

Где:

• yt.
  k-мерный вектор нестационарных
  переменных;

• xt.
  d-мерный вектор экзогенных
  переменных;

• et.
  k-мерный вектор случайных
  составляющих.

Модель можно представить в виде:

Где:

Ключевая теорема Гранжера гласит, что если матрица П имеет неполный
ранг r<k,
то существуют kxr
матрицы α и β, каждая ранга r,
такие, что П = α · βT,
ряд βT является
стационарным, и каждый столбец матрицы β является коинтеграционным
вектором, r — число коинтеграционных
связей. Элементы матрицы α называют сглаживающими параметрами модели коррекции
ошибок.

Если у вас имеется k эндогенных
переменных (каждая из которых содержит единичный корень), то может существовать
от нуля до k-1 линейно независимой
коинтеграционной связи. Если коинтеграционных
связей нет, к ряду в первых разностях может быть применен стандартный
анализ временных рядов. И наоборот, если в системе имеется одно коинтеграционное
уравнение, в каждое уравнение системы должна быть добавлена одна линейная
комбинация эндогенных переменных βTyt-1.
После умножения на коэффициент уравнения (т.е. на сглаживающий параметр
α) получается результирующая составляющая α · βT · yt-1,
которая и является составляющей коррекции ошибок. Каждое следующее коинтеграционное
уравнение будет вносить дополнительную составляющую коррекции ошибок,
уникальную по линейной комбинации параметров.

Если существует k коинтеграционных
связей, то ни один из рядов не имеет единичного корня и модель может быть
описана без взятия разностей.

Изучаемые ряды могут содержать ненулевое среднее, или тренд. Аналогично
коинтеграционные уравнения могут содержать константу и тренд. На практике
чаще используются следующие виды моделей:

Ряд y	Коинтеграционные уравнения	Модель
Тренда нет	Константы нет
Тренда нет	Константа есть
Линейный тренд	Константа есть
Линейный тренд	Линейный тренд
Квадратичный тренд	Линейный тренд

α’ — матрица, рассчитывающаяся из соотношения αT · α, = 0

В рамках такой схемы, при построении модели, можно варьировать два параметра.
Можно фиксировать вид модели и варьировать ранг. Или наоборот, фиксировать
ранг и выбирать наиболее подходящую форму модели. При построении помимо
статистических критериев следует руководствоваться экономической адекватностью
модели. Следует обратить внимание на нормализованные коинтеграционные
уравнения, чтобы убедится в том, что они отвечают вашим ожиданиям о природе
рассматриваемого процесса.

Модель также может быть приведена к более общему виду:

См. также:

Библиотека методов и моделей
| Коинтегрированные процессы |
Модель коррекции ошибок |
Модель «Векторная
модель коррекции ошибок» | ISmErrorCorrectionModel

An модель коррекции ошибок (ECM) принадлежит к категории множественных Временные ряды модели, наиболее часто используемые для данных, в которых базовые переменные имеют долгосрочный стохастический тренд, также известный как коинтеграция. ECM — это теоретически обоснованный подход, полезный для оценки как краткосрочного, так и долгосрочного воздействия одного временного ряда на другой. Термин исправление ошибок относится к тому факту, что отклонение последнего периода от долгосрочного равновесия, ошибка, влияет на его краткосрочную динамику. Таким образом, ECM напрямую оценивают скорость, с которой зависимая переменная возвращается в состояние равновесия после изменения других переменных.

История ECM

Йоль (1926) и Грейнджер и Ньюболд (1974) первыми привлекли внимание к проблеме ложная корреляция и найти решения, как решить эту проблему при анализе временных рядов.^[1][2] Учитывая два совершенно не связанных, но интегрированных (нестационарных) временных ряда, регрессивный анализ одного на другом, будет иметь тенденцию давать явно статистически значимую взаимосвязь, и поэтому исследователь может ошибочно полагать, что нашел доказательства истинной взаимосвязи между этими переменными. Обычный метод наименьших квадратов больше не будет согласованным, и часто используемая тестовая статистика будет недействительной. Особенно, Моделирование Монте-Карло покажи, что получишь очень высокий R в квадрате, очень высокий человек t-статистика и низкий Статистика Дарбина – Ватсона. С технической точки зрения Филлипс (1986) доказал, что оценки параметров не сходятся по вероятности, то перехватить будут расходиться, и наклон будет иметь невырожденное распределение по мере увеличения размера выборки.^[3] Однако может быть общий стохастический тренд к обеим сериям, которые действительно интересуют исследователя, потому что они отражают долгосрочную взаимосвязь между этими переменными.

Из-за стохастического характера тренда невозможно разбить интегрированный ряд на детерминированный (предсказуемый) тенденция и стационарный ряд, содержащий отклонения от тренда. Даже при детерминированном исключении тренда случайные прогулки в конечном итоге возникнут ложные корреляции. Таким образом, снятие тренда не решает проблему оценки.

Чтобы по-прежнему использовать Подход Бокса – Дженкинса, можно было различать ряды, а затем оценивать такие модели, как ARIMA, учитывая, что многие часто используемые временные ряды (например, в экономике) кажутся стационарными в первых разностях. Прогнозы на основе такой модели по-прежнему будут отражать циклы и сезонность, которые присутствуют в данных. Однако любая информация о долгосрочных корректировках, которую могут содержать данные в уровнях, опускается, и долгосрочные прогнозы будут ненадежными.

Это привело Сарган (1964) для разработки методологии ECM, которая сохраняет информацию об уровне.^[4][5]

Оценка

В литературе известно несколько методов оценки уточненной динамической модели, как описано выше. Среди них двухэтапный подход Энгла и Грейнджера, оценивающий их ECM за один шаг, и VECM на основе векторов с использованием Метод Йохансена.^[6]

Двухэтапный подход Энгла и Грейнджер

Первым шагом этого метода является предварительная проверка используемых индивидуальных временных рядов, чтобы подтвердить, что они нестационарный на первом месте. Это можно сделать стандартным единичный корень Пеленгационные испытания и Тест АПД (для решения проблемы серийно коррелированных ошибок). Возьмем случай двух разных серий. и . Если оба равны I (0), будет действителен стандартный регрессионный анализ. Если они интегрированы другого порядка, например один — I (1), а другой — I (0), необходимо преобразовать модель.

Если они оба интегрированы в одном порядке (обычно I (1)), мы можем оценить модель ECM в виде

Если обе переменные интегрированы, и этот ECM существует, они коинтегрируются теоремой Энгла – Грейнджера о представлении.

Затем на втором этапе оценивается модель с использованием обыкновенный метод наименьших квадратов: Если регрессия не является ложной, как определено критериями тестирования, описанными выше, Обычный метод наименьших квадратов будет не только актуально, но и по сути супер последовательный (Сток, 1987). Тогда прогнозируемые остатки из этой регрессии сохраняются и используются в регрессии разностных переменных плюс запаздывающий член ошибки

Затем можно протестировать коинтеграцию, используя стандартный t-статистика на Хотя этот подход прост в применении, существует множество проблем:

VECM

Подход Энгла – Грейнджера, описанный выше, имеет ряд недостатков. А именно, он ограничен только одним уравнением с одной переменной, обозначенной как зависимая переменная, объясненной другой переменной, которая, как предполагается, является слабо экзогенной для интересующих параметров. Он также основан на предварительном тестировании временных рядов, чтобы выяснить, являются ли переменные I (0) или I (1). Эти недостатки могут быть устранены с помощью процедуры Йохансена. Его преимущества заключаются в том, что предварительное тестирование не требуется, может существовать множество коинтегрирующих взаимосвязей, все переменные рассматриваются как эндогенные и возможны тесты, относящиеся к долгосрочным параметрам. Полученная модель известна как модель векторной коррекции ошибок (VECM), поскольку она добавляет функции коррекции ошибок в многофакторную модель, известную как векторная авторегрессия (VAR). Порядок действий следующий:

• Шаг 1: оцените неограниченную VAR с потенциально нестационарными переменными
• Шаг 2. Проверьте коинтеграцию с помощью Тест Йохансена
• Шаг 3: Сформируйте и проанализируйте VECM.

Пример ECM

Идея коинтеграции может быть продемонстрирована в простой макроэкономической обстановке. Предположим, потребление и располагаемый доход представляют собой макроэкономические временные ряды, которые связаны в долгосрочной перспективе (см. Гипотеза постоянного дохода ). В частности, пусть средняя склонность к потреблению быть 90%, то есть в долгосрочной перспективе . С точки зрения эконометриста, эта долгосрочная связь (также известная как коинтеграция) существует, если ошибки из регрессии площадь стационарный серия, хотя и нестационарны. Предположим также, что если внезапно меняется на , тогда изменения на , то есть, предельная склонность к потреблению равняется 50%. Наше последнее предположение состоит в том, что разрыв между текущим и равновесным потреблением уменьшается каждый период на 20%.

В этой настройке изменение по уровню потребления можно смоделировать как . Первый член в RHS описывает краткосрочное влияние изменения в на , второй член объясняет долгосрочное стремление к равновесному соотношению между переменными, а третий член отражает случайные шоки, которые получает система (например, шоки доверия потребителей, влияющие на потребление). Чтобы увидеть, как работает модель, рассмотрим два вида шоков: постоянные и временные (временные). Пусть для простоты равняться нулю для всех t. Предположим в период т — 1 система находится в равновесии, т.е. . Предположим, что в период t увеличивается на 10, а затем возвращается на предыдущий уровень. потом первый (в период t) увеличивается на 5 (половина от 10), но после второго периода начинает уменьшаться и сходится к исходному уровню. Напротив, если шок постоянно, то медленно сходится к значению, превышающему начальное на 9.

Эта структура общая для всех моделей ECM. На практике эконометристы часто сначала оценивают взаимосвязь коинтеграции (уравнение в уровнях), а затем вставляют его в основную модель (уравнение в разностях).

Рекомендации

дальнейшее чтение

• Доладо, Хуан Дж .; Гонсало, Хесус; Мармол, Франсеск (2001). «Коинтеграция». В Балтаги, Бади Х. (ред.). Компаньон теоретической эконометрики. Оксфорд: Блэквелл. стр.634 –654. Дои:10.1002 / 9780470996249.ch31. ISBN  0-631-21254-X.
• Эндерс, Уолтер (2010). Прикладные эконометрические временные ряды (Третье изд.). Нью-Йорк: Джон Вили и сыновья. С. 272–355. ISBN  978-0-470-50539-7.
• Люткеполь, Гельмут (2006). Новое введение в анализ множественных временных рядов. Берлин: Springer. стр.237 –352. ISBN  978-3-540-26239-8.
• Мартин, Вэнс; Херн, Стэн; Харрис, Дэвид (2013). Эконометрическое моделирование с использованием временных рядов. Нью-Йорк: Издательство Кембриджского университета. С. 662–711. ISBN  978-0-521-13981-6.

Векторные модели коррекции ошибок

Многомерные линейные модели, включая коинтегрирующие отношения и переменные экзогенного предиктора

Модели коррекции векторных ошибок (VEC), или cointegrated VAR models, адресуют нестационарность в многомерных временных рядах, возникающих в результате совместных движений нескольких рядов откликов. Для примера анализа с использованием инструментов моделирования VEC, смотрите Моделирование экономики США.

Темы

тип модели временного ряда

Модель коррекции ошибок (ECM) принадлежит к Категория нескольких моделей временных рядов , наиболее часто используемых для данных, в которых базовые переменные имеют долгосрочный стохастический тренд, также известный как коинтеграция. ECM — это теоретически обоснованный подход, полезный для оценки как краткосрочного, так и долгосрочного воздействия одного временного ряда на другой. Термин «исправление ошибок» относится к тому факту, что отклонение последнего периода от долгосрочного равновесия, ошибка, влияет на его краткосрочную динамику. Таким образом, ECM напрямую оценивают скорость, с которой зависимая переменная возвращается в состояние равновесия после изменения других переменных.

Содержание

• 1 История ECM
• 2 Оценка
  • 2.1 Двухэтапный подход Энгла и Грейнджера
  • 2.2 VECM
  • 2.3 Пример ECM
• 3 Ссылки
• 4 Далее чтение

История ECM

Юл (1926) и Грейнджер и Ньюболд (1974) первыми привлекли внимание к проблеме ложной корреляции и нашли решения, как ее решить. в анализе временных рядов. Учитывая два совершенно несвязанных, но интегрированных (нестационарных) временных ряда, регрессионный анализ одного из другого будет иметь тенденцию давать явно статистически значимую взаимосвязь, и, таким образом, исследователь может ошибочно полагать, что нашел доказательства существования истинная взаимосвязь между этими переменными. Обычный метод наименьших квадратов больше не будет согласованным, а часто используемая тестовая статистика будет недействительной. В частности, моделирования Монте-Карло показывают, что можно получить очень высокий R в квадрате, очень высокий индивидуальный t-статистический и низкий Дарбина – Ватсона. статистика. С технической точки зрения Филлипс (1986) доказал, что оценки параметров не будут сходиться по вероятности, точка пересечения будет расходиться, а наклон будет иметь невырожденное распределение по мере увеличения размера выборки. Однако может существовать общий стохастический тренд для обоих рядов, который искренне интересует исследователя, поскольку он отражает долгосрочную взаимосвязь между этими переменными.

Из-за стохастического характера тренда невозможно разбить интегрированный ряд на детерминированный (предсказуемый) тренд и стационарный ряд, содержащий отклонения от тренда. Даже при детерминированном удалении тренда случайных блужданий в конечном итоге возникнут ложные корреляции. Таким образом, детрендирование не решает проблему оценки.

Чтобы по-прежнему использовать подход Бокса – Дженкинса, можно было бы различать ряды, а затем оценивать такие модели, как ARIMA, учитывая, что многие часто используемые временные ряды ( например, в экономике) кажутся стационарными в первых разностях. Прогнозы на основе такой модели по-прежнему будут отражать циклы и сезонность, которые присутствуют в данных. Однако любая информация о долгосрочных корректировках, которую могут содержать данные в уровнях, опускается, и долгосрочные прогнозы будут ненадежными.

Это привело Саргана (1964) к разработке методологии ECM, которая сохраняет информацию об уровне.

Оценка

В литературе известно несколько методов. для оценки уточненной динамической модели, как описано выше. Среди них двухэтапный подход Энгла и Грейнджера, оценивающий их ECM за один этап, и векторный VECM с использованием метода Йохансена.

двухэтапного подхода Энгла и Грейнджера

Первый этап этот метод заключается в предварительном тестировании отдельных временных рядов, которые используются, чтобы подтвердить, что они нестационарны в первую очередь. Это можно сделать с помощью стандартного модульного корневого тестирования DF и теста ADF (для решения проблемы серийно коррелированных ошибок). Возьмем случай двух разных серий x t { displaystyle x_ {t}}и y t { displaystyle y_ {t}}. Если оба равны I (0), будет действителен стандартный регрессионный анализ. Если они интегрированы другого порядка, например один — I (1), а другой — I (0), необходимо преобразовать модель.

Если они оба интегрированы в одном порядке (обычно I (1)), мы можем оценить модель ECM в виде

A (L) Δ yt = γ + B (L) Δ xt + α (yt — 1 — β 0 — β 1 xt — 1) + ν t. { Displaystyle A (L) , Delta y_ {t} = gamma + B (L) , Delta x_ {t} + alpha (y_ {t-1} — beta _ {0} — beta _ {1} x_ {t-1}) + nu _ {t}.}

Если обе переменные интегрированы и этот ECM существует, они коинтегрируются теоремой Энгла – Грейнджера о представлении.

Затем на втором этапе оценивается модель с помощью обычных наименьших квадратов : yt = β 0 + β 1 xt + ε t { displaystyle y_ {t} = beta _ {0} + beta _ {1} x_ {t} + varepsilon _ {t}}Если регрессия не является ложной в соответствии с критериями тестирования, описанными выше, Обычный метод наименьших квадратов будет не только действительным, но и действительно супер согласованным (Stock, 1987). Тогда прогнозируемые остатки ε t ^ = yt — β 0 — β 1 xt { displaystyle { hat { varepsilon _ {t}}} = y_ {t} — beta _ {0} — beta _ {1} x_ {t}}из этой регрессии сохраняются и используются в регрессии разностных переменных плюс запаздывающий член ошибки

A (L) Δ yt = γ + B (L) Δ xt + α ε ^ t — 1 + ν t. { Displaystyle A (L) , Delta y_ {t} = gamma + B (L) , Delta x_ {t} + alpha { hat { varepsilon}} _ {t-1} + nu _ {t}.}

Затем можно протестировать коинтеграцию, используя стандартную t-статистику на α { displaystyle alpha}. Хотя этот подход прост в применении, однако существует множество проблем:

VECM

Энгл-Грейнджер описанный выше подход имеет ряд недостатков. А именно, он ограничен только одним уравнением с одной переменной, обозначенной как зависимая переменная, объясненной другой переменной, которая, как предполагается, является слабо экзогенной для интересующих параметров. Он также основан на предварительном тестировании временных рядов, чтобы выяснить, являются ли переменные I (0) или I (1). Эти недостатки могут быть устранены с помощью процедуры Йохансена. Его преимущества заключаются в том, что в предварительном тестировании нет необходимости, может быть множество коинтегрирующих взаимосвязей, все переменные рассматриваются как эндогенные, и возможны тесты, относящиеся к долгосрочным параметрам. Полученная модель известна как модель векторной коррекции ошибок (VECM), поскольку она добавляет функции коррекции ошибок в многофакторную модель, известную как векторная авторегрессия (VAR). Процедура выполняется следующим образом:

• Шаг 1: оценка неограниченной VAR, включающей потенциально нестационарные переменные
• Шаг 2: Тест на коинтеграцию с использованием теста Йохансена
• Шаг 3: Сформировать и проанализировать VECM.

Пример ECM

Идея коинтеграции может быть продемонстрирована в простых макроэкономических условиях. Предположим, потребление C t { displaystyle C_ {t}}и располагаемый доход Y t { displaystyle Y_ {t}}представляют собой макроэкономические временные ряды, которые связаны в долгосрочной перспективе (см. гипотезу о постоянном доходе ). В частности, пусть средняя склонность к потреблению составляет 90%, то есть в долгосрочной перспективе C t = 0,9 Y t { displaystyle C_ {t} = 0,9Y_ {t}}. С точки зрения эконометриста, эта долгосрочная связь (также известная как коинтеграция) существует, если ошибки из регрессии C t = β Y t + ε t { displaystyle C_ {t} = beta Y_ {t} + varepsilon _ {t}}— это стационарный ряд, хотя Y t { displaystyle Y_ {t}}и C t { displaystyle C_ {t}}нестационарны. Предположим также, что если Y t { displaystyle Y_ {t}}внезапно изменяется на Δ Y t { displaystyle Delta Y_ {t}}, то C t { displaystyle C_ {t}}изменяется на Δ C t = 0,5 Δ Y t { displaystyle Delta C_ {t} = 0,5 , Delta Y_ {t }}, то есть предельная склонность к потреблению равна 50%. Наше последнее предположение состоит в том, что разрыв между текущим и равновесным потреблением уменьшается каждый период на 20%.

В этой настройке изменение Δ C t = C t — C t — 1 { displaystyle Delta C_ {t} = C_ {t} -C_ {t-1}}в уровне потребления можно смоделировать как Δ C t = 0,5 Δ Y t — 0,2 (C t — 1 — 0,9 Y t — 1) + ε t { displaystyle Delta C_ {t} = 0,5 , Delta Y_ {t} -0.2 (C_ {t-1} -0.9Y_ {t-1}) + varepsilon _ {t}}. Первый член в правой части страницы описывает краткосрочное влияние изменения Y t { displaystyle Y_ {t}}на C t { displaystyle C_ {t}}, второй член объясняет долгосрочное стремление к равновесному соотношению между переменными, а третий член отражает случайные шоки, которые получает система (например, шоки доверия потребителей, влияющие на потребление). Чтобы увидеть, как работает модель, рассмотрим два вида шоков: постоянные и временные (временные). Для простоты пусть ε t { displaystyle varepsilon _ {t}}равно нулю для всех t. Предположим, что в период t — 1 система находится в равновесии, т.е. C t — 1 = 0.9 Y t — 1 { displaystyle C_ {t-1} = 0.9Y_ {t-1}}. Предположим, что в период t Y t { displaystyle Y_ {t}}увеличивается на 10, а затем возвращается на свой предыдущий уровень. Тогда C t { displaystyle C_ {t}}сначала (в период t) увеличивается на 5 (половина от 10), но после второго периода C t { displaystyle C_ { t}}начинает убывать и сходится к исходному уровню. Напротив, если удар Y t { displaystyle Y_ {t}}является постоянным, то C t { displaystyle C_ {t}}медленно сходится к значению, которое превышает исходное значение C t — 1 { displaystyle C_ {t-1}}на 9.

Эта структура является общей для всех моделей ECM. На практике эконометристы часто сначала оценивают взаимосвязь коинтеграции (уравнение в уровнях), а затем вставляют его в основную модель (уравнение в разностях).

Ссылки

Дополнительная литература

• Dolado, Juan J.; Гонсало, Хесус; Мармол, Франсеск (2001). «Коинтеграция». В Балтаги, Бади Х. (ред.). Компаньон теоретической эконометрики. Оксфорд: Блэквелл. Стр. 634 –654. doi : 10.1002 / 9780470996249.ch31. ISBN 0-631-21254-X.
• Эндерс, Уолтер (2010). Прикладные эконометрические временные ряды (Третье изд.). Нью-Йорк: Джон Вили и сыновья. С. 272–355. ISBN 978-0-470-50539-7.
• Lütkepohl, Helmut (2006). Новое введение в анализ множественных временных рядов. Берлин: Springer. Стр. 237 –352. ISBN 978-3-540-26239-8.
• Мартин, Вэнс; Херн, Стэн; Харрис, Дэвид (2013). Эконометрическое моделирование с использованием временных рядов. Нью-Йорк: Издательство Кембриджского университета. С. 662–711. ISBN 978-0-521-13981-6.

МАТЕМАТИЧЕСКИЕ И ИНСТРУМЕНТАЛЬНЫЕ МЕТОДЫ

ЭКОНОМИКИ

MATHEMATICAL AND INSTRUMENTAL METHODS

OF ECONOMICS

DOI: 10.18287/2542-0461-2021-12-3-147-154 ЮУ

НАУЧНАЯ СТАТЬЯ УДК 330.4

Дата поступления: 20.05.2021 рецензирования: 26.06.2021 принятия: 27.08.2021

Векторная модель коррекции ошибок при моделировании взаимосвязи показателей банковского кредитования и темпов роста российской

экономики

Д.Ю. Иванов

Самарский национальный исследовательский университет имени академика С.П. Королева,

г. Самара, Российская ФедерацияЕ-mail: ivanov.dyu@ssau.ru. ORCID: http://orcid.org/0000-0003-0619-9340

М.М.Т. Тали

Самарский национальный исследовательский университет имени академика С.П. Королева,

г. Самара, Российская Федерация E-mail: m.economic@mail.ru

Аннотация: В статье рассматривается проблема моделирования функциональной зависимости объема выданных кредитов и темпов роста российской экономики. Актуальность данного исследования обусловлена необходимостью выявления факторов, влияющих на рост показателя реального валового внутреннего продукта. Проанализированные отечественные и зарубежные источники не дают единого набора факторов, влияющих на темп роста национальной экономики, выделяя финансовые механизмы, производственные процессы, объемы кредитования физических и юридических лиц, инвестиционную активность и т. д. В статье отмечается проблема формирования многофакторной модели влияния различных параметров на показатель темпа роста национальной экономики. Процесс моделирования функциональной зависимости ВВП от элементов вектора влияния затрудняется из-за специфики статистических данных. С целью избежать подобных проблем, связанных с коинтеграцией рядов, была предложена векторная модель корректировки ошибок. Модель апробирована на статистических данных организаций банковского сектора и предприятий реального сектора российской экономики. Выявлено, что при существующих условиях организации процесса кредитования банковская система работает не столько на увеличение объемов производства, сколько на поддержание уровня финансового состояния хозяйствующих субъектов (поддержание уровня ликвидности и увеличение финансовых вложений), не способствуя при этом изменению общей структуры российской экономики. Разработанная векторная модель корректировки ошибок позволяет измерить отклонения от равновесия и скорость его восстановления, что указывает на большую эффективность данной методики. При этом приведенные результаты позволяют сделать вывод о том, что при наличии положительной взаимосвязи между объемами кредитования и основными показателями, степень влияния кредитования на экономический рост в целом незначительна.

Ключевые слова: векторная модель; корректировка ошибок; темп роста экономики; кредитование; эконометрическое моделирование; коинтеграция рядов.

Цитирование. Иванов Д.Ю., Тали М.М.Т. Векторная модель коррекции ошибок при моделировании взаимосвязи показателей банковского кредитования и темпов роста российской экономики // Вестник Самарского университета. Экономика и управление. 2021. Т. 12, № 3. С. 147-154. DOI: http://doi.org/10.18287/2542-0461-2021-12-3-147-54.

Информация о конфликте интересов: авторы заявляют об отсутствии конфликта интересов. © Иванов Д.Ю., Тали М.М.Т., 2021

Дмитрий Юрьевич Иванов — доктор экономических наук, профессор, заведующий кафедрой менеджмента и организации производства, Самарский национальный исследовательский университет имени академика С.П. Королева, 443086, Российская Федерация, г. Самара, Московское шоссе, 34.

Тали Махди Мохаммед Тали — аспирант, Самарский национальный исследовательский университет имени академика С.П. Королева, 443086, Российская Федерация, г. Самара, Московское шоссе, 34.

SCTENTTFTC ARTICLE

Submitted: 20.05.2021 Revised: 26.06.2021 Accepted: 27.08.2021

Vector model of error correction in modeling the relationship between bank lending indicators and the growth rates of the Russian economy

D.Yu. Ivanov

Samara National Research University, Samara, Russian Federation E-mail: ivanov.dyu@ssau.ru. ORCID: http://orcid.org/0000-0003-0619-9340

M.M.T. Tali

Samara National Research University, Samara, Russian Federation

E-mail: m.economic@mail.ru

Abstract: The article discusses the problem of modeling the functional dependence of the volume of loans issued and the growth rate of the Russian economy. The relevance of this study is due to the need to identify the factors affecting the growth of the indicator of real gross domestic product. The analyzed domestic and foreign sources do not provide a single set of factors affecting the growth rate of the national economy, highlighting financial mechanisms, production processes, lending volumes to individuals and legal entities, investment activity, etc. The article notes the problem of the formation of a multifactor model of the influence of various parameters on the indicator of the growth rate of the national economy. The process of modeling the functional dependence of GDP on the elements of the influence vector is complicated by the specifics of statistical data. In order to avoid such problems associated with series cointegration, a vector error correction model was proposed. The model was tested on statistical data of organizations in the banking sector and enterprises of the real sector of the Russian economy. It was revealed that under the existing conditions of organizing the lending process, the banking system works not so much to increase production volumes as to maintain the level of the financial condition of economic entities (maintaining the level of liquidity and increasing financial investments), while not contributing to a change in the overall structure of the Russian economy. The developed vector model of error correction makes it possible to measure deviations from equilibrium and the rate of its recovery, which indicates the greater efficiency of this technique. At the same time, the above results allow us to conclude that in the presence of a positive relationship between the volume of lending and the main indicators, the degree of influence of lending on economic growth is generally insignificant

Key words: vector model; error correction; economic growth topics; lending; econometric modeling; cointegration of series.

Citation. Ivanov D.Yu., Tali M.M.T. Vector model of error correction in modeling the relationship between bank lending indicators and the growth rates of the Russian economy. Vestnik Samarskogo universiteta. Ekonomika i upravlenie = Vestnik of Samara University. Economics and Management, 2021, vol. 12, no. 3, pp. 147-154. DOI: http://doi.org/10.18287/2542-0461-2021-12-3-147-154. (In Russ.) Information on the conflict of interest: authors declare no conflict of interest.

© Ivanov D.Yu., M.M.T. Tali, 2021

Dmitriy Yu. Ivanov — Doctor of Economics, professor, head of the Department of Management and Production Organization, Samara National Research University, 34, Moskovskoye shosse, Samara, 443086, Russian Federation.

Tali Mahdi Mohammed Tali — postgraduate student, Samara National Research University, 34, Moskovskoye shosse, Samara, 443086, Russian Federation.

Введение

Тем роста национальной экономики любого государства является важным показателем эффективности деятельности экономических, политических, финансовых и прочих механизмов в стране. Взаимное влияние различных факторов отражается в инвестиционной активности, объемах кредитования, в обороте организаций реального и финансового секторов экономики. Финансовые показатели инвестиционного процесса и кредитования физических и юридических лиц характеризуют развитие бизнеса и уровень доходов домохозяйств. Можно сказать, что коммерческие банки, которые действуют в соответствии с денежно-кредитной политикой государства, осуществляют регулировку движения денежных потоков, воздействуя на скорость их оборота, эмиссию, общую массу. Современный банковский сектор осуществляет управление финансовыми потоками в государственной системе платежей и расчетов, реализуя свою деятельность при помощи механизмов депозитов, инвестиций и кредитных операций.

Проблема влияния процессов банковского кредитования на темп роста национальной экономики рассматривался авторами применительно к различным факторам. Так, по мнению R.I. McKinnon, влияние кредитной системы на темпы роста экономики заключаются в росте следующих показателей: реальный ВВП на душу населения, скорость прироста материального капитала и т.д. [1]. D.S. Allen и L. Ndikumana определяют влияние как положительное изменение уровня создания товаров и национального дохода, которые предоставляются страной в течение определенного периода времени. Это обычно измеряется с точки зрения уровня производства в экономике [2].

Согласно теории V.R. Bencivenga и B.D. Smith, влияние кредитных ресурсов на рост экономики заключается в формировании труда и капитала. Предприниматель, который использует банковский кредит, с целью формирования капитала, инвестированного в бизнес, стимулирует производство товаров и услуг для экономического роста [3]. Как отмечали экономисты R.W. Goldsmith [4] и E.S. Shaw [5], банковское кредитование и экономический рост положительно коррелируют: в качестве основного фактора роста экономики они выделяют потребительское кредитование (кредиты населению). J.A. Schumpeter, напротив, полагал, что финансовые посредники способствуют росту путем выявления и перенаправления средств на инновационные проекты. Ученый отмечал, что существенная функция кредита состоит в том, чтобы позволить предпринимателю изъять необходимые ему товары, осуществляя спрос на них, и тем самым заставить экономическую систему перейти на новые каналы [6].

J.G. Gurley и E.S. Shaw утверждали, что если доход растет с гарантированной скоростью, то спрос на финансовые активы также растет с определенной скоростью. Кроме того, существует спрос на операции с деньгами, чтобы идти в ногу с растущим доходом [7]. Соответственно, накопление активов и рост доходов стимулируют спрос за счет расходных единиц на финансовые услуги во все большем разнообразии. Ученые утверждали, что влияние банковского кредитования на долгосрочные темпы экономического роста проявляется в виде мобилизации сбережений. Банковский сектор мобилизует сбережения, предлагая широкий спектр инструментов для деноминированных сбережений различных сумм.

Эконометрическое моделирование темпов роста российской экономики, валового внутреннего продукта и макроэкономических показателей представлено в ряде работ отечественных ученых [8 — 12].

Как видим, авторы отмечают влияние на экономику государства различных факторов: финансовых и производственных, кредитования физических и юридических лиц, рыночных

механизмов и т.д. При этом отсутствует единое мнение относительно набора этих факторов и степени их влияния. Процесс моделирования функциональной зависимости ВВП от элементов вектора влияния затрудняется из-за специфики статистических данных. С целью избежать подобных проблем, связанных с коинтеграцией рядов, была предложена векторная модель корректировки ошибок.

Разработка векторной модели корректировки ошибок

Новизна предлагаемой методики заключается в формировании подходов, подтверждающих наличие коинтеграции в многомерной модели, если рассматриваемых рядов больше двух. При этом было установлено, что для большого количества рядов будет существовать ряд коинтеграционных соотношений. Предлагается критерий выбора и оценки лучшего ко-интеграционного соотношения для модели. В рамках теста Йохансена была осуществлена проверка нулевой гипотезы о существовании максимума г коинтеграционных векторов, и альтернативной гипотезы в том, что их г+1. Если величина тестов оказывается значимой, то нулевая гипотеза отвергается. Найденное максимальное значение г является рангом коинтеграции. Для одиночных уравнений проверка на интегрированность заключается в выявлении равенства, указывающего на наличие единичных корней в соответствующей авторегрессии. В общем виде процедура тестирования коинтеграции выглядит следующим образом: рассматривается векторная модель авторегрессии (VAR):

Р

Ух = 1 AiУt-1 + Вхх + £ , (1)

I=1

где Ai — матрица, состоящая из коинтеграционных векторов, £ — стационарные процессы

гт! к

£ = а Ух = IЩУи . i=1

Модель (1) можно представить в виде векторной модели

Р

Лу = Пу-1 + I Г7 Лу — 7 + Вх1 + £, 7=1

РР

п= IА -1,г7 = — IА i=1 i=7+1

Из данного представления возможно предположить, что если первые разности рядов у стационарны, то Пум — тоже стационарна. Если ранг коинтеграции меньше числа переменных, матрицу П можно представить в виде произведения двух матриц а$ , где вторая матрица — матрица из коинтегрирующих векторов. Ранг матрицы П определяет ранг коинтеграции. Задача нахождения параметров $ эквивалентна задаче нахождения собственных векторов определенной матрицы. Для тестирования ранга коинтеграции использовался тест отношения правдоподобия (ЬЯ), показатели которого в данном случае сводятся к функции от собственных значений данной матрицы. Нулевая гипотеза заключается в предположении, что ранг коинтеграции равен данному значению г.

Векторная модель коррекции ошибок обусловлена тем, что проверка гипотезы начинается с ранга 0 до ранга к — 1. Если гипотеза не отвергается для ранга 0, то ранг считается нулевым, все переменные имеют интегрированность /(1) или кратность /(1) и отсутствие коинтеграции. Аналогично до г=к. В таком случае П обратима и принимается альтернативная гипотеза о стационарности исходных рядов, все переменные имеют порядок интегрированности /(0). Явление коинтеграции допустимо лишь при 0<г<1.

Рассмотрим подробнее случай, когда 0<г<1, коинтеграция присутствует и П представим в виде произведения двух матриц а$ . Имеются два ряда хх, у порядка интеграции 1(1), их ли-

нейная комбинация представима в виде: у — х6_ум = ^(х — хм) + или Ау = + Рассматриваемые ряды описывают некоторые экономические данные, которые могут не меняться с течением времени. Тогда у = _ум = … = у0 и х( = хм = … = х, то есть все члены рассматриваемой линейной комбинации равны нулю, а остатки е( будут стационарны. На практике найти такое соотношение между у и х не представляется возможным. С целью избежать подобных проблем, связанных с коинтеграцией рядов была предложена векторная модель корректировки ошибок («УЕСМ). Для вышеописанного случая она будет выглядеть следующим образом:

Ду = ДДх? + + 0з(У-1 — ^-1 — Ъ-1) + Ъ .

По своей сути «УЕСМ ограничивает в установленном временном периоде динамику эндогенных переменных и возвращает их к коинтеграционному отношению, при этом коррекци-онная динамика допускается. Коинтеграционный параметр является параметром коррекции ошибок, поскольку данные ошибки (нарушения) равновесия корректируются за счет изменений в зависимости от степени отклонения основных показателей.

Результаты моделирования

С целью выявления эффективности использования данной модели был представлен ряд стандартных диагностических тестов с константой и к=2, подтверждающих равенство нулю эндогенных переменных на данном лаге, которое (равенство) доказывается при помощи теста Вальда. Данный тест позволяет обнулить коэффициенты при каждых переменных на данном лаге и обеспечивает выделение статистики значимости обнуления. Переменные избыточны, если коэффициенты незначимы. Кроме того, тестирование показало, что «УЕСМ имеет гомоскедастичные и некоррелируемые остатки, однако это непринципиально для теста на коинтеграцию.

В рамках выявления ранга коинтеграции г, были проверены три нулевые гипотезы (НО): г = 0, г < 1 и г < 2, а также выделены две статистики, которые отвечают на вопрос: «коинте-грированы переменные или нет?». Обе статистики опровергают НО: г = 0 и не опровергают НО г <1 (таблица 1). Следовательно, наблюдается коинтеграция с г = 1. Тождественность указанных статистических данных при г < 2 подтверждает наличие единичного корня. При этом в ходе тестирования были выделены коинтегрирующий вектор (Ь) матрицы Р и корректирующий коэффициент (а) при параметре коррекции. Обеспечение единичного порядка позволило идентифицировать Ь и сформулировать его экономический смысл, при котором Ь может быть записано в рамках коинтегрирующего уравнения, подтверждающего долговременную равновесную взаимосвязь переменных и подлинность их корреляции.

Таблица 1 — Значения показателей векторной модели коррекции ошибок

Table 1 — Values of indicators of the vector error correction model

r След матрицы Максимальное число Коинтегрирующий вектор Корректирующий коэффициент

0 47,989 (0,000) 34,745 (0,000) 1, -0,00532, -0,00035 -1,142

1 13,244 (0,106) 13,221 (0,073)

2 0,023 (0,880) 0,023 (0,880)

В рамках апробации данной модели был проведен анализ деятельности банковского сектора и его влияния на экономический рост, который (анализ) позволил определить положительную корреляцию между коэффициентами финансовой глубины (и, в частности, объемами выданных кредитов) и показателями экономического роста. В качестве примера был рассмотрен реальный сектор — предприятия, работающие на внутреннем рынке (таблица 2).

Таблица 2 — Расчет коэффициентов корреляции между объемами выданных кредитов и показателями экономического роста

Table 2 — Calculation of correlation coefficients between the volume of loans issued and indicators of economic growth______

2015 2016 2017 2018 2019 Корреляция

Промышленность 35,88 9,03 20,36 10,25 10,68 0,81765

Сельское хозяйство 73,84 45,61 44,70 46,99 47,56 0,94296

Строительство -0,37 24,81 32,65 35,01 34,14 0,01243

Торговля и обществен- 50,57 31,29 26,50 19,96 19,70 0,23862

ное питание

Транспорт и связь 24,17 21,78 47,06 23,12 23,45 0,51606

Таблица 3 — Показатель задолженности предприятий основных отраслей экономики Table 3 — Indicator of indebtedness of enterprises in the main sectors of the ^ economy

2014 2015 2016 2017 2018 2019

Показатель задолженности предприятий основных отраслей экономики 5,43 8,05 7,9 7,8 6,2 6,5

Таблица 4 — Значения общих показателей кредитования в соотношении с совокупными активами и собственным капиталом банковских организаций

Table 4 — Values of general lending indicators in relation to total assets and equity of banking organizations_______

Показатель 2014 2015 2016 2017 2018 2019

Объемы выданных 20 778 21 423 22 146 24 033 26 992 27 199

кредитов банковски- 931 025 708 477 457 743

ми организациями,

млн. руб.

Объемы выданных 61,1 61,4 60,0 57,0 56,1 56,9

кредитов банковски-

ми организациями, % от общего объема

кредитов

Совокупные активы 77 653 82 999,7 800 63,3 814 29,9 801 34,7 815 60,4

банковских органи-

заций, млрд. руб.

Совокупные активы 98,0 99,7 93,0 93,6 92,1 92,7

банковских органи-

заций, % к ВВП

iНе можете найти то, что вам нужно? Попробуйте сервис подбора литературы.

Собственный капи- 7 928,4 9 008,6 9 387,1 9 144,3 9441,7 9 231,0

тал банковских орга-

низаций, млрд. руб.

Собственный капи- 10,0 10,8 10,9 10,5 10,4 10,5

тал банковских орга-

низаций, % к ВВП

Банки наиболее активно предоставляют кредитные ресурсы предприятиям экспортоори-ентированных отраслей (до 45% задолженности предприятий основных отраслей экономики (таблица 3), основная часть кредитов реальному сектору экономики носит преимущественно краткосрочный характер и направлена в большей степени на пополнение оборотных средств. Увеличение объемов долгосрочных кредитов, с одной стороны, сдерживает рост финансовой несбалансированности в реальном секторе: уменьшение сальдированного финансового ре-

зультата и, как возможное следствие, увеличение разрыва между динамикой доходов и предполагаемых выплат заемщиков. С другой стороны, очевидно несоответствие срочности ресурсной базы банковского сектора потребностям заемщиков и возможное увеличение конъюнктурного риска вследствие доминирования в масштабах среди клиентов банков предприятий сырьевых и экспортоориентированных секторов.

В рамках разработки векторной модели коррекции ошибок, а также развития функций импульсной реакции на вариацию переменных (подтверждающих наличие коинтеграции в многомерной модели, включающей более двух рядов), было отмечено, что при существующих условиях организации процесса кредитования банковская система работает не столько на увеличение объемов производства, сколько на поддержание уровня финансового состояния хозяйствующих субъектов (поддержание уровня ликвидности и увеличение финансовых вложений), не способствуя при этом изменению общей структуры российской экономики (таблица 4).

Заключение

Таким образом, объединяя в себе статическую долгосрочную и динамическую краткосрочную связи между переменными, VECM дает возможность измерить отклонения от равновесия и скорость его восстановления, что указывает на большую эффективность данной методики. При этом отметим, что приведенные результаты позволяют сделать вывод о том, что при наличии положительной взаимосвязи между объемами кредитования и основными показателями, степень влияния кредитования на экономический рост в целом незначительна.

Библиографический список

1. McKinnon R.I. Money and Capital in Economic Development. Washington, DC: Brooking Institution, 1973. 184 p. URL: https://www.brookings.edu/book/money-and-capital-in-economic-development/.

2. Allen D.S. Financial Intermediation and Economic Growth in Southern Africa / D.S. Allen, L. Ndikumana // Journal of African Economies. 2000. № 9. P. 132-160. DOI: http://dx.doi.org/10.1093/jae/9.2.132.

3. Bencivenga V.R. Financial Intermediation and Endogenous Growth / V.R. Bencivenga, B.D. Smith // The Review of Economic Studies. 1991. № 58. P. 195-209. URL: http://linksjstor.org/sici?sici=0034-6527%28199104%2958%3A2%3C195%3AFIAEG%3E2 0.C0%3B2-3.

4. Goldsmith R.W. Financial Structure and Development / R.W. Goldsmith. New Haven, CT: Yale University Press, 1969. 561 p.

5. Shaw E.S. Financial Deepening in Economic Development / E.S. Shaw. New York: Oxford University Press, 1973. 270 p.

6. Schumpeter J.A. The Theory of Economic Development // Harvard Economic Studies. 1911-1912. № 46. P. 72-74.

7. Gurley J.G. Financial Aspects of Economic Development / J.G. Gurley, E.S. Shaw // The American Economic Review. 1955. № 3. P. 515-538.

8. Андреева Е.Г., Сухова А.Н. Экономический рост. Модели экономического роста // Омский научный вестник. 2011. № 6 (102). С. 46-50. URL: https://elibrary.ru/item.asp?id=17942321.

9. Гогин, А.А. Многофакторная модель экономического роста и прогноз развития региона в среднесрочной перспективе: автореф. дис. … канд. экон. наук: 08.00.13 / Гогин Андрей Александрович. Иваново, 2013. 15 с. URL: https://dspace.kpfu.ru/xmlui/bitstream/handle/net/147187/0- 803711.pdf?sequence=-1&isAllowed=y.

10. Гиблова, Н.М. Влияние денежно-кредитной политики на экономический рост в условиях нестабильности // Банковское дело. 2015. № 2. С. 14-20. URL: http://www.library.fa.ru/files/Giblova.pdf; https://elibrary.ru/item. asp? id=23 098674.

11. Дембилов, О.Э. Роль денежно-кредитной политики Банка России в экономическом развитии государства // Российское предпринимательство. 2015. Т. 16. № 20. С. 3387-3398. DOI: http://doi.org/10.18334/rp.16.20.2009.

12. Иванов, Д.Ю., Орлова К.Ю. Моделирование взаимодействия участников банковской системы с учетом рисков // Известия Самарского научного центра Российской академии наук. 2013. Т. 15. № 6-4. С. 10741077. URL: http://www.ssc.smr.ru/media/joumals/izvestia/2013/2013_6_1074_1077.pdf; https://elibrary.ru/item.asp?id= 21834487.

References

1. McKinnon R.I. Money and Capital in Economic Development. Washington, DC: Brooking Institution, 1973, 184 p. Available at: https://www.brookings.edu/book/money-and-capital-in-economic-development/.

2. Allen D.S., Ndikumana L. Financial Intermediation and Economic Growth in Southern Africa. Journal of African Economies, 2000, no. 9, pp. 132-160. DOI: http://dx.doi.org/10.1093/jae/9.2.132.

3. Bencivenga V.R., Smith B.D. Financial Intermediation and Endogenous Growth. The Review of Economic Studies, 1991, no. 58, pp. 195-209. Available at: http://linksjstor.org/sici?sici=0034-6527%28199104%2958%3A2%3C195%3AFIAEG%3E2.0.C0%3B2-3.

4. Goldsmith R.W. Financial Structure and Development. New Haven, CT: Yale University Press, 1969, 561 p.

5. Shaw E.S. Financial Deepening in Economic Development. New York: Oxford University Press, 1973, 270 p.

6. Schumpeter J.A. The Theory of Economic Development. Harvard Economic Studies, 1911-1912, no. 46, pp. 72-74.

7. Gurley J.G., Shaw E.S. Financial Aspects of Economic Development. The American Economic Review, 1955, no. 3, pp. 515-538.

8. Andreeva E.G., Sukhova A.N. Economic growth. Models of economic growth. Omsk Scientific Bulletin, 2011, no. 6 (102), pp. 46-50. Available at: https://elibrary.ru/item.asp?id=17942321. (In Russ.)

9. Gogin A.A. A multifactor model of economic growth and a forecast for the development of the region in the medium term. Ivanovo, 2013, 15 p. Available at: https://dspace.kpfu.ru/xmlui/bitstream/handle/net/147187/0-803711.pdf?sequence=-1&isAllowed=y. (In Russ.)

10. Giblova N.M. The influence of monetary policy on economic growth in conditions of instability. Banking, 2015, no. 2, pp. 14-20. Available at: http://www.library.fa.ru/files/Giblova.pdf; https://elibrary.ru/ item.asp?id=23098674. (In Russ.)

11. Dembilov O.E. The role of monetary policy of the Bank of Russia in the state’s economic development. Russian Journal of Entrepreneurship, 2015, vol. 16, no. 20, pp. 3387-3398. DOI: https://doi.org/10.18334/rp.16.20.2009. (In Russ.)

12. Orlova C.Yu., Ivanov D.Y. Banking system participants interaction modeling with an allowance for risk. Izvestia of Samara Scientific Center of the Russian Academy of Sciences, 2013, vol. 15, no. 6-4, pp. 1074-1077. Available at: http://www.ssc.smr.ru/media/journals/izvestia/2013/2013_6_1074_1077.pdf; https://elibrary.ru/ item.asp?id=21834487. (In Russ.)

Модель исправления ошибок (ECM) относится к категории моделей нескольких временных рядов, наиболее часто используемых для данных, в которых базовые переменные имеют долгосрочный общий стохастический тренд, также известный как коинтеграция . ECM — это теоретически обоснованный подход, полезный для оценки как краткосрочных, так и долгосрочных эффектов одного временного ряда на другой. Термин «исправление ошибок» относится к тому факту, что отклонение последнего периода от долгосрочного равновесия, ошибка , влияет на его краткосрочную динамику. Таким образом, ECM напрямую оценивают скорость, с которой зависимая переменная возвращается в состояние равновесия после изменения других переменных.

История ECM

Юл (1926) и Грейнджер и Ньюболд (1974) были первыми, кто привлек внимание к проблеме ложной корреляции и нашел решения о том, как ее решать при анализе временных рядов. Учитывая два совершенно не связанных, но интегрированных (нестационарных) временных ряда, регрессионный анализ одного по другому будет иметь тенденцию давать явно статистически значимую взаимосвязь, и, таким образом, исследователь может ошибочно полагать, что нашел доказательства истинной взаимосвязи между этими переменными. Обычные методы наименьших квадратов больше не будут согласованными, а часто используемые тестовые статистические данные будут недействительными. В частности, моделирование методом Монте-Карло показывает, что можно получить очень высокий R-квадрат , очень высокую индивидуальную t-статистику и низкую статистику Дарбина – Ватсона . С технической точки зрения Филлипс (1986) доказал, что оценки параметров не будут сходиться по вероятности , точка пересечения будет расходиться, а наклон будет иметь невырожденное распределение по мере увеличения размера выборки. Однако может существовать общий стохастический тренд для обоих рядов, который искренне интересует исследователя, поскольку он отражает долгосрочную взаимосвязь между этими переменными.

Из-за стохастической природы тренда невозможно разбить интегрированный ряд на детерминированный (предсказуемый) тренд и стационарный ряд, содержащий отклонения от тренда. Даже при детерминированном исключении тренда случайного блуждания в конечном итоге возникнут ложные корреляции. Таким образом, снятие тренда не решает проблему оценки.

Чтобы по-прежнему использовать подход Бокса – Дженкинса , можно было бы различать ряды, а затем оценивать модели, такие как ARIMA , учитывая, что многие обычно используемые временные ряды (например, в экономике) кажутся стационарными в первых различиях. Прогнозы на основе такой модели по-прежнему будут отражать циклы и сезонность, которые присутствуют в данных. Однако любая информация о долгосрочных корректировках, которую могут содержать данные в уровнях, опускается, и долгосрочные прогнозы будут ненадежными.

Это привело Саргана (1964) к разработке методологии ECM, которая сохраняет информацию об уровне.

Предварительный расчет

В литературе известно несколько методов оценки уточненной динамической модели, как описано выше. К ним относятся двухэтапный подход Энгла и Грейнджера, оценивающий их ECM за один этап, и VECM на основе векторов с использованием метода Йохансена .

Двухэтапный подход Энгла и Грейнджер

Первым шагом этого метода является предварительная проверка отдельных используемых временных рядов, чтобы подтвердить, что они изначально нестационарны . Это можно сделать с помощью стандартного модульного корневого DF-тестирования и ADF-теста (для решения проблемы серийно коррелированных ошибок). Возьмем случай двух разных серий и . Если оба равны I (0), будет действителен стандартный регрессионный анализ. Если они интегрированы в другом порядке, например, один является I (1), а другой — I (0), необходимо преобразовать модель.

Если они оба интегрированы в одном порядке (обычно I (1)), мы можем оценить модель ECM в виде

Если обе переменные интегрированы и этот ЕСМ существует, они объединяются теоремой Энгла – Грейнджера о представлении.

Второй этап затем оценить модель с помощью обычных наименьших квадратов :
Если регрессия не поддельный, как определено в соответствии с критериями испытаний было описано выше, метод наименьших квадратов будет не только силу, но на самом деле очень последовательным (Шток, 1987). Затем прогнозируемые остатки из этой регрессии сохраняются и используются в регрессии разностных переменных плюс запаздывающий член ошибки.

Затем можно проверить коинтеграцию с помощью стандартного т-статистики на . Хотя этот подход прост в применении, существует множество проблем:

VECM

Подход Энгла – Грейнджера, описанный выше, страдает рядом недостатков. А именно, он ограничен только одним уравнением с одной переменной, обозначенной как зависимая переменная, объясненной другой переменной, которая, как предполагается, является слабо экзогенной для интересующих параметров. Он также основан на предварительном тестировании временных рядов, чтобы выяснить, являются ли переменные I (0) или I (1). Эти недостатки можно устранить с помощью процедуры Йохансена. Его преимущества заключаются в том, что предварительное тестирование не требуется, может существовать множество коинтегрирующих взаимосвязей, все переменные рассматриваются как эндогенные, и возможны тесты, относящиеся к долгосрочным параметрам. Полученная модель известна как модель векторной коррекции ошибок (VECM), поскольку она добавляет функции коррекции ошибок в многофакторную модель, известную как векторная авторегрессия (VAR). Процедура выполняется следующим образом:

• Шаг 1: оцените неограниченную VAR, включающую потенциально нестационарные переменные
• Шаг 2: Проверьте коинтеграцию с помощью теста Йохансена
• Шаг 3: Сформируйте и проанализируйте VECM.

Пример ECM

Идея коинтеграции может быть продемонстрирована в простой макроэкономической обстановке. Предположим, потребление и располагаемый доход — это макроэкономические временные ряды, которые связаны в долгосрочном плане (см. Гипотезу о постоянном доходе ). В частности, пусть средняя склонность к потреблению будет 90%, то есть в долгосрочной перспективе . С точки зрения эконометриста, эта долгосрочная взаимосвязь (также известная как коинтеграция) существует, если ошибки регрессии являются стационарными рядами, хотя и нестационарны. Предположим также, что если внезапно изменяется на , то изменяется на , то есть предельная склонность к потреблению равна 50%. Наше окончательное предположение состоит в том, что разрыв между текущим и равновесным потреблением уменьшается каждый период на 20%.

В этой настройке изменение уровня потребления можно смоделировать как . Первый член в правой части таблицы описывает краткосрочное влияние изменения на , второй член объясняет долгосрочное стремление к равновесному соотношению между переменными, а третий член отражает случайные шоки, которые получает система (например, шоки уверенности потребителей в том, что влияют на расход). Чтобы увидеть, как работает модель, рассмотрим два вида шоков: постоянные и временные (временные). Для простоты положим равным нулю для всех t. Предположим, что в период т  — 1 система находится в равновесии, то есть . Предположим, что за период t увеличивается на 10, а затем возвращается на прежний уровень. Затем первый (в период t) увеличивается на 5 (половина от 10), но после второго периода начинает уменьшаться и сходится к своему исходному уровню. Напротив, если шок является постоянным, то медленно приближается к значению, превышающему начальное на 9.

Эта структура общая для всех моделей ECM. На практике эконометристы часто сначала оценивают взаимосвязь коинтеграции (уравнение в уровнях), а затем вставляют его в основную модель (уравнение в разностях).

использованная литература

дальнейшее чтение

• Доладо, Хуан Дж .; Гонсало, Хесус; Мармол, Франсеск (2001). «Коинтеграция». В Балтаги, Бади Х. (ред.). Компаньон теоретической эконометрики . Оксфорд: Блэквелл. стр.  634 -654. DOI : 10.1002 / 9780470996249.ch31 . ISBN   0-631-21254-X .
• Эндерс, Уолтер (2010). Прикладные эконометрические временные ряды (Третье изд.). Нью-Йорк: Джон Вили и сыновья. С. 272–355. ISBN   978-0-470-50539-7 .
• Lütkepohl, Гельмут (2006). Новое введение в анализ множественных временных рядов . Берлин: Springer. стр.  237 -352. ISBN   978-3-540-26239-8 .
• Мартин, Вэнс; Херн, Стэн; Харрис, Дэвид (2013). Эконометрическое моделирование с использованием временных рядов . Нью-Йорк: Издательство Кембриджского университета. С. 662–711. ISBN   978-0-521-13981-6 .

Цель данной статьи — поделиться результатами сравнительного анализ двух тестов на коинтеграцию, теста Энгла-Гренджера и теста Йохансена. Для этого нам понадобится рассмотреть соотношение между двумя и более переменными, понять, что такое VAR процесс, как перейти к VECM модели, в чем заключается процедура Йохансена, и как интерпретировать результат статистического теста, полученного от стандартного пакета типа Matlab.

VAR процесс

Регрессия полезна, когда анализируются только два ряда, потому что в этом случае может быть не более одного коэффициента коинтеграции. В случае со многими переменными может быть более одного вектора коинтеграции. Следовательно, нужна методология, которая бы определила структуру всех векторов коинтеграции.

Векторный авторегрессионный (VAR) процесс, основанный на гауссовых (нормально распределенных) ошибках, часто использовался в качестве описания макроэкономических временных рядов. Причин для этого много: VAR-модель гибкая, легко оцениваемая и, как правило, хорошо вписывается в макроэкономические данные. Однако возможность объединения долгосрочной и краткосрочной информации с использованием свойств коинтеграции, вероятно, является наиболее важной причиной, по которой VAR-модель продолжает вызывать интерес как у эконометристов, так и у прикладных экономистов.

Теоретические экономические модели традиционно разрабатывались как неслучайные математические сущности и часто применялись к эмпирическим данным путем добавления процесса случайных ошибок в математическую модель.

С эконометрической точки зрения эти два подхода принципиально отличаются друг от друга: первый начинается с явной случайной формулировки всех данных, а затем сужает общую статистическую (динамическую) модель путем наложения поддающихся проверке ограничений на параметры, второй начинается с математической (статической) формулировки теоретической модели, а затем расширяет модель путем добавления случайных компонентов.

К сожалению, было доказано, что эти два подхода, даже если применяются к идентичным данным, дают очень разные результаты, поэтому приводят к различным выводам. С научной точки зрения это неудовлетворительно. Поэтому здесь мы попытаемся преодолеть разрыв между двумя точками зрения, начав с некоторых типичных вопросов, которые представляют теоретический интерес, а затем покажем, как можно ответить на эти вопросы на основе статистического анализа VAR-модели. Поскольку статистический анализ по своей конструкции «больше», чем теоретическая модель, он не только отвечает на конкретные теоретические вопросы, но и дает дополнительное представление о макроэкономической проблеме.

Теоретическую модель можно упростить, сделав допущение «при прочих равных условиях», то есть что «все остальное неизменно», в то время как статистически четкая эмпирическая модель должна решать теоретическую проблему в контексте «все остальное меняется». Встраивая теоретическую модель в более широкие эмпирические рамки, анализ статистически обоснованной модели может подтвердить наличие подводных камней в макроэкономическом рассуждении. В этом смысле VAR-анализ может быть полезен для создания новых гипотез или для изменения слишком узко заданных теоретических моделей.

На практике полезно классифицировать переменные, которые характеризуются высокой степенью персистентности во времени (незначительный возврат к среднему), как нестационарные, а переменные, характеризующиеся значительной тенденцией возврата к среднему, как стационарные. Однако важно подчеркнуть, что стационарность / нестационарность или, наоборот, порядок интегрирования являются не свойством экономической переменной, а удобным статистическим приближением для разграничения краткосрочных, среднесрочных и долгосрочных изменений в данных.

Перейдем к случаю, когда мы наблюдаем вектор переменных. В этом случае необходимо дополнительно обсудить ковариации между переменными в момент времени , а также их ковариации между моментами времени и . Ковариации содержат информацию о статических и динамических связях между переменными, которую мы хотели бы раскрыть с помощью эконометрики. Для простоты будет использоваться для обозначения как случайной величины, так и ее реализации.

Рассмотрим -мерный вектор :

Введем следующее обозначение на случай, когда не были сделаны упрощающие предположения:

Теперь предположим, что одно и то же распределение применимо ко всем и что распределение приблизительно нормально, поэтому первые два момента вокруг среднего значения (центральные моменты) являются достаточными для описания вариации в данных. Введем обозначение:

где — вектор размерности . Ковариационная матрица представлена следующим образом

где . Вышеприведенное обозначение дает полное общее описание многомерного нормального векторного случайного процесса. Поскольку параметров для оценки гораздо больше, чем наблюдений, то с практической точки зрения такое описание бесполезно, и необходимо упростить предположения для сокращения числа параметров. Эмпирические модели обычно основаны на следующих предположениях:

Теперь мы можем записать среднее значение и ковариации в более простой форме:

Два приведенных выше допущения для бесконечного определяют слабо стационарный процесс. Когда эти два предположения будут выполнены, VAR-модель будет иметь постоянные параметры.

Пусть — случайный процесс (упорядоченный ряд случайных переменных) для . Тогда считается стационарным в широком смысле. Стационарность в узком смысле требует, чтобы распределение было таким же, как для

Эмпирический анализ начинается с матрицы , где — это вектор переменных. Исходя из предположения, что наблюдаемые данные являются реализацией случайного процесса, можно выразить совместную вероятность при заданном начальном значении и значении параметра , описывающего случайный процесс:

Для данной функции вероятности оценки максимального правдоподобия могут быть найдены путем максимизации функции правдоподобия. Здесь мы ограничимся обсуждением многомерного нормального распределения. Для выражения совместной вероятности удобно использовать процесс вместо матрицы . Поскольку у размерность , а у — , то параметров гораздо больше, чем наблюдений без упрощения допущений. Но даже если мы вводим упрощающие ограничения на среднее значение и ковариации процесса, они не дают прямой информации об экономическом поведении. Поэтому, разложив совместный процесс на условный и частный, а затем последовательно повторяя разложение для частного процесса, мы можем получить более полезную формулировку:

где

Теперь покажем, что VAR-модель является условным процессом

Можно увидеть, как и связаны с и . Сначала разложим данные на два набора, вектор и условный набор , то есть

Запишем частный и условный процесс:

Теперь можно вывести параметры условной модели:

где

и

Разница между наблюдаемым значением процесса и его условным средним значением обозначена как :

Подставляя выражение для условного среднего значения, получаем:

Используя обозначение , и принимая, что , получаем векторную авторегрессионную модель -го порядка:

где — , а считаются заданными.

Если верно предположение, что является многомерным нормальным процессом, то из этого следует, что VAR-модель:

• линейна по параметрам;

• имеет постоянные параметры;

• имеет нормально распределенные ошибки .

Обратите внимание, что постоянство параметров зависит от постоянства ковариационных матриц и . Если какая-либо из них изменится в результате преобразования или вмешательства во время анализа выборки, вероятно, изменятся как свободный член , так и «коэффициенты наклона» . Таким образом, допущения о постоянстве параметров сильно зависят от контекста и обычно требуют, чтобы для соответствующего периода времени моделировались все основные известные структурные изменения.

Было показано, что VAR-модель по сути представляет собой переформулировку ковариаций данных. Вопрос заключается в том, можно ли интерпретировать модель с точки зрения рационального экономического поведения, и если да, то можно ли использовать модель в качестве «плана эксперимента», когда данные собираются путем пассивных наблюдений. Идея заключается в интерпретации условного среднего значения VAR-модели как описания планов агентов во время с учетом имеющейся информации . В соответствии с допущениями VAR-модели, разница между средним значением и фактической реализацией представляет собой процесс белого шума

Таким образом, допущение согласуется с экономическими агентами, которые рациональны в том смысле, что они не допускают систематических ошибок при составлении планов на время на основе имеющейся информации в момент времени . Например, VAR-модель с автокоррелированными и/или гетероскедастическими остатками описывает агентов, которые не используют всю информацию, содержащуюся в данных, как можно более эффективно. Это связано с тем, что, включив систематические изменения в остатки, агенты могут повысить точность, с которой они реализуют свои планы. Поэтому проверка предположений модели, то есть проверка остатков на соответствие белому шуму, имеет решающее значение не только для правильного статистического вывода, но и для экономической интерпретации модели как примерного описания поведения рациональных агентов.

К сожалению, во многих экономических приложениях допущение о многомерной нормальности для VAR-модели в ее простейшей форме не выполняется. Поскольку в целом статистические выводы справедливы только в той степени, в какой удовлетворяются предположения, заложенные в основу модели, это потенциально является серьезной проблемой. Поэтому нужно спросить, возможно ли модифицировать базовую VAR-модель таким образом, чтобы она сохраняла свою привлекательность в качестве удобного описания основных свойств данных и в то же время позволяла делать обоснованные выводы.

Исследования в области моделирования показали, что достоверные статистические выводы чувствительны к нарушению некоторых допущений, таких как параметрическая нестабильность, автокорреляция остатков (чем выше, тем хуже) и асимметричные остатки, при этом достаточно устойчивы к другим, таким как избыточный коэффициент эксцесса и гетероскедастичность остатков.

В любом случае, прямое или косвенное тестирование предположений имеет решающее значение для успеха эмпирического применения. Как только мы поймем причины, по которым модель не удовлетворяет допущениям, часто появляется возможность модифицировать модель, чтобы в итоге получить статистически «хорошо себя зарекомендовавшую» модель. Важными инструментами в этом контексте являются:

• использование интервенционных фиктивных переменных для объяснения значимых политических или институциональных событий в выборке;

• обусловленность слабо или сильно экзогенными переменными;

• проверка измерений выбранных переменных;

• коррекция периода выборки, чтобы избежать структурных изменений или разделить выборку на более однородные периоды.

ECM процесс

Так называемая векторная модель исправления ошибок (далее VECM) дает удобную переформулировку VAR-модели в терминах разностей, запаздывающих разностей и уровней процесса. У этой формулировки есть несколько преимуществ:

1. Эффект мультиколлинеарности, который обычно сильно проявляется в данных временных рядов, значительно снижается в форме исправления ошибок. Разности гораздо более «ортогональны», чем уровни переменных.

2. Вся информация о долгосрочных эффектах обобщается в матрице уровней (в дальнейшем обозначена как ). Следовательно, ей можно уделить особое внимание при решении проблемы коинтеграции.

3. Интерпретация оценок интуитивно более понятна, поскольку коэффициенты можно естественным образом разделить на краткосрочные и долгосрочные эффекты.

4. Формулировка VECM дает прямой ответ на вопрос, «почему цена актива изменилась с предыдущего по настоящий период в результате изменений в выбранном наборе информации».

Теперь рассмотрим модель VAR, сформулированную в общей форме VECM без константы и тренда:

где — целое число между 1 и , определяющее положение лага ECM-члена. Обратите внимание, что значение функции правдоподобия не меняется даже при изменении значения .

VAR(2)-модель в VECM формулировке при определена как:

где , а . В уравнении лагированная матрица уровней находится во времени .

CVAR процесс

Рассмотрим нестационарную VAR-модель и покажем, что наличие единичных корней (стохастических трендов) приводит к условию неполного ранга на матрице долгосрочных уровней .

Коинтеграция подразумевает, что определенные линейные комбинации переменных векторного процесса интегрированы более низким порядком, чем сам процесс. Таким образом, если нестационарность одной переменной соответствует нестационарности другой, то существует их линейная комбинация, которая становится стационарной. Другой способ выразить это взаимоотношение заключается в том, что когда две или несколько переменных имеют общие стохастические (и детерминистические) тренды, они будут иметь тенденцию двигаться вместе в долгосрочной перспективе. Такие векторы коинтеграции часто могут быть интерпретированы как долгосрочные равновесные соотношения переменных и, следовательно, представляют значительный экономический интерес.

В рамках VAR-модели гипотеза о коинтеграции может быть сформулирована в виде ограничения на неполный ранг матрицы . Воспроизведем ниже VAR(2)-модель в виде ECM с :

и дадим оценку неограниченной матрице .

Если , то . Из этого следует, что не может иметь полного ранга, так как обратное приведет к логическому несоответствию в уравнении. Рассмотрим как простую матрицу с полным рангом. В этом случае в каждом уравнении стационарная переменная будет равна нестационарной переменной плюс некоторые запаздывающие стационарные переменные и член со стационарной ошибкой. Поскольку стационарная переменная не может быть равна нестационарной переменной, то либо , либо матрица должна иметь неполный ранг:

где и — -матрицы, . Таким образом, при гипотезе имеем коинтегрированную VAR(2)-модель:

где — — вектор коинтеграции. интерпретируется как скорость приведения процесса к равновесию. В соответствии с гипотезой о том, что , все стохастические компоненты в модели являются стационарными, и система теперь логически непротиворечива.

Если , то стационарно, и применяется стандартный вывод. Если , то в существует автономных трендов, так что каждый является нестационарным со своим собственным индивидуальным трендом. По сути мы имеем VAR-процесс в ряде разностей. В этом случае векторный процесс управляется различными стохастическими трендами, и невозможно получить векторы коинтеграции между уровнями переменных. Мы говорим, что переменные не имеют общих стохастических трендов и, следовательно, не движутся вместе во времени.

В этом случае VAR-модель с уровнями может быть переформулирована в VAR-модель с разностями без потери долгосрочной информации. Поскольку , в модели с разностями применяется стандартный вывод. Если , то и существует направлений, по которым процесс можно сделать стационарным с помощью линейных комбинаций. Это и есть векторы коинтеграции. Причина нашего интереса к ним заключается в том, что они часто могут быть интерпретированы как отклонения от стабильных экономических отношений.

R процесс (консолидация общей VAR модели)

Рассмотрим VARмодель в форме ECM с :

где , — это вектор, , — количество детерминированных компонент, таких как константа или тренд, а начальные значения считаются заданными.

Мы используем следующие сокращенные обозначения:

тогда мы можем переписать VARмодель в более компактной форме:

где . Теперь мы консолидируем краткосрочные «транзитные» эффекты, , чтобы получить «чистую» модель долгосрочной коррекции. Чтобы объяснить идею «консолидации», которая используется во многих различных ситуациях в эконометрике, мы сначала проиллюстрируем ее использование в модели множественной регрессии.

Теорема Фриша-Во-Ловела (Frisch-Waugh-Lovell, FWL) гласит, что OLS-оценка в модели линейной регрессии, может быть получена в два этапа.

1. Построить регрессию от , получая остатки из .
   Построить регрессию от , получая остатки из .

2. Построить регрессию от , чтобы получить оценку , то есть .

Таким образом сначала мы консолидируем влияние на и , а затем строим регрессию для «очищенного» , то есть , от «очищенного» , то есть .

Воспользуемся той же идеей для VAR-модели. Сначала определим вспомогательные регрессии:

где , — МНК оценки, . Таким образом, это эмпирические аналоги ковариационных матриц .

Консолидированная модель

важна для понимания как статистических, так и экономических свойств VAR-модели. Путем консолидации исходная «грязная» VAR, содержащая краткосрочные эффекты коррекции и интервенции, была преобразована в «чистую» равновесную форму коррекции, в которой коррекция происходит исключительно в направлении долгосрочных равновесных отношений. Это означает, что мы не только преобразовали «грязную» эмпирическую модель в красивую статистическую модель, но и в более интерпретируемую экономическую форму.

Тест Йохансена

Тест Йохансена, также называемый LR-тестом на коинтеграционный ранг или тестом следа (трейс тестом), основан на VAR-модели в R-форме, где сконцентрирована вся краткосрочная динамика, фиктивные и другие детерминированные компоненты:

Тест Йохансена называется тестом следа, потому что асимптотическое распределение статистики является следом матрицы, основанной на функциях броуновского движения или стандартных винеровских процессах. Тест Йохансена для определения ранга коинтеграции включает следующие гипотезы:

Соответствующая LR-статистика имеет вид (статистика следа):

где можно интерпретировать как квадрат канонических корреляций между линейной комбинацией уровней и линейной комбинацией разностей . В этом смысле величина является показателем того, насколько сильно линейное отношение коррелирует со стационарной частью процесса . Когда , линейная комбинация нестационарна и не существует поправки на равновесие.

Процедура тестирования заключается в следующем. Сначала проверяется нулевая гипотеза о том, что существует один вектор коинтеграции, затем гипотеза о двух векторах и т.д. Мы отвергаем нулевую гипотезу, что — число векторов коинтеграции — меньше чем , если значение статистического критерия больше указанного критического значения.

Также возможна проверка нулевой гипотезы против альтернативной о том, что ранг на единицу больше, чем предполагается в нулевой гипотезе:

• ;

• .

В таком случае применяется статистика максимального собственного числа:

Пример: преобразование VAR(3) в ECM

Возьмем в качестве примера VAR(3) процесс:

Это достаточно сложное уравнение может быть выражено в матричной форме (опустим вектор с ошибками для краткости):

Далее мы должны преобразовать модель через разности. Это можно сделать следующим образом. Во-первых, мы вычитаем

из обеих частей уравнения, преобразуя левую сторону уравнения в разности:

Мы можем преобразовать это выражение следующим образом:

Открывая скобки, получаем:

Группируем члены с общими множителями:

В результате получим выражение:

Схожая процедура применяется по отношению к матрице :

Открывая скобки, получаем:

Группируем члены с общими множителями:

В результате получаем:

Обозначим , , , получим VAR(3) модель в ECM форме:

Мы видим, что VAR-процесс уровней рядов может быть записан как VAR-процесс разностей за исключением одного члена .

Ранг матрицы дает число векторов коинтеграции в рядах динамики (ранг матрицы — это число линейно независимых рядов). Таким образом, ранг матрицы говорит о том, что следует делать. Если имеет нулевой ранг, то матрица — нулевая. Это показывает, что коинтеграции в рядах данных нет, и для достижения стационарности требуется нахождение разностей.

Если матрица — полная, то ряды уже стационарны (матрица имеет обратную, и, таким образом, выражение может быть решено для уровней, выраженных в разностях. Это будет верным только если ряды уровней ).

Если ранг лежит между 0 и ( , в нашем случае , ), то существует векторов коинтеграции. Модель исправления ошибки включает в себя краткосрочные изменения, которые поддерживают долгосрочное равновесие.

Тест Йохансена в MATLAB

У нас есть два ряда цен акций, и . Мы хотим, чтобы и были коинтегрированными, то есть чтобы ранг коинтеграции был равен 1. Рассмотрим два тикера Московской биржи, TATN и TATNP за 2020 год:

Тест Йохансена выполняется с помощью функции jcitest, которая на вход принимает массив из временных рядов, в данном случае размера , где — количество торговых дней. На выходе функция возвращает логическое значение, равное 1, если нулевая гипотеза отвергается в пользу альтернативной, и 0 – иначе.

testPrices(:,1) = prices(:,indexY);
testPrices(:,2) = prices(:,indexX);
[hjt,pValuejt,statjt,cValuejt,mles] = jcitest(testPrices, 'model', 'H2');
[hjtm,pValuejtm,statjtm,cValuejtm,mlesm] = jcitest(testPrices, 'model', 'H2', 'test', 'maxeig');

Статистика следа

Дальше начинается самое интересное: программа выдает ответ, который обычному человеку сложно понять, потому что он приходит в виде массива логических значений.

Википедия нас к такому не готовила, поэтому давайте разберемся, что здесь происходит. Гипотетически тест следа может привести к трем различным вариантам ранга коинтеграции и, следовательно, количествам единичных корней.

1. , , когда

2. , , когда ,

3. , , когда ,

где — статистика следа, — соответствующие критические значения, в нашем случае равно 2, так как у нас две переменные, (TATN) и (TATNP). Поэтому, чтобы оценить значение , мы должны выполнить последовательность тестов.

Отметим, что асимптотические таблицы определяются так, что когда истинна, тогда , где задается как:

Рассмотрим результат теста для нулевого ранга. В чем здесь заключается нулевая гипотеза?

Из ответа матлаба мы видим, что нулевая гипотеза отвергается для нулевого ранга ( для ). Это означает, что асимптотически.

Рассмотрим результат теста для первого ранга. В чем здесь заключалась нулевая гипотеза?

Следующее значение соответствует , истинному коинтеграционному числу, а в соответствии с ответом матлаба о том, что нулевая гипотеза не отвергается для первого ранга ( для ). Таким образом последний вариант .

Резюмируем:

• 

• 

• 

Таким образом правильное значение асимптотически принимается в 95% всех случаев, что как раз и должна делать процедура 5%-ного теста.

Статистика максимального собственного числа

Практически тот же самый результат мы видим для статистики максимального собственного числа.

Здесь у нас есть следующие варианты:

где — статистика максимального собственного числа, — соответствующие критические значения.

Напомним, что задается как:

Рассмотрим результат теста для нулевого ранга. В чем здесь заключается нулевая гипотеза?

• 

• 

• 

Из ответа матлаба мы видим, что нулевая гипотеза отвергается для нулевого ранга ( для ). Это означает, что асимптотически.

Рассмотрим результат теста для первого ранга. В чем здесь заключалась нулевая гипотеза?

• 

• 

• 

Следующее значение соответствует истинному коинтеграционному числу, а в соответствии с ответом матлаба о том, что нулевая гипотеза не отвергается для первого ранга ( для ).

По результатам обеих статистик мы видим, что пара (TATN, TATNP) является коинтегрированной.

Тест Энгла-Грэнджера vs Тест Йохансена

Мной была проанализирована 1 621 пара акций Московской биржи за 2020 год на дневных данных. В 87% случаев результаты теста Энгла-Гренджера и теста Йохансена совпали.

Также было проанализировано 3 193 890 пар на американских биржах (NYSE, NASDAQ и AMEX) за 2020 год на дневных данных. Также в 87% случаев результаты теста Энгла-Гренджера и теста Йохансена совпали.

Еще было проанализировано 21 725 пар на криптобиржах (Poloniex, Binance, Kraken) за 2020 год на дневных данных. В 86% случаев результаты теста Энгла-Гренджера и теста Йохансена совпали.

С практической точки зрения для принятия решения о том, стоит ли добавлять пару активов в портфель, а также для оценки весовых коэффициентов лучше использовать оба теста на коинтеграцию.