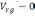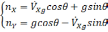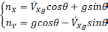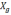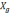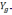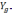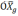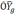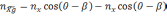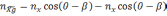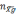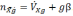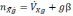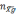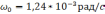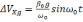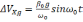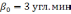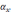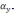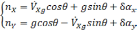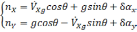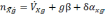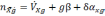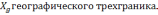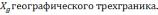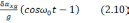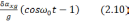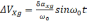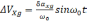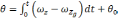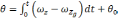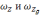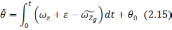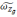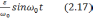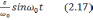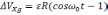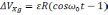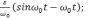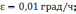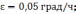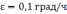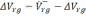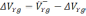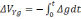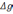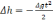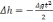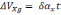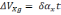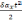Модель ошибок бинс - Не ошибается лишь тот, кто ничего не делает!

Список литературы

1. Ишлинский А.Ю. Ориентация, гироскопы и инерциальная навигация. М.: Наука, 1976. 672 с.

2. Ривкин С.С. Стабилизация измерительных устройств на качающемся основании. М.: Наука, 1978. 320 с.

3. Пельпор Д.С., Колосов Ю.А., Рахтеенко Е.Р. Расчёт и проектирование гироскопических стабилизаторов. М.: Машиностроение, 1972. 325 с.

4. Фабрикант Е.А., Журавлев Л.Д. Динамика следящего привода гироскопических стабилизаторов. М.: Машиностроение, 1984. 248 с.

5. Неусыпин А.К. Гироскопические приводы. М.: Машиностроение, 1978. 191 с

6. Родионов В. И. Гироскопические системы стабилизации и управления. Тула: Изд-во ТулГУ, 2000. 192 с.

V.I. Rodionov, D.A. Veterkov

GEOMETRY OF TARGET SEEKER WITH INCLINED CARDAN SUSPENSION

The geometiy two-axis stabilization system and control (SSaC) of target seeker is researched. There are results of the angular coordinate conversion. Ability of inclined SSaC to carry out homing in a forward hemisphere is shown.

Key words: homing head, target seeker, geometry.

Получено 3.12.12

УДК 629.7

В.В. Матвеев, канд. техн. наук, доц., (4872) 35-19-59, matweew.valery@yandex.ru (Россия, Тула, ТулГУ)

МОДЕЛЬ ПОГРЕШНОСТЕЙ БЕСПЛАТФОРМЕННОЙ ННЕРЦНАЛЬНОЙ НАВИГАЦИОННОЙ СИСТЕМЫ

Получена модель погрешностей бесплатформенной инерциалъной навигационной системы (БИНС), включающая уравнения погрешностей в определении скорости координат и ориентации. Приведена обобщенная структурная схема формирования погрешностей БИНС.

Ключевые слова: бесплатформенная инерциальная навигационная система, модель погрешностей.

Введение

Решение уравнений погрешностей позволяет предъявить требования к характеристикам гироскопов и акселерометров бесплатформенной инерциалъной навигационной системы (БИНС), если она должна обеспечить

заданную точность или рассчитать точность определения навигационных параметров, если характеристики элементов заданы. Изучение уравнений погрешностей позволяет обоснованно провести выбор алгоритма работы БИНС. Без анализа этих уравнений невозможно строгое обоснование допустимости тех или иных упрощений. Наконец, лишь на основании изучения свойств уравнений погрешностей можно судить о необходимости коррекции БИНС, а также ее эффективности [1].

Если структура БИНС неизменна, то ее погрешности могут быть сведены к некоторым эквивалентным погрешностям первичной информации, т.е. к погрешностям чувствительных элементов. В качестве таких характерных в БИНС обычно принимают инструментальные погрешности акселерометров и гироскопов.

Системы координат

Введем в рассмотрение следующие системы координат: i — инерциальная система координат (inertial frame), начало которой совпадает с центром Земли, а плоскость O’X’Y’ лежит в плоскости экватора Земли. Ось O’X’ — направлена в точку весеннего равноденствия, ось O’Z’ направлена к северному полюсу, а ось O’Y1 дополняет две предыдущие до правой системы координат;

e — земная система координат, центр которой помещен в центр Земли, причем плоскость OeXeYe совпадает с плоскостью экватора. Ось OeXe направлена в плоскости Гринвичского меридиана, ось OeZe — вдоль оси вращения Земли к северному полюсу, а ось OeYe дополняет две предыдущие до правой системы координат. Система координат OeXeYeZe вращается относительно инерциальной системы O1 XlYlZl с угловой скоростью суточного вращения Земли. Проекции вектора угловой скорости суточного вращения Земли на оси инерциальной земной систем координат определяются следующим равенством:

ю^ = ю% = ||о о u||t .

Здесь и далее для обозначения векторов будет применяться индексная форма записи [2], при которой верхний индекс обозначает наименование системы координат, в которой заданы проекции данного вектора, а два нижних соответственно определяют движение одной системы координат (второй индекс) по отношении к другой (первый индекс). Обозначим символом C e матрицу направляющих косинусов при переходе от системы координат i к системе координат е.

Географическая система координат (другие названия: нормальная система координат, в англоязычной литературе Local Navigation Frame) OXgYgZg ориентирована по сторонам света: ось OXg направлена по касательной к меридиану на север, OYg — вдоль истинной вертикали вверх, OZg

— по касательной к параллели на восток. Начало системы координат О совпадает с центом масс подвижного объекта, поэтому такую систему координат называют также сопровождающей. Географическую систему координат обозначим символом g.

Матрица перехода от земной системы координат е к географической g имеет вид

sin В cos L -sin В sin L cos В

Cg =

cos В cosL -sin L

cos В sin L cos L

sin В 0

где В, L — широта и долгота соответственно.

Связанная система координат OXYZ является подвижной системой координат, осями которой являются продольная ось ОХ, нормальная ось OY и поперечная ось OZ, фиксированные относительно подвижного объекта. Связанной системе координат присвоим символ Ъ (от английского термина «body»). Матрицу перехода от географической системы координат к связанной обозначим символом С

Схема переходов между системами координат иллюстрируется на

рис.1.

со = О

cot

со

Рис. 1. Схема переходов

В соответствии с рис. 1 имеют место следующие равенства:

/ е

™l=Ce™ie> = Cg™eg>

<4 = CgCe<*l>

А = ctdcoi + ct col + coi

(1)

Последнее из равенств (1) характеризует показания идеальных гироскопов.

Погрешности ориентации

Решение задачи ориентации в БИНС часто осуществляется на основе матричного уравнения Пуассона или его кватернионного аналога [3,4]

+ (2)

где [<4х], [со^х] — кососимметрические матрицы, соответствующие проекциям векторов абсолютной угловой скорости связанной Ъ и географине-

190

скои g систем координат, которые имеют вид:

0 ъ Ъ <Ъ, у 0 _ю Ъ ‘Ъ, 7 юЪ ‘Ъ, у

ь <Ъ = ь 0 Ъ _<iЪ, х юЪ = <ЪЪ, 7 0 _юЪ ‘Ъ, х

ь _<‘Ъ, у ъ <‘Ъ, X 0 _юЪ Щ, у юЪ ‘Ъ, х 0

(3)

Параметры ориентации подвижного объекта определяются из соответствующих элементов матрицы направляющих косинусов:

_ СЪ _ СЪ

#1,3 • ^Ъ СЪ 3,2 у = аг^—ъ-‘ ^ = arcsm^12, У = arctg—Ъ-

(4)

‘ЪМ Ъ 2,2

В основе алгоритма БИНС лежит пересчет данных, измеренных в связанной системе координат в нормальную. Этот пересчет возможен,

когда матрица перехода СЪ известна. Матрицу СЪ5 можно найти из решения обобщенного уравнения Пуассона:

5 (5)

С Ъ = _[<ъ х]С5 + сЪ к x],

где [юъъ х], [^Ъь х] — кососимметрические матрицы, соответствующие проекциям векторов абсолютной угловой скорости связанного и нормального трехгранников на свои ребра.

При решении уравнения (5) на компьютере используется информация об абсолютных угловых скоростях связанного и нормального трехгранников, содержащая погрешности. Вместо точных значений [юЪъ х] используют данные [<% ^ х], представляющие собой выходные сигналы

гироскопов с их погрешностями [АюЪъ х]. Таким образом, выходные сигналы гироскопов принимают вид

Ъ (6)

[<% Ъъ х] = [<Ъ х] + [А<Ъъ х].

Что касается матрицы [ю^ х], то вместо нее в алгоритмах использу-

ют матрицу

[<% Ъ х] = [<Ъ х] + [А<Ъ х],

(7)

которая соответствует вектору угловой скорости географического трехгранника, вычисленного с погрешностями [Аю^ х] посредством навигационного алгоритма БИНС. В результате в БИНС реализуется уравнение Пуассона вида [3,4]

СЪ = СЪ [<%ЪЪ х] _ [%Ъ х]СЪ, (8)

где ~ — расчетная географическая система координат, которая не совпадает с истинной географической системой ъ. Положение системы координат ~

относительно g зададим посредством углов Эйлера а, р, % и матрицы направляющих косинусов С^ (рис. 2).

Рис. 2. Взаимное положение систем координат

На основании рис. 2 следует матричное равенство [3,4]

С| = С|С^ (9)

связывающее матрицу преобразования при «идеальной» работе с расчетной, которая используется в алгоритмах БИНС. Дифференцируя по времени равенство (9), имеем

С|=С*<^ + С*С£. (10)

Подставляя в полученное равенство правые части уравнений (5) и (8), получим

= С*[о&х]С* — [й§х]С*С* — С|[4х]С* + С|С*[со§х].

Принимая во внимание соотношение (10), имеем

С| = С|С|[4х]С| — [&§х]С| — С* С# [о&х]с£ + С|[со|х].

Учитывая соотношение для выходных сигналов гироскопов [й^х], приведенное уравнение упрощается:

С| = С|С|[Дсо^х]С^-[а)|х]С| + С|[со|х]. (11)

В уравнении (11) матрица погрешностей гироскопов [Дсо^х] умножена слева и справа на две взаимно обратные матрицы, что является подобным преобразованием кососимметрических матриц, а это эквивалентно преобразованию вектора Лсо|, из системы Ь в систему координат g. В этом случае уравнение (11) с учетом (7) приобретает вид

С| = С|[Л со*х] — [Дсо|х]С| + С| [<и§х] — [<а|х]С|. (12)

Полученное уравнение характеризует динамику погрешностей алгоритма ориентации БИНС при любых значениях погрешностей инерциаль-ных чувствительных элементов, в том числе микромеханических гироскопов и акселерометров.

Рассмотрим вариант малого отклонения расчетной системы координат £ от g для случая применения инерциальных чувствительных элементов высокой и средней точности, но на ограниченном интервале времени.

iНе можете найти то, что вам нужно? Попробуйте сервис подбора литературы.

192

В этом случае углы а, в, х отклонения системы координат ~ относительно о имеют малые значения, что позволяет приближенно представить матрицу С|% в виде разности единичной и кососимметрической матриц:

1 0 0 0 -в а

с! « Е — [Фх] = о 0 1 0 — в 0 -х

0 0 1 -а х 0

Пренебрегая в уравнении (12) величинами второго порядка малости, получим линеаризованное матричное уравнение погрешностей ориентации БИНС в виде

[Ф х] = -[Аю* х] + [Аю§ х] + [Фх]^ х] — ^ х][Фх]. (13)

Если ввести вектор конечного поворота

Ф = ||х а в Г,

(14)

то разность матриц в правой части (13) [Фх][ю! х] — [ю^ х][Фх] эквива-

лентна векторному произведению Ф х юг!. Тогда векторное уравнение относительно погрешностей построения вертикали и азимутальной погрешности представляется в виде

Ф = — Аю! + Аю!о + Ф х ю!

Ш 1° 1°

или

Ф = Фхю* + Аю| — С!ДюЬь. (15)

Полученное уравнение показывает скорость изменения вектора конечного поворота, характеризующего положение системы координат ~ по отношению к системе о. Причиной изменения вектора Ф является погрешности гироскопов Аю;Ь, выраженные в проекциях на оси координат о и погрешности в определении угловой скорости географической системы координат АюЬь.

Если погрешности ориентации рассматривать по отношению к земной и инерциальной системе координат, то уравнение (15) принимает вид

Ф = Фхю^ -САю?ь, (16)

Ф = -СЬ АюЬь. (17)

В уравнении (16) отсутствует член Аю;ее, так как угловая скорость вращения Земли может быть учтена без ошибки.

Уравнение погрешностей в определении скорости координат

Скорости и координаты в БИНС определяются путем интегрирования сигналов акселерометров, пересчитанных в географическую систему

координат о. В соответствии с теоремой Кориолиса абсолютное ускорение объекта в географической системе координат имеет вид

а! = а° + а% + , (18) где а! = [ю£ х][юО, х]?о — переносное ускорение, = ^ + [ю!ох]у!0 — относительное ускорение, с0 = 2[ю! х]у0 — кориолисово ускорение, — вектор линейной скорости географической системы координат, заданный своими проекциями в географической системе координат, г! — радиус-вектор вершины системы координат о.

Переносное ускорение а!е складывается с ускорением силы тяготения Земли о’0, в результате чего образуется вектор ускорения силы тяжести

= а!е + 00 •

Складывая векторы абсолютного ускорения и ускорения силы тяжести, получим вектор кажущегося ускорения в географической системе координат

П°о = + [Юе0о х]у°о + 2[Ю! х]уе0о + О0 . (19)

Направление отклонения чувствительного элемента вертикального акселерометра под действием положительно направленного вверх ускорения движения и ускорения силы тяжести совпадают, отсюда и совпадение знаков у абсолютного ускорения ЛА и ускорения силы тяжести. Если пренебречь уклонением отвесных линий, то вектор ускорения силы тяжести направлен вдоль геодезической вертикали, и его проекции имеют вид:

0 о! 0

Из соотношения (19) выражаем производную по времени от линейной скорости перемещения вершины географического трехгранника g относительно земной системы координат e:

vgg = Cgng — (Kgg x] + 2[(g x])Vegg — gg. (20)

Перепишем уравнение (20), принимая во внимание, что входящие в него величины вычисляются с погрешностями:

V&egg = Cgb nig — ([&ggx] + 2[(Dgex])Vgg — gg . (21)

Вычитая из уравнения (21) алгоритм идеальной работы (20), получим

AVg, = Cgng — Cgng — ([A(gx] + 2[A(g x])vg, —

-([(gg x] + 2[fflg x])AVegg — Agg

Если принять во внимание соотношение (9), то уравнение (21) принимает вид

Д1>4 = (С| — Е) л * + с|Ди§ — Ди^, (23)

где Ди^ — вектор погрешностей компенсации скоростных членов и ускорения силы тяжести, Ап^ — погрешности акселерометров, пересчитанные в

географическую систему координат.

Полагая отклонение расчетной системы координат £ от истинной g

малым, когда допустимо приближенное равенство С^ « Е — [Ч’х], получаем уравнение (23) в виде

Лт>4 = -[^х]п| + Д4 — Дм^.

Пренебрегая погрешностями компенсации скоростных членов и ускорения силы тяжести, окончательно получаем векторное уравнение погрешностей БИНС в определении скорости

Дт>|=4х^ + С|Д4. (24)

Записываем уравнение погрешностей БИНС по координатам местоположения объекта в виде

Дг* =

где Дг^ — вектор погрешностей БИНС в счислении координат.

Блок-схема формирования погрешностей БИНС приведена на рис. 3.

её

Рис. 3. Блок-схема формирования погрешностей БИНС

Приведенная схема характеризует формирование погрешностей БИНС с географическим опорным трехгранником, которая может быть преобразована для любого опорного трехгранника. Ветвь «А» характеризует влияние погрешностей ориентации, на точность в определении линей-

ных скоростей и координат местоположения объекта. Наличие в блок-схеме векторов угловой скорости rag и кажущегося ускорения ng, а также

матрицы Cg говорит о том, что величина погрешностей БИНС зависит от динамики движения объекта.

Заключение

Знание модели погрешностей БИНС позволяет оценить общую погрешность БИНС по заданным погрешностям гироскопов и акселерометров либо решать обратную задачу: предъявить требования к инерциальным чувствительным элементам из условия заданной точности БИНС. Кроме того, модель погрешностей необходима при разработке структуры фильтра Калмана для решения задач комплексирования БИНС с другими навигационными устройствами.

Работа выполнена при поддержке гранта РФФИ №10-08-00230а «Научные основы построения малогабаритных систем ориентации и навигации для беспилотных вращающихся по крену летательных аппаратов».

Список литературы

1. Инерциальные навигационные системы морских объектов /Д.П. Лукьянов [и др.]; под. ред. Д.П. Лукьянова. Л.: Судостроение, 1989.184 с.

2. Groves P.D. Principles of GNSS, Inertial, and Multisensor Integrated Navigation Systems /Artech Hous. 2008. 505 p.

3. Матвеев В.В. Инерциальные навигационные системы: учеб. пособие. Тула: Изд-во ТулГУ, 2012.199 с.

4. Матвеев В.В, Распопов В.Я. Основы построения бесплатформенных инерциальных навигационных систем: учеб. пособие. СПб.: ГНЦ РФ ОАО «Концерн «ЦНИИ «Электроприбор», 2009.280с.

V. V. Matveev

MODEL OF ERRORS STRAPDOWN INERTIAL NAVIGATION SYSTEM

A model errors of strapdown inertial navigation system (SINS), including the equation of error in determining the speed of the coordinates and orientation. The generalized block diagram of SINS errors.

Key words: Strapdown inertial navigation system, model errors

Получено 3.12.12

Источник

Предложите, как улучшить StudyLib

(Для жалоб на нарушения авторских прав, используйте

другую форму
)

Ваш е-мэйл

Заполните, если хотите получить ответ

Оцените наш проект

Источник

Необходимо
проанализировать погрешности, возникающие
в процессе эксплуатации БИНС.

Режим
(алгоритм) работа ИНС, когда её элементы
и устройства идеальны (не имеют
инструментальных погрешностей) и
начальные условия функционирования
системы точно соответствуют начальным
обстоятельствам движения объекта,
называют режимом (алгоритмом) идеальной
работы. В реальных условиях инерциальным
чувствительным элементам присущи
различного рода погрешности.

Режим
работы ИНС, при котором её элементы
функционируют с погрешностями и начальные
условия не соответствуют начальным
обстоятельствам движения объекта
называют возмущением.

Уравнения
для отклонения переменных, характеризующих
состояния БИНС, от их значений при
идеальной работе, называют уравнением
погрешностей[31]. Анализируя погрешности,
можно в определенной степени упростить
алгоритмы, по которым работает
вычислительное устройство, а также
выработать обоснованные требования к
коррекции БИНС.

Ошибки
БИНС в случае неточного определения
вертикали.

Рассмотрим
случай, когда акселерометры и гироскоп
функционируют без ошибок, а вертикаль
в начальный момент задана с ошибкой. В
этом случае безошибочные показания
акселерометров определяются
равенствами[30](предполагается, что :

(2.1)

где
nx,
ny
–
величина кажущегося ускорения относительно
осей х и y,
VXg
—
скорость, θ — угол.

Для
определения местоположения БЛА (широты
φ) необходимо перепроектировать показания
акселерометров (2.1) в географическую
систему координат, т.е. на оси О
и О
Однако за счёт неточного задания
вертикали сигналы акселерометров (2.1)
будут пересчитываться не на оси
географического трехгранника, а на оси
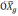
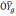
ивычисленной системы координат. В этом
случае получим:

(2.2)

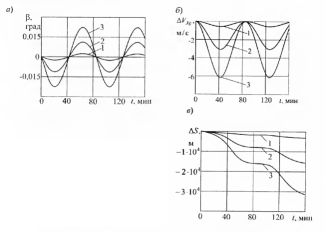
где
— проекция кажущегося ускорения на
географическую систему координат, β —
угол

Для
малого угла β, подставив (2.2) в (2.1), получим
проекцию кажущегося ускорения:

(2.3)

Таким
образом, после пересчёта данных в
географическую систему координат в
проекции кажущегося ускорения 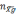содержится составляющая вектора
ускорения силы тяжести.

Согласно
дальнейшим расчетам [31]

β(t)=(2.4)

где

Эту
частоту можно трактовать, как частоту
малых незатухающих колебаний в поле
силы тяжести Земли физического маятника,
приведенная длина которого равна
расстоянию от центра Земли до объекта,
движущегостя на высоте h.
Числовое значение частоты Шулера равно
,
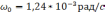
соответственно период Шулера Т=84,4[*].

Из
решения следует, что вычисленная
вертикаль будет совершать колебания
относительно истинной вертикали с
периодом Шулера.

Согласно
расчётам [31], ошибка определения скорости
связана с ошибкой построения вертикали.

(2.5)

Ошибка
определения широты:

Δφ=(2.6)

Ошибка
определения пройденного расстояния
ΔS:

ΔS=R
(2.7)

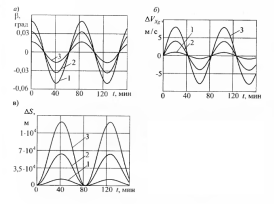
На
рисунке 2.1 показаны ошибки БИНС, вызванные
неточным заданием вертикали, таким
образом, отклонение аналитической
вертикали от истинной, ошибки в определении
скорости и местонахождения БЛА имеют
колебательный характер, период их
колебания равен периоду Шулера.

Рисунок
2.1 Ошибки БИНС, вызванные неточным
задание вертикали: а) ошибка построения
вертикали б) ошибка определения скорости,
в) ошибка в определении пройденного
расстояния; 1 — 2 —3 —.

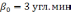
Ошибки
БИНС, вызванные погрешностью акселерометров.

Пусть
в БИНС начальные условия выдержаны
точно, а в показаниях акселерометров
имеются погрешности (смещение нуля)
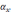
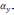
δи δВ этом случае уравнения(2.1) примут вид:

(2.8)

проекцию
кажущегося ускорения:

(2.9)

где
sinθ
– проекция ошибок акселерометров на
ребро О

β(t)=

Из
решения следует, что погрешности
акселерометра вызывают колебания
вертикали с периодом Шулера относительно
смещенного от истинной вертикали
положения равновесия на величену β(t)=
колебаний равна ошибке акселерометра
в доле ускорения силы тяжести.

Ошибка
определения скорости.

(2.11)

Ошибка
определения широты и пройденного
расстояния:

Δφ=(2.12)

ΔS=(2.13)

На
рисунке 2.2 показаны ошибки вызванные
погрешностью акселерометров.

Рисунок
2.2 Ошибки БИНС, вызванные погрешностью
акселерометра: а) ошибка построения
вертикали б) ошибка определения скорости,
в) ошибка в определении пройденного
расстояния; 1 — 2 —3 —.

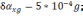
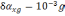
Ошибки
БИНС, вызванные дрейфом гироскопов

Пусть
теперь начальные данные выдержаны
точно, акселерометр функционирует
идеально, а датчик угловой скорости
измеряет абсолютную угловую скорость
БЛА с ошибкой ε. Найдем ошибку в определении
тангажа. Тангаж определяется[30], как
результат интегрирования относительно
угловой скорости связанного трехгранника

(2.14)

где
– ωx,
ωz-;
ε-собственный дрейф гироскопа

Наличие
собственного дрейфа гироскопа ε приведет
к погрешности в определении проекции
абсолютной
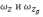
угловой скорости связанного и
географического трехгранников,
соответственно. Расчетное значение
угла тангажа можно представить в виде:

где
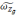
— рассчитанная с помощью БИНС проекция
угловой скорости географического
трехгранника.

После
некоторых преобразований [31] получаем
связь между истсинным и вычисленным
значением тангажа

θ-=β
или Δθ=β (2.16)

Таким
образом, при одноканальном анализе БИНС
ошибка выработки тангажа равно ошибке
построения вертикали с обратным знаком.

Ошибки
определение вертикали, скорости, широты
и пройденного пути:

β(t)=
—

(2.18)

Δφ=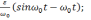(2.19)

ΔS=(2.20)

где-

Из
формул видно, что вычисленная вертикаль
по –прежнему совершает колебания
истинной вертикали с частотой Шулера
и амплитудой .
В ошибке определения скорости имеется
постоянная составляющая, пропорциональная
радиусу Земли. Нарастание со временем
погрешности БИНС является главным их
недостатком.

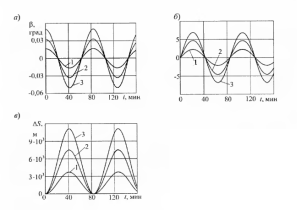
Рисунок
2.3 Ошибки БИНС, вызванные дрейфом
гироскопа: а) ошибка построения вертикали
б) ошибка определения скорости, в) ошибка
в определении пройденного расстояния;
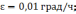
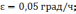
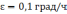
1 – 2 —3 —.

Ошибки
вертикального канала БИНС.

Рассмотрим
погрешности вертикального канала,
вызванные ошибкой компенсации ускорения
силы тяжести g

Положим,
гироскоп и акселерометры работают без
ошибок, а начальные данные введены
точно. В соответствии с принципом работы
вертикального канала найдем ошибку в
определении вертикальной скорости БЛА,
как разность между вычисленной и истинной
вертикальной скоростью

(2.21)

Из
[31] находим:

(2.22)

где
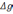
— ошибка компенсации ускорения силы
тяжести

Очевидно,
что ошибка в определении высоты выглядит
так

(2.23)

Из
формул можно заключить, что ошибки в
определении вертикальной скорости и
высоты с помощью БИНС растут неограниченно.
Беспредельный рост ошибок вертикального
канала БИНС называется неустойчивостью
этого канала.

Ошибки
определение вертикали, скорости, широты
и пройденного пути:

β(t)=-
—

(2.25)

ΔS=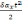(2.26)

Из
соотношений видно, что при отсутствии
вектора ускорения силы тяжести ошибка
построения вертикали, а также ошибки в
определении скорости и координаты,
вызванные смещением нуля акселерометра,
неограниченно возрастает.

Соседние файлы в предмете [НЕСОРТИРОВАННОЕ]

Источник

В.В. Матвеев, В.Я. Распопов
ОСНОВЫ ПОСТРОЕНИЯ
БЕСПЛАТФОРМЕННЫХ
ИНЕРЦИАЛЬНЫХ
НАВИГАЦИОННЫХ
СИСТЕМ
УДК 629.7
Публикуется по решению редакционной коллегии
ГНЦ РФ ОАО «Концерн «ЦНИИ «Электроприбор»
Рецензенты; д.т.н. профессор Ю. В. Филатов (Санкт-Петербургский го-
сударственный электротехнический университет «ЛЭТИ»),
д.т.н. профессор А А. Одинцов (ГНЦ РФ ОАО «Концерн
«ЦНИИ «Электроприбор».
Основы построения бесплатформенных инерциальных навигационных
систем / В.В.Матвеев, В.Я.Распопов / Под общ. ред. д.т.н. В Я. Распопова.
- СПб.: ГНЦ РФ ОАО «Концерн «ЦНИИ «Электроприбор», 2009. - 280 с.
ISBN 978-5-900780-73-3
В настоящем учебном пособии изложены принципы построения бес-
платформенных инерциальных навигационных систем (БИНС) с использо-
ванием различных кинематических параметров: углов Эйлера - Крылова,
направляющих косинусов, параметров Родрига - Гамильтона (кватернио-
нов).
Рассмотрены принципы работы акселерометров и гироскопических
приборов, используемых в БИНС. Уделено внимание анализу погрешно-
стей БИНС, приведены формулы для оценки точности БИНС.
Излагаются вопросы комплексирования БИНС с другими системами
навигационной информации. Приведены примеры использования фильтра
Калмана в интшрированных навигационных системах.
Уделяется внимание моделированию БИНС в среде Simulink - пакете
расширения системы MATLAB. Приведены схемы моделирования элемен-
тов БИНС с использованием различных кинематических параметров. Каж-
дая глава заканчивается вопросами для самоконтроля, позволяющими чи-
тателю оценить степень усвоения материала. Учебное пособие снабжено
многочисленными примерами.
Пособие предназначено для студентов вузов, обучающихся по специ-
альности «Приборы и системы ориентации, стабилизации и навигации» и
по направлениям подготовки «Приборостроение» и «Автоматизация и
управление». Учебное пособие может быть полезно аспирантам и инжене-
рам, начинающим работать в области автономной навигации.
Библиогр. 136. Ил. 179. Табл. 22.
Работа выполнена при поддержке гранта РФФИ 08-08-00082
ISBN 978-5-900780-73-3
© ГНЦ РФ ОАО «Концерн «ЦНИИ «Электроприбор», 2009
© В В. Матвеев, 2009
© В. Я. Распопов, 2009
ОГЛАВЛЕНИЕ
Предисловие......................................................................5
Введение....................................................................... 9
ГЛАВА 1. Принципы построения БИНС................................................17
1.1. БИНС с акселерометрами и ДУ С..................'.....................17
1.2. Акселерометрические БИНС.............................................22
1.3. БИНС на неуправляемых гироскопах.....................................23
ГЛАВА 2. Инерциальные чувствительные элементы...................................26
2.1. Акселерометры........................................................26
2.1.1. Общая характеристика...........................................26
2.1.2. Осевые и маятниковые акселерометры.............................29
2.1.3. Струнные акселерометры.........................................42
2.1.4. Конструкции и технические характеристики.......................47
2.2. Гироскопы............................................................62
2.2.1. Общая характеристика...........................................62
2.2.2. Лазерные и волоконно- оптические гироскопы.....................63
2.2.3. Волновые твердотельные гироскопы...............................75
2.2.4. Динамически настраиваемые гироскопы............................88
2.2.5. Микромеханическис гироскопы....................................98
ГЛАВА 3. БИНС на акселерометрах и ДУ С..........................................118
3.1. БИНС с углами Эйлера- Крылова.......................................118
3.2. БИНС с направляющими косинусами.....................................128
3.2.1. Уравнение Пуассона............................................128
3.2.2. БИНС с двумя уравнениями Пуассона.............................132
3.2.3. БИНС с одним уравнением Пуассона..............................136
3.3. БИНС с параметрами Родрига - Гамильтона.............................137
3.3.1. Ось конечного поворота........................................137
3.3.2. Параметры Родрига - Гамильтона................................140
3.3.3. Кватернионы...................................................141
3-3.4. Кватернионные матрицы.........................................151
3.3.5. Кинематическое уравнение для кватерниона......................154
3.3.6. БИНС с параметрами Родрига — Гамильтона.......................156
3.4. Анализ алгоритмов БИНС............................................. 159
3.5. Начальная выставка БИНС.............................................159
ГЛАВА 4. Модель ошибок БИНС....................................................161
4.1. Элементарный анализ ошибок БИНС.....................................168
4.2. Векторная модель ошибок БИНС........................................178
4.3. Скалярная модель ошибок БИНС........................................188
4.4. Уравнения ошибок БИНС в определении параметров ориентации...........193
3
ГЛАВА 5. Комплексные навигационные системы..................................198
5.1. Элементы теории случайных процессов..............................198
5.2. Принципы построения комплексных систем навигации.................210
5.3. Непрерывный фильтр Кал мана в комплексных навигационных системах.215
5.4. Дискретный фильтр Калмана в комплексных навигационных системах...232
5.5. Инерциально-спутниковые навигационные комплексы..................247
ГЛАВА 6. Моделирование алгоритмов БИНС в среде MATLABSimulink .............258
6.1. Алгоритмы ориентации..............................................258
6.1.1. Алгоритм ориентации с углами Эйлера - Крылова...............258
6.1.2. Алгоритм ориентации с направляющими косинусами...............263
6.1.3. Алгоритм ориентации с кватернионами.........................267
6.2. Калибровка инерциальных ЧЭ с помощью фильтра Калмана.............271
6.2.1. Блоки моделирования случайных воздействий в пакете Simulink.271
6.2.2. Реализация фильтра Калмана для калибровки инерциальных ЧЭ...273
Заключение .................................................................277
4
Посвящается 80-летию
Тульского государственного университета.
ПРЕДИСЛОВИЕ
Основы теории инерциальных навигационных систем (ИНС) являются од-
ной из дисциплин, включаемых в рабочие программы обучения специалистов
по направлению «Управление движением и навигация». Рабочие программы
этой дисциплины в различных вузах включают как типовые темы, так и специ-
альные, обусловленные, как правило, научными интересами кафедры и заказа-
ми потребителей.
Типовые темы включают рассмотрение принципов инерциального счисле-
ния текущих координат объекта и невозмущаемости навигационных систем
(принцип М. Шулера); основы теории и устройства инерциальных чувствитель-
ных элементов (акселерометров и гироскопов); основы построения геометриче-
ских, полуаналитических и аналитических ИНС, модели их ошибок и способы
начальной выставки.
Перечень доступных книг и статей по теории ИНС насчитывает не одну
сотню наименований. К сожалению, многие книги, издание которых относится
к периоду 50-х - 70-х годов прошлого столетия, стали библиографической ред-
костью, как, например, небольшие по объему, но емкие по охвату вопросов по-
строения ИНС книги Г. О. Фридлендера [27] и А. А. Якушенкова [29]. Фунда-
ментальные работы А. Ю. Ишлинского [14], П. В. Бромберга [6], видимо, не
преследовали учебные цели, но рассмотрение в них научных проблем является
образцом для написания учебников. Среди последних, несомненно, необходимо
обратить внимание на двухтомный труд В. Д. Андреева по теории ИНС [1], ко-
торый для своего изучения требует основательной подготовки и времени, так
как все материалы текстуально увязаны. Этим изданием можно воспользоваться
и как хорошо аргументированным справочным пособием по теории ИНС.
Ряд изданий последних десятилетий ориентированы прежде всего на спе-
циалистов в области ИНС, но работы С. П. Дмитриева, Л. П. Несенюка [10, 28]
вполне применимы в учебном процессе, так же как и работы О. Н. Анучина,
Г. И. Емельянцева, О. А. Степанова в области интегрированных навигационных
систем [2, 24].
Интенсификация работ в области бесплатформенных инерциальных навига-
ционных систем (БИНС) связана с развитием главным образом ракетно-
космической отрасли. Ученым, работающим в этой отрасли, и принадлежат ос-
5
новные публикации в области теории и проектирования БИНС. Здесь необхо-
димо указать на монографии В. Н Бранна и И. П. Шмыглевского [3, 4]. Однако
освоение излагаемого в них материала предполагает основательную математи-
ческую подготовку, которой явно недостаточно, к сожалению, у сегодняшних
студентов технических вузов, да и у многих специалистов, изрядно забывших и
общие и специальные разделы высшей математики, если этот инструмент, по
выражению акад. А. Н Крылова, какое-то время не используется. Интерес к
БИНС в последние годы заметно усиливается в связи с модернизацией авиони-
ки для самолетов 4-го поколения и переходу к самолетам 5-го и 6-го поколений
и необходимостью разработки бортовых систем управления высокодинамич-
ными летательными аппаратами, включая их беспилотные варианты. Уместно
отмстить также возрастающую роль автономных мобильных роботов самого
разно! о назначения, решение целевых задач которыми предполагает в их соста-
ве наличие БИНС.
Таким образом, два обстоятельства, во-первых, возрастающая потребность в
БИНС и, во-вторых, отсутствие доступного по применяемому математическому
аппарату учебного пособия по основам теории БИНС привели к появлению
данного учебного пособия, которое в основном ориентировано на студентов
вузов, обучающихся по направлению «Управление движением и навигация».
Основная идея книги - это доступное изложение принципов построения БИНС
В дальнейшем можно приступить к изучению более фундаментальных изданий,
указанных в списках литературы по главам.
Читателями книги могут быть также инженеры и специалисты, начинающие
работать в области создания бссплатформенных систем ориентации и навига-
ции, аспиранты и преподаватели учебных заведений.
Особенностью учебного пособия являются самодостаточность каждой гла-
вы и даже раздела и доступность излагаемого материала. Отдельная глава по-
священа моделированию БИНС в наиболее популярном среди студентов и спе-
циалистов программном продукте MATLAB и его пакете расширения Simulink.
Эта глава может стать частью расчетного лабораторного практикума по курсу
«Инерциальные навигационные системы».
При работе над учебным пособием авторы внимательно ознакомились, а
при необходимости и изучили материал ряда изданий, основные из которых от-
ражены в списках литературы. Авторы активно использовали материалы статей,
относящихся к тематике БИНС и публикуемые в сборниках материалов ежегод-
ных международных конференций по интегрированным навигационным систе-
мам, организуемым и проводимым ЦНИИ «Электроприбор» под руководством
акад. РАН В. Г. Пешехонова, а также в журнале «Гироскопия и навигация».
Авторы признательны за консультации и материалы по лазерным гироско-
пам и струнным акселерометрам д. ф.-м. н. заместителю директора НИИ
«Полюс» им. М. Ф. Стельмаха В. Г. Дмитриеву и д. т. н. профессору МАИ
В. А. Мельникову, а также за ценные советы доктору технических наук
О. А. Степанову (ОАО «Концерн «ЦНИИ «Электроприбор»).
Уместно заметить, что часть материала, которая вошла в учебное пособие,
была изложена в виде лекций, лабораторных и практических занятий на курсах
по повышению квалификации, которые были проведены на кафедре «Приборы
управления» Тульского государственного университета для инженеров ФГУП
РФЯЦ им. акад. Забабахина и ОАО «Мичуринский завод «Прогресс» (2006,
2007 гг.).
6
Авторы благодарят сотрудников отделов ОАО «Раменское приборострои-
тельное конструкторское бюро» (РПКБ), Раменского приборостроительного
завода (РПЗ), Пермской научно-производственной приборостроительной ком-
пании (ПНППК), завода «Прогресс» (г. Мичуринск) и др., предоставивших
комплекты информационно-рекламных материалов о продукции своих пред-
приятий.
Особая признательность за предоставленные образцы продукции, работа с
которыми позволила с большей основательностью осветить некоторые вопросы,
связанные с выбором элементной базы БИНС, заместителю директора по науч-
ной работе ОАО «Темп-Авиа», к.т.н. В. В. Лосеву зам. директора ПНППК, к.т.н.
В.С. Ермакову, генеральному директору ОАО «Мичуринский завод «Прогресс»,
к.э.н. В.А. Дмитриеву.
Главы 1, 2 и разделы 3.1, 3.2 написаны В.Я. Распоповым, главы 4, 5. 6 и раз-
делы 3.3, 3.4, 3.5 - В.В. Матвеевым.
Авторы благодарны сотрудникам кафедры «Приборы управления» Тульско-
го государе гвенного университета проф. д. т. н. Ю. В. Иванову, доценту, к. т. н.
Д. М. Малютину, доценту, к. т. н. Р. В. Алалуеву за обсуждение отдельных ма-
териалов учебного пособия и аспирантам кафедры А. В. Никулину,
В. В.Лихошерсту, Р. В. Ершову за большую работу по компьютерному набору
материалов учебного пособия.
Авторы признательны рецензентам д. т. н. профессору А. А. Одинцову и
д. т. н профессору Ю В . Филатову за ценные замечания, способствовавшие
улучшению содержания книги.
Выход книги в свет не был бы возможен без всесторонней поддержки ака-
демика РАН В Г. Пешехонова
БАЗОВАЯ ЛИТЕРАТУРА
1. Андреев В. Д. Теория инерциальной навигации. Кн. 1. Автономные системы. Кн.П. Коррек-
тируемые системы. - М.: Наука, 1966, 1967.
2. Анучин О.Н., Емельянцев Г.И. Интегрированные системы ориентации и навигации для
морских подвижных объектов / Под общ. ред. чл.- кор. РАН В.Г. Пешехонова.- СПб., 1999,-
357 с.
3. Бранец В.Н., Шмыглевский И.П. Применение кватернионов в задачах ориентации твердо-
го тела. М.:Наука. 1973.- 320 с.
4. Бранен В.Н., Шмыглевский И.П. Введение в теорию бесплатформенных инерциальных
навигационных систем. - М.: Наука, 1992. - 280 с.
5. Броксмейер Ч.Ф. Системы инерциальной навигации. - Л.: Судостроение, 1967.
6. Бромберг П.В. Теория инерциальных систем навигации. - М.: Наука, 1979- 296 с.
7. Бор юные системы навигации и ориентации искусственных спутников Земли / О. Н. Анучин,
И.Э. Комарова, Л.Ф. Порфирьев. - СПб.: ГНЦ РФ ЦНИИ «Электроприбор», 2004.- 326 с.
8. Горешпгейн И.А., Шульман И.А., Сафарьян А.С. Инерциальная навигация. - М.: Сов.
радио, 1962.
9. Гироскопические системы. Гироскопические приборы и системы: Учеб, для вузов
/Д.С.Пельпор , И.А.Михалев, В.А.Бауман и др. / Под род. Д.С.Пельпора. 2- е изд., перераб. и
доп,- М.:Высш. школа, 1988.-424 с.
10. Дмитриев С.П., Пелевин А.Е. Задачи навигации и управления при стабилизации судна на
траектории. - СПб: ГНЦ РФ ЦНИИ «Электроприбор», 2002. - 159 с.
11. Захарин М.И., Захарин Ф.М. Кинематика инерциальных систем навигации. - М.: Машино-
строение, 1968.
12. Инерциальные навигационные системы морских объектов/Д.П. Лукьянов, А.В Молчанов,
А.А. Одинцов, И.Б. Вайсгант/ Под. ред. Д.П. Лукьянова.- Л.: Судостроение, 1989,- 184 с.
13. Инерциальная навигация / Под род О’ Доннела. - М.: Наука, 1968.
7
14. Ишлинский А.Ю. Ориентация, гироскопы и инерциальная навигация. - М.: Наука, 1976,-
672 с.
15. Климов Д.М. Инерциальная навигация на море. - М.: Наука, 1984,- 118 с.
16. Лебедев Р.К. Стабилизация летательного аппарата бесплатформенной инерциальной систе-
мой. М Машиностроение, 1977. - 144с.
17. Лукомский Ю.А., Пешехонов В.Г., Скороходов Д.А. Навигация и управление движением
судов. - Спб: Элмор, 2002. - 360 с.
18. Лурье А. И. Аналитическая механика. - М.: Изд- во физ,- мат. лит., 1961,- 824 с.
19. Мак-Клур К.Л. Теория инерциальной навигации / Пер. с англ. - М.: Наука, 1964. - 300 с.
20. Пешехонов В.Г. Ключевые задачи современной автономной навигации // Гироскопия и на-
вигация. -1996. - № 1. - С. 48-55.
21. Помыкаев И.И., Селезнев В.П., Дмитроченко Л.А. Навигационные приборы и системы. -
М.: Машиностроение, 1983.
22. Ривкин С.С., Ивановский P-И., Костров А.В. Статистическая оптимизация навигационных
систем. - Л.: Судостроение, 1976. - 284 с.
23. Селезнев В.П. Навигационные устройства. - Л.: Машиностроение, 1974. - 660 с.
24. Степанов О.А. Применение теории нелинейной фильтрации в задачах обработки навигаци-
онной информации. - СПб.: ГНЦ РФ ЦНИИ «Электроприбор», 1998,- 370 с.
25. Степанов О.А. Особенности построения и перспективы развития навигационных инерци-
ально-спутниковых систем. /Интегрированные инерциально-спутниковые системы навига-
ции: Сб. статей. - СПб.: ГНЦ РФ ЦНИИ «Электроприбор», 2001.
26. Управление и наведение беспилотных маневренных летательных аппаратов на основе со-
временных информационных технологий /Под ред. М.Н. Крарилыцикова и Г.Г. Себрякова. -
М.:Физматлит. 2003. - 280 с.
27. Фридлендер Г.О. Инерциальные системы навигации. - М., Физматлит, 1961.
28. Челпанов И.Б., Несенюк Л.П., Брагинский М.В. Расчет характеристик навигационных
гироприборов - Л.: Судостроение. 1978. - 264 с.
29. Якушенков А.А. Основы инерциальной навигации. - М.: Морской транспорт, 1963,- 146 с.
8
ВВЕДЕНИЕ
Термин «навигация» (от лат. navigo - плыву на корабле) может быть пере-
веден как искусство кораблевождения. В настоящее время под навигацией по-
нимают теорию и практику вождения по заданному маршруту таких подвижных
объектов, как самолеты, ракеты, морские суда, подводные лодки, космические
аппараты и т.д. Под навигацией в узком смысле слова понимается решение на-
вигационной задачи, т.е. определение текущих координат местоположения объ-
екта. Под навигацией в широком смысле слова понимают решение навигацион-
ной задачи и использование полученной информации для управления центром
масс объекта. В учебном пособии рассматривается только решение навигацион-
ной задачи, т.е. определение текущих координат местоположения объекта.
Навигация, осуществляемая автономными средствами, т е. на основании
информации, полученной только на борту объекта от акселерометров, гироско-
пов и часов, называется инерциальной [В. 12]. Основная идея инерциальной на-
вигации — это двукратное интегрирование измеренных ускорений. Ускорение
носит абсолютный характер. Наблюдатель, находящийся внутри объекта, обна-
ружит ускоренное движение благодаря тому, что на него будет действовать си-
ла инерции. Все измерительные устройства, основанные на различных физиче-
ских принципах (механических, оптических и т.д.), будут реагировать на силу
инерции и тем самым установят факт ускоренного движения объекта без при-
влечения какой-либо внешней информации [В. 14]. Таким образом, инерциаль-
ный способ определения местоположения объекта можно уподобить свойству
часов и хронометров измерять время вне зависимости от контактов с внешним
миром [В6]. Другими словами, принципы инерциальной навигации основаны на
физических законах, действующих во Вселенной, независимо от установленных
человеком' связей с внешней средой.
Физические явления, связанные с инерцией тел и используемые в инерци-
альной навигации, подчиняются законам механики, которые справедливы по
отношению к инерциальной системе координат. В инерциальных навигацион-
ных системах производится искусственная материализация инерциальной коор-
динатной системы с точностью до приборных ошибок соответствующих уст-
ройств. Этим, по-видимому, и объясняется происхождение термина «инерци-
альная навигация» [В 17].
9
Самое простое объяснение инерциальной навигации следует из рассмотре-
ния задачи о движении тела под действием внешних сил на плоской поверхно-
сти. Второй закон Ньютона устанавливает связь между ускорением а, массой
тела т и приложенной силой F:
та - F. (В1)
В соответствии со вторым законом Ньютона информацию о координатах
тела принципиально можно получить, измерив внешние силы, приложенные к
телу. Произведя интегрирование уравнения (В.1) при известных начальных ус-
ловиях можно найти координаты тела (навигационную информацию). Однако
измерить приложенные к объекту внешние силы весьма сложно. Например, ес-
ли подвижным объектом является судно, то к нему прикладываются следующие
силы: сила, развиваемая движителем, сила сопротивления движению, различ-
ные возмущающие силы, не поддающиеся точному описанию. Поэтому целесо-
образно измерять не приложенные к объекту силы, а ускорения.
Если связать с рассматриваемой плоскостью систему координат ОАТ (рис.
dx
Bl, а), то в соответствии с определением скорости имеем . где у* - про-
dt
екция скорости на ось ОХ, х - перемещение вдоль оси ОХ.
Рис. В1. Движение тела на плоской поверхности:
а) оси чувствительности акселерометров параллельны осям ОХ и OY ;
б) оси чувствительности акселерометров повернуты на угол СХ относительно системы коор-
динат OXY
Проинтегрировав приведенное равенство, получим
x-x0=Jvvt//, (В2)
о
где х0 - начальное значение координаты.
По определению ускорения имеем
(ВЗ)
dt
где ах - проекция ускорения тела на ось ОХ.
10
Интегрируя уравнение (В.З), получаем
vr - уОл + J a, dt, (В4)
о
где vOv - проекция начальной скорости на ось ОХ.
Интегрируя уравнение (В.4) по времени и подставляя в полученный резуль-
тат равенство (В2), получаем
t t
х = х0+ vQxt + J J axdtdt. (B5)
о 0
Так как рассматривается задача на плоскости, то уравнение (В5) необходи-
мо дополнить уравнением по другой координате
t t
У = Уо + vo? + ff aydtdt, (B6)
о о
где а - проекция ускорения объекта на ось ОУ; у0, vOv - соответственно на-
чальная координата и скорость вдоль оси ОУ.
Таким образом, если оси чувствительности акселерометров совпадают с на-
правлением осей некоторой навигационной системы координат (в данном слу-
чае ОАУ), то задача навигации решается путем двукратного интегрирования
измеренных ускорений ах и ау . Однако на практике такой случай никогда не
реализуется и оси чувствительности акселерометров нс совпадают с направле-
нием осей системы координат ОАТ (рис. В 1,6). В связи с этим возникает задача
определения углового положения осей чувствительности акселерометров (угла
а ) относит ельно осей навигационной системы координат. Эта задача решается
с помощью гироскопов.
На основании изложенного можно заключить, что для инерциального опре-
деления координат местоположения объекта необходимо:
1) знать информацию о начальных значениях координат (х0,.у0) и скоро-
стей (vOa,vOv);
2) непрерывно измерять проекции ускорения объекта с помощью акселеро-
метров;
3) определять с помощью гироскопов ориентацию осей чувствительности
акселерометров относительно навигационной системы координат;
4) дважды интегрировать ускорения объекта по времени.
В действительности решение навигационной задачи инерциальным спосо-
бом вдоль поверхности Земли осложняется тем, что акселерометры измеряют
разность между ускорением объекта и гравитационным ускорением. Еще Эйн-
штейн обратил внимание на то, что наблюдатель, находящийся внутри объекта,
не сможет определить различие между ускорением объекта и ускорением
гравитационного поля путем измерений, проводимых только внутри объекта
(рис. В2).
Таким образом, реакция акселерометра на силу тяготения Земли эквива-
лентна силе инерции, т.е. фиктивной силе, вызванной вертикальным перемеще-
нием объекта с ускорением g.
Одним из возможных методов исключения гравитационной составляющей
является приведение осей чувствительности акселерометров в плоскость гори-
11
зонта с помощью гиростабилизированной платформы (ГСП). Эта платформа,
предохраняя акселерометры от влияния угловых перемещений объекта, имеет
ряд существенных недостатков: являясь прецизионным электромеханическим
устройством, она ненадежна, потребляет много энергии, имеет большую массу
и габариты, сложна при сборке и дорогостояща. Другим способом построения
инерциальной навигационной системы является размещение акселерометров и
гироскопов непосредственно на борту подвижного объекта, а функции ГСП вы-
полняет бортовое вычислительное устройство. В связи с этим такие устройства
называют бесплатформенными (бескарданными) инерциальными навигацион-
ными системами (БИНС).
Рис. В2. Одинаковые показания маятников: а) маятник находится на Земле;
б) маятник перемещается вертикально с ускорением g вдали от Земли
В БИНС используемые чувствительные элементы - акселерометры и изме-
рители параметров ориентации (гироскопы) - могут быть построены на различ-
ных физических принципах. При этом количество измерителей должно быть
таким, чтобы обеспечить получение информации о векторе кажущегося ускоре-
ния точки объекта, в котором установлены измерители, и о векторе абсолютной
угловой скорости, характеризующей вращение.
Идеи БИНС фактически были реализованы еще в начале 30-х годов, при ис-
следованиях вхождения самолета в штопор, в частности самолета Р-5 [В 16].
Группа советских инженеров во главе с В.С.Ведровым разработала инерциаль-
ную навигационную систему, в которой акселерометры и гироскопические из-
мерители угловой скорости устанавливались непосредственно на корпусе само-
лета. При такой аппаратурной реализации отпадала необходимость в сложной и
дорогой ГСП. В той фактически первой БИНС информация, получаемая с аксе-
лерометров и гироскопов, записывалась в полете с помощью самописцев, а за-
тем математически обрабатывалась на Земле с помощью механических ариф-
мометров, в результате чего рассчитывались координаты центра масс самолета
и параметры ориентации.
Одно из обстоятельств, сдерживающих широкое внедрение БИНС, - это
чрезвычайно высокие требования к инерциальным чувствительным элементам.
Гироскопы и акселерометры, будучи жестко установлены на борту объекта,
должны обладать заданной точностью в широком диапазоне угловых скоростей
и ускорений, а также функционировать в условиях вибраций, ударов и т.п. Сле-
дующим фактором, сдерживающим развитие БИНС, являлось отсутствие быст-
родействующих бортовых вычислительных машин. Именно благодаря появле-
12
нию цифровых вычислительных машин в дальнейшем оказалось возможным на
борту подвижного объекта в реальном масштабе времени реализовывать алго-
ритмы БИНС.
Практическая реализация первой БИНС была осуществлена в системе
управления движением и ориентации транспортного космического корабля
«Союз-Т». Появление первой БИНС в системе управления движением космиче-
ского аппарата является неслучайным. Это объясняется тем, что космический
аппарат после его выведения на орбиту находится в условиях свободного поле-
та при исчезающее малых возмущениях.
Изложение и математическое обоснование построения БИНС для различ-
ных конфигураций применяемых аппаратных средств и составляет основное
содержание учебного пособия. Вводимый математический аппарат для рас-
смотрения конкретных вопросов теории БИНС перед применением достаточно
подробно комментируется.
Учебное пособие состоит из шести глав.
В первой главе на основе рассмотрения одного канала приводятся прин-
ципы построения БИНС с акселерометрами и датчиками угловой скорости, ак-
селерометрические БИНС, БИНС с неуправляемыми гироскопами.
Во второй главе дано описание акселерометров и гироскопических прибо-
ров, используемых в БИНС, приведены упрощенные математические модели
для понимания измерительных свойств этих приборов.
В третьей главе подробно описываются алгоритмы БИНС с акселеромет-
рами и датчиками угловой скорости. Приведены алгоритмы БИНС с использо-
ванием различных кинематических параметров: углов Эйлера - Крылова, на-
правляющих косинусов, параметров Родрига - Гамильтона (кватернионов). Дан
сравнительный анализ алгоритмов БИНС. Рассматриваются вопросы начальной
выставки БИНС.
Четвертая глава посвящена погрешностям БИНС. Изложение ведется по
мере усложнения. Получены погрешности БИНС на основе одноканального
подхода, приводится полная модель погрешностей.
В пятой главе освещаются вопросы объединения БИНС с другими систе-
мами, в частности со спутниковыми навигационными системами. Рассмотрены
принципы построения комплексных навигационных систем, даны элементы
теории случайных процессов, приведены алгоритмы оптимальной фильтрации
Калмана.
В шестой главе описаны схемы для моделирования БИНС и ее отдельных
блоков в среде MATLABXSimulink. Приведены примеры для создания собствен-
ных блоков алгебры кватернионов. Рассмотрены примеры использования
фильтра Калмана.
ЛИТЕРАТУРА К ВВЕДЕНИЮ
В1. Андреев В. Д. Теория инерциальной навигации. Кн.1. Автономные системы. Кн.П. Коррек-
тируемые системы. - М.: Наука, 1966, 1967.
В2. Анучин О.Н., Емельянцев Г.И. Интегрированные системы ориентации и навигации для
морских подвижных объектов / Под общей ред. чл.-кор. РАН В.Г. Пешехонова.- СПб., 1999,-
357 с.
13
ВЗ. Бранец В.Н., Шмыглевский И.П. Введение в теорию бесплатформенных инерциальных
навигационных систем. - М.: Наука, 1992. - 280 с.
В4. Бромберг П.В. Теория инерциальных систем навигации. - М.: Наука, 1979. - 296 с.
В5. Гироскопические системы. Гироскопические приборы и системы: Учеб, для вузов
/Д.С.Пельпор , И.А.Михалев, В.А. Бауман и др. / Под ред. Д.С.Пельпора. 2- е изд., перераб. и
доп. - М.:Высш. шк., 1988. - 424 с.
В6. Дрейпер Ч.С., Ригли У. Интегрирующие поплавковые гироскопы / История механики гиро-
скопических систем: Сб. статей. - М.: Наука, 1975. - С. 61- 81.
В7. Инерциальные навигационные системы морских объектов/Д.П. Лукьянов, А.В. Молчанов,
А.А. Одинцов, И.Б. Вайсгант / Под. ред. Д.П. Лукьянова,- Л.: Судостроение. 1989,- 184 с.
В8. Инерциальная навигация / Под ред О’ Доннела. - М.: Наука, 1968.
В9. Ишлинский А.Ю. Ориентация, гироскопы и инерциальная навигация. - М.: Наука, 1976. -
672 с.
В10. Климов Д.М. Инерциальная навигация на море. - М.: Наука, 1984,- 118 с.
Bl 1.Красовский А. А., Белоглазов И. Н., Чигин Г. П. Теория корреляционно- экстремальных
навигационных систем. - М.: Наука, 1979. - 448 с.
В12 .Онищенко С.М. Применение гиперкомплексных чисел в теории инерциальной навигации.
Киев: Наук, думка, 1983.- 208 с.
В13. Пешехонов В.Г. Ключевые задачи современной автономной навигации И Гироскопия и на-
вигация. - 1996.- №1.- С. 48-55.
В14. Селезнев В.П. Навигационные устройства. - Машиностроение, 1974. - 660 с.
В15. Фридлендер Г.О. Инерциальные системы навигации. - М.: Физматлит, 1961.- 153 с.
В16. Шестов С.А. Гироскоп на земле, в небесах и на море. - М.: Знание, 1989. - 192 с.
В17. Якушенков А.А. Основы инерциальной навигации. - М.: Морской транспорт, 1963.- 146 с.
ПРИНЯТЫЕ СОКРАЩЕНИЯ
БИНС - бесплатфор.менная инерциальная навигационная система
ВОГ - волоконно-оптический гироскоп
ВТГ - волновой твердотельный гироскоп
ГСП - гиростабилизированная платформа
ДУС - датчик угловой скорости
ДНГ - динамически настраиваемый гироскоп
ИМ - инерционная масса
ИНС - инерциальная навигационная система
КЛГ - кольцевой лазерный гироскоп
КНС - комплексная навигационная система
ЛА - летательный аппарат
ММ А -микромеханический акселерометр
ММГ - микромеханический гироскоп
МЭМС - микроэлектронно-механическая система
НГ - неуправляемый (свободный) гироскоп
РВГ - роторный вибрационный гироскоп
ЧЭ - чувствительный элемент
14
СПИСОК ОСНОВНЫХ ОБОЗНАЧЕНИЙ
Системы координат (трехгранники):
OXgYgZg - географическая (нормальная);
OXgYgZg - вычисленная географическая;
OXYZ - связанная с летательным аппаратом;
OUXUYUZU - инерциальная;
— земная;
- неподвижная (используется при выводе уравнения Пуассона и параметров Родрига -
Гамильтона).
Кинематические параметры:
V -рыскание; 0 - тангаж; у -крен;
<р - широта; А - долгота; h - высота;
CO_y , (Оу , (0z - проекции вектора абсолютной угловой скорости связанной системы координат
на свои оси;
(dXg, (f>yg, (£>Zg - проекции вектора абсолютной угловой скорости географической системы
координат на свои оси;
VXg ’ ^Yg » VZg ~ проекции вектора линейной скорости ЛА на оси географической системы ко-
ординат;
пх, nY , nz - проекции вектора кажущегося ускорения на оси связанной системы координат;
nXg ’ nYg, nZg ~ проекции вектора кажущегося ускорения на оси географической системы коор-
динат;
g - ускорение силы тяжести;
R3 - радиус Земли; R - расстояние от центра Земли до центра масс ЛА;
а - азимутальная ошибка БИНС;
Р, % - ошибки построения вертикали;
Дф , ДА , ДА - ошибки в определении широты, долготы и высоты;
Дф , Д0, Ду - ошибки в определении рыскания, тангажа и крена;
£у, Еу , 8у - дрейфы гироскопов;
бог, 5 а у, 5az - ошибки акселерометров.
Матрицы ортогонального преобразования:
А - матрица перехода от географической системы координат к связанной;
В - матрица перехода от инерциальной системы координат к географической;
С - матрица перехода от связанной системы координат к географической (С = А? );
Си - матрица перехода от географической системы координат к инерциальной (Си = ВТ );
D - матрица перехода от связанной системы координат к инерциальной;
Е - единичная матрица;
Ег - матрица ошибок;
F - матрица перехода от географического трехгранника к вычисленному;
15
Кватернионы:
Л - собственный кватернион, характеризующий переход от географического трехгранника к
связанному;
, Л’ - отображения вектора кажущегося ускорения, заданного в географической и связанной
системах координат;
Q.g, Q - отображения векторов абсолютной угловой скорости географического и связанного
трехгранников соответственно.
® - кватернион ошибок.
Характеристика случайного процесса
mx(t) , Dx(t) , Kx(t,t') - математическое ожидание; дисперсия и корреляционная функция;
S(co) - спектральная плотность;
|Л - коэффициент затухания корреляционной функции;
Пространство состояний
x(t) — вектор состояния системы;
и>(7) - вектор возмущения;
z(t) - вектор измерения;
v(f) - вектор ошибки измерения,
A(t) - матрица состояния;
G(t) - матрицей возмущения;
H(t) - матрица наблюдения;
Q(t) , R(t) - матрицы интенсивностей возмущений и ошибок измерения.
В учебном пособии также принято:
• для кососимметрических матриц символ заключаются в квадратные скобки (например, [ со] );
• расчетные с помощью БИНС параметры снабжаются символом «~»(например, V );
• оцениваемые с помощью фильтра Калмана величины снабжаются знаком «Л» (например,
х);
• пример начинается и заканчивается символом ♦.
16
ГЛАВА 1
ПРИНЦИПЫ ПОСТРОЕНИЯ БИНС
В зависимости от состава инерциальных чувствительных элементов БИНС
могут быть построены с применением следующих приборов: датчиков угловой
скорости (ДУС) и акселерометров, только акселерометров, акселерометров и
неуправляемых гироскопов.
1.1. БИНС с акселерометрами и ДУС
Рассмотрим принцип действия бесплатформенной инерциальной навигаци-
онной системы при движении летательного аппарата (ЛА) вдоль плоскости ме-
ридиана сферической и невращающейся Земли.
Свяжем с исходным положением ЛА географическую систему координат
OXgGYg0Zg0 (рис. 1.1), где ось OXgQ лежит в плоскости горизонта и направлена
на север, ось OYg0 направлена вдоль истинной вертикали вверх, OZg0 - на-
правлена на восток (перпендикулярна плоскости чертежа). Предположим, что в
начальный момент времени координата и скорость ЛА известны и равны (р(/0)
и Ил^(г0) соответственно. С ЛА свяжем систему координат OXYZ, где ось ОХ
направлена по продольной оси ЛА, ось OZ - вдоль поперечной оси, а ось OY
перпендикулярна плоскости крыльев и направлена вверх. Предполагается, что в
начальный момент времени система координат OXYZ совпадает с O0Arg0yg0Zg0
Рис. 1.1. БИНС с акселерометрами и ДУС
17
На борту ЛА размещены два линейных акселерометра Ах и AY с осями чув-
ствительности, направленными вдоль продольной ОХ и нормальной осей OY
ЛА, и гироскопический датчик угловой скорости, измеряющий проекцию w7
абсолютной угловой скорости ЛА.
Пусть ЛА переместился из точки О0 в точку Ох с координатой ср, которая
подлежит определению. Из точки О{ направим текущую ОХ„, OYir и началь-
ную ориентацию OXg0, OYr{) осей географической системы координат. Оче-
видно, что если известно направление истинной вертикали OYg в каждый мо-
мент времени, то задача навигации будет решена измерением угла между осями
OY Q и OY (см. рис. 1.1). Таким образом, задача построения вертикали на
борту подвижного объекта и задача навигации эквивалентны по своему со-
держанию [1.7].
Предположим, что в точке О} связанная с ЛА система координат отклонена
от географической на угол тангажа 0. Известно, что акселерометры измеряют
не абсолютное ускорение объекта, а так называемое кажущееся ускорение, т.е.
равнодействующую между абсолютным ускорением объекта и ускорением си-
лы тяжести. Вектор кажущегося ускорения п может быть задан проекциями
и g на ребра OXg и OYg географического трехгранника OXgYgZg
(рис. 1.2).
Рис. 1.2. Взаимное положение географического и связанного трехгранников
С пдмощью акселерометров измеряются проекции вектора кажущегося ус-
корения п на оси ОХ и OY связанного трехгранника, совпадающие с осями
чувствительности акселерометров. В соответствии с рис. 1.1 (см. также рис. 1.2)
проекции кажущегося ускорения на оси чувствитсльностей акселерометров
имеют вид:
п v = V cos 0 + g sin 6;
. (1.1)
nY = g cos 0 - Vx sin 0,
где - ускорение ЛА в северном направлении; g - ускорение силы тяжести.
* *о
18
Если осуществить обратный переход, т.е. перепроектировать показания ак-
селерометров в географическую систему координат
nXg = пх:c°s0-«rsin0, (1.2)
то можно определить линейное ускорение ЛА в северном направлении. Подста-
вив (1.1) в (1.2), получим
nXg = (VXg cos 0 + g sin 0) cos 0 - (g cos 0 - KXg sin 0) sin 0 = VXg. (1.3)
Действительно, если имеется информация об угле 0, то, перепроектировав
показания акселерометров из связанной системы координат в географическую,
можно найти проекцию ускорения VПоследующее двукратное интегрирова-
ние ускорения Vx позволит найти координату и скорость ЛА. Процесс опреде-
ления скорости и координаты инерциальным способом иллюстрируется рис.
1.3.
Kvg(^o) <р(/0)
Рис. 1.3. Определение скорости и координаты инерциальным способом
После пересчета информации в соответствии с уравнением (1.2) получаем
ускорение п Xg представляющее собой северную составляющую горизонтально-
го ускорения ЛА. На выходе первого интегратора появляется приращение ли-
нейной скорости в северном направлении, которое складывается с начальной
скоростью ЛА VXg{to), и образуется линейная скорость VXg. Следующий по
структурной схеме блок осуществляет деление линейной скорости на радиус-
вектор R = R3 + h (R3 - радиус Земли, h - высота), после чего мы получаем
значение угловой скорости изменения широты ЛА ф. Последующее интегриро-
вание ф позволяет найти координату (р с учетом ее начального значения cp(f0).
Скорость VKg и широта ср ЛА найдены в предположении, что известен угол
тангажа 0 (см. рис. 1.2). Решим задачу определения угла 0 между связанной и
географической системами координат. Гироскопический ДУС измеряет проек-
цию абсолютной угловой скорости ЛА
' coz = coZg +0 = -ф + 0. (1.4)
Здесь со/1; и 0 - соответственно переносная и относительная угловая ско-
рость ребра OZ связанного трехгранника.
Для того чтобы найти угол 0, необходимо предварительно исключить из по-
казаний ДУС переносную угловую скорость coZg = -ф, после чего искомый угол
0 определяется в результате интегрирования
19
t t
0 = j(coz -a>Zg)dt + 0(7O) = JGdt + 0(/o),
'o zo
(1.5)
где 0(?o) - начальное значение угла тангажа.
Угловую скорость ф можно найти из алгоритма счисления координаты ме-
стоположения ЛА. Структурная схема северного канала БИНС представлена на
рие.1.4.
Рис. 1.4 Структурная схема северного канала БИНС
Структурная схема северного канала БИНС представляет собой так называе-
мый алгоритм идеальной работы, когда акселерометры и ДУС работают без по-
грешностей.
Рассмотрим вертикальный канал БИНС, позволяющий определить верти-
кальную скорость и высоту полета ЛА. Предположим, что ЛА имеет вертикаль-
ную составляющую ускорения . В этом случае проекции кажущегося уско-
рения на оси чувствительности акселерометров имеют вид:
пх = Vxg cos6 + (g + ^yg)sin0;
(1-6)
Пу = (g + VYg ) C0S 6 ~ VXg sin 0-
Спроектируем равенства (1.6) на ось OY
nYg = [HVg cos 0 + (g + VYg ) sin 0] sin 0 + [(g + VYg ) cos 0 - VXg sin 0] cos 0 = g + VYg .(1.7)
Если исключить из величины nYg ускорение силы тяжести g и дважды про-
интегрировать ускорение VYg, то можно получить вертикальную скорость VYg и
высоту полета h, если известны начальные данные о скорости VYg (/0) и высоте
Л(/о). Для компенсации ускорения силы тяжести необходимо иметь модель
гравитационного поля Земли. Блок-схема вертикального канала БИНС показана
на рис. 1.5.
20
Рис. 1.5. Вертикальный канал БИНС
Особенностью вертикального канала является его неустойчивость (неогра-
ниченный рост ошибок), в связи с чем в автономном режиме он практически не
используется (см. главу 4).
Заметим, что определение координат местоположения ЛА (широты (р, высо-
ты h ), линейных скоростей Vx , VYg, а также угла 6, характеризующего ориен-
тацию ЛА, основано только на измерениях акселерометров и гироскопа без
привлечения какой-либо внешней информации. Автономность инерциальных
методов навигации является главным их преимуществом по сравнению с дру-
гими методами (астрономическими, радиотехническими и др.).
Рис. 1.6. Обобщенная функциональная схема БИНС
На основе рассмотрения одного канала можно выделить следующие основ-
ные блоки, необходимые для построения БИНС (рис. 1.6):
• блок акселерометров — для определения проекций вектора кажущегося ус-
корения п на оси связанного трехгранника;
• блок пересчета - для преобразования проекций вектора кажущегося ускоре-
ния п на оси навигационной системы координат (в данном случае геогра-
фическая система координат);
• навигационный алгоритм - для выработки координат местоположения объ-
екта и скоростей и формирования компонент вектора абсолютной угловой
скорости географического трехгранника ;
21
• блок гироскопов - для определения проекций абсолютной угловой скорости
со на ребра связанного трехгранника;
• алгоритм ориентации - для решения задачи ориентации и формирования
матрицы перехода С, используемой в блоке пересчета. Алгоритм ориента-
ции может быть реализован с использованием различных кинематических
параметров, таких, как углы Эйлера - Крылова, направляющие косинусы,
кватернионы и др. (подробнее см. главу 3).
Следует также отметить, что БИНС обладают рядом несомненных преиму-
ществ перед инерциальными навигационными системами с гиростабилизиро-
ванной платформой. Прежде всего это - отсутствие ГСП. Вместе с тем к чувст-
вительным элементам БИНС предъявляются высокие требования, так как при
непосредственном закреплении на борту объекта чувствительные элементы
подвергаются значительно более сильным возмущениям, чем в инерциальной
навигационной системе платформенного типа [1.4].
1.2. Акселерометрические БИНС
Информацию о движении ЛА относительно центра масс в аксслерометричс-
ских БИНС определяют по сигналам акселерометров. В этом случае на каждую
ось связанной системы координат устанавливают два акселерометра. Сущест-
вуют два способа расположения осей чувствительности акселерометров [1.8]. В
первом способе вдоль каждой оси связанной системы координат устанавливает-
ся пара акселерометров, оси чувствительности которых перпендикулярны этой
оси. Для случая измерения угловой скорости тангажа компоновка акселеромет-
ров показана на рис. 1.7.
Рис. 1.7. Измерение угловой скорости тангажа
с помощью акселерометров
Акселерометры АХ1 и АХ2 на-
ходятся на расстоянии I от про-
дольной оси ЛА. Пользуясь рис.
1.7, находим показания акселеро-
метров (напомним, угловое уско-
рение в общем случае определя-
ется в виде сох I):
nv, =nY -0/;
' .. (1-8)
п V2 - +6/.
Здесь пх - проекция кажуще-
гося ускорения объекта на ось
11 х
Складывая и вычитая уравне-
ния (1.8) получаем кажущееся ус-
корение ЛА пх и угловое
ускорение 9
пх = у («ач + пхг 6 = “И%1 )'
(1-9)
22
Величина пх совместно с аналогично полученной nY используется для ре-
шения задачи навигации (см. раздел 1.1). Угол поворота 6 определяется двой-
ным интегрированием второго равенства (1.9) с учетом начального значения
6('о)-
Во втором варианте на каждую ось ЛА также устанавливается два акселеро-
метра, однако оси чувствительности последних параллельны соответствующей
оси ЛА (рис. 1.8). Показания акселеро-
метров для второго способа имеют вид
(напомним, центростремительное уско-
рение в общем случае определяется как
сох(сох/)):
(1.Ю)
/7Г1 = пу — 02Z;
nY2 ~nY+ О2^.
Из уравнений (1.10) нетрудно полу-
чить кажущееся ускорение пу и угло-
вую скорость 0
nY ~ 2 (,7у1 +Л>'2)’
Рис. 1.8. Второй способ компоновки
акселерометров
(1.11)
0 =
nY2 nY
21
Интегрируя второе выражение (1.11)
с учетом О(/о) можно определить угол тангажа 0. Недостатком этого способа
является трудность определения знака угловой скорости [1.8]. Однако для оп-
ределения параметров ориентации необходимо производить однократное ин-
тегрирование в отличие от первого способа.
Чувствительность акселерометрических БИНС к угловым движениям ЛА в
значительной степени определяется расстоянием между акселерометрами, сле-
довательно, необходимо увеличивать /, что не всегда возможно. Существенные
погрешности таких систем могут быть вызваны неточным заданием параметра
/, в связи с этим акселерометрические БИНС не нашли широкого применения.
Акселерометрические БИНС могут быть полезны в тех случаях, когда невоз-
можно измерить угловую скорость с помощью ДУС, например, некоторые бес-
пилотные ЛА совершают вращение по крену с угловой скоростью до 20 Гц. Для
измерения такой угловой скорости необходимы ДУС с диапазоном 7200 град/с,
однако измерителей угловой скорости с такими характеристиками не существу-
ет. Преодолеть трудности с измерением высокой угловой скорости позволяют
акселерометрические БИНС.
' 1.3. БИНС на неуправляемых гироскопах
В БИНС такого типа задача ориентации решается с помощью неуправляемых
(свободных) гироскопов (НГ). В общем случае для решения задачи ориентации
необходимо два НГ с кинетическими моментами, перпендикулярными друг
другу в начальный момент времени [1.4]. Рассмотрим по аналогии с разделом
1.1 движение ЛА в плоскости меридиана сферической и невращающейся Земли.
В данном случае задачу навигации и ориентации можно решить с помощью од-
ного НГ и двух акселерометров (рис. 1.9).
23
Рис. 1.9. БИНС на НГ
Пусть в начальный момент времени кинетический момент гироскопа Н
совпадает с вертикалью O0Yg0 . ЛА перемещается в точку О{, причем связанная
система координат повернута, как и прежде, на угол тангажа 6 вокруг оси
OZg. В силу свойства свободного гироскопа сохранять главную ось неизмен-
ной относительно инерциального пространства кинетический момент Н в точ-
ке О] будет иметь то же направление, что и в точке OG (понятно, что это воз-
можно только для идеального НГ). С датчика угла НГ снимается угол а, т.е.
угол между вертикальной осью OY ЛА и кинетическим моментом. На основа-
нии рис. 1.9 находим связь между показаниями НГ, широтой и углом тангажа 6
е = (р-а. (1.12)
Из соотношения (1.12) следует, что для определения угла тангажа необходи-
мо привлекать широту <р из навигационного алгоритма. Блок-схема северного
канала БИНС на НГ приведена на рис. 1.10.
Рис. 1.10. Структурная схема БИНС на НГ
24
В качестве НГ в БИНС такого типа, как правило, используются два гироско-
па с электростатическим подвесом ротора. Подробно функционирование бес-
платформенной системы ориентации на электростатических гироскопах рас-
смотрено в работе [1.3].
ЛИТЕРАТУРА К ГЛАВЕ 1
1. Андреев В. Д. Теория инерциальной навигации. Кн.1. Автономные системы. Кн.П. Коррек-
тируемые системы. - М.: Наука, 1966, 1967.
2. Бромберг П.В. Теория инерциальных систем навигации. - М.: Наука, 1979. - 296 с.
3. Гироскопические системы. Гироскопические приборы и системы: Учеб, для вузов
/Д.С.Пельпор , И.А.Михалев, В.А. Бауман и др./ Под ред. Д.С.Пельпора. 2-е изд., перераб. и
доп. - М.гВысш. шк., 1988.-424 с.
4. Инерциальные навигационные системы морских объектов/Д.П. Лукьянов, А.В. Молчанов,
А.А. Одинцов, И.Б Вайсгант; под. ред. Д.П. Лукьянова. - Л.: Судостроение, 1989.-184 с.
5. Инерциальная навигация. Под ред О’Доннела. - М.: Наука, 1968.
6. Ишлинский А.Ю. Ориентация, гироскопы и инерциальная навигация. М.: Наука, 1976. -
672 с.
7. Климов Д.М. Инерциальная навигация на море. - М.: Наука, 1984.-118 с.
8. Селезнев В.П. Навигационные устройства. - Машиностроение, 1974. - 660 с.
9. Фридлендер Г.О. Инерциальные системы навигации. - М., Физматлит, 1961. - 153 с.
10. Якушенков А.А. Основы инерциальной навигации. - М.: Морской транспорт. 1963. - 146 с.
Вопросы для самоконтроля
1. Какой набор чувствительных элементов применяется для
построения БИНС?
2. Каким образом ориентируются оси чувствительности акселе-
рометров и гироскопов в БИНС различных типов?
3. Для чего необходим блок пересчета в алгоритмах БИНС?
25
Глава 2
ИНЕРЦИАЛЬНЫЕ ЧУВСТВИТЕЛЬНЫЕ ЭЛЕМЕНТЫ
Инерциальными чувствительными элементами называют акселерометры и
гироскопы - приборы, измеряющие параметры линейных и угловых перемеще-
ний подвижных объектов для решения задач их ориентации, навигации и
управления.
2.1. Акселерометры
2.1.1. Общая характеристика
Чувствительный элемент (ЧЭ) большинства серийно выпускаемых акселе-
рометров состоит из массы, смонтированной в корпусе на элементах подвеса
различного конструктивного исполнения. По виду движения массы чувстви-
тельных элементов акселерометры делятся на осевые и маятниковые. В осевых
акселерометрах конструкция подвеса обеспечивает прямолинейное движение
массы, а в маятниковых - угловое.
В литературе зачастую указывается на то, что термин «акселерометр» имеет
неправильное употребление, так как акселерометр позволяет измерять не абсо-
лютное ускорение объекта, а лишь так называемое кажущееся ускорение - гео-
метрическую разность между абсолютным ускорением и ускорением силы тя-
готения. По этой причине чувствительные элементы, измеряющие кажущиеся
ускорение, академик А Ю Ишлинский назвал ньютонометрами. Однако в учеб-
ном пособии будет все же употребляться более привычный термин - акселеро-
метр.
У акселерометра выделяют ось чувствительности (эту ось также определяют
как измерительную) и перпендикулярные к ней поперечные оси. Ось чувстви-
тельности - это ось, в направлении которой возможно перемещение массы, обу-
словленное конструкцией подвеса. Акселерометры с одной осью чувствитель-
ности называют однокомпонентными. Принципиально возможно создание про-
странственных подвесов, обеспечивающих чувствительному элементу две
(двухкомпонентный акселерометр) или три (трехкомпонентный акселерометр)
оси чувствительности. В одном корпусе могут быть также установлены два или
три независимых ЧЭ с разным направлением осей чувствительности. Наиболее
просто двух - и трехкомпонентные акселерометры реализуются компоновкой
двух или трех однокомпонентных акселерометров. Если оси чувствительности
трех однокомпонентных акселерометров направить вдоль осей неинерциальной
системы координат XYZ, то измеряемые акселерометрами ускорения имеют вид:
ax=Vx-gx, ay=Uy-gy, a.=U_-gz, (2.1)
где Ux, Uv, U_ — проекции абсолютного ускорения движения объекта на оси
системы координат ATZ; gx, gy, g. - проекции ускорения силы тяжести на тс
же оси.
26
В соответствии с (2.1) для определения величин Ux, Uy, U. к показаниям
акселерометров необходимо добавить гравитационные составляющие gx, gy,
g.. Если акселерометры установлены на стабилизированной в плоскости гори-
зонта платформе, для двух акселерометров эта операция исключается. В ос-
тальных случаях необходима внешняя коррекция.
Акселерометры способны измерять линейное и угловое ускорения. Соответ-
ственно различают линейные и угловые акселерометры. В линейных акселеро-
метрах ось чувствительности параллельна вектору измеряемого ускорения. Для
измерения углового ускорения ось чувствительности должна быть параллельна
вектору линейного ускорения, обусловленного угловым ускорением.
По принципу измерения акселерометры делятся на приборы прямого и ком-
пенсационного измерения (действия, преобразования). Структурная схема аксе-
лерометра прямого измерения представляет собой последовательное соедине-
ние ЧЭ и элементов измерительной цепи. ЧЭ выполняет преобразование «уско-
рение - сила - перемещение», а измерительная цепь - преобразование «пере-
мещение - выходной сигнал». Выходной сигнал может быть непрерывным или
дискретным. ЧЭ и измерительная цепь равноценно влияют на метрологические
характеристики акселерометра прямого измерения, а его погрешность опреде-
ляется суммированием погрешностей отдельных звеньев ЧЭ и измерительной
цепи.
Акселерометры компенсационного (уравновешивающего) преобразования в
общем случае содержат цепь прямого преобразования с коэффициентом пере-
дачи К, цепь обратного преобразования с коэффициентом передачи Кои и
датчик неуравновешенности активной силы, действующей на подвес, и компен-
сирующей силы, также действующей на подвес, но с обратным знаком. Инер-
ционная масса ЧЭ, преобразующая ускорение в активную силу, находится вне
цепи уравновешивания. Роль датчика неуравновешенности выполняет подвес,
который вместе с инерционной массой ЧЭ образует колебательную систему.
Произведение К Коп называется глубиной уравновешивания. При глубокой
отрицательной обратной связи (К Коп > 1000) акселерометры компенсацион-
ного преобразования имеют следующие свойства:
1. Коэффициент преобразования рпределяется параметрами цепи обратного
преобразования Коп и звеньев, находящихся вне цепи уравновешивания.
Настройка коэффициента преобразования осуществляется изменением па-
раметров звеньев цепи обратной связи.
2. Погрешности цепи обратного преобразования и звеньев, находящихся вне
цепи уравновешивания, входят в погрешность акселерометра.
3. Нестабильность параметров звеньев, определяющих коэффициент К, не
оказывает существенного влияния на его стабильность. Главное, чтобы бы-
ла обеспечена высокая чувствительность и требуемое значение величины
/С-Лог,.
Отсюда следует, что при проектировании акселерометров компенсационного
преобразования главная задача заключается в обеспечении метрологических
характеристик цепи обратного преобразования, а тип датчика перемещений
инерционной массы не имеет принципиального значения.
Цепь обратного преобразования (уравновешивания, обратной связи) может
выполняться аналоговой или цифровой, реализующей широтно-, частот] ю- или
27
релейно-импульсную модуляцию сигнала.
Акселерометры с цифровой обратной связью имеют высокую точность и
применяются в основном в составе инерциальных навигационных систем плат-
форменного типа для измерения медленно изменяющихся ускорений.
В бесплатформенных инерциальных навигационных системах, а также в
других системах для измерения быстро изменяющихся ускорений, применяются
акселерометры с аналоговым контуром обратной связи. Если требуется частот-
ный выходной сигнал, в цепь обратной связи включается преобразователь «на-
пряжение - частота» (ПНЧ).
Акселерометры с аналоговым контуром обратной связи могут иметь струк-
туру с пропорциональным и интегральным регулированием.
В акселерометрах с пропорциональным регулированием на входе колеба-
тельной системы (датчик неуравновешенности) имеет место систематическая
ошибка регулирования, зависящая от разности инерционной и уравновеши-
вающей сил, которая, однако, не влияет на метрологические характеристики
акселерометра по следующим причинам:
• абсолютное значение ошибки мало при большой глубине уравновешивания;
• при нееденичной обратной связи система обладает астатизмом относитель-
но ошибки регулирования.
В акселерометрах с интегральным регулированием в цепь обратной связи
включают интегрирующий элемент. Такие акселерометры имеют малую глуби-
ну уравновешивания и неудовлетворительную виброустойчивость.
Точность преобразования акселерометрами ускорения в электрический сиг-
нал определяется величинами смещения нуля, погрешностью полной шкалы
(или чувствительности), а также температурным и временным дрейфом этих
параметров. Важными составляюгцими погрешности являются также погрешно-
сти линейности (нелинейность) и поперечная чувствительность. Смещение нуля
и чувствительность акселерометров при нормальных условиях корректируются
при изготовлении. Остаточная погрешность может быть уменьшена путем ка-
либровки и запоминания калибровочных констант в памяти микропроцессора.
Калибровка акселерометра возможна двумя способами: на вибростенде с образ-
цовым датчиком ускорения и с использованием силы тяжести.
Поперечная чувствительность характеризует способность датчика преобра-
зовывать в электрический сигнал ускорение, направленное под углом 90° к оси
чувствительности датчика. У идеального акселерометра поперечная чувстви-
тельность равна нулю.
Шум, содержащийся в выходном сигнале акселерометра, определяет разре-
шающую способность устройства, важную при определении малых ускорений.
Предельное разрешение в основном определяется уровнем шума измерения,
который включает внешний фоновый шум и шум собственно датчика. Уровень
шума непосредственно связан с шириной полосы пропускания датчика. Умень-
шение полосы пропускания н>тем включения фильтра нижних частот (ФНЧ) на
выходе датчика приводит к снижению уровня шума. Это улучшает отношение
сигнал/шум и увеличивает разрешающую способность, однако вносит ампли-
тудные и фазовые частотные искажения.
Акселерометры обладают большим конструктивным разнообразием, зави-
сящим от способа реализации ЧЭ, демпфера, дагчиков перемещений и силы
(момента), применяемых материалов и технологий и др.
Название акселерометра часто содержит ключевые слова, которые, по мне-
нию разработчиков, отражают его основные конструктивные и (или) функцио-
28
нальные особенности.
Например, «струнный акселерометр» имеет ЧЭ, выполненный в виде инер-
ционной массы на струне; «капиллярный акселерометр» имеет оригинальную
конструкцию демпфера. В названиях акселерометров: «емкостный», «пьезоре-
зистивный», «индуктивный», «на поверхностно-акустических волнах» и др. от-
ражен способ измерения перемещений инерционной массы. По виду материала,
из которого изготовлен ЧЭ, применяют названия: «кварцевый», «кремниевый»
акселерометры.
Примеры подобной, ненормированной, терминологии можно продолжать, но
нужно иметь в виду, что определяющими терминами являются: «осевой», «ма-
ятниковый», «линейный», «угловой», преобразование прямое или компенсаци-
онное.
Следует отметить еще одно обстоятельство, заключающееся в том, что с ис-
пользованием в качестве конструкционных материалов кремния, кварца и дру-
гих, которые возможно обрабатывать по технологиям микроэлектроники, поя-
вились, так называемые, микромеханические акселерометры. Если ЧЭ выпол-
нен из монокристаллической пластины, например кремниевой, а силовые эле-
менты компенсационного преобразователя и электроника - по традиционным
технологиям, то такие акселерометры принято называть интегральными, иногда
- гибридными. Необходимо обратить внимание также, что микросистемы, в том
числе и микроакселерометры, выполненные по технологиям микромеханики,
относят к микроэлектромеханическим системам (МЭМС - широко используе-
мая аббревиатура). При этом под МЭМС понимают не только изделия (систе-
мы), но и технологии их изготовления. Технологии МЭМС позволяют произво-
дить микроакселерометры в виде микросхем. При этом ЧЭ может не иметь под-
вижной инерционной массы на подвесе, а может использоваться, например,
пьезоэффект. Развитие МЭМС является перспективным направлением при раз-
работке акселерометров.
По совокупности конструктивно-технологических признаков изготовления
все акселерометры можно разделить на группы макромеханических, интеграль-
ных и микромеханических.
ЧЭ акселерометра, как отмечалось, представляет инерционную массу на
подвесе. К группе макромеханических можно отнести акселерометры, в кото-
рых подвес реализован в виде пружин, струны или керновых, шарикоподшип-
никовых, электромагнитных узлов, которые могут выполнять также роль изме-
рительных элементов в, так называемых, поплавковых акселерометрах с гидро-
статической разгрузкой узлов подвеса. Антиподом макромеханическим акселе-
рометрам по размерам являются микромеханические, а интегральные (гибрид-
ные) акселерометры являются продуктом совместного применения макро- и
МЭМС технологий.
2.1.2. Осевые и маятниковые акселерометры
2.1.2.1. Акселерометры прямого преобразования. Расчетная схема осевого
акселерометра представлена на рис. 2.1 в виде инерционной массы т, смонти-
рованной в корпусе на пружинах. Пружины, а также какой-либо центрирующий
элемент (не показан, но он может и отсутствовать) обеспечивают движение
массы только вдоль оси чувствительности у. Предполагается, что основание, на
котором установлен акселерометр, перемещается с линейным ускорением, век-
29
тор которого имеет проекции aх, ау, а. на оси х, у, z и вращается с угловой
скоростью, вектор которой имеет проекции сох, соу, со. на те же оси.
Рис. 2.1. Расчетная схема осевого акселерометра прямого преобразования
Вследствие действия сил на инерционную массу, последняя занимает поло-
жение, определяемое координатой у, которая содержит информацию об изме-
ряемом ускорении а. . Измерение перемещения у может быть реализовано раз-
личными типами датчиков: потенциометрическим, индуктивным, оптоэлек-
тронным и др.
Рассмотрим силы, приложенные к инерционной массе в направлении оси у.
Под действием силы F = тау, являющейся следствием ускорения ау, инерци-
онная масса перемещается по координате у со скоростью у и ускорением у. В
сторону, противоположную координате у и векторам у и у, действуют упругая
сила пружины Gyy (Gy — суммарная жесткость пружин в направлении оси у),
сила сопротивления перемещению массы клуу , которую называют также силой
демпфирования ( £ - абсолютный коэффициент демпфирования), инерционная
сила массы ту. В направлении перемещения массы действует центробежная
сила wy(or + со2). Сила демпфирования зависит от его способа: газовое, жид-
костное, электровихревое и др. Наряду с силой демпфирования, которую назы-
вают также силой вязкого трения, может быть учтено и сухое трение, возникно-
вение которого возможно в некоторых конструкциях.
В соответствии с методом кинетостатики, суммируя векторы сил по рис. 2.1.
со своими знаками, приравниваем сумму нулю и получаем уравнение движения
инерционной массы осевого акселерометра:
ту + кщу + Gvy - ту (от + со2 ) = тау . (2.2)
Перепишем уравнение (2.2) в форме
У + о? + - (со* + со2)] у = ау, (2.3)
/с"
где со ,0 = J—~ - собственная частота колебаний инерционной массы;
* V т
£ . = ——— — относительный коэффициент демпфирования инерционной мас-
У 2тау0
сы.
30
Очевидно, чтобы уменьшить влияние ускорений, обусловленных угловыми
скоростями соЛ, (£>_, необходимо выполнять условие
Ю>0 » + «£ • (2-4)
В соответствии с (2.2) и (2.3) ЧЭ осевого акселерометра является колеба-
тельным звеном, передаточная функция которого по отношению к вынуждаю-
щей силе при выполнении условия (2.4) имеет вид
У тау T2s2+2t>yTys+ 1
(2.5)
где
Gy (0j0 dt
В установившемся (стационарном) режиме имеет место смещение инерци-
онной массы
та
(2.6)
которое содержит информацию об измеряемом ускорении вдоль оси чувстви-
тельности.
В качестве примера на рис. 2.2 приведены ос-
новные элементы конструкции ЧЭ осевого акселе-
рометра, соответствующего расчетной схеме по
рис. 2.1, разработанного фирмой Texas Instruments
Inc. (США).
Инерционная масса (ИМ) 1 смонтирована отно-
сительно основания 4 на стойках 2 с помощью уп-
ругих элементов подвеса, выполненных в виде
плоских пружин 3, обеспечивающих ИМ переме-
щение только вдоль оси чувствительности вследст-
вие перемещения основания с ускорением ау. Из-
мерение перемещений ИМ реализуется датчиком,
состоящим из двух электродов 5, 6, емкость между
которыми изменяется при перемещении ИМ.
Расчетная схема маятникового акселерометра
приведена на рис. 2.3 Акселерометр представлен в
виде подпружиненной массы т, расположенной на
плече / относительно оси подвеса, смонтированной
в корпусе на узлах вращения (подшипники каче-
ния, скольжения, керновые опоры и др.) Подвес
может быть реализован в виде упругого элемента
Рис. 2.2. Основные элементы
конструкции ЧЭ осевого аксе-
лерометра фирмы Texas In-
struments Inc.:
1 - инерционная масса; 2 -
стойка;
3 - упругий элемент подвеса
(пружина); 4 - основание; 5. 6 -
неподвижный и подвижный
электроды емкостного датчика
перемещений инерционной
массы
(элементов), работающего на кручение.
Векторы линейного ускорения и угловой скорости, характеризующие пере-
мещение основания, на котором установлен акселерометр, имеют проекции на
оси х, у, z: ах, аг, а_ и сог, со^, со.. Инерционная масса вследствие движения
основания занимает положение, определяемое угловой координатой а, содер-
жащей информацию об измеряемом ускорении а, вектор которого совпадает с
осью чувствительности. Датчики углового положения маятника могут быть раз-
личных типов.
31
Рис. 2.3. Расчетная схема маятникового акселерометра прямого преобразования
Рассмотрим силы, действующие на ИМ, и моменты сил относительно оси
подвеса (качания) маятника. Считаем угловую скорость вращения основания
постоянной, а силы инерции Кориолиса пренебрежимо малыми по сравнению с
остальными.
К инерционной массе приложены силы, вызванные линейными ускорениями
основания ау и ах, ускорением силы тяжести g и центростремительным уско-
рением (со, + 0)2sin а, следствием которых являются моменты относительно
оси подвеса маятника:
М, = maj cos а, Мг — т £g - (—ах )] I sin а,
Л/3 = т [(со2 + а)2) I sin aj I cos а .
Движению маятника под действием указанных моментов препятствуют: мо-
мент упругих сил Gaa (Ga - суммарная жесткость подвеса вокруг оси z, обу-
словленная упругими силами), моме нт диссипативных сил, или сил демпфиро-
вания кДаа. (кДа - абсолютный коэффициент демпфирования) и инерционный
момент J.ii (J. - момент инерции маятника относительно оси z). Имея в виду,
что угол а — малая величина (sin а ~ а, cos а ~1), в соответствии с методом
кинетостатики получим уравнение движения ИМ по координате а :
' J + к^а + [<7а + т (g + ах}1 - т (со^ + со^)/2^а = тау1. (2.7)
Перепишем уравнение (2.7) в форме:
« + 2^a«a0« + <
2 ml Г
®aO +y~Lg +
ml
► a - —а
(2.8)
где о)и0
£
— собственная частота колебаний маятника; Е,(, = ——
z^af!
- от-
а
носительный коэффициент демпфирования маятника.
32
Для уменьшения влияния перекрестных ускорений необходимо выполнение
условия
Юа0
(2.9)
Передаточная функция ЧЭ маятникового акселерометра при выполнении ус-
ловия (2.9) по отношению к возмущающему моменту имеет вид
a (s) К
(5) = ---- = ’
mayl 7>2 + 2V> + l
(2.Ю)
,, 1 1
ГДе i ’
Ga Юа0
В установившемся режиме имеет место отклонение маятника на угол
та I
аСТ = ——, величина которого пропорциональна измеряемому ускорению
G„
вдоль оси чувствительности.
Очевидно, что колебательное движение ИМ можно описать и по линейной
координате, имея в виду что у = I sin а » 1а.
а)
Рис. 2.4. Монокристаллический ЧЭ маятнико-
вого акселерометра:
а - конструкция; б - общий вид; в - расчетная
схема;
1 - инерциднная масса; 2 - упругие элементы
подвеса; 3 — рамка
б)
В качестве примера на рис. 2.4 (а, б) показан ЧЭ маятникового акселеромет-
ра разработки Минского НИИ радиоматериалов, изготовленный методом хими-
ческого травления из монокристаллического кремния. ЧЭ представляет единую
33
конструкцию, которая состоит из ИМ 1, упругих элементов подвеса 2, выпол-
ненных в виде миниатюрных «балок», работающих на изгиб, и рамки 3, которая
защемляется между двумя крышками корпуса (не показаны). Между крышками
и ИМ остаются зазоры (по 10 мкм) с каждой стороны, в пределах которых пе-
ремещается ИМ под действием сил, обусловленных ускорением av. Мерой пе-
ремещения ИМ является изменение емкостей между электродами, нанесенными
на поверхности ИМ с обеих сторон и поверхности крышек, обращенные к ИМ.
Очевидно, что в реальных конструкциях ИМ нс сосредоточена в центре масс
на расстоянии / от оси качаний маятника и момент инерции ИМ относительно
оси z (J.) должен быть вычислен на основании теоремы Штейнера.
Заметим, что динамика ЧЭ с монокристаллическим маятником в общем слу-
чае отличается от динамики ЧЭ с маятником, имеющим фиксированную ось
колебаний (см. рис. 2.3). На рис. 2.4, в показана расчетная схема, из которой
следует, что положение ИМ - маятника в системе координат х, у определено
линейной координатой у его центра масс (ЦМ) и поворотом ИМ вокруг ЦМ на
угол а . Динамика маятника в этом случае описывается двумя уравнениями ко-
лебаний по координатам у и а [2.18]. Имея в виду, что длина упругих «балок»
значительно меньше длины ИМ, в первом приближении можно пренебречь ви-
лянием координаты у на угол а . Уравнение движения ИМ в этом случае иден-
тично (2.7), в котором параметр I - расстояние от ЦМ до оси z, a J. « Jo + ml2
(Jo - момент инерции ИМ относительно оси параллельной оси z и проходящей
через ЦМ). Следует также обратить внимание на то, что из-за упругости «ба-
лок» подвеса ИМ - маятник может иметь формы колебаний отличные от пока-
занной на рис. 2,4, в («первая» форма колебаний).
Рассмотрим измерительные цепи акселерометров прямого преобразования.
Последовательность преобразований физических величин в процессе измерения
ускорения осевым акселерометром может быть представлена в виде блок-схемы
измерительной цепи (рис. 2.5), на которой каждый элемент преобразования
представлен в виде звена с соответствующей передаточной функцией.
ау
Рис. 2.5. Блок-схема измерительной цепи осевого акселерометра
т
Величина т инерционной массы ЧЭ является коэффициентом передачи пер-
вого звена, на вход которого поступает измеряемое ускорение ау, а выходом
является инерционная сила F. На вход второго звена, передаточная функция
которого W определяется зависимостью (2.5), поступает инерционная сила F, а
выходом является перемещение у ИМ, равное изменению Д/г первоначального
зазора между электродами емкостного датчика (преобразователя) перемещений.
Выходом емкостного, дифференциального датчика перемещений с передаточ-
ной функцией Wn является напряжение Д£7 , которое затем посредством актив-
ного фильтра с передаточной функцией W. преобразуется в выходное напря-
жение ивых.
Известно [2.18], что передаточная функция емкостного дифференциального
датчика перемещений имеет вид
34
ли ипт1
Wn=------- =
ДА Ло
(2.Н)
где Uou - опорное напряжение питания дифференциального моста, в который
включены электроды датчика перемещений, образующие измерительные емко-
сти; h0 - начальный зазор между подвижным и неподвижным электродами.
Реализация фильтра может быть различной в зависимости от требований,
предъявляемых к качеству переходного процесса, полосе пропускания частот и
других. Как правило, передаточная функция фильтра соответствует колебатель-
ному звену
Ж, (5) = ,
ф ГфгГ+27^ + 1
(2.12)
где коэффициент передачи Кф, постоянная времени Тф и относительный коэф-
фициент демпфирования фильтра определяются номиналами электронных
компонентов схемы.
В соответствии с рис. 2.5 и с учетом (2.5), (2.11), (2.12) передаточная функ-
ция осевого акселерометра имеет вид:
jy fSy- ^вьа = _____________;_____________________
ол ау Л„(7;У+2^ + 1)(г>2+2^Г#5+|)'
Из передаточной функции (2.13) при s-О следует важнейший технический
В
(2.13)
параметр акселерометра - масштабный коэффициент
Км = = mU°"KyK*. (2.14)
ау h0
Важнейшей характеристикой акселерометра является также нестабильность
Км , в том числе его температурная нестабильность, определяемая в процентах
от номинала для заданных условий работы. Очевидно, этот параметр зависит от
нестабильности всех компонентов величины Км . Амплитудно-частотные, фа-
зочастотные характеристики и переходный процесс измерительной цепи могут
быть построены на основании известных процедур с передаточной функцией
измерительной цепи при формальной замене 5 = /со (со — частота).
Последовательность преобразования физических величин при измерении ус-
корения маятниковым акселерометром показана в виде блок-схемы измери-
тельной цепи на рис. 2.6.
Рис. 2.6. Блок-схема измерительной цепи маятникового акселерометра
Предполагается, что датчик перемещений и фильтр аналогичны описанным
выше. Звено с коэффициентом передачи / переводит угловую меру перемеще-
ний ИМ т в линейное изменение зазора между электродами емкостного датчи-
ка перемещений. Передаточная функция маятникового акселерометра в соот-
ветствии с рис. 2.6. и выражениями (2.10), (2.11), (2.12) имеет вид
35
ж ____________________________________________
“ Ъ (ту + + l)(r,V + 2^ + 1) ’
(2.15)
из которой следует (5 = 0) выражение для масштабного коэффициента
Ц,Ь1Х _ ^о.пКик,
Здесь следует напомнить, что маятниковый акселерометр более восприимчив
к ускорениям, действующим по перекрестным осям, и для него имеет место так
называемый вибрационный сдвиг нуля при «косой» вибрации основания, из-
вестный также, как эффект Максвелла - Капицы.
2.1.2.2. Акселерометры компенсационного преобразования. В акселеро-
метрах компенсационного преобразования (компенсационные акселерометры)
сила, инициируемая ускорением, воспринимаемым ИМ, уравновешивается (по-
этому компенсационные акселерометры называют также акселерометрами
уравновешивающего преобразования) силой, имеющей, как правило, электро-
статическую, магнитоэлектрическую или электромагнитную природу. Уравно-
вешивающее воздействие на ИМ создается с помощью цепи обратной связи
(цепь уравновешивания, компенсации).
Рассмотрим создание разностной электростатической силы, действующей на
ИМ акселерометра, выполняющей также роль подвижного электрода емкостно-
го датчика перемещений (дифференциальный конденсатор). Схема формирова-
ния электростатической обратной связи приведена на рис. 2.7.
Рис. 2.7. Схема формирования электростатической обратной связи
Измерительный мост образован дифференциальными емкостями С] и С2, у
которых общий провод («земля») соединен с электродом, расположенным на
ИМ акселерометра, и резисторами R. Генератор (Г) вырабатывает опорное на-
пряжение с амплитудой меандров Uo п, которое питает измерительный мост
(рис. 2.8, а). Напряжение АС , снимаемое с измерительного моста, через усили-
тель (У), синхронный детектор (СД) и фильтр (Ф) нижних частот, имеющих со-
ответственно коэффициенты передач К}, К2 и К3, поступает на выход (С/В14Х) и
по линии обратной связи - на сумматор (t/oc), на который подается также
опорное напряжение генератора. Очевидно, (7ВЫХ = -t/oc = K&U (К = К{К2КД
Напряжение обратной связи смещает опорное напряжение относительно обще-
го провода на величину t/oc (рис. 2.8, б), но величина питания измерительного
моста по амплитуде остается неизменной (2 Uo п), и, следовательно, напряжение
At/ в соответствии с (2.11) равно
At/ = U°n^h . (2.16)
Л)
36
Вследствие смещения опорного напряжения емкости Ct и С2 оказываются
Имея в виду разностную электростатическую силу, действующую на под-
вижный электрод — ИМ, а также равенство t/BbIX = -2(7ОС, запишем передаточ-
ную функцию канала обратной связи [2.18]
££ sU
IV =—= ° оп- (2.17)
о.с т , 1 2 ’ '
^вых
где £ - диэлектрическая проницаемость среды между электродами;
£0 - 8,85 10“12 Ф/м; 5 - площадь взаимного перекрытия электродов.
Блок-схемы измерительных цепей акселерометров с обратной связью приве-
дены на рис. 2.9.
Рис. 2.9. Блок-схемы измерительных цепей осевого (а) и маятникового (б) акселерометров
с электростатической обратной связью
Передаточные функции замкнутых цепей измерения акселерометров по от-
ношению к ускорению, воспринимаемому ИМ, имеют вид:
mWyW.^
1 +
- (осевой);
тГ-w^w,^
1 + /ЗДЛЛс
- (маятниковый).
Схема, иллюстрирующая формирование магнитоэлектрической обратной
связи, приведена на рис. 2.10. Магнитоэлектрический датчик силы образован
постоянными магнитами, укрепленными в корпусе (показан штриховкой), и ка-
тушками, установленными на ИМ акселерометра. ИМ с корпусом связана упру-
гим элементом подвеса с одной стороны (маятниковый акселерометр). Очевид-
37
но, снабдив ИМ симметричным упругим элементом, получим схему осевого
акселерометра. Измерительные емкости конденсаторов С] и С2 образованы
подвижными электродами, размещенными на ИМ и неподвижными, размещен-
ными на элементах конструкции (не показаны) акселерометра. Измерительные
емкости конденсаторов С, и С, включены во времязапаздывающис цепи гене-
ратора Г, который формирует на выходе напряжение Ц, поступающее на
фильтры 0J и Ф2, которые выделяют постоянную составляющую сигнала. На-
/. /?
пряжения С/ф1 и С/Ф2 пропорциональны отношениям у и -. н которых Z, и t2
- время, в течение которого напряжения на конденсаторах С] и С2 достигают
пороговых значений, а величина Т - +12 определяет период импульсной по-
следовательности генератора.
Рис. 2.10. Схема формирования магнитоэлектрической обратной связи
Напряжения 1/ф1 и иф2 поступают на масштабные усилители У1 и У2, вы-
ходные напряжения которых являются входами для усилителя УЗ: Z7BX1 и (7ВХ2.
Напряжение на выходе усилителя УЗ, равное Ь'вь|ХЗ = t/BX2 - ^ВХ1 включено в
последовательную цепь, образованную катушками датчика силы с общим со-
противлением Rl и сопротивлением нагрузки RH . По каналу (цепи) обратной
связи протекает ток /, пропорциональный перемещению ИМ и создающий силу
и момент, действующие заодно с упругим моментом подвеса ИМ. Ток / и на-
пряжение (7ВЫХ пропорциональны ускорению, действующему на ИМ акселеро-
метра. При соответствующем выборе элементов электронной схемы, соответст-
вующей рис. 2.10, учитывая, что 7?н » RL может быть обеспечено напряжение
Гвых = KU Сг ~С|-, (2.18)
ВЫХ ” с2 + С,
где К ,с - К{ - К2 - коэффициент усиления усилителей У1 и У2.
Таким образом, напряжение на выходе электронной схемы акселерометра
пропорционально относительному приращению величины измерительной емко-
сти и, следовательно, пропорционально действующему на него ускорению.
Имея в виду, что С, =--2— и С2 =------у—, в соответствии с (2.18) получим
h0 + ДА " h0 - ДА
38
В соответствии с рис. 2.10 ток, протекающий в канале обратной связи, равен:
/ = ^вых . (2.20)
R„ + R,
л L
Сила, развиваемая магнитоэлектрическим датчиком с учетом (2.19, 2.20)
равна
F^IB^K^h, (2.21)
К U}B3L
где лмэ = —; В3 - индукция в зазоре между катушками и магнита-
+Rl)
ми; L - длина провода обмоток катушек.
На рис. 2.11 приведены блок-схемы измерительных цепей маятникового ак-
селерометра с магнитоэлектрической обратной связью.
Рис. 2.11. Блок-схемы измерительных цепей осевого (а) и маятникового (б) акселерометров
с магнитоэлектрической обратной связью
Передаточная функция акселерометра по напряжению в соответствии с
(2.19) имеет вид:
(2.22)
,7
Х й/l Ло
Передаточная функция обратной связи в соответствии с (2.19, 2.21) опреде-
ляется выражением:
^ос = — = ВзЬ
ивых RH + Rl
Передаточные функции замкнутых цепей измерения по отношению к уско-
рению имеют вид:
(2.23)
Ф =
(2.24)
(2.25)
----------(осевой);
1 + Ж,ЖэсЖос
Ф = —^а^эс--------(маятниковый).
l+ZX^oc
В акселерометрах с обратной связью второе слагаемое в знаменателях пере-
даточных функций обычно значительно больше единицы. Заметим, что это пра-
вило затруднительно выполнить для акселерометров с электростатической об-
ратной связью.
Из выражений (2.24), (2.25) для статического режима с учетом замечания о
39
(2-26)
их знаменателях получим
. ^вых w(^h+7?l)
zTa _______________________ РЫЛ ___ 11 7
's=0" ау ~ B3L
Зависимость (2.26) определяет масштабный коэффициент и из нее следует:
—^ВЬ1Х—В L = та., т.е. IB L = та . (2.27)
Равенство (2.27) является общепринятым расчетным соотношением, которое
имеет простой физический смысл: сила, развиваемая магнитоэлектрическим
датчиком в цепи обратной связи, уравновешивает инерционную силу ЧЭ, обу-
словленную измеряемым ускорением. Из равенства (2.27) можно получить, на-
пример, требуемое значение индукции магнитной цепи В3 = —— при заданных
Рис. 2.12. Функциональная схема маятникового
акселерометра с подвесом ИМ на торсионах:
1 - ИМ-маятник; 2 - торсион; 3, 4 - электроды
емкостных преобразователей силы
и перемещений
значениях остальных параметров.
Варианты конструктивного оформления датчиков сил для цепей обратной
связи на примерах маятниковых акселерометров показаны на рис. 2.12 - 2.14.
На рис. 2.12 приведена функциональная схема маятникового акселерометра,
разработанного в Draper Laboratori (США) и изготовленного по технологиям
МЭМС.
ИМ-маятник 1 представляет собой
прямоугольную в плане пластину по-
стоянной толщины, подвешенную на
паре торсионных упругих элементов 2,
работающих на кручение. Маятнико-
вый эффект достигается ассиметрией
подвеса пластины на торсионах. Под
пластиной размещена пара электродов
4, изменение емкости которых проис-
ходит при вращении пластины на тор-
сионах при действии ускорения «о».
Под пластиной размещены также элек-
троды 3 контура компенсации. Пара-
мегры пластины и упругого подвеса подобраны под заданный диапазон изме-
ряемых ускорений. Акселерометр может работать в разомкнутом режиме (пря-
мое измерение) и с контуром обратной связи. Выбор режима работы зависит от
требований точности, диапазона измерений и стоимости прибора. С замкнутым
контуром коррекции ток, пропорциональный результирующему изменению ем-
кости, идет от гибкого элемента (торсиона) подвеса через усилитель (У), демо-
дулятор (Д) к сумматору (Е), в котором происходит алгебраическое сложение
опорного напряжения Uo и напряжения U, пропорционального перемещениям
маятника, обусловленным измеряемым ускорением а.
Акселерометры изготовлены с применением технологии травления кремние-
вой пластины. Полученная структура анодной сваркой прикреплена к подложке
из стекла Pyrex, на которой размещены электроды.
Акселерометры были изготовлены для применения в управляемых боепри-
пасах с диапазоном измеряемых ускорений от 100 до 1000 g, а также для ком-
мерческого применения с диапазоном измеряемых ускорений 0,1 - 1,5 g.
Фирма Sundstrand Data Control (США) разработала в начале 1980-х годов се-
рию маятниковых акселерометров компенсационного измерения Q-Flex (моде-
40
ли QA-1000, 1100, 1200, 2000 и т.д.), которые имеют кварцевый ЧЭ, изготов-
ленный из цельного диска.
Принципиальная схема акселерометра приведена на рис. 2.13. Акселерометр
имеет измерительные емкости С{, С2 и магнитоэлектрический датчик силы
(момента) цепи обратной связи. Датчик силы имеет традиционное (не планар-
ное) исполнение (интегральный, или гибридный акселерометр).
Рис. 2.13. Принципиальная схема акселерометра Q-Flex:
7 - кольцевое основание; 2 - упругий элемент подвеса; 3 - инерционная масса; 4 - постоян-
ный магнит;
5,7 - элементы магнитопровода; 6 - катушка датчика силы; 8,9- контактные площадки
датчика перемещений (угла) и силы (момента) соответственно
Рассматриваемый акселерометр от микромеханики имеет только кварцевый
маятник, но его конструкция интересна тем, что ее особенности использованы
другими разработчиками, а современные технологии позволяют выполнить и
другие элементы конструкции в микроисполенении.
Кольцевое основание 7, упругие элементы («балки») подвеса 2 и инерцион-
ная масса 3 (маятник) вытравлены из пластины аморфного плавленого кварца.
Маятник перемещается в пределах начального зазора h0 = 19 мкм при воздей-
ствии на него силы, обусловленной ускорением а. Демпфирование маятника -
газодинамическое и контурное — с помощью электрического корректирующего
устройства в усилителе цепи обратной связи. Металлизированные части квар-
цевого маятника и плоские поверхности магнитопроводов 7 являются электро-
дами емкостного преобразователя (датчика) перемещений. Непосредственно на
маятнике смонтирована катушка 6 магнитоэлектрического преобразователя
(датчика) силы, включающего также постоянные магниты 4 и магнитопроводы
5, 7. Токоподводы от датчиков перемещений и силы выведены через упругие
элементы 'подвеса к контактным площадкам 8 и 9. На узле ЧЭ установлен тер-
модатчик, что даёт возможность алгоритмической компенсации температурного
дрейфа параметров акселерометра.
Полоса пропускания акселерометра QA-2000 (без корректирующего устрой-
ства) 300 Гц. Акселерометры нашли применение в бесплатформенных инерци-
альных навигационных системах.
На рис. 2.14. приведена принципиальная схема маятникового компенсацион-
ного акселерометра, все элементы которого, включая керновые опоры маятни-
41
ка, могут быть изготовлены традиционными технологиями (акселерометр в
макромеханическом исполнении).
Рис. 2.14. Принципиальная схема маятникового акселерометра на керновых опорах:
1 - маятник; 2 - катушка датчика момента; 3 - корпус; 4 - керновая опора; 5 - якорь датчика угла;
6 - постоянный магнит; 7 - катушка датчика угла
Маятник 1 (инерционная масса) конструктивно объединен с катушкой 2 маг-
нитоэлектрического датчика момента (ДМ) и якорем 5 датчика угла (ДУ) ин-
дукционного типа. Этот узел смонтирован в корпусе 3 на керновых опорах 4.
Постоянный магнит 6 ДМ связан с корпусом (условно обозначен штриховкой) и
размещен внутри катушки 2. Корпус 3 выполняет также функцию магнитопро-
вода ДМ. Катушка 7 ДУ также размещена на корпусе. Цепь обратной связи по-
казана в виде усили >сля У и сопротивления R, на котором выделяется напряже-
ние {/вых , пропорциональное измеряемому ускорению а.
Уместно отметить, что подвес маятникового ЧЭ на керновых опорах реали-
зован в акселерометре ДА -11. Можно также указать, что в поплавковых маят-
никовых компенсационных акселерометрах, например типа АЛ2, ЧЭ представ-
ляет цилиндрический поплавок в жидкости со смещенным центром масс. Цен-
трирование ЧЭ в корпусе реализуется с помощью керновых, камневых (воз-
можно, с осевой растяжкой), шарикоподшипниковых или электромагнитных
опор.
2.1.3. Струнные акселерометры
2.1.З.1. Принцип работы. Струнные акселерометры относятся к приборам
прямого преобразования, но в силу присущих им особенностей их принято вы-
делять в отдельную группу. К этим особенностям относятся отсутствие под-
вижной ИМ и сам принцип формирования выходного сигнала, который основан
на зависимости частоты поперечных колебаний растянутых струн от силы их
натяжения, которая, в свою очередь, зависит от измеряемого ускорения. В об-
щей цепи преобразования всегда присутствует звено, связывающее механиче-
ское напряжение в струне с ее частотой. Эта зависимость определяется из урав-
нения динамики струны, представляющего собой уравнение в частных произ-
водных гиперболического типа (методы его решения подробно рассмотрены,
например, в работе [2.1]), и имеет вид
(2-28)
42
где f - частота гибкой струны длиной 1,Т- натяжение струны; р — линейная
плотность материала струны.
На рис. 2.15 приведена принципиальная схема двухструнного дифференци-
ального акселерометра осевого типа, представляющего собой конструкцию, в
которой инерционная масса 1 вывешена на продольных струнах 2 и поперечных
3, ограничивающих (препятствующих), перемещениям ИМ в направлениях осей
х, z. В процессе изготовления струнам 2 заданы начальные натяжения То, кото-
рые определяют заданную частоту^ их поперечных колебаний. При появлении
измеряемого ускорения а вдоль оси у появляется вариация силы в каждой из
iwa
струн ДГ =------ (ш - масса ИМ, s - площадь поперечного сечения струны),
вследствие чего натяжение одной из струн увеличивается, а другой - уменьша-
ется. Соответственно изменяются частоты их колебаний. Разность частот струн
Lf = f - f есть мера измеряемых ускорений.
Рис. 2.15. Принципиальная схема струнного дифференциального акселерометра:
1 - ИМ; 2 - продольные (рабочие) струны;
3 - поперечные (удерживающие) струны; (N - S) - магниты
Возбуждение поперечных колебаний струны, преобразование их в электри-
ческий сигнал и последующая его регистрация осуществляются устройствами
возбуждения - съема, которые могут быть реализованы на различных физиче-
ских принципах.
Известны системы возбуждения, построенные по разомкнутому и замкнуто-
му (автогенераторному) принципам. В схемах разомкнутого типа возбуждение
струны осуществляется импульсом силы, после чего струна совершает свобод-
ные затухающие колебания на частоте механического резонанса. Основной
трудностью метода свободных колебаний является регистрация частоты при
уменьшающейся амплитуде колебаний. Этот метод не позволяет иметь непре-
рывную информацию об измеряемом параметре. К разомкнутой схеме возбуж-
дения можно отнести схему с задающим генератором, когда о собственной час-
тоте колебаний струны можно судить по частоте генератора в момент достиже-
ния струной максимальной амплитуды АЧХ (амплитудно-частотной характери-
стики). Этот метод (метод АЧХ) также трудно реализуем.
Наиболее часто используются автогенераторные схемы возбуждения, в кото-
рых частотозадающий элемент струны находится в состоянии автоколебаний.
Функциональная схема струнного автогенератора с частотозадающим элемен-
том магнитоэлектрического типа (для одной струны) показана на рис. 2.16.
43
Рис. 2.16. Функциональная схема струнного автогенератора с магнитоэлектрическим частотоза-
дающим элементом: 1 - компенсационная струна; 2 - вибрирующая струна; 3 - усилитель
По струне 2 проходит знакопеременный ток, который взаимодействуя с маг-
нитным полем магнитов N- S , вызывает ее вибрацию. При колебаниях струны
в постоянном магнитном поле в ней наводится ЭДС. Струна включена в мосто-
вую схему, в другое плечо которой включена компенсационная (неподвижная)
струна 1, эквивалентная струне 2. Обе струны с резисторами R/ и R? образуют
равноплечий электрический мост, диагональ «а — а» которого подключена ко
входу усилителя 3 обратной связи, а диагональ «в - в» - к его выходу. Мостовая
схема включения устраняет составляющую обратной связи не зависящую от
частоты. Автогенератор обеспечивает колебания струны на ее собственной час-
тоте, которая при наличии ускорения изменяется в соответствии с (2.28)
f = — Т" ±та/s = JL 1Го1 АГ = |1+— (2.29)
21 у р 21 у р у То
[Ц та
где Л =— J— ; &Т =-------•
21 у р 5
Таким образом, частота выходного сигнала струнного акселерометра содер-
жит информацию об измеряемом ускорении.
Для двухструнного акселерометра (см. рис. 2.15) с двумя задающими эле-
ментами, схемы которых аналогичны рис. 2.16, выходной сигнал усилителя
представляет собой частотно-модулированный сигнал вида:
С7. = U. sin со/; £7, = £7 , sin соЛ,
1 mi 1 7 2 m2 2 7
где CD] - 2-nf}; со, - 2л/2 — частоты, определяемые зависимостью (2.29)).
Последующая обработка сигнала определяется требованиями, предъявляе-
мыми к акселерометру. При выборе способа формирования характеристик сле-
дует исходить из необходимости линеаризации нелинейной (квадратичной) ста-
тической характеристики (2.29); минимизации погрешностей, связанных со спе-
цификой работы струнных преобразователей, в частности, с релаксацией на-
пряжений в струне; минимизации погрешностей, связанных с технологическими
процессами изготовления, которые могут привести к неполной геометрической
или физической идентичности струны.
2.1.3.2. Методы формирования выходного сигнала. Выходной сигнал наи-
более очевидным образом может быть получен как приращение частоты. В со-
ответствии с (2.29) для однострунного преобразователя имеем
44
A/i = /и [1 - Vl + ЛГ/Г,,]; (2.30)
а для двухструнного
= /„, Vi ± дт; / ги - /02Vi + дг2 / тш, (2.31)
где fm, f02 - частоты собственных поперечных колебаний струн; Г01, Г02 -
предварительные натяжения струн.
Для одинаковых струн (f0l = f02 = fQ, TOi = T02 = Го) выражение (2.31) упро-
щается
ДГ2 = Л[Vi + дг/т; -71ТДГ/Г„]. (2.32)
При условии ДГ / То « 1 выражения (2.30, 2.32) могут быть разложены в
степенные ряды:
ДГ
ДА — fo
/ 2
ДГ] 1(м]
т.) 8^;
(2.33)
В выражениях (2.33) члены в квадратных скобках после единицы характери-
зуют отклонение статических характеристик струнных преобразователей от ли-
нейного закона. Можно ограничиться линейностью статической характеристики
с относительной погрешностью 8, определяемой следующими требованиями:
[X / •
дН с 1(ДГ]
--- — о ; — --
То J 81 Го J
и /щах и /1
(2-34)
Из (2.34) следуют предельно допустимые расстройки по натяжению для од-
нострунного и двухструнного (дифференциальных) преобразователей:
(АП < ЕЕ
---- <4о, - < у/оо . (2.35)
А) / max А) / max
При выполнении условий (2.35) статические характеристики струнных пре-
образователей можно считать линейными с относительной погрешностью 5.
Предельные приращения частот на границе диапазона измерения определяются
выражениями:
ДА = /128; Д/1 = Лл/88 .
J 1 шах J 0 v > У 2 шах J 0 4
Рассмотренный метод преобразования частот обеспечивает требуемую ли-
нейность статической характеристики при выполнении условий (2.34), но дает
относительно невысокую крутизну характеристики, особенно для однострунно-
го преобразователя (2.33).
Возможности этого метода для регистрации нестационарных низкочастот-
ных (разность частот) процессов ограничены. Кроме того, требуется высокая
стабильность величин /0, То, т.е. стабильность состояния струн, что не всегда
выполнимо.
В соответствии с (2.33) выходные сигналы однострунного и двухструнного
преобразователей с учетом (2.34) могут быть представлены в виде отношений
частот:
45
АД."!. (2.зб)
Л 2Г„ Л Г„
Из выражений (2.36) следует, что данный метод формирования выходного
сигнала исключает влияние на него собственной частоты колебаний струн, но
по-прежнему сохраняется влияние начального натяжения струн.
Существует еще один, наиболее удобный, метод формирования выходного
сигнала дифференциального струнного акселерометра, имеющего линейную
статическую характеристику.
Имея в виду (2.32), запишем разность квадратов частот
fi - f, = (/ - f,)(f + f2) = 2/Тп и с учетом (2.28) вычислим разность
частот:
А6=Л-Л = - ,Г7Г-Т- (237)
2р/ (/ + /2)
Выражение (2.37) устанавливает соответствие между разностью частот струн
и приращением их натяжения. Нелинейность этой зависимости определяется
нестабильностью суммы частот в процессе измерений. Если струнный преобра-
зователь снабдить устройством, которое в процессе измерений ускорения изме-
няет натяжение струн таким образом, что всегда выполняется условие:
Z + /2 = 2/0 = Z (const),
(2.38)
то
(2.39)
ДТ _ ДГ
Л " 2р/2/э " 4pZVo
и характеристика преобразователя будет линейной.
Домножим числитель и знаменатель выражения (2.39) на /0 и убедимся, что
оно эквивалентно следующему равенству
ЛГ2/ _ ДГ /0_ АГ______________
4р/!.Д Л 21^ Г°'
Из выражений (2.29, 2.33) следует, что линеаризация статической характери-
стики может быть обеспечена путем формирования по определенному закону
дополнительных усилий, растягивающих обе струны. Если эти дополнительные
корректирующие усилия формируются по закону
Тд =(ЛГ/2Т0)2, (2.41)
то частоты струн определяются выражениями:
/=/0(1 + ДТ/2Т0), /2 = /0(1-ДТ/2Г0),
а разность частот равна:
_ ДГ
А/3 = J1 — J2 = 7 о ~ >
^0
что совпадает с результатом выражения (2.40).
Из полученного результата следует, что для выполнения условия (2.38) в
конструкции преобразователя должен быть узел для формирования дополни-
тельного натяжения струн (2.41). Эта задача может быть решена либо с помо-
щью устройства, реализующего нелинейный закон (2.41), либо с помощью
замкнутой системы управления, структурная схема которого показана на рис.
2.17(2.20].
46
С выходов структурных автоге-
нераторов АГ (см. рис. 2.16) пере-
менные напряжения частот f и f2
поступают на смесители С1 и С2,
выходы которых подключены к по-
лосовым фильтрам Ф1 и Ф2, про-
пускающим соответственно раз-
ность fx- f2 и сумму fx+ f2 час-
тот. Разностная частота поступает в
накопительный реверсивный счет-
чик СИ, который подсчитывает им-
пульсы разностной частоты. По-
скольку число импульсов есть ин-
теграл от частоты, в СИ вырабаты-
вается число, пропорциональное
скорости объекта, где установлен
акселерометр, который, следова-
тельно, является интегрирующим.
Суммарная частота fx + f2 посту-
Рис. 2.17. Структурная схема струнного диффе-
ренциального акселерометра с линейной статиче-
ской характеристикой: АГ - автогенераторы; С1,
С2 - смесители; Ф1, Ф2 - полосовые фильтры; СИ
- счетчик импульсов; КГ - кварцевый (эталонный)
генератор; ФЧД - фазочастотный дискриминатор;
У - усилитель; ДС - датчик силы
пает на фазачастотный дискрими-
натор ФЧД, где сравнивается с эталонной частотой f3 от кварцевого генератора
КГ. Напряжение, пропорциональное отклонению суммарной частоты от эта-
лонной, после усилителя У поступает к датчику силы, который управляет натя-
жением струн, создавая корректирующее воздействие Ти в соответствии с за-
коном (2.41).
Известны струнные акселерометры типа КИ68-1 для систем управления из-
делий ракетно-космической техники.
Применение ручного труда в процессе сборки, подбора струнных преобразо-
вателей в дифференциальную пару, наряду с указанными выше трудностями
обеспечения линейности статической характеристики, делает струнные акселе-
рометры сложными и дорогостоящими. Кроме того, они эксплуатируются с ин-
дивидуальными амортизаторами, снижающими точность системы управления.
Вместе с тем следует отметить, что технологии МЭМС создают новые воз-
можности для акселерометров струнного типа.
2.1.4. Конструкции и технические характеристики
Рассмотрим особенности конструкций и технические характеристики неко-
торых отечественных и зарубежных серийно выпускаемых акселерометров, от-
носящихся к группам макромеханических, интегральных и микромеханических.
2.1.4.1 Макромеханические акселерометры. К акселерометрам этой груп-
пы, ЧЭ которых изготавливаются по традиционным технологиям, относятся
маятниковые компенсационные акселерометры для измерения линейных уско-
рений типа ДА-11, АК-5-15, АК-5-50, ДЛУК-3 (рис. 2.18), разработанные в се-
редине 70-х годов прошлого века, которые до настоящего времени находят ши-
рокое применение. Акселерометры ДА-11 и серии АК относятся к навигацион-
ному классу и применяются, в частности, в управляемых гиростабилизаторах
для авиационных носителей. К этой группе относятся также струнные и по-
плавковые акселерометры.
47
a)
б)
Рис. 2.18. Общий вид маятниковых компенсационных акселерометров
ДА-11 («) и АК-5; ДЛУК (б)
Электрокинематическая схема маятникового компенсационного акселеро-
метра ДА-11 приведена на рис. 2.19 (разработка Раменского приборостроитель-
ного конструкторского бюро).
Рис. 2.19. Электрокинематическая схема акселерометра ДА-11:
1 — инерционная масса (маятник); 2 — катушки датчика силы цепи обратной связи; 3 — магнит;
4 - магнитопровод; 5,6 — подвижная и неподвижная катушки датчика (преобразователя)
перемещений; 7 - корпус; 8 - электромагнит возбуждения опор; 9 - камневая опора;
10-керновая ось; zB - виброперемещение опор; ау - измеряемое ускорение
Расчетная схема механической части акселерометра, также как и всех после-
дующих, соответствует рис. 2.3. Инерционная масса 1 реагирует на ускорение
перемещения основания с корпусом 7 вдоль оси чувствительности у, которую
называют также измерительной осью. Угловое перемещение а ИМ-маятника
относительно оси z измеряется датчиком трансформаторного типа, который
состоит из неподвижных (стационарных) катушек 6, установленных в корпусах
непосредственно в симметричных магнитных системах, включающих магниты
3 и магнитопроводы 4, и бескаркасных подвижных (роторных) катушек 5, на-
48
клеенных на маятник. Напряжение питания подается на катушки б, магнитный
поток замыкается через магнитопроводы 4, ЭДС наводится в катушках 5. Двух-
секционная катушка 2 датчика силы цепи обратной связи на каркасе, изготов-
ленном из алюминиевого сплава, установлена на маятнике. Каркас катушки вы-
полняет роль электромагнитного демпфера. Ось вращения (подвеса) маятника
реализована в виде керновых осей 10 и камневых опор 9. В целях уменьшения
трения в опорах предусмотрено виброперемещение zB опор под действием
электромагнита 8.
Акселерометр выдерживает ударные ускорения в 25 g в количестве 10000 с
длительностью импульса 25 мс.
Магнитные системы имеют вставные стержневые термошунты для стабили-
зации магнитной индукции в рабочем зазоре датчика силы. Электропитание
осуществляется от трех источников: t/]=10B; /; = 12кГц; £72=2,5В;
/2 = 19,2 кГц; U. = 36 В; /3 = 400 Гц.
Электрокинематическая схема капиллярного маятникового компенсационно-
го акселерометра АК приведена на рис. 2.20 (разработка Арзамасского ОКБ
«Темп»).
НЧФ
^0
Рис. 2.20. Электрокинематическая схема акселерометра АК-5:
/ - инерционная масса (рамка); 2 - магнит; 3 - магнитопровод; 4 - катушки датчика перемещения
(угла); 5 - подвижная часть («флажок») датчика перемещений (угла); 6 - корпус; 7 - торсионный
подвес; 8 - капилляр-демпфер; ФЧВ - фазочувствительный выпрямитель; МУ - масштабный уси-
литель; КУ - корректирующее устройство; УМ - усилитель мощности; НЧФ - низкочастотный
фильтр; Г - генератор датчика перемещений; a у - измеряемое ускорение
Инерционная масса имеет форму рамки-маятника 1, смонтированной на кор-
пусе 6 с помощью торсионного подвеса 7, выполненного в виде растяжек из
бериллиевой бронзы БрБ2. Датчик перемещений вихретокового типа фиксирует
угловые отклонения а рамки и состоит из подвижной части 5 («флажок», вы-
полненный из алюминиевой фольги), закрепленной на рамке, и двух катушек
индуктивности 4, закрепленных на корпусе и включенных по дифференциаль-
ной схеме. Катушка датчика силы цепи обратной связи укреплена на рамке,
49
одна из ветвей которой (нижняя) размещена между полюсами магнитов 2, объе-
диненных магнитопроводом 3. К катушке датчика силы приклеены капилляры
8, в которых частично находятся торсионные растяжки. В капилляры закачана
кремнийорганическая жидкость (полиметилсилоксан) для демпфирования вер-
тикальных колебаний маятника. Электронный бок акселерометра содержит ге-
нератор питания (Г) датчика перемещений, фазочувствительный выпрямитель
(ФЧВ), масштабирующий усилитель (МУ), корректирующее устройство (КУ -
RC-цепь), низкочастотный фильтр (НЧФ) и усилитель мощности (УМ). АК-5
выпускается с тремя диапазонами измерения: ±15; ±50; ±100g (соответственно
АК-5-15, АК-5-50, АК-5-100). Частота напряжения питания датчика перемеще-
ний 3,5 МГц. Питание акселерометра осуществляется от одного источника пи-
тания напряжением ±15 В относительно средней точки. Акселерометры выдер-
живают одиночные удары до 80 g с длительностью импульса 2-6 мс.
Приведенные описания конструкций акселерометров рассматриваемой кон-
структорско-технологической (макромеханической) группы дают представле-
ние об их сложности, трудоемкости изготовления (следовательно, высокой
стоимости) и недостаточной виброустойчивости. обусловленной особенностями
подвеса ИМ. Характеристики акселерометров приведены в табл. 2.1.
Таблица 2.1
Характеристики акселерометров, изготавливаемых по традиционным технологиям
Параметры, размерность Модель (марка) акселерометра
А-Л2 ДА-9 ДА-10 ДА-11 АК-5 143-Б1 ки 68-1
Диапазон измере- ний, g ±7 ±12 ±15 ±1 - -±10 ±15; ±50; ±100 -10 + +50 ±22
Порог чувствитель- ности, g - 10'6 10'5 5 10 6 2 10 4 - -
Частотный диапазон измерений, Гц - - - - - 0-60 -
Крутизна статической характеристики (масштабный коэф- фициент). MAJg - 1,72± ±0,25 1,72± ±0,25 1,28± ±0,32 0,485± ±0.001 (АК-5- 15) - -
Нулевой сигнал,g ЗЮ3 ±5,8х хЮ'4 ±1,2х хЮ'3 ±0,58х х10’3 ±1,5х хЮ'3 (АК-5- 15) - -
Нелинейность функции преобразования (3 а), % - - - 0.044 - 0,2 -
Температурный коэффициент кру- тизны статической характеристики. %/°С 1,2-10'3 - - 2-Ю’3 4-10’3 (АК-5- 15) - -
50
Продолжение табл. 2.1
Температурный ко- эффициент нулевого сигнала, g/°C 5-10'6 - - 8,7-106 2-Ю’5 (АК-5- 15)
Потребляемый ток при <7=0, мА - 20 5 98 40 (АК-5- 15) - -
Диапазон рабочих температур, °C 0-68 -60- +85 -60- +80 -60- +85 -55 — +60 ±65 0- +40
Масса, г 220 38 120 45 50 (АК-5- 15) 800 4100
2.1.4.2. Интегральные акселерометры. К этой группе относятся акселеро-
метры, ЧЭ которых изготавливаются по технологиям МЭМС (применяются
также термины - технологии микроэлектроники, микромеханики, планарные,
кремниевые), а сервисная электроника, включая тонкопленочную, изготовляет-
ся, как правило, в виде отдельных конструктивных узлов.
По праву приоритета здесь нужно отметить маятниковые акселерометры ти-
па Q-Flex с магнитоэлектрическим датчиком силы в цепи обратной связи (см.
рис. 2.13), разработанные фирмой Sundstrand Data Control (США) в начале 80-х
годов, и разработанные в середине 90-х годов прошлого века фирмой LITEF
GmbH (Германия) маятниковые акселерометры В-290 с электростатическим
датчиком силы в цепи обратной связи. Принципиальная схема ЧЭ акселеромет-
ра В-290 приведена на рис. 2.21.
Акселерометр состоит из ИМ - маятника 7, упругих элементов подвеса 2,
основания 5, выполненных из монокристаллической кремниевой подложки ме-
тодом анизотропного травления и закрепленных между обкладками-крышками
3, изготовленными из проводящего монокремния. Крышки 3 и основание 5 раз-
делены легированным изолятором 4 (SiO2 или SiN4).
Рис. 2.21. Принципиальная схема ЧЭ акселерометра В-290 «TRIAD»:
1 - инерционная масса-маятник; 2 — упругие элементы подвеса;
3 - обкладки-крышки; 4 - изолятор; 5 - основание
Проводящая инерционная масса 7 и пара неподвижных электродов на крем-
ниевых крышках 3 образуют емкости С(, С2. Расстояние h0 определяет возмож-
ные перемещения маятника под действием сил инерции, обусловленных изме-
51
ряемым ускорением av в диапазоне ±10 или ±20 g. Акселерометр имеет контур
(цепь) обратной связи с преобразователем (датчиком) силы электростатическо-
го типа на тех же емкостях, что и датчик перемещений.
Цифровые блоки в контуре силовой компенсации выполнены на сигнальных
процессорах ADSP 2101, которые также осуществляют компенсацию темпера-
турного дрейфа нулевого сигнала и крутизны статической характеристики по
информации от встроенного термодатчика. Акселерометр выдерживает одиноч-
ные удары с ускорением 1000g. Диапазон температур от -40 до 100°С.
Раменское приборостроительное конструкторское бюро (РПКБ) выпускает
несколько моделей интегральных акселерометров [2.19]. На рис. 2.22 показан
общий вид цифрового акселерометра АЦ-1 прямого преобразования, который
состоит из кремниевого ЧЭ и дискретной электроники, выполненных в общем
корпусе в виде отдельных конструктивных узлов. Выходной сигнал - частот-
ный, с алгоритмической компенсацией погрешностей.
Акселерометр АЦ-1 имеет сле-
дующие характеристики и пара-
метры: диапазон измерений 40g;
крутизна выходной характеристи-
ки 1,5 кГц/g; погрешность при ал-
горитмической компенсации (не
более) 3%; диапазон рабочих тем-
ператур от -60 до ±80°С; Напря-
жение питания 5 В; габаритные
размеры 80x30x12 мм; масса 50 г.
Акселерометр предназначен для измерения линейных ускорений в инерци-
альных системах, курсовертикалях, системах управления различных подвиж-
ных объектов.
Рис. 2.22. Общий вид акселерометра АЦ-1
Общий вид акселеро-
метров серии А компенса-
ционного преобразования
показан на рис. 2.23. Чув-
ствительные элементы
этих акселерометров пред-
ставляют кремниевые ма-
ятники, изготовленные ме-
тодами объемной обработ-
ки. Так, на базе маятника
диаметром 18 мм и толщи-
Рис. 2.23. Общий вид акселерометра серии А НОЙ 0,38 ММ разработано
(А-15, А-16, А-17) несколько модификаций
акселерометров моделей А-12, 15, 16 и 17, которые, аналогично акселерометрам
Q-Flex, выполнены по гибридной (не планарной) технологии [2.6].
На маятник наплавляют металлические пластины (обкладки) конденсаторов
емкостного преобразователя перемещений и методом прецизионной микро-
сборки устанавливают обмотки (катушки) преобразователя (датчика) силы. Два
других электрода (пластины, обкладки) емкостного преобразователя перемеще-
ний напылены на элементах корпуса. Упругие элементы подвеса имеют разме-
ры 1,Зх0,12x0,008 мм. Зазор между маятником (подвижный электрод) и элек-
тродами на корпусе составляет 0,021 мм. Для увеличения маятниковое™ уста-
52
новлен груз. Акселерометры содержат электронику, выполненную по гибридно-
пленочной технологии. Основные характеристики акселерометров приведены в
табл. 2.2.
Таблица 2.2
Характеристики акселерометров серии А
Параметры, размерность Модель (марка) акселерометра
А-15 А-16 А-17
Диапазон измерений, g 20 35 10
Крутизна статической характеристики, мА/g 1,0-1,4 0,9-1,3 1,0-1,6
Нестабильность масштабного коэффициента, % <0,02 <0,02 <0,02
Температурный коэффициент крутизны ста- тической характеристики, %/°С <±210'2 <±2-10’2 <±210'2
Порог ЧуВСТВИТеЛЬНОСТИ, MKg 0,5 0,5 0,5
Дрейф нулевого сигнала, g/ч <510'5 <710’5 <2,5-10'5
Температурный коэффициент нуля (нулевого сигнала), g/°C <±31О'5 <±3-10'5 <±2 10’5
Тяжение (постоянная составляющая), Mg < 12 < 15 12
Стабильность тяжения, 10‘6g <300 <300 <300
Стабильность погрешности базовой плоско- сти, 10'6 рад < 100 < 100 < 100
Погрешность базовой плоскости, мрад <9 <9 <9
Диапазон рабочих температур, °C -60 - +80 -60 - +80 -60 - +80
Ударное воздействие: амплитуда g/длит., мс 50/1-5 50/1-5 30/15
Напряжение питания, В ±15 ±15 ±15
Габаритные размеры, мм 24x21x21 24x21x21 24x21x21
Масса (с электроникой), г <40 <40 <40
Акселерометры А-17 используются в термостатированных изделиях, и их
характеристики обеспечиваются при температуре +75±2°С. В акселерометры
А-16, А-15 встроен температурный датчик, и их характеристики обеспечивают-
ся алгоритмической компенсацией.
Акселерометры серии «А» предназначены для измерения линейного ускоре-
ния в инерциальных навигационных системах, курсовертикалях и системах
управления подвижными объектами.
ФГУП НИИ физических измерений (г. Пенза) имеет богатый опыт разработ-
ки и производства акселерометров прямого и компенсационного преобразова-
ния. В настоящее время на базе кремниевой технологии разработан универсаль-
ный ряд акселерометров серии АЛЕ с электростатическими преобразователями
перемещения и силы для измерения ускорений в пределах от ±0,18 до ±350 м/с2.
На рис. 2.24 показаны основные элементы конструкции акселерометра
АЛЕ-049.
53
]
Рис. 2.24. Основные элементы конструкции
акселерометра АЛЕ-049:
1 — стеклянные пластины; 2 — проводящая об-
кладка неподвижной пластины;
3 - опорный кремниевый элемент; 4 - инерци-
онная масса; 5 — упругие элементы подвеса;
6 - незащемляемая часть опорного элемента
Инерционная масса 4 с упругими элементами подвеса 5 и опорным элемен-
том 3 изготовлены из монокристаллического кремния анизотропным травлени-
ем. Инерционная масса является подвижным элементом емкостного преобразо-
вателя перемещений. Неподвижные пластины (обкладки) 2 выполнены напыле-
нием на стеклянных пластинах 1. Соединение пластин 1 с опорным элементом 3
осуществляется методом электростатической сварки. Часть опорного элемента
6 имеет меньшую толщину, чем основная пластина и не защемляется между
ci склянными пластинами.
Характеристики акселерометров приведены в табл. 2.3.
Таблица 2.3
Характеристики акселерометров серии АЛЕ
Параметры, размерность Тип акселерометра
АЛЕ 037 АЛЕ 048 АЛЕ 051 АЛЕ 044 АЛЕ 050 АЛЕ 049
Диапазон измерений, м/с2 ±0,18..±90 ±0,18..±220 ±1,4..±90 ±11..±90 ±5,6..±90 ±5,6..±1400
Выходное напряжение, В 0-6
Нелинейность функции преоб- разования, % 0,02 0,02 0,01 0,2 0,2 0,2
Коэффициенты влияния темпера- туры :на нуль, мВ/’С ца чувст- вительность. %/°С 1-0,1 0,1 1 3-1 3-1
0,01 0,008 0,02 0,01 0,01
Напряжение пи- тания, В ±15 28 ±12 28 ±12 28
Потребляемый ток, мА 30 60 25 5 10 20
Температура ок- ружающей среды, °C ±50 -50.+125 ±50 ±50 ±50
Габариты, мм 35x35x35 32x2x6 35x29x15 35x29x15 35x35x22
54
В середине 1990-х годов в Арзамасском НПП «Темп-Авиа» были созданы
первые образцы интегральных маятниковых акселерометров с емкостным дат-
чиком перемещений и магнитоэлектрическим датчиком силы в цепи (контуре)
обратной связи, совершенствование которых продолжается до настоящего вре-
мени.
Акселерометры выпускаются в сериях АТ (измерение линейных ускорений)
и АС (измерение угловых ускорений), имеют высокую временную стабильность
параметров, практически нечувствительны к поперечным ускорениям, встроен-
ный усилитель обеспечивает нормированный и усиленный по мощности сигнал.
На рис. 2.25 показана конструкция акселерометра АТ-1104, принципиальная
схема которой аналогична схеме акселерометра Q-Flcx (см. рис. 2.13) (размеры
указаны в миллиметрах).
Рис. 2.25. Конструкция акселерометра
с кремниевым чувствительным элементом-маятником:
1 - корпус; 2 - магнитопровод; 3 - магнит; 4 - наконечник из магнитомягкого материала;
5 - кронштейн крепления катушки; б - кремниевая пластина; 7 - подвижная часть кремниевой
пластины - маятник; 8 — катушка; 9 - оптическое стекло; 10 - втулка;
11 - герметичная крышка
Маятником акселерометра является подвижная часть 7 кремниевой пластины
6, соединенная с ней тремя упругими элементами. Изготовлен чувствительный
элемент (ЧЭ) методом анизотропного травления. Кремниевая пластина по пе-
риметру защемлена между стеклами 9. Пластина и стекла имеют примерно рав-
ные коэффициенты теплового расширения. С ЧЭ жестко скреплены кронштей-
ны 5, на которых смонтированы катушки 8. Очевидно, в силу этого увеличива-
ется маятниковость ЧЭ. Стекла с ЧЭ и катушками размещены между магнито-
проводами 2 цилиндрической формы и с помощью втулки 10 объединены в мо-
нолитную конструкцию. Соосно с катушками размещены магниты 3, на кото-
рых укреплены наконечники 4 из магнитомягкого материала. Вся конструкция
смонтирована на корпусе 7, внутри которого (на рис. 2.25 не показан) размеще-
ны элементы электронной схемы, и закрыта герметичной крышкой 77. Благо да-
55
ря герметизации возможно заполнение акселерометра инертным газом и созда-
ние внутреннего давления (если это необходимо).
На рис. 2.26 и 2.27 показаны элементы конструкции акселерометра.
Рис. 2.26. Элементы маятниковой системы:
1 - кремниевая пластина; 2 - чувствительный элемент (длина указана в миллиметрах);
3 - оптические стекла; 4 - кронштейн с катушкой
Рис. 2. 27. Элементы конструкции магнитоэлектрической системы:
I - магнитопровод; 2 - катушка с кронштейном на маятнике; 3 - магнит
в магнитопроводе; 4 - оптические стекла.
Между поверхностями ЧЭ и стеклами имеются зазоры в пределах (16±18)
мкм. Эти зазоры определяют возможность поворота ЧЭ относительно оси упру-
гих элементов (балок), которая лежит в плоскости ЧЭ. Поверхности ЧЭ-
маягника и стекол со стороны зазоров покрыты металлизированным слоем, и
таким образом получен дифференциальный емкостной датчик перемещений
ЧЭ-маятника. Катушки и магнитная система образуют магнитоэлектрический
датчик силы, который включен в цепь обратной связи и образует электриче-
скую «пружину».
Характеристики однотипных акселерометров АТ-1104 и QA-2000 (Q-Flex)
приведены в табл. 2.4
Таблица 2.4
Характеристики акселерометров АТ-П04 и QA-2000
Параметр, размерность Модель акселерометра
QA-2000 АТ-1104
Диапазон измеряемых ускорений, g ±1 +±20 ±1 +±10
Порог чувствительности, g 10'6 Ю'6
Крутизна статической характеристики, мА/g 1,33±О,13 1,0±=0,15
Дрейф нуля, g ±4-10'3 ±20-10'3
Нелинейность, % 0,0025 0,1
Температурный коэффициент крутизны статической характеристики, %/°С 1,2-10'2 1,5-10'2
Температурный коэффициент нулевого сигнала, g/°C ЗЮ'5 1-Ю'4
Потребляемый ток при нулевом измеряемом ускоре- нии, мА 20 30
Диапазон рабочих температур, °C -54 ++ 104 -55 ++120
Масса, г 80 35
56
Акселерометр AT-1104 относится к навигационному классу и может быть
использован в системах управления различных подвижных объектов, в том чис-
ле - в инерциальных навигационных системах, а также в системах точного по-
зиционирования. Другие модели серии АТ и АС могут быть использованы для
исследования, испытаний и диагностики машин и механизмов, горизонтирова-
ния элементов конструкций и др. Следует отметить также, что акселерометры
типа АТ-1104 и АТ-1112 имеют диапазон измерений от 0,5 до 50 g, что делает
возможным их применение на высокодинамичных объектах.
Идеология построения акселерометров типа Q-Flex применена также в аксе-
лерометрах. разработанных в МГТУ им. Н. Э. Баумана и НПО «Корпус» (г. Са-
ратов).
2.1.43. Микромеханические акселерометры. Микромеханические акселе-
рометры (ММА) имеют ЧЭ, включающий инерционную массу на упругом под-
весе, преобразователь ее перемещений и обслуживающую (сервисную) элек-
тронику. выполненные на одном чипе (кристалле) технологиями МЭМС. Разра-
боткой и серийным производством ММА занимаются фирмы: Analog Devices,
Motorola, Hitachi, Hilton Head и др. Наиболее широким спектром моделей и ха-
рактеристик обладают ММА серии ADXL (фирма Analog Devices). Акселеро-
метры этой серии являются осевыми и выпускаются в вариантах прямого и
компенсационного преобразований.
На рис 2.28 показана схема работы кремниевого ЧЭ, а на рис 2.29 - блок-
схема, поясняющая принцип измерения с аналоговым выходом.
внешние
пластины
Рис. 2.28. Конфигурация чувствительного элемента ММА:
а) в покое; б) при действии ускорения
Рис. 2.29. Блок-схема ММА с аналоговым выходом
57
На неподвижные пластины конденсатора ЧЭ от генератора подаются проти-
вофазные прямоугольные импульсы 1 МГц: амплитуды обоих импульсов рав-
ны, но сдвинуты по фазе на 180°. В спокойном состоянии емкости Ct и Сэ двух
конденсаторов одинаковы, поэтому выходное напряжение на их электрическом
центре (т. е. на подвижной пластине, присоединенной к ИМ) равно 0.
Когда ИМ начинает двигаться, разность емкостей приводит к появлению вы-
ходного сигнала на центральной пластине. Амплитуда сигнала будет увеличи-
ваться с увеличением ускорения, приложенного к ИМ. Центральная пластина
через усилитель У1 подключена к синхронному детектору. Направление движе-
ния ИМ влияет на фазу сигнала, поэтому синхронное детектирование использу-
ется для выделения информации об амплитуде. Выход синхронного детектора
через усилитель У2 обеспечивает выходное напряжение ускорения V.
На рис. 2.30, а показана упрощенная блок-схема двухосного акселерометра
ADXL202 с двумя ЧЭ - сенсорами по двум взаимно-перпендикулярным осям х
и у, поясняющая принцип формирования на выходе широтно-импульсного мо-
дулированного сигнала (ШИМ-сигнала) (рис. 2.30, б).
Рис. 2.30. Блок-схема (а) двухосного ММА с ШИМ-сигналом (б) на выходе
Такой типа выхода очень полезен из-за значительной защиты от шума (по-
мех), (данные передаются по одному проводу). Стандартные дешевые микро-
контроллеры имеют таймеры, которые могут быть с успехом применены для
измерения интервалов Т и 72 Ускорение, выраженное в g, в этом случае рас-
считывается по формуле
(Т А
3(g) = 8(—-0,5).
Следует отметить, что ШИМ в 50% (7’1 = 72) обозначает 0g на выходе. Нет
необходимости измерять 72 для каждого цикла измерений. Его необходимо об-
новлять для учета измерений, вызванных температурой. Так как период 72 рас-
пространяется (одинаков) как для канала X, так и для канала У, необходимо из-
мерять его только в одном канале. Период 72 может быть установлен от 0,5 до
10 мс с помощью внешнего резистора.
Аналоговое напряжение, соответствующее ускорению, можно затем полу-
чить с помощью усиления сигнала с выходов X и Y или пропуская сигнал ШИМ
через 7?С-фильтр для восстановления постоянной составляющей.
58
Прогресс в миниатюризации ММА серии ADXL иллюстрируется табл. 2.5 и
рис. 2.31.
Таблица 2.5
Эволюция характеристик ММА серии ADXL
Параметры, размерность Марка (модель) ММА. (год выпуска)
ADXL50 (1993) ADXL76 (1996) ADXL78 (2002) ADXL40 (2004)
Площадь чипа, мм2 10,8 5,4 2,7 2,5
Площадь ЧЭ (мм2)/ ее доля (%) от площади чипа 0,43/4,0 0,38/7,0 0,27/10 0,22/8,8
Емкость преобразователя перемеще- ний (фФ)/ частота питания (кГц) 100/25,0 100/24,5 40/24,5 160/12,5
Шум, Mg/yjTu 4,0 1,0 1,0 1,0
Смещение нуля, g 3,0 1,0 0,5 0,5
б)
г)
Рис. 2.31. ММА ф. Analog Devices:
а - ADXL76 (кристалл с ЧЭ и электроникой в корпусе; видна распайка от компонентов
электроники к выводам); б - микроструктура ЧЭ; в - ADXL 105 (кристалл с ЧЭ и электрони-
кой в корпусе; видна распайка); г - кристалл с микроструктурой (в центре) и компонентами
электроники (толстые линии - токоподводы)
Характеристики ММА серии ADXL приведены в табл. 2.6.
59
Таблица 2.6
Характеристики ММА серии ADXL
Марка ММА/ ко- личество осей чувст- вительности Параметры, размерность
Диапазон измере- ний, g Крутизна статической характери- стики, мВ/g Нелиней- ность ха- рактери- стики, % Плотность шума, Mg/Vfu Напряже- ние пита- ния, В/ ток потребле- ния, мА Вид сиг- нала: на- пряжение (V) или ШИМ
ADXL202/2 ±2 12,5 %/g 0,2 0,5 3—5/0,6 ШИМ
ADXL05/1 ±5 - 0,2 0,5 - V
ADXL105/1 ±5 250 0,2 0,175 2,7-5,2/2 V
ADXL210/2 ±10 - 0,2 0,5 - ШИМ
ADXL150/1 ±50 38 0,2 1,0 5/2 V
ADXL250/2 ±50 38 0,2 1,0 5/3,5 V
ADXL 190/1 ±100 18 0,2 - 5/2 V
ММА ADXL150 и ADXL250 относятся к прибором третьего поколения и об-
ладают абсолютной погрешностью 0,01g. По сравнению с другими моделями у
них уменьшенный дрейф нуля, не превышающий 0,4g в диапазоне температур (-
50 - +100) °C. Акселерометры выдерживают ускорение 2000g длительностью
0,5 мс без питания и ускорение 500g длительностью 0,5 мс с питанием.
Акселерометры этой серии находят применение: при измерении углов на-
клона в автомобильных сигнальных устройствах и мониторах пациентов; при
реакции на инерционные силы для защиты дисков компьютеров типа Notebook,
в чувствительных элементах подушек безопасности, в системах навигации ав-
томобиля, в системах контроля работы лифта; при наличии ударов и вибрации в
системах управления станками и контроля вибростендов. Они пригодны для
применения в системах ориентации и навигации роботов, в том числе - в бес-
пилотных летательных аппаратах.
Выводы
Существует широкий спектр отечественных серийных акселерометров с ха-
рактеристиками, обеспечивающими их применение в инерциальных навигаци-
онных системах (ИНС), в том числе - в бесплатформенных ИНС (БИНС). Важ-
нейшими характеристиками акселерометров навигационного класса являются
чувствительность и временная стабильность нулевого сигнала и масштабного
коэффициента.
Необходимым значениям этих характеристик отвечают поплавковые (интег-
рирующие) акселерометры, акселерометры серий ДА и АК и др., изготовляемые
по традиционным (макромеханическим) технологиям. Всем акселерометрам
этой группы присуща высокая стоимость, обусловленная сложными технологи-
ческими процессами их изготовления, а также низкая надежность узлов подвеса
инерционной массы, чувствительность к ускорениям по перекрестным осям,
отсутствие в некоторых моделях сервисной электроники или, наоборот, се ус-
ложнение из-за необходимости иметь несколько источников электропитания.
По этим причинам, общепринятый в настоящее время критерий оценки изделий
- «цена/качество», оказывается не в пользу акселерометров этой группы. Несо-
мненным является и то, что акселерометры этой группы имеют свои «ниши»
навигационного применения.
60
Интегральные акселерометры серий «А», «АЛЕ», «АТ» по критерию «це-
на/качество» превосходят акселерометры «макромеханической» группы благо-
даря, прежде всего, применению технологий МЭМС для изготовления ЧЭ. Бла-
годаря этим же технологиям, в сочетании с более современной электроникой
обработки сигналов, их характеристики достигли значений, которые переводят
некоторые модели интегральных акселерометров в класс навигационных при-
боров. Правда, в ряде моделей остается неудовлетворительной временная ста-
бильность этих характеристик.
Алгоритмическими методами и конструктивными решениями, например,
термостатированием, вакуумированием или газовым заполнением корпуса, уда-
ется уменьшить временную нестабильность характеристик до приемлемых зна-
чений, и интегральные акселерометры, например серии «А», успешно приме-
няются в ИНС и БИНС различных подвижных объектов, в том числе, авиаци-
онного применения.
Акселерометры серии «АТ» успешно используются в инклинометрии для
решения задач подземной навигации и могут быть применены в ИНС летатель-
ных аппаратов (ЛА) средней дальности, а также в БИНС беспилотных ЛА.
Акселерометры серии «АЛЕ» предназначены, главным образом, для реше-
ния задач ракетно-космической техники, в том числе, для выработки команды
на выключение стартовых двигателей ракет, которую можно отнести к классу
навигационных. Характеристики некоторых моделей этой серии делают воз-
можным их применение в БИНС беспилотных ЛА.
Микромеханические акселерометры в настоящее время серийно выпускают-
ся только за рубежными фирмами. Чувствительность, масштабный коэффици-
ент и его погрешность (нелинейность статической характеристики) вполне со-
поставимы с аналогичными характеристиками интегральных акселерометров.
Однако по стабильности характеристик во времени, их существенной темпера-
турной зависимости они уступают интегральным акселерометрам и акселеро-
метрам макромеханической группы. Существенным недостатком ММА являет-
ся зашумленность (шум) выходного сигнала, затрудняющая его обработку.
Можно ожидать, что по критерию «цена/качество» в обозримом будущем ММА
будут обладать приоритетом. Достигнутые в настоящее время характеристики,
особенно на фоне малых габаритов, массы и энергопотребления по сравнению с
акселерометрами других групп, делает ММА для ряда применений единственно
возможными, например, в системах микронавигации малоразмерных роботов, в
том числе, для мини-БПЛА с ограниченным временем работы.
В заключение материала по акселерометрам приведем укрупненные области
их навигационного применения и соответствующие им значения характеристик:
• ИНС и БИНС для ЛА большой дальности. Основные характеристики аксе-
лерометров: смещение нуля (H5)-lCT4g; погрешность масштаба - 0,05%;
диапазон измерения — до 30g (10g самолетный);
• ИНС и БИНС для ЛА средней и ближней дальности, включая БПЛА, а так-
же инклинометры, измерительные блоки. Основные характеристики акселе-
рометров: смещение нуля (l-H2)10'3g; погрешность масштаба - (0,1^0,2)%;
диапазон измерения - до 50 g.
Требуемые значения характеристик акселерометров для систем вибромет-
рии, диагностики, контроля аварийных режимов и др. значительно менее жест-
кие (по крайней мере, меньше на порядок) по сравнению с навигационными
системами.
61
2.2. Гироскопы
2.2.1. Общая характеристика.
Все гироскопы делятся на два основных класса: свободные гироскопы (аста-
тические), задача которых заключается в «хранении» заданного направления
(заданной системы координат), и датчики (измерители) угловой скорости (ДУС)
основания (объекта), на котором они установлены. Для астатических гироско-
пов основным показателем точности является остаточная скорость ухода
(дрейф) гироскопа, а для ДУ С — погрешности измерения угловой скорости, обу-
словленные различными причинами (конструктивными, технологическими,
температурными, эксплуатационными и пр.). Остаточная скорость ухода (име-
ется в виду наличие выходного сигнала при отсутствии измеряемой скорости)
присуща и ДУ С. В работе [2.16] обобщены сведения о состоянии на 1996 г. рос-
сийской и мировой гироскопии и приведена диаграмма (рис. 2.32) достигнутых
точностей различных типов гироскопов — свободных и ДУС. Несмотря на дос-
тигнутый прогресс за время, прошедшее с момента опубликования результатов,
приведенных в работе [2.16], порядок значений дрейфа и ранжировка гироско-
пов по точности сохранились.
Элсктростаз ичсские гироскопы
Гироскопы иа магнитных подвесах
Поплавковые интегрирующие гироскопы
Гироскопы на воздушном подвесе
Волновые твердотельные гироскопы
Кольцевые лазерные гироскопы
Волоконно-оптические гироскопы
Динамически настраиваемые гироскопы
Механические гироскопы
Микромеханические гироскопы
град/ч
1 Г~ 1 1 I 1 г
10’6 ИГ5 10'4 10’ 10'-’ 10'* 1 1,0 10 ю2 * * * * * В
Рис. 2.32. Остаточная скорость ухода (в градусах в час) гироскопов различных типов
Электростатические гироскопы (ЭСГ) нашли применение в сочетании с кар-
дановым подвесом в морских ИНС.
В России для целей морской навигации используются ЭСГ, разработанные в
ЦНИИ «Электроприбор» (Санкт-Петербург), в котором также проводятся рабо-
ты по созданию БИНС на базе ЭСГ
В США в 80-х годах прошлого века были созданы БИНС корабельного и
62
авиационного применения на базе ЭСГ. Для высокоточных систем навигации и
других применений, где требуется малый дрейф, могут быть использованы ги-
роскопы с магнитным и воздушным подвесом сферического резонатора и по-
плавковые гироскопы с магнитным центрированием поплавка. Указанные типы
гироскопов при построении ИНС требуют кардановых подвесов.
Цена перечисленных типов гироскопов велика. Механические гироскопы
(гироскопы с вращающимся ротором и с кардановым или сферическим шарико-
подшипниковым подвесами), видимо, с учетом технологии их производства,
достигли своих предельных возможностей по точности, а цена их по критерию
«цсна/качество» достаточна высока.
Микромеханические гироскопы (ММГ) - абсолютные лидеры по минимуму
массы, габаритов, энергопотребления и стоимости. ММГ военного применения
зарубежных фирм уже имеют «заявленный» остаточный дрейф на уровне
1 град/ч и имеют по прогнозам устойчивую тенденцию к уменьшению этой ха-
рактеристики ММГ уверенно занимают нишу чувствительных гироскопиче-
ских элементов в БИНС с небольшим временем функционирования. Неинерци-
альные источники информации (спутниковая навигация, магнитометры и т.д.)
существенно расширяют возможности БИНС на базе ММГ и ММА.
Динамически настраиваемые гироскопы (ДНГ) относятся к классу рот орных
вибрационных гироскопов (РВГ), имеют давнюю историю развития и успешно
применяются для решения разнообразных измерительных задач в машино-
строении, робототехнике и пр., а также широко используются для создания
ИНС, включая БИНС. Следует заметить, что в динамике ММГ и РВГ много об-
щего, начиная с того, что ММГ часто называют кориолисовыми вибрационны-
ми гироскопами, подчеркивая общий для них характер движения (вибрацион-
ный) ЧЭ в режиме измерения и роль кориолисовых сил в его формировании.
Разумеется, что и в РВГ силы инерции Кориолиса являются определяющими.
Интересно, что и в ММГ и в РВГ применяется режим динамической настройки.
Волновые твердотельные гироскопы (ВТГ) являются блестящим примером
построения гироскопа, не имеющего традиционного элемента - вращающегося
ротора, так же как лазерные гироскопы (ЛГ) и волоконно-оптические гироско-
пы (ВОГ). ВТГ, ЛГ и ВОГ являются гироскопами навигационного класса и ус-
пешно применяются в ИНС, включая БИНС, средней и выше точности.
Важнейшими характеристиками гироскопов являются диапазон измерений,
масштабный коэффициент и его стабильность (или погрешность, зависящая от
различных причин), остаточный дрейф, массогабаритные и эксплуатационные
параметры и характеристики.
2.2.2. Лазерные и волоконно-оптические гироскопы
Принцип действия ЛГ и ВОГ основан на эффекте, открытом Саньяком в
1913 г. при > исследовании свойств многозеркального кольцевого оптического
резонатора, называемого также пассивным интерферометром Саньяка. Принцип
действия кольцевого оптического резонатора можно рассмотреть исходя из не-
строгих, но наглядных представлений [2.6]. На рис. 2.33 приведена схема иде-
ального оптического кольцевого контура радиусом R. Свет от излучателя И в
точке А разделяется на два луча, которые распространяются по окружности в
противоположных направлениях и после обхода контура объединяются. В не-
подвижном интерферометре время обхода контура каждым из лучей одинаково
и равно t = 2п7? / с (с = 3 10 0 см/с - скорость света).
63
Рис 2.33. Принципиальная схема кольцевого резонатора (пассивный интерферометр Саньяка)
Во вращающемся интерферометре место встречи лучей приходится уже не
на точку А, а на точку А1. Считая скорость света неизменной, получаем, что для
волны, бегущей в направлении вращения,
для встречной волны
2л/? + RQ.t = ct+,
2 л А’ - RQ.t_ = ct_.
Находим разность времен
Д( = t+ - t_ =
2nR
c — RQ.
2nR ~ 4л/?2 q _ 4Sq
c + RC1 c2 c2
(2.42)
Важно отметить, что разность времен пропорциональна площади 5 контура
резонатора. При более строгом подходе к вычислению величины Л? можно по-
казать, что независимо от формы замкнутого контура и любого параллельного
расположения оси его вращения по отношению к оси симметрии, справедлива
формула (2.42).
Из-за исключительно малых значений величины Д/ прямые измерения ско-
рости вращения объектов с помощью пассивных интерферометров Саньяка
возможны только в волоконно-оптических гироскопах, содержащих 500-1000 м
оптического волокна, намотанного на катушку, благодаря чему резко возрастает
величина 5.
Изменение длины хода лучей приводит к фазовому сдвигу (фаза Саньякя)
встречных волн:
* л 45v 8 л 5 ,
Д<р - уД/ = —у—~ =----Q , (2.43)
с с Хс
А
где f — частота электромагнитного излучения; v = 2л/ - круговая частота;
X = - длина волны.
Из (2.43) (фаза Саньяка) следует возможность измерения скорости вращения
по сдвигу интерференционных полос, что используется в лазерных гироскопах.
2.2.2.1. Лазерные гироскопы. Кольцевой лазерный гироскоп (КЛГ) пред-
ставляет собой активный интерферометр - лазер с замкнутым контуром, на-
пример треугольным, схема которого приведена на рис. 2.34.
64
Внутри замкнутого контура-резонатора
находится активная среда, а по вершинам
размещены зеркала: А - плоское, В - сфе-
рическое, С - полупрозрачное. В резона-
торе возбуждаются когерентные волны.
Условие генерации в кольцевом резонато-
ре состоит в том, чтобы на длине Zo его
периметра укладывалось целое число п
длин волн X:
= пк - пс I f ; (п — £0 / X),
откуда следует частота генерируемого
излучения f = пс / L. При вращении ре-
Рис. 2.34. Схема активного интерферо-
метра
зонатора со скоростью Q вокруг оси О возникает разность длин волн, циркули-
рующих по направлению вращения (7Ч) и против него (Л,2). Учитывая изменение
эффективной длины оптического пути обоих лучей, которое в соответствии с
(2.42) равно АЛ = 4SQ / с, найдем разность частот
где
МР
(2-45)
масштабный коэффициент резонатора.
В соответствии с (2.44), разностная частота на выходе кольцевого резонатора
прямо пропорциональна угловой скорости основания, на котором размещен ре-
зонатор. Следует отметить, что разностная частота Л/ есть частота биений, воз-
никающих в результате наложения двух
встречных разночастотных бегущих волн.
Для выделения частоты биений встречные
волны, выходящие через одно из зеркал ре-
зонатора, совмещаются с помощью специ-
альной оптической схемы на фотоэлектрон-
ном устройстве (ФПУ) с двумя площадка-
ми, каждая шириной около 200 микрон, на-
пример, по схеме на рис. 2.35 [2.21].
Встречные волны с длинами Xi, кэ про-
ходят через полупрозрачное зеркало 1,
призму 2 и попадают на ФЭУ 3. Падающие
на ФЭУ лучи имеют малый угол расхожде-
ния £ и образуют интерференционную кар-
Рис. 2.35. Схема совмещения волн на
выходе интерферометра:
1 - зеркало; 2 - призма; 3 -- фотоэлек-
тронный умножитель
тину (вид «А-А»), которая при Af= 0 стационарна. Когда резонатор вращается,
интерференционная картина перемещается по площадкам ФПУ со скоростью,
определяемой частотой А/. Если используется ФПУ с размером чувствительной
площадки меньше расстояния между интерференционными полосами, можно
определить частоту биений по скорости прохождения максимумов интенсивно-
сти интерференционной картины по приемной площади ФПУ. Частота биений
определяется путем преобразования синусоидального сигнала, формируемого в
65
ФПУ, в последовательность прямоугольных импульсов. За каждый период из-
менения интенсивности интерференционной картины формируется один им-
пульс. Число импульсов N в единицу времени определяет частоту биений, кото-
рая представляется в цифровом виде. Переход к измеряемой скорости осущест-
вляется через масштабный коэффициент (2.44), (2.45).
Заметим, что КЛГ может применяться для измерения угла поворота основа-
ния, на котором он установлен. В этом случае его масштабный коэффициент
определяется числом импульсов при повороте КЛГ на единичный угол.
Выходная характеристика КЛГ зависит не только от скорости вращения ос-
нования, но и от многих процессов в резонаторе, заполненном активной средой.
Рис. 2.36. Частотная характеристика ЛГ
Зависимость частоты импульсов,
поступающих с выхода ФПУ, от уг-
ловой скорости вращения лазерного
гироскопа называется частотной
характеристикой гироскопа (рис.
2.36). В идеальном гироскопе такая
характеристика должна изображать-
ся прямой линией (пунктир на рис.
2.36). К сожалению, в лазерных ги-
роскопах присутствует целый ряд
вредных паразитных эффектов, при-
водящих к искажению этой линей-
ной зависимости. Наиболее существенным таким эффектом является, так назы-
ваемый «захват» встречных волн (английский термин mode-locking). Физику
захвата можно легко понять, если вспомнить, что зеркала лазерного гироскопа,
при всем их высочайшем качестве, все же обладают рассеянием. Это приводит к
тому, что, например, луч, распространяющийся по часовой стрелке, рассеиваясь
на зеркалах, «навязывает» свою фазу встречному лучу, распространяющемуся
против часовой стрелки; то же самое происходит и с лучом, распространяю-
щимся против часовой стрелки, который, рассеиваясь на тех же зеркалах, точно
так же навязывает свою фазу первому лучу. В результате при вращении гиро-
скопа кольцевой лазер генерирует встречные волны с одной и той же частотой,
как было бы в покоящемся гироскопе, хотя реально лазерный гироскоп враща-
ется и частоты встречных волн должны бы быть различными.
Таким образом, ничтожно малое рассеяние приводит к полной потере чувст-
вительности лазерного гироскопа к угловому вращению в определенной зоне
угловых скоростей, называемой зоной захвата. Зона захвата 2Q0 может быть
довольно большой. Отметим, что эта реальная частотная характеристика с уве-
личением угловой скорости вращения постепенно выходит на идеальную ли-
нейную зависимость, так что в первом приближении «захват» проявляется не во
всей области угловых скоростей, а лишь на ее начальном участке, вблизи нуля
угловых скоростей (от -Qo до +О0).
Для борьбы с захватом частот встречных волн предложено много способов.
Один из них очевиден - уменьшить или вовсе исключить рассеяние на диэлек-
трических зеркалах и других оптических элементах резонатора лазерного гиро-
скопа. Следует отметить, что на этом пути практически все возможности либо
уже исчерпаны, либо будут исчерпаны в самое ближайшее время. Так, коэффи-
циент отражения лазерных зеркал сегодня составляет 99,9995... 99,99995%, и
каждая «девятка» после запятой дается ценой огромных технологических уси-
лий и миллионных затрат в долларовом исчислении.
66
Другим способом снижения вредного влияния захвата является перевод «ра-
бочей точки» лазерного гироскопа в ту область частотной характеристики, где
она является практически линейной (например, в точку Q на рис. 2.36 при час-
тоте вращения £1п)- Это достигается, например, созданием вращения лазерного
гироскопа с постоянной угловой скоростью Г2П, соответствующей точке Q.
Одним из распространенных методов предотвращения явления захвата явля-
ется метод вибрационной подставки, реализация которого заключается в меха-
ническом покачивании резонатора вокруг оси чувствительности на частоте <1П-
В некоторых случаях для этого используется механический колебательный кон-
тур с упругим элементом типа торсиона. Механическая «виброподставка» не-
удобна в реализации и приводит к дополнительным погрешностям.
В лазерных гироскопах разработки ФГУП НИИ «Полюс» перевод рабочей
точки Q на линейный участок характеристики производится наложением по-
стоянного или переменного магнитного поля на активную среду лазера. Техни-
чески это реализуется намоткой специальной катушки (соленоида) на разряд-
ный промежуток гелий-неонового лазера. Создание такого «кажущегося» вра-
щения лазерного гироскопа с частотой Qn основано на магнитно-оптическом
эффекте Зеемана
Для создания электронной подставки (невзаимности) может быть использо-
ван и эффект Фарадея. Существует еще целый ряд погрешностей, приводящих к
нарушению линейности частотной характеристики ЛГ (сдвиг нуля частотной
характеристики, затягивание частот встречных волн и пр.). Совокупное дейст-
вие всех этих паразитных эффектов приводит к нелинейности частотной харак-
теристики и тем самым к зависимости масштабного коэффициента от угловой
скорости вращения гироскопа Q, благодаря чему одним из важнейших парамет-
ров лазерного гироскопа является нелинейность масштабного коэффициента.
Параметры лазерного (как и любого другого) гироскопа, как правило, неста-
бильны во времени, например, из-за тепловых нестационарных эффектов. Важ-
нейшим параметром гироскопа является дрейф нуля, где под нулем следует по-
нимать значение частоты выходного сигнала (числа импульсов реверсивного
счетчика Nq) в рабочей точке покоящегося гироскопа. Современные лазерные
гироскопы на гелий-неоновых кольцевых лазерах характеризуются дрейфом
нуля 0,005-10 град/ч, в зависимости от их габаритов и конструкции.
Фактически ЛГ является интегрирующим прибором, поскольку реверсивный
счетчик считает общее количество импульсов (с учетом их знака, т.е. направле-
ния вращения) за определенный промежуток времени; тем самым, гироскоп из-
меряет величину угла, на который повернулся объект по данной оси за этот
промежуток времени независимо от того, как менялась при этом угловая ско-
рость. Угловая скорость может быть вычислена дифференцированием угла по
времени. Вышеуказанный промежуток времени может быть различным - от до-
лей секунды до десятков минут (это определяется назначением гироскопа и ха-
рактеристиками той системы, где он применяется). В тех случаях, когда этот
промежуток времени по требованиям системы является малым, на первое место
выходят шумовые характеристики ЛГ, или, что то же самое, случайный дрейф
нуля. Этот параметр важен потому, что при малых временных интервалах (ма-
лом такте съема информации) шумовая составляющая дрейфа нуля может быть
воспринята системой обработки сигнала как истинное, быстро меняющееся во
времени вращение объекта. И чем больше интервал времени, отведенный для
обработки сигнала, тем меньше влияние случайного дрейфа, и наоборот.
67
Учет всех погрешностей ЛГ может быть проведен с использованием полной
адекватной физико-математической модели погрешностей. Погрешности гиро-
скопа могут быть условно подразделены на два вида - воспроизводимые и не-
воспроизводимые (случайные). Разумеется, все усилия разработчиков направ-
лены на снижение или устранение невоспроизводимых погрешностей. Что каса-
ется воспроизводимых ошибок, то при их тщательном изучении они могут быть
устранены методом алгоритмической коррекции, при которой в логическую
систему обработки сигнала заранее закладывается алгоритм обработки с учетом
воспроизводимых зависимостей.
Естественно, что следует ожидать сильной зависимости параметров гиро-
скопа от температуры, что особенно проявляется в существенно нестационар-
ном режиме работы лазерного гироскопа сразу после его включения. Это связа-
но с тем, что даже весьма малое изменение длины периметра резонатора лазер-
ного гироскопа приводит к весьма сильному изменению оптической частоты
генерации лазера, что будет воспринято системой обработки сигнала, как пово-
рот или вращение объекта. Так, для вышеупомянутого треугольного резонатора
кольцевого лазера со стороной 13 см необходимая точность поддержания дли-
ны периметра резонатора во всем диапазоне климатических воздействий долж-
на быть не хуже Х/ЗОО, т.е. не хуже 20 ангстрем! Тем не менее такая «сверхста-
билизация» длины периметра резонатора на практике реализуется за счет при-
менения прецизионных пьезокорректоров, корректирующих изменение длины
периметра резонатора и включенных в цепь обратной связи со сведением к ну-
лю сигнала ошибки.
Существенным является влияние внешних магнитных полей на дрейф нуля
гироскопа. С целью снижения этого влияния лазерный гироскоп помещается в
многослойный магнитный экран, после чего интегральная чувствительность к
магнитному полю падает до вполне приемлемой величины 0,5 - 1 град/ч/Э (для
дрейфов порядка 0,1 град/ч).
Рис. 2.37. Принципиальная схема чувствитель-
ного элемента КЛГ:
I - диафрагма; 2 - зеркала; 3 - оптический
канал с активной средой; 4 - установочные
элементы;5 — анод; 6 - катод; 7 - совмещающая
призма; ФЭУ, устройство обработки информа-
ции В одном из газоразрядных каналов
Интерферометр, который является
чувствительным элементом КЛГ,
представляет собой монолитный блок
из высококачественного кварца, прин-
ципиальная схема которого приведена
на рис. 2.37.
В монолитном кварцевом блоке
высверлены каналы 3 для лучей, обра-
зующих треугольный оптический кон-
тур. Резонансный контур в виде тре-
угольника обладает наименьшими по-
терями ввиду минимума отражающих
зеркал 2, расположенных в его верши-
нах. Резонатор с треугольным оптиче-
ским контуром имеет максимальную
добротность. В моноблоке высверле-
ны места для установки анодов 5 и
катода 6, необходимых для возбужде-
ния активной среды, состоящей из
смеси неона и гелия.
68
расположена диафрагма I для обеспечения одномодового режима работы КЛГ.
Задача диафрагмы заключается в создании условий, при которых увеличивают-
ся потери нежелательных мод.
Для выделения сигнала разностной частоты встречные лучи проходят через
совмещающую призму 7 и попадают на ФПУ (см. рис. 2.35). Для монтажа чув-
ствительного элемента в корпусе служат установочные элементы 4 (отверстия
или стойки). Чувствительный элемент КЛГ работает вместе с подсистемами:
регулировки мощности накачки активной газовой среды, стабилизации частоты
излучения, стабилизации периметра резонатора и многими другими.
В качестве примеров конструктивной реализации на рис. 2.38 показан общий
вид одноосного лазерного гироскопа ГЛ-1, а на рис. 2.39 - чувствительный эле-
мент лазерного трехосного гироскопа ОАО «Раменский приборостроительный
завод» [2.19] (разработчик РПКБ).
Рис. 2.39. Чувствительный элемент
трехосного лазерного гироскопа
Рис. 2.38. Лазерный гироскоп ГЛ-1
Гироскоп ГЛ-1 является основным измерителем (датчиком) угловой скоро-
сти с механической виброподставкой. В качестве отражательных элементов
(«зеркал») используются призмы полного внутреннего отражения и применена
электрическая накачка активной среды высокочастотным током. Гироскоп име-
ет встроенные датчики температуры, информация с которых используется для
алгоритмической компенсации температурной погрешности прибора. Гироскоп
имеет следующие характеристики: время готовности в нормальных условиях -
не более 7 мин.; систематически дрейф не более 0,6 град/ч; среднеквадратиче-
ское отклонение показаний в запуске от систематического дрейфа не более
0,05 град/ч; рабочий диапазон температур от -20 до ±55°С; габаритные размеры
0 206 мм х 106 мм; масса не превышает 4 кг.
Чувствительный элемент трехосного лазерного гироскопа обеспечивает сле-
дующие технические характеристики- диапазон измеряемых угловых скоростей
- ±400 град/с; диапазон измеряемых углов не ограничен; дискретность измере-
ния угла 0,5 угл. с.; случайная ошибка (шум) - 0,005 град / Л ; рабочий диапа-
зон температур ±60 °C; масса - 6 кг; потребляемая мощность не более 10 Вт.
В табл. 2.7 приведены характеристики КЛГ различных разработчиков [2.13].
69
Характеристики КЛГ
Таблица 2.7
Параметры, размерность LG-8028 GG-1342 ASLIG KM-11 БЛГ-1 ЛГ-1 «Морион»
Litton Inc. Honeywell Sperry НИИ «Полюс» ОКБ «Темп» МИЭА НПО «Астро- физика»
Диапазон изме- ряемых угловых скоростей, град/с ±600 ±800 ±100 - ±100 - ±200
Систематическая погрешность, град/ч 0,010,2 0,01 0,1 0,01 0,5-1,5 0,01 0,2-2,0
Случайная по- грешность, град/ч 0,003 0,003 0,05 0,003 - 0,003 0,03
Стабильность масштабного коэффициента 5-10 6 5-10 6 510 s - 10’5 5-10’6 -
Потребляемая мощность, Вт 3 - - - 6 - 9
Периметр, см 28 32 - 44 16 28 26
Ресурс, 103 ч 15 20 30 10 0,5-'1,0 - 5-7
Масса, кг 1,7 1,9 1,8 - 1,6 1,8 -
Количество изме- рительных осей 1 - - 1 3 1 3x2
В табл. 2.7 приведены характеристики КЛГ первого поколения, в которых, в
частности, применена механическая виброподставка, используемая и в совре-
менных разработках. Следует обратить внимание на трехосный ЛГ второго по-
коления (МТ-401МЭ), разработанный НИИ «Полюс», имеющий улучшенные
характеристики.
В настоящее время благодаря высокой точности, определяемой малым зна-
чением случайного дрейфа, стабильностью и линейностью масштабного коэф-
фициента в широком диапазоне измерений, а также благодаря вибрационной и
ударной устойчивости, КЛГ является основным гироскопическим прибором в
БИНС для разнообразных подвижных объектов.
Гироскопы с дрейфом нуля 0,005 - 0,01 град/ч обладают значительными га-
баритами, требуют весьма высокой технологии их изготовления и применяются
в автономных навигационных системах для объектов дальнего действия, на-
пример, для гражданских трансконтинентальных самолетов.
Лазерные гироскопы с дрейфом нуля 0,1-5 град/ч обладают значительно
меньшими габаритами, требуют также высокой технологии их изготовления и с
успехом могут быть использованы в системах навигации, интегрированных с
другими навигационными системами, например, со спутниковыми навигаци-
онными системами типа GPS (CIIL4) и ГЛОНАСС (Россия).
Лазерные гироскопы с дрейфом нуля 1-10 град/час обладают наименьшими
габаритами и могут быть использованы в системах управления движением вы-
сокоманевренных объектов малого радиуса действия.
2.2.2.2. Волоконно-оптические гироскопы. В волоконно-оптических гиро-
скопах (ВОГ) замкнутый оптический контур образован многовитковой катуш-
кой оптического волокна (оптоволокно). Если замкнутый контур образован оп-
товолокном, намотанным на цилиндрическую катушку, то в формуле (2.43) 5 =
N SB (N - число витков катушки, SB - средняя площадь витка катушки) и выра-
70
жение для фазы Саньяка принимает вид:
. SnNSn _ 2nLD
ф = Дф =------=---------Q
Хс Хс
(2-46)
где L,D- длина оптоволокна и диаметр оптоволоконного контура.
Волоконно-оптические гироскопы могут быть построены по схеме с разомк-
нутым или с замкнутым контуром. На рис. 2.40, а приведена принципиальная
схема ВОГ с разомкнутым контуром. Свет от излучателя И интенсивностью 70 с
оптической мощностью Ро через деполяризатор ДП и разветвитель 2 поступает
к волоконному контуру (катушка) в противоположных направлениях и, обойдя
его, через элемент 2 попадает на фотоприемник ФП и далее в блок электроники
БЭ. Если волновые фронты на выходе интерферометра совмещены идеально, то
зависимость оптической мощности, поступающей на фотоприемник, от фазы
Саньяка имеет известный вид Р - Ро (1 + cos фс).
Для повышения чувствительности ВОГ к малым измеряемым угловым ско-
ростям в контур включен фазовый модулятор ФМ, который вносит вспомога-
тельный фазовый сдвиг между встречными световыми волнами на л/2, и мощ-
ность на выходе фотоприемника будет пропорциональна величине sin фс.
Принципиальная схема ВОГ с замкнутым контуром (компенсационная схема
ВОГ) приведена на рис. 2.40, б.
а)
Рис. 2.40. Принципиальные схемы ВОГ:
а — с разомкнутым контуром; б — с замкнутым контуром; I — катушка; 2 — разветвитель
Оптическая схема ВОГ имеет так называемую минимальную конфигурацию,
обеспечивающую взаимность оптических путей двух встречно распространяю-
щихся световых волн.
Свет от излучателя И через оптические разветвители 2 поступает к оптово-
локну катушки 1, пройдя через которую объединяется элементом 2 и попадает
через фотоприемник ФП на синхронный детектор СД, который при наличии
вращения катушки со скоростью Q выделяет фазу Саньяка. Эта фаза компенси-
руется с помощью частотного фазового модулятора ФМ следующим образом.
Одна из световых волн, распространяющихся по волокну в противоположных
направлениях, попадает сначала на ФМ, а затем на катушку, а другая - сначала
на катушку, а потом на ФМ. Вследствие этого обе волны выходят с катушки с
одинаковой частотой, но с разностью по фазе, определяемой опережением по
фазе частоты, которую вырабатывает ФМ и которая зависит от длины волокна.
При появлении скорости вращения Q фаза Саньяка фс подавляется компенси-
рующей фазой фк, вырабатываемой ФМ с помошью регулировки частоты, кото-
рая определяется известным соотношением
71
fk=DQJnn, (2.47)
где X - длина волны света; ип - показатель преломления используемого волок-
на.
В результате работа ВОГ происходит при условии <рс - (рк ~ 0, что позволяет
считать ВОГ с замкнутым контуром линейной системой.
Блок электроники БЭ выполняет следующие функции: стабилизирует вы-
ходную мощность излучателя; усиливает и детектирует (СД) сигнал, посту-
пающий с ФП; формирует синусоидальное напряжение, подаваемое на ФМ для
внесения постоянного фазового сдвига на величину л/2 и формирует пилооб-
разное напряжение, создающее фазовый сдвиг, компенсирующий фазу Саньяка.
В соответствии с рис. 2.40, б и работой [2.7] на рис. 2.41 приведена струк-
турная схема ВОГ.
Рис. 2.41. Структурная схема одноосного ВОГ с замкнутым контуром
Структурная схема отображает последовательные преобразования входного
сигнала (угловая скорость Q) в выходной сигнал (напряжение (/вых). Коэффици-
ент передачи первого звена называется масштабным коэффициентом оптиче-
ского контура и определяется из (2.46): Кыик = 2nLD / Хс, рад/с“‘ .Коэффициент
преобразования фазы Саньяка в мощность излучения Ка (Вт/рад), поступающе-
го на фотоприемник, зависит от мощности излучения излучателя, от потерь в
оптическом тракте и его поляризационных характеристик. Фотоприемник как
устройство преобразования сигнала характеризуется чувствительностью А?ФП
(A/Вт) и коэффициентом усиления Ку. Передаточная функция синхронного де-
тектора может быть представлена апериодическим звеном первого порядка
Wa(S)=l/(TaS + t),
где S — d/dt', Тед < 1 / wc; ТСд — постоянная времени, vvc — частота среза разомк-
нутой системы.
После интегратора с коэффициентом передачи Ки в прямой цепи формирует-
ся выходное напряжение (/ВЬ1Х, которое содержит информацию об измеряемой
угловой скорости вращения Q. Контур обратной связи замыкается через фазо-
вый модулятор, на который подается пилообразное напряжение, формируемое в
электронном блоке с коэффициентом передачи Кп. Фазовая амплитуда пилооб-
разной модуляции автоматически поддерживается у значения 2л, а фаза Санья-
ка компенсируется пилообразным сигналом с частотой (2.47). Эффективность
фазового модулятора Л?ФМ - (рад/В), где С/л - полуволна напряжения.
Масштабный коэффициент ВОГ определяется из передаточной функции
замкнутой системы при 5=0 следующим выражением
Ки = InLD/fcK^K^, % ,. (2.48)
/ / рад с
Термозависимость масштабного коэффициента от его составляющих оче-
72
видна из (2.48). Имея в виду, что в выражении для КФМ величина Un пропорцио-
нальна X, приходим к заключению, что масштабный коэффициент не зависит от
X, что улучшает температурную зависимость ВОГ.
В настоящее время наиболее распространенными являются два конструктив-
ных типа ВОГ: на дискретных оптических элементах и с применением в опти-
ческом контуре многофункционального интегрального оптического элемента
(МИОЭ). В качестве излучателя применяется суперлюминесцентный диод
(СЛД). Для примера можно указать СЛД - ИЛПН-330-1Ж, изготавливаемый на
предприятии «Инжект» (г. Саратов) (филиал НИИ «Полюс»), имеющий мощ-
ность на выходе встроенного одномодового волоконного световода 3 мВТ, дли-
ну волны излучения 0,83 мкм с шириной спектральной характеристики ~ 25 нм
и встроенный фотодиод обратной связи для стабилизации мощности излучения.
Другой СЛД этого же изготовителя — ИЛПН-330-Ч — имеет мощность на воло-
конном выходе 1,5-2 мВт с шириной спектра =30-36 нм и встроенный фотоди-
од.
В качестве приемника излучения - фотоприемника (ФП) используется обыч-
но фотодиод на основе p-i-n структуры. Например, то же предприятие («Ин-
жект») выпускает ФП типа ФП1-850К, который имеет токовую чувствитель-
ность не менее 0,3 A/Вт на длине волны X = 0,835 мкм с временем нарастания и
спада фронта импульсного сигнала не более 2 нс.
Очевидно, что точность ВОГ существенно зависит от качества оптического
волокна, в качестве которого используется, например, волокно PANDA, сохра-
няющего состояние поляризации. Известно, что минимальная измеряемая ско-
рость вращения зависит от параметров волокна следующим образом:
где h — коэффициент перекрестной поляризационной связи (h-параметр); Lp —
длина поляризационных биений.
В табл. 2.8 приведены параметры волоконных световодов на базе волокна
PANDA, изготавливаемых на предприятии «Оптолинк» (г. Зеленоград) [2.17].
Таблица 2.8
Параметры волоконных световодов предприятия «Оптолинк»
Параметр, размерность Значение
Рабочая длина волны, мкм 0,83 1,55
Диаметр модового поля, мкм 4,5 6,5
Диаметр волокна, мкм 80
Диаметр волокна с покрытием, мкм 120-5-160
Числовая апертура 0,15 0,13
h-параметр, / м < 10’5 < 10'5
Потери, дБ/км <3 <2 ,
Длина волны отсечки, нм 680-5-780 1250-5-1450
Длина биений, нм <3
ВОГ на дискретных оптических элементах может быть выполнен по цельно-
волоконной технологии, т.е. все его элементы, за исключением излучателя и
фотоприемника, изготавливаются из оптоволокна [2.7].
МИОЭ выполняет функции: поляризацию световой волны для уменьшения
нестабильности смещения нуля вследствие поляризационной невзаимности;
расщепление световых волн на распространяющиеся в волоконном контуре в
73
противоположном направлении с равными мощностями; внесение фазового
сдвига между встречными световыми волнами с помощью электрооптического
фазового модулятора. Интегрирование МИОЭ в оптический блок производится
стыковкой его волноводов с концами волоконного контура и с одним из концов
•входного изотропного разветвителя. МИОЭ может быть изготовлен на кристал-
лах LiNbO3 методом высокотемпературного протонного обмена [2.17].
Для намотки оптоволокна может быть использован каркас из дюралюминия
Д16Т, имеющего температурный коэффициент расширения, близкий к кварцу.
Для заполнения межвиткового пространства и придания блоку прочности мо-
жет применяться виксинт К-68. Катушка с волокном располагается на тепло-
изолированной плате.
Предприятием «Оптолинк» разработана серия SRS одноосных ВОГ мини-
мальной конфигурации по схеме рис. 2.42 и трехосный ВОГ TRS-500, характе-
ристики которых приведены в табл. 2.9 [2.17].
Рис 2.42. Функциональная схема одноосного ВОГ минимальной конфигурации:
СЛД - суперлюминесцентный диод; ДП - деполяризатор; ВР - волоконный разветвитель; ФП -
фоюприемник; МИОЭ - многофункциональный интегрально-оптический элемент; ВК - волокон-
ный контур
Характеристики ВОГ предприятия «Оптолинк»
Таблица 2.9
Парамертр, размерность SRS-2000 SRS-1000 SRS-500 SRS-200 TRS-500
Диапазон изме- ряемых угловых скоростей, град/с ± 10 ±30 ± 100 ±200 ±500
Дрейф смещения при постоянной температуре, град/ч <0,01 <0,1 < 1,0 < 10,0 < 10,0
Погрешность масштабного ко- эффициента, °/о <0,01 <0,02 <0,02 <0,05 <0,5
Полоса пропуска- ния, Гц > 10 10-30 > 100 > 100 100ч-500
Шум, град!^[ч <0,001 < 0,003 < 0,005 <0,01 <0,05
Длина ВК, м 2000 1000 500 200 500
Масса, кг 1,2 0,8 0,8 0,8 1,1
Размеры, мм 0250 х 40 0150x40 0150x40 0150x40 110x110x90
Выход RS232 RS 232 RS 232 Аналоговый Аналоговый и RS-485
74
В табл. 2.10 приведены характеристики ВОГ разработки предприятия
«ФИЗОПТИКА» и Пермской научно-производственной приборостроительной
компании (ПНППК). Уместно заметить, что СЛД для ВОГ разработки
«ФИЗОПТИКА» поставляет НИИ «Полюс».
Таблица 2.10
Характеристики ВОГ
Характеристика, ВГ910Ф ВГ941-3 ВГ951 ДУС-500 Д-36
размерность «ФИЗОПТИКА» ПНППК
Диапазон изме- ряемых угловых скоростей, град/с ±300 ± 500 ±80 ±500 ±60
Систематическая погрешность, град/ч 5 30 1-3 2 36
Случайная по- грешность, град/ч 0,08 0,3 0,017 0,03 -
Нестабильность масштабного ко- эффициента, % 0,1 0,3 0,1 0,01 -
Потребляемая мощность, Вт 1,1 0,8 1,5 15 5
Габариты, мм 080 х 20 025,4 х 58 0150x30 - -
Масса, г НО 40 650 1500 -
Волоконно-оптические гироскопы, в настоящее время достигли показателей
точности, характерных для КЛГ, и могут использоваться в ИНС и БИНС для
высокоточной навигации (дрейф 0,01 — 0,1 град/ч), среднеточной навигации
(дрейф 0,1 ч- 1,0 град/ч) и для решения т актических задач (дрейф >1.0 град /ч).
2.2.3 Волновые твердотельные гироскопы
Принцип работы волновых твердотельных гироскопов (ВТГ) основан на ис-
пользовании инертных свойств упругих волн, возбуждаемых в виде радиаль-
ных колебаний на второй моде в полусферическом, цилиндрическом или коль-
цевом резонаторах.
Эффект инер гности упругих волн во вращающихся осесимметричных телах
открыл теоретически и подтвердил экспериментально Г.Х. Брайен в 1890 г.. Он
показал, что при вращении вибрирующей оболочки, в результате действия
инерционных сил Кориолиса, происходит расщепление собственной частоты
основной формы изгибных колебаний ее стенок, что приводит к прецессии
стоячей волны как относительно оболочки, так и в инерциальном пространстве.
Прецессия стоячей, волны во вращающемся резонаторе иллюстрируется
рис. 2.43. В' упругой полусферической оболочке-резонаторе (рис. 2.43, а) воз-
буждаются стоячие волны в двух взаимно-перпендикулярных направлениях х, у,
характеризуемые пучностями и узлами на кромке (или в сечении) резонатора
(рис. 2.43, б).
При вращении резонатора вокруг оси чувствительности, которая перпенди-
кулярна плоскости кольцевых сечений резонатора и является осью их симмет-
рии, волновая картина стоячих волн отстает от вращающегося резонатора, т.е.
узлы и пучности прецессируют относительно резонатора и инерциального про-
75
странства (рис. 2.43, в).
Возникновение моментов сил инерции Кориолиса, вызывающих прецессию
стоячей воны, иллюстрируется рис. 2.44.
а)
Рис. 2.43. Прецессия стоячей волны во вращающемся резонаторе:
а - стоячая волна в резонаторе; б - положение стоячей волны при неподвижном резонаторе;
в - положение стоячей волны при вращающемся резонаторе; Q - скорость вращения; 3 - угол
прецессии стоячей волны; а - угол поворота резонатора
«)
Рис. 2.44. К пояснению прецессии стоячей волны:
а - вибрирующий резонатор; б вращающийся резонатор
76
При вращении вибрирующего кольца с угловой скоростью О к каждой эле-
ментарной массе в точках А, В. С, D приложены силы инерции Кориолиса F^,
Fo, FKC, F'kd как реакция на ускорения Кориолиса аКА, акв, акс, ако, являющиеся
следствием наличия линейных виброскоростей VA, VB, V& Vd и переносной ско-
рости Q. Результирующий момент от разности пары сил F^, FKB, FKC и Fkd и
вызывает прецессию (вращение) стоячей волны относительно резонатора и в
инерциальном пространстве. Определяя положение стоячей волны, зависящее
от угловой скорости Q относительно корпуса, можно получить информацию об
угле поворота и угловой скорости основания в инерциальном пространстве.
Режим работы ВТГ в качестве датчика угловой скорости (ДУС) - ВТГ-ДУС,
или в качестве интегрирующего гироскопа (ИГ) - ВТГ-ИГ зависит от способа
возбуждения колебаний резонатора. Позиционное возбуждение (рис. 2.45F), при
котором на пару противоположных электродов подается переменное напряже-
ние с частотой, в два раза меньшей собственной частоты основной формы,
обеспечивает режим работы ВТГ-ДУС. При Q = О ориентация стоячих волн в
резонаторе постоянна и определяется ориентацией 90 электродов позиционно-
I о возбуждения 9 = 90. Следовательно, стоячая волна «привязана» к резонато-
ру. При вращении основания ориентация стоячей волны относительно резона-
тора определяется выражением [2.2]
9 = 90-^^fi, (2.49)
соо
где Q - —---добротность резонатора; £ - коэффициент затухания (демпфиро-
вания) материала резонатора; К - масштабный коэффициент резонатора; соо -
собственная частота колебаний резонатора.
«)
Рис. 2.45. Схемы позиционного (а) и параметрического (б) возбуждения
77
Z
Рис. 2.46. ВТГ фирмы Delco:
/ - внутренний корпус; 2 - резона-
тор; 3 - наружный корпус; 4 - воз-
будитель колебаний (емкостный
преобразователь силы); 5 - элек-
троды датчика преобразователя
перемещений
Режим ВТГ-ИГ обеспечивается параметрическим возбуждением резонатора
(рис. 2.456), кромка которого окружена кольцевым электродом, образующим
цилиндрический конденсатор. К конденсатору приложено напряжение с ампли-
тудой и0 и частотой Л, близкой к частоте собственных колебаний резонатора.
Ориентация стоячей волны относительно резонатора определяется выражением:
9 = 90 - К j О(т)сЛ, (2.50)
о
где К - масштабный коэффициент резонатора; 90 - начальная ориентация стоя-
чей волны.
ВТГ-ИГ является более перспективным чувствительным элементом для
БИНС, чем ВТГ-ДУС по причине более высокой точности.
Резонаторы ВТГ могут иметь форму полусферической или цилиндрической
оболочки (объемные резонаторы) с различными вариантами крепления к корпу-
су, а также могут выполняться в виде кольца (кольцевые резонаторы). Материал
резонаторов может быть различный: металл различных марок, кварцевое стек-
ло, кремний и др.
Наиболее полно теория волнового твердотельного гироскопа излагается в
работе [2.10].
2.2.3.1. ВТГ с объемным резонатором. В отечественной и зарубежной лите-
ратуре описаны ВТГ различных конструкций, отличающиеся резонатором, спо-
собом его закрепления, конструкцией емкостных преобразователей сил и пере-
мещений и др. (см. например [2.8, 2.11]). Разра-
боткой и исследованиями ВТГ за рубежом за-
нимаются фирмы Delco Electronics (CLLL4), Gen-
eral Motors Corp. (GMC), Marconi (Англия),
Badin-Crouzet (Франция).
Фирма Delco Electronics (СШТ) одной из
первых заявила о разработке ВТГ (рис. 2.4, 6),
где в качестве резонатора используется вибри-
рующая кварцевая кристаллическая полусфера
2, через вершину которой проходит стержень,
жестко закрепленный по концам во внутреннем
7 и наружном 3 корпусах прибора. Возбудитель
колебаний 4 состоит из шестнадцати электродов
емкостных датчиков возбуждения (ДВ), охваты-
вающих резонатор и размещенных в наружном
корпусе 3. Съем сигнала производится восемью
электродами 5 емкостных датчиков перемеще-
ния (ДП), расположенных под углом 45° и раз-
мещенных во внутреннем корпусе 1 по кругу и
охваченных резонатором. Основные элементы:
резонатор, стержень, корпуса — изготавливаются
из плавленого кварца путем медленного охлаж-
дения расплавленной окиси кремния для вос-
произведения одной резонансной частоты (мо-
ночастотность).
В экваториальном сечении резонатора у ос-
нования с помощью ДВ создаются радиальные
колебания из двух стоячих волн (4 пучности).
78
Вращение резонатора относительно измерительной оси, совпадающей с поляр-
ной осью z, вызывает поворот диаграммы колебаний, пропорциональный скоро-
сти поворота прибора в инерциальном пространстве, что фиксируется электро-
дами съема. Характеристики ВТГ приведены в табл. 2.11.
Характеристики ВТГ фирмы Delco
Таблица 2.11
Параметры, размерность Значение
Точность без компенсации ухода, град/ч 0,01
Случайный уход, град/ч 2,2-10'4
Диапазон ускорений, g 100
Время выхода на рабочий режим, с 1
Постоянная времени, с 900
Добротность резонатора 8,2-106
Мода колебаний Эллиптическая
Резонансная частота, Гц ЗЮ3
Диаметр резонатора, мм 65
Толщина стенки резонатора, мм 1,3
В середине 1980-х годов Э. Лопер и Д. Линч разработали конструкцию ВТГ,
которая выпускалась в США и послужила прототипом для разработки ВТГ
ФНПЦ РПКБ [2.12], показанного на рис. 2.47.
ВТГ состоит из внутреннего 1
и наружного 3 корпусов, в кото-
рых с помощью сквозной ножки
закреплен полусферический ре-
зонатор 2. На наружном корпусе
имеются 16 отдельных электро-
дов 5 и один кольцевой электрод
4, предназначенные для возбуж-
дения и управления стоячей вол-
ной. На внутреннем корпусе
размещены восемь электродов 6
системы съема информации
(датчик перемещений), форми-
рующих два измерительных ка-
нала, расположенных под углом
45° по отношению друг к другу.
Электроды выполнены напыле-
нием металлической пленки со-
Рис. 2.47. Конструктивная схема ВТГ разработки
РПКБ:
1 - внутренний корпус; 2 - резонатор; 3 - наружный
корпус; 4 - кольцевой электрод; 5 - электроды возбу-
ждения; 6 - электроды датчика перемещений;
7 - кожух; 8 - встроенный насос
ответствующей конфигурации.
Кожух 7 с ниппелем и встроен-
ным геттерным насосом 8 служат
для создания и поддержания в
полости прибора сверхвысокого
вакуума (~(1,33-0,133)-10"6 Па).
Основное отличие американского ВТГ состоит в конструкции резонатора,
который имеет по краю полусферической оболочки специальные зубцы, ис-
пользуемые для массовой балансировки и устранения расщепления собствен-
ных частот, с поверхности которых можно испарять лазером требуемое количе-
ство вещества, не изменяя добротность резонатора. В отечественных разработ-
79
ках лучшие результаты показал балансировочный процесс, основанный на ис-
пользовании ионного травления поверхности кварцевого стекла. Нарушения
структуры стекла при этом столь незначительны, что удаление несбалансиро-
ванной массы осуществляется прямо с поверхности полусферы, и балансиро-
вочные зубцы при этом не нужны [2.11].
Обычно металлизируется вся поверхность полусферического резонатора за
исключением его торцевой кромки, которая играет роль изолятора между по-
крытиями на внешней и внутренней поверхности полусферы. Эти покрытия
подключаются к электронному блоку ВТГ через внешнюю и внутреннюю нож-
ки. На рис. 2.48 показана распространенная электрическая схема подключения
Рис. 2.48. Электрическая схема подключения
резонатора к внешним цепям:
I - измерительный электрод; 2 - электрод
управления^ - кольцевой электрод возбуждения; 4
- выходной усилитель;5 - усилитель напряжения
управления
резонатора к внешним цепям
Электрическая схема включает
цепи: измерительную, управления и
параметрического возбуждения.
Измерительная цепь включает в
себя измерительные электроды 1
(обычно используют 4 пары внут-
ренних измерительных электродов,
расположенные через 45°), которые
образуют небольшую электриче-
скую емкость с металлическим по-
крытием внутренней полусферы, и
которые подключены к входам уси-
лителей 4 с высоким входным со-
противлением. Металлическое по-
крытие внутренней полусферы под-
ключается к источнику постоянного
напряжения с внутренним со-
противлением R.
Цепь управления включает в се-
бя управляющие электроды 2 (обычно используют 16 наружных управляющих
электродов, расположенных через 22,5° и соединенных по 4 крестом), на кото-
рые подаются управляющие напряжения (72 от внешних усилителей с выход-
ным сопротивлением R2. Металлическое покрытие внешней полусферы при
этом заземляется.
Цепь параметрического возбуждения включает в себя кольцевой электрод 3,
соединенный с внешним генератором прямоугольных импульсов Uj с выход-
ным сопротивлением Rj.
В соответствии с работой [2.10] для вращающегося идеального тонкого по-
лусферического резонатора ориентация стоячей волны (см. рис. 2.43) определя-
ется зависимостью
. _________________ t
2 + v - 7(2 + v)2 + 4(1 - v)k2 ] j ОДб/т, (2.51)
J о
где к - номер формы колебаний; v - коэффициент Пуассона.
Имея в виду, что к = 2 (вторая форма колебаний), v = 0,17 (материал резона-
тора - плавленый кварц), из (2.51) получим
/
ад « 0,312 , (2.52)
о
' ад =-----!—-Г
2(1 - ’}к L
80
т.е., в формуле (2.50) масштабный коэффициент К ~ 0,312.
Таким образом, при повороте резонатора вокруг оси чувствительности на
/
угол J П(т)б/т = 90° против часовой стрелки пучности стоячей волны будут
о
прецессировать по часовой стрелке на угол 9 ~ 0.312 • 90° ~ 28° или относи-
тельно инерциального пространства на угол а ~ 62° (см. рис. 2.43).
Таким образом, вращение резонатора в
инерциальной системе координат можно рас-
сматривать как причину уменьшения амплиту-
ды первичной вибрации и появление новой со-
ставляющей колебаний (вторичная волна), пуч-
ности которой расположены под углом 45° от-
носительно пучностей первичной волны, т.е.
эти пучности совпадают с узлами первичной
вибрации. Наложение этих составляющих при-
водит к образованию результирующей диа-
1раммы пучности, которая расположена под
углом ~ 28° относительно первоначальной диа-
Рис. 2.49. Общий вид ВТГ-ИГ
разработки РПКБ
граммы вибрации.
Общий вид ВТГ-ИГ разработки РПКБ показан на рис. 2.49, а в табл. 2.12
приведены его характеристики [2.9].
Таблица 2.12
Характеристики ВТГ-ИГ РПКБ
Параметры, размерность Значение
Систематический дрейф, град/ч 3,0
Случайный дрейф, град/ч 0,05 - 0,5
Нестабильность масштабного коэффициента, % 0,005 - 0,02
Резонансная частота (возбуждения), кГц 2,8 ± 0,2
Расщепление резонансной частоты, Гц 10’4
Напряжение питания ДП, В 40
Напряжение возбуждения, В 400
Добротность резонатора 5-Ю6
Постоянная времени, с >600
Габаритные размеры, мм 0 65 х 92
Масса, г 350
ВТГ фирмы Marconi (Великобритания) является датчиком угловой скорости,
в котором чувствительный элемент (рис. 2.50, а) выполнен в виде цилиндриче-
ского резонатора 2 диаметром 17 мм и длиной образующей цилиндра 24 мм,
укрепленного на основании 3 с помощью ножки [2.12]. На верхней кромке ре-
зонатора установлена система пьезокристаллов 1, из которых пара А-А' вклю-
чена в цепь позиционного возбуждения, В-В' - в цепь измерения, а пьезокри-
сталлы С-С' и D-D' включены в цепь обратной связи для демпфирования коле-
баний резонатора (рис. 2.50, б).
При вращении вибрирующего цилиндра (резонатора) вокруг оси чувстви-
тельности z в пьезокристаллах, находящихся в узлах колебаний, возникает элек-
трический сигнал, амплитуда которого пропорциональна скорости вращения
(см. (2.49)). Цилиндр вибрирует на основной частоте изгибной вибрации, обра-
зующей две полные длины волны по окружности цилиндра. При частоте виб-
рации 7400 Гц добротность резонатора равна 1500.
81
б)
Рис. 2.50. ВТГ-ДУС фирмы Marconi:
а - чувствительный элемент (/ - система пьезокристаллов, 2 - резонатор, 3 — основание);
б - схема подключения резонатора к внешним цепям
Затухание вибрации цилиндра, вызванное его механическими свойствами,
происходит достаточно медленно, поэтому для обеспечения бы ci рого срабаты-
вания необходимо использовать демпфирование. Для этого создана отрица-
тельная обратная связь, которая компенсирует вибрацию цилиндра, вызванную
вращением. Сигнал с датчиков С-С' усиливается и подается в датчики D-D' с
фазовым сдвигом, необходимым для сигнала обратной связи. Характеристики
ВТГ приведены в табл. 2.13.
Таблица 2.13
Характеристики ВТГ-ДУС фирмы Marconi
Параметры, размерность Значение
Диапазон измерений, град/с ±300
Чувствительность, град/с 0,02
Резонансная частота, Гц 7400
Полоса пропускания, Гц 100
Нелинейность характеристики в диапазоне измерений ±60 град/с, % <0,3
Время выхода на рабочий режим, с 0,3
Погрешность от перекрестных связей, % <0,1
Потребляемая мощность, мВТ 500
Можно указать на другие многочисленные варианты возможного конструк-
тивного исполнения ВТГ. Например, фирма Westinghouse Electric (CI1L4) рекла-
мирует ВТГ-ДУС, в котором резонатор - тонкостенный цилиндр с размерами
0 12,3x11,2 мм — выполнен из пьезокерамики и центральной частью через
стойку крепится к корпусу. Верхний и нижний торцы резонатора свободны. На
внешней поверхности цилиндра размещены электроды возбуждения и съема, а
внутренняя поверхность является общим электродом. К цилиндру подводится
синусоидальное электрическое поле, и его верхние и нижние торцы должны
совершать радиальные колебания расширения-сжатия в противофазе При вра-
щении резонатора вокруг продольной оси возникает реакция - изгибно-
крутильные колебания с узловым сжатием в средней части цилиндра. Возни-
кающие при этом механические напряжения преобразуются в электрическое
синусоидальное напряжение, амплитуда которого пропорциональна скорости
82
вращения. Резонансная частота цилиндра ~91 Гц. ВТГ может обеспечить диапа-
зон измерений в 1000 град/с при чувствительности 0,5 град/с и ожидаемом
дрейфе -150 град/ч.
Достигнутые значения характеристик точности ВТГ-ИГ делают возможным
их применение в БИНС среднего класса точности, и совершенствование их про-
должается в направлениях прежде всего материаловедческой базы и конструк-
торско-технологических решений. Ощутимые успехи в разработке ВТГ-ДУС
достигнуты в ОАО «Темп-Авиа» (г. Арзамас).
2.2.3.2. ВТГ с кольцевым резонатором. Кольцевой резонатор ВТГ состоит
из упругих кольца и элементов его подвеса в корпусе. Для изготовления резона-
тора могут быть применены различные материалы (никель, поликристалличе-
ский и монокристаллический кремний) и соответствующие им технологии. Для
возбуждения первичных колебаний применяют электростатические и магнито-
электрические датчики силы (возбуждения — ДВ), а для измерения вторичных
колебаний применяют электростатические (емкостные) датчики перемещений
(ДП). ВТГ этого типа могут изготавливаться полностью по технологиям
МЭМС, и в этом случае они относятся к классу микромеханических гироско-
пов. Так же как и акселерометры, ВТГ могут быть изготовлены в интегральном
варианте: резонатор с ДП - по технологиям МЭМС, а ДВ и сервисная электро-
ника - по обычным технологиям. На рис. 2.51, а показан кольцевой резонатор
фирмы BAE Systems, имеющей опыт разработки ВТГ, изготовленный из поли-
кристаллического кремния [2.22], а на рис. 2.51, б, в - положения стоячей волны
колебаний.
Резонатор состоит из кольца диаметром 1,1 мм и восьми упругих элементов
подвеса, которые обеспечивают две идентичные эллиптические формы стоячих
волн с одинаковыми частотами. Ширина кольца и упругих элементов - 4 мкм.
Толщина структуры - 80 мкм. Анкер диаметром 120 мкм обеспечивает соеди-
нение резонатора с основанием. Вокруг кольца равномерно расположены 16
электродов высотой около 60 мкм, длиной 150 мкм, отделенных от кольца воз-
душным зазором в 1,4 мкм.
Кольцо с помощью электростатических ДВ приводится в вибрационное
движение с постоянной амплитудой 0,15 мкм на резонансной частоте системы
«кольцо-подвес», равной 29 к! ц. При вращении резонатора вокруг оси чувстви-
тельности z со скоростью Q силы Кориолиса перераспределяют энергию пер-
вичной изгибной (стоячей) волны к вторичной, которая развернута относитель-
но первой на 45°, увеличивая тем самым амплитуду вторичных колебаний (пуч-
ности вторичных колебаний совпадают с узлами первичных колебаний).
Вибрация кольцевого резонатора приводит к изменению зазора между коль-
цом и электродом. Величина зазора определяется функцией времени и позицией
кольца относительно электрода. Чтобы кольцу придать вибрацию в форме пер-
вичной изгибной волны, которая имеет два узловых диаметра, синусоидальная
электростатическая возбуждающая сила прикладывается через окружающий
электрод, расположенный в начальной точке, соответствующей 0°. Идеальная
вибрирующая кольцевая структура имеет две идентичные изгибные волны с
одинаковыми собственными частотами. Каждый электрод соединяется с емко-
стным буферным усилителем входного сигнала низкого уровня с единичным
коэффициентом усиления (истоковый повторитель) для обнаружения неболь-
ших емкостных изменений между кольцом и чувствительным электродом ДП,
возникающих в результате вибрации
83
Рис. 2.51. Кольцевой резо-
натор:
а - общий вид; б, в - по-
ложения стоячей волны не
вращающегося и вращаю-
щегося резонатора
Любое рассогласование частот (расщепление) между первичными и вторич-
ными колебаниями, которое возникает из-за несовершенства технологии произ-
водства (несимметричность массы и жесткостей) может быть скомпенсировано
электронным способом с помощью компенсационных (регулирующих) элек-
тродов.
Амплитуда вторичных колебаний кольца пропорциональна измеряемой
скорости вращения Q и определяется выражением 5, = АК — 5,Q , где К ~ 0,37
(Оо
- масштабный коэффициент резонатора; 6, - амплитуда первичных колебаний
(режим возбуждения).
Структурная схема цепей возбуждения и регулирования, необходимых для
работы в разомкнутом контуре, показана на рис. 2.52. Она состоит из трех ос-
новных контуров (цепей). Основной контур управления базируется на схеме
фазово-синхронизированного контурного осциллятора, который работает на
резонансной частоте гироскопа. Такая схема фазовой автоподстройки частоты
(ФАПЧ) основывается на фазовом соотношении между возбуждающей силой и
выходным перемещением. При резонансе вибрационное перемещение кольце-
вой структуры отстает от приложенной возбуждающей силы на 90°. Эта разни-
ца фаз измеряется с использованием сбалансированного демодулятора. Второй
контур, который называется «контур управления амплитудой», необходим для
тщательного регулирования амплитуды эталонной (контрольной) вибрации с
целью минимизации ошибок по коэффициенту усиления в выходном сигнале
датчика. Таким образом, основной и амплитудный контуры управления дейст-
вуют совместно, чтобы поддерживать резонанс кольцевой структуры в соответ-
ствии с режимом первичных колебаний и постоянную амплитуду вибрации.
84
(эталон)
Рис. 2.52. Структурная схема контуров возбуждения, считывания и регулирования для кольцевого
ВТГ, работающего в разомкнутом контуре: АРУ — автоматическая регулировка усиления, У —
усилитель, ФНЧ - фильтр низких частот, ГУН - генератор, управляемый напряжением
После настройки электронной схемы на режим колебаний выполняется элек-
тронная подстройка структуры. Третий контур, который называется контуром
управления квадратурой, непрерывно регулирует одну пару балансирующих
напряжений, прикладываемых в позициях ±22,5°, сводя к нулю квадратурную
составляющую, т.е. нулевой выходной сигнал (выходной сигнал при отсутст-
вии измеряемой скорости), который отстает на 90° от выходного сигнала, вы-
званного кориолисовыми силами. Для работы ВТГ в замкнутом контуре необ-
ходимо использовать дополнительный контур для сведения выходного переме-
щения к нулю.
Конструкция резонатора и обслуживающей электроники выполняются по
технологии МЭМС и, следовательно, реализация данного ВТГ может быть от-
несена к классу микромеханических гироскопов.
Вариант интегрального исполнения ВТГ с кольцевым резонатором и магни-
тоэлектрическим ДВ фирмы BAE Systems [2.18] показан на рис. 2.53.
Чувствительный элемент (ЧЭ) выполнен на кремниевой пластине 3 (разме-
ром 10x10 мм), где размещен кольцевой резонатор (кольцо) диаметром 6 мм и
сечением 120x100 мкм, который с помощью восьми упругих элементов 2 под-
веса сечением 60x100 мкм соединен с пластиной. ЧЭ изготовлен методом плаз-
менного изотропного травления. Токопроводящие проводники нанесены только
на верхнюю поверхность, а контактные площадки 4 для соединения с провода-
ми нанесены на пластину.
Имеется восемь идентичных проводящих контуров, каждый из которых об-
разует цепочку: контактная площадка - упругий элемент подвеса - 1/8 длины
кольца - упругий элемент подвеса - контактная площадка. Таким образом, каж-
дый упругий элемент содержит два проводника, по одному от каждого смежно-
го контура, в дополнение к третьему проводнику 5, который находится между
85
ними, чтобы минимизировать емкостную связь. Кремниевая пластина имеет
связь, обеспечивающую «земляной» слой.
Рис. 2.53. ВТГ фирмы BAE Systems с кольцевым резонатором:
а - принципиальная схема чувствительного элемента микрогироскопа; б - фрагмент конструкции
кольцевого резонатора; в - принципиальная схема магнитоэлектрического преобразователя силы:
1 — кольцевой резонатор; 2 - упругий элемент подвеса; 3 - кремниевая пластина; 4 - контактная
площадка; 5 - проводник; 6 - верхний и нижний полюсные наконечники; 7 - стеклянная подлож-
ка; 8 - плата с электроникой; 9 - корпус; 10 — крышка
Фрагмент конструкции кольца с упругим элементом подвеса и частью крем-
ниевой пластины показан на рис. 2.53, б.
Кремниевая пластина 3 анодно соединена со стеклянной подложкой 7 (рис.
2.53, в), которые температурно согласованы между собой. На подложке распо-
ложена также магнитная система, включающая кобальт-самариевый магнит (N-
S) и магнитопровод из двух полюсных наконечников 6, в зазоре между которы-
ми находится кольцо 1. Сервисная электроника расположена на ситалловой
плате 8. Вся конструкция собрана в герметичном коваровом корпусе 9 с крыш-
кой 10.
Магнитоэлектрический преобразователь совместно с электроникой обеспе-
чивает эллиптическую моду колебаний кольца на частоте 14,5 кГц его механи-
ческого резонанса. Деформации кольца за один период колебаний создаются
следующим образом. В первый полупериод направление токов в секторах I и V
(показаны стрелками) во взаимодействии с магнитным потоком создают (по
правилу левой руки) растягивающие силы, а в секторах III и VII - сжимающие
силы. Во втором полупериоде характер сил меняется на противоположный. Ка-
nrBU
ждая пара проводящих секторов кольца создает силу FM -------, где г - ра-
4/?/у
диус кольца; В - магнитная индукция в зазоре между полюсными наконечника-
86
ми магнитной системы; t/np - напряжение, приложенное к проводящему сектору
кольца; Rtl - значение нагрузочного резистора, включенного последовательно с
Рис. 2.54. Внешний вид ВТГ с кольцевым
резонатором фирмы BAE Systems
проводящим сектором кольца.
Заметим, что проводящие секторы VI и
VIII кольца, вибрирующего на частоте со
под действием преобразователя силы, иг-
рают роль якоря индукционного преобразо-
вателя перемещений. При этом выделяется
лг5со8
напряжение ивых = —-—, где о - вибро-
перемещение кольца.
Секторы II и IV используются в контуре
силовой обратной связи для устранения де-
формаций смещения. Измерительные и
компенсационные секторы в каждом полу-
периоде меняются ролями.
Случайный дрейф гироскопа оценивается в ~0,2 град/с. Гироскоп вибро-
устойчив, а также выдерживает ускорения порядка 10000 g. Предположитель-
ная область применения - в системах управления высокоманевренных лета-
тельных аппаратов. Общий вид ВТГ приведен на рис. 2.54. Можно указать так-
же на ВТГ, который широко используется в автопилотах радиоуправляемых
моделей самолетов [2.23, 2.24] и имеет характеристики, приведенные в табл.
2.14.
Таблица 2.14
Характеристики ВТГ CRS03-01 с кольцевым резонатором
Параметры, размерность Значение
Измеряемый диапазон, 7с. ±100
Масштабный коэффициент, мВ/(7с.) 20
Питающее напряжение, В 5,00±0,25
Смещение, % от питающего напряжения 50
Начальная ошибка смещения, мВ ±60
Вариация смещения по температуре, мВ ±60
Вариация масштабного коэф-та по температуре, % ±3
Начальная точность масштабного коэф-та, % ±1
Нелинейность, % от измерительного диапазона <0,5
Шум покоя (среднеквадратичн.), мВ < 1
Рабочая температура, ° С -40~±85
Полоса пропускания, Гц >10
Момент включения, с. <0.5
Утечка тока, мА <50
Входной импеданс, Ом 100
Максимальный выходной ток, мА >0,5
Чувствительность по перекрестной оси, % <1
Размеры, мм 29x29x18,4
Устойчивость ударная, g 99
Страна-производитель Япония
Характеристики ВТГ с кольцевым резонатором вполне приемлемы для ис-
пользования их в составе БИНС малоразмерных БПЛА, интегрированных со
спутниковыми навигационными системами. Как зарубежные, так и отечествен-
ные разработчики («Оптолинк», г. Зеленоград) активно работают над улучше-
87
нием характеристик ВТГ с кольцевым резонатором, как в микромеханическом,
так и в интегральном исполнении. Гироскопы этого типа обладают возможно-
стями по улучшению точностных характеристик, а их малые габариты, масса и
стоимость гарантируют их использование в системах управления и навигации, в
том числе в БИНС различных робототехнических комплексов.
2.2.4. Динамически настраиваемые гироскопы
Динамически настраиваемые гироскопы (ДНГ) обладают рядом достоинств,
которые определили их успешное применение в качестве чувствительных эле-
ментов в БИНС и в гиростабилизаторах. К этим достоинствам следует отнести
характеристики точности, сопоставимые с КЛГ и ВОГ, малую массу, габариты
и потребляемую мощность, работоспособность в широком температурном диа-
пазоне и др. ДНГ посвящена обширная литература, например [2.3, 2.4, 2.15].
2.2.4.1 Принципиальные схемы, динамическая настройка и режимы ра-
боты. В любом известном ДНГ ротор смонтирован на валу (оси) двигателя
(привода) с помощью подвеса, обеспечивающего упругую связь ротора с вра-
щающимся валом.
Рис. 2.55. Принципиальные схемы ДНГ:
а - без промежуточных элементов подвеса ротора; б - одноколенный (однорамочный) подвес;
в - двухрамочный подвес; г - рамки подвеса; 1 - ротор; 2 - торсионы; 3 - вал; 4 - кольцо и рамки
На рис. 2.55 показаны наиболее распространенные принципиальные схемы
ДНГ. Одной из первых предложена схема гироскопа по рис. 2.55, а, в котором
ротор 1 смонтирован на валу 3 двигателя (не показан) с помощью упругих эле-
ментов 2, имеющих конечную жесткость на кручение вокруг оси х и бесконеч-
ную жесткость на изгиб вокруг осей у и z. Упругие элементы, обладающие та-
кой характеристикой, принято называть торсионами. Очевидно, ротор имеет
88
возможность малых угловых отклонений вокруг оси х, пропорционально кото-
рым к ротору будет приложен упругий момент относительно вращающегося
вала.
На рис. 2.55, б приведена схема гироскопа, названного по имени его изобре-
тателя Howe (в русской литературе - «Хоув», «Хау»), в котором ротор 1 смон-
тирован на валу 3 с помощью двух пар торсионов 2 и кольца 4. Торсионы обес-
печивают ротору малые угловые отклонения по отношению к валу вокруг осей
х и у, вследствие которых появятся упругие моменты, приложенные к ротору.
На рис. 2.55, в показана схема гироскопа, в котором подвес ротора 1 относи-
тельно вала 3 реализуется упругими элементами (торсионами) 2 и двумя рамка-
ми 4. Это гироскоп является развитием схемы Howe. Действительно, если в
схеме по рис. 2.55, б вместо кольца применить рамку 4 и, кроме того, устано-
вить еще одну, развернутую в экваториальной плоскости ротора на 90°, то при-
ходим к двухрамочной конструкции подвеса (рис. 2.55, г).
Рассмотрим физическую природу принципа динамической настройки гиро-
скопов и возможные режимы их работы при реализации этого принципа.
На рис. 2.56 для гироскопа по схеме рис. 2.55, а нанесены векторы основных
моментов сил, действующих вокруг оси х закрутки торсионов в связанной с ро-
тором системе координат xyz.
Рис. 2.56. К определению векторов моментов сил
Положение системы координат xyz относительно опорной системы коорди-
нат xoyozo, связанной с основанием, определено углом у = Q.t поворота вала
(Q - скорость вращения вала), с которым связана система координат xo_yozo, и
89
углом а поворота ротора относительно оси х (продольная ось торсиона) отно-
сительно вала. Основание, на котором установлен гироскоп, вращается вокруг
оси х0 со скоростью со « £1. При развороте ротора на малый угол а
(sin а ~ а, cos а ® 1 ) со скоростью сс и ускорением а вокруг продольной оси
торсиона действуют следующие моменты: Аа - инерционный момент (А -
экваториальный момент симметричного ротора); Ьа - момент демпфирования
колебаний ротора (b - абсолютный коэффициент демпфирования); са - упру-
гий момент торсионов (с - жесткость торсионов на кручение); моменты сил
инерции Кориолиса: МГ1 = CQcosa- eosin у » CQcosiny (С - осевой момент
инерции ротора),
Мг2 = (J£lsin a) £1 cos a « >4Q2a, МГ2 = (C£lcosa)£lsina « C£72a.
В соответствии с методом кинетостатики сложим векторы моментов сил со
своими знаками, приравняем полученную алгебраическую сумму нулю и полу-
чим уравнение движения гироскопа (ротора) по координате a
Аа + Ьа + са + (С - A) Q2a - CQcosin у = 0. (2.53)
Момент сил (С - A)Q а называют центробежным или квазиупругим.
Перепишем уравнение (2.53) в стандартной форме
а + 2nd. + с^а - Я,со sin Q.t, (2.54)
где 2п = b/А, = l-C + уА
Решение уравнения (2.54), соответствующее установившемуся режиму коле-
баний ротора, имеет известный вид:
уу
аст = . * cosin (£1/ - ф), (2.55)
7(c02-Q2)2+4n2Q2
где ф = arctg |^2hQ / (с(2 - Q2.
Из (2.55) следует, что амплитуда колебаний ротора на частоте £1 пропор-
циональна угловой скорости со основания. Так как гироскоп имеет частотный
(вибрационный), амплитудно-модулированный сигнал на выходе, его называют
роторным вибрационным гироскопом (РВГ).
Очевидно, что амплитуда колебаний ротора увеличится при условии резо-
нанса с0 = £7, откуда следует условие динамической настройки
устанавливающее связь между скоростью вращения ротора и конструктивными
параметрами гироскопа. Важно отметить, что при динамической настройке
(2.56) амплитуда колебаний ротора не зависит от скорости его вращения:
, a«Cco/Z?. (2.57)
Возможна такая реализация ДНГ, при которой демпфирующий момент рото-
ра будет существенно меньше остальных. Для этого случая и = 0 и решение
уравнения (2.54) при нулевых начальных условиях имеет вид
С
а ~-----со/ cos £ it,
2А
откуда следует, что амплитуда колебаний ротора на частоте его вращения про-
порциональна углу со/ поворота основания в инерциальном пространстве. Оче-
90
видно, угол а ограничен максимально возможной закруткой торсионов. Таким
образом, при выполнении условий с0 = Q, п = 0 реализуется прецессионно-
вибрационный режим работы РВГ.
Реакция РВГ на постоянную угловую скорость основания показана на рис.
2.57.
Рис. 2.57. Реакция РВГ на постоянную угловую скорость основания:
вибрационный (а) и прецессионно-вибрационный (б) режимы работы ДНГ
б)
Рис. 2.58. К определению условия динамической настройки гироскопа Howe
Для определения условия динамической настройки РВГ по схеме рис. 2.55, б
обратимся к рис. 2.58, на котором введены следующие системы координат (СК):
с основанием связана СК x'o_yozo, относительно которой углом <р = Q1 опреде-
лена СК xByBzB, связанная с валом; с кольцом связана СК , положение ко-
91
(2-59)
торой относительно СК xByBzB определено углом а поворота кольца вместе с
ротором за счет разворота вокруг продольной оси внутренней пары торсионов;
с ротором связана СК xyz, положение которой относительно СК x^Zj, опре-
делено углом Р разворота ротора относительно кольца вокруг продольной оси
внешней пары торсионов. Вектор кинетического момента Н направлен по
главной оси z гироскопа. Указанные построения СК справедливы, если инер-
ционность ротора настолько велика, что положение главной оси гироскопа не
меняется в течение нескольких оборотов вала. При этом положение главной оси
может быть определено углом А в плоскости xozo. Для малых значений углов
а, Р их векторная сумма будет равна постоянному углу А. при любом угле ф.
Для малых углов А , а, Р справедливы равенства:
а = A. coscp, Р = A.sin(p. (2.58)
Очевидно, чтобы сохранить направление главной оси гироскопа в инерци-
альном пространстве, необходимо иметь достаточно большой кинетический
момент ротора, устранить (или минимизировать) возмущающие моменты, дей-
ствующие на ротор со стороны упругих элементов подвеса (упругий элемент) и
со стороны кольца (динамический момент).
Проекции на оси л0 и у0 упругого момента, действующего на ротор со сто-
роны подвеса, имеют вид (cos а ~ 1):
М — са sin (р — cP cos ф;
М = ~са cos Ф — СР sin Ф,
где с — суммарная жесткость каждой пары торсионов на кручение.
Подстановка (2.58) в (2.59) приводит у результату:
Чл. =°-Ч». =~А- (2 б°)
Таким образом, упругий момент, действующий на ротор со стороны подвеса,
направлен в отрицательную сторону оси у0.
В соответствии с (2.53) со стороны кольца подвеса (аналог ротора в схеме по
рис. 2.55, а) к ротору относительно оси у, приложен динамический момент
(полагаем b = 0):
= + (с> “ 4)q2(X] ’
который, с учетом величин а из (2.51) и а = — AQ2 cosQz равен:
= (24 -CjQ^cosQf, (2.61)
где 4 , С] - экваториальный и осевой (относительно оси х1) моменты инерции
кольца подвеса.
Проекция динамического момента на ось xt со стороны кольца на ротор от-
сутствует, так как он компенсируется моментом, обусловленным большой же-
сткостью на изгиб внутренней пары торсионов относительно оси .
Запишем проекции вектора величины (2.61) на оси х0 и у0:
92
(2.62)
^дх0 = sin<P = ~|(24
МпУп = COS(P = |(2Л> " С,)П2Х(1 + cos2Qr).
Вычислим величины (2.62), осреднснные за время Т = 2л / Q одного оборо-
(2-63)
та вала:
<Х.) = -1 (24 - с,)7 jsin 2ntd< = °’
(м„.) = |(24 - C,)O2z| j(1 + cos2flz)rf/ = |(24 - С,)П2Х
2 1 0 2
Таким образом, любое отклонение ротора от оси вращения вала вызывает
динамический момент, действующий на ротор в сторону отклонения, и упругий
момент, направленный в противоположную сторону. Равенство этих моментов,
те компенсация упругих моментов инерционным и гироскопическим момен-
тами, и определяет условие динамической настройки РВГ с одноколейным под-
весом:
-(24-C,)Q2 =с, (2.64)
откуда следует
Q = ^c/(4 -0,5С,) . (2.65)
Равенство (2.64) есть условие компенсации упругих моментов в среднем за
один оборот вала, что показано на рис. 2.59, на котором видно, что упругий мо-
мент является постоянным М„, , а динамический меняется и по значению его
ДУо
величины, и по направлению.
Рис. 2.59. Изменение моментов, действующих на ротор, за один оборот вала привода
Его проекция на ось у0 имеет постоянную составляющую < Мщ,п > и пере-
менную М на удвоенной частоте вращения вала. Проекция этого момента на
93
ось х0 имеет только переменную составляющую на той же частоте .
1 аким образом, на ротор гироскопа с одноколейным подвесом даже при вы-
полнении условия динамической настройки будут действовать гармонические
моменты на двойной частоте вращения вала, что является причиной дрейфа ги-
роскопа, подверженного угловой вибрации основания на этой же частоте [2.3,
2.4, 2.15]. Для устранения влияния этой погрешности была предложена схема
гироскопа с двухрамочным (двухколейным) упругим подвесом ротора.
Можно показать, рассуждая аналогично выше приведенному, что при усло-
вии равенства экваториальных и аксиальных моментов инерции для первой и
второй рамок (Д = А2, Вх = В2,СХ = С2) и равенстве жесткостей каждой пары
торсионов, со стороны подвеса к ротору приложены только постоянные момен-
ты упругих и динамических сил относительно оси у0. Момент упругих сил ра-
вен удвоенной величине по сравнению с одноколейным подвесом, так как вдоль
каждой оси подвеса работают по две пары торсионов
Мууо=-2ск. (2.66)
Динамический момент также удвоенный по сравнению с аналогичным мо-
ментом (2.64) одноколечного подвеса имеет вид
=(4+B,-C,)£A. . (2.67)
Из равенства моментов (2.66) и (2.67) следует условие динамической на-
стройки РВГ с двухколенным (двухрамочным) подвесом:
(4+5,-CJQ2 =2с, (2.68)
откуда следует:
Q = ^2с/(4 + 5, - С,) . (2.69)
При выполнении условий (2.68) и (2.69) гироскоп становится астатическим
Несовпадение векторов кинетического момента ротора и момента двигателя,
который от вала через подвес передастся на ротор, приводит к известному эф-
фекту совмещения указанных векторов. На рис 2.60 вектор момента двигателя
А/дв совпадает с осью z0, а ротор отклонен относительно оси у0 (см. рис. 2.58)
на угол X, и, следовательно, имеют место проекции этого вектора на ось собст-
венного вращения ротора Л/дв cos X « Млв и на ось, ей перпендикулярную в
плоскости xQy0 Мав sin X » МДВХ .
Рис. 2.60. К пояснению эффекта совмещения осей вращения вала и ротора
94
Первая составляющая момента двигателя уравновешивается моментом сил
сопротивления вращению ротора, который для разряженной среды можно счи-
тать пропорциональным скорости его вращения Мав = КисО. (Кж - интеграль-
ный коэффициент, зависящий от параметров газовой среды, формы и характера
обтекания ротора). Вторая составляющая вызывает дрейф гироскопа вокруг оси
у0 в сторону уменьшения угла X со скоростью
= Х = -^^ = -^ = -^ X. (2.70)
да Н CQ С
Из (2.70) следует, что угловая скорость дрейфа исчезает при совмещении
осей z и z0. Поэтому ДН1 ’ следует применять в замкнутых системах, когда век-
тор /7 все время находится вблизи оси вращения вала, например, в гиростаби-
лизаторах.
Зависимость (2.70) иллюстрирует возможность применения ДНГ в качестве
датчика угловой скорости. Действительно, если основание разворачивается с
постоянной угловой скоростью (orO = А, вокруг оси у0, то из (2.70) следует
Кис
т.е. отклонение ротора от равновесного положения пропорционально измеряе-
мой угловой скорости основания. Очевидно, что масштабный коэффициент
ДНГ для режима датчика угловой скорости зависит от значений С и Кис.
На рис. 2.61 показаны реакции ДНГ с одноколейным и двухколенным подве-
сами ротора на постоянную угловую скорость основания.
«7 б)
Рис. 2.61. Реакция ДНГ на постоянную угловую скорость:
а - прецессионно-вибрационный режим работы (одноколейный подвес ротора); б - прецессион-
ный режим работы (двухколенный подвес ротора)
В ДНГ, реализующих прецессионно-вибрационный режим работы на моно-
тонно возрастающее отклонение ротора накладываются колебания с удвоенной
частотой вращения вала. Среднее значение угла отклонения ротора в начальный
момент можно считать пропорциональным интегралу от угловой скорости ос-
нования Через некоторый промежуток времени начинает проявляться демпфи-
рующий момент и устанавливается среднее значение угла, определяемое фор-
мулами (2.57) или (2.71). Таким образом, настроенный РВГ - ДНГ можно рас-
сматривать как астатический датчик угловой скорости после окончания пере-
ходного процесса (рис. 2.61 б).
2.2.4.2. Конструкции и технические характеристики. Конструкция любо-
го ДНГ содержит ротор с упругим подвесом, привод (двигатель), датчики угла и
момента, если гироскоп работает в замкнутом контуре. Возможно термостати-
рование ДНГ.
95
На рис. 2.62 приведена кинематиче-
ская схема ДНГ [2.15] с двухколенным
(двухрамочным) подвесом, соответст-
вующим принципиальной схеме по рис.
2.55, в, г. Ротор 7 с помощью двухра-
мочного подвеса 3 смонтирован на кон-
сольной части вала 7, установленного в
корпусе 77 в радиально-упорных шари-
коподшипниках 10 совмещенного типа,
имеющих предварительный осевой на-
тяг. В качестве привода используется
синхронный, гистерезисный электро-
двигатель, ротор 9 которого установлен
на валу 7, а статор 8 - в корпусе 77. Ин-
дукционные датчики угла 12 положения
ротора установлены в корпусе и попар-
но включены по дифференциальной
схеме. Датчик момента магнитоэлек-
трического типа включает кольцевой
магнит 13, установленный на роторе и
катушки 2, установленные на корпусе.
Винты 4 служат для динамической на-
стройки. ДНГ имеет герметичную
Рис. 2.62. Кинематическая схема ДНГ
с двухрамочным подвесом:
1 - ротор; 2 - катушка датчика момента;
3 — подвес; 4 — винт; 5 — крышка; 6 - гермо-
ввод;/ - вал привода; 8, 9 - статор и ротор
привода; 10- шарикоподшипник; 11- кор-
пус; 12 - датчик угла; 13 - магнит
крышку 5 и гермовводы б для соедине-
ния внутренних и внешних электрических цепей.
На рис. 2.63 приведены общие виды ДНГ разработки РПКБ и ПНППК
(Пермская научно-производственная приборостроительная компания).
Рис. 2.63. Общий вид ДНГ:п - ГВК-16 (РПКБ);
б- МГ-4 (РПКБ); в-ДНГ-12 (ПНППК)
Характеристики ДНГ отечественной разработки приведены в табл. 2.15.
96
Характеристики ДНГ
Таблица 2.15
Характеристики, размерность Модель, разработчик
КИ-05- 5А КИНД 05-049 РВГ-1М ГВК-6-1 ГВК-10 ГВК-16 ГВК-17 ГВК-18 МГ-4 ДНГ-4
НИИ ПМ ОКБ «Темп» РПКБ ПНППК
Диапазон измеряемых угловых скоростей, град/с ±15 ±30 ±150 ±160 ±50 ±200 ±120 - ±60 ±90
Случайный дрейф, град/ч (от запуска к запуску) ±0,3 ±0,15 ±5.0 ±0.01 ±(0,03-0,2) ±(0,1-1,0) ±(0,05-0,2) ±0,01 ±0.2 ±0,5
Дрейф, не зависящий от ускорения, град/ч - - - ±3 ±25 ±50 ±25 ±3 ±25 ±50
Дрейф, пропорциональный ускорению, град/ч - - - ±1 ±3 ±25 ±15 ±3 ±25 ±6
Нестабильность масштабного коэффициента, % 0,05 0.05 0.1 - 0,1 - - - - -
Крутизна датчиков момента, град/(с/1) - - - 23 130 1000 600 80 400 450±70
Питание; В кГц; двигатель датчики угла; обогрев - - - 18(11);0,48 2,5; 19.2 115;0.4 18(11);0,48 2,5; 19,2 115;0,4 18(11);0,48 2.5; 19.2 36;0,4 18(11);0,48 2,5; 19.2 36;0,4 18(11);0,48 2,5; 19,2 115;0,4 15(11);0,48 2,5; 19.2 115;0,4 7,4;0,5 2,5; 32
Время готовности, мин - - - 10 - - - 8 - -
Габаритные размеры, мм 054x78 033x27 025x30 054x45 056x63 032x31,5 039x33 054x45 042x46 -
Масса, г 430 80 50 265 460 85 125 250 200 80
Механическая прочность при воздействии ускорения,g - - - - - 100 100 - - 75
В заключение обзора конструкций ДНГ отметим следующее.
С точки зрения операции динамической настройки предпочтительнее
одноколейные гироскопы — роторные вибрационные гироскопы (РВГ). Кроме
того, они по сравнению с двухколенными обладают меньшей трудоемкостью
изготовления, более простой схемой съема и преобразования сигнала, менее
подвержены влиянию дрейфов нулевых сигналов датчика угла и усилителя об-
ратной связи. РВГ могут обеспечивать диапазоны измерения от нуля до ±180
.. .±600 град/с. К сожалению, все еще нет автономного (серийного) образца РВГ
и каждый образец индивидуален. Поэтому он может поставляться только в со-
ставе системы, т.е. с определенным видом акселерометров и, следовательно, с
заданным массивом констант для компенсации систематических погрешностей,
особенно от температуры и от небаланса по осям при наличии ускорений.
Точность двухколенных ДНГ выше, чем у РВГ. Например, ДНГ модели
ГВК-10 используется в стратегической крылатой ракете с алгоритмом огибания
местности и периодическим обнулением показаний и ошибок над контрольны-
ми точками.
Таким образом, отечественные потребители ДНГ располагают достаточно
обширным выбором гироскопов этого типа для многоцелевого применения, как
в составе платформенных ИНС, так и в БИНС. Следует отметить, что в послед-
ние годы значительные усилия направлены на разработку и применение ДНГ в
составе систем подземной и трубопроводной навигации для обеспечения на-
правленного бурения, каротажа скважин и оценки состояния трубопроводов.
2.2.5. Микромеханические гироскопы
Микромеханическими гироскопами (ММГ), так же как и ММА, называют
конструкции, в которых механически подвижные узлы, реализующие чувстви-
тельный элемент ММГ, а также сервисная электроника, обслуживающая его
работу, представляют единый чип, изготавливаемый с помощью специальных
(технологии микроэлектромеханических систем - МЭМС) и технологий микро-
электроники.
Микромеханические гироскопы являются электромеханическими системами,
в которых энергия вынужденных (первичных) колебаний инерционной массы
(ИМ) на упругом подвесе (резонатор) при появлении переносной угловой ско-
рости преобразуется в энергию вторичных колебаний, содержащих информа-
цию об измеряемой угловой скорости. Это преобразование осуществляется
вследствие воздействия на резонатор сил (или моментов) инерции Кориолиса
при вращении резонатора с переносной угловой скоростью, вектор которой
перпендикулярен вектору количества движения, или момента количества дви-
жения (кинетического момента), соответственно для поступательных или вра-
щательных первичных колебаний ИМ.
Первичные колебания называют также режимом движения (РД), или движе-
нием по координате возбуждения, а вторичные - режимом чувствительности
(РЧ), или движением по координате выходного сигнала.
По виду движения инерционных масс в РД и РЧ различают гироскопы LL-
типа (linear-linear), или LL-гироскопы; гироскопы RR-типа (rotarc-rotare), или
RR-гироскопы и гироскопы LR-типа, или LR-гироскопы. В LL-гироскопах
инерционные массы в РД и РЧ совершают поступательные перемещения, в RR-
гироскопах - вращательные перемещения, в LR (RL)-rnpocKonax - различные
комбинации поступательных и вращательных перемещений инерционных масс.
98
К этой группе принято относить также камертонные и волновые ММГ.
Отличительным признаком камертонных ММГ является наличие стержне-
вых структур («ножек»). Существенно и то, что инерционная масса «ножек»,
как правило, равномерно распределена вдоль их длины и имеется свободный,
незакрепленный конец. При появлении переносной угловой скорости, вектор
которой перпендикулярен векторам количеств движения элементарных масс,
распределенных вдоль «ножек», возникают силы инерции Кориолиса, которые
генерируют вторичные колебания «ножек» ММГ.
Отличительным признаком волновых ММГ является наличие резонаторов,
имеющих форму кольца, которое с помощью упругих элементов подвеса скреп-
лено с корпусом, либо имеющих форму стержня, закрепление которого в кор-
пусе не препятствует его продольным и поперечным колебаниям. Первый тип
волновых ММГ часто называют кольцевыми, а второй - стержневыми. В обоих
случаях используется инертность стоячих волн, возбуждаемых в кольце или
стержне. Волны прецессируют при появлении переносной угловой скорости,
вектор которой перпендикулярен плоскости вибрирующего кольца либо на-
правлен вдоль вибрирующего стержня (эффект Брайена).
Существующие образцы коммерчески доступных камертонных и волновых
ММГ в настоящее время выполнены по интегральным технологиям (см. п.
2.2.3.2). Имеются также публикации, посвященные этим типам ММГ, которые
могут быть полностью изготовлены по технологиям МЭМС.
Каждый вид ММГ характеризуется набором классификационных признаков,
важнейшими из которых являются: количество измерительных осей (соответст-
венно, одно- или двухкомпонентный ММГ); количество инерционных масс
(ИМ) (одно- и многомассовые ММГ); тип подвеса ИМ (контактный, неконтакт-
ный, внутренний, внешний); перемещение ИМ в одной плоскости, как в РД, так
и в РЧ, либо в различных для РД и РЧ; тип привода ИМ в РД (электростатиче-
ский, магнитоэлектрический и др.); тип датчика съема сигнала в РЧ.
Микромеханические гироскопы могут работать в режимах прямого и ком-
пенсационного преобразований (измерений).
Типовыми параметрами ММГ являются: диапазон измерений, чувствитель-
ность, полоса пропускания, масштабный коэффициент и его стабильность, пе-
рекрестная чувствительность, шум, температурная стабильность характеристик
и другие эксплуатационные параметры и характеристики.
2.2.5.1. Принципиальные схемы и режимы работы. Конструктивным уз-
лом, определяющим функциональные возможности ММГ, является чувстви-
тельный элемент (ЧЭ), которым можно называть инерционную массу (или мас-
сы) в подвесе с приводом, обеспечивющим ИМ режим движения. На ИМ при
наличии переносной угловой скорости, вследствие возникающего ускорения
Кориолиса и соответствующих ему сил инерции, генерируются вторичные ко-
лебания (режим чувствительности). На этом основании ММГ иногда называют
приборами для измерения ускорений Кориолиса.
Наиболее просто реализуются и имеют наибольшее распространение одно-
массовые ММГ LL- и RR-типа.
На рис. 2.64 приведена принципиальная схема ЧЭ ММГ LL-типа, который
состоит из ИМ 1 (величиной т) и подвеса из упругих элементов 3, 4, скреплен-
ных с основанием 5 (показано условно). Элементы 2 обеспечивают целостность
и жесткость в местах сопряжения упругих элементов. Привод какой-либо физи-
ческой природы (электростатический, электромагнитный и т. д. - на рисунке не
показан) функционально входит в состав ЧЭ.
99
В общем случае привод развивает силу F()sinpt (Fo, р - амплитуда силы и час-
тота ее генерации), которая направлена под некоторым малым углом е (sins « е,
cose ~ 1) к оси х и сообщает ИМ колебания х = а0 sin pt (х0 - амплитуда коле-
баний). Мгновенный вектор линейной скорости ИМ в РД имеет проекции на
оси х и у:
V ' = V cos е « V; V - V sin s ~ -Vе .
Л у
При появлении переносной угловой скорости Q., мгновенный вектор кото-
рой направлен в положи гельном направлении оси z, возникают ускорения Ко-
риолиса вдоль осей х и у:
акх = 2Q.Ke аку - 2F1.V ,
вследствие чего ИМ оказывается под действием сил инерции Кориолиса: та^
вдоль оси х, и таху вдоль оси у.
Рис. 2.64. Принципиальная схема одномассового чувствительного элемента ММГ LL-типа:
1 - инерционная масса; 2 - жесткий элемент; 3, 4 - упругие элементы подвеса;
5 - основание (показано условно)
С учетом сил инерции, демпфирования и упругих сил, действующих на ИМ,
уравнения ее движения в простейшем случае имеют вид:
тх + b х + G х - Fo sin pt — 2mV£l.E',
/ ч * (2.72)
ту + b у + Gyy = -(Fo s^nРЧг ~ 2mVQ_,
где bx, by — коэффициенты демпфирования ИМ в направлении соответствую-
щих осей; Gx, G - жесткости упругого подвеса в направлении соответствую-
щих осей.
Первое уравнение системы (2.72) описывает РД, а второе - РЧ, из которого
следует, что перемещение ИМ вдоль оси у под действием кориолисовой силы
искажается проекцией силы привода на эту же ось, что приводит к измеритель-
ной ошибке ММГ. Если пренебречь влиянием этого искажения, то в устано-
вившемся режиме движение ИМ в РЧ определяется выражением
Г =-----(2-73)
бу
из которого следует, что амплитуда вторичных колебаний ИМ пропорциональ-
на измеряемой угловой скорости основания, т.е. ММГ является датчиком угло-
100
вой скорости. Из (2.73) следует также необходимость поддержания постоянной
скорости х = V в РД, что, как следует из первого уравнения системы (2.72),
является не простой задачей.
Выполним оценку влияния величины £ на точность измерения Q.. Так как
V = х = хор cos pt, ускорение Кориолиса а = 2Q.xop cos pt. Проекция уско-
рения ИМ в режиме движения на ось у равна
av = хе = -Ехар2 sin pt - Ехор2 cos(pt + 90) и на эту составляющую ускорения
ИМ реагирует так же, как и на аку , что приводит к ошибке измерения, которую
принято называть квадратурной, т.к. между ускорениями ау и аку существует
сдвиг по фазе на 90°.
Запишем отношение амплитуд ускорений:
ау _ еР
a., 2Q.
ку А
из которого следует, что при одинаковом порядке ускорений точность соблю-
дения перпендикулярности между направлениями режима движения (РД) и ре-
жима чувствительности (РЧ) должна быть очень высокой. Например, при Qz=
0,05 рад/ с, р = 105 рад/с, ау = аку = 1 допустимое значение угла £ = 10'6рад, что
практически обеспечить нс удается.
Квадратурный сигнал имеет ту же частоту, что и частота привода, а это де-
лает затруднительным фильтрацию помехи. Однако из-за сдвига на 90° квадра-
турный сигнал может быть частично исключен с помощью фазочувствительно-
го детектора. Эффективность такой фильтрации зависит от того, насколько точ-
но фазовое соотношение может поддерживаться электроникой.
Следует обратить внимание, что в ММГ с одномассовым ЧЭ трудно отде-
лить полезный сигнал, обусловленный ускорением Кориолиса, от сигнала, вы-
званного линейным ускорением, вектор которого имеет составляющую вдоль
оси вторичных колебаний (выходная ось).
Рис. 2.65. Принципиальные схемы одномассовых чувствительных элементов ММГ:
а - ЧЭ со спаренными упругими элементами внешнего подвеса; 6 — ЧЭ с разделенными упругими
элементами внешнего подвеса и промежуточной рамкой;в — ЧЭ с сопряженными упругими эле-
ментами внутреннего подвеса с функцией механического усиления выходного сигнала; 7 - ИМ;
2 - жесткие элементы подвеса; 3, 4 - упругие элементы подвеса; 5 - основание; 6 - кинематиче-
ский элемент
На рис. 2.65, в дополнение к рис. 2.64, приведены принципиальные схемы
ЧЭ, которые применены в большинстве известных конструкций одномассовых
ММГ. В схеме ЧЭ по рис. 2.65, а подвес ИМ 7 относительно основания 5 вы-
полнен в виде упругих элементов 3, 4, расположенных вне контура ИМ. В отли-
101
чие от схемы ЧЭ по рис. 2.64, где все упругие элементы подвеса связаны между
собой через инерционную массу, ЧЭ по схеме рис.2.65, а имеет сопряженные с
помощью жестких элементов 2, пары упругих элементов подвеса.
В схеме по рис. 2.65, б ЧЭ имеет ИМ 1, которая упругими элементами 3 со-
единена с элементом подвеса 2 в форме рамки, который упругими элементами 4
соединен с основанием 5.
Во всех схемах ЧЭ измерительной является ось z, вокруг которой действует
измеряемая угловая скорость Qz. В схемах по рис. 2.65, а, б режим движения
может быть организован вдоль любой из осей х и у.
В ЧЭ по схеме рис. 2.65 в подвес ИМ 1 относительно основания 5 выполнен
в виде упругих элементов 3 и 4.
Упругие элементы 4 обеспечивают также подвес элемента 6. «Точка» сопря-
жения элементов 3 и 4 делит последний на два отрезка длиной 1 и 72-
Режим движения выполняется вдоль оси х и перемещения ИМ 1 обеспечи-
ваются упругими элементами 3. Элемент 6 при этом остается неподвижным.
При появлении угловой скорости Qz силы инерции Кориолиса вынуждают пе-
ремещения ИМ 1 вдоль оси у на величину yt. Кориолисовы силы преодолевают
силы упругости элементов 4, обусловленные их жесткостью и длиной элемента
12 , а также инерционные и силы демпфирования. Элемент 6 при этом переме-
щается на величину у2 =yI(l + 7l/Z2j пропорционально которой может быть
сформирован выходной сигнал ММГ.
Важнейшими параметрами ММГ являются собственные частоты ИМ в РД и
РЧ, их стабильность, а также возможность частотной настройки между режи-
мами. В простейшем случае собственные частоты колебаний ИМ, соответст-
вующие, например, ЧЭ по схеме рис. 2.65, б, если РД организован вдоль оси х, а
РЧ - вдоль оси у, имеют вид:
Чо = ,
где /Л), т2 - соответственно массы ИМ и рамки.
В микрогироскопах RR-типа движение инерционных масс в РД и РЧ носит
вращательный характер. Сочетание относительного, вращательного движения
ИМ в РД и ее переносного, вращательного движения в РЧ приводит к возник-
новению момента сил инерции Кориолиса, который носит название гироскопи-
ческого момента.
В микрогироскопах RR-типа реали-
зуется колебательное движение инер-
ционной массы (ротора) в режимах
первичных и вторичных колебаний. На
рис. 2.66 ротор 1 укреплен относитель-
но опоры-основания 3 на упругих эле-
ментах 2 подвеса, которые имеют ма-
лые жесткости на кручение вокруг оси
у и на изгиб вокруг оси z. Жесткость
упругих элементов вокруг оси х значи-
тельно больше. Таким образом, воз-
можны колебания ротора вокруг осей z
и у.
Привод обеспечивает колебатель-
ные движения ротора со скоростью
102
Рис. 2.66. Режимы работы микрогироскопа
RR-типа:
РД - режим движения; РЧ - режим чувстви-
тельности; 1 — ротор; 2 - упругие элементы;
у = Q вокруг оси z таким образом, что первую половину периода кинетический
момент направлен в положительную сторону оси z, а вторую половину Н-
направлен в отрицательную сторону. Достаточно точно соблюдается равенство
Нх = Н2 = Н = Jy£ (Jy - осевой момент инерции ротора). Это режим первич-
ных колебаний, т. е. режим движения (РД). При появлении переносной скоро-
сти со основания (для ротора это - прецессия) возникает гироскопический мо-
мент МГ] для первого полупериода РД и МГ2 — для второго полупериода РД
(Мп = MV2 = //со). Периодически меняющий направление гироскопический
момент вызывает колебания ротора вокруг оси у. Это режим вторичных колеба-
ний, т. е. режим чувствительности (РЧ).
Момент привода Мо sin pt (Мо, р - амплитуда и частота моменте) преодо-
левает инерционный момент демпфирования и момент сил упругости подвеса
вокруг оси z. Гироскопический момент преодолевает аналогичные моменты сил
вокруг оси у. Таким образом, простейшие уравнения движения ротора имеют
вид:
(2.74)
JrY + byy + Gyy = Мо sin pt
>
./с,а + bact + Gua = Н со,
где Jy, Ja — осевой и экваториальный моменты инерции ротора; Ьу, Ьа - ко-
эффициенты демпфирования ротора в РД и РЧ; Gy, G. - жесткости упругих
элементов подвеса вокруг осей z и у соответственно; у, a — углы колебаний
ротора в РД и РЧ.
Для установившегося РЧ из второго уравнения системы (2.74) следует угол
поворота ротора вокруг оси у
(2.75)
//со
а -----,
G.
который содержит информацию об угловой скорости вращения основания, на
котором находится гироскоп. Следовательно, ММГ RR-типа также является
датчиком угловой скорости.
Принципиальные схемы чувствительных элементов ММГ RR-типа приведе-
ны на рис. 2.67. Инерционная масса 1 (ротор) относительно анкеров 5, установ-
ленных на подложке, имеет подвес, включающий упругие элементы 2, 5 и про-
межуточный, жесткий элемент 4. ИМ 1 может иметь кольцевую форму, а также
конфигурации с разнесением масс для увеличения инерционности ротора. Уп-
ругие элементы 2 имеют малую жесткость на кручение и обеспечивают колеба-
ния ротора относительно выходных (измерительных) осей в РЧ. Упругие эле-
менты 5 имеют малую изгибную жесткость в плоскости первичных колебаний
ротора и обеспечивают РД. Элементы 5, показанные в виде прямолинейных
стержней, могут иметь более сложную форму, а также иное угловое расположе-
ние относительно входной (чувствительной) и выходной (измерительной) осей.
В любом случае расположение элементов 5 в плоскости ротора должно быть
таким, чтобы иметь минимальные жесткости относительно выходных осей.
В схемах рис. 2.67, а, б передача вращающего момента привода осуществля-
ется непосредственно на ротор. Элементы статора привода располагаются,
как правило, снаружи ротора. Промежуточный элемент 4 имеет размеры, зави-
сящие от элементов, располагающихся на нем, а также от размеров упругих
элементов 5. На рис. 2.67, а пунктиром показано возможное изменение разме-
103
ров элементов 2, 4, 5.
В схеме рис. 2.67, в привод, обеспечивающий РД ротору 1, предпочтительно
должен располагаться в пространствах, ограниченных внутренним контуром
элемента 4. В этом случае передача вращающего момента привода на ротор
реализуется через элемент 4 и торсионы 2. Очевидно, что возможно и непосред-
ственная передача вращающего момента привода на ротор.
Чувствительные элементы (схемы рис. 2.67, а, в) служат для измерения од-
ной переносной угловой скорости основания и на их основе могут быть по-
строены однокомпонентные ММГ. Осью чувствительности для них является
ось у, вокруг которой основание вращается со скоростью О.у. РД происходит
вокруг оси z, вдоль которой направлены векторы переменного кинетического
момента Н ротора. Переменные гироскопические моменты НО.У вызывают ко-
лебания ротора в РЧ вокруг выходных (измерительных) осей х (рис. 2.67, г, ё).
Рис. 2.67. Принципиальные схемы чувствительных элементов ММГ:
а, б - с непосредственной передачей момента привода на ротор
(а - однокомпонентный, б - двухкомпонентный); в - однокомпонентный с возможностью переда-
чи момента привода на ротор непосредственно и через промежуточный элемент; г, д, е - режимы
работы МГ; 1 - инерционная масса (ротор); 2. 5 - упругие элементы подвеса: 3 - анкер(элемент
крепления микроструктуры к подложке); 4 - промежуточный (кинематический) элемент подвеса
104
Уравнения движения ЧЭ однокомпонентных ММГ аналогичны системе
(2.74).
ЧЭ по схеме на рис. 2 67, б служит для измерения двух угловых скоростей
основания, и на его основе могут быть построены двухкомпонентные ММГ.
Осями чувствительности могут быть любая из осей х, у. РД вокруг оси z создает
переменный кинетический момент Н и при появлении угловых скоростей Qx,
Qy возникают гироскопический момент 77QX, генерирующий РЧХ, и гироскопи-
ческий момент 77Qy, генерирующий РЧУ (рис. 2.67, д).
Уравнения движения ЧЭ двухкомпонентного ММГ описываются также сис-
темой (2.74), к которой необходимо добавить уравнение движения ротора во-
круг второй измерительной оси:
Jad + Z?ad + Gua - HQ.
Jpp + fcpP + брр = HQx- >
(2.76)
где a, P, у - углы поворота ротора вокруг осей х, у и z соответственно; Ja,
Эр, Jy - моменты инерции всех элементов (тел), вращающихся вокруг осей х, у,
z; ba, bp,by — коэффициенты демпфирования относительно соответствующих
осей; Ga, Gp, Gy — жесткости всех элементов подвеса при их деформациях от-
(2.77)
носительно осей х, у, z соответственно; МB(t) - вибрационный момент привода.
Углы поворотов ротора относительно измерительных осей в установившемся
режиме определяются аналогично (2.75):
«Л;
G« G„
Из выражений (2.77) следует, что точность измерения переносных скоростей
основания зависит, в первую очередь, от стабильности и предсказуемости пара-
метров, определяющих величины Н , Ga, Gp (а также Ja, Jp).
Наряду с ЧЭ микрогироскопов, в которых РД ротора происходит в его плос-
кости, в Draper Laboratory (СИМ) был разработан, так называемый, рамочный
ММГ, принципиальная схема ЧЭ которого приведена на рис. 2.68.
Z.
Рис. 2.68. Принципиальная
схема «рамочного» чувстви-
тельного элемента ММГ:
1,2 - наружная и внутренняя
рамки; 3, 4- упругие элементы
(торсионы); 5 — дополнительная
масса; 6 - основание
105
Конструкция образована соединением двух рамок, конструктивно выпол-
ненных в виде внешнего 1 и внутреннего 2 плоских элементов, соединенных
между собой и с основанием 6 с помощью торсионов 3 и 4, оси которых пер-
пендикулярны друг другу. Для увеличения инерционности на внутреннем эле-
менте расположена дополнительная масса 5. С помощью электростатических
датчиков силы наружному элементу 7 сообщаются первичные угловые колеба-
ния относительно оси у (РД). Эти колебания через торсионы 3 передаются и на
внутренний элемент, сообщая ему колебательный кинетический момент Н .
При вращении прибора со скоростью Q. относительно оси z возникают момен-
ты сил Кориолиса Н£1_, которые заставляют колебаться внутренний элемент
относительно оси х (РЧ). Амплитуда этих колебаний, измеряемая расположен-
ным под внутренним элементом емкостным преобразователем, будет пропор-
циональна измеряемой угловой скорости.
Движение ЧЭ в простейшем случае описывается уравнениями (2.74), в кото-
рых следует полагать: у — угол колебания рамок 7 и 2 относительно оси у; а -
угол колебаний рамки 2 вокруг оси х; Jy - суммарный момент инерции тел 7, 2,
5 относительно оси у; Ja - суммарный момент инерции тел 2, 5 относительно
оси х; Ьу — коэффициент демпфирования рамок 7, 2 прц колебаниях относи-
тельно оси у; Ьа — коэффициент демпфирования рамки 2 при колебаниях вокруг
оси х; Gy, Ga - жесткость на кручение торсионов 4 и 3 соответственно.
Помимо описанных, наиболее часто цитируемых схем ЧЭ, существуют и
другие, в том числе с двумя роторами, вращающимися в РД синхронно и проти-
вофазно, аналогично ЧЭ двухмассовых ММГ LL - и LR-типа.
Рис. 2.69. Принципиальная схема ММГ Stark
Draper Lab.:
1 - жесткий элемент подвеса; 2 - инерционная мас-
са; 3, 4 - упругие элементы подвеса; 5 - анкер;
6, 7 - электроды емкостного измерителя переме-
щений в РЧ; 8 - неподвижные электроды электро-
статических приводов; 9,10- гребенчатые струк-
туры емкостного измерителя перемещений в РД
В большинстве известных схем
ММГ реализация РД и РЧ осуще-
ствляется с помощью электроста-
тических преобразователей, соз-
дающих электростатические силы,
вызывающие высокочастотное ко-
лебательное движение ИМ, а в ре-
жиме РЧ преобразуют параметры
колебаний ИМ в изменение емко-
сти. На рис. 2.69 приведена прин-
ципиальная схема микрогироскопа
(Патент США, №8.349.855. Дата
выдачи 27.09.1994. Владелец - The
Charles Stark Draper Lab.), кинема-
тика которого аналогична ЧЭ (рис.
2.65, а).
Инерционная масса 2, выпол-
ненная в виде рамочной структуры,
имеет подвес относительно анке-
ров 5, связанных с подложкой, со-
стоящий из четырех упругих элементов 3 и четырех упругих элементов 4, каж-
дая пара которых разделена жестким недеформируемым элементом 7. ИМ 2
имеет возможность перемещений вдоль оси х со скоростью V с помощью элек-
тростатических приводов, неподвижные, гребенчатые структуры 8 которых свя-
106
заны с подложкой, а подвижные электроды являются частью ИМ 2. Для изме-
рения перемещений ИМ 2 в РД служит емкостный измеритель, гребенчатая
структура 9 которого является частью ИМ 2, а две неподвижные структуры 10
электродов связаны с подложкой.
Появление угловой скорости Q. вокруг оси z вызывает перемещения ИМ 2
вместе с элементами 1 под действием сил инерции Кориолиса вдоль оси у (РЧ).
Перемещения в РЧ измеряются двумя емкостными измерителями перемещений
с двух сторон ИМ 2, которые состоят из неподвижных электродов 6, связанных
с подложкой, и подвижных электродов 7, являющихся частью ИМ 2.
Принципиальная схема ММГ (патент США, № 5.650 568 Дата публикации
22.07.1997. Владелец - The Charles Stark Draper Lab.), ЧЭ которой соответствует
схеме рис. 2.67, а, приведена на рис. 2.70. Ротор 1 с массивными участками,
разнесенными вдоль оси х, с помощью упругих элементов 5 подвеса, растяжск-
торсионов 2, промежуточного кинематического (опорного) элемента 4 и анке-
ров 3 смонтирован на подложке. Электростатический привод, гребенчатые
структуры ротора которого составляют единое целое с ИМ 1, а статорные
структуры 6. 8 размещены на подложке, обеспечивают колебательный РД во-
круг оси z. При появлении переносной угловой скорости основания пере-
менный гироскопический момент вызывает вторичные колебания ротора (РЧ)
вокруг оси у. Электроды 9, размещенные на подложке, и электроды, сформиро-
ванные, напротив, на роторе, образуют емкостные измерители перемещений.
Конструкция имеет особенности. Прежде всего, следует обратить внимание
на петлевые образования (длина петли около 200 мкм при ширине 20 мкм) уп-
ругих элементов 5, которые служат для того, чтобы уменьшить растягивающую
силу в упругих элементах при колебаниях ротора, так как растяжение упругих
элементов вызывает нелинейную зависимость между амплитудой колебаний
ротора и из жесткостью.
Рис. 2.70. Принципиальная схема ММГ Stark Draper Lab.:
1 - инерционная масса (ротор);
2 - упругие элементы-растяжки (торсионы);
3 - анкер; 4 - кинематический элемент подвеса;
5 - упругие элементы подвеса с петлевыми образованиями;
6, 8 - статоры электростатического привода;
7 - петля-компенсатор; 9 - электрод емкостного измерителя перемещений
107
Следует обратить внимание на продольные пустоты в анкерах, которые, по
сути, сформировали миниатюрные упругие элементы в местах соединения тор-
сионов 2 и анкеров 3. При возможных напряжениях в материале, и особенно в
местах соединения разнородных материалов, упругость в местах соединения
торсионов 2 и анкеров 3 должна создать более комфортные условия работы
торсионов. Далее, из-за необходимости присадки бора в кремний, из которого
выполнены ЧЭ (технологическая необходимость), в материале также могут воз-
никнуть дополнительные напряжения. Такая ситуация характерна для статоров
б, которые выполнены из двух половин, разъединенных петлей 7, выполняющей
роль компенсатора напряжений.
В реализованной микроструктуре диаметр (максимальный) ротора около
1 мм. Электроды выполнены в виде тонкопленочной металлизации на подложке
из стекла «Ругех». Имеется также электрод для компенсации момента сил Ко-
риолиса при работе гироскопа с обратной связью.
2.2.5.2 Настройка режимов колебаний. ММГ, как колебательная система,
может быть охарактеризован реюнансной частотой вынужденных колебаний,
частотами информативных колебаний и показателем качества, или добротно-
стью по демпфированию.
Рис. 2.71. К пояснению режимов настройки
ММГ: а -- нормированная амплитудная и фазовая
частотные характеристики;
б - режимы настройки
Когда резонансные частоты совпадают
Кроме добротности по демпфиро-
ванию для характеристики качества
механического осциллятора исполь-
зуется параметр добротности как
отношение амплитуды его колеба-
ний при резонансе к полосе пропус-
каемых частот измеряемого сигнала.
Так как ускорение Кориолиса -
это сигнал узкой полосы частот с
центром на частоте режима возбуж-
дения колебаний, механический ко-
эффициент усиления режима чувст-
вительности может быть настроен
соответствием или приблизительным
соответствием резонансных частот
режимов возбуждения колебаний и
чувствительности.
Существует несколько способов
установки резонансных частот ре-
жимов возбуждения колебаний и
чувствительности, показанных на
рис. 2.71.
На рис. 2.71, а показаны зависи-
мости отношения амплитуды у коле-
баний по информативной оси к ам-
плитуде Ау ускорения Кориолиса и
фазы этих колебаний от частоты, а
на рис. 2.71, б - возможные режимы
настройки ММГ.
со, = cov, механический коэффициент
108
усиления ММГ очень высок, но полоса частот входного (измеряемой скорости)
сигнала уменьшается, и существует фазовый сдвиг на выходе. Если частота
возбуждаемых колебаний намного меньше частоты колебаний режима чувстви-
тельности со « со ,, гироскоп имеет большую полосу пропускания и не имеет
фазового сдвига. Наконец, если резонансные частоты не совпадают на неболь-
шом отрезке (например, в 10%), механический коэффициент усиления ММГ
будет большим, а полоса пропускания по сравнению с первым случаем умень-
шится незначительно.
Из рис. 2.71 следует, что для динамики ММГ гораздо важнее отношение час-
тот, чем их абсолютные значения.
Настройка частоты вынужденных движений осуществляется соответст-
вующим подбором частоты питающего напряжения приводов. Настройка час-
тоты информативных колебаний (режим чувствительности) осуществляется из-
менением жесткости подвеса в направлении этих колебаний за счет использо-
вания электростатических сил на электродах «гребенок».
На рис. 2.72 для иллюстрации принципа
реализации динамической настройки показа-
на ИМ, которая относительно точек крепле-
ния (анкеров) 3 смонтирована на упругих
элементах 1, 2, между которыми включен
жесткий, недеформируемый элемент. Непод-
вижные 4 и подвижный 5 электроды являют-
ся частью электростатической «гребенки»,
включенной в электрическую цепь и соз-
дающей электростатическую силу
Смещение ИМ на величину Ду вызвано
ее перемещением со скоростью V в положи-
тельную сторону оси х и вращением основа-
ния со скоростью FL.
Очевидно, упругая сила Fynp элементов
подвеса направлена против смещения Ду, а
электростатическая сила F, электродов
Рис. 2.72. К пояснению настройки
ММГ в режиме чувствительности:
1,2 - упругие элементы; 3 - «точка»
крепления; 4, 5 - электроды «гребен-
ки»
«гребенки» - в сторону этого смещения.
Суммарная сила, действующая на ЧЭ:
Eyi]p - Fjy < Е>Т1р и, следовательно, уменьша-
ется жесткость подвеса и резонансная часто-
та информативных колебаний.
В общем случае «гребенки» могут содержать п пар конденсаторов и тогда
для схемы подвеса по рис. 2.72 резонансная частота для режима чувствительно-
сти (в направлении оси у) определяется формулой
2G„ ~1,-ГГи°
т
(2.78)
где СО1, ДуО1 - /-й пары конденсаторов и зазор между «пальцем» и электродом
«гребенки»; t/0- напряжение на конденсаторе; (7Ь,- жесткость упругою эле-
109
мента подвеса; т — масса ИМ.
Из (2.78) следует, что, изменяя параметры электростатической «гребенки» и
напряжения, можно изменять частоту колебаний ИМ в РД, добиваясь нужной
расстройки частот по отношению к резонансной частоте первичных колебаний
ИМ в РД.
Подробное исследование динамики ММГ выполнено в ряде работ, например
в [2.18] и в цитированной в ней литературе.
2.2.5.3 Конструкции и технические характеристики. Разработкой и вы-
пуском ММГ занимаются ряд зарубежных фирм и организаций, например
Bosch, MS Lab., Draper Lab., Epson, Analog Devieces, HSG-IMIT и др. В России
разработкой ММГ с различным уровнем достигнутых успехов занимаются ЗАО
«Гирооптика» (С.-Петербург), ЦНИИ «Электроприбор», РПКБ (г. Раменское),
ОАО «Темп-Авиа», МИЭТ (г. Зеленоград) и др.
Большое количество конструкций ММГ описано в работе [2.18]. Рассмотрим
некоторые из них, содержащие значительное количество технических решений,
повторяемых в других разработках.
Фирма Analog Devieces разработала и выпускает серию ADXRS ММГ LL-
типа на диапазон до 300 %.
Гироскоп ADXRS представляет собой
интегральную микросхему, выполнен-
ную на одном кристалле кремния и со-
держащую все необходимые электрон-
ные компоненты формирования выход-
ного сигнала (рис. 2.73). В центре мик-
росхемы находятся две микромеханиче-
ские структуры ЧЭ, принцип работы
которой соответствует рис. 2.65, б. ЧЭ
каждой из структур приводится в режим
движения электростатическими гребен-
чатыми двигателями. Съем сигнала
осуществляется при появлении угловой
скорости, перпендикулярной плоскости
кристалла аналогичными структурами.
Рис. 2.73. Внешний вид кристалла гироскопа В микроструктурах направления коле-
ADXRS (увеличено) с выделенными контура- баний ИМ в режимах движения и чув-
ми блоков электроники ствительности взаимно перпендикуляр-
ны. Это дает возможность избежать влияния постоянных и виброускорений на
выходной сигнал гироскопа.
Высокочастотный сигнал, полученный с емкостных датчиков перемещений,
поступает на каскады усиления и демодуляции, преобразующие его в выходное
напряжение, пропорциональное измеряемой угловой скорости. В состав микро-
схемы входят датчик температуры для компенсации температурных погрешно-
стей и калибровки, а также прецизионный источник опорного напряжения.
Толщина механической структуры — 6 мкм. Корпус ММГ не вакуумирован,
поэтому добротность резонатора по осям движения в РД и РЧ составляет ~ 45.
Благодаря этому ММГ работает в режиме прямого измерения, так как расстрой-
ка частот составляет большую величину, около 300 Гц. Частота недемпфиро-
ванных колебаний подвеса ~ 15 кГц.
ПО
При амплитуде напряжения 12 В электростатический гребенчатый двигатель
обеспечивает ИМ при резонансе амплитуду колебаний в 10 мкм, стабилизируе-
мую с помощью контура обратной связи. В РЧ перемещения ИМ составляют
порядок 1016 м. Высокочувствительная емкостная система съема сигнала по-
зволяет измерить эти перемещения с погрешностью порядка 16 10'1' м. Масса
ММГ менее 1 г, а размер керамического корпуса 7х7><3 мм. Случайный дрейф
составляет ~ 0,3 град/с. Характеристики ММГ серии ADXRS приведены в табл.
2.16.
Гироскопы ADXRS имеют стабильный выходной сигнал при ускорениях до
2000 g и могут использоваться, например, как автомобильные датчики перево-
рота. Кроме того, их можно применять в интегрированных с GPS системах на-
вигации, в системах стабилизации различных подвижных объектов и во многих
других случаях.
Одна из первых микроструктур, реализующая принцип LR-гироскопа, раз-
работана в Draper Laboratory и показана на рис. 2.74.
Гребенчатые
структуры
двигателя
Анкер
Упругие
элементы
подвеса
Рис. 2.74. Микроструктура LR-гироскопа Draper Laboratory
Чувствительный элемент (ЧЭ) состоит из двух инерционных масс, которые с
помощью упругих элементов подвеса и рамки связаны с анкерами, скреплен-
ными с подложкой, где расположены статоры гребенчатых структур электро-
статических двигателей (левого, правого и центрального) и неподвижные элек-
троды емкостных датчиков перемещений, подвижные электроды которых раз-
мещены на ЧЭ. Режим движения инерционных масс в противофазе осуществля-
ется в направлении оси х. При появлении угловой скорости Q вокруг оси у (ось
чувствительности) инерционные массы под действием сил Кориолиса выходят
из плоскости ху в противофазе, вызывая угловые колебания рамки вместе с
инерционными массами, которые измеряются емкостными датчиками переме-
щений. ,
Первые образцы прибора имели дрейф (0,5-1) град/с, который в дальнейшем
был уменьшен на порядок. Фирма Boeing освоила выпуск гироскопов и успеш-
но применила их в автомобильной промышленности. Подобные гироскопы бы-
ли использованы в разработанной Draper Laboratory' системе для управления и
наведения реактивных снарядов ВМФ США. Дрейф гироскопов, входящих в
систему, составлял 1000 град/ч.
Разработку гироскопов RR-типа наряду с Draper Laboratory ведут специали-
сты фирм Bosch GmbH и института HSG-IMIT (Германия).
111
Таблица 2.16
Характеристики ММГ серии ADXRS
Характеристика, размерность ADXRS150 ADXRS300 ADXRS401 ADXRS610 ADXRS612 ADXRS614
Диапазон измеряемых угловых скоростей, град/с ±150 ±300 ±75 ±300 ±300 ±75
Чувствительность, ,мВ/°/с 12,5 5 15 6 7 25
Нелинейность, % 0,1 0,1 0,1 0.1 0,1 0,1
Чувствительность от напряжения питания, %/В 0,7 - - - - -
Нулевой сигнал,В 2,5 2,5 2,5 2,5 2,5 2,5
Температурный дрейф нулевого сигнала, мВ max ±300 - - - — -
Время включения, мс 35 35 35 50 50 50
Чувствительность к линейному ускорению, %/g 0.2 0,2 0,2 0.1 0,1 0,1
Нулевой сигнал от напряжения питания, °/с/В 1 1 — - — -
Плотность шума, <ус/у]Гц 0,05 0,1 3 MB(rms) 0,05 0.06 0.04
Коэффициент передачи датчика температуры, мВ/°К 8,4 8,4 8.4 9 9 9
Температурный дрейф, мВ 5 5 — — — —
Рабочее напряжение питания. В 5 5 5 5 5 5
Потребляемый ток, мА 6 6 6 3,5 3,5 3,5
Диапазон рабочих температур, °C -40++85 -40-+85 -40-+85 -40-+105 -40-+105 -40-+105
На рис. 2.75 показан микрогироскоп, принцип работы которого аналогичен
гироскопу по рис. 2.70. Отличие заключается в подвесе, который выполнен в
виде двух упругих элементов разной длины. Длинный элемент своими концами
скреплен с вибрирующим ротором, а в средней части — с коротким элементом
подвеса, концы которого соединены с анкерами, связанными с подножкой.
Входная (ось чувствительности) и выходная оси расположены в плоскости ро-
тора, совершающего вибрационное «вращение».
б)
Рис. 2.75. RR-гироскоп фирм Bosch GmbH:
а - общий вид микроструктуры; б - фрагмент микроструктуры
Кинематическая схема другого варианта RR-гироскопа разработки института
HSG-IMIT приведена на рис. 2.76.
Рис. 2.76 Кинематическая схема RR-гироскопа института HSG-IMIT
Инерционные массы через внешние упругие элементы связаны с внешним
ободом внутреннего кольца, которое вместе с внутренним ободом и роторными
элементами гребенчатой структуры вибропривода (двигателя) представляют
единую структуру, которая, в свою очередь, через внутренние упругие элемен-
ты подвеса соединена с анкером, установленным на подложке. На подложке
сформированы также статорные элементы гребенчатого вибропривода. Вра-
щающий момент Мв вибропривода создает переменный кинетический момент
гироскопа, взаимодействие которого с измеряемой угловой скоростью Q при-
водит к возникновению переменного момента сил Кориолиса Мк , вызывающе-
го колебательное движение инерционных масс относительно выходной оси. Пе-
ремещение инерционных масс измеряется электростатическими датчиками, не-
подвижные электроды которых расположены на подложке под инерционными
массами.
113
Корпус гироскопа вакуумирован до давления 0.01 мБар. Частота колебаний
ротора (инерционных масс) в режиме движения 1420 Гц. Скорость дрейфа око-
ло 65 град/ч при полосе пропускания 50 Гц. Диапазон измеряемых скоростей до
200 град/с.
Гироскопы RR-типа активно исследуются отечественными разработчиками.
Некоторые разработки, видимо, близки к выпуску опытных партий, например, в
ЦНИИ «Электроприбор», ЗАО «Гирооптика» и др.
Следует обратить внимание, что в ряде применений не требуется ММГ изго-
товленный полностью по технологиям МЭМС, если требования по массе, габа-
ритам и стоимости не являются слишком критичными. Оказывается вполне
достаточным и даже предпочтительным гироскоп в интегральном исполнении,
как например ВТГ с кольцевым резонатором (см. п. 2.2.3.2) который сочетает
достоинства микромеханического ЧЭ и электроники, выполненной в отдельном
объеме.
Выводы
Современные механические гироскопы, история развития которых продол-
жается около 150 лет, практически достигли «потолка» своих возможностей,
как в плане физических принципов функционирования' так и используемого
конструктивно-технологического базиса.
История развития и практического применения динамически настраиваемых
гироскопов насчитывает нс более пятидесяти лет, а лазерных, волоконно-
оптических, волновых твердотельных и микромеханических и того меньше.
Достигнутые технические характеристики этих гироскопов не соответствуют
возможностям, заложенным в физических принципах их функционирования, а
их преимущества будут проявляться во все большем объеме особенно в тех об-
ластях применения, где точность выполнения функциональной задачи должна
сочетаться с малыми массой, габаритами, энергопотреблением, стоимостью и
сохранением стабильности своих характеристик.
Лазерные гироскопы первого поколения имеют механический виброподвес и
при дрейфе нуля порядка 0,01 град/ч обладают очевидными недостатками: сла-
бая устойчивость к механическим и климатическим воздействиям и ограниче-
ния по уменьшению такта съема информации. Именно на таких гироскопах бы-
ли построены первые автономные лазерно-гироскопические навигационные
системы фирм Litton и Honeywell для гражданских самолетов, так же как и пер-
вая советская БИНС на лазерных гироскопах КМ-11-1А разработки НИИ «По-
люс».
В лазерных гироскопах второго поколения вместо механического вибропод-
веса используются магнитооптические методы вывода рабочей точки из зоны
захвата на базе эффектов Фарадея и Зеемана. Отсутствие подвижных деталей и
узлов в этих гироскопах предопределяет их высокую устойчивость к жестким
эксплуатационным условиям. В настоящее время лазерные гироскопы с магни-
тооптической «виброподставкой» относят к гироскопам средней точности с
дрейфом порядка 1-10 град/ч, что делает возможным их использование в лазер-
но-гироскопических спутниково-навигационных БИНС. Но уже в ближайшем
будущем ожидается дрейф у гироскопов этого типа порядка 0,01-0,02 град/ч и,
следовательно, возможность создания на их базе БИНС, работающих в авто-
номном режиме без коррекции не менее часа (для отдельных применений).
Динамически настраиваемые гироскопы с двухрамочным подвесом относят-
114
ся к гироскопам среднего и выше классам точности и используются в ИНС и
БИНС для объектов различного назначения.
Видимо, для объектов с ограниченным временем работы целесообразно при
построении систем управления и навигации, включая БИНС, использовать ги-
роскопы с одноколечными подвесами. Следует отметить, что ряд конструктив-
ных решений при проектировании подвеса может быть реализован с использо-
ванием кремниевой технологии.
Отечественные разработчики (РПКБ, РПЗ, ПНППК, «Темп-Авиа») выпуска-
ют, и продолжают работать над их совершенствованием, широкую номенклату-
ру динамически настраиваемых гироскопов, используемых в ИНС собственной
разработки, а также применяемые другими разработчиками в качестве комплек-
тующих изделий.
Волоконно-оптические гироскопы, за немногими исключениями, относятся к
гироскопам среднего класса точности и в силу присущих им достоинств все
шире применяются в БИНС, интегрированных со спутниковыми навигацион-
ными системами.
Достигнутый дрейф в 0,01 град/ч и весьма привлекательные эксплуатацион-
ные качества волновых твердотельных гироскопов привлекают внимание все
большего числа разработчиков, особенно к конструкциям с кольцевым и стерж-
невым резонаторами. РПКБ, единственное пока в России предприятие, разрабо-
тавшее интегрирующий волновой твердотельный гироскоп с дрейфом порядка
3 град/ч для использования в БИНС гражданского применения. Это предпри-
ятие работает также над созданием БИНС на базе волновых твердотельных ги-
роскопов с кольцевым резонатором в качестве резервной навигационной систе-
мы. Следует отметить, что зарубежные фирмы, в частности BAE Systems, вы-
пускает доступные на российском рынке гироскопы этого типа с кольцевым
резонатором, успешно используемые, например, в корректируемых БИНС бес-
пилотных летательных аппаратов.
Микромеханические гироскопы, имеющие наименьшую историю развития,
относятся к грубым приборам, но имеют устойчивую и весьма прогрессивную
тенденцию к уменьшению систематического дрейфа. Уже сейчас в гироскопах
этого типа военного применения разработки фирмы Analog Devieces заявленный
дрейф не хуже 10 град/ч, что переводит их в гироскопы среднего класса точно-
сти. Даже с уровнем дрейфа более 100 град/ч возможно применение гироскопов
этого типа для решения ряда задач стабилизации и управления высокоманев-
ренными летательными аппаратами.
Участие в разработке этого типа гироскопов грандов отечественного гиро-
скопического приборостроения ЦНИИ «Электроприбор» (С.Петербург), РПКБ
(г. Раменское), ОАО «Темп-Авиа» (г. Арзамас), а также ЗАО «Гирооптика»,
МИЭТ (г. Зеленоград), МГТУ им. Баумана и других делают вполне реальным
приближение микромеханических гироскопов к точностям, приемлемым для их
использования, в БИНС малогабаритных, динамических объектов, включая ро-
боты различного назначения, с увеличенным временем автономной работы.
115
ЛИТЕРАТУРА К ГЛАВЕ 2
2.1. Абрамович И.Г., Левин В.И. Уравнения математической физики. - М.: Наука, 1964. - 286 с.
2.2. Басараб М.А., Кравченко В.Ф., Матвеев В.А. Математическое моделирование физических
процессов в гироскопии. - М.: Радиотехника, 2005. - 176 с.
2.3. Брозгуль Л.И. Смирнов Е.А. Вибрационные гироскопы. - М.: Машиностроение, 1970. -
216с.
2.4. Брозгуль В.Л. Динамически настраиваемые гироскопы. - М.: Машиностроение, 1989. - 229 с.
2.5. Будкин В.Л., Паршин В.А., Позоров С.А., Саломатин А.К., Соловьев В.М. // Гироскопия
и навигация. - 1988. - №3. - С. 149-153.
2.6. Волоконная оптика и приборостроение/ М.М. Бутусов, С.Л Галкин, С.П. Оробинский, Б.П.
Пал; Под общ ред. М.М. Бутусова. - Л.: Машиностроение. Ленингр. Отд-ние, 1987. - 328 с.
2.7. Гребенников В.И., Еремин Л.В., Мишин Б.А., Нахов С.Ф., Ермаков Р.В. Малогабарит-
ный трехкомпонентный волоконно-оптический измеритель угловой скорости средней точно-
сти / Сб. материалов XIII С.-Петербургской международной конференции по интегрирован-
ным навигационным системам. - 2006. - С. 219-225.
2.8. Гироскопы на новых физических принципах. Обзор по материалам отечественной и зару-
бежной печати. / Составил Чесноков Л.В. - ГОНТП, 1990. - 97 с.
2.9. Джанджгава Г.И., Бахонин К.А., Виш радов Г.М., Требухов А.В. Бесплатформснная инер-
циальная навигационная система на базе твердотельного волнового гироскопа. // Сб. мате-
риалов XIV С.-Петербургской международной конференции по интегрированным навигаци-
онным системам. - 2007. С. 116-125.
2. Ю.Журавлев В.Ф., Климов Д.М. Волновой твердотельный гироскоп. М.: Наука, 1985. - 126 с.
2.11 .Лунин Б.С. Физико-химические основы разработки полусферических резонаторов волновых
твердотельных гироскопов. - М.: Изд-во МАИ, 2005. - 223 с.
2.12. Матвеев В.А., Л и латников В.И., Алехин А.В. Проектирование волнового твердотельного
гироскопа. - М.: Изд-во МГТУ им. Баумана, 1907. - 165 с.
2.13. Ориентация и навигации подвижных объектов / Под общ. ред. Б.С. Алешина, К.К. Вереме-
енко, А.И. Черноморского. - М.: ФИЗМАТЛИТ, 2006. - 422 с.
2.14. Пельпор Д.С., Осокин Ю.Н., Рахтиенко Е.Р. Гироскопические приборы систем оринтации
и стабилизации. - М.: Машиностроение, 1977. - 207 с.
2.15. Пельпор Д.С., Матвеев В.В., Арсеньев В.Д. Динамически настраиваемые гироскопы. -
М.: Машиностроение, 1988. - 263 с.
2.16. Пешехонов В.Г. Ключевые задачи современной автономной навигации // Гироскопия и на-
вигация, - 1996. - №1. - С. 48.
2.17. Прилуцкий В.Б. Понамарев В.Г., Маргус В.Г., Фенюк М.А., Коркишко Ю.Н., Федоров
В.А. и др. Интерферометрические волоконно-оптические гироскопы с линейным выходом //
Сб. материалов XI С.-Петербургской международной конференции по интегрированным на-
вигационным системам. - 2004. С. 129-136.
2.18. Распопов В.Я. Микромеханические приборы. - М : Машиностроение, 2007. -400 с.
2.19. Рекламные материалы Раменского Приборостроительного конструкторского бюро, Рамен-
ского приборостроительного завода, Пермской научно-производственной приборостроитель-
ной компании, Мичуринского завода «Прогресс».
2.20. Самотокин Б.Б., Мелешко В.В., Степановский Ю.В. Навигационные приборы и системы. -
Киев.: «Вища школа», 1986. - 343 с.
2.21. Серегин В.В., Кукулиев Р.М. Лазерные гиромстры и их применение. - М.: Машинострое-
ние, 1990. 287 с.
2.22. Putty M.W. and Najafi К. “A Micromachined Vibrating Ring Gyroscope”, in Proc. Digest, Solid-
State Sensors and Actuators Workshop, Hilton Head, 1994. - P. 213-220.
2.23. Patent No. US 6282958 (2001) «Angular rate sensor» / С. P. Fell; Assignee BAE Systems PLC,
Farnborough (GB).
2.24. Rate Gyroscope CRS03 Features Data / Silicon Sensing Systems Japan, ltd //
http://www.spp.co.jp/sssj7qanda-e.html
116
Вопросы для самоконтроля
1. Классификация акселерометров.
2. Особенности измерительных цепей, акселерометров прямого и ком-
пенсационного преобразования.
3. Особенности конструкции и основные технические характеристи-
ки акселерометров серий АК, ДА.
4. Особенности конструкции и основные технические характеристи-
ки акселерометром серий А, А Т, АЛЕ.
5. Особенности конструкции и основные технические характеристи-
ки струнных акселерометров.
6. Особенности конструкции и основные технические характеристи-
ки микромеханических акселерометров.
7. Классификация гироскопов.
8. Принцип работы и особенности конструкции лазерных гироскопов.
9. Частотная характеристика и основные технические характери-
стики лазерных гироскопов.
10. Принцип работы разомкнутых и замкнутых волоконно-оптических
гироскопов.
11. Особенности конструкции и основные технические характеристи-
ки волоконно-оптических гироскопов.
12. Основные схемы и принцип работы роторных вибрационных гиро-
скопов.
13. Динамическая настройка и режимы работы роторных вибрацион-
ных гироскопов.
14. Особенности конструкции и основные технические характеристи-
ки роторных вибрационных гироскопов.
15. Принцип и режимы работы волновых твердотельных гироскопов. •
16. Особенности конструкции и основные технические характеристи-
ки волновых твердотельных гироскопов с объемным резонатором.
17. Особенности конструкции и основные технические характеристи-
ки волновых твердотельных гироскопов с кольцевым резонатором.
18. Классификация микромеханических гироскопов.
19. Принцип работы, особенности конструкции и основные техниче-
ские характеристики микромеханических гироскопов LL- , LR-, RR-
типов.
20. Области применения гироскопов различных типов в БИНС различ-
ного назначения.
117
Глава 3
БИНС НА АКСЕЛЕРОМЕТРАХ И ДУС
3.1. БИНС с углами Эйлера - Крылова
Для определения положения объекта на поверхности Земли наибольшее рас-
пространение получили географические координаты, с помощью которых по-
ложение некоторой точки О задается широтой ср и долготой X. Для летатель-
ных аппаратов вводится еще одна координата - высота над уровнем моря h.
Широта определяется углом, образуемым нормалью к земному сфероиду и
плоскостью экватора Земли. Долготу измеряют двугранным углом между плос-
костью меридиана, проходящего через точку О, и плоскостью Гринвичского
меридиана (рис. 3.1).
Рис. 3.1. Географические координаты точки
Введем нормальную систему координат OX Y Z (по ГОСТ 20058-80) с
вершиной, совмещенной с центром масс объекта, ось OXg которого направлена
на север по касательной к меридиану, ось OZg - по касательной к параллели на
восток, а ось OYg — вдоль вертикали места вверх. Оси нормальной системы ко-
ординат ориентированы по странам света, а точка О перемещается вместе с
объектом, поэтому такая система координат называется также географической
или географическим сопровождающим трехгранником.
Для построения алгоритмов БИНС необходимо найти кинематические эле-
менты его движения: проекции абсолютной угловой скорости вращения трех-
гранника на его оси и проекции абсолютного линейного ускорения его верши-
ны.
118
Пусть точка О перемещается с линейной скоростью V относительно по-
верхности Земли. Проекции вектора V на оси OXg , OYg , OZg обозначим VXg,
> vzg <РИС- 3-2)-
Рис. 3.2. Проекции векторов линейной скорости объекта (а) и угловой скорости Земли (б)
на ребра географического трехгранника
Исходя из рис. 3.2 проекции вектора линейной скорости на оси географиче-
ской системы координат имеют вид
^=Ггсо5К, V,s=h, VZg=VrsinK. (3.1)
где Гг - горизонтальная составляющая скорости ЛА; К — курсовой угол, т.е.
угол между направлением на север и вектором Иг.
Абсолютная угловая скорость трехгранника OX YgZg складывается из пере-
носной угловой скорости обусловленной вращением Земли вокруг своей оси и
относительной скорости вращения трехгранника вследствие перемещения объ-
екта вдоль земной поверхности. Вектор угловой скорости Земли U имеет сле-
дующие проекции на оси географической системы координат (рис. 3.2, б)
Ur -UXg ={7cos(p, UB -UYg = t/sin(p, UZg=Q. (3.2)
Здесь Ur, UB - горизонтальная и вертикальная составляющие угловой ско-
рости Земли.
Горизонтальная составляющая угловой скорости Земли U costp приводит к
вращению плоскости горизонта, причем если наблюдать это вращение с поло-
жительного направления оси OXg, то восточная часть плоскости горизонта бу-
дет опускаться, а западная - подниматься. Вертикальная составляющая угловой
скорости Земли U sin (р приводит к вращению плоскости горизонта вокруг ме-
стной вертикали против часовой стрелки, если наблюдать за вращением с по-
ложительного направления б? У (рис. 3.2, б).
При движении объекта вдоль параллели, широта ср остается постоянной, а
географическая система координат поворачивается вокруг оси вращения Земли
с угловой скоростью X (рис. 3.3, а). Изменение долготы можно представить
через восточную составляющую линейной скорости объекта (см. также рис. 3.1)
119
• У7 У7
к=-^=—L,
р /?cos<p
(3.3)
где R = R3 + h; R3 - геоцентрический радиус Земли, р — радиус соответст-
вующей параллели.
Если объект перемещается в плоскости меридиана, то долгота остается по-
стоянной, а приращение широты в единицу времени можно рассматривать как
угловую скорость вращения трехгранника OXgYgZx вокруг оси Zg (рис. 3.3, б).
Рис. 3.3. Угловые скорости: (а) А,; (б) ф
(3.5)
Вектор угловой скорости ф направлен в отрицательную сторону оси OZr,
т.е. на запад, а его модуль равен
У7
(3.4)
IX
Исходя из рис. 3.1 и 3.3 проекции абсолютной угловой скорости географиче-
ского трехгранника на его оси равны
coAg = (U + A,) cos ср;
(aYg = (L7 + A)sin(p; >
= -Ф-
Подставив правые части соотношений (3.3) и (3.4) в (3.5), получим
тт
coAg =t/cos<p + -J4
к
vz
coyg =(7sm(p + -^Zg(p; -
Zs R
Найдем проекции вектора абсолютного ускорения движущейся вершины
трехгранника OXgYgZ на его ребра. Абсолютное ускорение складывается из
(3.6)
следующих составляющих
а = а +аг +ас,
(3-7)
120
С Г -С
где а - переносное ускорение, а — относительное ускорение, а - кориоли-
сово ускорение.
Найдем каждую составляющую абсолютного ускорения а . Кориолисово ус-
корение вызвано переносной угловой скоростью вращения Земли и линейной
относительной скоростью объекта и выражается векторным произведением
ас =2UxVr =2
U cos ср U sin <р
Vxg
VYg
к
О
^g
(3.8)
где i, j, к - орты осей системы координат OXgYgZg .
Раскрывая определитель (3.8), находим проекции кориолисова ускорения на
оси OXgYgZg :
Относительное ускорение аг
скорости Vr = VXgi + VYgj + VZgk
верхности Земли с
со' = XcoscpZ + Xsincpj - фЛ :
acXg = 2t7KZgsin<p;
= -2UVZg coscp;
aZg = 2(VYgU cos cp - UVX sin cp).
вызвано изменением относительной линейной
и движением объекта вдоль сферической no-
относительной
угловой
(3-9)
скоростью
ar — Vr + со' х Vr = Vr +
* J
V V
R R
V V
-Vs r Yg
(З.Ю)
Из (3.10) находим проекции относительного ускорения на оси географиче-
ской системы координат:
axs = Yxg+^-‘g4> + ^L.
ar -и Xk к
R R'
ai =KZ
uZg Z£ R Д
(3.11)
Что касается переносного ускорения ае, то оно вызвано угловой скоростью
вращения Земли и определяется так:
, ае = U*(UxR). (3.12)
На основании (3.12), имеем:
aXg =t727?sin<pcoscp,
aYg = —U2R cos2 ср,
<4=0-
(3.13)
к
R
121
Сложим вектор переносного ускорения ае с вектором g ускорения гравита-
ционного поля Земли, вследствие чего образуется вектор ускорения силы тяже-
сти с компонентами (0, g, 0).
Примем во внимание, что акселерометры измеряют кажущееся ускорение,
поэтому сложим соответствующие компоненты вектора ускорения силы тяже-
сти с составляющими кориолисова (3 9) и переносного ускорения (3.11), в ре-
зультате чего получим проекции вектора кажущегося ускорения вершины трех-
гранника OX Y Z на его оси:
Г-Г К
nxg = vxg + ~~ %ч> + 8-+2uvZgsin ф;
К к
2 2
R -2Wzecos4> + g; (3.14)
nZg = vZg + D------'2Ф + 2(VYgU cos Ф - uvXg sin ф)-
К к
В действительности инерциальные чувствительные элементы БИНС жестко
установлены на борту подвижного объекта. В этом случае акселерометры изме-
ряют проекции вектора кажущегося ускорения на ребра связанного с объектом
трехгранника и показания акселерометров необходимо перепроектировать в
географическую систему координат в соответствии с информацией, выработан-
ной в блоке ориентации.
Допустим, что задача перепроектирования кажущихся ускорений из связан-
ного трехгранника в географический трехгранник решена и получены выраже-
ния (3.14). Однако при навигации вдоль поверхности Земли необходимо, чтобы
на входы первых интеграторов поступали только ускорения относительного
движения Vx , VYg > ^Zg Следовательно, ускорения Кориолиса и ускорения,
связанные с криволинейностью движения объекта вдоль сферической поверх-
ности Земли, должны быть скомпенсированы. Из выражений (3.14) следует, что
компенсирующие («вредные») составляющие ускорения равны:
aXg =^r-tg(p+ + 2UVZg sin ф;
а Л
г2 к2
а‘ =-^-^-2t/KZgcos<p+g; (3.15)
К к
aZg = V~~s - —tgip + 2(YYgUcosф-UVXg sinф).
К A
Таким образом, на входы первых интеграторов необходимо подавать сле-
дующие величины
nXg~aXg =^Xg'^
nYg~aYg~^Yg’ (3.16)
nZg ~ aZg ~ ^Zg ’
где nx, nYg, nZg - проекции вектора кажущегося ускорения на оси географи-
ческой системы координат.
122
Составляющие относительной скорости движения объекта образуются после
интегрирования ускорений (3.16), с учетом ввода начальных скоростей KVg(/0),
t t
^Xg ~'Kg (Ч ) "* | (nXg “ aXg № = ^Xg (?0 ) + J ^Xgd^’
(o *o
t t
VYS + )dt = VYg (k ) + J ^Ygdt>‘ (3 1 7)
4) f0
t t
VZg = ^({0) + (ПХ8- aZg )dt = VZg (k ) + J ^Ygdt-
'fl <0
Координаты местоположения объекта определяются с помощью вторичного
интегрирования (с учетом начальных значений координат и высоты ф(/0),
Ж), Ж)):
г К.
<р = <р('о) + ]-^
J к
г0
Х = 1(Г0)+[ Vzs—dt- (3.18)
J У?coscp
'о v
t
h = h(Q + v,sdt.
'о
Таким образом, уравнения (3.17) и (3.1.18) реализуют навигационный алго-
ритм БИНС, позволяющий определить текущие координаты местоположения и
скорость объекта.
Рис. 3.4. Взаимное положение связанной и географической систем координат
Рассмотрим задачу определения углов ориентации ЛА относительно геогра-
фической системы координат. Эти углы определим следующим образом
(рис. 3.4). Введем трехгранник OXYZ, ребра которого направим вдоль строи-
тельных осей ЛА. Ось ОХ совпадает с продольной осью ЛА и направлена к
123
носу, ось OZ совпадает с поперечной осью ЛА и направлена в сторону правого
крыла, ось OY перпендикулярна плоскости крыльев и направлена вверх.
Положение строительных осей ЛА (связанная система координат) относи-
тельно географического трехгранника определяется тремя углами, которые на-
зываются углами рыскания (курса), тангажа и крена. Угол рыскания vg - угол,
отсчитываемый в горизонтальной плоскости OXgZg от оси OXg против хода
стрелки часов до проекции продольной оси объекта на эту плоскость. Угол тан-
гажа 0 отсчитывают в вертикальной плоскости между осью ОХ и ее проекци-
ей на горизонтальную плоскость. Угол крена у отсчитывают в поперечной
плоскости между осью OZ и линией пересечения указанной плоскости с плос-
костью горизонта. Когда правое крыло ЛА находится ниже горизонтальной
плоскости, то крен считается
у у' положительным. Углы ориента-
L v ции vg, 0, у называют само-
летными углами, либо углами
Эйлера - Крылова.Определим
матрицы направляющих коси-
нусов при. переходе от геогра-
фической системы координат
OXgYgZg к связанной OXYZ.
Вначале трехгранники
х' OXgYgZg и OXYZ совпадали.
Первый поворот трехгранника
OXYZ осуществляется вокруг
оси OYg на угол у против хода
Рис. 3.5. Поворот на угол рыскания стрелки часов, если наблюдать
за этим перемещением с поло-
жительного конца оси OYg. При этом трехгранник OXYZ занимает некоторое
промежуточное положение OXY'Z' (рис. 3.5).
Нетрудно убедиться, обращаясь к рис. 3.5, что соответствующая таблица на-
правляющих косинусов имеет вид
Xg Yg Zg
X cosvg 0 — sinvp
Y' 0 1 0
Z' sinvg 0 COSKg
В соответствии с таблицей направляющих косинусов введем квадратную
матрицу размера 3x3
cos у
О
sin vg
О -sing
1 О
О cosg
(3.19)
Матрицу можно отождествить с некоторым линейным оператором, ко-
торый, действуя на координатный трехгранник OXgYgZg, переводит его в
124
трехгранник OX'Y'Z'. Символически это можно записать в виде
[XTZ']=4,[^grgzg], (3.20)
Кроме того, символы X', Y' ,Z' и Xg , Yg, Zg можно трактовать как коор-
динаты вектора, заданного соответственно в системах координат XYZ' и
g s g ’
Для анализа угловых перемещений А.Ю. Ишлинским предложена условная
запись [3.9], которая применительно к только что рассмотренному перемеще-
нию имеет вид
^-+OXYZ-
какого
Над
оси,
°Wg—
В этой записи стрелка показывает, из
последующее переходит трехгранник,
стрелкой приводятся две совпадающие
вокруг которых совершается конечный пово-
рот, а под стрелкой - угол этого поворота.
Второй поворот на угол 6 (рис. 3.6) про-
ведем относительно промежуточной оси OZ'
против хода стрелки часов.
Аналогично рассмотренному
вому повороту, введем матрицу
щих косинусов
выше пер-
направляю-
Z'
cos О
-sin О
sin 6
COS0
О
О
1
(3-21)
исходного положения и в какое
Поворот на угол тангажа
Z’.Z”
Рис. 3.6.
Последний поворот осуществим на
угол крена у вокруг оси ОХ”, которая
одновременно является продольной осью
ЛА (рис. 3.7).
Третий поворот переводит трехгран-
ник OX Y Z в конечное положение
OXYZ. Матрица поворота в этом случае
имеет вид
cosy
О
sin у
(3.22)
-sin у
cosy
Ле = Г
Z
О
О
У
1
о
О
О
Z
Полная цепочка преобразований выглядит следующим образом:
YgX Z',Z
ОХYZ —-----------> OX'Y'Z'-----—
g k s V 0

---> OXYZ
У
125
[ATZ] = Л/XT'Z"] = Aq[XYZ'] = A7AQAw[XgYgZg]. (3.23)
Введем обозначение A = , где матрица А является искомой матрицей
преобразования от трехгранника OXgYgZg к OXYZ
cos 6 cos у
sin0 -cos0siny
А= - cosy cosy sin 0 +sin у sin у
sin у cos у sin 0 + cos у sin у
cosycosO cosy sin у sin 0 +sin у cos у (3.24)
- sin у cos 6 - sin у sin у sin 0 + cos у cos у
Так как в алгоритмах бесплатформенных систем навигации осуществляется
преобразование информации из связанного трехгранника в географическую
систему координат, то рассмотрим обратную матрицу
l^gYgZg] = A,[XYZ].
Важно подчеркнуть, что матрицы направляющих косинусов являются орто-
гональными, т.е. для них выполняется равенство
А~' = АТ,
(3.25)
где Т — символ транспонирования.
Введем матрицу С - Аг, которая на основании (3.24) имеет следующий вид
cos 0 cos у
sin0
- cos 0 sin у
- cos у cos у sin 0 + sin у sin у
cos у cos 0
cos у sin у sin 0 + sin у cos у
sin у cos у sin 0 + cos у sin у
- sin у cos 0
- sin у sin у sin 0 + cos у cos у
(3.26)
С =
Таким образом, матрица С осуществляет переход от связанного трех-
гранника OXYZ к географическому OXgY?Z,
[XgYgZg] = C[XYZ].
Найдем проекции вектора абсолютной угловой скорости связанного трех-
гранника на свои ребра. В соответствии с последовательностью поворотов
(3.23), имеем
(3.27)
где со v, wyg , co/g - проекции абсолютной угловой скорости географической
системы координат на соответствующие оси.
Равенство (3.27) с учетом матриц С, А и А^ может быть переписано в ви-
де
у + у sin 0
0 sin у + у cos у cos 0
- у sin у cos 0 + 0 cos у
(3.28)
Первое слагаемое правой части (3.28) представляет собой переносную угло-
вую скорость связанного трехгранника, а второе - относительную. Для опреде-
ления параметров ориентации ЛА необходимо алгоритмически скомпенсиро-
вать составляющие переносной угловой скорости, вызванной вращением Земли
и перемещением ЛА вдоль ее поверхности. Составляющие переносной угловой
126
скорости вырабатываются на основе показаний акселерометров (это будет пока-
зано ниже). Если эти составляющие скомпенсированы, то проекции угловой
скорости трехгранника OXYZ относительно географической системы коорди-
нат OX Y Za имеют вид:
g S S
ы°™ - у + ф sin 0;
со°™ =0siny + ki/cosycos0; >
со™ = -ф sin у cos 6 + 0 cos у.
(3.29)
Разрешая уравнения (3.29) относительно ф , 6 и у, несложно получить из-
вестную систему уравнений:
V = —[оф™ cos у - со™ sin у];
COS0
0 = со™ sin у + со™ cos у;
у = <тн - /g0[co°;H cos у - со°™ sin у ].
(3.30)
Уравнения (3.30) называются кинематическими уравнениями в углах Эйле-
ра-Крылова. Проинтегрировать систему дифференциальных уравнений (3.30)
можно численными методами, в результате чего будут определены параметры
ориентации у , 0, у.
Рис. 3.8. Структурная схема горизонтальных каналов БИНС
127
Структурная схема горизонтальных каналов БИНС представлена на рис. 3.8.
Работа БИНС происходит следующим образом. Блок акселерометров выраба-
тывает проекции вектора кажущегося ускорения пх , nY, nz на ребра связанно-
го трехгранника. Пересчет компонент вектора кажущегося ускорения из связан-
ного трехгранника в географический осуществляется с помощью матрицы С,
которая вычисляется на основании показаний ДУ С. В результате пересчета об-
разуются проекции кажущегося ускорения nXg и nZg на оси географической
системы координат. Из составляющих пх, nZg исключаются компенсирующие
ускорения акХе и aZg , сформированные на основании равенств (3.15), в резуль-
тате чего образуются ускорения относительного движения ЛА Vx и Vz . Дву-
кратное интегрирование ускорений и VZg на основании уравнений (3.17) и
(3.18) позволяет определить координаты местоположения и скорости объекта.
По информации об угловых скоростях ф, Z., широте ср и угловой скорости
Земли U вырабатываются проекции вектора абсолютной угловой скорости
географического трехгранника на свои оси сод. , coyg, coZg на основе соотноше-
ний (3.5). Составляющие угловой скорости coXg, coyg, coZg после пересчета с по-
мощью матрицы С1 поступают в алгоритм ориентации.
Выработка параметров ориентации у , 0, у происходит на основе измере-
ний ДУС. Три ДУС измеряют проекции вектора абсолютной угловой скорости
ЛА cov , еоу, coz на ребра связанного трехгранника. Из показаний ДУС вычита-
ются проекции вектора угловой скорости географического трехгранника на оси
связанной системы координат со"?р, соуер, coz р, которые для ЛА являются пере-
носной угловой скоростью, вследствие чего образуются относительные угловые
скорости со°™, сэутн, cdz™ • По информации о проекциях со°™ > ®°гн> «ZH выраба-
тываются углы рыскания г/ , тангажа 0 и крена у интегрированием уравнений
(3.30). На основании значений углов у, 0, у формируются матрицы С и
Ст - С 1.
Принципиально возможно интегрировать сигналы акселерометров в связан-
ной системе и далее пересчитывать полученные данные в навигационную сис-
тему координат с учетом влияния ускорения силы тяжести и поворотных уско-
рений. В этом варианте заметно больший объем вычислений и его применяют
реже [3.7].
3.2. БИ ИС с направляющими косинусами
3.2.1. Уравнение Пуассона
Одними из распространенных параметров ориентации, используемых в бес-
платформенных системах ориентации и навигации, являются направляющие
косинусы (directional cosines'). Девять косинусов углов между шестью осями ко-
ординат однозначно определяют их взаимную ориентацию.
При принятой ранее последовательности поворотов ЛА на углы у , 0, у и
переходе от связанной с ЛА системы координат к географической OXgYgZg по-
лучена матрица перехода С
128
cos0cos|/ - cos у cos у sin 0 +sin у sin у
sin у cos v sin 6 + cos у sin
sinO
cosycos6
— sin у cos 0
.(3.31)
-cos6sin|/ cos у sin у sin 0 +sin у cosy
- sin у sin v sin 0 + cos у cos у
Метод определения направляющих косинусов через углы последовательных
поворотов приводит к необходимости вычисления произведений двух или трех
функций синусов и косинусов угловых параметров ориентации, что представля-
ет достаточно сложный и громоздкий процесс. Поэтому направляющие косину-
сы чаше используются в качестве самостоятельных параметров ориентации,
поскольку они могут быть вычислены аналитически, если Известны их началь-
ные значения и угловые скорости со v, со,, coz с которыми система OXYZ вра-
щается относительно осей системы OXsYgZg [3.5]. Если матрица (3.31) извест-
на, то углы рыскания, тангажа и крена определяются через се элементы:
~С..
V = arctg—— ;
сп
0 = arcsin с2);
(3.32)
у = arctg——.
С?2
где сн , с2|, с22, с23, с31 - элементы матрицы С .
Рассмотрим способы вычисления матрицы направляющих косинусов [3.5].
Из теоретической механики известно, что дифференцирование вектора г , опре-
деляющего координаты точки в некоторой системе координат OXYZ (коорди-
наты х, у, z), дает линейную скорость
dr
v = — = r (3.33)
dt
с проекциями vx, vr, vz на оси OXYZ.
Если эта система координат вращается с угловой скоростью со относительно
некоторой неподвижной системы координат 0£>т]С,, то абсолютная линейная
скорость точки определяется следующим образом
dr dr
v= — = — + coxr. (3.34)
dt dt
В правой части равенства (3.34) первое слагаемое, отмеченное знаком «~»,
представляет собой скорость точки в системе координат OXYZ, а второе учи-
тывает факт вращения этой системы относительно неподвижной системы коор-
динат О^г]^.
Векторному уравнению (3.34) соответствуют три скалярные, определяющие
проекции вектора v абсолютной линейной скорости точки на оси подвижной
системы OXYZ в виде
vx = x + corz-coz/
vy = y + ci)zx-(oxz; -
(3.35)
vz =z + (йху - CO, X.
В матричном виде операция дифференцирования вектора г по времени в
системе координат определяется выражением
129
dr
dt
(3.36)
где , r], Q - координаты точки в системе координат ОЕ,х] £.
Дифференцирование вектора г во вращающейся системе координат OXYZ
представляется так:
v =
(3.37)
Векторному произведению сох г в матричной форме записи соответствует
произведение кососимметрической матрицы
[со]- 0 со* ~^z 0 соу -cov (3.38)
на матрицу-столбец сог г - со X У Z V 0 (3.39)
Поэтому уравнение (3.35) можно переписать в матричной форме
Координаты точки в подвижной и неподвижной системах координат связаны
матричной зависимостью
а2
а32 a33
(3.41)
которая характеризует преобразование координат, т.е. переход от координат
точки в неподвижной системе координат OEjrfc к координатам той же точки в
подвижной системе координат OXYZ. Матрица А с элементами atj (i,j = 1,2,3)
характеризует именно этот переход.
При обратном переходе от координат точки в системе OXYZ к координатам
в системе ОЕ^С, используется матрица С — Ат, транспонированная по отноше-
нию к матрице А. Соответствующее преобразование координат выражается
зависимостью вида
г = Сг', (3.42)
130
где r =
- матрица столбец из координат точки в системе О^г]^; г'
- то
П
же в системе OXYZ; С — матрица преобразования координат при переходе от
системы OXYZ к системе Ot^C,.
Для установления связи направляющих косинусов с угловыми скоростями
соЛ., cor, coz, с которыми подвижная система координат вращается относитель-
но неподвижной, продифференцируем по времени выражение (3.42)
rCr' + Cr (3.43)
Умножим обе части равенства (3.43) на матрицу А и, учитывая, что
АС = Е, (3.44)
где Е - единичная матрица, перепишем уравнение (3.43) в виде
Аг - г' + АСг'. (3.45)
В уравнении (3.45) левая часть Аг представляет собой абсолютную линей-
ную скорость точки v в подвижной системе координат, вследствие чего урав-
нения (2.40) и (2.45) эквивалентны. Из их сравнения следует, что
АС = [а>], • (3.46)
или
С = С[со]. (3.47)
Уравнение (3.47) можно записать относительно матрицы 4
А = -[(о]А. (3.48)
Уравнение (3.47) или (3.48) хорошо известно в теории инерциальной навига-
ции как матричное дифференциальное уравнение Пуассона, связывающее про-
изводную от матрицы направляющих косинусов с самой матрицей и вектором
угловой скорости со, с которыми система OXYZ вращается относительно не-
подвижной О^гС,.
Таким образом, если имеется информация о проекциях вектора абсолютной
угловой скорости, на оси подвижной системы координат OXYZ, в виде со v, сог,
coz, то направляющие косинусы по отношению к неподвижной системе коор-
динат б?£,т}<2, могут быть рассчитаны путем интегрирования матричного уравне-
ния Пуассона
Ai А 2 Аз А1 С12 Аз 0 -coz СОу
Ai Аз Аз = А. б?22 Аз coz 0 (3.49)
Al Аг Аз Al ^32 Аз -СОу СО у 0
эквивалентно девяти дифференциальным урав-
^13 Al^A Аг^А'’
Аз Al®r С22СОу,
А3 —С?3|СОу С32СОу.
Матричное уравнение (3.49)
нениям первого порядка
А1 ~ АзЮГ’ Аг — Аз®А' — A1®Z’
С2] = C22®z ~ С;,СОГ, с,, = с23соЛ — c21coz,
Ai — c32coz — с33соу, с32 — с33сол. — c3lcoz,
(3.50)
Скалярный вид уравнения Пуассона показывает, что совокупность (3.50)
распадается на три отдельно интегрируемые системы (триады) из трех уравне-
ний каждая. Первая триада имеет переменные сн , с|2, с13, вторая - с21, с2,, с23,
третья - с31, с3,, с33.
131
Следует отмстить, что вектор со - ||со% соу coz||r и соответствующая ему
кососимметрическая матрица [со] в математике называются дуальными объек-
тами, которые связаны между собой посредством символа Леви-Чивита

(3 51)
Если поставить в соответствие вектору угловой скорости со, заданного про-
екциями со., сот;, со, в системе координат > кососимметрическую матрицу
О -со, соп
со, 0 -со,
-СОП со, О
то преобразование компонент вектора
со из системы координат <9£>г|^ в OXYZ
будет осуществлять по закону
0 — <oz соу 0 — СО,
C0z 0 -cov = А со, 0 -со, Аг
— сог (0 х 0 -% (0- 0
(3.52)
3.2.2. БИНС с двумя уравнениями Пуассона
Рис. 3.9. Взаимное положение инерциальной, земной
и географической систем координат
На борту ЛА необходимо
определять его ориентацию
относительно географиче-
ской системы координат
OXgYgZs, вращающейся от-
носительно инерциального
пространства с составляю-
щими вектора абсолютной
угловой скорости coVg, со, ,
coZg . В связи с этим уравне-
нием (3.47) непосредственно
нельзя воспользоваться для
определения параметров
ориентации ЛА, так как оно
записано в предположении
неподвижности системы ко-
ординат О^гС,.
Для решения задачи ори-
ентации ЛА относительно
* Символ Леви - Чивита Eik/ определяется следующими правилами: если значения хотя бы двух
индексов совпадают, то е,и = 0; если все индексы разные и образуют циклическую перестановку
последовательности 1 2 3, то ем = +1; если все индексы разные и образуют циклическую пере-
становку 3 2 1, то е,л, = -1
132
географической системы координат OXgYgZg введем инерциальную систему
координат OUXUYUZU, начало которой поместим в центр Земли, ось OuZu — на-
правим вдоль оси вращения Земли к северному полюсу, ОиХи - по линии пере-
сечения плоскостей экватора и Гринвичского меридиана в начальный момент
времени /0, а ось OUYU образует с первыми двумя правый ортогональный трех-
гранник (рис. 3.9).
Введем земную систему координат OtiX0Y0Z0, оси которой в начальный мо-
мент времени совпадают с инерциальной системой координат OuXuYuZu и вра-
щаются относительно последней с угловой скоростью U + X. Мгновенное по-
ложение системы координат OQXGY0Z0 относительно OuXuYuZu определим с
помощью угла X., называемого инерциальной долготой. Инерциальная долгота
X. связана с географической долготой X соотношением
X. =U(t-t0) + X (3.53)
Совместим вершину трехгранника OXgYgZg с трехгранниками OuXiXuZu,
O0X0Y0Z0 (рис.3.10) и найдем матрицы преобразования между их ребрами
Рис.3.10. Инерциальная OuXuYuZu, земная O0X0Y0Z0 и географическая OXgYgZg
системы координат
Результирующий переход от инерциального трехгранника к географическо-
му найдем как произведение матриц и :
133
В = ВЦ>В}.
-sin (poos X. -sincpsinX. coscp
coscp cos X. coscp sin X. sincp
-sinX. cosX. 0
(3.55)
Рассмотрим обратный переход от географической системы координат
OXgYgZg к инерциальной OuXt<YuZu. Этому переходу поставим в соответствие
матрицу преобразования Си
си=вг = -sincpcosX, coscpcosX. -sincpsinX.. coscp sin X. coscp sinep -sinX, cosX. 0 (3.56)
Введем матрицу преобразования D от связанного с ЛА трехгранника OXYZ
к инерциальному OuXuYuZu
[XuYZu] = D[XYZ]. (3.57)
Используя следующие схемы преобразований
ИЛА] - С [XgYgZg]; HgKgZg] = C[XYZ}, (3.58)
нетрудно показать, что связь между матрицами D, Си и С определяется сле-
дующим равенством
Л = С„С. (3.59)
Так как ДУСы измеряют проекции вектора абсолютной угловой скорости на
ребра связанного трехгранника, то имеет место уравнение Пуассона
Р = Р[<о], (3.60)
где [со] - кососимметрическая матрица, соответствующая проекциям вектора
абсолютной угловой скорости связанного трехгранника на свои оси.
Для определения матрицы Си можно записать второе уравнение Пуассона
Си =C[cog],
(3.61)
где [cog ] - кососимметрическая матрица, составленная из проекций вектора аб-
солютной угловой скорости географического трехгранника на свои оси
0 aYg
[<og] = ®Zg 0 "^g (3.62)
™xs 0
Полученная из решения уравнения (3.61) матрица Си позволяет найти широ-
ту и долготу. Широта ср местоположения объекта на земной сфере может при-
нимать значения в интервале (—л/2, л/2). В этом интервале элементы
c„3i= coscp или CH32=s’n(P матрицы (3.56) определяют широту однозначно
[3.9]. Для определения угла ср обычно используется функция арктангенса:
С
ср = arctg—.
См31
(3.63)
Долгота объекта X принимает значения в интервале (0,2л) и связана с
инерциальной долготой X. соотношением (3.53), из которого получаем
Х = Х.-£/(/-/„).
134
Для определения X. нельзя непосредственно воспользоваться элементом
cul3=-sinX., так как функция arcsinfx) принимает значения (—л/2,л/2). Для
преодоления этой трудности в работе [3.9] предложено воспользоваться функ-
X
цией ctg-^~, которая монотонно убывает в интервале (0,2л) и рационально вы-
ражается через функции cosX. и sinX.
X. 1 + COSX. 1 + Cu9,
ctg— = ——------=------— . (3.64)
2 smX* ~си}3
Таким образом, определяя соответствующие элементы матрицы Си из реше-
ния уравнения Пуассона (3.61) можно найти широту и долготу местоположения
объекта.
Полученные из решений уравнений (3.60) и (3.61) матрицы D и Си позво-
ляют найти матрицу перехода от связанного трехгранника к географическому,
и, следовательно, решить задачу ориентации
C = DCTU. (3.65)
Блок-схема алгоритма БИНС с двумя уравнениями Пуассона для горизон-
тальных каналов представлена на рис. 3.11.
135
3.2.3. БИНС с одним уравнением Пуассона
Рассмотрим другой способ определения параметров ориентации. Обратимся
к матричному уравнению D = Z)[co] и, подставив в него значение матрицы
D = СиС, получим
CUC + СиС = СиС[со], (3.66)
или что то же самое
СнС = С„С[<о]-СиС. (3.67)
Подставим вместо матрицы Си правую часть уравнения Пуассона (3.61):
С = С~1 {С„С[<о]- C„[(og]C}, (3.68)
и, раскрыв фигурные скобки в соответствии с дистрибутивным свойством мат-
риц, окончательно получим
C = C[(D]-[coe]C. (3.69)
Таким образом, для получения матрицы С достаточно решить одно уравне-
ние (3.69), называемое обобщенным уравнением Пуассона. Блок-схема алго-
ритма БИНС с использованием обобщенного уравнения Пуассона приведена на
рис. 3.12.
Рис. 3.12. Блок-схема БИНС с одним уравнением Пуассона
Эффективным средством повышения точности и экономичности алгоритмов
БИНС является использование вместо направляющих косинусов параметров
136
Родрига-Гамильтона. Использование этих алгоритмов вместо равноценных по
точности алгоритмов, основанных на уравнениях Пуассона, позволяет умень-
шить объем вычислений в среднем на 30% [3.7].
3.3. БИНС с параметрами Родрига — Гамильтона
3.3.1. Ось конечного поворота
Следуя работе [3.9]
рассмотрим понятие оси
конечного поворота.
Пусть система координат
Oxyz поворачивается от-
носительно некоторой не-
подвижной системы коор-
динат на произволь-
ный угол <р вокруг неко-
торой оси и, называемой
осью конечного поворота.
Обозначим через I, т, п -
косинусы углов, которые
образует ось конечного
поворота и с осями сис-
темы координат ,
тогда эти же величины
являются соответственно
косинусами углов между
осью и и осями системы
координат Oxyz
Рис. 3.13 Поворот системы координат Oxyz
относительно ОЕу]^ вокруг оси и
cos(w,E>) = cos(w,x) = /,
cos(i/,p) = cos(w, = m, >
cos(n,Q = cos(w,z) = n.
В частности, имеем
I = cosp,
(3.70)
(3-71)
где ц - угол, который образует ось вращения и одновременно и с осью £, сис-
темы координат ^т]^ и с осью х системы координат xyz (рис. 3.13).
Обозначим направляющие косинусы оси х относительно системы координат
ОЕ,т|^ соответственно через а, Ь, с:
cos(x,£) = n, cos(x,r]) = Z>, cos(x,£) = c. (3.72)
Направляющие косинусы удовлетворяют уравнению
а2 +Ь2 +с2 =1.
(3.73)
137
Выразим направляющие косинусы оси х через направляющие косинусы /,
т, п оси конечного поворота и и угол поворота <р. Очевидно, что проекции
единичного вектора х0 оси х на оси системы координат ОЕ^С, равны а, Ь, с,
тогда разложение этого вектора по базису ОЕ^туС, имеет вид
-*-о й£о + ССо ’
где , т)0, £0 - орты координатных осей OE,tyC,.
(3-74)
В свою очередь единичный вектор и0 оси конечного поворота и по этому
же базису имеет следующее разложение:
ho=^o+wt|o + <o- (3-75)
Найдем скалярное произведение векторов х0 и «0
иохо cos(w0, х0) = la + mb + пс, (3.76)
или с учетом первого соотношения (3.70)
la + mb + nc = l. (3.77)
Для определения трех искомых величин а, Ь, с кроме уравнений (3.73) и
(3.74) требуется еще одно уравнение. Для вывода этого уравнения можно вос-
пользоваться тем обстоятельством, что плоскость хи повернута относительно
плоскости Е^и вокруг оси вращения и на угол (р. Так как двугранный угол из-
меряется углом между двумя перпендикулярами к образующим его плоскостям,
то введем два вектора h и к, первый из которых перпендикулярен плоскости
Еи , а второй — плоскости хи (рис. 3.13). Согласно свойству скалярного произ-
ведения двух векторов имеем
hkcostp = А.А. + h к + h.kQ (3.78)
где /г, , Л. - проекции на оси ^т|<^ вектора h ; А,, к^, — проекции на те же
оси вектора к.
В качестве вектора h возьмем векторное произведение единичных векторов
«О И £о
Л = «ох = ъ по ;0 1 т п 1 0 0
(3.79)
Таким образом,
А. =0, = л, = -т. (3.80)
В качестве вектора к можно взять векторное произведение векторов и0 и
*0
к = и0 х х0 - /
По Со
т п
b с
(3-81)
Раскрывая определитель (3.81), получаем следующие равенства
k.^=mc-nb, кл - —(1с - па), к^=1Ь-ат. (3.82)
138
Модули векторных произведений (3.79) и (3.81) одинаковы и равны синусу
угла р. между осями и и или, что то же, между осями х и и. Таким образом,
учитывая формулу (3.71), имеем
к - h = sinр = V1-72. (3.83)
С учетом найденных проекций (3.80) и (3.82) уравнение (3.78) принимает
вид
(1 -Z2)coscp = а(п2 + m2)-l(nc + mb), (3.84)
которое и является недостающим третьим уравнением, помимо (3.73) и (3.77).
Так как
72 +т2 + п2 = 1,
то
т2+п2 = 1-72. (3.85)
Из (3.77) вытекает равенство
nc + mb = 7(1-а). (3.86)
Тогда уравнение (3.84) с учетом (3.85) и (3.86) принимает вид
(1 -12) cos ф = а(1 - 72) -12 (1 - а). (3.87)
После несложных преобразований находим величину а, выраженную через
7 и ф
а = 72(1-со8ф) + со8ф. (3.88)
Для определения величины Ь исключим из соотношения (3.73) косинусы а
и с посредством формул (3.77) и (3.88). В результате придем к квадратному
уравнению
Ъ2 -27>7/и(1-со8ф) + 72/и2(1-со8ф)2 -п2 sin2 ф = 0 (3.89)
Из двух корней этого уравнения
= 7/и(1 — созф) + л sin ф, Т>2 = 7w(l-cosф)-zzsin ф (3.90)
следует остановиться на первом. Действительно, рассмотрим частный случай:
ось и совпадает с осью С>, а угол ф = л/2. В этом случае направляющие коси-
нусы оси конечного поворота (рис. 3.14) равны
7 = cos(w,^) = cos(ti/2) = 0,
tn - cos(n,r|) = cos(rc/2) = 0,
n = cos(w,Q = cos(O) = 1.
Тогда Z>,'=+1; b2 =-l. Так как 7? = cos(x,г]), а исходя из рис. 3.14 оси х и г|
совпадают, то однозначно b = +1. Таким образом, в общем случае
7> = 7ш(1-со8ф) + л8тф. (3-91)
Подставив выражения (3.88) и (3.91) для а и b в уравнение (3.77), получим
формулу для определения величины с
с = л7(1-со8ф)-/и8Шф. (3.92)
139
Рис. 3.14. Поворот системы координат Oxyz на угол ф = л/2 вокруг оси С,
Аналогично определяются косинусы углов между осью у и осями £, т], £ и
далее между осью z и теми же осями , т], С,. В итоге таблица косинусов уг-
лов между осями систем координат xyz и £,Т]^ может быть представлена в сле-
дующем виде [3.9]:
л £
X (1 — COS ф)/2 + COS ф (1 — cos y)ml + п sin ф (1 - cos ф)и/ - т sin ф
У (1 - cos ф)/ли - п sin ф (1 — cos ф)ли2 + cos ф (1 - cos ф)/ии + / sin ф
Z (1 — cos ф)лг/ + ли sin ф (1 — cos ф)/ии — 1 sin ф (1 - cos ф)и2 + cos ф
(3.93)
В этой таблице величины I, т , п — косинусы углов, которые образует ось
поворота и с осями ОЕ^С,, а также с осями Oxyz.
3.3.2. Параметры Родрига - Гамильтона
Каждому повороту тела на угол <р вокруг оси и с направляющими косину-
сами I, т и п, заданными относительно исходной системы координат £,т](^
ставятся в соответствие четыре числа, называемые параметрами Родрига-
Г амильтона, [3.9]:
Z.n=cos—, A,. =/sin—,
2 2
2 2 (3.94)
. . <р . . ф
А, = ли sin —, Л. = nsm—.
2 2 3 2
Параметры Родрига - Гамильтона связаны друг с другом очевидным соот-
ношением
140
X2 + X2 + Л.2 + Л.2 = 1. (3.95)
Представим таблицу направляющих косинусов (3.93) через параметры Хо,
X,, Х2, Х3. Учитывая, что
, а • гФ ~ 7 ф .
l-cos<p = 2sin у, cos<p = 2cos у-1,
элемент (1,1) таблицы (3.93) может быть представлен в виде
(l-coscp)/2 +cos<p = 2sin2-^Z2 +2cos2y-l = 2Х2 +2Х2 -1.
__ . _ . ф <р
Учитывая, что зшф = 2sin—cos —, получим элемент (1,2) таблицы (3.93)
(1 - cos q>)ml + п sin ф = 2 sin2 у ml + 2п sin у cos у = 2ХД., + 2ХОХ3.
Аналогичным образом могут быть найдены остальные элементы таблицы
(3.93), которую можно представить в виде
П С
X 2Х2+2Х2-1 2А.]Л.2 + 2ХоА,3 2Х]Х3 — 2A.0Z2
у 2Л.1Х2 — 2А.оХ3 2Х2+212-1 2Л,2Х3 + 2А.О
Z 2А.[Х3 + 2Х0Х2 2Х2Х3 -2АД, 2А,2+2Л.3-1
(3.96)
Если, например, вместо осей % , т) , приять оси географической системы
координат OXgYgZg, а вместо х, у, z - оси связанной системы координат
OXYZ, то матрица (3.96) явится аналогом матрицы направляющих косинусов,
полученной в п. 3.1.1:
A =
COS0COS|/
sin0 - cos 0 sin ф
- cosy cos ф sin 0 + sin у sin ф
cosycos0 cos у sin ф sin 0 +sin у cos ф
(3.97)
sin у созф sin 0 + cosy sin ф
— sinycos0 —8ту8Щф8т0 + СО8уСО8ф
Таким образом, взаимное положение двух систем координат помимо трех
углов Эйлера - Крылова, девяти направляющих косинусов, можно определить с
помощью четырех параметров Родрига - Гамильтона.
3.3.3. Кватернионы
Определенную систематизацию вычислений, связанных с нахождением па-
раметров Родрига - Гамильтона и сложением конечных поворотов дают, так
называемые, кватернионы — гиперкомплексные числа вида
141
Л — 7An + iX, + jk-> 4* ЛХ3
(3.98)
с одной действительной 1 и тремя мнимыми единицами i , j, к .
Кватернионы впервые были введены в математику в 1843г. В.Р. Гамильто-
ном при разработке нового аппарата гиперкомплексных чисел, аналогичного
аппарату комплексных чисел на плоскости.
Величины 7Л0 и + у’Х2 + АА3 называются соответственно скалярной и
векторной частями кватерниона и обозначаются
5(Л) = 7Х0;
К (Л) = + к^.
Следовательно, кватернион (3.98) можно представить в виде
Л = 5(Л) + К(Л). (3.99)
Кватернионом, сопряженным данному кватерниону Л , является кватернион,
обозначаемый Л и определяемый следующим образом
Л = 5(A) - К(Л) = 7Х0 - а, - ,/л2 - АХ3. (3.100)
Кватернион можно рассматривать как вектор в четырехмерном пространст-
ве, длина которого называется тензором (tensor) или модулем кватерниона [3.2,
3.21] и обозначается
|л| = 7^ + х2 +х2+х23 - (З.Ю1)
Следуя работам [3.2, 3.21] рассмотрим основные свойства кватернионов.
Пусть даны два кватерниона Р = 7р0 + ^ + jp2 + Ар3, Q = lq(i+icp+ jq2 + kq2.
1. Суммой P + Q кватернионов P и Q называется кватернион
P + Q^lP^+iPx +JP2 +кРз+1(10+Щ +j^2 +кЧз = (3 W2)
= i(p0+qJ+i(Px + qj+j(p2 + q2)+k(p2 + q2)-
Сумма кватернионов подчиняется свойствам
а) коммутативности Р + Q - Q + Р;
б) ассоциативности P + (Q + R) = (P + Q) + R.
2. Разностью PQ кватернионов Р и Q называется кватернион
Р - Q = 1р0 + iPi + jp2 + кр2 - lq0 - iqx - jq2 - kq5 = (3 103)
=i(p0-q0)+i(P!-qj+j( p2-q2)+k( p2-qJ
3. Произведение кватернионов обозначается символом «°» и определяется
правилами умножения мнимых единиц
7 ° i = i ° 7 = i, 1° j - j ° 1 = j, l°k — kol = k, 7 ° 7 = 7,
i2=-l, /=-1, X2=—1, (3.104)
io j - —j ° i = k, j<>k = -k°j = i, koi = —i°k= j.
Гамильтон для обозначения тензора кватерниона использовал литеру Т, т.е.
Т(А) ~ Xq -+ X] + А.2 + X3 (см. [3.21]).
142
Правила умножения мнимых единиц могут быть по-
лучены циклической перестановкой мнимых единиц по
схеме представленной на рис. 3.15.
В соответствии со схемой на рис. 3.15 при умножении
двух единиц, расположенных по стрелке, получается
третья единица с плюсом; при движении против стрелки
единица берется с минусом.
♦77 р и м е р 3.3.1. Найти произведение двух кватер-
нионов М - р01 + р3Л и N - v01 + V]Z.
Решение.
Рис. 3.15. Правила ум-
ножения мнимых единиц
Пользуясь правилами умножения мнимых единиц (3.104) (либо схемой на
рис. 3.15), получим
М °7V = (ц0/ + МзЛ)°(v07 + v,i) = pnv07 ° 1 + p0v,7 °i + p3vn/r ° 1 + p3v,k-i =
i ♦
= 1W + nov,7 + p3vj + p3v0£
Из примера 3.3.1 видно, что компонент 1 ведет себя как обычный скаляр,
поэтому его будем в дальнейшем опускать при написании кватернионов.
♦/7 р и м е р 3.3.2. Найти произведение кватернионов Р = рп + ip} + jp2 + кр3
и 2 = + М2 + кЯз-
Решение.
р„ + ipx + jp2 + кр3 множимое о
Чо + Ч + 'РР + кЧз множитель
+ РоЯо + Ч^Чу + 'НуЧ2 + кРу>Чз
~РхЯх + Ф/7о - ГРуЧз + kptq2
- p2q2 + ip2q3 + jp2q0 -kp2qx
~ РзЧз - ip3q2 + jp3qx + kp3qa
РоЯо ~ РхЯу - Р2Я2 - Рз<7з + i( Р»Я + РхЯ0 + РгЧз ~ Р3Ч2) +
+ К Р0Я2 ~ РхЯз + Р2Ч0 + РзЯх ) + к( РоЯз + РуЯ2 ~ Р2Ях + Рз^о )
Результат произведения кватернионов можно представить в виде
р ° Q = РоЯо -Pi4t~ Р2Я2 - РзЯз + Ро <‘Я1 + J41 + ^/з) + Яо (iPi + JP2 + кр3) + } Q5
+ КР2Я3 ~ РзЯ 2)+ ЛРзЯх -РЯз) + к(рхч2 -p24i)
♦
Замечая, что последние три слагаемые в (3.105) образуют определитель,
произведение (3.105) перепишем следующим образом:
i J к
р ° Q = РоЧо -РхЯ- Р2Я2 - РзЯз + Роу (Q) + Я (У (Р) + Рх Р2 Рз (3.106)
Я Я2 Яз
143
Если ввести векторы р = (рх,р2,р2) и q=(q},q2,q2), то произведение ква-
тернионов можно представить в виде
P'Q= РоЯо~Р Ч + А/(0 + 4(/(р) + РХЯ (3.107)
Здесь символами «•» и «х» обозначено соответственно скалярное и вектор-
ное произведение введенных выше векторов.
С помощью символов S и V можно получить еще одно представление произ-
ведения кватернионов
Р - Q = S(P)S(Q) + S(P)V(Q) + V(P)S(Q) + V(P) о F(0). (3.108)
Из сравнения правых частей (3.107) и (3.108) следует, что
V(P)°V(Q) = -pq + p*q. (3.109)
Таким образом, произведение векторных частей кватернионов Р и Q вклю-
чает сразу и скалярное и векторное произведения.
Наличие в равенстве (3.106) определителя (или, что то же самое, в равенстве
(3.107) векторного произведения) указывает на некоммутативность произведе-
ния квач ернионов
PvQ^QoP. (3.110)
Произведение кватернионов
а)ассоциативно
Л°(М Л) = (ДоЛ/)°7У; (3.111)
б) дистрибутивно относительно сложения
Л-(М+ 7V) = A°Af+ До Д. (3.112)
Найдем произведение кватерниона Л и сопряженного кватерниона Л
Л ° Л = [*V(A) + Г (Л)] о [5(Д) - Г(Л)] = 5(A)2 - Г (Л)2.
Исходя из того, что
S(A)2=X2;
Г(Л)2 = У(Л) о Е(Л) = (-Х • X + X X X) = -X X = -(X2 + X2 + X2).
следует
АоЛ = ЛоЛ-Х20+Х2+Х22+Х23=|л|2. (3.113)
Число |л|2 называется нормой кватерниона и обозначается ||л||
||л||=|а|2=х2+х2+х2+х2. (З.П4)
Если норма ||л|| = 1, то кватернион Л называется нормированным.
Рассмотрим произведение кватернионов Р и Q имеющих нулевые скаляр-
ные части, т.е. S(P) - 0 и S(Q} = 0 . На основании соотношения (3.109), имеем
Р°Q = -p q + p*q . (3.115)
Так как скалярное произведение р q коммутативно, то
Q°P = -p q-p*q. (3.116)
Складывая и вычитая равенства (3.115) и (3.116), получаем кватернионные
аналоги скалярного и векторного произведений векторов:
144
p g = ~(P°Q + Q°JJ),
P^4 = 6pQ-QP)
(3.117)
В табл. 3.1 приводятся формулы векторной алгебры, где слева написаны
обычные векторные формулы, справа их кватернионные аналоги.
Таблица 3.1
Формулы векторной алгебры и их кватернионные аналоги
Векторные обозначения Кватернионные обозначения
Вектор
Р Р
Модуль вектора
А = Р Р =Р
Сумма векторов
p + q = r P + Q = R
Скалярное произведение
Р Я -^(PoQ + Qop)
Векторное произведение
РХЯ ^(P.Q-Q.P)
Косинус угла между векторами
Р Я cos<p РЯ P°Q+Q°P cos ср = — 2PQ
Условие ортогональности векторов
РЯ = ® PQ=QP
Условие коллинеарности векторов
p*q = 0 PQ=QoP
Смешанное произведение векторов
> Р (Яхг) ^(RoQoP-PoQoR)
Условие компланарности векторов
Р (я*г) = 0 RQP - P°Q R
4. Обратный кватернион Л 1 определяется из условия
Л Л 1 =Л '°А-1.
145
(3.118)
Умножим обе части равенства Л 1 ° Л = 1 справа на сопряженный кватерни-
он Л,получим
Д’ оДоД = 1°Л.
С учетом ассоциативности произведения кватернионов и равенства (3.113)
находим выражение для обратного кватерниона
Для нормированного кватерниона справедливы соотношения
A = A4, Л°Л = Л°Л = 1. (3.120)
5. Собственным кватернионом называется кватернион, компонентами кото-
рого являются параметры Родрига - Гамильтона. Так как параметры Родрига -
Гамильтона связаны соотношением (3.95), то собственный кватернион является
нормированным.
Найдем собственные кватернионы для последовательности поворотов, ха-
рактеризующих ориентацию JIA относительно географической системы коор-
динат OXgYgZg , рассмотренных в разделе 3.1. Итак, первый поворот связанной
системы координат OXYZ происходит вокруг оси OYg против часовой стрелки,
вследствие чего связанная система координат заняла промежуточное положение
OXYZ' . Следовательно, осью первого конечного поворота их является направ-
ление оси OYg (рис. 3.16).
Рис. 3.16. Ось конечного поворота при вращении на угол
Найдем направляющие косинусы Z,, тх, п} оси конечного поворота их:
/, = cos(w,, Xg ) = cos(7i / 2) = 0,
тх = cos(W],Yg) - cos(O) = 1,
nx - cgs(ux ,Zg) = cos(tt / 2) = 0.
146
(3.121)
w
Следовательно, из четырех параметров Родрига - Гамильтона p0=cos—,
р, = l} sm у, р2 = тх sin = sin 2 отличных от НУЛЯ будут только два
/>(1=cos^-, p2=sin^-. (3.122)
Совокупности параметров (3.122) поставим в соответствие собственный ква-
тернион
Р = cos-^- + ysin-y. (3.123)
Аналогично могут быть получены кватернионы, характеризуй >щие повороты
на углы 0 и у. В табл. 3.2 приведены направляющие косинусы оси конечного
поворота и параметры Родрига - Гамильтона для этих поворотов.
Таблица 3.2
К составлению собственных кватернионов при повороте на углы 0 и у
Иллюстрация конечного поворота
Направляющие косинусы
оси конечного поворота;
параметры Родрига - Гамильтона
/2 = cos(w,, х'} = cos(7l / 2) = О,
т2 = cos(i/2, у’) = cos(n: / 2) = О,
п2 = cos(z/2, z') = cos(O) = 1.
0 . 0
<7o=cos-> ?3=sin-
/3 = cos(w3,x") = cos(O) = 1,
w3 - cos(w3, y") = cos(ti / 2) = 0,
n2 - cos(i/3, z") = cos(7l / 2) = 0.
у . у
rn=cos—, r. = sin—
0 2 1 2
147
Пользуясь табл. 3.2, введем кватернионы, характеризующие повороты свя-
занной с ЛА системы координат на углы тангажа и крена вокруг осей Z',Z" и
ХХ
0 0 у V
Q — cos — + Asin —, 7? = cos—+ /sin—. (3.124)
2 2 2 2
При определенных навыках составления собственных кватернионов, отве-
чающих последовательности конечных поворотов можно, опускать определение
направляющих косинусов оси конечного поворота и формально руководство-
ваться следующим правилом. Скалярная часть кватерниона всегда отлична от
нуля, за исключением случая поворота на угол л. В векторной части кватер-
ниона отлична от нуля компонента, соответствующая оси, вокруг которой про-
исходит поворот. Например, если поворот происходит вокруг оси X, то отлич-
на от нуля компонента при мнимой единице i , аналогично У -> j, Z к . Если
конечный поворот происходит по ходу стрелки часов, то векторная часть ква-
терниона пишется со знаком «минус» - образуется сопряженный кватернион.
Для того чтобы определить результирующий кватернион
А = Хо + ТА-! + у’Х2 + Ал3, характеризующий взаимное расположение трехгранни-
ков OXgY„Z и OXYZ, необходимо найти произведение [3.9]
A = Po£°/?. (3.125)
Пользуясь правилами умножения кватернионов найдем компоненты , X,,
Х2, Х3 результирующего кватерниона А. Так как произведение кватернионов
ассоциативно, то найдем первоначально произведение PQ
п „ f v . v3 ( 0 . . 03
P°Q- cos—ь /sin— ° cos— + Asm— =
( 2 2) V 2 2)
Ш 0, Ш . 0 . . W 0...W.0
= cos-— cos— + Acos—sin—+ /sin—cos—+ /^Asm—sin —=
22 22 2 2^22
l
w 0..W.0 . . w 0, w . 0
= cos—cos—+1 sin—sin —+ /sin—cos— + к cos—sin—.
22 22 22 22
Далее найдем результирующий кватернион A
. ( и/ 0 . . w . 0 . . w 6, V • 6 ’ ( у . • уЗ
A= cos—cos—+ <sm—sin —+ /sm—cos—+ Acos—sin— P cos—+ism — =
(22 22 22 2 2j < 2 2)
V 6 У . v 0 . у . . V . 0 V., .W.0.Y
= cos—cos—cos— +1 cos—cos—sin — +1 sm—sin—cos — + г sm—sin - sin — +
222 222 222 222
. . w 0 у . , . w 0 . у » Ш.0 У , . w . 0 . у
+ /sm—cos,—cos —+ /°isin—cos—sin —+ «cos—sin—cos— + к ° icos—sm—sin— =
222 222 222 2 2 2
W 0 Y - V • 0 • У ( V 6-У . V . 0 уЗ
= cos—cos—cos—-sm—sm—sin —+ / cos—cos—sin —+ sm—sm—cos— +
222 2 2 2 ( 2 2 2 2 2 2)
.(VI/ 0 У V . 0 . у , ( ч/. 0 Y . V 0 . Y
+ / sm — cos—cos—+ cos—sm—sin — +A cos—sm—cos—-sm —cos—sin— .
{ 2 2 2 2 2 2) ( 2 2 2 2 2 2)
Приравняв составляющие при мнимых единицах, получим:
148
, • V 0 y . V . О . у
А„ - cos—cos—cos—-sin—sin—sin—,
0 2 2 2 2 2 2
, V 0 . Y . v . О у
A. =cos—cos—sin— + sin — sin—cos—,
2 2 2 2 2 2 (3.126)
, .у 0 Y V . 6 . у
A, - sin—cos—cos— + cos—sin—sin—,
2 2 2 2 2 2 2
. w . 0 y -V 6 • У
A. = cos—sin—cos—-sin—cos—sin—.
3 2 2 2 2 2 2
6. Рассмотрим, как преобразуются компоненты некоторого неизменного век-
тора г при переходе от системы координат OXgY Z к системе OXYZ. Введем
следующие квач ернионы, составленные из компонент вектора в системах коор-
динат OXgYgZg и OXYZ:
R = rv i + rY i + п. к,
s XS YSJ * (5.ПТ)
R = rxi + fyj + r2k.
Кватернионы R и R называются гиперкомплексными отображениями (или
просто отображениями) вектора г на базисы OXgY Z и OXYZ. Если переход
от системы координат OX.YgZ. к системе OXYZ осуществляется посредством
кватерниона Л, то имеет место следующее равенство [3.2, 3.3]
й = ЛоЛ?оЛ. (3.128)
Соотношение (3.128) - это, так называемое, равенство перепроектирования
[3.3], которое позволяет найти компоненты неизменного вектора г в системе
координат OXYZ по компонентам этого же вектора, заданного в системе коор-
динат OX YgZg .
Умножим обе части равенства (3.128) справа на Л, а слева на Л
Ло/?ол = АоДо/г? о д о д
Учитывая свойства нормированного кватерниона (Л ° Л = Л ° Д = 1), полу-
чим
R =До/?оД. (3.129)
Формула (3.129) является обратным равенством перепроектирования и по-
зволяет по известным проекциям вектора г на оси системы координат OXYZ
найти проекции г на оси системы OX Y Z
^Пример 3.3.3. Вектор кажущегося ускорения п задан проекциями
(EVg,g,0) в географической системе координат OX..YZg. Связанная система
координат OXYZ повернута на угол 0 вокруг оси Z (рис. 3.17). Требуется
найти компоненты вектора кажущегося ускорения п в связанной системе коор-
динат.
149
Решение.
Так как осью поворота являются две совпадающие оси Z и Z', то собствен-
ный кватернион преобразования имеет вид (см. формулу (3.124)):
е , - е
О = cos— + KSin— .
2 2
Обозначим через JV, гиперкомплексное отображение вектора ng ;
JVg=VXgi + gj.
e . e,)
cos— + sin—к -
2 2 J
17 w -W|-Ir/-W w I ’ Г 0 6 ,
K, cos—+ gsin — k+ -rv, sin — + gcos— / ° cos— + sin—к
Afi э Ц A* 2 2 J J V 2 2
e ( TZ . e eV e
cos—+ -VY sin—+ gcos— sin— i +
2 L 2 2) 2
01 •
2 J
e ev
Найдем компоненты вектора п в новой системе координат, пользуясь равен-
ством перепроектирования:
JV = Q ° Jfg ° Q = ^cos у - sin у А:"] ° (VXgi + gy)
X - .°. -.ov
7 Afi 2 °’ 2у
7г/ 0
= I rA-gCOS- + gSin- I'
’ V 6 - 6 I • -
+ - cos— + gsin— sm —+
I s 2 2 J 2
2 ° "2
. e
e
2
. e
2
r/ . e еЛ e
-V.. sin—+ geos— cos—
Ag 2 2) 2
2
После несложных тригонометрических преобразований получим
Л - (VAg cos 6 + g sin 0)i + (-VXg sin 0 + g cos 0) j,
откуда искомые компоненты вектора кажущегося ускорения и в связанной сис-
теме координат имеют вид
пх = FVg cos 0 + g sin 0; пу = -ГИ sin 0 + g cos 0..
Правильность полученных проекций нетрудно проверить, пользуясь непо-
средственно рис. 3.17. ♦
150
3.3.4. Кватернионные матрицы
Для сокращения объема вычислений, связанных с произведением кватер-
нионов, удобно пользоваться кватернионными матрицами (quaternionic matrix)
размера 4x4, составленных из компонент кватерниона. Для собственного ква-
терниона вращения Л = Хо + + jk2 + кк3 такая матрица имеет вид [3.14]
к -к -х2 -к
К К -X. к
М(Х) = 3 2.
Х2 Х3 ^0 — Х1
к -х2 к к
(3.130)
Аналогично можно поставить кватернионную матрицу в соотвехсгвие ото-
бражению вектора. Если гиперкомплексное отображение вектора со имеет вид
Q = icov + jcOy + Atoz, (3.131)
то соответствующая кватернионная матрица составляется следующим образом:
0 - СО у - СОу -coz
со.. 0 — со7 СОу
М(со) = (Оу coz 0 -СО у (3 132)
coz -СОу СОу 0
Матрица (3.132) имеет на главной диагонали нули в силу того, что скалярная
часть отображения вектора равна нулю, и представляет собой кососимметриче-
скую матрицу размера 4x4. В матрице (3.132) показан минор элемента (1,1),
т.е. матрица, полученная вычеркиванием первой строки и первого столбца. Ес-
ли вспомнить кососимметрическую матрицу [со], введенную в разделе 3.2, то
нетрудно заметить, что она совпадает с указанным минором матрицы Л/(со).
Следовательно, матрицу (3.132) можно представить в виде клеточной матрицы*
[3-14]
0
— СОу — coz
М(со) =
<оА,
сог
[со]
(3.133)
coz
Матрица [со] называется векторным ядром матрицы 7И(со) [3.14].
Наряду с ^матрицами Л/(Л.) и Л/(со) вводятся столбцевые матрицы размера
4x1 (4-мерные векторы), составленные их элементов кватерниона. Так, для
кватерниона Л и отображения вектора Q (3.131) такие столбцевые матрицы
имеют вид
Клеточной или блочной матрицей называется матрица, элементы которой (клетки) являются
некоторыми матрицами. Любую матрицу можно представить в блочной и клеточной форме и
притом многими способами.
151
М(Х),
(3.134)
С помощью кватернионных матриц
(3.134) произведение кватернионов
Af(co) и столбцевых матриц
представляется в виде
РКМ
Ро Хо -Х2 -Х3 Цо
Р х0 -Х3 х2 Mi
Р2 х2 Л3 хо -м М2
Рз х3 -Х2 >-0 Мз
(3.135)
Таким образом, произведению кватернионов Л и М соответствует умно-
жение кватернионной М(X) и столбцевой матрицы р.
Л о М М(Х)р,
(3.136)
где знаком <-> показана эквивалентность (изоморфность) операций умноже-
ния кватернионов с одной стороны и матриц с другой стороны.
♦77 р и м е р 3.3.4. Найти произведение двух кватернионов М = р0 + рЛ и
7V = v0+v1i, рассмотренных в примере 3.3.1, с помощью кватернионной и
столбцевой матрицы.
Решение.
Пользуясь правилом составления кватернионной (3.130) и столбцевой (3.134)
матриц, находим
М-о
0
о
Из
Но
Мз
о
О
в
Сравнивая с примером 3.3.1 можно убедиться
зультатов. ♦
совпадении полученных рс-
Кроме матриц Л7(Х) и Л/(со) вводятся также матрицы Л7(Х) и Л/(со) [3.14]
Хо -к — Х2 0 - сох - со -со.
М(Х) = к Х2 Хо — Х3 Х3 *0 — Х2 , 2И(со) = “х J [cof , (3.137)
Х3 Х2 -к Хо со. ;
отличающиеся от матриц Л/(Х) и М (со) своими транспонированными вектор-
ными ядрами.
Отметим несколько свойств матриц 7И(Х) и Л/(Х) [3.14].
152
1. Подобно матрицам направляющих косинусов матрицы М(А) и М(Л.) ор-
тогональны, т.е.
М '(А) = ЛГ(А), Л/ ’(А) = ЛГ(А), (3.138)
причем матрица Мт(к) соответствует сопряженному кватерниону Л.
2. Матрицы Л/(А) и 7И(А) коммутируют между собой
Л/(А)М(А) = 2И(А)Л/(А). (3.139)
3. Через матрицы 7И(А) и М(А.) легко выражается матрица направляющих
косинусов А в параметрах Родрига-Гамильтона
7W(A)7Wr(A) = 1 i 0 0 0
0 (3.140)
0 А 0
Существует еще один способ задания кватернионных матриц вида:
К -К -Х2
А, А„ -а3 -А,
Ж(А) = 1 ^2 А3 к 2 К (3.141)
Х2 -к к
Матрица .41 (К) отличается от кватернионной матрицы Л£(А) знаком при
элементе А3 в первой строке и в первом столбце и знаками в векторном ядре.
Произведению кватернионов Л и М соответствует умножение кватернионных
матриц Л^(А) и Ж(р)

(3.142)
♦ Пример 3.3.5. Найти произведение двух кватернионов М - ц0 + р3Л и
TV = v0 + vj, рассмотренных в примерах 3.3.1 и 3.3.4 с помощью кватернион-
ных матриц Ж(А).
Решение.
В соответствии с определением матрицы (3.141), имеем
Мо 0 0 Мз Vo -Vj 0 0 Movo -Movi -M3V1 M3V0
0 Мо “Из 0 V) vo 0 0 Movi Movo -M3v0 -M3V1
0 Из Мо 0 0 0 Vo Vi M3vi M3v0 Movo Movi
~Мз 0 0 Мо 0 0 -V! Vo -M3V0 M3V1 -M0V1 Movo
Обращаясь, например, к первому столбцу полученной матрицы, находим ква-
тернион соответствующий результату произведения кватернионов М и Л
Movo + Pov1f + p3v1j + p3vo^.
153
Сравнивая полученный результат с кватернионом, найденным в примере
3.3.4, приходим к выводу об изоморфности операций умножения с помощью
матриц Ж(Д) и Л/(Х). ♦
Следует отметить, что матрица подобно матрице Л/(Л) является ор-
тогональной (проверьте это свойство).
3.3.5. Кинематическое уравнение для кватерниона
В разделах 3.1 и 3.2 для построения БИНС использовались кинематические
уравнения для углов Эйлера-Крылова и направляющих косинусов (уравнения
Пуассона). Получим кватернионный эквивалент матричного уравнения Пуассо-
на, рассмотренного в разделе 3.2. Заменим векторное уравнение абсолютной
линейной скорости точки
dr
v= —+ сохг (3.143)
его кватернионным аналогом. Используя формулу векторного произведения в
пространстве кватернионов (3.117), уравнение (3.143) запишем в виде:
Г= — + -(Q- о Q), (3.144)
dt 2
где V , О,, R - гиперкомплексные отображения вектора абсолютной линейной
скорости v, вектора угловой скорости со и вектора г . Пусть переход от непод-
вижной системы координат к подвижной XYZ осуществляется кватернио-
ном Л, тогда преобразование компонент вектора г' из системы координат
OXYZ в компоненты вектора в системе Ofy]Q подчиняется обратному равенст-
ву перепроектирования (3.129)
R = Л R' ° Л .
Продифференцируем обе части последнего равенства по времени
Я = Л°Я' оЛ+ДоЛ'оЛ + ЛоЯ'оЛ. (3.145)
Умножим уравнение (3.145) слева на кватернион Л, а справа на Л и полу-
чим
Л ° Л = Л ° Л ° Л ° Л + АЛ ° Л’ °Л ° Л + Л Aj °Л°А. (3.146)
Учитывая свойство нормированных кватернионов A°A = A°A = 1 и, меняя
последовательность членов правой части равенства (3.146), имеем
A°R°A = R' + A°A°R' + R'°A°A. (3.147)
В уравнении (3.147) величина A°R°A есть абсолютная линейная скорость
V , поэтому правые части (3.144) и (3.147) равны. Приравнивая вторые слагае-
мые в правых частях уравнений (3.144) и (3.147), получим
Л°Л=—Q,
2
или
2A = A°Q. (3.148)
154
Равенство (3.148) и есть искомое кинематическое уравнение для кватернио-
на. Приравняв третьи слагаемые в уравнениях (3.144) и (3.147), получим диф-
ференциальное уравнение относительно сопряженного кватерниона
2A = -Q°A. (3.149)
Запишем уравнение (3.148) в матричной
Хо A.Q А.^ А.2 А.3 0
2 А. 2 -- Х| Xq — А.3 А,2 А-2 А,3 Xq — X] е е ч * (3.150)
^3 ^-3 ^1 ^0 со.
и в скалярной форме
2Х0 = —XjCO^ — Х,соу — X3<oz,
2A.J =A,o(ov — Z,3(oy + X2coz, (з 151)
2Z2 = Х3со у + XqCDj, — ,
2Х3 — — Х2(о v + Xtcoy + Xocoz.
Кинематические уравнения (3.151) позволяют по известным проекциям сод.,
соу, coz вектора абсолютной угловой скорости <о на оси подвижной системы
координат найти параметры Родрига - Гамильтона Хо, X,, Л,2, Х3, характери-
зующие положение подвижной системы координат XYZ , относительно непод-
вижной сад.
При численном решении кинематических уравнений могут возникнуть вы-
числительные погрешности, связанные с уходом нормы кватерниона [3.2], т.е.
когда перестает выполняться равенство Л ° Л = 1. Для автоматической норми-
ровки кватерниона необходимо вместо уравнения (3.151) решать уравнение ви-
да [3.2]
2Л = Л°П + Л(1-||Л||). (3.152)
В отличие от (3.151) уравнение (3.152) снабжено членомЛ(1 - ||Л||), который
обеспечивают автоматическую коррекцию нормы кватерниона.
Уравнение (3.152) в скалярной форме имеет вид:
2Х0 = —Х.|(о% — Х2соу — X3coz + Хо[1— (Х20 + А.2 + Л,2 + А.2)],
2A.J = А,осоа. — А.3(оу + A.2coz + Xj [1 — (А?о + А,2 + А.2 + А,2)],
2А.2 = А.3сол. + А,осоу — + А,2[1 — (АД + А,2 + А,2 + А.3)],
2А,3 = — А.,со v + XjCOy + A.ocoz + A.3[l — (А.2 + A/j + А,2 + А.3)].
(3.153)
Кинематические уравнения (3.153) с коррекцией нормы кватерниона не-
сколько сложнее уравнений (3.151), однако член Л(1—||Л||) обеспечивает под-
держание нормы кватерниона близкой к единице.
155
3.3.6. БИНС с параметрами Родрига — Гамильтона
Рассмотрим принципы построения БИНС с использованием кватернионов.
Введем кватернионы для последовательно выполненных преобразований от
инерциального трехгранника OuXuYuZu к географическому OXgYgZgn от гео-
графического к связанному OXYZ. Переход от трехгранника к
ход от трехгранника OuXY Zu к
OXgYeZ обозначим посредством кватерниона К, а переход от OXgY Z к
связанному трехграннику OXYZ - обозначим через Л. Результирующий пере-
OXgY,Z обозначим через кватернион М
Условная схема преобразований приведена
на рис. 3.18.
Так как К - кватернион первого преоб-
разования (поворота), а Л - кватернион
второго преобразования, то результирую-
щий кватернион М определяется следую-
щим произведением
М-К-Х. (3.154)
Для реализации алгоритмов БИНС не-
обходимо в каждый момент времени иметь
информацию о положении связанного
трехгранника относительно географическо-
го. Эта информация может быть получена из кватерниона Л, являющегося ана-
логом матрицы направляющих косинусов А (см. матрицу (3.97)). Зная кватер-
нион Л , можно пересчитать кажущееся ускорение J1A, измеренное в связанных
с ЛА осях, в географическую систему координат и определить параметры ори-
ентации гр, 0, у. Обратимся к матрицам направляющих косинусов (3 96) и
(3.97), первая из которых выражена через параметры Родрига - Гамильтона, а
вторая - непосредственно через косинусы углов гр , 0, у. В силу эквивалентно-
сти (3.96) и (3.97) искомые углы рыскания, тангажа и крена могут быть выра-
жены через параметры Родрига - Гамильтона следующим образом:
гр = arctg
- arctg -
— '2X^2
2Х“+2Х2о-1
0 = arcsin(«p) = arcsin(2X]X2 + 22.0X3),
(3.155)
у — arctg —— - arctg -
2X?7.3 —2A.qX|
2A,q + 2л, — 1
Рассмотрим процедуру вычисления кватерниона A. Выразим из соотноше-
ния (3.154) кватернион А , для чего умножим обе части равенства (3.154) слева
на сопряженный кватернион К, получим
А = К°М (3.156)
Исходя из соотношения (3.156), для определения кватерниона А необходи-
мо определять кватернионы К и М с последующим их перемножением. Ква-
тернионы К и М могут быть найдены интегрированием кинематических
уравнений вида (3.149) и (3.148):
156
2K=-Ci.g°K, K(t0) = K0, (3.157)
2Л7 ЛЬП, M(t0) = M0, (3.158)
где Q.g, Г2 - гиперкомплексные отображения векторов абсолютной угловой
скорости географического и связанного трехгранников соответственно.
Уравнения (3.157) и (3.158) для простоты изложения приведены без коррек-
ции нормы кватерниона; для реализации численных алгоритмов целесообразно
эти уравнения снабжать корректирующим членом.
По элементам кватерниона К могут быть найдены инерциальная долгота и
широта из сравнения матриц (3.55) и (3.97). Компоненты вектора абсолютной
угловой скорости географического трехгранника cog, а, следовательно, и ото-
бражения , могут быть найдены из навигационного алгоритма аналогично
схеме БИНС с двумя уравнениями Пуассона (см. п. 3.2). Что касается вектора
абсолютной угловой скорости со связанного трехгранника и его отображения
Q, то его компоненты непосредственно измеряются триадой ДУС.
Так как кватернион Л характеризует преобразование географического трех-
гранника в связанный, а в алгоритмах БИНС осуществляется обратный пересчет
информации из связанной системы координат в географическую, то и операция
преобразования гиперкомплексного отображения JVg вектора кажущегося ус-
корения ng также будет обратной
jVg=AoJVoA} (3.159)
где Jfg, JV — отображения вектора кажущегося ускорения, заданного в геогра-
фической и в связанной системах координат.
Блок схема алгоритма БИНС с интегрированием двух кинематических урав-
нений в кватернионах представлена на рис. 3.19.
Рассмотрим еще одну схему БИНС, основанную на интегрировании одного
дифференциального уравнения относительно кватерниона Л. Для вывода этого
уравнения продифференцируем по времени обе части равенства (3.156)
Л = К°М + К°М. (3.160)
Заменим производные К и М правыми частями уравнений (3.157) и (3.158)
Л = -—Q °К °М +-К °М oQ. (3.161)
2 2
Учитывая, что К ° М = Л, получим следующее уравнение
2A = A°Q-Qg°A. (3.162)
Уравнение (3.162) является аналогом обобщенного уравнения Пуассона и
позволяет непосредственно отыскивать кватернион Л, не прибегая к решению
двух кинематических уравнений (3.157) и (3.158).
Структурная схема БИНС, основанная на решении уравнения (3.162) пред-
ставлена на рис. 3.20.
157
Рис. 3.19. БИНС с решением двух кинематических уравнений в кватернионах
Рис. 3.20. БИНС, основанная на решении одного кинематического уравнения в кватернионах
158
3.4. Анализ алгоритмов БИНС
Для описания взаимного положения сопровождающего и связанного с объ-
ектом трехгранников могут быть использованы различные кинематические па-
раметры: углы Эйлера - Крылова, направляющие косинусы, параметры Родрига
- Гамильтона, параметры Кейли — Клейна и др. С математической точки зрения
для описания алгоритмов идеальной работы БИНС все эти параметры приводят
к одинаковым результатам. Различные кинематические параметры можно трак-
товать, как элементы соответствующего линейного пространства, так как все
они допускают операции сложения и умножения на число. В каждом линейном
пространстве задана операция ортогонального преобразования, позволяющая
определить компоненты вектора (элемента пространства) при повороте системы
координат. Другими словами, все пространства кинематических параметров
изоморфны, т.е. все элементы и операции над ними в одном пространстве име-
ют взаимно-однозначные аналоги во всех остальных пространствах [3.14]. Ха-
рактеристика некоторых кинематических параметров приведена в табл. 3.3.
Векторное трехмерное матричное пространство Ч) образует множество век-
торов заданных в виде разложения по осям некоторого ортонормированного
базиса, либо множество одностолбцевых матриц rT = |rv rY rz||.
Элементами матричного трехмерного пространства Л3 является множество
кососимметрических матриц [г], которые, как уже отмечалось, являются ду-
альным представлением столбцевых матриц (векторов) г. Кинематическое
уравнение в пространстве представляет собой известное из теоретической
механики матричное уравнение Пуассона.
Кватернионное (гиперкомплексное) пространство образует множество ги-
перкомплексных чисел - кватернионов. Для описания ортогонального преобра-
зования здесь используются так называемые собственные кватернионы Л, эле-
ментами которых являются параметры Родрига - Гамильтона. Гипсркомплскс-
ное отображение вектора R на четырехмерное пространство 91 совпадает с
самим вектором г, если ортонормированный базис пространства V совмещас г-
ся с мнимыми единицами i, j, к .
Другим способом вычислений с параметрами Родрига - Гамильтона являют-
ся кватернионные матрицы М(Х), М(г) размера 4x4 и столбцевые матрицы
г размера 4x1 (чстырехмерныс векторы). В пространстве Л4 умножение ква-
тернионов сводится к умножению матриц М(X) и г, кроме того, здесь легко
выражается матрица направляющих косинусов Л . С точки зрения реализации
численных алгоритмов предпочтение отдается параметрам Родрига - Гамиль-
тона или их систематизирующей гиперкомплексной конструкции — кватернио-
ну. Кинематические уравнения в параметрах Родрига - Гамильтона линейные,
имеют четвертый порядок и определены для любых углов рыскания, тангажа и
крена. Параметры Родрига - Гамильтона подчиняются одному уравнению нор-
мирования (3.95), что делает их одними из самых удобных в БИНС [3.14].
Кинематические уравнения в углах Эйлера - Крылова имеют невысокий по-
рядок (третий) и понятную структуру, но содержат тригонометрические функ-
ции от искомых углов и допускают вырождение при угле тангажа, равное 90°.
Все это обусловливает Их непригодность в БИНС. Уравнения БИНС, записан-
ные с использованием матрицы направляющих косинусов, - линейные, опреде-
лены для любых углов рыскания, тангажа и крена, однако уравнения Пуассона
имеют достаточно высокий - девятый порядок. Кроме того, уравнения Пуассо-
на должны быть дополнены шестью уравнениями связи.
159
Таблица 3.3
Характеристика кинематических параметров
Линейное пространство Элементы пространс1ва Формулы ортогонального преобразования Кинематическое уравнение
Векторное трехмерное V г = rxi + rYj + r,k, r'=h r7|| r = Х“и'Ь';=Ха*Л' а„ =со5(Х,Л;), г' = Аг, г = А1 г'. 1 г у= -[со, cosy-сог sin у]; COS0 6 = cor sin у + coz cosy; у = со v +/gO[co1,cosy-cozsiny], |/(7()) = |/|„0«|) = 0о; у(/()) = у1Г
Матричное трехмерное Ж3 и= 0 -rz rY 0 ~rx -rY rx 0 [Г>] = А[г]Аг,[г] = А7[г,]А А = -[ю]Л, Л(/0) = Л0
Кватернионное Н R = rxi + r>j + r7k, A = Xo + X,/ + X, j + yk. < |< о о ° о К < " II 2А = А°О A(Z0) = A0
Четырехмерное маличное пространство М4 M(X) = r r -- Xo X, X2 X3 X| Xn — X3 X2 X, X3 Xo — X! X3 - X2 X, Xo = 0 rx rY rz||. г' = М(Х)М7'(Х)г. г = М(Х)М/(Х)г. 2А = М(Х)щ M(t0) = M0
3.5. Начальная выставка БИНС
Для запуска алгоритмов БИНС необходимо ввести начальные значения ко-
ординат местоположения ЛА, его скорости и параметров ориентации. Опреде-
ление углового положения ЛА по отношению к географической системе коор-
динат в период подготовки БИНС к запуску и составляет суть начальной вы-
ставки (ориентирования) [3.5]. Начальная выставка может быть автономной и с
привлечением информации от других навигационных систем (ма1 чигомстров,
систем спутниковой навигации и др.).
Рассмотрим автономный способ начальной выставки БИНС на неподвижном
относительно Земли ЛА. В данном случае входной измерительной информаци-
ей являются ускорение силы тяжести для акселерометров и угловая скорость
суточного вращения Земли для ДУС. Допустим, в начальный момент времени
ЛА занимает произвольное положение относительно географического трех-
гранника OX Y Z , определяемое углами Vo, Y0 (Рис- 3.21). Углы у0, 0О,
у0 являются искомыми для решения задачи начальной выставки.
Рис. 3.21. Взаимное положение связанного и географического трехгранников
в начальный момент времени
Пользуясь рис. 3.21 или матрицей направляющих косинусов (3.24), найдем
проекции вектора ускорения силы тяжести на оси связанной системы координат
Sx 0 gsine0
gy = А g - gcosy0 cos0o
gz 0 -gsiny0 cos0(
о
(3.163)
Пользуясь показаниями акселерометров, нетрудно найти начальные углы
тангажа и крена
161
O'
0O = arcsin ;
g
( (3.164)
Yo = arctg •
I gy J
Из выражений (3.164) видно, что из сигналов акселерометров невозможно
найти ориентацию ЛА в азимуте (по углу к/0). Для определения начального уг-
ла рыскания привлечем сигналы ДУС
(0у
coz
Ur cos 0О cos Vo + sin 0O
UT (- cos y0 cos Vo sin % + sin y0 sin Vo) + cos Yo cos
Ur (sin y0 cos Vo sin % + cos Yo s’n Vo ) _ sin Yo cos ®o
(3.165)
Начальное значение угла рыскания может быть получено по сигналу одного
продольного ДУС и найденному выше углу тангажа 0О.
Из (3.165) следует
(3.166)
со у - sin 0()t/„ со v - U sin 0n sin ф
V - arccos——-------—- = arccos—-----------------—
Uг cos 0О U cos (р cos 0О
После определения начальных значений углов Vo > и Yo можно рассчи-
тать начальную матрицу перехода С(/о) либо начальный кватернион А(/()) в
зависимости от используемого алгоритма. Важно отметить, что начальную вы-
ставку по углу рыскания на Северном полюсе осуществить не представляется
возможным, так как <р -л/2 и горизонтальная составляющая угловой скорости
Земли равна нулю.
ЛИТЕРАТУРА К ГЛАВЕ 3
3.L Анучин О.Н., Емельянцев Г.И. Интегрированные системы ориентации и навигации для
морских подвижных объектов / Под общей ред. чл.-кор. РАН В.Г. Пешехонова. - СПб., 1999.
-357 с.
3.2. Бранен В.Н., Шмыглевский И.П. Применение кватернионов в задачах ориентации твердого
тела. М.:Наука. 1973. - 320 с.
3.3. Бранец В.Н., Шмыглевский И.П. Введение в теорию бесплатформенных инерциальных
навигационных систем. - М.: Наука, 1992. - 280 с.
3.4. Бромбер! П.В. Теория инерциальных систем навигации. - М.: Наука, 1979-296 с.
3.5. Гироскопические системы. Гироскопические приборы и системы: Учеб, для вузов
/Д.С.Пельпор, И.А.Михалев, В.А. Бауман и др. / Под ред. Д.С.Пельпора. 2-е изд., перераб. и
доп. - М.:Высш. шк., 1988.- 424 с.
3.6. Дмитриев С.П., Пелевин А.Е. Задачи навигации и управления при стабилизации судна на
траектории. - СПб: ГНЦ РФ ЦНИИ «Электроприбор», 2002. - 159с.
3.7. Инерциальные навигационные системы морских объектов/Д.П. Лукьянов, А.В. Молчанов,
А.А. Одийцов, И.Б. Вайсгант; под. ред. Д.П. Лукьянова. - Л.: Судостроение, 1989.-184 с.
3.8. Инерциальная навигация. Под ред О’Доннела. - М.: Наука, 1968.
3.9. Ишлинский А.Ю. Ориентация, гироскопы и инерциальная навигация. М.: Наука, 1976. -
672 с.
3.10. Климов Д.М. Инерциальная навигация на море. - М.: Наука, 1984.-118 с.
3.11. Комплекснозначные и гиперкомплексные системы в задачах обработки многомерных сиг-
налов /Под ред. Я.А. Фурмана. - М.:Физматлит, 2004. - 456 с.
3.12. Кузовков Н.Т., Салычев О.С. Инерциальная навигация и оптимальная фильтрация. - М.:
Машиностроение, 1982. - 216 с.
162
3.13. Лебедев Р.К. Стабилизация летательного аппарата бесплатформенной инерциальной систе-
мой. - М.: Машиностроение. 1977. -144 с.
3.14. Лурье А.И. Аналитическая механика. - М.: Изд-во физ.-мат. лит., 1961.-824 с.
3.15. Онищенко С.М. Применение гиперкомплексных чисел в теории инерциальной навигации. -
Киев: Наук, думка, 1983.-208с.
3.16. Пешехонов В.Г. Ключевые задачи современной автономной навигации // Гироскопия и на-
вигация. - 1996. - №1. - С. 48-55.
3.17. Помыкаев И.И., Селезнев В.П., Дмитроченко Л.А. Навигационные приборы и системы. -
М.: Машиностроение, 1983.
3.18. Селезнев В.П. Навигационные устройства. - Машиностроение, 1974. -660 с.
3.19. Управление и наведение беспилотных маневренных летательных аппаратов на основе со-
временных информационных технологий /Под ред. М.Н. Красилыцикова и Г.Г. Себрякова. -
М.:Физматлит. 2003. - 280 с.
3.20. Фролов В.С. Радиоинерциальные системы наведения. М.: Сов. радио, 1976. - 184 с.
3.21. Hamilton W.R. Lectures on Quaternions. Dublin. Hodges and Smith, 1853.
4“
Вопросы и задачи для самоконтроля к главе 3
1. Какая проекция абсолютной угловой скорости географического
трехгранника характеризует приращение широты?
2. Что характеризует матрица С ?
3. Возможно ли вычисление параметров ориентации посредством
алгоритма с углами Эйлера-Крылова, если значение угла танга-
жа равно 9(f?
4. Составить матрицу направляющих косинусов между системами
координат xyz и xlylzl (см. рисунок)
Рисунок к вопросу 4
5. Проекции абсолютной угловой скорости трехгранника xyz на
свои оси равны (Лх,вду,сдг. Относительно xyz вращается трех-
гранник xlylzl с относительными угловыми скоростями а и Р
(см. рис.). Найти проекции абсолютной угловой скорости трех-
гранника xlylzl на свои оси с помощью непосредственного про-
ектирования векторов и с помощью матричных преобразований.
Составить условную запись преобразований.
163
б. Какая матрица называется ортогональной?
7. Летательный аппарат вращается по крену с угловой скоро-
стью у, измеряемой с помощью ДУС (см. рис.). Составить
уравнения Пуассона для определения угла у. .
8. Составить кососимметрическую матрицу [со] для вектора
“ = Ц1 2 f.
9. Взаимное положение систем координат xyz и xiylzl определяет-
ся символической записью
У, У
—.....- W,
В системе координат xyz задан вектор « = |<7ч av я.|| .
Найти компоненты вектора а в системе координат xlyIzl с
помощью подобного преобразования. Указание: воспользовать-
ся формулой 3.52.
10. Найти:
a) joi°k, б)j°k + k°j
164
11. Даны два кватерниона: P = 2 + 3i + 5j + 2k и
0 = -1 + 4z -3j + к Найти:
a)S(P)V(Q); б) S(Q)P; в) Q; e)V(P)oV(Q).
12. Найти решения уравнений
a) (3xi + 2ук) ° j-2i° j = -4/ + 4к,
б) 5xi ° j о к + i ° (3xi + 2yj) + j°i = -8Z2 + 5к .
13 Найти норму и тензор кватерниона
а) Л = 2 + 2у/ i + 5/3^ j + к,
б) A = 3i-^3k
14. Какие поверхности описываются следующими уравнениями.
a) (jx + jy + kz) ° (ix + jy + kz) + 1=0,
6) ||K(2 + /x + jy + Az)|| = 5,
в) |K(l + ix +jy+ kz)| = S(4 + 7i).
75. Составить кватернионную матрицу для кватерниона
Л = 0,5 +1 + 2/ + ЗА .
16. В условиях задачи 7 составить кинематические уравнения в
параметрах Родрига-Гамилътона для определения угла у.
17. Дана цепочка преобразований
.y,x, z,,z2
xyz а----" X'y'z' ---7—* x2y2z2
Р
Составить собственный кватернион вращения, характеризующий поло-
жение системы координат x2y2z2 относительно xyz.
18. Доказать, что М(Х)МГ (X) = Е .
cos a D -sin a
Ответы. 2. [А,У Z,] = QATZ]. 3. нет. 4 0 1 0
sin a 3 cos a
41 1 0 0 |||1 cos a sin а 0|||сос 1 0 ° 1111° ₽
5. = 0 cosP sin Р -since cos а 0' со + 0 cosP sinp |||0 + 0
41 0 -sinp cosP 0 0 l|||coz 0 -sinp cosp||||d 0
со rl ~ coxcosa + co sina + P;
41 = -cox cos p sin a + co, cosP cos a + (co z +d)sinP;
со. 1 — сол sin P sin a - co^, sin p cos a + (coT + a) cos p
6. Удовлетворяющая условию: АГ = А 1.
7- с22=с23у; с23=-с22у или с32=с33у; с33=-с32у, где с22, с23, с32, с33
элементы матрицы
165
1
с = < = о
о
о
cosy
- sin у
sin у . 8.
cosy
[<о] =
О
3
-2
-3
О
1
2
-1
О
О
9. ахХ -ах cosa-a, since; avl = av; a.x =axsina + G: cosa.
10 a) 1, 6) 0. 11. a)8i-6j + 2k; 6) -2-3i-5j-2k; -l-4i + 3j-k:
+ lli + 5j-29k.
12. a) x = 2, у = 2, 6) x = -1, у = 3. 13. а) ||л|| = 16, |л| = 4, б) ||л|| = 12,
|л| = 2у[з . 14. а) сфера радиуса г = 1 с центром в начале координат, б) сфера
радиуса г = 4$ с центром в начале координат, в) сфера радиуса г = 4 с цен-
тром в начале координат.
0,5 -1 -2 -3
1 0,5 -3 2
75. 7И(Х) =
2 3 0,5 -1
3 -2 1 0,5
16. 2r0=-r,y, 2rI=/'oy, где г0 и гх компоненты кватерниона
У . . У
R = cos—4-ISin —.
2 2
a p..a p . . a . P a.p
17. cos—cos—+ isin—cos-- /sin—sin — + «cos—sin—.
22 22 22 22
166
ГЛАВА 4
МОДЕЛЬ ОШИБОК БИНС
Рассмотренные выше принципы построения БИНС характеризуют функцио-
нирование БИНС в том случае, когда все элементы работают без ошибок, а на-
чальные условия определены и введены идеально. Навигационные параметры,
вырабатываемые БИНС, при «идеальных» измерениях абсолютных ускорений и
угловых скоростей объекта также будут безошибочными. В силу этого такие
алгоритмы вычисления навигационных параметров получили наименование
алгоритма идеальной работы ИНС [4.1, 4.9]. Погрешности инерциальных чувст-
вительных элементов и ввода начальных условий служат возмущениями для
БИНС, а движение БИНС, обусловленное ими, называют возмущенным. В воз-
мущенном движении интерес представляет его отклонение от невозмущенного.
Уравнения для отклонения переменных, характеризующих состояние БИНС, от
их значений при отсутствии возмущений называют уравнениями ошибок [4.1].
Анализ свойств уравнений ошибок составляет одну из основных задач теории
БИНС.
Цель расчета ошибок заключается в определении связи между погрешностя-
ми элементов и неточным вводом начальных условий, с одной стороны, и по-
грешностями выходных данных БИНС, с другой [4.5].
Установление такой связи позволяет рассчитать погрешности БИНС, в кото-
рой используют элементы с известными характеристиками ошибок, или, наобо-
рот, исходя из заданной точности, определить требования к элементам системы
и к погрешностям начальной выставки. Анализируя ошибки, можно в опреде-
ленной степени упростить алгоритмы, по которым работает вычислительное
устройство, а также выработать обоснованные требования к коррекции БИНС.
Заметим, что было бы методически неправильным вводить в уравнения
ошибок погрешности возможно большего числа элементов, входящих в ИНС.
Целесообразно иметь наименьшее число независимых параметров, определяю-
щих состояние системы. Как правило, в ИНС в качестве такого рода параметров
берут инструментальные погрешности гироскопов и акселерометров и погреш-
ности задания начальных условий. Другие погрешности можно свести к пере-
численным.
Анализ погрешностей БИНС базируется на решении уравнений ошибок, ча-
ще всего получаемых с помощью, так называемых, уравнений в вариациях [4.5],
представляющих собой линеаризованные уравнения первого приближения от-
носительно возмущений, действующих на систему. Такие уравнения выводят
либо формальной вариацией алгоритмов БИНС, либо подстановкой в алгорит-
мы вместо независимых переменных суммы самой переменной и ее прираще-
ния. Из образующихся выражений вычитают первоначальные уравнения и пре-
небрегают квадратами приращений и их произведениями. В общем случае по-
лучают неоднородные линейные обыкновенные дифференциальные уравнения
девятого порядка с переменными коэффициентами.
167
4.1. Элементарный анализ ошибок БИНС
Рассмотрим возникновение погрешностей в северном канале БИНС. Пусть
ЛА перемещается в плоскости меридиана вдоль поверхности неподвижной сфе-
рической Земли. На борту ЛА размещены два линейных акселерометра с осями
чувствительности, направленными по продольной ОХ и вертикальной оси OY
ЛА, и гироскопический ДУС, способный измерять абсолютную угловую ско-
рость coz ЛА. Как и прежде, введем географическую систему координат
OXс направлением осей на север, вдоль истинной вертикали вверх и на
восток соответственно (рис.4.1).
Рис. 4.1. К выводу уравнений ошибок одноканальной БИНС
Предполагается, что в начальный момент времени связанная система коор-
динат совпадает с географической О0Хg0yg0Zg0.
Пусть ЛА переместился из точки О0 в О. С точкой О свяжем текущую
OXg, OYS и начальную ориентацию (?0Xg0, О0К?0 географических осей. По-
нятно, что если известно направление вертикали OYg в каждый момент време-
ни, то задача навигации была бы решена точно. Однако алгоритмы БИНС реа-
лизуют вертикаль OYg с точностью до малой ошибки р (ошибки построения
вертикали). В связи с этим введем вычисленную систему координат OXgYgZg,
повернутую относительно OX YgZg вокруг оси OZ на упомянутый выше угол
р (см. рис. 4.1). Здесь и далее расчетные с помощью БИНС параметры будем
снабжать знаком «~». Положим, что ЛА в точке О набирает высоту с углом
тангажа 0.
168
Ошибки БИНС в случае неточного определения вертикали
(4-1)
Рассмотрим случай, когда акселерометры и гироскоп функционируют без
ошибок, а вертикаль в начальный момент задана с ошибкой. В этом случае без-
ошибочные показания акселерометров определяются равенствами, полученны-
ми в главе 1 (предполагается, что VYg = 0:
пх = Vxg cos 0 + g sin
nY = g cos 0 - Vx sin 0.
Для определения местоположения JIA (широты (p) необходимо перепроек-
тировать показания акселерометров (4.1) в географическую систему координат,
т.е. на оси OXg и OYg . Однако за счет неточного задания вертикали сигналы
акселерометров (4.1) будут пересчитываться не на оси географического трех-
гранника, а на оси ОХ„ и OYP вычисленной системы координат OX Y Z . В
о о ооо
этом случае получим
nXg = пх cos(0 - Р) - nY sin(0 - Р).
(4-2)
Подставим в соотношение (4.2) сигналы акселерометров (4.1):
n~g = cos 0 + g sin 0) cos(0 - P) - (g cos 0 - VXg sin 0)sin(0 - P). (4.3)
После несложных преобразований получим
nxg =^cos₽ + gsinp.
(4.4)
Для малого угла Р можно приближенно записать
nxg^xg+g^- (4-5)
Таким образом, после пересчета данных в географическую систему коорди-
нат в проекции кажущегося ускорения n*g содержится составляющая вектора
ускорения силы тяжести.
На основании рис. 4.1 получим
Р = <р — <р (4.6)
где <р - значение широты, выработанной с помощью БИНС.
Дифференцируя обе части равенства (4.6), получим
р = -<р + ф. (4.7)
ч
Приборное значение широты <р вырабатывается в результате интегрирова-
ния n^g, поэтому соотношение (4.7) запишем следующим образом
₽ = -тЖ+?₽)Л + Ч>- (4.8)
О
у
Учитывая, что ф = -%-, уравнение (4.8) перепишем в виде
169
о
(4.9)
Дифференцируя по времени обе части уравнения (4.9), имеем
(4.Ю)
где <о0 =
- часто га Шулера. Эту частоту можно трактовать, как частоту ма-
лых незатухающих колебаний в поле силы тяжести Земли физического маятни-
ка, приведенная длина которого равна расстоянию от центра Земли до объекта,
движущегося на высоте h. Числовое значение частоты Шулера при h«R3
равно соо -
9 81
-----——— = 1,24-10'3 рад/с, соответственно период Шулера
6371-103
Т = 2л/соо =84,4 мин.
Если в начальный момент времени 0(0) = 0, 0(0) = 0, то ошибка построения
вертикали равна нулю. В случае, когда в начальный момент времени вертикаль
задана с ошибкой 0(0) = 0О, решение уравнения (4.10) имеет вид
Р = 0О cosco0/. (4.11)
Из решения (4.11) следует, что вычисленная вертикаль будет совершать ко-
лебания относительно истинной вертикали с периодом Шулера.
Найдем ошибку в определении скорости ЛА как разность между приборной
скоростью, полученной при однократном интегрировании сигналов акселеро-
метров, и истинной скоростью ЛА
(4.12)
о
о
о
(4-13)
Согласно (4.12) ошибка в определении скорости связана с ошибкой построе-
ния вертикали. Для случая неточного задания начального значения вертикали
подставим решение (4.11) в соотношение (4.12), получим
А = g ГРо cos= -—sin ш0/.
° Ь “о
АГ.
Интегрируя Аф =---—, нетрудно получить ошибку определения широты
R
cosco0/).
(4-14)
о
Умножив слева и справа соотношение (4.14) на радиус-вектор R, получим
ошибку пройденного расстояния AS
AS = А<рА = 0О7?(1 - cos co0t).
(4.15)
Таким образом, отклонение аналитической вертикали от истинной, ошибки в
определении скорости и местоположения ЛА имеют колебательный характер,
период их колебаний равен периоду Шулера. Амплитуда же колебаний опреде-
ляется начальным отклонением вычисленной вертикали от истинной (рис. 4.2).
170
Рис. 4.2. Ошибки БИНС, вызванные
неточным заданием вертикали:
а) ошибка построения вертикали;
б) ошибка в определении скорости;
в) ошибка в определении пройденного
расстояния;
1 - Ро = 1 угл. мин;
2 - Ро = 2 угл. мин;
3 - Ро = 3 угл. мин
Ошибки БИНС, вызванные погрешностями акселерометров
Пусть теперь в БИНС начальные условия выдержаны точно, а в показаниях
акселерометров имеются погрешности (смещение нуля) 8av и 8ау. В этом слу-
чае уравнения (4.1) примут вид:
пх = VXg cos 0 + g sin 0 + Ъах;
nY = gcos0-PA-gsin0 + 8ay.
(4-16)
После перепроектирования сигналов акселерометров на ось OXg, получим
nxg = cos Р + £ sin Р + ^ах cos(0 - Р) - 8ау sin(0 - Р). (4.17)
Представим в соотношении (4.17) тригонометрические функции разности
аргументов с учетом малости угла Р по известным формулам тригонометрии
cos(0-P) = cos0cosР + sin0sinp ® cos0 + Psin0;
sin(0-P) = sin0cosp-cos0sinp ® sin0-pcos0.
(4.18)
С учетом (4.18) кажущееся ускорение (4.17) перепишем в виде
л ~ = VXg + gP + Sax (cos 0 + p sin 0) - 8ar (sin 0 + P cos 0) « VXg + gP + SaXg ,(4.19)
где 8ax = cos0-8ar sin0 - проекция ошибок акселерометров на ребро
OXg географического трехгранника.
171
В соотношении (4.19) пренебрежем произведением ошибок 8ал(3 и 8аг|3.
Пользуясь равенством (4.9), получим уравнение для ошибки построения верти-
кали
₽ = --H(S₽ + &J.Vs)A. (4.20)
Дифференцируя по времени обе части уравнения (4.20) получим
, да Vp
p+<oj₽=—(4.21)
К
Для малого угла тангажа 0 приближенно можно записать
8а « 8аЛ- - 8ar0 ® 8ау,
т.е. на погрешности БИНС влияют только ошибки акселерометра A v. Полагая
дах = const, решение уравнения (4.21) при нулевых начальных условиях имеет
вид
P=^L(cosco0/-l). (4.22)
g
Из решения (4.22) следует, что погрешности акселерометра вызывают коле-
бания вычисленной вертикали с периодом Шулера относительно смещенного от
" о S^ V л
истинной вертикали положения равновесия на величину р = ——. Амплитуда
g
колебаний равна ошибке акселерометра в долях ускорения силы тяжести
8aA./g.
Получим ошибки БИНС в определении скорости, широты и пройденного
расстояния, вызванные погрешностью акселерометра Ах. Вычитая из вычис-
ленной линейной скорости истинную, находим
8a v .
—— sina>0/
co0
A = J (Vxg + gP + Sa v )dl - j VXgdt =
о 0
(423)
Таким образом, ошибка в измерении скорости также имеет характер колеба-
ний с периодом Шулера и амплитудой, пропорциональной величине смещения
нулевого отсчета акселерометра. Погрешности БИНС в определении широты и
пройденного расстояния имеют вид:
A 'Xg да v
-----dt =—— (1 -cos(D0O;
R g
(4.24)
AS = —4_(1 - coscofl/).
(4.25)
Из выражений (4.24) и (4.25) видно, что погрешность счисления координат ы
местоположения ЛА носит также колебательный характер с периодом Шулера.
Ошибки БИНС для различных значений погрешности акселерометра приве-
дены на рис. 4.3.
172
Рис. 4.3. Ошибки БИНС, вызванные
смещением нуля акселерометра:
а) ошибка построения вертикали;
б) ошибка в определении скорости; в)
ошибка в определении координаты;
1 - 8а х = НУ4 g;
2- 8ах = 5 4 g;
3 - 8а х = 10'3 g
Ошибки БИНС, вызванные дрейфом гироскопов
Пусть теперь начальные данные выдержаны точно, акселерометр функцио-
нирует идеально, а датчик угловой скорости измеряет абсолютную угловую
скорость ЛА с ошибкой е . Найдем ошибку в определении угла тангажа. В со-
ответствии с блок-схемой, приведенной в разделе 1.1, тангаж определяется как
результат интегрирования относительной угловой скорости связанного трех-
гранника
t
е = |(<о7-ш2г)Л+«0. (4.26)
о
Наличие собственного дрейфа гироскопа s приведет к погрешности в опре-
делении проекций coz и (oZg абсолютной угловой скорости связанного и гео-
графического трехгранников соответственно. Расчетное значение угла тангажа
можно представить в виде
t
0 = j (coz + £ - (5Zg )dt +0n, (4.27)
о
где (£>Zg - рассчитанная с помощью БИНС проекция угловой скорости геогра-
фического трехгранника. В уравнении (4.27) положено, что начальное значение
угла тангажа 0О введено точно.
Вычтем из расчетного тангажа (4.27) истинное значение (4.26), в результате
чего получим ошибку в определении угла 0
173
ДО = 6 - 6 = j (coz + 'E-cbZg)dt +0O - j (coz ~(aZg)dt -Qo.
о о
Отсюда сразу находим
Д0 = j(e-AcoZg)^, (4.28)
о
где AcoZg =SZg — coZg.
Дифференцируя обе части равенства (4.28), имеем
A0 = £-AcoZg. (4.29)
В соответствии с рис. 4.1 вычисленное значение угла тангажа 6 определяет-
ся как угол между осью OXg вычисленного трехгранника и продольной оси ЛА
ОХ. Тогда связь между истинным и вычисленным значением тангажа опреде-
ляется равенством
е-е=р, (4.зо)
или
де=-р. • (4.31)
Таким образом, при одноканальном анализе БИНС ошибка выработки тан-
гажа равна ошибке построения вертикали с обратным знаком. Уравнение (4.29)
с учетом соотношения (4.31) принимает вид
P-AcoZg-E. (4.32)
Так как AcoZg = -
R
, находим уравнение для ошибки построения вертика-
ли с учетом дрейфа гироскопа
ДИ,,
₽ =---(4.33)
Уравнение для ошибки построения вертикали (4.33) отличается от аналогич-
ного уравнения платформенной ИНС знаком перед членом е, выражающим
дрейф гироскопа [4.9].
/
Учитывая, что ACVg = JgP^t (см. формулу (4.12)), уравнение (4.33) прини-
0
мает вид
₽ = “[?₽-с. (4.34)
л о
Найдем решение уравнения (4.34) для случая постоянного дрейфа
(е = const). Как видно из уравнения (4.34), в момент t = 0 0(0) - -е (определен-
ный интеграл с равными пределами обращается в нуль). Иначе говоря, в на-
чальный момент отклонение вычисленной вертикали от истинной происходит с
угловой скоростью, равной скорости дрейфа гироскопа. Дифференцируя по
времени обе части уравнения (4.34), получим
Р + ®оР = О.
(4.35)
Приняв Р(0) = 0, получим решение уравнения (4.35) в виде
174
Р = ——sinco0f. (4.36)
со0
По аналогии с предыдущим материалом находим ошибки в определении
скорости, широты и пройденного расстояния:
=£T?(cosco0r-l); (4.37)
£
Atp = —(sinсо,/- соо/); (4.38)
«о
eJ?
AS =—(sincoo/ -<о0?). (4.39)
соо
Из формул (4.37) - (4.39) видно, что вычисленная вертикаль по-прежнему
совершает колебания около истинной вертикали с частотой Шулера и амплиту-
дой £ / со0. В ошибке определения скорости имеется постоянная составляющая,
пропорциональная радиусу Земли. Наличие этой постоянной составляющей
приводит к накапливающейся погрешности при определении широты и прой-
денного расстояния (рис. 4.4). Нарастание со временем погрешностей БИНС
является главным их недостатком.
Рис. 4.4. Ошибки БИНС, вызванные дрейфом гиро-
скопа:
а) ошибка построения вертикали;
б) ошибка в определении скорости;
в) ошибка в определении координаты;
1 -Е = 0,01 град/ч;
2 - £ = 0,05 град/ч;
3 - £ = 0,1 град/ч
Ошибки вертикального канала БИНС
Рассмотрим погрешности вертикального канала, вызванные ошибкой ком-
пенсации ускорения силы тяжести g .
Положим, гироскоп и акселерометры работают без ошибок, а начальные
данные введены точно. В соответствии с принципом работы вертикального ка-
нала (см. п. 1.1) найдем ошибку в определении вертикальной скорости ЛА как
разность между вычисленной и истинной вертикальной скоростью
175
4^=1-^ “fCr, +g-g)dt-^rtdl. (4.40)
0 0
Здесь g — ускорение силы тяжести, вводимое в алгоритм вертикального ка-
нала БИНС на основе модели гравитационного поля Земли, для компенсации
истинного значения g .
Из соотношения (4.40) находим погрешность в определении вертикальной
скорости
t
AV^-fadl, (4.41)
о
где Ag = g - g - ошибка компенсации ускорения силы тяжести
Очевидно, что ошибка в определении высоты выглядит так
А/г=|дИу/С (4.42)
о
Полагая Ag = const, получаем
Др/2
AKrg=-AgC АЛ = -—. (4.43)
Из формул (4.43) можно заключить, что ошибки в определении вертикаль-
ной скорости и высоты с помощью БИНС растут неограниченно. Аналогичные
ошибки будет иметь вертикальный канал БИНС в случае смещения нуля аксе-
лерометров. Беспредельный рост ошибок вертикального канала БИНС называ-
ется неустойчивостью этого канала.
Ограниченность ошибок горизонтальных каналов (в данном случае северно-
го) обусловлено исключительно лишь действием на акселерометры вектора ус-
корения силы тяжести g . Гравитационные силы играют в алгоритмах БИНС
такую же положительную роль, как и в платформенных ИНС [4.8. 4.9]: благода-
ря вектору ускорения силы тяжести ошибки БИНС остаются ограниченными.
Действительно, положив g = 0 в уравнении для ошибки построения вертикали
(4.20), записанной с учетом ошибок акселерометров, имеем
Р = (4.44)
о
Решив уравнение (4.44) при 8aXg = const, получим
₽ = (4-45)
Найдем также ошибки БИНС в определении скорости и пройденного рас-
стояния без учета вектора ускорения силы тяжести:
A VXg = J (Kg + )dt “J ^xgdt = (4-46)
о 0
Д5 = ]Д^Л = ^^-. (4.47)
0
Из соотношений (4.45)- (4.47) видно, что при отсутствии вектора ускорения
силы тяжести ошибка построения вертикали, а также ошибки в определении
скорости и координаты, вызванные смещением нуля акселерометра, неограни-
176
ченно возрастают. Напомним, с присутствием вектора ускорения силы тяжести
в показаниях акселерометров эти ошибки БИНС носят колебательный характер
с периодом Шулера.
Структурная схема ошибок северного канала БИНС
Подводя итог анализу точности работы БИНС на основе одноканального
анализа, приведем систему уравнений, характеризующую ошибки северного
канала:
Р = -^-е;
R
^A'g =gP + SaYg; (4.48)
AV •„
Л<р = —
R
де=- р
С учетом уравнений (4.48) и алгоритмов идеальной работы, изложенных в
разделе 1.1 структурную схему северного канала БИНС с учетом погрешностей
акселерометров и гироскопа можно представить в виде, показанном на рис. 4.5.
Рис. 4.5. Структурная схема северного канала БИНС с учетом погрешностей
акселерометров и гироскопа
177
На приведенной структурной схеме символ s необходимо рассматривать как
оператор Лапласа, а все переменные как изображения по Лапласу. Пользуясь
правилами преобразования структурных схем, замкнутый контур ошибок БИНС
можно представить так (рис. 4.6).
Рис. 4.6. Структурная схема ошибок БИНС
Из рис. 4.6 можно заключить, что вектор ускорения силы тяжести приводит
к образованию отрицательной обратной связи на структурной схеме ошибок
БИНС.
4.2. Векторная модель ошибок БИНС
Получим векторную модель ошибок БИНС с географическим опорным трех-
гранником. В основе алгоритма БИНС лежит пересчет данных, измеренных в
связанной с подвижным объектом системе координат в географическую. Этот
пересчет возможен, когда матрица перехода С известна [4.9]. Напомним, мат-
рицу С можно найти из решения обобщенного уравнения Пуассона
C = C[co]-[cog]C, (4 49)
где [со], [сос. ] - кососимметрические матрицы, соответствующие проекциям
векторов абсолютной угловой скорости связанного и географического трех-
гранников на свои ребра.
При решении уравнения (4.9) в ЭВМ используется информация об абсолют-
ных угловых скоростях связанного и географического трехгранников, содер-
жащая ошибки. Вместо точных значений cov, соу, coz в ЭВМ используются
данные <ov , йу, coz, представляющие собой выходные сигналы ДУС. В этих
данных содержатся дрейфы гироскопов £ v, еу, ez, так что вводя кососим-
метрическую матрицу
получим следующее выражение для расчетной с помощью БИНС кососиммет-
рической матрицы, составленной из проекций абсолютной угловой скорости
связанного трехгранника
[со] = [<о] + [в].
(451)
178
Что касается фигурирующей в уравнении (4.49) матрицы [cog], то вместо нес
в алгоритмах используется матрица [сб^], соответствующая вектору угловой
скорости географического трехгранника, вычисленного с помощью навигаци-
онного алгоритма БИНС.
В этом случае в процессе вычислений будет получена матрица направляю-
щих косинусов С, нс равная фактической матрице С . Использование матрицы
С в алгоритмах БИНС для пересчета измерений векторных величин приведет к
тому, что все измерения будут пересчитаны к осям трехгранника, не совпадаю-
щего с географическим, т.е. к вычисленному OX^Z^. Определим положение
вычисленного трехгранника OX Y Z относительно географического OX Y Zp
ООО ООО
посредством трех малых углов а, р, х (рис. 4.7). Угол а характеризует ази-
мутальную ошибку БИНС, а углы Р и / - ошибки построения вертикали.
Рис. 4.7. Взаимное положение географического и вычисленного трехгранников
Итак, вначале вычисленный трехгранник OX YgZ совпадал с географиче-
ским OX Y Z Первый поворот трехгранника OX YZV совершим на угол а
вокруг ребра OYg против хода стрелки часов, если наблюдать за вращением со
179
стороны положительного направления оси OYg . Этот угол характеризует ази-
мутальную ошибку БИНС. В результате поворота на угол а трехгранник
OX Y Z займет некоторое промежуточное положение OX'Y'Z' причем ось
OYg является одновременно осью OY„. Этому повороту соответствует таблица
направляющих косинусов
Yg 0Q
x'g cos a 0 -sin a
Yg 0 1 0
N sin a 0 cos a
В соответствии с таблицей направляющих косинусов введем матрицу преоб-
разования
cos а
sin а
О -sin а
1 О
О cos а
(4-52)
Применительно к только что рассмотренному перемещению условная запись
в соответствии с [3 9] имеет вид
Vi
OX Y Z ---------► OX'Y'Z'
* а а
С помощью введенной матрицы преобразования (4.52) рассматриваемый по-
ворот можно также записать следующим образом:
^Kz^=FJVgzJ- (4.53)
Аналогично следующий поворот осуществим на угол р вокруг ребра OZ'g .
Обозначим через OX''Y"Z" положение трехгранника OX YPZ соответствую-
ООО 000
щее второму повороту. Наконец, последний поворот осуществим на угол % во-
круг ребра ОХ”, при котором трехгранник OX”Y"Z"g переходит в вычисленный
трехгранник OXgYgZ .
Переход от трехгранника OX OY Z к OXYZP и введенные матрицы пре-
О О О ООО
образования иллюстрируется табл. 4.1.
О
В этой таблице обозначено: Е - единичная матрица; [FJ =
О
-а
О а
О О
О О
О
О -р О
О
О О
[^] = Р О
, [Fz] =
-х
О
- кососимметрические матрицы, соответ-
0
О О
О О
О X
ствующие матрицам перехода Fa, Ff., F .
180
Таблица 4.1
Конечные повороты на углы СС, [3, /
oxjvz.,--------
-——► ox'xz:
f) о о о
*- OXJZ
ООО

или в матричной форме
Пренебрегая произведением матриц малых углов, найдем результирующую
матрицу перехода от географического трехгранника к вычисленному

181
Из соотношения (4.54) находим
а
Р -а
1 X
-X 1
(4.55)
Следует отметить, что матрица (4.55) обладает ортогональными свойствами
(FT = F~'), так как произведения углов а , Р, х являются малыми величинами
по сравнению с 1, что читатель может проверить самостоятельно, т.е. показать,
что FTF = Е .
В силу ортогональности матрицы F , запишем
<4-56)
Введем матрицу ошибок (error matrix) Ег, определяемую из соотношения
(4.56):
~Р а
1 -х
X 1
(4-57)
Таким образом, матрица Ег характеризует переход от вычисленного трех-
гранника OX Y Z к географическому OX„Y Z:
“ ооо ооо
Er(XgYgZg]=(XgYgZg}. (4.58)
Матрицу (4.58) можно также представить в виде суммы единичной и косо-
симметрической матриц
Приступим теперь непосредственно к выводу уравнений ошибок БИНС.
Вспомним назначение матрицы преобразования С
[XgYgZg] = C[XYZ]. (4.60)
Подставив в соотношение (4.60) выражение (4.58), получим
= (4.61)
Умножим слева обе части равенства (4.61) на матрицу Егх = Етг :
[XgYgZg] = E^C[XYZ] = C[XYZ]. (4.62)
где С - ETr С - вычисленная матрица преобразования. Откуда получим
С ЕС. (4.63)
Равенство (4.63) связывает «идеальную» матрицу преобразования, исполь-
зуемую в алгоритме «идеальной» работы, и вычисленную, которая фактически
используется в алгоритмах БИНС.
Обратимся к обобщенному уравнению Пуассона, реализующему алгоритм
идеальной работы
C = C[<o]-[<oJC. (4.64)
Подставим равенство (4.63) в левую часть уравнения Пуассона (4 64)
182
£rC + £C = C[<o]-[cog]C. (4.65)
Для матрицы С также можно записать обобщенное уравнение Пуассона
C = C[o]-[5g]C (4.66)
Уравнение (4.65) с учетом (4.66) примет вид
= + . (4.67)
Учитывая, что ЕгС = С (см. формулу (4.63)), получим
ЁГС = С{[со] - [5]} - [<og ]С + Er [S* ]С . (4.68)
Разность в фигурных скобках представляет собой кососимметрическую мат-
рицу дрейфов гироскопов (см. формулу (4.51)). Умножив справа обе части
уравнения (4.68) на матрицу С”1, получим
Ёг =-С[е]Сг - [cog ]ССТ + £ [cog]. (4.69)
Из формулы (4.63) вытекает Ст = Ст'Ег; ССТ = Ег, тогда уравнение (4.69)
перепишем так
Ёг=-С[е]СтЕг -[cog]£r + Е [cog]. (4.70)
Кососимметрическую матрицу [®g], соответствующую вектору угловой
скорости вычисленного трехгранника, представим следующей суммой
[Sg] = [cog] + [Acog], (4.71)
где [Acog] - кососимметрическая матрица ошибок выработки угловых скоро-
стей географического трехгранника.
В уравнении (4.71) матрица дрейфов гироскопов [е] умножена слева и спра-
ва на две взаимно обратные матрицы, что является подобным преобразованием
в пространстве кососимметрических матриц (см. формулу (3.52)) и эквивалент-
но преобразованию вектора е к географической системе координат OXgYgZg.
В этом случае уравнение (4.70) с учетом (4.71) можно представить в следующем
виде
Ёг =-[eg]£ -[(og]^ + F [cog] + £ [Acog], (4.72)
где [eg] — кососимметрическая матрица, элементами которой являются
дрейфы гироскопов спроектированных в географическую систему координат.
Пренебрегая в уравнении (4.72) величинами второго порядка малости:
[eg]^=[Eg]{£-+[£-r]}«[egi;
F[Acog] = {£'+[£]}[A(og]-[A(og]
и учитывая, что J?r[co ]-[со ]£r = ][£,]> получаем
[^] = -[eg] + [^][(og]-[cDg][£r] + [A(Og]. (4.73)
Уравнение (4.73) характеризует азимутальную ошибку и ошибки построения
вертикали БИНС в линейном пространстве, элементами которого являются ко-
сосимметрические матрицы размера 3x3 (см. раздел 3.4).
183
Представим уравнение (4.73) в векторном пространстве. В уравнении (4.73)
найдем явный вид разности [£ ][cog J — [<»][£,. ]:

+X4-g
-P«Ag+XWZg
₽coVg-xcoZg
0 p<or - acoZg
-p(org+a<oZs 0
Если ввести вектор конечного поворота
ег ~ 7.‘ + Ч/ + ,
(4.74)
(4.75)
где i , j, к - орты координатных осей OXg , OYg , OZ, , то матрица в правой
части (4.74) эквивалентна векторному произведению er х (ot (проверьте это).
Векторное уравнение относительно ошибок построения вертикали и ошибки
ориентации в азимуте можно представить в виде
ёг = е. х cog -Е„ + Acog . (4.76)
Таким образом, уравнение (4.76) является аналогом уравнения (4.73) в век-
торном прост ранствс.
Найдем аналог уравнений (4 73) и (4.76) в пространстве кватернионов Для
этого введем кватернион-отображение, компонентами которого являются дрей-
фы ДУС:
£ = ie v + jcy + kez , (4.77)
где i, j, к - мнимые единицы.
Получим следующее выражение для кватерниона-отображения вектора аб-
солютной угловой скорости связанного трехгранника:
Q = Q-r£, (4.78)
где £1, Q - отображения векторов истинной и расчетной с помощью БИНС
абсолютной угловой скорости связанного трехгранника.
Представим кватернион-отображение вектора абсолютной угловой скорости
географического трехгранника в виде
Qg=fig+AQg, (4 79)
где AQg — отображение вектора ошибок абсолютной угловой скорости геогра-
фического трехгранника.
Введем расчетный собственный кватернион Л~ нс равный истинному ква-
терниону Л вследствие ошибок чувствительных элементов БИНС. Переход от
географической системы координат OX Y Z к вычисленному трехграннику
OXgYgZ„ в соответствии с рис. 4.1 осуществлен тремя конечными поворотами
на углы a , [3, у. Каждому конечному повороту можно поставить в соответст-
вие собственный кватернион вращения:
ot (X В В У У
О =cos—г/sin—; 0„ = cos—+ Asin—; 0 = cos—+/sin—. (4.80)
a 2 2* 2 2 х 2 2
Так как углы a, р, у считаются малыми, перепишем кватернионы (4.80) в
виде
0a«l + j-; O(l~l + A--; О «1 + Д.
a / 2 Р 2 х 2
(4.81)
184
Пренебрегая величинами более высокого порядка малости, найдем кватер-
нион результирующего перехода от системы координат OX YZa к ОХ УZ„,
произведением кватернионов (4.81)
0 = 0 <0 о© J1+ |о| 1 + Д0 |о| 1 + /1+ + j- + k^- .(4.82)
р х V 2} < 2) t 2) 2 2 2
Кватернион 0 есть кватернион ошибок, являющийся аналогом матрицы Ег,
и имеет вид
0 = 1+-|е,., (4.83)
где ег - г/ + уа + Ар.
Ортогональные преобразования с помощью кватернионов 0, Л можно ус-
ловно записать следующим образом:
Л°(2ГУ7)оД = (У KZJ,
___________ (4.84)
^gYgZg} = ®^XsYgZgy®.
Исключая из соотношений (4.84) величину {XgYg Zg), получим
(^gi;Zg)-0°A°(ATZ),°A°O. (4.85)
Введем расчетный кватернион ориентации Л~, определяемый из соотноше-
ния (4.85), следующим образом
Л~=О°Л, Л~=Ло©. (4.86)
Здесь Л - сопряженный расчетный кватернион ориентации.
С учетом обозначений (4.86) равенство (4.85) принимает вид
(XgYg Zg) = Л~ о (XYZ) о Л~ . (4.87)
Из второго соотношения (4.86) выразим кватернион ошибок 0
О = Л°Л~. (4.88)
Продифференцируем по времени обе части равенства (4.88):
О = Л°Л~+Л°Л~. (4.89)
Производные кватернионов Л и Л~ можно найти на основании решения
кинематических уравнений
2Л = Л ° Q — О ° Л,
~ ~ _ (4.90)
2Л = Л — Q°A~.
Подставив уравнения (4.90) в (4.89), получим
20 = (A°Q-Qg оЛ)°Л + Л°(Л~ -Q°A~). (4.91)
Раскроем скобки в соответствии с дистрибутивным свойством кватернионов,
сгруппируем члены с конструкцией Л°(...)°Л~ и получим
20 = A°(Q-Q)°A~ -Qg °Л°Л~+Л°Л~ . (4.92)
Учитывая, что Q-Q = -£ (см. формулу (4.78)) и в силу соотношения (4.88)
уравнение (4.92) перепишем в виде
2О = -Ло£°Л~+0 ng-Q^o©_ (4.93)
Принимая во внимание, что
185
20 = ёг;
Л о £ о Д~ = До£оДо0 = £^ ° 0 = £g о
1 + -е,
2 '

(4.94)
0 Q -Q °® = ®°(Q + AQ )-Q °®«— (е °Q -О °е ) + Д£2 ,
<5 <5 v <5 & ' 6 <5 ’ &
уравнение (4.2.44) можно представить в виде
ёг =~(^г °er)~^g
Уравнение (4.94) и есть искомое дифференциальное уравнение в пространст-
ве кватернионов относительно ошибок построения вертикали и ошибки ориен-
тации в азимуте. Следует отметить, что слагаемое в правой части (4.94), снаб-
женное множителем ’Л, является аналогом векторного произведения в обычном
векторном пространстве (см. формулы (3.117) и таблицу 3.1):
-~(er °Qg -Qg oer)^erxwg.
Отсюда становится понятным, что уравнение (4.94) совпадает с аналогичным
уравнением (4.76), записанным в векторном пространстве.
Найдем погрешности определения вектора кажущегося ускорения п. Алго-
ритм идеального режима работы имеет вид
nxg
ПУ8
nzg
(4-95)
где пх, nY, nz - проекции кажущегося ускорения на ребра связанного трех-
гранника; пх, nYg, nZg - проекции кажущегося ускорения на ребра геогра-
фического трехгранника.
В БИНС фактически реализуется следующее матричное равенство
nxg
nYg
nzg
+ 8ах
+ 8aY
+ 5az
(4.96)
где n^g - проекции кажущегося ускорения на ребра вычисленного
трехгранника; 8ах , 8aY, 8az - смещение нулей акселерометров.
Вычтем из равенства (4.96) алгоритм идеальной работы (4.95)
&”xg nxg nXg nx+dax nx
^nYg = nYg — nYg = C Пу -C nY (4-97)
*nzg nzg nzg Hz+8az nz
Учитывая, что С = Е, С, Er = Е +[1?,. ], получим
nx+^>ax nx+^ax 5a
Anrg = {E + [Er]}TC nY + -C nY = [ETr]C nY + daY + C 5a
^zg hz+8«z nz nz+daz 8a
.(4.98)
186
Полагая погрешности акселерометров малыми величинами, пренебрежем в
правой части (4.98) членами, содержащими произведения малых углов а , 0, %
на смещение нулей 8а х, 8ау , 8az. Принимая во внимание, что [Е? ] = — [Ег ],
уравнение (4.98) перепишем в виде
^xg nxg
^Yg nYg +
^zg nzg dazg
(4.99)
Здесь 8аXg , 8aYg, 8aZg — проекции ошибок акселерометров на ребра геогра-
фического трехгранника.
Вспомним, что произведение кососимметрической матрицы на столбцевую
матрицу эквивалентно векторному произведению, поэтому матричное уравне-
ние (4.99) можно представить в векторных обозначениях
Ang = -er *ng+ 8а g. (4.100)
Представим вектор Ang в виде суммы
bng=bVg+bak; (4.101)
где &Vg — вектор ошибок выработки линейной скорости объекта относительно
географической системы координат; - вектор ошибок компенсации «вред-
ных» ускорений.
С учетом (4.101) уравнения ошибок выработки скорости в векторной форме
можно представить в виде
A Vg = -ег + 8а g -как. (4.102)
К уравнению (4.102) можно прийти с использованием аппарата кватернио-
нов. Алгоритм идеального режима работы имеет вид
JVg=A°JV оЛ, (4.103)
где JV — отображение вектора кажущегося ускорения заданного в осях связан-
ного трехгранника; JVg - отображение вектора кажущегося ускорения, заданно-
го в осях географического трехгранника.
Фактически алгоритм реализуется в виде
JVg =Л~оЛ:оЛ~, (4.104)
где ,
JV = JV + 8a. (4.105)
Здесь 8CL — i8a v + j8ar + k8az - отображение вектора ошибок акселеромет-
ров, i, j, к - по-прежнему мнимые единицы.
Вычтем из равенства (4.104) выражение (4.103) для алгоритма идеальной ра-
боты
187
AJV, = Л ' °Л'°Д~ + Л <'6CZ<-Л -Лс Л’ -Л . (4 106)
С учетом равенства (4.86) соотношение (4.106) принимает вид
ДЛ, = 0оДоЛ^оД<-® + 0°Ло 8CL °Л°О — A^JV°A. (4 107)
Учитывая равенство перепроектирования Л ° (...) ° Л, имеем
=0-JV 00 + 008^00-^. (4.108)
Подставим в уравнение (4.108) кватернион ошибок 0 = 1+ 0,5ег, пренебре-
жем нелинейными членами относительно ег и произведениями углов а, , %
на ошибки акселерометров 8а х, 8ау , 8аг и получим
ДЛ =-Цл °JVJ+56Z. (4.109)
Представим отображение ДЛ^ в виде суммы
&Afg=bVg+8ak, (4.110)
где ДК„ - отображение вектора ошибок выработки скорости ЛА относительно
сопровождающего трехгранника; 8С1к — отображение вектора ошибок компен-
сации «вредных» ускорений.
Перепишем уравнение (4.109) с учетом соотношения (4.110)
ДГ= 1( V е -е °JVР)+8С1-8dk. (4.111)
о 'о * ' а • о
Слагаемое -^(Лгг °er -er °JVg) в правой части (4.111) аналогично векторно-
му произведению ng х ег — — ег х пг, что говорит о том, что уравнение (4.111)
полностью совпадает с векторным уравнением (4.102).
4.3. Скалярная модель ошибок БИНС
Определим скалярный вид уравнений:
ёг =егхаа -ее + Дсо •
’ " (4.112)
ЛГ₽ - -er xnf + 8а g - Аак.
Найдем компоненты вектора ошибок угловой скорости географического
трехгранника Дсо как разности между расчетными и истинными значениями
угловых скоростей географического трехгранника
188
rz rz
АсоА£ = cox - coA£ = U cos cp + - U cos cp-—;
R R
~ Vz ~ vz
AcoZg =t/ sin<p + -^-tgcp-£/ sincp--Zgcp;
R R
(4.113)
AcoZg =

R I T? )
Представим в соотношениях (4.3.2) вычисленные параметры в виде суммы
истинного значения этого параметра и малой ошибки
ср = <р + Аср; rVg=rVg+ArAg; VZg = VZg + AKZg; R=R + AR, (4.114)
и, пренебрегая величинами второго и более высокого порядка малости, получа-
ем
—— - C/Acp sin cp —AT?;
R~
( V
т r r Ze
tgq + U cos ср ч-------т—
k 7? cos cp
I wvZe
A<P---
(4.115)
R
. _ AVXg AT?
R + R2 Xg'
Учитывая, что er =yi + aj + РЛ, ng=nXgi + nYgj+ nZgk, и вычисляя вектор-
ные произведения ег х сл? и er х ng, получаем следующую систему уравнений
ошибок БИНС:
R ггл ^vzetg^> vzg^> А7?г/
a = “vgP - “zx X - £ Yg + ^Acp cos <P+-Z------+ ——2-------r Vzgt&V,
R 7? cos cp R~
^Xg ЛR
R + R2 Xg’
A^z AT?
-^-t/Acpsin cp-—VZg,
A VXg = nYg^ -nzg°- + §axg - ^axg;
A^ =nZgx-nXg^ + 8aYg-Aa}g;
A^zg = ”xga -'hgX + 8aZg - AaZg.
P = K>ygX-«v^cc-£zg
X = (OZga-coygP-eA,g
(4.116)
Погрешности компенсации «вредных» ускорений можно также найти как
разности между расчетными и истинными значениями ускорений, подлежащих
компенсации с последующим разложением в ряд Тэйлора около истинных зна-
чений. В линейном приближении ошибки компенсации «вредных» ускорений
имеют вид
= 2 ——tgip + Т/ sin ф ДИ7„ +
( V
Aa*g = -2l + U cos <р Л V2
И2
yzg
R cos2 ср
2V.
rzg —a vXg + 2t/ sin <рд<р+
к
Vr V г
+ 2t7coscp Аср + ——ЛК- +-^-ДИГа;
R Хё R ё

189

(z, A fjz A (у >
—^-tgg) ДГ^ + —— +20’coscp Д1^ - ——Zgcp+2Osincp ДИ^
R ! R j { R
V,
IkJk
r R
Vv V7
jS ,s + 2UVXp coscp + 20 К sin(p Дер,
/?cos2cp g )
-'g
(4.H7)
R
где Rg — погрешность компенсации ускорения силы тяжести. В соотношениях
(4.117) не учтены погрешности в определении радиус-вектора R
Аналогично определим погрешности счисления координат ср, Л., А:
*• Гп сп Г
А<Р — СР — СО = ——--=-----------— А/С.
R R R R~
ДЛ, = JZs-----^—= ^Vze-+- Kzg--A(p-----------^—RR; (4.118)
7?coscp A coscp A coscp 7?cos"cp R~ coscp
Таким образом, полная система уравнений ошибок БИНС в скалярной форме
имеет вид:
о г,л AKz/g<P rz?A(P Д^г/ f
а = сол,Р - со/Д - Eyg + О Дер cos ср + r - + -^-у- - -^r^Zgcp;
p = corgX-^a-£Zg
X = ®Zga-wrgp-E%g
R R2 Ag’
RVZ RR
^-C/Acpsincp-—HZg;
= "r8P - nZga + s«
^Yg = nzgX - nxgP + daYg - ^aYg^
^Zg = "xgO- - "rgX + §aZg - ^aZg ;
(4 119)
Д^ У*,
Дср = ——^-RR:
R R2
RV V V
RX =---+------L A(p---A7?;
Acoscp Rcos cp R" coscp
Rh = RVyg.
Входящие в уравнения (4.119) проекции инструментальных погрешностей
гироскопов и акселерометров определяются следующим образом
eAg =ех cos 6 coscp + £у (sin у sin р- cos у coscp sin 0) +
+ ez sin у cos cp sin 0 + cos у sin cp;
exg =£%sin0 + £y cosy cos 0 — ez sin у cos 0; (4 120)
EA,g =-£x cos0sincp + Er(cosysincpsin0 + sinycoscp) +
+ £z (cos у cos cp - sin у sin cp sin 0);
190
daXg - Ъах cos 0 cos + &aY (sin у sin у - cos у cos у sin 0) +
+ 5a z sin у cos v/ sin 0 + cos у sin g;
baYg = 5a v sin 0 + 5a y cos у cos 0 - 5az sin у cos 0; (4.121)
5aZs, = -5a v cos 0 sin у + 5a y (cosy sin |/ sin 0 + sin у cos у) +
+ 5az(cosycosy - sin у sin у sin 0).
Математическая модель погрешностей БИНС (4.119) представляет собой
систему неоднородных линейных обыкновенных дифференциальных уравнений
с переменными коэффициентами. Неоднородность модели (4.119) вызвана по-
грешностями акселерометров и гироскопов, которые являются входными по-
грешностями БИНС. Погрешности инерциальных чувствительных элементов
могут быть постоянными по величине, но чаще всего описываются случайными
функциями времени. Погрешности гироскопов и акселерометров входят в сис-
тему (4.119) в виде проекций на ребра географического трехгранника, т.с. по-
грешности инерциальных ЧЭ пересчитываются в географическую систему ко-
ординат вместе с полезной информацией, получаемой в связанной системе ко-
ординат. Вследствие этого погрешности гироскопов и акселерометров из-за нс-
стационарности матрицы перехода С будут нестационарными случайными
процессами даже при стационарности случайных процессов, представляющих
реальные погрешности инерциальных чувствительных элементов [4.9]. Кроме
того, в модель погрешностей БИНС входят проекции абсолютной угловой ско-
рости географического трехгранника и проекции кажущегося ускорения его
вершины на ребра. В таком случае погрешности БИНС зависят от траектории
движения центра масс ЛА и его перемещения относительно центра масс, по-
этому аналитическое решение системы (4.119) возможно только для частных
случаев движения.
В связи с этим рассмотрим погрешности БИНС для неподвижного объекта,
находящегося на экваторе. В этом случае проекции абсолютной угловой скоро-
сти географического трехгранника и проекции кажущегося ускорения его вер-
шины на ребра определяются только угловой скоростью суточного вращения
Земли и ускорением силы тяжести:
-С; wy?=0; coZg =0;
”zg=°-
(4.122)
В этих условиях математическая модель погрешностей БИНС (4.121) распа-
дается на две независимые системы уравнений

(4.123)
191
d = C'P - £}g + C/Aip;
ДК,
P = -4Ax-£Zg —A
А^л-g = ^P+^;
A’
R
(4.124)
Рассмотрим сначала решение системы уравнений (4.123). Структура уравне-
ний (4.123) совпадает с точностью до знаков с моделью погрешностей северно-
го канала, рассмотренного в разделе 4.1. Дифференцируя по времени обе части
первого уравнения системы (4.123) в предположении = const и подставляя
в него второе, получаем
Х + «а = -^. (4.125)
к
Если в начальный момент времени вертикаль в плоскости экватора была вы-
ставлена с ошибкой /(О) = %0, то, учитывая, что х(0) - -£ v, решение уравнения
(4.125) имеет вид
<5tfz £ Ve
X = Хо cos (£)ot +-— (1 - cos <o0/) —— sin <o0Z. (4.126)
S “o
Подставив во втором уравнении системы (4.123) вместо величины х реше-
ние (4.126), найдем погрешность в определении восточной составляющей ско-
рости
Д Vz = ---------sin со0/ - £ v„ 7?(cos w0 t -1) <4.1Z Z J
co0
Наконец, пользуясь третьим уравнением системы (4.124) находим погреш-
ность в определении долготы
АХ= Хо-
^t2z Vp
----— (cos <о0/ -1) —— (sin <о0( - соо/).
g J wo
(4.128)
В рассматриваемых условиях погрешности БИНС в определении восточной
скорости и долюты аналогичны погрешностям северного канала, рассмотрен-
ного в п. 4.1. Как и следовало ожидать, дрейф гироскопов £Xg вызывает расту-
щую со временем погрешность выработки долготы.
Рассмотрим теперь систему уравнений (4.124). Во втором уравнении систе-
мы (4.124) пренебрежем перекрестной связью Ua , тогда ошибки северного ка-
нала БИНС независимы от погрешности а азимутального канала. Дифферен-
циальное уравнение относительно азимутальной ошибки запишем в виде
' d = С/(Р + А<р) —£yg . (4.129)
Складывая второе уравнение системы (4.124) с четвертым, находим
р + Дф = -£^. (4.130)
Интегрируя обе части равенства (4.130) в предположении £Zr = const, имеем
Р + А(р = р0 + А(р0 - zZgt, (4.131)
где Дф0 - начальная погрешность значения широты.
192
Подставляя правую часть уравнения (4.131) в (4.129) и интегрируя получен-
ное уравнение, находим
Ut2
а = а0 - eYgt + poU + Atp0Ut -£Zg — .
(4.132)
Из уравнения (4.132) можно заключить, что азимутальная погрешность
БИНС возрастает пропорционально времени и квадрату времени. Следует отме-
тить, что три последних слагаемых имеют в качестве множителя угловую ско-
рость суточного вращения Земли, поэтому они начинают оказывать влияние на
погрешности БИНС после примерно двух часов непрерывной работы [4.4].
4.4. Уравнения ошибок БИНС в определении параметров ориентации
Представим формулу (4.63) в виде
ОЕ,С (4.133)
Заменим в равенстве (4.133) матрицу Ег суммой единичной и кососиммет-
рической матриц
С = {£, + [£Г]}ГС = {£-[£'Г]}С. (4.134)
Уравнение (4.134) можно представить в виде
ДС = -[ЕГ]С, (4.135)
где АС = С - С - ошибка выработки матрицы направляющих косинусов.
Уравнение (4.135) позволяет определить погрешности выработки элементов
матрицы направляющих косинусов, а, следовательно, и погрешности выработки
параметров ориентации объекта.
Найдем погрешности выработки параметров ориентации для случая малых
углов тангажа 0 и крена у. В этом случае матрица преобразования С прибли-
женно имеет вид
COSY/ - ©cos v + у sin sin y/
С~ 6 1 ~Y
-sin у у cosy/ COSY/
(4.136)
Представим в матрице (4.136) углы рыскания, тангажа и крена в виде суммы
истинных значений этих углов и малых приращений. В результате матрица АС
примет вид
AC« - Ay/ sin Y/ A0 - A0 cos y/ + Ay sin Yp + Ay/ COSY/ + 0 sin y/Ay/ + у COS YpAY|/ 0 -Ay (4.137)
4 -Ay/COSY/ AyCOSYg-ysinY|/AYg -Ay/SHIY/
С другой стороны, эти элементы определяются правой частью уравнения
(4.135) 0 -P a COSY/ — 0 COS Y|7 + у Sin Yp sinY/
— P 0 -x 0 1 ~Y (4.138)
-a X 0 -sinYg У COSY/ COSY/
193
Приравнивая величины ДСИ, ДС21,ДС23 соответствующим элементам мат-
рицы, полученной в результате произведения (4.138), имеем
Avj/ sin = -рО - a sin ;
ДО = —х sin — р cos *4/; (4.139)
Ду = Р sin v|/ - % cos vj/.
Пренебрегая в первом уравнении (4.139) произведением малых величин рО,
получаем ошибки выработки параметров ориентации БИНС
Д V = -а;
ДО = -/sin -pcosv; (4.140)
Ду ~ Р sin у - % cos vg.
Из уравнений (4.140) можно заключить, что для определения ошибок выра-
ботки параметров ориентации необходимо найти ошибки азимутальной ориен-
тации и ошибки построения вертикали в соответствии с уравнениями (4.119).
Следует отметить, что ошибка выработки рыскания Avy определяется только
азимутальной ошибкой а
Получим формулы (4.140), пользуясь алгеброй кватернионов. Из уравнения
(4.88) имеем
Л~=0оЛ. (4.141)
Подставив в уравнение (4.141) кватернион ошибок 0 =1-0,5е,., получим
Д' =(1-0,5ег)оЛ. (4.142)
После преобразований имеем
ЛА--()>,. оД, (4.143)
где ДА = Л~ - Л - ошибка выработки кватерниона Л .
Уравнение (4.143) является кватернионным аналогом матричного уравнения
(4.135). Положим, как и выше, углы 0 и у малыми. В этом случае элементы
истинного кватерниона Л можно представить в виде (см. соотношения (3.126)):
0 у
„ vy 0 у . vi/ . 0 . у V
А,, - cos — cos—cos—-sm—sin—sin— ~ cos—;
о non 2 2 2 2
. vy . 0 у у vy 0 . vy
-- p'n — cos — «—cos— +—sm—,
2 2222 222
у VI/ . 0 . у .VI/
-OS —firL- Sin— ~ Sin — ,
2 2 2 2 2
. V • - У vy 0 . у 0 vy у . vy
A, = cos—sin—cos— -sin—cos—sin — ~— cos-sin—.
3 n n 2 2222222

2 2
Y
2
W 4Z . J . ±z . vz r
A, =cos—cos—sm — + sin—sin—cos—
1 2 n n n n n
V
2
A, = sin—cos—cos—+ cos—sin—sin—
2 2 2 2 2 2
2
V|Z . 0
2 2
Найдем элементы кватерниона ДЛ
д. Av|/ . v .. Ду vy Д0 . vy
ДАП ---—sin —; ДА. = —cos—+—sin—;
2 2 2 2 2 2
А. Avy v|/ ДО vy Ду . vy
ДА, =——cos—; АА, =—cos— -sin—.
2 2 2 2 2 2
(4.144)
(4.145)
Для определения правой части (4.143) воспользуемся, к примеру, кватерни-
онными матрицами (см. п. 3.3.4)
194
о
-ox
°А = -О,5
-х -а -р Ао -хА!-аА2-рХ3 -аХ2
0 ~Р а К = -0,5 xAq РХ2 + аА3 «-0,5 хА0-РА2
Р о -х А9 аА0 +pAj -хА3 аА0 +рА|
-а х 0 А3 pXQ-aXj +хА2 РА0 +хА2
х
а
(4.146)
Из сравнения (4.145) и (4.146) получим алгебраические уравнения:
ДА0 -0,5аА2; ДА] = -О,5(хАо ~рА2);
ДА 2 = -О,5(аАо + рА]); ДА3 =-О,5(РАо +/А2).
(4.147)
Из первого уравнения системы (4.147) получим Д|/ = -а . Второе и четвер-
тое уравнение системы (4.147) в развернутой записи имеют вид
_ . ы 1/ _ . ш 1/
Д0 sin— + Ду cos — = р sin-х cos—'>
2 2 2 (4.148)
„11/ . W „ W .11/
Д0 cos -у - Ду sin — = -p cos — - % sm—.
Разрешая уравнения (4.148) относительно ДО и Ду, находим
Д0 = ~X$in |/ ~Pcosi/;
л y н y, (4.149)
Ду = Р sin ц/- х cos у,
что повторяет соотношения (4.140).
Уравнения (4.135) и (4.143) связывают ошибку в вычислении матрицы на-
правляющих косинусов, либо собственного кватерниона ориентации с ошибка-
ми в азимуте и построения вертикали. Найдем дифференциальные уравнения
относительно ДС и ДА . Продифференцируем по времени обе части равенства
(4.135)
ДС = -[СГ]С-[С,.]С. (4.150)
Подставим в полученное уравнение вместо матрицы [Д.] правую часть
дифференциального уравнения (4.73), учитывая также, что С = C[co]-[o)g]C,
имеем
AC = [eJC + [cog][Cr]C-[£r][coJC-[A(Og]C-[£r]{C[ci)]-[Cr][cogJC}.
(4-151)
Принимая во внимание, что ДС = -_ЕГ ]С , имеем
ДС = [е* ]С - [со* ] ДС - [Дсо., ]С + ДС[со]. (4.152)
Умножим слева первое слагаемое правой части уравнения (4.152) [£*]С на
единичную матрицу Е = ССТ:
ССг[е*]С. (4.153)
В соотношении (4.153) кососимметрическая матрица [eg] умножена слева и
справа на две взаимно обратные матрицы, что эквивалентно преобразованию
компонент вектора е о из географического трехгранника в связанный, поэтому
ССг[е*]С = С[е]. (4.154)
195
Меняя последовательность членов в уравнении (4.152) и принимая во вни-
мание равенство (4.154), получаем дифференциальное уравнение относительно
матрицы ошибок ДС
ДС = ДС[(о] + С[£]-[Д(о?]С-[со?]ДС. (4 155)
Следует отметить, что в уравнении (4.155) матрица дрейфов гироскопов за-
писана в осях связанного трехгранника, в отличие от уравнений (4.73).
Дифференциальное уравнение (4.155) достаточно просто получить на осно-
вании понятия вариации функций. Если из некоторого класса функций выбраны
две функции р(/) и y(t), то разность этих функций называется вариацией
функции у(/). Вариацию функций обозначают 5у(0 или бу. Вариация функ-
ции аналогична приращению Д/ или дифференциалу dt аргумента обычной
функции. В связи с этим уравнение (4.155) можно получить, осуществив фор-
мальную вариацию уравнения Пуассона С = С[со] - [(og ]С
6С = 8С[со] + С[6со]-[5(оДС-[со J5C. (4 156)
Заметим, что в уравнении (4.156) вариация [Зсо] соответствует приращению
вектора абсолютной угловой скорости, заданного своими проекциями в связан-
ной системе координат, поэтому очевидно [бсо] = [е] .
ЬПри м е р 4.4.1. Найти дифференциальное уравнение относительно ошиб-
ки выработки кватерниона Л .
Решение.
Обратимся к уравнению (3.78)
2Л = Л ° Q — ° д.
Варьируя это уравнение, находим
2дл = 8л а+л<(5о ю), л а обл. (4.157)
Замечая, что 6Q = Р (см. формулу (4.78)), окончательно находим
28A = 8Aof2 + Ao£-5QgoA-Qeo8A . (4 158)
Метод получения ошибок БИНС, основанный на вариации функции, являет-
ся достаточно продуктивным и позволяет сравнительно просто получать урав-
нения ошибок навигационных систем.
ЛИТЕРАТУРА К ГЛАВЕ 4
4.1 Андреев В. Д. Теория инерциальной навигации. Кн. 1. Автономные системы. Кн.2 Корректи-
руемые системы. - М.: Наука, 1966, 1967.
4.2 Ahj чин, О.Н., Емельянцев Г.И. Интегрированные системы ориентации и навигации для
морских подвижных объектов/Под общей ред. чл.-кор. РАН В.Г. Пешехонова. - С-Пб.. 1999.
-357 с.
4.3. Бранец В.Н., Шмыглевский И.П. Введение в теорию бесплатформснных инерциальных
навигационных систем. - М.: Наука, 1992. - 280 с.
4.4. Бромберг П.В. Теория инерциальных систем навигации. -М.: Наука, 1979-296 с.
4.5. Инерциальные навигационные системы морских объсктов/Д.П. Лукьянов, А.В. Молчанов,
А А Одинцов, И.Б. Вайсгант; под. ред. Д.П. Лукьянова. - Л.: Судостроение, 1989.-184 с.
4.6. Ишлинский А.Ю. Ориентация, гироскопы и инерциальная навигация. М.: Наука 1976. -
672 с.
196
4.7. Каракашев В.А. Обобщенные уравнения ошибок инерциальных навигационных систем
//Изв. Вузов. Приборостроение. - 1973.-№3.
4.8. Климов Д.М. Инерциальная навигация на море. - М.: Наука, 1984.-118 с.
4.9. Кузовков Н.Т., Салычев О.С. Инерциальная навигация и оптимальная фильтрация. - М.:
Машиностроение, 1982. - 216 с.
4.10. Помыкаев И.И., Селезнев В.П., Дмитроченко Л.А. Навигационные приборы и системы. -
М.: Машиностроение, 1983.
4.11 .Селезнев В.П. Навигационные устройства. - Машиностроение, 1974. - 660 с.
4.12. Степанов О.А. Особенности построения и перспективы развития навигационных инерци-
ально-спутниковых систем. /Интегрированные инерциально-спутниковые системы навига-
ции. Сб. статей докл. СПб. 2001.
4.13. Управление и наведение беспилотных маневренных летательных аппаратов на основе со-
временных информационных технологий /Под редакцией М.Н. Красильщикова и Г.Г. Себря-
кова. - М.:Физматлит. 2003. - 280 с.
4.14. Якушенков А,А.Основы инерциальной навигации. М.: Морской транспорт, 1963.-146с.
Вопросы для самоконтроля
1. Каково влияние погрешностей акселерометров на ошибки
БИНС.
2. Как оценить влияние дрейфов гироскопов на ошибки БИНС.
3. Как связаны ошибки в выработке параметров ориентации
с ошибками построения вертикали и ошибкой в азимуте?
4. Почему вертикальный канал БИНС называют неустойчи-
вым?
197
Глава 5
КОМПЛЕКСНЫЕ НАВИГАЦИОННЫЕ СИСТЕМЫ
Хотя инерциальная навигация обладает такими неоспоримыми преимущест-
вами, как автономность и помехозащищенность, она имеет главный недостаток
— накопление погрешностей с течением времени. Для устранения этого недос-
татка инерциальные системы навигации объединяются в навигационные ком-
плексы с навигационными системами, основанными на других физических
принципах (спутниковые навигационные системы (СНС), астронавигационные
и радионавигационные системы, корреляционно-экстремальные системы и др.).
Объединение информации навигационных систем осуществляется на основе
моделей их погрешностей, которые в общем случае представляют собой слу-
чайные функции времени.
5.1. Элементы теории случайных процессов
Погрешности инерциальных чувствительных элементов
как случайный процесс
На практике встречаются случайные величины, которые изменяют свои зна-
чения с течением времени. Особенностью таких случайных величин является
то, что практически ничего нельзя сказать об их поведении в будущем, даже
если известен характер поведения в прошлом [5.22]. Возьмем, к примеру, не-
сколько однотипных гироскопических датчиков угловой скорости, запустим их
на неподвижном основании и будем записывать их выходные сигналы, начиная
с некоторого момента времени. Так как основание неподвижно (вращением
Земли пренебрегаем), то записи будут представлять собой погрешности (шумы)
гироскопов. Несмотря на то, что гироскопы однотипные, их погрешности будут
принимать разные значения в разные моменты времени в силу всевозможных
причин: нсидентичности геометрических параметров конструкции, систем воз-
буждения и съема сигнала; различия установки и многих других неконтроли-
руемых факторов. Все это приведет к тому, что после записи будет получена
картина, приведенная на рис. 5.1.
198
Примерно такая же картина будет получена, если записывать шум одного
гироскопа и затем совместить записанные интервалы. Значение каждой кон-
кретной записи в определенный момент времени t' будет представлять случай-
ную величину (эти значения отмечены точками на рис. 5.1). Таким образом,
случайная величина, меняющаяся со временем, представляет собой случайный
процесс.
Случайным процессом (функцией) называется такая функция, значение кото-
рой при каждом фиксированном значении времени является случайной величи-
ной. Сечением случайного процесса называются значения случайного процесса
в некоторый фиксированный момент времени. Так, значения погрешностей ги-
роскопов в момент времени t' и есть сечение случайного процесса.
Отдельная запись на рис 5.1 называется реализацией случайного процесса.
При изучении случайных процессов исследуют не свойства каждой реализации
е,(0 отдельно, характеризующей процесс е(/), а свойства всего множества
реализаций в целом.
Для описания случайных процессов вводятся вероятностные характеристи-
ки, аналогичные случайным величинам. В отличие от числовых характеристик
случайных величин, характеристики случайных процессов в общем случае -
неслучайные функции времени [5 22].
В основу теории случайных процессов (функций) положено пять неслучай-
ных функций, характеризующих процесс [5.6, 5.22, 5.23]:
1) математическое ожидание случайного процесса - характеризует поведение
процесса в среднем;
2) дисперсия случайного процесса - характеризует рассеивание значений про-
цесса во времени относительно среднего значения;
3) плотность распределения - дает представление о распределении случайного
процесса в фиксированные моменты времени;
4) корреляционная функция - характеризует степень линейной зависимости
между двумя сечениями случайного процесса;
5) спектральная плотность - дает спектральное представление случайного
процесса.
Рассмотрим более подробно основные характеристики случайного процесса
[5.6,5.21,5.22].
Рис 5.2. Случайный процесс X(Z) и его математическое ожидание т (/)
199
Первой и важнейшей характеристикой случайного процесса является его ма-
тематическое ожидание, т.е. «средняя» неслучайная функция времени
вокруг которой происходит разброс реализаций случайного процесса (рис. 5.2).
Таким образом, если взять сечение случайного процесса X(t) в произволь-
ный момент времени t, то в этом сечении имеем случайную величину, матема-
тическое ожидание которой
mx(t) = M[X(tJ] (5.1)
есть функция времени.
Используя понятие математического ожидания, вводится центрированный
случайный процесс
Z(0 = Х(0-«(0- (5-2)
Дисперсия и среднее квадратическое отклонение
По аналогии со случайными величинами вводится дисперсия случайного
процесса
Dx(/) = M[(%(0-mA(0)2] = ^[W]- (5-3)
Следовательно, дисперсия случайного процесса Dx (t) характеризует степень
разброса реализаций около его математического ожидания mx(t) и равна дис-
персии соответствующего сечения случайного процесса Размерность диспер-
сии равна квадрату размерности случайного процесса X(t).
Чтобы иметь характеристику разброса случайного процесса в его размерно-
сти, вводится среднеквадратическое отклонение. Среднеквадратическое откло-
нение (СКО) есть арифметическое значение квадратного корня из дисперсии
случайного процесса
= (5.4)
Функция распределения и плотность распределения
По аналогии со случайными величинами в теории случайных процессов вво-
дится функция распределения, которая определяется вероятностью того, что
сечение случайного процесса X(f) в момент времени t примет значение менее
заданного х
F(t,x) = P{X(t)<x}, (5.5)
где функция F(t,x) - называется одномерным законом распределения.
Функция F(t,x) зависит от двух аргументов: времени t, когда берется сече-
ние, йот X) меньше которого должна быть случайная величина X(t).
Более точной характеристикой случайных процессов является двумерный
закон распределения
F(Z1,Z2,x1,x2) = P{A(r1)<xl,X(/2)<x2}.
Аналогично случайным величинам вводится плотное гь распределения (диф-
ференциальный закон распределения) случайного процесса
200
. . . dF(t,x) .. . dF^t^t^x^x,)
fxM = — /,(У2,*„х2) = V‘ - '-—. (5.6)
dx cx}ox2
Следует отметить, что наиболее полную характеристику случайного процес-
са может дать многомерный закон распределения, однако в инженерных при-
ложениях обычно ограничиваются одномерным, иногда двухмерным законом
распределения случайного процесса [5.6].
Существует большой класс процессов, так называемые нормальные, или га-
уссовские, случайные процессы. Если X(t) — нормальный случайный процесс,
то одномерная плотность распределения определяется формулой
1 1
Г (t, х) = .. ехр]------------[х - rn (Z)]
V2nD,(r) I 2D,(t)
(5.7)
Известно, что вероятность попадания случайной величины в полосу ±3о
равна 0,997. Это же свойство можно отнести и к нормально распределенным
случайным процессам (рис. 5.3), для которых границы отклонения реализаций
хДг) от математического ожидания приблизительно равны 3сг(0 [5.18].
mv(/)-3ay(0
Рис. 5.3. Границы отклонений случайного процесса при нормальном законе распределения
Корреляционная функция
Одной из важнейших характеристик случайного процесса является корреля-
ционная функция, устанавливающая степень зависимости между двумя сече-
ниями случайного процесса. Корреляционной функцией случайного процесса
X(t) называется неслучайная функция двух аргументов определяемая
по формуле
Kx(t.t') = M[X(t)X(j')],
(5-8)
где X(t), X(t‘)
- центрированные случайные функции
X(t) = X(t)-mx(f),
X(t') = X(t')-mx(t').
201
Отметим некоторые свойства корреляционной функции. Из определения
корреляционной функции (5.8) вытекает
А(Г,Г) = А(Лт), (5.9)
т.е. корреляционная функция симметрична относительно своих аргументов
Если положить t ~ t', то из (5.8) следует
Кх= М[X(t) X(t)] = М[Х2(Z)] = Dx(t). (5.10)
Итак, при равенстве аргументов корреляционная функция равна дисперсии
случайного процесса.
Векторный случайный процесс
Рассмотрим векторный случайный процесс, т.е. вектор, у которого каждый
элемент представляет собой случайный процесс (под вектором по-прежнему
понимаем столбцевую матрицу):
Xr(')=W0, (5.11)
Пусть случайный процесс Xt(t) имеет математическое ожидание w ® и
корреляционную функцию X.(r,f) (z = 1,2,...Л’). Характеристики w,(0 и
описывают поведение только отдельного случайного процесса Xt(t) и нс опре-
деляют «взаимных характеристик» - зависимости между составляющими век-
торного случайного процесса X(t). В качестве такой характеристики рассмат-
ривается взаимная корреляционная функция Kv(t,f) двух случайных (скаляр-
ных) процессов X.(t) и Х}({') [5.6]
К/Ли') = М[Х^)Х^')]. (5.12)
Из (5.12) следует, что при равенстве индексов j = i взаимная корреляцион-
ная функция равна корреляционной функции случайного процесса Xt).
Взаимную корреляционную функцию можно представить в виде квадратной
матрицы размера к х к
Р(ЛП = А/[Х(0Хг(Г)] = ХИ(/,П K2l (1,0 X12(f,Z) К22М - K2kM (5-13)
хи(лО к,2(м') .
На главной диагонали матрицы (5.13) стоят к корреляционных функций со-
ответствующих случайных процессов. Случайные процессы X.(f) и Xj(t) на-
зываются некоррелированными, если взаимная корреляционная функция
равна нулю при любых значениях аргументов t и t' для i' * j. В этом
случае матрица (5.13) является диагональной. Если t = t', то матрица P(t,t}
обозначается с одним аргументом P(z) и называется корреляционной матрицей
202
(correlation matrix) случайного векторного процесса X(t) [5.17]. Очевидно, что
в этом случае на главной диагонали матрицы P(t) находятся дисперсии эле-
ментов векторного случайного процесса X(t).
Для двух случайных векторных процессов X(t) и Y(t) вводится взаимная
матричная корреляционная функция
Рху =M{(X(t)-m^[Y(t}-my(tyT}, (5.14)
где т,(/), mv(i) - векторы, составленные из математических ожиданий ком-
понент векторов X(t) и Y(t) .
Стационарные случайные процессы
Среди случайных процессов выделяют процессы, которые протекают во
времени приблизительно однородно и вероятностные характеристики которых
значительно нс изменяются со временем. Такие случайные процессы называют
стационарными. Случайный процесс называется стационарным, если его мате-
матическое ожидание и дисперсия не зависят от времени (более строгое опре-
деление стационарных случайных процессов можно найти в работе [5.6]):
mx(t) = const, Dx(t) = const. (5.15)
Из (5.15) следует, что при записи математического ожидания и дисперсии
стационарного случайного процесса аргумент t можно опустить.
Рассмотрим корреляционную функцию стационарного случайного процесса.
В этом случае корреляционная функция при смещении аргументов на один и
тот же интервал времени Д/ остается неизменной:
Kx(t,t ) = Kx(t + At,t + Д/). (5.16)
Если положить Д/ = —/, то равенство (5.16) можно переписать в виде
Kx(t,t') = Kx(O,t'-t). (5.17)
Из соотношения (5.17) следует, что корреляционная функция стационарного
случайного процесса зависит только от промежутка между t и t'. Таким обра-
зом корреляционная функция стационарного случайного процесса есть функция
одного аргумента
X (0,/'-/) = К,(т),
где x-t'-t - интервал между двумя сечениями случайного процесса.
Так как корреляционная функция симметрична относительно своих аргумен-
тов, то для стационарного случайного процесса
Kx(z) = Kx(-t), (5.18)
ч
т.е. корреляционная функция является четной функцией.
В общем случае дисперсия случайною процесса определяется так
Dx(t) = Kx(t,t),
тогда для стационарного случайного процесса имеет место равенство
DX=KX(O). (5.19)
203
Спектральное представление случайных процессов
Рассмотрим спектральное представление стационарных случайных процес-
сов, основанное на паре преобразований Фурье
f(t} = р((о)Лсо, (5.20)
—ос
1 +ос
ЭД = —(5.21)
Интеграл (5.20) позволяет представить непериодическую функцию /(Z) в
виде суммы синусоид с непрерывной последовагельностью частот. Функция
S(co) называется спектральной плотностью и характеризует «плотность» ам-
плитуд, приходящихся в интервале частот (со, со+ Jco).
Получим одно важное соотношение, которое понадобится в дальнейшем.
Найдем спектральную плотность 5-функции Дирака, обладающей следующими
свойствами:
1) =
со, t - О,
0. !*0.
2) f S(l)/(r)dt = /(O).
Второе свойство называется фильтрующим («выхватывающим») свойством
5-функции, используя которое получаем спектральную плотность 5-функции
J +00 । j
ЭД=-!-= —е-*'| =—. (5.22)
2л J 2л h-° 2л
—СО
Таким образом, спектральная плотность 5-функции постоянна и равна 1/2л.
Подставив спектральную плотность 5-функции из (5.22) в (5.20), получим
Ко .
5(/) = [—Л/со
Д)2л
или
2л5(0=|Л<о. (5.23)
—ос
Формула (5.23) будет полезна в дальнейшем и связывает 5-функцию с инте-
гралом с бесконечными пределами от показательной функции с мнимым пока-
зателем.
В спектральной теории стационарных случайных процессов вместо функции
/(/) вводится корреляционная функция КДт). В этом случае соотношения
(5.20) и (5.21) принимают следующий вид:
* Преобразования Фурье (5.20) и (5.21) могут отличаться коэффициентами при интегра-
лах. Множитель 1/2л может содержаться в равенстве (5.20), а в (5.21) отсутствовать.
Иногда применяется симметричная форма записи преобразований Фурье, когда оба равенства
снабжаются множителем 1/(2тг),/2.
204
Кх(т) = р(<о)Лсо,
-со
(5.24)
1 +ЮО
5((о)=— |Х(т)е Z“W/.
2л J
(5.25)
Учитывая связь между корреляционной функцией и дисперсией стационар-
ного случайного процесса, из (5.24) получаем дисперсию стационарного слу-
чайного процесса
Z), = Кх (0) = J S(cd>7(o . (5.26)
Из соотношения (5.26) следует, что дисперсия стационарного случайного
процесса равна сумме элементарных слагаемых 5,(со)<7(о. Если интеграл (5.26)
представить в виде бесконечной суммы, то на k-ю гармонику будет приходиться
дисперсия
D4 = 5(<oJAco, (5.27)
где Аси - интервал между соседними частотами.
Равенство (5 27) показывает, что спектральная плотность стационарного
случайного процесса характеризует плотность распределения дисперсий по
частотам непрерывного спектра [5.6]. Размерность спектральной плотности
есть отношение дисперсии случайного процесса к частоте, т.е.
‘ед!
с'1
= [ед2 - с].
Белый шум
Модель случайного процесса типа белого шума нашла широкое применение
для описания широкополосных погрешностей чувствительных элементов БИНС
и для конструирования так называемых формирующих фильтров, рассмотри-
ваемых ниже. Понятие белого шума рассмотрим на основе следующего приме-
ра.
♦ Пример 5.1.1. Найти корреляционную функцию случайного процесса, у
которого спектральная плотность постоянна на всех частотах S(co) = 50 = const.
Решение.
Пользуясь соотношением (5.24), имеем
Кх(у) = j ЗДЛсо = So Je/Mdco.
—со —оо
Так как из формулы (5.23) следует, что
Je/wtJco = 2n5(x),
то корреляционная функция белого шума имеет вид
Кл(т) = 2лЭДт). (5.28)
205
Стационарный случайный процесс, у которого спектральная плотность по-
стоянна на всех частотах, называется стационарным белым шумом. Стационар-
ный белый шум представляет собой случайные колебания на всех частотах, от-
сюда и происхождение термина «белый шум» по аналогии с «белым светом»,
включающим все частоты видимого диапазона Из соотношения (5.28) следует,
что дисперсия белого шума (при т = 0) стремится к бесконечности, поэтому на
практике реализовать случайный процесс с бесконечной дисперсией невозмож-
но. Однако белый шум нашел широкое применение, в частности, в теории оп-
тимальной фильтрации, так как отдельные случайные процессы в некотором
диапазоне частот имеют постоянную спектральную плотность и вследствие чс-
этого в этом диапазоне могут быть аппроксимированы белым шумом.
Представим равенство (5.28) в виде
А(т) = q&(x),
где
<7 = 2л50. (5.29)
Величина q называется интенсивностью белого шума [5.6, 5.21] и имеет
размерность спектральной плотности.
Экспоненциа чъно-коррелированный случайный процесс
Экспоненциально-коррелированный случайный процесс является следую-
щим по сложности случайным процессом после белого шума и описывается
корреляционной функцией вида
х;.(т) = г>хм|т|, (5.30)
где Dx — дисперсия случайного процесса, ц - коэффициент затухания корре-
ляционной функции.
♦ Пример 5.1.2. Корреляционная функция стационарного случайного про-
цесса имеет вид К(т) = Т>ге-'''т'. Требуется найти спектральную плотность слу-
чайного процесса.
Решение.
По определению спектральной плотности имеем
1 7") +х
5(со) = -L j Dxe~^'e Jwxch = J c
X —ОС
(5.31)
Пользуясь свойством модуля
-т, т < О,
т, т > О,
интеграл (5.31) представим в виде суммы интегралов, после вычисления кото-
рых получим
5(со) = f eV™ dt + ТeW = —-— + —-—] =---------.
2 л Jr J 2л^р-/со p + jcoJ л(р-+со-)
Таким образом, экспоненциально-коррелированному случайному процессу
(5.30) соответствует спектральная плотность
S(«>) = °'Р - . (5.32)
л(ц" + (1Г )
206
Вид корреляционной функции (5.30) и спектральной плотности (5.32) пока-
зан на рис. 5.4.
Рис. 5.4. Характеристики экспоненциально-коррелированного
случайного процесса: а) корреляционная функция;б) спектральная плотность
Прохождение случайного процесса через линейную систему
На практике достаточно часто возникает задача определения спектральной
плотности 5вых((в) случайного процесса на выходе динамической системы,
описываемой передаточной функцией FT(jco), по известной спектральной
плотности 5вх(со) входного стационарного случайного процесса (рис. 5 .5)
Динамическая
система
5пх(со)
$вых («)
> №( /со)
Рис. 5.5. К задаче о связи спектральных плотностей
на входе и выходе динамической системы
Для решения этой задачи необходимо воспользоваться известным соотноше-
нием [5.18]
s,„(<o)=|’r(;ffl)| (5.33)
где |И'(уо>)|2 - квадрат модуля частотной передаточной функции И'(усо).
Достаточно часто в задачах оптимизации систем управления (в том числе и
комплексных навигационных систем) необходимо оптимальным образом выби-
рать параметры системы из условия минимума ее дисперсии (либо СКО) ошиб-
ки. В этом случае необходимо знать дисперсию случайного процесса на выходе
системы. Подставим в соотношение (5.26) вместо спектральной плотности пра-
вую часть равенства (5.33) и получим
+со
(5.34)
207
Формула (5.34) позволяет определить дисперсию выходного сигнала в уста-
новившемся режиме, если известна частотная передаточная функция системы и
спектральная плотность входного случайного процесса.
Для вычисления дисперсии в соответствии с (5.34) необходимо подынте-
гральное выражение привести к виду
(5.35)
где
B^^b^jcd)2"-2 +Ь^)2п-4 ..
(5 36)
Л(7®) = а0 + ...ап.
Если подынтегральное выражение приведено к виду (5.35), то значение ин-
теграла (5.34) выражается через коэффициенты Ьп,Ь},..., Ьп_х, а0, ау,..., ап и
приводится в специальных таблицах [5.18].
♦ Пример. 5.1.3. Динамическая система описывается дифференциальным
уравнением первого порядка
—х(0 + их(0 = МО, (5-37)
dt
где w(Z) - стационарный белый шум единичной интенсивности (q = 1). Требу-
ется определить спектральную плотность процесса x(t)
Решение.
Составляем передаточную функцию по уравнению (5.37)
^(5)=-^, (5.38)
5 + Ц
где 5 - оператор Лапласа.
Записываем частотную передаточную функцию формальной заменой 5 = усо
ГГ(усо) = к-.-_
усо + ц
Находим квадрат модуля частотной передаточной функции
/ю+М (Vco2+p2)2 со2+ц2
Пользуясь определением интенсивности белого шума q = 27bS0, находим
спектральную плотность случайного процесса на входе
s.x(®)=7-
2л
1
2л
(5-40)
Наконец, определяем спектральную плотность случайного процесса на вы-
ходе
с, . . к2 1
Л_.._ (со) = — -----z------
вылх z 2 . 2 о
со + ц 2л
(5-41)
Положим в формуле (5 38) к = y]2Dxp., тогда спектральная плотность слу-
чайного процесса x(t) имеет вид
208
s.(“>)= <5 42>
я(ог +рг)
что совпадает с (5.32). ♦
Формирующий фильтр
Обращаясь к примеру 5.1.2, можно заключить, что процессу со спектральной
плотностью (5.42) соответствует корреляционная функция К*(т) = Та-
ким образом, если пропустить белый шум единичной интенсивности через зве-
но с передаточной функцией
[y(5) = 3^£iE, (5.43)
5 + Ц
то на выходе образуется экспоненциально-коррелированный случайный про-
цесс (5.30) (рис. 5.6).
Белый шум М /0Э.+ ц Случайный процесс
г/ = 1 Ф>) = , Г'4" 2. л(со + ц )
Рис. 5.6. Пропускание белого шума через систему первого порядка
В этой связи уравнение
4 ДО + иДО = 7wZw(0 (5.44)
dt
называется уравнением формирующего фильтра, а белый шум единичной ин-
тенсивности и’(/) -порождающим белым шумом
Понятие формирующего фильтра широко используется в оптимальной
фильтрации, основным требованием которой является условие, чюбы на входе
некоторой динамической системы действовали возмущения в виде белого шу-
ма. В тех случаях, когда входные возмущения отличны от белого шума (окра-
шенный шум), необходимо в физическую динамическую систему ввести фик-
тивную линейную систему, описываемую уравнением соответствующего фор-
мирующего фильтра, возбуждаемую фиктивным белым шумом единичной ин-
тенсивности (рис. 5.7).
Порождающий Реальный случайный Выходной
белый шум Фиктивная процесс Реальная сигнал
а _ 1 ДИ Нс1М И Ч С С кзя ДИ НЗМИ ч сс кяя
У 1 система система
Рис. 5.7. Процесс «отбеливания» входного воздействия
209
Модели погрешностей инерциальных чувствительных элементов
Приведем модели случайных процессов, которые наиболее широко исполь-
зуются для описания погрешностей инерциальных чувствительных элементов
{5.21,5.27].
1) Случайная константа. Используется для описания систематических (ква-
зипостоянных) составляющих погрешностей чувствительных элементов. На-
пример, систематический дрейф гироскопа есист в некоторых случаях можно
рассматривать как нормальную случайную величину с нулевым математиче-
ским ожиданием (Л/[есист] = 0) и дисперсией De. Очевидно, что случайная кон-
станта удовлетворяет дифференциальному уравнению
Ёс,,ст=0. (5.45)
2) Белый шум. Используется для описания широкополосных составляющих
погрешностей инерциальных чувствительных элементов и, как правило, задает-
ся интенсивностью белого шума q.
3) Винеровский случайный процесс. Случайный процесс этого типа описыва-
ется формирующим фильтром вида
Д7) = и(Г), (5.46)
где и’(/) -гауссовский белый шум с интенсивностью q .
Винсровскис процессы применяются для описания ошибок инерциальных
чувствительных элементов и позволяют передать наличие систематических со-
ставляющих ошибок и в простейшем виде учесть возможную их изменчивость
[5.27].
4) Экспоненциально-коррелированный случайный процесс. Этот случайный
процесс используется для описания низкочастотных составляющих погрешно-
стей инерциальных чувствительных элементов и называется также марковским
процессом первого порядка. Уравнение формирующего фильтра имеет вид
а(/) = -|1т(0 + ^2Dxpw(t). (5.47)
Для определения коэффициента затухания корреляционной функции ц и
дисперсии Dx осуществляют запись погрешности чувствительного элемента и
строят корреляционную функцию и спектральную плотность (см. рис. 5.4). Из
полученных графиков рассчитывают параметры ц и Dx .
5.2. Принципы построения комплексных систем навигации
При объединении нескольких навигационных измерителей наиболее широ-
кое применение получили две схемы комплексирования, известные как способ
компенсации и фильтрации [5.30, 5.32].
Способ компенсации
Рассмотрим объединение двух навигационных измерителей, определяющих
один и тот же навигационный параметр x(t) по способу компенсации [5.30,
5.32]. Идея этого способа заключается в формировании разностных измерений,
210
при которых исключается из рассмотрения навигационный параметр ^полезное
сообщение). Структурная схема комплексирования по способу компенсации
приведена на рис. 5.8.
Рис. 5.8. Структурная схема комплексирования по способу компенсации
Сигналы на выходе первого и второго навигационных измерителей имеет
вид:
x}(t) = х(0 + и,(0, (5.48)
х2 (0 = х(г)+ «,(/), (5.49)
где x(t) - измеряемый навигационный параметр (полезный сигнал), и
и,(/) - погрешности навигационных измерителей, которые предполагаются
стационарными случайными процессами. Пусть спектральная плотность S'Дсо)
погрешности первого навигационного измерителя сосредоточена в низкочас-
тотной области, а спектральная плотность погрешности второго измерителя
5э(со) является широкополос-
ной (рис. 5.9).
В соответствии с принципом
комплексирования по способу
компенсации сигналы x{(t) и
x2(t) подаются на вычитающее
устройство ВУ}, на выходе ко-
торого образуется разностный
сигнал (точка А на рис. 5.8)
(/) = nx(t) -п, (Г), (5.50)
Рис. 5.9. Спектральные плотности погрешностей
навигационных измерителей
не содержащий измеряемого навигационного параметра.
Разностный сигнал x4(t) поступает в линейный фильтр, передаточная функ-
ция F(s) которого должна быть такой, чтобы он в соответствии с выбранным
критерием д наибольшей степени подавлял помеху n2(t) и в минимальной сте-
пени искажал помеху (t). Сигнал на выходе фильтра с передаточной функци-
ей F(s) имеет вид (точка В на рис. 5.8)
Xe(5) = F(5)Xj4(5) = [n1(5)-772(5)]F(5).
(5.51)
211
На вычитающем устройстве ВУ2 образуется разность
J’(.v) = X] (5) - хв (.S') = Л'(л) + /7, ($) - [/7] (л) - П2 (s)]F(s) =
= л-(л) + [1 - Ffs)]/?! (л) + F(s)n2 (s).
(5.52)
Выходной сигнал комплексной навигационной системы (КНС) может быть
представлен в виде
у(5) = л-(5) + £(5), (5.53)
где £(л) - результирующая погрешность КНС, определяемая следующим обра-
зом:
£(5) = £1(5) + £2(5)=Ф(5)/71(5) + Г(5)/72(5) . (5.54)
Из соотношения (5.54) можно заключить, что е(л) не зависит от x(f), вслед-
ствие чего системы, в которых погрешность не зависит от полезного сообщения
x(t), называются инвариантными по отношению к x(f). Результирующая по-
грешность КНС состоит из двух составляющих: £,(Г) и е9(^), где еД?) - со-
ставляющая, обусловленная процессом а £,(0—составляющая, обуслов-
ленная процессом п2 (t). Дисперсия результирующей погрешности е(.у) в соот-
ветствии с формулой (5.34) на выходе равна
О.
Ч = f [11 - I2 S. (<о)+1 I2 («)]</ю. (5.55)
величины De .
На практике комплсксирование
навигационных измерителей на
основе взаимной компенсации и
фильтрации их ошибок осуществ-
ляется, как правило, с применени-
ем критерия минимума среднего
квадратического значения резуль-
тирующей ошибки. В таком слу-
чае передаточная функция F(s)
линейного фильтра выбирается
такой, чтобы обеспечить минимум
Можно показать, что для рассматриваемых в качестве иллюстрации спек-
тральных плотностей 5](со) и 52(со) (см. рис. 5.9) линейный фильтр является
фильтром нижних частот. Пусть его амплитудно-частотная характеристика
имеет вид, представленный на рис. 5.10.
На этом же рисунке изображена амплитудно-частотная характеристика
фильтра верхних частот Ф(усо) = 1 - F(yco). Практически фильтры в подобных
КНС нс являются оптимальными. Они часто реализуются просто с помощью
апериодического звена, передаточная функция которого имеет вид
F(s) =
I
7 + 1
(5.56)
где Т- постоянная времени фильтра.
Тогда передаточная функция фильтра верхних частот
212
(5.57)
0(5)=1-F(5)=—-
Ts +1
В идеальном случае, когда спектральные плотности S,(co) и S', (со) не пере-
крываются, сигнал на выходе линейного фильтра имеет вид
*в (s) = F(s)xA (л) = [и, (5) - п2 (5)] = п} (5). (5.58)
Тогда выходной сигнал КНС в идеальном случае был бы равен
у(л) = х, (5) - хв(л) = xfs) + и, (5) - л, (5) , (5.59)
т. е. полезный сигнал воспроизводился бы без ошибок. В действительности
спектры S', (со) и 52(со) перекрываются, поэтому в выходном сигнале y(t} при-
сутствует погрешность e(t), дисперсия которой определяется согласно (5.55).
Дисперсия Z) графически характеризуется суммой площадей заштрихованных
участков (рис. 5.11, 5.12).
Рис. 5.12. Ошибка КНС, обусловленная
помехой (t).
Из анализа рис. 5.11 и 5.12 видно, что на выходе КНС результирующая по-
грешность e(z) существенно меньше, чем погрешности отдельных измерителей
n}(f) и n2(t). Таким образом, выходной сигнал в рассмотренной КНС состоит
из трех частей: полезного сигнала x(Z); ошибки £,(/), обусловленной помехой
лД?), прошедшей через фильтр верхних частот, и ошибки e2(Z) , обусловленной
помехой и,(/), прошедшей через фильтр нижних частот.
Выигрыш в точности и помехоустойчивости при комплексировании навига-
ционных измерителей тем выше, чем больше различие в спектральных характе-
ристиках помех и, (с) и п2 (/). Фильтр является безынерционным относительно
x(Z) [5.32].
Способ фильтрации
Другим возможным способом комплексирования навигационных измерите-
лей является объединение их по схеме фильтрации. Структурная схема фильтра
при комплексировании N измерителей представлена на рис. 5.13.
Сигналы на выходе навигационных измерителей имеют вид:
x,(Z) = x(Z) + w,(Z),
x,(t) = x(t) + n2(t),
(5.60)
xN(t) = x(t) + nN (Г),
213
где x(t) - истинное значение измеряемого навигационного параметра; и((/) —
ошибка на выходе z-ro измерителя; i = 1, 2,...,N. Сигналы всех TV измерителей по-
ступают на входы соответствующих линейных фильтров с передаточными
функциями F}(s), F2(s),..., Fn(s) . Сигнал на выходе КНС в соответствии с рис.
5.13 имеет вид
= (5.61)
/=1
Рис. 5.13. Структурная схема комплексирования по схеме фильтрации
При реализации КНС, построенных по способу фильтрации необходимо,
чтобы фильтр не вносил динамических погрешностей в измерение x(t), т. е.
должно выполниться условие инвариантности
N
£ВД = 1- (5-62)
1=1
Когда условие (5.62) выполняется, то выходной сигнал КНС имеет вид
N
y(s) = A'(.s) + F^sjn^s). (5.63)
Z=1
Из соотношения (5.63) видно, что результирующая погрешность измерения
имеет вид
N
E(s') = y(s}-x(s)^'^Fi{s)ni{s'). (5.64)
Z=1
В часто встречающемся на практике случае двух измерителей уравнение
(5.64) принимает вид
Я-0 = x(s) + Fx (s)^ (s) + F2 (s)n2 (5). (5.65)
Согласно условию инвариантности (5.62) F{(s) = 1 -F2(s), тогда
y(s) = x(5) + [1 - F2 (5)]^! (5) + F2 (s)n2 (s). (5.66)
Очевидно, что (5.66) совпадает с (5.52), т. е. способы компенсации и фильт-
рации в рассмотренном частном случае эквивалентны друг другу.
214
5.3. Непрерывный фильтр Калмана в комплексных
навигационных системах
Модель системы в пространстве состояний
По своему назначению любой фильтр обязан подавлять помехи и с наи-
меньшими искажениями пропускать
полезный сигнал. Другими словами,
фильтр дает оценку полезного сигнала
(рис. 5.14).
На рис. 5.14 через x(t) обозначен
полезный сигнал, зашумленный поме-
-Ф)
£(/)
Рис. 5.14. Работа любого фильтра
хой v(Z), которая складывается с x(t) и в результате чего образуется входной
сигнал фильтра z(t). На основе сигнала z(Z), «засоренного» помехой v(Z),
фильтр должен дать оценку x(t) полезного сообщения x(t). Здесь и далее
оценку будем обозначать с помощью символа «л». Под оценкой понимается
приближенное значение полезного сообщения. Очевидно, чем ближе оценка к
полезному сигналу, тем качественнее работа фильтра. Если фильтр удовлетво-
ряет определенному критерию качества (доставляет экстремум заранее задан-
ному функционалу), то он называется оптимальным.
Чрезвычайно широкое применение в комплексных навигационных системах
получил оптимальный фильтр Калмана, созданный Рудольфом Калманом (Ru-
dolf Kalman) в 1960г. Преимуществом фильтра Калмана является то, что он
представляет собой легко реализуемый на ЭВМ рекуррентный алгоритм (т.е. от
шага к шагу), вырабатывающий оптимальную оценку параметров динамической
системы.
Классический фильтр Калмана является линейной системой и формируется в
терминах пространства состояний, т.е. алгоритм фильтрации представляет со-
бой систему линейных дифференциальных уравнений представленных в форме
Коши (разрешенных относительно первых производных).
Как будет показано ниже, составной частью фильтра Калмана является ди-
намическая модель системы, поэтому рассмотрим физические системы, дина-
мика которых может описываться системой обыкновенных линейных диффе-
ренциальных уравнений вида [5.17]
x(t) = A(t)x(t) + G(t)w(t) + B(t)u(t), (5.67)
Здесь x(t) - и-мерный вектор (далее и-всктор). называемый вектором со-
стояния системы. Под вектором, как и ранее, понимается столбцевая матрица с
п элементами.
В уравнении (5.67) также обозначено: w(t) -/7-вектор, называемый векто-
ром возмущения', u(t) — r-вектор. называемый вектором управления', t — время;
A(t) — матрица размера п х п, называемая матрицей состояния', G(t) — матри-
ца размера пх р , называемая матрицей возмущения', B(t) — матрица размера
пх г, называемая матрицей управления.
Также предполагается, что начальное время Го фиксировано и начальное со-
стояние x(t0) известно.
215
Элементы вектора х(/) называются переменными состояния, а элементы
векторов H’(z) и u(t) соответственно переменными возмущения и управления.
Предположим, что выходные сигналы датчиков, предназначенных для на-
блюдения за поведением системы (5.67), можно описать с помощью соотноше-
ния
z(Z) = H(Ox(/) + v(O, (5.68)
где z(t) - m-вектор, называемый вектором измерения, v(t) - m-вектор, назы-
ваемый вектором ошибки измерения, H(t) - непрерывная матрица размера
т х п, которая связывает состояние и измерение. Ее обычно называют матри-
цей измерения. Вектор z(t) иногда называют вектором выхода системы.
Компоненты z{t) называют измерениями или измеряемыми переменными, а
компоненты v(t) - ошибками измерения или переменными шума измерения.
^Пример 5.3.1. Система характеризуется переменными состояния xt),
x2(t), х3(Г), Л'4(0 (Рис- 5.15). Измерительная система, состоящая из трех дат-
чиков, измеряет переменные состояния х, (t), х2 (/), х4 (t) и выдает их значения
зашумленные помехами гДО, v2(r), v3 (f). Требуется найти матрицу измерения
(наблюдения) H(t).
Динамическая Измерительная
система система
Рис. 5.15. Система и датчики, наблюдающие за переменными состояния
Решение.
В соответствии с рис. 5.15 составим уравнения измерений
гДО^х, (O + v/0,
z2(t) = x2(t) + v2(t),
z3(0 = x4(O + v3(r).
(5 69)
Запишем уравнения (5.69) в векторно-матричной форме (для сокращения за-
писи аргумент время опущен)
216
(5.70)
В уравнении (5.70) снизу показаны размерности матриц и векторов. Сравни-
вая (5.70) с общим уравнением измерений (5.68), получаем искомую матрицу
измерения
Н = 0
о
ООО
1 о о
0 О 1
(5 71)
Таким образом, матрица измерения (5.71) с помощью своих элементов рас-
пределяет переменные состояния на подлежащие измерению и нсизмсряемые.Ф
♦ Пример 5.3.2. [5.17] Упрощенная модель
управления плоским движением самолета по уг-
лу рыскания в горизонтальном полете имеет вид
(рис. 5.16)
Уф = -Ахр + и’(0, (5-72)
где J — момент инерции самолета относительно
оси 3, |/ - угол рыскания, <р - отклонение ру-
ля, к — коэффициент пропорциональности ме-
жду отклонением руля и восстанавливающим
моментом (А >0); w(t) - момент, вызываемый
порывами ветра.
Предполагая, что рыскание и скорость его из-
менения можно измерять на борту самолета с
помощью инерциальной системы, составим мо-
дель динамики самолета в пространстве состоя-
ний, если измерения засорены помехами ^(г) и
у2(0-
Решение.
Разделим уравнение (5.69) на момент инерции
J и обозначив b = -к/ J , u(f) = ср(т), получим:
ф = £>«(/) + — w(t) .
Рис. 5.16. Схематическая модель
динамики самолета:
I - - самолет; 2 - расчетное
направление; 3 - ось рыскания;
4 - руль
(5.73)
Представим уравнение (5.73) в пространстве
новые переменные:
х, = у,
х2 = ф.
состояний, для этого введем
(5 74)
217
С учетом новых переменных (5.74), дифференциальное уравнение второго
порядка (5.73) представим в виде системы двух уравнений первого порядка:
X, = х2,
х2 - bu(t) + — w(t).
(5.75)
Вводя вектор состояния хТ = Цх]
матричной форме
х2||, запишем уравнения (5.75) в векторно-
d
dt х2
0 х2
0
17 J
w(/) +
w(0-
(5.76)
0
0
0
b
Из уравнения (5.76) получаем матрицы состояния, возмущения и управления
соответственно
0 1
0 0’
°
|1/7 ’
Составим уравнения измерений. Так как инерциальной системой измеряются
угол у и производная ф с ошибками Vj (t) и v2 (f), то уравнения измерений
имеют вид
A(t) =
G(t) =
= V + v,(0,
z2 =v + v2(0-
Если ввести вектор измерения zT -||zj ;
= ||vi v21| > т0 уравнения (5.78) можно переписать в виде
1 0
0 1
На основании уравнения (5.79) находим матрицу измерения
1 0
0 1
z(0 =
Я(0 =
(5-77)
(5.78)
z2|| и вектор ошибок измерений
x(f) + v(Z) .
(5-79)
(5.80)
0
Btf) = и'
b
Система, описываемая уравнениями (5.67) и (5.68), называется непрерывной
шчейной системой, где под непрерывностью понимается непрерывность вре-
мени t. Структурная схема такой системы показана на рис. 5.17.
w(Z)
Z(Z)
Рис. 5.17. Структурная схема непрерывной линейной системы
218
При исследовании таких систем будет предполагаться, что известны только
векторы измерения z(Z) и управления u(t).
Исходные предпосылки
Векторно-матричные уравнения (5.67) и (5.68) записаны в форме, которая
соответствует исходным уравнениям для калмановской фильтрации и является
математической моделью состояния исследуемой навигационной системы. Ин-
формацию о векторе состояния x(t), который, как правило, не может быть из-
мерен непосредственно, можно получить из совокупности сигналов измерения
(наблюдения) z(f), образованных линейными комбинациями составляющих
вектора состояния навигационной системы.
Основными допущениями калмановской фильтрации является то, что вход-
ные возмущения h’(Z) и ошибки измерения v(t) должны быть гауссовскими
белыми шумами с нулевым математическим ожиданием
= 0;'
M[v(Z)] = 0, /
и корреляционными матрицами
M[v(t)vT (/')] = R(t)6(t' - Z),
где Q(t), R(t) — матрицы интенсивностей входных шумов w(t) и ошибок из-
мерения v(t) - являются симметричными неотрицательно-определенной и по-
ложительно-определенной матрицами интенсивности белых шумов размером
рх р и т х т соответственно.
Кроме того, векторы v(t) и »v(z) должны быть статистически независимы,
т.е. их взаимная корреляционная матрица равна нулю
A/[v(Z)H-r(z')] = 0.
(5.81)
(5.82)
(5.83)
Начальный момент времени z0 характеризуется наличием исходного состоя-
ния системы (5.67) x(Z0), которое представляет собой векторную случайную
величину с заданным математическим ожиданием
W'('o)] = *o (5-84)
и корреляционной матрицей
Ро = M{[x(Z0)-x0][x(Z0)-x0]r}. (5.85)
Матрица Ро является симметричной и на своей главной диагонали содержит
дисперсии элементов начального вектора состояния x(Z0) (см. раздел 5.1) . На-
чальное состояние системы (5.67) определяется предысторией и не зависит от
поступающих в моменты времени Z > Zo возмущающих воздействий и измере-
ний.
Соотношения (5.81) — (5.85) содержат достаточный объем исходной инфор-
мации, в рамках которой ведется рассмотрение задачи оптимальной фильтрации
Калмана.
Сформулируем задачу оптимальной фильтрации: располагая данными изме-
рения z(Z) на интервале (Z0,Z), модель которых соответствует уравнениям (5.67)
219
и (5.68), определить наилучшую оценку x(t) вектора состояния x(t) системы
(5.67), удовлетворяющую определенному критерию качества. Чтобы ответить
на вопрос о качестве работы фильтра, введем вектор ошибки оценки x(t), оп-
ределяемый равенством
х(/) = x(t) - х(/) . (5.86)
и имеющий нулевое среднее
М[х(Г)] = 0. (5.87)
Разности (5.86) можно дать геометриче-
скую интерпретацию, показанную на рис.
(5.18).
Если оценка точная, то вектор x(f) сов-
падает с вектором x(t) и вектор ошибки
оценки х(/) равен нулю, или, что то же са-
мое, длина вектора x(t) равна нулю. Таким
образом, чем меньше длина вектора ошибки
оценки х(/), тем точнее оценка и качествсн-
Рис. 5.18. Геометрическая интерпрета-
ция ошибки оценки нее работа фильтра. В связи с этим за крите-
рий качества работы фильтра можно принять
минимизацию квадрата модуля вектора ошибки оценки
|х|2 =хгх = х2+х22+... + х2 —>0. (5.88)
Так как х(/) и х(Г) - случайные векторы, то и вектор х(Г) также случай-
ный, поэтому минимизируют нс квадрат модуля вектора х(Г), а его среднее
значение (математическое ожидание). В связи с этим критерий качества можно
представить в виде
J(t) = Л7[хг(/)х(/)] = min. (5.89)
Запишем критерий качества оценки в виде квадратичной формы
ДО = M[xT(t)x(t)] = М {Sp[x(t)xT (t)]} =
и " (5 90)
= 5p{M[x(0xr(r)]} = SpP(i) =
1=1 <=1
где Р(/) - корреляционная матрица ошибок оценки размера п х п ; Sp обозна-
п
чает след матрицы, т.с. сумму ее диагональных элементов, — сумма дис-
1=1
псрсий элементов вектора х(/). В соотношении (5.90) учитывается, что вектор
ошибок оценки имеет нулевое математическое ожидание.
Корреляционная матрица P(t) = М[х(/)хг(г)] симметрична и содержит на
своей главной диагонали дисперсии ошибок оценок. Это позволяет судить об
эффективности применения оптимального фильтра в конкретной системе по
величинам диагональных элементов корреляционной матрицы P(t).
Задача оценки имеет несколько частных случаев, определяемых соотноше-
нием моментов времени измерения z(/]) и выработки оценки x(t) [5.17,5.21].
Так, использование всех сигналов измерения до z(^) включительно для выра-
ботки вектора оценок в момент времени t приводит к задаче фильтрации. Для
220
обозначения оценки используется обозначение с двумя аргументами x(t |t), где
первый аргумент t относится к моменту выработки вектора оценок, второй - к
использованным для этого измерениям. При t < tx имеем задачу сглаживания, т.
е. получение вектора оценок в некоторый прошедший момент времени t на ос-
новании всей имеющейся к моменту tx информации. Попытка предсказать зна-
чения компонент вектора оценок x(t) после поступления последнего измерения
z(tx), т. е. при t > tx, приводит к задаче упреждения или предсказания (также
используются термины прогнозирование и экстраполяция) [5.21].
Непрерывный фильтр Калмана
Ниже без вывода приведен алгоритм оптимального фильтра Калмана для не-
прерывного времени [5.17, 5.21].
1) Оптимальная оценка для системы (5.67), (5.68) удовлетворяет уравнению
х(0 = Я(Ох(0 + А(0[г(0-Я(Г)х(0], (5.91)
где х(?0) = 0, a K(t) - матрица передачи фильтра размера п х т .
2) Матрица K(t) определяется с помощью соотношения
K(t) = P(t)HT(t)R~t), (5.92)
где P(t) - корреляционная матрица ошибки фильтрации
x(f) = x(t) - x(t)
размера п х п .
3) Корреляционная матрица P(Z), удовлетворяет матричному дифференци-
альному уравнению
P(t) = A(t)P(t) + P(t)AT(t) - P(t)HT (t)R~l(f)H(t)P(t) + G(t)Q(t)GT(t) (5.93)
с начальным условием P(Z0) = M[x(Z0)xr(Z0)].
Структурная схема оптимального фильтра приведена на рис. 5.19.
Рис. 5.19. Структурная схема оптимального линейного фильтра
для непрерывных линейных систем
Из рис. 5.19 следует, что фильтр представляет собой модель динамики сис-
темы x(Z) = A(f)x(t), возбуждаемую сигналом коррекции от цепи обратной свя-
зи K(t)z(t), где z(t) = z(t)-z(t) - невязка измерения, z(t) = H(t)x(t) - оценка
измерения.
221
Для вычисления матрицы передачи оптимального фильтра K(t) необходимо
определить корреляционную матрицу ошибки фильтрации, которая является
решением уравнения (5.93). Это уравнение представляет собой систему обык-
новенных нелинейных дифференциальных уравнений первого порядка типа
уравнений Риккати. Хотя матрица P(t) имеет п~ элементов, достаточно рас-
смотреть только /?(/? + !)/2 уравнений системы (5.93), поскольку Р(/) являет-
ся корреляционной и поэтому симметричной матрицей.
Для того чтобы оценить качество работы фильтра, нет необходимости моде-
лировать фильтр или хотя бы определять матрицу K(t). Для этой цели доста-
точно решить уравнения (5.93) и рассмотреть диагональные элементы мат-
рицы P(t).
Анализ уравнений оптимального фильтра позволяет решить еще одну зада-
чу, часто встречающуюся в практических приложениях - задачу предсказания.
Задача предсказания состоит в нахождении наилучшей оценки x(t) после по-
лучения последнего измерения в момент времени t > Г, , т.е. оценки x(t | Z,). Та-
кая задача просто решается в предположении, что отсутствие сигналов измере-
ния после момента времени tx можно учесть устремлением матрицы интенсив-
ностей шумов измерения R(t) к бесконечности при t > tx или приравниванием
Н(Z) к нулю
Приведем также без доказательства алгоритм прогнозирования для непре-
рывного времени [5.17, 5.21].
Г) При известной текущей оценке х(у рД для некоторого оптималь-
ное предсказание удовлетворяет уравнению
хрр,) = Л(Г)х(/|/,) (5.94)
для всех / > /, с начальным условием x(t} р,).
2) Корреляционная матрица ошибки прогнозирования P(t | t{) удовлетворяет
дифференциальному уравнению
Р(1 11,) = A(l)P(l M+P(t[ l,)Ar(t) + (5.95)
для t > tx с начальным условием Р(Г] p1)=M[x(z1 pjx7"^ p,)].
Сравнение уравнение (5.93) и (5.95) для корреляционных матриц ошибки
фильтрации и предсказания показывает, что они отличаются только членом
- P(t)H (t)R t)H(t)P(t), который фигурирует лишь в уравнении (5.93). Это
слагаемое можно рассматривать как корректирующий член, ограничивающий
рост корреляционной матрицы ошибки фильтрации Ясно, что если R(t) —> со,
то измерения настолько зашумлены, что их можно считать бесполезными. Из
уравнения (5.94) видно, что оптимальный предсказатель является однородной
частью оптимального фильтра, а это можно предполагать из общих физических
соображений [5.17].
♦ Пример 5.3.3. На выходе измерительного преобразователя образуется
сумма полезного сигнала x(t) и помехи v(r). Известны спектральные плотно-
сти полезного сигнала

Ля
л(со2 + р2)
222
и помехи Sv(со) = So = const. Полезный сигнал и помеха некоррелированны.
Математическое ожидание помехи и полезного сигнала нулевое. Необходимо
найти структуру фильтра Калмана для оценивания полезного сигнала x(t).
Решение.
На входе оптимального фильтра образуется сумма полезного сигнала и по-
мехи
z(t) = x(t) + v(t). (5.96)
Основным требованием калмановской фильтрации является то, чтобы вход-
ные воздействия и ошибки измерения были белошумными, поэтому полезный
сигнал x(t) представим как результат прохождения белого шума единичной
интенсивности и’(/) через формирующий фильтр первого порядка:
х + |ix = y]2Dxpw(t). (5.97)
Перенося в уравнении (5.97) член цх вправо, сразу находим матрицу со-
стояния и возмущения
Л(0 = -ц, G(t) = j2Dxp. (5.98)
Из уравнения измерения (5.96) определяем матрицу измерения H(f) = 1.
Найдем теперь матрицы интенсивностей входного шума и шума измерения.
По определению имеем (см. пример 5.1.1 и формулу (5.29)):
A/[»v(/) (/')] = M[w(t)w(t')] = Kx(t,t') = Кх(т) = 27i5w5(t) = ?5(т) = 18(f -/),
M[v(0vr(f)] = )] = Kv(t,t') = Kv(t) = 2дЭДт) = r5(f -t).
(5.99)
Отсюда получаем искомые матрицы интенсивностей (в данном случае это
скалярные величины):
С(П = 1, R(t) = r, (5.100)
где г = 2tiSv - интенсивность измерительного шума.
Теперь все готово для определения фильтра Калмана. Записываем корреля-
ционное уравнение
P(t) = A(t)P(t) + P(t)AT(t) - P(t)HT(t)R-1 + G(t)Q(t)GT(t)
и подставляем в него полученные матрицы. Так как порядок оцениваемого про-
цесса - первый, то и корреляционная матрица вырождается в скаляр p(t). В
результате имеем
^ = -2рр--р2 +2Dxv (5.101)
dt г
с начальным условием p(t0) = р0, где р0 - начальная дисперсия оцениваемого
процесса.
Решим уравнение (5.98) методом разделения переменных
> —----------------= --dt. (5.102)
/Г + 2prp - 2Dxpr г
Обозначая через pt и р2 корни уравнения р2 + 2xrp - 2Dxpr = 0, получаем
-------------= --dt, (5.103)
(/’-Р1ХР-Р2) г
где р12 =-pr±-J|Jr2 + 2Dxpr
223
Представим правую часть (5 103) через элементарные дроби
1 dp dp 1 dl (5
P1-P2 _P~P| P - P2 J Г
104)
Приняв во внимание, что р2 -pt = -2д/ц2/-2 + 2Zpr , получим
Р-Р1 Р-Р2
(5.105)
где а -
7 2D р
ц"+---*-
Интегрируя обе части уравнения (5.105), после несложных преобразований
получаем дисперсию ошибки фильтрации
1-ае~2а'
(5.106)
где а = ——— .
Ро - Р2
На основе (5.106) находим коэффициент передачи оптимального фильтра
K(t) = P(t)HT(t)R~l(t)-рЛ-— = —. (5.107)
г г
В соответствии с уравнением (5.91) записываем уравнение оптимального
фильтра для оценки полезного сигнала v(Z)
ад=-рад+^4ад - ад], <5. Ю8)
г
причем дисперсия /?(/) определяется в соответствии с (5.106). При достаточно
большом времени (t -»ос) p{t) —> р(, а коэффициент передачи принимает по-
стоянное значение
К(0 = —= -p + Jp2+^^. (5.109)
г У г
Если г —> оо, то K(t) -> 0, если Dx = 0 (сигнал детерминированный), то так-
же K(t) = 0.4
♦ Пример. 5.3.4. В условиях примера 5.3.3 положить, что в некоторый мо-
мент времени tx > /0 происходит сбой в приеме полезного сигнала. При этом в
момент времени tx была получена последняя оценка x(tx} — x(tx |0 и известна
дисперсия ошибки оценивания p(tx)~ p(tx |/j). Требуется найти ошибку пред-
сказания и экстраполированную (спрогнозированную) оценку для t > .
Решение.
Запишем корреляционное уравнение для ошибки предсказания
P(t IZ,) = A(l)P(l IZ,) + Р(11 /,)АТ (I) + G(z)e(z)Gr(z).
Подставив в это уравнение матрицы A(t), G(t), Q(t) из примера 5.3.3, по-
лучим
p(t | tx) + 2xp(t | ) = 2Dxp (5.110)
224
для t > tx, с начальным условием p(tx | tx).
Следует отметить, что уравнение (5.110) линейное, поэтому будем искать его
решение в виде суммы общего решения соответствующего однородного урав-
нения (5.110) и некоторого частного, определяемого правой частью (5.110).
Общее решение линейного дифференциального уравнения первого порядка
имеет известный вид
A'l6)«ta=Ce-2‘", (5.111)
где С - постоянная интегрирования.
Так как правая часть уравнения (5.110) постоянна, то частное решение нахо-
дим, положив нулю производную в уравнении (5.110)
(5.112)
Пр-
окладывая (5.111) с (5.112) получаем общий вид решения уравнения (5.110)
p(ttx) = Ce-2iXl +DX. (5.113)
Используя начальное (граничное) условие p(tx | tx), определяем постоянную
интегрирования С
С учетом (5.114) решение (5.113) принимает вид
р(Ф1)ЧХШ)-ЛК!|‘<м,’+о«. (5.115)
для t > tx.
Для достаточно большого времени предсказания t»tx ошибка предсказа-
ния стремится к дисперсии Dx.
Найдем уравнение оптимального фильтра в режиме предсказания, который
соответствует уравнению (5.108) при K(t) - 0
х(?|/,) = -цх(Г|/1). (5.116)
Решение уравнения (5.116) имеет вид
х(Г|^) = Се-р/ (5.117)
для t > tx, где С - постоянная интегрирования.
Используя начальное условие x(tx | tx) для момента времени tx, находим по-
стоянную интегрирования
C=^li. (5.118)
Перепишем решение уравнения (5.117) с учетом (5.118)
JcG|fj) = Jc(Zj t>tx (5.119)
Таким образом, оптимальный предсказатель экстраполирует самую послед-
нюю оптимальную оценку для получения оптимального предсказания. ♦
Наблюдаемост ъ
Понятие наблюдаемости системы введено Калманом и позволяет ответить на
вопрос: при каких условиях можно восстановить поведение вектора состояния
225
x(t) динамической системы на конечном интервале времени, зная поведение
вектора измерения z(t) на этом же интервале.
Для пояснения наблюдаемости рассмотрим динамическую систему 5, со-
стоящую из подсистем 5] и S2. Система S харак гсризуется вектором состоя-
ния x(t), включающим два подвектора х,(Г) и x2(f), причем к подсистеме
относится подвектор xf(Z), а к подсистеме S2 - подвектор x2(t) (рис. 5.20).
Измерения z(z) сформированы только посредством подвектора Xj (t) подсисте-
Рис. 5.20. Ненаблюдаемая система
блюдаема.
На рис. 5.20 через j(f) обо-
значен вектор, компонентами
которого являются часть или все
компоненты подвектора Xj (/).
Видно, что подвектор хэ(0
нельзя оценить, исследуя только
измерения z(t), поскольку под-
вектор x2(t) не влияет на под-
систему Sj и не включен в изме-
рения z(t) В этом случае
говорят, что система S нена-
Для того чтобы проверить является ли система наблюдаемой, существует
критерий [5.14, 5.17], согласно которому стационарная линейная система п-го
порядка полностью наблюдаема тогда и только тогда, когда матрица размера
пхтп
НТ АТНТ ... (АГУ^НТ
(5.120)
имеет ранг и.
♦ Пример 5.3.5. Определить, является ли система, рассмотренная в примере
5.3.2, наблюдаемой.
Решение.
В примере 5.3.2 были получены следующие матрицы состояния и измерения:
0 1
/ф) =
0 0
1
0
0
1
Я(Г) =
В данном случае п = 2, m = 2 значит должна быть образована матрица
(5.120) размера пхтп = 2x4 . В соответствии с (5.120) находим
Н
о о
1 О'
Тогда
Напомним, матрица имеет ранг п, если все миноры порядка выше п, которые можно составить
из матрицы, равны нулю, а среди миноров порядка п хотя бы один был отличен от нуля.
226
1
paiirll//7
Л z Я г || = ранг
О
О О О
= 2,
1 1 0
и поэтому система полностью наблюдаема.
Рассмотрим случай, когда измеряется только скорость изменения угла рыс-
кания, тогда матрица измерения равна Н = ||0 1||. Проверим систему на наблю-
даемость для этого случая, имеем
ранг||.Нт = Ранг| о|= 1
Следовательно, в этом случае система ненаблюдаема. ♦
♦ Пример 5.3.6. Разработать алгоритм оценивания высоты полета летатель-
ного аппарата по сигналам вертикального канала бесплатформеной инерциаль-
ной навигационной системы и радиовысотомера. Комплексную обработку ин-
формации осуществить по схеме компенсации Грис. 5.21). Погрешности в выра-
ботке высоты БИНС описываются уравнениями:
=5aKg;
где Д/?Б , Д VYg — ошибка выработки высоты вертикальной скорости БИНС;
6aYg — погрешность акселерометров - белый шум со спектральной плотностью
= const, причем M[5ayj(f (f)] = 0 .
Погрешность радиовысотомера vp(7) принять белым шумом (Л/[гр(/)] = 0)
со спектральной плотностью 5р = const.
Рис. 5.21. Объединение вертикального канала БИНС и радиовысотомера
по схеме компенсации
Решение.
Найдем все необходимые матрицы для построения оптимального фильтра
Калмана. Введем вектор состояния системы
лм
х1
х2
(5.122)
Обозначим входной шум системы w(Z) = 6aYg(t), тогда модель ошибок БИНС
в векторно-матричной форме имеет вид
227
(5.123)
Отсюда находим матрицы состояния и возмущения
ЭД =
0 °11
1 °Г
С(')=|о
(5.124)
В соответствии со структурной схемой (рис. 5.21) запишем уравнение изме-
рения
z(t) = zl-z2=h + hb -h- vp(t) = Д/?Б + v(z), (5.125)
где v(t) - —v (Z) - погрешность радиовысотомера принята как шум измерения.
Представим уравнение измерений в матричной форме
ЭД = ||0
+ v(Z),
(5.126)
откуда находим матрицу измерения
Я«=||0 1||. (5.127)
Найдем матрицы интенсивностей входных шумов системы Q(t) и шумов
измерения R(t):
M[H’(;)wr(',)] = e(')8(/'-z),
Так как входной шум v(t) и шум измерения v(t) — скалярные величины, то
и матрицы Q(t) и 7?(z) будут также скалярами (см. формулы (5.28), (5.29)):
М[ w(t) w(t')] = qb(t' -t);
Л/(v(Z)v(Z')] = r8(Z' - Z),
где q = 2л56(2 - интенсивность шума акселерометра, г - 2л5р — интенсивность
шума радиовысотомера (интенсивность измерительного шума).
Таким образом,
эд=г.
Перед разработкой фильтра проверим наблюдаемость системы. Так как сис-
тема имеет второй порядок, то для полной наблюдаемости необходимо
ранг||яг ЛГЯГ| = 2.
Для данной системы имеем
_ О
“ 1 ’
нт
Ат
° 1. лтнт
о о
1
Ю
Тогда
О 1
1 о
ранг||я т
ЛгЯг|| = ранг
= 2,
следовательно, система полностью наблюдаема.
Перейдем теперь к разработке структуры фильтра Калмана. Найдем скаляр-
ный вид матричного уравнения (5.93).
Составим уравнения относительно элементов вектора ошибки оценивания
ЭД-
228
Xj2(Z) Xj(Ox2(Z)
x2(r)Xj(0 х2(0
*1(0
|х2(г)
Xj (t) =&Vyg- = Xj (0 - Xj (0,
x2 (0 = ДЛБ - ЛЬ£ = x2 (t) - x2 (t).
Корреляционная матрица P(t) равна
P(t) = M[x(t)xT(t)] = M
Так как вектор x(t) имеет нулевое математическое ожидание, то из послед-
него равенства видно, что диагональные элементы - это дисперсии ошибок
оценивания. Вследствие того что матрица P(t) симметрична
(= р2}),необходимо решить нс четыре уравнения (5.93), а три.
Найдем в отдельности каждое слагаемое уравнения (5.93):
1) Л(/)Р(/) =
2) P(t)AT (t)-
Ai
Рп
Ai
Р12
Рп
Р12
А2
Р12
о о
А. Рп
0 Ai
О р12
О О
1 О
0 1
О о
Рп РпР12
3) P(t)HT(t)R~l(t)H(t)P(t)= г г2
РпР22 Р22
Г Г
4) G(z)e(/)GrW= ' 0.
На основании полученных слагаемых правой части (5.93) находим скаляр-
ный вид корреляционного уравнения:
Рп
А. =---- + А
г
_ п РпР22
Рп ~~ Р\
(5.128)
_ О ^22
Р22 ~~ 2Рп
Для того чтобы проинтегрировать систему уравнений (5.128), необходимо
знать начальную матрицу P(t0) = M[x(t0)xT(t0)]. Как правило, начальная кор-
реляционная матрица задается в виде диагональной матрицы. В данном приме-
ре на главной диагонали корреляционной матрицы находятся начальные дис-
персии ошибок БИНС в определении вертикальной скорости и высоты
ЛА) =
О
^дл
IIА i(A) 0
I О А? (А)
0
Найдем матрицу передачи оптимального фильтра K(t)
229
K(t) = P(t)HT(f)R~l(t) =
Pn
Pn
Pn
P22
Pn
r
P22
r
(5.129)
0 1
1 r
Наконец, найдем уравнения оптимального фильтра в соответствии с (5.91)
d А'1
dt х2
О 0 %]
1 0 х2
или в скалярной форме:
Х{ = -(z-x2),
г (5.130)
X, = Х( +^^-(z-X,).
Г
Решение уравнений оптимального фильтра (5.130) должны осуществляться
при нулевых начальных условиях. ♦
♦ Пример 5.3.7. Рыскание у летательного аппарата измеряется двумя дат-
чиками, один из которых грубый, а второй - точный. Рыскание vg представляет
собой случайный процесс с корреляционной функцией К(т} = De , парамет-
ры D и ц известны. Информация о рыскании, засоренная шумами Vj с интен-
сивностью л] и v2 с интенсивностью г2, с датчиков поступает в фильтр Калма-
на. Шумы v1 и v2 независимы. Интенсивность шума гх грубого датчика в 2 раза
больше чем интенсивность г2 точного датчика. Требуется найти уравнение оп-
тимального фильтра и определить, во сколько раз «вес» измерения кх грубого
датчика меньше «веса» измерения к2 сигнала точного датчика.
Решение.
Представим случайный процесс с корреляционной функцией K(x) = De
как результат прохождения белого шума иф) единичной интенсивности через
формирующий фильтр первого порядка
ф = -ц|/ + -j2Dpw(t).
Отсюда находим
A(t) = -p, G(t) = -j2D^, Q(t) = l-
Уравнения измерений имеют вид
Zi(Z) = v|/W+v,0),
z2(f) = v(f)+v2(z).
Приведенные уравнения представим в матричной форме
1
1
v(0+v(0,
z(0 =
230
где zT = Ц^! z,||, vT =||v] v2|| - вектор измерения и вектор ошибок измерения
соответственно.
Найдем матрицу интенсивностей ошибок измерения
ViO) г
v20) L.
1И0')
Л
V20')||
7
откуда
Л/[v, (/>](/')] M[v,0)v20')]
M[v20)v10')] M[v20)v20')]
'i
О
60-f),
*0) =
'1
О
О
12
Корреляционное уравнение имеет вид
р = -2цр-
—+ —V+2r>|i.
/1 r2j
Найдем матрицу передачи фильтра Калмана

о
1/г2
р_
г
р
Г2
M[v(t)vT(t')] = M
Обозначим
А,=Д к2 = Р
<1 ч
Найдем уравнение фильтра Калмана
фО) = -цфО) + ||£1
z.O)
z20)
1 _
VO) ,
1
или
ФО) = -рфО) + К [z} 0) - ФО)] + k2[z2 0) - ФО)] • (5.131)
Структурная схема системы, соответствующая уравнению (5.131), показана
на рис. 5.22.
Рис. 5.22. Объединение сигналов грубого и точного датчиков
231
Теперь найдем отношение коэффициентов передачи (весов) грубого и точно-
го датчиков, с которыми измерения поступают в фильтр
Р,г Г2 _ 1
plr2 гх 2
Таким образом, сигнал точного датчика входит в фильтр с большим весом, а
сигнал грубого датчика — с малым весом. ♦
Для повышения надежности системы можно ввести автоматическое диагно-
стирование датчиков на возможность отказа [5.26]. Предположим, что в фильтр
калмана поступают измерения от нескольких датчиков, измеряющих один и тот
же навигационный параметр. В этом случае оценка навигационного параметра
х формируется по сигналам от всех датчиков и при отказе одного из них оцен-
ка х не может измениться мгновенно. При этом невязка измерения zk (t) отка-
завшего датчика (к - номер датчика), равная
zk(t) = zk(t)-z(t), (5.132)
сильно возрастает. Это возрастание невязки и можно принять за признак отказа
А'-го датчика. Если невязка превышает некоторое пороговое значение, то проис-
ходит автоматическое отключение этого датчика. Однако в этом случае необхо-
димо соответствующим образом перестроить алгоритм оценивания. При диаго-
нальной матрице R(f) выключение сигнала А-го датчика можно имитировать
обращением в нуль элементов R~l(t)kk матрицы R l(t) [5.26]. Например, при
отказе точного датчика в примере 5.3.7 необходимо перестроить матрицу
R~l(t) так

о
0
1/г.
О
О
1/г2
1/г,
о
(5.133)

Эта перестройка матрицы R~'(f) приведет к тому, что коэффициент переда-
чи точного датчика обратится в нуль (к2 = 0 ) и его сигнал будет автоматически
отключен. На рис. 5.22 через zx(f) и z2(t) обозначены невязки измерений соот-
ветствующих датчиков.
5.4. Дискретный фильтр Калмана в комплексных навигационных системах
Непрерывный фильтр Калмана имеет ограниченное практическое примене-
ние, так как алгоритмы оптимальной фильтрации должны быть реализованы на
цифровых вычислительных машинах (ЦВМ). В системах с ЦВМ используются
дискретные сигналы в виде последовательности импульсов, поэтому наиболь-
ший интерес представляет именно дискретный фильтр Калмана. Непрерывный
фильтр Калмана имеет скорее научный интерес и позволяет в некоторых случа-
ях более наглядно и просто провести предварительный анализ качества процес-
са фильтрации.
При реализации дискретного фильтра Калмана с использованием ЦВМ не-
обходима дискретная форма матричного уравнения (5.67), поэтому в следую-
щем подразделе излагается переход от непрерывного матричного уравнения
232
состояния (5.67) к его дискретному аналогу - матричному разностному уравне-
нию состояния.
Переходная матрица состояния
Точный переход от векторно-матричного дифференциального уравнения
(5.67) к разностному векторно-матричному уравнению основан на получении
решения дифференциального уравнения (5.67) [5.14, 5.17].
Получим решение уравнения
x(t) = A(t)x + G(t)iv(t)+B(t)u(t). (5.134)
Это легко сделать с помощью так называемой переходной матрицы состоя-
ния [5.14, 5.17]. Предположим, что t0, x(t0), w(t), u(t) известны, причем по-
следние две функции непрерывны и ограниченны для всех t > t0 .
Так как система (5.134) линейная и неоднородная, то ее общее решение
представляет собой сумму общего решения соответствующей однородной сис-
темы и частного решения неоднородной системы. Первое решение иногда на-
зывают также свободным, а второе - вынужденным.
Вначале получим общее решение соответствующей однородной системы
уравнений
х(/) = Л(/)х (5.135)
для t > t0 и произвольного х(/0).
Общее решение уравнения (5.135) будем искать в виде
х(/) = Х(ОС, (5.136)
где X (Z) - неизвестная матрица размера п х п; С - столбцевая матрица по-
стоянных интегрирования высотой п.
Частное решение уравнения (5.134) будем искать методом вариации произ-
вольных постоянных. Подставим (5.136) в (5.134), получим
Х(Г)С + X(t}C = Л(г)Х(/)С + 6(^(0 + B(0«(0 , (5.137)
или
Х(ОС + [Х(0 - Л(/)Х(/)]С = <7(r>(0 + В(о«(О-
Выражение в квадратных скобках тождественно равно нулю, т.к. оно экви-
валентно однородному уравнению (5.135). В связи с этим матрицу С можно
найти следующим образом:
С = j X"1 (т)[<7(т>(т) + В(г)«(т) Jx. (5.138)
го
Тогда частное решение уравнения (5.138) имеет вид
х(/) = Х(0 j X1 (т)[(7(т>(т) + Л(т)«(т)с?т. (5.139)
' 'о
Сложив общее решение (5.136) с частным (5.139), получим
x(t) = X(t)C + X(/)j Х-1(т)[С?(т>(т) + В(т)и(х)с!т. (5.140)
Зная начальное состояние системы x(Z0), найдем матрицу
C = X'‘(Ox(fo). (5.141)
233
С учетом (5.141) получим решение уравнения (5.140)
х(0 = %(/)%-' (/0)х(Г0) + X(Z) J (т)[6(т>(т) + В(т)И(т)Л. (5.142)
(с
Здесь матрица Х(Г) называется фундаментальной матрицей системы [5.17].
Заметим, что она зависит только от матрицы состояния системы A(t). Обозна-
чим
<H(t,x) = X(t)X~'(x) (5.143)
и назовем матрицу Ф(1,т) размера пхп переходной матрицей состояния сис-
темы (5.134).
Перепишем уравнение (5.142) в виде
х(/) = Ф(/,/0)х(^0) + J Ф(/,т)[6(т)и>(т) + 1?(т)н(т)]б/т, (5.144)
'о
где t > t0.
Системы с постоянными коэффициентами
Если матрицы A(t), G(t) и H(t) постоянны, то систему называют системой
с постоянными коэффициентами или стационарной системой [5.17] Уравне-
ния такой системы имеют вид
x(t) = Ax(t) + Gw(t) + Bu(t); (5.145)
z(t) = Hx(t) + v(t). (5.146)
Для удобства начальное время положим равным нулю.
Для уравнения вида (5.145) переходная матрица состояния принимает срав-
нительно простой вид. Чтобы убедиться в этом, введем матричную экспоненту
(матричный экспоненциал) [5.17]:
эп.п 00 Antn
еА‘ = Е + Л/ + ... + ^- + ... = У-—. (5.147)
п-
Очевидно, что матрица
X(t) = eAl
является решением дифференциального уравнения
Х = АХ.
Так как
X“*(T) = e“4x, (5.148)
то из соотношения (5.143) следует, что переходная матрица принимает вид
Ф(/,с) = еЛ(,т), (5.149)
С учетом (5.148) и (5.149) получаем решение системы с постоянными коэф-
фициентами
x(t) = еАгх(0) + jеА u~T}[Gw(x) + Bu(x)]dx. (5.150)
о
234
Дискретная модель
Предположим, что векторы возмущения и управления являются кусочно-
постоянными функциями времени, причем оба они изменяют свои значения в
одни и те же моменты времени. Далее предположим, что измерения проводятся
в те же моменты времени [5.17].
Компоненты векторов и’(/) и «(/) изображены на рис. 5.23, где жирными
линиями показано, что интервалы между дискретными моментами времени не
обязательно постоянны.
Рис. 5.23. Компоненты кусочно-постоянных функций и’(7) и u(t) для дискретной модели
Рассмотрим интервал времени tk <t<tk+x для некоторого к = 0,.... Предпо-
ложим, что x(tk) известно, w(f) = w(k) = const и u(t) = и(к) = const для интер-
вала tk <t< tk_ ]. Тогда из уравнения (5.144) следует
*(О = ф('л+1 Л )*('*) +
4+1
. 4
w(Ar) +
4+1
]ф(/м,т)Я(т)А
Обозначив:
х(^+1) = х(£ + 1);
(5.152)
x(4) = x(fc);
(5.153)
4+i
j Ф(/Л+1, t)G(t)Jt = Г(£ + 1, Jt); (5.154)
4+i
]ф(г11|,т)В(г)Л = Ч'(А + 1Л),
4
(5.155)
уравнение (5.151) можно переписать в виде
х(к +1) = Ф(к +1, к)х(к) + Г (к +1, k)w(k) + У (к +1, к)и(к) (5.156)
для к = 0.1 Заметим, что в равенствах (5.154), (5.155) для вычисления
Г(£ + 1Л) и ЧДАг-ИЛ) необходимо иметь переходную матрицу состояния в
«(А-).(5.151)
235
виде, в котором ее первый аргумент является постоянным, а второй — перемен-
ным.
В уравнении (5.156) матрица Г(£ + 1,к) размера пхр называется переход-
ной матрицей возмущения, матрица 4Z(Z: + 1,A') размера лхг - переходной
матрицей управления.
Последовательность {и>(0), и>(1),...,} называется возмущающей последова-
тельностью, а {и(0),н(1),...,} — управляющей последовательностью. Зная эти
две последовательности и вектор х(0), можно с использованием уравнения
(5.151) вычислить последовательность состояния {х(1),х(2),...}.
Допустим, измерительная система описывается уравнением
z(O = ^(f)x(Z) + v(r), (5.156)
причем измерения проводятся в те же дискретные моменты времени, в какие
определено состояние системы (5.151). Тогда в каждый момент времени t = tk+l,
к = 0,1..., уравнение измерений принимает вид
2(Д+1) = Н (ZA+1 WA.+1) + v(^+1)
или с использованием обозначений принятых в формулах (5.152), (5.154)
z(k + 1) = Н(к + ])х(к +1) + v(k + Г). (5.157)
Последовательность {z(l),z(2),...} называется последовательностью измере-
ний или выходной последовательностью системы, a {v(l),v(2),...} — последова-
тельностью ошибок измерения.
Описание системы вида (5.151), (5.157) называется дискретной линейной
системой. Структурная схема модели приведена на рис. 5.24.
Рис. 5.24. Структурная схема дискретной линейной системы
Здесь блок «Задержка на 1 шаг» соответствует блоку хранения (памяти) или
задержки значения х из предыдущего вычислительного цикла для использова-
ния в последующем цикле. В отличие от непрерывных линейных систем опера-
236
ции дифференцирования и интегрирования для дискретных линейных систем не
определены. В дискретной линейной системе существуют только две операции:
усиление и единичное запаздывание (запаздывание на один шаг). Оператор зве-
на единичного запаздывания обозначается z-1. Выходной сигнал этого звена
равен входному сигналу в предыдущий дискретный момент времени [5.14].
♦ Пример 5 4.1. [5.17]. Требуется получить дискретную модель системы вто-
рого порядка из примера 5.3.2.
Решение.
Положим, что дискретные моменты отсчета отстоят друг от друга на посто-
янные промежутки времени Т. Тогда £ + 1 соответствует моменту времени
(к + 1)Т , а к - моменту кТ.
Найдем переходную матрицу состояния, пользуясь тем обстоятельством, что
система стационарная. Учитывая соотношение (5.149), имеем
Ф(/, т) = Ф(Г - т) = еА (,-т) = Е + А • (/ - т) +-—— + ... + .
А =
Так как матрица состояния имеет вид
О
О
1
О
то нетрудно показать, что
А" - 0, для всех п > 2 . В связи с этим, имеем
Ф(М) = 1 0 + 0 1 (t-x) = 1 t-x
0 1 0 0 0 1
Отсюда получаем
ф(к+1,к)= ‘
(к + 1)Т-кТ
1
II1 Т
11° 1
(5.158)
Определяем переходную матрицу возмущения
Г(£ + 1Л)= |ф(/А+1,т)6(т)б?т =
(4+1)Г
(к + 1)Т-т
1
О
1/J
dx -
(А+1)Т
кТ
у[(А+1)Г-т]
7
и
т
j
Аналогично находим переходную матрицу управления
7' (А71)Г||1 (к + 1)Т - т|
W + U) = ]Ф(ГА+1,тЖт)Л= J I '
w<u)- ]ф(/„„т)адл= |
Ч кт I'
!Т =
(*^Г||ВД + 1)Г-т]
.1 ь
dx =
кТ
ЬТ2
2
ЬТ
Следовательно, динамика системы описывается уравнением
237
Т2
х(к +1) =
2 х(к) +
2J
Т
и(/с) +
ЬТ2
2
ЬТ
и(к).
(5.159)
1
О
Т
Соответствующее уравнение модели измерения имеет вид
1
О
1
z(k +1) =
х(к +1) + v(k +1).
(5.160)
О
На практике для получения дискретной системы можно воспользоваться ме-
тодом первых разностей. Согласно этому методу необходимо x(t), w(f) и м(г)
замени гь на х(к), w(k), и(к), а вместо x(t) подставить выражение
х(0 = Х(А? + 1^~Х^> (5.161)
где Т- период дискретизации.
Тогда стационарную линейную систему можно представить в виде
х(£П) = (£ + Л7)х(/) + 67М>)+ B7w(/), (5.162)
где Е - единичная матрица размера п^п . Из уравнения (5.162) можно по-
лучить приближенные значения переходной матрицы состояния, возмущения и
управления:
Ф(к + ,к)~Е + АТ. Yk + ,k)*GT, Ч(к + ,к)*ВТ. (5.163)
♦ Пример 5.4.2. Найти дискретную модель для уравнения формирующего
фильтра первого порядка
x(t) + рх(/) = ^2Z)Ypw(r). (5.164)
Решение.
Представим производную в виде
;.(0 = х(Л+р-хда
Осуществим замены
x(t) —> х(к), w(Z) —> w(k).
Тогда уравнение (5.164) можно представить в виде
х(к +1) = (1 - рГ)х(А) + T^2Dxpw(k). (5.165)
Отсюда получаем
Ф(£ + 1Л)«(1-рТ), T(£ + l,A)«7/2Z)ji. (5.166)
Действительно, в общем случае
Ф(к + !,£) = = е^т = 1 - цГ + + ... + ; (5.167)
______________________(А + 1)Т rzyz
Г (к + 1Л) = yl2Dxp j e-g[(*+l)r-T1Jx = У-------^-(1 - е^т) =
кТ
= VwM1_gr+(=^+...+]!.
ц 2!
238
Если удержать в рядах (5.167) и (5.168) только первые члены, получим фор-
мулы (5.166). ♦
Алгоритм дискретного фильтра Колмана
Рассмотрим без вывода алгоритм дискретного фильтра Калмана. В теории
оценивании дискретных процессов также используются обозначения с двумя
аргументами, например х(к | у), где к - шаг формирования оценки вектора
состояния, j - шаг приема измерений. По аналогии с разделом 5.3 различают
следующие задачи: если к > j , то это задача предсказания, если к = j, это за-
дача фильтрации, а если к < j, то это задача сглаживания или интерполяции.
Введем аналогично вектор ошибки оценки x(kj), определяемый соотно-
шением
x(kj) = x(k)-x(kj). (5.169)
Следуя введенным обозначениям, если, например к - у , то х(к | к) - вектор
ошибки фильтрации.
Аналогично введем критерий качества
М[хТ(к | j)x(k | у)] = min,’ (5.170)
или словами: среднее значение квадрата модуля вектора ошибки должно быть
минимальным.
Пусть линейная дискретная система описывается уравнениями:
х(к +1) = Ф(к +1, А')х(Аг) + Г(£ +1, k)w(k); (5.171)
z(k + 1) = Н(к + 1)х(А- +1) + v(k +1), (5.172)
где х(к) - /7-мсрный вектор состояния; w(k) - /2-вектор возмущения; z -
/л-вектор измерения; v — /л-векюр ошибки измерения; А'= 0,1... — дискретное
время; Ф(к + 1,к) - переходная матрица состояния размера пхп; H(k + Y) -
матрица измерения размера тхп.
Полагается, что возмущающая последовательность w(k) является р — мер-
ной гауссовской белой последовательностью с нулевым средним
М|>(А:)] = 0 (5.173)
и корреляционной матрицей
M[K(j)wT(k)] = Q(k)S/t, (5.174)
где Q(k) - неотрицательно определенная матрица размера р*р, - символ
Кронексра, определяемый так:
1, если j = Аг;
> 8,*=Р J (5.175)
7 [О, если j = к.
Последовательность ошибок измерения v(k +1) представляет собой т —
мерную гауссовскую белую последовательность, для которой
М[у(Аг + 1)] = 0 (5.176)
при любом А' = 0,1... и
M[y(j + 1>г(* +1)] = R(k +1)8# , (5.177)
239
где к = 0,1..., j =0,1..., Л(£+1) - неотрицательно определенная матрица раз-
мера т х т . Полагается, что случайные процессы v и w независимы, так что
М[у(У>г(£)] = 0 (5.178)
при любых j = 1,2... и к = 0,1...
Начальное состояние системы х(0) принимается в виде гауссовского слу-
чайного, п — вектор с нулевым математическим ожиданием и корреляционной
матрицей
Л/[х(0)хг(0)] = Р(0) . (5.179)
Предполагас юя, что начальное состояние х(0) не зависит от векторов w(k)
и v(k +1).
Дополнительные свойства, которым должны удовлетворять уравнения
(5.171), (5.172), приведены в работах [5.14, 5.17, 5.27].
Далее без вывода приведем алгоритм оптимального фильтра Калмана для
дискретных систем [5.17, 5.27].
1. Оптимальная текущая оценка х(к +11 к +1) описывается рекуррентным
соотношением
х(к +11 к +1) = Ф(£ + ,к)х(к | к) +
+ К (к + l)[z(Ar +1) - Н(к + 1)Ф(£ +1, к)£(к | £)] (5’180)
для к =0,1,..., где х(0|0) = 0.
2. К(к + ) — матрица размера их/и, определяемая с помощью следующих
соотношений:
К(к +1) = Р(к +11 к}НТ(к + 1)[Я(£ + )Р(к +11 k)HT (к +1) + R(k +1)]’1; (5.181)
Р(к +11 к) = Ф(к + 1,к)Р(к | к)Фг(к +1,£) + Г(£ + l,k)Q(k)Tr(k + 1,£); (5.182)
Р(к +11 к +1) = [Е - К (к + 1)Н(к + 1)]Р(£ +11 к), (5.183)
где Е — единичная матрица размера п х п, а начальное условие для уравнения
(5.182) имеет вид /ДО|0) = Р(0).
Вычислительные аспекты дискретного фильтра Калмана
Одной из наиболее важных особенностей дискретного фильтра Калмана яв-
ляется его рекуррентная форма, что делает этот фильтр исключительно полез-
ным для оптимальной фильтрации при обработке результатов измерения с по-
мощью ЭВМ [5.17]. Измерения можно обрабатывать по мере их поступления, и
не требуется хранить какие-либо измерительные данные в памяти. Однако ал-
горитм требует хранения в памяти матриц Ф(£ + 1,£), Г(£ + 1,£), Н(к + 1),
Q(k) и R(k + ) для всех £ = 0,1,...
Информационное взаимодействие блоков фильтра легко понять на основе
структурной схемы (рис. 5.25).
240
Рис. 5.25. Структурная схема дискретного фильтра Калмана
Предположим, что оценка х(к | к) известна для некоторого к , и требуется
определить х(к +11 к +1) при известном z(k +1). Общая схема вычислительно-
го цикла имеет следующий вид [5.17].
1. Оценка х(к | к) «прогнозируется на шаг вперед» с помощью умножения се
слева на переходную матрицу состояния Ф(А + 1,А), что позволяет получить
предсказание х(к +11 к). Этот шаг можно рассматривать как динамическую
экстраполяцию предыдущей оценки.
2. Предсказанная оценка х(& + 1| к) умножается справа на Н(к + 1), что дает
в результате предсказание измерения £(& + ! |£). Вычитая его из истинного из-
мерения z(k +1), получаем невязку измерения z(k +11 к).
3. Невязка измерения умножается на матрицу К (к +1), и результат склады-
вается с х(к +11 к) для получения х(к +11 к + 1).
4. Оценка х(к +11 к +1) хранится в памяти до тех пор, пока нс будет получе-
но следующее измерение. После этого цикл повторяется.
241
Описанный здесь фильтр работает по методу «коррекции предсказания», т.е.
«корректирующий» член К(к: + V)z(k +11 к) складывается с предсказанием
х(к +11 к) для вычисления оценки х(к +1| к +1). Корректирующий член состо-
ит из невязки измерения, взвешенной с помощью матрицы К(к + Х). В связи с
этим матрицу К (к +1) называют весовой матрицей, матрицей передачи
фильтра или матрицей передачи Калмана [5.17].
Уравнение (5.180) может быть расщеплено на два уравнения:
х(А' + 1|£) = Ф(А'П,ад£|£);
х(Л + 1|^ + 1)-^(Л + 1|А0 + ^ + 1)[г(^ + 1)-Я(А + 1)л-(Л + 1|А-)]- ( }
Алгоритм фильтрации начинает свою работу со значения х(010) = 0, причем
после поступления первого измерения сразу получаем первую оценку
x(l|l) = tf(l)z(l).
Многократно повторяя описанный выше вычислительный цикл, состоящий
из четырех шагов, последовательно получаем оценки х(212), х(313)...
Следует отметить, что в соответствии с рис. 5.25 оптимальный фильтр со-
стоит из модели динамического процесса, выполняющей функцию предсказа-
ния, и корректирующей цепи обратной связи, с помощью которой в модель в
качестве возмущения вводится слагаемое, состоящее из взвешенной невязки
измерения.
Теперь рассмотрим вычисление матрицы передачи фильтра К(к + 1) и двух
корреляционных матриц Р(к +11 к) и Р(к +11 к: +1) [5.17].
1. По известным Р(кк), Q(k). Ф(к + },к) и Г(Л + 1,А) с использованием
уравнения (5.182) вычисляется матрица Р(к +11 к).
2. Матрицы P(k + ik), Н(к + ) и R(k + Y) подставляются в уравнение
(5.181) для получения матрицы К (к +1), которая используется описанным
выше способом на третьем шаге вычислительного цикла фильтрации.
3. Матрицы Р(к + \к), К(к + ) и Н(к + 1) подставляются в уравнение
(5.183) для получения матрицы Р(к +11 к +1). Эта матрица хранится в па-
мяти до тех пор, пока не будет получено следующее измерение. После этого
цикл повторяется.
Уравнения (5.181) - (5.183) описывают алгоритм рекуррентного вычисления
матрицы передачи оптимального фильтра. Матрицы Р(к +11 к) и Р(к +11 к +1)
- корреляционные матрицы гауссовских марковских процессов х(к +11 к) и
х(к +11 к +1), имеющих нулевые математические ожидания. Следовательно,
при вычислении матрицы передачи фильтра одновременно определяются пара-
метры распределения вероятностей ошибок предсказания и фильтрации. Диаго-
нальные элементы матриц Р(к +11 к) и Р(к +11 к +1) представляют собой со-
ответственно дисперсии компонент векторов ошибки предсказания и ошибки
фильтрации. В связи с этим матрицу Р(к +11 к) называют априорной матрицей
ошибок оценивания, а матрицу Р(к +11 к +1) — апостериорной матрицей оши-
бок оценивания.
242
Для анализа качества фильтрации необязательно реализовать фильтр в пол-
ном составе, для этого достаточно реализовать уравнения (5.181) — (5.183),
Точнее, для изучения того, как изменяются во времени дисперсии ошибок,
можно исследовать диагональные элементы двух корреляционных матриц.
Важно подчеркнуть, что матрицы Q(k) и R(k + ) имеют другую размер-
ность в отличие от матриц интенсивностей Q(t) и R(t) для непрерывного вре-
мени. Чтобы мощность случайных воздействий дискретной и непрерывных сис-
тем в предельном случае при Т —> 0 была одинакова, матрицы Q(k) и R(k +1)
связаны с соответствующими матрицами непрерывной системы следующим
образом [5.14]:
(>(£) = + = (5.185)
Здесь Q(tk), R(tk+i) — значения матриц интенсивностей непрерывной сис-
темы в моменты времени tk и ZA+1 соответственно. Из соотношений (5.185) ста-
новится понятным, что матрицы О(к} и R(k+1) имеют размерность дисперсии
(напомним, Q(t) и R(t) имеют размерность спектральной плотности).
Следует отметить, что в отличие от случая непрерывного белого щума дис-
персия дискретного белого шума нс является бесконечной, а потому такой шум
физически реализуем.
♦ Пример 5.4.3. [5.4]. Для повышения точности автономной работы БИНС
обычно осуществляют ее калибровку, под которой понимается процесс уточне-
ния различного рода систематических составляющих погрешностей инерциаль-
ных чувствительных элементов. В ряде случаев погрешность чувствительных
элементов можно представить как сумму систематической ес (к +1) и белошум-
ной v(k + Г) составляющих. Будем интерпретировать систематическую погреш-
ность как вектор состояния х(к), а белошумную составляющую как ошибки
измерения.
Уравнения состояния и измерения в этом случае можно представить в виде
Ес(к +1) = Ес(к),
z(k + V) = Ec(k + l) + v(k + l)
Тогда задачу калибровки можно сформулировать как оценку систематиче-
ской составляющей по измерениям «засоренным» белым шумом.
Примем дисперсию белого шума v(£ + l) равной 4 [ед2]. Относительно сис-
тематической погрешности известно, что ее дисперсия равна 9 [ед2]. Проана-
лизировать работу фильтра Калмана для оценки систематической составляю-
щей.
Решение.
Сравняв уравнения (5.186) с общими уравнениями состояния и измерения
динамической системы (5.171), (5.172), найдем следующие матрицы
Ф(£ + 1Л) = 1; Г(Л + 1Л) = 0; Я(£ + 1) = 1. (5.187)
Исходя из того, что возмущающая последовательность в первом уравнении
системы (5.186) отсутствует, то
(5.186)
243
Q(k) = O. (5.188)
Так как дисперсия белого шума (ошибок измерения) равна 4 [ед2], то
7?(А+1) = 4 [ед2]. (5.189)
Положим начальную дисперсию Ро =9 [ед2]. Допустим, в результате данно-
го запуска ЧЭ систематическая составляющая составила 3 [ед], которую и не-
обходимо оценить с помощью фильтра Калмана. Однако, как следует из усло-
вий задачи, систематическая составляющая принимается совместно с белым
шумом с дисперсией 4 [ед2]. Для того чтобы получить модель входного сигна-
ла z(k +1), необходимо наложить на систематическую составляющую величи-
ной 3 [ед] белый шум с дисперсией 4 [ед2]. Грубую модель входного сигнала
z(k +1) можно получить, подбрасывая монету. При этом орел, к примеру, будет
соответствовать значению у = +2 [ед], а решка у = -2 [ед] (рис. 5.26).
Рис. 5.26. Формирование модели измерений
к • v(A + l), к = 0,1...
1 Решка -2
2 Решка -2
3 Орел +2
4 Орел +2
5 Решка -2
Запишем уравнения оптимального фильтра (5.180) - (5.183) с учетом матриц
(5.187) - (5.189) в последовательности их вычисления:
1) Р(к +11 к) = Р(к | к), Р(010) = Ро = 9[ед2];
2) /С(А + 1) =
Р(А + 1|А)
Р(£ + 1| £) + /?(£ + !)’
3) Р(к + 11А + 1) =[1 -АДА + 1)]Р(А + 11к)
4) х(к +11 к +1) = х(к | к) + К(к + l)[z(A +1) - х(к | А)], £(010) = 0.
Структурная схема фильтра Калмана приведена на рис. 5.27.
Рассмотрим первый вычислительный цикл при к = 0.
1) Первре измерение на шаге к = 0 еще не получено, поэтому определяем
априорную корреляционную матрицу
Р(110) = Р(0| 0) = 9[ед2].
2) . Находим коэффициент передачи оптимального фильтра
= Р(1|0)
Р(110) + ад 9 + 4
244
3) . Принимаем первое измерение. Определим апостериорную корреляцион-
ную матрицу
Р(111) = [1 - WO10) = (1 - 0,69) • 9 = 2,77 [ед2 ].
4) . Оптимальный фильтр формирует первую оценку
1(111) = 1(010) + 7C(l)[z(l) - 1(010)] = 0,69 + 0,69 • (1 - 0) = 0,69[ед].
Рис. 5.27. Структурная схема калибровки ЧЭ
Приведем следующий вычислительный цикл.
1) Р(2|1) = Р(1|1) = 2,77[ед2].
2) . К(2) =----------= • 2,77 = 0,41.
Р(211) + А(2) 2,77 + 4
3) . Р(212) = [1 -К(2)]Р(211) = (1 - 0,41) • 2,77 = 1,63[ед2].
4) . 1(212) = 1(111) + K(2)[z(2) -1(111)] = 0,69 + 0,41 • (1 - 0,69) = 0,82[ед].
Несколько следующих вычислительных циклов сведены в табл. 5.4.1.
Таблица 5.4.1
Вычисления в фильтре Калмана
к P(ltl|*) К (к +1) Р(1 + 1| 1 + 1) 1(1 + 111 + 1)
3 1,64 0,29 1,2 2,03
4 1,16 0,23 0,90 2,70
5 0,90 0,18 0,74 2,39
Графическое изображение оценки 1(1 +11 k +1) систематической состав-
ляющей £с(1) и измерения z(l + l) представлено на рис. 5.28.
245
Из рис. 5.28 видно, что оценка постепенно приближается к систематической
погрешности ЧЭ. На шаге 5 происходит некоторое ухудшение оценки, однако
при дальнейших измерениях систематическая погрешность может быть оценена
достаточно точно.
Графики дисперсии ошибок предсказания и фильтрации, а также коэффици-
ента передачи приведены на рис. 5.29.
Рис. 5.29. Результаты моделирования фильтра Калмана:
а) дисперсии ошибок предсказания и фильтрации
б) коэффициент передачи оптимального фильтра
Из анализа рис. 5.29 можно отметить следующее:
а) Первое измерение приводит к значительному уменьшению ошибки
фильтрации Р(к +1| к +1) (рис. 5.29, а). Одно измерение уменьшает дисперсию с
9 [ед2] до 2,77 [ед2].
б) На первых тактах работы фильтра измерения принимаются с большим ве-
сом, что определяется большими значениями коэффициента передачи К(к + 1),
затем следует уменьшение коэффициента передачи (см. рис. 5.29. б) — фильтр
все более «доверяет» модели. ♦
^Пример 5.4.4. [5.17] Динамическая система описывается следующими
уравнениями
х(к +1) = Фа(А) +
z(k +1) = х(к +1) + v(k +1)
для & = 0,1,..., где w(k) - гауссовская белая последовательность с нулевым
средним и постоянной дисперсией Q, v(k +1) - гауссовская белая последова-
246
тельность с нулевым средним и постоянной дисперсией R, х(0) - гауссовская
случайная величина с нулевым средним и дисперсией Р(0), а Ф = const. Пред-
полагается, что обе гауссовские последовательности ш(А)и v(A 4-1) независи-
мы. Проанализировать оптимальный фильтр.
Уравнения оптимального фильтра имеет вид:
х(к +11 к +1) = Фл(А1А) + К(к + l)[z(A +1) - Фх(А | А)]. (5.190)
Находим априорную дисперсию ошибки оценивания и коэффициент переда-
чи оптимального фильтра:
АЧА + 1|А) = Ф2Р(А|А) + 2; (5.191)
К(к +1) = [Ф2Р(А | А) + Q] [Ф2 Р(к | к) + Q + Я]"1 =
_ Ф2Р(А|А) + 2 (5.192)
~ Ф2Р(кк) + д + Р'
Тогда уравнения для дисперсии ошибки фильтрации принимает вид
Р(А + 1|А+1) =
Ф2 Р(к к)+ Q
Ф2Р(А| А)+ £> + /?
[Ф2Р(А|А) + 2] =
/?[Ф2Р(А|А) + 2]
Ф2ПА | k) + Q + R
(5.193)
при начальном условии Р(010) = Р(0).
Из уравнения (5.191) ясно, что Р(к +11 А) > Q, так как Р(к | А) > 0. Это озна-
чает, что предельная точность предсказания определяется дисперсией возмуще-
ния.
Из уравнения (5.192) следует, что коэффициент передачи фильтра изменяет-
ся в пределах 0 < АДА + 1) < 1. Если подставить уравнение (5.192) в (5.193):
Р(А + 1|А + 1) = 7?/С(А + 1),
то становится очевидным, что 0 < Р(к +11 к +1) < R . В результате получим, что
если Р(0) » R, то первое измерение приведет к значительному уменьшению
дисперсии ошибки фильтрации от Р(0) до 0 < Р( 11) < R < Р(0). ♦
5.5. Инерциально-спутниковые навигационные комплексы
Достичь заданного уровня точности, помехозащищенности и надежности по-
зволяют комплексные навигационные системы, основные схемы построения
которых, приведены в разделе 5.2. Комплексные навигационные системы реа-
лизуют принцип избыточности, когда один и тот же навигационный параметр
определяется несколькими навигационными системами, основанными на раз-
личных физических принципах. К числу основных навигационных систем раз-
личных подвижных объектов уже давно относятся инерциальные навигацион-
ные системы (ИНС) . Они автономны, не требуют информации о магнитном
Здесь под ИНС понимается инерциальная система любого типа, в том числе и БИНС.
247
поле Земли, не излучают энергию, однако имеют тенденцию к накоплению по-
грешностей. Объединение ИНС с навигационными системами, основанных на
других физических принципах позволяет, позволяет устранить этот недостаток.
Помимо ИНС подвижные объекты все чаще снабжаются спутниковыми навига-
ционными системами (СНС). Навигационные параметры, полученные с помо-
щью СНС, не имеют тенденции к накоплению погрешностей как ИНС, однако в
большей степени подвержены различным случайным помехам. Интеграция
ИНС (а следовательно, и БИНС) и СНС позволяет создать высокоточный на-
дежный навигационный комплекс, сочетающий в себе преимущества ИНС и
СНС. Основные достоинства и недостатки ИНС и СНС приведены в табл. 5.5.1
[5.28, 5.30].
Таблица 5.5.1
Сравнительная характеристика ИНС и СНС
Тип системы Достоинства Недостатки
СНС Высокая точность; погрешности не имеют тенденции к рос- ту; малое время готовности Низкая скорость обновления ин- формации (1 - 10Гц); подверженность помехам; .потеря сигналов
ИНС Автономность; высокая скорость выдачи информации (до 100 Гц); непо зверженность внешним помехам Неограниченный рост погрешно- стей; необходимость знания грави- тационного поля Земли; проблема начальной выставки и калибровки
В настоящее время известны четыре основных типа инерциально-
спутниковых комплекса, отличающиеся уровнем интеграции [5.30]:
• раздельная схема;
• слабосвязанная схема;
• сильносвязанная схема;
• глубокоинтегрированная схема.
Варианты комплексирования ИНС и СНС
Самый простой вариант построения инерциально-спутниковой системы - это
раздельная схема комплексирования (рис. 5.30). В этой схеме ИНС и СНС неза-
висимо друг от друга вырабатывают скорости Иинс, Иснс и координаты место-
положения 5ИНС, 5СНС объекта.
Рис. 5.30. Раздельная схема комплексирования ИНС и СНС
248
Для ограничения роста погрешностей ИНС производится периодический пе-
резапуск алгоритмов ИНС с новыми начальными условиями по скорости и ко-
ординатам, привлекаемым от СНС. В целом система обладает достаточно высо-
кой точностью и надежностью: выход из строя одного из навигационных изме-
рителей нс влечет за собой выход другого навигационного измерителя. Объеди-
нение ИНС и СНС по этой схеме требует минимальных изменений в аппарат-
ных средствах и программном обеспечении уже имеющихся на борту систем
[5.8].
Следующая по уровню интеграции — это слабосвязанная схема комплсксиро-
вания. в которой сигналы ИНС и СНС объединяются по схеме компенсации
(рис. 5.31), рассмотренной в разделе 5.2. Этот способ основан на формировании
разностных измерений сигналов ИНС и СНС, согласно которому из рассмотре-
ния исключаются сами навигационные параметры
~ ^инс _ ^снс = А^инс _ А^снс’ 194)
г2 = *5инс — *$СНС ~ А^ИНС — А^СНС’
где z}, z2 - составляющие общего вектора измерения z ; Иинс, Д|1НС - векто-
ры скорости и координат местоположения, выработанные с помощью ИНС;
Кгнс, ‘S'chc аналогичны предыдущим векторам, но выработанные СНС; ДИ[1НС,
ДИСНС, ДУ11НС, Д5СНГ - векторы погрешностей в определении скорости и ко-
ординат ИНС и СНС.
В соответствии с соотношениями (5.194) не требуется статистического опи-
сания динамики навигационных параметров. Очевидно, что при использовании
этой схемы необходимы сигналы не менее чем от четырех спутников. Цен-
тральной частью комплексной системы является фильтр Калмана, решающий
задачу оценивания по поступающим разностным измерениям. Так как в состав
СНС также входит фильтр Калмана, то образуется последовательное включение
фильтров, поэтому другое название этого варианта комплексирования - каскад-
ная схема.
Рис. 5.31. Слабосвязанная схема комплексирования
В фильтре Калмана заложена модель погрешностей ИНС и СНС, степень
подробности которой определяется требованиями к точности вырабатываемых
навигационных параметров. В модель погрешностей ИНС включаются дрейф
гироскопов, смещение нуля акселерометров, а также погрешности в определе-
нии координат местоположения, скорости и параметров ориентации. В резуль-
249
тате фильтр Калмана формирует оценки погрешностей ИНС в определении
скорости АИинс и координаты Д5'11НС, которые вычитаются из сигналов ИНС.
Точность работы КНС во многом определяется качеством оценок ДИ[111С и
Д5ИНС • Кроме этого, на основе тех же разностных измерений фильтр Калмана
формирует оценки погрешностей инерциальных чувствительных элементов:
дрейф гироскопов е и смешение нуля акселерометров да, которые с целью
компенсации поступают в ИНС. В этом случае погрешности гироскопов и аксе-
лерометров остаются в линейной области, что позволяет пользоваться линейной
моделью погрешностей ИНС. Отмстим, что целесообразно передавать инфор-
мацию о скорости и координатах, определяемых ИНС в СНС, для ускорения
захвата сигналов спутников и сужения полосы пропускания (пунктирная линия
на рис. 5.31) [5.8]. При пропадании сигнала от СНС фильтр Калмана переводит-
ся в режим предсказания погрешностей ИНС (см. раздел 5.3).
Следующей по уровню интеграции является так называемая сильносвязаная
схема комплексирования (рис. 5.32). В сильносвязанном варианте также фор-
мируются разностные измерения, как и в предыдущем случае, однако здесь
сравниваются пссвдодальности и пссвдоскорости (рис. 5.32).
Г +А1'И|1С - д ИII (С
Рис. 5.32. Сильносвязанная схема комплексирования
Здесь, как и прежде ИНС вырабатывает вектор скорости ДИинс и вектор ко-
ординат местоположения 5ИНС с погрешностями ДИПНС и Д5|1НС - По значени-
ям Иинс и 5ИНС вычисляются псевдодальнос ги £> и пссвдоскорости
каждого наблюдаемого /-го спутника. Для определения и ZX||ir необхо-
дима информация о координатах и скоростях спутника в геоцентрической сис-
теме координат (эфемериды), этим обусловлена связь между блоком вычисле-
ния и СНС (рис. 5.32). Затем следует сравнение псевдоскоростей и пссвдодаль-
ностсй, вычисленных с помощью ИНС и полученных от СНС:
с, = D -D. = ЫХ -&D, ,
Ч 'ИПС lCHC 'ИНС 'СНС
Z. = Ь, -Д = ,
А 'инс 'СНС 'ИНС 'СНС
(5.195)
250
где AD , AD. , AD. , AD. - noi решности в определении пссвдодаль-
ностей и пссвдоскоросюй с помощью ИНС и СНС соответственно; с, , ь, _
элементы общего вектора измерения z, i — номер наблюдаемого спутника.
Как и в предыдущем случае, разностные измерения поступают в фильтр
Калмана, который оценивает погрешности ИНС в определении скорости и ко-
ординат, а также погрешности инерциальных чувствительных элементов, по-
ступающие в ИНС для их компенсации. Информация о пссвдоскоростях и пссв-
додальностях, вычисляемых с помощью ИНС, поступает в СНС для ускорения
захвата сигналов спутников и сужения полосы пропускания (пунктирная линия
на рис. 5.32).
Так как в приведенной схеме измерения строятся по разности пссвдоскоро-
стей и пссвдодальностсй, то в приемнике СНС нс требуется реализации фильтра
Калмана для определения скорости V и координат местоположения объекта S.
Это обстоятельство несколько упрощает приемник СНС, однако выход из строя
ИНС приведет к неработоспособности всего комплекса. Преимуществом силь-
носвязанной схемы по сравнению с слабосвязанной является то, что теперь нет
необходимости наблюдать как минимум четыре спутника - комплексная систе-
ма позволяет использовать информацию даже от одного спутника.
Что касается глубокоинтсгрированной схемы комплексирования [5.25, 5.30],
то в приемнике СНС вообще отсутствуют контуры слежения за D, и D, (рис.
5.33).
Рис. 5.33. Глубокоинтегрированная схема комплексирования
Глубокоин гсгрированная схема комплексирования включает упрошенный
приемник СНС, блок гироскопов и акселерометров и вычислительное устройст-
во, реализующее фильтр Калмана. В фильтр Калмана непосредственно посту-
пают сигналы гироскопов и акселерометров и выход коррелятора приемника
СНС. На фильтр возложены задачи оценивания как навигационных параметров
навигации и ориентации V,S ,ф,6,у, так и пссвдодальностсй D( и псевдоско-
ростей D,, которые являются данными для поиска сигналов спутников. Кроме
того, фильтр Калмана оценивает инструментальные погрешности гироскопов и
акселерометров в целях компенсации. Реализация глубокоинтсгрированной
схемы требует весьма мощных вычислительных устройств, поскольку для опи-
251
сания системы требуется высокая размерность вектора состояния (до 40 и бо-
лее) в условиях достаточно быстрых изменений Dz.
♦ Пример 5.5.1. БИНС и СНС объединяются по слабосвязанной схеме ком-
плексирования, причем от СНС привлекается только позиционная информация.
СНС работает в обычном режиме и вырабатывает координаты местоположения
ЛА с частотой 1Гц и погрешностью 20 м. ЛА совершает горизонтальный полет
в направлении на север, поэтому eZg = £z и 8а х = &ах (в формировании оши-
бок БИНС участвует погрешность продольного акселерометра и одного попе-
речного гироскопа). Полагается, что в БИНС используются ДНГ типа ГВК-16, и
микроакселерометры типа ADXL202, основные характеристики которых, при-
ведены в табл. 5.5.2.
Таблица 5.5.2
Характеристики инерциальных ЧЭ
Чувствительный элемент Погрешность
Систематическая составляющая Случайная состав- ляющая (СКО)
ДНГ 40°/ч (2,4-10'4рад/с) 17ч (4,8-10’6рад/с)
Микроакселерометр 10'3g (1(Г2 м/с2) 200 pg (2-10’4 м/с2)
Требуется проанализировать работу фильтра на основе северного канала
БИНС.
Решение.
Воспользуемся БИНС (4.1.48): приближенной моделью погрешностей северного канала Р R ez> AKXg=gP + 8ax; (5.196)
Алвине — ^Xg-
С учетом табл. 5.5.2 модель погрешностей инерциальных чувствительных
элементов можно представить в виде:
ez = £Z,CT +£/ ;
8а v = 8асгист + 8асгл
(5.197)
где ez ст, 8аСуст - систематическая составляющая погрешностей гироскопов и
акселерометров соответственно, ez , §асх — случайная составляющая погреш-
ностей гироскопов и акселерометров соответственно.
Для систематических погрешностей можно записать очевидные дифферен-
циальные уравнения
ecz,,CT=0, 8а7т=0. (5.198)
252
Случайные составляющие погрешностей ЧЭ будем считать гауссовым белым
шумом. Объединяя уравнения (5.196) и (5.198), с учетом (5.197) получим мо-
дель погрешностей северного канала БИНС:
P = -^i-£czHCT-E^;
R
s“,CT=0;
5«с;,ст = 0;
Л^вИНС = ^Xs-
Сформируем измерения как разность сигналов БИНС и СНС
Z = ^БИНС — *^СНС = + Д^БЫНС — S — Л5СИС = Левине — Л^СНС
Погрешности СНС AxS'chc- будем рассматривать как шум измерения.
Введя вектор состояния
хг=||р г»" &Г А$винс|,
представим уравнения (5.199) и (5.201) в векторно-матричной форме:
(5.199)
(5.200)
(5.201)
Р 0 -1 0 0 р -1 0
Л g R 0 0 1 0 0 1 II рсл
(1 dt сист bZ - 0 0 0 0 0 о N W + 0 0 ez |§67СЛ
8azICT 0 0 0 0 0 §4,ст 0 0
Левине 0 1 0 0 0 Левине 0 0
(5.202)
z = ||0 0 0
ЛИ,
сист
fcZ
5«",ст
Левине
Л^снс •
(5.203)
Из уравнений (5.202) и (5.203) находим матрицы состояния, возмущения и
наблюдения:
0 -1 0 0 1 0
R g 0 0 1 0 0 1
А = 0 0 0 0 0 ; G = 0 0 ; н = ||о о о о 1||
0 0 0 0 0 0 0
0 1 0 0 0 0 0
Находим матрицы интенсивностей возмущений и ошибок измерения:
гсл
fcz
5ясл
Чг
5(С-0

И &>?|
о
253
M[v(z)vr(OJ = М[Д5снс(0Л5снс('')] = -').
где q, и q - интенсивности шумов гироскопов и акселерометров, г - интен
сивность шума СНС.
а)
Рис. 5.34. Реализация фильтра Калмана
при комплексировании БИНС и СНС:
а) оценка ошибки построения вертикали;
б) оценка ошибки по скорости;
в) оценка систематической составляющей
дрейфа гироскопа;
г) оценка систематической составляющей
смещения нуля акселерометра;
д) оценка ошибки БИНС по координате
Так как приемник СНС вырабатывает позиционную информацию с частотой
1 Гц, примем период дискретизации для реализации фильтра Калмана Т~ 1 с.
Находим переходные матрицы состояния и возмущения (см. формулы
(5.163))
254
фхЕ + АТ; Г-GT,
где Т- период дискретизации.
1 0 0 0 о| 0 - -10 0
6371000
0 10 0 0 9,8 0 0 10
Ф~Е+АТ= 0 0 10 0 + 0 0 0 0 0
0 0 0 1 0 0 0 0 0 0
0 0 0 0 1 0 1 0 0 0
— 1 0
0 1
V~GT = 0 0 -1
0 0
0 0
Найдем матрицы интенсивностей Q(k) и R(k +1)
для дискретного времени
(см. формулы (5.185))
O(t) WqJT О
С(^) = -^2= *
Т И 0 q-JT
О
О
Я(Л + 1) = -^ = - = Р(
V Z
где D, и £>6а - дисперсии случайной составляющей гироскопа и акселеро-
метра соответственно; £>снс - дисперсия шума СНС.
Дисперсии случайной составляющей гироскопа и акселерометра примем со-
ответственно £>Е =(К/ч)2 и Dda =(200pg)2. Результаты моделирования ФК
приведены на рис. 5.34.
Из анализа результатов моделирования можно сделать следующие выводы:
• Оценка ошибки построения вертикали принимает установившееся значение
к моменту времени оценивания —100 с. Ошибка оценивания составляет 0,2°.
• Оценивание ошибки по скорости происходит достаточно точно, причем
время переходного процесса составляет около 30 с.
• При оценивании систематической составляющей дрейфа гироскопа в на-
чальный момент времени происходит интенсивное «списание» ошибки, при
котором происходит грубое оценивание. На интервале 100-250 с ФК уточ-
няет грубую оценку и достаточно точно вырабатывает оценку «системати-
ки» гироскопа.
• Для систематической составляющей погрешности акселерометра ФК нс вы-
рабатывает оценку, так как эта переменная состояния ненаблюдаема.
• Оценка погрешности БИНС в определении координаты принимает устано-
вившееся значение через 25-30 с. Ошибка оценивания определяется
точностью СНС и составляет около 20 м.
255
Чтобы подтвердить нснаблюдасмость систематической составляющей ошиб-
ки акселерометра, необходимо составить матрицу |//г АтНг ... (ЛГ)"_|ЯГ|| и
определить се ранг. Можно показать, что для данной системы ранг будет равен
4, что меньше порядка системы (п = 5). Если исключить из системы 4-е уравне-
ние (5.199), то ранг матрицы наблюдаемости будет равен 4, что соответствует
полной наблюдаемости системы. ♦
ЛИТЕРАТУРА К ГЛАВЕ 5
5.1. Анучин О.Н., Емельянцсв Г.И. Интегрированные системы ориентации и навигации для
морских подвижных объектов/Под общей ред. чл.-кор. РАН В.Г. Пешехонова. - СПб.: ГНЦ
ЦНИИ «Электроприбор», 1999. - 357 с.
5.2. Бабич О.А. Обработка информации в навигационных комплексах. М.Машиностроение,
1991.-512с.
5.3. Белоглазов II. Н., Джанджава Г. И., Чигин Г. П. Основы навигации по геофизическим
полям - М.: Наука. 1985. - 328 с.
5.4. Браммер К., Зиффлинг Г. Фильтр Калмана - Бьюси. -М.: Наука, 1982. - 200 с.
5.5. Борювые системы навигации и ориентации искусственных спутников Земли/ О.Н. Анучин,
Комарова И.Э.. Порфирьев Л.Ф.. - СПб.: ГНЦ РФ ЦНИИ «Электроприбор», 2004.-326с.
5.6. Вентцель Е.С., Овчаров Л.А. Теория случайных процессов и ее инженерные приложения. -
Учеб, пособие для втузов. - М.: Высш. шк„ 2000. - 383 с.
5.7. Дмшриев С.П., Пелевин А.Е. Задачи навигации и управления при стабилизации судна на
траектории. - СПб: ГНЦ РФ ЦНИИ «Электроприбор», 2002. - 159 с.
5.8. Дмитриев С.П., Степанов О.А., Кошаев Д.А. Исследование способов комплексирования
данных при построении инерциально-спутниковых систем /Интегрированные инерциально-
спутниковые системы навигации: Сб. статей и докл. - СПб.: ГНЦ РФ ЦНИИ «Электропри-
бор», 2001. - С. 43-60.
5.9. Иванов Ю.П. Комплсксированис информационно-измерительных устройств летательных
аппаратов: Учеб, пособие для вузов. - Л.Машиностроение, 1984.-207 с.
5.10. Информационная на (ежность, контроль и диагнастика навигационных систсм/С.П. Дмит-
риев, Н.В. Колесов, А.В. Осипов. Изд. 2-е, переработанное - Спб: ГНЦ РФ ЦНИИ «Электро-
прибор», 2004.- 208 с.
5.11. Казаков I1.E. Статистическая теория систем управления в пространстве состояний.
М.:Наука, 1975.-432 с.
5.12. Климов Д.М Инерциальная навигация на море. - М.: Наука, 1984.-118 с.
5.13. Красовский А. А., Белоглазов И И., Чигин Г. И. Теория корреляционно-экстремальных
навигационных систем - М.: Наука, 1979 г. -448 с.
5.14. Кузовков Н.Т., Карабанов С.В., Салычев О.С. Непрерывные и дискретные системы управ-
ления и методы идентификации. - М.: Машиностроение, 1978. - 222 с.
5.15. Кузовков Н.Т., Салычев О.С. Инерциальная навигация и оптимальная фильтрация. - М.:
Машиностроение, 1982. - 216с.
5.16. Лукомский Ю.А., Пешехонов В.Г., Скороходов Д.А. Навигация и управление движением
судов. - СПб.: Элмор. 2002. -360 с.
5.17. Медич Дж. Статистически оптимальные линейные оценки и управление. - М.: Энергия,
1973.-440 с.
5.18Л 1егоды классической и современной теории автоматического управления. Учебник в 3-х т.
Т1: Анализ и статистическая динамика систем автоматического управления /Под ред. Н.Д.
Егупова. - М.: Изд-во МГТУ им. Н.Э. Баумана, 2000. -748 с.
5.19. Пешехонор В.Г. Ключевые задачи современной автономной навигации // Гироскопия и на-
вигация. 1996. №1 (12). С. 48-55.
5.20. Помыг.аев И.И., Селезнев В.П.. Дмигроченко Л.А. Навигационные приборы и системы. -
М.: Машиностроение, 1983.
5.21. Ривкин С.С., Ивановский Р.И., Костров А.В. Статистическая оптимизация навигационных
систем. - Л.: Судостроение, 1976. - 284 с.
5.22. Свеглицкий В.А Случайные колебания механических систем. - М. Машиностроение. 1976. -
216с.
5.23. Селезнев В.П. Навигационные устройства. - М.Машиностроение. 1974. - 660 с.
256
5.24 Сетевые спутниковые радионавигационные системы/ Под. Ред. В.С. Шебшаевича. - М.: Ра-
дио и связь, 1993. - 272 с.
5.25. Соловьев Ю.А. Системы спутниковой навигации. - М.: Эко-Трендз, 2000. - 268 с.
5.2б. Справочник по теории автоматического управления/Под ред. А.А. Красовского. - М.: Наука,
1987,-712 с.
5.27. Степанов О.А. Основы теории оценивания с приложениями к задачам обработки навигаци-
онной информации. Ч. I. Введение в теорию оценивания. - СПб.: ГНЦ РФ ЦНИИ «Электро-
прибор», 2008. - 500 с.
5.28. Степанов О.А. Особенности построения и перспективы развития навигационных инерци-
ально-спутниковых систем. /Интегрированные инерциально-спутниковые системы навига-
ции: Сб. статей и докл. - СПб.% ГНЦ РФ ЦНИИ «Электроприбор», 2001. С. 25-43.
5.2ФС гепанов О.А. Применение теории нелинейной фильтрации в задачах обработки навигаци-
онной информации. - С.-Пб.: ГНЦ РФ - ЦНИИ «Электроприбор», 1998.-370с.
5.30. Управление и наведение беспилотных маневренных летательных аппаратов на основе со-
временных информационных технологий /Под редакцией М.Н. Красилыцикова и Г.Г. Ссбря-
кова. - М.: Физматлит. 2003. - 280 с.
5.31. Фролов В.С. Радиоинсрциальные системы наведения. М.Советское радио. 1976. 184с.
5.32. Челпанов И.Б., Несенюк Л.П., Брагинский М.В. Расчет характеристик навигационных
гироприборов. - Л.: Судостроение. 1978. - 264 с.
5.33. Ярлыков М.С. Статистическая теория радионавигации. М.: Радио и связь. 1985. - 344с.
5.34. Яценков В.С. Основы спутниковой навигации. Система GPS NAVSTAR и ГЛОНАСС. - М_:
Горячая линия - Телеком, 2005. - 272 с.
5.35. Global Positioning Systems, Inertial Navigation, and Integration/ Mohinder S. Grewal, Lawrence
R. Weill, Angus P. Andrews. John Wiley & Sons, Inc. -2001.
Вопросы для самоконтроля
1.
2.
3.
Что характеризует оценка x(t /1}), если t>tx?
Вектор состояния содержит 8 элементов. Сколько необхо-
димо решить дифференциальных уравнений для определения
корреляционной матрицы ошибок оценивания?
Для построения оптимальной системы стабилизации ЛА по
тангажу необходимо получать информацию об углах атаки
а, тангажа 0 и угловой скорости 0 по тангажу. Движение
ЛА в продольной плоскости описывается системой уравнений
0 + tfj0 + а2а = а3Бе
0-а-а4а = а4сцг,

, где 6в — управление по рулю вы-
соты; ан. — приведенное к углу атаки возмущающее воздей-
ствие турбулентной атмосферы; а{, а2, а3, а4 - постоян-
ные коэффициенты. Положить а„. стационарным белым
шумом с интенсивностью ц. Найти структуру оптимального
фильтра для оценки вектора состояния
х = ||х| х, x3f = ||а 0 0|| по измерениям тангажа 0 и угловой
скорости тангажа 0. Измерения 0 и 0 проводятся на фоне
белых шумов с интенсивностями i] и р.
257
Глава 6
МОДЕЛИРОВАНИЕ АЛГОРИТМОВ БИНС В СРЕДЕ
MATLABSimulink
В соответствии с обобщенной функциональной схемой (см. рис. 1.6) алго-
ритмы БИНС укрупнено можно разделить на следующие блоки:
• алгоритм ориентации;
• блок пересчета;
• навигационный алгоритм.
Одним из ответственных блоков БИНС является алгоритм ориентации, так
как от него зависит точность выработки параметров ориентации и, кроме того,
по информации этого блока осуществляется пересчет вектора кажущегося уско-
рения из связанной системы координат в географическую. Поэтому рассмотрим
реализацию алгоритмов БИНС на примере этого блока.
6.1. Алгоритмы ориентации
6.1.1. Алгоритм ориентации с углами Эйлера-Крылова
Источником информации алгоритма ориентации с углами Эйлера-Крылова
являются проекции вектора относительной угловой скорости ю"н, •, по-
лучаемые на основе сигналов трех ДУС и проекций абсолютной угловой скоро-
сти географического трехгранника. Выходом алгоритма ориентации являются
углы рыскания у , тангажа 0 и крена у. Для того чтобы иметь возможность
сравнивать углы |/, 0, у, вырабатываемые алгоритмом ориентации с истин-
ными значениями этих углов создадим блок позволяющий формировать проек-
ции го",н, го“1Н, о>”™ , по сигналам у , 0, у . Обратимся к уравнениям (3.29) осу-
ществляющих СВЯЗЬ углов , 0, у С угловыми скоростями (0°™ , (I)}””' , со™1
= у + sin 0;
= Osin у + vj/cosycos0;
= -ф sin у cos 0 + 0 cos у.
(6.1)
Примем законы изменения углов рыскания, тангажа и крена синусоидаль-
ными со следующими параметрами:
а) рыскание: амплитуда 1°, частота 0,1 Гц,
б) тангаж: амплитуда 1,5°, частота 0,15 Гц,
в) крен: амплитуда 0,3°, частота 0,2 Гц.
Запустим пакет Simulink программы MATLAB и откроем пустое окно но-
вой модели нажатием кнопки Create a new model на панели инструментов брау-
зера библиотек Simulink. Для реализации законов изменения углов рыскания,
тангажа и крена из библиотеки Sources перетащим мышью три источника сину-
соидального сигнала Sine Wave. Сменим название блоков на psi, theta, gamma.
258
Двойным щелчком откроем каждый из блоков и введем заданные значения ам-
плитуды и частоты в единицах СИ в соответствующие поля ввода Amplitude
(амплитуда) и Frequency (частота). Для перевода в единицы СИ можно вос-
пользоваться встроенной константой pi, которая соответствует числу л (рис.
6.1).
Block Parameters: psi
Sine Wave
psi Output a sine wave where the sine tjpe determines the computational
technique used The parameters in the two types are related through:
> Samples per period = 2’pi / (Frequency " Sample time)
th eta Number of offset samples - Phase “ Samples per period f (2"pi)
______ Use the sample-based sine type if numerical problems due to running for
p , large times (eg. overflow in absolute time) occur.
gamma Parameters
S me type. Tpne based -
Amplitude
jl'pi/160
Bias
' 1° |
Frequency (iad/sec):
(iirzp и
Phase (rad]'
1°
Sample time
1°
•г Interpret vector parameters at 1-D
°* Cancel ] Нф> | |
Рис. 6.1. Блоки синусоидального сигнала и окно параметров одного из блоков
Для формирования соотношений (6.1) потребуются блоки дифференцирова-
ния, произведения, суммирования и тригонометрических функций синуса и ко-
синуса. Блок дифференцирования Derivative находится в библиотеке Continu-
ous', суммирование, произведение и тригонометрические функции реализуются
с помощью блоков Sum, Product и Trigonometric Function соответственно, на-
ходящиеся в библиотеке Math Operations Модель, соответствующая системе
уравнений (6.1) приведена на рис. 6.2.
К выходу каждой составляющей угловой скорости подключен осциллограф
Scope из библиотеки виртуальных регистраторов Sinks.
Войдем в раздел меню Simulation (Моделирование) окна модели и выберем
команду Singulation parameters... (Параметры моделирования), в результате бу-
дет выведено окно, показанное на рис. 6.3.
Установим размер максимального шага интегрирования (Max step size) le-3
(т.е. 103 с) и конечное время интегрирования (Stop time) 100с. Запустим полу-
ченную модель на исполнение нажатием кнопки ► (Start simulations) на панели
инструментов окна модели. Открывая двойным щелчком осциллографы можно
просмотреть результаты моделирования (рис. 6.4, а). Важно подчеркнуть, для
того чтобы осциллограф не ограничивал число выводимых точек необходимо
259
нажать кнопку Parameters панели инструментов блока Scope и в открывшемся
окне вкладки Data History сбросить флажок Limit data points to last (рис. 6.4, б).
Trigonometric
FunctionB
Рис. 6.2. Реализация уравнений 6.1
Рис. 6.3. Окно параметров моделирования
260
a)
Рис. 6.4. Результаты моделирования составляющей угловой скорости СО™1 (а)
и окно параметров-блока Scope (б)
Выделим модель, за исключением блоков синусоидального сигнала и вирту-
альных осциллографов, затем правой кнопкой мыши вызовем контекстное ме-
ню и выберем команду Create subsystem («Создать подсистему»), в результате
чего модель формирования составляющих угловой скорости будет выглядеть в
виде одного блока (рис. 6.5). Откроем двойным щелчком созданную подсисте-
му, сменим названия входов и выходов.
да mma
Рис. 6.5. Подсистема формирования
проекций вектора относительной
угловой скорости из углов Эйлера-
Крылова:
Для реализации алгоритма ориентации с уг-
лами Эйлера-Крылова необхочимо решить об-
ратную задачу, т.е. из составляющих угловой
скорости cog, со™', со™1 получить углы рыс-
кания, тангажа и крена. Данный алгоритм ос-
нован на решении системы уравнений (3.30),
воспроизведем се еще раз
ф = —-—[со™1 cosy - со™1 sin у];
cos 0
6 = со™1 sin у + со™1 cos у;
у = со™* - ZgOfco™1 cosy - со*'" sin у].
(6.2)
Уравнения (6.2) разрешены относительно первых производных от углов |/,
0, у, поэтому если сформировать правые части (6.2) и проинтегрировать их, то
получим искомые углы рыскания, тангажа и крена. Следует отметить, что урав-
нения (6.2) связаны между собой по углам тангажа и крена.
Необходимый для решения уравнений (6.2) блок интегрирования (Integrator}
находится в библиотеке Continuous. Модель алгоритма ориентации с углами
Эйлера-Крылова приведена на рис. 6.6.
261
gamma!
Рис. 6.6. Алгоритм ориентации с углами Эйлера-Крылова
Для осуществления операции деления необходимо в окне параметров блока
Product ввести символы */. Следует также отметить, что на интеграторах по
умолчанию установлены нулевые начальные условия (Initial condition) (рис.
6.7, а), соответствующие начальным значениям углов рыскания, тангажа и кре-
на (так как была принята синусоидальная форма изменения этих углов).
Рис. 6.7. Окно параметров интегратора (д)
и интегратор с внешним источником начальных условий (б)
262
В противном случае в интеграторах необходимо устанавливать начальные
значения углов , 0, у. Начальные значения интегратора можно нс только
устанавливать в поле Initial condition окна параметров, но и подавать их от
внешнего источника, например с блока Constant. Для этого необходимо из спи-
ска Initial condition source (источник начальных условий) окна параметров бло-
ка Integrator выбрать альтернативу external (внешний) (рис. 6.7, б).
Убедившись, в том, что на выходе алгоритма углы у , 0, у совпадают с со-
ответствующими углами на входе, объединим алгоритм ориентации в подсис-
тему и подключим к выходу виртуальные авиационные приборы из библиотеки
Diah&Gauges Blockset Global Majic ActiveX Library Dejno Aircraft Instruments
(рис. 6.8). Следует отмстить, что виртуальные авиагоризонт и курсовой индика-
тор регистрируют углы в градусах, поэтому выходные сигналы алгоритма ори-
ентации переведены в градусы включением блоков (Radians to Degrees), нахо-
дящихся в библиотеке Simulink Extras Transformations. Для объединения сиг-
налов тангажа и крена применяется блок мультиплексора Мих, находящийся в
библиотеке Signal Routing.
Atificiat Horizon
Рис. 6.8. Алгоритм ориентации с подключенными к нему
виртуальными авиационными приборами
6.1.2. Алгоритм ориентации с направляющими косинусами
Алгоритм ориентации с направляющими косинусами основан на решении
обобщенного уравнения Пуассона (см. п. 3.2.3)
C = C[®J-[cogJC. (6.3)
263
Рассмотрим случай, когда можно пренебречь вектором угловой скорости
географического трехгранника: со v„ = co/g = a>Zg - 0 . В этом случае уравнение
(6.3) принимает вид
С = С[со]. (6.4)
Решим уравнение (6.4) в Simulink для законов изменения углов рыскания,
тангажа и крена, принятых в п. 6.1. Начнем решение поставленной задачи с
формирования кососимметрической матрицы [со]
0 -coz СОу
[со] = coz 0 -CDV
-сог СОЛ, 0
На рис. 6.9 показан способ формирования кососимметрической матрицы
[со].
С помощью блоков тих с тремя входами формируются столбцы кососим-
метрической матрицы, а с помощью блока Matrix Concatenate (местоположение
- библиотека Math Operations) происходит объединение столбцов в матрицу
размера 3x3. Реализация алгоритма ориентации с направляющими косинусами в
соответствии с уравнением (6.4) приведена на рис. 6.10.
Selector4
Рис. 6.10. Алгоритм ориентации с направляющими косинусами
264
В блок-схеме (рис. 6.10) использован уже созданный блок формирования уг-
ловых скоростей из углов Эйлера-Крылова. В центральной части блок-схемы
реализуется матричное уравнение (6.4), в результате чего образуется матрица
направляющих косинусов С . Произведение матриц осуществляется посредст-
вом блока Matrix Multiply, находящимся в библиотеке DSP BlocksetMath Func-
tions Matrices and Linear AlgebraMatrix Operation. Для извлечения необходи-
мых элементов из матрицы направляющих косинусов служат блоки Selector
(местоположение библиотека Signal Routing'). В окне параметров блока Selector
необходимо сменить тип входа (Input Туре) с векторного (Vector) на матричный
(Matrix), и установить соответствующие значения номера строки и столбца
матрицы в поля ввода Rows и Columns (рис. 6.11, а). После установки типа вхо-
да Matrix внешний вид блока сменится на тот, который представлен внизу на
рис. 6.11, а
) CU(R.C) >
Рис. 6.11. Блок Selector и его окно параметров (а); окно параметров блока Integrator (б)

Важно отметить, что начальными условиями для интегрирования матрично-
го уравнения (6.4) является начальная матрица направляющих косинусов С(/(|).
Так как в начальный момент времени у0 ~ 0, = 0, у0 = 0 в силу синусои-
дальных законов изменения углов у, 0, у, то матрица С(/(|) будет единичной
С(/„) =
cos 0() cos |/0 - cos yn cos 0 sin 0О + sin у0 sin ip0 sin у0 cos р0 sin 0О + cos у„ sin t|/0
sin 0'о cos у0 cos 0О - sin y(l cos Оо
- cos 0О sin i|/0 cos y0 sin i|/() sin 0O + sin y0 cos |/n - sin y0 sin sin 0O + cos yfl cos vp0
1 0 0
0 1 0
0 0 1
265
Окно параметров интегратора приведено на рис. 6.11, б. Для задания матри-
цы следует в квадратных скобках записывать строки матрицы, отделяя их «точ-
кой с запятой». Для разделения элементов в строке матрицы применяется про-
бел. Блок-схема алгоритма ориентации с направляющими косинусами, осно-
ванного на обобщенном уравнении Пуассона (6.3) приведена на рис. 6.12.
Рис. 6.12. Блок-схема алгоритма ориентации на основе обобщенного уравнения Пуассона
Рис. 6.13. Блок формирования матрицы направляющих косинусов из углов Эйлера - Крылова
266
Для формирования кососимметрической матрицы cog] использован создан-
ный выше блок Skew-symmetric matrix, на который в данном случае подаются
нулевые значения проекций со v, cor , coZg (напомним, в БИНС эти составляю-
щие подаются из навигационного алгоритма). Интегратор на рис. 6.12 реализо-
ван с внешним приемом начальных условий, т.е. матрицей C(f0). Для формиро-
вания матрицы направляющих косинусов из углов Эйлера-Крылова использует-
ся предварительно разработанный блок Krylov Angles to Direction Cosine
Matrix, представленный на рис. 6.13.
На рис. 6.13 блок Fen из библиотеки User-Defined Function позволяет реали-
зовать произвольную функцию, задаваемую пользователем. В данном случае
этот блок осуществляет умножение соответствующих входов u[l]...u[6] для
формирования матрицы направляющих косинусов. Для преобразования матри-
цы направляющих косинусов С в углы ig, 0, у используется созданный блок
Direct Cosine Matrix to Krylov Angles, представляющий собой объединение в
подсистему правой части блок-схемы, представленной на рис. 6.10
Следует отметить, что в разделе TransformationsAxes библиотеки Aerospace
Blockset содержатся блоки преобразований углов Эйлера в матрицу направ-
ляющие косинусов, углов Эйлера в кватернион и т.д. (рис. 6.14, а). Однако в
этих блоках используется другая последовательность поворотов на углы рыска-
ния, тангажа и крена в отличие от принятой в учебном пособии, поэтому непо-
средственное применение этих блоков может привести к некорректным резуль-
татам (рис. 6.14, б).
Ports & Subsyst- А
Signal Attributes
Signal Routing
Й- Sinks
2с Soirees
- 5т- User-Defined Fu
w Aerospace Blockset
2^ Actuators
2l-' Alteration
♦ Environment
♦ Equations of Mo
5> GNC
2)- Propulsion
- Transformations
tb Axes
Un*s
Рис. 6.14. Раздел TransferinationsAxes библиотеки Aerospace Blockset (a);
блоки формирования матрицы направляющих косинусов (б)
На рис. 6.14, б блок Krylov Angles to Direction Cosine Matrix, созданный в
соответствии с рис. 6.13, а — блок Euler Angles to Direction Cosine Matrix,
вставлен из библиотеки Aerospace Blockset, откуда видны различные значения
матриц'направляющих косинусов.
6.1.3. Алгоритм ориентации с кватернионами
Напомним, алгоритм ориентации с кватерниоными основан на решении ки-
нематического уравнения (см. раздел 3.3.6)
Л = ЛоП-ЦоД + л(1- ||Л||,
(6 6)
267
где Л - собственный кватернион, характеризующий ориентацию связанной
системы координат относительно географической.
Уравнение (6.6) снабжено корректирующим членом А(1 - ||Л||) для автома-
тической коррекции нормы кватерниона. Решение уравнения (6.6) в среде Simu-
link начнем с разработки блока умножения кватернионов с помощью кватерни-
онных матриц. В разделе 3.3.4 показано, что умножению кватернионов Л и П
соответствует умножению матриц вида
М(Х) =
-К
К
к
-к
-х2
-А,3
К
к
-к
х2
-К
К
о
соЛ.
сог
(6.7)
Пример формирования матриц М(Х)
и М(Х) приведен на рис. 6.15.
Рис. 6.15. Блок-схема формирования матриц М(Х) и М(Х)
Отметим, что блок Submatrix (местоположение: DSP BlocksetMath Func-
tions Matrices and Linear AlgebraXMatrix Operation) выделяет векторное ядро
матрицы М(Х)
Объединим блок-схему на рис. 6.15 в подсистему и создадим блок Matrix
Quaternions (кватернионная матрица). Пример произведения произвольных
кватернионов с помощью самостоятельно разработанного блока произведения
кватернионов приведен на рис. 6.16.
268
Constant!
Рис. 6.16. Произведение кватернионов с помощью матрицы Л/(Х)
При выполнении вычислений связанных с кватернионными матрицами поле-
зен блок преобразования вектора в гиперкомплексное отображение этого векто-
ра, для чего необходимо формально добавить нулевую компоненту к вектору
(рис. 6.17). _________________________________
Рис. 6.17. Создание блока преобразования вектора в отображение
Блок-схема алгоритма ориентации с кватернионами представлена на рис.
6.18.
Рис. 6.18. Блок-схема алгоритм ориентации с кватернионами
269
В центральной части блок-схемы представлен созданный предварительно
блок, реализующий уравнение (6.6), на вход которого подаются отображения
векторов абсолютной угловой скорости связанного и географического трех-
гранников. На рис. 6.19 приведена подсистема, реализующая уравнение (6.6).
Krylov Angles to
Quaternions
Рис. 6.19. Подсистема решения кинематического уравнения в кватернионах
На рис. 6.19 темным цветом обозначены блоки, формирующие член
Л(1 — ||д||) для автоматической коррекции нормы кватерниона. Блок Reshape
включен в систему для корректной работы модели. Блок Krylov Angles—> Quat
— это также предварительно разработанный блок для преобразования начальных
углов рыскания, тангажа и крена в кватернион в соответствии с формулами
3.126. Структура блока Krylov Angles—> Quat представлена на рис. 6.20.
Рис. 6.20. Структура блока Krylov Angles —> Quat
270
Отметим еще раз, что аналогичный блок находится в библиотеке Aerospace
Blockset TransformationsAxes, но он не соответствует приятой последователь-
ности разворотов на углы рыскания, тангажа и крена, поэтому перед использо-
ванием его необходимо модернизировать.
6.2. Калибровка инерциальных ЧЭ с помощью фильтра Калмана
6.2.1. Блоки моделирования случайных воздействий в пакете Simulink
В библиотеке Sources основной библиотеки блоков находятся три блока для
моделирования случайных воздействий: Uniform Random Number, Random
Number. Band-Limited White Noise.
Источник случайного сигнала Uniform Random Number
Источник случайного сигнала Uniform Random Number служит для генера-
ции случайного сигнала с равномерным распределением. Уровень сигнала ог-
раничен сверху и снизу значениями Maximum и Minimum. Применение этого
источника и окно установки его параметров представлены на рис 6.21.
Unl'orm Rardonr Scope
Number
f*r>i.l. Pararfteier*: Itnifcrrn Raiwta.v: Nun ber
I Iniforn Rrtirlmn Number
Output a urifnrmljr dktrih jfnrl random signal Pulpit is repeatable fnr a
given seed.
Рис. 6.21. Источник случайного сигнала с равномерным распределением
Необходимо помнить, что осциллограмма сигнала не будет повторяться при
различных запусках модели.
Источник случайного сигнала Random Number
Источник случайного сигнала Random Number служит для создания случай-
ного сигнала с равномерным распределением уровня. Применение источника
271
иллюстрирует рис. 6.22. Специфическими параметрами этого источника являет-
ся среднее значение сигнала Mean и дисперсия Variance.
Random Scope
Number
Olocfc Pat Rahcbm M »be
Random Number
Output a normally (Gaussian) distributed random signal. Output is
repeatable for a given seed.
Рис. 6.22. Источник случайного сигнала с нормальным распределением
Источник случайного сигнала Band-Limited White Noise
Генератор белого шума Band-Limited White Noise служит для создания шу-
мового сигнала типа белого шума с заданной мощностью. Рисунок 6.23 показы-
вает работу этого блока и окно установки его параметров.
Scoae
Band-Limited
White Noise
лоск Parameters: E'aod-I imited Vbite Noise
Continuous V^iite Njise. (iucskJ (link) -•—
V/hi.e noise :dr continuous (s-domain| systems. Band-limited using
zero-order-hold.
Рис.6.23. Генератор белого шума
272
Генератор характеризуется мощностью шума Noise Power (спектральной
плотностью), временем дискретизации Sample time и числом Seed, служащим
для инициализации генератора случайных чисел. Генератор фактически являет-
ся квантователем непрерывного сигнала, представляющего белый шум.
6.2.2. Реализация фильтра Калмана для калибровки
инерциальных ЧЭ
В разделе 5.4 рассматривался пример 5.4.3 поясняющий калибровку инерци-
альных ЧЭ с помощью фильтра Калмана. Воспроизведем этот пример в пакете
Simulink. Напомним, погрешность ЧЭ представлялась в виде суммы системати-
ческой £с(Л + 1) и белошумной у(Л + 1) составляющих:
ес(А- + 1) = £С(А),
z(k + 1) = £С(Л+ 1) + v(k: + 1).
(6.7)
Получим модель погрешности ЧЭ в виде постоянной составляющей равной 1
(не будем принимать во внимание размерности величин (для датчика угловой
скорости это [рад/с]) и белого шума с дисперсией также равной 1 ед" (рис. 6.24).
Время дискретизации {sample time) примем 0,01 с. Находим мощность шума
(спектральную плотность), которую необходимо установить в блоке Band-
Limited White Noise. I2 • 0,01 = 0,01 ед2 • с .
Bard-Lirrited
White Noise
Рис. 6.24. Модель погрешности ЧЭ
Проверяем дисперсию белого шума с помощью блока Variance (местополо-
жение DSP Blockset Statistics) (рис. 6.25). В параметрах блока Variance поста-
вим флажок Running variance.
273
Рис. 6.25. Расчет дисперсии белой последовательности
Уравнения оптимального фильтра для данной модели имеют вид
Р(к +11 к) = Р(к | к), Р(010) = Ро = 1[ед2];
(6-8)
K(k+})=
Р(к + 1к) + Я(к+})
(6.9)
Р(к: +11 к +1) = [1 - К (к + 1)]Р(Л +11 к);
(6 10)
x(A: + l|A: + l) = x(A:|A:) + /C(A + l)[z(^ + l)-i(A'|I')], ?(010) = 0. (6.11)
Матрице R(k +1) приравняем значение найденной дисперсии белого шума
(в данном случае: 1.017).
Функцию задержки на один шаг можно осуществить с помощью блока
Memory либо Unit Delay (библиотека Discrete). Работа блока Memory и его па-
раметры показаны на рис. 6.26.
М error*
Арр^ о one integration otep delay. The oclpU ig the previaua input value, j
Parameters —
| nitisl comSticn
I
✓ Inherit eanple the
Direct feeihough of rout duenq tnearcation
•1_________________ _________ ______ ________________________________
□K. | Cance [ Help | I
Рис. 6.26. Работа блока Memory
Параметр Inherit sample time означает «Принять время дискретизации при
выполнении функции задержки». Строка Initial condition позволяет задавать
274
начальное значение. Начальное значение определяется дисперсией системати-
ческой составляющей, которую примем равной 1.
Модель уравнений (6.8) - (6.10) и характер изменения коэффициента пере-
дачи представлен на рис. 6.27.
Рис. 6.27. Изменение коэффициента передачи оптимального фильтра
Реализация полного алгоритма фильтра Калмана на основании уравнений
(6.8) - (6.11) представлена на рис. 6.28.
Рис. 6.28. Структурная схема ФК
275
Оценка систематической составляющей и измерения, поступающие в
фильтр, представлены на рис. 6.29.
Рис. 6.29. Оценка систематической составляющей с помощью фильтра Калмана
Из рис. 6.29 следует, что фильтр Калмана достаточно точно вырабатывает
оценку систематической составляющей погрешности инерциального ЧЭ.
ЛИТЕРАТУРА К ГЛАВЕ 6
6.1. Дьяконов В.П. MATLAB 6: учебный курс. - СПб.: Питер, 2002.
6.2. Дьяконов В., Круглов В. Математические пакеты расширения MATLAB: Спец, справочник.
-СПб.: Питер, 2001.
6.3. Дьяконов В., Круглов В. MATLAB. Анализ, идентификация и моделирование систем: Спец,
справочник. - СПб.: Питер, 2002.
276

Источник