Абсолютная и относительная погрешности (ошибки).
Пусть некоторая
величина x
измерена n
раз. В результате получен ряд значений
этой величины: x1,
x2,
x3,
…, xn
Величиной, наиболее
близкой к действительному значению,
является среднее арифметическое этих
результатов:
Отсюда следует,
что каждое физическое измерение должно
быть повторено несколько раз.
Разность между
средним значением
измеряемой
величины и значением отдельного измерения
называется абсолютной
погрешностью отдельного измерения:
(13)
Абсолютная
погрешность может быть как положительной,
так и отрицательной и измеряется в тех
же единицах, что и измеряемая величина.
Средняя абсолютная
ошибка результата — это среднее
арифметическое значений абсолютных
погрешностей отдельных измерений,
взятых по абсолютной величине (модулю):
(14)
Отношения
называются относительными погрешностями
(ошибками) отдельных измерений.
Отношение средней
абсолютной погрешности результата
к среднему арифметическому значению
измеряемой величины называют относительной
ошибкой результата и выражают в процентах:
Относительная
ошибка характеризует точность измерения.
Законы распределения случайных величин.
Результат измерения
физической величины зависит от многих
факторов, влияние которых заранее учесть
невозможно. Поэтому значения, полученные
в результате прямых измерений какого
— либо параметра, являются случайными,
обычно не совпадающие между собой.
Следовательно, случайные
величины —
это такие величины, которые в зависимости
от обстоятельств могут принимать те
или иные значения. Если случайная
величина принимает только определенные
числовые значения, то она называется
дискретной.
Например,
количество заболеваний в данном регионе
за год, оценка, полученная студентом на
экзамене, энергия электрона в атоме и
т.д.
Непрерывная
случайная величина принимает любые
значения в данном интервале.
Например: температура
тела человека, мгновенные скорости
теплового движения молекул, содержание
кислорода в воздухе и т.д.
Под событием
понимается всякий результат или исход
испытания. В теории вероятностей
рассматриваются события, которые при
выполнение некоторых условий могут
произойти, а могут не произойти. Такие
события называются
случайными.
Например, событие, состоящее в появлении
цифры 1 при выполнении условия — бросания
игральной кости, может произойти, а
может не произойти.
Если событие
неизбежно происходит в результате
каждого испытания, то оно называется
достоверным.
Событие называется невозможным,
если оно вообще не происходит ни при
каких условиях.
Два события,
одновременное появление которых
невозможно, называются несовместными.
Пусть случайное
событие А в серии из n
независимых испытаний произошло m
раз, тогда отношение:
называется
относительной частотой события А. Для
каждой относительной частоты выполняется
неравенство:
При небольшом
числе опытов относительная частота
событий в значительной мере имеет
случайный характер и может заметно
изменяться от одной группы опытов к
другой. Однако при увеличении числа
опытов частота событий все более теряет
свой случайный характер и приближается
к некоторому постоянному положительному
числу, которое является количественной
мерой возможности реализации случайного
события А. Предел, к которому стремится
относительная частота событий при
неограниченном увеличении числа
испытаний, называется статистической
вероятностью события:
Например, при
многократном бросании монеты частота
выпадения герба будет лишь незначительно
отличаться от ½. Для достоверного события
вероятность Р(А) равна единице. Если
Р=0, то событие невозможно.
Математическим
ожиданием
дискретной случайной величины называется
сумма произведений всех ее возможных
значений хi
на вероятность этих значений рi:
Статистическим
аналогом математического ожидания
является среднее арифметическое значений
:
,
где mi
— число дискретных случайных величин,
имеющих значение хi.
Для непрерывной
случайной величины математическим
ожиданием служит интеграл:
,
где р(х) — плотность
вероятности.
Отдельные значения
случайной величины группируются около
математического ожидания. Отклонение
случайной величины от ее математического
ожидания (среднего значения) характеризуется
дисперсией,
которая для дискретной случайной
величины определяется формулой:
(15)
(16)
Дисперсия имеет
размерность случайной величины. Для
того, чтобы оценивать рассеяние
(отклонение) случайной величины в
единицах той же размерности, введено
понятие среднего
квадратичного отклонения
σ(Х), которое
равно корню квадратному из дисперсии:
(17)
Вместо среднего
квадратичного отклонения иногда
используется термин «стандартное
отклонение».
Всякое отношение,
устанавливающее связь между всеми
возможными значениями случайной величины
и соответствующими им вероятностями,
называется законом
распределения случайной величины.
Формы задания закона распределения
могут быть разными:
а) ряд распределения
(для дискретных величин);
б) функция
распределения;
в) кривая распределения
(для непрерывных величин).
Существует
относительно много законов распределения
случайных величин.
Нормальный
закон распределения случайных
величин (закон
Гаусса).
Случайная величина
распределена по
нормальному закону, если ее плотность
вероятности f(x)
определяется формулой:
(18),
где <x>
— математическое ожидание (среднее
значение) случайной величины <x>
= M
(X);
—
среднее квадратичное отклонение;
—
основание натурального логарифма
(неперово число);
f
(x)
– плотность вероятности (функция
распределения вероятностей).
Многие случайные
величины (в том числе все случайные
погрешности) подчиняются нормальному
закону распределения (закону Гаусса).
Для этого распределения наиболее
вероятным значением
измеряемой
величины
является
её среднее
арифметическое
значение.
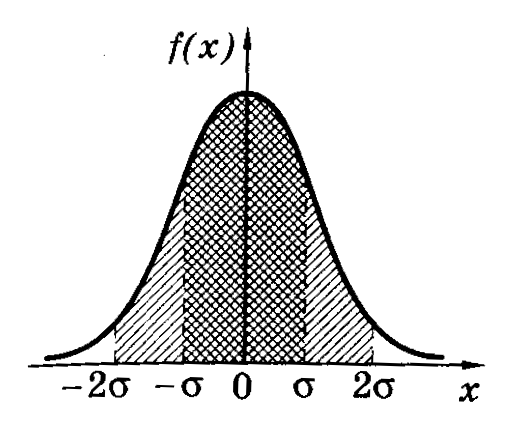
График нормального
закона распределения изображен на
рисунке (колоколообразная кривая).
Кривая симметрична
относительно прямой х=<x>=α,
следовательно, отклонения случайной
величины вправо и влево от <x>=α
равновероятны. При х=<x>±
кривая асимптотически приближается к
оси абсцисс. Если х=<x>,
то функция распределения вероятностей
f(x)
максимальна и принимает вид:
(19)
Таким образом,
максимальное значение функции fmax(x)
зависит от величины среднего квадратичного
отклонения. На рисунке изображены 3
кривые распределения. Для кривых 1 и 2
<x>
= α = 0 соответствующие значения среднего
квадратичного отклонения различны, при
этом 2>1.
(При увеличении
кривая распределения становится более
пологой, а при уменьшении
– вытягивается вверх). Для кривой 3 <x>
= α ≠ 0 и 3
= 2.
Закон
распределения
молекул в газах по скоростям называется
распределением
Максвелла.
Функция плотности вероятности попадания
скоростей молекул в определенный
интервал
теоретически была определена в 1860 году
английским физиком Максвеллом
. На рисунке
распределение Максвелла представлено
графически. Распределение движется
вправо или влево в зависимости от
температуры газа (на рисунке Т1
< Т2).
Закон распределения Максвелла определяется
формулой:
(20),
где mо
– масса молекулы, k
– постоянная Больцмана, Т – абсолютная
температура газа,
—
скорость молекулы.
Распределение
концентрации молекул газа в атмосфере
Земли (т.е.
в силовом поле) в зависимости от высоты
было дано австрийским физиком Больцманом
и называется
распределением
Больцмана:
(21)
Где n(h)
– концентрация молекул газа на высоте
h,
n0
– концентрация у поверхности Земли, g
– ускорение свободного падения, m
– масса молекулы.
Распределение
Больцмана.
Совокупность всех
значений случайной величины называется
простым
статистическим рядом.
Так как простой статистический ряд
оказывается большим, то его преобразуют
в вариационный
статистический
ряд или интервальный
статистический ряд. По интервальному
статистическому ряду для оценки вида
функции распределения вероятностей по
экспериментальным данным строят
гистограмму
– столбчатую
диаграмму. (Гистограмма – от греческих
слов “histos”–
столб и “gramma”–
запись).
n
-
h
Гистограмма
распределения Больцмана.
Для построения
гистограммы интервал, содержащий
полученные значения случайной величины
делят на несколько интервалов xi
одинаковой ширины. Для каждого интервала
подсчитывают число mi
значений случайной величины, попавших
в этот интервал. После этого вычисляют
плотность частоты случайной величины
для каждого интервала xi
и среднее значение случайной величины
<xi
> в каждом интервале.
Затем по оси абсцисс
откладывают интервалы xi,
являющиеся основаниями прямоугольников,
высота которых равна
(или
высотой
– плотностью относительной частоты
).
Расчетами показано,
что вероятность попадания нормально
распределенной случайной величины в
интервале значений от <x>–
до <x>+
в среднем равна 68%. В границах вдвое
более широких (<x>–2;
<x>+2)
размещается в среднем 95% всех значений
измерений, а в интервале (<x>–3;<x>+3)
– уже 99,7%. Таким образом, вероятность
того, что отклонение значений нормально
распределенной случайной величины
превысит 3
(
– среднее квадратичное отклонение)
чрезвычайно мала (~0,003). Такое событие
можно считать практически невозможным.
Поэтому границы <x>–3
и <x>+3
принимаются за границы практически
возможных значений нормально распределенной
случайной величины («правило трех
сигм»).
Если число измерений
(объем выборки) невелико (n<30),
дисперсия вычисляется по формуле:
(22)
Уточненное среднее
квадратичное отклонение отдельного
измерения вычисляется по формуле:
(23)
Напомним, что для
эмпирического распределения по выборке
аналогом математического ожидания
является среднее арифметическое значение
<x>
измеряемой величины.
Чтобы дать
представление о точности и надежности
оценки измеряемой величины, используют
понятия доверительного интервала и
доверительной вероятности.
Доверительным
интервалом
называется интервал (<x>–x,
<x>+x),
в который по определению попадает с
заданной вероятностью действительное
(истинное) значение измеряемой величины.
Доверительный интервал характеризует
точность полученного результата: чем
уже доверительный интервал, тем меньше
погрешность.
Доверительной
вероятностью
(надежностью)
результата серии измерений называется
вероятность того, что истинное значение
измеряемой величины попадает в данный
доверительный интервал (<x>±x).
Чем больше величина доверительного
интервала, т.е. чем больше x,
тем с большей надежностью величина <x>
попадает в этот интервал. Надежность
выбирается самим исследователем
самостоятельно, например, =0,95;
0,98. В медицинских и биологических
исследованиях, как правило, доверительную
вероятность (надежность) принимают
равной 0,95.
Если величина х
подчиняется нормальному закону
распределения Гаусса, а <x>
и <>
оцениваются по выборке (числу измерений)
и если объем выборки невелик (n<30),
то интервал (<x>
– t,n<>,
<x>
+ t,n<>)
будет доверительным интервалом для
известного параметра х с доверительной
вероятностью .
Коэффициент t,n
называется коэффициентом
Стьюдента
(этот коэффициент был предложен в 1908 г.
английским математиком и химиком В.С.
Госсетом, публиковавшим свои работы
под псевдонимом «Стьюдент» – студент).
Значении коэффициента
Стьюдента t,n
зависит от доверительной вероятности
и числа измерений n
(объема выборки). Некоторые значения
коэффициента Стьюдента приведены в
таблице 1.
Таблица 1
|
n |
|
||||||
|
0,6 |
0,7 |
0,8 |
0,9 |
0,95 |
0,98 |
0,99 |
|
|
2 |
1,38 |
2,0 |
3,1 |
6,3 |
12,7 |
31,8 |
63,7 |
|
3 |
1,06 |
1,3 |
1,9 |
2,9 |
4,3 |
7,0 |
9,9 |
|
4 |
0,98 |
1,3 |
1,6 |
2,4 |
3,2 |
4,5 |
5,8 |
|
5 |
0,94 |
1,2 |
1,5 |
2,1 |
2,8 |
3,7 |
4,6 |
|
6 |
0,92 |
1,2 |
1,5 |
2,0 |
2,6 |
3,4 |
4,0 |
|
7 |
0,90 |
1,1 |
1,4 |
1,9 |
2,4 |
3,1 |
3,7 |
|
8 |
0,90 |
1,1 |
1,4 |
1,9 |
2,4 |
3,0 |
3,5 |
|
9 |
0,90 |
1,1 |
1,4 |
1,9 |
2,3 |
2,9 |
3,4 |
|
10 |
0,88 |
1,1 |
1,4 |
1,9 |
2,3 |
2,8 |
3,3 |
В таблице 1 в верхней
строке заданы значения доверительной
вероятности
от 0,6 до 0,99, в левом столбце – значение
n.
Коэффициент Стьюдента следует искать
на пересечении соответствующих строки
и столбца.
Окончательный
результат измерений записывается в
виде:
(25)
Где
– полуширина доверительного интервала.
Результат серии
измерений оценивается относительной
погрешностью:
(26)
Соседние файлы в предмете [НЕСОРТИРОВАННОЕ]
- #
- #
- #
- #
- #
- #
- #
- #
- #
- #
- #
Систематические погрешности вызываются или известными причинами, или такими, которые могут быть установлены при детальном анализе процедуры измерений. Систематические погрешности либо постоянны, либо изменяются по определенному закону в ходе измерений. Поскольку систематические погрешности, как правило, не единичны, общий результат измерений может содержать суммарную положительную или отрицательную погрешность, абсолютное значение которой может быть велико. [c.806]
Необходимо отметить, что критерием точности данных является не отношение разности абсолютных значений положительной и отрицательной площадей к одному из них, как это иногда считают, а абсолютное значение этой разности, которое выражает среднюю во всем диапазоне концентраций погрешность [c.159]
Под погрешностью показаний индикатора в пределах данного участка понимают сумму абсолютных величин наибольших (положительной и отрицательной) погрешностей, накопленных на данном участке при прямом и обратном ходе измерительного стержня. Допускаются следующие погрешности показаний в пределах участка шкалы, равного 0,1 мм в начале второго оборота стрелки — 6 мкм в пределах 1 мм на любом участке измерения—12 мкм в пределах всего интервала измерений на участках О—2 О—3 О—5 О—10 мм—соответственно 12, 15, 18, 22 мкм. Вариация показаний составляет 3 мкм. [c.188]
Имеется несколько вариантов классификации систематических погрешностей. Так, по природе различают аналитические и инструментальные систематические погрешности. По влиянию на результат анализа систематические погрешности делят на положительные, которые приводят к завышению значений аналитического сигнала и, следовательно, к завышенным значениям определяемых содержаний элемента, и на отрицательные, которые приводят к занижению значений определяемых содержаний элемента. Помимо этого их подразделяют на постоянные (аддитивные), значение которых не связано с абсолютным значением аналитического сигнала (массой аналитической навески), и пропорциональные (мультипликативные), значение которых пропорционально значению аналитического сигнала. [c.24]
Случайные ошибки отличаются от систематических тем, что увеличением числа измерений можно уменьшить их величину. Эта особенность обусловлена тем, что значения случайных ошибок с одинаковой степенью вероятности могут быть положительными и отрицательными. Казалось бы, это позволяет осуществить количественную оценку случайных ошибок. Однако это не так число повторных измерений, как правило, невелико, поэтому методы теории вероятности неприменимы. Как же следует обрабатывать результаты отдельных измерений (каждое из которых содержит случайную ошибку) для того, чтобы получить величину, более всего приближающуюся к точному значению Приступая к решению этой задачи, предполагаем, что систематические ошибки исключены. Прежде всего следует определить абсолютную и относительную погрешности измерения данной величины. [c.465]
При большом числе равноточных испытаний числа положительных (Х — й > 0) и отрицательных (А», — ц < 0) погрешностей, равных по абсолютному значению, одинаковы. Иначе говоря, в генеральной совокупности одинаково часто должны [c.822]
Абсолютная погрешность приближенных чисел может быть как положительной, так и отрицательной. Поэтому при сложении этих чисел возможна взаимная компенсация погрешностей, в результате которой абсолютная погрешность суммы может оказаться меньше суммы абсолютных погрешностей слагаемых. Во всяком случае абсолютная погрешность суммы не может быть больше суммы абсолютных погрешностей слагаемых, т. е. если а — абсолютная погрешность суммы а = а + аа — -. . . а и а , а ,.. ., а — абсолютные погрешности приближенных величин а , аз,.. ., а , то [c.762]
Когда параметр шероховатости меньше определяемой по формуле (6.6) величины, погрешность положительна и уменьшается с уменьшением толщины неровного слоя. При увеличении толщины слоя больше указанного значения погрешность также уменьшается и даже может стать отрицательной. Абсолютное значение неровностей поверхности, оказывающих влияние на точность измерения толщины, составляет 0,01 мм и более на частоте 2 МГц. [c.696]
Как уже указывалось, относительная и абсолютная погрешность определения элемента растворимого вещества для такого рода материалов всегда будет отрицательной. Она не зависит от относительных количеств определяемых веществ в смеси и поэтому для каждого конкретного случая, т. е. при известном и постоянном а, будет величиной постоянной. Таким [c.52]
Случайные ошибки направлены как в большую, так и меньшую сторону, они связаны с разбросом измеряемых показаний от средней величины. Обычно полностью исключить эти ошибки нельзя, так как любую величину абсолютно точно измерить в большинстве случаев невозможно, всегда допускается определенная погрешность. Распределение случайных ошибок соответствует кривой нормального распределения вероятностей, из которых следует, что положительные и отрицательные отклонения равновероятны и что меньшие отклонения встречаются значительно чаще, чем большие. [c.213]
График, построенный для большого числа случайных погрешностей, носит название закона нормального распределения (рис. ЙЛ 1). Из рис. 2.1 Ь видно, что случайные погрешности, равные по абсолютному значению, но различные по знаку, встречаются одинаково часто, т. е. число отрицательных погрешностей равно числу положительных [c.35]
Систематические погрешности подразделяют на положительные, которые приводят к завышению значений аналитического сигнала (Л) и, следовательно, к завышенным значениям определяемых содержаний элемента, и на отрицательные, которые приводят к занижению значений определяемых содержаний элемента. Помимо этого их подразделяют на постоянные (аддитивные), значение которых не связано с абсолютным значением аналитического сигнала, и пропорциональные (мультипликативные), значение которых пропорционально значению аналитического сигнала. [c.93]
Абсолютная погрешность показания прибора — это разность между его показанием, и значением измеряемой величины, установленным по образцовым мерам или приборам. Погрешность может быть положительной и отрицательной. [c.16]
Температурные коэффициенты теплот диссоциации при всех значениях ионной силы остаются отрицательными и постоянными в пределах указанной погрешности, однако с увеличением концентрации фонового электролита можно говорить о некоторой тенденции к уменьшению значения А Ср по абсолютной величине по всем ступеням (табл. 2). [c.21]
Из выражения (46) следует, что абсолютная погрешность регулирования при неизменном перепаде давления п — ) растет с увеличением нагрузки горелки и зависит от жесткости пружины. Погрешность регулирования имеет отрицательный знак (рв>р2)- [c.62]
Уравнение (21.14) показывает, что абсолютная погрешность, допущенная при определении пропускания, т. е. отношения Р/Р , вызывает в 0,434/TlgT раз большую относительную погрешность результата анализа. Зависимость множителя —0,434/Т1 Т (lgT имеет отрицательный знак) от светопоглощения А показана на рис. 79. Видно, [c.296]
Рассмотрим зависимость результатов определения от наличия систематических погрешностей. В одних случаях результат может отличаться от истинного всегда на одно и то же значение, т. с. погрешность будет постоянной независимо от размера навески. Так, определяя свинец, его осаждают в виде PbSOi и промывают осадок водой. В результат вносится постоянная отрицательная систематическая погрешность, связанная с потерями за счет заметной растворимости сульфата свинца. Эта погрешность по абсолютному значению всегда будет одна и та же, независимо от количества находящегося на фильтре [c.59]
В аналитической практике выделяют три разновидности погрешностей, которые могут искажать результаты анализов при проявлении причин различной природы случайные погрешности, систематические погрешности и промахи. Случайные погрешности обусловлены неявными факторами, меняющимися от опыта к опыту, и характеризуют понятие воспроизводимости метода (методики) анализа. Систематическая погрешность обусловлена причинами известной природы (или же причинами, которые могут быть выявлены при детальном рассмотрении методики). Ей соответствует понятие правильность метода анализа . Понятие точность объединяет воспроизводимость и правильность метода анализа. Разница между случайными и систематическими отклонениями ( ,) заключается в том, что первые могут принимать различные значения с различными знаками, и для выборки достаточно большого объема число положительных отклонений должно быть равно числу отрицательных, вторые постоянны как по значению, так и по знаку, хотя постоянство их по значению может быть абсолютным или относительным. Наконец, третий вид погрешности — промах — предст авляет собой отклонение, которое резко отличается по значению от других отклонений выборки и причиной которого является невнимательность или некомпетентность аналитика. Промахи и систематические ошибки, присутствующие в выборке результатов анализа, выявляются в результате ее статистической обработки. [c.84]
Искажения, которые получаются при всяком измерении, носят название погрешностей (ошибок) измерения. Каждое измерение имеет ценность только тогда, когда известна его погрешность или указаны ее возможные пределы. Погрешность, выраженную в единицах измеряемой величины, называют абсолютной. Она бывает как положительная, так и отрицательная. Погрешность, выраженную в процентах (или долях) от действительного значения, называют относительной. На рис. 1-1 представлена в общем виде классифи-каци погрешностей. [c.6]
Необходимо отметить, что критерием точности да)анЬ1х является не отношение разности абсолютных значений положительной и отрицательной площадей к одному из них, как это иногда считают, а абсолютное значение этой разности, которое выражает среднюю во всем диапазоне концентраций погрешность в определении Yl/Y2 и, соответственно, а. При этом следует помнить, что погрешности возможны преимущественно в какой-нибудь ограни- [c.208]
Качество измерительного прибора характеризуется рядом факторов, из которых основными являются точность, чувствительность и инерционность (время запаздывания). Точность измерительного прибора определяется степенью приближения результата измерения к действительному значению измеряемой величины. Отклонение измеренного значения от действительного называется погрешностью измерения. Погрешность измерения выражается абсолютной или относительной величиной. Она может быть положительной или отрицательной,. .бсолютная погрещность [c.9]
При нормальном законе распределения погрешностей малые по абсолютной величине погрешности появляются чаще больших. Большие погрешности (грубые промахи) встречаются редко. Если их исключить из рассмотрения, то случайные погрешности не должны превосходить некоторого предела — максимальной погрешности измерения (Дмакс). Положительные погреш ности появляются так же часто, как н равные им по абсолютной величине отрицательные- погрешности. На основании этого свойства погрешностей наиболее досто-28 [c.28]
В подшипниках и демпферах смазка заполняет обширные полости и чаще всего разрывается уже при давлении, близком к давлению насыщенных паров, или при отрицательном давлении порядка нескольких десятых долей атмосферы. Без большой погрешности можно полагать, что смазка разрывается при падении абсолютной величины давления до нуля. По соотношениям (10), (14) у подшипников с торцовой ванной (см. рис. 4, а), нагруженных в отрицательном направлении оси у (см. рис. 3), наибольшее падение давления и разрыв смазки происходят в некотором месте в центральной зоне подшипника вдали от его краев в окрестности координат 2 = О, ф я/2. Непосредственной причиной разрыва являются либо статическая нагрузка подшипника силой Ру = С, либо колебания цапфы ротора. Последние могут быть вызваны внешней динамической нагрузкой Рр(0 (в простейшем случае Ре(0 = Ррсов т, т = 1) или же возникать самопроизвольно. Если бы давленне в слое смазки не зависело от осевой координаты 2 и гармонически изменялось по окружности цапфы, то разрыв смазки наступил бы тогда, когда сумма относительных нагрузок Г и О - [c.46]
Переходя к объяснению способов, которыми разочтены центры поверхности и населенности России, должно прежде всего заметить, что некоторые ее части или подразделения непременно следовало при этом признать равномерно населенными. Признание это, конечно, нельзя считать абсолютно точным, потому что равномерного распределения людей на поверхности земли нельзя даже и на минуту представить, но когда дело идет о больших величинах, реализм не может успевать иначе, как допуская известного )ода небольшие погрешности в определении всяких величин. Логрешности бывают положительного и отрицательного свойства, и, слагаясь, одни отчасти уничтожаются другими,, и результат, выведенный из множества данных, должен заключать вероятную погрешность, гораздо меньшую, чем в отдельных входящих величинах. Признаем, например, два уезда заселенными с одинаковою степенью скученности и определим по карте центр тяжести каждого тогда должно-полагать, что вследствие действительной неравномерности в одном уезде центр населенности будет лежать севернее или восточнее найденного центра тяжести, а в другом — [c.504]
Первая теплота растворения, как мы помним из предыдущего, может быть при т = О представлена уравнением ДЯ = ДЯреш + + ДЯ [с. 58, уравнение (IV. ) ]. Здесь все не относящиеся к энергии решетки экзо- и эндо-эффекты входят в суммарную химическую теплоту гидратации ионов АЯ . Энергию решетки в пределах интересующей нас точности можно считать в диапазоне изученных нами температур не зависящей от температуры. Ориентировочный расчет показывает, что d .H JdT в интервале 20—50 °С составляет меньше /зо от обычной вероятной погрешности в абсолютных значениях АЯреш- Таким образом, все наблюдаемое влияние температуры на АЯо следует отнести за счет изменений с температурой. Во всех рассматриваемых случаях с повышением температуры ДЯ становится более экзотермичной, так как отрицательны. Гидратация ионов, как в целом экзотермический процесс, должна с ростом температуры уменьшаться при т = О энергетически, а не координационно. Поэтому увеличение экзотермичности ДЯд можно объяснить только уменьшением какого-то эндотермического члена, входящего в ДЯ . [c.169]
Водяные (водородно-кислородные) кулонометры дают все же отрицательные ошибки при измерении малых количеств электричества в случае, когда используется ток с плотностью <2,0 ма1см [124, 126]. Так, Соестберген [126] показал, что объем выделившегося на 1 к газа в водородно-кислородном кулонометре с раствором NaOH (2 М) и платиновыми электродами (1 см ) в интервале 0,4—100 ма меньше теоретического значения. Абсолютное значение отрицательного отклонения растет с увеличением силы тока, однако относительная погрешность при этом убывает. В кулонометре с указанным электролитом теоретическое значение фактора в формуле (7), равное 0,1741, достигается лишь при силе тока 3000 ма. При больших плотностях тока (проволочные электроды длиной 0,5 см и диаметром 0,1 мм) практическое совпадение экспериментального и теоретического значений фактора наблюдается уже при силе тока 1650 ма. [c.16]
Применение одноизотопных металлов с нечетными массовыми номерами, использованных для изготовления зондов и тиглей, позволило исключить перекрытия в масс-спектрах анализируемых веществ, однако оставалась нерешенной вторая половина задачи уменьшение абсолютного вклада ионов материала зондов в суммарный ионный ток образца, что могло бы внести погрешности в результаты определения. Кроме того, доля вклада ионов материала зонда свидетельствует об уровне вносимых им примесей. В работе [12] предложено оригинальное решение проблемы путем реализации униполярного разряда, схема которого представлена на рис. 4.3. В данном случае зонд всегда находится под отрицательным потенциалом, а образец под положительным. Такой подход дает возможность уменьшить вклад ионов материала зонда в суммарный ионный ток образца до Ы0 — 5-10 %. Кроме того, оказалось возможным практически без замены зонда осуществлять анализ двух-трех образцов. При этом вклад примесей, содержащихся в материале зонда, в масс-спектры анализируемых образцов составил (в % ат.) железо, натрий и калий до 1-10 — 3-10 хром, марганец и ванадий до 5 10 —10 никель, медь и цинк до 10 —З-Ю остальные элементы — меньше 3-10 — 3-10- °. Следовательно, вносимые количества примесей находятся за пределами чувствительности метода ИМС. [c.122]
Прибор УЗИС-6 — относительного отсчета, т. е. но величине сдвига импульса на экране трубки осуществляется измерение величины относительного изменения скорости ультразвука. Абсолютная величина определяется сравнением с эталоном — жидкостью с достаточно точно известной скоростью распространения ультразвука. Лабораторный датчик (кювета) имеет подвижный излучающий пьезоэлемент, благодаря чему можно изменять длину пути, проходимого ультразвуковыми импульсами в нсследуемой среде. В этом случае абсолютное значение скорости распространения ультразвука может быть измерено без применения эталонной жидкости с погрешностью не более 1,0%. Блок-схема прибора представлена на рнс. 10-5. Временное соотношение характерных импульсных сигналов (напряжений) в отдельных узлах блок-схемы приводится на рис. 10-6. Синхронизатор вырабатывает отрицательные пусковые импульсы 1 для запуска возбудителя и 2 для запуска генератора развертки. Возбудитель в момент поступления на него пускового импульса 1 возбуждает передающий пьезоэлемент электрическим импульсом малой длительности 3. При втом пьезоэлемент излучает в исследуемую среду короткий ультразвуковой импульс. [c.218]
Результатом
измерения
в стандарте названо значение измеряемой
величины, найденное путем ее измерения.
Это значение должно быть дополнено
указанием степени его недостоверности
в виде оценки погрешности или
неопределенности. Не следует забывать
о том, что результат измерения размерной
физической величины представляет собой
именованное
число.
Погрешность
результата измерения
(краткая форма термина – погрешность
измерения) исходно определяется как
отклонение результата измерения xизм
от истинного
значения
xист
измеряемой величины. Таким образом,
погрешность (абсолютная) равна Δx
= xизм
– xист.
Термин “абсолютная
погрешность”
используется, если нужно подчеркнуть,
что погрешность выражена в единицах
измеряемой величины. Качество измерения
лучше характеризует относительная
погрешность
δx
= Δx/xист
≈ Δx/xизм,
которая может быть выражена в долях
единицы, в процентах или в единицах ppm
(см. параграф 3.5). Не следует смешивать
абсолютную погрешность (которая может
быть как положительной, так и отрицательной)
с абсолютным значением погрешности
│Δx│.
Отметим,
что и абсолютная погрешность может
оказаться выраженной в процентах, если
сама измеряемая величина является
относительной (как, например, относительная
влажность H,
всегда выражаемая тоже в процентах). В
таких случаях необходимо обязательно
оговаривать, имеются ли в виду “абсолютные
проценты” относительной влажности ΔH
или “проценты от процентов”, т. е.
относительная погрешность относительной
влажности (ΔH/H)·100
%.
Понятие
истинного значения измеряемой величины,
на которое опирается определение
погрешности, связано с непростыми
философскими вопросами: ведь оно при
измерении неизвестно и не
может быть найдено!
Сам объект всегда обладает какой-то
неопределенностью; единицу величины
тоже нельзя задать идеально (а ведь
значение величины определяется как ее
отношение к единице!). Любое измерение
дает результат с конечным числом значащих
цифр; бесконечно точное измерение, если
бы и было возможно, потребовало бы
бесконечного времени для получения
бесконечного числа знаков после запятой…
Все эти соображения приводят к выводу
(который многие метрологи и философы
не разделяют), что истинное значение
могут иметь только математические
величины (см. параграф 2.10), физические
же величины его не имеют.
Тем
не менее, приведенное выше определение
погрешности сохраняет смысл в тех
случаях, когда измеряемая величина
могла бы быть
измерена более точно.
Результат такого возможного, а иногда
и фактически выполняемого более точного
измерения, в какой-то степени заменяющий
воображаемое истинное значение, называют
действительным
значением
измеряемой величины xд,
или иногда “условно истинным” значением.
В итоге определение погрешности несколько
изменяют и записывают следующим образом:
Δx
= xизм
– xд.
Погрешность
каждого конкретного измерения, конечно,
остается неизвестной, – если бы было
иначе, следовало бы вычислить xд
= xизм
– Δx
и устранить погрешность.
Поэтому результат измерения всегда
дополняется не значением
погрешности, а ее оценкой.
Для
западной философской традиции исходное
определение погрешности измерения,
опирающееся на ненаблюдаемое
истинное значение, оказалось неприемлемым
– оно противоречит позитивистским
установкам, на которых воспитываются
западные ученые. Поэтому было введено
другое понятие – неопределенность
измерения (uncertainty
of measurement).
Ему посвящен международный документ
Guide to the
expression of uncertainty in measurement
(Руководство по выражению неопределенности
в измерении), опубликованный в 1993 г.
Международной организацией по
стандартизации ISO с участием шести
других организаций, включая Международное
бюро мер и весов. Имеется русский перевод
этого документа, однако мы будем для
краткости называть его просто “Гайд”.
Согласно этому “Гайду” неопределенность
измерения есть параметр,
связанный с результатом измерения,
характеризующий рассеяние значений,
которые могли бы быть разумным образом
приписаны измеряемой величине.
Таким образом, авторы “Гайда”, изгнав
пресловутое ненаблюдаемое истинное
значение, ввели в определение элемент
субъективности в виде слов “которые
могли бы быть разумным образом приписаны…”
(в оригинале
– that could reasonably be
attributed…). Кроме того,
слово “рассеяние” маскирует возможностьсистематического смещенияполучаемых
при измерении результатов.
И тот, и другой недостаток, конечно,
нельзя приписать недосмотру авторов.
Дело в серьезных философско-методологических
трудностях и парадоксах, возникающих
при анализе измерения с теоретико-познавательных
позиций
4.4.
Источники и составляющие погрешности
или неопределенности
Существует
ряд причин, приводящих к появлению
отдельных составляющих погрешности
или неопределенности измерения (для
краткости часто слово “составляющие”
опускают, и говорят о частных
погрешностях,
которые в сумме образуют результирующую
погрешность
измерения). Студенту, работающему с
данным пособием, рекомендуется
самостоятельно выявлять эти причины
при анализе знакомых ему измерительных
процедур. Отметим одно обстоятельство,
которое может смутить читателя в
последующем тексте: некоторые факторы
удобнее считать источниками составляющих
неопределенности, а другие – источниками
составляющих погрешности. Далее будут
использоваться без специальных пояснений
оба термина.
Начнем
с того, что сами объекты всегда обладают
некоторой неопределенностью,
расплывчатостью.
Н
рис. 4.1 представлен примерный вид пика
сигнала, зарегистрированного каким-либо
прибором. Предположим, что исследователь
(например, в диагностических целях)
должен определить амплитуду этого пика
и его длительность. Максимум пика
прорисован достаточно четко, но от
какого “пьедестала” отсчитывать его
высоту? Между какими точками сигнала
отсчитывать длительность? Ясно, что
дать однозначные ответы на эти вопросы
нельзя. Для получения общезначимых
результатов нужнодоговариваться
о принятых способах отсчета. А если бы
сигнал был еще и зашумлен высокочастотной
случайной помехой?
Особый
случай неопределенности объекта имеет
место тогда, когда конкретный экземпляр
объекта или некоторая выборка
из совокупности объектов рассматривается
как представитель типа
объектов и
по результатам измерения на этом
экземпляре или выборке приходится
судить о свойствах всего типа. В этом
случае роль объекта, имеющего
неопределенность, играет весь этот тип
или, как говорят статистики, генеральная
совокупность,
а сама неопределенность обусловливается
неизбежным статистическим
разбросом свойств
экземпляров, образующих выборку.
Далее,
свойства объекта могут зависеть от
условий,
в которых он находится, а эти условия
не всегда можно контролировать, что
приводит к еще одной составляющей
неопределенности. Так, пульс некоторого
пациента может быть учащенным просто
потому, что окружающая обстановка и
само ожидание диагноза заставляют его
волноваться.
Во
многих случаях исследовательская задача
требует подготовки
объекта к выполнению измерений.
Биологические объекты нужно препарировать;
выполнению химического анализа
предшествует пробоподготовка.
Эти операции вносят специфические
составляющие погрешности и неопределенности,
которые при каждом конкретном эксперименте
следует специально изучать.
Когда
объект подготовлен, начинается собственно
измерение, которое невозможно без
взаимодействия
средства измерения с объектом. Это
взаимодействие неизбежно изменяет
свойства объекта, в том числе измеряемую
величину, – отсюда еще одна характерная
составляющая погрешности или
неопределенности.
Ряд составляющих погрешности или
неопределенности связан с
пространственно-временной локализациейизмерения.
Очень часто измерение выполняется не
там, где хотелось бы: температура
измеряется не внутри тела, а на его
поверхности; по энцефалограмме, снимаемой
тоже с поверхности, приходится судить
о процессах в мозге, и т. д.
В ряде случаев результат измерения
характеризует в усредненном виде слишком
большую область объекта, а хотелось бы
получить информацию “в точке”. Бывает
и наоборот: по результатам измерений в
малых областях приходится судить об
объекте в целом.
Периодичность измерений, затрачиваемое
на них время (в течение которого объект
успевает измениться), случайные задержки
и т. д. – все это тоже может сказаться
на неопределенности результата.
В
некоторых случаях используется метод
измерения,
упрощенный по сравнению с теоретически
правильным (или, в другой ситуации, в
основу эксперимента кладется чрезмерно
упрощенная модель
объекта).
Эти упрощения приводят к появлению
характерных составляющих погрешности.
Целый
ряд составляющих погрешности вносится
самой измерительной аппаратурой.
Им в данном пособии посвящена отдельная
глава 5.
Часто
существенная составляющая погрешности
вносится внешними или внутренними
(свойственными самому объекту) помехами.
Некоторые разновидности помех и способы
борьбы с ними также будут рассмотрены
далее.
При малой степени автоматизации измерений
(см. параграф 4.2) определенные составляющие
погрешности вносит персонал,
выполняющий измерительные операции.
Его невнимательность может быть даже
причиной крупных ошибок (промахов),
например, вызванных перестановкой цифр
или записью неверной цифры при регистрации
показаний приборов вручную.
При высокой степени автоматизации могут
остаться незамеченными сбоиаппаратуры, приводящие к таким же
результатам, как промахи операторов.
Наконец,
обработка
первичных данных
тоже может внести свои составляющие в
общую погрешность. Кроме того, она
каким-то образом трансформирует ранее
внесенные составляющие.
Итак, источники, вносящие вклад в общую
погрешность или неопределенность
результата, многочисленны, и одна из
задач метрологического образования
состоит в том, чтобы выработать у студента
навык контролировать каждый элемент
эксперимента, будь то концепция, метод,
прибор или операция, на предмет его
возможного несовершенства, приводящего
к появлению неопределенности или
погрешности результата.
Следует каждый раз задавать себе примерно
такие вопросы: почему в предлагаемой
методике эксперимента выбрана именно
такая скорость вращения центрифуги? К
чему приведет нестабильность этой
скорости?
Широко
используется обобщенная классификация
составляющих погрешности по признаку
их происхождения: эти составляющие
делят на инструментальные
(или аппаратурные), методические
и личные.
Несколько упрощая этот вопрос, можно
сказать, что за инструментальные
составляющие отвечает изготовитель
аппаратуры, за методические – организатор
эксперимента (или составитель методики
выполнения измерений – МВИ), а за личные
– персонал, проводящий эксперимент.
4.5.
Классификация составляющих погрешности
по характеру проявления
Характер
проявления составляющих погрешности
(о составляющих неопределенности
будет сказано в главе 6) является очень
важным классификационным признаком,
поскольку от него зависят способы
снижения этих составляющих, как путем
надлежащей организации эксперимента,
так и путем обработки первичных данных.
Основной
признак, позволяющий классифицировать
составляющие погрешности по характеру
проявления, – это их поведение в
последовательности измерений. По этому
признаку в классической метрологии
различают случайную
составляющую погрешности, изменяющуюся
непредсказуемым образом в ряду результатов
последовательных измерений, и
систематические
составляющие, которые остаются постоянными
или меняются закономерным образом как
функции времени и влияющих факторов
(иногда из состава систематических
выделяют прогрессирующую
составляющую). В практике встречаются
также составляющие погрешности, не
являющиеся случайными в математическом
смысле слова, но вместе с тем и не
изменяющиеся закономерным образом.
Отдельно рассматривают упоминавшиеся
выше промахи
(или, в автоматической аппаратуре, сбои).
Повышение
быстродействия измерительных устройств
и широкое распространение динамических
измерений вызвало к жизни представление
погрешности в целом как реализации
непрерывного случайного
процесса,
высокочастотные компоненты которого
соответствуют прежнему понятию случайной
составляющей, а низкочастотные (медленно
меняющиеся) – систематической составляющей
погрешности. Погрешности результатов
последовательных измерений рассматриваются
как отсчеты этого непрерывного процесса.
При
таком подходе граница между систематическими
и случайными составляющими делается
нечеткой (она лежит в области среднечастотных
компонентов случайного процесса).
П
измерении изменяющейся величины
характеристики случайного процесса
ξ(t),
представляющего погрешность, могут,
вообще говоря, зависеть от текущего
размера измеряемой величины. Часто
считают, что такой зависимости нет, и
что реализация случайного процесса
ξ(t)
просто суммируется с измеряемой величиной
x(t).
Тогда говорят, что погрешность аддитивна.
Для
описания случайной составляющей
погрешности естественно выбрать
теоретико-вероятностную математическую
модель в виде случайной величины или
случайного процесса с некоторыми (обычно
только частично известными) вероятностными
характеристиками. Полной характеристикой
какой-либо непрерывной случайной
величины ζ
является
плотность распределения, которую будем
обозначать либо pζ
(ξ),
где ξ
теперь обозначает
вспомогательную переменную, а имя
случайной величины указано с помощью
индекса, либо в упрощенном виде – p(ζ)
или p(x).
Важно
понимать, что погрешность
не обязана “подчиняться
теории вероятностей”.
Зачастую нельзя даже ставить вопрос о
том, каково “истинное распределение
вероятностей” случайной погрешности.
Мы просто подбираем
математическую модель, которая не
противоречит результатам опыта.
Однако
бывают случаи, когда механизм возникновения
отдельных компонентов случайной
составляющей погрешности достаточно
прост и сам поддается математическому
описанию. Тогда, если факторы, не
учитываемые математической моделью
этого механизма (а они всегда есть),
несущественны, можно говорить о
теоретическом
законе распределения
соответствующего компонента погрешности.
Приведем
несколько примеров.
Н
рис. 4.2 изображен возможный график
постоянного измеряемого напряженияUx.
и наложенной на него синусоидальной
помехи с амплитудой Um.
Допустим, что измерения производятся
в случайные моменты времени, которые
могут с одинаковой вероятностью попасть
в любую точку цикла изменения помехи.
Абсолютная погрешность, вызванная
помехой, будет равна мгновенному значению
помехи в момент измерения. Можно найти
распределение вероятностей ее значений
как распределение неслучайной
функции Umsinφ
случайной
величины –
фазы помехи φ в момент измерения. В
соответствии со сделанным выше допущением
фаза распределена равномерно в пределах
цикла помехи и, следовательно, имеет
плотность распределения
p(φ)
= 1/(2π).
Для
нахождения распределения функции
случайной величины необходимо знать
обратную функцию, в данном случае это
арксинус. Поскольку интервалы возрастания
и убывания синуса симметричны, удобно
рассматривать не целый цикл изменения
фазы, а его половину, в пределах ±π/2, где
синус возрастает. Тогда плотность
распределения погрешности будет равна
удвоенной плотности распределения
фазы, умноженной на производную обратной
функции. В результате получаем
Это
выражение справедливо, если переменная
x,
соответствующая погрешности Δ, изменяется
в диапазоне, определяемом неравенствами:
– Um
< x <
Um;за его пределами,
естественно, p(x)
= 0.
Графики
рассчитанной нами плотности вероятности
погрешности p(x),
а также и ее интегральной функции
распределения F(x),
приведены на рис. 4.3. Распределение
такого вида называется арксинусоидальным.
Отметим, что плотность вероятности p(x)
получается
в “обратных вольтах”.
Это
же распределение погрешности получается,
если при гармонической помехе моменты
измерения располагаются во времени не
случайно, а следуют периодически, но не
синхронно с помехой, или просто очень
часто.
“
полученный результат можно объяснить
просто: синусоидальная помеха относительно
большее время принимает значения,
близкие к экстремумам, и меньшее время
находится вблизи нуля.
Другая
ситуация, в которой теоретическое
распределение погрешности можно найти
как распределение неслучайной функции
случайного аргумента, связана с
квантованием (округлением), выполняемым
при измерении.
В
результат измерения содержит конечное
число десятичных (или двоичных) разрядов
и может пониматься как результатокругления
измеряемой величины, непрерывной по
размеру. При неавтоматизированном
измерении округление выполняет оператор
при считывании показаний, при
автоматизированном и автоматическом
измерении оно происходит в аналого-цифровом
преобразователе АЦП.
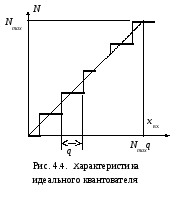
Для
многих типов АЦП (и цифровых приборов),
имея в виду идеальный случай отсутствия
других погрешностей, можно изобразить
ступенчатую характеристику, форма
которой показана на рис. 4.4. Здесь xвх
– входная
величина АЦП (чаще всего это электрическое
напряжение);
N – числовое
значение кодового результата
преобразования, q
– ступень
квантования
или, как говорят для краткости, “квант”.
Погрешность,
вызванная квантованием (ее принято
называть погрешностью
квантования),
в каждой точке этой характеристики
равна разности между ступенчатой
функцией и непрерывной линейной функцией,
проведенной на рис. 4.4 через середины
ступеней. В пределах каждой ступени
квантования эта разность, приведенная
к входу квантователя, линейно убывает
от +q/2
до –q/2
.
Предположим
теперь, что входная величина АЦП
изменяется
случайным образом в широких пределах,
так что ее плотность распределения
внутри каждой (малой по размеру!) ступени
квантования приблизительно постоянна.
Плотность
распределения погрешности квантования
при условии попадания величины xвх
в данный квант также будет постоянной,
поскольку погрешность квантования в
пределах кванта линейно
зависит от xвх.
Границами равномерного распределения
погрешности при том же условии будут
–q/2
и +q/2.
Суммарное ее распределение (при попадании
величины xвх
в другие кванты) будет тоже равномерным.
Его плотность составит p(x)
= 1/q
при –q/2<
x
<q/2
и p(x)
= 0 вне этих пределов (рис. 4.5).
В
многих случаях распределение погрешности
разумно считатьнормальным
или гауссовым
(рис. 4.6). Так, при измерениях малых
величин различной физической природы
определя-ющим источником погрешности
оказывается тепловой
шум – как
бы всеобщее дрожание физических объектов.
Термин
“шум” заимствован из радиотехники,
где он действительно проявляется как
слышимое (например, в наушниках) шуршание.
Наглядно тепловой шум можно представить
себе как сумму очень большого числа
бесконечно коротких импульсов случайной
амплитуды. В соответствии с центральной
предельной теоремой теории вероятностей
распределение мгновенных значений
такой суммы должно быть нормальным.
П
нормального распределения описывается
формулой
где σ – среднее квадратическое
или (другой термин) стандартное отклонение.
Нормальное распределение
играет очень важную роль в теории
вероятностей и с ним связан целый ряд
других распределений, например:
сумма квадратов n
нормально распределенных независимых
случайных величин распределяется по
так называемому закону χ2
(читается хи квадрат)
с n степенями
свободы;
модуль вектора на плоскости,
проекции которого распределены нормально,
распределяется по закону
Релея;
отношение двух нормально
распределенных величин распределяется
по закону Коши.
Краткие сведения об этих, а
также и других важных распределениях
можно найти, например, в справочнике
[29]. В будущей исследовательской
деятельности нынешнему студенту,
возможно, придется обратиться также к
обширным статистическим таблицам [4].
Ясно, что форма закона
распределения может служить важным
признаком для классификации случайных
составляющих погрешности по характеру
проявления. Этот общий признак можно
расчленить на ряд частных.
В
в разных ситуациях законы могут бытьнепрерывными
(как все, упомянутые выше) и дискретными.
Например, при многократном измерении
длительности повторяющегося
интервала времени
классическим цифровым методом (путем
счета импульсов независимого генератора,
укладывающихся в интервал) округление
происходит с определенными вероятностями
P1
и P2
как вниз, так
и вверх. Погрешность квантования
принимает с теми же вероятностями два
дискретных значения, различающихся на
единицу счета q
(рис. 4.7).
Во-вторых, законы
распределения могут быть ограниченными
(как арксинусоидальный и равномерный)
и неограниченными
(как нормальный). В первом случае можно
четко указать предельное значение
погрешности, во втором этого сделать
нельзя, и остается найти только некоторое
значение, превышение которого имеет
малую вероятность.
В-третьих, законы распределения
могут быть симметричными
(как на рис. 4.3, 4.5, 4.6) и несимметричными.
Так, плотность распределения Релея
отлична от нуля только в положительной
области переменной x и
имеет один максимум, причем возрастающая
и убывающая части функции p(x)
различны.
Далее, закон распределения
называют одномодальным,
если функция p(x)
имеет один максимум (в терминах теории
вероятности – моду).
Бывают также двухмодальные и многомодальные
распределения. Равномерное распределение
не имеет моды, а арксинусоидальное
распределение антимодально.
Одномодальные распределения
могут иметь разную “степень
остроконечности”; в теории вероятности
она характеризуется параметром,
называемым эксцессом.
В
реальных условиях, когда источников
погрешностей много, отдельные, различно
распределенные составляющие складываются,
и распределение результирующей
погрешности получается как композиция
(в общей математической терминологии
– свертка)
распределений составляющих. Вопросам
деформации распределений в результате
свертки уделено много внимания в книге
Петра Васильевича Новицкого и Ирины
Аркадьевны Зограф [21], где рассмотрены
также общие вопросы классификации
погрешностей, а для случайных составляющих
предложена классификация законов
распределения по двум параметрам,
характеризующим их форму.
4.6.
Принципы борьбы с систематическими и
случайными составляющими погрешности
С
точки зрения экспериментатора
систематические погрешности (здесь и
далее слово “составляющие” опускаем)
опаснее случайных. Последние проявляются
в виде разброса результатов измерений
и хорошо видны экспериментатору, а
систематические в большинстве случаев
требуют специальных приемов для их
обнаружения и (или) исключения.
Имеются типовые приемы борьбы с
систематическими погрешностями;
некоторые из них перечислены в учебнике
[23] и справочнике [5].
Метод
замещения
заключается в замене исследуемого
объекта регулируемой мерой измеряемой
величины. Выходную величину меры
регулируют так, чтобы используемые
средства измерений пришли в точно то
же состояние, в каком они были при наличии
исследуемого объекта.
Например,
если к не вполне исправному измерителю
электрического сопротивления подключить
вместо исследуемого резистора Rx
точный магазин сопротивлений и
отрегулировать его так, чтобы при
некотором сопротивлении R0
показание
измерителя осталось точно таким же, как
и при подключении Rx,
то получим Rx
= R0,
несмотря на неправильность работы
измерителя.
Обобщением
этого метода можно считать метод
калибровки
измерительного канала, основанный на
предположении о линейности зависимости
показаний N
от измеряемой величины.
В
качестве примера рассмотрим снова
измерение сопротивления прибором,
чувствительность которого не вполне
точно известна.
Предположим,
что в распоряжении исследователя имеются
образцовые резисторы R1
и R2
(желательно, чтобы было R1
< Rx
< R2),
причем показания измерителя при
поочередном подключении резисторов
R1,
Rx,
R2
составляют соответственно N1,
Nx,
N2.
При
линейной функции N(R),
независимо от ее параметров, получим
пропорцию:
(Rx
– R1)/(Nx
– N1)
= (R2
– R1)/(N2
– N1).
Из нее
следует
Это
выражение очевидным образом упрощается,
если можно взять R1
= 0 (при этом
в общем случае получится N1
≠
0).
Метод
калибровки дает менее точные результаты,
чем метод замещения, но реализуется
обычно проще. Отметим, что и метод
замещения не устраняет некоторых
погрешностей, связанных с особенностями
как измерительной аппаратуры, так и
самого объекта исследования.
Метод
противопоставления,
в изложении справочника [5], заключается
в следующем: “измерение выполняется с
двумя наблюдениями, проводимыми так,
чтобы причина систематической погрешности
оказывала разные, но известные по
закономерности воздействия на результаты
наблюдений”.
В
качестве примера приводится способ
взвешивания на рычажных весах по Гауссу:
взвешивают исследуемое тело (масса
которого mx)
дважды,
помещая его на разные чашки весов. При
неравенстве длин плеч коромысла
результаты взвешивания m1
и m2
не совпадают. Легко вывести формулу для
правильного результата, не зависящего
от отношения длин плеч: mx
= √
m1·
m2
.
М
компенсации погрешности по знаку,
опять-таки по [5], “предусматривает
измерение с двумя наблюдениями,
выполняемыми так, чтобы систематическая
погрешность входила в результат каждого
из них с разными знаками”. Результаты
этих двух наблюдений усредняют. Типичный
пример – переключение полярности малого
измеряемого напряжения для исключения
влияния паразитных термоэлектродвижущих
сил.
Метод
рандомизации
(от random
– случайный) состоит в том, чтобы сделать
влияние фактора, вызывающего систематическую
погрешность, случайным. В качестве
одного из примеров в справочнике [5]
приведено косвенное измерение площади
основания кругового цилиндра: для
исключения влияния некруглости цилиндра
его диаметр измеряют несколько раз в
различных направлениях и результаты
усредняют.
Пожалуй, более типичны примеры из области
биологических исследований. Так, если
при сравнении двух методов лечения один
из них испытывать в одной клинике, а
второй – в другой, то на результат
сравнения повлияют систематические
различия в стиле работы персонала. Нужно
распределить оба метода по обеим
клиникам.
Другой
пример: если нужно сравнить действие
какой-либо процедуры на различных
испытуемых, то не следует подвергать
их этой процедуре в одном и том же порядке
– лучше при повторении эксперимента
каждый раз случайным образом выбирать
новый порядок. (Аналогично, при повторении
описанного выше измерения с калибровкой
целесообразно изменять порядок
подключения резисторов R1,
Rx,
R2
).
Подобных
примеров можно подобрать очень много.
Идея такой рандомизации – одна из
основных в теории планирования
эксперимента.
Разновидностью
рандомизации можно считать прием
добавления случайного шума к полезному
сигналу для уменьшения погрешности,
вызванной квантованием измеряемой
величины. Это позволяет получать довольно
точные результаты при весьма грубом
квантовании.
Метод
симметричных наблюдений применяется
при наличии прогрессирующих
погрешностей, линейно изменяющихся во
времени. Он заключается в усреднении
результатов пар наблюдений, симметричных
относительно середины tср
общего
интервала измерения. Усредненные
результаты оказываются приведенными
к одному и тому же моменту времени
tср.
Метод
разделения стимула и отклика
не упомянут в большинстве литературных
источников как общий метод, но частные
его случаи хорошо известны.
Один
такой очень типичный случай – это выбор
четырехзажимного способа включения
резистора при измерении его сопротивления
(рис. 4.8).
Роль
стимула играет в данном случае ток I,
пропускаемый через резистор; роль
отклика – напряжение U
на резисторе.
Искомое сопротивление находится как R
=
U/I.
Резистор снабжен выводами, соединяющимися
с внешними цепями с помощью контактов,
обозначенных черными точками. Сопротивления
контактов и подводящих проводов
обозначены r.
П
сначала, что
используется двухзажимное
включение
резистора, показанное на рис. 4.8,а.
Ясно, что при этом U/I
= R
+ 2r.
Если сопротивление R
мало, влияние неизвестных и нестабильных
сопротивлений 2r
может породить значительную по размеру
погрешность.
Для
ее исключения делают по два вывода с
каждой стороны резистора (рис. 4.8,б).
Одна пара выводов (токовая) служит для
подачи стимула, а другая (потенциальная)
– для получения отклика. Контакты и
подводящие провода в токовой цепи
оказываются вне области, с которой
снимается отклик, а контакты и провода
в потенциальной цепи вносят незначительную
погрешность, поскольку ток, протекающий
по ним, обычно очень мал.
Кстати,
последнее обстоятельство позволяет
при отсутствии заранее выполненных
четырех выводов у резистора присоединять
к нему потенциальные провода простейшими
средствами, – например, с помощью
“крокодилов”.
В
эпоху неавтоматизированных измерений
была предложена схема двойного моста
постоянного тока (Томсона), которая, в
отличие от одинарного моста (Уитстона),
позволяет измерять очень малые
сопротивления именно потому, что
обеспечивает разделение токовых и
потенциальных цепей. В современных
цифровых омметрах, как правило, тоже
имеется возможность разделить эти цепи:
для подключения исследуемого объекта
предусматриваются четыре зажима. Приборы
с двухзажимным подключением исследуемого
резистора не следует применять для
измерения малых сопротивлений.
Если
ставится задача измерить сопротивление
какой-либо среды через
ее поверхность
с помощью накладных контактов (зондов),
то можно исключить влияние контактных
сопротивлений, используя “четырехзондовое”
присоединение, опять-таки разделяющее
стимул и отклик (рис. 4.9).
Т
же метод разделения стимула и отклика
используют при изучении магнитных
характеристик материалов в режиме
переменного намагничивания. Можно было
бы нанести на исследуемый образец (как
на сердечник) одну обмотку и измерять
индуктивность этой обмотки, зависящую
от магнитных свойств сердечника. Но
тогда возникает систематическая
погрешность, обусловленная сопротивлением
обмотки. Лучше наносить две обмотки,
используя одну из них в качестве
намагничивающей (для подачи стимула),
а другую в качестве измерительной (для
получения отклика), и измерять взаимную
индуктивность – при этом будет исключено
влияние сопротивления первой обмотки.
Аналогично,
при измерении акустического сопротивления
(например, при диагностике заболеваний
слухового анализатора), используют не
один обратимый электроакустический
преобразователь, а два: один в качестве
излучателя, а другой – приемника звука.
Довольно
часто в биологических исследованиях
используется стимул в виде короткого
импульса, а изучаемый отклик является
запаздывающей реакцией биологического
объекта на этот стимул. В таких случаях,
даже если цепи стимула и отклика
разделены, возможно появление сильной
помехи – “наводки” из цепи стимула в
цепь отклика, например, через “паразитные”
емкости. Для борьбы с этим явлением
принудительно уменьшают чувствительность
устройства, воспринимающего отклик, на
время действия стимула. Таким образом
стимул и отклик надежно разделяются во
времени.
Встречаются
ситуации, в которых систематическое
смещение результата измерения вызывается
случайной помехой, которая сама по себе
не имеет постоянной составляющей. Это
бывает в тех случаях, когда в измерительном
канале (см. параграф 5.2) имеется звено с
нелинейной характеристикой, разложение
которой в степенной ряд содержит
слагаемые с четными
степенями аргумента.
Можно
показать, что такое звено действует на
помеху подобно электрическому выпрямителю
– результатом этого действия и является
систематическое смещение результата
измерения. “Выпрямляющими” свойствами
могут обладать и биологические объекты.
Способы борьбы с этим явлением различны
и мы их здесь не будем рассматривать;
главное – чтобы оно было обнаружено.
В
какой-либо определенной составляющей
систематической погрешности настолько
ясен, что ее можно исключить расчетным
путем.
Излюбленный,
даже в какой-то степени затасканный
пример – измерение напряжения стрелочным
вольтметром, сопротивление которого
RV
нельзя считать бесконечно большим по
сравнению с сопротивлением цепи, к
которой он присоединен (рис. 4.10).
В
данном случае при
отключенном вольтметре
действительное напряжение на резисторе
R2
составило бы Uд
= U0R2/(R1
+
R2),
как это следует из схемы рис. 4.10,а.
Присоединяемый вольтметр “видит перед
собой” (рис. 4.10,б)
эквивалентное выходное сопротивление
цепи, равное Rвых
= R1R2/(R1
+
R2),
и образует вместе с ним делитель
напряжения эквивалентного источника
Uд.
В результате показания вольтметра
составят
UV
= UдRV/(Rвых
+
RV).
Отсюда получается значение абсолютной
систематической погрешности:
ΔU
= UV
– Uд
= Uд·[RV/(Rвых
+
RV)
– 1] = – UдRвых/(Rвых
+
RV)
=
=
– UVRвых/RV.
Зная
Rвых
и
RV,
легко вычислить поправку (– ΔU)
= UVRвых/RV,
которую нужно внести в показания
вольтметра, чтобы получить исправленный
результат измерения,
который не содержал бы систематической
погрешности, если бы все использованные
в расчете величины были известны точно.
Довольно
общим методом борьбы с систематическими
погрешностями является учет изменений
влияющих
факторов
(температуры, влажности, атмосферного
давления и т. п.) путем измерения
соответствующих величин и внесения
поправок в результат измерения. Для
расчета этих поправок необходимо заранее
определить коэффициенты
влияния
учитываемых факторов.
В ряде случаев
оказывается возможным устранить
систематическую погрешность известного
происхождения без расчетов, – путем
рационального построения экспериментальной
установки. Коэффициенты влияния при
этом учитываются автоматически.
Иллюстрирующий пример
показан на рис. 4.11. На нем изображен
некоторый датчик, используемый для
получения электрического сигнала с
напряжением Uвых,
пропорциональным измеряемой величине
xвх.
Датчик питается от источника, напряжение
которого Uпит
недостаточно
стабильно.
Рассмотрим
систематическую погрешность, вызываемую
зависимостью напряжения Uвых
от напряжения питания датчика Uпит
, которое в
данном случае выступает в роли влияющего
фактора. У многих датчиков – например,
построенных на основе потенциометра
или неравновесного моста, – эта
зависимость от питания тоже имеет вид
прямой пропорциональности.
Данный пример основан
на предположении, что реализуются именно
упомянутые зависимости, то есть Uвых
= kxвхUпит,
где k
– размерный коэффициент пропорциональности.
Для исключения погрешности, вызываемой
зависимостью Uвых
от Uпит,
можно использовать (как это и показано
на рис. 4.11) имеющийся у некоторых цифровых
вольтметров режим измерения
отношения напряжений.
Например, цифровой
прибор В7-34 имеет две пары входных
зажимов, и высвечиваемый на его табло
результат измерения выражается при
работе в этом режиме как
Nвых
=
N0·Ux
/Uy,
где
N0
– константа, зависящая от выбранных
пределов измерения, Ux
– напряжение на зажимах Hx,
Lx,
а Uy
– напряжение на зажимах Hy,
Ly.
В схеме, приведенной
на рис. 4.11, Ux
= Uвых,
Uy
= Uпит,
и прибор показывает
Nвых
= N0·Uвых
/Uпит
= N0·kxвхUпит
/Uпит
= N0·kxвх,
с
независимо от изменения напряжения
питания.
Приборы, предназначенные
исключительно для измерения отношений
двух входных величин, называются
логометрами
(не путать с
логгерами
– приборами для “сбора данных”!), а
режим измерения отношения, имеющийся
у многих цифровых приборов, часто
называют логометрическим.
Невредно знать англоязычный термин для
этого режима: ratiometric
mode, произведенный
от латинского корня в отличие от русского
слова, в котором использован греческий
корень того же смысла.
***
Из сказанного видно, насколько разнообразны
источники систематических погрешностей,
и соответственно способы борьбы с ними.
Напомним, что бороться с систематической
погрешностью можно лишь тогда, когда
есть основание подозревать ее наличие!
Поэтому следует при постановке
эксперимента специально искатьвозможные источники систематических
погрешностей.
Напротив,
случайные
погрешности явно
обнаруживаются в эксперименте в виде
разброса результатов измерения при
постоянной измеряемой величине. К ним
применим более формальный и единообразный
подход, принципы которого изложены в
следующих параграфах.
При
статических многократных измерениях
их влияние оценивают и уменьшают
статистической
обработкой результатов;
при динамических измерениях статистическая
обработка переходит в фильтрацию,
которая будет рассмотрена в главе 7.
4.7. Выбор
оценок центра и протяженности
эмпирических
распределений
Рассмотрим одну из
простейших статистических задач. Пусть
имеется выборка однородных первичных
данных, в которой
наблюдается некоторое рассеяние. Если
эти данные суть результаты многократных
измерений одной и той же величины, то
разумно искать приближенную оценку
“истинного” значения величины где-то
вблизи центра интервала рассеяния. При
этом протяженность самого этого интервала
или какой-либо иной параметр, характеризующий
рассеяние, будет оценкой размера
случайных погрешностей первичных
данных.
Начнем с некоторых простых понятий
теории оценок. Прежде всего, важно хорошо
понимать различие между функциями и их
параметрами, относящимися к вероятностной
модели, и приближенными, не повторяющимися
от опыта к опытустатистическими
аналогами(оценками) этих функций и
пара-метров.
По результатам экспериментов построить
точную вероятностную модель так же
невозможно, как найти истинное значение
измеряемой величины (между прочим,
являющееся одним из параметров этой
модели). Получаемые в эксперименте
статистические характеристики
рассматриваются как оценки возможных“истинных” вероятностных параметров.
Для того чтобы отличить статистические
(выборочные, эмпирические) функции и
параметры от вероятностных, используют
два способа. Один из них состоит в том,
что при одинаковыхбуквенных
обозначениях статистический аналог
снабжают верхним индексом в виде
звездочки или ставят над буквой волну
( ~ ). Например,D– дисперсия
(вероятностный параметр), аD*– его статистическая оценка.
Другой способ заключается в том, что за
вероятностными параметрами и их
статистическими оценками закрепляются
различныебуквы. Так,принято
обозначать среднее квадратическое
отклонение (вероятностный параметр)
греческой буквой σ, а его статистическую
оценку – соответствующей латинской
буквойs.
Далее, не следует путать эмпирическое
распределение первичных данныхв
одной серии измерений с расчетнымираспределениями оценок, полученных
на основе этого ряда – ведь любые
статистические оценки сами являются
случайными величинами на множестве
возможных серий измерений.
Всякие оценки могут
быть либо точечными,
либо интервальными.
Так, положение центра распределения
первичных данных можно оценить либо
одним числом, либо интервалом, в котором
этот центр с заданной вероятностью
должен находиться при повторении серий
измерений. То же можно сказать и о
протяженности распределения первичных
данных. Однако в данном случае точечная
оценка сама по себе характеризует
некоторый интервал, а интервальная
должна с известной вероятностью накрывать
ряд эмпирических интервалов (см.
параграф 6.9).
При выборе точечных оценок интерес
представляют такие их свойства как
состоятельность, несмещенность и
эффективность.
Оценка называется
состоятельной,
если она при увеличении объема выборки
стремится к истинному значению
оцениваемого параметра.
Оценка называется
несмещенной,
если при любом объеме выборки ее
математическое ожидание (определенное
на бесконечном множестве возможных
серий измерений заданного конечного
объема) совпадает с истинным значением
параметра.
Оценка называется
эффективной,
если она (на множестве серий измерений)
характеризуется минимальной дисперсией
среди возможных оценок данного параметра.
Может показаться, что состоятельность
и несмещенность – одно и то же свойство,
но это не так: оценка может быть
состоятельной, но смещенной, если она,
например, приближается к искомому
параметру с одной стороны.
Напротив, несмещенная,
но не состоятельная оценка может,
например, колебаться вокруг искомого
параметра при любом объеме выборки, не
приближаясь к нему.
Важным классификационным
признаком оценки является ее зависимость
или независимость от предполагаемого
закона распределения выборки и его
параметров. Зависимые оценки называют
параметрическими,
независимые – непараметрическими.
Конструируя ту или
иную оценку, иногда исходят из соображений
такого типа, которые принято называть
эвристическими, и только после этого
интересуются свойствами сконструированной
оценки. Другой подход состоит в том, что
сам вид оценки получают из некоторых
теоретических соображений или принципов.
Говоря об эвристическом
подходе к выбору оценок, уместно упомянуть
интересное обобщение, содержащееся в
книге Виктора Яковлевича Розенберга
[24]. Этот автор рассматривает, в числе
других, задачу “измерения функционалов
положения и протяженности обобщенного
импульса”. При этом под обобщенным
импульсом может пониматься действительный
импульсный сигнал, а также различные
функции, своей формой напоминающие
импульс, в том
числе и функции плотности распределения.
Таким образом, задача выбора параметров,
характеризующих положение центра и
протяженность эмпирического распределения,
сводилась бы к частному случаю задачи,
описанной В.Я. Розенбергом, если бы
плотность распределения была полностью
известна.
Перечислим методы
назначения указанных функционалов,
рассмотренные В.Я. Розенбергом. Для
функционалов положения это метод
выбранных точек
(по точке
максимума, по точкам наибольшей крутизны,
по положению одного или обоих фронтов)
и метод моментов
(функционал определяется абсциссой
центра тяжести обобщенного импульса).
В качестве функционалов протяженности
В.Я. Розенберг тоже рассмотрел метод
выбранных точек
с вариантами в виде метода сечений,
метода нулей и метода условных границ
(в пределах которых интеграл от выбранной
степени нормированной функции составляет
заданную долю единицы, например, 0,99) и
метод моментов
(функционал определяется, в частности,
как момент инерции фигуры, ограниченной
импульсом). Кроме того, им упомянут
довольно сложный метод
нормированных функционалов
(оставим этот термин без пояснений).
Эвристический подход
характерен также для работ П.В. Новицкого
и его учеников, в частности, он используется
в книге [21], которая будет часто упоминаться
в дальнейшем.
Среди теоретических
принципов, используемых для вычисления
оценок, кратко рассмотрим принцип
максимального
правдоподобия.
Пусть выборка x1 , x2
, x3 , … xn
характеризуется известным или
предполагаемым распределением с
плотностьюp(α,x),
зависящей от оцениваемого параметра
α. Совместная плотность при условии
взаимной независимости отсчетов
выражается произведениемL=p(α,x1)·p(α,x2)·p(α,x3)·…·p(α,xn),
которое называетсяфункцией
правдоподобия. За оценку α*(повторим: здесь оценка, в отличие от
“истинного” параметра, отмечена
звездочкой) принимают такое значение
параметра, при котором функция
правдоподобия достигает максимума, т.
е. полученная выборка наиболее вероятна.
Обычно проще вычисляется положение
максимума функцииlogL,
для чего приравнивается нулю частная
производная этой функции по оцениваемому
параметру α.
В ряде случаев
определяющим критерием при выборе
оценки является степень ее чувствительности
к промахам. Оценки, мало чувствительные
к “выпадающим” отсчетам или иным
отклонениям от предположений, положенных
в основу выбранного метода обработки
данных, называют робастными
(с ударением на а)
от английского robust
– крепкий, жесткий.
4.8.
Точечные оценки положения центра
распределения
первичных
данных
Три параметра
теоретической функции плотности
распределения непрерывной случайной
величины (или распределения вероятностей
дискретной случайной величины), которые,
вообще говоря, можно непосредственно
использовать в качестве центра
распределения, – это математическое
ожидание (центр тяжести), медиана (центр
по площади) и мода (центр по максимуму).
Сразу же, чтобы не возвращаться к этому
вопросу, рассмотрим применимость этих
параметров с точки зрения репрезентационной
теории, а именно, понятия адекватных
операций (см. параграф 2.8). Это важно при
обработке данных, получаемых в
неметрических шкалах.
Как говорилось в
параграфе 2.6, допустимые преобразования
номинальной
шкалы образуют
группу перестановок. Преобразования
этой группы в общем случае изменяют и
математическое ожидание, и медиану,
оставляя неизменной только моду, если
она есть у распределения. Оценка моды
и является адекватной статистикой для
данных, получаемых в номинальной шкале.
В качестве примера
нередко приводят исследование частостей
букв в каком-либо тексте. Мода – это
наиболее часто встречающаяся буква;
она не изменяется при допустимом
преобразовании (которое в данном случае
сводится к изменению нумерации букв в
алфавите).
Для шкалы
упорядоченных классов
допустима группа положительных монотонных
преобразований. Они в общем случае
изменяют математическое ожидание, но
оставляют на месте медиану и моду.
Предпочтительным параметром является
медиана, которая, в отличие от моды, есть
у всех распределений. Оценка математического
ожидания, в вычислении которой участвуют
операции суммирования или интегрирования,
не определенные для порядковых шкал,
не является в данном случае адекватной
статистикой.
Однако, если
упорядоченных классов, на которые
разбиваются данные, немного, медиана
мало информативна. Рассмотрим, например,
данные об оценках членов студенческой
группы. Медиана оценок каждого из
студентов сможет принять только значения
3, 4, и 5 (реже 3½ и 4½), что затруднит
ранжирование студентов по успеваемости.
Всем известно, что работники деканата
в этой ситуации идут на нарушение
требований репрезентационной теории
и вычисляют средний балл – оценку
математического ожидания. Авторам
пособия неизвестно, исследовал ли
кто-нибудь последствия этой теоретической
некорректности.
Чисто порядковые
шкалы, используемые
при ранжировании ряда одновременно
рассматриваемых объектов, не общезначимы,
и указание объекта, занявшего среднее
положение в некотором конкретном
ранжировании, обычно не представляет
интереса.
При ранжировании
чаще приходится решать другую задачу,
уже упоминавшуюся в параграфе 2.6: если
несколько экспертов ранжируют одну и
ту же совокупность объектов, и их
результаты не совпадают, то как найти
“среднее” ранжирование?
Для решения этой
задачи вводится понятие расстояния
между ранжированиями, и отыскивается
ранжирование, характеризуемое минимальной
суммой расстояний между первичными
ранжированиями. В одной из работ теоретика
“нового поколения” Сергея Васильевича
Муравьева из Томска приведен пример
усреднения пяти первичных ранжирований
шести пронумерованных объектов:
1, 2, 6, 4, 3, 5;
4, 5, 1, 2, 3, 6;
2, 5, 1, 3, 4, 6;
6, 3, 4, 2, 1, 5;
3, 4, 2, 6, 5, 1.
Среднее ранжирование
у С.В. Муравьева получилось в виде 4, 2,
1, 3, 6, 5. Именно такую процедуру (в
вычислительном отношении довольно
сложную) этот ученый рассматривает как
измерение в шкале порядка.
Читателю, интересующемуся
методами обработки результатов экспертных
оценок, рекомендуется обратиться к
книге [18].
Для метрических
шкал все три
упомянутых параметра, которые можно
принимать за центр распределения,
адекватны. С точки зрения обработки
реальных данных, имеющих статистический
разброс, наименее
удачным
параметром является мода. Она есть даже
не у всех теоретических распределений;
тем более трудно ее оценку искать по
гистограмме, которая бывает “изрезана”
локальными минимумами.
Чаще других используется
оценка, получаемая методом моментов –
оценка первого начального момента
(математического ожидания), вычисляемая
в виде среднего арифметического первичных
данных xi:
Для нормального
закона распределения первичных данных
она эффективна и является оценкой
максимального правдоподобия.
Однако ряд достоинств
имеет и медианная оценка xmed*.
Ее проще находить: при нечетном числе
n членов
вариационного ряда (т. е. выборки,
упорядоченной по возрастанию) это есть
просто средний член; при четном числе
n –
полусумма двух членов, наиболее близких
к середине ряда.
Оценка xmed*
по сравнению с
менее чувствительна к “выпадающим”
отсчетам, в том числе промахам: ее
возможный сдвиг из-за однократного
промаха не превышает расстояния между
соседними членами вариационного ряда
в его средней части, где отсчеты обычно
расположены наиболее густо.
Следует упомянуть и
о теоретических распределениях, у
которых не существует математического
ожидания (см. [21], с. 45 и 132 –135), в частности,
распределении Коши.
Наконец, оценка
медианы оказывается эффективнее
оценки математического ожидания для
островершинных распределений (например,
распределения Лапласа), при которых
густота отсчетов в середине вариационного
ряда наиболее велика (см. [21], с. 144 – 145).
Как известно, медиана
есть частный случай квантили
распределения. Вообще 100P-процентной
квантилью
распределения, характеризуемого
интегральной функцией F(x),
называют такое значение xP,
при котором
F(xP)
= P.
Конкретно, медиана есть 50-процентная
квантиль.
Можно сконструировать
и ряд других оценок центра распределения,
основанных на квантилях, – например, в
виде полусуммы эмпирических оценок
100(1 – P)-процентной
и 100P-процентной
квантилей.
4.9. Оценки
протяженности распределения первичных
данных
Работу читателя с этим параграфом
рекомендуется начать с обдумывания его
заголовка. Если оценка центра распределения,
рассмотренная в предыдущем параграфе,
принимается за результат измерения, то
оценка протяженности распределения
первичных данныхявляется оценкой
погрешности самих этих данных, но не
результата! Тем не менее, ее полезно
рассмотреть.
В основном для оценивания протяженности
распределений используются те же два
типа параметров, что и при нахождении
центра – имеются в виду моментные и
квантильные (близкие к “условным
границам” В.Я. Розенберга) оценки.
Оценкой моментного типа является оценка
дисперсииDx
– по определению второго центрального
(т. е. отсчитываемого не от начала
координат, а от математического ожидания
случайной величины) момента:
Но реально
математическое ожидание неизвестно;
его оценку
приходится находитьпо той же выборке,
что и оценку дисперсии. Можно показать,
что, если в предыдущую формулу вместоmx подставить
,
оценка дисперсии получится смещенной,
а именно – заниженной. Доказано, что
это смещение корректируется заменой в
знаменателеn наn– 1 (число
степеней свободыуменьшается на
единицу из-за вычисления
по
той же выборке):
Р
дисперсии – это размерностьквадрата
величины x,
а удобно иметь оценку протяженности
распределения, совпадающую по размерности
с измеряемой величиной. Квадратный
корень из дисперсии σx
= √Dx
называют среднеквадратическим,
среднеквадратичным
или стандартным
отклонением
случайной
величины, сокращенно СКО.
П
извлечение корня – нелинейная операция,
а оценка дисперсии имеет статистический
разброс, при вычислении оценкиsx
среднеквадратического
отклонения (СКО) по формуле sx
= √D*x
возникает
дополнительное смещение в сторону
занижения. Для его коррекции можно
ввести поправочный множитель, который
уменьшается от 1,13 при n
= 3 до 1,03 при n
= 20 (см. [25],
с. 209 или [26], с. 166).
На
практике часто эту поправку не вводят,
считая, что она мала по сравнению со
статистической погрешностью оценки
среднеквадратического отклонения.
Н
почти для всех возможных распределений
случайной погрешности заметная доля
отсчетов отличается от математического
ожидания больше, чем на СКО. Для нормального
распределения, как известно, только 68
% генеральной совокупности находится
в пределах ±σ от математического
ожидания, остальные 32 % выходят из этого
интервала. Для равномерного распределения
с размахом 2a,
у которого σ = a/√3,
из интервала ±σ выходит в среднем 42 %
выборки.
Если
требуется указать протяженность
распределения таким образом, чтобы
только заданная малая доля отсчетов ΔP
выходила из указанного интервала,
переходят к квантильным оценкам.
Распространенным
способом получения квантильных оценок
при симметричных законах распределения
первичных данных является умножение
их СКО σ (практически известна только
его экспериментальная оценка s)
на некоторый коэффициент, зависящий от
предполагаемого закона распределения
и выбранной доверительной
вероятности Pд
= 1 –
ΔP.
Доверительная вероятность характеризует
среднюю долю отсчетов, отклоняющихся
от центра распределения не более, чем
на вычисляемую оценку.
С
учетом предполагаемой симметрии закона
распределения упомянутый коэффициент
можно найти как 100ΔP/2-процентную
квантиль этого распределения. Очевидно,
такие “доверительные” оценки относятся
к классу параметрических.
При
выборе Pд
= 0,9 для широкого класса распределений
приближенно справедлива оценка в виде
Δд
= ±1,6σ (см. [21], с. 82 – 84); для ее использования
необходимо знать истинное СКО
распределения. Вычисление оценок (любым
методом) для Pд
> 0,9 требует знания формы закона
распределения в области его “хвостов”,
где сведения
о законе наименее надежны.
Теоретические соображения приведены
на с. 84 – 86 цитируемой книги [21].
Непараметрическую
квантильную оценку протяженности
распределения можно получить
непосредственно из вариационного ряда
(см. параграф 6.4) в виде разности его
крайних или других симметрично
расположенных членов.
Если
распределение первичных данных является
теоретически неограниченным, а к тому
же среди отсчетов могут оказаться
промахи, оценка в
виде разности крайних членов ряда
(т. е. в виде размаха эмпирического
распределения)
не только
ненадежна,
но имеет тенденцию расти с увеличением
объема выборки.. Более устойчивы
непараметрические оценки, получаемые
отбрасыванием с каждого конца вариационного
ряда определенной доли отсчетов (см.
[21], с. 51 – 53).
Однако,
если известно, что распределение строго
ограничено (например, является равномерным
или арксинусоидальным) и данные не
содержат промахов, оценка его протяженности
в виде размаха оказывается наилучшей.
Особое место среди оценок протяженности
распределения данных занимает
разработанная П.В. Новицким (правда, в
качестве характеристики погрешностей
средств измерений) и подробно
исследованная его ученицей Валентиной
Яковлевной Галочкинойэнтропийнаяоценка.
В статистической теории информации,
созданной Клодом Эльвудом Шенноном,
энтропиянекоторого вероятностного
ансамбля сообщений характеризует
неопределенность этого ансамбля.
Энтропия непрерывного распределения
записывается в виде (см. [21], с. 56):
Это выражение некорректно в двух
отношениях – во-первых, содержит под
знаком логарифма размерную величину
и, во-вторых, принимает бесконечно
большое числовое значение. Действительно,
сигнал с непрерывным случайно изменяющимся
информативным параметром потенциально
содержит бесконечную информацию.
Обе эти некорректности исчезают при
вычислении разности энтропий, а
интерес представляет именно эта разность.
Дело в том, что суть измерения, в трактовке
П.В. Новицкого, заключается в сужении
интервала неопределенности измеряемой
величины – до измерения он определялся
априорными сведениями о ней и был
довольно широким; после измерения этот
интервал стал определяться вероятным
диапазоном значений результата измерения,
т. е. по сути дела распределением его
погрешности.
И
из этих соображений П.В. Новицкий
предложил называтьэнтропийным
значением погрешностиполуширину
равномерного распределения, эквивалентного
по энтропии реальному распределению
погрешности. Для нормального распределения,
имеющего среднеквадратическое отклонение
σ, эта полуширина составляет Δэ= σ√πe/2 ≈ 2,066σ. Отношениеk= Δэ/σ,
зависящее от формы закона распределения
погрешности, П.В. Новицкий назвалэнтропийным коэффициентоми
использовал для построения своей
классификации законов распределения.
Теория информации в форме К. Шеннона
немногое дала теории измерений; однако
информационный подход к измерению
остается перспективным, по крайней мере
в качественном смысле. Исследователю
рекомендуется при постановке задачи
эксперимента задавать себе примерно
такие вопросы: какая информация мне
нужна для получения требуемого результата?
не упускаю ли я какую-либо существенную
информацию?
4.10.
Недостоверность результата классификационной
процедуры,
основанной
на измерении
Как
было сказано в параграфе 1.2, недостоверность
данных
классификационного
типа
определяется как вероятность
ложного решения.
Знание распределения случайной
составляющей погрешности измерения
(систематическая составляющая должна
быть скорректирована) позволяет оценить
вероятность принятия неправильного
решения при выполнении классификационной
процедуры, основанной на этом измерении.
Предположим,
например, что речь идет о контроле
некоторого объекта, который считается
годным при условии, что значение параметра
x,
полученное при однократном
его измерении, превышает принятое за
норму значение xн
или по крайней мере равно ему. Если
оказывается x
< xн,
объект должен быть забракован. (Нужно
заметить, что это формальное рассуждение
не учитывает неопределенности самого
объекта и обстановки, в которой он должен
работать).
На
рис. 4.12 показаны две возможные ситуации.
В первом случае действительное значение
параметра xд
больше нормы, то есть объект “на самом
деле” годен (рис. 4.12,а).
Но из-за случайного разброса результатов
измерения некоторые из них могут
оказаться и ниже нормирующего значения,
и при получении такого результата объект
будет ошибочно забракован. Вероятность
этого ошибочного решения (ложной
тревоги или
ошибки первого
рода) может
быть найдена как заштрихованная площадь
под графиком плотности вероятности
погрешности измерения слева от xн
на рис. 4.12,а.
В
втором случае (рис. 4.12,б)
в действительности xд
< xн,
и объект должен быть забракован. Но
некоторые результаты, вероятность
которых соответствует заштрихованной
площади справа от xн
на рисунке, приведут к тому, что негодный
объект будет принят за годный –
произойдет ошибка второго
рода.
Заметим, что “цена”
ошибок первого и второго рода, как
правило, различна: чаще всего ошибка
второго рода более опасна.
Для
надежного
вычисления вероятностей ошибок нужны
достоверные сведения о “хвостах”
плотности распределения погрешности,
которые зачастую отсутствуют, так как
для их экспериментального получения
требуются очень большие объемы выборок.
Здесь
был рассмотрен простейший случай
контроля одного
объекта. Часто интерес представляют
оценки вероятностных характеристик
контроля некоторой совокупности объектов
(например, партии изделий). Тогда для
определения доли ошибочно забракованных
или ошибочно пропущенных изделий нужно
учитывать еще и распределение параметров
самих контролируемых изделий, что
существенно усложняет вычисления.
113
I am trying to calculate the relative error between one model and another as follows:
(model1 - model2)/ (1 - model2)
where model1 and model2 are the correct predictions of the models, respectively.
model1 is better than model2 and I use this formula to calculate how much model1 reduces the error. The only thing I am not sure about is how to interpret the results: since model1 predicts more correct classes than model2, my relative error is negative. Let’s say I have
relative error = -54%
how can I interpret the result? Does it mean that model1 reduces the error by 54%, compared with model2?
EDIT:
model1 and model2 are the correct predictions of two neural networks on a language task: the neural networks pick the correct word among a limited set of words. model1has a better performance than model2: therefore the error from this formula will be negative.
Example: given 200 examples, model1 exactly predicts 150, model2 only 55. The result should be:
(150 - 55)/(1 - 55) = -1.76 (if we calculate the percentage = -175%)
Обновлено: 04.06.2023
Погрешность процесса – мера точности или в некотором роде мера качества. Увеличение допустимой погрешности приводит к ухудшению свойств воздействий (точность механизмов, КПД, веса и др.), но снижает себестоимость. Поэтому выбор допустимого уровня погрешностей зависит от состояния цена-качество и назначения продукции.
Допуск – допускаемая погрешность, норма точности, которая устанавливается чертежом или другой нормативно-технической документацией.
Установление допусков (норм точности) называют НОРМИРОВАНИЕМ ТОЧНОСТИ. Допуск определяет допустимый диапазон рассеяния, колебания значений задаваемого параметра. Допуск всегда является величиной положительной (равным нулю быть не может).
Допуск обозначается буквой (первая буква от французского слова Tolerance, что означает допустимый, терпимый).
Допуск размера выражают разность между наибольшим и наименьшим предельными размерами:
где – допуск размера .
Числовое значение допуска записывают с необходимым количеством цифр после запятой, в том числе с нулями в конце, в зависимости от необходимого порядка точности, например: 0,1 мм, 0,10 мм, 0,100 мм.
Чем меньше допуск размера, тем выше норма точности размера, выше эксплуатационные свойства изделия, но труднее и дороже получение такого размера (нужны более точные и дорогие технологическое оборудование, инструменты, трудоемкость получения размера возрастает, необходима более высокая квалификация рабочего, увеличивается возможное количество брака). Например, в зависимости от метода обработки детали с уменьшением допуска размера с 0,1 до 0,05 мм (т.е. в 2 раза) относительная стоимость получения размера может возрасти в 2,8 раза. Поэтому перед конструктором или технологом всегда стоит задача нахождения оптимального решения — разрешения противоречия межу эксплуатационными и конструктивными требованиями с одной стороны и возможностями и экономикой производства с другой. Таким образом, правильно установленным допуском следует считать такой возможно больший допуск, при котором полностью удовлетворяются конструктивные эксплуатационные требования к изделию.
Конструкторский допуск ( ) – заданная точность элемента, детали, изделия — устанавливают исходя из условия обеспечения нужного качества продукции и, прежде всего, эксплуатационных требований при длительной эксплуатации изделия, но с учетом технологических, метрологических и экономических возможностей (ориентируясь на передовую технологию). При установлении конструкторского допуска необходимо создавать запас точности на определенную длительность эксплуатации, так как со временем детали изнашиваются и точность снижается. Поэтому
где — конструктивная часть допуска, расчетная, необходимая для нормальной работы конструкции;
— допускаемая погрешность измерения размера;
-запас точности на длительную эксплуатацию.
Необходимо помнить, что допуски элементов деталей станков, приспособлений, инструментов, от которых зависит точность изготовленных с их помощью деталей изделий, должны быть значительно более жесткими, чем допуски деталей изделий.
Технологический допуск — точность, обеспечиваемая технологическим оборудованием – устанавливают на основе конструкторского допуска с учетом технологических требований, метрологических и экономических возможностей.
Технологический допуск рекомендуется устанавливать с некоторым технологическим запасом точности по сравнению с конструкторским допуском (т.е. технологический допуск должен быть более жестким, чем конструкторский). Обычно рекомендуется , т.е. должен быть не менее чем на 20% меньше конструкторского.
Как конструкторский, так и технологический допуски линейных размеров должны учитывать допускаемые погрешности измерений, которые составляют 20-40% от допуска линейного размера (т.е. 20-40% допуска идет на компенсацию погрешностей измерения).
Станки, приспособления и обрабатывающие инструменты должны соответствовать технологическому допуску изделия, т.е. рассеяние действительных размеров данным технологическим комплексом не должно превышать технологического допуска изделия.
В чертежах и других нормативно-технических документах непосредственно допуски размеров, как правило, не указывают. Чаще всего допуски размеров выражают через предельно допустимые отклонения от номинального размера:
ES(es)-верхнее предельное отклонение размера отверстия вала);
EI(ei)-нижнее предельное отклонение размера отверстия (вала).
Предельные отклонения размера определяются по формулам:
Числовые значения предельных отклонений записываются с необходимым количеством цифр после запятой, в том числе к нулями в конце, в зависимости от необходимого порядка точности (так же, как и допуски).
Верхнее и нижнее предельные отклонения могут быть оба положительными, оба отрицательными, верхнее может быть положительным, а нижнее отрицательным, одно из них может быть равным нулю (оба равным нулю быть не могут!).
Знаки отклонений, даже если они положительные, обязательно указывают, так как предельные отклонения представляют собой величины направленные (а не просто положительные числа).
Так как на чертежах допуски, как правило, выражают через предельные отклонения, то допуск размера можно выразить так:
Может. Разность между результатом измерения и номинальным размером называется отклонением размера – положительным, если размер больше номинального, и отрицательным, если размер меньше номинального.
5*y =ikghdjh
lirueeeety5u7 3y4
число по модулю всегда положительно
I-5I=5
I-10I= 10
5*10:5+3= 50:5+3= 10+3=13
Для приготовления варенья на 2 части сахара берут 3 таких же по весу части ягод.Сколько надо взять сахара и ягод для 10кг варень
Длины сторон треугольника пропорциональны числам 4 7 и 14. Найди разность большей и меньшей сторон треугольника если его перимет
У треугольника две стороны имеют одинаковую длину.периметр треугольника 16см,а третья сторона-4см.какова длина первой и второй с
После неудачного ремонта обе стрелки механических часов стали двигаться на 20% быстрее. Какое время покажут часы в 5 утра, если
В парке посадили 64 саженца берёзы и дуба,причём берёз посадили в 3 раза больше,чем дубов.Сколько саженцев берёз посадили ?решит
Размер — числовое значение линейной величины (диаметра, длины и т.п.) в выбранных единицах измерения.
Различают действительный, номинальный и предельные размеры.
Действительный размер – размер, установленный измерением с помощью средства измерения с допускаемой погрешностью измерения.
Под погрешностью измерения понимается отклонение результата измерения от истинного значения измеряемой величины. Истинный размер – размер, полученный в результате изготовления и значение которого нам не известно.
Номинальный размер — размер, относительно которого определяются предельные размеры и который служит началом отсчета отклонений.
Номинальный размер указывается на чертеже и является общий для отверстия и вала, образующих соединение и определяется на стадии разработки изделия исходя из функционального назначения деталей путем выполнения кинематических, динамических и прочностных расчетов с учетом конструктивных, технологических, эстетических и других условий.
В каждом десятичном интервале для каждого ряда содержится соответственно номеру ряда 5; 10; 20; 40 и 80 чисел. При установлении номинальных размеров предпочтение должно отдаваться рядам с более крупной градацией, например ряд Ra 5 следует предпочесть ряду Ra 10, ряд Ra 10 — ряду Ra 20 и т.д. Ряды нормальных линейных размеров построены на базе рядов предпочтительных чисел (ГОСТ 8032-84) с некоторым округлением. Например, по R5 (знаменатель 1,6) берутся значения 10; 16; 25; 40; 63; 100; 250; 400; 630 и т.д.
Стандарт на нормальные линейные размеры имеет большое экономическое значение, состоящее в том, что при сокращении числа номинальных размеров сокращается потребная номенклатура мерных режущих и измерительных инструментов (сверла, зенкеры, развертки, протяжки, калибры), штампов, приспособлений и другой технологической оснастки. При этом создаются условия для организации централизованного изготовления названных инструментов и оснастки на специализированных машиностроительных заводах.
Стандарт не распространяется на технологические межоперационные размеры и на размеры, связанные расчетными зависимостями с другими принятыми размерами или размерами стандартных комплектующих изделий.
Предельные размеры — два предельно допустимых размера, между которыми должен находиться или которым может быть равен действительный размер.
Когда необходимо изготовить деталь, то размер должен задаваться двумя значениями, т.е. предельными допустимыми значениями. Больший из двух предельных размеров называется наибольшим предельным размером, а меньший — наименьшим предельным размером. Размер годного элемента детали должен находиться между наибольшим и наименьшим допускаемыми предельными размерами.
Нормировать точность размера — это значит указать два его возможных (допускаемых) предельных размера.
Принято обозначать номинальный, действительный и предельные размеры соответственно: для отверстий — D, DД, Dmax, Dmin; для валов — d, dД, dmax, dmln.
Сравнивая действительный размер с предельными, можно судить о годности элемента детали. Условиями годности являются соотношения: для отверстий Dmin
Верхнее отклонение обозначается ES (Ecart Superieur) для отверстий и es — для валов; нижнее отклонение обозначается El (Ecart Interieur) для отверстий и ei — для валов.
Согласно определениям: для отверстий ES=Dmax-D; EI= Dmin -D; для валов es=dmax–d; ei= dmln-d
Особенность отклонений заключается в том, что они всегда имеют знак (+) или (-). В частном случае одно из отклонений может быть равно нулю, т.е. один из предельных размеров может совпадать с номинальным значением.
Допуском размера называется разность между наибольшим и наименьшим предельными размерами или алгебраическая разность между верхним и нижним отклонениями.
Допуск обозначается IT (International Tolerance) или TD — допуск отверстия и Td — допуск вала.
Согласно определению: допуск отверстия TD=Dmax-Dmin; допуск вала Td=dmax-dmin. Допуск размера всегда положительная величина.
Допуск размера выражает разброс действительных размеров в пределах от наибольшего до наименьшего предельных размеров, физически определяет величину официально разрешенной погрешности действительного размера элемента детали в процессе его изготовления.
Поле допуска — это поле, ограниченное верхним и нижним отклонениями. Поле допуска определяется величиной допуска и его положением относительно номинального размера. При одном и том же допуске для одного и того же номинального размера могут быть разные поля допусков.
Для графического изображения полей допусков, позволяющего понять соотношения номинального и предельных размеров, предельных отклонений и допуска, введено понятие нулевой линии.
Нулевой линией называется линия, соответствующая номинальному размеру, от которой откладываются предельные отклонения размеров при графическом изображении полей допусков. Положительные отклонения откладываются вверх, а отрицательные — вниз от нее (рис. 1.4 и 1.5)
Рис. 1.4. Схема расположения полей допусков отверстий
Поля допусков отверстий и валов могут занимать различное расположение относительно нулевой линии, что необходимо для образования различных посадок.
Рис. 1.5. Схема расположения полей допусков валов
Чем меньше допуск, тем точнее будет изготовлен элемент детали. Чем больше допуск, тем грубее элемент детали. Но в то же время, чем меньше допуск, тем труднее, сложнее и отсюда дороже изготовление элемента деталей; чем допуски больше, тем проще и дешевле изготовить элемент детали.
Размер — числовое значение линейной величины (диаметра, длины и т.п.) в выбранных единицах измерения.
Различают действительный, номинальный и предельные размеры.
Действительный размер – размер, установленный измерением с помощью средства измерения с допускаемой погрешностью измерения.
Под погрешностью измерения понимается отклонение результата измерения от истинного значения измеряемой величины. Истинный размер – размер, полученный в результате изготовления и значение которого нам не известно.
Номинальный размер — размер, относительно которого определяются предельные размеры и который служит началом отсчета отклонений.
Номинальный размер указывается на чертеже и является общий для отверстия и вала, образующих соединение и определяется на стадии разработки изделия исходя из функционального назначения деталей путем выполнения кинематических, динамических и прочностных расчетов с учетом конструктивных, технологических, эстетических и других условий.
В каждом десятичном интервале для каждого ряда содержится соответственно номеру ряда 5; 10; 20; 40 и 80 чисел. При установлении номинальных размеров предпочтение должно отдаваться рядам с более крупной градацией, например ряд Ra 5 следует предпочесть ряду Ra 10, ряд Ra 10 — ряду Ra 20 и т.д. Ряды нормальных линейных размеров построены на базе рядов предпочтительных чисел (ГОСТ 8032-84) с некоторым округлением. Например, по R5 (знаменатель 1,6) берутся значения 10; 16; 25; 40; 63; 100; 250; 400; 630 и т.д.
Стандарт на нормальные линейные размеры имеет большое экономическое значение, состоящее в том, что при сокращении числа номинальных размеров сокращается потребная номенклатура мерных режущих и измерительных инструментов (сверла, зенкеры, развертки, протяжки, калибры), штампов, приспособлений и другой технологической оснастки. При этом создаются условия для организации централизованного изготовления названных инструментов и оснастки на специализированных машиностроительных заводах.
Стандарт не распространяется на технологические межоперационные размеры и на размеры, связанные расчетными зависимостями с другими принятыми размерами или размерами стандартных комплектующих изделий.
Предельные размеры — два предельно допустимых размера, между которыми должен находиться или которым может быть равен действительный размер.
Когда необходимо изготовить деталь, то размер должен задаваться двумя значениями, т.е. предельными допустимыми значениями. Больший из двух предельных размеров называется наибольшим предельным размером, а меньший — наименьшим предельным размером. Размер годного элемента детали должен находиться между наибольшим и наименьшим допускаемыми предельными размерами.
Нормировать точность размера — это значит указать два его возможных (допускаемых) предельных размера.
Принято обозначать номинальный, действительный и предельные размеры соответственно: для отверстий — D, DД, Dmax, Dmin; для валов — d, dД, dmax, dmln.
Сравнивая действительный размер с предельными, можно судить о годности элемента детали. Условиями годности являются соотношения: для отверстий Dmin
Однако задавать на чертеже два размера неудобно, поэтому в дополнение к номинальному размеру на чертеже проставляют его предельные отклонения — верхнее и нижнее.
Отклонением называют алгебраическую разность между размером (действительным или предельным) и соответствующим номинальным размером. Отклонения отверстий обозначают Е, валов е.
Верхнее отклонение (ES, es) — это алгебраическая разность между наибольшим предельным и номинальным размерами.
Нижнее отклонение (EI, ei) — это алгебраическая разность между наименьшим предельным и номинальным размерами.
Определение отклонений как алгебраической разности числовых величин означает, что они всегда имеют знак: плюс ( + ) или минус (—).
Отклонения являются алгебраическими величинами и могут быть положительными, если предельный или действительный размер больше номинального; отрицательными, если предельный или действительный размер меньше номинального, и равными нулю — при равенстве указанных размеров. Поэтому всегда следует учитывать знак отклонения, и в формулах не допускается перестановка вычитаемых.
Среднее отклонение (Ет, ет) равно полусумме верхнего и нижнего отклонений.
Введем и еще одно понятие. После того как деталь изготовлена и при помощи измерения установлен ее действительный размер, можно говорить о действительном отклонении
Действительное отклонение (Еr еr) равно алгебраической разности действительного и номинального размеров:
Пример.
Определим верхнее и нижнее отклонения для штифтов с номинальным диаметром 20 мм, если известны: dmax= 20,010 и dmin= 19,989 мм.
В работе технолога чаще необходимо определять значения предельных размеров, зная величины верхнего и нижнего отклонений. Поэтому записываем также формулы предельных размеров:
Правила указания отклонений на чертежах:
1. Значения верхних и нижних предельных отклонений на чертежах и в других технических документах проставляют в миллиметрах с их знаками непосредственно после номинального размера.
2. Отклонения помещают одно над другим (верхнее над нижним) и пишут меньшими цифрами, чем те, которые приняты для номинальных размеров:
3. Число знаков в верхнем и нижнем отклонениях после запятой обязательно выравнивают:
4. Перед величиной предельного отклонения указывается знак плюс или минус
5. Если отклонения имеют одинаковые абсолютные значения, но разные знаки, то указывают только одно отклонение со знаком ±, например, ±0,011. При симметричном двустороннем поле допуска числовая величина отклонения записывается тем же шрифтом, что и номинальный размер (исключение):
6. Если вернее или нижнее отклонения равны нулю, их можно не указывать.
Номинальный размер 16 мм с различными предельными отклонениями на чертеже может обозначаться так:
а) ; б) 16 +0,1 ; в) 16-0,1; г) 16±0,2; д) ; е) .
Предельные отклонения, как и предельные размеры, характеризуют точность действительных размеров и погрешности обработки деталей.
Следовательно, для обработки деталей и оценки точности их изготовления должны быть заданы или предельные размеры, или предельные отклонения.
Для составления стандартных таблиц по допускам и посадкам, при выполнении ряда расчетов и проведении многих измерений гораздо удобнее пользоваться предельными отклонениями, а не предельными размерами, поэтому в стандартных таблицах допусков и посадок приведены числовые значения верхних и нижних отклонений. В таблицах отклонения приводят, как правило, в микрометрах и обязательно со знаками.
Зная понятия предельных размеров и отклонений, необходимо уточнить формулировку номинального размера:
Номинальный размер — это размер, относительно которого определяются предельные размеры и который служит началом отсчета всех отклонений, как предельных (верхнего и нижнего), так и действительных.
Читайте также:
- Закрывают ли группу на карантин при коронавирусе в детском саду если заболел воспитатель
- Школа 1062 педагогический состав
- Какие календарно обрядовые песни можно назвать самыми веселыми почему кратко
- Что делает заведующая детским садом после предъявления на ее имя претензии
- Какую роль играет маховик в двигателе внутреннего сгорания кратко