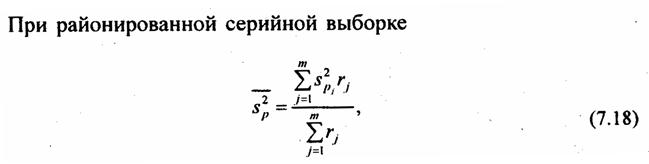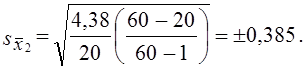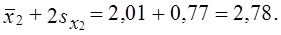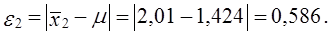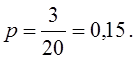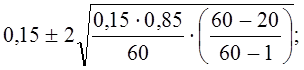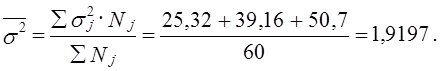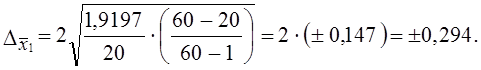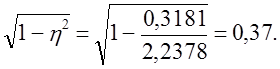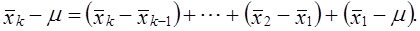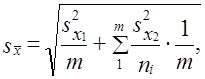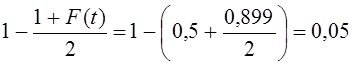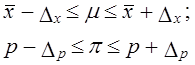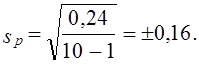На величину средней ошибки выборки не оказывает влияния

Другие вопросы по предмету Статистика

1. К основным
задачам статистики в государственном
и муниципальном
управлении
относят…

1.информирование
населения о состоянии экономической
и социальной сферы

2.обеспечение
информационных запросов управленческих
структур

3.формирование
предложений по планированию и
прогнозированию развития
социально-экономической сферы

4. корректировку
деятельности органов власти

Ответ: 1,2,3

2. Колеблемость,
многообразие, изменчивость значения
признака у отдельных единиц совокупности
называется

1. разбросом

2. множеством

3. рассеиванием

4. вариацией

Ответ: 4

3.Исследование
взаимосвязей варьирующих признаков в
пределах однородной
совокупности
называется группировкой.

1. типологической

2. аналитической

3. множественной

4.
структурной

Ответ:1

4. Вероятность
попадания каждой единицы генеральной
совокупности в выборочную совокупность
остается постоянной при … отборе.

1. бесповторном

2. механическом

3. повторном

4. безвозвратном

Ответ: 1

5. На величину
средней ошибки выборки не оказывает
влияния …

1. численность
выборки

2. способ отбора

3. степень вероятности

4. степень вариации
признака

Ответ: 3

6. Если вариационный
ряд имеет следующий вид:

Х	30	40	50
f	2	5	4

то медиана равна
…

Ответ:40

7. Если средняя
арифметическая признака равна 200, а
дисперсия 400, то коэффициент вариации
(в %) равен …

Ответ: 200

Произведение
цепных индивидуальных индексов…

1. меньше последнего
базисного индекса

2. больше последнего
базисного индекса

3. равно последнему
базисному индексу

4. равно единице

Ответ: 3

8.Учитывая что
на планируемый период затраты на 1 руб,
произведенной продукции увеличатся
на 20%, а объем произведенной продукции
увеличится на 30%, себестоимость продукции
предприятия…

Ответ: увеличится
на 56%

9.Если значение
коэффициента корреляции составляет
0,8, то связь между взаимосвязанными
признаками ________.

1. умеренная

2. слабая

3. заметная

4. тесная

Ответ: 4

10.
Параметр «а₁»
в уравнении прямой линии, по которому
проводилось выравнивание динамического
ряда, характеризует среднегодовой …

1. темп роста

2. темп прироста

3. абсолютный
прирост

4. уровень ряда

Ответ: 3

11.Отрицательное
значение коэффициента детерминации
означает …

1. ошибку в расчетах

2. отсутствие связи
между признаками

3. обратный характер
связи между признаками

4. тесную связь
между признаками

Ответ: 3

12. В теории
статистики по аналитическому выражению
выделяют следующие виды связей между
признаками

1. прямолинейные

2. обратные

3. умеренные

4. нелинейные

Ответ: 1;4

13. Коэффициент
вариации, равный 50% означает, что …

1. допущена ошибка
в расчетах

2. совокупность
неоднородна

3. размах вариации
составляет 50% от средней

4. совокупность
однородна

14. К условно –
натуральным единицам измерения
абсолютных статистических показателей
можно отнести …

1. килограммы

2. эталонные
тракторы

3. киловатт-часы

4. человеко-часы

Ответ: 2

15. В статистике
производства продукции используется
индекс промышленного производства –
это относительный показатель,
характеризующий изменение масштабы
производства в …

1. связи с ростом
цен

2. сравниваемых
периодов

3. периоде, который
наступит после текущего

4. связи с ликвидацией
предприятий

Ответ: 2

Соседние файлы в предмете [НЕСОРТИРОВАННОЕ]

• #
• #
• #
• #
• #
• #
• #
• #
• #
• #
• #

Выборочное наблюдение. общей дисперсии

2.2 Выборочное наблюдение

1. Методом жеребьевки осуществляется отбор:

— собственно-случайный;

— типический;

— серийный;

— механический.

2. Между объемом выборочной совокупности и ошибками выборки:

— существует обратная зависимость;

— существует прямая зависимость;

— существует тесная зависимость;

— отсутствует зависимость.

3. Расчет случайной ошибки одинаков для выборки:

— собственно-случайной;

— типической;

— серийной;

— ступенчатой.

4. Равная вероятность попадания единиц в выборочную совокупность является основным принципом:

— любой случайной выборки;

— собственно-случайной;

— серийной выборки при случайном отборе серий;

— механической.

5. При недостаточно равномерном представлении в выборочной совокупности различных категорий генеральной совокупности возникают:

— случайные ошибки репрезентативности;

— систематические ошибки репрезентативности;

— средние ошибки репрезентативности;

— предельные ошибки репрезентативности.

6. Вероятность попадания каждой единицы генеральной совокупности в выборочную совокупность остается постоянной при___________отборе:

— повторном

— бесповторном

— безвозвратном

— механическом

7. Расчет средней ошибки выборки при механическом отборе невозможенбез

— общей дисперсии

— средней из внутригрупповых дисперсий

— случайной дисперсии

— межгрупповой дисперсии

8. Предельная и средняя ошибки выборки равны при соответствующем уровне:

— вероятности;

— вариации признака;

— численности выборочной совокупности;

— численности генеральной совокупности.

9. По таблице случайных чисел осуществляется отбор ____________выборки:

— собственно-случайной;

— механической;

—  типической;

— серийной.

10. При типическом отборе внутри групп обследуются единицы, отобранные____________способом:

— собственно-случайным и механическим

— комбинированным и серийным

— механическим  и серийным

— всеми

11. Малая выборка – это выборочное наблюдение, при котором число обследуемых единиц:

— колеблется от 5 до 30;

— больше 100;

— составляет 5-10% генеральной совокупности;

— составляет > 10% генеральной совокупности.

12. Чем больше вариация признака, тем при прочих равных условиях ошибка выборки:

— больше;

— меньше;

— равна единице;

— не зависит от вариации признака.

13. После разбивки генеральной совокупности на группы из каждой группы в выборку попадает лишь одна единица при ________________отборе:

— механическом;

— типическом;

— серийном;

— собственно-случайном.

14. Только на основе бесповторного отбора может быть осуществлена________________________ выборка:

— механическая;

— собственно-случайная;

— типическая;

— серийная.

15. Статистически могут быть измерены:

— случайные ошибки репрезентативности;

— случайные ошибки регистрации;

— систематические ошибки репрезентативности;

— систематические ошибки регистрации.

16. На величину средней ошибки выборки не оказывает влияния:

— степень вероятности;

— способ отбора;

— степень вариации признака;

— численность выборки.

17. При увеличении численности собственно-случайной повторной выборки в 4 раза, допустимая ошибка выборки:

— уменьшится в 2 раза;

— увеличится в 2 раза;

— увеличится в 4 раза;

— уменьшится в 16 раз.

18. При уровне вероятности, превышающем 0,7, предельная ошибка выборки:

— больше средней ошибки выборки;

— меньше средней ошибки выборки;

— равна средней ошибки выборки;

— равна нулю.

19. Расчет предельной ошибки выборки при любом способе отбора невозможенбез

— уровня вероятности

— коэффициента корреляции

— коэффициента вариации

— t — критерия Стьюдента

!End

7. Если средняя арифметическая признака равна 200, а дисперсия 400, то коэффициент вариации (в %) равен …

Ответ: 200

Произведение цепных индивидуальных индексов…

1. меньше последнего базисного индекса

2. больше последнего базисного индекса

3. равно последнему базисному индексу

4. равно единице

Ответ: 3
8.Учитывая что на планируемый период затраты на 1 руб, произведенной продукции увеличатся на 20%, а объем произведенной продукции увеличится на 30%, себестоимость продукции предприятия…

Ответ: увеличится на 56%

9.Если значение коэффициента корреляции составляет 0,8, то связь между взаимосвязанными признаками ________.

1. умеренная

2. слабая

3. заметная

4. тесная

Ответ: 4
10. Параметр «а₁» в уравнении прямой линии, по которому проводилось выравнивание динамического ряда, характеризует среднегодовой …

1. темп роста

2. темп прироста

3. абсолютный прирост

4. уровень ряда

Ответ: 3
11.Отрицательное значение коэффициента детерминации означает …

1. ошибку в расчетах

2. отсутствие связи между признаками

3. обратный характер связи между признаками

4. тесную связь между признаками

Ответ: 3
12. В теории статистики по аналитическому выражению выделяют следующие виды связей между признаками

1. прямолинейные

2. обратные

3. умеренные

4. нелинейные

Ответ: 1;4
13. Коэффициент вариации, равный 50% означает, что …

1. допущена ошибка в расчетах

2. совокупность неоднородна

3. размах вариации составляет 50% от средней

4. совокупность однородна
14. К условно – натуральным единицам измерения абсолютных статистических показателей можно отнести …

1. килограммы

2. эталонные тракторы

3. киловатт-часы

4. человеко-часы

Ответ: 2
15. В статистике производства продукции используется индекс промышленного производства – это относительный показатель, характеризующий изменение масштабы производства в …

1. связи с ростом цен

2. сравниваемых периодов

3. периоде, который наступит после текущего

4. связи с ликвидацией предприятий

Ответ: 2

Вариант 3

1. Система органов государственной статистики включает следующие организации из нижеперечисленных…

1. районные управления статистики

2. федеральная служба государственной статистики

3. внутриорганизационные службы статистики

4.территориальные органы Федеральной службы государственной статистики

Ответ: 1,2,4
2. Задачей статистического наблюдения является…

1. выявление количественных закономерностей
2. сбор массовых данных об изучаемых явлениях (процессах)
3. первичная обработка и сводка данных
4. расчет обобщающих показателей

Ответ: 2
3. В статистике используются _____________ измерители.

1. стоимостные и натуральные

2. количественные и неколичественные

3. качественные и расчетные

4. количественные и качественные

Ответ: 4
4. Особенность представления цифрового материала в статистике состоит в том, что цифры являются …

1. абсолютными

2. именованными, относящимися к определенному месту и времени

3. именованными

4. агрегированными

Ответ: 1,2
5. Абсолютные величины могут выражаться в …

1. коэффициентах

2. промилле

3. километрах

4. процентах

Ответ: 3
6. Коэффициент вариации, равный 50% означает, что …

1. допущена ошибка в расчетах

2. совокупность неоднородна

3. размах вариации составляет 50% от средней

4. совокупность однородна

Ответ: 2
7.В теории статистики агрегатный индекс представляет собой отношение сумм произведений двух величин …

1. показателя интенсивности

2. индексируемого показателя

3. показателя, выбранного в качестве соизмерителя (веса)

4. показателя сравнения

Ответ: 2;3
8.В территориальных индексах физического объема продукции в качестве весов
обычно применяются цены.

1. суммарные
2. примерные
3. относительные
4. средние

Ответ: 3
9.Для определения тесноты связи двух качественных признаков, каждый из которых состоит только из двух групп применяются коэффициенты _____.

1. коэффициент знаков (Фехнера)

2. эластичности

3. эмпирическое корреляционное отношение

4. ассоциации

Ответ: 4
10. Если линейный коэффициент корреляции имеет положительное значение, то значение коэффициента регрессии …

1. равно нулю

2. положительное

3. не зависит от знака коэффициента корреляции

4. отрицательное

Ответ: 2
11. Корреляционное отношение используется для определения …

1. динамики явления

2. тесноты связи

3. остаточной вариации

4. факторной вариации

Ответ: 2

12. В теории статистики в зависимости от причинно-следственных связей статистические признаки разделяют на следующие виды …

1. динамические

2. результативные

3. статистические

4. факторные

Ответ: 2;4
13. Коэффициент вариации, равный 50% означает, что …

1. допущена ошибка в расчетах

2. совокупность неоднородна

3. размах вариации составляет 50% от средней

4. совокупность однородна
14. К условно – натуральным единицам измерения абсолютных статистических показателей можно отнести …

1. килограммы

2. эталонные тракторы

3. киловатт-часы

4. человеко-часы

Ответ: 2
15. По данным статистике прибыль предприятия увеличилась за первый год на 30%, за второй — на 40%. Увеличение объема прибыли за два года может быть выражена следующими из нижеприведенных данных…

1. на 35%

2. в 1,35 раза

3. на 82%

4. в 1,82 раза

Ответ: 1;2

Вариант 4

1. Элементы статистической совокупности характеризуются…

1. независимостью

2. массовостью

3. однородностью

4. системностью

Ответ: 2,3

2. В теории статистики различают следующие виды статистической сводки в зависимости от глубины обработки данных…

1. качественная

2. количественная

3. простая

4. сложная

Ответ: 3,4

3. К условно – натуральным единицам измерения абсолютных статистических показателей можно отнести …

1. килограммы

2. эталонные тракторы

3. киловатт-часы

4. человеко-часы

Ответ: 2

4. Относительная величина уровня экономического развития является частным случаем относительной величины …

1. координации

2. динамики

3. интенсивности

4. сравнения

Ответ: 3

5. Варьирующим признаком является …

1. цена одного килограмма товара

2. число π

3 пол человека

4. температура кипения воды

Ответ: 1
6. При недостаточно равномерном представлении в выборочной совокупности различных категорий генеральной совокупности возникают _______ошибки репрезентативности

1. систематические

2. случайные

3. средние

4. предельные

Ответ: 2
7. В статистике производства продукции используется индекс промышленного производства – это относительной показатель. Характеризующий изменение масштабов производства в …

1. сравниваемых периодах

2. связи с ростом цен

3. периоде, который наступил после текущего

4. связи с ликвидацией предприятий

Ответ: 1
8. В общем индексе цен индексируемой величиной будет выступать:

1. структура объема произведенной продукции

2. объем произведенной продукции

3. затраты на 1 руб. произведенной продукции

4. цена на единицу продукции

Ответ: 4
9. По данным статистике прибыль предприятия увеличилась за первый год на 30%, за второй — на 40%. Увеличение объема прибыли за два года может быть выражена следующими из нижеприведенных данных…

1. на 35%

2. в 1,35 раза

3. на 82%

4. в 1,82 раза

Ответ: 1;2
10.Расчет коэффициента детерминации невозможен без значения коэффициента

1. ассоциации

2. корреляции

3. эластичности

4. контингенции

Ответ: 2
11. В теории статистики функциональную зависимость среднего значения результативного признака от значения факторного признака характеризуют следующие утверждения …

1. аналитически выражается дисперсионным уравнением

2. это – корреляционная зависимость

3. это – вариационная зависимость

4. аналитически выражается уравнением регрессии

Ответ: 2;4
12. В теории статистики при исследовании взаимосвязи от двух и более признаков используются следующие виды коэффициентов корреляции …

1. парный

2. частный

3. общий

4. множественный

Ответ: 1;4

13. По средней ___________ определяется средний уровень моментного ряда.

1. арифметической

2. квадратической

3. геометрической

4. хронологической

Ответ:

14. Количественная модель, выражающая основную тенденцию изменения явления во времени, определяется на основе …

1. скользящей средней

2. аналитического выравнивания

3. укрупнения периодов

4. расчета среднегодового темпа прироста

Ответ: 2
15. . Если значение коэффициента корреляции составляет 0,8, то связь между взаимосвязанными признаками …

1. умеренная

2. слабая

3. заметная

4. тесна

Вариант 5

1. Заполните пропуск. Термин «статистика» был введен в науку Готфридом Ахенвалем в _____ веке.

1. 18

2. 15

3. 16

4. 17

Ответ: 1

2. К атрибутивным признакам группировок относят…

1. среднедушевой доход

2. уровень образования

3. возраст

4. пол

Ответ: 2,4

3.К относительным показателям, характеризующим просроченные кредиты, относится …

1.удельный вес предприятий, имеющих задолженность по кредитам в общем числе кредитуемых предприятий

2. сумма кредитов, погашенных несвоевременно

3. сумма кредитов, подлежащих погашению за отчетный период

4. удельный вес кредитов, погашенных несвоевременно

Ответ: 1

4. Сумма относительных показателей структуры, рассчитанных по одной совокупности, должна быть _____________

1. меньше 100%

2. меньше 100% или равной 100%

3. больше 100%

4. строго равной 100%

Ответ:4

6. Выборка, включающая несколько стадий отбора и на всех ступенях которой сохраняется одна и та же единица отбора, называется …

1.многообъектной

2. многорядной

3. многоступенчатой

4. многофазной

Ответ: 4

7. Подсчитайте количество изделий, которые нужно обследовать при повторном отборе для определения доли нестандартной продукции с предельной точностью 2% при вероятности 0,954. Доля нестандартной продукции по данным пробного обследования составляет 10%.

1. 900

2. 18

3. 81

4. 439

Ответ: 3

8.Индекс, характеризующий влияние изменения структуры изучаемого явления на динамику среднего уровня этого явления, называется …

1. индексом постоянного состава

2. индексом структурных сдвигов

3.индексом переменного состава

4.усредненным индексом

Ответ: 2

9.. По средней ___________ определяется средний уровень моментного ряда.

1. арифметической

2. квадратической

3. геометрической

4. хронологической

Ответ: 4

10.Отношение уровней ряда динамики называется…

Ответ: коэффициентом роста

11. Количественная модель, выражающая основную тенденцию изменения явления во времени, определяется на основе …

1. скользящей средней

2. аналитического выравнивания

3. укрупнения периодов

4. расчета среднегодового темпа прироста

Ответ: 2

12. Если значение коэффициента корреляции составляет 0,8, то связь между взаимосвязанными признаками …

1. умеренная

2. слабая

3. заметная

4. тесна

13. Если темп роста оплаты труда составил в 2007г. – 107,5%, в 2008г. – 108%, то заработная плата за два года увеличилась на…

1. 16,1%

2. 115,5%

3. 15,1%

4. 6%

Ответ: 1
14. . Значение медианы для ряда распределения

группы семей по размеру жилой площади, приходящейся на 1 человека, кв.м.	3-5	5-7	7-9	9-11	11 и более
число семей	10	22	28	30	26

Ответ: от 7 до 9
15.Для определения общей средней из групповых средних (удельный вес групп
неодинаков) следует применить формулу средней .

1. арифметической простой
2. гармонической взвешенной
3. гармонической простой
4. арифметической взвешенной

Ответ: 4

Вариант 6
1. К основным задачам статистики в государственном и муниципальном управлении относят …

1. обеспечение информационных запросов управленческих структур

2. корректировку деятельности органов власти

3. формирование предложений по планированию и прогнозированию развития социально-экономической сферы

4. информирование населения о состоянии экономической и социальной сферы

Ответ: 1,4

2. В теории статистики различают следующие виды сложных группировок…

1. первичные

2. комбинационные

3. многомерные

4. вторичные

Ответ: 2,3

3. Взаимосвязь относительных величин динамики ОВД, планового задания ОВПЗ и выполнения плана ОВВП выражается соотношением:

1. ОВВП = ОВД х ОВПЗ

2. ОВПЗ = ОВД х ОВВП

3. ОВД = ОВПЗ х ОВВП

4. ОВД = ОВПЗ : ОВВП

Ответ: 3

4. Качественные статистические признаки подразделяются на …

1. агрегатные

2. номинальные

3. альтернативные

4. комплексные

Ответ: 3,4

5. Подсчитайте необходимую численность выборки при определении среднего вклада населения в отделениях коммерческих банков города, чтобы с вероятностью 0.954 предельная ошибка выборки не превысила 50 руб. Ориентировочная дисперсия вкладов равна 200000.

1. 1600

2. 800

3. 160

4. 320

Ответ: 4

6. К способам отбора единиц в выборочную совокупность относят способы …

1. аналитический

2. типический

3. комбинированный

4. серийный

5. альтернативный

Ответ: 2;3;4

7. В теории статистики различают следующие виды ошибок статистического наблюдения в зависимости от причин возникновения …

1. ошибки репрезентативности

2. ошибки регистрации

3. частные ошибки

4. общие ошибки

Ответ: 1;2

8.Индекс – это относительный показатель, который выражает соотношение величин какого-либо явления …

1. только во времени

2. во времени, пространстве и в сравнении с любым эталоном

3.только в пространстве

4.только в сравнении с каким-либо эталоном (планом, нормативом, прогнозом)

Ответ: 2

9.Если темп роста оплаты труда составил в 2007г. – 107,5%, в 2008г. – 108%, то заработная плата за два года увеличилась на…

1. 16,1%

2. 115,5%

3. 15,1%

4. 6%

Ответ: 1
10. Ряд динамики, характеризующий экспорт страны по каждому году за период с 2000 по 2006 годы, по виду относится к ________ рядам динамики.
1. производным

2. произвольным

3. интервальным

4. моментальным

Ответ: 3

11.Средний уровень интервального ряда динамики определяется как средняя

1. геометрическая
2. квадратическая
3. арифметическая
4. хронологическая

Ответ: 3

12.Коэффициент контингенции рассчитывается по зависимости …

1. _2.

3. 4.

_{Ответ: 2}
13.Индекс ____________ выражается отношением средних величин за два периода (по двум объектам).

1. произвольного состава

2. переменного состава

3. постоянного состава

4. структурных сдвигов

Ответ: 2

Вариант 7

1. Федеральная служба государственной статистики выполняет

функции по …

1. сопоставлению основных социально-экономических показателей России с аналогичными показателями других стран

2. разработке основных направлений экономического развития общества

3.организация государственных статистических наблюдений по разработанным программам

4. заполнению форм государственного статистического наблюдения для предприятий и организаций

Ответ: 1,3

2. Статистической группировкой называются…

1. выявление количественных закономерностей развития явлений

2. разделение изучаемой совокупности на группы и подгруппы по определенным признакам

3. комплекс последовательных операций по обобщению единичных фактов

4. сбор данных по отдельным единицам совокупности

Ответ: 2

3. Относительная величина выполнения бизнес-плана фирмы определяется отношением фактического уровня к _______________

1. факту за прошлый период

2. плановому

3. плану за прошлый период

4. базисному

Ответ: 2

4.. В результате типической пропорциональной 1%-ной выборки в лесничестве отобрано 50 сосен и 50 елей. Средний диаметр одной сосны в выборке 136 мм, ели – 120 мм. Общая дисперсия диаметра деревьев в выборке – 289. Определите ошибку выборки с вероятностью 0,954.

1. 1,7

2. 3

3. 3,4

4. 1,5

Ответ: 3

5.Для определения общей средней из групповых средних (удельный вес групп
неодинаков) следует применить формулу средней .

1. арифметической простой
2. гармонической взвешенной
3. гармонической простой
4. арифметической взвешенной

Ответ: 4

6. Значение медианы для ряда распределения

группы семей по размеру жилой площади, приходящейся на 1 человека, кв.м.	3-5	5-7	7-9	9-11	11 и более
число семей	10	22	28	30	26

Ответ: от 7 до 9

7.Медиана в ряду распределения рабочих по уровню заработной платы равна 12 тыс. руб., следовательно…

Ответ: 50% рабочих имеют заработную плату 12 тыс. руб. и выше

8..Мода = … для значений признака: 3,3,3,5,5,6,9,11,12,13

Ответ: 3

9.Индекс ____________ выражается отношением средних величин за два периода (по двум объектам).

1. произвольного состава

2. переменного состава

3. постоянного состава

4. структурных сдвигов

Ответ: 2

10.К причинам вызывающим не сопоставимость рядов динамики относят…

1. изменение единиц измерения показателей

2. несовершенство методического аппарата наблюдения

3. ограниченность объема наблюдения

4. недостаточная квалификация исполнителей

Ответ: 1

11. В теории статистики при исследовании рядов динамики применяют следующие виды средних…

1. геометрическая

2. структурная

3. хронологическая

4. сложная

Ответ: 1,3

12.Параметр « » в уравнении прямой линии, по которому проводилось выравнивание динамического ряда, характеризует среднегодовой …

1. темп роста

2. темп прироста

3. абсолютный прирост

4. уровень ряда

13.По аналитическому выражению связи в статистике классифицируются на

1. линейные и криволинейные
2. сильные и слабые
3. прямые и обратные
4. закономерные и произвольные

Ответ: 1

14.При расчета среднего коэффициента роста с помощью средней геометрической подкоренное выражение представляет собой ___________цепных коэффициентов роста.

1. произведение

2. сумму

3. разность

4. частное

Ответ: 1

15. Для сравнения уровня вариации двух признаков необходимо использовать:

1. среднее квадратическое отклонение

2. коэффициент вариации

3. размах вариации

4. среднее линейное отклонение

Ответ: 3

Вариант 8

1. Предметом изучения статистики являются статистические …

1. таблицы
2. совокупности
3. показатели

4. единицы

Ответ: 4
2. Группировка, в которой для характеристики групп применяется только один показатель – численность групп, называется

1. аналитической группировкой

2. многомерной группировкой

3. рядом распределения

4. сводкой

Ответ: 3
3. В теории статистики для абсолютных статистических показателей используются следующие единицы измерения …

1. натуральные

2. процентные

3. относительные

4. стоимостные

Ответ: 1;4
4. В теории статистики для расчета относительного показателя плана необходимы следующие данные …

1. показатели базисного периода

2. показатели плана

3. показатели основной тенденции

4. показатели типичной части совокупности

Ответ: 1;2
5. Относительные статистические величины выражаются в …

1. процентах

2. промилле

3. стоимостных единицах измерения

4. натуральных единицах измерения

5. виде кратного отношения

Ответ: 1;2;5
6. В статистике производства продукции используется индекс промышленного производства – это относительный показатель, характеризующий изменение масштабы производства в …

1. связи с ростом цен

2. сравниваемых периодов

3. периоде, который наступит после текущего

4. связи с ликвидацией предприятий

Ответ: 2

7. В теории статистики для вычисления средней ошибки выборки для доли используют следующие данные …

1. выборочная средняя

2. генеральная средняя

3. объем выборки

4. выборочная доля

Ответ: 3;4
8.Дисперсия признака = … при условии:

показатель	значение признака
средняя величина признака, руб.	20
коэффициент вариации, %	25

Ответ: 25
9. Дисперсия -…( с точностью до 0,0001 ), если при осмотре 200 деталей среди них оказалось 10 бракованных изделий.

Ответ: 0,0475

10.. Коэффициент износа на конец года (с точностью до 0,1%) = …% при условии:

— коэффициент износа основных фондов на начало года = 25%

— коэффициент годности основных фондов на конец года = 72%

Ответ: 28
11. Среднегодовые темпы прироста фондоемкости =…% (с точностью до 0,1%) при условии, что в 2004 г. уровень фондоемкости продукции составил 108% к её уровню в 2002 г.

Ответ: 103,9
12.Остатки задолженности по кредиту на 1 января – 100 млн.руб., 1 февраля – 120 млн.руб., на 1 марта – 126 млн.руб., на 1 апреля – 140 млн.руб. Тогда средние остатки задолженности по кредиту за 1 квартал составляет___ млн.руб.

1. 125

2. 136,5

3. 122

4. 105

Ответ: 3
13.При расчета среднего коэффициента роста с помощью средней геометрической подкоренное выражение представляет собой ___________цепных коэффициентов роста.

1. произведение

2. сумму

3. разность

4. частное

Ответ: 1
14.Параметр a1 (a1= -1,04) линейного уравнения регрессии y_x=36,5 — l,04x показывает, что:

1. С снижением признака «х» на 1 признак «у» уменьшается на 1,04

2. С увеличением признака «х» на 1 признак «у» уменьшается на 1,04

3. не измениться

4. нет правильного ответа

Ответ: 2
15.Тесноту связи между двумя альтернативными признаками можно измерить с помощью коэффициентов …

Ответ: контингенции, ассоциации

Вариант 9
1. Документальный способ наблюдения применяется при…

1.переписи населения

2.определения степени выполнения плана по выпуску продукции сельскохозяйственными предприятиями области

3.переписи скота, находящегося в личном пользовании граждан

4.учете численности промышленно-производственного персонала

Ответ: 1
2. Интервал группировки, когда имеется и нижняя и верхняя граница, называется …

1. открытым

2. равным

3. неравным

4. закрытым

Ответ: 4
3. Если имеются данные о размере посевных площадей и урожайности по 20-ти предприятиям района, то расчёт средней урожайности осуществляется по формуле средней …

1. геометрической

2. арифметической простой

3. арифметической взвешенной

4. гармонической

Ответ: 3
4. Для сравнения уровня вариации двух признаков необходимо использовать:

1. среднее квадратическое отклонение

2. коэффициент вариации

3. размах вариации

4. среднее линейное отклонение

Ответ: 3
5.Объем повторной случайной выборки увеличится в … раза (с точностью до 0,01), если вероятность, гарантирующую результат, увеличить с 0,954(t=2) до 0.997(t=3). Формула для расчета объема выборки:

Ответ: 2.25 или 9/4
6. Межгрупповая дисперсия составляет 61% от общей дисперсии. Эмпирическое корреляционное отношение = … (с точностью до 0,01).

Ответ: 0,78
7. В теории статистики для вычисления сводного индекса товарооборота по формуле средней арифметической взвешенной используют

1.товарооборот базисного периода

2. индивидуальный индекс физического объёма товара

3. индивидуальный индекс цены

4. индивидуальный индекс товарооборота

Ответ: 2;3

8. В теории статистики для вычисления сводного индекса физического объема товаров по формуле средней арифметической взвешенной используют следующие данные по каждому виду товаров …

1.товарооборот текущего периода

2. товарооборот базисного периода

3. индивидуальный индекс физического объема товара

4. индивидуальный индекс товарооборота

Ответ: 2;3
9. При сопоставлении показателей каждого последующего уровня с предыдущим определяются показатели динамики _________ методом.

1. цепным

2. базисным

3. интервальным

4. индивидуальным

Ответ: 1

10. С точки зрения теории статистики ряд динамики включает следующие составные элементы…

1. значения изучаемого показателя

2. показатели времени

3. интервалы изменения признака

4. частоты

Ответ: 3,4
11.Коэффициент детерминации представляет собой долю …

Ответ: Межгрупповой дисперсии в общей дисперсии

12.Множественный коэффициент корреляции может принимать значение …

Ответ: 0 до 1
13.Индекс ____________ выражается отношением средних величин за два периода (по двум объектам).

1. произвольного состава

2. переменного состава

3. постоянного состава

4. структурных сдвигов

Ответ: 2

14.Отдельное значение группированного признака, положенного в основу ряда распределения, называют …

1. вариантой

2. частотностью

3. частотой

4. подлежащим

Ответ: 4
15.По таблице случайных чисел осуществляется отбор … выборки.

1. собственно-случайной

2. типической

3. механической

4. серийной

Ответ: 2

Вариант 10
1. В зависимости от числа положенных в основание группировки признаков различают группировки …

1. количественные и качественные

2. первичные и вторичные

3. простые и многомерные

4. типологические, аналитические и структурные

Ответ: 3
2. Статистические группировки, которые научно обоснованы, практически проверены и утверждены официально для применения, называются …

1. кластерами

2. нормативами

3. классификациями

4. рекомендациями

Ответ: 2

3. По форме организации обработки данных различают сводку …

1. централизованную и децентрализованную

2. ручную и механическую

3. типологическую и аналитическую

4. сплошную и выборочную

Ответ: 2
4. Отдельное значение группированного признака, положенного в основу ряда распределения, называют …

1. вариантой

2. частотностью

3. частотой

4. подлежащим

Ответ: 4
5. Если известна численность населения за равные интервалы времени, то для определения средней численности населения используется формула расчета средней …

1. арифметической взвешенной

2. хронологической взвешенной

3. арифметической простой

4. хронологической простой

Ответ: 3
6. По таблице случайных чисел осуществляется отбор … выборки.

1. собственно-случайной

2. типической

3. механической

4. серийной

Ответ: 2

7. Коэффициент механического (миграционного) прироста населения = …‰ (с точностью до 0,1‰) при условии:

Показатель	тыс.чел.
численность населения на начало года	120
численность населения на конец года	122
число родившихся за год	1,2
число умерших за год	1,0

Ответ: 14,8
8.Показатель изменения затрат на один рубль продукции выражается в процентах и определяется как отношение разности между фактическими затратами на рубль продукции данного года и затратами на рубль продукции за предыдущий год к затратам на рубль продукции …

1. будущего периода

2. 2000 года

3. отчетного периода

4. предыдущего года

Ответ: 4

9.В теории статистики в зависимости от выбранной базы сравнения показатели рядов динамики разделяют на …

1. абсолютные

2. относительные

3. цепные

4. базисные

Ответ: 3,4
10. В теории статистики интервальный ряд динамики может содержать следующие из нижеперечисленных данных…

1. объем вкладов населения в региональных банках на начало года

2. естественный прирост населения за период

3. численность населения региона на начало года

4. ежемесячные доходы населения

Ответ: 2,4

11.В результате проведения регрессионного анализа получают функцию, описывающую… показателей.

Ответ: Взаимосвязь

12.Для сравнения уровня вариации двух признаков необходимо использовать:

1. среднее квадратическое отклонение

2. коэффициент вариации

3. размах вариации

4. среднее линейное отклонение

Ответ: 3

13.Параметр « » в уравнении прямой линии, по которому проводилось выравнивание динамического ряда, характеризует среднегодовой …

1. темп роста

2. темп прироста

3. абсолютный прирост

4. уровень ряда

14. Для сравнения уровня вариации двух признаков необходимо использовать:

1. среднее квадратическое отклонение

2. коэффициент вариации

3. размах вариации

4. среднее линейное отклонение

Ответ: 3
15. Интервал группировки, когда имеется и нижняя и верхняя граница, называется …

1. открытым

2. равным

3. неравным

4. закрытым

Ответ: 4

7.4. Влияние вида выборки на величину ошибки выборки

Как указывалось в п. 7.2, при проведении выборочного наблюдения используются различные способы формирования выборочной совокупности: случайный отбор — повторный или бесповторный, механический, серийный, типический. Вид выборки влияет на величину ошибки выборки. При бесповторном отборе формула средней ошибки выборки дополняется множителем

который корректирует величину ошибки выборки и в связи с изменением состава совокупности и вероятности попадания единиц в выборку. В серийной выборке дисперсия определяется как колеблемость между сериями:

 (7.14)

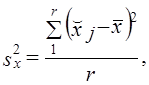
где x̌_j — среднее значение признака х в у-й серии;

х̅ — среднее значение в целом по выборке;

r — число отобранных серий.

Формула (7.14) предполагает равенство серий по числу единиц, если это условие не выполняется, то в числитель выражения (7.14) вводится вес — число единиц в j-й серии, f_j; тогда в  знаменателе указывается не r, а 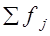. Межсерийная дисперсия представляет часть общей дисперсии признака х, и потому ее использование направлено на уменьшение ошибки выборки. Однако значение г намного меньше п, так как число отобранных гнезд намного меньше числа единиц наблюдения. Этот фактор увеличивает ошибку выборки. Его действие более значительно, нежели понижающее влияние межсерийной дисперсии — в результате ошибка серийной выборки в среднем больше ошибки выборки при отборе единицами.

При типическом отборе (стратифицированная или районированная выборка) дисперсия рассчитывается как средняя из внутрирайонных дисперсий:

                                                        (7.15′)

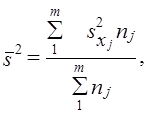
где     s²_ji — выборочная дисперсия признака х в j-м районе;

                                                              

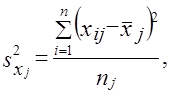
где     п_j — объем выборки в j-м районе;

т — число районов.

Очевидно, что по правилу сложения дисперсий величина s² меньше, чем величина общей дисперсии.

Величина ошибки районированной выборки меньше величины ошибки простой (нерайонированной выборки).

Часто используется сочетание районированного отбора с отбором сериями. Такой вид выборки обеспечивает преимущества в организации выборки и уменьшение ошибки выборки. Дисперсия такой выборки представляет среднюю из межсерийных дисперсий для каждого j-го района:

                                                            (7.16)

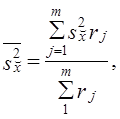
где s²_x̌j — межсерийная дисперсия в j-м районе;

 ,

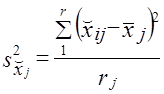
х̌_ij — средняя в i-й серии  j-го района;

х̅_j — средняя ву-м районе;

r— число серий, отобранных в j-м районе;

т — число районов.

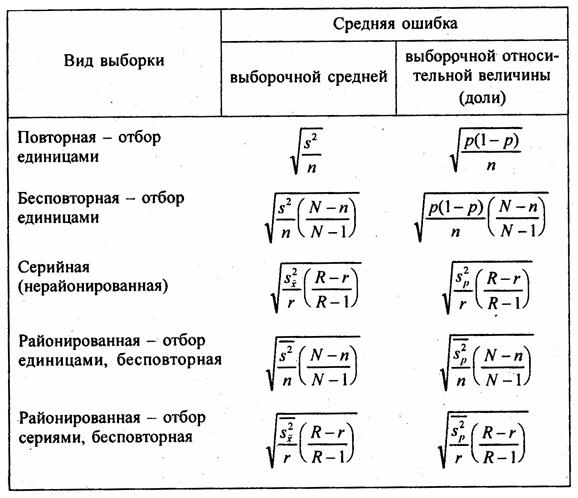
Табл. 7.2 содержит формулы средней ошибки выборки для выборочной средней и выборочной относительной величины для разных видов выборки. В приведенных формулах требуют пояснения выражения дисперсий выборочной относительной величины.

При нерайонированной серийной выборке

,

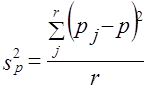
где     р_j — доля единиц определенной категории в у-й серии;

р — доля единиц этой категории в выборке.

Таблица 7.2

Формулы средней ошибки выборочной средней и выборочной относительной величины

 

Рассмотрим на примере влияние вида выборки на величину ошибки выборки. Исходные данные представлены в табл. 7.3.

Таблица 7.3

Показатели 60 предприятий легкой промышленности Санкт-Петербурга (по данным статистической отчетности за I полугодие 1995 г.)

№ пп	Форма Собственнос-ти	Оборачиваемость запасов, х1	Коэффициент покрытия, х2	№ пп	Форма собственности	Оборачиваемость запасов, х1	Коэффициент покрытия, х2
1	государственная	5,65	0,22	31	Частная	1,23	1,18
2	«	2,86	0,35	32	«	0,82	1,59
3	«	1,61	1,06	33	«	2,83	0,74
4	«	3,99	1,01	34	«	1,83	1,52
5	«	2,17	8,88	35	«	2,26	2,43
6	«	1,52	1,06	36	«	2,33	3,28
7	«	0,40	0,99	37	«	2,35	1,13
8	«	2,18	1,07	38	«	1,68	0,89
9	«	1,36	4,62	39	«	2,00	1,67
10	«	3,69	1,40	40	«	2,64	1,48
11	частная	0,45	1,34	41	«	2,75	1,51
12	«	1,0	1,16	42	«	3,29	5,96
13	«	2,05	2,00	43	«	1,6	1,38
14	«	2,36	1,43	44	«	1,90	2,39
15	«	4,90	1,76	45	«	3,27	3,62
16	«	3,12	1,26	46	«	3,49	0,46
17	«	1,36	1,89	47	«	2,92	1,26
18	«	1,56	12,36	48	смешання	3,22	0,78
19	«	4,84	1,23	49	«	2,61	1,67
20	«	1,23	3,26	50	«	5,17	0,95
21	«	0,81	2,22	51	«	8,63	0,96
22	«	0,7	1,16	52	«	1,06	2,51
23	«	0,87	1,21	53	«	2,13	3,49
24	«	0,20	1,45	54	«	2,03	1,22
25	«	1,71	4,04	55	«	1,82	2,92
26	«	1,83	2,07	56	«	3,12	1,54
27	«	1,32	0,69	57	«	0,77	0,97
28	«	1,95	1,97	58	«	4,15	0,93
29	«	1,46	1,31	59	«	3,62	1,34
30	«	2,96	5,32	60	«	3,89	3,51

Предприятия легкой промышленности примем за генеральную совокупность. Ее характеристики:

численность N = 60;

генеральные средние: μ₁ = 2,40 число оборотов;

       μ₂ = 1,424;

генеральные дисперсии: σ²₁ = 2,24;

                                          σ²₂ = 4,38;

средние квадратические σ₁ = 1,49 оборотов;

отклонения:                      σ₂ = 2,09.

Остановимся на смысле характеристик предприятий: оборачиваемость запасов рассчитывается делением продолжительности периода (полгода) на среднюю продолжительность одного периода оборота запасов. Очевидно, чем скорее оборачиваются запасы, тем выше их отдача. Коэффициент покрытия рассчитывается как отношение суммы всех источников покрытия запасов к стоимости запасов. Если значение этого показателя меньше единицы, то текущее финансовое состояние предприятия рассматривается как неустойчивое. В нашем примере вариация этого признака примерно в 2 раза превосходит вариацию предприятий по уровню оборачиваемости запасов: ν₂ = 147%, ν₁ = 62%.

Произведем 30%-ную выборку. Объем выборки составит п = 20 предприятий. При формировании выборки методом механического отбора каждое третье предприятие попадет в выборку. Отбор начинаем с полушага отбора, т. е. первым предприятием, попавшим в выборку, является второе по списку. Средние по выборке равны:

оборачиваемость запасов x̅₁ =2,16 оборотов, коэффициент покрытия x̅₂=2,01.

Средняя ошибка выборочной средней оборачиваемости запасов

   оборотов.

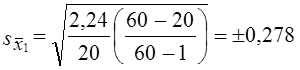
Средняя ошибка выборочного среднего коэффициента покрытия

 

С вероятностью 0,954 можно утверждать, что средняя оборачиваемость запасов на предприятиях легкой промышленности не ниже

x̅₁ — 2s_x1 = 2,16 — 0,55 = 1,61 оборотов и не выше x̅₁+2s_x1 = 2,16 +  0,55 = 2,71 оборотов.

Действительно генеральная средняя (μ₁ = 2,40) попадает в этот интервал.

Фактическая ошибка репрезентативности

  оборотов.

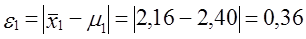
Эта величина меньше предельной ошибки выборки, гарантированной с принятой доверительной вероятностью, 0,36 < 0,55. Следовательно, выборка репрезентативна по этому признаку.

Вычислим предельную ошибку выборки коэффициента покрытия и определим доверительный интервал для этой характеристики. Его нижняя граница с той же вероятностью

;

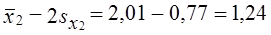
верхняя граница:

 

Генеральная средняя (μ₂ = 1,424) так же попадает в доверительный интервал.

Фактическая ошибка репрезентативности составляет:

Эта величина меньше предельной ошибки выборки (0,77), что дает основание считать выборку репрезентативной и по этому признаку.

В генеральной совокупности доля единиц с неустойчивым финансовым положением (х₂ < 1) составила 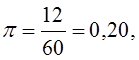  в выборке  

Доверительный интервал для оценки доли таких предприятий в генеральной совокупности составляет с вероятностью 0,954:

 

0,15 ± 0,076,

т. е. таких предприятий должно быть не меньше 7,4% и не больше 22,6%. Фактически их оказалось 20% от общего числа предприятии, т. е. выборка дает репрезентативный результат и по этому показателю.

Выполненная выборка формировалась как простая бесповторная механическая. Однако, наверняка статистик будет стремиться учесть структуру генеральной совокупности, поэтому  более естественной была бы выборка, учитывающая выделение предприятий разных форм собственности. Тогда выборка должна быть районированной.

Рассмотрим пример. Генеральная совокупность состоит из 11 государственных предприятий, 36 частных, 13 смешанных. В выборке эти пропорции соблюдаются следующим образом: отобраны по 4 предприятия государственных и смешанных и 12 — частных:

Предприятия	Генеральные характеристики	Выборочные характеристики
средние	доли	средние	доли
Государственные	μ1 = 2.35	π1 = 0,27	х̅1 = 1,92	Р1 = 0,25
Частные	μ1 =2,11	π2 = 0,11	х̅1  = 1,79	Р2=0,08
Смешанные	μ1 =3,25	π3 = 0,38	х̅1  =3,51	Рз — 0,25

Средняя из внутрирайонных дисперсий, рассчитанных по каждой группе предприятий в генеральной совокупности:

Эта величина меньше общей дисперсии без учета районирования (σ² = 2,24). Следовательно, и величина ошибки выборки при районированном отборе будет меньше:

 

Итак, с вероятностью 0,954 генеральная средняя оборачиваемости запасов находится в интервале 2,16 ± 0,294; 1,866 £ μ £ 2,454.

Чтобы понять, насколько целесообразно в том или ином случае применение районированного отбора, можно воспользоваться корреляционным отношением ц. Согласно правилу сложения дисперсий средняя из внутригрупповых дисперсий может быть представлена как

где h² — квадрат корреляционного отношения, равный б²:s².

Следовательно, применение районированной (типической) выборки изменяет предельную ошибку на 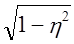 . В нашем примере для первой переменной (оборачиваемость) имеем:

          

Сопоставим полученный результат с изменением предельной ошибки выборки: 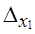 (без учета районирования) =0,55;

∆_x (при районировании) = 0,294, т. е. ошибка уменьшилась примерно вполовину.

Корреляционное отношение используется и при корректировке величины

                                                  (7.18′)

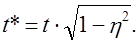
Тогда при вероятности 0,954 и t = 2; t*=2 — Ö0̅,8̅6̅ = 1,85, т. е. вместо t = 2 достаточно взять t = 1,85.

Многие выборки формируются как многоступенчатые. Ошибка многоступенчатой выборки может быть представлена как

Она складывается из ошибок отдельных ступеней. Поэтому практически используется не больше 2-3 ступеней отбора.

Средняя ошибка выборки при двухступенчатом отборе рассчитывается по формуле

где s_x1 ² — дисперсия признака х по совокупности «крупных» единиц;

s_x2² — дисперсия признака х в каждой из отобранных «крупных» единиц;

п_i — число отобранных единиц наблюдения в <-й «крупной» единице;

т — число отобранных «крупных» единиц.

Таким образом, применение многоступенчатой выборки улучшает организацию выборки, но увеличивает ее ошибку.

Кроме рассмотренных, применяется многофазовая выборка, когда одни сведения собираются на основе изучения всех единиц выборки, а другие — только на основании изучения некоторых из этих единиц, отобранных так, что они составляют подвыборки из единиц первоначальной выборки.

При периодическом повторении выборочных обследований с целью изучения динамики явлений применяются либо независимые выборки — через определенные промежутки времени отбор каждый раз производится независимо от предыдущих выборок; либо фиксированные выборки — в этом случае повторные обследования проводятся по одной и той же выборке. В связи с тем, что в фиксированной выборке могут происходить изменения (прежде всего за счет выбытия единиц) практикуют периодическую адаптацию фиксированной выборки происходящим изменениям. Чаще для целей изучения динамики используется промежуточный вариант — ротационная выборка (частичное замещение). При этом нужно следовать определенному плану замещения, например, каждый раз замещать четверть выборки, тогда каждая первоначальная единица останется в выборке в четырех следующих друг за другом обследованиях.

Названные виды выборок ориентированы на отбор конкретных материальных явлений. Кроме них следует назвать как особый вид выборки метод моментных наблюдений.Сущность метода моментных наблюдений состоит в периодической фиксации состояний .наблюдаемых единиц в отобранные моменты времени. Расчет объема такой выборки дает количество моментов. Этот вид выборочного наблюдения применяется при изучении использования производственного оборудования, либо рабочего времени (см. п. 7.13).

7.5. Задачи, решаемые при применении выборочного метода

При применении выборочного наблюдения возникают три основные задачи:

• определение объема выборки, необходимого для получения требуемой точности результатов с заданной вероятностью;

• определение возможного предела ошибки репрезентативности, гарантированного с заданной вероятностью, и сравнение его с величиной допустимой погрешности.

• определение вероятности того, что Ошибка выборки не превысит допустимой погрешности.

Все эти задачи решаются на основе теоремы Чебышева, согласно которой Р {[ х — μ | < e } ³ 1 — h, когда п — достаточно большое число; e и h — сколь угодно малые положительные числа. Это соотношение, как было показано в п. 7.3, может быть выражено через формулу предельной ошибки выборки ∆_x = ts_x или ∆_p = ts. Решение указанных задач зависит от того, какие величины в формуле предельной ошибки заданы, а какие нужно найти.

Объем выборки рассчитывается на стадии проектирования выборочного обследования. Так как

                                                      

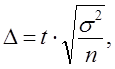
то

 ,                                                                (7.20)

где   ∆ — допустимая погрешность,, которая задается исследователем исходя из требуемой точности результатов проектируемой выборки;

t — табличная величина, соответствующая заданной доверительной вероятности F(t), с которой будут гарантированы оценки генеральной совокупности по данным выборочного обследования;

σ² — генеральная дисперсия.

Последняя величина, как правило, неизвестна. Используются какие-либо ее оценки: результаты прошлых обследований той же совокупности, если ее структура и условия развития достаточно стабильны, или же зная примерную величину средней, находят дисперсию из соотношения  ;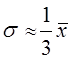

если известны x_max и х_min, то можно определить среднее квадратическое отклонение в соответствии с правилом «трех сигм»

   ,

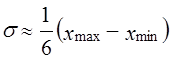
так как в нормальном распределении в размахе вариации «укладывается» 6σ(±3σ). Если распределение заведомо асимметричное, то

 .

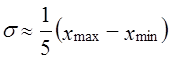
Для относительной величины принимают максимальную величину дисперсии σ²_max = 0,5∙0,5 = 0,25.

При расчете п не следует гнаться за большими значениями t и малыми значениями ∆, так как это приведет к увеличению объема выборки, а следовательно, к увеличению затрат средств, труда и времени, вовсе не являющемуся необходимым.

Формула (7.20) не учитывает бесповторности отбора и дает максимальную величину выборки, которую можно скорректировать «на бесповторность». Так как

  ,

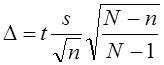
то на основе (7.20) получаем выражение скорректированного объема выборки (п):

  ,                                         (7.21)

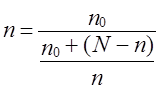
где

 .

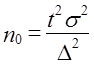
При больших размерах генеральной совокупности скорректированный Объем выборки незначительно отличается от n₀.

Например, для изучения структуры и стоимости покупок в универмаге из 10 000 покупателей следует отобрать определенное число человек, которое бы обеспечивало с вероятностью 0,95 определение средней стоимости покупок с точностью не менее 2 тыс. руб. Дисперсию примем по прошлому обследованию равной 625.

   человек;

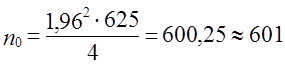
тогда скорректированная численность

   человек (≈ 570 человек).

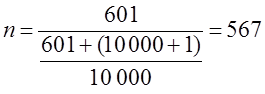
При проектировании районированной выборки рассчитанный объем выборки распределяют пропорционально численности районов (пропорциональный отбор):

  ,                                                              (7.22)

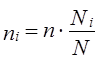
где  п_i — объем выборки для i-го района;

N_i — объем i-го района в генеральной совокупности;

п — общий объем выборки;

N — общий объем генеральной совокупности.

При различиях в однородности выделенных районов лучшие результаты дает распределение запланированного объема выборки между районами не только с учетом их объема, но и с учетом дисперсии признака (оптимальный отбор). В этом случае объем выборки в i-м районе определяется как

 ,                                                      (7.23)

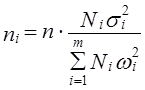
где σ²_i — дисперсия признака х в i-м районе.

При любом виде проектируемой выборки расчет объема выборки начинают по формуле повторного отбора (7.20). Если в результате расчета п доля отбора превысит 5%, проводят второй вариант расчета по формуле бесповторного отбора, либо по формуле (7.21), либо как

 .

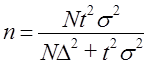
Если доля отбора меньше 5%, к формуле бесповторного отбора не переходят, так как это не скажется существенно на величине п.

Выборка должна быть такой, чтобы выборочные показатели по всем основным характеристикам были репрезентативны. Поэтому численность выборки рассчитывают многократно исходя из допустимых ошибок разных показателей, значения которых в генеральной совокупности известны.

Например, при выборочном учете детей школьного возраста требуется определить число семей, которые надо обследовать. При этом надо учесть: а) число детей в возрасте 6-7 лет, б) число детей в возрасте 6-15 лет; в) число детей в возрасте 16-17 лет;

г) среднедушевой доход (например, для решения вопроса о строительстве базы отдыха).

Так как репрезентируемые признаки могут иметь разную размерность, то допустимая погрешность для каждого их них задается в виде относительной величины (∆ : х̅) (например, планируется, что в определении среднего размера семьи ошибка должна быть не больше 2%, в определении дохода — не больше 3% и т.д.). В этом случае вместо дисперсии в формуле (7.20) берется квадрат коэффициента вариации.

Вычислив значение п, на основе каждой из характеристик получаем разные объемы выборки: 1200; 300; 700; 100. Обследовать необходимо 1200 семей, т.е. из рассчитанных численностей берется максимальная. При резких различиях необходимых объемов выборки для разных вопросов программы проводится многофазный отбор. В рассмотренном примере среднедушевой доход достаточно учитывать в одной из каждых 12 семей, попавших в выборку.

Многофазный отбор, как правило, довольно сложно организовать, может быть нарушен принцип случайности отбора. Поэтому для обеспечения репрезентативности оказывается выгоднее затратить больше средств на учет большего числа единиц совокупности. Многофазный отбор целесообразно применять, если соотношение между рассчитанными объемами выборки по крайней мере 1:6.

Поскольку расчет необходимой численности выборки основан не на точных, а на предположительных данных о колеблемости в совокупности, следует соблюдать следующие рекомендации: абсолютную величину п округлять только вверх; долю отбора округлять только вниз, т.е. из предосторожности планировать несколько больший объем выборки, чем показывают расчеты.

Объем многоступенчатой выборки рекомендуется увеличить не менее чем на 10% от рассчитанной численности, поскольку, как было показано в предыдущем параграфе, многоступенчатость отбора увеличивает ошибку выборки.

После проведения выборки рассчитывают возможные ошибки . выборочных показателей (ошибки репрезентативности), которые используются для оценки результатов выборки и для получения характеристик генеральной совокупности.

Пример. На электроламповом заводе взято для проверки 100 ламп. Средняя продолжительность их горения оказалась 1420 ч со средним квадратическим отклонением 61,03 ч. Поскольку приемщика продукции интересует качество всей партии (50 тыс. электроламп), оценивают точность полученной средней. Средняя возможная ошибка вычисленной выборочной средней

  ч.

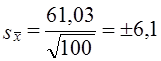
С вероятностью 0,954 предел возможной ошибки

∆_х = 2∙6,1 = ± 12,2 ч.

С вероятностью 0,954 можно утверждать, что средняя продолжительность горения 1 электролампы во всей партии будет находиться в пределах от 1408 до 1432 ч; 46 электроламп из 1000 могут иметь срок горения, выходящий за эти пределы.

Приемщика продукции интересуют отклонения от вычисленных пределов только в сторону сокращения продолжительности горения. Меньше чем 1408 ч могут гореть 23 лампы из 1000. На основании этого приемщик продукции решает вопрос о годности всей партии электроламп.

Решение вопроса может быть уточнено: определим, у какой доли ламп срок службы окажется меньше установленного лимита. Для потребителя продукции таким лимитом являются  1410 ч, продукция с меньшим сроком горения неприемлема.

При контрольной проверке 100 ламп 100 ламп горели менее 1410 ч, их удельный вес р = 0,1, или 10%. Средняя возможная ошибка этой доли

, или ± 3%.

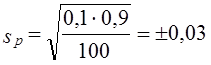
С вероятностью 0,954 предел ошибки доли Д^ = 2 • 0,03 = ± 0,06, или ±6%. Следовательно, во всей партии можно ожидать от 4 до 16% некачественных электроламп.

Чаще всего делают заключение об удовлетворительности выборки, сопоставляя получившиеся пределы ошибок выборочных показателей с величинами допустимых погрешностей. Может получиться, что предел ошибки, рассчитанный с заданной вероятностью, окажется выше допустимого размера погрешности. В этих случаях определяют вероятность того, что ошибка выборки не превзойдет допускаемую погрешность. Решение этой задачи и заключается в отыскании Fft) на основе формулы предела ошибки выборки:

,

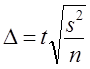
где ∆ — допустимый размер погрешности оцениваемого показателя;

s² — дисперсия показателя, рассчитанная по данным выборочного наблюдения;

п — объем проведенной выборки.

Продолжим пример с оценкой качества электроламп. Если при приемке партии электроламп ставится условие, что минимальный срок горения электроламп 1410 ч, то, учитывая среднюю продолжительность горения по выборке (х= 1420 ч), допустимая погрешность равна 10 ч: 1410 — 1420 = — 10 ч.

Как было установлено выше, с вероятностью 0,954 предел возможной ошибки выборочной средней составил 12,2 ч, что превосходит допустимую погрешность. Является ли это основанием для браковки всей партии? Для ответа на этот вопрос определяют вероятность риска при приемке продукции:

 , отсюда t= 1,64.

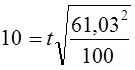
Соответствующая доверительная вероятность 0,899 (см. приложение, табл. 1). Вероятность того, что средний срок горения лампы меньше 1410 ч, равна:

 

Следовательно, из 100 ламп 5 могут гореть менее 1410 ч — риск появления некачественной продукции достаточно высок.

Аналогично можно определить вероятность того, что предел ошибки доли не превысит допускаемую погрешность доли.

Оценки надежности выборочных показателей, как показано на примере, позволяют принять обоснованные решения в отношении генеральной совокупности.

7.6. Распространение данных выборочного наблюдения на генеральную совокупность

Конечной целью выборочного наблюдения является характеристика генеральной совокупности на основе данных, полученных по выборке. При этом исходят из того, что все средние и относительные показатели, полученные по выборке, являются несмещенными и эффективными характеристиками генеральной совокупности.

Выборочные средние и относительные величины распространяются на генеральную совокупность обязательно с учетом предела их возможной ошибки. Приводится выборочный показатель со справкой о пределах ошибки с указанием доверительной вероятности:  x̅ ± ∆_x, p ± ∆_p.  Или же указывают границы значений генеральной характеристики с определенной вероятностью F(t):

 

Последняя форма записи является основной.

Иногда требуется указать только один (верхний или нижний) предел характеристики генеральной совокупности. При испытании качества продукции часто нас не интересуют положительные ошибки выборки (качество фактически выше, чем получилось по выборке), беспокоит нижний предел, как в примере, рассмотренном в предыдущем параграфе. В некоторых случаях, напротив, интерес вызывают верхние границы оцениваемых показателей, например при анализе расхода материалов. Так что при характеристике генеральной совокупности всегда указывают неблагоприятный предел.

На основе выборки могут быть получены и значения объемных показателей, т. е. подсчетов для генеральной совокупности. Такой расчет осуществляется двумя способами: путем прямого расчета и способом коэффициентов. Прямой расчет заключается в том, что выборочная средняя или доля умножается на объем генеральной совокупности:

 .

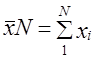
Так как средняя величина имеет ошибку репрезентативности ± А д то можно считать, что итоговый подсчет в генеральной совокупности находится в пределах

                                  (7.24)

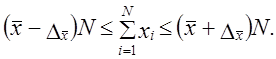
Итоговый подсчет по генеральной совокупности можно получить на основе итогового подсчета по выборке, разделив его на долю отбора единиц совокупности

 

Прежде чем проводить расчет объемных показателей для генеральной совокупности, нужно убедиться, что структура выборки соответствует структуре генеральной совокупности. При наличии значительных смещений в структуре выборки в долях отдельных групп (0,03 и выше) следует применить метод перевзвешивания, г. в. рассчитывать генеральную среднюю на основе выборочных средних по группам и удельного веса этих групп в генеральной совокупности:

  ,

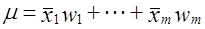
где w_i = N_iN.

При способе коэффициентов также используются не только выборочные данные, но и сведения о генеральной совокупности.

Этот способ основан на связи признаков друг с другом. Например, в результате выборочного обследования семей города получены размер среднедушевого дохода (х̅), средний доход семьи (у̅) и среднее число человек в семье (z̅). Так что x̅ = y̅ / z̅.

Зная численность населения города, требуется рассчитать общую величину денежного дохода населения. Очевидно, это можно сделать, умножив душевой доход на общее число жителей в городе: x̅N. Общий доход можно получить, суммируя доход отдельных семей; численность населения можно получить, суммируя данные о числе членов семей. Тогда

 .

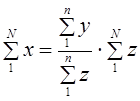
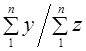
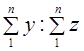
Средний душевой расход  представляет собой коэффициент, подсчитанный по выборке, который связывает две характеристики. Этот коэффициент рассчитывается как отношение двух итоговых подсчетов по выборке:

 .

Следовательно,

 .      

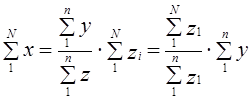
Последний сомножитель не что иное, как обратная величина доли отбора, рассчитанной по значениям признака z.

Итак, итоговый подсчет по генеральной совокупности может быть получен делением соответствующего итогового подсчета по выборке на долю отбора. При прямом расчете берется доля отбора единиц совокупности, при способе коэффициентов — доля отбора по значению какого-либо признака.

Эффективность способа коэффициентов по сравнению с методом прямого расчета зависит от того, насколько тесно связаны между собой признаки, лежащие в основе расчета коэффициента, т.е. признак, по которому подсчитывается итог, и признак, по которому определяется доля отбора. Эффект проявляется, если коэффициент корреляции между ними больше 0,8.

Способ коэффициентов используется для корректировки данных сплошного наблюдения. Например, перепись скота дала сведения, что поголовье свиней в районе составляет 10 000, в том числе в тех хозяйствах, которые потом были охвачены контрольным обходом, сплошное наблюдение показало число свиней 1100. Контрольный обход дал уточненную цифру: не 1100, а 1107 свиней. Тогда поправочный коэффициент

  .

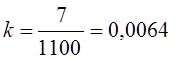
Отсюда скорректированная численность поголовья свиней во всем районе

N =N¢+∆N;  ∆N = kN¢ = ∙10 000 = 64.

N = 10 000 + 64 = 10 064 голов.

Таблицы интеграла вероятностей используются для выборок большого объема из бесконечно большой генеральной совокупности. Но уже при п <  00 получается несоответствие между табличными данными и вероятностью предела; при п < 100 погрешность становится значительной. Несоответствие вызывается главным образом характером распределения единиц генеральной совокупности. При большом объеме выборки особенность распределения в генеральной совокупности не имеет значения, так как распределение отклонений выборочного показателя от генеральной характеристики при большой выборке всегда оказывается нормальным.

В выборках небольшого объема п £ 30 характер распределения генеральной совокупности сказывается на распределении ошибок выборки. Поэтому для расчета ошибки выборки при небольшом объеме наблюдения (уже менее 100 единиц) отбор должен проводиться из совокупности, имеющей нормальное распределение.

Теория малых выборок разработана английским статистиком В. Госсетом (писавшим под псевдонимом Стьюдент) в начале XX в. В 1908 г. им построено специальное распределение, которое позволяет и при малых выборках соотносить t и доверительную вероятность F(t). При п > 100 таблицы распределения Стьюдента дают те же результаты, что и таблицы интеграла вероятностей Лапласа, при 30 £ п £ 100 различия незначительны. Поэтому практически к малым выборкам относят выборки объемом менее 30 единиц (безусловно, большой считается выборка с объемом более 100 единиц).

Использование малых выборок в ряде случаев обусловлено характером обследуемой совокупности. Так, в селекционной работе «чистого» опыта легче добиться на небольшом числе  делянок. Производственный и экономический эксперимент, связанный с экономическими затратами, также проводится на небольшом числе испытаний.

Как уже отмечалось, в случае малой выборки только для нормально распределенной генеральной совокупности могут быть рассчитаны и доверительные вероятности, и доверительные пределы генеральной средней.

Плотность вероятностей распределения Стьюдента описывается функцией

,                               (7.25)

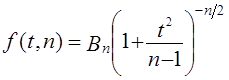
где  t — текущая переменная;

п — объем выборки;

В — величина, зависящая лишь от п.

Распределение Стьюдента имеет только один параметр: d.f. —число степеней свободы (иногда обозначается k).

Это распределение, как и нормальное, симметрично относительно точки t = 0, но оно более пологое. При увеличении объема выборки, а следовательно, и числа степеней свободы распределение Стьюдента быстро приближается к нормальному. Число степеней свободы равно числу тех индивидуальных значений признаков, которыми нужно располагать для определения искомой характеристики.

Так, для расчета дисперсии должна быть известна средняя величина. Поэтому при расчете дисперсии d.f. = п — 1

Таблицы распределения Стьюдента публикуются в двух вариантах:

1) аналогично таблицам интеграла вероятностей приводятся значения t и соответствующие вероятности F(t) при разном числе степеней свободы;

2) значения t приводятся для наиболее употребимых доверительных вероятностей 0,90; 0,95 и 0,99 или для 1 — 0,9 = 0,1, 1 — 0,95 = = 0,05 и 1 — 0,99 == 0,01 при разном числе степеней свободы. Такого рода таблица приведена в приложении (табл. 2), а также значение t-критерия Стьюдента при уровне значимости 0,10; 0,05; 0,01.

При малых выборках расчет средней возможной ошибки основан на выборочных дисперсиях, поэтому

 .

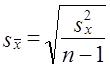
Приведенная формула используется для определения предела возможной ошибки выборочного показателя:

.

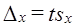
Порядок расчетов тот же, что и при больших выборках.

Пример. Для изучения интенсивности труда было организовано наблюдение за 10 отобранными рабочими. Доля работавших все время оказалась равной 0,40, дисперсия 0,4∙0,6 = 0,24. По табл. 2 приложения находим для F(t) = 0,95 и d.f. = n — 1 = 9, t = 2,26. Рассчитаем среднюю ошибку выборки доли работавших все время:

 

Тогда предельная ошибка выборки ∆_p = 2,26∙0,16 = ± 0,36. Таким образом, с вероятностью 0,95 доля рабочих, работавших без простоев, в данном цехе предприятия находится в пределах

39,64% £ π £ 40,36%

или

39,6% £ π £ 40,4%.

Если бы мы использовали для расчета доверительных границ генерального параметра таблицу интеграла вероятностей, то t было бы равно 1,96 и ∆_p — ± 0,31, т. е. доверительный интервал был бы несколько уже.

Малые выборки широко используются для решения задач, связанных с испытанием статистических гипотез, особенно гипотез о средних величинах.