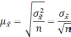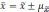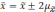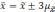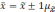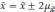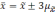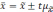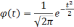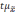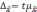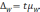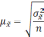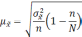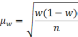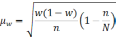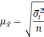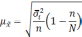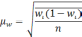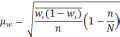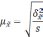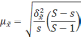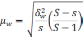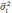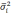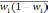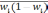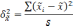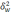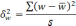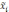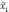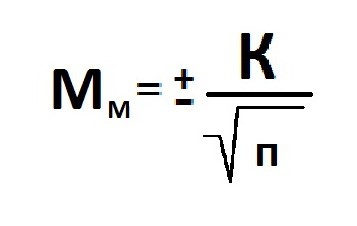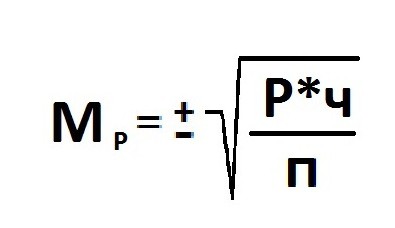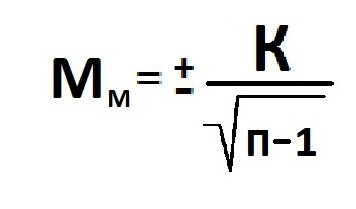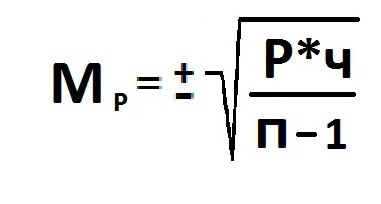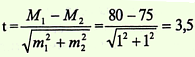В
статистике выделяют два основных метода
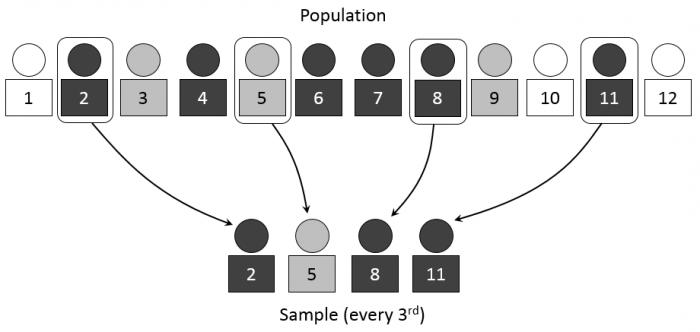
исследования — сплошной и выборочный.
При проведении выборочного исследования
обязательным является соблюдение
следующих требований: репрезентативность
выборочной совокупности и достаточное
число единиц наблюдений. При выборе
единиц наблюдения возможны ошибки
смещения,
т.е. такие события, появление которых
не может быть точно предсказуемым. Эти
ошибки являются объективными и
закономерными. При определении степени
точности выборочного исследования
оценивается величина ошибки, которая
может произойти в процессе выборки
— случайная
ошибка репрезентативности (m) — является
фактической разностью между средними
или относительными величинами, полученными
при проведении выборочного исследования
и аналогичными величинами, которые были
бы получены при проведении исследования
на генеральной совокупности.
Оценка
достоверности результатов исследования
предусматривает определение:
1.
ошибки репрезентативности
2.
доверительных границ средних (или
относительных) величин в генеральной
совокупности
3.
достоверности разности средних (или
относительных) величин (по критерию t)
Расчет
ошибки репрезентативности
(mм)
средней арифметической величины
(М):

где σ
— среднее квадратическое отклонение; n
— численность выборки (>30).
Расчет
ошибки репрезентативности (mР)
относительной величины (Р):

где Р — соответствующая относительная
величина (рассчитанная, например, в %);
q
=100 — Ρ%
— величина, обратная Р; n — численность
выборки (n>30)
В
клинических и экспериментальных работах
довольно часто приходится использовать
малую
выборку, когда
число наблюдений меньше или равно 30.
При малой выборке для расчета ошибок
репрезентативности, как средних, так
и относительных величин,
число
наблюдений уменьшается на единицу,
т.е.
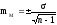

Величина
ошибки репрезентативности зависит от
объема выборки: чем больше число
наблюдений, тем меньше ошибка. Для оценки
достоверности выборочного показателя
принят следующий подход: показатель
(или средняя величина) должен в 3 раза
превышать свою ошибку, в этом случае он
считается достоверным.
21. Оценка достоверности разности статистических величин.
Достоверность
разности между двумя средними величинами
определяется по формуле:

где
М1
и М2
– две средних арифметических величины,
полученные в двух самостоятельных
независимых группах наблюдений;
m1
и m2
— их средние ошибки (выражение
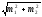
средних).
При
t ≥ 2 разность средних арифметических
может быть признана существенной и
неслучайной, то есть достоверной. Это
значит, что и в генеральной совокупности
средние величины отличаются, и что при
повторении подобных наблюдений будут
получены аналогичные различия. При t =
2 надежность также увеличивается, а риск
ошибки уменьшается. При t< 2 достоверность
разности средних величин считается
недоказанной.
23. Понятие о корреляционном анализе.
Корреляционная
связь может быть прямолинейной и
криволинейной.
Прямолинейная
связь характеризуется относительно
равномерным изменением средних значений
одного признака при равных изменениях
другого.
При
криволинейной связи – при равномерном
изменении одного признака могут
наблюдаться возрастающие и убывающие
значения другого признака.
Методы
вычисления коэффициентов корреляции:
рангов, квадратов, путем составления
корреляционной решетки.
Соседние файлы в предмете [НЕСОРТИРОВАННОЕ]
- #
- #
- #
- #
- #
- #
- #
- #
- #
19.02.201618.05 Mб137patofiziologiya_sist_krovi_2010.doc
- #
- #
Ошибка выборки или, иначе говоря, ошибка репрезентативности — это разница между значением показателя, полученного по выборке, и генеральным параметром. Так, ошибка репрезентативности выборочной средней равна ег = х — ц, выборочной относительной величины гг=р-п, дисперсии едЛ = s1 — а2, коэффициента корреляции ЕГ = г — р. [c.165]
Если представить, что было проведено бесконечное число выборок равного объема из одной и той же генеральной совокупности, то показатели отдельных выборок образовали бы ряд возможных значений выборочных средних величин х,, х-,, х3,. … относительных величин / ,, р2, ръ. … дисперсий s, s 2, s . .., и т. д. Каждая выборка имеет свою ошибку репрезентативности. Следовательно, можно построить ряды распределения выборок по величине ошибки репрезентативности для каждого показателя для средней, относительной величины и т.д. В таких распределениях улавливается тенденция к концентрации ошибок около центрального значения. Число выборок с той или иной величиной ошибки репрезентативности может быть симметрично или асимметрично относительно этого центрального значения. При бесконечно большом числе выборок получится кривая частот, которая представляет кривую выборочного распределения. Свойства таких распределений используются для получения статистических заключений, установления вероятности той или иной величины ошибки репрезентативности. [c.165]
Фактическая ошибка репрезентативности [c.177]
Фактическая ошибка репрезентативности составляет [c.177]
После проведения выборки рассчитывают возможные ошибки выборочных показателей (ошибки репрезентативности), которые используются для оценки результатов выборки и для получения характеристик генеральной совокупности. [c.185]
Так как средняя величина имеет ошибку репрезентативности Ах, то можно считать, что итоговый подсчет в генеральной совокупности находится в пределах [c.188]
Оценку генерального параметра получают на основе выборочного показателя с учетом ошибки репрезентативности. В другом случае в отношении свойств генеральной совокупности выдвигается некоторая гипотеза о величине средней, дисперсии, характере распределения, форме и тесноте связи между переменными. Проверка гипотезы осуществляется на основе выявления согласованности эмпирических данных с гипотетическими (теоретическими). Если расхождение между сравниваемыми величинами не выходит за пределы случайных ошибок, гипотезу принимают. При этом не делается никаких заключений о правильности самой гипотезы, речь идет лишь о согласованности сравниваемых данных. Основой проверки статистических гипотез являются данные случайных выборок. При этом безразлично, оцениваются ли гипотезы в отношении реальной или гипотетической генеральной совокупности. Последнее открывает путь применения этого метода за пределами собственно выборки при анализе результатов эксперимента, данных сплошного наблюдения, но малой численности. В этом случае рекомендуется проверить, не вызвана ли установленная закономерность стечением случайных обстоятельств, насколько она характерна для того комплекса условий, в которых находится изучаемая совокупность. [c.193]
Расхождение между расчетным и действительным значением изучаемых величин называется ошибкой наблюдения. В зависимости от причин возникновения различают ошибки регистрации и ошибки репрезентативности. [c.21]
В отличие от ошибок регистрации ошибки репрезентативности характерны только для несплошного наблюдения. Они возникают потому, что отобранная и обследованная совокупность недостаточно точно воспроизводит генеральную совокупность в целом. [c.22]
Отклонение значения показателя обследованной совокупности от его величины в генеральной совокупности называется ошибкой репрезентативности. [c.22]
Ошибки репрезентативности также бывают случайными и систематическими. Случайные ошибки репрезентативности возникают, если отобранная совокупность неполно воспроизводит совокупность в целом. Величина этих ошибок может быть оценена. [c.22]
Систематические ошибки репрезентативности появляются вследствие нарушения принципов отбора единиц из исходной совокупности, которые должны быть подвергнуты наблюдению. Для устранения ошибок наблюдения необходимо осуществить контроль полученной информации. [c.22]
Поскольку / указывает на вероятность расхождения х-х , т.е. на вероятность того, на какую величину генеральная средняя будет отличаться от выборочной средней, то это может быть прочитано так с вероятностью 0,683 можно утверждать, что разность между выборочной и генеральной средними не превышает одной величины средней ошибки выборки. Другими словами, в 68,3% случаев ошибка репрезентативности не выйдет за пределы ц. С вероятностью 0,954 можно утверждать, что ошибка репрезентативности не превышает 2ц, (т.е. в 95% случаев). С вероятностью 0,997, т.е. довольно близкой к единице, можно ожидать, что разность между выборочной и генеральной средней не превзойдет трехкратной средней ошибки выборки и т.д. Логически связь здесь выглядит довольно ясно чем больше пределы, в которых допускается возможная ошибка, тем с большей вероятностью судят о ее величине. [c.132]
Среднее значение удельных приведенных затрат для внутризаводских сетей промышленной канализации на 1 м3 часовой суммарной пропускной способности равно 99,36 руб/м3/ч. Вследствие небольшого объема представленной выборки определили, можно ли пользоваться найденным средним значением, используя для определения ошибки репрезентативности малой выборки критерий t — Стьюдента. . [c.39]
Д, , — ошибка репрезентативности выборки, зависящая от уровня доверительной вероятности [c.147]
Степень варьирования оценивается дисперсией G 2, а ошибка репрезентативности [c.147]
Разность между результатами выборочного и сплошного наблюдения называется ошибками репрезентативности. На основе применения математики можно заранее рассчитать репрезентативность выборки информации, ее соответствие генеральной совокупности. [c.481]
Предельная ошибка выборки А= Л ц. Доверительное число t показывает, что расхождение не превышает кратную ему ошибку выборки. С вероятностью 0,954 можно утверждать, что разность между выборочной и генеральной не превысит двух величин средней ошибки выборки, т.е. в 954 случаях ошибка репрезентативности не выйдет за 2ц. [c.222]
Ошибки наблюдения подразделяются на два вида ошибки регистрации и ошибки репрезентативности. [c.36]
Ошибки репрезентативности возникают при несплошном обследовании в силу того, что состав отобранной для него части единиц совокупно- [c.36]
Ошибки репрезентативности. Основные проблемы выборочного наблюдения сводятся к тому, что при его применении могут возникать определенные ошибки. Следовательно, аудиторы вынуждены учитывать риски, свойственные выборочному наблюдению, а также знать, как необходимо минимизировать эти риски. Аудиторы называют это риском ошибочного принятия (непринятия) результатов выборки. При этом в аудиторской практике различают риски первого и второго рода для тестов системы контроля и проверки верности оборотов и сальдо по счетам [там же]. [c.49]
Главные ошибки, возникающие при выборочном наблюдении, — это ошибки репрезентативности. Аудитор обязан обеспечить представительную (репрезентативную) выборку для данной совокупности. Проявляя должную тщательность в работе, он стремится точно установить и зарегистрировать в своей выборке факты хозяйственной жизни экономического субъекта, остатки по счетам, статьи баланса и т.д., но тем не менее по окончании всех [c.49]
Случайные ошибки репрезентативности. Риск (опасность) возникновения этих ошибок проистекает из собственно случайных обстоятельств (типа арифметических ошибок при отсутствии контроля, описок и т.д.). Но мы сознательно оставляем в стороне и не анализируем здесь тривиальные ошибки наблюдения, которые выражаются, скажем, в описках и которые может допустить любой ассистент аудитора, осуществляющий выборку. [c.50]
Систематические ошибки репрезентативности. Если же аудитор или его ассистент нарушают принцип случайности при отборе, то они рискуют получить систематические ошибки репрезентативности. Например, из всей совокупности дебиторской задолженности аудитор отобрал только просроченную (такой было 10%) и на основании других свидетельств установил, что половина отобранных им остатков по счетам — это задолженность безнадежная. Если на основе такой выборки аудитор будет считать, что безнадежная задолженность составляет 50% всех дебиторов проверяемого экономического субъекта, то скорее всего он глубоко ошибается (она вполне может быть на уровне, близком к 5%), поскольку уровень вероятности появления безнадежной задолженности намного выше именно в просроченной задолженности. Другими словами, аудитор рискует получить подобные погрешности в тех случаях, когда выборочная совокупность недостаточно точно воспроизводит те особенности и пропорции, которые имеются в проверяемой совокупности. [c.51]
Систематические ошибки репрезентативности — это неточности, которые аудитор может получить в процессе статистического выборочного наблюдения по вполне определенным причинам. Такие ошибки могут возникнуть как следствие преднамеренного или непреднамеренного искажения информации. Систематические ошибки репрезентативности тоже могут привести к искажению полученных результатов (как в сторону увеличения, так и в сторону уменьшения), по которым аудитор будет судить о всей проверяемой совокупности. Таким образом, в основе систематических ошибок репрезентативности лежит именно выборка, именно сам несплошной характер наблюдения. [c.51]
Ошибка репрезентативности — разница между результатами выборочного и сплошного наблюдения. [c.546]
Выборочному обследованию свойственна некоторая погрешность в сравнении со сплошным, которая органически присуща вообще любому выборочному наблюдению. Указанная погрешность или ошибка носит название ошибки репрезентативности. [c.101]
Выборочной средней и выборочной доле свойственны, как указано выше, ошибки репрезентативности. Теория выборочного метода дает возможность определить средние этих ошибок. [c.102]
Сравнивая выборочную среднюю с генеральной средней, видим расхождение — 0,8 млн. руб. (11,6—10,8 = = 0,8). Это так называемая ошибка репрезентативности случайного бесповторного отбора. [c.106]
В среднем объем строительно-монтажных работ по этим трестам составил 10,6 млн. руб. Ошибка репрезентативности — 1,0 млн. руб. [c.107]
В среднем по 16 отобранным трестам объем строительно-монтажных работ составил 10,5 млн. руб. Ошибка репрезентативности 1,1 млн. руб. [c.108]
Выше разобраны пять основных способов отбора выборочной совокупности. Каждый из них имеет свою ошибку репрезентативности. Наименьшие ошибки репрезентативности получены при механическом отборе и при случайной выборке и наибольшая — при серийном отборе. В других случаях результаты могут получиться иные. В учебниках по статистике указывается, что теоретически наименьшая ошибка должна наблюдаться при типическом, затем при механическом отборах и случайной выборке. Наибольшая ошибка — при серийном отборе. [c.108]
Практически при пользовании выборочным методом остаются неизвестными ошибки репрезентативности, так как неизвестна бывает генеральная средняя. В связи с этим необходимо теоретически определить возможную величину этой ошибки. [c.108]
Разность между показателями выборочной и генеральной совокупности называется ошибкой выборки. Ошибки выборки подразделяются на ошибки регистрации и ошибки репрезентативности. [c.22]
Ошибки репрезентативности также могут быть систематическими и случайными. Систематические ошибки репрезентативности возникают из-за неправильного, тенденциозного отбора единиц, при котором нарушается основной принцип научно организованной выборки — принцип случайности. Случайные ошибки репрезентативности означают, что, несмотря на принцип случайности отбора единиц, все же имеются расхождения между [c.22]
Разность между показателями выборочной и генеральной совокупности и будет случайной ошибкой репрезентативности. Ошибки репрезентативности [c.23]
При определении ошибки репрезентативности и объема выборки [c.16]
Как видно из приведенных расчетов, метод высшей и низшей точек довольно прост в применении. Его цель состоит в том, чтобы спрогнозировать поведение издержек при изменении деловой активности предприятия. Как и в любом прогнозе, здесь существует некоторая вероятность ошибки. Это связано с тем, что значение двух крайних показателей не всегда имеет репрезентативный характер. Поэтому из расчета следует исключать случайные, нехарактерные данные. [c.64]
Эта величина меньше предельной ошибки выборки, гарантированной с принятой доверительной вероятностью, 0,36 < 0,55. Следовательно, выборка репрезентативна по этому признаку. [c.177]
Ошибки репрезентативности, т.е. расхождения между данными выборочного наблюдения и данными всей совокупности, могут быть получены только при несплошном наблюдении, они про-изводны от самой сути выборочного наблюдения. При этом существуют и, соответственно, аудиторы должны различать две разные группы ошибок репрезентативности случайные и систематические. [c.50]
В среднем объем по этим 16 трестам к = 12,2 млн. руб. Отклонение от генеральной средней — 0,6 млн. руб. (11,6 — 12,2 — — 0,6). Ошибка репрезентативности случайного повторного итоора получилась в данном случае несколько меньше, чем в бесповторпом. [c.106]
Такая же опасность возникает при замене по какой-либо причине единиц, попавших в выборку, другими единицами (например, вместо отобранного домохозяйства, где в момент прихода интервьюера никто не открыл дверь, был проведен опрос в соседней квартире или интервьюер встретил решительный отказ участвовать в опросе и был вынужден пойти на замену домохозяйства). Как отмечает социолог В. И. Паниотто, систематические ошибки представляют собой некоторое постоянное смещение, которое не уменьшается с увеличением числа опрошенных и вызвано недостатками и просчетами в системе отбора респондентов. Если, например, для изучения общественного мнения жителей города в архитектурном управлении получить сведения о жилом фонде и из всех имеющихся в городе квартир отобрать случайным образом 400 квартир, а затем предложить интервьюерам опросить всех, кого они застанут в момент посещения в этих квартирах, то полученные данные не будут репрезентативны. Допущена систематическая ошибка более подвижная часть населения попадает в выборку в меньшей пропорции, а менее подвижная — в большей пропорции, чем в генеральной совокупности. Пенсионеров, например, можно чаще застать дома, чем студентов-вечерников. При увеличении выборки эта ошибка не устраняется если мы проведем опрос в 800 квартирах или даже во всех квартирах города (сплошной опрос), то полученные данные будут репрезентативны для населения, находящегося дома в момент прихода интервьюера, а не для всех жителей города. [c.164]
Ошибка
репрезентативности
— расхождение между выборочной
характеристикой и характеристикой
генеральной совокупности.
Ошибки
репрезентативности
-
Систематические
— возникают в результате нарушения
научных принципов отбора единиц
совокупности (преднамеренные и
непреднамеренные). -
Случайные
возникают в результате несплошного
характера наблюдения (средняя и
предельная ошибки выбора).
Случайные
ошибки могут быть доведены до незначительных
размеров, а главное, их размеры и пределы
можно определить с достаточной точностью
на основании закона больших чисел.
Средняя
ошибка выборки
— такое расхождение между средними
выборочной и генеральной совокупностями,
которое не превышает ±.
В
математической статистике доказывается,
что значения средней ошибки выборки
определяются по формулам:
Формула
для определения величины средней ошибки
выборки для количественного признака:
Формула
для определения величины средней ошибки
выборки для альтернативного признака:
Полученное
значение средней ошибки необходимо для
установления возможного значения 
Которое определяется по формуле:
Но
такое суждение можно гарантировать не
с абсолютной
достоверностью, а лишь с определенной
степенью
вероятности.
В
математической статистике доказывается,
что пределы значений характеристик
генеральной совокупности отличаются
от характеристик выборочной совокупности
лишь с вероятностью, которая определена
числом 0,683.
Это
означает, что в 683 случаях из 1000 генеральная
средняя будет находиться в установленных
пределах, т.е. отклонение ГС от ВС не
превысит однократной средней ошибки
выборки. В остальных 317 случаях они могут
выйти за эти пределы. Вероятность можно
повысить, если расширить пределы
отклонений. Так, при удвоенном значении

вероятность достигает 0,954 (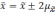
Если утроить значение то вероятность
увеличится до 0,997 (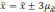
|
Возможное |
Вероятность |
|
|
0,683 |
|
|
0,954 |
|
|
0,997 |
Если
обозначить значение увеличения
за
t,
то можно записать в общем виде:
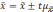
Множитель
t
называется коэффициентом
доверия.
Известный русский математик А.М.Ляпунов
дал выражение конкретных значений
множителя t
для различных степеней вероятности в
виде функции:
На
практике пользуются готовыми таблицами
этой функции.
|
t |
0 |
0,1 |
0,5 |
1 |
1,5 |
2 |
2,5 |
2,6 |
3 |
4 |
|
(t) |
0,1 |
0,0797 |
0,3829 |
0,6827 |
0,8664 |
0,9545 |
0,9876 |
0,9907 |
0,9973 |
0,99994 |
Из
вышесказанного следует, что лишь с
определенной степенью вероятности
можно утверждать, что показатели
генеральной совокупности и их отклонения
не превысят величину 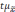
Полученную величину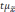
ошибкой выборки.
Предельная
ошибка выборки
—
максимально
возможное расхождение выборочной и
генеральной средних,
т.е.
максимум ошибки при заданной вероятности
ее появления.
Предельная
ошибка выборки для количественного
признака:
Предельная
ошибка выборки для альтернативного
признака:
В
связи с тем, что существуют различные
методы, виды и способы отбора единиц из
генеральной совокупности формулы для
расчета средней ошибки выборки также
будут различаться:
|
Способ |
Оцениваемый |
Повторный |
Бесповторный |
|
Собственно случайный механический |
Средняя |
|
|
|
Доля |
|
|
|
|
Типический |
Средняя |
|
|
|
Доля |
|
|
|
|
Серийный |
Средняя |
|
|
|
Доля |
|
|
— средняя из групповых дисперсий;
wi
— доля
единиц совокупности, обладающих изучаемым
признаком в i-й
типической
группе;
— средняя из групповых дисперсий для
доли. В табл. 6.6 представлены формулы
для исчисления средней ошибки выборки
при типическом отборе;
S
– общее число серий;
s
– число отобранных серий;
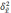
межгрупповая дисперсия средних,
определяемая по формуле:
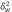
межгрупповая дисперсия доли, определяемая
по формуле:
— средняя
i-й
серии;
—
средняя по всей выборочной совокупности;
w
— доля признака i-й
серии;
— общая доля признака во всей выборочной
совокупности.
Соседние файлы в предмете [НЕСОРТИРОВАННОЕ]
- #
- #
- #
- #
- #
- #
- #
- #
- #
- #
- #
Понятие репрезентативности часто встречается в статистических отчетностях и при подготовке выступлений и докладов. Пожалуй, без нее трудно представить себе какой-либо из видов подачи информации на обозрение.
Репрезентативность — что это?
Репрезентативность отражает, насколько выбранные объекты или части соответствуют содержанию и смыслу совокупности данных, из которой они были выбраны.
Другие определения
Понятие репрезентативности можно раскрывать в разных контекстах. Но по своему смыслу репрезентативность – это соответствие черт и свойств выбранных единиц из общей совокупности, которые точно отражают характеристики всей генеральной базы данных в целом.
Также репрезентативность информации определяют как способность выборочных данных представить параметры и свойства совокупности, важные с точки зрения проводимого исследования.
Репрезентативная выборка
Принцип формирования выборки заключается в избрании наиболее важных и точно отображающих свойства общей совокупности данных. Для этого используются различные методы, которые позволяют получать точные результаты и общее представление о генеральной совокупности, используя только выборочные материалы, описывающие качества всех данных.
Таким образом, нет необходимости изучать весь материал, а достаточно рассмотреть выборочную репрезентативность. Что это? Это выборка отдельных данных для того, чтобы иметь понятие об общей массе информации.
Их в зависимости от способа различают как вероятностные и невероятностные. Вероятностная – это выборка, которая производится путем вычисления наиболее важных и интересных данных, являющихся в дальнейшем представителями генеральной совокупности. Это обдуманный выбор или случайная выборка, тем не менее, обоснованная своим содержанием.
Невероятностная – это одна из разновидностей случайной выборки, составляющаяся по принципу обычной лотереи. В таком случае не учитывается мнение того, кто составляет такую выборку. Используется лишь слепой жребий.
Вероятностная выборка
Вероятностные выборки также могут подразделяться на несколько видов:
- Одна из самых простых и понятных принципов – это нерепрезентативная выборка. К примеру, такой способ часто используется при проведении социальных опросов. При этом участники опроса не выбираются из толпы по каким-либо определенным признакам, и получение информации производится у первых 50 людей, принявших участие в нём.
- Преднамеренные выборки отличаются тем, что имеют ряд требований и условий при отборе, однако все же полагаются на случайное совпадение, не преследуя своей целью достижение хорошей статистики.
- Выборка на основании квот – это еще одна из вариаций невероятностной выборки, которая часто используется для исследования больших совокупностей данных. Для нее используется множество условий и норм. Подбираются объекты, которые должны им соответствовать. То есть на примере социального опроса можно предположить, что опрошены будут 100 человек, но только мнение некоторого числа людей, которые будут соответствовать установленным требованиям, будут учтены при составлении статистического отчета.
Вероятностные выборки
Для вероятностных выборок исчисляется ряд параметров, которым объекты в выборке будут соответствовать, и среди них разными способами могут избираться именно те факты и данные, которые будут представлены как репрезентативность данных выборки. Такими способами вычисления нужных данных могут быть:
- Простая случайная выборка. Заключается в том, что среди выбранного сегмента совершенно случайным методом лотереи выбирается необходимое количество данных, которые будут являться репрезентативной выборкой.
- Систематическая и случайная выборка дает возможность составить систему вычисления необходимых данных на основе случайно выбранного сегмента. Таким образом, если первое случайное число, которое указывает на порядковый номер данных, выбранных из общей совокупности, будет 5, то последующими данными, которые будут выбраны, могут стать, например, 15, 25, 35 и так далее. Этот пример наглядно объясняет, что даже случайный выбор может основываться на систематических вычислениях необходимых исходных данных.
Выборка потребителей
Осмысленная выборка – это способ, который заключается в рассмотрении каждого отдельного сегмента, и на основании его оценки составляется совокупность, отражающая характеристики и свойства общей базы данных. Таким образом набирается большее количество данных, соответствующих требованиям репрезентативной выборки. Можно легко отобрать некоторое количество вариантов, которые не войдут в общее число, не потеряв при этом качество отобранных данных, представляющих общую совокупность. Таким способом определяется репрезентативность результатов исследования.
Размер выборки
Не последний вопрос, который необходимо решить, – это размер выборки для репрезентативного представления генеральной совокупности. Размер выборки не всегда зависит от количества исходников в генеральной совокупности. Однако репрезентативность выборочной совокупности напрямую зависит от того, на сколько сегментов должен быть в итоге разделён результат. Чем больше таких сегментов, тем больше данных попадает в результативную выборку. Если результаты требуют общего обозначения и не требуют конкретики, тогда, соответственно, выборка становится меньше, поскольку, не вдаваясь в детали, информация излагается более поверхностно, а значит, ее прочтение будет общим.
Понятие ошибки репрезентативности
Ошибка репрезентативности – это конкретные расхождения между характеристиками генеральной совокупности и выборочных данных. При проведении любого выборочного исследования невозможно получить абсолютно точные данные, как при полном исследовании генеральных совокупностей и выборки, представленной лишь частью сведений и параметров, тогда как более детальное изучение возможно только при исследовании всей совокупности. Таким образом, неизбежны некоторые погрешности и ошибки.
Виды ошибок
Различают некоторые ошибки, которые возникают при составлении репрезентативной выборки:
- Систематические.
- Случайные.
- Преднамеренные.
- Непреднамеренные.
- Стандартные.
- Предельные.
Основанием для появления случайных ошибок может быть несплошной характер исследования общей совокупности. Обычно случайная ошибка репрезентативности имеет незначительный размер и характер.
Систематические ошибки между тем возникают при нарушении правил отбора данных из общей совокупности.
Средняя ошибка – это разница между усредненными значениями выборки и основной совокупностью. Она не зависит от количества единиц в выборке. Она обратно пропорциональна объему выборки. Тогда чем больше объем, тем меньше значение средней ошибки.
Предельная ошибка – это наибольшая возможная разница между усредненными значениями сделанной выборки и общей совокупностью. Такая ошибка охарактеризовывается как максимум вероятных ошибок при заданных условиях их появления.
Преднамеренные и непреднамеренные ошибки репрезентативности
Ошибки смещения данных бывают преднамеренными и непреднамеренными.
Тогда причинами появления преднамеренных ошибок является подход к подбору данных по методу определения тенденций. Непреднамеренные ошибки возникают еще на стадии подготовки выборочного наблюдения, формирования репрезентативной выборки. Для недопущения подобных ошибок необходимо создать хорошую основу для выборки, составляющей списки единиц отбора. Она должна полностью соответствовать целям проведения выборки, быть достоверной, охватывающей все аспекты исследования.
Валидность, надежность, репрезентативность. Расчет ошибок
Расчет ошибки репрезентативности (Мм) средней арифметической величины (М).
Среднее квадратическое отклонение: численность выборки (>30).
Ошибка репрезентативности (Мр) и относительная величина (Р): численность выборки (n>30).
В том случае, когда приходится изучать совокупность, где количество выборки мало и составляет меньше 30 единиц, тогда число наблюдений станет меньше на одну единицу.
Величина ошибки прямо порциональна объему выборки. Репрезентативность информации и вычисление степени возможности составления точного прогноза отражает определенная величина предельной ошибки.
Репрезентативные системы
Не только в процессе оценки подачи информации используется репрезентативная выборка, но и сам человек, получающий информацию, использует репрезентативные системы. Таким образом, мозг обрабатывает некоторое количество информации, создавая репрезентативную выборку из всего потока информации, чтобы качественно и быстро оценить подаваемые данные и понять суть вопроса. Ответить на вопрос: «Репрезентативность — что это?» — в масштабах человеческого сознания довольно просто. Для этого мозг использует все подвластные органы чувств, в зависимости от того, какую именно информацию необходимо вычленить из общего потока. Таким образом, различают:
- Визуальную репрезентативную систему, где задействуются органы зрительного восприятия глаза. Люди, часто использующие подобную систему, называются визуалами. С помощью этой системы человек обрабатывает информацию, поступающую в виде изображений.
- Аудиальная репрезентативная система. Главный орган, который используется – это слух. Информация, подаваемая в виде звуковых файлов или речи, обрабатываются именно этой системой. Люди, лучше воспринимающие информацию на слух, называются аудиалами.
- Кинестетическая репрезентативная система представляет собой обработку потока информации, путем восприятия его с помощью обонятельных и осязательных каналов.
- Дигитальная репрезентативная система используется вместе с другими как средство получения информации извне. Это субъективно-логическое восприятие и осмысление полученных данных.
Итак, репрезентативность — что это? Простая выборка из множества или неотъемлемая процедура при обработке информации? Однозначно можно сказать, что репрезентативность во многом определяет наше восприятие потоков данных, помогая вычленить из него наиболее веские и значимые.
Концепция репрезентативности часто встречается в статистических отчетах и при подготовке выступлений и отчетов. Пожалуй, без него сложно представить какое-либо представление информации для ознакомления.
Содержание
- 1 Репрезентативность — что это?
- 2 Другие определения
- 3 Репрезентативная выборка
- 4 Вероятностная выборка
- 5 Вероятностные выборки
- 6 Выборка потребителей
- 7 Размер выборки
- 8 Понятие ошибки репрезентативности
- 9 Виды ошибок
- 10 Преднамеренные и непреднамеренные ошибки репрезентативности
- 11 Валидность, надежность, репрезентативность. Расчет ошибок
- 12 Репрезентативные системы
Репрезентативность — что это?
Репрезентативность отражает степень, в которой выбранные объекты или части соответствуют содержанию и значению набора данных, из которого они были выбраны.
Другие определения
Репрезентативность можно понимать в разных контекстах. Но по своему смыслу репрезентативность — это соответствие характеристик и свойств выбранных единиц генеральной совокупности, которые точно отражают характеристики всей генеральной базы данных в целом.
Кроме того, репрезентативность информации определяется как способность данных выборки представлять параметры и свойства совокупности, которые важны с точки зрения проводимых исследований.
Репрезентативная выборка
Принцип выборки заключается в выборе наиболее важных свойств, которые точно отражают общую совокупность данных. Для этого используются различные методы, позволяющие получить точные результаты и общее представление о генеральной совокупности, используя только выборочные материалы, описывающие качество всех данных.
Таким образом, нет необходимости изучать весь материал, но достаточно учесть выборочную репрезентативность. Что это? Это набор отдельных данных, чтобы получить представление об общей массе информации.
В зависимости от метода они делятся на вероятностные и маловероятные. Вероятностный — это выборка, которая создается путем вычисления наиболее важных и интересных данных, которые в будущем будут репрезентативными для генеральной совокупности. Это осознанный выбор или случайная выборка, однако оправданная своим содержанием.
Маловероятно — это одна из разновидностей случайной выборки, составленной по принципу обычной лотереи. В этом случае мнение лица, взявшего такую пробу, не принимается во внимание. Используется только слепая жребий.
Вероятностная выборка
Вероятностные выборки также можно разделить на несколько типов:
- Один из самых простых и понятных принципов — нерепрезентативная выборка. Например, этот метод часто используется при проведении социальных опросов. При этом участники опроса не выбираются из общей массы по каким-либо конкретным критериям, а информация берется от первых 50 человек, принявших участие.
- Выборка вероятностей — это еще одна разновидность выборки невероятности, которая часто используется для исследования больших наборов данных. Для этого используется множество условий и правил. Выбираются объекты, которые должны им соответствовать. То есть на примере социального опроса можно предположить, что будет опрошено 100 человек, но при составлении статистического отчета будет учитываться только мнение определенного количества людей, которые будут соответствовать установленным требованиям.
- Преднамеренные выборки отличаются тем, что они имеют ряд требований и условий для отбора, но все же полагаются на совпадения, не преследуя цели получения хорошей статистики.
Вероятностные выборки
Для вероятностных выборок рассчитывается ряд параметров, которым будут соответствовать объекты в выборке, и среди них различными способами могут быть выбраны именно те факты и данные, которые будут представлены как репрезентативность данных выборки. Эти методы расчета требуемых данных могут быть:
- Простая случайная выборка. Он заключается в том, что среди выделенного сегмента методом полностью случайной лотереи выбирается необходимый объем данных, который будет репрезентативной выборкой.
- Систематическая и случайная выборка позволяет составить систему расчета необходимых данных на основе случайно выбранного сегмента. Итак, если первое случайное число, указывающее порядковый номер данных, выбранных из общей совокупности, равно 5, следующими данными для выбора могут быть, например, 15, 25, 35 и так далее. Этот пример ясно объясняет, что даже случайный выбор может быть основан на систематических вычислениях требуемых входных данных.
Выборка потребителей
Осмысленная выборка — это способ взглянуть на каждый отдельный сегмент, и на основе его оценки составляется генеральная совокупность, отражающая характеристики и свойства всей базы данных. Таким образом, собирается больше данных, отвечающих требованиям репрезентативной выборки. Легко выбрать набор параметров, которые не будут включены в общее количество, без потери качества выбранных данных, представляющих генеральную совокупность. Таким образом определяется репрезентативность результатов исследования.
Размер выборки
Не последняя проблема, которую необходимо решить, — это размер выборки для репрезентативной репрезентативности населения. Размер выборки не всегда зависит от количества источников в генеральной совокупности. Однако репрезентативность выборки напрямую зависит от того, на сколько сегментов в конечном итоге следует разделить результат. Чем больше таких сегментов, тем больше данных включается в итоговую выборку. Если результаты требуют общих обозначений и не требуют конкретики, то в результате выборка становится меньше, поскольку, не вдаваясь в детали, информация представлена более поверхностно, а значит, ее прочтение будет общим.
Понятие ошибки репрезентативности
Репрезентативная систематическая ошибка — это конкретное несоответствие между характеристиками населения и данными выборки. При проведении выборочного исследования невозможно получить абсолютно точные данные, как при полном изучении генеральных популяций и выборки, представленной только частью информации и параметров, в то время как более детальное изучение возможно только при изучении всей совокупности численность населения. Поэтому некоторые ошибки и ошибки неизбежны.
Виды ошибок
При составлении репрезентативной выборки возникают некоторые ошибки:
- Случайный.
- Стандарт.
- Не намеренно.
- Систематический.
- Предел.
- Умышленное.
Причиной появления случайных ошибок может быть прерывистый характер исследования генеральной совокупности. Обычно ошибка случайной репрезентативности незначительна по величине и характеру.
Между тем систематические ошибки возникают, когда нарушаются правила отбора данных из генеральной совокупности.
Средняя ошибка — это разница между средним значением выборки и основной совокупностью. Это не зависит от количества единиц в выборке. Он обратно пропорционален размеру выборки. Таким образом, чем больше объем, тем меньше среднее значение ошибки.
Предельная ошибка — это наибольшая возможная разница между средним значением выполненной выборки и всей генеральной совокупностью. Эта ошибка характеризуется как максимум возможных ошибок в данных условиях их возникновения.
Преднамеренные и непреднамеренные ошибки репрезентативности
Ошибки искажения данных могут быть преднамеренными или непреднамеренными.
Итак, причины появления преднамеренных ошибок — это подход к отбору данных с использованием метода выявления трендов. Непреднамеренные ошибки возникают и на этапе подготовки выборочного наблюдения, формирования репрезентативной выборки. Чтобы избежать таких ошибок, необходимо создать хорошую основу выборки для списков единиц выборки. Он должен полностью соответствовать целям выборки, быть надежным и охватывать все аспекты исследования.
Валидность, надежность, репрезентативность. Расчет ошибок
Расчет ошибки репрезентативности (Mm) среднего арифметического (M).
Стандартное отклонение: размер выборки (> 30).
Репрезентативная ошибка (Мр) и относительная величина (Р): размер выборки (n> 30).
В случае, если необходимо изучить совокупность, где размер выборки невелик и менее 30 единиц, количество наблюдений уменьшится на одну единицу.
Величина ошибки прямо пропорциональна размеру выборки. Репрезентативность информации и расчет степени возможности составления точного прогноза отражает определенное значение предельной погрешности.
Репрезентативные системы
В процессе оценки представления информации используется не только репрезентативная выборка, но и лицо, получающее информацию, также использует репрезентативные системы. Таким образом, мозг обрабатывает определенный объем информации, создавая репрезентативную выборку всего потока информации, чтобы качественно и быстро оценить предоставленные данные и понять суть проблемы. Ответьте на вопрос: «Представление — что это?» — В масштабе человеческого сознания это довольно просто. Для этого мозг использует все подчиненные органы чувств, в зависимости от типа информации, которую необходимо изолировать от общего потока. Поэтому проводится различие между:
- Система визуального представления, в которой задействованы органы зрительного восприятия глаза. Людей, которые часто используют эту систему, называют визуалами. С помощью этой системы человек обрабатывает информацию, поступающую в виде изображений.
- Система кинестетической репрезентации — это обработка потока информации путем ее восприятия через обонятельные и тактильные каналы.
- Система слухового представления. Основной используемый орган — слух. Информация, предоставленная в виде аудио- или голосового файла, обрабатывается именно этой системой. Людей, которые лучше всего воспринимают информацию на слух, называют аудиалами.
- Система цифрового представления используется вместе с другими как средство получения информации извне. Это субъективно-логическое восприятие и понимание полученных данных.
Так что же такое репрезентативность? Простая выборка из набора или целостная процедура обработки информации? Мы можем однозначно сказать, что репрезентативность во многом определяет наше восприятие потоков данных, помогая выделить самые тяжелые и наиболее важные из них.
В практической и научно-практической работе
врачи обобщают результаты, полученные как правило на выборочных
совокупностях.
Для более широкого распространения и применения полученных при изучении
репрезентативной выборочной совокупности данных и выводов
надо уметь по части явления судить о явлении и его закономерностях в
целом.
Учитывая, что врачи, как правило, проводят исследования на
выборочных совокупностях, теория статистики позволяет с помощью
математического аппарата (формул) переносить данные с выборочного
исследования на генеральную совокупность. При этом врач должен
уметь не только воспользоваться математической формулой, но сделать
вывод, соответствующий каждому способу оценки достоверности
полученных данных. С этой целью врач должен знать способы оценки
достоверности.
Применяя метод оценки достоверности результатов исследования для изучения общественного здоровья и деятельности учреждений
здравоохранения, а также в своей научной деятельности, исследователь должен уметь правильно выбрать способ данного метода.
Среди методов оценки достоверности различают параметрические и непараметрические.
Параметрическими называют количественные методы статистической обработки данных, применение которых требует обязательного
знания закона распределения изучаемых признаков в совокупности и вычисления их основных параметров.
Непараметрическими являются количественные методы статистической обработки данных, применение которых не требует знания
закона распределения изучаемых признаков в совокупности и вычисления их основных параметров.
Как параметрические, так и непараметрические методы, используемые
для сравнения результатов исследований, т.е. для сравнения
выборочных совокупностей, заключаются в применении определенных формул и
расчете определенных показателей в соответствии с
предписанными алгоритмами. В конечном результате высчитывается
определенная числовая величина, которую сравнивают с табличными
пороговыми значениями. Критерием достоверности будет результат сравнения
полученной величины и табличного значения при данном числе
наблюдений (или степеней свободы) и при заданном уровне безошибочного
прогноза.
Таким образом, в статистической процедуре оценки основное
значение имеет полученный критерий достоверности, поэтому сам способ
оценки достоверности в целом иногда называют тем или иным критерием по
фамилии автора, предложившего его в качестве основы метода.
Применение параметрических методов
При проведении выборочных исследований полученный результат не обязательно совпадает с результатом, который мог бы быть получен
при исследовании всей генеральной совокупности. Между этими величинами существует определенная разница, называемая ошибкой
репрезентативности, т.е. это погрешность, обусловленная переносом результатов выборочного исследования на всю генеральную
совокупность.
Определение доверительных границ средних
и относительных величин
Формулы определения доверительных границ представлены следующим образом:
- для средних величин (М): Мген = Мвыб ± tm
- для относительных показателей (Р): Рген = Рвыб ± tm
где Мген и Рген — соответственно, значения средней величины и относительного показателя генеральной
совокупности;
Мвы6 и Рвы6 — значения средней величины и относительного показателя выборочной совокупности;
m — ошибка репрезентативности;
t — критерий достоверности (доверительный коэффициент).
Данный способ применяется в тех случаях, когда по результатам выборочной совокупности необходимо судить о размерах изучаемого
явления (или признака) в генеральной совокупности.
Обязательным условием для применения способа является репрезентативность выборочной совокупности. Для переноса результатов,
полученных при выборочных исследованиях, на генеральную совокупность необходима степень вероятности безошибочного прогноза (Р),
показывающая, в каком проценте случаев результаты выборочных исследований по изучаемому признаку (явлению) будут иметь место в
генеральной совокупности.
При определении доверительных границ средней величины или относительного показателя генеральной совокупности, исследователь сам
задает определенную (необходимую) степень вероятности безошибочного прогноза (Р).
Для большинства медико-биологических исследований считается
достаточной степень вероятности безошибочного прогноза, равная 95%,
а число случаев генеральной совокупности, в котором могут наблюдаться
отклонения от закономерностей, установленных при выборочном
исследовании, не будут превышать 5%. При ряде исследований, связанных,
например, с применением высокотоксичных веществ, вакцин,
оперативного лечения и т.п., в результате чего возможны тяжелые
заболевания, осложнения, летальные исходы, применяется степень
вероятности Р = 99,7%, т.е. не более чем у 1% случаев генеральной
совокупности возможны отклонения от закономерностей,
установленных в выборочной совокупности.
Заданной степени вероятности (Р) безошибочного прогноза соответствует определенное, подставляемое в формулу, значение критерия
t, зависящее также и от числа наблюдений.
При n>30 степени вероятности безошибочного прогноза Р = 99,7% — соответствует значение t = 3, а при Р = 95,5% — значение
t = 2.
При п<30 величина t при соответствующей степени вероятности безошибочного прогноза определяется по специальной таблице
(Н.А. Плохинского).
на определение ошибок репрезентативности (m) и доверительных границ средней величины генеральной совокупности (Мген)
при числе наблюдений больше 30
Условие задачи: при изучении комбинированного воздействия шума и низкочастотной вибрации на организм человека было
установлено, что средняя частота пульса у 36 обследованных водителей сельскохозяйственных машин через 1 ч работы составила 80
ударов в 1 минуту; σ = ± 6 ударов в минуту.
Задание: определить ошибку репрезентативности (mM) и доверительные границы средней величины генеральной
совокупности (Мген).
Решение.
- Вычисление средней ошибки средней арифметической (ошибки репрезентативности) (m):
m = σ / √n =
6 / √36 =
±1 удар в минуту - Вычисление доверительных границ средней величины генеральной совокупности (Мген). Для этого необходимо:
- а) задать степень вероятности безошибочного прогноза (Р = 95 %);
- б) определить величину критерия t. При заданной степени вероятности (Р=95%) и числе наблюдений меньше 30 величина критерия t,
определяемого по таблице, равна 2 (t = 2). Тогда Мген = Мвыб ± tm = 80 ± 2×1 = 80 ± 2
удара в минуту.
Вывод. Установлено с вероятностью безошибочного прогноза Р =
95%, что средняя частота пульса в генеральной совокупности,
т.е. у всех водителей сельскохозяйственных машин, через 1 ч работы в
аналогичных условиях будет находиться в пределах от 78 до 82
ударов в минуту, т.е. средняя частота пульса менее 78 и более 82 ударов в
минуту возможна не более, чем у 5% случаев генеральной
совокупности.
на определение ошибок репрезентативности (m) и доверительных границ относительного показателя генеральной совокупности
(Рген)
Условие задачи: при медицинском осмотре 164 детей 3 летнего возраста, проживающих в одном из районов городе Н., в 18%
случаев обнаружено нарушение осанки функционального характера.
Задание: определить ошибку репрезентативности (mp) и доверительные границы относительного показателя
генеральной совокупности (Рген).
Решение.
- Вычисление ошибки репрезентативности относительного показателя:
m = √P x q / n =
√18 x (100 — 18) / 164 =
± 3% - Вычисление доверительных границ средней величины генеральной совокупности (Рген) производится следующим образом:
- необходимо задать степень вероятности безошибочного прогноза (Р=95%);
- при заданной степени вероятности и числе наблюдений больше 30, величина критерия t равна 2 (t = 2).
Тогда Рген = Рвыб± tm = 18% ± 2 х 3 = 18% ± 6%.
Вывод. Установлено с вероятностью безошибочного прогноза Р=95%, что частота нарушения осанки функционального характера у
детей 3 летнего возраста, проживающих в городе Н., будет находиться в пределах от 12 до 24% случаев.
Оценка достоверности разности результатов исследования
Данный способ применяется в тех случаях, когда необходимо определить, случайны или достоверны (существенны), т.е. обусловлены
какой-то причиной, различия между двумя средними величинами или относительными показателями.
Обязательным условием для применения данного способа является репрезентативность выборочных совокупностей, а также наличие
причинно-следственной связи между сравниваемыми величинами (показателями) и факторами, влияющими на них.
Формулы определения достоверности разности представлены следующим образом:
Если вычисленный критерий t более или равен 2 (t ≥ 2), что соответствует вероятности безошибочного прогноза Р равном или
более 95% (Р ≥ 95%), то разность следует считать достоверной (существенной), т.е. обусловленной влиянием какого-то фактора, что
будет иметь место и в генеральной совокупности.
При t < 2, вероятность безошибочного прогноза Р < 95%, это означает, что разность недостоверна, случайна, т.е. не
обусловлена какой-то закономерностью (не обусловлена влиянием какого-то фактора).
Поэтому полученный критерий должен всегда оцениваться по отношению к конкретной цели исследования.
на оценку достоверности разности средних величин
Условие задачи: при изучении комбинированного воздействия шума
и низкочастотной вибрации на организм человека было
установлено, что средняя частота пульса у водителей сельскохозяйственных
машин через 1 ч после начала работы составила 80 ударов в
минуту; m = ± 1 удар в мин. Средняя частота пульса у этой же группы
водителей до начала работы равнялась 75 ударам в минуту;
m = ± 1 удар в минуту.
Задание: оценить достоверность различий средних значений пульса у водителей сельскохозяйственных машин до и после 1 ч
работы.
Решение.
Вывод. Значение критерия t = 3,5 соответствует вероятности безошибочного прогноза Р > 99,7%, следовательно можно
утверждать, что различия в средних значениях пульса у водителей сельскохозяйственных машин до и после 1 ч работы не случайно, а
достоверно, существенно, т.е. обусловлено влиянием воздействия шума и низкочастотной вибрации.
на оценку достоверности разности относительных показателей
Условие задачи: при медицинском осмотре детей 3 летнего возраста в 18% (m = ± 3%) случаях обнаружено нарушение
осанки функционального характера. Частота аналогичных нарушений осанки при медосмотре детей 4-летнего возраста составила 24%
(m = ± 2,64%).
Задание: оценить достоверность различий в частоте нарушения осанки у детей 2 возрастных групп.
Решение.
Вывод. Значение критерия t=1,5 соответствует вероятности безошибочного прогноза Р<95%. Следовательно, различие в
частоте нарушений осанки среди детей, сравниваемых возрастных групп случайно, недостоверно, несущественно, т.е. не обусловлено
влиянием возраста детей.
Типичные ошибки, допускаемые исследователями при
применении способа оценки достоверности разности результатов исследования
- При оценке достоверности разности результатов исследования по критерию t часто делается вывод о достоверности (или
недостоверности) самих результатов исследования. В действительности же этот способ позволяет судить только о достоверности
(существенности) или случайности различий между результатами исследования. - При полученном значении критерия t<2 часто делается вывод о необходимости увеличения числа наблюдений. Если же
выборочные совокупности репрезентативны, то нельзя делать вывод о необходимости увеличения числа наблюдений, т.к. в данном
случае значение критерия t<2 свидетельствует о случайности, недостоверности различия между двумя сравниваемыми результатами
исследования.
Применение методов статистического анализа для изучения общественного здоровья и здравоохранения.
Под ред. чл.-корр. РАМН, проф. В.З.Кучеренко. М., «Гэотар-Медиа», 2007, учебное пособие для вузов
- Власов В.В. Эпидемиология. — М.: ГЭОТАР-МЕД, 2004. — 464 с.
- Лисицын Ю.П. Общественное здоровье и здравоохранение. Учебник для вузов. — М.: ГЭОТАР-МЕД, 2007. — 512 с.
- Медик В.А., Юрьев В.К. Курс лекций по общественному здоровью
и здравоохранению: Часть 1. Общественное здоровье. — М.: Медицина,
2003. — 368 с. - Миняев В.А., Вишняков Н.И. и др. Социальная медицина и организация здравоохранения (Руководство в 2 томах). — СПб, 1998. -528 с.
- Кучеренко В.З., Агарков Н.М. и др.Социальная гигиена и организация здравоохранения (Учебное пособие) — Москва, 2000. — 432 с.
- С. Гланц. Медико-биологическая статистика. Пер с англ. — М., Практика, 1998. — 459 с.