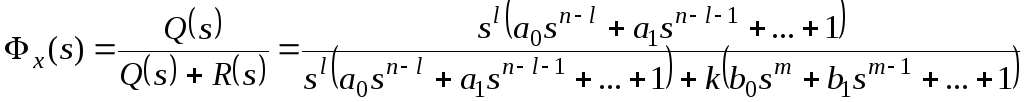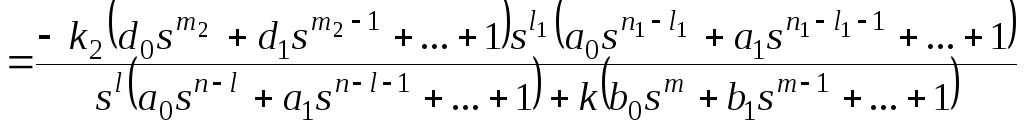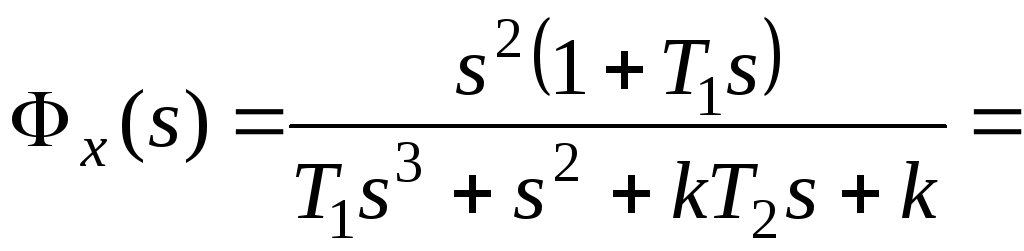Лекция 17.
Расчет
установившейся ошибки в системах
управления. Структурные признаки
астатизма. Коэффициенты ошибок
Установившейся
(статической) ошибкой называют постоянное
значение сигнала ошибки x(t)=g(t)-y(t),
которое она приобретает по окончании
переходного процесса:
,
рисунок 116.
Очевидно,
установившаяся ошибка зависит от законов
изменения и численных характеристик
входных сигналов системы. Поэтому при
ее определении принято рассматривать
так называемые типовые входные сигналы,
законы изменения которых составляют
степенной ряд относительно времени.
Например, для задающего воздействия:
,
,
и так далее.
При наличии
нескольких воздействий на линейную
систему для определения xуст
используется принцип суперпозиции –
реакция линейной системы на совокупность
входных сигналов совпадает с алгебраической
суммой ее реакций на каждый из сигналов
в отдельности:
,
где каждое слагаемое,
или составляющая сигнала ошибки,
определяется
для i-го
входного сигнала при условии, что
остальные тождественно равны нулю.
Такой подход полностью соответствует
определению передаточной функции и
позволяет выполнять расчет установившейся
ошибки на основе структурной схемы
системы.
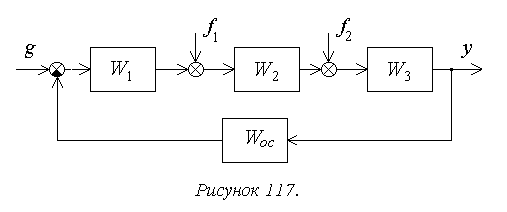
Рассмотрим порядок
расчета установившейся ошибки на
следующем достаточно общем примере
(рисунок 117).
В соответствии с
принципом суперпозиции установившаяся
ошибка будет определяться здесь в виде
суммы трех составляющих
.
Изображение по
Лапласу ошибки от задающего воздействия
получают через передаточную функцию
замкнутой системы по ошибке
при известном изображении задающего
воздействия G(s):
,
где (s)
– основная передаточная функция
замкнутой системы. Для структурной
схемы на рисунке 117
,
где
— передаточная функция разомкнутой
системы, или прямой цепи системы, для
рассматриваемого примера.
Непосредственно
для расчета установившегося значения
ошибки от задающего воздействия
используют теорему о конечном значении
для преобразования Лапласа:
В результате:
.
Изображение по
Лапласу ошибки от возмущающего воздействия
получают через передаточную функцию
замкнутой системы по ошибке от возмущения
при известном изображении возмущающего
воздействия F(s):
,
где f(s)
–передаточная функция замкнутой системы
по возмущающему воздействию,
;
Wf(s)
– передаточная функция разомкнутой
системы по возмущению (передаточная
функция участка прямой цепи системы от
точки приложения возмущающего воздействия
до выхода системы).
Для структурной
схемы на рисунке 8 необходимо учитывать
два возмущающих воздействия, приложенные
в различные точки системы.
Для f1:
,
,

Для f2:
,
,

Расчет упрощается
для системы с единичной отрицательной
обратной связью (рисунок 118):


где k=k1k2k3
– коэффициент передачи разомкнутой
системы.
Найдем установившуюся
ошибку для некоторых типовых вариантов
задающего воздействия.
При
получим:

При
получим:

При
получим:
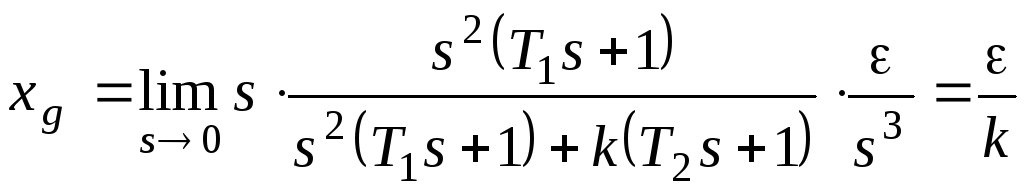
Если установившаяся
ошибка тождественно равна нулю при
каком-либо типовом варианте входного
сигнала, независимо от его численных
характеристик, систему называют
астатической по рассматриваемому
входному сигналу.
Количество типовых
вариантов входного сигнала – членов
степенного ряда, при которых установившаяся
ошибка тождественно равна нулю, определяет
порядок астатизма.
Рассматриваемая
система обладает свойством астатизма
второго порядка по задающему воздействию.
Рассмотрим
установившуюся ошибку от возмущения
f1:
,

где
– коэффициент передачи разомкнутой
системы по возмущению f1.
При
получим:

При
получим:

При
получим тот же результат.
Отметим, что по
возмущению f1
рассматриваемая система не является
астатической. Кроме того, она не в
состоянии отработать два последних
варианта входного сигнала.
Рассмотрим
установившуюся ошибку от возмущения
f2:
,
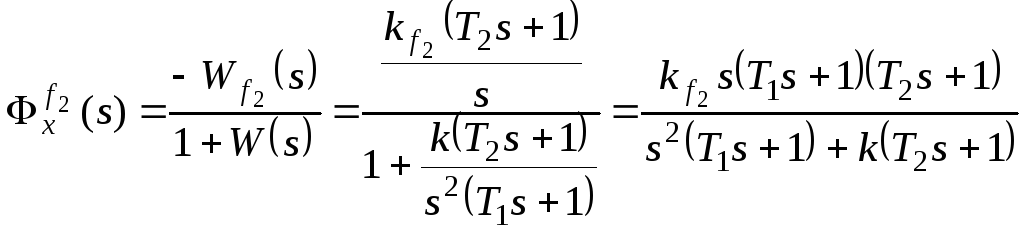
где
– коэффициент передачи разомкнутой
системы по возмущению f2.
При
получим:

При
получим:

При
получим:

По возмущению f2
рассматриваемая система имеет астатизм
первого порядка. Она не в состоянии
отработать возмущающее воздействие,
изменяющееся во времени с постоянным
ускорением.
Подведем некоторые
итоги:
1. Наличие и глубина
свойства астатизма зависят от точки
приложения входного сигнала.
2. Постоянные
времени звеньев системы не влияют на
ее точность.
3. Увеличение
значения коэффициента передачи
разомкнутой системы приводит к снижению
величины установившейся ошибки.
Для систем с
единичной отрицательной обратной связью
существуют достаточно простые структурные
признаки астатизма.
Рассмотрим
структуру, показанную на рисунке 119.
В общем случае
передаточная функция разомкнутой
системы может быть представлена в
следующей форме:

где l0.
Тогда получим:
и для общего вида
задающего воздействия
,
которому соответствует изображение
,

Результат нахождения
этого предела зависит от соотношения
показателей степени:
— при l>v
установившаяся ошибка равна нулю
независимо от остальных параметров, то
есть имеет место астатизм;
— при l=v
получаем константу;
— при l<v
установившаяся ошибка стремится к
бесконечности, то есть система не в
состоянии отработать входной сигнал.
Учитывая, что
минимальное значение v
нулевое, получаем условие астатизма по
задающему воздействию: l>0.
Таким образом,
структурный признак астатизма по
задающему воздействию в системе с
единичной отрицательной обратной связью
состоит в наличии нулевых корней в
знаменателе передаточной функции
разомкнутой системы, или интегрирующих
звеньев в прямой цепи системы.
Нетрудно также
убедиться, что положительное значение
l
совпадает с порядком астатизма.
Для получения
признака астатизма по возмущающему
воздействию представим передаточные
функции на рисунке 10 в форме:


где l1+l2=l,
k1k2=k,
m1+m2=m,
n1+n2=n,
причем
и
.
Тогда получим:
и для общего вида
возмущающего воздействия
,
которому соответствует изображение
,

Все вышеприведенные
выводы можно повторить для показателя
степени l1.
Таким образом,
структурный признак астатизма по
возмущающему воздействию в системе с
единичной отрицательной обратной связью
состоит в наличии нулевых корней в
знаменателе передаточной функции
участка системы до точки приложения
воздействия, или интегрирующих звеньев
на том же участке.
Более общий подход
к оценке точности линейных систем
управления основан на получении и
использовании коэффициентов ошибок.
Рассмотрим его на примере анализа
реакции системы на задающее воздействие.
Если рассматривать
произвольный закон изменения задающего
воздействия g(t),
то эта функция времени может быть
разложена в степенной ряд относительно
аргумента t.
Члены степенного ряда, как известно,
находятся через производные
,
,
…,
,
…
В общем случае ряд
бесконечен. Поэтому с практической
точки зрения рассматривать такое
представление сигнала целесообразно
только при достаточно плавном его
изменении, когда можно ограничиться
конечным числом членов ряда, имея в
виду, что при n
большем некоторого m
можно принять
,
n>m.
Для задачи оценки
установившейся ошибки при
с формулированное допущение вполне
корректно, так как в противном случае
эта задача не имеет смысла.
Коэффициенты
ошибки получают разложением передаточной
функции замкнутой системы по ошибке в
степенной ряд (ряд Тейлора) относительно
аргумента s:
,
где коэффициенты
разложения в общем случае находят как
значения производных в точке s=0:

Передаточные
функции, представляющие собой отношения
полиномов, при достаточно высоком
порядке системы могут оказаться слишком
сложными для дифференцирования. Поэтому
на практике коэффициенты их разложения
в ряд чаще находят путем деления полиномов
– числителя на знаменатель.
С учетом разложения
передаточной функции в ряд можно записать
изображение по Лапласу сигнала ошибки
в следующей форме:
.
Отметим, что с
учетом сформулированного выше допущения
такое представление сигнала ошибки
соответствует
или
.
Перейдя к оригиналу
с учетом теоремы дифференцирования
получим:
.
Вернемся к
рассмотренному выше примеру и предположим,
что задающее воздействие изменяется
по произвольному закону, но при достаточно
больших значениях времени этот закон
аппроксимируется выражением
.
Найдем коэффициенты
разложения передаточной функции по
ошибке
в степенной ряд.
Здесь сразу можно
отметить, что номер первого ненулевого
члена ряда определяется низшей степенью
аргумента s
в числителе дроби, то есть первые два
коэффициента c0
и c1
здесь получаем тождественно равными
нулю.
Далее получим:
В результате
получаем
,
,
,
и так далее.
Найдем производные
задающего воздействия:
,
,
.
Ясно, что для
определения установившейся ошибки
достаточно первых трех коэффициентов:
.
В заключение
отметим, что порядок астатизма системы
по какому-либо входному сигналу совпадает
с количеством нулевых коэффициентов
ошибки, получаемых в разложении в ряд
передаточной функции по ошибке от
данного входного сигнала.
Соседние файлы в папке Конспект ТАУ
- #
- #
- #
- #
- #
- #
- #
- #
- #
- #
- #
Лекция 17.
Расчет
установившейся ошибки в системах
управления. Структурные признаки
астатизма. Коэффициенты ошибок
Установившейся
(статической) ошибкой называют постоянное
значение сигнала ошибки x(t)=g(t)-y(t),
которое она приобретает по окончании
переходного процесса:
,
рисунок 116.
Очевидно,
установившаяся ошибка зависит от законов
изменения и численных характеристик
входных сигналов системы. Поэтому при
ее определении принято рассматривать
так называемые типовые входные сигналы,
законы изменения которых составляют
степенной ряд относительно времени.
Например, для задающего воздействия:
,
,
и так далее.
При наличии
нескольких воздействий на линейную
систему для определения xуст
используется принцип суперпозиции –
реакция линейной системы на совокупность
входных сигналов совпадает с алгебраической
суммой ее реакций на каждый из сигналов
в отдельности:
,
где каждое слагаемое,
или составляющая сигнала ошибки,
определяется
для i-го
входного сигнала при условии, что
остальные тождественно равны нулю.
Такой подход полностью соответствует
определению передаточной функции и
позволяет выполнять расчет установившейся
ошибки на основе структурной схемы
системы.
Рассмотрим порядок
расчета установившейся ошибки на
следующем достаточно общем примере
(рисунок 117).
В соответствии с
принципом суперпозиции установившаяся
ошибка будет определяться здесь в виде
суммы трех составляющих
.
Изображение по
Лапласу ошибки от задающего воздействия
получают через передаточную функцию
замкнутой системы по ошибке
при известном изображении задающего
воздействия G(s):
,
где (s)
– основная передаточная функция
замкнутой системы. Для структурной
схемы на рисунке 117
,
где
— передаточная функция разомкнутой
системы, или прямой цепи системы, для
рассматриваемого примера.
Непосредственно
для расчета установившегося значения
ошибки от задающего воздействия
используют теорему о конечном значении
для преобразования Лапласа:
В результате:
.
Изображение по
Лапласу ошибки от возмущающего воздействия
получают через передаточную функцию
замкнутой системы по ошибке от возмущения
при известном изображении возмущающего
воздействия F(s):
,
где f(s)
–передаточная функция замкнутой системы
по возмущающему воздействию,
;
Wf(s)
– передаточная функция разомкнутой
системы по возмущению (передаточная
функция участка прямой цепи системы от
точки приложения возмущающего воздействия
до выхода системы).
Для структурной
схемы на рисунке 8 необходимо учитывать
два возмущающих воздействия, приложенные
в различные точки системы.
Для f1:
,
,

Для f2:
,
,

Расчет упрощается
для системы с единичной отрицательной
обратной связью (рисунок 118):


где k=k1k2k3
– коэффициент передачи разомкнутой
системы.
Найдем установившуюся
ошибку для некоторых типовых вариантов
задающего воздействия.
При
получим:

При
получим:

При
получим:
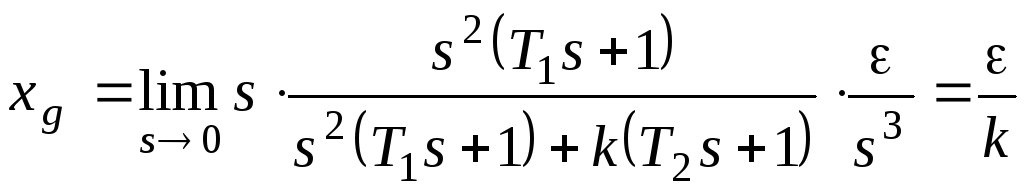
Если установившаяся
ошибка тождественно равна нулю при
каком-либо типовом варианте входного
сигнала, независимо от его численных
характеристик, систему называют
астатической по рассматриваемому
входному сигналу.
Количество типовых
вариантов входного сигнала – членов
степенного ряда, при которых установившаяся
ошибка тождественно равна нулю, определяет
порядок астатизма.
Рассматриваемая
система обладает свойством астатизма
второго порядка по задающему воздействию.
Рассмотрим
установившуюся ошибку от возмущения
f1:
,

где
– коэффициент передачи разомкнутой
системы по возмущению f1.
При
получим:

При
получим:

При
получим тот же результат.
Отметим, что по
возмущению f1
рассматриваемая система не является
астатической. Кроме того, она не в
состоянии отработать два последних
варианта входного сигнала.
Рассмотрим
установившуюся ошибку от возмущения
f2:
,
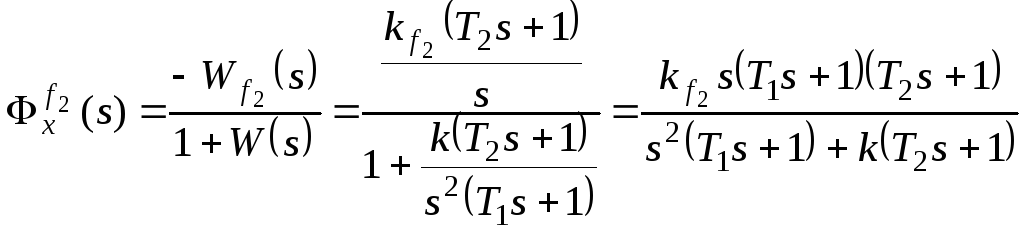
где
– коэффициент передачи разомкнутой
системы по возмущению f2.
При
получим:

При
получим:

При
получим:

По возмущению f2
рассматриваемая система имеет астатизм
первого порядка. Она не в состоянии
отработать возмущающее воздействие,
изменяющееся во времени с постоянным
ускорением.
Подведем некоторые
итоги:
1. Наличие и глубина
свойства астатизма зависят от точки
приложения входного сигнала.
2. Постоянные
времени звеньев системы не влияют на
ее точность.
3. Увеличение
значения коэффициента передачи
разомкнутой системы приводит к снижению
величины установившейся ошибки.
Для систем с
единичной отрицательной обратной связью
существуют достаточно простые структурные
признаки астатизма.
Рассмотрим
структуру, показанную на рисунке 119.
В общем случае
передаточная функция разомкнутой
системы может быть представлена в
следующей форме:

где l0.
Тогда получим:
и для общего вида
задающего воздействия
,
которому соответствует изображение
,

Результат нахождения
этого предела зависит от соотношения
показателей степени:
— при l>v
установившаяся ошибка равна нулю
независимо от остальных параметров, то
есть имеет место астатизм;
— при l=v
получаем константу;
— при l<v
установившаяся ошибка стремится к
бесконечности, то есть система не в
состоянии отработать входной сигнал.
Учитывая, что
минимальное значение v
нулевое, получаем условие астатизма по
задающему воздействию: l>0.
Таким образом,
структурный признак астатизма по
задающему воздействию в системе с
единичной отрицательной обратной связью
состоит в наличии нулевых корней в
знаменателе передаточной функции
разомкнутой системы, или интегрирующих
звеньев в прямой цепи системы.
Нетрудно также
убедиться, что положительное значение
l
совпадает с порядком астатизма.
Для получения
признака астатизма по возмущающему
воздействию представим передаточные
функции на рисунке 10 в форме:


где l1+l2=l,
k1k2=k,
m1+m2=m,
n1+n2=n,
причем
и
.
Тогда получим:
и для общего вида
возмущающего воздействия
,
которому соответствует изображение
,

Все вышеприведенные
выводы можно повторить для показателя
степени l1.
Таким образом,
структурный признак астатизма по
возмущающему воздействию в системе с
единичной отрицательной обратной связью
состоит в наличии нулевых корней в
знаменателе передаточной функции
участка системы до точки приложения
воздействия, или интегрирующих звеньев
на том же участке.
Более общий подход
к оценке точности линейных систем
управления основан на получении и
использовании коэффициентов ошибок.
Рассмотрим его на примере анализа
реакции системы на задающее воздействие.
Если рассматривать
произвольный закон изменения задающего
воздействия g(t),
то эта функция времени может быть
разложена в степенной ряд относительно
аргумента t.
Члены степенного ряда, как известно,
находятся через производные
,
,
…,
,
…
В общем случае ряд
бесконечен. Поэтому с практической
точки зрения рассматривать такое
представление сигнала целесообразно
только при достаточно плавном его
изменении, когда можно ограничиться
конечным числом членов ряда, имея в
виду, что при n
большем некоторого m
можно принять
,
n>m.
Для задачи оценки
установившейся ошибки при
с формулированное допущение вполне
корректно, так как в противном случае
эта задача не имеет смысла.
Коэффициенты
ошибки получают разложением передаточной
функции замкнутой системы по ошибке в
степенной ряд (ряд Тейлора) относительно
аргумента s:
,
где коэффициенты
разложения в общем случае находят как
значения производных в точке s=0:

Передаточные
функции, представляющие собой отношения
полиномов, при достаточно высоком
порядке системы могут оказаться слишком
сложными для дифференцирования. Поэтому
на практике коэффициенты их разложения
в ряд чаще находят путем деления полиномов
– числителя на знаменатель.
С учетом разложения
передаточной функции в ряд можно записать
изображение по Лапласу сигнала ошибки
в следующей форме:
.
Отметим, что с
учетом сформулированного выше допущения
такое представление сигнала ошибки
соответствует
или
.
Перейдя к оригиналу
с учетом теоремы дифференцирования
получим:
.
Вернемся к
рассмотренному выше примеру и предположим,
что задающее воздействие изменяется
по произвольному закону, но при достаточно
больших значениях времени этот закон
аппроксимируется выражением
.
Найдем коэффициенты
разложения передаточной функции по
ошибке
в степенной ряд.
Здесь сразу можно
отметить, что номер первого ненулевого
члена ряда определяется низшей степенью
аргумента s
в числителе дроби, то есть первые два
коэффициента c0
и c1
здесь получаем тождественно равными
нулю.
Далее получим:
В результате
получаем
,
,
,
и так далее.
Найдем производные
задающего воздействия:
,
,
.
Ясно, что для
определения установившейся ошибки
достаточно первых трех коэффициентов:
.
В заключение
отметим, что порядок астатизма системы
по какому-либо входному сигналу совпадает
с количеством нулевых коэффициентов
ошибки, получаемых в разложении в ряд
передаточной функции по ошибке от
данного входного сигнала.
Problem 1
For the unity feedback system shown in Figure P7.1. where $$G(s)=frac{450(s+8)(s+12)(s+15)}{s(s+38)left(s^{2}+2 s+28right)}$$ find the steady-state errors for the following iest inputs: $25 u(t), 37 t u(t)$ $47 t^{2} u(t)$
Problem 2
For the unity feedback system shown in Figure $mathbf{P} 7 . mathbf{1},$ where $$G(s)=frac{20(s+3)(s+4)(s+8)}{s^{2}(s+2)(s+15)}$$ find the steady-state error if the imput is $30 t^{2}$.
Problem 3
For the system shown in Figure P7.2, what steady-state error can be expected for the following test inputs: $15 u(t)$. 15 tu $(t) . ~ 15 t^{2} u(t)$.
Problem 4
For the unity feedback system shown in Figure $mathbf{P} 7.1$, where $$G(s)=frac{500}{(s+20)left(s^{2}+4 s+10right)}$$ find the steady-state error for inputs of $40 u(t), 70 t u(t),$ and $80 t^{2} u(t)$.
Problem 5
An input of $12 t^{3} u(t)$ is applied to the input of a Type 3 unity feedback system, as shown in Figure $P 7.1$, where $$G(s)=frac{200(s+2)(s+5)(s+7)(s+9)}{s^{3}(s+3)(s+10)(s+15)}$$ Find the steady-state error in position.
Problem 6
The steady-state error in velocity of a system is defined to be $$left.left(frac{d r}{d t}-frac{d c}{d t}right)right|_{t rightarrow infty}$$ where $r$ is the system input, and $c$ is the system output. Find the steady-state error in velocity for an input of $t^{3} u(t)$ to a unity feedback system with a forward transfer function of $$G(s)=frac{100(s+1)(s+2)}{s^{2}(s+3)(s+10)}$$
Cinsy Krehbiel
Numerade Educator
Problem 7
What is the steady-siate error for a step inpur of 15 units applied to the unity feedback system of Figure $mathbf{P} 7 . mathbf{1}$, where $$G(s)-frac{1000(s+12)(s+25)(s+32)}{(s+61)(s+73)(s+87)}$$
Problem 8
A system has $K_{p}=3 .$ What steady state error can be expected for inputs of $8 u(t)$ and $8 t u(t) ?$
Cinsy Krehbiel
Numerade Educator
Problem 9
For the unity feedback system shown in Figure $mathrm{P} 7.1$, where $$G(s)=frac{5000}{s(s+75)}$$
a. What is the expected percent overshoot for a unit step input?
b. What is the settling time for a unit step input?
c. What is the steady-state error for an input of $5 u(t) ?$
d. What is the steady-state error for an input of $5 t u(t) ?$
e. What is the steady-state error for an input of $5 t^{2} u(t) ?$
Problem 10
Given the unity feedback system shown in Figure P7.1, where $$G(s)=frac{10^{5}(s+3)(s+10)(s+20)}{s(s+25)(s+alpha)(s+30)}$$ find the value of $alpha$ to yield a $K_{v}=10^{4}$.
Problem 11
For the unity feedback system of Figure $mathbf{P} 7.1$, where $$G(s)=frac{K(s+2)(s+4)(s+6)}{s^{2}(s+5)(s+7)}$$ find the value of $K$ to yield a static error constant of 10,000.
Problem 12
For the system shown in Figure $mathrm{P} 7.3$
a. Find $K_{p}, K_{nu}$ and $K_{a}$
b, Find the steady-state error for an input of $50 u(t), 50 mathrm{ru}(t),$ and $50 t^{2} u(t)$
c. State the system type.
Anurag Kumar
Numerade Educator
Problem 13
A Type 3 unity feedback system has $r(t)=t^{3}$ applied to its input. Find the steady-state position error for this input if the forward transfer function is $$G(s)=frac{1000left(s^{2}+4 s+20right)left(s^{2}+20 s+15right)}{s^{3}(s+2)(s+10)}$$
Ernest Castorena
Numerade Educator
Problem 14
Find the system type for the system of Figure $mathbf{P} 7.4$
Swati Agarwal
Numerade Educator
Problem 15
The steady-state error is defined to be the difference in position between input and output as time approaches infinity. Let us define a steady-state velocity error, which is the difference in velocity between input and output Derive an expression for the error in velocity, $dot{e}(infty)=i(infty)-dot{c}(infty),$ and complete Table $mathrm{P} 7.1$ for the error in velocity.
Arpit Gupta
Numerade Educator
Problem 16
For the system shown in Figure $mathbf{P} 7.5$.
a. What value of $K$ will yield a steady-state error in position of 0.01 for an input of $(mathbf{1} / 10) ?$
b. What is the $K_{v}$ for the value of $K$ found in $(a) ?$
c. What is the minimum possible steady-state position error for the input given in (a)?
Shubham Kumar
Numerade Educator
Problem 17
Given the unity feedback system of Figure $P 7.1$, where $$G(s)=frac{K(s+a)}{s(s+1)(s+10)}$$ find the value of $K a$ so that a ramp input of slope 15 will yield an error of 0.003 in the steady state when compared to the output.
Problem 18
Given the system of Figure P7.6, design the value of $K$ so that for an input of $100 t u(t)$, there will be a 0.01 error in the steady state.
Problem 19
Find the value of $K$ for the unity feedback system shown in Figure $mathbf{P} 7.1$, where $$G(s)=frac{K(s+2)}{s^{2}(s+4)}$$ if the input is $10 t^{2} u(t)$, and the desired steady-state error is 0.01 for this input.
Problem 20
The unity feedback system of Figure $mathbf{P} 7.1$, where $$G(s)=frac{Kleft(s^{2}+3 s+30right)}{s^{n}(s+5)}$$ is to have 1 /6000 error between an input of $10 t u(t)$ and the output in the steady state.
a. Find $K$ and $n$ to meet the specification.
b. What are $K_{p}, K_{v},$ and $K_{a} ?$
Problem 21
For the unity feedback system of Figure $mathbf{P} 7.1$, where $$G(s)=frac{Kleft(s^{2}+2 s+5right)}{(s+2)^{2}(s+3)}$$
a. Find the system type.
b. What error can be expected for an input of $10 u(t) ?$
c. What error can be expected for an input of $10 tu(t) ?$
Ahmad Reda
Numerade Educator
Problem 22
For the unity feedback system of Figure $mathbf{P} 7.1$, where $$G(s)=frac{K(s+10)(s+15)}{s(s+3)(s+7)(s+20)}$$ find the value of $K$ to yield a steady-state error of 0.1 for a ramp input of $25 t u(t)$.
Problem 23
Given the unity feedback system of Figure $mathbf{P} 7.1$, where $$G(s)=frac{K(s+4)}{(s+1)left(s^{2}+10 s+26right)}$$ find the value of $K$ to yield a steady-state error of $5 %$..
Problem 24
For the unity feedback system of Figure $P 7.1$, where $$G(s)-frac{K}{s(s+4)(s+8)(s+10)}$$ find the minimum possible steady-state position error if a unit ramp is applied. What places the constraint upon the error?
GA
Gordon Ayadju
Numerade Educator
Problem 25
The unity feedback system of Figure $mathbf{P} 7.1$, where $$G(s)=frac{K(s+alpha)}{(s+beta)^{2}}$$ is to be designed to meet the following specifications. steady-state error for unit step input $=0.1 ;$ damping ratio $=0.5 ;$ natural frequency $=sqrt{10} .$ Find $K, alpha,$ and $beta$.
Problem 26
A second-order, unity feedback system is to follow a ramp input with the following specifications: the steady-state output position shall differ from the input position by 0.01 of the input velocity; the natural frequency of the closed-loop system shall be 10 rad/s. Find the following:
a. The system type
b. The exact expression for the forward-path transfer function
c. The closed-loop system’s damping ratio
Problem 27
The unity feedback system of Figure $mathbf{P} 7 . mathbf{1}$, where $$G(s)=frac{K(s+alpha)}{s(s+bar{beta})}$$ is to be designed to meet the following requirements: The steady-state position error for a unit ramp input equals 1 , 10 ; the closed-loop poles will be located at $-1 pm j 1 .$ Frnd $K, alpha,$ and $beta$ in order to meet the specifications.
Problem 28
Given the unity feedback control system of Figure P7.1, where $$G(s)=frac{K}{s^{n}(s+a)}$$ find the values of $n, K,$ and $a$ in order 10 meet specifications of $10 %$ over shoot and $boldsymbol{K}_{v}=100$.
Problem 29
Given the unity feedback control system of Figure P7.1. where $$G(s)=frac{K}{s(s+a)}$$ find the following:
a. $K$ and $a$ to yield $K_{nu}=1000$ and a $20 %$ overshoot
b. $K$ and $a$ to yield a $1 %$ error in the steady state and a $10 %$ overshoot
Problem 30
Given the system in Figure $mathrm{P} 7.7,$ find the following:
a. The closed-loop transfer function
b. The system type
c. The steady-state error for an input of $5 u(t)$
d. The steady-state error for an input of $5 tu(t)$
e. Discuss the validity of your answers to (c) and (d).
Artemisa Mazón
Numerade Educator
Problem 31
Repeat Problem 30 for the system shown in Figure P7.8.
Khoobchandra Agrawal
Numerade Educator
Problem 32
For the system shown in Figure $mathrm{P} 7.9$, use MATLAB to find the following:
a. The system type
b. $K_{0}, K_{v},$ and $K_{0}$
c. The steady state error for inputs of $30 u(t), 30 t u(t),$ and $30 t^{2} v(t)$
Uma Kumari
Numerade Educator
Problem 33
The system of Figure $P 7.10$ is to have the following specifications: $K_{v}=10$ $zeta=0.5 .$ Find the values of $K_{1}$ and $K_{f}$ required for the specifications of the system to be met.
Adriano Chikande
Numerade Educator
Problem 34
Find the total steady-state error due to a unit step input and a unit step disturbance in the system of Figure $mathbf{P 7 . 1 1}$.
Problem 35
Design the values of $K_{1}$ and $K_{2}$ in the system of Figure $P 7.12$ to meet the following specifications: Steady-state error component due to a unit step disturbance is $-0.000012 ;$ steady-state error component due to a unit ramp input is 0.003.
Problem 36
Derive Eq. (7.72) in the text, the final value of the actuating signal for nonunity feedback systems.
Nikolaos Alexandrakis
Numerade Educator
Problem 37
For each of the systems shown in Figure $mathbf{P} 7.13,$ find the following:
a. The system type
b. The appropriate static error constant
c. The input waveform to yield a constant error
The steady-state error for a unit input of the waveform found in (c)
The steady-state value of the actuating signal
KG
Kajal Gautam
Numerade Educator
Problem 38
For each of the systems shown in Figure $mathbf{P} 7.14$, find the appropriate static error constant as well as the steady-state error, $r(infty)-c(x),$ for unit step ramp, and parabolic inputs.
Problem 39
Given the system shown in Figure $mathbf{P} 7.15,$ find the following:
a. The system type
b. The value of $K$ to yield $0.1 %$ error in the steady state
Adriano Chikande
Numerade Educator
Problem 40
For the system shown in Figure $mathbf{P} 7.16$
a. What is the system type?
b. What is the appropriate static error constant?
c. What is the value of the appropriate static error constant?
What is the steady-state error for a unit step input?
Prabhu Ramji
Numerade Educator
Problem 41
For the system shown in Figure $mathrm{P} 7.17$, use MATLAB to find the following for $K=10$, and $K=10^{5}:$
a. The system type
b. $K_{0}, K_{v},$ and $K_{v}$
c. The steady-state error for inputs of $30 u(t), 30 t u(t),$ and $30 t^{2} u(t)$
Problem 42
Derive Eq. (7.69) in the text.
Arpit Gupta
Numerade Educator
Problem 43
Given the system shown in Figure $mathbf{P} 7.18$, do the following:
a. Derive the expression for the error, $E(s)=R(s)-C(s)$, in terms of $R(s)$ and $D(s)$
b. Derive the steady-state error, $e(infty),$ if $R(s)$ and $D(s)$ are unit step functions.
c. Determine the attributes of $G_{1}(s), G_{2}(s),$ and $H(s)$ necessary for the steady-state error to become zero.
Problem 44
Given the system shown in Figure $P 7.19$, find the sensitivity of the steady-state error to parameter $a$. Assume a step input. Plot the sensitivity as a function of parameter $a$.
Problem 45
For the system shown in Figure $mathbf{P} 7.20,$ find the sensitivity of the steady-state error for changes in $K_{1}$ and in $K_{2},$ when $K_{1}=100$ and $K_{2}=0.1 .$ Assume step inputs for both the input and the disturbance.
Problem 46
For each of the following closed-loop systems, find the steady-state error for unit step and unit ramp inputs. Use both the final value theorem and input substitution methods.
a. $dot{mathbf{x}}=left[begin{array}{rrr}-5 & -4 & -2 \ -3 & -10 & 0 \ -1 & 1 & -5end{array}right] mathbf{x}+left[begin{array}{l}1 \ 1 \ 0end{array}right] r ; quad y=left[begin{array}{lll}-1 & 2 & 1end{array}right] mathbf{x}$
b. $dot{mathbf{x}}=left[begin{array}{rrr}0 & 1 & 0 \ -5 & -9 & 7 \ -1 & 0 & 0end{array}right] mathbf{x}+left[begin{array}{l}0 \ 0 \ 1end{array}right] r: quad y=left[begin{array}{lll}1 & 0 & 0end{array}right] mathbf{x}$
c. $mathbf{x}=left[begin{array}{rrr}-9 & -5 & -1 \ 1 & 0 & -2 \ -3 & -2 & -5end{array}right] mathbf{x}+left[begin{array}{l}2 \ 3 \ 5end{array}right] r ; quad y=left[begin{array}{llll}1 & -2 & 4 & 1end{array}right]left[begin{array}{ll}x \ 1end{array}right]$
Vishal Parmar
Numerade Educator
Problem 47
An automobile guidance system yields an actual output distance, $X(s)$, for a desired input distance, $X_{c}(s),$ as shown in Figure $mathbf{P} 7.21(a) .$ Any difference, $X_{t}(s),$ between the commanded distance and the actual distance is converted into a velocity command, $V_{c}(s),$ by the controller and applied to the vehicle accelerator. The vehicle responds to the velocity command with a velocity, $V(s)$ and a displacement. $X(s)$. is realized. The velocity control, $G_{2}(s)$, is itself a closed-loop system, as shown in Figure $mathbf{P} 7.21(b) .$ Here the difference, $V_{e}(s),$ between the commanded velocity, $V_{c}(s),$ and the actual vehicle velocity, $V(s),$ drives a motor that displaces the automobile’s accelerator by $Y_{c}(s)$ (Stefani, 1978 ). Find the steady-state error for the velocity control loop if the motor and amplifier transfer function $G_{3}(s)=K[s(s+1)] .$ Assume $G_{4}(s)$ to be a first-order system, where a maximum possible 1 -foot displacement of the accelerator linkage yields a steady-state velocity of 100 miles/hour, with the automobile reaching 60 miles/hour in 10 seconds.
mj
Manish Jain
Numerade Educator
Problem 48
A simplified block diagram of a meter used to measure oxygen concentration is shown in Figure $mathrm{P} 7.22 .$ The meter uses the paramagnetic properties of a stream of oxygen. A small body is placed in a stream of oxygen whose concentration is $R(s),$ and it is subjected to a magnetic field. The torque on the body, $K_{1} R(s)$, due to the magnetic field is a function of the concentration of the oxygen. The displacement of the body, $theta(s)$. is detected, and a voltage. $boldsymbol{C}(s)$, is developed proportional to the displacement. This voltage is used to develop an electrostatic field that places a torque, $K_{3} C(s),$ on the body opposite to that developed by the magnetic field. When the body comes to rest. the output voltage represents the strength of the magnetic torque, which in turn is related to the concentration of the oxygen (Chesmond, 1982 ). Find the steady-state error between the output voltage, representing oxygen concentration, and the input oxygen concentration. How would you reduce the error to zero?
Mayukh Banik
Numerade Educator
Problem 49
A space station, shown in Figure $mathrm{P} 7.23(a),$ will keep its solar arays facing the sun. If we assume that the simplified block diagram of Figure $mathrm{P} 7.23(b)$ represents the solar tracking control system that will be used to rotate the array via rotary joints called solar alpha rotary joints (Figure $mathbf{P} 7.23(mathrm{c})$ ). Find $(mathrm{Kumar}, 1992)$
a. The steady-state error for step commands
b. The steady-state error for ramp commands
c. The steady-state error for parabolic commands
d. The range of $K_{c}$, $J$ to make the system stable
Narayan Hari
Numerade Educator
Problem 50
The following specification applies to a position control: $K_{v}=10 .$ On hand is an amplifier with a variable gain, $K_{2}$, with which to drive a motor. Two one-turn pots to convert shaft position into voltage are also available, where $pm 3 pi$ volts are placed across the pots. A motor is available whose transfer function is $$frac{theta_{m}(s)}{E_{a}(s)}=frac{K}{s(s+alpha)}$$ where $theta_{m}(s)$ is the motor armature position and $E_{c}(s)$ is the armature voltage. The components are interconnected as shown in Figure P7.24. The transfer function of the motor is found experimentally as follows. The motor and load are driven separately by applying a large, short square wave (a unit impulse) to the armature. An oscillograph of the response shows that the motor reached $63 %$ of its final output value 0.5 second after application of the impulse, Furthermore, with 10 volts dc applied to the armature. the constant output speed was 100 rad/s. Draw the completed block diagram of the system, specifying the transfer function of each component of the block diagram.
Keshav Singh
Numerade Educator
Problem 51
A boat is circling a ship that is using a tracking radar. The speed of the boat is 20 knots, and it is circling the ship at a distance of 1 nautical mile, as shown in Figure $mathbf{P} 7.25(a) .$ A simplified model of the tracking system is shown in Figure $mathbf{P} 7.25(b) .$ Find the value of $K$ so that the boat is kept in the center of the radar beam with no more than 0.1 degree error.
Arushi Sahay
Numerade Educator
Problem 52
Figure $mathbf{P} 7.26$ shows a simplified block diagram of a pilot in a loop to control the roll attitude of an Army UH-60A Black Hawk twin-engine helicopter with a single main rotor (Hess. 1993 ).
a. Find the system type.
b. The pilot’s response determines $K_{1}$. Find the value of $K_{1}$ if an appropriate static error constant value of 700 is required.
Would a pilot whose $K_{1}$ is the value found in (b) be hired to fly the helicopter? Note: In the block diagram $G_{D}(s)$ is a delay of about 0.154 second and can be represented by a Pade approximation of $G_{n}(s)=-(s-13)$, $(s+13)$
Khoobchandra Agrawal
Numerade Educator
Problem 53
Motion control, which includes position or force control, is used in robotics and machining. Force control requires the designer to consider two phases: contact and noncontact motions. Figure $mathbf{P} 7.27(a)$ is a diagram of a mechanical system for force control under contact motion. A force command, $F_{c m d}(s),$ is the input to the system, while the output, $F(s),$ is the controlled contact force. In the figure a motor is used as the force actuator. The force output from the actuator is applied to the object through a force sensor. A block diagram representation of the system is shown in Figure $mathrm{P} 7.27(b) . K_{2}$ is velocity feedback used to improve the transient response. The loop is actually implemented by an electrical loop (not shown) that controls the armature current of the motor to yield the desired torgue at the output. Recall that $T_{m}=K_{t} i_{a}$ (Ohnishi, 1996 ). Find an expression for the range of $K_{2}$ to keep the steady state force error below $10 %$ for ramp inputs of commanded force.
Yaqub Khan
Numerade Educator
Problem 54
Problem 50 in Chapter 4 describes an open-loop swivel controller and plant for an industrial robot. The transfer function for the controller and plant is $$G_{e}(s)=frac{omega_{d}(s)}{V_{t}(s)}=frac{K}{(s+10)left(s^{2}+4 s+10right)}$$ where $omega_{b}(mathrm{s})$ is the Laplace transform of the robot’s angular swivel velocity and $V_{i}(mathrm{s})$ is the input voltage to the controller. Assume $G_{e}(s)$ is the forward transfer function of a velocity control loop with an input transducer and sensor, each represented by a constant gain of 3 (Schneider, 1992 ).
a. Find the value of gain, $K$, to minimize the steady-state error between the input commanded angular swivel velocity and the output actual angular swivel velocity.
b. What is the steady-state error for the value of $K$ found in $(a) ?$
c. For what kind of input does the design in (a) apply?
Khoobchandra Agrawal
Numerade Educator
Problem 55
Problem 17 in Chapter 1 discusses the active control of a pantograph mechanism for high-speed rail systems, In Problem $62(a)$ Chapter $5,$ you found the block diagram for the active pantograph control system. Use your solution for Problem $62(a)$ in Chapter 5 to perform steady-state error analysis and design as follows (O’Connor, 1997):
a. Find the system type.
b. Find the value of controller gain, $K$, that minimizes the steady-state force error
c. What is the minimum steady-state force error?
Dading Chen
Numerade Educator
Лекция № 18
Тема:
Анализ вынужденных процессов в импульсных системах.
План лекции:
1. Вынужденные процессы при степенных входных воздействиях.
2. Установившиеся ошибки при типовых входных сигналах.
3. Коэффициенты ошибок дискретной системы.
1. Вынужденные процессы при степенных входных воздействиях.
Рассмотрим вынужденные процессы, возникающие в дискретных системах при степенных воздействиях и оценим точность воспроизведения входного сигнала.
Пусть входной сигнал является постоянным, т.е. 


В соответствии с формулой (94)
Рекомендуемые материалы

т.е. вынужденный процесс при постоянном входном воздействии также является постоянной величиной. Пусть

т.е. входной сигнал изменяется по линейному закону. Тогда
Из выражения (93) получим

где 
т.е. вынужденный процесс при линейном входном воздействии является также сигналом, изменяющимся по линейному закону, параметры которого определяются коэффициентами передаточной функции системы.
Продолжая рассмотрение, можно прийти к следующему результату: вынужденный процесс при степенном воздействии является полиномом, той же степени, что и входной сигнал. Коэффициенты этого полинома определяются коэффициентами входного воздействия и параметрами передаточной функции системы.
Оценим точность воспроизведения степенного входного сигнала замкнутой импульсной системой. Структурная схема системы представлена на рис.40. Входное воздействие имеет вид
 |

Рис.40
2. Установившиеся ошибки при типовых входных сигналах.
Найдем установившуюся ошибку системы 

где 
Определим передаточную функцию ошибки замкнутой импульсной системы:
или
где 
Установившееся значение сигнала ошибки найдем по теореме о предельном значении решетчатой функции:

где 
Из формулы (98) и таблиц z-преобразования получим

где P(z) — полином степени 

Тогда зависимость для установившейся ошибки принимает вид

Из анализа формула (99) видно, что могут представиться три случая:

т.е. ошибка неограниченно увеличивается с увеличением времени»

т.е. установившееся значение ошибки является постоянной величиной, отличной от нуля;
3) 

т.е. в этом случае установившееся значение ошибки равно нулю.
Если система является статической 

Величина W(1) представляет собой коэффициент передачи разомкнутой дискретной системы K. Нетрудно показать, что для случая экстраполятора нулевого порядка он совпадает со значением коэффициента передачи приведенной непрерывной части 
Для системы с астатизмом первого порядка 


где К — коэффициент передачи системы по скорости,
В импульсных системах в установившемся режиме могут возникать колебания внутри интервала квантования (так называемые «скрытые колебания»). Отметим, что в линейных импульсных системах с экстраполятором нулевого порядка в качестве формирующего звена появление таких колебаний принципиально невозможно. Возникновение «скрытых колебаний» связано с использованием формирующего звена, поддерживающего величину импульса на интервале 

При необходимости их исследования выходной сигнал рассматривают в смещенные моменты времени 

дискретной системы.
3. Коэффициенты ошибок дискретной системы
Для анализа точности непрерывных систем при степенных входных воздействиях успешно применяется метод, основанный на понятии коэффициентов ошибок. Этот же метод может быть применен и для дискретных систем.
Рассмотрим вынужденный процесс в замкнутой системе. Передаточная функция системы по ошибке имеет вид

где W(z)- передаточная функция разомкнутой системы. Пусть

Тогда для сигнала ошибки системы в вынужденном процессе можно записать уравнение, аналогичное зависимости (90):

Выразим значение смещенной функции 

где
Подставив выражение (101) в уравнение (100), получим
Меняя порядок суммирования, будем иметь

Введем коэффициенты 
Тогда выражение (102) приобретает вид

Коэффициенты 


Продифференцировав последнюю зависимость по Z , получим для i-й производной
или

При вычислении коэффициентов ошибок производные 

Коэффициенты разложения легко находятся переходом от переменной z к переменной 
В качестве примера рассмотрим определение ошибки, устанавливающейся в импульсной системе, если

Введя новую переменную 
Обратите внимание на лекцию «15. Безопасность оборудования и производственные процессы».
Разделив числитель на знаменатель, найдем разложение функции 


Отсюда 
Отметим, что, кроме коэффициентов ошибок, для определения величины 


Анализ точности при гармоническом входном сигнале при необходимости его проведения выполняется с помощью частотных характеристик импульсной системы аналогично тому, как это делалось для непрерывных систем. При этом для перехода от ЛАФЧХ разомкнутой дискретной системы к частотным характеристикам по сигналу ошибки могут использоваться те же номограммы замыкания, что и для непрерывных систем.