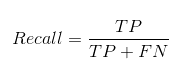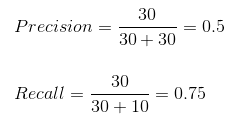Назначение матрицы источников ошибок

Мы уже рассказывали, как машинное обучение применяется для прогнозирования будущих событий в финансовом секторе, нефтегазовой промышленности, логистике, HR-менеджменте, девелопменте, страховании, муниципальном управлении, маркетинге, ритейле и других отраслях экономики. Сегодня рассмотрим еще несколько практических примеров такого приложения Machine Learning и в этом контексте разберем одно из ключевых понятий Data Science по оценке моделей. Читайте в нашей статье, что такое матрица ошибок (confusion matrix) и как она помогает измерить эффективность используемых ML-алгоритмов и других инструментов бизнес-аналитики, оценив потенциальные убытки и выгоды от возможных сценариев будущего в задаче прогнозирования спроса.

От ритейла до банка: 5 примеров применения Big Data и Machine Learning в задачах прогнозирования спроса и предложения

Вообще сегодня задача прогнозирования спроса стала довольно обыденным приложением методов Machine Learning (ML) в реальном бизнесе. В частности, в декабре 2019 года сервис объявлений «Юла» ускорил публикацию объявлений по продаже товаров с помощью функции их распознавания по фотографии. Помимо собственно распознавания того, что сфотографировано, нейросетевые модели предлагают пользователю уточнить характеристики продукта и оценивают его стоимость в среднем по рынку. При этом пользователю выдается прогноз, насколько быстро он продаст товар при различных ценах [1].

Другой пример, московский сервис приготовления и доставки еды навынос «Кухня на районе» с помощью нейросетей и ежедневной статистики продаж рассчитывает, сколько продуктов нужно привезти на каждую точку, чтобы минимизировать количество остатков. Анализируя данные по проданным позициям в разных локациях, нейросеть из 3 500 вариантов отбирает сотню блюд, которые будут максимально востребованы, чтобы готовить именно их на районных кухнях в течение следующей недели [2].

Подобным образом, на основе постоянного анализа продаж, машинное обучение позволяет эффективно решить задачу ценообразования, установив наиболее оптимальную стоимость на отдельные продукты и целые товарные категории. Например, именно это было сделано в отечественном интернет-магазине детских игрушек Babadu.ru, когда методы Machine Learning помогли разработать несколько маркетинговых стратегий, наиболее выгодных для ритейлера [3]. Аналогично строятся ML-модели эластичного спроса в другом российском гиганте интернет-торговли, Ozon.ru. Разработанный алгоритм анализирует значения более 150 признаков в истории продаж, чтобы на выходе предоставить точный прогноз по будущим заказам. При этом в модели заложена функция минимизации денежных потерь на покупку и хранение лишних товаров на складе или отток клиента (Churn Rate) из-за отсутствия нужного продукта [4].

Похожая задача прогнозирования спроса актуальна и для банков, которые стремятся оптимизировать процессы работы с наличными деньгами в своих банкоматах. Финансовые корпорации хотят, с одной стороны, чтобы средства не лежали в банкоматах «без дела»: гораздо выгоднее, например, разместить их на краткосрочном депозите. Но, клиенты будут недовольны, когда столкнутся с отказом из-за недостаточного количества денег в банкомате. Это грозит репутационными потерями, поэтому банк стремится решить данную проблему с помощью точного предсказания спроса на наличность в каждой точке расположения банкоматов. При этом нужно учитывать, что спрос на наличные зависит от множества параметров: макроэкономические факторы, политические новости, социальные события, расположение банкомата, прогноз погоды, время года, день недели и т.д. Чтобы предсказать завтрашнюю потребность в наличных для конкретного банкомата, Сбербанк, например, с 2016 года использует адаптивные алгоритмы машинного обучения вместе с классическими методами анализа временных рядов. Такие модели обеспечивают динамическое перестроение всех анализируемых параметров, предоставляя на выходе эффективный план оптимального распределения и перемещения наличных между банкоматами [5].

Что такое матрица ошибок и зачем она нужна: пример расчета стоимости ошибки прогнозирования

Поскольку в бизнесе поиск баланса между спросом и предложением напрямую конвертируется в деньги, возникает вопрос, насколько выгодно применение методов Machine Learning для решения этой задачи. С целью сопоставления предсказаний и реальности в Data Science используется матрица ошибок (confusion matrix) – таблица с 4 различными комбинациями прогнозируемых и фактических значений. Прогнозируемые значения описываются как положительные и отрицательные, а фактические – как истинные и ложные [6]. Вообще матрица ошибок используется для оценки точности моделей в задачах классификации. Но прогнозирование и распознавание образов можно рассматривать как частный случай этой проблемы, поэтому confusion matrix актуальна и для измерения точности предсказаний. Важно, что матрица ошибок позволяет оценить эффективность прогноза не только в качественном, но и в количественном выражении, т.е. измерить стоимость ошибки в деньгах. Например, каковы будут расходы на удержание пользователя, если машинное обучение предсказало, что он перестанет приносить компании пользу [7]? Аналогичный вопрос по предсказанию оттока (Churn Rate) актуален и в HR-сфере для удержания ключевых сотрудников, мотивация которых снижается. Впрочем, матрица ошибок может использоваться не только в рамках применения Machine Learning. По сути, этот метод оценки стоимости прогноза является универсальным аналитическим инструментом.

Прогноз	Реальность
+	—
+	True Positive (истинно-положительное решение): прогноз совпал с реальностью, результат положительный произошел, как и было предсказано ML-моделью	False Positive (ложноположительное решение): ошибка 1-го рода, ML-модель предсказала положительный результат, а на самом деле он отрицательный
—	False Negative (ложноотрицательное решение): ошибка 2-го рода – ML-модель предсказала отрицательный результат, но на самом деле он положительный	True Negative (истинно-отрицательное решение): результат отрицательный, ML-прогноз совпал с реальностью

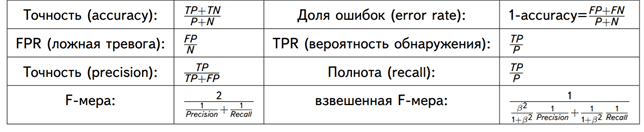
С математической точки зрения оценить точность ML-модели можно с помощью следующих метрик [8]:

• Точность – сколько всего результатов было предсказано верно;
• Доля ошибок;
• Полнота – сколько истинных результатов было предсказано верно;
• F-мера, которая позволяет сравнить 2 модели, одновременно оценив полноту и точность. Здесь используется среднее гармоническое вместо среднего арифметического, сглаживая расчеты за счет исключения экстремальных значений.

В количественном выражении это будет выглядеть так:

• P – число истинных результатов, P = TP + FN;
• N – число ложных результатов, N = TN + FP.

Рассмотрим матрицу ошибок на практическом примере для задачи прогнозирования спроса на скоропортящуюся продукцию, которая должна быть продана конечному пользователю в течение суток. Например, букеты цветов, продающиеся по цене k рублей при закупочной стоимости в p рублей. Предположим, с помощью Machine Learning было предложена 2 варианта:

• Положительный прогноз (+), что по цене k будут полностью раскуплены все цветы в количестве n букетов.
• Отрицательный прогноз (+), что по цене k будут полностью раскуплены не все цветы, останется m не проданных букетов.

Соответственно, матрица ошибок для этого случая будет выглядеть следующим образом:

Прогноз	Реальность
Проданы все букеты цветов	Остались не проданные m букетов
+: Проданы все n букетов по k рублей c ценой закупки p	True Positive: прогноз совпал с реальностью, все закупленные n букетов проданы Выручка = n*k Затраты = n*p Прибыль = n*(k-p) Стоимость ошибки = 0	False Positive: ошибка 1-го рода, ML-модель предсказала, что будет n продаж, а на самом деле их было (n-m), осталось m не проданных букетов, которые пропали и не вернули затраты на их покупку Выручка = (n-m)*k Затраты = n*p Прибыль = n*(k-p) – m*k Стоимость ошибки = m*p
—: Остались не проданные m букетов c ценой закупки p	False Negative: ошибка 2-го рода – ML-модель предсказала, что n букетов не будет продано, поэтому закупили (n-m) букетов, но спрос был на n букетов. Эффект недополученной прибыли Выручка = (n-m)*k Затраты = (n-m)*p Прибыль = (n-m)*(k-p) Стоимость ошибки = m*k	True Negative: ML-прогноз совпал с реальностью, было раскуплено (n-m) букетов по цене k, сколько и было изначально закуплено по цене p Выручка = (n-m)*k Затраты = (n-m)*p Прибыль = (n-m)*(k-p) Стоимость ошибки = 0

Таким образом, с помощью confusion matrix можно измерить эффективность прогноза в денежном выражении, что весьма актуально для практического бизнес-приложения Machine Learning. Впрочем, отметим еще раз, что данный метод предварительной оценки будущих сценариев можно использовать и вне сферы Data Science, оценивая риски и перспективы в рамках классического бизнес-анализа.

Другие практические вопросы системного и бизнес-анализа рассматриваются в рамках нашей Школы прикладного бизнес-анализа. А особенности практического применения больших данных и машинного обучения разбираются на наших образовательных курсах в лицензированном учебном центре обучения и повышения квалификации ИТ-специалистов (менеджеров, архитекторов, инженеров, администраторов, Data Scientist’ов и аналитиков Big Data) в Москве:

• Аналитика больших данных для руководителей
• Машинное обучение на Python

Источники

1. https://www.the-village.ru/village/city/news-city/371179-tseny
2. https://www.the-village.ru/village/business/businessmen/371631-kuhnya-na-rayone
3. https://chernobrovov.ru/articles/kak-mashinnoe-obuchenie-pomogaet-pravilno-ustanavlivat-pravilnye-ceny.html
4. https://habr.com/ru/company/ozontech/blog/431950/
5. http://futurebanking.ru/post/3213
6. https://hranalytic.ru/kak-ponyat-matrica-nesootvetstvij-confusion-matrix/
7. https://chernobrovov.ru/articles/kak-izmerit-effektivnost-machine-learning-schitaem-metriki-i-dengi-na-primere-prognozirovaniya-ottoka-polzovatelej.html
8. http://www.machinelearning.ru/wiki/images/archive/5/54/20151001162720!Kitov-ML-05-Model_evaluation.pdf

Матрица ошибок – это метрика производительности классифицирующей модели Машинного обучения (ML).

Когда мы получаем данные, то после очистки и предварительной обработки, первым делом передаем их в модель и, конечно же, получаем результат в виде вероятностей. Но как мы можем измерить эффективность нашей модели? Именно здесь матрица ошибок и оказывается в центре внимания.

Матрица ошибок – это показатель успешности классификации, где классов два или более. Это таблица с 4 различными комбинациями сочетаний прогнозируемых и фактических значений.

Давайте рассмотрим значения ячеек (истинно позитивные, ошибочно позитивные, ошибочно негативные, истинно негативные) с помощью «беременной» аналогии.

Истинно позитивное предсказание (True Positive, сокр. TP)
Вы предсказали положительный результат, и женщина действительно беременна.

Истинно отрицательное предсказание (True Negative, TN)
Вы предсказали отрицательный результат, и мужчина действительно не беременен.

Ошибочно положительное предсказание (ошибка типа I, False Positive, FN)
Вы предсказали положительный результат (мужчина беременен), но на самом деле это не так.

Ошибочно отрицательное предсказание (ошибка типа II, False Negative, FN)
Вы предсказали, что женщина не беременна, но на самом деле она беременна.

Давайте разберемся в матрице ошибок с помощью арифметики.

Пример. Мы располагаем датасетом пациентов, у которых диагностируют рак. Зная верный диагноз (столбец целевой переменной «Y на самом деле»), хотим усовершенствовать диагностику с помощью модели Машинного обучения. Модель получила тренировочные данные, и на тестовой части, состоящей из 7 записей (в реальных задачах, конечно, больше) и изображенной ниже, мы оцениваем, насколько хорошо прошло обучение.

Модель сделала свои предсказания для каждого пациента и записала вероятности от 0 до 1 в столбец «Предсказанный Y». Мы округляем эти числа, приводя их к нулю или единице, с помощью порога, равного 0,6 (ниже этого значения – ноль, пациент здоров). Результаты округления попадают в столбец «Предсказанная вероятность»: например, для первой записи модель указала 0,5, что соответствует нулю. В последнем столбце мы анализируем, угадала ли модель.

Теперь, используя простейшие формулы, мы рассчитаем Отзыв (Recall), точность результата измерений (Precision), точность измерений (Accuracy), и наконец поймем разницу между этими метриками.

Отзыв

Из всех положительных значений, которые мы предсказали правильно, сколько на самом деле положительных? Подсчитаем, сколько единиц в столбце «Y на самом деле» (4), это и есть сумма TP + FN. Теперь определим с помощью «Предсказанной вероятности», сколько из них диагностировано верно (2), это и будет TP.

$$Отзыв = frac{TP}{TP + FN} = frac{2}{2 + 2} = frac{1}{2}$$

Точность результата измерений (Precision)

В этом уравнении из неизвестных только FP. Ошибочно диагностированных как больных здесь только одна запись.

$$Точностьspaceрезультатаspaceизмерений = frac{TP}{TP + FP} = frac{2}{2 + 1} = frac{2}{3}$$

Точность измерений (Accuracy)

Последнее значение, которое предстоит экстраполировать из таблицы – TN. Правильно диагностированных моделью здоровых людей здесь 2.

$$Точностьspaceизмерений = frac{TP + TN}{Всегоspaceзначений} = frac{2 + 2}{7} = frac{4}{7}$$

F-мера точности теста

Эти метрики полезны, когда помогают вычислить F-меру – конечный показатель эффективности модели.

$$F-мера = frac{2 * Отзыв * Точностьspaceизмерений}{Отзыв + Точностьspaceизмерений} = frac{2 * frac{1}{2} * frac{2}{3}}{frac{1}{2} + frac{2}{3}} = 0,56$$

Наша скромная модель угадывает лишь 56% процентов диагнозов, и такой результат, как правило, считают промежуточным и работают над улучшением точности модели.

SkLearn

С помощью замечательной библиотеки Scikit-learn мы можем мгновенно определить множество метрик, и матрица ошибок – не исключение.

from sklearn.metrics import confusion_matrix
y_true = [2, 0, 2, 2, 0, 1]
y_pred = [0, 0, 2, 2, 0, 2]
confusion_matrix(y_true, y_pred)

Выводом будет ряд, состоящий из трех списков:

array([[2, 0, 0],
       [0, 0, 1],
       [1, 0, 2]])

Значения диагонали сверху вниз слева направо [2, 0, 2] – это число верно  предсказанных значений.

Фото: @opeleye

Были ли вы в ситуации, когда вы ожидали, что ваша модель машинного обучения должна работать очень хорошо, но у нее была низкая точность? Вы проделали всю тяжелую работу — так где же модель классификации сработала не так? Как это исправить?

Существует множество способов оценить эффективность вашей модели классификации, но ни один из них не выдержал испытания временем, кроме матрицы ошибок. Она помогает нам оценить, как наша модель работала, где она пошла не туда, и предлагает нам рекомендации по исправлению нашего пути.

В этой статье мы рассмотрим, как матрица ошибок дает целостное представление об эффективности вашей модели. И, в отличие от названия, вы поймете, что матрица ошибок — довольно простая, но мощная концепция. Итак, давайте раскроем тайну матрицы ошибок!

Что такое матрица ошибок?

Вопрос на миллион долларов — что такое, в конце концов, матрица ошибок?

Матрица ошибок — это матрица размером N x N, используемая для оценки эффективности модели классификации, где N — количество целевых классов. Матрица сравнивает фактические целевые значения с предсказанными моделью машинного обучения. Это дает нам целостное представление о том, насколько хорошо работает наша классификационная модель и какие ошибки она допускает.

Для задачи двоичной классификации у нас будет матрица 2 x 2, как показано ниже, с 4 значениями:

Расшифруем матрицу:

Но подождите — что здесь TP, FP, FN и TN? Это важнейшая часть матрицы ошибок. Давайте разберемся с каждым термином ниже.

Понимание True Positive, True Negative, False Positive и False Negative в матрице ошибок

True Positive (TP)

True Negative (TN)

False Positive (FP) — ошибка 1-го типа

False Negative (FN) — ошибка 2-го типа

Позвольте мне привести пример, чтобы лучше это понять. Предположим, у нас есть набор данных классификации с 1000 точками данных. Мы подгоняем на нем классификатор и получаем следующую матрицу ошибок:

Различные значения матрицы ошибок будут следующими:

Это оказался довольно приличный классификатор для нашего набора данных, учитывая относительно большее количество истинно положительных и истинно отрицательных значений.

Помните об ошибках 1-го и 2-го типа. Интервьюеры любят спрашивать, в чем разница между ними!

Зачем нам нужна матрица ошибок?

Прежде чем ответить на этот вопрос, давайте подумаем о проблеме гипотетической классификации.

Допустим, вы хотите предсказать, сколько людей инфицировано заразным вирусом, до того, как у них проявятся симптомы, и изолировать их от здорового населения. Двумя значениями для нашей целевой переменной будут: Sick и Not Sick.

Теперь вы, должно быть, задаетесь вопросом — зачем нам матрица ошибок, когда у нас есть наш вечный друг — Точность? Что ж, посмотрим, где точность не работает.

Наш набор данных является примером несбалансированного набора данных. Имеется 947 точек данных для отрицательного класса и 3 точки данных для положительного класса. Вот как мы рассчитаем точность:

Посмотрим, как работает наша модель:

Общие значения результатов:

TP = 30, TN = 930, FP = 30, FN = 10

Итак, точность для нашей модели:

96%! Неплохо!

Но это дает неверное представление о результате. Подумайте об этом.

Наша модель гласит: «Я могу предсказать заболевание в 96% случаев». Однако она делает наоборот. Это предсказание людей, которые не заболеют с точностью 96%, пока больные распространяют вирус!

Как вы думаете, это правильный показатель для нашей модели, учитывая серьезность проблемы? Разве мы не должны измерять, сколько положительных случаев мы можем правильно предсказать, чтобы остановить распространение заразного вируса? Или, из правильно спрогнозированных случаев сколько положительных случаев для проверки надежности нашей модели?

Здесь мы сталкиваемся с двойным понятием «точность (Precision) и полнота (Recall)».

Precision vs. Recall

Точность говорит нам, сколько из правильно предсказанных случаев действительно оказались положительными.

Вот как рассчитать точность:

Это определило бы надежность нашей модели.

Полнота сообщает нам, сколько реальных положительных случаев мы смогли правильно предсказать с помощью нашей модели.

А вот как мы можем рассчитать полноту:

Мы можем легко рассчитать точность и полноту для нашей модели, подставив значения в приведенные выше уравнения:

50% процентов правильно предсказанных случаев оказались положительными. В то время как 75% положительных результатов были успешно предсказаны нашей моделью. Потрясающие!

Точность — полезный показатель в тех случаях, когда ложноположительный результат важнее, чем ложноотрицательный.

Точность важна в системах рекомендаций по музыке или видео, на веб-сайтах электронной коммерции и т. д. Неправильные результаты могут привести к оттоку клиентов и нанести вред бизнесу.

Полнота — полезный показатель в случаях, когда ложноотрицательный результат важнее ложноположительного.

Полнота важна в медицинских случаях, когда не имеет значения, что возникает ложная тревога, но реальные положительные случаи не должны оставаться незамеченными!

В нашем примере полнота была бы лучшим показателем, потому что мы не хотим, чтобы случайно выписали инфицированного человека и позволили ему смешаться со здоровым населением, тем самым распространяя заразный вирус. Теперь вы можете понять, почему точность была плохим показателем для нашей модели.

Но будут случаи, когда нет четкой разницы между тем, что важнее: точность или полнота. Что нам делать в таких случаях? Мы их совмещаем!

F1-Score

На практике, когда мы пытаемся повысить точность нашей модели, полнота снижается, и наоборот. F1-Score отражает обе тенденции в одном значении:

F1-Score представляет собой гармоничное среднее значение точности и полноты, поэтому дает общее представление об этих двух показателях. Оно максимально, когда точность равно полноте.

Но здесь есть одна загвоздка. Интерпретируемость оценки F1 оставляет желать лучшего. Это означает, что мы не знаем, чего добивается наш классификатор — точности или полноты? Итак, мы используем его в сочетании с другими оценочными метриками, что дает нам полную картину результата.

Матрица ошибок с использованием scikit-learn в Python

Вы знаете теорию — теперь давайте применим ее на практике. Давайте запрограммируем матрицу ошибок с помощью библиотеки Scikit-learn (sklearn) на Python.

# confusion matrix in sklearn

from sklearn.metrics import confusion_matrix

3 from sklearn.metrics import classification_report

# actual values

actual = [1,0,0,1,0,0,1,0,0,1]

# predicted values

predicted = [1,0,0,1,0,0,0,1,0,0]

# confusion matrix

matrix = confusion_matrix(actual,predicted, labels=[1,0])

print(‘Confusion matrix : n’,matrix)

# outcome values order in sklearn

tp, fn, fp, tn = confusion_matrix(actual,predicted,labels=[1,0]).reshape(-1)

print(‘Outcome values : n’, tp, fn, fp, tn)

# classification report for precision, recall f1-score and accuracy

matrix = classification_report(actual,predicted,labels=[1,0])

print(‘Classification report : n’,matrix)

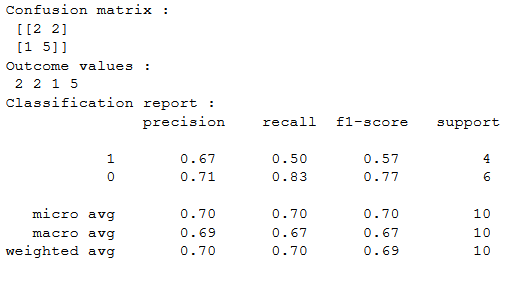
Sklearn имеет две отличные функции: confusion_matrix() и classification_report().

Mirco average — это оценка точности/полноты/f1, рассчитанная для всех классов.

Macro average — это среднее значение точности/полноты/f1-score.

Weighted average — это просто средневзвешенное значение точности/полноты/f1-score.

Матрица ошибок для мультиклассовой классификации

Как матрица ошибок будет работать для задачи классификации нескольких классов? Мы рассмотрим и этот случай.

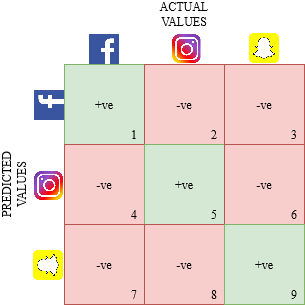
Давайте нарисуем матрицу ошибок для мультиклассовой задачи, в которой мы должны предсказать, любит ли человек Facebook, Instagram или Snapchat. Матрица ошибок будет иметь вид 3 x 3:

true positive, true negative, false positive и false negative для каждого класса будут вычисляться путем сложения значений ячеек следующим образом:

Вот и все! Вы готовы расшифровать любую матрицу ошибок размером N x N!

Заключение

И вдруг матрица ошибок перестает быть такой запутанной! Эта статья должна дать вам прочную основу для интерпретации и использования матрицы ошибок для алгоритмов классификации в машинном обучении.

Вскоре мы выпустим статью о кривой AUC-ROC и продолжим наше обсуждение там. До этого не теряйте надежды на свою модель классификации, возможно, вы просто используете неправильную метрику оценки!

Для классификационных моделей, как и для моделей регрессии, актуальна задача оценки их качества для определения работоспособности моделей и их сравнения. Однако решение этой задачи для моделей классификации вообще, и бинарной классификации в частности, сложнее, чем для регрессии. Связано это с тем, что целевая переменная (метка класса) является категориальным (дискретным) значением, и, следовательно, ошибка классификации не может быть выражена числовым значением.

Поэтому в основе оценки качества классификационных моделей лежит статистика результатов классификации обучающих примеров. С ее помощью вычисляются метрики качества — показатели, которые зависят от результатов классификации и не зависят от внутреннего состояния модели.

Среди наиболее популярных методов оценки качества классификаторов можно выделить следующие:

1. Матрица ошибок (Сonfusion matrix).
2. Меткость (Accuracy).
3. Точность (Precision).
4. Полнота (Recall).
5. Специфичность (Specificity).
6. F1-мера (F1-score).
7. Метрика P₄ .
8. Площадь под ROC-кривой (Area under ROC-curve, AUC-ROC).
9. Площадь под кривой полнота-точность (Area under precision-recall curve, AUC-PR).
10. Коэффициент корреляции Мэтьюса (Matthews correlation coefficient, MCC).
11. Функция потерь логистической регрессии (Logistic loss function, Log Loss).

Матрица ошибок

Прежде чем переходить к описанию собственно метрик качества бинарных классификаторов, рассмотрим методику описания этих метрик в терминах ошибок классификации. Пусть заданы два класса y=left { 0,1 right } и алгоритм, предсказывающий принадлежность каждого объекта одному из классов. Эта задача анализа известна как бинарная классификация.

Приведем пример. Пусть в страховой компании используется аналитическая платформа для поддержки принятия решений о целесообразности страхования того или иного объекта. Если риск наступления страхового события выше определенного порога, то такие объекты страховать нецелесообразно. Именно выявление таких объектов и является целью анализа. Тогда для объектов, страхование которых целесообразно, система должна установить класс 0, а объектам, в страховании которых отказано, — класс 1.

Любой реальный классификатор совершает ошибки. В нашем случае таких ошибок может быть две:

• класс 0 распознается классификатором как класс 1, что можно интерпретировать как «ложную тревогу»;
• класс 1 распознается как класс 0, что можно трактовать как «пропуск цели».

Очевидно, что приведенные ошибки неравноценны по связанным с ними издержкам классификации. В случае «ложной тревоги» компания потеряет только потенциальную страховую премию, т.е. будет иметь место всего лишь упущенная выгода. В случае «пропуска цели» возможна потеря значительной суммы из-за наступления страхового случая. Поэтому важнее не допустить «пропуск цели», чем «ложную тревогу».

Иными словами, важнее правильно определить объект, нежелательный для страхования из-за высокого риска, чем ошибиться в распознавании желательного. Будем называть соответствующий исход классификации положительным (объект не подлежит страхованию y=1), а противоположный — отрицательным (объект подлежит страхованию y=0). Тогда возможны следующие исходы классификации:

1. Объект, нежелательный для страхования, классифицирован как нежелательный, т.е. «положительный» класс распознан как положительный. Такой исход классификации (а также пример, для которого он получен) называют истинноположительным.
2. Объект, желательный для страхования, распознан как желательный, т.е. «отрицательный» класс распознан как отрицательный. Такой исход классификации называют истинноотрицательными.
3. Объект, желаемый для страхования, классифицирован как не желаемый, т.е. имела место ошибка, в результате которой отрицательный класс был распознан как положительный. Данный исход классификации называют ложноположительным, а ошибка классификации называется ошибкой I рода.
4. Нежелательный объект распознан как желательный, т.е. имела место ошибка, в результате которой положительный класс был распознан как отрицательный. Такой исход классификации называется ложноотрицательным, а ошибка классификации — ошибкой II рода.

Таким образом, ошибка I рода, или ложноположительный исход классификации, имеет место, когда пример, с которым связано отрицательное событие распознан моделью как положительный. Ошибкой II рода, или ложноотрицательным исходом классификации, называют случай, когда пример, с которым связано положительное событие, распознан как отрицательный. Поясним это с помощью матрицы ошибок классификации, называемой также таблицей сопряженности:

	y=0	y=1
widehat{y}=0	Истинноположительный (True Positive — TP)	Ложноположительный (False Positive — FP)
widehat{y}=1	Ложноотрицательный (False Negative — FN)	Истинноотрицательный (True Negative — TN)

Здесь widehat{y} — отклик модели, а y — фактическое значение. Таким образом, ошибки классификации бывают двух видов: False Negative (FN) и False Positive (FP). В данном случае P означает, что классификатор определяет класс объекта как положительный, а N как — отрицательный. T значит, что класс предсказан правильно, соответственно, F — неправильно. Каждая строка в матрице ошибок представляет предсказанный класс, а каждый столбец — фактически наблюдаемый класс.

Идеальный классификатор, если бы он существовал, выдавал бы только истиннополо­жительные и истинноотрицательные классификации, и его матрица ошибок содержала бы значения, отличные от нуля, только на главной диа­гонали.

Меткость

Представляет собой долю правильных классификаций модели:

ACC=frac{TP+TN}{TP+TN+FP+FN}.

Несложно увидеть, что сумма в знаменателе формулы представляет собой общее число классифицируемых примеров. Графически это можно интерпретировать следующим образом:

В английском языке этот термин обозначается как «accuracy», поэтому в интернете он часто упоминается как «аккуратность», хотя это слово и не передает смыслового значения данной величины.

Несмотря на то, что эта мера хорошо интерпретируется, на практике она используется достаточно редко, поскольку плохо работает в случае дисбаланса классов в обучающей выборке.

Поясним это на примере кредитного скоринга. Пусть требуется классифицировать заемщиков на добросовестных (не допустивших просрочку) и недобросовестных (допустивших просрочку). Целью является выявление недобросовестных заемщиков, поскольку связанные с ними издержки выше. Следовательно, классификация заемщика как недобросовестного является положительным событием, а как добросовестного — отрицательным.

Выборка содержит 1000 добросовестных заемщиков, 900 из которых классификатор предсказал правильно (TN=900, FP=100), и 100 недобросовестных, 50 из которых классификатор также определил верно (TP=50, FN=50).

Несложно вычислить, что:

ACC=frac{50+900}{50+900+100+50}=0.866.

Однако, если построить «наивную» модель, которая просто будет классифицировать всех клиентов, как добросовестных (на основании того, что таковых большинство), то меткость такой модели окажется:

ACC=frac{0+1000}{0+1000+0+100}=0.909.

Таким образом, оказалось, что меткость «бесполезной» модели, не имеющей предсказательной силы, выше, чем «рабочей» модели. Это противоречит здравому смыслу. Поэтому на практике стараются использовать альтернативные меры качества.

Точность

Точность равна доле истинноположительных классификаций к общему числу положительных классификаций. Данная величина часто упоминается как positive predictive value (PPV) или положительное прогностическое значение:

Pr=PPV=frac{TP}{TP+FP}.

Поясним данное выражение с помощью рисунка:

Несложно увидеть, что попытка отнести все объекты к одному классу неизбежно приведет к росту FP и уменьшению значения точности.

Полнота

Полнота, известная еще как чувствительность или доля истинноположительных примеров (TPR — true positive rate), определяется как число истинноположительных классификаций относительно общего числа положительных наблюдений:

Re=TPR=frac{TP}{TP+FN}.

Таким образом, полноту можно рассматривать как способность классификатора обнаруживать определенный класс. Графически полноту можно проиллюстрировать с помощью рисунка:

Точность и полноту для каждого класса легко определять с помощью матрицы ошибок. Точность равна отношению соответствующего диагонального элемента матрицы и суммы элементов всей строки класса, а полнота — отношению диагонального элемента матрицы и суммы элементов всего столбца класса.

PPV_{c}=frac{A_{cc}}{sumlimits_{i=1}^{n}A_{ci}},

TPR_{c}=frac{A_{cc}}{sumlimits_{i=1}^{n}A_{ic}},

где c — класс, n — число элементов столбца (равно числу классов), i — номер элемента в столбце, A — элемент матрицы ошибок.

Специфичность

Специфичность классификатора — это доля истинноотрицательных (True Negative Rate — TNR) классификаций в общем числе отрицательных классификаций:

Sp=TNR=frac{TN}{TN+FP}.

TNR показывает, насколько хорошо модель классифицирует отрицательные примеры. Поясним это с помощью рисунка.

Очевидно, что если все отрицательные примеры классифицированы правильно (т.е. число ложноположительных случаев равно 0), то TPR=1.

F1-мера

Точность и полнота, в отличие от меткости, не зависят от соотношения классов и, следовательно, могут применяться в условиях несбалансированных выборок. На практике часто встречается задача поиска оптимального баланса между точностью и полнотой. Действительно, улучшая настройку модели на один класс, например, путем изменения дискриминационного порога, мы тем самым ухудшаем настройку на другой.

Чем выше точность и полнота, тем лучше модель. Но на практике их максимальные значения одновременно недостижимы, поэтому приходится искать баланс между ними. Для этого используется метрика, объединяющая в себе информацию о точности и полноте. Она называется F1-мера и вычисляется следующим образом:

F1=frac{2cdot PPVcdot TPR}{PPV+TPR}=frac{2cdot TP}{2cdot TP+FP+FN}.

В данном выражении точность PPV и полнота TPR имеют одинаковый вес, поэтому при их уменьшении F1-мера сокращается пропорционально.

Однако на практике чаще используется сбалансированная F1-мера, в которой точности и полноте присваиваются разные веса с целью найти оптимальный баланс между данными метриками. Для этого в формулу для F1-меры вводится дополнительный балансировочный параметр, обозначаемый β. Сбалансированная F1-мера вычисляется следующим образом:

F1=frac{(1-beta ^{2})cdot PPVcdot TPR}{beta ^{2}cdot PPV+TPR}.

Если параметр принимает значения из диапазона 0< beta < 1, то приоритет имеет точность, а если beta> 1, то полнота.

Еще одним источником критики F1-меры является отсутствие симметрии. Это означает, что она может изменить свое значение при инверсии положительного и отрицательного классов.

Метрика P₄

Метрика P_{4} была разработана как расширение F1-меры, обладающее симметрией относительно инверсии классов. Вычисляется по формуле:

P_{4}=frac{4cdot TPcdot TN}{4cdot TPcdot TN+(TP+TN)cdot (FP+FN)}.

Метрика P_{4} изменяется в диапазоне от 0 до 1. Чем ближе значение метрики к 1, тем лучше работает модель. Очевидно, что значение меры стремится к 0, если хотя бы один из множителей в числителе становится равным нулю, т.е. когда модель теряет способность правильно распознавать положительные или отрицательные примеры.

AUC-ROC

ROC-кривая, или кривая рабочих характеристик приемника (Receiver Operating Characteristics curve), позволяет не только оценить качество работы классификатора, но и исследовать его поведение при различных значениях дискриминационного порога. Технология оценки качества моделей бинарной классификации с помощью ROC-кривых известна как ROC-анализ.

Рассмотрим совместно TPR и TNR классификатора. TPR показывает, насколько хорошо модель классифицирует положительные примеры. Очевидно, что если все положительные примеры классифицированы правильно (т.е. число ложноотрицательных случаев равно 0), то TPR=1. TNR показывает, насколько хорошо модель классифицирует отрицательные примеры. Очевидно, что если все отрицательные примеры классифицированы правильно (т.е. число ложноположительных случаев равно 0), то TPR=1.

Таким образом, по отдельности TPR и TNR характеризуют способность модели распознавать только один из классов. Но их совместное использование помогает создать метрику, которая позволяет выбирать значение дискриминационного порога, который оптимально балансирует модель между способностью распознавать положительные и отрицательные примеры. Именно эта задача и решается с помощью ROC-кривой.

Действительно, если изменять дискриминационный порог от 0 до 1 и наносить по оси абсцисс точки 1−TNR, а по оси ординат TPR, то полученный график и будет ROC-кривой. Величину 1−TNR называют долей ложноположительных классификаций (false positive rate) или показателем ложной тревоги. Она вычисляется следующим образом:

1-TNR=FPR=frac{FP}{FP+TN}.

При пороге, равном 1, все примеры будут классифицированы как отрицательные (FPR=1, TPR=1), а при пороге, равном 0, — как положительные (FPR=0, TPR=0). Поэтому ROC-кривая всегда идет от точки (0,0) до точки (1,1).

Несложно увидеть, что для идеальной модели ROC-кривая превращается в ломаную, проходящую через точки (0,0), (0,1) и (1,1). При этом площадь под ROC-кривой (AUC — Area Under Curve) окажется равной 1. Площадь под кривой выделена на рисунке светло-серым цветом.

Точка (0,1) соответствует идеальному состоянию модели, в котором и TPR, и TNR одновременно равны 1. Т.е. модель одинаково хорошо «научилась» работать как с положительными, так и с отрицательными примерами при существующем в обучающей выборке балансе классов.

Идеальная модель является скорее гипотетической и на практике, как правило, недостижима. Поэтому обычно приходится иметь дело с ROC-кривыми, которые не проходят через точку (0,1), а приближаются к ней на определенное расстояние. Соответственно и AUC−ROC оказывается меньше 1.

Таким образом показатель AUC−ROC является удобной мерой качества классификатора относительно идеального. Принята следующая шкала оценки качества.

AUC	Оценка
0.9 — 1	Отличное
0.8 — 0.9	Очень хорошее
0.7 — 0.8	Хорошее
0.6 — 0.7	Удовлетворительное
0.5 — 0.7	Плохое

Если AUC-ROC=0.5, то ROC-кривая превращается в линию, проходящую через точки (0,0) и (1,1), которая соответствует бесполезному классификатору, работающему как случайный предсказатель. Если AUC-ROC< 0.5, то получается модель, которая работает хуже случайного предсказателя и от ее использования следует отказаться.

AUC-PR

PR-кривые определяются аналогично ROC-кривым, но только по оси абсцисс у них откладываются значения полноты, а по оси ординат — точности.

Точность и полнота — две наиболее важные метрики, на которые следует обращать внимание при оценке качества модели бинарной классификации в условиях несбалансированности классов. Они помогают увидеть, какая часть фактически положительных наблюдений была классифицирована правильно, и какие среди классифицированных как положительные, были истинноположительными.

Если точность равна 1, то ложноположительные классификации отсутствуют. Но это ничего не говорит о том, были ли распознаны все положительные примеры. Если полнота равна 1, то все положительные объекты были распознаны правильно, а ложноотрицательные классификации отсутствуют. При этом ничего не говорится о том, сколько было допущено ложноположительных классификаций.

Таким образом, точность и полнота не особенно полезны для оценки качества классификатора, если их использовать по отдельности. В задаче классификации оценка точности, равная 1 для класса C, означает, что каждый элемент, помеченный как принадлежащий классу C, действительно принадлежит к классу C, но ничего не говорит о количестве элементов из класса
C, которые не были правильно классифицированы. Тогда как полнота, равная 1, означает, что каждый элемент из класса C был помечен как принадлежащий к классу C, но ничего не говорит о том, сколько элементов из других классов были также неправильно классифицированы как принадлежащие к классу C.

Обычно показатели точности и полноты не используются по отдельности. Вместо этого либо значения одной меры сравниваются с фиксированным уровнем другой (например, точность на уровне полноты 0.75), либо обе меры объединяются в один показатель. Примерами такой комбинации и является F1-мера — взвешенное гармоническое среднее точности и полноты.

Еще одним способом комбинирования точности и полноты в задаче оценки качества классификации являются так называемые кривые полнота-точность, которые строятся в системе координат, где по оси абсцисс откладывается полнота, а по оси ординат — точность. Кривая точность-полнота показывает, как выбор порога влияет на точность классификатора, а также помогает выбрать лучшее значение дискриминационного порога для определенного баланса классов.

Каждая точка PR-кривой представляет определенное значение дискриминационного порога, а ее расположение соответствует результирующей точности и полноте, когда этот порог выбран. Точка 1 на рисунке соответствует значению дискриминационного порога, равному 1, а точка 3 — значению порога 0. Точка 2 соответствует идеальному классификатору и совпадает с координатами (1,1), а точка 4 — оптимальному значению порога (точка кривой, наиболее близкая к идеальной точке (1,1)).

Преимущества PR-кривой по сравнению с ROC:

1. ROC-кривая, как правило, дает чрезмерно оптимистичную картину в условиях несбалансированности классов.
2. При изменении распределения классов ROC-кривая не меняется, а PR-кривая отражает изменение.

Аналогично ROC-кривой, площадь под PR-кривой (для отличия от ROC ее часто называют PR−AUC) отражает качество классификатора и позволяет сравнивать кривые, соответствующие различным балансам классов и значениям порога. Чем выше площадь, тем лучше работает модель.

Пунктирная линия внизу графика соответствует бесполезному классификатору (no-skill model — модель без навыков, или базовая модель), уровень которой изменяется при изменении баланса классов. Такая модель будет присваивать рейтинг 0.5 для любого примера.

На рисунке ниже представлена линия, соответствующая балансу классов, когда положительные примеры составляют 10% от обучающей выборки.

На рисунке точка 1 соответствует порогу 0.5, точка 2 соответствует порогу [0, 0.5). Для порогов (0.5, 1] точность не определена из-за деления на ноль. Можно увидеть, что точность здесь является константой, то есть PPV=0.1 (соответствует доле положительного класса), PR−AUC=0.1.

Таким образом, полнота базовой модели лежит в диапазоне (0.5, 1] независимо от дисбаланса классов, а точность равна доле положительного класса в обучающей выборке.

На следующем рисунке представлена PR-кривая для идеальной модели. На ней точка 1 соответствует порогу (0, 1], точка 2 соответствует порогу 0. Очевидно, что PR−AUC=1.

И, наконец, на рисунке ниже отображена PR-кривая (красная линия) для модели, которая работает хуже, чем базовая модель «без навыков» (синяя пунктирная линия). Она расположена ниже линии базовой модели.

Очевидный способ повысить качество «плохой» модели без каких-либо настроек — просто инвертировать классы (класс 0 изменить на класс 1). Это автоматически приведет к повышению точности по сравнению с базовой моделью.

Обычно «плохая» PR-кривая классификатора указывает на то, что в обучающих данных присутствуют проблемы: они содержат шум или классы в них плохо выражены (модель не может выявить закономерность, в соответствии с которой один класс отличается от другого). В этом случае PR−AUC не превышает доли положительных примеров обучающей выборке.

Возможен гибридный случай, когда «плохая» модель работает лучше, чем модель «без навыков», но для определенных пороговых значений.

Коэффициент корреляции Мэтьюса

Коэффициент используется в качестве показателя качества бинарных классификаторов. Он учитывает истинные и ложные классификации и обычно рассматривается как сбалансированная мера, которую можно использовать даже в условиях сильного дисбаланса классов.

MCC, по сути, коэффициент корреляции между фактическими и предсказанными моделью бинарными классификациями. Он изменяется в диапазоне от -1 до 1. MCC=1 указывает на идеальную классификацию, когда фактические и предсказанные классы совпадают для всех обучающих примеров (т.е. ложноположительные и ложноотрицательные классификации отсутствуют). Модель, для которой MCC=0, соответствует случайному предсказателю. MCC=−1 указывает на полное расхождение между фактом и предсказанием (т.е. вместо положительного класса модель всегда предсказывает отрицательный, и наоборот), следовательно, истинноположительные и истинноотрицательные классификации отсутствуют.

Формула для расчета MCC имеет вид:

MCC=frac{TPcdot TN-FPcdot FN}{sqrt{(TP+FP)(TP+FN)(TN+FP)(TN+FN)}}.

Несложно увидеть, что если в этой формуле обнулить все ложные классификации, то MCC=1, что соответствует ранее сделанным заключениям. Если число истинных и ложных классификаций равны, то числитель формулы становится равным 0 и MCC=0. И, наконец, если число истинных классификаций равно нулю, то числитель становится отрицательным, и делает таковым результат формулы.

Если какая-либо из четырех сумм в знаменателе равна нулю, знаменатель можно произвольно установить равным единице, это приводит к нулевому коэффициенту корреляции Мэтьюса.

Функция потерь логистической регрессии (Logistic loss function, Log Loss).

Функция потерь в задачах классификации показывает, какую «цену» придется заплатить за неточность предсказаний классификационной модели. Для логистической регрессии, решающей задачу бинарной классификации, она может быть вычислена следующим образом:

Log Loss=-frac{1}{l}sumlimits_{i=1}^{l}(y_{i}cdot log(widehat{y_{i}})+(1-y_{i})cdot log(1-widehat{y_{i}})),

где l — размер выборки, y_{i}=left { 0,1 right } — бинарная метка класса, заданная в примере, widehat{y_{i}} — предсказание модели.

Несложно увидеть, что функция потерь получается путем суммирования логарифма потерь на каждом примере. Потери на каждом примере определяются следующим образом: если предсказанный класс совпадает с фактическим, то потери равны 0, в противном случае потери равны 1. Очевидно, чем больше будет неправильных классификаций, тем больше будет значение LogLoss и тем хуже будет модель. Таким образом, чтобы получить лучшую модель, нужно минимизировать функцию потерь.

Преимуществом метрики LogLoss является устойчивость к выбросам и аномальным значениям в данных и простота вычисления. Недостатком — сложность интерпретации из-за нелинейного характера.

Сравнение метрик

Подведем итоги, кратко резюмируя преимущества и недостатки рассмотренных мер качества классификационных моделей.

Мера	Преимущества	Недостатки
Меткость	Хорошо интерпретируется.	Чувствительна к дисбалансу классов. Неадекватно отражает точность классификации.
Точность	Не чувствительна к дисбалансу классов.	Отражает качество классификации только для положительного класса.
Полнота	Не чувствительна к дисбалансу классов.	Не учитывает отрицательные классификации.
Специфичность	Просто вычисляется и интерпретируется.	Характеризует способность модели распознавать только один класс.
F1-мера	Позволяет найти баланс между точностью и полнотой.	Чувствительность к дисбалансу, отсутствие симметрии.
P4	Симметрична относительно инверсии классов.	Чувствительность к дисбалансу классов.
AUC-ROC	Наглядна, хорошо интерпретируется.	В условиях дисбаланса классов завышает качество модели. Не отражает изменения баланса классов.
AUC-PR	Наглядна, хорошо интерпретируется.	Не учитывает отрицательные классификации.
Коэффициент Мэтьюса	Более информативен, поскольку использует все типы результатов классификации.	Не может применяться, если один из множителей в знаменателе обращается в 0.
LogLoss	Устойчивость к выбросам в данных, простота вычисления.	Сложность интерпретации из-за нелинейного характера.

В статье рассмотрены наиболее общие меры оценки качества моделей бинарной классификации, отмечены их преимущества и недостатки. Однако в литературе авторы предлагают и другие подходы, которые показали хорошие результаты при решении конкретных задач и не претендующие на универсальность.

Другие материалы по теме:

Метрики качества линейных регрессионных моделей

Отбор переменных в моделях линейной регрессии

Репрезентативность выборочных данных

Перевод статьи – Understanding Confusion Matrix – Sarang Narkhede

Когда мы получаем данные после очистки, предварительной обработки и обработки данных, первым шагом, который мы делаем, является создание модели  и, конечно, получение результатов в вероятностях. Но держись! Как, черт возьми, мы можем измерить эффективность нашей модели? Лучшая эффективность, лучшая производительность и это именно то, что мы хотим. В данном случае мы начинаем использовать матрицу ошибок. Матрица ошибок (Confusion Matrix) – это измерение производительности для классификации машинного обучения.

Этот пост призван ответить на следующие вопросы:

• Что такое Матрица ошибок и зачем она нужна?
• Как вычислить матрицу ошибок для задач бинарной классификации?

Сегодня давайте разберемся с матрицей путаницы раз и навсегда.

Что такое матрица ошибок, и зачем она нужна?

Ну, это измерение производительности для задачи классификации машинного обучения, где выходной может быть два или более классов. Это таблица с 4 различными комбинациями прогнозируемых и фактических значений.

Это чрезвычайно полезно для вычисления Полноты, Точности, Специфичность, Точность и, что наиболее важно кривой ошибок AUC-ROC.

Давайте поймем термины TP, FP, FN, TN  на примере аналогии с  беременностью.

TP — истино-положительное решение:

Интерпретация: Вы предсказали положительное, и это правда.

Вы предсказали, что женщина беременна, и она на самом деле беременна.

TN — истино-отрицательное решение:

Интерпретация: Вы прогнозировали отрицательное значения, и это правда.

Вы предсказали, что мужчина не беременен, а он на самом деле не беременен.

FP — ложно-положительное решение (Ошибка типа 1):

Интерпретация: Вы предсказали положительное значение, и это неверно.

Вы предсказали, что мужчина беременен, но на самом деле это не так.

FN— ложно-отрицательное решение (Ошибка Типа 2):

Интерпретация: Вы предсказали отрицательное значение, и это неверно.

Вы предсказали, что женщина не беременна, но она на самом деле беременная.

Только помните, мы описываем прогнозируемые значения как положительные и отрицательные, а фактические значения как истинные и ложные.

How to Calculate Confusion Matrix for a 2-class classification problem?

Как вычислить матрицу ошибок  для задачи классификации с бинарными классами?

Давайте разберемся с матрицей ошибок посредством математик

Полнота Recall

Из всех положительных классов, сколько мы предсказали правильно. Это должно быть как можно выше.

Точность Precision

Из всех классов, сколько мы предсказали правильно. Это должно быть как можно выше.

F-мера

Трудно сравнить две модели с низкой точностью и высокой отзывчивостью или наоборот. Поэтому, чтобы сделать их сопоставимыми, мы используем F-меру. F-мера помогает измерять Полноту и Точность одновременно. Она использует гармоническое среднее вместо среднего арифметического, наказывая экстремальные значения больше.

https://towardsdatascience.com/understanding-confusion-matrix-a9ad42dcfd62