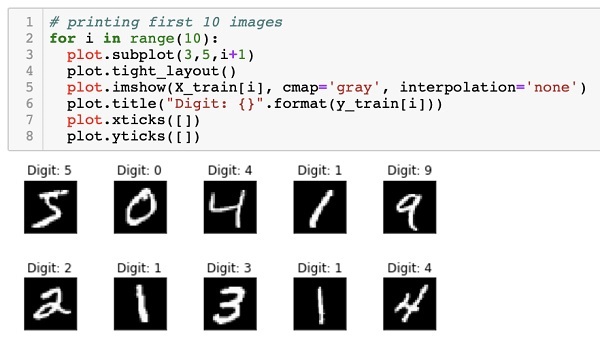
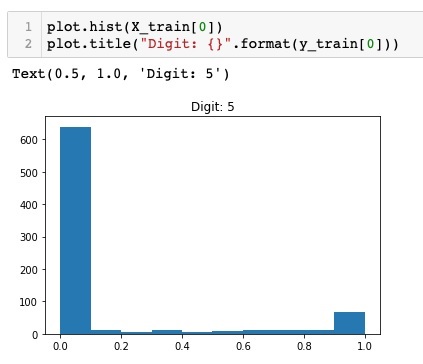
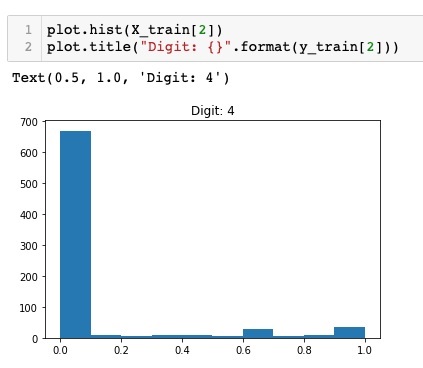
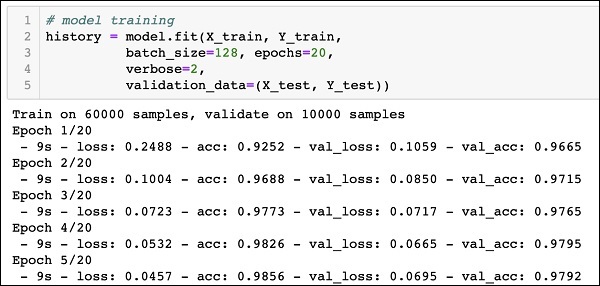
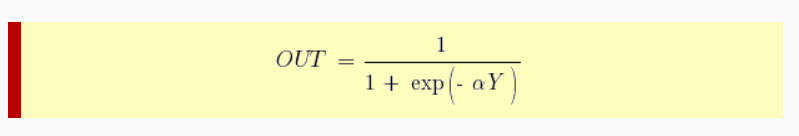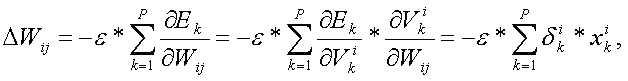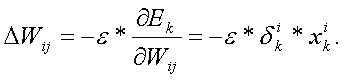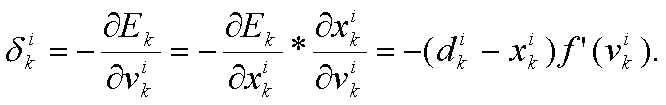Знакомимся с методом обратного распространения ошибки
Время на прочтение
6 мин
Количество просмотров 44K
Всем привет! Новогодние праздники подошли к концу, а это значит, что мы вновь готовы делиться с вами полезным материалом. Перевод данной статьи подготовлен в преддверии запуска нового потока по курсу «Алгоритмы для разработчиков».
Поехали!
Метод обратного распространения ошибки – вероятно самая фундаментальная составляющая нейронной сети. Впервые он был описан в 1960-е и почти 30 лет спустя его популяризировали Румельхарт, Хинтон и Уильямс в статье под названием «Learning representations by back-propagating errors».
Метод используется для эффективного обучения нейронной сети с помощью так называемого цепного правила (правила дифференцирования сложной функции). Проще говоря, после каждого прохода по сети обратное распространение выполняет проход в обратную сторону и регулирует параметры модели (веса и смещения).
В этой статья я хотел бы подробно рассмотреть с точки зрения математики процесс обучения и оптимизации простой 4-х слойной нейронной сети. Я считаю, что это поможет читателю понять, как работает обратное распространение, а также осознать его значимость.
Определяем модель нейронной сети
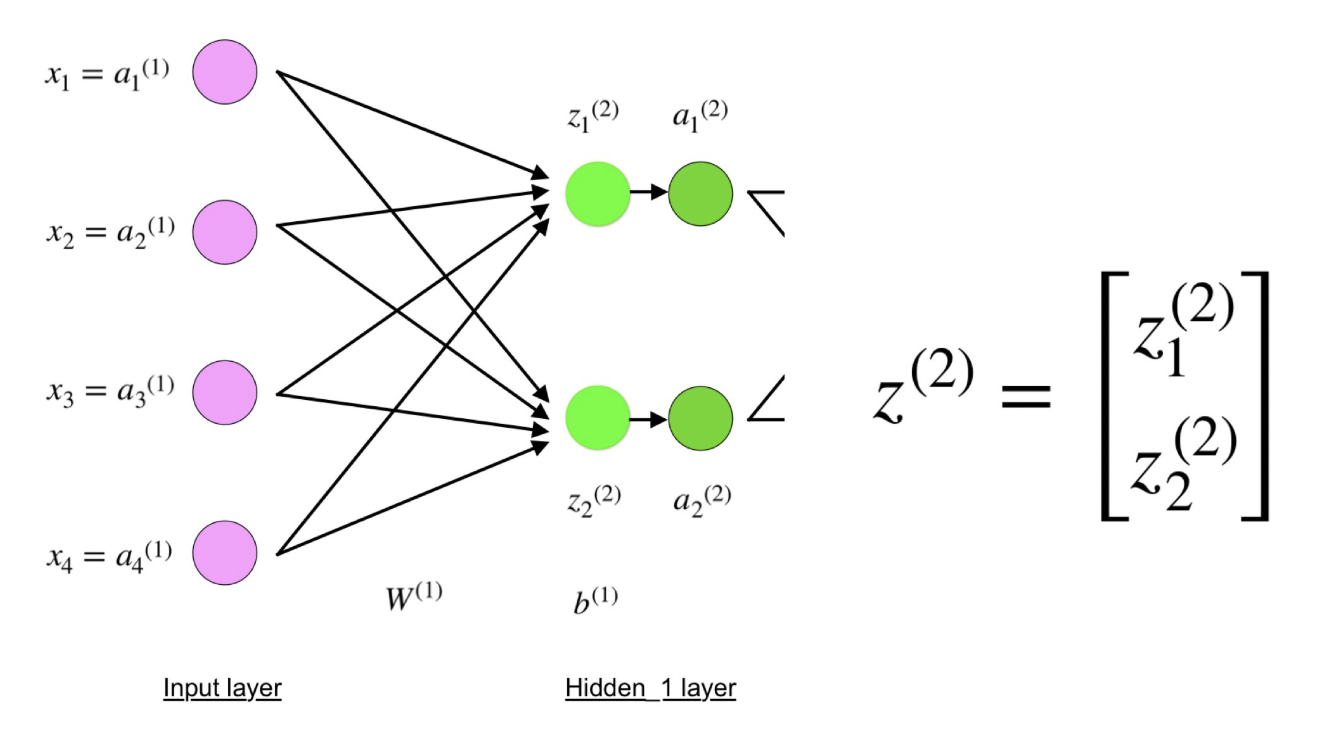
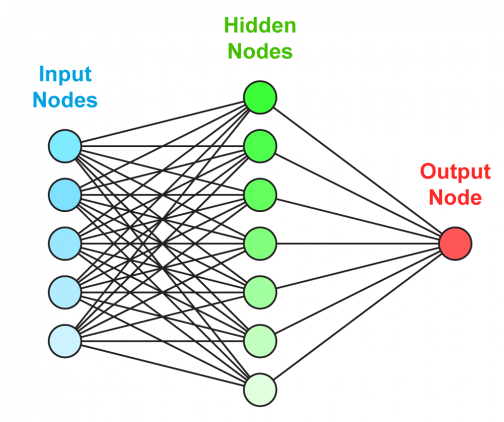
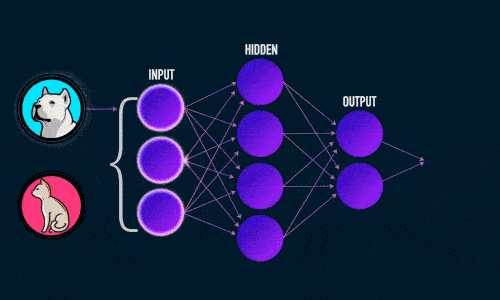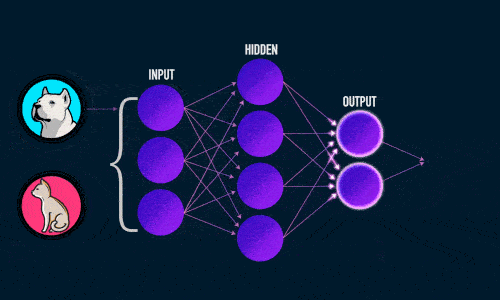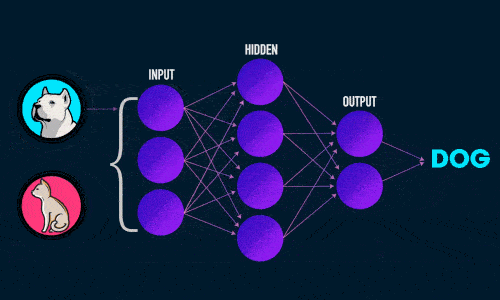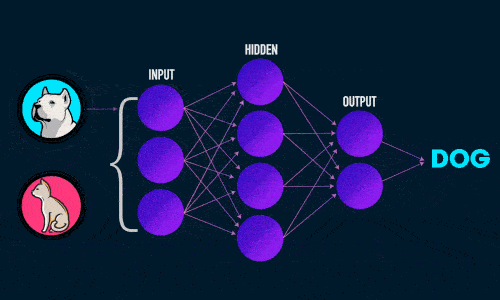
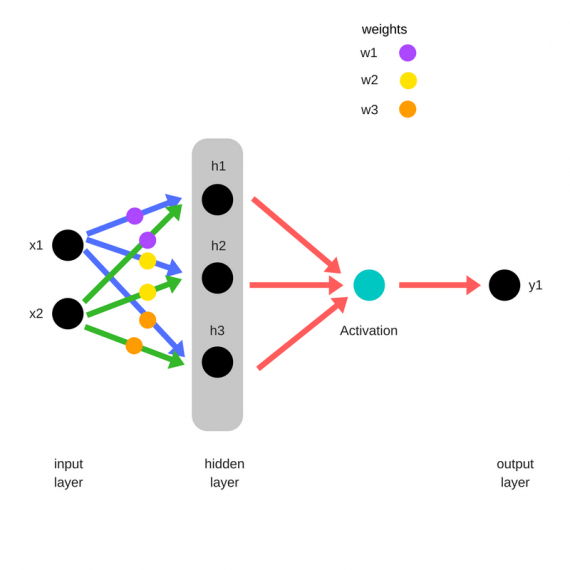
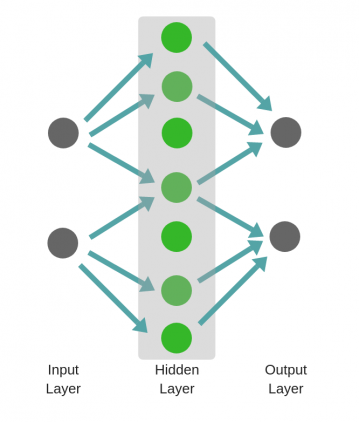
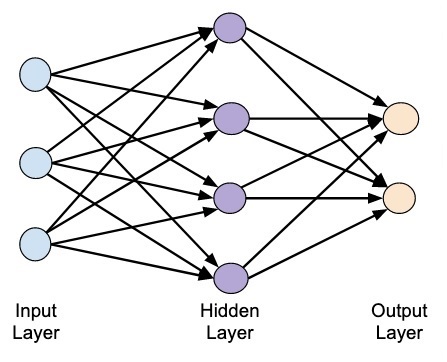
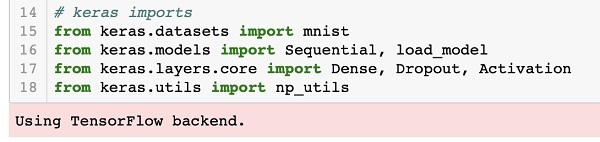
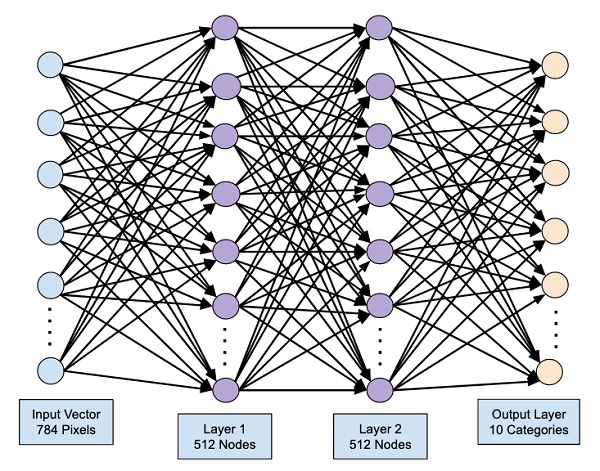
Четырехслойная нейронная сеть состоит из четырех нейронов входного слоя, четырех нейронов на скрытых слоях и 1 нейрона на выходном слое.
Простое изображение четырехслойной нейронной сети.
Входной слой
На рисунке нейроны фиолетового цвета представляют собой входные данные. Они могут быть простыми скалярными величинами или более сложными – векторами или многомерными матрицами.
Уравнение, описывающее входы xi.
Первый набор активаций (а) равен входным значениям. «Активация» — это значение нейрона после применения функции активации. Подробнее смотрите ниже.
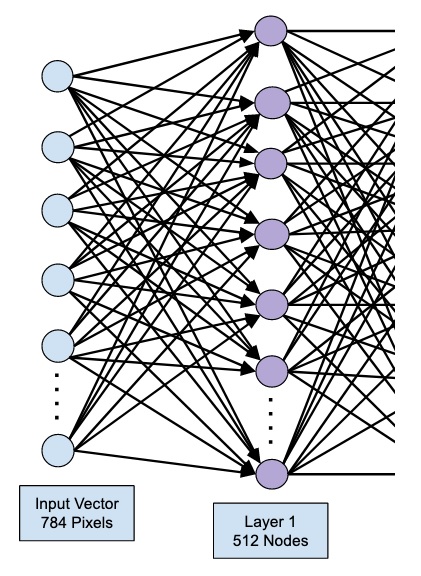
Скрытые слои
Конечные значения в скрытых нейронах (на рисунке зеленого цвета) вычисляются с использованием zl – взвешенных входов в слое I и aI активаций в слое L. Для слоев 2 и 3 уравнения будут следующими:
Для l = 2:
Для l = 3:
W2 и W3 – это веса на слоях 2 и 3, а b2 и b3 – смещения на этих слоях.
Активации a2 и a3 вычисляются с помощью функции активации f. Например, эта функция f является нелинейной (как сигмоид, ReLU и гиперболический тангенс) и позволяет сети изучать сложные паттерны в данных. Мы не будем подробно останавливаться на том, как работают функции активации, но, если вам интересно, я настоятельно рекомендую прочитать эту замечательную статью.
Присмотревшись внимательно, вы увидите, что все x, z2, a2, z3, a3, W1, W2, b1 и b2 не имеют нижних индексов, представленных на рисунке четырехслойной нейронной сети. Дело в том, что мы объединили все значения параметров в матрицы, сгруппированные по слоям. Это стандартный способ работы с нейронными сетями, и он довольно комфортный. Однако я пройдусь по уравнениям, чтобы не возникло путаницы.
Давайте возьмем слой 2 и его параметры в качестве примера. Те же самые операции можно применить к любому слою нейронной сети.
W1 – это матрица весов размерности (n, m), где n – это количество выходных нейронов (нейронов на следующем слое), а m – число входных нейронов (нейронов в предыдущем слое). В нашем случае n = 2 и m = 4.
Здесь первое число в нижнем индексе любого из весов соответствует индексу нейрона в следующем слое (в нашем случае – это второй скрытый слой), а второе число соответствует индексу нейрона в предыдущем слое (в нашем случае – это входной слой).
x – входной вектор размерностью (m, 1), где m – число входных нейронов. В нашем случае m = 4.
b1 – это вектор смещения размерности (n, 1), где n – число нейронов на текущем слое. В нашем случае n = 2.
Следуя уравнению для z2 мы можем использовать приведенные выше определения W1, x и b1 для получения уравнения z2:
Теперь внимательно посмотрите на иллюстрацию нейронной сети выше:
Как видите, z2 можно выразить через z12 и z22, где z12 и z22 – суммы произведений каждого входного значения xi на соответствующий вес Wij1.
Это приводит к тому же самому уравнению для z2 и доказывает, что матричные представления z2, a2, z3 и a3 – верны.
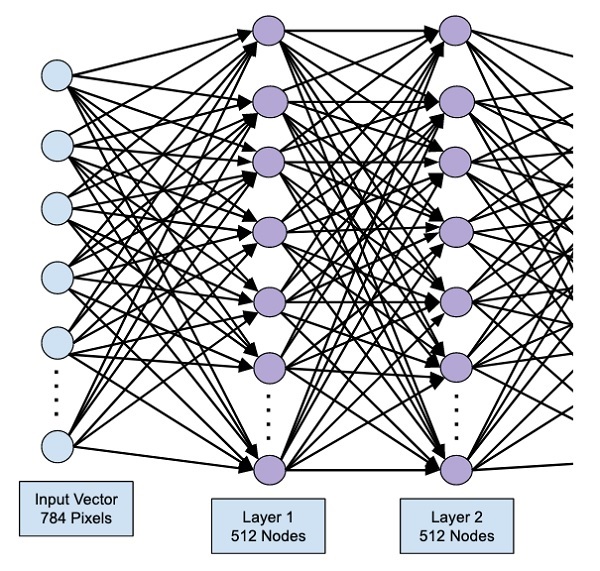
Выходной слой
Последняя часть нейронной сети – это выходной слой, который выдает прогнозируемое значение. В нашем простом примере он представлен в виде одного нейрона, окрашенного в синий цвет и рассчитываемого следующим образом:
И снова мы используем матричное представление для упрощения уравнения. Можно использовать вышеприведенные методы, чтобы понять лежащую в их основе логику.
Прямое распространение и оценка
Приведенные выше уравнения формируют прямое распространение по нейронной сети. Вот краткий обзор:
(1) – входной слой
(2) – значение нейрона на первом скрытом слое
(3) – значение активации на первом скрытом слое
(4) – значение нейрона на втором скрытом слое
(5) – значение активации на втором скрытом уровне
(6) – выходной слой
Заключительным шагом в прямом проходе является оценка прогнозируемого выходного значения s относительно ожидаемого выходного значения y.
Выходные данные y являются частью обучающего набора данных (x, y), где x – входные данные (как мы помним из предыдущего раздела).
Оценка между s и y происходит через функцию потерь. Она может быть простой как среднеквадратичная ошибка или более сложной как перекрестная энтропия.
Мы назовем эту функцию потерь С и обозначим ее следующим образом:
Где cost может равняться среднеквадратичной ошибке, перекрестной энтропии или любой другой функции потерь.
Основываясь на значении С, модель «знает», насколько нужно скорректировать ее параметры, чтобы приблизиться к ожидаемому выходному значению y. Это происходит с помощью метода обратного распространения ошибки.
Обратное распространение ошибки и вычисление градиентов
Опираясь на статью 1989 года, метод обратного распространения ошибки:
Постоянно настраивает веса соединений в сети, чтобы минимизировать меру разности между фактическим выходным вектором сети и желаемым выходным вектором.
и
…дает возможность создавать полезные новые функции, что отличает обратное распространение от более ранних и простых методов…
Другими словами, обратное распространение направлено на минимизацию функции потерь путем корректировки весов и смещений сети. Степень корректировки определяется градиентами функции потерь по отношению к этим параметрам.
Возникает один вопрос: Зачем вычислять градиенты?
Чтобы ответить на этот вопрос, нам сначала нужно пересмотреть некоторые понятия вычислений:
Градиентом функции С(x1, x2, …, xm) в точке x называется вектор частных производных С по x.
Производная функции С отражает чувствительность к изменению значения функции (выходного значения) относительно изменения ее аргумента х (входного значения). Другими словами, производная говорит нам в каком направлении движется С.
Градиент показывает, насколько необходимо изменить параметр x (в положительную или отрицательную сторону), чтобы минимизировать С.
Вычисление этих градиентов происходит с помощью метода, называемого цепным правилом.
Для одного веса (wjk)l градиент равен:
(1) Цепное правило
(2) По определению m – количество нейронов на l – 1 слое
(3) Вычисление производной
(4) Окончательное значение
Аналогичный набор уравнений можно применить к (bj)l:
(1) Цепное правило
(2) Вычисление производной
(3) Окончательное значение
Общая часть в обоих уравнениях часто называется «локальным градиентом» и выражается следующим образом:
«Локальный градиент» можно легко определить с помощью правила цепи. Этот процесс я не буду сейчас расписывать.
Градиенты позволяют оптимизировать параметры модели:
Пока не будет достигнут критерий остановки выполняется следующее:
Алгоритм оптимизации весов и смещений (также называемый градиентным спуском)
- Начальные значения w и b выбираются случайным образом.
- Эпсилон (e) – это скорость обучения. Он определяет влияние градиента.
- w и b – матричные представления весов и смещений.
- Производная C по w или b может быть вычислена с использованием частных производных С по отдельным весам или смещениям.
- Условие завершение выполняется, как только функция потерь минимизируется.
Заключительную часть этого раздела я хочу посвятить простому примеру, в котором мы рассчитаем градиент С относительно одного веса (w22)2.
Давайте увеличим масштаб нижней части вышеупомянутой нейронной сети:
Визуальное представление обратного распространения в нейронной сети
Вес (w22)2 соединяет (a2)2 и (z2)2, поэтому вычисление градиента требует применения цепного правила на (z3)2 и (a3)2:
Вычисление конечного значения производной С по (a2)3 требует знания функции С. Поскольку С зависит от (a2)3, вычисление производной должно быть простым.
Я надеюсь, что этот пример сумел пролить немного света на математику, стоящую за вычислением градиентов. Если захотите узнать больше, я настоятельно рекомендую вам посмотреть Стэндфордскую серию статей по NLP, где Ричард Сочер дает 4 замечательных объяснения обратного распространения.
Заключительное замечание
В этой статье я подробно объяснил, как обратное распространение ошибки работает под капотом с помощью математических методов, таких как вычисление градиентов, цепное правило и т.д. Знание механизмов этого алгоритма укрепит ваши знания о нейронных сетях и позволит вам чувствовать себя комфортно при работе с более сложными моделями. Удачи вам в путешествии по глубокому обучению!
На этом все. Приглашаем всех на бесплатный вебинар по теме «Дерево отрезков: просто и быстро».
Нейронные сети обучаются с помощью тех или иных модификаций градиентного спуска, а чтобы применять его, нужно уметь эффективно вычислять градиенты функции потерь по всем обучающим параметрам. Казалось бы, для какого-нибудь запутанного вычислительного графа это может быть очень сложной задачей, но на помощь спешит метод обратного распространения ошибки.
Открытие метода обратного распространения ошибки стало одним из наиболее значимых событий в области искусственного интеллекта. В актуальном виде он был предложен в 1986 году Дэвидом Э. Румельхартом, Джеффри Э. Хинтоном и Рональдом Дж. Вильямсом и независимо и одновременно красноярскими математиками С. И. Барцевым и В. А. Охониным. С тех пор для нахождения градиентов параметров нейронной сети используется метод вычисления производной сложной функции, и оценка градиентов параметров сети стала хоть сложной инженерной задачей, но уже не искусством. Несмотря на простоту используемого математического аппарата, появление этого метода привело к значительному скачку в развитии искусственных нейронных сетей.
Суть метода можно записать одной формулой, тривиально следующей из формулы производной сложной функции: если $f(x) = g_m(g_{m-1}(ldots (g_1(x)) ldots))$, то $frac{partial f}{partial x} = frac{partial g_m}{partial g_{m-1}}frac{partial g_{m-1}}{partial g_{m-2}}ldots frac{partial g_2}{partial g_1}frac{partial g_1}{partial x}$. Уже сейчас мы видим, что градиенты можно вычислять последовательно, в ходе одного обратного прохода, начиная с $frac{partial g_m}{partial g_{m-1}}$ и умножая каждый раз на частные производные предыдущего слоя.
Backpropagation в одномерном случае
В одномерном случае всё выглядит особенно просто. Пусть $w_0$ — переменная, по которой мы хотим продифференцировать, причём сложная функция имеет вид
$$f(w_0) = g_m(g_{m-1}(ldots g_1(w_0)ldots)),$$
где все $g_i$ скалярные. Тогда
$$f'(w_0) = g_m'(g_{m-1}(ldots g_1(w_0)ldots))cdot g’_{m-1}(g_{m-2}(ldots g_1(w_0)ldots))cdotldots cdot g’_1(w_0)$$
Суть этой формулы такова. Если мы уже совершили forward pass, то есть уже знаем
$$g_1(w_0), g_2(g_1(w_0)),ldots,g_{m-1}(ldots g_1(w_0)ldots),$$
то мы действуем следующим образом:
-
берём производную $g_m$ в точке $g_{m-1}(ldots g_1(w_0)ldots)$;
-
умножаем на производную $g_{m-1}$ в точке $g_{m-2}(ldots g_1(w_0)ldots)$;
-
и так далее, пока не дойдём до производной $g_1$ в точке $w_0$.
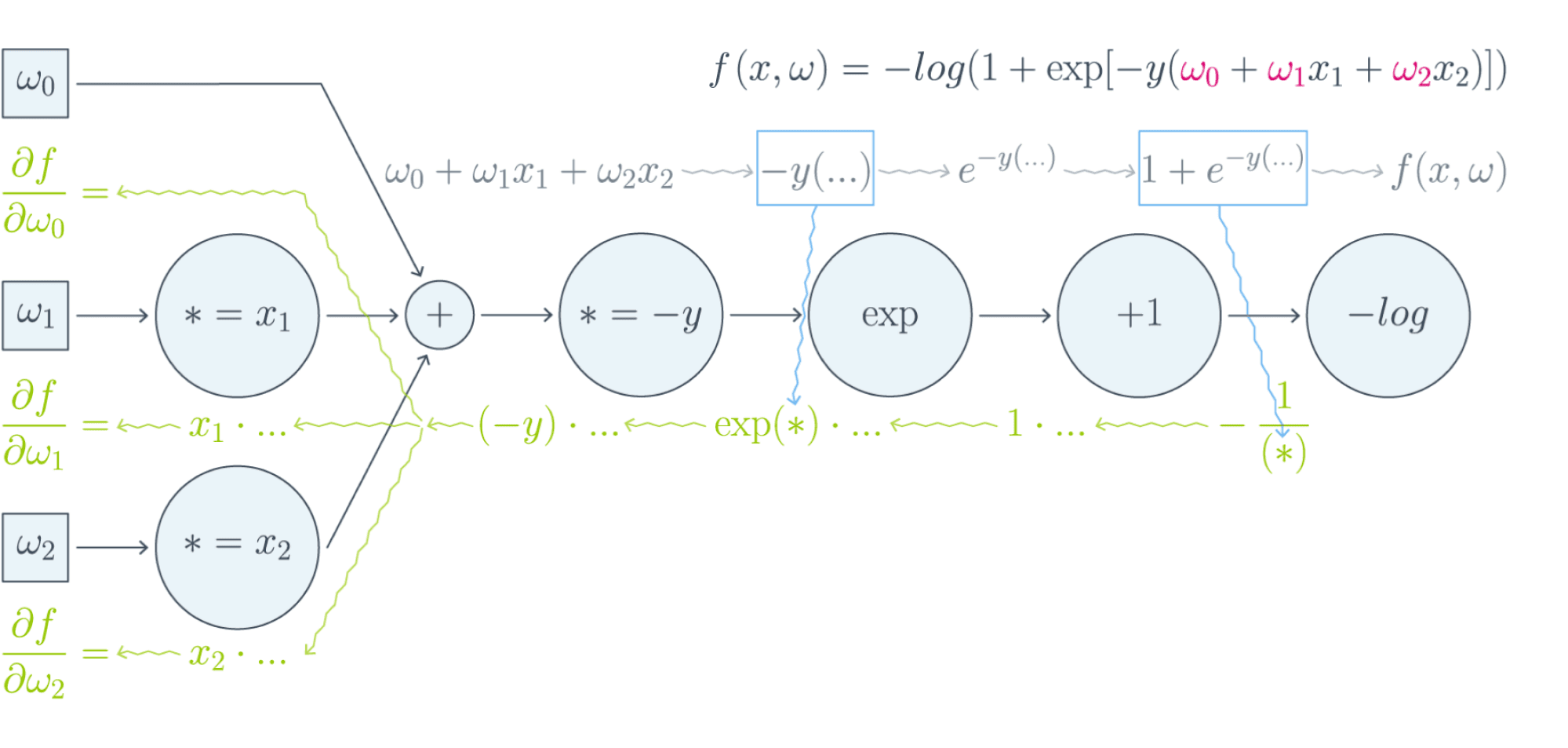
Проиллюстрируем это на картинке, расписав по шагам дифференцирование по весам $w_i$ функции потерь логистической регрессии на одном объекте (то есть для батча размера 1):
Собирая все множители вместе, получаем:
$$frac{partial f}{partial w_0} = (-y)cdot e^{-y(w_0 + w_1x_1 + w_2x_2)}cdotfrac{-1}{1 + e^{-y(w_0 + w_1x_1 + w_2x_2)}}$$
$$frac{partial f}{partial w_1} = x_1cdot(-y)cdot e^{-y(w_0 + w_1x_1 + w_2x_2)}cdotfrac{-1}{1 + e^{-y(w_0 + w_1x_1 + w_2x_2)}}$$
$$frac{partial f}{partial w_2} = x_2cdot(-y)cdot e^{-y(w_0 + w_1x_1 + w_2x_2)}cdotfrac{-1}{1 + e^{-y(w_0 + w_1x_1 + w_2x_2)}}$$
Таким образом, мы видим, что сперва совершается forward pass для вычисления всех промежуточных значений (и да, все промежуточные представления нужно будет хранить в памяти), а потом запускается backward pass, на котором в один проход вычисляются все градиенты.
Почему же нельзя просто пойти и начать везде вычислять производные?
В главе, посвящённой матричным дифференцированиям, мы поднимаем вопрос о том, что вычислять частные производные по отдельности — это зло, лучше пользоваться матричными вычислениями. Но есть и ещё одна причина: даже и с матричной производной в принципе не всегда хочется иметь дело. Рассмотрим простой пример. Допустим, что $X^r$ и $X^{r+1}$ — два последовательных промежуточных представления $Ntimes M$ и $Ntimes K$, связанных функцией $X^{r+1} = f^{r+1}(X^r)$. Предположим, что мы как-то посчитали производную $frac{partialmathcal{L}}{partial X^{r+1}_{ij}}$ функции потерь $mathcal{L}$, тогда
$$frac{partialmathcal{L}}{partial X^{r}_{st}} = sum_{i,j}frac{partial f^{r+1}_{ij}}{partial X^{r}_{st}}frac{partialmathcal{L}}{partial X^{r+1}_{ij}}$$
И мы видим, что, хотя оба градиента $frac{partialmathcal{L}}{partial X_{ij}^{r+1}}$ и $frac{partialmathcal{L}}{partial X_{st}^{r}}$ являются просто матрицами, в ходе вычислений возникает «четырёхмерный кубик» $frac{partial f_{ij}^{r+1}}{partial X_{st}^{r}}$, даже хранить который весьма болезненно: уж больно много памяти он требует ($N^2MK$ по сравнению с безобидными $NM + NK$, требуемыми для хранения градиентов). Поэтому хочется промежуточные производные $frac{partial f^{r+1}}{partial X^{r}}$ рассматривать не как вычисляемые объекты $frac{partial f_{ij}^{r+1}}{partial X_{st}^{r}}$, а как преобразования, которые превращают $frac{partialmathcal{L}}{partial X_{ij}^{r+1}}$ в $frac{partialmathcal{L}}{partial X_{st}^{r}}$. Целью следующих глав будет именно это: понять, как преобразуется градиент в ходе error backpropagation при переходе через тот или иной слой.
Вы спросите себя: надо ли мне сейчас пойти и прочитать главу учебника про матричное дифференцирование?
Встречный вопрос. Найдите производную функции по вектору $x$:
$$f(x) = x^TAx, Ain Mat_{n}{mathbb{R}}text{ — матрица размера }ntimes n$$
А как всё поменяется, если $A$ тоже зависит от $x$? Чему равен градиент функции, если $A$ является скаляром? Если вы готовы прямо сейчас взять ручку и бумагу и посчитать всё, то вам, вероятно, не надо читать про матричные дифференцирования. Но мы советуем всё-таки заглянуть в эту главу, если обозначения, которые мы будем дальше использовать, покажутся вам непонятными: единой нотации для матричных дифференцирований человечество пока, увы, не изобрело, и переводить с одной на другую не всегда легко.
Мы же сразу перейдём к интересующей нас вещи: к вычислению градиентов сложных функций.
Градиент сложной функции
Напомним, что формула производной сложной функции выглядит следующим образом:
$$left[D_{x_0} (color{#5002A7}{u} circ color{#4CB9C0}{v}) right](h) = color{#5002A7}{left[D_{v(x_0)} u right]} left( color{#4CB9C0}{left[D_{x_0} vright]} (h)right)$$
Теперь разберёмся с градиентами. Пусть $f(x) = g(h(x))$ – скалярная функция. Тогда
$$left[D_{x_0} f right] (x-x_0) = langlenabla_{x_0} f, x-x_0rangle.$$
С другой стороны,
$$left[D_{h(x_0)} g right] left(left[D_{x_0}h right] (x-x_0)right) = langlenabla_{h_{x_0}} g, left[D_{x_0} hright] (x-x_0)rangle = langleleft[D_{x_0} hright]^* nabla_{h(x_0)} g, x-x_0rangle.$$
То есть $color{#FFC100}{nabla_{x_0} f} = color{#348FEA}{left[D_{x_0} h right]}^* color{#FFC100}{nabla_{h(x_0)}}g$ — применение сопряжённого к $D_{x_0} h$ линейного отображения к вектору $nabla_{h(x_0)} g$.
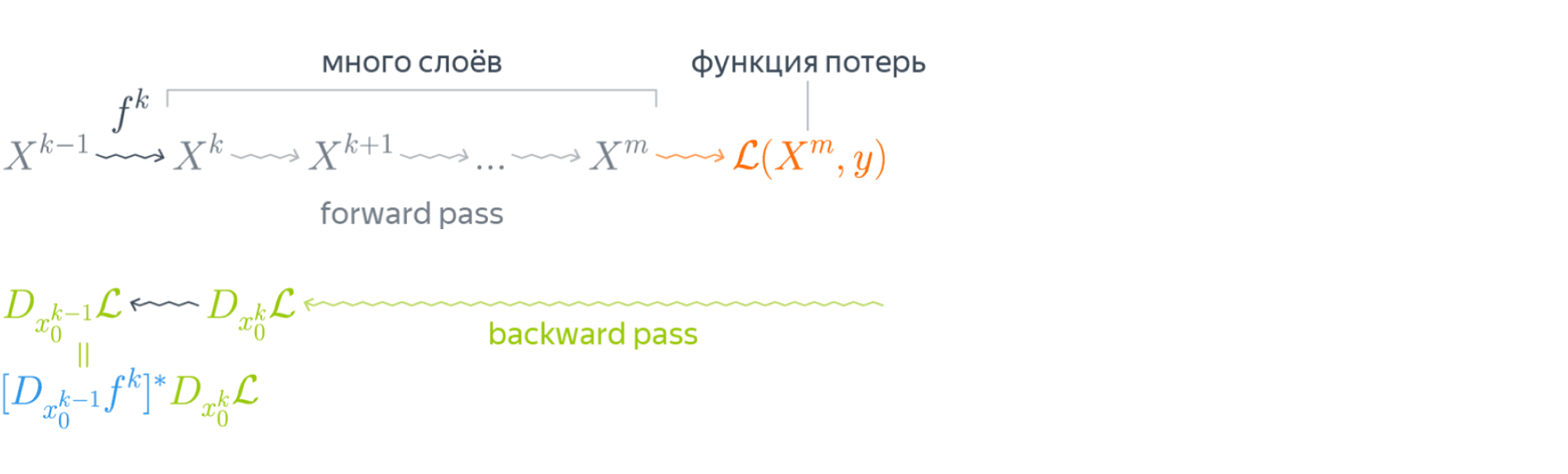
Эта формула — сердце механизма обратного распространения ошибки. Она говорит следующее: если мы каким-то образом получили градиент функции потерь по переменным из некоторого промежуточного представления $X^k$ нейронной сети и при этом знаем, как преобразуется градиент при проходе через слой $f^k$ между $X^{k-1}$ и $X^k$ (то есть как выглядит сопряжённое к дифференциалу слоя между ними отображение), то мы сразу же находим градиент и по переменным из $X^{k-1}$:
Таким образом слой за слоем мы посчитаем градиенты по всем $X^i$ вплоть до самых первых слоёв.
Далее мы разберёмся, как именно преобразуются градиенты при переходе через некоторые распространённые слои.
Градиенты для типичных слоёв
Рассмотрим несколько важных примеров.
Примеры
-
$f(x) = u(v(x))$, где $x$ — вектор, а $v(x)$ – поэлементное применение $v$:
$$vbegin{pmatrix}
x_1 \
vdots\
x_N
end{pmatrix}
= begin{pmatrix}
v(x_1)\
vdots\
v(x_N)
end{pmatrix}$$Тогда, как мы знаем,
$$left[D_{x_0} fright] (h) = langlenabla_{x_0} f, hrangle = left[nabla_{x_0} fright]^T h.$$
Следовательно,
$$
left[D_{v(x_0)} uright] left( left[ D_{x_0} vright] (h)right) = left[nabla_{v(x_0)} uright]^T left(v'(x_0) odot hright) =\
$$$$
= sumlimits_i left[nabla_{v(x_0)} uright]_i v'(x_{0i})h_i
= langleleft[nabla_{v(x_0)} uright] odot v'(x_0), hrangle.
,$$где $odot$ означает поэлементное перемножение. Окончательно получаем
$$color{#348FEA}{nabla_{x_0} f = left[nabla_{v(x_0)}uright] odot v'(x_0) = v'(x_0) odot left[nabla_{v(x_0)} uright]}$$
Отметим, что если $x$ и $h(x)$ — это просто векторы, то мы могли бы вычислять всё и по формуле $frac{partial f}{partial x_i} = sum_jbig(frac{partial z_j}{partial x_i}big)cdotbig(frac{partial h}{partial z_j}big)$. В этом случае матрица $big(frac{partial z_j}{partial x_i}big)$ была бы диагональной (так как $z_j$ зависит только от $x_j$: ведь $h$ берётся поэлементно), и матричное умножение приводило бы к тому же результату. Однако если $x$ и $h(x)$ — матрицы, то $big(frac{partial z_j}{partial x_i}big)$ представлялась бы уже «четырёхмерным кубиком», и работать с ним было бы ужасно неудобно.
-
$f(X) = g(XW)$, где $X$ и $W$ — матрицы. Как мы знаем,
$$left[D_{X_0} f right] (X-X_0) = text{tr}, left(left[nabla_{X_0} fright]^T (X-X_0)right).$$
Тогда
$$
left[ D_{X_0W} g right] left(left[D_{X_0} left( ast Wright)right] (H)right) =
left[ D_{X_0W} g right] left(HWright)=\
$$ $$
= text{tr}, left( left[nabla_{X_0W} g right]^T cdot (H) W right) =\
$$ $$
=
text{tr} , left(W left[nabla_{X_0W} (g) right]^T cdot (H)right) = text{tr} , left( left[left[nabla_{X_0W} gright] W^Tright]^T (H)right)
$$Здесь через $ast W$ мы обозначили отображение $Y hookrightarrow YW$, а в предпоследнем переходе использовалось следующее свойство следа:
$$
text{tr} , (A B C) = text{tr} , (C A B),
$$где $A, B, C$ — произвольные матрицы подходящих размеров (то есть допускающие перемножение в обоих приведённых порядках). Следовательно, получаем
$$color{#348FEA}{nabla_{X_0} f = left[nabla_{X_0W} (g) right] cdot W^T}$$
-
$f(W) = g(XW)$, где $W$ и $X$ — матрицы. Для приращения $H = W — W_0$ имеем
$$
left[D_{W_0} f right] (H) = text{tr} , left( left[nabla_{W_0} f right]^T (H)right)
$$Тогда
$$
left[D_{XW_0} g right] left( left[D_{W_0} left(X astright) right] (H)right) = left[D_{XW_0} g right] left( XH right) =
$$ $$
= text{tr} , left( left[nabla_{XW_0} g right]^T cdot X (H)right) =
text{tr}, left(left[X^T left[nabla_{XW_0} g right] right]^T (H)right)
$$Здесь через $X ast$ обозначено отображение $Y hookrightarrow XY$. Значит,
$$color{#348FEA}{nabla_{X_0} f = X^T cdot left[nabla_{XW_0} (g)right]}$$
-
$f(X) = g(softmax(X))$, где $X$ — матрица $Ntimes K$, а $softmax$ — функция, которая вычисляется построчно, причём для каждой строки $x$
$$softmax(x) = left(frac{e^{x_1}}{sum_te^{x_t}},ldots,frac{e^{x_K}}{sum_te^{x_t}}right)$$
В этом примере нам будет удобно воспользоваться формализмом с частными производными. Сначала вычислим $frac{partial s_l}{partial x_j}$ для одной строки $x$, где через $s_l$ мы для краткости обозначим $softmax(x)_l = frac{e^{x_l}} {sum_te^{x_t}}$. Нетрудно проверить, что
$$frac{partial s_l}{partial x_j} = begin{cases}
s_j(1 — s_j), & j = l,
-s_ls_j, & jne l
end{cases}$$Так как softmax вычисляется независимо от каждой строчки, то
$$frac{partial s_{rl}}{partial x_{ij}} = begin{cases}
s_{ij}(1 — s_{ij}), & r=i, j = l,
-s_{il}s_{ij}, & r = i, jne l,
0, & rne i
end{cases},$$где через $s_{rl}$ мы обозначили для краткости $softmax(X)_{rl}$.
Теперь пусть $nabla_{rl} = nabla g = frac{partialmathcal{L}}{partial s_{rl}}$ (пришедший со следующего слоя, уже известный градиент). Тогда
$$frac{partialmathcal{L}}{partial x_{ij}} = sum_{r,l}frac{partial s_{rl}}{partial x_{ij}} nabla_{rl}$$
Так как $frac{partial s_{rl}}{partial x_{ij}} = 0$ при $rne i$, мы можем убрать суммирование по $r$:
$$ldots = sum_{l}frac{partial s_{il}}{partial x_{ij}} nabla_{il} = -s_{i1}s_{ij}nabla_{i1} — ldots + s_{ij}(1 — s_{ij})nabla_{ij}-ldots — s_{iK}s_{ij}nabla_{iK} =$$
$$= -s_{ij}sum_t s_{it}nabla_{it} + s_{ij}nabla_{ij}$$
Таким образом, если мы хотим продифференцировать $f$ в какой-то конкретной точке $X_0$, то, смешивая математические обозначения с нотацией Python, мы можем записать:
$$begin{multline*}
color{#348FEA}{nabla_{X_0}f =}\
color{#348FEA}{= -softmax(X_0) odot text{sum}left(
softmax(X_0)odotnabla_{softmax(X_0)}g, text{ axis = 1}
right) +}\
color{#348FEA}{softmax(X_0)odot nabla_{softmax(X_0)}g}
end{multline*}
$$
Backpropagation в общем виде
Подытожим предыдущее обсуждение, описав алгоритм error backpropagation (алгоритм обратного распространения ошибки). Допустим, у нас есть текущие значения весов $W^i_0$ и мы хотим совершить шаг SGD по мини-батчу $X$. Мы должны сделать следующее:
- Совершить forward pass, вычислив и запомнив все промежуточные представления $X = X^0, X^1, ldots, X^m = widehat{y}$.
- Вычислить все градиенты с помощью backward pass.
- С помощью полученных градиентов совершить шаг SGD.
Проиллюстрируем алгоритм на примере двуслойной нейронной сети со скалярным output’ом. Для простоты опустим свободные члены в линейных слоях.
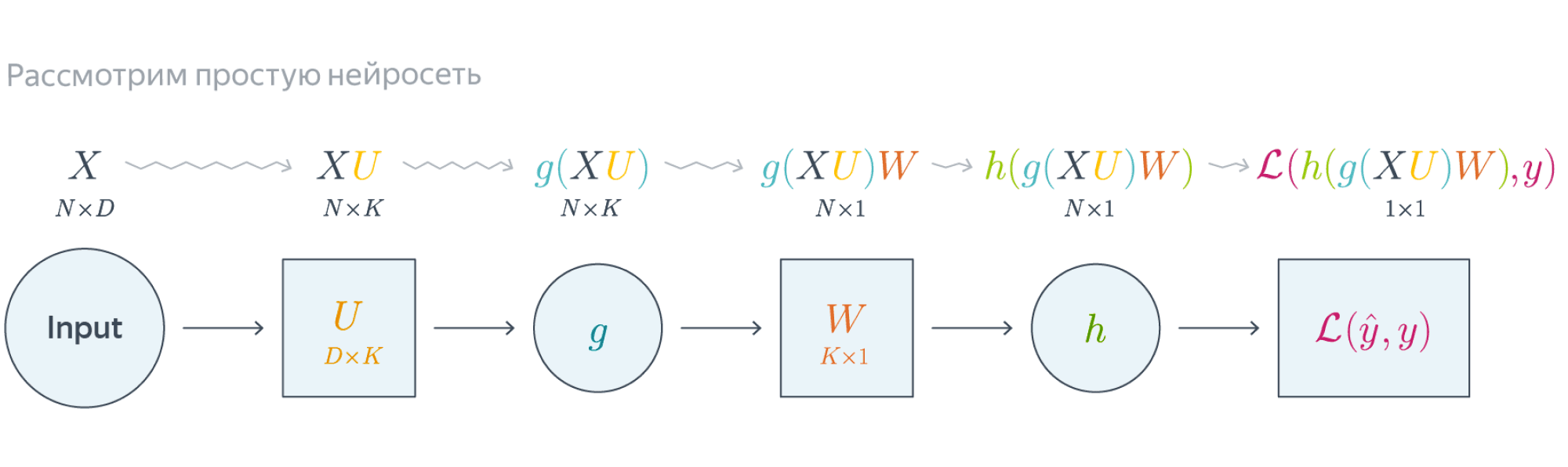
$$nabla_{W_0}mathcal{L} = nabla_{W_0}{left({vphantom{frac12}mathcal{L}circ hcircleft[Wmapsto g(XU_0)Wright]}right)}=$$
$$=g(XU_0)^Tnabla_{g(XU_0)W_0}(mathcal{L}circ h) = underbrace{g(XU_0)^T}_{ktimes N}cdot
left[vphantom{frac12}underbrace{h’left(vphantom{int_0^1}g(XU_0)W_0right)}_{Ntimes 1}odot
underbrace{nabla_{hleft(vphantom{int_0^1}g(XU_0)W_0right)}mathcal{L}}_{Ntimes 1}right]$$
Итого матрица $ktimes 1$, как и $W_0$
$$nabla_{U_0}mathcal{L} = nabla_{U_0}left(vphantom{frac12}
mathcal{L}circ hcircleft[Ymapsto YW_0right]circ gcircleft[ Umapsto XUright]
right)=$$
$$=X^Tcdotnabla_{XU^0}left(vphantom{frac12}mathcal{L}circ hcirc [Ymapsto YW_0]circ gright) =$$
$$=X^Tcdotleft(vphantom{frac12}g'(XU_0)odot
nabla_{g(XU_0)}left[vphantom{in_0^1}mathcal{L}circ hcirc[Ymapsto YW_0right]
right)$$
$$=ldots = underset{Dtimes N}{X^T}cdotleft(vphantom{frac12}
underbrace{g'(XU_0)}_{Ntimes K}odot
underbrace{left[vphantom{int_0^1}left(
underbrace{h’left(vphantom{int_0^1}g(XU_0)W_0right)}_{Ntimes1}odotunderbrace{nabla_{h(vphantom{int_0^1}gleft(XU_0right)W_0)}mathcal{L}}_{Ntimes 1}
right)cdot underbrace{W^T}_{1times K}right]}_{Ntimes K}
right)$$
Итого $Dtimes K$, как и $U_0$
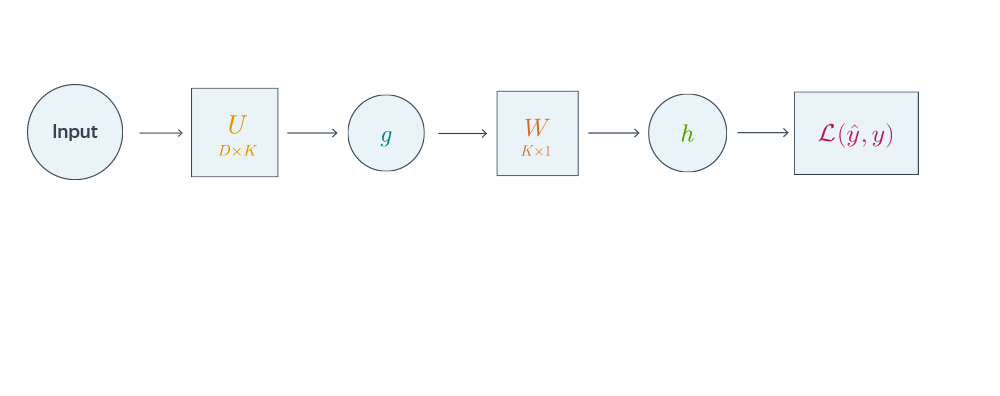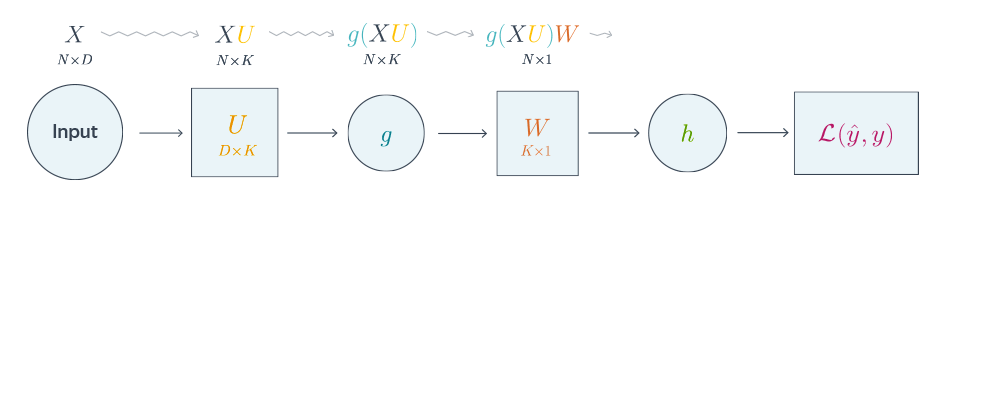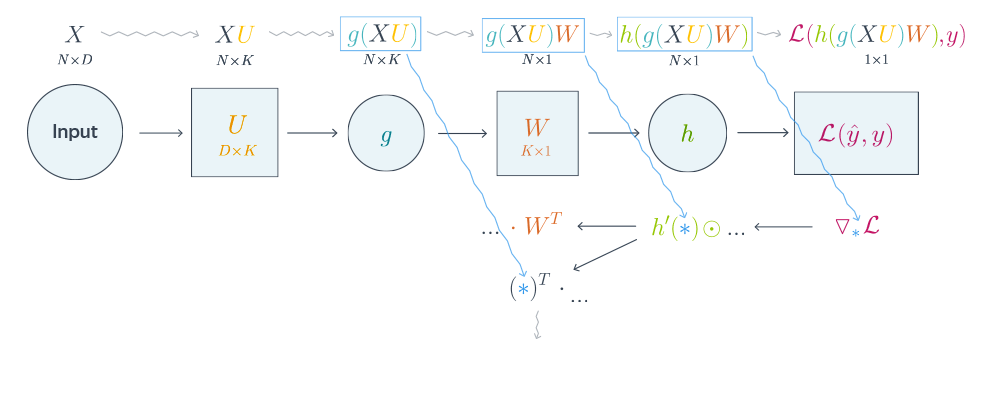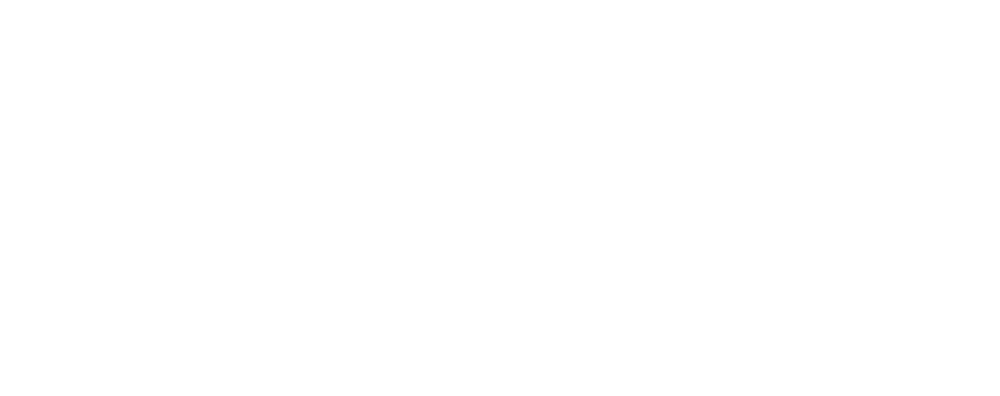
Схематически это можно представить следующим образом:
Backpropagation для двуслойной нейронной сети
Подробнее о предыдущих вычисленияхЕсли вы не уследили за вычислениями в предыдущем примере, давайте более подробно разберём его чуть более конкретную версию (для $g = h = sigma$).
Рассмотрим двуслойную нейронную сеть для классификации. Мы уже встречали ее ранее при рассмотрении линейно неразделимой выборки. Предсказания получаются следующим образом:
$$
widehat{y} = sigma(X^1 W^2) = sigmaBig(big(sigma(X^0 W^1 )big) W^2 Big).
$$
Пусть $W^1_0$ и $W^2_0$ — текущее приближение матриц весов. Мы хотим совершить шаг по градиенту функции потерь, и для этого мы должны вычислить её градиенты по $W^1$ и $W^2$ в точке $(W^1_0, W^2_0)$.
Прежде всего мы совершаем forward pass, в ходе которого мы должны запомнить все промежуточные представления: $X^1 = X^0 W^1_0$, $X^2 = sigma(X^0 W^1_0)$, $X^3 = sigma(X^0 W^1_0) W^2_0$, $X^4 = sigma(sigma(X^0 W^1_0) W^2_0) = widehat{y}$. Они понадобятся нам дальше.
Для полученных предсказаний вычисляется значение функции потерь:
$$
l = mathcal{L}(y, widehat{y}) = y log(widehat{y}) + (1-y) log(1-widehat{y}).
$$
Дальше мы шаг за шагом будем находить производные по переменным из всё более глубоких слоёв.
-
Градиент $mathcal{L}$ по предсказаниям имеет вид
$$
nabla_{widehat{y}}l = frac{y}{widehat{y}} — frac{1 — y}{1 — widehat{y}} = frac{y — widehat{y}}{widehat{y} (1 — widehat{y})},
$$где, напомним, $ widehat{y} = sigma(X^3) = sigmaBig(big(sigma(X^0 W^1_0 )big) W^2_0 Big)$ (обратите внимание на то, что $W^1_0$ и $W^2_0$ тут именно те, из которых мы делаем градиентный шаг).
-
Следующий слой — поэлементное взятие $sigma$. Как мы помним, при переходе через него градиент поэлементно умножается на производную $sigma$, в которую подставлено предыдущее промежуточное представление:
$$
nabla_{X^3}l = sigma'(X^3)odotnabla_{widehat{y}}l = sigma(X^3)left( 1 — sigma(X^3) right) odot frac{y — widehat{y}}{widehat{y} (1 — widehat{y})} =
$$$$
= sigma(X^3)left( 1 — sigma(X^3) right) odot frac{y — sigma(X^3)}{sigma(X^3) (1 — sigma(X^3))} =
y — sigma(X^3)
$$ -
Следующий слой — умножение на $W^2_0$. В этот момент мы найдём градиент как по $W^2$, так и по $X^2$. При переходе через умножение на матрицу градиент, как мы помним, умножается с той же стороны на транспонированную матрицу, а значит:
$$
color{blue}{nabla_{W^2_0}l} = (X^2)^Tcdot nabla_{X^3}l = (X^2)^Tcdot(y — sigma(X^3)) =
$$$$
= color{blue}{left( sigma(X^0W^1_0) right)^T cdot (y — sigma(sigma(X^0W^1_0)W^2_0))}
$$Аналогичным образом
$$
nabla_{X^2}l = nabla_{X^3}lcdot (W^2_0)^T = (y — sigma(X^3))cdot (W^2_0)^T =
$$$$
= (y — sigma(X^2W_0^2))cdot (W^2_0)^T
$$ -
Следующий слой — снова взятие $sigma$.
$$
nabla_{X^1}l = sigma'(X^1)odotnabla_{X^2}l = sigma(X^1)left( 1 — sigma(X^1) right) odot left( (y — sigma(X^2W_0^2))cdot (W^2_0)^T right) =
$$$$
= sigma(X^1)left( 1 — sigma(X^1) right) odotleft( (y — sigma(sigma(X^1)W_0^2))cdot (W^2_0)^T right)
$$ -
Наконец, последний слой — это умножение $X^0$ на $W^1_0$. Тут мы дифференцируем только по $W^1$:
$$
color{blue}{nabla_{W^1_0}l} = (X^0)^Tcdot nabla_{X^1}l = (X^0)^Tcdot big( sigma(X^1) left( 1 — sigma(X^1) right) odot (y — sigma(sigma(X^1)W_0^2))cdot (W^2_0)^Tbig) =
$$$$
= color{blue}{(X^0)^Tcdotbig(sigma(X^0W^1_0)left( 1 — sigma(X^0W^1_0) right) odot (y — sigma(sigma(X^0W^1_0)W_0^2))cdot (W^2_0)^Tbig) }
$$
Итоговые формулы для градиентов получились страшноватыми, но они были получены друг из друга итеративно с помощью очень простых операций: матричного и поэлементного умножения, в которые порой подставлялись значения заранее вычисленных промежуточных представлений.
Автоматизация и autograd
Итак, чтобы нейросеть обучалась, достаточно для любого слоя $f^k: X^{k-1}mapsto X^k$ с параметрами $W^k$ уметь:
- превращать $nabla_{X^k_0}mathcal{L}$ в $nabla_{X^{k-1}_0}mathcal{L}$ (градиент по выходу в градиент по входу);
- считать градиент по его параметрам $nabla_{W^k_0}mathcal{L}$.
При этом слою совершенно не надо знать, что происходит вокруг. То есть слой действительно может быть запрограммирован как отдельная сущность, умеющая внутри себя делать forward pass и backward pass, после чего слои механически, как кубики в конструкторе, собираются в большую сеть, которая сможет работать как одно целое.
Более того, во многих случаях авторы библиотек для глубинного обучения уже о вас позаботились и создали средства для автоматического дифференцирования выражений (autograd). Поэтому, программируя нейросеть, вы почти всегда можете думать только о forward-проходе, прямом преобразовании данных, предоставив библиотеке дифференцировать всё самостоятельно. Это делает код нейросетей весьма понятным и выразительным (да, в реальности он тоже бывает большим и страшным, но сравните на досуге код какой-нибудь разухабистой нейросети и код градиентного бустинга на решающих деревьях и почувствуйте разницу).
Но это лишь начало
Метод обратного распространения ошибки позволяет удобно посчитать градиенты, но дальше с ними что-то надо делать, и старый добрый SGD едва ли справится с обучением современной сетки. Так что же делать? О некоторых приёмах мы расскажем в следующей главе.
Нейронная сеть — попытка с помощью математических моделей воспроизвести работу человеческого мозга для создания машин, обладающих искусственным интеллектом.
Искусственная нейронная сеть обычно обучается с учителем. Это означает наличие обучающего набора (датасета), который содержит примеры с истинными значениями: тегами, классами, показателями.
Неразмеченные наборы также используют для обучения нейронных сетей, но мы не будем здесь это рассматривать.
Например, если вы хотите создать нейросеть для оценки тональности текста, датасетом будет список предложений с соответствующими каждому эмоциональными оценками. Тональность текста определяют признаки (слова, фразы, структура предложения), которые придают негативную или позитивную окраску. Веса признаков в итоговой оценке тональности текста (позитивный, негативный, нейтральный) зависят от математической функции, которая вычисляется во время обучения нейронной сети.
Раньше люди генерировали признаки вручную. Чем больше признаков и точнее подобраны веса, тем точнее ответ. Нейронная сеть автоматизировала этот процесс.
Искусственная нейронная сеть состоит из трех компонентов:
- Входной слой;
- Скрытые (вычислительные) слои;
- Выходной слой.
Обучение нейросетей происходит в два этапа:
- Прямое распространение ошибки;
- Обратное распространение ошибки.
Во время прямого распространения ошибки делается предсказание ответа. При обратном распространении ошибка между фактическим ответом и предсказанным минимизируется.
Прямое распространение ошибки
Зададим начальные веса случайным образом:
- w1
- w2
- w3
Умножим входные данные на веса для формирования скрытого слоя:
- h1 = (x1 * w1) + (x2 * w1)
- h2 = (x1 * w2) + (x2 * w2)
- h3 = (x1 * w3) + (x2 * w3)
Выходные данные из скрытого слоя передается через нелинейную функцию (функцию активации), для получения выхода сети:
- y_ = fn(h1 , h2, h3)
Обратное распространение
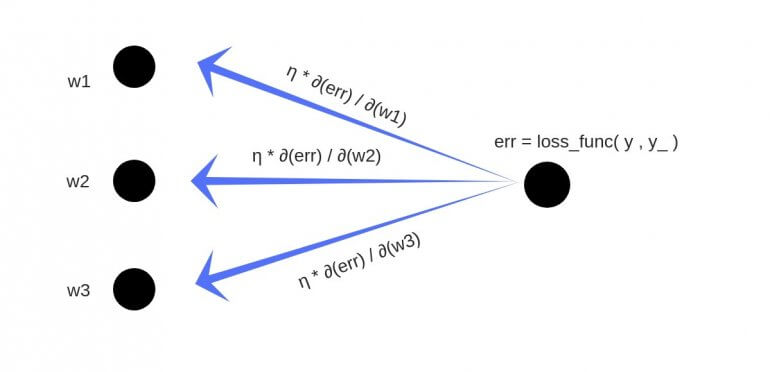
- Суммарная ошибка (total_error) вычисляется как разность между ожидаемым значением «y» (из обучающего набора) и полученным значением «y_» (посчитанное на этапе прямого распространения ошибки), проходящих через функцию потерь (cost function).
- Частная производная ошибки вычисляется по каждому весу (эти частные дифференциалы отражают вклад каждого веса в общую ошибку (total_loss)).
- Затем эти дифференциалы умножаются на число, называемое скорость обучения или learning rate (η).
Полученный результат затем вычитается из соответствующих весов.
В результате получатся следующие обновленные веса:
- w1 = w1 — (η * ∂(err) / ∂(w1))
- w2 = w2 — (η * ∂(err) / ∂(w2))
- w3 = w3 — (η * ∂(err) / ∂(w3))
То, что мы предполагаем и инициализируем веса случайным образом, и они будут давать точные ответы, звучит не вполне обоснованно, тем не менее, работает хорошо.
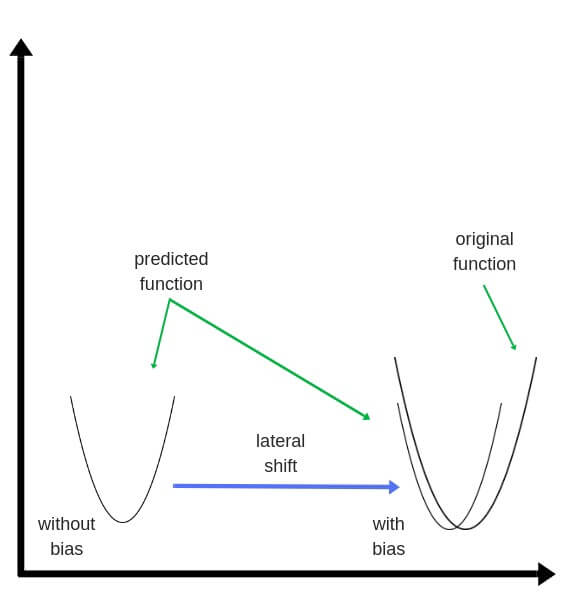
Смещения – это веса, добавленные к скрытым слоям. Они тоже случайным образом инициализируются и обновляются так же, как скрытый слой. Роль скрытого слоя заключается в том, чтобы определить форму базовой функции в данных, в то время как роль смещения – сдвинуть найденную функцию в сторону так, чтобы она частично совпала с исходной функцией.
Частные производные
Частные производные можно вычислить, поэтому известно, какой был вклад в ошибку по каждому весу. Необходимость производных очевидна. Представьте нейронную сеть, пытающуюся найти оптимальную скорость беспилотного автомобиля. Eсли машина обнаружит, что она едет быстрее или медленнее требуемой скорости, нейронная сеть будет менять скорость, ускоряя или замедляя автомобиль. Что при этом ускоряется/замедляется? Производные скорости.
Разберем необходимость частных производных на примере.
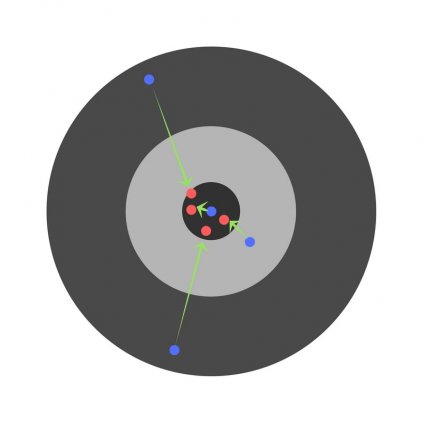
Предположим, детей попросили бросить дротик в мишень, целясь в центр. Вот результаты:
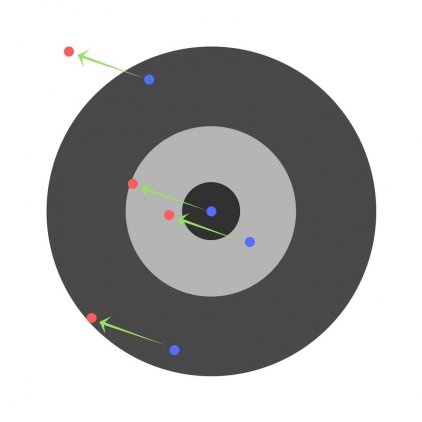
Теперь, если мы найдем общую ошибку и просто вычтем ее из всех весов, мы обобщим ошибки, допущенные каждым. Итак, скажем, ребенок попал слишком низко, но мы просим всех детей стремиться попадать в цель, тогда это приведет к следующей картине:
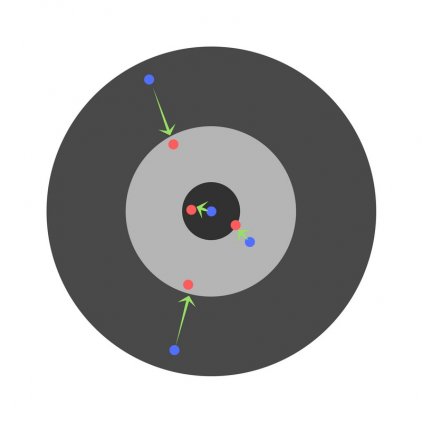
Ошибка нескольких детей может уменьшиться, но общая ошибка все еще увеличивается.
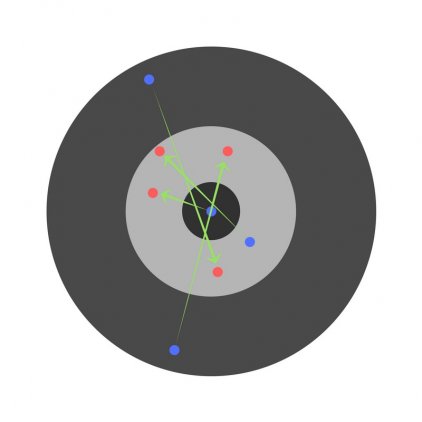
Найдя частные производные, мы узнаем ошибки, соответствующие каждому весу в отдельности. Если выборочно исправить веса, можно получить следующее:
Гиперпараметры
Нейронная сеть используется для автоматизации отбора признаков, но некоторые параметры настраиваются вручную.
Скорость обучения (learning rate)
Скорость обучения является очень важным гиперпараметром. Если скорость обучения слишком мала, то даже после обучения нейронной сети в течение длительного времени она будет далека от оптимальных результатов. Результаты будут выглядеть примерно так:
С другой стороны, если скорость обучения слишком высока, то сеть очень быстро выдаст ответы. Получится следующее:
Функция активации (activation function)
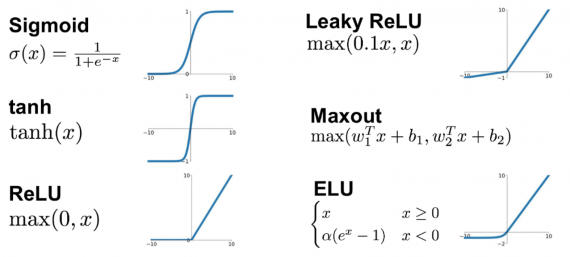
Функция активации — это один из самых мощных инструментов, который влияет на силу, приписываемую нейронным сетям. Отчасти, она определяет, какие нейроны будут активированы, другими словами и какая информация будет передаваться последующим слоям.
Без функций активации глубокие сети теряют значительную часть своей способности к обучению. Нелинейность этих функций отвечает за повышение степени свободы, что позволяет обобщать проблемы высокой размерности в более низких измерениях. Ниже приведены примеры распространенных функций активации:
Функция потери (loss function)
Функция потерь находится в центре нейронной сети. Она используется для расчета ошибки между реальными и полученными ответами. Наша глобальная цель — минимизировать эту ошибку. Таким образом, функция потерь эффективно приближает обучение нейронной сети к этой цели.
Функция потерь измеряет «насколько хороша» нейронная сеть в отношении данной обучающей выборки и ожидаемых ответов. Она также может зависеть от таких переменных, как веса и смещения.
Функция потерь одномерна и не является вектором, поскольку она оценивает, насколько хорошо нейронная сеть работает в целом.
Некоторые известные функции потерь:
- Квадратичная (среднеквадратичное отклонение);
- Кросс-энтропия;
- Экспоненциальная (AdaBoost);
- Расстояние Кульбака — Лейблера или прирост информации.
Cреднеквадратичное отклонение – самая простая фукция потерь и наиболее часто используемая. Она задается следующим образом:
Функция потерь в нейронной сети должна удовлетворять двум условиям:
- Функция потерь должна быть записана как среднее;
- Функция потерь не должна зависеть от каких-либо активационных значений нейронной сети, кроме значений, выдаваемых на выходе.
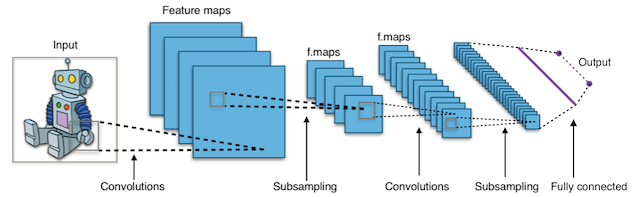
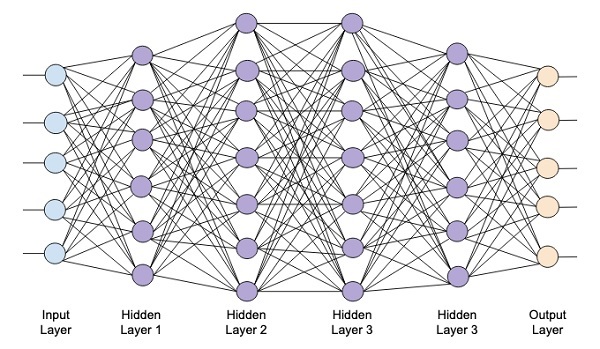
Глубокие нейронные сети
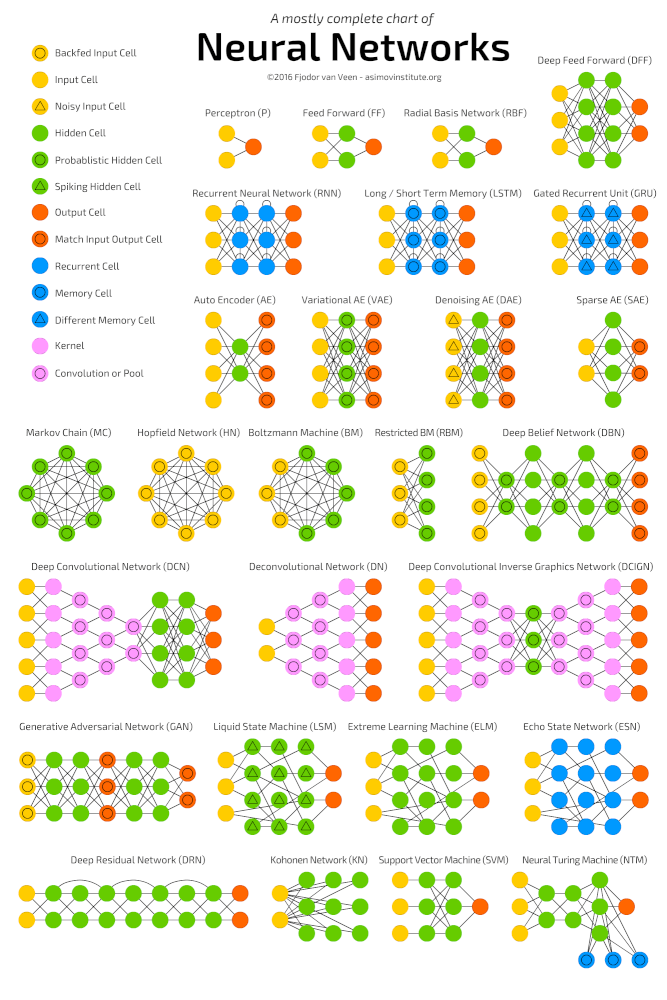
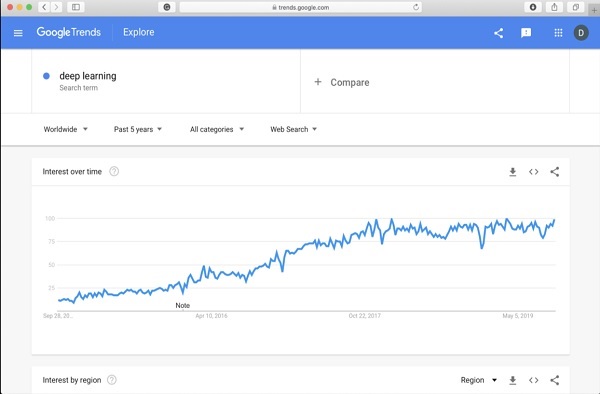
Глубокое обучение (deep learning) – это класс алгоритмов машинного обучения, которые учатся глубже (более абстрактно) понимать данные. Популярные алгоритмы нейронных сетей глубокого обучения представлены на схеме ниже.
Более формально в deep learning:
- Используется каскад (пайплайн, как последовательно передаваемый поток) из множества обрабатывающих слоев (нелинейных) для извлечения и преобразования признаков;
- Основывается на изучении признаков (представлении информации) в данных без обучения с учителем. Функции более высокого уровня (которые находятся в последних слоях) получаются из функций нижнего уровня (которые находятся в слоях начальных слоях);
- Изучает многоуровневые представления, которые соответствуют разным уровням абстракции; уровни образуют иерархию представления.
Пример
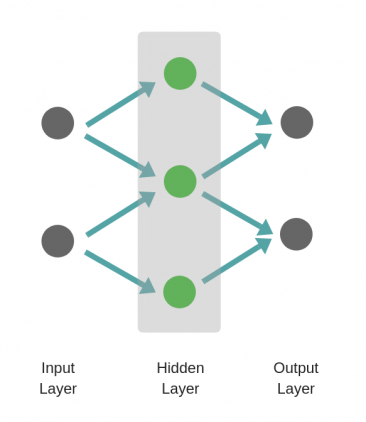
Рассмотрим однослойную нейронную сеть:
Здесь, обучается первый слой (зеленые нейроны), он просто передается на выход.
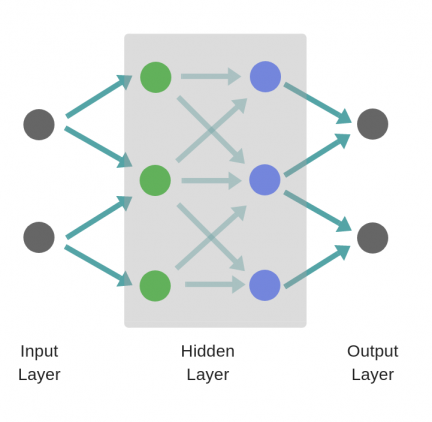
В то время как в случае двухслойной нейронной сети, независимо от того, как обучается зеленый скрытый слой, он затем передается на синий скрытый слой, где продолжает обучаться:
Следовательно, чем больше число скрытых слоев, тем больше возможности обучения сети.
Не следует путать с широкой нейронной сетью.
В этом случае большое число нейронов в одном слое не приводит к глубокому пониманию данных. Но это приводит к изучению большего числа признаков.
Пример:
Изучая английскую грамматику, требуется знать огромное число понятий. В этом случае однослойная широкая нейронная сеть работает намного лучше, чем глубокая нейронная сеть, которая значительно меньше.
Но
В случае изучения преобразования Фурье, ученик (нейронная сеть) должен быть глубоким, потому что не так много понятий, которые нужно знать, но каждое из них достаточно сложное и требует глубокого понимания.
Главное — баланс
Очень заманчиво использовать глубокие и широкие нейронные сети для каждой задачи. Но это может быть плохой идеей, потому что:
- Обе требуют значительно большего количества данных для обучения, чтобы достичь минимальной желаемой точности;
- Обе имеют экспоненциальную сложность;
- Слишком глубокая нейронная сеть попытается сломать фундаментальные представления, но при этом она будет делать ошибочные предположения и пытаться найти псевдо-зависимости, которые не существуют;
- Слишком широкая нейронная сеть будет пытаться найти больше признаков, чем есть. Таким образом, подобно предыдущей, она начнет делать неправильные предположения о данных.
Проклятье размерности
Проклятие размерности относится к различным явлениям, возникающим при анализе и организации данных в многомерных пространствах (часто с сотнями или тысячами измерений), и не встречается в ситуациях с низкой размерностью.
Грамматика английского языка имеет огромное количество аттрибутов, влияющих на нее. В машинном обучении мы должны представить их признаками в виде массива/матрицы конечной и существенно меньшей длины (чем количество существующих признаков). Для этого сети обобщают эти признаки. Это порождает две проблемы:
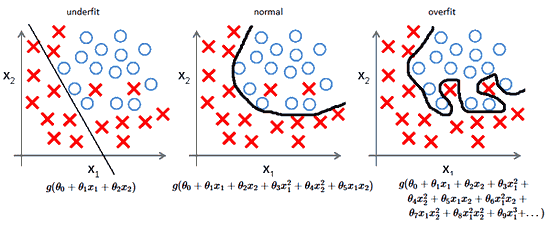
- Из-за неправильных предположений появляется смещение. Высокое смещение может привести к тому, что алгоритм пропустит существенную взаимосвязь между признаками и целевыми переменными. Это явление называют недообучение.
- От небольших отклонений в обучающем множестве из-за недостаточного изучения признаков увеличивается дисперсия. Высокая дисперсия ведет к переобучению, ошибки воспринимаются в качестве надежной информации.
Компромисс
На ранней стадии обучения смещение велико, потому что выход из сети далек от желаемого. А дисперсия очень мала, поскольку данные имеет пока малое влияние.
В конце обучения смещение невелико, потому что сеть выявила основную функцию в данных. Однако, если обучение слишком продолжительное, сеть также изучит шум, характерный для этого набора данных. Это приводит к большому разбросу результатов при тестировании на разных множествах, поскольку шум меняется от одного набора данных к другому.
Действительно,
алгоритмы с большим смещением обычно в основе более простых моделей, которые не склонны к переобучению, но могут недообучиться и не выявить важные закономерности или свойства признаков. Модели с маленьким смещением и большой дисперсией обычно более сложны с точки зрения их структуры, что позволяет им более точно представлять обучающий набор. Однако они могут отображать много шума из обучающего набора, что делает их прогнозы менее точными, несмотря на их дополнительную сложность.
Следовательно, как правило, невозможно иметь маленькое смещение и маленькую дисперсию одновременно.
Сейчас есть множество инструментов, с помощью которых можно легко создать сложные модели машинного обучения, переобучение занимает центральное место. Поскольку смещение появляется, когда сеть не получает достаточно информации. Но чем больше примеров, тем больше появляется вариантов зависимостей и изменчивостей в этих корреляциях.
Рад снова всех приветствовать, и сегодня продолжим планомерно двигаться в выбранном направлении. Речь, конечно, о масштабном разборе искусственных нейронных сетей для решения широкого спектра задач. Продолжим ровно с того момента, на котором остановились в предыдущей части, и это означает, что героем данного поста будет ключевой процесс — обучение нейронных сетей.
- Градиентный спуск
- Функция ошибки
- Метод обратного распространения ошибки
- Пример расчета
Тема эта крайне важна, поскольку именно процесс обучения позволяет сети начать выполнять задачу, для которой она, собственно, и предназначена. То есть нейронная сеть функционирует не по какому-либо жестко заданному на этапе проектирования алгоритму, она совершенствуется в процессе анализа имеющихся данных. Этот процесс и называется обучением нейронной сети. Математически суть процесса обучения заключается в корректировке значений весов синапсов (связей между имеющимися нейронами). Изначально значения весов задаются случайно, затем производится обучение, результатом которого будут новые значения синаптических весов. Это все мы максимально подробно разберем как раз в этой статье.
На своем сайте я всегда придерживаюсь концепции, при которой теоретические выкладки по максимуму сопровождаются практическими примерами для максимальной наглядности. Так мы поступим и сейчас 👍
Итак, суть заключается в следующем. Пусть у нас есть простейшая нейронная сеть, которую мы хотим обучить (продолжаем рассматривать сети прямого распространения):

То есть на входы нейронов I1 и I2 мы подаем какие-либо числа, а на выходе сети получаем соответственно новое значение. При этом нам необходима некая выборка данных, включающая в себя значения входов и соответствующее им, правильное, значение на выходе:
| bold{I_1} | bold{I_2} | bold{O_{net}} |
|---|---|---|
| x_{11} | x_{12} | y_{1} |
| x_{21} | x_{22} | y_{2} |
| x_{31} | x_{32} | y_{3} |
| … | … | … |
| x_{N1} | x_{N2} | y_{N} |
Допустим, сеть выполняет суммирование значений на входе, тогда данный набор данных может быть таким:
| bold{I_1} | bold{I_2} | bold{O_{net}} |
|---|---|---|
| 1 | 4 | 5 |
| 2 | 7 | 9 |
| 3 | 5 | 8 |
| … | … | … |
| 1000 | 1500 | 2500 |
Эти значения и используются для обучения сети. Как именно — рассмотрим чуть ниже, пока сконцентрируемся на идее процесса в целом. Для того, чтобы иметь возможность тестировать работу сети в процессе обучения, исходную выборку данных делят на две части — обучающую и тестовую. Пусть имеется 1000 образцов, тогда можно 900 использовать для обучения, а оставшиеся 100 — для тестирования. Эти величины взяты исключительно ради наглядности и демонстрации логики выполнения операций, на практике все зависит от задачи, размер обучающей выборки может спокойно достигать и сотен тысяч образцов.
Итак, итог имеем следующий — обучающая выборка прогоняется через сеть, в результате чего происходит настройка значений синаптических весов. Один полный проход по всей выборке называется эпохой. И опять же, обучение нейронной сети — это процесс, требующий многократных экспериментов, анализа результатов и творческого подхода. Все перечисленные параметры (размер выборки, количество эпох обучения) могут иметь абсолютно разные значения для разных задач и сетей. Четкого правила тут просто нет, в этом и кроется дополнительный шарм и изящность )
Возвращаемся к разбору, и в результате прохода обучающей выборки через сеть мы получаем сеть с новыми значениями весов синапсов.
Далее мы через эту, уже обученную в той или иной степени, сеть прогоняем тестовую выборку, которая не участвовала в обучении. При этом сеть выдает нам выходные значения для каждого образца, которые мы сравниваем с теми верными значениями, которые имеем.
Анализируем нашу гипотетическую выборку:

Таким образом, для тестирования подаем на вход сети значения x_{(M+1)1}, x_{(M+1)2} и проверяем, чему равен выход, ожидаем очевидно значение y_{(M+1)}. Аналогично поступаем и для оставшихся тестовых образцов. После чего мы можем сделать вывод, успешно или нет работает сеть. Например, сеть дает правильный ответ для 90% тестовых данных, дальше уже встает вопрос — устраивает ли нас данная точность или процесс обучения необходимо повторить, либо провести заново, изменив какие-либо параметры сети.
В этом и заключается суть обучения нейронных сетей, теперь перейдем к деталям и конкретным действиям, которые необходимо осуществить для выполнения данного процесса. Двигаться снова будем поэтапно, чтобы сформировать максимально четкую и полную картину. Поэтому начнем с понятия градиентного спуска, который используется при обучении по методу обратного распространения ошибки. Обо всем этом далее…
Обучение нейронных сетей. Градиентный спуск.
Рассмотрев идею процесса обучения в целом, на данном этапе мы можем однозначно сформулировать текущую цель — необходимо определить математический алгоритм, который позволит рассчитать значения весовых коэффициентов таким образом, чтобы ошибка сети была минимальна. То есть грубо говоря нам необходима конкретная формула для вычисления:
Здесь Delta w_{ij} — величина, на которую необходимо изменить вес синапса, связывающего нейроны i и j нашей сети. Соответственно, зная это, необходимо на каждом этапе обучения производить корректировку весов связей между всеми элементами нейронной сети. Задача ясна, переходим к делу.
Пусть функция ошибки от веса имеет следующий вид:
Для удобства рассмотрим зависимость функции ошибки от одного конкретного веса:

В начальный момент мы находимся в некоторой точке кривой, а для минимизации ошибки попасть мы хотим в точку глобального минимума функции:
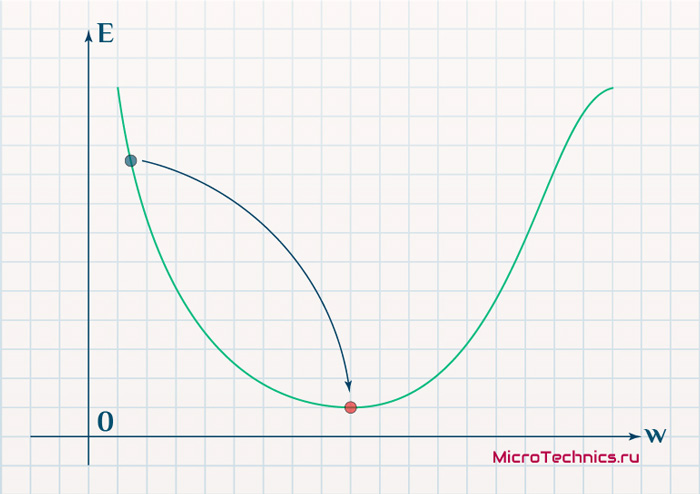
Нанесем на график вектора градиентов в разных точках. Длина векторов численно равна скорости роста функции в данной точке, что в свою очередь соответствует значению производной функции по данной точке. Исходя из этого, делаем вывод, что длина вектора градиента определяется крутизной функции в данной точке:
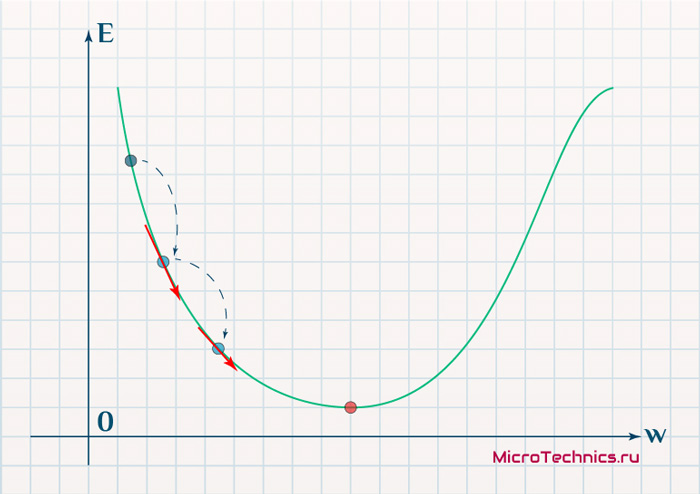
Вывод прост — величина градиента будет уменьшаться по мере приближения к минимуму функции. Это важный вывод, к которому мы еще вернемся. А тем временем разберемся с направлением вектора, для чего рассмотрим еще несколько возможных точек:
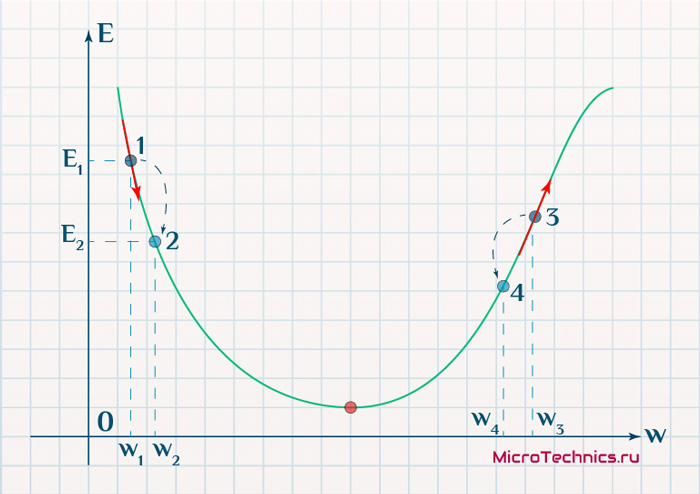
Находясь в точке 1, целью является перейти в точку 2, поскольку в ней значение ошибки меньше (E_2 < E_1), а глобальная задача по-прежнему заключается в ее минимизации. Для этого необходимо изменить величину w на некое значение Delta w (Delta w = w_2 — w_1 > 0). При всем при этом в точке 1 градиент отрицательный. Фиксируем данные факты и переходим к точке 3, предположим, что мы находимся именно в ней.
Тогда для уменьшения ошибки наш путь лежит в точку 4, а необходимое изменение значения: Delta w = w_4 — w_3 < 0. Градиент же в точке 3 положителен. Этот факт также фиксируем.
А теперь соберем воедино эту информацию в виде следующей иллюстрации:
| Переход | bold{Delta w} | Знак bold{Delta w} | Градиент |
|---|---|---|---|
| 1 rArr 2 | w_2 — w_1 | + | — |
| 3 rArr 4 | w_4 — w_3 | — | + |
Вывод напрашивается сам собой — величина, на которую необходимо изменить значение w, в любой точке противоположна по знаку градиенту. И, таким образом, представим эту самую величину в виде:
Delta w = -alpha cdot frac{dE}{dw}
Имеем в наличии:
- Delta w — величина, на которую необходимо изменить значение w.
- frac{dE}{dw} — градиент в этой точке.
- alpha — скорость обучения.
Собственно, логика метода градиентного спуска и заключается в данном математическом выражении, а именно в том, что для минимизации ошибки необходимо изменять w в направлении противоположном градиенту. В контексте нейронных сетей имеем искомый закон для корректировки весов синаптических связей (для синапса между нейронами i и j):
Delta w_{ij} = -alpha cdot frac{dE}{dw_{ij}}
Более того, вспомним о важном свойстве, которое мы отдельно пометили. И заключается оно в том, что величина градиента будет уменьшаться по мере приближения к минимуму функции. Что это нам дает? А то, что в том случае, если наша текущая дислокация далека от места назначения, то величина, корректирующая вес связи, будет больше. А это обеспечит скорейшее приближение к цели. При приближении к целевому пункту, величина frac{dE}{dw_{ij}} будет уменьшаться, что поможет нам точнее попасть в нужную точку, а кроме того, не позволит нам ее проскочить. Визуализируем вышеописанное:
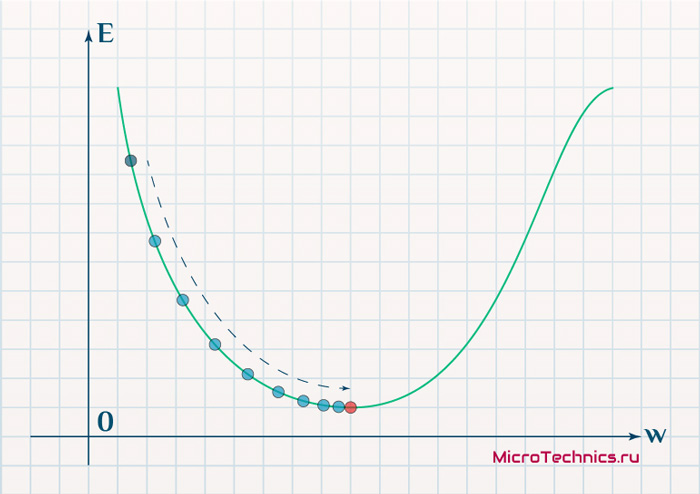
Скорость же обучения несет в себе следующий смысл. Она определяет величину каждого шага при поиске минимума ошибки. Слишком большое значение приводит к тому, что точка может «перепрыгнуть» через нужное значение и оказаться по другую сторону от цели:
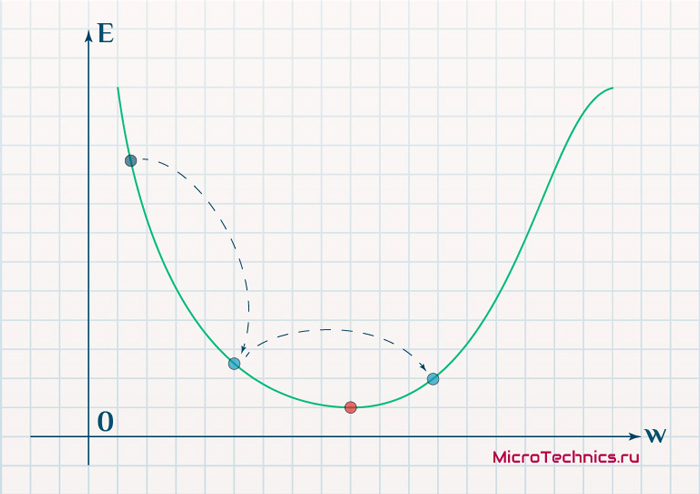
Если же величина будет мала, то это приведет к тому, что спуск будет осуществляться очень медленно, что также является нежелательным эффектом. Поэтому скорость обучения, как и многие другие параметры нейронной сети, является очень важной величиной, для которой нет единственно верного значения. Все снова зависит от конкретного случая и оптимальная величина определяется исключительно исходя из текущих условий.
И даже на этом еще не все, здесь присутствует один важный нюанс, который в большинстве статей опускается, либо вовсе не упоминается. Реальная зависимость может иметь совсем другой вид:
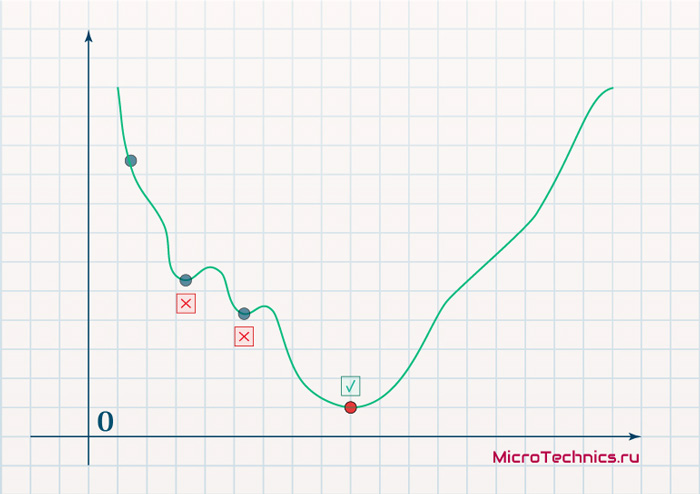
Из чего вытекает потенциальная возможность попадания в локальный минимум, вместо глобального, что является большой проблемой. Для предотвращения данного эффекта вводится понятие момента обучения и формула принимает следующий вид:
Delta w_{ij} = -alpha cdot frac{dE}{dw_{ij}} + gamma cdot Delta w_{ij}^{t - 1}
То есть добавляется второе слагаемое, которое представляет из себя произведение момента на величину корректировки веса на предыдущем шаге.
Итого, резюмируем продвижение к цели:
- Нашей задачей было найти закон, по которому необходимо изменять величину весов связей между нейронами.
- Наш результат — Delta w_{ij} = -alpha cdot frac{dE}{dw_{ij}} + gamma cdot Delta w_{ij}^{t — 1} — именно то, что и требовалось 👍
И опять же, полученный результат логичным образом перенаправляет нас на следующий этап, ставя вопросы — что из себя представляет функция ошибки, и как определить ее градиент.
Обучение нейронных сетей. Функция ошибки.
Начнем с того, что определимся с тем, что у нас в наличии, для этого вернемся к конкретной нейронной сети. Пусть вид ее таков:
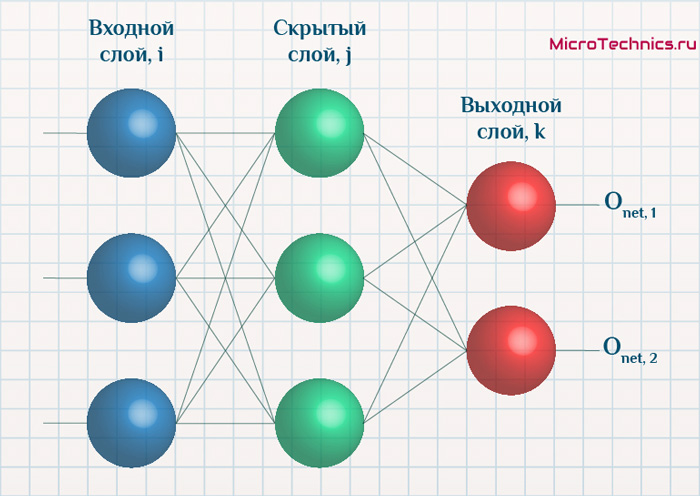
Интересует нас, в первую очередь, часть, относящаяся к нейронам выходного слоя. Подав на вход определенные значения, получаем значения на выходе сети: O_{net, 1} и O_{net, 2}. Кроме того, поскольку мы ведем речь о процессе обучения нейронной сети, то нам известны целевые значения: O_{correct, 1} и O_{correct, 2}. И именно этот набор данных на этом этапе является для нас исходным:
- Известно: O_{net, 1}, O_{net, 2}, O_{correct, 1} и O_{correct, 2}.
- Необходимо определить величины Delta w_{ij} для корректировки весов, для этого нужно вычислить градиенты (frac{dE}{dw_{ij}}) для каждого из синапсов.
Полдела сделано — задача четко сформулирована, начинаем деятельность по поиску решения.
В плане того, как определять ошибку, первым и самым очевидным вариантом кажется простая алгебраическая разность. Для каждого из выходных нейронов:
E_k = O_{correct, k} - O_{net, k}
Дополним пример числовыми значениями:
| Нейрон | bold{O_{net}} | bold{O_{correct}} | bold{E} |
|---|---|---|---|
| 1 | 0.9 | 0.5 | -0.4 |
| 2 | 0.2 | 0.6 | 0.4 |
Недостатком данного варианта является то, что в том случае, если мы попытаемся просуммировать ошибки нейронов, то получим:
E_{sum} = e_1 + e_2 = -0.4 + 0.4 = 0
Что не соответствует действительности (нулевая ошибка, говорит об идеальной работе нейронной сети, по факту оба нейрона дали неверный результат). Так что вариант с разностью откидываем за несостоятельностью.
Вторым, традиционно упоминаемым, методом вычисления ошибки является использование модуля разности:
E_k = | O_{correct, k} - O_{net, k} |
Тут в действие вступает уже проблема иного рода:
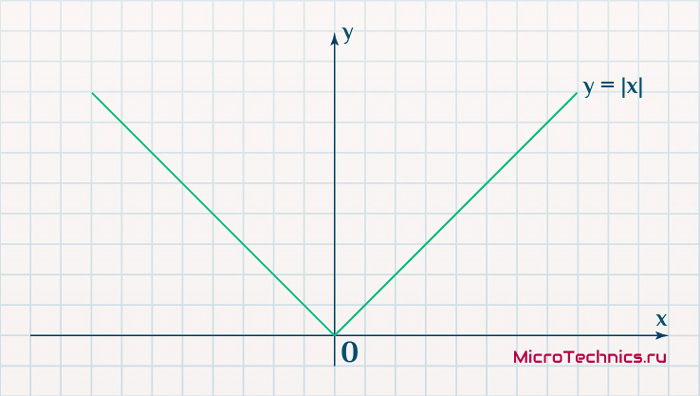
Функция, бесспорно, симпатична, но при приближении к минимуму ее градиент является постоянной величиной, скачкообразно меняясь при переходе через точку минимума. Это нас также не устраивает, поскольку, как мы обсуждали, концепция заключалась в том числе в том, чтобы по мере приближения к минимуму значение градиента уменьшалось.
В итоге хороший результат дает зависимость (для выходного нейрона под номером k):
E_k = (O_{correct, k} - O_{net, k})^2
Функция по многим своим свойствам идеально удовлетворяет нуждам обучения нейронной сети, так что выбор сделан, остановимся на ней. Хотя, как и во многих аспектах, качающихся нейронных сетей, данное решение не является единственно и неоспоримо верным. В каких-то случаях лучше себя могут проявить другие зависимости, возможно, что какой-то вариант даст большую точность, но неоправданно высокие затраты производительности при обучении. В общем, непаханное поле для экспериментов и исследований, это и привлекательно.
Краткий вывод промежуточного шага, на который мы вышли:
- Имеющееся: frac{dE}{dw_{jk}} = frac{d}{d w_{jk}}(O_{correct, k} — O_{net, k})^2.
- Искомое по-прежнему: Delta w_{jk}.
Несложные диффернциально-математические изыскания выводят на следующий результат:
frac{dE}{d w_{jk}} = -(O_{correct, k} - O_{net, k}) cdot f{Large{prime}}(sum_{j}w_{jk}O_j) cdot O_j
Здесь эти самые изыскания я все-таки решил не вставлять, дабы не перегружать статью, которая и так выходит объемной. Но в случае необходимости и интереса, отпишите в комментарии, я добавлю вычисления и закину их под спойлер, как вариант.
Освежим в памяти структуру сети:
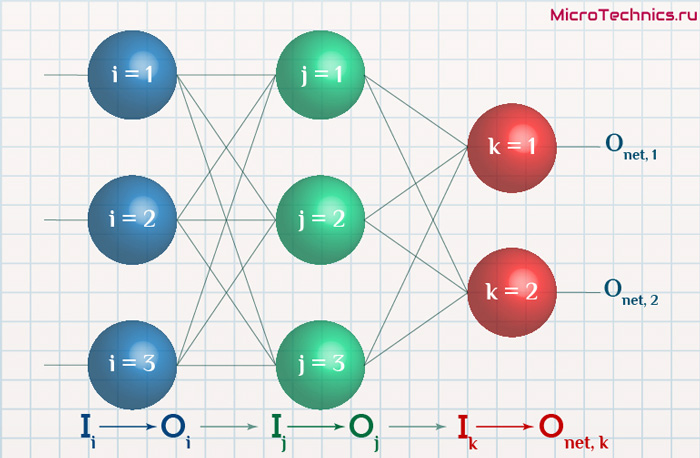
Формулу можно упростить, сгруппировав отдельные ее части:
- (O_{correct, k} — O_{net, k}) cdot f{Large{prime}}(sum_{j}w_{jk}O_j) — ошибка нейрона k.
- O_j — тут все понятно, выходной сигнал нейрона j.
f{Large{prime}}(sum_{j}w_{jk}O_j) — значение производной функции активации. Причем, обратите внимание, что sum_{j}w_{jk}O_j — это не что иное, как сигнал на входе нейрона k (I_{k}). Тогда для расчета ошибки выходного нейрона: delta_k = (O_{correct, k} — O_{net, k}) cdot f{Large{prime}}(I_k).
Итог: frac{dE}{d w_{jk}} = -delta_k cdot O_j.
Одной из причин популярности сигмоидальной функции активности является то, что ее производная очень просто выражается через саму функцию:
f{'}(x) = f(x)medspace (1medspace-medspace f(x))
Данные алгебраические вычисления справедливы для корректировки весов между скрытым и выходным слоем, поскольку для расчета ошибки мы используем просто разность между целевым и полученным результатом, умноженную на производную.
Для других слоев будут незначительные изменения, касающиеся исключительно первого множителя в формуле:
frac{dE}{d w_{ij}} = -delta_j cdot O_i
Который примет следующий вид:
delta_j = (sum_{k}{}{delta_kmedspace w_{jk}}) cdot f{Large{prime}}(I_j)
То есть ошибка для элемента слоя j получается путем взвешенного суммирования ошибок, «приходящих» к нему от нейронов следующего слоя и умножения на производную функции активации. В результате:
frac{dE}{d w_{ij}} = -(sum_{k}{}{delta_kmedspace w_{jk}}) cdot f{Large{prime}}(I_j) cdot O_i
Снова подводим промежуточный итог, чтобы иметь максимально полную и структурированную картину происходящего. Вот результаты, полученные нами на двух этапах, которые мы успешно миновали:
- Ошибка:
- выходной слой: delta_k = (O_{correct, k} — O_{net, k}) cdot f{Large{prime}}(I_k)
- скрытые слои: delta_j = (sum_{k}{}{delta_kmedspace w_{jk}}) cdot f{Large{prime}}(I_j)
- Градиент: frac{dE}{d w_{ij}} = -delta_j cdot O_i
- Корректировка весовых коэффициентов: Delta w_{ij} = -alpha cdot frac{dE}{dw_{ij}} + gamma cdot Delta w_{ij}^{t — 1}
Преобразуем последнюю формулу:
Delta w_{ij} = alpha cdot delta_j cdot O_i + gamma cdot Delta w_{ij}^{t - 1}
Из этого мы делаем вывод, что на данный момент у нас есть все, что необходимо для того, чтобы произвести обучение нейронной сети. И героем следующего подраздела будет алгоритм обратного распространения ошибки.
Метод обратного распространения ошибки.
Данный метод является одним из наиболее распространенных и популярных, чем и продиктован его выбор для анализа и разбора. Алгоритм обратного распространения ошибки относится к методам обучение с учителем, что на деле означает необходимость наличия целевых значений в обучающих сетах.
Суть же метода подразумевает наличие двух этапов:
- Прямой проход — входные сигналы двигаются в прямом направлении, в результате чего мы получаем выходной сигнал, из которого в дальнейшем рассчитываем значение ошибки.
- Обратный проход — обратное распространение ошибки — величина ошибки двигается в обратном направлении, в результате происходит корректировка весовых коэффициентов связей сети.
Начальные значения весов (перед обучением) задаются случайными, есть ряд методик для выбора этих значений, я опишу в отдельном материале максимально подробно. Пока вот можно полистать — ссылка.
Вернемся к конкретному примеру для явной демонстрации этих принципов:
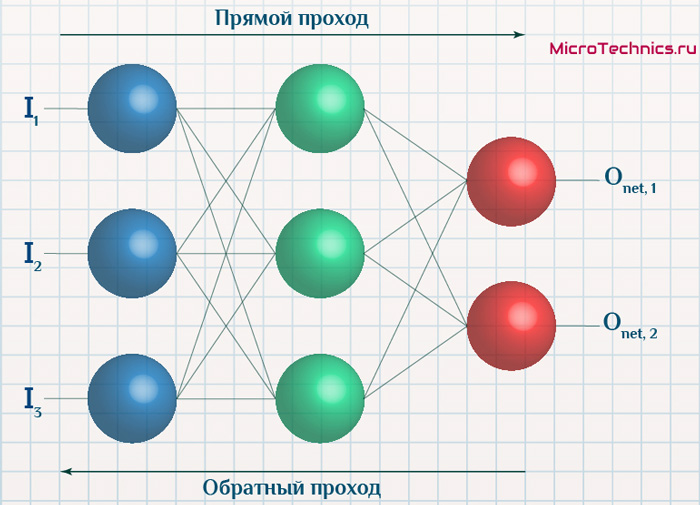
Итак, имеется нейронная сеть, также имеется набор данных обучающей выборки. Как уже обсудили в начале статьи — обучающая выборка представляет из себя набор образцов (сетов), каждый из которых состоит из значений входных сигналов и соответствующих им «правильных» значений выходных величин.
Процесс обучения нейронной сети для алгоритма обратного распространения ошибки будет таким:
- Прямой проход. Подаем на вход значения I_1, I_2, I_3 из обучающей выборки. В результате работы сети получаем выходные значения O_{net, 1}, O_{net, 2}. Этому целиком и полностью был посвящен предыдущий манускрипт.
- Рассчитываем величины ошибок для всех слоев:
- для выходного: delta_k = (O_{correct, k} — O_{net, k}) cdot f{Large{prime}}(I_k)
- для скрытых: delta_j = (sum_{k}{}{delta_kmedspace w_{jk}}) cdot f{Large{prime}}(I_j)
- Далее используем полученные значения для расчета Delta w_{ij} = alpha cdot delta_j cdot O_i + gamma cdot Delta w_{ij}^{t — 1}
- И финишируем, рассчитывая новые значения весов: w_{ij medspace new} = w_{ij} + Delta w_{ij}
- На этом один цикл обучения закончен, данные шаги 1 — 4 повторяются для других образцов из обучающей выборки.
Обратный проход завершен, а вместе с ним и одна итерация процесса обучения нейронной сети по данному методу. Собственно, обучение в целом заключается в многократном повторении этих шагов для разных образцов из обучающей выборки. Логику мы полностью разобрали, при повторном проведении операций она остается в точности такой же.
Таким образом, максимально подробно концентрируясь именно на сути и логике процессов, мы в деталях разобрали метод обратного распространения ошибки. Поэтому переходим к завершающей части статьи, в которой разберем практический пример, произведя полностью все вычисления для конкретных числовых величин. Все в рамках продвигаемой мной концепции, что любая теоретическая информация на порядок лучше может быть осознана при применении ее на практике.
Пример расчетов для метода обратного распространения ошибки.
Возьмем нейронную сеть и зададим начальные значения весов:
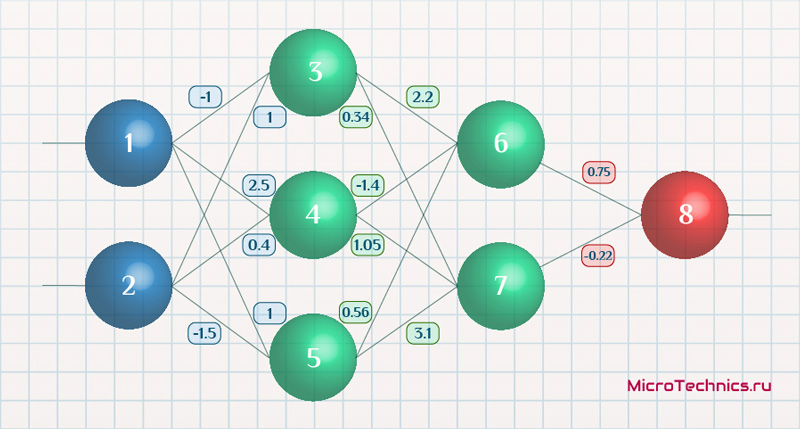
Здесь я задал значения не в соответствии с существующими на сегодняшний день методами, а просто случайным образом для наглядности примера.
В качестве функции активации используем сигмоиду:
f(x) = frac{1}{1 + e^{-x}}
И ее производная:
f{Large{prime}}(x) = f(x)medspace (1medspace-medspace f(x))
Берем один образец из обучающей выборки, пусть будут такие значения:
- Входные: I_1 = 0.6, I_1 = 0.7.
- Выходное: O_{correct} = 0.9.
Скорость обучения alpha пусть будет равна 0.3, момент — gamma = 0.1. Все готово, теперь проведем полный цикл для метода обратного распространения ошибки, то есть прямой проход и обратный.
Прямой проход.
Начинаем с выходных значений нейронов 1 и 2, поскольку они являются входными, то:
O_1 = I_1 = 0.6 \ O_2 = I_2 = 0.7
Значения на входе нейронов 3, 4 и 5:
I_3 = O_1 cdot w_{13} + O_2 cdot w_{23} = 0.6 cdot (-1medspace) + 0.7 cdot 1 = 0.1 \
I_4 = 0.6 cdot 2.5 + 0.7 cdot 0.4 = 1.78 \
I_5 = 0.6 cdot 1 + 0.7 cdot (-1.5medspace) = -0.45
На выходе этих же нейронов первого скрытого слоя:
O_3 = f(I3medspace) = 0.52 \ O_4 = 0.86\ O_5 = 0.39
Продолжаем аналогично для следующего скрытого слоя:
I_6 = O_3 cdot w_{36} + O_4 cdot w_{46} + O_5 cdot w_{56} = 0.52 cdot 2.2 + 0.86 cdot (-1.4medspace) + 0.39 cdot 0.56 = 0.158 \
I_7 = 0.52 cdot 0.34 + 0.86 cdot 1.05 + 0.39 cdot 3.1 = 2.288 \
O_6 = f(I_6) = 0.54 \
O_7 = 0.908
Добрались до выходного нейрона:
I_8 = O_6 cdot w_{68} + O_7 cdot w_{78} = 0.54 cdot 0.75 + 0.908 cdot (-0.22medspace) = 0.205 \
O_8 = O_{net} = f(I_8) = 0.551
Получили значение на выходе сети, кроме того, у нас есть целевое значение O_{correct} = 0.9. То есть все, что необходимо для обратного прохода, имеется.
Обратный проход.
Как мы и обсуждали, первым этапом будет вычисление ошибок всех нейронов, действуем:
delta_8 = (O_{correct} - O_{net}) cdot f{Large{prime}}(I_8) = (O_{correct} - O_{net}) cdot f(I_8) cdot (1-f(I_8)) = (0.9 - 0.551medspace) cdot 0.551 cdot (1-0.551medspace) = 0.0863 \
delta_7 = (sum_{k}{}{delta_kmedspace w_{jk}}) cdot f{Large{prime}}(I_7) = (delta_8 cdot w_{78}) cdot f{Large{prime}}(I_7) = 0.0863 cdot (-0.22medspace) cdot 0.908 cdot (1 - 0.908medspace) = -0.0016 \
delta_6 = 0.086 cdot 0.75 cdot 0.54 cdot (1 - 0.54medspace) = 0.016 \
delta_5 = (sum_{k}{}{delta_kmedspace w_{jk}}) cdot f{Large{prime}}(I_5) = (delta_7 cdot w_{57} + delta_6 cdot w_{56}) cdot f{Large{prime}}(I_7) = (-0.0016 cdot 3.1 + 0.016 cdot 0.56) cdot 0.39 cdot (1 - 0.39medspace) = 0.001 \
delta_4 = (-0.0016 cdot 1.05 + 0.016 cdot (-1.4)) cdot 0.86 cdot (1 - 0.86medspace) = -0.003 \
delta_3 = (-0.0016 cdot 0.34 + 0.016 cdot 2.2) cdot 0.52 cdot (1 - 0.52medspace) = -0.0087
С расчетом ошибок закончили, следующий этап — расчет корректировочных величин для весов всех связей. Для этого мы вывели формулу:
Delta w_{ij} = alpha cdot delta_j cdot O_i + gamma cdot Delta w_{ij}^{t - 1}
Как вы помните, Delta w_{ij}^{t — 1} — это величина поправки для данного веса на предыдущей итерации. Но поскольку у нас это первый проход, то данное значение будет нулевым, соответственно, в данном случае второе слагаемое отпадает. Но забывать о нем нельзя. Продолжаем калькулировать:
Delta w_{78} = alpha cdot delta_8 cdot O_7 = 0.3 cdot 0.0863 cdot 0.908 = 0.0235 \
Delta w_{68} = 0.3 cdot 0.0863 cdot 0.54= 0.014 \
Delta w_{57} = alpha cdot delta_7 cdot O_5 = 0.3 cdot (−0.0016medspace) cdot 0.39= -0.00019 \
Delta w_{47} = 0.3 cdot (−0.0016medspace) cdot 0.86= -0.0004 \
Delta w_{37} = 0.3 cdot (−0.0016medspace) cdot 0.52= -0.00025 \
Delta w_{56} = alpha cdot delta_6 cdot O_5 = 0.3 cdot 0.016 cdot 0.39= 0.0019 \
Delta w_{46} = 0.3 cdot 0.016 cdot 0.86= 0.0041 \
Delta w_{36} = 0.3 cdot 0.016 cdot 0.52= 0.0025 \
Delta w_{25} = alpha cdot delta_5 cdot O_2 = 0.3 cdot 0.001 cdot 0.7= 0.00021 \
Delta w_{15} = 0.3 cdot 0.001 cdot 0.6= 0.00018 \
Delta w_{24} = alpha cdot delta_4 cdot O_2 = 0.3 cdot (-0.003medspace) cdot 0.7= -0.00063 \
Delta w_{14} = 0.3 cdot (-0.003medspace) cdot 0.6= -0.00054 \
Delta w_{23} = alpha cdot delta_3 cdot O_2 = 0.3 cdot (−0.0087medspace) cdot 0.7= -0.00183 \
Delta w_{13} = 0.3 cdot (−0.0087medspace) cdot 0.6= -0.00157
И самый что ни на есть заключительный этап — непосредственно изменение значений весовых коэффициентов:
w_{78 medspace new} = w_{78} + Delta w_{78} = -0.22 + 0.0235 = -0.1965 \
w_{68 medspace new} = 0.75+ 0.014 = 0.764 \
w_{57 medspace new} = 3.1 + (−0.00019medspace) = 3.0998\
w_{47 medspace new} = 1.05 + (−0.0004medspace) = 1.0496\
w_{37 medspace new} = 0.34 + (−0.00025medspace) = 0.3398\
w_{56 medspace new} = 0.56 + 0.0019 = 0.5619 \
w_{46 medspace new} = -1.4 + 0.0041 = -1.3959 \
w_{36 medspace new} = 2.2 + 0.0025 = 2.2025 \
w_{25 medspace new} = -1.5 + 0.00021 = -1.4998 \
w_{15 medspace new} = 1 + 0.00018 = 1.00018 \
w_{24 medspace new} = 0.4 + (−0.00063medspace) = 0.39937 \
w_{14 medspace new} = 2.5 + (−0.00054medspace) = 2.49946 \
w_{23 medspace new} = 1 + (−0.00183medspace) = 0.99817 \
w_{13 medspace new} = -1 + (−0.00157medspace) = -1.00157\
И на этом данную масштабную статью завершаем, конечно же, не завершая на этом деятельность по использованию нейронных сетей. Так что всем спасибо за прочтение, любые вопросы пишите в комментариях и на форуме, ну и обязательно следите за обновлениями и новыми материалами, до встречи!
Применение алгоритма обратного распространения ошибки — один из известных методов, используемых для глубокого обучения нейронных сетей прямого распространения (такие сети ещё называют многослойными персептронами). Этот метод относят к методу обучения с учителем, поэтому требуется задавать в обучающих примерах целевые значения. В этой статье мы рассмотрим, что собой представляет метод обратного распространения ошибки, как он реализуется, каковы его плюсы и минусы.
Сегодня нейронные сети прямого распространения используются для решения множества сложных задач. Если говорить об обучении нейронных сетей методом обратного распространения, то тут пользуются двумя проходами по всем слоям нейросети: прямым и обратным. При выполнении прямого прохода осуществляется подача входного вектора на входной слой сети, после чего происходит распространение по нейронной сети от слоя к слою. В итоге должна осуществляться генерация набора выходных сигналов — именно он, по сути, является реакцией нейронной сети на этот входной образ. При прямом проходе все синаптические веса нейросети фиксированы. При обратном проходе все синаптические веса настраиваются согласно правил коррекции ошибок, когда фактический выход нейронной сети вычитается из желаемого, что приводит к формированию сигнала ошибки. Такой сигнал в дальнейшем распространяется по сети, причём направление распространения обратно направлению синаптических связей. Именно поэтому соответствующий метод и называют алгоритмом с обратно распространённой ошибкой. Синаптические веса настраивают с целью наибольшего приближения выходного сигнала нейронной сети к желаемому.
Общее описание алгоритма обратного распространения ошибки
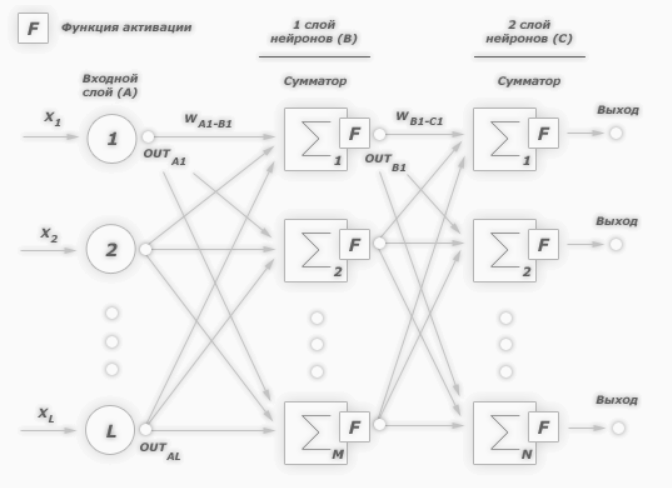
К примеру, нам надо обучить нейронную сеть по аналогии с той, что представлена на картинке ниже. Естественно, задачу следует выполнить, применяя алгоритм обратного распространения ошибки:
В многослойных персептронах в роли активационной функции обычно применяют сигмоидальную активационную функция, в нашем случае — логистическую. Формула:
Причём «альфа» здесь означает параметр наклона сигмоидальной функции. Меняя его, мы получаем возможность строить функции с разной крутизной.
Сигмоид может сужать диапазон изменения таким образом, чтобы значение OUT лежало между нулем и единицей. Нейронные многослойные сети характеризуются более высокой представляющей мощностью, если сравнивать их с однослойными, но это утверждение справедливо лишь в случае нелинейности. Нужную нелинейность и обеспечивает сжимающая функция. Но на практике существует много функций, которые можно использовать. Говоря о работе алгоритма обратного распространения ошибки, скажем, что для этого нужно лишь, чтобы функция была везде дифференцируема, а данному требованию как раз и удовлетворяет сигмоид. У него есть и дополнительное преимущество — автоматический контроль усиления. Если речь идёт о слабых сигналах (OUT близко к нулю), то кривая «вход-выход» характеризуется сильным наклоном, дающим большое усиление. При увеличении сигнала усиление падает. В результате большие сигналы будут восприниматься сетью без насыщения, а слабые сигналы будут проходить по сети без чрезмерного ослабления.
Цель обучения сети
Цель обучения нейросети при использовании алгоритма обратного распространения ошибки — это такая подстройка весов нейросети, которая позволит при приложении некоторого множества входов получить требуемое множество выходов нейронов (выходных нейронов). Можно назвать эти множества входов и выходов векторами. В процессе обучения предполагается, что для любого входного вектора существует целевой вектор, парный входному и задающий требуемый выход. Эту пару называют обучающей. Работая с нейросетями, мы обучаем их на многих парах.
Также можно сказать, что алгоритм использует стохастический градиентный спуск и продвигается в многомерном пространстве весов в направлении антиградиента, причём цель — это достижение минимума функции ошибки.
При практическом применении метода обучение продолжают не до максимально точной настройки нейросети на минимум функции ошибки, а пока не будет достигнуто довольно точное его приближение. С одной стороны, это даёт возможность уменьшить количество итераций обучения, с другой — избежать переобучения нейронной сети.
Пошаговая реализация метода обратного распространения ошибки
Необходимо выполнить следующие действия:
1. Инициализировать синаптические веса случайными маленькими значениями.
2. Выбрать из обучающего множества очередную обучающую пару; подать на вход сети входной вектор.
3. Выполнить вычисление выходных значений нейронной сети.
4. Посчитать разность между выходом нейросети и требуемым выходом (речь идёт о целевом векторе обучающей пары).
5. Скорректировать веса сети в целях минимизации ошибки.
6. Повторять для каждого вектора обучающего множества шаги 2-5, пока ошибка обучения нейронной сети на всём множестве не достигнет уровня, который является приемлемым.
Виды обучения сети по методу обратного распространения
Сегодня существует много модификаций алгоритма обратного распространения ошибки. Возможно обучение не «по шагам» (выходная ошибка вычисляется, веса корректируются на каждом примере), а «по эпохам» в offline-режиме (изменения весовых коэффициентов происходит после подачи на вход нейросети всех примеров обучающего множества, а ошибка обучения neural сети усредняется по всем примерам).
Обучение «по эпохам» более устойчиво к выбросам и аномальным значениям целевой переменной благодаря усреднению ошибки по многим примерам. Зато в данном случае увеличивается вероятность «застревания» в локальных минимумах. При обучении «по шагам» такая вероятность меньше, ведь применение отдельных примеров создаёт «шум», «выталкивающий» алгоритм обратного распространения из ям градиентного рельефа.
Преимущества и недостатки метода
К плюсам можно отнести простоту в реализации и устойчивость к выбросам и аномалиям в данных, и это основные преимущества. Но есть и минусы:
• неопределенно долгий процесс обучения;
• вероятность «паралича сети» (при больших значениях рабочая точка функции активации попадает в область насыщения сигмоиды, а производная величина приближается к 0, в результате чего коррекции весов почти не происходят, а процесс обучения «замирает»;
• алгоритм уязвим к попаданию в локальные минимумы функции ошибки.
Значение метода обратного распространения
Появление алгоритма стало знаковым событием и положительно отразилось на развитии нейросетей, ведь он реализует эффективный с точки зрения вычислительных процессов способ обучения многослойного персептрона. В то же самое время, было бы неправильным сказать, что алгоритм предлагает наиболее оптимальное решение всех потенциальных проблем. Зато он действительно развеял пессимизм относительно машинного обучения многослойных машин, который воцарился после публикации в 1969 году работы американского учёного с фамилией Минский.
Источники:
— «Алгоритм обратного распространения ошибки»;
— «Back propagation algorithm».
Использование функций потерь
Функция потерь (или объективная функция, или функция оценки результатов оптимизации) является одним из двух параметров, необходимых для компиляции модели:
model.compile(loss=’mean_squared_error’, optimizer=’sgd’)
from keras import losses
model.compile(loss=losses.mean_squared_error, optimizer=’sgd’)
Можно либо передать имя существующей функции потерь, либо передать символическую функцию TensorFlow/Theano, которая возвращает скаляр для каждой точки данных и принимает следующие два аргумента:
y_true: истинные метки. Тензор TensorFlow/Theano.
y_pred: Прогнозы. Тензор TensorFlow/Theano той же формы, что и y_true.
Фактически оптимизированная цель — это среднее значение выходного массива по всем точкам данных.
Доступные функции потери
mean_squared_error
keras.losses.mean_squared_error(y_true, y_pred)
mean_absolute_error
keras.losses.mean_absolute_error(y_true, y_pred)
mean_absolute_percentage_error
keras.losses.mean_absolute_percentage_error(y_true, y_pred)
mean_squared_logarithmic_error
keras.losses.mean_squared_logarithmic_error(y_true, y_pred)
squared_hinge
keras.losses.squared_hinge(y_true, y_pred)
hinge
keras.losses.hinge(y_true, y_pred)
categorical_hinge
keras.losses.categorical_hinge(y_true, y_pred)
logcosh
keras.losses.logcosh(y_true, y_pred)
Логарифм гиперболического косинуса ошибки прогнозирования.
log(cosh(x)) приблизительно равен (x ** 2) / 2 для малого x и abs(x) — log(2) для большого x. Это означает, что ‘logcosh’ работает в основном как средняя квадратичная ошибка, но не будет так сильно зависеть от случайного сильно неправильного предсказания.
Аргументы
- y_true: тензор истинных целей.
- y_pred: тензор прогнозируемых целей.
Возвращает
Тензор с одной записью о скалярной потере на каждый сэмпл.
huber_loss
keras.losses.huber_loss(y_true, y_pred, delta=1.0)
categorical_crossentropy
keras.losses.categorical_crossentropy(y_true, y_pred, from_logits=False, label_smoothing=0)
sparse_categorical_crossentropy
keras.losses.sparse_categorical_crossentropy(y_true, y_pred, from_logits=False, axis=-1)
binary_crossentropy
keras.losses.binary_crossentropy(y_true, y_pred, from_logits=False, label_smoothing=0)
kullback_leibler_divergence
keras.losses.kullback_leibler_divergence(y_true, y_pred)
poisson
keras.losses.poisson(y_true, y_pred)
cosine_proximity
keras.losses.cosine_proximity(y_true, y_pred, axis=-1)
is_categorical_crossentropy
keras.losses.is_categorical_crossentropy(loss)
Примечание: при использовании потери categorical_crossentropy ваши данные должны быть в категориальном формате (например, если у вас 10 классов, то целью для каждой выборки должен быть 10-мерный вектор, который является полностью нулевым, за исключением 1 в индексе, соответствующем классу выборки). Для того, чтобы преобразовать целые данные в категорические, можно использовать утилиту Keras to_categorical:
from keras.utils import to_categorical
categorical_labels = to_categorical(int_labels, num_classes=None)
При использовании переменной sparse_categorical_crossentropy loss, ваши данные должны быть целыми. Если у вас есть категориальные данные, следует использовать categoryical_crossentropy.
categoryical_crossentropy — это еще один термин для обозначения потери лога по нескольким классам.
You’ve created a deep learning model in Keras, you prepared the data and now you are wondering which loss you should choose for your problem.
We’ll get to that in a second but first what is a loss function?
In deep learning, the loss is computed to get the gradients with respect to model weights and update those weights accordingly via backpropagation. Loss is calculated and the network is updated after every iteration until model updates don’t bring any improvement in the desired evaluation metric.
So while you keep using the same evaluation metric like f1 score or AUC on the validation set during (long parts) of your machine learning project, the loss can be changed, adjusted and modified to get the best evaluation metric performance.
You can think of the loss function just like you think about the model architecture or the optimizer and it is important to put some thought into choosing it. In this piece we’ll look at:
- loss functions available in Keras and how to use them,
- how you can define your own custom loss function in Keras,
- how to add sample weighing to create observation-sensitive losses,
- how to avoid nans in the loss,
- how you can monitor the loss function via plotting and callbacks.
Let’s get into it!
Keras loss functions 101
In Keras, loss functions are passed during the compile stage, as shown below.
In this example, we’re defining the loss function by creating an instance of the loss class. Using the class is advantageous because you can pass some additional parameters.
from tensorflow import keras from tensorflow.keras import layers model = keras.Sequential() model.add(layers.Dense(64, kernel_initializer='uniform', input_shape=(10,))) model.add(layers.Activation('softmax')) loss_function = keras.losses.SparseCategoricalCrossentropy(from_logits=True) model.compile(loss=loss_function, optimizer='adam')
If you want to use a loss function that is built into Keras without specifying any parameters you can just use the string alias as shown below:
model.compile(loss='sparse_categorical_crossentropy', optimizer='adam')
You might be wondering how does one decide on which loss function to use?
There are various loss functions available in Keras. Other times you might have to implement your own custom loss functions.
Let’s dive into all those scenarios.
Which loss functions are available in Keras?
Binary Classification
Binary classification loss function comes into play when solving a problem involving just two classes. For example, when predicting fraud in credit card transactions, a transaction is either fraudulent or not.
Binary Cross Entropy
The Binary Cross entropy will calculate the cross-entropy loss between the predicted classes and the true classes. By default, the sum_over_batch_size reduction is used. This means that the loss will return the average of the per-sample losses in the batch.
y_true = [[0., 1.], [0.2, 0.8],[0.3, 0.7],[0.4, 0.6]] y_pred = [[0.6, 0.4], [0.4, 0.6],[0.6, 0.4],[0.8, 0.2]] bce = tf.keras.losses.BinaryCrossentropy(reduction='sum_over_batch_size') bce(y_true, y_pred).numpy()
The sum reduction means that the loss function will return the sum of the per-sample losses in the batch.
bce = tf.keras.losses.BinaryCrossentropy(reduction='sum')
bce(y_true, y_pred).numpy()
Using the reduction as none returns the full array of the per-sample losses.
bce = tf.keras.losses.BinaryCrossentropy(reduction='none') bce(y_true, y_pred).numpy() array([0.9162905 , 0.5919184 , 0.79465103, 1.0549198 ], dtype=float32)
In binary classification, the activation function used is the sigmoid activation function. It constrains the output to a number between 0 and 1.
Multiclass classification
Problems involving the prediction of more than one class use different loss functions. In this section we’ll look at a couple:
Categorical Crossentropy
The CategoricalCrossentropy also computes the cross-entropy loss between the true classes and predicted classes. The labels are given in an one_hot format.
cce = tf.keras.losses.CategoricalCrossentropy() cce(y_true, y_pred).numpy()
Sparse Categorical Crossentropy
If you have two or more classes and the labels are integers, the SparseCategoricalCrossentropy should be used.
y_true = [0, 1,2] y_pred = [[0.05, 0.95, 0], [0.1, 0.8, 0.1],[0.1, 0.8, 0.1]] scce = tf.keras.losses.SparseCategoricalCrossentropy() scce(y_true, y_pred).numpy()
The Poison Loss
You can also use the Poisson class to compute the poison loss. It’s a great choice if your dataset comes from a Poisson distribution for example the number of calls a call center receives per hour.
y_true = [[0.1, 1.,0.8], [0.1, 0.9,0.1],[0.2, 0.7,0.1],[0.3, 0.1,0.6]] y_pred = [[0.6, 0.2,0.2], [0.2, 0.6,0.2],[0.7, 0.1,0.2],[0.8, 0.1,0.1]] p = tf.keras.losses.Poisson() p(y_true, y_pred).numpy()
Kullback-Leibler Divergence Loss
The relative entropy can be computed using the KLDivergence class. According to the official docs at PyTorch:
KL divergence is a useful distance measure for continuous distributions and is often useful when performing direct regression over the space of (discretely sampled) continuous output distributions.
y_true = [[0.1, 1.,0.8], [0.1, 0.9,0.1],[0.2, 0.7,0.1],[0.3, 0.1,0.6]] y_pred = [[0.6, 0.2,0.2], [0.2, 0.6,0.2],[0.7, 0.1,0.2],[0.8, 0.1,0.1]] kl = tf.keras.losses.KLDivergence() kl(y_true, y_pred).numpy()
In a multi-class problem, the activation function used is the softmax function.
Object Detection
The Focal Loss
In classification problems involving imbalanced data and object detection problems, you can use the Focal Loss. The loss introduces an adjustment to the cross-entropy criterion.
It is done by altering its shape in a way that the loss allocated to well-classified examples is down-weighted. This ensures that the model is able to learn equally from minority and majority classes.
The cross-entropy loss is scaled by scaling the factors decaying at zero as the confidence in the correct class increases. The factor of scaling down weights the contribution of unchallenging samples at training time and focuses on the challenging ones.
import tensorflow_addons as tfa y_true = [[0.97], [0.91], [0.03]] y_pred = [[1.0], [1.0], [0.0]] sfc = tfa.losses.SigmoidFocalCrossEntropy() sfc(y_true, y_pred).numpy() array([0.00010971, 0.00329749, 0.00030611], dtype=float32)
Generalized Intersection over Union
The Generalized Intersection over Union loss from the TensorFlow add on can also be used. The Intersection over Union (IoU) is a very common metric in object detection problems. IoU is however not very efficient in problems involving non-overlapping bounding boxes.
The Generalized Intersection over Union was introduced to address this challenge that IoU is facing. It ensures that generalization is achieved by maintaining the scale-invariant property of IoU, encoding the shape properties of the compared objects into the region property, and making sure that there is a strong correlation with IoU in the event of overlapping objects.
gl = tfa.losses.GIoULoss() boxes1 = tf.constant([[4.0, 3.0, 7.0, 5.0], [5.0, 6.0, 10.0, 7.0]]) boxes2 = tf.constant([[3.0, 4.0, 6.0, 8.0], [14.0, 14.0, 15.0, 15.0]]) loss = gl(boxes1, boxes2)
Regression
In regression problems, you have to calculate the differences between the predicted values and the true values but as always there are many ways to do it.
Mean Squared Error
The MeanSquaredError class can be used to compute the mean square of errors between the predictions and the true values.
y_true = [12, 20, 29., 60.] y_pred = [14., 18., 27., 55.] mse = tf.keras.losses.MeanSquaredError() mse(y_true, y_pred).numpy()
Use Mean Squared Error when you desire to have large errors penalized more than smaller ones.
Mean Absolute Percentage Error
The mean absolute percentage error is computed using the function below.
It is calculated as shown below.
y_true = [12, 20, 29., 60.] y_pred = [14., 18., 27., 55.] mape = tf.keras.losses.MeanAbsolutePercentageError() mape(y_true, y_pred).numpy()
Consider using this loss when you want a loss that you can explain intuitively. People understand percentages easily. The loss is also robust to outliers.
Mean Squared Logarithmic Error
The mean squared logarithmic error can be computed using the formula below:
Here’s an implementation of the same:
y_true = [12, 20, 29., 60.] y_pred = [14., 18., 27., 55.] msle = tf.keras.losses.MeanSquaredLogarithmicError() msle(y_true, y_pred).numpy()
Mean Squared Logarithmic Error penalizes underestimates more than it does overestimates. It’s a great choice when you prefer not to penalize large errors, it is, therefore, robust to outliers.
Cosine Similarity Loss
If your interest is in computing the cosine similarity between the true and predicted values, you’d use the CosineSimilarity class. It is computed as:
The result is a number between -1 and 1 . 0 indicates orthogonality while values close to -1 show that there is great similarity.
y_true = [[12, 20], [29., 60.]] y_pred = [[14., 18.], [27., 55.]] cosine_loss = tf.keras.losses.CosineSimilarity(axis=1) cosine_loss(y_true, y_pred).numpy()
LogCosh Loss
The LogCosh class computes the logarithm of the hyperbolic cosine of the prediction error.
Here’s its implementation as a stand-alone function.
y_true = [[12, 20], [29., 60.]] y_pred = [[14., 18.], [27., 55.]] l = tf.keras.losses.LogCosh() l(y_true, y_pred).numpy()
LogCosh Loss works like the mean squared error, but will not be so strongly affected by the occasional wildly incorrect prediction. — TensorFlow Docs
Huber loss
For regression problems that are less sensitive to outliers, the Huber loss is used.
y_true = [12, 20, 29., 60.] y_pred = [14., 18., 27., 55.] h = tf.keras.losses.Huber() h(y_true, y_pred).numpy()
Learning Embeddings
Triplet Loss
You can also compute the triplet loss with semi-hard negative mining via TensorFlow addons. The loss encourages the positive distances between pairs of embeddings with the same labels to be less than the minimum negative distance.
import tensorflow_addons as tfa model.compile(optimizer='adam', loss=tfa.losses.TripletSemiHardLoss(), metrics=['accuracy'])
Creating custom loss functions in Keras
Sometimes there is no good loss available or you need to implement some modifications. Let’s learn how to do that.
A custom loss function can be created by defining a function that takes the true values and predicted values as required parameters. The function should return an array of losses. The function can then be passed at the compile stage.
def custom_loss_function(y_true, y_pred): squared_difference = tf.square(y_true - y_pred) return tf.reduce_mean(squared_difference, axis=-1) model.compile(optimizer='adam', loss=custom_loss_function)
Let’s see how we can apply this custom loss function to an array of predicted and true values.
import numpy as np y_true = [12, 20, 29., 60.] y_pred = [14., 18., 27., 55.] cl = custom_loss_function(np.array(y_true),np.array(y_pred)) cl.numpy()
Use of Keras loss weights
During the training process, one can weigh the loss function by observations or samples. The weights can be arbitrary, but a typical choice is class weights (distribution of labels). Each observation is weighted by the fraction of the class it belongs to (reversed) so that the loss for minority class observations is more important when calculating the loss.
One of the ways to do this is to pass the class weights during the training process.
The weights are passed using a dictionary that contains the weight for each class. You can compute the weights using Scikit-learn or calculate the weights based on your own criterion.
weights = { 0:1.01300017,1:0.88994364,2:1.00704935, 3:0.97863318, 4:1.02704553, 5:1.10680686,6:1.01385603,7:0.95770152, 8:1.02546573,
9:1.00857287}
model.fit(x_train, y_train,verbose=1, epochs=10,class_weight=weights)
The second way is to pass these weights at the compile stage.
weights = [1.013, 0.889, 1.007, 0.978, 1.027,1.106,1.013,0.957,1.025, 1.008] model.compile(optimizer=tf.keras.optimizers.SGD(), loss=tf.keras.losses.SparseCategoricalCrossentropy(), loss_weights=weights, metrics=['accuracy'])
How to monitor Keras loss function [example]
It is usually a good idea to monitor the loss function on the training and validation set as the model is training. Looking at those learning curves is a good indication of overfitting or other problems with model training.
There are two main options of how this can be done.
Monitor Keras loss using console logs
The quickest and easiest way to log and look at the losses is simply printing them to the console.
import tensorflow as tf
mnist = tf.keras.datasets.mnist
(x_train, y_train), (x_test, y_test) = mnist.load_data()
x_train, x_test = x_train / 255.0, x_test / 255.0
model = tf.keras.models.Sequential([
tf.keras.layers.Flatten(input_shape=(28, 28)),
tf.keras.layers.Dense(512, activation='relu'),
tf.keras.layers.Dropout(0.2),
tf.keras.layers.Dense(10, activation='softmax')
])
model.compile(optimizer='sgd',
loss='sparse_categorical_crossentropy',
metrics=['accuracy'])
model.fit(x_train, y_train,verbose=1, epochs=10)The problem with this approach is that those logs can be easily lost, it is difficult to see progress, and when working on remote machines, you may not have access to it.
Monitor Keras loss using a callback
Another cleaner option is to use a callback that will log the loss somewhere on every batch and epoch ended.
You need to decide where and what you would like to log, but it is really simple.
For example, logging Keras loss to neptune.ai could look like this:
from keras.callbacks import Callback
class NeptuneCallback(Callback):
def on_batch_end(self, batch, logs=None):
for metric_name, metric_value in logs.items():
neptune_run[f"{metric_name}"].log(metric_value)
def on_epoch_end(self, epoch, logs=None):
for metric_name, metric_value in logs.items():
neptune_run[f"{metric_name}"].log(metric_value)You can create the monitoring callback yourself or use one of the many available Keras callbacks both in the Keras library and in other libraries that integrate with it, like neptune.ai, TensorBoard, and others.
Once you have the callback ready, you simply pass it to the model.fit(...):
pip install neptune-tensorflow-keras# the same as above
import neptune.new as neptune
from neptune.new.integrations.tensorflow_keras import NeptuneCallback
run = neptune.init_run()
neptune_callback = NeptuneCallback(run=run)
model.fit(
x_train,
y_train,
validation_split=0.2,
epochs=10,
callbacks=[neptune_callback],
)
And monitor your experiment learning curves in the web app:
Note: For the most up-to-date code examples, please refer to the Neptune-Keras integration docs.
With neptune.ai, you can not only track losses, but also other metrics and parameters, as well as artifacts, source code, system metrics and more.
Why Keras loss nan happens
Most of the time, losses you log will be just some regular values, but sometimes you might get nans when working with Keras loss functions.
When that happens, your model will not update its weights and will stop learning, so this situation needs to be avoided.
There could be many reasons for nan loss but usually, what happens is:
- nans in the training set will lead to nans in the loss,
- NumPy infinite in the training set will also lead to nans in the loss,
- Using a training set that is not scaled,
- Use of very large l2 regularizers and a learning rate above 1,
- Use of the wrong optimizer function,
- Large (exploding) gradients that result in a large update to network weights during training.
So in order to avoid nans in the loss, ensure that:
- Check that your training data is properly scaled and doesn’t contain nans;
- Check that you are using the right optimizer and that your learning rate is not too large;
- Check whether the l2 regularization is not too large;
- If you are facing the exploding gradient problem, you can either: re-design the network or use gradient clipping so that your gradients have a certain “maximum allowed model update”.
Vanishing and Exploding Gradients in Neural Network Models: Debugging, Monitoring, and Fixing
Understanding Gradient Clipping (and How It Can Fix Exploding Gradients Problem)
Final thoughts
Hopefully, this article gave you some background into loss functions in Keras.
We’ve covered:
- Built-in loss functions in Keras,
- Implementation of your own custom loss functions,
- How to add sample weighing to create observation-sensitive losses,
- How to avoid loss nans,
- How you can visualize loss as your model is training.
For more information, check out the Keras Repository and the TensorFlow Loss Functions documentation.
При обучении нейронной сети на обучающей выборке на выходе нейросети вычисляются два ключевых параметра эффективности обучения — ошибка и точность предсказания. Для этого используются функция потери (loss) и метрика точности. Эти метрики различаются в зависимости от поставленной задачи (классификация или сегментация изображения, детекция объекта, регрессия). В Keras мы можем определить свои собственные функцию потери и метрики точности под свою конкретную задачу. О таких кастомных функциях и пойдет речь в статье. Кому интересно, прошу под кат.
Для примера предположим, что нам необходимо реализовать функцию ошибки Mean Average Error (MAE). Кастомную функцию потерь MAE можно реализовать следующим образом:
from keras import backend as K
def mae(y_true, y_pred):
true_value = K.sum(y_true * K.arange(0, 100, dtype="float32"), axis=-1)
pred_value = K.sum(y_pred * K.arange(0, 100, dtype="float32"), axis=-1)
mae = K.mean(K.abs(true_value - pred_value))
return mae
Здесь мы используем функции sum, arange, mean и abs, определенные в Keras.
Точно так же можно определить свою метрику точности. К примеру определим метрику earth_movers_distance для сравнения двух гистограмм:
from keras import backend as K
def earth_movers_distance(y_true, y_pred):
cdf_true = K.cumsum(y_true, axis=-1)
cdf_pred = K.cumsum(y_pred, axis=-1)
emd = K.sqrt(K.mean(K.square(cdf_true - cdf_pred), axis=-1))
return K.mean(emd)
Чтобы использовать наши метрики mae и earth_movers_distance импортируем соответствующие функции из отдельного модуля и добавим их в параметры loss и metrics при компиляции модели:
from utils.metrics import mae, earth_movers_distance
loss = earth_movers_distance
model.compile(optimizer=optimizer, loss=loss, metrics=[mae, "accuracy"])
Загрузка модели Keras с кастомной функцией потери
При обучении модели в Keras можно сохранять веса модели в h5 файл для последующей загрузки обученной модели на этапе предсказания. Если мы используем кастомные функции потерь и метрики качества, то мы можем столкнуться с проблемой. Когда мы загружаем обученные веса из файла h5 для модели с помощью метода load_weights мы можем получить такую ошибку:
ValueError: Unknown loss function:earth_movers_distance
Это известный баг в Keras (о нем писали в официальном репозитории на github).
Чтобы решить проблему нужно добавить наши кастомные функции потери и метрики качества в Keras:
from keras.utils.generic_utils import get_custom_objects
get_custom_objects().update({"earth_movers_distance": earth_movers_distance, "age_mae": age_mae})Пока на этом все. Всем удачи и до новых встреч!
Все курсы > Вводный курс > Занятие 21
В завершающей лекции вводного курса ML мы изучим основы нейронных сетей (neural network), более сложных алгоритмов машинного обучения.
Алгоритмы нейронных сетей принято относить к области глубокого обучения (deep learning). Все изученные нами ранее алгоритмы относятся к так называемому традиционному машинному обучению (traditional machine learning).
Прежде чем перейти к этому занятию, настоятельно рекомендую пройти предыдущие уроки вводного курса.
Смысл, структура и принцип работы
Смысл алгоритма нейронной сети такой же, как и у классических алгоритмов. Мы также имеем набор данных и цель, которой хотим добиться, обучив наш алгоритм (например, предсказать число или отнести объект к определенному классу).
Отличие нейросети от других алгоритмов заключается в ее структуре.
Как мы видим, нейронная сеть состоит из нейронов, сгруппированных в слои (layers), у нее есть входной слой (input layer), один или несколько скрытых слоев (hidden layers) и выходной слой (output layer). Каждый нейрон связан с нейронами предыдущего слоя через определенные веса.
Количество слоев и нейронов не ограничено. Эта особенность позволяет нейронной сети моделировать очень сложные закономерности, с которыми бы не справились, например, линейные модели.
Функционирует нейросеть следующим образом.
На первом этапе данные подаются в нейроны входного слоя (x и y) и умножаются на соответствующие веса (w1, w2, w3, w4). Полученные произведения складываются. К результату прибавляется смещение (bias, в данном случае b1 и b2).
$$ w_{1}cdot x + w_{3}cdot y + b_{1} $$
$$ w_{2}cdot x + w_{4}cdot y + b_{2} $$
Получившаяся сумма подаётся в функцию активации (activation function) для ограничения диапазона и стабилизации результата. Этот результат записывается в нейроны скрытого слоя (h1 и h2).
$$ h_{1} = actfun(w_{1}cdot x + w_{3}cdot y + b_{1}) $$
$$ h_{2} = actfun(w_{2}cdot x + w_{4}cdot y + b_{2}) $$
На втором этапе процесс повторяется для нейронов скрытого слоя (h1 и h2), весов (w5 и w6) и смещения (b3) до получения конечного результата (r).
$$ r = actfun(w_{5}cdot h_{1} + w_{6}cdot h_{2} + b_{3}) $$
Описанная выше нейронная сеть называется персептроном (perceptron). Эта модель стремится повторить восприятие информации человеческим мозгом и учитывает три этапа такого процесса:
- Восприятие информации через сенсоры (входной слой)
- Создание ассоциаций (скрытый слой)
- Реакцию (выходной слой)
Основы нейронных сетей на простом примере
Приведем пример очень простой нейронной сети, которая на входе получает рост и вес человека, а на выходе предсказывает пол. Скрытый слой в данном случае мы использовать не будем.
В качестве функции активации мы возьмём сигмоиду. Ее часто используют в задачах бинарной (состоящей из двух классов) классификации. Приведем формулу.
$$ f(x) = frac{mathrm{1} }{mathrm{1} + e^{-x}} $$
График сигмоиды выглядит следующим образом.
Эта функция преобразует любые значения в диапазон (или вероятность) от 0 до 1. В случае задачи классификации, если результат (вероятность) близок к нулю, мы отнесем наблюдение к одному классу, если к единице, то к другому. Граница двух классов пройдет на уровне 0,5.
Общее уравнение нейросети выглядит следующим образом.
$$ r = sigmoid(w_{1}cdot weight + w_{2}cdot height + bias) $$
Теперь предположим, что у нас есть следующие данные и параметры нейросети.
Откроем ноутбук к этому занятию⧉
|
# даны вес и рост трех человек # единицей мы обозначим мужской пол, а нулем — женский. data = { ‘Иван’: [84, 180, 1], ‘Мария’: [57, 165, 0], ‘Анна’: [62, 170, 0] } |
|
# и даны следующие веса и смещение w1, w2, b = 0.3, 0.1, —39 |
Пропустим первое наблюдение через нашу нейросеть. Следуя описанному выше процессу, вначале умножим данные на соответствующие веса и прибавим смещение.
|
r = w1 * data[‘Иван’][0] + w2 * data[‘Иван’][1] + b |
Теперь к полученному результату (r) применим сигмоиду.
|
np.round(1 / (1 + np.exp(—r)), 3) |
Результат близок к единице, значит пол мужской. Модель сделала верный прогноз. Повторим эти вычисления для каждого из наблюдений.
|
# пройдемся по ключам и значениям нашего словаря с помощью метода .items() for k, v in data.items(): # вначале умножим каждую строчку данных на веса и прибавим смещение r1 = w1 * v[0] + w2 * v[1] + b # затем применим сигмоиду r2 = 1 / (1 + np.exp(—r1)) # если результат больше 0,5, модель предскажет мужской пол if r2 > 0.5: print(k, np.round(r2, 3), ‘male’) # в противном случае, женский else: print(k, np.round(r2, 3), ‘female’) |
|
Иван 0.985 male Мария 0.004 female Анна 0.032 female |
Как мы видим, модель отработала верно.
Обучение нейронной сети
В примере выше был описан первый этап работы нейронной сети, называемый прямым распространением (forward propagation).
И кажется, что этого достаточно. Модель справилась с поставленной задачей. Однако, обратите внимание, веса были подобраны заранее и никаких дополнительных действий от нас не потребовалось.
В реальности начальные веса выбираются случайно и отклонение истинного результата от расчетного (т.е. ошибка) довольно велико.
Как и с обычными алгоритмами ML, для построения модели, нам нужно подобрать идеальные веса или заняться оптимизацией. Применительно к нейронным сетям этот процесс называется обратным распространением (back propagation).
В данном случае мы как бы двигаемся в обратную сторону и, уже зная результат (и уровень ошибки), с учётом имеющихся данных рассчитываем, как нам нужно изменить веса и смещения, чтобы уровень ошибки снизился.
Для того чтобы математически описать процесс оптимизации, нам не хватает знаний математического анализа (calculus) и, если говорить более точно, понятия производной (derivative).
Затем, уже с новыми весами, мы снова повторяем весь процесс forward propagation слева направо и снова рассчитываем ошибку. После этого мы вновь меняем веса в ходе back propagation.
Эти итерации повторяются до тех пор, пока ошибка не станет минимальной, а веса не будут подобраны идеально.
Создание нейросети в библиотеке Keras
Теперь давайте попрактикуемся в создании и обучении нейронной сети с помощью библиотеки Keras. В первую очередь установим необходимые модули и библиотеки.
|
# установим библиотеку tensorflow (через нее мы будем пользоваться keras) и модуль mnist !pip install tensorflow mnist |
И импортируем их.
|
# импортируем рукописные цифры import mnist # и библиотеку keras from tensorflow import keras |
1. Подготовка данных
Как вы вероятно уже поняли, сегодня мы снова будем использовать уже знакомый нам набор написанных от руки цифр MNIST (только на этот раз воспользуемся не библиотекой sklearn, а возьмем отдельный модуль).
В модуле MNIST содержатся чёрно-белые изображения цифр от 0 до 9 размером 28 х 28 пикселей. Каждый пиксель может принимать значения от 0 (черный) до 255 (белый).
Данные в этом модуле уже разбиты на тестовую и обучающую выборки. Посмотрим на обучающий набор данных.
|
# сохраним обучающую выборку и соответсвующую целевую переменную X_train = mnist.train_images() y_train = mnist.train_labels() # посмотрим на размерность print(X_train.shape) print(y_train.shape) |
Как мы видим, обучающая выборка содержит 60000 изображений и столько же значений целевой переменной. Теперь посмотрим на тестовые данные.
|
# сделаем то же самое с тестовыми данными X_test = mnist.test_images() y_test = mnist.test_labels() # и также посмотрим на размерность print(X_test.shape) print(y_test.shape) |
Таких изображений и целевых значений 10000.
Посмотрим на сами изображения.
|
# создадим пространство для четырех картинок в один ряд fig, axes = plt.subplots(1, 4, figsize = (10, 3)) # в цикле for создадим кортеж из трех объектов: id изображения (всего их будет 4), самого изображения и # того, что на нем представлено (целевой переменной) for ax, image, label in zip(axes, X_train, y_train): # на каждой итерации заполним соответствующее пространство картинкой ax.imshow(image, cmap = ‘gray’) # и укажем какой цифре соответствует изображение с помощью f форматирования ax.set_title(f‘Target: {label}’) |
Нейросети любят, когда диапазон входных значений ограничен (нормализован). В частности, мы можем преобразовать диапазон [0, 255] в диапазон от [–1, 1]. Сделать это можно по следующей формуле.
$$ x’ = 2 frac {x-min(x)}{max(x)-min(x)}-1 $$
Применим эту формулу к нашим данным.
|
# функция np.min() возвращает минимальное значение, # np.ptp() — разницу между максимальным и минимальным значениями (от англ. peak to peak) X_train = 2. * (X_train — np.min(X_train)) / np.ptp(X_train) — 1 X_test = 2. * (X_test — np.min(X_test)) / np.ptp(X_test) — 1 |
Посмотрим на новый диапазон.
|
# снова воспользуемся функцией np.ptp() np.ptp(X_train) |
Теперь нам необходимо «вытянуть» изображения и превратить массивы, содержащие три измерения, в двумерные матрицы. Мы уже делали это на занятии по компьютерному зрению.
Применим этот метод к нашим данным.
|
# «вытянем» (flatten) наши изображения, с помощью метода reshape # у нас будет 784 столбца (28 х 28), количество строк Питон посчитает сам (-1) X_train = X_train.reshape((—1, 784)) X_test = X_test.reshape((—1, 784)) # посмотрим на результат print(X_train.shape) print(X_test.shape) |
Посмотрим на получившиеся значения пикселей.
|
# выведем первое изображение [0], пиксели с 200 по 209 X_train[0][200:210] |
|
array([—1. , —1. , —1. , —0.61568627, 0.86666667, 0.98431373, 0.98431373, 0.98431373, 0.98431373, 0.98431373]) |
Наши данные готовы. Теперь нужно задать конфигурацию модели.
2. Конфигурация нейронной сети
Существует множество различных архитектур нейронных сетей. Пока что мы познакомились с персептроном или в более общем смысле нейросетями прямого распространения (Feed Forward Neural Network, FFNN), в которых данные (сигнал) поступают строго от входного слоя к выходному.
Такую же сеть мы и будем использовать для решения поставленной задачи. В частности, на входе мы будем одновременно подавать 784 значения, которые затем будут проходить через два скрытых слоя по 64 нейрона каждый и поступать в выходной слой из 10 нейронов (по одному для каждой из цифр или классов).
В первую очередь воспользуемся классом Sequential библиотеки Keras, который укажет, что мы задаём последовательно связанные между собой слои.
|
# импортируем класс Sequential from tensorflow.keras.models import Sequential # и создадим объект этого класса model = Sequential() |
Далее нам нужно прописать сами слои и связи между нейронами.
Тип слоя Dense, который мы будем использовать, получает данные со всех нейронов предыдущего слоя. Функцией активации для скрытых слоев будет уже известная нам сигмоида.
|
# импортируем класс Dense from tensorflow.keras.layers import Dense # и создадим первый скрытый слой (с указанием функции активации и размера входного слоя) model.add(Dense(64, activation = ‘sigmoid’, input_shape = (784,))) # затем второй скрытый слой model.add(Dense(64, activation = ‘sigmoid’)) # и наконец выходной слой model.add(Dense(10, activation = ‘softmax’)) |
Выходной слой будет состоять из 10 нейронов, по одному для каждого из классов (цифры от 0 до 9). В качестве функции активации будет использована новая для нас функция softmax (softmax function).
Если сигмоида подходит для бинарной классификации, то softmax применяется для задач многоклассовой классификации. Приведем формулу.
$$ text{softmax}(vec{z})_{i} = frac{e^{z_i}}{sum_{j=1}^K e^{z_i}} $$
Функция softmax на входе принимает вектор действительных чисел (z), применяет к каждому из элементов zi экспоненциальную функцию и нормализует результат через деление на сумму экспоненциальных значений каждого из элементов.
На выходе получается вероятностное распределение любого количества классов (K), причем каждое значение находится в диапазоне от 0 до 1, а сумма всех значений равна единице. Приведем пример для трех классов.
Очевидно, вероятность того, что это кошка, выше. Теперь, когда мы задали архитектуру сети, необходимо заняться ее настройками.
Работа над ошибками. Внимательный читатель безусловно обратил внимание, что вероятности на картинке не соответствуют приведенным в векторе значениям. Если подставить эти числа в формулу softmax вероятности будут иными.
|
z = ([1, 2, 0.5]) np.exp(z) / sum(np.exp(z)) |
|
array([0.2312239 , 0.62853172, 0.14024438]) |
Впрочем, алгоритм по-прежнему уверен, что речь идет о кошке.
3. Настройки
Настроек будет три:
- тип функции потерь (loss function) определяет, как мы будем считать отклонение прогнозного значения от истинного
- способ или алгоритм оптимизации этой функции (optimizer) поможет снизить потерю или ошибку и подобрать правильные веса в процессе back propagation
- метрика (metric) покажет, насколько точна наша модель
Функция потерь
В первую очередь, определимся с функцией потерь. Раньше, например, в задаче регрессии, мы использовали среднеквадратическую ошибку (MSE). Для задач классификации мы будем использовать функцию потерь, называемую перекрестной или кросс-энтропией (cross-entropy). Продолжим пример с собакой, кошкой и попугаем.
Функция перекрестной энтропии (D) показывает степень отличия прогнозного вероятностного распределения (которое мы получили на выходе функции softmax (S)) от истинного (наша целевая переменная (L)). Чем больше отличие, тем выше ошибка.
Также обратите внимание, наша целевая переменная закодирована, вместо слова «кошка» напротив соответсвующего класса стоит единица, а напротив остальных классов — нули. Такая запись называется унитарным кодом, хотя чаще используется анлийский термин one-hot encoding.
Когда мы будем обучать наш алгоритм, мы также применим эту кодировку к нашим данным. Например, если в целевой переменной содержится цифра пять, то ее запись в one-hot encoding будет следующей.
В дополнение замечу, что функция кросс-энтропии, в которой применяется one-hot encoding, называется категориальной кросс-энтропией (categorical cross-entropy).
Отлично! С тем как мы будем измерять уровень ошибки (качество обучения) нашей модели, мы определились. Теперь нужно понять, как мы эту ошибку будем минимизировать. Для этого существует несколько алгоритмов оптимизации.
Алгоритм оптимизации
Классическим алгоритмом является, так называемый, метод стохастического градиентного спуска (Stochastic Gradient Descent или SGD).
Если предположить для простоты, что наша функция потерь оптимизирует один вес исходной модели, и мы находимся изначально в точке А (с неидеальным случайным весом), то наша задача — оказаться в точке B, где ошибка (L) минимальна, а вес (w) оптимален.
Спускаться мы будем вдоль градиента, то есть по кратчайшему пути. Идею градиента проще увидеть на функции с двумя весами. Такая функция имеет уже три измерения (две независимых переменных, w1 и w2, и одну зависимую, L) и графически похожа на «холмистую местность», по которой мы будем спускаться по наиболее оптимальному маршруту.
Стохастичность (или случайность) этого алгоритма заключается в том, что мы берем не всю выборку для обновления весов модели, а лишь одно или несколько случайных наблюдений. Такой подход сильно сокращает время оптимизации.
Метрика
Остается определиться с метрикой качества. Здесь мы просто возьмём знакомую нам метрику accuracy, которая посчитает долю правильно сделанных прогнозов.
Посмотрим на используемый код.
|
model.compile( loss = ‘categorical_crossentropy’, optimizer = ‘sgd’, metrics = [‘accuracy’] ) |
4. Обучение модели
Теперь давайте соберём все описанные выше элементы и посмотрим на работу модели в динамике. Повторим ещё раз изученные выше шаги.
- Значения пикселей каждого изображения поступают в 784 нейрона входного слоя
- Далее они проходят через скрытые слои, где они умножаются на веса, складываются, смещаются и поступают в соответствующую функцию активации
- На выходе из функции softmax мы получаем вероятности для каждой из цифр
- После этого результат сравнивается с целевой переменной с помощью функции перекрестной энтропии (функции потерь); делается расчет ошибки
- На следующем шаге алгоритм оптимизации стремится уменьшить ошибку и соответствующим образом изменяет веса
- После этого процесс повторяется, но уже с новыми весами.
Давайте выполним все эти операции в библиотеке Keras.
|
# вначале импортируем функцию to_categorical, чтобы сделать one-hot encoding from tensorflow.keras.utils import to_categorical |
|
# обучаем модель model.fit( X_train, # указываем обучающую выборку to_categorical(y_train), # делаем one-hot encoding целевой переменной epochs = 10 # по сути, эпоха показывает сколько раз алгоритм пройдется по всем данным ) |
|
1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 18 19 20 21 |
Epoch 1/10 1875/1875 [==============================] — 4s 2ms/step — loss: 2.0324 — accuracy: 0.4785 Epoch 2/10 1875/1875 [==============================] — 3s 2ms/step — loss: 1.2322 — accuracy: 0.7494 Epoch 3/10 1875/1875 [==============================] — 3s 2ms/step — loss: 0.7617 — accuracy: 0.8326 Epoch 4/10 1875/1875 [==============================] — 3s 2ms/step — loss: 0.5651 — accuracy: 0.8663 Epoch 5/10 1875/1875 [==============================] — 3s 2ms/step — loss: 0.4681 — accuracy: 0.8827 Epoch 6/10 1875/1875 [==============================] — 3s 2ms/step — loss: 0.4121 — accuracy: 0.8923 Epoch 7/10 1875/1875 [==============================] — 3s 2ms/step — loss: 0.3751 — accuracy: 0.8995 Epoch 8/10 1875/1875 [==============================] — 3s 2ms/step — loss: 0.3487 — accuracy: 0.9045 Epoch 9/10 1875/1875 [==============================] — 3s 2ms/step — loss: 0.3285 — accuracy: 0.9090 Epoch 10/10 1875/1875 [==============================] — 3s 2ms/step — loss: 0.3118 — accuracy: 0.9129 <keras.callbacks.History at 0x7f36c3f09490> |
На обучающей выборке мы добились неплохого результата, 91.29%.
5. Оценка качества модели
На этом шаге нам нужно оценить качество модели на тестовых данных.
|
# для оценки модели воспользуемся методом .evaluate() model.evaluate( X_test, # который применим к тестовым данным to_categorical(y_test) # не забыв закодировать целевую переменную через one-hot encoding ) |
|
313/313 [==============================] — 1s 1ms/step — loss: 0.2972 — accuracy: 0.9173 [0.29716429114341736, 0.9172999858856201] |
Результат «на тесте» оказался даже чуть выше, 91,73%.
6. Прогноз
Теперь давайте в качестве упражнения сделаем прогноз.
|
# передадим модели последние 10 изображений тестовой выборки pred = model.predict(X_test[—10:]) # посмотрим на результат для первого изображения из десяти pred[0] |
|
array([1.0952151e-04, 2.4856537e-04, 1.5749732e-03, 7.4032680e-03, 6.2553445e-05, 8.7646207e-05, 9.4199123e-07, 9.7065586e-01, 5.3100550e-04, 1.9325638e-02], dtype=float32) |
Работа над ошибками. На видео я говорю про первые десять изображений. Разумеется, это неверно. Срез [-10:] выводит последние десять изображений.
В переменной pred содержится массив numpy с десятью вероятностями для каждого из десяти наблюдений. Нам нужно выбрать максимальную вероятность для каждого изображения и определить ее индекс (индекс и будет искомой цифрой). Все это можно сделать с помощью функции np.argmax(). Посмотрим на примере.
Теперь применим к нашим данным.
|
# для кажого изображения (то есть строки, axis = 1) # выведем индекс (максимальное значение), это и будет той цифрой, которую мы прогнозируем print(np.argmax(pred, axis = 1)) # остается сравнить с целевой переменной print(y_test[—10:]) |
|
[7 8 9 0 1 2 3 4 5 6] [7 8 9 0 1 2 3 4 5 6] |
Для первых десяти цифр модель сделала верный прогноз.
7. Пример улучшения алгоритма
Существует множество параметров модели, которые можно настроить. В качестве примера попробуем заменить алгоритм стохастического градиентного спуска на считающийся более эффективным алгоритм adam (суть этого алгоритма выходит за рамки сегодняшней лекции).
Посмотрим на результат на обучающей и тестовой выборке.
|
# снова укажем настройки модели model.compile( loss = ‘categorical_crossentropy’, optimizer = ‘adam’, # однако заменим алгоритм оптимизации metrics = [‘accuracy’] ) # обучаем модель методом .fit() model.fit( X_train, # указываем обучающую выборку to_categorical(y_train), # делаем one-hot encoding целевой переменной epochs = 10 # прописываем количество эпох ) |
|
1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 18 19 20 21 |
Epoch 1/10 1875/1875 [==============================] — 4s 2ms/step — loss: 0.2572 — accuracy: 0.9252 Epoch 2/10 1875/1875 [==============================] — 4s 2ms/step — loss: 0.1738 — accuracy: 0.9497 Epoch 3/10 1875/1875 [==============================] — 4s 2ms/step — loss: 0.1392 — accuracy: 0.9588 Epoch 4/10 1875/1875 [==============================] — 4s 2ms/step — loss: 0.1196 — accuracy: 0.9647 Epoch 5/10 1875/1875 [==============================] — 4s 2ms/step — loss: 0.1062 — accuracy: 0.9685 Epoch 6/10 1875/1875 [==============================] — 4s 2ms/step — loss: 0.0960 — accuracy: 0.9708 Epoch 7/10 1875/1875 [==============================] — 4s 2ms/step — loss: 0.0883 — accuracy: 0.9732 Epoch 8/10 1875/1875 [==============================] — 4s 2ms/step — loss: 0.0826 — accuracy: 0.9747 Epoch 9/10 1875/1875 [==============================] — 4s 2ms/step — loss: 0.0766 — accuracy: 0.9766 Epoch 10/10 1875/1875 [==============================] — 4s 2ms/step — loss: 0.0699 — accuracy: 0.9780 <keras.callbacks.History at 0x7f36c3d74590> |
|
# и оцениваем результат «на тесте» model.evaluate( X_test, to_categorical(y_test) ) |
|
313/313 [==============================] — 1s 1ms/step — loss: 0.1160 — accuracy: 0.9647 [0.11602973937988281, 0.9646999835968018] |
Как вы видите, с помощью одного изменения мы повысили долю правильных прогнозов до 96,47%.
Более подходящие для работы с изображениями сверточные нейронные сети (convolutional neural network, CNN) достигают свыше 99% точности на этом наборе данных, как это видно в примере⧉ на официальном сайте библиотеки Keras.
Подведем итог
На сегодняшнем занятии изучили основы нейронных сетей. В частности, мы узнали, что такое нейронная сеть, какова ее структура и алгоритм функционирования. Многие шаги, например, оценка уровня ошибки через функцию кросс-энтропии или оптимизация методом стохастического градиентного спуска, разумеется, требуют отдельного занятия. Эти уроки еще впереди.
При этом, я надеюсь, у вас сложилось целостное представление о том, что значит создать и обучить нейросеть, и какие шаги для этого требуются.
Вопросы для закрепления
Перечислите типы слоев нейронной сети
Посмотреть правильный ответ
Ответ: обычно используется входной слой, один или несколько скрытых слоев и выходной слой.
Из каких двух этапов состоит обучение нейронной сети?
Посмотреть правильный ответ
Ответ: вначале (1) при forward propagation мы пропускаем данные от входного слоя к выходному, затем, рассчитав уровень ошибки, (2) начинается обратный процесс back propagation, при котором, мы улучшаем веса исходной модели.
Для чего используются сигмоида и функция softmax в выходном слое нейронной сети в задачах классификации?
Посмотреть правильный ответ
Ответ: сигмоида используется, когда нужно предсказать один из двух классов, если классов больше двух, применяется softmax.
Ответы на вопросы
Вопрос. Что означает число 1875 в результате работы модели?
Ответ. Я планировал рассказать об этом на курсе по оптимизации, но попробую дать общие определения уже сейчас. Как я уже сказал, при оптимизации методом градиентного спуска мы можем использовать (1) все данные, (2) часть данных или (3) одно наблюдение для каждого обновления весов. Это регулируется параметром batch_size (размер партии).
- в первом случае, количество наблюдений (batch, партия) равно размеру датасета, веса не обновляются пока мы не пройдемся по всем наблюдениям, это простой градиентный спуск
- во втором случае, мы берем часть наблюдений (mini-batch, мини-партия), и когда обработаем их, то обновляем веса; после этого мы обрабатываем следующую партию
- и наконец мы можем взять только одно наблюдение и сразу после его анализа обновить веса, это классический стохастический градиентный спуск (stochastic gradient descent), параметр batch_size = 1
В чем преимущество каждого из методов? Если мы берем всю партию и по результатам ее обработки обновляем веса, то двигаемся к минимуму функции потерь наиболее плавно. Минус в том, что на расчет требуется время и вычислительные мощности.
Если берем только одно наблюдение, то считаем все быстро, но расчет минимума функции потерь менее точен.
В библиотеке Keras (и нашей нейросети) по умолчанию используется второй подход и размер партии равный 32 наблюдениям (
batch_size = 32). С учетом того, что в обучающей выборке 60000 наблюдений, разделив 60000 на 32 мы получим 1875 итераций или обновлений весов в рамках одной эпохи. Отсюда и число 1875.
Повторим, алгоритм обрабатывает 32 наблюдения, обновляет веса и после этого переходит к следующей партии (batch) из 32-х наблюдений. Обработав таким образом 60000 изображений, алгоритм заканчивает первую эпоху и начинает вторую. Размер партии и количество эпох регулируется параметрами batch_size и epochs соответственно.
Keras Tutorial: Руководство для начинающих по глубокому обучению на Python 3
В этом пошаговом руководстве по Keras вы узнаете, как построить сверточную нейронную сеть на Python!
Фактически, мы будем обучать классификатор для рукописных цифр, который может похвастаться более чем 99% точностью в известном наборе данных MNIST.
Прежде чем мы начнем, мы должны отметить, что это руководство ориентировано на новичков, которые заинтересованы в прикладном глубокого изучения.
Наша цель — познакомить вас с одной из самых популярных и мощных библиотек для построения нейронных сетей на Python. Это означает, что мы разберем большую часть теории и математики, но мы также укажем вам на большие ресурсы для их изучения.
Для начала изучения машинного обучения на Python с библиотекой Keras, желательно, чтобы Вы:
- Понимали основные концепции машинного обучения
- Имели навыки программирования на Python
Почему Keras?
Keras — рекомендуемая библиотека для глубокого изучения Python, особенно для начинающих. Его минималистичный, модульный подход позволяет с легкостью построить и запустить глубокие нейронные сети.
Типичные рабочие процессы Keras выглядят так:
- Определите ваши тренировочные данные: входной тензор и целевой тензор.
- Определите сеть слоев (или модель), которая отображает входные данные для наших целей.
- Настройте процесс обучения, выбрав функцию потерь, оптимизатор и некоторые показатели для мониторинга.
- Повторяйте данные тренировки, вызывая метод fit() вашей модели.
Что такое глубокое обучение?
Глубокое обучение относится к нейронным сетям с несколькими скрытыми слоями, которые могут изучать все более абстрактные представления входных данных. Это явное упрощение, но для нас это практическое определение для старта в этой дисциплине.
Например, глубокое обучение привело к значительным достижениям в области компьютерного зрения. Теперь мы можем классифицировать изображения, находить в них объекты и даже помечать их заголовками. Для этого глубокие нейронные сети со многими скрытыми слоями могут последовательно изучать более сложные функции из исходного входного изображения:
- Первые скрытые слои могут изучать только локальные контуры.
- Затем каждый последующий слой (или фильтр) изучает более сложные представления.
- Наконец, последний слой может классифицировать изображение как кошку или кенгуру.
Эти типы глубоких нейронных сетей называются сверточными нейронными сетями.
Что такое сверточные нейронные сети (Convolutional Neural Networks CNN)?
Короче говоря, сверточные нейронные сети (CNN) представляют собой многослойные нейронные сети (иногда до 17 или более слоев), которые предполагают, что входные данные являются изображениями.
Типичная архитектура CNN:
Удовлетворяя это требование, CNN могут резко сократить количество параметров, которые должны быть настроены. Следовательно, CNN могут эффективно справляться с высокой размерностью необработанных изображений.
Их основная механика выходит за рамки этого урока, но вы можете прочитать о них здесь.
Чем эта статья не является
Это не полный курс по глубокому обучению. Это руководство предназначено для того, чтобы перенести вас с нуля в вашу первую сверточную нейронную сеть с минимально возможной головной болью!
Если вы заинтересованы в овладении теорией глубокого обучения, мы рекомендуем этот замечательный курс из Стэнфорда:
- CS231n: сверточные нейронные сети для визуального распознавания
О моделях Keras
В Keras доступно два основных типа моделей: последовательная модель и класс Model, используемый с функциональным API .
Эти модели имеют ряд общих методов и атрибутов:
model.layersэто плоский список слоев, составляющих модель.model.inputsсписок входных тензоров модели.model.outputsсписок выходных тензоров модели.model.summary()печатает краткое представление вашей модели.model.get_config()возвращает словарь, содержащий конфигурацию модели.model.get_weights()возвращает список всех весовых тензоров в модели в виде массивов Numpy.model.set_weights(weights)устанавливает значения весов модели из списка массивов Numpy. Массивы в списке должны иметь ту же форму, что и возвращаемыеget_weights().model.to_json()возвращает представление модели в виде строки JSON. Обратите внимание, что представление не включает веса, только архитектуру.model.to_yaml()возвращает представление модели в виде строки YAML. Обратите внимание, что представление не включает веса, только архитектуру.model.save_weights(filepath)сохраняет вес модели в виде файла HDF5.model.load_weights(filepath, by_name=False)загружает вес модели из файла HDF5 (созданногоsave_weights). По умолчанию ожидается, что архитектура не изменится.
Методы API последовательной модели (Sequential model API)
Компиляция — Compile
compile(
optimizer,
loss=None,
metrics=None,
loss_weights=None,
sample_weight_mode=None,
weighted_metrics=None,
target_tensors=None
)
Настраивает модель для обучения.
Аргументы:
- optimizer: строка (имя оптимизатора) или экземпляр оптимизатора.
- loss (потеря): строка (имя целевой функции) или целевая функция или
Lossэкземпляр. Смотрите потери. Если модель имеет несколько выходов, вы можете использовать разные потери на каждом выходе, передав словарь или список потерь. Значение потерь, которое будет минимизировано моделью, будет тогда суммой всех индивидуальных потерь. - metrics: список метрик, которые будут оцениваться моделью во время обучения и тестирования. Как правило, вы будете использовать
metrics=['accuracy']. Чтобы указать разные метрики для разных выходов модели с несколькими выходами, вы также можете передать словарь, напримерmetrics={'output_a': 'accuracy', 'output_b': ['accuracy', 'mse']}. Вы также можете передать список (len = len (выводы)) списков метрик, таких какmetrics=[['accuracy'], ['accuracy', 'mse']]илиmetrics=['accuracy', ['accuracy', 'mse']]. - loss_weights: необязательный список или словарь, задающий скалярные коэффициенты (числа Python) для взвешивания вкладов потерь в различные выходные данные модели. Значение потерь, которое будет минимизировано моделью, будет затем взвешенной суммой всех индивидуальных потерь, взвешенных по
loss_weightsкоэффициентам. Если список, ожидается, что он будет иметь соотношение 1: 1 к выходам модели. Если это диктат, ожидается, что выходные имена (строки) будут сопоставлены скалярным коэффициентам. - sample_weight_mode: Если вам нужно сделать взвешивание выборки по временным шагам (2D веса), установите это значение
"temporal".Noneпо умолчанию используются веса выборки (1D). Если модель имеет несколько выходов, вы можете использовать разныеsample_weight_modeна каждом выходе, передав словарь или список режимов. - weighted_metrics: список метрик, которые будут оцениваться и взвешиваться по sample_weight или class_weight во время обучения и тестирования.
- target_tensors: по умолчанию Keras создаст заполнители для цели модели, которые будут снабжены целевыми данными во время обучения. Если вместо этого вы хотите использовать свои собственные целевые тензоры (в свою очередь, Keras не будет ожидать внешних данных Numpy для этих целей во время обучения), вы можете указать их с помощью
target_tensorsаргумента. Это может быть один тензор (для модели с одним выходом), список тензоров или точные сопоставления выходных имен с целевыми тензорами. - **kwargs: при использовании бэкэндов Theano / CNTK эти аргументы передаются в
K.function. При использовании бэкэнда TensorFlow эти аргументы передаются вtf.Session.run.
fit
Обучает модель для фиксированного числа эпох (итераций в наборе данных).
fit(
x=None,
y=None,
batch_size=None,
epochs=1,
verbose=1,
callbacks=None,
validation_split=0.0,
validation_data=None,
shuffle=True,
class_weight=None,
sample_weight=None,
initial_epoch=0,
steps_per_epoch=None,
validation_steps=None,
validation_freq=1,
max_queue_size=10,
workers=1,
use_multiprocessing=False
)
Аргументы:
- x: входные данные. Это может быть:
- Массив Numpy (или похожий на массив) или список массивов (в случае, если модель имеет несколько входов).
- Диктовое отображение (dict mapping) входных имен в соответствующий массив / тензоры, если модель имеет именованные входы.
- Генератор или
keras.utils.Sequenceвозвращение(inputs, targets)или(inputs, targets, sample weights). - None (default) — Нет (по умолчанию) при подаче из тензоров, встроенных в каркас (например, тензоры данных TensorFlow).
- y: целевые данные. Как и входные данные
x, это могут быть либо массив (ы) Numpy, тензор (ы), встроенные в платформу, список массивов Numpy (если модель имеет несколько выходных данных), либо None (по умолчанию), если они поступают из тензоров, встроенных в платформу (например, TensorFlow) тензоры данных). Если выходным слоям в модели присвоены имена, вы также можете передать словарь, отображающий выходные имена в массивы Numpy. Ifxявляется генератором илиkeras.utils.Sequenceэкземпляром,yуказывать не следует (поскольку цели будут получены изx). - batch_size: целое число или
None. Количество образцов на обновление градиента. Еслиbatch_sizeне указан, по умолчанию будет 32. Не указывайте,batch_sizeесли ваши данные представлены в виде символических тензоров, генераторов илиSequenceэкземпляров (так как они генерируют пакеты). - epochs: целочисленные. Количество эпох для обучения модели. Эпоха — это итерация по всему
xиyпредоставленным данным. Обратите внимание, что в сочетании сinitial_epoch,epochsследует понимать как «конечную эпоху». Модель не обучается для ряда итераций, заданныхepochs, а просто до тех пор, пока неepochsбудет достигнута эпоха индекса . - verbose: Integer. 0, 1 или 2. Режим многословия. 0 = тихий, 1 = индикатор выполнения, 2 = одна строка за эпоху.
- callbacks: список
keras.callbacks.Callbackэкземпляров. Список обратных вызовов, применяемых во время обучения и проверки (если). Смотрите обратные вызовы. - validation_split: с плавающей точкой от 0 до 1. Доля данных обучения, которые будут использоваться в качестве данных проверки. Модель выделит эту часть обучающих данных, не будет обучаться им и будет оценивать потери и любые метрики модели на этих данных в конце каждой эпохи. Данные проверки выбираются из последних выборок
xиyпредоставленных данных перед перетасовкой. Этот аргумент не поддерживается, когда онxявляется генератором илиSequenceэкземпляром. - validation_data:
данные для оценки потерь и любые метрики модели в конце каждой эпохи. Модель не будет обучаться на этих данных.
validation_dataперекроетvalidation_split.validation_dataможет быть: — кортеж(x_val, y_val)массивов или тензоров(x_val, y_val, val_sample_weights)Numpy — кортеж массивов Numpy — набор данных или итератор набора данныхДля первых двух случаев,
batch_sizeдолжны быть предоставлены. Для последнего случая,validation_stepsдолжны быть предоставлены. -
shuffle: Boolean (следует ли перемешивать данные тренировки перед каждой эпохой) или str (для «партии»). «пакетная» — это специальная опция для работы с ограничениями данных HDF5; он тасуется кусками размером с партию. Не имеет эффекта, когда
steps_per_epochнетNone. -
class_weight: необязательный словарь, отображающий индексы класса (целые числа) на значение веса (с плавающей запятой), используемое для взвешивания функции потерь (только во время обучения). Это может быть полезно для того, чтобы сказать модели «уделять больше внимания» выборкам из недопредставленного класса.
- sample_weight: необязательный массив весов Numpy для обучающих выборок, используемый для взвешивания функции потерь (только во время обучения). Вы можете либо передать плоский (1D) массив Numpy такой же длины, что и входные выборки (отображение весов и выборок 1: 1), либо в случае временных данных вы можете передать двумерный массив с формой
(samples, sequence_length), чтобы применить разный вес для каждого временного шага каждого образца. В этом случае вы должны обязательно указатьsample_weight_mode="temporal"вcompile(). Этот аргумент не поддерживается, когдаxгенератор илиSequenceэкземпляр вместо этого предоставляют sample_weights в качестве третьего элементаx. - initial_epoch: целое число. Эпоха, с которой начинается тренировка (полезно для возобновления предыдущего тренировочного заезда).
- steps_per_epoch: целое число или
None. Общее количество шагов (партий образцов) до объявления одной эпохи законченной и начала следующей эпохи. При обучении с использованием входных тензоров, таких как тензоры данных TensorFlow, значение по умолчаниюNoneравно числу выборок в вашем наборе данных, деленному на размер пакета, или 1, если это невозможно определить. - validation_steps: только релевантно, если
steps_per_epochуказано. Общее количество шагов (партий образцов) для проверки перед остановкой. - validation_steps: релевантно, только если
validation_dataпредоставлено и является генератором. Общее количество шагов (партий образцов), которые нужно нарисовать перед остановкой при выполнении проверки в конце каждой эпохи. - validation_freq: уместно, только если предоставлены данные проверки. Целое число или список / кортеж / набор. Если целое число, указывает, сколько тренировочных эпох должно быть выполнено до того, как будет выполнен новый прогон проверки, например,
validation_freq=2выполняет проверку каждые 2 эпохи. Если в списке, кортеже или наборе указываются эпохи, в которых нужно выполнять проверку, например,validation_freq=[1, 2, 10]выполняет проверку в конце 1-й, 2-й и 10-й эпох. - max_queue_size: целое число. Используется только для генератора или
keras.utils.Sequenceвхода. Максимальный размер очереди генератора. Если не указано, поmax_queue_sizeумолчанию будет 10. - workers: целое число. Используется только для генератора или
keras.utils.Sequenceвхода. Максимальное количество процессов, которые могут ускоряться при использовании потоков на основе процессов. Если не указан, поworkersумолчанию будет 1. Если 0, будет запускать генератор в основном потоке. - use_multiprocessing: Boolean. Используется только для генератора или
keras.utils.Sequenceвхода. ЕслиTrue, используйте процессные потоки. Если не указано, поuse_multiprocessingумолчаниюFalse. Обратите внимание, что, поскольку эта реализация опирается на многопроцессорность, вы не должны передавать невыгружаемые аргументы генератору, так как они не могут быть легко переданы дочерним процессам. - **kwargs: используется для обратной совместимости.
Краткий обзор учебника/статьи по Keras
Вот перечень шагов для создания вашей первой сверточной нейройнной сети (CNN) с использованием Keras:
- Настройте свою среду.
- Установите Керас / Keras.
- Импорт библиотек и модулей.
- Загрузить данные изображения из MNIST.
- Предварительная обработка входных данных для Keras.
- Метки препроцесс-класса для Keras.
- Определите архитектуру модели.
- Скомпилируйте модель.
- Подгонка модели по тренировочным данным.
- Оценить модель по данным испытаний.
Шаг 1: Настройте свою рабочую среду
убедитесь, что на вашем компьютере установлено следующее:
- Python 2.7+ (Python 3 тоже хорошо, но Python 2.7 все еще более популярен для науки о данных в целом)
- SciPy с NumPy
- Matplotlib (необязательно, рекомендуется для исследовательского анализа)
- Theano * ( Инструкция по установке )
Theano — это библиотека Python, которая позволяет нам так эффективно оценивать математические операции, включая многомерные массивы. В основном он используется при создании проектов глубокого обучения. Он работает намного быстрее на графическом процессоре (GPU), чем на CPU. Theano достигает высоких скоростей, что создает жесткую конкуренцию реализациям на языке C для задач, связанных с большими объемами данных.
Theano знает, как брать структуры и преобразовывать их в очень эффективный код, который использует numpy и некоторые нативные библиотеки. Он в основном предназначен для обработки типов вычислений, требуемых для алгоритмов больших нейронных сетей, используемых в Deep Learning. Именно поэтому, это очень популярная библиотека в области глубокого обучения.
Рекомендуется установить Python, NumPy, SciPy и matplotlib через дистрибутив Anaconda. Он поставляется со всеми этими пакетами.
Conda Cheatsheet: command line package and environment manager.pdf
Краткий обзор как настроить Анаконду здесь:
Инструкция по Anaconda & Conda. Как управлять и настроить среду для Python?
* Примечание: TensorFlow также поддерживается (как альтернатива Theano), но мы придерживаемся Theano для простоты. Основное отличие состоит в том, что вам необходимо изменить данные немного по-другому, прежде чем передавать их в свою сеть.
Еще раз пробежимся по устанавливаемым библиотекам:
SciPy (произносится как сай пай) — это пакет прикладных математических процедур, основанный на расширении Numpy Python. С SciPy интерактивный сеанс Python превращается в такую же полноценную среду обработки данных и прототипирования сложных систем, как MATLAB, IDL, Octave, R-Lab и SciLab.
Matplotlib — библиотека на языке программирования Python для визуализации данных.
Theano — библиотека, которая используется для разработки систем машинного обучения как сама по себе, так и в качестве вычислительного бекэнда для более высокоуровневых библиотек, например, Lasagne, Keras или Blocks.
NumPy — это библиотека языка Python, добавляющая поддержку больших многомерных массивов и матриц, вместе с большой библиотекой высокоуровневых (и очень быстрых) математических функций для операций с этими массивами.
Проверим правильно ли мы все установили
Переходим в Jupyter Notebook в среде, которая имеет установленные библиотеки/пакеты. Запускаем следующие команды:
1. Для проверки среды:
import sys print(sys.version) print(sys.base_prefix)
Результата:
3.7.5 (default, Oct 31 2019, 15:18:51) [MSC v.1916 64 bit (AMD64)] C:UsersUser.condaenvsMyNewEnvironmentName
2. Для проверки библиотек:
import numpy as np
import theano as th
import keras as kr
import matplotlib as mpl
print('numpy:' + np.__version__)
print('theano:' + th.__version__)
print('keras:' + kr.__version__)
print('matplotlib:' + mpl.__version__)
Результат:
numpy:1.17.4 theano:1.0.4 keras:2.2.4 matplotlib:3.1.1
Как это выглядит в Jupyter Notebook:
Шаг 2. Импортируем библиотеки и модули для нашего проекта
Удаляем предыдущие проверочные шаги из Notebook.
Теперь начнем с импорта numpy и установки начального числа для генератора псевдослучайных чисел на компьютере. Это позволяет нам воспроизводить результаты из нашего скрипта:
import numpy as np np.random.seed(123) # for reproducibility
Далее мы импортируем тип модели Sequential из Keras. Это просто линейный набор слоев нейронной сети, и он идеально подходит для того типа CNN с прямой связью, который мы строим в этом руководстве.
from keras.models import Sequential
Далее, давайте импортируем «основные» слои из Keras. Это слои, которые используются практически в любой нейронной сети:
from keras.layers import Dense, Dropout, Activation, Flatten
Затем мы импортируем слои CNN из Keras. Это сверточные слои, которые помогут нам эффективно тренироваться на данных изображения:
from keras.layers import Convolution2D, MaxPooling2D
Наконец, мы импортируем некоторые утилиты. Это поможет нам преобразовать наши данные позже:
from keras.utils import np_utils
Теперь у нас есть все необходимое для построения архитектуры нейронной сети.
Полный текст скрипта после шага 2:
import numpy as np np.random.seed(123) # for reproducibility from keras.models import Sequential from keras.layers import Dense, Dropout, Activation, Flatten from keras.layers import Convolution2D, MaxPooling2D from keras.utils import np_utils
Шаг 3. Загружаем изображения из MNIST
MNIST — отличный набор данных для начала глубокого обучения и компьютерного зрения. Это достаточно сложная задача, чтобы гарантировать нейронные сети, но она управляема на одном компьютере.
Библиотека Keras удобно уже включает это. Мы можем загрузить это так:
from keras.datasets import mnist # Load pre-shuffled MNIST data into train and test sets (X_train, y_train), (X_test, y_test) = mnist.load_data()
Мы можем посмотреть на форму набора данных:
print(X_train.shape)
Результат:
(60000, 28, 28)
Отлично, получается, что в нашем обучающем наборе 60 000 сэмплов, и размер каждого изображения составляет 28 х 28 пикселей. Мы можем подтвердить это, построив первый пример в matplotlib:
from matplotlib import pyplot as plt plt.imshow(X_train[0])
Вывод изображения:
В целом, при работе с компьютерным зрением полезно визуально отобразить данные, прежде чем выполнять какую-либо работу алгоритма. Это быстрая проверка работоспособности, которая может предотвратить легко предотвратимые ошибки (например, неверную интерпретацию измерений данных).
Полный скрипт после шага 3
import numpy as np np.random.seed(123) # for reproducibility from keras.models import Sequential from keras.layers import Dense, Dropout, Activation, Flatten from keras.layers import Convolution2D, MaxPooling2D from keras.utils import np_utils from keras.datasets import mnist from matplotlib import pyplot as plt # Загрузка предварительно перемешанных данных MNIST в наборы trains и tests (X_train, y_train), (X_test, y_test) = mnist.load_data() # Форма набора данных print(X_train.shape) # Вывод изображения plt.imshow(X_train[0])
Шаг 4: Предварительная обработка входных данных для Keras
При использовании бэкэнда Theano вы должны явно объявить размер для глубины входного изображения. Например, полноцветное изображение со всеми 3 каналами RGB будет иметь глубину 3.
Наши изображения MNIST имеют глубину только 1, но мы должны явно объявить это.
Другими словами, мы хотим преобразовать наш набор данных из формы (n, ширина, высота) в (n, глубина, ширина, высота).
Вот как мы можем сделать это легко:
X_train = X_train.reshape(X_train.shape[0], 1, 28, 28) X_test = X_test.reshape(X_test.shape[0], 1, 28, 28)
Чтобы подтвердить, мы можем снова напечатать размеры X_train:
print(X_train.shape)
Результат:
(60000, 1, 28, 28)
Последний шаг предварительной обработки для входных данных — преобразовать наш тип данных в float32 и нормализовать наши значения данных в диапазоне [0, 1].
X_train = X_train.astype('float32')
X_test = X_test.astype('float32')
X_train /= 255
X_test /= 255
Теперь наши входные данные готовы к обучению модели.
Полный текст скрипта после 4 шага
import numpy as np
np.random.seed(123) # для воспроизводимости
from keras.models import Sequential
from keras.layers import Dense, Dropout, Activation, Flatten
from keras.layers import Convolution2D, MaxPooling2D
from keras.utils import np_utils
from keras.datasets import mnist
from matplotlib import pyplot as plt
# Загрузка предварительно перемешанных данных MNIST в наборы trains и tests
(X_train, y_train), (X_test, y_test) = mnist.load_data()
# Форма набора данных
print("=== Результат X_train.shape ===")
print(X_train.shape)
# Вывод изображения
plt.imshow(X_train[0])
# Преобразование набора данных из формы (n, ширина, высота) в (n, глубина, ширина, высота)
X_train = X_train.reshape(X_train.shape[0], 1, 28, 28)
X_test = X_test.reshape(X_test.shape[0], 1, 28, 28)
# Вывод размеров X_train
print("=== Результат X_train.shape ===")
print(X_train.shape)
# Преобразование типа данных в float32
X_train = X_train.astype('float32')
X_test = X_test.astype('float32')
# Нормализация значений данных в диапазоне [0, 1]
X_train /= 255
X_test /= 255
Шаг 5. Предварительная обработка меток классов для Keras
Далее, давайте посмотрим на форму наших данных меток классов:
print(y_train.shape)
Результат:
(60000,)
Хм … это может быть проблематично. У нас должно быть 10 разных классов, по одному на каждую цифру, но, похоже, у нас есть только одномерный массив. Давайте посмотрим на ярлыки для первых 10 учебных образцов:
print(y_train[:10])
Результат:
[5 0 4 1 9 2 1 3 1 4]
И есть проблема. Данные y_train и y_test не разделены на 10 различных меток классов, а представлены в виде одного массива со значениями классов.
Мы можем это легко исправить:
# Convert 1-dimensional class arrays to 10-dimensional class matrices Y_train = np_utils.to_categorical(y_train, 10) Y_test = np_utils.to_categorical(y_test, 10)
Метод np_utils.to_categorical — Преобразует вектор класса (целые числа) в двоичную матрицу классов.
Теперь мы можем взглянуть еще раз:
print(Y_train.shape)
Результат:
(60000, 10)
Полный текст скрипта после 5 шага
import numpy as np
np.random.seed(123) # для воспроизводимости
from keras.models import Sequential
from keras.layers import Dense, Dropout, Activation, Flatten
from keras.layers import Convolution2D, MaxPooling2D
from keras.utils import np_utils
from keras.datasets import mnist
from matplotlib import pyplot as plt
# Загрузка предварительно перемешанных данных MNIST в наборы trains и tests
(X_train, y_train), (X_test, y_test) = mnist.load_data()
# Форма набора данных
print("=== Результат X_train.shape ===")
print(X_train.shape)
# Вывод изображения
plt.imshow(X_train[0])
# Преобразование набора данных из формы (n, ширина, высота) в (n, глубина, ширина, высота)
X_train = X_train.reshape(X_train.shape[0], 1, 28, 28)
X_test = X_test.reshape(X_test.shape[0], 1, 28, 28)
# Вывод размеров X_train
print("=== Результат X_train.shape ===")
print(X_train.shape)
# Преобразование типа данных в float32
X_train = X_train.astype('float32')
X_test = X_test.astype('float32')
# Нормализация значений данных в диапазоне [0, 1]
X_train /= 255
X_test /= 255
# Просмотр формы меток классов наших данных
print("=== Результат y_train.shape ===")
print(y_train.shape)
print("=== Результат y_train[:10] ===")
print(y_train[:10])
# Преобразование одномерных массивов классов в 10-мерные матрицы классов
Y_train = np_utils.to_categorical(y_train, 10)
Y_test = np_utils.to_categorical(y_test, 10)
# Вывод после преобразования
print("=== Результат Y_train.shape после np_utils.to_categorical ===")
print(Y_train.shape)
Результат:
=== Результат X_train.shape === (60000, 28, 28) === Результат X_train.shape === (60000, 1, 28, 28) === Результат y_train.shape === (60000,) === Результат y_train[:10] === [5 0 4 1 9 2 1 3 1 4] === Результат Y_train.shape после np_utils.to_categorical === (60000, 10)
Шаг 6: Зададим архитектуру модели нейронной сети
Теперь мы готовы определить архитектуру нашей модели. В реальной научно-исследовательской работе исследователи потратят значительное количество времени на изучение архитектуру моделей.
Чтобы продолжать этот урок, мы не будем обсуждать здесь теорию или математику.
Когда вы только начинаете, вы можете просто воспроизвести проверенную архитектуру из академических работ или использовать существующие примеры. Вот список примеров реализации в Keras.
Начнем с объявления последовательного формата модели:
model = Sequential()
Далее мы объявляем входной слой:
model.add(Conv2D(32,(3, 3), activation = 'relu', input_shape=(1,28,28), data_format='channels_first'))
Входной параметр shape должен иметь форму 1 образца. В этом случае это то же самое (1, 28, 28), которое соответствует (глубина, ширина, высота) каждого изображения цифры.
Но что представляют собой первые 3 параметра? Они соответствуют количеству используемых фильтров свертки, количеству строк в каждом ядре свертки и количеству столбцов в каждом ядре свертки соответственно.
* Примечание. Размер шага по умолчанию равен (1,1), и его можно настроить с помощью параметра «subsample».
Мы можем подтвердить это, напечатав форму текущей модели:
print(model.output_shape)
Результат:
(None, 32, 26, 26)
Затем мы можем просто добавить больше слоев в нашу модель, как будто мы строим legos:
model.add(Conv2D(32, (3, 3), activation='relu')) model.add(MaxPooling2D(pool_size=(2,2))) model.add(Dropout(0.25))
Опять же, мы не будем слишком углубляться в теорию, но важно выделить слой Dropout, который мы только что добавили. Это метод регуляризации нашей модели с целью предотвращения переоснащения. Вы можете прочитать больше об этом здесь .
MaxPooling2D — это способ уменьшить количество параметров в нашей модели, переместив фильтр пула 2×2 по предыдущему слою и взяв максимум 4 значения в фильтре 2×2.
Пока что для параметров модели мы добавили два слоя свертки. Чтобы завершить архитектуру нашей модели, давайте добавим полностью связанный слой, а затем выходной слой:
model.add(Flatten()) model.add(Dense(128, activation='relu')) model.add(Dropout(0.5)) model.add(Dense(10, activation='softmax'))
Для плотных слоев первым параметром является выходной размер слоя. Keras автоматически обрабатывает связи между слоями.
Обратите внимание, что конечный слой имеет выходной размер 10, соответствующий 10 классам цифр.
Также обратите внимание, что веса из слоев Convolution должны быть сплющены (сделаны одномерными) перед передачей их в полностью связанный плотный слой.
Вот как выглядит вся архитектура модели:
model = Sequential() model.add(Conv2D(32,(3, 3), activation = 'relu', input_shape=(1,28,28), data_format='channels_first')) model.add(Conv2D(32, (3, 3), activation='relu')) model.add(MaxPooling2D(pool_size=(2,2))) model.add(Dropout(0.25)) model.add(Flatten()) model.add(Dense(128, activation='relu')) model.add(Dropout(0.5)) model.add(Dense(10, activation='softmax'))
Теперь все, что нам нужно сделать, это определить функцию потерь и оптимизатор, и тогда мы будем готовы обучить ее.
Шаг 7. Скомпилируем модель
Сложная часть уже закончилась.
Теперь нам просто нужно скомпилировать модель, и мы будем готовы обучать ее. Когда мы компилируем модель, мы объявляем функцию потерь и оптимизатор (SGD, Adam и т.д.).
model.compile(loss='categorical_crossentropy',
optimizer='adam',
metrics=['accuracy'])
Keras имеет множество функций потери и встроенных оптимизаторов на выбор.
Шаг 8. Обучим модель на тестовых данных (тренировочных данных)
Чтобы соответствовать модели, все, что нам нужно сделать, это объявить размер партии и количество эпох для обучения, а затем передать наши данные обучения.
model.fit(X_train, Y_train,
batch_size=32, epochs=10, verbose=1)
Результат:
Epoch 1/10 60000/60000 [==============================] - 38100s 635ms/step - loss: 0.2253 - acc: 0.9337 Epoch 2/10 60000/60000 [==============================] - 728s 12ms/step - loss: 0.1195 - acc: 0.9650 Epoch 3/10 60000/60000 [==============================] - 964s 16ms/step - loss: 0.0927 - acc: 0.9724 Epoch 4/10 60000/60000 [==============================] - 1169s 19ms/step - loss: 0.0778 - acc: 0.9768 Epoch 5/10 60000/60000 [==============================] - 1223s 20ms/step - loss: 0.0709 - acc: 0.9794 Epoch 6/10 60000/60000 [==============================] - 730s 12ms/step - loss: 0.0640 - acc: 0.9809 Epoch 7/10 60000/60000 [==============================] - 749s 12ms/step - loss: 0.0578 - acc: 0.9828 Epoch 8/10 60000/60000 [==============================] - 730s 12ms/step - loss: 0.0554 - acc: 0.9825 Epoch 9/10 60000/60000 [==============================] - 728s 12ms/step - loss: 0.0528 - acc: 0.9848 Epoch 10/10 60000/60000 [==============================] - 719s 12ms/step - loss: 0.0495 - acc: 0.9852
Вы также можете использовать различные обратные вызовы для установки правил ранней остановки, сохранения весов моделей по ходу дела или регистрации истории каждой эпохи обучения.
Шаг 9: Оценка работы модели на тестовых данных
Наконец, мы можем оценить нашу модель по тестовым данным:
score = model.evaluate(X_test, Y_test, verbose=0) score
Результат:
[2.3163251502990723, 0.0986]
4.4
9
голоса
Рейтинг статьи
В
наших занятиях по пакету Keras мы часто использовали метод compile(), через
который связывали модель с оптимизатором, функцией потерь и метриками:
model = keras.Sequential([ layers.Input(shape=(784,)), layers.Dense(128, activation='relu'), layers.Dense(64, activation='relu'), layers.Dense(10, activation='softmax'), ]) model.compile(optimizer='adam', loss='categorical_crossentropy', metrics=['accuracy'])
Чаще
всего мы их определяли через строки, используя параметры по умолчанию. Если же
требуется более тонкая настройка, то следует использовать соответствующие
классы. В частности, для оптимизаторов частым выбором являются следующие
классы:
- SGD – стохастический
градиентный спуск (с моментами, в том числе и Нестерова); - RMSprop – оптимизатор RMSprop;
- Adam
– оптимизатор
Adam; - Adadelta
– оптимизатор
Adadelta; - Adagrad
– оптимизатор
Adagrad.
У
каждого из этих оптимизаторов есть свой набор параметров, подробнее о них можно
почитать в официальной документации:
https://keras.io/api/optimizers/
Например,
класс наиболее популярного оптимизатора Adam имеет следующий
синтаксис:
tf.keras.optimizers.Adam(learning_rate=0.001,
beta_1=0.9, beta_2=0.999, epsilon=1e-07, amsgrad=False, name=»Adam»,
**kwargs)
Именно
с такими параметрами он вызывается по умолчанию. Если требуются другие
значения, то мы должны создать экземпляр этого класса и указать нужные
параметры, например, так:
model.compile(optimizer=keras.optimizers.Adam(learning_rate=0.01), loss='categorical_crossentropy', metrics=['accuracy'])
То
же самое и с функциями потерь. Существует их стандартный набор в пакете Keras, например:
- BinaryCrossentropy
– бинарная кросс-энтропия; - CategoricalCrossentropy
– категориальная кросс-энтропия; - KLDivergence
– дивергенция Кульбака-Лейблера; - MeanSquaredError
– средний квадрат ошибки; - MeanAbsoluteError
– средняя абсолютная ошибка.
Полный
перечень этих классов можно посмотреть на странице:
https://keras.io/api/losses/
Также
на занятиях по курсу «Нейронные сети» мы подробно говорили когда (для каких
задач) какую функцию лучше применять. Если вы этого не знаете, то рекомендую
этот курс к просмотру.
Соответственно,
если нам нужно обратиться непосредственно к классу, то это можно реализовать,
следующим образом:
model.compile(optimizer=keras.optimizers.Adam(learning_rate=0.01), loss=keras.losses.CategoricalCrossentropy(), metrics=['accuracy'])
Наконец,
метрики также можно задавать с помощью различных предопределенных классов:
- Accuracy
- BinaryAccuracy
- CategoricalAccuracy
Полный
перечень этих классов можно посмотреть на странице:
https://keras.io/api/metrics/
Применяются
они очевидным образом:
model.compile(optimizer=keras.optimizers.Adam(learning_rate=0.01), loss=keras.losses.CategoricalCrossentropy(), metrics=[keras.metrics.CategoricalAccuracy()])
Собственные функции потерь
Конечно,
при необходимости, оптимизаторы, функции потерь и метрики мы можем
конструировать свои собственные. Чаще всего это относится к функциям потерь и
реже к метрикам. Создавать свои «хорошие» оптимизаторы – это уже удел избранных
и мы оставим это за рамками текущего курса (в принципе, встроенных вполне
достаточно для большинства реальных проектов).
Итак,
собственные потери в Kerasможно определить двумя способами:
- непосредственно
через функцию; - с
помощью класса, унаследованного от keras.losses.Loss.
Начнем
с наиболее простого варианта – определение своей функции потерь. Для этого
достаточно объявить функцию с двумя аргументами y_true, y_pred и
математическими операциями над этими тензорами, например, так:
def myloss(y_true, y_pred): return tf.reduce_mean(tf.square(y_true - y_pred))
Здесь
мы вычисляем средний квадрат рассогласования значений между требуемым выходом y_true и
спрогнозированным сетью y_pred. Все вычисления
лучше всего делать через функции Tensorflow, так как они, затем, будут
участвовать в автоматическом дифференцировании для вычисления градиентов. А эта
операция гарантированно корректно работает именно с функциями пакета Tensorflow (например,
функции NumPy здесь использовать
нельзя).
После
того, как функция объявлена, мы должны передать ссылку на нее в методе compile, следующим
образом:
model.compile(optimizer=keras.optimizers.Adam(learning_rate=0.001), loss=myloss, metrics=[keras.metrics.CategoricalAccuracy()])
Все,
теперь параметры модели будут подстраиваться для минимизации указанной функции
потерь.
Второй
способ определения потерь – это описание дочернего класса от базового keras.losses.Loss.
Зачем это нужно?Например, если мы хотим передавать дополнительные параметры для
вычисления потерь. Давайте предположим, что функция потерь имеет вид:
то
есть, здесь два дополнительных параметра α и β. Как раз их можно
определить, используя класс в качестве функции потерь, следующим образом:
class MyLoss(keras.losses.Loss): def __init__(self, alpha=1.0, beta=1.0): super().__init__() self.alpha = alpha self.beta = beta def call(self, y_true, y_pred): return tf.reduce_mean(tf.square(self.alpha * y_true - self.beta * y_pred))
Здесь
в конструкторе создаются два локальных свойства alpha и beta, а затем, в
методе call() производится
вычисление среднего квадрата ошибок с учетом этих параметров.
В
методе compile() мы можем
воспользоваться этим классом, например, так:
model.compile(optimizer=keras.optimizers.Adam(learning_rate=0.001), loss=MyLoss(0.5, 2.0), metrics=[keras.metrics.CategoricalAccuracy()])
Опять
же, это лишь пример того, как можно задавать пользовательские потери в пакете Keras. Необходимость
в этом возникает редко – в нестандартных задачах. Как правило, мы пользуемся
уже встроенными функциями или классами.
Пользовательские метрики
Наряду
с потерями можно создавать и собственные метрики. Для этого описывается класс
на основе базового tf.keras.metrics.Metric со следующим набором методов:
- __init__(self)
– конструктор для инициализации метрики; - update_state(self, y_true, y_pred, sample_weight=None) – обновление переменных состояния,
которые, затем, используются в методе result() для
окончательного вычисления метрики; - result(self)
– метод для вычисления метрики на основе переменных состояния; - reset_states(self)
– сброс переменных состояния (например, при переходе к новой эпохе при обучении
нейронной сети).
Давайте
на конкретном примере посмотрим, как это все работает. Я взял за основу
довольно удачный пример из документации:
https://www.tensorflow.org/guide/keras/train_and_evaluate
и
видоизменил его для подсчета доли правильно классифицированных данных, то есть,
фактически, повторил метрику CategoricalAccuracy. Сам класс имеет
следующий вид:
class CategoricalTruePositives(keras.metrics.Metric): def __init__(self, name="my_metric"): super().__init__(name=name) self.true_positives = self.add_weight(name="acc", initializer="zeros") self.count = tf.Variable(0.0) def update_state(self, y_true, y_pred, sample_weight=None): y_pred = tf.reshape(tf.argmax(y_pred, axis=1), shape=(-1, 1)) y_true = tf.reshape(tf.argmax(y_true, axis=1), shape=(-1, 1)) values = tf.cast(y_true, "int32") == tf.cast(y_pred, "int32") if sample_weight is not None: sample_weight = tf.cast(sample_weight, "float32") values = tf.multiply(values, sample_weight) values = tf.cast(values, "float32") self.true_positives.assign_add(tf.reduce_mean(values)) self.count.assign_add(1.0) def result(self): return self.true_positives / self.count def reset_states(self): self.true_positives.assign(0.0) self.count.assign(0.0)
Смотрите,
вначале в конструкторе мы формируем две переменные состояния: true_positives – сумма долей
верной классификации; count – общее число долей. Затем, в методе update_state() мы для
каждого мини-батча вычисляем вектор верной классификации (values), определяем
долю правильной классификации и увеличиваем счетчик count на единицу. В методе result() делаем
окончательные вычисления для метрики (вычисляем среднюю долю верной
классификации), а в методе reset_states() сбрасываем
переменные true_positives и count в ноль.
После
этого, мы можем добавить наш класс метрики к списку метрик:
model.compile(optimizer=keras.optimizers.Adam(learning_rate=0.001), loss=keras.losses.CategoricalCrossentropy(), metrics=[keras.metrics.CategoricalAccuracy(), CategoricalTruePositives()])
И
при обучении сети обе метрики должны показывать одинаковые результаты. По
аналогии можно создавать самые разные метрики для контроля за процессом подбора
параметров моделей.
Настройка сети с несколькими выходами
Давайте
теперь представим, что мы проектируем сеть с несколькими выходами. Например,
это может быть модель автоэнкодера с дополнительным выходом для классификации
изображений:
Описать
такую архитектуру достаточно просто, используя функциональный подход:
enc_input = layers.Input(shape=(28, 28, 1)) x = layers.Conv2D(32, 3, activation='relu')(enc_input) x = layers.MaxPooling2D(2, padding='same')(x) x = layers.Conv2D(64, 3, activation='relu')(x) x = layers.MaxPooling2D(2, padding='same')(x) x = layers.Flatten()(x) hidden_output = layers.Dense(8, activation='linear')(x) x = layers.Dense(7 * 7 * 8, activation='relu')(hidden_output) x = layers.Reshape((7, 7, 8))(x) x = layers.Conv2DTranspose(64, 5, strides=(2, 2), activation="relu", padding='same')(x) x = layers.BatchNormalization()(x) x = layers.Conv2DTranspose(32, 5, strides=(2, 2), activation="linear", padding='same')(x) x = layers.BatchNormalization()(x) dec_output = layers.Conv2DTranspose(1, 3, activation="sigmoid", padding='same', name="dec_output")(x) x2 = layers.Dense(128, activation='relu')(hidden_output) class_output = layers.Dense(10, activation='softmax', name="class_output")(x2) model = keras.Model(enc_input, [dec_output, class_output])
Смотрите,
здесь классификатор представляет собой обычную полносвязную сеть с десятью
выходами. Затем, с помощью класса Model мы создаем
модель сети с одним входом и двумя выходами.
Далее,
нам бы хотелось обучить эту сеть, но функции потерь для выходов следует брать
разными:
- для
первого выхода – средний квадрат ошибок рассогласований между входом и выходом; - для
второго выхода – категориальную кросс-энтропию.
Сделать
это можно, по крайней мере, двумя способами. В первом случае в методе compile() указать
список соответствующих функций для параметра loss:
model.compile(optimizer='adam', loss=['mean_squared_error', 'categorical_crossentropy'] )
Тогда
средний квадрат ошибок будет связан с первым выходом модели, а категориальная
кросс-энтропия – со вторым. Кроме того, при обучении в методе fit() также нужно
будет указать список требуемых выходных данных для обоих выходов:
model.fit(x_train, [x_train, y_train], epochs=1)
Во
втором случае мы можем в методах compile() и fit() словари,
вместо списков, что может быть несколько удобнее. Например, функции потерь
можно связать с выходами по их именам, следующим образом:
model.compile(optimizer='adam', loss={ 'dec_output': 'mean_squared_error', 'class_output': 'categorical_crossentropy' } )
И с метриками:
model.compile(optimizer='adam', loss={ 'dec_output': 'mean_squared_error', 'class_output': 'categorical_crossentropy' }, metrics={ 'dec_output': None, 'class_output': 'acc' } )
Обратите
внимание, мы для первого выхода указали метрику None, то есть, она
отсутствует. По идее, можно было бы вообще не указывать первую строчку в
словаре для metrics, а оставить
только вторую.
И
то же самое в методе fit() – для указания выходных значений
воспользуемся словарем:
model.fit(x_train, {'dec_output': x_train, 'class_output': y_train}, epochs=1)
Как
видите, все достаточно удобно. При этом, общая функция потерь будет
складываться из значений функция для обоих выходов. Если нам нужно
дополнительно указать веса loss_weightsпри их сложении:
то
это можно сделать через параметр loss_weights, следующим образом:
model.compile(optimizer='adam', loss={ 'dec_output': 'mean_squared_error', 'class_output': 'categorical_crossentropy' }, loss_weights = [1.0, 0.5], metrics={ 'dec_output': None, 'class_output': 'acc' } )
Здесь
использован список, но также можно указать словарь.
Давайте
в конце этой программы пропустим через обученный автоэнкодер первое тестовое
изображение и оценим полученные выходы:
p = model.predict(tf.expand_dims(x_test[0], axis=0)) print( tf.argmax(p[1], axis=1).numpy() ) plt.subplot(121) plt.imshow(x_test[0], cmap='gray') plt.subplot(122) plt.imshow(p[0].squeeze(), cmap='gray') plt.show()
После
запуска (с весами loss_weights = [1.0, 1.0]), увидим максимальное значение на 7-м
выходе классификатора и следующее восстановленное изображение на декодере:
Конечно,
одной эпохи обучения для такой задачи мало, это лишь пример того, как можно
независимо настраивать параметры для модели с множеством разнотипных выходов.
И, я надеюсь, вы теперь хорошо себе это представляете.
Видео по теме
Deep Learning with Keras — Introduction
Deep Learning has become a buzzword in recent days in the field of Artificial Intelligence (AI). For many years, we used Machine Learning (ML) for imparting intelligence to machines. In recent days, deep learning has become more popular due to its supremacy in predictions as compared to traditional ML techniques.
Deep Learning essentially means training an Artificial Neural Network (ANN) with a huge amount of data. In deep learning, the network learns by itself and thus requires humongous data for learning. While traditional machine learning is essentially a set of algorithms that parse data and learn from it. They then used this learning for making intelligent decisions.
Now, coming to Keras, it is a high-level neural networks API that runs on top of TensorFlow — an end-to-end open source machine learning platform. Using Keras, you easily define complex ANN architectures to experiment on your big data. Keras also supports GPU, which becomes essential for processing huge amount of data and developing machine learning models.
In this tutorial, you will learn the use of Keras in building deep neural networks. We shall look at the practical examples for teaching. The problem at hand is recognizing handwritten digits using a neural network that is trained with deep learning.
Just to get you more excited in deep learning, below is a screenshot of Google trends on deep learning here −
As you can see from the diagram, the interest in deep learning is steadily growing over the last several years. There are many areas such as computer vision, natural language processing, speech recognition, bioinformatics, drug design, and so on, where the deep learning has been successfully applied. This tutorial will get you quickly started on deep learning.
So keep reading!
Deep Learning with Keras — Deep Learning
As said in the introduction, deep learning is a process of training an artificial neural network with a huge amount of data. Once trained, the network will be able to give us the predictions on unseen data. Before I go further in explaining what deep learning is, let us quickly go through some terms used in training a neural network.
Neural Networks
The idea of artificial neural network was derived from neural networks in our brain. A typical neural network consists of three layers — input, output and hidden layer as shown in the picture below.
This is also called a shallow neural network, as it contains only one hidden layer. You add more hidden layers in the above architecture to create a more complex architecture.
Deep Networks
The following diagram shows a deep network consisting of four hidden layers, an input layer and an output layer.
As the number of hidden layers are added to the network, its training becomes more complex in terms of required resources and the time it takes to fully train the network.
Network Training
After you define the network architecture, you train it for doing certain kinds of predictions. Training a network is a process of finding the proper weights for each link in the network. During training, the data flows from Input to Output layers through various hidden layers. As the data always moves in one direction from input to output, we call this network as Feed-forward Network and we call the data propagation as Forward Propagation.
Activation Function
At each layer, we calculate the weighted sum of inputs and feed it to an Activation function. The activation function brings nonlinearity to the network. It is simply some mathematical function that discretizes the output. Some of the most commonly used activations functions are sigmoid, hyperbolic, tangent (tanh), ReLU and Softmax.
Backpropagation
Backpropagation is an algorithm for supervised learning. In Backpropagation, the errors propagate backwards from the output to the input layer. Given an error function, we calculate the gradient of the error function with respect to the weights assigned at each connection. The calculation of the gradient proceeds backwards through the network. The gradient of the final layer of weights is calculated first and the gradient of the first layer of weights is calculated last.
At each layer, the partial computations of the gradient are reused in the computation of the gradient for the previous layer. This is called Gradient Descent.
In this project-based tutorial you will define a feed-forward deep neural network and train it with backpropagation and gradient descent techniques. Luckily, Keras provides us all high level APIs for defining network architecture and training it using gradient descent. Next, you will learn how to do this in Keras.
Handwritten Digit Recognition System
In this mini project, you will apply the techniques described earlier. You will create a deep learning neural network that will be trained for recognizing handwritten digits. In any machine learning project, the first challenge is collecting the data. Especially, for deep learning networks, you need humongous data. Fortunately, for the problem that we are trying to solve, somebody has already created a dataset for training. This is called mnist, which is available as a part of Keras libraries. The dataset consists of several 28×28 pixel images of handwritten digits. You will train your model on the major portion of this dataset and the rest of the data would be used for validating your trained model.
Project Description
The mnist dataset consists of 70000 images of handwritten digits. A few sample images are reproduced here for your reference
Each image is of size 28 x 28 pixels making it a total of 768 pixels of various gray scale levels. Most of the pixels tend towards black shade while only few of them are towards white. We will put the distribution of these pixels in an array or a vector. For example, the distribution of pixels for a typical image of digits 4 and 5 is shown in the figure below.
Each image is of size 28 x 28 pixels making it a total of 768 pixels of various gray scale levels. Most of the pixels tend towards black shade while only few of them are towards white. We will put the distribution of these pixels in an array or a vector. For example, the distribution of pixels for a typical image of digits 4 and 5 is shown in the figure below.
Clearly, you can see that the distribution of the pixels (especially those tending towards white tone) differ, this distinguishes the digits they represent. We will feed this distribution of 784 pixels to our network as its input. The output of the network will consist of 10 categories representing a digit between 0 and 9.
Our network will consist of 4 layers — one input layer, one output layer and two hidden layers. Each hidden layer will contain 512 nodes. Each layer is fully connected to the next layer. When we train the network, we will be computing the weights for each connection. We train the network by applying backpropagation and gradient descent that we discussed earlier.
Deep Learning with Keras — Setting up Project
With this background, let us now start creating the project.
Setting Up Project
We will use Jupyter through Anaconda navigator for our project. As our project uses TensorFlow and Keras, you will need to install those in Anaconda setup. To install Tensorflow, run the following command in your console window:
>conda install -c anaconda tensorflow
To install Keras, use the following command −
>conda install -c anaconda keras
You are now ready to start Jupyter.
Starting Jupyter
When you start the Anaconda navigator, you would see the following opening screen.
Click ‘Jupyter’ to start it. The screen will show up the existing projects, if any, on your drive.
Starting a New Project
Start a new Python 3 project in Anaconda by selecting the following menu option −
File | New Notebook | Python 3
The screenshot of the menu selection is shown for your quick reference −
A new blank project will show up on your screen as shown below −
Change the project name to DeepLearningDigitRecognition by clicking and editing on the default name “UntitledXX”.
Deep Learning with Keras — Importing Libraries
We first import the various libraries required by the code in our project.
Array Handling and Plotting
As typical, we use numpy for array handling and matplotlib for plotting. These libraries are imported in our project using the following import statements
import numpy as np import matplotlib import matplotlib.pyplot as plot
Suppressing Warnings
As both Tensorflow and Keras keep on revising, if you do not sync their appropriate versions in the project, at runtime you would see plenty of warning errors. As they distract your attention from learning, we shall be suppressing all the warnings in this project. This is done with the following lines of code −
# silent all warnings
import os
os.environ['TF_CPP_MIN_LOG_LEVEL']='3'
import warnings
warnings.filterwarnings('ignore')
from tensorflow.python.util import deprecation
deprecation._PRINT_DEPRECATION_WARNINGS = False
Keras
We use Keras libraries to import dataset. We will use the mnist dataset for handwritten digits. We import the required package using the following statement
from keras.datasets import mnist
We will be defining our deep learning neural network using Keras packages. We import the Sequential, Dense, Dropout and Activation packages for defining the network architecture. We use load_model package for saving and retrieving our model. We also use np_utils for a few utilities that we need in our project. These imports are done with the following program statements −
from keras.models import Sequential, load_model from keras.layers.core import Dense, Dropout, Activation from keras.utils import np_utils
When you run this code, you will see a message on the console that says that Keras uses TensorFlow at the backend. The screenshot at this stage is shown here −
Now, as we have all the imports required by our project, we will proceed to define the architecture for our Deep Learning network.
Creating Deep Learning Model
Our neural network model will consist of a linear stack of layers. To define such a model, we call the Sequential function −
model = Sequential()
Input Layer
We define the input layer, which is the first layer in our network using the following program statement −
model.add(Dense(512, input_shape=(784,)))
This creates a layer with 512 nodes (neurons) with 784 input nodes. This is depicted in the figure below −
Note that all the input nodes are fully connected to the Layer 1, that is each input node is connected to all 512 nodes of Layer 1.
Next, we need to add the activation function for the output of Layer 1. We will use ReLU as our activation. The activation function is added using the following program statement −
model.add(Activation('relu'))
Next, we add Dropout of 20% using the statement below. Dropout is a technique used to prevent model from overfitting.
model.add(Dropout(0.2))
At this point, our input layer is fully defined. Next, we will add a hidden layer.
Hidden Layer
Our hidden layer will consist of 512 nodes. The input to the hidden layer comes from our previously defined input layer. All the nodes are fully connected as in the earlier case. The output of the hidden layer will go to the next layer in the network, which is going to be our final and output layer. We will use the same ReLU activation as for the previous layer and a dropout of 20%. The code for adding this layer is given here −
model.add(Dense(512))
model.add(Activation('relu'))
model.add(Dropout(0.2))
The network at this stage can be visualized as follows −
Next, we will add the final layer to our network, which is the output layer. Note that you may add any number of hidden layers using the code similar to the one which you have used here. Adding more layers would make the network complex for training; however, giving a definite advantage of better results in many cases though not all.
Output Layer
The output layer consists of just 10 nodes as we want to classify the given images in 10 distinct digits. We add this layer, using the following statement −
model.add(Dense(10))
As we want to classify the output in 10 distinct units, we use the softmax activation. In case of ReLU, the output is binary. We add the activation using the following statement −
model.add(Activation('softmax'))
At this point, our network can be visualized as shown in the below diagram −
At this point, our network model is fully defined in the software. Run the code cell and if there are no errors, you will get a confirmation message on the screen as shown in the screenshot below −
Next, we need to compile the model.
Deep Learning with Keras — Compiling the Model
The compilation is performed using one single method call called compile.
model.compile(loss='categorical_crossentropy', metrics=['accuracy'], optimizer='adam')
The compile method requires several parameters. The loss parameter is specified to have type ‘categorical_crossentropy’. The metrics parameter is set to ‘accuracy’ and finally we use the adam optimizer for training the network. The output at this stage is shown below −
Now, we are ready to feed in the data to our network.
Loading Data
As said earlier, we will use the mnist dataset provided by Keras. When we load the data into our system, we will split it in the training and test data. The data is loaded by calling the load_data method as follows −
(X_train, y_train), (X_test, y_test) = mnist.load_data()
The output at this stage looks like the following −
Now, we shall learn the structure of the loaded dataset.
The data that is provided to us are the graphic images of size 28 x 28 pixels, each containing a single digit between 0 and 9. We will display the first ten images on the console. The code for doing so is given below −
# printing first 10 images
for i in range(10):
plot.subplot(3,5,i+1)
plot.tight_layout()
plot.imshow(X_train[i], cmap='gray', interpolation='none')
plot.title("Digit: {}".format(y_train[i]))
plot.xticks([])
plot.yticks([])
In an iterative loop of 10 counts, we create a subplot on each iteration and show an image from X_train vector in it. We title each image from the corresponding y_train vector. Note that the y_train vector contains the actual values for the corresponding image in X_train vector. We remove the x and y axes markings by calling the two methods xticks and yticks with null argument. When you run the code, you would see the following output −
Next, we will prepare data for feeding it into our network.
Deep Learning with Keras — Preparing Data
Before we feed the data to our network, it must be converted into the format required by the network. This is called preparing data for the network. It generally consists of converting a multi-dimensional input to a single-dimension vector and normalizing the data points.
Reshaping Input Vector
The images in our dataset consist of 28 x 28 pixels. This must be converted into a single dimensional vector of size 28 * 28 = 784 for feeding it into our network. We do so by calling the reshape method on the vector.
X_train = X_train.reshape(60000, 784) X_test = X_test.reshape(10000, 784)
Now, our training vector will consist of 60000 data points, each consisting of a single dimension vector of size 784. Similarly, our test vector will consist of 10000 data points of a single-dimension vector of size 784.
Normalizing Data
The data that the input vector contains currently has a discrete value between 0 and 255 — the gray scale levels. Normalizing these pixel values between 0 and 1 helps in speeding up the training. As we are going to use stochastic gradient descent, normalizing data will also help in reducing the chance of getting stuck in local optima.
To normalize the data, we represent it as float type and divide it by 255 as shown in the following code snippet −
X_train = X_train.astype('float32')
X_test = X_test.astype('float32')
X_train /= 255
X_test /= 255
Let us now look at how the normalized data looks like.
Examining Normalized Data
To view the normalized data, we will call the histogram function as shown here −
plot.hist(X_train[0])
plot.title("Digit: {}".format(y_train[0]))
Here, we plot the histogram of the first element of the X_train vector. We also print the digit represented by this data point. The output of running the above code is shown here −
You will notice a thick density of points having value close to zero. These are the black dot points in the image, which obviously is the major portion of the image. The rest of the gray scale points, which are close to white color, represent the digit. You may check out the distribution of pixels for another digit. The code below prints the histogram of a digit at index of 2 in the training dataset.
plot.hist(X_train[2])
plot.title("Digit: {}".format(y_train[2])
The output of running the above code is shown below −
Comparing the above two figures, you will notice that the distribution of the white pixels in two images differ indicating a representation of a different digit — “5” and “4” in the above two pictures.
Next, we will examine the distribution of data in our full training dataset.
Examining Data Distribution
Before we train our machine learning model on our dataset, we should know the distribution of unique digits in our dataset. Our images represent 10 distinct digits ranging from 0 to 9. We would like to know the number of digits 0, 1, etc., in our dataset. We can get this information by using the unique method of Numpy.
Use the following command to print the number of unique values and the number of occurrences of each one
print(np.unique(y_train, return_counts=True))
When you run the above command, you will see the following output −
(array([0, 1, 2, 3, 4, 5, 6, 7, 8, 9], dtype=uint8), array([5923, 6742, 5958, 6131, 5842, 5421, 5918, 6265, 5851, 5949]))
It shows that there are 10 distinct values — 0 through 9. There are 5923 occurrences of digit 0, 6742 occurrences of digit 1, and so on. The screenshot of the output is shown here −
As a final step in data preparation, we need to encode our data.
Encoding Data
We have ten categories in our dataset. We will thus encode our output in these ten categories using one-hot encoding. We use to_categorial method of Numpy utilities to perform encoding. After the output data is encoded, each data point would be converted into a single dimensional vector of size 10. For example, digit 5 will now be represented as [0,0,0,0,0,1,0,0,0,0].
Encode the data using the following piece of code −
n_classes = 10 Y_train = np_utils.to_categorical(y_train, n_classes)
You may check out the result of encoding by printing the first 5 elements of the categorized Y_train vector.
Use the following code to print the first 5 vectors −
for i in range(5): print (Y_train[i])
You will see the following output −
[0. 0. 0. 0. 0. 1. 0. 0. 0. 0.] [1. 0. 0. 0. 0. 0. 0. 0. 0. 0.] [0. 0. 0. 0. 1. 0. 0. 0. 0. 0.] [0. 1. 0. 0. 0. 0. 0. 0. 0. 0.] [0. 0. 0. 0. 0. 0. 0. 0. 0. 1.]
The first element represents digit 5, the second represents digit 0, and so on.
Finally, you will have to categorize the test data too, which is done using the following statement −
Y_test = np_utils.to_categorical(y_test, n_classes)
At this stage, your data is fully prepared for feeding into the network.
Next, comes the most important part and that is training our network model.
Deep Learning with Keras — Training the Model
The model training is done in one single method call called fit that takes few parameters as seen in the code below −
history = model.fit(X_train, Y_train, batch_size=128, epochs=20, verbose=2, validation_data=(X_test, Y_test)))
The first two parameters to the fit method specify the features and the output of the training dataset.
The epochs is set to 20; we assume that the training will converge in max 20 epochs — the iterations. The trained model is validated on the test data as specified in the last parameter.
The partial output of running the above command is shown here −
Train on 60000 samples, validate on 10000 samples Epoch 1/20 - 9s - loss: 0.2488 - acc: 0.9252 - val_loss: 0.1059 - val_acc: 0.9665 Epoch 2/20 - 9s - loss: 0.1004 - acc: 0.9688 - val_loss: 0.0850 - val_acc: 0.9715 Epoch 3/20 - 9s - loss: 0.0723 - acc: 0.9773 - val_loss: 0.0717 - val_acc: 0.9765 Epoch 4/20 - 9s - loss: 0.0532 - acc: 0.9826 - val_loss: 0.0665 - val_acc: 0.9795 Epoch 5/20 - 9s - loss: 0.0457 - acc: 0.9856 - val_loss: 0.0695 - val_acc: 0.9792
The screenshot of the output is given below for your quick reference −
Now, as the model is trained on our training data, we will evaluate its performance.
Evaluating Model Performance
To evaluate the model performance, we call evaluate method as follows −
loss_and_metrics = model.evaluate(X_test, Y_test, verbose=2)
To evaluate the model performance, we call evaluate method as follows −
loss_and_metrics = model.evaluate(X_test, Y_test, verbose=2)
We will print the loss and accuracy using the following two statements −
print("Test Loss", loss_and_metrics[0])
print("Test Accuracy", loss_and_metrics[1])
When you run the above statements, you would see the following output −
Test Loss 0.08041584826191042 Test Accuracy 0.9837
This shows a test accuracy of 98%, which should be acceptable to us. What it means to us that in 2% of the cases, the handwritten digits would not be classified correctly. We will also plot accuracy and loss metrics to see how the model performs on the test data.
Plotting Accuracy Metrics
We use the recorded history during our training to get a plot of accuracy metrics. The following code will plot the accuracy on each epoch. We pick up the training data accuracy (“acc”) and the validation data accuracy (“val_acc”) for plotting.
plot.subplot(2,1,1)
plot.plot(history.history['acc'])
plot.plot(history.history['val_acc'])
plot.title('model accuracy')
plot.ylabel('accuracy')
plot.xlabel('epoch')
plot.legend(['train', 'test'], loc='lower right')
The output plot is shown below −
As you can see in the diagram, the accuracy increases rapidly in the first two epochs, indicating that the network is learning fast. Afterwards, the curve flattens indicating that not too many epochs are required to train the model further. Generally, if the training data accuracy (“acc”) keeps improving while the validation data accuracy (“val_acc”) gets worse, you are encountering overfitting. It indicates that the model is starting to memorize the data.
We will also plot the loss metrics to check our model’s performance.
Plotting Loss Metrics
Again, we plot the loss on both the training (“loss”) and test (“val_loss”) data. This is done using the following code −
plot.subplot(2,1,2)
plot.plot(history.history['loss'])
plot.plot(history.history['val_loss'])
plot.title('model loss')
plot.ylabel('loss')
plot.xlabel('epoch')
plot.legend(['train', 'test'], loc='upper right')
The output of this code is shown below −
As you can see in the diagram, the loss on the training set decreases rapidly for the first two epochs. For the test set, the loss does not decrease at the same rate as the training set, but remains almost flat for multiple epochs. This means our model is generalizing well to unseen data.
Now, we will use our trained model to predict the digits in our test data.
Predicting on Test Data
To predict the digits in an unseen data is very easy. You simply need to call the predict_classes method of the model by passing it to a vector consisting of your unknown data points.
predictions = model.predict_classes(X_test)
The method call returns the predictions in a vector that can be tested for 0’s and 1’s against the actual values. This is done using the following two statements −
correct_predictions = np.nonzero(predictions == y_test)[0] incorrect_predictions = np.nonzero(predictions != y_test)[0]
Finally, we will print the count of correct and incorrect predictions using the following two program statements −
print(len(correct_predictions)," classified correctly") print(len(incorrect_predictions)," classified incorrectly")
When you run the code, you will get the following output −
9837 classified correctly 163 classified incorrectly
Now, as you have satisfactorily trained the model, we will save it for future use.
Deep Learning with Keras — Saving Model
We will save the trained model in our local drive in the models folder in our current working directory. To save the model, run the following code −
directory = "./models/"
name = 'handwrittendigitrecognition.h5'
path = os.path.join(save_dir, name)
model.save(path)
print('Saved trained model at %s ' % path)
The output after running the code is shown below −
Now, as you have saved a trained model, you may use it later on for processing your unknown data.
Loading Model for Predictions
To predict the unseen data, you first need to load the trained model into the memory. This is done using the following command −
model = load_model ('./models/handwrittendigitrecognition.h5')
Note that we are simply loading the .h5 file into memory. This sets up the entire neural network in memory along with the weights assigned to each layer.
Now, to do your predictions on unseen data, load the data, let it be one or more items, into the memory. Preprocess the data to meet the input requirements of our model as what you did on your training and test data above. After preprocessing, feed it to your network. The model will output its prediction.
Deep Learning with Keras — Conclusion
Keras provides a high level API for creating deep neural network. In this tutorial, you learned to create a deep neural network that was trained for finding the digits in handwritten text. A multi-layer network was created for this purpose. Keras allows you to define an activation function of your choice at each layer. Using gradient descent, the network was trained on the training data. The accuracy of the trained network in predicting the unseen data was tested on the test data. You learned to plot the accuracy and error metrics. After the network is fully trained, you saved the network model for future use.
Среди инструментов трейдера уже довольно давно присутствуют машинное обучение и, в частности, нейронные сети. В свою очередь, среди нейронных сетей, в той части их классификации, которая объединяет так называемые методы «обучения с учителем», особое место занимают сети с обратным распространением ошибки (backpropagation neural network, BPNN). Существует множество различных модификаций подобных алгоритмов. На их основе построены, например, глубокие, рекуррентные и сверточные нейронные сети. Так что, нас не должно удивлять обилие материалов на данную тему (как и статей на данном сайте). Сегодня мы разовьем её в относительно новом для MQL5 направлении. Дело в том, что некоторое время назад в MQL5 появились новые возможности API, предназначенные для работы с матрицами и векторами. Они позволяют реализовать расчеты в нейронной сети в пакетном режиме, когда данные обрабатываются целиком (или блоками), а не поэлементно.
Благодаря матричным операциям существенно упрощаются программные инструкции, воплощающие формулы прямого и обратного распространения сигналов в сети. Фактически они преобразуются в однострочные выражения. За счет этого мы сможем уделить внимание другим важным аспектам по усовершенствованию алгоритма.
В данной статье мы напомним вкратце теорию сетей с обратным распространением ошибки и создадим на её основе универсальные классы для построения сетей: приведенные формулы будут почти «зеркально» отражены в исходном коде. Таким образом, новички смогут пройти полный «путь» по освоению данной технологии, не ища сторонние публикации.
Если же вы знакомы с теорией, то можете смело переходить ко второй части статьи, где рассматриваются примеры использования классов на практике — в скрипте, индикаторе и эксперте.
Введение в теорию нейронных сетей
Напомним, что нейронные сети (НС) состоят из простых вычислительных элементов — нейронов, как правило, логически объединенных в слои и соединенных связями (синапсами), по которым «проходит сигнал». Сигнал является математической абстракцией, с помощью которой можно представить ситуации из любой прикладной области, не исключая и трейдинг.
Синапс соединяет выход одного нейрона со входом другого и характеризуется величиной, называемой весом wi. Текущее состоянием нейрона получается, как взвешенная сумма сигналов, поступивших на его связи (входы).
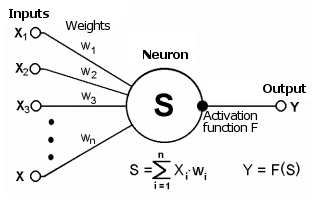
Схема нейрона
Это состояние дополнительно обрабатывается с помощью нелинейной активационной функции, формирующей выходное значение конкретного нейрона, откуда сигнал пойдет далее по синапсам следующих подключенных нейронов (если они есть) или станет компонентой в «ответе» нейронной сети (если текущий нейрон расположен в последнем слое).
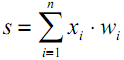 |
(1) |
| |
(2) |
Наличие нелинейности усиливает вычислительные возможности сети. В качестве активационных функций может использоваться, например, гиперболический тангенс или логистическая (обе относятся к так называемым S-образным или сигмоидальным функциям):
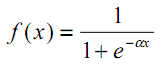 |
(3) |
Как мы увидим далее, MQL5 предоставляет большой набор встроенных активационных функций. Выбор конкретной функции следует делать на основе специфики задачи (регрессия, классификация). Как правило, для любой задачи можно подобрать несколько функций и далее экспериментальным путем найти оптимальную из них.
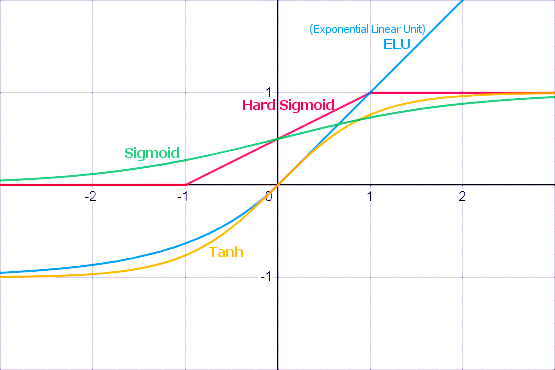
Популярные функции активации
Активационные функции могут иметь различные диапазоны значений — ограниченные или неограниченные. В частности, сигмоида (3) отображает данные в диапазон [0,+1] (лучше подходит для задач классификации), а гиперболический тангенс — в диапазон [-1,+1] (лучше подходит для задач регрессии и прогнозирования).
Одно из важных свойств функции активации — то, как определена её производная на всей оси. Наличие конечной, ненулевой производной является критически необходимым для алгоритма обратного распространения ошибки, который будет рассмотрен в дальнейшем. В частности, S-образные функции удовлетворяют этому требованию. Более того, стандартные функции активации, как правило, имеют довольно простую аналитическую запись производной, что гарантирует их эффективный расчет. Например, для сигмоиды (3) получим:
| |
(4) |
Нейронная сеть из одного слоя представлена на следующем рисунке.
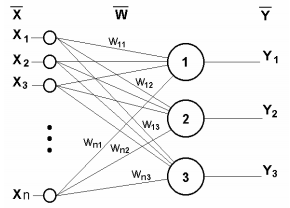
Однослойная нейронная сеть
Принцип её работы математически описывает такое уравнение:
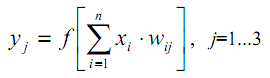 |
(5) |
Очевидно, что все весовые коэффициенты одного слоя можно свести в матрицу W, в которой каждый элемент wij задает величину i-ой связи j-ого нейрона. Таким образом, процесс, происходящий в НС, может быть записан в матричной форме:
| Y = F(X W) | (6) |
где X и Y — соответственно входной и выходной сигнальные векторы, F(V) — активационная функция, применяемая поэлементно к компонентам вектора V.
Число слоев и число нейронов в каждом слое сети зависит от входных данных: их размерности, объема выборки, закона распределения и многих других факторов. Как правило, конфигурацию сети выбирают методом проб.
Для иллюстрации приведем схему сети из двух слоев.
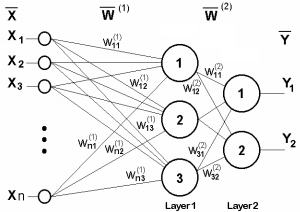
Двухслойная нейронная сеть
Теперь рассмотрим один нюанс, опущенный ранее. Из рисунка активационных функций очевидно, что существует некое значение T, где S-образные функции имеют максимальный наклон и хорошо передают сигналы, а прочие функции имеют характерную точку перелома (или несколько таких точек). Поэтому основная работа каждого нейрона происходит в окрестности T. Обычно T=0 или лежит возле 0, а потому желательно иметь средство для автоматического сдвига аргумента активационной функции к T.
Данное явление не было отражено в формуле (1), которая должна была бы выглядеть так:
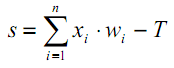 |
(7) |
Такое смещение обычно вводится путем добавления к слою нейронов еще одного псевдо-входа, значение которого всегда равно 1. Присвоим этому входу номер 0. Тогда:
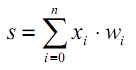 |
(8) |
где w0 = –T, x0 = 1.
Обучение НС с «учителем» предполагает наличие обучающих данных, заранее подготовленных и «размеченных» человеком-экспертом. В этих данных входным векторам сопоставлены желаемые выходные.
Само обучение производится по следующим этапам.
1. Проинициализировать элементы весовой матрицы (обычно небольшими случайными значениями);
2. Подать на входы один из векторов и вычислить реакцию сети; это фаза прямого распространения сигнала, которая будет использоваться и при штатной эксплуатации уже обученной сети;
3. Вычислить разницу между идеальным и полученным значениями выхода, то есть ошибку сети, после чего подстроить веса по некоторой формуле (см. далее) в зависимости от этой ошибки;
4. Продолжать в цикле с пункта 2 для всех входных векторов набора данных, пока ошибка не станет меньше заданного минимального уровня (успешное завершение обучения) или не будет достигнуто предопределенное максимальное количество циклов обучения (НС не справилась с задачей).
Для случая однослойной НС формула для модификации весов довольно очевидна:
| |
(9) |
| |
(10) |
где δ — ошибка сети (разница между полученным ответом сети и идеалом), t и t+1 — номера соответственно текущей и следующей итераций; ν — коэффициент скорости обучения, 0<ν<1; i — номер входа; j — номер нейрона в слое.
Однако, что делать, когда сеть многослойная? Здесь мы и подходим к идее обратного распространения ошибки.
Алгоритм обратного распространения ошибки
Среди различных структур нейронных сетей одной из наиболее известных является многослойная структура, в которой каждый нейрон конкретного слоя связан со всеми нейронами предыдущего слоя или, в случае первого слоя, со всеми входами НС. Такие НС называются полносвязными, и именно для их структуры приводится дальнейшее изложение. Во многих других типах НС, в частности, в сверточных, связи устанавливаются между ограниченными областями слоев, так называемыми ядрами, что несколько усложняет адресацию элементов сети, но не сказывается на применимости метода обратного распространения.
Интуитивно понятно, что информацию об ошибке следует передавать неким образом от выходов нейронной сети к её входам, постепенно «размазывая» по всем слоям, с учетом «проводимости» связей, то есть весов.
Согласно методу наименьших квадратов, минимизируемой целевой функцией ошибки НС является величина:
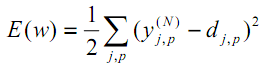 |
(11) |
где yjpᴺ — реальное выходное состояние нейрона j выходного слоя N нейронной сети при подаче на ее входы p-го образа; djp — идеальное (желаемое) выходное состояние этого нейрона.
Суммирование ведется по всем нейронам выходного слоя и по всем обрабатываемым образам. Коэффициент 1/2 вставлен только для получения «красивой» производной от E (двойки сокращаются), которая будет использоваться далее для обучения (см. формулу (12)) и в любом случае «взвешивается» важным параметром алгоритма — скоростью (которую можно увеличить в 2 раза или даже менять динамически по некоторым условиям).
Один из наиболее эффективных способов минимизации функции основывается на том, что наилучшие локальные направления к экстремумам указывают производные от этой функции в конкретной её точке. Производная со знаком плюс приведет нас к максимуму, а производная со знаком минус — к минимуму. Конечно, максимумы и минимумы могут оказаться локальными, и для «перепрыгивания» в глобальный минимум могут потребоваться дополнительные приемы, но мы здесь пока оставим данную проблему за кадром.
Описанный метод называется методом градиентного спуска, и означает подстройку весовых коэффициентов на основе производной E, следующим образом:
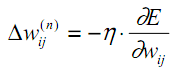 |
(12) |
Здесь wij — весовой коэффициент связи, соединяющей i-ый нейрон слоя n-1 с j-ым нейроном слоя n, η — коэффициент скорости обучения.
Вспомним внутреннее устройство нейрона и на его основе выделим в формуле (12) каждый этап вычислений в частную производную:
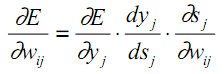 |
(13) |
Здесь под yj, как и раньше, подразумевается выход нейрона j, а под sj — взвешенная сумма его входных сигналов, то есть аргумент активационной функции. Так как множитель dyj/dsj является производной этой функции, из этого следует требование дифференцируемости активационной функции на всей оси абсцисс для использования в рассматриваемом алгоритме обратного распространения ошибки.
Например, в случае гиперболического тангенса:
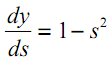 |
(14) |
Третий множитель в (13) ∂sj/∂wij равен выходу нейрона yi предыдущего слоя (n-1). Почему это так? Напомним, что в многослойной сети сигнал попадает с выхода нейрона предыдущего слоя на вход нейрона текущего слоя. Поэтому формулу (1) для sj можно в более общем виде переписать так:
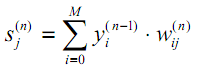 |
(15) |
где M — число нейронов в слое n-1 с учетом нейрона с постоянным выходным состоянием +1, задающего смещение; yi(n-1)=xij(n) — i-ый вход нейрона j слоя n, связанный с выходом i-го нейрона (n-1)-го слоя;
Что касается первого множителя в (13), его логично разложить по приращениям ошибок в соседнем, более старшем слое (ведь значения ошибок распространяются в обратную сторону):
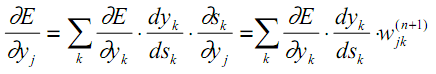 |
(16) |
Здесь суммирование по k выполняется среди нейронов слоя n+1.
Нетрудно заметить, что первые два множителя в (13) для одного слоя (с индексами j при нейронах) повторяются в (16) для следующего слоя (с индексами k) в виде коэффициента перед весом wjk.
Введем промежуточную переменную, включающую эти два множителя:
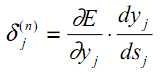 |
(17) |
В результате мы получим рекурсивную формулу для расчетов величин δj(n) слоя n из величин δk(n+1) более старшего слоя n+1.
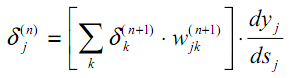 |
(18) |
Для выходного же слоя новая переменная, как и раньше, вычисляется на основе разницы между полученным и желаемым результатом сети.
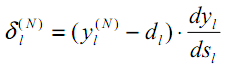 |
(19) |
По сравнению с (9) здесь, формально более строго, добавлена производная активационной функции. Правда, в выходном слое НС, в зависимости от задачи, АФ может и отсутствовать.
Теперь мы можем записать формулу (12) для коррекции весов в процессе обучения в раскрытом виде:
| |
(20) |
Иногда для придания процессу коррекции весов некоторой инерционности, сглаживающей резкие скачки производной при перемещении по поверхности целевой функции, формула (20) дополняется значением изменения веса на предыдущей итерации:
| |
(21) |
где µ — коэффициент инерционности, t — номер текущей итерации.
Таким образом, полный алгоритм обучения НС с помощью процедуры обратного распространения строится так:
1. Проинициализировать весовые матрицы малыми случайными числами.
2. Подать на входы сети один из векторов данных и в режиме обычного функционирования, когда сигналы распространяются от входов к выходам, рассчитать послойно общий результат НС по формулам взвешенного суммирования (15) и активации f:
| |
(22) |
Причем нейроны 0-го, входного слоя используются только для подачи входных сигналов и не имеют синапсов и активационных функций.
| |
(23) |
Iq — q-ая компонента входного вектора, поданная на 0-ой слой.
3. Если ошибка сети меньше заданной малой величины, останавливаем процесс с признаком успеха. Если ошибка существенна, продолжаем следующие шаги.
4. Рассчитать для выходного слоя N: δ по формуле (19), а также изменения весов Δw по формулам (20) или (21).
5. Для всех остальных слоев, в обратном порядке, n=N-1,…1 рассчитать δ и Δw по формулам (18) и (20) (или (18) и (21)) соответственно.
6. Скорректировать все веса в НС, для итерации t на основе предыдущей итерации t-1.
| |
(24) |
7. Повторяем процесс в цикле с шага 2.
Диаграмма сигналов в сети при обучении по алгоритму обратного распространения приведена на следующем рисунке.
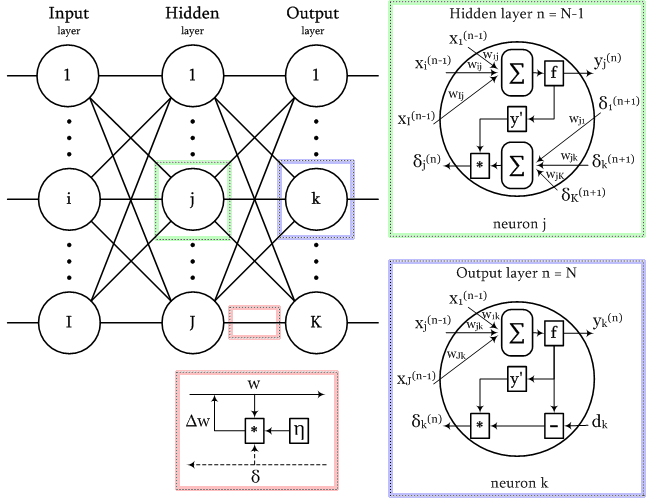
Схема сигналов в алгоритме обратного распространения ошибки
На вход сети попеременно предъявляются все тренировочные образы, чтобы она, образно говоря, не забывала одни по мере запоминания других. Обычно это делается в случайном порядке, но из-за того, что у нас данные будут помещены в матрицы и обсчитываться целиком как единый набор, в нашей реализации мы введем другой элемент случайности, но обсудим его чуть позднее.
Использование матриц означает, что веса всех слоев, а также входные и целевые обучающие данные будут представлены матрицами, а вышеприведенные формулы, и соответственно, алгоритмы получат матричную форму. Другими словами, мы не сможем оперировать отдельными векторами входных и обучающих данных, и весь цикл со 2-го по 7-ой шаги будет рассчитываться сразу для всего набора данных. Один такой цикл называется эпохой обучения.
Обзор активационных функций
К статье прилагается скрипт AF.mq5, который выводит на график миниатюрные изображения всех поддерживаемых в MQL5 активационных функций (синим цветом) и их производных (красным цветом). Скрипт автоматически масштабирует миниатюры так, чтобы в окно уместились все функции, поэтому для получения более детальных изображений рекомендуется предварительно увеличить или максимизировать окно. Пример изображения, полученного с помощью скрипта, приведен ниже.
Правильный выбор активационной функции зависит от типа нейронной сети и решаемой задачи. Более того, в одной сети может применяться несколько разных АФ. Например, SoftMax отличается от прочих функций тем, что обрабатывает выходные значения слоя не поэлементно, а во взаимной увязке — нормализует их таким образом, что величины можно интерпретировать как вероятности (их сумма равна 1), что используется для множественной классификации.
Данная тема настолько обширна, что потребовала отдельной статьи или цикла статей. Здесь мы лишь ограничимся предупреждением, что все функции имеют как положительные, так и отрицательные стороны, которые потенциально могут приводить к неработоспособности сети. В частности, для S-образных функций характерна так называемая проблема обнуления градиента («vanishing gradient», когда сигналы начинают попадать на участки «насыщения» S-кривой и потому подстройка весов стремится к нулю), а для монотонно возрастающих — проблема взрывного роста градиента («exploding gradient», то есть постоянно увеличивающиеся веса, вплоть до численного переполнения и получения NaN (Not A Number)). Обе упомянутые проблемы становятся тем более вероятны, чем больше количество слоев в сети. Для их решения можно использовать различные приемы, такие как нормализация данных (в том числе, не только на входе, но и в промежуточных слоях), алгоритмы прореживания сетей (выбрасывание нейронов («dropout»), пропуск связей), обучение пакетами данных, зашумление и прочие варианты регуляризации — некоторые из них мы рассмотрим и реализуем далее.
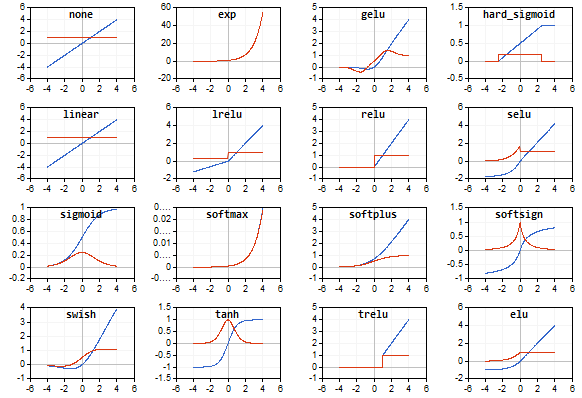
Демо-скрипт со всеми функциями активации
Реализация нейронной сети в классе MatrixNet
Приступим к написанию класса нейронной сети на основе матриц MQL5. Поскольку сеть состоит из слоев, опишем массивы весовых коэффициентов и выходных значений нейронов каждого слоя. Количество слоев будет храниться в переменной n, а веса нейронов в слоях и сигналы на выходе каждого слоя — в матрицах weights и outputs, соответственно. Обратите внимание, что термин outputs обозначает сигналы на выходах нейронов любого слоя, а не только на выходе сети. Так что outputs[i] описывают и промежуточные слои, и даже 0-й слой, куда подаются входные данные.
Индексация массивов weights и outputs иллюстрируется следующей схемой (связи каждого нейрона с источником смещения +1 не показаны для упрощения):
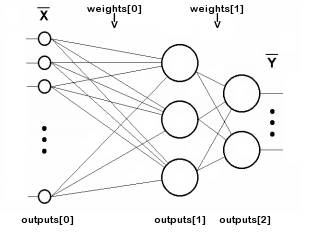
Схема индексации массивов матриц в двухслойной сети
Количество n не включает входной слой, потому что он не требует весов.
class MatrixNet { protected: const int n; matrix weights[]; matrix outputs[]; ENUM_ACTIVATION_FUNCTION af; ENUM_ACTIVATION_FUNCTION of; double speed; bool ready; ...
В нашей сети будут поддерживаться 2 типа активационных функций (на выбор пользователя): один — для всех слоев, кроме выходного (хранится в af), и отдельный — для выходного слоя (в переменной of). В переменной speed хранится скорость обучения (коэффициент η из формулы (20)).
Переменная ready содержит признак успешной инициализации объекта сети.
Конструктор сети принимает целочисленный массив layers, который определяет количество и размеры всех слоев. 0-й элемент задает размер входного псевдо-слоя, то есть количество признаков в каждом векторе входных данных. Последний элемент определяет размер выходного слоя, все остальные — промежуточных скрытых слоев. Количество слоев не может быть меньше двух. Для выделения памяти под массивы матриц написан вспомогательный метод allocate (мы будем его далее дополнять по мере расширения самого класса).
public: MatrixNet(const int &layers[], const ENUM_ACTIVATION_FUNCTION f1 = AF_TANH, const ENUM_ACTIVATION_FUNCTION f2 = AF_NONE): ready(false), af(f1), of(f2), n(ArraySize(layers) - 1) { if(n < 2) return; allocate(); for(int i = 1; i <= n; ++i) { weights[i - 1].Init(layers[i - 1] + 1, layers[i]); } ... } protected: void allocate() { ArrayResize(weights, n); ArrayResize(outputs, n + 1); ... }
Для инициализации каждой матрицы весов в качестве количества строк берется размер предыдущего слоя layers[i — 1] и к нему добавляется один синапс для постоянного регулируемого источника смещения +1. В качестве количества колонок берется размер текущего слоя layers[i]. В каждой матрице весов первый индекс относится к слою слева от матрицы, а второй — к слою справа.
Такая нумерация обеспечивает простую запись умножения векторов сигналов на матрицы слоев при прямом распространении (штатная работа сети). При обратном распространении ошибки (в режиме обучения) потребуется умножать вектор ошибок каждого старшего слоя на его транспонированную матрицу весов, чтобы пересчитать в ошибки для младшего слоя.
Иными словами, из-за того, что информация внутри сети движется в двух противоположных направлениях — рабочие сигналы от входов к выходам, а ошибки от выходов ко входам — весовые матрицы в каком-то из этих двух направлений должны использоваться в обычном виде, а во втором — транспонированными. Мы взяли за нормальную конфигурацию такую разметку матрицы, которая облегчает расчет прямого сигнала.
Матрицы outputs мы будем заполнять непосредственно в процессе прохождения сигнала по сети. А вот веса следует случайным образом инициализировать: для этого в конце конструктора вызывается метод randomize.
public: MatrixNet(const int &layers[], const ENUM_ACTIVATION_FUNCTION f1 = AF_TANH, const ENUM_ACTIVATION_FUNCTION f2 = AF_NONE): ready(false), af(f1), of(f2), n(ArraySize(layers) - 1) { ... ready = true; randomize(); } void randomize(const double from = -0.5, const double to = +0.5) { if(!ready) return; for(int i = 0; i < n; ++i) { weights[i].Random(from, to); } }
Наличия весовых матриц уже достаточно, чтобы реализовать прямой проход сигналов со входа сети на выход. Тот факт, что веса пока не обучены, не принципиален: обучением мы займемся позднее.
bool feedForward(const matrix &data) { if(!ready) return false; if(data.Cols() != weights[0].Rows() - 1) { PrintFormat("Column number in data %d <> Inputs layer size %d", data.Cols(), weights[0].Rows() - 1); return false; } outputs[0] = data; for(int i = 0; i < n; ++i) { if(!outputs[i].Resize(outputs[i].Rows(), weights[i].Rows()) || !outputs[i].Col(vector::Ones(outputs[i].Rows()), weights[i].Rows() - 1)) return false; matrix temp = outputs[i].MatMul(weights[i]); if(!temp.Activation(outputs[i + 1], i < n - 1 ? af : of)) return false; } return true; }
Количество столбцов во входной матрице data должно совпадать с количеством строк в 0-й матрице весов за вычетом 1 (вес к сигналу смещения).
Прочитать результат штатной работы сети позволяет метод getResults. По умолчанию он возвращает матрицу состояний выходного слоя.
matrix getResults(const int layer = -1) const { static const matrix empty = {}; if(!ready) return empty; if(layer == -1) return outputs[n]; if(layer < -1 || layer > n) return empty; return outputs[layer]; }
Оценить текущее качество модели можно методом test: он принимает на вход не только матрицу входных данных, но и матрицу с желаемым откликом сети.
double test(const matrix &data, const matrix &target, const ENUM_LOSS_FUNCTION lf = LOSS_MSE) { if(!ready || !feedForward(data)) return NaN(); return outputs[n].Loss(target, lf); }
После выполнения прямого прохода сигнала с помощью feedForward, мы здесь вычисляем меру «потерь» заданного типа. По умолчанию, это среднеквадратическая ошибка (LOSS_MSE), которая применима для задач регрессии и прогнозирования. Однако если сеть будет использоваться для классификации образов, следует выбрать другой тип оценки, например, кроссэнтропию LOSS_CCE.
В случае ошибки вычислений метод возвращает «не число» (NaN).
Теперь займемся обратным распространением ошибки. Метода backProp также начинается с проверки совпадения размеров целевых данных и выходного слоя. Затем для выходного слоя вычисляется производная активационной функции (если она есть) и «потери» сети на выходе, относительно целевых данных.
bool backProp(const matrix &target) { if(!ready) return false; if(target.Rows() != outputs[n].Rows() || target.Cols() != outputs[n].Cols()) return false; matrix temp; if(!outputs[n].Derivative(temp, of)) return false; matrix loss = (outputs[n] - target) * temp;
Матрица loss содержит величины δ из формулы (19).
Далее для всех слоев кроме выходного выполняется такой цикл:
for(int i = n - 1; i >= 0; --i) { if(i < n - 1) loss.Resize(loss.Rows(), loss.Cols() - 1); matrix delta = speed * outputs[i].Transpose().MatMul(loss);
Здесь мы видим «один в один» формулу (20): получаем приращения весов на основе скорости обучения η, δ текущего слоя и соответствующих выходов предыдущего (младшего) слоя.
Далее для каждого слоя вычисляем формулу (18), рекурсивно получая остальные δ: в ход опять идет производная АФ и умножение более старшей δ на транспонированную весовую матрицу. Следует напомнить, что индекс i в массиве outputs[] соответствует слою с весами в (i-1)-й матрице weights[], потому что входной псевдо-слой (outputs[0]) не имеет весов. Другими словами, при прямом прохождении сигнала матрица weights[0], будучи применена к outputs[0], производит outputs[1], weights[1] производит outputs[2] и так далее, а при обратном распространении ошибки индексы совпадают: например, outputs[2] (после дифференцирования) умножается на транспонированную weights[2].
if(!outputs[i].Derivative(temp, af)) return false; loss = loss.MatMul(weights[i].Transpose()) * temp;
Только после того как мы подсчитали loss δ для младшего слоя, можно подстраивать веса матрицы weights[i], то есть корректировать их на полученную выше delta.
weights[i] -= delta;
}
return true;
}
Теперь у нас почти все готово, чтобы реализовать полный алгоритм обучения с циклом по эпохам и вызовом методов feedForward и backProp. Однако сперва необходимо вновь обратиться к теории, потому что некоторые важные нюансы мы ранее отложили.
Обучение и регуляризация
Обучение НС производится на тренировочных данных, доступных на текущий момент. На основе этих данных выбирается конфигурация сети (количество слоев, количество нейронов по слоям и т.д.), скорость обучения и прочие характеристики. Поэтому, в принципе, всегда можно сконструировать достаточно мощную сеть, чтобы она давала любую достаточно малую ошибку на тренировочных данных. Однако главная сила НС и цель применения НС в том, чтобы она хорошо работала на будущих неизвестных данных (с теми же неявными зависимостями, что и тренировочный набор).
Эффект, когда обученная НС слишком хорошо подстраивается под обучающие данные, но проваливает «форвард-тест», называется переобучением, и должен всячески искореняться. Для этой цели применяют так называемую регуляризацию — добавление в модель или метод обучения неких дополнительных условий, оценивающих обобщающую способность сети. Существует множество различных способов регуляризации, в частности:
- анализ работы обучаемой сети на дополнительном валидационном наборе данных (отличном от обучающего);
- случайное отбрасывание части нейронов или связей во время обучения;
- прореживание (pruning) сети после обучения;
- привнесение шума во входные данные;
- искусственное размножение данных;
- слабое постоянное уменьшение амплитуды весов при обучении;
- экспериментальный подбор объема и конфигурации сети по тонкой грани, когда сеть еще способна обучаться, но уже не переобучается на имеющихся данных;
Мы реализуем некоторые из них в своем классе.
Для начала предусмотрим передачу в метод обучения не только входных и выходных обучающих данных (параметры data и target, соответственно), но также валидационного набора (он тоже состоит из входных и парных им выходных векторов: validation и check).
По мере обучения ошибка сети на обучающих данных, как правило, достаточно монотонно убывает (фраза «как правило» использована, потому что при неверном подборе скорости обучения или емкости сети, процесс может пойти нестабильно). Однако если параллельно подсчитывать ошибку сети на валидационном наборе, она сперва тоже будет уменьшаться (пока сеть выявляет наиболее важные закономерности в данных), а затем начнет расти по мере переобучения (когда сеть адаптируется уже к частным особенностям обучающей выборки, но не валидационной). Таким образом, процесс обучения следует остановить, когда ошибка валидации начнёт расти. Данный подход называется «ранней остановкой».
Помимо двух наборов данных, метод train позволяет задать максимальное количество эпох обучения (epochs), желаемую точность (accuracy, т.е. среднюю минимальную ошибку, которой нам достаточно: при этом обучение также заканчивается с признаком успеха) и способ подсчета ошибки (lf).
Скорость обучения speed устанавливается равной точности accuracy, но для повышения гибкости настроек, их можно при необходимости разнести. Так сделано потому, что далее мы поддержим автоматическую подстройку скорости, и начальное приблизительное значение не столь важно.
double train(const matrix &data, const matrix &target, const matrix &validation, const matrix &check, const int epochs = 1000, const double accuracy = 0.001, const ENUM_LOSS_FUNCTION lf = LOSS_MSE) { if(!ready) return NaN(); speed = accuracy; ...
Величины ошибок сети в текущей эпохе сохраним в переменных mse и msev — для обучающего и валидационного наборов. Но чтобы не реагировать на неизбежные случайные флуктуации, потребуется усреднять ошибки за некоторый период p, рассчитываемый из общего заданного числа эпох. Сглаженные значения ошибок будут храниться в переменных msema и msevma, а их предыдущие значения — в переменных msemap и msevmap.
double mse = DBL_MAX; double msev = DBL_MAX; double msema = 0; double msemap = 0; double msevma = 0; double msevmap = 0; double ema = 0; int p = 0; p = (int)sqrt(epochs); ema = 2.0 / (p + 1); PrintFormat("EMA for early stopping: %d (%f)", p, ema);
Далее запускаем цикл по эпохам обучения. Мы разрешаем не предоставлять валидационные данные, т.к. впоследствии реализуем другой способ регуляризации «dropout». Если валидационная выборка не пуста, рассчитываем msev вызовом метода test на ней. В любом случае рассчитываем mse с помощью вызова test на обучающей выборке. Напоминаем, что test осуществляет вызов метода feedForward и расчет ошибки результата сети относительно целевых значений.
int ep = 0; for(; ep < epochs; ep++) { if(validation.Rows() && check.Rows()) { msev = test(validation, check, lf); msevma = (msevma ? msevma : msev) * (1 - ema) + ema * msev; } mse = test(data, target, lf); msema = (msema ? msema : mse) * (1 - ema) + ema * mse; ...
Прежде всего проверяем, чтобы значение ошибки было валидным числом. В противном случае в сети произошло переполнение или на вход поданы некорректные данные.
if(!MathIsValidNumber(mse)) { PrintFormat("NaN at epoch %d", ep); break; }
Если новая ошибка стала больше прежней с некоторым «запасом», который определяется из соотношения размеров обучающей и валидационной выборок, цикл прерывается.
const int scale = (int)(data.Rows() / (validation.Rows() + 1)) + 1; if(msevmap != 0 && ep > p && msevma > msevmap + scale * (msemap - msema)) { PrintFormat("Stop by validation at %d, v: %f > %f, t: %f vs %f", ep, msevma, msevmap, msema, msemap); break; } msevmap = msevma; msemap = msema; ...
Если же ошибка продолжает уменьшаться или, как минимум не растет, запоминаем новые значения ошибок для сравнения в следующей эпохе.
Если ошибка достигла требуемой точности, считаем обучение завершенным и также выходим из цикла.
if(mse <= accuracy) { PrintFormat("Done by accuracy limit %f at epoch %d", accuracy, ep); break; }
Кроме того, в цикле вызывается виртуальный метод progress, который можно переопределить в производных классах сети, и с помощью него прерывать обучения в ответ на некоторые действия пользователя. Стандартную реализацию progress мы покажем чуть ниже.
if(!progress(ep, epochs, mse, msev, msema, msevma)) { PrintFormat("Interrupted by user at epoch %d", ep); break; }
Наконец, если цикл не был прерван ни по одному из вышеприведенных условий, запускаем обратный проход ошибки по сети с помощью backProp.
if(!backProp(target)) { mse = NaN(); break; } } if(ep == epochs) { PrintFormat("Done by epoch limit %d with accuracy %f", ep, mse); } return mse; }
Предоставленный по умолчанию метод progress выводит в журнал показатели обучения один раз в секунду.
virtual bool progress(const int epoch, const int total, const double error, const double valid = DBL_MAX, const double ma = DBL_MAX, const double mav = DBL_MAX) { static uint trap; if(GetTickCount() > trap) { PrintFormat("Epoch %d of %d, loss %.5f%s%s%s", epoch, total, error, ma == DBL_MAX ? "" : StringFormat(" ma(%.5f)", ma), valid == DBL_MAX ? "" : StringFormat(", validation %.5f", valid), valid == DBL_MAX ? "" : StringFormat(" v.ma(%.5f)", mav)); trap = GetTickCount() + 1000; } return !IsStopped(); }
Возвращаемое значение true продолжает обучение, в то время как false приведет к прерыванию цикла.
Помимо «ранней остановки», класс MatrixNet умеет случайным образом «отключать» часть связей а-ля «dropout».
Канонический метод «dropout» предполагает временное исключение из сети случайно выбранных нейронов. Однако мы не можем это реализовать без больших накладных расходов, поскольку алгоритм использует матричные операции. Для исключения нейронов из слоя потребовалось бы на каждой итерации переформатировать матрицы весов и частично копировать их. Гораздо проще и эффективнее устанавливать случайные веса в 0, то есть обрывать связи. Разумеется, в начале каждой эпохи программа должна восстановить временно отключенные веса до их предыдущего состояния, а потом выбрать несколько новых для отключения в следующей эпохе.
Количество временно обнуляемых связей задается с помощью метода enableDropOut, как процент от общего числа весов сети. По умолчанию, переменная dropOutRate равна 0, и режим отключен.
void enableDropOut(const uint percent = 10) { dropOutRate = (int)percent; }
Принцип работы «dropout» заключается в сохранении текущего состояния весовых матриц в некоем дополнительно хранилище (его реализует класс DropOutState) и обнулении случайно выбранных связей сети. После обучения сети в полученном модифицированном виде на протяжении одной эпохи, обнуленные элементы матриц восстанавливаются из хранилища, и процедура повторяется: выбираются и обнуляются другие случайные веса, сеть обучается с ними, и так далее. С устройством и применением класса DropOutState предлагается разобраться самостоятельно.
Адаптивная скорость обучения
До сих пор подразумевалось, что у нас используется постоянная скорость обучения (переменная speed), но это непрактично (обучение может идти очень медленно при малой скорости или «возбуждаться» при большой).
Одну из разновидностей адаптации скорости обучения можно «подсмотреть» в особой модификации алгоритма обратного распространения, которая называется «rprop» (от resilient propagation, то есть эластичное распространение). Суть заключается в том, чтобы для каждого веса проверять, совпадает ли знак приращений delta на предыдущей и текущей итерации. Совпадение знака означает, что направление градиента сохранилось, и в этом случае скорость можно повысить, причем избирательно для данного веса. Для тех весов, где знак градиента поменялся, имеет смысл, наоборот, «замедлиться».
Поскольку у нас в матрицах на каждой эпохе обсчитываются сразу все данные, значение и знак градиента для каждого веса аккумулируют (и «усредняют») поведение всего пакета данных. Поэтому более точно технология называется «batch rprop».
Все строки кода в классе MatrixNet, которые реализуют это усовершенствование, обложены макросами BATCH_PROP. Перед включением заголовочного файла MatrixNet.mqh в ваш исходный код рекоменуется включать адаптивную скорость с помощью директивы:
#define BATCH_PROP
Для начала обратим внимание, что вместо переменной speed в этом режиме используется массив матриц speed, а также потребуется запоминать приращения весов с прошлой эпохи в массиве матриц deltas.
class MatrixNet { protected: ... #ifdef BATCH_PROP matrix speed[]; matrix deltas[]; #else double speed; #endif
Кроме того, коэффициенты ускорения и торможения, а также максимальная и минимальные скорости задаются выделенными для этого 4-мя переменными.
double plus; double minus; double max; double min;
Выделение памяти под новые массивы и установка значений по умолчанию новым переменным производится в уже знакомом нам методе allocate.
void allocate() { ArrayResize(weights, n); ArrayResize(outputs, n + 1); ArrayResize(bestWeights, n); dropOutRate = 0; #ifdef BATCH_PROP ArrayResize(speed, n); ArrayResize(deltas, n); plus = 1.1; minus = 0.1; max = 50; min = 0.0; #endif }
Для установки других значений этим переменным перед запуском обучения воспользуйтесь методом setupSpeedAdjustment.
В конструкторе MatrixNet массивы матриц speed и deltas инициализируются копированием массива матриц weights — просто так удобнее получить матрицы аналогичных размеров по слоям сети. Заполнение speed и deltas значащими данными происходит на последующих этапах. В частности, в начале метода train вместо простого присваивания точности (accuracy) в скалярную переменную speed теперь производится заполнение этим значением всех матриц в массиве speed.
double train(const matrix &data, const matrix &target, const matrix &validation, const matrix &check, const int epochs = 1000, const double accuracy = 0.001, const ENUM_LOSS_FUNCTION lf = LOSS_MSE) { ... #ifdef BATCH_PROP for(int i = 0; i < n; ++i) { speed[i].Fill(accuracy); deltas[i].Fill(0); } #else speed = accuracy; #endif ... }
Внутри метода backProp выражение с вычислением приращений теперь ссылается на матрицу соответствующего слоя, а не на скаляр. Сразу же после получения приращений delta вызывается метод adjustSpeed (приведен далее), в который для сопоставления прежнего и нового направления передается произведение delta * deltas[i]. Наконец, новые приращения весов сохраняются в deltas[i], чтобы анализировать их на следующей эпохе.
bool backProp(const matrix &target) { ... for(int i = n - 1; i >= 0; --i) { ... #ifdef BATCH_PROP matrix delta = speed[i] * outputs[i].Transpose().MatMul(loss); adjustSpeed(speed[i], delta * deltas[i]); deltas[i] = delta; #else matrix delta = speed * outputs[i].Transpose().MatMul(loss); #endif ... } ... }
Метод adjustSpeed довольно прост. Положительный знак в элементе матричного произведения означает сохранение градиента, и скорость увеличивается в plus раз, но не более чем до величины max. Отрицательный знак означает смену градиента, и скорость уменьшается в minus раз, но не менее величины min.
void adjustSpeed(matrix &subject, const matrix &product) { for(int i = 0; i < (int)product.Rows(); ++i) { for(int j = 0; j < (int)product.Cols(); ++j) { if(product[i][j] > 0) { subject[i][j] *= plus; if(subject[i][j] > max) subject[i][j] = max; } else if(product[i][j] < 0) { subject[i][j] *= minus; if(subject[i][j] < min) subject[i][j] = min; } } } }
Сохранение и восстановление лучшего состояния обученной сети
Итак, обучение сети проводится в цикле по итерациям, называемым эпохами: в каждой эпохе через сеть проходят все вектора обучающего набора, помещенные в матрицу, где по строкам лежат записи, а по колонкам — их признаки. Например, в каждой записи может храниться бар котировок, а по столбцам — цены OHLC и объемы.
Процесс подстройки весов, хотя и выполняется по градиенту, носит случайных характер в том смысле, что из-за неровности целевой функции решаемой задачи и переменной скорости мы можем периодически попадать на более «плохие» настройки, прежде чем «обнаружить» новый минимум ошибки сети. В принципе, у нас нет гарантии, что с увеличением номера эпохи, качество обученной модели будет непременно улучшаться, а ошибка сети — уменьшаться.
В связи с этим имеет смысл постоянно контролировать общую ошибку сети, и если после текущей эпохи ошибка обновляет минимум, найденные веса следует запомнить. Для этих целей определен еще один массив матриц весов, а также структура с показателями обучения Stats.
class MatrixNet { ... public: struct Stats { double bestLoss; int bestEpoch; int epochsDone; }; Stats getStats() const { return stats; } protected: matrix bestWeights[]; Stats stats; ...
Внутри метода train, перед началом цикла по эпохам инициализируем структуру со статистикой.
double train(const matrix &data, const matrix &target, const matrix &validation, const matrix &check, const int epochs = 1000, const double accuracy = 0.001, const ENUM_LOSS_FUNCTION lf = LOSS_MSE) { ... stats.bestLoss = DBL_MAX; stats.bestEpoch = -1; DropOutState state(dropOutRate);
Внутри самого цикла при обнаружении величины ошибки меньше минимальной известной мы запоминаем все весовые матрицы в bestWeights.
int ep = 0; for(; ep < epochs; ep++) { ... const double candidate = (msev != DBL_MAX) ? msev : mse; if(candidate < stats.bestLoss) { stats.bestLoss = candidate; stats.bestEpoch = ep; for(int i = 0; i < n; ++i) { bestWeights[i].Assign(weights[i]); } } } ...
После обучения легко запросить как финальные веса сети, так и лучшие веса.
bool getWeights(matrix &array[]) const { if(!ready) return false; ArrayResize(array, n); for(int i = 0; i < n; ++i) { array[i] = weights[i]; } return true; } bool getBestWeights(matrix &array[]) const { if(!ready) return false; if(!n || !bestWeights[0].Rows()) return false; ArrayResize(array, n); for(int i = 0; i < n; ++i) { array[i] = bestWeights[i]; } return true; }
Эти массивы матриц можно сохранить в файл для последующего восстановления уже обученной и готовой к работе сети. Для этого предусмотрен отдельный конструктор.
MatrixNet(const matrix &w[], const ENUM_ACTIVATION_FUNCTION f1 = AF_TANH, const ENUM_ACTIVATION_FUNCTION f2 = AF_NONE): ready(false), af(f1), of(f2), n(ArraySize(w)) { if(n < 2) return; allocate(); for(int i = 0; i < n; ++i) { weights[i] = w[i]; #ifdef BATCH_PROP speed[i] = weights[i]; deltas[i] = weights[i]; #endif } ready = true; }
Позднее мы покажем сохранение и чтение готовых сетей в одном из практических примеров.
Визуализация прогресса обучения сети
Наличие метода progress, выводящего периодические сообщения в журнал, не особо наглядно. Поэтому в файле MatrixNet.mqh также реализован производный от MatrixNet класс MatrixNetVisual, выводящий в окно график с изменяющимися величинами ошибок обучения по эпохам.
Графическое отображение предоставляет стандартный класс CGraphic (поставляемый с MetaTrader 5), а точнее — небольшой производный от него класс CMyGraphic.
Объект данного класса является частью MatrixNetVisual. Также внутри «визуализируемой» сети описан массив из 5-ти кривых и массивы типа double, предназначенные непосредственно для отображаемых линий.
class MatrixNetVisual: public MatrixNet { CMyGraphic graphic; CCurve *c[5]; double p[], x[], y[], z[], q[], b[]; ...
Здесь:
В методе graph, вызываемом из конструкторов MatrixNetVisual, создается графический объект размером на все окно и добавляются 5 вышеописанных кривых (CCurve).
void graph() { ulong width = ChartGetInteger(0, CHART_WIDTH_IN_PIXELS); ulong height = ChartGetInteger(0, CHART_HEIGHT_IN_PIXELS); bool res = false; const string objname = "BPNNERROR"; if(ObjectFind(0, objname) >= 0) res = graphic.Attach(0, objname); else res = graphic.Create(0, objname, 0, 0, 0, (int)(width - 0), (int)(height - 0)); if(!res) return; c[0] = graphic.CurveAdd(p, x, CURVE_LINES, "Training"); c[1] = graphic.CurveAdd(p, y, CURVE_LINES, "Validation"); c[2] = graphic.CurveAdd(p, z, CURVE_LINES, "Val.EMA"); c[3] = graphic.CurveAdd(p, q, CURVE_LINES, "Train.EMA"); c[4] = graphic.CurveAdd(p, b, CURVE_POINTS, "Best/Minimum"); ... } public: MatrixNetVisual(const int &layers[], const ENUM_ACTIVATION_FUNCTION f1 = AF_TANH, const ENUM_ACTIVATION_FUNCTION f2 = AF_NONE): MatrixNet(layers, f1, f2) { graph(); }
В переопределенном методе progress аргументы добавляются в соответствующие массивы double, а затем вызывается метод plot для актуализации изображения.
virtual bool progress(const int epoch, const int total, const double error, const double valid = DBL_MAX, const double ma = DBL_MAX, const double mav = DBL_MAX) override { PUSH(p, epoch); PUSH(x, error); if(valid != DBL_MAX) PUSH(y, valid); else PUSH(y, nan); if(ma != DBL_MAX) PUSH(q, ma); else PUSH(q, nan); if(mav != DBL_MAX) PUSH(z, mav); else PUSH(z, nan); plot(); return MatrixNet::progress(epoch, total, error, valid, ma, mav); }
Метод plot производит пополнение и отображение кривых.
void plot() { c[0].Update(p, x); c[1].Update(p, y); c[2].Update(p, z); c[3].Update(p, q); double point[1] = {stats.bestEpoch}; b[0] = stats.bestLoss; c[4].Update(point, b); ... graphic.CurvePlotAll(); graphic.Update(); }
С технической стороной визуализации предлагается разобраться самостоятельно. Как это выглядит на экране, мы скоро увидим.
Тестовый скрипт
Классы семейства MatrixNet готовы для первой проверки. Ею станет скрипт MatrixNet.mq5, в котором исходные данные генерируются искусственно на основе известной аналитической записи. Формула взята из раздела справки про машинное обучение, где приведен собственный пример обучения по алгоритму обратного распространения ошибки — не столь универсальный, как наши классы, и потому требующий значительного кодирования (сравните далее количество строк с использованием класса и без).
f = ((x + y + z)^2 / (x^2 + y^2 + z^2)) / 3
Единственное маленькое отличие нашей формулы заключается в делении значения на 3, что дает диапазон функции от 0 до 1.
Форму функции можно оценить с помощью следующего рисунка, где поверхности (x<->y) показаны для трех разных значений z: 0.05, 0.5 и 5.0.
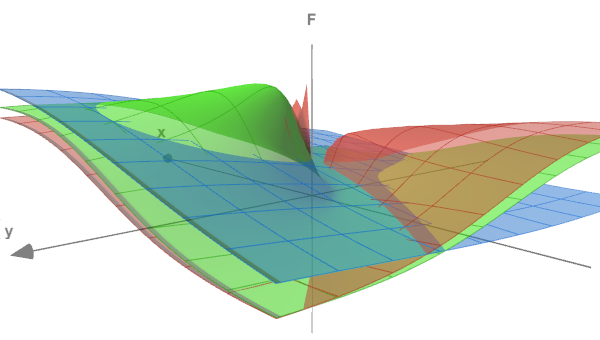
Тестовая функция в 3-х сечениях
Во входных переменных скрипта зададим количество эпох обучения, точность (терминальную ошибку), а также интенсивность шума, которую мы можем по желанию добавить в генерируемые данные (это приблизит эксперимент к реальным задачам и продемонстрирует, как наличие шума усложняет выявлении зависимостей). По умолчанию параметр RandomNoise равен 0, и шум отсутствует.
input int Epochs = 1000; input double Accuracy = 0.001; input double RandomNoise = 0.0;
Генерацией экспериментальных данных «заведует» функция CreateData. Её параметры-матрицы data и target будут заполнены точками описанной выше функции, в количестве count. Один входной вектор (строка матрицы data) имеет 3 колонки (для x, y, z). Выходной вектор (строка матрицы target) — это единственное значение f. Точки (x,y,z) генерируются случайно в диапазоне от -10 до +10.
bool CreateData(matrix &data, matrix &target, const int count) { if(!data.Init(count, 3) || !target.Init(count, 1)) return false; data.Random(-10, 10); vector X1 = MathPow(data.Col(0) + data.Col(1) + data.Col(2), 2); vector X2 = MathPow(data.Col(0), 2) + MathPow(data.Col(1), 2) + MathPow(data.Col(2), 2); if(!target.Col(X1 / X2 / 3.0, 0)) return false; if(RandomNoise > 0) { matrix noise; noise.Init(count, 3); noise.Random(0, RandomNoise); data += noise - RandomNoise / 2; noise.Resize(count, 1); noise.Random(-RandomNoise / 2, RandomNoise / 2); target += noise; } return true; }
Интенсивность шума в RandomNoise задается как амплитуда дополнительного разброса правильных координат и полученного для них значения функции. Учитывая, что функция имеет максимальную величину 1.0, такой уровень шума сделает её практически нераспознаваемой.
Для использования нейронной сети подключим заголовочный файл MatrixNet.mqh и перед этой директивой препроцессора определим макрос BATCH_PROP, чтобы задействовать ускоренное обучения с переменной скоростью.
#define BATCH_PROP #include <MatrixNet.mqh>
В главной функции скрипта определяем конфигурацию сети (количество слоев и их размеры) с помощью массива layers, который передаем в конструктор MatrixNetVisual. Наборы обучающих и валидационных данных генерируем двукратным вызовом CreateData.
void OnStart() { const int layers[] = {3, 11, 7, 1}; MatrixNetVisual net(layers); matrix data, target; CreateData(data, target, 100); matrix valid, test; CreateData(valid, test, 25); ...
На практике исходные данные следует нормализовать, очистить от выбросов, проверить факторы на независимость, прежде чем отправлять в сеть, но в данном случае мы сами генерируем данные.
Обучение выполняется методом train на матрицах data и target. Ранняя остановка произойдет по мере ухудшения показателей на наборе valid/test, однако на незашумленных данных мы, скорее всего, достигнем требуемой точности или же предельного числа циклов, в зависимости от того, что случится быстрее.
Print("Training result: ", net.train(data, target, valid, test, Epochs, Accuracy)); matrix w[]; if(net.getBestWeights(w)) { MatrixNet net2(w); if(net2.isReady()) { Print("Best copy on training data: ", net2.test(data, target)); Print("Best copy on validation data: ", net2.test(valid, test)); } }
После обучения запрашиваем матрицы лучших найденных весов и ради проверки конструируем на их основе другой экземпляр сети — объект net2, после чего выполняем рабочий прогон сети на обоих наборах данных и выводим величины ошибок для них в журнал.
Поскольку в скрипте используется сеть с визуализацией прогресса обучения, запускаем цикл ожидания команды пользователя на завершения скрипта, чтобы пользователь мог ознакомиться с графиком.
while(!IsStopped()) { Sleep(1000); } }
При запуске скрипта с параметрами по умолчанию можем получить примерно следующую картину (каждый запуск будет отличаться от других из-за случайной генерации данных и инициализации сети).
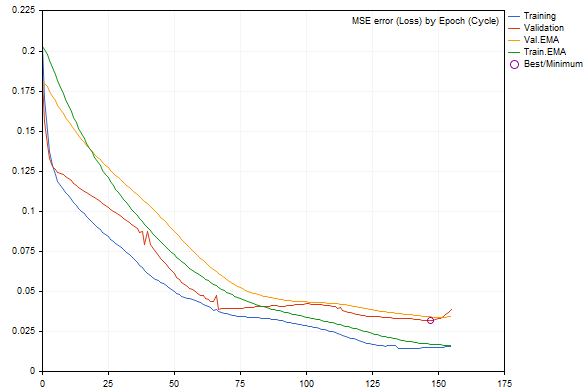
Динамика изменения ошибки сети при обучении
Ошибки на обучающем и валидационном наборе отображены синей и красной линиями, соответственно, а их сглаженные версии — зеленая и желтая. Наглядно видно, что по мере обучения все типы ошибок уменьшаются, но после некоторого момента ошибка валидации становится больше ошибки обучающего набора, а ближе к правому краю графика заметно её возрастание, в результате чего происходит «ранняя остановка». Лучшая конфигурация сети помечена кружком.
В журнале увидим похожие записи:
EMA for early stopping: 31 (0.062500)
Epoch 0 of 1000, loss 0.20296 ma(0.20296), validation 0.18167 v.ma(0.18167)
Epoch 120 of 1000, loss 0.02319 ma(0.02458), validation 0.04566 v.ma(0.04478)
Stop by validation at 155, v: 0.034642 > 0.034371, t: 0.016614 vs 0.016674
Training result: 0.015707719706513287
Best copy on training data: 0.015461956812387292
Best copy on validation data: 0.03211748853774414
Если начать добавлять в данные шум с помощью параметра RandomNoise, темпы обучения заметно снизятся, а при слишком большом шуме ошибка обученной сети возрастет или она вовсе перестанет обучаться.
Вот, например, как выглядит график при добавлении шума 3.0.
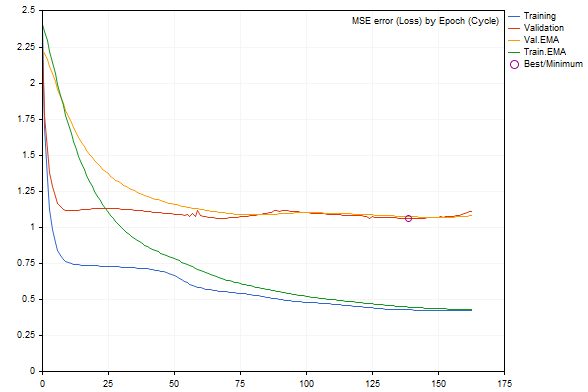
Динамика изменения ошибки сети при обучении с добавленным шумом
Показатель ошибки, согласно журналу, на порядок хуже.
Epoch 0 of 1000, loss 2.40352 ma(2.40352), validation 2.23536 v.ma(2.23536) Stop by validation at 163, v: 1.082419 > 1.080340, t: 0.432023 vs 0.432526 Training result: 0.4244786772678285 Best copy on training data: 0.4300476339855798 Best copy on validation data: 1.062895214094978
Убедившись, что нейросетевой инструментарий работает, перейдем к более практичным примерам: индикатору и эксперту.
Прогнозирующий индикатор
В качестве примера прогнозирующего индикатора на основе НС рассмотрим BPNNMatrixPredictorDemo.mq5 — это модификация готового индикатора из кодовой базы, в котором НС реализована на MQL5 без применения матриц, путем портирования с языка C++ другой, более ранней версии того же индикатора (с подробным описанием, включая релевантные части теории НС).
Принцип работы индикатора заключается в формировании входных векторов заданной длины из прошлых приращений EMA-усредненной цены на отрезках между барами, отстоящими друг от друга по последовательности Фибоначчи (1,2,3,5,8,13,21,34,55,89,144…). По этой информации требуется предсказать приращение цены на следующем баре (справа от исторических баров, попавших в соответствующий вектор). Размер вектора определяется заданным пользователем размером входного слоя НС (_numInputs). Количество слоев (вплоть до 6) и их размеры вводятся в другие входные переменные.
input int _lastBar = 0; input int _futBars = 10; input int _smoothPer = 6; input int _numLayers = 3; input int _numInputs = 12; input int _numNeurons1 = 5; input int _numNeurons2 = 1; input int _numNeurons3 = 0; input int _numNeurons4 = 0; input int _numNeurons5 = 0; input int _ntr = 500; input int _nep = 1000; input int _maxMSEpwr = -7;
Также здесь указывается размер обучающей выборки (_ntr), максимальное количество эпох (_nep) и минимальная MSE-ошибка (_maxMSEpwr).
Период EMA-усреднения цены задается в _smoothPer.
По умолчанию, индикатор берет обучающие данные, начиная с последнего бара (_lastBar равно 0), и делает прогноз на _futBars вперед (очевидно, что имея на выходе сети прогноз на 1 бар, мы можем его поэтапно «задвигать» во входной вектор, чтобы предсказывать несколько последующих баров). Если ввести в _lastBar положительное число, получим прогноз по состоянию на соответствующее количество баров в прошлом, что позволит его визуально оценить (сравнить с уже имеющимися котировками).
Индикатор выводит 3 буфера:
- светло-зеленая линия с целевыми значениями обучающей выборки;
- синяя линия с выходом сети на обучающей выборке;
- красная линия с прогнозом;
Прикладная часть индикатора по формированию наборов данных и визуализации результатов (как исходных данных, так и прогноза) не претерпела изменений.
Основные преобразования произошли в двух функциях Train и Test — теперь они полностью делегируют работу НС объектам класса MatrixNet. Train обучает сеть на основе собранных данных и возвращает массив с весами сети (при запуске в тестере обучение делается лишь однажды, а при запуске онлайн открытие нового бара вызывает повторное обучение — это легко поменять в исходном коде). Test воссоздает сеть по весам и выполняет штатный однократный расчет прогноза. В принципе, более оптимально было бы сохранить объект обученной сети, и эксплуатировать его без воссоздания. Мы сделаем так в следующем примере эксперта, а в случае индикатора специально оставлена исходная структура кода старой версии, чтобы было удобнее сравнивать подходы кодирования с матрицами и без. В частности, можно обратить внимание на то, что в матричной версии мы избавлены от необходимости «прогонять» векторы через сеть в цикле по одному и вручную делать «reshape» массивов с данными, в соответствии с их размерностью.
С настройками по умолчанию индикатор выглядит на графике EURUSD,H1 следующим образом.
Прогноз нейросетевого индикатора
Следует отметить, что индикатор является лишь демонстрацией работы НС и не рекомендуется в текущем упрощенном виде для принятия торговых решений.
Хранение сетей в файлах
Исходные данные, поступающие с рынка, могут быстро меняться, и некоторые трейдеры считают целесообразным обучать сеть оперативно (каждый день, каждую сессию, и т.д.) на наиболее свежих образцах. Однако это может быть накладно, да и не столь актуально для среднесрочных и долгосрочных торговых систем, оперирующих днями. В подобных случаях обученную сеть желательно сохранить для последующей загрузки и быстрого использования.
Для этой цели в рамках статьи создан класс MatrixNetStore, определенный в заголовочном файле MatrixNetStore.mqh. В классе имеются шаблонные методы save и load, предполагающие в качестве параметра шаблона M любой класс из семейства MatrixNet (пока их у нас только два, с учетом MatrixNetVisual, но желающие могут расширить набор). Оба метода имеют аргумент с именем файла и оперируют стандартными данными НС: количеством слоев, их размером, весовыми матрицами, функциями активации.
Вот как делается сохранения сети.
class MatrixNetStore { static string signature; public: template<typename M> static bool save(const string filename, const M &net, Storage *storage = NULL, const int flags = 0) { matrix w[]; if(!net.getBestWeights(w)) { if(!net.getWeights(w)) { return false; } } int h = FileOpen(filename, FILE_WRITE | FILE_BIN | FILE_SHARE_READ | FILE_SHARE_WRITE | FILE_ANSI | flags); if(h == INVALID_HANDLE) return false; FileWriteString(h, signature); FileWriteInteger(h, net.getActivationFunction()); FileWriteInteger(h, net.getActivationFunction(true)); FileWriteInteger(h, ArraySize(w)); for(int i = 0; i < ArraySize(w); ++i) { matrix m = w[i]; FileWriteInteger(h, (int)m.Rows()); FileWriteInteger(h, (int)m.Cols()); double a[]; m.Swap(a); FileWriteArray(h, a); } if(storage) { if(!storage.store(h)) Print("External info wasn't saved"); } FileClose(h); return true; } ... }; static string MatrixNetStore::signature = "BPNNMS/1.0";
Отметим пару моментов. В начале файла пишется сигнатура, чтобы по ней можно было проверять правильность формата файла (сигнатуру можно менять: для этого в классе предусмотрены методы). Кроме того, метод save позволяет при необходимости дописать к стандартной информации о сети любые дополнительные пользовательские данные: достаточно передать указатель на объект специального интерфейса Storage.
class Storage { public: virtual bool store(const int h) = 0; virtual bool restore(const int h) = 0; };
«Зеркальным» образом сеть можно восстановить из файла.
class MatrixNetStore { ... template<typename M> static M *load(const string filename, Storage *storage = NULL, const int flags = 0) { int h = FileOpen(filename, FILE_READ | FILE_BIN | FILE_SHARE_READ | FILE_SHARE_WRITE | FILE_ANSI | flags); if(h == INVALID_HANDLE) return NULL; const string header = FileReadString(h, StringLen(signature)); if(header != signature) { FileClose(h); Print("Incorrect file header"); return NULL; } const ENUM_ACTIVATION_FUNCTION f1 = (ENUM_ACTIVATION_FUNCTION)FileReadInteger(h); const ENUM_ACTIVATION_FUNCTION f2 = (ENUM_ACTIVATION_FUNCTION)FileReadInteger(h); const int size = FileReadInteger(h); matrix w[]; ArrayResize(w, size); for(int i = 0; i < size; ++i) { const int rows = FileReadInteger(h); const int cols = FileReadInteger(h); double a[]; FileReadArray(h, a, 0, rows * cols); w[i].Swap(a); w[i].Reshape(rows, cols); } if(storage) { if(!storage.restore(h)) Print("External info wasn't read"); } M *m = new M(w, f1, f2); FileClose(h); return m; }
Теперь у нас все готово, чтобы обратиться к завершающему примеру статьи — торговому роботу.
Прогнозирующий эксперт
В качестве стратегии для прогнозирующего эксперта TradeNN.mq5 возьмем достаточно простой принцип: торговать в предсказанном направлении следующего бара. Нам важно продемонстрировать нейросетевые технологии в действии, а не исследовать все обозримые факторы на применимость в контексте прибыльности.
Исходными данными станут приращения цен на заданном количестве баров, причем опционально можно анализировать не только текущий символ, но и дополнительные, что теоретически позволит выявить взаимозависимости (например, если один тикер опосредованно «следует» за другим или их комбинациями). Единственный выход сети не будет интерпретироваться как целевая цена, а вместо этого, с целью упрощения системы, будет анализироваться знак: положительный — покупка, отрицательный — продажа.
Иными словами, схема работы сети в некотором смысле гибридная: с одной стороны сеть будет решать задачу регрессии, но с другой стороны торговое действие выбирается из двух, как при классификации. В перспективе можно увеличить число нейронов в выходном слое до количества торговых ситуаций и применить активационную функцию SoftMax — правда, чтобы обучать такую сеть, потребуется автоматически или вручную разметить котировки согласно ситуациям.
Выбор стратегии специально сделан максимально простым, чтобы сосредоточиться на параметрах сети, а не стратегии.
Перечень анализируемых инструментов вводится во входной параметр Symbols через запятую. Первым должен идти символ текущего графика — именно на этом символе ведется торговля.
input string Symbols = "XAGUSD,XAUUSD,EURUSD"; input int Depth = 5; input int Reserve = 250;
Выбор символов по умолчанию обусловлен тем, что серебро и золото считаются коррелированными активами, и по ним относительно мало возмутительных новостей (по сравнению с валютами), так что, в принципе, можно пробовать анализировать как серебро по золоту (как сейчас), так и золото по серебру. Что же касается EURUSD, то эта пара добавлена в качестве основы всего рынка, и в данном случае наличие новостей по ней не важно, так как она работает как предиктор, а не прогнозируемая переменная.
Среди других наиболее важных параметров — количество баров (Depth) по каждому инструменту, формирующих вектор. Например, если в строке Symbols задано 3 тикера, а в Depth стоит 5 (по умолчанию), значит общий размер входного вектора НС равен 15.
Параметр Reserve позволяет задать длину выборки (количество векторов, формируемых из ближайшей истории котировок). Значение 250 выбрано по умолчанию, потому что в нашем тесте будет использоваться дневной таймфрейм, и 250 составляет примерно 1 год. Соответственно, Depth, равный 5 — это неделя.
Разумеется, все настройки можно менять, как и таймфрейм, но на старших таймфремах, вроде D1, предположительно, более выражены фундаментальные закономерности, нежели спонтанные реакции рынка на сиюминутные обстоятельства.
Важно также напомнить, что при запуске в тестере заранее подгружается примерно 1 год котировок, поэтому увеличение объема запрашиваемых обучающих данных на D1+ потребует пропускать некоторое количество начальных баров, ожидая накопления их достаточного количества.
По аналогии с предыдущими примерами, в параметрах следует задать количество эпох обучения и точность (по совместительству, начальную скорость, а далее скорость будет динамически выбираться для каждого синапса по «rprop»).
input int Epochs = 1000; input double Accuracy = 0.0001;
В данном эксперте НС получит 5 слоев: один входной, 3 скрытых и выходной. Размер входного слоя определяет входной вектор, а второй и третий слои выделяются с коэффициентом HiddenLayerFactor. Для предпоследнего слоя будет использована эмпирическая формула (см. далее исходный код), чтобы его размер лежал между предыдущим и выходным (единичным).
input double HiddenLayerFactor = 2.0; input int DropOutPercentage = 0;
Также на примере данной НС мы испытаем способ регуляризации «dropout»: процент случайно выбираемых для обнуления весов задается в параметре DropOutPercentage. Валидационная выборка здесь не предусморена, хотя желающие смогут совмещать оба метода: класс это позволяет.
Для загрузки сети из файла предназначен параметр NetBinFileName. Файлы всегда ищутся относительно общей папки терминалов, поскольку иначе для тестирования эксперта в тестере потребовалось бы указывать заранее имена всех нужных сетей в исходном коде, в директиве #property tester_file — только так они отправились бы на агент.
Когда параметр NetBinFileName пуст, эксперт обучает новую сеть и сохраняет её в файле с уникальным временным именем. Это делается даже в процессе оптимизации, что позволяет генерировать большое количество конфигураций сети (для разных размеров векторов, слоев, «dropout»-а, глубины истории).
input string NetBinFileName = ""; input int Randomizer = 0;
Более того, параметр Randomizer дает возможность по-разному инициализировать случайный генератор и тем самым обучать много экземпляров сетей для одних и тех же прочих настроек. Напомним, что каждая сеть уникальна за счет рандомизации. Потенциально, использование комитетов НС, из которых считывается консолидированное решение или по принципу большинства, является еще одной разновидностью регуляризации.
Вместе с тем, установка конкретного значения в Randomizer позволит воспроизводить один и тот же процесс обучения в целях отладки.
Хранение ценовой информации по символам организовано с помощью структуры Closes и массива таких структур CC: в результате получим что-то вроде массива массивов.
struct Closes { double C[]; }; Closes CC[];
Под рабочие инструменты и их количество зарезервированы глобальный массив S и переменная Q: они заполняются в OnInit.
string S[]; int Q; int OnInit() { Q = StringSplit(StringLen(Symbols) ? Symbols : _Symbol, ',', S); ArrayResize(CC, Q); MathSrand(Randomizer); ... return INIT_SUCCEEDED; }
Запросить котировки на заданную глубину Depth от конкретного бара offset позволяет функция Calc: именно в ней заполняется массив CC. Как эта функция вызывается, мы увидим чуть дальше.
bool Calc(const int offset) { const datetime dt = iTime(_Symbol, _Period, offset); for(int i = 0; i < Q; ++i) { const int bar = iBarShift(S[i], PERIOD_CURRENT, dt); const int n = CopyClose(S[i], PERIOD_CURRENT, bar, Depth + 2, CC[i].C); for(int j = 0; j < n - 1; ++j) { CC[i].C[j] = (CC[i].C[j + 1] - CC[i].C[j]) / SymbolInfoDouble(S[i], SYMBOL_TRADE_TICK_SIZE) * SymbolInfoDouble(S[i], SYMBOL_TRADE_TICK_VALUE); } ArrayResize(CC[i].C, n - 1); } return true; }
Затем для конкретного массива CC[i].C специальная функция Diff сможет рассчитать приращения цен, которые и попадут во входные векторы для сети. Особенностью функции является то, что все приращения, кроме последнего, она записывает в переданный по ссылке массив d, а последнее приращение, которое будет выступать целевым значением прогноза, возвращается напрямую.
double Diff(const double &a[], double &d[]) { const int n = ArraySize(a); ArrayResize(d, n - 1); double overall = 0; for(int j = 0; j < n - 1; ++j) { int k = n - 2 - j; overall += a[k]; d[j] = overall / sqrt(j + 1); } ... return a[n - 1]; }
Здесь следует отметить, что в соответствии с теорией «случайного блуждания» временных рядов, мы нормируем разницы квадратным корнем расстояния в барах (пропорционально доверительному интервалу, если рассматривать прошлое, как уже отработанный прогноз). Это не является каноническим приемом, но работа с НС зачастую сродни исследовательской.
Вся процедура выбора факторов (например, не только цен, но индикаторов, объемов) и подготовки данных для сети (нормализация, кодирование) — это отдельная обширная тема. Важно максимально облегчить для НС вычислительную работу, в противном случае она может не справиться с задачей.
В главной функции эксперта OnTick все операции выполняются только по открытию бара. Учитывая, что эксперт анализирует котировки разных инструментов, требуется синхронизировать их бары, прежде чем продолжать штатную работу. Синхронизацию выполняет функция Sync, здесь не показанная. Однако интересно отметить, что примененная синхронизация на базе функции Sleep, подходит даже для тестирования в режиме цен открытия. И мы позднее воспользуемся этим режимом из соображений эффективности.
void OnTick() { ... static datetime last = 0; if(last == iTime(_Symbol, _Period, 0)) return; ...
Экземпляр сети хранится в переменной run типа авто-указателя (заголовочный файл AutoPtr.mqh), что избавляет нас от необходимости контролировать освобождение памяти. Переменная std предназначена для хранения дисперсии, рассчитываемой на наборе данных, полученном из рассмотренных выше функций Calc и Diff. Дисперсия потребуется для нормализации данных.
static AutoPtr<MatrixNet> run; static double std;
Если пользователь задал в NetBinFileName имя файла для загрузки, программа попытается загрузить сеть с помощью LoadNet (см. далее). Эта функция в случае успеха возвращает указатель на объект сети.
if(NetBinFileName != "") { if(!run[]) { run = LoadNet(NetBinFileName, std); if(!run[]) { ExpertRemove(); return; } } }
При наличии сети выполняем прогнозирование и осуществляем торговлю: за всё это отвечает TradeTest (см. далее).
if(run[]) { TradeTest(run[], std); } else { run = TrainNet(std); } last = iTime(_Symbol, _Period, 0); }
Если сети еще нет, формируем обучающую выборку и обучаем на ней сеть с помощью вызова TrainNet: эта функция также возвращает указатель на новый объект сети, а кроме того, заполняет переданную по ссылке переменную std рассчитанной дисперсией данных.
Обратите внимание, что сеть сможет обучаться только после того, как в истории по всем рабочим символам окажется как минимум запрошенное количество баров. Для онлайн-графика это произойдет, скорее всего, сразу после размещения эксперта (если только пользователь не ввел запредельное число), а в тестере предзагруженная история, как правило, ограничена одним годом, и потому может потребоваться сдвинуть старт прохода в прошлое, чтобы к интересующему вас моменту накопить нужное количество баров для обучения.
Проверка на достаточное количество баров вставлена в начало OnTick, но в статье не приводится (см. полные исходные коды).
После того как сеть обучена, эксперт начнет торговать. Для тестера это означает, что мы получим своего рода форвард-тест обученной сети. Полученные финансовые показатели можно использовать для оптимизации с целью выбора наиболее подходящей конфигурации сети или селекции комитета сетей (одинаковых по конфигурации).
А вот и сама функция TrainNet (обратите внимание на вызовы Calc и Diff).
MatrixNet *TrainNet(double &std) { double coefs[]; matrix sys(Reserve, Q * Depth); vector model(Reserve); vector t; datetime start = 0; for(int j = Reserve - 1; j >= 0; --j) { if(!Calc(j + 1)) { return NULL; } if(start == 0) start = iTime(_Symbol, _Period, j); ArrayResize(coefs, 0); for(int i = 0; i < Q; ++i) { double temp[]; double m = Diff(CC[i].C, temp); if(i == 0) { model[j] = m; } int dest = ArraySize(coefs); ArrayCopy(coefs, temp, dest, 0); } t.Assign(coefs); sys.Row(t, j); } std = sys.Std() * 3; Print("Normalization by 3 std: ", std); sys /= std; matrix target = {}; target.Col(model, 0); target /= std; int layers[] = {0, 0, 0, 0, 1}; layers[0] = (int)sys.Cols(); layers[1] = (int)(sys.Cols() * HiddenLayerFactor); layers[2] = (int)(sys.Cols() * HiddenLayerFactor); layers[3] = (int)fmax(sqrt(sys.Rows()), fmax(sqrt(layers[1] * layers[3]), sys.Cols() * sqrt(HiddenLayerFactor))); ArrayPrint(layers); MatrixNetVisual *net = new MatrixNetVisual(layers); net.setupSpeedAdjustment(SpeedUp, SpeedDown, SpeedHigh, SpeedLow); net.enableDropOut(DropOutPercentage);
Print("Training result: ", net.train(sys, target, Epochs, Accuracy));
...
Мы используем класс сети с визуализацией, в результате чего прогресс обучения будет виден на графике. После обучения вы можете вручную удалить объект-картинку, когда она станет ненужной. При выгрузке эксперта картинка удаляется автоматически.
Далее требуется прочитать из сети лучшие весовые матрицы. Дополнительно мы проверяем возможность успешно воссоздать сеть по этим весам и тестируем её производительность на тех же данных.
matrix w[]; if(net.getBestWeights(w)) { MatrixNet net2(w); if(net2.isReady()) { Print("Best result: ", net2.test(sys, target)); ... } } return net; }
Наконец, сеть сохраняется в файл вместе со специально подготовленной строкой, описывающей условия обучения: интервал истории, список символов и таймфрейм, размер данных, настройки сети.
const string context = StringFormat("rn%s %s %s-%s", _Symbol, EnumToString(_Period),
TimeToString(start), TimeToString(iTime(_Symbol, _Period, 0))) + "rn" +
Symbols + "rn" + (string)Depth + "/" + (string)Reserve + "rn" +
(string)Epochs + "/" + (string)Accuracy + "rn" +
(string)HiddenLayerFactor + "/" + (string)DropOutPercentage + "rn";
const string tempfile = "bpnnmtmp" + (string)GetTickCount64() + ".bpn";
MatrixNetStore store;
BinFileNetStorage writer(context, net.getStats(), std);
store.save(tempfile, *net, &writer);
...
Упомянутый здесь класс BinFileNetStorage является специфическим для нашего эксперта и с помощью переопределенных методов store/restore (родительский интерфейс Storage) обрабатывает наше дополнительное описание, величину нормализации (она потребуется для штатной работы на новых данных), а также статистику обучения в виде структуры MatrixNet::Stats (приводилась выше).
Далее поведение эксперта зависит от того, работает ли он в режиме оптимизации или нет. При оптимизации мы отправим файл сети с агента в терминал с помощью механизма фреймов (см. исходный код). Такие файлы складируются в локальной папке MQL5/Files/, в подпапке с именем эксперта.
if(!MQLInfoInteger(MQL_OPTIMIZATION)) { string filename = "bpnnm" + TimeStamp((datetime)FileGetInteger(tempfile, FILE_MODIFY_DATE)) + StringFormat("(%7g)", net.getStats().bestLoss) + ".bpn"; if(!FileMove(tempfile, 0, filename, FILE_COMMON)) { PrintFormat("Can't rename temp-file: %s [%d]", tempfile, _LastError); } } else { ... }
В остальных случаях (простое тестирование или работа онлайн) файл перемещается в общую папку терминалов. Так сделано, чтобы облегчить последующую загрузку через параметр NetBinFileName. Дело в том, что для работы в тестере нам потребовалось бы в исходном коде указывать директиву #property tester_file с конкретным именем файла, который планируется вводить в параметр NetBinFileName, и перекомпилировать эксперт. Без этих манипуляций файл сети не будет скопирован на агент. Поэтому более практичным является использование общей папки, доступной из всех локальных агентов.
Функция LoadNet реализована следующим образом:
MatrixNet *LoadNet(const string filename, double &std, const int flags = FILE_COMMON) { BinFileNetStorage reader; MatrixNetStore store; MatrixNet *net; std = 1.0; Print("Loading ", filename); ResetLastError(); net = store.load<MatrixNet>(filename, &reader, flags); if(net == NULL) { Print("Failed: ", _LastError); return NULL; } MatrixNet::Stats s[1]; s[0] = reader.getStats(); ArrayPrint(s); std = reader.getScale(); Print(std); Print(reader.getDescription()); return net; }
Функция TradeTest вызывает Calc(0), чтобы затем получить вектор из актуальных приращений цен.
bool TradeTest(MatrixNet *net, const double std) { if(!Calc(0)) return false; double coefs[]; for(int i = 0; i < Q; ++i) { double temp[]; Diff(CC[i].C, temp, true); ArrayCopy(coefs, temp, ArraySize(coefs), 0); } vector t; t.Assign(coefs); matrix data = {}; data.Row(t, 0); data /= std; ...
На основании вектора сеть должна сделать прогноз, но прежде принудительно закрывается имеющаяся открытая позиция — анализ совпадения прежнего и нового направлений здесь не производится. Используемый для закрытия метод ClosePosition будет показан ниже. Затем, по результатам прямого прогона сети, открываем новую позицию в предполагаемом направлении.
ClosePosition();
if(net.feedForward(data))
{
matrix y = net.getResults();
Print("Prediction: ", y[0][0] * std);
OpenPosition((y[0][0] > 0) ? ORDER_TYPE_BUY : ORDER_TYPE_SELL);
return true;
}
return false;
}
Функции OpenPosition и ClosePosition реализованы схожим образом. Приведем только ClosePosition.
bool ClosePosition() { MqlTradeRequest request = {}; if(!PositionSelect(_Symbol)) return false; const string pl = StringFormat("%+.2f", PositionGetDouble(POSITION_PROFIT)); request.action = TRADE_ACTION_DEAL; request.position = PositionGetInteger(POSITION_TICKET); const ENUM_ORDER_TYPE type = (ENUM_ORDER_TYPE)(PositionGetInteger(POSITION_TYPE) ^ 1); request.type = type; request.price = SymbolInfoDouble(_Symbol, type == ORDER_TYPE_BUY ? SYMBOL_ASK : SYMBOL_BID); request.volume = PositionGetDouble(POSITION_VOLUME); request.deviation = 5; request.comment = pl; ResetLastError(); MqlTradeResult result[1]; const bool ok = OrderSend(request, result[0]); Print("Status: ", _LastError, ", P/L: ", pl); ArrayPrint(result); if(ok && (result[0].retcode == TRADE_RETCODE_DONE || result[0].retcode == TRADE_RETCODE_PLACED)) { return true; } return false; }
Настало время для практических исследований. Запустим эксперт в тестере с настройками по умолчанию, на графике XAGUSD,D1, в режиме по ценам открытия. Начальной датой теста поставим 2022.01.01. Это означает, что сразу после старта эксперта сеть начнет обучаться на ценах предыдущего 2021-го года и затем по её сигналам будет торговать. Чтобы видеть график изменения ошибки по эпохам, тестер следует запускать в визуальном режиме.
В журнале появятся записи следующего вида, связанные с обучением НС.
Sufficient bars at: 2022.01.04 00:00:00 Normalization by 3 std: 1.3415995381755823 15 30 30 21 1 EMA for early stopping: 31 (0.062500) Epoch 0 of 1000, loss 2.04525 ma(2.04525) Epoch 121 of 1000, loss 0.31818 ma(0.36230) Epoch 243 of 1000, loss 0.16857 ma(0.18029) Epoch 367 of 1000, loss 0.09157 ma(0.09709) Epoch 479 of 1000, loss 0.06454 ma(0.06888) Epoch 590 of 1000, loss 0.04875 ma(0.05092) Epoch 706 of 1000, loss 0.03659 ma(0.03806) Epoch 821 of 1000, loss 0.03043 ma(0.03138) Epoch 935 of 1000, loss 0.02721 ma(0.02697) Done by epoch limit 1000 with accuracy 0.024416 Training result: 0.024416206367547762 Best result: 0.024416206367547762 Check-up of saved and restored copy: bpnnm202302121707(0.0244162).bpn Loading bpnnm202302121707(0.0244162).bpn [bestLoss] [bestEpoch] [trainingSet] [validationSet] [epochsDone] [0] 0.024 999 250 0 1000 1.3415995381755823 XAGUSD PERIOD_D1 2021.01.18 00:00-2022.01.04 00:00 XAGUSD,XAUUSD,EURUSD 5/250 1000/0.0001 2.0/0 Best result restored: 0.024416206367547762
Пока обратите внимание на величину финальной ошибки. Позднее мы повторим тест с включенным режимом «dropout» разной интенсивности и сравним результаты.
Торговый отчет выглядит таким образом.
Пример отчета торговли по прогнозу
Очевидно, что на большей части 2022 года торговля пошла неудовлетворительно. Однако в левой части, непосредственно после 2021 года, который предоставил обучающую выборку, заметен непродолжительный прибыльный период. Вероятно, закономерности, найденные сетью, продолжали действовать некоторое время. Так ли это, и не следует ли каким-либо образом изменить настройки сети или обучающего набора, чтобы улучшить показатели, — можно выяснить для каждой конкретной торговой системы только в ходе разносторонних исследований. Это большая кропотливая работа, не связанная с внутренней реализацией нейросетевых алгоритмов. Здесь мы ограничимся минимальным анализом.
В журнале нам сообщается название файла с обученной сетью. Введем его в тестере в параметр NetBinFileName, а время тестирования расширим, начав с 2021 года. В таком режиме все входные параметры, кроме двух первых (Symbols и Depth), не имеют значения.
Тестовая торговля на увеличенном интервале показывает следующую динамику баланса (желтым подсвечена обучающая выборка).
Кривая баланса при торговле на расширенном интервале, включая обучающую выборку
Как и следовало ожидать, сеть «научилась» специфике конкретного интервала, но вскоре после его завершения перестает приносить прибыль.
Давайте повторим обучение сети дважды: с «dropout»-ом в размере 25% и 50% (параметр DropOutPercentage должен быть последовательно выставлен в 25, а потом — в 50). Для инициирования обучения новых сетей очистим параметр NetBinFileName, а начало теста вернем на дату 2022.01.01.
При «dropout» 25% получим ошибку заметно больше, чем в первом случае. Но это ожидаемо, так как мы пытаемся за счет огрубления модели расширить её применимость на данные вне выборки (out-of-sample).
Epoch 0 of 1000, loss 2.04525 ma(2.04525) Epoch 125 of 1000, loss 0.46777 ma(0.48644) Epoch 251 of 1000, loss 0.36113 ma(0.36982) Epoch 381 of 1000, loss 0.30045 ma(0.30557) Epoch 503 of 1000, loss 0.27245 ma(0.27566) Epoch 624 of 1000, loss 0.24399 ma(0.24698) Epoch 744 of 1000, loss 0.22291 ma(0.22590) Epoch 840 of 1000, loss 0.19507 ma(0.20062) Epoch 930 of 1000, loss 0.18931 ma(0.19018) Done by epoch limit 1000 with accuracy 0.182581 Training result: 0.18258059873803228
При «dropout» 50% ошибка еще больше увеличивается.
Epoch 0 of 1000, loss 2.04525 ma(2.04525) Epoch 118 of 1000, loss 0.54929 ma(0.55782) Epoch 242 of 1000, loss 0.43541 ma(0.45008) Epoch 367 of 1000, loss 0.38081 ma(0.38477) Epoch 491 of 1000, loss 0.34920 ma(0.35316) Epoch 611 of 1000, loss 0.30940 ma(0.31467) Epoch 729 of 1000, loss 0.29559 ma(0.29751) Epoch 842 of 1000, loss 0.27465 ma(0.27760) Epoch 956 of 1000, loss 0.25901 ma(0.26199) Done by epoch limit 1000 with accuracy 0.251914 Training result: 0.25191436104184456
На следующем изображении совмещены графики обучения в 3-х вариантах.
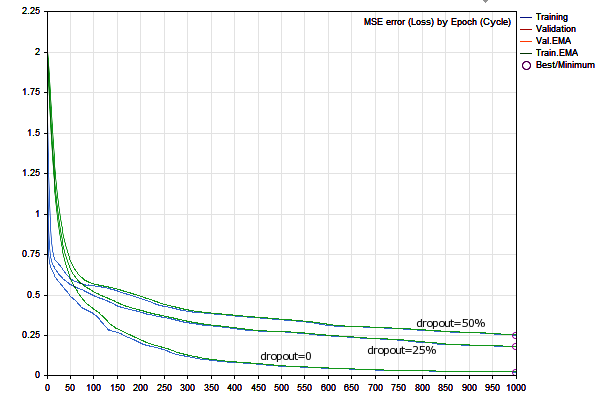
Динамика обучения при различной величине dropout
А вот каковы кривые балансов (желтым подсвечена обучающая выборка).
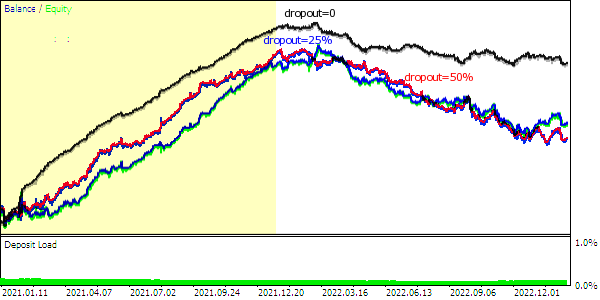
Кривые балансов торговли по прогнозам сетей с разным dropout
Из-за случайного отключения весов при «dropout» линия баланса на обучающем периоде становится не такой гладкой, как на полной сети, и общая прибыль, разумеется, уменьшается.
В данном эксперименте все варианты довольно быстро (в течение месяца-двух) теряют связь с рынком, но суть эксперимента была в проверке созданного нейросетевого инструментария, а не в выработке законченной системы.
В целом, средняя величина «dropout» 25% кажется более оптимальной, потому что меньшая степень регуляризации возвращает нас к переобучению, а бОльшая степень — разрушает вычислительные способности сети. Однако, основной вывод, который мы можем предварительно сделать — нейросетевой подход не является панацеей, способной «вытянуть» любую торговую систему. Причиной неудач могут быть как неверные предположения о наличии конкретных зависимостей, так и в параметрах разных модулей алгоритма и подготовки данных.
Прежде чем отбросить эту (или любую другую ТС) следует попробовать различные способы поиска лучших настроек для сети, как мы обычно делаем для настроек экспертов без ИИ. Для хорошо обусловленных выводов потребуется собрать гораздо больше статистики.
В частности, мы можем искать другие кластеры символов или таймфреймов, запустить оптимизацию по доступным сейчас публичным переменным или расширить их перечень (например, активационными функциями, способами формирования векторов, фильтрацией по дням недели и т.д.).
В этом плане использование НС никоим образом не освобождает трейдера от задачи выдвижения гипотез, проверки идей и значащих факторов. Единственное отличие заключается в том, что оптимизация настроек торговой системы дополняется мета-параметрами НС.
В качестве эксперимента запустим оптимизацию по размеру вектора, количеству векторов, фактору размера скрытых слоев и «dropout». Кроме того, включим в оптимизацию и параметр Randomizer — это позволит для каждого сочетания прочих настроек сгенерировать несколько экземпляров сетей.
- Vector size (Depth) — с 1 по 5
- Training set (Reserve) — с 50 по 400 с шагом 50
- Hidden Layer Factor — с 1 по 5
- DropOut — 0, 25%, 50%
- Randomizer — с 0 по 9
set-файл с настройками прилагается. Интервал дат от 2022.01.01 до 2023.02.15.
Критерием оптимизации выберем, например, Profit Factor, хотя с учетом малого количества сочетаний (6000) и их полного перебора (в отличие от генетики), это не важно.
Анализ результатов оптимизации можно проводить, экспортировав в файл XML или непосредственно из opt-файла, например, как это предлагается в OLAP-программе из статьи Количественный и визуальный анализ отчетов тестера или другими скриптами (opt-формат открыт).
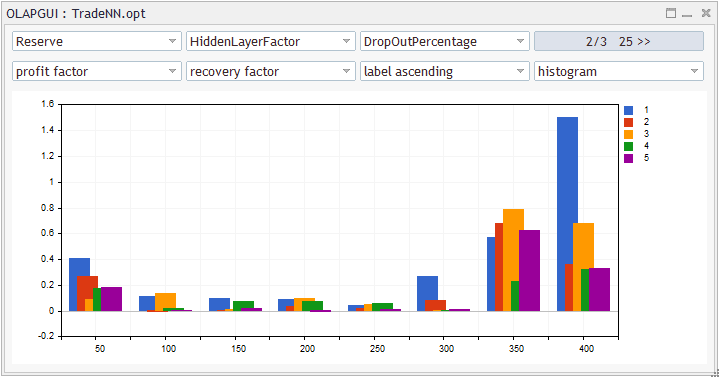
Статистический анализ отчета оптимизации
Для этого скриншота агрегирование показателей в запрошенных разбивках (Reserve по X (горизонтальная ось) относительно HiddenLayerFactor по Y (помечено цветом) при DropOutPercentage 25% по Z) осуществлялось с помощью специфического расчета профит-фактора (по ячейкам в осях X/Y/Z) от фактора восстановления (из каждого прохода тестера в рамках оптимизации). Такая искусственная мера добротности не идеальна, но зато доступна «из коробки».
Аналогичные или более привычные статистики можно рассчитать в Excel.
Статистически более выигрышным является фактор скрытых слоев, равный 1 (а не 2, как было по умолчанию), а размер вектора — равный 4 (вместо 5). При этом рекомендуемая величина «dropout» — 25% или 50%, но не 0%.
Также ожидаемо, более глубокая история предпочтительнее (350 или 400 отсчетов и, вероятно, дальнейшее увеличение оправдано).
Подытожим найденные рабочие настройки:
- Vector size = 4
- Training set = 400
- Hidden Layer Factor = 1
Поскольку в оптимизации был задействован параметр Randomizer, у нас есть 30 экземпляров сетей, обученных в данной конфигурации, — по 10 сетей для каждого уровня «dropout» (0%, 25%, 50%). Нам нужны 25% и 50%. Выгрузив отчет оптимизации в XML, мы можем отфильтровать нужные записи и получим таблицу (сортировка по прибыльности с фильтром больше 1):
Pass Result Profit Expected Profit Recovery Sharpe Custom Equity Trades Depth Reserve Hidden DropOut Randomizer Payoff Factor Factor Ratio DD % LayerF Perc 3838 1.35 336.02 2.41741 1.34991 1.98582 1.20187 1 1.61 139 4 400 1 25 6 838 1.23 234.40 1.68633 1.23117 0.81474 0.86474 1 2.77 139 4 400 1 25 1 3438 1.20 209.34 1.50604 1.20481 0.81329 0.78140 1 2.47 139 4 400 1 50 5 5838 1.17 173.88 1.25094 1.16758 0.61594 0.62326 1 2.76 139 4 400 1 50 9 5038 1.16 167.98 1.20849 1.16070 0.51542 0.60483 1 3.18 139 4 400 1 25 8 3238 1.13 141.35 1.01691 1.13314 0.46758 0.48160 1 2.95 139 4 400 1 25 5 2038 1.11 118.49 0.85245 1.11088 0.38826 0.41380 1 2.96 139 4 400 1 25 3 4038 1.10 107.46 0.77309 1.09951 0.49377 0.38716 1 2.12 139 4 400 1 50 6 1438 1.10 104.52 0.75194 1.09700 0.51681 0.37404 1 1.99 139 4 400 1 25 2 238 1.07 73.33 0.52755 1.06721 0.19040 0.26499 1 3.69 139 4 400 1 25 0 2838 1.03 34.62 0.24907 1.03111 0.10290 0.13053 1 3.29 139 4 400 1 50 4 2238 1.02 21.62 0.15554 1.01927 0.05130 0.07578 1 4.12 139 4 400 1 50 3
Возьмем лучшую, первую строку.
Напомним, что в ходе оптимизации все обученные сети сохраняются в папке MQL5/Files/<имя эксперта>/<дата оптимизации>. В принципе, этого можно не делать, учитывая, что по значению Randomizer можно вновь обучить аналогичную сеть, но только при условии полного соответствия входных данных. Если же история котировок изменится (например, другой брокер), воспроизвести сеть именно с такими характеристиками не получится.
Файлы в указанной папке имеют имена, состоящие из названий и значений оптимизируемых параметров. Поэтому достаточно выполнить поиск в файловой системе:
Depth=4-Reserve=400-HiddenLayerFactor=1-DropOutPercentage=25-Randomizer=6
Допустим, файл имеет имя:
Depth=4-Reserve=400-HiddenLayerFactor=1-DropOutPercentage=25-Randomizer=6-3838(0.428079).bpn
где число в круглых скобках — ошибка сети, число перед скобками — номер прохода.
Заглянем внутрь файла: несмотря на то, что файл бинарный, в его концовке сохранены в виде текста наши мета-данные обучения, в частности указано, что интервал обучения составил 2021.01.12 00:00-2022.07.28 00:00 (400 баров D1).
Скопируем файл под более кратким именем, например, test3838.bpn, в общую папку терминалов.
Введем имя test3838.bpn в параметр NetBinFileName, а в параметр Vector size (Depth) — 4 (все остальные параметры неважны, если работа ведется исключительно в режиме прогнозирования).
Проверим торговлю эксперта на еще более увеличенном периоде: поскольку 2022—2023 год выступил в роли валидационного форвард-теста, захватим 2020 в качестве неизвестного периода.
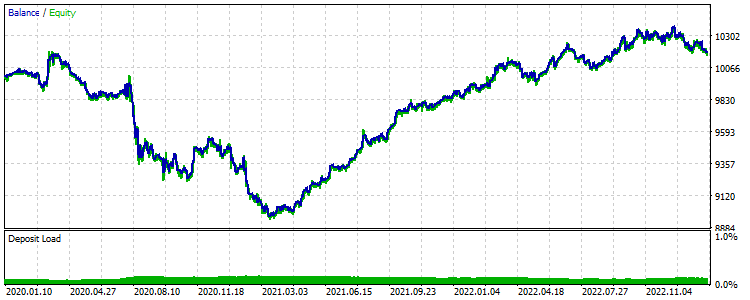
Пример неудачного теста торговли по прогнозам вне обучающей выборки
Чуда не случилось — система убыточна на «новых» данных. Нетрудно убедиться, что подобная картина характерна и для других настроек.
Итак, у нас две новости: хорошая и плохая.
Плохая заключается в том, что предложенная идея не работает — может быть, не работает вообще, а может быть это артефакт ограниченности обследованного пространства факторов в нашем демо-примере (все-таки мы не запускали супер-мега-оптимизацию на миллиарды сочетаний и сотни символов).
А хорошая новость — в том, что предложенный нейросетевой инструментарий позволяет оценивать идеи и выдает ожидаемые (с технической точки зрения) результаты.
Заключение
В данной статье представлены классы нейронных сетей с обратным распространением ошибки на матрицах MQL5. Реализация не требует зависимости от внешних программ, таких как Python, и специальных программно-аппаратных средств (графических ускорителей с поддержкой OpenCL). Помимо штатных режимов обучения и последующей эксплуатации сетей, классы обеспечивают визуализацию процесса, сохранение и восстановление сетей в файлах.
Благодаря подобным классам использование НС довольно легко интегрируется в любую программу, однако следует помнить, что сеть — это лишь инструмент, применяемый к некоторому материалу (в нашем случае: финансовым данным). Если материал не содержит достаточно информации, сильно зашумлен или нерелевантен, никакая нейронная сеть, не сможет найти в нем грааль.
Алгоритм обратного распространения ошибки является одним из наиболее распространенных базовых методов обучения, на основе которого можно конструировать более сложные нейросетевые технологии: рекуррентные сети, сверточные сети, обучение с подкреплением.
Метод обратного распространения ошибки — метод обучения многослойного перцептрона. Впервые метод был описан в 1974 г. Полем Дж. Вербосом[1], а также независимо и одновременно А. И. Галушкиным[2]. Далее существенно развит в 1986 г. Дэвидом И. Румельхартом, Дж. Е. Хинтоном и Рональдом Дж. Вильямсом[3] и независимо и одновременно С. И. Барцевым и В. А. Охониным (Красноярская группа)[4]. Это итеративный градиентный алгоритм, который используется с целью минимизации ошибки работы многослойного перцептрона и получения желаемого выхода.
Основная идея этого метода состоит в распространении сигналов ошибки от выходов сети к её входам, в направлении, обратном прямому распространению сигналов в обычном режиме работы. Барцев и Охонин предложили сразу общий метод («принцип двойственности»), приложимый к более широкому классу систем, включая системы с запаздыванием, распределённые системы, и т. п.[5]
Для возможноcти применения метода обратного распространения ошибки передаточная функция нейронов должна быть дифференцируема.
Cигмоидальные функции активации[]
Наиболее часто в качестве функций активации используются следующие виды сигмоид:
Функция Ферми (экспоненциальная сигмоида):

Рациональная сигмоида:

Гиперболический тангенс:

где s — выход сумматора нейрона, 
Менее всего, сравнительно с другими сигмоидами, процессорного времени требует расчет рациональной сигмоиды. Для вычисления гиперболического тангенса требуется больше всего тактов работы процессора. Если же сравнивать с пороговыми функциями активациями, то сигмоиды расчитываются очень медленно. Если после суммирования в пороговой функции сразу можно начинать сравнение с определенной величиной (порогом), то в случае сигмоидальной функции активации — нужно расчитать сигмоид (затратить время в лучшем случае на три операции: взятие модуля, сложение и деление), и только потом сравнивать с пороговой величиной (например, нулем). Если считать, что все простейшие операции расчитываются процессором за примерно одинаковое время, то работа сигмоидальной функции активации после произведенного суммирования (которое займет одинаковое время) будет медленее пороговой функции активации как 1:4.
Функция оценки работы сети[]
В тех случаях, когда удается оценить работу сети обучение нейронных сетей можно представить как задачу оптимизации. Оценить — означает указать количественно хорошо или плохо сеть решает поставленные ей задачи. Для этого строится функция оценки. Она, как правило, явно зависит от выходных сигналов сети и неявно (через функционирование) — от всех ее параметров. Простейший и самый распространенный пример оценки — сумма квадратов расстояний от выходных сигналов сети до их требуемых значений:

где 
Метод наименьших квадратов далеко не всегда является лучшим выбором оценки. Тщательное конструирование функции оценки позволяет на порядок поысить эффективность обучения сети, а также получать дополнительную информацию — «уровень уверенности» сети в даваемом ответе[6].
Описание алгоритма[]
Файл:Neuro.PNG Архитектура многослойного перцептрона
Алгоритм обратного распространения ошибки применяется для многослойного перцептрона. У сети есть входы 





Как модифицировать веса? Мы будем реализовывать стохастический градиентный спуск, то есть будем подправлять веса после каждого тестового примера. Нам нужно двигаться в сторону, противоположную градиенту, то есть добавлять к каждому весу 

где

Производная считается следующим образом. Пусть сначала 



Аналогично, 


Если же j-й узел — не на последнем уровне, то у него есть выходы; обозначим их через Children(j). В этом случае

и

Ну а 



поправок алгоритм называется алгоритмом обратного распространения ошибки (backpropagation). Краткое резюме проделанной работы:
- для узла последнего уровня

- для внутреннего узла сети

- для всех узлов

Получающийся алгоритм представлен ниже. На вход алгоритму, кроме указанных параметров, нужно также подавать в каком-нибудь формате структуру сети. На практике очень хорошие результаты показывают сети достаточно простой структуры, состоящие из двух уровней нейронов — скрытого уровня (hidden units) и нейронов-выходов (output units); каждый вход сети соединен со всеми скрытыми нейронами, а результат работы каждого скрытого нейрона подается на вход каждому из нейронов-выходов. В таком случае достаточно подавать на вход количество нейронов скрытого уровня.
Алгоритм[]
Алгоритм:
BackPropagation 
- Инициализировать
маленькими случайными значениями.
- Повторить NUMBER_OF_STEPS раз:
- Для всех d от 1 до m:
- Подать
на вход сети и подсчитать выходы
каждого узла.
- Для всех
.
- Для каждого уровня l, начиная с предпоследнего:
- Для каждого узла j уровня l вычислить
.
- Для каждого ребра сети {i, j}
.
- Выдать значения
.
Математическая интерпретация обучения нейронной сети[]
На каждой итерации алгоритма обратного распространения весовые коэффициенты нейронной сети модифицируются так, чтобы улучшить решение одного примера. Таким образом, в процессе обучения циклически решаются однокритериальные задачи оптимизации.
Обучение нейронной сети характеризуется четырьмя специфическими ограничениями, выделяющих обучение нейросетей из общих задач оптимизации: астрономическое число параметров, необходимость высокого параллелизма при обучении, многокритериальность решаемых задач, необходимость найти достаточно широкую область, в которой значения всех минимизируемых функций близки к минимальным. В остальном проблему обучения можно, как правило, сформулировать как задачу минимизации оценки. Осторожность предыдущей фразы («как правило») связана с тем, что на самом деле нам неизвестны и никогда не будут известны все возможные задачи для нейронных сетей, и, быть может, где-то в неизвестности есть задачи, которые несводимы к минимизации оценки. Минимизация оценки — сложная проблема: параметров астрономически много (для стандартных примеров, реализуемых на РС — от 100 до 1000000), адаптивный рельеф (график оценки как функции от подстраиваемых параметров) сложен, может содержать много локальных минимумов.
Недостатки алгоритма[]
Несмотря на многочисленные успешные применения обратного распространения, оно не является панацеей. Больше всего неприятностей приносит неопределенно долгий процесс обучения. В сложных задачах для обучения сети могут потребоваться дни или даже недели, она может и вообще не обучиться. Причиной может быть одна из описанных ниже.
Паралич сети[]
В процессе обучения сети значения весов могут в результате коррекции стать очень большими величинами. Это может привести к тому, что все или большинство нейронов будут функционировать при очень больших значениях OUT, в области, где производная сжимающей функции очень мала. Так как посылаемая обратно в процессе обучения ошибка пропорциональна этой производной, то процесс обучения может практически замереть. В теоретическом отношении эта проблема плохо изучена. Обычно этого избегают уменьшением размера шага η, но это увеличивает время обучения. Различные эвристики использовались для предохранения от паралича или для восстановления после него, но пока что они могут рассматриваться лишь как экспериментальные.
Локальные минимумы[]
Обратное распространение использует разновидность градиентного спуска, то есть осуществляет спуск вниз по поверхности ошибки, непрерывно подстраивая веса в направлении к минимуму. Поверхность ошибки сложной сети сильно изрезана и состоит из холмов, долин, складок и оврагов в пространстве высокой размерности. Сеть может попасть в локальный минимум (неглубокую долину), когда рядом имеется гораздо более глубокий минимум. В точке локального минимума все направления ведут вверх, и сеть неспособна из него выбраться. Статистические методы обучения могут помочь избежать этой ловушки, но они медленны.
Размер шага[]
Внимательный разбор доказательства сходимости[3] показывает, что коррекции весов предполагаются бесконечно малыми. Ясно, что это неосуществимо на практике, так как ведет к бесконечному времени обучения. Размер шага должен браться конечным, и в этом вопросе приходится опираться только на опыт. Если размер шага очень мал, то сходимость слишком медленная, если же очень велик, то может возникнуть паралич или постоянная неустойчивость. П. Д. Вассерман[7] описал адаптивный алгоритм выбора шага, автоматически корректирующий размер шага в процессе обучения. В книге А. Н. Горбаня[8] предложена разветвлённая технология оптимизации обучения.
См. также[]
- Сигмоид
- Многослойный перцептрон
Литература[]
- Уоссермен Ф. Нейрокомпьютерная техника: Теория и практика. — М.: «Мир», 1992.
- Хайкин С. Нейронные сети: Полный курс. Пер. с англ. Н. Н. Куссуль, А. Ю. Шелестова. 2-е изд., испр. — М.: Издательский дом Вильямс, 2008, 1103 с.
Внешние ссылки[]
- Копосов А.И., Щербаков И.Б., Кисленко Н.А., Кисленко О.П., Варивода Ю.В. и др. Отчет по научно-исследовательской работе «Создание аналитического обзора информационных источников по применению нейронных сетей для задач газовой технологии». — Москва: ВНИИГАЗ, 1995.
- Миркес Е. М., Нейроинформатика: Учеб. пособие для студентов с программами для выполнения лабораторных работ. Красноярск: ИПЦ КГТУ, 2002, 347 с. Рис. 58, табл. 59, библиогр. 379 наименований. ISBN 5-7636-0477-6
Примечания[]
- ↑ Werbos P. J., Beyond regression: New tools for prediction and analysis in the behavioral sciences. Ph.D. thesis, Harvard University, Cambridge, MA, 1974.
- ↑ Галушкин А. И. Синтез многослойных систем распознавания образов. — М.: «Энергия», 1974.
- ↑ 3,0 3,1 Rumelhart D.E., Hinton G.E., Williams R.J., Learning Internal Representations by Error Propagation. In: Parallel Distributed Processing, vol. 1, pp. 318—362. Cambridge, MA, MIT Press. 1986.
- ↑ Барцев С. И., Охонин В. А. Адаптивные сети обработки информации. Красноярск : Ин-т физики СО АН СССР, 1986. Препринт N 59Б. — 20 с.
- ↑ Барцев С. И., Гилев С. Е., Охонин В. А., Принцип двойственности в организации адаптивных сетей обработки информации, В кн.: Динамика химических и биологических систем. — Новосибирск: Наука, 1989. — С. 6-55.
- ↑ Миркес Е. М., — Новосибирск: Наука, Сибирская издательская фирма РАН, 1999. — 337 с. ISBN 5-02-031409-9 Другие копии онлайн: [1]
- ↑ Wasserman P. D. Experiments in translating Chinese characters using backpropagation. Proceedings of the Thirty-Third IEEE Computer Society International Conference.. — Washington: D. C.: Computer Society Press of the IEEE, 1988.
- ↑ Горбань А. Н. Обучение нейронных сетей.. — Москва: СП ПараГраф, 1990.
Главное отличие
и преимущество нейросетей перед
классическими средствами прогнозирования
и классификации заключается в их
способности к обучению. Так что же такое
обучение нейросетей?
На этапе
обучения происходит вычисление
синаптических коэффициентов в процессе
решения нейронной сетью задач, в которых
нужный ответ определяется не по правилам,
а с помощью примеров, сгруппированных
в обучающие множества. Так что нейросеть
на этапе обучения сама выполняет роль
эксперта в процессе подготовки данных
для построения экспертной системы.
Предполагается, что правила находятся
в структуре обучающих данных.
Для
обучения нейронной сети требуются
обучающие данные. Они должны отвечать
свойствам представительности и
случайности или последовательности.
Все зависит от класса решаемой задачи.
Такие данные представляют собой ряды
примеров с указанием для каждого из них
значением выходного параметра, которое
было бы желательно получить. Действия,
которые при этом происходят, можно
назвать контролируемым обучением:
«учитель» подаем на вход сети вектор
исходных данных, а на выходной узел
сообщает желаемое значение результата
вычислений.
Контролируемое
обучение нейросети можно рассматривать
как решение оптимизационной задачи. Ее
целью является минимизация функции
ошибок Е на данном множестве примеров
путем выбора значений весов W. Достижение
минимума называется сходимостью процесса
обучения. Именно возможность этого и
доказал Розенблатт.
Поскольку
ошибка зависит от весов нелинейно,
получить решение в аналитической форме
невозможно, и поиск глобального минимума
осуществляется посредством итерационного
процесса- так называемого обучающего
алгоритма. Разработано уже более сотни
разных обучающих алгоритмов, отличающихся
друг от друга стратегией оптимизации
и критерием ошибок. Обычно в качестве
меры погрешности берется средняя
квадратичная ошибка (СКО):
где М – число
примеров в обучающем множестве.
Минимизация величины Е осуществляется
с помощью градиентных методов. Изменение
весов происходит в направлении, обратном
к направлению наибольшей крутизны для
функции:
Здесь e —
определяемый пользователем параметр,
который называется коэффициентом
обучения.
Обратное
распространение ошибки
Одним из самых
распространенных алгоритмов обучения
нейросетей прямого распространения
является алгоритм обратного распространения
ошибки (BackPropagation, BP). Этот алгоритм был
переоткрыт и популяризован в 1986 г.
Румельхартом и МакКлелландом из группы
по изучению параллельных распределенных
процессов в Массачусетском технологическом
институте. Здесь я хочу подробно изложить
математическую суть алгоритма, так как
очень часто в литературе ссылаются на
какой-то факт или теорему, но никто не
приводит его доказательства или
источника. Честно говоря, то же самое
относится к Теореме об отображении
нейросетью любой функциональной
зависимости, на которой основываются
все попытки применить нейросети к
моделированию реальных процессов. Я бы
хотел посмотреть на ее доказательство,
но еще нигде его не смог найти. Вот, чтобы
у Вас не возникало такого чувства
неудовлетворенности в полноте понимания
работы нейросети, я решил привести этот
алгоритм полностью, хотя честно сознаюсь,
что не совсем понимаю его логику.
Итак,
это алгоритм градиентного спуска,
минимизирующий суммарную квадратичную
ошибку:
Здесь индекс i
пробегает все выходы многослойной сети.
Основная идея ВР состоит в том,
чтобы вычислять чувствительность ошибки
сети к изменениям весов. Для этого нужно
вычислить частные производные от ошибки
по весам. Пусть обучающее множество
состоит из Р образцов, и входы k-го образца
обозначены через {xi k}. Вычисление частных
производных осуществляется по правилу
цепи: вес входа i-го нейрона, идущего от
j-го нейрона, пересчитывается по формуле:
где e — длина шага
в направлении, обратном к градиенту.
Если рассмотреть отдельно k-тый
образец, то соответствующиее изменение
весов равно:
Множитель
«эпсилан ik» вычисляется через
аналогичные множители из последующего
слоя, и ошибка, таким образом, передается
в обратном направлении.
Для выходных
элементов получим:
Для скрытых
элементов множитель «эпсилан ik»
определяется так:
где индекс h
пробегает номера всех нейронов, на
которые воздействует i-ый нейрон.
Чтобы
наглядно представить себе алгоритм
обратного распространения ошибки, можно
посмотреть следующий рисунок 7:
Соседние файлы в предмете [НЕСОРТИРОВАННОЕ]
- #
- #
- #
- #
- #
- #
- #
- #
- #
- #
- #