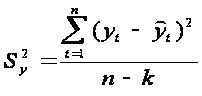Нормальность распределения ошибок

Тестирование данных на нормальность часто является первым этапом их анализа, так как большое количество статистических методов исходит из предположения нормальности распределения изучаемых данных.

Например, пусть необходимо проверить гипотезу о равенстве средних значений в двух независимых выборках. Для этой цели подходит критерий Стьюдента. Но применение критерия Стьюдента обосновано, только если данные подчиняются нормальному распределению. Поэтому перед применением критерия необходимо проверить гипотезу о нормальности исходных данных. Или проверка остатков линейной регрессии на нормальность — позволяет проверить, соответствует ли применяемая модель регрессии исходным данным.

Нормальное распределение естественным образом возникает практически везде, где речь идёт об измерении с ошибками. Более того, в силу центральной предельной теоремы, распределение многих выборочных величин (например, выборочного среднего) при достаточно больших объёмах выборки хорошо аппроксимируется нормальным распределением вне зависимости от того, какое распределение было у выборки исходно. В связи с этим становится понятным, почему проверке распределения на нормальность стоит уделить особое внимание. В дальнейшем речь пойдёт о так называемых критериях согласия (goodness-of-fit tests). Проверяться будет не просто факт согласия с нормальным распределением с определёнными фиксированными значениями параметров, а несколько более общий факт принадлежности распределения к семейству нормальных распределений со всевозможными значениями параметров.

Проверку выборки на нормальность можно производить несколькими путями. Для начала можно вспомнить, какой вид у графика нормального распределения (гистограмма, график плотности и т.п.), как в нормальном распределении соотносятся среднее, мода, медиана, какими должны быть асимметрия и эксцесс, выполняется ли «правило 3-х сигм». Про всё это мы писали в статье про нормальное распределение. Вот с помощью такой описательной статистики можно оценить выборку на нормальность (обычно приемлемо отклонение на порядок ошибки рассчитываемого параметра). Вторая группа методов — критерии нормальности.

Критерии нормальности

Список критериев нормальности:

  • Критерий Шапиро-Уилка
  • Критерий асимметрии и эксцесса
  • Критерий Дарбина
  • Критерий Д’Агостино
  • Критерий Васичека
  • Критерий Дэвида-Хартли-Пирсона
  • Критерий хи-квадрат
  • Критерий Андерсона-Дарлинга
  • Критерий Филлибена
  • Критерий Колмогорова-Смирнова
  • Критерий Мартинса-Иглевича
  • Критерий Лина-Мудхолкара
  • Критерий Шпигельхальтера
  • Критерий Саркади
  • Критерий Смирнова-Крамера-фон Мизеса
  • Критерий Локка-Спурье
  • Критерий Оя
  • Критерий Хегази-Грина
  • Критерий Муроты-Такеучи

Подробно эти критерии с формулами и таблицами можно посмотреть здесь.

Проверка на нормальность в R (источник)

Самый простой графический способ проверки характера распределения данных — построение гистограммы (с помощью функции hist() — это сделать несложно). Если гистограмма имеет колоколообразный симметричный вид, можно сделать заключение о том, что анализируемая переменная имеет примерно нормальное распределение. Однако при интерпретации гистограмм следует соблюдать осторожность, поскольку их внешний вид может сильно зависеть как от числа наблюдений, так и от шага, выбранного для разбиения данных на классы.

норм распределение

Другим очень часто используемым графическим способом проверки характера распределения данных является построение т.н. графиков квантилей (Q-Q plots, Quantile-Quantile plots). На таких графиках изображаются квантили двух распределений — эмпирического (т.е. построенного по анализируемым данным) и теоретически ожидаемого стандартного нормального распределения. При нормальном распределении проверяемой переменной точки на графике квантилей должны выстраиваться в прямую линию, исходящую под улом 45 градусов из левого нижнего угла графика. Графики квантилей особенно полезны при работе с небольшими по размеру совокупностями, для которых невозможно построить гистограммы, принимающие какую-либо выраженную форму.

В R для построения графиков квантилей можно использовать базовую функцию qqnorm(), которая в качестве основного аргумента принимает вектор со значениями анализируемой переменной.

x <- rnorm(500) # генерация нормально распределенной совокупности с n = 500
qqnorm(x)

qq plot

Следует отметить, что интерпретация графиков квантилей при работе с небольшими выборками, происходящими из нормально распределенных генеральных совокупностей, требует определенного навыка. Дело в том, что при небольшом числе наблюдений точки на графике квантилей могут не всегда образовывать четко выраженную прямую линию. В качестве иллюстрации этого утверждения на следующем рисунке приведены графики квантилей для 5 случайным образом сгенерированных нормально распределенных выборок по 20 наблюдений каждая (если использованный в примере пакет DAAG у Вас не установлен, выполните команду install.packages(«DAAG»)):

library(DAAG)
qreference(m = 20, seed = 145, nrep = 5, nrows = 1)

квантили

Фигура, в которую выстраиваются точки на некоторых графиках далека от прямой линии. Причина данного эффекта — в небольшом объеме наблюдений.

Тесты проверки на нормальность в R

Существует целый ряд статистических тестов, специально разработанных для проверки нормальности распределения данных. В общем виде проверяемую при помощи этих тестов нулевую гипотезу можно сформулировать так: «Анализируемая выборка происходит из генеральной совокупности, имеющей нормальное распределение». Если получаемая при помощи того или иного теста вероятность ошибки Р оказывается меньше некоторого заранее принятого уровня значимости (например, 0.05), нулевая гипотеза отклоняется.

В R реализованы практически все имеющиеся тесты на нормальность — либо в виде стандарных функций, либо в виде функций, входящих в состав отдельных пакетов. Примером базовой функции является shapiro.test(), при помощи которой можно выполнить широко используемый тест Шапиро-Уилка:

shapiro.test(rnorm(500))
Shapiro-Wilk normality test
data: rnorm(500)
W = 0.9978, p-value = 0.7653 # P > 0.05 - нулевая гипотеза не отвергается

Основные классические критерии проверки на нормальность собраны в пакете nortest. Пакет можно установить с CRAN при помощи вызова функции install.packages():

> install.packages(pkgs=c("nortest"))

Подключить установленный пакет можно при помощи функции library():

> library(nortest)

Может возникнуть вопрос: «А зачем столько много разных критериев для проверки одного факта? Нельзя ли выбрать наилучший и всегда его использовать?». Ответ на этот вопрос не утешителен: «В общем случае, к сожалению, нельзя».

Критерий Лиллифорса

Критерий Лиллифорса (Lilliefors) является вариантом известного классического критерия Колмогорова-Смирнова, специально модифицированного для проверки нормальности. Эта модификация существенна. Для проверки гипотезы нормальности нельзя использовать классический непараметрический критерий Колмогорова-Смирнова, реализованный в функции ks.test(). Критерий Лиллифорса реализован в функции lillie.test():

> lillie.test(rnorm(100, mean = 6, sd = 4));
Lilliefors (Kolmogorov-Smirnov) normality test
data: rnorm(100, mean = 6, sd = 4)
D = 0.0463, p-value = 0.8621
> lillie.test(runif(100, min = 2, max = 4));
Lilliefors (Kolmogorov-Smirnov) normality test
data: runif(100, min = 2, max = 4)
D = 0.0732, p-value = 0.2089

Критерии Крамера-фон Мизеса и Андерсона-Дарлинга

Эти критерии менее известны, но обычно работают гораздо лучше, нежели критерий Лиллифорса. Они реализованы в функциях cvm.test() и ad.test() соответственно:

> cvm.test(rnorm(50, mean = 6, sd = 4));
Cramer-von Mises normality test
data: rnorm(50, mean = 6, sd = 4)
W = 0.0321, p-value = 0.8123
> ad.test(runif(50, min = 2, max = 4));
Anderson-Darling normality test
data: runif(50, min = 2, max = 4)
A = 1.5753, p-value = 0.0004118

Критерий Шапиро-Франсиа

Этот критерий работает достаточно хорошо в большинстве не очень «сложных» случаев. Получить p-значение можно посредством функции sf.test():

> sf.test(rexp(50, rate = 2));
Shapiro-Francia normality test
data: rexp(50, rate = 2)
W = 0.7803, p-value = 2.033e-06

Критерий хи-квадрат Пирсона

В отличие от задач проверки пропорций, критерий хи-квадрат обычно очень плохо работает в задачах проверки распределения на нормальность. Вероятность ошибки второго рода очень велика для достаточно широкого класса альтернативных распределений. В связи с этим, использовать его не рекомендуется. Тем не менее реализация его предоставлена функцией pearson.test(). У этой функции есть булевская опция adjusted, которая позволяет внести поправки в p-значение из-за наличия двух неизвестных параметров. Рекомендуемая последовательность действий такая: получить два p-значения, одно, соответствующее adjusted=TRUE, второе — adjusted=FALSE. Истинное p-значение обычно находится между. Кроме того, полезно поварьировать объем выборки и посмотреть, насколько сильно меняется p-значение. Если влияние объёма выборки сильное, то от использования критерия стоит отказаться во избежание ошибок.

> pearson.test(rnorm(50, mean = 6, sd = 4));
Pearson chi-square normality test
data: rnorm(50, mean = 6, sd = 4)
P = 5.2, p-value = 0.6356
> pearson.test(runif(50, min = -1, max = 1));
Pearson chi-square normality test
data: runif(50, min = -1, max = 1)
P = 7.6, p-value = 0.3692

Дополнительнаая информация: проверка на нормальность

Источник

  1. Предположение о нормальном распределении случайной ошибки в рамках классической линейной регрессии и его следствия.

Предложение
об ошибках в классической модели
формируются наиболее жестким и не всегда
реалистичным путем:

Предполагается,
что ошибка (

(
= 1 … N))
образует так называемый слабый белый
шум – последовательность центрированных
(
)
и не коррелированных случайных величин
с одинаковыми дисперсиями

Свойство
центрированности практически не является
ограничением, так как при наличии
постоянного регрессора среднее значение
ошибки можно было бы включить в
соответствующий коэффициент (
)В
ряде случаев сделанные предложения об
ошибках будут дополняться свойствами
нормальности – случайный вектор 
имеет нормальное распределение. Эту
модель мы будем называть классической
моделью с нормально распределительными
ошибками.

Многомерное
нормальное распределение задается
своим вектором и матрицей ковариации
– здесь она имеет вид

,
где 1 – единичная матрица. Если компоненты
вектора корелированы, следовательно,
автоматически независимы, следовательно,
ошибки в модели образуют последовательность
независимых одинаково нормально
распределенных случайных величин N
(0;
).Если
каждая из величин

нормально
распределена, то вектор ,
из них составленный, ну обязан быть
нормально распределенным.

  1. Доверительные
    интервалы оценок параметров и проверка
    гипотез об их значимости    .

Доверительные
интервалы параметров регрессии
определяются следующим образом.

Здесь
td
— значение t-статистики
для выбранного уровня значимости d.
Величина p=1-d
называется
доверительной вероятностью или уровнем
надежности, нередко выражаемым в
процентах. Это показатель, характеризует
вероятность того, что теоретическое
значение параметра регрессии будет
находиться в полученном доверительном
интервале.

С
лекции:

=b0
– b1*X1
– это случайные величины, поэтому
необходимо найти доверительные интервалы
для истинных значений b0
и b1.

Bi
принадлежит (bi
+- дельта bi),
где дельта bi
= Sbi*tкрит

B0
принадлежит ( b0
+- Sb0
* t
крит)

B1
принадлжет (b1
+- Sb1
* t
крит)

  1. Прогнозирование по регрессионной модели и его точность. Доверительные и интервалы прогноза (с лекции)

 Мы получили
регрессионную математическую модель
и можем прогнозировать процесс путем
вычислений. Основным   фактором   в   прогнозировании   чаще   всего   оказывается   трендовая
компонента. Он особен давать достаточно
надежные прогнозы и на 4-5
шагов,следовательно,идёт расчет оценок
среднесрочных и долгосрочных прогнозов.

Линейный
метод наименьших квадратов позволяет
по серии наблюдений Xi и Yi установить
параметры линейного уравнения вида

где Yc,i –
расчетное значение отклика при заданном
моменте времени Xi, а b0 и b1 —
параметры линейной модели.

Для
оценки(проверки) прогноза возможны след
способы: 1)По реальным прогнозируемым
данным. 2)Построение точечного и
интервального прогноза.

P
(прогноз)
= b0+b1*Xp

Дельта
(предельная
ошибка) = t
критич * S
р

Доверительный
интервал, учитывающий неопределенность,
связанную с положением тренда, и
возможность отклонения от этого тренда,
определяется в виде:

где
n — длина временного ряда; L -период
упреждения; yn+L -точечный прогноз на
момент n+L; ta- значение t-статистики
Стьюдента; Sp- средняя квадратическая
ошибка прогноза. Предположим, что тренд
характеризуется прямой:

Так
как оценки параметров определяются по
выборочной совокупности, представленной
временным рядом, то они содержат
погрешность.

Тогда
доверительный интервал можно представить
в виде:

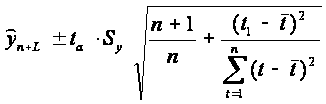
Дисперсия
отклонений фактических наблюдений от
расчетных определяется выражением:


 где yt-
фактические значения уровней ряда,

Соседние файлы в предмете [НЕСОРТИРОВАННОЕ]

  • #
  • #
  • #
  • #
  • #
  • #
  • #
  • #
  • #
  • #
  • #
Источник

$begingroup$

The Wikipedia page on ANOVA lists three assumptions, namely:

  • Independence of cases – this is an assumption of the model that simplifies the statistical analysis.
  • Normality – the distributions of the residuals are normal.
  • Equality (or «homogeneity») of variances, called homoscedasticity…

Point of interest here is the second assumption. Several sources list the assumption differently. Some say normality of the raw data, some claim of residuals.

Several questions pop up:

  • are normality and normal distribution of residuals the same person (based on Wikipedia entry, I would claim normality is a property, and does not pertain residuals directly (but can be a property of residuals (deeply nested text within brackets, freaky)))?
  • if not, which assumption should hold? One? Both?
  • if the assumption of normally distributed residuals is the right one, are we making a grave mistake by checking only the histogram of raw values for normality?

kjetil b halvorsen's user avatar

asked Jan 18, 2011 at 19:07

Roman Luštrik's user avatar

Roman LuštrikRoman Luštrik

3,3684 gold badges32 silver badges39 bronze badges

$endgroup$

5

$begingroup$

Let’s assume this is a fixed effects model. (The advice doesn’t really change for random-effects models, it just gets a little more complicated.)

First let us distinguish the «residuals» from the «errors:» the former are the differences between the responses and their predicted values, while the latter are random variables in the model. With sufficiently large amounts of data and a good fitting procedure, the distributions of the residuals will approximately look like the residuals were drawn randomly from the error distribution (and will therefore give you good information about the properties of that distribution).

The assumptions, therefore, are about the errors, not the residuals.

  1. No, normality (of the responses) and normal distribution of errors are not the same. Suppose you measured yield from a crop with and without a fertilizer application. In plots without fertilizer the yield ranged from 70 to 130. In two plots with fertilizer the yield ranged from 470 to 530. The distribution of results is strongly non-normal: it’s clustered at two locations related to the fertilizer application. Suppose further the average yields are 100 and 500, respectively. Then all residuals range from -30 to +30, and so the errors will be expected to have a comparable distribution. The errors might (or might not) be normally distributed, but obviously this is a completely different distribution.

  2. The distribution of the residuals matters, because those reflect the errors, which are the random part of the model. Note also that the p-values are computed from F (or t) statistics and those depend on residuals, not on the original values.

  3. If there are significant and important effects in the data (as in this example), then you might be making a «grave» mistake. You could, by luck, make the correct determination: that is, by looking at the raw data you will seeing a mixture of distributions and this can look normal (or not). The point is that what you’re looking it is not relevant.

ANOVA residuals don’t have to be anywhere close to normal in order to fit the model. However, unless you have an enormous amount of data, near-normality of the residuals is essential for p-values computed from the F-distribution to be meaningful.

answered Jan 18, 2011 at 19:45

whuber's user avatar

$endgroup$

16

$begingroup$

Standard Classical one-way ANOVA can be viewed as an extension to the classical «2-sample T-test» to an «n-sample T-test». This can be seen from comparing a one-way ANOVA with only two groups to the classical 2-sample T-test.

I think where you are getting confused is that (under the assumptions of the model) the residuals and the raw data are BOTH normally distributed. However the raw data consist of normal distributions with different means (unless all the effects are exactly the same) but the same variance. The residuals on the other hand have the same normal distribution. This comes from the third assumption of homoscedasticity.

This is because the normal distribution is decomposable into a mean and variance components. If $Y_{ij}$ has a normal distribution with mean $mu_{j}$ and variance $sigma^2$ can be written as $Y_{ij}=mu_{j}+sigmaepsilon_{ij}$ where $epsilon_{ij}$ has a standard normal distribution.

While ANOVA is derivable from the assumption of normality, I think (but am unsure) it can be replaced by an assumption of linearity (along the Best Linear Unbiased Estimator (BLUE) lines of estimation, where «BEST» is interpreted as minimum mean square error). I believe this basically involves replacing the distribution for $epsilon_{ij}$ with any mutually independent distribution (over all i and j) which has mean 0 and variance 1.

In terms of looking at your raw data, it should look normal when plotted separately for each factor level in your model. This means plotting $Y_{ij}$ for each j on a separate graph.

answered Jan 18, 2011 at 23:06

probabilityislogic's user avatar

$endgroup$

3

$begingroup$

In the one-way case with $p$ groups of size $n_{j}$:
$F = frac{SS_{b} / df_{b}}{SS_{w} / df_{w}}$ where

$SS_{b} = sum_{j=1}^{p}{n_{j} (M — M_{j}})^{2}$ and

$SS_{w} = sum_{j=1}^{p}sum_{i=1}^{n_{j}}{(y_{ij} — M_{j})^{2}}$

$F$ follows an $F$-distribution if $SS_{b} / df_{b}$ and $SS_{w} / df_{w}$ are independent, $chi^{2}$-distributed variables with $df_{b}$ and $df_{w}$ degrees of freedom, respectively. This is the case when $SS_{b}$ and $SS_{w}$ are the sum of squared independent normal variables with mean $0$ and equal scale. Thus $M-M_{j}$ and $y_{ij}-M_{j}$ must be normally distributed.

$y_{i(j)} — M_{j}$ is the residual from the full model ($Y = mu_{j} + epsilon = mu + alpha_{j} + epsilon$), $y_{i(j)} — M$ is the residual from the restricted model ($Y = mu + epsilon$). The difference of these residuals is $M — M_{j}$.

EDIT to reflect clarification by @onestop: under $H_{0}$ all true group means are equal (and thus equal to $M$), thus normality of the group-level residuals $y_{i(j)} — M_{j}$ implies normality of $M — M_{j}$ as well. The DV values themselves need not be normally distributed.

answered Jan 18, 2011 at 20:01

caracal's user avatar

caracalcaracal

11.7k53 silver badges66 bronze badges

$endgroup$

2

Источник

Многие статистические тесты требуют, чтобы одна или несколько переменных были нормально распределены , чтобы результаты теста были надежными.

В этом руководстве объясняется несколько методов, которые вы можете использовать для проверки нормальности переменных в Stata.

Для каждого из этих методов мы будем использовать встроенный набор данных Stata с именем auto.Вы можете загрузить этот набор данных с помощью следующей команды:

сисус авто

Метод 1: гистограммы

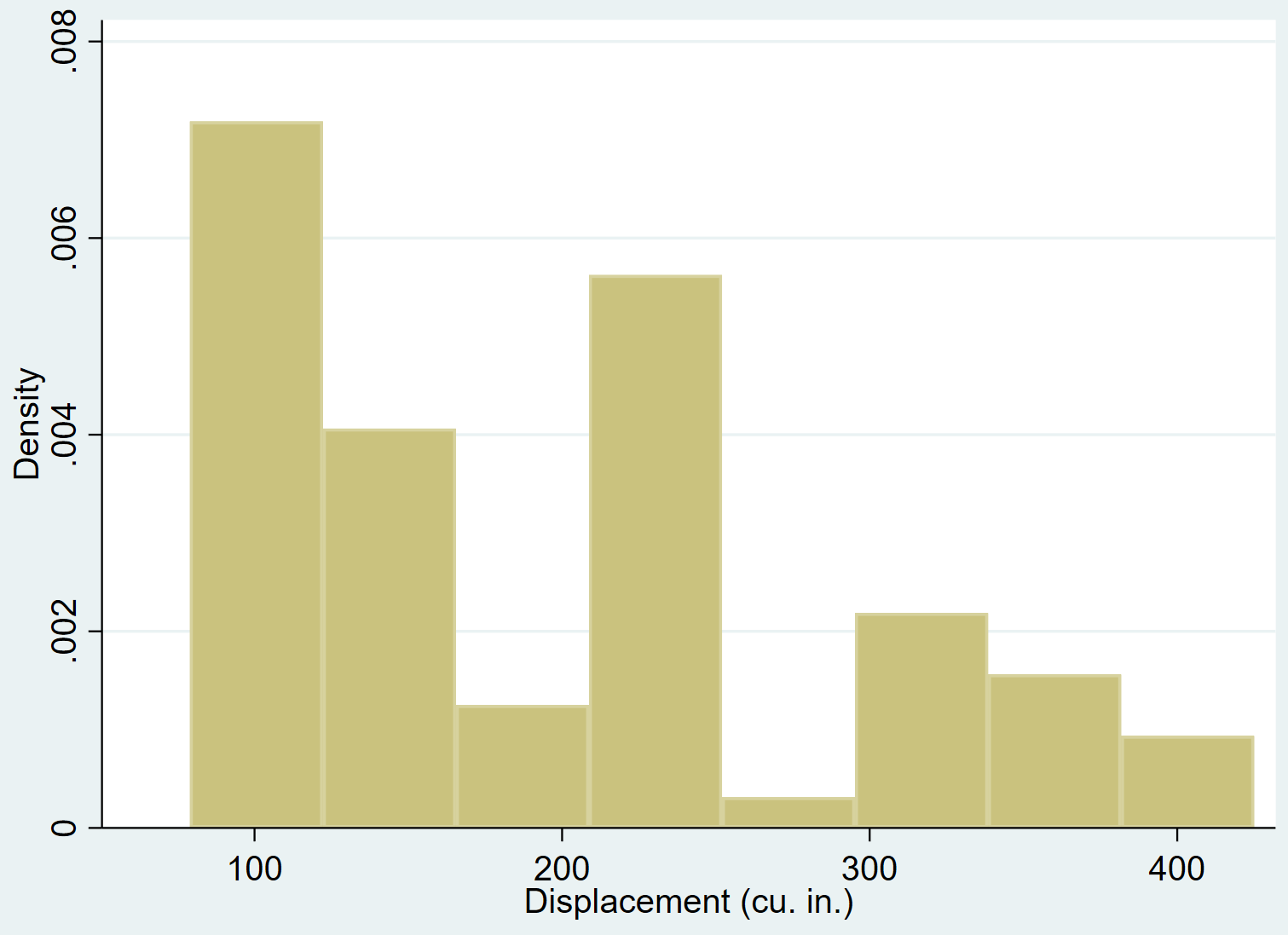
Один неформальный способ увидеть, нормально ли распределена переменная, — это создать гистограмму для просмотра распределения переменной.

Если переменная распределена нормально, гистограмма должна принять форму «колокола» с большим количеством значений, расположенных ближе к центру, и меньшим количеством значений, расположенных на хвостах.

Мы можем использовать команду hist для создания гистограммы для переменного смещения :

его смещение

Пример гистограммы в Stata

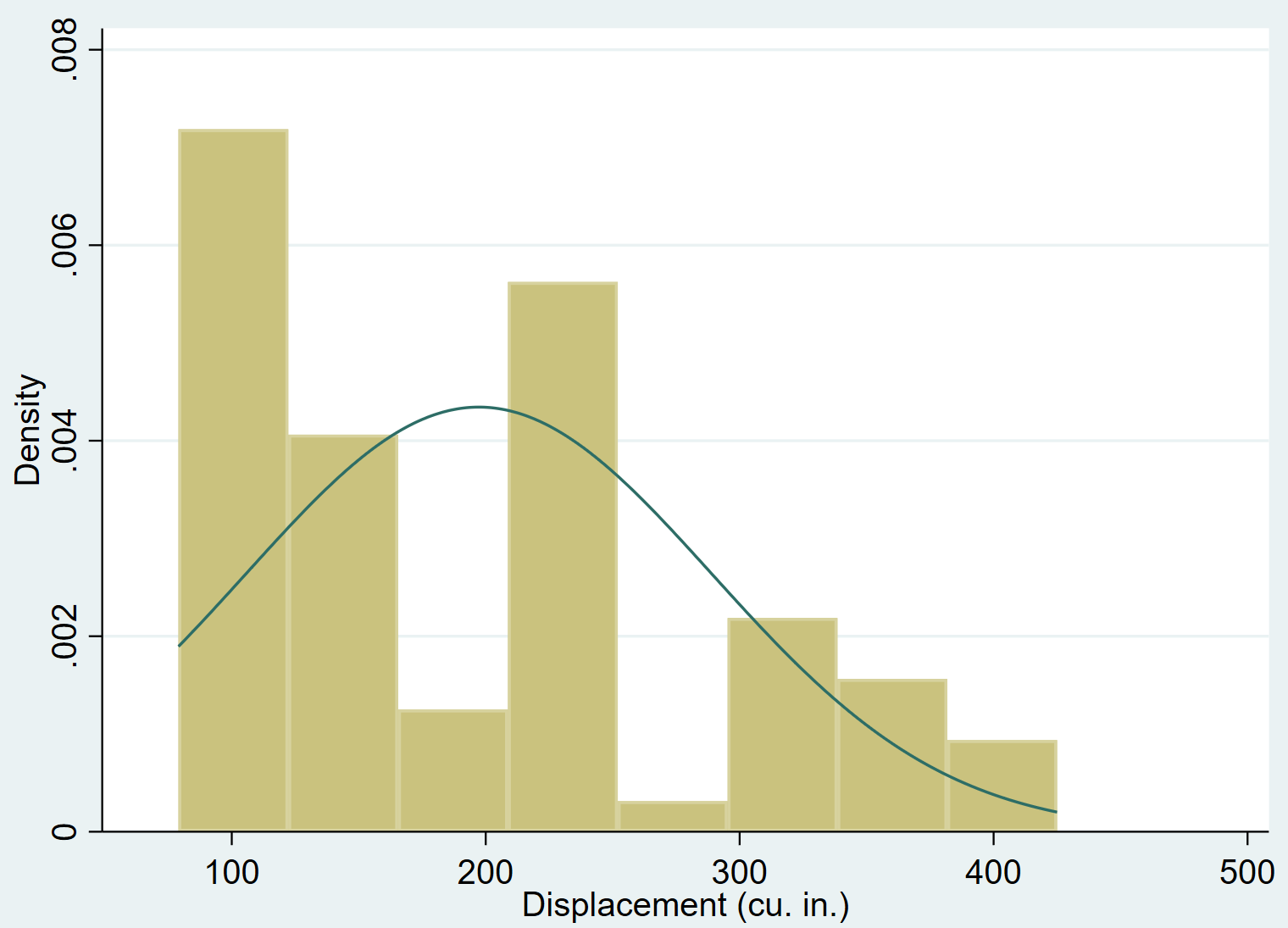
Мы можем добавить кривую нормальной плотности к гистограмме с помощью команды normal :

смещение, нормальное

Гистограмма с нормальной кривой в Stata

Совершенно очевидно, что смещение переменной смещено вправо (например, большинство значений сконцентрировано слева, а длинный «хвост» значений простирается вправо) и не подчиняется нормальному распределению.

Связанный: Левостороннее и правостороннее распределение

Метод 2: Тест Шапиро-Уилка

Формальный способ проверить нормальность — использовать тест Шапиро-Уилка .

Нулевая гипотеза для этого теста состоит в том, что переменная имеет нормальное распределение. Если p-значение теста меньше некоторого уровня значимости (обычный выбор включает 0,01, 0,05 и 0,10), то мы можем отклонить нулевую гипотезу и сделать вывод, что имеется достаточно доказательств того, что переменная не имеет нормального распределения.

*Этот тест можно использовать, когда общее количество наблюдений составляет от 4 до 2000.

Мы можем использовать команду swilk для выполнения теста Шапиро-Уилка для переменного смещения :

водоизмещение

Вывод теста Shapiro Wilk в Stata

Вот как интерпретировать вывод теста:

Obs: 74. Это количество наблюдений, использованных в тесте.

Вт: 0,92542. Это тестовая статистика для теста.

Вероятность z: 0,00031. Это p-значение, связанное со статистикой теста.

Поскольку p-значение меньше 0,05, мы можем отклонить нулевую гипотезу теста. У нас есть достаточно доказательств, чтобы сказать, что переменное смещение не имеет нормального распределения.

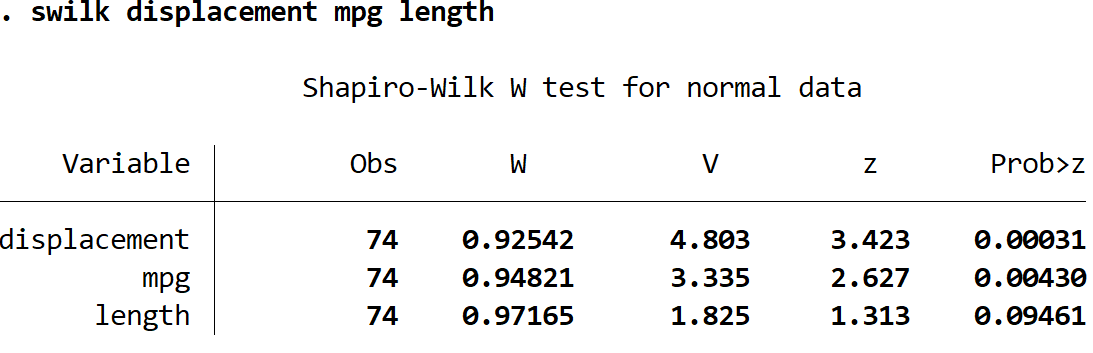
Мы также можем выполнить тест Шапиро-Уилка для более чем одной переменной одновременно, указав несколько переменных после команды swilk :

объем двигателя swilk длина миль на галлон

Несколько тестов Шапиро-Уилка одновременно в Stata

Используя уровень значимости 0,05, мы пришли бы к выводу, что смещение и мили на галлон распределены ненормально, но у нас нет достаточных доказательств, чтобы сказать, что длина распределена ненормально.

Метод 3: Тест Шапиро-Франсиа

Другой формальный способ проверить нормальность — использовать тест Шапиро-Франсиа .

Нулевая гипотеза для этого теста состоит в том, что переменная имеет нормальное распределение. Если p-значение теста меньше некоторого уровня значимости, то мы можем отклонить нулевую гипотезу и сделать вывод, что имеется достаточно доказательств того, что переменная не имеет нормального распределения.

*Этот тест можно использовать, когда общее количество наблюдений составляет от 10 до 5000.

Мы можем использовать команду sfrancia для выполнения теста Шапиро-Уилка для переменного смещения :

смещение

Вывод теста Shapiro-Francia в Stata

Вот как интерпретировать вывод теста:

Obs: 74. Это количество наблюдений, использованных в тесте.

W’: 0,93011. Это тестовая статистика для теста.

Вероятность z: 0,00094. Это p-значение, связанное со статистикой теста.

Поскольку p-значение меньше 0,05, мы можем отклонить нулевую гипотезу теста. У нас есть достаточно доказательств, чтобы сказать, что переменное смещение не имеет нормального распределения.

Подобно тесту Шапиро-Уилка, вы можете выполнить тест Шапиро-Франсиа одновременно для нескольких переменных, указав несколько переменных после команды sfrancia .

Метод 4: Тест на асимметрию и эксцесс

Другой способ проверить нормальность — использовать тест асимметрии и эксцесса, который определяет, согласуется ли асимметрия и эксцесс переменной с нормальным распределением.

Нулевая гипотеза для этого теста состоит в том, что переменная имеет нормальное распределение. Если p-значение теста меньше некоторого уровня значимости, то мы можем отклонить нулевую гипотезу и сделать вывод, что имеется достаточно доказательств того, что переменная не имеет нормального распределения.

*Для этого теста требуется минимум 8 наблюдений.

Мы можем использовать команду sktest для выполнения теста на асимметрию и эксцесс для переменного смещения :

смещение

Асимметрия и эксцесс для нормальности в Stata

Вот как интерпретировать вывод теста:

Obs: 74. Это количество наблюдений, использованных в тесте.

прил чи (2): 5,81. Это статистика теста хи-квадрат для теста.

Prop>chi2: 0,0547. Это p-значение, связанное со статистикой теста.

Поскольку значение p не менее 0,05, мы не можем отвергнуть нулевую гипотезу теста. У нас нет достаточных доказательств, чтобы сказать, что смещение не распределяется нормально.

Подобно другим тестам на нормальность, вы можете выполнить тест на асимметрию и эксцесс одновременно с несколькими переменными, указав несколько переменных после команды sktest .

Источник

Понравилась статья? Поделить с друзьями:
  • Нормальное количество ошибок
  • Ноутбук выдает ошибку и не выключается
  • Ноутбук выдает ошибку видеокарты
  • Нормал мод форд фокус 3 ошибка
  • Норма стандартной ошибки