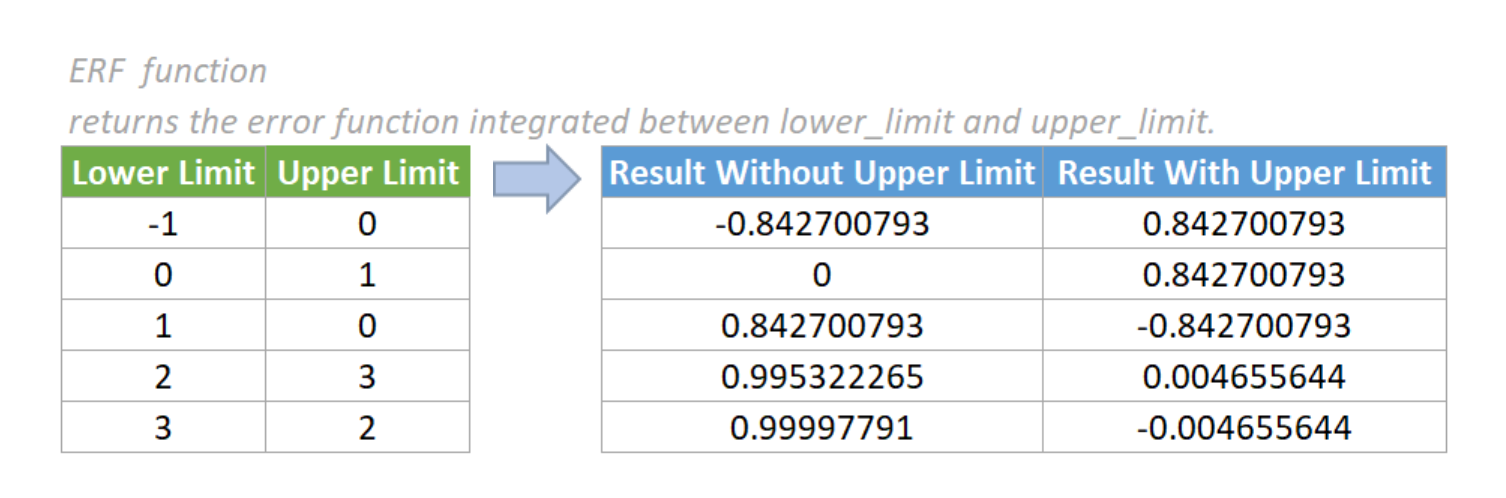
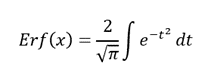Функция ФОШ возвращает функцию ошибки, проинтегрированную от значения аргумента «нижний_предел» до значения аргумента «верхний_предел».
Описание функции ФОШ
Возвращает функцию ошибки, проинтегрированную от значения аргумента «нижний_предел» до значения аргумента «верхний_предел».
Синтаксис
=ФОШ(нижний_предел; [верхний_предел])Аргументы
нижний_пределверхний_предел
Обязательный аргумент. Нижний предел интегрирования ФОШ.
Необязательный аргумент. Верхний предел интегрирования ФОШ. Если аргумент «верхний_предел» опущен, функция ФОШ выполняет интегрирование в пределах от 0 до значения аргумента «нижний_предел».
Замечания
- Если аргумент «нижний_предел» не является числом, функция ФОШ возвращает значение ошибки #ЗНАЧ!.
- Если аргумент «верхний_предел» не является числом, функция ФОШ возвращает значение ошибки #ЗНАЧ!.
Пример
Функция ERF возвращает функцию ошибки, интегрированную между нижним_пределом и верхним_пределом.
Синтаксис
=ERF (lower_limit, [upper_limit])
аргументы
- Нижний предел (обязательно): Нижний предел интегрирования.
- Верхний предел (необязательно): Верхний предел интегрирования. Если опущено, будет возвращена интеграция между 0 и нижним_пределом.
Возвращаемое значение
Функция ERF возвращает числовое значение.
Примечания к функциям
- Функция ERF была улучшена в Excel 2010, и теперь она может вычислять отрицательные значения.
В Excel 2007 функция ERF принимает только положительные значения. Если какой-либо из предоставленных аргументов имеет отрицательное значение, функция ERF вернет ошибку #ЧИСЛО! значение ошибки. - Значение! значение ошибки возникает, если какой-либо из предоставленных аргументов не является числовым.
- Когда верхний_предел опущен, ERF интегрируется между нулем (значение нижнего_предела) и нижним_пределом (значение верхнего_предела). Следовательно, когда нижний предел положительный, ERF возвращает положительный результат. Наоборот.
Более того, когда нижний_предел больше верхнего_предела, ERF возвращает отрицательный результат. Наоборот. - Результирующий диапазон, возвращаемый функцией ERF, находится между -1 и 1.
- Уравнение функции ошибки:
Примеры
Пример первый: результат без верхнего предела
В этом случае мы хотим вычислить функцию ошибки, когда аргумент upper_limit опущен. Это означает, что функция ERF интегрируется между нулем и нижним_пределом. Пожалуйста, сделайте следующее.
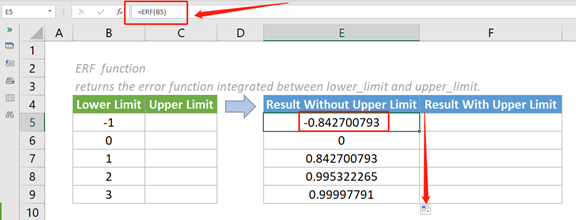
1. Пожалуйста, скопируйте приведенную ниже формулу в ячейку E5, затем нажмите клавишу Enter, чтобы получить результат.
=ERF (B5)
2. Выберите эту ячейку результатов и перетащите ее маркер автозаполнения вниз, чтобы получить остальные результаты.
Заметки:
- Как показано на приведенном выше снимке экрана, когда единственный аргумент нижний_лимит отрицательный, возвращаемый результат также отрицательный. Наоборот.
- Когда единственный аргумент нижний_предел равен нулю (0), ERF возвращает в качестве результата ноль (0).
- Аргумент в каждой из приведенных выше формул предоставляется в виде ссылки на ячейку, содержащей числовое значение.
- Мы также можем напрямую ввести значение в формулу. Например, формулу в ячейке E5 можно изменить на:
=ERF (-1)
Пример второй: результат с верхним пределом
В этом случае мы хотим вычислить функцию ошибки, когда предоставлены аргументы lower_limit и upper_limit. Пожалуйста, сделайте следующее.
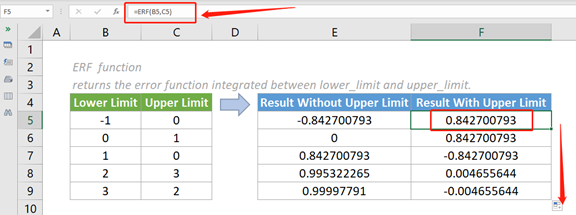
1. Пожалуйста, скопируйте приведенную ниже формулу в ячейку F5, затем нажмите клавишу Enter, чтобы получить результат.
=ERF (B5, C5)
2. Выберите эту ячейку результатов и перетащите ее маркер автозаполнения вниз, чтобы получить остальные результаты.
Заметки:
- Как видно из приведенного выше снимка экрана, когда верхний_предел больше нижнего_предела, ERF возвращает положительный результат. Наоборот.
- Аргументы в каждой из приведенных выше формул предоставляются в виде ссылок на ячейки, содержащих числовые значения.
- Мы также можем напрямую вводить значения в формулу. Например, формулу в ячейке F5 можно изменить на:
=ERF (-1, 0)
Относительные функции:
-
Excel EVEN Функция
Функция EVEN округляет числа от нуля до ближайшего четного целого числа.
-
Excel EXP Функция
Функция EXP возвращает результат возведения константы e в энную степень.
Лучшие инструменты для работы в офисе
Kutools for Excel — Помогает вам выделиться из толпы
Хотите быстро и качественно выполнять свою повседневную работу? Kutools for Excel предлагает 300 мощных расширенных функций (объединение книг, суммирование по цвету, разделение содержимого ячеек, преобразование даты и т. д.) и экономит для вас 80 % времени.
- Разработан для 1500 рабочих сценариев, помогает решить 80% проблем с Excel.
- Уменьшите количество нажатий на клавиатуру и мышь каждый день, избавьтесь от усталости глаз и рук.
- Станьте экспертом по Excel за 3 минуты. Больше не нужно запоминать какие-либо болезненные формулы и коды VBA.
- 30-дневная неограниченная бесплатная пробная версия. 60-дневная гарантия возврата денег. Бесплатное обновление и поддержка 2 года.
Вкладка Office — включение чтения и редактирования с вкладками в Microsoft Office (включая Excel)
- Одна секунда для переключения между десятками открытых документов!
- Уменьшите количество щелчков мышью на сотни каждый день, попрощайтесь с рукой мыши.
- Повышает вашу продуктивность на 50% при просмотре и редактировании нескольких документов.
- Добавляет эффективные вкладки в Office (включая Excel), точно так же, как Chrome, Firefox и новый Internet Explorer.
Комментарии (0)
Оценок пока нет. Оцените первым!
Функция ERF возвращает функцию ошибки, интегрированную между нижним_пределом и верхним_пределом.
Синтаксис
=ERF (lower_limit, [upper_limit])
аргументы
- Нижний предел (обязательно): Нижний предел интегрирования.
- Верхний предел (необязательно): Верхний предел интегрирования. Если опущено, будет возвращена интеграция между 0 и нижним_пределом.
Возвращаемое значение
Функция ERF возвращает числовое значение.
Примечания к функциям
- Функция ERF была улучшена в Excel 2010, и теперь она может вычислять отрицательные значения.
В Excel 2007 функция ERF принимает только положительные значения. Если какой-либо из предоставленных аргументов имеет отрицательное значение, функция ERF вернет ошибку #ЧИСЛО! значение ошибки. - Значение! значение ошибки возникает, если какой-либо из предоставленных аргументов не является числовым.
- Когда верхний_предел опущен, ERF интегрируется между нулем (значение нижнего_предела) и нижним_пределом (значение верхнего_предела). Следовательно, когда нижний предел положительный, ERF возвращает положительный результат. Наоборот.
Более того, когда нижний_предел больше верхнего_предела, ERF возвращает отрицательный результат. Наоборот. - Результирующий диапазон, возвращаемый функцией ERF, находится между -1 и 1.
- Уравнение функции ошибки:
Примеры
Пример первый: результат без верхнего предела
В этом случае мы хотим вычислить функцию ошибки, когда аргумент upper_limit опущен. Это означает, что функция ERF интегрируется между нулем и нижним_пределом. Пожалуйста, сделайте следующее.
1. Пожалуйста, скопируйте приведенную ниже формулу в ячейку E5, затем нажмите клавишу Enter, чтобы получить результат.
=ERF (B5)
2. Выберите эту ячейку результатов и перетащите ее маркер автозаполнения вниз, чтобы получить остальные результаты.
Заметки:
- Как показано на приведенном выше снимке экрана, когда единственный аргумент нижний_лимит отрицательный, возвращаемый результат также отрицательный. Наоборот.
- Когда единственный аргумент нижний_предел равен нулю (0), ERF возвращает в качестве результата ноль (0).
- Аргумент в каждой из приведенных выше формул предоставляется в виде ссылки на ячейку, содержащей числовое значение.
- Мы также можем напрямую ввести значение в формулу. Например, формулу в ячейке E5 можно изменить на:
=ERF (-1)
Пример второй: результат с верхним пределом
В этом случае мы хотим вычислить функцию ошибки, когда предоставлены аргументы lower_limit и upper_limit. Пожалуйста, сделайте следующее.
1. Пожалуйста, скопируйте приведенную ниже формулу в ячейку F5, затем нажмите клавишу Enter, чтобы получить результат.
=ERF (B5, C5)
2. Выберите эту ячейку результатов и перетащите ее маркер автозаполнения вниз, чтобы получить остальные результаты.
Заметки:
- Как видно из приведенного выше снимка экрана, когда верхний_предел больше нижнего_предела, ERF возвращает положительный результат. Наоборот.
- Аргументы в каждой из приведенных выше формул предоставляются в виде ссылок на ячейки, содержащих числовые значения.
- Мы также можем напрямую вводить значения в формулу. Например, формулу в ячейке F5 можно изменить на:
=ERF (-1, 0)
Относительные функции:
-
Excel EVEN Функция
Функция EVEN округляет числа от нуля до ближайшего четного целого числа.
-
Excel EXP Функция
Функция EXP возвращает результат возведения константы e в энную степень.
Лучшие инструменты для работы в офисе
Kutools for Excel — поможет вам выделиться из толпы
Хотите быстро и качественно выполнять свою повседневную работу? Kutools for Excel предлагает мощные расширенные функции 300 (объединение книг, суммирование по цвету, разделение содержимого ячеек, преобразование даты и т. д.) и экономит для вас 80% времени.
- Разработан для 1500 рабочих сценариев, помогает решить 80% проблем с Excel.
- Уменьшите количество нажатий на клавиатуру и мышь каждый день, избавьтесь от усталости глаз и рук.
- Станьте экспертом по Excel за 3 минуты. Больше не нужно запоминать какие-либо болезненные формулы и коды VBA.
- 30-дневная неограниченная бесплатная пробная версия. 60-дневная гарантия возврата денег. Бесплатное обновление и поддержка 2 года.
Вкладка Office — включение чтения и редактирования с вкладками в Microsoft Office (включая Excel)
- Одна секунда для переключения между десятками открытых документов!
- Уменьшите количество щелчков мышью на сотни каждый день, попрощайтесь с рукой мыши.
- Повышает вашу продуктивность на 50% при просмотре и редактировании нескольких документов.
- Добавляет эффективные вкладки в Office (включая Excel), точно так же, как Chrome, Firefox и новый Internet Explorer.
Комментарии (0)
Оценок пока нет. Оцените первым!
Оставляйте свои комментарии
The ERF function is an Engineering formula that calculates and returns the error function, integrated between specified lower and upper limits. In this guide, we’re going to show you how to use the ERF function, and also go over some tips and error handling methods.
Supported versions
- All Excel versions (The function was improved in Excel 2010 to include support for negative numbers.)
ERF Function Syntax
ERF(lower_limit, [upper_limit])
Arguments
| lower_limit | The lower bound of the integration. |
| [upper_limit] | Optional. The upper bound of the integral. If omitted, ERF returns the integration between 0 and the lower_limit. |
Examples
Lower limit only
The lower_limit is the only required argument for the ERF function. If you want to calculate the integral between 0 and a numeric value. You only need to enter a lower_limit value The ERF function accepts negative numerical values in Excel 2010 and newer versions. Below is an example set,
=ERF(1) integrates between 0 and 1
Lower Limit and Upper Limit
Enter an [upper_limit] argument to set both lower and upper limits to be used in the error function. The [upper_limit] argument is very similar to the lower_limit as it accepts numerical values without a sign (in Excel 2010 and later). Here is how you can use the ERF function with both arguments:
=ERF(1,2) integrates between 1 and 2
If you look at the screenshots, you can see ERF(1) and ERF(0,1) returns same value.
Download Workbook
Tips
- Other related Excel functions:
- ERF.PRECISE returns the error function between 0 and the entered argument.
- ERFC and ERFC.PRECISE functions return complementary error function integrated between x and infinity. (Both functions work similarly. The ERFC.PRECISE function was added to provide consistency between function names.)
- You can find further details on Wikipedia’s Error Function page.
Issues
- If the lower_limit is non-numeric, the ERF returns the #VALUE! error value.
- If the [upper_limit] is non-numeric, the ERF returns the #VALUE! error value.
- The ERF function returns the #NUM! error value if one or both of the arguments are negative in Excel 2007 or earlier versions.
The ERF function is an Engineering formula that calculates and returns the error function, integrated between specified lower and upper limits. In this guide, we’re going to show you how to use the ERF function, and also go over some tips and error handling methods.
Supported versions
- All Excel versions (The function was improved in Excel 2010 to include support for negative numbers.)
ERF Function Syntax
ERF(lower_limit, [upper_limit])
Arguments
| lower_limit | The lower bound of the integration. |
| [upper_limit] | Optional. The upper bound of the integral. If omitted, ERF returns the integration between 0 and the lower_limit. |
Examples
Lower limit only
The lower_limit is the only required argument for the ERF function. If you want to calculate the integral between 0 and a numeric value. You only need to enter a lower_limit value The ERF function accepts negative numerical values in Excel 2010 and newer versions. Below is an example set,
=ERF(1) integrates between 0 and 1
Lower Limit and Upper Limit
Enter an [upper_limit] argument to set both lower and upper limits to be used in the error function. The [upper_limit] argument is very similar to the lower_limit as it accepts numerical values without a sign (in Excel 2010 and later). Here is how you can use the ERF function with both arguments:
=ERF(1,2) integrates between 1 and 2
If you look at the screenshots, you can see ERF(1) and ERF(0,1) returns same value.
Download Workbook
Tips
- Other related Excel functions:
- ERF.PRECISE returns the error function between 0 and the entered argument.
- ERFC and ERFC.PRECISE functions return complementary error function integrated between x and infinity. (Both functions work similarly. The ERFC.PRECISE function was added to provide consistency between function names.)
- You can find further details on Wikipedia’s Error Function page.
Issues
- If the lower_limit is non-numeric, the ERF returns the #VALUE! error value.
- If the [upper_limit] is non-numeric, the ERF returns the #VALUE! error value.
- The ERF function returns the #NUM! error value if one or both of the arguments are negative in Excel 2007 or earlier versions.
3.3.Температурное
поле непрерывного неподвижного точечного
источника в неограниченной среде.
Функция ошибок Гаусса (функция erf(x)).
Если в точке с
координатами x‘,
y‘,
z‘
в интервале времени от t‘
= 0 до t‘
= t
работает источник тепла мощностью
W,
то температурное поле этого источника,
как указано выше, может быть найдено
интегрированием фундаментального
решения по t‘
от 0 до t
(т.е. от момента включения до момента
выключения источника). Поместим начало
координат в точку, где находится источник
тепла. Тогда x’
= y’
= z’
= 0, и формула
для температуры принимает вид:
,
(3.3.1)
где r2
= (x — x’)2
+ (y — y’)2
+ (z — z’)2
= x2
+ y2
+ z2
— квадрат расстояния от источника до
точки наблюдения.
Произведем в
интеграле (3.3.1) замену переменных:
r2/[4a(t
— t’)] = 2.
Тогда: (t —
t’)3/2
= r3/(8a3/23),
dt’ = r2d/(2a3),
пределы интегрирования: t’
= 0
,
t’ = t
= ,
и формула (3.3.1) принимает вид:
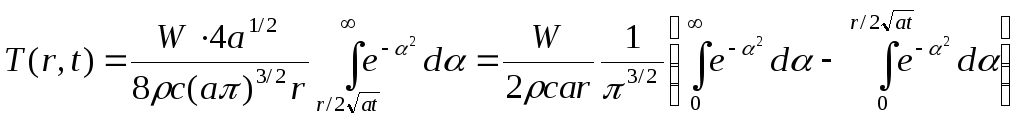
(3.3.2)
Первый интеграл,
стоящий в скобках, известен из курса
высшей математики:
(интеграл
Пуассона),
а второй интеграл
через элементарные функции не выражается
и определяет специальную функцию,
которая называется функцией
ошибок Гаусса,
или интегралом
вероятностей,
или функцией эрфектум:
(3.3.3)
(читается «эрфектум»
или сокращенно: «эрф»). Через эту
функцию выражаются решения многих
задач в теории теплопроводности, да и
в других областях физики она играет
важную роль.
Из определения
(3.3.3) видно, что erf(0)
= 0, а erf()
= 1, т.е. erf(x)
— это монотонно возрастающая
функция, вид которой изображен
на Рис.3.3. Функция erf(x)
табулирована, и ее значения
приводятся в различных
справочниках; в таблице 3.1 приведены
несколько значений этой функции. В
библиотеках некоторых
языков программирования имеются
готовые подпрограммы для
вычисления функции erf(x).
Если готовой подпрограммы
нет, функцию erf(x)
можно
вычислить с помощью степенного
ряда. «Стандартное»
разложение этой функции в
степенной ряд, которое обычно
приводится в математических
справочниках, имеет вид:
.
(3.3.4)
Э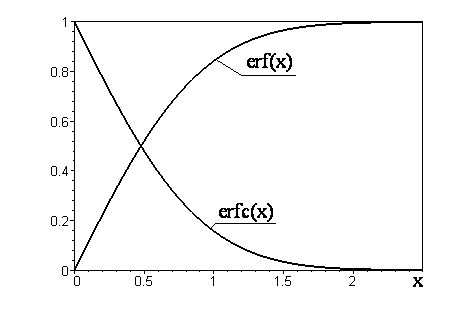
ряд удобен для анализа свойств функции,
но для практических расчетов он неудобен,
т.к. является знакопеременным, что
при вычислениях приводит к потере
точности. Более удобен следующий
ряд:
,
(3.3.5)
где
,
.
С
Рис. 3.3.
помощью этого ряда легко составить
программу вычисления erf(x)
на любом языке программирования
и даже на программируемом
микрокалькуляторе. Суммирование
надо прекращать, когда при
добавлении очередного an-го
слагаемого сумма перестанет меняться
(будет достигнута «машинная
точность»).
Если большой
точности не требуется, то можно
использовать приближенную формулу:
erf(x)
[1 — exp(-4x2/)]1/2.
(3.3.6)
Формула (3.3.6) дает
значения, абсолютная погрешность которых
не более 6.310-3,
а относительная погрешность
не более 0.71%.
Иногда требуется
определить erf(x)
в области отрицательных значений x.
Из формулы (3.3.3) очевидно, что erf(-x)
= — erf(x).
Заметим, что хотя
функция erf(x)
не является «элементарной», с точки
зрения ее свойств и способов
вычисления она проще, чем многие
«элементарные» функции, например,
тригонометрические.
С функцией erf(x)
связано еще несколько функций, часто
встречающихся в теплофизических
задачах. Это прежде всего дополнительный
интеграл вероятностей:
,
(3.3.7)
который встречается
настолько часто, что для него используется
специальное обозначение: erfc(x)
(сокращенно читается «эрфик»). Вид
этой функции также приведен на рис.3.3.
Довольно часто
функцию erf(x)
приходится дифференцировать и
интегрировать. Из определения
(3.3.3) следует, что
,
(3.3.8)
а интеграл от
erfc(x)
(обозначается как ierfc(x))
равен:
.
(3.3.9)
Вернемся к формуле
(3.3.2). Замечая, что ca
= ,
запишем эту формулу в виде:
.
(3.3.10)
При t
значение функции
0,
1, и формула (3.3.10), как и должно быть,
совпадает с формулой для
стационарного решения (если T0
принять за начало отсчета
температуры), т.к. при t
достигается стационарное
распределение температуры
в безграничной среде.
Таблица 3.1.
Некоторые значения функции erf(x).
|
x |
erf(x) |
x |
erf(x) |
x |
erf(x) |
x |
erf(x) |
x |
erf(x) |
|
0.0 |
0.0 |
0.3 |
0.32863 |
0.6 |
0.60386 |
0.9 |
0.79691 |
2.0 |
0.99532 |
|
0.1 |
0.11246 |
0.4 |
0.42839 |
0.7 |
0.67780 |
1.0 |
0.84270 |
2.5 |
0.99959 |
|
0.2 |
0.22270 |
0.5 |
0.52050 |
0.8 |
0.74210 |
1.5 |
0.96611 |
Соседние файлы в папке КраткийКонспектЛекций
- #
- #
- #
- #
- #
- #
- #
- #
- #
- #
- #

Функция ошибок (также называемая функция ошибок Гаусса) — неэлементарная функция (b) , возникающая в теории вероятностей (b) , статистике (b) и теории дифференциальных уравнений в частных производных (b) . Она определяется как
- .
Дополнительная функция ошибок, обозначаемая (иногда применяется обозначение ), определяется через функцию ошибок:
- .
Комплексная функция ошибок, обозначаемая , также определяется через функцию ошибок:
- .
Свойства
- Функция ошибок нечётна (b) :
- Для любого комплексного выполняется
- где черта обозначает комплексное сопряжение (b) числа .
- Функция ошибок не может быть представлена через элементарные функции (b) , но, разлагая интегрируемое выражение в ряд Тейлора (b) и интегрируя почленно, мы можем получить её представление в виде ряда:
- Это равенство выполняется (и ряд сходится) как для любого вещественного (b) , так и на всей комплексной плоскости (b) , согласно признаку Д’Аламбера (b) . Последовательность знаменателей образует последовательность A007680 в OEIS (b) .
- Для итеративного вычисления элементов ряда полезно представить его в альтернативном виде:
- поскольку — сомножитель, превращающий -й член ряда в -й, считая первым членом .
- Функция ошибок на бесконечности равна единице; однако это справедливо только при приближении к бесконечности по вещественной оси, так как:
- При рассмотрении функции ошибок в комплексной плоскости точка будет для неё существенно особой.
- Производная функции ошибок выводится непосредственно из определения функции:
- Первообразная (b) функции ошибок, получаемая способом интегрирования по частям (b) :
- Обратная функция ошибок представляет собой ряд
- где c0 = 1 и
- Поэтому ряд можно представить в следующем виде (заметим, что дроби сокращены):
- Последовательности числителей и знаменателей после сокращения — A092676 и A132467 в OEIS; последовательность числителей до сокращения — A002067 в OEIS.
Применение
Если набор случайных величин подчиняется нормальному распределению (b) со стандартным отклонением (b) , то вероятность, что величина отклонится от среднего не более чем на , равна .
Функция ошибок и дополнительная функция ошибок встречаются в решении некоторых дифференциальных уравнений, например, уравнения теплопроводности (b) с начальными условиями, (b) описываемыми функцией Хевисайда (b) («ступенькой»).
В системах цифровой оптической коммуникации, вероятность ошибки на бит также выражается формулой, использующей функцию ошибок.
Асимптотическое разложение
При больших полезно асимптотическое разложение (b) для дополнительной функции ошибок:
Хотя для любого конечного этот ряд расходится, на практике первых нескольких членов достаточно для вычисления с хорошей точностью, в то время как ряд Тейлора сходится очень медленно.
Другое приближение даётся формулой
где
Родственные функции
С точностью до масштаба и сдвига, функция ошибок совпадает с нормальным интегральным распределением, обозначаемым
Обратная функция (b) к , известная как нормальная квантильная функция (b) , иногда обозначается (b) и выражается через нормальную функцию ошибок как
Нормальное интегральное распределение чаще применяется в теории вероятностей и математической статистике, в то время как функция ошибок чаще применяется в других разделах математики.
Функция ошибок является частным случаем функции Миттаг-Леффлера (b) , а также может быть представлена как вырожденная гипергеометрическая функция (функция Куммера (b) ):
Функция ошибок выражается также через интеграл Френеля (b) . В терминах регуляризованной неполной гамма-функции P (b) и неполной гамма-функции (b) ,
Обобщённые функции ошибок
серая линия:
красная линия:
зелёная линия:
синяя линия:
жёлтая линия: .
Некоторые авторы обсуждают более общие функции
Примечательными частными случаями являются:
- — прямая линия, проходящая через начало координат:
- — функция ошибок .
После деления на все с нечётными выглядят похоже (но не идентично), это же можно сказать про с чётными . Все обобщённые функции ошибок с выглядят похоже на полуоси .
На полуоси все обобщённые функции могут быть выражены через гамма-функцию (b) :
Следовательно, мы можем выразить функцию ошибок через гамма-функцию:
Повторные интегралы дополнительной функции ошибок
Повторные интегралы дополнительной функции ошибок определяются как[1]
- ,
- для .
Их можно разложить в ряд:
откуда следуют свойства симметрии
и
Реализации
В стандарте языка Си (b) (ISO/IEC 9899:1999, пункт 7.12.8) предусмотрены функция ошибок и дополнительная функция ошибок . Функции объявлены в заголовочных файлах math.h (b) (для Си (b) ) или cmath (для C++ (b) ). Там же объявлены пары функций erff(), erfcf() и erfl(), erfcl(). Первая пара получает и возвращает значения типа float, а вторая — значения типа long double. Соответствующие функции также содержатся в библиотеке Math проекта «Boost (b) ».
В языке Java (b) стандартная библиотека математических функций java.lang.Math (b) не содержит[2] функцию ошибок. Класс Erf можно найти в пакете org.apache.commons.math.special из не стандартной библиотеки, поставляемой[3]Apache Software Foundation (b) .
Системы компьютерной алгебры (b) Maple (b) , Matlab (b) , Mathematica (b) и Maxima (b) содержат обычную и дополнительную функции ошибок, а также обратные к ним функции.
В языке Python (b) функция ошибок доступна[4] из стандартной библиотеки math, начиная с версии 2.7. Также функция ошибок, дополнительная функция ошибок и многие другие специальные функции определены в модуле Special проекта SciPy (b) .
В языке Erlang (b) функция ошибок и дополнительная функция ошибок доступны из стандартного модуля math[5].
В Excel функция ошибок представлена, как ФОШ и ФОШ.ТОЧН[6]
См. также
- Функция Гаусса (b)
- Функция Доусона (b)
- Гауссов интеграл (b)
Примечания
- ↑ Carslaw, H. S. (b) & Jaeger, J. C. (b) (1959), Conduction of Heat in Solids (2nd ed.), Oxford University Press, ISBN 978-0-19-853368-9, p 484
- ↑ Math (Java Platform SE 6). Дата обращения: 28 марта 2008. Архивировано 29 августа 2009 года.
- ↑ Архивированная копия. Дата обращения: 28 марта 2008. Архивировано из оригинала 9 апреля 2008 года.
- ↑ 9.2. math — Mathematical functions — Python 2.7.10rc0 documentation
- ↑ Язык Erlang (b) . ОписаниеАрхивная копия от 20 июня 2012 на Wayback Machine (b) функций стандартного модуля
math. - ↑ Функция ФОШ. support.microsoft.com. Дата обращения: 15 ноября 2021. Архивировано 15 ноября 2021 года.
Литература
- Press, William H.; Teukolsky, Saul A.; Vetterling, William T. & Flannery, Brian P. (2007), Section 6.2. Incomplete Gamma Function and Error Function, Numerical Recipes: The Art of Scientific Computing (3rd ed.), New York: Cambridge University Press, ISBN 978-0-521-88068-8
- Milton Abramowitz and Irene A. Stegun, eds. Handbook of Mathematical Functions with Formulas, Graphs, and Mathematical Tables. — New York: Dover, 1972. — Т. 7.
- Nikolai G. Lehtinen. Error functions (апрель 2010). Дата обращения: 25 мая 2019.
Ссылки
- MathWorld — Erf
- Онлайновый калькулятор Erf и много других специальных функций (до 6 знаков)
- Онлайновый калькулятор, вычисляющий в том числе Erf
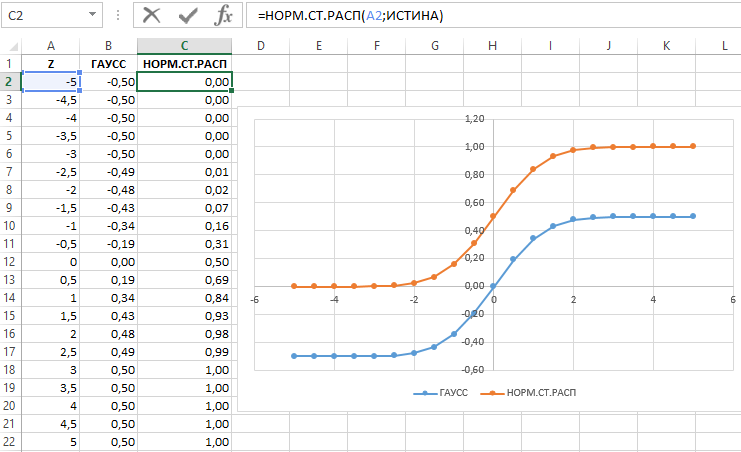
Функция ГАУСС, подлежащая применению в версиях Excel начиная от 2013 года или новее. Она позволяет вычислить такую вероятность, с которой элемент стандартной нормальной совокупности будет находиться в интервале между средними и стандартными отклонениями от среднего.
Синтаксис рассматриваемой функции не представляет из себя ничего сложного, ведь функции ГАУСС присущ всего один обязательный аргумент – Z – возвращающий число.
Важно отметить, что существует определенная связь между функцией ГАУСС и такой статистической функцией, как стандартное нормальное распределение, иначе говоря – НОРМ.СТ.РАСП.
Итак, всегда функция НОРМ.СТ.РАСП (0; Истина) делает возврат 0,5, тогда как ГАУСС (z) имеет в результате значение меньше на 0,5, чем результат функции НОРМ.СТ.РАСП. На рисунке, расположенном ниже, приведен пример использования данных статистических функций для возвращения числа 1,5.
Для наглядности продемонстрируем зависимость между значениями функций графическим способом. Для этого – сформируем таблицу с выборкой чисел, например на интервале от -5 до 5 с шагом 0,5, а затем по имеющимся данным построим график:
На графике четко прослеживается пропорциональная корреляция результатов вычислений функций ГАУСС и НОРМ.СТ.РАСП.
Решение системы вероятности методом ГАУССА в Excel
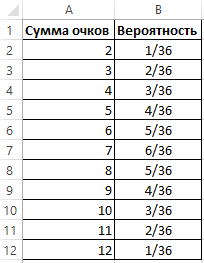
Задача представляет собой вычисление вероятности возможных значений при бросании двух костей.
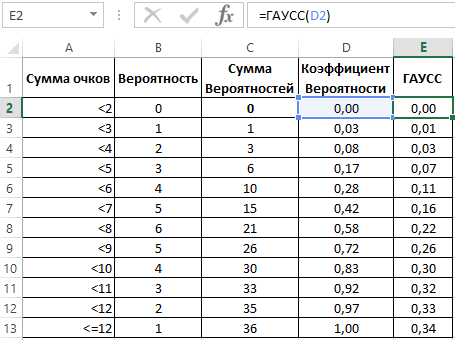
Пример с игрой в кости является наиболее наглядным, так как мы имеем ограниченный набор данных, которые соответствуют вероятностям. Так, вероятность имеет значение от нуля до единицы, к которому стремится наблюдаемая частота при бесконечно большой выборке или повторении эксперимента.
Существует 36 возможных комбинаций. При этом, вероятность того, что при бросании двух костей выпадет 2 очка равна 1/36, а 7 очков – 1/6. Отобразим перечень возможных значений бросания двух игральных костей в таблице, приведя при этом все вероятности к общему знаменателю.
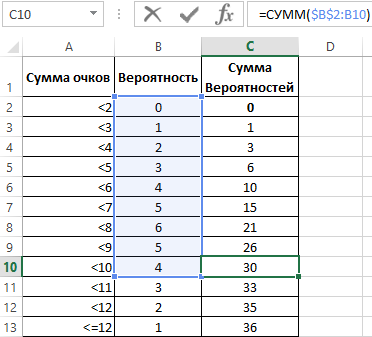
Однако, такой ряд данных не дает возможности для выявления полного распределения, поэтому следует отобразить данные об отдельных вероятностях в рассчитанную по функции распределения. Так необходимо, все вероятности просуммировать последовательно (1+2+3+4+5+6+5+4+3+2+1).
Теперь определяем коэффициент вероятности разделив по отдельности последовательную сумму вероятностей на максимально возможное количество комбинаций 36.
В первом случае нами были рассмотрены отдельные вероятности, во втором – сумма вероятностей от первого возможного значения до заданного.
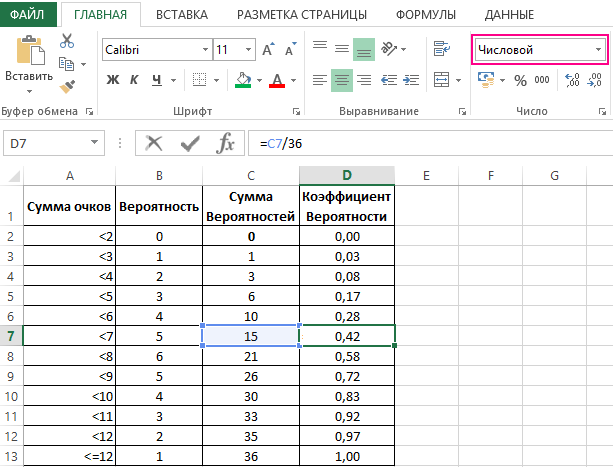
Необходимо преобразовать диапазон ячеек D2:D13 в числовой формат данных, иначе при обращении на них функции ГАУСС будет иметь место ошибка.
В созданный рядом с первоначальной таблицей столбец E введем формулу, которая в качестве аргумента делает обращение к ячейке D2.
Далее, протянем формулу вниз по столбцу, и получим ряд вероятностей с использованием функции ГАУСС.
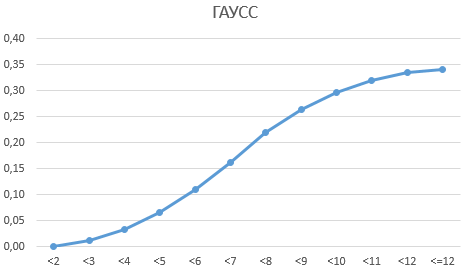
Для более наглядной визуализации, построим график вероятности:
Решение вероятности методом распределения кривой Гаусса в Excel
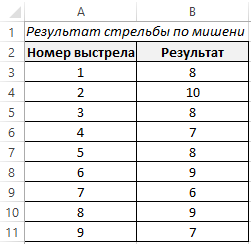
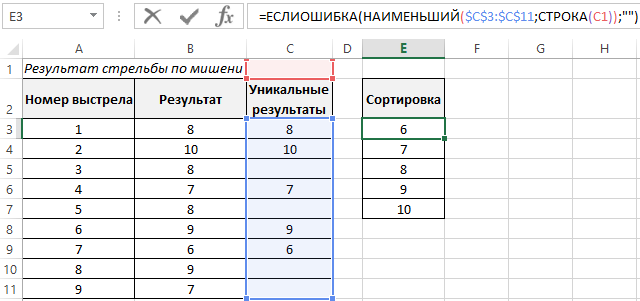
Теперь в качестве примера нормального распределения с помощью функции ГАУСС решим задачу о вероятностном соотношении результатов стрельбы по мишени.
Для этого построим базовую таблицу, которая отражает результаты стрельбы по мишени в девяти подходах.
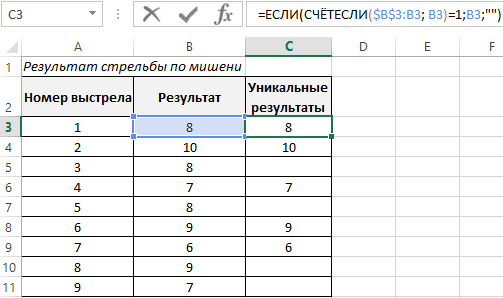
Затем, выберем только уникальные результаты, для этого используем хитрую формулу:
Делаем сортировку формулой для результатов по возрастанию и выводим в отдельную табличку:
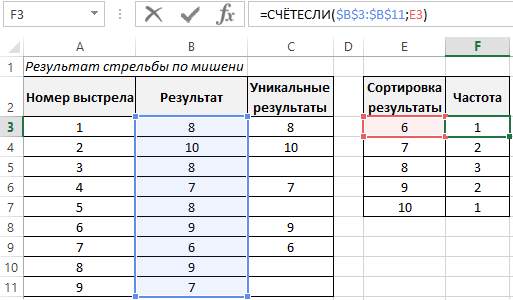
После чего определим частоту встречающихся только для уникальных результатов:
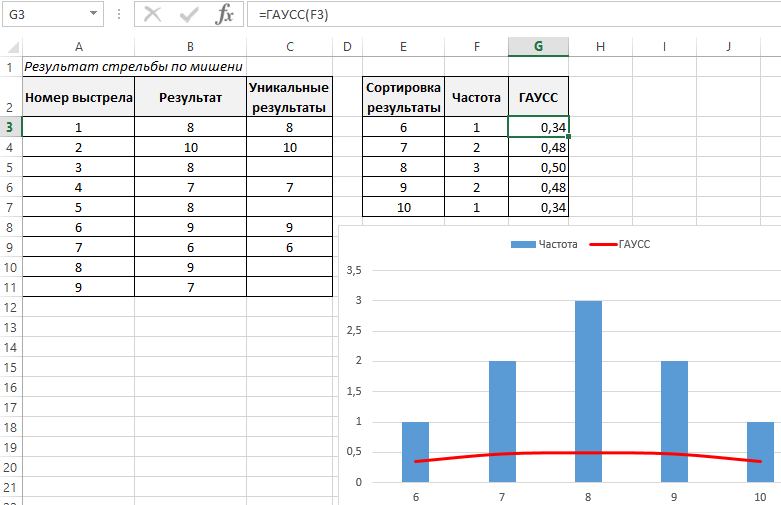
Далее применим функцию ГАУСС к значениям ячеек с частотой встречаемости. Отразим результаты вычислений на графике:
На графике красной линией определено нормальное распределение кривой Гаусса.
Функция ЕСЛИОШИБКА() в MS EXCEL
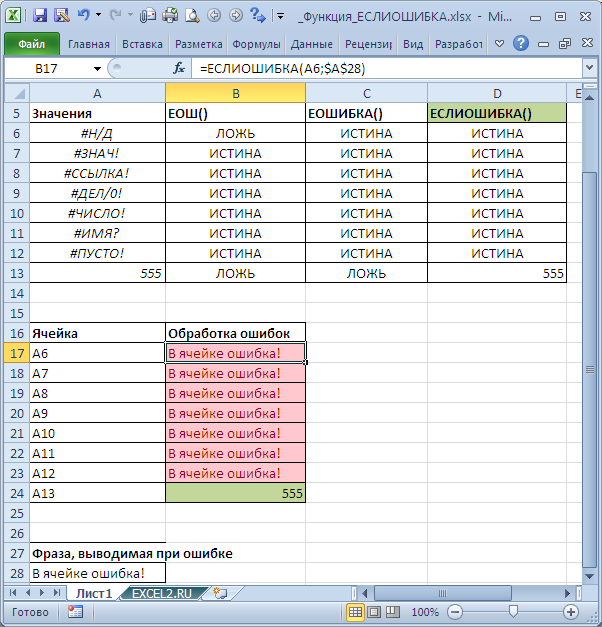
Функция ЕСЛИОШИБКА() , английский вариант IFERROR(), проверяет выражение на равенство значениям #Н/Д, #ЗНАЧ!, #ССЫЛКА!, #ДЕЛ/0!, #ЧИСЛО!, #ИМЯ? или #ПУСТО! Если проверяемое выражение или значение в ячейке содержит ошибку, то функция возвращает определенное для этого случая значение, в противном случае — результат вычисления выражения или содержимое ячейки.
Функция ЕСЛИОШИБКА() впервые появилась в EXCEL 2007.
Синтаксис функции
ЕСЛИОШИБКА(значение;значение_при_ошибке)
Значение — аргумент, проверяемый на возникновение ошибок.
Значение_при_ошибке — значение, возвращаемое при ошибке.
Для обработки ошибок #Н/Д, #ЗНАЧ!, #ССЫЛКА!, #ДЕЛ/0!, #ЧИСЛО!, #ИМЯ? или #ПУСТО! обычно используют формулу вида (см. файл примера ):
=ЕСЛИОШИБКА(A2/B2;»Ошибка расчете»)
Формула проверяет на предмет ошибки результат вычисления A2/B2.
Если результат вычисления не является ошибкой #Н/Д, #ЗНАЧ!, #ССЫЛКА!, #ДЕЛ/0!, #ЧИСЛО!, #ИМЯ? или #ПУСТО! , то формула возвращает результат вычисления A2/B2 , если обнаруживает, то возвращает строку Ошибка в расчете.
Функция ЕСЛИОШИБКА() vs ЕОШИБКА()
В отличие от функции ЕСЛИОШИБКА() функция ЕОШИБКА() не умеет самостоятельно обрабатывать ошибку — приходится задействовать функцию ЕСЛИ() :
=ЕСЛИ(ЕОШИБКА(A2/B2);»Ошибка в расчетах»;A2/B2)
Т.к. функция ЕСЛИОШИБКА() впервые появилась в EXCEL 2007, то в более ранних версиях придется использовать функцию ЕОШИБКА() .
Обратите внимание, что использована именно ЕОШИБКА() , а не ЕОШ() , т.к. для последней ошибка #Н/Д ошибкой не является (см. рисунок выше).
Примеры формул ЕСЛИОШИБКА и ЕДН для обработки ошибок в Excel
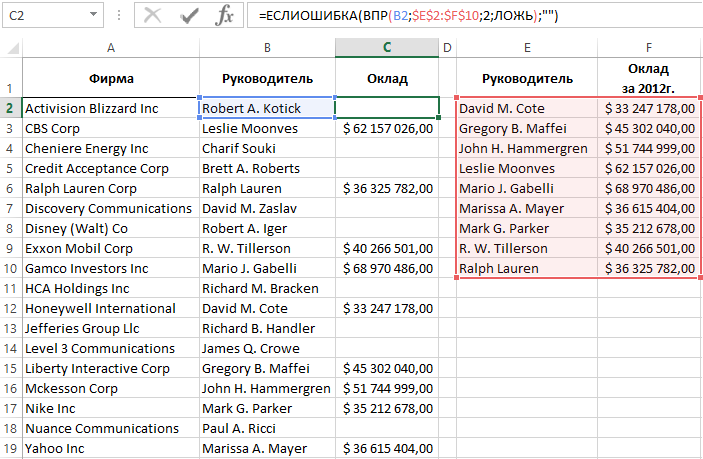
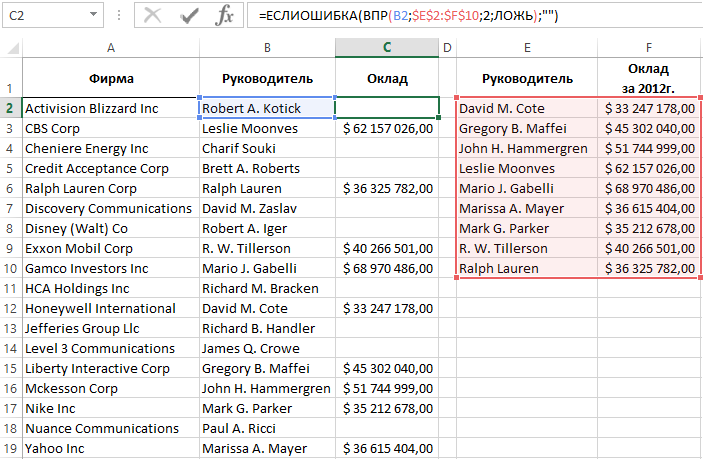
В поисковых функциях Excel: ВПР, ГПР, ПОИСКПОЗ чаще всего в третьем аргументе используется значение ЛОЖЬ или 0. Так пользователь заставляет искать в исходной таблице только точные совпадения значений при поиске. Если в поисковой функции будет в третьем аргументе определено точное совпадение, а искомое значение не будет найдено в таблице, тогда функция возвращает ошибку с кодом #Н/Д!
Формула ЕСЛИОШИБКА обработки ошибок функции ВПР в Excel
Ошибка #Н/Д! пригодится в анализе моделей данных Excel, так как информирует пользователя и программу о том, что не было найдено соответственное значение. Однако если большая часть такой модели данных будет использована в отчетах, то код ошибки #Н/Д! будет смотреться некорректно. Для этого Excel предлагает функции, которые проверяют результаты вычислений на ошибки и позволяют возвращать другие альтернативные значения.
Ниже на рисунке представлена таблица фирм с фамилиями их руководителей. Вторая таблица содержит те же фамилии и соответствующие им оклады. Функция ВПР используется для соединения двух таблиц в одну. Но не по всем руководителям имеются данные об их окладах, поэтому часто встречается код ошибки #Н/Д! в результатах вычисления функции ВПР.
Формула, изображенная на следующем рисунке уже изменена. Она использует функцию ЕСЛИОШИБКА и возвращает пустую строку в том случае если искомое значение не найдено в исходной таблице:
Пользователи часто называют эту функцию «скрывающая ошибки». Так как она позволяет определить и укрыть любые ошибки, которые можно после этого воспринимать по-другому. А не сметить этими некрасивыми кодами в отчетах для презентации.
Первый аргумент функции ЕСЛИОШИБКА – это выражение или формула, а во втором аргументе следует указать альтернативное значение, которое должно отображаться при возникновении ошибки. Если в первом аргументе выражение или формула вернет ошибку, тогда функция вместо его значения возвратит второй аргумент. В противные случаи будет возвращено значение первого аргумента.
В данном примере альтернативным значением является пустая строка (двойные кавычки без каких-либо символов между ними). Благодаря этому отчет более читабельный и имеет презентабельный вид. Данная функция может возвращать любое значение, например, «Нет данных» или число 0.
Функции для работы с кодами ошибок в Excel
Функция ЕСЛИОШИБКА проверяет каждую ошибку, которую способна вернуть формула в Excel. Но следует использовать ее с определенной осторожностью. Ведь она способна скрывать все ошибки без разбора и даже такие важные как: #ДЕЛ/0! или #ЧИСЛО! и т.п.
Чтобы скрывать только определенную группу ошибок Excel предлагает еще 3 других функций:
- ЕОШИБКА – возвращает логическое значение ИСТИНА если ее аргумент содержит ошибку: #Н/Д, #ЗНАЧ!, #ССЫЛКА!, #ДЕЛ/0!, #ЧИСЛО!, #ИМЯ? или #ПУСТО.
- ЕОШ – функция возвращает ИСТИНА если ее аргумент содержит любую ошибку, кроме #Н/Д!
- ЕНД – возвращает значение ИСТИНА если ее аргумент содержит ошибку с кодом #Н/Д! или ЛОЖЬ если аргумент содержит любое значение или любую другую ошибку.
Три выше описанные функции для обработки ошибок в Excel возвращают логические значения ИСТИНА или ЛОЖЬ наиболее часто используются вместе с функцией ЕСЛИ.
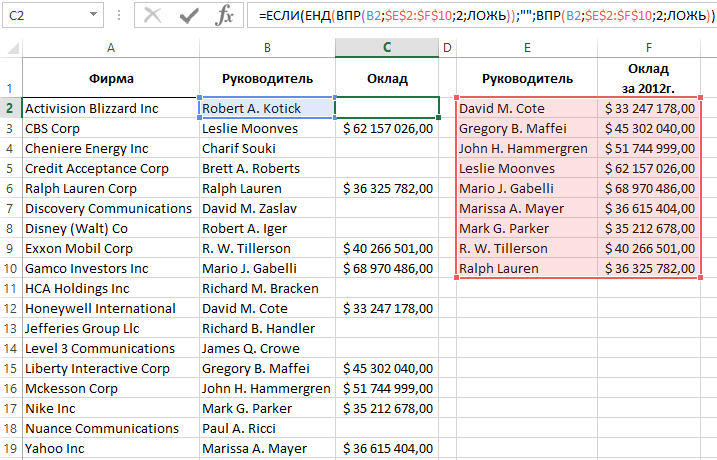
Формула ЕСЛИ и ЕДН для ошибок ВПР без функции ЕСЛИОШИБКА в Excel
Бескомпромиссная функция обработки ошибок ЕСЛИОШИБКА появилась в программе Excel начиная с 2010-й версии. Для проверки ошибок в старших версиях Excel наиболее часто использовалась функция ЕНД:
Функция ЕНД возвращает логическое значение ИСТИНА если в ее аргументе находится только один тип ошибок – #Н/Д! Или же значение ЛОЖЬ при любых других значениях. В данной формуле функция ЕСЛИ помогает функции ЕНД. Если была получена ошибка #Н/Д! формула возвращает пустую строку – указано во втором аргументе функции ЕСЛИ. В противные случаи возвращается результат вычисления функции ВПР – указано в третьем аргументе ЕСЛИ.
Главным недостатком такой формулы является необходимость дублировать функцию ВПР:
- первый разу внутри функции ЕНД;
- второй раз в третьем аргументе ЕСЛИ.
Это значит, что Excel должен два раза выполнять функцию ВПР для одной и той же ячейки. Если на листе содержится множество таких формул, тогда их пересчет требует много времени и системных ресурсов. Очень неудобно будет работать с такими файлами. Возникнет необходимость отключения автоматического пересчета формул: «ФОРМУЛЫ»-«Вычисления»-«Параметры вычислений»-«Вручную».
Перехват ошибок в формулах функцией ЕСЛИОШИБКА (IFERROR)
Тот, кто никогда не ошибался — опасен.
(Книга самурая)
Ошибки случаются. Вдвойне обидно, когда они случаются не по твоей вине. Так в Microsoft Excel, некоторые функции и формулы могут выдавать ошибки не потому, что вы накосячили при вводе, а из-за временного отсутствия данных или копирования формул «с запасом» на избыточные ячейки. Классический пример — ошибка деления на ноль при вычислении среднего:
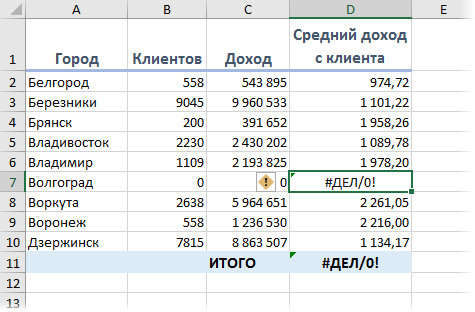
Причем заметьте, что итоги в нашей таблице тоже уже не считаются — одна ошибка начинает порождать другие, передаваясь по цепочке от одной зависимой формулы к другой. Так что из-за одной ошибочной ячейки, в конце концов, может перестать работать весь расчет.
Для лечения подобных ситуаций в Microsoft Excel есть мегаполезная функция ЕСЛИОШИБКА (IFERROR), которая умеет проверять заданную формулу или ячейку и, в случае возникновения любой ошибки, выдавать вместо нее заданное значение: ноль, пустую текстовую строку «» или что-то еще.
Синтаксис функции следующий:
=ЕСЛИОШИБКА( Что_проверяем ; Что_выводить_вместо_ошибки )
Так, в нашем примере можно было бы все исправить так:
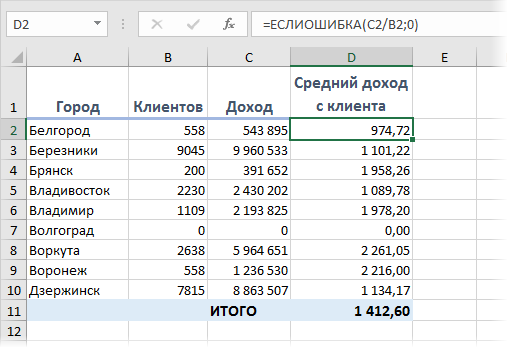
Все красиво и ошибок больше нет.
Обратите внимание, что эта функция появилась только с 2007 версии Microsoft Excel. В более ранних версиях приходилось использовать функции ЕОШ (ISERROR) и ЕНД (ISNA) . Эти функции похожи на ЕСЛИОШИБКА, но они только проверяют наличие ошибок и не умеют заменять их на что-то еще. Поэтому приходилось использовать их обязательно в связке с функцией проверки ЕСЛИ (IF) , создавая вложенные конструкции типа:
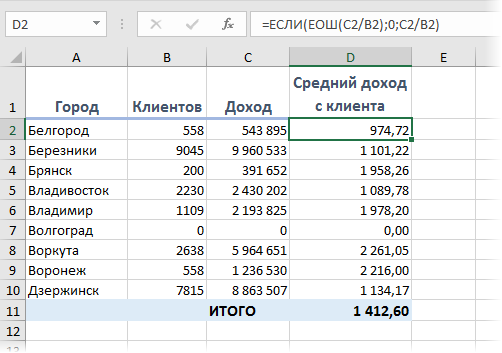
Такой вариант ощутимо медленне работает и сложнее для понимания, так что лучше использовать новую функцию ЕСЛИОШИБКА, если это возможно.
ЕСЛИОШИБКА (функция ЕСЛИОШИБКА)
Функцию ЕСЛИОШИБКА можно использовать для треппинга и обработки ошибок в формуле. ЕСЛИОШИБКА возвращает значение, которое вы указываете, если формула оценивается как ошибка. в противном случае возвращается результат формулы.
Аргументы функции ЕСЛИОШИБКА описаны ниже.
значение Обязательный аргумент. Аргумент, проверяемый на наличие ошибки.
валуе_иф_еррор Обязательный. Возвращаемое значение, если формула возвращает ошибку. Оцениваются следующие типы ошибок: #N/A, #VALUE!, #REF!, #DIV/0!, #NUM!, #NAME? и #NULL!.
Если «значение» или «валуе_иф_еррор» является пустой ячейкой, ЕСЛИОШИБКА рассчитает ее как пустую строку («»).
Если значение является формулой массива, ЕСЛИОШИБКА возвращает массив результатов для каждой ячейки в диапазоне, указанном в значении. Ознакомьтесь со вторым примером ниже.
Скопируйте образец данных из следующей таблицы и вставьте их в ячейку A1 нового листа Excel. Чтобы отобразить результаты формул, выделите их и нажмите клавишу F2, а затем — ВВОД.
=ЕСЛИОШИБКА(A2/B2;»Ошибка при вычислении»)
Выполняет проверку на предмет ошибки в формуле в первом аргументе (деление 210 на 35), не обнаруживает ошибок и возвращает результат вычисления по формуле
=ЕСЛИОШИБКА(A3/B3;»Ошибка при вычислении»)
Выполняет проверку на предмет ошибки в формуле в первом аргументе (деление 55 на 0), обнаруживает ошибку «деление на 0» и возвращает «значение_при_ошибке»
Ошибка при вычислении
=ЕСЛИОШИБКА(A4/B4;»Ошибка при вычислении»)
Выполняет проверку на предмет ошибки в формуле в первом аргументе (деление «» на 23), не обнаруживает ошибок и возвращает результат вычисления по формуле.
Ошибка при вычислении
Выполняет проверку на предмет ошибки в формуле в первом аргументе в первом элементе массива (A2/B2 или деление 210 на 35), не обнаруживает ошибок и возвращает результат вычисления по формуле
Выполняет проверку на предмет ошибки в формуле в первом аргументе во втором элементе массива (A3/B3 или деление 55 на 0), обнаруживает ошибку «деление на 0» и возвращает «значение_при_ошибке»
Ошибка при вычислении
Выполняет проверку на предмет ошибки в формуле в первом аргументе в третьем элементе массива (A4/B4 или деление «» на 23), не обнаруживает ошибок и возвращает результат вычисления по формуле
Примечание. Если у вас установлена текущая версия Office 365, вы можете ввести формулу в левую верхнюю ячейку диапазона вывода, а затем нажмите клавишу ВВОД, чтобы подтвердить формулу как формулу динамических массивов. В противном случае необходимо ввести формулу в качестве устаревшей формулы массива, сначала выделив диапазон вывода, введите формулу в верхнюю левую ячейку выходного диапазона, а затем нажмите клавиши CTRL + SHIFT + ВВОД, чтобы подтвердить его. Excel автоматически вставляет фигурные скобки в начале и конце формулы. Дополнительные сведения о формулах массива см. в статье Использование формул массива: рекомендации и примеры.
Дополнительные сведения
Вы всегда можете задать вопрос специалисту Excel Tech Community, попросить помощи в сообществе Answers community, а также предложить новую функцию или улучшение на веб-сайте Excel User Voice.
Примечание: Эта страница переведена автоматически, поэтому ее текст может содержать неточности и грамматические ошибки. Для нас важно, чтобы эта статья была вам полезна. Была ли информация полезной? Для удобства также приводим ссылку на оригинал (на английском языке).
Типы ошибок в формулах Excel: какие бывают и как исправить
Каждый, кто более-менее часто имеет дело с формулами Excel (пишет сам или пользуется файлами, созданными другими), знает, что иногда в этих формулах появляются крайне неприятные ошибки, которые приводят к их полной неработоспособности. В разнообразии ошибок легко запутаться. Но чтобы уметь быстро их исправлять, нужно знать, почему возникает та или иная ошибка и что с ней делать. Разберем их основные виды.
Если ячейка вдруг целиком заполнилась символами решётки, то варианта всего два: либо значение ячейки не помещается в нее, либо в ней введено отрицательное значение времени (случается, если формат ячейки — «Время»).
В первом случае достаточно расширить столбец или уменьшить шрифт, а во втором — исправить значение времени. Например, если в формуле из меньшего времени вычитается большее, то нужно сделать наоборот (или взять результат вычислений по модулю).
Эту ошибку часто зовут «дело», хотя говорит она не о делах а о том, что нельзя делить на ноль. Возникает, если в формуле происходит деление на 0 или на пустую ячейку. Соответственно, исправив нулевой или пустой знаменатель, можно исправить ошибку.
Самая распространенная ошибка. Возникает тогда, когда функция поиска данных не находит искомое значение в диапазоне. Функции поиска данных это: ВПР, ГПР, ПОИСКПОЗ, ПРОСМОТР. Соответственно, решается либо изменением поискового запроса («что ищем»), либо внесением в диапазон искомого значения. Однако, чаще всего эта ошибка вполне ожидаема и просто помогает проверить наличие того или иного значения в списке. Многие пользователи предпочитают выводить вместо нее пустые значения или какой-то значимый текст с помощью функции ЕСЛИОШИБКА. Например:
=ЕСЛИОШИБКА(ВПР(A1;B:C;2;0);»Отсутствует в справочнике»)
Возникает, когда в формуле используется нераспознанное программой имя. Именем Excel считает любой текст, не являющийся названием функции, ссылкой на ячейку/диапазон и не взятый в кавычки. Например, в формуле =СЕГОДНЯ()+СЕГ-A4 слово СЕГ будет распознано как имя.
Когда распознанного имени нет в списке именованных диапазонов, появляется данная ошибка. Способы решения:
- Создать нужное имя в диспетчере имен;
- Проверить правильность написания уже существующего имени;
- Проверить, верно ли написаны функции рабочего листа (опечатки приведут к возникновению ошибки)
Данная ошибка возникает в случае, когда ячейка или диапазон, на который ссылается формула, был удален, перемещен или стал недоступным. Например, если есть формула
и Вы удалите столбец С, то формула выдаст ошибку #ССЫЛКА!, так как вместе со столбцом С была удалена и ячейка C3. Обратите внимание, что на листе по-прежнему есть ячейка с таким адресом, но физически это уже не та ячейка, которая раньше располагалась на этом месте (хотя адрес тот же).
Чтобы исправить ошибку, нужно отменить удаление ячейки (если есть такая возможность) или заново сослаться на нужный диапазон. Другой вариант — использовать функцию ДВССЫЛ для тех ячеек, которые могут быть удалены. Например, формула =A1+ДВССЫЛ(«C3») будет работать даже тогда, когда мы удалим столбец C.
Другой вариант возникновения — файлы, на которые есть ссылки были перемещены, удалены или переименованы. Любое из этих действий при последующем обновлении связей выдаст указанную ошибку. Вывод — будьте аккуратнее с файлами, на которые делаете ссылки.
Возникает чаще всего тогда, когда в формуле использован неверный тип данных. Помните, что текст, число или дата — разные типы данных и обрабатываются по разному. Если передать, например, функции ДЕНЬНЕД() ссылку на ячейку с текстом, то появится указанная ошибка. То же самое произойдет, если попытаетесь вычесть из 100 слово «десять». Для исправления — проверьте все аргументы Соответствуют ли они требуемым типам данных? Если нет — укажите правильные типы.
Крайне редкая ошибка, так как мало кто использует в работе оператор пересечения диапазонов (про него можно почитать тут ). Собственно, возникает тогда, когда диапазоны не пересекаются. Для исправления — укажите пересекающиеся диапазоны. Например, формула:
выдаст ошибку. А формула:
будет работать безошибочно и вернет диапазон A5:B5
Еще одна не самая распространенная ошибка. Встречается, если задан недопустимый числовой аргумент. То есть, тип данных указан верно (поэтому не #ЗНАЧ!), но само число выбрано недопустимое. Чаще всего встречается в финансовых функциях. Например, формула:
выдаст эту ошибку, так как аргумент «Ставка» не может быть отрицательным.
Для исправления — введите допустимый числовой аргумент.
Знать, что означают ошибки — полбеды. Нужно еще понять, какая именно часть формулы генерирует ошибку. Для этого формулу нужно проанализировать. Советы на эту тему можно найти в этой статье . Желаем Вам только исправных формул!
Видеоверсию данной статьи смотрите на нашем канале на YouTube
Чтобы не пропустить новые уроки и постоянно повышать свое мастерство владения Excel — подписывайтесь на наш канал в Telegram Excel Everyday
Много интересного по другим офисным приложениям от Microsoft (Word, Outlook, Power Point, Visio и т.д.) — на нашем канале в Telegram Office Killer
Вопросы по Excel можно задать нашему боту обратной связи в Telegram @ExEvFeedbackBot
Вопросы по другому ПО (кроме Excel) задавайте второму боту — @KillOfBot
Перейти к содержанию
Получение антилогов
На чтение 1 мин. Просмотров 157 Опубликовано 12.05.2021
Excel позволяет использовать на листах довольно много различных тригонометрических функций. Если вы хорошо разбираетесь в триггерах, вы можете задаться вопросом, почему нет функций, производящих антиблоги.
Антилог в Excel технически определяется как функция, обратная функции LOG10. Функция LOG10 означает логарифм числа по основанию 10. Учитывая это определение, антилогарифмический или обратный логарифм любого числа просто возводится в 10 до этого числа. Например, логарифм по основанию 10 для 4 равен 0,60206, а антилогарифм по основанию 10 для 4 равен 10,000 (10 в четвертой степени). Это также означает, что антилогарифм по основанию 10 логарифма 4 по основанию 10 снова равен 4. (Повышение 10 до степени 0.60206 равно 4.)
В следующей таблице показано, как вы могли бы это сделать. получить антиблоги различных функций журнала в Excel.
| Base | Number | Журнал | Antilog (Power) | |||
|---|---|---|---|---|---|---|
| x | y | = LOG ( x, y) | =x^y | |||
| e | y | = LN (y) | =e^y | |||
| 10 | y | = LOG10 (y) | =10^y |