Are there any pure-python implementations of the inverse error function?
I know that SciPy has scipy.special.erfinv(), but that relies on some C extensions. I’d like a pure python implementation.
I’ve tried writing my own using the Wikipedia and Wolfram references, but it always seems to diverge from the true value when the arg is > 0.9.
I’ve also attempted to port the underlying C code that Scipy uses (ndtri.c and the cephes polevl.c functions) but that’s also not passing my unit tests.
Edit: As requested, I’ve added the ported code.
Docstrings (and doctests) have been removed because they’re longer than the functions. I haven’t yet put much effort into making the port more pythonic — I’ll worry about that once I get something that passes unit tests.
Supporting functions from cephes polevl.c
def polevl(x, coefs, N):
ans = 0
power = len(coefs) - 1
for coef in coefs[:N]:
ans += coef * x**power
power -= 1
return ans
def p1evl(x, coefs, N):
return polevl(x, [1] + coefs, N)
Main Inverse Error Function
def inv_erf(z):
if z < -1 or z > 1:
raise ValueError("`z` must be between -1 and 1 inclusive")
if z == 0:
return 0
if z == 1:
return math.inf
if z == -1:
return -math.inf
# From scipy special/cephes/ndrti.c
def ndtri(y):
# approximation for 0 <= abs(z - 0.5) <= 3/8
P0 = [
-5.99633501014107895267E1,
9.80010754185999661536E1,
-5.66762857469070293439E1,
1.39312609387279679503E1,
-1.23916583867381258016E0,
]
Q0 = [
1.95448858338141759834E0,
4.67627912898881538453E0,
8.63602421390890590575E1,
-2.25462687854119370527E2,
2.00260212380060660359E2,
-8.20372256168333339912E1,
1.59056225126211695515E1,
-1.18331621121330003142E0,
]
# Approximation for interval z = sqrt(-2 log y ) between 2 and 8
# i.e., y between exp(-2) = .135 and exp(-32) = 1.27e-14.
P1 = [
4.05544892305962419923E0,
3.15251094599893866154E1,
5.71628192246421288162E1,
4.40805073893200834700E1,
1.46849561928858024014E1,
2.18663306850790267539E0,
-1.40256079171354495875E-1,
-3.50424626827848203418E-2,
-8.57456785154685413611E-4,
]
Q1 = [
1.57799883256466749731E1,
4.53907635128879210584E1,
4.13172038254672030440E1,
1.50425385692907503408E1,
2.50464946208309415979E0,
-1.42182922854787788574E-1,
-3.80806407691578277194E-2,
-9.33259480895457427372E-4,
]
# Approximation for interval z = sqrt(-2 log y ) between 8 and 64
# i.e., y between exp(-32) = 1.27e-14 and exp(-2048) = 3.67e-890.
P2 = [
3.23774891776946035970E0,
6.91522889068984211695E0,
3.93881025292474443415E0,
1.33303460815807542389E0,
2.01485389549179081538E-1,
1.23716634817820021358E-2,
3.01581553508235416007E-4,
2.65806974686737550832E-6,
6.23974539184983293730E-9,
]
Q2 = [
6.02427039364742014255E0,
3.67983563856160859403E0,
1.37702099489081330271E0,
2.16236993594496635890E-1,
1.34204006088543189037E-2,
3.28014464682127739104E-4,
2.89247864745380683936E-6,
6.79019408009981274425E-9,
]
s2pi = 2.50662827463100050242
code = 1
if y > (1.0 - 0.13533528323661269189): # 0.135... = exp(-2)
y = 1.0 - y
code = 0
if y > 0.13533528323661269189:
y = y - 0.5
y2 = y * y
x = y + y * (y2 * polevl(y2, P0, 4) / p1evl(y2, Q0, 8))
x = x * s2pi
return x
x = math.sqrt(-2.0 * math.log(y))
x0 = x - math.log(x) / x
z = 1.0 / x
if x < 8.0: # y > exp(-32) = 1.2664165549e-14
x1 = z * polevl(z, P1, 8) / p1evl(z, Q1, 8)
else:
x1 = z * polevl(z, P2, 8) / p1evl(z, Q2, 8)
x = x0 - x1
if code != 0:
x = -x
return x
result = ndtri((z + 1) / 2.0) / math.sqrt(2)
return result
Существуют ли какие-либо реализации pure-python функции обратной ошибки?
Я знаю, что SciPy имеет scipy.special.erfinv(), но это зависит от некоторых расширений C. Мне нужна чистая реализация python.
Я пробовал писать свои собственные, используя ссылки Википедии и Вольфрама, но он всегда кажется отличным от истинного значения, когда arg> 0.9.
Я также попытался перенести базовый код C, который использует Scipy ( ndtri.c и cephes polevl.c), но также не передает мои модульные тесты.
Изменение: по запросу я добавил портированный код.
Докстры (и доктрины) были удалены, потому что они длиннее функций. Я еще не приложил много усилий, чтобы сделать порт более pythonic — я буду беспокоиться об этом, как только я получу что-то, что проходит модульные тесты.
Вспомогательные функции от cephes polevl.c
def polevl(x, coefs, N):
ans = 0
power = len(coefs) - 1
for coef in coefs[:N]:
ans += coef * x**power
power -= 1
return ans
def p1evl(x, coefs, N):
return polevl(x, [1] + coefs, N)
Основная функция инверсной ошибки
def inv_erf(z):
if z < -1 or z > 1:
raise ValueError("'z' must be between -1 and 1 inclusive")
if z == 0:
return 0
if z == 1:
return math.inf
if z == -1:
return -math.inf
# From scipy special/cephes/ndrti.c
def ndtri(y):
# approximation for 0 <= abs(z - 0.5) <= 3/8
P0 = [
-5.99633501014107895267E1,
9.80010754185999661536E1,
-5.66762857469070293439E1,
1.39312609387279679503E1,
-1.23916583867381258016E0,
]
Q0 = [
1.95448858338141759834E0,
4.67627912898881538453E0,
8.63602421390890590575E1,
-2.25462687854119370527E2,
2.00260212380060660359E2,
-8.20372256168333339912E1,
1.59056225126211695515E1,
-1.18331621121330003142E0,
]
# Approximation for interval z = sqrt(-2 log y ) between 2 and 8
# i.e., y between exp(-2) = .135 and exp(-32) = 1.27e-14.
P1 = [
4.05544892305962419923E0,
3.15251094599893866154E1,
5.71628192246421288162E1,
4.40805073893200834700E1,
1.46849561928858024014E1,
2.18663306850790267539E0,
-1.40256079171354495875E-1,
-3.50424626827848203418E-2,
-8.57456785154685413611E-4,
]
Q1 = [
1.57799883256466749731E1,
4.53907635128879210584E1,
4.13172038254672030440E1,
1.50425385692907503408E1,
2.50464946208309415979E0,
-1.42182922854787788574E-1,
-3.80806407691578277194E-2,
-9.33259480895457427372E-4,
]
# Approximation for interval z = sqrt(-2 log y ) between 8 and 64
# i.e., y between exp(-32) = 1.27e-14 and exp(-2048) = 3.67e-890.
P2 = [
3.23774891776946035970E0,
6.91522889068984211695E0,
3.93881025292474443415E0,
1.33303460815807542389E0,
2.01485389549179081538E-1,
1.23716634817820021358E-2,
3.01581553508235416007E-4,
2.65806974686737550832E-6,
6.23974539184983293730E-9,
]
Q2 = [
6.02427039364742014255E0,
3.67983563856160859403E0,
1.37702099489081330271E0,
2.16236993594496635890E-1,
1.34204006088543189037E-2,
3.28014464682127739104E-4,
2.89247864745380683936E-6,
6.79019408009981274425E-9,
]
s2pi = 2.50662827463100050242
code = 1
if y > (1.0 - 0.13533528323661269189): # 0.135... = exp(-2)
y = 1.0 - y
code = 0
if y > 0.13533528323661269189:
y = y - 0.5
y2 = y * y
x = y + y * (y2 * polevl(y2, P0, 4) / p1evl(y2, Q0, 8))
x = x * s2pi
return x
x = math.sqrt(-2.0 * math.log(y))
x0 = x - math.log(x) / x
z = 1.0 / x
if x < 8.0: # y > exp(-32) = 1.2664165549e-14
x1 = z * polevl(z, P1, 8) / p1evl(z, Q1, 8)
else:
x1 = z * polevl(z, P2, 8) / p1evl(z, Q2, 8)
x = x0 - x1
if code != 0:
x = -x
return x
result = ndtri((z + 1) / 2.0) / math.sqrt(2)
return result
Существуют ли чисто Python реализации функции обратной ошибки?
Я знаю, что SciPy имеет scipy.special.erfinv (), но это зависит от некоторых расширений Си. Я хотел бы чистую реализацию Python.
Я пытался написать свои собственные, используя ссылки на Википедию и Вольфрама, но всегда кажется, что они отличаются от истинного значения, когда аргумент> 0,9.
Я также попытался портировать основной код C, который использует Scipy (ndtri.c и cephes polevl.c функции), но это также не проходит мои юнит-тесты.
Изменить: По запросу я добавил портированный код.
Строки документации (и тесты документов) были удалены, потому что они длиннее функций. Я еще не приложил много усилий, чтобы сделать порт более питоническим — я буду беспокоиться об этом, как только получу что-то, что проходит модульные тесты.
Вспомогательные функции от cephes polevl.c
def polevl(x, coefs, N):
ans = 0
power = len(coefs) - 1
for coef in coefs[:N]:
ans += coef * x**power
power -= 1
return ans
def p1evl(x, coefs, N):
return polevl(x, [1] + coefs, N)
Главная обратная функция ошибок
def inv_erf(z):
if z < -1 or z > 1:
raise ValueError("`z` must be between -1 and 1 inclusive")
if z == 0:
return 0
if z == 1:
return math.inf
if z == -1:
return -math.inf
# From scipy special/cephes/ndrti.c
def ndtri(y):
# approximation for 0 <= abs(z - 0.5) <= 3/8
P0 = [
-5.99633501014107895267E1,
9.80010754185999661536E1,
-5.66762857469070293439E1,
1.39312609387279679503E1,
-1.23916583867381258016E0,
]
Q0 = [
1.95448858338141759834E0,
4.67627912898881538453E0,
8.63602421390890590575E1,
-2.25462687854119370527E2,
2.00260212380060660359E2,
-8.20372256168333339912E1,
1.59056225126211695515E1,
-1.18331621121330003142E0,
]
# Approximation for interval z = sqrt(-2 log y ) between 2 and 8
# i.e., y between exp(-2) = .135 and exp(-32) = 1.27e-14.
P1 = [
4.05544892305962419923E0,
3.15251094599893866154E1,
5.71628192246421288162E1,
4.40805073893200834700E1,
1.46849561928858024014E1,
2.18663306850790267539E0,
-1.40256079171354495875E-1,
-3.50424626827848203418E-2,
-8.57456785154685413611E-4,
]
Q1 = [
1.57799883256466749731E1,
4.53907635128879210584E1,
4.13172038254672030440E1,
1.50425385692907503408E1,
2.50464946208309415979E0,
-1.42182922854787788574E-1,
-3.80806407691578277194E-2,
-9.33259480895457427372E-4,
]
# Approximation for interval z = sqrt(-2 log y ) between 8 and 64
# i.e., y between exp(-32) = 1.27e-14 and exp(-2048) = 3.67e-890.
P2 = [
3.23774891776946035970E0,
6.91522889068984211695E0,
3.93881025292474443415E0,
1.33303460815807542389E0,
2.01485389549179081538E-1,
1.23716634817820021358E-2,
3.01581553508235416007E-4,
2.65806974686737550832E-6,
6.23974539184983293730E-9,
]
Q2 = [
6.02427039364742014255E0,
3.67983563856160859403E0,
1.37702099489081330271E0,
2.16236993594496635890E-1,
1.34204006088543189037E-2,
3.28014464682127739104E-4,
2.89247864745380683936E-6,
6.79019408009981274425E-9,
]
s2pi = 2.50662827463100050242
code = 1
if y > (1.0 - 0.13533528323661269189): # 0.135... = exp(-2)
y = 1.0 - y
code = 0
if y > 0.13533528323661269189:
y = y - 0.5
y2 = y * y
x = y + y * (y2 * polevl(y2, P0, 4) / p1evl(y2, Q0, 8))
x = x * s2pi
return x
x = math.sqrt(-2.0 * math.log(y))
x0 = x - math.log(x) / x
z = 1.0 / x
if x < 8.0: # y > exp(-32) = 1.2664165549e-14
x1 = z * polevl(z, P1, 8) / p1evl(z, Q1, 8)
else:
x1 = z * polevl(z, P2, 8) / p1evl(z, Q2, 8)
x = x0 - x1
if code != 0:
x = -x
return x
result = ndtri((z + 1) / 2.0) / math.sqrt(2)
return result
Время чтения 3 мин.
Метод Python math.erf() вернет ошибку в точке x. Функция ошибки также известна как функция ошибки Гаусса: она выдает ошибку, если в качестве параметра передается любое не числовое значение.
Python math.erfc() — это встроенный метод, определенный в математическом модуле, который используется для поиска дополнительной функции ошибок в точке x, если x — переданный параметр. Например, если x передается в качестве параметра в функцию erf(erf(x)), она возвращает дополнительную функцию ошибки.
Содержание
- Что такое функция erf() в Python?
- Синтаксис
- Параметры
- Возвращаемое значение
- Примеры программ по методу erf() в Python
- Пример 1. Программа, демонстрирующая работу метода erf()
- Пример 2. Программа для передачи значения вне допустимого диапазона из функции и отображения вывода
- Что такое функция erfc() в Python?
- Синтаксис
- Параметры
- Возвращаемое значение
- Примеры программ
- Пример 1. Программа, показывающая работу метода erfc()
- Пример 2. Передача значения вне допустимого диапазона из функции и отображения вывода
Python erf() — это встроенный метод, определенный в математическом модуле, который используется для поиска функции ошибки в точке x, если x является переданным параметром. Например, если x передается в качестве параметра в функцию erf(erf(x)), она возвращает функцию ошибки. Мы можем использовать математический модуль, импортировав его.
Синтаксис
Здесь var — это переменная, функцию ошибки которой мы должны найти.
Параметры
Имеет один аргумент var, который принимает значения числового типа данных и выдает TypeError, если передается аргумент любого другого типа данных.
Возвращаемое значение
Возвращает значение функции ошибки числа в типе данных float.
См. следующий пример кода.
|
import math var = 0.6 print(math.erf(var)) |
Примеры программ по методу erf() в Python
Пример 1. Программа, демонстрирующая работу метода erf()
|
import math a1 = 0.3 b1 = 0.9 c1 = 0.7 d1 = 0.2 print(«Value for parameter «, a1, » is «, math.erf(a1)) print(«Value for parameter «, b1, » is «, math.erf(b1)) print(«Value for parameter «, c1, » is «, math.erf(c1)) print(«Value for parameter «, d1, » is «, math.erf(d1)) |
Выход:
|
Value for parameter 0.3 is 0.3286267594591274 Value for parameter 0.9 is 0.796908212422832 Value for parameter 0.7 is 0.6778011938374183 Value for parameter 0.2 is 0.22270258921047847 |
В этом примере кода мы видели, что, передавая параметр vaild, который отличается для разных примеров, мы получаем желаемое решение метода erf().
Пример 2. Программа для передачи значения вне допустимого диапазона из функции и отображения вывода
См. следующий код.
|
import math x = ‘b’ print(math.erf(x)) |
Выход:
|
TypeError: must be real number, not str |
В этом примере мы видим, что при передаче параметра, который не имеет числового типа, функция выдает ошибку.
Python erfc() — это встроенный метод, определенный в математическом модуле, который используется для поиска дополнительной функции ошибок в точке x, если x — переданный параметр. Например, если x передается в качестве параметра в функцию erf(erf(x)), она возвращает дополнительную функцию ошибки.
Что такое функция erfc() в Python?
Функция Python math.erfc() возвращает дополнительную функцию ошибки в точке x. Функция ошибки также известна как функция ошибки Гаусса, и функция выдает ошибку, если в качестве параметра передается любое не числовое значение. Определяется как 1,0 – erf(x). Используется для большого значения x, если мы вычтем из 1, то это приведет к потере значимости.
Мы можем использовать математический модуль, импортировав его. После импорта мы используем для вызова этой функции статический объект.
Синтаксис
Здесь var — это переменная, для которой мы должны найти дополнительную функцию ошибки.
Параметры
Он принимает один параметр var, который принимает значения числового типа данных и выдает ошибку типа, если передается аргумент любого другого типа данных.
Возвращаемое значение
Он возвращает значение функции ошибки числа в типе данных float.
См. следующий код.
|
import math var = 0.6 print(math.erfc(var)) |
Примеры программ
Пример 1. Программа, показывающая работу метода erfc()
|
import math a1 = 0.3 b1 = 0.9 c1 = 0.7 d1 = 0.2 print(«Value for parameter «, a1, » is «, math.erfc(a1)) print(«Value for parameter «, b1, » is «, math.erfc(b1)) print(«Value for parameter «, c1, » is «, math.erfc(c1)) print(«Value for parameter «, d1, » is «, math.erfc(d1)) |
Выход:
|
Value for parameter 0.3 is 0.6713732405408726 Value for parameter 0.9 is 0.20309178757716786 Value for parameter 0.7 is 0.32219880616258156 Value for parameter 0.2 is 0.7772974107895215 |
В этом примере мы видели, что, передавая параметр vaild, который отличается для разных примеров, мы получаем желаемое решение метода erfc(), которое является дополнительным значением функции ошибок.
Пример 2. Передача значения вне допустимого диапазона из функции и отображения вывода
|
import math x = ‘b’ print(math.erfc(x)) |
Выход:
|
TypeError: must be real number, not str |
В этом примере мы видели, что при передаче параметра, который не имеет числового типа, функция выдает ошибку.

Мы редко получаем скрипт, работающий без каких-либо ошибок с первой попытки, что абсолютно нормально при написании кода. Важной и иногда сложной частью является исправление этих ошибок.
Процесс исправления ошибок и обеспечения ожидаемой работы скрипта может занять много итераций в зависимости от опыта программиста и имеющейся у нас информации об ошибке. Языки программирования дают нам некоторые подсказки относительно того, что может быть причиной ошибки, что в основном и делает трассировка Python.
Трассировку в Python можно рассматривать как отчет, который помогает нам понять и устранить проблему в коде. В этой статье мы узнаем, что такое обратная трассировка в Python, как читать сообщения обратной трассировки, чтобы иметь возможность использовать их более эффективно, и различные типы ошибок.
Обратная трассировка в Python
Программа на Python останавливает выполнение, когда она сталкивается с ошибкой, которая может быть в форме синтаксической ошибки или исключения. Синтаксические ошибки возникают, когда интерпретатор обнаруживает недопустимый синтаксис, и их относительно легче исправить.
Примером синтаксической ошибки может быть несоответствующая скобка. С другой стороны, исключение возникает, когда синтаксис правильный, но программа выдает ошибку.
Обратная трассировка — это отчет, который помогает нам понять причину исключения. Он содержит вызовы функций, выполненные в коде, вместе с номерами их строк, чтобы мы не были в неведении о проблеме, вызывающей сбой кода.
Давайте рассмотрим простой пример.
Приведенный ниже фрагмент кода создает функцию, которая складывает два числа и умножает сумму на первое число. Затем он вызывает функцию с аргументами 5 и 4. Однако 4 передается как строка, так что на самом деле это не число.
def add_and_multiply(x, y):
return (x + y) * x
add_and_multiply(5, "4")Когда этот код выполняется, Python вызывает следующее исключение:
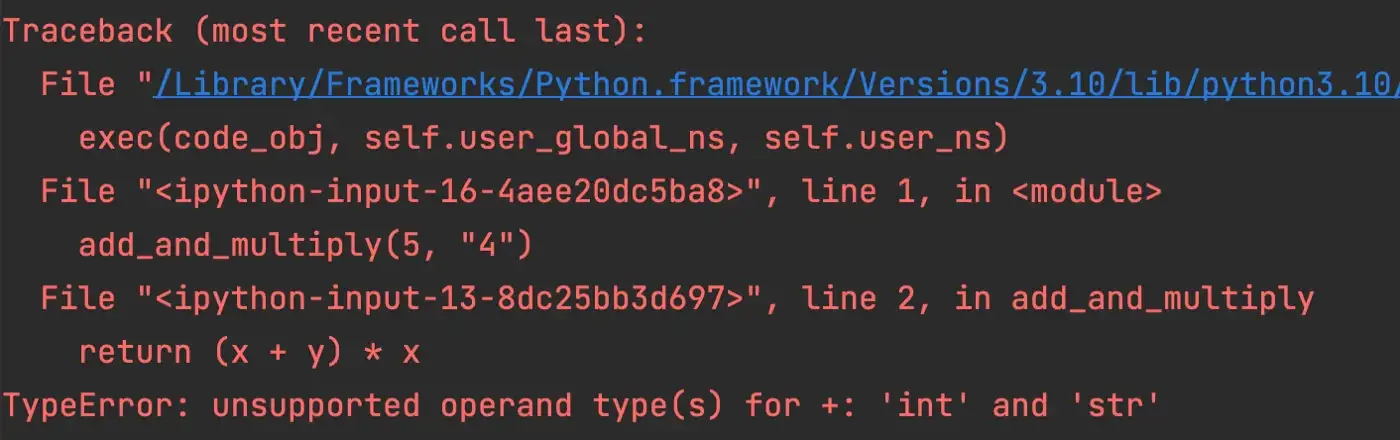
В последней строке показан тип ошибки вместе с кратким объяснением. Ошибка в этом случае — это ошибка типа, вызванная неподдерживаемым операндом между целыми числами и строками. Оператор плюс не может быть использован для добавления строки к целому числу, поэтому код приводит к исключению.
Строки над последней сообщают нам, где произошло исключение, с точки зрения имени функции и номера строки. Приведенный здесь пример очень прост, но при работе с очень длинными сценариями или программой с несколькими сценариями информация об именах функций и номерах строк весьма полезна для диагностики и устранения проблемы.
Обратная трассировка также показывает имена модулей и файлов, что очень полезно при работе со сценариями, которые импортируют модули из других файлов или скриптов. Способ отображения имен файлов и модулей немного меняется в зависимости от вашей рабочей среды (например, терминала или ОТВЕТА).
Например, когда я сохраняю приведенный выше фрагмент кода как «sample_script.py» и пытаюсь запустить его в терминале, я получаю следующую трассировку:
Traceback (most recent call last):
File "/Users/sonery/sample_script.py", line 6, in <module>
add_and_multiply(5, "6")
File "/Users/sonery/sample_script.py", line 2, in add_and_multiply
print((x + y) * x)
TypeError: unsupported operand type(s) for +: 'int' and 'str'В любом случае, мы получаем информативную зацепку в сообщениях обратной связи.
Распространенные типы обратной трассировки
Значительное количество времени при создании эффективных программ и поддержании их в рабочем состоянии тратится на отладку ошибок. Следовательно, крайне важно использовать обратные трассировки Python.
В противном случае на поиск и устранение неполадок могут потребоваться часы, что может иметь серьезные последствия, если программа уже запущена в производство.
Наиболее важной частью сообщения об обратном отслеживании является тип ошибки, поскольку он дает нам подсказки о том, какая ошибка приводит к остановке выполнения скрипта.
Давайте рассмотрим некоторые из часто встречающихся типов ошибок в сообщениях обратной трассировки.
TypeError
Ошибка типа возникает, когда тип данных объекта несовместим с определенной операцией. Пример, который мы сделали в начале, где добавляются целое число и строка, является примером этой ошибки.
AttributeError
В Python все является объектом с таким типом, как целое число, строка, список, кортеж, словарь и так далее. Типы определяются с помощью классов, которые также имеют атрибуты, используемые для взаимодействия с объектами класса.
Классы могут иметь атрибуты данных и процедурные атрибуты (т.е. методы):
- Атрибуты данных: что необходимо для создания экземпляра класса
- Методы (т.е. процедурные атрибуты): Как мы взаимодействуем с экземплярами класса.
Предположим, у нас есть объект типа list. Мы можем использовать метод append для добавления нового элемента в список. Если у объекта нет атрибута, который мы пытаемся использовать, возникает исключение ошибки атрибута.
Вот пример:
mylist = [1, 2, 3, 4, 5]
mylist.add(10)
# output
Traceback (most recent call last):
File "<file>", line 3378, in run_code
exec(code_obj, self.user_global_ns, self.user_ns)
File "<ipython-input-25-4ad0ec665b52>", line 3, in <module>
mylist.add(10)
AttributeError: 'list' object has no attribute 'add'Поскольку класс list не имеет атрибута с именем “add”, мы получаем трассировку, показывающую ошибку атрибута.
ImportError и ModuleNotFoundError
Python имеет огромный выбор сторонних библиотек (т.е. модулей), что позволяет выполнять множество задач за несколько строк кода.
Чтобы использовать такие библиотеки, а также встроенные библиотеки Python (например, ОС, запросы), нам необходимо их импортировать. Если при их импорте возникает проблема, возникает исключение importerror или module not found error.
Например, в следующем фрагменте кода мы пытаемся импортировать класс логистической регрессии из Scikit-learn.
from sklearn import LogisticRegression
# output
Traceback (most recent call last):
File "<file>", line 3378, in run_code
exec(code_obj, self.user_global_ns, self.user_ns)
File "<ipython-input-22-b74afc1ba453>", line 1, in <module>
from sklearn import LogisticRegression
ImportError: cannot import name 'LogisticRegression' from 'sklearn' (/Library/Frameworks/Python.framework/Versions/3.10/lib/python3.10/site-packages/sklearn/__init__.py)Возникает исключение ошибки импорта, поскольку класс логистической регрессии доступен в модуле линейной модели. Правильный способ импорта следующий.
from sklearn.linear_model import LogisticRegressionИсключение ошибки модуля не найдено возникает, если модуль недоступен в рабочей среде.
import openpyxl
# output
Traceback (most recent call last):
File "<file>", line 3378, in run_code
exec(code_obj, self.user_global_ns, self.user_ns)
File "<ipython-input-23-f5ea1cbb6934>", line 1, in <module>
import openpyxl
File "/Applications/PyCharm CE.app/Contents/plugins/python-ce/helpers/pydev/_pydev_bundle/pydev_import_hook.py", line 21, in do_import
module = self._system_import(name, *args, **kwargs)
ModuleNotFoundError: No module named 'openpyxl'IndexError
Некоторые структуры данных имеют индекс, который можно использовать для доступа к их элементам, таким как списки, кортежи и кадры данных Pandas. Мы можем получить доступ к определенному элементу, используя индекс последовательности.
names = ["John", "Jane", "Max", "Emily"]
# Get the third item
names[2]
# output
"Max"Если индекс выходит за пределы допустимого диапазона, возникает исключение ошибки индекса.
names = ["John", "Jane", "Max", "Emily"]
# Get the sixth item
names[5]
# output
Traceback (most recent call last):
File "<file>", line 3378, in run_code
exec(code_obj, self.user_global_ns, self.user_ns)
File "<ipython-input-30-3033b2837dcd>", line 3, in <module>
names[5]
IndexError: list index out of rangeПоскольку список содержит 4 элемента, возникает исключение, когда мы пытаемся получить доступ к шестому элементу, которого не существует.
Давайте рассмотрим другой пример, используя фрейм данных Pandas.
import pandas as pd
import numpy as np
df = pd.DataFrame(np.random.randint(10, size=(5, 2)), columns=["A", "B"])
df
# output
A B
0 1 6
1 6 3
2 8 8
3 3 5
4 5 6Переменная df представляет собой DataFrame с 5 строками и 2 столбцами. Следующая строка кода пытается получить значение в третьем столбце первой строки.
df.iloc[0, 3]
# output
Traceback (most recent call last):
File "<file>", line 3378, in run_code
exec(code_obj, self.user_global_ns, self.user_ns)
File "<file>", line 1, in <module>
df.iloc[0, 3]
File "<file>", line 960, in __getitem__
return self.obj._get_value(*key, takeable=self._takeable)
File "<file>", line 3612, in _get_value
series = self._ixs(col, axis=1)
File "<file>", line 3439, in _ixs
label = self.columns[i]
File "<file>", line 5039, in __getitem__
return getitem(key)
IndexError: index 3 is out of bounds for axis 0 with size 2Как мы видим в последней строке трассировки, это сообщение об ошибке говорит само за себя.
NameError
Исключение ошибки имени возникает, когда мы ссылаемся на переменную, которая не определена в нашем коде.
Вот пример:
members = ["John", "Jane", "Max", "Emily"]
member[0]
# output
Traceback (most recent call last):
File "<file>", line 3378, in run_code
exec(code_obj, self.user_global_ns, self.user_ns)
File "<ipython-input-35-9fcefb83a26f>", line 3, in <module>
name[5]
NameError: name 'member' is not definedИмя переменной — члены, поэтому мы получаем ошибку, когда пытаемся использовать член вместо членов.
ValueError
Исключение ошибки значения возникает, когда мы пытаемся присвоить неправильное значение переменной. Вспомните наш DataFrame с 5 строками и 2 столбцами.
import pandas as pd
import numpy as np
df = pd.DataFrame(np.random.randint(10, size=(5, 2)), columns=["A", "B"])
df
# output
A B
0 1 6
1 6 3
2 8 8
3 3 5
4 5 6Допустим, мы хотим добавить новый столбец в этот DataFrame.
df["C"] = [1, 2, 3, 4]
# output
Traceback (most recent call last):
File "<file>", line 3378, in run_code
exec(code_obj, self.user_global_ns, self.user_ns)
File "<file>", line 1, in <module>
df["C"] = [1, 2, 3, 4]
File "<file>", line 3655, in __setitem__
self._set_item(key, value)
File "<file>", line 3832, in _set_item
value = self._sanitize_column(value)
File "<file>", line 4535, in _sanitize_column
com.require_length_match(value, self.index)
File "<file>", line 557, in require_length_match
raise ValueError(
ValueError: Length of values (4) does not match length of index (5)Как объясняется в сообщении об ошибке, фрейм данных содержит 5 строк, поэтому каждый столбец имеет 5 значений. Когда мы пытаемся создать новый столбец со списком из 4 элементов, мы ошибку значения.
Заключительные мысли
Сообщения об ошибках очень полезны при отладке кода или его правильном выполнении в первый раз. К счастью, трассировка Python имеет четкие и поясняющие сообщения об ошибках.
В этой статье мы узнали, что такое обратная трассировка, как ее читать и некоторые из распространенных типов обратных трассировок.


