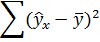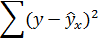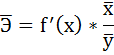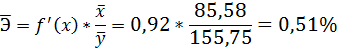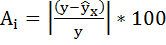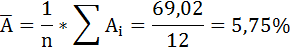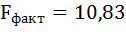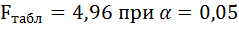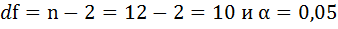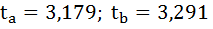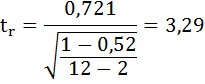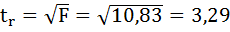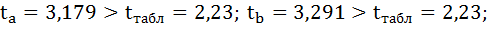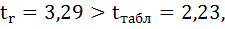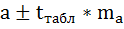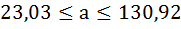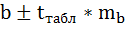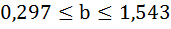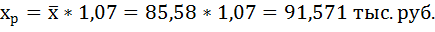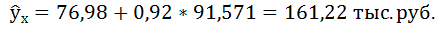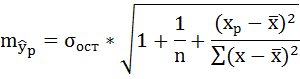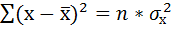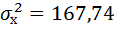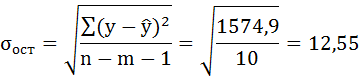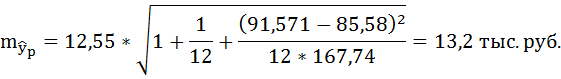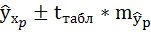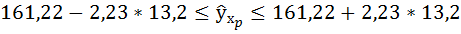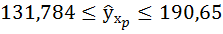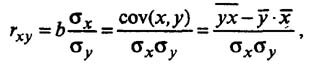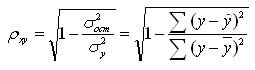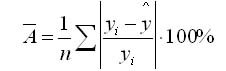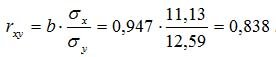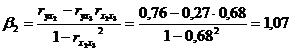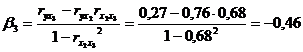-
Оценим качество уравнений с помощью средней ошибки аппроксимации
Средняя ошибка аппроксимации — среднее
отклонение расчетных (теоретических)
значений зависимой переменной y
от фактических (эмпирических) значений
Допустимый предел значений
не
более 10-12 %.
А. Для линейной регрессии Б. Для
степенной регрессии
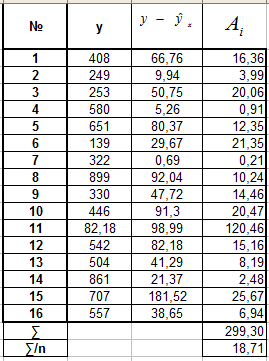
В. Для экспоненциальной регрессии
Г. Для полулогарифмической регрессии
Е. Для гиперболической регрессии
Вывод: для каждой из построенных
моделей ошибка аппроксимации превышает
допустимые пределы, что говорит о плохом
качестве моделей регрессии.
Наименьшей (хотя и недопустимой) она
является для уравнения полулогарифмической
регрессии
.
-
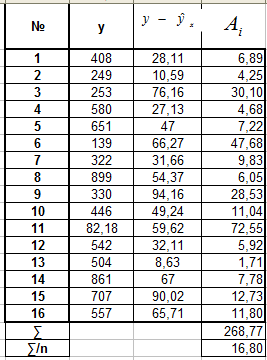
Оценим статистическую надежность результатов регрессионного моделирования с помощью f-критерия Фишера.
Н0 — гипотеза о статистической
незначимости показателя детерминации
R²
(Fфакт = 0) и уравнения
регрессии.
n – общее число наблюдений
(n=16); m –
число параметров при переменной x
(m=1)/
По таблице значений F-критерия
Фишера при условии значимости
= 0,05 и число степеней свободы k1
= m = 1, k2
= n – m
– 1 = 16-1-1= 14 находим Fкр
— максимально возможное значение
критерия под влиянием случайных факторов
при данных степенях свободы и уровне
значимости : Fкр
= 4,60.
А. Для линейной регрессии
(
)
Так как
то гипотеза Н0 отвергается,
т.е. R²
статистически значим, как и уравнение
линейной регрессии.
Б. Для степенной регрессии
(
)
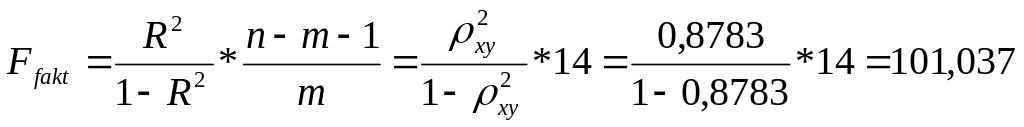
Так как
то гипотеза Н0 отвергается,
т.е. R²
статистически значим, как и уравнение
степенной регрессии.
В. Для экспоненциальной регрессии
(
)
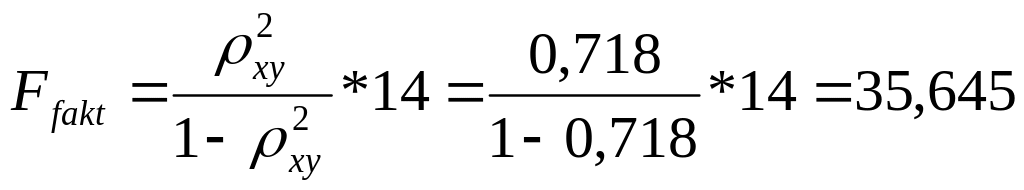
Так как
то гипотеза Н0 отвергается,
т.е. R²
статистически значим, как и уравнение
полулогарифмической регрессии.
Д. Для гиперболической регрессии
(
)
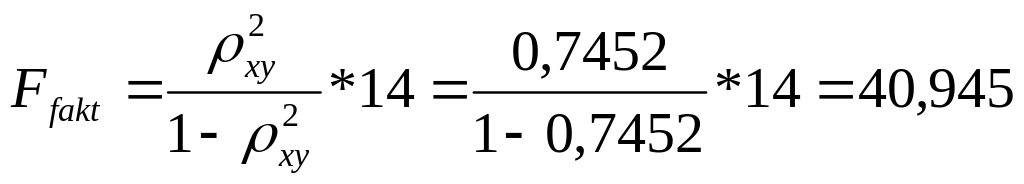
Так как
то гипотеза Н0 отвергается,
т.е. R²
статистически значим, как и уравнение
гиперболической регрессии.
Вывод: F-критерия
Фишера показывает, во сколько раз
уравнение регрессии предсказывает
результаты наблюдений лучше, чем прямая
.
Статистически значимыми являются
уравнения линейной, степенной,
экспоненциальной, гиперболической
регрессии, из них всех лучше предсказывает
результаты наблюдений уравнение
степенной регрессии (
)
-
По значениям характеристик, рассчитанных в пп. 4,6,7 выберем лучшее уравнение регрессии и дадим его обоснование.
П.4. Наибольшее значение коэффициента
эластичности имеет уравнение
степенной регрессии (
.
П.6. Наименьшую ошибку аппроксимации
(хотя и не допустимую) имеет уравнение
полулогарифмической регрессии
.
Уравнение степенной регрессии
отличается на небольшую величину:
П.7. Согласно F-критерию
Фишера лучше всех предсказывает
результаты наблюдений уравнение
степенной регрессии (
)
Вывод: Лучше всех описывает данные
наблюдений (зависимость между средней
заработанной платой и выплатами
социального характера x
и потребительскими расходами на душу
населения y) уравнение
степенной регрессии
Качество модели плохое, так как
>10%,
возможно из-за небольшого числа наблюдений
(n=16).
-
По линейному уравнению регрессии
рассчитаем прогнозное значение
результата (y), если
прогнозное значение фактора (x)
увеличивается на 7% от его среднего
уровня:
Уравнение линейной регрессии y=a
+ b*x (
).
n – общее число
наблюдений (n=16); m
– число параметров при переменной x
(m=1);
tкр
= 2,1448
Прогнозное значение фактора (x):
xпр =
тыс.
руб.;
xпр —
= 44,25 – 885 = -840,75; (xпр —
= (-840,75)² = 706860,5625.
Прогнозное значение фактора (y):
yпр = a
+ b* xпр =
160,48 + 0,39*44,25 = 177,74 тыс. руб.
Стандартная ошибка прогноза:
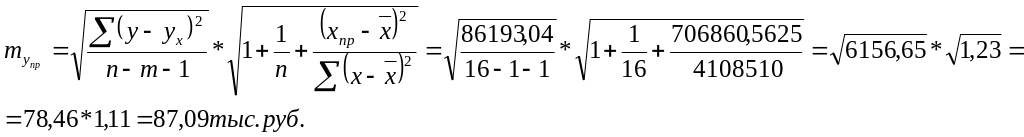
Предельная ошибка прогноза, которая
в 95% случаев не будет превышена, составит:
Доверительный интервал прогноза для
уровня значимости
=0,05:
(min
max
или
(
=
(177,74 – 186,79; 177,74 + 186,79) = (-9,05; 364,53)
11
Соседние файлы в предмете [НЕСОРТИРОВАННОЕ]
- #
- #
- #
- #
- #
- #
- #
- #
- #
- #
- #
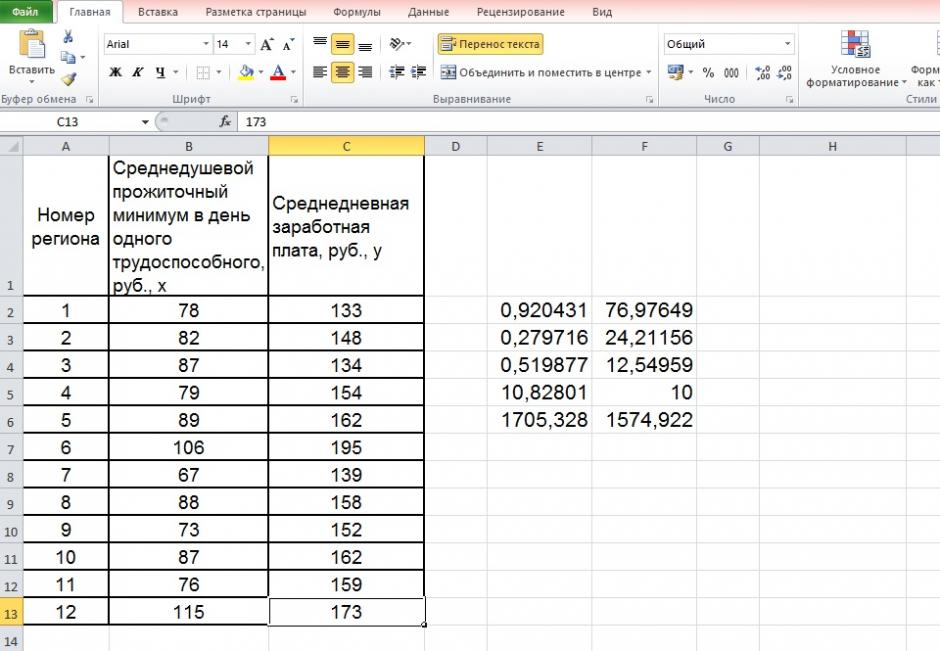
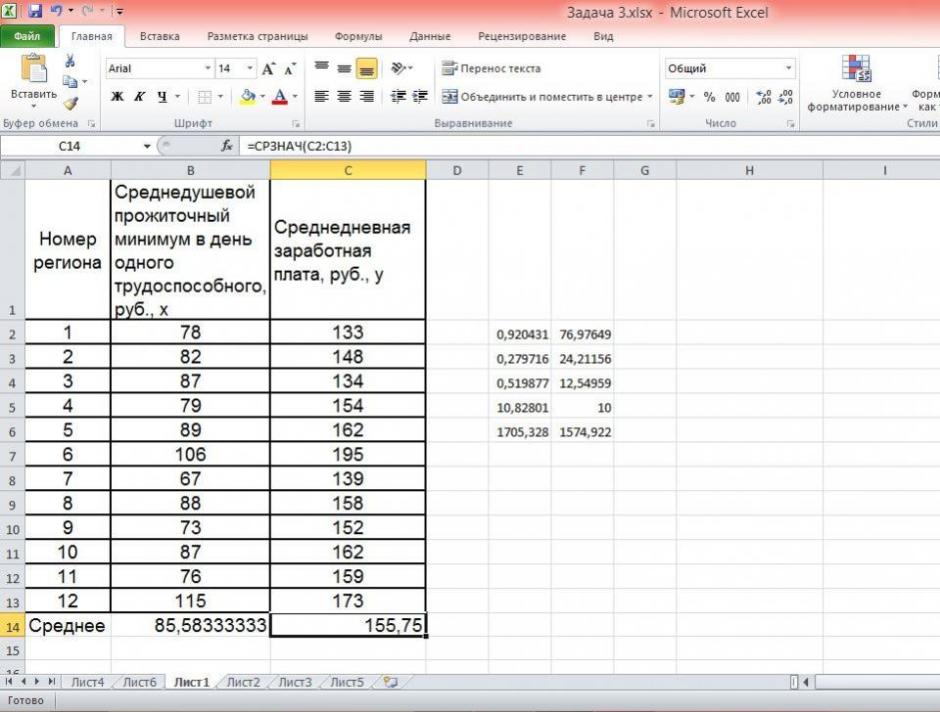
По территориям региона приводятся данные за 200Х г.
| Номер региона | Среднедушевой прожиточный минимум в день одного трудоспособного, руб., х | Среднедневная заработная плата, руб., у |
|---|---|---|
| 1 | 78 | 133 |
| 2 | 82 | 148 |
| 3 | 87 | 134 |
| 4 | 79 | 154 |
| 5 | 89 | 162 |
| 6 | 106 | 195 |
| 7 | 67 | 139 |
| 8 | 88 | 158 |
| 9 | 73 | 152 |
| 10 | 87 | 162 |
| 11 | 76 | 159 |
| 12 | 115 | 173 |
Задание:
1. Постройте поле корреляции и сформулируйте гипотезу о форме связи.
2. Рассчитайте параметры уравнения линейной регрессии
.
3. Оцените тесноту связи с помощью показателей корреляции и детерминации.
4. Дайте с помощью среднего (общего) коэффициента эластичности сравнительную оценку силы связи фактора с результатом.
5. Оцените с помощью средней ошибки аппроксимации качество уравнений.
6. Оцените с помощью F-критерия Фишера статистическую надёжность результатов регрессионного моделирования.
7. Рассчитайте прогнозное значение результата, если прогнозное значение фактора увеличится на 10% от его среднего уровня. Определите доверительный интервал прогноза для уровня значимости 
.
8. Оцените полученные результаты, выводы оформите в аналитической записке.
Решение:
Решим данную задачу с помощью Excel.
1. Сопоставив имеющиеся данные х и у, например, ранжировав их в порядке возрастания фактора х, можно наблюдать наличие прямой зависимости между признаками, когда увеличение среднедушевого прожиточного минимума увеличивает среднедневную заработную плату. Исходя из этого, можно сделать предположение, что связь между признаками прямая и её можно описать уравнением прямой. Этот же вывод подтверждается и на основе графического анализа.
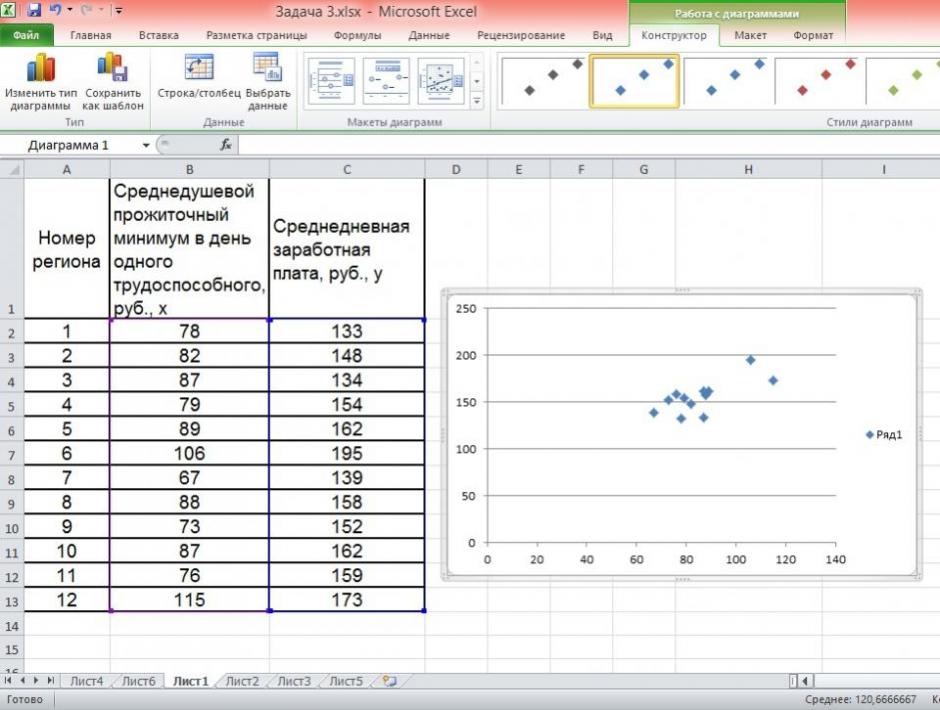
Чтобы построить поле корреляции можно воспользоваться ППП Excel. Введите исходные данные в последовательности: сначала х, затем у.
Выделите область ячеек, содержащую данные.
Затем выберете: Вставка / Точечная диаграмма / Точечная с маркерами как показано на рисунке 1.
Рисунок 1 Построение поля корреляции
Анализ поля корреляции показывает наличие близкой к прямолинейной зависимости, так как точки расположены практически по прямой линии.
2. Для расчёта параметров уравнения линейной регрессии
воспользуемся встроенной статистической функцией ЛИНЕЙН.
Для этого:
1) Откройте существующий файл, содержащий анализируемые данные;
2) Выделите область пустых ячеек 5×2 (5 строк, 2 столбца) для вывода результатов регрессионной статистики.
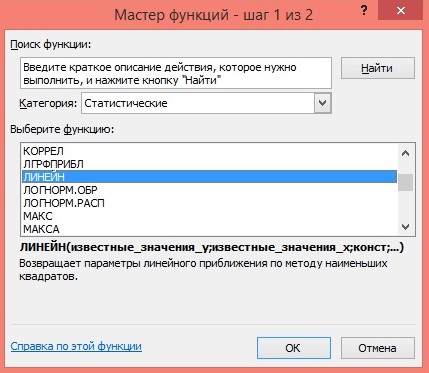
3) Активизируйте Мастер функций: в главном меню выберете Формулы / Вставить функцию.
4) В окне Категория выберете Статистические, в окне функция – ЛИНЕЙН. Щёлкните по кнопке ОК как показано на Рисунке 2;
Рисунок 2 Диалоговое окно «Мастер функций»
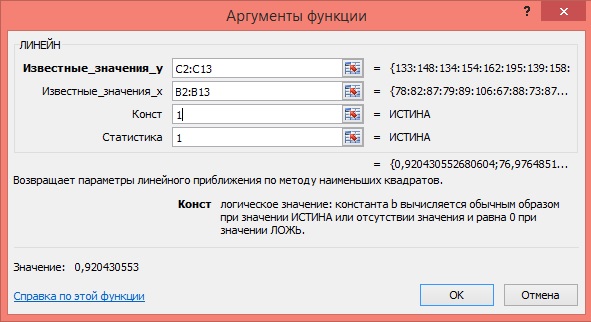
5) Заполните аргументы функции:
Известные значения у – диапазон, содержащий данные результативного признака;
Известные значения х – диапазон, содержащий данные факторного признака;
Константа – логическое значение, которое указывает на наличие или на отсутствие свободного члена в уравнении; если Константа = 1, то свободный член рассчитывается обычным образом, если Константа = 0, то свободный член равен 0;
Статистика – логическое значение, которое указывает, выводить дополнительную информацию по регрессионному анализу или нет. Если Статистика = 1, то дополнительная информация выводится, если Статистика = 0, то выводятся только оценки параметров уравнения.
Щёлкните по кнопке ОК;
Рисунок 3 Диалоговое окно аргументов функции ЛИНЕЙН
6) В левой верхней ячейке выделенной области появится первый элемент итоговой таблицы. Чтобы раскрыть всю таблицу, нажмите на клавишу <F2>, а затем на комбинацию клавиш <Ctrl>+<Shift>+<Enter>.
Дополнительная регрессионная статистика будет выводиться в порядке, указанном в следующей схеме:
| Значение коэффициента b | Значение коэффициента a |
| Стандартная ошибка b | Стандартная ошибка a |
| Коэффициент детерминации R2 | Стандартная ошибка y |
| F-статистика | Число степеней свободы df |
| Регрессионная сумма квадратов
|
Остаточная сумма квадратов
|
Рисунок 4 Результат вычисления функции ЛИНЕЙН
Получили уровнение регрессии:
Делаем вывод: С увеличением среднедушевого прожиточного минимума на 1 руб. среднедневная заработная плата возрастает в среднем на 0,92 руб.
3. Коэффициент детерминации 
означает, что 52% вариации заработной платы (у) объясняется вариацией фактора х – среднедушевого прожиточного минимума, а 48% — действием других факторов, не включённых в модель.
По вычисленному коэффициенту детерминации можно рассчитать коэффициент корреляции: 
.
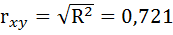
Связь оценивается как тесная.
4. С помощью среднего (общего) коэффициента эластичности определим силу влияния фактора на результат.
Для уравнения прямой 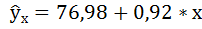средний (общий) коэффициент эластичности определим по формуле:
Средние значения найдём, выделив область ячеек со значениями х, и выберем Формулы / Автосумма / Среднее, и то же самое произведём со значениями у.
Рисунок 5 Расчёт средних значений функции и аргумент
Таким образом, при изменении среднедушевого прожиточного минимума на 1% от своего среднего значения среднедневная заработная плата изменится в среднем на 0,51%.
С помощью инструмента анализа данных Регрессия можно получить:
— результаты регрессионной статистики,
— результаты дисперсионного анализа,
— результаты доверительных интервалов,
— остатки и графики подбора линии регрессии,
— остатки и нормальную вероятность.
Порядок действий следующий:
1) проверьте доступ к Пакету анализа. В главном меню последовательно выберите: Файл/Параметры/Надстройки.
2) В раскрывающемся списке Управление выберите пункт Надстройки Excel и нажмите кнопку Перейти.
3) В окне Надстройки установите флажок Пакет анализа, а затем нажмите кнопку ОК.
• Если Пакет анализа отсутствует в списке поля Доступные надстройки, нажмите кнопку Обзор, чтобы выполнить поиск.
• Если выводится сообщение о том, что пакет анализа не установлен на компьютере, нажмите кнопку Да, чтобы установить его.
4) В главном меню последовательно выберите: Данные / Анализ данных / Инструменты анализа / Регрессия, а затем нажмите кнопку ОК.
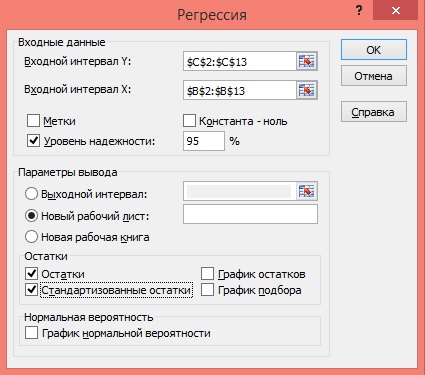
5) Заполните диалоговое окно ввода данных и параметров вывода:
Входной интервал Y – диапазон, содержащий данные результативного признака;
Входной интервал X – диапазон, содержащий данные факторного признака;
Метки – флажок, который указывает, содержит ли первая строка названия столбцов или нет;
Константа – ноль – флажок, указывающий на наличие или отсутствие свободного члена в уравнении;
Выходной интервал – достаточно указать левую верхнюю ячейку будущего диапазона;
6) Новый рабочий лист – можно задать произвольное имя нового листа.
Затем нажмите кнопку ОК.
Рисунок 6 Диалоговое окно ввода параметров инструмента Регрессия
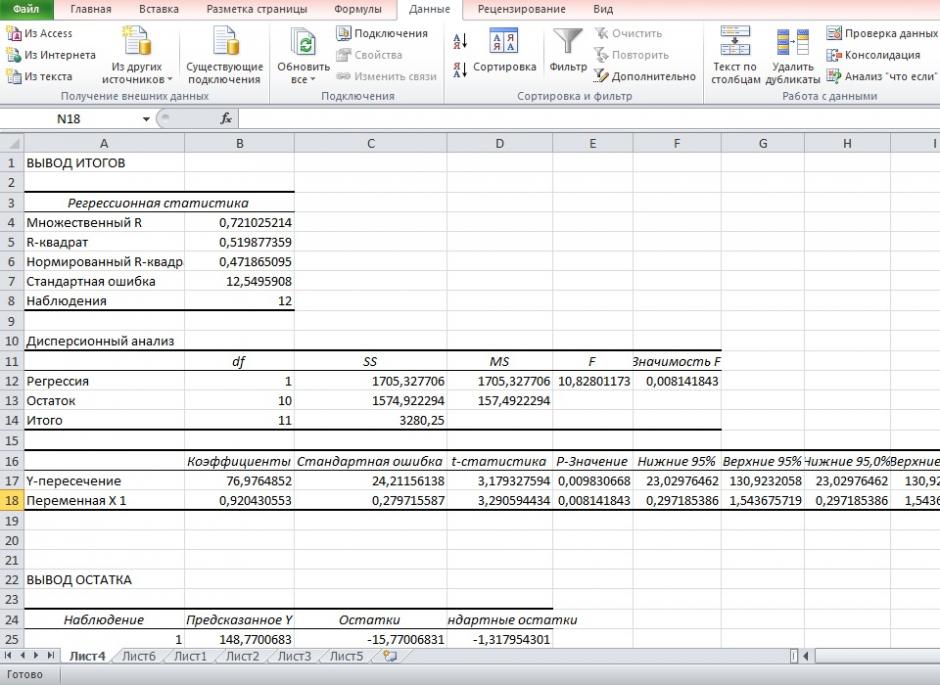
Результаты регрессионного анализа для данных задачи представлены на рисунке 7.
Рисунок 7 Результат применения инструмента регрессия
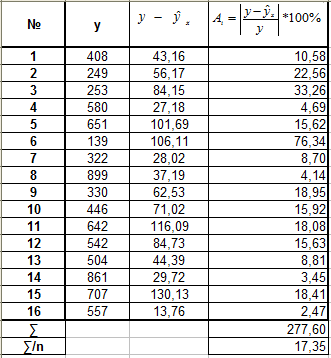
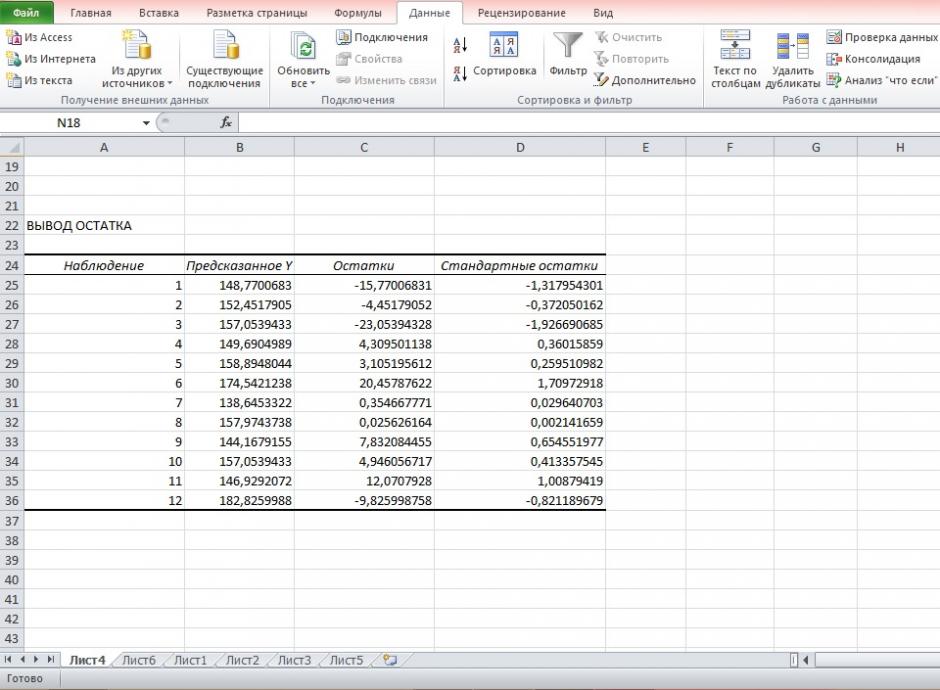
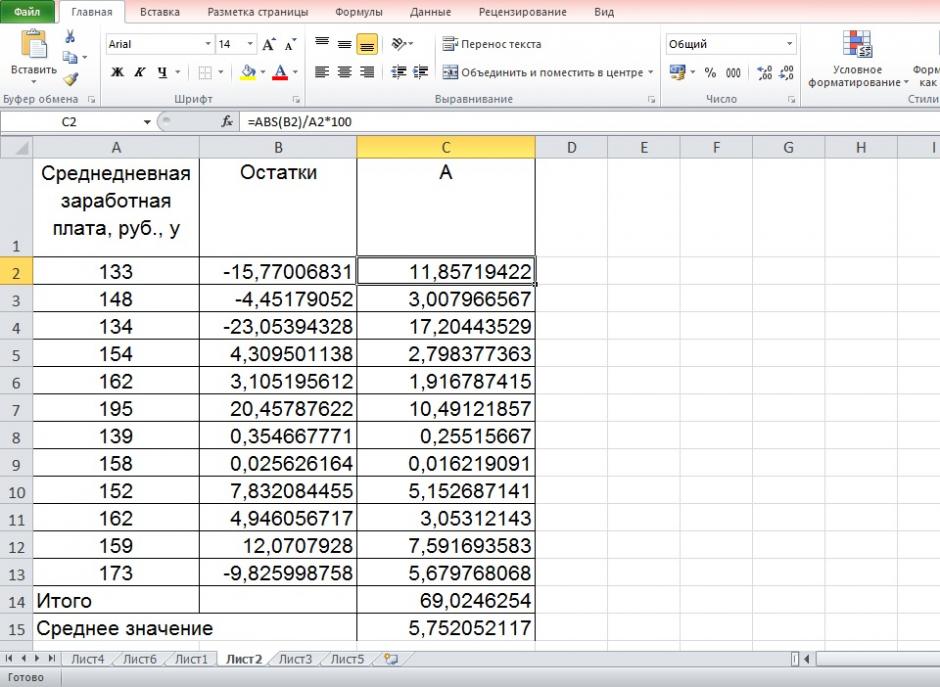
5. Оценим с помощью средней ошибки аппроксимации качество уравнений. Воспользуемся результатами регрессионного анализа представленного на Рисунке 8.
Рисунок 8 Результат применения инструмента регрессия «Вывод остатка»
Составим новую таблицу как показано на рисунке 9. В графе С рассчитаем относительную ошибку аппроксимации по формуле:
Рисунок 9 Расчёт средней ошибки аппроксимации
Средняя ошибка аппроксимации рассчитывается по формуле:
Качество построенной модели оценивается как хорошее, так как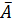 
не превышает 8 – 10%.
6. Из таблицы с регрессионной статистикой (Рисунок 4) выпишем фактическое значение F-критерия Фишера: 
Поскольку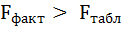 
при 5%-ном уровне значимости, то можно сделать вывод о значимости уравнения регрессии (связь доказана).
8. Оценку статистической значимости параметров регрессии проведём с помощью t-статистики Стьюдента и путём расчёта доверительного интервала каждого из показателей.
Выдвигаем гипотезу Н0 о статистически незначимом отличии показателей от нуля:
.
для числа степеней свободы 
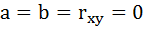
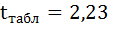
На рисунке 7 имеются фактические значения t-статистики:
t-критерий для коэффициента корреляции можно рассчитать двумя способами:
I способ: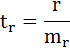 
где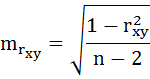 
– случайная ошибка коэффициента корреляции.
Данные для расчёта возьмём из таблицы на Рисунке 7.
II способ: 
Фактические значения t-статистики превосходят табличные значения:
Поэтому гипотеза Н0 отклоняется, то есть параметры регрессии и коэффициент корреляции не случайно отличаются от нуля, а статистически значимы.
Доверительный интервал для параметра a определяется как
Для параметра a 95%-ные границы как показано на рисунке 7 составили:
Доверительный интервал для коэффициента регрессии определяется как
Для коэффициента регрессии b 95%-ные границы как показано на рисунке 7 составили:
Анализ верхней и нижней границ доверительных интервалов приводит к выводу о том, что с вероятностью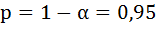 
параметры a и b, находясь в указанных границах, не принимают нулевых значений, т.е. не являются статистически незначимыми и существенно отличны от нуля.
7. Полученные оценки уравнения регрессии позволяют использовать его для прогноза. Если прогнозное значение прожиточного минимума составит:
Тогда прогнозное значение прожиточного минимума составит:
Ошибку прогноза рассчитаем по формуле:
где 
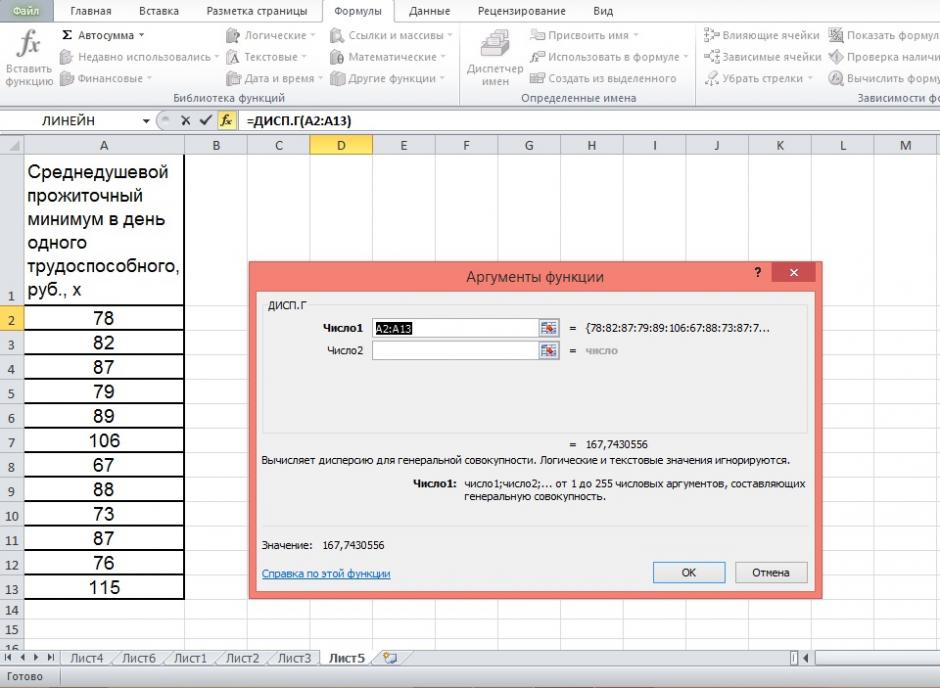
Дисперсию посчитаем также с помощью ППП Excel. Для этого:
1) Активизируйте Мастер функций: в главном меню выберете Формулы / Вставить функцию.
2) В окне Категория выберете Статистические, в окне функция – ДИСП.Г. Щёлкните по кнопке ОК.
3) Заполните диапазон, содержащий числовые данные факторного признака. Нажмите ОК.
Рисунок 10 Расчёт дисперсии
Получили значение дисперсии 
Для подсчёта остаточной дисперсии на одну степень свободы воспользуемся результатами дисперсионного анализа как показано на Рисунке 7.
Доверительные интервалы прогноза индивидуальных значений у при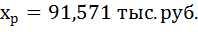 
с вероятностью 0,95 определяются выражением:
Интервал достаточно широк, прежде всего, за счёт малого объёма наблюдений. В целом выполненный прогноз среднемесячной заработной платы оказался надёжным.
Условие задачи взято из: Практикум по эконометрике: Учеб. пособие / И.И. Елисеева, С.В. Курышева, Н.М. Гордеенко и др.; Под ред. И.И. Елисеевой. – М.: Финансы и статистика, 2003. – 192 с.: ил.
Средняя ошибка аппроксимации
По семи территориям Уральского района за 199Х г. известны значения двух признаков.
| Район | Расходы на покупку продовольственных товаров в общих расходах, %, у | Среднедневная заработная плата одного работающего, руб., х |
| Удмуртская респ. | 68,8 | 45,1 |
| Свердловская обл. | 61,2 | 59,0 |
| Башкортостан | 59,9 | 57,2 |
| Челябинская обл. | 56,7 | 61,8 |
| Пермская обл. | 55,0 | 58,8 |
| Курганская обл. | 54,3 | 47,2 |
| Оренбургская обл. | 49,3 | 55,2 |
Требуется:
1. Для характеристики зависимости у от х рассчитать параметры следующих функций:
а) линейной;
б) степенной;
в) показательной;
г) равносторонней гиперболы (так же нужно придумать как предварительно линеаризовать данную модель).
2. Оценить каждую модель через среднюю ошибку аппроксимации Аср и F-критерий Фишера.
Решение проводим при помощь онлайн калькулятора Линейное уравнение регрессии.
а) линейное уравнение регрессии;
Использование графического метода.
Этот метод применяют для наглядного изображения формы связи между изучаемыми экономическими показателями. Для этого в прямоугольной системе координат строят график, по оси ординат откладывают индивидуальные значения результативного признака Y, а по оси абсцисс — индивидуальные значения факторного признака X.
Совокупность точек результативного и факторного признаков называется полем корреляции.
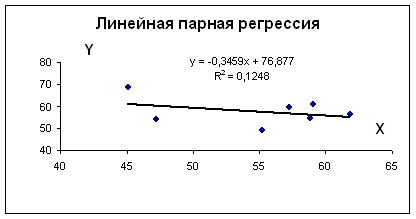
Для наших данных система уравнений имеет вид
Из первого уравнения выражаем а и подставим во второе уравнение
Получаем b = -0.35, a = 76.88
Уравнение регрессии: y = -0.35 x + 76.88
| x | y | x 2 | y 2 | x • y | y(x) | (y i -y cp ) 2 | (y-y(x)) 2 | |y — y x |:y |
| 45,1 | 68,8 | 2034,01 | 4733,44 | 3102,88 | 61,28 | 119,12 | 56,61 | 0,1094 |
| 59 | 61,2 | 3481 | 3745,44 | 3610,8 | 56,47 | 10,98 | 22,4 | 0,0773 |
| 57,2 | 59,9 | 3271,84 | 3588,01 | 3426,28 | 57,09 | 4,06 | 7,9 | 0,0469 |
| 61,8 | 56,7 | 3819,24 | 3214,89 | 3504,06 | 55,5 | 1,41 | 1,44 | 0,0212 |
| 58,8 | 55 | 3457,44 | 3025 | 3234 | 56,54 | 8,33 | 2,36 | 0,0279 |
| 47,2 | 54,3 | 2227,84 | 2948,49 | 2562,96 | 60,55 | 12,86 | 39,05 | 0,1151 |
| 55,2 | 49,3 | 3047,04 | 2430,49 | 2721,36 | 57,78 | 73,71 | 71,94 | 0,172 |
| 384,3 | 405,2 | 21338,41 | 23685,76 | 22162,34 | 405,2 | 230,47 | 201,71 | 0,5699 |
Примечание: значения y(x) находятся из полученного уравнения регрессии:
y(45.1) = -0.35*45.1 + 76.88 = 61.28
y(59) = -0.35*59 + 76.88 = 56.47
. . .
Ошибка аппроксимации
Оценим качество уравнения регрессии с помощью ошибки абсолютной аппроксимации. Средняя ошибка аппроксимации — среднее отклонение расчетных значений от фактических:
F-статистики. Критерий Фишера.
Проверка значимости модели регрессии проводится с использованием F-критерия Фишера, расчетное значение которого находится как отношение дисперсии исходного ряда наблюдений изучаемого показателя и несмещенной оценки дисперсии остаточной последовательности для данной модели.
Если расчетное значение с k1=(m) и k2=(n-m-1) степенями свободы больше табличного при заданном уровне значимости, то модель считается значимой.
где m – число факторов в модели.
Оценка статистической значимости парной линейной регрессии производится по следующему алгоритму:
1. Выдвигается нулевая гипотеза о том, что уравнение в целом статистически незначимо: H0: R 2 =0 на уровне значимости α.
2. Далее определяют фактическое значение F-критерия:
где m=1 для парной регрессии.
3. Табличное значение определяется по таблицам распределения Фишера для заданного уровня значимости, принимая во внимание, что число степеней свободы для общей суммы квадратов (большей дисперсии) равно 1 и число степеней свободы остаточной суммы квадратов (меньшей дисперсии) при линейной регрессии равно n-2.
4. Если фактическое значение F-критерия меньше табличного, то говорят, что нет основания отклонять нулевую гипотезу.
В противном случае, нулевая гипотеза отклоняется и с вероятностью (1-α) принимается альтернативная гипотеза о статистической значимости уравнения в целом.
Табличное значение критерия со степенями свободы k1=1 и k2=5, Fkp = 6.61
Поскольку фактическое значение F b
в) показательная регрессия;
г) модель равносторонней гиперболы.
Система нормальных уравнений.
Для наших данных система уравнений имеет вид
7a + 0.1291b = 405.2
0.1291a + 0.0024b = 7.51
Из первого уравнения выражаем а и подставим во второе уравнение
Получаем b = 1054.67, a = 38.44
Уравнение регрессии:
y = 1054.67 / x + 38.44
Ошибка аппроксимации.
Оценим качество уравнения регрессии с помощью ошибки абсолютной аппроксимации.
Задача №3. Расчёт параметров регрессии и корреляции с помощью Excel
По территориям региона приводятся данные за 200Х г.
| Номер региона | Среднедушевой прожиточный минимум в день одного трудоспособного, руб., х | Среднедневная заработная плата, руб., у |
|---|---|---|
| 1 | 78 | 133 |
| 2 | 82 | 148 |
| 3 | 87 | 134 |
| 4 | 79 | 154 |
| 5 | 89 | 162 |
| 6 | 106 | 195 |
| 7 | 67 | 139 |
| 8 | 88 | 158 |
| 9 | 73 | 152 |
| 10 | 87 | 162 |
| 11 | 76 | 159 |
| 12 | 115 | 173 |
Задание:
1. Постройте поле корреляции и сформулируйте гипотезу о форме связи.
2. Рассчитайте параметры уравнения линейной регрессии
.
3. Оцените тесноту связи с помощью показателей корреляции и детерминации.
4. Дайте с помощью среднего (общего) коэффициента эластичности сравнительную оценку силы связи фактора с результатом.
5. Оцените с помощью средней ошибки аппроксимации качество уравнений.
6. Оцените с помощью F-критерия Фишера статистическую надёжность результатов регрессионного моделирования.
7. Рассчитайте прогнозное значение результата, если прогнозное значение фактора увеличится на 10% от его среднего уровня. Определите доверительный интервал прогноза для уровня значимости .
8. Оцените полученные результаты, выводы оформите в аналитической записке.
Решение:
Решим данную задачу с помощью Excel.
1. Сопоставив имеющиеся данные х и у, например, ранжировав их в порядке возрастания фактора х, можно наблюдать наличие прямой зависимости между признаками, когда увеличение среднедушевого прожиточного минимума увеличивает среднедневную заработную плату. Исходя из этого, можно сделать предположение, что связь между признаками прямая и её можно описать уравнением прямой. Этот же вывод подтверждается и на основе графического анализа.
Чтобы построить поле корреляции можно воспользоваться ППП Excel. Введите исходные данные в последовательности: сначала х, затем у.
Выделите область ячеек, содержащую данные.
Затем выберете: Вставка / Точечная диаграмма / Точечная с маркерами как показано на рисунке 1.
Рисунок 1 Построение поля корреляции
Анализ поля корреляции показывает наличие близкой к прямолинейной зависимости, так как точки расположены практически по прямой линии.
2. Для расчёта параметров уравнения линейной регрессии
воспользуемся встроенной статистической функцией ЛИНЕЙН.
1) Откройте существующий файл, содержащий анализируемые данные;
2) Выделите область пустых ячеек 5×2 (5 строк, 2 столбца) для вывода результатов регрессионной статистики.
3) Активизируйте Мастер функций: в главном меню выберете Формулы / Вставить функцию.
4) В окне Категория выберете Статистические, в окне функция – ЛИНЕЙН. Щёлкните по кнопке ОК как показано на Рисунке 2;
Рисунок 2 Диалоговое окно «Мастер функций»
5) Заполните аргументы функции:
Известные значения у – диапазон, содержащий данные результативного признака;
Известные значения х – диапазон, содержащий данные факторного признака;
Константа – логическое значение, которое указывает на наличие или на отсутствие свободного члена в уравнении; если Константа = 1, то свободный член рассчитывается обычным образом, если Константа = 0, то свободный член равен 0;
Статистика – логическое значение, которое указывает, выводить дополнительную информацию по регрессионному анализу или нет. Если Статистика = 1, то дополнительная информация выводится, если Статистика = 0, то выводятся только оценки параметров уравнения.
Щёлкните по кнопке ОК;
Рисунок 3 Диалоговое окно аргументов функции ЛИНЕЙН
6) В левой верхней ячейке выделенной области появится первый элемент итоговой таблицы. Чтобы раскрыть всю таблицу, нажмите на клавишу , а затем на комбинацию клавиш + + .
Дополнительная регрессионная статистика будет выводиться в порядке, указанном в следующей схеме:
| Значение коэффициента b | Значение коэффициента a |
| Стандартная ошибка b | Стандартная ошибка a |
| Коэффициент детерминации R 2 | Стандартная ошибка y |
| F-статистика | Число степеней свободы df |
| Регрессионная сумма квадратов |
Остаточная сумма квадратов
Рисунок 4 Результат вычисления функции ЛИНЕЙН
Получили уровнение регрессии:
Делаем вывод: С увеличением среднедушевого прожиточного минимума на 1 руб. среднедневная заработная плата возрастает в среднем на 0,92 руб.
3. Коэффициент детерминации означает, что 52% вариации заработной платы (у) объясняется вариацией фактора х – среднедушевого прожиточного минимума, а 48% — действием других факторов, не включённых в модель.
По вычисленному коэффициенту детерминации можно рассчитать коэффициент корреляции: .
Связь оценивается как тесная.
4. С помощью среднего (общего) коэффициента эластичности определим силу влияния фактора на результат.
Для уравнения прямой средний (общий) коэффициент эластичности определим по формуле:
Средние значения найдём, выделив область ячеек со значениями х, и выберем Формулы / Автосумма / Среднее, и то же самое произведём со значениями у.
Рисунок 5 Расчёт средних значений функции и аргумент
Таким образом, при изменении среднедушевого прожиточного минимума на 1% от своего среднего значения среднедневная заработная плата изменится в среднем на 0,51%.
С помощью инструмента анализа данных Регрессия можно получить:
— результаты регрессионной статистики,
— результаты дисперсионного анализа,
— результаты доверительных интервалов,
— остатки и графики подбора линии регрессии,
— остатки и нормальную вероятность.
Порядок действий следующий:
1) проверьте доступ к Пакету анализа. В главном меню последовательно выберите: Файл/Параметры/Надстройки.
2) В раскрывающемся списке Управление выберите пункт Надстройки Excel и нажмите кнопку Перейти.
3) В окне Надстройки установите флажок Пакет анализа, а затем нажмите кнопку ОК.
• Если Пакет анализа отсутствует в списке поля Доступные надстройки, нажмите кнопку Обзор, чтобы выполнить поиск.
• Если выводится сообщение о том, что пакет анализа не установлен на компьютере, нажмите кнопку Да, чтобы установить его.
4) В главном меню последовательно выберите: Данные / Анализ данных / Инструменты анализа / Регрессия, а затем нажмите кнопку ОК.
5) Заполните диалоговое окно ввода данных и параметров вывода:
Входной интервал Y – диапазон, содержащий данные результативного признака;
Входной интервал X – диапазон, содержащий данные факторного признака;
Метки – флажок, который указывает, содержит ли первая строка названия столбцов или нет;
Константа – ноль – флажок, указывающий на наличие или отсутствие свободного члена в уравнении;
Выходной интервал – достаточно указать левую верхнюю ячейку будущего диапазона;
6) Новый рабочий лист – можно задать произвольное имя нового листа.
Затем нажмите кнопку ОК.
Рисунок 6 Диалоговое окно ввода параметров инструмента Регрессия
Результаты регрессионного анализа для данных задачи представлены на рисунке 7.
Рисунок 7 Результат применения инструмента регрессия
5. Оценим с помощью средней ошибки аппроксимации качество уравнений. Воспользуемся результатами регрессионного анализа представленного на Рисунке 8.
Рисунок 8 Результат применения инструмента регрессия «Вывод остатка»
Составим новую таблицу как показано на рисунке 9. В графе С рассчитаем относительную ошибку аппроксимации по формуле:
Рисунок 9 Расчёт средней ошибки аппроксимации
Средняя ошибка аппроксимации рассчитывается по формуле:
Качество построенной модели оценивается как хорошее, так как не превышает 8 – 10%.
6. Из таблицы с регрессионной статистикой (Рисунок 4) выпишем фактическое значение F-критерия Фишера:
Поскольку при 5%-ном уровне значимости, то можно сделать вывод о значимости уравнения регрессии (связь доказана).
8. Оценку статистической значимости параметров регрессии проведём с помощью t-статистики Стьюдента и путём расчёта доверительного интервала каждого из показателей.
Выдвигаем гипотезу Н0 о статистически незначимом отличии показателей от нуля:
.
для числа степеней свободы
На рисунке 7 имеются фактические значения t-статистики:
t-критерий для коэффициента корреляции можно рассчитать двумя способами:
I способ:
где – случайная ошибка коэффициента корреляции.
Данные для расчёта возьмём из таблицы на Рисунке 7.
II способ:
Фактические значения t-статистики превосходят табличные значения:
Поэтому гипотеза Н0 отклоняется, то есть параметры регрессии и коэффициент корреляции не случайно отличаются от нуля, а статистически значимы.
Доверительный интервал для параметра a определяется как
Для параметра a 95%-ные границы как показано на рисунке 7 составили:
Доверительный интервал для коэффициента регрессии определяется как
Для коэффициента регрессии b 95%-ные границы как показано на рисунке 7 составили:
Анализ верхней и нижней границ доверительных интервалов приводит к выводу о том, что с вероятностью параметры a и b, находясь в указанных границах, не принимают нулевых значений, т.е. не являются статистически незначимыми и существенно отличны от нуля.
7. Полученные оценки уравнения регрессии позволяют использовать его для прогноза. Если прогнозное значение прожиточного минимума составит:
Тогда прогнозное значение прожиточного минимума составит:
Ошибку прогноза рассчитаем по формуле:
где
Дисперсию посчитаем также с помощью ППП Excel. Для этого:
1) Активизируйте Мастер функций: в главном меню выберете Формулы / Вставить функцию.
2) В окне Категория выберете Статистические, в окне функция – ДИСП.Г. Щёлкните по кнопке ОК.
3) Заполните диапазон, содержащий числовые данные факторного признака. Нажмите ОК.
Рисунок 10 Расчёт дисперсии
Получили значение дисперсии
Для подсчёта остаточной дисперсии на одну степень свободы воспользуемся результатами дисперсионного анализа как показано на Рисунке 7.
Доверительные интервалы прогноза индивидуальных значений у при с вероятностью 0,95 определяются выражением:
Интервал достаточно широк, прежде всего, за счёт малого объёма наблюдений. В целом выполненный прогноз среднемесячной заработной платы оказался надёжным.
Условие задачи взято из: Практикум по эконометрике: Учеб. пособие / И.И. Елисеева, С.В. Курышева, Н.М. Гордеенко и др.; Под ред. И.И. Елисеевой. – М.: Финансы и статистика, 2003. – 192 с.: ил.
Средней ошибки аппроксимации качество уравнений
Оценка этой формы связи по коэффициенту множественной корреляции и средней ошибке аппроксимации показывает, что адекватность данной модели не подтверждается. Действительно, хотя значение коэффициента достаточно высокое (0,92), средняя ошибка аппроксимации составляет более 10% (I = 14,5%). Поэтому данная форма должна быть исключена из перебора известных уравнений регрессии. [c.29]
Анализ полученной формы связи по той же причине, что и в первом случае, позволяет сделать вывод о непригодности и этой модели. Коэффициент множественной корреляции хотя и имеет более высокое значение, чем в линейной зависимости (0,93), но по величине средней ошибки аппроксимации (б = 12,4%) это уравнение регрессии подлежит исключению из дальнейшего перебора. [c.29]
Последняя модель себестоимости добычи нефти, как показывает оценка ее по известным критериям, удовлетворяет условиям адекватности. Коэффициент множественной корреляции R составляет 0,98, что свидетельствует о том, что колеблемость исследуемого показателя более чем на 96 % определяется факторами, включенными в эту модель. При оценке по f-критерию (t R = 30,5) можно утверждать, что с вероятностью 0,99 факторы, включенные в модель, имеют существенную связь с исследуемым показателем (t a n = 2,58). Средняя ошибка аппроксимации составляет всего лишь 2,9 %, а F-критерий, характеризующий уровень остаточной дисперсии, превышает критическое (табличное) значение в четыре раза. К этому следует добавить, что полученная модель себестоимости добычи нефти представляет собой достаточно простую форму связи, легко решается и поддается экономической интерпретации. [c.30]
Оценка полученной модели по статистическим характеристикам показывает, что колеблемость затрат исследуемой подсистемы на 85 % обусловлена колеблемостью факторов, включенных в модель, коэффициент множественной корреляции высокий (/ = 0,92) и существенный (f = = 39,8), модель является адекватной, средняя ошибка аппроксимации (ё = 5,7%) меньше 10%. [c.39]
Статистический анализ показывает, что уравнение значимо Рф = 5,054 при /»табл = 3,01, корреляционное отношение равно 0,9959, ее»стандартная ошибка равна 0,0015. Среднее квадратическое отклонение расчетной себестоимости от фактической равно 0,018. Средняя ошибка аппроксимации 1,1%. [c.90]
Средняя ошибка аппроксимации [c.94]
Средняя ошибка аппроксимации. [c.95]
В случаях, когда трудно обосновать форму зависимости, решение задачи можно провести по разным моделям и сравнить полученные результаты. Адекватность разных моделей фактическим зависимостям проверяется по критерию Фишера, показателю средней ошибки аппроксимации и величине множественного коэффициента детерминации, о которых речь пойдет несколько позже (см. 7.4). [c.144]
Эти сведения вводятся в ПЭВМ и рассчитываются матрицы парных и частных коэффициентов корреляции, уравнение множественной регрессии, а также показатели, с помощью которых оценивается надежность коэффициентов корреляции и уравнения связи критерий Стьюдента, критерий Фишера, средняя ошибка аппроксимации, множественные коэффициенты корреляции и детерминации. [c.145]
Для того чтобы убедиться в надежности уравнения связи и правомерности его использования для практической цели, необходимо дать статистическую оценку надежности показателей связи. Для этого используются критерий Фишера (F-отношение), средняя ошибка аппроксимации ( ), коэффициенты множественной корреляции (/ ) и детерминации (D). [c.151]
Для статистической оценки точности уравнения связи используется также средняя ошибка аппроксимации [c.152]
Чем меньше теоретическая линия регрессии (рассчитанная по уравнению) отклоняется от фактической (эмпиричной), тем меньше средняя ошибка аппроксимации. В нашем примере она составляет 0,0364, или 3,64 %. Учитывая, что в экономических расчетах допускается погрешность 5-8 %, можно сделать вывод, что исследуемое уравнение связи довольно точно описывает изучаемые зависимости. [c.152]
После построения уравнения регрессии необходимо сделать проверку его значимости с помощью специальных критериев установить, не является ли полученная зависимость, выраженная уравнением регрессии, случайной, т.е. можно ли ее использовать в прогнозных целях и для факторного анализа. В статистике разработаны методики строгой проверки значимости коэффициентов регрессии с помощью дисперсионного анализа и расчета специальных критериев (например, F-критерия). Нестрогая проверка может быть выполнена путем расчета среднего относительного линейного отклонения (ё), называемого средней ошибкой аппроксимации [c.123]
Модель считается адекватной, т.е. пригодной для практического использования, если средняя ошибка аппроксимации не превосходит 15%. [c.123]
Оценку качества построенной модели даст коэффициент (индекс) детерминации, а также средняя ошибка аппроксимации. [c.6]
Средняя ошибка аппроксимации — среднее отклонение расчетных значений от фактических [c.6]
Подставляя в данное уравнение фактические значения х, получаем теоретические значения результата ух. По ним рассчитаем показатели тесноты связи — индекс корреляции рху и среднюю ошибку аппроксимации 7, [c.13]
Рассчитать линейный коэффициент парной корреляции и среднюю ошибку аппроксимации. [c.16]
Это означает, что 52% вариации заработной латы (у) объясняется вариацией фактора х — среднедушевого прожиточного минимума. Качество модели определяет средняя ошибка аппроксимации [c.18]
Оцените с помощью средней ошибки аппроксимации качество уравнений. [c.38]
Оцените качество уравнений с помощью средней ошибки аппроксимации. [c.42]
Оцените качество уравнения через среднюю ошибку аппроксимации. [c.92]
Оцените качество каждого тренда через среднюю ошибку аппроксимации, линейный коэффициент автокорреляции отклонений. [c.166]
СРЕДНЯЯ ОШИБКА АППРОКСИМАЦИИ [c.87]
Представим расчет средней ошибки аппроксимации для уравнения ух = 9,876 + 5,129 hue в табл. 2.7. А = — 7,3 = 1,2%, что [c.88]
Расчет средней ошибки аппроксимации [c.88]
В стандартных программах чаще используется первая формула для расчета Средней ошибки аппроксимации. [c.88]
В чем смысл средней ошибки аппроксимации и как она определяется [c.89]
Средняя ошибка аппроксимации [c.10]
Выбор вида модели основан на логическом анализе изучаемых показателей, сравнении статистических характеристик (средняя ошибка аппроксимации, критерий Фишера, коэффициенты множественной корреляции и детерминации), рассчитанных для различных функций по одним и тем же первичным данным. [c.31]
Проверка приведенной в формуле (154) себестоимости по фактическим данным 103 СМУ показала, что средняя ошибка аппроксимации, определяющая степень соответствия расчетных значений фактическим, составила всего 1,5%, что вполне допустимо. [c.227]
Исчисляемый коэффициент детерминации получился равным 0,869. Это говорит о том, что размер заработной платы водителей на 86,9% зависит от Р и Л ри на 13,1% — от неучтенных в модели факторов. Средняя ошибка аппроксимации составила всего лишь 0,17%. Модель была получена на основе конкретных показателей ряда автотранспортных предприятий Владимирского транспортного управления, поэтому она может -быть использована в практической работе только на этих предприятиях. Предлагаемая же методика может быть использована в любом транспортном управлении, министерстве при планировании и анализе себестоимости автомобильных перевозок и установлении нормативов по заработной плате водителей за время работы на линии. [c.36]
http://ecson.ru/economics/econometrics/zadacha-3.raschyot-parametrov-regressii-i-korrelyatsii-s-pomoschju-excel.html
http://economy-ru.info/info/119599/
Выдвигаем две гипотезы:
Н0: коэффициенты регрессии
статистически не значимы, т.е. равны о;
Н1: коэффициенты регрессии
статистически значимы, т.е. отличны от
нуля.
Значения случайных ошибок параметров
с учетом округления равны (рисунок 3):
Они показывают, какое значение данной
характеристики сформировались под
влиянием случайных факторов. Эти значения
используются для расчета t-критерия
Стьюдента (рисунок 3):
.
Если значения t-критерия
больше 2,13, можно сделать вывод о
существенности параметра, который
формируется под воздействием неслучайных
причин. Здесь параметр b4
является статистически значимым при
уровне значимости 5%, а все остальные
параметры являются статистически не
значимыми.
На это же указывает показатель вероятности
случайных значений параметров регрессии
(Р – значимость): если α меньше
принятого нами уровня (обычно 0,1; 0,05 или
0,01), делают вывод о неслучайной природе
данного значения параметра, т.е. о том,
что он статистически значим и надежен.
В противном случае принимается гипотеза
о случайной природе значения коэффициентов
уравнения.
5. Оцените качество уравнения через среднюю ошибку аппроксимации.
Рассчитаем среднюю ошибку аппроксимации
по формуле :
Таблицу расчета средней ошибки
аппроксимации представим на рисунке
6.
Рисунок 6 – Таблица расчета среднего
коэффициента аппроксимации
— множественная модель регрессии обладает
хорошим аппроксимирующим качеством.
6. Рассчитайте матрицу парных коэффициентов корреляции и отберите информативные факторы в модели. Укажите коллинеарные факторы.
О коллинеарности факторов можно судить
о величине парного коэффициента
корреляции (
)
между факторными признаками.
Матрицу парных коэффициентов корреляции
переменных можно рассчитать, используя
инструмент анализа данных Корреляция.
Для этого:
1) в главном меню последовательно выберете
пункты Сервис / Анализ данных /
Корреляция. Щелкните по кнопке ОК;
2) заполните диалоговое окно ввода данных
и параметров вывода (рисунок 7);
3) результаты вычислений – матрица
парных коэффициентов корреляции –
представлены на рисунке 8.
Рисунок 7. Диалоговое окно ввода параметров
инструмента Корреляция
Рисунок 8 – Матрица парных коэффициентов
корреляции
Cвязь у с фактором х3
можно охарактеризовать как умеренную,
с остальными факторами, как слабую.
Однако,
,
и
указывают на тесную связь между факторами.
При отборе факторов в модель предпочтение
отдается фактору, который при достаточно
тесной связи с результатом имеет
наименьшую тесноту связи с другими
факторами. Из трех факторов х1,
х2, х3 из анализа,
на наш взгляд, можно удалить факторы
х1, х2,
как наиболее коррелируемые с факторами
х4, х5. Таким
образом, информативными являются факторы
х3, х4, х5.
7. Постройте модель в естественной форме только с информативными факторами и оцените ее параметры.
Алгоритмические шаги нахождения
параметров множественного уравнения
регрессии с отобранными факторами и
его параметров выполняются соответственно
с пунктом 1 лабораторной работы.
Результаты анализа представлены на
рисунке 9.
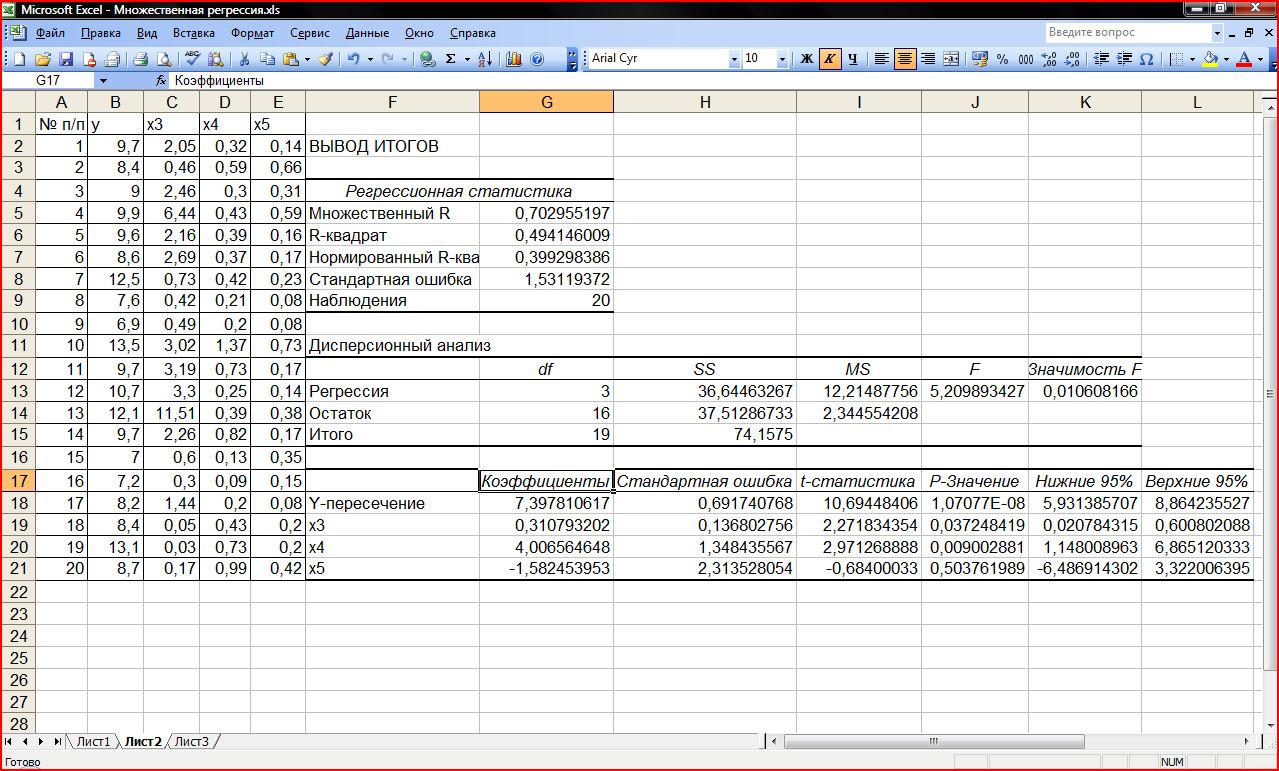
Рисунок 9 – Результат применения
инструмента Регрессия для переменных
х3, х4, х5
Уравнение регрессии имеет вид (в скобках,
под коэффициентами, обычно указывают
t-статистику):
(10,69) (2,27) (2,97) (-0,68)
Уравнение в целом и его параметры
статистически значимы, кроме b5.
Отрицательный знак b5
не поддается экономической интерпретации,
из чего следует, что повышение насыщенности
средствами оздоровления растений
отрицательно сказывается на урожайности.
Если в результате получается, что
некоторые коэффициенты не значимы, как
в нашем случае незначим b5,
то необходимо вернуться к пункту 6 и
исключить его из анализа.
Результаты регрессионного анализа с
факторными переменными х3,
х4 представлены на рисунке
10.
Рисунок 10 – Результат применения
инструмента Регрессия для переменных
х3, х4
Получаем уравнение вида:
(11,01)
(2,20) (3,22)
Уравнение в целом и его параметры
статистически значимы. При этом можем
наблюдать, что коэффициент детерминации
R2=0,47 незначительно
снизился, зато скорректированный
увеличился
по сравнению с результатами регрессии
с полным перечнем факторов. Что
свидетельствует об улучшении качества
модели.
Соседние файлы в предмете [НЕСОРТИРОВАННОЕ]
- #
- #
- #
- #
- #
- #
- #
- #
- #
- #
- #
По территориям региона приводятся данные за 200Х г.
| Номер региона | Среднедушевой прожиточный минимум в день одного трудоспособного, руб., х | Среднедневная заработная плата, руб., у |
|---|---|---|
| 1 | 78 | 133 |
| 2 | 82 | 148 |
| 3 | 87 | 134 |
| 4 | 79 | 154 |
| 5 | 89 | 162 |
| 6 | 106 | 195 |
| 7 | 67 | 139 |
| 8 | 88 | 158 |
| 9 | 73 | 152 |
| 10 | 87 | 162 |
| 11 | 76 | 159 |
| 12 | 115 | 173 |
Задание:
1. Постройте поле корреляции и сформулируйте гипотезу о форме связи.
2. Рассчитайте параметры уравнения линейной регрессии
.
3. Оцените тесноту связи с помощью показателей корреляции и детерминации.
4. Дайте с помощью среднего (общего) коэффициента эластичности сравнительную оценку силы связи фактора с результатом.
5. Оцените с помощью средней ошибки аппроксимации качество уравнений.
6. Оцените с помощью F-критерия Фишера статистическую надёжность результатов регрессионного моделирования.
7. Рассчитайте прогнозное значение результата, если прогнозное значение фактора увеличится на 10% от его среднего уровня. Определите доверительный интервал прогноза для уровня значимости .
8. Оцените полученные результаты, выводы оформите в аналитической записке.
Решение:
Решим данную задачу с помощью Excel.
1. Сопоставив имеющиеся данные х и у, например, ранжировав их в порядке возрастания фактора х, можно наблюдать наличие прямой зависимости между признаками, когда увеличение среднедушевого прожиточного минимума увеличивает среднедневную заработную плату. Исходя из этого, можно сделать предположение, что связь между признаками прямая и её можно описать уравнением прямой. Этот же вывод подтверждается и на основе графического анализа.
Чтобы построить поле корреляции можно воспользоваться ППП Excel. Введите исходные данные в последовательности: сначала х, затем у.
Выделите область ячеек, содержащую данные.
Затем выберете: Вставка / Точечная диаграмма / Точечная с маркерами как показано на рисунке 1.
Рисунок 1 Построение поля корреляции
Анализ поля корреляции показывает наличие близкой к прямолинейной зависимости, так как точки расположены практически по прямой линии.
2. Для расчёта параметров уравнения линейной регрессии
воспользуемся встроенной статистической функцией ЛИНЕЙН.
Для этого:
1) Откройте существующий файл, содержащий анализируемые данные;
2) Выделите область пустых ячеек 5×2 (5 строк, 2 столбца) для вывода результатов регрессионной статистики.
3) Активизируйте Мастер функций: в главном меню выберете Формулы / Вставить функцию.
4) В окне Категория выберете Статистические, в окне функция – ЛИНЕЙН. Щёлкните по кнопке ОК как показано на Рисунке 2;
Рисунок 2 Диалоговое окно «Мастер функций»
5) Заполните аргументы функции:
Известные значения у – диапазон, содержащий данные результативного признака;
Известные значения х – диапазон, содержащий данные факторного признака;
Константа – логическое значение, которое указывает на наличие или на отсутствие свободного члена в уравнении; если Константа = 1, то свободный член рассчитывается обычным образом, если Константа = 0, то свободный член равен 0;
Статистика – логическое значение, которое указывает, выводить дополнительную информацию по регрессионному анализу или нет. Если Статистика = 1, то дополнительная информация выводится, если Статистика = 0, то выводятся только оценки параметров уравнения.
Щёлкните по кнопке ОК;
Рисунок 3 Диалоговое окно аргументов функции ЛИНЕЙН
6) В левой верхней ячейке выделенной области появится первый элемент итоговой таблицы. Чтобы раскрыть всю таблицу, нажмите на клавишу <F2>, а затем на комбинацию клавиш <Ctrl>+<Shift>+<Enter>.
Дополнительная регрессионная статистика будет выводиться в порядке, указанном в следующей схеме:
| Значение коэффициента b | Значение коэффициента a |
| Стандартная ошибка b | Стандартная ошибка a |
| Коэффициент детерминации R2 | Стандартная ошибка y |
| F-статистика | Число степеней свободы df |
| Регрессионная сумма квадратов
|
Остаточная сумма квадратов
|
Рисунок 4 Результат вычисления функции ЛИНЕЙН
Получили уровнение регрессии:
Делаем вывод: С увеличением среднедушевого прожиточного минимума на 1 руб. среднедневная заработная плата возрастает в среднем на 0,92 руб.
3. Коэффициент детерминации означает, что 52% вариации заработной платы (у) объясняется вариацией фактора х – среднедушевого прожиточного минимума, а 48% — действием других факторов, не включённых в модель.
По вычисленному коэффициенту детерминации можно рассчитать коэффициент корреляции: .
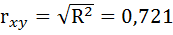
Связь оценивается как тесная.
4. С помощью среднего (общего) коэффициента эластичности определим силу влияния фактора на результат.
Для уравнения прямой 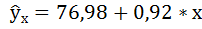средний (общий) коэффициент эластичности определим по формуле:
Средние значения найдём, выделив область ячеек со значениями х, и выберем Формулы / Автосумма / Среднее, и то же самое произведём со значениями у.
Рисунок 5 Расчёт средних значений функции и аргумент
Таким образом, при изменении среднедушевого прожиточного минимума на 1% от своего среднего значения среднедневная заработная плата изменится в среднем на 0,51%.
С помощью инструмента анализа данных Регрессия можно получить:
— результаты регрессионной статистики,
— результаты дисперсионного анализа,
— результаты доверительных интервалов,
— остатки и графики подбора линии регрессии,
— остатки и нормальную вероятность.
Порядок действий следующий:
1) проверьте доступ к Пакету анализа. В главном меню последовательно выберите: Файл/Параметры/Надстройки.
2) В раскрывающемся списке Управление выберите пункт Надстройки Excel и нажмите кнопку Перейти.
3) В окне Надстройки установите флажок Пакет анализа, а затем нажмите кнопку ОК.
• Если Пакет анализа отсутствует в списке поля Доступные надстройки, нажмите кнопку Обзор, чтобы выполнить поиск.
• Если выводится сообщение о том, что пакет анализа не установлен на компьютере, нажмите кнопку Да, чтобы установить его.
4) В главном меню последовательно выберите: Данные / Анализ данных / Инструменты анализа / Регрессия, а затем нажмите кнопку ОК.
5) Заполните диалоговое окно ввода данных и параметров вывода:
Входной интервал Y – диапазон, содержащий данные результативного признака;
Входной интервал X – диапазон, содержащий данные факторного признака;
Метки – флажок, который указывает, содержит ли первая строка названия столбцов или нет;
Константа – ноль – флажок, указывающий на наличие или отсутствие свободного члена в уравнении;
Выходной интервал – достаточно указать левую верхнюю ячейку будущего диапазона;
6) Новый рабочий лист – можно задать произвольное имя нового листа.
Затем нажмите кнопку ОК.
Рисунок 6 Диалоговое окно ввода параметров инструмента Регрессия
Результаты регрессионного анализа для данных задачи представлены на рисунке 7.
Рисунок 7 Результат применения инструмента регрессия
5. Оценим с помощью средней ошибки аппроксимации качество уравнений. Воспользуемся результатами регрессионного анализа представленного на Рисунке 8.
Рисунок 8 Результат применения инструмента регрессия «Вывод остатка»
Составим новую таблицу как показано на рисунке 9. В графе С рассчитаем относительную ошибку аппроксимации по формуле:
Рисунок 9 Расчёт средней ошибки аппроксимации
Средняя ошибка аппроксимации рассчитывается по формуле:
Качество построенной модели оценивается как хорошее, так как 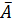не превышает 8 – 10%.
6. Из таблицы с регрессионной статистикой (Рисунок 4) выпишем фактическое значение F-критерия Фишера:
Поскольку 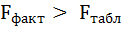при 5%-ном уровне значимости, то можно сделать вывод о значимости уравнения регрессии (связь доказана).
8. Оценку статистической значимости параметров регрессии проведём с помощью t-статистики Стьюдента и путём расчёта доверительного интервала каждого из показателей.
Выдвигаем гипотезу Н0 о статистически незначимом отличии показателей от нуля:
.
для числа степеней свободы
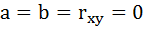
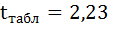
На рисунке 7 имеются фактические значения t-статистики:
t-критерий для коэффициента корреляции можно рассчитать двумя способами:
I способ: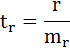
где 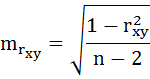– случайная ошибка коэффициента корреляции.
Данные для расчёта возьмём из таблицы на Рисунке 7.
II способ:
Фактические значения t-статистики превосходят табличные значения:
Поэтому гипотеза Н0 отклоняется, то есть параметры регрессии и коэффициент корреляции не случайно отличаются от нуля, а статистически значимы.
Доверительный интервал для параметра a определяется как
Для параметра a 95%-ные границы как показано на рисунке 7 составили:
Доверительный интервал для коэффициента регрессии определяется как
Для коэффициента регрессии b 95%-ные границы как показано на рисунке 7 составили:
Анализ верхней и нижней границ доверительных интервалов приводит к выводу о том, что с вероятностью 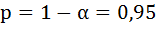параметры a и b, находясь в указанных границах, не принимают нулевых значений, т.е. не являются статистически незначимыми и существенно отличны от нуля.
7. Полученные оценки уравнения регрессии позволяют использовать его для прогноза. Если прогнозное значение прожиточного минимума составит:
Тогда прогнозное значение прожиточного минимума составит:
Ошибку прогноза рассчитаем по формуле:
где
Дисперсию посчитаем также с помощью ППП Excel. Для этого:
1) Активизируйте Мастер функций: в главном меню выберете Формулы / Вставить функцию.
2) В окне Категория выберете Статистические, в окне функция – ДИСП.Г. Щёлкните по кнопке ОК.
3) Заполните диапазон, содержащий числовые данные факторного признака. Нажмите ОК.
Рисунок 10 Расчёт дисперсии
Получили значение дисперсии
Для подсчёта остаточной дисперсии на одну степень свободы воспользуемся результатами дисперсионного анализа как показано на Рисунке 7.
Доверительные интервалы прогноза индивидуальных значений у при 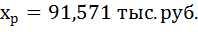с вероятностью 0,95 определяются выражением:
Интервал достаточно широк, прежде всего, за счёт малого объёма наблюдений. В целом выполненный прогноз среднемесячной заработной платы оказался надёжным.
Условие задачи взято из: Практикум по эконометрике: Учеб. пособие / И.И. Елисеева, С.В. Курышева, Н.М. Гордеенко и др.; Под ред. И.И. Елисеевой. – М.: Финансы и статистика, 2003. – 192 с.: ил.
Коэффициент корреляции
Тесноту (силу) связи изучаемых показателей в предмете эконометрика оценивают с помощью коэффициента корреляции Rxy, который может принимать значения от -1 до +1.
Если Rxy > 0,7 — связь между изучаемыми показателями сильная, можно проводить анализ линейной модели
Если 0,3 < Rxy < 0,7 — связь между показателями умеренная, можно использовать нелинейную модель при отсутствии Rxy > 0,7
Если Rxy < 0,3 — связь слабая, модель строить нельзя
Для нелинейной регрессии используют индекс корреляции (0 < Рху < 1):
Средняя ошибка аппроксимации
Для оценки качества однофакторной модели в эконометрике используют коэффициент детерминации и среднюю ошибку аппроксимации.
Средняя ошибка аппроксимации определяется как среднее отклонение полученных значений от фактических
Допустимая ошибка аппроксимации не должна превышать 10%.
В эконометрике существует понятие среднего коэффициента эластичности Э – который говорит о том, на сколько процентов в среднем изменится показатель у от своего среднего значения при изменении фактора х на 1% от своей средней величины.
Пример нахождения коэффициента корреляции
Исходные данные:
|
Номер региона |
Среднедушевой прожиточный минимум в день одного трудоспособного, руб., |
Среднедневная заработная плата, руб., |
|
1 |
81 |
124 |
|
2 |
77 |
131 |
|
3 |
85 |
146 |
|
4 |
79 |
139 |
|
5 |
93 |
143 |
|
6 |
100 |
159 |
|
7 |
72 |
135 |
|
8 |
90 |
152 |
|
9 |
71 |
127 |
|
10 |
89 |
154 |
|
11 |
82 |
127 |
|
12 |
111 |
162 |
Рассчитаем параметры парной линейной регрессии, составив таблицу
| x |
x2 |
y |
xy |
y2 |
|
|
1 |
81 |
6561 |
124 |
10044 |
15376 |
|
2 |
77 |
5929 |
131 |
10087 |
17161 |
|
3 |
85 |
7225 |
146 |
12410 |
21316 |
|
4 |
79 |
6241 |
139 |
10981 |
19321 |
|
5 |
93 |
8649 |
143 |
13299 |
20449 |
|
6 |
100 |
10000 |
159 |
15900 |
25281 |
|
7 |
72 |
5184 |
135 |
9720 |
18225 |
|
8 |
90 |
8100 |
152 |
13680 |
23104 |
|
9 |
71 |
5041 |
127 |
9017 |
16129 |
|
10 |
89 |
7921 |
154 |
13706 |
23716 |
|
11 |
82 |
6724 |
127 |
10414 |
16129 |
|
12 |
111 |
12321 |
162 |
17982 |
26244 |
|
Среднее |
85,8 |
7491 |
141,6 |
12270,0 |
20204,3 |
|
Сумма |
1030,0 |
89896 |
1699 |
147240 |
242451 |
| σ |
11,13 |
12,59 |
|||
| σ2 |
123,97 |
158,41 |
формула расчета дисперсии σ2 приведена здесь.
Коэффициенты уравнения y = a + bx определяются по формуле
Получаем уравнение регрессии: y = 0,947x + 60,279.
Коэффициент уравнения b = 0,947 показывает, что при увеличении среднедушевого прожиточного минимума в день одного трудоспособного на 1 руб. среднедневная заработная плата увеличивается на 0,947 руб.
Коэффициент корреляции рассчитывается по формуле:
Значение коэффициента корреляции более — 0,7, это означает, что связь между среднедушевым прожиточным минимумом в день одного трудоспособного и среднедневной заработной платой сильная.
Коэффициент детерминации равен R2 = 0.838^2 = 0.702
т.е. 70,2% результата объясняется вариацией объясняющей переменной x.
Классическая модель линейной регрессии
Лабораторная
работа № 2
Тема
«Классическая модель линейной регрессии»
Задания По данным приложения А:
1) рассчитайте параметры линейного уравнения
множественной регрессии с полным перечнем факторов по данным о деятельности
крупнейших компаний США в 2007 г.
2) дайте сравнительную оценку силы связи факторов с
результатом с помощью средних (общих) коэффициентов эластичности.
) оцените с помощью F-критерия Фишера —
Снедекора значимость уравнения линейной регрессии и показателя тесноты связи.
) оцените статистическую значимость коэффициентов
регрессии с помощью t — критерия Стьюдента.
) оцените качество уравнения через среднюю ошибку
аппроксимации.
) рассчитайте матрицу парных коэффициентов корреляции
и отберите информативные факторы в модели. Укажите коллинеарные факторы.
) постройте модель в естественной форме только с
информативными факторами и оцените ее параметры.
) постройте модель в стандартизованном масштабе и
проинтерпретируйте ее параметры.
9) рассчитайте прогнозное значение
результата, если прогнозное значение факторов составляют 80% от их максимальных
значений.
10) рассчитайте ошибки и доверительный интервал прогноза для
уровня значимости 
.
) по полученным результатам сделайте экономический вывод.
Реализация
типовых заданий
1. Рассчитайте параметры линейного уравнения
множественной регрессии с полным перечнем факторов по данным о деятельности
крупнейших компаний США в 2007 г.
Имеются данные о деятельности 25 крупнейших компаний США
(таблица 8.2.1).
Построим уравнение множественной линейной регрессии
следующего вида:
.
Для этого проведем регрессионный анализ данных факторов с помощью
табличного редактора МС Excel.
Таблица 8.2.1 — Исходные данные для проведения
корреляционного и регрессионного анализа
|
№ п/п |
|
|||||
|
1 |
45,9 |
34 |
68 |
12,5 |
43,3 |
2,3 |
|
2 |
46,7 |
16,1 |
49,3 |
18,8 |
42,9 |
3,9 |
|
3 |
45,7 |
7,2 |
66,6 |
7 |
41,3 |
1,7 |
|
4 |
46,7 |
12,7 |
17,3 |
14,6 |
40,9 |
2,6 |
|
5 |
47,6 |
22,7 |
78,5 |
30,7 |
39,7 |
3,1 |
|
6 |
46,3 |
17,7 |
20,9 |
28 |
28,9 |
0,6 |
|
7 |
49,1 |
139,8 |
356,4 |
100,6 |
39,4 |
5,1 |
|
8 |
20,6 |
72,4 |
24,8 |
39,2 |
2,6 |
|
|
9 |
51,9 |
168,1 |
218,2 |
216,1 |
38,7 |
4,5 |
|
10 |
45,4 |
4,7 |
5 |
1,2 |
37,7 |
1,9 |
|
11 |
46,3 |
9,5 |
28,8 |
7,8 |
37,7 |
3 |
|
12 |
46,9 |
29,8 |
68 |
12,4 |
37,4 |
3,6 |
|
13 |
46,9 |
16,1 |
47,5 |
17,9 |
28,6 |
3,7 |
|
14 |
46,4 |
12,5 |
45,4 |
61,5 |
35,5 |
2,5 |
|
15 |
45,4 |
22,2 |
43,9 |
30,5 |
35,1 |
3,1 |
|
16 |
45,8 |
9,5 |
11,5 |
9,7 |
34,5 |
0,3 |
|
17 |
46,8 |
29,7 |
46,8 |
41,2 |
32,9 |
2,2 |
|
18 |
45,9 |
24,8 |
27,8 |
32,2 |
3,5 |
|
|
19 |
46,1 |
20,4 |
54 |
40,6 |
27,8 |
4,1 |
|
20 |
46,9 |
15,4 |
42,8 |
17,2 |
31,7 |
4,3 |
|
21 |
44,1 |
24,1 |
5,8 |
38 |
31,6 |
2,9 |
|
22 |
46,3 |
16,2 |
31 |
20,5 |
31,6 |
3,5 |
|
23 |
47 |
16,1 |
41,4 |
19 |
31,5 |
4 |
|
24 |
45,6 |
6,9 |
6,8 |
6,7 |
30,3 |
2,6 |
|
25 |
45,7 |
18,2 |
20,9 |
23,4 |
29,6 |
4 |
где y — чистый доход, млрд. долл. x1 — оборот капитала, млрд.
долл. x2 — использованный капитал, млрд. долл. x3 — численность служащих,
тыс. чел. x4 — рыночная капитализация компаний, млрд. долл. x5 — заработная плата
служащих, тыс. долл.
Для построения модели можно воспользоваться инструментом
анализа данных Регрессия. Порядок действий следующий:
а) в главном меню выберите Сервис/Анализ данных/Регрессия.
Щелкните по кнопке ОК;
б) заполните диалоговое окно ввода данных и параметров ввода
(рисунок 8.2.1):
классическая модель линейная регрессия
Рисунок 8.2.1 — Диалоговое окно ввода параметров инструмента
«Регрессия»
Входной интервал Y — диапазон, содержащий
данные результативного признака;
Входной интервал Х — диапазон, содержащий
данные всех пяти факторов;
Метки — флажок, который указывает, содержит ли первая
строка названия столбцов или нет;
Константа — ноль — флажок, указывающий на
наличие или отсутствие свободного члена в уравнении;
Выходной интервал — достаточно указать
левую верхнюю ячейку будущего диапазона;
Новый рабочий лист — можно задать
произвольное имя нового листа.
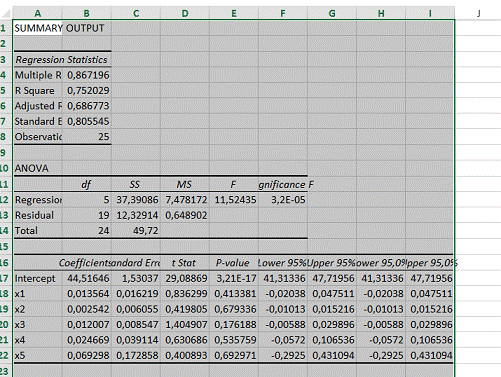
Результаты регрессионного анализа представлены на рисунке
8.2.2.
Рисунок 8.2.2 — Результат применения инструмента Регрессия
для факторов
Составим уравнение множественной регрессии:
Коэффициенты регрессии показывают среднее изменение результативного
признака с изменением на 1 единицу своего измерения данного фактора при условии
постоянства всех остальных.
Таким образом, коэффициент регрессии при х1 показывает,
что с увеличением оборотного капитала на 1 млрд. долл. чистый доход увеличится
в среднем на 0,0136 млрд. долл., при х2 показывает, что с
увеличением оборотного капитала на 1 млрд. долл. чистый доход увеличится в
среднем на 0,003 млрд. долл., х3 показывает, что с увеличением
оборотного капитала на 1 млрд. долл. чистый доход увеличится в среднем на 0,012
тыс. чел., х4 показывает, что с увеличением оборотного капитала на 1
млрд. долл. чистый доход увеличится в среднем на 0,025 млрд. долл., х5
показывает, что с увеличением оборотного капитала на 1 млрд. долл. чистый доход
увеличится в среднем на 0,07 тыс. долл., при фиксированном значении остальных
факторов.
Параметр 
экономического смысла не имеет.
2. Дайте сравнительную оценку силы связи факторов с
результатом с помощью средних (общих) коэффициентов эластичности.
Средние коэффициенты эластичности 
показывают, на сколько процентов от значения своей средней 
изменяется результат при изменении
фактора 
на 1 % от своей средней 
и при фиксированном воздействии на y всех прочих факторов, включенных в уравнение регрессии.
Для линейной зависимости
,
где 
— коэффициент регрессии при в уравнении множественной регрессии.
Результаты вычисления соответствующих показателей для каждого
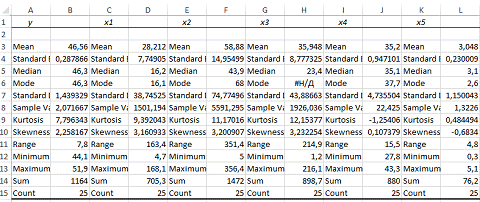
признака представлены на рисунке 8.2.3.
Рисунок 8.2.3 — Результат применения инструмента
«Описательная статистика»
Здесь 
,
,
,
,
.
По значениям средних коэффициентов эластичности можно сделать
вывод о более сильном влиянии на результат y признаков факторов 
и 
, чем признаков факторов 
, 
и 
.
Средний коэффициент эластичности 
, показывает, что с увеличением оборотного капитала на 1 %, чистый
доход увеличивается в среднем на 0,008 %, при условии, что другие факторы
остаются постоянными, 
, показывает, что с увеличением оборотного
капитала на 1 %, чистый доход увеличивается в среднем на 0,003 %, при условии,
что другие факторы остаются постоянными, 
, показывает, что с увеличением оборотного капитала на 1 %, чистый
доход увеличивается в среднем на 0,009 %, при условии, что другие факторы
остаются постоянными, 
, показывает, что с увеличением оборотного
капитала на 1 %, чистый доход увеличивается в среднем на 0,019 %, при условии,
что другие факторы остаются постоянными, 
, показывает, что с увеличением оборотного капитала на 1 %, чистый
доход увеличивается в среднем на 0,005 %, при условии, что другие факторы
остаются постоянными.
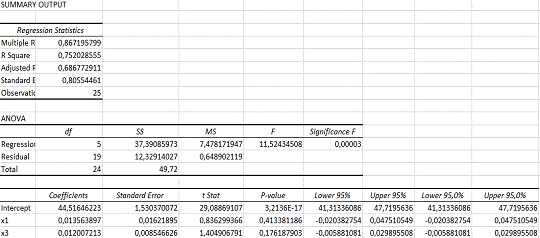
3. Оцените с помощью F-критерия Фишера-Снедекора значимость
уравнения линейной регрессии и показателя тесноты связи.
Оценку надежности уравнения регрессии в целом и показателя тесноты
связи 
дает F-критерий Фишера:
.
Для проверки значимости уравнения выдвигаем две гипотезы:
Н0: уравнение регрессии статистически не значимо;
Н1: уравнение регрессии статистически значимо.
По данным таблиц дисперсионного анализа, представленным на рисунке
8.2.2, 
=11.52. Вероятность случайно получить
такое значение F-критерия составляет 0,00003, что не
превышает допустимый уровень значимости 5 %; об этом свидетельствует величина P — значение из этой же таблицы. Следовательно, полученное
значение не случайно, оно сформировалось под влиянием существенных факторов,
т.е. подтверждается статистическая значимость всего уравнения и показателя
тесноты связи . 
=0,00003. > следовательно уравнение регрессии является статистически
значимым.
4. Оцените статистическую значимость
коэффициентов регрессии с помощью t — критерия Стьюдента.
Выдвигаем две гипотезы: Н0: коэффициенты регрессии статистически
не значим, т.е. равны о; Н1: коэффициенты регрессии статистически
значимы, т.е. отличны от нуля. Значения случайных ошибок параметров 
с учетом округления равны (рисунок
8.2.2):
Они показывают, какое значение данной характеристики
сформировались под влиянием случайных факторов. Эти значения используются для
расчета t-критерия Стьюдента (рисунок 8.2.2):
.
Если значения t-критерия
меньше 2,09, можно сделать вывод о неслучайной природе данного значения
параметра, т. е о том, что он статистически значим и надежен. Tтабл=
5. Оцените качество уравнения через среднюю ошибку
аппроксимации.
Рассчитаем среднюю ошибку аппроксимации по формуле средней
арифметической простой:
Таблица 8.2.2 — Данные для расчета средней ошибки аппроксимации
|
№ п/п |
|
||
|
1 |
2 |
3 |
4 |
|
1 |
45,9 |
46,58 |
1,48 |
|
2 |
46,7 |
46,46 |
0,52 |
|
3 |
45,7 |
46,05 |
0,77 |
|
4 |
46,7 |
46,12 |
1,23 |
|
5 |
47,6 |
46,64 |
2,01 |
|
6 |
46,3 |
45,92 |
0,81 |
|
7 |
49,1 |
50,04 |
1,91 |
|
8 |
46,6 |
0,26 |
|
|
9 |
51,9 |
51,34 |
1,09 |
|
10 |
45,4 |
45,69 |
0,64 |
|
11 |
46,3 |
46,82 |
1,13 |
|
12 |
46,9 |
46,47 |
0,93 |
|
13 |
46,9 |
46,07 |
1,77 |
|
14 |
46,4 |
46,63 |
0,49 |
|
15 |
45,4 |
46,41 |
2,23 |
|
16 |
45,8 |
45,68 |
0,25 |
|
17 |
46,8 |
46,54 |
0,57 |
|
18 |
45,9 |
46,18 |
0,62 |
|
19 |
46,1 |
46,43 |
0,71 |
|
20 |
46,9 |
46,16 |
1,58 |
|
21 |
44,1 |
46,36 |
5,12 |
|
22 |
46,3 |
46,11 |
0,40 |
|
23 |
47 |
46,16 |
1,79 |
|
24 |
45,6 |
45,65 |
0,12 |
|
25 |
45,7 |
46,13 |
0,94 |
|
1164,00 |
29,38 |
Таким образом, фактические значения результативного признака
отличаются от теоретических значений на 117,5 %. Следовательно, построенная
модель не является удовлетворительной.
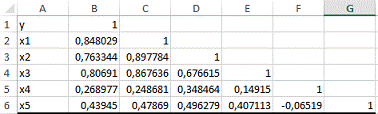
i. Рассчитайте матрицу парных коэффициентов
корреляции и отберите информативные факторы в модели. Укажите коллинеарные
факторы.
Значения линейных коэффициентов парной корреляции определяют
тесноту попарно связанных переменных, использованных в данном уравнении множественной
регрессии.
Парные коэффициенты корреляции рассчитываются по формулам:
; 
.
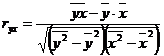
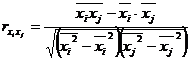
Рисунок 8.2.4 — Матрица коэффициентов парной корреляции
Из матрицы можно заметить, что факторы 
и 
, и мультиколлинеарны, т.к. коэффициенты корреляции превышают 0,7.
Таким образом, можно сказать, что они дублируют друг друга.
При отборе факторов в модель предпочтение отдается фактору,
который при достаточно тесной связи с результатом имеет наименьшую тесноту
связи с другими факторами. В нашем примере получаем, информативными факторами
являются: и .
Построим новое уравнение множественной регрессии с информативными
факторами.
7. Постройте модель в естественной форме только с
информативными факторами и оцените ее параметры.
Построим уравнение множественной линейной регрессии следующего
вида:
.
Параметры вычисляем аналогично пункту 1 (рисунок 8.2.7).
Рисунок 8.2.7 — Результат применения инструмента
«Регрессия»
Получаем уравнение следующего вида: 
.
Уравнение в целом, а также его параметры являются статистически
значимыми.
8. Постройте модель в стандартизованном масштабе и
проинтерпретируйте ее параметры.
Уравнение в стандартизованном масштабе
имеет вид:
.
Расчет β —
коэффициентов выполним по формулам
; 
.
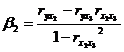
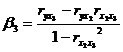
Парные коэффициенты корреляции берутся из матрицы (рисунок 8.2.6):
Получим уравнение 
.
Стандартизованные коэффициенты регрессии показывают, на
сколько сигм изменится в среднем результативный признак, если соответствующий
фактор изменится на 1 сигму при неизменном среднем уровне других факторов.
В нашем случае, при увеличении использования капитала на 1
сигму чистый доход увеличится на 1,07 сигм, при условии, что численность
служащих остаются на прежнем уровне, при увеличении использования капитала на 1
сигму чистый доход уменьшится на 0,46 сигм, при условии, что численность
служащих остаются на прежнем уровне.
9. Рассчитайте прогнозное
значение результата, если прогнозное значение факторов составляют 80% от их
максимальных значений.
Рассчитаем ожидаемое прогнозное значение
чистого дохода как точечный прогноз путем подстановки в уравнение регрессии
прогнозные значения факторов:
1) найдем максимальное значение для фактора (рисунок 8.2.4): 
) найдем максимальное значение для фактора (рисунок 8.2.4): 
) найдем прогнозные значения факторов:
для фактора : 
для фактора : 
4) подставим прогнозные значения
факторов в уравнение
В результате получим:
Таким образом, при прогнозных значениях использованного капитала
356 млдр. долл. и численности служащих 216,1 тыс. чел. чистый доход крупнейших
компаний США составит 92,21 млрд. долл.