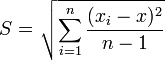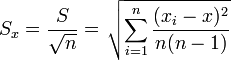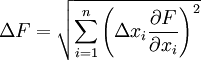Абсолютная и относительная погрешность

4.2
Средняя оценка: 4.2
Всего получено оценок: 2201.
4.2
Средняя оценка: 4.2
Всего получено оценок: 2201.
Абсолютную и относительную погрешность используют для оценки неточности в производимых расчетах с высокой сложностью. Также они используются в различных измерениях и для округления результатов вычислений. Рассмотрим, как определить абсолютную и относительную погрешность.
Опыт работы учителем математики — более 33 лет.
Абсолютная погрешность
Абсолютной погрешностью числа называют разницу между этим числом и его точным значением.
Рассмотрим пример: в школе учится 374 ученика. Если округлить это число до 400, то абсолютная погрешность измерения равна 400-374=26.
Для подсчета абсолютной погрешности необходимо из большего числа вычитать меньшее.
Существует формула абсолютной погрешности. Обозначим точное число буквой А, а буквой а – приближение к точному числу. Приближенное число – это число, которое незначительно отличается от точного и обычно заменяет его в вычислениях. Тогда формула будет выглядеть следующим образом:
Δа=А-а. Как найти абсолютную погрешность по формуле, мы рассмотрели выше.
На практике абсолютной погрешности недостаточно для точной оценки измерения. Редко когда можно точно знать значение измеряемой величины, чтобы рассчитать абсолютную погрешность. Измеряя книгу в 20 см длиной и допустив погрешность в 1 см, можно считать измерение с большой ошибкой. Но если погрешность в 1 см была допущена при измерении стены в 20 метров, это измерение можно считать максимально точным. Поэтому в практике более важное значение имеет определение относительной погрешности измерения.
Записывают абсолютную погрешность числа, используя знак ±. Например, длина рулона обоев составляет 30 м ± 3 см. Границу абсолютной погрешности называют предельной абсолютной погрешностью.
Относительная погрешность
Относительной погрешностью называют отношение абсолютной погрешности числа к самому этому числу. Чтобы рассчитать относительную погрешность в примере с учениками, разделим 26 на 374.
Получим число 0,0695, переведем в проценты и получим 7 %. Относительную погрешность обозначают процентами, потому что это безразмерная величина. Относительная погрешность – это точная оценка ошибки измерений. Если взять абсолютную погрешность в 1 см при измерении длины отрезков 10 см и 10 м, то относительные погрешности будут соответственно равны 10 % и 0,1 %. Для отрезка длиной в 10 см погрешность в 1 см очень велика, это ошибка в 10 %. А для десятиметрового отрезка 1 см не имеет значения, всего 0,1 %.
Различают систематические и случайные погрешности. Систематической называют ту погрешность, которая остается неизменной при повторных измерениях. Случайная погрешность возникает в результате воздействия на процесс измерения внешних факторов и может изменять свое значение.
Правила подсчета погрешностей
Для номинальной оценки погрешностей существует несколько правил:
- при сложении и вычитании чисел необходимо складывать их абсолютные погрешности;
- при делении и умножении чисел требуется сложить относительные погрешности;
- при возведении в степень относительную погрешность умножают на показатель степени.
Приближенные и точные числа записываются при помощи десятичных дробей. Берется только среднее значение, поскольку точное может быть бесконечно длинным. Чтобы понять, как записывать эти числа, необходимо узнать о верных и сомнительных цифрах.
Верными называются такие цифры, разряд которых превосходит абсолютную погрешность числа. Если же разряд цифры меньше абсолютной погрешности, она называется сомнительной. Например, для дроби 3,6714 с погрешностью 0,002 верными будут цифры 3,6,7, а сомнительными – 1 и 4. В записи приближенного числа оставляют только верные цифры. Дробь в этом случае будет выглядеть таким образом – 3,67.
Что мы узнали?
Абсолютные и относительные погрешности используются для оценки точности измерений. Абсолютной погрешностью называют разницу между точным и приближенным числом. Относительная погрешность – это отношение абсолютной погрешности числа к самому числу. На практике используют относительную погрешность, так как она является более точной.
Тест по теме
Доска почёта

Чтобы попасть сюда — пройдите тест.
-
Светлана Лобанова-Асямолова
10/10
-
Валерий Соломин
10/10
-
Анастасия Юшкова
10/10
-
Ксюша Пономарева
7/10
-
Паша Кривов
10/10
-
Евгений Холопик
9/10
-
Guzel Murtazina
10/10
-
Максим Аполонов
10/10
-
Olga Bimbirene
9/10
-
Света Колодий
10/10
Оценка статьи
4.2
Средняя оценка: 4.2
Всего получено оценок: 2201.
А какая ваша оценка?
Погре́шность измере́ния — оценка отклонения величины измеренного значения величины от её истинного значения. Погрешность измерения является характеристикой (мерой) точности измерения.
Поскольку выяснить с абсолютной точностью истинное значение любой величины невозможно, то невозможно и указать величину отклонения измеренного значения от истинного. (Это отклонение принято называть ошибкой измерения. В ряде источников, например, в БСЭ, термины ошибка измерения и погрешность измерения используются как синонимы.) Возможно лишь оценить величину этого отклонения, например, при помощи статистических методов. При этом за истинное значение принимается среднестатистическое значение, полученное при статистической обработке результатов серии измерений. Это полученное значение не является точным, а лишь наиболее вероятным. Поэтому в измерениях необходимо указывать, какова их точность. Для этого вместе с полученным результатом указывается погрешность измерений. Например, запись T=2.8±0.1 c. означает, что истинное значение величины T лежит в интервале от 2.7 с. до 2.9 с. некоторой оговоренной вероятностью (см. доверительный интервал, доверительная вероятность, стандартная ошибка).
В 2006 году на международном уровне был принят новый документ, диктующий условия проведения измерений и установивший новые правила сличения государственных эталонов. Понятие «погрешность» стало устаревать, вместо него было введено понятие «неопределенность измерений».
Содержание
- 1 Определение погрешности
- 2 Классификация погрешностей
- 2.1 По форме представления
- 2.2 По причине возникновения
- 2.3 По характеру проявления
- 2.4 По способу измерения
- 3 См. также
- 4 Литература
Определение погрешности
В зависимости от характеристик измеряемой величины для определения погрешности измерений используют различные методы.
- Метод Корнфельда, заключается в выборе доверительного интервала в пределах от минимального до максимального результата измерений, и погрешность как половина разности между максимальным и минимальным результатом измерения:
- Средняя квадратическая погрешность:
- Средняя квадратическая погрешность среднего арифметического:
Классификация погрешностей
По форме представления
- Абсолютная погрешность — ΔX является оценкой абсолютной ошибки измерения. Величина этой погрешности зависит от способа её вычисления, который, в свою очередь, определяется распределением случайной величины Xmeas. При этом равенство:
ΔX = | Xtrue − Xmeas | ,
где Xtrue — истинное значение, а Xmeas — измеренное значение, должно выполняться с некоторой вероятностью близкой к 1. Если случайная величина Xmeas распределена по нормальному закону, то, обычно, за абсолютную погрешность принимают её среднеквадратичное отклонение. Абсолютная погрешность измеряется в тех же единицах измерения, что и сама величина.
- Относительная погрешность — отношение абсолютной погрешности к тому значению, которое принимается за истинное:

Относительная погрешность является безразмерной величиной, либо измеряется в процентах.
- Приведенная погрешность — относительная погрешность, выраженная отношением абсолютной погрешности средства измерений к условно принятому значению величины, постоянному во всем диапазоне измерений или в части диапазона. Вычисляется по формуле
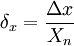
где Xn — нормирующее значение, которое зависит от типа шкалы измерительного прибора и определяется по его градуировке:
— если шкала прибора односторонняя, т.е. нижний предел измерений равен нулю, то Xn определяется равным верхнему пределу измерений;
— если шкала прибора двухсторонняя, то нормирующее значение равно ширине диапазона измерений прибора.
Приведенная погрешность — безразмерная величина (может измеряться в процентах).
По причине возникновения
- Инструментальные / приборные погрешности — погрешности, которые определяются погрешностями применяемых средств измерений и вызываются несовершенством принципа действия, неточностью градуировки шкалы, ненаглядностью прибора.
- Методические погрешности — погрешности, обусловленные несовершенством метода, а также упрощениями, положенными в основу методики.
- Субъективные / операторные / личные погрешности — погрешности, обусловленные степенью внимательности, сосредоточенности, подготовленности и другими качествами оператора.
В технике применяют приборы для измерения лишь с определенной заранее заданной точностью – основной погрешностью, допускаемой нормали в нормальных условиях эксплуатации для данного прибора.
Если прибор работает в условиях, отличных от нормальных, то возникает дополнительная погрешность, увеличивающая общую погрешность прибора. К дополнительным погрешностям относятся: температурная, вызванная отклонением температуры окружающей среды от нормальной, установочная, обусловленная отклонением положения прибора от нормального рабочего положения, и т.п. За нормальную температуру окружающего воздуха принимают 20°С, за нормальное атмосферное давление 01,325 кПа.
Обобщенной характеристикой средств измерения является класс точности, определяемый предельными значениями допускаемых основной и дополнительной погрешностей, а также другими параметрами, влияющими на точность средств измерения; значение параметров установлено стандартами на отдельные виды средств измерений. Класс точности средств измерений характеризует их точностные свойства, но не является непосредственным показателем точности измерений, выполняемых с помощью этих средств, так как точность зависит также от метода измерений и условий их выполнения. Измерительным приборам, пределы допускаемой основной погрешности которых заданы в виде приведенных основных (относительных) погрешностей, присваивают классы точности, выбираемые из ряда следующих чисел: (1; 1,5; 2,0; 2,5; 3,0; 4,0; 5,0; 6,0)*10n, где n = 1; 0; -1; -2 и т.д.
По характеру проявления
- Случайная погрешность — погрешность, меняющаяся (по величине и по знаку) от измерения к измерению. Случайные погрешности могут быть связаны с несовершенством приборов (трение в механических приборах и т.п.), тряской в городских условиях, с несовершенством объекта измерений (например, при измерении диаметра тонкой проволоки, которая может иметь не совсем круглое сечение в результате несовершенства процесса изготовления), с особенностями самой измеряемой величины (например при измерении количества элементарных частиц, проходящих в минуту через счётчик Гейгера).
- Систематическая погрешность — погрешность, изменяющаяся во времени по определенному закону (частным случаем является постоянная погрешность, не изменяющаяся с течением времени). Систематические погрешности могут быть связаны с ошибками приборов (неправильная шкала, калибровка и т.п.), неучтёнными экспериментатором.
- Прогрессирующая (дрейфовая) погрешность — непредсказуемая погрешность, медленно меняющаяся во времени. Она представляет собой нестационарный случайный процесс.
- Грубая погрешность (промах) — погрешность, возникшая вследствие недосмотра экспериментатора или неисправности аппаратуры (например, если экспериментатор неправильно прочёл номер деления на шкале прибора, если произошло замыкание в электрической цепи).
По способу измерения
- Погрешность прямых измерений
- Погрешность косвенных измерений — погрешность вычисляемой (не измеряемой непосредственно) величины:
Если F = F(x1,x2…xn), где xi — непосредственно измеряемые независимые величины, имеющие погрешность Δxi, тогда:
См. также
- Измерение физических величин
- Класс точности
- Метрология
- Система автоматизированного сбора данных со счетчиков по радиоканалу
- Методы электроаналитической химии
Литература
- Назаров Н. Г. Метрология. Основные понятия и математические модели. М.: Высшая школа, 2002. 348 с.
- Лабораторные занятия по физике. Учебное пособие/Гольдин Л. Л., Игошин Ф. Ф., Козел С. М. и др.; под ред. Гольдина Л. Л. — М.: Наука. Главная редакция физико-математичекой литературы, 1983. — 704 с.
Wikimedia Foundation.
2010.
Абсолютная и относительная погрешности (ошибки).
Пусть некоторая
величина x
измерена n
раз. В результате получен ряд значений
этой величины: x1,
x2,
x3,
…, xn
Величиной, наиболее
близкой к действительному значению,
является среднее арифметическое этих
результатов:
Отсюда следует,
что каждое физическое измерение должно
быть повторено несколько раз.
Разность между
средним значением
измеряемой
величины и значением отдельного измерения
называется абсолютной
погрешностью отдельного измерения:
(13)
Абсолютная
погрешность может быть как положительной,
так и отрицательной и измеряется в тех
же единицах, что и измеряемая величина.
Средняя абсолютная
ошибка результата — это среднее
арифметическое значений абсолютных
погрешностей отдельных измерений,
взятых по абсолютной величине (модулю):
(14)
Отношения
называются относительными погрешностями
(ошибками) отдельных измерений.
Отношение средней
абсолютной погрешности результата
к среднему арифметическому значению
измеряемой величины называют относительной
ошибкой результата и выражают в процентах:
Относительная
ошибка характеризует точность измерения.
Законы распределения случайных величин.
Результат измерения
физической величины зависит от многих
факторов, влияние которых заранее учесть
невозможно. Поэтому значения, полученные
в результате прямых измерений какого
— либо параметра, являются случайными,
обычно не совпадающие между собой.
Следовательно, случайные
величины —
это такие величины, которые в зависимости
от обстоятельств могут принимать те
или иные значения. Если случайная
величина принимает только определенные
числовые значения, то она называется
дискретной.
Например,
количество заболеваний в данном регионе
за год, оценка, полученная студентом на
экзамене, энергия электрона в атоме и
т.д.
Непрерывная
случайная величина принимает любые
значения в данном интервале.
Например: температура
тела человека, мгновенные скорости
теплового движения молекул, содержание
кислорода в воздухе и т.д.
Под событием
понимается всякий результат или исход
испытания. В теории вероятностей
рассматриваются события, которые при
выполнение некоторых условий могут
произойти, а могут не произойти. Такие
события называются
случайными.
Например, событие, состоящее в появлении
цифры 1 при выполнении условия — бросания
игральной кости, может произойти, а
может не произойти.
Если событие
неизбежно происходит в результате
каждого испытания, то оно называется
достоверным.
Событие называется невозможным,
если оно вообще не происходит ни при
каких условиях.
Два события,
одновременное появление которых
невозможно, называются несовместными.
Пусть случайное
событие А в серии из n
независимых испытаний произошло m
раз, тогда отношение:
называется
относительной частотой события А. Для
каждой относительной частоты выполняется
неравенство:
При небольшом
числе опытов относительная частота
событий в значительной мере имеет
случайный характер и может заметно
изменяться от одной группы опытов к
другой. Однако при увеличении числа
опытов частота событий все более теряет
свой случайный характер и приближается
к некоторому постоянному положительному
числу, которое является количественной
мерой возможности реализации случайного
события А. Предел, к которому стремится
относительная частота событий при
неограниченном увеличении числа
испытаний, называется статистической
вероятностью события:
Например, при
многократном бросании монеты частота
выпадения герба будет лишь незначительно
отличаться от ½. Для достоверного события
вероятность Р(А) равна единице. Если
Р=0, то событие невозможно.
Математическим
ожиданием
дискретной случайной величины называется
сумма произведений всех ее возможных
значений хi
на вероятность этих значений рi:
Статистическим
аналогом математического ожидания
является среднее арифметическое значений
:
,
где mi
— число дискретных случайных величин,
имеющих значение хi.
Для непрерывной
случайной величины математическим
ожиданием служит интеграл:
,
где р(х) — плотность
вероятности.
Отдельные значения
случайной величины группируются около
математического ожидания. Отклонение
случайной величины от ее математического
ожидания (среднего значения) характеризуется
дисперсией,
которая для дискретной случайной
величины определяется формулой:
(15)
(16)
Дисперсия имеет
размерность случайной величины. Для
того, чтобы оценивать рассеяние
(отклонение) случайной величины в
единицах той же размерности, введено
понятие среднего
квадратичного отклонения
σ(Х), которое
равно корню квадратному из дисперсии:
(17)
Вместо среднего
квадратичного отклонения иногда
используется термин «стандартное
отклонение».
Всякое отношение,
устанавливающее связь между всеми
возможными значениями случайной величины
и соответствующими им вероятностями,
называется законом
распределения случайной величины.
Формы задания закона распределения
могут быть разными:
а) ряд распределения
(для дискретных величин);
б) функция
распределения;
в) кривая распределения
(для непрерывных величин).
Существует
относительно много законов распределения
случайных величин.
Нормальный
закон распределения случайных
величин (закон
Гаусса).
Случайная величина
распределена по
нормальному закону, если ее плотность
вероятности f(x)
определяется формулой:
(18),
где <x>
— математическое ожидание (среднее
значение) случайной величины <x>
= M
(X);
—
среднее квадратичное отклонение;
—
основание натурального логарифма
(неперово число);
f
(x)
– плотность вероятности (функция
распределения вероятностей).
Многие случайные
величины (в том числе все случайные
погрешности) подчиняются нормальному
закону распределения (закону Гаусса).
Для этого распределения наиболее
вероятным значением
измеряемой
величины
является
её среднее
арифметическое
значение.
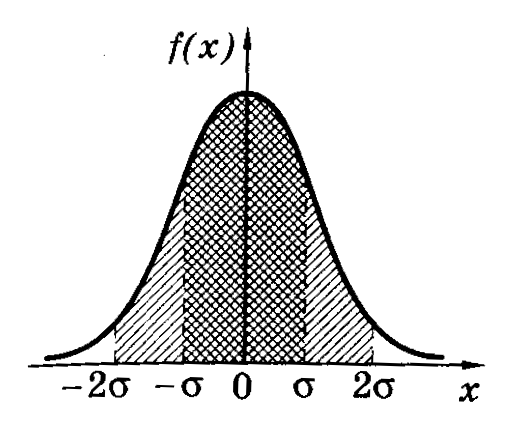
График нормального
закона распределения изображен на
рисунке (колоколообразная кривая).
Кривая симметрична
относительно прямой х=<x>=α,
следовательно, отклонения случайной
величины вправо и влево от <x>=α
равновероятны. При х=<x>±
кривая асимптотически приближается к
оси абсцисс. Если х=<x>,
то функция распределения вероятностей
f(x)
максимальна и принимает вид:
(19)
Таким образом,
максимальное значение функции fmax(x)
зависит от величины среднего квадратичного
отклонения. На рисунке изображены 3
кривые распределения. Для кривых 1 и 2
<x>
= α = 0 соответствующие значения среднего
квадратичного отклонения различны, при
этом 2>1.
(При увеличении
кривая распределения становится более
пологой, а при уменьшении
– вытягивается вверх). Для кривой 3 <x>
= α ≠ 0 и 3
= 2.
Закон
распределения
молекул в газах по скоростям называется
распределением
Максвелла.
Функция плотности вероятности попадания
скоростей молекул в определенный
интервал
теоретически была определена в 1860 году
английским физиком Максвеллом
. На рисунке
распределение Максвелла представлено
графически. Распределение движется
вправо или влево в зависимости от
температуры газа (на рисунке Т1
< Т2).
Закон распределения Максвелла определяется
формулой:
(20),
где mо
– масса молекулы, k
– постоянная Больцмана, Т – абсолютная
температура газа,
—
скорость молекулы.
Распределение
концентрации молекул газа в атмосфере
Земли (т.е.
в силовом поле) в зависимости от высоты
было дано австрийским физиком Больцманом
и называется
распределением
Больцмана:
(21)
Где n(h)
– концентрация молекул газа на высоте
h,
n0
– концентрация у поверхности Земли, g
– ускорение свободного падения, m
– масса молекулы.
Распределение
Больцмана.
Совокупность всех
значений случайной величины называется
простым
статистическим рядом.
Так как простой статистический ряд
оказывается большим, то его преобразуют
в вариационный
статистический
ряд или интервальный
статистический ряд. По интервальному
статистическому ряду для оценки вида
функции распределения вероятностей по
экспериментальным данным строят
гистограмму
– столбчатую
диаграмму. (Гистограмма – от греческих
слов “histos”–
столб и “gramma”–
запись).
n
-
h
Гистограмма
распределения Больцмана.
Для построения
гистограммы интервал, содержащий
полученные значения случайной величины
делят на несколько интервалов xi
одинаковой ширины. Для каждого интервала
подсчитывают число mi
значений случайной величины, попавших
в этот интервал. После этого вычисляют
плотность частоты случайной величины
для каждого интервала xi
и среднее значение случайной величины
<xi
> в каждом интервале.
Затем по оси абсцисс
откладывают интервалы xi,
являющиеся основаниями прямоугольников,
высота которых равна
(или
высотой
– плотностью относительной частоты
).
Расчетами показано,
что вероятность попадания нормально
распределенной случайной величины в
интервале значений от <x>–
до <x>+
в среднем равна 68%. В границах вдвое
более широких (<x>–2;
<x>+2)
размещается в среднем 95% всех значений
измерений, а в интервале (<x>–3;<x>+3)
– уже 99,7%. Таким образом, вероятность
того, что отклонение значений нормально
распределенной случайной величины
превысит 3
(
– среднее квадратичное отклонение)
чрезвычайно мала (~0,003). Такое событие
можно считать практически невозможным.
Поэтому границы <x>–3
и <x>+3
принимаются за границы практически
возможных значений нормально распределенной
случайной величины («правило трех
сигм»).
Если число измерений
(объем выборки) невелико (n<30),
дисперсия вычисляется по формуле:
(22)
Уточненное среднее
квадратичное отклонение отдельного
измерения вычисляется по формуле:
(23)
Напомним, что для
эмпирического распределения по выборке
аналогом математического ожидания
является среднее арифметическое значение
<x>
измеряемой величины.
Чтобы дать
представление о точности и надежности
оценки измеряемой величины, используют
понятия доверительного интервала и
доверительной вероятности.
Доверительным
интервалом
называется интервал (<x>–x,
<x>+x),
в который по определению попадает с
заданной вероятностью действительное
(истинное) значение измеряемой величины.
Доверительный интервал характеризует
точность полученного результата: чем
уже доверительный интервал, тем меньше
погрешность.
Доверительной
вероятностью
(надежностью)
результата серии измерений называется
вероятность того, что истинное значение
измеряемой величины попадает в данный
доверительный интервал (<x>±x).
Чем больше величина доверительного
интервала, т.е. чем больше x,
тем с большей надежностью величина <x>
попадает в этот интервал. Надежность
выбирается самим исследователем
самостоятельно, например, =0,95;
0,98. В медицинских и биологических
исследованиях, как правило, доверительную
вероятность (надежность) принимают
равной 0,95.
Если величина х
подчиняется нормальному закону
распределения Гаусса, а <x>
и <>
оцениваются по выборке (числу измерений)
и если объем выборки невелик (n<30),
то интервал (<x>
– t,n<>,
<x>
+ t,n<>)
будет доверительным интервалом для
известного параметра х с доверительной
вероятностью .
Коэффициент t,n
называется коэффициентом
Стьюдента
(этот коэффициент был предложен в 1908 г.
английским математиком и химиком В.С.
Госсетом, публиковавшим свои работы
под псевдонимом «Стьюдент» – студент).
Значении коэффициента
Стьюдента t,n
зависит от доверительной вероятности
и числа измерений n
(объема выборки). Некоторые значения
коэффициента Стьюдента приведены в
таблице 1.
Таблица 1
|
n |
|
||||||
|
0,6 |
0,7 |
0,8 |
0,9 |
0,95 |
0,98 |
0,99 |
|
|
2 |
1,38 |
2,0 |
3,1 |
6,3 |
12,7 |
31,8 |
63,7 |
|
3 |
1,06 |
1,3 |
1,9 |
2,9 |
4,3 |
7,0 |
9,9 |
|
4 |
0,98 |
1,3 |
1,6 |
2,4 |
3,2 |
4,5 |
5,8 |
|
5 |
0,94 |
1,2 |
1,5 |
2,1 |
2,8 |
3,7 |
4,6 |
|
6 |
0,92 |
1,2 |
1,5 |
2,0 |
2,6 |
3,4 |
4,0 |
|
7 |
0,90 |
1,1 |
1,4 |
1,9 |
2,4 |
3,1 |
3,7 |
|
8 |
0,90 |
1,1 |
1,4 |
1,9 |
2,4 |
3,0 |
3,5 |
|
9 |
0,90 |
1,1 |
1,4 |
1,9 |
2,3 |
2,9 |
3,4 |
|
10 |
0,88 |
1,1 |
1,4 |
1,9 |
2,3 |
2,8 |
3,3 |
В таблице 1 в верхней
строке заданы значения доверительной
вероятности
от 0,6 до 0,99, в левом столбце – значение
n.
Коэффициент Стьюдента следует искать
на пересечении соответствующих строки
и столбца.
Окончательный
результат измерений записывается в
виде:
(25)
Где
– полуширина доверительного интервала.
Результат серии
измерений оценивается относительной
погрешностью:
(26)
Абсолютная погрешность
- Причины возникновения погрешности измерения
- Систематическая и случайная погрешности
- Определение абсолютной погрешности
- Алгоритм оценки абсолютной погрешности в серии прямых измерений
- Значащие цифры и правила округления результатов измерений
- Примеры
Причины возникновения погрешности измерения
Погрешность измерения – это отклонение измеренного значения величины от её истинного (действительного) значения.
Обычно «истинное» значение неизвестно, и можно только оценить погрешность, приняв в качестве «истинного» среднее значение, полученное в серии измерений. Таким образом, процесс оценки проводится статистическими методами.
Виды погрешности измерений
Причины
Инструментальная погрешность
Определяется погрешностью инструментов и приборов, используемых для измерений (принципом действия, точностью шкалы и т.п.)
Погрешность метода
Определяется несовершенством методов и допущениями в методике.
Теоретическая погрешность
Определяется теоретическими упрощениями, степенью соответствия теоретической модели и реальности.
Погрешность оператора
Определяется субъективным фактором, ошибками экспериментатора.
Систематическая и случайная погрешности
Систематической погрешностью называют погрешность, которая остаётся постоянной или изменяется закономерно во времени при повторных измерениях одной и той же величины.
Систематическая погрешность всегда имеет знак «+» или «-», т.е. говорят о систематическом завышении или занижении результатов измерений.
Систематическую погрешность можно легко определить, если известно эталонное (табличное) значение измеряемой величины. Для других случаев разработаны эффективные статистические методы выявления систематических погрешностей. Причиной систематической погрешности может быть неправильная настройка приборов или неправильная оценка параметров (завышенная или заниженная) в расчётных формулах.
Случайной погрешностью называют погрешность, которая не имеет постоянного значения при повторных измерениях одной и той же величины.
Случайные погрешности неизбежны и всегда присутствуют при измерениях.
Определение абсолютной погрешности
Абсолютная погрешность измерения – это модуль разности между измеренным и истинным значением измеряемой величины:
$$ Delta x = |x_{изм}-x_{ист} | $$
Например:
При пяти взвешиваниях гири с маркировкой 100 г были получены различные значения массы. Если принять маркировку за истинное значение, то получаем следующие значения абсолютной погрешности:
$m_i,г$
98,4
99,2
98,1
100,3
98,5
$Delta m_i, г$
1,6
0,8
1,9
0,3
1,5
Граница абсолютной погрешности – это величина h: $ |x-x_{ист}| le h $
Для оценки границы абсолютной погрешности на практике используются статистические методы.
Алгоритм оценки абсолютной погрешности в серии прямых измерений
Шаг 1. Проводим серию из N измерений, в каждом из которых получаем значение измеряемой величины $x_i, i = overline{1, N}$.
Шаг 2. Находим оценку истинного значения x как среднее арифметическое данной серии измерений:
$$ a = x_{cp} = frac{x_1+x_2+ cdots +x_N}{N} = frac{1}{N} sum_{i = 1}^N x_i $$
Шаг 3. Рассчитываем абсолютные погрешности для каждого измерения:
$$ Delta x_i = |x_i-a| $$
Шаг 4. Находим среднее арифметическое абсолютных погрешностей:
$$ Delta x_{cp} = frac{Delta x_1+ Delta x_2+ cdots + Delta x_N}{N} = frac{1}{N} sum_{i = 1}^N Delta x_i $$
Шаг 5. Определяем инструментальную погрешность при измерении как цену деления прибора (инструмента) d.
Шаг 6. Проводим оценку границы абсолютной погрешности серии измерений, выбирая большую из двух величин:
$$ h = max {d; Delta x_{cp} } $$
Шаг 7. Округляем и записываем результаты измерений в виде:
$$ a-h le x le a+h или x = a pm h $$
Значащие цифры и правила округления результатов измерений
Значащими цифрами – называют все верные цифры числа, кроме нулей слева. Результаты измерений записывают только значащими цифрами.
Например:
0,00501 — три значащие цифры 5,0 и 1.
5,01 — три значащие цифры.
5,0100 – пять значащих цифр; такая запись означает, что величина измерена с точностью 0,0001.
Внимание!
Правила округления.
Погрешность измерения округляют до первой значащей цифры, всегда увеличивая ее на единицу (округление по избытку, “ceiling”).
Округлять результаты измерений и вычислений нужно так, чтобы последняя значащая цифра находилась в том же десятичном разряде, что и абсолютная погрешность измеряемой величины.
Например: если при расчетах по результатам серии измерений получена оценка истинного значения a=1,725, а оценка абсолютной погрешности h = 0,11, то результат записывается так:
$$ a approx 1,7; h approx ↑0,2; 1,5 le x le 1,9 или x = 1,7 pm 0,2 $$
Примеры
Пример 1. При измерении температура воды оказалась в пределах от 11,55 ℃ до 11,63 ℃. Какова абсолютная погрешность этих измерений?
По условию $11,55 le t le 11,63$. Получаем систему уравнений:
$$ {left{ begin{array}{c} a-h = 11,55 \ a+h = 11,63 end{array} right.} Rightarrow {left{ begin{array}{c} 2a = 11,55+11,63 = 23,18 \ 2h = 11,63-11,55 = 0,08 end{array} right.} Rightarrow {left{ begin{array}{c} a = 11,59 \ h = 0,04end{array} right.} $$
$$ t = 11,59 pm 0,04 ℃ $$
Ответ: 0,04 ℃
Пример 2. По результатам измерений найдите границы измеряемой величины. Инструментальная погрешность d = 0,1.
$x_i$
15,3
16,4
15,3
15,8
15,7
16,2
15,9
Находим среднее арифметическое:
$$ a = x_{ср} = frac{15,3+16,4+ cdots +15,9}{7} = 15,8 $$
Находим абсолютные погрешности:
$$ Delta x_i = |x_i-a| $$
$ Delta x_i$
0,5
0,6
0,5
0
0,1
0,4
0,1
Находим среднее арифметическое:
$$ Delta x_{ср} = frac{0,5+0,6+ cdots + 0,1}{7} approx 0,31 gt d $$
Выбираем большую величину:
$$ h = max {d; Delta x_{ср} } = max {0,1; 0,31} = 0,31 $$
Округляем по правилам округления по избытку: $h approx ↑0,4$.
Получаем: x = 15, $8 pm 0,4$
Границы: $15,4 le x le 16,2$
Ответ: $15,4 le x le 16,2$
Пример 3*. В первой серии экспериментов было получено значение $x = a pm 0,3$. Во второй серии экспериментов было получено более точное значение $x = 5,631 pm 0,001$. Найдите оценку средней a согласно полученным значениям x.
Более точное значение определяет более узкий интервал для x. По условию:
$$ {left{ begin{array}{c} a-0,3 le x le a+0,3 \ 5,630 le x le 5,632 end{array} right.} Rightarrow a-0,3 le 5,630 le x le 5,632 le a+0,3 Rightarrow $$
$$ Rightarrow {left{ begin{array}{c} a-0,3 le 5,630 \ 5,632 le a+0,3 end{array} right.} Rightarrow {left{ begin{array}{c} a le 5,930 \ 5,332 le a end{array} right.} Rightarrow 5,332 le a le 5,930 $$
Т.к. a получено в серии экспериментов с погрешностью h=0,3, следует округлить полученные границы до десятых:
$$ 5,3 le a le 5,9 $$
Ответ: $ 5,3 le a le 5,9 $
| Напечатано:: | Гость |
| Дата: | понедельник, 5 июня 2023, 09:59 |
Описание
1. Понятие о погрешности измерения.
2. Классификация погрешностей измерения.
3. Систематические погрешности
Оглавление
- 1. Понятие о погрешности измерения
- 2. Классификация погрешностей измерения
- 3. Систематические погрешности
1. Понятие о погрешности измерения
Всякий процесс измерения независимо от условий, в которых его проводят, сопряжен с погрешностями, которые искажают представление о действительном значении измеряемой величины.
Погрешностью называют отличие между объективно существующим истинным значением физической величины и найденным в результате измерения действительным значением физической величины.
Истинное значение физической величины идеальным образом отражает соответствующее свойство объекта. Практически получено быть не может.
Действительное значение физической величины находится как результат измерения и приближается к истинному значению настолько, что для данной цели может применяться вместо него.
Источниками появления погрешностей при измерениях могут служить различные факторы, основными из которых являются: несовершенство конструкции средств измерений или принципиальной схемы метода измерения; неточность изготовления средств измерений; несоблюдение внешних условий при измерениях; субъективные погрешности и др.
2. Классификация погрешностей измерения
В зависимости от обстоятельств, при которых проводились измерения, а также в зависимости от целей измерения, выбирается та или иная классификация погрешностей. Иногда используют одновременно несколько взаимно пересекающихся классификаций, желая по нескольким признакам точно охарактеризовать влияющие на результат измерения физические величины. В таком случае рассматривают, например, инструментальную составляющую неисключённой систематической погрешности. При выборе классификаций важно учитывать наиболее весомые или динамично меняющиеся или поддающиеся регулировке влияющие величины. Ниже приведены общепринятые классификации согласно типовым признакам и влияющим величинам.
По виду представления, различают абсолютную, относительную и приведённую погрешности.
Абсолютная погрешность это разница между результатом измерения X и истинным значением Q измеряемой величины. Абсолютная погрешность находится как D = X — Q и выражается в единицах измеряемой величины.
Относительная погрешность это отношение абсолютной погрешности измерения к истинному значению измеряемой величины: d = D / Q = (X – Q) / Q .
Приведённая погрешность это относительная погрешность, в которой абсолютная погрешность средства измерения отнесена к условно принятому нормирующему значению QN , постоянному во всём диапазоне измерений или его части. Относительная и приведённая погрешности – безразмерные величины.
В зависимости от источника возникновения, различают субъективную, инструментальную и методическую погрешности.
Субъективная погрешность обусловлена погрешностью отсчёта оператором показаний средства измерения.
Инструментальная погрешность обусловлена несовершенством применяемого средства измерения. Иногда эту погрешность называют аппаратурной. Метрологические характеристики средств измерений нормируются согласно ГОСТ 8.009 – 84, при этом различают четыре составляющие инструментальной погрешности: основная, дополнительная, динамическая, интегральная. Согласно этой классификации, инструментальная погрешность зависит от условий и режима работы, а также от параметров сигнала и объекта измерения.
Методическая погрешность обусловлена следующими основными причинами:
– отличие принятой модели объекта измерения от модели, адекватно описывающей его метрологические свойства;
– влияние средства измерения на объект измерения;
– неточность применяемых при вычислениях физических констант и математических соотношений.
В зависимости от измеряемой величины, различают погрешность аддитивную и мультипликативную. Аддитивная погрешность не зависит от измеряемой величины. Мультипликативная погрешность меняется пропорционально измеряемой величине.
В зависимости от режима работы средства измерений, различают статическую и динамическую погрешности.
Динамическая погрешность обусловлена реакцией средства измерения на изменение параметров измеряемого сигнала (динамический режим).
Статическая погрешность средства измерения определяется при параметрах измеряемого сигнала, принимаемых за неизменные на протяжении времени измерения (статический режим).
По характеру проявления во времени, различают случайную и систематическую погрешности.
Систематической погрешностью измерения называют погрешность, которая при повторных измерениях одной и той же величины в одних и тех же условиях остаётся постоянной или закономерно меняется.
Случайной погрешностью измерения называют погрешность, которая при повторных измерениях одной и той же величины в одних и тех же условиях изменяется случайным образом.
3. Систематические погрешности
Систематические погрешности при повторных измерениях остаются постоянными или изменяются по определенному закону.
Когда судят о погрешности, подразумевают не значение, а интервал значений, в котором с заданной вероятностью находится истинное значение. Поэтому говорят об оценке погрешности. Если бы погрешность оказалась измеренной, т.е. стали бы известны её знак и значение, то её можно было бы исключить из действительного значения измеряемой физической величины и получить истинное значение.
Для получения результатов, минимально отличающихся от истинного значения измеряемой физической величины, проводят многократные наблюдения и проводят математическую обработку полученного массива с целью определения и минимизации случайной составляющей погрешности.
Минимизация систематической погрешности в процессе наблюдений выполняется следующими методами: метод замещения (состоит в замещении измеряемой величины мерой), метод противопоставления (состоит в двух поочерёдных измерениях при замене местами меры и измеряемого объекта), метод компенсации погрешности по знаку (состоит в двух поочерёдных измерениях, при которых влияющая величина становится противоположной).
При многократных наблюдениях возможно апостериорное (после выполнения наблюдений) исключение систематической погрешности в результате анализа рядов наблюдений. Рассмотрим графический анализ. При этом результаты последовательных наблюдений представляются функцией времени либо ранжируются в порядке возрастания погрешности.
Рассмотрим временную зависимость. Будем проводить наблюдения через одинаковые интервалы времени. Результаты последовательных наблюдений являются случайной функцией времени. В серии экспериментов, состоящих из ряда последовательных наблюдений, получаем одну реализацию этой функции. При повторении серии получаем новую реализацию, отличающуюся от первой.
Реализации отличаются преимущественно из-за влияния факторов, определяющих случайную погрешность, а факторы, определяющие систематическую погрешность, одинаково проявляются для соответствующих моментов времени в каждой реализации. Значение, соответствующее каждому моменту времени, называется сечением случайной функции времени. Для каждого сечения можно найти среднее по всем реализациям значение. Очевидно, что эта составляющая и определяет систематическую погрешность. Если через значения систематической погрешности для всех моментов времени провести плавную кривую, то она будет характеризовать временную закономерность изменения погрешности. Зная закономерность изменения, можем определить поправку для исключения систематической погрешности. После исключения систематической погрешности получаем «исправленный ряд результатов наблюдений».
Известен ряд способов исключения систематических погрешностей, которые условно можно разделить па 4 основные группы:
- устранение источников погрешностей до начала измерений;
- исключение почетностей в процессе измерения способами замещения, компенсации погрешностей по знаку, противопоставления, симметричных наблюдений;
- внесение известных поправок в результат измерения (исключение погрешностей начислением);
- оценка границ систематических погрешностей, если их нельзя исключить.
По характеру проявления систематические погрешности подразделяют на постоянные, прогрессивные и периодические.
Постоянные систематические погрешности сохраняют свое значение в течение всего времени измерений (например, погрешность в градуировке шкалы прибора переносится на все результаты измерений).
Прогрессивные погрешности – погрешности, которые в процессе измерении подрастают или убывают (например, погрешности, возникающие вследствие износа контактирующих деталей средств измерения).
И группу систематических погрешностей можно отнести: инструментальные погрешности; погрешности из-за неправильной установки измерительного устройства; погрешности, возникающие вследствие внешних влияний; погрешности метода измерения (теоретические погрешности); субъективные погрешности.