Введя предположение о случайном характере оцениваемого вектора x и ошибок измерения v и задаваясь их статистическими свойствами, представляется логичным не только использовать этот факт при анализе точности того или иного алгоритма, но и попытаться учесть сделанные предположения уже на этапе постановки и решения задачи. Иными словами, попытаться построить алгоритм «хорошего» качества с точки зрения уровня и свойств соответствующих ему ошибок оценивания. Именно такие алгоритмы и будут рассматриваться в последующих разделах.
2.3.1 Постановка задачи получения оптимальных линейных оценок.
Итак, будем полагать, что задача оценивания (2.1.20), (2.1.21) решается в условиях, когда оцениваемый вектор x и ошибки измерения v считаются случайными. Количественная характеристика качества оценивания может быть введена с помощью скалярной функции
− ~
L(x x ( y)) , устанавливающей определенный штраф за отличие оценки от истинного значения
оцениваемого параметра и называемой функцией потерь. Наибольшее распространение при анализе качества оценок в задачах обработки навигационной информации получила
квадратичная функция потерь, имеющая вид
|
~ |
~ |
т |
(x |
~ |
n |
~ |
2 |
. |
||||
|
L(x − x ( y)) = (x − x ( y)) |
− x ( y)) |
= ∑(xi − xi ( y)) |
||||||||||
|
i=1 |
||||||||||||
|
Введем связанный с этой функцией потерь критерий в виде |
||||||||||||
|
~ |
( y)) |
т |
~ |
~ |
(2.3.1) |
|||||||
|
J = M x,y {(x − x |
(x − x ( y))}= M x,y {SpP}, |
|||||||||||
|
где |
||||||||||||
|
~ |
~ |
~ |
( y)) |
т |
(2.3.2) |
|||||||
|
P = M x,y (x |
− x ( y))(x − x |
|||||||||||
|
~ |
||||||||||||
|
матрица ковариаций ошибок ε( y) = x − x ( y) . |
||||||||||||
|
Сформулируем задачу оценивания вектора |
x |
по измерениям (2.1.21) |
следующим образом: |
найти такую оценку, которая обеспечит минимум математического ожидания для квадратичной функции потерь, т.е.
|
xˆ( y) = arg min M |
n |
~ |
2 |
||
|
x, y ∑ |
(x − x ( y)) |
. |
|||
|
~ |
i |
||||
|
x |
( y) |
i =1 |
|||
Таким образом, сформулированная задача нахождения оценки сводится к минимизации следа матрицы ковариаций ее ошибок или, что то же самое, к минимизации суммы дисперсий ошибок оценивания. Этот критерий получил наименование среднеквадратического критерия, а оценка,
обеспечивающая его минимум – оптимальной в среднеквадратическом смысле оценкой. Такую оценку называют еще оценкой с минимальной дисперсией (minimum variance estimate).
44
Заметим, что критерий (2.3.1) принципиально отличается от наблюдаемых критериев, поскольку цель решения задачи заключается в обеспечении определенных требований к ошибкам оценки искомого вектора, а не к вычисленным значениям измеряемых параметров.
Введем составной случайный вектор z = (xт , y т )т , включающий вектор оцениваемых
параметров и вектор измерений. Из выражения для критерия (2.3.1) следует, что для его
вычисления в общем случае требуется располагать совместной ф.п.р.в. fx,y (x, y) . Обычно при
решении задач обработки навигационной информации статистические свойства задаются для оцениваемого вектора и ошибок измерения, которые в наиболее полном объеме характеризуются
совместной ф.п.р.в. fx,v (x, v) . При наличии fx,v (x, v) плотность fx,y (x, y) в принципе может
быть получена с использованием соотношения (2.1.21) и правил преобразования случайных векторов, рассмотренных в 1.4. Однако, следует заметить, что, во-первых, не всегда имеются
достаточные основания для введения той или иной ф.п.р.в. fx,v (x, v) , а во-вторых, даже при наличии fx,v (x, v) нахождение fx,y (x, y) не является тривиальной задачей.
С целью упрощения задачи будем считать, что имеется информация лишь о первых двух
|
моментах вектора z , представленная в виде его математического ожидания z = (x т |
, y т )т и |
||||||||||
|
матрицы ковариаций |
|||||||||||
|
z |
P x |
P xy |
|||||||||
|
P |
= |
xy |
т |
, |
(2.3.3) |
||||||
|
) |
P |
y |
|||||||||
|
(P |
|||||||||||
|
а при нахождении оценки используется линейное относительно измерений выражение вида |
|||||||||||
|
~ |
= x + K ( y |
− y) . |
(2.3.4) |
||||||||
|
x ( y) |
Нетрудно заметить, что при таком виде оценки выполняется следующее равенство
~ =
M y x ( y) x .
Оценка, удовлетворяющая такому условию, называется несмещенной. Это весьма важное свойство оценки, более подробно будет обсуждаться в последующих разделах.
Подставляя (2.3.4) в (2.3.2), можем записать
J = M x,y {(x − x + K ( y − y))т (x − x + K ( y − y))}=
{ } (2.3.5)
= M x,y Sp(x − x + K ( y − y))(x − x + K ( y − y))т .
Из этого выражения вытекает, что для вычисления математического ожидания в (2.3.5) теперь уже достаточно знать только z = (x т , y т )т и P z . Введенные ограничения позволяют сформулировать следующую задачу.
Располагая математическим ожиданием и матрицей ковариации для вектора z = (x т , y т )т ,
найти несмещенную оценку вида (2.3.4), обеспечивающую минимум среднеквадратического критерия (2.3.5). Поскольку предполагается линейная зависимость оценки от измерений, то речь
45
таким образом пойдет о линейных несмещенных оценках с минимальной дисперсией или, что то же самое об оптимальных в среднеквадратическом смысле линейных оценках.
2.3.2 Решение задачи нахождения оптимальных линейных оценок
Опираясь на результаты, полученные в теории оценивания, можно получить следующий весьма важный результат.
Для того, чтобы линейная оценка (2.3.4) при решении задачи (2.1.20), (2.1.21)
|
обеспечивала минимум критерия (2.3.5) необходимо и достаточно, чтобы матрица |
K opt , |
|
используемая при вычислении этой оценки, удовлетворяла уравнению |
|
|
K opt P y = P xy . |
(2.3.6) |
Убедимся в справедливости этого утверждения. Для начала в целях упрощения будем считать, что векторы центрированные, т.е. их математические ожидания нулевые и таким образом вместо
|
~ |
||||||||||||||||||||||
|
(2.3.4) можно использовать выражение x ( y) = Ky . |
||||||||||||||||||||||
|
Необходимость. Представим произвольную матрицу |
~ |
|||||||||||||||||||||
|
K в виде |
||||||||||||||||||||||
|
~ |
~ |
(2.3.7) |
||||||||||||||||||||
|
K = K opt |
+δK , |
|||||||||||||||||||||
|
где K opt — матрица, удовлетворяющая (2.3.6), |
а δ |
— малый скалярный параметр. Подставляя |
||||||||||||||||||||
|
(2.3.7) в (2.3.5) и раскрывая скобки, получим |
}= |
|||||||||||||||||||||
|
~ |
(K |
opt |
~ |
(K |
opt |
~ |
т |
|||||||||||||||
|
J = M x,y {Sp(x − |
+ δK ) y)(x − |
+ δK ) y) |
||||||||||||||||||||
|
= Sp[P x |
− K opt P yx − P xy (K opt )т |
+ K opt (K opt )т ]− |
||||||||||||||||||||
|
~ |
yx |
+ P |
xy ~ т |
~ y |
(K |
opt |
) |
т |
− K |
opt |
P |
y ~ т |
)+ δ |
2 |
~ y ~ т |
. |
||||||
|
− δSp(KP |
K |
− KP |
K |
SpKP K |
Принимая во внимание, что следы прямой и транспонированной матриц совпадают, это выражение удобно преобразовать как
|
~ |
= Sp[P |
x |
− 2P |
xy |
(K |
opt |
) |
т |
+ K |
opt |
(K |
opt |
) |
т |
] − |
|||||
|
J |
||||||||||||||||||||
|
− 2δSp(P |
xy ~ т |
− K |
opt |
P |
y ~ т |
) + δ |
2 |
~ |
y |
~ |
||||||||||
|
K |
K |
SpKP |
K. |
Поскольку матрица K opt по предположению минимизирует выбранный критерий, то должно выполняться условие
|
~ |
~ |
~ |
~ |
|||||
|
dJ |
||||||||
|
= |
2Sp(P xy K т − K opt P y K |
т )= 2Sp(P xy − K opt P y )K т = 0 . |
||||||
|
dδ |
||||||||
|
δ=0 |
||||||||
|
~ |
K opt должна |
|||||||
|
Очевидно, что для выполнения этого условия при |
любой |
матрице |
||||||
|
K , |
||||||||
|
удовлетворять уравнению (2.3.6). |
||||||||
|
Достаточность |
||||||||
|
Предположим теперь, что K opt удовлетворяет (2.3.6). |
Покажем, что оценка |
xˆ( y) = K opt y |
||||||
|
минимизирует критерий (2.3.5). |
||||||||
|
Подставляя эту оценку в (2.3.5), запишем |
46
J opt =( M x,y {Sp(x − K opt y)(x − K opt y)т}=).
= Sp P x − 2P xy (K opt )т + K opt P y (K opt )т
~
Для произвольной матрицы K , заданной в виде (2.3.7), получим
|
~ |
~ |
~ ~ |
т . |
|
J |
= J opt − 2δSp((P xy − K opt P y )K |
т )+ δ2SpKP y K |
Поскольку по предположению второе слагаемое обращается в ноль, а третье — в силу
неотрицательности P y неотрицательно, то
|
~ |
|
|
J opt ≤ J , |
|
|
что и завершает доказательство достаточности. |
|
|
Если матрица P y не вырождена, то тогда из (2.3.6) следует |
|
|
K opt = P xy (P y )−1 , |
(2.3.8) |
|
и таким образом |
|
|
xˆ( y) = Pxy (P y )−1 y. |
(2.3.9) |
|
Сняв требование о центрированном характере векторов x и |
y , нетрудно убедиться в том, что |
приведенное доказательство полностью сохранится и на этот случай, если в качестве оптимальной
|
оценки принять выражение (2.3.4), в котором K = K opt , т.е. |
|
|
xˆ( y) = x + K opt ( y − y), |
(2.3.10) |
|
где K — матрица соответствующей размерности. |
|
|
Используя (2.3.10), нетрудно получить выражение для матрицы ковариаций |
|
|
Popt = M x, y{(x − xˆ( y))(x − xˆ( y))T } = |
|
|
= Px + K opt P y (K opt )T − K opt P yx − Pxy (K opt )T . |
|
|
Преобразуя это выражение с использованием (2.3.8), получаем |
|
|
Popt = P x − P xy (P y )-1 P yx . |
(2.3.11) |
Таким образом, алгоритм вычисления оптимальных в среднеквадратическом смысле линейных оценок и соответствующей им матрицы ковариаций при решении задачи оценивания (2.1.20), (2.1.21) задается соотношениями (2.3.10), (2.3.11).
Необходимо обратить внимание на одно весьма важное следствие из доказанного утверждения, имеющее существенное прикладное значение – алгоритм вычисления линейных оптимальных
|
оценок |
полностью определяется первыми двумя моментами для составного вектора |
|
z = (xт |
, y т )т и не зависит от вида ф.п.р.в. fx,y (x, y) . Иными словами при произвольном виде |
этих функций, имеющих одинаковые первые два момента, алгоритмы вычисления оптимальных в среднеквадратическом смысле линейных оценок и соответствующих им матриц ковариаций также будут одинаковыми.
47

2.3.3 Решение линейной задачи
Из предыдущего раздела следует, что для получения линейных оптимальных оценок необходимо располагать математическим ожиданием и матрицей ковариации для вектора
z = (x т , y т )т . Как отмечалось выше, при решении задач обработки навигационной информации считаются известными статистические свойства оцениваемого вектора и ошибок измерения. В
нелинейном случае даже при известном виде совместной ф.п.р.в. fx,v (x, v) возникает проблема
нахождения первых двух моментов вектора z = (x т , y т )т . Эта проблема легко решается для линейной задачи (2.1.10), (2.1.11), если заданы соответствующие характеристики для вектора
(x т , v т )т .
B , где матрица B определяет взаимную корреляцию x и v , то
R
|
P |
x |
P |
xy |
|||||
|
P z = |
= |
|||||||
|
(P xy )т |
P y |
.(2.3.12) |
||||||
|
P x |
P x H т + B |
|||||||
|
= |
HPx + Bт |
|||||||
|
HPx H т + HB + BтH т + R |
|
Принимая во внимание |
тот факт, что в этом случае P xy = P x H т |
+ B , |
|
P y = HP x H т + HB + B тH т + R , |
нетрудно конкретизировать выражения (2.3.10), (2.3.11) |
(см. |
задачу 2.3.1).
В частности, в случае, когда x и v некоррелированы, т.е. B = 0 , соотношения для оптимальной оценки и матрицы ковариаций ее ошибок могут быть представлены как
K opt = (P x H т )(HP x H т + R)−1 ,
Popt = P x − P x H т (HP x H т + R)−1 HP x .
Учитывая справедливость (1.6.27), (1.6.28) можем также записать
Popt = (P x )−1 + H тR−1H −1 ,
K opt = Popt H тR −1 .
(2.3.13)
(2.3.14)
(2.3.15)
(2.3.16)
Интересным представляется сопоставление оптимального в среднеквадратическом смысле
линейного алгоритма с алгоритмами, рассмотренными в предыдущем разделе, т.е. с алгоритмами метода наименьших квадратов и его модификациями. Нетрудно заметить, что при B = 0 выражение (2.3.10) при подстановке в него выражения (2.3.16) и выражение (2.3.15) совпадают с выражениями (2.2.28), (2.2.29), и таким образом полученный алгоритм совпадет с
алгоритмом ММНК, если в его критерии принять D = (P x )−1 , Q = R −1 . Причины такого совпадения обсуждаются в подразделе 2.5.4. Сопоставление между собой различных вариантов
48

МНК было проведено в подразделе 2.2.4. Поскольку при сделанных предположениях линейная оптимальная оценка совпадает с ММНК, полученные в этом разделе выводы относительно взаимосвязи ММНК с ОМКН и МНК в полном объеме распространяются на оптимальные в среднеквадратическом смысле линейные оценки.
В частности, если считать выполненным условие
|
(P x )−1 << H тR−1H |
(2.3.17) |
|
и, кроме того, принять R = r 2 E , т.е. полагать, что ошибки представляют |
собой |
некорррелированные случайные величины с одинаковыми дисперсиями, то тогда можно говорить о практическом совпадении оптимальных в среднеквадратическом смысле линейных оценок с оценками обычного МНК.
Важно подчеркнуть, что вывод о совпадении оптимальных в среднеквадратическом смысле линейных оценок с оценками ММНК справедлив лишь при отсутствии корреляции между оцениваемым вектором и ошибками измерений. При появлении такой корреляции оптимальный алгоритм изменяется, в то время как ММНК сохраняется прежним, поскольку в его критерии учет этого фактора не предусмотрен.
Проиллюстрируем сказанное на примере оценивания коэффициентов полинома первой степени по измерениям (2.1.3), считая, что ошибки измерения являются некоррелированными между собой центрированными случайными величинами с одинаковыми дисперсиями, равными r 2 , а
оцениваемые коэффициенты представляют собой центрированные ( x = 0 ), некоррелированные между собой и с ошибками измерений случайные величины с матрицей ковариаций
0
1 . Пример реализации измерений типа (2.1.3) приведен на рис. 2.3.1.
σ 12
Используя соотношения (2.3.15), (2.3.16), легко получить следующие выражения для оценок и матрицы ковариаций
|
1 |
+ |
m |
||||||||||||
|
1 |
σ2 |
r 2 |
||||||||||||
|
opt |
||||||||||||||
|
xˆ |
= |
0 |
m |
|||||||||||
|
r |
2 |
|||||||||||||
|
1 |
∑ti |
|||||||||||||
|
r 2 |
||||||||||||||
|
i=1 |
||||||||||||||
|
1 |
+ |
m |
||||||||||||
|
σ02 |
r 2 |
|||||||||||||
|
Popt = |
||||||||||||||
|
1 |
m |
1 |
||||||||||||
|
∑ti |
σ2 |
|||||||||||||
|
r 2 |
||||||||||||||
|
i=1 |
1 |
|
1 |
m |
−1 |
m |
||||||||||
|
∑ti |
∑yi |
||||||||||||
|
2 |
, |
||||||||||||
|
r |
i=1 |
i=1 |
|||||||||||
|
1 |
1 |
m |
m |
||||||||||
|
+ |
∑ti2 |
∑ti yi |
|||||||||||
|
σ2 |
r 2 |
||||||||||||
|
1 |
i=1 |
i=1 |
|||||||||||
|
1 |
m |
−1 |
|||||||||||
|
∑ti |
|||||||||||||
|
2 |
|||||||||||||
|
r |
i=1 |
||||||||||||
|
1 |
m |
. |
|||||||||||
|
+ |
∑ti2 |
||||||||||||
|
r 2 |
|||||||||||||
|
i=1 |
49

|
50 |
||||||||||
|
40 |
измеренные значения |
|||||||||
|
30 |
||||||||||
|
20 |
||||||||||
|
10 |
||||||||||
|
0 |
||||||||||
|
-10 |
линейный тренд |
|||||||||
|
-20 |
||||||||||
|
-30 |
1 |
2 |
3 |
4 |
5 |
6 |
7 |
8 |
9 |
10 |
|
0 |
||||||||||
|
номер измерения |
Рис.2.3.1 Пример реализации ошибок измерений, содержащих линейный тренд.
Критерий МНК, соответствующая ему оценка и матрица ковариаций ее ошибок в этой задаче будут определяться как
|
m |
||||||||||||||||||||
|
J мнк (x) = ∑( yi − x0 − x1ti )2 , |
(2.3.18) |
|||||||||||||||||||
|
i=1 |
||||||||||||||||||||
|
и таким образом можно записать |
||||||||||||||||||||
|
m |
−1 |
m |
m |
−1 |
||||||||||||||||
|
xˆ |
мнк |
m |
∑ti |
∑yi |
мнк |
2 |
m |
∑ti |
||||||||||||
|
0 |
= |
i=1 |
i=1 |
, |
P |
= r |
i=1 |
. |
||||||||||||
|
ˆ |
мнк |
m |
m |
m |
m |
m |
||||||||||||||
|
x |
∑ti |
2 |
∑ti yi |
∑ti |
2 |
|||||||||||||||
|
1 |
∑ti |
∑ti |
||||||||||||||||||
|
i=1 |
i=1 |
i=1 |
i=1 |
i=1 |
В ОМНК при диагональной матрице Q в (2.3.18) появятся сомножители qi , и соответственно выражения для оценки и матрицы ковариаций преобразуются к виду
m∑qi
xˆ омнк = mi=1
∑qi ti
i=1
|
m |
−1 |
m |
||
|
∑qiti |
∑qi yi |
|||
|
i=1 |
i=1 |
, |
||
|
m |
m |
|||
|
∑qi ti2 |
∑qi ti yi |
|||
|
i=1 |
i=1 |
m∑qi
Pомнк = mi=1
∑qi ti
i=1
|
m |
−1 |
|
∑qi ti |
|
|
i=1 |
. |
|
m |
|
|
∑qi ti2 |
|
|
i=1 |
|
Нетрудно заметить, что при qi = |
1 |
, i = |
, |
эти выражения совпадут с выражениями для |
||||||
|
1.m |
||||||||||
|
r 2 |
||||||||||
|
1 |
0 |
|||||||||
|
МНК, а, положив дополнительно D |
2 |
и учитывая, что x = 0 , легко убедиться, что |
||||||||
|
= |
σ0 |
|||||||||
|
0 |
1 |
|||||||||
|
σ2 |
||||||||||
|
1 |
50
оценки ММНК совпадут с оптимальными оценками.
|
1 |
m |
1 |
1 |
m |
||||
|
Условие (2.3.17) в этом примере сводится к неравенствам |
<< |
, |
<< |
∑ti2 , при |
||||
|
σ2 |
r 2 |
σ2 |
r 2 |
|||||
|
0 |
1 |
j=1 |
выполнении которых все рассматриваемые оценки будут между собой совпадать.
2.3.4 Свойство ортогональности оптимальных линейных оценок
Докажем следующее весьма важное свойство линейной оптимальной в среднеквадратическом смысле оценки xˆ( y) . В целях простоты сделаем это для случая x = 0 .
Для того, чтобы линейная оценка xˆ( y) = Ky была оптимальной, необходимо и достаточно
|
выполнение условия |
|
|
M{(x − xˆ( y)) y т} = M{εy т} = 0, |
(2.3.19) |
означающего, что ошибка оценки ε = x − xˆ( y) не коррелирована с вектором измерений y .
Когда два вектора некоррелированы, то, как отмечалось в 1.3.5, говорят также об их ортогональности. В связи с этим сформулированное свойство линейной оптимальной оценки называют также свойством или условием ортогональности [1.9].
|
Необходимость. Пусть оценка оптимальна, |
т. е. матрица K = K opt = P xy (P y )−1 , |
определяется |
|||
|
в соответствии с выражением (2.3.8). Отсюда с очевидностью следует, что |
|||||
|
M{(x − xˆ( y)) y т} = M{xy т − K opt yy т} = 0. |
|||||
|
Достаточность. |
|||||
|
Пусть равенство (2.3.19) выполнено. Тогда можем записать |
|||||
|
M{(x − Ky) y т} = 0 , |
|||||
|
т.е. P xy = KP y , откуда для матрицы |
K |
получаем выражение (2.3.8), подтверждающее |
|||
|
оптимальность оценки, удовлетворяющей уравнению (2.3.19). |
|||||
|
Приведенное утверждение будет также справедливо, если вместо (2.3.19) записать |
|||||
|
M{(x − xˆ( y))xˆ т ( y)} = M{εxˆ т ( y)} = 0, |
(2.3.20) |
||||
|
или |
|||||
|
M{(x − xˆ( y)(Ly)т} = M{ε(Ly)т} = 0, |
(2.3.21) |
||||
|
где L — произвольная матрица размерности n ×m . |
|||||
|
В частности, при L = L j = (0,…0,1,0000)т |
из (2.3.21) вытекает, что |
||||
|
j |
|||||
|
M{εyiт} = 0, |
i = |
. |
(2.3.22) |
||
|
1.m |
Равенства (2.3.19), (2.3.20), (2.3.21) означают тот факт, что ошибка оценки ε = x − xˆ( y)
ортогональна вектору оценки xˆ( y) , вектору измерений y , произвольной линейной
комбинации его компонент и каждой компоненте по отдельности.
51
Соседние файлы в предмете [НЕСОРТИРОВАННОЕ]
- #
- #
- #
- #
- #
- #
- #
- #
- #
- #
- #
Многие статистические задачи требуют оценки ковариационной матрицы совокупности, которую можно рассматривать как оценку формы диаграммы разброса набора данных. В большинстве случаев такая оценка должна выполняться на выборке, свойства которой (размер, структура, однородность) имеют большое влияние на качество оценки. Пакет sklearn.covariance предоставляет инструменты для точной оценки ковариационной матрицы для данной популяции в различных условиях.
Мы предполагаем, что наблюдения независимы и одинаково распределены (iid).
2.6.1. Эмпирическая ковариация
Ковариационная матрица набора данных хорошо аппроксимируется классической оценкой максимального правдоподобия (или «эмпирической ковариацией») при условии, что количество наблюдений достаточно велико по сравнению с количеством признаков (переменных, описывающих наблюдения). Точнее, оценщик максимального правдоподобия выборки — это асимптотически несмещенный оценщик ковариационной матрицы соответствующей совокупности.
Эмпирическая ковариационная матрица выборки может быть вычислена с использованием empirical_covariance функции пакета или путем подгонки EmpiricalCovariance объекта к выборке данных с помощью EmpiricalCovariance.fit метода. Будьте осторожны, чтобы результаты зависели от центрирования данных, поэтому можно использовать assume_centered параметр точно. Точнее, если assume_centered=False, то предполагается, что тестовый набор имеет тот же средний вектор, что и обучающий набор. В противном случае оба должны быть центрированы пользователем и assume_centered=True использоваться.
Примеры
- См. В разделе Оценка ковариации усадки: LedoitWolf против OAS и максимальное правдоподобие пример того, как подогнать
EmpiricalCovarianceобъект к данным.
2.6.2. Уменьшение ковариации
2.6.2.1. Базовая усадка
Несмотря на то, что он является асимптотически несмещенным оценщиком ковариационной матрицы, оценщик максимального правдоподобия не является хорошим оценщиком собственных значений ковариационной матрицы, поэтому матрица точности, полученная в результате ее обращения, не является точной. Иногда даже оказывается, что эмпирическая ковариационная матрица не может быть инвертирована по числовым причинам. Для того, чтобы избежать такой проблемы инверсии, преобразование эмпирической ковариационной матрицы было введено: shrinkage.
В scikit-learn это преобразование (с определяемым пользователем коэффициентом усадки) можно напрямую применить к предварительно вычисленной ковариации с помощью shrunk_covariance метода. Кроме того, сжатая оценка ковариации может быть адаптирована к данным с помощью ShrunkCovariance объекта и его ShrunkCovariance.fit метода. Опять же, результаты зависят от того, центрированы ли данные, поэтому можно использовать assume_centered параметр точно.
Математически это сжатие состоит в уменьшении отношения между наименьшим и наибольшим собственными значениями эмпирической ковариационной матрицы. Это можно сделать, просто сдвинув каждое собственное значение в соответствии с заданным смещением, что эквивалентно нахождению оценщика максимального правдоподобия со штрафом l2 ковариационной матрицы. На практике усадка сводится к простому выпуклому преобразованию: $Sigma_{rm shrunk} = (1-alpha)hat{Sigma} + alphafrac{{rm Tr}hat{Sigma}}{p}rm Id$.
Выбирая величину усадки, $alpha$ сводится к установлению компромисса смещения/дисперсии и обсуждается ниже.
Примеры
- См. В разделе Оценка ковариации усадки: LedoitWolf против OAS и максимальное правдоподобие пример того, как подогнать
ShrunkCovarianceобъект к данным.
2.6.2.2. Усадка Ледуа-Вольфа
В своей статье 1 2004 г. О. Ледуа и М. Вольф предлагают формулу для расчета оптимального коэффициента усадки.α который минимизирует среднеквадратичную ошибку между оценочной и реальной ковариационной матрицей.
Оценщик Ледойта-Вольфа ковариационной матрицы может быть вычислен на выборке с ledoit_wolf функцией sklearn.covariance пакета, или ее можно получить иным способом, подгоняя LedoitWolf объект к той же выборке.
Примечание Случай, когда ковариационная матрица популяций изотропна
Важно отметить, что когда количество образцов намного превышает количество элементов, можно ожидать, что усадка не потребуется. Интуиция, лежащая в основе этого, заключается в том, что если ковариация совокупности имеет полный ранг, когда количество выборок растет, ковариация выборки также станет положительно определенной. В результате усадка не потребуется, и метод должен делать это автоматически.
Однако это не так в процедуре Ледуа-Вольфа, когда ковариация совокупности оказывается кратной единичной матрице. В этом случае оценка усадки Ледуа-Вольфа приближается к 1 по мере увеличения количества образцов. Это указывает на то, что оптимальная оценка ковариационной матрицы в смысле Ледуа-Вольфа кратна единице. Поскольку ковариация населения уже кратна единичной матрице, решение Ледуа-Вольфа действительно является разумной оценкой.
Примеры
- См. В разделе Оценка ковариации усадки: LedoitWolf против OAS и максимальное правдоподобие пример того, как подогнать
LedoitWolfобъект к данным и визуализировать характеристики оценщика Ледуа-Вольфа с точки зрения правдоподобия.
Рекомендации
О. Ледойт и М. Вольф, «Хорошо обусловленная оценка для многомерных ковариационных матриц», Журнал многомерного анализа, том 88, выпуск 2, февраль 2004 г., страницы 365-411.
2.6.2.3. Приблизительная усадка Oracle
Предполагая, что данные распределены по Гауссу, Chen et al. 2 выведена формула, направленная на выбор коэффициента усадки, который дает меньшую среднеквадратичную ошибку, чем та, которая дается формулой Ледуа и Вольфа. Результирующая оценка известна как оценка ковариации Oracle Shrinkage Approximating.
Оценщик OAS ковариационной матрицы может быть вычислен на выборке с помощью oas функции sklearn.covariance пакета, или он может быть получен иным образом путем подгонки OAS объекта к той же выборке.
Компромисс смещения и дисперсии при установке усадки: сравнение вариантов оценок Ледуа-Вольфа и OAS
Рекомендации
Чен и др., «Алгоритмы сжатия для оценки ковариации MMSE», IEEE Trans. на знак. Proc., Volume 58, Issue 10, October 2010.
Примеры
- См. В разделе Оценка ковариации усадки: LedoitWolf против OAS и максимальное правдоподобие пример того, как подогнать
OASобъект к данным. - См. Оценку Ледуа-Вольфа и OAS для визуализации разницы среднеквадратических ошибок между a
LedoitWolfиOASоценкой ковариации.
2.6.3. Редкая обратная ковариация
Матрица, обратная ковариационной матрице, часто называемая матрицей точности, пропорциональна матрице частичной корреляции. Это дает частичную независимость отношениям. Другими словами, если два признака независимы друг от друга условно, соответствующий коэффициент в матрице точности будет равен нулю. Вот почему имеет смысл оценивать матрицу разреженной точности: оценка ковариационной матрицы лучше обусловлена изучением отношений независимости от данных. Это называется ковариационным отбором .
В ситуации с малой выборкой, в которой n_samples порядок n_features или меньше, разреженные оценки обратной ковариации, как правило, работают лучше, чем оценки сжатой ковариации. Однако в противоположной ситуации или для сильно коррелированных данных они могут быть численно нестабильными. Кроме того, в отличие от оценщиков усадки, разреженные оценщики могут восстанавливать недиагональную структуру.
Оценщик GraphicalLasso использует l1 штраф для обеспечения разреженности на высокоточной матрице: тем выше его alpha параметр, тем более разреженной прецизионную матрицу. Соответствующий GraphicalLassoCV объект использует перекрестную проверку для автоматической установки alpha параметра.
Сравнение максимального правдоподобия, усадки и разреженных оценок ковариации и матрицы точности в настройках очень малых выборок.
Примечание Восстановление структуры
Восстановление графической структуры из корреляций в данных — непростая задача. Если вы заинтересованы в таком восстановлении, имейте в виду, что:
- Восстановление легче из корреляционной матрицы, чем из ковариационной матрицы: стандартизируйте свои наблюдения перед запуском
GraphicalLasso - Если в нижележащем графе есть узлы с гораздо большим количеством соединений, чем в среднем узле, алгоритм пропустит некоторые из этих соединений.
- Если количество ваших наблюдений невелико по сравнению с количеством ребер в вашем нижележащем графе, вы не сможете его восстановить.
- Даже если вы находитесь в благоприятных условиях восстановления, альфа-параметр, выбранный путем перекрестной проверки (например, с использованием
GraphicalLassoCVобъекта), приведет к выбору слишком большого количества ребер. Однако соответствующие ребра будут иметь больший вес, чем нерелевантные.
Математическая формулировка следующая:
$$hat{K} = mathrm{argmin}_K big( mathrm{tr} S K — mathrm{log} mathrm{det} K + alpha |K|_1 big)$$
Где $K$ — матрица точности, которую необходимо оценить, и $S$ — это выборочная ковариационная матрица. $|K|_1$ — сумма модулей недиагональных коэффициентов $K$. Для решения этой проблемы используется алгоритм GLasso из статьи Friedman 2008 Biostatistics. Это тот же алгоритм, что и в glasso пакете R.
Примеры
- Оценка разреженной обратной ковариации: пример синтетических данных, показывающих восстановление структуры и сравнение с другими оценками ковариации.
- Визуализация структуры фондового рынка: пример реальных данных фондового рынка, определение наиболее связанных символов.
Рекомендации
- Фридман и др., «Оценка разреженной обратной ковариации с помощью графического лассо» , Biostatistics 9, стр. 432, 2008 г.
2.6.4. Оценка робастной ковариации
Реальные наборы данных часто подвержены ошибкам измерения или записи. Регулярные, но необычные наблюдения также могут появляться по разным причинам. Наблюдения, которые случаются очень редко, называются выбросами. Эмпирическая оценка ковариации и сжатая оценка ковариации, представленные выше, очень чувствительны к наличию выбросов в данных. Следовательно, следует использовать надежные оценщики ковариации для оценки ковариации реальных наборов данных. В качестве альтернативы можно использовать робастные оценщики ковариации для обнаружения выбросов и отбрасывания / уменьшения веса некоторых наблюдений в соответствии с дальнейшей обработкой данных.
В sklearn.covariance пакете реализована надежная оценка ковариации, определитель минимальной ковариации 3 .
2.6.4.1. Определитель минимальной ковариации
Оценщик, определяющий минимальную ковариацию, — это надежный оценщик ковариации набора данных, представленный PJ Rousseeuw в 3 . Идея состоит в том, чтобы найти заданную пропорцию (h) «хороших» наблюдений, которые не являются выбросами, и вычислить их эмпирическую ковариационную матрицу. Эта эмпирическая ковариационная матрица затем масштабируется, чтобы компенсировать выполненный выбор наблюдений («этап согласованности»). Вычислив оценку определителя минимальной ковариации, можно присвоить веса наблюдениям в соответствии с их расстоянием Махаланобиса, что приведет к повторной оценке ковариационной матрицы набора данных («этап повторного взвешивания»).
Rousseeuw и Van Driessen 4 разработали алгоритм FastMCD для вычисления определителя минимальной ковариации. Этот алгоритм используется в scikit-learn при подгонке объекта MCD к данным. Алгоритм FastMCD также одновременно вычисляет надежную оценку местоположения набора данных.
Сырые оценки могут быть доступны как raw_location_ и raw_covariance_ атрибутами из MinCovDet надежного объекта ковариационной оценивани.
Рекомендации
- 3 PJ Rousseeuw. Наименьшая медиана квадратов регрессии. Дж. Ам Стат Асс, 79: 871, 1984.
- 4 Быстрый алгоритм для определения определителя минимальной ковариации, 1999, Американская статистическая ассоциация и Американское общество качества, TECHNOMETRICS.
Примеры
- См. Пример надежной и эмпирической ковариационной оценки, чтобы узнать, как подогнать
MinCovDetобъект к данным, и посмотрите, насколько оценка остается точной, несмотря на наличие выбросов. - См оценку ковариационной Robust и Махаланобиса расстояния Актуальность визуализировать разницу между
EmpiricalCovarianceиMinCovDetковариации оценок с точки зрения расстояния Махаланобиса (так мы получим более точную оценку точности матрицы тоже).
В предыдущих параграфах данной главы мы рассматривали случай отказа от одной предпосылки классической линейной модели множественной регрессии. Теперь мы расширим наш анализ и откажемся сразу от двух предпосылок: от предпосылок №№4-5 (о постоянстве дисперсии случайной ошибки и о некоррелированности разных случайных ошибок между собой). В техническом смысле этот параграф несколько сложнее предыдущих (в частности, тут более широко используется линейная алгебра). Поэтому, если вы заинтересованы в том, чтобы разобраться только в прикладных аспектах множественной регрессии, а в соответствующих вычислениях готовы полностью довериться эконометрическому пакету, можете его пропустить.
Отказ от указанных двух предпосылок означает, что ковариационная матрица вектора случайных ошибок (таблица, в которой записаны все ковариации между (varepsilon_{i}) и (varepsilon_{j}), см. параграф 3.3) больше не является диагональной матрицей с одинаковыми числами на главной диагонали, как это было в первоначальной классической модели. Теперь ковариационная матрица вектора случайных ошибок Ω — это произвольная ковариационная матрица (разумеется, так как это не совсем любая матрица, а именно ковариационная матрица, то по своим свойствам она является симметричной и положительно определенной).
Модель, в которой сохранены только первые три предпосылки классической линейной модели множественной регрессии, называется обобщенной линейной моделью множественной регрессии.
Проанализируем, к каким последствиям приводит отказ от предпосылок №№4-5.
Во-первых, полученная обычным методом наименьших квадратов оценка ({widehat{beta} = left( {X^{‘}X} right)^{- 1}}X’y) остается несмещенной (это свойство мы доказывали, опираясь как раз лишь на первые три предпосылки).
Во-вторых, МНК-оценки хоть и остаются несмещенными, но больше не являются эффективными.
В-третьих, если мы оцениваем ковариационную матрицу вектора оценок коэффициентов (которая нужна для тестирования всевозможных гипотез), то оценка (widehat{V}{{(widehat{beta})} = left( {X^{‘}X} right)^{- 1}}S^{2}) смещена и больше не является корректной.
Чтобы убедиться в этом, посчитаем ковариационную матрицу от (widehat{beta}) в условиях обобщенной модели (при этом мы используем свойства ковариационной матрицы, перечисленные в параграфе 3.3):
(V{left( widehat{beta} right) = V}{leftlbrack {{({X^{‘}X})}^{- 1}X’y} rightrbrack = V}{leftlbrack {{({X^{‘}X})}^{- 1}X'{({mathit{Xbeta} + varepsilon})}} rightrbrack =})
({}V{leftlbrack {{({{({X^{‘}X})}^{- 1}X’})}varepsilon} rightrbrack = left( {X^{‘}X} right)^{- 1}}X^{‘}Vlbrackvarepsilonrbrack{left( {left( {X^{‘}X} right)^{- 1}X^{‘}} right)^{‘} = {({X^{‘}X})}^{- 1}}X^{‘}Omega{left( {left( {X^{‘}X} right)^{- 1}X^{‘}} right)^{‘} = {({X^{‘}X})}^{- 1}}X^{‘}Omega X{({X^{‘}X})}^{- 1})
Так выглядит ковариационная матрица вектора МНК-оценок в обобщенной модели. Ясно, что она не может быть корректно оценена стандартной оценкой (left( {X^{‘}X} right)^{- 1}S^{2}). Следовательно, прежней формулой пользоваться нельзя: если мы будем использовать стандартные ошибки, рассчитанные по обычной формуле (предполагая выполнение предпосылок классической линейной модели), то получим некорректные стандартные ошибки, что может привести нас к неверным выводам по поводу значимости или незначимости тех или иных регрессоров.
Таким образом, последствия перехода к обобщенной модели аналогичны тем, что мы наблюдали для случая гетероскедастичности. Это неудивительно, так как гетероскедастичность — частный случай обобщенной линейной модели.
Поэтому для получения эффективных оценок обычный МНК не подойдет, и придется воспользоваться альтернативным методом — обобщенным МНК (ОМНК, generalized least squares, GLS). Формулу для расчета оценок коэффициентов при помощи ОМНК позволяет получить специальная теорема.
Теорема Айткена
Если
- модель линейна по параметрам и правильно специфицирована
({y = {mathit{Xbeta} + varepsilon}},) - матрица Х — детерминированная матрица, имеющая максимальный ранг k,
- (E{(varepsilon) = overrightarrow{0}}),
- (V{(varepsilon) = Omega}) — произвольная положительно определенная и симметричная матрица,
то оценка вектора коэффициентов модели ({{widehat{beta}}^{} = {({X’Omega^{- 1}X})}^{- 1}}X’Omega^{- 1}y) является:
- несмещенной
- и эффективной, то есть имеет наименьшую ковариационную матрицу в классе всех несмещенных и линейных по y оценок.
Предпосылки теоремы Айткена — это предпосылки обобщенной линейной модели множественной регрессии. Из них первые три — стандартные, как в классической модели, а четвертая ничего особого не требует (у вектора случайных ошибок может быть любая ковариационная матрица без каких-либо дополнительных специальных ограничений). Сама теорема Айткена является аналогом теоремы Гаусса — Маркова для случая обобщенной модели.
Докажем эту теорему.
Из линейной алгебры известно: если матрица (Omega) симметрична и положительно определена, то существует такая матрица P, что
(P’bullet{P = Omega^{- 1}}) ⇔ ({P^{‘} = Omega^{- 1}}bullet P^{- 1})
А раз такое представление возможно, то воспользуемся им для замены переменных. От вектора значений зависимой переменной (y), перейдем к вектору (Pbullet y), обозначив его как вектор ({y^{} = P}bullet y). Аналогичным образом введем матрицу ({X^{} = P}bullet X) и вектор ошибок ({varepsilon^{} = P}bulletvarepsilon).
Вернемся к исходной модели, параметры которой нас и интересуют:
({y = X}{beta + varepsilon})
Умножим левую и правую части равенства на матрицу (P):
({mathit{Py} = mathit{PX}}{beta + mathit{Pvarepsilon}})
С учетом новых обозначений это равенство можно записать так:
({y^{} = X^{}}{beta + varepsilon^{}})
Для новой модели (со звездочками) выполняются предпосылки теоремы Гаусса-Маркова. Чтобы в этом убедиться, достаточно показать, что математическое ожидание вектора случайных ошибок является нулевым вектором (третья предпосылка классической модели) и ковариационная матрица вектора случайных ошибок является диагональной с одинаковыми элементами на главной диагонали (четвертая и пятая предпосылки).
Для этого вычислим математическое ожидание нового вектора ошибок:
(E{left( varepsilon^{} right) = E}{left( mathit{Pvarepsilon} right) = P}bullet E{(varepsilon) = P}bullet{overrightarrow{0} = overrightarrow{0}})
Теперь вычислим ковариационную матрицу вектора (varepsilon^{}):
(V{left( varepsilon^{} right) = V}{left( {Pbulletvarepsilon} right) = P}bullet V(varepsilon)bullet{P^{‘} = P}bulletOmegabullet{P^{‘} = P}bulletOmegabulletOmega^{- 1}bullet{P^{- 1} = I_{n}})
Здесь (I_{n}) обозначает единичную матрицу размера n на n.
Следовательно, для модели со звездочками выполняются все предпосылки теоремы Гаусса — Маркова. Поэтому получить несмещенную и эффективную оценку вектора коэффициентов можно, применив к этой измененной модели обычный МНК:
({{widehat{beta}}^{} = left( {{X^{}}^{‘}X^{}} right)^{- 1}}{X^{}}^{‘}y^{})
Теперь осталось вернуться к исходным обозначениям, чтобы получить формулу несмещенной и эффективной оценки интересующего нас вектора в терминах обобщенной модели:
({{widehat{beta}}^{} = left( {{X^{}}^{‘}X^{}} right)^{- 1}}{X^{}}^{‘}{y^{} = left( {{(mathit{PX})}^{‘}mathit{PX}} right)^{- 1}}left( mathit{PX} right)^{‘}{mathit{Py} = left( {X’P’mathit{PX}} right)^{- 1}}X^{‘}P^{‘}{mathit{Py} =}left( {X’Omega^{- 1}P^{- 1}mathit{PX}} right)^{- 1}X’Omega^{- 1}P^{- 1}{mathit{Py} = {({X’Omega^{- 1}X})}^{- 1}}X’Omega^{- 1}y)
Что и требовалось доказать.
Взвешенный МНК, который мы обсуждали ранее, — это частный вариант обобщенного МНК (для случая, когда только предпосылка №4 нарушена, а предпосылка №5 сохраняется).
Как и при использовании взвешенного МНК в ситуации применения ОМНК коэффициент R-квадрат не обязан лежать между нулем и единицей и не может быть интерпретирован стандартным образом.
Слабая сторона ОМНК состоит в том, что для его реализации нужно знать не только матрицу регрессоров X с вектором значений зависимой переменной y, но и ковариационную матрицу вектора случайных ошибок (Omega). На практике, однако, эта матрица почти никогда не известна. Поэтому в прикладных исследованиях практически всегда вместо ОМНК используется, так называемый, доступный ОМНК (его ещё называют практически реализуемый ОМНК, feasible GLS). Идея доступного ОМНК состоит в том, что следует сначала оценить матрицу (Omega) (традиционно обозначим её оценку (widehat{Omega})), а уже затем получить оценку вектора коэффициентов модели, заменив в формуле ОМНК (Omega) на (widehat{Omega}):
({{widehat{beta}}^{} = {({X'{widehat{Omega}}^{- 1}X})}^{- 1}}X'{widehat{Omega}}^{- 1}y.)
Применение этого подхода осложняется тем, что (widehat{Omega}) не может быть оценена непосредственно без дополнительных предпосылок, так как в ней слишком много неизвестных элементов. Действительно, в матрице размер (n) на (n) всего (n^{2}) элементов, и оценить их все, имея всего (n) наблюдений, представляется слишком амбициозной задачей. Даже если воспользоваться тем, что матрица (Omega) является симметричной, в результате чего достаточно оценить только элементы на главной диагонали и над ней, мы все равно столкнемся с необходимостью оценивать (left( {n + 1} right){n/2}) элементов, что всегда больше числа доступных нам наблюдений.
Поэтому процедура доступного ОМНК устроена так:
- Делаются некоторые предпосылки по поводу того, как устроена ковариационная матрица вектора случайных ошибок (Omega). На основе этих предпосылок оценивается матрица (widehat{Omega}).
- После этого по формуле ({({X'{widehat{Omega}}^{- 1}X})}^{- 1}X'{widehat{Omega}}^{- 1}y) вычисляется вектор оценок коэффициентов модели.
Из сказанного следует, что доступный ОМНК может быть реализован только в ситуации, когда есть разумные основания сформулировать те или иные предпосылки по поводу матрицы (widehat{Omega}). Рассмотрим некоторые примеры таких ситуаций.
Пример 5.4. Автокорреляция и ОМНК-оценка
Рассмотрим линейную модель ({y = X}{beta + varepsilon}), для которой дисперсия случайных ошибок постоянна, однако наблюдается так называемая автокорреляция первого порядка:
(varepsilon_{i} = {{rho ast varepsilon_{i — 1}} + u_{i}})
Здесь (u_{i}) — независимые и одинаково распределенные случайные величины с дисперсией (sigma_{u}^{2}), а (rhoin{({{- 1},1})}) — коэффициент автокорреляции.
(а) Найдите ковариационную матрицу вектора случайных ошибок для представленной модели.
(б) Запишите в явном виде формулу ОМНК-оценки вектора коэффициентов модели, предполагая, что коэффициент (rho) известен.
Примечание: в отличие от гетероскедастичности, автокорреляция случайных ошибок обычно наблюдается не в пространственных данных, а во временных рядах. Для временных рядов вполне естественна подобная связь будущих случайных ошибок с предыдущими их значениями.
Решение:
(а) Используя условие о постоянстве дисперсии случайной ошибки, то есть условие (mathit{var}{{(varepsilon_{i})} = mathit{var}}{(varepsilon_{i — 1})}), найдем эту дисперсию:
(mathit{var}{{(varepsilon_{i})} = mathit{var}}{({{rho ast varepsilon_{i — 1}} + u_{i}})})
(mathit{var}{{(varepsilon_{i})} = rho^{2}}mathit{var}{{(varepsilon_{i — 1})} + mathit{var}}{(u_{i})})
(mathit{var}{{(varepsilon_{i})} = rho^{2}}mathit{var}{{(varepsilon_{i})} + sigma_{u}^{2}})
(mathit{var}{left( varepsilon_{i} right) = frac{sigma_{u}^{2}}{1 — rho^{2}}}.)
Тем самым мы нашли элементы, которые будут стоять на главной диагонали ковариационной матрицы вектора случайных ошибок. Теперь найдем элементы, которые будут находиться непосредственно на соседних с главной диагональю клетках:
(mathit{cov}{left( {varepsilon_{i},varepsilon_{i — 1}} right) = mathit{cov}}{left( {{{rho ast varepsilon_{i — 1}} + u_{i}},varepsilon_{i — 1}} right) = {rho ast mathit{cov}}}{left( {varepsilon_{i — 1},varepsilon_{i — 1}} right) + mathit{cov}}{left( {u_{i},varepsilon_{i — 1}} right) = {rho ast mathit{var}}}{{left( varepsilon_{i — 1} right) + 0} = frac{rho ast sigma_{u}^{2}}{1 — rho^{2}}})
По аналогии легко убедиться, что
(mathit{cov}{left( {varepsilon_{i},varepsilon_{i — k}} right) = frac{rho^{k} ast sigma_{u}^{2}}{1 — rho^{2}} = frac{sigma_{u}^{2} ast rho^{k}}{1 — rho^{2}}}.)
Следовательно, ковариационная матрица вектора случайных ошибок имеет вид:
({Omega = frac{sigma_{u}^{2}}{1 — rho^{2}}}begin{pmatrix} begin{matrix} 1 & rho rho & 1 end{matrix} & ldots & begin{matrix} rho^{n — 2} & rho^{n — 1} rho^{n — 3} & rho^{n — 2} end{matrix} ldots & ldots & ldots begin{matrix} rho^{n — 2} & rho^{n — 3} rho^{n — 1} & rho^{n — 2} end{matrix} & ldots & begin{matrix} 1 & rho rho & 1 end{matrix} end{pmatrix})
(б) Вектор ОМНК-оценок коэффициентов имеет вид:
({{widehat{beta}}^{} = {({X’Omega^{- 1}X})}^{- 1}}X^{‘}Omega^{- 1}{y =}{left( {X’begin{pmatrix} begin{matrix} 1 & rho rho & 1 end{matrix} & ldots & begin{matrix} rho^{n — 2} & rho^{n — 1} rho^{n — 3} & rho^{n — 2} end{matrix} ldots & ldots & ldots begin{matrix} rho^{n — 2} & rho^{n — 3} rho^{n — 1} & rho^{n — 2} end{matrix} & ldots & begin{matrix} 1 & rho rho & 1 end{matrix} end{pmatrix}^{- 1}X} right)^{- 1} ast}X’begin{pmatrix} begin{matrix} 1 & rho rho & 1 end{matrix} & ldots & begin{matrix} rho^{n — 2} & rho^{n — 1} rho^{n — 3} & rho^{n — 2} end{matrix} ldots & ldots & ldots begin{matrix} rho^{n — 2} & rho^{n — 3} rho^{n — 1} & rho^{n — 2} end{matrix} & ldots & begin{matrix} 1 & rho rho & 1 end{matrix} end{pmatrix}^{- 1}y)
Обратите внимание, что дробь (frac{sigma_{u}^{2}}{1 — rho^{2}}) при расчете представленной оценки сокращается. Поэтому для вычисления оценки знать величину (sigma_{u}^{2}) не нужно.
Примечание: если коэффициент автокорреляции (rho) неизвестен, то его можно легко оценить. Например, для этого можно применить обычный МНК к исходной регрессии, получить вектор остатков и оценить регрессию ({widehat{e}}_{i} = {widehat{rho} ast e_{i — 1}}). Полученной оценки (widehat{rho}) достаточно, чтобы вычислить ОМНК-оценку вектора параметров модели. Тем самым в представленном примере для применения доступного ОМНК достаточно оценить всего один параметр ковариационной матрицы вектора оценок коэффициентов.
Пример 5.5. Гетероскедастичность и ОМНК-оценка
Рассмотрим линейную модель ({y = X}{beta + varepsilon}), для которой выполнены все предпосылки классической линейной модели множественной регрессии за одним исключением: дисперсия случайной ошибки прямо пропорциональна квадрату некоторой известной переменной
(mathit{var}{left( varepsilon_{i} right) = sigma_{i}^{2} = sigma_{0}^{2}}{z_{i}^{2} > 0}.)
(а) Найдите ковариационную матрицу вектора случайных ошибок для представленной модели.
(б) Запишите в явном виде формулу ОМНК-оценки вектора коэффициентов модели.
Решение:
(а) Так как в этом случае нарушена только четвертая предпосылка классической линейной модели множественной регрессии, то вне главной диагонали ковариационной матрицы вектора случайных ошибок будут стоять нули.
(Omega = begin{pmatrix} begin{matrix} {sigma_{0}^{2}z_{1}^{2}} & 0 0 & {sigma_{0}^{2}z_{2}^{2}} end{matrix} & begin{matrix} ldots & 0 ldots & 0 end{matrix} begin{matrix} ldots & ldots 0 & 0 end{matrix} & begin{matrix} ldots & ldots ldots & {sigma_{0}^{2}z_{n}^{2}} end{matrix} end{pmatrix})
(б) Обратите внимание, что при подстановке в общую формулу для ОМНК-оценки величина (sigma_{0}^{2}) сокращается, следовательно, для оценки вектора коэффициентов знать её не нужно:
({{widehat{beta}}^{} = {({X’Omega^{- 1}X})}^{- 1}}X^{‘}Omega^{- 1}{y =}left( {X’begin{pmatrix} begin{matrix} z_{1}^{2} & 0 0 & z_{2}^{2} end{matrix} & begin{matrix} ldots & 0 ldots & 0 end{matrix} begin{matrix} ldots & ldots 0 & 0 end{matrix} & begin{matrix} ldots & ldots ldots & z_{n}^{2} end{matrix} end{pmatrix}^{- 1}X} right)^{- 1}X’begin{pmatrix} begin{matrix} z_{1}^{2} & 0 0 & z_{2}^{2} end{matrix} & begin{matrix} ldots & 0 ldots & 0 end{matrix} begin{matrix} ldots & ldots 0 & 0 end{matrix} & begin{matrix} ldots & ldots ldots & z_{n}^{2} end{matrix} end{pmatrix}^{- 1}y)
* * *
Ещё одна важная ситуация, когда с успехом может быть применен доступный ОМНК — это модель со случайными эффектами, которую мы рассмотрим в главе, посвященной панельным данным.
Dynamic Model Development
P.W. Oxby, … T.A. Duever, in Computer Aided Chemical Engineering, 2003
3.2 An Optimality Property of the Determinant Criterion
Equation (12) can be generalized by replacing the inverse of the estimate of the error covariance matrix,
Σ^εn−1, with an arbitrary symmetric positive definite weight matrix, W:
(14)Δθ^(k)=(XTWX)−1XTWz(θ^(k))
The estimate of the parameter covariance is:
(15)Σ^θ=(XTWX)−1XTWΣ^εn(XTWX)−1
If the determinant of the estimate of the parameter covariance matrix,
|Σ^θ|, is minimized with respect to the elements of W, the solution is independent of X and is simply
(16)W=Σ^εn−1
Substitution of (16) back into (14) gives (12) which, as has been shown, is equivalent to the determinant criterion. Therefore of all weighting schemes in the form of (14), it is the one equivalent to the determinant criterion that minimizes
|Σ^θ|, the determinant of the estimate of the parameter covariance matrix when the error covariance is unknown. This appears to be a rather strong result in support of the determinant criterion. It might also be noted that, unlike derivations based on likelihood, this result does not depend on the measurement errors being normally distributed. But it will be shown that the practical usefulness of the result does depend on the assumption that the residual covariance
Z(θ^)Z(θ^)T/n, is a good estimate of the true error covariance. Ideally one would want W to be the inverse of the error covariance matrix. The determinant in effect makes a compromise and substitutes an estimate of it. The potential problem here is that if the data set is not large, the residual covariance matrix may be a poor estimate of the error covariance matrix. A poor estimate of the error covariance matrix will lead to a poor estimate of the parameter covariance matrix. Therefore, although the determinant criterion gives the minimum determinant of the estimate of the parameter covariance matrix, if this estimate is poor, then the optimality property may be of little significance. This suggests that the optimality of the determinant criterion may be more relevant for large data sets than small ones. The simulation studies presented in Section 4 will confirm this to be true.
Read full chapter
URL:
https://www.sciencedirect.com/science/article/pii/S1570794603800706
Kalman Filters and Nonlinear Filters
Vytas B. Gylys, in Encyclopedia of Physical Science and Technology (Third Edition), 2003
IV.B Square Root Filtering
By far the greatest trouble spot in computer mechanization of the KF is the updating of state error covariance matrix P, that is, the computation of Pk∣k according to Eq. (18). As the estimation process progresses, the elements of Pk∣k typically continue to decrease in magnitude and so matrix Pk∣k keeps approaching the zero matrix, although theoretically it should forever remain positive definite, no matter how small in magnitude its elements become. Hence, unless special measures are taken, accumulation of roundoff error in the repetitive use of Eq. (18) may cause the computed Pk∣k to lose its positive definiteness. As suggested by the matrix inversion operation appearing on the right-hand side of Eq. (16) for computing the Kalman gain, this situation is aggravated if several components of the measurement vector are very accurate and consequently the positive definite measurement error covariance matrix R is ill conditioned, that is, if R has eigenvalues of both relatively very large and small magnitudes.
Let A be a nonnegative definite symmetric matrix; then there exists a matrix S such that A = SST. Matrix S is often called the square root of A. The Cholesky decomposition algorithm provides a method of constructing from A the matrix S so that S is lower triangular; that is, all elements of S above the main diagonal are zero. Square root filtering is motivated by the observations that, if the state error covariance matrix P = SST, then (a) since SST is always nonnegative definite, matrix P expressed as SST cannot become negative definite, and (b) matrix S is generally less ill conditioned than matrix P.
Several versions of the square root filtering algorithm are known. The earliest form was developed by J. E. Potter in 1964 for applications in which the process noise is absent (i.e., covariance matrix Q is zero) and the measurements are sequentially processed as scalars. In 1967 J. F. Bellantoni and K. W. Dodge extended Potter’s results to vector-valued measurements. A. Andrews in 1968 and then S. F. Schmidt in 1970 published two alternative procedures for handling the process noise. In 1973 N. A. Carlson described a procedure that considerably improved the speed and decreased the memory requirements of square root filtering and in which, as in Potter’s algorithm, vector-valued measurements are processed sequentially as scalars. Finally, the so-called UDUT covariance factorization method is the most recent major milestone in numerical handling of KFs. This method, developed by G. J. Bierman and C. L. Thornton, represents the state error covariances before and after the measurement update step asPk|k−1=Uk|k−1Dk|k−1Uk|k−1TandPk|k=Uk|kDk|kUk|kT,with D being a diagonal matrix and U an upper triangular matrix with 1’s on its main diagonal. In this method, the square root of the covariance matrix, which now would correspond to UD1/2, is never computed explicitly, which avoids numerical computation of square roots. Like Carlson’s algorithm, the UDUT factorization method maintains the covariance matrix in factored form and so (like Carlson’s algorithm) is considerably more efficient in processor time and storage than the original Potter algorithm.
As a quick comparison of computational efficiency, the conventional Kalman method, the less efficient form of Carlson’s algorithm, and the UDUT factorization method are roughly equal: The processing of each time step (consisting of one time propagation and one measurement update) requires of the order of 16[9ns3 + 9ns2nm + 3ns2nw] adds and about the same number of multiplies, plus a relatively modest number of divides and square roots (square roots are required only in some, as in Potter’s or Carlson’s square root algorithms). Here, as before, ns is the length of the state vector, nm the length of the measurement vector, and nw the lenght of the process noise vector w. The faster version of Carlson’s algorithm is more efficient and requires only of the order of 16[5ns3 + 9ns2nm + 3ns2nw] adds and 16[5ns3 + 12ns2nm + 3ns2nw] multiplies, plus 2nsnm divides and nsnm square roots, at each time point. The stable (Joseph) form of the KF [as given by Eq. (18′)] fares more poorly: At each time step, it requires of the order of 16[18ns3 + 15ns2nm + 3ns2nw] adds and about the same number of multiplies.
As a summary, (a) a square root filter is a numerically stable form for performing the KF covariance–gain processing defined by Eqs. (15), (16), and (18); (b) the efficiency of its more recent versions roughly compares with that of these three equations; (c) the increased stability allows one to use relatively low-precision arithmetic in the KF gain–covariance processing, with a possible exception of some dot products.
Real-time implementation of a filter involves additional issues that are unimportant in the non-real-time environment. Besides the adequacy of functional performance, the most important of these issues is the requirement to produce timely responses to external stimuli. Thus, resorting to a parallel or concurrent processing may be the only way out. This usually implies the use of special hardware architectures such as parallel, vector pipelined, or systolic processors.
As one example, consider the use of a filter in the tracking of multiple objects in a hard real-time environment characterized by strict deadlines. In such a case one may want to maintain simultaneously many estimation processes, each handling a single object. Parallel processors may seem to be a suitable hardware architecture for this problem, but if separate estimation processes in such an application progress at different rates and at any time some of them require a great amount of special handling, then parallel architecture, such as a single-instruction multiple-data stream computer, may not be the best choice. As another example, consider a KF to be implemented as part of a navigation system on a small airborne computer (uniprocessor). Suppose that the navigation measurements come at a certain fixed rate. If the filtering process cannot keep up with the arrival rate of measurements and so not all of them can be utilized, the estimation performance may deteriorate. In this problem, if there is an upper bound on hardware resources, the only solution may be to decompose the estimation algorithm into concurrently executable processes. For instance, the time-propagation step (which, say, is to be executed at a relatively high rate) may constitute one process and the measurement-update step (which needs to be executed only at some lower rate, say, at the rate of measurement arrivals) may constitute another. Such a decomposition of an estimation algorithm into concurrent procedures often creates a surrogate algorithm that performs more poorly than the original algorithm.
The effects of the finite-length word computing is another issue that must be considered in filter implementation for real-time applications. The computer on which a filter is developed and validated through successive off-line simulations is often more powerful and uses higher-precision arithmetic and number representations than the ultimate real-time processor. Hence, one must in advance determine in advance what effect a shorter word length will have on performance.
Read full chapter
URL:
https://www.sciencedirect.com/science/article/pii/B0122274105003574
Batch track estimators for multistatic target motion analysis
Ngoc Hung Nguyen, Kutluyıl Doğançay, in Signal Processing for Multistatic Radar Systems, 2020
8.7 Asymptotic efficiency analysis
In this section, the WIVE is analytically shown to be asymptotically efficient (i.e., its error covariance matrix approaches the CRLB matrix as M→∞) in the presence of small measurement noise.
The error covariance matrix of the WIVE is given by
(8.71a)CWIVE=E{(ξˆWIVE−ξ)(ξˆWIVE−ξ)T}
(8.71b)=E{(GTW−1F)−1GTW−1eeTW−1G(FTW−1G)−1}.
Assuming the observability of the target (i.e., GTW−1F is nonsingular), the asymptotic error covariance of the WIVE is given by
(8.72)CWIVE=plim{1M(GTW−1FM)−1GTW−1eeTW−1GM(FTW−1GM)−1}
where the probability limit (plim) is defined by [101]
plimxˆ(M)=x⁎⇔limM→∞P{|x(M)−x⁎|>ϵ}=0
for every ϵ>0. Applying Slutsky’s theorem [100] to (8.72), we obtain
(8.73)CWIVE=plim{1M}plim{GTW−1FM}−1plim{GTW−1eeTW−1GM}×plim{FTW−1GM}−1.
We can rewrite the term inside the second plim in the right-hand side of (8.73) as
(8.74)GTW−1FM=1M∑k=0M−1GkTWk−1Fk.
Since the measurement noise vector ηk is finite and statistically independent over k, GkTWk−1Fk is also statistically independent over k and the entries of GkTWk−1Fk (denoted as κij,k) have finite variances. Using the inequality
(8.75)∑k=0M−1E{κij,k2}(k+1)2⩽max{E{κij,k2}}∑k=0M−11(k+1)2
and noting that ∑k=0M−11(k+1)2 converges to π2/6 as M→∞ [102], ∑k=0M−1E{κij,k2}(k+1)2 converges as M→∞. Therefore, the Kolmogorov criterion is satisfied for each entry κij,k of GkTWk−1Fk. Consequently, following Kolmogorov’s strong law of large numbers [103], 1M∑k=0M−1GkTWk−1Fk almost surely converges to 1M∑k=0M−1E{GkTWk−1Fk} as M→∞. This implies that the sample covariance matrix GTW−1FM almost surely converges to E{GTW−1FM} as M→∞. Therefore, we obtain
(8.76)plim{GTW−1FM}−1=E{GTW−1FM}−1.
For small measurement noise, the BCPLE estimate ξˆBCPLE, which is used to compute G and W for the WIVE, has a small bias. In addition, the covariances of the estimates dˆi,k, θˆi,k and vˆk computed from ξˆBCPLE vanish as M→∞. Therefore, G and W can be approximated by their noise-free versions G∘ and W∘ as M→∞ under the small measurement noise assumption. Note that G∘=F∘. Consequently, we have
(8.77)plim{GTW−1FM}−1≈E{F∘TW∘−1FM}−1.
Using the approximation E{F}≈F∘ (by neglecting the second- and higher-order noise terms) leads to
(8.78)E{F∘TW∘−1FM}=F∘TW∘−1E{F}M≈F∘TW∘−1F∘M.
From (8.77) and (8.78), we obtain
(8.79)plim{GTW−1FM}−1≈M(F∘TW∘−1F∘)−1.
Similarly, we have
(8.80)plim{FTW−1GM}−1≈M(F∘TW∘−1F∘)−1.
Using a similar approach that leads to (8.76), we can use the strong law of large numbers to show that
(8.81)plim{GTW−1eeTW−1GM}=E{GTW−1eeTW−1GM}.
Using small noise approximations, we obtain
(8.82)plim{GTW−1eeTW−1GM}≈F∘TW∘−1E{eeTM}W∘−1F∘≈F∘TW∘−1W∘W∘−1F∘M≈F∘TW∘−1F∘M.
By substituting (8.79), (8.80) and (8.82) into (8.73), we obtain the asymptotic error covariance of the WIVE as M→∞:
(8.83)CWIVE≈(F∘TW∘−1F∘)−1.
Since it is proved in Section 8.11 (Appendix A) that
(8.84)F∘TW∘−1F∘=J∘TK−1J∘
we have
(8.85a)CWIVE≈(J∘TK−1J∘)−1
(8.85b)≈Cξ.
This concludes the proof for the asymptotic efficiency of the WIVE under the small measurement noise assumption.
It is also shown in Section 8.11 (Appendix C) that the CRLB for the TMA problem under consideration is independent of the choice of TDOA/FDOA reference receiver. As a result, the asymptotic performance of the WIVE is independent of the choice of reference receiver.
Read full chapter
URL:
https://www.sciencedirect.com/science/article/pii/B9780128153147000184
Computer Techniques and Algorithms in Digital Signal Processing
K. Giridhar, … Ronald A. Iltis, in Control and Dynamic Systems, 1996
A Appendix – Time Updates for the Blind MAPSD Algorithm
In this Appendix, we derive the one-step time updates of the channel estimate and the associated error covariance matrix for the blind MAP symbol detector developed in Section 4.2. Recall from Eq. (51) that
(A.1)pfk+1|dik+1,Nf,rk=∑j:djk,Nf∈dik+1,Nfαjp(fk+1|djk,Nf,rk)
where αj is given by Eq. (52). Using Eq. (49), this Gaussian sum can be explicitly written as follows:
(A.2)pfk+1|dik+1,Nf,rk=∑j:djk,Nf∈dik+1,NfαjNfk+1;Ff^jk|k,FPjk|kFH+Q
which defines the one-step prediction of the mean vector f^ik+1|k and the covariance matrix Pik+1|k. Some basic results about sums of Gaussian p.d.f.s can be used to derive these one-step predictions.
Lemma: Let the p.d.f. of the random vector x be a weighted sum of N multivariate Gaussian p.d.f.s as follows:
(A.3)px=∑j=1NαjNx;xj,Pj
where αj , xj, and Pj are, respectively, the jth weight, mean, and covariance. (i) The mean value of x is given by
(A.4)xa=∑j=1Nαjxj.
(ii) The error covariance is given by
(A.5)Pa=∑j=1NαjPj+xa–xjxa–xjH.
Proof: The first part of the lemma is easily proved from the definition of xa, i.e.,
(A.6)xa=Ex=∫xx∑j=1NαjNx;xj,Pjdx=∑j=1Nαjxj.
To prove the second part of the lemma, consider
(A.7)Pa=Ex−xax−xaH=∑j=1Nαj∫xxxHNjdx+xaxaH−∫xxxaHNjdx−∫xxaxHNjdx
where, for convenience, we have used the notation Nj to represent the p.d.f. N(x; xj, Pĵ). Observe that ∫xxaHNjdx=xjxaHand∫xaxHNjdx=xaxjH. By adding and subtracting the term xjxjH to the expression inside the square brackets, we obtain
(A.8)Pa=∑j=1Nαj∫xxxHNjdx−xjxjH+xaxaH−xjxaH−xaxjH+xjxjH=∑j=1Nαj∫xxxHNjdx−xjxjH+xa−xjxa−xjH..
It is straightforward to show that
(A.9)∑j=1Nαj∫xxxHNjdx−xjxjH=∑j=1Nαj∫xx−xj(x−xj)HNjdx=∑j=1NαjPj.
Substituting this result into Eq. (A.8 ), we obtain the result in Eq. (A.5 ) for the error covariance Pa, which completes the proof.
To obtain the one-step predicted mean vector of the blind MAPSD algorithm, Eq. (A.4 ) is used with xj=Ff^jk|k. The summation is performed over the M predecessor subsequences djk,Nf, yielding
(A.10)f^ik+1|k)=∑j:djk,Nf∈dik+1,NfαjFf^jk|k.
By substituting αj=pdjk,Nf|rk−1/qik, the final expression in Eq. (53) is obtained. Similarly, the one-step error covariance update in Eq. (54) is obtained by substituting FPjk|kFH+Q=Pj and
(A.11)νj,ikνj,iHk=xa−xjxa−xjH
into Eq. (A.5 ) where xa=f^ik+1|k (and xj=Ff^jk|k as above).
Read full chapter
URL:
https://www.sciencedirect.com/science/article/pii/S0090526796800454
Waveform selection for multistatic target tracking in clutter
Ngoc Hung Nguyen, Kutluyıl Doğançay, in Signal Processing for Multistatic Radar Systems, 2020
3.5 Summary
In this chapter, the optimal waveform selection problem was considered for multistatic tracking of a single target in clutter. Since the exact track error covariance matrix is not available during the waveform selection process (i.e., prior to the actual waveform transmission) due to the presence of false-alarm measurements, an expected track error covariance matrix is calculated (utilizing the degradation factor (3.26)) and used for waveform selection. It was demonstrated via simulation examples that the presented waveform selection scheme achieves a significantly reduced RMSE for the target state estimate compared to those of the fixed waveforms.
Read full chapter
URL:
https://www.sciencedirect.com/science/article/pii/B9780128153147000111
State Estimation
Jay Farrell, in The Electrical Engineering Handbook, 2005
4.3 Recursive State Estimation
Equations 4.4 through 4.5 provide the mean and the covariance of the state through time based only on the initial mean state vector and its error covariance matrix. When measurements y(k) are available, the measurements can be used to improve the accuracy of an estimate of the state vector at time k. The symbols xˆ−(k) and xˆ+(k) are used to denote the estimate of x(k) before and after incorporating the measurement, respectively.
Similarly, the symbols Pxˆ−(k) and Pxˆ+(k) are used to denote the error covariance matrices corresponding to xˆ−(k) and xˆ+(k), respectively. This section presents the time propagation and measurement update equations for both the state estimate and its error covariance. The equations are presented in a form that is valid for any linear unbiased measurement correction. These equations contain a gain matrix K that determines the estimator performance. The choice of K to minimize the error covariance Pxˆ+(k) will be of interest.
For an unbiased linear measurement, the update will have the form:
(4.8)xˆ+(k)=xˆ−(k)+K(k)(y(k)−yˆ−(k)),
where yˆ−(k)=H(k)xˆ−(k).. The error covariance of xˆ+(k) is the following:
(4.9)Pxˆ+(k)=(I−K(k)H(k))Pxˆ−(k)(I−K(k)H(k))T +K(k)R(k)KT(k).
K(k) is a possibly time-varying state estimation gain vector to be designed. If no measurement is available at time k, then K(k) = 0, which yields xˆ+(k)=xˆ−(k) and Pxˆ+(k)=Pxˆ−(k). If a measurement is available, and the state estimator is designed well, then Pxˆ+(k)≤Pxˆ−(k). In either case, the time propagation of the state estimate and its error covariance matrix is achieved by:
(4.10)xˆ−(k+1)=Φ(k)xˆ+(k)+Γˆuu(k)
(4.11)Pxˆ−(k+1)=Φ(k)Pxˆ+(k)ΦT(k)+ΓωQd(k)ΓωT.
At least two issues are of interest relative to the state estimation problem. First, does there exist a state estimation gain vector K(k) such that xˆ is guaranteed to converge to x regardless of initial condition and the sequence u(k)? Second, how should the designer select the gain vector K(k)?
The first issue raises the question of observability. A linear time-invariant system is observable if the following matrix has rank n:
[HT, ΦTHT, …,( ΦT)nHT].
When a system is observable, then it is guaranteed that a stabilizing gain vector K exists. Assuming that the system of interest is observable, the remainder of this chapter discusses the design and analysis of state estimators.
Figure 4.1 portrays the state estimator in conjunction with the system of interest. The system of interest is depicted in the upper left. The state estimator is superimposed on a gray background in the lower right.
FIGURE 4.1. State Estimation System Block Diagram
This interconnected system will be referred to as the state estimation system. The figure motivates several important comments. First, although the state estimator has only n states, the state estimation system has 2n states. Second, the inputs to the state estimation system are the deterministic input u and the stochastic inputs ω and v. Third, the inputs to the state estimator are the deterministic input u and the measured plant output y. The state space model for the state estimation system is the following:
(4.12)[x(k+1)xˆ−(k+1)]=[Φx0LHxΦ−LH][x(k)xˆ−(k)]+[ΓuΓω0Γˆu0L][u(k)ω(k)v(k)],
where L = ΦK.
Based on this state-space model, with the assumption that the system is time invariant, the transfer function from v to yˆ is as written here:
(4.13)Gv(z)=H[zI−(Φ−LH)]−1L,
where z is the discrete-time unit advance operator. Assuming that H = Hx, the transfer function from u to r is as follows:
(4.14)Gu(z)=H[zI−(Φ−LH)]−1 [(zI−Φ)(zI−Φx)−1Γu−(zI−Φx)(zI−Φx)−1Γˆu].
Therefore, if Γu=Γˆu and Φx = Φ, then this transfer function is identically zero. Assuming again that H = Hx, the transfer function from ω to r is the following:
(4.15)Gω(z)=H[zI−(Φ−LH)]−1[zI−Φ][zI−Φx]−1Γω.
In the special case where, in addition, Φx = Φ, the transfer function Gω(z) has n identical poles and zeros. This transfer functions is often stated as:
(4.16)Gω(z)=H[zI−(Φ−LH)]−1Γω,
where n pole and zero cancellations have occurred. These pole-zero cancellations and therefore the validity of equation 4.16 are dependent on the exact modeling assumption and the stability of the canceled poles.
Read full chapter
URL:
https://www.sciencedirect.com/science/article/pii/B9780121709600500815
Waveform selection for multistatic tracking of a maneuvering target
Ngoc Hung Nguyen, Kutluyıl Doğançay, in Signal Processing for Multistatic Radar Systems, 2020
2.5 Adaptive waveform selection
The main motivation behind adaptive waveform selection is that the tracking performance (i.e., the state estimation error covariance matrix) is dependent on the transmitted waveform parameters. To see this relationship more clearly, we recall from (2.20) that, at time instant k+1, the measurement covariance matrix Rk+1(ψk+1) is a function of the transmitted waveform parameter vector ψk+1. As a result, the error covariance of filtered state estimate Pm,k+1|k+1(ψk+1) for the mth EKF component of the IMM-EKF algorithm is explicitly dependent on ψk+1 as seen in (2.22). Consequently, the combined state error covariance matrix PIMM,k+1|k+1 is also a function of ψk+1. Based on this dependence, the tracking performance can be optimized by adaptively adjusting the parameters of the waveform transmitted at the next time instant k+1.
The criterion for our adaptive waveform selection scheme is to minimize the MSE of the target state estimate which is equivalent to minimizing the trace of the state estimate’s error covariance matrix. Since there exist more than one error covariance matrix for the maneuvering target tracking problem under consideration, i.e., P1,k+1|k+1,P2,k+1|k+1,…,PM,k+1|k+1 for the hypothesized models and PIMM,k+1|k+1 for the combined state estimate, one matrix must be chosen to characterize the tracking performance. Three options are available [44]:
- (i)
-
The most-likely covariance which corresponds to the dynamic model with the highest predicted probability of being the correct model:
(2.31)PMost-likely,k+1|k+1=Pm⋄,k+1|k+1
where
(2.32)m⋄=arg maxmμm,k+1|k.
- (ii)
-
The minimax covariance which corresponds to the covariance with the largest trace value:
(2.33)PMinimax,k+1|k+1=Pm▹,k+1|k+1
where
(2.34)m▹=arg maxm{trace(Pm,k+1|k+1)}.
- (iii)
-
The predicted combined covariance matrix PIMM,k+1|k defined by
(2.35a)xˆIMM,k+1|k=∑m=1Mμm,k+1|kxˆm,k+1|k,
(2.35b)PIMM,k+1|k=∑m=1Mμm,k+1|k(Pm,k+1|k+1+(xˆm,k+1|k−xˆIMM,k+1|k)(xˆm,k+1|k−xˆIMM,k+1|k)T).
Note that the error covariance of filtered IMM estimate, PIMM,k+1|k+1, cannot be used because the measurement vector y˜k+1 is not available during the waveform selection step at time instant k.
By denoting Pk+1|k+1⋆ as the covariance matrix chosen from the three above covariance matrices for using in adaptive waveform selection, the waveform optimization problem is defined as
(2.36)ψk+1opt=arg minψ∈Ψ{trace(Pk+1|k+1⋆(ψ))},
where Ψ is a library of possible waveforms. The waveform library may include a number of different radar waveform classes or a single radar waveform class with various waveform parameters. Note that this waveform selection step is performed at the end of the processing at time instant k and prior to the waveform transmission at the next time instant k+1.
Read full chapter
URL:
https://www.sciencedirect.com/science/article/pii/B978012815314700010X
Communication network operation for CPSs
Husheng Li, in Communications for Control in Cyber Physical Systems, 2016
-
1: forEach time slot do
-
2: forEach transmitter having packets to transmit do
-
3: Estimate the set of received measurementsY
-
4: forEach measurement y in the queue do
-
5: Use delay-tolerant Kalman filtering toestimate the error covariance matrices Σ and ΣY,y
-
6: Use Eqs.(7.56) and(7.58)to compute the number of equivalentbits.
-
7: end for
-
8: Compute the total length of the virtual queue and broadcastit.
-
9: end for
-
10: Broadcast the lengths of the virtual and actual queue lengths.
-
11: Compute the back pressure using Eq.(7.60).
-
12: Transmit the measurement having the maximum information, or do nottransmit.
-
13: end for
Read full chapter
URL:
https://www.sciencedirect.com/science/article/pii/B978012801950400007X
Optimal sensor configuration methods for state estimation
Ch. Venkateswarlu, Rama Rao Karri, in Optimal State Estimation for Process Monitoring, Fault Diagnosis and Control, 2022
6.2 Brief review on sensor configuration methods
Various techniques have been reported for sensor selection in linear and nonlinear systems. The sensor selection methods reported for linear systems include sensor network design based on steady-state behavior of the systems [1], sensor location techniques for dynamic systems based on minimization of error covariance matrices of Kalman filters [2], analysis of observability matrices [3], and techniques based on minimization of measurement cost [4]. Optimal sensor location for linear or linearized systems has also been reported by various other researchers [5,6]. However, a linearized model may not represent the actual dynamics of the process over the entire region of operation.
Most processes are accurately described by nonlinear dynamic models and the sensor location techniques based on these models would be more desirable for nonlinear systems. The issue of sensor selection for state estimation in nonlinear systems has been addressed by several researchers which include the observability analysis of nonlinear systems based on geometric approach [7], use of observability functions [8], and methods for distributed systems [9,10]. Sensor selection for state estimation in nonlinear systems has also been performed by using empirical observability gramians or observability covariance matrices [11,12]. These observability covariance matrices reflect the influence of process states on the measurements and they provide a comprehensive description of the state to output behavior of the system. Certain scalar measures computed from the error covariance matrices are used to quantify the degree of observability based on which the sensors that provide maximum amount of information are ranked [13]. This chapter primarly focuses on sensor selection methods for optimal estimation of states, which serve as inferential measurements for process operational strategies.
Sensor configuration methods are broadly classified into classical methods and gramian-based methods. The gramian-based methods include both the observability and empirical observability gramians. These methods are discussed as follows.
Read full chapter
URL:
https://www.sciencedirect.com/science/article/pii/B9780323858786000051
Special Volume: Computational Methods for the Atmosphere and the Oceans
Jacques Blum, … I. Michael Navon, in Handbook of Numerical Analysis, 2009
7.3 The KF formulation
The KF is a recursive filter that estimates the state of a dynamic system from a series of incomplete and noisy measurements.
Consider a linear observation process described by
(7.1)yko=Hkxkt+ek,
where k is a multiple of the number of time-steps between two consecutive observations in time. yk0 is the vector of observations while the vector ek is an additive noise representing the error in observations due for instance to instrumental error. Random noise ek is assumed white in time with mean 0 and covariance Rk, i.e.,
(7.2)E(ekekT)=RkdkdkT,
All the time, we consider a discrete in time stochastic dynamic system
(7.3)xkt=Mk−1xk−1t+ηk−1,
where Mk represents model dynamics while ηk is model error white in time with mean zero and covariance Qk,
(7.4)E(hkhkT)=QkdkdkT,
One can show that the linear KF (Gelb, Kasper, Nash, Price and Sutherland [1974], Jazwinski [1970], Todling [1999]) consists of following stages:
- •
-
Advance in time:
(7.5){xkf=Mk−1xk−1aPkf=Mk−1Pk−1aMk−1T+Qk−1,
where the forecast and analysis error covariance matrices at time k are given by
(7.6){Pkf=E{(xkt−xkf)(xkt−xkf)T}Pka=E{(xkt−xka)(xkt−xka)T}.
Qk−1 is the model error covariance matrix at time t = tk−1, and Mk−1 is the model dynamics.
xk−1a and
xk−1f are the analysis and the forecast at time t = tk−1. - •
-
Compute the Kalman gain:
(7.7)Kk=PkfHkT(HkPkfHkT+Rk)−1.
The matrix Kk is the optimal weighting matrix known as the Kalman gain matrix.
- •
-
Update the state:
(7.8)xka=xkf+Kk(yko−Hkxkf),
where
y0k is the observation at time t = tk, Hk is the observation matrix at time t= tk. - •
-
Update error covariance matrix:
(7.9)Pka=(I−KkHk)Pkf.
Read full chapter
URL:
https://www.sciencedirect.com/science/article/pii/S1570865908002093
Введя предположение о случайном характере оцениваемого вектора x и ошибок измерения v и задаваясь их статистическими свойствами, представляется логичным не только использовать этот факт при анализе точности того или иного алгоритма, но и попытаться учесть сделанные предположения уже на этапе постановки и решения задачи. Иными словами, попытаться построить алгоритм «хорошего» качества с точки зрения уровня и свойств соответствующих ему ошибок оценивания. Именно такие алгоритмы и будут рассматриваться в последующих разделах.
2.3.1 Постановка задачи получения оптимальных линейных оценок.
Итак, будем полагать, что задача оценивания (2.1.20), (2.1.21) решается в условиях, когда оцениваемый вектор x и ошибки измерения v считаются случайными. Количественная характеристика качества оценивания может быть введена с помощью скалярной функции
− ~
L(x x ( y)) , устанавливающей определенный штраф за отличие оценки от истинного значения
оцениваемого параметра и называемой функцией потерь. Наибольшее распространение при анализе качества оценок в задачах обработки навигационной информации получила
квадратичная функция потерь, имеющая вид
|
~ |
~ |
т |
(x |
~ |
n |
~ |
2 |
. |
||||
|
L(x − x ( y)) = (x − x ( y)) |
− x ( y)) |
= ∑(xi − xi ( y)) |
||||||||||
|
i=1 |
||||||||||||
|
Введем связанный с этой функцией потерь критерий в виде |
||||||||||||
|
~ |
( y)) |
т |
~ |
~ |
(2.3.1) |
|||||||
|
J = M x,y {(x − x |
(x − x ( y))}= M x,y {SpP}, |
|||||||||||
|
где |
||||||||||||
|
~ |
~ |
~ |
( y)) |
т |
(2.3.2) |
|||||||
|
P = M x,y (x |
− x ( y))(x − x |
|||||||||||
|
~ |
||||||||||||
|
матрица ковариаций ошибок ε( y) = x − x ( y) . |
||||||||||||
|
Сформулируем задачу оценивания вектора |
x |
по измерениям (2.1.21) |
следующим образом: |
найти такую оценку, которая обеспечит минимум математического ожидания для квадратичной функции потерь, т.е.
|
xˆ( y) = arg min M |
n |
~ |
2 |
||
|
x, y ∑ |
(x − x ( y)) |
. |
|||
|
~ |
i |
||||
|
x |
( y) |
i =1 |
|||
Таким образом, сформулированная задача нахождения оценки сводится к минимизации следа матрицы ковариаций ее ошибок или, что то же самое, к минимизации суммы дисперсий ошибок оценивания. Этот критерий получил наименование среднеквадратического критерия, а оценка,
обеспечивающая его минимум – оптимальной в среднеквадратическом смысле оценкой. Такую оценку называют еще оценкой с минимальной дисперсией (minimum variance estimate).
44
Заметим, что критерий (2.3.1) принципиально отличается от наблюдаемых критериев, поскольку цель решения задачи заключается в обеспечении определенных требований к ошибкам оценки искомого вектора, а не к вычисленным значениям измеряемых параметров.
Введем составной случайный вектор z = (xт , y т )т , включающий вектор оцениваемых
параметров и вектор измерений. Из выражения для критерия (2.3.1) следует, что для его
вычисления в общем случае требуется располагать совместной ф.п.р.в. fx,y (x, y) . Обычно при
решении задач обработки навигационной информации статистические свойства задаются для оцениваемого вектора и ошибок измерения, которые в наиболее полном объеме характеризуются
совместной ф.п.р.в. fx,v (x, v) . При наличии fx,v (x, v) плотность fx,y (x, y) в принципе может
быть получена с использованием соотношения (2.1.21) и правил преобразования случайных векторов, рассмотренных в 1.4. Однако, следует заметить, что, во-первых, не всегда имеются
достаточные основания для введения той или иной ф.п.р.в. fx,v (x, v) , а во-вторых, даже при наличии fx,v (x, v) нахождение fx,y (x, y) не является тривиальной задачей.
С целью упрощения задачи будем считать, что имеется информация лишь о первых двух
|
моментах вектора z , представленная в виде его математического ожидания z = (x т |
, y т )т и |
||||||||||
|
матрицы ковариаций |
|||||||||||
|
z |
P x |
P xy |
|||||||||
|
P |
= |
xy |
т |
, |
(2.3.3) |
||||||
|
) |
P |
y |
|||||||||
|
(P |
|||||||||||
|
а при нахождении оценки используется линейное относительно измерений выражение вида |
|||||||||||
|
~ |
= x + K ( y |
− y) . |
(2.3.4) |
||||||||
|
x ( y) |
Нетрудно заметить, что при таком виде оценки выполняется следующее равенство
~ =
M y x ( y) x .
Оценка, удовлетворяющая такому условию, называется несмещенной. Это весьма важное свойство оценки, более подробно будет обсуждаться в последующих разделах.
Подставляя (2.3.4) в (2.3.2), можем записать
J = M x,y {(x − x + K ( y − y))т (x − x + K ( y − y))}=
{ } (2.3.5)
= M x,y Sp(x − x + K ( y − y))(x − x + K ( y − y))т .
Из этого выражения вытекает, что для вычисления математического ожидания в (2.3.5) теперь уже достаточно знать только z = (x т , y т )т и P z . Введенные ограничения позволяют сформулировать следующую задачу.
Располагая математическим ожиданием и матрицей ковариации для вектора z = (x т , y т )т ,
найти несмещенную оценку вида (2.3.4), обеспечивающую минимум среднеквадратического критерия (2.3.5). Поскольку предполагается линейная зависимость оценки от измерений, то речь
45
таким образом пойдет о линейных несмещенных оценках с минимальной дисперсией или, что то же самое об оптимальных в среднеквадратическом смысле линейных оценках.
2.3.2 Решение задачи нахождения оптимальных линейных оценок
Опираясь на результаты, полученные в теории оценивания, можно получить следующий весьма важный результат.
Для того, чтобы линейная оценка (2.3.4) при решении задачи (2.1.20), (2.1.21)
|
обеспечивала минимум критерия (2.3.5) необходимо и достаточно, чтобы матрица |
K opt , |
|
используемая при вычислении этой оценки, удовлетворяла уравнению |
|
|
K opt P y = P xy . |
(2.3.6) |
Убедимся в справедливости этого утверждения. Для начала в целях упрощения будем считать, что векторы центрированные, т.е. их математические ожидания нулевые и таким образом вместо
|
~ |
||||||||||||||||||||||
|
(2.3.4) можно использовать выражение x ( y) = Ky . |
||||||||||||||||||||||
|
Необходимость. Представим произвольную матрицу |
~ |
|||||||||||||||||||||
|
K в виде |
||||||||||||||||||||||
|
~ |
~ |
(2.3.7) |
||||||||||||||||||||
|
K = K opt |
+δK , |
|||||||||||||||||||||
|
где K opt — матрица, удовлетворяющая (2.3.6), |
а δ |
— малый скалярный параметр. Подставляя |
||||||||||||||||||||
|
(2.3.7) в (2.3.5) и раскрывая скобки, получим |
}= |
|||||||||||||||||||||
|
~ |
(K |
opt |
~ |
(K |
opt |
~ |
т |
|||||||||||||||
|
J = M x,y {Sp(x − |
+ δK ) y)(x − |
+ δK ) y) |
||||||||||||||||||||
|
= Sp[P x |
− K opt P yx − P xy (K opt )т |
+ K opt (K opt )т ]− |
||||||||||||||||||||
|
~ |
yx |
+ P |
xy ~ т |
~ y |
(K |
opt |
) |
т |
− K |
opt |
P |
y ~ т |
)+ δ |
2 |
~ y ~ т |
. |
||||||
|
− δSp(KP |
K |
− KP |
K |
SpKP K |
Принимая во внимание, что следы прямой и транспонированной матриц совпадают, это выражение удобно преобразовать как
|
~ |
= Sp[P |
x |
− 2P |
xy |
(K |
opt |
) |
т |
+ K |
opt |
(K |
opt |
) |
т |
] − |
|||||
|
J |
||||||||||||||||||||
|
− 2δSp(P |
xy ~ т |
− K |
opt |
P |
y ~ т |
) + δ |
2 |
~ |
y |
~ |
||||||||||
|
K |
K |
SpKP |
K. |
Поскольку матрица K opt по предположению минимизирует выбранный критерий, то должно выполняться условие
|
~ |
~ |
~ |
~ |
|||||
|
dJ |
||||||||
|
= |
2Sp(P xy K т − K opt P y K |
т )= 2Sp(P xy − K opt P y )K т = 0 . |
||||||
|
dδ |
||||||||
|
δ=0 |
||||||||
|
~ |
K opt должна |
|||||||
|
Очевидно, что для выполнения этого условия при |
любой |
матрице |
||||||
|
K , |
||||||||
|
удовлетворять уравнению (2.3.6). |
||||||||
|
Достаточность |
||||||||
|
Предположим теперь, что K opt удовлетворяет (2.3.6). |
Покажем, что оценка |
xˆ( y) = K opt y |
||||||
|
минимизирует критерий (2.3.5). |
||||||||
|
Подставляя эту оценку в (2.3.5), запишем |
46
J opt =( M x,y {Sp(x − K opt y)(x − K opt y)т}=).
= Sp P x − 2P xy (K opt )т + K opt P y (K opt )т
~
Для произвольной матрицы K , заданной в виде (2.3.7), получим
|
~ |
~ |
~ ~ |
т . |
|
J |
= J opt − 2δSp((P xy − K opt P y )K |
т )+ δ2SpKP y K |
Поскольку по предположению второе слагаемое обращается в ноль, а третье — в силу
неотрицательности P y неотрицательно, то
|
~ |
|
|
J opt ≤ J , |
|
|
что и завершает доказательство достаточности. |
|
|
Если матрица P y не вырождена, то тогда из (2.3.6) следует |
|
|
K opt = P xy (P y )−1 , |
(2.3.8) |
|
и таким образом |
|
|
xˆ( y) = Pxy (P y )−1 y. |
(2.3.9) |
|
Сняв требование о центрированном характере векторов x и |
y , нетрудно убедиться в том, что |
приведенное доказательство полностью сохранится и на этот случай, если в качестве оптимальной
|
оценки принять выражение (2.3.4), в котором K = K opt , т.е. |
|
|
xˆ( y) = x + K opt ( y − y), |
(2.3.10) |
|
где K — матрица соответствующей размерности. |
|
|
Используя (2.3.10), нетрудно получить выражение для матрицы ковариаций |
|
|
Popt = M x, y{(x − xˆ( y))(x − xˆ( y))T } = |
|
|
= Px + K opt P y (K opt )T − K opt P yx − Pxy (K opt )T . |
|
|
Преобразуя это выражение с использованием (2.3.8), получаем |
|
|
Popt = P x − P xy (P y )-1 P yx . |
(2.3.11) |
Таким образом, алгоритм вычисления оптимальных в среднеквадратическом смысле линейных оценок и соответствующей им матрицы ковариаций при решении задачи оценивания (2.1.20), (2.1.21) задается соотношениями (2.3.10), (2.3.11).
Необходимо обратить внимание на одно весьма важное следствие из доказанного утверждения, имеющее существенное прикладное значение – алгоритм вычисления линейных оптимальных
|
оценок |
полностью определяется первыми двумя моментами для составного вектора |
|
z = (xт |
, y т )т и не зависит от вида ф.п.р.в. fx,y (x, y) . Иными словами при произвольном виде |
этих функций, имеющих одинаковые первые два момента, алгоритмы вычисления оптимальных в среднеквадратическом смысле линейных оценок и соответствующих им матриц ковариаций также будут одинаковыми.
47

2.3.3 Решение линейной задачи
Из предыдущего раздела следует, что для получения линейных оптимальных оценок необходимо располагать математическим ожиданием и матрицей ковариации для вектора
z = (x т , y т )т . Как отмечалось выше, при решении задач обработки навигационной информации считаются известными статистические свойства оцениваемого вектора и ошибок измерения. В
нелинейном случае даже при известном виде совместной ф.п.р.в. fx,v (x, v) возникает проблема
нахождения первых двух моментов вектора z = (x т , y т )т . Эта проблема легко решается для линейной задачи (2.1.10), (2.1.11), если заданы соответствующие характеристики для вектора
(x т , v т )т .
B , где матрица B определяет взаимную корреляцию x и v , то
R
|
P |
x |
P |
xy |
|||||
|
P z = |
= |
|||||||
|
(P xy )т |
P y |
.(2.3.12) |
||||||
|
P x |
P x H т + B |
|||||||
|
= |
HPx + Bт |
|||||||
|
HPx H т + HB + BтH т + R |
|
Принимая во внимание |
тот факт, что в этом случае P xy = P x H т |
+ B , |
|
P y = HP x H т + HB + B тH т + R , |
нетрудно конкретизировать выражения (2.3.10), (2.3.11) |
(см. |
задачу 2.3.1).
В частности, в случае, когда x и v некоррелированы, т.е. B = 0 , соотношения для оптимальной оценки и матрицы ковариаций ее ошибок могут быть представлены как
K opt = (P x H т )(HP x H т + R)−1 ,
Popt = P x − P x H т (HP x H т + R)−1 HP x .
Учитывая справедливость (1.6.27), (1.6.28) можем также записать
Popt = (P x )−1 + H тR−1H −1 ,
K opt = Popt H тR −1 .
(2.3.13)
(2.3.14)
(2.3.15)
(2.3.16)
Интересным представляется сопоставление оптимального в среднеквадратическом смысле
линейного алгоритма с алгоритмами, рассмотренными в предыдущем разделе, т.е. с алгоритмами метода наименьших квадратов и его модификациями. Нетрудно заметить, что при B = 0 выражение (2.3.10) при подстановке в него выражения (2.3.16) и выражение (2.3.15) совпадают с выражениями (2.2.28), (2.2.29), и таким образом полученный алгоритм совпадет с
алгоритмом ММНК, если в его критерии принять D = (P x )−1 , Q = R −1 . Причины такого совпадения обсуждаются в подразделе 2.5.4. Сопоставление между собой различных вариантов
48

МНК было проведено в подразделе 2.2.4. Поскольку при сделанных предположениях линейная оптимальная оценка совпадает с ММНК, полученные в этом разделе выводы относительно взаимосвязи ММНК с ОМКН и МНК в полном объеме распространяются на оптимальные в среднеквадратическом смысле линейные оценки.
В частности, если считать выполненным условие
|
(P x )−1 << H тR−1H |
(2.3.17) |
|
и, кроме того, принять R = r 2 E , т.е. полагать, что ошибки представляют |
собой |
некорррелированные случайные величины с одинаковыми дисперсиями, то тогда можно говорить о практическом совпадении оптимальных в среднеквадратическом смысле линейных оценок с оценками обычного МНК.
Важно подчеркнуть, что вывод о совпадении оптимальных в среднеквадратическом смысле линейных оценок с оценками ММНК справедлив лишь при отсутствии корреляции между оцениваемым вектором и ошибками измерений. При появлении такой корреляции оптимальный алгоритм изменяется, в то время как ММНК сохраняется прежним, поскольку в его критерии учет этого фактора не предусмотрен.
Проиллюстрируем сказанное на примере оценивания коэффициентов полинома первой степени по измерениям (2.1.3), считая, что ошибки измерения являются некоррелированными между собой центрированными случайными величинами с одинаковыми дисперсиями, равными r 2 , а
оцениваемые коэффициенты представляют собой центрированные ( x = 0 ), некоррелированные между собой и с ошибками измерений случайные величины с матрицей ковариаций
0
1 . Пример реализации измерений типа (2.1.3) приведен на рис. 2.3.1.
σ 12
Используя соотношения (2.3.15), (2.3.16), легко получить следующие выражения для оценок и матрицы ковариаций
|
1 |
+ |
m |
||||||||||||
|
1 |
σ2 |
r 2 |
||||||||||||
|
opt |
||||||||||||||
|
xˆ |
= |
0 |
m |
|||||||||||
|
r |
2 |
|||||||||||||
|
1 |
∑ti |
|||||||||||||
|
r 2 |
||||||||||||||
|
i=1 |
||||||||||||||
|
1 |
+ |
m |
||||||||||||
|
σ02 |
r 2 |
|||||||||||||
|
Popt = |
||||||||||||||
|
1 |
m |
1 |
||||||||||||
|
∑ti |
σ2 |
|||||||||||||
|
r 2 |
||||||||||||||
|
i=1 |
1 |
|
1 |
m |
−1 |
m |
||||||||||
|
∑ti |
∑yi |
||||||||||||
|
2 |
, |
||||||||||||
|
r |
i=1 |
i=1 |
|||||||||||
|
1 |
1 |
m |
m |
||||||||||
|
+ |
∑ti2 |
∑ti yi |
|||||||||||
|
σ2 |
r 2 |
||||||||||||
|
1 |
i=1 |
i=1 |
|||||||||||
|
1 |
m |
−1 |
|||||||||||
|
∑ti |
|||||||||||||
|
2 |
|||||||||||||
|
r |
i=1 |
||||||||||||
|
1 |
m |
. |
|||||||||||
|
+ |
∑ti2 |
||||||||||||
|
r 2 |
|||||||||||||
|
i=1 |
49

|
50 |
||||||||||
|
40 |
измеренные значения |
|||||||||
|
30 |
||||||||||
|
20 |
||||||||||
|
10 |
||||||||||
|
0 |
||||||||||
|
-10 |
линейный тренд |
|||||||||
|
-20 |
||||||||||
|
-30 |
1 |
2 |
3 |
4 |
5 |
6 |
7 |
8 |
9 |
10 |
|
0 |
||||||||||
|
номер измерения |
Рис.2.3.1 Пример реализации ошибок измерений, содержащих линейный тренд.
Критерий МНК, соответствующая ему оценка и матрица ковариаций ее ошибок в этой задаче будут определяться как
|
m |
||||||||||||||||||||
|
J мнк (x) = ∑( yi − x0 − x1ti )2 , |
(2.3.18) |
|||||||||||||||||||
|
i=1 |
||||||||||||||||||||
|
и таким образом можно записать |
||||||||||||||||||||
|
m |
−1 |
m |
m |
−1 |
||||||||||||||||
|
xˆ |
мнк |
m |
∑ti |
∑yi |
мнк |
2 |
m |
∑ti |
||||||||||||
|
0 |
= |
i=1 |
i=1 |
, |
P |
= r |
i=1 |
. |
||||||||||||
|
ˆ |
мнк |
m |
m |
m |
m |
m |
||||||||||||||
|
x |
∑ti |
2 |
∑ti yi |
∑ti |
2 |
|||||||||||||||
|
1 |
∑ti |
∑ti |
||||||||||||||||||
|
i=1 |
i=1 |
i=1 |
i=1 |
i=1 |
В ОМНК при диагональной матрице Q в (2.3.18) появятся сомножители qi , и соответственно выражения для оценки и матрицы ковариаций преобразуются к виду
m∑qi
xˆ омнк = mi=1
∑qi ti
i=1
|
m |
−1 |
m |
||
|
∑qiti |
∑qi yi |
|||
|
i=1 |
i=1 |
, |
||
|
m |
m |
|||
|
∑qi ti2 |
∑qi ti yi |
|||
|
i=1 |
i=1 |
m∑qi
Pомнк = mi=1
∑qi ti
i=1
|
m |
−1 |
|
∑qi ti |
|
|
i=1 |
. |
|
m |
|
|
∑qi ti2 |
|
|
i=1 |
|
Нетрудно заметить, что при qi = |
1 |
, i = |
, |
эти выражения совпадут с выражениями для |
||||||
|
1.m |
||||||||||
|
r 2 |
||||||||||
|
1 |
0 |
|||||||||
|
МНК, а, положив дополнительно D |
2 |
и учитывая, что x = 0 , легко убедиться, что |
||||||||
|
= |
σ0 |
|||||||||
|
0 |
1 |
|||||||||
|
σ2 |
||||||||||
|
1 |
50
оценки ММНК совпадут с оптимальными оценками.
|
1 |
m |
1 |
1 |
m |
||||
|
Условие (2.3.17) в этом примере сводится к неравенствам |
<< |
, |
<< |
∑ti2 , при |
||||
|
σ2 |
r 2 |
σ2 |
r 2 |
|||||
|
0 |
1 |
j=1 |
выполнении которых все рассматриваемые оценки будут между собой совпадать.
2.3.4 Свойство ортогональности оптимальных линейных оценок
Докажем следующее весьма важное свойство линейной оптимальной в среднеквадратическом смысле оценки xˆ( y) . В целях простоты сделаем это для случая x = 0 .
Для того, чтобы линейная оценка xˆ( y) = Ky была оптимальной, необходимо и достаточно
|
выполнение условия |
|
|
M{(x − xˆ( y)) y т} = M{εy т} = 0, |
(2.3.19) |
означающего, что ошибка оценки ε = x − xˆ( y) не коррелирована с вектором измерений y .
Когда два вектора некоррелированы, то, как отмечалось в 1.3.5, говорят также об их ортогональности. В связи с этим сформулированное свойство линейной оптимальной оценки называют также свойством или условием ортогональности [1.9].
|
Необходимость. Пусть оценка оптимальна, |
т. е. матрица K = K opt = P xy (P y )−1 , |
определяется |
|||
|
в соответствии с выражением (2.3.8). Отсюда с очевидностью следует, что |
|||||
|
M{(x − xˆ( y)) y т} = M{xy т − K opt yy т} = 0. |
|||||
|
Достаточность. |
|||||
|
Пусть равенство (2.3.19) выполнено. Тогда можем записать |
|||||
|
M{(x − Ky) y т} = 0 , |
|||||
|
т.е. P xy = KP y , откуда для матрицы |
K |
получаем выражение (2.3.8), подтверждающее |
|||
|
оптимальность оценки, удовлетворяющей уравнению (2.3.19). |
|||||
|
Приведенное утверждение будет также справедливо, если вместо (2.3.19) записать |
|||||
|
M{(x − xˆ( y))xˆ т ( y)} = M{εxˆ т ( y)} = 0, |
(2.3.20) |
||||
|
или |
|||||
|
M{(x − xˆ( y)(Ly)т} = M{ε(Ly)т} = 0, |
(2.3.21) |
||||
|
где L — произвольная матрица размерности n ×m . |
|||||
|
В частности, при L = L j = (0,…0,1,0000)т |
из (2.3.21) вытекает, что |
||||
|
j |
|||||
|
M{εyiт} = 0, |
i = |
. |
(2.3.22) |
||
|
1.m |
Равенства (2.3.19), (2.3.20), (2.3.21) означают тот факт, что ошибка оценки ε = x − xˆ( y)
ортогональна вектору оценки xˆ( y) , вектору измерений y , произвольной линейной
комбинации его компонент и каждой компоненте по отдельности.
51
Соседние файлы в предмете [НЕСОРТИРОВАННОЕ]
- #
- #
- #
- #
- #
- #
- #
- #
- #
- #
- #
Чтобы понять, как устроена ковариационная матрица вектора случайных ошибок (Omega) в модели со случайными эффектами, вычислим её элементы. Для этого определим дисперсии (varepsilon_{text{it}}) и случайных эффектов следующим образом: (text{var}left( varepsilon_{text{it}} right) = sigma_{varepsilon}^{2}), (text{var}left( mu_{i} right) = sigma_{mu}^{2}). Элементами ковариационной матрицы (Omega) являются коэффициенты ковариации:
(ctext{ov}left( v_{text{it}},v_{text{jp}} right), i,j = 1,2,ldots,n, t,p = 1,2,ldots,T.)
С учетом наших обозначений:
(ctext{ov}left( v_{text{it}},v_{text{jp}} right) = ctext{ov}left( mu_{i} + varepsilon_{text{it}},mu_{j} + varepsilon_{text{jp}} right) =)
(= ctext{ov}left( mu_{i},mu_{j} right) + ctext{ov}left( mu_{i},varepsilon_{text{jp}} right) + ctext{ov}left( varepsilon_{text{it}},mu_{j} right) + ctext{ov}left( varepsilon_{text{it}},varepsilon_{text{jp}} right) =)
(= ctext{ov}left( mu_{i},mu_{j} right) + ctext{ov}left( varepsilon_{text{it}},varepsilon_{text{jp}} right))
Здесь в последнем переходе мы использовали предпосылку №2 модели со случайными эффектами, в силу которой случайные ошибки (varepsilon_{text{it}}) не коррелированы с (mu_{i}).
Если (i = j) и (t = p), то
(ctext{ov}left( v_{text{it}},v_{text{jp}} right) = ctext{ov}left( mu_{i},mu_{i} right) + ctext{ov}left( varepsilon_{text{it}},varepsilon_{text{it}} right) = sigma_{mu}^{2} + sigma_{varepsilon}^{2} = sigma_{v}^{2}.)
Поэтому на главной диагонали ковариационной матрицы вектора случайных ошибок стоят суммы (sigma_{v}^{2} = sigma_{mu}^{2} + sigma_{varepsilon}^{2}).
Если (i = j) и (t neq p), то
(ctext{ov}left( v_{text{it}},v_{text{jp}} right) = ctext{ov}left( mu_{i},mu_{i} right) + ctext{ov}left( varepsilon_{text{it}},varepsilon_{text{ip}} right) = sigma_{mu}^{2} + 0 = sigma_{mu}^{2}.)
Если же (i neq j), то
(ctext{ov}left( v_{text{it}},v_{text{jp}} right) = ctext{ov}left( mu_{i},mu_{j} right) + ctext{ov}left( varepsilon_{text{it}},varepsilon_{text{jp}} right) = 0 + 0 = 0.)
Таким образом, ковариационная матрица вектора случайных ошибок представляет собой блочную матрицу размера n на n блоков:
(Omega = begin{pmatrix} begin{matrix} Sigma & mathbf{0} \ mathbf{0} & Sigma \ end{matrix} & cdots & begin{matrix} mathbf{0} \ mathbf{0} \ end{matrix} \ vdots & ddots & vdots \ begin{matrix} mathbf{0} & mathbf{0} \ end{matrix} & cdots & Sigma \ end{pmatrix})
Здесь (mathbf{0}) обозначает нулевую квадратную матрицу размера T на T, а (Sigma) — квадратную матрицу размера t на t, на главной диагонали которой стоят числа (sigma_{mu}^{2} + sigma_{varepsilon}^{2}), а вне главной диагонали — числа (sigma_{mu}^{2}):
(Sigma = begin{pmatrix} begin{matrix} sigma_{mu}^{2} + sigma_{varepsilon}^{2} & sigma_{mu}^{2} \ sigma_{mu}^{2} & sigma_{mu}^{2} + sigma_{varepsilon}^{2} \ end{matrix} & cdots & begin{matrix} sigma_{mu}^{2} \ sigma_{mu}^{2} \ end{matrix} \ vdots & ddots & vdots \ begin{matrix} text{ }sigma_{mu}^{2}text{ } & text{ }sigma_{mu}^{2}text{ } \ end{matrix} & cdots & sigma_{mu}^{2} + sigma_{varepsilon}^{2} \ end{pmatrix} = begin{pmatrix} begin{matrix} sigma_{v}^{2} & sigma_{mu}^{2} \ sigma_{mu}^{2} & sigma_{v}^{2} \ end{matrix} & cdots & begin{matrix} sigma_{mu}^{2} \ sigma_{mu}^{2} \ end{matrix} \ vdots & ddots & vdots \ begin{matrix} sigma_{mu}^{2} & sigma_{mu}^{2} \ end{matrix} & cdots & sigma_{v}^{2} \ end{pmatrix})
Представим, например, что в выборке имеются данные про три объекта ((n = 3)), и про каждый из них доступна информация за два периода времени (T = 2). В этом случае
(Sigma = begin{pmatrix} sigma_{mu}^{2} + sigma_{varepsilon}^{2} & sigma_{mu}^{2} \ sigma_{mu}^{2} & sigma_{mu}^{2} + sigma_{varepsilon}^{2} \ end{pmatrix}.)
И, следовательно, ковариационная матрица вектора случайных ошибок будет иметь вид:
(Omega = begin{pmatrix} begin{matrix} sigma_{mu}^{2} + sigma_{varepsilon}^{2} & sigma_{mu}^{2} \ sigma_{mu}^{2} & sigma_{mu}^{2} + sigma_{varepsilon}^{2} \ end{matrix} & begin{matrix} 0 & 0 \ 0 & 0 \ end{matrix} & begin{matrix} 0 & 0 \ 0 & 0 \ end{matrix} \ begin{matrix} 0 & 0 \ 0 & 0 \ end{matrix} & begin{matrix} sigma_{mu}^{2} + sigma_{varepsilon}^{2} & sigma_{mu}^{2} \ sigma_{mu}^{2} & sigma_{mu}^{2} + sigma_{varepsilon}^{2} \ end{matrix} & begin{matrix} 0 & 0 \ 0 & 0 \ end{matrix} \ begin{matrix} 0 & 0 \ 0 & 0 \ end{matrix} & begin{matrix} 0 & 0 \ 0 & 0 \ end{matrix} & begin{matrix} sigma_{mu}^{2} + sigma_{varepsilon}^{2} & sigma_{mu}^{2} \ sigma_{mu}^{2} & sigma_{mu}^{2} + sigma_{varepsilon}^{2} \ end{matrix} \ end{pmatrix}.)
С учетом этого результата процедура реализации доступного ОМНК для оценки параметров модели со случайными эффектами устроена так:
-
Находим оценки ({widehat{sigma}}_{v}^{2} = {widehat{sigma}}_{varepsilon}^{2} + {widehat{sigma}}_{mu}^{2}) и ({widehat{sigma}}_{mu}^{2}). Зная их, вычисляем оценку ковариационной матрицы вектора случайных ошибок (widehat{mathrm{Omega}}).
-
Находим оценку вектора коэффициентов модели со случайными эффектами при помощи доступного ОМНК (см. параграф 5.5):
(widehat{beta^{text{RE}}} = begin{pmatrix} begin{matrix} widehat{beta_{1}^{text{RE}}} \ widehat{beta_{2}^{text{RE}}} \ end{matrix} \ begin{matrix} ldots \ widehat{beta_{k}^{text{RE}}} \ end{matrix} \ end{pmatrix} = left( X^{T}{widehat{mathrm{Omega}}}^{- 1}X right)^{- 1}X^{T}{widehat{mathrm{Omega}}}^{- 1}y)
Поясним детали первого пункта описанной процедуры. Оценка ковариационной матрицы может быть вычислена по формуле:
(widehat{Omega} = begin{pmatrix} begin{matrix} widehat{Sigma} & mathbf{0} \ mathbf{0} & widehat{Sigma} \ end{matrix} & cdots & begin{matrix} mathbf{0} \ mathbf{0} \ end{matrix} \ vdots & ddots & vdots \ begin{matrix} mathbf{0} & mathbf{0} \ end{matrix} & cdots & widehat{Sigma} \ end{pmatrix}, где widehat{Sigma} = begin{pmatrix} begin{matrix} {widehat{sigma}}_{v}^{2} & {widehat{sigma}}_{mu}^{2} \ {widehat{sigma}}_{mu}^{2} & {widehat{sigma}}_{v}^{2} \ end{matrix} & cdots & begin{matrix} {widehat{sigma}}_{mu}^{2} \ {widehat{sigma}}_{mu}^{2} \ end{matrix} \ vdots & ddots & vdots \ begin{matrix} {widehat{sigma}}_{mu}^{2} & {widehat{sigma}}_{mu}^{2} \ end{matrix} & cdots & {widehat{sigma}}_{v}^{2} \ end{pmatrix}.)
Чтобы определить (widehat{Omega}), нужно получить состоятельные оценки ({widehat{sigma}}_{v}^{2}) и ({widehat{sigma}}_{mu}^{2}). Это можно сделать по следующим формулам:
({widehat{sigma}}_{v}^{2} = frac{1}{nT — k}sum_{i = 1}^{n}{sum_{t = 1}^{T}e_{text{it}}^{2}} (9.6),)
({widehat{sigma}}_{mu}^{2} = frac{1}{nT*frac{T — 1}{2} — k}sum_{i = 1}^{n}{sum_{t = 1}^{T — 1}{sum_{s = t + 1}^{T}{e_{text{it}}e_{text{is}}}}} (9.7).)
Здесь (e_{text{it}}) — остатки, полученные в ходе оценки параметров модели со случайными эффектами при помощи обычного МНК (pooled regression).
В статистике, иногда ковариационная матрица многомерной случайная величина неизвестна, но должна быть оценена. Оценка ковариационных матриц затем занимается вопросом о том, как аппроксимировать фактическую ковариационную матрицу на основе выборки из многомерного распределения. Простые случаи, когда наблюдения завершены, могут быть обработаны с помощью выборочной ковариационной матрицы. Примерная ковариационная матрица (SCM) представляет собой несмещенную и эффективную оценку ковариационной матрицы, если пространство ковариационных матриц рассматривается как внешняя выпуклая конус в R ; однако, измеренный с использованием внутренней геометрии положительно определенных матриц, SCM является смещенным и неэффективным оценщиком. Кроме того, если случайная величина имеет нормальное распределение, выборочная ковариационная матрица имеет распределение Уишарта, а его версия с немного другим масштабом — оценка максимального правдоподобия. Случаи с отсутствующими данными требуют более глубокого рассмотрения. Другой проблемой является устойчивость к выбросам, к которым выборочные ковариационные матрицы очень чувствительны.
Статистический анализ многомерных данных часто включает исследовательские исследования того, как переменные изменяются по отношению друг к другу, и это может сопровождаться явными статистическими моделями, включающими ковариационную матрицу переменных. Таким образом, оценка ковариационных матриц непосредственно на основе данных наблюдений играет две роли:
-
- для получения начальных оценок, которые могут использоваться для изучения взаимосвязей;
- для предоставления выборочных оценок, которые могут использоваться для проверки модели.
Оценки ковариационных матриц требуются на начальных этапах анализа главных компонентов и факторного анализа, а также используются в версиях регрессионного анализа, которые обрабатывают зависимые переменные в наборе данных вместе с независимой переменной как результат случайной выборки.
Содержание
- 1 Оценка в общем контексте
- 2 Оценка максимального правдоподобия для многомерного нормального распределения
- 2.1 Первые шаги
- 2.2 Трассировка матрицы 1 × 1
- 2.3 Использование спектральная теорема
- 2.4 Заключительные шаги
- 2.5 Альтернативный вывод
- 3 Оценка внутренней ковариационной матрицы
- 3.1 Внутреннее ожидание
- 3.2 Смещение выборочной ковариационной матрицы
- 4 Оценка усадки
- 5 Ближайшее допустимое матрица
- 6 См. также
- 7 Ссылки
Оценка в общем контексте
Дана выборка, состоящая из n независимых наблюдений x 1,…, x n p-мерного случайного вектора x ∈ R (ap × 1 вектор-столбец), несмещенный оценка ковариационной матрицы (p × p)
- Σ = E [(X — E [X]) (X — E [X]) T] { displaystyle OperatorName { Sigma} = operatorname {E} left [ left (X- operatorname {E} [X] right) left (X- operatorname {E} [X] right) ^ { mathrm {T}} right]}
— это образец ковариационной матрицы
- Q = 1 n — 1 ∑ i = 1 n (xi — x ¯) (xi — x ¯) T, { displaystyle mathbf {Q} = {1 over {n-1}} sum _ {i = 1} ^ {n} (x_ {i} — { overline {x}}) (x_ {i} — { overline {x}}) ^ { mathrm {T}},}
где xi { displaystyle x_ {i}}
- x ¯ = 1 n ∑ i = 1 nxi { displaystyle { overline {x}} = {1 over {n}} sum _ {i = 1} ^ {n} x_ {i}}
— выборочное среднее. Это верно независимо от распределения случайной величины X, конечно, при условии, что теоретические средние значения и ковариации существуют. Причина для фактора n — 1, а не n, по существу та же, что и причина того же фактора, появляющегося в несмещенных оценках выборочных дисперсий и выборочных ковариаций, что связано с фактом что среднее значение неизвестно и заменено выборочным средним.
В случаях, когда известно, что распределение случайной величины X находится в пределах определенного семейства распределений, другие оценки могут быть получены на основе этого предположения. Хорошо известен случай, когда случайная величина X нормально распределена : в этом случае оценка максимального правдоподобия ковариационной матрицы немного отличается от несмещенной оценки и определяется выражением
- Q n = 1 n ∑ i = 1 n (xi — x ¯) (xi — x ¯) T. { displaystyle mathbf {Q_ {n}} = {1 over n} sum _ {i = 1} ^ {n} (x_ {i} — { overline {x}}) (x_ {i} — { overline {x}}) ^ { mathrm {T}}.}
Вывод этого результата приведен ниже. Ясно, что разница между несмещенной оценкой и оценкой максимального правдоподобия уменьшается при больших n.
В общем случае несмещенная оценка ковариационной матрицы обеспечивает приемлемую оценку, когда все векторы данных в наблюдаемом наборе данных полны: то есть они не содержат недостающих элементов. Один из подходов к оценке ковариационной матрицы состоит в том, чтобы обрабатывать оценку каждой дисперсии или попарной ковариации отдельно и использовать все наблюдения, для которых обе переменные имеют допустимые значения. Предполагая, что отсутствующие данные отсутствуют случайно, это приводит к оценке ковариационной матрицы, которая является несмещенной. Однако для многих приложений эта оценка может оказаться неприемлемой, поскольку не гарантируется, что оцененная матрица ковариации будет положительной полуопределенной. Это может привести к расчетным корреляциям, имеющим абсолютные значения больше единицы, и / или необратимой ковариационной матрице.
При оценке кросс-ковариации пары сигналов, которые являются стационарными в широком смысле, отсутствующие выборки не обязательно должны быть случайными (например, подвыборка
Оценка максимального правдоподобия для многомерного нормального распределения
Случайный вектор X ∈ R (ap × 1 «вектор-столбец») имеет многомерное нормальное распределение с невырожденной ковариационной матрицей Σ в точности, если Σ ∈ R является положительно определенной матрицей и функция плотности вероятности X равна
- е (Икс) знак равно (2 π) — п 2 det (Σ) — 1 2 ехр (- 1 2 (x — μ) T Σ — 1 (x — μ)) { displaystyle f (x) = (2 pi) ^ {- { frac {p} {2}}} , det ( Sigma) ^ {- { frac {1} {2}}} exp left (- {1 over 2 } (x- mu) ^ { mathrm {T}} Sigma ^ {- 1} (x- mu) right)}
где μ ∈ R — это ожидаемое значение X. Ковариационная матрица Σ является многомерным аналогом того, что в одном измерении было бы дисперсией, а
- (2 π) — p 2 det ( Σ) — 1 2 { displaystyle (2 pi) ^ {- { frac {p} {2}}} det ( Sigma) ^ {- { frac {1} {2}}}}
нормализует плотность f (x) { displaystyle f (x)}
Предположим теперь, что X 1,…, X n — независимые и идентично распределенные выборки из приведенного выше распределения. На основании наблюдаемых значений x1,…, x n этого образца, мы хотим оценить Σ.
Первые шаги
Функция правдоподобия:
- L (μ, Σ) = (2 π) — np 2 ∏ i = 1 n det (Σ) — 1 2 exp (- 1 2 (xi — μ) T Σ — 1 (xi — μ)) { displaystyle { mathcal {L}} ( mu, Sigma) = (2 pi) ^ {- { frac {np } {2}}} , prod _ {i = 1} ^ {n} det ( Sigma) ^ {- { frac {1} {2}}} exp left (- { frac { 1} {2}} (x_ {i} — mu) ^ { mathrm {T}} Sigma ^ {- 1} (x_ {i} — mu) right)}
Это довольно легко показано, что оценка максимального правдоподобия среднего вектора μ является вектором «выборочного среднего »:
- x ¯ = x 1 + ⋯ + xnn. { displaystyle { overline {x}} = { frac {x_ {1} + cdots + x_ {n}} {n}}.}
См. раздел об оценке в статье о нормальное распределение для подробностей; здесь процесс аналогичен.
Поскольку оценка x ¯ { displaystyle { bar {x}}}
- L (x ¯, Σ) ∝ det (Σ) — n 2 exp (- 1 2 ∑ i = 1 n (xi — x ¯) T Σ — 1 (xi — x ¯))), { displaystyle { mathcal {L}} ({ overline {x}}, Sigma) propto det ( Sigma) ^ {- { frac {n} {2}}} exp left (- {1 over 2} sum _ {i = 1} ^ {n} (x_ {i} — { overline {x}}) ^ { mathrm {T}} Sigma ^ {- 1} (x_ {i} — { overline {x}}) right),}
, а затем найдите значение Σ, которое максимизирует вероятность данных (на практике легче работать с log L { displaystyle { mathcal {L}}}
След матрицы 1 × 1
Теперь мы подошли к первому удивительному шагу: рассмотрим скаляр (xi — x ¯) T Σ — 1 (xi — x ¯) { displaystyle (x_ {i} — { overline {x}}) ^ { mathrm {T}} Sigma ^ {- 1} (x_ {i} — { overline {x }})}
- L (x ¯, Σ) ∝ det (Σ) — n 2 exp (- 1 2 ∑ i = 1 n tr ((xi — x ¯) T Σ — 1 (xi — x ¯)))) = det (Σ) — n 2 exp (- 1 2 ∑ i = 1 n tr ((xi — x ¯) (xi — x ¯) T Σ — 1)) = det (Σ) — n 2 exp (- 1 2 tr (∑ i = 1 n (xi — x ¯) (xi — x ¯) T Σ — 1)) = det (Σ) — n 2 exp (- 1 2 tr (S Σ — 1)) { Displaystyle { begin {align} { mathcal {L}} ({ overline {x}}, Sigma) propto det ( Sigma) ^ {- { frac {n } {2}}} exp left (- {1 over 2} sum _ {i = 1} ^ {n} operatorname {tr} left ( left (x_ {i} — { overline { x}} right) ^ { mathrm {T}} Sigma ^ {- 1} left (x_ {i} — { overline {x}} right) right) right) \ = det ( Sigma) ^ {- { frac {n} {2}}} exp left (- {1 over 2} sum _ {i = 1} ^ {n} operatorname {tr} left ( left (x_ {i} — { overline {x}} right) left (x_ {i} — { overline {x}} right) ^ { mathrm {T}} Sigma ^ {- 1} right) right) \ = det ( Sigma) ^ {- { frac {n} {2}}} exp left (- {1 over 2} operatorname {tr} left ( sum _ {i = 1} ^ {n} left (x_ {i} — { overline {x}} right) left (x_ {i} — { overline {x}} right) ^ { mathrm {T}} Sigma ^ {- 1} right) right) \ = det ( Sigma) ^ {- { frac {n} {2}}} exp left (- {1 over 2} operatorname {tr} left (S Sigma ^ {- 1} right) right) end {align}}}
где
- S = ∑ i = 1 n ( xi — x ¯) (xi — x ¯) T ∈ R p × p. { displaystyle S = sum _ {i = 1} ^ {n} (x_ {i} — { overline {x}}) (x_ {i} — { overline {x}}) ^ { mathrm { T}} in mathbf {R} ^ {p times p}.}
S { displaystyle S}

Использование спектральной теоремы
Из спектральной теоремы из линейной алгебры следует, что положительно определенная симметричная матрица S имеет единственную положительную — определенный симметричный квадратный корень S. Мы снова можем использовать «циклическое свойство» следа для записи
- det (Σ) — n 2 exp (- 1 2 tr (S 1 2 Σ — 1 S 1 2)). { displaystyle det ( Sigma) ^ {- { frac {n} {2}}} exp left (- {1 over 2} operatorname {tr} left (S ^ { frac {1 } {2}} Sigma ^ {- 1} S ^ { frac {1} {2}} right) right).}
Пусть B = S Σ S. Тогда приведенное выше выражение принимает вид
- det (S) — n 2 det (B) n 2 exp (- 1 2 tr (B)). { displaystyle det (S) ^ {- { frac {n} {2}}} det (B) ^ { frac {n} {2}} exp left (- {1 over 2} operatorname {tr} (B) right).}
Положительно определенная матрица B может быть диагонализована, а затем проблема поиска значения B, которое максимизирует
- det (B) n 2 exp ( — 1 2 тр (B)) { displaystyle det (B) ^ { frac {n} {2}} exp left (- {1 over 2} operatorname {tr} (B) right)}
Поскольку след квадратной матрицы равен сумме собственных значений («след и собственные значения» ), уравнение сводится к задаче поиска собственных значений λ 1,…, λ p, которые максимизируют
- λ за 2 exp (- λ i 2). { displaystyle lambda _ {i} ^ { frac {n} {2}} exp left (- { frac { lambda _ {i}} {2}} right).}
Это — это просто задача исчисления, и мы получаем λ i = n для всех i. Таким образом, предположим, что Q — матрица собственных векторов, тогда
- B = Q (n I p) Q — 1 = n I p { displaystyle B = Q (nI_ {p}) Q ^ {- 1} = nI_ {p}}
т. е. n раз больше единичной матрицы p × p.
Завершение шагов
Наконец, мы получаем
- Σ = S 1 2 B — 1 S 1 2 = S 1 2 (1 n I p) S 1 2 = S n, { displaystyle Sigma = S ^ { frac {1} {2}} B ^ {- 1} S ^ { frac {1} {2}} = S ^ { frac {1} {2}} left ( { frac {1} {n}} I_ {p} right) S ^ { frac {1} {2}} = { frac {S} {n}},}
то есть p × p «образец ковариационной матрицы»
- S n = 1 n ∑ i = 1 n (X i — X ¯) (X i — X ¯) T { displaystyle {S over n} = {1 over n} sum _ {i = 1} ^ {n} (X_ {i} — { overline {X}}) (X_ {i} — { overline {X}}) ^ { mathrm {T}}}
— это оценка максимального правдоподобия «матрицы ковариаций совокупности» Σ. На этом этапе мы используем прописную букву X, а не строчную букву x, потому что мы думаем о ней «как об оценке, а не как об оценке», т.е. как о чем-то случайном, распределение вероятностей которого мы могли бы получить, зная. Можно показать, что случайная матрица S имеет распределение Уишарта с n — 1 степенями свободы. То есть:
- ∑ i = 1 n (X i — X ¯) (X i — X ¯) T ∼ W p (Σ, n — 1). { displaystyle sum _ {я = 1} ^ {n} (X_ {i} — { overline {X}}) (X_ {i} — { overline {X}}) ^ { mathrm {T} } sim W_ {p} ( Sigma, n-1).}
Альтернативный вывод
Альтернативный вывод оценки максимального правдоподобия может быть выполнен с помощью формул матричного исчисления ( см. также дифференциал определителя и дифференциал обратной матрицы ). Он также проверяет вышеупомянутый факт об оценке максимального правдоподобия среднего. Перепишите вероятность в журнал, используя трюк с трассировкой:
- ln L (μ, Σ) = const — n 2 ln det (Σ) — 1 2 tr [Σ — 1 ∑ i = 1 n (xi — μ) (xi — μ) T]. { displaystyle ln { mathcal {L}} ( mu, Sigma) = operatorname {const} — {n over 2} ln det ( Sigma) — {1 over 2} operatorname { tr} left [ Sigma ^ {- 1} sum _ {i = 1} ^ {n} (x_ {i} — mu) (x_ {i} — mu) ^ { mathrm {T}} right].}
Дифференциал этого логарифмического правдоподобия равен
- d ln L (μ, Σ) = — n 2 tr [Σ — 1 {d Σ}] — 1 2 tr [- Σ — 1 {d Σ} Σ — 1 ∑ i = 1 n (xi — μ) (xi — μ) T — 2 Σ — 1 ∑ i = 1 n (xi — μ) {d μ} T]. { displaystyle d ln { mathcal {L}} ( mu, Sigma) = — { frac {n} {2}} operatorname {tr} left [ Sigma ^ {- 1} left {d Sigma right } right] — {1 over 2} operatorname {tr} left [- Sigma ^ {- 1} {d Sigma } Sigma ^ {- 1} sum _ {i = 1} ^ {n} (x_ {i} — mu) (x_ {i} — mu) ^ { mathrm {T}} -2 Sigma ^ {- 1} sum _ {i = 1} ^ {n} (x_ {i} — mu) {d mu } ^ { mathrm {T}} right].}
Это, естественно, разбивается на части, связанные с оценкой среднего и части, относящейся к оценке дисперсии. условие первого порядка для максимума, d ln L (μ, Σ) = 0 { displaystyle d ln { mathcal {L}} ( mu, Sigma) = 0}



- ∑ i = 1 n ( xi — μ) = 0, { displaystyle sum _ {i = 1} ^ {n} (x_ {i} — mu) = 0,}
, что приводит к оценке максимального правдоподобия
- μ ^ = X ¯ = 1 n ∑ i = 1 n X i. { displaystyle { widehat { mu}} = { bar {X}} = {1 over n} sum _ {i = 1} ^ {n} X_ {i}.}
Это позволяет нам упростить
- ∑ я знак равно 1 N (xi — μ) (xi — μ) T = ∑ i = 1 n (xi — x ¯) (xi — x ¯) T = S { displaystyle sum _ {i = 1} ^ {n} (x_ {i} — mu) (x_ {i} — mu) ^ { mathrm {T}} = sum _ {i = 1} ^ {n} (x_ {i} — { bar {x}}) (x_ {i} — { bar {x}}) ^ { mathrm {T}} = S}
, как определено выше. Тогда термины, содержащие d Σ { displaystyle d Sigma}

- — 1 2 tr (Σ — 1 {d Σ} [n I p — Σ — 1 S]). { displaystyle — {1 over 2} operatorname {tr} left ( Sigma ^ {- 1} left {d Sigma right } left [nI_ {p} — Sigma ^ {- 1 } S right] right).}
Условие первого порядка d ln L (μ, Σ) = 0 { displaystyle d ln { mathcal {L}} ( mu, Sigma) = 0}


- Σ ^ = 1 n S, { displaystyle { widehat { Sigma}} = {1 over n} S,}
, что, конечно, совпадает с каноническим выводом, приведенным ранее.
Дуайер указывает, что разложение на два члена, как показано выше, является «ненужным», и выводит оценщик за две строки работы. Обратите внимание, что может быть нетривиальной задачей показать, что такая производная оценка является уникальным глобальным максимизатором для функции правдоподобия.
Оценка внутренней ковариационной матрицы
Внутреннее ожидание
Для выборки из n независимых наблюдений x 1,…, x n p-мерной гауссовской случайной величины X с нулевым средним и ковариацией R, оценка максимального правдоподобия из R определяется как
- R ^ = 1 n i = 1 nxixi T. { displaystyle { hat { mathbf {R}}} = {1 over n} sum _ {i = 1} ^ {n} x_ {i} x_ {i} ^ { mathrm {T}}. }
Параметр R принадлежит набору положительно определенных матриц, который является римановым многообразием, а не векторным пространством , следовательно, обычные понятия векторного пространства математического ожидания, то есть «E [R ^]», и смещение оценки должны быть обобщены на многообразия, чтобы иметь смысл проблемы оценки ковариационной матрицы. Это можно сделать, определив математическое ожидание многозначной оценки R ^ по отношению к многозначной точке R как
- ER [R ^] = def exp R E [ехр R — 1 R ^] { displaystyle mathrm {E} _ { mathbf {R}} [{ hat { mathbf {R}}}] { stackrel { mathrm {def} } {=}} exp _ { mathbf {R}} mathrm {E} left [ exp _ { mathbf {R}} ^ {- 1} { hat { mathbf {R}}} right]}
где
- ехр R (R ^) = R 1 2 ехр (R — 1 2 R ^ R — 1 2) R 1 2 { displaystyle exp _ { mathbf {R }} ({ hat { mathbf {R}}}) = mathbf {R} ^ { frac {1} {2}} exp left ( mathbf {R} ^ {- { frac {1 } {2}}} { hat { mathbf {R}}} mathbf {R} ^ {- { frac {1} {2}}} right) mathbf {R} ^ { frac {1 } {2}}}
- ехр R — 1 (R ^) = R 1 2 (журнал R — 1 2 R ^ R — 1 2) R 1 2 { displaystyle exp _ { mathbf {R }} ^ {- 1} ({ hat { mathbf {R}}}) = mathbf {R} ^ { frac {1} {2}} left ( log mathbf {R} ^ {- { frac {1} {2}}} { hat { mathbf {R}}} mathbf {R} ^ {- { frac {1} {2}}} right) mathbf {R} ^ { frac {1} {2}}}
— экспоненциальный map и обратная экспоненциальная карта, соответственно, «exp» и «log» обозначают обычную матричную экспоненту и матричный логарифм, а E [·] — это обычный оператор математического ожидания, определенный в векторном пространстве, в данном случае касательном пространстве многообразия.
Смещение выборочной ковариационной матрицы
Векторное поле Оценка SCM R ^ { displaystyle { hat { mathbf {R}}}}
- B (R ^) = exp R — 1 ER [R ^ ] = Е [ехр R — 1 R ^] { Displaystyle mathbf {B} ({ hat { mathbf {R}}}) = exp _ { mathbf {R}} ^ {- 1} mathrm {E} _ { mathbf {R}} left [{ hat { mathbf {R}}} right] = mathrm {E} left [ exp _ { mathbf {R}} ^ { -1} { hat { mathbf {R}}} right]}
Внутреннее смещение оценки тогда определяется как exp R B (R ^) { displaystyle exp _ { mathbf { R}} mathbf {B} ({ hat { mathbf {R}}})}
Для сложных гауссовских случайных величин это векторное поле смещения может быть показано равным
- B (R ^) = — β (p, n) R { displaystyle mathbf {B} ({ hat { mathbf {R}}}) = — beta (p, n) mathbf {R}}
где
- β (p, n) = 1 p (p log n + p — ψ (n — p + 1) + (n — p + 1) ψ (n — p + 2) + ψ (n + 1) — (n + 1) ψ (n + 2)) { displaystyle beta (p, n) = { frac {1} {p}} left (p log n + p- psi (n-p + 1) + (n-p + 1) psi (n-p + 2) + psi (n + 1) — (n + 1) psi (n + 2) right)}
и ψ (·) — это дигамма функция. Внутреннее смещение выборочной ковариационной матрицы равно
- exp R B (R ^) = e — β (p, n) R { displaystyle exp _ { mathbf {R}} mathbf {B} ({ hat { mathbf {R}}}) = e ^ {- beta (p, n)} mathbf {R}}
, и SCM асимптотически несмещен при n → ∞.
Аналогично, внутренняя неэффективность выборочной ковариационной матрицы зависит от римановой кривизны пространства положительно определенных матриц.
Оценка усадки
Если размер выборки n невелик, а количество рассматриваемых переменных p велико, указанные выше эмпирические оценки ковариации и корреляции очень нестабильны. В частности, можно предоставить оценки, которые значительно улучшают оценку максимального правдоподобия с точки зрения среднеквадратичной ошибки. Более того, для n < p (the number of observations is less than the number of random variables) the empirical estimate of the covariance matrix becomes сингулярное число, то есть его нельзя инвертировать для вычисления матрицы точности.
. В качестве альтернативы было предложено множество способов для улучшения оценки ковариационной матрицы. Все эти подходы основаны на концепции усадки. Это подразумевается в байесовских методах и в штрафных методах максимального правдоподобия и явно в методе усадки типа Стейна.
Простая версия оценки усадки ковариационной матрицы представлен оценкой усадки Ледуа-Вольфа. Рассматривается выпуклая комбинация эмпирической оценки (A { displaystyle A}



Были предложены различные цели сокращения:
- единичная матрица, масштабированная по средней выборочной дисперсии ;
- одноиндексная модель ;
- модель с постоянной корреляцией, в которой выборочные дисперсии сохраняются, но предполагается, что все парные коэффициенты корреляции равны друг другу;
- двухпараметрическая матрица, где все дисперсии идентичны, и все ковариации идентичны друг другу (хотя и не идентичны дисперсиям);
- диагональная матрица, содержащая выборочные дисперсии по диагонали и нули везде;
- единичная матрица.
Оценщик усадки может быть обобщен на многоцелевой оценщик усадки, который использует несколько целевых объектов одновременно. Программное обеспечение для вычисления оценки ковариационной усадки доступно в R (пакеты corpcor и ShrinkCovMat ), в Python (библиотека scikit -learn ), а в MATLAB.
Ближайшая допустимая матрица
В некоторых приложениях (например, построение моделей данных только из частично наблюдаемых данных) требуется найти «ближайшую» ковариационную матрицу или корреляционная матрица с заданной симметричной матрицей (например, наблюдаемых ковариаций). В 2002 году Хайэм формализовал понятие близости, используя взвешенную норму Фробениуса и предоставил метод для вычисления ближайшей корреляционной матрицы.
См. Также
Ссылки
- ^ Смит, Стивен Томас (май 2005 г.). «Ковариация, подпространство и внутренние границы Крамера – Рао». IEEE Trans. Сигнальный процесс. 53 (5): 1610–1630. doi : 10.1109 / TSP.2005.845428.
- ^Надежная статистика, Питер Дж. Хубер, Wiley, 1981 (переиздано в мягкой обложке, 2004)
- ^«Современная прикладная статистика with S «, Брайан Д. Рипли, Springer, 2002, ISBN 0-387-95457-0, ISBN 978 -0-387-95457-8, стр. 336
- ^Девлин, Сьюзан Дж. ; Gnanadesikan, R.; Кеттенринг, Дж. Р. (1975). «Робастная оценка и обнаружение выбросов с помощью коэффициентов корреляции». Биометрика. 62(3): 531–545. doi : 10.1093 / biomet / 62.3.531.
- ^К.В. Mardia и (1979) Multivariate Analysis, Academic Press.
- ^Дуайер, Пол С. (июнь 1967). «Некоторые приложения матричных производных в многомерном анализе». Журнал Американской статистической ассоциации. 62 (318): 607–625. doi : 10.2307 / 2283988. JSTOR 2283988.
- ^О. Ледойт и М. Вольф (2004a) «Хорошо обусловленная оценка для крупномерных ковариационных матриц Архивировано 05.12.2014 в Wayback Machine » Журнал многомерного анализа 88(2): 365—411.
- ^ А. Тулумис (2015) «Непараметрические оценки ковариационной матрицы усадки типа Штейна в параметрах большой размерности « Вычислительная статистика и анализ данных 83: 251–261.
- ^О. Ледойт и М. Вольф (2003) «Улучшенная оценка ковариационной матрицы доходности акций с приложением для выбора портфеля Архивировано 05.12.2014 на Wayback Machine «Журнал эмпирических финансов 10 (5): 603—621».
- ^О. Ледойт и М. Вольф (2004b) «Дорогая, я сжал образец ковариационной матрицы Архивировано 05.12.2014 в Wayback Machine » Журнал управления портфелем 30(4): 110—119.
- ^Т. Ланцевики и М. Аладжем (2014) «Многоцелевой анализ сжатия для матриц ковариации », Транзакции IEEE по обработке сигналов, том: 62, выпуск 24, страницы: 6380-6390.
- ^corpcor: Эффективная оценка ковариации и (частичной) корреляции, CRAN
- ^ShrinkCovMat: Матрицы оценки ковариации усадки, CRAN
- ^Код MATLAB для целей усадки: масштабированная идентичность, одноиндексная модель, модель постоянной корреляции, двухпараметрическая матрица и диагональная матрица.
- ^Хайэм, Николас Дж. (2002). «Вычисление ближайшей корреляционной матрицы — задача из финансов». Журнал численного анализа IMA. 22 (3): 329–343. CiteSeerX 10.1.1.661.2180. doi :10.1093/imanum/22.3.329.

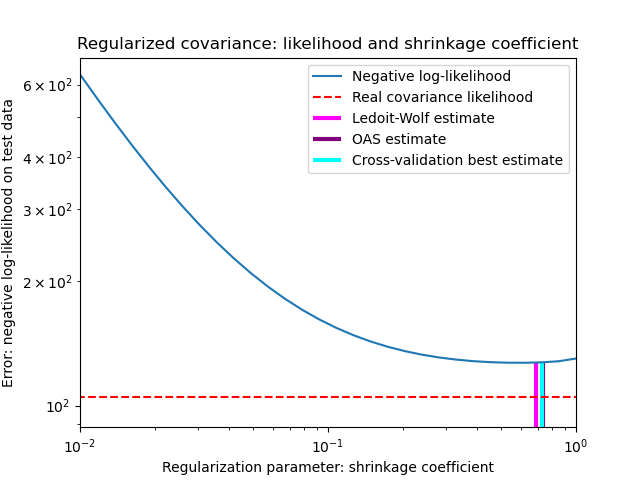
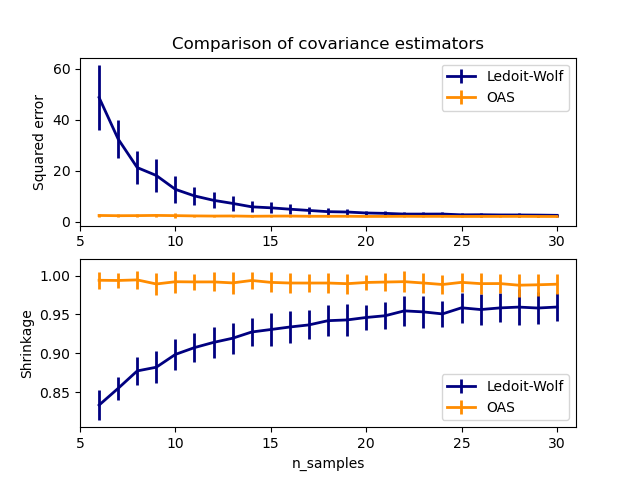
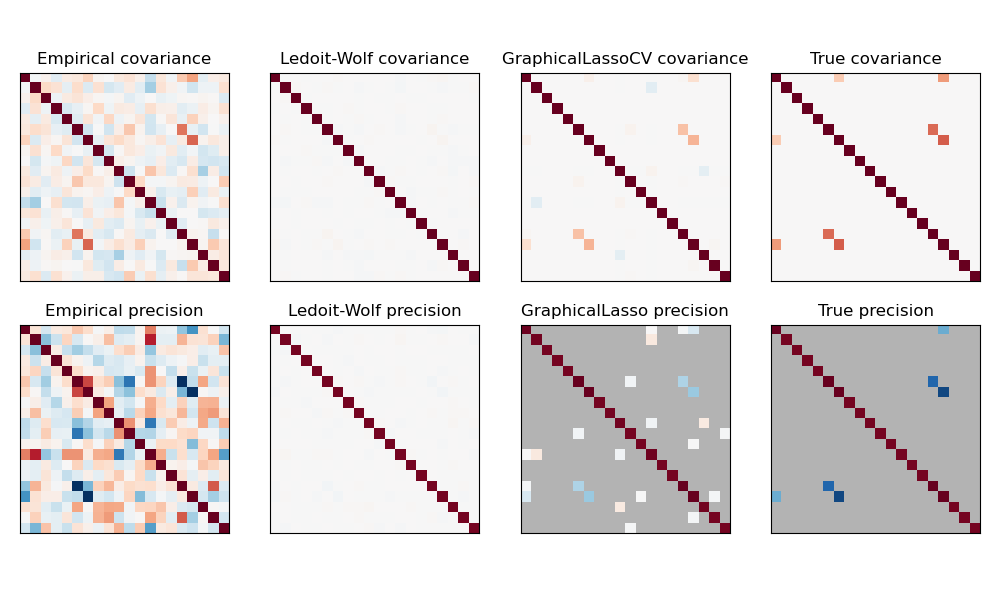

![{ displaystyle operatorname { Sigma} = operatorname {E} left [ left (X - operatorname {E} [X] right) left (X- operatorname {E} [X] right) ^ { mathrm {T}} right]}](https://wikimedia.org/api/rest_v1/media/math/render/svg/cdd1400b2d5e8baf3d9a79011f1452bb1d83c274)


















![ln { mathcal {L}} ( mu, Sigma) = operatorname {const} - {n over 2} ln det ( Sigma) - {1 over 2} operatorname {tr} left [ Sigma ^ {{- 1}} sum _ {{i = 1}} ^ {n} (x_ {i} - mu) (x_ {i} - mu) ^ {{ mathrm {T}}} right].](https://wikimedia.org/api/rest_v1/media/math/render/svg/19a132ab3db51593d7fba1786566392c2089f173)
![{ displaystyle d ln { mathcal {L}} ( mu, Sigma) = - { frac {n} {2}} operatorname {tr} left [ Sigma ^ {- 1} left {d Sigma right } right] - {1 over 2} operatorname {tr} left [- Sigma ^ {- 1} {d Sigma } Sigma ^ {- 1} sum _ {i = 1} ^ {n} (x_ {i} - mu) (x_ {i} - mu) ^ { mathrm {T }} -2 Sigma ^ {- 1} sum _ {i = 1} ^ {n} (x_ {i} - mu) {d mu } ^ { mathrm {T}} right].}](https://wikimedia.org/api/rest_v1/media/math/render/svg/8e05b9dbd637f1304a2e7781fa63fb813f8a5f3d)



![- {1 over 2} operatorname {tr} left ( Sigma ^ {{- 1}} left {d Sigma right } left [nI_ {p} - Sigma ^ {{- 1}} S right] right).](https://wikimedia.org/api/rest_v1/media/math/render/svg/1724960e30912702239cb54b5d90b71c4f89ce07)


![{ mathrm {E}} _ {{{ mathbf {R}}}} [{ hat {{ mathbf {R}} }}] { stackrel {{ mathrm {def}}} {=}} exp _ {{{ mathbf {R}}}} { mathrm {E}} left [ exp _ {{ { mathbf {R}}}} ^ {{- 1}} { hat {{ mathbf {R}}}} right]](https://wikimedia.org/api/rest_v1/media/math/render/svg/71ec1f6bcb105144b3b61dc03f28d46445b83064)


![{ mathbf {B}} ({ hat {{ mathbf {R}}}}) = exp _ {{{ mathbf {R}}}} ^ {{- 1}} { mathrm {E}} _ {{{ mathbf {R}}}} left [{ hat {{ mathbf {R}}}} right] = { mathrm {E}} left [ exp _ {{{ mathbf {R}}}} ^ {{- 1}} { hat {{ mathbf {R}}}} right ]](https://wikimedia.org/api/rest_v1/media/math/render/svg/c3e09f12f16b646e19a2737456dce7e5f5c89472)


