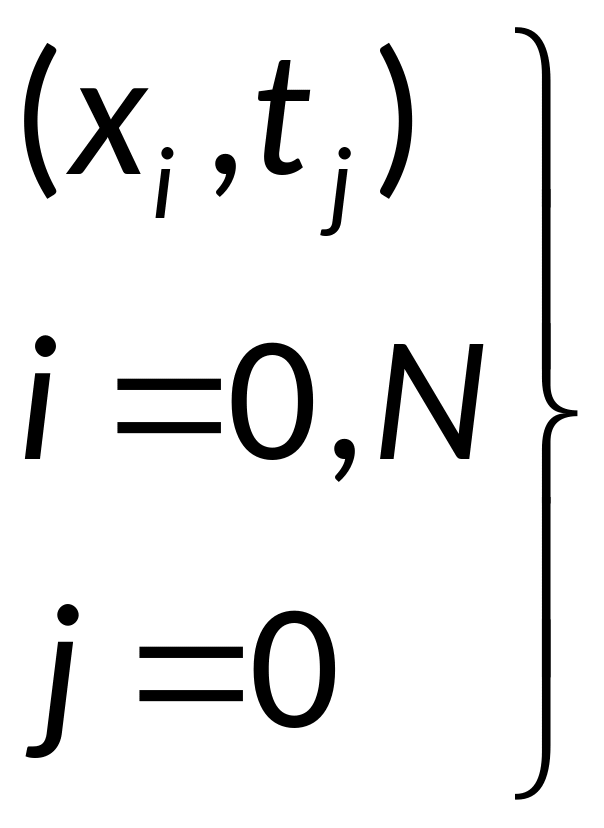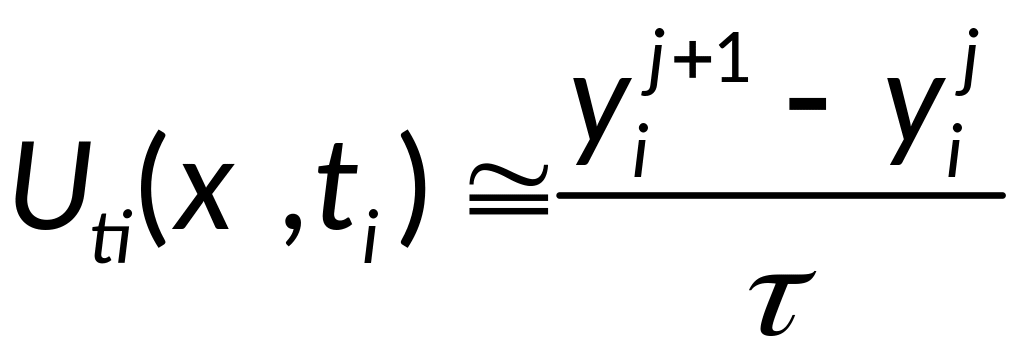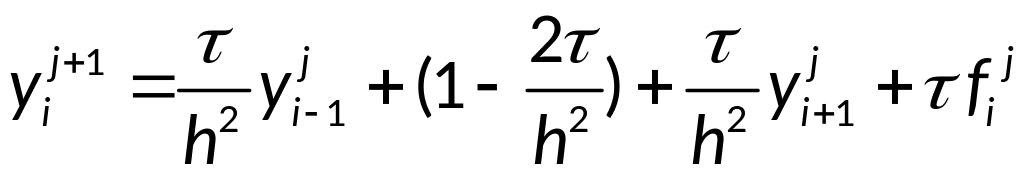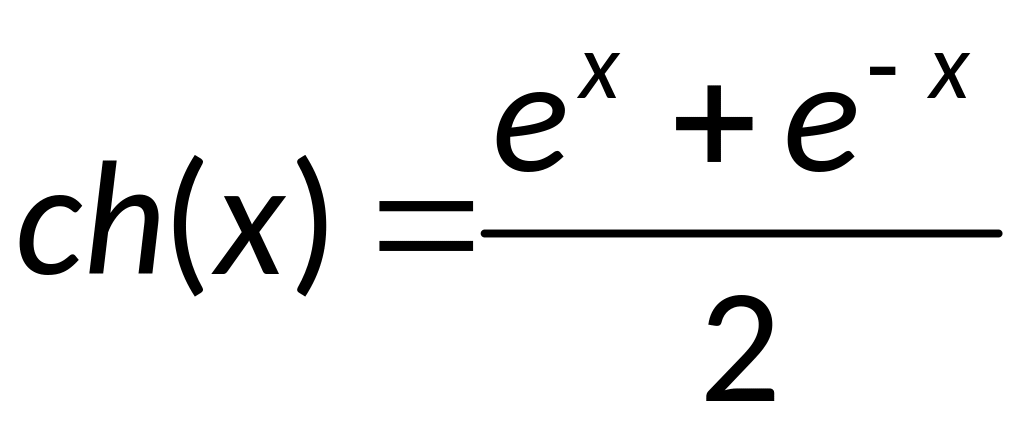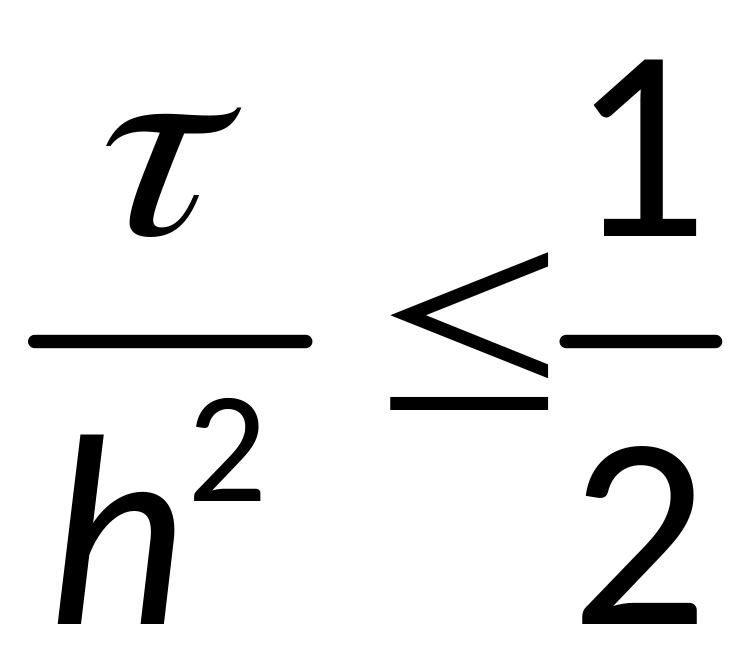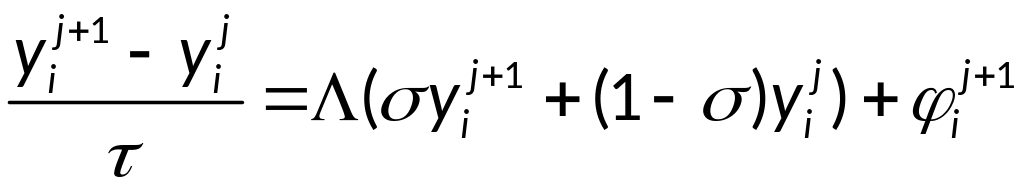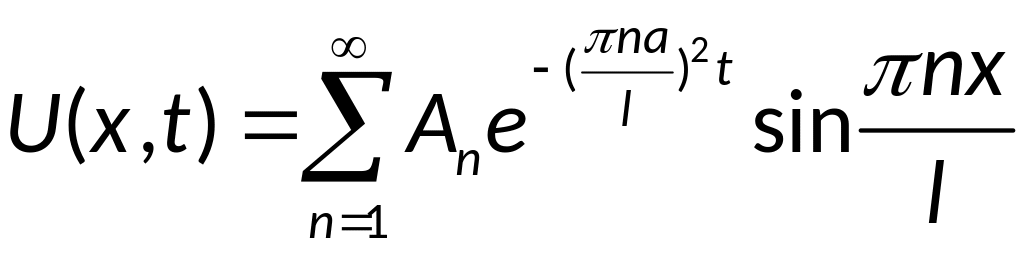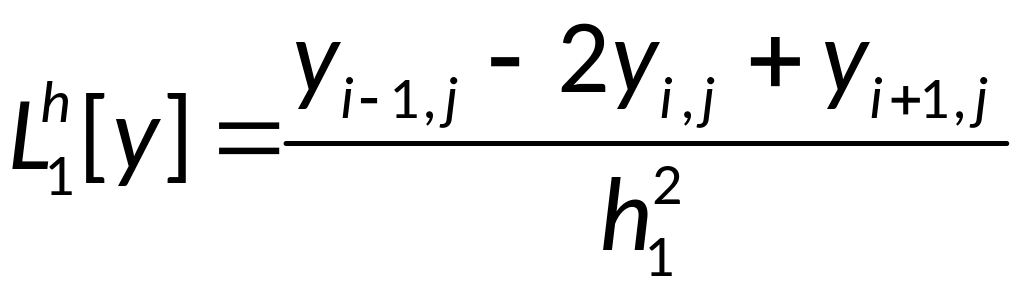ВЕСТН. САМАР. ГОС. ТЕХН. УН-ТА. СЕР. ТЕХНИЧЕСКИЕ НАУКИ. 2014. № 1 (41)
УДК 621.315.01
ПОГРЕШНОСТЬ АППРОКСИМАЦИИ УРАВНЕНИЯ НЕСТАЦИОНАРНОЙ ТЕПЛОПРОВОДНОСТИ ПЛАСТИНЫ С ГРАНИЧНЫМИ УСЛОВИЯМИ ТРЕТЬЕГО РОДА
В.И. Котенев, А.В. Котенев, А.Н. Татарников
Самарский государственный технический университет Россия, 443100, г. Самара, ул. Молодогвардейская, 244
E-mail: akotenev@samgtu.ru
Рассматривается одноэлементная аппроксимация уравнения нестационарной теплопроводности пластины при теплообмене с граничными условиями третьего рода с применением метода интегральных элементов, в котором использована квадратичная координатная функция. Динамика теплообмена пластины представлена типовым звеном второго порядка, для которого построены разностные частотные характеристики в заданном диапазоне относительных частот. Этот диапазон частот позволяет определить область, в которой допустима одноэлементная аппроксимация. Погрешность аппроксимации оценивается исходя из условия обеспечения заданной величины частоты среза системы автоматического управления температурой пластины. Рассмотрен пример определения частоты среза системы при Bi=1 и заданных значениях размеров и коэффициента температуропроводности материала пластины. Показано, что в диапазоне относительных частот от 0 до 4 погрешность аппроксимации амплитудно-частотной характеристики не превышает 1 дБ, а фазо-частотной характеристики — 5°.
Ключевые слова: уравнение нестационарной теплопроводности пластины, аппроксимация, система управления, одноэлементная аппроксимация, метод интегральных элементов, оценка погрешности аппроксимации.
Известно [1], что точное решение задачи нестационарной теплопроводности, даже для тела простой геометрической формы, выражается в виде бесконечного функционального ряда. Причем, если точное решение получено, то в практических расчетах используются только несколько членов этого ряда. Получение точного решения для тела сложной геометрической формы практически невозможно.
Поэтому разработка приближенных методов решений [2-5] имеет большое прикладное значение. Особенно эта проблема актуальна в решениях задач синтеза систем управления тепловыми процессами, так как модели их объектов управления содержат не только обыкновенные дифференциальные уравнения, но и уравнения в частных производных.
Существующие методы интегральных преобразований, ортогональной проекции [4] и ряд других методов, хотя и позволяют получать сравнительно простые приближенные модели, но они существенно отличаются от тех моделей,
Виктор Иванович Котенев (д.т.н., проф.), профессор кафедры «Электроснабжение промышленных предприятий».
Александр Викторович Котенев (к.т.н., доц.), доцент кафедры «Электроснабжение промышленных предприятий».
Алексей Николаевич Татарников, аспирант.
которые используются в теории систем автоматического управления, и по этой причине их применение крайне ограничено.
Из сравнения модели метода интегральных элементов [6] с точной моделью [7] по переходным характеристикам при скачкообразном изменении граничных условий следует, что они незначительно отличаются лишь на начальных участках, что практически не отражается на конечной температуре нагреваемого тела. Однако, это может негативно отразится на качестве процесса системы управления, и тем сильнее, чем выше ее быстродействие.
Поэтому погрешность аппроксимации недостаточно оценивать только по временным характеристикам. Удобно ее оценивать еще и по частотным характеристикам объекта управления, исходя из заданного быстродействия системы управления.
Данный подход рассматривается на примере уравнения нестационарной теплопроводности пластины
дЭ( г, г)_д 29( г
г, XI
дг
дг2
г> 0, 0 < г < 1
(1)
с краевыми условиями
дЭ(1, г)
дг
Э( г,0)_ 0; ^ [Эс (1, г)-Э(1, г)]_ 0; дЭ( 0, г)
(2)
дг
_ 0,
где Bi _ а/АЯп — число В1;
г _ аг/Я — относительное время;
Я _ Я / Яп — относительная толщина пластины;
а — коэффициент теплоотдаМи;
X, а — коэффициенты теплопроводности и температуропроводности;
Яп — толщина половины пластины;
Э, Э с — температуры шара и окружающей среды.
В [6] приведены системы обыкновенных дифференциальных и операторных уравнений, которые получены с помощью метода, изложенного в [5]. При однолинейной аппроксимации уравнения пластины система операторных уравнений представлена двумя уравнениями. Одно из них составлено для центра пластины
»1 (Р)_
а второе — для поверхности
»2 ( Р )_
»с ( Р )- Г21 р&2 ( р ) Гц р + 1
»с ( Р )- Т12 Р»1 ( Р) Гц Р + 1
где
(2) ь(1) (2) ь(1) ь(1) ь(1)
Г _ Ь(2)+ Г _ Ь(2) + Г _ Г _ Ь11 •
Гп _ьп + в. ; Г21 _Ь21 + в. ; Г22 _ в. ; Г12 _ в. ;
; й«—^ Ь(2)_ т (т + 3) ; . (2) т +1 т +1
¿г ; _ —
2 (т + 1)(т + 2)’ 11 (т + 1)(т + 2)’
»с ( Р) = ЭМ ; », (Р)_М£) ; _ 1,2.
Из этих уравнений можно выразить температуру поверхности пластины относительно температуры греющей среды:
»2 (Р) _ (Р)»с (р) ; (3)
(Гц — Г12 ) Р +1
(Г11Г22 — Г12Г21) р2 +(Гп + Г22 ) Р +1
(4)
где
Г11 _ 13/12 ; Г21 _ 23 ; Г22 _ 1/3; Г21 _ 5/12; Bi _ 1; т _ 2. Из точного решения уравнения (1) [7] следует, что
»2т (Р)_ ^2 (р)»с (р) . (5)
Передаточная функция, соответствующая точному решению является трансцендентной функцией комплексного переменного р
еЬд/р_
^2т _
сИ^/р + В1 1Л/р Частотная передаточная функция
сЪуЛа
^2т ( Р )_
Подставив в (6)
77 _72 _ * +7^
(6)
после несложных преобразований получим:
12т (П)_ 20lg
^2 2 а7 + а8
2
а5 + а6
V /
Ф2т («) _ arctg
^ а ^ а8
(7)
(8)
где
а7 _ а1а2а3 + аза4а5; а8 _ а1а2а5 — Оза4а6; а5 _ а3а4 + Bi х (а2а3 — а1а4);
а6 _ а1а2 + х Bi (а1а4 + а2а3); а1 _ sin х ; а2 _ 8И х; а3 _ со8 х; а4 _ сИ х ;
а7
в2
х =./— ; О = ю ; V 2 а
; ю — круговая частота.
Переходные характеристики, точные &2т (т) (оригинал выражения (5)) и приближенные &2 (т) (оригинал выражения (3)), при Bi = 1, т = 1, приведены на рис.1.
Мт),0.5
МО
0.4
0.3
0.2
0.1
0
А
// // / /
/ / г
0.1
Мх)’0.8
&2т (т)о.7 0.6 0.5 0.4 0.3 0.2 0.1 0
0
iНе можете найти то, что вам нужно? Попробуйте сервис подбора литературы.
0.5
0.2 0.3 0.4 0.5
//
п 1
Рис. 1. Точные $2т (т) (сплошные линии) и приближенные $2 (пунктирные линии) характеристики
Разностные логарифмические амплитудная АЬ (О) = ¿2 (О)-(О) и фазовая Аф(О) = ф2т (О) — ф2 (О) частотные характеристики представлены на рис. 2. Характеристики Ь (О) , ф (О) построены по выражению (4), а ¿2т (О), ф2т (О) — по соотношениям (7), (8).
Из анализа частотных характеристик следует, что в диапазоне частот 0<О<О1 (О1 = 100,6 «4) погрешность составляет: фазовой частотной характеристики ф<5°, амплитудной частотной характеристики — АЬ< 1 дБ. Погреш-
ность Лф(П) при частотах П>Ц растет почти по линейной зависимости, достигая Лф( 101’7 I = 30° , что необходимо учитывать при синтезе регуляторов.
Рис. 2. Погрешность частотных характеристик: фазовой Лф(П) — 1; логарифмической амплитудной ЛL (П) — 2
Например, при управлении температурой стальной пластины, толщина которой составляет
Яп = 0,03 м ,
а коэффициент температуропроводности
а = 1,25 -10″5 м2/с,
частота среза системы автоматического управления не должна превышать
а Ц 1,25 -10-5 • 4
®ср =—о =-2-= 0,0561 1 с.
ср Яп2 0,032
Для повышения быстродействия системы управления может быть использована более сложная математическая модель [6], которая получена при разбиении пластины на большое число частей.
Выводы. Дана количественная оценка погрешности аппроксимации уравнения нестационарной теплопроводности пластины с граничными условиями третьего рода обыкновенными линейными дифференциальными уравнениями. Показано, что однолинейная аппроксимация допустима при относительных частотах среза систем автоматического управления, не превышающих значений П = 4.
БИБЛИОГРАФИЧЕСКИЙ СПИСОК
1. Канторович Л.В., Крылов В.И. Приближенные методы высшего анализа. М.: Физматгиз, 1962 -708 с.
2. Кудинов В.А., Карташов Э.М., Калашников В.В. Аналитические решения задач тепломассопе-реноса и термоупругости для многослойных конструкций. — М.: Высшая школа, 2005. — 432с.
3. Цой П.В. Методы расчета задач тепломассопереноса. М.: Энергоатомиздат, 1984. — 416с.
4. Сегерлинд Л. Применение метода конечных элементов. М.: Мир, 1979. — 392с.
5. Котенев В.И. Приближенный метод решения задач нестационарной теплопроводности // Известия Академии наук СССР. Энергетика и транспорт. — 1983. — №3. — С. 111-116.
6. Котенев В.И., Котенев А.В. Аппроксимация уравнений теплопроводности конечным числом типовых динамических звеньев // Вестник СамГТУ Техн. науки. — 2013. — Вып№2 (38). — С. 158 — 163.
7. Лыков А.В. Теория теплопроводности. М.: Высшая школа, 1967. — 599 с.
Статья поступила 27 января 2014 г.
ACCURACY APPROXIMATION OF UNSTEADY HEAT CONDUCTION PLATE WITH BOUNDARY CONDITIONS OF THE THIRD KIND
V.I. Kotenev, A.V. Kotenev, A.N. Tatarnikov
Samara State Technical University
244, Molodogvardeyskaya st., Samara, 443100, Russia
In the paper one-element approximation of the equation of transient heat conduction of plate at heat exchange with boundary conditions of the third kind with application of the method of integral elements in which square coordinate function is used is considered. Dynamics of heat exchange of plate is presented by a standard second order dynamic unit for which difference frequency characteristics in the given range of the relative frequencies are constructed. This frequency range allows determining area in which one-element approximation is admissible. The error of approximation is estimated proceeding from a condition of ensuring the given value of the cutoff frequency of automatic control system of the plate temperature. An example of the system cutoff frequency determination is presented at Bi=1 and the preset values of the plate size and the thermal diffusivity of the material of the plate. It is shown that in the range of relative frequencies from 0 to 4 the error of approximation of the amplitude-frequency characteristic does not exceed 1 dB, and the phase-frequency characteristic — 5
Keywords: equation of a transient heat conduction of a plate, approximation, control system, one-element approximation, method of integral elements, approximation error estimation.
Viktor I. Kotenev (Dr. Sci. (Techn.)), Professor. Alexander V. Kotenev (Ph.D. (Techn.)), Associate Professor. Aleksey N. Tatarnikov, Postgraduate Student.
Постановка задачи:
найти U(x,t)
(1)
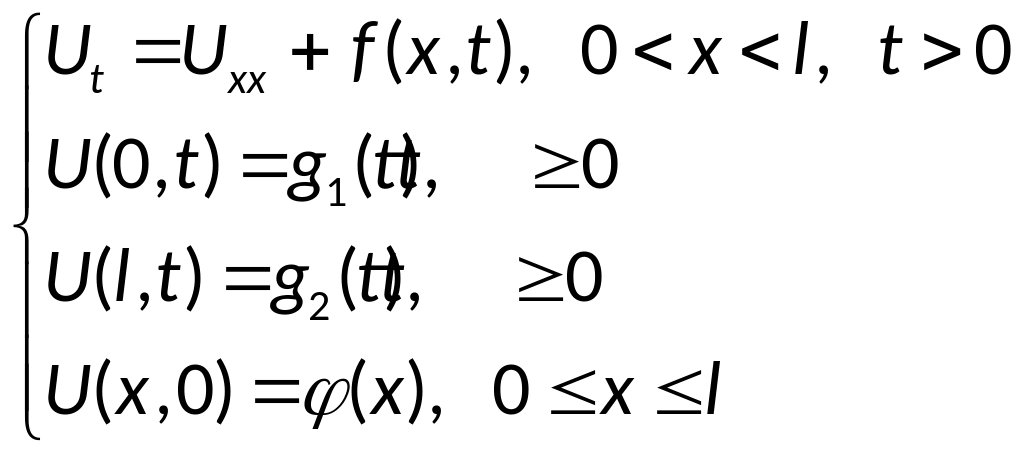
Функция U(x,t)
имеет смысл температуры, а задача (1)
описывает процесс теплопроводности в
стержне длины l.
,
— температура в концах стержня (ГУ 1-го
рода)
— начальная
температура
Дискретизация
задачи (1):
;
;
;
;
— сетка узлов

Множество узлов
,
,…,
(2)
Называется j-ым
слоем.
— граничные узлы
— дискретное
множество точек, представленное матрицей
Пострим разностную
схему методом конечных разностей:
— правая разностная
аппроксимация

Явная разностная
схема для уравнения теплопроводности:
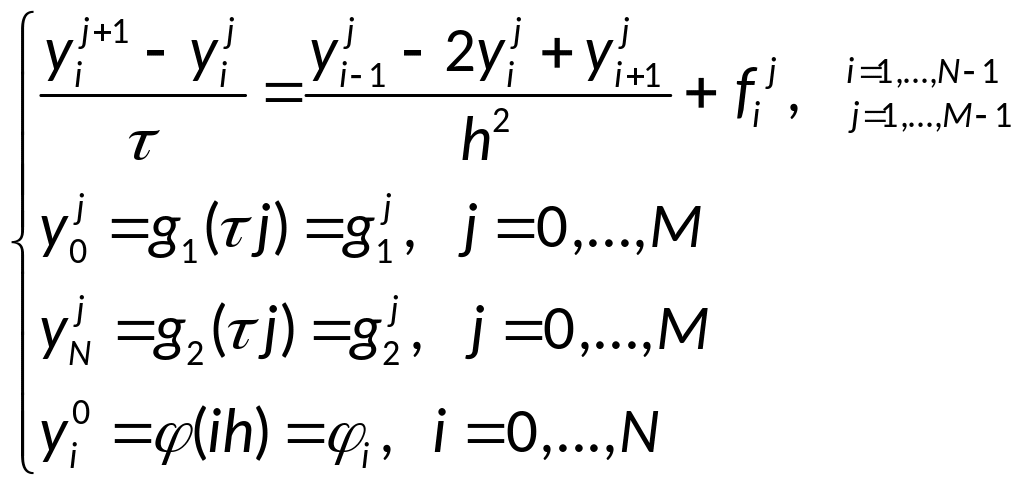
Разностная схема
(2) называется явной, так как решение
неизвестной
находится по явной формуле, используя
следующий четырёхточечный шаблон
(смотри картинку).
;
— коэффициент
33. Метод конечных разностей решения первой начально-краевой задачи для одномерного уравнения теплопроводности: условная устойчивость явной схемы.
Рассмотрим основное
уравнение разностной схемы:
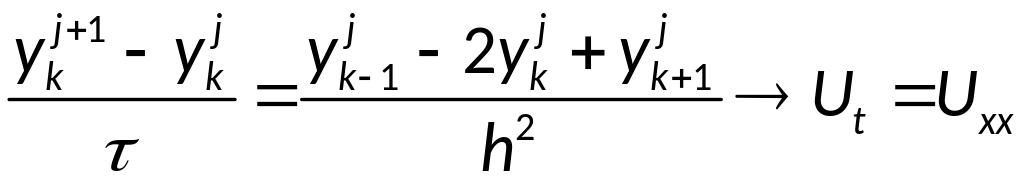
Предположим, что
решение задачи можно представить в
виде:
,
где
i
– мнимая единица
k
– индекс точки
h
– шаг
p
– константа
q>1
– погрешность растёт
неустойчивость
q
1
– погрешность
не растёт
устойчивость



Воспользуемся
формулами:
;
;
;
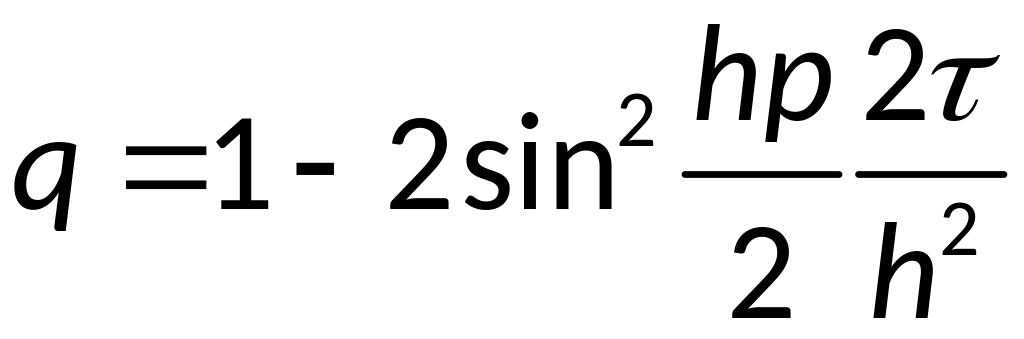
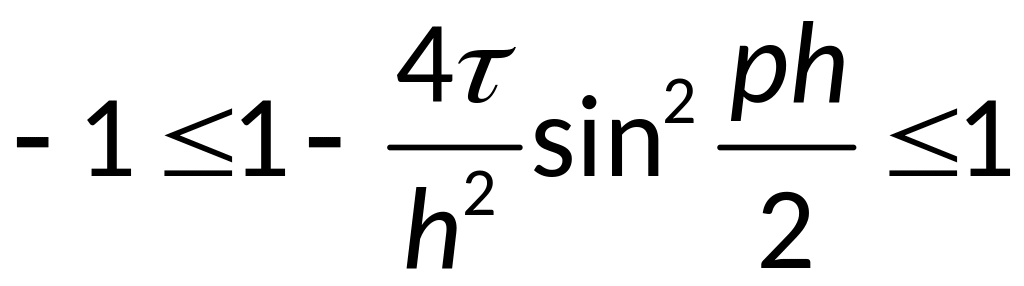
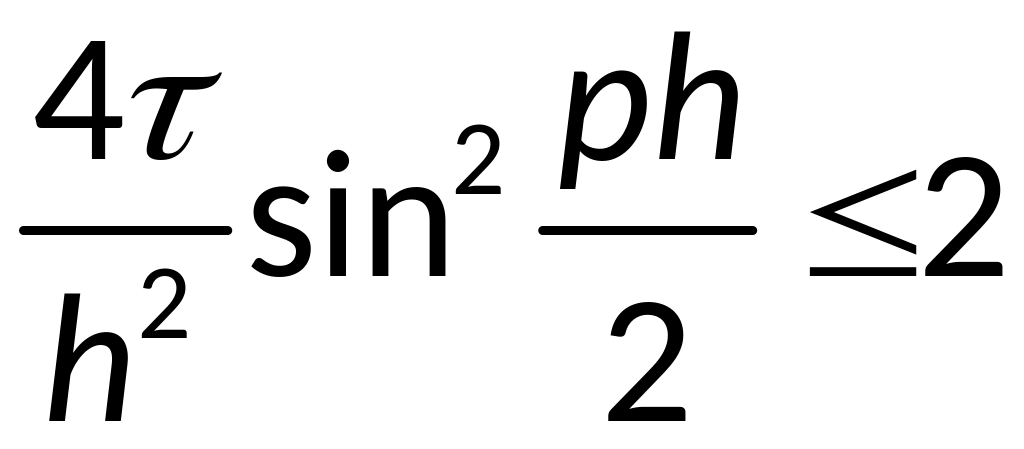
— условие
явной разностной схемы

34. Метод конечных разностей решения первой начально-краевой задачи для одномерного уравнения теплопроводности: неявная схема, абсолютная устойчивость неявной схемы.
(1)
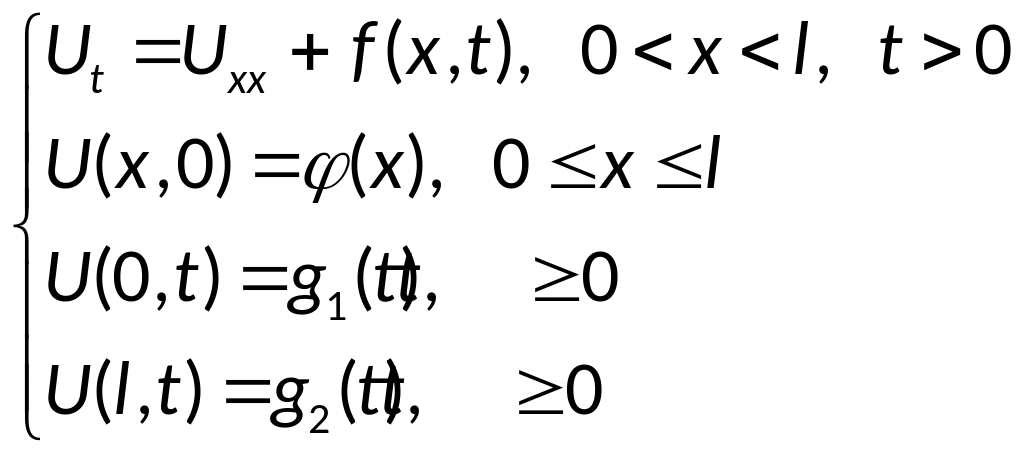
;
— условия согласования
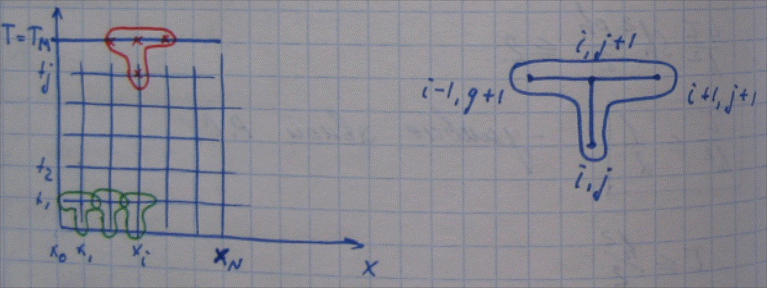
Посредством метода
конечных разностей, строим неявную
разностную схему:

(2)
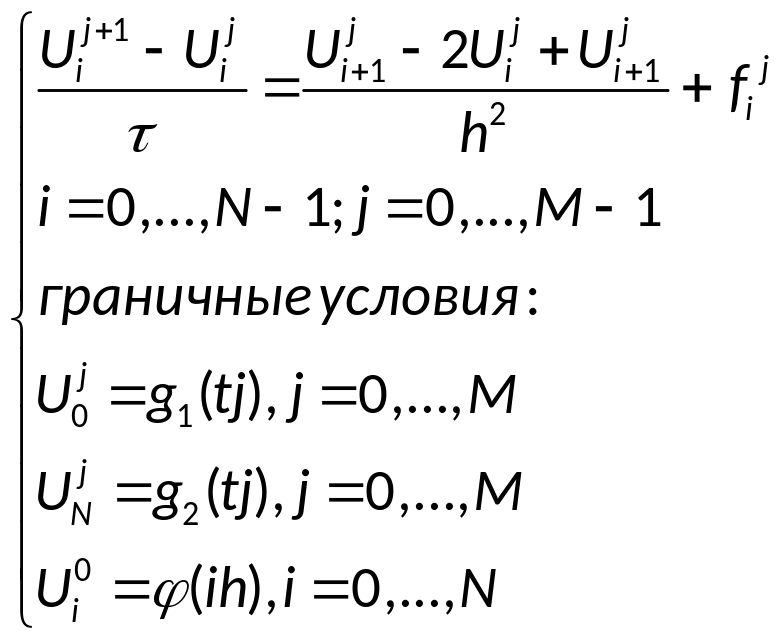
Для каждой точки
напишем систему уравнений:
AU=F 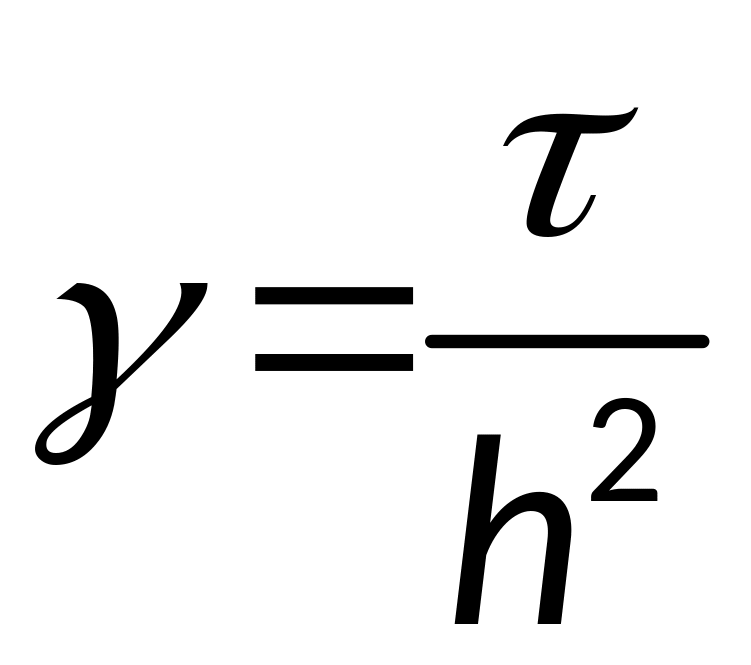
Однопараметрическое
семейство разностных схем имеет вид:
,
где
σ – произвольный
вещественный параметр (вес верхнего
слоя
);
;
при σ=0
получаем явную разностную схему;
при σ≠0 получаем
неявную разностную схему;
Рассмотрим неявную
разностную схему при σ=1
и выпишем СЛАУ в
традиционном виде:

Алгоритм решения
задачи:
1. Решением задачи
является
2. Первоначально
заполняются начальный слой и граничные
слои
3. Для каждого слоя
j
будем формировать правую часть F.
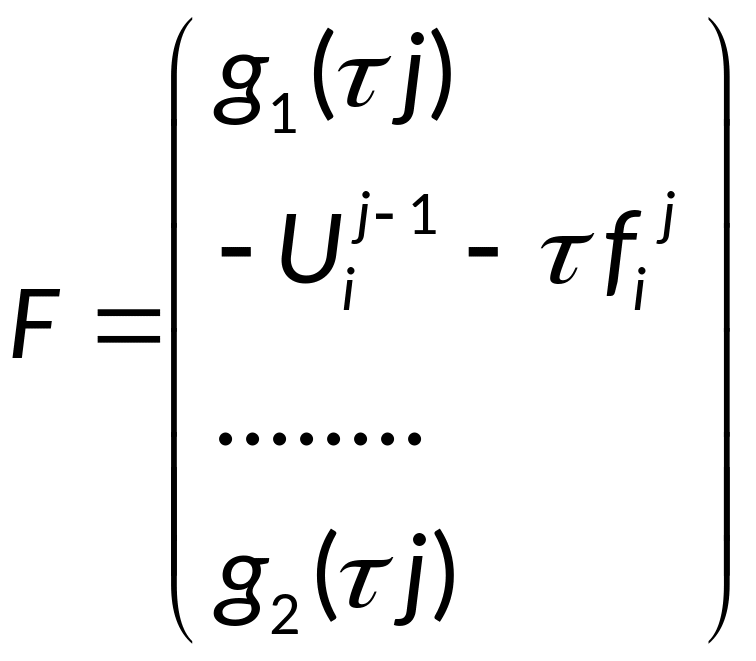
4. Решаем
систему Ay=F
5. Обработка
результатов
— исследование
сходимости
— построение
графиков
Аналитическое
решение имеет вид:
,
где An
находится в виде:

Доказательство
устойчивости неявной разностной схемы:
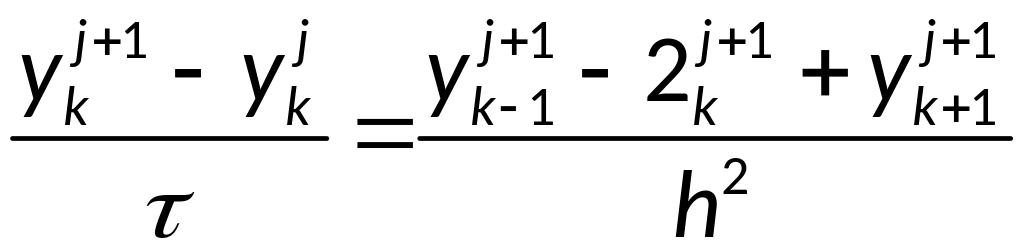
,
— схема
неустойчива
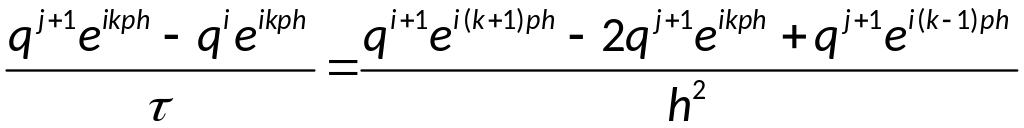
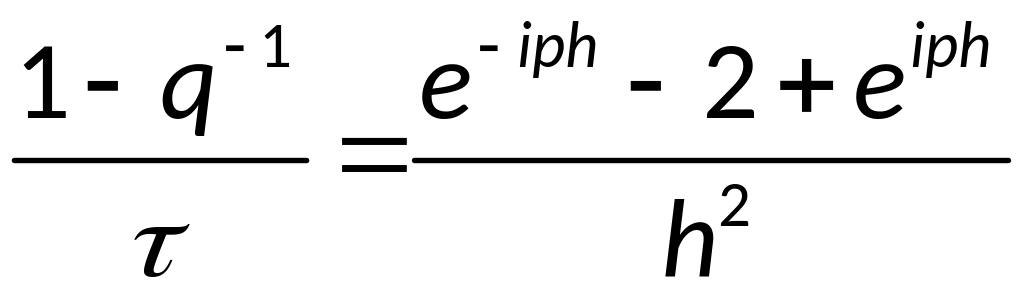
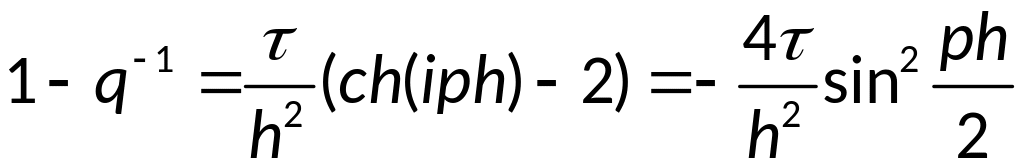
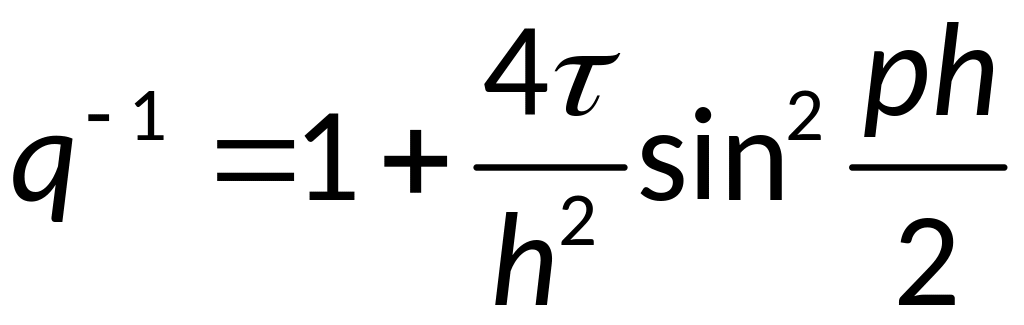
,
схема
является абсолютно устойчивой
35.Метод переменных направлений решения двумерной начально-краевой задачи для уравнений теплопроводности.
Будем рассматривать
поставленную задачу – нагревание
мембраны:
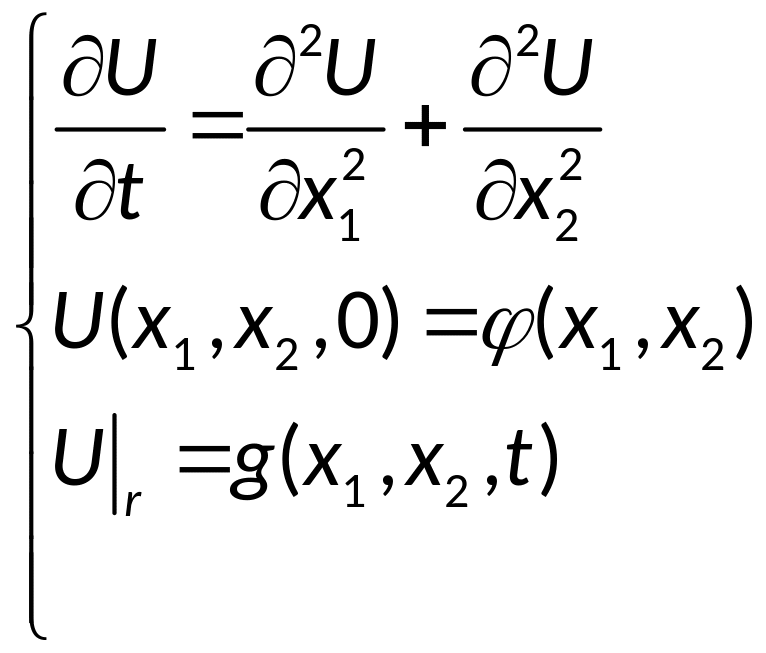
—
разностный
оператор


Операторная запись
разностной схемы:
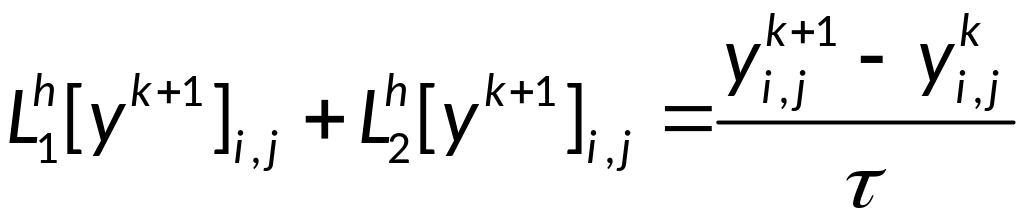
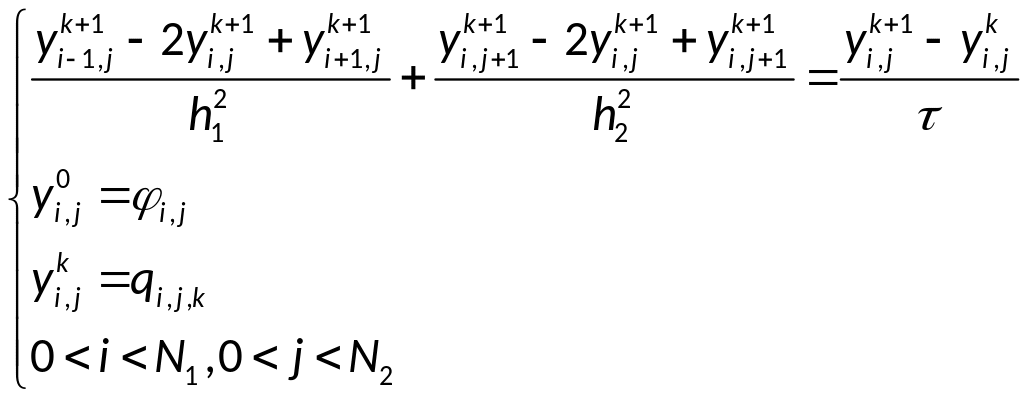
Будем реализовывать
разностную схему в два этапа, введя
половинный слой по времени:
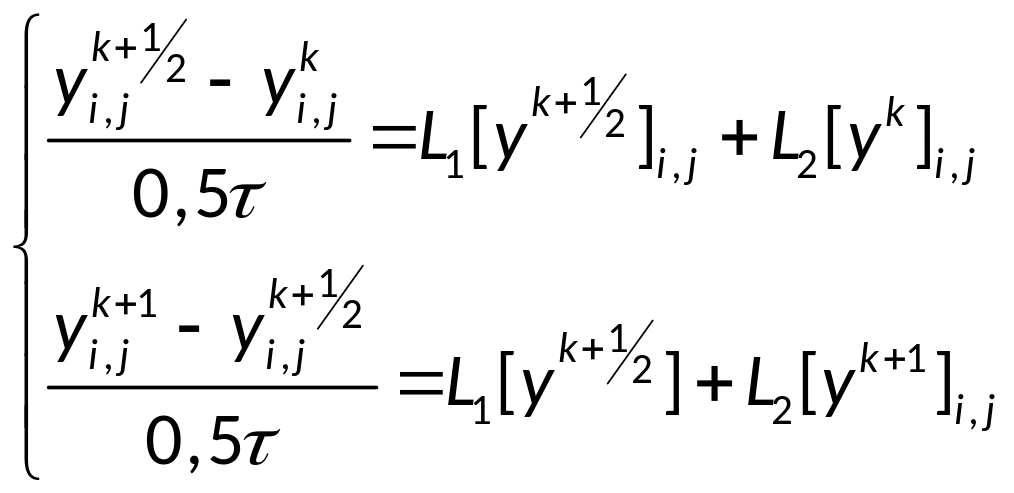
Первое уравнение:

При каждом
фиксированном j
выполняется прогонка по направлению
x1.
Общее число арифметическиех действий
Разностные схемы
в которых число арифметических действий
N
равно числу узлов на слое – называются
экономичными. Метод переменных
направлений является экономичной
разностной схемой.
Другой способ
решения этой задачи – применение
локально-одномерных задач.
Локально-одномерная
схема (трёхмерная и большее число
пространственных измерений)
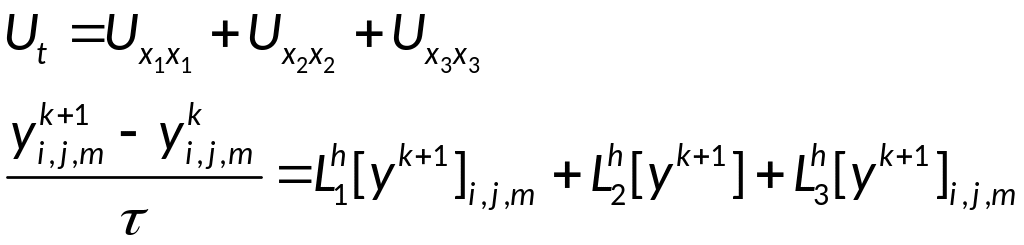
Локально-одномерная
схема:
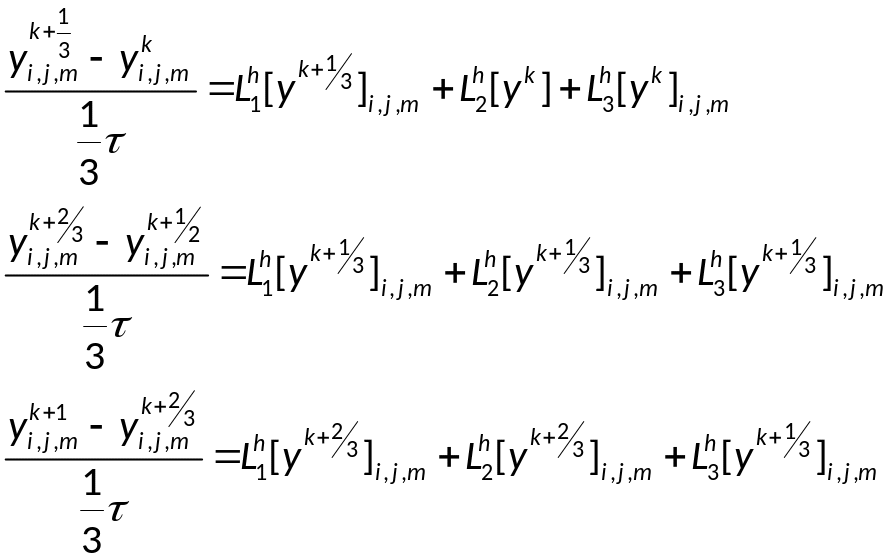
36. Метод конечных
разностей решения начально-краевой
задачи для уравнения колебаний струны:
схема крест, порядок аппроксимации.
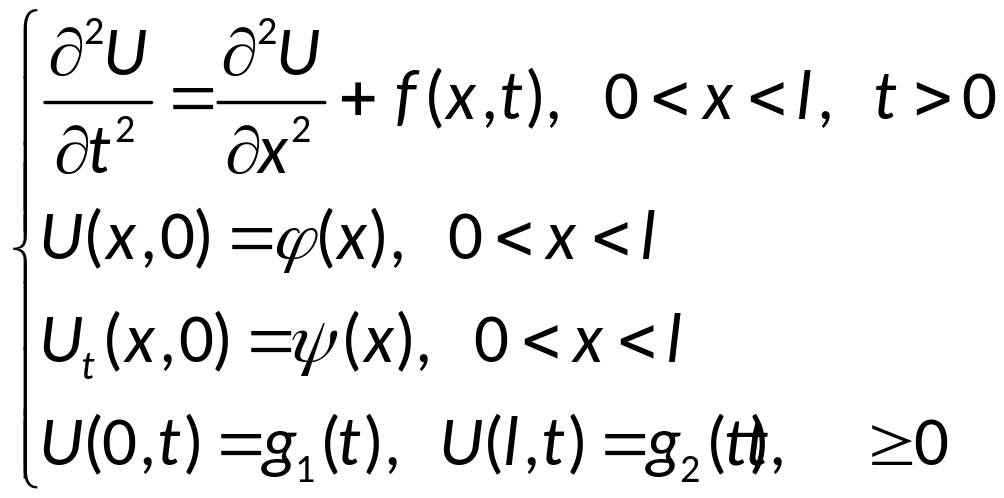
Условие согласования:
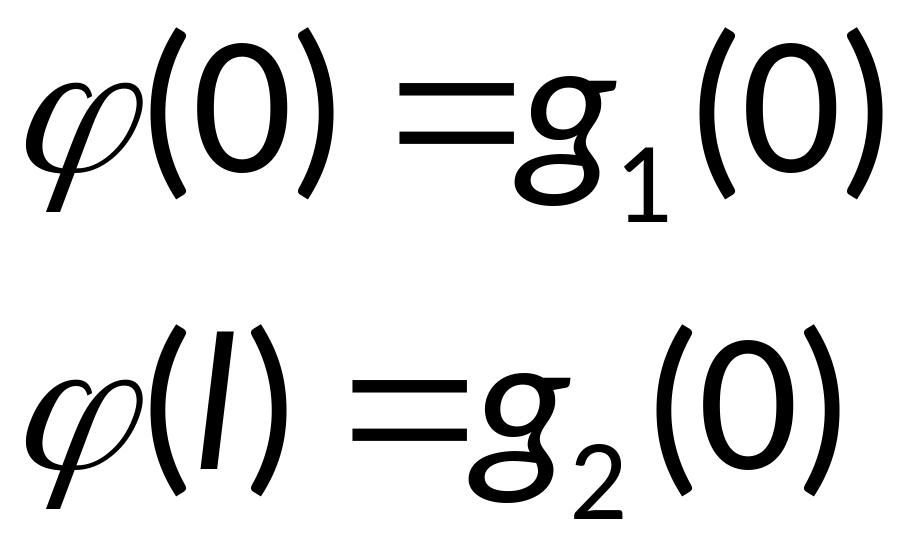

Это уравнение
написано на пяти-точечном шаблоне.
Необходимо вычислить значения на слое
Очевидно, что
находится из условия
находим из условия

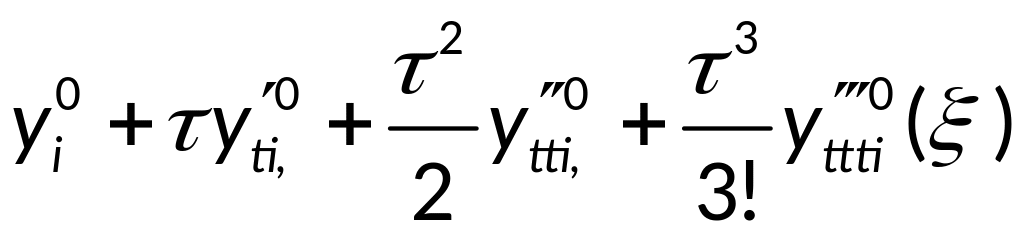
Тогда аппроксимация
примет вид:
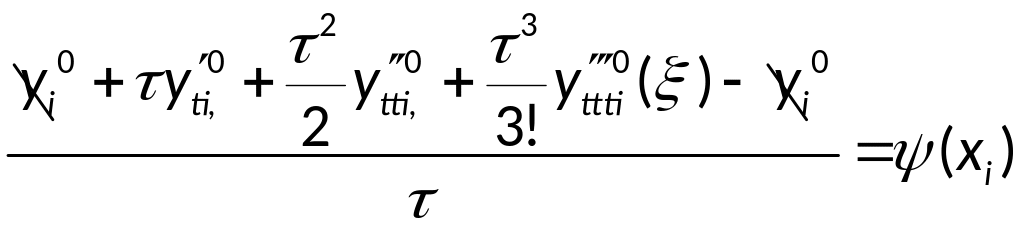
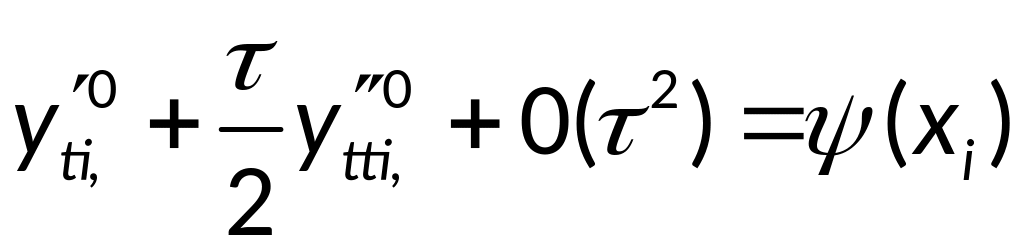

Алгоритм и разностная
схема для уравнения колебаний:
1. 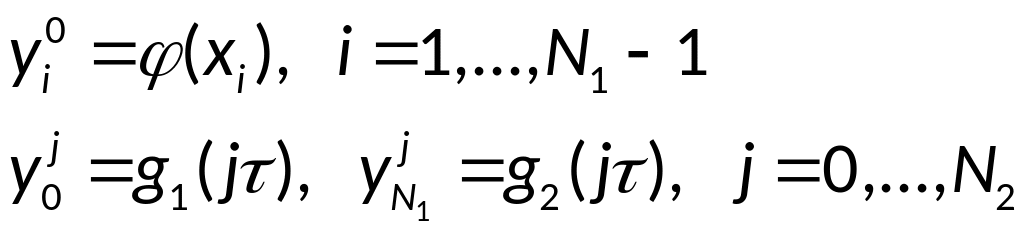
2. Значения на
первом слое: 
3. 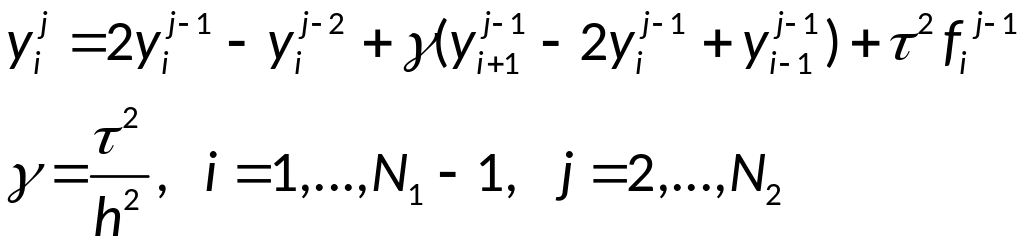
37.Метод конечных
разностей решения начально-краевой
задачи для уравнения колебаний струны:
условная устойчивость схемы.
Докажем, что схема
является условно-устойчивой, методом
гармоник:
для этого рассмотрим
разностную схему для одного уравнения:
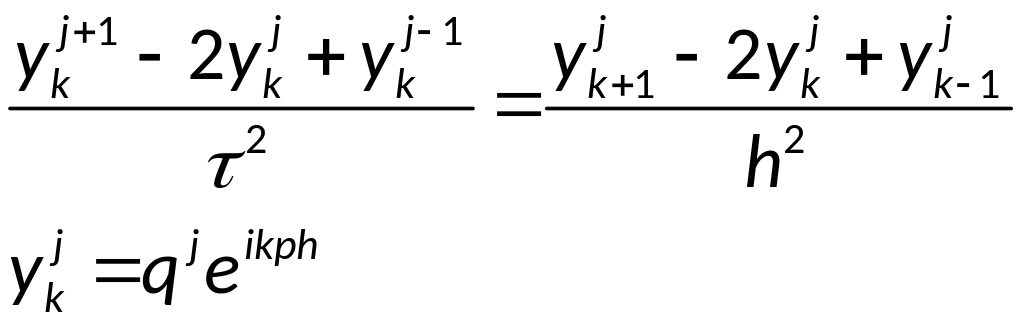
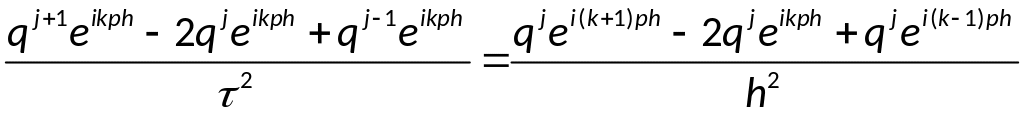
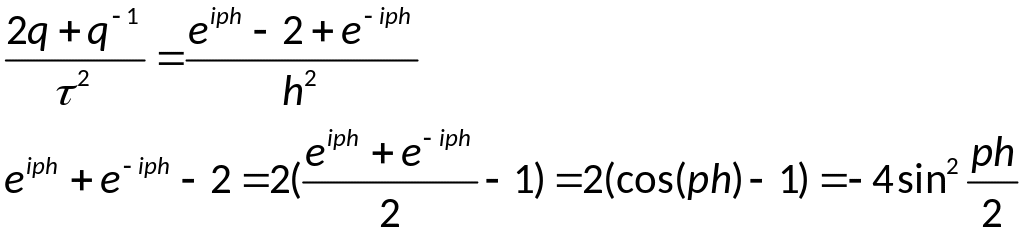
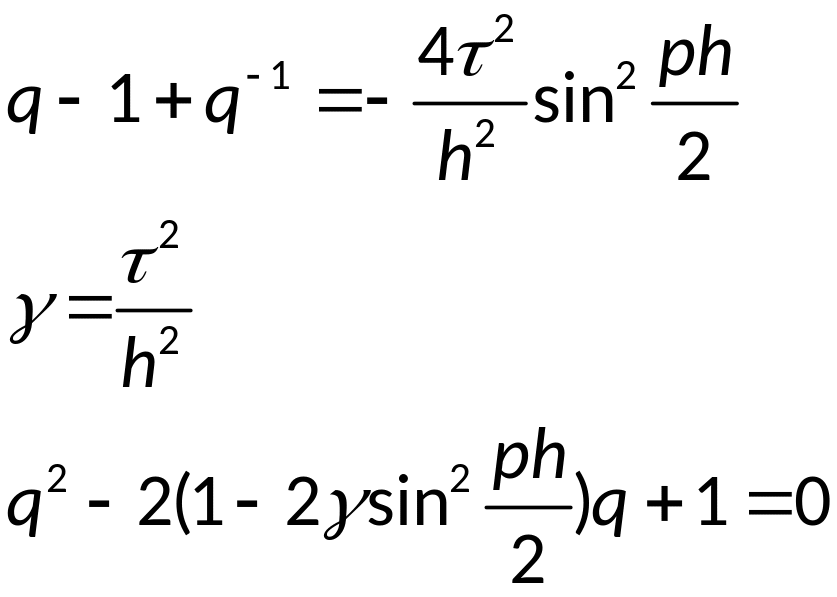
По теореме Виета:


38. Метод конечных
разностей решения задачи Дирихле для
уравнения Пуассона. Порядок аппроксимации
схемы.
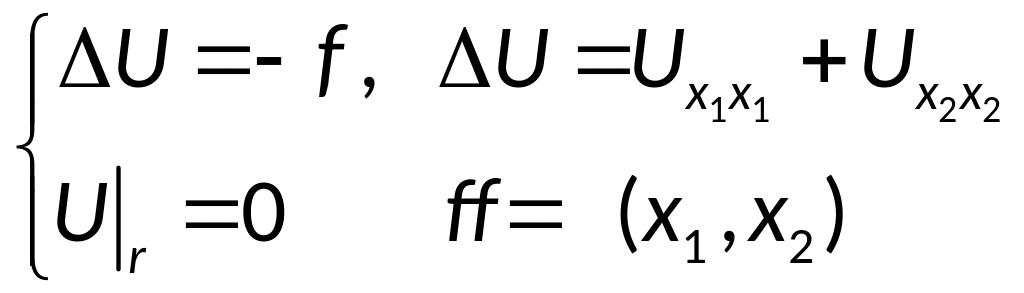
Разностная схема
выглядит следующим образом:
Разностное уравнение
– аппроксимация исходного дифференциального
уравнения:
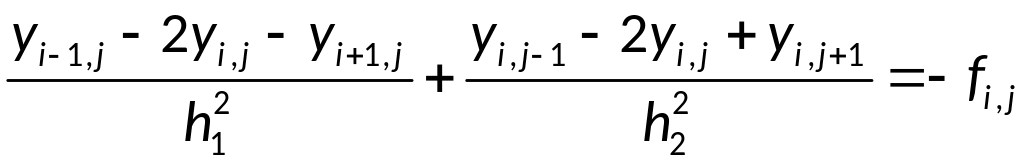
Дальнейшее
разложение элементов уравнения в ряд
Тейлора даст нам искомый порядок
аппроксимации (будем рассматривать
случай
).
39. Метод конечных
разностей решения задачи Дирихле для
уравнения Пуассона. Итерационные методы
решения сеточных уравнений: простой
итерации.
Задача Дирихле
для уравнения Пуассона определяется,
как задача нахождения
, удовлетворяющей в области определения
D
уравнению:
и
(f
и g
задаются в задаче). Подобная
модель может применяться для описания
установившегося течения жидкости,
стационарных тепловых полей, процессов
теплопередачи с внутренними источниками
тепла и деформации упругих пластин.
Одним из наиболее
распространенных подходов к численному
решению дифференциальных уравнений
является метод
конечных разностей (метод сеток).
Следуя этому подходу, область решения
D
можно представить в виде дискретного
(как правило, равномерного) набора
(сетки) точек (узлов). Так, например,
прямоугольная сетка в области D
может быть задана в виде пятиточечного
шаблона.
Разностная схема
выглядит следующим образом:
Разностное
уравнение-аппроксимация исходного
дифференциального уравнения:
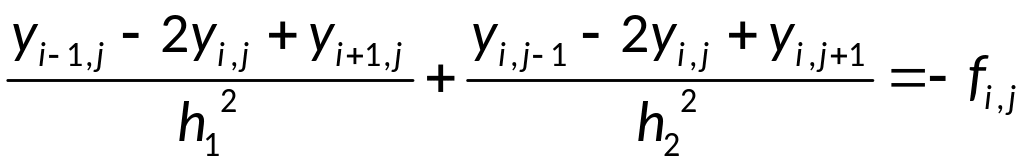
Простой итерации:
Расчетная формула
метода простой итерации:
Соседние файлы в предмете [НЕСОРТИРОВАННОЕ]
- #
- #
- #
- #
- #
- #
- #
- #
- #
- #
- #
disserCat — электронная библиотека диссертаций работаем для вас с 2009 года
- Корзина пуста
Вход
|
Регистрация
Вы робот?
Мы заметили, что с вашего адреса поступает очень много запросов.
Подтвердите, что вы не робот