Оценка погрешностей измерений виды измерений причины ошибок

2.1. Погрешности измерений, их классификация

Истинное значение
физической величины
– значение физической величины, которое
идеальным образом отражало бы в
количественном и качественном отношениях
соответствующее свойство объекта.

Результат любого
измерения отличается от истинного
значения физической величины на некоторое
значение, зависящее от точности средств
и методов измерения, квалификации
оператора, условий, в которых проводилось
измерение, и т. д. Отклонение результата
измерения от истинного значения
физической величины называется
погрешностью
измерения.

Поскольку определить
истинное значение физической величины
в принципе невозможно, так как это
потребовало бы применения идеально
точного средства измерений, то на
практике вместо понятия истинного
значения физической величины применяют
понятие действительного
значения измеряемой величины,
которое настолько точно приближается
к истинному значению, что может быть
использовано вместо него. Это может
быть, например, результат измерения
физической величины образцовым средством
измерения.

Абсолютная
погрешность измерения
(Δ) – это разность между результатом
измерения х
и действительным (истинным) значением
физической величины х_и:

Δ
= х –
х_и.
(2.1)

Относительная
погрешность измерения
(δ) – это отношение абсолютной погрешности
к действительному (истинному) значению
измеряемой величины (часто выраженное
в процентах):

δ
= (Δ / х_и)·100 %
(2.2)

Приведенная
погрешность (γ)
– это выраженное в процентах отношение
абсолютной погрешности к нормирующему
значению Х_N
– условно принятому значению физической
величины, постоянному во всем диапазоне
измерений:

γ =
(Δ /Х_N)·100 %
(2.3)

Для приборов с
нулевой отметкой на краю шкалы нормирующее
значение Х_N
равно конечному значению диапазона
измерений. Для приборов с двухсторонней
шкалой, т. е. с отметками шкалы,
расположенными по обе стороны от нуля
значение Х_N
равно арифметической сумме модулей
конечных значений диапазона измерения.

Погрешность
измерения (результирующая
погрешность)
является суммой двух составляющих:
систематической
и случайной
погрешностей.

Систематическая
погрешность
– это составляющая погрешности измерения,
остающаяся постоянной или закономерно
изменяющаяся при повторных измерениях
одной и той же величины. Причинами
появления систематической погрешности
могут являться неисправности средств
измерений, несовершенство метода
измерений, неправильная установка
измерительных приборов, отступление
от нормальных условий их работы,
особенности самого оператора.
Систематические погрешности в принципе
могут быть выявлены и устранены. Для
этого требуется проведение тщательного
анализа возможных источников погрешностей
в каждом конкретном случае.

Систематические
погрешности подразделяются на:

• методические;

• инструментальные;

• субъективные.

Методические
погрешности
происходят от несовершенства метода
измерения, использования упрощающих
предположений и допущений при выводе
применяемых формул, влияния измерительного
прибора на объект измерения. Например,
измерение температуры с помощью термопары
может содержать методическую погрешность,
вызванную нарушением температурного
режима объекта измерения вследствие
внесения термопары.

Инструментальные
погрешности
зависят от погрешностей применяемых
средств измерения. Неточность градуировки,
конструктивные несовершенства, изменения
характеристик прибора в процессе
эксплуатации и т. д. являются причинами
основных погрешностей инструмента
измерения.

Субъективные
погрешности
вызываются неправильными отсчетами
показаний прибора человеком (оператором).
Например, погрешность от параллакса,
вызванная неправильным направлением
взгляда при наблюдении за показаниями
стрелочного прибора. Использование
цифровых приборов и автоматических
методов измерения позволяет исключить
такого рода погрешности.

Во многих случаях
систематическую погрешность в целом
можно представить как сумму двух
составляющих: аддитивной
(∆_а)
и
мультипликативной
(∆_м).

Если реальная
характеристика средства измерения
смещена относительно номинальной так,
что при всех значениях преобразуемой
величины Х
выходная величина Y
оказывается больше (или меньше) на одну
и ту же величину Δ, то такая погрешность
называется аддитивной
погрешностью нуля (рис.
2.1).

Мультипликативная
погрешность
– это погрешность чувствительности
средства измерения.

Такой подход
позволяет легко скомпенсировать влияние
систематической погрешности на результат
измерения путем введения раздельных
поправочных коэффициентов для каждой
из этих двух составляющих.

Рис.
2.1. К пояснению понятий аддитивной

и
мультипликативной погрешностей

Случайная
погрешность (∆_с)
– это составляющая погрешности измерения,
изменяющаяся случайным образом при
повторных измерениях одной и той же
величины. Наличие случайных погрешностей
выявляется при проведении ряда измерений
постоянной физической величины, когда
оказывается, что результаты измерений
не совпадают друг с другом. Часто
случайные погрешности возникают из-за
одновременного действия многих
независимых причин, каждая из которых
в отдельности слабо влияет на результат
измерения.

Во многих случаях
влияние случайных погрешностей можно
уменьшить путем выполнения многократных
измерений с последующей статистической
обработкой полученных результатов.

В некоторых случаях
оказывается, что результат одного
измерения резко отличается от результатов
других измерений, выполненных при тех
же контролируемых условиях. В этом
случае говорят о грубой погрешности
(промахе измерения). Причиной могут
послужить ошибка оператора, возникновение
сильной кратковременной помехи, толчок,
нарушение электрического контакта и
т. д. Такой результат, содержащий
грубую
погрешность
необходимо выявить, исключить и не
учитывать при дальнейшей статистической
обработке результатов измерений.

Причины
возникновения погрешностей измерений

Имеется ряд
слагаемых погрешностей, которые являются
доминирующими в общей погрешности
измерений. К ним относятся:

1. Погрешности,
   зависящие от средств измерений.
   Нормируемую допустимую погрешность
   средства измерения следует рассматривать
   как погрешность измерения при одном
   из возможных вариантов использования
   этого средства
   измерения.

2. Погрешности,
   зависящие от установочных мер.
   Установочные меры могут быть универсальными
   (концевые меры) и специальными
   (изготовленными по виду измеряемой
   детали). Погрешность измерения будет
   меньшее, если установочная мера будет
   максимально подобна измеряемой детали
   о конструкции, массе, материалу, его
   физическим свойствам, способу базирования
   и т. д. Погрешности от концевых мер длины
   возникают из-за погрешности изготовления
   или погрешности аттестации, а также
   из-за погрешности их притирки.

3. Погрешности,
   зависящие от измерительного усилия.
   При оценке влияния измерительного
   усилия на погрешность измерения
   необходимо выделить упругие деформации
   установочного узла и деформации в зоне
   контакта измерительного наконечника
   с деталью.

4. Погрешности,
   происходящие от температурных деформаций.
   Погрешности возникают из-за разности
   температур объекта измерения и
   измерительного средства. Существует
   два основных источника, обуславливающих
   погрешность от температурных деформаций:
   отклонение температуры воздуха от
   20 °С и кратковременные колебания
   температуры воздуха в процессе измерения.

5. Погрешности,
   зависящие от оператора
   (субъективные погрешности). Возможны
   четыре вида субъективных погрешностей:

• погрешность
  отсчитывания
  (особенно важна, когда обеспечивается
  погрешность измерения, не превышающая
  цену деления);

• погрешность
  присутствия
  (проявляется в виде влияния теплоизлучения
  оператора на температуру окружающей
  среды, а тем самым и на измерительное
  средство);

• погрешность
  действия
  (вносится оператором при настройке
  прибора);

• профессиональные
  погрешности
  (связаны с квалификацией оператора, с
  отношением его к процессу измерения).

1. Погрешности при
   отклонениях от правильной геометрической
   формы.

2. Дополнительные
   погрешности при измерении внутренних
   размеров.

При характеристике
погрешностей средств измерений часто
пользуются

понятием
предела допускаемой погрешности средств
измерений.

Предел допускаемой
погрешности средства измерений
– это наибольшая, без учета знака,
погрешность средства измерений, при
котором оно может быть признано и
допущено к применению. Определение
применимо к основной и дополнительной
погрешности средств измерений.

Учет всех нормируемых
метрологических характеристик средств
измерений является сложной и трудоемкой
процедурой. На практике такая точность
не нужна. Поэтому для средств измерений,
используемых в повседневной практике,
принято деление на классы
точности,
которые дают их обобщенную метрологическую
характеристику.

Требования к
метрологическим характеристикам
устанавливаются в стандартах на средства
измерений конкретного типа.

Классы точности
присваиваются средствам измерений с
учетом результатов государственных
приемочных испытаний.

Класс точности
средства измерений
– обобщенная характеристика средства
измерений, определяемая пределами
допускаемых основных и дополнительных
погрешностей. Класс точности может
выражаться одним числом или дробью
(если аддитивная и мультипликативная
погрешности сопоставимы – например,
0,2/0,05 – адд./мульт.).

Обозначения классов
точности наносятся на циферблаты, щитки
и корпуса средств измерений, приводятся
в нормативно-технических документах.
Классы точности могут обозначаться
буквами (например, М, С и т. д.) или
римскими цифрами (I,
II,
III
и т. д.). Обозначение классов точности
по ГОСТу 8.401-80 может сопровождаться
дополнительными условными знаками:

• 0,5;
  1,6; 2,5 и т. д. – для приборов, приведенная
  погрешность которых составляет 0,5; 1,6;
  2,5 % от нормирующего значения X_N.
  При этом X_N
  принимается равным большему из модулей
  пределов измерений, если нулевое
  значение входного (выходного) сигнала
  находится на краю или вне диапазона
  измерений;

• 0,1,
  0,4, 1,0 и т. д. – для приборов, у которых
  относительная
  погрешность
  составляет 0,1; 0,4; 1,0 % непосредственно
  от полученного значения измеряемой
  величины x;

• 0,02/0,01 – для
  приборов, у которых измеряемая величина
  не может отличаться от значения x,
  показанного указателем, больше, чем на
  [С+d(|X_N/x|-1)]%,
  где C
  и d
  – числитель и знаменатель соответственно
  в обозначении класса точности; X_N
  – больший
  (по модулю) из пределов измерений
  прибора.

Примеры обозначения
классов точности приведены на рис. 2.2.

Рис.
2.2. Лицевые панели приборов:

а
– вольтметра
класса точности 0,5; б
– амперметра
класса точности 1,5;

в
– амперметра
класса точности 0,02/0,01;

г
– мегомметра класса точности 2,5 с
неравномерной шкалой

Метрологическая
надежность средств измерения

В процессе
эксплуатации любого средства измерения
может возникнуть неисправность или
поломка, называемые отказом.

Метрологическая
надежность
средств
измерения
– это свойство средств измерений
сохранять установленные значения
метрологических характеристик в течение
определенного времени при нормальных
режимах и рабочих условиях эксплуатации.
Она характеризуется интенсивностью
отказов, вероятностью безотказной
работы и наработкой на отказ.

Интенсивность
отказов
определяется выражением:

,
(2.1)

где
L
– число отказов; N
– число однотипных элементов; ∆t
– промежуток времени.

Для средств
измерения, состоящего из
n
типов элементов, интенсивность
отказов
рассчитывается как

(2.2)

где
m_i
–
количество элементов i-го
типа.

Вероятность
безотказной работы:

(2.3)

Наработка на
отказ:

(2.4)

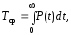
Для внезапного
отказа, интенсивность отказов которого
не зависит от времени работы средства
измерения:

(2.5)

Межповерочный
интервал, в
течение которого обеспечивается заданная
вероятность безотказной работы,
определяется по формуле:

,
(2.6)

где
P_мо
– вероятность метрологического отказа
за время между поверками; P(t)
– вероятность безотказной работы.

В процессе
эксплуатации может производиться
корректировка межповерочного интервала.

Поверка средств
измерения

В основе обеспечения
единообразия средств измерений лежит
система передачи размера единицы
измеряемой величины. Технической формой
надзора за единообразием средств
измерений является государственная
(ведомственная) поверка средств измерений,
устанавливающая их метрологическую
исправность.

Поверка
– определение метрологическим органом
погрешностей средства измерений и
установление его пригодности к применению.

Пригодным к
применению в течение определенного
межповерочного
интервала
времени признают те СИ, поверка которых
подтверждает их соответствие
метрологическим и техническим требованиям
к данному СИ.

Средства измерений
подвергают первичной, периодической,
внеочередной, инспекционной и экспертной
поверкам.

Первичной поверке
подвергаются
СИ при выпуске из производства или
ремонта, а также СИ, поступающие по
импорту.

Периодической
поверке подлежат
СИ, находящиеся в эксплуатации или на
хранении через определенные межповерочные
интервалы, установленные с расчетом
обеспечения пригодности к применению
СИ на период между поверками.

Инспекционную
поверку производят
для выявления пригодности к применению
СИ при осуществлении госнадзора и
ведомственного метрологического
контроля за состоянием и применением
СИ.

Экспертную
поверку выполняют
при возникновении спорных вопросов по
метрологическим характеристикам (MX),
исправности СИ и пригодности их к
применению.

Достоверная
передача размера единиц во всех звеньях
метрологической цепи от эталонов или
от исходного образцового средства
измерений к рабочим средствам измерений
производится в определенном порядке,
приведенном в поверочных схемах.

Поверочная схема
– это утвержденный в установленном
порядке документ, регламентирующий
средства, методы и точность передачи
размера единицы физической величины
от государственного эталона или исходного
образцового средства измерений рабочим
средствам.

Различают
государственные, ведомственные и
локальные поверочные схемы органов
государственной или ведомственных
метрологических служб.

Государственная
поверочная схема
распространяется на все средства
измерений данной ФВ, имеющиеся в стране.
Устанавливая многоступенчатый порядок
передачи размера единицы ФВ от
государственного эталона, требования
к средствам и методам поверки,
государственная поверочная схема
представляет собой структуру
метрологического обеспечения определённого
вида измерений в стране. Эти схемы
разрабатываются главными центрами
эталонов и оформляются одним ГОСТом
ГСИ.

Локальные
поверочные схемы
распространяются на средства измерений,
подлежащие поверке в данном метрологическом
подразделении на предприятии, имеющем
право поверки средств измерений, и
оформляются в виде стандарта предприятия.
Ведомственные и локальные поверочные
схемы не должны противоречить
государственным и должны учитывать их
требования применительно к специфике
конкретного предприятия.

Ведомственная
поверочная схема
разрабатывается органом ведомственной
метрологической службы, согласовывается
с главным центром эталонов – разработчиком
государственной поверочной схемы
средств измерений данной ФВ и
распространяется только на средства
измерений, подлежащие внутриведомственной
поверке.

Поверочная схема
устанавливает передачу размера единиц
одной или нескольких взаимосвязанных
величин. Она должна включать не менее
двух ступеней передачи размера. Поверочную
схему для СИ одной и той же величины,
существенно отличающихся по диапазонам
измерений, условиям применения и методам
поверки, а также для СИ нескольких ФВ
допускается подразделять на части. На
чертежах поверочной схемы должны быть
указаны:

• наименования СИ
  и методов поверки;

• номинальные
  значения ФВ или их диапазоны;

• допускаемые
  значения погрешностей СИ;

• допускаемые
  значения погрешностей методов поверки.
  Правила расчета параметров поверочных
  схем и оформления чертежей поверочных
  схем приведены в ГОСТ 8.061-80 «ГСИ.
  Поверочные схемы. Содержание и построение»
  и в рекомендациях МИ 83-76 «Методика
  определения параметров поверочных
  схем».

Калибровка
средств измерения

Калибровка
средства измерений
– это
совокупность операций, выполняемых
калибровочной лабораторией с целью
определения и подтверждения действительных
значений метрологических характеристик
и (или) пригодности средства измерений
к применению в сферах, не подлежащих
государственному метрологическому
контролю и надзору в соответствии с
установленными требованиями.

Результаты
калибровки средств измерений удостоверяются
калибровочным
знаком,
наносимым на средства измерений, или
сертификатом
о калибровке,
а также записью
в эксплуатационных документах.

Поверку (обязательная
госповерка) может выполнять, как правило,
орган государственной метрологической
службы, а калибровку –
любая
аккредитованная и неаккредитованная
организация.

Поверка обязательна
для средств измерений, применяемых в
сферах, подлежащих государственному
метрологическому контролю (ГМК),
калибровка же –
процедура
добровольная, поскольку относится к
средствам измерений, не подлежащим ГМК.
Предприятие вправе самостоятельно
решать вопрос о выборе форм и режимов
контроля состояния средств измерений,
за исключением тех областей применения
средств измерений, за которыми государства
всего мира устанавливают свой контроль
– это
здравоохранение, безопасность труда,
экология и др.

Освободившись от
государственного контроля, предприятия
попадают под не менее жёсткий контроль
рынка. Это означает, что свобода выбора
предприятия по «метрологическому
поведению» является относительной, все
равно необходимо соблюдать метрологические
правила.

В развитых странах
устанавливает и контролирует исполнение
этих правил негосударственная организация,
именуемая «национальной калибровочной
службой». Эта служба берёт на себя
функции регулирования и разрешения
вопросов, связанных со средствами
измерений, не подпадающими под контроль
государственных метрологических служб.

Желание иметь
конкурентоспособную продукцию побуждает
предприятия иметь измерительные
средства, дающие достоверные результаты.

Внедрение системы
сертификации продукции дополнительно
стимулирует поддержание измерительных
средств на соответствующем уровне. Это
согласуется с требованиями систем
качества, регламентируемыми стандартами
ИСО серии 9000.

Построение
Российской системы калибровки (РСК)
основывается на следующих принципах:

• добровольность
  вступления;

• обязательность
  получения размеров единиц от
  государственных эталонов;

• профессионализм
  и компетентность персонала;

• самоокупаемость
  и самофинансирование.

Основное звено
РСК –
калибровочная
лаборатория. Она представляет собой
самостоятельное предприятие или
подразделение в составе метрологической
службы предприятия, которое может
осуществлять калибровку средств
измерений для собственных нужд или для
сторонних организаций. Если калибровка
проводится для сторонних организаций,
то калибровочная лаборатория должна
быть аккредитована органом РСК.
Аккредитацию осуществляют государственные
научные метрологические центры или
органы Государственной метрологической
службы в соответствии со своей компетенцией
и требованиями, установленными в ГОСТе
51000.2-95 «Общие требования к аккредитующему
органу».

Порядок аккредитации
метрологической службы утвержден
постановлением Госстандарта РФ от 28
декабря 1995 г. № 95 «Порядок аккредитации
метрологических служб юридических лиц
на право проведения калибровочных
работ».

Методы поверки
(калибровки) средств измерения

Допускается
применение четырех методов
поверки
(калибровки) средств измерений:

• непосредственное
  сличение с эталоном;

• сличение с помощью
  компаратора;

• прямые измерения
  величины;

• косвенные измерения
  величины.

Метод
непосредственного сличения
поверяемого (калибруемого) средства
измерения с эталоном соответствующего
разряда широко применяется для различных
средств измерений в таких областях, как
электрические и магнитные измерения,
для определения напряжения, частоты и
силы тока. В основе метода лежит проведение
одновременных измерений одной и той же
физической величины поверяемым
(калибруемым) и эталонным приборами.
При этом определяют погрешность как
разницу показаний поверяемого и
эталонного средств измерений, принимая
показания эталона за действительное
значение величины. Достоинства этого
метода в его простоте, наглядности,
возможности применения автоматической
поверки (калибровки), отсутствии
потребности в сложном оборудовании.

Метод сличения
с помощью компаратора
основан на использовании прибора
сравнения, с помощью которого сличаются
поверяемое (калибруемое) и эталонное
средства измерения. Потребность в
компараторе возникает при невозможности
сравнения показаний приборов, измеряющих
одну и ту же величину, например, двух
вольтметров, один из которых пригоден
для постоянного тока, а другой –
переменного.
В подобных ситуациях в схему поверки
(калибровки) вводится промежуточное
звено –
компаратор.
Для приведенного примера потребуется
потенциометр, который и будет компаратором.
На практике компаратором может служить
любое средство измерения, если оно
одинаково реагирует на сигналы как
поверяемого (калибруемого), так и
эталонного измерительного прибора.
Достоинством данного метода специалисты
считают последовательное во времени
сравнение двух величин.

Метод прямых
измерений
применяется, когда имеется возможность
сличить испытуемый прибор с эталонным
в определенных пределах измерений. В
целом этот метод аналогичен методу
непосредственного сличения, но методом
прямых измерений производится сличение
на всех числовых отметках каждого
диапазона (и поддиапазонов, если они
имеются в приборе). Метод прямых измерений
применяют, например, для поверки или
калибровки вольтметров постоянного
электрического тока.

Метод косвенных
измерений
используется, когда действительные
значения измеряемых величин невозможно
определить прямыми измерениями либо
когда косвенные измерения оказываются
более точными, чем прямые. Этим методом
определяют вначале не искомую
характеристику, а другие, связанные с
ней определенной зависимостью. Искомая
характеристика определяется расчетным
путем. Например, при поверке (калибровке)
вольтметра постоянного тока эталонным
амперметром устанавливают силу тока,
одновременно измеряя сопротивление.
Расчетное значение напряжения сравнивают
с показателями калибруемого (поверяемого)
вольтметра. Метод косвенных измерений
обычно применяют в установках
автоматизированной поверки (калибровки).

Погрешности измерений и их
классификация .

При
измерении физических величии с помощью даже самых точных и совершенных средств
и методов их результат всегда отличается от истин­ного
значения измеряемой физической величины, т.е. определяется с неко­торой
погрешностью. Источниками погрешностей измерения являются сле­дующие
причины: несовершенство используемых методов и средств измере­ний,
нестабильность измеряемых физических величин, непостоянство климатических
условий, внешние и внутренние помехи, а также различные субъек­тивные факторы
экспериментатора.

Определение
«погрешность» является одним из центральных в метрологии, в котором
используются понятия «погрешность результата измере­ния» и «погрешность
средства измерения».

Погрешностью результата измерения (погрешностью измерения) называется отклонение
результата измерения от истинного значения измеряемой физической величины. Так
как истинное значение измеряемой величины неизвестно, то при количественной
оценке погрешности пользуются дейст­вительным значением физической
величины.

Это
значение находится экспериментальным путем и настолько близко к истинному
значению, что для поставленной измерительной задачи может быть использовано
вместо него.

Погрешность средства измерения (СИ) — разность между показаниями СИ
и истинным (действительным) значением измеряемой физической величины. Она
характеризует точность результатов измерений, проводимых дан­ным средством

Существует пять основных
признаков, по
которым классифицируются погрешности измерения.

По
способу количественного выражения погрешности измерения делятся на абсолютные,
относительные и приведенные.

Абсолютной погрешностью △, выражаемой в единицах
измеряемой величины, называется отклонение результата измерения х от истинного зна­чения х_н:                                (1.1)

и знак полученной
погрешности, но не определяет качество самого проведенного измерения.

Понятие
погрешности характеризует как бы несовершенство измере­ния.
Характеристикой качества измерения является используемое в метроло­гии понятие точности измерений, отражающее меру близости результатов измерений к истинному
значению измеряемой физической величины. Точ­ность и погрешность связаны
обратной зависимостью. Иначе говоря, высо­кой точности измерений соответствует
малая погрешность. Так, например, измерение силы тока в 10 А и 100 А может быть
выполнено с идентичной аб­солютной погрешностью ∆ = ±1 А. Однако качество
(точность) первого из­мерения ниже второго. Поэтому, чтобы иметь возможность
сравнивать каче­ство измерений, введено понятие относительной погрешности.

Относительной погрешностью δ называется отношение
абсолютной погрешности измерения к истинному значению измеряемой величины:

                                                                   (1.2)

Мерой
точности измерений служит величина,
обратная модулю отно­сительной погрешности, т.е. 1/|δ|. Погрешность δ часто выражают в
про­центах:

δ
= 100△/х_н (%). Поскольку обычно △⋍х_н, то относительная по­грешность
может быть определена как δ ⋍ △/х или δ = 100△/х (%).

Если
измерение выполнено однократно и за
абсолютную погрешность результата измерения △ принята разность между
показанием прибора и ис­тинным значением измеряемой величины х_Н то из соотношения (1.2)
следу­ет, что значение относительной погрешности δ уменьшается с ростом вели­чины
х_н  (здесь предполагается
независимость △ от х_н). Поэтому для изме­рений
целесообразно выбирать такой прибор, показания которого были бы в последней
части его шкалы (диапазона измерений), а для сравнения различ­ных приборов
использовать понятие приведенной погрешности.

Приведенной погрешностью δ_пр, выражающей
потенциальную точ­ность измерений, называется отношение абсолютной погрешности △ к неко­торому нормирующему
значению X_N (например, к конечному
значению шкалы прибора или сумме конечных значений шкал при двусторонней шка­ле).     

По
характеру (закономерности) изменения погрешности измерений подразделяются на
систематические, случайные и грубые (промахи).

Систематические погрешности △_с — составляющие погрешности из­мерений,
остающиеся постоянными или закономерно изменяющиеся , при многократных (повторных)
измерениях одной и той же величины в одних и тех же условиях. Такие погрешности
могут быть выявлены путем детального анализа возможных их источников и
уменьшены (применением более точных приборов, калибровкой приборов с помощью
рабочих мер и пр.). Однако полностью их устранить нельзя.

По
характеру изменения во времени систематические погрешности подразделяются на постоянные (сохраняющие величину и
знак), прогресси­рующие (возрастающие или убывающие во времени), периодические, а также изменяющиеся во
времени по сложному непериодическому закону. Основ­ные из этих погрешностей —
прогрессирующие.

Прогрессирующая (дрейфовая) погрешность — это непредсказуемая по­грешность,
медленно меняющаяся во времени. Прогрессирующие погрешно­сти характеризуются
следующими особенностями:

•        
возможна
их коррекция поправками только в данный момент времени, а далее эти погрешности
вновь непредсказуемо изменяются;

•          
изменения
прогрессирующих погрешностей во времени представляют со­бой нестационарный
случайный процесс (характеристики которого изменяются во времени), и поэтому в
рамках достаточно полно разработанной теории стационарных случайных процессов
они могут быть описаны лишь с некоторыми ограничениями.

Случайные погрешности 
— составляющие погрешности измерений, изменяющиеся случайным образом при
повторных (многократных) измере­ниях одной и той же величины в одних и тех же
условиях. В появлении таких погрешностей нет каких-либо закономерностей, они
проявляются при повторных измерениях одной и той же величины в виде некоторого
разброса получаемых результатов. Практически случайные погрешности неизбежны,
неустранимы и всегда имеют место в результатах измерений. Описание случайных
погрешностей возможно только на основе теории случайных процессов и
математической статистики. В отличие от систематических случайные погрешности
нельзя исклю­чить из результатов измерений путем введения поправки, однако их
можно существенно уменьшить путем многократного измерения этой величины и
последующей статистической обработкой полученных результатов.

Грубые погрешности (промахи) —
погрешности, существенно превы­шающие ожидаемые при данных условиях измерения.
Такие погрешности возникают из-за ошибок оператора или неучтенных внешних
воздействий. Их выявляют при обработке результатов измерений и исключают из рас­смотрения,
пользуясь определенными правилами.

По причинам возникновения погрешности измерения подразделяются
на методические, инструментальные, внешние и субъективные.

Методические
погрешности возникают обычно из-за
несовершенства метода измерений, использования неверных теоретических
предпосылок (допущений) при измерениях, а также из-за влияния выбранного
средства изме­рения на измеряемые физические величины. При подключении
электроизме­рительного прибора от источника сигнала потребляется некоторая
мощность. Это приводит к искажению режима работы источника сигнала и вызывает
погрешность метода измерения (методическую погрешность).

Так,
например, если вольтметр обладает недостаточно высоким входным сопротивлением,
то его подключение к исследуемой схеме способно из­менить в ней распределение
токов и напряжений. При этом результат изме­рения может существенно отличаться
от действительного. Для расчета мето­дической погрешности при измерении токов и
напряжений необходимо знать внутренние сопротивления амперметров R_A
и вольтметров R_v. Методическую
погрешность можно уменьшить путем применения бо­лее точного метода измерения.

Инструментальные
(аппаратурные, приборные) погрешности
возни­кают из-за несовершенства средств измерения» т.е. из-за погрешностей
средств измерений. Источниками инструментальных погрешностей могут быть,
например, неточная градуировка прибора и смещение нуля, вариация показаний
прибора в процессе эксплуатации и т.д. Уменьшают инструмен­тальные погрешности
применением более точного прибора.

Внешняя
погрешность — важная составляющая погрешности
измере­ния, связанная с отклонением одной или
нескольких влияющих величин от нормальных значений или выходом их за пределы нормальной области (на­пример,
влияние влажности, температуры, внешних электрических и
магнит­ных полей, нестабильности источников питания, механических воздействий и
т.д.). В большинстве случаев внешние погрешности являются систематиче­скими и
определяются дополнительными погрешностями применяемых средств измерений. .

Субъективные
погрешности вызываются ошибками оператора при от­счете
показаний средств измерения (погрешности от небрежности и невни­мания
оператора, от параллакса, т.е. от неправильного направления взгляда при отсчете
показаний стрелочного прибора и пр.). Подобные погрешности устраняются
применением современных цифровых приборов или автомати­ческих методов
измерения.

По характеру поведения измеряемой физической величины в процессе
измерений различают статические и динамические погрешности.

Статические
погрешности возникают при измерении
установившего­ся значения измеряемой величины, т.е. когда эта величина
перестает изме­няться во времени.

Динамические
погрешности имеют место при динамических
измерени­ях, когда измеряемая величина
изменяется во времени и требуется установить закон ее изменения. Причина
появления динамических погрешностей состо­ит в несоответствии скоростных
(временных) характеристик прибора и ско­рости изменения измеряемой величины.

Средства измерений
могут применяться в нормальных и рабочих усло­виях.

Эти
 условия для
конкретных видов СИ (средств  измерения) установлены в
стандартах или технических условиях.

Нормальным
 условиям применения средств измерений должен
удовлетворять ряд следующих (основных) требований:

температура
окружающего воздуха (20±5) °С;  

относительная
влажность (65±15) %;  

атмосферное
давле­ние (100±4) кПа;  

напряжение
питающей сети (220±4) В и (115±2,5) В;  

частота
сети (50±1) Гц и (400±12) Гц.

Как
следует из перечисленных требований, нормальные условия применения СИ
характеризуются диапазоном значений влияющих на них величин типа климатических
факторов и параметров элек­тропитания.

Рабочие
условия применения СИ определяются диапазоном
значений влияющих величин не только климатического характера и параметров
электропитания, но и типа механических воздействий. В частности, диапазон климатических
воздействий делится на ряд групп, охватывающих широкий диапазон изменения
окружающей температуры.

В зависимости от обстоятельств, при которых проводились измерения, а также в зависимости от целей измерения, выбирается та или иная классификация погрешностей. Иногда используют одновременно несколько взаимно пересекающихся классификаций, желая по нескольким признакам точно охарактеризовать влияющие на результат измерения физические величины. В таком случае рассматривают, например, инструментальную составляющую неисключённой систематической погрешности. При выборе классификаций важно учитывать наиболее весомые или динамично меняющиеся или поддающиеся регулировке влияющие величины. Ниже приведены общепринятые классификации согласно типовым признакам и влияющим величинам.

По виду представления, различают абсолютную, относительную и приведённую погрешности.

Абсолютная погрешность это разница между результатом измерения X и истинным значением Q измеряемой величины. Абсолютная погрешность находится как D = X — Q и выражается в единицах измеряемой величины.

Относительная погрешность это отношение абсолютной погрешности измерения к истинному значению измеряемой величины: d = D / Q = (X – Q) / Q .

Приведённая погрешность это относительная погрешность, в которой абсолютная погрешность средства измерения отнесена к условно принятому нормирующему значению Q_N , постоянному во всём диапазоне измерений или его части. Относительная и приведённая погрешности – безразмерные величины.

В зависимости от источника возникновения, различают субъективную, инструментальную и методическую погрешности.

Субъективная погрешность обусловлена погрешностью отсчёта оператором показаний средства измерения.

Инструментальная погрешность обусловлена несовершенством применяемого средства измерения. Иногда эту погрешность называют аппаратурной. Метрологические характеристики средств измерений нормируются согласно ГОСТ 8.009 – 84, при этом различают четыре составляющие инструментальной погрешности: основная, дополнительная, динамическая, интегральная. Согласно этой классификации, инструментальная погрешность зависит от условий и режима работы, а также от параметров сигнала и объекта измерения.

Методическая погрешность обусловлена следующими основными причинами:

– отличие принятой модели объекта измерения от модели, адекватно описывающей его метрологические свойства;

– влияние средства измерения на объект измерения;

– неточность применяемых при вычислениях физических констант и математических соотношений.

В зависимости от измеряемой величины, различают погрешность аддитивную и мультипликативную. Аддитивная погрешность не зависит от измеряемой величины. Мультипликативная погрешность меняется пропорционально измеряемой величине.

В зависимости от режима работы средства измерений, различают статическую и динамическую погрешности.

Динамическая погрешность обусловлена реакцией средства измерения на изменение параметров измеряемого сигнала (динамический режим).

Статическая погрешность средства измерения определяется при параметрах измеряемого сигнала, принимаемых за неизменные на протяжении времени измерения (статический режим).

По характеру проявления во времени, различают случайную и систематическую погрешности.

Систематической погрешностью измерения называют погрешность, которая при повторных измерениях одной и той же величины в одних и тех же условиях остаётся постоянной или закономерно меняется.

Случайной погрешностью измерения называют погрешность, которая при повторных измерениях одной и той же величины в одних и тех же условиях изменяется случайным образом.