Оценка случайной погрешности. Доверительный интервал
Методика
оценки случайной погрешности основана
на положениях теории вероятностей и
математической статистики. Оценить
случайную ошибку можно только в том
случае, когда проведено неоднократное
измерение одной и той же величины.
Пусть
в результате проделанных измерений
получено п значений величины х:
х1 , х2 , …, хп .
Обозначим через
среднеарифметическое значение
.
(3)
В
теории вероятностей доказано, что при
увеличении числа измерений п
среднеарифметическое значение измеряемой
величины приближается к истинному:
При
небольшом числе измерений (п 10)
среднее значение может существенно
отличаться от истинного. Для того, чтобы
знать, насколько точно значение
характеризует измеряемую величину,
необходимо определить так называемый
доверительный интервал полученного
результата.
Поскольку
абсолютно точное измерение невозможно,
то вероятность правильности утверждения
«величина х имеет значение, в точности
равное
»
равна нулю. Вероятность же утверждения
«величина х имеет какое-либо значение»
равна единице (100%). Таким образом,
вероятность правильности любого
промежуточного утверждения лежит в
пределах от 0 до 1. Цель измерения – найти
такой интервал, в котором с наперед
заданной вероятностью
(0 < < 1)
находится истинное значение измеряемой
величины. Этот интервал называется
доверительным интервалом, а
неразрывно связанная с ним величина
– доверительной вероятностью
(или коэффициентом надежности). За
середину интервала принимается среднее
значение, рассчитанное по формуле (3).
Очевидно,
что ширина
доверительного интервала (а следовательно,
и ошибка s x)
зависит от того, насколько сильно
отличаются отдельные измерения величины
хi от среднего
значения
.
«Разброс» результатов измерений
относительно среднего характеризуется
среднеквадратичной ошибкой ,
которую находят по формуле
,
(4)
где
.
Ширина
искомого доверительного интервала
прямо пропорциональна среднеквадратичной
ошибке:
.
(5)
Коэффициент
пропорциональности tn,
называется коэффициентом Стьюдента;
он зависит от числа опытов п и
доверительной вероятности .
Следует
отметить, что доверительная вероятность
никак не связана с точностью результата
измерений. Величиной
задаются заранее, исходя из требований
к их надежности. В большинстве технических
экспериментов и в лабораторном практикуме
значение
принимается равным 0,95.
Расчет
случайной погрешности измерения величины
х проводится в следующем порядке:
1) вычисляется
сумма измеренных значений, а затем –
среднее значение величины
по формуле (3);
2) для
каждого i-го опыта
рассчитываются разность между измеренным
и средним значениями
,
а также квадрат этой разности (отклонения)
( хi)2 ;
3) находится
сумма квадратов отклонений, а затем –
средне-квадратичная ошибка
по формуле (4);
4) по
заданной доверительной вероятности
и числу проведенных опытов п из
таблицы на с. 149 приложений выбирается
соответствующее значение коэффициента
Стьюдента tn,
и определяется случайная погрешность
s x
по формуле (5).
Значения
коэффициента Стьюдента tn,
|
|
Ч |
||||||||||
|
3 |
4 |
5 |
6 |
7 |
8 |
9 |
10 |
15 |
20 |
25 |
|
|
0,90 |
2,92 |
2,35 |
2,13 |
2,02 |
1,94 |
1,90 |
1,86 |
1,83 |
1,76 |
1,73 |
1,71 |
|
0,95 |
4,30 |
3,18 |
2,78 |
2,57 |
2,45 |
2,36 |
2,31 |
2,26 |
2,14 |
2,09 |
2,06 |
|
0,99 |
9,92 |
5,84 |
4,60 |
4,03 |
3,71 |
3,50 |
3,36 |
3,25 |
2,98 |
2,86 |
2,80 |
Плотность
веществ
|
Вещество |
Вода |
Глицерин |
Ртуть |
Свинец |
|
, |
1000 |
1260 |
13600 |
11350 |
Соседние файлы в предмете [НЕСОРТИРОВАННОЕ]
- #
- #
- #
- #
- #
- #
- #
- #
- #
- #
- #
Обновлено: 04.06.2023
Доверительный интервал – предельные значения статистической величины, которая с заданной доверительной вероятностью γ будет находится в этом интервале при выборке большего объема. Обозначается как P(θ — ε γ из достаточно близких к единице значений γ = 0.9 , γ = 0.95 , γ = 0.99 .
- доверительный интервал для генерального среднего, доверительный интервал для дисперсии;
- доверительный интервал для среднего квадратического отклонения, доверительный интервал для генеральной доли;
Если требуется найти доверительный интервал для вариационного ряда, то необходимо воспользоваться этим онлайн-калькулятором. Возможно, перед началом расчетов необходимо будет сгруппировать данные. Также существует возможность найти интервальный прогноз.
Классификация доверительных интервалов
По виду оцениваемого параметра:
По типу выборки:
- Доверительный интервал для бесконечной выборки;
- Доверительный интервал для конечной выборки;
По виду критической области:
- двусторонняя область: =2*(1-НОРМСТРАСП(Χнабл))
- левосторонняя область: =НОРМСТРАСП(Χнабл)
- правосторонняя область: =1-НОРМСТРАСП(Χнабл)
Примеры применения
Расчет средней ошибки выборки при случайном отборе
Расхождение между значениями показателей, полученных по выборке, и соответствующими параметрами генеральной совокупности называется ошибкой репрезентативности.
Обозначения основных параметров генеральной и выборочной совокупности.
| Характеристики | Генеральная совокупность | Выборочная совокупность |
| Объем совокупности (численность единиц) | N | n |
| Численность единиц, обладающих обследуемым качеством (признаком) | M | m |
| Доля единиц, обладающих обследуемым качеством (признаком), выборочная доля |
| Формулы средней ошибки выборки | |||
| повторный отбор | бесповторный отбор | ||
| для средней | для доли | для средней | для доли |
Соотношение между пределом ошибки выборки (Δ), гарантируемым с некоторой вероятностью Р(t), и средней ошибкой выборки имеет вид: или Δ = t·μ, где t– коэффициент доверия, определяемый в зависимости от уровня вероятности Р(t) по таблице интегральной функции Лапласа.
Формулы расчета численности выборки при собственно-случайном способе отбора
| Способ отбора | Формулы определения численности выборки |
| для средней | для доли |
| Повторный | |
| Бесповторный |
Найти численность выборки можно, использовав калькулятор.
Метод доверительных интервалов
- задается доверительная вероятность γ (надежность).
- по выборке определяется оценка параметра a .
- из соотношения P(α1 a находится ошибка ε.
- рассчитывается доверительный интервал (a — ε ; a + ε).
Пример №1 . При проверке годности партии таблеток (250 шт.) оказалось, что средний вес таблетки 0,3 г, а СКО веса 0,01 г. Найти доверительный интервал, в который с вероятностью 90% попадает норма веса таблетки.
Решение.
Определяем значение tkp по таблицам функции Лапласа.
В этом случае 2Ф(tkp) = 1 — γ
Ф(tkp) = γ/2 = (1- 0.05)/2 = 0.475
По таблице функции Лапласа найдем, при каком tkp значение Ф(tkp) = 0.475
tkp(γ) = Ф(0.475) = 1.96
(0.3 — 0.206;0.3 + 0.206) = (0.094;0.51)
С вероятностью 0.9 можно утверждать, что среднее значение при выборке большего объема не выйдет за пределы найденного интервала.
Пример №2 . На площади в 70 га, занятой пшеницей, определяется с помощью выборочного метода доля посева, пораженная насекомыми вредителями. Сколько проб надо взять в выборку, чтобы при вероятности 0,997 определить искомую величину с точностью до 4%, если пробная выборка показывает, что доля пораженной посевной площади составляет 9%?
Решение ищем по формуле определения численности выборки для повторного отбора.
Ф(tkp) = γ/2 = 0.997/2 = 0,4985 и этому значению по таблице Лапласа соответствует tkp =2.96.
w = 9% = 0,09
Δ = 4% = 0,04
Итого: n = 2.96 2 *0,09(1-0,09)/0,04 2 = 448,4844 ≈ 449
Пример . При проверке веса импортируемого груза на таможне методом случайной повторной выборки было отобрано 100 изделий. В результате был установлен средний вес изделия 5000 г при среднем квадратическом отклонении 40 г. С вероятностью 0,950 определить пределы, в которых находится средний вес изделия в генеральной совокупности.
Решение
Поскольку n>30, то определяем значение tkp по таблицам функции Лапласа.
В этом случае 2Ф(tkp) = γ
Ф(tkp) = γ/2 = 0.95/2 = 0.475
По таблице функции Лапласа найдем, при каком tkp значение Ф(tkp) = 0.475
tkp(γ) = (0.475) = 1.96
(5000 — 78.4;5000 + 78.4) = (4921.6;5078.4)
С вероятностью 0.95 можно утверждать, что среднее значение при выборке большего объема не выйдет за пределы найденного интервала.
Пример . С надежностью γ=0.954 построить доверительный интервал для генеральной доли
Пример №1
1. Используя результаты расчетов, выполненных в задании № 2 и полагая, что эти данные получены при помощи собственно-случайного 10-ти процентного бесповторного отбора, определить:
а) пределы, за которые с доверительной вероятностью 0,954 не выйдет среднее значение признака, рассчитанное по генеральной совокупности;
б) как нужно изменить объем выборки, чтобы снизить предельную ошибку средней величины на 50%.
2. Используя результаты расчетов, выполненных в задании № 2 и полагая, что эти данные получены при помощи повторного отбора, определить:
а) пределы, за которые в генеральной совокупности не выйдет значение доли предприятий, у которых индивидуальные значения признака превышают моду с доверительной вероятностью 0,954;
б) как изменить объем выборки, чтобы снизить предельную ошибку доли на 20 %.
Методические указания
Задание. Поточная линия по производству однотипных деталей подвергалась реконструкции Заданы две выборки отображающие процент брака в партиях деталей выпускаемых на данной линии до и после реконструкции Можно ли достоверно утверждать, что после реконструкции процент брака в партиях деталей снизился?
- провести выборку собственно случайным способом объемом n=5;
- определить интервальные значения среднего генеральной совокупности (X) по рассчитанным выборочным показателям (X, s 2 ) с помощью функции t-распределения Стьюдента при уровне значимости α=0.05;
- определить точечное значение среднего генеральной совокупности (X) по исходным данным;
- оценить правильность интервальных расчетов, сравнивая точечное значение (X) с интервальным значением, рассчитанным по выборке;
2. Вводим исходные данные.
Нажимаем кнопку Далее .
Задание №2: В целях изучения затрат времени на изготовление одной детали рабочими завода проведена 10% -ная случайная бесповторная выборка, в результате которой получено распределение деталей по затратам времени, представленное в прил. Б.
На основании этих данных вычислите:
а) средние затраты времени на изготовление одной детали;
б) средний квадрат отклонений (дисперсию) и среднее квадратическое отклонение;
в) коэффициент вариации;
г) с вероятностью 0,954 предельную ошибку выборочной средней и возможные границы, в которых ожидаются средние затраты времени на изготовление одной детали на заводе;
д) с вероятностью 0,954 предельную ошибку выборочной доли и границы удельного веса числа деталей с минимальными затратами времени на их изготовление. Перед тем как производить расчеты, необходимо записать условия задачи и заполнить табл. 2.1
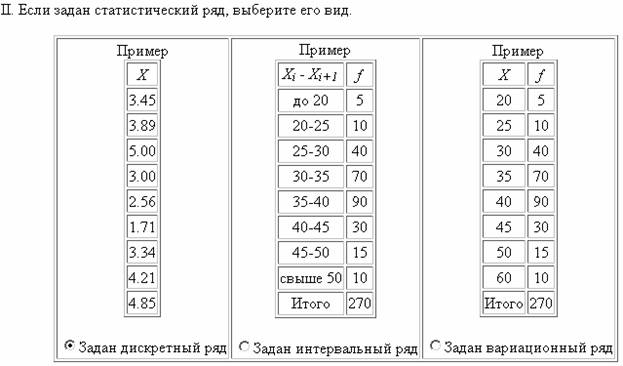
- Вид статистического ряда: Задан дискретный ряд ;
- Количество групп: не делать группировку ;
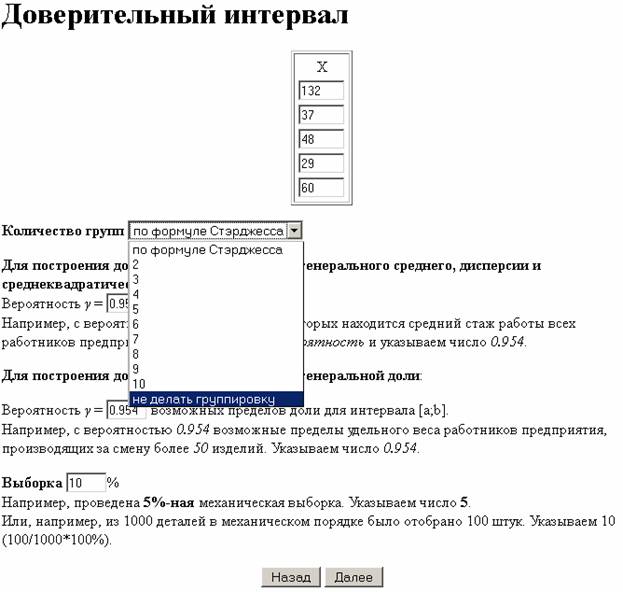
- Для построения доверительного интервала генерального среднего, дисперсии и среднеквадратического отклонения: y= 0.954 ;
- Для построения доверительного интервала генеральной доли: y= 0.954 ;
- Выборка: 10 ;
- Выводить в отчет: Доверительный интервал для генерального среднего , Доверительный интервал для генеральной доли ;
Задание №3: Используя результаты расчетов, выполненных в задании №2 и полагая, что эти данные получены при помощи повторного отбора, определить:
а) пределы, за которые в генеральной совокупности не выйдет значение доли предприятий, у которых индивидуальные значения признака превышают моду с доверительной вероятностью 0.954 ;
б) как изменить объем выборки, чтобы снизить предельную ошибку доли на 20% .
Решение.
Используя результаты расчетов, выполненных в задании № 2 и полагая, что эти данные получены при помощи повторного отбора, определить:
а) пределы, за которые в генеральной совокупности не выйдет значение доли предприятий, у которых индивидуальные значения признака превышают моду с доверительной вероятностью 0.954 ;
б) как изменить объем выборки, чтобы снизить предельную ошибку доли на 20%.
- Вид статистический ряда: Задан интервальный ряд ;
- Для построения доверительного интервала генерального среднего, дисперсии и среднеквадратического отклонения: y = 0.95 ;
- Выборка: 20 ;
- Выводить в отчет: Доверительный интервал для генерального среднего .
Задание №5: На заводе электроламп из партии продукции в количестве 16000 шт. ламп взято на выборку 1600 шт. (случайный, бесповторный отбор), из которых 40 шт. оказались бракованными. Определить с вероятностью 0.997 пределы, в которых будет находиться процент брака для всей партии продукции.
Решение.
Здесь N = 16000 , n = 1600 , w = d / n = 40/1600 = 0.025.
Для количественной оценки случайных погрешностей и установления границ случайной погрешности результата измерения могут использоваться: предельная погрешность, интервальная оценка, числовые характеристики закона распределения. Выбор конкретной оценки определяется необходимой полнотой сведений о погрешности, назначением измерений и характером использования их результатов.
Предельная погрешность Δm – погрешность, больше которой в данном измерительном эксперименте не может появиться. Теоретически, такая оценка погрешности правомерна только для распределений, границы которых четко выражены и существует такое значение ± Δm , которое ограничивает возможные значения случайных погрешностей с обеих сторон от центра распределения (например, равномерное). На практике такая оценка есть указание наибольшей погрешности, которая может встретиться при многократных измерениях одной и той же величины. Недостатком такой оценки является то, что она не содержит информации о характере закона распределения случайных погрешностей. При арифметическом суммировании предельных погрешностей получаемая сумма может значительно превышать действительные погрешности.
Более универсальными и информативными являются квантильные оценки. Площадь, заключенная под всей кривой плотности распределения погрешностей, отражает вероятность всех возможных значений погрешности и по условиям нормирования равна единице. Эту площадь можно разделить вертикальными линиями на части. Абсциссы таких линий называются квантилями. Так, на рис.16 Δx1, есть 25%-ная квантиль, так как площадь под кривой f (Δx) слева от нее составляет 25% всей площади. Абсцисса Δx2 соответствует 75%-ной квантили. Между Δx1, и Δx2 заключено 50% всех возможных значений погрешности, а остальные лежат вне этого интервала.
Рис. 16. Квантильные оценки случайной величины
Квантильная оценка погрешности представляется интервалом от − Δx(P) до + Δx(P), на котором с заданной вероятностью Ρ встречаются Ρ⋅100% всех возможных значений случайной погрешности. Интервал с границами ± Δx(P) называется доверительным интервалом случайной погрешности, между границами которого с заданной доверительной вероятностью
где q – уровень значимости; xН , xВ – нижняя и верхняя границы интервала, находится истинное значение оцениваемого параметра. Принято границы доверительного интервала (доверительные границы) указывать симметричными относительно результата измерения.
В метрологической практике используют главным образом квантильные оценки доверительного интервала. Под Р-процентным квантилем xP понимают абсциссу такой вертикальной линии, слева от которой площадь под кривой плотности распределения равна Р %. Иначе говоря, квантиль –это значение случайной величины (погрешности) с заданной доверительной вероятностью Р. Так как квантили, ограничивающие доверительный интервал погрешности могут быть выбраны различными, то при оценивании случайной погрешности доверительными границами необходимо одно -временно указывать значение принятой доверительной вероятности (например, ±0,3 В при Ρ = 0,95). Доверительные границы случайной погрешности Δx(P), соответствующие доверительной вероятности Р, находят по формуле-
где t – коэффициент, зависящий от Ρ и формы закона распределения
Рис. 17. К понятию доверительных интервалов
На графике нормального распределения погрешностей (рис. 4.11) по оси абсцисс отложены интервалы с границами ±σ, ±2σ, ±3σ, ±4σ. Доверительные вероятности для этих интервалов приведены в табл.
Границы доверительных интервалов и соответствующие им доверительные вероятности
Как видно из этой таблицы, оценка случайной погрешности группы наблюдений интервалом ±1σ соответствует доверительной вероятности 0,68. Такая оценка не дает уверенности в высоком качестве измерений, поскольку 32% от всего числа наблюдений может выйти за пределы указанного интервала, что совершенно неприемлемо при однократных измерениях и дезинформирует потребителя измерительной информации. Доверительному интервалу ±3σ соответствует Ρ = 0,997. Это означает, что практически с вероятностью очень близкой к единице ни одно из возможных значений погрешности при нормальном законе ее распределения не выйдет за границы интервала. Поэтому, при нормальном распределении погрешностей, принято считать случайную погрешность с границами ±3σ предельной (максимально возможной) погрешностью. Погрешности, выходящие за эти границы, классифицируют как грубые или промахи. В целях единообразия в оценивании случайных погрешностей интервальными оценками при технических измерениях доверительна вероятность принимается равной 0,95. Лишь для особо точных и ответственных измерений (важных, например, для безопасности и здоровья людей) допускается применять более высокую доверительную вероятность. Итак, для получения интервальной оценки многократных наблюдений нормально распределенной случайной величины необходимо:
− определить точечные оценки МО и СКО Sx случайной величины по формулам (4.3) и (4.6) соответственно;
− выбрать доверительную вероятность Р из рекомендуемого ряда значений 0,90; 0,95; 0,99;
Значения xН и xВ определяются из таблиц значений интегральной функции распределения F(t) или функции Лапласа Ф(t ). Полученный доверительный интервал удовлетворяет условию
где n – число измеренных значений; zр – аргумент функции Лапласа Ф(t ), отвечающей вероятности P/ 2. В данном случае zр называется квантильным множителем. Половина длины доверительного интервала называется доверительной границей погрешности результата измерений. При отличии закона распределения случайной величины от нормального необходимо построить его математическую модель ММ и определять доверительный интервал с ее использованием.
Рассмотренный способ нахождения доверительных интервалов справедлив для достаточно большого числа наблюдений n , когда σ = Sx . Следует помнить, что вычисляемая оценка СКО Sx является лишь некоторым приближением к истинному значению σ . Определение доверительного интервала при заданной вероятности оказывается тем менее надежным, чем меньше число наблюдений. Расчет доверительных интервалов для случая, когда распределение результатов наблюдений нормально, но их дисперсия неизвестна, т.е. при малом числе наблюдений n , можно выполнить с использованием распределения Стьюдента S(t, k ). Оно описывает плотность распределения отношения (дроби Стьюдента):
где Q – истинное значение измеряемой величины. Величины вычисляются на основании опытных данных и представляют собой точечные оценки МО, СКО результатов измерений и СКО среднего арифметического значения. Вероятность того, что дробь Стьюдента в результате выполненных наблюдений примет некоторое значение в интервале [ − tр ; + tр],
где k – число степеней свободы, равное (n −1). Величины t р (называемые коэффициентами Стьюдента), рассчитанные с помощью двух последних формул для различных значений доверительной вероятности и числа измерений, табулированы. Следовательно, с помощью распределения Стьюдента можно найти вероятность того, что отклонение среднего арифметического от истинного значения измеряемой величины не превышает,
ε – половина длины доверительного интервала, или доверительная граница погрешности измерений. В тех случаях, когда распределение случайных погрешностей не является нормальным, все же часто пользуются распределением Стьюдента с приближением, степень которого остается неизвестной. Распределение Стьюдента применяют при числе измерений n
Вспомним первый урок по теме (там же внизу оглавление) и основной метод математической статистики. Он состоит в том, что для изучения генеральной совокупности объёма из неё производится выборка, состоящая из элементов, которая хорошо характеризует всю совокупность (свойство представительности). И на основании исследования этой выборочной совокупности мы с высокой достоверностью можем оценить генеральные характеристики. Чаще всего требуется выявить закон распределения генеральной совокупности (о чём пойдёт речь позже) и оценить его важнейшие числовые параметры, такие как генеральная средняя , генеральная дисперсия и среднее квадратическое отклонение .
Очевидно, что для оценки этих параметров нужно вычислить соответствующие выборочные значения. Так, выборочная средняя позволяет нам оценить генеральную среднюю , причём, оценить её точечно. Почему точечно? Потому что – это отдельно взятое, конкретное значение. Если из той же генеральной совокупности мы будем проводить многократные выборки, то в общем случае у нас будут получаться различные выборочные средние, и каждая из них представляет собой точечную оценку генерального значения .
Аналогично, несмещённой точечной оценкой генеральной дисперсии является исправленная выборочная дисперсия , и соответственно, стандартного отклонения – исправленное стандартное отклонение .
…что-то не понятно / недопонятно в терминах? Срочно изучать предыдущие уроки!
Недостаток точечных оценок состоит в том, что при небольшом объёме выборки (как оно часто бывает), мы можем получать выборочные значения, которые далеки от истины.
И в этих случаях логично потребовать, чтобы выборочная характеристика (средняя, дисперсия или какая-то другая) отличалась от генерального значения не более чем на некоторое положительное значение . А точнее, менее.
Значение называется точностью оценки, и озвученное выше требование можно записать с помощью модуля:
А теперь я раскрою модуль:
и сформулирую суть:
На данном уроке будут рассмотрены:
- доверительный интервал для… – заголовок параграфа в поле зрения; – быстрая ссылка для опытных читателей.
Доверительный интервал для оценки генеральной средней
нормально распределённой генеральной совокупности
…да-да, пример уже 21-й!
Известно, что генеральная совокупность распределена нормально со средним квадратическим отклонением . Найти доверительный интервал для оценки математического ожидания с надежностью 0,95, если выборочная средняя , а объем выборки .
Внимание! Важное замечание: если в задаче указан тип выборки (повторная / бесповторная), то решение будет иметь свои особенности – читайте 10-ю статью об оценках по повторной и бесповторной выборке.
А теперь принципиальный момент непосредственно по задаче:
здесь известно стандартное отклонение генеральной совокупности.
Дело в том, что в похожих задачах оно бывает не известно, и тогда решение будет отличаться!
Но сейчас решение таково, разбираемся в ситуации:
– из генеральной совокупности попугаев проведена выборка в особей и по её результатам найдена выборочная средняя: (средняя масса попугая, например).
Выборочная средняя – это точечная оценка неизвестной нам генеральной средней . Как отмечалось выше, недостаток точечной оценки состоит в том, что она может оказаться далёкой от истины. И по условию, требуется найти интервал , которой с вероятностью накроет истинное значение .
Именно так! Здесь будет неверным сказать, что попадёт в этот интервал.
Решаем. Точность оценки рассчитывается по формуле , где – коэффициент доверия. Этот коэффициент отыскивается из соотношения , где – функция Лапласа.
В данном случае , следовательно:
И по таблице значений функции Лапласа либо пользуясь расчётным макетом (пункт 5*), выясняем, что значению соответствует аргумент .
Таким образом, точность оценки:
и искомый доверительный интервал:
Этот интервал с вероятностью (надёжностью) накрывает истинное генеральное значение среднего веса попугая. Но всё же остаётся 5%-ная вероятность, что генеральная средняя окажется вне найденного интервала.
Ответ: .
И тут возникает светлая мысль уменьшить этот интервал – чтобы получить более точную оценку. Что для этого можно сделать? Давайте посмотрим на формулу .
Очевидно, что чем меньше стандартное отклонение (мера разброса значений), тем короче доверительный интервал. Но это в отдельно взятой задаче ни на что не влияет – ведь нам известно конкретное значение , и изменить его нельзя.
, то есть о том, что этот более узкий интервал накроет генеральную среднюю, мы теперь можем утверждать лишь с вероятностью 68,26%. Что, конечно, неудовлетворительно, для серьёзного статистического исследования.
Поэтому для уменьшения доверительного интервала (при том же значении ) остаётся увеличивать объём выборки . Что совершенно понятно и без формулы , ведь чем больше объём выборки, тем точнее она характеризует генеральную совокупность (при прочих равных условиях). Об объёме мы поговорим на уроке об оценках по повторной и бесповторной выборке, ну а пока продолжаем.
Творческая задача для самостоятельного решения:
По результатам выборочного исследования объектов найдена выборочная средняя .
1) С какой вероятностью можно утверждать, что генеральная средняя отличается от найденного значения менее чем на 3, если известно, что генеральная совокупность распределения нормально с дисперсией 400?
2) Определить доверительный интервал, который с надежностью накроет истинное значение генеральной средней.
Расчётный макет (пункты 5 и 5*) – в помощь. Краткое решение в конце урока.
И тут, наверное, у вас назрели вопросы – а откуда известно, что генеральная совокупность распределена нормально, и тем более, откуда известно её стандартное отклонение?
Обычно эта информация известна из предыдущих исследований. Классический пример – измерительный прибор. Очевидно, что его случайные погрешности удовлетворяют условию теоремы Ляпунова, а значит, распределены нормально. Кроме того, производитель, как правило, тестирует прибор, и указывает в его паспорте стандартное отклонение случайных погрешностей измерений, которое можно принять за .
Но если установить нормальность распределения достаточно просто (в том числе статистическими методами), то с генеральным значением всё сложнее – зачастую вычислить его трудно или невозможно.
В такой ситуации остаётся ориентироваться на исправленное стандартное отклонение , и решение несколько изменится. Ещё одна классическая задача, которая уже встретилась ранее:
В результате 10 независимых измерений некоторой величины , выполненных с одинаковой точностью, полученные опытные данные, которые представлены в таблице:
Предполагая, что результаты измерений подчинены нормальному закону распределения вероятностей, оценить истинное значение величины при помощи доверительного интервала, покрывающего это значение с доверительной вероятностью 0,95.
Не путать со случайными ошибками измерительного прибора! Здесь речь идёт об измерениях и помимо технических, велико влияние других, в частности, человеческого фактора, особенно, если вы используете махрово-аналоговый прибор – что-нибудь вроде механического секундомера или линейки.
Теперь построим доверительный интервал для оценки истинного (генерального) значения величины .
Если генеральное стандартное отклонение не известно
(наш случай), то этот интервал строится по похожей формуле:
, с той поправкой, что коэффициент доверия рассчитывается с помощью распределения Стьюдента. В рамках курса теорвера я не рассказывал об этом распределении, и поэтому ограничусь технической стороной вопроса.
Значение можно найти с помощью таблицы значений распределения Стьюдента, в частности, популярна таблица, специально адаптированная для данной задачи*. И, согласно этой таблице, доверительной вероятности и объёму выборки соответствует коэффициент доверия:
* В стандартной же таблице приводятся значения для так называемого уровня значимости и числа степеней свободы .
Вычислим точность оценки:
Таким образом, искомый доверительный интервал:
– данный интервал с вероятностью накрывает истинное значение измеряемой величины .
Ответ:
Для самостоятельного решения:
На основании испытаний установлено, что в среднем для изготовления шавермы полупроводникового диода требуется секунд, а исправленное среднее квадратическое отклонение составляет секунд. Предположив, что время изготовления диода есть нормальная случайная величина, определить с надежностью доверительный интервал для оценки среднего времени изготовления диода
Краткое решение и ответ в конце урока – расчётный макет (Пункт 10б) – в помощь.
Итак, что главное в разобранных задачах? Главное, обратить внимание, генеральное ли нам дано отклонение или исправленное выборочное . От этого зависит, какую формулу нужно использовать, эту:
, где ,
или эту:
, где отыскивается с помощью распределения Стьюдента.
И быстренько более редкая задача:
Доверительный интервал для оценки
генеральной дисперсии и стандартного отклонения
Этот интервал можно построить несколькими способами, которые я постараюсь уместить буквально в пару экранов. И сейчас последует продолжение той же задачи об измерениях:
По равноточным измерениям найдено исправленное среднее квадратическое отклонение . Предполагая, что результаты измерений распределены нормально, построить доверительный интервал для оценки истинного значения (генерального стандартного отклонения) с надёжностью .
Обратите внимание, что для решения этой задачи нам не обязательно знать выборочную среднюю (хотя в Примере 23 мы её нашли).
Данный интервал с вероятностью (надёжностью) накрывает истинное значение . И если из всех частей неравенства извлечь корни, то получим соответствующий интервал для оценки генерального стандартного отклонения:
Значения известны, и осталось разобраться с нижним этажом. Во-первых, вычислим:
и теперь, по таблице критических значений распределения или с помощью расчётного макета (Пункт 11б) находим:
Способ второй. Другой, более простой подход состоит в построении симметричного интервала по формуле:
, где значение отыскивается по соответствующей таблице.
Согласно таблице, доверительной вероятности и объёму соответствует значение , таким образом:
В результате мы получили примерно такой же по размаху интервал. Для малых выборок может даже получиться , в таких случаях принимают ещё более грубую интервальную оценку:
Ответ: 1) , 2) .
Как и для распределения Стьюдента, при увеличении распределение хи-квадрат стремится к нормальному, и уже при можно использовать приближенную формулу:
, где коэффициент доверия определяется из знакомого лапласовского соотношения .
Точнее завершаю, и ради исследовательского интереса предлагаю продолжить вам – экзаменационный Пример 20:
В результате обработки экспериментальных данных объёма мы получили следующие выборочные характеристики: .
В предположении о нормальном распределении генеральной совокупности, с надёжностью определить доверительные интервалы:
1) для оценки неизвестной генеральной средней ;
2) для оценки генерального среднего квадратического отклонения двумя способами – с помощью распределения хи-квадрат: и приближённо, по формуле , где .
Краткое решение и примерный образец оформления в конце урока, который подошёл к концу. В следующей небольшой статье я разберу частную, но весьма популярную задачку по этой же теме – Оценка вероятности биномиального распределения, ну а если вам не терпится, то сразу к послеследующей статье.
До скорых встреч!
Решения и ответы:
Пример 22. Решение:
1) По условию, точность оценки равна и дисперсия .
Из формулы найдём коэффициент доверия:
Вычислим соответствующую доверительную вероятность:
– таким образом, с вероятностью 86,64% можно утверждать, что генеральная средняя отличается от менее чем на (т.е. находится в доверительном интервале от 90 до 96)
2) Для доверительной вероятности :
– этому значению функции Лапласа соответствует аргумент: .
Вычислим точность оценки:
Определим доверительный интервал:
– данный интервал с вероятностью 99% накрывает истинное значение .
Пример 24. Решение: доверительный интервал для оценки истинного значения измеряемой величины имеет вид:
Для заданного уровня доверительной вероятности и количества степеней свободы по таблице распределения Стьюдента находим: .
Вычислим точность оценки:
сек.
Таким образом, искомый доверительный интервал:
– данный интервал с вероятностью 99,9% накрывает истинное значение среднего времени изготовления одного диода.
Пример 26. Решение: вычислим исправленное среднеквадратическое отклонение:
1) Определим доверительный интервал , где .
Для уровня доверительной вероятности и объёма выборки по соответствующей таблице найдём .
Вычислим точность оценки:
Таким образом:
– с вероятностью данный интервал накроет генеральное среднее значение .
2) Найдём доверительный интервал для генерального стандартного отклонения .
а) С помощью распределения :
Вычислим и с помощью соответствующей функции Экселя (Пункт 11б) найдём:
Таким образом:
– искомый интервал, накрывающий генеральное значение с вероятностью .
б) Дадим интервальную оценку приближенно, с помощью формулы:
Коэффициент доверия найдём из соотношения . В данном случае:
, и с помощью таблицы или расчётного макета (Пункт 5*), выясняем, что .
Таким образом:
– искомый интервал.
Ответ:
1) ,
2) с помощью распределения и приближённо.
Автор: Емелин Александр
(Переход на главную страницу)
cкидкa 15% на первый зaкaз, при оформлении введите прoмoкoд: 5530-hihi5
Читайте также:
- Нотариат история возникновения кратко
- Леохар аполлон бельведерский кратко
- Назначение мониторинга и прогнозирования чс кратко
- Акционерное общество на английском кратко
- Парашютная акробатика это кратко
Погрешность и доверительный интервал: в чем разница?
17 авг. 2022 г.
читать 2 мин
Часто в статистике мы используем доверительные интервалы для оценки значения параметра совокупности с определенным уровнем достоверности.
Каждый доверительный интервал принимает следующий вид:
Доверительный интервал = [нижняя граница, верхняя граница]
Погрешность равна половине ширины всего доверительного интервала.
Например, предположим, что у нас есть следующий доверительный интервал для среднего значения генеральной совокупности:
95% доверительный интервал = [12,5, 18,5]
Ширина доверительного интервала составляет 18,5 – 12,5 = 6. Допустимая погрешность равна половине ширины, которая будет равна 6/2 = 3 .
В следующих примерах показано, как рассчитать доверительный интервал вместе с погрешностью для нескольких различных сценариев.
Пример 1: Доверительный интервал и допустимая погрешность для среднего значения генеральной совокупности
Мы используем следующую формулу для расчета доверительного интервала для среднего значения генеральной совокупности:
Доверительный интервал = x +/- z*(s/ √n )
куда:
- x : выборочное среднее
- z: z-критическое значение
- s: стандартное отклонение выборки
- n: размер выборки
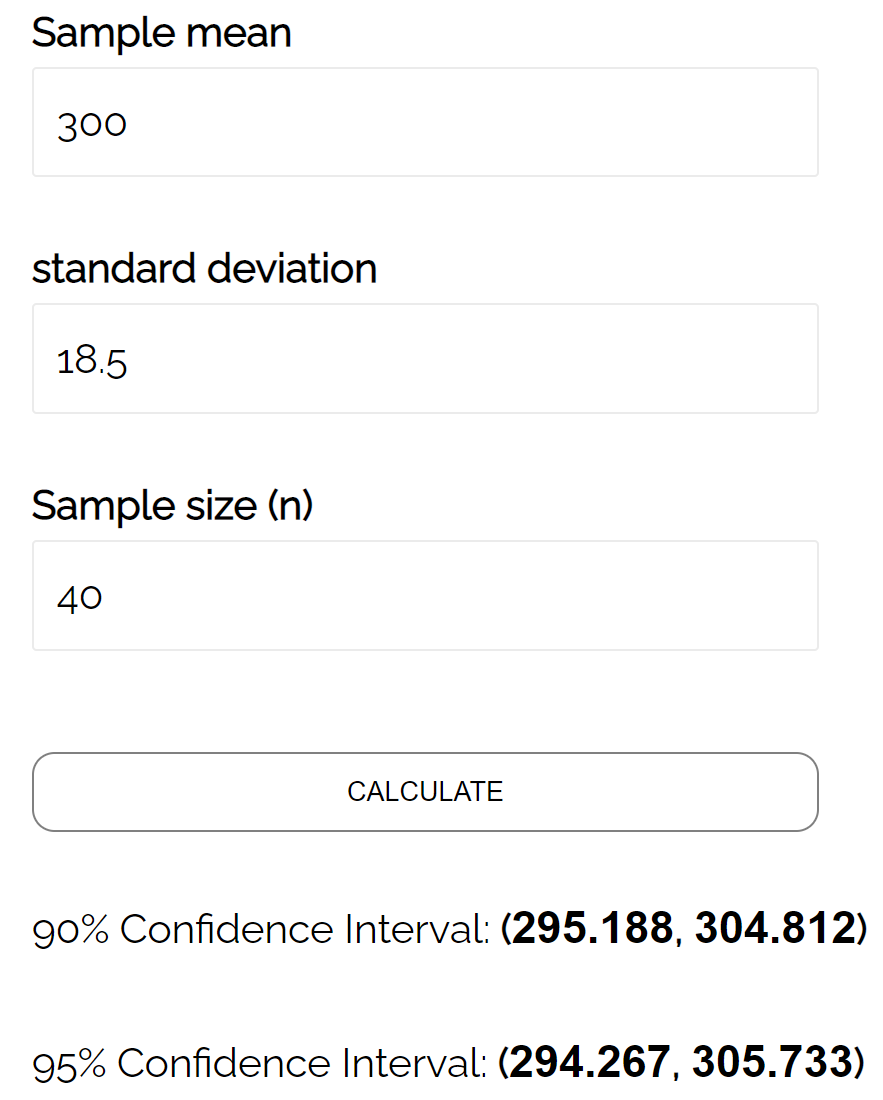
Пример: Предположим, мы собираем случайную выборку дельфинов со следующей информацией:
- Размер выборки n = 40
- Средний вес выборки x = 300
- Стандартное отклонение выборки s = 18,5
Мы можем подставить эти числа в калькулятор доверительного интервала , чтобы найти 95% доверительный интервал:
95% доверительный интервал для истинного среднего веса популяции черепах составляет [294,267, 305,733] .
Погрешность будет равна половине ширины доверительного интервала, который равен:
Погрешность: (305,733 – 294,267) / 2 = 5,733 .
Пример 2: Доверительный интервал и допустимая погрешность для доли населения
Мы используем следующую формулу для расчета доверительного интервала для доли населения:
Доверительный интервал = p +/- z * (√ p (1-p) / n )
куда:
- p: доля выборки
- z: выбранное значение z
- n: размер выборки
Пример: Предположим, мы хотим оценить долю жителей округа, поддерживающих определенный закон. Мы выбираем случайную выборку из 100 жителей и спрашиваем их об их отношении к закону. Вот результаты:
- Размер выборки n = 100
- Доля в пользу закона p = 0,56
Мы можем подставить эти числа в доверительный интервал для калькулятора пропорций , чтобы найти 95% доверительный интервал:
95% доверительный интервал для истинной доли населения составляет [0,4627, 0,6573] .
Погрешность будет равна половине ширины доверительного интервала, который равен:
Погрешность: (0,6573 – 0,4627) / 2 = 0,0973 .
Дополнительные ресурсы
Погрешность и стандартная ошибка: в чем разница?
Как найти погрешность в Excel
Как найти погрешность на калькуляторе TI-84