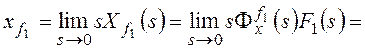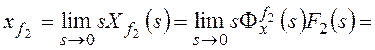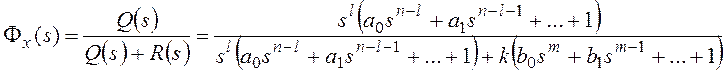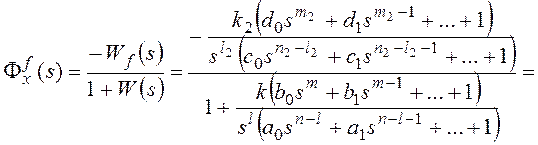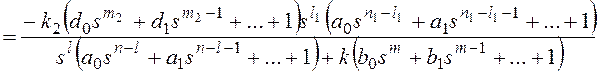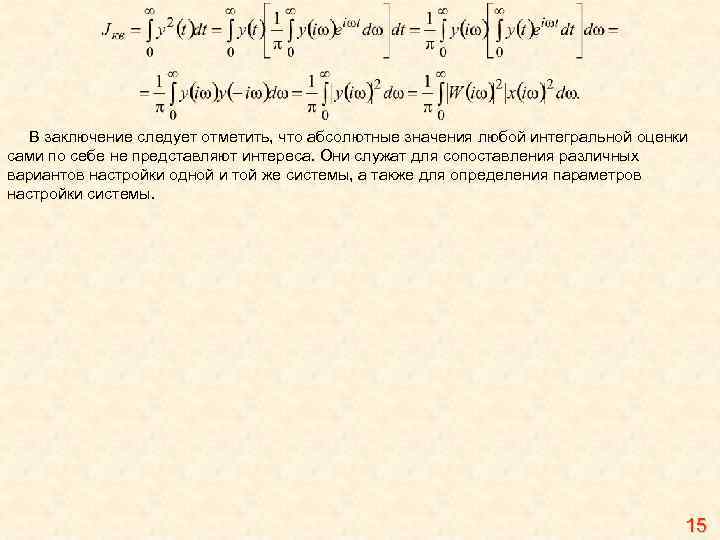По отношению к нескольким параметрическим возмущениям применяют принцип суперпозиции, который можно проиллюстрировать следующим примером.
Пусть система управления описывается дифференциальным уравнением первого порядка
|
Ту’(t) + у(t) = k х(t) или |
dy |
= − |
1 |
y(t) + |
k |
x(t) , |
|
|
dt |
T |
T |
|||||
ДЛЯ КОТОРОЙ ВВОДЯТСЯ ДВЕ ФУНКЦИИ ЧУВСТВИТЕЛЬНОСТИ
Vkу(t) = ∂y∂(kt) ; VTy (t) = ∂∂yT(t) .
Если продифференцировать исходноеуравнение по параметрам k и Т
|
∂ dy |
= |
−1 ∂ |
y(t) + |
1 |
x(t); |
||||||
|
∂k dt |
T ∂k |
T |
|||||||||
|
k |
|||||||||||
|
∂ |
dy = − |
−1 |
∂y |
+ |
1 |
y(t) |
− |
x(t) |
|||
|
T 2 |
T 2 |
||||||||||
|
∂T dt |
T |
∂T |
и произвести в полученных выражениях замену через функции чувствительности, то получают уравнения чувствительности рассматриваемой системы:
|
dV y |
(t) |
1 |
V y (t) + |
1 |
||||||
|
k |
= − |
x(t); |
||||||||
|
dt |
T |
T |
||||||||
|
k |
||||||||||
|
dV y |
(t) |
1 |
V y (t) + |
1 |
||||||
|
T |
= − |
(y(t) − kx(t)). |
||||||||
|
dt |
T |
T 2 |
||||||||
|
T |
Определив Vky (t) и VTy (t) , можно найти изменение хода процесса управления за счет изменения параметров k и Т:
∆у(t) = Vky (t) ∆k + Vky (t) ∆Т.
Функции чувствительности применяют для проектирования системы с наименьшим изменением качественных показателей при отклонении значений параметров системы от расчетных.
8.4 Понятие об управляемости и наблюдаемости объекта
При проектировании систем управления необходимо предварительно оценивать такие структурные свойства объектов как управляемость и наблюдаемость.
Объект называется полностью управляемым, если его с помощью некоторого ограниченного управляющего воздействия можно перевести в течение конечного интервала времени из любого начального состояния в заданное конечное состояние. Для осуществления такого перевода объекта необходимо, но не достаточно, чтобы каждая из координат состояния зависела хотя бы от одной из составляющих управляющего воздействия.
Линейный стационарный объект называется полностью наблюдаемым, если по результатам наблюдения (измерения или измерения и вычисления) выходных координат можно определить (восстановить) предыдущие значения координат состояния. Для полной наблюдаемости или восстанавливаемости объекта необходимо (но не достаточно), чтобы каждая координата состояния была связана по меньшей мере с одним из наблюдаемых сигналов.
8.5 Тренировочные задания
1НАРЯДУ С ПРОБЛЕМОЙ УСТОЙЧИВОСТИ ПРИ СИНТЕЗЕ СИСТЕМ АВТОМАТИЧЕСКОГО РЕГУЛИРОВАНИЯ ЯВЛЯЕТСЯ ПРОБЛЕМА КАЧЕСТВА РЕГУЛИРОВАНИЯ, ХАРАКТЕРИЗУЮЩАЯ ТОЧНОСТЬ И ПЛАВНОСТЬ ПРОТЕКАНИЯ ПЕРЕХОДНОГО ПРОЦЕССА. ДЛЯ ОЦЕНКИ КАЧЕСТВА РЕГУЛИРОВАНИЯ В КОЛИЧЕСТВЕННОЙ ФОРМЕ ИСПОЛЬЗУЮТСЯ ПОКАЗАТЕЛИ КАЧЕСТВА, КОТОРЫЕ ПОДРАЗДЕЛЯЮТСЯ НА ПРЯМЫЕ, КОСВЕННЫЕ, ЧАСТОТНЫЕ, ИНТЕГРАЛЬНЫЕ.
А Какие показатели качества называются прямыми и почему?
В Какой из косвенных показателей качества регулирования используют для оценки качества колебательных переходных процессов?
С Что является положительным фактом использования интегральных критериев качества регулирования?
2В ИНЖЕНЕРНОЙ ПРАКТИКЕ ШИРОКО ИСПОЛЬЗУЮТСЯ ЧАСТОТНЫЕ МЕТОДЫ ИССЛЕДОВАНИЯ СИСТЕМ УПРАВЛЕНИЯ, КОТОРЫЕ ПОЗВОЛЯЮТ ОЦЕНИТЬ КАЧЕСТВО РЕГУЛИРОВАНИЯ ПО ВЕЩЕСТВЕННЫМ ЧАСТОТНЫМ ХАРАКТЕРИСТИКАМ.
А Если ВЧХ представлена суммой, то что представляет собой переходный процесс?
В Если ВЧХ по оси координат увеличили в a раз, то как поведет себя переходный процесс? С Как определить начальное и конечное значения переходного процесса?
8.6Тест
1КАКОЙ ПОКАЗАТЕЛЬ ОТНОСИТСЯ К ГРУППЕ ПРЯМЫХ ПОКАЗАТЕЛЕЙ КАЧЕСТВА РЕГУЛИРОВАНИЯ?
А Степень устойчивости. В Время регулирования. С Начальное отклонение.
2КАКОЙ ПОКАЗАТЕЛЬ КАЧЕСТВА НАЗЫВАЕТСЯ СТАТИЧЕСКОЙ ОШИБКОЙ?
А Максимальное отклонение от заданного значения.
В Отклонение от заданного значения вустановившемся состоянии.
С Разность между максимальным и минимальным значениями переходного процесса.
3 СТЕПЕНЬ ЗАТУХАНИЯ ОПРЕДЕЛЯЕТСЯ КАК…
А ψ = y1 − y3 100 %. y1
В ψ = y1 − y3 100 %. y3
С ψ = y1 − y3 100 %, y2
где y1, y2, y3 − амплитуды выходных колебаний.
4 ЕСЛИ η − СТЕПЕНЬ УСТОЙЧИВОСТИ, ТО ВРЕМЯ РЕГУЛИРОВАНИЯ АПЕРИОДИ-
ЧЕСКИХ ПЕРЕХОДНЫХ ПРОЦЕССОВ ОПРЕДЕЛЯЕТСЯ КАК…
А Tp > η3 . В Tp = 3η. С Tp ≤ η3 .
5 ОЦЕНКА СТАТИЧЕСКОЙ ОШИБКИ МОЖЕТ БЫТЬ ПОЛУЧЕНА КАК…
А yст = lim y(t).
t →∞
В yст = max y(t). С yст = min y(t).
|
6 |
ИНТЕГРАЛЬНЫЙ КВАДРАТИЧНЫЙ КРИТЕРИЙ КАЧЕСТВА РЕГУЛИРОВА- |
|||
|
НИЯ − ЭТО… |
||||
|
∞ |
||||
|
А |
J = ∫ |
′ |
2 |
dt. |
|
(y(t) + y (t)) |
||||
|
0 |
||||
|
∞ |
В J = ∫y2 (t)dt.
0
С J = ∞∫(y′(t)2 + y(t))dt.
0
7 ПРИ АНАЛИЗЕ ПЕРЕХОДНОГО ПРОЦЕССА С ПОМОЩЬЮ ВЧХ НЕОБХОДИМО ПРИВЕСТИ В СООТВЕТСТВИЕ МАСШТАБЫ ПО ОСИ КООРДИНАТ. ЕСЛИ ВЧХ УВЕЛИЧИЛАСЬ В α РАЗ, Т.Е. СТАЛА αRE(ω), ТО ПЕРЕХОДНЫЙ ПРОЦЕСС…
А Увеличится в α раз − α y(t). В Уменьшится в α раз − α1 y(t) .
ССожмется в α раз − y t .
α
8 УСЛОВИЕМ МОНОТОННОСТИ ПРОТЕКАНИЯ ПЕРЕХОДНОГО ПРОЦЕССА ЯВЛЯЕТСЯ…
А Re(ω) > 0; d Re(dωω) < 0 .
В Re(ω) > 0; d Re(dωω) > 0 .
С Re(ω) < 0; d Re(ω)dω < 0.
9 СИНТЕЗ СИСТЕМ АВТОМАТИЧЕСКОГО РЕГУЛИРОВАНИЯ
9.1 Задачи синтеза
Рассмотренные выше задачи относятся к задачам анализа автоматических систем. Задачи синтеза можно рассматривать как обратные задачам анализа. Они подразделяются на два вида: во-первых, требуется определить структуру, во-вторых, параметры системы по заданным показателям качества.
Синтез является важнейшим этапом проектирования и конструирования систем, основным и наиболее важным приложением результатов, полученных теорией автоматического управления. При решении задачи полного синтеза необходимо определить алгоритмическую и функциональную структуры системы.
Алгоритмическую структуру системы находят при помощи математических методов на основании требований, записанных в математической форме. В связи с этим процедуру отыскания алгоритмической структуры называют теоретическим синтезом или аналитическим конструированием системы управления.
Синтез функциональной структуры заключается в выборе конкретных элементов системы и согласовании их характеристик. Этот этап проектирования не имеет пока строгой математической основы и относится к области инженерного искусства. Последовательность решения задач полного синтеза может быть различной.
В простых случаях задачу иногда удается решить с методологической точки зрения в идеальной последовательности. При проектировании сложных промышленных систем управления применить такую последовательность, как правило, оказывается невозможно, поэтому в большинстве случаев задачу синтеза решают следующим образом.
Вначале, исходя из требований назначения системы и учитывая условия ее работы, по каталогам серийного оборудования выбирают функционально необходимые элементы: регулирующий орган, исполнительное устройство, датчики, которые вместе с объектом управления образуют неизменную часть системы. Затем на основании требований к статическим и динамическим свойствам системы определяют ее изменяемую часть, алгоритмическая структура которой находится с учетом свойств выбранных функционально необходимых элементов. Техническая же реализация осуществляется с использованием стандартных унифицированных регуляторов и различных корректирующих и компенсирующих устройств. Процессы определения алгоритмической и функциональной структур системы управления тесно переплетаются между собой, их приходится выполнять по несколько раз. Окончательное решение о структуре системы принимается на основе компромисса между точностью и качеством работы системы, с одной стороны, и простотой и надежностью – с другой.
Заключительным этапом проектирования системы управления является расчет настроечных параметров выбранного регулятора. В разделе 7 отмечалось, что под синтезом устойчивых систем понималось определение параметров настроек регуляторов при известной структуре. Ниже приводятся методы расчета настроечных параметров для одноконтурной системы автоматического управления.
В настоящее время разработано много методов расчета настроек регулятора, одни из них являются более точными, но трудоемкими, другие – простыми, но приближенными. Во всех методах необходимо обеспечить процесс регулирования, какправило, удовлетворяющий двум выбранным критериям, один из которых позволяет обеспечить заданный запас устойчивости, а второй – обеспечить качество регулирования.
9.2 Выбор оптимальных настроек регуляторов методом незатухающих колебаний
Метод незатухающих колебаний, предложенный учеными Циглером иНикольсом, является приближенным методом определения оптимальных настроекрегуляторов, обеспечивающим необходимый запасустойчивости, некоторую степень затухания инебольшую динамическую ошибку.
Расчет регуляторов с одним параметром настройки производится в один этап и основывается на расчете критического значения настройки пропорциональной составляющей, при которой АСР будет находиться на границе устойчивости. Уравнение для расчета этой настройки выводится из критерия устойчивости Найквиста, чтобы обеспечить запас устойчивости. Для некоторого значения частоты ωкр должно выполняться соотношение Wp.c (iωкp) = – 1.
Таким образом, П-регулятор рассчитывается по обычным частотным характеристикам объекта. Уравнения для расчета критических значений настройки S1кp и частоты ωкр имеют вид:
|
ϕоб(ωкp) = –π; |
(9.1) |
1 |
||
|
S1кp= |
. |
(9.2) |
||
|
M об (ωкр ) |
||||
|
Оптимальная настройка П-регулятора: |
||||
|
S1опт |
= 0,55 S1кр. |
(9.3) |
Расчет регуляторов с двумя и более параметрами настройки производится в два этапа: на первом – определяется критическое значение пропорциональной составляющей; на втором – обеспечивается степень затухания ψ = 0,8 … 0,9.
Оптимальные настройки регуляторов находят по следующим формулам:– ПИ-регулятор
|
S опт = 0,45 S |
1кр |
; |
(9.4) |
|
1 |
S0опт = 0,086S1крωкр;
|
– ПИД-регулятор |
S1опт = 0,6 S1кр; |
|
S0опт = 0,192S1крωкр; |
(9.5) |
S2опт = 0,471 S1кр .
ωкр
9.3Алгоритм расчета области настроек типовых регуляторов методом РАФХ
Метод расширенных частотных характеристик описан в разделе 7 и использован при синтезе систем с заданным запасом устойчивости.
Методика расчета оптимальных настроек регуляторов методом РАФХ аналогична. Под оптимальными настройками в данном методе понимают настройки регулятора, обеспечивающие заданную степень колебательности mзад процесса регулирования при минимуме интегрального квадратичного критерия Jкв. В связи с этим расчет настроечных параметров регулятора распадается на два этапа: определение настроек, обеспечивающих заданный запас устойчивости – заданную степень колебательности, и определение настроек, обеспечивающих качество регулирования, оцениваемое по интегральному квадратичному критерию.
Первый этап подробно описан в разделе 7. Расчет регуляторов с одним настроечным параметром (П- и И-регуляторы) выполняется в один (первый) этап. Для регуляторов с двумя настроечными параметрами на первом этапе рассчитывается линия равной степени колебательности в плоскости параметров настроек S0, S1. На втором этапе необходимо выбрать только одну пару настроек S0опт, S1опт, соответ-
ствующую минимальному значению интегрального квадратичного критерия качества. Расчет этого критерия для различных процессов регулирования показывает, что его минимуму для ПИ-регулятора соответствует точка на кривой равной степени колебательности, расположенная несколько правее вершины (рис. 9.1, а). Такой точкой является точка 3. Разным точкам на кривой равной степени колебательности соответствуют различные процессы регулирования (рис. 9.1, б).
|
y |
1 |
б) |
|||||||
|
а) |
|||||||||
|
S0 |
|||||||||
|
2 |
3 |
||||||||
|
1 |
4 |
2 |
|||||||
|
3 |
4 |
||||||||
|
0 |
m = mзад |
5 S1 |
5 |
||||||
|
0 |
|||||||||
|
t |
|||||||||
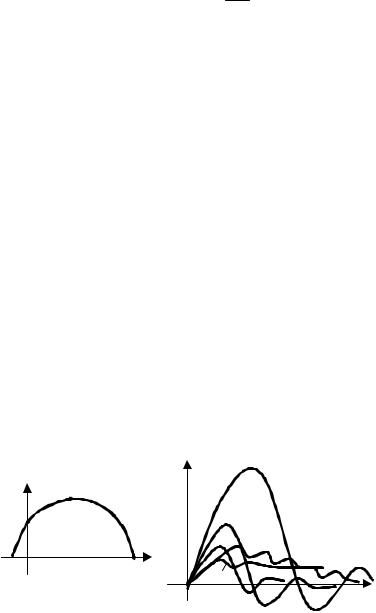
Рис. 9.1 Выбор оптимальных настроек ПИ-регулятора:
a – кривая равной степени колебательности; б – графики переходных процессов регулирования для различных настроек ПИ-регулятора
В точке 1 отсутствует пропорциональная составляющая, регулятор работает как интегральный, особенностью которого является наибольшая динамическая ошибка. В точках 2 и 3 регулятор работает как ПИ-регулятор, причем из сравнения этих двух процессов видно, что с точки зрения заданного качества регулирования переходный процесс в точке 3 лучше, чем в точке 2. Так как при движении вдоль кривой равной степени колебательности пропорциональная составляющая возрастает, возрастает рабочая частота, следовательно, уменьшается динамическая ошибка регулирования, но с некоторого момента (точка 2) начинает уменьшаться и величина настройки интегральной составляющей S0, которая определяет скорость устранения статической ошибки. Чем меньше величина S0 , тем медленнее выбирается статическая ошибка, т.е. наблюдается затягивание «хвоста» переходного процесса (точка 4). В точке 5 от-
сутствует интегральная составляющая, регулятор работает как пропорциональный, его особенностью является наличие статической ошибки регулирования.
Оптимальные настройки регулятора S0опт и S1опт рассчитываются по минимуму Jкв. Для их выбора
необходимо рассчитывать критерий Jкв для всех пар настроек регулятора вдоль кривой равной степени колебательности. Эта процедура трудоемка и на практике прибегают к инженерной методике определения местонахождения точки 3. Рабочая частота определяется, исходя из соотношений
ωр = 1,2 ω0 или ωр 0,8 ωп,
где ω0 – частота, соответствующая вершине кривой m = mзад; ωп – частота, соответствующая пропорциональному закону регулирования. После этого по формулам (7.18) рассчитываются S0опт , S1опт .
|
y |
б) |
|||
|
а) |
||||
|
S1 |
2 |
3 |
||
|
m = mзад |
||||
|
1 |
||||
|
1 |
3 |
|||
|
2 |
||||
|
0 |
S2 |
yзад |
t |
|
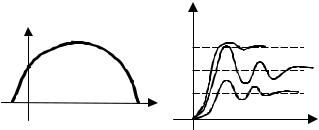
Рис. 9.2 Выбор оптимальных настроек ПД-регулятора:
а – линия равной степени колебательности; б – графики процессов регулирования для различных настроек ПД-регулятора
Процедура расчета оптимальных параметров настроек ПД-регу-лятора аналогична расчету ПИрегулятора. В плоскости параметров S1 и S2 строится кривая заданной степени колебательности (рис. 9.2, а). При движении вдоль кривой вправо увеличивается дифференцио-нальная составляющая S2 и частота. Следовательно, чем больше S2, тем меньше динамическая ошибка регулирования. Величина настройки, пропорциональная составляющей S1, сначала увеличивается, а затем уменьшается, причем, чем больше S2, тем меньше статическая ошибка. Вышесказанное хорошо иллюстрируется графиками процессов регули-рования для различных настроек регуляторов, изображенных на рис. 9.2, б.
Оптимальные настройки S1*, S2* определяются из условия минимума Jкв, которому на кривой равной степени колебательности соответствует точка, расположенная на ее вершине.
9.4 Графоаналитический метод синтеза систем
Рассматриваемый метод относится к группе графоаналитических методов, разработанных В. Я. Ротачем, в основу которого заложены следующие положения.
Во-первых, считается, что система регулирования обладает необходимым запасом устойчивости, если ее показатель колебательности не превышает величины М = 1,1 … 1,6, т.е. одним из критериев оптимальности является обеспечение заданного показателя колебательности Мзад.
Во-вторых, линейную систему регулирования можно рассматривать как своеобразный частотный фильтр, через который проходят составляющие гармоники входных воздействий. В зависимости от динамических свойств АСР гармоники с различными частотами претерпевают различные изменения, т.е. амплитуда и фаза выходного сигнала будут другие, чем на входе.
Идеальной системой регулирования считается система, обладающая абсолютными фильтрующими свойствами. Амплитудно-частотная характеристика такой системы относительно возмущающих воздействий равна нулю во всем диапазоне частот от 0 до ∞, а относительно управляющего воздействия она
равна 1, т.е. Мв(ω) = 0; Му(ω) = 1.
Задача выбора оптимальных параметров настроек системы заключается в том, чтобы в наибольшей степени приблизить АЧХ реальной системы к АХЧ идеальной системы. Так как в реальных системах практически невозможно добиться, чтобы выполнялось условие Мв(ω) = 0, то параметры на-
стройки должны выбираться таким образом, чтобы система наиболее интенсивно фильтровала «опасные» гармоники. Так как производственные объекты являются низкочастотным фильтром, то целесообразно выбрать такой метод, который гарантировал бы наилучшее приближение частотных характеристик системы в окрестности точки с нулевой частотой. Приближение реальной системы к идеальной осуществляется путем разложения в ряд Тейлора. Условие оптимальности можно записать в виде:
|
– относительно возмущающего воздействия |
d |
||||||
|
Мв(0) = 0; |
Mв(0) = 0 ; |
(9.6) |
|||||
|
dω |
|||||||
|
– относительно управляющего воздействия |
|||||||
|
d |
|||||||
|
Му(0) = 1; |
M у(0) = 0 . |
(9.7) |
|||||
|
dω |
|||||||
Уравнения (9.6), (9.7) служат для определения оптимальных параметров настроек системы. Расчет проводится в следующем порядке.
1В пространстве параметров настроек регулятора определяется граница области, в которой система обладает достаточным запасом устойчивости.
2В этой области определяется точка, удовлетворяющая минимуму отклонения частотных характеристик реальной системы от характеристик идеальной.
Исходными данными являются частотные характеристики объекта, в частности, амплитуднофазовая.
Для построения границы заданного запаса устойчивости используется следующий подход. Как известно, запас устойчивости может определяться двумя числовыми величинами: запасом устойчивости по модулю и запасом устойчивости по фазе, характеризующими степень удаления АФХ разомкнутой системы от «опасной» точки (–1, i0). Но оказывается, что степень удаления АФХ разомкнутой системы от точки (–1, i0) может быть определена по величине максимума амплитудно-частотной характеристики замкнутой системы (см. 7.3.2).
Таким образом, требование, чтобы максимум АЧХ замкнутой системы не превышал некоторой заранее заданной величины, сводится к требованию, чтобы АФХ разомкнутой системы не заходила внутрь области, ограниченной радиусом r и с центром на расстоянии R от начала координат, расположенной на отрицательной вещественной полуоси.
После определения области заданного запаса устойчивости производится определение точки в этой области, соответствующей оптимальным настройкам регулятора.
9.4.1П-РЕГУЛЯТОР
Передаточная функция П-регулятора записывается в виде
|
W(s) = kр. |
|
|
Амплитудно-фазовая характеристика разомкнутой системы с |
П-регулятором: |
|
Wр.с (iω) = kp Wоб (iω). |
Определение оптимальной настройки kр производится в следующем порядке.
Строится АФХ разомкнутой системы при kp = 1, что соответствует W(i ω) = Wоб(iω), т.е.построению АФХ регулируемого объекта (рис. 9.3). Далее, из начала координат проводится луч под углом
|
β = arcsin |
1 |
(9.8) |
|
|
M |
|||
к отрицательной вещественной полуоси.
Вычерчивается окружность с центром на вещественной отрицательной полуоси, касающаяся одновременно АФХ объекта и этого луча:
|
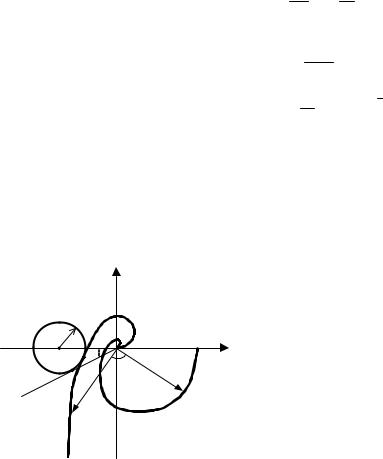
rkp = |
M |
, т.е. kp = |
M |
1 . |
(9.9) |
|
|
M 2 −1 |
||||||
|
M 2 −1 r |
В большинстве случаев расчет систем автоматического регулирования проводится на обеспечение показателя коле-бательности М = 1,62, что га-рантирует запас устойчивости по модулю d = 0,38 и по фазе
γ = 36°, а степень затухания пе-реходного процесса в колеба-тельном звене Мз.c(0) = 1: γ = 0,9. В соответствии с этим формулы (9.8) и (9.9) принимают вид
|
1 |
° |
|||||
|
β = arcsin |
= 38 |
; |
||||
|
1,62 |
||||||
|
1 |
(9.10) |
|||||
|
. |
||||||
|
kp = |
r |
|||||
Найденное значение коэффициента передачи является оптимальным значением.
9.4.2 И–РЕГУЛЯТОР
Передаточная функция И-регулятора:
Wи(s) = kp , где kp = εp . Tps Tp
Амплитудно-фазовая характеристика разомкнутой системы:
Wp.c (iω) = iωkpTp Wоб(iω);
Wp.c (iω) = εωp Wоб(iω)e−i π2 .
Расчет П-регулятора производится в два этапа:
1 По АФХ регулируемого объекта строится АФХ разомкнутой системы для kр = 1 и некоторого значения постоянной времени Тр, величина которой выбирается любой, удобнойдля построения характеристики:
|
W 1 |
Wp.c (iω) |
1 |
W (iω)e−i |
π |
||||
|
(iω) = |
= |
2 |
. |
|||||
|
iωT |
ωT |
|||||||
|
p.c |
об |
|||||||
|
p |
p |
|
Im |
||
|
r |
||
|
β |
90° |
Re |
|
Wоб(i ω) |
||
|
ω1 |
||
|
ω1 |
||
|
Wр.с(i ω) |
Рис. 9.4 Определение предельного коэффициента передачи И- регулятора
ЧЕНИЕМ, ОПРЕДЕЛЯЕТСЯ КАК
|
εp = |
kp |
= |
1 M |
1 |
. |
||
|
Tp |
Tp M 2 |
−1 r |
|||||
Последнюю удобно строить, поворачивая каждый вектор АФХ объекта на угол 90° по часовой стрелке и уменьшая его длину в Тр ω раз (рис. 9.4).
2 ПРОВОДИТСЯ ЛИНИЯ ПОД УГЛОМ β К ОТ-
РИЦАТЕЛЬНОЙ ВЕЩЕСТВЕННОЙ ПОЛУОСИ И ВЫЧЕРЧИВАЕТСЯ ОКРУЖНОСТЬ С ЦЕНТРОМ, РАСПОЛОЖЕННЫМ НА ЭТОЙ ОСИ, КАСАЮЩАЯСЯ ОДНОВРЕМЕННО ПОСТРОЕННОЙ ЛИНИИ И АФХ Wр1.с (Iω). ВЕЛИЧИНА КОЭФФИЦИЕНТА ПЕ-
РЕДАЧИ KР, ОБЕСПЕЧИВАЮЩАЯ ЗАДАННУЮ ВЕЛИЧИНУ МАКСИМУМА АЧХ ЗАМКНУТОЙ СИСТЕМЫ (ЗАДАННЫЙ ПОКАЗАТЕЛЬ КОЛЕБАТЕЛЬНОСТИ МЗАД ОПРЕДЕЛЯЕТСЯ ПО ФОРМУЛЕ (9.9)), И, СЛЕДОВАТЕЛЬНО, ВЕЛИЧИНА ПРЕДЕЛЬНОГО КОЭФФИЦИЕНТА ПЕРЕДАЧИ И-РЕГУЛЯТОРА, КОТОРАЯ ЯВЛЯЕТСЯ И ЕГО ОПТИМАЛЬНЫМ ЗНА-
(9.11)
|
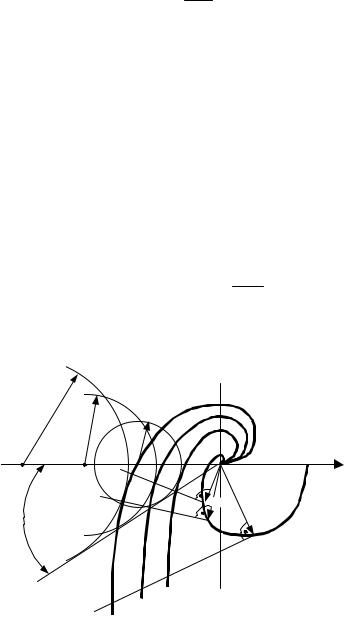
Если M зад =1,62 , то |
|||||||||||
|
β = 38°; kp = |
1 |
; |
εp = |
1 |
. |
(9.12) |
|||||
|
r |
Tp r |
||||||||||
|
9.4.3 |
ПИ-РЕГУЛЯТОР |
||||||||||
|
Передаточная функция ПИ-регулятора: |
|||||||||||
|
W |
(s) = k |
+ |
1 |
||||||||
|
1 |
. |
||||||||||
|
пи |
p |
Tиs |
Амплитудно-фазовая характеристика разомкнутой системы:
Wp.c (iω) = kp 1+ iω1Tи Wоб(iω) .
Расчет ПИ-регулятора производится в следующем порядке:
1 Строится семейство АФХ разомкнутой системы при kр = 1 и некоторых различных значениях времени изодрома Tиl (l = 1, 2, 3, …), выбираемых произвольно, но с точки зрения удобства построения:
Wpl.c (iω) =Wоб(iω) −i WобT(iω) .
ω иl
Для определения границы области устойчивости ПИ-регулятора первоначально вычерчивается АФХ объекта W(i ω), которую достаточно иметь в пределах III квадранта комплексной плос-
кости W (рис. 9.5).
НА ЭТОЙ ХАРАКТЕРИСТИКЕ ВЫБИРАЮТСЯ ТОЧКИ А1, А2, А3, … С ЧАСТОТАМИ ω 1, ω 2, ω3, …, КОТОРЫЕ СОЕДИНЯЮТСЯ С НАЧАЛОМ КООРДИНАТ ОТРЕЗКАМИ ОА1, ОА2,
ОА3, … . К ЭТИМ ОТРЕЗКАМ В ТОЧКАХ А1, А2, А3, … ВОССТАНАВЛИВАЮТСЯ ПЕРПЕНДИКУЛЯРЫ. ДАЛЕЕ ОПРЕДЕЛЯЮТСЯ ПОЛОЖЕНИЯ ТОЧЕК ВJ АФХ РАЗОМКНУТОЙ СИСТЕМЫ. С ЭТОЙ ЦЕЛЬЮ НА ВОССТАНОВЛЕННЫХ ПЕРПЕНДИКУЛЯРАХ ОТКЛАДЫВА-
ЮТСЯ ОТРЕЗКИ АJВJ, ОПРЕДЕЛЯЕМЫЕ, КАК Aj Bj = OAj . СОЕДИНЯЯ ТОЧКИ ВJ С ВРЕМЕ-
ωjTиl
НЕМ ИЗОДРОМА ТИL ПЛАВНОЙ КРИВОЙ, ПОЛУЧАЮТ АФХ РАЗОМКНУТОЙ СИСТЕМЫ. АНАЛОГИЧНЫМ ОБРАЗОМ СТРОЯТСЯ АФХ РАЗОМКНУТОЙ СИСТЕМЫ ДЛЯ ДРУГИХ ЗНАЧЕНИЙ ТИL.
Im
r3
|
r2 |
r1 |
|||
|
B3 |
Re |
|||
|
Wоб(i ω) |
||||
|
B2 A3 |
ω3 |
|||
|
ββ |
ω2 |
|||
|
ω1 |
||||
|
A2 |
A1
B1
Tи1
Tи2
Tи3
РИС. 9.5 К ОПРЕДЕЛЕНИЮ КОЭФФИЦИЕНТОВ ПЕРЕДАЧИ
ПИ-регулятора для различных Тиl
2Проводится линия под углом β к вещественной отрицательной полуоси и строятся окружности
сцентром на этой оси, касающиеся АФХ разомкнутой системы для различных Тиl и этой прямой. Для каждого значения Тиl определяется предельное значение коэффициента передачи
|
kpl = |
M |
1 |
, |
|
|
M 2 −1 rl |
если M зад =1,62, то β = 38°, kpl = 1r l .
Рис. 9.6 Определение оптимальной настройки ПИрегулятора
3 В плоскости параметров настроек kр – Ти строится граница области, в которой максимум АЧХ замкнутой системы относительно управляющего воздействия не превышает заданной величины. С этой целью используются полученные данные kpl, Тиl (рис. 9.6).
Оптимальным настройкам регулятора соответствует точка, для
которой отношение kр будет максимальным, так как именно в ней
Tи
выполняется условие (9.7). Такой точкой является точка касания касательной к границе области допустимого запаса устойчивости, проведенной через начало координат. Действительно, любая другая
прямая, выходящая из начала координат с большим отношением kр ,
Tи
которое определяет угловой коэффициент, не будет проходить через область допустимого запаса устойчивости, и поэтому получить большую величину отношения в данной системе невозможно без уменьшенияееустойчивости ниже необходимой величины.
9.5Тренировочные задания
1Важнейшим этапом проектирования и конструирования систем является синтез, когда необходимо определить алгоритмическую и функциональную структуру. Если структура известна, то синтез сводится к определению параметров настроек регуляторов. Все методы расчета последних подразделяются на точные, но трудоемкие, и простые, но приближенные. Наиболее распространенными являются метод незатухающих колебаний, метод РАФХ и графоаналитический метод.
АВ чем заключается синтез функциональной структуры?
В Какие методы расчета параметров настроек регуляторов относятся к точным методам? С Как называется синтез, заключающийся в расчете параметров настроек регуляторов?
2 Одним из точных методов расчета параметров настроек регуляторов является метод РАФХ, основанный на аналоге критерия Найквиста. Расчет распадается на два этапа: определение настроек, обеспечивающих заданный запас устойчивости, и определение настроек, обеспечивающих качество регулирования.
А Какие параметры настроек регуляторов называются оптимальными согласно методу РАФХ? В Каким показателем оценивается качество регулирования в методе РАФХ?
СКак выбираются оптимальные настройки в методе РАФХ для регуляторов с двумя настроечными параметрами?
3 Вторым точным методом расчета оптимальных настроек регулятора является графоаналитический метод, основанный на использовании АФХ регулируемого объекта.
А Каким показателем оценивается запас устойчивости в графоаналитическом методе? В Как в графоаналитическом методе оценивается качество регулирования?
СКак определить оптимальные настройки ПИ-регулятора?
9.6Тест
Точность системы автоматического управления Статическая ошибка системы
В системах
автоматического управления часто
приходится решать задачу стабилизации
управляемой величины. Точность поддержания
требуемого значения управляемой величины
в такой системе можно оценить как разницу
между заданным значением управляемой
величины и её установившимся значением
в системе после окончания переходного
процесса:
.
Эта величина
получила название статической ошибки
системы. При вычислении статической
ошибки предполагается, что система
находится в статике и все сигналы в ней
имеют постоянные величины. Статическая
ошибка используется для оценки точности
установления в системе заданной
постоянной выходной величины после
окончания переходного процесса.
Используя
передаточную функцию замкнутой системы
по ошибке, для изображения ошибки в
системе можно записать
,
где
передаточная
функция замкнутой системы по ошибке,
изображение
задающего воздействия.
Для статики,
когда все сигналы в системе неизменны,
выражение для ошибки можно перенести
в область оригиналов
.
Поскольку
,
гдеW(p)
– передаточная функция разомкнутой
системы, то статическую ошибку системы
можно вычислить, зная передаточную
функцию разомкнутой системы:
,
где
.
Вместо
абсолютного значения статической ошибки
часто используют относительную
статическую ошибку
.
Если система
статическая (т.е. не содержит интегрирующих
звеньев), то передаточную функцию
разомкнутой системы можно представить
в следующем нормированном виде:
,
гдеK– коэффициент
усиления системы,A*(p),B*(p)
– нормированные полиномыA(p)
иB(p).
При этом
и
.
Тогда
и статическая ошибка в статической
системе
.
Статическая
ошибка в статической системе уменьшается
с увеличением коэффициента усиления
системы. Статическая система всегда
будет иметь некоторую ошибку. Физический
смысл такой ошибки заключается в
необходимости некоторого рассогласования
между задающей и выходной величинами
системы для получения сигнала управления.
Если в системе
управления имеются интегрирующие
звенья, то система будет астатической.
Для астатической системы первого порядка
(содержащей одно интегрирующее звено)
передаточная функция разомкнутой
системы
и передаточная функция замкнутой системы
по ошибке
.
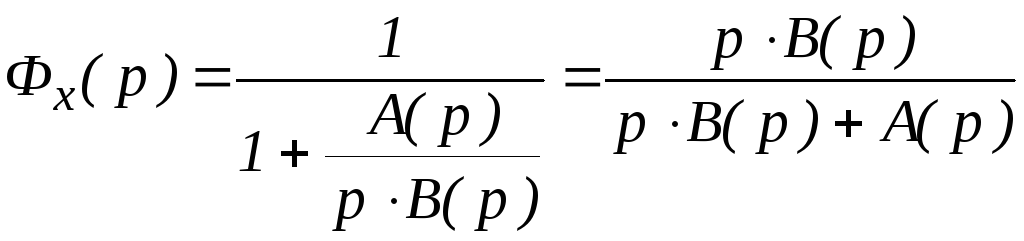
В этом случае всегда
и, следовательно, статическая ошибка
астатической системы будет равна нулю.
Таким образом, статическая ошибка в
астатической системе в принципе
отсутствует, что обуславливает более
высокую точность астатических систем,
по сравнению со статическими системами.
В астатической системе автоматического
управления установившееся значение
управляемой величины равно заданному
значению этой величины.
Вынужденная ошибка системы
Процесс в
системе складывается из свободного
процесса и вынужденного процесса:
.
Для
устойчивой системы свободный процесс
по истечении времениtпзатухает и в системе устанавливается
вынужденный процесс
Точность
поддержания заданного значения
управляемой величины в вынужденном
режиме характеризуется вынужденной
ошибкой системы
.
Вынужденная
ошибка хорошо характеризует работу
системы автоматического управления в
том случае, когда изменения управляющего
воздействия происходят существенно
медленнее собственных переходных
процессов в системе и последними можно
пренебречь.
Рассмотрим
вычисление вынужденной ошибки системы
автоматического управления. Изображение
для вынужденной ошибки
.
В общем случае
является дробно-рациональной функцией
отpи ее можно разложить
в ряд Тейлора по степенямрвблизи
, тогда
и
выражение для вынужденной ошибки системы
примет вид
где
постоянные
коэффициенты.
Для полученного
изображения вынужденной ошибки на
основе свойств преобразования Лапласа
легко находится выражение для оригинала
ошибки
где
,
,
…коэффициенты
ошибок, полученные выше (C0– коэффициент статической ошибки,C1
– коэффициент скоростной ошибки и
т. д.).
Коэффициенты
ошибки могут быть также получены делением
числителя передаточной функции на ее
знаменатель. Полученное выражение для
вынужденной ошибки позволяет оценить
точность системы автоматического
управления в установившемся режиме.
Вынужденная ошибка, например, хорошо
характеризует точность работы следящих
систем автоматического управления.
Соседние файлы в папке ТАУ
- #
- #
- #
Лекция 17. Расчет установившейся ошибки в системах управления.
Структурные признаки астатизма
Установившейся (статической) ошибкой называют
постоянное значение сигнала ошибки x(t)=g(t)-y(t),
которое она приобретает по окончании переходного процесса: 
, рисунок 116.
Очевидно, установившаяся ошибка зависит от законов
изменения и численных характеристик входных сигналов системы. Поэтому при ее
определении принято рассматривать так называемые типовые входные сигналы,
законы изменения которых составляют степенной ряд относительно времени.
Например, для задающего воздействия:
, 
, 
и так
далее.
При наличии нескольких воздействий на линейную систему
для определения xуст используется
принцип суперпозиции – реакция линейной системы на совокупность входных
сигналов совпадает с алгебраической суммой ее реакций на каждый из сигналов в
отдельности:
, где
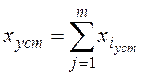
каждое слагаемое, или составляющая сигнала ошибки, 
определяется
для i-го входного сигнала при условии, что остальные
тождественно равны нулю. Такой подход полностью соответствует определению
передаточной функции и позволяет выполнять расчет установившейся ошибки на
основе структурной схемы системы.
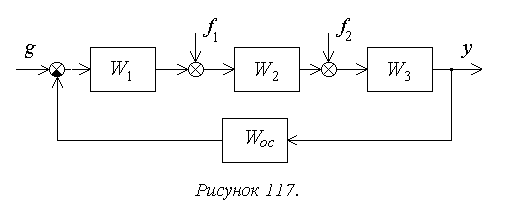
Рассмотрим порядок расчета установившейся ошибки на
следующем достаточно общем примере (рисунок 117).
В соответствии с принципом суперпозиции установившаяся
ошибка будет определяться здесь в виде суммы трех составляющих 
.
Изображение по Лапласу ошибки от задающего воздействия
получают через передаточную функцию замкнутой системы по ошибке 
при известном изображении задающего
воздействия G(s):
, где
F(s) – основная передаточная функция замкнутой системы.
Для структурной схемы на рисунке 117
, где 
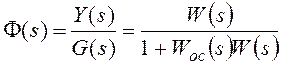
— передаточная функция
разомкнутой системы, или прямой цепи системы, для рассматриваемого примера.
Непосредственно для расчета
установившегося значения ошибки от задающего воздействия используют теорему о
конечном значении для преобразования Лапласа:
В результате:
.
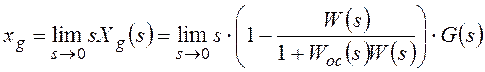
Изображение по Лапласу ошибки от возмущающего
воздействия получают через передаточную функцию замкнутой системы по ошибке от
возмущения 
при известном изображении возмущающего
воздействия F(s):
, где
Ff(s) –передаточная функция замкнутой системы по
возмущающему воздействию,
;
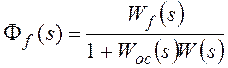
Wf(s)
– передаточная функция разомкнутой системы по возмущению (передаточная функция
участка прямой цепи системы от точки приложения возмущающего воздействия до
выхода системы).
Для структурной схемы на рисунке 8 необходимо
учитывать два возмущающих воздействия, приложенные в различные точки системы.
Для f1:
,
,
.
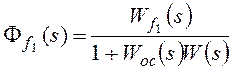
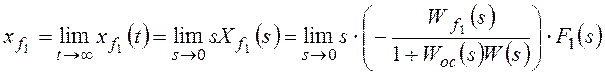
Для f2:
,
,
.
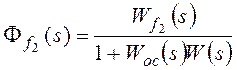
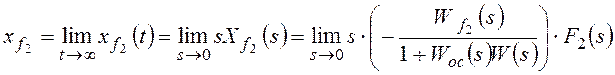
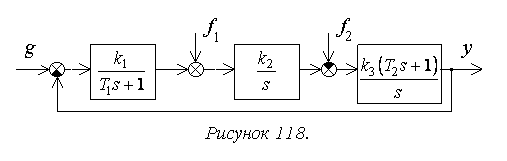
Расчет упрощается для
системы с единичной отрицательной обратной связью (рисунок 118):
,
, где k=k1k2k3 – коэффициент передачи
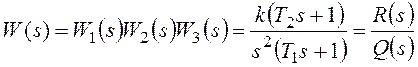
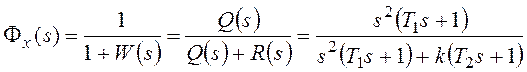
разомкнутой системы.
Найдем установившуюся ошибку
для некоторых типовых вариантов задающего воздействия.
При получим:
.
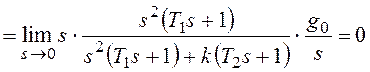
При получим:
.
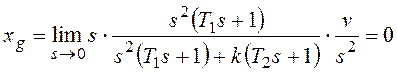
При получим:
.
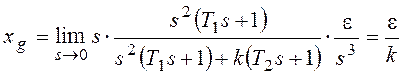
Если установившаяся ошибка
тождественно равна нулю при каком-либо типовом варианте входного сигнала,
независимо от его численных характеристик, систему называют астатической по
рассматриваемому входному сигналу.
Количество типовых вариантов
входного сигнала – членов степенного ряда, при которых установившаяся ошибка
тождественно равна нулю, определяет порядок астатизма.
Рассматриваемая система
обладает свойством астатизма второго порядка по задающему воздействию.
Рассмотрим установившуюся
ошибку от возмущения f1:
,
, где 
–
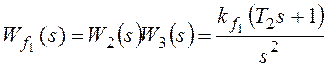
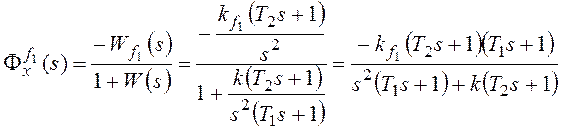
коэффициент передачи разомкнутой системы по возмущению f1.
При 
получим:
.
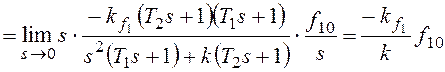
При 
получим:
.
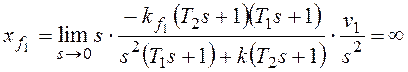
При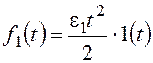 
получим
тот же результат.
Отметим, что по возмущению f1 рассматриваемая система
не является астатической. Кроме того, она не в состоянии отработать два последних
варианта входного сигнала.
Рассмотрим установившуюся
ошибку от возмущения f2:
,
, где 
–
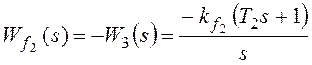
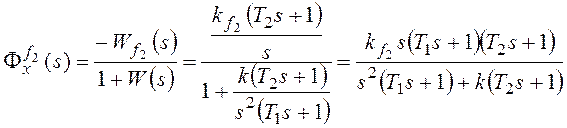
коэффициент передачи разомкнутой системы по возмущению f2.
При 
получим:
.
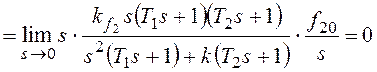
При 
получим:
.
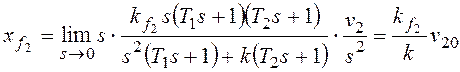
При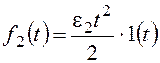 
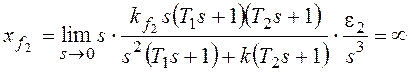
получим:
.
По возмущению f2 рассматриваемая система имеет
астатизм первого порядка. Она не в состоянии отработать возмущающее
воздействие, изменяющееся во времени с постоянным ускорением.
Подведем некоторые итоги:
1. Наличие и глубина
свойства астатизма зависят от точки приложения входного сигнала.
2. Постоянные времени
звеньев системы не влияют на ее точность.
3. Увеличение значения
коэффициента передачи разомкнутой системы приводит к снижению величины
установившейся ошибки.
Для систем с единичной
отрицательной обратной связью существуют достаточно простые структурные
признаки астатизма.
Рассмотрим структуру,
показанную на рисунке 119.
В общем случае передаточная
функция разомкнутой системы может быть представлена в следующей форме:
, где l³0.
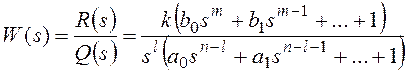
Тогда получим:
и для общего вида задающего воздействия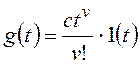 
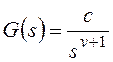
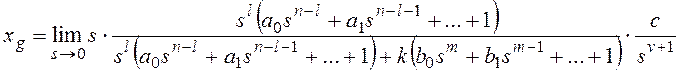
, которому соответствует изображение 
,
.
Результат нахождения этого
предела зависит от соотношения показателей степени:
— при l>v установившаяся
ошибка равна нулю независимо от остальных параметров, то есть имеет место
астатизм;
— при l=v получаем
константу;
— при l<v установившаяся
ошибка стремится к бесконечности, то есть система не в состоянии отработать
входной сигнал.
Учитывая, что минимальное
значение v нулевое,
получаем условие астатизма по задающему воздействию: l>0.
Таким образом, структурный
признак астатизма по задающему воздействию в системе с единичной отрицательной
обратной связью состоит в наличии нулевых корней в знаменателе передаточной
функции разомкнутой системы, или интегрирующих звеньев в прямой цепи системы.
Нетрудно также убедиться,
что положительное значение l совпадает
с порядком астатизма.
Для получения признака
астатизма по возмущающему воздействию представим передаточные функции на
рисунке 10 в форме:
,
, где l1+l2=l,
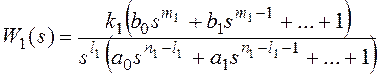
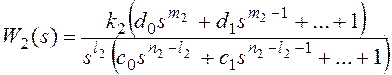
k1k2=k, m1+m2=m,
n1+n2=n,
причем 
и 
.
Тогда получим:
и для общего вида возмущающего воздействия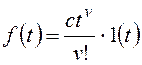 
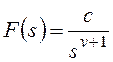
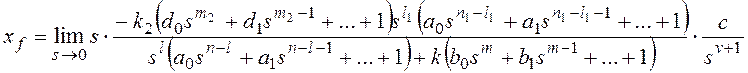
, которому соответствует изображение 
,
.
Все вышеприведенные выводы
можно повторить для показателя степени l1.
Таким образом, структурный
признак астатизма по возмущающему воздействию в системе с единичной
отрицательной обратной связью состоит в наличии нулевых корней в знаменателе
передаточной функции участка системы до точки приложения воздействия, или
интегрирующих звеньев на том же участке.
Величина — статическая ошибка
Cтраница 1
Величина статической ошибки зависит как от настройки регулятора, так и от характеристики и режима работы объекта.
[1]
Стремление уменьшить величину статической ошибки иногда неизбежно приводит к увеличению перерегулирования и времени регулирования. Уменьшение перерегулирования иногда приводит к увеличению статической ошибки.
[2]
В статических системах величина статической ошибки зависит от величины ступенчатой нагрузки. Эта зависимость, называемая статической характеристикой, имеет большое значение для анализа работы САР.
[3]
В астатических системах величина статической ошибки определяется значением нечувствительности регулятора.
[4]
При большом числе компрессоров величина статической ошибки может выйти за допустимые пределы.
[5]
Статическая точность передачи характеризуется величиной статической ошибки, определяемой углом рассогласования между осями датчика и приемника при отсутствии вращения. Величина статической ошибки зависит от нагрузки или момента на валу приемника, а также от собственной погрешности сельсинов.
[6]
Статическая точность передачи характеризуется величиной статической ошибки, определяемой углом пяссогласования между осями датчика и приемника при отсутствии вращения. Величина статической ошибки зависит от нагрузки или момента на валу приемника, а также от собственной погрешности сельсинов.
[7]
По мере увеличения коэффициента усиления величина статической ошибки уменьшается. В то же время степень колебания повышается и соответственно увеличивается динамическая ошибка регулирования. Оптимальная величина должна выбираться как с учетом статической, так и динамической ошибки. Причем статическая ошибка регулирования может быть исключена за счет введения интегральной составляющей в закон регулирования.
[8]
Нужно иметь в виду, что величина статической ошибки зависит как от настройки регулятора, так и от характеристики и режима работы объекта.
[9]
Получается противоречие между требованиями обеспечения устойчивости и величиной статической ошибки.
[10]
Определим границу ОНР, исходя из предположения, что величина статической ошибки не должна превышать величины 0 5 % от входного сигнала при полном перемещении исполнительного механизма.
[11]
Таким образом, давление в приемном канале 2 с точностью до величины статической ошибки, определяемой коэффициентом усиления струйного усилителя, поддерживается постоянным. При постоянном сечении потока этим способом измеряют расход вещества, определяемого как произведение скорости на площадь поперечного сечения потока.
[13]
По оси ординат откладывается отношение максимальной динамической ошибки в переходном процессе к величине статической ошибки, которая имела бы место, если бы в системе использовался пропорциональный регулятор, и была бы равна KLI ( K) при единичном ступенчатом изменении нагрузки. Это значение принято считать наилучшим. Нижняя кривая соответствует декременту затухания, равному 0 46, который получается, если коэффициент усиления выбрать близким к максимальному.
[15]
Страницы:
1
2
3
4
В автоматической системе с симметричной нелинейностью могут иметь место несимметричные автоколебания с некоторой постоянной составляющей 
при приложении постоянного внешнего воздействия. При этом величина амплитуды и частота автоколебаний, существовавших до приложения внешнего воздействия, во многом определяют величину постоянной составляющей. Но, наличие постоянного внешнего воздействия изменяет величину амплитуды и частоты автоколебаний.
Величина 
в случае статической системы определяет собой статическую ошибку, в астатической системе — установившуюся ошибку при постоянной скорости, а в дважды астатической — установившуюся ошибку при постоянном ускорении. Основная задача, таким образом, сводится к определению зависимости между величинами постоянного внешнего воздействия (или постоянной скорости его изменения) и установившейся ошибки, или же к такому выбору параметров системы, например, коэффициента усиления 
при котором величина статической ошибки не превышает заданного значения.
Практический интерес представляет также определение зависимости амплитуды и частоты автоколебаний от величины постоянного внешнего воздействия.
Уравнение нелинейной автоматической системы
где 
— приложенное в любой точке ее внешнее воздействие в данном случае может быть записано в виде
В статической системе будет 
, где 
, а в астатической, когда 
имеем 
, где 
(постоянная скорость изменения внешнего воздействия). В дважды астатической системе 
и при 
будет 
Решение уравнения 
вследствие несимметричности автоколебаний необходимо искать в виде [16], [13]
где 
— постоянная составляющая автоколебаний, х — периодическая (колебательная) составляющая.
Вследствие наличия смещения 
при разложении нелинейной функции 
в ряд Фурье добавится член, характеризующий
постоянную составляющую; при этом выражение для гармонической линеаризации нелинейности приобретает вид
здесь 
— соответственно постоянная составляющая и коэффициенты гармонической линеаризации, определяемые по формулам
где 
В частном случае, когда нелинейность 
является однозначной (не петлевой) 
то формула (Х.59) принимает вид
Определив по формулам 
коэффициенты гармонической линеаризации 
и подставив в уравнение 
вместо 
выражение 
получим гармонически линеаризованное уравнение системы
Это уравнение можно представить в виде системы двух уравнений соответственно для постоянной и колебательной составляющих решения:
Уравнение 
описывает смещение центра колебаний системы в зависимости от величины постоянного внешнего воздействия М. Уравнение (Х.64) описывает периодическое движение системы по координате х относительно центра колебаний, определяемого величиной смещения 
Однако оба уравнения линейно взаимосвязаны, так как коэффициенты 
уравнения 
зависят от величины смещения 
а величина 
в уравнении 
зависит от амплитуды автоколебаний А.
Из уравнения 
можно определить величину статической ошибки в функции от амплитуды автоколебаний А, внешнего воздействия М и параметров системы, например, k:
Подставляя найденное выражение 
в уравнение 
полагая 
и выделяя вещественную и мнимую части, получим два уравнения
Решить аналитически уравнения 
относительно А и 
обычно затруднительно. Целесообразно в данном случае применение какого-либо из графических приемов. Часто бывает удобно из уравнений 
найти выражение для 
. Приравнивая полученные значения 
, получим новое уравнение с тремя неизвестными 
:
Из уравнения 
как правило, можно определить какую-либо из величин как функцию двух остальных. Например,
Полученное уравнение 
дает возможность построить семейство кривых 
при разных значениях М. Затем по одной из формул 
легко определить 
при 
Если какая-либо из искомых величин входит только в одно из уравнений 
то описанное решение значительно упрощается.
Поскольку после построения графиков станет известной зависимость амплитуды автоколебаний 
от значения параметра 
и величины внешнего воздействия М, то из формулы 
определяются искомые зависимости 
при 
или 
при 
Таким образом определяется величина статической ошибки 
в зависимости от величины внешнего воздействия М и значения определяемого параметра системы 
Если полученные значений статической ошибки и амплитуды автоколебаний на входе нелинейного звена 
не являются непосредственно интересующими проектировщика величинами, то пересчет в любую точку системы производится через передаточные функции соответствующих звеньев системы.
Решение уравнений 
возможно и другим способом: подставив в уравнение 
и выделив вещественную и мнимую части, получим два алгебраических уравнения с тремя неизвестными 
Эти уравнения дают возможность определить амплитуду А и частоту 
автоколебаний как функцию постоянной составляющей 
Подставив значения амплитуды и частоты автоколебаний в выражение для 
[первая формула (Х.60)], получим функцию смещения
которая является характеристикой данного нелинейного звена по отношению к постоянной составляющей 
при наличии автоколебаний. Важно отметить, что функция смещения 
не зависит ни от числа внешних воздействий на систему, ни от характера их изменения (он может быть не постоянной, а медленно меняющейся, что рассматривается ниже в § 5).
После определения функции смещения из уравнения 
с подстановкой 
сразу определяется искомая зависимость статической ошибки 
от величины постоянного внешнего воздействия М.
Возможен случай, когда к нелинейной системе приложено несколько внешних воздействий:
Методика расчетов при этом сохраняется. В отличие от линейных систем в данном случае складывать статические ошибки от отдельных воздействий нельзя. Это обусловлено нелинейной зависимостью 
от величины внешнего воздействия, как это следует из уравнения 
которое в данном случае принимает вид
Для облегчения практических расчетов в табл. 1 и 2 приложения IV приведены значения коэффициентов гармонической линеаризации для некоторых типоб нелинейных звеньев. Более полные сведения по гармонической линеаризации при наличии внешнего воздействия приведены в работе [13].
Несимметричные колебания в нелинейных автоматических системах могут возникать не только при наличии внешнего воздействия, но и при несимметричных характеристиках самого нелинейного элемента 
без внешнего воздействия.
В этом случае правая часть уравнения 
равна нулю:
При несимметричных характеристиках нелинейного звена 
возникает постоянная составляющая
Поэтому решение уравнения 
как и прежде, надо искать в виде суммы постоянной и периодической составляющих:
Уравнения 
в данном случае имеют вид
Решение уравнений 
выполняется таким же образом, как это делалось для симметричной характеристики нелинейного звена, при наличии постоянного внешнего воздействия.
Для облегчения использования описанной выше методики в табл. 3 приложения II приведены готовые выражения 
для некоторых типов несимметричных нелинейностей [13].
Пример 4. Для иллюстрации описанной выше методики определения установившихся ошибок в автоколебательных нелинейных системах рассмотрим систему, блок-схема которой приведена на рис. Х.20.
Рис. Х.20. Блок-схема релейной системы автоматического регулирования
Уравнения этой системы имеют вид:
Нелинейность представляет собой характеристику идеального симметричного реле
Уравнение системы будет
Предположим, что функция 
является управляющим воздействием, изменяющимся с постоянной скоростью
которое должна воспроизвести система на выходе. Второе внешнее воздействие 
является возмущающим и имеет постоянную величину (например, постоянная нагрузка на выходном валу системы), т. е.
Необходимо определить установившуюся ошибку на выходе системы. Правая часть характеристического уравнения будет при этом постоянной и установившееся решение для X с учетом автоколебаний следует искать в виде выражений 
Тогда уравнения для постоянных и периодических составляющих будут иметь вид:
В соответствии с изложенной выше методикой из уравнений 
определим
Откуда
или
Для определения амплитуды А периодической составляющей используется уравнение 
для которого запишем характеристическое уравнение
Подставив 
и выделив вещественную и мнимую части, получим 
Из уравнений 
найдем
Исключая из уравнений 
величину 
определим частоту автоколебаний
Подставив полученные значения 
в уравнение 
определим амплитуду автоколебаний
Здесь величина
является амплитудой симметричных автоколебаний при отсутствии внешних воздействий 
Подставив полученное значение амплитуды А в формулу 
определим искомую величину смещения
Из формулы (Х.82) видно, что автоколебания в системе существуют только до тех пор, пока внешние воздействия удовлетворяют условию
причем амплитуда автоколебаний уменьшается 
с увеличением внешних воздействий.
Так, в результате расчета определена величина смещения на входе реле. Однако практически больший интерес представляет установившаяся ошибка на выходе системы. Поскольку на выходе системы должно воспроизводиться внешнее воздействие 
то, согласно рис. Х.20, ошибка данной системы выражается величиной 
Запишем переменную 
через х, которая уже известна.
Из заданных уравнений системы 
имеем
Учитывая, что 
уравнение 
запишем в виде
В соответствии с характером правой части нужно искать установившееся решение этого линейного уравнения в виде
где 
— постоянные величины;
— периодическая составляющая.
Подставляя выражение 
получим три уравнения
Из уравнения (X.87) определим
Затем из уравнения 
найдем
Наконец, из уравнения 
получим
где 
определяются соответственно из формул 
Итак, в системе содержатся все три составляющие ошибки 
зависящие от величины внешних воздействий и от параметров системы. Наиболее нежелательной составляющей ошибки является составляющая 
возрастающая с течением времени. Для исключения этой ошибки необходимо в системе жесткую обратную связь заменить гибкой
Лекция 8 Составитель: Шендалева Е. В. , к. т. н. , доцент каф. ТХНГСС Ом. ГТУ
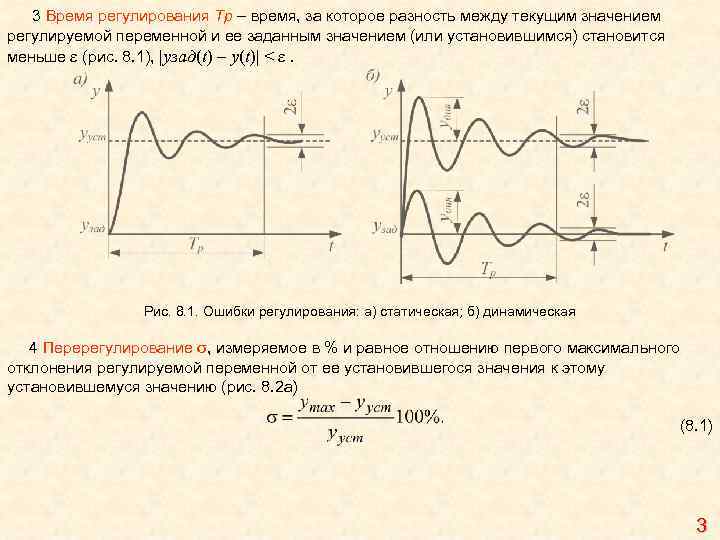
Исследование качества процессов регулирования Одной из проблем, возникающих при построении систем автоматического регулирования, наряду с проблемой устойчивости, является качество регулирования, характеризующее точность и плавность протекания переходного процесса. Система автоматического регулирования называется качественной, если она удовлетворяет определенным технологическим требованиям: например, как будет меняться реакция системы, если на ее вход действуют различного рода возмущения как по каналу управления, так и по каналу возмущения, т. е. обеспечивается ли принципиальная возможность прихода системы в некоторое установившееся состояние. Такое понятие качества автоматической системы охватывает ее статические и динамические свойства, выраженные в количественной форме и получившие название показателей качества управления. Для оценки качества регулирования в количественной форме используются показатели качества, которые подразделяются на прямые, косвенные, частотные, интегральные. Показатели качества управления Прямые показатели: Наиболее распространенными прямыми показателями или критериями качества, применяемыми в системах управления, являются: 1 Статическая ошибка регулирования ycт, определяемая как разность между установившимся значением регулируемой переменной и ее заданным значением (рис. 8. 1 а), т. е. yст = yуст– узад. 2 Динамическая ошибка регулирования yдин, определяемая как наибольшее отклонение в переходном процессе регулируемой переменной от ее установившегося значения (рис. 8. 1 б). 2
3 Время регулирования Тр – время, за которое разность между текущим значением регулируемой переменной и ее заданным значением (или установившимся) становится меньше ε (рис. 8. 1), |узад(t) – у(t)| < ε. Рис. 8. 1. Ошибки регулирования: а) статическая; б) динамическая 4 Перерегулирование σ, измеряемое в % и равное отношению первого максимального отклонения регулируемой переменной от ее установившегося значения к этому установившемуся значению (рис. 8. 2 а) (8. 1) 3
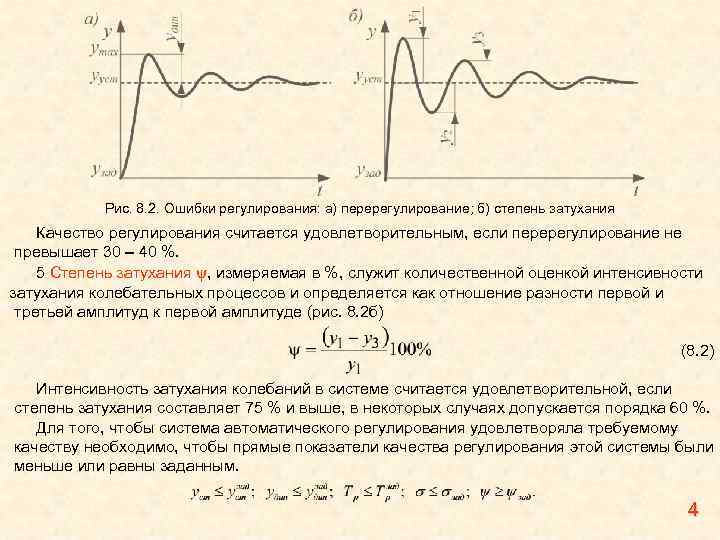
Рис. 8. 2. Ошибки регулирования: а) перерегулирование; б) степень затухания Качество регулирования считается удовлетворительным, если перерегулирование не превышает 30 – 40 %. 5 Степень затухания ψ, измеряемая в %, служит количественной оценкой интенсивности затухания колебательных процессов и определяется как отношение разности первой и третьей амплитуд к первой амплитуде (рис. 8. 2 б) (8. 2) Интенсивность затухания колебаний в системе считается удовлетворительной, если степень затухания составляет 75 % и выше, в некоторых случаях допускается порядка 60 %. Для того, чтобы система автоматического регулирования удовлетворяла требуемому качеству необходимо, чтобы прямые показатели качества регулирования этой системы были меньше или равны заданным. 4
Иногда требования по качеству регулирования могут быть более жесткие, например, переходный процесс должен быть монотонным или монотонным и без перегибов. Прямые показатели качества удобно использовать в тех случаях, когда имеется график переходного процесса y(t), который может быть получен экспериментально в реальной системе регулирования или путем моделирования на ЭВМ. Если же такой возможности нет, т. е. не удается никаким образом получить кривую переходного процесса, то пользуются косвенными показателями качества, которые вычисляются без построения графика переходного процесса по коэффициентам уравнений или по частотным характеристикам. Косвенные показатели качества Основную группу среди косвенных показателей качества составляют корневые показатели качества регулирования, к которым относятся степень устойчивости и степень колебательности. С точки зрения качества регулирования можно сделать следующие выводы. 1 Степень устойчивости характеризует интенсивность затухания наиболее медленно затухающей неколебательной составляющей переходного процесса, которая определяется как yк(t) = Ске–ηt. Пусть рассматриваемая система описывается дифференциальным уравнением второго порядка, характеристическое уравнение которого имеет два действительных различных корня s 1 = – α 1, s 2 = – α 2 и α 1 < α 2 (рис. 8. 3 а). Последним соответствуют две элементарные составляющие свободного движения системы (рис. 8. 3 б). Как видно из графиков переходных процессов, чем меньше абсолютное значение корня характеристического уравнения, тем медленнее затухает соответствующая ему составляющая. 5
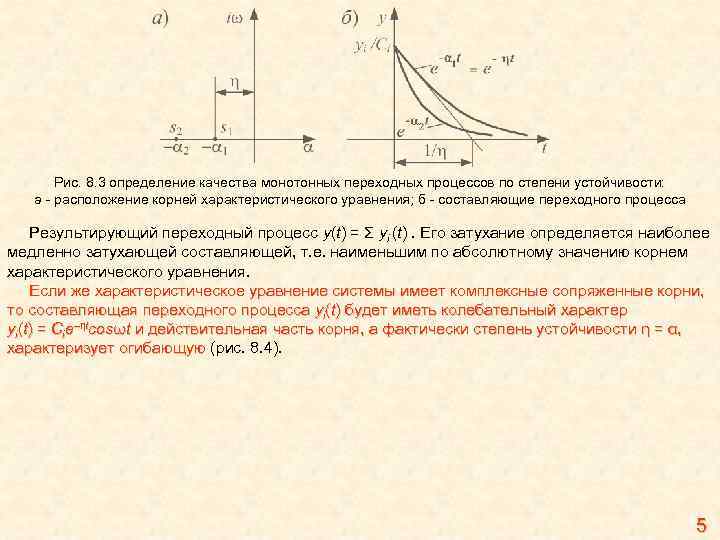
Рис. 8. 3 определение качества монотонных переходных процессов по степени устойчивости: а — расположение корней характеристического уравнения; б — составляющие переходного процесса Результирующий переходный процесс y(t) = Σ yi (t). Его затухание определяется наиболее медленно затухающей составляющей, т. е. наименьшим по абсолютному значению корнем характеристического уравнения. Если же характеристическое уравнение системы имеет комплексные сопряженные корни, то составляющая переходного процесса yi(t) будет иметь колебательный характер –ηt yi(t) = Сie–ηtcosωt и действительная часть корня, а фактически степень устойчивости η = α, характеризует огибающую (рис. 8. 4). 5
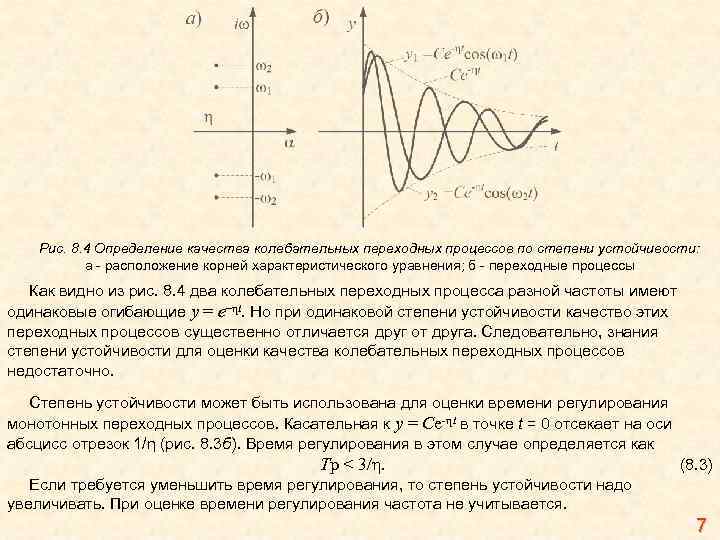
Рис. 8. 4 Определение качества колебательных переходных процессов по степени устойчивости: а — расположение корней характеристического уравнения; б — переходные процессы Как видно из рис. 8. 4 два колебательных переходных процесса разной частоты имеют одинаковые огибающие y = е–ηt. Но при одинаковой степени устойчивости качество этих переходных процессов существенно отличается друг от друга. Следовательно, знания степени устойчивости для оценки качества колебательных переходных процессов недостаточно. Степень устойчивости может быть использована для оценки времени регулирования монотонных переходных процессов. Касательная к y = Cе-ηt в точке t = 0 отсекает на оси абсцисс отрезок 1/η (рис. 8. 3 б). Время регулирования в этом случае определяется как Tp < 3/η. (8. 3) Если требуется уменьшить время регулирования, то степень устойчивости надо увеличивать. При оценке времени регулирования частота не учитывается. 7
2 Степень колебательности так же, как и степень устойчивости, используется и для оценки запаса устойчивости и для оценки качества регулирования. Степень колебательности m − это модуль минимального отношения действительной и мнимой частей корня sj характеристического уравнения (8. 4) Степень колебательности характеризует затухание наиболее медленно затухающей составляющей y(t) = Ae–mωtsinωt, откуда следует, что изменение частоты влечет и изменение амплитуды колебаний. Степень колебательности однозначно связана со степенью затухания. Действительно, в момент времени t 0 амплитуда свободной составляющей определяется как момент времени t 0 + Т, т. е. через период, , ав . В этом случае степень затухания, согласно (8. 2), запишется (8. 4) так как T = 2 p/w, y = 1 – e-2 pm Степень затухания изменяется от 0 до 1, а степень колебательности — от 0 до ∞. Наиболее часто используются следующие их значения: m = 0, 141 (y = 0, 61); m = 0, 221 (y = 0, 75); m = 0, 366 (y = 0, 9); m = 0, 478 (y = 0, 95). 8
3 Оценка статической ошибки может быть получена по предельной теореме (8. 5) где передаточная функция замкнутой системы по каналу ошибки; X(s) изображение задающего воздействия, в большинстве случаев x(t) = С = const и X(s) = С/s. С учетом вышесказанного Например, для систем с интегральным регулятором статическая ошибка отсутствует а для систем с пропорциональным регулятором равна Если в Wоб(s) коэффициент передачи равен k, то Из последнего соотношения видно, что в системах с П-регулятором статическая ошибка уменьшается с увеличением значения параметра настройки регулятора. В реальных системах берется максимально возможное значение S 1, исходя из обеспечения запаса устойчивости. В заключение следует заметить, что динамическая ошибка корневыми методами не оценивается. 9
Интегральные критерии качества представляют собой определенные интегралы по времени в пределах от 0 до ∞ от некоторой функции переходного процесса y(t) или ошибки ε(t) и вычисляются непосредственно, либо по переходным функциям системы, или по коэффициентам передаточной функции системы. Целью использования этих критериев является получение общей оценки быстродействия и отклонения регулируемой величины от установившегося значения. К интегральным критериям качества предъявляются два требования: а) простота вычисления интеграла; б) несложность выражения через коэффициенты дифференциального уравнения. 1 Линейный интегральный критерий (8. 6) служит для оценки качества неколебательных процессов. Геометрически этот критерий характеризует площадь, заключенную между кривой переходного процесса и осью абсцисс (рис. 8. 5 а), он учитывает как время регулирования, так и величину динамических отклонений. Если неизвестна кривая переходного процесса, но известна передаточная функция замкнутой системы Wзамк(s) и входная переменная x(t) = 1(t), то значение линейного интегрального критерия определяется с использованием теоремы о конечном значении функции. Действительно, формулу (8. 6) можно записать иначе и тогда 10
Рис. 8. 5 Интегральные оценки качества регулирования: а — линейная; б — модульная; в — квадратичная Линейный интегральный критерий качества можно вычислить и другими методами. Например, если даны дифференциальное уравнение и начальные условия any(n)(t) + an – 1 y (n – 1)(t) +. . . + a 0 y(t) = 0, y(n– 1)(0), . . . , y′(0), y(0), то, проинтегрировав его, получим Для устойчивых систем y(i)(∞) = 0 для i = 1, 2, . . . , n. Тогда – any(n– 1)(0) – an– 1 y(n– 2)(0) –. . . – a 0 Jл = 0, откуда а при нулевых начальных условиях 11
Существуют модификации линейного интегрального критерия, которые применяются в тех случаях, когда начальный участок переходного процесса является менее ответственным, например, Выведем формулу, позволяющую вычислять такой критерий. Для этого продифференцируем по s функцию осуществляющую преобразование по Лапласу функции y(t) Если перейти к пределу при s → 0, то получим Следует отметить, что для вычисления таких критериев не требуется знание переходного процесса. Чем меньше значение линейного интегрального критерия, тем лучше качество процесса регулирования. Однако использование данного типа критериев для знакопеременных переходных процессов не дает объективной картины, так, например, для незатухающей синусоиды Jл = 0. Поэтому для оценки качества регулирования таких процессов используют интегральные оценки, знакопеременность подынтегральной функции которых устранена каким-либо способом. 12
Пример 8. 1 Требуется вычислить Так как для системы с передаточной функцией , а 2 Модульный интегральный критерий (8. 7) применяется для оценки качества колебательных процессов, а для неколебательных процессов он совпадает с линейным интегральным критерием. Для его вычисления требуется знание переходного процесса. На практике этот критерий используется при численном исследовании систем на моделях с применением вычислительной техники, т. е. там, где операция взятия модуля не представляет трудности. Геометрически критерий равен площади, заключенной между кривой y(t) и осью абсцисс (рис. 8. 5 б). В некоторых случаях используют модификацию модульного интегрального критерия которая придает больший вес значениям переходного процесса в его конце. 13
3 Интегральный квадратичный критерий (8. 9) является наиболее распространенным критерием качества и представляет собой площадь под кривой y 2(t) (рис. 8. 5 в). Как видно из (8. 9), разные по величине ординаты переходного процесса входят в критерий с разным весом, что приводит к тому, что начальный участок переходного процесса приобретает наибольшее значение, чем его «хвост», который практически не влияет на квадратичный критерий. Стремясь минимизировать (8. 9), фактически минимизируют наибольшие отклонения регулируемой величины, поэтому минимальные значения критерия всегда соответствуют колебательным процессам с малым затуханием. С целью устранения этого недостатка применяют улучшенную квадратичную оценку (8. 10) которая, кроме самих отклонений, учитывает с весовым коэффициентом их производную. Весовой коэффициент выбирается равным желаемому времени нарастания или применяется в пределах Tр/6 ≤ Т ≤ Tр/3, (8. 11) где Тр — желаемая длительность переходного процесса. Квадратичный критерий, как и линейный, можно вычислить без построения переходного процесса по частотной характеристике замкнутой системы и преобразованию по Фурье от входного сигнала. Используя формулу Релея, получают 14
В заключение следует отметить, что абсолютные значения любой интегральной оценки сами по себе не представляют интереса. Они служат для сопоставления различных вариантов настройки одной и той же системы, а также для определения параметров настройки системы. 15