Оценка точности прогноза модельная ошибка - Не ошибается лишь тот, кто ничего не делает!

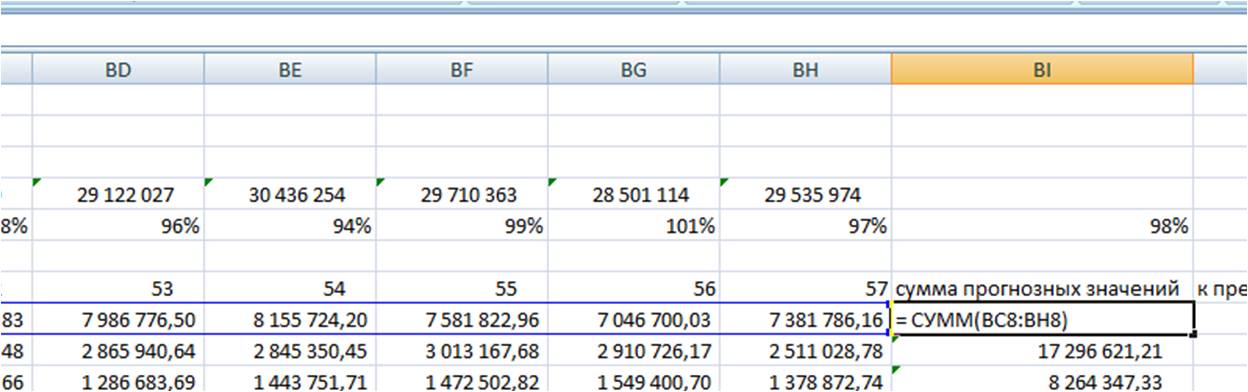
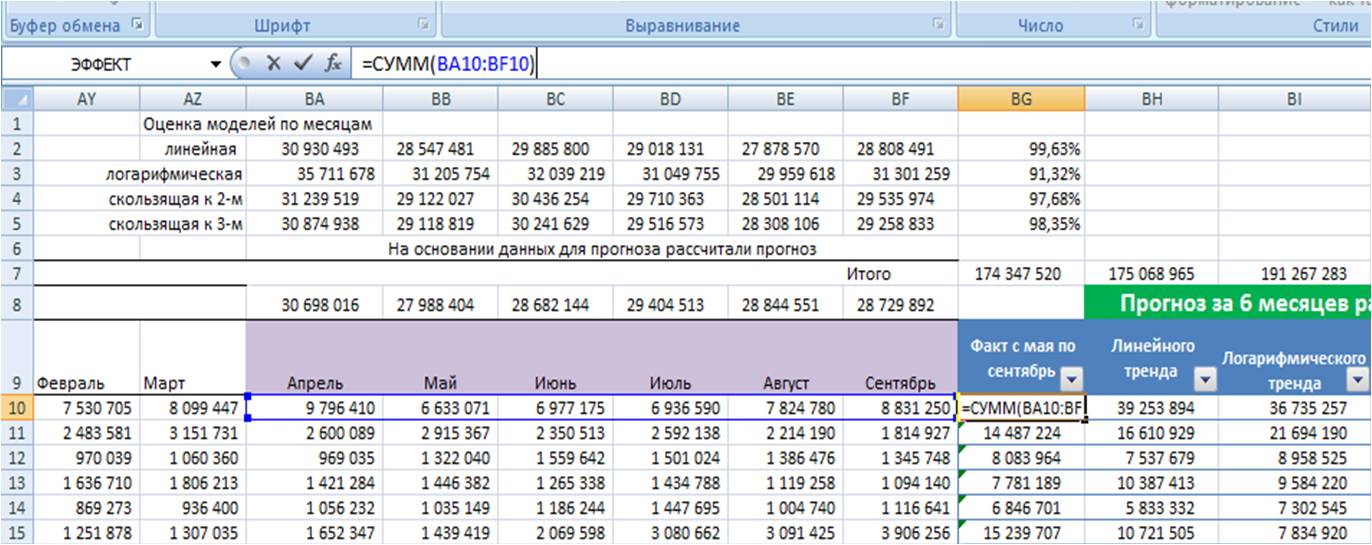
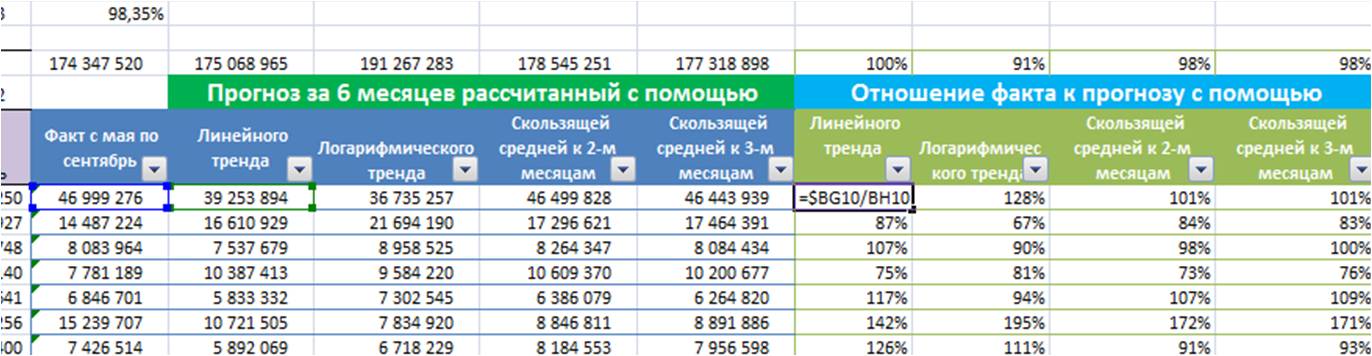
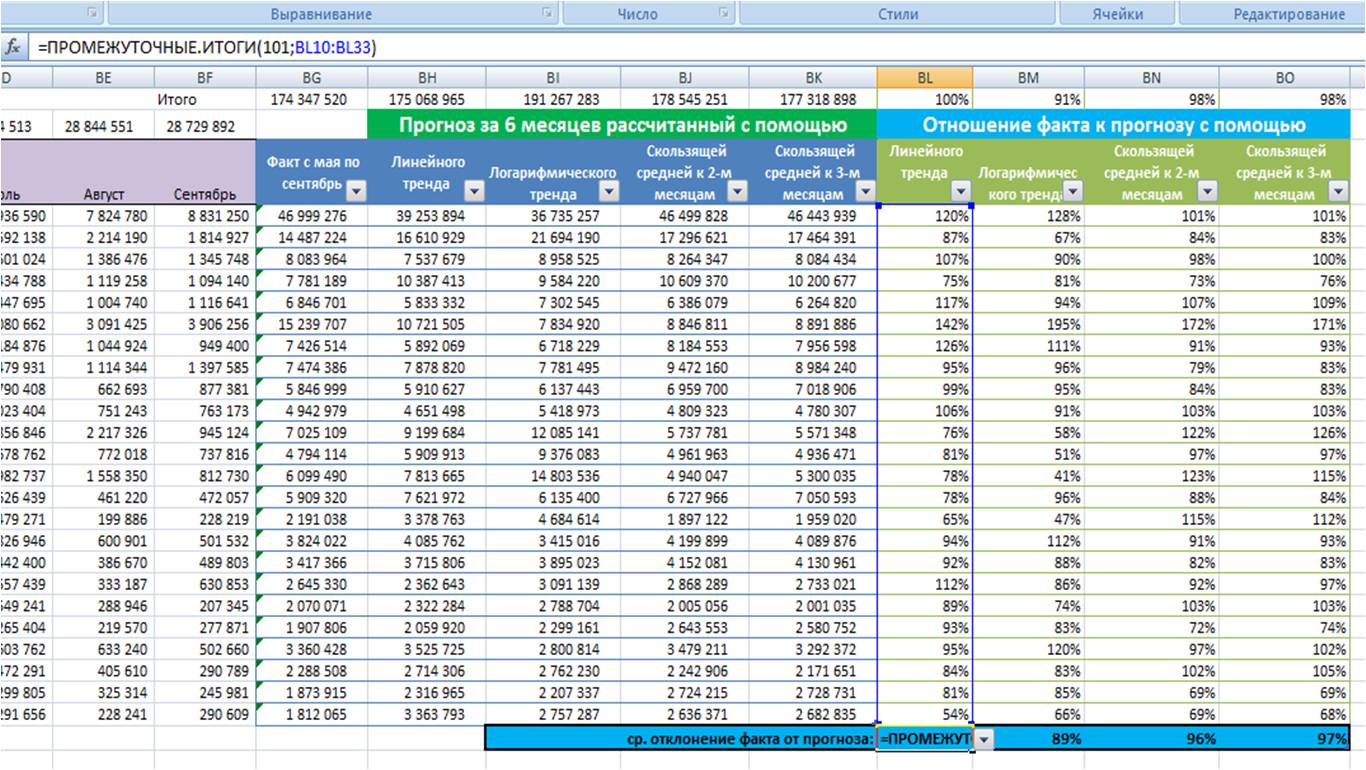
Анализ временных рядов

Общее введение
Две основные цели
Идентификация модели
временных рядов
- Систематическая
  составляющая и случайный шум
- Два общих типа компонент
  временных рядов
- Анализ тренда
- Анализ сезонности
АРПСС (Бокс и Дженкинс) и
автокорреляции
- Общее введение
- Два основных процесса
- Модель АРПСС
- Идентификация
- Оценивание параметров
- Оценивание модели
Прерванные временные ряды
Экспоненциальное
сглаживание
- Общее введение
- Простое экспоненциальное
  сглаживание
- Выбор лучшего значения
  параметра a (альфа)
- Индексы качества подгонки
- Сезонная и несезонная модели
  с трендом или без тренда
Сезонная декомпозиция (метод
Census I)
- Общее введение
- Вычисления
Сезонная корректировка X-11
(метод Census II)
- Сезонная корректировка:
  основные идеи и термины
- Метод Census II
- Таблицы результатов
  корректировки X-11
- Подробное описание всех
  таблиц результатов, вычисляемых в методе X-11
Анализ распределенных лагов
- Общая цель
- Общая модель
- Распределенный лаг Алмона
Одномерный анализ Фурье
Кросс-спектральный анализ
- Общее введение
- Основные понятия и принципы
- Результаты для каждой
  переменной
- Кросс-периодограмма,
  кросс-плотность, квадратурная плотность и
  кросс-амплитуда
- Квадрат когерентности,
  усиление и фазовый сдвиг
- Как создавались данные для
  примера
Спектральный анализ —
Основные понятия и принципы
- Частота и период
- Общая структура модели
- Простой пример
- Периодограмма
- Проблема рассеяния
- Добавление констант во
  временной ряд (пэддинг)
- Косинус-сглаживание
- Окна данных и оценки
  спектральной плотности
- Подготовка данных к анализу
- Результаты для случая, когда в
  ряде отсутствует периодичность
Быстрое преобразование Фурье
- Общее введение
- Вычисление БПФ во временных
  рядах

В следующих разделах мы вначале представим
обзор методов, используемых для идентификации
моделей временных рядов (таких как сглаживание,
подгонка и автокорреляции). Затем опишем общий
класс моделей, которые могут быть использованы
для описания рядов и построения прогнозов
(модели авторегрессии и скользящего среднего).
Наконец, расскажем о некоторых простых, но часто
используемых методах, основанных на линейной
регрессии. За дальнейшей информацией обратитесь
к соответствующим разделам.

Общее введение

Вначале дадим краткий обзор методов анализа
данных, представленных в виде временных рядов,
т.е. в виде последовательностей измерений,
упорядоченных в неслучайные моменты времени. В
отличие от анализа случайных выборок, анализ
временных рядов основывается на предположении,
что последовательные значения в файле данных
наблюдаются через равные промежутки времени
(тогда как в других методах нам не важна и часто
не интересна привязка наблюдений ко времени).

Подробное обсуждение этих методов можно найти
в следующих работах: Anderson (1976), Бокс и Дженкинс
(1976), Kendall (1984), Kendall and Ord (1990), Montgomery, Johnson, and Gardiner (1990),
Pankratz (1983), Shumway (1988), Vandaele (1983), Walker (1991), Wei (1989).

Две основные цели

Существуют две основные цели анализа временных
рядов: (1) определение природы ряда и (2)
прогнозирование (предсказание будущих значений
временного ряда по настоящим и прошлым
значениям). Обе эти цели требуют, чтобы модель
ряда была идентифицирована и, более или менее,
формально описана. Как только модель определена,
вы можете с ее помощью интерпретировать
рассматриваемые данные (например, использовать в
вашей теории для понимания сезонного изменения
цен на товары, если занимаетесь экономикой). Не
обращая внимания на глубину понимания и
справедливость теории, вы можете
экстраполировать затем ряд на основе найденной
модели, т.е. предсказать его будущие значения.

Идентификация модели временных
рядов

Систематическая
составляющая и случайный шум
Два общих типа компонент
временных рядов
Анализ тренда
Анализ сезонности

За более полной информацией о простых
автокорреляциях (обсуждаемых в этом разделе) и
других автокорреляциях, см. Anderson (1976), Box and Jenkins
(1976), Kendall (1984), Pankratz (1983), and Vandaele (1983). См. также:

АРПСС (Бокс и Дженкинс) и
автокорреляции
Прерванные временные ряды
Экспоненциальное
сглаживание
Сезонная декомпозиция (метод
Census I)
Сезонная корректировка X-11
(метод Census II)
Таблицы результатов
корректировки X-11
Анализ распределенных лагов
Одномерный анализ Фурье
Кросс-спектральный анализ
Основные понятия и принципы
Быстрое преобразование Фурье

Систематическая составляющая и
случайный шум

Как и большинство других видов анализа, анализ
временных рядов предполагает, что данные
содержат систематическую составляющую (обычно
включающую несколько компонент) и случайный шум
(ошибку), который затрудняет обнаружение
регулярных компонент. Большинство методов
исследования временных рядов включает различные
способы фильтрации шума, позволяющие увидеть
регулярную составляющую более отчетливо.

Два общих типа компонент
временных рядов

Большинство регулярных составляющих временных
рядов принадлежит к двум классам: они являются
либо трендом, либо сезонной составляющей. Тренд
представляет собой общую систематическую
линейную или нелинейную компоненту, которая
может изменяться во времени. Сезонная
составляющая — это периодически повторяющаяся
компонента. Оба эти вида регулярных компонент
часто присутствуют в ряде одновременно.
Например, продажи компании могут возрастать из
года в год, но они также содержат сезонную
составляющую (как правило, 25% годовых продаж
приходится на декабрь и только 4% на август).

Эту общую модель можно понять на
«классическом» ряде — Ряд G (Бокс и
Дженкинс, 1976, стр. 531), представляющем месячные
международные авиаперевозки (в тысячах) в
течение 12 лет с 1949 по 1960 (см. файл Series_g.sta).
График месячных перевозок ясно показывает почти
линейный тренд, т.е. имеется устойчивый рост
перевозок из года в год (примерно в 4 раза больше
пассажиров перевезено в 1960 году, чем в 1949). В то же
время характер месячных перевозок повторяется,
они имеют почти один и тот же характер в каждом
годовом периоде (например, перевозок больше в
отпускные периоды, чем в другие месяцы). Этот
пример показывает довольно определенный тип
модели временного ряда, в которой амплитуда
сезонных изменений увеличивается вместе с
трендом. Такого рода модели называются моделями
с мультипликативной сезонностью.

Анализ тренда

Не существует «автоматического» способа
обнаружения тренда в временном ряде. Однако если
тренд является монотонным (устойчиво возрастает
или устойчиво убывает), то анализировать такой
ряд обычно нетрудно. Если временные ряды
содержат значительную ошибку, то первым шагом
выделения тренда является сглаживание.

Сглаживание. Сглаживание всегда включает
некоторый способ локального усреднения данных,
при котором несистематические компоненты
взаимно погашают друг друга. Самый общий метод
сглаживания — скользящее среднее, в котором
каждый член ряда заменяется простым или
взвешенным средним n соседних членов, где n
— ширина «окна» (см. Бокс и Дженкинс, 1976; Velleman
and Hoaglin, 1981). Вместо среднего можно использовать
медиану значений, попавших в окно. Основное
преимущество медианного сглаживания, в
сравнении со сглаживанием скользящим средним,
состоит в том, что результаты становятся более
устойчивыми к выбросам (имеющимся внутри окна).
Таким образом, если в данных имеются выбросы
(связанные, например, с ошибками измерений), то
сглаживание медианой обычно приводит к более
гладким или, по крайней мере, более
«надежным» кривым, по сравнению со
скользящим средним с тем же самым окном. Основной
недостаток медианного сглаживания в том, что при
отсутствии явных выбросов, он приводит к более
«зубчатым» кривым (чем сглаживание
скользящим средним) и не позволяет использовать
веса.

Относительно реже, когда ошибка измерения
очень большая, используется метод сглаживания
методом наименьших квадратов, взвешенных
относительно расстояния или метод отрицательного
экспоненциально взвешенного сглаживания. Все
эти методы отфильтровывают шум и преобразуют
данные в относительно гладкую кривую (см.
соответствующие разделы, где каждый из этих
методов описан более подробно). Ряды с
относительно небольшим количеством наблюдений и
систематическим расположением точек могут быть
сглажены с помощью бикубических сплайнов.

Подгонка функции. Многие монотонные
временные ряды можно хорошо приблизить линейной
функцией. Если же имеется явная монотонная
нелинейная компонента, то данные вначале следует
преобразовать, чтобы устранить нелинейность.
Обычно для этого используют логарифмическое,
экспоненциальное или (менее часто)
полиномиальное преобразование данных.

Анализ сезонности

Периодическая и сезонная зависимость
(сезонность) представляет собой другой общий тип
компонент временного ряда. Это понятие было
проиллюстрировано ранее на примере
авиаперевозок пассажиров. Можно легко видеть,
что каждое наблюдение очень похоже на соседнее;
дополнительно, имеется повторяющаяся сезонная
составляющая, это означает, что каждое
наблюдение также похоже на наблюдение, имевшееся
в том же самом месяце год назад. В общем,
периодическая зависимость может быть формально
определена как корреляционная зависимость
порядка k между каждым i-м элементом ряда и
(i-k)-м элементом (Kendall, 1976). Ее можно измерить с
помощью автокорреляции (т.е. корреляции между
самими членами ряда); k обычно называют лагом
(иногда используют эквивалентные термины:
сдвиг, запаздывание). Если ошибка измерения не
слишком большая, то сезонность можно определить
визуально, рассматривая поведение членов ряда
через каждые k временных единиц.

Автокорреляционная коррелограмма. Сезонные
составляющие временного ряда могут быть найдены
с помощью коррелограммы. Коррелограмма
(автокоррелограмма) показывает численно и
графически автокорреляционную функцию (AКФ),
иными словами коэффициенты автокорреляции (и их
стандартные ошибки) для последовательности
лагов из определенного диапазона (например, от 1
до 30). На коррелограмме обычно отмечается
диапазон в размере двух стандартных ошибок на
каждом лаге, однако обычно величина
автокорреляции более интересна, чем ее
надежность, потому что интерес в основном
представляют очень сильные (а, следовательно,
высоко значимые) автокорреляции (см. Элементарные
понятия статистики).

Исследование коррелограмм. При изучении
коррелограмм следует помнить, что
автокорреляции последовательных лагов
формально зависимы между собой. Рассмотрим
следующий пример. Если первый член ряда тесно
связан со вторым, а второй с третьим, то первый
элемент должен также каким-то образом зависеть
от третьего и т.д. Это приводит к тому, что
периодическая зависимость может существенно
измениться после удаления автокорреляций
первого порядка, т.е. после взятия разности с
лагом 1).

Частные автокорреляции. Другой полезный
метод исследования периодичности состоит в
исследовании частной автокорреляционной
функции (ЧАКФ), представляющей собой
углубление понятия обычной автокорреляционной
функции. В ЧАКФ устраняется зависимость между
промежуточными наблюдениями (наблюдениями внутри
лага). Другими словами, частная автокорреляция на
данном лаге аналогична обычной автокорреляции,
за исключением того, что при вычислении из нее
удаляется влияние автокорреляций с меньшими
лагами (см. Бокс и Дженкинс, 1976; см. также McDowall,
McCleary, Meidinger, and Hay, 1980). На лаге 1 (когда нет
промежуточных элементов внутри лага), частная
автокорреляция равна, очевидно, обычной
автокорреляции. На самом деле, частная
автокорреляция дает более «чистую» картину
периодических зависимостей.

Удаление периодической зависимости. Как
отмечалось выше, периодическая составляющая для
данного лага k может быть удалена взятием
разности соответствующего порядка. Это означает,
что из каждого i-го элемента ряда вычитается (i-k)-й
элемент. Имеются два довода в пользу таких
преобразований.

Во-первых, таким образом можно определить
скрытые периодические составляющие ряда.
Напомним, что автокорреляции на
последовательных лагах зависимы. Поэтому
удаление некоторых автокорреляций изменит
другие автокорреляции, которые, возможно,
подавляли их, и сделает некоторые другие
сезонные составляющие более заметными.

Во-вторых, удаление сезонных составляющих
делает ряд стационарным,
что необходимо для применения АРПСС
и других методов, например, спектрального
анализа.

АРПСС

Общее введение
Два основных процесса
Модель АРПСС
Идентификация
Оценивание параметров
Оценивание модели

Дополнительная информация о методах Анализа
временных рядов дана также в следующих
разделах:

Идентификация модели
временных рядов
Прерванные временные ряды
Экспоненциальное
сглаживание
Сезонная декомпозиция (метод
Census I)
Сезонная корректировка X-11
(метод Census II)
Таблицы результатов
корректировки X-11
Анализ распределенных лагов
Одномерный анализ Фурье
Кросс-спектральный анализ
Основные понятия и принципы
Быстрое преобразование Фурье

Общее введение

Процедуры оценки параметров и прогнозирования,
описанные в разделе Идентификация
модели временных рядов, предполагают, что
математическая модель процесса известна. В
реальных данных часто нет отчетливо выраженных
регулярных составляющих. Отдельные наблюдения
содержат значительную ошибку, тогда как вы
хотите не только выделить регулярные компоненты,
но также построить прогноз. Методология АРПСС,
разработанная Боксом и Дженкинсом (1976), позволяет
это сделать. Данный метод чрезвычайно популярен
во многих приложениях, и практика подтвердила
его мощность и гибкость (Hoff, 1983; Pankratz, 1983; Vandaele, 1983).
Однако из-за мощности и гибкости, АРПСС — сложный
метод. Его не так просто использовать, и
требуется большая практика, чтобы овладеть им.
Хотя часто он дает удовлетворительные
результаты, они зависят от квалификации
пользователя (Bails and Peppers, 1982). Следующие разделы
познакомят вас с его основными идеями. Для
интересующихся кратким, рассчитанным на
применение, (нематематическим) введением в АРПСС,
рекомендуем книгу McCleary, Meidinger, and Hay (1980).

Два основных процесса

Процесс авторегрессии. Большинство
временных рядов содержат элементы, которые
последовательно зависят друг от друга. Такую
зависимость можно выразить следующим
уравнением:

x_t =
+ ₁*x_(t-1) + ₂*x_(t-2) + ₃*x_(t-3) + … +

Здесь:
—
константа (свободный член),
₁,
₂,
₃
— параметры авторегрессии.

Вы видите, что каждое наблюдение есть сумма
случайной компоненты (случайное воздействие, ) и линейной
комбинации предыдущих наблюдений.

Требование стационарности. Заметим, что
процесс авторегрессии будет стационарным
только, если его параметры лежат в определенном
диапазоне. Например, если имеется только один
параметр, то он должен находиться в интервале -1<<+1. В противном случае,
предыдущие значения будут накапливаться и
значения последующих x_t могут быть
неограниченными, следовательно, ряд не будет стационарным.
Если имеется несколько параметров
авторегрессии, то можно определить аналогичные
условия, обеспечивающие стационарность (см.
например, Бокс и Дженкинс, 1976; Montgomery, 1990).

Процесс скользящего среднего. В отличие от
процесса авторегрессии, в процессе скользящего
среднего каждый элемент ряда подвержен
суммарному воздействию предыдущих ошибок. В
общем виде это можно записать следующим образом:

x_t = µ + _t — ₁*_(t-1) — ₂*_(t-2) — ₃*_(t-3) — …

Здесь:
µ —
константа,
₁,
₂,
₃ —
параметры скользящего среднего.

Другими словами, текущее наблюдение ряда
представляет собой сумму случайной компоненты
(случайное воздействие, ) в данный момент и линейной
комбинации случайных воздействий в предыдущие
моменты времени.

Обратимость. Не вдаваясь в детали, отметим,
что существует «двойственность» между
процессами скользящего среднего и авторегрессии
(см. например, Бокс и Дженкинс, 1976; Montgomery, Johnson, and
Gardiner, 1990). Это означает, что приведенное выше
уравнение скользящего среднего можно переписать
(обратить) в виде уравнения авторегрессии
(неограниченного порядка), и наоборот. Это так
называемое свойство обратимости. Имеются
условия, аналогичные приведенным выше условиям стационарности,
обеспечивающие обратимость модели.

Модель АРПСС

Модель авторегрессии и скользящего среднего. Общая
модель, предложенная Боксом и Дженкинсом (1976)
включает как параметры авторегрессии, так и
параметры скользящего среднего. Именно, имеется
три типа параметров модели: параметры
авторегрессии (p), порядок разности (d), параметры
скользящего среднего (q). В обозначениях Бокса
и Дженкинса модель записывается как АРПСС (p, d, q).
Например, модель (0, 1, 2) содержит 0
(нуль) параметров авторегрессии (p) и 2
параметра скользящего среднего (q), которые
вычисляются для ряда после взятия разности с
лагом 1.

Идентификация. Как отмечено ранее, для
модели АРПСС необходимо, чтобы ряд был стационарным,
это означает, что его среднее постоянно, а
выборочные дисперсия и автокорреляция не
меняются во времени. Поэтому обычно необходимо
брать разности ряда до тех пор, пока он не станет
стационарным
(часто также применяют логарифмическое
преобразование для стабилизации дисперсии).
Число разностей, которые были взяты, чтобы
достичь стационарности, определяются параметром
d (см. предыдущий раздел). Для того чтобы
определить необходимый порядок разности, нужно
исследовать график ряда и автокоррелограмму.
Сильные изменения уровня (сильные скачки вверх
или вниз) обычно требуют взятия несезонной
разности первого порядка (лаг=1). Сильные
изменения наклона требуют взятия разности
второго порядка. Сезонная составляющая требует
взятия соответствующей сезонной разности (см.
ниже). Если имеется медленное убывание
выборочных коэффициентов автокорреляции в
зависимости от лага, обычно берут разность
первого порядка. Однако следует помнить, что для
некоторых временных рядов нужно брать разности
небольшого порядка или вовсе не брать их.
Заметим, что чрезмерное количество взятых
разностей приводит к менее стабильным оценкам
коэффициентов.

На этом этапе (который обычно называют идентификацией
порядка модели, см. ниже) вы также должны
решить, как много параметров авторегрессии (p)
и скользящего среднего (q) должно
присутствовать в эффективной и экономной модели
процесса. (Экономность модели означает, что в
ней имеется наименьшее число параметров и
наибольшее число степеней свободы среди всех
моделей, которые подгоняются к данным). На
практике очень редко бывает, что число
параметров p или q больше 2 (см. ниже более
полное обсуждение).

Оценивание и прогноз. Следующий, после
идентификации, шаг (Оценивание) состоит в
оценивании параметров модели (для чего
используются процедуры минимизации функции
потерь, см. ниже; более подробная информация о
процедурах минимизации дана в разделе Нелинейное оценивание).
Полученные оценки параметров используются на
последнем этапе (Прогноз) для того, чтобы
вычислить новые значения ряда и построить
доверительный интервал для прогноза. Процесс
оценивания проводится по преобразованным данным
(подвергнутым применению разностного оператора).
До построения прогноза нужно выполнить обратную
операцию (интегрировать данные). Таким
образом, прогноз методологии будет сравниваться
с соответствующими исходными данными. На
интегрирование данных указывает буква П в
общем названии модели (АРПСС = Авторегрессионное
Проинтегрированное Скользящее Среднее).

Константа в моделях АРПСС. Дополнительно
модели АРПСС могут содержать константу,
интерпретация которой зависит от подгоняемой
модели. Именно, если (1) в модели нет параметров
авторегрессии, то константа есть среднее значение ряда, если (2)
параметры авторегрессии имеются, то константа
представляет собой свободный член. Если бралась
разность ряда, то константа представляет собой
среднее или свободный член преобразованного
ряда. Например, если бралась первая разность
(разность первого порядка), а параметров
авторегрессии в модели нет, то константа
представляет собой среднее значение
преобразованного ряда и, следовательно, коэффициент
наклона линейного тренда исходного.

Идентификация

Число оцениваемых параметров. Конечно, до
того, как начать оценивание, вам необходимо
решить, какой тип модели будет подбираться к
данным, и какое количество параметров
присутствует в модели, иными словами, нужно
идентифицировать модель АРПСС. Основными
инструментами идентификации порядка модели
являются графики, автокорреляционная функция
(АКФ), частная автокорреляционная функция (ЧАКФ).
Это решение не является простым и требуется
основательно поэкспериментировать с
альтернативными моделями. Тем не менее,
большинство встречающихся на практике временных
рядов можно с достаточной степенью точности
аппроксимировать одной из 5 основных моделей (см.
ниже), которые можно идентифицировать по виду
автокорреляционной (АКФ) и частной
автокорреляционной функции (ЧАКФ). Ниже дается
список этих моделей, основанный на рекомендациях
Pankratz (1983); дополнительные практические советы
даны в Hoff (1983), McCleary and Hay (1980), McDowall, McCleary, Meidinger, and Hay
(1980), and Vandaele (1983). Отметим, что число параметров
каждого вида невелико (меньше 2), поэтому нетрудно
проверить альтернативные модели.

Один параметр (p): АКФ — экспоненциально
убывает; ЧАКФ — имеет резко выделяющееся значение
для лага 1, нет корреляций на других лагах.
Два параметра авторегрессии (p): АКФ имеет
форму синусоиды или экспоненциально убывает;
ЧАКФ имеет резко выделяющиеся значения на лагах 1,
2, нет корреляций на других лагах.
Один параметр скользящего среднего (q): АКФ
имеет резко выделяющееся значение на лаге 1,
нет корреляций на других лагах. ЧАКФ
экспоненциально убывает.
Два параметра скользящего среднего (q): АКФ
имеет резко выделяющиеся значения на лагах 1, 2,
нет корреляций на других лагах. ЧАКФ имеет форму
синусоиды или экспоненциально убывает.
Один параметр авторегрессии (p) и один параметр
скользящего среднего (q): АКФ экспоненциально
убывает с лага 1; ЧАКФ — экспоненциально
убывает с лага 1.

Сезонные модели. Мультипликативная сезонная
АРПСС представляет естественное развитие и
обобщение обычной модели АРПСС на ряды, в которых
имеется периодическая сезонная компонента. В
дополнении к несезонным параметрам, в модель
вводятся сезонные параметры для определенного
лага (устанавливаемого на этапе идентификации
порядка модели). Аналогично параметрам простой
модели АРПСС, эти параметры называются: сезонная
авторегрессия (ps), сезонная разность (ds) и
сезонное скользящее среднее (qs). Таким
образом, полная сезонная АРПСС может быть
записана как АРПСС (p,d,q)(ps,ds,qs).
Например, модель (0,1,2)(0,1,1) включает 0
регулярных параметров авторегрессии, 2
регулярных параметра скользящего среднего и 1
параметр сезонного скользящего среднего. Эти
параметры вычисляются для рядов, получаемых
после взятия одной разности с лагом 1 и далее
сезонной разности. Сезонный лаг, используемый
для сезонных параметров, определяется на этапе
идентификации порядка модели.

Общие рекомендации относительно выбора
обычных параметров (с помощью АКФ и ЧАКФ)
полностью применимы к сезонным моделям. Основное
отличие состоит в том, что в сезонных рядах АКФ и
ЧАКФ имеют существенные значения на лагах,
кратных сезонному лагу (в дополнении к
характерному поведению этих функций,
описывающих регулярную (несезонную) компоненту
АРПСС).

Оценивание параметров

Существуют различные методы оценивания
параметров, которые дают очень похожие оценки, но
для данной модели одни оценки могут быть более
эффективны, а другие менее эффективны. В общем, во
время оценивания порядка модели используется
так называемый квазиньютоновский алгоритм
максимизации правдоподобия (вероятности)
наблюдения значений ряда по значениям
параметров (см. Нелинейное
оценивание). Практически это требует
вычисления (условных) сумм квадратов (SS)
остатков модели. Имеются различные способы
вычисления суммы квадратов остатков SS; вы
можете выбрать: (1) приближенный метод
максимального правдоподобия МакЛеода и Сейлза
(1983), (2) приближенный метод максимального
правдоподобия с итерациями назад, (3)точный метод
максимального правдоподобия по Meларду (1984).

Сравнение методов. В общем, все методы дают
очень похожие результаты. Также все методы
показали примерно одинаковую эффективность на
реальных данных. Однако метод 1 (см. выше) —
самый быстрый, и им можно пользоваться для
исследования очень длинных рядов (например,
содержащих более 30,000 наблюдений). Метод Меларда
(номер 3) может оказаться неэффективным, если
оцениваются параметры сезонной модели с большим
сезонным лагом (например, 365 дней). С другой
стороны, вы можете использовать вначале
приближенный метод максимального правдоподобия
(для того, чтобы найти прикидочные оценки
параметров), а затем точный метод; обычно
требуется только несколько итераций точного
метода (номер 3, выше), чтобы получить
окончательные оценки.

Стандартные ошибки оценок. Для всех оценок
параметров вычисляются так называемые асимптотические
стандартные ошибки, для вычисления которых
используется матрица частных производных
второго порядка, аппроксимируемая конечными
разностями (см. также раздел Нелинейное
оценивание).

Штраф. Процедура оценивания минимизирует
(условную) сумму квадратов остатков модели. Если
модель не является адекватной, может случиться
так, что оценки параметров на каком-то шаге
станут неприемлемыми — очень большими (например,
не удовлетворяют условию стационарности). В
таком случае, SS будет приписано очень большое
значение (штрафное значение). Обычно это
«заставляет» итерационный процесс удалить
параметры из недопустимой области. Однако в
некоторых случаях и эта стратегия может
оказаться неудачной, и вы все равно увидите на
экране (во время процедуры оценивания) очень
большие значения SS на серии итераций. В таких
случаях следует с осторожностью оценивать
пригодность модели. Если модель содержит много
параметров и, возможно, имеется интервенция (см.
ниже), то следует несколько раз испытать процесс
оценивания с различными начальными. Если модель
содержит много параметров и, возможно,
интервенцию (см. ниже), вам следует повторить
процедуру с различными начальными значениями
параметров.

Оценивание модели

Оценки параметров. Если значения
вычисляемой t статистики не значимы,
соответствующие параметры в большинстве случаев
удаляются из модели без ущерба подгонки.

Другой критерий качества. Другой обычной
мерой надежности модели является сравнение
прогноза, построенного по урезанному ряду с
«известными (исходными) данными».

Однако качественная модель должна не только
давать достаточно точный прогноз, но быть
экономной и иметь независимые остатки,
содержащие только шум без систематических
компонент (в частности, АКФ остатков не должна
иметь какой-либо периодичности). Поэтому
необходим всесторонний анализ остатков. Хорошей
проверкой модели являются: (a) график остатков и
изучение их трендов, (b) проверка АКФ остатков (на
графике АКФ обычно отчетливо видна
периодичность).

Анализ остатков. Если остатки
систематически распределены (например,
отрицательны в первой части ряда и примерно
равны нуля во второй) или включают некоторую
периодическую компоненту, то это
свидетельствует о неадекватности модели. Анализ
остатков чрезвычайно важен и необходим при
анализе временных рядов. Процедура оценивания
предполагает, что остатки не коррелированы и
нормально распределены.

Ограничения. Следует напомнить, что модель
АРПСС является подходящей только для рядов,
которые являются стационарными
(среднее, дисперсия и автокорреляция примерно
постоянны во времени); для нестационарных рядов
следует брать разности. Рекомендуется иметь, как
минимум, 50 наблюдений в файле исходных данных.
Также предполагается, что параметры модели
постоянны, т.е. не меняются во времени.

Прерванные временные ряды

Обычный вопрос, возникающий при анализе
временных рядов, состоит в следующем,
воздействует или нет внешнее событие на
последовательность наблюдений. Например,
привела ли новая экономическая политика к росту
экономики, как обещалось; изменил ли новый закон
интенсивность преступлений и т.д. В общем, нужно
оценивать воздействия одного или нескольких
дискретных событий на значения ряда. Этот вид
анализа прерванных временных рядов подробно
описан в книге McDowall, McCleary, Meidinger, and Hay (1980).
Различают следующие три типа воздействий: (1)
устойчивое скачкообразное, (2) устойчивое
постепенное, (3) скачкообразное временное. См.
также следующие разделы:

Идентификация модели
временных рядов
АРПСС
Экспоненциальное
сглаживание
Сезонная декомпозиция (метод
Census I)
Сезонная корректировка X-11
(метод Census II)
Таблицы результатов
корректировки X-11
Анализ распределенных лагов
Одномерный анализ Фурье
Кросс-спектральный анализ
Основные понятия и принципы
Быстрое преобразование Фурье

Экспоненциальное сглаживание

Общее введение
Простое экспоненциальное
сглаживание
Выбор лучшего значения
параметра a (альфа)
Индексы качества подгонки
Сезонная и несезонная модели
с трендом или без тренда

См. также:

Идентификация модели
временных рядов
АРПСС (Бокс и Дженкинс) и
автокорреляции
Прерванные временные ряды
Сезонная декомпозиция (метод
Census I)
Сезонная корректировка X-11
(метод Census II)
Таблицы результатов
корректировки X-11
Анализ распределенных лагов
Одномерный анализ Фурье
Кросс-спектральный анализ
Основные понятия и принципы
Быстрое преобразование Фурье

Общее введение

Экспоненциальное сглаживание — это очень
популярный метод прогнозирования многих
временных рядов. Исторически метод был
независимо открыт Броуном и Холтом. Броун служил
на флоте США во время второй мировой войны, где
занимался обнаружением подводных лодок и
системами наведения. Позже он применил открытый
им метод для прогнозирования спроса на запасные
части. Свои идеи он описал в книге, вышедшей в
свет в 1959 году. Исследования Холта были
поддержаны Департаментом военно-морского флота
США. Независимо друг от друга, Броун и Холт
открыли экспоненциальное сглаживание для
процессов с постоянным трендом, с линейным
трендом и для рядов с сезонной составляющей.

Gardner (1985), предложил «единую» классификацию
методов экспоненциального сглаживания.
Превосходное введение в эти методы можно найти в
книгах Makridakis, Wheelwright, and McGee (1983), Makridakis and Wheelwright (1989),
Montgomery, Johnson, and Gardiner (1990).

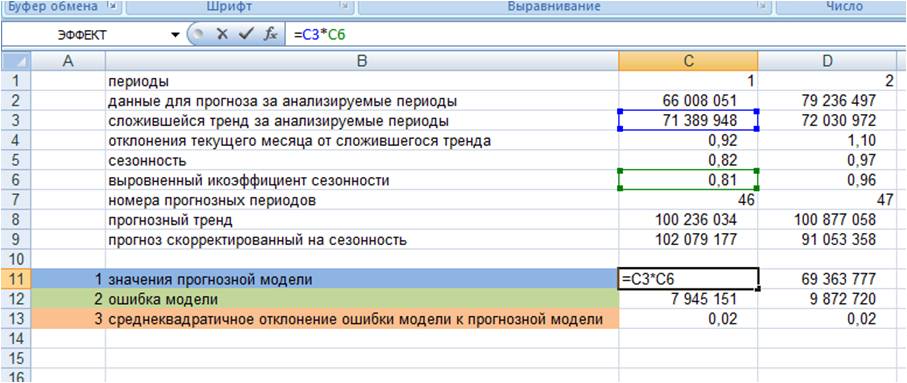
Простое экспоненциальное
сглаживание

Простая и прагматически ясная модель
временного ряда имеет следующий вид: X_t = b + _t, где b —
константа и
(эпсилон) — случайная ошибка. Константа b относительно
стабильна на каждом временном интервале, но
может также медленно изменяться со временем.
Один из интуитивно ясных способов выделения b
состоит в том, чтобы использовать сглаживание
скользящим средним, в котором последним
наблюдениям приписываются большие веса, чем
предпоследним, предпоследним большие веса, чем
пред-предпоследним и т.д. Простое
экспоненциальное именно так и устроено. Здесь
более старым наблюдениям приписываются
экспоненциально убывающие веса, при этом, в
отличие от скользящего среднего, учитываются все
предшествующие наблюдения ряда, а не те, что
попали в определенное окно. Точная формула
простого экспоненциального сглаживания имеет
следующий вид:

S_t = *X_t + (1-)*S_t-1

Когда эта формула применяется рекурсивно, то
каждое новое сглаженное значение (которое
является также прогнозом) вычисляется как
взвешенное среднее текущего наблюдения и
сглаженного ряда. Очевидно, результат
сглаживания зависит от параметра (альфа). Если равно 1, то
предыдущие наблюдения полностью игнорируются.
Если равно 0, то
игнорируются текущие наблюдения. Значения между 0, 1 дают
промежуточные результаты.

Эмпирические исследования Makridakis и др. (1982;
Makridakis, 1983) показали, что весьма часто простое
экспоненциальное сглаживание дает достаточно
точный прогноз.

Выбор лучшего значения
параметра (альфа)

Gardner (1985) обсуждает различные теоретические и
эмпирические аргументы в пользу выбора
определенного параметра сглаживания. Очевидно,
из формулы, приведенной выше, следует, что должно попадать в интервал между 0
(нулем) и 1 (хотя Brenner et al., 1968, для дальнейшего
применения анализа АРПСС считают, что 0<<2). Gardner (1985)
сообщает, что на практике обычно рекомендуется
брать меньше .30.
Однако в исследовании Makridakis et al., (1982), большее .30, часто
дает лучший прогноз. После обзора литературы,
Gardner (1985) приходит к выводу, что лучше оценивать
оптимально по данным
(см. ниже), чем просто «гадать» или
использовать искусственные рекомендации.

Оценивание лучшего значения с помощью данных. На
практике параметр сглаживания часто ищется с поиском
на сетке. Возможные значения параметра
разбиваются сеткой с определенным шагом.
Например, рассматривается сетка значений от = 0.1 до = 0.9, с шагом 0.1.
Затем выбирается ,
для которого сумма квадратов (или средних
квадратов) остатков (наблюдаемые значения минус
прогнозы на шаг вперед) является минимальной.

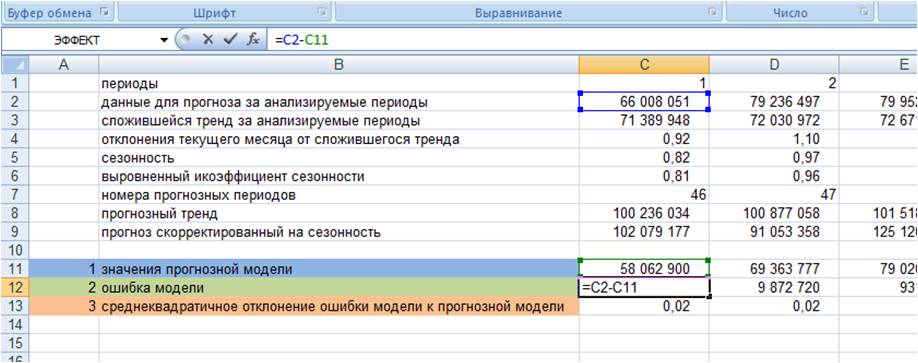
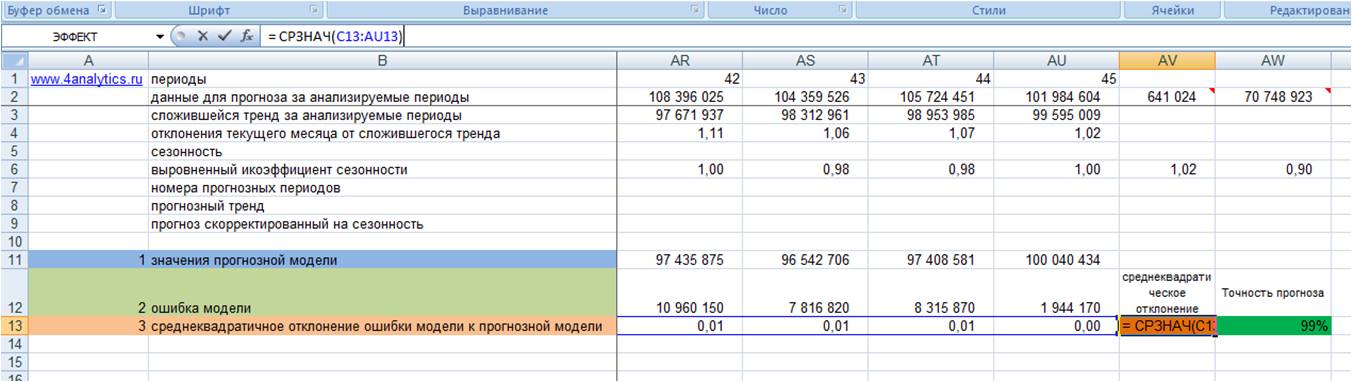
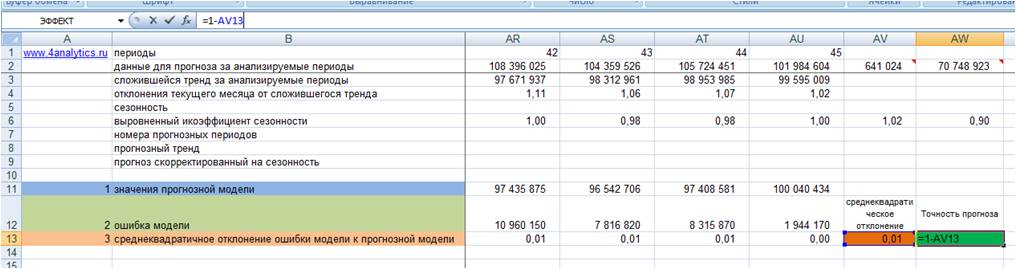
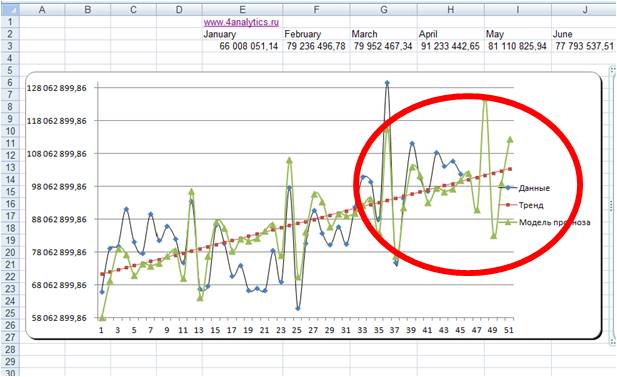
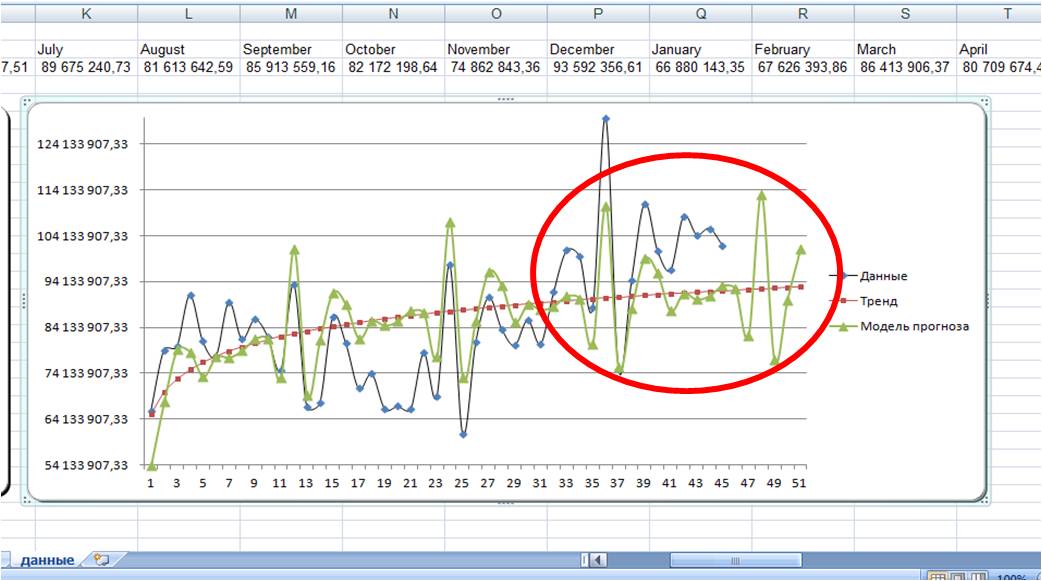
Индексы качества подгонки

Самый прямой способ оценки прогноза,
полученного на основе определенного значения — построить график
наблюдаемых значений и прогнозов на один шаг
вперед. Этот график включает в себя также остатки
(отложенные на правой оси Y). Из графика ясно
видно, на каких участках прогноз лучше или хуже.

Такая визуальная проверка точности прогноза
часто дает наилучшие результаты. Имеются также
другие меры ошибки, которые можно использовать
для определения оптимального параметра (см. Makridakis, Wheelwright, and McGee,
1983):

Средняя ошибка. Средняя ошибка (СО)
вычисляется простым усреднением ошибок на
каждом шаге. Очевидным недостатком этой меры
является то, что положительные и отрицательные
ошибки аннулируют друг друга, поэтому она не
является хорошим индикатором качества прогноза.

Средняя абсолютная ошибка. Средняя
абсолютная ошибка (САО) вычисляется как среднее абсолютных
ошибок. Если она равна 0 (нулю), то имеем
совершенную подгонку (прогноз). В сравнении со
средней квадратической ошибкой, эта мера
«не придает слишком большого значения»
выбросам.

Сумма квадратов ошибок (SSE),
среднеквадратическая ошибка. Эти величины
вычисляются как сумма (или среднее) квадратов
ошибок. Это наиболее часто используемые индексы
качества подгонки.

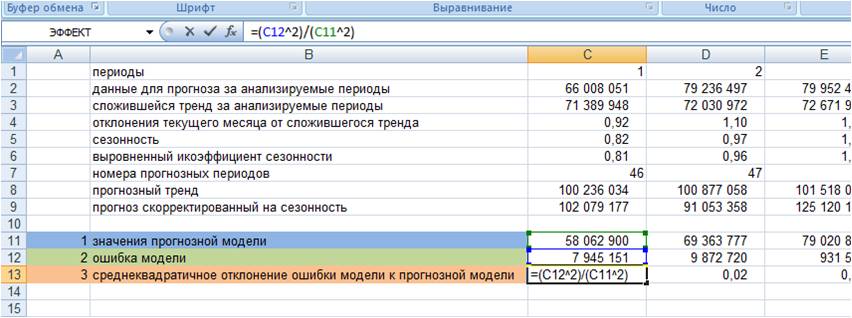
Относительная ошибка (ОО). Во всех
предыдущих мерах использовались действительные
значения ошибок. Представляется естественным
выразить индексы качества подгонки в терминах относительных
ошибок. Например, при прогнозе месячных продаж,
которые могут сильно флуктуировать (например, по
сезонам) из месяца в месяц, вы можете быть вполне
удовлетворены прогнозом, если он имеет точность
?10%. Иными словами, при прогнозировании
абсолютная ошибка может быть не так интересна
как относительная. Чтобы учесть относительную
ошибку, было предложено несколько различных
индексов (см. Makridakis, Wheelwright, and McGee, 1983). В первом
относительная ошибка вычисляется как:

ОО_t = 100*(X_t — F_t )/X_t

где X_t — наблюдаемое
значение в момент времени t, и F_t — прогноз (сглаженное
значение).

Средняя относительная ошибка (СОО).
Это значение вычисляется как среднее
относительных ошибок.

Средняя абсолютная относительная ошибка
(САОО). Как и в случае с обычной средней
ошибкой отрицательные и положительные
относительные ошибки будут подавлять друг друга.
Поэтому для оценки качества подгонки в целом (для
всего ряда) лучше использовать среднюю абсолютную
относительную ошибку. Часто эта мера более
выразительная, чем среднеквадратическая ошибка.
Например, знание того, что точность прогноза ±5%,
полезно само по себе, в то время как значение 30.8
для средней квадратической ошибки не может быть
так просто проинтерпретировано.

Автоматический поиск лучшего параметра.
Для минимизации средней квадратической ошибки,
средней абсолютной ошибки или средней
абсолютной относительной ошибки используется
квази-ньютоновская процедура (та же, что и в АРПСС). В большинстве случаев
эта процедура более эффективна, чем обычный
перебор на сетке (особенно, если параметров
сглаживания несколько), и оптимальное значение можно быстро
найти.

Первое сглаженное значение S₀.
Если вы взгляните снова на формулу простого
экспоненциального сглаживания, то увидите, что
следует иметь значение S₀ для
вычисления первого сглаженного значения
(прогноза). В зависимости от выбора параметра (в частности, если близко к 0), начальное
значение сглаженного процесса может оказать
существенное воздействие на прогноз для многих
последующих наблюдений. Как и в других
рекомендациях по применению экспоненциального
сглаживания, рекомендуется брать начальное
значение, дающее наилучший прогноз. С другой
стороны, влияние выбора уменьшается с длиной
ряда и становится некритичным при большом числе
наблюдений.

Сезонная и несезонная модели с
трендом или без тренда

В дополнение к простому экспоненциальному
сглаживанию, были предложены более сложные
модели, включающие сезонную компоненту и
трендом. Общая идея таких моделей состоит в том,
что прогнозы вычисляются не только по предыдущим
наблюдениям (как в простом экспоненциальном
сглаживании), но и с некоторыми задержками, что
позволяет независимо оценить тренд и сезонную
составляющую. Gardner (1985) обсудил различные модели в
терминах сезонности (отсутствует, аддитивная
сезонность, мультипликативная) и тренда
(отсутствует, линейный тренд, экспоненциальный,
демпфированный).

Аддитивная и мультипликативная
сезонность. Многие временные ряды имеют
сезонные компоненты. Например, продажи игрушек
имеют пики в ноябре, декабре и, возможно, летом,
когда дети находятся на отдыхе. Эта
периодичность имеет место каждый год. Однако
относительный размер продаж может слегка
изменяться из года в год. Таким образом, имеет
смысл независимо экспоненциально сгладить
сезонную компоненту с дополнительным
параметром, обычно обозначаемым как (дельта). Сезонные
компоненты, по природе своей, могут быть
аддитивными или мультипликативными. Например, в
течение декабря продажи определенного вида
игрушек увеличиваются на 1 миллион долларов
каждый год. Для того чтобы учесть сезонное
колебание, вы можете добавить в прогноз на каждый
декабрь 1 миллион долларов (сверх
соответствующего годового среднего). В этом
случае сезонность — аддитивная. Альтернативно,
пусть в декабре продажи увеличились на 40%, т.е. в 1.4
раза. Тогда, если общие продажи малы, то
абсолютное (в долларах) увеличение продаж в
декабре тоже относительно мало (процент роста
константа). Если в целом продажи большие, то
абсолютное (в долларах) увеличение продаж будет
пропорционально больше. Снова, в этом случае
продажи увеличатся в определенное число раз, и
сезонность будет мультипликативной (в данном
случае мультипликативная сезонная составляющая
была бы равна 1.4). На графике различие между двумя
видами сезонности состоит в том, что в аддитивной
модели сезонные флуктуации не зависят от
значений ряда, тогда как в мультипликативной
модели величина сезонных флуктуаций зависит от
значений временного ряда.

Параметр сезонного сглаживания . В общем, прогноз
на один шаг вперед вычисляется следующим образом
(для моделей без тренда; для моделей с линейным и
экспоненциальным трендом, тренд добавляется; см.
ниже):

Аддитивная модель:

Прогноз_t = S_t + I_t-p

Мультипликативная модель:

Прогноз_t = S_t*I_t-p

В этой формуле S_t
обозначает (простое) экспоненциально сглаженное
значение ряда в момент t, и I_t-p обозначает сглаженный
сезонный фактор в момент t
минус p (p —
длина сезона). Таким образом, в сравнении с
простым экспоненциальным сглаживанием, прогноз
«улучшается» добавлением или умножением
сезонной компоненты. Эта компонента оценивается
независимо с помощью простого экспоненциального
сглаживания следующим образом:

Аддитивная модель:

I_t = I_t-p + *(1-)*e_t

Мультипликативная модель:

I_t = I_t-p + *(1-)*e_t/S_t

Обратите внимание, что предсказанная сезонная
компонента в момент t
вычисляется, как соответствующая компонента на
последнем сезонном цикле плюс ошибка (e_t,
наблюдаемое минус прогнозируемое значение в
момент t). Ясно, что параметр принимает значения
между 0 и 1. Если он равен нулю, то сезонная
составляющая на следующем цикле та же, что и на
предыдущем. Если
равен 1, то сезонная составляющая
«максимально» меняется на каждом шаге из-за
соответствующей ошибки (множитель (1-) не
рассматривается из-за краткости введения). В
большинстве случаев, когда сезонность
присутствует, оптимальное значение лежит между 0 и 1.

Линейный, экспоненциальный,
демпфированный тренд. Возвращаясь к примеру
с игрушками, мы можем увидеть наличие линейного
тренда (например, каждый год продажи
увеличивались на 1 миллион), экспоненциального
(например, каждый год продажи возрастают в 1.3
раза) или демпфированного тренда (в первом году
продажи возросли на 1 миллион долларов; во втором
увеличение составило только 80% по сравнению с
предыдущим, т.е. на $800,000; в следующем году вновь
увеличение было только на 80%, т.е. на $800,000 * .8 = $640,000
и т.д.). Каждый тип тренда по-своему проявляется в
данных. В целом изменение тренда — медленное в
течение времени, и опять (как и сезонную
компоненту) имеет смысл экспоненциально
сгладить его с отдельным параметром
[обозначаемым (гамма)
— для линейного и экспоненциального тренда, (фи) — для
демпфированного тренда].

Параметры сглаживания (линейный и экспоненциальный тренд) и (демпфированный тренд). Аналогично
сезонной компоненте компонента тренда
включается в процесс экспоненциального
сглаживания. Сглаживание ее производится в
каждый момент времени независимо от других
компонент с соответствующими параметрами. Если равно 0, то тренд
постоянен для всех значений временного ряда (и
для всех прогнозов). Если равно 1, то тренд «максимально»
определяется ошибками наблюдений. Параметр учитывает, как сильно
изменяется тренд, т.е. как быстро он
«демпфируется» или, наоборот, возрастает.

Сезонная декомпозиция (метод Census I)

Общее введение
Вычисления

См. также:

Идентификация модели
временных рядов
АРПСС (Бокс и Дженкинс) и
автокорреляции
Прерванные временные ряды
Экспоненциальное
сглаживание
Сезонная корректировка X-11
(метод Census II)
Таблицы результатов
корректировки X-11
Анализ распределенных лагов
Одномерный анализ Фурье
Кросс-спектральный анализ
Основные понятия и принципы
Быстрое преобразование Фурье

Общее введение

Предположим, что у вас имеются ежемесячные
данные о пассажиропотоке на международных
авиалиниях за 12 лет (см. Бокс и Дженкинс, 1976). Если
изобразить эти данные на графике, то будет хорошо
видно, что (1) объем пассажиропотока имеет во
времени возрастающий линейный тренд, и (2) в ряде
имеется ежегодно повторяющаяся закономерность — сезонность
(большинство перевозок приходится на летние
месяцы, кроме того, имеется пик меньшей высоты в
районе декабрьских каникул). Цель сезонной
декомпозиции и корректировки как раз и состоит в
том, чтобы отделить эти компоненты, то есть
разложить ряд на составляющую тренда, сезонную
компоненту и оставшуюся нерегулярную
составляющую. «Классический» прием,
позволяющий выполнить такую декомпозицию,
известен как метод Census I. Этот метод
описывается и обсуждается в работах Makridakis,
Wheelwright, and McGee (1983) и Makridakis and Wheelwright (1989).

Общая модель. Основная идея сезонной
декомпозиции проста. В общем случае временной
ряд типа того, который описан выше, можно
представить себе состоящим из четырех различных
компонент: (1) сезонной компоненты (обозначается S_t,
где t обозначает момент времени), (2) тренда (T_t),
(3) циклической компоненты (C_t) и (4)
случайной, нерегулярной компоненты или
флуктуации (I_t). Разница между
циклической и сезонной компонентой состоит в
том, что последняя имеет регулярную (сезонную)
периодичность, тогда как циклические факторы
обычно имеют более длительный эффект, который к
тому же меняется от цикла к циклу. В методе Census I
тренд и циклическую компоненту обычно
объединяют в одну тренд-циклическую компоненту
(TC_t). Конкретные функциональные
взаимосвязи между этими компонентами могут
иметь самый разный вид. Однако, можно выделить
два основных способа, с помощью которых они могут
взаимодействовать: аддитивно и мультипликативно:

Аддитивная модель:

X_t = TC_t + S_t + I_t

Мультипликативная модель:

X_t = T_t*C_t*S_t*I_t

Здесь X_t обозначает
значение временного ряда в момент времени t. Если имеются какие-то априорные сведения
о циклических факторах, влияющих на ряд
(например, циклы деловой конъюнктуры), то можно
использовать оценки для различных компонент для
составления прогноза будущих значений ряда.
(Однако для прогнозирования предпочтительнее экспоненциальное
сглаживание, позволяющее учитывать сезонную
составляющую и тренд.)

Аддитивная и мультипликативная
сезонность. Рассмотрим на примере различие
между аддитивной и мультипликативной сезонными
компонентами. График объема продаж детских
игрушек, вероятно, будет иметь ежегодный пик в
ноябре-декабре, и другой — существенно меньший по
высоте — в летние месяцы, приходящийся на
каникулы. Такая сезонная закономерность будет
повторяться каждый год. По своей природе
сезонная компонента может быть аддитивной или
мультипликативной. Так, например, каждый год
объем продаж некоторой конкретной игрушки может
увеличиваться в декабре на 3 миллиона долларов.
Поэтому вы можете учесть эти сезонные изменения, прибавляя
к своему прогнозу на декабрь 3 миллиона. Здесь
мы имеем аддитивную сезонность. Может
получиться иначе. В декабре объем продаж
некоторой игрушки может увеличиваться на 40%, то
есть умножаться на множитель 1.4. Это значит,
например, что если средний объем продаж этой
игрушки невелик, то абсолютное (в денежном
выражении) увеличение этого объема в декабре
также будет относительно небольшим (но в
процентном исчислении оно будет постоянным);
если же игрушка продается хорошо, то и абсолютный
(в долларах) рост объема продаж будет
значительным. Здесь опять, объем продаж
возрастает в число раз, равное определенному множителю,
а сезонная компонента, по своей природе,
мультипликативная компонента (в данном случае
равная 1.4). Если перейти к графикам временных
рядов, то различие между этими двумя видами
сезонности будет проявляться так: в аддитивном
случае ряд будет иметь постоянные сезонные
колебания, величина которых не зависит от общего
уровня значений ряда; в мультипликативном случае
величина сезонных колебаний будет меняться в
зависимости от общего уровня значений ряда.

Аддитивный и мультипликативный тренд-цикл. Рассмотренный
пример можно расширить, чтобы проиллюстрировать
понятия аддитивной и мультипликативной
тренд-циклических компонент. В случае с
игрушками, тренд «моды» может привести к
устойчивому росту продаж (например, это может
быть общий тренд в сторону игрушек
образовательной направленности). Как и сезонная
компонента, этот тренд может быть по своей
природе аддитивным (продажи ежегодно
увеличиваются на 3 миллиона долларов) или
мультипликативным (продажи ежегодно
увеличиваются на 30%, или возрастают в 1.3 раза).
Кроме того, объем продаж может содержать
циклические компоненты. Повторим еще раз, что
циклическая компонента отличается от сезонной
тем, что она обычно имеет большую временную
протяженность и проявляется через неравные
промежутки времени. Так, например, некоторая
игрушка может быть особенно «горячей» в
течение летнего сезона (например, кукла,
изображающая персонаж популярного мультфильма,
которая к тому же агрессивно рекламируется). Как
и в предыдущих случаях, такая циклическая
компонента может изменять объем продаж
аддитивно, либо мультипликативно.

Вычисления

В вычислительном отношении процедура метода Сезонной
декомпозиции (Census I) следует стандартным
формулам, см. Makridakis, Wheelwright, and McGee (1983) или Makridakis and
Wheelwright (1989).

Скользящее среднее. Сначала
вычисляется скользящее среднее для временного
ряда, при этом ширина окна берется равной периоду
сезонности. Если период сезонности — четное
число, пользователь может выбрать одну из двух
возможностей: брать скользящее среднее с
одинаковыми весами или же с неравными весами так,
что первое и последнее наблюдения в окне имеют
усредненные веса.

Отношения или разности. После взятия
скользящих средних вся сезонная (т.е. внутри
сезона) изменчивость будет исключена, и поэтому
разность (в случае аддитивной модели) или
отношение (для мультипликативной модели) между
наблюдаемым и сглаженным рядом будет выделять
сезонную составляющую (плюс нерегулярную
компоненту). Более точно, ряд скользящих средних
вычитается из наблюдаемого ряда (в аддитивной
модели) или же значения наблюдаемого ряда
делятся на значения скользящих средних (в
мультипликативной модели).

Сезонная составляющая. На следующем
шаге вычисляется сезонная составляющая, как
среднее (для аддитивных моделей) или урезанное
среднее (для мультипликативных моделей) всех
значений ряда, соответствующих данной точке
сезонного интервала.

Сезонная корректировка ряда. Исходный
ряд можно скорректировать, вычитая из него
(аддитивная модель) или деля его значения на
(мультипликативная модель) значения сезонной
составляющей.

Получающийся в результате ряд называется
сезонной корректировкой ряда (из ряда убрана
сезонная составляющая)..

Тренд-циклическая компонента.
Напомним, что циклическая компонента отличается
от сезонной компоненты тем, что
продолжительность цикла, как правило, больше, чем
один сезонный период, и разные циклы могут иметь
разную продолжительность. Приближение для
объединенной тренд-циклической компоненты можно
получить, применяя к ряду с сезонной поправкой
процедуру 5-точечного (центрированного)
взвешенного скользящего среднего с весами 1, 2, 3, 2,
1.

Случайная или нерегулярная компонента.
На последнем шаге выделяется случайная или
нерегулярная компонента (погрешность) путем
вычитания из ряда с сезонной поправкой
(аддитивная модель) или делением этого ряда
(мультипликативная модель) на тренд-циклическую
компоненту.

Сезонная корректировка X-11 (метод Census II)

Общие идеи, лежащие в основе сезонной
декомпозиции и корректировки, изложены в
разделе, посвященном методу сезонной
корректировки Census I (см. Сезонная
декомпозиция (метод Census I)). Метод Census II (2)
является развитием и уточнением обычного метода
корректировки. На протяжении многих лет
различные варианты метода Census II развивались в
Бюро Переписи США (US Census Bureau); один из вариантов
этого метода, получивший широкую известность и
наиболее часто применяемый в государственных
органах и сфере бизнеса, называется «вариант X-11
метода Census II» (см. Shiskin, Young, and Musgrave, 1967).
Впоследствии этот усовершенствованный вариант
метода Census II стал называться просто X-11.
Помимо документации, которую можно получить из
Census Bureau, подробное описание метода дано в работах
Makridakis, Wheelwright and McGee (1983), Makridakis and Wheelwright (1989).

За дополнительной информацией обратитесь к
следующим разделам:

Сезонная корректировка:
основные идеи и термины
Метод Census II
Таблицы результатов
корректировки X-11
Подробное описание всех
таблиц результатов, вычисляемых в методе X-11

За дальнейшей информацией обратитесь к Анализу временных рядов и
следующим разделам:

Идентификация модели
временных рядов
АРПСС (Бокс и Дженкинс) и
автокорреляции
Прерванные временные ряды
Экспоненциальное
сглаживание
Сезонная декомпозиция (метод
Census I)
Анализ распределенных лагов
Одномерный анализ Фурье
Кросс-спектральный анализ
Основные понятия и принципы
Быстрое преобразование Фурье

Сезонная корректировка: основные идеи и
термины

Предположим, что у вас имеются ежемесячные
данные о пассажиропотоке на международных
авиалиниях за 12 лет (см. Бокс и Дженкинс, 1976). Если
изобразить эти данные на графике, то будет хорошо
видно, что (1) объем пассажиропотока имеет во
времени возрастающий линейный тренд, и что (2) в
ряде имеется ежегодно повторяющаяся
закономерность — сезонность (большинство
перевозок приходится на летние месяцы, кроме
того, имеется пик меньшей высоты в районе
декабрьских каникул). Цель сезонной декомпозиции
и корректировки как раз и состоит в том, чтобы
отделить эти компоненты, то есть разложить ряд на
составляющую тренда, сезонную компоненту и
оставшуюся нерегулярную составляющую.
«Классический» прием, позволяющий выполнить
такую декомпозицию, известен как метод Census I
(см. раздел Census I). Этот метод
описывается и обсуждается в работах Makridakis,
Wheelwright, and McGee (1983) и Makridakis and Wheelwright (1989).

Аддитивная модель:

X_t = TC_t + S_t + I_t

Мультипликативная модель:

X_t = T_t*C_t*S_t*I_t

Здесь X_t обозначает
значение временного ряда в момент времени t.

Если имеются какие-то априорные сведения о
циклических факторах, влияющих на ряд (например,
циклы деловой конъюнктуры), то можно
использовать оценки для различных компонент для
составления прогноза будущих значений ряда.
(Однако для прогнозирования предпочтительнее экспоненциальное
сглаживание, позволяющее учитывать сезонную
составляющую и тренд.)

Аддитивный и мультипликативный тренд-цикл.
Рассмотренный пример можно расширить, чтобы
проиллюстрировать понятия аддитивной и
мультипликативной тренд-циклических компонент.
В случае с игрушками, тренд «моды» может
привести к устойчивому росту продаж (например,
это может быть общий тренд в сторону игрушек
образовательной направленности). Как и сезонная
компонента, этот тренд может быть по своей
природе аддитивным (продажи ежегодно
увеличиваются на 3 миллиона долларов) или
мультипликативным (продажи ежегодно
увеличиваются на 30%, или возрастают в 1.3 раза).
Кроме того, объем продаж может содержать
циклические компоненты. Повторим еще раз, что
циклическая компонента отличается от сезонной
тем, что она обычно имеет большую временную
протяженность и проявляется через неравные
промежутки времени. Так, например, некоторая
игрушка может быть особенно «горячей» в
течение летнего сезона (например, кукла,
изображающая персонаж популярного мультфильма,
которая к тому же агрессивно рекламируется). Как
и в предыдущих случаях, такая циклическая
компонента может изменять объем продаж
аддитивно, либо мультипликативно.

Метод Census II

Основной метод сезонной декомпозиции и
корректировки, рассмотренный в разделе Сезонная корректировка:
основные идеи и термины, может быть
усовершенствован различными способами. На самом
деле, в отличие от многих методов моделирования
временных рядов (в частности, АРПСС),
которые основаны на определенной теоретической
модели, вариант X-11 метода Census II представляет
собой просто результат многочисленных специально
разработанных приемов и усовершенствований,
которые доказали свою работоспособность в
многолетней практике решения реальных задач (см.
Burman, 1979, Kendall and Ord, 1990, Makridakis and Wheelwright, 1989; Wallis, 1974).
Некоторые из наиболее важных усовершенствований
перечислены ниже.

Поправка на число рабочих дней. В
месяцах разное число дней и разное число рабочих
дней. Если мы анализируем, например, цифры
ежемесячной выручки парка аттракционов, то
разница в числе суббот и воскресений (пиковые
дни) в разных месяцах существенным образом
скажется на различиях в ежемесячных показателях
дохода. Вариант X-11 метода Census II дает
пользователю возможность проверить,
присутствует ли во временном ряду этот эффект
числа рабочих дней, и если да, то внести
соответствующие поправки.

Выбросы. Большинство реальных
временных рядов содержит выбросы, то есть резко
выделяющиеся наблюдения, вызванные какими-то
исключительными событиями. Например, забастовка
персонала может сильно повлиять на месячные или
годовые показатели выпуска продукции фирмы.
Такие выбросы могут исказить оценки сезонной
компоненты и тренда. В процедуре X-11
предусмотрены корректировки на случай появления
выбросов, основанные на использовании
«принципов статистического контроля»:
значения, выходящие за определенный диапазон
(который определяется в терминах, кратных сигма,
т.е. стандартных отклонений), могут быть
преобразованы или вовсе пропущены, и только
после этого будут вычисляться окончательные
оценки параметров сезонности.

Последовательные уточнения.
Корректировки, связанные с наличием выбросов и
различным числом рабочих дней можно производить
многократно, чтобы последовательно получать для
компонент оценки все лучшего качества. В методе X-11
делается несколько последовательных уточнений
оценок для получения окончательных компонент
тренд-цикличности и сезонности, нерегулярной
составляющей, и самого временного ряда с
сезонными поправками.

Критерии и итоговые статистики. Помимо
оценки основных компонент ряда, можно вычислить
различные сводные статистики. Например, можно
сформировать таблицы дисперсионного анализа для
проверки значимости фактора сезонной
изменчивости и ряда и фактора рабочих дней (см.
выше), процедура метода X-11 вычисляет также
ежемесячные относительные изменения в случайной
и тренд-циклической компонентах. С увеличением
продолжительности временного промежутка,
измеряемого в месяцах или, в случае квартального
варианта метода X-11 — в кварталах года,
изменения в тренд-циклической компоненте, вообще
говоря, будут нарастать, в то время как изменения
случайной составляющей должны оставаться
примерно на одном уровне. Средняя длина
временного интервала, на котором изменения
тренд-циклической компоненты становятся
примерно равными изменениям случайной
компоненты, называется месяцем (кварталом)
циклического доминирования, или сокращенно
МЦД (соответственно КЦД). Например, если МЦД равно
двум, то на сроках более двух месяцев
тренд-циклическая компонента станет
доминировать над флуктуациями нерегулярной
(случайной) компоненты. Эти и другие результаты
более подробно будут обсуждаться далее.

Таблицы результатов
корректировки X-11

Вычисления, которые производятся в процедуре
X-11, лучше всего обсуждать в контексте
таблиц результатов, которые при этом выдаются.
Процедура корректировки разбивается на семь
этапов, которые обычно обозначаются буквами A
— G.

Априорная корректировка (помесячная сезонная
корректировка). Перед тем, как к временному
ряду, содержащему ежемесячные значения, будет
применяться какая-либо сезонная корректировка,
могут быть произведены различные корректировки,
заданные пользователем. Можно ввести еще один
временной ряд, содержащий априорные
корректирующие факторы; значения этого ряда
будут вычитаться из исходного ряда (аддитивная
модель), или же значения исходного ряда будут
поделены на значения корректирующего ряда
(мультипликативная модель). В случае
мультипликативной модели пользователь может
также определить свои собственные поправочные
коэффициенты (веса) на число рабочих дней. Эти
веса будут использоваться для корректировки
ежемесячных наблюдений, так чтобы учитывалось
число рабочих дней в этом месяце.
Предварительное оценивание вариации числа
рабочих дней (месячный вариант X-11) и весов. На
следующем шаге вычисляются предварительные
поправочные коэффициенты на число рабочих дней
(только в месячном варианте X-11) и веса,
позволяющие уменьшить эффект выбросов.
Окончательное оценивание вариации числа
рабочих дней и нерегулярных весов (месячный
вариант X-11). Поправки и веса, вычисленные в
пункте B, используются для построения
улучшенных оценок тренд-циклической и сезонной
компонент. Эти улучшенные оценки используются
для окончательного вычисления факторов числа
рабочих дней (в месячном варианте X-11) и весов.
Окончательное оценивание сезонных факторов,
тренд-циклической, нерегулярной и сезонно
скорректированной компонент ряда. Окончательные
значения факторов рабочих дней и весов,
вычисленные в пункте C, используются для
вычисления окончательных оценок для компонент
ряда.
Модифицированные ряды: исходный, сезонно
скорректированный и нерегулярный. Исходный и
окончательный сезонно скорректированный ряды, а
также нерегулярная компонента модифицируются
путем сглаживания выбросов. Полученные в
результате этого, модифицированные ряды
позволяют пользователю проверить устойчивость
сезонной корректировки.
Месяц (квартал) циклического доминирования
(МЦД, КЦД), скользящее среднее и сводные
показатели. IНа этом этапе вычислений
рассчитываются различные сводные
характеристики (см. далее), позволяющие
пользователю исследовать относительную
важность разных компонент, среднюю флуктуацию от
месяца к месяцу (от квартала к кварталу), среднее
число идущих подряд изменений в одну сторону и
др.
Графики. Наконец, вы можете построить
различные графики итоговых результатов.
Например, можно построить окончательно
скорректированный ряд в хронологическом порядке
или по месяцам (см. ниже).

Подробное описание всех таблиц
результатов, вычисляемых в методе X-11

На каждом из этапов A — G (см. раздел Таблицы результатов
корректировки X-11) вычислялись различные
таблицы результатов. Обычно все они нумеруются, а
также им приписывается буква, соответствующая
этапу анализа. Например, таблица B 11 содержит
предварительно сезонно скорректированный ряд; C
11 — это более точно сезонно скорректированный
ряд, а D 11 — окончательный сезонно
скорректированный ряд. Далее приводится
перечень всех таблиц. Таблицы, помеченные
звездочкой (*), недоступны (или неприменимы) при
анализе квартальных показателей. Кроме того, в
случае квартальной корректировки некоторые из
описанных ниже вычислений несколько
видоизменяются. Так, например, для вычисления
сезонных факторов вместо 12-периодного (т.е.
12-месячного) скользящего среднего используется
4-периодное (4-квартальное) скользящее среднее;
предварительная тренд-циклическая компонента
вычисляется по центрированному 4-периодному
скользящему среднему, а окончательная оценка
тренд-циклической компоненты вычисляется по
5-точечному среднему Хендерсона.

В соответствии со стандартом метода X-11,
принятым Бюро переписи США, предусмотрены три
степени подробности вывода: Стандартный (17 — 27
таблиц), Длинный (27 — 39 таблиц) и Полный (44 —
59 таблиц). Имеется также возможность выводить
только таблицы результатов, выбранные
пользователем. В следующих далее описаниях
таблиц, буквы С, Д и П рядом с
названием таблицы указывают, какие таблицы
выводятся и/или распечатываются в
соответствующем варианте вывода. (Для графиков
предусмотрены два уровня подробности вывода: Стандартный
и Все.)

Щелкните на имени таблицы для
получения информации о ней.

* A 1.
Исходный ряд (С)

*
A 2. Априорные месячные поправки (С)

*
A 3. Исходный ряд, скорректированный с помощью
априорных месячных поправок (С)

* A
4. Априорные поправки на рабочие дни (С)

B
1. Ряд после априорной корректировки либо
исходный ряд (С)

B 2.
Тренд-цикл (Д)

B
3. Немодифицированные S-I разности или отношения (П)

B
4. Значения для замены выбросов S-I разностей
(отношений) (П)

B 5.
Сезонная составляющая (П)

B 6.
Сезонная корректировка ряда (П)

B 7.
Тренд-цикл (Д)

B 8.
Немодифицированные S-I разности (отношения) (П)

B
9. Значения для замены выбросов S-I разностей
(отношений) (П)

B 10.
Сезонная составляющая (Д)

B 11.
Сезонная корректировка ряда (П)

B 12. (не используется)

B 13.
Нерегулярная составляющая ряда (Д)

Таблицы B 14 — B 16, B 18 и B 19: Поправка на число
рабочих дней. Эти таблицы доступны только при
анализе ежемесячных данных. Число разных дней
недели (понедельников, вторников и т.д.)
колеблется от месяца к месяцу. Бывают ряды, в
которых различия в числе рабочих дней в месяце
могут давать заметный разброс ежемесячных
показателей (например, месячный доход парка
аттракционов сильно зависит от того, сколько в
этом месяце было выходных дней). Пользователь
имеет возможность определить начальные веса для
каждого дня недели (см. A
4), и/или эти веса могут быть оценены по данным
(пользователь также может сделать использование
этих весов условным, т.е. только в тех случаях,
когда они объясняют значительную часть
дисперсии).

*
B 14. Выбросы нерегулярной составляющей,
исключенные из регрессии рабочих дней (Д)

* B
15. Предварительная регрессия рабочих дней (Д)

*
B 16. Поправки на число рабочих дней, полученные из
коэффициентов регрессии (П)

B
17. Предварительные веса нерегулярной компоненты (Д)

*
B 18. Поправки на число рабочих дней, полученные из
комбинированных весов дней недели (П)

*
B 19. Исходный ряд с поправками на рабочие дни и
априорную вариацию (П)

C
1. Исходный ряд, модифицированный с помощью
предварительных весов, с поправкой на рабочие
дни и априорную вариацию (Д)

C 2.
Тренд-цикл (П)

C 3. (не используется)

C
4. Модифицированные S-I разности (отношения) (П)

C 5.
Сезонная составляющая (П)

C 6.
Сезонная корректировка ряда (П)

C 7.
Тренд-цикл (Д)

C 8. (не используется)

C
9. Модифицированные S-I разности (отношения) (П)

C 10.
Сезонная составляющая (Д)

C 11.
Сезонная корректировка ряда (П)

C 12. (не используется)

C 13.
Нерегулярная составляющая (С)

Таблицы C 14 — C 16, C 18 и C 19: Поправка на число
рабочих дней. Эти таблицы доступны только при
анализе ежемесячных данных и если при этом
требуется поправка на различное число рабочих
дней. В этом случае поправки на число рабочих
дней вычисляются по уточненным значениям
сезонно скорректированных рядов аналогично
тому, как это делалось в пункте B (B 14 — B 16,
B 18, B 19).

*
C 14. Выбросы нерегулярной составляющей,
исключенные из регрессии рабочих дней (С)

* C
15. Регрессия рабочих дней — окончательный вариант
(С)

*
C 16. Поправки на число рабочих дней, полученные из
коэффициентов регрессии, — окончательный вариант
(С)

C
17. Окончательные веса нерегулярной компоненты (С)

*
C 18. Поправки на число рабочих дней, полученные из
комбинированных весов дней недели —
окончательный вариант (С)

*
C 19. Исходный ряд с поправками на рабочие дни и
априорную вариацию (С)

D
1. Исходный ряд, модифицированный с помощью
окончательных весов, с поправкой на рабочие дни и
априорную вариацию (Д)

D 2.
Тренд-цикл (П)

D 3. (не используется)

D
4. Модифицированные S-I разности (отношения) (П)

D 5.
Сезонная составляющая (П)

D 6.
Сезонная корректировка ряда (П)

D 7.
Тренд-цикл (Д)

D
8. Немодифицированные S-I разности (отношения) —
окончательный вариант (С)

D
9. Окончательные значения для замены выбросов S-I
разностей (отношений) (С)

D 10.
Сезонная составляющая — окончательный вариант (С)

D
11. Сезонная корректировка ряда — окончательный
вариант (С)

D 12.
Тренд-циклическая компонента — окончательный
вариант (С)

D 13.
Нерегулярная составляющая — окончательный
вариант (С)

E 1.
Модифицированный исходный ряд (С)

E 2.
Модифицированный ряд с сезонной поправкой (С)

E 3.
Модифицированная нерегулярная составляющая (С)

E
4. Разности (отношения) годовых сумм (С)

E
5. Разности (относительные изменения) исходного
ряда (С)

E
6. Разности (относительные изменения)
окончательного варианта ряда с сезонной
поправкой (С)

F 1.
МЦД (КЦД) скользящее среднее (С)

F 2.
Сводные показатели (С)

G 1. График (С)

G 2. График (С)

G 3. График (В)

G 4. График (В)

Анализ распределенных лагов

Общая цель
Общая модель
Распределенный лаг Алмона

За дальнейшей информацией обратитесь к Анализу временных рядов и
следующим разделам:

Идентификация модели
временных рядов
АРПСС (Бокс и Дженкинс) и
автокорреляции Вводный обзор АРПСС
Прерванные временные ряды
Экспоненциальное
сглаживание
Сезонная декомпозиция (метод
Census I)
Сезонная корректировка X-11
(метод Census II)
Таблицы результатов
корректировки X-11
Одномерный анализ Фурье
Кросс-спектральный анализ
Основные понятия и принципы
Быстрое преобразование Фурье

Общая цель

Анализ распределенных лагов — это специальный
метод оценки запаздывающей зависимости между
рядами. Например, предположим, вы производите
компьютерные программы и хотите установить
зависимость между числом запросов, поступивших
от покупателей, и числом реальных заказов. Вы
могли бы записывать эти данные ежемесячно в
течение года и затем рассмотреть зависимость
между двумя переменными: число запросов и число
заказов зависит от запросов, но зависит с
запаздыванием. Однако очевидно, что запросы
предшествуют заказам, поэтому можно ожидать, что
число заказов. Иными словами, в зависимости между
числом запросов и числом продаж имеется

временной сдвиг (лаг) (см. также автокорреляции и
кросскорреляции).

Такого рода зависимости с запаздыванием
особенно часто возникают в эконометрике.
Например, доход от инвестиций в новое
оборудование отчетливо проявится не сразу, а
только через определенное время. Более высокий
доход изменяет выбор жилья людьми; однако эта
зависимость, очевидно, тоже проявляется с
запаздыванием. [Подобные задачи возникают в
страховании, где временной ряд клиентов и ряд
денежных поступлений сдвинуты друг относительно
друга].

Во всех этих случаях, имеется независимая или объясняющая
переменная, которая воздействует на зависимые
переменные с некоторым запаздыванием (лагом).
Метод распределенных лагов позволяет
исследовать такого рода зависимость.

Подробные обсуждения зависимостей с
распределенными лагами имеются в
эконометрических учебниках, например, в Judge, Griffith,
Hill, Luetkepohl, and Lee (1985), Maddala (1977), and Fomby, Hill, and Johnson (1984).
Ниже дается краткое описание этих методов.
Предполагается, что вы знакомы с понятием
корреляции (см. Основные
статистики и таблицы), кросскорреляции и
основными идеями множественной регрессии (см. Множественная регрессия).

Общая модель

Пусть y — зависимая переменная, a независимая
или объясняющая x. Эти переменные измеряются
несколько раз в течение определенного отрезка
времени. В некоторых учебниках по эконометрике
зависимая переменная называется также эндогенной
переменной, a зависимая или объясняемая
переменная экзогенной переменной.
Простейший способ описать зависимость между
этими двумя переменными дает следующее линейное
уравнение:

Y_t = _i*x_t-i

В этом уравнении значение зависимой переменной
в момент времени t является
линейной функцией переменной x,
измеренной в моменты t, t-1,
t-2 и т.д. Таким образом, зависимая
переменная представляет собой линейные функции x и x, сдвинутых на
1, 2, и т.д. временные периоды. Бета коэффициенты
(i) могут
рассматриваться как параметры наклона в этом
уравнении. Будем рассматривать это уравнение как
специальный случай уравнения линейной регрессии
(см. раздел Множественная
регрессия). Если коэффициент переменной с
определенным запаздыванием (лагом) значим, то
можно заключить, что переменная y
предсказывается (или объясняется) с
запаздыванием.

Распределенный лаг Алмона

Обычная проблема, возникающая в множественной
регрессии, состоит в том, что соседние значения x
сильно коррелируют. В самом крайнем случае, это
приводит к тому, что корреляционная матрица не
будет обратимой и коэффициенты бета не могут
быть вычислены. В менее экстремальных ситуациях
вычисления этих коэффициентов и их стандартные
ошибки становятся ненадежными из-за
вычислительных ошибок (ошибок округления). В
контексте множественной регрессии эта проблема
хорошо известна как проблема мультиколлинеарности
(см. раздел Множественная
регрессия).

Алмон (1965) предложил специальную процедуру,
которая в данном случае уменьшает
мультиколлинеарность. Именно, пусть каждый
неизвестный коэффициент записан в виде:

_i =
₀ + ₁*i + … + _q*i^q

Алмон показал, что во многих случаях (в
частности, чтобы избежать мультиколлинеарности)
легче оценить коэффициенты альфа, чем
непосредственно коэффициенты бета. Такой
метод оценивания коэффициентов бета
называется полиномиальной аппроксимацией.

Неправильная спецификация. Общая
проблема полиномиальной аппроксимации, состоит
в том, что длина лага и степень полинома
неизвестны заранее. Последствия
неправильного определения (спецификации) этих
параметров потенциально серьезны (в силу
смещения, возникающего в оценках при
неправильном задании параметров). Этот вопрос
подробно обсуждается в книгах Frost (1975), Schmidt and Waud
(1973), Schmidt and Sickles (1975) и Trivedi and Pagan (1979).

Одномерный анализ Фурье

В спектральном анализе исследуются
периодические модели данных. Цель анализа —
разложить комплексные временные ряды с
циклическими компонентами на несколько основных
синусоидальных функций с определенной длиной
волн. Термин «спектральный» — своеобразная
метафора для описания природы этого анализа.
Предположим, вы изучаете луч белого солнечного
света, который, на первый взгляд, кажется
хаотически составленным из света с различными
длинами волн. Однако, пропуская его через призму,
вы можете отделить волны разной длины или
периодов, которые составляют белый свет.
Фактически, применяя этот метод, вы можете теперь
распознавать и различать разные источники света.
Таким образом, распознавая существенные
основные периодические компоненты, вы узнали
что-то об интересующем вас явлении. В сущности,
применение спектрального анализа к временным
рядам подобно пропусканию света через призму. В
результате успешного анализа можно обнаружить
всего несколько повторяющихся циклов различной
длины в интересующих вас временных рядах,
которые, на первый взгляд, выглядят как случайный
шум.

Наиболее известный пример применения
спектрального анализа — циклическая природа
солнечных пятен (например, см. Блумфилд, 1976 или
Шамвэй, 1988). Оказывается, что активность
солнечных пятен имеет 11-ти летний цикл. Другие
примеры небесных явлений, изменения погоды,
колебания в товарных ценах, экономическая
активность и т.д. также часто используются в
литературе для демонстрации этого метода. В
отличие от АРПСС или метода экспоненциального
сглаживания (см. разделы АРПСС
и Экспоненциальное
сглаживание), цель спектрального анализа —
распознать сезонные колебания различной длины, в
то время как в предшествующих типах анализа,
длина сезонных компонент обычно известна (или
предполагается) заранее и затем включается в
некоторые теоретические модели скользящего
среднего или автокорреляции.

Классический текст по спектральному анализу —
Bloomfield (1976); однако другие подробные обсуждения
могут быть найдены в Jenkins and Watts (1968), Brillinger (1975), Brigham
(1974), Elliott and Rao (1982), Priestley (1981), Shumway (1988) или Wei (1989).

За дальнейшей информацией обратитесь к Анализу временных рядов и
следующим разделам:

Основные понятия и принципы
Быстрое преобразование Фурье
Идентификация модели
временных рядов
АРПСС (Бокс и Дженкинс) и
автокорреляции Вводный обзор АРПСС
Прерванные временные ряды
Анализ распределенных лагов
Сезонная декомпозиция (метод
Census I)
Экспоненциальное
сглаживание
Кросс-спектральный анализ

Кросс-спектральный анализ

Общее введение
Основные понятия и принципы
Результаты для каждой
переменной
Кросс-периодограмма,
кросс-плотность, квадратурная плотность и
кросс-амплитуда
Квадрат когерентности,
усиление и фазовый сдвиг
Как создавались данные для
примера

За дальнейшей информацией обратитесь к Анализу временных рядов и
следующим разделам:

Идентификация модели
временных рядов
АРПСС (Бокс и Дженкинс) и
автокорреляции Вводный обзор АРПСС
Прерванные временные ряды
Экспоненциальное
сглаживание
Сезонная декомпозиция (метод
Census I)
Сезонная корректировка X-11
(метод Census II)
Таблицы результатов
корректировки X-11
Анализ распределенных лагов
Одномерный анализ Фурье
Основные понятия и принципы
Быстрое преобразование Фурье

Общее введение

Кросс-спектральный анализ развивает Одномерный анализ Фурье и
позволяет анализировать одновременно два ряда.
Мы предполагаем, что вы уже прочитали введение к
разделу одномерного спектрального анализа.
Подробное обсуждение кросс-спектрального
анализа можно найти в книгах Bloomfield (1976), Jenkins and Watts
(1968), Brillinger (1975), Brigham (1974), Elliott and Rao (1982), Priestley (1981),
Shumway (1988), or Wei (1989).

Периодичность ряда на определенных
частотах. Наиболее известный пример
применения спектрального анализа — циклическая
природа солнечных пятен (например, см. Блумфилд,
1976 или Шамвэй, 1988). Оказывается, что активность
солнечных пятен имеет 11-ти летний цикл. Другие
примеры небесных явлений, изменения погоды,
колебания в товарных ценах, экономическая
активность и т.д. также часто используются в
литературе для демонстрации этого метода.

Основные понятия и принципы

Простой пример. Рассмотрим следующие два
ряда с 16 наблюдениями:

	ПЕРЕМ1	ПЕРЕМ2
1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16	1.000 1.637 1.148 -.058 -.713 -.383 .006 -.483 -1.441 -1.637 -.707 .331 .441 -.058 -.006 .924	-.058 -.713 -.383 .006 -.483 -1.441 -1.637 -.707 .331 .441 -.058 -.006 .924 1.713 1.365 .266

С первого взгляда нелегко рассмотреть
взаимосвязь между двумя рядами. Тем не менее, как
показано ниже, ряды создавались так, что содержат
две сильно коррелируемые периодичности. Далее
показаны части таблицы результатов из
кросс-спектрального анализа (спектральные
оценки были сглажены окном Парзена ширины 3).

Незавмсимая (X): ПЕРЕМ1 Зависимая (Y): ПЕРЕМ2
Частота	Период	X плотность	Y плотность	Кросс плотность	Кросс квадр.	Кросс амплит.
0.000000 .062500 .125000 .187500 .250000 .312500 .375000 .437500 .500000	16.00000 8.00000 5.33333 4.00000 3.20000 2.66667 2.28571 2.00000	.000000 8.094709 .058771 3.617294 .333005 .091897 .052575 .040248 .037115	.024292 7.798284 .100936 3.845154 .278685 .067630 .036056 .026633 0.000000	-.00000 2.35583 -.04755 -2.92645 -.26941 -.07435 -.04253 -.03256 0.00000	0.00000 -7.58781 .06059 2.31191 .14221 .02622 .00930 .00342 0.00000	.000000 7.945114 .077020 3.729484 .304637 .078835 .043539 .032740 0.000000

Результаты для каждой
переменной

Полная таблица результатов содержит все
спектральные статистики, вычисленные для
каждого ряда, как описано в разделе Одномерный анализ Фурье.
Взглянув на приведенные выше результаты,
очевидно, что оба ряда имеют основные
периодичности на частотах .0625 и .1875.

Кросс-периодограмма,
кросс-плотность, квадратурная плотность и
кросс-амплитуда

Аналогично результатам для одной переменной,
полная итоговая таблица результатов также
покажет значения периодограммы для
кросс-периодограммы. Однако кросс-спектр состоит
из комплексных чисел,
которые могут быть разделены на действительную и
мнимую части. Они могут быть сглажены для
вычисления оценок кросс-плотности и
квадратурной плотности (квадр-плотность для
краткости), соответственно. (Причины сглаживания
и различные функции весов для сглаживания
обсуждаются в разделе Одномерный
анализ Фурье.) Квадратный корень из суммы
квадратов значений кросс-плотности и
квадр-плотности называется кросс-амплитудой.
Кросс-амплитуда может интерпретироваться как
мера ковариации между соответствующими
частотными компонентами двух рядов. Таким
образом из результатов, показанных в таблице
результатов выше, можно заключить, что частотные
компоненты .0625 и .1875 двух рядов взаимосвязаны.

Квадрат когерентности, усиление
и фазовый сдвиг

Существуют дополнительные статистики, которые
будут показаны в полной итоговой таблице
результатов.

Квадрат когерентности. Можно
нормировать значения кросс-амплитуды, возведя их
в квадрат и разделив на произведение оценок
спектральной плотности каждого ряда. Результат
называется квадратом когерентности, который
может быть проинтерпретирован как квадрат
коэффициента корреляции (см. раздел Корреляции); т.е.
значение когерентности — это квадрат корреляции
между циклическими компонентами двух рядов
соответствующей частоты. Однако значения
когерентности не следует объяснять таким
образом; например, когда оценки спектральной
плотности обоих рядов очень малы, могут
получиться большие значения когерентности
(делитель в выражении когерентности может быть
очень маленьким), даже если нет существенных
циклических компонент в каждом ряду
соответствующей частоты.

Усиление. Значение усиления в анализе
вычисляется делением значения кросс-амплитуды
на оценки спектральной плотности одного или двух
рядов. Следовательно, может быть вычислено два
значения усиления, которые могут
интерпретироваться как стандартные
коэффициенты регрессии, соответствующей
частоты, полученные методом наименьших
квадратов.

Фазовый сдвиг. В заключение, оценки
фазового сдвига вычисляются как арктангенс (tan**-1)
коэффициента пропорциональности оценки
квадр-плотности и оценки кросс-плотности. Оценки
фазового сдвига (обычно обозначаемые греческой
буквой y) измеряют, насколько каждая частотная
компонента одного ряда опережает частотные
компоненты другого.

Как создавались данные для
примера

Теперь вернемся к примеру данных, приведенному
выше. Большие оценки спектральной плотности для
обоих рядов и значения кросс-амплитуды для
частот = 0.0625 и = .1875 предполагают две
существенных синхронных периодичности с этими
частотами в обоих рядах. Фактически, два ряда
создавались как:

v1 = cos(2**.0625*(v0-1))
+ .75*sin(2**.2*(v0-1))

v2 = cos(2**.0625*(v0+2)) +
.75*sin(2**.2*(v0+2))

(где v0 — номер наблюдения).
Действительно, анализ, представленный в этом
обзоре, очень хорошо воспроизводит
периодичность, заложенную в данные.

Спектральный анализ — Основные понятия и
принципы

Частота и период
Общая структура модели
Простой пример
Периодограмма
Проблема рассеяния
Добавление констант во
временной ряд (пэддинг)
Косинус-сглаживание
Окна данных и оценки
спектральной плотности
Подготовка данных к анализу
Результаты для случая, когда в
ряде отсутствует периодичность

За дальнейшей информацией обратитесь к Анализу временных рядов и
следующим разделам:

Идентификация модели
временных рядов
АРПСС (Бокс и Дженкинс) и
автокорреляции Вводный обзор АРПСС
Прерванные временные ряды
Экспоненциальное
сглаживание
Сезонная декомпозиция (метод
Census I)
Сезонная корректировка X-11
(метод Census II)
Таблицы результатов
корректировки X-11
Анализ распределенных лагов
Одномерный анализ Фурье
Кросс-спектральный анализ
Быстрое преобразование Фурье

Частота и период

Длина волны функций синуса или косинуса, как
правило, выражается числом циклов (периодов) в
единицу времени (Частота), часто обозначается
греческой буквой ню (; в некоторых учебниках также
используют f). Например, временной ряд,
состоящий из количества писем, обрабатываемых
почтой, может иметь 12 циклов в году. Первого числа
каждого месяца отправляется большое количество
корреспонденции (много счетов приходит именно
первого числа каждого месяца); затем, к середине
месяца, количество корреспонденции уменьшается;
и затем вновь возрастает к концу месяца. Поэтому
каждый месяц колебания в количестве
корреспонденции, обрабатываемой почтовым
отделением, будут проходить полный цикл. Таким
образом, если единица анализа — один год, то будет равно 12 (поскольку
имеется 12 циклов в году). Конечно, могут быть и
другие циклы с различными частотами. Например,
годичные циклы (=1)
и, возможно, недельные циклы (=52 недели в год).

Период Т функций синуса или косинуса
определяется как продолжительность по времени
полного цикла. Таким образом, это обратная
величина к частоте: T = 1/. Возвратимся к примеру с почтой из
предыдущего абзаца, здесь месячный цикл будет
равен 1/12 = 0.0833 года. Другими словами, это период
составляет 0.0833 года.

Общая структура модели

Как было отмечено ранее, цель спектрального
анализа — разложить ряд на функции синусов и
косинусов различных частот, для определения тех,
появление которых особенно существенно и
значимо. Один из возможных способов сделать это —
решить задачу линейной множественной
регрессии (см. раздел Множественная
регрессия), где зависимая переменная
-наблюдаемый временной ряд, а независимые
переменные или регрессоры: функции синусов всех
возможных (дискретных) частот. Такая модель
линейной множественной регрессии может быть
записана как:

x_t = a₀ + [a_k*cos(_k*t) + b_k*sin(_k*t)] (для k = 1 до q)

Следующее общее понятие классического
гармонического анализа в этом уравнении — (лямбда) -это
круговая частота, выраженная в радианах в
единицу времени, т.е. = 2**_k, где — константа пи =
3.1416 и _k = k/q. Здесь
важно осознать, что вычислительная задача
подгонки функций синусов и косинусов разных длин
к данным может быть решена с помощью
множественной линейной регрессии. Заметим, что
коэффициенты a_k при
косинусах и коэффициенты b_k
при синусах — это коэффициенты регрессии,
показывающие степень, с которой соответствующие
функции коррелируют с данными [заметим, что сами
синусы и косинусы на различных частотах не
коррелированы или, другим языком, ортогональны.
Таким образом, мы имеем дело с частным случаем
разложения по ортогональным полиномам.] Всего
существует q различных синусов
и косинусов (см. также Множественная регрессия);
интуитивно ясно, что число функций синусов и
косинусов не может быть больше числа данных в
ряде. Не вдаваясь в подробности, отметим, если n —
количество данных, то будет n/2+1 функций
косинусов и n/2-1 функций синусов. Другими
словами, различных синусоидальных волн будет
столько же, сколько данных, и вы сможете
полностью воспроизвести ряд по основным
функциям. (Заметим, если количество данных в ряде
нечетно, то последнее наблюдение обычно
опускается. Для определения синусоидальной
функции нужно иметь, по крайней мере, две точки:
высокого и низкого пика.)

В итоге, спектральный анализ определяет
корреляцию функций синусов и косинусов
различной частоты с наблюдаемыми данными. Если
найденная корреляция (коэффициент при
определенном синусе или косинусе) велика, то
можно заключить, что существует строгая
периодичность на соответствующей частоте в
данных.

Комплексные числа (действительные и мнимые
числа). Во многих учебниках по спектральному
анализу структурная модель, показанная выше,
представлена в комплексных числах; т.е. параметры
оцениваемого процесса описаны с помощью
действительной и мнимой части преобразования
Фурье. Комплексное число состоит из
действительного и мнимого числа. Мнимые числа, по
определению, — это числа, умноженные на константу i,
где i определяется как квадратный корень из -1.
Очевидно, корень квадратный из -1 не существует в
обычном сознании (отсюда термин мнимое число);
однако арифметические операции над мнимыми
числами могут производиться естественным
образом [например, (i*2)**2= -4]. Полезно представление
действительных и мнимых чисел, образующих
двумерную координатную плоскость, где
горизонтальная или X-ось представляет все
действительные числа, а вертикальная или Y-ось
представляет все мнимые числа. Комплексные числа
могут быть представлены точками на двумерной
плоскости. Например, комплексное число 3+i*2 может
быть представлено точкой с координатами {3,2} на
этой плоскости. Можно также представить
комплексные числа как углы; например, можно
соединить точку, соответствующую комплексному
числу на плоскости с началом координат
(комплексное число 0+i*0), и измерить угол наклона
этого вектора к горизонтальной оси. Таким
образом интуитивно ясно, каким образом формула
спектрального разложения, показанная выше, может
быть переписана в комплексной области. В таком
виде математические вычисления часто более
изящны и проще в выполнении, поэтому многие
учебники предпочитают представление
спектрального анализа в комплексных числах.

Простой пример

Шамвэй (1988) предлагает следующий простой пример
для объяснения спектрального анализа. Создадим
ряд из 16 наблюдений, полученных из уравнения,
показанного ниже, а затем посмотрим, каким
образом можно извлечь из него информацию.
Сначала создадим переменную и определим ее как:

x = 1*cos(2**.0625*(v0-1))
+ .75*sin(2**.2*(v0-1))

Эта переменная состоит из двух основных
периодичностей — первая с частотой =.0625 (или периодом 1/=16; одно наблюдение
составляет 1/16-ю длины полного цикла, или весь
цикл содержит каждые 16 наблюдений) и вторая с
частотой =.2 (или
периодом 5). Коэффициент при косинусе (1.0) больше
чем коэффициент при синусе (.75). Итоговая таблица
результатов спектрального анализа показана
ниже.

	Спектральный анализ: ПЕРЕМ1 (shumex.sta) Число наблюдений: 16
t	Час- тота	Период	Косинус корэфф.	Синус корэфф.	Периодо- грамма
0 1 2 3 4 5 6 7 8	.0000 .0625 .1250 .1875 .2500 .3125 .3750 .4375 .5000	16.00 8.00 5.33 4.00 3.20 2.67 2.29 2.00	.000 1.006 .033 .374 -.144 -.089 -.075 -.070 -.068	0.000 .028 .079 .559 -.144 -.060 -.031 -.014 0.000	.000 8.095 .059 3.617 .333 .092 .053 .040 .037

Теперь рассмотрим столбцы таблицы результатов.
Ясно, что наибольший коэффициент при косинусах
расположен напротив частоты .0625. Наибольший
коэффициент при синусах соответствует частоте
.1875. Таким образом, эти две частоты, которые были
«внесены» в данные, отчетливо проявились.

Периодограмма

Функции синусов и косинусов независимы (или
ортогональны); поэтому можно просуммировать
квадраты коэффициентов для каждой частоты, чтобы
вычислить периодограмму. Более часто,
значения периодограммы вычисляются как:

P_k = синус-коэффициент_k²
+ косинус-коэффициент_k² * N/2

где P_k — значения
периодограммы на частоте _k , и N — общая
длина ряда. Значения периодограммы можно
интерпретировать как дисперсию (вариацию) данных
на соответствующей частоте. Обычно значения
периодограммы изображаются в зависимости от
частот или периодов.

Проблема рассеяния

В примере, приведенном выше, функция синуса с
частотой 0.2 была «вставлена» в ряд. Однако
из-за того, что длина ряда равна 16, ни одна из
частот, полученных в таблице результатов, не
совпадает в точности с этой частотой. На практике
в этих случаях часто оказывается, что
соответствующая частота «рассеивается» на
близкие частоты. Например, могут быть найдены
большие значения периодограммы для двух близких
частот, когда в действительности существует
только одна основная функция синуса или косинуса
с частотой, которая попадает на одну из этих
частот или лежит между найденными частотами.
Существует три подхода к решению проблемы
рассеяния:

При помощи добавление констант во временной
ряда ряда можно увеличить частоты,
Применяя сглаживание ряда перед анализом,
можно уменьшить рассеяние или
Применяя сглаживание периодограммы, можно
идентифицировать основные частотные области или
(спектральные плотности), которые
существенно влияют на циклическое поведение
ряда.

Ниже смотрите описание каждого из этих
подходов.

Добавление констант во
временной ряд (пэддинг)

Так как частотные величины вычисляются как N/t,
можно просто добавить в ряд константы (например,
нули), и таким образом получить увеличение
частот. Фактически, если вы добавите в файл
данных, описанный в примере выше, десять нулей,
результаты не изменятся; т.е. наибольшие пики
периодограммы будут находиться по-прежнему на
частотах близких к .0625 и .2. (Добавление констант
во временной ряд также часто желательно для
увеличения вычислительной эффективности; см.
ниже.)

Косинус-сглаживание

Так называемый процесс косинус-сглаживания —
рекомендуемое преобразование ряда,
предшествующее спектральному анализу. Оно
обычно приводит к уменьшению рассеяния в
периодограмме. Логическое обоснование этого
преобразования подробно объясняется в книге
Bloomfield (1976, стр. 80-94). По существу, количественное
отношение (p) данных в начале и в конце ряда
преобразуется при помощи умножения на веса:

w_t = 0.5*{1-cos[*(t — 0.5)/m]} (для t=0 до m-1)
w_t = 0.5*{1-cos[*(N — t +
0.5)/m]} (для t=N-m до N-1)

где m выбирается так, чтобы 2*m/N было равно коэффициенту
пропорциональности сглаживаемых данных (p).

Окна данных и оценки
спектральной плотности

На практике, при анализе данных обычно не очень
важно точно определить частоты основных функций
синусов или косинусов. Скорее, т.к. значения
периодограммы — объект существенного случайного
колебания, можно столкнуться с проблемой многих
хаотических пиков периодограммы. В этом случае
хотелось бы найти частоты с большими спектральными
плотностями, т.е. частотные области, состоящие
из многих близких частот, которые вносят
наибольший вклад в периодическое поведение
всего ряда. Это может быть достигнуто путем
сглаживания значений периодограммы с помощью
преобразования взвешенного скользящего
среднего. Предположим, ширина окна скользящего
среднего равна m (должно быть нечетным
числом); следующие наиболее часто используемые
преобразования (заметим: p = (m-1)/2).

Окно Даниэля (равные веса). Окно
Даниэля (Daniell, 1946) означает простое (с равными
весами) сглаживание скользящим средним значений
периодограммы; т.е. каждая оценка спектральной
плотности вычисляется как среднее m/2
предыдущих и последующих значений
периодограммы.

Окно Тьюки. В окне Тьюки (Blackman and Tukey, 1958)
или Тьюки-Ханна (Hanning) (названное в честь Julius Von Hann),
для каждой частоты веса для взвешенного
скользящего среднего значений периодограммы
вычисляются как:

w_j = 0.5 + 0.5*cos(*j/p) (для j=0 до p)
w_-j = w_j (для j 0)

Окно Хемминга. В окне Хемминга
(названного в честь R. W. Hamming) или Тьюки-Хемминга
(Blackman and Tukey, 1958), для каждой частоты, веса для
взвешенного скользящего среднего значений
периодограммы вычисляются как:

w_j = 0.54 + 0.46*cos(*j/p) (для j=0 до p)
w_-j = w_j (для j 0)

Окно Парзена. В окне Парзена (Parzen, 1961),
для каждой частоты, веса для взвешенного
скользящего среднего значений периодограммы
вычисляются как:

w_j = 1-6*(j/p)² + 6*(j/p)³    (для
j = 0 до p/2)
w_j = 2*(1-j/p)³    (для j = p/2 + 1 до p)
w_-j = w_j    (для j 0)

Окно Бартлетта. В окне Бартлетта (Bartlett,
1950) веса вычисляются как:

w_j = 1-(j/p) (для j = 0 до p)
w_-j = w_j (для j 0)

За исключением окна Даниэля, все весовые
функции приписывают больший вес сглаживаемому
наблюдению, находящемуся в центре окна и меньшие
веса значениям по мере удаления от центра. Во
многих случаях, все эти окна данных получают
очень похожие результаты.

Подготовка данных к анализу

Теперь рассмотрим несколько других
практических моментов спектрального анализа.
Обычно, полезно вычесть среднее из значений ряда
и удалить тренд (чтобы добиться стационарности)
перед анализом. Иначе периодограмма и
спектральная плотность «забьются» очень
большим значением первого коэффициента при
косинусе (с частотой 0.0). По существу, среднее — это
цикл частоты 0 (нуль) в единицу времени; т.е.
константа. Аналогично, тренд также не
представляет интереса, когда нужно выделить
периодичность в ряде. Фактически оба этих
эффекта могут заслонить более интересные
периодичности в данных, поэтому и среднее, и
(линейный) тренд следует удалить из ряда перед
анализом. Иногда также полезно сгладить данные
перед анализом, чтобы убрать случайный шум,
который может засорять существенные
периодические циклы в периодограмме.

Результаты для случая, когда в
ряде отсутствует периодичность

В заключение, зададим вопрос: что, если
повторяющихся циклов в данных нет, т.е. если
каждое наблюдение совершенно независимо от всех
других наблюдений? Если распределение
наблюдений соответствует нормальному, такой
временной ряд может быть белым шумом (подобный
белый шум можно услышать, настраивая радио). Если
исходный ряд — белый шум, то значения
периодограммы будут иметь экспоненциальное
распределение. Таким образом, проверкой на
экспоненциальность значений периодограммы
можно узнать, отличается ли исходный ряд от
белого шума. Пользователь может также построить
одновыборочную статистику d статистику
Колмогорова-Смирнова (cм. также раздел Непараметрическая статистика и
распределения).

Проверка, что шум — белый в ограниченной
полосе частот. Заметим, что также можно
получить значения периодограммы для
ограниченной частотной области. Снова, если
введенный ряд — белый шум с соответствующими
частотами (т.е. если нет существенных
периодических циклов этих частот), то
распределение значений периодограммы должно
быть снова экспоненциальным.

Быстрое преобразование Фурье (БПФ)

Общее введение
Вычисление БПФ во временных
рядах

За дальнейшей информацией обратитесь к Анализу временных рядов и
следующим разделам:

Идентификация модели
временных рядов
АРПСС (Бокс и Дженкинс) и
автокорреляции Вводный обзор АРПСС
Прерванные временные ряды
Экспоненциальное
сглаживание
Сезонная декомпозиция (метод
Census I)
Сезонная корректировка X-11
(метод Census II)
Таблицы результатов
корректировки X-11
Анализ распределенных лагов
Одномерный анализ Фурье
Кросс-спектральный анализ
Основные понятия и принципы

Общее введение

Интерпретация результатов спектрального
анализа обсуждается в разделе Основные
понятия и принципы, однако там мы не
обсуждали вычислительные проблемы, которые в
действительности очень важны. До середины 1960-х
для представления спектрального разложения
использовались точные формулы для нахождения
параметров синусов и косинусов. Соответствующие
вычисления требовали как минимум N**2 (комплексных)
умножений. Таким образом, даже сегодня
высокоскоростному компьютеру потребовалось бы
очень много времени для анализа даже небольшого
временного ряда (для 8,000 наблюдений
потребовалось бы по меньшей мере 64 миллиона
умножений).

Ситуация кардинально изменилась с открытием
так называемого алгоритма
быстрого преобразования Фурье, или БПФ для
краткости. Достаточно сказать, что при
применении алгоритма БПФ время выполнения
спектрального анализа ряда длины N стало
пропорционально N*log2(N) что конечно
является огромным прогрессом.

Однако недостаток стандартного алгоритма БПФ
состоит в том, что число данных ряда должно быть
равным степени 2 (т.е. 16, 64, 128, 256, …). Обычно это
приводит к необходимости добавлять нули во
временной ряд, который, как описано выше, в
большинстве случаев не меняет характерные пики
периодограммы или оценки спектральной
плотности. Тем не менее, в некоторых случаях,
когда единица времени значительна, добавление
констант во временной ряд может сделать
результаты более громоздкими.

Вычисление БПФ во временных
рядах

Выполнение быстрого преобразования Фурье
чрезвычайно эффективно. На большинстве
стандартных компьютеров, ряд с более чем 100,000
наблюдений легко анализируется. Однако
существует несколько моментов, которые надо
помнить при анализе рядов большого размера.

Как упоминалось ранее, для применения
стандартного (и наиболее эффективного) алгоритма
БПФ требуется, чтобы длина исходного ряда была
равна степени 2. Если это не так, должны быть
проведены дополнительные вычисления. Будут
использоваться простые точные вычислительные
формулы, пока исходный ряд относительно мал, и
вычисления можно выполнить за относительно
короткое время. Для длинных временных рядов,
чтобы применить алгоритм БПФ, используется
основной подход, описанный Monro и Branch (1976). Этот
метод требует значительно больше памяти; однако
ряд рассматриваемой длины может анализироваться
все еще очень быстро, даже если число наблюдений
не является степенью 2.

Для временных рядов, длина которых не равна
степени 2, мы можем дать следующие рекомендации:
если размер исходного ряда не превосходит
средний размер (т.е. имеется только несколько
тысяч наблюдений), не стоит беспокоиться. Анализ
займет несколько секунд. Для анализа средних и
больших рядов (например, содержащих свыше 100,000
наблюдений), добавьте в ряд константы (например
нули) до тех пор, пока длина ряда не станет
степенью 2 и затем примените косинус-сглаживание
ряда в разведочной части анализа ваших данных.

Дополнительная информация по методам анализа данных, добычи данных,
визуализации и прогнозированию содержится на
Портале StatSoft (http://www.statsoft.ru/home/portal/default.asp)
и в Углубленном Учебнике StatSoft (Учебник с формулами).

Все права на материалы электронного учебника принадлежат компании StatSoft

Источник

Ошибка прогнозирования: виды, формулы, примеры

Ошибка прогнозирования — это такая величина, которая показывает, как сильно прогнозное значение отклонилось от фактического. Она используется для расчета точности прогнозирования, что в свою очередь помогает нам оценивать как точно и корректно мы сформировали прогноз. В данной статье я расскажу про основные процентные «ошибки прогнозирования» с кратким описанием и формулой для расчета. А в конце статьи я приведу общий пример расчётов в Excel. Напомню, что в своих расчетах я в основном использую ошибку WAPE или MAD-Mean Ratio, о которой подробно я рассказал в статье про точность прогнозирования, здесь она также будет упомянута.

В каждой формуле буквой Ф обозначено фактическое значение, а буквой П — прогнозное. Каждая ошибка прогнозирования (кроме последней!), может использоваться для нахождения общей точности прогнозирования некоторого списка позиций, по типу того, что изображен ниже (либо для любого другого подобной детализации):

Алгоритм для нахождения любой из ошибок прогнозирования для такого списка примерно одинаковый: сначала находим ошибку прогнозирования по одной позиции, а затем рассчитываем общую. Итак, основные ошибки прогнозирования!

MPE — Mean Percent Error

MPE — средняя процентная ошибка прогнозирования. Основная проблема данной ошибки заключается в том, что в нестабильном числовом ряду с большими выбросами любое незначительное колебание факта или прогноза может значительно поменять показатель ошибки и, как следствие, точности прогнозирования. Помимо этого, ошибка является несимметричной: одинаковые отклонения в плюс и в минус по-разному влияют на показатель ошибки.

Для каждой позиции рассчитывается ошибка прогноза (из факта вычитается прогноз) — Error
Для каждой позиции рассчитывается процентная ошибка прогноза (ошибка прогноза делится на фактический показатель) — Percent Error
Находится среднее арифметическое всех процентных ошибок прогноза (процентные ошибки суммируются и делятся на количество) — Mean Percent Error

MAPE — Mean Absolute Percent Error

MAPE — средняя абсолютная процентная ошибка прогнозирования. Основная проблема данной ошибки такая же, как и у MPE — нестабильность.

Для каждой позиции рассчитывается абсолютная ошибка прогноза (прогноз вычитается из факта по модулю) — Absolute Error
Для каждой позиции рассчитывается абсолютная процентная ошибка прогноза (абсолютная ошибка прогноза делится на фактический показатель) — Absolute Percent Error
Находится среднее арифметическое всех абсолютных процентных ошибок прогноза (абсолютные процентные ошибки суммируются и делятся на количество) — Mean Absolute Percent Error

Вместо среднего арифметического всех абсолютных процентных ошибок прогноза можно использовать медиану числового ряда (MdAPE — Median Absolute Percent Error), она наиболее устойчива к выбросам.

WMAPE / MAD-Mean Ratio / WAPE — Weighted Absolute Percent Error

WAPE — взвешенная абсолютная процентная ошибка прогнозирования. Одна из «лучших ошибок» для расчета точности прогнозирования. Часто называется как MAD-Mean Ratio, то есть отношение MAD (Mean Absolute Deviation — среднее абсолютное отклонение/ошибка) к Mean (среднее арифметическое). После упрощения дроби получается искомая формула WAPE, которая очень проста в понимании:

Для каждой позиции рассчитывается абсолютная ошибка прогноза (прогноз вычитается из факта, по модулю) — Absolute Error
Находится сумма всех фактов по всем позициям (общий фактический объем)
Сумма всех абсолютных ошибок делится на сумму всех фактов — WAPE

Данная ошибка прогнозирования является симметричной и наименее чувствительна к искажениям числового ряда.

Рекомендуется к использованию при расчете точности прогнозирования. Более подробно читать здесь.

RMSE (as %) / nRMSE — Root Mean Square Error

RMSE — среднеквадратичная ошибка прогнозирования. Примерно такая же проблема, как и в MPE и MAPE: так как каждое отклонение возводится в квадрат, любое небольшое отклонение может значительно повлиять на показатель ошибки. Стоит отметить, что существует также ошибка MSE, из которой RMSE как раз и получается путем извлечения корня. Но так как MSE дает расчетные единицы измерения в квадрате, то использовать данную ошибку будет немного неправильно.

Для каждой позиции рассчитывается квадрат отклонений (разница между фактом и прогнозом, возведенная в квадрат) — Square Error
Затем рассчитывается среднее арифметическое (сумма квадратов отклонений, деленное на количество) — MSE — Mean Square Error
Извлекаем корень из полученного результат — RMSE
Для перевода в процентную или в «нормализованную» среднеквадратичную ошибку необходимо:
1. Разделить на разницу между максимальным и минимальным значением показателей
2. Разделить на разницу между третьим и первым квартилем значений показателей
3. Разделить на среднее арифметическое значений показателей (наиболее часто встречающийся вариант)

MASE — Mean Absolute Scaled Error

MASE — средняя абсолютная масштабированная ошибка прогнозирования. Согласно Википедии, является очень хорошим вариантом для расчета точности, так как сама ошибка не зависит от масштабов данных и является симметричной: то есть положительные и отрицательные отклонения от факта рассматриваются в равной степени.

Важно! Если предыдущие ошибки прогнозирования мы могли использовать для нахождения точности прогнозирования некого списка номенклатур, где каждой из которых соответствует фактическое и прогнозное значение (как было в примере в начале статьи), то данная ошибка для этого не предназначена: MASE используется для расчета точности прогнозирования одной единственной позиции, основываясь на предыдущих показателях факта и прогноза, и чем больше этих показателей, тем более точно мы сможем рассчитать показатель точности. Вероятно, из-за этого ошибка не получила широкого распространения.

Здесь данная формула представлена исключительно для ознакомления и не рекомендуется к использованию.

Суть формулы заключается в нахождении среднего арифметического всех масштабированных ошибок, что при упрощении даст нам следующую конечную формулу:

Также, хочу отметить, что существует ошибка RMMSE (Root Mean Square Scaled Error — Среднеквадратичная масштабированная ошибка), которая примерно похожа на MASE, с теми же преимуществами и недостатками.

Это основные ошибки прогнозирования, которые могут использоваться для расчета точности прогнозирования. Но не все! Их очень много и, возможно, чуть позже я добавлю еще немного информации о некоторых из них. А примеры расчетов уже описанных ошибок прогнозирования будут выложены через некоторое время, пока что я подготавливаю пример, ожидайте.

Об авторе

HeinzBr

Автор статей и создатель сайта SHTEM.RU

Источник

Оценка ошибки прогнозирования временного ряда

Работая с научными публикациями, сталкиваюсь с различными показателями ошибок прогнозирования временных рядов. Среди всех встречающихся оценок ошибки прогнозирования стоит отметить две, которые в настоящее время, являются самыми популярными: MAE и MAPE.
Пусть ошибка есть разность:
,
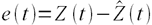
где Z(t) – фактическое значение временного ряда, а – прогнозное.
Тогда формулы для оценок ошибки прогнозирования временных рядов для N отчетов можно записать в следующем виде.

MAPE – средняя абсолютная ошибка в процентах

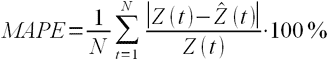
Данная оценка применяется для временных рядов, фактические значения которых значительно больше 1. Например, оценки ошибки прогнозирования энергопотребления почти во всех статьях приводятся как значения MAPE.

Если же фактические значения временного ряда близки к 0, то в знаменателе окажется очень маленькое число, что сделает значение MAPE близким к бесконечности – это не совсем корректно. Например, фактическая цена РСВ = 0.01 руб/МВт.ч, a прогнозная = 10 руб/МВт.ч, тогда MAPE = (0.01 – 10)/0.01 = 999%, хотя в действительности мы не так уж сильно ошиблись, всего на 10 руб/МВт.ч. Для рядов, содержащих значения близкие к нулю, применяют следующую оценку ошибки прогноза.

MAE – средняя абсолютная ошибка

Для оценки ошибки прогнозирования цен РСВ и индикатора БР корректнее использовать MAE.

После того, как получены значения для MAPE и/или MAE, то в работах обычно пишут: «Прогнозирование временного ряда энергопотребления с часовым разрешение проводилось на интервале с 01.01.2001 до 31.12.2001 (общее количество отсчетов N ~ 8500). Для данного прогноза значение MAPE = 1.5%». При этом, просматривая статьи, можно сложить общее впечатление об ошибки прогнозирования энергопотребления, для которого MAPE обычно колеблется от 1 до 5%; или ошибки прогнозирования цен на электроэнергию, для которого MAPE колеблется от 5 до 15% в зависимости от периода и рынка. Получив значение MAPE для собственного прогноза, вы можете оценить, насколько здорово у вас получается прогнозировать.

Кроме указанных иногда используют другие оценки ошибки, менее популярные, но также применимые. Подробнее об этих оценках ошибки прогноза читайте указанные статьи в Википедии.

MSE – среднеквадратичная ошибка

RMSE – квадратный корень из среднеквадратичной ошибки

ME – средняя ошибка

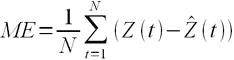
SD – стандартное отклонение

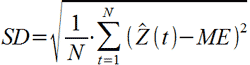
, где ME – есть средняя ошибка, определенная по формуле выше.

Связь точности и ошибки прогнозирования

Точность прогнозирования есть понятие прямо противоположное ошибке прогнозирования. Если ошибка прогнозирования велика, то точность мала и наоборот, если ошибка прогнозирования мала, то точность велика. По сути дела оценка ошибки прогноза MAPE есть обратная величина для точности прогнозирования — зависимость здесь простая.

Точность прогноза в % = 100% – MAPE

Величину точности оценивать не принято, говоря о прогнозировании всегда оценивают, то есть определяют значение именно ошибки прогноза, то есть величину MAPE и/или MAE. Однако нужно понимать, что если MAPE = 5%, то точность прогнозирования = 95%. Говоря о высокой точности, мы всегда говорим о низкой ошибки прогноза и в этой области недопонимания быть не должно. Вы практически не найдете материалов о прогнозировании, в которых приведены оценки именно точности прогноза, хотя с точки зрения здравого маркетинга корректней говорить именно о высокой точности. В рекламных статьях всегда будет написано о высокой точности.

При этом величина MAPE является количественной оценкой именно ошибки, и эта величина нам ясно говорит и о точности прогнозирования, исходя из приведенной выше простой формулы. Таким образом, оценивая ошибку, мы всегда оцениваем точность прогнозирования.

Источник

Существует множество моделей прогноза, но как выбрать среди них ту, которая наиболее точно сделает прогноз?

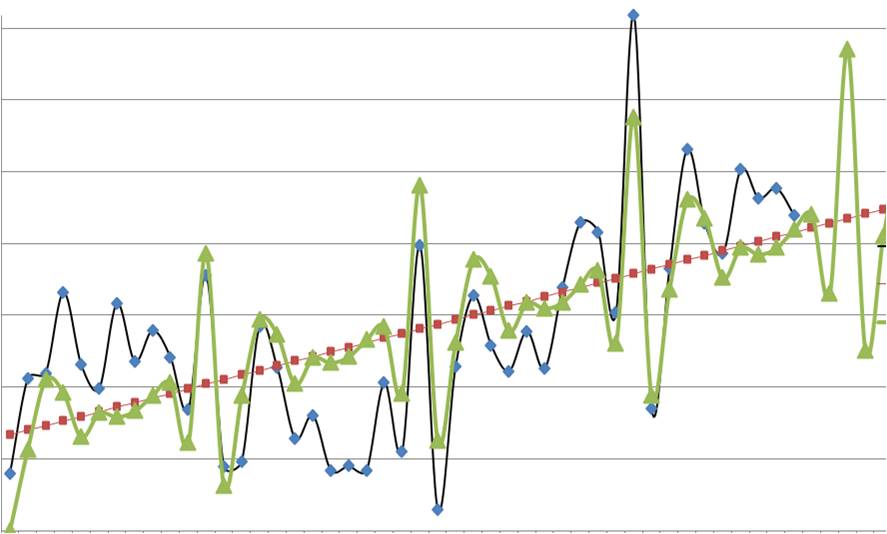
Из данной статьи вы узнаете:

Какие способы оценки прогноза вы можете использовать?
Как выбрать оптимальную модель, которая поможет вам сделать максимально точный прогноз?
Как рассчитать показатель «Точность прогноза»?

Какие способы оценки прогнозной модели вы можете использовать:

1. Оценить отношение фактических продаж к прогнозу;

2. Расчет показателя точность прогноза — оценка на сколько точно выбранная модель описывает анализируемые данные;

3. Графический анализ — строим график и визуально оцениваем адекватность модели прогноза относительно фактических продаж за последний период ;

1-й способ — Расчет отношения фактических продаж к прогнозу.

Сначала рассчитываем прогноз разными способами и оцениваем отношение фактических продаж к прогнозу. ВАЖНО протестировать модели не по одному товару или направлению продаж, а сразу взять 10 и более товарных позиций или направлений продаж и рассчитать прогноз по ним на минимум на 3 периода вперед (количество периодов и направления прогноза зависят от ваших задач. Если задача — сделать точный прогноз на 6 месяцев, то рассчитываем прогноз на 6 месяцев несколькими вариантами и оцениваем отношение факта к прогнозу по сумме полугода).

Рассчитаем прогноз 4 способами на полгода. Протестируем следующие модели:

Линейный тренд + сезонность — лист «Линейный» в приложенном файле (см. статью «Как рассчитать прогноз с учетом роста и сезонности в Excel»)
Логарифмический тренд + сезонность — лист «Логарифмический» в приложенном файле (см. статью «5 способов расчета значений логарифмического тренда»)
Скользящая средняя с сезонностью к 2-м месяцам — лист «Скользящая к 2-м» (см. статью «Как рассчитать прогноз по методу скользящей средней»);
Скользящяя средняя с сезонностью к 3-м месяцам — лист «Скользящая к 3-м»;

Для каждой из 4-х прогнозных моделей в листе «Оценка моделей»:

Суммируем прогноз по каждой модели за 6 месяцев;

Суммируем фактические продажи, которые мы будем сравнивать с прогнозом;

Рассчитываем отношение факта к прогнозу по каждой позиции для каждой модели;

Рассчитываем по каждой модели среднее отношение факта к прогнозу;

Выбираем модель прогноза, которая по показателю «среднее отношение факта к прогнозу» оказалась максимально приближена к 100%;

Для наших данных самой точной моделью оказалась скользящая средняя к 3-м месяцам с сезонностью, среднее отклонение факта от прогноза 97%.

Мы протестировали каждую модель прогноза на реальных данных и выбрали для себя оптимальную, которая в среднем показала минимальное отклонение от факлических продаж.

2-й способ оценки модели прогноза — расчет показателя точность прогноза.

Показатель точность прогноза показывает, на сколько точно выбранная модель прогноза описывает данные. Идея в том, чем точнее выбранная модель описывает фактические данные, тем точнее она сделает прогноз.

Как рассчитать точность прогноза? Рассмотрим на примере расчета для модели прогноза с линейным трендом и сезонностью.

1. Рассчитываем значения прогнозной модели для каждого анализируемого момента времени в прошлом.

Для этого значения тренда для анализируемых периодов умножаем на выровненные коэффициенты сезонности (см. файл с примером)

2. Рассчитываем ошибку прогнозной модели. Для этого за каждый период от фактических значений вычитаем значения прогнозной модели.

3. Рассчитываем квадратическое отклонение ошибки от значений прогнозной модели (см. файл с примером);

4. Рассчитываем среднее значение квадратического отклонения, т.е. среднеквадратическое отклонение

5. Точность прогноза = (1- среднеквадратическое отклонение ошибки прогнозной модели)*100 (см. файл с примером).

Показатель точности прогноза выражается в процентах:

Если точность прогноза равна 100%, то выбранная модель описывает фактические значения на 100%, т.е. очень точно.
Если 0% или отрицательное число, то совсем не описывает, и данной модели доверять не стоит.

Выбрать подходящую модель прогноза можно с помощью расчета показателя точность прогноза. Модель прогноза, у которой показатель точность прогноза будет ближе к 100%, с большей вероятностью сделает более точный прогноз. Такую модель можно назвать оптимальной для выбранного временного ряда.

3. Способ оценки прогнозной модели — визуальный.

На график выводим анализируемые данные, тренд, значение модели и прогноз (см. вложенный файл). Обычно визуально видно, какая модель адекватнее строит прогноз . 3-й способ по своей сути схож с 1-м и вторым, только мы верим не цифрам, а тому что мы видим на графике.

Линейная модель:

Логарифмическая модель:

По последним периодам видно, что линейная модель более точно описывает данные за последние месяцы, и она, вероятнее всего, сделает более точный прогноз.

Какую модель прогноза выбрать?

1. Которая на основании тестирования на реальных данных для выбранного промежутка времени (месяца, 3-х месяцев, полугода, года) будет делать максимально точный прогноз, т.е. отношение факта к прогнозу будет близко к 1 или 100%.

2. Модель, которая будет максимально точно описывать фактические данные, т.е. показатель точность прогноза будет приближаться к 1, но не всегда модели точно описывающие данные делают адекватные прогнозы (это надо понимать и оценивать графически).

3. Модель, которой визуально вы больше доверяете с точки зрения описания входящих данных и продления прогнозной модели в будущее.

Для повышения точности прогноза я в своей практике стараюсь использовать 3 этих способа параллельно:

По завершении прогнозного периода и в промежутках всегда оцениваю отношение фактических продаж к прогнозу.
При построении прогноза анализирую показатель «среднеквадратическое отклонение» и рассчитываю показатель «точность прогноза» для оценки данных и модели.
А также на график вывожу анализируемые данные и прогнозную модель, для визуального контроля.

Оценивая прогноз по факту или в промежуточные периоды в случае значительных отклонений фактических продаж от прогнозных, разбираю ситуацию и выясняю причины, в случае необходимости вношу корректировки в прогнозную модель.

С помощью программы Forecast4AC PRO вы можете рассчитать показатель точность прогноза автоматически.

Также Forecast4AC умеет автоматически выбирать оптимальную модель прогноза для каждого временного ряда.

+ одним нажатием строить график «Анализируемые данные + модель прогноза», на котором вы можете оценить, как соотносятся между собой:

анализируемые данные;
выбранный тренд;
модель прогноза;

как в анализируемом периоде, так и в будущем.

Точных прогнозов!

Присоединяйтесь к нам!

Скачивайте бесплатные приложения для прогнозирования и бизнес-анализа:

Novo Forecast Lite — автоматический расчет прогноза в Excel.
4analytics — ABC-XYZ-анализ и анализ выбросов в Excel.
Qlik Sense Desktop и QlikView Personal Edition — BI-системы для анализа и визуализации данных.

Тестируйте возможности платных решений:

Novo Forecast PRO — прогнозирование в Excel для больших массивов данных.

Получите 10 рекомендаций по повышению точности прогнозов до 90% и выше.

Зарегистрируйтесь и скачайте решения

Статья полезная? Поделитесь с друзьями

Источник

Методы оценки качества прогноза

Время на прочтение
3 мин

Количество просмотров 29K

Часто при составлении любого прогноза — забывают про способы оценки его результатов. Потому как часто бывает, прогноз есть, а сравнение его с фактом отсутствует. Еще больше ошибок случается, когда существуют две (или больше) модели и не всегда очевидно — какая из них лучше, точнее. Как правило одной цифрой (R²) сложно обойтись. Как если бы вам сказали — этот парень ходит в синей футболке. И вам сразу все стало про него ясно )

В статьях о методах прогнозирования при оценке полученной модели я постоянно использовал такие аббревиатуры или обозначения.

R²
MSE
MAPE
MAD
Bias

Попробую объяснить, что я имел в виду.

Остатки

Итак, по порядку. Основная величина, через которую оценивается точность прогноза это остатки (иногда: ошибки, error, e). В общем виде это разность между спрогнозированными значениями и исходными данными (либо фактическими значениями). Естественно, что чем больше остатки тем сильнее мы ошиблись. Для вычисления сравнительных коэффициентов остатки преобразуют: либо берут по модулю, либо возводят в квадрат (см. таблицу, колонки 4,5,6). В сыром виде почти не используют, так как сумма отрицательных и положительных остатков может свести суммарную ошибку в ноль. А это глупо, сами понимаете.

Суровые MSE и R²

Когда нам требуется подогнать кривую под наши данные, то точность этой подгонки будет оцениваться программой по среднеквадратической ошибке (mean squared error, MSE). Рассчитывается по незамысловатой формуле

где n-количество наблюдений.

Соотвественно, программа, рассчитывая кривую подгонки, стремится минимизировать этот коэффициент. Квадраты остатков в числителе взяты именно по той причине, чтобы плюсы и минусы не взаимоуничтожились. Физического смысла MSE не имеет, но чем ближе к нулю, тем модель лучше.

Вторая абстрактная величина это R² — коэффициент детерминации. Характеризует степень сходства исходных данных и предсказанных. В отличии от MSE не зависит от единиц измерения данных, поэтому поддается сравнению. Рассчитывается коэффициент по следующей формуле:

где Var(Y) — дисперсия исходных данных.

Безусловно коэффициент детерминации — важный критерий выбора модели. И если модель плохо коррелирует с исходными данными, она вряд ли будет иметь высокую предсказательную силу.

MAPE и MAD для сравнения моделей

Статистические методы оценки моделей вроде MSE и R², к сожалению, трудно интерпретировать, поэтому светлые головы придумали облегченные, но удобные для сравнения коэффициенты.

Среднее абсолютное отклонение (mean absolute deviation, MAD) определяется как частное от суммы остатков по модулю к числу наблюдений. То есть, средний остаток по модулю. Удобно? Вроде да, а вроде и не очень. В моем примере MAD=43. Выраженный в абсолютных единицах MAD показывает насколько единиц в среднем будет ошибаться прогноз.

MAPE призван придать модели еще более наглядный смысл. Расшифровывается выражение как средняя абсолютная ошибка в процентах (mean percentage absolute error, MAPE).

где Y — значение исходного ряда.

Выражается MAPE в процентах, и в моем случае означает, что в модель может ошибаться в среднем на 16%. Что, согласитесь, вполне допустимо.

Наконец, последняя абсолютно синтетическая величина — это Bias, или просто смещение. Дело в том, что в реальном мире отклонения в одну сторону зачастую гораздо болезненнее, чем в другую. К примеру, при условно неограниченных складских помещениях, важнее учитывать скачки реального спроса вверх от спрогнозированных значений. Поэтому случаи, где остатки положительные относятся к общему числу наблюдений. В моем случае 44% спрогнозированных значений оказались ниже исходных. И можно пожертвовать другими критериями оценки, чтобы минимизировать этот Bias.

Можете попробовать это сами в Excel и Numbers

Интересно узнать — какие методы оценки качества прогнозирования вы используете в своей работе?

Подробности на блоге

Источник

Важным этапом прогнозирования
социально-экономических явлений
является оценка точности и надежности
прогнозов.

Эмпирической мерой точности прогноза,
служит величина его ошибки, которая
определяется как разность между
прогнозными ()
и фактическими (у_t)
значениями исследуемого показателя.
Данный подход возможен только в двух
случаях:

а) период упреждения известен, уже
закончился и исследователь располагает
необходимыми фактическими значениями
прогнозируемого показателя;

б) строится ретроспективный прогноз,
то есть рассчитываются прогнозные
значения показателя для периода времени
за который уже имеются фактические
значения. Это делается с целью проверки
разработанной методики прогнозирования.

В данном случае вся имеющаяся информация
делится на две части в соотношении 2/3
к 1/3. Одна часть информации (первые 2/3
от исходного временного ряда) служит
для оценивания параметров модели
прогноза. Вторая часть информации
(последняя 1/3 части исходного ряда)
служит для реализации оценок прогноза.

Полученные, таким образом, ретроспективно
ошибки прогноза в некоторой степени
характеризуют точность предлагаемой
и реализуемой методики прогнозирования.
Однако величина ошибки ретроспективного
прогноза не может в полной мере и
окончательно характеризовать используемый
метод прогнозирования, так как она
рассчитана только для 2/3 имеющихся
данных, а не по всему временному ряду.

В случае если, ретроспективное
прогнозирование осуществлять по связным
и многомерным динамическим рядам, то
точность прогноза, соответственно,
будет зависеть от точности определения
значений факторных признаков, включенных
в многофакторную динамическую модель,
на всем периоде упреждения. При этом,
возможны следующие подходы к
прогнозированию по связным временным
рядам: можно использовать как фактические,
так и прогнозные значения признаков.

Все показатели оценки точности
статистических прогнозов условно можно
разделить на три группы:

аналитические;
сравнительные;
качественные.

Аналитические показатели точности
прогноза позволяют количественно
определить величину ошибки прогноза.
К ним относятся следующие показатели
точности прогноза:

Абсолютная ошибка прогноза (D^*)
определяется как разность между
эмпирическим и прогнозным значениями
признака и вычисляется по формуле:

, (16.1)

где у_t– фактическое
значение признака;

—
прогнозное значение признака.

Относительная ошибка прогноза (d^*_отн)
может быть определена как отношение
абсолютной ошибки прогноза (D^*):

к
фактическому значению признака (у_t_):

(16.2)

— к прогнозному
значению признака ()

(16.3)

Абсолютная и относительная ошибки
прогноза являются оценкой проверки
точности единичного прогноза, что
снижает их значимость в оценке точности
всей прогнозной модели, так как на
изучаемое социально-экономическое
явление подвержено влиянию различных
факторов внешнего и внутреннего
свойства. Единично удовлетворительный
прогноз может быть получен и на базе
реализации слабо обусловленной и
недостаточно адекватной прогнозной
модели и наоборот – можно получить
большую ошибку прогноза по достаточно
хорошо аппроксимирующей модели.

Поэтому на практике иногда определяют
не ошибку прогноза, а некоторый
коэффициент качества прогноза (К_к),
который показывает соотношение между
числом совпавших (с) и общим числом
совпавших (с) и несовпавших (н) прогнозов
и определяется по формуле:

(16.4)

Значение К_к= 1 означает, что имеет
место полное совпадение значений
прогнозных и фактических значений и
модель на 100% описывает изучаемое
явление. Данный показатель оценивает
удовлетворительный вес совпавших
прогнозных значений в целом по временному
ряду и изменяющегося в пределах от 0 до
1.

Следовательно, оценку точности получаемых
прогнозных моделей целесообразно
проводить по совокупности сопоставлений
прогнозных и фактических значений
изучаемых признаков.

Средним показателем точности прогноза
является средняя абсолютная ошибка
прогноза (),
которая определяется как средняя
арифметическая простая из абсолютных
ошибок прогноза по формуле вида:

, (16.5)

де n– длина временного
ряда.

Средняя абсолютная ошибка прогноза
показывает обобщенную характеристику
степени отклонения фактических и
прогнозных значений признака и имеет
ту же размерность, что и размерность
изучаемого признака.

Для оценки точности прогноза используется
средняя квадратическая ошибка прогноза,
определяемая по формуле:

(16.6)

Размерность средней квадратической
ошибки прогноза также соответствует
размерности изучаемого признака. Между
средней абсолютной и средней квадратической
ошибками прогноза существует следующее
примерное соотношение:

(16.7)

Недостатками средней абсолютной и
средней квадратической ошибками
прогноза является их существенная
зависимость от масштаба измерения
уровней изучаемых социально-экономических
явлений.

Поэтому на практике в качестве
характеристики точности прогноза
определяют среднюю ошибку аппроксимации,
которая выражается в процентах
относительно фактических значений
признака, и определяется по формуле
вида:

(16.8)

Данный показатель является относительным
показателем точности прогноза и не
отражает размерность изучаемых
признаков, выражается в процентах и на
практике используется для сравнения
точности прогнозов полученных как по
различным моделям, так и по различным
объектам. Интерпретация оценки точности
прогноза на основе данного показателя
представлена в следующей таблице:

Интерпретация
точности

< 10

10 – 20

20 – 50

> 50

Высокая

Хорошая

Удовлетворительная

Не удовлетворительная

В качестве сравнительного показателя
точности прогноза используется
коэффициент корреляции между прогнозными
и фактическими значениями признака,
который определяется по формуле:

, (16.9)

где
—
средний уровень ряда динамики прогнозных
оценок.

Используя данный коэффициент в оценке
точности прогноза следует помнить, что
коэффициент парной корреляции в силу
своей сущности отражает линейное
соотношение коррелируемых величин и
характеризует лишь взаимосвязь между
временным рядом фактических значений
и рядом прогнозных значений признаков.
И даже если коэффициент корреляции R= 1, то это еще не предполагает полного
совпадения фактических и прогнозных
оценок, а свидетельствует лишь о наличии
линейной зависимости между временными
рядами прогнозных и фактических значений
признака.

Одним из показателей оценки точности
статистических прогнозов является
коэффициент несоответствия (КН), который
был предложен Г. Тейлом и может
рассчитываться в различных модификациях:

Коэффициент несоответствия (КН₁),
определяемый как отношение средней
квадратической ошибки к квадрату
фактических значений признака:

(16.10)

КН = о, если
,
то есть полное совпадение фактических
и прогнозных значений признака.

КН = 1, если при прогнозировании получают
среднюю квадратическую ошибку адекватную
по величине ошибке, полученной одним
из простейших методов экстраполяции
неизменности абсолютных цепных
приростов.

КН > 1, когда прогноз дает худшие
результаты, чем предположение о
неизменности исследуемого явления.
Верхней границы коэффициент несоответствия
не имеет.

2.Коэффициент несоответствия КН₂определяется как отношение средней
квадратической ошибки прогноза к сумме
квадратов

отклонений
фактических значений признака от
среднего уровня исходного временного
ряда за весь рассматриваемый период:

, (16.11)

где — средний уровень исходного ряда
динамики.

Если КН > 1, то прогноз на уровне среднего
значения признака дал бы лучший
результат, чем имеющийся прогноз.

3.Коэффициент несоответствия (КН₃),
определяемый как отношение средней
квадратической ошибке прогноза к сумме
квадратов отклонений фактических
значений признака от теоретических,
выравненных по уравнению тренда:

, (16.12)

где — теоретические уровни временного ряда,
полученные по

модели тренда.

Если КН > 1, то прогноз методом
экстраполяции тренда дает хороший
результат.

Источник

17 авг. 2022 г.
читать 2 мин

Одной из наиболее распространенных метрик, используемых для измерения точности прогнозирования модели, является средняя абсолютная ошибка в процентах , часто обозначаемая аббревиатурой MAPE .

Он рассчитывается как:

MAPE = (1/n) * Σ(|факт – прогноз| / |факт|) * 100

куда:

Σ — символ, означающий «сумма».
n – размер выборки
фактический – фактическое значение данных
прогноз – прогнозируемое значение данных

MAPE обычно используется, потому что его легко интерпретировать. Например , значение MAPE, равное 14 %, означает, что средняя разница между прогнозируемым значением и фактическим значением составляет 14 %.

В следующем примере показано, как рассчитать и интерпретировать значение MAPE для данной модели.

Пример: интерпретация значения MAPE для данной модели

Предположим, сеть продуктовых магазинов строит модель для прогнозирования будущих продаж. На следующей диаграмме показаны фактические продажи и прогнозируемые продажи по модели за 12 последовательных периодов продаж:

Мы можем использовать следующую формулу для расчета абсолютной процентной ошибки каждого прогноза:

Абсолютная ошибка в процентах = |фактический-прогноз| / |фактическое| * 100

Затем мы можем вычислить среднее значение абсолютных процентных ошибок:

MAPE для этой модели оказывается равным 5,12% .

Это говорит нам о том, что средняя абсолютная процентная ошибка между продажами, предсказанными моделью, и фактическими продажами составляет 5,12% .

Чтобы определить, является ли это хорошим значением для MAPE , необходимо использовать отраслевые стандарты.

Если стандартная модель в продовольственной отрасли дает значение MAPE, равное 2%, то это значение 5,12% можно считать высоким.

И наоборот, если большинство моделей прогнозирования в продуктовой промышленности дают значения MAPE от 10% до 15%, то значение MAPE, равное 5,12%, можно считать низким, и эта модель может считаться отличной для прогнозирования будущих продаж.

Сравнение значений MAPE для разных моделей

MAPE особенно полезен для сравнения соответствия различных моделей.

Например, предположим, что сеть продуктовых магазинов хочет построить модель для прогнозирования будущих продаж и найти наилучшую из возможных моделей.

Предположим, они соответствуют трем различным моделям и находят соответствующие им значения MAPE:

MAPE модели 1: 14,5%
MAPE модели 2: 16,7%
MAPE модели 3: 9,8%

Модель 3 имеет самое низкое значение MAPE, что говорит нам о том, что она способна прогнозировать будущие продажи наиболее точно среди трех потенциальных моделей.

Дополнительные ресурсы

Как рассчитать MAPE в Excel
Как рассчитать MAPE в R
Как рассчитать MAPE в Python
Калькулятор MAPE

Источник

Оценка точности выбранных моделей прогнозирования Показатели точности

Оценка точности выбранных моделей прогнозирования

Показатели точности характеризуют качество модели. О точности можно судить по величине ошибки (погрешности) прогноза. Ошибка прогноза – величина, характеризующая расхождение между фактическим и прогнозным значением показателя. 1) абсолютная ошибка прогноза – Имеет ту же размерность, что и прогнозируемый показатель и зависит от масштаба измерения уровней ряда.

2) Обобщающий показатель точности модели (Mean Absolute Derivation (MAD)), получен усреднением модулей абсолютных отклонений – Используют в случае, когда оценку нужно получить в тех же единицах, в которых измерены уровни ряда.

3) Относительная ошибка прогноза, выражена в процентах Показывает, насколько велика ошибка по сравнению с фактическим значением уровня исходного ряда. Если абсолютная и относительная ошибка больше нуля – то прогнозная оценка завышена и наоборот.

4) Mean Absolute Persentage Error (MAPE). Получена усреднением модулей относительных ошибок: Позволяет сравнивать точность прогнозных оценок, полученных с помощью одной и той же модели применительно к двум различным временным рядам, имеющим даже различные единицы измерения.

Механический подход к оценке качества модели Если -высокая точность модели; — точность признать хорошей; — точность удовлетворительная.

5) Mean Percentage Error (MPE) – как показатель 4), но нет модуля. Значение этого показателя может указывать на наличие систематического смещения в прогнозных оценках (например, последовательное завышение или занижение получаемых с помощью модели расчетных уровней временного ряда.

Все рассмотренные показатели можно вычислить 1) после того, как период упреждения закончился и имеются фактические данные о прогнозируемом показателе; 2) при рассмотрении показателя на ретроспективном участке. В этом случае: А) вся информация делится на 2 части В) по первой части оцениваются параметры модели С) данные второй части рассматриваются как фактические. Ошибки прогноза, полученные ретроспективно (на втором участке) характеризуют точность применяемой модели.

На практике при сравнении моделей могут использоваться: 6) Средняя квадратическая ошибка S; Или 7) Суммы квадратов ошибок (Sums of Squared Errors (SSE)) или RSS (остаточная сумма квадратов) или средние квадраты ошибок. , где m – число параметров в модели; Эти показатели чувствительны к наличию больших ошибок прогнозов

Для исследователя предпочтительнее модель, постоянно дающая средние по величине ошибки, чем модель, допускающая наряду с малыми ошибками серьезные отклонения от фактических уровней. Чем меньше значения всех показателей, тем выше точность модели. О точности модели нельзя судить по одному значению ошибки прогноза. О качестве применяемых моделей можно судить лишь по совокупности сопоставлений прогнозных значений с фактическими.

Источник

В прогнозировании есть одна простая истина, к которой прогнозисты пришли достаточно давно: высокая точность аппроксимации данных не гарантирует высокую точность прогнозов. Это означает, что модель, дающая наименьшие ошибки по обучающей выборке, не обязательно даст такие же наименьшие ошибки по тестовой выборке. Противоположное («чем лучше аппроксимация, тем точнее прогноз») вообще возможно лишь для обратимых процессов, в которых никаких качественных изменений не происходит. Но, как мы знаем, в мире нет ничего более постоянного, чем перемены.

Впрочем, помимо этой простой истины есть ещё и другая: модель, заведомо плохо аппроксимирующая ряд данных, навряд ли даст точный прогноз. Это в свою очередь означает, что для получения более точных прогнозов, модель должна точно описывать ряд по внутренней выборке, быть адекватной поставленной задаче и включать все существенные переменные. Потому что, если модель представляет собой очень грубое и условное описание объекта, то по ней нельзя сделать адекватных выводов о самом объекте исследования.

Как видим, перед нами противоречие: модель должна хорошо описывать данные, но хорошее описание не гарантирует получения точных прогнозов. Противоречие решается достаточно легко, если следовать одному из базовых буддистский принципов — придерживаться срединного пути. Но как же найти эту середину? Для этого надо просто научиться оценивать качество построенной модели. А в этом нам помогут различные графики и ряд коэффициентов.

Графический анализ моделей

С графическим анализом всё просто. Все те инструменты, которые мы рассмотрели ранее в параграфе «Графический анализ данных«, сейчас нам пригодятся для того, чтобы понять, какая из моделей лучше и почему. Как всё это сделать в R мы так же уже рассматривали ранее, так что не будем тратить в этот раз время на примеры.

Самый простой метод оценки полученной модели — линейный график. На него достаточно нанести фактические значения, расчётные и прогнозные. Так мы сможем увидеть, как модель описала данные и насколько полученный прогноз соответствует сложившейся динамике. Более того, так можно понять (на основе знаний о прогнозируемом процессе), насколько полученные прогноз правдоподобен.

Очень простой пример с линейным графиком показан наследующем рисунке.

Линейный график по несезонной модели ETS(M,N,N)

На нём показан ряд фактических значений (чёрная сплошная линия «Series»), ряд расчётных (фиолетовая пунктирная линия «Fitted values»), точечный прогноз (синяя сплошная линия «Point forecast») и 95% прогнозный интервал («95% prediction interval»). Уже глядя на этот график можно сделать несколько выводов:

Ряд фактических значений был описан моделью неплохо, хотя основные характеристики ряда выявлены не были — это видно потому что расчётные значения всё время как будто отстают от фактических на один шаг. К тому же, ряд расчётных значений не такой гладкий, как хотелось бы и в ряде наметились элементы сезонности (это особенно чётко видно с 1986 года) — каждый четвёртый квартал виден пик показателя. Это не криминал, но может говорить о том, что стоило бы обратиться к другой модели либо другому методу оценивания.
Прогноз по нашей модели представляет собой прямую линию, параллельную оси абсцисс. Это хороший прогноз в случае, если ряд данных не имеет явной тенденции к росту либо снижению. Однако в нашем случае ряд данных явно демонстрирует увеличение показателя во времени. Поэтому такая тенденция в будущем хоть и возможна, но, скорее всего, не соответствует ожиданиям. Для того, чтобы здесь сделать какой-то однозначный вывод, нужно, конечно, понимать, с каким показателем мы имеем дело, и насколько реалистичен такой сценарий на практике.
Прогнозные интервалы значительно расширяются и к последнему наблюдению составляют 5800 — 6500. Опять же, такие широкие интервалы — это не страшно, но одна из потенциальных причин этой ширины — неправильно выбранная (или специфицированная) модель. Так же на возможно неправильно выбранную модель указывает неровность прогнозного интервала при таком ровном прогнозе. Возможно, всё-таки надо было использовать другую модель (с трендом и сезонностью), а, может быть, мы не учли какие-то важные факторы.

На основе этих пунктов уже можно заключить, что стоит попробовать ещё какую-нибудь модель для прогнозирования этого ряда данных.

Если мы используем для выбора модели процедуру ретропрогноза, то на тот же самый график стоит нанести значения из проверочной выборки. Другая модель, построенная по тому же ряду данных, показана на рисунке ниже.

Линейный график по сезонной модели ETS(M,A,M)

По этому рисунку тоже можно сделать ряд выводов:

Фактические значения описаны этой моделью лучше, чем предыдущей, но всё ещё есть ряд промежутков, аппроксимированных моделью не очень хорошо (как, например, наблюдение в начале 1984 года). Возможно, это говорит о том, что в это время происходили какие-то события, которые наша экстраполяционная модель не может уловить, а, может быть, нужно просто изменить метод оценки модели. При прогнозировании на практике стоит выяснить, что происходило в эти моменты, чтобы понять, носят ли эти события чисто случайный характер.
Прогноз по модели получился с учётом сезонности, и, как видно по тестовой выборке, это сыграло модели на руку — она дала прогноз точнее, чем это сделала бы предыдущая модель ETS(M,N,N).
Прогнозный интервал оказался уже, чем в предыдущем случае и по своей динамике соответствует поведению точечного прогноза (что говорит о том, что мы смогли уловить важные элементы ряда).

В общем, всё в этом графике указывает на то, что стоит обратиться к модели с трендом и сезонностью.

В ряде случаев по одному лишь линейному графику бывает сложно сделать выводы о качестве модели. Например, те же самые выбросы оценить по нему на глаз непросто. В этом случае нужно обратиться к графикам по остаткам модели. Даже простой линейный график по остаткам может дать много полезной информации.

Однако прежде чем приступать к непосредственному анализу, надо понять, что нам нужно. В идеальной модели остатки ни от чего не зависят, выглядят распределёнными случайно и желательно даже нормально. Графически это должно выражаться отсутствием какой-либо предсказуемости в остатках и ровными гистограммами и ящичковыми диаграммами.

На следующих рисунках приведены четыре графика по остаткам модели ETS(M,N,N) (той, которая соответствует первому графику в этой статье).

Линейный график по остаткам модели ETS(M,N,N)

Гистограмма по остаткам модели ETS(M,N,N)

Ящичковая диаграмма по остаткам модели ETS(M,N,N)

Точечная диаграмма по остаткам модели ETS(M,N,N)

Взглянем критически на эти графики и попробуем вынести какую-нибудь полезную информацию.

Линейный график по остаткам демонстрирует периодические колебания (которые особенно заметны примерно с 1986 года) — это всё из-за того, что мы не учли в модели сезонность. По остаткам она видна более явно, чем по графику по исходному ряду.
Гистограмма по остаткам демонстрирует явную асимметрию: очень много ошибок лежит выше нуля (справа). Это так же указывает на неправильную спецификацию модели. Обычно исследователи при построении разных моделей стараются добиваться нормально распределённых остатков, но это требование на практике очень сложно удовлетворить. Именно поэтому нам нужно, чтобы они были хотя бы симметрично распределены относительно нуля. Это будет указывать на то, что модель построена без систематических ошибок.
Ящичковая диаграмма показывает то же, что и гистограмма: мы имеем дело с асимметричным распределением. Помимо этого она ещё показала, что практически все отрицательные остатки можно статистически считать выбросами — то есть они настолько редко случаются, что играют небольшую роль в описательной способности модели. На себя так же обращает внимание завышенное среднее значение ошибки (красная точка по середине ящичка) — это так же сигнализирует о неправильной спецификации.
Точечная диаграмма, построенная по расчётным значениям (Fitted) и абсолютным остаткам модели была построена для дополнительной информации. Она нам может показать, есть ли в модели гетероскедастичность. Другими словами, постоянна ли дисперсия остатков модели. Видно, что при меньших расчётных значениях остатки лежат в пределах от нуля до 0.015, в то время как при достижении 6000 по оси абсцисс разброс увеличивается. Это указывает на непостоянность дисперсии, что в свою очередь опять говорит о возможных проблемах модели.

Теперь рассмотрим точно такие же графики, но уже по модели с трендом и сезонностью.

Линейный график по остаткам модели ETS(M,A,M)

Гистограмма по остаткам модели ETS(M,A,M)

Точечная диаграмма по остаткам модели ETS(M,A,M)

Ящичковая диаграмма по остаткам модели ETS(M,A,M)

По ним можно заключить следующее:

Линейный график демонстрирует более случайный характер распределения остатков, чем в предыдущем примере. Та самая пресловутая сезонность уже менее заметна. Но на себя обращают внимание три отрицательные ошибки, соответствующие 1984, 1989 и 1990 годам. Возможно, у таких ошибок есть какое-то объяснение. На практике стоило бы выяснить, что происходило в эти кварталы для того, чтобы улучшить описательные и прогнозные свойства модели.
Гистограмма имеет более симметричный вид. Если бы не те несколько отрицательных ошибок, она бы выглядела вообще прекрасно.
Ящичковая диаграмма так же демонстрирует большую симметрию относительно нуля (по сравнению с предыдущей моделью), а так же указывает на наличие нескольких выбросов. Это те самые отрицательные ошибки, которые мы отметили ранее. Всё-таки что-то с ними надо сделать!
Последний график всё так же, как и в предыдущем примере указывает на наличие гетероскедастичности. Это значит, что при построении прогнозных интервалов сей неприятный эффект надо учесть, иначе интервалы могут оказаться либо слишком узкими, либо излишне широкими.

Как видим, на основе такого небольшого анализа можно получить много полезной информации об аппроксимационных свойствах модели и принять решение о том, что делать с моделью либо к какой модели обратиться.

Но помимо приведённых графиков есть ещё один, специализированный, который позволяет сравнивать распределение случайной величины с некоторым заданным. Называется он «квантиль-квантиль» потому что позволяет проводить поквантильное сравнение фактических и теоретических значений. Пример такого графика представлен на этом рисунке:

График квантиль-квантиль по остаткам

По нему видно, что наблюдения, находящиеся в хвостах распределения выбиваются и из-за них распределение остатков оказывается непохожим на нормальное. В идеале мы хотели бы, чтобы все точки на графике находились если не непосредственно на прямой линии, то хотя бы близко к ней, вокруг неё.

Как это сделать в R

В R такой график можно построить с помощью функций qqplot() и qqline(). Если нас интересует сравнение с нормальным распределением, то можно так же использовать функцию qqnorm(). Например:

x <- rnorm(100,0,1)
qqnorm(x)
qqline(x)

Попробуйте и посмотрите, какой получится график.

Коэффициенты для оценки качества моделей

Но, конечно же, одним графическим анализом ограничиваться не стоит. Очевидно, что глаз не всегда может увидеть то, что легко показал бы какой-нибудь коэффициент.

Первая группа коэффициентов, которые могут использоваться для оценки качества, обычно используется на остатках модели. Это все те статистические показатели, которые мы рассмотрели раньше в параграфе «Статистический анализ данных». Ничего нового и интересного относительно них сказать нельзя, поэтому здесь на них мы останавливаться не будем.

Добавим в нашу коллекцию два коэффициента, которые могут помочь при оценке описательной способности модели. Первый — это коэффициент корреляции, рассчитанный по фактическим и расчётным значениям. Чем ближе коэффициент к единице, тем в среднем ближе связь между этими значениями к линейной, то есть тем точнее описаны данные нашей моделью. Этот коэффициент мы уже обсуждали в параграфе «Выявление связей между переменными».

Второй полезный коэффициент — коэффициент детерминации. Он показывает процент объяснённой моделью дисперсии и рассчитывается по формуле:

begin{equation} label{eq:mq_Rsquared}
R^2 = 1 -frac{SSE}{TSS} ,
end{equation}
где ( SSE = sum_{t=1}^T e_t^2 ) — это сумма квадратов ошибок модели (иногда обозначается ещё как RSS, SSR), (TSS = sum_{t=1}^T (y_t -bar{y})^2) — сумма квадратов отклонений фактических значений от средней величины. Здесь SSE соответствует «Sum of Squared Errors», RSS — «Residuals Sum of Squares», SSR — «Sum of Squared Ressiduals», TSS — «Total Sum of Squares». Все эти суммы квадратов на самом деле близки по смыслу к дисперсии остатков и дисперсии по исходному ряду данных. Просто в формуле eqref{eq:mq_Rsquared} не происходит деление на число наблюдений.

Коэффициент детерминации более популярен в регрессионном анализе, нежели в других разделах прогнозирования, но может спокойно использоваться и при оценке экстраполяционных моделей. В случае, если модель идеально описывает ряд данных, SSE становится равной нулю, в результате чего (R^2) становится равен единице. Если же модель ряд совсем не описывает, а представляет собой просто прямую линию, то коэффициент детерминации становится равным нулю. В случаях с нелинейными моделями коэффициент может так же становиться отрицательным, но при этом неинтерпретируемым.

Несмотря на то, что коэффициент детерминации показывает этот самый процент той самой объяснённой дисперсии, сильно полагаться на него не стоит. Во-первых, он считается по обучающей части выборки, а значит просто показывает, насколько хорошо мы описали данные. При этом точность описания не гарантирует точность прогнозов. В некоторых случаях даже наоборот: излишне точное описание приводит к ухудшению прогнозных свойств модели (так как та начинает слишком сильно реагировать на шум). Простой пример — полиномы: чем выше степень полинома, тем выше (R^2), но тем обычно хуже точность прогнозов. Во-вторых, коэффициент детерминации будет всегда тем выше, чем выше число параметров в модели. То есть (R^2) у модели (y = a_0 + a_1 x_1 + e) будет всегда ниже, чем у модели (y = a_0 + a_1 x_1 + a_2 x_2 + e), даже если (x_2) в принципе ненужен. Именно поэтому иногда в эконометрике обращаются к так называемому скорректированному коэффициенту детерминации — (R^2)-adjusted. Но о нём мы поговорим в следующем параграфе.

В заключение по коэффициенту детерминации хотелось бы лишь добавить, что при построении моделей он не должен являться самоцелью: «Посмотрите, какая у меня хорошая модель получилась: (R^2=0,936)!» — типичная ошибка начинающих аналитиков. (R^2) может выступать лишь индикатором того, насколько модель адекватна. Низкие значения коэффциента детерминации могут указывать на то, что модель особого смысла не имеет, но при этом высокие значения не говорят о том, что перед нами хорошая модель.

По коэффициентам аппроксимации у меня всё. Но, если бы мы ограничивались лишь анализом аппроксимационных свойств моделей, то не было бы смысла вообще писать этот параграф. Нас, ведь, на самом деле больше интересует оценка точности прогнозов. Оценить её можно при использовании процедуры ретропрогноза. В этом случае наш интерес сдвигается с того, как модель себя повела на обучающей выборке на то, как она себя повела на тестовой. И здесь уже есть, куда развернуться.

Конечно, анализ этот можно проводить по аналогии с анализом обычной случайной величины, а значит и использовать весь стандартный набор коэффициентов, но в некоторых случаях стандартные методы просто неприменимы, а в других случаях не дадут полной информации о прогнозных свойствах моделей.

Например, коэффициент MAE, к которому мы обращались в параграфе «Простые методы оценки параметров моделей», будет в этом случае рассчитываться так:

begin{equation} label{eq:mq_MAE}
text{MAE} = frac{1}{h} sum_{j=1}^h | e_{T+j} |,
end{equation}
где (e_{T+j}) — ошибка на прогнозном шаге j, h — срок прогнозирования, T — номер последнего наблюдения в обучающей выборке.

У этого коэффициента есть два недостатка, которые проявляются только в случае анализа прогнозной точности моделей:

Его значение сложно интерпретировать. Вот, допустим, получилось, что (MAE = 1547.13). О чём это говорит? Это много или мало? Если сравнить с другой моделью, то станет, конечно, ясно. Но какова будет реакция начальника, когда на вопрос прогнозисту: «Штурман, приборы?» — он услышит: «1547.13»?
С помощью этого коэффициента можно проводить сравнение только между моделями по одному ряду данных. Но на практике часто стоит задача понять, как себя ведёт модель по нескольким рядам данных по сравнению с другими моделями. И тут уже полученные по разным рядам MAE складывать друг с другом нельзя, так как при сложении яблок с гвоздями получается абсурд.

Для того, чтобы так или иначе справиться с одной из или обеими этими проблемами, было разработано несколько коэффициентов.

MAPE — «Mean Absolute Percentage Error» — Средняя абсолютная процентная ошибка:

begin{equation} label{eq:mq_MAPE}
text{MAPE} = frac{1}{h} sum_{j=1}^h frac{| e_{T+j} |}{y_{T+j}},
end{equation}

Это коэффициент, не имеющий размерности, с очень простой интерпретацией. Его можно измерять в долях или процентах. Если у вас получилось, например, что (MAPE = 11.4%), то это говорит о том, что ошибка составила 11,4% от фактических значений. Этот коэффициент можно легко складывать по разным рядам. Можно даже рассчитать MAPE и изучить его распределение, используя инструменты статистического анализа. С другой стороны, можно отбросить в eqref{eq:mq_MAPE} часть, отвечающую за «Mean»:

begin{equation} label{eq:mq_APE}
text{APE} = frac{| e_{T+j} |}{y_{T+j}},
end{equation}
и изучить распределение прогнозных ошибок на некоторый шаг j, используя всё те же статистические методы. Можно вместо «M», средней, посчитать «Md», медиану. Можно обратиться к квантилям… В общем, ни в чём себе не отказывайте, чувствуйте себя как дома!

Но, конечно же, без проблем быть не может. Из-за деления на фактические значения этот коэффициент оказался чувствительным к масштабу. Так, в случае, если (y_{T+j}) близко к нулю, то значение eqref{eq:mq_APE} из-за деления на очень маленькое число взлетит. А уж если (y_{T+j}=0), то нас вообще ждёт бедствие вселенского масштаба.

Но на этом ещё не всё. Коэффициент по разному относится к положительным и отрицательным ошибкам. Допустим, что наш точечный прогноз на 137-м наблюдении составил (hat{y}_{137} = 20), а фактическое значение при этом было (y_{137}=10). Какой будет ошибка APE в этом случае? Подставим эти значения в формулу eqref{eq:mq_APE}, чтобы получить (frac{|10-20|}{10}=1=100%). А какой была бы ошибка, если бы фактическое значение было равно 30? Очевидно, что (frac{|30-20|}{30}=0,33(3)=33.(3)%). Вроде бы ошибка та же, но, по объективным причинам, она во втором случае составляет 33.3% от фактического значения, а не 100%. Получается, что этот коэффициент жестче относится к случаям завышенных прогнозов, чем заниженных. В случае с агрегированием прогнозов по разным значениям, это приводит к искажениям — прогнозист не получает достоверной информации о том, насколько его прогноз точен. Такая асимметрия не могла не привести к появлению других коэффициентов.

Один из вариантов решения проблемы предложили Spyros Makridakis и Michele Hibon, назвав коэффициент SMAPE — «Symmetric MAPE» — симметричная MAPE:

begin{equation} label{eq:mq_SMAPE}
text{SMAPE} = frac{1}{h} sum_{j=1}^h frac{2 | e_{T+j} |}{|y_{T+j}| + |hat{y}_{T+j}|} .
end{equation}

Число «2» в этой формуле не случайно. Дело в том, что в соответствии с первоначальной задумкой в знаменателе должно быть среднее между фактическим и расчётным значениями: (bar{y_t} = frac{y_t + hat{y}_t}{2} ). При подстановке этого значения в знаменатель, двойка переносится в числитель, поэтому мы и получаем то, что получаем.

Трактовка у коэффициента примерно такая же, как и у MAPE: какой процент составляет ошибка от этой самой величины (bar{y_t}).

Идея, надо сказать, хорошая, но, конечно же, всё так же не лишена проблем. Коэффициент должен бы быть симметричным, но таковым до конца не является. Рассмотрим это на примере. Пусть наш прогноз на всё том же 137-м наблюдении составил (hat{y}_{137} = 110), а фактическое значение было (y_{137} = 100). SMAPE в этом случае составит (frac{2 cdot |100 — 110|}{100+110} = 9.52%). Если же прогноз оказался заниженным и составил (hat{y}_{137} = 90), то SMAPE получится равным (frac{2 cdot |100 — 90|}{100+90} = 10.53%). То есть, опять же, коэффициент демонстрирует смещение, только в этот раз в сторону завышенных прогнозов: завышенные прогнозы приводят к меньшей ошибке, чем заниженные. Сейчас уже в среде прогнозистов сложилось более-менее устойчивое понимание, что SMAPE на является хорошей ошибкой. Тут дело не только в завышении прогнозов, но ещё и в том, что наличие прогноза в знаменателе позволяет манипулировать результатами оценки. Кроме того, неясно, что именно минимизирует SMAPE. Поэтому я бы лично рекомендовал эту ошибку не использовать при оценки прогнозов (да, мы её активно использовали в нашем учебнике по прогнозированию, но сейчас я бы этого не стал делать).

Это, конечно же, не могло не привести к появлению ещё нескольких коэффициентов.

MASE расшифровывается как «Mean Absolute Scaled Error» и переводится как «Средняя абсолютная масштабированная ошибка». Предложена была Робом Хайндманом и Анной Коелер и рассчитывается так:

begin{equation} label{eq:mq_MASE}
text{MASE} = frac{T-1}{h} frac{sum_{j=1}^h | e_{T+j} |}{sum_{t=2}^T |y_{t} — y_{t-1}|} .
end{equation}

Обратите внимание, что в eqref{eq:mq_MASE} мы имеем дело с двумя суммами: та, что в числителе, соответствует тестовой выборке, та, что в знаменателе — обучающей. Вторая фактически представляет собой среднюю абсолютную ошибку прогноза по методу Naive. Она же соответствует среднему абсолютному отклонению ряда в первых разностях. Эта величина, по сути, показывает, насколько обучающая выборка предсказуема. Она может быть равна нулю только в том случае, когда все значения в обучающей выборке равны друг другу, что соответствует отсутствию каких-либо изменений в ряде данных, ситуации на практике почти невозможной. Кроме того, если ряд имеет тендецию к росту либо снижению, его первые разности будут колебаться около некоторого фиксированного уровня. В результате этого по разным рядам с разной структурой, знаменатели будут более-менее сопоставимыми. Всё это, конечно же, является очевидными плюсами MASE, так как позволяет складывать разные значения по разным рядам и получать несмещённые оценки.

Но, конечно же, без минусов нельзя. Проблема MASE в том, что её тяжело интерпретировать. Например, (MASE = 1.21) ни о чём, по сути, не говорит. Это просто означает, что ошибка прогноза оказалась в 1.21 раза выше среднего абсолютного отклонения ряда в первых разностях, и ничего более. Показывать шефу эти цифры опасно для жизни аналитика.

Можно, конечно, знаменатель eqref{eq:mq_MASE} заменить на простую среднюю по всему ряду, чтобы получить другую среднюю абсолютную масштабированную (относительно среднего уровня ряда) ошибку (sMAE — scaled MAE, иногда обозначается как MAE/mean). Для пущей безопасности в знаменателе можно взять среднее абсолютное значение ряда:

begin{equation} label{eq:mq_MASALE}
text{sMAE} = frac{T}{h} frac{sum_{j=1}^h | e_{T+j} |}{sum_{t=1}^T |y_{t}|} .
end{equation}

Модуль в знаменателе нужен для ситуаций, когда мы имеем дело как с положительными, так и отрицательными величинами, средняя величина по которым может быть близка к нулю. Если в такой ситуации брать просто среднюю, мы столкнёмся со всё той же проблемой масштаба. В общем случае значение eqref{eq:mq_MASALE} будет показывать, какой процент от средней составляют ошибки прогноза. Эта величина всё так же будет несмещённой (по сравнению с MAPE и SMAPE), и может легко складываться с другими такими же величинами. Единственная проблема — тренд в ряде данных может влиять на итоговое значение eqref{eq:mq_MASALE}. Но зато такой коэффициент легче интерпретировать, чем eqref{eq:mq_MASE} — эта ошибка может легко измеряться в процентах.

Заметим, знаменатель sMAE может быть равен нулю только в одном случае — если все фактические значения в обучающей выборке оказались равны нулю. Такое возможно лишь в ситуациях с целочисленным спросом, если в распоряжении исследователя ещё не было ни одного ненулевого значения. В общем, очень экзотическая ситуация, в которой надо обращаться к нестатистическим методам прогнозирования. А так ошибка может использоваться как при прогнозировании положительных, так и отрицательных значений.

sMAE — практически идеальный показатель. У него есть лишь один небольшой недостаток — он никак не ограничен сверху. То есть теоретически возможны ситуации, когда (sMAE = 1000%) (например, когда в проверочной выборке продажи неожиданно взлетели в разы, а в обучающей до этого составляли единицы), и с этим ничего не поделать. Такие ситуации, впрочем, тоже необычны, нечасто встречаются и будут приводить к похожим результатам во всех рассмотренных выше ошибках.

Ну, и не забываем о том, что вместо средней «M» в eqref{eq:mq_MASE} и eqref{eq:mq_MASALE} можно использовать и что-нибудь другое…

Но и даже на этом ещё не всё. Роберт Файлдс в 1992 году предложил нечто под названием «GMRAE» — «Geometric Mean Relative Absolute Error»:

begin{equation} label{eq:mq_GMRAE}
text{GMRAE} = prod_{j=1}^h left( frac{| e_{a,T+j} |}{| e_{b,T+j} |} right)^{frac{1}{h}} ,
end{equation}
где (e_{b,T+j}) — ошибка по некоторой второй модели.

GMRAE показывает, во сколько раз наша модель оказалась хуже (или лучше), чем выбранная для сравнения (модель-бенчмарк). Если (GMRAE>1), то наша модель оказалась менее точной, в противоположной ситуации — более точной. В качестве той самой второй модели для простоты можно выбрать Naive. Однако, можно и не ограничиваться Naive. Что именно выбрать обычно остаётся на совести прогнозиста, и в свою очередь может вызывать некоторые сложности. Действительно, почему именно Naive? Почему бы не модель экспоненциального сглаживания с демпфированным трендом или какая-нибудь ARIMA(2,1,3)?! Вопрос открытый. Но важно, чтобы по разным рядам происходило сравнение с одной и той же моделью.

Как видно, GMRAE легче интерпретировать, чем MASE, но сложнее, чем MAPE, SMAPE или sMAE. Впрочем, она всё так же не ограничена сверху и может теоретически достигать заоблачных величин.

Но без ложки дёгтя не обошлось. Из-за того, что эта ошибка представляет собой среднюю геометрическую, она не может использоваться в ситуациях, когда хотя бы одна из ошибок одной из моделей оказалась равной нулю — в этом случае GMRAE становится равной либо нулю, либо бесконечности.

Одна из модификаций этой ошибки — rMAE — Relative MAE (относительная MAE):
begin{equation} label{eq:mq_rMAE}
text{rMAE} = frac{text{MAE}_a}{text{MAE}_b} .
end{equation}
Здесь мы фактически просто рассчитываем MAE двух моделей, и дальше делим одну величину на другую. Интерпретация получается похожей на интерпретацию GMRAE, но сама ошибка при этом оказывается более робастной (так как ситуация, когда MAE=0 оказывается значительно менее вероятной, чем ситуация, когда одна какая-то ошибка оказалась нулевой).

Последний коэффициент, который мы рассмотрим, призван оценивать не точность прогноза, а его смещение. Называется он «Mean Percentage Error» — средняя процентная ошибка:

begin{equation} label{eq:mq_MPE}
text{MPE} = frac{1}{h} sum_{j=1}^h frac{ e_{T+j} }{y_{T+j}}
end{equation}

Можно заметить, что он похож на eqref{eq:mq_MAPE}, но отличается лишь отсутствием модулей в числителе. Он показывает процент смещения прогноза. Положительные значения MPE указывают на систематическое занижение прогноза (то есть, мы недооценили спрос), а отрицательные — на завышения. Его значение так же, как и MAPE eqref{eq:mq_MAPE} может измеряться в процентах. Он обладает теми же преимуществами и недостатками, что и MAPE.

На основе этой идеи со средними ошибками можно предложить и симметричную MPE, и среднюю масштабированную ошибку sME. Подробней на этом мы останавливаться не будем.

Ну, и совсем уж напоследок. Иногда в литературе встречается сравнение моделей на основе RMSE («Root Mean Squared Error» — «Корня из средней квадратичной ошибки»):

begin{equation} label{eq:mq_RMSE}
text{RMSE} = sqrt{ frac{1}{h} sum_{j=1}^h { e_{T+j} }^2}
end{equation}

Раньше бытовало мнение, что такое сравнение некорректно (см. Armstrong and Colopy, 1992), так как обычно приводит к выбору неправильной модели (то есть не самой точной). Всё из-за того, что эта ошибка сильно подвержена влиянию выбросов (из-за квадрата в формуле). Однако сейчас уже есть понимание, что проблема тут не в корректности и правильности, а в том, с чем именно мы имеем дело. Дело в том, что ошибки на основе MSE минимизируются с помощью средней величины, в то время как ошибки на основе MAE минимизируются медианами. Так что всё сводится к тому, что именно вы хотите увидеть.

Один из примеров эффективного использования ошибок на основе MSE — это прогнозирование прерывистого спроса. В этом случае число нулей в выборке может быть настолько большим (может легко перевалить за 50%), что все ошибки, основанные на модулях будут отдавать предпочтение нулевому прогнозу (мы ничего не продадим, поэтому нечего запасать — депрессивный прогноз). Это всё из-за того самого эффекта со средними и медианами (см. параграф методы оценки моделей).

На основе eqref{eq:mq_RMSE} можно, например, предложить rRMSE:
begin{equation} label{eq:mq_rRMSE}
text{rRMSE} = frac{text{RMSE}_a}{text{RMSE}_b} ,
end{equation}
которая может интерпретироваться аналогично rMAE.

На этом все самые популярные и полезные коэффициенты заканчиваются. В жизни встречаются, конечно же, и другие, но они обычно либо обладают большим количеством недостатков, либо значительно менее популярны среди прогнозистов.

Пример в R

В пакете smooth рассмотренные выше коэффициенты уже реализованы. Подключим пакет:

library("smooth")

И посмотрим, как они работают на примере следующих двух моделей:

x <- es(M3$N1234$x,model="MNN",h=8)$forecast
y <- es(M3$N1234$x,model="MAN",h=8)$forecast

Переменные x и y теперь содержат прогнозы на 8 наблюдений вперёд по моделям ETS(M,N,N) и ETS(M,A,N) по ряду N1234 базы M3-Competition.

Ряд N1234 и модель ETS(M,A,N)

График исходного ряда (см. выше) демонстрирует рост, и, откровенно говоря, модель ETS(M,A,N) выглядит на обучающей выборке неплохо. Она улавливает тенденцию к росту. Если не прибегать ни к какому фундаментальному анализу, то можно заключить, что возрастающий тренд — это то, что нас ждёт в ближайшем будущем. Но будущее таки не предопределено, именно об этом нам в очередной раз говорит следующий график, на котором показана модель ETS(M,N,N) и значения из проверочной выборки.

Ряд N1234 и модель ETS(M,N,N)

И именно поэтому прогнозирование всегда должно осуществляться параллельно с фундаментальным анализом.

Тем не менее, посмотрим, насколько точными оказались прогнозы по этим двум моделям. Для начала рассчитаем MPE:

MPE(M3$N1234$xx,x)
[1] -0.009
MPE(M3$N1234$xx,y)
[1] -0.037

Как видим, прогноз по второй модели оказался более смещённым — он составил -3,7%, по сравнению с -0,9% первой модели. Не удивительно — ситуация в проверочной выборке изменилась кардинально по сравнению с тем, что мы видели в обучающей!

Что же там с точностью прогнозов?

MAPE(M3$N1234$xx,x)
[1] 0.009
MAPE(M3$N1234$xx,y)
[1] 0.037

Из-за того, что прогнозы по обеим моделям оказались завышенными, значение MPE оказывается равным по модулю значению MAPE. Вторая модель ошиблась сильнее, чем первая.

Симметричная MAPE даст нам примерно то же самое:

SMAPE(M3$N1234$xx,x)
[1] 0.009
SMAPE(M3$N1234$xx,y)
[1] 0.036

Для MASE нам понадобится значение, по которому мы будем масштабировать ошибки. Рассмотрим классические вариант со средней абсолютной ошибкой в знаменателе:

MASE(M3$N1234$xx,x,mean(abs(diff(M3$N1234$x))))
[1] 1.218
MASE(M3$N1234$xx,y,mean(abs(diff(M3$N1234$x))))
[1] 4.820

Очевидно, что вторая модель ошиблась по сравнению с первой в четыре раза. Но, к сожалению, по MASE особо больше нечего сказать.

А теперь масштабируем её относительно среднего абсолютного уровня (sMAE):

MASE(M3$N1234$xx,x,mean(abs(M3$N1234$x)))
[1] 0.011
MASE(M3$N1234$xx,y,mean(abs(M3$N1234$x)))
[1] 0.043

Получили примерно ту же картину, только эти значения можно измерять в процентах и они несут чуть больше смысла.

Ну, и напоследок рассчитаем GMRAE. Для этого для сначала дадим прогноз по модели Naive, чтобы было, с чем сравнивать:

es(M3$N1234$x,model="ANN",persistence=1,h=8)$forecast->z

А теперь посчитаем GMRAE:

GMRAE(M3$N1234$xx,x,z)
[1] 1
GMRAE(M3$N1234$xx,y,z)
[1] 4.877

Первая модель, как видим, дала точно такой же прогноз, как и Naive — GMRAE оказалась равной единице. Вторая же модель спрогнозировала ряд в несколько раз хуже, чем это сделала Naive.

В этом нашем примере все ошибки дали примерно один и тот же результат. Однако на других рядах данных результаты могут различаться. Попробуйте, например, используя всё те же модели, сравнить прогнозы на следующем условном ряде данных:

example <- rnorm(100,2,1)

Источник

MPE — Mean Percent Error

MAPE — Mean Absolute Percent Error

WMAPE / MAD-Mean Ratio / WAPE — Weighted Absolute Percent Error

RMSE (as %) / nRMSE — Root Mean Square Error

MASE — Mean Absolute Scaled Error

Об авторе

HeinzBr

Оценка ошибки прогнозирования временного ряда

MAPE – средняя абсолютная ошибка в процентах

MAE – средняя абсолютная ошибка

MSE – среднеквадратичная ошибка

RMSE – квадратный корень из среднеквадратичной ошибки

ME – средняя ошибка

SD – стандартное отклонение

Связь точности и ошибки прогнозирования

1-й способ — Расчет отношения фактических продаж к прогнозу.

Для каждой из 4-х прогнозных моделей в листе «Оценка моделей»:

2-й способ оценки модели прогноза — расчет показателя точность прогноза.

3. Способ оценки прогнозной модели — визуальный.

Какую модель прогноза выбрать?

Для повышения точности прогноза я в своей практике стараюсь использовать 3 этих способа параллельно:

Точных прогнозов!

Присоединяйтесь к нам!

<img loading="lazy" decoding="async" src="https://4analytics.ru/images/images/NovoForecast/box_pro_white_2.png" alt="Novo Forecast - прогноз в Excel - точно, легко и быстро!" width="237" height="237" />

Зарегистрируйтесь и скачайте решения

Статья полезная? Поделитесь с друзьями

Методы оценки качества прогноза

Остатки

Суровые MSE и R2

MAPE и MAD для сравнения моделей

Пример: интерпретация значения MAPE для данной модели

Сравнение значений MAPE для разных моделей

Дополнительные ресурсы

Оценка точности выбранных моделей прогнозирования Показатели точности

Графический анализ моделей

Коэффициенты для оценки качества моделей

Суровые MSE и R²