одиночная ошибка
- одиночная ошибка
-
одиночная ошибка
одиночная неисправность
—
[Л.Г.Суменко. Англо-русский словарь по информационным технологиям. М.: ГП ЦНИИС, 2003.]Тематики
- информационные технологии в целом
Синонимы
- одиночная неисправность
Справочник технического переводчика. – Интент.
2009-2013.
Смотреть что такое «одиночная ошибка» в других словарях:
-
одиночная (двойная, тройная…) ошибка в цифровом сигнале данных — одиночная (двойная, тройная…) ошибка Ошибка в цифровом сигнале данных, при которой один (два, три…) ошибочных единичных элемента находятся в последовательности из n единичных элементов. [ГОСТ 17657 79 ] Тематики передача данных Обобщающие… … Справочник технического переводчика
-
ошибка в одном разряде — одиночная битовая ошибка — [Л.Г.Суменко. Англо русский словарь по информационным технологиям. М.: ГП ЦНИИС, 2003.] Тематики информационные технологии в целом Синонимы одиночная битовая ошибка EN single bit error … Справочник технического переводчика
-
одиночная — 79 одиночная [двойная, тройная] ошибка (в цифровом сигнале данных) Источник: ПР 45.02 97: Отраслевая система стандартизации. Принципы разработки нормативных документов Смотри также родственные термины: 79. Одиночная (двойная, тройная …) ош … Словарь-справочник терминов нормативно-технической документации
-
Одиночная (двойная, тройная …) ошибка в цифровом сигнале данных — 79. Одиночная (двойная, тройная …) ошибка в цифровом сигнале данных Одиночная (двойная, тройная …) ошибка E. Single, double, triple … error Ошибка в цифровом сигнале данных, при которой один (два, три …) ошибочных единичных элемента… … Словарь-справочник терминов нормативно-технической документации
-
Одиночная (двойная, тройная…) ошибка в цифровом сигнале данных — 1. Ошибка в цифровом сигнале данных, при которой один (два, три …) ошибочных единичных элемента находятся в последовательности из п единичных элементов Употребляется в документе: ГОСТ 17657 79 Передача данных. Термины и определения … Телекоммуникационный словарь
-
ВЫБОРКИ ОШИБКА — (SAMPLING ERROR) Многие социологические исследования основаны на использовании случайной выборки из населения. Однако одиночная выборка может быть недостаточно репрезентативной в этом случае говорят об ошибке выборки. Повторные выборки в конечном … Социологический словарь
-
ошибочный бит — одиночная ошибка цифровая ошибка — [Л.Г.Суменко. Англо русский словарь по информационным технологиям. М.: ГП ЦНИИС, 2003.] Тематики информационные технологии в целом Синонимы одиночная ошибкацифровая ошибка EN bit error … Справочник технического переводчика
-
Код Хемминга — Коды Хемминга наиболее известные и, вероятно, первые из самоконтролирующихся и самокорректирующихся кодов. Построены они применительно к двоичной системе счисления. Содержание 1 История 2 Самоконтролирующиеся коды … Википедия
-
Гибридизация ДНК — У этого термина существуют и другие значения, см. гибридизация. Гибридизация ДНК, гибридизация нуклеиновых кислот соединение in vitro комплементарных одноцепочечных нуклеиновых кислот в одну молекулу. При полной комплементарности… … Википедия
-
Код Хэмминга — Эта статья или раздел нуждается в переработке. Пожалуйста, улучшите статью в соответствии с правилами написания статей … Википедия
Любая
принятая по каналу связи кодовая
комбинация h(x),
возможно
содержащая ошибку, может быть представлена
в виде суммы по модулю два неискаженной
комбинации кода f(x)
и
вектора ошибки ξ(x):
h(x)
= f(x)
ξ(x).
При
делении h(x)
на
образующий многочлен g(x)
остаток,
указывающий на наличие ошибки,
обнаруживается только в том случае,
если многочлен, соответствующий вектору
ошибки, не делится на g(x):
f(x)-неискаженная
комбинация кода и, следовательно, на
g(x)
делится
без остатка.
Вектор
одиночной ошибки имеет единицу в
искаженном разряде и нули во всех
остальных разрядах. Ему соответствует
многочлен ξ(x)
= xi.
Последний
не должен делиться на g(x).
Среди
неприводимых многочленов, входящих в
разложении хn+1,
многочленом
наименьшей степени, удовлетворяющим
указанному условию, является x
+ 1. Остаток от деления любого многочлена
на x
+ 1 представляет собой многочлен нулевой
степени и может принимать только два
значения: 0 или 1. Все кольцо в данном
случае состоит из идеала, содержащего
многочлены с четным числом членов, и
одного класса вычетов, соответствующего
единственному остатку, равному 1. Таким
образом, при любом числе информационных
разрядов необходим только один проверочный
разряд. Значение символа этого разряда
как раз и обеспечивает четность числа
единиц в любой разрешенной кодовой
комбинации, а, следовательно, и делимость
ее на xn
+ 1.
Полученный
циклический код с проверкой на четность
способен обнаруживать не только одиночные
ошибки в отдельных разрядах, но и ошибки
в любом нечетном числе разрядов.
-
Исправление одиночных или обнаружение двойных ошибок
Прежде
чем исправить одиночную ошибку в принятой
комбинации из п
разрядов,
необходимо определить, какой из разрядов
был искажен. Это можно сделать только
в том случае, если каждой одиночной
ошибке в определенном разряде соответствуют
свой класс вычетов и свой опознаватель.
Так как в циклическом коде опознавателями
ошибок являются остатки от деления
многочленов ошибок на образующий
многочлен кода g(x),
то
g(x)
должно
обеспечить требуемое число различных
остатков при делении векторов ошибок
с единицей в искаженном разряде. Как
отмечалось, наибольшее число остатков
дает неприводимый многочлен. При степени
многочлена m
= n-k
он может дать 2n—k
— 1 ненулевых остатков (нулевой остаток
является опознавателем безошибочной
передачи).
Следовательно,
необходимым условием исправления любой
одиночной ошибки является выполнение
неравенства
2n—k
— 1
=
n,
где
—
общее
число разновидностей одиночных ошибок
в кодовой комбинации из п
символов;
отсюда находим степень образующего
многочлена кода
m = n
– k
log2(n+1)
и общее
число символов в кодовой комбинации.
Наибольшие значения k
и
п
для
различных m
можно найти пользуясь табл. 7.8.
Таблица 7.8.
|
M |
1 |
2 |
3 |
4 |
5 |
6 |
7 |
8 |
9 |
10 |
|
N |
1 |
3 |
7 |
15 |
31 |
63 |
127 |
255 |
511 |
1023 |
|
K |
0 |
1 |
4 |
11 |
26 |
57 |
120 |
247 |
502 |
1013 |
Как
указывалось, образующий многочлен g(x)
должен
быть делителем двучлена хn+1.
Доказано,
что любой двучлен типа х2m-1+
1
= хn+1
может
быть представлен произведением всех
неприводимых многочленов, степени
которых являются делителями числа т
(от
1 до т
включительно).
Следовательно, для любого т
существует
по крайней мере один неприводимый
многочлен степени т,
входящий
сомножителем в разложение двучлена
хn+1.
Пользуясь
этим свойством, а также имеющимися в
ряде книг таблицами многочленов,
неприводимых при двоичных коэффициентах,
выбрать образующий многочлен при
известных n
и m
несложно. Определив образующий многочлен,
необходимо убедиться в том, что он
обеспечивает заданное число остатков.
Пример
7.16.
Выберем образующий многочлен для случая
n
= 15 и m
= 4.
Двучлен
x15
+ 1 можно записать в виде произведения
всех неприводимых многочленов, степени
которых являются делителями числа 4.
Последнее делится на 1, 2, 4.
В
таблице неприводимых многочленов
находим один многочлен первой степени,
а именно x+1,
один многочлен второй степени x2
+
x
+ 1 и три многочлена четвертой степени:
х4
+ x
+ 1, х4
+ х3
+ 1, х4
+ х3
+ х2
+ х + 1. Перемножив все многочлены, убедимся
в справедливости соотношения (х + 1)(х2
+
х + 1)(х4
+ х
+
1)(х4
+ х3+
1)(х4
+ х3
+ х2
+ х + 1) = x15
+
1
Один
из сомножителей четвертой степени может
быть принят за образующий многочлен
кода. Возьмем, например, многочлен х4
+ х3
+ 1, или в виде двоичной последовательности
11001.
Чтобы
убедиться, что каждому вектору ошибки
соответствует отличный от других
остаток, необходимо поделить каждый из
этих векторов на 11001.Векторы ошибок m
младших разрядов имеют вид: 00…000,
00…0010, 00…0100, 00…1000.
Степени
соответствующих им многочленов меньше
степени образующего многочлена g(x).
Поэтому они сами являются остатками
при нулевой целой части. Остаток,
соответствующий вектору ошибки в
следующем старшем разряде, получаем
при делении 00…10000 на 11001, т.е.
Аналогично
могут быть найдены и остальные остатки.
Однако их можно получить проще, деля на
g(x)
комбинацию в виде единицы с рядом нулей
и выписывая все промежуточные остатки:
При последующем
делении остатки повторяются.
Таким
образом, мы убедились в том, что число
различных остатков при выбранном g(x)
равно п = 15, и, следовательно, код,
образованный таким g(x),
способен исправить любую одиночную
ошибку. С тем же успехом за образующий
многочлен кода мог быть принят и многочлен
х4
+
х + 1. При этом был бы получен код,
эквивалентный выбранному.
Однако
использовать для тех же целей многочлен
х4
+ х3
+ x2
+ х + 1 нельзя. При проверке числа различных
остатков обнаруживается, что их у него
не 15, а только 5. Действительно,
Это
объясняется тем, что многочлен x4
+ х3
+ х2
+ х + 1 входит в разложение не только
двучлена x15+
1, но и двучлена x5
+ 1.
Из
приведенного примера следует, что в
качестве образующего следует выбирать
такой неприводимый многочлен g(x)
(или
произведение таких многочленов), который,
являясь делителем двучлена хп
+ 1,
не входит в разложение ни одного двучлена
типа хλ+
1, степень
которого λ
меньше
п.
В
этом случае говорят, что многочлен g(x)
принадлежит
показателю степени п.
В табл.
7.9 приведены основные характеристики
некоторых кодов, способных исправлять
одиночные ошибки или обнаруживать все
одиночные и двойные ошибки.
Таблица
7.9.
|
Показатель |
Образующий |
Число |
Длина |
|
2 3 3 4 4 5 5 |
x2
x3
x3
x4
x4
x5
x5 |
3 7 7 15 15 31 31 |
3 7 7 15 15 31 31 |
Это
циклические коды Хэмминга для исправления
одной ошибки, в которых в отличие от
групповых кодов Хэмминга все проверочные
разряды размещаются в конце кодовой
комбинации.
Эти
коды могут быть использованы для
обнаружения любых двойных ошибок.
Многочлен, соответствующий вектору
двойной ошибки, имеет вид ξ(х)
= хi
– хj,
или
ξ(x)
= хi(хj
– i
+
1) при j>i.
Так как j
– i<n,
a
g(x)
не
кратен х
и
принадлежит показателю степени п,
то
ξ(x)
не
делится
на g(x),
что
и позволяет обнаружить двойные ошибки.
Исправление — одиночная ошибка
Cтраница 1
Исправление одиночной ошибки основано на том, что одна комбинация может быть смешана с другой лишь в том случае, если изменены значения не менее чем трех кодовых элементов.
[1]
Для исправления одиночных ошибок и обнаружения любых двойных ошибок при длине исходной комбинации т разрядов образующее число должно состоять из k l разрядов, а полная кодовая комбинация — из nm k разрядов.
[3]
Для исправления одиночной ошибки каждой разрешенной кодовой комбинации необходимо сопоставить подмножество запрещенных кодовых комбинаций. Чтобы эти подмножества не пересекались, хэммингово расстояние между разрешенными кодовыми комбинациями должно быть не менее трех.
[4]
Для исправления одиночной ошибки расстояние между разрешенными комбинациями должно составлять три единицы. Способ позволяет обнаружить; непересекающихся ошибок, при / р в данной кодовой группе.
[5]
Для исправления одиночной ошибки нужно допустить столько избыточных знаков в каждой кодовой группе, чтобы получить еще больше возможных кодовых комбинаций и отобрать в качестве 2 разрешенных кодовых групп только такие, которые различаются друг от друга тремя и более знаками.
[6]
При исправлении одиночной ошибки ( минимальное расстояние 3) каждое сообщение можно окружить единичной сферой, и эти сферы не перекрываются.
[8]
Для обнаружения и исправления одиночной ошибки применяют разнообразные корректирующие коды. Каждый корректирующий код рассчитан на обнаружение и исправление определенного класса ошибок. В ЭЦВМ находит широкое применение для обнаружения и исправления однократных ошибок код Хэмминга.
[9]
Так, для исправления одиночной ошибки расстояние Хэмминга между разрешенными кодовыми комбинациями должно быть не менее трех.
[10]
Для обнаружения и исправления одиночной ошибки необходимо использовать меньшее количество разрешенных кодовых комбинаций и выбрать их таким образом, чтобы они отличались друг от друга не менее чем на три единицы.
[11]
Когда говорят об исправлении одиночной ошибки, считают, что вероятность двойной ошибки в канале связи пренебрежимо мала. Если такая вероятность достаточно велика, то код с d 3 можно использовать для обнаружения двойных ошибок, но при этом исправить одиночную ошибку он уже не может.
[12]
Это циклические коды для исправления одиночных ошибок, эквивалентные групповым кодам Хэмминга.
[13]
Минимальное расстояние 3 дает исправление одиночных ошибок; каждая одиночная ошибка оставляет точку, расположенную ближе к первоначальному положению, чем к любому другому посылаемому сообщению. Ясно, что код с этим минимальным расстоянием может использоваться также для обнаружения двойных ошибок. Минимальное расстояние 4 дает исправление одиночных ошибок, а также обнаружение двойных ошибок. Минимальное расстояние 5 дает исправление двойных ошибок. Обратно, для того чтобы обнаруживать или исправлять ошибки соответствующей кратности, код должен иметь соответствующее минимальное расстояние.
[15]
Страницы:
1
2
3
4
І – орфографическая ошибка
Это ошибки в словах (буквенные, постановка дефиса, слитное и раздельное написание) (Орфография)
Как (-) то рас пашол снег. Прелители грачи. Учиникам пара здавать икзамены. Он неуспел ра(с)строит(ь)ся.
V – пунктуационная ошибка
Это ошибки в постановке знаков препинания (запятая, точка, тире, двоеточие, вопросительный и восклицательный знаки, точка с запятой, кавычки, скобки, троеточие) (Синтаксис)
Когда солнце встало(,) он увидел свою ошибку. Многие писатели(,) художники(,) певцы с радостью откликнулись на приглашение. Билет(,) купленный дядей на прошлой неделе(,) оказался недействительным. Каждый день (–) это возможность изменить мир к лучшему. Все(:) деревья, кусты, листва на земле (–) трепетало от порывистого ветра. Инспектор ответил(: «)Я не согласен(»).
Г – грамматическая ошибка
Это ошибки в образовании и употреблении формы слова, т.е. сочетаемости в грамматических формах (Морфология)
бессмертность, заместо, англичаны, на мосте, Гринев жил недорослью, Он не боялся опасностей и рисков, Во дворе построили большую качель, Один брат был богатей другого, Эта книга более интереснее, Я пошел к ему, ихний дом, Он ни разу не ошибился, Мама всегда радовается гостям, Вышев на середину комнаты, он заговорил, В дальнем углу сидел улыбающий ребенок, Мы ставим елку на середину комнаты и украшиваем ее. Первых два места определились в бескомпромиссной борьбе.
Р – речевая ошибка
Это употребление не соответвующих смыслу слов или форм слова (Лексика) Здесь и непонимание значения слова, тавтология, неправильное употребление синонимов, омонимов, паронимов и т.д.
С – стилистическая ошибка
Это ошибки в употреблении стилистически окрашенных слов в инородном стиле. Единство стиля – важная компонента любой работы. (Лексика и Развитие речи). Как правило, ученики используют сниженную лексику: разговорные, жаргонные слова, просторечную лексику.
Попечитель богоугодных заведений подлизывается к ревизору (Попечитель богоугодных заведений заискивает перед ревизором). В этом эпизоде главный герой накосячил. (В этом эпизоде главный герой допустил просчет / совершил ошибку).
Стилистический и смысловой разнобой между частями предложения:
Рыжий, толстый, здоровый, с лоснящимся лицом, певец Таманьо привлекал Серова как личность огромной внутренней энергии. – Огромная внутренняя энергия, которой привлекал Серова певец Таманьо, сказывалась и в его внешности: массивный, с буйной рыжей шевелюрой, с брызжущим здоровьем лицом.
Л – логическая ошибка
Это ошибки логического построения текста. Среди них наиболее часто встечающаяся – отсутствие причинно-следственной связи:
Обломов воспитывался в деревне, поэтому ничего не умел делать сам.
К логическим ошибкам также следует отнести порядок слов в предложении, ведущий к искажению смысла:
Есть немало произведений, повествующих о детстве автора, в мировой литературе. – В мировой литературе есть немало произведений, повествующих о детстве автора.
Ф – фактическая ошибка
Это ошибки смысловые, искажение исходного содержания текста (в сочинении и изложении) (Развитие речи)
Z – нарушение абзацного членения
Текст неверно разделен на микротемы, абзацы (Синтаксис и Развитие речи)
Отдельным видом ошибок следует, пожалуй, выделить бедность и однообразие используемых синтаксических конструкций.
Мужчина был одет в прожженный ватник. Он был грубо заштопан. Сапоги были почти новые. Носки изъедены молью. – Мужчина был одет в грубо заштопанный прожженный ватник, хотя сапоги были почти новые, носки оказались изъедены молью.
Это очень серьезный недостаток ученических работ. И очень распространенный.
Просмотр содержимого документа
«Классификация ошибок по русскому языку.»

Самые распространенные ошибки в ЕГЭ по русскому языку:
Классификация ошибок по ФИПИ
- Грамматические ошибки.
- Речевые ошибки.
- Логические ошибки
- Фактические ошибки.
- Орфографические ошибки.
- Пунктуационные ошибки.
- Графические ошибки.
Грамматические ошибки
Грамматическая ошибка – это ошибка в структуре языковой единицы: в структуре слова, словосочетания или предложения; это нарушение какой-либо грамматической нормы: словообразовательной, морфологической, синтаксической.
Например:
- подскользнуться вместо поскользнуться, благородность вместо благородство – здесь допущена ошибка в словообразовательной структуре слова, использована не та приставка или не тот суффикс;
- без комментарий, едь вместо поезжай, более легче – неправильно образована форма слова, т. е. нарушена морфологическая норма;
- оплатить за проезд, удостоен наградой – нарушена структура словосочетания (не соблюдаются нормы управления);
- Покатавшись на катке, болят ноги; В сочинении я хотел показать значение спорта и почему я его люблю – неправильно построены предложения с деепричастным оборотом (1) и с однородными членами (2), т. е. нарушены синтаксические нормы.
В отличие от грамматических, речевые ошибки – это ошибки не в построении, не в структуре языковой единицы, а в ее использовании, чаще всего в употреблении слова. По преимуществу это нарушения лексических норм, например:
- Штольц – один из главных героев одноименного романа Гончарова «Обломов»;
- Они потеряли на войне двух единственных сыновей.
Речевую ошибку можно заметить только в контексте, в этом ее отличие от ошибки грамматической, для обнаружения которой контекст не нужен.
Ниже приводятся общепринятые классификаторы грамматических и речевых ошибок.
Виды грамматических ошибок:
- Ошибочное словообразование — Трудолюбимый, надсмехаться.
- Ошибочное образование формы существительного — Многие чуда техники, не хватает время.
- Ошибочное образование формы прилагательного — Более интереснее, красивше.
- Ошибочное образование формы числительного — С пятистами рублями.
- Ошибочное образование формы местоимения — Ихнего пафоса, ихи дети.
- Ошибочное образование формы глагола — Они ездиют, хочут, пиша о жизни природы.
- Нарушение согласования — Я знаком с группой ребят, серьезно увлекающимися джазом.
- Нарушение управления — Нужно сделать свою природу более красивую.
Повествует читателей. - Нарушение связи между подлежащим и сказуемым — Большинство возражали против такой оценки его творчества.
- Нарушение способа выражения сказуемого в отдельных конструкциях — Он написал книгу, которая эпопея.
Все были рады, счастливы и веселые. - Ошибки в построении предложения с однородными членами — Страна любила и гордилась поэтом.
В сочинении я хотел сказать о значении спорта и почему я его люблю. - Ошибки в построении предложения с деепричастным оборотом — Читая текст, возникает такое чувство…
- Ошибки в построении предложения с причастным оборотом — Узкая дорожка была покрыта проваливающимся снегом под ногами.
- Ошибки в построении сложного предложения — Эта книга научила меня ценить и уважать друзей, которую я прочитал еще в детстве. Человеку показалось то, что это сон.
- Смешение прямой и косвенной речи — Автор сказал, что я не согласен с мнением рецензента.
- Нарушение границ предложения — Когда герой опомнился. Было уже поздно.
- Нарушение видовременной соотнесенности глагольных форм — Замирает на мгновение сердце и вдруг застучит вновь.
Речевые ошибки
Виды речевых ошибок:
- Типичные грамматические ошибки (К9)Употребление слова в несвойственном ему значении — Мы были шокированы прекрасной игрой актеров.
Мысль развивается на продолжении всего текста. - Неразличение оттенков значения, вносимых в слово приставкой и суффиксом — Мое отношение к этой проблеме не поменялось. Были приняты эффектные меры.
- Неразличение синонимичных слов — В конечном предложении автор применяет градацию.
- Употребление слов иной стилевой окраски — Автор, обращаясь к этой проблеме, пытается направить людей немного в другую колею.
- Неуместное употребление эмоционально-окрашенных слов и фразеологизмов — Астафьев то и дело прибегает к употреблению метафор и олицетворений.
- Неоправданное употребление просторечных слов — Таким людям всегда удается объегорить других.
- Нарушение лексической сочетаемости — Автор увеличивает впечатление. Автор использует художественные >особенности (вместо средства).
- Употребление лишних слов, в том числе плеоназм — Красоту пейзажа автор передает нам с помощью художественных приемов. Молодой юноша, очень прекрасный.
- Употребление однокоренных слов в близком контексте (тавтология) — В этом рассказе рассказывается о реальных событиях.
- Неоправданное повторение слова — Герой рассказа не задумывается над своим поступком. Герой даже не понимает всей глубины содеянного.
- Бедность и однообразие синтаксических конструкций — Когда писатель пришел в редакцию, его принял главный редактор. Когда они поговорили, писатель отправился в гостиницу.
- Неудачное употребление местоимений — Данный текст написал В. Белов. Он относится к художественному стилю. У меня сразу же возникла картина в своем воображении.
Это ошибки, связанные с употреблением глагола, глагольных форм, наречий, частиц:
- Ошибки в образовании личных форм глаголов: Им двигает чувство сострадания (следует: движет);
- Неправильное употребление видовременных форм глаголов: Эта книга дает знания об истории календаря, научит делать календарные расчеты быстро и точно (следует: …даст.., научит… или …дает.., учит…);
- Ошибки в употреблении действительных и страдательных причастий: Ручейки воды, стекаемые вниз, поразили автора текста (следует: стекавшие);
- Ошибки в образовании деепричастий: Вышев на сцену, певцы поклонились (норма: выйдя);
- Неправильное образование наречий: Автор тута был не прав (норма: тут);
Эти ошибки связаны обычно с нарушением закономерностей и правил грамматики и возникают под влиянием просторечия и диалектов.
К типичным можно отнести и грамматико-синтаксические ошибки:
- Нарушение связи между подлежащим и сказуемым: Главное, чему теперь я хочу уделить внимание, это художественной стороне произведения (норма: … это художественная сторона произведения); Чтобы приносить пользу Родине, нужно смелость, знания, честность (норма: … нужны смелость, знания, честность);
- Ошибки, связанные с употреблением частиц, например, неоправданный повтор: Хорошо было бы, если бы на картине стояла бы подпись художника; отрыв частицы от того компонента предложения, к которому она относится (обычно частицы ставятся перед теми членами предложения, которые они должны выделять, но эта закономерность часто нарушается в сочинениях): В тексте всего раскрываются две проблемы» (ограничительная частица «всего» должна стоять перед подлежащим: «… всего две проблемы»);
- Неоправданный пропуск подлежащего (эллипсис): Его храбрость, (?) постоять за честь и справедливость привлекают автора текста;
- Неправильное построение сложносочиненного предложения: Ум автор текста понимает не только как просвещенность, интеллигентность, но и с понятием «умный» связывалось представление о вольнодумстве.
Типичные речевые ошибки (К10)
Это нарушения, связанные с неразвитостью речи: плеоназм, тавтология, речевые штампы; немотивированное использование просторечной лексики, диалектизмов, жаргонизмов; неудачное использование экспрессивных средств, канцелярит, неразличение (смешение) паронимов; ошибки в употреблении омонимов, антонимов, синонимов; не устраненная контекстом многозначность.
К наиболее частотным речевым ошибкам относятся:
- Неразличение (смешение) паронимов: В таких случаях я взглядываю в «Философский словарь» (глагол взглянуть обычно требует управления существительным или местоимением с предлогом «на» («взглянуть на кого-нибудь или на что-нибудь»), а глагол заглянуть («быстро или украдкой посмотреть куда-нибудь, взглянуть с целью узнать, выяснить что-нибудь»), который необходимо употребить в приведённом предложении, управляет существительным или местоимением с предлогом «в»);
- Ошибки в выборе синонима: Имя этого поэта знакомо во многих странах (вместо слова известно в предложении ошибочно употреблен его синоним знакомо); Теперь в нашей печати отводится значительное пространство для рекламы, и это нам не импонирует (в данном случае вместо слова пространство лучше употребить его синоним – место; иноязычное слово импонирует также требует синонимической замены);
- Ошибки в подборе антонимов при построении антитезы: В третьей части текста веселый, а не мажорный мотив заставляет нас задуматься (антитеза требует точности при выборе слов с противоположными значениями, а слова«веселый» и «мажорный» антонимами не являются;
- Разрушение образной структуры фразеологизмов, что случается в неудачно организованном контексте: Этому, безусловно, талантливому писателю Зощенко палец в рот не клади, а дай только посмешить читателя.
Логические ошибки
Логические ошибки связаны с нарушением логической правильности речи. Они возникают в результате нарушения законов логики, допущенного как в пределах одного предложения, суждения, так и на уровне целого текста.
- сопоставление (противопоставление) двух логически неоднородных (различных по объему и по содержанию) понятий в предложении;
- в результате нарушения логического закона тождества, подмена одного суждения другим.
Композиционно-текстовые ошибки
- Неудачный зачин. Текст начинается предложением, содержащим указание на предыдущий контекст, который в самом тексте отсутствует, наличием указательных словоформ в первом предложении, например: В этом тексте автор…
- Ошибки в основной части.
- Сближение относительно далеких мыслей в одном предложении.
- Отсутствие последовательности в изложении; бессвязность и нарушение порядка предложений.
- Использование разнотипных по структуре предложений, ведущее к затруднению понимания смысла.
- Неудачная концовка. Дублирование вывода, неоправданное повторение высказанной ранее мысли.
Фактические ошибки
Фактические ошибки — разновидность неязыковых ошибок, заключающаяся в том, что пишущий приводит факты, противоречащие действительности, дает неправильную информацию о фактических обстоятельствах, как связанных, так и не связанных с анализируемым текстом (фоновые знания)
- Искажение содержания литературного произведения, неправильное толкование, неудачный выбор примеров.
- Неточность в цитате. Отсутствие указания на автора цитаты. Неверно названный автор цитаты.
- Незнание исторических и др. фактов, в том числе временное смещение.
- Неточности в именах, фамилиях, прозвищах литературных героев. Искажения в названиях литературных произведений, их жанров, ошибка в указании автора.
Орфографические, пунктуационные, графические ошибки
При проверке грамотности (К7-К8) учитываются ошибки
- На изученные правила;
- Негрубые (две негрубые считаются за одну):
- в исключениях из правил;
- в написании большой буквы в составных собственных наименованиях;
- в случаях раздельного и слитного написания не с прилагательными и причастиями,
- выступающими в роли сказуемого;
- в написании и и ы после приставок;
- в трудных случаях различения не и ни (Куда он только не обращался! Куда он ни обращался, никто не мог дать ему ответ. Никто иной не …; не кто иной, как…; ничто иное не …; не что иное, как … и др.);
- в случаях, когда вместо одного знака препинания поставлен другой;
- в пропуске одного из сочетающихся знаков препинания или в нарушении их последовательности;
Необходимо учитывать также повторяемость и однотипность ошибок. Если ошибка повторяется в одном и том же слове или в корне однокоренных слов, то она считается за одну ошибку.
- Однотипные (первые три однотипные ошибки считаются за одну ошибку, каждая следующая подобная ошибка учитывается как самостоятельная): ошибки на одно правило, если условия выбора правильного написания заключены в грамматических (в армии, в роще; колют, борются) и фонетических (пирожок, сверчок) особенностях данного слова. Важно!!!
- Понятие об однотипных ошибках не распространяется на пунктуационные ошибки.
- Не считаются однотипными ошибки на такое правило, в котором для выяснения
- Повторяющиеся (считается за одну ошибку повтор в одном и том же слове или в корне однокоренных слов)
| Орфографические ошибки |
|
| Пунктуационные ошибки |
|
| Графические ошибки |
Графические ошибки – различные приемы сокращения слов, использование пробелов между словами, различных подчеркиваний и шрифтовых выделений. К ним относятся: различные описки и опечатки, вызванные невнимательностью пишущего или поспешностью написания. Распространенные графические ошибки:
|
Смотри также:
- Критерии оценивания сочинения
- Решай задания и варианты ЕГЭ по русскому языку с ответами.
Классификация ошибок
Грамматические ошибки
Грамматическая ошибка – ошибка в структуре языковой единицы: словосочетания или предложения; нарушение какой-либо грамматической нормы – словообразовательной, морфологической, синтаксической и др.
|
№ п/п |
Вид ошибки |
Примеры |
|
1 |
Ошибочное словообразование |
Трудолюбимый, надсмехаться |
|
2 |
Ошибочное образование формы существительного |
Многие чуда техники, не хватает время |
|
3 |
Ошибочное образование формы прилагательного |
Более интереснее |
|
4 |
Ошибочное образование формы числительного |
С пятистами рублями |
|
5 |
Ошибочное образование формы местоимения |
Ихнего пафоса |
|
6 |
Ошибочное образование формы глагола |
Они хочут, пиша о жизни |
|
7 |
Нарушение согласования |
Я знаком с группой ребят, увлекающимися джазом |
|
8 |
Нарушение управления |
Повествует читателей. Нужно сделать свою природу более красивую. |
|
9 |
Нарушение связи между подлежащим и сказуемым |
|
|
10 |
Нарушение способа выражения сказуемого в отдельных конструкциях |
Он написал книгу, которая эпопея. Мы были рады, счастливы и веселые. |
|
11 |
Ошибки в построении предложения с однородными членами |
Страна любила и гордилась поэтом. |
|
12 |
Ошибки в построении предложения с деепричастным оборотом |
Читая текст, возникает такое чувство … |
|
13 |
Ошибки в построении предложения с причастным оборотом |
Узкая дорожка была покрыта проваливающимся снегом под ногами. |
|
14 |
Ошибки в построении сложного предложения |
Эта книга научила меня ценить и уважать друзей, которую я прочла еще в детстве. |
|
15 |
Смешение прямой и косвенной речи |
Автор сказал, что я не согласен с мнением рецензента. |
|
16 |
Нарушение границ предложения |
Когда герой опомнился. Было уже поздно. |
|
17 |
Нарушение видовременной соотнесенности глагольных форм |
Замирает на мгновение сердце и вдруг застучит вновь. |
|
18 |
Неудачное употребление местоимений |
Данный текст написал В.Белов. Он относится к художественному стилю. У меня сразу же возникла картина в своем воображении. |
Речевые ошибки
Речевая ошибка – ошибка в использовании языковых единиц, чаще всего в употреблении слова. Речевую ошибку можно обнаружить только в контексте.
|
№ п/п |
Вид ошибки |
Примеры |
|
1 |
Употребление слова в несвойственном ему значении |
Мы были шокированы прекрасной игрой актеров. Мысль развивается на продолжении всего текста. |
|
2 |
Неразличение оттенков значения, вносимых в слово приставкой и суффиксом |
Мое отношение к этой проблеме не поменялось. Были приняты эффектные меры. |
|
3 |
Неразличение синонимичных слов |
В конечном предложении автор употребляет градацию. |
|
4 |
Употребление слов иной стилевой окраски |
Автор, обращаясь к этой проблеме, пытается направить людей немного в другую колею. |
|
5 |
Неуместное употребление эмоционально-окрашенных слов и фразеологизмов |
Астафьев то и дело прибегает к употреблению метафор и олицетворений. |
|
6 |
Неоправданное употребление просторечных слов |
Таким людям всегда удается объегорить других. |
|
7 |
Нарушение лексической сочетаемости |
Автор увеличивает впечатление. Автор использует художественные особенности. |
|
8 |
Употребление лишних слов, в том числе плеоназм |
Молодой юноша, очень прекрасный |
|
9 |
Употребление рядом или близко однокоренных слов (тавтология) |
В этом рассказе рассказывается о реальных событиях. |
|
10 |
Неоправданное повторение слова |
Герой рассказа не задумывается под своим поступком. Герой даже не понимает всей глубины содеянного. |
|
11 |
Бедность и однообразие синтаксических конструкций |
Когда писатель пришел в редакцию, его принял главный редактор. Когда они поговорили, писатель отправился в гостиницу. |
Орфографические и пунктуационные ошибки
На оценку сочинения распространяются положения об однотипных и негрубых ошибках (см. Нормы оценки знаний, умений, навыков по русскому языку).
Среди ошибок выделяются негрубые, т.е. не имеющие существенного значения для характеристики грамотности. При подсчете ошибок две негрубые считаются за одну.
К негрубым ошибкам относятся:
— в исключениях из правил
— в написании большой буквы в составных собственных наименованиях
— в случаях раздельного и слитного написания НЕ с прилагательными и причастиями, выступающими в роли сказуемого
— в написании И и Ы после приставок
— в трудных случаях различения НЕ и НИ (Куда он только не обращался! Куда он ни обращался! Никто иной не… Не кто иной, как Не что иное, как и др)
— в случаях, когда вместо одного знака поставлен другой
— в пропуске одного из сочетающихся знаков препинания или в нарушении их последовательности
Необходимо учитывать повторяемость и однотипность ошибок. Если ошибка повторяется в одном и том же слове или в корне однокоренных слов, то она считается за одну ошибку.
Однотипными считаются ошибки на одно правило, если условия выбора заключены в грамматических (в армии, в роще; колют, борются) и фонетических (пирожок, сверчок) особенностях данного слова.
Не считаются однотипными ошибки на такое правило, в котором для выяснения правильного написания слова требуется подобрать другое (опорное) слово или его форму (вода – воды, грустить – грусть)
Первые три однотипные ошибки считаются за одну ошибку, каждая следующая подобная считается за самостоятельную. Если в одном непроверяемом слове допущены две и более ошибки, то все они считаются за одну ошибку.
Понятие об однотипных ошибках не распространяется на пунктуационные ошибки.
Ошибки графические (не учитывается при проверке) – разновидность ошибок, связанных с графикой, описки.
К числу наиболее распространенных относятся:
— пропуски букв
— перестановки букв
— замены одних буквенных знаков другими
— добавление лишних букв
Орфографические и пунктуационные ошибки,
не влияющие на оценку работы
Орфография
— в переносе слов
— буквы э/е после согласных в иноязычных словах (рэкет, пленэр) и после гласных в собственных именах (Мариетта)
— прописная /строчная буквы в названиях, связанных с религией (М(м)асленица, Р(р)ождество, Б(б)ог)
— прописная /строчная буквы в собственных именах нерусского происхождения; написание фамилий с первыми частями дон, Ван, сент .. (дон Педро и Дон Кихот)
— слитное/раздельное/дефисное написание сложных существительных без соединительной гласной (чаще всего заимствования), не регулируемые правилами и не входящие в словарь-минимум (ленд-лиз, ноу-хау, папье-маше, пресс-папье, перекати-поле, гуляй-город, но портшез, метрдотель)
— на правила, которые не включены в школьную программу (например, правило слитного / раздельного написания наречных единиц / наречий с приставкой / предлогом, например, в разлив, под стать, в бегах, в рассрочку, на попятную, на ощупь,на подхвате)
Пунктуация
— тире в неполном предложении
— обособление несогласованных определений, относящихся к нарицательным именам существительным
— запятые при ограничительно-выделительных оборотов
— различение омонимичных частиц и междометий и, соответственно, невыделение и выделение их запятыми
— в передаче авторской пунктуации
Этические ошибки
Соблюдение этических норм
Этическая ошибка выносится в случаях, когда в работе содержатся высказывания, унижающие человеческое достоинство, выражающие циничное отношение к человеческой личности, проявления речевой агрессии (речевая агрессия может быть внешне выражена, может быть скрытой).
Речевая агрессия связана с словесным выражением негативных эмоций, чувств, намерений в неприемлемой в данной речевой ситуации форме: оскорбление, угроза, грубое требование, обвинение, насмешка, употребление бранных слов, жаргонизмов и др.
Например: «Этот текст меня бесит», «Судя по тому, что говорит автор, он маньяк», «Михалков в своем репертуаре! Пишет детские книги, поэтому и требует, чтобы читали именно в детстве. Это настоящий пиар! Нечего морочить людям мозги устаревшими истинами»
Наши курсы призваны помочь школьникам успешно подготовиться к ЕГЭ и стать студентами медицинских вузов. Мы предлагаем глубокие знания как для подготовки к профильным ЕГЭ по химии и биологии, так и к ЕГЭ по русскому языку.
В этой статье познакомимся с классификацией типичных ошибок в русском языке и разберем их на конкретных примерах.
Классификация ошибок по ФИПИ
Составители КИМов ЕГЭ по русскому языку предлагают следующую классификацию, которая используется при проверке письменного задания. Итак, типичные ошибки подразделяются на:
-
Грамматические
-
Речевые
-
Логические
-
Фактические
-
Орфографические, пунктуационные и графические
Рассмотрим каждый вид подробнее.
Виды грамматических ошибок
Грамматические ошибки заключаются в неправильном образовании слов и их грамматических форм, в нарушении синтаксической связи между словами в словосочетании и предложении.
Ознакомимся с типичными грамматическими ошибками в русском языке.
-
Ошибочное словообразование
Подскользнуться (нужно писать поскользнуться).
-
Неправильное образование формы существительного
Многочисленные договора (нужно: многочисленные договоры).
-
Неверное образование формы прилагательного
Не более громче, а более громкий, не самый старейший, а самый старый
-
Неправильное образование формы числительного
Около пятиста участников вместо пятисот участников
-
Неверное образование формы местоимения
Ихний сын (правильно: их сын).
-
Неправильное образование форм глаголов, причастий, деепричастий
Махает (правильно: машет)
Скакающий (верно: скачущий),
Положа трубку вместо положив
-
Нарушение согласования
Он восхищается студентами, напролом идущих к своей цели (правильно: студентами, идущими к своей цели).
-
Нарушение управления
Анна Александровна не поздравила с день рожденья.
(правильно: не поздравила с днём рождения).
-
Нарушение связи между подлежащим и сказуемым
Все, кто советуют не пользоваться гаджетами перед сном, обычно сами пренебрегают этим правилом (правильно: кто советует).
-
Ошибочное построение предложений с причастным и деепричастным оборотами
Классический пример: Подъезжая к станции, у меня слетела шляпа.
-
Смешение прямой и косвенной речи
Директор заявил, что я накажу виновных.
(Правильно: директор заявил, что он накажет виновных).
-
Нарушение границ предложения
Аня, наверное, испугалась. Потому что вздрогнула и обернулась (необходимо оформить как сложноподчиненное предложение).
Виды речевых ошибок
Речевая ошибка – это нарушение в структуре употребления и сочетаемости слов.
Постарайтесь запомнить типичные речевые ошибки в русском языке и не употреблять их в своих высказываниях.
-
Употребление слова в не подходящем для него значении
Благодаря землетрясению, были разрушены сотни жилых домов (следовало употребить предлог из-за).
-
Плеоназм
Он откликается на всесвободные вакансии (слово вакансия означает свободное рабочее место).
-
Тавтология
В своем рассказе автор рассказывает о событиях прошлого лета.
-
Неудачное употребление местоимений
Лена очень любила свою подругу. Она была очень доброй и заботливой.
-
Неправильное употребление паронимов
В решении этого вопроса были приняты эффектные меры (следует употребить эффективные меры).
-
Нарушение лексической сочетаемости
Евгений постоянно пополняет свой кругозор. Работа занимает важную роль в его жизни (правильно: кругозор расширяют; занимает важное место либо играет важную роль).
-
Неоправданное употребление просторечий, жаргонизмов
Автор не ожидал такого кринжа.
Логические ошибки – это высказывания, в которых есть внутреннее противоречие, нарушение логики изложения мысли. Такие ошибки тоже не редко встречаются в работах ЕГЭ по русскому языку.
-
Подмена понятий
Автор поднимает проблему патриотизма. Эта тема очень важна в наше время (тема и проблема – далеко не одно и то же).
-
Нарушение причинно-следственных связей
Вскоре она перестала плакать, так как успокоилась.
-
Отсутствие связи между высказываниями
Автор задумывается о роли воспитания в жизни ребенка. И действительно, детям нужно заботиться о животных, чтобы привить чувство ответственности.
Фактические ошибки
Фактическая ошибка – это искажение информации о событиях и лицах, упоминаемых в тексте сочинения.
-
Искажение фактов, содержащихся в тексте.
Автор с упоением отзывается о писателе А. Эйнштейне.
-
Неверное упоминание фактов биографии автора или героя текста, даты, фамилии, цитаты.
Все смешалось в доме Обломовых.
Орфографические, графические, пунктуационные ошибки
Орфографическая ошибка – это неправильное написание слова. К типичным орфографическим ошибкам в русском языке относятся:
-
Правописание букв в слабой позиции перехот(переход)
-
Нарушения в переносе слов рад-ость
-
Слитное или раздельное написание слов какбудто, не чем (как будто, нечем)
-
Правописание чередующихся корней умерать (умирать)
-
Правописание словарных слов. Например, поменяться кординально (кардинально)
Совет: если вы сомневаетесь в написании слова, не используйте его, а замените синонимом, в написании которого вы уверены.
Графические ошибки – это перестановка (полувер) либо пропуск букв (рассморение), а иногда добавление лишних букв (дажбе). Чаще всего эти недочёты связаны с невнимательностью пишущего либо с торопливостью.
Пунктуационные ошибки связаны с неправильной постановкой знаков препинания, неверного их выбора (запятая на месте тире).
К типичным ошибкам в ЕГЭ по русскому языку, связанным с пунктуацией, относятся:
-
неверное оформление прямой речи на письме,
-
невыделение уточняющих слов, причастных и деепричастных оборотов.
Хотя наиболее частыми являются именно грамматические ошибки в ЕГЭ по русскому языку, обратите внимание и на все остальные.
Совет: найдите в интернете текст с ошибками и отредактируйте его, выделив в нем все виды ошибок. Такое упражнение поможет вам стать грамотнее и прибавит чувство уверенности при написании сочинения на ЕГЭ.
А если ваша подготовка к ЕГЭ зашла в тупик и вы не знаете, с чего начать, либо у вас остались вопросы, то скорее записывайтесь на наши курсы!
Речь – это канал развития интеллекта,
чем раньше будет усвоен язык,
тем легче и полнее будут усваиваться знания.
Николай Иванович Жинкин,
советский лингвист и психолог
Речь мыслится нами как абстрактная категория, недоступная для непосредственного восприятия. А между тем это – важнейший показатель культуры человека, его интеллекта и мышления, способ познания сложных связей природы, вещей, общества и передачи этой информации путём коммуникации.
Очевидно, что и обучаясь, и уже пользуясь чем-либо, мы в силу неумения или незнания совершаем ошибки. И речь, как и другие виды деятельности человека (в которых язык – важная составляющая часть), в данном отношении не является исключением. Ошибки делают все люди, как в письменной, так и в устной речи. Более того, понятие культуры речи, как представление о «речевом идеале», неразрывно связано с понятием речевой ошибки. По сути это – части одного процесса, а, значит, стремясь к совершенству, мы должны уметь распознавать речевые ошибки и искоренять их.
Что такое ошибки в языке? Зачем говорить грамотно?
Сто лет назад человек считался грамотным, если он умел писать и читать на родном языке. Сейчас грамотным называют того, кто не только читает и говорит, но и пишет в соответствии с правилами языка, которые нам дают филологи и система образования. В устаревшем смысле мы все грамотные. Но далеко не все из нас всегда правильно ставят знаки препинания или пишут трудные слова.
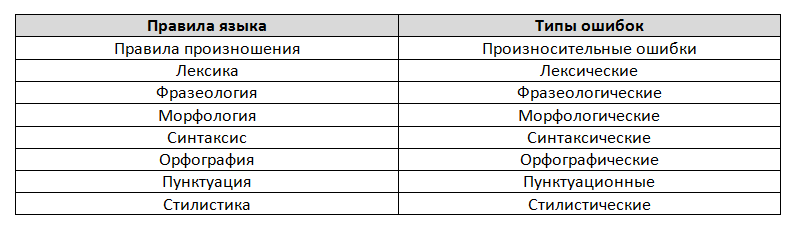
Виды речевых ошибок
Сначала разберёмся с тем, что такое речевые ошибки. Речевые ошибки – это любые случаи отклонения от действующих языковых норм. Без их знания человек может нормально жить, работать и настраивать коммуникацию с другими. Но вот эффективность совершаемых действий в определённых случаях может страдать. В связи с этим возникает риск быть недопонятым или понятым превратно. А в ситуациях, когда от этого зависит наш личный успех, подобное недопустимо.
Автором приведённой ниже классификации речевых ошибок является доктор филологических наук Ю. В. Фоменко. Его деление, по нашему мнению, наиболее простое, лишённое академической вычурности и, как следствие, понятное даже тем, кто не имеет специального образования.
Виды речевых ошибок:
Примеры и причины возникновения речевых ошибок
С. Н. Цейтлин пишет: «В качестве фактора, способствующего возникновению речевых ошибок, выступает сложность механизма порождения речи». Давайте рассмотрим частные случаи, опираясь на предложенную выше классификацию видов речевых ошибок.
Произносительные ошибки
Произносительные или орфоэпические ошибки возникают в результате нарушения правил орфоэпии. Другими словами, причина кроется в неправильном произношении звуков, звукосочетаний, отдельных грамматических конструкций и заимствованных слов. К ним также относятся акцентологические ошибки – нарушение норм ударения. Примеры:
Произношение: «конечно» (а не «конешно»), «пошти» («почти»), «плотит» («платит»), «прецендент» («прецедент»), «иликтрический» («электрический»), «колидор» («коридор»), «лаболатория» («лаборатория»), «тыща» («тысяча»), «щас» («сейчас»).
Неправильное ударение: «зво́нит», «диа́лог», «до́говор», «ката́лог», «путепро́вод», «а́лкоголь», «свекла́», «феноме́н», «шо́фер», «э́ксперт».
Лексические ошибки
Лексические ошибки – нарушение правил лексики, прежде всего – употребление слов в несвойственных им значениях, искажение морфемной формы слов и правил смыслового согласования. Они бывают нескольких видов.
Употребление слова в несвойственном ему значении. Это самая распространённая лексическая речевая ошибка. В рамках этого типа выделяют три подтипа:
- Смешение слов, близких по значению: «Он обратно прочитал книжку».
- Смешение слов, близких по звучанию: экскаватор – эскалатор, колос – колосс, индианка – индейка, одинарный – ординарный.
- Смешение слов, близких по значению и звучанию: абонент – абонемент, адресат – адресант, дипломат – дипломант, сытый – сытный, невежа – невежда. «Касса для командировочных» (нужно – командированных).
Словосочинительство. Примеры ошибок: грузинец, героичество, подпольцы, мотовщик.
Нарушение правил смыслового согласования слов. Смысловое согласование – это взаимное приспособление слов по линии их вещественных значений. Например, нельзя сказать: «Я поднимаю этот тост», поскольку «поднимать» значит «перемещать», что не согласовывается с пожеланием. «Через приоткрытую настежь дверь», – речевая ошибка, потому что дверь не может быть и приоткрыта (открыта немного), и настежь (широко распахнута) одновременно.
Сюда же относятся плеоназмы и тавтологии. Плеоназм – словосочетание, в котором значение одного компонента целиком входит в значение другого. Примеры: «май месяц», «маршрут движения», «адрес местожительства», «огромный мегаполис», «успеть вовремя». Тавтология – словосочетание, члены которого имеют один корень: «Задали задание», «Организатором выступила одна общественная организация», «Желаю долгого творческого долголетия».
Фразеологические ошибки
Фразеологические ошибки возникают, когда искажается форма фразеологизмов или они употребляются в несвойственном им значении. Ю. В. Фоменко выделяет 7 разновидностей:
- Изменение лексического состава фразеологизма: «Пока суть да дело» вместо «Пока суд да дело»;
- Усечение фразеологизма: «Ему было впору биться об стенку» (фразеологизм: «биться головой об стенку»);
- Расширение лексического состава фразеологизма: «Вы обратились не по правильному адресу» (фразеологизм: обратиться по адресу);
- Искажение грамматической формы фразеологизма: «Терпеть не могу сидеть сложив руки». Правильно: «сложа»;
- Контаминация (объединение) фразеологизмов: «Нельзя же все делать сложа рукава» (объединение фразеологизмов «спустя рукава» и «сложа руки»);
- Сочетание плеоназма и фразеологизма: «Случайная шальная пуля»;
- Употребление фразеологизма в несвойственном значении: «Сегодня мы будем говорить о фильме от корки до корки».
Морфологические ошибки
Морфологические ошибки – неправильное образование форм слова. Примеры таких речевых ошибок: «плацкарт», «туфель», «полотенцев», «дешевше», «в полуторастах километрах».
Синтаксические ошибки
Синтаксические ошибки связаны с нарушением правил синтаксиса – конструирования предложений, правил сочетания слов. Их разновидностей очень много, поэтому приведём лишь некоторые примеры.
- Неправильное согласование: «В шкафу стоят много книг»;
- Неправильное управление: «Оплачивайте за проезд»;
- Синтаксическая двузначность: «Чтение Маяковского произвело сильное впечатление» (читал Маяковский или читали произведения Маяковского?);
- Смещение конструкции: «Первое, о чём я вас прошу, – это о внимании». Правильно: «Первое, о чём я вас прошу, – это внимание»;
- Лишнее соотносительное слово в главном предложении: «Мы смотрели на те звёзды, которые усеяли всё небо».
Орфографические ошибки
Этот вид ошибок возникает из-за незнания правил написания, переноса, сокращения слов. Характерен для письменной речи. Например: «сабака лаяла», «сидеть на стули», «приехать на вогзал», «русск. язык», «грамм. ошибка».
Пунктуационные ошибки
Пунктуационные ошибки – неправильное употребление знаков препинания при письме.
Стилистические ошибки
Этой теме мы посвятили отдельный материал.
Пути исправления и предупреждения речевых ошибок
Как предупредить речевые ошибки? Работа над своей речью должна включать:
- Чтение художественной литературы.
- Посещение театров, музеев, выставок.
- Общение с образованными людьми.
- Постоянная работа над совершенствованием культуры речи.
Онлайн-курс «Русский язык»
Речевые ошибки – одна из самых проблемных тем, которой уделяется мало внимания в школе. Тем русского языка, в которых люди чаще всего допускают ошибки, не так уж много — примерно 20. Именно данным темам мы решили посвятить курс «Русский язык». На занятиях вы получите возможность отработать навык грамотного письма по специальной системе многократных распределенных повторений материала через простые упражнения и специальные техники запоминания.
Подробнее Купить сейчас
Источники
- Беззубов А. Н. Введение в литературное редактирование. – Санкт-Петербург, 1997.
- Савко И. Э. Основные речевые и грамматические ошибки
- Сергеева Н. М. Ошибки речевые, грамматические, этические, фактологические…
- Фоменко Ю. В. Типы речевых ошибок. – Новосибирск: НГПУ, 1994.
- Цейтлин С. Н. Речевые ошибки и их предупреждение. – М.: Просвещение, 1982.
Отзывы и комментарии
А теперь вы можете потренироваться и найти речевые ошибки в данной статье или поделиться другими известными вам примерами. Кроме того, обратите внимание на наш курс по развитию грамотности.
В латыни есть слово lapsus. Оно обозначает ошибку в речи человека. От этого слова появилось всем известное сокращение ляп. Только если ляп считают грубым нарушением норм речи, то lapsus имеет не настолько строгое значение. К сожалению, аналога этого слова, которое обозначает речевые ошибки, в современном русском языке нет. Но lapsus встречаются повсеместно.
Содержание
- Типы речевых ошибок
- Виды нормативных ошибок
- Орфоэпическая ошибка
- Морфологическая ошибка
- Орфографическая ошибка
- Синтаксически-пунктуационные ошибки
- Стилистические ошибки
- Лексические речевые ошибки
Типы речевых ошибок
Речевые ошибки подразделяются на нормативные ошибки и опечатки. Опечатками называют механические ошибки. В тексте слово может быть написано неверно, что усложнит восприятие информации. Или же вместо одного слова случайно используют другое. Опечатки встречаются и в устной речи. Это оговорки, которые можно услышать от людей каждый день.
Механические ошибки происходят неосознанно, но от них многое зависит. Ошибки в написании цифр создают искажение фактической информации. А неправильное написание слов может полностью изменить смысл сказанного. Хорошо демонстрирует проблему опечаток одна сцена из фильма «Александр и ужасный, кошмарный, нехороший, очень плохой день» режиссера Мигеля Артета. В типографии перепутали буквы «п» и «с» и в детской книжке написали вместо «Можно прыгнуть на кровать» фразу «Можно срыгнуть на кровать». И по сюжету кинокартины эта ситуация вылилась в скандал.
Особое внимание уделяли опечаткам во времена сталинских репрессий, когда неверно написанное слово стоило человеку жизни. Искоренить проблему опечаток, невозможно, так как человек делает их неосознанно. Единственный способ, при помощи которого вы избежите этого типа речевых ошибок, быть внимательным при написании текста, тщательно подбирать слова, которые вы произнесете.
Виды нормативных ошибок
Речевые ошибки связаны с нарушением норм русского языка. Виды речевых ошибок:
- орфоэпические;
- морфологические;
- орфографические;
- синтаксически-пунктуационные;
- стилистические;
- лексические.
Орфоэпическая ошибка
Произносительная ошибка связана с нарушением норм орфоэпии. Она проявляется только в устной речи. Это ошибочное произношение звуков, слов или же словосочетаний. Также к ошибкам в произношении относят неправильное ударение.
Искажение слов происходит в сторону сокращения количества букв. К примеру, когда вместо «тысяча» произносится слово «тыща». Если вы хотите говорить грамотно и красиво, стоит избавить речь от подобных слов. Распространено также ошибочное произношение слова «конечно» — «конешно».
Произносить правильное ударение не только правильно, но и модно. Наверняка вы слышали, как люди поправляют неправильное ударение в словах «Алкоголь», «звОнит», «дОговор» на верные – «алкогОль», «звонИт» и «договОр». Неправильная постановка ударения в последнее время заметнее, чем раньше. И мнение о вашей эрудиции зависит от соблюдения норм произношения.
Морфологическая ошибка
Морфологией называют раздел лингвистики, в котором объектом изучения являются слова и их части. Морфологические ошибки получаются из-за неправильного образования форм слов различных частей речи. Причинами являются неправильное склонение, ошибки в употреблении рода и числа.
К примеру, «докторы» вместо «доктора». Это морфологическая ошибка в употреблении множественного числа.
Часто употребляют неверную форму слова при изменении падежа. Родительный падеж слова яблоки – яблок. Иногда вместо этого слова употребляют неверную форму «яблоков».
Распространенные морфологические ошибки – неверное написание числительных:
«Компания владела пятьюстами пятьдесят тремя филиалами». В этом примере слово «пятьдесят» не склонили. Верное написание: «Компания владела пятьюстами пятьюдесятью тремя филиалами».
В употреблении прилагательных распространена ошибка неверного употребления сравнительной степени. К примеру, такое использование: «более красивее» вместо «более красивый». Или же «самый высочайший» вместо «самого высокого» или «высочайшего».
Орфографическая ошибка
Орфографические ошибки – это неправильное написание слов. Они возникают тогда, когда человек не знает правильного написания слова. Вы получали когда-либо сообщение, где находили грамматические ошибки. Распространенный пример: написание слова «извини» через «е». Чтобы с вами не случалось подобных орфографических ошибок, как можно больше читайте. Чтение стимулирует восприятие правильного написания слов. И если вы привыкли читать правильно написанный текст, то и писать вы будете, не делая грамматические ошибки.
Орфографические ошибки, в принципе, случаются из-за незнания правильности слов. Поэтому если вы не уверены в написанном слове, стоит обратиться к словарю. На работе узнавайте тот перечень специфических для вашей области слов, который нужно запомнить и в котором ни в коем случае нельзя совершать грамматические ошибки.
Синтаксически-пунктуационные ошибки
Эти виды речевых ошибок возникают при неправильной постановке знаков препинания и неверном соединении слов в словосочетаниях и предложениях.
Пропуск тире, лишние запятые – это относится к ошибкам пунктуации. Не поленитесь открыть учебник, если вы не уверены в постановке запятой. Опять же, это та проблема, с которой можно справиться, читая много книг. Вы привыкаете к правильной постановке знаков препинания и уже на интуитивном уровне вам сложно совершить ошибку.
Нарушение правил синтаксиса встречается часто. Распространены ошибки в согласовании. «Человеку для счастья нужно любимое место для отдыха, работа, счастливая семья». Слово «нужно» в этом предложении не подходит при перечислении. Необходимо употребить «нужны».
Профессиональные редакторы считают, что часто встречается ошибка в управлении. Когда слово заменяется на синоним или же похожее слово, но управление с новым словом не согласуется.
Пример ошибки в управлении: «Они хвалили и приносили поздравления Алине за победу».
Они хвалили Алину. Они приносили поздравления Алине. Части предложения не согласуются из-за неправильного управления. После «хвалили» необходимо добавить слово «ее», чтобы исправить ошибку.
Стилистические ошибки
В отличие от других видов ошибок, стилистические основываются на искажении смысла текста. Классификация основных стилистических речевых ошибок:
- Плеоназм. Явление встречается часто. Плеоназм — это избыточное выражение. Автор выражает мысль, дополняя ее и так всем понятными сведениями. К примеру, «прошла минута времени», «он сказал истинную правду», «за пассажиром следил секретный шпион». Минута – это единица времени. Правда – это истина. А шпион в любом случае является секретным агентом.
- Клише. Это устоявшиеся словосочетания, которые очень часто используются. Клише нельзя полностью отнести к речевым ошибкам. Иногда их употребление уместно. Но если они часто встречаются в тексте или же клише разговорного стиля используется в деловом – это серьезная речевая ошибка. К клише относят выражения «одержать победу», «золотая осень», «подавляющее большинство».
- Тавтология. Ошибка, в которой часто повторяются одни и те же либо однокоренные слова. В одном предложении одно и тоже слово не должно повторяться. Желательно исключить повторения в смежных предложениях.
Предложения, в которых допущена эта ошибка: «Он улыбнулся, его улыбка наполнила помещение светом», «Катя покраснела от красного вина», «Петя любил ходить на рыбалку и ловить рыбу».
- Нарушение порядка слов. В английском языке порядок слов намного строже, чем в русском. Он отличается четким построением частей предложения в определенной последовательности. В русском языке можно менять местами словосочетания так, как вам бы хотелось. Но при этом важно не потерять смысл высказывания.
Для того, чтобы этого не случилось, руководствуйтесь двумя правилами:
- Порядок слов в предложении может быть прямым и обратным в зависимости от подлежащего и сказуемого.
- Второстепенные члены предложения должны согласоваться с теми словами, от которых они зависят.
Лексические речевые ошибки
Лексика – это словарный запас языка. Ошибки возникают тогда, когда вы пишите либо говорите о том, в чем не разбираетесь. Чаще ошибки в значениях слов происходят по нескольким причинам:
- Слово устарело и редко используется в современном русском языке.
- Слово относится к узкоспециализированной лексике.
- Слово является неологизмом и его значение не распространено.
Классификация лексических речевых ошибок:
- Ложная синонимия. Человек считает синонимами несколько слов, которые ими не являются. Например, авторитет не есть популярность, а особенности не являются различиями. Примеры, где допущена ошибка: «Певица была авторитетом среди молодежи» вместо «Певица была популярной среди молодежи». «У брата и сестры было много особенностей в характерах» вместо «У брата и сестры было много различий в характерах».
- Употребление похожих по звучанию слов. Например, употребление слова «одинарный», когда необходимо сказать «ординарный». Вместо слова «индианка» могут написать ошибочное «индейка».
- Путаница в близких по значению словах. «Интервьюер» и «Интервьюируемый», «Абонент» и «Абонемент», «Адресат» и «Адресант».
- Непреднамеренное образование новых слов.
Допустить речевую ошибку просто. Иногда это получается в случае оговорки, а иной раз проблема заключается в незнании какой-либо нормы русского языка либо из-за путаницы значений слов. Читайте много книг, правильно говорить и не стесняйтесь лишний раз обратиться к словарю или учебнику. Постоянно работайте над устной и письменной речью, чтобы количество ошибок было приближено к нулю.
Рекомендации по квалификации ошибок при проверке итоговых сочинений (изложений)
При проверке сочинения (изложения) учитываются следующие виды ошибок:
- несоответствие содержания сочинения теме или подмена темы;
- фактические ошибки, связанные с отсутствием у пишущего достоверной информации по обсуждаемой теме, незнанием (или слабым знанием) текстов художественных произведений, историко-литературного и культурно-исторического контекста, неверным или неточным использованием терминов и понятий;
- логические ошибки, связанные с нарушением законов логики как в пределах одного предложения, суждения, так и в пределах целого текста, например: сопоставление (противопоставление) различных по объему и содержанию понятий, использование взаимоисключающих понятий, подмена одного суждения другим, необоснованное противопоставление, установление неверных причинно-следственных связей, несоответствие аргументации заявленному тезису; неправильное формирование контраргументов; отсутствие связи между сформулированной проблемой и высказанным мнением в связи с обозначенной в сочинении проблемой; неиспользование или неправильное использование средств логической связи, неправильное деление текста на абзацы;
- речевые (в том числе стилистические) ошибки, нарушение стилевого единства текста;
- грамматические ошибки;
- орфографические и пунктуационные ошибки;
- несоблюдение требуемого объема.
на сайте
Предлагаемый ниже материал не носит исчерпывающего характера, но может помочь учителю квалифицировать наиболее типичные ошибки, допускаемые выпускниками в сочинениях (изложениях).
Ошибки, связанные с содержанием и логикой работы выпуфильмы онлайнскника
Фактические ошибки
Нарушение требования достоверности в передаче фактического материала вызывает фактические ошибки, представляющие собой искажение изображаемой в высказывании ситуации или отдельных ее деталей.
Выделяются две категории фактических ошибок.
1. Фактические ошибки, связанные с привлечением литературного материала (искажение историко-литературных фактов, неверное именование героев, неправильное обозначение времени и места события; ошибки в передаче последовательности действий, в установлении причин и следствий событий и т. п.); неверное указание даты жизни писателя или времени создания художественного произведения, неверные обозначения топонимов, ошибки в употреблении терминологии, неправильно названные жанры, литературные течения и направления и т. д.
2. Ошибки в фоновом материале – различного рода искажения фактов, не связанных с литературным материалом.
Фактические ошибки можно разделить на грубые и негрубые. Если экзаменуемый утверждает, что автором «Евгения Онегина» является Лермонтов, или называет Татьяну Ларину Ольгой – это грубые фактические ошибки. Если же вместо «Княжна Мери», выпускник написал «Княжна Мэри», то эта ошибка может оцениваться экспертом как фактическая неточность или описка и не учитываться при оценивании работы.
Логические ошибки
Логическая ошибка – нарушение правил или законов логики, признак формальной несостоятельности определений, рассуждений, доказательств и выводов. Логические ошибки включают широкий спектр нарушений в построении развернутого монологического высказывания на заданную тему, начиная с отступлений от темы, пропуска необходимых частей работы, отсутствия связи между частями и заканчивая отдельными логическими несообразностями в толковании фактов и явлений. К характерным логическим ошибкам экзаменуемых относятся:
1) нарушение последовательности высказывания;
2) отсутствие связи между частями высказывания;
3) неоправданное повторение высказанной ранее мысли;
4) раздробление микротемы другой микротемой;
5) несоразмерность частей высказывания;
6) отсутствие необходимых частей высказывания и т. п.;
7) нарушение причинно-следственных связей;
нарушение логико-композиционной структуры текста.
Текст представляет собой группу тесно взаимосвязанных по смыслу и грамматически предложений, раскрывающих одну микротему. Текст имеет, как правило, следующую логико-композиционную структуру: зачин (начало мысли, формулировка темы), средняя часть (развитие мысли, темы) и концовка (подведение итога). Следует отметить, что данная композиция является характерной, типовой, но не обязательной. В зависимости от структуры произведения или его фрагментов возможны тексты без какого-либо из этих компонентов. Текст, в отличие от единичного предложения, имеет гибкую структуру, поэтому при его построении есть некоторая свобода выбора форм. Однако она не беспредельна. При написании сочинения необходимо логично и аргументированно строить монологическое высказывание, делать обобщения.
Примеры логических ошибок в разных частях текста
Неудачный зачин
Текст начинается предложением, содержащим указание на предыдущий контекст, который в самом тексте отсутствует, например: С особенной силой этот эпизод описан в романе… Наличие указательных словоформ в данных предложениях отсылает к предшествующему тексту, таким образом, сами предложения не могут служить началом сочинения.
Ошибки в средней части
1. В одном предложении сближаются относительно далекие мысли, например: Большую, страстную любовь она проявляла к сыну Митрофанушке и исполняла все его прихоти. Она всячески издевалась над крепостными, как мать она заботилась о его воспитании и образовании.
2. Отсутствует последовательность в мыслях, нарушен порядок предложений, что приводит к бессвязности, например: Из Митрофанушки Простакова воспитала невежественного грубияна. Комедия «Недоросль» имеет большое значение в наши дни. В комедии Простакова является отрицательным типом. Или: В своем произведении «Недоросль» Фонвизин показывает помещицу Простакову, ее брата Скотинина и крепостных. Простакова – властная и жестокая помещица. Ее имение взято в опеку.
3. Использованы разнотипные по структуре предложения, что ведет к затруднению понимания смысла, например: Общее поднятие местности над уровнем моря обусловливает суровость и резкость климата. Холодные, малоснежные зимы, сменяющиеся жарким летом. Весна коротка с быстрым переходом к лету. Правильный вариант: Общее поднятие местности над уровнем моря обусловливает суровость и резкость климата. Холодные, малоснежные зимы сменяются короткой весной, быстро переходящей в жаркое лето.
4. Экзаменуемый не различает причину и следствие, часть и целое, смежные явления и другие отношения, например: Так как Обломов – человек ленивый, у него был Захар – его слуга.
Неудачная концовка
Вывод продублирован: Итак, Простакова горячо и страстно любит сына, но своей любовью вредит ему. Таким образом, Простакова своей слепой любовью воспитывает в Митрофанушке лень, распущенность и бессердечие.
Ошибки, связанные с нарушением речевых, грамматических,
орфографических и пунктуационных норм
При проверке и оценке итогового сочинения (изложения) учитывается грамотность выпускника. Приведенный ниже материал поможет при квалификации разных типов ошибок.
Речевые ошибки
Речевая (в том числе стилистическая) ошибка – это ошибка не в построении, не в структуре языковой единицы, а в ее использовании, чаще всего в употреблении слова. По преимуществу это нарушения лексических норм, например: Штольц – один из главных героев одноименного романа Гончарова «Обломов»; Они потеряли на войне двух единственных сыновей. Само по себе слово одноименный (или единственный) ошибки не содержит, оно лишь неудачно употреблено, не «вписывается» в контекст, не сочетается по смыслу со своим ближайшим окружением.
К речевым (в том числе стилистическим) ошибкам следует относить:
1) употребление слова в несвойственном ему значении;
2) употребление иностилевых слов и выражений;
3) неуместное использование экспрессивных, эмоционально окрашенных средств;
4) немотивированное применение диалектных и просторечных слов и выражений;
5) смешение лексики разных исторических эпох;
6) нарушение лексической сочетаемости (слова в русском языке сочетаются друг с другом в зависимости от их смысла; от традиций употребления, вызванных языковой практикой (слова с ограниченной сочетаемостью);
7) употребление лишнего слова (плеоназм);
повторение или двойное употребление в словесном тексте близких по смыслу синонимов без оправданной необходимости (тавтология);9) необоснованный пропуск слова;
10) бедность и однообразие синтаксических конструкций;
11) порядок слов, приводящий к неоднозначному пониманию предложения.
Разграничение видов речевых (в том числе стилистических) ошибок особенно важно при оценивании работ отличного и хорошего уровня. В то же время следует помнить, что соблюдение единства стиля – самое высокое достижение пишущего. Поэтому отдельные стилистические погрешности, допущенные школьниками, предлагается считать стилистическими недочетами. Речевые ошибки следует отличать от ошибок грамматических (об этом см. далее).
Проведенная апробация выявила следующие речевые ошибки: нарушения, связанные с неразвитостью речи: плеоназм, тавтология, речевые штампы, немотивированное использование просторечной лексики, диалектизмов, жаргонизмов; неудачное использование экспрессивных средств, канцелярит, неразличение (смешение) паронимов, ошибки в употреблении омонимов, антонимов, синонимов, не устраненная контекстом многозначность.
К наиболее частотным ошибкам относятся следующие:
1. Неразличение (смешение) паронимов: Хищное (вместо хищническое) истребление лесов привело к образованию оврагов; В конце собрания слово представили (вместо предоставили) известному ученому; В таких случаях я взглядываю в «Философский словарь» (глагол взглянуть обычно имеет при себе дополнение с предлогом на: взглянуть на кого-нибудь или на что-нибудь, а глагол заглянуть, который необходимо употребить в этом предложении, имеет дополнение с предлогом в).
2. Ошибки в выборе синонима: Имя этого поэта знакомо во многих странах (вместо слова известно в предложении ошибочно употреблен его синоним знакомо); Теперь в нашей печати отводится значительное пространство для рекламы, и это нам не импонирует (в данном случае вместо слова пространство лучше употребить его синоним место; иноязычное слово импонирует также требует синонимической замены).
3. Ошибки при употреблении антонимов в построении антитезы: В третьей части текста не веселый, но и не мажорный мотив заставляет нас задуматься (антитеза требует четкости и точности в сопоставлении контрастных слов, а не веселый и мажорный не являются даже контекстуальными антонимами, поскольку не выражают разнополярных проявлений одного и того же признака).
4. Нарушение лексической сочетаемости: В этом книжном магазине очень дешевые цены; Леонид вперед меня выполнил задание; Узнав об аварии, начальник скоропостижно прибыл на объект.
Грамматические ошибки
Грамматическая ошибка – это ошибка в структуре языковой единицы: в структуре слова, словосочетания или предложения; это нарушение какой-либо грамматической нормы – словообразовательной, морфологической, синтаксической. Для обнаружения грамматической ошибки не нужен контекст, и в этом ее отличие от ошибки речевой, которая выявляется в контексте. Не следует также смешивать ошибки грамматические и орфографические.
Грамматические ошибки состоят в ошибочном словообразовании, ошибочном образовании форм частей речи, в нарушении согласования, управления, видовременной соотнесенности глагольных форм, в нарушении связи между подлежащим и сказуемым, ошибочном построении предложения с деепричастным или причастным оборотом, однородными членами, а также сложных предложений, в смешении прямой и косвенной речи в нарушении границ предложения. Например:
– подскользнуться вместо поскользнуться, благородность вместо благородство (здесь допущена ошибка в словообразовательной структуре слова, использована не та приставка или не тот суффикс);
– без комментарий вместо без комментариев, едь вместо поезжай, более легче (неправильно образована форма слова, т.е. нарушена морфологическая норма);
– заплатить за квартплату, удостоен наградой (нарушена структура словосочетания: не соблюдаются нормы управления);
– Покатавшись на катке, болят ноги; В сочинении я хотел показать значение спорта и почему я его люблю (неправильно построены предложения с деепричастным оборотом (1) и с однородными членами (2), т.е. нарушены синтаксические нормы).
Одними из наиболее типичных грамматических ошибок являются ошибки, связанные с употреблением глагольных форм, наречий, частиц:
1) ошибки в образовании личных форм глаголов: Им двигает чувство сострадания (норма для употребленного в тексте значения глагола движет);
2) неправильное употребление временных форм глаголов: Эта книга дает знания об истории календаря, научит делать календарные расчеты быстро и точно (следует …даст.., научит… или …дает…, учит…);
3) ошибки в употреблении действительных и страдательных причастий: Ручейки воды, стекаемые вниз, поразили автора текста (следует стекавшие);
4) ошибки в образовании деепричастий: Вышев на сцену, певцы поклонились (норма выйдя);
5) неправильное образование наречий: Автор тута был не прав (норма тут);
6) ошибки, связанные с нарушением закономерностей и правил грамматики, возникающие под влиянием просторечия и диалектов.
Кроме того, к типичным можно отнести и синтаксические ошибки, а именно:
1) нарушение связи между подлежащим и сказуемым: Главное, чему теперь я хочу уделить внимание, это художественной стороне произведения (правильно это художественная сторона произведения); Чтобы приносить пользу Родине, нужно смелость, знания, честность (вместо нужны смелость, знания, честность);
2) ошибки, связанные с употреблением частиц: Хорошо было бы, если бы на картине стояла бы подпись художника; отрыв частицы от того компонента предложения, к которому она относится (обычно частицы ставятся перед теми членами предложения, которые они должны выделять, но эта закономерность часто нарушается в сочинениях): В тексте всего раскрываются две проблемы (ограничительная частица всего должна стоять перед подлежащим: … всего две проблемы);
3) неоправданный пропуск подлежащего (эллипсис): Его храбрость, (?) постоять за честь и справедливость привлекают автора текста;
4) неправильное построение сложносочиненного предложения: Ум автор текста понимает не только как просвещенность, интеллигентность, но и с понятием «умный» связывалось представление о вольнодумстве.
Орфографические ошибки
Орфографическая ошибка – это неправильное написание слова; она может быть допущена только на письме, обычно в слабой фонетической позиции (для гласных – в безударном положении, для согласных – на конце слова или перед другим согласным) или в слитно-раздельно-дефисных написаниях, например: на площаде, о синим карандаше, небыл, кто то, полапельсина. На оценку сочинения распространяются положения об однотипных и негрубых ошибках. Напомним соответствующий фрагмент из «Норм оценки знаний, умений и навыков по русскому языку».
Среди орфографических ошибок следует выделять негрубые, т.е. не имеющие существенного значения для характеристики грамотности. При подсчете ошибок две негрубые считаются за одну. К негрубым относятся ошибки
1) в исключениях из правил;
2) в написании большой буквы в составных собственных наименованиях;
3) в случаях раздельного и слитного написания не с прилагательными и причастиями, выступающими в роли сказуемого;
4) в написании и и ы после приставок;
5) в трудных случаях различения не и ни (Куда он только не обращался! Куда он ни обращался, никто не мог дать ему ответ. Никто иной не …; не кто иной, как …; ничто иное не …; не что иное, как … и др.).
Необходимо учитывать также повторяемость и однотипность ошибок. Если ошибка повторяется в одном и том же слове или в корне однокоренных слов, то она считается за одну ошибку. Однотипными считаются ошибки на одно правило, если условия выбора правильного написания заключены в грамматических (в армии, в роще; колют, борются) и фонетических (пирожок, сверчок) особенностях данного слова.
Не считаются однотипными ошибки на такое правило, в котором для выяснения правильного написания одного слова требуется подобрать другое (опорное) слово или его форму (вода – воды, рот – ротик, грустный – грустить, резкий – резок).
Первые три однотипные ошибки считаются за одну ошибку, каждая следующая подобная ошибка учитывается как самостоятельная. Если в одном непроверяемом слове допущены две и более ошибки, то все они считаются за одну ошибку.
При оценке сочинения исправляются, но не учитываются следующие ошибки:
1. В переносе слов.
2. Буквы э/е после согласных в иноязычных словах (рэкет, пленэр) и после гласных в собственных именах (Мариетта).
3. В названиях, связанных с религией: М(м)асленица, Р(р)ождество, Б(б)ог.
4. При переносном употреблении собственных имен (Обломовы и обломовы).
5. В собственных именах нерусского происхождения; написание фамилий с первыми частями дон, ван, сент… (дон Педро и Дон Кихот).
6. Сложные существительные без соединительной гласной (в основном заимствования), не регулируемые правилами и не входящие в словарь-минимум (ленд-лиз, люля-кебаб, ноу-хау, папье-маше, перекати-поле, гуляй-город пресс-папье, но бефстроганов, метрдотель, портшез, прейскурант).
7. На правила, которые не включены в школьную программу (например, правило слитного / раздельного написания наречных единиц / наречий с приставкой / предлогом, например: в разлив, за глаза ругать, под стать, в бегах, в рассрочку, на попятную, в диковинку, на ощупь, на подхвате, на попа ставить (ср. действующее написание напропалую, врассыпную).
В отдельную категорию выделяются графические ошибки, т.е. различные описки, вызванные невнимательностью пишущего или поспешностью написания. Например, неправильные написания, искажающие звуковой облик слова (рапотает вместо работает, мемля вместо земля). Эти ошибки связаны с графикой, т.е. средствами письменности данного языка, фиксирующими отношения между буквами на письме и звуками устной речи. К графическим средствам помимо букв относятся различные приемы сокращения слов, использование пробелов между словами, различные подчеркивания и шрифтовые выделения.
Одиночные графические ошибки не учитываются при проверке, но если таких ошибок больше 5 на 100 слов, то работу следует признать безграмотной.
Пунктуационные ошибки
Пунктуационная ошибка – это неиспользование пишущим необходимого знака препинания или его употребление там, где он не требуется, а также необоснованная замена одного знака препинания другим.
В соответствии с «Нормами оценки знаний, умений и навыков по русскому языку» исправляются, но не учитываются следующие пунктуационные ошибки:
1) тире в неполном предложении;
2) обособление несогласованных определений, относящихся к нарицательным именам существительным;
3) запятые при ограничительно-выделительных оборотах;
4) различение омонимичных частиц и междометий и, соответственно, невыделение или выделение их запятыми;
5) в передаче авторской пунктуации.
Среди пунктуационных ошибок следует выделять негрубые, т.е. не имеющие существенного значения для характеристики грамотности. При подсчете ошибок две негрубые считаются за одну.
К негрубым относятся ошибки
1) в случаях, когда вместо одного знака препинания поставлен другой;
2) в пропуске одного из сочетающихся знаков препинания или в нарушении их последовательности.
Правила подсчета однотипных и повторяющихся ошибок на пунктуацию не распространяется.
[1] Подробнее о квалификации ошибок см. в «Учебно-методических материалах для председателей и членов региональных предметных комиссий по проверке выполнения заданий с развернутым ответом экзаменационных работ ЕГЭ по русскому языку». Данный материал размещен на сайте ФИПИ (http://fipi.ru/ege-i-gve-11/dlya-predmetnyh-komissiy-subektov-rf).
Памятка
эксперту «Классификация ошибок»
К
7. Орфографические ошибки
Орфографические ошибки-
неправильное написание слова, допущенное на письме, обычно в слабой
фонетической позиции.
Однотипные и неоднотипные орфографические
ошибки:
·
Однотипные- ошибки
на одно и то же орфографическое правило. Эти ошибки исправляются, но при
подсчете общего количества допущенных ошибок считаются 3 за 1, каждая
последующая считается самостоятельной ошибкой. Примечание: не считаются
однотипными ошибки, допущенные в словах с проверяемыми гласными в корне слова.
·
Повторяющиеся-
ошибки в одном и том же повторяющемся слове или в корне однокоренных слов. Эти
ошибки также считаются за одну.
Грубые и негрубые орфографические ошибки:
К негрубым орфографическим ошибкам
относятся:
·
исключения из правил;
·
строчная и прописная буквы в собственных
наименованиях;
·
не регулируемые правилами слитные и
раздельные написания наречий;
·
слитное и раздельное написание НЕ с
прилагательными и причастиями, выступающими в роли сказуемых;
·
различение НЕ и Ни в оборотах никто
иной не…, ничто иное не…, не кто иной, как…, не что иное, как…, а также во
фразах типа: Куда только он не обращался! Куда только он ни обращался, никто
не мог дать ему ответ;
·
написание собственных имен нерусского
происхождения;
·
написание И и Ы после приставок.
Другие виды ошибок:
·
Графические ошибки ( пи проверке не
учитываются)- разновидность ошибок, связанных с
графикой ( различные приемы сокращения слов, использование пробелов между
словами, различные подчеркивания, шрифтовые выделения).
·
Описки-ошибки,
вызванные невнимательностью пишущего или поспешностью написания. Они исправляются,
но не выносятся на поля и не учитываются при подсчете ошибок. К опискам
относятся:
ü пропуски
букв;
ü перестановка
букв;
ü замена
одних букв другими;
ü добавление
лишних букв.
К
8. Пунктуационные ошибки
Пунктуационные ошибки-ошибки,
связанные с нарушением пунктуационных правил. 2 негрубые пунктуационные
ошибки считаются за 1.
К негрубым пунктуационным ошибкам
относятся :
ü употребление
одного знака препинания вместо другого;
ü пропуск
одного из двойных знаков препинания;
ü нарушение
последовательности сочетающихся знаков или пропуск одного из сочетающихся
знаков;
ü не
относится к ошибкам авторская пунктуация.
Понятие об однотипных ошибках НЕ
распространяется на пунктуационные ошибки.
К
9. Классификация грамматических ошибок
·
ошибки в образовании слов,
связанных с нарушением словообразовательных форм;
·
ошибки в образовании форм различных частей
речи, связанные с нарушением морфологических
норм;
·
ошибки в построении словосочетаний, связанные
с нарушением синтаксических норм;
·
ошибки в построении простого предложения, связанные
с нарушением синтаксических норм;
·
ошибки в построении сложного предложения, связанные
с нарушением синтаксических норм.
|
I. |
|
|
1. |
Неправильное |
|
2. |
Неправильное |
|
3. |
Ошибки |
|
4. |
Неправильное |
|
5. |
Неправильная |
|
6. |
Неправильная |
|
7. |
Нарушение ( вм. |
|
8. |
Неправильное много |
|
9. |
Ошибки в Я |
|
10. |
Склонение |
|
11. |
Неверное Вывод |
|
12. |
Ошибки ( вм. |
|
13. |
Неправильное |
|
14. |
Ошибки в |
|
15 |
Ошибки в |
|
16. |
Неверное |
|
17. |
Неправильное Изделия, |
|
18. |
Ошибки |
|
19. |
Ошибки |
|
II. |
|
|
1. |
Неправильное |
|
2. |
Неправильное |
|
3. |
Согласование |
|
III. |
|
|
1. |
Употребление |
|
IV. |
|
|
1. |
Личное |
|
2. |
Расположение |
|
V. |
|
|
1. |
Рассогласование |
|
2. |
Объединение |
|
3. |
Парное |
|
4. |
Не Проявление |
|
5. |
Объединение |
|
VI. |
|
|
1. |
Употребление Тигр |
|
2. |
Употребление |
|
VII. |
|
|
1. |
Одновременное |
|
2. |
Пропуск |
|
3. |
Тавтологическое |
v При
вынесении грамматической ошибки эксперту необходимо делать на полях работы выпускника
подробную запись, например: Г VII
. 3
К
9. Классификация речевых ошибок
|
1. |
|
2. · · · |
|
3. |
|
4. |
|
5. |
|
6. по |
|
7. |
|
8. |
|
9. |
|
10. Следует сказать |
|
11. А. Блок-мастер звукозаписи. |
v При
вынесении речевой ошибки эксперту необходимо делать на полях работы выпускника
подробную запись, например: Р2
Классификация
фактических ошибок
|
Ф1. |
|
Ф2. «Век |
|
Ф3. Великая |
|
Ф4 |
v При
вынесении фактической ошибки эксперту необходимо делать на полях работы
выпускника подробную запись, например: Ф2
Этические
ошибки:
|
Речевая Проявление грубое, |
Мне Этот Это |
Логические
ошибки
|
Л1. Сопоставление |
На уроке |
|
Л2.Нарушение |
В |
|
Л3. Пропуск |
Людской |
|
Л4. Перестановка |
Пора |
|
Л5. Неоправданная |
Автор |
|
Л6.Сопоставление |
Синтаксис энциклопедических статей |
|
Композиционно-текстовые ошибки |
|
|
Л7.Неудачный |
В |
|
Л8. Ошибка в · · · |
|
|
Л9. Неудачная |
v При
вынесении логической ошибки эксперту необходимо делать на полях работы
выпускника подробную запись, например: Л2
Так как каждая из 2k разрешенных комбинаций в результате действия помех может трансформироваться в любую другую, то всегда имеется 2k*2n возможных случаев передачи. В это число входят:
-
2k случаев безошибочной передачи;
-
2k(2k –1) случаев перехода в другие разрешенные комбинации, что соответствует необнаруженным ошибкам;
-
2k(2n – 2k) случаев перехода в неразрешенные комбинации, которые могут быть обнаружены.
Следовательно, часть обнаруживаемых ошибочных кодовых комбинаций от общего числа возможных случаев передачи составляет
.
Пример22: Определить обнаруживающую способность кода, каждая комбинация которого содержит всего один избыточный символ (n=k+1).
Решение : 1. Общее число выходных последовательностей составляет 2k+1, т.е. вдвое больше общего числа кодируемых входных последовательностей.
2. За подмножество разрешенных кодовых комбинаций можно принять, например, подмножество 2k комбинаций, содержащих четное число единиц (или нулей).
3. При кодировании к каждой последовательности из k информационных символов добавляют один символ (0 или 1), такой, чтобы число единиц в кодовой комбинации было четным. Исполнение любого нечетного числа символов переводит разрешенную кодовую комбинацию в подмножество запрещенных комбинаций, что обнаруживается на приемной стороне по нечетности числа единиц. Часть опознанных ошибок составляет
.
Любой метод декодирования можно рассматривать как правило разбиения всего множества запрещенных кодовых комбинаций на 2k пересекающихся подмножеств Mi, каждая из которых ставится в соответствие одной из разрешенных комбинаций. При получении запрещенной комбинации, принадлежащей подмножеству Mi, принимают решение, что передавалась запрещенная комбинация Ai. Ошибка будет исправлена в тех случаях, когда полученная комбинация действительно образовалась из Ai, т.е. 2n-2k cлучаях.
Всего случаев перехода в неразрешенные комбинации 2k(2n – 2k). Таким образом, при наличии избыточности любой код способен исправлять ошибки.
Отношение числа исправляемых кодом ошибочных кодовых комбинаций к числу обнаруживаемых ошибочных комбинаций равно
.
Способ разбиения на подмножества зависит от того, какие ошибки должны направляться конкретным кодом.
Большинство разработанных кодов предназначено для корректирования взаимно независимых ошибок определенной кратности и пачек (пакетов) ошибок.
Взаимно независимыми ошибками называют такие искажения в передаваемой последовательности символов, при которых вероятность появления любой комбинации искаженных символов зависит только от числа искаженных символов r и вероятности искажения обычного символа p.
При взаимно независимых ошибках вероятность искажения любых r символов в n-разрядной кодовой комбинации:
,
где p – вероятность искажения одного символа;
r – число искаженных символов;
n – число двоичных символов на входе кодирующего устройства;
– число ошибок порядка r.
Если учесть, что p<<1, то в этом случае наиболее вероятны ошибки низшей кратности. Их следует обнаруживать и исправлять в первую очередь.
4.3 Связь корректирующей способности кода с кодовым расстоянием
При взаимно независимых ошибках наиболее вероятен переход в кодовую комбинацию, отличающуюся от данной в наименьшем числе символов.
Степень отличия любых двух кодовых комбинаций характеризуется расстоянием между ними в смысле Хэмминга или просто кодовым расстоянием.
Кодовое расстояние выражается числом символов, в которых комбинации отличаются одна от другой, и обозначается через d.
Ч
тобы получить кодовое расстояние между двумя комбинациями двоичного кода, достаточно подсчитать число единиц в сумме этих комбинаций по модулю 2. Например
(Сложение ”по модулю 2”: y= х1 х2, сумма равна 1 тогда и только тогда, когда х1 и x2 не совпадают ).
Минимальное расстояние, взятое по всем парам кодовых разрешенных комбинаций кода, называют минимальным кодовым расстоянием.
Более полное представление о свойствах кода дает матрица расстояний D, элементы которой dij (i,j = 1,2,…,m) равны расстояниям между каждой парой из всех m разрешенных комбинаций.
Пример23: Представить симметричной матрицей расстояний код х1 = 000; х2 = 001; х3 = 010; х4 = 111.
Решение. 1. Минимальное кодовое расстояние для кода d=1.
-
Симметричная матрица четвертого порядка для кода
Таблица 4.1.
|
x1 |
x2 |
x3 |
x4 |
||
|
000 |
001 |
010 |
111 |
||
|
x1 |
000 |
1 |
1 |
3 |
|
|
x2 |
001 |
1 |
2 |
2 |
|
|
x3 |
010 |
1 |
2 |
2 |
|
|
x4 |
111 |
3 |
2 |
2 |
Декодирование после приема производится таким образом, что принятая кодовая комбинация отождествляется с той разрешенной, которая находится от нее на наименьшем кодовом расстоянии.
Такое декодирование называется декодированием по методу максимального правдоподобия.
Очевидно, что при кодовом расстоянии d=1 все кодовые комбинации являются разрешенными.
Например, при n=3 разрешенные комбинации образуют следующее множество: 000, 001, 010, 011, 100, 101, 110, 111.
Любая одиночная ошибка трансформирует данную комбинацию в другую разрешенную комбинацию. Это случай безызбыточного кода, не обладающего корректирующей способностью.
Если d = 2, то ни одна из разрешенных кодовых комбинаций при одиночной ошибке не переходит в другую разрешенную комбинацию. Например, подмножество разрешенных кодовых комбинаций может быть образовано по принципу четности в нем числа единиц. Например, для n=3:
000, 011, 101, 110 – разрешенные комбинации;
001, 010, 100, 111 – запрещенные комбинации.
Код обнаруживает одиночные ошибки, а также другие ошибки нечетной кратности (при n=3 тройные).
В общем случае при необходимости обнаруживать ошибки кратности до r включительно минимальное хэммингово расстояние между разрешенными кодовыми комбинациями должно быть по крайней мере на единицу больше r, т.е d0 minr+1.
Действительно, в этом случае ошибка, кратность которой не превышает r, не в состоянии перевести одну разрешенную кодовую комбинацию в другую.
Для исправления одиночной ошибки кодовой комбинации необходимо сопоставить подмножество запрещенных кодовых комбинаций.
Чтобы эти подмножества не пересекались, хэммингово расстояние между разрешенными кодовыми комбинациями должно быть не менее трех. При n=3 за разрешенные кодовые комбинации можно, например, принять 000 и 111. Тогда разрешенной комбинации 000 необходимо приписать подмножество запрещенных кодовых комбинаций 001, 010, 100, образующихся в результате двоичной ошибки в комбинации 000.
Подобным же образом разрешенной комбинации 111 необходимо приписать подмножество запрещенных кодовых комбинаций: 110, 011, 101, образующихся в результате возникновения единичной ошибки в комбинации 111:
Рис. 4.1.
В общем случае для обеспечения возможности исправления всех ошибок кратности до s включительно при декодировании по методу максимального правдоподобия, каждая из ошибок должна приводить к запрещенной комбинации, относящейся к подмножеству исходной разрешенной кодовой комбинации.
Любая n-разрядная двоичная кодовая комбинация может быть интерпретирована как вершина m-мерного единичного куба, т.е. куба с длиной ребра, равной 1.
При n=2 кодовые комбинации располагаются в вершинах квадрата:
Рис. 4.2.
При n=3 кодовые комбинации располагаются в вершинах единичного куба:
Рис. 4.3.
В общем случае n-мерный единичный куб имеет 2n вершин, что равно наибольшему возможному числу кодовых комбинаций.
Такая модель дает простую геометрическую интерпретацию и кодовому расстоянию между отдельными кодовыми комбинациями. Оно соответствует наименьшему числу ребер единичного куба, которые необходимо пройти, чтобы попасть от одной комбинации к другой.
Ошибка будет не только обнаружена, но и исправлена, если искаженная комбинация остается ближе к первоначальной, чем к любой другой разрешенной комбинации, то есть должно быть: или
В общем случае для того, чтобы код позволял обнаруживать все ошибки кратности r и исправлять все ошибки кратности s (r>s), его кодовое расстояние должно удовлетворять неравенству d r+s+1 (rs).
Метод декодирования при исправлении одиночных независимых ошибок можно пояснить следующим образом. В подмножество каждой разрешенной комбинации относят все вершины, лежащие в сфере с радиусом (d-1)/2 и центром в вершине, соответствующей данной разрешенной кодовой комбинации. Если в результате действия помехи комбинация переходит в точку, находящуюся внутри сферы (d-1)/2, то такая ошибка может быть исправлена.
Если помеха смещает точку разрешенной комбинации на границу двух сфер (расстояние d/2) или больше (но не в точку, соответствующую другой разрешенной комбинации), то такое искажение может быть обнаружено.
Для кодов с независимым искажением символов лучшие корректирующие коды – это такие, у которых точки, соответствующие разрешенным кодовым комбинациям, расположены в пространстве равномерно.
Проиллюстрируем построение корректирующего кода на следующем примере. Пусть исходный алфавит, состоящий из четырех букв, закодирован двоичным кодом: х1 = 00; х2 = 01; х3 = 10; х4 = 11. Этот код использует все возможные комбинации длины 2, и поэтому не может обнаруживать ошибки (так как d=1).
Припишем к каждой кодовой комбинации один элемент 0 или 1 так, чтобы число единиц в нем было четное, то есть х1 = 000; х2 = 011; х3 = 101; х4 = 110.
Для этого кода d=2, и, следовательно, он способен обнаруживать все однократные ошибки. Так как любая запрещенная комбинация содержит нечетное число единиц, то для обнаружения ошибки достаточно проверить комбинацию на четность (например, суммированием по модулю 2 цифр кодовой комбинации). Если число единиц в слове четное, то сумма по модулю 2 его разрядов будет 0, если нечетное – то 1. Признаком четности называют инверсию этой суммы.
Рассмотрим общую схему организации контроля по четности (контроль по нечетности, parity check – контроль по паритету).

Рис. 4.4.
На n-входовом элементе формируется признак четности Р числа, который в качестве дополнительного, (n+1)-го контрольного разряда (parity bit) отправляется вместе с передаваемым словом в линию связи или запоминающее устройство. Передаваемое (n+1)-разрядное слово имеет всегда нечетное число единиц. Если в исходном слове оно было нечетным, то инверсия функции М2 от такого слова равна 0, и нулевое значение контрольного разряда не меняет число единиц при передаче слова. Если же число единиц в исходном слове было четным, то контрольный разряд Р для такого числа будет равен 1, и результирующее число единиц в передаваемом (n+1)-разрядном слове станет нечетным. Вид контроля, когда по линии передается нечетное число единиц, по строгой терминологии называют контролем по нечетности.
На приемном конце линии или из памяти от полученного (n+1)-разрядного слова снова берется свертка по четности, Если значение этой свертки равно 1, то или в передаваемом слове, или в контрольном разряде при передаче или хранении произошла ошибка. Столь простой контроль не позволяет исправить ошибку, но он, по крайней мере, дает возможность при обнаружении ошибки исключить неверные данные, затребовать повторную передачу и т.д.
Систему контроля можно построить на основе не только инверсии функции М2, но и прямой функции М2 (строго контроль по четности). Однако, в этом случае исходный код “все нули” будет иметь контрольный разряд, равный 0. В линию отправится посылка из сплошных нулей, и на приемном конце она будет неотличима от весьма опасной неисправности – полного пропадания связи. Поэтому контроль по четности в своем чистом виде почти никогда не применяют, контрольный разряд формируют как четности, и в нестрогой терминологии “контролем по четности” называют то, что, строго говоря, на самом деле является контролем по нечетности.
Контроль по четности основан на том, что одиночная ошибка (безразлично – пропадание единицы или появление линией) инвертирует признак четности. Однако две ошибки проинвертируют его дважды, то есть оставят без изменения, поэтому двойную ошибку контроль по четности не обнаруживает. Рассуждая аналогично, легко прийти к выводу, что контроль по четности обнаруживает все нечетные ошибки и не реагирует на любые четные. Пропуск четных ошибок – это не какой-либо дефект системы контроля. Это следствие предельно малой избыточности, равной всего одному разряду. Для более глубокого контроля требуется соответственно и большая избыточность. Если ошибки друг от друга не зависят, то из не обнаруживаемых чаще всего будет встречаться двойная ошибка, а при вероятности одиночной ошибки, равной Р, вероятность двойной будет Р2. Поскольку в нормальных цифровых устройствах P<<1, необнаруженные двойные ошибки встречаются значительно реже, чем обнаруженные одиночные. Поэтому далее при таком простом контроле качество работы устройства существенно возрастает. Это верно лишь для взаимно независимых ошибок.
Признаки четности можно использовать для контроля только неизменяемых данных. При выполнении над данными каких-либо логических операций признаки четности слов в общем изменяются, и попытки компенсировать эти изменения оказываются неэффективными. Счастливое исключение – операция арифметического сложения: сумма по модулю 2 признаков четности двоичных слагаемых и всех, возникших в процессе сложения переносов, равна признаку четности кода арифметической суммы этих слагаемых.
Контроль по четности – самый дешевый по аппаратурным затратам вид контроля, и применяется он очень широко. Практически любой канал передачи цифровых данных или запоминающее устройство, если они не имеют какого-либо более сильного метода контроля, защищены контролем по четности.
Продолжим рассмотрение примера построения корректирующего метода. Чтобы код был способен и исправлять однократные ошибки, необходимо добавить еще не менее двух разрядов. Это можно сделать различными способами, например, повторить первые две цифры:
х1 = 00000; х2 = 01101; х3 = 10110; х4 = 11011;
Матрица расстояний этого кода:
Таблица 4.2.
|
x1 |
x2 |
x3 |
x4 |
||
|
D= |
3 |
3 |
4 |
x1 |
|
|
3 |
4 |
3 |
x2 |
||
|
3 |
4 |
3 |
x3 |
||
|
4 |
3 |
3 |
x4 |
Видно, что d 3, что отвечает неравенству (d 2+3+1).
Пример23: Постройте корректирующий код для передачи двух сообщений:
-
обнаруживающий одну ошибку;
-
обнаруживающий и исправляющий одну ошибку;
-
обнаруживающий две и исправляющий одну ошибку.
КОНТРОЛЬ ПРАВИЛЬНОСТИ РАБОТЫ ЦИФРОВЫХ УСТРОЙСТВ
Общие сведения
В процессе работы цифрового устройства возникают ошибки, искажающие информацию. Причинами таких ошибок могут быть:
◙ выход из строя какого-либо элемента, из-за чего устройство теряет работоспособность;
◙ воздействие различного рода помех, возникающих из-за проникновения сигналов из одних цепей в другие через различные паразитные связи.
Выход из строя элемента устройства рассматривается как неисправность. При этом в устройстве наблюдается постоянное искажение информации.
Иной характер искажений информации имеет место под воздействием помех. Вызвав ошибку, помехи могут затем в течение длительного времени не проявлять себя. Такие ошибки называют случайными сбоями.
В связи с возникновением ошибок необходимо снабжать цифровые устройства системой контроля правильности циркулирующей в ней информации. Такие системы контроля могут предназначаться для решения задач двух типов:
◙ задачи обнаружения ошибок;
◙ задачи исправления ошибок.
Система обнаружения ошибок, производя контроль информации, способна лишь выносить решения: нет ошибок и есть ошибка, причем в последнем случае она не указывает, какие разряды слов искажены.
Система исправления ошибок сигнализирует о наличии ошибок и указывает, какие из разрядов искажены. При этом непосредственное исправление цифр искаженных разрядов представляет собой уже несложную операцию. Если известно, что некоторый разряд двоичного слова ошибочен, то появление в нем ошибочного лог.0 означает, что правильное значение — лог. 1 и наоборот.
Трудно локализовать ошибку, т.е. указать, в каких разрядах слова она возникла. После решения этой задачи само исправление сводится лишь к инверсии цифр искаженных разрядов, поэтому обычно под исправлением ошибок понимают решение задачи локализации ошибок.
При постоянном нарушении правильности информации, обнаружив ошибку, можно принять меры для поиска неисправного элемента и заменить его исправным. Причины же случайных сбоев обычно выявляются чрезвычайно трудно, и такие изредка возникающие ошибки желательно было бы устранять автоматически, восстанавливая правильное значение слов с помощью системы исправления ошибок. Однако следует иметь в виду, что система исправления ошибок требует значительно большего количества оборудования, чем система обнаружения ошибок.
Ниже раздельно рассматриваются методы контроля:
◙ цифровых устройств хранения и передачи информации;
◙ цифровых устройств обработки информации.
К устройствам первого типа могут быть отнесены запоминающие устройства, регистры, цепи передачи и другие устройства, в которых информация не должна изменяться. На выходе этих устройств информация та же, что и на входе. К устройствам второго типа относятся устройства, у которых входная информация не совпадает с выходной и в тех случаях, когда ошибки не возникают. Примером могут служить арифметические и логические устройства.
Обнаружение одиночных ошибок в устройствах хранения и передачи информации
Для дальнейшего изложения потребуется понятие кодовое расстояние по Хеммингу. Для двух двоичных слов кодовое расстояние по Хеммингу есть число разрядов, в которых разнятся эти слова. Так, для слов 11011 и 10110 кодовое расстояние d = 3, так как эти слова различаются в трех разрядах (первом, третьем и четвертом).
Пусть используемые слова имеют m разрядов. Для представления информации можно использовать все 2 возможных комбинаций от 00 … 0 до 11 … 1. Тогда для каждого слова найдутся другие такие слова, которые отличаются от данного не более чем в одном разряде. Например, для некоторого слова 1101 можно найти следующие слова: 0101, отличающиеся только в четвертом разряде; 1001, отличающееся только в третьем разряде, и т.д. Таким образом, минимальное кодовое расстояние d
= 1. Обнаружить ошибки в таких словах невозможно. Например, если передавалось слово N
= 1101, а принято N
= 0101, то в принятом слове невозможно обнаружить никаких признаков наличия ошибки (ведь могло бы быть передано и слово N
= 0101). Для того чтобы можно было обнаружить одиночные ошибки (ошибки, возникающие не более чем в одном из разрядов слова), минимальное кодовое расстояние должно удовлетворять условию d
≥ 2. Это условие требует, чтобы любая пара используемых слов отличалась друг от друга не менее чем в двух разрядах. При этом, если возникает ошибка, она образует такую комбинацию цифр, которая не используется для представления слов, т.е. образует так называемую запрещенную комбинацию.
Для получения d = 2 достаточно к словам, использующим любые комбинации из m информационных двоичных разрядов, добавить один дополнительный разряд, называемый контрольным. При этом значение цифры контрольного разряда выбирают таким, чтобы общее число единиц в слове было четным. Например:
В первом из приведенных примеров число единиц информационной части четно (8), поэтому контрольный разряд должен содержать 0. Во втором примере число единиц в информационной части слова нечетно (7), и для того, чтобы общее число единиц в слове было четным, контрольный разряд должен содержать единицу. Таким способом во все слова вводится определенный признак — четность числа единиц. Принятые слова проверяются на наличие в них этого признака, и, если он оказывается нарушенным (т.е. обнаруживается, что число содержащихся в разрядах слова единиц нечетно), принимается решение, что слово содержит ошибку.
Этот метод позволяет обнаруживать ошибку. Но с его помощью нельзя определить, в каком разряде слова содержится ошибка, т.е. нельзя исправить ее. Кроме того, при этом методе не могут обнаруживаться ошибки четной кратности, т.е. ошибки одновременно в двух, четырех и т.д. разрядах, так как при таком четном числе ошибок не нарушается четность числа единиц в разрядах слова. Однако наряду с одиночными ошибками могут обнаруживаться ошибки, возникающие одновременно в любом нечетном числе разрядов.
На практике часто вместо признака четности используется признак нечетности, т.е. цифра контрольного разряда выбирается такой, чтобы общее число единиц в разрядах слова было нечетным. При этом, если имеет место, например, обрыв линии связи, это обнаруживается, так как принимаемые слова будут иметь 0 во всех разрядах и нарушится принцип нечетности числа единиц.
Рассмотрим схемы, выполняющие операцию проверки на четность (нечетность). Проверка на четность требует суммирования по модулю 2 цифр разрядов слова. Если а , а
,…, а
— цифры разрядов, результат проверки на четность определится выражением р = а
а
а
,…, а
. Если р = 0, то число единиц в разрядах слова четно, в противном случае оно нечетно.
Наиболее просто эта операция реализуется, когда контролируемое слово передается в последовательной форме. Суммирование в этом случае может быть выполнено в последовательности р = …((a а
) а
) … а
. К результату суммирования р
первых разрядов прибавляется цифра очередного поступающего разряда (i + 1), находится результат суммирования (i + 1) разрядов p
= p
а
, и так до тех пор, пока не будут просуммированы цифры всех разрядов.
Из таблицы истинности
Таблица 1

для операции p = p
а
(табл. 1) видно, что лог.0 не должен менять состояния устройства суммирования (p
= p
), лог.1 переводит устройство в новое состояние (p
=
). Эта логика соответствует работе триггера со счетным входом (рис.1).

Рис.1. Триггер со счетным входом.
Действительно, пусть триггер был предварительно установлен в состояние 0, после чего на его синхронизирующий вход стали поступать логические уровни, соответствующие цифрам контролируемого слова. При этом первая лог.1 переведет триггер в состояние 1, вторая лог. 1 вернет триггер в состояние 0 и т.д. Следовательно, после подачи четного числа единиц триггер окажется в состоянии р = 0; при поступлении нечетного числа единиц — в состоянии р = 1.
Если разряды контролируемого слова передаются в параллельной форме, то последовательность действий при проверке на четность может быть следующая:
Согласно этому выражению для нахождения р вначале попарно суммируются по модулю 2 цифры разрядов контролируемого слова, далее полученные результаты также суммируются попарно и т.д.
Этот принцип вычисления р использован в схеме проверки на четность на рис.2.

Рис.2. Схема проверки на четность.
Цифры разрядов (и их инверсии) поступают на входы элементов (на рис.2 обозначены =1) первого яруса схемы, в которых они попарно суммируются по модулю 2. Полученные результаты попарно суммируются в элементах второго яруса и т.д.
Результат проверки на четность образуется на выходе элемента старшего яруса. Каждый из элементов схемы реализует следующую логическую функцию:
Построенная по данному выражению схема элемента, выполняющего операцию суммирования по модулю 2, приведена на рис.3.

Рис.3.Схема элемента, выполняющего операцию суммирования по модулю 2.
Определим число ярусов и число элементов в этой схеме проверки на четность. Пусть число разрядов n контролируемого слова составляет целую степень двух. Число элементов в отдельных ярусах а составляет геометрическую прогрессию 1,2,4,8,…, n/2, знаменатель которой q = 2. Для последнего k-то яруса а
= 1, для первого яруса а
=a
q
откуда 2
= n/2 или 2
= n.
Из этого соотношения можно найти число ярусов k. Число суммирующих элементов в схеме равно сумме членов приведенной выше геометрической прогрессии:
Контроль арифметических операций
В устройствах хранения и передачи информации одиночная ошибка вызывала искажение цифры лишь одного разряда слова. При выполнении арифметических операций одиночная ошибка в получаемом результате может вызвать искажение одновременно группы разрядов. Пусть в суммирующем счетчике хранится число N = 10111 и на вход поступает очередная единица. Произойдет сложение: N
= N
+1. При этом

Пусть в процессе суммирования из-за ошибочной работы устройства не будет передан перенос из 2-го разряда в 3-й. Такая одиночная ошибка приведет к следующему результату:

Сравнивая ошибочный результат N с правильным N
, видим, что они различаются в двух разрядах. Тем не менее считаем, что в N
содержится одиночная ошибка. Во всех случаях, когда ошибочный результат связан с арифметическим прибавлением (или вычитанием) ошибочной единицы к одному из разрядов, имеет место одиночная ошибка. И если ошибочный результат может быть получен из правильного результата путем арифметического суммирования (или вычитания) единицы не менее чем в k разрядах, кратность ошибки равна k.
Для контроля арифметических операций чаще всего используется контроль по модулю q. Этот метод более универсален и годится также для контроля устройств хранения и передачи информации. Сущность метода состоит в следующем.
Контролируемое число N арифметически делится на q, и выделяется остаток r . Остаток вписывается в контрольные разряды числа N вслед за его информационными разрядами. Принятое число N* делится на q и выделяется остаток r
*. Эту операцию выполняет устройство свертки по модулю q (рис.4).

Рис.4. Устройство свертки по модулю q.
Устройство сравнения сравнивает r и r
*, в случае их несовпадения выносит решение о наличии ошибки в принятом слове. Схема на рис. 5 иллюстрирует принцип контроля суммирующего устройства.

Рис.5. Схема, иллюстрирующая принцип контроля суммирующего устройства.
Пусть в результате суммирования чисел N и N
получено N*. Остатки r
и r
также суммируются с выделением остатка r
. Если остаток r
*, полученный от деления числа N* на модуль q, не совпадает с r
, то элемент сравнения сигнализирует о наличии ошибок в работе устройства.
Чаще всего используется q = 3, иногда выбирается q = 7. При увеличении значения q возрастает способность метода к обнаружению ошибок, но одновременно увеличивается объем контролирующего оборудования.
Рассмотрим пример применительно к схеме на рис. 5. Пусть q = 3, N = 32
= 100000
, N
= 29
= 011101
. Соответствующие этим числам остатки равны r
= 2
= 10
, r
= 2
= 10
(при q = 3 остатки могут принимать значения 0, 1, 2 и для их представления в двоичной форме достаточно двух контрольных разрядов). При отсутствии ошибок в работе устройства результат суммирования чисел N* = N
+ N
= 61
= = 111101
, значение свертки по модулю 3 равно r
* = 01
. Суммируя r
и r
и выделяя остаток по модулю 3, получаем r
= 01
. Совпадение r
* = r
указывает на отсутствие ошибок. При наличии ошибок не имело бы места совпадение остатков r
* и r
.
Эффективность контроля по модулю характеризуется данными, приведенными в табл. 2.
Таблица 2

В таблице указано, какую часть всех возможных комбинаций ошибок составляют ошибки, которые не обнаруживаются при контроле по модулю. Как видно из приведенных данных, обнаруживаются все однократные ошибки; доля ошибок высокой кратности, оказывающихся необнаруженными, при модуле 7 меньше, чем при модуле 3. Тем самым эффективность контроля по модулю 7 выше, чем при модуле 3. Однако при контроле по модулю 7 контрольная часть слов содержит три двоичных разряда (вместо двух разрядов при модуле 3) и, кроме того, сложнее схемы формирования остатков (схемы свертки).
В заключение рассмотрим построение схем свертки по модулю 3. Общим для этих схем является следующий метод получения остатка. Каждый разряд числа вносит определенный вклад в формируемый остаток. В табл. 3 приведены остатки от деления на 3 значений, выражаемых единицами отдельных разрядов (т.е. весовых коэффициентов разрядов). Эти остатки для единиц нечетных разрядов равны 1, для четных разрядов они равны 2. Следовательно, для получения остатка от деления на 3 всего числа достаточно просуммировать остатки для единиц отдельных его разрядов и затем для получения суммы найти остаток от деления на 3.
Таблица 3

Например, пусть N = 11001011 ; сумма остатков, создаваемых отдельными разрядами, S=1·2+1·1 + 0·2 + 0·1 + 1·2+0·1+1·2+1·1 = 8; далее, деля 8 на 3, получаем остаток r
= 2.
Схема свертки по модулю 3 для последовательной формы передачи чисел
Схема может быть выполнена в виде двухразрядного счетчика с циклом 3, построенного таким образом, что единицы нечетных разрядов поступающего на вход числа вызывают увеличение содержимого счетчика на единицу, а единицы четных разрядов вызывают увеличение числа в счетчике на два. Функционирование такого счетчика описывается табл. 4.
Здесь b— код, определяющий четность номера очередного разряда числа, поступающего на вход счетчика; примем для четных разрядов b = 0, для нечетных разрядов b = 1.
Таблица 4

Таблица 5

По этой таблице и таблице переходов JK-триггера (табл. 5) построены приведенные на рис. 6 карты, по которым находят логические выражения для входов триггеров ТТ1 и ТТ2 счетчика:


Рис.6. Карты, по которым находят логические выражения для входов триггеров ТТ1 и ТТ2 счетчика.
Представив выражения для J и J
в базисе И-НЕ:
получим схему межтриггерных связей на рис.7. Логическая переменная b формируется триггером 3.
Этот триггер переключается тактовыми импульсами (ТИ), следующими с частотой поступления разрядов числа на вход счетчика. Таким образом, в моменты поступления нечетных разрядов триггер 3 устанавливается в состояние 1 и b = 1, в моменты поступления четных разрядов b= 0.

Рис.7. Схема межтриггерных связей.
Схема свертки для параллельной формы представления числа
При параллельной форме представления числа обычно используется пирамидальный способ построения схемы свертки, показанный на рис. 8.

Элементы А первого яруса формируют остатки для пар разрядов числа, выдавая уровень лог. 1 на один из выходов А ,А
,А
в зависимости от значения остатка (0,1,2). В последующих ярусах используются однотипные элементы В, которые формируют остатки по результатам, выдаваемым парой элементов предыдущего яруса. На выходе элемента последнего яруса образуется остаток для всего числа.
Выходы элементов определяются следующими логическими выражениями: для первого яруса

для остальных ярусов

Если число разрядов n = 2 , то число ярусов в схеме свертки равно k, а число элементов составляет (n – 1).
4.4 Понятие качества корректирующего кода
Одной из основных характеристик корректирующего кода является избыточность кода, указывающая степень удлинения кодовой комбинации для достижения определенной корректирующей способности.
Если на каждые m символов выходной последовательности кодера канала приходится k информационных и (m-k) проверочных, то относительная избыточность кода может быть выражена одним из соотношений: Rm = (m-k)/m или Rk = (m-k)/k.
Величина Rk, изменяющаяся от 0 до , предпочтительнее, так как лучше отвечает смыслу понятия избыточности. Коды, обеспечивающие заданную корректирующую способность при минимально возможной избыточности, называют оптимальными.
В связи с нахождением оптимальных кодов оценим, например, возможное наибольшее число Q разрешенных комбинаций m-значного двоичного кода, обладающего способностью исправлять взаимно независимые ошибки кратности до s включительно. Это равносильно отысканию числа комбинаций, кодовое расстояние между которыми не менее d=2s+1.
Общее число различных исправляемых ошибок для каждой разрешающей комбинации составляет
,
где Cmi – число ошибок кратности i.
Каждая из таких ошибок должна приводить к запрещенной комбинации, относящейся к подмножеству данной разрешенной комбинации. Совместно с этой комбинацией подмножество включает комбинаций.
1+
Однозначное декодирование возможно только в том случае, когда названные подмножества не пересекаются. Так как общее число различных комбинаций m-значного двоичного кода составляет 2m, число разрешенных комбинаций не может превышать
Или .
Эта верхняя оценка найдена Хэммингом. Для некоторых конкретных значений кодового расстояния d, соответствующие Q укажем в таблице:
Таблица 4.3.
|
d |
Q |
d |
Q |
|
1 |
|
5 |
|
|
2 |
|
… |
… |
|
3 |
|
… |
… |
|
4 |
|
… |
|
Коды, для которых в приведенном соотношении достигается равенство, называют также плотноупакованными.
Однако не всегда целесообразно стремиться к использованию кодов, близких к оптимальным. Необходимо учитывать другой, не менее важный показатель качества корректирующего кода – сложность технической реализации процессов кодирования и декодирования.
Если информация должна передаваться по медленно действующей и дорогостоящей линии связи, а кодирующее и декодирующее устройства предполагается выполнить на высоконадежных и быстродействующих элементах, то сложность этих устройств не играет существенной роли. Решающим фактором в этом случае является повышение эффективности пользования линией связи, поэтому желательно применение корректирующих кодов с минимальной избыточностью.
Если же корректирующий код должен быть применен в системе, выполненной на элементах, надежность и быстродействие которых равны или близки надежности и быстродействию элементов кодирующей и декодирующей аппаратуры. Это возможно, например, для повышения достоверности воспроизведения информации с запоминающего устройства ЭВМ. Тогда критерием качества корректирующего кода является надежность системы в целом, то есть с учетом возможных искажений и отказов в устройствах кодирования и декодирования. В этом случае часто более целесообразны коды с большей избыточностью, но простые в технической реализации.
4.5 Линейные коды
Самый большой класс разделимых кодов составляют линейные коды, у которых значения проверочных символов определяются в результате проведения линейных операций над определенными информационными символами. Для случая двоичных кодов каждый проверочный символ выбирают таким образом, чтобы его сумма с определенными информационными символами была равна 0. Символ проверочной позиции имеет значение 1, если число единиц информационных разрядов, входящих в данное проверочное равенство, нечетно, и 0, если оно четно. Число проверочных равенств (а следовательно, и число проверочных символов) и номера конкретных информационных разрядов, входящих в каждое из равенств, определяется тем, какие и сколько ошибок должен исправлять или обнаруживать данный код. Проверочные символы могут располагаться на любом месте кодовой комбинации. При декодировании определяется справедливость проверочных равенств. В случае двоичных кодов такое определение сводится к проверкам на четность числа единиц среди символов, входящих в каждое из равенств (включая проверочные). Совокупность проверок дает информацию о том, имеется ли ошибка, а в случае необходимости и о том, на каких позициях символы искажены.
Любой двоичный линейный код является групповым, так как совокупность входящих в него кодовых комбинаций образует группу. Уточнение понятий линейного и группового кода требует ознакомления с основами линейной алгебры.
4.6 Математическое введение к линейным кодам
Основой математического описания линейных кодов является линейная алгебра (теория векторных пространств, теория матриц, теория групп). Кодовые комбинации рассматривают как элементы множества, например, кодовые комбинации двоичного кода принадлежат множеству положительных двоичных чисел.
Множества, для которых определены некоторые алгебраические операции, называют алгебраическими системами. Под алгебраической операцией понимают однозначные сопоставление двум элементам некоторого третьего элемента по определенным правилам. Обычно основную операцию называют сложением (обозначают a+b=c) или умножением (обозначают a*b=c), а обратную ей – вычитанием или делением, даже, если эти операции проводятся не над числами и не идентичны соответствующим арифметическим операциям.
Рассмотрим кратко основные алгебраические системы, которые широко используют в теории корректирующих кодов.
Группой множество элементов, в котором определена одна основная операция и выполняются следующие аксиомы:
-
В результате применения операции к любым двум элементам группы образуется элемент этой же группы (требование замкнутости).
-
Для любых трех элементов группы a,b,c удовлетворяется равенство (a+b)+c=a+(b+c), если основная операция – сложение, и равенство a(bc)=(ab)c, если основная операция – умножение.
-
В любой группе Gn существует однозначно определенный элемент, удовлетворяющий при всех значениях a из Gn условию а+0=0+а, если основная операция – сложение, или условию а*1=1*а=а, если основная операция – умножение. В первом случае этот элемент называют нулем и обозначают символом 0, а во втором – единицей и обозначают символом 1.
-
Всякий элемент а группы обладает элементом, однозначно определенным уравнением а+(-а)=-а+а=0, если основная операция – сложение, или уравнением а*а-1= а-1*а=1, если основная операция – умножение.
В первом случае этот элемент называют противоположным и обозначают (-а), а во втором – обратным и обозначают а-1.
Если операция, определенная в группе, коммутативна, то есть справедливо равенство a+b=b+a (для группы по сложению) или равенство a*b=b*a (для группы по умножению), то группу называют коммутативной или абелевой.
Группу, состоящую из конечного числа элементов, называют порядком группы.
Чтобы рассматриваемое нами множество n-разрядных кодовых комбинаций было конечной группой, при выполнении основной операции число разрядов в результирующей кодовой комбинации не должно увеличиваться. Этому условию удовлетворяет операция символического поразрядного сложения по заданному модулю q (q – простое число), при которой цифры одинаковых разрядов элементов группы складываются обычным порядком, а результатом сложения считается остаток от деления полученного числа по модулю q.
При рассмотрении двоичных кодов используется операция сложения по модулю 2. Результатом сложения цифр данного разряда является0, если сумма единиц в нем четная, и 1, если сумма единиц в нем нечетная, например,
Выбранная нами операция коммутативна, поэтому рассматриваемые группы будут абелевыми.
Нулевым элементом является комбинация, состоящая из одних нулей. Противоположным элементом при сложении по модулю 2 будет сам заданный элемент. Следовательно, операция вычитания по модулю 2 тождественна операции сложения.
Пример24. Определить, являются ли группами следующие множества кодовых комбинаций:
-
0001, 0110, 0111, 0011;
-
0000, 1101, 1110, 0111;
-
000, 001, 010, 011, 100, 101, 110, 111.
Решение: Первое множество не является группой, так как не содержит нулевого элемента.
Второе множество не является группой, так как не выполняется условие замкнутости, например, сумма по модулю 2 комбинаций 1101 и 1110 дает комбинацию 0011, не принадлежащую исходному множеству.
Третье множество удовлетворяет всем перечисленным условиям и является группой.
Подмножества группы, являющиеся сами по себе группами относительно операции, определенной в группе, называют подгруппами. Например, подмножество трехразрядных кодовых комбинаций: 000, 001, 010, 011 образуют подгруппу указанной в примере группы трехразрядных кодовых комбинаций.
Пусть в абелевой группе Gn задана определенная подгруппа А. Если В – любой, не входящий в А элемент из Gn, то суммы (по модулю 2) элементов В с каждым из элементов подгруппы А образуют определенный класс группы Gn по подгруппе А, порождаемый элементом В.
Элемент В, естественно, содержится в этом смежном классе, так как любая подгруппа содержит нулевой элемент. Взяв последовательно некоторые элементы Bj группы, не вошедшие в уже образованные смежные классы, можно разложить всю группу на смежные классы по подгруппе А.
Элементы Bj называют образующими элементами смежных классов по подгруппам.
В таблице разложения, иногда называемой групповой таблицей, образующие элементы обычно располагают в крайнем левом столбце, причем крайним левым элементом подгруппы является нулевой элемент.
Пример25: Разложить группу трехразрядных двоичных кодовых комбинаций по подгруппе двухразрядных кодовых комбинаций.
Решение: Разложение выполняют в соответствии с таблицей:
Таблица 4.4.
|
A1=0 |
A2 |
A3 |
A4 |
|
000 |
001 |
010 |
011 |
|
B1 |
A2B1 |
A3B1 |
A4B1 |
|
100 |
101 |
110 |
111 |
Пример26: Разложить группу четырехразрядных двоичных кодовых комбинаций по подгруппе двухразрядных кодовых комбинаций.
Решение: Существует много вариантов разложения в зависимости от того, какие элементы выбраны в качестве образующих смежных классов.
Один из вариантов:
Таблица 4.5.
|
A1=0 |
A2 |
A3 |
A4 |
|
0000 |
0001 |
0110 |
0111 |
|
B1 0100 |
A2B1 0101 |
A3B1 0110 |
A4B1 0111 |
|
B2 1010 |
A2B2 1011 |
A3B2 1000 |
A4B2 1001 |
|
B3 1100 |
A2B3 1101 |
A3B3 1110 |
A4B3 1111 |
Кольцом называют множество элементов R, на котором определены две операции (сложение и умножение), такие, что
-
множество R является коммутативной группой по отношению;
-
произведение элементов аR и bR есть элемент R (замкнутость по отношению и умножению);
-
для любых трех элементов a,b,c из R справедливо равенство a(bc)=(ab)c (ассоциативный закон для умножения);
-
для любых трех элементов a,b,c из R выполняются соотношения a(b+c)=ab+ac и (b+c)a=ba+ca (дистрибутивные законы);
Если для любых двух элементов кольца справедливо соотношение ab=ba, то кольцо называют коммутативным.
Кольцо может не иметь единичного элемента по умножению и обратных элементов.
Примером кольца может служить множество действительных четных целых чисел относительно обычных операций сложения и умножения.
Полем F называют множество, по крайней мере, двух элементов, в котором определены две операции – сложение и умножение, и выполняются следующие аксиомы:
-
множество элементов образуют коммутативную группу по сложению;
-
множество ненулевых элементов образуют коммутативную группу по умножению;
-
для любых трех элементов множества a,b,c выполняется соотношение (дистрибутивный закон) a(b+c)=ab+ac.
Поле F является, следовательно, коммутативным кольцом с единичным элементом по умножению, в котором каждый ненулевой элемент обладает обратным элементом. Примером поля может служить множество всех действительных чисел.
Поле GF(P), состоящее из конечного числа элементов Р, называют конечным полем или полем Галуа. Для любого числа Р, являющегося степенью простого числа q, существует поле, насчитывающее р элементов. Например, совокупность чисел по модулю q, если q — простое число, является полем.
Поле не может содержать менее двух элементов, поскольку в нем должны быть по крайней мере единичный элемент относительно операции сложения (0) и единичный элемент относительно операции умножения (1). Поле, включающее только 0 и 1, обозначим GF(2). Правила сложения и умножения в поле с двумя элементами следующие:
|
+ |
0 |
1 |
× |
0 |
1 |
|
|
0 |
0 |
1 |
0 |
0 |
0 |
|
|
1 |
1 |
0 |
1 |
0 |
1 |
Рис. 4.5 Правила сложения и умножения в поле с двумя элементами
Двоичные кодовые комбинации, являющиеся упорядоченными последовательностями из n Элементов поля GF(2), рассматриваются в теории кодирования как частный случай последовательностей из n элементов поля GF(P). Такой подход позволяет строить и анализировать коды с основанием, равным степени простого числа. В общем случае суммой кодовых комбинаций Aj и Ai называют комбинацию Af = Ai + Aj, в которой любой символ Ak (k=1,2,…,n) представляет собой сумму k-х символов комбинаций, причем суммирование производится по правилам поля GF(P). При этом вся совокупность n-разрядных кодовых комбинаций оказывается абелевой группой.
В частном случае, когда основанием кода является простое число q, правило сложения в поле GF(q) совпадает с правилом сложения по заданному модулю q.
4.7 Линейный код как пространство линейного векторного пространства
В рассмотренных алгебраических системах (группа, кольцо, поле) операции относились к единому классу математических объектов (элементов). Такие операции называют внутренними законами композиции элементов.
В теории кодирования широко используются модели, охватывающие два класса математических объектов (например, L и ). Помимо внутренних законов композиции в них задаются внешние законы композиции элементов, по которым любым двум элементам и аL ставится в соответствие элемент сL.
Линейным векторным пространством над полем элементов F (скаляров) называют множество элементов V (векторов), если для него выполняются следующие аксиомы:
-
множество V является коммутативной группой относительно операции сложения;
-
для любого вектора v изV и любого скаляра с из F определено произведение cv, которое содержится в V (замкнутость по отношению умножения на скаляр);
-
если u и v из V векторы, а с и d из F скаляры, то справедливо с(с+v)=cu+cv; (c+d)v=cv+dv (дистрибутивные законы);
-
если v-вектор, а с и d-скаляры, то (cd)v=c(dv) и 1*v=v
(ассоциативный закон для умножения на скаляр).
Выше было определено правило поразрядного сложения кодовых комбинаций, при котором вся их совокупность образует абелеву группу. Определим теперь операцию умножения последовательности из n элементов поля GF(P) (кодовой комбинации) на элемент поля ai GF(P)аналогично правилу умножения вектора на скаляр: ai(a1, a2, … , an)= (ai a1, ai a2, … , ai an)
(умножение элементов производится по правилам поля GF(P)).
Поскольку при выбранных операциях дистрибутивные законы и ассоциативный закон (п.п.3.4) выполняются, все множество n-разрядных кодовых комбинаций можно рассматривать как векторное линейное пространство над полем GF(2) (т.е. 0 и 1). Сложение производят поразрядно по модулю 2. При умножении вектора на один элемент поля (1) он не изменяется, а умножение на другой (0) превращает его в единичный элемент векторного пространства, обозначаемый символом 0=(0 0…0).
Если в линейном пространстве последовательностей из n элементов поля GF(P) дополнительно задать операцию умножения векторов, удовлетворяющую определенным условиям (ассоциативности, замкнутости, билинейности по отношению к умножению на скаляр), то вся совокупность n-разрядных кодовых комбинаций превращается в линейную коммутативную алгебру над полем коэффициентов GF(P).
Подмножество элементов векторного пространства, которое удовлетворяет аксиомам векторного пространства, называют подпространством.
Линейным кодом называют множество векторов, образующих подпространства векторного пространства всех n-разрядных кодовых комбинаций над полем GF(P).
В случае двоичного кодирования такого подпространства комбинаций над полем GF(2) образует любая совокупность двоичных кодовых комбинаций, являющаяся подгруппой группы всех n-разрядных двоичных кодовых комбинаций. Поэтому любой двоичный линейный код является групповым.
4.8 Построение двоичного группового кода
Построение конкретного корректирующего кода производят, исходя из требуемого объема кода Q, т. е. необходимого числа передаваемых команд или дискретных значений измеряемой величины и статистических данных о наиболее вероятных векторах ошибок в используемом канале связи.
Вектором ошибки называют n-разрядную двоичную последовательность, имеющую единицы в разрядах, подвергшихся искажению, и нули во всех остальных разрядах. Любую искаженную кодовую комбинацию можно рассматривать теперь как сумму (или разность) но модулю 2 исходной разрешенной кодовой комбинации и вектора ошибки.
Исходя из неравенства 2k – l Q (нулевая комбинация часто не используется, так как не меняет состояния канала связи), определяем число информационных разрядов k, необходимое для передачи заданного числа команд обычным двоичным кодом.
Каждой из 2k — 1 ненулевых комбинаций k -разрядного безызбыточного кода нам необходимо поставить в соответствие комбинацию из п символов. Значения символов в п – k проверочных разрядах такой комбинации устанавливаются в результате суммирования по модулю 2 значений символов в определенных информационных разрядах.
Поскольку множество 2k комбинаций информационных символов (включая нулевую) образует подгруппу группы всех n-разрядных комбинаций, то и множество 2k n-разрядных комбинаций, полученных по указанному правилу, тоже является подгруппой группы n-разрядных кодовых комбинаций. Это множество разрешенных кодовых комбинаций и будет групповым кодом.
Нам надлежит определить число проверочных разрядов и номера информационных разрядов, входящих в каждое из равенств для определения символов в проверочных разрядах.
Разложим группу 2n всех n-разрядных комбинаций на смежные классы по подгруппе 2k разрешенных n-разрядных кодовых комбинаций, проверочные разряды в которых еще не заполнены. Помимо самой подгруппы кода в разложении насчитывается 2n—k – 1 смежных классов. Элементы каждого класса представляют собой суммы по модулю 2 комбинаций кода и образующих элементов данного класса. Если за образующие элементы каждого класса принять те наиболее вероятные для заданного канала связи вектора ошибок, которые должны быть исправлены, то в каждом смежном классе сгруппируются кодовые комбинации, получающиеся в результате воздействия на все разрешенные комбинации определенного вектора ошибки. Для исправления любой полученной на выходе канала связи кодовой комбинации теперь достаточно определить, к какому классу смежности она относится. Складывая ее затем (по модулю 2) с образующим элементом этого смежного класса, получаем истинную комбинацию кода.
Ясно, что из общего числа 2n – 1 возможных ошибок групповой код может исправить всего 2n—k – 1 разновидностей ошибок по числу смежных классов.
Чтобы иметь возможность получить информацию о том, к какому смежному классу относится полученная комбинация, каждому смежному классу должна быть поставлена в соответствие некоторая контрольная последовательность символов, называемая опознавателем (синдромом).
Каждый символ опознавателя определяют в результате проверки на приемной стороне справедливости одного из равенств, которые мы составим для определения значений проверочных символов при кодировании.
Ранее указывалось, что в двоичном линейном коде значения проверочных символов подбирают так, чтобы сумма по модулю 2 всех символов (включая проверочный), входящих в каждое из равенств, равнялась нулю. В таком случае число единиц среди этих символов четное. Поэтому операции определения символов опознавателя называют проверками на четность. При отсутствии ошибок в результате всех проверок на четность образуется опознаватель, состоящий из одних нулей. Если проверочное равенство не удовлетворяется, то в соответствующем разряде опознавателя появляется единица. Исправление ошибок возможно лишь при наличии взаимно однозначного соответствия между множеством опознавателей и множеством смежных классов, а следовательно, и множеством подлежащих исправлению векторов ошибок.
Таким образом, количество подлежащих исправлению ошибок является определяющим для выбора числа избыточных символов п – k . Их должно быть достаточно для того, чтобы обеспечить необходимое число опознавателей. Если, например, необходимо исправить все одиночные независимые ошибки, то исправлению подлежат п ошибок:
000…01
000…10
……….
010…00
100…00
Различных ненулевых опознавателей должно быть не менее п. Необходимое число проверочных разрядов, следовательно, должно определяться из соотношения
2n—k -1 n или 2n—k -1
Если необходимо исправить не только все единичные, но и все двойные независимые ошибки, соответствующее неравенство принимает вид
2n—k-l
+
В общем случае для исправления всех независимых ошибок кратности до s включительно получаем
2n—k-l
+
+…+
Стоит подчеркнуть, что в приведенных соотношениях указывается теоретический предел минимально возможного числа проверочных символов, который далеко не во всех случаях можно реализовать практически. Часто проверочных символов требуется больше, чем следует из соответствующего равенства.
Одна из причин этого выяснится при рассмотрении процесса сопоставления каждой подлежащей исправлению ошибки с ее опознавателем.
4.8.1 Составление таблицы опознавателей
Начнем для простоты с установления опознавателей для случая исправления одиночных ошибок. Допустим, что необходимо закодировать 15 команд. Тогда требуемое число информационных разрядов равно четырем. Пользуясь соотношением 2n—k — 1= п, определяем общее число разрядов кода, а следовательно, и число ошибок, подлежащих исправлению (n = 7). Три избыточных разряда позволяют использовать в качестве опознавателей трехразрядные двоичные последовательности.
В данном случае ненулевые последовательности в принципе могут быть сопоставлены с подлежащими исправлению ошибками в любом порядке. Однако более целесообразно сопоставлять их с ошибками в разрядах, начиная с младшего, в порядке возрастания двоичных чисел (табл. 4.6).
Таблица 4.6.
|
Векторы ошибок |
Опознаватели |
Векторы ошибок |
Опознаватели |
|
0000001 |
001 |
0010000 |
101 |
|
0000010 |
010 |
0100000 |
110 |
|
0000100 |
011 |
1000000 |
111 |
|
0001000 |
100 |
При таком сопоставлении каждый опознаватель представляет собой двоичное число, указывающее номер разряда, в котором произошла ошибка.
Коды, в которых опознаватели устанавливаются по указанному принципу, известны как коды Хэмминга.
Возьмем теперь более сложный случай исправления одиночных и двойных независимых ошибок. В качестве опознавателей одиночных ошибок в первом и втором разрядах можно принять, как и ранее, комбинации 0…001 и 0…010.
Однако в качестве опознавателя одиночной ошибки в третьем разряде комбинацию 0…011 взять нельзя. Такая комбинация соответствует ошибке одновременно в первом и во втором разрядах, а она также подлежит исправлению и, следовательно, ей должен соответствовать свой опознаватель 0…011.
В качестве опознавателя одиночной ошибки в третьем разряде можно взять только трехразрядную комбинацию 0…0100, так как множество двухразрядных комбинаций уже исчерпано. Подлежащий исправлению вектор ошибки 0…0101 также можно рассматривать как результат суммарного воздействия двух векторов ошибок 0…0100 и 0…001 и, следовательно, ему должен быть поставлен в соответствие опознаватель, представляющий собой сумму по модулю 2 опознавателей этих ошибок, т.е. 0…0101.
Аналогично находим, что опознавателем вектора ошибки 0…0110 является комбинация 0…0110.
Определяя опознаватель для одиночной ошибки в четвертом разряде, замечаем, что еще не использована одна из трехразрядных комбинаций, а именно 0…0111. Однако, выбирая в качестве опознавателя единичной ошибки в i-м разряде комбинацию с числом разрядов, меньшим i, необходимо убедиться в том, что для всех остальных подлежащих исправлению векторов ошибок, имеющих единицы в i-м и более младших разрядах, получатся опознаватели, отличные от уже использованных. В нашем случае подлежащими исправлению векторами ошибок с единицами в четвертом и более младших разрядах являются: 0…01001, 0…01010, 0…01100.
Если одиночной ошибке в четвертом разряде поставить в соответствие опознаватель 0…0111, то для указанных векторов опознавателями должны были бы быть соответственно
0…0111
0…0111
0…0111
0…0001 0…0010 0…0100
_______ ________ _______
0…0110 0…0101 0…0011
Однако эти комбинации уже использованы в качестве опознавателей других векторов ошибок, а именно: 0…0110, 0…0101, 0…0011.
Следовательно, во избежание неоднозначности при декодировании в качестве опознавателя одиночной ошибки в четвертом разряде следует взять четырехразрядную комбинацию 1000. Тогда для векторов ошибок
0…01001, 0…01010, 0…01100
опознавателями соответственно будут:
0…01001, 0…01010, 0…01100.
Аналогично можно установить, что в качестве опознавателя одиночной ошибки в пятом разряде может быть выбрана не использованная ранее четырехразрядная комбинация 01111.
Действительно, для всех остальных подлежащих исправлению векторов ошибок с единицей в пятом и более младших разрядах получаем опознаватели, отличающиеся от ранее установленных:
Векторы ошибок Опознаватели
0…010001 0…01110
0…010010 0…01101
0…010100 0…01011
0…011000 0…00111
Продолжая сопоставление, можно получить таблицу опознавателей для векторов ошибок данного типа с любым числом разрядов. Так как опознаватели векторов ошибок с единицами в нескольких разрядах устанавливаются как суммы по модулю 2 опознавателей одиночных ошибок в этих разрядах, то для определения правил построения кода и составления проверочных равенств достаточно знать только опознаватели одиночных ошибок в каждом из разрядов. Для построения кодов, исправляющих двойные независимые ошибки, таблица таких опознавателей определена с помощью вычислительной машины вплоть до 29-го разряда [Теория кодирования. Сборник. – М.:Мир, 1964]. Опознаватели одиночных ошибок в первых пятнадцати разрядах приведены в табл. 4.7.
По тому же принципу аналогичные таблицы определены и для ошибок других типов, например для тройных независимых ошибок, пачек ошибок в два и три символа.
4.8.2 Определение проверочных равенств
Итак, для любого кода, имеющего целью исправлять наиболее вероятные векторы ошибок заданного канала связи (взаимно независимые ошибки или пачки ошибок), можно составить таблицу опознавателей одиночных ошибок в каждом из разрядов. Пользуясь этой таблицей, нетрудно определить, символы каких разрядов должны входить в каждую из проверок на четность.
Таблица 4.7.
|
Номер разряда |
Опознаватель |
Номер разряда |
Опознаватель |
Номер разряда |
Опознаватель |
|
1 |
00000001 |
6 |
00010000 |
11 |
01101010 |
|
2 |
00000010 |
7 |
00100000 |
12 |
10000000 |
|
3 |
00000100 |
8 |
00110011 |
13 |
10010110 |
|
4 |
00001000 |
9 |
01000000 |
14 |
10110101 |
|
5 |
00001111 |
10 |
01010101 |
15 |
11011011 |
Рассмотрим в качестве примера опознаватели для кодов, предназначенных исправлять единичные ошибки (табл. 4.8).
Таблица 4.8.
|
Номер разрядов |
Опознаватель |
Номер разрядов |
Опознаватель |
Номер разрядов |
Опознаватель |
|
1 |
0001 |
7 |
0111 |
12 |
1100 |
|
2 |
0010 |
8 |
1000 |
13 |
1101 |
|
3 |
0011 |
9 |
1001 |
14 |
1110 |
|
4 |
0100 |
10 |
1010 |
15 |
1111 |
|
5 |
0101 |
11 |
1011 |
16 |
10000 |
|
6 |
0110 |
В принципе можно построить код, усекая эту таблицу на любом уровне. Однако из таблицы видно, что оптимальными будут коды (7, 4), (15, 11), где первое число равно n, а второе k, и другие, которые среди кодов, имеющих одно и то же число проверочных символов, допускают наибольшее число информационных символов.
Усечем эту таблицу на седьмом разряде и найдем номера разрядов, символы которых должны войти в каждое из проверочных равенств.
Предположим, что в результате первой проверки на четность для младшего разряда опознавателя будет получена единица. Очевидно, это может быть следствием ошибки в одном из разрядов, опознаватели которых в младшем разряде имеют единицу. Следовательно, первое проверочное равенство должно включать символы 1, 3, 5 и 7-го разрядов: a1 a3
a5
a7=0.
Единица во втором разряде опознавателя может быть следствием ошибки в разрядах, опознаватели которых имеют единицу во втором разряде. Отсюда второе проверочное равенство должно иметь вид a2 a3
a6
a7= 0 .
Аналогично находим и третье равенство: a4 a5
a6
a7= 0 .
Чтобы эти равенства при отсутствии ошибок удовлетворялись для любых значений информационных символов в кодовой комбинации, в нашем распоряжении имеется три проверочных разряда. Мы должны так выбрать номера этих разрядов, чтобы каждый из них входил только в одно из равенств. Это обеспечит однозначное определение значений символов в проверочных разрядах при кодировании. Указанному условию удовлетворяют разряды, опознаватели которых имеют по одной единице. В нашем случае это будут первый, второй и четвертый разряды.
Таким образом, для кода (7, 4), исправляющего одиночные ошибки, искомые правила построения кода, т. е. соотношения, реализуемые в процессе кодирования, принимают вид:
a1=a3 a5
a7,
a2=a3 a6
a7, (4.1)
a4=a5 a6
a7 .
Поскольку построенный код имеет минимальное хэммингово расстояние dmin = 3, он может использоваться с целью обнаружения единичных и двойных ошибок. Обращаясь к табл. 4.8, легко убедиться, что сумма любых двух опознавателей единичных ошибок дает ненулевой опознаватель, что и является признаком наличия ошибки.
Пример 27. Построим групповой код объемом 15 слов, способный исправлять единичные и обнаруживать двойные ошибки.
В соответствии с dи 0 min r+s+1код должен обладать минимальным хэмминговым расстоянием, равным 4. Такой код можно построить в два этапа. Сначала строим код заданного объема, способный исправлять единичные ошибки. Это код Хэмминга (7, 4). Затем добавляем еще один проверочный разряд, который обеспечивает четность числа единиц в разрешенных комбинациях.
Таким образом, получаем код (8, 4). В процессе кодирования реализуются соотношения:
a1=a3 a5
a7,
a2=a3 a6
a7,
a4=a5 a6
a7 .
a8=a1 a2
a3
a4
a5
a6
a7,
Обозначив синдром кода (7, 4) через S1, результат общей проверки на четность — через S2(S2 = ) и пренебрегая возможностью возникновения ошибок кратности 3 и выше, запишем алгоритм декодирования:
при S1= 0 и S2= 0 ошибок нет;
при S1= 0 и S2= 1 ошибка в восьмом разряде;
при S1 0 и S2= 0 двойная ошибка (коррекция блокируется, посылается запрос повторной передачи);
при S1 0 и S2= 1 одиночная ошибка (осуществляется ее исправление).
Пример 28. Используя табл. 4.8, составим правила построения кода (8,2), исправляющего все одиночные и двойные ошибки.
Усекая табл. 4.7 на восьмом разряде, найдем следующие проверочные равенства:
a1 a5
a8=0,
a2 a5
a8=0,
a3 a5=0,
a4 a5=0,
a6 a8=0,
a7 a8=0.
Соответственно правила построения кода выразим соотношениями
a1=a5 a8 (4.2 а)
a2=a5 a8 (4.2 б)
a3=a5 (4.2 в)
a4=a5 (4.2 г)
a6=a8 (4.2 д)
a7=a8 (4.2 е)
Отметим, что для построенного кода dmin = 5, и, следовательно, он может использоваться для обнаружения ошибок кратности от 1 до 4.
Соотношения, отражающие процессы кодирования и декодирования двоичных линейных кодов, могут быть реализованы непосредственно с использованием сумматоров по модулю два. Однако декодирующие устройства, построенные таким путем для кодов, предназначенных исправлять многократные ошибки, чрезвычайно громоздки. В этом случае более эффективны другие принципы декодирования.
4.8.3 Мажоритарное декодирование групповых кодов
Для линейных кодов, рассчитанных на исправление многократных ошибок, часто более простыми оказываются декодирующие устройства, построенные по мажоритарному принципу. Это метод декодирования называют также принципом голосования или способом декодирования по большинству проверок. В настоящее время известно значительное число кодов, допускающих мажоритарную схему декодирования, а также сформулированы некоторые подходы при конструировании таких кодов.
Мажоритарное декодирование тоже базируется на системе проверочных равенств. Система последовательно может быть разрешена относительно каждой из независимых переменных, причем в силу избыточности это можно сделать не единственным способом.
Любой символ аi выражается d (минимальное кодовое расстояние) различными независимыми способами в виде линейных комбинаций других символов. При этом может использоваться тривиальная проверка аi = аi. Результаты вычислений подаются на соответствующий этому символу мажоритарный элемент. Последний представляет собой схему, имеющую d входов и один выход, на котором появляется единица, когда возбуждается больше половины его входов, и нуль, когда возбуждается число таких входов меньше половины. Если ошибки отсутствуют, то проверочные равенства не нарушаются и на выходе мажоритарного элемента получаем истинное значение символа. Если число проверок d 2s+ 1 и появление ошибки кратности s и менее не приводит к нарушению более s проверок, то правильное решение может быть принято по большинству неискаженных проверок. Чтобы указанное условие выполнялось, любой другой символ aj(j
i) не должен входить более чем в одно проверочное равенство. В этом случае мы имеем дело с системой разделенных проверок.
Пример 29. Построим систему разделенных проверок для декодирования информационных символов рассмотренного ранее группового кода (8,2).
Поскольку код рассчитан на исправление любых единичных и двойных ошибок, число проверочных равенств для определения каждого символа должно быть не менее 5. Подставив в равенства (4.2 а) и (4.2 б) значения а8, полученные из равенств (4.2 д) и (4.2 е) и записав их относительно a5 совместно с равенствами (4.2 в) и (4.2 г) и тривиальным равенством a5 = a5, получим следующую систему разделенных проверок для символа a5:
a5 = a6 a1,
a5 = a7 a2,
а5 = а3,
а5 = a4,
а5 = а5.
Для символа a8 систему разделенных проверок строим аналогично:
a8 = a3 a1,
a8 = a4 a2,
a8 = а6,
a8 = a7,
a8 = а8.
4.8.4 Матричное представление линейных кодов
Матрицей размерности l n называют упорядоченное множество l
n элементов, расположенных в виде прямоугольной таблицы с l строками и n столбцами:
Транспонированной матрицей к матрице А называют матрицу, строками которой являются столбцы, а столбцами строки матрицы А:
Матрицу размерности n n называют квадратной матрицей порядка n. Квадратную матрицу, у которой по одной из диагоналей расположены только единицы, а все остальные элементы равны нулю, называют единичной матрицей I. Суммой двух матриц А
|аij| и В
|bij| размерности l
n называют матрицу размерности l
n:
А + В |аij| + |bij|
|аij + bij|.
Умножение матрицы А |аij| размерности l
n на скаляр с дает матрицу размерности l
n: сА
c |аij|
|c аij|.
Матрицы А |аij| размерности l
n и В
|bjk| размерности n
m могут быть перемножены, причем элементами cik матрицы — произведения размерности l
m являются суммы произведений элементов l-й строки матрицы А на соответствующие элементы k-го столбца матрицы В:
cik =
В теории кодирования элементами матрицы являются элементы некоторого поля GF(P), а строки и столбцы матрицы рассматриваются как векторы. Сложение и умножение элементов матриц осуществляется по правилам поля GF(P).
Пример 30. Вычислим произведение матриц с элементами из поля GF (2):
Элементы cik матрицы произведения М = M1M2 будут равны:
c11 = (011) (101) = 0 + 0 + 1 = 1
c12 = (011) (110) = 0 + 1 + 0 = 1
c13 = (011) (100) = 0 + 0 + 0 = 0
c21 = (100) (101) = 1 + 0 + 0 = 1
c22 = (100) (110) = 1 + 0 + 0 = 1
c23 = (100) (100) = 1 + 0 + 0 = 1
c31 = (001) (101) = 0 + 0 + 1 = 1
c32 = (001) (110) = 0 + 0 + 0 = 0
c33 = (001) (100) = 0 + 0 + 0 = 0
Следовательно,
Зная закон построения кода, определим все множество разрешенных кодовых комбинаций. Расположив их друг под другом, получим матрицу, совокупность строк которой является подпространством векторного пространства n-разрядных кодовых комбинаций (векторов) из элементов поля GF(P). В случае двоичного (n, k)-кода матрица насчитывает n столбцов и 2k—1 строк (исключая нулевую). Например, для рассмотренного ранее кода (8,2), исправляющего все одиночные и двойные ошибки, матрица имеет вид
При больших n и k матрица, включающая все векторы кода, слишком громоздка. Однако совокупность векторов, составляющих линейное пространство разрешенных кодовых комбинаций, является линейно зависимей, так как часть векторов может быть представлена в виде линейной комбинации некоторой ограниченной совокупности векторов, называемой базисом пространства.
Совокупность векторов V1, V2, V3, …, Vn называют линейно зависимой, когда существуют скаляры с1,..сn (не все равные нулю), при которых
c1V1 + c2V2+…+ cnVn= 0
В приведенной матрице, например, третья строка представляет собой суммы по модулю два первых двух строк. Для полного определения пространства разрешенных кодовых комбинаций линейного кода достаточно записать в виде матрицы только совокупность линейно независимых векторов. Их число называют размерностью векторного пространства.
Среди 2k – 1 ненулевых двоичных кодовых комбинаций — векторов их только k. Например, для кода (8,2)
Матрицу, составленную из любой совокупности векторов линейного кода, образующей базис пространства, называют порождающей (образующей) матрицей кода.
Если порождающая матрица содержит k строк по n элементов поля GF(q), то код называют (n, k)-кодом. В каждой комбинации (n, k)-кода k информационных символов и n – k проверочных. Общее число разрешенных кодовых комбинаций (исключая нулевую) Q = qk-1.
Зная порождающую матрицу кода, легко найти разрешенную кодовую комбинацию, соответствующую любой последовательности Аki из k информационных символов.
Она получается в результате умножения вектора Аki на порождающую матрицу Мn,k:
Аni = Аki • Мn,k .
Найдем, например, разрешенную комбинацию кода (8,2), соответствующую информационным символам a5=l, a8 = 1:
.
Пространство строк матрицы остается неизменным при выполнении следующих элементарных операций над строками: 1) перестановка любых двух строк; 2) умножение любой строки на ненулевой элемент поля; 3) сложение какой-либо строки с произведением другой строки на ненулевой элемент поля, а также при перестановке столбцов.
Если образующая матрица кода M2 получена из образующей матрицы кода M1 с помощью элементарных операций над строками, то обе матрицы порождают один и тот же код. Перестановка столбцов образующей матрицы кода приводит к образующей матрице эквивалентного кода. Эквивалентные коды весьма близки по своим свойствам. Корректирующая способность таких кодов одинакова.
Для анализа возможностей линейного (n, k)-кода, а также для упрощения процесса кодирования удобно, чтобы порождающая матрица (Мn,k) состояла из двух матриц: единичной матрицы размерности k k и дописываемой справа матрицы-дополнения (контрольной подматрицы) размерности k • (n – k), которая соответствует n – k проверочным разрядам:
(4.3)
Разрешенные кодовые комбинации кода с такой порождающей матрицей отличаются тем, что первые k символов в них совпадают с исходными информационными, а проверочными оказываются (n — k) последних символов. Действительно, если умножим вектор-строку Ak,i = = (a1 a2…ai…ak) на матрицу Мn,k= [IkPk,n—k], получим вектор
An,i = (a1a2…ai…ak…ak+1…aj…an),
где проверочные символы аj(k +1 j
n) являются линейными комбинациями информационных:
(4.4)
Коды, удовлетворяющие этому условию, называют систематическими. Для каждого линейного кода существует эквивалентный систематический код. Как следует из (4.3), (4.4), информацию о способе построения такого кода содержит матрица-дополнение. Если правила построения кода (уравнения кодирования) известны, то значения символов любой строки матрицы-дополнения получим, применяя эти правила к символам соответствующей строки единичной матрицы.
Пример 31. Запишем матрицы Ik, Рk,n—k_и Mn,k для двоичного кода (7,4).
Единичная матрица на четыре разряда имеет вид
Один из вариантов матрицы дополнения можно записать, используя соотношения (4.1)
Тогда для двоичного кода Хэммннга имеем:
Запишем также матрицу для систематического кода (7,4):
В свою очередь, по заданной матрице-дополнению Pk,n-k можно определить равенства, задающие правила построения кода. Единица в первой строке каждого столбца указывает на то, что в образовании соответствующего столбцу проверочного разряда участвовал первый информационный разряд. Единица в следующей строке любого столбца говорит об участии в образовании проверочного разряда второго информационного разряда и т, д.
Так как матрица-дополнение содержит всю информацию о правилах построения кода, то систематический код с заданными свойствами можно синтезировать путем построения соответствующей матрицы-дополнения.
Так как минимальное кодовое расстояние d для линейного кода равно минимальному весу его ненулевых векторов, то в матрицу-дополнение должны быть включены такие k строк, которые удовлетворяли бы следующему общему условию: вектор-строка образующей матрицы, получающаяся при суммировании любых l (1 l
k) строк, должна содержать не менее d – l отличных от нуля символов.
Действительно, при выполнении указанного условия любая разрешенная кодовая комбинация, полученная суммированием l строк образующей матрицы, имеет не менее d ненулевых символов, так как l ненулевых символов она всегда содержит в результате суммирования строк единичной матрицы. Синтезируем таким путем образующую матрицу двоичного систематического кода (7,4) с минимальным кодовым расстоянием d = 3. В каждой вектор-строке матрицы-дополнения согласно сформулированному условию (при l=1) должно быть не менее двух единиц. Среди трехразрядных векторов таких имеется четыре: 011, 110, 101, 111.
Эти векторы могут быть сопоставлены со строками единичной матрицы в любом порядке. В результате получим матрицы систематических кодов, эквивалентных коду Хэмминга, например:
Нетрудно убедиться, что при суммировании нескольких строк такой матрицы (l>1) получим вектор-строку, содержащую не менее d=3 ненулевых символов.
Имея образующую матрицу систематического кода Мn,k= [IkPk,n—k], можно построить так называемую проверочную (контрольную) матрицу Н размерности (n – k) n:
При умножении неискаженного кодового вектора Аni на матрицу, транспонированную к матрице Н, получим вектор, все компоненты которого равны нулю:
Каждая компонента Sj является результатом проверки справедливости соответствующего уравнения декодирования:
В общем случае, когда кодовый вектор Аni =(a1, a2,…, ai,…,ak,ak+1,…,aj,…,an) искажен вектором ошибки ξni =(ξ1, ξ2,…, ξi,…,ξk,aξk+1,…,ξj,…,ξn), умножение вектора (Аni + ξni) на матрицу Нт дает ненулевые компоненты:
Отсюда видно, что Sj(k +1 j
n) представляют собой символы, зависящие только от вектора ошибки, а вектор S = (Sk + 1, Sk + 2, …,, Sj, …, Sn) является не чем иным, как опознавателем ошибки (синдромом).
Для двоичных кодов (операция сложения тождественна операции вычитания) проверочная матрица имеет вид
Пример 32. Найдем проверочную матрицу Н для кода (7,4) с образующей матрицей М:
Определим синдромы в случаях отсутствия и наличия ошибки в кодовом векторе 1100011.
Выполним транспонирование матрицы P4,3
Запишем проверочную матрицу:
Умножение на Нт неискаженного кодового вектора 1100011 дает нулевой синдром:
При наличии в кодовом векторе ошибки, например, в 4-м разряде (1101011) получим:
Следовательно, вектор-строка 111 в данном коде является опознавателем (синдромом) ошибки в четвертом разряде. Аналогично можно найти и синдромы других ошибок. Множество всех опознавателей идентично множеству опознавателей кода Хэмминга (7,4), но сопоставлены они конкретным векторам ошибок по-иному, в соответствии с образующей матрицей данного (эквивалентного) кода.
4.8.5 Технические средства кодирования и декодирования для групповых кодов
Кодирующее устройство строится на основании совокупности равенств, отражающих правила построения кода. Определение значений символов в каждом из n – k проверочных разрядов в кодирующем устройстве осуществляется посредством сумматоров по модулю два.
На каждый разряд сумматора (кроме первого) используется четыре элемента И (вентиля) и два элемента ИЛИ.
Сумматор по модулю два выпускают в виде отдельного логического элемента, который на схеме изображается прямоугольником с надписью внутри — М2. Приведем несколько примеров реализации кодирующих и декодирующих устройств групповых кодов.
Пример 33. Рассмотрим техническую реализацию кода (7,4), имеющего целью исправление одиночных ошибок.
Правила построения кода определяются равенствами
a1=a3 a5
a7,
a2=a3 a6
a7,
a4=a5 a6
a7.
Схема кодирующего устройства приведена на рис. 4.6.
Рис. 4.6.
При поступлении импульса синхронизации со схемы управления подлежащая кодированию k-разрядная комбинация неизбыточного кода переписывается, например, с аналого-кодового преобразователя в информационные разряды n-разрядного регистра. Предположим, что в результате этой операции триггеры регистра установились в состояния, указанные в табл. 4.9.
С некоторой задержкой формируются выходные импульсы сумматоров С1, С2 С3, которые устанавливают триггеры проверочных разрядов в положение 0 или 1 в соответствии с приведенными выше равенствами. Например, в нашем случае ко входам сумматора C1 подводится информация, записанная в 3, 5 и 7-разрядах и, следовательно, триггер Тг1 первого проверочного разряда устанавливается в положение 1, аналогично триггер Тг2 устанавливается в положение 0, а триггер Тг4 — в положение 1.
Сформированная в регистре разрешенная комбинация (табл. 4.10) импульсом, поступающим с блока управления, последовательно или параллельно считывается в линию связи. Далее начинается кодирование следующей комбинации.
Рассмотрим теперь схему декодирования и коррекции ошибок (рис. 4.7), строящуюся на основе совокупности проверочных равенств. Для кода (7, 4) они имеют вид:
a1 a3
a5
a7= 0 ,
a2 a3
a6
a7= 0,
a4 a5
a6
a7= 0 .
Таблица 4.9.
|
Тr1 |
Тr2 |
Tr3 |
Тr4 |
Тr5 |
Tr6 |
Тr7 |
|
— |
— |
1 |
— |
0 |
1 |
0 |
Кодовая комбинация, возможно содержащая ошибку, поступает на n-разрядный приемный регистр (на рис. 4.7 триггеры Тг1 –Тг7). По окончании переходного процесса в триггерах с блока управления на каждый из сумматоров (C1 – С3) поступает импульс опроса.
Таблица 4.10.
|
Тг1 |
Тг2 |
Тг3 |
Тг4 |
Тг5 |
Tг6 |
Тг7 |
|
1 |
0 |
1 |
1 |
0 |
1 |
0 |
Рис. 4.7.
Выходные импульсы сумматоров устанавливают в положение 0 или 1 триггеры регистра опознавателей. Если проверочные равенства выполняются, все триггеры регистра опознавателей устанавливаются в положение 0, что соответствует отсутствию ошибок. При наличии ошибки в регистр опознавателей запишется опознаватель этого вектора ошибки. Дешифратор ошибки DC ставит в соответствие множеству опознавателей множество векторов ошибок. При опросе выходных вентилей дешифратора сигналы коррекции поступают только на те разряды, в которых вектор ошибки, соответствующий записанному на входе опознавателю, имеет единицы. Сигналы коррекции воздействуют на счетные входы триггеров. Последние изменяют свое состояние, и, таким образом, ошибка исправлена. На триггеры проверочных разрядов импульсы коррекции можно не посылать, если после коррекции информация списывается только с информационных разрядов. Для кода Хэмминга (7,4) любой опознаватель представляет собой двоичное трехразрядное число, равное номеру разряда приемного регистра, в котором записан ошибочный символ.
Предположим, что сформированная ранее в кодирующем устройстве комбинация при передаче исказилась и на приемном регистре была зафиксирована в виде, записанном в табл. 4.11.
Таблица 4.11.
|
Тг1 |
Тг2 |
Тг3 |
Тг4 |
Тг5 |
Тг6 |
Tг7 |
|
1 |
0 |
1 |
1 |
1 |
1 |
0 |
По результатам опроса сумматоров получаем:
на выходе С1 a1 a3
a5
a7= 1+1+1+0=1,
на выходе С2 a2 a3
a6
a7= 0+1+1+0=0,
на выходе С3 a4 a5
a6
a7= 1+1+1+0=1 .
Рис. 4.8.
Следовательно, номер разряда, в котором произошло искажение, 101 или 5. Импульс коррекции поступит на счетный вход триггера Тг5, и ошибка будет исправлена.
Пример 34. Реализуем мажоритарное декодирование для группового кода (8,2), рассчитанного на исправление двойных ошибок.
В случае мажоритарного декодирования сигналы с триггеров приемного регистра поступают непосредственно или после сложения по модулю два в соответствии с уравнениями системы разделённых проверок на мажоритарные элементы М, формирующие скорректированные информационные символы.
Схема декодирования представлена на рис. 4.8. На входах мажоритарных элементов указаны сигналы, соответствующие случаю поступления из канала связи кодовой информации, искаженной в обоих информационных разрядах (5-м и 8-м). Реализуя принцип решения «по большинству», мажоритарные элементы восстанавливают на выходе правильные значения информационных символов.
4.9 Построение циклических кодов
4.9.1 Общие понятия и определения
Любой групповой код (n, k) может быть записан в виде матрицы, включающей k линейно независимых строк по n символов и, наоборот, любая совокупность k линейно независимых n-разрядных кодовых комбинаций может рассматриваться как образующая матрица некоторого группового кода. Среди всего многообразия таких кодов можно выделить коды, у которых строки образующих матриц связаны дополнительным условием цикличности.
Все строки образующей матрицы такого кода могут быть получены циклическим сдвигом одной комбинации, называемой образующей для данного кода. Коды, удовлетворяющие этому условию, получили название циклических кодов.
Сдвиг осуществляется справа налево, причем крайний левый символ каждый раз переносится в конец комбинации. Запишем, например, совокупность кодовых комбинаций, получающихся циклическим сдвигом комбинации 001011:

Число возможных циклических (n, k)-кодов значительно меньше числа различных групповых (n, k)-кодов.
При описании циклических кодов n-разрядные кодовые комбинации представляются в виде многочленов фиктивной переменной х. Показатели степени у x соответствуют номерам разрядов (начиная с нулевого), а коэффициентами при х в общем случае являются элементы поля GF(q). При этом наименьшему разряду числа соответствует фиктивная переменная х0 = 1. Многочлен с коэффициентами из поля GF(q) называют многочленом над полем GF(q). Так как мы ограничиваемся рассмотрением только двоичных кодов, то коэффициентами при х будут только цифры 0 и 1. Иначе говоря, будем оперировать с многочленами над полем GF(2). Запишем, например, в виде многочлена образующую кодовую комбинацию 01011:
G(x) = 0·x4 + 1·x3 + 0·x2 + 1·x + 1
Поскольку члены с нулевыми коэффициентами при записи многочлена опускаются, образующий многочлен:
G(x) = x3 + x + 1
Наибольшую степень х в слагаемом с ненулевым коэффициентом называют степенью многочлена. Теперь действия над кодовыми комбинациями сводятся к действиям над многочленами. Суммирование многочленов осуществляется с приведением коэффициентов по модулю два.
Указанный циклический сдвиг некоторого образующего многочлена степени n — k без переноса единицы в конец кодовой комбинации соответствует простому умножению на х. Умножив, например, первую строку матрицы (001011), соответствующую многочлену g0(х) = x3 + x + 1, на х, получим вторую строку матрицы (010110), соответствующую многочлену х • g0(x).
Нетрудно убедиться, что кодовая комбинация, получающаяся при сложении этих двух комбинаций, также будет соответствовать результату умножения многочлена x3 + x + 1 на многочлен x+1. Действительно,

Циклический сдвиг строки матрицы с единицей в старшем (n-м) разряде (слева) равносилен умножению соответствующего строке многочлена на х с одновременным вычитанием из результата многочлена хn + 1= хn – 1, т. е. с приведением по модулю хn + 1.
Отсюда ясно, что любая разрешенная кодовая комбинация циклического кода может быть получена в результате умножения образующего многочлена на некоторый другой многочлен с приведением результата по модулю xn + l. Иными словами, при соответствующем выборе образующего многочлена любой многочлен циклического кода будет делиться на него без остатка.
Ни один многочлен, соответствующий запрещенной кодовой комбинации, на образующий многочлен без остатка не делится. Это свойство позволяет обнаружить ошибку. По виду остатка можно определить и вектор ошибки.
Умножение и деление многочленов весьма просто осуществляется на регистрах сдвига с обратными связями, что и явилось причиной широкого применения циклических кодов.
4.9.2 Математическое введение к циклическим кодам
Так как каждая разрешенная комбинация n-разрядного циклического кода есть произведение двух многочленов, один из которых является образующим, то эти комбинации можно рассматривать как подмножества всех произведений многочленов степени не выше n—1. Это наталкивает на мысль использовать для построения этих кодов еще одну ветвь теории алгебраических систем, а именно теорию колец.
Как следует из приведенного ранее определения, для образования кольца на множестве n-разрядных кодовых комбинаций необходимо задать две операции: сложение и умножение.
Операция сложения многочленов уже выбрана нами с приведением коэффициентов по модулю два.
Определим теперь операцию умножения. Нетрудно видеть, что операция умножения многочленов по обычным правилам с приведением подобных членов по модулю два может привести к нарушению условия замкнутости. Действительно, в результате умножения могут быть получены многочлены более высокой степени, чем n—1, вплоть до 2(n-1), а соответствующие им кодовые комбинации будут иметь число разрядов, превышающее n и, следовательно, не относятся к рассматриваемому множеству. Поэтому операция символического умножения задается так:
1) многочлены перемножаются по обычным правилам, но с приведением подобных членов по модулю два;
2) если старшая степень произведения не превышает n-1, то оно и является результатом символического умножения;
3) если старшая степень произведения больше или равна n, то многочлен произведения делится на заранее определенный многочлен степени n и результатом символического умножения считается остаток от деления.
Степень остатка не превышает n—1, и, следовательно, этот многочлен принадлежит к рассматриваемому множеству k-разрядных кодовых комбинаций.
При анализе циклического сдвига с перенесением единицы в конец кодовой комбинации установлено, что таким многочленом n-й степени является многочлен хn + 1.
Действительно, в результате умножения многочлена степени n-1 на х получим
G(x) = (xn-1 + xn-2 + … + x + 1)x = xn + xn-1 + … + x
Следовательно, чтобы результат умножения и теперь соответствовал кодовой комбинации, образующейся путем циклического сдвига исходной кодовой комбинации, в нем необходимо заменить хn на 1. Такая замена эквивалентна делению полученного при умножении многочлена на xn + 1 с записью в качестве результата остатка от деления, что обычно называют взятием остатка или приведением по модулю xn + 1 (сам остаток при этом называют вычетом).
Выделим теперь в нашем кольце подмножество всех многочленов, кратных некоторому многочлену g(x). Такое подмножество называют идеалом, а многочлен g(x)-порождающим многочленом идеала.
Количество различных элементов в идеале определяется видом его порождающего многочлена. Если на порождающий многочлен взять 0, то весь идеал будет составлять только этот многочлен, так как умножение его на любой другой многочлен дает 0.
Если за порождающий многочлен принять 1[g(x) = 1], то в идеал войдут все многочлены кольца. В общем случае число элементов идеала, порожденного простым многочленом степени n-k, составляет 2k.
Теперь становится понятным, что циклический двоичный код в построенном нами кольце n-разрядных двоичных кодовых комбинаций является идеалом. Остается выяснить, как выбрать многочлен g(x), способный породить циклический код с заданными свойствами.
4.9.3 Требования, предъявляемые к образующему многочлену
Согласно определению циклического кода все многочлены, соответствующие его кодовым комбинациям, должны делиться на g(x) без остатка. Для этого достаточно, чтобы на g(x) делились без остатка многочлены, составляющие образующую матрицу кода. Последние получаются циклическим сдвигом, что соответствует последовательному умножению g(x) на х с приведением по модулю xn + 1.
Следовательно, в общем случае многочлен gi(x) является остатком от деления произведения g(x)·хi на многочлен xn + 1 и может быть записан так:
gi(x)=g(x)xi + c(xn + 1)
где с =1, если степень g(x) хi превышает п-1; с = 0, если степень g(x) хi не превышает п-1.
Отсюда следует, что все многочлены матрицы, а поэтому и все многочлены кода будут делиться на g(x) без остатка только в том случае, если на g(x) будет делиться без остатка многочлен xn + 1.
Таким образом, чтобы g(x) мог породить идеал, а, следовательно, и циклический код, он должен быть делителем многочлена xn + 1.
Поскольку для кольца справедливы все свойства группы, а для идеала — все свойства подгруппы, кольцо можно разложить на смежные классы, называемые в этом случае классами вычетов по идеалу.
Первую строку разложения образует идеал, причем нулевой элемент располагается крайним слева. В качестве образующего первого класса вычетов можно выбрать любой многочлен, не принадлежащий идеалу. Остальные элементы данного класса вычетов образуются путем суммирования образующего многочлена с каждым многочленом идеала.
Если многочлен g(x) степени m = n-k является делителем xn + 1, то любой элемент кольца либо делится на g(x) без остатка (тогда он является элементом идеала), либо в результате деления появляется остаток r(х), представляющий собой многочлен степени не выше m-1.
Элементы кольца, дающие в остатке один и тот же многочлен ri(x), относятся к одному классу вычетов. Приняв многочлены r(х) за образующие элементы классов вычетов, разложение кольца по идеалу с образующим многочленом g(x) степени m можно представить табл. 4.12, где f(x)-произвольный многочлен степени не выше n-m-1.
Таблица 4.12.
|
0 |
g(x) |
x·g(x) |
(x+1)·g(x) |
… |
f(x)·g(x) |
|
r1(x) r2(x) … … rn(x) |
g(x) + r1(x) g(x) + r2(x) … … g(x) + rn(x) |
x·g(x) + r1(x) x·g(x) + r2(x) … … x·g(x) + rn(x) |
(x+1)·g(x) + r1(x) (x+1)·g(x) + r2(x) … … (x+1)·g(x) + rn(x) |
… … … … … |
f(x)·g(x) + r1(x) f(x)·g(x) + r2(x) … … f(x)·g(x) + rn(x) |
Как отмечалось, групповой код способен исправить столько разновидностей ошибок, сколько различных классов насчитывается в приведенном разложении. Следовательно, корректирующая способность циклического кода будет тем выше, чем больше остатков может быть образовано при делении многочлена, соответствующего искаженной кодовой комбинации, на образующий многочлен кода.
Наибольшее число остатков, равное 2m — 1 (исключая нулевой), может обеспечить только неприводимый (простой) многочлен, который делится сам на себя и не делится ни на какой другой многочлен (кроме 1).
4.10 Выбор образующего многочлена по заданному объему кода и заданной корректирующей способности
По заданному объему кода однозначно определяется число информационных разрядов k. Далее необходимо найти наименьшее n, обеспечивающее обнаружение или исправление ошибок заданной кратности. В случае циклического кода эта проблема сводится к нахождению нужного многочлена g(x).
Начнем рассмотрение с простейшего циклического кода, обнаруживающего все одиночные ошибки.
4.10.1 Обнаружение одиночных ошибок
Любая принятая по каналу связи кодовая комбинация h(x), возможно содержащая ошибку, может быть представлена в виде суммы по модулю два неискаженной комбинации кода f(x) и вектора ошибки ξ(x):
h(x) = f(x) ξ(x)
При делении h(x) на образующий многочлен g(x) остаток, указывающий на наличие ошибки, обнаруживается только в том случае, если многочлен, соответствующий вектору ошибки, не делится на g(x): f(x)-неискаженная комбинация кода и, следовательно, на g(x) делится без остатка.
Вектор одиночной ошибки имеет единицу в искаженном разряде и нули во всех остальных разрядах. Ему соответствует многочлен ξ(x) = xi. Последний не должен делиться на g(x). Среди неприводимых многочленов, входящих в разложении хn+1, многочленом наименьшей степени, удовлетворяющим указанному условию, является x + 1. Остаток от деления любого многочлена на x + 1 представляет собой многочлен нулевой степени и может принимать только два значения: 0 или 1. Все кольцо в данном случае состоит из идеала, содержащего многочлены с четным числом членов, и одного класса вычетов, соответствующего единственному остатку, равному 1. Таким образом, при любом числе информационных разрядов необходим только один проверочный разряд. Значение символа этого разряда как раз и обеспечивает четность числа единиц в любой разрешенной кодовой комбинации, а, следовательно, и делимость ее на xn + 1.
Полученный циклический код с проверкой на четность способен обнаруживать не только одиночные ошибки в отдельных разрядах, но и ошибки в любом нечетном числе разрядов.
4.10.2 Исправление одиночных или обнаружение двойных ошибок
Прежде чем исправить одиночную ошибку в принятой комбинации из п разрядов, необходимо определить, какой из разрядов был искажен. Это можно сделать только в том случае, если каждой одиночной ошибке в определенном разряде соответствуют свой класс вычетов и свой опознаватель. Так как в циклическом коде опознавателями ошибок являются остатки от деления многочленов ошибок на образующий многочлен кода g(x), то g(x) должно обеспечить требуемое число различных остатков при делении векторов ошибок с единицей в искаженном разряде. Как отмечалось, наибольшее число остатков дает неприводимый многочлен. При степени многочлена m = n-k он может дать 2n—k — 1 ненулевых остатков (нулевой остаток является опознавателем безошибочной передачи).
Следовательно, необходимым условием исправления любой одиночной ошибки является выполнение неравенства
2n—k — 1 = n,
где — общее число разновидностей одиночных ошибок в кодовой комбинации из п символов; отсюда находим степень образующего многочлена кода
m = n – k log2(n+1)
и общее число символов в кодовой комбинации. Наибольшие значения k и п для различных m можно найти пользуясь табл. 4.13.
Таблица 4.13.
|
M |
1 |
2 |
3 |
4 |
5 |
6 |
7 |
8 |
9 |
10 |
|
N |
1 |
3 |
7 |
15 |
31 |
63 |
127 |
255 |
511 |
1023 |
|
K |
0 |
1 |
4 |
11 |
26 |
57 |
120 |
247 |
502 |
1013 |
Как указывалось, образующий многочлен g(x) должен быть делителем двучлена хn+1. Доказано, что любой двучлен типа х2m-1+ 1 = хn+1 может быть представлен произведением всех неприводимых многочленов, степени которых являются делителями числа т (от 1 до т включительно). Следовательно, для любого т существует по крайней мере один неприводимый многочлен степени т, входящий сомножителем в разложение двучлена хn+1.
Пользуясь этим свойством, а также имеющимися в ряде книг таблицами многочленов, неприводимых при двоичных коэффициентах, выбрать образующий многочлен при известных n и m несложно. Определив образующий многочлен, необходимо убедиться в том, что он обеспечивает заданное число остатков.
Пример 35. Выберем образующий многочлен для случая n = 15 и m = 4.
Двучлен x15 + 1 можно записать в виде произведения всех неприводимых многочленов, степени которых являются делителями числа 4. Последнее делится на 1, 2, 4.
В таблице неприводимых многочленов находим один многочлен первой степени, а именно x+1, один многочлен второй степени x2 + x + 1 и три многочлена четвертой степени: х4 + x + 1, х4 + х3 + 1, х4 + х3 + х2 + х + 1. Перемножив все многочлены, убедимся в справедливости соотношения (х + 1)(х2 + х + 1)(х4 + х + 1)(х4 + х3+ 1)(х4 + х3 + х2 + х + 1) = x15 + 1
Один из сомножителей четвертой степени может быть принят за образующий многочлен кода. Возьмем, например, многочлен х4 + х3 + 1, или в виде двоичной последовательности 11001.
Чтобы убедиться, что каждому вектору ошибки соответствует отличный от других остаток, необходимо поделить каждый из этих векторов на 11001.Векторы ошибок m младших разрядов имеют вид: 00…000, 00…0010, 00…0100, 00…1000.
Степени соответствующих им многочленов меньше степени образующего многочлена g(x). Поэтому они сами являются остатками при нулевой целой части. Остаток, соответствующий вектору ошибки в следующем старшем разряде, получаем при делении 00…10000 на 11001, т.е.

Аналогично могут быть найдены и остальные остатки. Однако их можно получить проще, деля на g(x) комбинацию в виде единицы с рядом нулей и выписывая все промежуточные остатки:

При последующем делении остатки повторяются.
Таким образом, мы убедились в том, что число различных остатков при выбранном g(x) равно п = 15, и, следовательно, код, образованный таким g(x), способен исправить любую одиночную ошибку. С тем же успехом за образующий многочлен кода мог быть принят и многочлен х4 + х + 1. При этом был бы получен код, эквивалентный выбранному.
Однако использовать для тех же целей многочлен х4 + х3 + x2 + х + 1 нельзя. При проверке числа различных остатков обнаруживается, что их у него не 15, а только 5. Действительно,

Это объясняется тем, что многочлен x4 + х3 + х2 + х + 1 входит в разложение не только двучлена x15+ 1, но и двучлена x5 + 1.
Из приведенного примера следует, что в качестве образующего следует выбирать такой неприводимый многочлен g(x) (или произведение таких многочленов), который, являясь делителем двучлена хп + 1, не входит в разложение ни одного двучлена типа хλ+ 1, степень которого λ меньше п. В этом случае говорят, что многочлен g(x) принадлежит показателю степени п.
В табл. 4.14 приведены основные характеристики некоторых кодов, способных исправлять одиночные ошибки или обнаруживать все одиночные и двойные ошибки.
Таблица 4.14.
|
Показатель неприводимого многочлена |
Образующий многочлен |
Число остатков |
Длина кода |
|
2 3 3 4 4 5 5 |
x2 + x + 1 x3 + x + 1 x3 + x2 + 1 x4 + x3 + 1 x4 + x + 1 x5 + x2 + 1 x5 + x3 + 1 |
3 7 7 15 15 31 31 |
3 7 7 15 15 31 31 |
Это циклические коды Хэмминга для исправления одной ошибки, в которых в отличие от групповых кодов Хэмминга все проверочные разряды размещаются в конце кодовой комбинации.
Эти коды могут быть использованы для обнаружения любых двойных ошибок. Многочлен, соответствующий вектору двойной ошибки, имеет вид ξ(х) = хi – хj, или ξ(x) = хi(хj – i + 1) при j>i. Так как j – ig(x) не кратен х и принадлежит показателю степени п, то ξ(x) не делится на g(x), что и позволяет обнаружить двойные ошибки.
4.10.3 Обнаружение ошибок кратности три и ниже
Образующие многочлены кодов, способных обнаруживать одиночные, двойные и тройные ошибки, можно определить, базируясь на следующем указании Хэмминга. Если известен образующий многочлен р(хт) кода длины п, позволяющего обнаруживать ошибки некоторой кратности z, то образующий многочлен g(x) кода, способного обнаруживать ошибки следующей кратности (z + 1), может быть получен умножением многочлена р(хт) на многочлен х + 1, что соответствует введению дополнительной проверки на четность. При этом число символов в комбинациях кода за счет добавления еще одного проверочного символа увеличивается до n + l.
В табл. 4.15 приведены основные характеристики некоторых кодов, способных обнаруживать ошибки кратности три и менее.
Таблица 4.15.
|
Показатель неприводимого многочлена |
Образующий многочлен |
Число информационных символов |
Длина кода |
|
3 4 5 |
(x+1)(x3 + x + 1) (x+1)(x4+ x + 1) (x+1)(x5+ x + 1) |
4 11 26 |
8 16 32 |
4.10.4 Обнаружение и исправление независимых ошибок произвольной кратности
Важнейшим классом кодов, используемых в каналах, где ошибки в последовательностях символов возникают независимо, являются коды Боуза-Чоудхури-Хоквингема. Доказано, что для любых целых положительных чисел m и sп = 2т—1 с числом проверочных символов не более ms, который способен обнаруживать ошибки кратности 2s или исправлять ошибки кратности s. Для понимания теоретических аспектов этих кодов необходимо ознакомиться с рядом новых понятий высшей алгебры.
4.10.5 Обнаружение и исправление пачек ошибок
Для произвольного линейного блокового (п, k)-кода, рассчитанного на исправление пакетов ошибок длины b или менее, основным соотношением, устанавливающим связь корректирующей способности с числом избыточных символов, является граница Рейджера: n – k 2b
При исправлении линейным кодом пакетов длины b или менее с одновременным обнаружением пакетов длины l b или менее требуется по крайней мере b + l проверочных символов.
Из циклических кодов, предназначенных для исправления пакетов ошибок, широко известны коды Бартона, Файра и Рида-Соломона.
Первые две разновидности кодов служат для исправления одного пакета ошибок в блоке. Коды Рида-Соломона способны исправлять несколько пачек ошибок.
Особенности декодирования циклических кодов, исправляющих пакеты ошибок, рассмотрены далее на примере кодов Файра.
4.10.6 Методы образования циклического кода
Существует несколько различных способов кодирования. Принципиально наиболее просто комбинации циклического кода можно получить, умножая многочлены а(х), соответствующие комбинациям безызбыточного кода (информационным символам), на образующий многочлен кода g(x). Такой способ легко реализуется. Однако он имеет тот существенный недостаток, что получающиеся в результате умножения комбинации кода не содержат информационные символы в явном виде. После исправления ошибок такие комбинации для выделения информационных символов приходится делить на образующий многочлен кода.
Применительно к циклическим кодам принято (хотя это и не обязательно) отводить под информационные k символов, соответствующих старшим степеням многочлена кода, а под проверочные n—k символов низших разрядов. Чтобы получить такой систематический код, применяется следующая процедура кодирования.
Многочлен а(х), соответствующий k-разрядной комбинации безызбыточного кода, умножаем на хт, где m = n—k. Степень каждого одночлена, входящего в а(х), увеличивается, что по отношению к комбинации кода означает необходимость приписать со стороны младших разрядов m нулей. Произведение а(х)хт делим на образующий многочлен g(x). В общем случае при этом получаем некоторое частное q(x) той же степени, что и а(х) и остаток r(х). Последний прибавляем к а(х)хт. В результате получаем многочлен
f(x) = a(x)xm + r(x)
Поскольку степень g(x) выбираем равной т, степень остатка r(х) не превышает m – 1. В комбинации, соответствующей многочлену а(х)хт, т младших разрядов нулевые, и, следовательно, указанная операция сложения равносильна приписыванию r(х) к а(х) со стороны младших разрядов.
Покажем, что f(x) делится на g(x) без остатка, т. е. является многочленом, соответствующим комбинации кода. Действительно, запишем многочлен а(х)хт в виде
a(x)xm = q(x)g(x) + r(x)
Так как операции сложения и вычитания по модулю два идентичны, r(х) можно перенести влево, тогда что и требовалось доказать.
a(x)xm+ r(x) = f(x) = q(x)g(x)
Таким образом, циклический код можно строить, приписывая к каждой комбинации безызбыточного кода остаток от деления соответствующего этой комбинации многочлена на образующий многочлен кода. Для кодов, число информационных символов в которых больше числа проверочных, рассмотренный способ реализуется наиболее просто.
Следует указать еще на один способ кодирования. Так как циклический код является разновидностью группового кода, то его проверочные символы должны выражаться через суммы по модулю два определенных информационных символов.
Равенства для определения проверочных символов могут быть получены путем решения рекуррентных соотношений:
(4.5)
где h—двоичные коэффициенты так называемого генераторного многочлена h(x), определяемого так
h(x) = (xn + 1)/g(x) = h0 + h1x + … + hkxk
Соотношение (4.5) позволяет по заданной последовательности информационных сигналов a0, a1, …, ak-1 вычислить n—k проверочных символов ak, ak+1, … …, an-1. Проверочные символы, как и ранее, размещаются на местах младших разрядов. При одних и тех же информационных символах комбинации кода, получающиеся таким путем, полностью совпадают с комбинациями, получающимися при использовании предыдущего способа кодирования. Применение данного способа целесообразно для кодов с числом проверочных символов, превышающим число информационных, например для кодов Боуза-Чоудхури-Хоквингема.
4.10.7 Матричная запись циклического кода
Полная образующая матрица циклического кода Mn,k составляется из двух матриц: единичной Ik (соответствующей k информационным разрядам) и дополнительной Сk,n—k (соответствующей проверочным разрядам):
Mn,k = || IkCk,n—k ||
Построение матрицы Ik трудностей не представляет. Если образование циклического кода производится на основе решения рекуррентных соотношений, то его дополнительную матрицу можно определить, воспользовавшись правилами, указанными ранее. Однако обычно строки дополнительной матрицы циклического кода Сk,n—k определяются путем вычисления многочленов r(х). Для каждой строки матрицы Ik соответствующий r(х) находят делением информационного многочлена а(х)хт этой строки на образующий многочлен кода g(x).
Дополнительную матрицу можно определить и не строя Ik. Для этого достаточно делить на g(x) комбинацию в виде единицы с рядом нулей и получающиеся остатки записывать в качестве строк дополнительной матрицы. При этом если степень какого-либо r(х) оказывается меньше n – k – 1, то следующие за этим остатком строки матрицы получают путем циклического сдвига предыдущей строки влево до тех пор, пока степень r(х) не станет равной п-k— 1. Деление производится до получения k строк дополнительной матрицы.
Пример 36. Запишем образующую матрицу для циклического кода (15,11) с порождающим многочленом g(x) = х4 + х3 + 1.
Воспользовавшись результатами ранее проведенного деления, получим

Существует другой способ построения образующей матрицы, базирующийся на основной особенности циклического (n, k)-кода. Он проще описанного, но получающаяся матрица менее удобна.
Матричная запись кодов достаточно широко распространена.
4.10.8 Укороченные циклические коды
Корректирующие возможности циклических кодов определяются степенью т образующего многочлена. В то время как необходимое число информационных символов может быть любым целым числом, возможности в выборе разрядности кода весьма ограничены.
Если, например, необходимо исправить единичные ошибки при k = 5, то нельзя взять образующий многочлен третьей степени, поскольку он даст только семь остатков, а общее число разрядов получится равным 8.
Следовательно, необходимо брать многочлен четвертой степени и тогда n= 15. Такой код рассчитан на 11 информационных разрядов.
Однако можно построить код минимальной разрядности, заменив в (n, k) -коде j первых информационных символов нулями и исключив их из кодовых комбинаций. Код уже не будет циклическим, поскольку циклический сдвиг одной разрешенной кодовой комбинации не всегда приводит к другой разрешенной комбинации того же кода. Получаемый таким путем линейный (n—j, k—j)-код называют укороченным циклическим кодом. Минимальное расстояние этого кода не менее, чем минимальное кодовое расстояние (n, k)-кода, из которого он получен. Матрица укороченного кода получается из образующей матрицы (n, k)-кода исключением j строк и столбцов, соответствующих старшим разрядам. Например, образующая матрица кода (9,5), полученная из матрицы кода (15,11), имеет вид

4.11 Технические средства кодирования и декодирования для циклических кодов
4.11.1 Линейные переключательные схемы
Основу кодирующих и декодирующих устройств циклических кодов составляют регистры сдвига с обратными связями, позволяющие осуществлять как умножение, так и деление многочленов с приведением коэффициентов по модулю два. Такие регистры также называют многотактными линейными переключательными схемами и линейными кодовыми фильтрами Хаффмена. Они состоят из ячеек памяти, сумматоров по модулю два и устройств умножения на коэффициенты многочленов множителя или делителя. В случае двоичных кодов для умножения на коэффициент, равный 1, требуется только наличие связи в схеме. Если коэффициент равен 0, то связь отсутствует. Сдвиг информации в регистре осуществляется импульсами, поступающими с генератора продвигающих импульсов, который на схеме, как правило, не указывается. На вход устройств поступают только коэффициенты многочленов, причем начиная с коэффициента при переменной в старшей степени.
Рис. 4.9.
На рис. 4.9 представлена схема, выполняющая умножение произвольного (например, информационного) многочлена
a(x) = a0 + a1x + … + ak-1xk-1
на некоторый фиксированный (например, образующий) многочлен
g(x) = g0 + g1x + … + gn-kxn-k.
Произведение этих многочленов равно
a(x)g(x)=a0g0 + (a0g1 + a1g0)x + … +(ak-2gn-k + ak-1gn-k-1)xn-2 +ak-1gn-kxn-1
Предполагаем, что первоначально ячейки памяти находятся в нулевом состоянии и что за коэффициентами множимого следует n—k нулей.
На первом такте на вход схемы поступает первый коэффициент аk-1 многочлена а(х) и на выходе появляется первый коэффициент произведения, равный
ak-1gn—k
На следующем такте на выход поступит сумма
ak-2gn-k + ak-1gn-k-1 ,
т.е. второй коэффициент произведения, и т. д. На n-м такте все ячейки, кроме последней, будут в нулевом состоянии и на выходе получим последний коэффициент а0g0
Используется также схема умножения многочленов при поступлении множимого младшим разрядом вперед (рис. 4.10).
На рис. 4.11 представлена схема, выполняющая деление произвольного многочлена, например
a(x)xm = a0 + a1x + … + an-1xn-1
на некоторый фиксированный (например, образующий) многочлен
g(x) = g0 + g1x + … + gn-kxn-k
Обратные связи регистра соответствуют виду многочлена g(x). Количество включаемых в него сумматоров равно числу отличных от нуля коэффициентов g(x), уменьшенному на единицу. Это объясняется тем, что сумматор сложения коэффициентов старших разрядов многочленов делимого и делителя в регистр не включается, так как результат сложения заранее известен (он равен 0).
Рис. 4.10.
Рис. 4.11.
За первые n—k тактов коэффициенты многочлена-делимого заполняют регистр, причем коэффициент при х в старшей степени достигает крайней правой ячейки. На следующем такте «единица» делимого, выходящая из крайней ячейки регистра, по цепи обратной связи подается к сумматорам по модулю два, что равносильно вычитанию многочлена-делителя из многочлена-делимого. Если в результате предыдущей операции коэффициент при старшей степени х у остатка оказался равным нулю, то на следующем такте делитель не вычитается. Коэффициенты делимого только сдвигаются вперед по регистру на один разряд, что находится в полном соответствии с тем, как это делается при делении многочленов столбиком.
Деление заканчивается с приходом последнего символа многочлена-делимого. При этом разность будет иметь более низкую степень, чем делитель. Эта разность и есть остаток.
Отметим, что если в качестве многочлена-делителя выбран простой многочлен степени m = n—k, то, продолжая делить образовавшийся остаток при отключенном входе, будем получать в регистре по одному разу каждое из ненулевых m-разрядных двоичных чисел. Затем эта последовательность чисел повторяется.
Пример 37. Рассмотрим процесс деления многочлена а(х)хт =(x3+1)x3 на образующий многочлен g(x) = х3+ х2+1. Схема для этого случая представлена на рис. 4.12, где 1, 2, 3-ячейки регистра. Работа схемы поясняется табл. 4.16.
Рис. 4.12.
Вычисление остатка начинается с четвертого такта и заканчивается после седьмого такта. Последующие сдвиги приводят к образованию в регистре последовательности из семи различных ненулевых трехразрядных чисел. В дальнейшем эта последовательность чисел повторяется.
Рассмотренные выше схемы умножения и деления многочленов непосредственно в том виде, в каком они представлены на рис. 4.10, 4.11, в качестве кодирующих устройств циклических кодов на практике не применяются: первая — из-за того, что образующаяся кодовая комбинация в явном виде не содержит информационных символов, а вторая — из-за того, что между информационными и проверочными символами образуется разрыв в n — k разрядов.
4.11.2 Кодирующие устройства
Все известные кодирующие устройства для любых типов циклических кодов, выполненные на регистрах сдвига, можно свести к двум типам схем согласно рассмотренным ранее методам кодирования.
Таблица 4.16.
|
Номер такта |
Вход |
Состояние ячеек регистра |
Номер такта |
Вход |
Состояние ячеек регистра |
||||
|
1 |
2 |
3 |
1 |
2 |
3 |
||||
|
1 2 3 4 5 6 7 |
1 0 0 1 0 0 0 |
1 0 0 0 1 1 1 |
0 1 0 0 0 1 1 |
0 0 1 1 1 1 0 |
8 9 10 11 12 13 14 |
— — — — — — — |
0 1 0 0 1 1 1 |
1 0 1 0 0 1 1 |
1 0 0 1 1 1 0 |
Схемы первого типа вычисляют значения проверочных символов путем непосредственного деления многочлена а(х)хт на образующий многочлен g(x). Это делается с помощью регистра сдвига, содержащего n—k разрядов (рис. 4.13).
Рис. 4.13.
Схема отличается от ранее рассмотренной тем, что коэффициенты кодируемого многочлена участвуют в обратной связи не через n—k сдвигов, а сразу с первого такта. Это позволяет устранить разрыв между информационными и проверочными символами.
В исходном состоянии ключ К1 находится в положении 1. Информационные символы одновременно поступают как в линию связи, так и в регистр сдвига, где за k тактов образуется остаток. Затем ключ K1 переходит в положение 2 и остаток поступает в линию связи.
Пример 38. Рассмотрим процесс деления многочлена а(х)хт = (х3 + 1)x3 на многочлен g(x) = x3 + х2+ 1 за k тактов.
Схема кодирующего устройства для заданного g(x) приведена на рис. 4.14. Процесс формирования кодовой комбинации шаг за шагом представлен в табл. 4.17, где черточками отмечены освобождающиеся ячейки, занимаемые новыми информационными символами.
С помощью схем второго типа вычисляют значения проверочных символов как линейную комбинацию информационных символов, т. е. они построены на использовании основного свойства систематических кодов. Кодирующее устройство строится на основе k-разрядного регистра сдвига (рис. 4.15).
Рис. 4.14.
Таблица 4.17.
|
Номер такта |
Вход |
Состояние ячеек регистра |
Выход |
||
|
1 |
2 |
3 |
|||
|
1 2 3 4 5 6 7 |
1 0 0 1 0 0 0 |
1 1 1 1 — — — |
0 1 1 1 1 — — |
1 1 0 0 1 1 — |
1 01 001 1001 01001 101001 1101001 |
Выходы ячеек памяти подключаются к сумматору в цепи обратной связи в соответствии с видом генераторного многочлена
h(x) = (xn + 1)/g(x) = h0 + h1x + … + hkxk
В исходном положении ключ К1 находится в положении 1. За первые k тактов поступающие на вход информационные символы заполняют все ячейки регистра. После этого ключ переводят в положение 2. На каждом из последующих тактов один из информационных символов выдается в канал связи и одновременно формируется проверочный символ, который записывается в последнюю ячейку регистра. Через n—k тактов процесс формирования проверочных символов заканчивается и ключ K1 снова переводится в положение 1.
В течение последующих k тактов содержимое регистра выдается в канал связи с одновременным заполнением ячеек новой последовательности информационных символов.
Пример 39. Рассмотрим процесс формирования кодовой комбинации с использованием генераторного многочлена для случая g(x) = x3 + x2 + 1 и а(x) = x3 + 1.
Определяем генераторный многочлен:
Рис. 4.15.
Рис. 4.16.
Соответствующая h(x) схема кодирующего устройства приведена на рис. 4.16. Формирование кодовой комбинации поясняется табл. 4.18. Оно начинается после заполнения регистра информационными символами.
4.11.3 Декодирующие устройства
Декодирование комбинаций циклического кода можно проводить различными методами. Существуют методы, основанные на использовании рекуррентных соотношений, на мажоритарном принципе, на вычислении остатка от деления принятой комбинации на образующий многочлен кода и др. Целесообразность применения каждого из них зависит от конкретных характеристик используемого кода.
Рассмотрим сначала устройства декодирования, в которых для обнаружения и исправления ошибок производится деление произвольного многочлена f(x), соответствующего принятой комбинации, на образующий многочлен кода g0(x). В этом случае при декодировании могут использоваться те же регистры сдвига, что и при кодировании.
Таблица 4.18.
|
Номер такта |
Состояние ячеек регистра |
Выход |
|||
|
1 |
2 |
3 |
4 |
||
|
1 2 3 4 5 6 7 |
1 0 1 1 — — — |
0 1 0 1 1 — — — |
0 0 1 0 1 1 — — |
1 0 0 1 0 1 1 — |
1 01 001 1001 01001 101001 1101001 |
Рис. 4.17.
Декодирующие устройства для кодов, обнаруживающих ошибки, по существу ничем не отличаются от схем кодирующих устройств. В них добавляется лишь буферный регистр для хранения принятого сообщения на время проведения операции деления. Если остатка не обнаружено (случай отсутствия ошибки), то информация с буферного регистра считывается в дешифратор сообщения. Если остаток обнаружен (случай наличия ошибки), то информация в буферном регистре уничтожается и на передающую сторону посылается импульс запроса повторной передачи.
В случае исправления ошибок схема несколько усложняется. Информацию о разрядах, в которых произошла ошибка, несет, как и ранее, остаток. Схема декодирующего устройства представлена на рис. 4.17.
Символы подлежащей декодированию кодовой комбинации, возможно, содержащей ошибку, последовательно, начиная со старшего разряда, вводятся в n-разрядный буферный регистр сдвига и одновременно в схему деления, где за n тактов определяется остаток, который в случае непрерывной передачи сразу же переписывается в регистр второй аналогичной схемы деления.
Начиная с (n + 1)-го такта в буферный регистр и первую схему деления начинают поступать символы следующей кодовой комбинации. Одновременно на каждом такте буферный регистр покидает один символ, а в регистре второй схемы деления появляется новый остаток (синдром). Детектор ошибок, контролирующий состояния ячеек этого регистра, представляет собой комбинаторно-логическую схему, построенную с таким расчетом, чтобы она отмечала все те синдромы («выделенные синдромы»), которые появляются в схеме деления, когда каждый из ошибочных символов занимает крайнюю правую ячейку в буферном регистре. При последующем сдвиге детектор формирует сигнал «1», который, воздействуя на сумматор коррекции, исправляет искаженный символ.
Одновременно по цепи обратной связи с выхода детектора подается сигнал «1» на входной сумматор регистра второй схемы деления. Этот сигнал изменяет выделенный синдром так, чтобы он снова соответствовал более простому типу ошибки, которую еще подлежит исправить. Продолжая сдвиги, обнаружим и другие выделенные синдромы. После исправления последней ошибки все ячейки декодирующего регистра должны оказаться в нулевом состоянии. Если в результате автономных сдвигов состояние регистра не окажется нулевым, это означает, что произошла неисправимая ошибка.
Для декодирования кодовых комбинаций, разнесенных во времени, достаточно одной схемы деления, осуществляющей декодирование за 2n тактов.
Сложность детектора ошибок зависит от числа выделенных синдромом. Простейшие детекторы получаются при реализации кодов, рассчитанных на исправление единичных ошибок.
Выделенный синдром появляется в схеме деления раньше всего в случае, когда ошибка имеет место в старшем разряде кодовой комбинации, так как он первым достигает крайней правой ячейки буферного регистра. Поскольку неискаженная кодовая комбинация делится на g0(x) без остатка, то для определения выделенного синдрома достаточно разделить на g0(x) вектор ошибки с единицей в старшем разряде. Остаток, получающийся на n-м такте, и является искомым выделенным синдромом.
В зависимости от номера искаженного разряда после первых тактов будем получать различные остатки (опознаватели соответствующих векторов ошибок). Вследствие этого выделенный синдром будет появляться в регистре схемы деления через различное число последующих тактов, обеспечивая исправление искаженного символа.
В качестве схем деления в декодирующем устройстве могут быть использованы как схемы, определяющие остаток за n тактов (см. рис. 4.11), так и схемы, определяющие остаток за k тактов (рис. 4.13). При использовании схемы деления за k тактов векторам одиночных ошибок ξ(х) будут соответствовать другие остатки на n-м такте, являющиеся результатом деления на образующий многочлен кода векторов ξ(х)хт, а на ξ(x). Поэтому выделенные синдромы, а следовательно, и детекторы ошибок для указанных схем будут различны.
Пример 40. Рассмотрим процесс исправления единичной ошибки при использовании кода (7,4) с образующим многочленом g(x) = х3 + х2 + 1 и применении в декодирующем устройстве схем деления за n и k тактов.
Определим опознаватели ошибок и выделенный синдром для случая использования схемы деления за n тактов:

Детектор ошибки, обеспечивающий формирование на выходе сигнала только в случае появления в схеме деления остатка 110, можно реализовать посредством двух логических элементов НЕ и одного логического элемента ИЛИ-НЕ.
На рис. 4.18 приведена схема соответствующего декодирующего устройства. В табл. 4.19 представлен процесс исправления ошибки для случая, когда кодовая комбинация 1001011 (см. табл. 4.18) поступила на вход декодирующего устройства с искаженным символом в 4-м разряде (1000011).
После n (в данном случае 7) тактов в схему деления II переписывается опознаватель ошибки 101.
Рис. 4.18.
Таблица 4.19.
|
Номер такта |
Вход |
Состояние ячеек схем деления |
Выход после коррекции |
||
|
1 |
2 |
3 |
|||
|
1 2 3 4 5 6 7 8 9 10 11 12 13 14 |
1 0 0 0 0 1 1 0 0 0 0 0 0 0 |
1 0 0 1 1 0 1 1 1 0 0 0 0 0 |
0 1 0 0 1 1 0 1 1 1 0 0 0 0 |
0 0 1 1 1 0 1 1 0 1 0 0 0 0 |
Переписывается в схему деления II 1 01 001 1001 01001 101001 1101001 |
На каждом последующем такте на выходе буферного регистра появляется неискаженный символ корректируемой кодовой комбинации, а в схеме деления II новый остаток. Выделенный синдром появится в схеме деления на 10-м такте, когда искаженный символ займет крайнюю правую ячейку регистра. На следующем такте он попадет в корректирующий сумматор и будет там исправлен импульсом, поступающим с выхода детектора ошибки. Этот же импульс по цепи обратной связи приводит ячейки схемы деления II в нулевое состояние (корректирует выделенный синдром). При использовании схемы деления за k тактов соответствие между векторами ошибок и остатками на n-м такте иное.

Рис. 4.19.
Таблица 4.20.
|
Номер такта |
Вход |
Состояние ячеек схем деления |
Выход после коррекции |
||
|
1 |
2 |
3 |
|||
|
1 2 3 4 5 6 7 8 9 10 11 12 13 14 |
1 0 0 0 0 1 1 0 0 0 0 0 0 0 |
1 1 1 0 1 1 0 1 0 0 0 0 0 0 |
0 1 1 1 0 1 1 0 1 0 0 0 0 0 |
1 1 0 1 0 1 1 0 0 1 0 0 0 |
Переписывается в схему деления II 1 01 001 1001 01001 101001 1101001 |
Детектор для выделенного синдрома 100 можно построить из одного логического элемента НЕ и одного элемента ИЛИ-НЕ.
На рис. 4.19 представлена схема декодирующего устройства для этого случая. Табл. 4.20 позволяет проследить по тактам процесс исправления ошибки в кодовой комбинации 1000011 (искажен символ в 4-м разряде).
Сравнение показывает, что использование в декодирующем устройстве схемы деления за k тактов предпочтительнее, так как выделенный синдром в этом случае при любом объеме кода содержит единицу в старшем и нули во всех остальных разрядах, что приводит к более простому детектору ошибки.
Пример 41. Рассмотрим более сложный случай исправления одиночных и двойных смежных ошибок. Для этой цели может использоваться циклический код (7,3) с образующим многочленом g(x) = (х + 1)(x3 + x2+1).
Ориентируясь на схему деления за k тактов, найдем выделенный синдром для двойных смежных ошибок:

Для одиночных ошибок соответственно получим

Детектор ошибок в этом случае должен формировать сигнал коррекции при появлении каждого выделенного синдрома. Схема декодирующего устройства представлена на рис. 4.20.
Процесс исправления кодовой комбинации 1000010 с искаженными символами в 4-м и 5-м разрядах поясняется табл. 4.21.
На 9-м такте в схеме деления II появляется первый выделенный синдром 1100. На следующем такте на выходе аналогично обозначенного элемента ИЛИ-НЕ детектора ошибок формируется импульс коррекции, который исправляет 5-й разряд кодовой комбинации и одновременно по цепи обратной связи изменяет остаток в схеме деления II, приводя его в соответствие выделенному синдрому еще не исправленной одиночной ошибки в 4-м разряде (1000). На 11-м такте импульс коррекции формирует элемент ИЛИ-НЕ детектора ошибок, соответствующий указанному выделенному синдрому. Этим импульсом обеспечивается исправление 4-го разряда кодовой комбинации и получение нулевого остатка в схеме деления II.
Рис. 4.20.
Таблица 4.21.
|
Номер такта |
Вход |
Состояние ячеек схем деления |
Выход после коррекции |
|||
|
1 |
2 |
3 |
4 |
|||
|
1 2 3 4 5 6 7 8 9 10 11 12 13 14 |
1 0 0 0 1 0 0 0 0 0 0 0 0 0 |
1 0 1 1 1 0 1 0 0 0 0 0 0 0 |
1 1 1 0 0 1 1 1 0 0 0 0 0 0 |
1 1 0 0 1 0 0 1 1 0 0 0 0 0 |
0 1 1 0 0 1 0 0 1 1 0 0 0 0 |
Переписывается в схему деления II 1 01 101 1101 11101 011101 0011101 |
Список литературы
-
Дмитриев В.И. Прикладная теория информации. Учебник для студентов ВУЗов по специальности «Автоматизированные системы обработки информации и управления». – М.: Высшая школа, 1989 – 320 с.