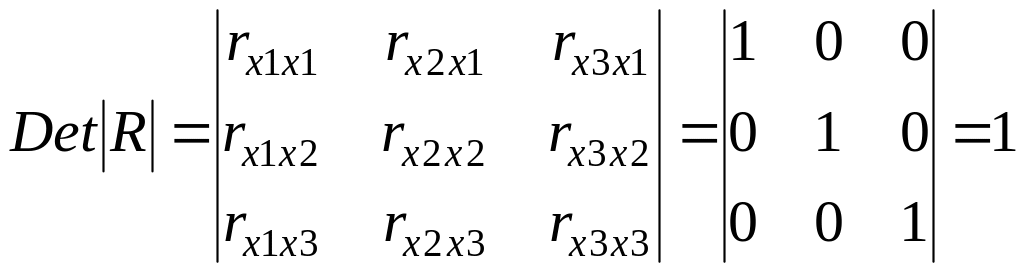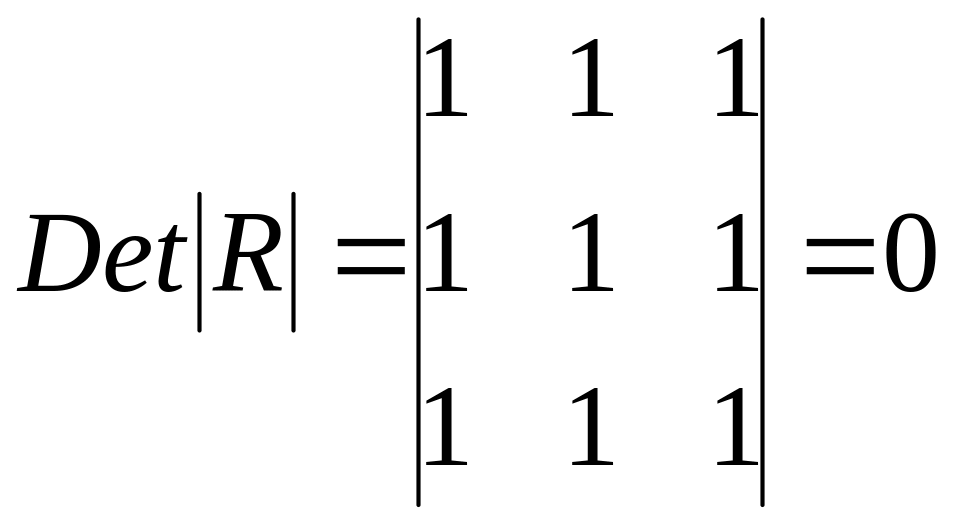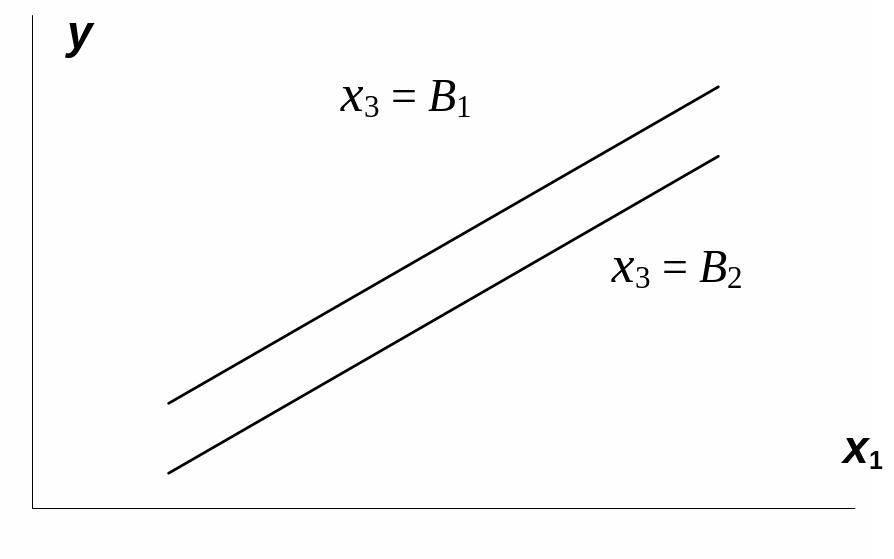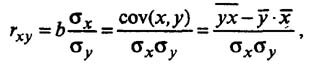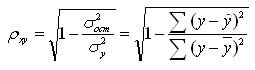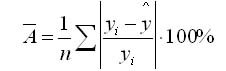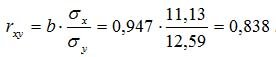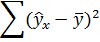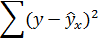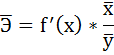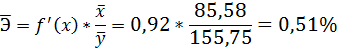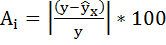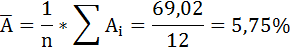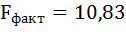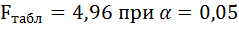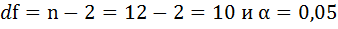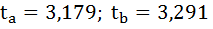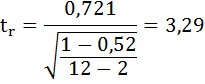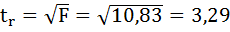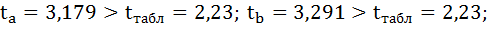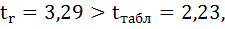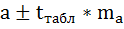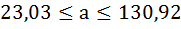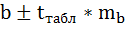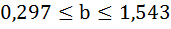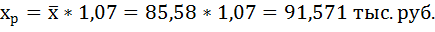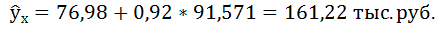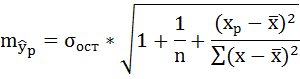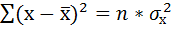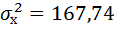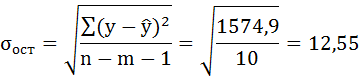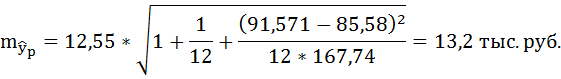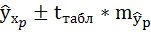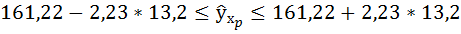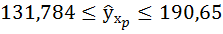Средняя ошибка аппроксимации
Фактические
значения результативного признака
отличаются от теоретических, рассчитанных
по уравнению регрессии. Чем меньше эти
отличия, тем ближе теоретические значения
к эмпирическим данным, тем лучше качество
модели. Величина отклонений фактических
и расчетных значений результативного
признака каждому наблюдению представляет
собой ошибку аппроксимации. В отдельных
случаях ошибка аппроксимации может
оказаться равной нулю. Отклонения (y
–
)
несравнимы между собой, исключая
величину, равную нулю. Так, если для
одного наблюдения y
–
= 5, а для другого – 10, то это не означает,
что во втором случае модель дает вдвое
худший результат. Для сравнения
используются величины отклонений,
выраженные в процентах к фактическим
значениям. Например, если для первого
наблюдения y
= 20, а для второго y
= 50, ошибка аппроксимации составит 25 %
для первого наблюдения и 20 % – для
второго.
Поскольку
(y
–
)
может быть величиной как положительной,
так и отрицательной, ошибки аппроксимации
для каждого наблюдения принято определять
в процентах по модулю.
Отклонения
(y
–
)
можно рассматривать как абсолютную
ошибку аппроксимации, а
– как
относительную ошибку аппроксимации.
Для того, чтобы иметь общее суждение о
качестве модели из относительных
отклонений по каждому наблюдению,
находят среднюю ошибку аппроксимации
как среднюю арифметическую простую
. (2.38)
По
нашим данным представим расчет средней
ошибки аппроксимации для уравнения Y
= 6,136
Х0,474
в следующей таблице.
Таблица.
Расчет средней ошибки аппроксимации
|
y |
yx |
y |
|
|
6 |
6,135947 |
-0,135946847 |
0,022658 |
|
9 |
8,524199 |
0,475801308 |
0,052867 |
|
10 |
10,33165 |
-0,331653106 |
0,033165 |
|
12 |
11,84201 |
0,157986835 |
0,013166 |
|
13 |
13,164 |
-0,163999272 |
0,012615 |
|
Итого |
0,134471 |
A
= (0,1345 / 5)
100 = 2,69 %, что говорит о хорошем качестве
уравнения регрессии, ибо ошибка
аппроксимации в пределах 5-7 % свидетельствует
о хорошем подборе модели к исходным
данным.
Возможно
и другое определение средней ошибки
аппроксимации:
(2.39)
Для
нашего примера эта величина составит:
.
Для
расчета средней ошибки аппроксимации
в стандартных программах чаще используется
формула (2.39).
Аналогично
определяется средняя ошибка аппроксимации
и для уравнения параболы.
№11
Факторы,
включаемые во множественную регрессию,
должны отвечать следующим требованиям:
1)
быть количественно измеримы. Если
необходимо включить в модель качественный
фактор, не имеющий количественного
измерения, то нужно придать ему
количественную определенность (например,
в модели урожайности качество почвы
задается в виде баллов; в модели стоимости
объектов недвижимости учитывается
место нахождения недвижимости: районы
могут быть проранжированы);
2)
не должны быть коррелированны между
собой и тем более находиться в точной
функциональной связи.
Включение
в модель факторов с высокой интеркорреляцией,
когда ryx1
< rx1x2,
для зависимости y
= a
+ b1
x1
+ b2
x2
+ ,
может привести к нежелательным
последствиям – система нормальных
уравнений может оказаться плохо
обусловленной и повлечь за собой
неустойчивость и ненадежность оценок
коэффициентов регрессии.
Если
между факторами существует высокая
корреляция, то нельзя определить их
изолированное влияние на результативный
показатель, и параметры уравнения
регрессии оказываются неинтерпретируемыми.
Так, в уравнении y
= a
+ b1
x1
+ b2
x2
+ ,
предполагается, что факторы x1
и x2
независимы друг от друга, т.е. rx1x2
= 0. Тогда можно говорить, что параметр
b1
измеряет силу влияния фактора x1
на результат y
при неизменном значении фактора x2.
Если же rx1x2
= 1, то с изменением фактора x1
фактор x2
не может оставаться неизменным. Отсюда
b1
и b2
нельзя интерпретировать как показатели
раздельного влияния x1
и x2
на y.
Пример
3.2. При
изучении зависимости y
= f(x,
z,
v)
матрица парных коэффициентов корреляции
оказалась следующей:
|
y |
x |
z |
v |
|
|
y |
1 |
|||
|
x |
0,8 |
1 |
||
|
z |
0,7 |
0,8 |
1 |
|
|
v |
0,6 |
0,5 |
0,2 |
1 |
Очевидно,
что факторы x
и z
дублируют друг друга. В анализ целесообразно
включить фактор z,
а не x,
так как корреляция z,
с результатом y
слабее, чем корреляция фактора x
с y
(ryz
< ryx),
но зато слабее межфакторная корреляция
rzv
< rxv.
Поэтому в данном случае в уравнение
множественной регрессии включаются
факторы z,
и v.
По
величине парных коэффициентов корреляции
обнаруживается лишь явная коллинеарность
факторов. Наибольшие трудности в
использовании аппарата множественной
регрессии возникают при наличии
мультиколлинеарности
факторов, когда более чем два фактора
связаны между собой линейной зависимостью,
т.е. имеет место совокупное воздействие
факторов друг на друга. Наличие
мультиколлинеарности факторов может
означать, что некоторые факторы всегда
будут действовать в унисон. В результате
вариация в исходных данных перестает
быть полностью независимой и нельзя
оценить воздействие каждого фактора в
отдельности. Чем сильнее мультиколлинеарность
факторов, тем менее надежна оценка
распределения суммы объясненной вариации
по отдельным факторам с помощью метода
наименьших квадратов.
Если
рассматривается регрессия y
= a
+ b
x
+ c
z
+ d
v
+ ,
то для расчета параметров с применением
МНК предполагается равенство
S2y
= S2факт
+ S2,
где
S2y
– общая сумма квадратов отклонений
;
S2факт
– факторная (объясненная) сумма квадратов
отклонений
;
S2
– остаточная сумма квадратов отклонений
.
В
свою очередь, при независимости факторов
друг от друга выполнимо равенство
S2факт
= S2x
+ S2z
+ S2v,
где
S2x,
S2z,
S2v
– суммы квадратов отклонений, обусловленные
влиянием соответствующих факторов.
Если
же факторы интеркоррелированы, то данное
равенство нарушается.
Включение
в модель мультиколлинеарных факторов
нежелательно по следующим причинам:
– затрудняется
интерпретация параметров множественной
регрессии как характеристик действия
факторов в «чистом» виде, ибо факторы
коррелированны; параметры линейной
регрессии теряют экономический смысл;
– оценки
параметров ненадежны, обнаруживают
большие стандартные ошибки и меняются
с изменением объема наблюдений (не
только по величина, но и по знаку), что
делает модель непригодной для анализа
и прогнозирования.
Для
оценки факторов может использоваться
определитель матрицы
парных коэффициентов корреляции между
факторами.
Если
бы факторы не коррелировали между собой,
то матрицы парных коэффициентов
корреляции между ними была бы единичной,
поскольку все недиагональные элементы
rxixj
(xi
xj)
были бы равны нулю. Так, для уравнения,
включающего три объясняющих переменных,
y
= a
+ b1
x1
+ b2
x2
+ b3
x3
+ ,
матрица
коэффициентов корреляции между факторами
имела бы определитель, равный единице
,
поскольку
rx1x1
= rx2x2
= rx3x3
= 1 и rx1x2
= rx1x3
= rx2x3
= 0.
Если
же между факторами существует полная
линейная зависимость и все коэффициенты
корреляции равны единице, то определитель
такой матрицы равен нулю
.
Чем
ближе к нулю определитель матрицы
межфакторной корреляции, тем сильнее
мультиколлинеарность факторов и
ненадежнее результаты множественной
регрессии. И, наоборот, чем ближе к
единице определитель матрицы межфакторной
корреляции, тем меньше мультиколлинеарность
факторов.
Оценка
значимости мультиколлинеарности
факторов может быть проведена методом
испытания гипотезы о независимости
переменных H0:
DetR
= 1. Доказано, что величина
имеет приближенное распределение 2
с df
= m
(m
– 1)/2 степенями
свободы. Если фактическое значение 2
превосходит табличное (критическое):
2факт
> 2табл(df,)
то гипотеза H0
отклоняется. Это означает, что DetR
1, недиагональные ненулевые коэффициенты
корреляции указывают на коллинеарность
факторов. Мультиколлинеарность считается
доказанной.
Через
коэффициенты множественной детерминации
можно найти переменные, ответственные
за мультиколлинеарность факторов. Для
этого в качестве зависимой переменной
рассматривается каждый из факторов.
Чем ближе значение коэффициента
множественной детерминации к единице,
тем сильна проявляется мультиколлинеарность
факторов. Сравнивая между собой
коэффициенты множественной детерминации
факторов
R2x1x2x3…xp;
R2x2x1x3…xp
и т.п., можно выделить переменные,
ответственные за мультиколлинеарность,
следовательно, можно решать проблему
отбора факторов, оставляя в уравнении
факторы с минимальной величиной
коэффициента множественной детерминации.
Имеется
ряд подходов преодоления сильной
межфакторной корреляции. Самый простой
из них состоит в исключении из модели
одного или нескольких факторов. Другой
путь связан с преобразованием факторов,
при котором уменьшается корреляция
между ними. Например, при построении
модели на основе рядов динамики переходят
от первоначальных данных к первым
разностям уровней y
= yt
– yt–1,
чтобы исключить влияние тенденции, или
используются такие методы, которые
сводят к нулю межфакторную корреляцию,
т.е. переходят от исходных переменных
к их линейным комбинациям, не коррелированным
друг с другом (метод главных компонент).
Одним
из путей учета внутренней корреляции
факторов является переход к совмещенным
уравнениям регрессии, т.е. к уравнениям,
которые отражают не только влияние
факторов, но и их взаимодействие. Так,
если y
= f(x1,
x2,
x3).
то можно построить следующее совмещенное
уравнение:
y
= a
+ b1
x1
+ b2
x2
+ b3
x3
+ b12
x1
x2
+ b13
x1
x3
+ b23
x2
x3
+ .
Рассматриваемое
уравнение включает эффект взаимодействия
первого порядка. Можно включать в модель
и взаимодействие более высоких порядков,
если будет доказана его статистическая
значимость, например включение
взаимодействия второго порядка b123
x1
x2
x3
и т.д. Как правила, взаимодействие
третьего и более высоких порядков
оказывается статистически незначимым;
совмещенные уравнения регрессии
ограничиваются взаимодействием первого
и второго порядков. Но и оно может
оказаться несущественным. Тогда
нецелесообразно включать в модель
взаимодействие всех факторов и всех
порядков. Так, если анализ совмещенного
уравнения показал значимость только
взаимодействия факторов x1и
x3,
то уравнение будет иметь вид:
y
= a
+ b1
x1
+ b2
x2
+ b3
x3
+ b13
x1
x3
+ .
Взаимодействие
факторов x1и
x3
означает, что на разных уровнях фактора
x3
влияние фактора x1на
y
будет неодинаково, т.е. оно зависит от
значений фактора x3.
На рис. 3.1 взаимодействие факторов
представляется непараллельными линиями
связи x1с
результатом y.
И, наоборот, параллельные линии влияния
фактора x1на
y
при разных уровнях фактора x3
означают отсутствие взаимодействия
факторов x1и
x3.
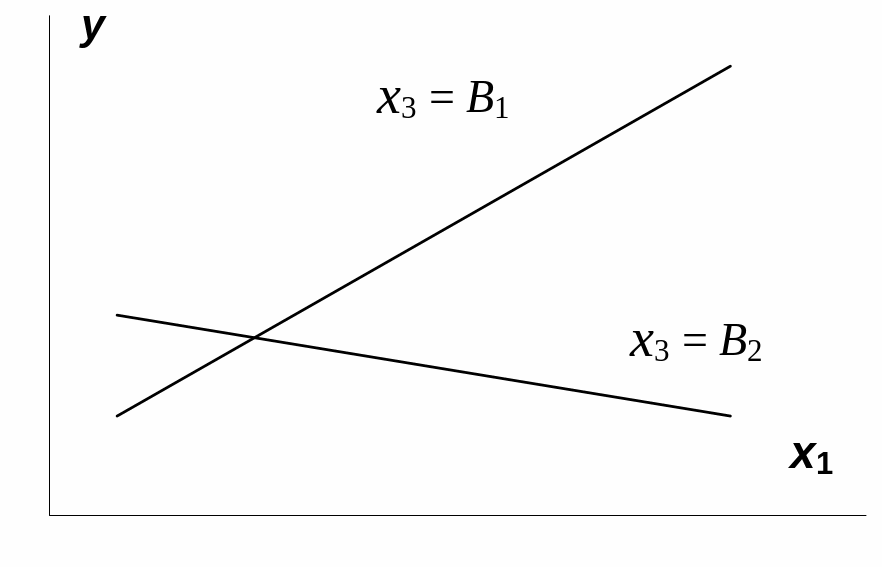
Рис.
3.1. Графическая иллюстрация взаимодействия
факторов
Совмещенные
уравнения регрессии строятся, например,
при исследовании эффекта влияния на
урожайность разных видов удобрений
(комбинаций азота и фосфора).
Решению
проблемы устранения мультиколлинеарности
факторов может помочь и переход к
уравнениям приведенной формы. С этой
целью в уравнение регрессии подставляют
рассматриваемый фактор, выраженный из
другого уравнения.
Пусть,
например, рассматривается двухфакторная
регрессия вида yx
= a
+ b1
x1
+ b2
x2,
для которой факторы x1и
x2
обнаруживают высокую корреляцию. Если
исключить один из факторов, то мы придем
к уравнению парной регрессии. Вместе с
тем можно оставить факторы в модели, но
исследовать данное двухфакторное
уравнение регрессии совместно с другим
уравнением, в котором фактор (например,
x2)
рассматривается как зависимая переменная.
Предположим, что x2
= A
+ B
y
+ C
x3.
Подставив это уравнение в искомое вместо
x2,
получим:
yx
= a
+ b1
x1
+ b2
(A
+ B
y
+ C
x3)
или
yx
(1 – b2
B)
= (a
+ b2
A)
+ b1
x1
+ C
b2
x3.
Если
(1 – b2
B)
0, то, разделив обе части равенства на
(1 – b2
B),
получим уравнение вида
,
которое
принято называть приведенной формой
уравнения для определения результативного
признака y.
Это уравнение может быть представлено
в виде
yx
= a’
+ b’1
x1
+ b’3
x3.
К
нему для оценки параметров может быть
применен метод наименьших квадратов.
Отбор
факторов, включаемых в регрессию,
является одним из важнейших этапов
практического использования методов
регрессии. Подходы к отбору факторов
на основе показателей корреляции могут
быть разные. Они приводят построение
уравнения множественной регрессии
соответственно к разным методикам. В
зависимости от того, какая методика
построения уравнения регрессии принята,
меняется алгоритм её решения на
компьютере.
Наиболее
широкое применение получили следующие
методы построения уравнения множественной
регрессии:
– метод
исключения;
– метод
включения;
– шаговый
регрессионный анализ.
Каждый
из этих методов по-своему решает проблему
отбора факторов, давая в целом близкие
результаты – отсев факторов из полного
его набора (метод исключения), дополнительное
введение фактора (метод включения),
исключение ранее введенного фактора
(шаговый регрессионный анализ).
На
первый взгляд может показаться, что
матрица парных коэффициентов корреляции
играет главную роль в отборе факторов.
Вместе с тем вследствие взаимодействия
факторов парные коэффициенты корреляции
не могут в полной мере решать вопрос о
целесообразности включения в модель
того или иного фактора. Эту роль выполняют
показатели частной корреляции, оценивающие
в чистом виде тесноту связи фактора с
результатом. Матрица частных коэффициентов
корреляции наиболее широко используется
в процедуре отсева факторов. Отсев
факторов можно проводить и по t-критерию
Стьюдента для коэффициентов регрессии:
из уравнения исключаются факторы с
величиной t-критерия
меньше табличного. Так, например,
уравнение регрессии составило:
y
= 25 + 5x1
+ 3x2
+ 4x3
+ .
(4,0) (1,3) (6,0)
В
скобках приведены фактические значения
t-критерия
для соответствующих коэффициентов
регрессии, как правило, при t
< 2 коэффициент регрессии незначим и,
следовательно, рассматриваемый фактор
не должен присутствовать в регрессионной
модели. В данном случае – это фактор
x2.
При
отборе факторов рекомендуется пользоваться
следующим правилом: число включаемых
факторов обычно в 6-7 раз меньше объема
совокупности, по которой строится
регрессия. Если это соотношение нарушено,
то число степеней свободы остаточной
вариации очень мало. Это приводит к
тому, что параметры уравнения регрессии
оказываются статистически незначимыми,
а F-критерий
меньше табличного значения.
Соседние файлы в предмете [НЕСОРТИРОВАННОЕ]
- #
- #
- #
- #
- #
- #
- #
- #
- #
- #
- #
Содержание
- Общие сведения аппроксимации характеристик
- Полиномиальная аппроксимация
- Кусочно-линейная аппроксимация
- Аппроксимация трансцендентными функциями
- Линейная регрессия
- Квадратичная регрессия
- Кубическая регрессия
- Вывод формул
- Средняя ошибка аппроксимации
- Пример нахождения коэффициента корреляции
- Аппроксимация опытных данных. Метод наименьших квадратов
- Классификация методов наименьших квадратов
- Выполнение аппроксимации
- Способ 1: линейное сглаживание
- Способ 2: экспоненциальная аппроксимация
- Способ 3: логарифмическое сглаживание
- Способ 4: полиномиальное сглаживание
- Способ 5: степенное сглаживание
Общие сведения аппроксимации характеристик
Ранее отмечалось, что нелинейный преобразователь может быть описан с помощью вольт-амперной характеристики, которую, как правило, получают экспериментальным путем и затем представляют в виде графической зависимости тока от напряжения. Однако использовать вольт-амперную характеристику в графической форме неудобно. Поэтому возникает задача аппроксимации, под которой понимают приближенное представление нелинейной характеристики математическими методами.
Аппроксимирующая функция должна удовлетворять следующим требованиям:
- быть простой, но допускать последующую математическую обработку;
- достаточно точно отображать экспериментально полученную характеристику.
Исходя из указанных требований в ТЭС применяются следующие методы аппроксимации вольт-амперных характеристик:
- полиномиальная (степенная);
- кусочно-линейная;
- аппроксимация трансцендентными функциями (экспоненциальными, тригонометрическими и др.).
Полиномиальная аппроксимация
Данный метод аппроксимации удобно применять при рассмотрении принципов действия многих нелинейных преобразователей: модуляторов, демодуляторов, генераторов и других при воздействии на них одного либо нескольких гармонических колебаний.
Степенная аппроксимация заключается в записи вольт-амперной характеристики i = f(u) в виде полинома (многочлена) n-й степени:
(Формула).
С помощью такого полинома можно произвести аппроксимацию с любой степенью точности. При этом точность будет выше, если использовать полиномы высоких порядков. Однако это неудобно для анализа.
На практике применяют следующие полиномы:
Рис. 3.1. Аппроксимация вольт-амперной характеристики нелинейного преобразователя прямой линией (1) и параболой (2)
Отметим, что аппроксимация многочленом первой степени, которая приводит к получению прямой линии 1 (см. рис. 3.1), не позволяет изучать нелинейные преобразования, например перенос спектра сигнала на другую частоту. Данный вид аппроксимации применяется только при изучении линейных процессов, например усиления. Полином второй степени (квадратичная парабола 2) уже позволяет изучать нелинейные процессы, но только при воздействии слабых сигналов.
В общем случае для использования степенной аппроксимации необходимо знать коэффициенты (Формула) полинома, которые обычно определяют с помощью «метода выбранных точек». Иными словами, коэффициенты (Формула) находят из условия равенства значений ординат аппроксимированной и действительной характеристик в выбранных точках.
Для аппроксимации полинома n-й степени в пределах интервала ΔU, задаваемого диапазоном изменения напряжения u, выбирают n+1 значений напряжения (Формула) и определяют значения токов
В простейшем случае значения (Формула) находят делением интервала ΔU на n равных частей Δ, как показано на рис. 3.2. При n = 4 значение Δ = (u5 − u1) / 4. Далее составляется следующая система уравнений:
Рис. 3.2. Определение ординат нелинейной характеристики методом выбранных точек
Решение данной системы уравнений определяют коэффициенты (Формула). Если значение u = 0 располагается внутри интервала аппроксимации ΔU, то коэффициент a0 находят как значение тока при u = 0.
При вычислении коэффициентов (Формула) иногда предъявляется дополнительное требование равенства не только ординат действительной и аппроксимированной характеристик, но и их производных.
Следует иметь в виду, что аппроксимированная характеристика может резко отличаться от действительной за пределами интервала аппроксимации ΔU. Поэтому степенная аппроксимация широко применяется при анализе работы нелинейных устройств, на которые поступают относительно небольшие сигналы. Использовать этот метод при больших отклонениях мгновенных значений входного сигнала от рабочей точки нецелесообразно по причине ухудшения точности.
Кусочно-линейная аппроксимация
Данный метод основан на приближенной замене реальной плавно изменяющейся вольт-амперной характеристики i = f(u) отрезками прямых линий с различными наклонами.
На рис. 3.3 показана аппроксимированная характеристика, содержащая два линейных участка.
Рис. 3.3. Аппроксимация вольт-амперной характеристики нелинейного преобразователя отрезками прямых линий
Математически эту аппроксимированную характеристику можно записать в виде
(Формула),
где U0 — напряжение отсечки; S — крутизна характеристики, имеющая размерность проводимости (См или А / В).
На рис. 3.3 методом проекций построены импульсы тока, получаемые при воздействии гармонического колебания с большой амплитудой. При разложении импульсов в ряд Фурье постоянная составляющая и амплитуды нескольких первых гармоник также близки друг к другу. Иными словами, при больших сигналах кусочно-линейная аппроксимация дает достаточную точность расчетов. При малых сигналах точность падает, и результаты могут быть неверными.
Таким образом, метод кусочно-линейной аппроксимации обычно применяется при анализе процессов нелинейных преобразований в случае больших амплитуд входных сигналов.
Аппроксимация трансцендентными функциями
В данном методе в качестве аппроксимирующих функций используются экспоненты либо их суммы (но не более чем из двух слагаемых), гиперболические, тригонометрические и некоторые другие функции. Чаще всего применяется показательная аппроксимация. Так, в частности, характеристику полупроводникового диода можно аппроксимировать экспонентой:
где (Формула) — обратный ток насыщения; α — постоянная, характеризующая температурный потенциал.
Данное выражение хорошо определяет начальный участок характеристики. Иными словами, показательная аппроксимация достаточно точна при небольших амплитудах входных сигналов. В противном случае погрешность расчетов оказывается значительной.
Для определения пригодности этого метода аппроксимации для расчета применяют так называемое приведение к линейному виду, сущность которого заключается в следующем. Сначала представленное ранее выражение для тока i логарифмируется:
Далее по реальной вольт-амперной характеристике строится зависимость
Затем в диапазоне напряжений ΔU проверяется степень отличия этой характеристики от прямой линии. Если это отличие оказывается небольшим, то исходную характеристику нелинейного элемента (полупроводникового диода) можно аппроксимировать экспонентой.
Нелинейные зависимости более сложного вида можно аппроксимировать суммой двух трансцендентных функций. Например, характеристика туннельного диода описывается выражением
в котором первое слагаемое определяет туннельный ток, а второе — диффузионный.
Рис. 3.4. Пример аппроксимации характеристики туннельного диода трансцендентными функциями
Графическое изображение этой характеристики приведено на рис. 3.4, где сплошной линией показан суммарный ток, а штриховой — его компоненты.
Линейная регрессия
Уравнение регрессии:
Коэффициент a:
Коэффициент b:
Коэффициент линейной парной корреляции:
Коэффициент детерминации:
Средняя ошибка аппроксимации:
Квадратичная регрессия
Уравнение регрессии:
Система уравнений для нахождения коэффициентов a, b и c:
Коэффициент корреляции:

где
Коэффициент детерминации:
Средняя ошибка аппроксимации:
Кубическая регрессия
Уравнение регрессии:
Система уравнений для нахождения коэффициентов a, b, c и d:
Коэффициент корреляции, коэффициент детерминации, средняя ошибка аппроксимации — используются те же формулы, что и для квадратичной регрессии.
Вывод формул
Сначала сформулируем задачу:
Пусть у нас есть неизвестная функция y=f(x), заданная табличными значениями (например, полученными в результате опытных измерений).
Нам необходимо найти функцию заданного вида (линейную, квадратичную и т. п.) y=F(x), которая в соответствующих точках принимает значения, как можно более близкие к табличным.
На практике вид функции чаще всего определяют путем сравнения расположения точек с графиками известных функций.
Полученная формула y=F(x), которую называют эмпирической формулой, или уравнением регрессии y на x, или приближающей (аппроксимирующей) функцией, позволяет находить значения f(x) для нетабличных значений x, сглаживая результаты измерений величины y.
Для того, чтобы получить параметры функции F, используется метод наименьших квадратов. В этом методе в качестве критерия близости приближающей функции к совокупности точек используется суммы квадратов разностей значений табличных значений y и теоретических, рассчитанных по уравнению регрессии.
Таким образом, нам требуется найти функцию F, такую, чтобы сумма квадратов S была наименьшей:
Рассмотрим решение этой задачи на примере получения линейной регрессии F=ax+b.
S является функцией двух переменных, a и b. Чтобы найти ее минимум, используем условие экстремума, а именно, равенства нулю частных производных.
Используя формулу производной сложной функции, получим следующую систему уравнений:
Для функции вида 

Подставив производные, получим:
Далее:
Откуда, выразив a и b, можно получить формулы для коэффициентов линейной регрессии, приведенные выше.
Аналогичным образом выводятся формулы для остальных видов регрессий.

Средняя ошибка аппроксимации
Для оценки качества однофакторной модели в эконометрике используют коэффициент детерминации и среднюю ошибку аппроксимации.
Средняя ошибка аппроксимации определяется как среднее отклонение полученных значений от фактических
Допустимая ошибка аппроксимации не должна превышать 10%.
В эконометрике существует понятие среднего коэффициента эластичности Э – который говорит о том, на сколько процентов в среднем изменится показатель у от своего среднего значения при изменении фактора х на 1% от своей средней величины.
Пример нахождения коэффициента корреляции
Исходные данные:
|
Номер региона |
Среднедушевой прожиточный минимум в день одного трудоспособного, руб., |
Среднедневная заработная плата, руб., |
|
1 |
81 |
124 |
|
2 |
77 |
131 |
|
3 |
85 |
146 |
|
4 |
79 |
139 |
|
5 |
93 |
143 |
|
6 |
100 |
159 |
|
7 |
72 |
135 |
|
8 |
90 |
152 |
|
9 |
71 |
127 |
|
10 |
89 |
154 |
|
11 |
82 |
127 |
|
12 |
111 |
162 |
Рассчитаем параметры парной линейной регрессии, составив таблицу
| x |
x2 |
y |
xy |
y2 |
|
|
1 |
81 |
6561 |
124 |
10044 |
15376 |
|
2 |
77 |
5929 |
131 |
10087 |
17161 |
|
3 |
85 |
7225 |
146 |
12410 |
21316 |
|
4 |
79 |
6241 |
139 |
10981 |
19321 |
|
5 |
93 |
8649 |
143 |
13299 |
20449 |
|
6 |
100 |
10000 |
159 |
15900 |
25281 |
|
7 |
72 |
5184 |
135 |
9720 |
18225 |
|
8 |
90 |
8100 |
152 |
13680 |
23104 |
|
9 |
71 |
5041 |
127 |
9017 |
16129 |
|
10 |
89 |
7921 |
154 |
13706 |
23716 |
|
11 |
82 |
6724 |
127 |
10414 |
16129 |
|
12 |
111 |
12321 |
162 |
17982 |
26244 |
|
Среднее |
85,8 |
7491 |
141,6 |
12270,0 |
20204,3 |
|
Сумма |
1030,0 |
89896 |
1699 |
147240 |
242451 |
| σ |
11,13 |
12,59 |
|||
| σ2 |
123,97 |
158,41 |
формула расчета дисперсии σ2 приведена здесь.
Коэффициенты уравнения y = a + bx определяются по формуле
Получаем уравнение регрессии: y = 0,947x + 60,279.
Коэффициент уравнения b = 0,947 показывает, что при увеличении среднедушевого прожиточного минимума в день одного трудоспособного на 1 руб. среднедневная заработная плата увеличивается на 0,947 руб.
Коэффициент корреляции рассчитывается по формуле:
Значение коэффициента корреляции более — 0,7, это означает, что связь между среднедушевым прожиточным минимумом в день одного трудоспособного и среднедневной заработной платой сильная.
Коэффициент детерминации равен R2 = 0.838^2 = 0.702
т.е. 70,2% результата объясняется вариацией объясняющей переменной x.
Аппроксимация опытных данных. Метод наименьших квадратов
Аппроксимация опытных данных – это метод, основанный на замене экспериментально полученных данных аналитической функцией наиболее близко проходящей или совпадающей в узловых точках с исходными значениями (данными полученными в ходе опыта или эксперимента). В настоящее время существует два способа определения аналитической функции:
— с помощью построения интерполяционного многочлена n-степени, который проходит непосредственно через все точки заданного массива данных. В данном случае аппроксимирующая функция представляется в виде: интерполяционного многочлена в форме Лагранжа или интерполяционного многочлена в форме Ньютона.
— с помощью построения аппроксимирующего многочлена n-степени, который проходит в ближайшей близости от точек из заданного массива данных. Таким образом, аппроксимирующая функция сглаживает все случайные помехи (или погрешности), которые могут возникать при выполнении эксперимента: измеряемые значения в ходе опыта зависят от случайных факторов, которые колеблются по своим собственным случайным законам (погрешности измерений или приборов, неточность или ошибки опыта). В данном случае аппроксимирующая функция определяется по методу наименьших квадратов.
Метод наименьших квадратов (в англоязычной литературе Ordinary Least Squares, OLS) — математический метод, основанный на определении аппроксимирующей функции, которая строится в ближайшей близости от точек из заданного массива экспериментальных данных. Близость исходной и аппроксимирующей функции F(x) определяется числовой мерой, а именно: сумма квадратов отклонений экспериментальных данных от аппроксимирующей кривой F(x) должна быть наименьшей.
Рис.1. Аппроксимирующая кривая, построенная по методу наименьших квадратов
Метод наименьших квадратов используется:
— для решения переопределенных систем уравнений, когда количество уравнений превышает количество неизвестных;
— для поиска решения в случае обычных (не переопределенных) нелинейных систем уравнений;
— для аппроксимации точечных значений некоторой аппроксимирующей функцией.
Аппроксимирующая функция по методу наименьших квадратов определяется из условия минимума суммы квадратов отклонений
Квадратичный критерий обладает рядом «хороших» свойств, таких, как дифференцируемость, обеспечение единственного решения задачи аппроксимации при полиномиальных аппроксимирующих функциях.
В зависимости от условий задачи аппроксимирующая функция представляет собой многочлен степени m
Степень аппроксимирующей функции
∙ В случае если степень аппроксимирующей функции m=1, то мы аппроксимируем табличную функцию прямой линией (линейная регрессия).
∙ В случае если степень аппроксимирующей функции m=2, то мы аппроксимируем табличную функцию квадратичной параболой (квадратичная аппроксимация).
∙ В случае если степень аппроксимирующей функции m=3, то мы аппроксимируем табличную функцию кубической параболой (кубическая аппроксимация).
В общем случае, когда требуется построить аппроксимирующий многочлен степени m для заданных табличных значений, условие минимума суммы квадратов отклонений по всем узловым точкам переписывается в следующем виде:
Необходимым условием существования минимума функции является равенству нулю ее частных производных по неизвестным переменным
Преобразуем полученную линейную систему уравнений: раскроем скобки и перенесем свободные слагаемые в правую часть выражения. В результате полученная система линейных алгебраических выражений будет записываться в следующем виде:
Данная система линейных алгебраических выражений может быть переписана в матричном виде:
В результате была получена система линейных уравнений размерностью m+1, которая состоит из m+1 неизвестных. Данная система может быть решена с помощью любого метода решения линейных алгебраических уравнений (например, методом Гаусса). В результате решения будут найдены неизвестные параметры аппроксимирующей функции, обеспечивающие минимальную сумму квадратов отклонений аппроксимирующей функции от исходных данных, т.е. наилучшее возможное квадратичное приближение. Следует помнить, что при изменении даже одного значения исходных данных все коэффициенты изменят свои значения, так как они полностью определяются исходными данными.
Аппроксимация исходных данных линейной зависимостью
(линейная регрессия)
В качестве примера, рассмотрим методику определения аппроксимирующей функции, которая задана в виде линейной зависимости. В соответствии с методом наименьших квадратов условие минимума суммы квадратов отклонений записывается в следующем виде:
Необходимым условием существования минимума функции является равенству нулю ее частных производных по неизвестным переменным. В результате получаем следующую систему уравнений:
Преобразуем полученную линейную систему уравнений.
Решаем полученную систему линейных уравнений. Коэффициенты аппроксимирующей функции в аналитическом виде определяются следующим образом (метод Крамера):
Данные коэффициенты обеспечивают построение линейной аппроксимирующей функции в соответствии с критерием минимизации суммы квадратов аппроксимирующей функции от заданных табличных значений (экспериментальные данные).
Алгоритм реализации метода наименьших квадратов
1. Начальные данные:
— задан массив экспериментальных данных
— задана степень аппроксимирующего многочлена (m)
2. Алгоритм вычисления:
2.1. Определяются коэффициенты для построения системы уравнений размерностью
2.2. Формирование системы линейных уравнений размерностью
2.3. Решение системы линейных уравнений с целью определения неизвестных коэффициентов аппроксимирующего многочлена степени m.
2.4.Определение суммы квадратов отклонений аппроксимирующего многочлена от исходных значений по всем узловым точкам
Найденное значение суммы квадратов отклонений является минимально-возможным.
Аппроксимация с помощью других функций
Следует отметить, что при аппроксимации исходных данных в соответствии с методом наименьших квадратов в качестве аппроксимирующей функции иногда используют логарифмическую функцию, экспоненциальную функцию и степенную функцию.
Логарифмическая аппроксимация
Рассмотрим случай, когда аппроксимирующая функция задана логарифмической функцией вида:
Поиск неизвестных коэффициентов осуществляется по методу наименьших квадратов в соответствии со следующей системой уравнений.
Решаем полученную систему линейных уравнений. Коэффициенты аппроксимирующей функции в аналитическом виде определяются следующим образом:
Экспоненциальная аппроксимация
Рассмотрим случай, когда аппроксимирующая функция задана экспоненциальной функцией вида:
Для применения метода наименьших квадратов экспоненциальная функция линеаризуется:
Поиск неизвестных коэффициентов осуществляется по методу наименьших квадратов в соответствии со следующей системой уравнений.
Решаем полученную систему линейных уравнений. Коэффициенты аппроксимирующей функции в аналитическом виде определяются следующим образом:
Степенная аппроксимация
Рассмотрим случай, когда аппроксимирующая функция задана степенной функцией вида:
Для применения метода наименьших квадратов степенная функция линеаризуется:
Поиск неизвестных коэффициентов осуществляется по методу наименьших квадратов в соответствии со следующей системой уравнений.
Решаем полученную систему линейных уравнений. Коэффициенты аппроксимирующей функции в аналитическом виде определяются следующим образом:
Выбор наилучшей аппроксимирующей функции определяется значением среднеквадратического отклонения. В связи с этим следует по методу наименьших квадратов определить несколько аппроксимирующих функций, а затем по критерию наименьшего среднеквадратического отклонения выбрать наиболее подходящую функцию.
Классификация методов наименьших квадратов
- Метод наименьших квадратов.
- Метод максимального правдоподобия (для нормальной классической линейной модели регрессии постулируется нормальность регрессионных остатков).
- Обобщенный метод наименьших квадратов ОМНК применяется в случае автокорреляции ошибок и в случае гетероскедастичности.
- Метод взвешенных наименьших квадратов (частный случай ОМНК с гетероскедастичными остатками).
Проиллюстрируем суть классического метода наименьших квадратов графически. Для этого построим точечный график по данным наблюдений (xi, yi, i=1;n) в прямоугольной системе координат (такой точечный график называют корреляционным полем). Попытаемся подобрать прямую линию, которая ближе всего расположена к точкам корреляционного поля. Согласно методу наименьших квадратов линия выбирается так, чтобы сумма квадратов расстояний по вертикали между точками корреляционного поля и этой линией была бы минимальной. 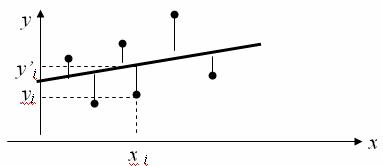
Математическая запись данной задачи: 
Значения yi и xi=1…n нам известны, это данные наблюдений. В функции S они представляют собой константы. Переменными в данной функции являются искомые оценки параметров — ,
. Чтобы найти минимум функции 2-ух переменных необходимо вычислить частные производные данной функции по каждому из параметров и приравнять их нулю, т.е.

В результате получим систему из 2-ух нормальных линейных уравнений: 
Решая данную систему, найдем искомые оценки параметров: 
Правильность расчета параметров уравнения регрессии может быть проверена сравнением сумм (возможно некоторое расхождение из-за округления расчетов).
Для расчета оценок параметров ,
можно построить таблицу 1.
Знак коэффициента регрессии b указывает направление связи (если b>0, связь прямая, если b <0, то связь обратная). Величина b показывает на сколько единиц изменится в среднем признак-результат -y при изменении признака-фактора — х на 1 единицу своего измерения.
Формально значение параметра а – среднее значение y при х равном нулю. Если признак-фактор не имеет и не может иметь нулевого значения, то вышеуказанная трактовка параметра а не имеет смысла.
Оценка тесноты связи между признаками осуществляется с помощью коэффициента линейной парной корреляции — rx,y. Он может быть рассчитан по формуле: 

Область допустимых значений линейного коэффициента парной корреляции от –1 до +1. Знак коэффициента корреляции указывает направление связи. Если rx, y>0, то связь прямая; если rx, y<0, то связь обратная.
Если данный коэффициент по модулю близок к единице, то связь между признаками может быть интерпретирована как довольно тесная линейная. Если его модуль равен единице ê rx , y ê =1, то связь между признаками функциональная линейная. Если признаки х и y линейно независимы, то rx,y близок к 0.
Для расчета rx,y можно использовать также таблицу 1.
Таблица 1
| N наблюдения | xi | yi | xi·yi | (xi-x)² | (yi-y)² |
| 1 | x1 | y1 | x1·y1 | (x1-x)² | (y1-y)² |
| 2 | x2 | y2 | x2·y2 | (x2-x)² | (y2-y)² |
| … | |||||
| n | xn | yn | xn·yn | (xn-x)² | (yn-y)² |
| Сумма по столбцу | ∑x | ∑y | ∑x·y | ∑(xi-x)² | ∑(yi-y)² |
| Среднее значение |  |
 |
 |
 |
 |
Для оценки качества полученного уравнения регрессии рассчитывают теоретический коэффициент детерминации – R2yx: 
где d2 – объясненная уравнением регрессии дисперсия ye2— остаточная (необъясненная уравнением регрессии) дисперсия ys2y — общая (полная) дисперсия y.
Коэффициент детерминации характеризует долю вариации (дисперсии) результативного признака y, объясняемую регрессией (а, следовательно, и фактором х), в общей вариации (дисперсии) y. Коэффициент детерминации R2yx принимает значения от 0 до 1. Соответственно величина 1-R2yx характеризует долю дисперсии y, вызванную влиянием прочих неучтенных в модели факторов и ошибками спецификации.
При парной линейной регрессии R2yx=r2yx.
Выполнение аппроксимации
Наименование данного метода происходит от латинского слова proxima – «ближайшая» Именно приближение путем упрощения и сглаживания известных показателей, выстраивание их в тенденцию и является его основой. Но данный метод можно использовать не только для прогнозирования, но и для исследования уже имеющихся результатов. Ведь аппроксимация является, по сути, упрощением исходных данных, а упрощенный вариант исследовать легче.
Главный инструмент, с помощью которого проводится сглаживания в Excel – это построение линии тренда. Суть состоит в том, что на основе уже имеющихся показателей достраивается график функции на будущие периоды. Основное предназначение линии тренда, как не трудно догадаться, это составление прогнозов или выявление общей тенденции.
Но она может быть построена с применением одного из пяти видов аппроксимации:
- Линейной;
- Экспоненциальной;
- Логарифмической;
- Полиномиальной;
- Степенной.
Способ 1: линейное сглаживание
Прежде всего, давайте рассмотрим самый простой вариант аппроксимации, а именно с помощью линейной функции. На нем мы остановимся подробнее всего, так как изложим общие моменты характерные и для других способов, а именно построение графика и некоторые другие нюансы, на которых при рассмотрении последующих вариантов уже останавливаться не будем.
Прежде всего, построим график, на основании которого будем проводить процедуру сглаживания. Для построения графика возьмем таблицу, в которой помесячно указана себестоимость единицы продукции, производимой предприятием, и соответствующая прибыль в данном периоде. Графическая функция, которую мы построим, будет отображать зависимость увеличения прибыли от уменьшения себестоимости продукции.
- Для построения графика, прежде всего, выделяем столбцы «Себестоимость единицы продукции» и «Прибыль». После этого перемещаемся во вкладку «Вставка». Далее на ленте в блоке инструментов «Диаграммы» щелкаем по кнопке «Точечная». В открывшемся списке выбираем наименование «Точечная с гладкими кривыми и маркерами». Именно данный вид диаграмм наиболее подходит для работы с линией тренда, а значит, и для применения метода аппроксимации в Excel.
- График построен.
- Для добавления линии тренда выделяем его кликом правой кнопки мыши. Появляется контекстное меню. Выбираем в нем пункт «Добавить линию тренда…».
Существует ещё один вариант её добавления. В дополнительной группе вкладок на ленте «Работа с диаграммами» перемещаемся во вкладку «Макет». Далее в блоке инструментов «Анализ» щелкаем по кнопке «Линия тренда». Открывается список. Так как нам нужно применить линейную аппроксимацию, то из представленных позиций выбираем «Линейное приближение».
- Если же вы выбрали все-таки первый вариант действий с добавлением через контекстное меню, то откроется окно формата.
В блоке параметров «Построение линии тренда (аппроксимация и сглаживание)» устанавливаем переключатель в позицию «Линейная».
При желании можно установить галочку около позиции «Показывать уравнение на диаграмме». После этого на диаграмме будет отображаться уравнение сглаживающей функции.Также в нашем случае для сравнения различных вариантов аппроксимации важно установить галочку около пункта «Поместить на диаграмму величину достоверной аппроксимации (R^2)». Данный показатель может варьироваться от 0 до 1. Чем он выше, тем аппроксимация качественнее (достовернее). Считается, что при величине данного показателя 0,85 и выше сглаживание можно считать достоверным, а если показатель ниже, то – нет.
После того, как провели все вышеуказанные настройки. Жмем на кнопку «Закрыть», размещенную в нижней части окна.
- Как видим, на графике линия тренда построена. При линейной аппроксимации она обозначается черной прямой полосой. Указанный вид сглаживания можно применять в наиболее простых случаях, когда данные изменяются довольно быстро и зависимость значения функции от аргумента очевидна.
Сглаживание, которое используется в данном случае, описывается следующей формулой:
y=ax+b
В конкретно нашем случае формула принимает такой вид:
y=-0,1156x+72,255
Величина достоверности аппроксимации у нас равна 0,9418, что является довольно приемлемым итогом, характеризующим сглаживание, как достоверное.
Способ 2: экспоненциальная аппроксимация
Теперь давайте рассмотрим экспоненциальный тип аппроксимации в Эксель.
- Для того, чтобы изменить тип линии тренда, выделяем её кликом правой кнопки мыши и в раскрывшемся меню выбираем пункт «Формат линии тренда…».
- После этого запускается уже знакомое нам окно формата. В блоке выбора типа аппроксимации устанавливаем переключатель в положение «Экспоненциальная». Остальные настройки оставим такими же, как и в первом случае. Щелкаем по кнопке «Закрыть».
- После этого линия тренда будет построена на графике. Как видим, при использовании данного метода она имеет несколько изогнутую форму. При этом уровень достоверности равен 0,9592, что выше, чем при использовании линейной аппроксимации. Экспоненциальный метод лучше всего использовать в том случае, когда сначала значения быстро изменяются, а потом принимают сбалансированную форму.
Общий вид функции сглаживания при этом такой:
y=be^x
где e – это основание натурального логарифма.
В конкретно нашем случае формула приняла следующую форму:
y=6282,7*e^(-0,012*x)
Способ 3: логарифмическое сглаживание
Теперь настала очередь рассмотреть метод логарифмической аппроксимации.
- Тем же способом, что и в предыдущий раз через контекстное меню запускаем окно формата линии тренда. Устанавливаем переключатель в позицию «Логарифмическая» и жмем на кнопку «Закрыть».
- Происходит процедура построения линии тренда с логарифмической аппроксимацией. Как и в предыдущем случае, такой вариант лучше использовать тогда, когда изначально данные быстро изменяются, а потом принимают сбалансированный вид. Как видим, уровень достоверности равен 0,946. Это выше, чем при использовании линейного метода, но ниже, чем качество линии тренда при экспоненциальном сглаживании.
В общем виде формула сглаживания выглядит так:
y=a*ln(x)+b
где ln – это величина натурального логарифма. Отсюда и наименование метода.
В нашем случае формула принимает следующий вид:
y=-62,81ln(x)+404,96
Способ 4: полиномиальное сглаживание
Настал черед рассмотреть метод полиномиального сглаживания.
- Переходим в окно формата линии тренда, как уже делали не раз. В блоке «Построение линии тренда» устанавливаем переключатель в позицию «Полиномиальная». Справа от данного пункта расположено поле «Степень». При выборе значения «Полиномиальная» оно становится активным. Здесь можно указать любое степенное значение от 2 (установлено по умолчанию) до 6. Данный показатель определяет число максимумов и минимумов функции. При установке полинома второй степени описывается только один максимум, а при установке полинома шестой степени может быть описано до пяти максимумов. Для начала оставим настройки по умолчанию, то есть, укажем вторую степень. Остальные настройки оставляем такими же, какими мы выставляли их в предыдущих способах. Жмем на кнопку «Закрыть».
- Линия тренда с использованием данного метода построена. Как видим, она ещё более изогнута, чем при использовании экспоненциальной аппроксимации. Уровень достоверности выше, чем при любом из использованных ранее способов, и составляет 0,9724.
Данный метод наиболее успешно можно применять в том случае, если данные носят постоянно изменчивый характер. Функция, описывающая данный вид сглаживания, выглядит таким образом:
y=a1+a1*x+a2*x^2+…+an*x^nВ нашем случае формула приняла такой вид:
y=0,0015*x^2-1,7202*x+507,01 - Теперь давайте изменим степень полиномов, чтобы увидеть, будет ли отличаться результат. Возвращаемся в окно формата. Тип аппроксимации оставляем полиномиальным, но напротив него в окне степени устанавливаем максимально возможное значение – 6.
- Как видим, после этого наша линия тренда приняла форму ярко выраженной кривой, у которой число максимумов равно шести. Уровень достоверности повысился ещё больше, составив 0,9844.
Формула, которая описывает данный тип сглаживания, приняла следующий вид:
y=8E-08x^6-0,0003x^5+0,3725x^4-269,33x^3+109525x^2-2E+07x+2E+09
Способ 5: степенное сглаживание
В завершении рассмотрим метод степенной аппроксимации в Excel.
- Перемещаемся в окно «Формат линии тренда». Устанавливаем переключатель вида сглаживания в позицию «Степенная». Показ уравнения и уровня достоверности, как всегда, оставляем включенными. Жмем на кнопку «Закрыть».
- Программа формирует линию тренда. Как видим, в нашем случае она представляет собой линию с небольшим изгибом. Уровень достоверности равен 0,9618, что является довольно высоким показателем. Из всех вышеописанных способов уровень достоверности был выше только при использовании полиномиального метода.
Данный способ эффективно используется в случаях интенсивного изменения данных функции. Важно учесть, что этот вариант применим только при условии, что функция и аргумент не принимают отрицательных или нулевых значений.
Общая формула, описывающая данный метод имеет такой вид:
y=bx^n
В конкретно нашем случае она выглядит так:
y = 6E+18x^(-6,512)
Как видим, при использовании конкретных данных, которые мы применяли для примера, наибольший уровень достоверности показал метод полиномиальной аппроксимации с полиномом в шестой степени (0,9844), наименьший уровень достоверности у линейного метода (0,9418). Но это совсем не значит, что такая же тенденция будет при использовании других примеров. Нет, уровень эффективности у приведенных выше методов может значительно отличаться, в зависимости от конкретного вида функции, для которой будет строиться линия тренда. Поэтому, если для этой функции выбранный метод наиболее эффективен, то это совсем не означает, что он также будет оптимальным и в другой ситуации.
Если вы пока не можете сразу определить, основываясь на вышеприведенных рекомендациях, какой вид аппроксимации подойдет конкретно в вашем случае, то есть смысл попробовать все методы. После построения линии тренда и просмотра её уровня достоверности можно будет выбрать оптимальный вариант.
Источники
- https://pue8.ru/svyaz-elektricheskaya/metody-approksimacii-xarakteristik-nelinejnyx-preobrazovatelej-signalov.html
- https://planetcalc.ru/5992/
- http://univer-nn.ru/ekonometrika/koefficient-korrelyacii-srednyaya-oshibka-approksimacii-koefficient-elastichnosti/
- http://simenergy.ru/math-analysis/digital-processing/85-ordinary-least-squares
- https://math.semestr.ru/corel/linepar.php
- https://lumpics.ru/approximation-in-excel/
Средняя ошибка аппроксимации
Фактические
значения результативного признака
отличаются от теоретических, рассчитанных
по уравнению регрессии. Чем меньше эти
отличия, тем ближе теоретические значения
к эмпирическим данным, тем лучше качество
модели. Величина отклонений фактических
и расчетных значений результативного
признака каждому наблюдению представляет
собой ошибку аппроксимации. В отдельных
случаях ошибка аппроксимации может
оказаться равной нулю. Отклонения (y
–
)
несравнимы между собой, исключая
величину, равную нулю. Так, если для
одного наблюдения y
–
= 5, а для другого – 10, то это не означает,
что во втором случае модель дает вдвое
худший результат. Для сравнения
используются величины отклонений,
выраженные в процентах к фактическим
значениям. Например, если для первого
наблюдения y
= 20, а для второго y
= 50, ошибка аппроксимации составит 25 %
для первого наблюдения и 20 % – для
второго.
Поскольку
(y
–
)
может быть величиной как положительной,
так и отрицательной, ошибки аппроксимации
для каждого наблюдения принято определять
в процентах по модулю.
Отклонения
(y
–
)
можно рассматривать как абсолютную
ошибку аппроксимации, а
– как
относительную ошибку аппроксимации.
Для того, чтобы иметь общее суждение о
качестве модели из относительных
отклонений по каждому наблюдению,
находят среднюю ошибку аппроксимации
как среднюю арифметическую простую
. (2.38)
По
нашим данным представим расчет средней
ошибки аппроксимации для уравнения Y
= 6,136
Х0,474
в следующей таблице.
Таблица.
Расчет средней ошибки аппроксимации
|
y |
yx |
y |
|
|
6 |
6,135947 |
-0,135946847 |
0,022658 |
|
9 |
8,524199 |
0,475801308 |
0,052867 |
|
10 |
10,33165 |
-0,331653106 |
0,033165 |
|
12 |
11,84201 |
0,157986835 |
0,013166 |
|
13 |
13,164 |
-0,163999272 |
0,012615 |
|
Итого |
0,134471 |
A
= (0,1345 / 5)
100 = 2,69 %, что говорит о хорошем качестве
уравнения регрессии, ибо ошибка
аппроксимации в пределах 5-7 % свидетельствует
о хорошем подборе модели к исходным
данным.
Возможно
и другое определение средней ошибки
аппроксимации:
(2.39)
Для
нашего примера эта величина составит:
.
Для
расчета средней ошибки аппроксимации
в стандартных программах чаще используется
формула (2.39).
Аналогично
определяется средняя ошибка аппроксимации
и для уравнения параболы.
№11
Факторы,
включаемые во множественную регрессию,
должны отвечать следующим требованиям:
1)
быть количественно измеримы. Если
необходимо включить в модель качественный
фактор, не имеющий количественного
измерения, то нужно придать ему
количественную определенность (например,
в модели урожайности качество почвы
задается в виде баллов; в модели стоимости
объектов недвижимости учитывается
место нахождения недвижимости: районы
могут быть проранжированы);
2)
не должны быть коррелированны между
собой и тем более находиться в точной
функциональной связи.
Включение
в модель факторов с высокой интеркорреляцией,
когда ryx1
< rx1x2,
для зависимости y
= a
+ b1
x1
+ b2
x2
+ ,
может привести к нежелательным
последствиям – система нормальных
уравнений может оказаться плохо
обусловленной и повлечь за собой
неустойчивость и ненадежность оценок
коэффициентов регрессии.
Если
между факторами существует высокая
корреляция, то нельзя определить их
изолированное влияние на результативный
показатель, и параметры уравнения
регрессии оказываются неинтерпретируемыми.
Так, в уравнении y
= a
+ b1
x1
+ b2
x2
+ ,
предполагается, что факторы x1
и x2
независимы друг от друга, т.е. rx1x2
= 0. Тогда можно говорить, что параметр
b1
измеряет силу влияния фактора x1
на результат y
при неизменном значении фактора x2.
Если же rx1x2
= 1, то с изменением фактора x1
фактор x2
не может оставаться неизменным. Отсюда
b1
и b2
нельзя интерпретировать как показатели
раздельного влияния x1
и x2
на y.
Пример
3.2. При
изучении зависимости y
= f(x,
z,
v)
матрица парных коэффициентов корреляции
оказалась следующей:
|
y |
x |
z |
v |
|
|
y |
1 |
|||
|
x |
0,8 |
1 |
||
|
z |
0,7 |
0,8 |
1 |
|
|
v |
0,6 |
0,5 |
0,2 |
1 |
Очевидно,
что факторы x
и z
дублируют друг друга. В анализ целесообразно
включить фактор z,
а не x,
так как корреляция z,
с результатом y
слабее, чем корреляция фактора x
с y
(ryz
< ryx),
но зато слабее межфакторная корреляция
rzv
< rxv.
Поэтому в данном случае в уравнение
множественной регрессии включаются
факторы z,
и v.
По
величине парных коэффициентов корреляции
обнаруживается лишь явная коллинеарность
факторов. Наибольшие трудности в
использовании аппарата множественной
регрессии возникают при наличии
мультиколлинеарности
факторов, когда более чем два фактора
связаны между собой линейной зависимостью,
т.е. имеет место совокупное воздействие
факторов друг на друга. Наличие
мультиколлинеарности факторов может
означать, что некоторые факторы всегда
будут действовать в унисон. В результате
вариация в исходных данных перестает
быть полностью независимой и нельзя
оценить воздействие каждого фактора в
отдельности. Чем сильнее мультиколлинеарность
факторов, тем менее надежна оценка
распределения суммы объясненной вариации
по отдельным факторам с помощью метода
наименьших квадратов.
Если
рассматривается регрессия y
= a
+ b
x
+ c
z
+ d
v
+ ,
то для расчета параметров с применением
МНК предполагается равенство
S2y
= S2факт
+ S2,
где
S2y
– общая сумма квадратов отклонений
;
S2факт
– факторная (объясненная) сумма квадратов
отклонений
;
S2
– остаточная сумма квадратов отклонений
.
В
свою очередь, при независимости факторов
друг от друга выполнимо равенство
S2факт
= S2x
+ S2z
+ S2v,
где
S2x,
S2z,
S2v
– суммы квадратов отклонений, обусловленные
влиянием соответствующих факторов.
Если
же факторы интеркоррелированы, то данное
равенство нарушается.
Включение
в модель мультиколлинеарных факторов
нежелательно по следующим причинам:
– затрудняется
интерпретация параметров множественной
регрессии как характеристик действия
факторов в «чистом» виде, ибо факторы
коррелированны; параметры линейной
регрессии теряют экономический смысл;
– оценки
параметров ненадежны, обнаруживают
большие стандартные ошибки и меняются
с изменением объема наблюдений (не
только по величина, но и по знаку), что
делает модель непригодной для анализа
и прогнозирования.
Для
оценки факторов может использоваться
определитель матрицы
парных коэффициентов корреляции между
факторами.
Если
бы факторы не коррелировали между собой,
то матрицы парных коэффициентов
корреляции между ними была бы единичной,
поскольку все недиагональные элементы
rxixj
(xi
xj)
были бы равны нулю. Так, для уравнения,
включающего три объясняющих переменных,
y
= a
+ b1
x1
+ b2
x2
+ b3
x3
+ ,
матрица
коэффициентов корреляции между факторами
имела бы определитель, равный единице
,
поскольку
rx1x1
= rx2x2
= rx3x3
= 1 и rx1x2
= rx1x3
= rx2x3
= 0.
Если
же между факторами существует полная
линейная зависимость и все коэффициенты
корреляции равны единице, то определитель
такой матрицы равен нулю
.
Чем
ближе к нулю определитель матрицы
межфакторной корреляции, тем сильнее
мультиколлинеарность факторов и
ненадежнее результаты множественной
регрессии. И, наоборот, чем ближе к
единице определитель матрицы межфакторной
корреляции, тем меньше мультиколлинеарность
факторов.
Оценка
значимости мультиколлинеарности
факторов может быть проведена методом
испытания гипотезы о независимости
переменных H0:
DetR
= 1. Доказано, что величина
имеет приближенное распределение 2
с df
= m
(m
– 1)/2 степенями
свободы. Если фактическое значение 2
превосходит табличное (критическое):
2факт
> 2табл(df,)
то гипотеза H0
отклоняется. Это означает, что DetR
1, недиагональные ненулевые коэффициенты
корреляции указывают на коллинеарность
факторов. Мультиколлинеарность считается
доказанной.
Через
коэффициенты множественной детерминации
можно найти переменные, ответственные
за мультиколлинеарность факторов. Для
этого в качестве зависимой переменной
рассматривается каждый из факторов.
Чем ближе значение коэффициента
множественной детерминации к единице,
тем сильна проявляется мультиколлинеарность
факторов. Сравнивая между собой
коэффициенты множественной детерминации
факторов
R2x1x2x3…xp;
R2x2x1x3…xp
и т.п., можно выделить переменные,
ответственные за мультиколлинеарность,
следовательно, можно решать проблему
отбора факторов, оставляя в уравнении
факторы с минимальной величиной
коэффициента множественной детерминации.
Имеется
ряд подходов преодоления сильной
межфакторной корреляции. Самый простой
из них состоит в исключении из модели
одного или нескольких факторов. Другой
путь связан с преобразованием факторов,
при котором уменьшается корреляция
между ними. Например, при построении
модели на основе рядов динамики переходят
от первоначальных данных к первым
разностям уровней y
= yt
– yt–1,
чтобы исключить влияние тенденции, или
используются такие методы, которые
сводят к нулю межфакторную корреляцию,
т.е. переходят от исходных переменных
к их линейным комбинациям, не коррелированным
друг с другом (метод главных компонент).
Одним
из путей учета внутренней корреляции
факторов является переход к совмещенным
уравнениям регрессии, т.е. к уравнениям,
которые отражают не только влияние
факторов, но и их взаимодействие. Так,
если y
= f(x1,
x2,
x3).
то можно построить следующее совмещенное
уравнение:
y
= a
+ b1
x1
+ b2
x2
+ b3
x3
+ b12
x1
x2
+ b13
x1
x3
+ b23
x2
x3
+ .
Рассматриваемое
уравнение включает эффект взаимодействия
первого порядка. Можно включать в модель
и взаимодействие более высоких порядков,
если будет доказана его статистическая
значимость, например включение
взаимодействия второго порядка b123
x1
x2
x3
и т.д. Как правила, взаимодействие
третьего и более высоких порядков
оказывается статистически незначимым;
совмещенные уравнения регрессии
ограничиваются взаимодействием первого
и второго порядков. Но и оно может
оказаться несущественным. Тогда
нецелесообразно включать в модель
взаимодействие всех факторов и всех
порядков. Так, если анализ совмещенного
уравнения показал значимость только
взаимодействия факторов x1и
x3,
то уравнение будет иметь вид:
y
= a
+ b1
x1
+ b2
x2
+ b3
x3
+ b13
x1
x3
+ .
Взаимодействие
факторов x1и
x3
означает, что на разных уровнях фактора
x3
влияние фактора x1на
y
будет неодинаково, т.е. оно зависит от
значений фактора x3.
На рис. 3.1 взаимодействие факторов
представляется непараллельными линиями
связи x1с
результатом y.
И, наоборот, параллельные линии влияния
фактора x1на
y
при разных уровнях фактора x3
означают отсутствие взаимодействия
факторов x1и
x3.

Рис.
3.1. Графическая иллюстрация взаимодействия
факторов
Совмещенные
уравнения регрессии строятся, например,
при исследовании эффекта влияния на
урожайность разных видов удобрений
(комбинаций азота и фосфора).
Решению
проблемы устранения мультиколлинеарности
факторов может помочь и переход к
уравнениям приведенной формы. С этой
целью в уравнение регрессии подставляют
рассматриваемый фактор, выраженный из
другого уравнения.
Пусть,
например, рассматривается двухфакторная
регрессия вида yx
= a
+ b1
x1
+ b2
x2,
для которой факторы x1и
x2
обнаруживают высокую корреляцию. Если
исключить один из факторов, то мы придем
к уравнению парной регрессии. Вместе с
тем можно оставить факторы в модели, но
исследовать данное двухфакторное
уравнение регрессии совместно с другим
уравнением, в котором фактор (например,
x2)
рассматривается как зависимая переменная.
Предположим, что x2
= A
+ B
y
+ C
x3.
Подставив это уравнение в искомое вместо
x2,
получим:
yx
= a
+ b1
x1
+ b2
(A
+ B
y
+ C
x3)
или
yx
(1 – b2
B)
= (a
+ b2
A)
+ b1
x1
+ C
b2
x3.
Если
(1 – b2
B)
0, то, разделив обе части равенства на
(1 – b2
B),
получим уравнение вида
,
которое
принято называть приведенной формой
уравнения для определения результативного
признака y.
Это уравнение может быть представлено
в виде
yx
= a’
+ b’1
x1
+ b’3
x3.
К
нему для оценки параметров может быть
применен метод наименьших квадратов.
Отбор
факторов, включаемых в регрессию,
является одним из важнейших этапов
практического использования методов
регрессии. Подходы к отбору факторов
на основе показателей корреляции могут
быть разные. Они приводят построение
уравнения множественной регрессии
соответственно к разным методикам. В
зависимости от того, какая методика
построения уравнения регрессии принята,
меняется алгоритм её решения на
компьютере.
Наиболее
широкое применение получили следующие
методы построения уравнения множественной
регрессии:
– метод
исключения;
– метод
включения;
– шаговый
регрессионный анализ.
Каждый
из этих методов по-своему решает проблему
отбора факторов, давая в целом близкие
результаты – отсев факторов из полного
его набора (метод исключения), дополнительное
введение фактора (метод включения),
исключение ранее введенного фактора
(шаговый регрессионный анализ).
На
первый взгляд может показаться, что
матрица парных коэффициентов корреляции
играет главную роль в отборе факторов.
Вместе с тем вследствие взаимодействия
факторов парные коэффициенты корреляции
не могут в полной мере решать вопрос о
целесообразности включения в модель
того или иного фактора. Эту роль выполняют
показатели частной корреляции, оценивающие
в чистом виде тесноту связи фактора с
результатом. Матрица частных коэффициентов
корреляции наиболее широко используется
в процедуре отсева факторов. Отсев
факторов можно проводить и по t-критерию
Стьюдента для коэффициентов регрессии:
из уравнения исключаются факторы с
величиной t-критерия
меньше табличного. Так, например,
уравнение регрессии составило:
y
= 25 + 5x1
+ 3x2
+ 4x3
+ .
(4,0) (1,3) (6,0)
В
скобках приведены фактические значения
t-критерия
для соответствующих коэффициентов
регрессии, как правило, при t
< 2 коэффициент регрессии незначим и,
следовательно, рассматриваемый фактор
не должен присутствовать в регрессионной
модели. В данном случае – это фактор
x2.
При
отборе факторов рекомендуется пользоваться
следующим правилом: число включаемых
факторов обычно в 6-7 раз меньше объема
совокупности, по которой строится
регрессия. Если это соотношение нарушено,
то число степеней свободы остаточной
вариации очень мало. Это приводит к
тому, что параметры уравнения регрессии
оказываются статистически незначимыми,
а F-критерий
меньше табличного значения.
Соседние файлы в предмете [НЕСОРТИРОВАННОЕ]
- #
- #
- #
- #
- #
- #
- #
- #
- #
- #
- #
Коэффициент корреляции
Тесноту (силу) связи изучаемых показателей в предмете эконометрика оценивают с помощью коэффициента корреляции Rxy, который может принимать значения от -1 до +1.
Если Rxy > 0,7 — связь между изучаемыми показателями сильная, можно проводить анализ линейной модели
Если 0,3 < Rxy < 0,7 — связь между показателями умеренная, можно использовать нелинейную модель при отсутствии Rxy > 0,7
Если Rxy < 0,3 — связь слабая, модель строить нельзя
Для нелинейной регрессии используют индекс корреляции (0 < Рху < 1):
Средняя ошибка аппроксимации
Для оценки качества однофакторной модели в эконометрике используют коэффициент детерминации и среднюю ошибку аппроксимации.
Средняя ошибка аппроксимации определяется как среднее отклонение полученных значений от фактических
Допустимая ошибка аппроксимации не должна превышать 10%.
В эконометрике существует понятие среднего коэффициента эластичности Э – который говорит о том, на сколько процентов в среднем изменится показатель у от своего среднего значения при изменении фактора х на 1% от своей средней величины.
Пример нахождения коэффициента корреляции
Исходные данные:
|
Номер региона |
Среднедушевой прожиточный минимум в день одного трудоспособного, руб., |
Среднедневная заработная плата, руб., |
|
1 |
81 |
124 |
|
2 |
77 |
131 |
|
3 |
85 |
146 |
|
4 |
79 |
139 |
|
5 |
93 |
143 |
|
6 |
100 |
159 |
|
7 |
72 |
135 |
|
8 |
90 |
152 |
|
9 |
71 |
127 |
|
10 |
89 |
154 |
|
11 |
82 |
127 |
|
12 |
111 |
162 |
Рассчитаем параметры парной линейной регрессии, составив таблицу
| x |
x2 |
y |
xy |
y2 |
|
|
1 |
81 |
6561 |
124 |
10044 |
15376 |
|
2 |
77 |
5929 |
131 |
10087 |
17161 |
|
3 |
85 |
7225 |
146 |
12410 |
21316 |
|
4 |
79 |
6241 |
139 |
10981 |
19321 |
|
5 |
93 |
8649 |
143 |
13299 |
20449 |
|
6 |
100 |
10000 |
159 |
15900 |
25281 |
|
7 |
72 |
5184 |
135 |
9720 |
18225 |
|
8 |
90 |
8100 |
152 |
13680 |
23104 |
|
9 |
71 |
5041 |
127 |
9017 |
16129 |
|
10 |
89 |
7921 |
154 |
13706 |
23716 |
|
11 |
82 |
6724 |
127 |
10414 |
16129 |
|
12 |
111 |
12321 |
162 |
17982 |
26244 |
|
Среднее |
85,8 |
7491 |
141,6 |
12270,0 |
20204,3 |
|
Сумма |
1030,0 |
89896 |
1699 |
147240 |
242451 |
| σ |
11,13 |
12,59 |
|||
| σ2 |
123,97 |
158,41 |
формула расчета дисперсии σ2 приведена здесь.
Коэффициенты уравнения y = a + bx определяются по формуле
Получаем уравнение регрессии: y = 0,947x + 60,279.
Коэффициент уравнения b = 0,947 показывает, что при увеличении среднедушевого прожиточного минимума в день одного трудоспособного на 1 руб. среднедневная заработная плата увеличивается на 0,947 руб.
Коэффициент корреляции рассчитывается по формуле:
Значение коэффициента корреляции более — 0,7, это означает, что связь между среднедушевым прожиточным минимумом в день одного трудоспособного и среднедневной заработной платой сильная.
Коэффициент детерминации равен R2 = 0.838^2 = 0.702
т.е. 70,2% результата объясняется вариацией объясняющей переменной x.
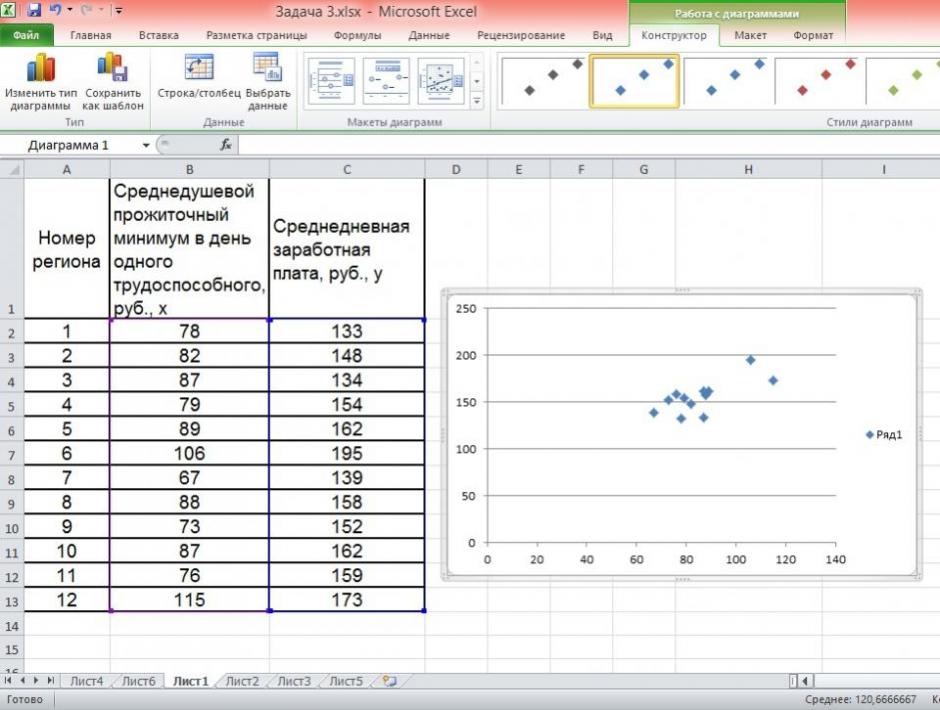
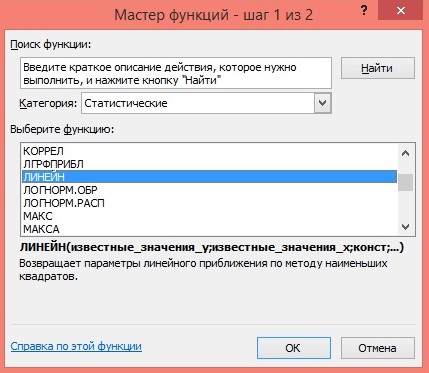
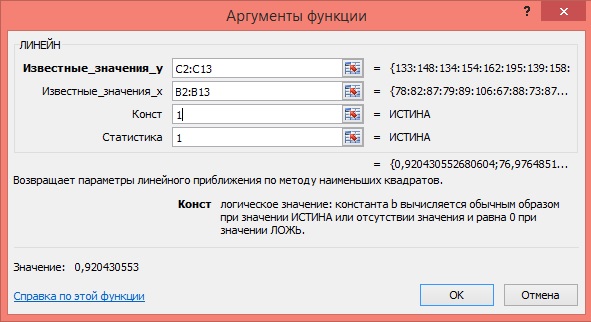
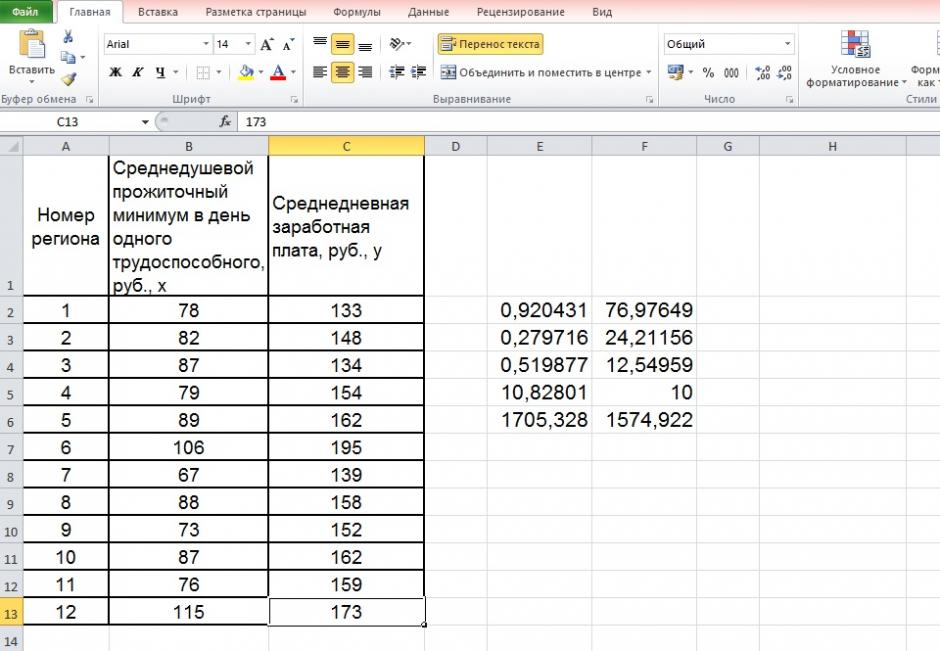
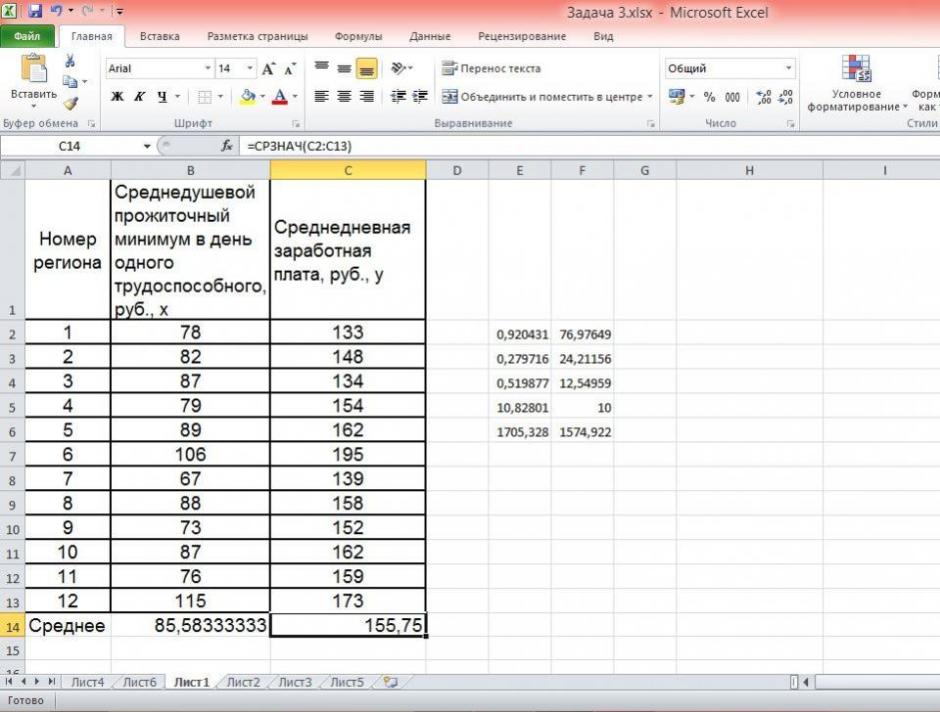
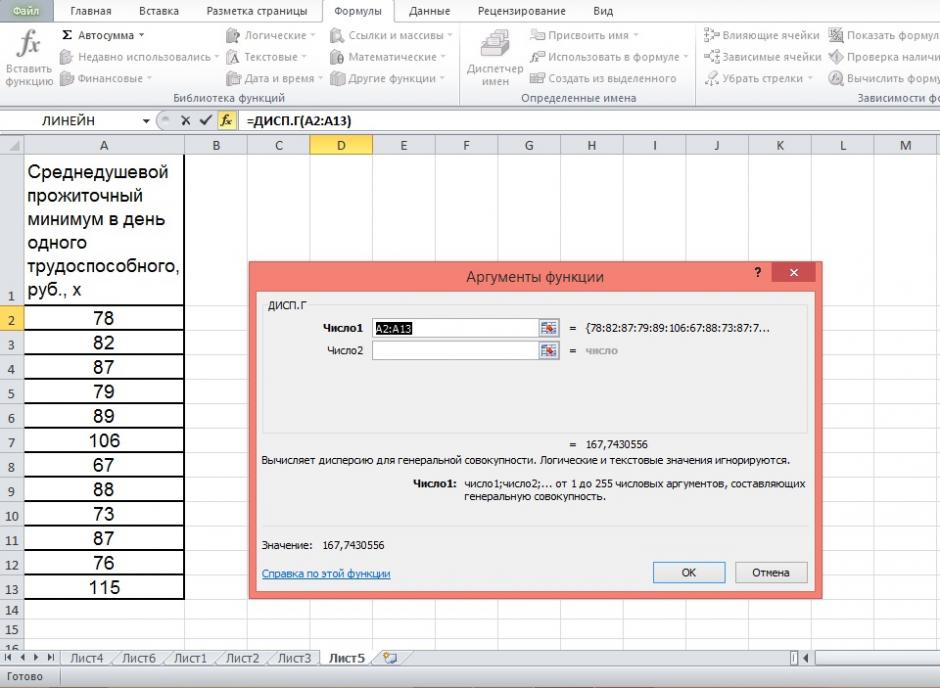
По территориям региона приводятся данные за 200Х г.
| Номер региона | Среднедушевой прожиточный минимум в день одного трудоспособного, руб., х | Среднедневная заработная плата, руб., у |
|---|---|---|
| 1 | 78 | 133 |
| 2 | 82 | 148 |
| 3 | 87 | 134 |
| 4 | 79 | 154 |
| 5 | 89 | 162 |
| 6 | 106 | 195 |
| 7 | 67 | 139 |
| 8 | 88 | 158 |
| 9 | 73 | 152 |
| 10 | 87 | 162 |
| 11 | 76 | 159 |
| 12 | 115 | 173 |
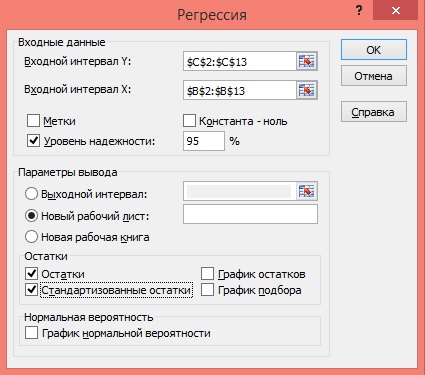
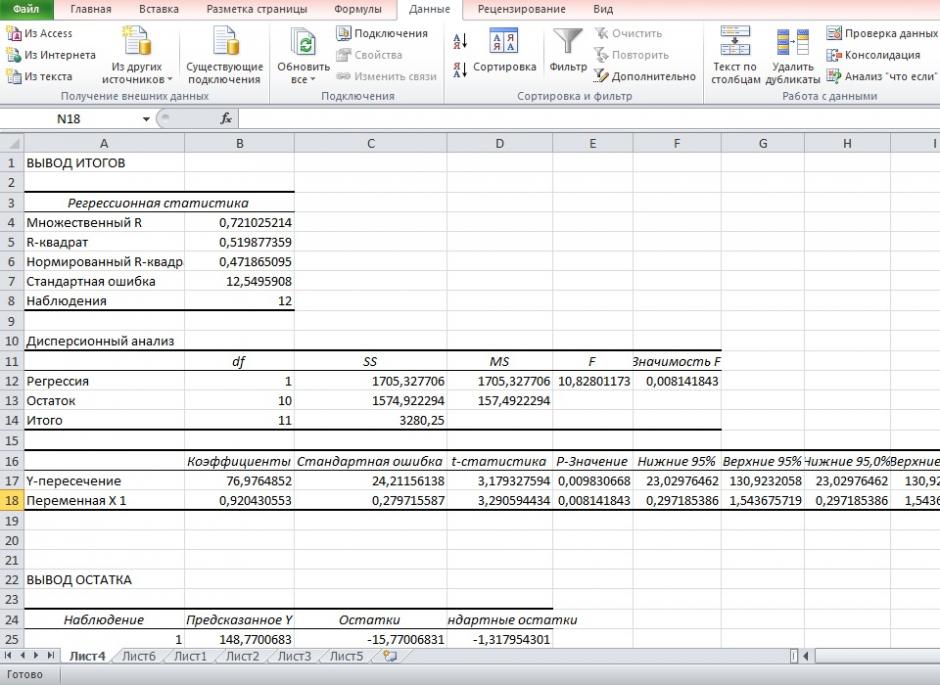
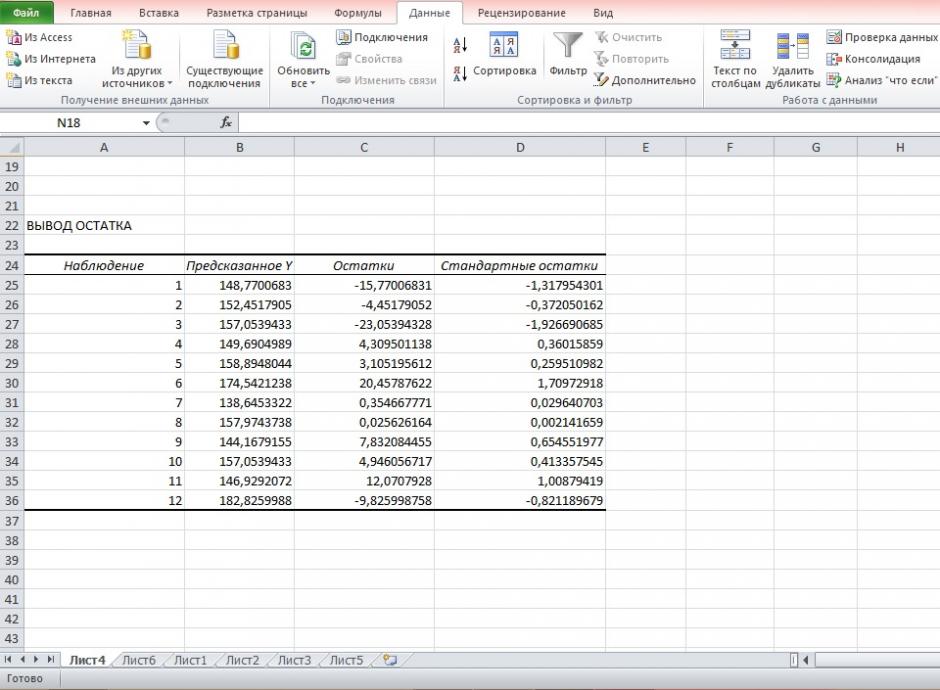
Задание:
1. Постройте поле корреляции и сформулируйте гипотезу о форме связи.
2. Рассчитайте параметры уравнения линейной регрессии

3. Оцените тесноту связи с помощью показателей корреляции и детерминации.
4. Дайте с помощью среднего (общего) коэффициента эластичности сравнительную оценку силы связи фактора с результатом.
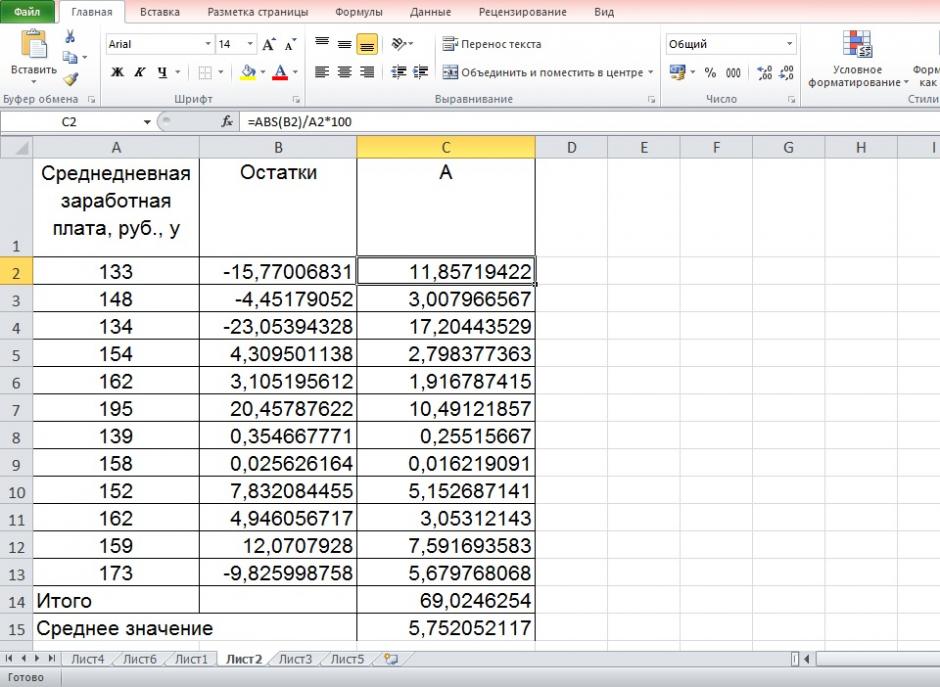
5. Оцените с помощью средней ошибки аппроксимации качество уравнений.
6. Оцените с помощью F-критерия Фишера статистическую надёжность результатов регрессионного моделирования.
7. Рассчитайте прогнозное значение результата, если прогнозное значение фактора увеличится на 10% от его среднего уровня. Определите доверительный интервал прогноза для уровня значимости 
8. Оцените полученные результаты, выводы оформите в аналитической записке.
Решение:
Решим данную задачу с помощью Excel.
1. Сопоставив имеющиеся данные х и у, например, ранжировав их в порядке возрастания фактора х, можно наблюдать наличие прямой зависимости между признаками, когда увеличение среднедушевого прожиточного минимума увеличивает среднедневную заработную плату. Исходя из этого, можно сделать предположение, что связь между признаками прямая и её можно описать уравнением прямой. Этот же вывод подтверждается и на основе графического анализа.
Чтобы построить поле корреляции можно воспользоваться ППП Excel. Введите исходные данные в последовательности: сначала х, затем у.
Выделите область ячеек, содержащую данные.
Затем выберете: Вставка / Точечная диаграмма / Точечная с маркерами как показано на рисунке 1.
Рисунок 1 Построение поля корреляции
Анализ поля корреляции показывает наличие близкой к прямолинейной зависимости, так как точки расположены практически по прямой линии.
2. Для расчёта параметров уравнения линейной регрессии
воспользуемся встроенной статистической функцией ЛИНЕЙН.
Для этого:
1) Откройте существующий файл, содержащий анализируемые данные;
2) Выделите область пустых ячеек 5×2 (5 строк, 2 столбца) для вывода результатов регрессионной статистики.
3) Активизируйте Мастер функций: в главном меню выберете Формулы / Вставить функцию.
4) В окне Категория выберете Статистические, в окне функция – ЛИНЕЙН. Щёлкните по кнопке ОК как показано на Рисунке 2;
Рисунок 2 Диалоговое окно «Мастер функций»
5) Заполните аргументы функции:
Известные значения у – диапазон, содержащий данные результативного признака;
Известные значения х – диапазон, содержащий данные факторного признака;
Константа – логическое значение, которое указывает на наличие или на отсутствие свободного члена в уравнении; если Константа = 1, то свободный член рассчитывается обычным образом, если Константа = 0, то свободный член равен 0;
Статистика – логическое значение, которое указывает, выводить дополнительную информацию по регрессионному анализу или нет. Если Статистика = 1, то дополнительная информация выводится, если Статистика = 0, то выводятся только оценки параметров уравнения.
Щёлкните по кнопке ОК;
Рисунок 3 Диалоговое окно аргументов функции ЛИНЕЙН
6) В левой верхней ячейке выделенной области появится первый элемент итоговой таблицы. Чтобы раскрыть всю таблицу, нажмите на клавишу <F2>, а затем на комбинацию клавиш <Ctrl>+<Shift>+<Enter>.
Дополнительная регрессионная статистика будет выводиться в порядке, указанном в следующей схеме:
| Значение коэффициента b | Значение коэффициента a |
| Стандартная ошибка b | Стандартная ошибка a |
| Коэффициент детерминации R2 | Стандартная ошибка y |
| F-статистика | Число степеней свободы df |
| Регрессионная сумма квадратов
|
Остаточная сумма квадратов
|
Рисунок 4 Результат вычисления функции ЛИНЕЙН
Получили уровнение регрессии:
Делаем вывод: С увеличением среднедушевого прожиточного минимума на 1 руб. среднедневная заработная плата возрастает в среднем на 0,92 руб.
3. Коэффициент детерминации 
По вычисленному коэффициенту детерминации 
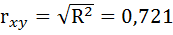
Связь оценивается как тесная.
4. С помощью среднего (общего) коэффициента эластичности определим силу влияния фактора на результат.
Для уравнения прямой 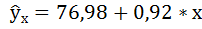
Средние значения найдём, выделив область ячеек со значениями х, и выберем Формулы / Автосумма / Среднее, и то же самое произведём со значениями у.
Рисунок 5 Расчёт средних значений функции и аргумент
Таким образом, при изменении среднедушевого прожиточного минимума на 1% от своего среднего значения среднедневная заработная плата изменится в среднем на 0,51%.
С помощью инструмента анализа данных Регрессия можно получить:
— результаты регрессионной статистики,
— результаты дисперсионного анализа,
— результаты доверительных интервалов,
— остатки и графики подбора линии регрессии,
— остатки и нормальную вероятность.
Порядок действий следующий:
1) проверьте доступ к Пакету анализа. В главном меню последовательно выберите: Файл/Параметры/Надстройки.
2) В раскрывающемся списке Управление выберите пункт Надстройки Excel и нажмите кнопку Перейти.
3) В окне Надстройки установите флажок Пакет анализа, а затем нажмите кнопку ОК.
• Если Пакет анализа отсутствует в списке поля Доступные надстройки, нажмите кнопку Обзор, чтобы выполнить поиск.
• Если выводится сообщение о том, что пакет анализа не установлен на компьютере, нажмите кнопку Да, чтобы установить его.
4) В главном меню последовательно выберите: Данные / Анализ данных / Инструменты анализа / Регрессия, а затем нажмите кнопку ОК.
5) Заполните диалоговое окно ввода данных и параметров вывода:
Входной интервал Y – диапазон, содержащий данные результативного признака;
Входной интервал X – диапазон, содержащий данные факторного признака;
Метки – флажок, который указывает, содержит ли первая строка названия столбцов или нет;
Константа – ноль – флажок, указывающий на наличие или отсутствие свободного члена в уравнении;
Выходной интервал – достаточно указать левую верхнюю ячейку будущего диапазона;
6) Новый рабочий лист – можно задать произвольное имя нового листа.
Затем нажмите кнопку ОК.
Рисунок 6 Диалоговое окно ввода параметров инструмента Регрессия
Результаты регрессионного анализа для данных задачи представлены на рисунке 7.
Рисунок 7 Результат применения инструмента регрессия
5. Оценим с помощью средней ошибки аппроксимации качество уравнений. Воспользуемся результатами регрессионного анализа представленного на Рисунке 8.
Рисунок 8 Результат применения инструмента регрессия «Вывод остатка»
Составим новую таблицу как показано на рисунке 9. В графе С рассчитаем относительную ошибку аппроксимации по формуле:
Рисунок 9 Расчёт средней ошибки аппроксимации
Средняя ошибка аппроксимации рассчитывается по формуле:
Качество построенной модели оценивается как хорошее, так как 
6. Из таблицы с регрессионной статистикой (Рисунок 4) выпишем фактическое значение F-критерия Фишера:
Поскольку 
8. Оценку статистической значимости параметров регрессии проведём с помощью t-статистики Стьюдента и путём расчёта доверительного интервала каждого из показателей.
Выдвигаем гипотезу Н0 о статистически незначимом отличии показателей от нуля:
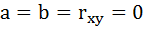
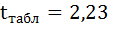
На рисунке 7 имеются фактические значения t-статистики:
t-критерий для коэффициента корреляции можно рассчитать двумя способами:
I способ: 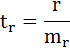
где 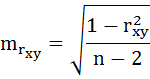
Данные для расчёта возьмём из таблицы на Рисунке 7.
II способ:
Фактические значения t-статистики превосходят табличные значения:
Поэтому гипотеза Н0 отклоняется, то есть параметры регрессии и коэффициент корреляции не случайно отличаются от нуля, а статистически значимы.
Доверительный интервал для параметра a определяется как
Для параметра a 95%-ные границы как показано на рисунке 7 составили:
Доверительный интервал для коэффициента регрессии определяется как
Для коэффициента регрессии b 95%-ные границы как показано на рисунке 7 составили:
Анализ верхней и нижней границ доверительных интервалов приводит к выводу о том, что с вероятностью 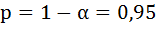
7. Полученные оценки уравнения регрессии позволяют использовать его для прогноза. Если прогнозное значение прожиточного минимума составит:
Тогда прогнозное значение прожиточного минимума составит:
Ошибку прогноза рассчитаем по формуле:
где
Дисперсию посчитаем также с помощью ППП Excel. Для этого:
1) Активизируйте Мастер функций: в главном меню выберете Формулы / Вставить функцию.
2) В окне Категория выберете Статистические, в окне функция – ДИСП.Г. Щёлкните по кнопке ОК.
3) Заполните диапазон, содержащий числовые данные факторного признака. Нажмите ОК.
Рисунок 10 Расчёт дисперсии
Получили значение дисперсии
Для подсчёта остаточной дисперсии на одну степень свободы воспользуемся результатами дисперсионного анализа как показано на Рисунке 7.
Доверительные интервалы прогноза индивидуальных значений у при 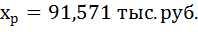
Интервал достаточно широк, прежде всего, за счёт малого объёма наблюдений. В целом выполненный прогноз среднемесячной заработной платы оказался надёжным.
Условие задачи взято из: Практикум по эконометрике: Учеб. пособие / И.И. Елисеева, С.В. Курышева, Н.М. Гордеенко и др.; Под ред. И.И. Елисеевой. – М.: Финансы и статистика, 2003. – 192 с.: ил.