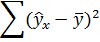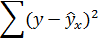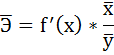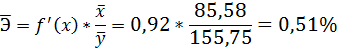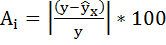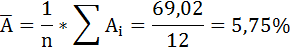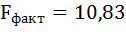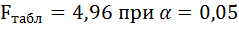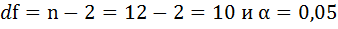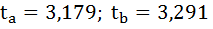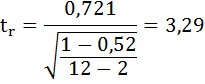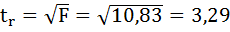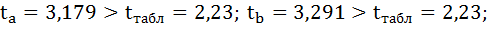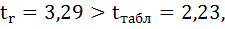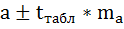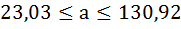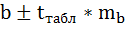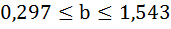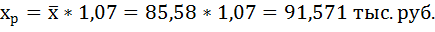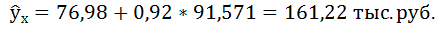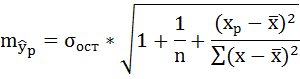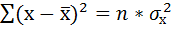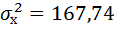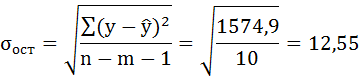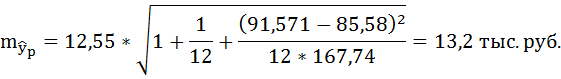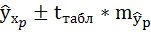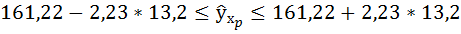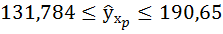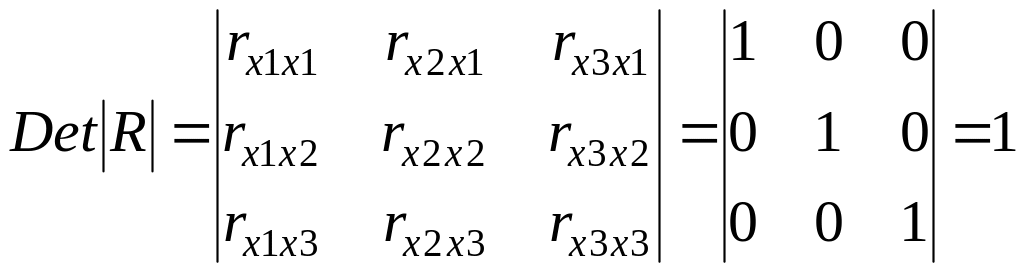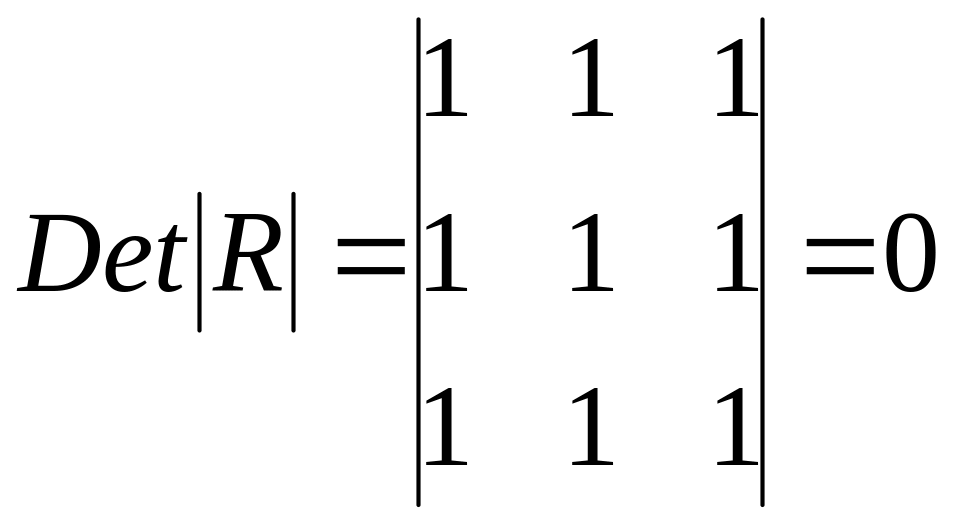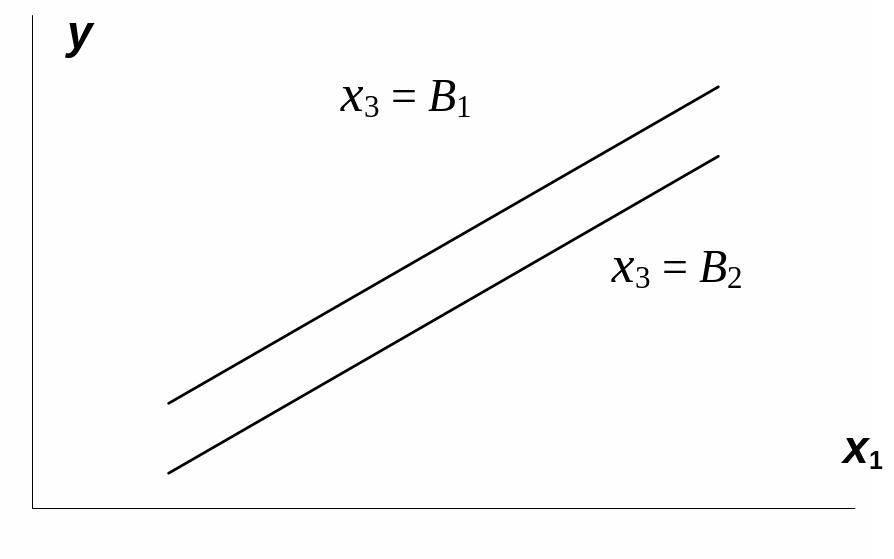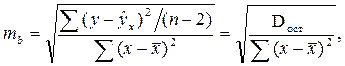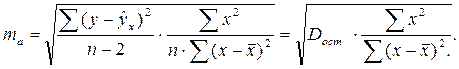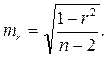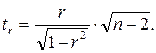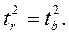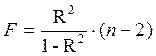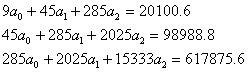По территориям региона приводятся данные за 200Х г.
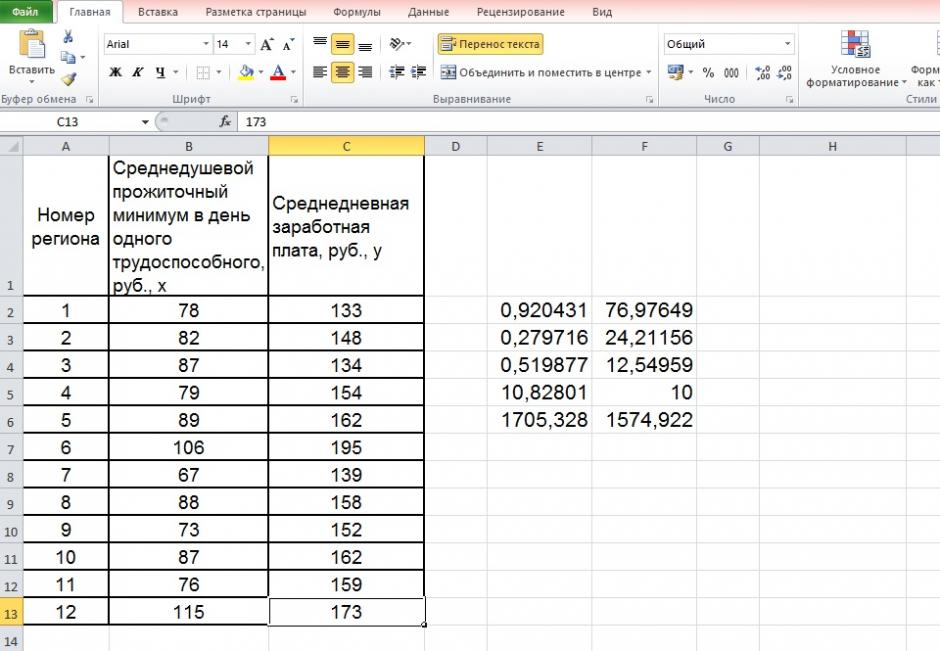
| Номер региона | Среднедушевой прожиточный минимум в день одного трудоспособного, руб., х | Среднедневная заработная плата, руб., у |
|---|---|---|
| 1 | 78 | 133 |
| 2 | 82 | 148 |
| 3 | 87 | 134 |
| 4 | 79 | 154 |
| 5 | 89 | 162 |
| 6 | 106 | 195 |
| 7 | 67 | 139 |
| 8 | 88 | 158 |
| 9 | 73 | 152 |
| 10 | 87 | 162 |
| 11 | 76 | 159 |
| 12 | 115 | 173 |
Задание:
1. Постройте поле корреляции и сформулируйте гипотезу о форме связи.
2. Рассчитайте параметры уравнения линейной регрессии

3. Оцените тесноту связи с помощью показателей корреляции и детерминации.
4. Дайте с помощью среднего (общего) коэффициента эластичности сравнительную оценку силы связи фактора с результатом.
5. Оцените с помощью средней ошибки аппроксимации качество уравнений.
6. Оцените с помощью F-критерия Фишера статистическую надёжность результатов регрессионного моделирования.
7. Рассчитайте прогнозное значение результата, если прогнозное значение фактора увеличится на 10% от его среднего уровня. Определите доверительный интервал прогноза для уровня значимости 
8. Оцените полученные результаты, выводы оформите в аналитической записке.
Решение:
Решим данную задачу с помощью Excel.
1. Сопоставив имеющиеся данные х и у, например, ранжировав их в порядке возрастания фактора х, можно наблюдать наличие прямой зависимости между признаками, когда увеличение среднедушевого прожиточного минимума увеличивает среднедневную заработную плату. Исходя из этого, можно сделать предположение, что связь между признаками прямая и её можно описать уравнением прямой. Этот же вывод подтверждается и на основе графического анализа.
Чтобы построить поле корреляции можно воспользоваться ППП Excel. Введите исходные данные в последовательности: сначала х, затем у.
Выделите область ячеек, содержащую данные.
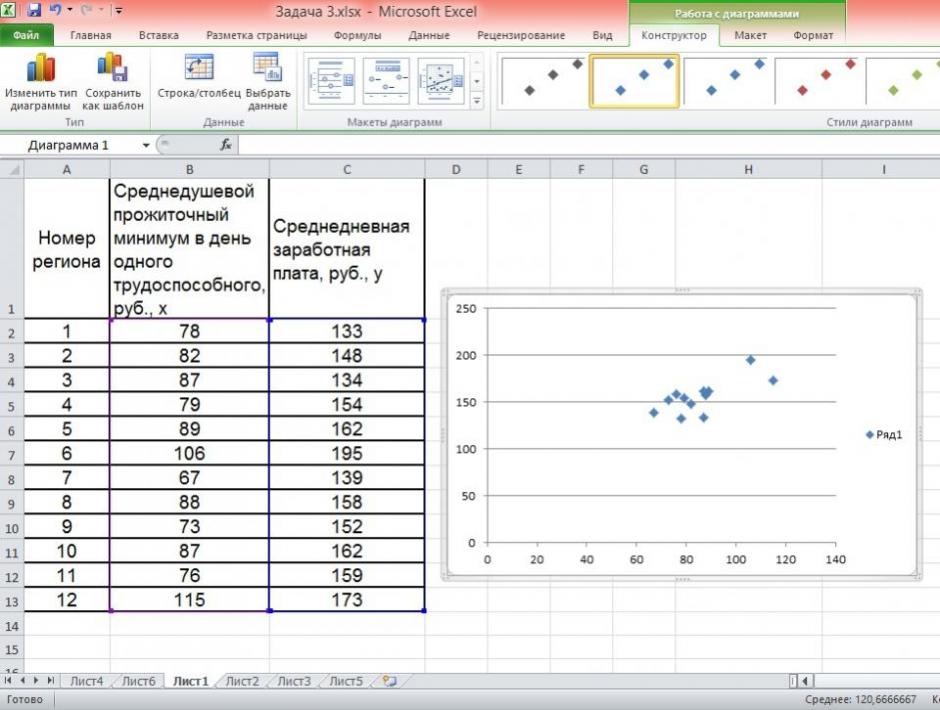
Затем выберете: Вставка / Точечная диаграмма / Точечная с маркерами как показано на рисунке 1.
Рисунок 1 Построение поля корреляции
Анализ поля корреляции показывает наличие близкой к прямолинейной зависимости, так как точки расположены практически по прямой линии.
2. Для расчёта параметров уравнения линейной регрессии
воспользуемся встроенной статистической функцией ЛИНЕЙН.
Для этого:
1) Откройте существующий файл, содержащий анализируемые данные;
2) Выделите область пустых ячеек 5×2 (5 строк, 2 столбца) для вывода результатов регрессионной статистики.
3) Активизируйте Мастер функций: в главном меню выберете Формулы / Вставить функцию.
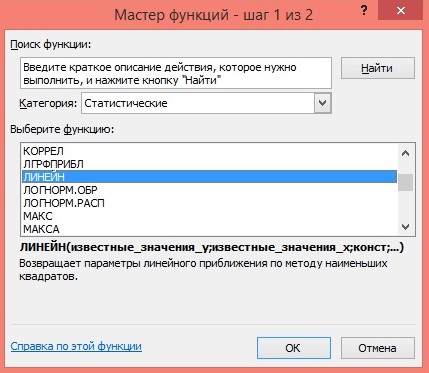
4) В окне Категория выберете Статистические, в окне функция – ЛИНЕЙН. Щёлкните по кнопке ОК как показано на Рисунке 2;
Рисунок 2 Диалоговое окно «Мастер функций»
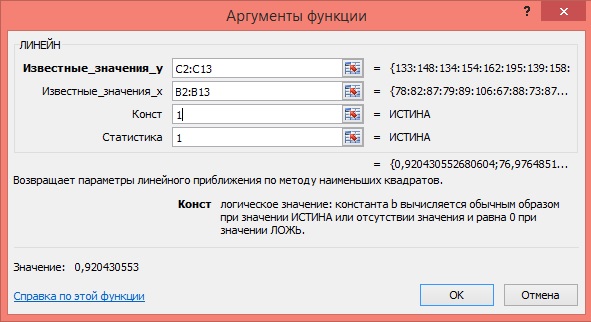
5) Заполните аргументы функции:
Известные значения у – диапазон, содержащий данные результативного признака;
Известные значения х – диапазон, содержащий данные факторного признака;
Константа – логическое значение, которое указывает на наличие или на отсутствие свободного члена в уравнении; если Константа = 1, то свободный член рассчитывается обычным образом, если Константа = 0, то свободный член равен 0;
Статистика – логическое значение, которое указывает, выводить дополнительную информацию по регрессионному анализу или нет. Если Статистика = 1, то дополнительная информация выводится, если Статистика = 0, то выводятся только оценки параметров уравнения.
Щёлкните по кнопке ОК;
Рисунок 3 Диалоговое окно аргументов функции ЛИНЕЙН
6) В левой верхней ячейке выделенной области появится первый элемент итоговой таблицы. Чтобы раскрыть всю таблицу, нажмите на клавишу <F2>, а затем на комбинацию клавиш <Ctrl>+<Shift>+<Enter>.
Дополнительная регрессионная статистика будет выводиться в порядке, указанном в следующей схеме:
| Значение коэффициента b | Значение коэффициента a |
| Стандартная ошибка b | Стандартная ошибка a |
| Коэффициент детерминации R2 | Стандартная ошибка y |
| F-статистика | Число степеней свободы df |
| Регрессионная сумма квадратов
|
Остаточная сумма квадратов
|
Рисунок 4 Результат вычисления функции ЛИНЕЙН
Получили уровнение регрессии:
Делаем вывод: С увеличением среднедушевого прожиточного минимума на 1 руб. среднедневная заработная плата возрастает в среднем на 0,92 руб.
3. Коэффициент детерминации 
По вычисленному коэффициенту детерминации 
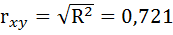
Связь оценивается как тесная.
4. С помощью среднего (общего) коэффициента эластичности определим силу влияния фактора на результат.
Для уравнения прямой 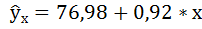
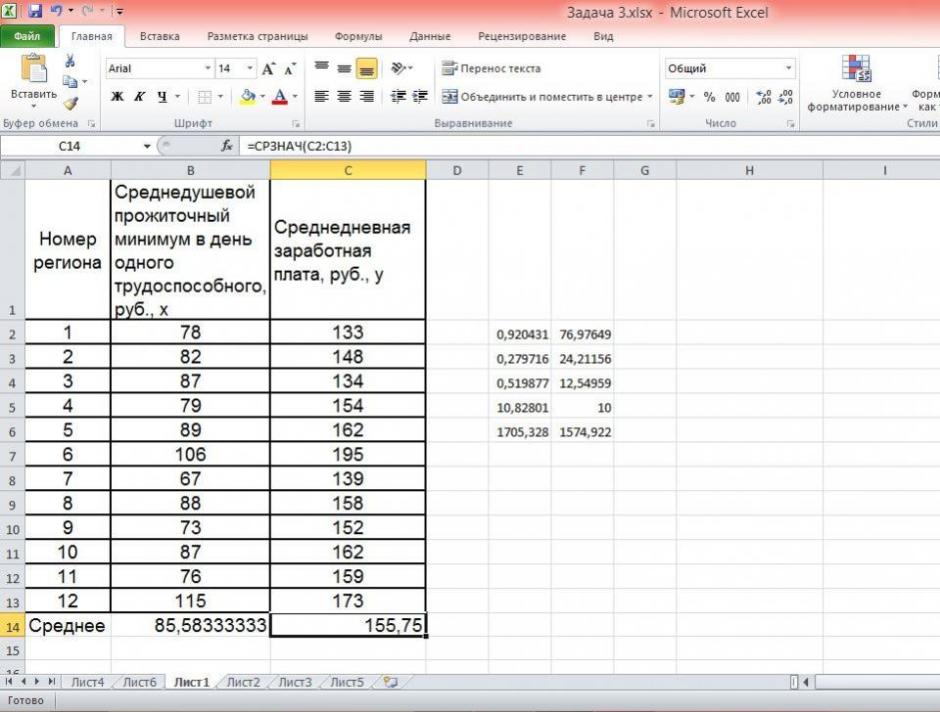
Средние значения найдём, выделив область ячеек со значениями х, и выберем Формулы / Автосумма / Среднее, и то же самое произведём со значениями у.
Рисунок 5 Расчёт средних значений функции и аргумент
Таким образом, при изменении среднедушевого прожиточного минимума на 1% от своего среднего значения среднедневная заработная плата изменится в среднем на 0,51%.
С помощью инструмента анализа данных Регрессия можно получить:
— результаты регрессионной статистики,
— результаты дисперсионного анализа,
— результаты доверительных интервалов,
— остатки и графики подбора линии регрессии,
— остатки и нормальную вероятность.
Порядок действий следующий:
1) проверьте доступ к Пакету анализа. В главном меню последовательно выберите: Файл/Параметры/Надстройки.
2) В раскрывающемся списке Управление выберите пункт Надстройки Excel и нажмите кнопку Перейти.
3) В окне Надстройки установите флажок Пакет анализа, а затем нажмите кнопку ОК.
• Если Пакет анализа отсутствует в списке поля Доступные надстройки, нажмите кнопку Обзор, чтобы выполнить поиск.
• Если выводится сообщение о том, что пакет анализа не установлен на компьютере, нажмите кнопку Да, чтобы установить его.
4) В главном меню последовательно выберите: Данные / Анализ данных / Инструменты анализа / Регрессия, а затем нажмите кнопку ОК.
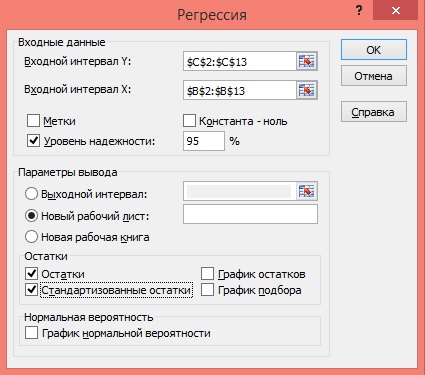
5) Заполните диалоговое окно ввода данных и параметров вывода:
Входной интервал Y – диапазон, содержащий данные результативного признака;
Входной интервал X – диапазон, содержащий данные факторного признака;
Метки – флажок, который указывает, содержит ли первая строка названия столбцов или нет;
Константа – ноль – флажок, указывающий на наличие или отсутствие свободного члена в уравнении;
Выходной интервал – достаточно указать левую верхнюю ячейку будущего диапазона;
6) Новый рабочий лист – можно задать произвольное имя нового листа.
Затем нажмите кнопку ОК.
Рисунок 6 Диалоговое окно ввода параметров инструмента Регрессия
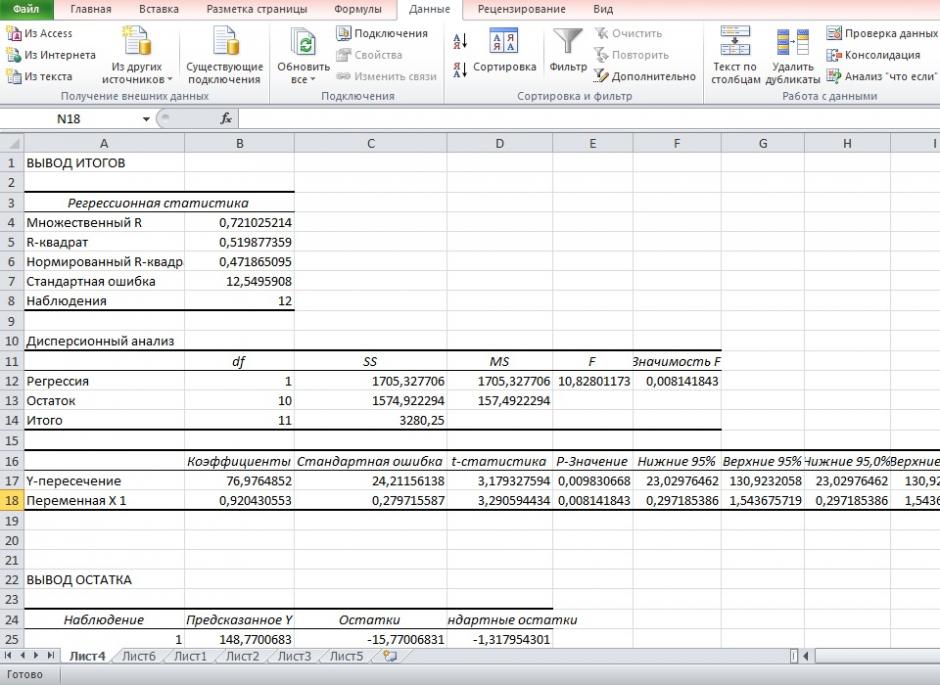
Результаты регрессионного анализа для данных задачи представлены на рисунке 7.
Рисунок 7 Результат применения инструмента регрессия
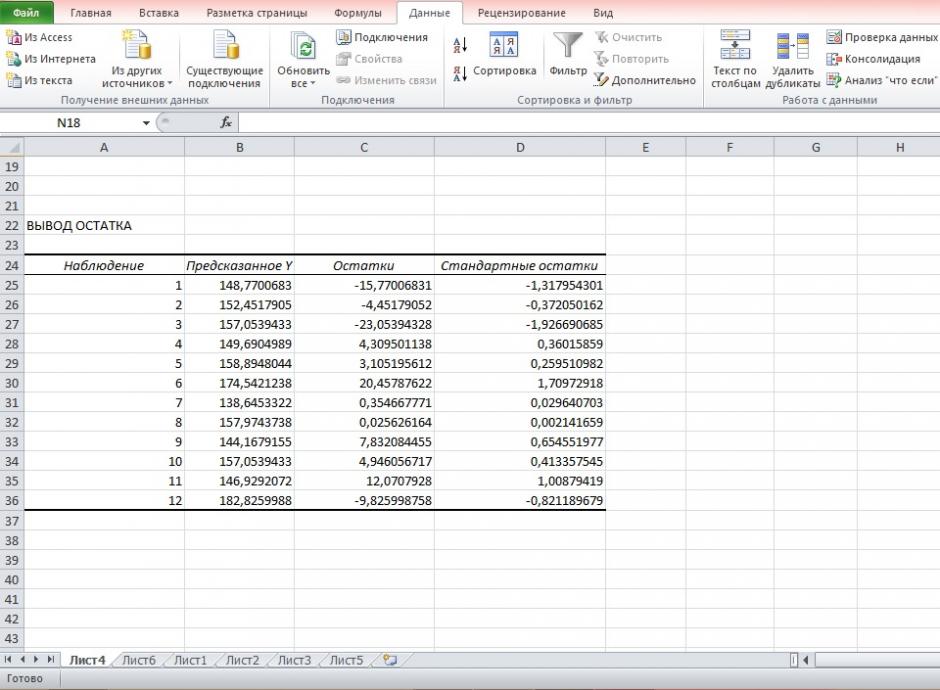
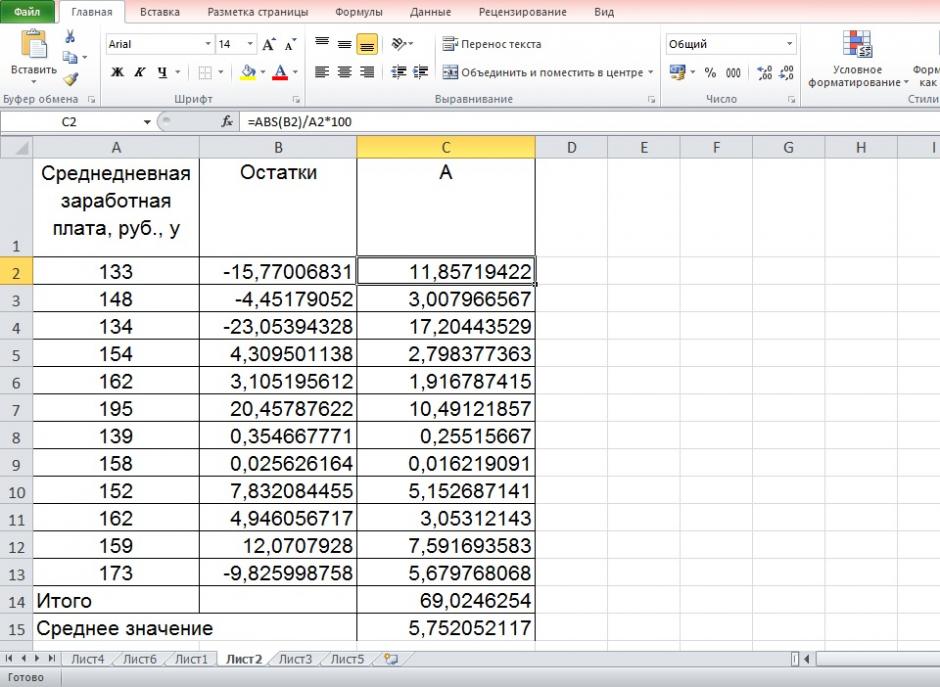
5. Оценим с помощью средней ошибки аппроксимации качество уравнений. Воспользуемся результатами регрессионного анализа представленного на Рисунке 8.
Рисунок 8 Результат применения инструмента регрессия «Вывод остатка»
Составим новую таблицу как показано на рисунке 9. В графе С рассчитаем относительную ошибку аппроксимации по формуле:
Рисунок 9 Расчёт средней ошибки аппроксимации
Средняя ошибка аппроксимации рассчитывается по формуле:
Качество построенной модели оценивается как хорошее, так как 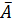
6. Из таблицы с регрессионной статистикой (Рисунок 4) выпишем фактическое значение F-критерия Фишера:
Поскольку 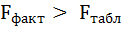
8. Оценку статистической значимости параметров регрессии проведём с помощью t-статистики Стьюдента и путём расчёта доверительного интервала каждого из показателей.
Выдвигаем гипотезу Н0 о статистически незначимом отличии показателей от нуля:
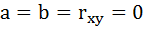
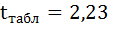
На рисунке 7 имеются фактические значения t-статистики:
t-критерий для коэффициента корреляции можно рассчитать двумя способами:
I способ: 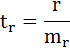
где 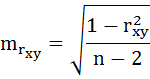
Данные для расчёта возьмём из таблицы на Рисунке 7.
II способ:
Фактические значения t-статистики превосходят табличные значения:
Поэтому гипотеза Н0 отклоняется, то есть параметры регрессии и коэффициент корреляции не случайно отличаются от нуля, а статистически значимы.
Доверительный интервал для параметра a определяется как
Для параметра a 95%-ные границы как показано на рисунке 7 составили:
Доверительный интервал для коэффициента регрессии определяется как
Для коэффициента регрессии b 95%-ные границы как показано на рисунке 7 составили:
Анализ верхней и нижней границ доверительных интервалов приводит к выводу о том, что с вероятностью 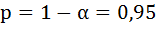
7. Полученные оценки уравнения регрессии позволяют использовать его для прогноза. Если прогнозное значение прожиточного минимума составит:
Тогда прогнозное значение прожиточного минимума составит:
Ошибку прогноза рассчитаем по формуле:
где
Дисперсию посчитаем также с помощью ППП Excel. Для этого:
1) Активизируйте Мастер функций: в главном меню выберете Формулы / Вставить функцию.
2) В окне Категория выберете Статистические, в окне функция – ДИСП.Г. Щёлкните по кнопке ОК.
3) Заполните диапазон, содержащий числовые данные факторного признака. Нажмите ОК.
Рисунок 10 Расчёт дисперсии
Получили значение дисперсии
Для подсчёта остаточной дисперсии на одну степень свободы воспользуемся результатами дисперсионного анализа как показано на Рисунке 7.
Доверительные интервалы прогноза индивидуальных значений у при 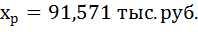
Интервал достаточно широк, прежде всего, за счёт малого объёма наблюдений. В целом выполненный прогноз среднемесячной заработной платы оказался надёжным.
Условие задачи взято из: Практикум по эконометрике: Учеб. пособие / И.И. Елисеева, С.В. Курышева, Н.М. Гордеенко и др.; Под ред. И.И. Елисеевой. – М.: Финансы и статистика, 2003. – 192 с.: ил.
Средняя ошибка аппроксимации
Фактические
значения результативного признака
отличаются от теоретических, рассчитанных
по уравнению регрессии. Чем меньше эти
отличия, тем ближе теоретические значения
к эмпирическим данным, тем лучше качество
модели. Величина отклонений фактических
и расчетных значений результативного
признака каждому наблюдению представляет
собой ошибку аппроксимации. В отдельных
случаях ошибка аппроксимации может
оказаться равной нулю. Отклонения (y
–
)
несравнимы между собой, исключая
величину, равную нулю. Так, если для
одного наблюдения y
–
= 5, а для другого – 10, то это не означает,
что во втором случае модель дает вдвое
худший результат. Для сравнения
используются величины отклонений,
выраженные в процентах к фактическим
значениям. Например, если для первого
наблюдения y
= 20, а для второго y
= 50, ошибка аппроксимации составит 25 %
для первого наблюдения и 20 % – для
второго.
Поскольку
(y
–
)
может быть величиной как положительной,
так и отрицательной, ошибки аппроксимации
для каждого наблюдения принято определять
в процентах по модулю.
Отклонения
(y
–
)
можно рассматривать как абсолютную
ошибку аппроксимации, а
– как
относительную ошибку аппроксимации.
Для того, чтобы иметь общее суждение о
качестве модели из относительных
отклонений по каждому наблюдению,
находят среднюю ошибку аппроксимации
как среднюю арифметическую простую
. (2.38)
По
нашим данным представим расчет средней
ошибки аппроксимации для уравнения Y
= 6,136
Х0,474
в следующей таблице.
Таблица.
Расчет средней ошибки аппроксимации
|
y |
yx |
y |
|
|
6 |
6,135947 |
-0,135946847 |
0,022658 |
|
9 |
8,524199 |
0,475801308 |
0,052867 |
|
10 |
10,33165 |
-0,331653106 |
0,033165 |
|
12 |
11,84201 |
0,157986835 |
0,013166 |
|
13 |
13,164 |
-0,163999272 |
0,012615 |
|
Итого |
0,134471 |
A
= (0,1345 / 5)
100 = 2,69 %, что говорит о хорошем качестве
уравнения регрессии, ибо ошибка
аппроксимации в пределах 5-7 % свидетельствует
о хорошем подборе модели к исходным
данным.
Возможно
и другое определение средней ошибки
аппроксимации:
(2.39)
Для
нашего примера эта величина составит:
.
Для
расчета средней ошибки аппроксимации
в стандартных программах чаще используется
формула (2.39).
Аналогично
определяется средняя ошибка аппроксимации
и для уравнения параболы.
№11
Факторы,
включаемые во множественную регрессию,
должны отвечать следующим требованиям:
1)
быть количественно измеримы. Если
необходимо включить в модель качественный
фактор, не имеющий количественного
измерения, то нужно придать ему
количественную определенность (например,
в модели урожайности качество почвы
задается в виде баллов; в модели стоимости
объектов недвижимости учитывается
место нахождения недвижимости: районы
могут быть проранжированы);
2)
не должны быть коррелированны между
собой и тем более находиться в точной
функциональной связи.
Включение
в модель факторов с высокой интеркорреляцией,
когда ryx1
< rx1x2,
для зависимости y
= a
+ b1
x1
+ b2
x2
+ ,
может привести к нежелательным
последствиям – система нормальных
уравнений может оказаться плохо
обусловленной и повлечь за собой
неустойчивость и ненадежность оценок
коэффициентов регрессии.
Если
между факторами существует высокая
корреляция, то нельзя определить их
изолированное влияние на результативный
показатель, и параметры уравнения
регрессии оказываются неинтерпретируемыми.
Так, в уравнении y
= a
+ b1
x1
+ b2
x2
+ ,
предполагается, что факторы x1
и x2
независимы друг от друга, т.е. rx1x2
= 0. Тогда можно говорить, что параметр
b1
измеряет силу влияния фактора x1
на результат y
при неизменном значении фактора x2.
Если же rx1x2
= 1, то с изменением фактора x1
фактор x2
не может оставаться неизменным. Отсюда
b1
и b2
нельзя интерпретировать как показатели
раздельного влияния x1
и x2
на y.
Пример
3.2. При
изучении зависимости y
= f(x,
z,
v)
матрица парных коэффициентов корреляции
оказалась следующей:
|
y |
x |
z |
v |
|
|
y |
1 |
|||
|
x |
0,8 |
1 |
||
|
z |
0,7 |
0,8 |
1 |
|
|
v |
0,6 |
0,5 |
0,2 |
1 |
Очевидно,
что факторы x
и z
дублируют друг друга. В анализ целесообразно
включить фактор z,
а не x,
так как корреляция z,
с результатом y
слабее, чем корреляция фактора x
с y
(ryz
< ryx),
но зато слабее межфакторная корреляция
rzv
< rxv.
Поэтому в данном случае в уравнение
множественной регрессии включаются
факторы z,
и v.
По
величине парных коэффициентов корреляции
обнаруживается лишь явная коллинеарность
факторов. Наибольшие трудности в
использовании аппарата множественной
регрессии возникают при наличии
мультиколлинеарности
факторов, когда более чем два фактора
связаны между собой линейной зависимостью,
т.е. имеет место совокупное воздействие
факторов друг на друга. Наличие
мультиколлинеарности факторов может
означать, что некоторые факторы всегда
будут действовать в унисон. В результате
вариация в исходных данных перестает
быть полностью независимой и нельзя
оценить воздействие каждого фактора в
отдельности. Чем сильнее мультиколлинеарность
факторов, тем менее надежна оценка
распределения суммы объясненной вариации
по отдельным факторам с помощью метода
наименьших квадратов.
Если
рассматривается регрессия y
= a
+ b
x
+ c
z
+ d
v
+ ,
то для расчета параметров с применением
МНК предполагается равенство
S2y
= S2факт
+ S2,
где
S2y
– общая сумма квадратов отклонений
;
S2факт
– факторная (объясненная) сумма квадратов
отклонений
;
S2
– остаточная сумма квадратов отклонений
.
В
свою очередь, при независимости факторов
друг от друга выполнимо равенство
S2факт
= S2x
+ S2z
+ S2v,
где
S2x,
S2z,
S2v
– суммы квадратов отклонений, обусловленные
влиянием соответствующих факторов.
Если
же факторы интеркоррелированы, то данное
равенство нарушается.
Включение
в модель мультиколлинеарных факторов
нежелательно по следующим причинам:
– затрудняется
интерпретация параметров множественной
регрессии как характеристик действия
факторов в «чистом» виде, ибо факторы
коррелированны; параметры линейной
регрессии теряют экономический смысл;
– оценки
параметров ненадежны, обнаруживают
большие стандартные ошибки и меняются
с изменением объема наблюдений (не
только по величина, но и по знаку), что
делает модель непригодной для анализа
и прогнозирования.
Для
оценки факторов может использоваться
определитель матрицы
парных коэффициентов корреляции между
факторами.
Если
бы факторы не коррелировали между собой,
то матрицы парных коэффициентов
корреляции между ними была бы единичной,
поскольку все недиагональные элементы
rxixj
(xi
xj)
были бы равны нулю. Так, для уравнения,
включающего три объясняющих переменных,
y
= a
+ b1
x1
+ b2
x2
+ b3
x3
+ ,
матрица
коэффициентов корреляции между факторами
имела бы определитель, равный единице
,
поскольку
rx1x1
= rx2x2
= rx3x3
= 1 и rx1x2
= rx1x3
= rx2x3
= 0.
Если
же между факторами существует полная
линейная зависимость и все коэффициенты
корреляции равны единице, то определитель
такой матрицы равен нулю
.
Чем
ближе к нулю определитель матрицы
межфакторной корреляции, тем сильнее
мультиколлинеарность факторов и
ненадежнее результаты множественной
регрессии. И, наоборот, чем ближе к
единице определитель матрицы межфакторной
корреляции, тем меньше мультиколлинеарность
факторов.
Оценка
значимости мультиколлинеарности
факторов может быть проведена методом
испытания гипотезы о независимости
переменных H0:
DetR
= 1. Доказано, что величина
имеет приближенное распределение 2
с df
= m
(m
– 1)/2 степенями
свободы. Если фактическое значение 2
превосходит табличное (критическое):
2факт
> 2табл(df,)
то гипотеза H0
отклоняется. Это означает, что DetR
1, недиагональные ненулевые коэффициенты
корреляции указывают на коллинеарность
факторов. Мультиколлинеарность считается
доказанной.
Через
коэффициенты множественной детерминации
можно найти переменные, ответственные
за мультиколлинеарность факторов. Для
этого в качестве зависимой переменной
рассматривается каждый из факторов.
Чем ближе значение коэффициента
множественной детерминации к единице,
тем сильна проявляется мультиколлинеарность
факторов. Сравнивая между собой
коэффициенты множественной детерминации
факторов
R2x1x2x3…xp;
R2x2x1x3…xp
и т.п., можно выделить переменные,
ответственные за мультиколлинеарность,
следовательно, можно решать проблему
отбора факторов, оставляя в уравнении
факторы с минимальной величиной
коэффициента множественной детерминации.
Имеется
ряд подходов преодоления сильной
межфакторной корреляции. Самый простой
из них состоит в исключении из модели
одного или нескольких факторов. Другой
путь связан с преобразованием факторов,
при котором уменьшается корреляция
между ними. Например, при построении
модели на основе рядов динамики переходят
от первоначальных данных к первым
разностям уровней y
= yt
– yt–1,
чтобы исключить влияние тенденции, или
используются такие методы, которые
сводят к нулю межфакторную корреляцию,
т.е. переходят от исходных переменных
к их линейным комбинациям, не коррелированным
друг с другом (метод главных компонент).
Одним
из путей учета внутренней корреляции
факторов является переход к совмещенным
уравнениям регрессии, т.е. к уравнениям,
которые отражают не только влияние
факторов, но и их взаимодействие. Так,
если y
= f(x1,
x2,
x3).
то можно построить следующее совмещенное
уравнение:
y
= a
+ b1
x1
+ b2
x2
+ b3
x3
+ b12
x1
x2
+ b13
x1
x3
+ b23
x2
x3
+ .
Рассматриваемое
уравнение включает эффект взаимодействия
первого порядка. Можно включать в модель
и взаимодействие более высоких порядков,
если будет доказана его статистическая
значимость, например включение
взаимодействия второго порядка b123
x1
x2
x3
и т.д. Как правила, взаимодействие
третьего и более высоких порядков
оказывается статистически незначимым;
совмещенные уравнения регрессии
ограничиваются взаимодействием первого
и второго порядков. Но и оно может
оказаться несущественным. Тогда
нецелесообразно включать в модель
взаимодействие всех факторов и всех
порядков. Так, если анализ совмещенного
уравнения показал значимость только
взаимодействия факторов x1и
x3,
то уравнение будет иметь вид:
y
= a
+ b1
x1
+ b2
x2
+ b3
x3
+ b13
x1
x3
+ .
Взаимодействие
факторов x1и
x3
означает, что на разных уровнях фактора
x3
влияние фактора x1на
y
будет неодинаково, т.е. оно зависит от
значений фактора x3.
На рис. 3.1 взаимодействие факторов
представляется непараллельными линиями
связи x1с
результатом y.
И, наоборот, параллельные линии влияния
фактора x1на
y
при разных уровнях фактора x3
означают отсутствие взаимодействия
факторов x1и
x3.
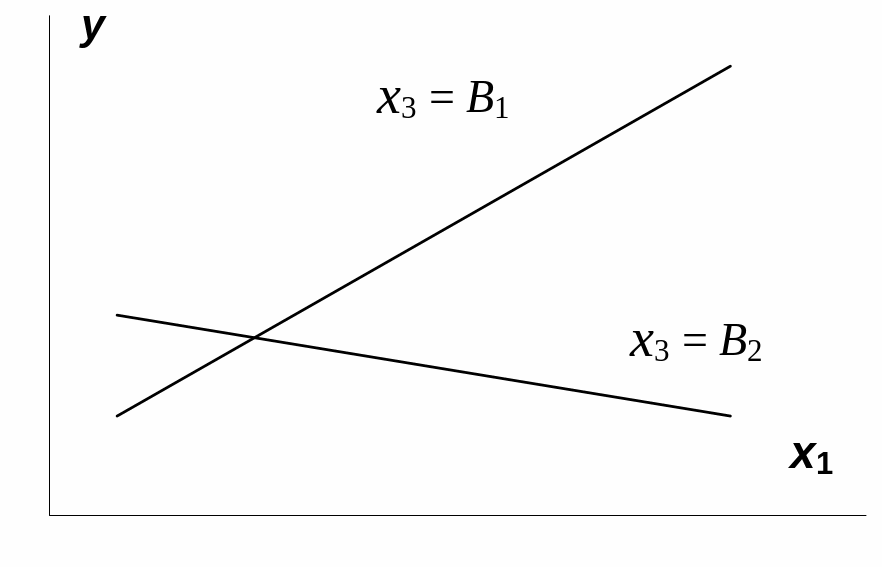
Рис.
3.1. Графическая иллюстрация взаимодействия
факторов
Совмещенные
уравнения регрессии строятся, например,
при исследовании эффекта влияния на
урожайность разных видов удобрений
(комбинаций азота и фосфора).
Решению
проблемы устранения мультиколлинеарности
факторов может помочь и переход к
уравнениям приведенной формы. С этой
целью в уравнение регрессии подставляют
рассматриваемый фактор, выраженный из
другого уравнения.
Пусть,
например, рассматривается двухфакторная
регрессия вида yx
= a
+ b1
x1
+ b2
x2,
для которой факторы x1и
x2
обнаруживают высокую корреляцию. Если
исключить один из факторов, то мы придем
к уравнению парной регрессии. Вместе с
тем можно оставить факторы в модели, но
исследовать данное двухфакторное
уравнение регрессии совместно с другим
уравнением, в котором фактор (например,
x2)
рассматривается как зависимая переменная.
Предположим, что x2
= A
+ B
y
+ C
x3.
Подставив это уравнение в искомое вместо
x2,
получим:
yx
= a
+ b1
x1
+ b2
(A
+ B
y
+ C
x3)
или
yx
(1 – b2
B)
= (a
+ b2
A)
+ b1
x1
+ C
b2
x3.
Если
(1 – b2
B)
0, то, разделив обе части равенства на
(1 – b2
B),
получим уравнение вида
,
которое
принято называть приведенной формой
уравнения для определения результативного
признака y.
Это уравнение может быть представлено
в виде
yx
= a’
+ b’1
x1
+ b’3
x3.
К
нему для оценки параметров может быть
применен метод наименьших квадратов.
Отбор
факторов, включаемых в регрессию,
является одним из важнейших этапов
практического использования методов
регрессии. Подходы к отбору факторов
на основе показателей корреляции могут
быть разные. Они приводят построение
уравнения множественной регрессии
соответственно к разным методикам. В
зависимости от того, какая методика
построения уравнения регрессии принята,
меняется алгоритм её решения на
компьютере.
Наиболее
широкое применение получили следующие
методы построения уравнения множественной
регрессии:
– метод
исключения;
– метод
включения;
– шаговый
регрессионный анализ.
Каждый
из этих методов по-своему решает проблему
отбора факторов, давая в целом близкие
результаты – отсев факторов из полного
его набора (метод исключения), дополнительное
введение фактора (метод включения),
исключение ранее введенного фактора
(шаговый регрессионный анализ).
На
первый взгляд может показаться, что
матрица парных коэффициентов корреляции
играет главную роль в отборе факторов.
Вместе с тем вследствие взаимодействия
факторов парные коэффициенты корреляции
не могут в полной мере решать вопрос о
целесообразности включения в модель
того или иного фактора. Эту роль выполняют
показатели частной корреляции, оценивающие
в чистом виде тесноту связи фактора с
результатом. Матрица частных коэффициентов
корреляции наиболее широко используется
в процедуре отсева факторов. Отсев
факторов можно проводить и по t-критерию
Стьюдента для коэффициентов регрессии:
из уравнения исключаются факторы с
величиной t-критерия
меньше табличного. Так, например,
уравнение регрессии составило:
y
= 25 + 5x1
+ 3x2
+ 4x3
+ .
(4,0) (1,3) (6,0)
В
скобках приведены фактические значения
t-критерия
для соответствующих коэффициентов
регрессии, как правило, при t
< 2 коэффициент регрессии незначим и,
следовательно, рассматриваемый фактор
не должен присутствовать в регрессионной
модели. В данном случае – это фактор
x2.
При
отборе факторов рекомендуется пользоваться
следующим правилом: число включаемых
факторов обычно в 6-7 раз меньше объема
совокупности, по которой строится
регрессия. Если это соотношение нарушено,
то число степеней свободы остаточной
вариации очень мало. Это приводит к
тому, что параметры уравнения регрессии
оказываются статистически незначимыми,
а F-критерий
меньше табличного значения.
Соседние файлы в предмете [НЕСОРТИРОВАННОЕ]
- #
- #
- #
- #
- #
- #
- #
- #
- #
- #
- #
Средняя ошибка аппроксимации
Фактические
значения результативного признака
отличаются от теоретических, рассчитанных
по уравнению регрессии. Чем меньше эти
отличия, тем ближе теоретические значения
к эмпирическим данным, тем лучше качество
модели. Величина отклонений фактических
и расчетных значений результативного
признака каждому наблюдению представляет
собой ошибку аппроксимации. В отдельных
случаях ошибка аппроксимации может
оказаться равной нулю. Отклонения (y
–
)
несравнимы между собой, исключая
величину, равную нулю. Так, если для
одного наблюдения y
–
= 5, а для другого – 10, то это не означает,
что во втором случае модель дает вдвое
худший результат. Для сравнения
используются величины отклонений,
выраженные в процентах к фактическим
значениям. Например, если для первого
наблюдения y
= 20, а для второго y
= 50, ошибка аппроксимации составит 25 %
для первого наблюдения и 20 % – для
второго.
Поскольку
(y
–
)
может быть величиной как положительной,
так и отрицательной, ошибки аппроксимации
для каждого наблюдения принято определять
в процентах по модулю.
Отклонения
(y
–
)
можно рассматривать как абсолютную
ошибку аппроксимации, а
– как
относительную ошибку аппроксимации.
Для того, чтобы иметь общее суждение о
качестве модели из относительных
отклонений по каждому наблюдению,
находят среднюю ошибку аппроксимации
как среднюю арифметическую простую
. (2.38)
По
нашим данным представим расчет средней
ошибки аппроксимации для уравнения Y
= 6,136
Х0,474
в следующей таблице.
Таблица.
Расчет средней ошибки аппроксимации
|
y |
yx |
y |
|
|
6 |
6,135947 |
-0,135946847 |
0,022658 |
|
9 |
8,524199 |
0,475801308 |
0,052867 |
|
10 |
10,33165 |
-0,331653106 |
0,033165 |
|
12 |
11,84201 |
0,157986835 |
0,013166 |
|
13 |
13,164 |
-0,163999272 |
0,012615 |
|
Итого |
0,134471 |
A
= (0,1345 / 5)
100 = 2,69 %, что говорит о хорошем качестве
уравнения регрессии, ибо ошибка
аппроксимации в пределах 5-7 % свидетельствует
о хорошем подборе модели к исходным
данным.
Возможно
и другое определение средней ошибки
аппроксимации:
(2.39)
Для
нашего примера эта величина составит:
.
Для
расчета средней ошибки аппроксимации
в стандартных программах чаще используется
формула (2.39).
Аналогично
определяется средняя ошибка аппроксимации
и для уравнения параболы.
№11
Факторы,
включаемые во множественную регрессию,
должны отвечать следующим требованиям:
1)
быть количественно измеримы. Если
необходимо включить в модель качественный
фактор, не имеющий количественного
измерения, то нужно придать ему
количественную определенность (например,
в модели урожайности качество почвы
задается в виде баллов; в модели стоимости
объектов недвижимости учитывается
место нахождения недвижимости: районы
могут быть проранжированы);
2)
не должны быть коррелированны между
собой и тем более находиться в точной
функциональной связи.
Включение
в модель факторов с высокой интеркорреляцией,
когда ryx1
< rx1x2,
для зависимости y
= a
+ b1
x1
+ b2
x2
+ ,
может привести к нежелательным
последствиям – система нормальных
уравнений может оказаться плохо
обусловленной и повлечь за собой
неустойчивость и ненадежность оценок
коэффициентов регрессии.
Если
между факторами существует высокая
корреляция, то нельзя определить их
изолированное влияние на результативный
показатель, и параметры уравнения
регрессии оказываются неинтерпретируемыми.
Так, в уравнении y
= a
+ b1
x1
+ b2
x2
+ ,
предполагается, что факторы x1
и x2
независимы друг от друга, т.е. rx1x2
= 0. Тогда можно говорить, что параметр
b1
измеряет силу влияния фактора x1
на результат y
при неизменном значении фактора x2.
Если же rx1x2
= 1, то с изменением фактора x1
фактор x2
не может оставаться неизменным. Отсюда
b1
и b2
нельзя интерпретировать как показатели
раздельного влияния x1
и x2
на y.
Пример
3.2. При
изучении зависимости y
= f(x,
z,
v)
матрица парных коэффициентов корреляции
оказалась следующей:
|
y |
x |
z |
v |
|
|
y |
1 |
|||
|
x |
0,8 |
1 |
||
|
z |
0,7 |
0,8 |
1 |
|
|
v |
0,6 |
0,5 |
0,2 |
1 |
Очевидно,
что факторы x
и z
дублируют друг друга. В анализ целесообразно
включить фактор z,
а не x,
так как корреляция z,
с результатом y
слабее, чем корреляция фактора x
с y
(ryz
< ryx),
но зато слабее межфакторная корреляция
rzv
< rxv.
Поэтому в данном случае в уравнение
множественной регрессии включаются
факторы z,
и v.
По
величине парных коэффициентов корреляции
обнаруживается лишь явная коллинеарность
факторов. Наибольшие трудности в
использовании аппарата множественной
регрессии возникают при наличии
мультиколлинеарности
факторов, когда более чем два фактора
связаны между собой линейной зависимостью,
т.е. имеет место совокупное воздействие
факторов друг на друга. Наличие
мультиколлинеарности факторов может
означать, что некоторые факторы всегда
будут действовать в унисон. В результате
вариация в исходных данных перестает
быть полностью независимой и нельзя
оценить воздействие каждого фактора в
отдельности. Чем сильнее мультиколлинеарность
факторов, тем менее надежна оценка
распределения суммы объясненной вариации
по отдельным факторам с помощью метода
наименьших квадратов.
Если
рассматривается регрессия y
= a
+ b
x
+ c
z
+ d
v
+ ,
то для расчета параметров с применением
МНК предполагается равенство
S2y
= S2факт
+ S2,
где
S2y
– общая сумма квадратов отклонений
;
S2факт
– факторная (объясненная) сумма квадратов
отклонений
;
S2
– остаточная сумма квадратов отклонений
.
В
свою очередь, при независимости факторов
друг от друга выполнимо равенство
S2факт
= S2x
+ S2z
+ S2v,
где
S2x,
S2z,
S2v
– суммы квадратов отклонений, обусловленные
влиянием соответствующих факторов.
Если
же факторы интеркоррелированы, то данное
равенство нарушается.
Включение
в модель мультиколлинеарных факторов
нежелательно по следующим причинам:
– затрудняется
интерпретация параметров множественной
регрессии как характеристик действия
факторов в «чистом» виде, ибо факторы
коррелированны; параметры линейной
регрессии теряют экономический смысл;
– оценки
параметров ненадежны, обнаруживают
большие стандартные ошибки и меняются
с изменением объема наблюдений (не
только по величина, но и по знаку), что
делает модель непригодной для анализа
и прогнозирования.
Для
оценки факторов может использоваться
определитель матрицы
парных коэффициентов корреляции между
факторами.
Если
бы факторы не коррелировали между собой,
то матрицы парных коэффициентов
корреляции между ними была бы единичной,
поскольку все недиагональные элементы
rxixj
(xi
xj)
были бы равны нулю. Так, для уравнения,
включающего три объясняющих переменных,
y
= a
+ b1
x1
+ b2
x2
+ b3
x3
+ ,
матрица
коэффициентов корреляции между факторами
имела бы определитель, равный единице
,
поскольку
rx1x1
= rx2x2
= rx3x3
= 1 и rx1x2
= rx1x3
= rx2x3
= 0.
Если
же между факторами существует полная
линейная зависимость и все коэффициенты
корреляции равны единице, то определитель
такой матрицы равен нулю
.
Чем
ближе к нулю определитель матрицы
межфакторной корреляции, тем сильнее
мультиколлинеарность факторов и
ненадежнее результаты множественной
регрессии. И, наоборот, чем ближе к
единице определитель матрицы межфакторной
корреляции, тем меньше мультиколлинеарность
факторов.
Оценка
значимости мультиколлинеарности
факторов может быть проведена методом
испытания гипотезы о независимости
переменных H0:
DetR
= 1. Доказано, что величина
имеет приближенное распределение 2
с df
= m
(m
– 1)/2 степенями
свободы. Если фактическое значение 2
превосходит табличное (критическое):
2факт
> 2табл(df,)
то гипотеза H0
отклоняется. Это означает, что DetR
1, недиагональные ненулевые коэффициенты
корреляции указывают на коллинеарность
факторов. Мультиколлинеарность считается
доказанной.
Через
коэффициенты множественной детерминации
можно найти переменные, ответственные
за мультиколлинеарность факторов. Для
этого в качестве зависимой переменной
рассматривается каждый из факторов.
Чем ближе значение коэффициента
множественной детерминации к единице,
тем сильна проявляется мультиколлинеарность
факторов. Сравнивая между собой
коэффициенты множественной детерминации
факторов
R2x1x2x3…xp;
R2x2x1x3…xp
и т.п., можно выделить переменные,
ответственные за мультиколлинеарность,
следовательно, можно решать проблему
отбора факторов, оставляя в уравнении
факторы с минимальной величиной
коэффициента множественной детерминации.
Имеется
ряд подходов преодоления сильной
межфакторной корреляции. Самый простой
из них состоит в исключении из модели
одного или нескольких факторов. Другой
путь связан с преобразованием факторов,
при котором уменьшается корреляция
между ними. Например, при построении
модели на основе рядов динамики переходят
от первоначальных данных к первым
разностям уровней y
= yt
– yt–1,
чтобы исключить влияние тенденции, или
используются такие методы, которые
сводят к нулю межфакторную корреляцию,
т.е. переходят от исходных переменных
к их линейным комбинациям, не коррелированным
друг с другом (метод главных компонент).
Одним
из путей учета внутренней корреляции
факторов является переход к совмещенным
уравнениям регрессии, т.е. к уравнениям,
которые отражают не только влияние
факторов, но и их взаимодействие. Так,
если y
= f(x1,
x2,
x3).
то можно построить следующее совмещенное
уравнение:
y
= a
+ b1
x1
+ b2
x2
+ b3
x3
+ b12
x1
x2
+ b13
x1
x3
+ b23
x2
x3
+ .
Рассматриваемое
уравнение включает эффект взаимодействия
первого порядка. Можно включать в модель
и взаимодействие более высоких порядков,
если будет доказана его статистическая
значимость, например включение
взаимодействия второго порядка b123
x1
x2
x3
и т.д. Как правила, взаимодействие
третьего и более высоких порядков
оказывается статистически незначимым;
совмещенные уравнения регрессии
ограничиваются взаимодействием первого
и второго порядков. Но и оно может
оказаться несущественным. Тогда
нецелесообразно включать в модель
взаимодействие всех факторов и всех
порядков. Так, если анализ совмещенного
уравнения показал значимость только
взаимодействия факторов x1и
x3,
то уравнение будет иметь вид:
y
= a
+ b1
x1
+ b2
x2
+ b3
x3
+ b13
x1
x3
+ .
Взаимодействие
факторов x1и
x3
означает, что на разных уровнях фактора
x3
влияние фактора x1на
y
будет неодинаково, т.е. оно зависит от
значений фактора x3.
На рис. 3.1 взаимодействие факторов
представляется непараллельными линиями
связи x1с
результатом y.
И, наоборот, параллельные линии влияния
фактора x1на
y
при разных уровнях фактора x3
означают отсутствие взаимодействия
факторов x1и
x3.

Рис.
3.1. Графическая иллюстрация взаимодействия
факторов
Совмещенные
уравнения регрессии строятся, например,
при исследовании эффекта влияния на
урожайность разных видов удобрений
(комбинаций азота и фосфора).
Решению
проблемы устранения мультиколлинеарности
факторов может помочь и переход к
уравнениям приведенной формы. С этой
целью в уравнение регрессии подставляют
рассматриваемый фактор, выраженный из
другого уравнения.
Пусть,
например, рассматривается двухфакторная
регрессия вида yx
= a
+ b1
x1
+ b2
x2,
для которой факторы x1и
x2
обнаруживают высокую корреляцию. Если
исключить один из факторов, то мы придем
к уравнению парной регрессии. Вместе с
тем можно оставить факторы в модели, но
исследовать данное двухфакторное
уравнение регрессии совместно с другим
уравнением, в котором фактор (например,
x2)
рассматривается как зависимая переменная.
Предположим, что x2
= A
+ B
y
+ C
x3.
Подставив это уравнение в искомое вместо
x2,
получим:
yx
= a
+ b1
x1
+ b2
(A
+ B
y
+ C
x3)
или
yx
(1 – b2
B)
= (a
+ b2
A)
+ b1
x1
+ C
b2
x3.
Если
(1 – b2
B)
0, то, разделив обе части равенства на
(1 – b2
B),
получим уравнение вида
,
которое
принято называть приведенной формой
уравнения для определения результативного
признака y.
Это уравнение может быть представлено
в виде
yx
= a’
+ b’1
x1
+ b’3
x3.
К
нему для оценки параметров может быть
применен метод наименьших квадратов.
Отбор
факторов, включаемых в регрессию,
является одним из важнейших этапов
практического использования методов
регрессии. Подходы к отбору факторов
на основе показателей корреляции могут
быть разные. Они приводят построение
уравнения множественной регрессии
соответственно к разным методикам. В
зависимости от того, какая методика
построения уравнения регрессии принята,
меняется алгоритм её решения на
компьютере.
Наиболее
широкое применение получили следующие
методы построения уравнения множественной
регрессии:
– метод
исключения;
– метод
включения;
– шаговый
регрессионный анализ.
Каждый
из этих методов по-своему решает проблему
отбора факторов, давая в целом близкие
результаты – отсев факторов из полного
его набора (метод исключения), дополнительное
введение фактора (метод включения),
исключение ранее введенного фактора
(шаговый регрессионный анализ).
На
первый взгляд может показаться, что
матрица парных коэффициентов корреляции
играет главную роль в отборе факторов.
Вместе с тем вследствие взаимодействия
факторов парные коэффициенты корреляции
не могут в полной мере решать вопрос о
целесообразности включения в модель
того или иного фактора. Эту роль выполняют
показатели частной корреляции, оценивающие
в чистом виде тесноту связи фактора с
результатом. Матрица частных коэффициентов
корреляции наиболее широко используется
в процедуре отсева факторов. Отсев
факторов можно проводить и по t-критерию
Стьюдента для коэффициентов регрессии:
из уравнения исключаются факторы с
величиной t-критерия
меньше табличного. Так, например,
уравнение регрессии составило:
y
= 25 + 5x1
+ 3x2
+ 4x3
+ .
(4,0) (1,3) (6,0)
В
скобках приведены фактические значения
t-критерия
для соответствующих коэффициентов
регрессии, как правило, при t
< 2 коэффициент регрессии незначим и,
следовательно, рассматриваемый фактор
не должен присутствовать в регрессионной
модели. В данном случае – это фактор
x2.
При
отборе факторов рекомендуется пользоваться
следующим правилом: число включаемых
факторов обычно в 6-7 раз меньше объема
совокупности, по которой строится
регрессия. Если это соотношение нарушено,
то число степеней свободы остаточной
вариации очень мало. Это приводит к
тому, что параметры уравнения регрессии
оказываются статистически незначимыми,
а F-критерий
меньше табличного значения.
Соседние файлы в предмете [НЕСОРТИРОВАННОЕ]
- #
- #
- #
- #
- #
- #
- #
- #
- #
- #
- #
По территориям региона приводятся данные за 200Х г.
| Номер региона | Среднедушевой прожиточный минимум в день одного трудоспособного, руб., х | Среднедневная заработная плата, руб., у |
|---|---|---|
| 1 | 78 | 133 |
| 2 | 82 | 148 |
| 3 | 87 | 134 |
| 4 | 79 | 154 |
| 5 | 89 | 162 |
| 6 | 106 | 195 |
| 7 | 67 | 139 |
| 8 | 88 | 158 |
| 9 | 73 | 152 |
| 10 | 87 | 162 |
| 11 | 76 | 159 |
| 12 | 115 | 173 |
Задание:
1. Постройте поле корреляции и сформулируйте гипотезу о форме связи.
2. Рассчитайте параметры уравнения линейной регрессии

3. Оцените тесноту связи с помощью показателей корреляции и детерминации.
4. Дайте с помощью среднего (общего) коэффициента эластичности сравнительную оценку силы связи фактора с результатом.
5. Оцените с помощью средней ошибки аппроксимации качество уравнений.
6. Оцените с помощью F-критерия Фишера статистическую надёжность результатов регрессионного моделирования.
7. Рассчитайте прогнозное значение результата, если прогнозное значение фактора увеличится на 10% от его среднего уровня. Определите доверительный интервал прогноза для уровня значимости 
8. Оцените полученные результаты, выводы оформите в аналитической записке.
Решение:
Решим данную задачу с помощью Excel.
1. Сопоставив имеющиеся данные х и у, например, ранжировав их в порядке возрастания фактора х, можно наблюдать наличие прямой зависимости между признаками, когда увеличение среднедушевого прожиточного минимума увеличивает среднедневную заработную плату. Исходя из этого, можно сделать предположение, что связь между признаками прямая и её можно описать уравнением прямой. Этот же вывод подтверждается и на основе графического анализа.
Чтобы построить поле корреляции можно воспользоваться ППП Excel. Введите исходные данные в последовательности: сначала х, затем у.
Выделите область ячеек, содержащую данные.
Затем выберете: Вставка / Точечная диаграмма / Точечная с маркерами как показано на рисунке 1.
Рисунок 1 Построение поля корреляции
Анализ поля корреляции показывает наличие близкой к прямолинейной зависимости, так как точки расположены практически по прямой линии.
2. Для расчёта параметров уравнения линейной регрессии
воспользуемся встроенной статистической функцией ЛИНЕЙН.
Для этого:
1) Откройте существующий файл, содержащий анализируемые данные;
2) Выделите область пустых ячеек 5×2 (5 строк, 2 столбца) для вывода результатов регрессионной статистики.
3) Активизируйте Мастер функций: в главном меню выберете Формулы / Вставить функцию.
4) В окне Категория выберете Статистические, в окне функция – ЛИНЕЙН. Щёлкните по кнопке ОК как показано на Рисунке 2;
Рисунок 2 Диалоговое окно «Мастер функций»
5) Заполните аргументы функции:
Известные значения у – диапазон, содержащий данные результативного признака;
Известные значения х – диапазон, содержащий данные факторного признака;
Константа – логическое значение, которое указывает на наличие или на отсутствие свободного члена в уравнении; если Константа = 1, то свободный член рассчитывается обычным образом, если Константа = 0, то свободный член равен 0;
Статистика – логическое значение, которое указывает, выводить дополнительную информацию по регрессионному анализу или нет. Если Статистика = 1, то дополнительная информация выводится, если Статистика = 0, то выводятся только оценки параметров уравнения.
Щёлкните по кнопке ОК;
Рисунок 3 Диалоговое окно аргументов функции ЛИНЕЙН
6) В левой верхней ячейке выделенной области появится первый элемент итоговой таблицы. Чтобы раскрыть всю таблицу, нажмите на клавишу <F2>, а затем на комбинацию клавиш <Ctrl>+<Shift>+<Enter>.
Дополнительная регрессионная статистика будет выводиться в порядке, указанном в следующей схеме:
| Значение коэффициента b | Значение коэффициента a |
| Стандартная ошибка b | Стандартная ошибка a |
| Коэффициент детерминации R2 | Стандартная ошибка y |
| F-статистика | Число степеней свободы df |
| Регрессионная сумма квадратов
|
Остаточная сумма квадратов
|
Рисунок 4 Результат вычисления функции ЛИНЕЙН
Получили уровнение регрессии:
Делаем вывод: С увеличением среднедушевого прожиточного минимума на 1 руб. среднедневная заработная плата возрастает в среднем на 0,92 руб.
3. Коэффициент детерминации 
По вычисленному коэффициенту детерминации 
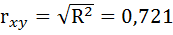
Связь оценивается как тесная.
4. С помощью среднего (общего) коэффициента эластичности определим силу влияния фактора на результат.
Для уравнения прямой 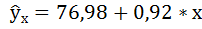
Средние значения найдём, выделив область ячеек со значениями х, и выберем Формулы / Автосумма / Среднее, и то же самое произведём со значениями у.
Рисунок 5 Расчёт средних значений функции и аргумент
Таким образом, при изменении среднедушевого прожиточного минимума на 1% от своего среднего значения среднедневная заработная плата изменится в среднем на 0,51%.
С помощью инструмента анализа данных Регрессия можно получить:
— результаты регрессионной статистики,
— результаты дисперсионного анализа,
— результаты доверительных интервалов,
— остатки и графики подбора линии регрессии,
— остатки и нормальную вероятность.
Порядок действий следующий:
1) проверьте доступ к Пакету анализа. В главном меню последовательно выберите: Файл/Параметры/Надстройки.
2) В раскрывающемся списке Управление выберите пункт Надстройки Excel и нажмите кнопку Перейти.
3) В окне Надстройки установите флажок Пакет анализа, а затем нажмите кнопку ОК.
• Если Пакет анализа отсутствует в списке поля Доступные надстройки, нажмите кнопку Обзор, чтобы выполнить поиск.
• Если выводится сообщение о том, что пакет анализа не установлен на компьютере, нажмите кнопку Да, чтобы установить его.
4) В главном меню последовательно выберите: Данные / Анализ данных / Инструменты анализа / Регрессия, а затем нажмите кнопку ОК.
5) Заполните диалоговое окно ввода данных и параметров вывода:
Входной интервал Y – диапазон, содержащий данные результативного признака;
Входной интервал X – диапазон, содержащий данные факторного признака;
Метки – флажок, который указывает, содержит ли первая строка названия столбцов или нет;
Константа – ноль – флажок, указывающий на наличие или отсутствие свободного члена в уравнении;
Выходной интервал – достаточно указать левую верхнюю ячейку будущего диапазона;
6) Новый рабочий лист – можно задать произвольное имя нового листа.
Затем нажмите кнопку ОК.
Рисунок 6 Диалоговое окно ввода параметров инструмента Регрессия
Результаты регрессионного анализа для данных задачи представлены на рисунке 7.
Рисунок 7 Результат применения инструмента регрессия
5. Оценим с помощью средней ошибки аппроксимации качество уравнений. Воспользуемся результатами регрессионного анализа представленного на Рисунке 8.
Рисунок 8 Результат применения инструмента регрессия «Вывод остатка»
Составим новую таблицу как показано на рисунке 9. В графе С рассчитаем относительную ошибку аппроксимации по формуле:
Рисунок 9 Расчёт средней ошибки аппроксимации
Средняя ошибка аппроксимации рассчитывается по формуле:
Качество построенной модели оценивается как хорошее, так как 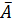
6. Из таблицы с регрессионной статистикой (Рисунок 4) выпишем фактическое значение F-критерия Фишера:
Поскольку 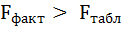
8. Оценку статистической значимости параметров регрессии проведём с помощью t-статистики Стьюдента и путём расчёта доверительного интервала каждого из показателей.
Выдвигаем гипотезу Н0 о статистически незначимом отличии показателей от нуля:
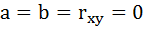
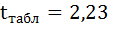
На рисунке 7 имеются фактические значения t-статистики:
t-критерий для коэффициента корреляции можно рассчитать двумя способами:
I способ: 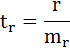
где 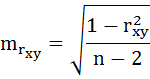
Данные для расчёта возьмём из таблицы на Рисунке 7.
II способ:
Фактические значения t-статистики превосходят табличные значения:
Поэтому гипотеза Н0 отклоняется, то есть параметры регрессии и коэффициент корреляции не случайно отличаются от нуля, а статистически значимы.
Доверительный интервал для параметра a определяется как
Для параметра a 95%-ные границы как показано на рисунке 7 составили:
Доверительный интервал для коэффициента регрессии определяется как
Для коэффициента регрессии b 95%-ные границы как показано на рисунке 7 составили:
Анализ верхней и нижней границ доверительных интервалов приводит к выводу о том, что с вероятностью 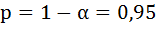
7. Полученные оценки уравнения регрессии позволяют использовать его для прогноза. Если прогнозное значение прожиточного минимума составит:
Тогда прогнозное значение прожиточного минимума составит:
Ошибку прогноза рассчитаем по формуле:
где
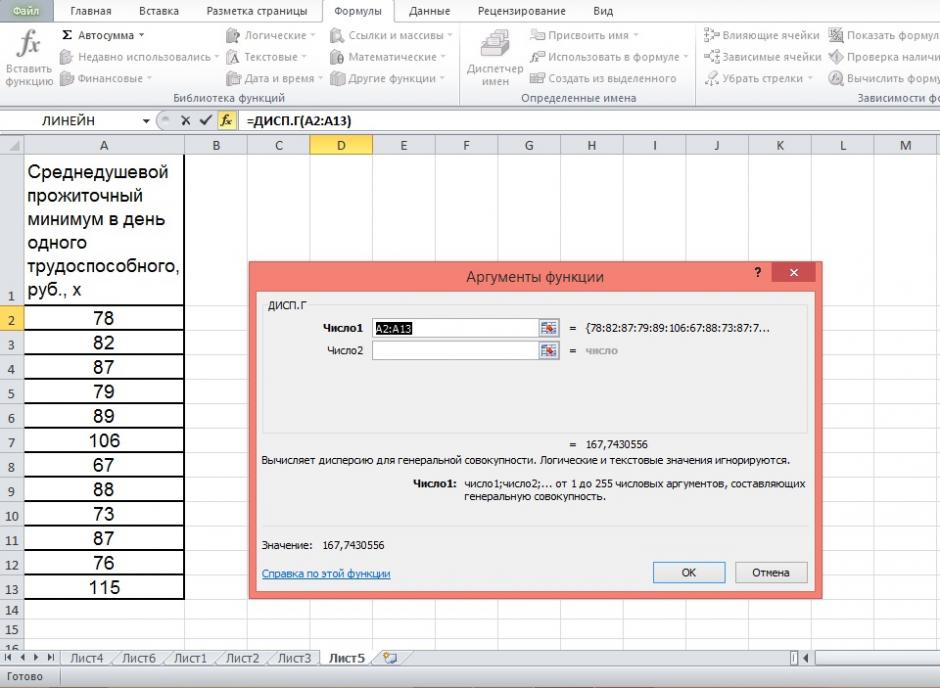
Дисперсию посчитаем также с помощью ППП Excel. Для этого:
1) Активизируйте Мастер функций: в главном меню выберете Формулы / Вставить функцию.
2) В окне Категория выберете Статистические, в окне функция – ДИСП.Г. Щёлкните по кнопке ОК.
3) Заполните диапазон, содержащий числовые данные факторного признака. Нажмите ОК.
Рисунок 10 Расчёт дисперсии
Получили значение дисперсии
Для подсчёта остаточной дисперсии на одну степень свободы воспользуемся результатами дисперсионного анализа как показано на Рисунке 7.
Доверительные интервалы прогноза индивидуальных значений у при 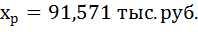
Интервал достаточно широк, прежде всего, за счёт малого объёма наблюдений. В целом выполненный прогноз среднемесячной заработной платы оказался надёжным.
Условие задачи взято из: Практикум по эконометрике: Учеб. пособие / И.И. Елисеева, С.В. Курышева, Н.М. Гордеенко и др.; Под ред. И.И. Елисеевой. – М.: Финансы и статистика, 2003. – 192 с.: ил.
Расчет доверительных интервалов и прогнозов для линейного уравнения регрессии
Как правило, в линейной регрессии обычно оценивается значимость не только уравнения в целом, но и отдельных его параметров.Показатели корреляционной связи, вычисленные по ограниченной совокупности (по выборке), являются лишь оценками той или иной статистической закономерности, поскольку в любом параметре сохраняется элемент не полностью погасившейся случайности, присущей индивидуальным значениям признаков. Поэтому необходима статистическая оценка степени точности и надежности параметров корреляции. Под надежностью здесь понимается вероятность того, что значение проверяемого параметра не равно нулю, не включает в себя величины противоположных знаков.
Вероятностная оценка параметров корреляции производится по общим правилам проверки статистических гипотез, разработанным математической статистикой, в частности путем сравнения оцениваемой величины со средней случайной ошибкой оценки. Для коэффициента парной регрессии b средняя ошибка оценки вычисляется как:
где Dост – остаточная дисперсия на одну степень свободы.
Для нашего примера величина стандартной ошибки коэффициента регрессии составила:
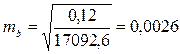
Для оценки того, насколько точные значения показателей могут отличаться от рассчитанных, осуществляется построение доверительных интервалов. Они определяют пределы, в которых лежат точные значения определяемых показателей с заданной степенью точности, соответствующей заданному уровню значимости α (α – вероятность отвергнуть правильную гипотезу при условии, что она верна, обычно принимается равной 0,05 или 0,01).
Для оценки статистической значимости коэффициента линейной регрессии и линейного коэффициента парной корреляции, а также для расчета доверительных интервалов b, применяется t – критерий Стьюдента.
Для оценки существенности коэффициента регрессии его величина сравнивается с его стандартной ошибкой, т.е. определяется фактическое значение t-критерия Стьюдента: 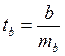
В рассматриваемом примере фактическое значение t-критерия для коэффициента регрессии составило:
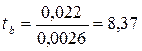
Этот же результат получим, извлекая квадратный корень из найденного F-критерия, т.е.
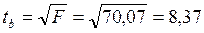
Действительно, справедливо равенство 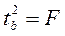
При 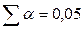
Для расчета доверительных интервалов для параметров a и b уравнения линейной регрессии определяем предельную ошибку ∆ для каждого показателя:
Формулы для расчета доверительных интервалов имеют вид:
Если границы интервала имеют разные знаки, т.е. в эти границы попадает ноль, то оцениваемый параметр принимается нулевым.
Доверительный интервал для коэффициента регрессии определяется как 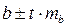
0,022 ± 2,16·0,0026 = 0,022 ± 0,0057, т.е.
Поскольку коэффициент регрессии в эконометрических исследованиях имеет четкую экономическую интерпретацию, то доверительные границы интервала для коэффициента регрессии не должны содержать противоречивых результатов, например, -10 ≤ b ≤ 40. Такого рода запись указывает, что истинное значение коэффициента регрессии одновременно содержит положительные и отрицательные величины и даже ноль, чего не может быть.
Стандартная ошибка параметра а определяется по формуле:
Процедура оценивания существенности данного параметра не отличается от рассмотренной выше для коэффициента регрессии; вычисляется t-критерий: 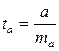
Значимость линейного коэффициента корреляции проверяется на основе величины ошибки коэффициента корреляции mr:
Фактическое значение t-критерия Стьюдента определяется как
Данная формула свидетельствует, что в парной линейной регрессии 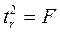
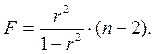
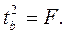
Таким образом, проверка гипотез о значимости коэффициентов регрессии и корреляции равносильна проверке гипотезы о существенности линейного уравнения регрессии.
В рассматриваемом примере tr совпало с tb. Величина tr =8,37 значительно превышает табличное значение 2,16 при а=0,05. Следовательно, коэффициент корреляции существенно отличен от нуля и зависимость является достоверной.
Прогноз, полученный подстановкой в уравнение регрессии ожидаемого значения фактора, называют точечным прогнозом. Вероятность точной реализации такого прогноза крайне мала. Необходимо сопроводить его значением средней ошибки прогноза или доверительным интервалом прогноза с достаточно большой вероятностью.
Точечный прогноз заключается в получении прогнозного значения yp, которое определяется путем подстановки в уравнение регрессии
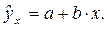
Интервальный прогноз заключается в построении доверительного интервала прогноза, т.е. верхней и нижней границы ypmin, ypmax интервала, содержащего точную величину для прогнозного значения 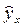
(ypmin 2 – индекс детерминации;
n – число наблюдений;
m – число параметров при переменных х.
Величина m характеризует число степеней свободы для факторной суммы квадратов, а (n – m — 1) – число степеней свободы для остаточной суммы квадратов.
Для степенной функции 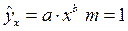
Для параболы второй степени y=a + b·x + c·x 2 + ε m=2 и 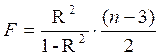
Для оценки качества построенной модели используется также средняя ошибка аппроксимации. Фактические значения результативного признака отличаются от теоретических, рассчитанных по уравнению регрессии, т.е. у и 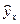
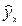
Поскольку (у— 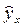
Чтобы иметь общее суждение о качестве модели из относительных отклонений по каждому наблюдению, определяют среднюю ошибку аппроксимации как среднюю арифметическую простую:
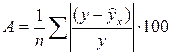
Для нашего примера представим расчет средней ошибки аппроксимации в таблице 4.
Пример нахождения доверительных интервалов коэффициентов регрессии
1. Постройте поле корреляции и сформулируйте гипотезу о форме связи.
2. Постройте уравнение зависимости экспорта нефти от цены на нефть.
3. Рассчитайте среднюю ошибку аппроксимации и коэффициент детерминации. Оценить статистическую значимость параметров регрессии и уравнения в целом.
4. Оцените полученные результаты, выводы оформите в аналитической записке.
Таблица 5
Цена нефти марки Urals (Россия), долл/барр.
Экспорт нефти и нефтепродуктов, млн.т.
Решение:
Уравнение имеет вид y = ax + b
1. Параметры уравнения регрессии.
Средние значения
Связь между признаком Y фактором X сильная и прямая
Уравнение регрессии
| x | y | x 2 | y 2 | x ∙ y | y(x) | (y- y ) 2 | (y-y(x)) 2 | (x-x p ) 2 |
| 119 | 298.12 | 14161 | 88875.53 | 35476.28 | 219.63 | 232120.8 | 6160.56 | 24362.01 |
| 203 | 481.03 | 41209 | 231389.86 | 97649.09 | 521.16 | 89328.76 | 1610.26 | 5196.01 |
| 281 | 539.12 | 78961 | 290650.37 | 151492.72 | 801.15 | 57979.42 | 68658.51 | 35.01 |
| 305 | 653.57 | 93025 | 427153.74 | 199338.85 | 887.3 | 15961.59 | 54628.94 | 895.01 |
| 381 | 987.66 | 145161 | 975472.28 | 376298.46 | 1160.11 | 43160.41 | 29738.57 | 11218.34 |
| 363 | 1252.85 | 131769 | 1569633.12 | 454784.55 | 1095.5 | 223673.03 | 24760.35 | 7729.34 |
| 389 | 1276.88 | 151321 | 1630422.53 | 496706.32 | 1188.83 | 246980.01 | 7753.57 | 12977.01 |
| 387 | 1396.70 | 149769 | 1950770.89 | 540522.9 | 1181.65 | 380430.93 | 46248.04 | 12525.34 |
| 315 | 952.03 | 99225 | 906361.12 | 299889.45 | 923.19 | 29625.58 | 831.49 | 1593.34 |
| 217 | 619.96 | 47089 | 384350.4 | 134531.32 | 571.41 | 25583.74 | 2356.85 | 3373.67 |
| 149 | 384.40 | 22201 | 147763.36 | 57275.6 | 327.32 | 156427.5 | 3258.23 | 15897.01 |
| 192 | 516.59 | 36864 | 266865.23 | 99185.28 | 481.67 | 69336.98 | 1219.24 | 6902.84 |
| 3301 | 9358.91 | 1010755 | 8869708.45 | 2943150.82 | 9358.91 | 1570608.75 | 247224.62 | 102704.92 |
По таблице Стьюдента находим Tтабл
Tтабл (n-m-1;a) = (10;0.05) = 1.812
Поскольку Tнабл > Tтабл , то отклоняем гипотезу о равенстве 0 коэффициента корреляции. Другими словами, коэффициента корреляции статистически — значим.
Анализ точности определения оценок коэффициентов регрессии
S a = 0.4906
Доверительные интервалы для зависимой переменной
Рассчитаем границы интервала, в котором будет сосредоточено 95% возможных значений Y при неограниченно большом числе наблюдений и X = 1
(-587.75;179.86)
Проверка гипотез относительно коэффициентов линейного уравнения регрессии
1) t-статистика
Статистическая значимость коэффициента регрессии a подтверждается (7.32>1.812)
Статистическая значимость коэффициента регрессии b не подтверждается (1.46 Fkp, то коэффициент детерминации статистически значим.
Доверительные интервалы для зависимой переменной
Уравнение тренда имеет вид y = at 2 + bt + c
1. Находим параметры уравнения методом наименьших квадратов.
Система уравнений
Для наших данных система уравнений имеет вид (см. таблицу).
Получаем a0 = -11.37, a1 = 88.47, a2 = 2151.09
Уравнение тренда: y = -11.37t 2 +88.47t+2151.09
Оценим качество уравнения тренда с помощью ошибки абсолютной аппроксимации.
Поскольку ошибка больше 15%, то данное уравнение не желательно использовать в качестве тренда
Средние значения
т.е. в 87.35 % случаев влияет на изменение данных. Другими словами — точность подбора уравнения тренда — высокая
| t | y | t 2 | y 2 | x ∙ y | y(t) | (y-y cp ) 2 | (y-y(t)) 2 | (t-t p ) 2 | (y-y(t)) : y | t 3 | t 4 | t 2 y |
| 1 | 2225.3 | 1 | 4951960.09 | 2225.3 | 2228.19 | 65.6099 | 8.352 | 16 | 6431.117 | 1 | 1 | 2225.3 |
| 2 | 2254.9 | 4 | 5084574.01 | 4509.8 | 2282.55 | 462.25 | 764.5225 | 9 | 62347.985 | 8 | 16 | 9019.6 |
| 3 | 2332.3 | 9 | 5439623.29 | 6996.9 | 2314.17 | 9781.21 | 328.6969 | 4 | 42284.599 | 27 | 81 | 20990.7 |
| 4 | 2365.8 | 16 | 5597009.64 | 9463.2 | 2323.05 | 17529.76 | 1827.5625 | 1 | 101137.95 | 64 | 256 | 37852.8 |
| 5 | 2295.4 | 25 | 5268861.16 | 11477 | 2309.19 | 3844 | 190.1641 | 0 | 31653.566 | 125 | 625 | 57385 |
| 6 | 2303.9 | 36 | 5307955.21 | 13823.4 | 2272.59 | 4970.25 | 980.3161 | 1 | 72135.109 | 216 | 1296 | 82940.4 |
| 7 | 2166.7 | 49 | 4694588.89 | 15166.9 | 2213.25 | 4448.89 | 2166.9025 | 4 | 100859.885 | 343 | 2401 | 106168.3 |
| 8 | 2080.4 | 64 | 4328064.16 | 16643.2 | 2131.17 | 23409 | 2577.5929 | 9 | 105621.908 | 512 | 4096 | 133145.6 |
| 9 | 2075.9 | 81 | 4309360.81 | 18683.1 | 2026.35 | 24806.25 | 2455.2025 | 16 | 102860.845 | 729 | 6561 | 168147.9 |
| 45 | 20100.6 | 285 | 44981997.26 | 98988.8 | 20100.51 | 89317.2199 | 11299.312 | 60 | 625332.964 | 4050 | 30666 | 1235751.2 |
2. Анализ точности определения оценок параметров уравнения тренда.
Анализ точности определения оценок параметров уравнения тренда
S a = 4.8518
Доверительные интервалы для зависимой переменной
По таблице Стьюдента находим Tтабл
Tтабл (n-m-1;a) = (7;0.05) = 1.895
Рассчитаем границы интервала, в котором будет сосредоточено 95% возможных значений Y при неограниченно большом числе наблюдений и t = 6
2151.09 + 88.47*6 + -11.37*62 — 1.895*39.911 ; 2151.09 + 88.47*6 + -11.37*62 — 1.895*39.911
(-55.3814;95.8814)
Интервальный прогноз.
Определим среднеквадратическую ошибку прогнозируемого показателя.
где L — период упреждения; уn+L — точечный прогноз по модели на (n + L)-й момент времени; n — количество наблюдений во временном ряду; Sy — стандартная ошибка прогнозируемого показателя; Tтабл — табличное значение критерия Стьюдента для уровня значимости а и для числа степеней свободы, равного n — 2.
Точечный прогноз, t = 10: y(10) = -11.37*10 2 + 88.47* + 2151.09 = 1898.79
K1 = 247.4924
1898.79 — 247.4924 = 1651.2976 ; 1898.79 + 247.4924 = 2146.2824
t = 10: (1651.2976;2146.2824)
Точечный прогноз, t = 11: y(11) = -11.37*11 2 + 88.47* + 2151.09 = 1748.49
K2 = 261.9213
1748.49 — 261.9213 = 1486.5687 ; 1748.49 + 261.9213 = 2010.4113
t = 11: (1486.5687;2010.4113)
Точечный прогноз, t = 12: y(12) = -11.37*12 2 + 88.47* + 2151.09 = 1575.45
K3 = 278.0099
1575.45 — 278.0099 = 1297.4401 ; 1575.45 + 278.0099 = 1853.4599
t = 12: (1297.4401;1853.4599)
Точечный прогноз, t = 13: y(13) = -11.37*13 2 + 88.47* + 2151.09 = 1379.67
K4 = 295.4871
1379.67 — 295.4871 = 1084.1829 ; 1379.67 + 295.4871 = 1675.1571
t = 13: (1084.1829;1675.1571)
Точечный прогноз, t = 14: y(14) = -11.37*14 2 + 88.47* + 2151.09 = 1161.15
K5 = 314.1213
1161.15 — 314.1213 = 847.0287 ; 1161.15 + 314.1213 = 1475.2713
t = 14: (847.0287;1475.2713)
3. Проверка гипотез относительно коэффициентов линейного уравнения тренда.
1) t-статистика. Критерий Стьюдента.
Статистическая значимость коэффициента уравнения подтверждается
Статистическая значимость коэффициента тренда подтверждается
Доверительный интервал для коэффициентов уравнения тренда
Определим доверительные интервалы коэффициентов тренда, которые с надежность 95% будут следующими (tтабл=1.895):
(a — tтабл·Sa; a + tтабл·Sa)
(-20.5642;-2.1758)
(b — t табл·Sb; b + tтаблS·b)
(36.7313;140.2087)
2) F-статистика. Критерий Фишера.
Fkp = 5.32
Поскольку F > Fkp, то коэффициент детерминации статистически значим
4. Тест Дарбина-Уотсона на наличие автокорреляции остатков для временного ряда.
| y | y(x) | e i = y-y(x) | e 2 | (e i — e i-1 ) 2 |
| 2225.3 | 2228.19 | -2.89 | 8.3521 | 0 |
| 2254.9 | 2282.55 | -27.65 | 764.5225 | 613.0576 |
| 2332.3 | 2314.17 | 18.13 | 328.6969 | 2095.8084 |
| 2365.8 | 2323.05 | 42.75 | 1827.5625 | 606.1444 |
| 2295.4 | 2309.19 | -13.79 | 190.1641 | 3196.7716 |
| 2303.9 | 2272.59 | 31.31 | 980.3161 | 2034.01 |
| 2166.7 | 2213.25 | -46.55 | 2166.9025 | 6062.1796 |
| 2080.4 | 2131.17 | -50.77 | 2577.5929 | 17.8084 |
| 2075.9 | 2026.35 | 49.55 | 2455.2025 | 10064.1024 |
| 11299.3121 | 24689.8824 |
Критические значения d1 и d2 определяются на основе специальных таблиц для требуемого уровня значимости a, числа наблюдений n и количества объясняющих переменных m.
Не обращаясь к таблицам, можно пользоваться приблизительным правилом и считать, что автокорреляция остатков отсутствует, если 1.5
Задача №3. Расчёт параметров регрессии и корреляции с помощью Excel
По территориям региона приводятся данные за 200Х г.
| Номер региона | Среднедушевой прожиточный минимум в день одного трудоспособного, руб., х | Среднедневная заработная плата, руб., у |
|---|---|---|
| 1 | 78 | 133 |
| 2 | 82 | 148 |
| 3 | 87 | 134 |
| 4 | 79 | 154 |
| 5 | 89 | 162 |
| 6 | 106 | 195 |
| 7 | 67 | 139 |
| 8 | 88 | 158 |
| 9 | 73 | 152 |
| 10 | 87 | 162 |
| 11 | 76 | 159 |
| 12 | 115 | 173 |
Задание:
1. Постройте поле корреляции и сформулируйте гипотезу о форме связи.
2. Рассчитайте параметры уравнения линейной регрессии

3. Оцените тесноту связи с помощью показателей корреляции и детерминации.
4. Дайте с помощью среднего (общего) коэффициента эластичности сравнительную оценку силы связи фактора с результатом.
5. Оцените с помощью средней ошибки аппроксимации качество уравнений.
6. Оцените с помощью F-критерия Фишера статистическую надёжность результатов регрессионного моделирования.
7. Рассчитайте прогнозное значение результата, если прогнозное значение фактора увеличится на 10% от его среднего уровня. Определите доверительный интервал прогноза для уровня значимости 
8. Оцените полученные результаты, выводы оформите в аналитической записке.
Решение:
Решим данную задачу с помощью Excel.
1. Сопоставив имеющиеся данные х и у, например, ранжировав их в порядке возрастания фактора х, можно наблюдать наличие прямой зависимости между признаками, когда увеличение среднедушевого прожиточного минимума увеличивает среднедневную заработную плату. Исходя из этого, можно сделать предположение, что связь между признаками прямая и её можно описать уравнением прямой. Этот же вывод подтверждается и на основе графического анализа.
Чтобы построить поле корреляции можно воспользоваться ППП Excel. Введите исходные данные в последовательности: сначала х, затем у.
Выделите область ячеек, содержащую данные.
Затем выберете: Вставка / Точечная диаграмма / Точечная с маркерами как показано на рисунке 1.
Рисунок 1 Построение поля корреляции
Анализ поля корреляции показывает наличие близкой к прямолинейной зависимости, так как точки расположены практически по прямой линии.
2. Для расчёта параметров уравнения линейной регрессии
воспользуемся встроенной статистической функцией ЛИНЕЙН.
1) Откройте существующий файл, содержащий анализируемые данные;
2) Выделите область пустых ячеек 5×2 (5 строк, 2 столбца) для вывода результатов регрессионной статистики.
3) Активизируйте Мастер функций: в главном меню выберете Формулы / Вставить функцию.
4) В окне Категория выберете Статистические, в окне функция – ЛИНЕЙН. Щёлкните по кнопке ОК как показано на Рисунке 2;
Рисунок 2 Диалоговое окно «Мастер функций»
5) Заполните аргументы функции:
Известные значения у – диапазон, содержащий данные результативного признака;
Известные значения х – диапазон, содержащий данные факторного признака;
Константа – логическое значение, которое указывает на наличие или на отсутствие свободного члена в уравнении; если Константа = 1, то свободный член рассчитывается обычным образом, если Константа = 0, то свободный член равен 0;
Статистика – логическое значение, которое указывает, выводить дополнительную информацию по регрессионному анализу или нет. Если Статистика = 1, то дополнительная информация выводится, если Статистика = 0, то выводятся только оценки параметров уравнения.
Щёлкните по кнопке ОК;
Рисунок 3 Диалоговое окно аргументов функции ЛИНЕЙН
6) В левой верхней ячейке выделенной области появится первый элемент итоговой таблицы. Чтобы раскрыть всю таблицу, нажмите на клавишу , а затем на комбинацию клавиш + + .
Дополнительная регрессионная статистика будет выводиться в порядке, указанном в следующей схеме:
| Значение коэффициента b | Значение коэффициента a |
| Стандартная ошибка b | Стандартная ошибка a |
| Коэффициент детерминации R 2 | Стандартная ошибка y |
| F-статистика | Число степеней свободы df |
| Регрессионная сумма квадратов |
Остаточная сумма квадратов
Рисунок 4 Результат вычисления функции ЛИНЕЙН
Получили уровнение регрессии:
Делаем вывод: С увеличением среднедушевого прожиточного минимума на 1 руб. среднедневная заработная плата возрастает в среднем на 0,92 руб.
3. Коэффициент детерминации 
По вычисленному коэффициенту детерминации 
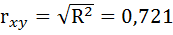
Связь оценивается как тесная.
4. С помощью среднего (общего) коэффициента эластичности определим силу влияния фактора на результат.
Для уравнения прямой 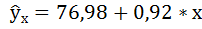
Средние значения найдём, выделив область ячеек со значениями х, и выберем Формулы / Автосумма / Среднее, и то же самое произведём со значениями у.
Рисунок 5 Расчёт средних значений функции и аргумент
Таким образом, при изменении среднедушевого прожиточного минимума на 1% от своего среднего значения среднедневная заработная плата изменится в среднем на 0,51%.
С помощью инструмента анализа данных Регрессия можно получить:
— результаты регрессионной статистики,
— результаты дисперсионного анализа,
— результаты доверительных интервалов,
— остатки и графики подбора линии регрессии,
— остатки и нормальную вероятность.
Порядок действий следующий:
1) проверьте доступ к Пакету анализа. В главном меню последовательно выберите: Файл/Параметры/Надстройки.
2) В раскрывающемся списке Управление выберите пункт Надстройки Excel и нажмите кнопку Перейти.
3) В окне Надстройки установите флажок Пакет анализа, а затем нажмите кнопку ОК.
• Если Пакет анализа отсутствует в списке поля Доступные надстройки, нажмите кнопку Обзор, чтобы выполнить поиск.
• Если выводится сообщение о том, что пакет анализа не установлен на компьютере, нажмите кнопку Да, чтобы установить его.
4) В главном меню последовательно выберите: Данные / Анализ данных / Инструменты анализа / Регрессия, а затем нажмите кнопку ОК.
5) Заполните диалоговое окно ввода данных и параметров вывода:
Входной интервал Y – диапазон, содержащий данные результативного признака;
Входной интервал X – диапазон, содержащий данные факторного признака;
Метки – флажок, который указывает, содержит ли первая строка названия столбцов или нет;
Константа – ноль – флажок, указывающий на наличие или отсутствие свободного члена в уравнении;
Выходной интервал – достаточно указать левую верхнюю ячейку будущего диапазона;
6) Новый рабочий лист – можно задать произвольное имя нового листа.
Затем нажмите кнопку ОК.
Рисунок 6 Диалоговое окно ввода параметров инструмента Регрессия
Результаты регрессионного анализа для данных задачи представлены на рисунке 7.
Рисунок 7 Результат применения инструмента регрессия
5. Оценим с помощью средней ошибки аппроксимации качество уравнений. Воспользуемся результатами регрессионного анализа представленного на Рисунке 8.
Рисунок 8 Результат применения инструмента регрессия «Вывод остатка»
Составим новую таблицу как показано на рисунке 9. В графе С рассчитаем относительную ошибку аппроксимации по формуле:
Рисунок 9 Расчёт средней ошибки аппроксимации
Средняя ошибка аппроксимации рассчитывается по формуле:
Качество построенной модели оценивается как хорошее, так как 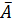
6. Из таблицы с регрессионной статистикой (Рисунок 4) выпишем фактическое значение F-критерия Фишера:
Поскольку 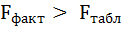
8. Оценку статистической значимости параметров регрессии проведём с помощью t-статистики Стьюдента и путём расчёта доверительного интервала каждого из показателей.
Выдвигаем гипотезу Н0 о статистически незначимом отличии показателей от нуля:
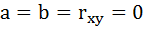
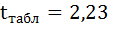
На рисунке 7 имеются фактические значения t-статистики:
t-критерий для коэффициента корреляции можно рассчитать двумя способами:
I способ:
где 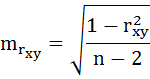
Данные для расчёта возьмём из таблицы на Рисунке 7.
II способ:
Фактические значения t-статистики превосходят табличные значения:
Поэтому гипотеза Н0 отклоняется, то есть параметры регрессии и коэффициент корреляции не случайно отличаются от нуля, а статистически значимы.
Доверительный интервал для параметра a определяется как
Для параметра a 95%-ные границы как показано на рисунке 7 составили:
Доверительный интервал для коэффициента регрессии определяется как
Для коэффициента регрессии b 95%-ные границы как показано на рисунке 7 составили:
Анализ верхней и нижней границ доверительных интервалов приводит к выводу о том, что с вероятностью 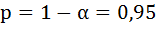
7. Полученные оценки уравнения регрессии позволяют использовать его для прогноза. Если прогнозное значение прожиточного минимума составит:
Тогда прогнозное значение прожиточного минимума составит:
Ошибку прогноза рассчитаем по формуле:
где
Дисперсию посчитаем также с помощью ППП Excel. Для этого:
1) Активизируйте Мастер функций: в главном меню выберете Формулы / Вставить функцию.
2) В окне Категория выберете Статистические, в окне функция – ДИСП.Г. Щёлкните по кнопке ОК.
3) Заполните диапазон, содержащий числовые данные факторного признака. Нажмите ОК.
Рисунок 10 Расчёт дисперсии
Получили значение дисперсии
Для подсчёта остаточной дисперсии на одну степень свободы воспользуемся результатами дисперсионного анализа как показано на Рисунке 7.
Доверительные интервалы прогноза индивидуальных значений у при 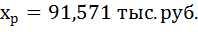
Интервал достаточно широк, прежде всего, за счёт малого объёма наблюдений. В целом выполненный прогноз среднемесячной заработной платы оказался надёжным.
Условие задачи взято из: Практикум по эконометрике: Учеб. пособие / И.И. Елисеева, С.В. Курышева, Н.М. Гордеенко и др.; Под ред. И.И. Елисеевой. – М.: Финансы и статистика, 2003. – 192 с.: ил.
источники:
http://math.semestr.ru/corel/prim1.php
http://ecson.ru/economics/econometrics/zadacha-3.raschyot-parametrov-regressii-i-korrelyatsii-s-pomoschju-excel.html