Ошибка Даламбера
Другой великий француз – Даламбер – вошел в историю теории вероятностей со своей знаменитой ошибкой, суть которой в том, что он неверно определил равновозможность исходов.
Задача: Какова вероятность, что подброшенные вверх две правильные монеты упадут на одну и ту же сторону?
Решение, предложенное Даламбером: Опыт имеет три равновозможных исхода:
1. обе монеты упали на «орла»;
2. обе монеты упали на «решку»;
3. одна из монет упала на «орла», другая на «решку».
Из них благоприятными для нашего события будут два исхода, поэтому искомая вероятность равна 2/3.
Правильное решение: Опыт имеет четыре равновозможных исхода:
1. первая монета упала на «орла», вторая тоже на «орла»;
2. первая монета упала на «решку», вторая тоже на «решку»;
3. первая монета упала на «орла», а вторая на — «решку»;
4. первая монета упала на «решку», а вторая на — «орла».
Из них благоприятными для нашего события будут два исхода, поэтому искомая вероятность равна = .
Даламбер совершил одну из самых распространенных ошибок, допускаемую при вычислении вероятности: он объединил два принципиально разных исхода в один. Чтобы не повторить эту ошибку, помните, что природа различает все предметы, даже если внешне они для нас неотличимы.
Ошибка Даламбера
Другой великий француз – Даламбер – вошел в историю теории вероятностей со своей знаменитой ошибкой, суть которой в том, что он неверно определил равновозможность исходов.
Задача: Какова вероятность, что подброшенные вверх две правильные монеты упадут на одну и ту же сторону?
Решение, предложенное Даламбером: Опыт имеет три равновозможных исхода:
1. обе монеты упали на «орла»;
2. обе монеты упали на «решку»;
3. одна из монет упала на «орла», другая на «решку».
Из них благоприятными для нашего события будут два исхода, поэтому искомая вероятность равна 2/3.
Правильное решение: Опыт имеет четыре равновозможных исхода:
1. первая монета упала на «орла», вторая тоже на «орла»;
2. первая монета упала на «решку», вторая тоже на «решку»;
3. первая монета упала на «орла», а вторая на — «решку»;
4. первая монета упала на «решку», а вторая на — «орла».
Из них благоприятными для нашего события будут два исхода, поэтому искомая вероятность равна = .
Даламбер совершил одну из самых распространенных ошибок, допускаемую при вычислении вероятности: он объединил два принципиально разных исхода в один. Чтобы не повторить эту ошибку, помните, что природа различает все предметы, даже если внешне они для нас неотличимы.
Каждый год учителя жалуются на то, что падает
интерес у учеников к учебе, и каждый год
усложняются задания ГИА и ЕГЭ. Вот уже и элементы
теории вероятностей стали полноправными
заданиями в тестах. Этой теме в школьном курсе не
уделялось должного внимания и казалось, что
сложно будет побороть страх учеников перед этими
задачами. Но мы, учителя, поняли, что т.к. изменить
ситуацию невозможно, под нее надо
подстраиваться.
Проанализировав демонстрационные варианты,
убедилась, что для успешного решения указанных
задач необходимо повторить (а может быть выучить)
основные положения теории вероятностей.
Прежде всего, напомним учащимся, что же изучает
этот раздел математики?
Наблюдая со стороны за различными явлениями
или участвуя в проведении опытов, мы замечаем,
что некоторое явление может произойти, а может и
нет. Те события, исход которых предсказать
нельзя, назовем случайным.
Например, нельзя заранее предсказать будет ли
цифра «6» в номере машины, проезжающей сейчас
мимо вас, будет ли вынут именно красный шар из
коробки, в которой 4 шара разного цвета?
Предсказать исход одного испытания мы не можем, а
вот подсчитать вероятность его наступления при
большом количестве произведенных однородных
испытаний – это под силу теории вероятностей.
Основная формула классической вероятности
всего одна: , где n
– число благоприятных исходов, m – общее число
исходов.
При этом надо подчеркивать, что общее число
исходов конечно и все исходы равнозначны (в
противном случае применение этой формулы
невозможно, т.к. получим неверный результат).
Ученики школы среднего и старшего звена
знакомятся только со случайными событиями.
Причем, это знакомство в основном опирается на их
жизненный опыт, интуицию.
В своей повседневной жизни мы часто повторяем:
«с достаточной долей вероятности…», «мне
кажется невероятно, что это произойдет», «почти
со 100% вероятностью можно утверждать…». Этими
фразами мы, опираясь на знания предыдущих лет (а
иногда и на интуицию) прогнозируем исход
какого-то события. Однако, не смотря на наш
прогноз, указанное событие может произойти, а
может и нет. Так, купив лотерейный билет, мы
рассчитываем, конечно, на выигрыш. Подбрасывая
монету, скажем, 4 раза, предполагаем, что «орел» и
«решка» выпадут по 2 раза. Но проделав этот
нехитрый опыт, убеждаемся, что это совсем не так в
реальности. Вот тогда и возникает вопрос: а
сколько раз надо бросить монету, что б
вероятность выпадения нужной стороны её была
почти 50%?
На все эти вопросы и отвечает теория
вероятностей. Она дает возможность численно
характеризовать возможность наступления того
или иного события.
Еще очень важным моментом в подсчете
вероятности наступления события, является то,
что все испытания и их исход договорились
считать равновозможными (равновероятными).
Что это значит?
Рассмотрим, например, опыт, с однократным
подбрасыванием монеты. В реальной жизни может
быть несколько исходов: выпадет «орел», выпадет
«решка», монета встанет на ребро, укатится
куда-нибудь. Кроме того, при многократном
подбрасывании, может оказаться, что выпадение,
скажем, «орла» намного чаще, чем «решки».При
детальном исследовании монеты оказалось, что на
сторону «герба»ушло больше металла(при отливке
монеты) и эта сторона тяжелее. Может сказаться и
неоднородность металла при плавке, порыв ветра
при бросании монеты, неровность поверхности, на
которую падает монета и т.д. Чтоб исход испытания
не зависел от этих частностей, договорились
считать монету «правильной» или «симметричной»,
т.е. одинаковой по весу с обеих сторон, падающей
на одну и ту же плоскость в безветренную погоду.
Аналогично надо считать симметричными игральный
кубик и игральные кости при бросании их во время
эксперимента.
Следует предостеречь учеников от неверного
способа решения задач рассуждением, без учета
всех возможностей исходов. Приведу пример.
Задача. Бросают два игральных кубика.
Найти вероятность того, что сумма выпавших очков
будет равна пяти.
Ошибочное решение. В данной ситуации
возможны два исхода: либо сумма будет равна пяти,
либо не будет. Значит, общее число исходов – два,
а из них благоприятных – один (т.е. сумма равна
пяти). Значит, по формуле вероятности:
В чем ошибка ученика? Как мы знаем, каждый кубик
имеет 6 граней, на которых расположены точки от
одной до шести. Бросая оба кубика одновременно,
число очков, выпавших на первом кубике, не
зависит от того, какое число очков в это время
выпадет на втором. Т.е. шесть исходов первого
кубика сочетаются с шестью исходами второго. И
общее число равновозможных исходов: 6 • 6 = 36.
Тогда, благоприятных исходов, т.е. сумма равна
пяти будет 4 : 3+2; 2+3; 1+4; 4+1. Следовательно, ответ на
вопрос задачи:
Очень уместно здесь познакомить учеников со
знаменитой ошибкой Даламбера.
Пример. Ошибка Даламбера. Какова
вероятность, что подброшенные, вверх две
правильные монеты упадут на одну и ту же сторону?
Решение, предложенное Даламбером. Опыт
имеет три равновозможных исхода:
1) обе монеты упали на «орла»;
2) обе монеты упали на «решку»;
3) одна из монет упала на «орла», другая на
«решку».
Из них благоприятными для нашего событиями
будут два исхода, поэтому искомая вероятность
равна .
Правильное решение. Опыт имеет четыре
равновозможных исхода:
1) первая монета упала на «орла», вторая тоже на
«орла»;
2) первая монета упала на «решку», вторая тоже на
«решку»;
3) первая монета упала на «орла», вторая – на
«решку»;
5) первая монета упала на «решку», вторая – на
«орла».
Из них благоприятными для нашего события будут
два исхода, поэтому искомая вероятность равна
Даламбер совершил одну из самых
распространенных ошибок, допускаемую при
вычислении вероятности: он объединил два
принципиально разных исхода в один. Чтобы не
повторить эту ошибку, помните, что природа
различает все предметы, даже если внешне
они для нас неотличимы.
Надо напоминать учащимся, что нужно
анализировать полученный результат: найденная
вероятность не может быть больше 1, как не может,
например, упасть на землю яблок больше, чем их
находится на дереве. Что при бросании монеты,
вероятность выпадения «орла» или «решки» почти
одинакова, а вот вероятность, скажем, отказа
тормозов у автомобиля добросовестного водителя,
крайне мала. Поэтому учащиеся должны помнить, что
p є [0;1].
Крайне редко, но бывают задания, где
вероятность оказывается равной нулю (нулевая
вероятность). События, вероятность которых равна
нулю называются невозможными. Например,
сумма выпавших очков на двух костях равна 13 (мы
знаем, что максимальное число очков одной грани
– 6, значит для двух граней – 12).
Если же вероятность равна 1 (иногда говорят
«стопроцентная вероятность»), то событие
называем достоверным. Примером может служить
опыт с игральным кубиком и утверждение, что при
подбрасывании выпало не более 6 очков.
Все остальные события, вероятность которых
находится в интервале (0;1), будем называть случайными.
Они и составляют основную часть задач в теории
вероятностей. Их-то и решают по уже упомянутой
формуле.
Хочется еще раз напомнить, что половина успеха
в решении той или иной задачи (совсем
необязательно по теории вероятностей) заложена
во внимательном чтении условия. Очень много
ошибок допускают ученики торопясь сделать
задание, которое, как кажется, им знакомо и, не
вникнув в исходные данные, допускают
непростительные ошибки.
Приведу пример двух похожих, но абсолютно
разных по смыслу (и, естественно, по способу
решения) задач.
Задача №1. Фабрика выпускает сумки. В
среднем, на 100 сумок, приходится 8 сумок со
скрытыми дефектами. Найдите вероятность того,
что купленная сумка окажется качественной. (Если
необходимо, результат округлите до сотых).
Решение. Вероятность найдем по
формуле: .
Здесь из 100 сумок 8 некачественных, следовательно,
остальные качественные, т.е. 100 – 8 = 92 сумки.
m = 100,
n = 92
Ответ: 0,92
Задача №2. Фабрика выпускает сумки. В
среднем, на каждые 100 качественных сумок
приходится 8 сумок со скрытыми дефектами. Найдите
вероятность того, что купленная сумка окажется
качественной. (Если необходимо, результат
округлите до сотых).
Решение. Вероятность найдем по формуле: . В этой задаче, в
отличие от предыдущей общее количество сумок
складывается из качественных ( 100 штук) и
некачественных (8 штук), т.е. m = 100 + 8 = 108 .
Среди этих 108 сумок, качественных было 100 штук, n
= 100
Ответ: 0,93
Литература.
- Бунимович Е.А., Булычев В.А. «Вероятность и
статистика» .М «Дрофа». 2002г. - Колмогоров А.Н.и др. Введение в теорию
вероятностей.. М. «Наука» 1982г. - Скопец З.А. «Дополнительные главы по курсу
математики». М. «Просвещение» .1974г. - Чистяков В.П. «Курс теории вероятностей». М.
«Наука» 1982г.

Статистическое |
|
определение |
|
вероятности |
|
Вероятность как предельное |
|
значение частоты. |

|
Самостоятельная работа |
|||
|
Вариант 1 |
Вариант 2 |
Вариант 3 |
Вариант 4 |
|
1. |
На столе 12 |
1. В коробке 24 |
1.В лотерее 100 |
1.В вазе 7 |
|
|
кусков пирога. В |
карандаша, из |
билетов, из них 5 |
цветков, из них 3 |
||
|
трех |
них 3 красного |
выигрышных. |
розы. Из букета |
||
|
«счастливых» из |
цвета. Из |
Какова |
наугад |
||
|
них запечены |
коробки наугад |
вероятность |
вынимается |
||
|
призы. Какова |
вынимается |
выигрыша? |
цветок. Какова |
||
|
вероятность |
карандаш. |
вероятность того, |
|||
|
взять |
Какова |
что это роза? |
|||
|
«счастливый» |
вероятность того, |
||||
|
кусок пирога? |
что он красный? |
||||
|
2. В урне 15 |
2. Из чисел от 1 |
2. В корзине |
2. В корзине 10 |
||
|
белых и 25 |
до 25 наудачу |
лежат 5 яблок и 3 |
яблок, из них 4 |
||
|
черных шаров. |
выбрано число. |
груши. Из |
червивых. |
||
|
Из урны наугад |
Какова |
корзины наугад |
Какова |
||
|
выбирается один |
вероятность того, |
вынимается один |
вероятность того, |
||
|
шар. Какова |
что оно окажется |
фрукт. Какова |
что любое взятое |
||
|
вероятность того, |
кратным 5? |
вероятность того, |
наугад яблоко |
||
|
что он будет |
что это яблоко? |
окажется не |
|||
|
белым? |
червивым? |

СТАТИСТИЧЕСКОЕ
ОПРЕДЕЛЕНИЕ
ВЕРОЯТНОСТИ

Ошибка Даламбера.
Жан Лерон Даламбер
(1717 -1783)
Великий французский философ и математик Даламбер вошел в историю теории вероятностей со своей знаменитой ошибкой, суть которой в том, что он неверно определил равновозможность исходов в опыте всего с двумя монетами!

Ошибка Даламбера.

|
Решение Даламбера: |
Правильное решение: |
||
|
Опыт имеет три |
Опыт имеет четыре |
||
|
равновозможных исхода: |
равновозможных исхода: |
||
|
1) |
обе монеты упадут на |
1) |
обе монеты упадут на «орла»; |
|
«орла»; |
2) |
обе монеты упадут на |
|
|
2) |
обе монеты упадут на |
«решку»; |
|
|
«решку»; |
3) |
первая монета упадет на |
|
|
3) |
одна из монет упадет на |
«орла», вторая на «решку»; |
|
|
«орла», другая на |
4) |
первая монета упадет на |
|
|
«решку». |
«решку», вторая на «орла». |
|
Из них благоприятными |
Из них благоприятными будут |
||||||
|
будут два исхода. |
2 |
два исхода. |
2 |
1 |
|||
|
n 3, m 2, P(A) m |
n 4, m 2, P(A) m |
||||||
|
n |
3 |
n |
4 |
2 |
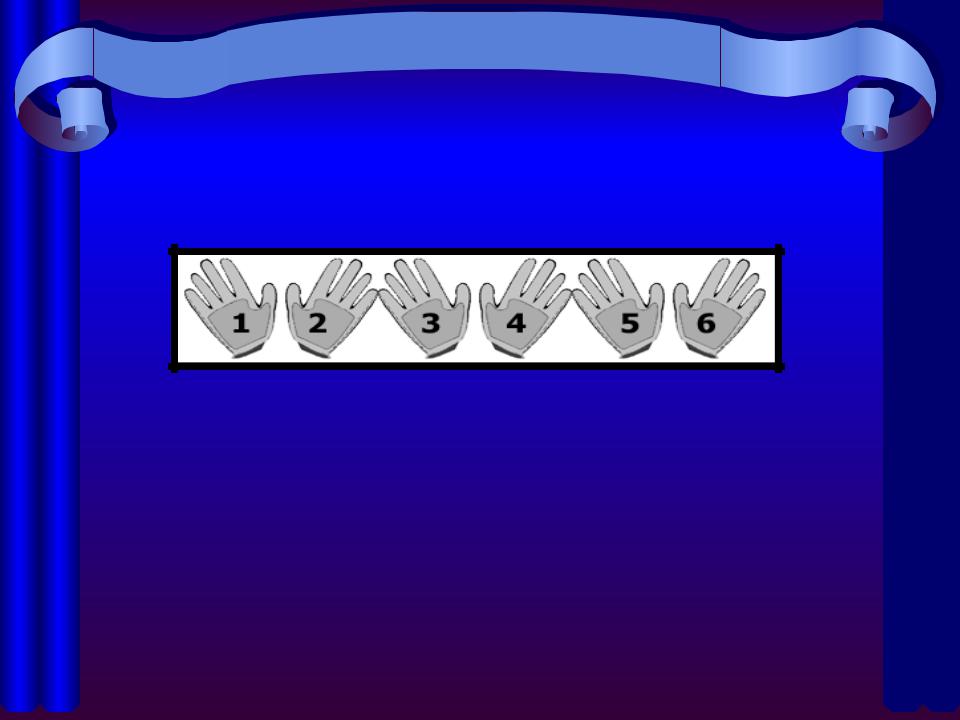
Опыт «Выбор перчаток». В коробке лежат 3 пары |
|
одинаковых перчаток. Из нее, не глядя, вынимаются |
|
две перчатки. Перечислите все равновозможные |
|
исходы. |
Какой вариант решения правильный:
|
1-ый вариант: |
2-ой вариант: |
||
|
3 исхода: |
4 исхода: |
||
|
1) «обе перчатки на левую руку», |
1) «обе перчатки на левую руку», |
||
|
2) «обе |
2) «обе |
||
|
перчатки на правую руку», |
перчатки на правую руку», |
||
|
3) «перчатки на |
3) «первая |
||
|
разные руки». |
перчатка на левую руку, вторая на |
||
|
правую», |
4) «первая |
||
|
перчатка на правую руку, вторая |
|
|
Правило: природа различает все предметы, даже если внешне они |
|
|
для нас неотличимы. |
на левую». |

Вывод:
Формула классической вероятности дает очень простой способ вычисления вероятностей. Однако простота этой формулы обманчива. При ее использовании возникают два очень непростых вопроса:
1.Как выбрать систему исходов опыта так, чтобы они были равновозможными, и можно ли это сделать вообще?
2.Как найти числа т и п и убедиться в том, что они найдены верно?

ПРОБЛЕМНЫЙ ВОПРОС 1: А можно ли вычислить вероятность события с помощью ряда экспериментов?

Опыт человечества.
Вероятность попасть под дождь в Лондоне гораздо выше, чем в пустыне Сахара.
Весь наш жизненный опыт подсказывает, что любое событие считается тем более вероятным, чем чаще оно происходит. Значит, вероятность должна быть каким- то образом связана с частотой.

Частота случайного события. |
|
Абсолютной частотой |
|
случайного события А в серии |
|
из N случайных опытов |
|
называется число NA , которое |
показывает, сколько раз в этой серии произошло событие А.
Соседние файлы в папке Пз 1
- #
- #
- #
- #
Пример 1. Правильная монета подбрасывается 2 раза.
Событие A: Выпадение хотя бы одного “орла”.
Решение. Число возможных исходов в серии из двух испытаний равно 4:
ОО, ОР, РО, РР.
Число исходов, благоприятствующих событию A, равно 3:
ОО, ОР, РО.
Следовательно,
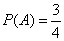
Пример 2. В семье имеется 2 ребенка.
Событие A: Хотя бы один из детей – мальчик.
Решение. Задача по своей сути не отличается от предыдущей. Только под испытанием теперь следует понимать рождение ребенка. Если рождение мальчика или девочки в одном испытании представляют собой случайные события, то число равновероятных исходов равно 4:
ММ, МД, ДМ, ДД.
Только первые 3 исхода благоприятствуют событию A. Поэтому
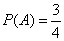
Ошибочное решение. Число возможных вариантов в серии из двух испытаний равно 3:
ММ, МД, ДД.
Первые два исхода благоприятствуют событию A. Поэтому
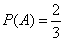
Анализ. Три события:
“2 мальчика”,
“1 мальчик и одна девочка” и
“2 девочки”
не являются равновозможными, поскольку ММ и ДД представляют собой элементарные события, тогда как событие “1 мальчик и одна девочка” – составное событие, которое разлагается на 2 исхода: МД и ДМ.
Любопытно, что подобную ошибку в рассуждениях допустил в свое время великий математик Даламбер, рассматривая задачу о подбрасывании монеты (см. Пример 1).
Авторы проекта
- Учащиеся 9″Е» класса
- Шляпникова Дарья
- Ревина Дарья
Руководитель проекта
- учитель математики
- Сиськова Наталья Алексеевна
Цель
Воспользовавшись различными источниками информации дать наиболее полное представление о применении теории вероятности и статистики в различных средах жизнедеятельности человека.
Задачи
- 1)История возникновения и развития теории вероятности и статистики.
- 2)Определение теории вероятности и исследование «Вероятность сдачи ЕГЭ по алгебре».
- 3)Определение статистики и статистические исследования.
Из истории возникновения теории вероятностей и статистики
Первыми открывателями теории вероятности считают Пьера Ферма и Блеза Паскаля, эти французские учёные открыли ключ к составлению количественной оценки. Они использовали метод, который позже был назван комбинаторным анализом, или проще комбинаторикой. В ХХ веке появилась математическая статистика — наука, основанная на законах теории вероятности.
-
Блез Паскаль(19.06.1623 — 19.08.1662)
Определение теории вероятностей
Вероятностью события называется отношение числа благоприятных для него исходов к числу всех равновозможных исходов. Это определение называют классическим определением вероятности.
• Статистическое: вероятность приближенно равна частоте появление события А в длинной серии экспериментов.
• Классическое: вероятность – это отношение числа благоприятных для события А исходов к числу к числу всех исходов эксперимента.
• Геометрическое: вероятность – это отношение площади события А ко всей площади области, где случайно выбирается точка.
Примеры вероятностных исследований
Другой французский учёный вошёл в историю со своей знаменитой ошибкой.
Ошибка Даламбера
Задача: Какова вероятность, что подброшенные вверх две правильные монеты упадут на одну и ту же сторону?
Решение, предложенное Даламбером:
Опыт имеет три возможных исхода:
- 1) Обе монеты упали на «орла»;
- 2) Обе монеты упали на «решку»;
- 3) Одна из монет упала на «орла», другая на «решку».
Из них благоприятными для нашего события будут 2 исхода, поэтому вероятность равна 2/3.
Ошибкак сосотиот в том, что Даламбер определил два принципиально разных исхода в один, поэтому опыт будет иметь четыре возможных исхода:
- 1) Обе монеты упали на «орла»;
- 2) Обе монеты упали на «решку»;
- 3)Первая монета упала на «орла», а вторая – на «решку».
- 4)Первая монета упала на «решку», а вторая – на «орла».
Из них благоприятными для нашего события будут 2 исхода, поэтому искомая вероятность равна 2/4=1/2
«Вероятность сдачи ЕГЭ по алгебре»
Дано: в 2008-2009 году
положительные годовые оценки: 57 человек.
подтвердили: 56 человек.
Решение:
P(А) – вероятность сдачи экзамена на «4»и«5».
m(A) – сколько человек подтвердят свою отметку.
n – кол-во человек.
-вероятность сдачи экзамена на положительную отметку.
Дано:
На «4»и«5»: 2009-2010 год – 53 человека.
m(A) — ? человек(подтвердили свою отметку)
Решение:
Ответ: 52 ученика подтвердят свою отметку.
Определение и виды статистики
Статистика — (от лат. Status — состояние) – наука, изучающая, обрабатывающая и анализирующая количественные данные о самых разнообразных массовых явлениях, происходящих в природе и обществе.
Наш словарик:
- 1. Среднее арифметическое (Х) ряда чисел– это частное от деления суммы этих чисел на число слагаемых.
- 2. Размах (A) ряда чисел — это разность между наибольшим и наименьшим из этих чисел.
- 3. Модой (Мо) ряда чисел — называется число, наиболее часто встречающееся в данном ряду.
- 4. Медианой (Ме) ряда чисел – называется число этого ряда
(или полусумму двух его чисел), справа и слева от которого на числовой прямой лежит одинаковое количество членов ряда.
Виды статистики
- Математическая
- Медицинска
- Экономическая
- Демографическая
- Налоговая
- Метеорологическая
- Финансовая
- Биологическая
Статистические исследования
Исследование по результатам проведения зимней олимпиады в Ванкувере в 2010 году
Исследование по теме «Крупнейшие реки»
Выводы
- Теория вероятностей устанавливает закономерности для случайных событий.
- Теория вероятностей и статистика представляют средство для одной из важнейших способностей ума – способности представлять явления в разных комбинациях.
- Статистика и теория вероятностей неразрывно связаны с нашей повседневной жизнью, помогает решить насущные задачи: выбор наилучшего из возможных вариантов, оценка степени риска, шансов на успех.
Источники
- 1.Ю.Н.Макарычев, Н.Г.Миндюк. Начальные сведения из теории вероятностей в школьном курсе алгебры. “Математика в школе”. № 7. 2004 г. стр. 24.
- 2.В.А.Булычев, Е.А.Бунимович. Изучение теории вероятностей и статистики в школьном курсе математики. “Математика в школе”. № 4. 2003 г. стр. 59.
- 3.Бунимович Е.А., Булычев В.А. Основы статистики и вероятность. М. «Дрофа», 2004.
- 4.http://www.hi-edu.ru.
- 5.http://www.BankReferatov.ru
- 6.Большев Л.Н., Смирнов Н.В. Таблицы математической статистики.- М.: Наука,1983.
- 7.Боровков А.А. Математическая статистика.- М.: Наука, 1984.
- 8.Боровков А.А. Теория вероятностей.- М.: Наука, 1986.
- 9.Володин И.Н. «Лекции по теории вероятностей и математической статистике».
- 10.Е.А. Буминович, В.А. Булычев «Вероятность и статистика в курсе математики общеобразовательной школы»
- 11.Крамер Г. Математические методы статистики.- М.: Мир, 1975.
- 12.Лютикас В.С. Факультативный курс по математике. Теория вероятностей. М.«Просвещение» 1990.
- 13.Статистика. В.С. Мхитарян, 2002 год.
- 14.Ткачева М.В. Домашняя математика. М.«Просвещение», 1994.
- 15.Элементы статистики и вероятности. М.В.Ткачева, Н. Е. Федорова. Просвещение, 2004 год.
Описание презентации по отдельным слайдам:
-
-
2 слайд
Статистическое определение вероятности
Вероятность как предельное значение частоты.
-
3 слайд
Ошибка Даламбера.
Великий французский философ и математик Даламбер вошел в историю теории вероятностей со своей знаменитой ошибкой, суть которой в том, что он неверно определил равновозможность исходов в опыте всего с двумя монетами!
Жан Лерон Даламбер
(1717 -1783) -
4 слайд
Ошибка Даламбера.
Опыт. Подбрасываем две одинаковые монеты. Какова вероятность того, что они упадут на одну и ту же сторону?Решение Даламбера:
Опыт имеет три
равновозможных исхода:
1) обе монеты упадут на «орла»;
2) обе монеты упадут на «решку»;
3) одна из монет упадет на «орла», другая на «решку».
Из них благоприятными
будут два исхода.Правильное решение:
Опыт имеет четыре
равновозможных исхода:
1) обе монеты упадут на «орла»;
2) обе монеты упадут на «решку»;
3) первая монета упадет на «орла», вторая на «решку»;
4) первая монета упадет на «решку», вторая на «орла».
Из них благоприятными будут
два исхода. -
5 слайд
Вывод:
Формула классической вероятности дает очень простой способ вычисления вероятностей. Однако простота этой формулы обманчива. При ее использовании возникают два очень непростых вопроса:
Как выбрать систему исходов опыта так, чтобы они были равновозможными, и можно ли это сделать вообще?
Как найти числа т и п и убедиться в том, что они найдены верно? -
6 слайд
ПРОБЛЕМНЫЙ ВОПРОС 1:
А можно ли вычислить вероятность события с помощью ряда экспериментов? -
7 слайд
Опыт человечества.
Вероятность попасть под дождь в Лондоне гораздо выше, чем в пустыне Сахара.
Весь наш жизненный опыт подсказывает, что любое событие считается тем более вероятным, чем чаще оно происходит. Значит, вероятность должна быть каким-то образом связана с частотой. -
8 слайд
Частота случайного события.
Абсолютной частотой случайного события А в серии из N случайных опытов называется число NA , которое показывает, сколько раз в этой серии произошло событие А. -
9 слайд
Частота случайного события.
Относительной частотой случайного события называют отношение числа появлений этого события к общему числу проведенных экспериментов:где А – случайное событие по отношению к некоторому испытанию,
N раз проведено испытание и при этом событие А наступило в NA случаях. -
10 слайд
Пример
Наблюдения показывают, что в среднем среди 1000 новорожденных детей 515 мальчиков. Какова частота рождения мальчика в такой серии наблюдений?
Ответ: 0,515 -
11 слайд
ПРОБЛЕМНЫЙ ВОПРОС 2:
Может быть, относительную частоту и нужно принять за вероятность? -
12 слайд
Фундаментальным свойством относительных частот является тот факт, что с увеличением числа опытов относительная частота случайного события постепенно стабилизируется и приближается к вполне определенному числу, которое и следует считать его вероятностью.
-
13 слайд
Статистическая вероятность
Вероятность случайного события приближенно равна частоте этого события, полученной при проведении большого числа случайных экспериментов: , где — число испытаний, в которых наступило событие А, N – общее число испытаний. -
14 слайд
По статистике, на каждые 1000 лампочек приходится 3 бракованные. Какова вероятность купить исправную лампочку?
Решение:
3/1000 = 0,0031 – 0,003 = 0,997
Задача.
Слайд 1Понятие вероятности
Теория вероятностей, 9 класс.

Слайд 2Статистическое определение вероятности
Вероятность как предельное значение частоты.

Слайд 4СТАТИСТИЧЕСКОЕ
ОПРЕДЕЛЕНИЕ
ВЕРОЯТНОСТИ

Слайд 5Ошибка Даламбера.
Великий французский философ и математик Даламбер вошел
в историю теории вероятностей со своей знаменитой ошибкой, суть которой в том, что он неверно определил равновозможность исходов в опыте всего с двумя монетами!
Жан Лерон Даламбер
(1717 -1783)

Слайд 6Ошибка Даламбера.
Опыт. Подбрасываем две одинаковые монеты. Какова вероятность того, что они
упадут на одну и ту же сторону?
Решение Даламбера:
Опыт имеет три
равновозможных исхода:
1) обе монеты упадут на «орла»;
2) обе монеты упадут на «решку»;
3) одна из монет упадет на «орла», другая на «решку».
Из них благоприятными
будут два исхода.
Правильное решение:
Опыт имеет четыре
равновозможных исхода:
1) обе монеты упадут на «орла»;
2) обе монеты упадут на «решку»;
3) первая монета упадет на «орла», вторая на «решку»;
4) первая монета упадет на «решку», вторая на «орла».
Из них благоприятными будут
два исхода.

Слайд 7Опыт «Выбор перчаток». В коробке лежат 3 пары одинаковых перчаток. Из
нее, не глядя, вынимаются две перчатки. Перечислите все равновозможные исходы.
Какой вариант решения правильный:
Правило: природа различает все предметы, даже если внешне они для нас неотличимы.
1-ый вариант: 3 исхода: 1) «обе перчатки на левую руку», 2) «обе перчатки на правую руку», 3) «перчатки на разные руки».
2-ой вариант: 4 исхода: 1) «обе перчатки на левую руку», 2) «обе перчатки на правую руку», 3) «первая перчатка на левую руку, вторая на правую», 4) «первая перчатка на правую руку, вторая на левую».

Слайд 8Вывод:
Формула классической вероятности дает очень простой способ вычисления
вероятностей. Однако простота этой формулы обманчива. При ее использовании возникают два очень непростых вопроса:
Как выбрать систему исходов опыта так, чтобы они были равновозможными, и можно ли это сделать вообще?
Как найти числа т и п и убедиться в том, что они найдены верно?

Слайд 9ПРОБЛЕМНЫЙ ВОПРОС 1:
А можно ли вычислить вероятность события с помощью ряда
экспериментов?

Слайд 10Опыт человечества.
Весь наш жизненный опыт подсказывает, что любое событие
считается тем более вероятным, чем чаще оно происходит. Значит, вероятность должна быть каким-то образом связана с частотой.

Слайд 11Частота случайного события.
Абсолютной частотой случайного события А в серии из N
случайных опытов называется число NA , которое показывает, сколько раз в этой серии произошло событие А.

Слайд 12Частота случайного события.
Относительной частотой случайного события называют отношение числа появлений этого
события к общему числу проведенных экспериментов:
где А – случайное событие по отношению к некоторому испытанию,
N раз проведено испытание и при этом событие А наступило в NA случаях.

Слайд 13Примеры
Пример 1. Наблюдения показывают, что в среднем среди 1000
новорожденных детей 515 мальчиков. Какова частота рождения мальчика в такой серии наблюдений?
Ответ: 0,515

Слайд 14Примеры
Пример 2. За лето на Черноморском побережье было 67
солнечных дней. Какова частота солнечных дней на побережье за лето? Частота пасмурных дней?
Ответ: 0,728; 0,272.

Слайд 15Примеры
Пример 3. Отдел технического контроля обнаружил 5 бракованных изделий
в партии из 1000 изделий. Найдите частоту изготовления бракованных изделий.
Ответ: 0,005

Слайд 16Примеры
Пример 4. Для выяснения качества семян было отобрано и
высеяно в лабораторных условиях 1000 штук. 980 семян дали нормальные всходы. Найдите частоту нормального всхода семян.
Ответ: 0,98

Слайд 17ПРОБЛЕМНЫЙ ВОПРОС 2:
Может быть, относительную частоту и нужно
принять за вероятность?

Слайд 18Фундаментальным свойством относительных частот является тот факт, что с увеличением числа
опытов относительная частота случайного события постепенно стабилизируется и приближается к вполне определенному числу, которое и следует считать его вероятностью.

Слайд 19Проверка
Пример 5. Подбрасывание монеты. А – выпадает герб.
Классическая вероятность: всего 2 исхода,
1 исход события А:

Слайд 20Проверка
Пример 5. Французский естествоиспытатель Бюффон (XVIII в.) бросил монету 4040 раз,
и при этом герб выпал в 2048 случаях. Следовательно, частота выпадения герба в данной серии испытаний равна:
Жорж Бюффон

Слайд 21Проверка
Пример 5. Английский математик Карл Пирсон (1857-1936) бросал монету 24000 раз,
причем герб выпал 12012 раз. Следовательно, частота выпадения герба в данной серии испытаний равна:
Карл Пирсон

Слайд 22Результаты
Вывод
Пример 5 подтверждает естественное предположение о том, что вероятность выпадения герба
при одном бросании монеты равна 0,5.

Слайд 23Статистическая вероятность
Вероятность случайного события приближенно равна частоте этого события,
полученной при проведении большого числа случайных экспериментов: , где — число испытаний, в которых наступило событие А, N – общее число испытаний.

Слайд 24Задача №1.
Чтобы определить, как часто встречаются в лесопарке деревья разных
пород, ребята провели следующие эксперименты. Каждый выбрал свою тропинку и по пути следования записывал породу каждого десятого дерева.
Результаты были занесены в таблицу:
Породы Сосна Дуб Береза Ель Осина Всего
Число деревьев 315 217 123 67 35 757
Оцените вероятность того, что выбранное наугад в этом парке дерево будет:
а) сосной;
б) хвойным;
в) лиственным.
Указание. Ответ запишите в виде десятичной дроби с тремя знаками после запятой.

Слайд 25Задача №1.
Решение:
а) A={выбранное наугад в парке дерево — сосна}
NА = 315, N = 757, Р(А) = 315/757 ≈ 0,416;
б) В ={выбранное наугад в парке дерево — хвойное} NА = 315 + 67 = 382, N = 757.
Р(А) = 382/757 ≈ 0,505;
в) C = {выбранное наугад в парке дерево — лиственное} NА = 217 + 123 + 35 = 375, N = 757.
Р(А) = 375/757 ≈ 0,495.

Слайд 26 По статистике, на каждые 1000 лампочек приходится 3 бракованные.
Какова вероятность купить исправную лампочку?
Решение:
3/1000 = 0,003
1 – 0,003 = 0,997
Задача №2.

Слайд 27 Демографы утверждают, что вероятность рождения близнецов равна 0,012. в
скольких случаях из 10 000 рождений можно ожидать появление близнецов?
Решение:
Ответ: в 120 случаях.
Задача №3.

Слайд 28Вопросы:
Запишите формулу вычисления вероятности случайного события в классической модели. Поясните, что
означает каждая буква в этой формуле.
Запишите формулу вычисления вероятности случайного события в статистической модели. Поясните, что означает каждая буква в этой формуле.
Какому условию должны удовлетворять исходы опыта, чтобы можно было воспользоваться классическим определением вероятности?
Чему равна частота достоверного события?
Что такое абсолютная частота? относительная частота?
Как частота связана с вероятностью?
После 100 опытов частота события А оказалась равна 0, а частота события В равна 1. Можно ли сказать, что событие А невозможное, а событие В – достоверное?

Слайд 29Домашнее задание.
Задача №1. По статистике в городе Новинске
за год из каждой 1000 автомобилистов два попадают в аварию. Какова вероятность того, что автомобилист в этом городе весь год проездит без аварий?
Задача №2. Чтобы определить, какой цвет волос встречается в городе чаще, а какой реже, студенты за полчаса провели следующий эксперимент. Каждый выбрал свой маршрут и записывал по пути следования цвет волос каждого пятого встречного. Результаты были занесены в следующую таблицу:
Цвет волос Брюнеты Шатены Рыжие Блондины Всего
Число людей 198 372 83 212 865
Оцените вероятность того, что выбранный наугад житель этого города будет:
а) шатеном;
б) рыжим;
в) не рыжим.

Слайд 1Понятие вероятности
Теория вероятностей, 9 класс.

Слайд 2Статистическое определение вероятности
Вероятность как предельное значение частоты.

Слайд 4Ошибка Даламбера.
Великий французский философ и математик Даламбер вошел
в историю теории вероятностей со своей знаменитой ошибкой, суть которой в том, что он неверно определил равновозможность исходов в опыте всего с двумя монетами!
Жан Лерон Даламбер
(1717 -1783)

Слайд 5Ошибка Даламбера.
Опыт. Подбрасываем две одинаковые монеты. Какова вероятность того, что они
упадут на одну и ту же сторону?
Решение Даламбера:
Опыт имеет три
равновозможных исхода:
1) обе монеты упадут на «орла»;
2) обе монеты упадут на «решку»;
3) одна из монет упадет на «орла», другая на «решку».
Из них благоприятными
будут два исхода.
Правильное решение:
Опыт имеет четыре
равновозможных исхода:
1) обе монеты упадут на «орла»;
2) обе монеты упадут на «решку»;
3) первая монета упадет на «орла», вторая на «решку»;
4) первая монета упадет на «решку», вторая на «орла».
Из них благоприятными будут
два исхода.

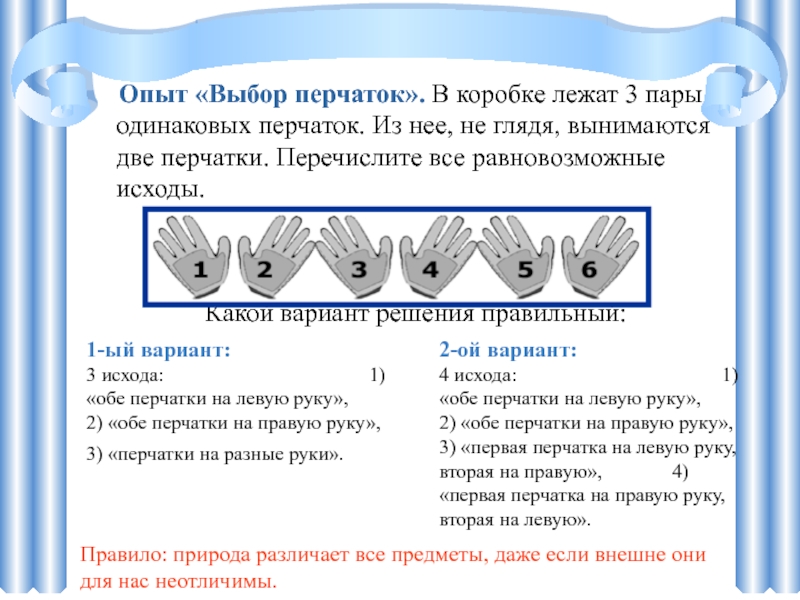
Слайд 6Опыт «Выбор перчаток». В коробке лежат 3 пары одинаковых перчаток. Из
нее, не глядя, вынимаются две перчатки. Перечислите все равновозможные исходы.
Какой вариант решения правильный:
Правило: природа различает все предметы, даже если внешне они для нас неотличимы.
1-ый вариант: 3 исхода: 1) «обе перчатки на левую руку», 2) «обе перчатки на правую руку», 3) «перчатки на разные руки».
2-ой вариант: 4 исхода: 1) «обе перчатки на левую руку», 2) «обе перчатки на правую руку», 3) «первая перчатка на левую руку, вторая на правую», 4) «первая перчатка на правую руку, вторая на левую».
Слайд 7Вывод:
Формула классической вероятности дает очень простой способ вычисления
вероятностей. Однако простота этой формулы обманчива. При ее использовании возникают два очень непростых вопроса:
Как выбрать систему исходов опыта так, чтобы они были равновозможными, и можно ли это сделать вообще?
Как найти числа т и п и убедиться в том, что они найдены верно?

Слайд 8Опыт человечества.
Вероятность попасть под дождь
в Лондоне гораздо выше, чем в пустыне Сахара.
Весь наш жизненный опыт подсказывает, что любое событие считается тем более вероятным, чем чаще оно происходит. Значит, вероятность должна быть каким-то образом связана с частотой.

Слайд 9Частота случайного события.
Абсолютной частотой случайного события А в серии из N
случайных опытов называется число NA , которое показывает, сколько раз в этой серии произошло событие А.

Слайд 10Частота случайного события.
Относительной частотой случайного события называют отношение числа появлений этого
события к общему числу проведенных экспериментов:
где А – случайное событие по отношению к некоторому испытанию,
N раз проведено испытание и при этом событие А наступило в NA случаях.

Слайд 11Примеры
Пример 1. Наблюдения показывают, что в среднем среди 1000
новорожденных детей 515 мальчиков. Какова частота рождения мальчика в такой серии наблюдений?
Ответ: 0,515

Слайд 12Примеры
Пример 2. За лето на Черноморском побережье было 67
солнечных дней. Какова частота солнечных дней на побережье за лето? Частота пасмурных дней?
Ответ: 0,728; 0,272.

Слайд 13Примеры
Пример 3. Отдел технического контроля обнаружил 5 бракованных изделий
в партии из 1000 изделий. Найдите частоту изготовления бракованных изделий.
Ответ: 0,005

Слайд 14Примеры
Пример 4. Для выяснения качества семян было отобрано и
высеяно в лабораторных условиях 1000 штук. 980 семян дали нормальные всходы. Найдите частоту нормального всхода семян.
Ответ: 0,98

Слайд 15Фундаментальным свойством относительных частот является тот факт, что с увеличением числа
опытов относительная частота случайного события постепенно стабилизируется и приближается к вполне определенному числу, которое и следует считать его вероятностью.

Слайд 16Проверка
Пример 5. Подбрасывание монеты. А – выпадает герб.
Классическая вероятность: всего 2 исхода,
1 исход события А:

Слайд 17Проверка
Пример 5. Французский естествоиспытатель Бюффон (XVIII в.) бросил монету 4040 раз,
и при этом герб выпал в 2048 случаях. Следовательно, частота выпадения герба в данной серии испытаний равна:
Жорж Бюффон

Слайд 18Проверка
Пример 5. Английский математик Карл Пирсон (1857-1936) бросал монету 24000 раз,
причем герб выпал 12012 раз. Следовательно, частота выпадения герба в данной серии испытаний равна:
Карл Пирсон

Слайд 19Результаты
Вывод
Пример 5 подтверждает естественное предположение о том, что вероятность выпадения герба
при одном бросании монеты равна 0,5.

Слайд 20Статистическая вероятность
Вероятность случайного события приближенно равна частоте этого события,
полученной при проведении большого числа случайных экспериментов: , где — число испытаний, в которых наступило событие А, N – общее число испытаний.

Слайд 21Задача №1.
Чтобы определить, как часто встречаются в лесопарке деревья разных
пород, ребята провели следующие эксперименты. Каждый выбрал свою тропинку и по пути следования записывал породу каждого десятого дерева.
Результаты были занесены в таблицу:
Породы Сосна Дуб Береза Ель Осина Всего
Число деревьев 315 217 123 67 35 757
Оцените вероятность того, что выбранное наугад в этом парке дерево будет:
а) сосной;
б) хвойным;
в) лиственным.
Указание. Ответ запишите в виде десятичной дроби с тремя знаками после запятой.

Слайд 22Задача №1.
Решение:
а) A={выбранное наугад в парке дерево — сосна}
NА = 315, N = 757, Р(А) = 315/757 0,416;
б) В ={выбранное наугад в парке дерево — хвойное} NА = 315 + 67 = 382, N = 757.
Р(А) = 382/757 0,505;
в) C = {выбранное наугад в парке дерево — лиственное} NА = 217 + 123 + 35 = 375, N = 757.
Р(А) = 375/757 0,495.

Слайд 23 По статистике, на каждые 1000 лампочек приходится 3 бракованные.
Какова вероятность купить исправную лампочку?
Решение:
3/1000 = 0,003
1 – 0,003 = 0,997
Задача №2.

Слайд 24 Демографы утверждают, что вероятность рождения близнецов равна 0,012. в
скольких случаях из 10 000 рождений можно ожидать появление близнецов?
Решение:
Ответ: в 120 случаях.
Задача №3.

Слайд 25Домашнее задание.
Задача №1. По статистике в городе Новинске
за год из каждой 1000 автомобилистов два попадают в аварию. Какова вероятность того, что автомобилист в этом городе весь год проездит без аварий?
Задача №2. Чтобы определить, какой цвет волос встречается в городе чаще, а какой реже, студенты за полчаса провели следующий эксперимент. Каждый выбрал свой маршрут и записывал по пути следования цвет волос каждого пятого встречного. Результаты были занесены в следующую таблицу:
Цвет волос Брюнеты Шатены Рыжие Блондины Всего
Число людей 198 372 83 212 865
Оцените вероятность того, что выбранный наугад житель этого города будет:
а) шатеном;
б) рыжим;
в) не рыжим.

Каждый год учителя жалуются на то, что падает
интерес у учеников к учебе, и каждый год
усложняются задания ГИА и ЕГЭ. Вот уже и элементы
теории вероятностей стали полноправными
заданиями в тестах. Этой теме в школьном курсе не
уделялось должного внимания и казалось, что
сложно будет побороть страх учеников перед этими
задачами. Но мы, учителя, поняли, что т.к. изменить
ситуацию невозможно, под нее надо
подстраиваться.
Проанализировав демонстрационные варианты,
убедилась, что для успешного решения указанных
задач необходимо повторить (а может быть выучить)
основные положения теории вероятностей.
Прежде всего, напомним учащимся, что же изучает
этот раздел математики?
Наблюдая со стороны за различными явлениями
или участвуя в проведении опытов, мы замечаем,
что некоторое явление может произойти, а может и
нет. Те события, исход которых предсказать
нельзя, назовем случайным.
Например, нельзя заранее предсказать будет ли
цифра «6» в номере машины, проезжающей сейчас
мимо вас, будет ли вынут именно красный шар из
коробки, в которой 4 шара разного цвета?
Предсказать исход одного испытания мы не можем, а
вот подсчитать вероятность его наступления при
большом количестве произведенных однородных
испытаний – это под силу теории вероятностей.
Основная формула классической вероятности
всего одна: , где n
– число благоприятных исходов, m – общее число
исходов.
При этом надо подчеркивать, что общее число
исходов конечно и все исходы равнозначны (в
противном случае применение этой формулы
невозможно, т.к. получим неверный результат).
Ученики школы среднего и старшего звена
знакомятся только со случайными событиями.
Причем, это знакомство в основном опирается на их
жизненный опыт, интуицию.
В своей повседневной жизни мы часто повторяем:
«с достаточной долей вероятности…», «мне
кажется невероятно, что это произойдет», «почти
со 100% вероятностью можно утверждать…». Этими
фразами мы, опираясь на знания предыдущих лет (а
иногда и на интуицию) прогнозируем исход
какого-то события. Однако, не смотря на наш
прогноз, указанное событие может произойти, а
может и нет. Так, купив лотерейный билет, мы
рассчитываем, конечно, на выигрыш. Подбрасывая
монету, скажем, 4 раза, предполагаем, что «орел» и
«решка» выпадут по 2 раза. Но проделав этот
нехитрый опыт, убеждаемся, что это совсем не так в
реальности. Вот тогда и возникает вопрос: а
сколько раз надо бросить монету, что б
вероятность выпадения нужной стороны её была
почти 50%?
На все эти вопросы и отвечает теория
вероятностей. Она дает возможность численно
характеризовать возможность наступления того
или иного события.
Еще очень важным моментом в подсчете
вероятности наступления события, является то,
что все испытания и их исход договорились
считать равновозможными (равновероятными).
Что это значит?
Рассмотрим, например, опыт, с однократным
подбрасыванием монеты. В реальной жизни может
быть несколько исходов: выпадет «орел», выпадет
«решка», монета встанет на ребро, укатится
куда-нибудь. Кроме того, при многократном
подбрасывании, может оказаться, что выпадение,
скажем, «орла» намного чаще, чем «решки».При
детальном исследовании монеты оказалось, что на
сторону «герба»ушло больше металла(при отливке
монеты) и эта сторона тяжелее. Может сказаться и
неоднородность металла при плавке, порыв ветра
при бросании монеты, неровность поверхности, на
которую падает монета и т.д. Чтоб исход испытания
не зависел от этих частностей, договорились
считать монету «правильной» или «симметричной»,
т.е. одинаковой по весу с обеих сторон, падающей
на одну и ту же плоскость в безветренную погоду.
Аналогично надо считать симметричными игральный
кубик и игральные кости при бросании их во время
эксперимента.
Следует предостеречь учеников от неверного
способа решения задач рассуждением, без учета
всех возможностей исходов. Приведу пример.
Задача. Бросают два игральных кубика.
Найти вероятность того, что сумма выпавших очков
будет равна пяти.
Ошибочное решение. В данной ситуации
возможны два исхода: либо сумма будет равна пяти,
либо не будет. Значит, общее число исходов – два,
а из них благоприятных – один (т.е. сумма равна
пяти). Значит, по формуле вероятности:
В чем ошибка ученика? Как мы знаем, каждый кубик
имеет 6 граней, на которых расположены точки от
одной до шести. Бросая оба кубика одновременно,
число очков, выпавших на первом кубике, не
зависит от того, какое число очков в это время
выпадет на втором. Т.е. шесть исходов первого
кубика сочетаются с шестью исходами второго. И
общее число равновозможных исходов: 6 • 6 = 36.
Тогда, благоприятных исходов, т.е. сумма равна
пяти будет 4 : 3+2; 2+3; 1+4; 4+1. Следовательно, ответ на
вопрос задачи:
Очень уместно здесь познакомить учеников со
знаменитой ошибкой Даламбера.
Пример. Ошибка Даламбера. Какова
вероятность, что подброшенные, вверх две
правильные монеты упадут на одну и ту же сторону?
Решение, предложенное Даламбером. Опыт
имеет три равновозможных исхода:
1) обе монеты упали на «орла»;
2) обе монеты упали на «решку»;
3) одна из монет упала на «орла», другая на
«решку».
Из них благоприятными для нашего событиями
будут два исхода, поэтому искомая вероятность
равна .
Правильное решение. Опыт имеет четыре
равновозможных исхода:
1) первая монета упала на «орла», вторая тоже на
«орла»;
2) первая монета упала на «решку», вторая тоже на
«решку»;
3) первая монета упала на «орла», вторая – на
«решку»;
5) первая монета упала на «решку», вторая – на
«орла».
Из них благоприятными для нашего события будут
два исхода, поэтому искомая вероятность равна
Даламбер совершил одну из самых
распространенных ошибок, допускаемую при
вычислении вероятности: он объединил два
принципиально разных исхода в один. Чтобы не
повторить эту ошибку, помните, что природа
различает все предметы, даже если внешне
они для нас неотличимы.
Надо напоминать учащимся, что нужно
анализировать полученный результат: найденная
вероятность не может быть больше 1, как не может,
например, упасть на землю яблок больше, чем их
находится на дереве. Что при бросании монеты,
вероятность выпадения «орла» или «решки» почти
одинакова, а вот вероятность, скажем, отказа
тормозов у автомобиля добросовестного водителя,
крайне мала. Поэтому учащиеся должны помнить, что
p є [0;1].
Крайне редко, но бывают задания, где
вероятность оказывается равной нулю (нулевая
вероятность). События, вероятность которых равна
нулю называются невозможными. Например,
сумма выпавших очков на двух костях равна 13 (мы
знаем, что максимальное число очков одной грани
– 6, значит для двух граней – 12).
Если же вероятность равна 1 (иногда говорят
«стопроцентная вероятность»), то событие
называем достоверным. Примером может служить
опыт с игральным кубиком и утверждение, что при
подбрасывании выпало не более 6 очков.
Все остальные события, вероятность которых
находится в интервале (0;1), будем называть случайными.
Они и составляют основную часть задач в теории
вероятностей. Их-то и решают по уже упомянутой
формуле.
Хочется еще раз напомнить, что половина успеха
в решении той или иной задачи (совсем
необязательно по теории вероятностей) заложена
во внимательном чтении условия. Очень много
ошибок допускают ученики торопясь сделать
задание, которое, как кажется, им знакомо и, не
вникнув в исходные данные, допускают
непростительные ошибки.
Приведу пример двух похожих, но абсолютно
разных по смыслу (и, естественно, по способу
решения) задач.
Задача №1. Фабрика выпускает сумки. В
среднем, на 100 сумок, приходится 8 сумок со
скрытыми дефектами. Найдите вероятность того,
что купленная сумка окажется качественной. (Если
необходимо, результат округлите до сотых).
Решение. Вероятность найдем по
формуле: .
Здесь из 100 сумок 8 некачественных, следовательно,
остальные качественные, т.е. 100 – 8 = 92 сумки.
m = 100,
n = 92
Ответ: 0,92
Задача №2. Фабрика выпускает сумки. В
среднем, на каждые 100 качественных сумок
приходится 8 сумок со скрытыми дефектами. Найдите
вероятность того, что купленная сумка окажется
качественной. (Если необходимо, результат
округлите до сотых).
Решение. Вероятность найдем по формуле: . В этой задаче, в
отличие от предыдущей общее количество сумок
складывается из качественных ( 100 штук) и
некачественных (8 штук), т.е. m = 100 + 8 = 108 .
Среди этих 108 сумок, качественных было 100 штук, n
= 100
Ответ: 0,93
Литература.
- Бунимович Е.А., Булычев В.А. «Вероятность и
статистика» .М «Дрофа». 2002г. - Колмогоров А.Н.и др. Введение в теорию
вероятностей.. М. «Наука» 1982г. - Скопец З.А. «Дополнительные главы по курсу
математики». М. «Просвещение» .1974г. - Чистяков В.П. «Курс теории вероятностей». М.
«Наука» 1982г.

Статистическое |
|
определение |
|
вероятности |
|
Вероятность как предельное |
|
значение частоты. |

|
Самостоятельная работа |
|||
|
Вариант 1 |
Вариант 2 |
Вариант 3 |
Вариант 4 |
|
1. |
На столе 12 |
1. В коробке 24 |
1.В лотерее 100 |
1.В вазе 7 |
|
|
кусков пирога. В |
карандаша, из |
билетов, из них 5 |
цветков, из них 3 |
||
|
трех |
них 3 красного |
выигрышных. |
розы. Из букета |
||
|
«счастливых» из |
цвета. Из |
Какова |
наугад |
||
|
них запечены |
коробки наугад |
вероятность |
вынимается |
||
|
призы. Какова |
вынимается |
выигрыша? |
цветок. Какова |
||
|
вероятность |
карандаш. |
вероятность того, |
|||
|
взять |
Какова |
что это роза? |
|||
|
«счастливый» |
вероятность того, |
||||
|
кусок пирога? |
что он красный? |
||||
|
2. В урне 15 |
2. Из чисел от 1 |
2. В корзине |
2. В корзине 10 |
||
|
белых и 25 |
до 25 наудачу |
лежат 5 яблок и 3 |
яблок, из них 4 |
||
|
черных шаров. |
выбрано число. |
груши. Из |
червивых. |
||
|
Из урны наугад |
Какова |
корзины наугад |
Какова |
||
|
выбирается один |
вероятность того, |
вынимается один |
вероятность того, |
||
|
шар. Какова |
что оно окажется |
фрукт. Какова |
что любое взятое |
||
|
вероятность того, |
кратным 5? |
вероятность того, |
наугад яблоко |
||
|
что он будет |
что это яблоко? |
окажется не |
|||
|
белым? |
червивым? |

СТАТИСТИЧЕСКОЕ
ОПРЕДЕЛЕНИЕ
ВЕРОЯТНОСТИ

Ошибка Даламбера.
Жан Лерон Даламбер
(1717 -1783)
Великий французский философ и математик Даламбер вошел в историю теории вероятностей со своей знаменитой ошибкой, суть которой в том, что он неверно определил равновозможность исходов в опыте всего с двумя монетами!

Ошибка Даламбера.

|
Решение Даламбера: |
Правильное решение: |
||
|
Опыт имеет три |
Опыт имеет четыре |
||
|
равновозможных исхода: |
равновозможных исхода: |
||
|
1) |
обе монеты упадут на |
1) |
обе монеты упадут на «орла»; |
|
«орла»; |
2) |
обе монеты упадут на |
|
|
2) |
обе монеты упадут на |
«решку»; |
|
|
«решку»; |
3) |
первая монета упадет на |
|
|
3) |
одна из монет упадет на |
«орла», вторая на «решку»; |
|
|
«орла», другая на |
4) |
первая монета упадет на |
|
|
«решку». |
«решку», вторая на «орла». |
|
Из них благоприятными |
Из них благоприятными будут |
||||||
|
будут два исхода. |
2 |
два исхода. |
2 |
1 |
|||
|
n 3, m 2, P(A) m |
n 4, m 2, P(A) m |
||||||
|
n |
3 |
n |
4 |
2 |

Опыт «Выбор перчаток». В коробке лежат 3 пары |
|
одинаковых перчаток. Из нее, не глядя, вынимаются |
|
две перчатки. Перечислите все равновозможные |
|
исходы. |
Какой вариант решения правильный:
|
1-ый вариант: |
2-ой вариант: |
||
|
3 исхода: |
4 исхода: |
||
|
1) «обе перчатки на левую руку», |
1) «обе перчатки на левую руку», |
||
|
2) «обе |
2) «обе |
||
|
перчатки на правую руку», |
перчатки на правую руку», |
||
|
3) «перчатки на |
3) «первая |
||
|
разные руки». |
перчатка на левую руку, вторая на |
||
|
правую», |
4) «первая |
||
|
перчатка на правую руку, вторая |
|
|
Правило: природа различает все предметы, даже если внешне они |
|
|
для нас неотличимы. |
на левую». |

Вывод:
Формула классической вероятности дает очень простой способ вычисления вероятностей. Однако простота этой формулы обманчива. При ее использовании возникают два очень непростых вопроса:
1.Как выбрать систему исходов опыта так, чтобы они были равновозможными, и можно ли это сделать вообще?
2.Как найти числа т и п и убедиться в том, что они найдены верно?

ПРОБЛЕМНЫЙ ВОПРОС 1: А можно ли вычислить вероятность события с помощью ряда экспериментов?

Опыт человечества.
Вероятность попасть под дождь в Лондоне гораздо выше, чем в пустыне Сахара.
Весь наш жизненный опыт подсказывает, что любое событие считается тем более вероятным, чем чаще оно происходит. Значит, вероятность должна быть каким- то образом связана с частотой.

Частота случайного события. |
|
Абсолютной частотой |
|
случайного события А в серии |
|
из N случайных опытов |
|
называется число NA , которое |
показывает, сколько раз в этой серии произошло событие А.
Соседние файлы в папке Пз 1
- #
- #
- #
- #
Пример 1. Правильная монета подбрасывается 2 раза.
Событие A: Выпадение хотя бы одного “орла”.
Решение. Число возможных исходов в серии из двух испытаний равно 4:
ОО, ОР, РО, РР.
Число исходов, благоприятствующих событию A, равно 3:
ОО, ОР, РО.
Следовательно,
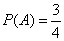
Пример 2. В семье имеется 2 ребенка.
Событие A: Хотя бы один из детей – мальчик.
Решение. Задача по своей сути не отличается от предыдущей. Только под испытанием теперь следует понимать рождение ребенка. Если рождение мальчика или девочки в одном испытании представляют собой случайные события, то число равновероятных исходов равно 4:
ММ, МД, ДМ, ДД.
Только первые 3 исхода благоприятствуют событию A. Поэтому
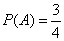
Ошибочное решение. Число возможных вариантов в серии из двух испытаний равно 3:
ММ, МД, ДД.
Первые два исхода благоприятствуют событию A. Поэтому
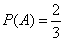
Анализ. Три события:
“2 мальчика”,
“1 мальчик и одна девочка” и
“2 девочки”
не являются равновозможными, поскольку ММ и ДД представляют собой элементарные события, тогда как событие “1 мальчик и одна девочка” – составное событие, которое разлагается на 2 исхода: МД и ДМ.
Любопытно, что подобную ошибку в рассуждениях допустил в свое время великий математик Даламбер, рассматривая задачу о подбрасывании монеты (см. Пример 1).
Разработка урока по теории вероятности
Тема: Классическое определение вероятности
Цель:
Создать условия для осознания и осмысления блока новой учебной информации.
Задачи:
— Способствовать запоминанию основной терминологии, умению устанавливать события вероятности;
— формировать умение упорядочить полученные знания для рационального применения;
— развитие навыков учащихся в вычислении классической вероятности;
формирование вероятностного мышления;
— способствовать развитию интереса к математике; умений применять новый материал на практике и в жизни.
Оборудование к уроку: доска, компьютер с проектором, игральные кубики, монеты.
Ход урока:
Урок сопровождается компьютерной презентацией.
1. Организационный момент.
Сообщить тему урока и сформулировать его цели.
2. Вступительное слово учителя.
Случай, случайность – с ними мы встречаемся повседневно: случайная встреча, случайная поломка, случайная находки, случайная ошибка. Этот ряд можно продолжать бесконечно. Казалось бы, тут нет места для математики – какие уж законы в царстве Случая! Но и здесь наука обнаружила интересные закономерности – они позволяют человеку уверенно чувствовать себя при встрече со случайными событиями.
Как наука теория вероятности зародилась в 17в. Возникновение понятия вероятности было связано как с потребностями страхования, получившего значительное распространение в ту эпоху, когда заметно росли торговые связи и морские путешествия, так и в связи с запросами азартных игр.
Слово “азарт”, под которым обычно понимается сильное увлечение, горячность, является транскрипцией французского слова hazard, буквально означающего “случай”, “риск”. Азартными называют те игры, а которых выигрыш зависит главным образом не от умения игрока, а от случайности.
Схема азартных игр была очень проста и могла быть подвергнута всестороннему логическому анализу. Первые попытки этого рода связаны с именами известных учёных – алгебраиста Джероламо Кардано (1501 – 1576) и Галилео Галилея (1564 – 1642). Однако честь открытия этой теории, которая не только даёт возможность сравнивать случайные величины, но и производить определенные математические операции с ними, принадлежит двум выдающимися ученым – Блезу Паскалю (1623 – 1662) и Пьеру Ферма. Ещё в древности было замечено, что имеются явления, которые обладают особенностью: при малом числе наблюдений над ними не наблюдается никакой правильности, но по мере увеличения числа наблюдений всё яснее проявляется определенная закономерность. Всё началось с игры в кости.
Азартные игры практиковались в ту пору главным образом среди знати, феодалов и дворян. Особенно распространенной была игра в кости. Было замечено. что при многократном бросании однородного кубика, все шесть граней которой отмечены соответственно числами 1, 2, 3, 4, 5, 6 число очков от 1 до 6 выпадают в среднем одинаково часто, иными словами, выражаясь языком математики, выпадение определённого числа очков имеет вероятность, равную 1/6 (т.е. отношению числа случаев, благоприятствующих событию к общему числу всех случаев). Аналогично вероятность появления на верхней грани кости чётного числи очков равна 3/6 ,так как из шести равновозможных случаев чётное число появляется только в трёх.
Решение порой довольно сложных задач, с которыми обращались заинтересованные лица к Паскалю, Ферма, Гюйгенсу, способствовало разработке основных понятий и общих принципов теории вероятностей, в том числе и правил действия над ними. Отсюда не следует, конечно, заключать, что основоположники теории вероятностей рассматривали азартные игры как единственный или главный предмет разрабатывавшейся ими новой отрасли науки.
На развитие теории вероятностей оказали влияние более серьёзные потребности науки и запросы практики, в первую очередь страховое дело, начатое в некоторых странах ещё в 16в. В 16-17вв. учреждение страховых обществ и страхование судов от пожара распространились во многих европейских странах.
Азартные игры были для ученых только удобной моделью для решения задач и анализа понятий теории вероятности. Об этом заметил ещё Гюйгенс в своей книге “О расчётах в азартной игре” (1657), которая была первой книгой в мире по теории вероятностей. Он писал: “…при — внимательном изучении предмета читатель заметит, что он занимается не только игрой, а что здесь даются основы глубокой и весьма интересной”. Гюйгенс впервые ввёл важное для теории вероятностей понятие математического ожидания, которое получило дальнейшее развитие а трудах Даниила Бернулли, Даламбера и др. Понятие математического ожидания находит немало применений а разных других областях человеческой деятельности.
Таким образом, в 60-е годы 17в. были выработаны первые понятия и некоторые элементы теории вероятностей. В последующие два века учёные столкнулись с множеством новых задач, связанных с исследованием случайных явлений.
Во второй половине XIX века основной вклад внесли русские учёные П. Л. Чебышев, А. А. Марков и А. М. Ляпунов. В это время были доказаны закон больших чисел, центральная предельная теорема, а также разработана теория цепей Маркова. Современный вид теория вероятностей получила благодаря аксиоматизации, предложенной Андреем Николаевичем Колмогоровым. В результате теория вероятностей приобрела строгий математический вид и окончательно стала восприниматься как один из разделов математики.
Классическое определение теории вероятности
Вероятностью события является сумма вероятностей исходов, благоприятствующих этому событию.
Ну а если же вероятное пространство построено из равно возможных исходов — то класическая теорема примет вид:
Вероятностью события называется отношение числа благоприятствующих этому событию исходов к общему числу равновозможных исходов.
Другими словами если мы кидаем одну игральную кость, то шанс выпада четверки будет 1/6.
Где 1 — число благоприятствующих событий (четверка ведь в кости одна), а 6 — общее число исходов (всего 6 сторон у игральной кости).
Так же вероятность представляется в виде:
- Простой дроби: 1/6
- Десятичной дроби: 0.1666666(6)
- Процентах 16.66%
А как подсчитать вероятность случайного события? Ведь оно произошло случайно, значит, не подчиняется закономерностям. Оказывается, и в мире случайного действуют определенные законы.
Этим занимается раздел математики, который называется «теорией вероятностей».
Возьмите в руки кубики.
При бросании кубика сколько различных элементарных событий может произойти? (6)
Сколько событий благоприятных событию «выпадет 4»? (1)
Сформулируем правило:
- Число всех возможных исходов –n
- Все исходы равновозможны
- Количество благоприятных исходов – m
- P(A) – вероятность события А
P(A) = mn
Слово вероятность по-французски — probabilite, по-английски – probability.
Учащимся предлагается по учебнику прочитать правило вычисления вероятностей.
Первичное закрепление изученного.
Событием называется результаты опытов, испытаний или наблюдений.
Задача: исследовать виды событий. Для этого:
1. Приведите примеры событий.
Пользуясь образцом: играется шахматная партия – испытание. Выигрыш, ничья, проигрыш его возможные исходы события.
У больного определили 1-ую группу крови. Проверка группы крови – испытание, 1-я группа крови событие.
2. Какие бывают события?
Достоверное – если оно обязательно произойдет, например, в ящике 10 белых шаров, то событие извлеченный шар – белый – достоверное.
Невозможное — если оно заведомо не может произойти в данном испытании, например, в ящике 10 белых шаров, то событие вытащить черный шар — невозможное.
Случайное событие – которое в данном испытании может произойти, а может и не произойти, например, если при бросании монеты событие – выпал герб — случайное. Попробуйте придумать свои примеры и оформить все, что вы узнали в виде схемы.
Справка: Событие называют случайным, если оно может произойти, а может и не произойти.
Выполните следующие испытания:
1) Подбросьте монету 50 раз. Посчитайте сколько раз
а) выпадет орел.
б) Подбросьте монету 20 раз. Посчитайте сколько раз выпал орел.
в) Как сравнить результаты?
Может вы приведете свои примеры?
На учениях по стрельбе из винтовки стрелок попадал 8 раз из 10 выстрелов.
Какова частота поражения цели у этого спортсмена и сколько попаданий в цель можно ожидать от него на соревнованиях, если каждый участник будет стрелять 30 раз?
Возможные исходы испытаний можно найти путем правдоподобных рассуждений основанных на практическом опыте и здравом смысле.
Пример: Возьмем игральный кубик, то при бросании этого кубика каковы шансы выпадения на его верхней грани 1, 2, 3, 4, 5, 6 очков (одинаковы, т.к. нет оснований считать, что выпадение одного из очков, например 6 более вероятно, чем 2).
Говорят, что вероятность выпадения на верхней грани кубика одного числа очков, например 3 равна 1/6.
А события, имеющие одинаковую вероятность называются равновозможными.
Так что такое вероятность события?
От какого слова произошло это понятие?
Задача Даламбера – французский математик (1717-1783). Найти вероятность того, что при подбрасывании двух монет на обеих монетах выпадут цифры.
После выполнения заданий в группах переходим к отчету групп и подведению итогов.
Теперь давайте ответим на вопросы:
1. Какие события вы узнали? И что такое событие?
2. Что такое относительная частота события?
3. Какова вероятность невозможного события?
4. Какова вероятность достоверного события?
5. В каких пределах находится вероятность?
6. Как называются 2 события, имеющие одинаковую вероятность?
II этап.
А теперь попытаемся выполнить работу.
1. В каждое из приведенных ниже предложении впиши наиболее подходящее по смыслу слово, выбрав его из слов возможно, невозможно, наверняка, маловероятно.
1) Завтра солнце … взойдет на востоке.
2) …, что бутерброд упадет маслом вниз.
3) …, что у Анастасии день рождения 30 февраля.
4) …, что в Самаре на улице ты встретишь тигра.
2. Запиши номера тех пар событий, которые, по твоему мнению имеют равные шансы произойти в результате одного испытания (т.е. равновозможны).
1) Появление орла и появление решки в результате одного испытания.
2) Выпадения одного очка и выпадение шести очков в результате броска игрального кубика.
3) выпадение одного очка и выпадение одного из четных очков (т.е. 2, либо 4, либо 6).
3. В ящике лежат 1 черная и 2 белых шашки. Саша хочет, не глядя, вытащить черную шашку, он вынимает и это оказывается белая шашка, после чего он кладет ее в карман и делает еще одну попытку. Как ты думаешь, при второй попытке шансы Саши вытащить черную шашку
1) увеличились.
2) уменьшились.
3) остались прежними.
Запиши номер нужного ответа.
Задача
Бросают одну игральную кость. Вычислить вероятность события «выпало четное число очков».
Решение: N = 6; N(A) = 3; P(A) = .
Задача: Ошибка Даламбера
Какова вероятность, что подброшенные вверх две правильные монеты упадут на одну и ту же сторону?
Решение, предложенное Даламбером.
Опыт имеет три равновозможных исхода:
- Обе монеты упали на «орла».
- Обе монеты упали на «решку».
- Одна из монет упала на «орла», другая на «решку».
N = 3; N(A) = 2; P(A) = .
Учащимся предложить подбросить две монеты и найти ошибку в предложенном решении.
Правильное решение.
- Орел, орел
- Решка, решка
- Орел, решка
- Решка, орел
N = 4; N(A) = 2; P(A) = .
Нельзя объединять два принципиально разных исхода в один. Природа различает все предметы.
Какие из следующих событий – случайные, достоверные, невозможные:
- черепаха научиться говорит;
- вода в чайнике, стоящим на горячей плите закипит;
- ваш день рождения – 19 октября
- день рождение вашего друга – 30 февраля;
- вы выиграете участвуя в лотереи;
- вы не выигрываете, участвуя в беспроигрышной лотереи;
- вы проиграете партию в шахматы;
- на следующей недели испортиться погода;
- вы нажали на звонок, а он не зазвонил;
- после четверга будет пятница;
- после пятницы будет воскресенье.
Для каждого из перечисленных событий определите, какое оно: достоверное, возможное, невозможное
- летом у школьников будут каникулы;
- 1 июля в Норильске будет солнечно;
- после уроков дежурные уберут кабинет;
- в 11-м классе школьники не будут изучать алгебру;
- зимой выпадает снег;
- при включении света, лампочка перегорит;
- вы выходите на улицу, а на встречу вам идет слон.
Придумайте и запишите в тетрадь события, чтобы они соответствовали знакам в таблице например, событие 8 должно быть очень вероятным.
|
Событие |
1 |
2 |
3 |
4 |
5 |
6 |
7 |
8 |
|
Достоверное |
|
|
|
|||||
|
Возможное |
|
|
|
|||||
|
невозможное |
|
|
V. Подведение итогов.
Какие ключевые слова урока можно выделить?
Объясните их значение.
Какой ключевой факт сегодня изучен?
Что общего и в чем отличие статистики и вероятности?
Завершить урок хочется такой историей.
— Доктор, — спрашивает пациент – пойдут ли у меня дела на поправку?
— Несомненно, — отвечает врач, — потому что статистика говорит, что один из ста выздоравливает при этой болезни.
— Но почему же при этом именно я должен выздороветь?
— Потому что вы как раз и есть мой сотый пациент.
Домашнее задание:
Составить 2 задачи на вероятность.
Разбить учеников на тройки. Каждая тройка пишет реферат на одну из тем:
- Даниил Бернулли и его вклад в развитие теории вероятностей.
- Гюйгенс и его вклад в развитие теории вероятностей
- Блез Паскаль и его вклад в развитие теории вероятностей
- Ферма и его вклад в развитие теории вероятностей
Литература
- Ю.Н.Макарычев, Н.Г.Миндюк. Начальные сведения из теории вероятностей в школьном курсе алгебры. “Математика в школе”. № 7. 2004 г. стр. 24.
- В.А.Булычев, Е.А.Бунимович. Изучение теории вероятностей и статистики в школьном курсе математики. “Математика в школе”. № 4. 2003 г. стр. 59.
Электронные источники информации
- Бунимович Е.А., Булычев В.А. Вероятность и статистика 5-9. Электронное учебное пособие на CD-ROM. – М.: Дрофа, 2003.
- www.teorver.ru
- http://ru.wikipedia.org/wiki/Теория_вероятности.
Описание презентации по отдельным слайдам:
-
-
2 слайд
Статистическое определение вероятности
Вероятность как предельное значение частоты.
-
3 слайд
Ошибка Даламбера.
Великий французский философ и математик Даламбер вошел в историю теории вероятностей со своей знаменитой ошибкой, суть которой в том, что он неверно определил равновозможность исходов в опыте всего с двумя монетами!
Жан Лерон Даламбер
(1717 -1783) -
4 слайд
Ошибка Даламбера.
Опыт. Подбрасываем две одинаковые монеты. Какова вероятность того, что они упадут на одну и ту же сторону?Решение Даламбера:
Опыт имеет три
равновозможных исхода:
1) обе монеты упадут на «орла»;
2) обе монеты упадут на «решку»;
3) одна из монет упадет на «орла», другая на «решку».
Из них благоприятными
будут два исхода.Правильное решение:
Опыт имеет четыре
равновозможных исхода:
1) обе монеты упадут на «орла»;
2) обе монеты упадут на «решку»;
3) первая монета упадет на «орла», вторая на «решку»;
4) первая монета упадет на «решку», вторая на «орла».
Из них благоприятными будут
два исхода. -
5 слайд
Вывод:
Формула классической вероятности дает очень простой способ вычисления вероятностей. Однако простота этой формулы обманчива. При ее использовании возникают два очень непростых вопроса:
Как выбрать систему исходов опыта так, чтобы они были равновозможными, и можно ли это сделать вообще?
Как найти числа т и п и убедиться в том, что они найдены верно? -
6 слайд
ПРОБЛЕМНЫЙ ВОПРОС 1:
А можно ли вычислить вероятность события с помощью ряда экспериментов? -
7 слайд
Опыт человечества.
Вероятность попасть под дождь в Лондоне гораздо выше, чем в пустыне Сахара.
Весь наш жизненный опыт подсказывает, что любое событие считается тем более вероятным, чем чаще оно происходит. Значит, вероятность должна быть каким-то образом связана с частотой. -
8 слайд
Частота случайного события.
Абсолютной частотой случайного события А в серии из N случайных опытов называется число NA , которое показывает, сколько раз в этой серии произошло событие А. -
9 слайд
Частота случайного события.
Относительной частотой случайного события называют отношение числа появлений этого события к общему числу проведенных экспериментов:где А – случайное событие по отношению к некоторому испытанию,
N раз проведено испытание и при этом событие А наступило в NA случаях. -
10 слайд
Пример
Наблюдения показывают, что в среднем среди 1000 новорожденных детей 515 мальчиков. Какова частота рождения мальчика в такой серии наблюдений?
Ответ: 0,515 -
11 слайд
ПРОБЛЕМНЫЙ ВОПРОС 2:
Может быть, относительную частоту и нужно принять за вероятность? -
12 слайд
Фундаментальным свойством относительных частот является тот факт, что с увеличением числа опытов относительная частота случайного события постепенно стабилизируется и приближается к вполне определенному числу, которое и следует считать его вероятностью.
-
13 слайд
Статистическая вероятность
Вероятность случайного события приближенно равна частоте этого события, полученной при проведении большого числа случайных экспериментов: , где — число испытаний, в которых наступило событие А, N – общее число испытаний. -
14 слайд
По статистике, на каждые 1000 лампочек приходится 3 бракованные. Какова вероятность купить исправную лампочку?
Решение:
3/1000 = 0,0031 – 0,003 = 0,997
Задача.
Слайд 1Понятие вероятности
Теория вероятностей, 9 класс.

Слайд 2Статистическое определение вероятности
Вероятность как предельное значение частоты.

Слайд 4СТАТИСТИЧЕСКОЕ
ОПРЕДЕЛЕНИЕ
ВЕРОЯТНОСТИ

Слайд 5Ошибка Даламбера.
Великий французский философ и математик Даламбер вошел
в историю теории вероятностей со своей знаменитой ошибкой, суть которой в том, что он неверно определил равновозможность исходов в опыте всего с двумя монетами!
Жан Лерон Даламбер
(1717 -1783)

Слайд 6Ошибка Даламбера.
Опыт. Подбрасываем две одинаковые монеты. Какова вероятность того, что они
упадут на одну и ту же сторону?
Решение Даламбера:
Опыт имеет три
равновозможных исхода:
1) обе монеты упадут на «орла»;
2) обе монеты упадут на «решку»;
3) одна из монет упадет на «орла», другая на «решку».
Из них благоприятными
будут два исхода.
Правильное решение:
Опыт имеет четыре
равновозможных исхода:
1) обе монеты упадут на «орла»;
2) обе монеты упадут на «решку»;
3) первая монета упадет на «орла», вторая на «решку»;
4) первая монета упадет на «решку», вторая на «орла».
Из них благоприятными будут
два исхода.

Слайд 7Опыт «Выбор перчаток». В коробке лежат 3 пары одинаковых перчаток. Из
нее, не глядя, вынимаются две перчатки. Перечислите все равновозможные исходы.
Какой вариант решения правильный:
Правило: природа различает все предметы, даже если внешне они для нас неотличимы.
1-ый вариант: 3 исхода: 1) «обе перчатки на левую руку», 2) «обе перчатки на правую руку», 3) «перчатки на разные руки».
2-ой вариант: 4 исхода: 1) «обе перчатки на левую руку», 2) «обе перчатки на правую руку», 3) «первая перчатка на левую руку, вторая на правую», 4) «первая перчатка на правую руку, вторая на левую».

Слайд 8Вывод:
Формула классической вероятности дает очень простой способ вычисления
вероятностей. Однако простота этой формулы обманчива. При ее использовании возникают два очень непростых вопроса:
Как выбрать систему исходов опыта так, чтобы они были равновозможными, и можно ли это сделать вообще?
Как найти числа т и п и убедиться в том, что они найдены верно?

Слайд 9ПРОБЛЕМНЫЙ ВОПРОС 1:
А можно ли вычислить вероятность события с помощью ряда
экспериментов?

Слайд 10Опыт человечества.
Весь наш жизненный опыт подсказывает, что любое событие
считается тем более вероятным, чем чаще оно происходит. Значит, вероятность должна быть каким-то образом связана с частотой.

Слайд 11Частота случайного события.
Абсолютной частотой случайного события А в серии из N
случайных опытов называется число NA , которое показывает, сколько раз в этой серии произошло событие А.

Слайд 12Частота случайного события.
Относительной частотой случайного события называют отношение числа появлений этого
события к общему числу проведенных экспериментов:
где А – случайное событие по отношению к некоторому испытанию,
N раз проведено испытание и при этом событие А наступило в NA случаях.

Слайд 13Примеры
Пример 1. Наблюдения показывают, что в среднем среди 1000
новорожденных детей 515 мальчиков. Какова частота рождения мальчика в такой серии наблюдений?
Ответ: 0,515

Слайд 14Примеры
Пример 2. За лето на Черноморском побережье было 67
солнечных дней. Какова частота солнечных дней на побережье за лето? Частота пасмурных дней?
Ответ: 0,728; 0,272.

Слайд 15Примеры
Пример 3. Отдел технического контроля обнаружил 5 бракованных изделий
в партии из 1000 изделий. Найдите частоту изготовления бракованных изделий.
Ответ: 0,005

Слайд 16Примеры
Пример 4. Для выяснения качества семян было отобрано и
высеяно в лабораторных условиях 1000 штук. 980 семян дали нормальные всходы. Найдите частоту нормального всхода семян.
Ответ: 0,98

Слайд 17ПРОБЛЕМНЫЙ ВОПРОС 2:
Может быть, относительную частоту и нужно
принять за вероятность?

Слайд 18Фундаментальным свойством относительных частот является тот факт, что с увеличением числа
опытов относительная частота случайного события постепенно стабилизируется и приближается к вполне определенному числу, которое и следует считать его вероятностью.

Слайд 19Проверка
Пример 5. Подбрасывание монеты. А – выпадает герб.
Классическая вероятность: всего 2 исхода,
1 исход события А:

Слайд 20Проверка
Пример 5. Французский естествоиспытатель Бюффон (XVIII в.) бросил монету 4040 раз,
и при этом герб выпал в 2048 случаях. Следовательно, частота выпадения герба в данной серии испытаний равна:
Жорж Бюффон

Слайд 21Проверка
Пример 5. Английский математик Карл Пирсон (1857-1936) бросал монету 24000 раз,
причем герб выпал 12012 раз. Следовательно, частота выпадения герба в данной серии испытаний равна:
Карл Пирсон

Слайд 22Результаты
Вывод
Пример 5 подтверждает естественное предположение о том, что вероятность выпадения герба
при одном бросании монеты равна 0,5.

Слайд 23Статистическая вероятность
Вероятность случайного события приближенно равна частоте этого события,
полученной при проведении большого числа случайных экспериментов: , где — число испытаний, в которых наступило событие А, N – общее число испытаний.

Слайд 24Задача №1.
Чтобы определить, как часто встречаются в лесопарке деревья разных
пород, ребята провели следующие эксперименты. Каждый выбрал свою тропинку и по пути следования записывал породу каждого десятого дерева.
Результаты были занесены в таблицу:
Породы Сосна Дуб Береза Ель Осина Всего
Число деревьев 315 217 123 67 35 757
Оцените вероятность того, что выбранное наугад в этом парке дерево будет:
а) сосной;
б) хвойным;
в) лиственным.
Указание. Ответ запишите в виде десятичной дроби с тремя знаками после запятой.

Слайд 25Задача №1.
Решение:
а) A={выбранное наугад в парке дерево — сосна}
NА = 315, N = 757, Р(А) = 315/757 ≈ 0,416;
б) В ={выбранное наугад в парке дерево — хвойное} NА = 315 + 67 = 382, N = 757.
Р(А) = 382/757 ≈ 0,505;
в) C = {выбранное наугад в парке дерево — лиственное} NА = 217 + 123 + 35 = 375, N = 757.
Р(А) = 375/757 ≈ 0,495.

Слайд 26 По статистике, на каждые 1000 лампочек приходится 3 бракованные.
Какова вероятность купить исправную лампочку?
Решение:
3/1000 = 0,003
1 – 0,003 = 0,997
Задача №2.

Слайд 27 Демографы утверждают, что вероятность рождения близнецов равна 0,012. в
скольких случаях из 10 000 рождений можно ожидать появление близнецов?
Решение:
Ответ: в 120 случаях.
Задача №3.

Слайд 28Вопросы:
Запишите формулу вычисления вероятности случайного события в классической модели. Поясните, что
означает каждая буква в этой формуле.
Запишите формулу вычисления вероятности случайного события в статистической модели. Поясните, что означает каждая буква в этой формуле.
Какому условию должны удовлетворять исходы опыта, чтобы можно было воспользоваться классическим определением вероятности?
Чему равна частота достоверного события?
Что такое абсолютная частота? относительная частота?
Как частота связана с вероятностью?
После 100 опытов частота события А оказалась равна 0, а частота события В равна 1. Можно ли сказать, что событие А невозможное, а событие В – достоверное?

Слайд 29Домашнее задание.
Задача №1. По статистике в городе Новинске
за год из каждой 1000 автомобилистов два попадают в аварию. Какова вероятность того, что автомобилист в этом городе весь год проездит без аварий?
Задача №2. Чтобы определить, какой цвет волос встречается в городе чаще, а какой реже, студенты за полчаса провели следующий эксперимент. Каждый выбрал свой маршрут и записывал по пути следования цвет волос каждого пятого встречного. Результаты были занесены в следующую таблицу:
Цвет волос Брюнеты Шатены Рыжие Блондины Всего
Число людей 198 372 83 212 865
Оцените вероятность того, что выбранный наугад житель этого города будет:
а) шатеном;
б) рыжим;
в) не рыжим.















