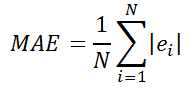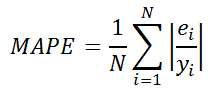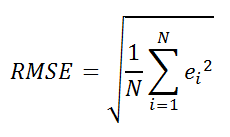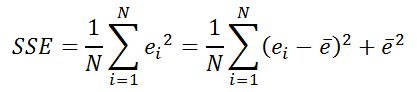history 20 февраля 2021 г.
- Группы статей
Как показано в соответствующих статьях на нашем сайте excel2.ru, исходный ряд можно сгладить разными методами:
- скользящее среднее;
- взвешенное скользящее среднее и его модификации (центрированное скользящее среднее и взвешенное центрированное скользящее среднее);
- экспоненциальное сглаживание
Какой из методов лучше сглаживает исходный ряд? Как правило, для ответа на этот вопрос вычисляются ошибки (разности) между соответствующими точками рядов (исходного и скользящего среднего), т.е. ei=yi-ŷi. Интуитивно понятно, что лучше тот метод сглаживания, суммарная ошибка которого меньше.
Виды ошибок
Суммарную ошибку можно найти несколькими способами:
Средняя абсолютная ошибка (англ. Mean Absolute Error, MAE)
Средняя абсолютная процентная ошибка (англ. Mean Absolute Percentage Error, MAPE)
Среднеквадратичная ошибка (англ. Root Mean Squared Error, RMSE)
В наших вычислениях будем использовать RMSE. Для вычисления этой ошибки в EXCEL используется следующий алгоритм:
- вычисляются ошибки (разности) между соответствующими точками рядов (исходного и скользящего среднего), т.е. ei=yi-ŷi;
- вычисляются квадраты этих ошибок (Errors Squared);
- затем находят сумму этих квадратов ошибок — SSE (Sum of the Squared Errors);
- разделив SSE на количество точек ряда скользящего среднего, получим ошибку, которая в англоязычной литературе называется MSE (Mean Squared Error). SSE имеет размерность дисперсии. Математически можно показать, что SSE равна дисперсии ошибок плюс квадрат средней ошибки (дисперсия вычисляется как для генеральной совокупности, а не как для выборки);
- И, наконец, Среднеквадратичная ошибка (RMSE) вычисляется путем извлечения квадратного корня из MSE.
Примечание: Формула для расчета Среднеквадратичной ошибки (RMSE) практически совпадает с формулой для стандартной ошибки регрессии (Standard Error of the Regression). Отличие состоит в том, что стандартная ошибка регрессии учитывает поправку на количество оцениваемых параметров (сумма квадратов ошибок делится не на n, а на n-p, где p – количество оцениваемых параметров модели). Т.к. количество параметров обычно невелико (1, 2 или 3), то при больших n различие этих значений ошибок незначительно.
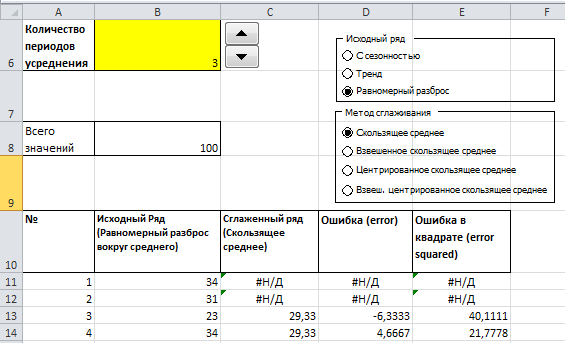
Для удобства сравнения методов сглаживания в файле примера создана соответствующая форма.
С помощью Переключателей в форме можно выбрать тип исходного ряда (С сезонностью, Растущий тренд или Равномерный разброс). Также можно выбрать один из 5 методов сглаживания и количество периодов сглаживания.
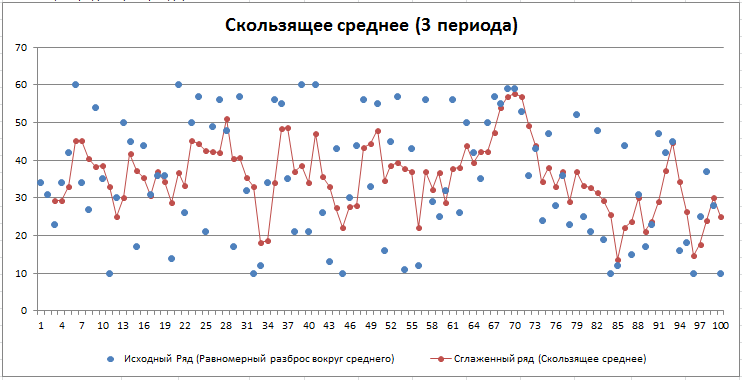
В зависимости от выбранных опций будет автоматически выведена диаграмма с исходным рядом и сглаженной кривой.
Также будет вычислена среднеквадратичная ошибка RMSE (ячейка K9 в файле примера).
Если метод сглаживания «уловил» тренд исходного ряда, то
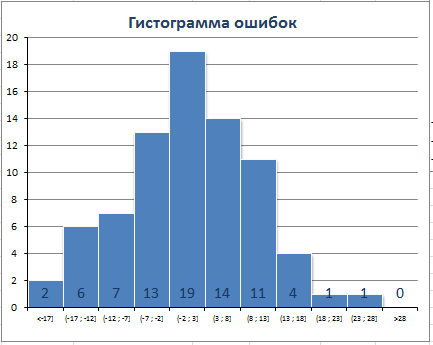
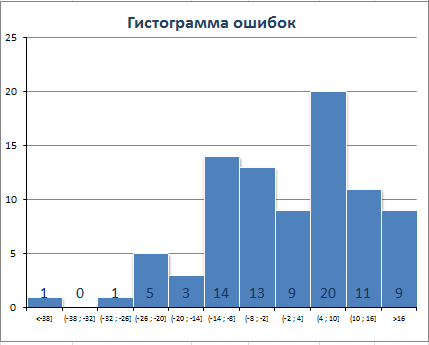
1) распределение ошибок (или остатки, англ. residuals) должно быть приблизительно нормальным со средним значением близким к 0.
Примечание: В случае, если исходный ряд представляет собой случайный равномерный разброс вокруг некоторого среднего (в MS EXCEL это можно реализовать с помощью функции СЛУЧМЕЖДУ()), то очевидно, что распределение ошибок не будет нормальным. Используя форму EXCEL для генерации трендов можно убедиться в этом непосредственно.
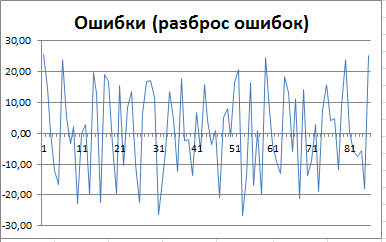
2) Разброс ошибок не должен меняться в зависимости от периода.
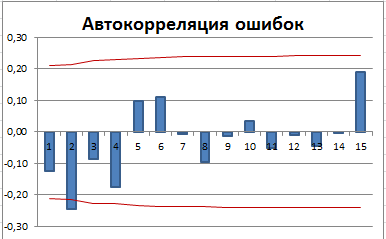
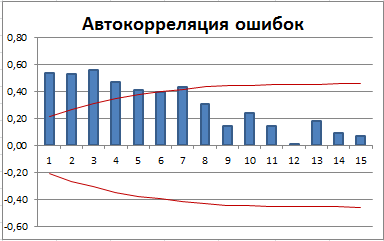
3) Должна отсутствовать автокорреляция ошибок (ошибки должны быть независимыми случайными величинами).
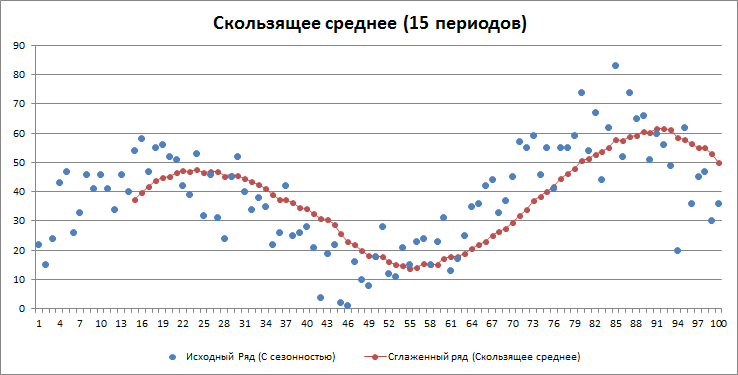
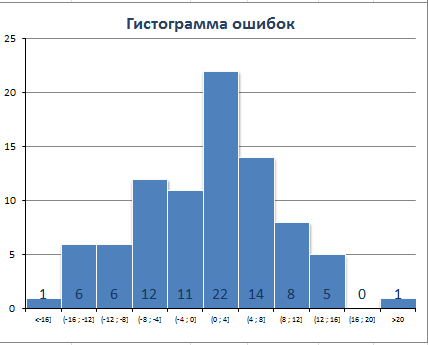
Очевидно, что при сглаживании рядов с сезонностью методом скользящего среднего ошибки не будут удовлетворять этим требованиям. Например:
Очевидно, что имеется сдвиг вправо сглаженного ряда. Это приводит к тому, что гистограмма ошибок смещена влево (левый хвост длиннее).
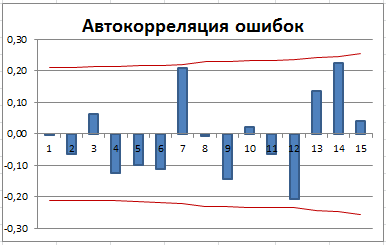
Имеется автокорреляция ошибок (для первых лагов значения автокорреляции вышли за границы 95% доверительного интервала).
Совершенно иная картина для центрированного взвешенного среднего.
Вернемся к среднеквадратичной ошибке (RMSE).
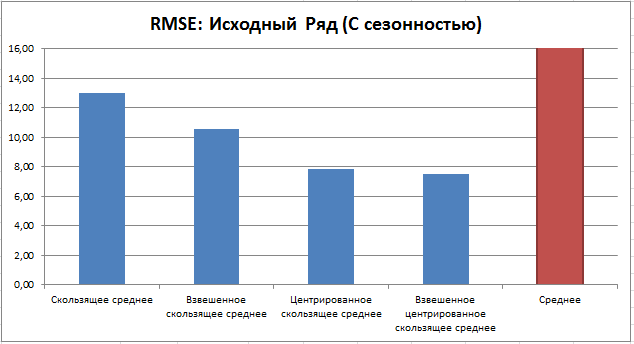
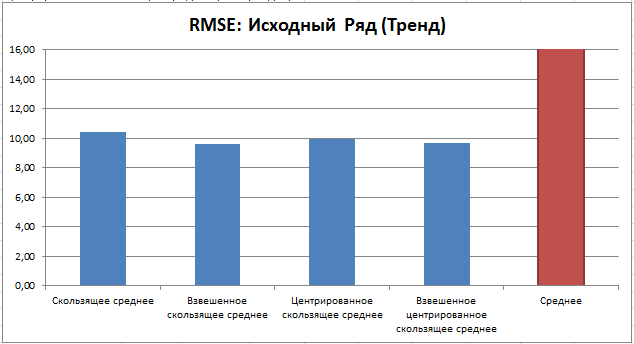
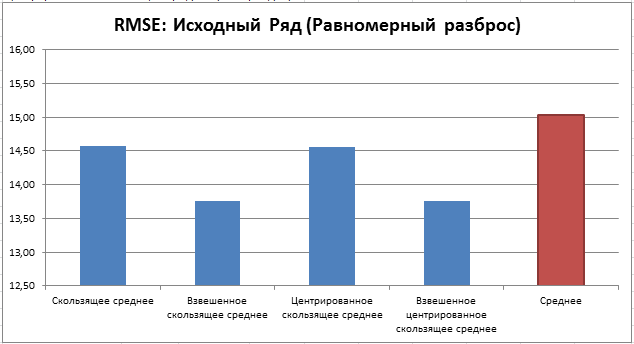
Сравним эту ошибку для различных типов исходного ряда. Сглаживание будем производить всеми 4-мя методами скользящего среднего (15 периодов) плюс вычислим среднеквадратичную ошибку относительно среднего значения исходного ряда. В итоге будем иметь 3 диаграммы:
Для рядов с сезонностью (или цикличностью), похоже, наилучшим методом сглаживания является взвешенное центрированное скользящее среднее.
В случае равномерного разброса наименьшую ошибку дают взвешенное скользящее среднее и взвешенное центрированное скользящее среднее.
|
Уравнение линии тренда дает неверный результат |
||||||||
Ответить |
||||||||
Ответить |
||||||||
Ответить |
||||||||
Ответить |
||||||||
Ответить |
Доверительный интервал для тренда в общем виде определяется как
,
(8.17)
где
— значениеt-статистики
Стьюдента;
—
средняя квадратическая ошибка тренда.
Для
учета неопределенности, связанной не
только с положением тренда, но и с
возможностью отклонения от этого
тренда, вводится средняя квадратическая
ошибка прогноза
.
Тогда доверительный интервал прогноза
будет равен:
,
(8.18)
где
L
— период
упреждения.
Основная трудность при определении
доверительного интервала прогноза
состоит в том, что не для всех классов
моделей имеются аналитические выражения
оценки границ доверительного интервала.
Также все аналитические выражения для
определения доверительных интервалов
исходят из предположения о нормальном
распределении ошибок аппроксимации,
что не всегда выполняется.
Рассмотрим построение доверительных
интервалов для разных типов кривых.
Отметим, что аналитическое выражение
доверительного интервала удалось
получить не во всех случаях. В частности,
доверительные интервалы для сложных
кривых, отличающихся от полиномов, имеют
достаточно условный характер. Для
определения доверительных интервалов
полиномов необходимо получить
среднеквадратическую ошибку прогноза.
Будем исходить из того, что ошибки
прогноза связаны только с ошибками в
оценках параметров.
Покажем определение доверительных
интервалов прогноза для трендов,
описываемых соответственно прямой,
квадратической и кубической параболами.
Для получения среднеквадратических
ошибок прогноза полиномов удобно
воспользоваться матричным выражением
дисперсии множественной регрессии
(формула 8.13). Заменив переменные Хна характеристики времениt,
получим:
,
(8.19)
где
—
оценка дисперсии,
— для прямой,
— для квадратичной параболы,
— для кубической параболы,
—
время, для которого производится
экстраполяция.
Матрицы нормальных уравнений для этих
кривых при условии, что начало отсчета
времени приходится на середину ряда,
имеют следующий вид:
,


После
ряда преобразований получим для прямой:

для
параболы второй степени:

для
параболы третьей степени:

Для того чтобы учесть рассеяние вокруг
кривых в суммарную дисперсию включим
дисперсию случайной компоненты ,
то есть.
Таким образом, получили формулу для
расчета средней квадратической ошибки
прогноза:
.
(8.20)
Для прямой, параболы второго и третьего
порядка формулы для расчета средней
квадратической ошибки прогноза имеют
вид:

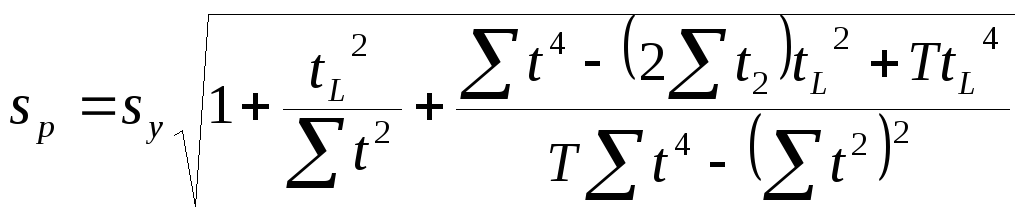

Среднеквадратическая
ошибка прогноза оказывает преобладающее
влияние на ширину доверительного
интервала. При одной и той же величине
доверительный интервал прогноза тем
шире, чем выше степень полинома,
характеризующего тренд. Также ширина
доверительного интервала для кривых
зависит от уровня значимости, периода
упреждения, среднего квадратического
отклонения от тренда и степени полинома.
Уравнения
экспоненты
и
логарифмической параболыс
помощью логарифмирования легко приводятся
соответственно к линейному и параболическому
виду:
,
.
Для приведенных
выражений можно найти среднеквадратические
ошибки оценок параметров и
среднеквадратическую ошибку прогноза.
Доверительный интервал определяется
выражением:
.
(8.21)
Такой
же подход возможен при экстраполяции
модифицированной экспоненты и S-образных
кривых, в случае, если значение асимптоты
задано. Тогда модифицированную экспоненту
можно записать как
.
Откуда
.
Параметры
loga
и logb
оцениваются обычным методом наименьших
квадратов. Располагая значениями границ
доверительного интервала для
,
легко определяются доверительные
интервалы прогноза для:
.
Доверительные интервалы, полученные с
помощью логарифмического преобразования
исходной модели, являются несимметричными
относительно величины, определенной
по уравнению тренда (точечного прогноза).
Оценка доверительных интервалов в
адаптивных моделях.
При прогнозировании с использованием
адаптивных методов модель используется
в двух значениях: как модель временного
ряда, выражающая закон генерирования
уровней ряда, и как прогнозная модель
или предиктор. Отличие этих двух типов
моделей в том, что на выходе модели
временного ряда оценки фактических
уровней ряда, а на выходе прогнозной
модели – оценки будущих уровней ряда.
Прогнозная модель формируется на
последнем шаге вычислений по последним
значениям коэффициентов.
Прогнозная модель
Хольта-Уинтерса аддитивного типа имеет
вид:
,
(8.22)
где
— период
упреждения, а
— прогнозное значение уровня ряда в
момент времениn
на
— шагов
вперед,
— аддитивный коэффициент сезонности,
наиболее поздняя оценка коэффициента
для аналогичного периода года.
Прогнозная модель
Хольта-Уинтерса мультипликативного
типа имеет вид:
,
(8.23)
где
— период
упреждения, а
— прогнозное значение уровня ряда в
момент времениn
на
— шагов
вперед,
— мультипликативный коэффициент
сезонности, наиболее поздняя оценка
коэффициента для аналогичного периода
года.
Каждая сезонная
компонента характеризует изменение
уровня временного ряда для какого-либо
одного периода. Сезонные колебания
обычно изменяются не только из года в
год, но у них может наблюдаться значительная
колеблемость коэффициентов сезонности
в различные периоды года. Например, в
летние месяцы будет наблюдаться большая
вариация коэффициентов сезонности, а
в зимние месяцы небольшая. Отсюда
следует, что при интервальном оценивании
необходимо учесть дисперсию сезонной
компоненты именно того периода, на
момент которого дается прогноз.
Для
подтверждения того, что различие
дисперсий сезонных компонент значимо
и не может быть объяснено случайными
причинами, можно воспользоваться
критерием Фишера-Снедекора или критерием
Бартлетта.
В случае выборок
одинакового размера по критерию
Фишера-Снедекора сравнивают наибольшую
и наименьшую дисперсию:
и
по таблице критических точек распределения
Фишера-Снедекора, по заданному уровню
значимости и числам степеней свободы
находится критическая точка
.
Если,
то различие между сравниваемыми
дисперсиями незначимо.
Если окажется,
что различие между сравниваемыми
дисперсиями незначимо, то подавно
незначимо и различие между остальными
дисперсиями. Недостаток этого метода
в том, что информация, которую содержат
остальные дисперсии, кроме наибольшей
и наименьшей, не учитывается.
Данного недостатка
лишен критерий Бартлетта, критерий
проверки однородности двух и большего
числа дисперсий. Данный критерий
заключается в сравнении логарифма
средней дисперсии с суммой логарифмов
отдельных дисперсий.
Бартлетт показал,
что величина
,
где


примерно
подчиняется 2
–распределению с n-1
степенями свободы. Если вычисленное 2
значение превышает значение 1-2
для n-1
степени свободы, то гипотеза отвергается.
Для
частного случая, когда все
равны,
так что:

где
.
Для
проверки значимости отличия дисперсий
сезонных компонент был рассмотрен
типичный представитель тренд-сезонного
временного ряда «Денежная масса М0» за
интервал времени 1996-2001 годы (рис. 8.2,8.3).
Рис.
8.2. Наличные деньги (М0) за период 1996-2001
гг.
Р
График, построенный методом наложения.
Наличные деньги
(М0) за период 1996-2001 гг.
В формировании
уровней этого ряда существенную роль
играют сезонные факторы. После выравнивания
тренда с помощью 13-членной центрированной
скользящей средней, было выделена
сезонная компонента аддитивного и
мультипликативного типа.
Наблюдаемое
значение Фишера-Снедекора составило
70,67 и 101,41 для дисперсий сезонных компонент
аддитивного и мультипликативного типа
соответственно, критическое значение
составило 4,107 для уровня значимости
0,1. Наблюдаемое значение критерия
Бартлетта – 18,74 и 36,03 для дисперсий
сезонных компонент аддитивного и
мультипликативного типа соответственно,
критическое значение составило 17,275 для
уровня значимости 0,1.
Итак,
исследование показало, что дисперсии
сезонных компонент для отдельных месяцев
значимо отличаются друг от друга,
следовательно, при построении интервального
прогноза правомочно учесть дисперсию
сезонной компоненты именно того периода,
на момент которого дается прогноз.
Важное
значение при интервальном оценивании
имеет зависимость компонент. Степень
тесноты линейной связи между двумя
переменными определяется коэффициентом
парной корреляции. Чем выше значение
коэффициента корреляции, тем теснее
связь. Для определения существенности
коэффициентов корреляции, их необходимо
проверить на значимость по t-критерию
Стьюдента. Наблюдаемое значение
t-критерия
вычисляется по формуле:
и
по таблице критических точек распределения
Стьюдента, по заданному уровню значимости
и числу степеней свободы k
находят критическую точку
.
Если,
то коэффициент корреляции значимо
отличается от нуля и переменные
коррелированы. Коэффициенты корреляции
между трендовой составляющей и сезонной
составляющей как аддитивного, так и
мультипликативного характера, незначимо
отличаются от нуля, следовательно,
данные компоненты независимы.
Проверив
предположения о различии дисперсий
сезонных компонент и независимости
трендовой и сезонной составляющих
временного ряда, рассмотрим построение
доверительного интервала для моделей
Хольта-Уинтерса. Используя свойство
независимости компонент тренд-сезонного
временного ряда, дисперсию прогноза
для аддитивной модели Хольта-Уинтерса
получаем как сумму дисперсии тренда и
сезонной компоненты. Дисперсия сезонной
компоненты определяется по следующему
соотношению:

где
—
дисперсия сезонной компоненты для j
— месяца
(квартала),
–
объем выборки сезонных коэффициентов
за j
— месяц
(квартал).
Таким образом,
дисперсия прогноза для аддитивной
модели Хольта-Уинтерса определяется
как:

где
—
оценка дисперсии сезонной компоненты.
Совокупность
вычисленных сезонных коэффициентов,
как правило, небольшая, она в 4 или в 12
раз меньше общей выборки. Значения
среднего и дисперсии, полученные для
выборки небольшого размера, могут
существенно отличаться от точных
(неизвестных) значений. Отклонения
выборочных значений от точных сами
являются случайными величинами,
распределенными по каким-то законам.
Очевидно, что вероятность больших
отклонений невелика и стремится к нулю
при увеличении размеров выборки.
Стьюдентом была разработана теория
распределения отклонений выборочных
значений от точных в зависимости от
размеров выборки. В теории вероятностей
показано, что усреднение функции
распределения по всем возможным значениям
этих отклонений с учетом законов
распределений выборочного среднего и
выборочной дисперсии приводит к
расширению плотности распределения —
дисперсия увеличивается в
раз, гдеk
– размер выборки. С учетом последних
обстоятельств, дисперсию сезонных
коэффициентов следует скорректировать
на размер выборки. Окончательно формула
оценки доверительного интервала для
аддитивной модели Хольта-Уинтерса
примет вид:

(8.24)
Для
определения доверительного интервала
для мультипликативной модели
Хольта-Уинтерса, логарифмированием
приводим ее к модели аддитивного вида:
.
Далее определяются
доверительные интервалы для аддитивной
модели, полученной с помощью логарифмического
преобразования, а затем потенцированием,
производится обратный переход – расчет
доверительного интервала исходной
модели по следующему выражению:

(8.25)
где
,
— дисперсии тренда и сезонной компоненты
в логарифмах.
Оценка
доверительных интервалов в многофакторных
моделях. При
прогнозировании экономических процессов
часто бывает удобно расчленить временной
ряд на составляющие (компоненты). В этом
случае становится более очевидным
воздействие каждого фактора на
формирование результирующего признака.
Прогноз результирующего признака в
таком случае получается объединением
(в виде сумм или произведения) прогнозов
отдельных компонент.
Для построения
интервального прогноза сумм или
произведений показателей нужно иметь
представление о наличии или отсутствии
зависимостей слагаемых или сомножителей.
Предположение о зависимости показателей
может быть вынесено из содержательного
анализа показателей или получено из
корреляционно-регрессионного анализа
данных.
При прогнозировании
по аддитивной модели необходимо
рассмотреть два варианта: когда слагаемые
независимые величины и когда они зависимы
друг от друга. Рассмотрим первый случай.
Воспользуемся теоремой математической
статистики, согласно которой дисперсия
суммы независимых величин равна сумме
дисперсий слагаемых.
,
Тогда при условии
независимости переменных, входящих в
аддитивную модель, имеем:
,
(8.26)
где
—
дисперсия прогноза j-составляющей,
N
– число
суммируемых прогнозов.
Во втором случае, в случае зависимости
слагаемых, по теореме математической
статистики дисперсия суммы нескольких
случайных величин равна сумме всех
возможных корреляционных моментов, то
есть необходимо определение коэффициентов
корреляции между попарно взятыми
слагаемыми.
Для двух слагаемых
имеем:
.
Дисперсия
суммы увеличивается, следовательно,
увеличивается и интервал прогнозирования.
Для
определения доверительного интервала
для мультипликативной модели можно
применить переход к аддитивной модели
логарифмированием. Затем строятся
доверительные интервалы в логарифмах
для аддитивной модели, и потенцируя
полученные результаты переходим к
доверительным интервалам исходной
модели.
Используя предложенный выше подход,
рассмотрим построение доверительных
интервалов для обобщенной аддитивной
модели, представляющей тренд-сезонный
временной ряд:
,
,
(8.27)
где
—
тренд (регулярная компонента);
—
сезонная компонента;
—
случайная компонента.
При прогнозировании по аддитивной
модели отдельно рассчитываются прогнозные
значения каждой компоненты временного
ряда (тренда и сезонной компоненты) с
последующим их суммированием. Наиболее
часто на практике тренд аппроксимируют
полиномом, а периодическую — функцию
отрезком ряда Фурье по наиболее значимым
гармоникам. В таком случае обобщенную
аддитивную модель можно записать в
виде:
,
(8.28)
где
р– порядок полинома,k– количество гармоник,
— частота. Все элементы в модели являются
функциями от времени. Если через
обозначить
набор факторов, влияющих на зависимую
переменную Y, то данную
модель можно рассматривать как
многофакторную. Параметры модели
определяются по методу наименьших
квадратов по формуле:
.
Доверительные интервалы для прогнозного
значения Yt+1оцениваются по формуле:
,
(8.29)
где
— ожидаемый
вектор-столбец в периоде
.
Мультипликативная
модель, представляющей тренд-сезонный
временной ряд, имеет вид:
,
(8.30)
где
—
“годовая” составляющая (тренд);
—
постоянная пропорциональности для j-го
месяца (квартала), не меняющаяся от года
к году;
—
случайная ошибка.
При прогнозировании
по мультипликативной модели также
отдельно рассчитывается прогнозное
значение каждой компоненты временного
ряда (тренда и сезонной компоненты) с
последующим их умножением. Тренд, как
и в аддитивной модели, чаще всего
аппроксимируют полиномом. Сезонная
компонента представляет собой индексы
сезонности. Для прогноза обычно используют
средние индексы за анализируемый период.
Для
определения
доверительного интервала при использовании
мультипликативной модели переходим к
аддитивной модели логарифмированием:
.
Доверительный
интервал в этом случае определим по
формуле:

(8.31)
где
,
— дисперсии тренда и сезонной компоненты
в логарифмах. Обратным преобразованием
оцениваем доверительный интервал для
мультипликативной модели.
Сегодня мы будем изучать тренды. Постараюсь максимально полно и доступно изложить всю известную мне информацию по данной теме. Мы часто слышим, что тренд — наш друг, но как уже многие поняли, эта фраза не является учебным пособием, да и воротить миллионами она нам не поможет. В чём же заключается эта дружба, какое преимущество мы получаем в тренде, где находятся лучшие точки входа в рынок по тренду?
Большинство трейдеров совершают множество ошибок при торговле по тренду, которые напрочь рушат всю прибыльность их торговли, а казалось бы, тренды — это так легко! Надеюсь, эта статья со множеством различных примеров расставит всё на свои места.
Как определить тренд?
Стоит отметить, что метод торговли по тренду не является стратегией, это лишь руководство к действию, небольшой урок к пониманию рынка, который в недалёком будущем должен помочь вам облегчить процесс принятия решений.
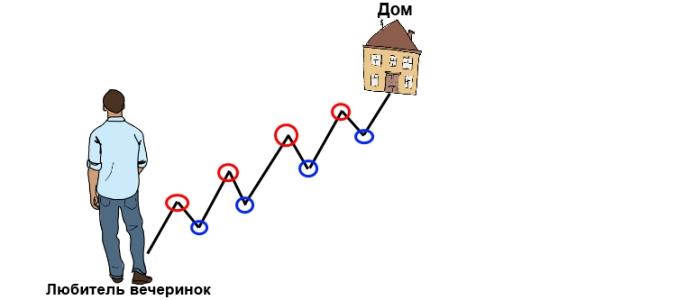
Как я уже писал, консолидация — это коридор, а цена — это пьяный человек, вернувшийся с вечеринки, который пытается добраться в свою спальню передвигаясь от стенки к стенке по нашему флэтовому коридору. Так вот, если попытаться представить тренд подобным образом, то мы получим подобную картину:
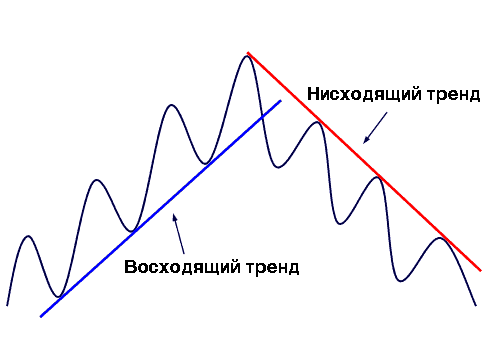
Цена — это любитель вечеринок, а тренд — это его путь домой. И если вы вспомните как ходят выпившие — 3 шага вперёд, 1 шаг назад, то вы получите полное понимание движения цены по тренду. При этом, наш герой, каждый раз добирается к новым максимумам. Вот и выходит, что восходящий тренд — это образование ценой более высоких максимумов и минимумов, а нисходящий — это образование более низких минимумов и максимумов.
Восходящий тренд — это направленное движение рынка вверх с повышающимися максиумами и миниумами.
Нисходящий тренд — это направленное движение рынка вниз с понижающимися максиумами и миниумами.
Миниумы в восходящем тренде или максиумы в нисходящем — это откаты тренда, которые почти всегда происходят, если только тренд не очень стремительный.
Тренды могут отличаться на разных таймфреймах одного инструмента. К примеру, на дневном графике может быть восходящий тренд, а на пятиминутном в то же самое время нисходящий. Чем старше таймфрейм, тем тренд является более сильным и надежным.
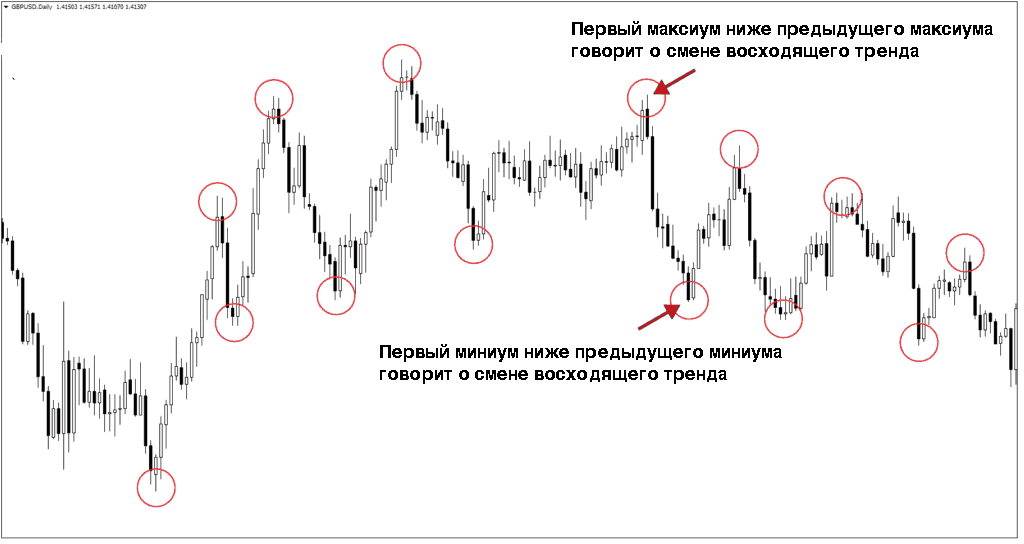
О смене текущего тренда можно говорить, если нарушается последовательность восходящих максиумов и миниумов.
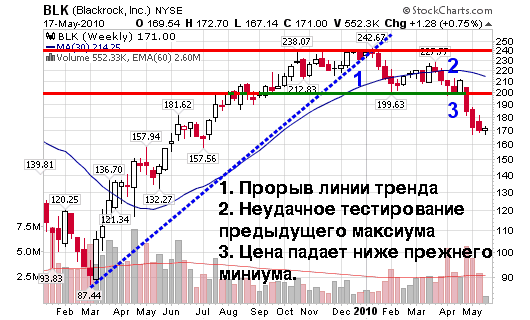
На графике выше первый нижний максимум был первым признаком того, что восходящий тренд начал выдыхаться. Но только после первого нижнего минимума у нас появляется убедительное доказательство, что произошла смена тенденции.
Находить тренды также можно с помощью линий тренда.
Чем чаще цена касается линии тренда, тем тренд длительней и сильнее. Если линия тренда очень крутая, то такие тренды обычно недолговечны.
Разворот тренда определяется прорывом линии тренда с последующим неудачным тестированием предыдущего максиума или миниума, после которого цена уходит выше или ниже прежнего максиума или миниума.
Всегда нужно помнить, что ситуация на рынке может поменяться очень быстро, и любой тренд может внезапно закончиться, перейдя в консолидацию или дать начало противоположному тренду. Также тренд может продолжаться очень долгое время. Поэтому важно знать, как обычно ведет себя инструмент, которым вы торгуете. Характерны ли для него периоды длительных консолидаций или большую часть времени он движется в тренде.
В периоды, когда непросто определить, есть ли на графике тренд или нет, лучше вообще воздержаться от торговли.
Характеристики тренда
Как и всё остальное, тренд имеет свои правила и определённые черты поведения.
Главный плюс заключается в том, что цена делает сильные рывки в сторону целенаправленного движения, после чего она останавливается и консолидируется (делает небольшой перерыв). Уверен, что многие из вас открывали сделки перед этими сильными скачками, и получали неплохую прибыль, а после этого, смотрели как она исчезает в консолидирующемся рынке. Стоит помнить, что тренд состоит из нескольких частей, и нужно уметь «предсказывать» его последующие действия.
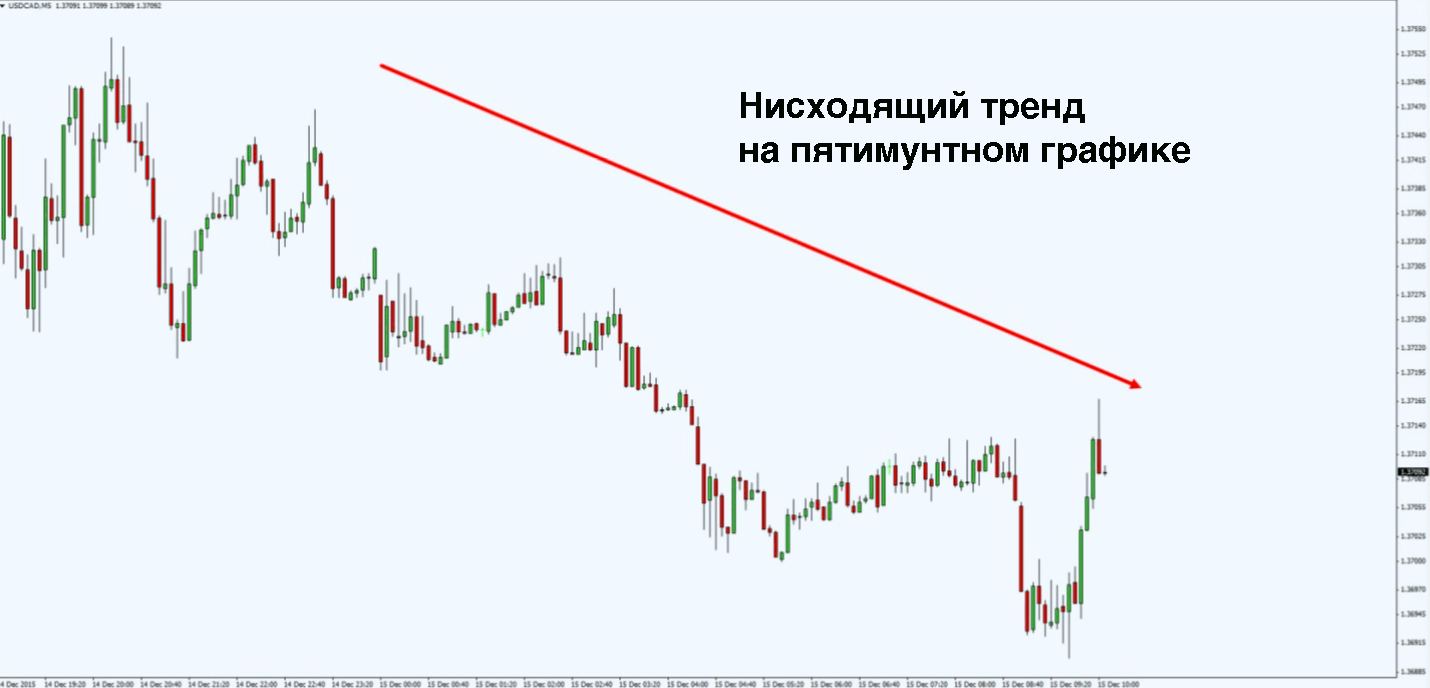
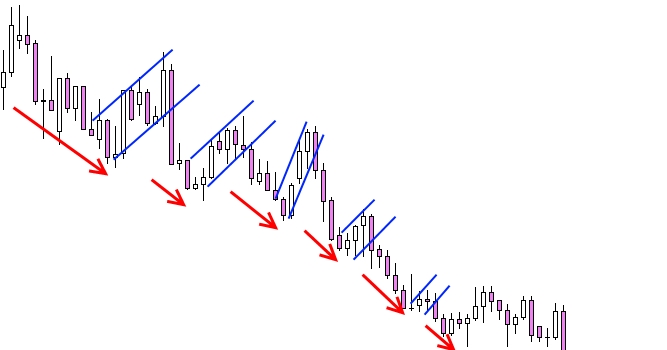
Выше изображён график с нисходящим движением цены. Красными стрелочками обозначены резкие падения, а синими границами отмечены зоны консолидации. Рынок камнем падает вниз, а после этого делает перерыв. Все условия соблюдены, присутствует движение по основному шаблону.
Стоит обратить пристальное внимание на зоны консолидации, ведь они являются своеобразным граалем для каждого трейдера, ведь эти зоны являются наилучшими точками для входа в трендовый рынок. Вновь обратимся к нашему примеру, но посмотрим на него с позиции уровней поддержки и сопротивления.
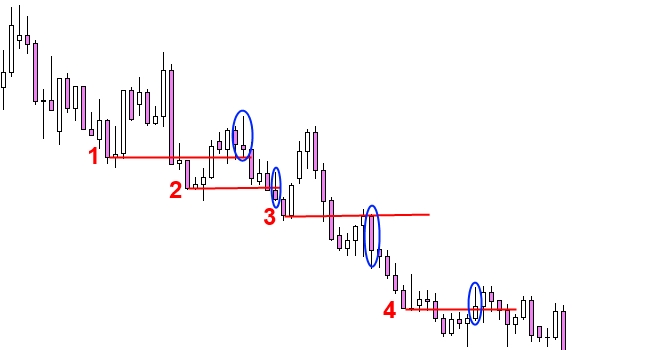
- Мы устанавливаем уровень сопротивления и видим, что через некоторое время рынок образует медвежий пин бар в данной зоне, который приводит к снижению цены на 125 пунктов.
- На очередном уровне возникает пин бар, его можно использовать как дополнительную точку входа, так как он является подтверждением первому сигналу.
- На графике появился сигнал доминирующая свеча от уровня сопротивления, после которого рынок снизился ещё на 100 пунктов.
- Очередной пин бар от сильного уровня, дополнительные 50 пунктов прибыли.
Подобные принципы торговли подходят и для восходящего рынка, только рисовать мы уже будем не сопротивление, а поддержку.
Динамические уровни
Если всё-таки у вас возникают трудности с определением тренда классическим способом, тогда динамические уровни — ваш путь. Что это такое?
Это обычные скользящие средние, только с экспоненциальным методом сглаживания, периоды можно выставлять любые, но я рекомендую 8 и 21, или 8 и 18. Возможно, для некоторых это было секретом, но данные линии могут играть роль уровней поддержки и сопротивления. Если они находятся над ценой, значит они играют роль сопротивления, если наоборот, тогда они являются поддержкой.
Вы только посмотрите, как же много точек входа по тренду. Да, я согласен, это идеальная ситуация, такое редко встречается, но нам необходимо знать, что делать в подобных ситуациях, и тут нам на помощь приходит закон уровней, который гласит: от сопротивления продавай, от поддержки покупай.
Вы можете использовать:
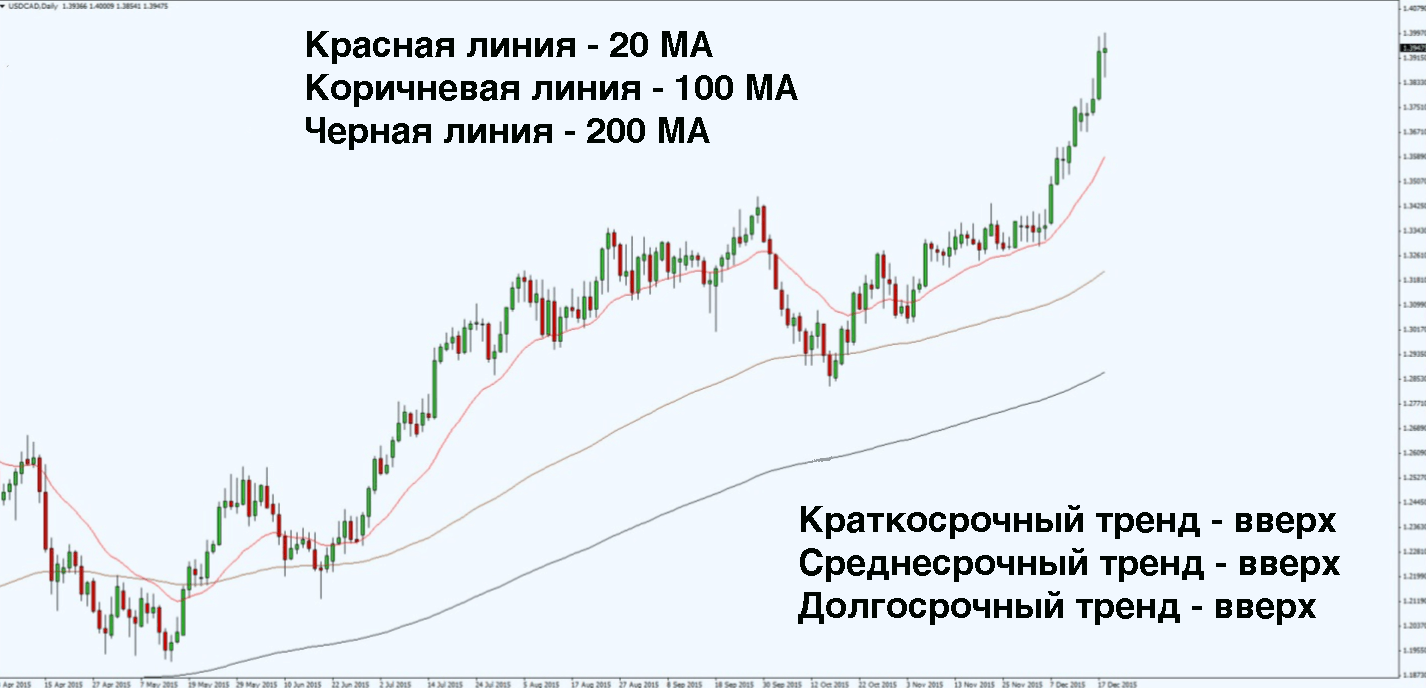
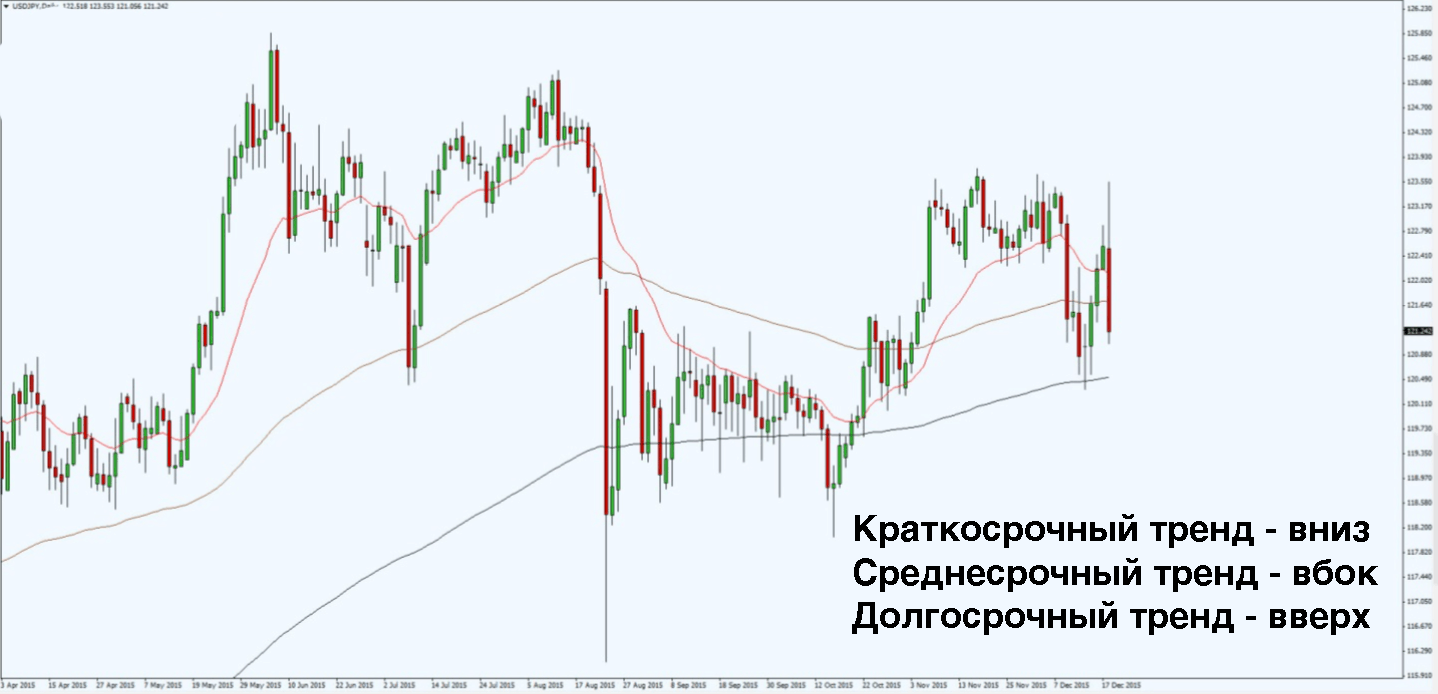
- 20 MA для краткосрочных тенденций.
- 100 MA — для среднесрочных тенденций.
- 200 MA — для долгосрочных тенденций.
Если скользящая средняя направлена вверх и цена находится выше нее — значит тренд восходящий. Обратное справедливо для нисходящего тренда.
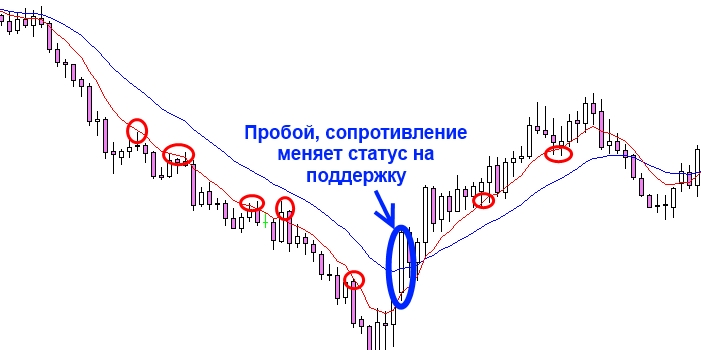
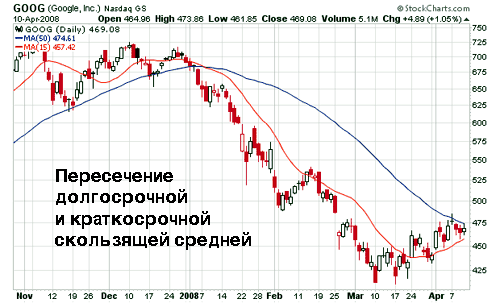
Хорошей точкой для выхода и определения смены текущего направления тренда может служить пересечение скользящих средних. Сигнал возникает, когда кратковременная линия скользящего среднего пересекает выше или ниже долгосрочную линию скользящего среднего. Этот метод может также служить указанием на то, набирает ли тренд силу или собирается в ближайшее время развернуться.
Не открывайте ордера сразу после того, как увидели пробой, ждите подтверждения. «Большие дяди» знают, что новички любят торговать в таких ситуациях, и поверьте, этими знаниями они пользуются вовсю. Достаточно спровоцировать цену на пробой, подождать до тех пор пока будет открыто достаточно ордеров, и можно разворачивать рынок. В подобных ситуациях, лучше всего продолжать искать сигналы прайс экшен в направлении предыдущего тренда до образования нового.
Информация для фанатов торговли против тренда
Если рассматривать долгосрочную перспективу подобных сделок, то через некоторое время, они приведут вас к разорению, хотя полностью исключать их не стоит. Идеальный трейдер это тот, у кого не более 35% сделок заключены против тренда, а остальные открыты в сторону его направления.
Ведь, возвращаясь к примеру с нашим любителем вечеринок, вероятность того, что он в таком состоянии пойдёт обратно, очень мала.
Торговля по тренду — это простейший способ получения прибыли. Если вам действительно хочется научиться зарабатывать, тогда освойте этот метод. К сожалению, цена не находится постоянно в подвижном состоянии, иначе, рынок стал бы чем-то простым. Поэтому, запаситесь терпением, отработайте свою стратегию и протестируйте её.
Смертельная ошибка при торговле по тренду
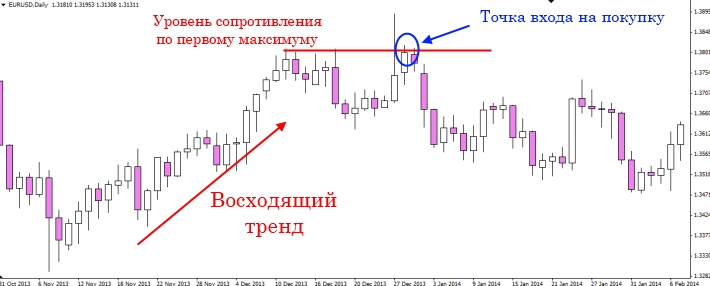
Во многих статьях по прайс экшен, часто акцентировалось внимание на том, что от сопротивления мы продаём, а от поддержки мы покупаем, но почему-то многие пропускают это мимо ушей, чем портят весь потенциал трендового рынка. И после этого мы видим такие точки входа:
Даже если представить, что там нет такого большого пин бара, то почему там заключена сделка на покупку? Неужели не видно сопротивления? Или вся логика открытия этого ордера заключается в том, что у нас на графике восходящий тренд? А вот ещё один пример, очередная ошибка:
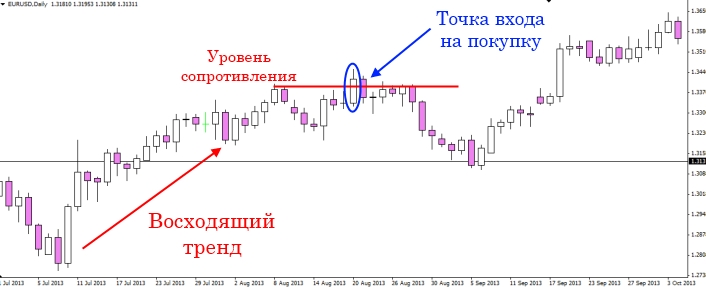
В этой точке входа есть хоть капля логики, но некоторые вопросы остаются. Почему вход от сопротивления? А если сделка открывалась на пробой, то почему не дождались подтверждения истинности?
Эта ошибка очень распространена среди начинающих трейдеров, да что уж там, даже среди прожжённых опытом и слитыми депозитами есть те, кто до сих пор так торгует, но вот почему-то этого не осознаёт.
Поздний вход
Если говорить рифмованной фразой, то можно выразиться так «сделка открывается — мозг трейдера отключается», поэтому я и советую торговать по принципу установил и забыл. А сейчас перейдём непосредственно к решению проблемы.
Что плохого в том, что мы торгуем на пробой сопротивления в восходящем тренде? Плохо в этом то, что таким образом мы лишаем себя того преимущества, которое дарит нам такое состояние рынка.
- У нас получается большой уровень стоп-лосс.
- Если стоп установлен за пробивающей свечой, то он считается необоснованно рискованным.
- Уменьшается соотношение риска и прибыли, из потенциальных 1:4, мы еле-еле получаем 1:2.
- Мы лишаемся поддержки быков (в восходящем движении).
- Есть вероятность входа на пике тренда.
Как можно заметить, мы действительно лишаем себя слишком большого количества различных полезностей, и это всё из-за неправильного подхода к торговле. Надеюсь, сейчас мы всё исправим.
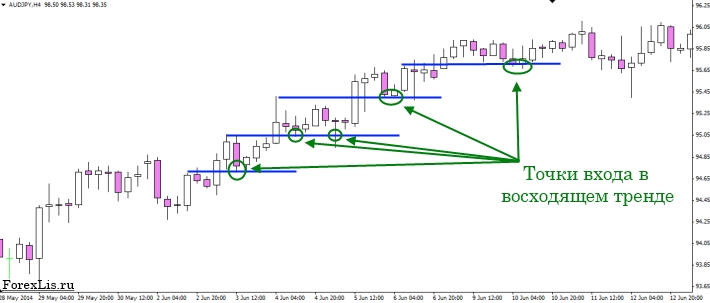
Торгуем в растущем рынке
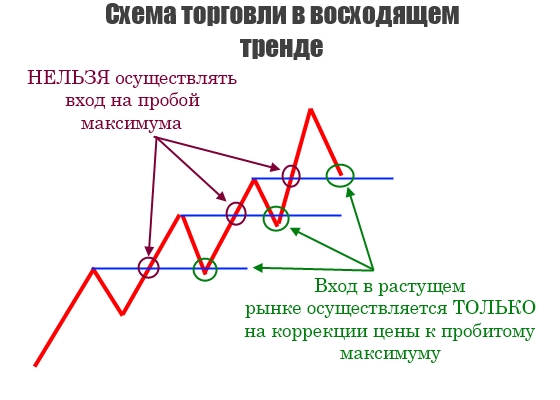
Начнём с изучения простой схемы:
Нельзя осуществлять входы на пробой максимумов в восходящем тренде, так как в долгосрочной перспективе, это приведёт к потери депозита из-за вероятности входа на покупку на пике растущего движения. В такие моменты человеческий фактор начинает играть против вас, и вы пытаетесь всячески избежать убытка путём перемещения уровня стоп-лосс, что приводит к ещё большим потерям. Чтобы таких ситуаций не случалось, лучше всего входить после коррекции рынка к уровню поддержки.
На графике это выглядит так:
Все точки входа располагаются на уровнях поддержки, которые установлены по локальным максимумам восходящего тренда. Стоит отметить один большой минус торговли на пробой сопротивления: каждый раз при таком входе, рынок возвращается на уровень открытия вашего ордера, закрывает вас в безубытке и продолжает своё предыдущее движение.
Прям небольшое разоблачение, теперь вы знаете причину, по которой так вредно переносить стоп в безубыток, тем более, если ещё не совсем осознаёте свои действия. Больше сетовать на своего брокера по этому поводу не будете. Продолжаем.
Давайте разберём ещё несколько входов для тренда на форекс по другим валютным парам.
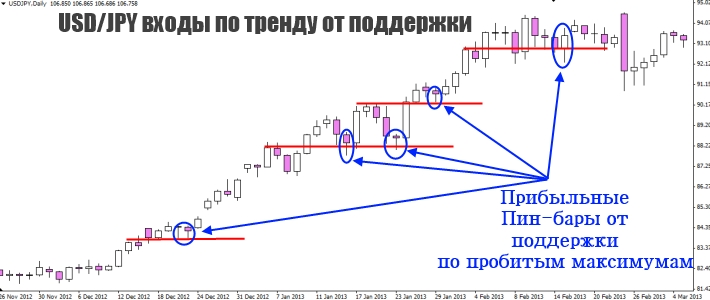
Ниже расположен график валютной пары USD/JPY, дневной таймфрейм.
Неужели это так сложно? Наносим уровни поддержки и сопротивления по максимумам, ждём коррекции цены к отмеченным местам, далее либо входим отложенным ордером, что является не самой лучшей тактикой, либо ждём сигнала по прайс экшен на вход в направлении тренда на форекс, что даёт нам наибольшую вероятность на получение прибыли.
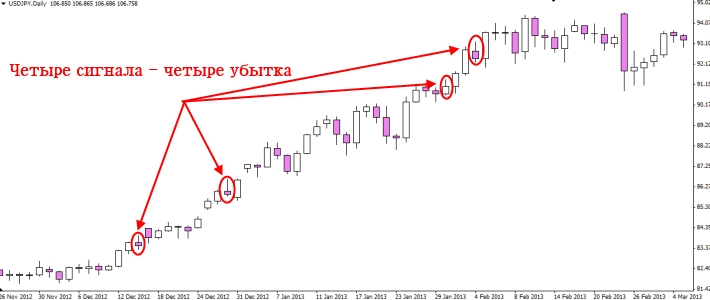
Для того, чтобы подтвердить то, что я сказал о разворотных сигналах, вернёмся к этому же примеру и посмотрим, сколько убыточных Пинов находится на графике.
Не так здорово, как вы себе это представляли. Но, это так, на заметку, меньше входов на разворот — целее будет ваш депозит.
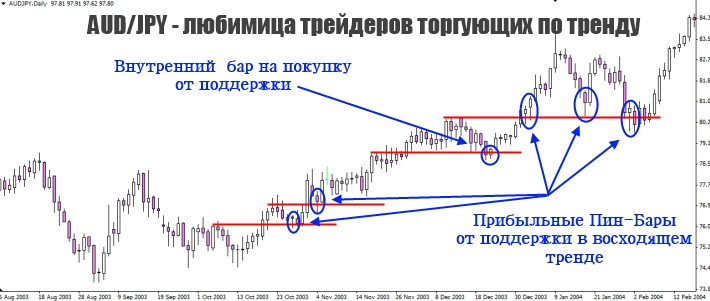
AUD/JPY — пара, которую очень сильно любят те, кто торгует в направлении тренда на форекс. А всё потому, что она практически всегда корректируется к пробитым максимумам или минимумам, а после этого, рисует прайс экшен сигнал в направлении общего движения цены, сейчас вы сами в этом убедитесь.
Как вы можете видеть, или не видеть, так как график получился мелковат, цена рисует максимум, пробивает его, корректируется к нему, рисует сигнал на вход и продолжает своё движение. Это просто наилучший вариант входа в рынок с минимальным риском и большой вероятностью закрытия в прибыль. На некоторых поддержках мы получали по 2 пин бара в направлении тренда. Также, на графике есть один внутренний бар, который полностью себя отработал.
Надеюсь, данная статья прояснила для вас общую картину и вы не станете совершать столь глупые ошибки в торговле по тренду на форекс.
Как понимать угол движения цены по тренду?
Сайты по трейдингу наводнены разговорами о пин барах, внутренних барах и внешних барах. Но часто при этом упускается из внимания история изменения цены на графике. И дело не только в ключевых уровнях. Я имею в виду угол движения цены.
Стать успешным трейдером прайс экшен — это нечто большее, чем просто научиться искать пин бары на уровнях. Важно научиться понимать общий рыночный контекст и оценивать силу тренда. Все это позволит вам выбирать только лучшие торговые настройки и забирать максимум прибыли с рынка.
Угол, под которым рынок движется вверх или вниз указывает на соотношение спроса и предложения.
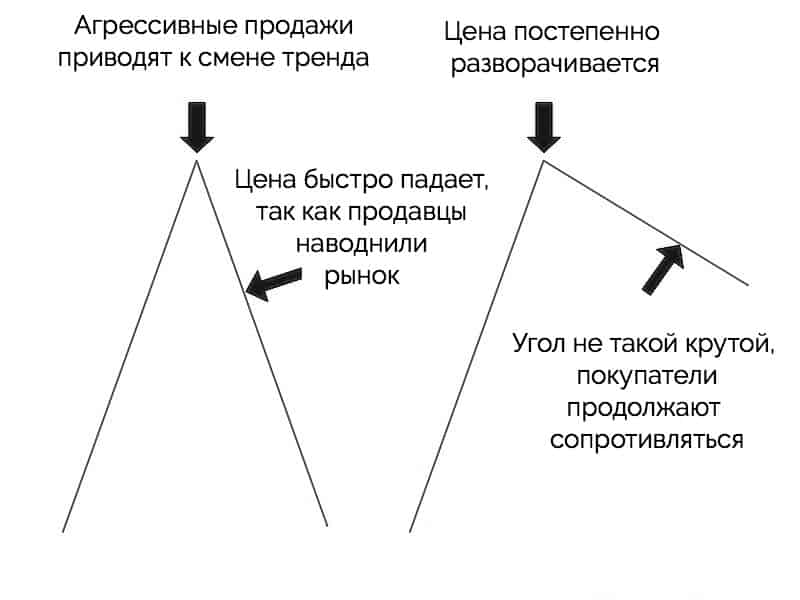
Ниже приведена иллюстрация двух рынков. Первый показывает рынок, на котором предложение значительно превышает спрос. Другими словами, количество продавцов намного больше, чем количество покупателей. Это выглядит в виде крутого падения цены. Вторая иллюстрация показывает рынок, где продавцов не намного больше, чем покупателей.
Первая иллюстрация показывает рынок, где предложение намного превышает спрос, и поэтому цена стремительно падает. Вторая показывает рынок, на котором предложение все еще превышает спрос, однако оно не является односторонним. Этот тип рынка говорит нам, что покупатели все еще готовы покупать по новым, еще более высоким ценам.
Вы должны научиться читать углы наклона рынка, чтобы увеличить свои шансы на поиск выгодных торговых сетапов.
Давайте рассмотрим пример рынка, на котором было агрессивное ралли, за которым последовал крутой спад:
С одной стороны очевидно, что мы ищем сигналы на покупку в восходящем тренде и сигналы на продажу в нисходящем. Но иллюстрация выше — это нечто большее, чем просто понимание, когда следует покупать или продавать на трендовом рынке.
Речь идет о том, чтобы научиться читать график, используя углы наклона бычьего или медвежьего движения цены.
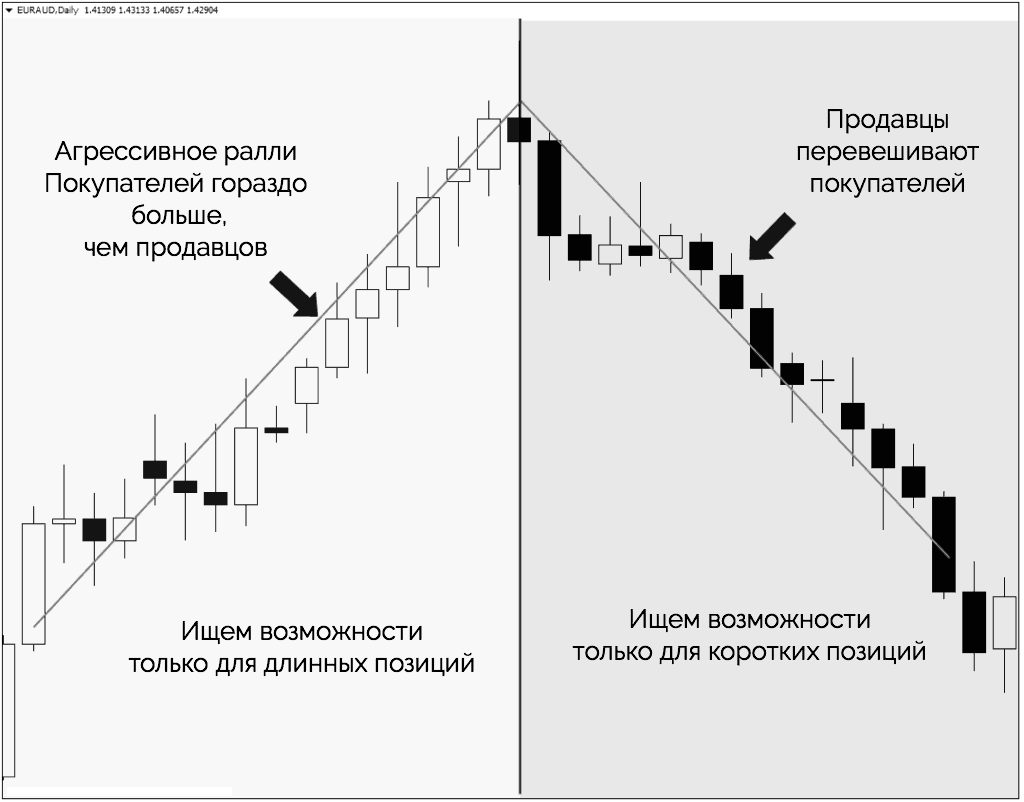
График выше иллюстрирует две части рынка. Одна показывает бычий рынок, а другой — медвежий. Поскольку угол обоих движений одинаково крутой, мы можем определить две вещи:
- Покупатели значительно перевешивают продавцов во время бычьего движения.
- Продавцы значительно перевешивают покупателей во время медвежьего движения.
Хотя эти два истины являются не являются новаторскими, многие трейдеры все равно продолжают не обращать внимания на очевидные вещи и пытаются продавать на бычьем рынке и покупать на медвежьем.
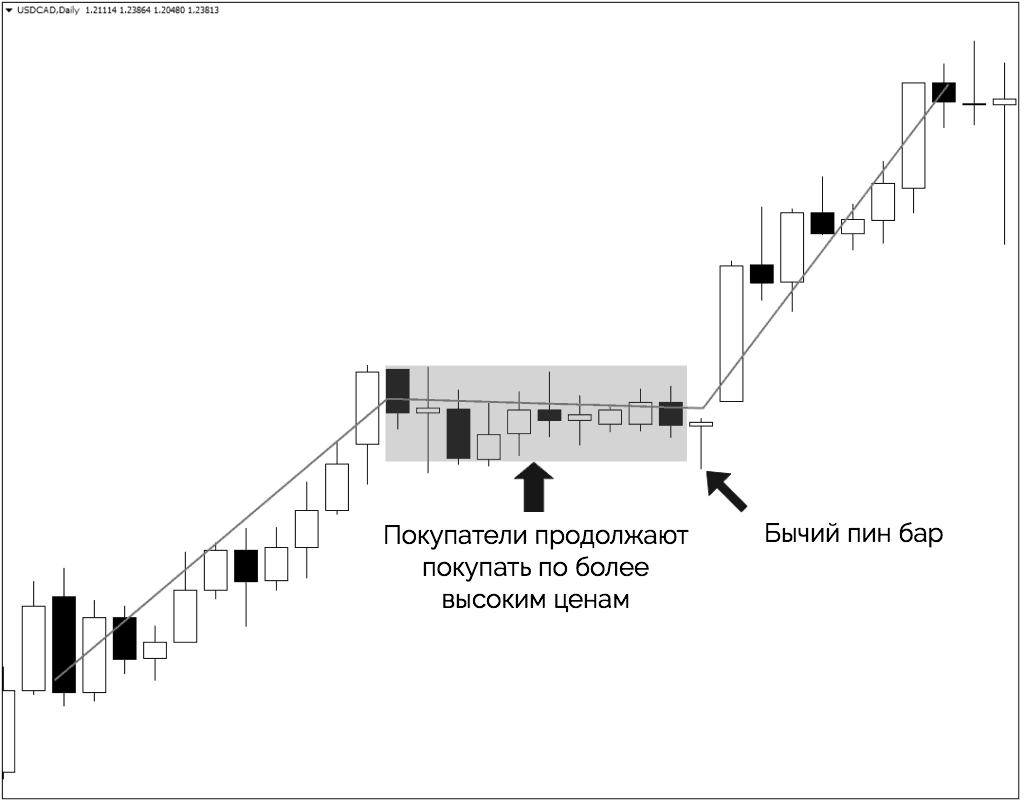
Чтобы понять важность углов, давайте взглянем на рынок, где покупатели продолжают покупать даже по более высоким ценам:
После продолжительного движения вверх покупатели все еще готовы поддерживать цену. Это отличная информация для открытия сделок в лонг.
Это не означает, что тренды не могут испытывать агрессивных откатов — иногда они происходят. Тем не менее, боковое ценовое движение является верным признаком того, что движение в сторону предшествующего восходящего тренда наиболее вероятно.
Мы можем использовать эту информацию в сочетании с сигналами прайс экшен в виде пин бара, чтобы найти благоприятную точку для входа в рынок.